Modified SSR-NET: A Shallow Convolutional Neural Network for Efficient Hyperspectral Image Super-Resolution

A fast and shallow convolutional neural network is proposed for hyperspectral image super-resolution inspired by Spatial-Spectral Reconstruction Network (SSR-NET). The feature extraction ability is improved compared to SSR-NET and other state-of-the-art methods, while the proposed network is also shallow. Numerical experiments show both the visual and quantitative superiority of our method. Specifically, for the fusion setup with two inputs, obtained by 32× spatial downsampling for the low-resolution hyperspectral (LR HSI) input and 25× spectral downsampling for high-resolution multispectral (HR MSI) input, a significant improvement of the quality of super-resolved HR HSI over 4 dB is demonstrated as compared with SSR-NET. It is also shown that, in some cases, our method with a single input, HR MSI, can provide a comparable result with that achieved with two inputs, HR MSI and LR HSI.

1 Introduction

The hyperspectral image super-resolution is a fast-growing research area in computer vision, particularly due to technical difficulties of high-resolution hyperspectral data acquisition with both high spatial and spectral resolutions. Unlike conventional cameras capturing images with three spectral bands (RGB), hyperspectral imaging systems capture hundreds of spectral bands of different wavelengths. Due to the significant increase of information that hyperspectral images (HSI) provide with respect to RGB images, they are considered beneficial for many computer vision tasks, especially in cases when three channels of RGB images are not enough to identify and distinguish objects and materials (Segl et al., 2003; Khan et al., 2018; Cavalli, 2021). Hyperspectral imaging is widely used in areas such as anti-spoofing (Kaichi and Ozasa, 2021), food quality and safety assessment (Feng and Sun, 2012), medical diagnosis (Fei, 2020), precision agriculture (Rascher et al., 2007). Moreover, for extracting more information, some methods apply HSI super-resolution (SR) as a preprocessing step for other computer vision tasks, such as dehazing (Makarau et al., 2014; Gan et al., 2016; Mehta et al., 2020, 2021) and object detection (Pham et al., 2019; Yan et al., 2021).

Unfortunately, hyperspectral imaging systems mainly focus on captioning higher spectral resolution because of the hardware limitations, which adversely affect spatial resolution. Instead, multispectral cameras capture multispectral images (MSI) with much higher spatial resolution than HSI cameras. Therefore, the most practical way to obtain higher resolution imaging for both spatial and spectral domains is to fuse these two types of inputs, HR MSI and LR HSI, by taking advantage of spatial information of the first input, and a correlation among the spectral bands of the second input. There are two special cases of hyperspectral image super-resolution when only one of the inputs (HR MSI or LR HSI) is given.

In this paper, a novel two-input fusion HSI SR method is proposed as a modification of the baseline method, SSR-NET (Zhang X. et al., 2021) architecture, which is a state-of-the-art HSI SR network. To improve the spatio-spectral feature extraction ability of this baseline method and at the same time to keep the network shallow, we add long and short skip connections and two convolutional blocks. As a result, the proposed method, modified SSR-NET (MSSR-NET), outperforms the baseline SSR-NET and other state-of-the-art methods quantitatively and qualitatively. We demonstrate the efficiency and robustness of our network by training and testing it for different types of input data formation.

Perhaps the biggest problem in HSI super-resolution is the absence of real input and output data pairs, which are necessary for training a neural network. It is almost impossible to capture exactly the same scene in two different spatial and spectral resolutions (Chen et al., 2015; Pan and Shen, 2019; Zhou et al., 2020). The standard approach to overcome this image co-registration issue is to generate HR MSI and LR HSI directly from HR HSI. The drawback of this approach is a mismatch of this modeling with respect to reality and, as a result, unpredictable behavior of even state-of-the-art methods in real-life applications. Another problem is a lack of hyperspectral data due to acquisition difficulties. Only a few public datasets are available for training and testing HSI SR methods which mainly contain only a single large image. To be able to apply the proposed method in a real-life scenario, we train and evaluate it for different methods of input data generation.

To summarize, the main contributions of this work are:

1. A novel fast CNN is proposed as a modification of SSR-NET for hyperspectral image super-resolution. It has a simple architecture and comparable or smaller model size compared with the state-of-the-art methods.

2. For different types of input data formation, the proposed method has a superior reconstruction quality visually and numerically compared with SSR-NET and other state-of-the-art methods.

3. The proposed network has been modified and trained to work also with single-input data: HR MSI or LR HSI. It is shown that for HR MSI input data, the reconstruction accuracy in some cases is very close to the accuracy achieved in the two-input scenario.

The rest of the paper is organized as follows: Section 2 provides the formal definition of HSI SR and its sub-tasks, summarizes the main approaches for each of them, describes in detail the baseline SSR-NET and proposed methods. The experiments on remote sensing datasets are described in Section 3. Finally, the conclusions are given in Section 4.

2 Materials and Methods

2.1 Problem Formulation

Let $Z\in {\mathbb{R}}^{H\times W\times L}$ be a target HR HSI that need to be recovered by fusing LR HSI $X\in {\mathbb{R}}^{h\times w\times L}(h\ll H,w\ll W)$ and HR MSI $Y\in {\mathbb{R}}^{H\times W\times l}(l\ll L)$, where H, W and L denote the height, width and number of the bands in the spectral cube HR HSI, respectively. Correspondingly, h and w are the spatial dimensions of LR HSI, and l is the number of spectral bands of HR MSI.

For simplicity of mathematical formulation, the reshaped versions (mode-3 unfolding matrices) of Z, X and Y will be denoted as $\mathcal{Z}\in {\mathbb{R}}^{HW\times L}$, $\mathcal{X}\in {\mathbb{R}}^{hw\times L}$, $\mathcal{Y}\in {\mathbb{R}}^{HW\times l}$. The observations for modeling of the fusion based super-resolution are given by the following equations:

$\mathcal{X}=\mathcal{Z}D(\mathrm{1a})$

$\mathcal{Y}=C\mathcal{Z}(\mathrm{1b})$

where $D\in {\mathbb{R}}^{HW\times hw}$ is a downsampling operator along the spatial dimension to obtain LR HSI by downsampling HR HSI, and $C\in {\mathbb{R}}^{l\times L}$ is the camera spectral response function that maps the L spectral channels into l channels.

The reconstruction of Z from these observations is the super-resolution (SR) problem. HSI SR methods can be classified into the following categories, corresponding to three cases of super-resolution in the spatial domain (only Eq. 1a is used), in the spectral domain (only Eq. 1b is used), and in both spatial and spectral domains (both observations of Eq. 1 are exploited):

1. HSI-from-MSI spectral reconstruction, with the goal to reconstruct HSI from a given MSI, which, in particular, can be an RGB image. Here the spatial resolution of HSI and MSI are the same, and the number of channels in the output HSI is larger than that of MSI, i.e., generating HSI with dimensions H × W × L from the MSI with dimensions H × W × l, where l ≪ L.

2. HR-from-LR HSI super-resolution, with the aim to produce a HR HSI from the given LR HSI. Here spatial resolution increases, while the number of channels is kept the same, i.e., generating HSI with dimensions H × W × L from LR HSI with dimensions h × w × l, where h ≪ H, w ≪ W.

3. Fusion-based super-resolution, with the aim to estimate HR HSI from two inputs: HR MSI and LR HSI. Here, the final HSI shall have the same spatial resolution as HR MSI and have the same number of spectral bands (channels) as LR HSI. Thus, the goal of HSI super-resolution is to recover HR HSI with dimensions H × W × L by fusing LR HSI with dimensions h × w × L (h ≪ H, w ≪ W) and HR MSI with dimensions H × W × l (l ≪ L).

2.2 Related Work

There are three main approaches for HSI SR: bayesian-based (Bungert et al., 2017; Chang et al., 2020; Vella et al., 2021), tensor-based (Gao et al., 2021; Peng et al., 2021; Xue et al., 2021), and matrix factorization-based (Liu J. et al., 2020; Borsoi et al., 2020; Li X. et al., 2021) methods. The drawbacks of these model-based methods are the hand-crafted priors and the inference time as they mainly use alternating direction method of multipliers algorithm for optimization. The learning-based methods outperform the traditional ones due to better spatial information extraction, especially in the case of complex scenes.

Due to the powerful feature extraction ability, deep learning approaches make up the majority of recent state-of-the-art methods. Most of them belong to supervised learning. Some learning-based methods try to extract spatio-spectral features, the correlation among spectral bands simultaneously with spatial information, by exploiting 3D convolutions (Mei et al., 2017; Li et al., 2020; Fu et al., 2021; Li et al., 2021b,d). This approach is mainly used for the feature extraction from input LR HSIs. The drawback of this technique is the computational complexity which leads to large model size and long reconstruction time. Some of them are hybrid frameworks, i.e., the network tries to learn parameters of a model-based method (Dian et al., 2021; Vella et al., 2021; Ma et al., 2022). They mainly use the alternating direction method of multipliers algorithm to estimate the coefficients, which leads to slow performance.

However, because of the data insufficiency problem, there exists also an interest in semi-supervised (Li K. et al., 2021) and unsupervised (Qu et al., 2018; Fubara et al., 2020; Zhang L. et al., 2021; Zheng et al., 2021) learning approaches. Some recent works try to tackle the problem of image co-registration (Wang et al., 2019; Zhou et al., 2020; Qu et al., 2022).

2.3 Baseline Method: SSR-NET

As a baseline method, we have selected the learning-based method, Spatial–Spectral Reconstruction Network (SSR-NET) (Zhang X. et al., 2021), which is the state-of-the-art among shallow CNN-based methods developed for remote sensing datasets. In terms of the number of model parameters and test speed, SSR-NET outperforms other state-of-the-art methods. SSR-NET consists of three main parts: cross-mode message inserting (CMMI) network, spatial reconstruction network (SpatRN) and spectral reconstruction network (SpecRN).

Each of the networks–building blocks of SSR-NET, consists of a standard 3 × 3 convolutional layer and a ReLU activation function, and in the case of SpatRN and SpecRN, skip-connections are applied. The architectures of SpatRN and SpecRN are similar, and they differ only with their sub-network-specific loss functions.

The goal of CMMI block is to generate a so-called hypermultiple spectral image (HMSI) which contains the essential information of LR HSI and HR MSI. For that purpose, it firstly generates the preliminary fused version by taking all the known values for pre-fixed bands, and then takes values for other bands by applying upsampling of LR HSI. After applying convolution, the obtained hypermultiple spectral image passes through the next blocks, SpatRN and SpecRN, which use spatial and spectral edge losses, respectively. The overall loss function is a sum of three losses: spatial edge loss, spectral edge loss and fusion loss. Spatial edge loss is the weighted sum of the mean squared errors between the edge maps of the ground-truth and initial super-resolved HSI, which is the output of SpatRN, for the horizontal and vertical directions. Spectral edge loss calculates the mean squared error between the ground-truth edge map and edge map of the output of SpecRN, along the spectral dimension. Fusion loss computes mean squared error between the reconstructed and ground-truth HSIs.

The input LR data is generated by a bilinear downsampling operation from HR HSI, which is in advance blurred by a Gaussian filter. HR MSI is obtained by sampling equal intervals of bands from HR HSI.

2.4 Proposed Method: MSSR-NET

As it was mentioned in SSR-NET paper (Zhang X. et al., 2021), the network capacity to reconstruct complex spatial information is decreasing along with increasing scene complexity. The reason behind this limitation is the network’s very shallow structure. To overcome the issue mentioned above, we propose a network with a more powerful feature extraction ability that alleviates these problems.

Our proposed network can be seen as a modification of SSR-NET. The main contributions to the baseline architecture are the following: 1) long and short skip-connections to reuse convolved hypermultiple feature map, and 2) two extra conv + ReLU blocks. The first convolution is applied on LR HSI before the hypermultiple spectral image construction block, and the second one follows that block. The intuition behind these two additional convolutions is to strengthen the feature extraction capability, which is one of the main drawbacks of SSR-NET due to its shallow structure. We added those blocks to the spatial reconstruction part because the spatial context is more complex than the spectral one. The structure of the MSSR-NET is depicted in Figure 1, where blue blocks and arrows indicate our modifications.

FIGURE 1

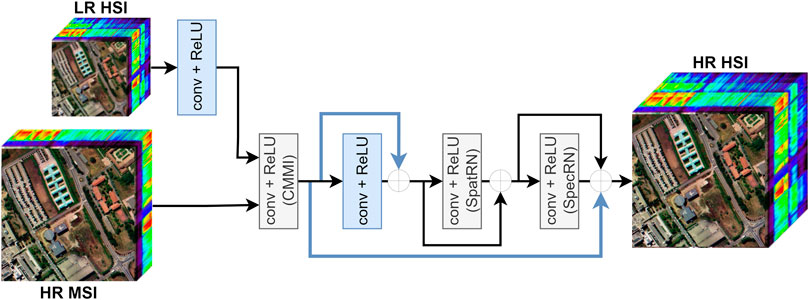
FIGURE 1. MSSR-NET architecture. The operation types are written in each block and the arrows with plus sign denote skip-connections. The blue arrows and blocks are our modifications to the baseline scheme.

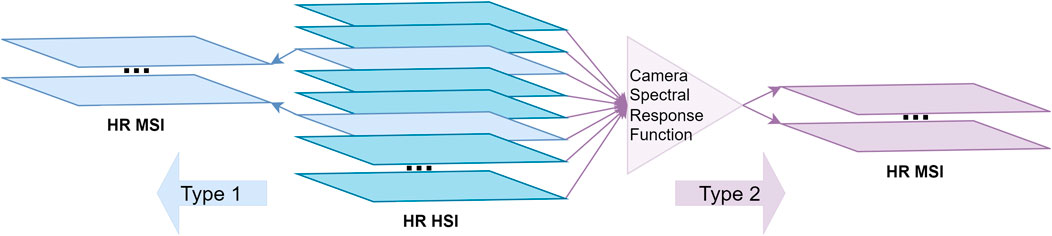
We consider two different data formation models for HR MSI (Type 1 and Type 2), which are illustrated in Figure 2. In Type 1, we apply the data formation strategy used in Zhang X. et al. (2021). In this case, HR MSI is generated by direct sampling of five spectral bands located at equal intervals of GT HR HSI without any modification of spectrum. As a result, five spectral bands of ground-truth data are directly involved in training and testing. In Type 2, the spectral response function corresponding to IKONOS sensor is applied on GT HR HSI to obtain HR MSI with four spectral channels, and therefore the spectral bands of the ground-truth data are smoothed according to the spectral properties of the sensor.

FIGURE 2

FIGURE 2. Two different data formation strategies for HR MSI generation.

Moreover, the single input scenarios are discussed, and the impact of each input component will be shown in the next section. Specifically, the experiments showed that the scores of evaluation metrics are slightly changed when we remove LR HSI as an input. In particular, the difference between the PSNR values in the case of two inputs and single HR MSI is less than 1 dB on Pavia University dataset in the case of our method.

3 Results

3.1 Experimental Setup

The experiments are done on remote sensing datasets, each of which contains a single image. Table 1 provides more details about the datasets used in the experiments. Following SSR-NET’s train-test splitting strategy, the central patch 128 × 128 is cropped for testing in Botswana, Pavia Centre, Pavia University, Urban datasets, and the rest is used for training. As Indian Pines consists of a single small hyperspectral image, the central 64 × 64 patch will be used for testing. The inputs, HR MSI and LR HSI, are generated from the ground-truth (GT) HR HSI. Following SSR-NET image formation strategy, the input LR HSI is generated by bilinear downsampling operation from the GT HR HSI, which is in advance blurred by a 5 × 5 Gaussian filter with standard deviation 2 in the spatial domain.

TABLE 1

TABLE 1. Remote sensing datasets for hyperspectral image super-resolution.

Four evaluation metrics are used for quantitative comparisons: Peak Signal-to-Noise Ratio (PSNR), Erreur Relative Globale Adimensionnelle de Synthèse (ERGAS) (Thomas and Wald, 2006) and Spectral Angle Mapper (SAM).

3.2 HSI SR Experiments for Two Different Models of HR MSI Data

3.2.1 Experiments for Type 1 Data Formation

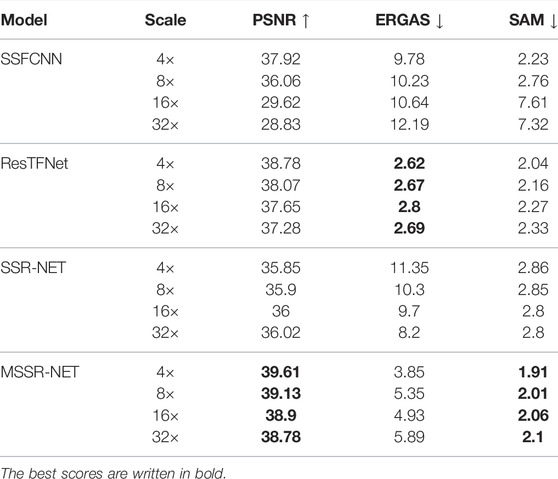
Here we have five spectral bands at equal intervals without any modification. From Table 2 one can see that the improvement over the baseline method in the case of Botswana dataset is about 4 dB in PSNR for 4× spatial downsampling while both networks have comparable model sizes. As mentioned in SSR-NET, because of the very shallow structure of their network, it is hard to reconstruct less uniform scenes, as well as more complex architectures can do. Botswana dataset has a relatively more complex structure compared with other remote sensing datasets, which leads to the lower PSNR values for SSR-NET. The result of ResTFNet (Liu X. et al., 2020) is about 1 dB less than ours, but also it has a deeper structure. Our network consists of five convolutional layers, while ResTFNet has four times more layers. SSFCNN has very unstable behavior on some datasets. Specifically, the PSNRs corresponding to SSFCNN (Han et al., 2018) for Pavia University dataset have values from 30 to 42 dB. Moreover, the higher the spatial downsampling ratio is, the higher PSNR can be. A possible reason can be not proper utilization of LR HSI data. Figure 3 shows the difference images between GT HSI and the outputs of each network for three selected spectral bands. Especially from that difference images can be seen that the MSSR-NET significantly outperforms the results of SSR-NET and SSFCNN. The errors are clearly visible near the edges. As the results of ResTFNet and MSSR-NET are close, it is hard to see the difference from their difference images.

TABLE 2

TABLE 2. Quantitative results on Botswana dataset. HR MSI is generated according to Type 1 model.

FIGURE 3

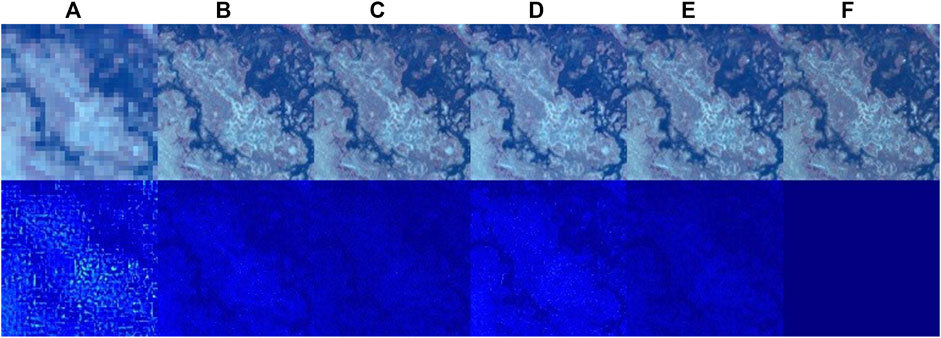
FIGURE 3. Qualitative comparison on Botswana dataset in case of 4× spatial downsampling. For visualization purposes, three spectral bands (47-14-3) are selected from the output data and difference images are calculated based on that preselected three bands. The first row shows (A) input LR HSI, (B) SSFCNN output, (C) ResTFNet output, (D) SSR-NET output, (E) MSSR-NET output, (F) GT HR HSI; the second row shows corresponding difference images between the GT HR HSI and (A–F), respectively.

Table 3 shows that for Pavia University dataset, which has a relatively simple context, the capability of the shallow network can be enough for a good reconstruction quality. Due to that property, the results of our method are slightly better than those for the baseline method.

TABLE 3

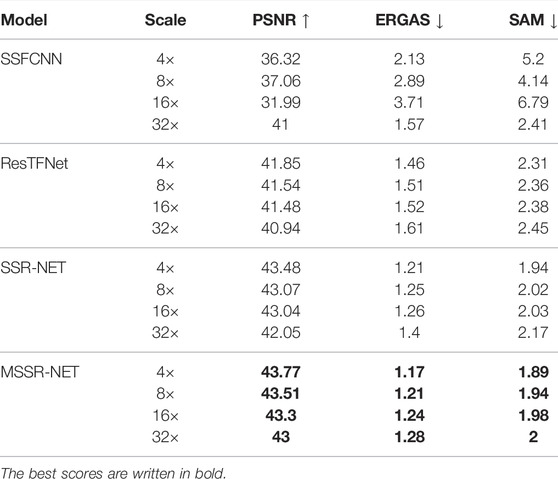
TABLE 3. Quantitative results on Pavia University dataset. HR MSI is generated according to Type 1 model by taking five spectral bands.

From Table 4 can be seen that the difference between the baseline and our method is about 3.6 dB in terms of PSNR for Indian Pines dataset. Figure 4 illustrates the outputs and their corresponding difference images for three spectral channels. The figure shows that the outputs of SSFCNN, ResTFNet and SSR-NET are blurry compared with the output HSI of our method. Corresponding difference maps verify the superiority of our method over other methods.

TABLE 4

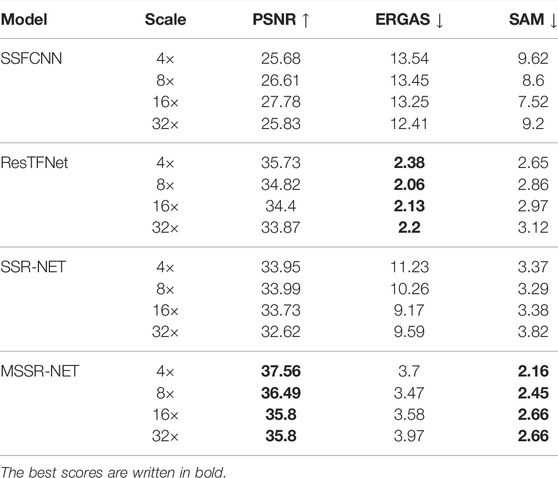
TABLE 4. Quantitative results on Indian Pines dataset. HR MSI is generated according to Type 1 model.

FIGURE 4

FIGURE 4. Qualitative comparison on Indian Pines dataset in case of 4× spatial downsampling. For visualization purposes, three spectral bands (28-14-3) are selected from the output data and difference images are calculated based on that preselected three bands. The first row shows (A) input LR HSI, (B) SSFCNN output, (C) ResTFNet output, (D) SSR-NET output, (E) MSSR-NET output, (F) GT HR HSI; the second row shows corresponding difference images between the GT HR HSI and (A–F), respectively.

The experiments on Pavia Center (Table 5) and Urban (Table 6) datasets also confirm that the MSSR-NET has better values of evaluation metrics compared to others.

TABLE 5

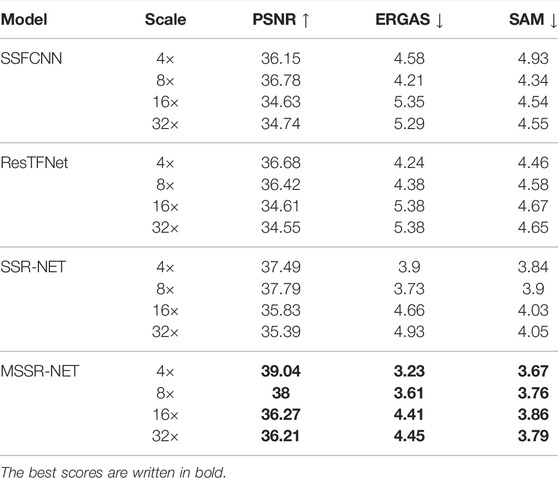
TABLE 5. Quantitative results on Pavia Center dataset. HR MSI is generated according to Type 1 model.

TABLE 6

TABLE 6. Quantitative results on Urban dataset. HR MSI is generated according to Type 1 model.

3.2.2 Experiments for Type 2 Data Formation

For these experiments, Pavia University dataset is used, which consists of a single huge image with 610, ×, 340 spatial resolution and 103 spectral bands. LR HSI generation part remains the same as in Zhang X. et al. (2021): HR HSI is blurred by 5 × 5 Gaussian filter with standard deviation 2, and LR HSI is obtained by spatially downsampling the blurred HR HSI by bilinear interpolation at a factor of 4, 8, 16, 32.

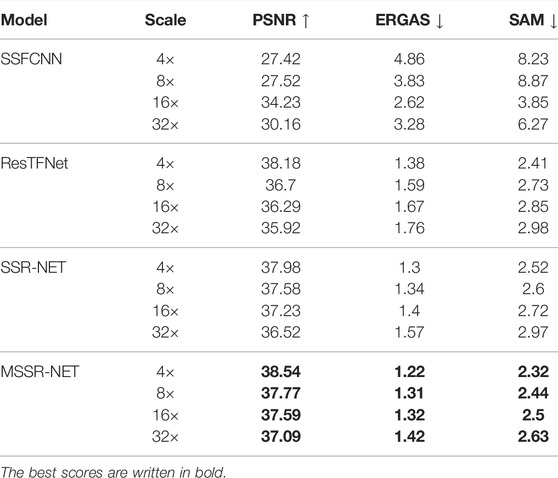
It can be seen from Table 7, that the advantage of our proposed method over SSR-NET becomes more significant than it was for the observations based on the model Type 1. The differences can be easily seen from the difference images illustrated in jet colormap in Figure 5. The lighter the color, the bigger is the difference. From the difference image corresponding to the output of SSR-NET, Figure 5D, it can be seen that especially near the edges, the difference is bigger compared with our method. Similar observations can be made about ResTFNet and SSFCNN.

TABLE 7

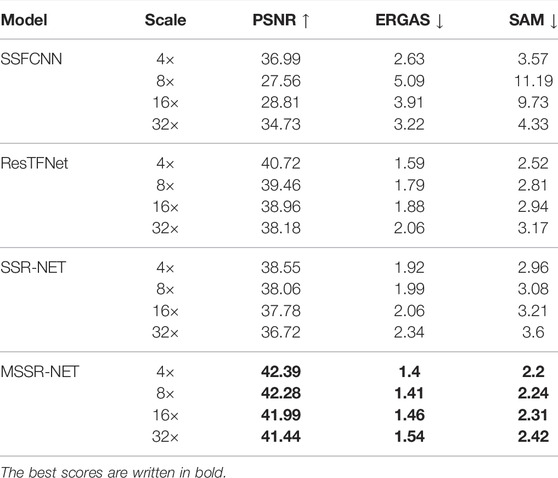
TABLE 7. Quantitative results on Pavia University dataset. HR MSI is generated according to Type 2 model.

FIGURE 5

FIGURE 5. Qualitative comparison on Pavia University dataset in case of 32× spatial downsampling and Type 2 spectral downsampling. For visualization purposes three spectral bands (66-28-0) are selected from the output data and difference images are calculated based on that preselected three bands. The first row shows (A) input LR HSI, (B) SSFCNN output, (C) ResTFNet output, (D) SSR-NET output, (E) MSSR-NET output, (F) GT HR HSI; the second row shows corresponding difference images between the GT HR HSI and (A–F), respectively.

Moreover, it is worth mentioning that compared with the results corresponding to the first data formation strategy (Table 3), the PSNR of the baseline method drops by 5 dB. Thus, the baseline method is not capable of reconstructing slightly modified HR MSI as well as in the case of unmodified ground-truth spectral bands. Unlike the baseline method, our method could reconstruct the HSI with almost the same quality in both data formation cases. For 32× spatial and about 25× spectral downsampling, the difference between the baseline method and ours is 4.7 dB.

Table 8 shows a comparison of the model size, inference time and FLOPs [approximately twice of multiply–accumulate operations (Mac)] corresponding to each method. The measurements are done on Urban dataset test image using NVIDIA GeForce RTX 3090 GPU. The FLOPs of MSSR-NET are 1.6 times more than the FLOPs of SSR-NET.

TABLE 8

TABLE 8. Model complexity analysis on Urban datset using NVIDIA GeForce RTX 3090 GPU.

Additionally, to investigate a comparative robustness of SSR-NET and MSSR-NET with respect to noise we train HR MSI with noiseless data and noisy LR HSI with the additive Gaussian noise. HR MSI is generated by taking four spectral bands based on Type 1 data formation, and additive Gaussian noise with σ = 100 standard deviation is added to LR HSI. From Table 9 can be seen that MSSR-NET is more noise resistant than the baseline SSR-NET, PSNR corresponding to MSSR-NET is decreased about 1.5 dB when we consider a noisy case, meanwhile, that gap for SSR-NET is more than 4 dB. But in general, even for this kind of high σ, PSNR values are still high. The reason of such a behavior can be explained by higher correlation between spectral bands than the spatial correlation within each spectral band. As it is mentioned above, the network mainly relies on the input HR MSI, and even aggressive downsampling of the second input (LR HSI) by a factor of 32 does not affect much on the results.

TABLE 9

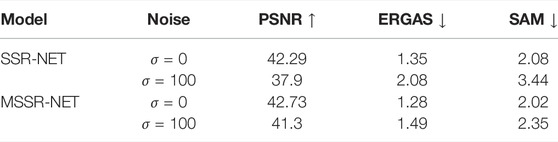
TABLE 9. Qualitative results on Pavia University dataset in case of two inputs: HR MSI and noisy LR HSI with σ standard deviation. Four spectral bands of HR MSI are generated according to Type 1 model and LR HSI is 4× downsampled.

3.3 HSI SR With Single Input Data

As can be seen from the tables mentioned above, the changes in the downsampling ratio in the spatial domain do not affect much on the results. So as a next step, single input cases are discussed to find out the impact of each input component. For that purpose, we feed to the network only one input, LR HSI or HR MSI.

Firstly, we feed spatially downsampled image, LR HSI, with different downsampling ratios. One can see by comparing Tables 8 and 10, that even in the case of 4× downsampling, PSNR drops by about 10 dB when we remove input HR MSI and leave only LR HSI. From Table 10 one can see that the results with a single input LR HSI lead to inferior results for all the methods, i.e., the input information is not enough for good reconstruction.

TABLE 10

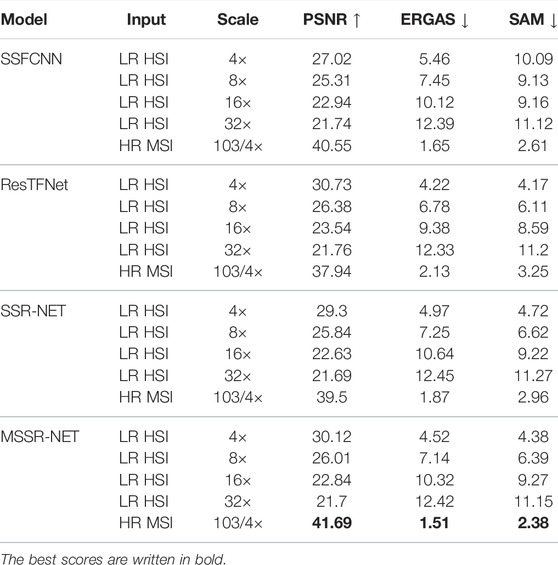
TABLE 10. Quantitative results on Pavia University dataset in case of single inputs. HR MSI is generated according to Type 2 model.

Secondly, let HR MSI, formed by Type 2, be fed to the network. By comparing the results of the two-input case (Table 8) with the lines of Table 10 corresponding to a single HR MSI input, we can see that the scores of evaluation metrics are very close. So, the network mainly learns from HR MSI, and feeding LR HSI to the network only slightly improves the results. Specifically, for MSSR-NET, the impact of the two-input case over a single HR MSI input case is less than 1 dB in terms of PSNR, which can also be seen by comparing the outputs illustrated in Figures 5 and 6.

FIGURE 6

FIGURE 6. Qualitative comparison on Pavia University dataset in case of single input HR MSI and Type 2 spectral downsampling. For visualization purposes, three spectral bands (66-28-0) are selected from the output data and difference images are calculated based on that preselected three bands. The first row shows (A) SSFCNN output, (B) ResTFNet output, (C) SSR-NET output, (D) MSSR-NET output, (E) GT HR HSI; the second row shows corresponding difference images between the GT HR HSI and (A–E), respectively.

A possible reason behind this high accuracy performance of the method with a single input data, HR MSI, is a high correlation among the spectral channels, so even four high-resolution spectral bands are enough to reconstruct 103 bands with very high quality. The correlations in the spatial domain are much weaker, so the spatial quality is much more critical for the learning process.

3.4 Ablation Study

Ablation experiments are done to show the impact of each component of MSSR-NET architecture. During the experiments we have seen that adding convolutional layers to the spectral reconstruction block does not provide any improvements, so we make changes before the spectral reconstruction block. A spatial reconstruction block is modified to allow better feature extraction and from Table 11 can be seen that it leads to improvements over the baseline method. Notations used in the first column of Table 11 are the followings: each addition means that we add only that part to the baseline network excluding others, e.g., “first conv” denotes the convolutional layer + ReLU applied on LR HSI just before CMMI block, “econd conv” is the convolution + ReLU layer between CMMI block and SpatRN.

TABLE 11

TABLE 11. Ablation experiments on Pavia Center dataset. Four spectral bands of HR MSI are generated according to Type 1 model and LR HSI is 4× downsampled.

4 Discussion

In this paper, a shallow convolutional neural network-based method was proposed to fuse LR HSI and HR MSI for HSI SR. Based on SSR-NET we proposed MSSR-NET of the shallow structure, small model size and short inference time. MSSR-NET demonstrates an essentially better performance due to a more powerful feature extraction capability. The quantitative and qualitative comparisons demonstrate the superiority of MSSR-NET on different remote sensing scenes.Experiments with different data formation strategies show that MSSR-NET is more robust with respect to different types of data formations than other state-of-the-art methods. Specifically for Botswana and Indian Pines datasets, the difference between PSNR values corresponding to the baseline SSR-NET and MSSR-NET is more than 3 dB in case of Type 1 data formation. That gap is about 4 dB for Pavia University dataset for Type 2 data formation. Moreover, with the increase of the downsampling ratio, that gap becomes bigger.Furthermore, we add additive Gaussian noise to the second input, LR MSI, to investigate MSSR-NET behaviour for both blurry and noisy LR HSI. Table 9 shows that MSSR-NET is more robust to noise than the baseline SSR-NET. The PSNR values corresponding to baseline SSR-NET are decreased by more than 4 dB when we consider a noisy case, meanwhile, that gap for MSSR-NET is about 1.5 dB. However, even for aggressive noise with standard deviation σ = 100 the PSNRs are still high.As a result of such behavior, we investigated the importance of the input LR HSI. We show that the network mainly relies on the input HR MSI. Specifically, for Pavia University dataset, the PSNR of our method will drop less than 1 dB when we remove input LR HSI. In the future, we plan to extend our shallow network to solve combined HSI enhancement problems, such as denoising and demosaicing.

5 Conclusion

This paper proposes a shallow CNN, MSSR-NET, for HSI SR based on SSR-NET architecture. MSSR-NET outperforms state-of-the-art HSI SR methods on five remote sensing datasets. Moreover, MSSR-NET shows its superiority in different data formation setups. Another property that we discovered is that the difference between the results corresponding to a single HR MSI input and two input cases is little.

Data Availability Statement

Publicly available datasets were analyzed in this study. The data can be found here: (https://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes).

Author Contributions

SA developed the method, the programs, and the numerical experiments under the guidance and with critical feedback of VK and KE. SA wrote the paper, which was then reviewed in depth by VK and KE.

Funding

The study is supported by the Doctoral School of Industry Innovations, Tampere University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Borsoi, R. A., Imbiriba, T., and Bermudez, J. C. M. (2020). Super-resolution for Hyperspectral and Multispectral Image Fusion Accounting for Seasonal Spectral Variability. IEEE Trans. Image Process. 29, 116–127. doi:10.1109/TIP.2019.2928895

PubMed Abstract | CrossRef Full Text | Google Scholar

Bungert, L., Coomes, D. A., Ehrhardt, M. J., Rasch, J., Reisenhofer, R., and Schönlieb, C.-B. (2017). Blind Image Fusion for Hyperspectral Imaging with the Directional Total Variation. Bristol, United Kingdom: IOP Publishing. ArXiv abs/1710.05705.

Google Scholar

Cavalli, R. M. (2021). Capability of Remote Sensing Images to Distinguish the Urban Surface Materials: A Case Study of Venice City. Remote Sens. 13, 3959. doi:10.3390/rs13193959

CrossRef Full Text | Google Scholar

Chang, Y., Yan, L., Zhao, X.-L., Fang, H., Zhang, Z., and Zhong, S. (2020). Weighted Low-Rank Tensor Recovery for Hyperspectral Image Restoration. IEEE Trans. Cybern. 50, 4558–4572. doi:10.1109/TCYB.2020.2983102

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, C., Li, Y., Liu, W., and Huang, J. (2015). Sirf: Simultaneous Satellite Image Registration and Fusion in a Unified Framework. IEEE Trans. Image Process. 24, 4213–4224. doi:10.1109/TIP.2015.2456415

PubMed Abstract | CrossRef Full Text | Google Scholar

Dian, R., Li, S., and Kang, X. (2021). Regularizing Hyperspectral and Multispectral Image Fusion by Cnn Denoiser. IEEE Trans. Neural Netw. Learn. Syst. 32, 1124–1135. doi:10.1109/TNNLS.2020.2980398

PubMed Abstract | CrossRef Full Text | Google Scholar

Fei, B. (2019). Hyperspectral Imaging in Medical Applications. Data Handl. Sci. Technol. 32, 523–565. doi:10.1016/B978-0-444-63977-6.00021-3

CrossRef Full Text | Google Scholar

Feng, Y.-Z., and Sun, D.-W. (2012). Application of Hyperspectral Imaging in Food Safety Inspection and Control: A Review. Crit. Rev. Food Sci. Nutr. 52, 1039–1058. doi:10.1080/10408398.2011.651542

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, Y., Liang, Z., and You, S. (2021). Bidirectional 3d Quasi-Recurrent Neural Network for Hyperspectral Image Super-resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 14, 2674–2688. doi:10.1109/JSTARS.2021.3057936

CrossRef Full Text | Google Scholar

Fubara, B. J., Sedky, M., and Dyke, D. (2020). “Rgb to Spectral Reconstruction via Learned Basis Functions and Weights,” in Proceeding of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 1984–1993. doi:10.1109/CVPRW50498.2020.00248

CrossRef Full Text | Google Scholar

Gan, Y., Hu, B., Wen, D., and Wang, S. (2016). “Dehazing Method for Hyperspectral Remote Sensing Imagery with Hyperspectral Linear Unmixing,” in Hyperspectral Remote Sensing Applications and Environmental Monitoring and Safety Testing Technology (Bellingham, WA: International Society for Optics and Photonics SPIE, SPIE Digital Library), 10156, 296–301. doi:10.1117/12.2246656

CrossRef Full Text | Google Scholar

Gao, H., Zhang, G., and Huang, M. (2021). Hyperspectral Image Superresolution via Structure-Tensor-Based Image Matting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 14, 7994–8007. doi:10.1109/JSTARS.2021.3102579

CrossRef Full Text | Google Scholar

Han, X.-H., Shi, B., and Zheng, Y. (2018). “Ssf-cnn: Spatial and Spectral Fusion with Cnn for Hyperspectral Image Super-resolution,” in Proceeding of the 2018 25th IEEE International Conference on Image Processing (ICIP), 2506–2510. doi:10.1109/ICIP.2018.8451142

CrossRef Full Text | Google Scholar

Kaichi, T., and Ozasa, Y. (2021). “A Hyperspectral Approach for Unsupervised Spoof Detection with Intra-sample Distribution,” in Proceeding of the 2021 IEEE International Conference on Image Processing (ICIP), 839–843. doi:10.1109/ICIP42928.2021.9506625

CrossRef Full Text | Google Scholar

Khan, M. J., Khan, H. S., Yousaf, A., Khurshid, K., and Abbas, A. (2018). Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 6, 14118–14129. doi:10.1109/ACCESS.2018.2812999

CrossRef Full Text | Google Scholar

Li, K., Dai, D., Konukoglu, E., and Gool, L. V. (2021a). Hyperspectral Image Super-resolution with Spectral Mixup and Heterogeneous Datasets. ArXiv abs/2101.07589. Available at: https://arxiv.org/abs/2101.07589.

Google Scholar

Li, Q., Wang, Q., and Li, X. (2021b). Exploring the Relationship between 2d/3d Convolution for Hyperspectral Image Super-resolution. IEEE Trans. Geosci. Remote Sens. 59, 8693–8703. doi:10.1109/TGRS.2020.3047363

CrossRef Full Text | Google Scholar

Li, Q., Wang, Q., and Li, X. (2020). Mixed 2d/3d Convolutional Network for Hyperspectral Image Super-resolution. Remote Sens. 12, 1660. doi:10.3390/rs12101660

CrossRef Full Text | Google Scholar

Li, X., Zhang, Y., Ge, Z., Cao, G., Shi, H., and Fu, P. (2021c). Adaptive Nonnegative Sparse Representation for Hyperspectral Image Super-resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 14, 4267–4283. doi:10.1109/JSTARS.2021.3072044

CrossRef Full Text | Google Scholar

Li, Y., Iwamoto, Y., Lin, L., Xu, R., Tong, R., and Chen, Y.-W. (2021d). Volumenet: A Lightweight Parallel Network for Super-resolution of Mr and Ct Volumetric Data. IEEE Trans. Image Process. 30, 4840–4854. doi:10.1109/tip.2021.3076285

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, J., Wu, Z., Xiao, L., Sun, J., and Yan, H. (2020a). A Truncated Matrix Decomposition for Hyperspectral Image Super-resolution. IEEE Trans. Image Process. 29, 8028–8042. doi:10.1109/TIP.2020.3009830

CrossRef Full Text | Google Scholar

Liu, X., Liu, Q., and Wang, Y. (2020b). Remote Sensing Image Fusion Based on Two-Stream Fusion Network. Inf. Fusion 55, 1–15. doi:10.1016/j.inffus.2019.07.010

CrossRef Full Text | Google Scholar

Ma, Q., Jiang, J., Liu, X., and Ma, J. (2022). Deep Unfolding Network for Spatiospectral Image Super-resolution. IEEE Trans. Comput. Imaging 8, 28–40. doi:10.1109/TCI.2021.3136759

CrossRef Full Text | Google Scholar

Makarau, A., Richter, R., Müller, R., and Reinartz, P. (2014). Haze Detection and Removal in Remotely Sensed Multispectral Imagery. IEEE Trans. Geosci. Remote Sens. 52, 5895–5905. doi:10.1109/TGRS.2013.2293662

CrossRef Full Text | Google Scholar

Mehta, A., Sinha, H., Mandal, M., and Narang, P. (2021). “Domain-aware Unsupervised Hyperspectral Reconstruction for Aerial Image Dehazing,” in Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), 413–422. doi:10.1109/wacv48630.2021.00046

CrossRef Full Text | Google Scholar

Mehta, A., Sinha, H., Narang, P., and Mandal, M. (2020). “Hidegan: A Hyperspectral-Guided Image Dehazing gan,” in Proceeding of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 846–856. doi:10.1109/CVPRW50498.2020.00114

CrossRef Full Text | Google Scholar

Mei, S., Yuan, X., Ji, J., Zhang, Y., Wan, S., and Du, Q. (2017). Hyperspectral Image Spatial Super-resolution via 3d Full Convolutional Neural Network. Remote Sens. 9, 1139. doi:10.3390/rs9111139

CrossRef Full Text | Google Scholar

Pan, Z.-W., and Shen, H.-L. (2019). Multispectral Image Super-resolution via Rgb Image Fusion and Radiometric Calibration. IEEE Trans. Image Process. 28, 1783–1797. doi:10.1109/TIP.2018.2881911

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, Y., Li, W., Luo, X., and Du, J. (2021). Hyperspectral Image Superresolution Using Global Gradient Sparse and Nonlocal Low-Rank Tensor Decomposition with Hyper-Laplacian Prior. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 14, 5453–5469. doi:10.1109/JSTARS.2021.3076170

CrossRef Full Text | Google Scholar

Pham, T. T., Takalkar, M. A., Xu, M., Hoang, D. T., Truong, H. A., Dutkiewicz, E., et al. (2019). “Airborne Object Detection Using Hyperspectral Imaging: Deep Learning Review,” in Computational Science and its Applications – ICCSA 2019. Editors S. Misra, O. Gervasi, B. Murgante, E. Stankova, V. Korkhov, C. Torreet al. (Cham: Springer International Publishing), 306–321. doi:10.1007/978-3-030-24289-3_23

CrossRef Full Text | Google Scholar

Qu, Y., Qi, H., and Kwan, C. (2018). “Unsupervised Sparse Dirichlet-Net for Hyperspectral Image Super-resolution,” in Proceeding of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2511–2520. doi:10.1109/CVPR.2018.00266

CrossRef Full Text | Google Scholar

Qu, Y., Qi, H., Kwan, C., Yokoya, N., and Chanussot, J. (2022). Unsupervised and Unregistered Hyperspectral Image Super-resolution with Mutual Dirichlet-Net. IEEE Trans. Geosci. Remote Sens. 60, 1–18. doi:10.1109/TGRS.2021.3079518

CrossRef Full Text | Google Scholar

Rascher, U., Nichol, C. J., Small, C., and Hendricks, L. (2007). Monitoring Spatio-Temporal Dynamics of Photosynthesis with a Portable Hyperspectral Imaging System. Photogrammetric Eng. Remote Sens. 73, 45–56. doi:10.14358/pers.73.1.45

CrossRef Full Text | Google Scholar

Segl, K., Roessner, S., Heiden, U., and Kaufmann, H. (2003). Fusion of Spectral and Shape Features for Identification of Urban Surface Cover Types Using Reflective and Thermal Hyperspectral Data. ISPRS J. Photogrammetry Remote Sens. 58, 99–112. Algorithms and Techniques for Multi-Source Data Fusion in Urban Areas. doi:10.1016/S0924-2716(03)00020-0

CrossRef Full Text | Google Scholar

Thomas, C., and Wald, L. (2006). “Comparing Distances for Quality Assessment of Fused Images,” in 26th EARSeL Symposium. Editor E. Bochenek (Varsovie, Poland: Millpress), 101–111.(

Google Scholar

Vella, M., Zhang, B., Chen, W., and Mota, J. F. C. (2021). “Enhanced Hyperspectral Image Super-resolution via Rgb Fusion and Tv-Tv Minimization,” in Proceeding of the 2021 IEEE International Conference on Image Processing (ICIP), 3837–3841. doi:10.1109/ICIP42928.2021.9506715

CrossRef Full Text | Google Scholar

Wang, W., Zeng, W., Huang, Y., Ding, X., and Paisley, J. (2019). “Deep Blind Hyperspectral Image Fusion,” in Proceeding of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), 4149–4158. doi:10.1109/ICCV.2019.00425

CrossRef Full Text | Google Scholar

Xue, J., Zhao, Y.-Q., Bu, Y., Liao, W., Chan, J. C.-W., and Philips, W. (2021). Spatial-spectral Structured Sparse Low-Rank Representation for Hyperspectral Image Super-resolution. IEEE Trans. Image Process. 30, 3084–3097. doi:10.1109/TIP.2021.3058590

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, L., Zhao, M., Wang, X., Zhang, Y., and Chen, J. (2021). Object Detection in Hyperspectral Images. IEEE Signal Process. Lett. 28, 508–512. doi:10.1109/LSP.2021.3059204

CrossRef Full Text | Google Scholar

Zhang, L., Nie, J., Wei, W., Li, Y., and Zhang, Y. (2021a). Deep Blind Hyperspectral Image Super-resolution. IEEE Trans. Neural Netw. Learn. Syst. 32, 2388–2400. doi:10.1109/TNNLS.2020.3005234

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Huang, W., Wang, Q., and Li, X. (2021b). SSR-NET: Spatial-Spectral Reconstruction Network for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 59, 5953–5965. doi:10.1109/TGRS.2020.3018732

CrossRef Full Text | Google Scholar

Zheng, K., Gao, L., Liao, W., Hong, D., Zhang, B., Cui, X., et al. (2021). Coupled Convolutional Neural Network with Adaptive Response Function Learning for Unsupervised Hyperspectral Super Resolution. IEEE Trans. Geosci. Remote Sens. 59, 2487–2502. doi:10.1109/TGRS.2020.3006534

CrossRef Full Text | Google Scholar

Zhou, Y., Rangarajan, A., and Gader, P. D. (2020). An Integrated Approach to Registration and Fusion of Hyperspectral and Multispectral Images. IEEE Trans. Geosci. Remote Sens. 58, 3020–3033. doi:10.1109/TGRS.2019.2946803

CrossRef Full Text | Google Scholar