A Cross-Check of the Reflectance Models to Be Used in Interpretation of Observations of Regolith-Like Surfaces

Many current and proposed programs of satellite remote sensing of the Earth and other celestial bodies rely upon measurements of the intensity and polarization of light scattered by these bodies. These measurement data are interpreted by searching for the best fits to light-scattering characteristics precalculated with some theoretical models. For regolith-like surfaces, i.e., discrete densely packed random media, the light-scattering models are still under development and they work under different approaches. Here, to estimate the difference between the reflectance characteristics yielded by these procedures, we compare the results of simulations performed according to five frequently used approximate models of a semi-infinite particulate medium. Special attention is paid to taking into account the weak-localization effect. The models differ by the scattering matrixes of a volume element and the dependence of the imaginary part of the effective refractive index on the filling factor. The volume element is an individual spherical particle or a randomly oriented cluster of particles. The cases of modifying the scattering matrix by the static structure factor correction or by subtracting the contribution of the mean field are also considered. The values for the size parameter of particles or monomers in the clusters and the refractive index were assumed at 1.76 and 1.50 + i0.0001, respectively; and two values for the filling factor (defined as a volume fraction occupied by particles in the medium), 20 and 10%, were considered. Our analysis shows that the angular dependences of the intensity and the linear polarization degree obtained with the considered models are rather close to each other. Moreover, they agree with the corresponding characteristics for a large cloud of particles (N is equal to or exceeds 10⁶) with the filling factor up to 20%, which were obtained by approximate methods but well follow the trends found in rigorous simulations for smaller ensembles of particles (Penttilä et al., J. Quant. Spectrosc. Radiat. Transfer, 2021, 262, 107524). Hence, these approximate models are equally acceptable to the interpretation of the results of observations.

1 Introduction

To gain insight into the nature, origin, and evolution of various bodies in the Solar System, including the Earth, photometric and polarimetric data obtained in space-borne and ground-based observations are widely used. From the perspective of the present analysis of the light-scattering properties of regolith-like surfaces, it is worth mentioning, for example, the Cassini–Huygens space mission, which acquired a huge data amount while orbiting Saturn and studying the planet and its system for 13 years. To continue research of satellites of the giant planets, the Jupiter Icy Moons Explorer mission (JUICE) is planned to be implemented in the nearest future. However, for many celestial bodies, the surfaces of which are covered with a regolith—a powder-like material composed of grains of different sizes and packing density—the interpretation of the results of observations in terms of the sizes, refractive index, and packing density of regolith particles requires the use of an adequate model to determine the characteristics of electromagnetic radiation reflected from a densely packed discrete random medium.

To calculate the light scattering characteristics of a densely packed discrete random medium is an extremely complex problem that cannot currently be solved at the theoretical level. The difficulty in the theoretical consideration of this problem is mainly connected with peculiarities of the light scattering in the near field (Mishchenko et al., 2011; Tishkovets et al., 2013). The matter is that, as distinct from sparse media, densely packed media exhibit the effects, which cannot be described only by contributions of the ladder and cyclic diagrams to the scattered radiation, since these effects are caused by the interference of inhomogeneous waves of different scattering orders. The interference of this kind manifests itself in the mutual shadowing and may considerably influence the opposition effects (Tishkovets et al., 2013). While the description of the light scattering by densely packed media in terms of the ladder and cyclic diagrams has been considerably improved in recent years [see (Tishkovets et al., 2011; Doicu and Mishchenko, 2019b; Doicu and Mishchenko, 2019c) and references therein], the contribution of the diagrams corresponding to the interference of waves of different scattering orders has not been taken into account yet.

At the same time, as has been noted above, there is a pressing need for models that correctly describe the light scattering characteristics of densely packed media. Because of this, attempts are being made to develop such models on the base of the well-elaborated theory of light scattering by sparse media [see (Mishchenko, 1994; Barrowes et al., 2000; Tishkovets and Mishchenko, 2004; Mishchenko et al., 2006; Mishchenko et al., 2013; Tishkovets and Petrova, 2013; Muinonen et al., 2017; Ito et al., 2018; Muinonen et al., 2018; Tishkovets and Petrova, 2020; Penttilä et al., 2021) and references therein].

For sparse media, it is assumed that the waves propagating between scatterers in the medium are spherical, which essentially simplifies the theoretical analysis. Moreover, in this case, it is relatively easy to obtain the ensemble-averaged reflection matrix analytically for a plane-parallel medium (Tishkovets and Mishchenko, 2004; Mishchenko et al., 2006; Tishkovets et al., 2011; Tishkovets and Petrova, 2013; Doicu and Mishchenko, 2019b; Doicu and Mishchenko, 2019c; Tishkovets and Petrova, 2020) or numerically with the Monte-Carlo technique for a spherical volume (Muinonen et al., 2017; Muinonen et al., 2018; Penttilä et al., 2021). To adapt these models to the problems of light scattering by densely packed media, the scattering characteristics of “a volume element” are modified. Specifically, it is suggested that the mean (coherent) field should be excluded [see (Barrowes et al., 2000; Muinonen et al., 2017; Muinonen et al., 2018; Penttilä et al., 2021) and the references therein], or the static structure factor correction should be made (Mishchenko, 1994; Mishchenko et al., 2013; Ito et al., 2018), or the scattering characteristics of randomly oriented clusters of particles should be considered as those of a volume element (Tishkovets and Petrova, 2013; Ito et al., 2018).

Unfortunately, the limits of applicability of the above specified models are unknown, since the data on the light-scattering characteristics measured in laboratory for the samples with thoroughly controlled parameters are still very rare (Mishchenko et al., 2013). Particularly, in the paper by Mishchenko et al. (2013), the solution of the vector radiative transfer equation was verified by the well-controlled experiment with a medium of monodisperse spherical particles suspended in water. It was found that, for the filling factor values below 0.1, all of the reflection matrix elements calculated with the static structure correction of a volume element very neatly fit the laboratory data. Some differences are observed only for the element R₄₄.

Given the laboratory data limitation, the quality of the model may be estimated with the methods that allow the scattering characteristics to be rigorously calculated for some cases. Such an attempt was recently made by Penttilä et al. (2021). They considered clusters composed of 10³ to 10⁵ spherical particles and compared their light-scattering characteristics obtained with the rigorous numerical method and with the model, according to which the mean field contribution was excluded (Muinonen et al., 2017; Muinonen et al., 2018; Penttilä et al., 2021). The calculations were performed for the backscattering domain, where the weak-localization effect reveals itself. For this relatively small clusters, the results of the rigorous simulations and the model approximation well agreed. For the clusters containing much more particles (from 10⁶ to 10⁹), the light-scattering characteristics were calculated within the frames of the assumed model approximation. It was found that, with growing the number of particles in a cluster, the intensity and the polarization of scattered light asymptotically tend to some limit that seems to be achieved when the number of particles in a cluster is 10⁹. In the opinion of Penttilä et al. (2021), the backward-scattered properties of this cluster represent the properties of a macroscopic, almost infinite system. Because of this, it would be interesting to compare the results reported by Penttilä et al. (2021) to the intensity and the linear polarization degree of light reflected by a semi-infinite discrete medium, the calculation technique for which is well-developed and does not require large computational resources (Tishkovets and Petrova, 2020). This comparison would allow us to estimate the applicability of the model (Tishkovets and Petrova, 2020) to densely packed media, the parameters of which are at least close to those used by Penttilä et al. (2021).

The purpose of this paper is to determine whether the differences between the reflectance characteristics yielded by different approximate procedures are substantial. For this, we compare the light-scattering characteristics in the back-scattering domain calculated by the models of a semi-infinite discrete medium with different versions of a volume element to each other and to the results reported by Penttilä et al. (2021). The parameters of all of the models considered below are assumed to be the same as those considered by Penttilä et al. (2021): the medium are composed of monodisperse spherical particles with the size parameter x = 1.76 (x ≡ 2πa/λ, where λ is the wavelength and a is the particle radius) and the refractive index m = 1.50 + i0.0001. As regards the filling factor (or the packing density) in the medium, which is a volume fraction occupied by particles in the medium, two values, ξ = 20 and 10%, were considered. The first value of ξ was used by Penttilä et al. (2021) for calculating the weak-localization contribution, while the second one, by Mishchenko et al. (2013) for verifying the applicability of the vector radiative transfer equation to densely packed media. (It is worth noting that Mishchenko et al. (2013) considered the other parameters of particles and the oblique radiation incidence). The simulations performed with two values of the parameter ξ will make it possible to follow the influence of the concentration of particles on the manifestation of the weak-localization effect in the models with different versions of a volume element of the medium.

2 Models of a Medium

In this paper we consider five models of a discrete random densely-packed medium (from A to E below), which differ by both the scattering characteristics of a volume element and the behavior of the extinction in a medium. The medium is considered as a semi-infinite layer, and the incident radiation is assumed to propagate perpendicularly to its boundary, since the theory for a more general case of the obliquely incident radiation is still at an early stage of development [see, e.g., (Tishkovets et al., 2011; Doicu and Mishchenko, 2019a)]. We compare the results of these models to each other and to the simulation results reported by Penttilä et al. (2021). To calculate the intensity and the linear polarization degree of light reflected by a semi-infinite discrete medium, we use the procedure and the fast algorithm described by Tishkovets and Petrova (2020). This procedure allows us to consider both the diffuse and coherent-backscattering components of the reflected light.

2.1 Model A

This model is simplest. The scattering matrix of a volume element in this model medium is equal to the scattering matrix of an individual particle of the medium. The size parameter and the refractive index of these particles were specified above (see the Introduction). To describe the propagation of radiation in a discrete random medium, a concept of the so-called complex effective refractive index $m_{\mathrm{eff}}$ is used [see, e.g., (Tishkovets et al., 2011; Doicu and Mishchenko, 2019a), and the references therein]. Its imaginary part $\mathrm{Im}\left(m_{\mathrm{eff}}\right)$ is directly related to the extinction coefficient of the medium, and this dependence differs for sparse and densely packed media. Within model A, it is assumed that $\mathrm{Im}\left(m_{\mathrm{eff}}\right)$ linearly depends on the concentration (or the number density) of particles in the medium η, analogously to that in a sparse medium model (Bohren and Huffman, 1983; Mishchenko et al., 2006; Tishkovets et al., 2011; Doicu and Mishchenko, 2019a):

$\mathrm{Im}\left(m_{\mathbf{eff}}\right)=\frac{\eta }{2k_0}{C}_{\mathrm{ext}}=\frac{3\xi }{8\pi x^3}{k}_0^2{C}_{\mathrm{ext}}=\frac{3\xi }{4x^3}{\displaystyle \sum }_l\left(2l+1\right)\mathrm{Re}\left(a_l+b_l\right).(1)$

Here, $k_0=2\pi /\lambda$, $C_{\mathrm{ext}}$ is the extinction cross-section of a particle, and $a_l$ and $b_l$ are the Mie coefficients (Bohren and Huffman, 1983), while $\xi =4\pi \eta a^3/3$ is the filling factor. The single-scattering albedo is determined as usual, $\omega =C_{\mathrm{sca}}/C_{\mathrm{ext}}$, where $C_{\mathrm{sca}}$ is the scattering cross-section of a particle.

2.2 Model B

This model differs from model A only by the behavior of the extinction in dependence on the concentration of scatterers. In a densely packed medium, this dependence is nonlinear. If this medium is composed of identical spherical particles, $\mathrm{Im}\left(m_{\mathrm{eff}}\right)$ can be determined from the following system of equations, which stems from the analysis of the mean field in a medium [see, e.g., (Tishkovets et al., 2011) and the references therein]

$X_{Ln}^{\left(pn\right)}+\frac{3\xi }{2x^3}{\displaystyle \sum }_q\left(a_l+pq{b}_l\right){\displaystyle \sum }_l\left(2l+1\right)X_{ln}^{\left(qn\right)}{F}_{Lln}^{\left(q\right)}=0.(2)$

Here, $p,q=\pm 1$; n can take one of the values, $\pm 1$;

$F_{LlM}^{\left(q\right)}={\displaystyle \sum }_s{C}_{LMl-M}^{s0}{C}_{Lql-q}^{s0}{f}_s,$

where the quantities C with indexes are the Clebsch–Gordan coefficients (Varshalovich et al., 1988);

$f_l=\underset{\rho }{\overset{\infty }{{\displaystyle \int }}}\left(g\left(y\right)-1\right)h_l\left(y\right)j_l\left(y{m}_{\mathrm{eff}}\right)y^2\mathrm{d}y-\frac{{\rho }^2}{1-m_{\mathrm{eff}}^2}\left[m_{\mathrm{eff}}{h}_l\left(\rho \right)j_l^{\prime }\left(\rho m_{\mathrm{eff}}\right)-h_l^{\prime }\left(\rho \right)j_l\left(\rho m_{\mathrm{eff}}\right)\right]$

where ρ = 2x, the $j$ and $h$ designations are for the Bessel and Hankel spherical functions and their derivatives, respectively, $g\left(y\right)$ is the pair correlation function for the system of identical solid spheres (Balescu, 1975).

The linear homogeneous system of Eq. 2 has a non-trivial solution if its determinant is equal to zero. This condition allows us to determine the effective refractive index $m_{\mathrm{eff}}$, which depends on the properties of the medium: the shape, sizes, refractive index, and filling factor of the particles. The dependences of $\mathrm{Im}\left(m_{\mathrm{eff}}\right)$ on the filling factor of particles ξ calculated according to Eqs 1, 2 for the particles’ parameters specified above are shown inFigure 1.

FIGURE 1

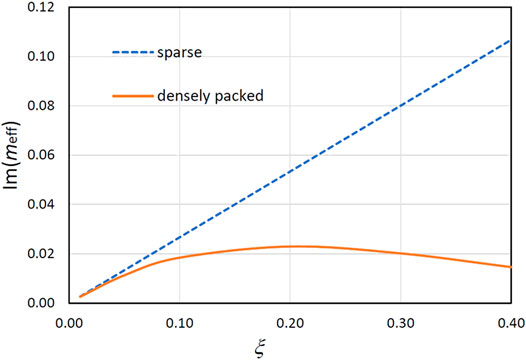
FIGURE 1. The imaginary part of the effective refractive index of a medium composed of identical spherical particles with x = 1.76 and m = 1.50 + i0.0001 in dependence on the filling factor of particles according to Eqs 1, 2 for sparse (dashed line) and densely packed (solid line) media, respectively.

As is seen from the figure, when the concentration of particles is high, $\mathrm{Im}\left(m_{\mathrm{eff}}\right)$ of a densely packed medium may be substantially lower than the values predicted by Eq. 1 that is valid for the sparse media approximation. For example, for a case of ξ = 20% and the particle parameters considered here, the value of $\mathrm{Im}\left(m_{\mathrm{eff}}\right)$ in model A is more than twice that in model B: 0.0534 versus 0.0229.

2.3 Model C

In this model, the scattering matrix of a volume element of the medium coincides with that of a randomly oriented cluster of spherical particles. According to Tishkovets and Petrova (2013), when the number of particles in clusters is large, the intensity and the degree of linear polarization of light reflected by a semi-infinite medium composed of such clusters becomes almost independent on the further increase of this number. The imaginary part of the effective refractive index of the medium is assumed to be determined as

$\mathrm{Im}\left(m_{\mathrm{eff}}\right)=\frac{{\eta }_1}{2k_0}{C}_{\mathrm{ext}},(3)$

where ${\eta }_1$ and $C_{\mathrm{ext}}$ are the concentration of clusters in the medium and the extinction cross-section of the clusters, respectively. The filling factor of particles (not clusters) in the medium is defined as

$\xi =\frac{4}{3}\pi {\eta }_1{a}_v^3,(4)$

where $a_v$ is the radius of a volume-equivalent sphere of the cluster ($a_v^3=N{a}^3$, where N is the number of particles with radii $a$ in the cluster). The single scattering albedo is determined analogously to that in model A.

Earlier, model C was successfully applied to the media with relatively low values of the filling factor of particles in a medium (ξ ≤ 4%) (Tishkovets and Petrova, 2013).

2.4 Model D

This model is analogous to that considered by Mishchenko (1994), Mishchenko et al. (2013), and Ito et al. (2018); i.e., the scattering characteristics of a volume element of the medium are corrected with accounting for the so-called static structure factor. According to the Percus−Yevick approximation (Balescu, 1975), the structure factor is given by (Balescu, 1975; Mishchenko, 1994; Ito et al., 2018)

$S\left(\vartheta \right)=\frac{1}{1-C\left(u\right)},$

where $u=4x\sin \frac{\vartheta }{2}$, ϑ is the scattering angle, and

$C\left(u\right)=24\xi W\left(u\right).$

If $u\ne 0$,

$\begin{array}{l}W\left(u\right)=\frac{\alpha +\beta +\delta }{u^2}\cos u-\frac{\alpha +2\beta +4\delta }{u^3}\sin u-\frac{2\left(\beta +6\delta \right)}{u^4}\cos u+\\ +\frac{2\beta }{u^4}+\frac{24\delta }{u^5}\sin u+\frac{24\delta }{u^6}\left(\cos u-1\right).\end{array}$

If u = 0,

$W\left(0\right)=-\left(\frac{\alpha }{3}+\frac{\beta }{4}+\frac{\delta }{6}\right).$

The coefficients $\alpha ,\beta ,\delta$ are

$\alpha =\frac{{\left(1+2\xi \right)}^2}{{\left(1-\xi \right)}^4},$

$\beta =-6\xi \frac{{\left(1+\xi /2\right)}^2}{{\left(1-\xi \right)}^4},$

$\delta =\alpha \xi /2.$

Then, with accounting for the structure factor, the normalized scattering matrix of a particle in the medium $\mathbf{F}\left(\vartheta \right)$ is connected with the matrix of an individual isolated particle $\mathbf{Z}\left(\vartheta \right)$ by the following relationship (Ito et al., 2018)

$\mathbf{F}\left(\vartheta \right)=\frac{4\pi }{k_0^2{C}_{\mathrm{sca}}^{\mathrm{s}}}\mathbf{Z}\left(\vartheta \right)\mathit{S}\left(\vartheta \right),(5)$

where

$k_0^2{C}_{\mathrm{sca}}^{\mathrm{s}}={\displaystyle \underset{4\pi }{\int }{Z}_{11}\left(\vartheta \right)S\left(\vartheta \right)\mathrm{d}\Omega }=2\pi \underset{0}{\overset{\pi }{{\displaystyle \int }}}{Z}_{11}\left(\vartheta \right)S\left(\vartheta \right)\sin \vartheta \mathrm{d}\vartheta .(6)$

The imaginary part of the effective refractive index of the medium is determined as

$\mathrm{Im}\left(m_{\mathrm{eff}}\right)=\frac{\eta }{2k_0}\left(C_{\mathrm{sca}}^{\mathrm{s}}+C_{\mathrm{abs}}\right)=\frac{3\xi }{8\pi x^3}{k}_0^2\left(C_{\mathrm{sca}}^{\mathrm{s}}+C_{\mathrm{abs}}\right),(7)$

where $C_{\mathrm{abs}}$ is the absorption cross-section of a particle calculated according to the Mie theory, while the scattering cross-section $C_{\mathrm{sca}}^{\mathrm{s}}$ is obtained from Eq. 6, which takes into account the structure factor. The single-scattering albedo of particles in this model is determined as

$\omega =\frac{C_{\mathrm{sca}}^{\mathrm{s}}}{C_{\mathrm{sca}}^{\mathrm{s}}+C_{\mathrm{abs}}}.(8)$

The results of this modeling for the noncoherent part of the reflected radiation, which is determined by the radiative transfer equation, were compared to those of laboratory measurements. This comparison showed that, for the concentrations up to 10%, all of the elements of the reflectance matrix of the medium (except R₄₄) well agree with the measurement results (Mishchenko et al., 2013).

2.5 Model E

This model corresponds to that developed by the researchers from the University of Helsinki [see (Muinonen et al., 2017; Muinonen et al., 2018; Penttilä et al., 2021) and references therein]. In this model, the contribution of the coherent (or mean) field is subtracted from the scattering characteristics of a volume element. The field scattered by some volume containing particles (a cluster of particles) in the medium ${\mathbf{E}}^{\left(\mathrm{s}\right)}$ is represented by a sum of the incoherent ${\mathbf{E}}^{\left(\mathrm{in}\right)}$ and coherent ${\mathbf{E}}^{\left(\mathrm{c}\right)}$ parts [see, e.g., (Barrowes et al., 2000; Muinonen et al., 2017; Muinonen et al., 2018; Penttilä et al., 2021), and the references therein]

${\mathbf{E}}^{\left(\mathrm{s}\right)}={\mathbf{E}}^{\left(\mathrm{in}\right)}+{\mathbf{E}}^{\left(\mathrm{c}\right)}.$

Since the locations of scatterers in the medium are random, the equality $\mathrm{<}{\mathbf{E}}^{\left(\mathrm{in}\right)}>=0$ should be fulfilled. Here the angle brackets mean the ensemble-averaging over a large number of volume-element realizations. Then, the average of the second moment of the field ${\mathbf{E}}^{\left(\mathrm{in}\right)}$ is determined by the relationship

$<|{\mathbf{E}}^{\left(\mathrm{in}\right)}{|}^2>=<|{\mathbf{E}}^{\left(\mathrm{s}\right)}{|}^2>-<|{\mathbf{E}}^{\left(\mathrm{c}\right)}{|}^2>.(9)$

The terms in the right part of Eq. 9 can be averaged numerically by generating clusters with sufficiently large number of particles with the concentration and parameters of particles required. In this averaging procedure, some function $H\left(\vartheta \right)$ is derived; by multiplying this function by the scattering matrix of an individual particle, the scattering matrix of a volume element is obtained. The whole technique is described at length by Muinonen et al. (2017). The procedure of calculating the scattering characteristics, which are required to find the reflectance matrix of a medium (or a cluster containing a large number of particles), is the same as that for relationships Eqs 5–8 in the previous model. The only difference is that the normalized function $H\left(\vartheta \right)$ should be used instead of the structure factor.

This model yields the results that rather well agree with those of rigorous calculations of the intensity and the degree of linear polarization of light scattered by clusters of spherical particles, the number of which is N ≤ 10⁵ (note that the clusters were generated by filling a spherical volume by small constituents with the packing density specified) (Penttilä et al., 2021).

3 Results and Discussion

To solve the radiative transfer and weak localization equations, the scattering matrix of a volume element of the medium is usually presented as a series expansion in generalized spherical functions (Mishchenko et al., 2006). The algorithms and codes to solve these equations by using these expansions are available on the web-sites https://www.giss.nasa.gov/staff/mmishchenko/brf/ and http://rian.kharkov.ua/index.php/en/software-en, respectively. Here we use these codes to calculate the normalized intensity and the degree of linear polarization of radiation reflected by a semi-infinite medium.

The simulations according to model C required that clusters with the assumed filling factor should be constructed. For this, we randomly placed N identical non-overlapping spherical particles of the specified size into a spherical volume, the size of which provides the required filling factor ξ for a given value of N. To calculate the single-scattering matrix of clusters, we used the publicly available FORTRAN code (MSTM) (Mackowski and Mishchenko, 2011), which is based on the superposition T-matrix method, one of the most versatile and efficient direct computer solvers of the macroscopic Maxwell equations for an arbitrary multi-sphere configuration in random or fixed orientation. The parameters of clusters’ constituents and the filling factor are the same as those considered by Penttilä et al. (2021): x = 1.76, m = 1.50 + i0.0001, and ξ = 20%. The values of $\mathrm{Im}\left(m_{\mathrm{eff}}\right)$ were derived according to Eqs 3, 4; and they are 0.0798, 0.0771, and 0.0720 for N = 20, 40, and 80, respectively.

In Figure 2, as an illustration of the results of model C, we present the intensity normalized to a value at opposition (the scattering angle is ϑ = 180°) I/I₀ and the degree of linear polarization P of light reflected from a medium composed of randomly oriented clusters. These quantities are shown in dependence on the scattering angle, and the curves for different numbers of particles in the clusters are compared. For each of the assumed values of N, we actually generated several configurations of the clusters, but the angular dependences of I/I₀ and P obtained for the medium composed of these clusters turned out to be very close under a given N. Consequently, we show here the phase curves only for one of the configurations for a specified N. Moreover, as it became clear from the model calculations, the growth of N to the values exceeding ∼50 does not influence much the angular behavior of the considered quantities (Figure 2).

FIGURE 2

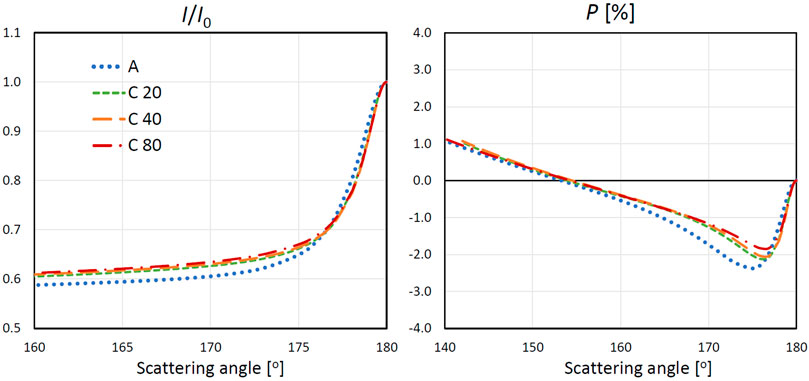
FIGURE 2. The intensity normalized to a value at ϑ = 180° I/I₀ and the degree of linear polarization P of light reflected by a semi-infinite medium composed of clusters in dependence on the scattering angle. The curves for different numbers of particles in the clusters (model C) are compared to each other and those for individual particles in a medium (model A) with ξ = 20%. The values of x, m, and Im (m_eff) are specified in the text.

Let us turn to comparison of the results of different models. The normalized intensity and the linear polarization degree calculated by the above described models A−D for the packing density of the medium ξ = 10% are shown in Figure 3 in dependence on the scattering angle ϑ. To avoid overloading the diagrams, we present here models C only by the results for clusters with 40 constituents. The reason is that, as has been noted above, the further growth of the clusters induces only very weak changes in the angular dependences of the intensity and the linear polarization degree of light scattered by a medium composed of these clusters (Figure 2). As is seen from Figure 3, all of the models with the packing density ξ = 10% yield rather close results. It should be reminded that, when verifying the applicability of the radiative transfer equation to a densely packed medium, model D perfectly fitted the phase curves measured in the laboratory (Mishchenko et al., 2013). Since the weak-localization equation was derived under the same conditions as the classic radiative transfer equation (Tishkovets et al., 2011), a good agreement between models A–D in Figure 3 suggests that all of them may be used to estimate the parameters of a medium at least in the cases, when the properties of particles in a medium are close to those specified here and the packing density of particles is less than 10%.

FIGURE 3

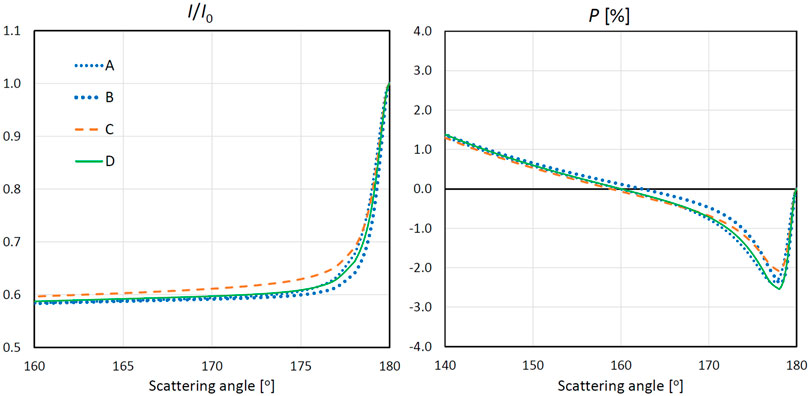
FIGURE 3. The normalized intensity I/I₀ and the degree of linear polarization P of light reflected by a discrete random medium in dependence on the scattering angle, which were obtained with models A−D and ξ = 10%. The values of x and m are specified in the text.

Let us consider the results of simulations with the packing density ξ = 20% according to all of the models, including model E, in more detail. The obtained phase curves of the normalized intensity and the linear polarization degree are shown in Figure 4.

FIGURE 4

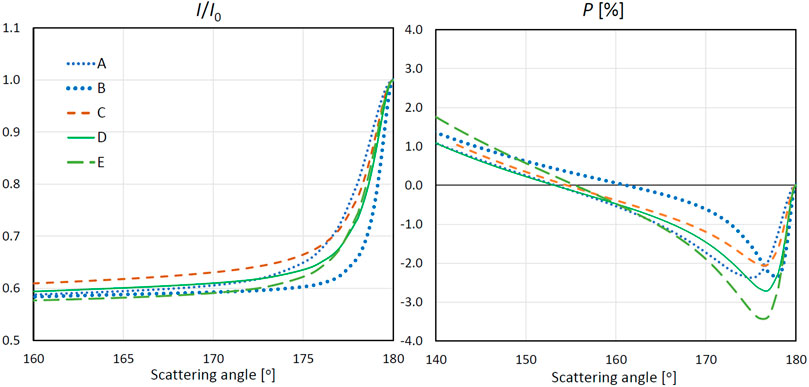
FIGURE 4. The normalized intensity I/I₀ and the degree of linear polarization P of light reflected by a discrete random medium in dependence on the scattering angle, which were obtained with models A−E and ξ = 20%. The values of x and m are specified in the text.

The values of $\mathrm{Im}\left(m_{\mathrm{eff}}\right)$ in each of the models and the parameters of the phase curves of the normalized intensity I/I₀ and the polarization P are listed in Table 1. These parameters are the angular halfwidth of the intensity peak Δϑ at a level of 0.8 of its maximum, the inversion angle ${\vartheta }_{\mathrm{inv}}$, at which the linear polarization changes its sign, the polarization value $P_{\min }$ at the minimum of the so-called negative branch observed at high scattering angles (or low phase angles φ = 180° − ϑ), and the angular position of this minimum ${\vartheta }_{\min }$.

TABLE 1

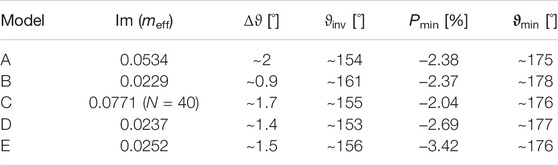
TABLE 1. The values of Im (m_eff) in models A−E and the parameters of the phase curves of the normalized intensity and the linear polarization degree for ξ = 20%.

There are two characteristic features in the phase curves of the characteristics of radiation reflected by a medium, which are reproduced by each of the considered models. They are a narrow interference peak in the intensity, which is rigorously centered at the backscattering direction, and a branch of negative polarization, the minimum of which is close to the opposition. The dependence of these features on the properties of a scattering medium was analyzed at length in many papers [see, e.g. (Tishkovets et al., 2011; Tishkovets and Petrova, 2013), and references therein]. Specifically, it was shown that the halfwidth of the interference peak and the phase angle at the polarization minimum (${\phi }_{\min }$ = 180° – ${\vartheta }_{\min }$) under nonzero polarization of the noncoherent component are in direct proportion to the concentration of scatterers (or the filling factor ξ). When the concentration of particles decreases, the angular range, within which the weak-localization effect manifests itself, also decreases, while the inversion scattering angle ${\vartheta }_{\mathrm{inv}}$ grows (compare Figures 3, 4). As might be expected, with increasing the packing density, the difference between the model curves becomes more noticeable, though all of them exhibit qualitatively the same behavior. Moreover, the models C, D, and E well agree in terms of the inversion angle of polarization and the position of the polarization minimum.

As is also seen from Figure 4 and Table 1, the decrease in the value of $\mathrm{Im}\left(m_{\mathrm{eff}}\right)$ in model B relative to that in model A (0.0229 versus 0.0534) results in narrowing the intensity peak (Δϑ becomes ∼0.9° instead of ∼2°) and in moving the polarization minimum to opposition (${\vartheta }_{\min }$ becomes ∼178° instead of ∼175°). This is explained by the fact that the decrease in the imaginary part of the effective refractive index $\mathrm{Im}\left(m_{\mathrm{eff}}\right)$ under the same characteristics of a volume element (an individual spherical particle) of a medium yields the equivalent decrease (by a factor of ∼2.3) in the concentration of scatterers. According to the above mentioned studies, more porous media should exhibit narrower opposition features due to the weak-localization effect.

Unfortunately, since the experimental data on the scattering by discrete random densely-packed media with thoroughly controlled parameters (the sizes and shape of particles, the packing density, and the other parameters of a medium) are limited, it is currently impossible to determine unambiguously which of these models more correctly describes the light scattering by a densely packed particulate media. Because of this, we compare the results of these models to those reported by Penttilä et al. (2021). They describe the simulations for the intensity and the linear polarization degree of light scattered by a large spherical volume randomly filled with spherical particles, the sizes, the refractive index, and the filling factor (or the packing density) of which are equal to the parameters considered here. In the cited paper, the number of particles N in the volume was varied within 10³–10⁹. For ensembles containing more than 10⁵ particles, the calculations were performed with an approximate method under the assumption that the waves propagating between scatterers in the medium are spherical, while numerically rigorous methods were used for smaller ensembles. In addition, in the approximate method, the contribution of the mean field to the scattering matrix of a volume element and the imaginary part of the effective refractive index was removed (Muinonen et al., 2017; Muinonen et al., 2018; Penttilä et al., 2021). The results of the approximate and exact calculations for N < 10⁵ turned out to be in satisfactory agreement.

To facilitate the comparison of our models (Figure 4) with the results of Penttilä et al. (2021), we show them together in Figure 5. To avoid overloading the diagrams, only the data for the particles’ number N = 10⁵, 10⁶, and 10⁹ from Penttilä et al. (2021) are given in Figure 5.

FIGURE 5

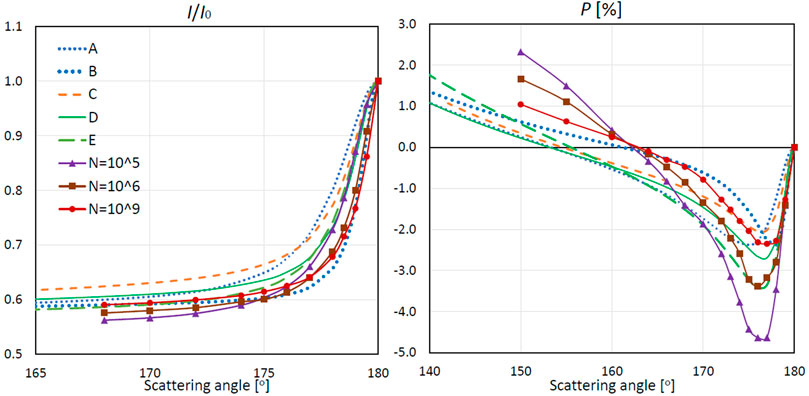
FIGURE 5. The same as in Figure 4 but compared to the specified models for a cloud of particles considered by Penttilä et al. (2021).

When analyzing the phase curves in Figure 5, it is important to have in mind that the geometry of the light-scattering simulations for a spherical cloud of particles and a semi-infinite layer differs, i.e., the scattering media are different in shape. Because of this, the agreement between the angular profiles for model E and a cloud of 10⁹ particles (Penttilä et al., 2021), for which the light-scattering characteristics of a volume element are the same, is worse than it could be expected. In addition, an assumption on the exponential decrease of the intensity with depth in a medium, which was made when deriving the weak localization equations for a semi-infinite layer (Tishkovets and Petrova, 2020), may play a certain role in this discrepancy. Consequently, the fact that, among models A–E, model B appears to agree best of all with the data for a cloud of 10⁹ particles should not be considered as a decisive factor in favor of using this model in the interpretation of measurements. Most likely, this agreement resulted from a particular combination of the parameters of particles and might not be relevant to the other parameters’ values.

The comparison of the phase curves of polarization produced by models C–E and those for a large cloud of particles suggests that the angular position of the polarization minimum ${\vartheta }_{\min }$ turns out to be almost independent of the model type. This circumstance makes this parameter most reliable for the interpretation of the measured phase curves of polarization.

4 Conclusion

At present, it is a challenge to describe theoretically the light scattering process for densely packed random media, where particles are not in far zones of each other, as in sparse media. Because of this, to estimate the light scattering properties of densely packed media, researchers turn to approximate methods and models that stem from the light-scattering theory for sparse media. However, it is not clear yet whether the results of this approximate modeling are correct, since the experimental data for the samples with thoroughly controlled parameters are limited so far.

To estimate the difference between the results yielded by the approximate procedures, we considered five approximate models, which are most frequently used to calculate the reflection matrix of a densely packed semi-infinite medium, and compared their results to each other and to those of the rigorous and approximate simulations for a large spherical cloud of particles (Penttilä et al., 2021). In our models, the incident radiation is assumed to propagate perpendicularly to its boundary. The parameters of particles were chosen according to those assumed by Penttilä et al. (2021). The input parameters of our models differ by the scattering matrix of a volume element of the medium and the dependence of the extinction on the concentration of particles. For our computations, we used the fast algorithm proposed by Tishkovets and Petrova (2020).

It was found that the reflectance characteristics obtained with different models for a semi-infinite medium (Figure 4) qualitatively agree with each other and with those for a cloud containing 10⁶ and more particles (Penttilä et al., 2021; Figure 5). Hence, these approximate models are equally acceptable to the interpretation of the results of measurements. It should also be noted that the approximate simulations performed both in this study and by Penttilä et al. (2021) are based on the same assumption that the waves propagating between scatterers in the medium are spherical. Consequently, the qualitative agreement between their results could be expected. However, the difference between the intensity and linear polarization profiles obtained here and by Penttilä et al. (2021) may be caused by different shapes of the media considered.

One of the purposes of developing the reflectance models for densely packed particulate media with accounting for the weak-localization effect is to apply them to the interpretation of different measurement results, in particular, numerous observations of atmosphereless bodies of the Solar System. Consequently, the used model should allow a lot of parameters’ cases to be tested rather quickly. For example, even in the simplest model A, there are four input parameters (the size of particles, the real and imaginary parts of their refractive index, and the filling factor) that should be varied when fitting the experimental data with the model. Because of this, together with the reliability and effectiveness of the model, the time required to calculate the reflectance matrix of a medium becomes one of the key parameters. In this regard and given the results of the present analysis, the model and the fast algorithm presented by Tishkovets and Petrova (2020) are particularly appealing for the use in interpretation of the data concerning the media composed, at least, of weakly absorbing particles comparable to the wavelength in size with the filling factor less than 20%.

It is worth noting that, as any approximate model, the above models may be used only within some particular ranges of the parameters describing the properties of a medium. However, at present, to determine these ranges is impossible, since laboratory measurements of samples with thoroughly controlled characteristics, which could serve as a reference, are still severely lacking. We may expect that the present models will naturally work correctly for rather loosely packed media (i.e., for ξ < 20%), while their applicability to denser media or those containing particles with the other parameters should additionally be verified. We are planning to estimate the discrepancy between the parameters of the observed objects resulted from fitting their light-scattering characteristics with different models in our future studies.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

VT: Conceptualization, Methodology, Investigation, Software. EP: Methodology, Validation, Investigation, Visualization.

Funding

The work by VT was supported by the Marie Skłodowska-Curie Research Innovation and Staff Exchange (RISE) (the GRASP-ACE grant no. 778349). EP acknowledges the support of Ministry of Science and Higher Education of the Russian Federation under the grant 075-15-2020-780 (N13.1902.21.0039).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to M. Mishchenko and D. Mackowski for making available the T-matrix computational codes (https://www.giss.nasa.gov/staff/mmishchenko/t_matrix.html, www.eng.auburn.edu/∼dmckwski/scatcodes/) and to M. Mishchenko for providing us with the code to compute the diffuse component of the reflection matrix, a complete version of which is freely accessible on https://www.giss.nasa.gov/staff/mmishchenko/brf/.

References

Balescu, R. (1975). Equilibrium and Nonequilibrium Statistical Mechanics. NY: Wiley.

Google Scholar

Barrowes, B. E., Ao, C. O., Teixeira, F. L., Kong, J. A., and Tsang, L. (2000). Monte Carlo Simulations of Electromagnetic Wave Propagation in Dense Random Media with Dielectric Spheroids. IEICE Trans. Electron. E83-C (12), 1797–1802.

Google Scholar

Bohren, C. F., and Huffman, D. R. (1983). Absorption and Scattering of Light by Small Particles. New York: Wiley.

Google Scholar

Doicu, A., and Mishchenko, M. I. (2019a). Electromagnetic Scattering by Discrete Random Media. II: The Coherent Field. J. Quant. Spectrosc. Radiat. Transfer 230, 86–105. doi:10.1016/j.jqsrt.2019.03.011

CrossRef Full Text | Google Scholar

Doicu, A., and Mishchenko, M. I. (2019b). Electromagnetic Scattering by Discrete Random Media. III: The Vector Radiative Transfer Equation. J. Quant. Spectrosc. Radiat. Transfer 236, 106564. doi:10.1016/j.jqsrt.2019.07.007

CrossRef Full Text | Google Scholar

Doicu, A., and Mishchenko, M. I. (2019c). Electromagnetic Scattering by Discrete Random Media. IV: Coherent Backscattering. J. Quant. Spectrosc. Radiat. Transfer 236, 106565. doi:10.1016/j.jqsrt.2019.07.008

CrossRef Full Text | Google Scholar

Ito, G., Mishchenko, M. I., and Glotch, T. D. (2018). Radiative-Transfer Modeling of Spectra of Planetary Regoliths Using Cluster-Based Dense Packing Modifications. J. Geophys. Res. Planets 123, 1203–1220. doi:10.1029/2018je005532

CrossRef Full Text | Google Scholar

Mackowski, D. W., and Mishchenko, M. I. (2011). A Multiple Sphere T-Matrix Fortran Code for Use on Parallel Computer Clusters. J. Quant. Spectrosc. Radiat. Transfer 112, 2182–2192. doi:10.1016/j.jqsrt.2011.02.019

CrossRef Full Text | Google Scholar

Mishchenko, M. I., Travis, L. D., and Lacis, A. A. (2006). Multiple Scattering of Light by Particles: Radiative Transfer and Coherent Backscattering. Cambridge, UK: Cambridge University Press.

Google Scholar

Mishchenko, M. I. (1994). Asymmetry Parameters of the Phase Function for Densely Packed Scattering Grains. J. Quant. Spectrosc. Radiat. Transfer 52, 95–110. doi:10.1016/0022-4073(94)90142-2

CrossRef Full Text | Google Scholar

Mishchenko, M. I., Goldstein, D. H., Chowdhary, J., and Lompado, A. (2013). Radiative Transfer Theory Verified by Controlled Laboratory Experiments. Opt. Lett. 38 (18), 3522–3525. doi:10.1364/ol.38.003522

PubMed Abstract | CrossRef Full Text | Google Scholar

Mishchenko, M. I., Tishkovets, V. P., Travis, L. D., Cairns, B., Dlugach, J. M., Liu, L., et al. (2011). Electromagnetic Scattering by a Morphologically Complex Object: Fundamental Concepts and Common Misconceptions. J. Quant. Spectrosc. Radiat. Transfer 112, 671–692. doi:10.1016/j.jqsrt.2010.03.016

CrossRef Full Text | Google Scholar

Muinonen, K., Markkanen, J., Väisänen, T., Peltoniemi, J. I., and Penttilä, A. (2017). Multiple Scattering in Discrete Random media Using First-Order Incoherent Interactions. Radio Sci. 52 (11), 1419–1431. doi:10.1002/2017RS006419

CrossRef Full Text | Google Scholar

Muinonen, K., Markkanen, J., Väisänen, T., Peltoniemi, J., and Penttilä, A. (2018). Multiple Scattering of Light in Discrete Random media Using Incoherent Interactions. Opt. Lett. 43 (4), 683–686. doi:10.1364/OL.43.000683

PubMed Abstract | CrossRef Full Text | Google Scholar

Penttilä, A., Markkanen, J., Väisänen, T., Räbinä, J., Yurkin, M. A., and Muinonen, K. (2021). How Much Is Enough? The Convergence of Finite Sample Scattering Properties to Those of Infinite media. J. Quant. Spectrosc. Radiat. Transfer 262, 107524. doi:10.1016/j.jqsrt.2021.107524

CrossRef Full Text | Google Scholar

Tishkovets, V. P., and Mishchenko, M. I. (2004). Coherent Backscattering of Light by a Layer of Discrete Random Medium. J. Quant. Spectrosc. Radiat. Transfer 86, 161–180. doi:10.1016/s0022-4073(03)00281-4

CrossRef Full Text | Google Scholar

Tishkovets, V. P., and Petrova, E. V. (2020). An Algorithm and Codes for Fast Computations of the Opposition Effects in a Semi-infinite Discrete Random Medium. J. Quant. Spectrosc. Radiat. Transfer 255, 107252. doi:10.1016/j.jqsrt.2020.107252

CrossRef Full Text | Google Scholar

Tishkovets, V. P., and Petrova, E. V. (2013). Coherent Backscattering by Discrete Random media Composed of Clusters of Spherical Particles. J. Quant. Spectrosc. Radiat. Transfer 127, 192–206. doi:10.1016/j.jqsrt.2013.05.017

CrossRef Full Text | Google Scholar

Tishkovets, V. P., and Petrova, E. V. (2013). “Light Scattering by Densely Packed Systems of Particles: Near-Field Effects,” in Light Scattering Reviews 7: Radiative Transfer and Optical Properties of Atmosphere and Underlying Surface. Editor A Kokhanovsky (Chichester, UK: Springer), 7, 3–36. doi:10.1007/978-3-642-21907-8_1

CrossRef Full Text | Google Scholar

Tishkovets, V. P., Petrova, E. V., and Mishchenko, M. I. (2011). Scattering of Electromagnetic Waves by Ensembles of Particles and Discrete Random Media. J. Quant. Spectrosc. Radiat. Transfer 112, 2095–2127. doi:10.1016/j.jqsrt.2011.04.010

CrossRef Full Text | Google Scholar

Varshalovich, D. A., Moskalev, A. N., and Khersonskii, V. K. (1988). Quantum Theory of Angular Momentum. Singapore: World Scientific.

Google Scholar