Mind the Gap - Part 3: Doppler Velocity Measurements From Space

Convective motions and hydrometeor microphysical properties are highly sought-after parameters for evaluating atmospheric numerical models. With most of Earth’s surface covered by water, space-borne Doppler radars are ideal for acquiring such measurements at a global scale. While these systems have proven to be useful tools for retrieving cloud microphysical and dynamical properties from the ground, their adequacy and specific requirements for spaceborne operation still need to be evaluated. Comprehensive forward simulations enable us to assess the advantages and drawbacks of six different Doppler radar architectures currently planned or under consideration by space agencies for the study of cloud dynamics. Radar performance is examined against the state-of-the-art numerical model simulations of well-characterized shallow and deep, continental, and oceanic convective cases. Mean Doppler velocity (MDV) measurements collected at multiple frequencies (13, 35, and 94 GHz) provide complementary information in deep convective cloud systems. The high penetration capability of the 13 GHz radar enables to obtain a complete, albeit horizontally under-sampled, view of deep convective storms. The smaller instantaneous field of view (IFOV) of the 35 GHz radar captures more precise information about the location and size of convective updrafts above 5–8 km height of most systems which were determined in the portion of storms where the mass flux peak is typically located. Finally, the lower mean Doppler velocity uncertainty of displaced phase center antenna (DPCA) radars makes them an ideal system for studying microphysics in shallow convection and frontal systems, as well as ice and mixed-phase clouds. It is demonstrated that a 94 GHz DCPA system can achieve retrieval errors as low as 0.05–0.15 mm for raindrop volume-weighted mean diameter and 25% for rime fraction (for a −10 dBZ echo).

1 Introduction

Improvements in weather and forecast models require thorough understanding of processes occurring in cloud and precipitation systems (Zelinka et al., 2017; Satoh et al., 2018). An accurate representation of cloud-scale dynamics and hydrometeor fall velocities is an important step toward understanding these processes. Convective clouds serve as a primary mechanism for the transfer of thermal energy, moisture, and momentum through the troposphere, significantly impacting the large-scale atmospheric circulation and local environment and also affecting the probability of subsequent cloud formation (Hartmann et al., 2018; Gasparini et al., 2021). Furthermore, several different assumptions for hydrometeor terminal fall velocities are used for different processes in models whether in large-scale parameterized clouds and precipitation (vanZanten et al., 2011). Climate models are very sensitive to the specification of fall speeds. For example, Sanderson et al., 2008 found that the ice fall speed was the second most important parameter for determining climate sensitivity. A decrease in the fall velocity of ice crystals can affect upper tropospheric water vapor amounts (Mitchell and Finnegan, 2009) while changes to the fall velocity of raindrops can induce changes in the evaporation rate and hence affect the temperature structure in the lower part of the atmosphere (vanZanten et al., 2011).

Despite their importance, there are considerable measurement gaps in convective updrafts and hydrometeor fall velocities. These gaps limit our ability to constrain these important aspects of model parameterization and verification. Observations of the number and magnitude of updrafts contributing to vertical transport in deep convection are not available over the tropical oceans and are rarely available over land. Measuring convective motions from surface-based observatories remains challenging owing to a shortage of profiling sensors and the shortcoming of multi-Doppler radar retrievals (Oue et al., 2021). On the other hand, surface-based observatories can provide high-quality, long-term records of hydrometeor fall velocities (Kalesse and Kollias, 2013); however, such measurements are sparse in the southern hemisphere and over the oceans.

Spaceborne Doppler radar observations can offer global observations of Doppler velocities, thus providing an unprecedented opportunity to help constrain weather and climate models (Battaglia et al., 2020a). The Earth Cloud Aerosol and Radiation Explorer (EarthCARE) satellite is a joint European Space Agency (ESA) and Japanese Aerospace Exploration Agency (JAXA) mission scheduled to launch in 2023. EarthCARE (EC) will host the first 94-GHz Doppler cloud profiling radar (CPR) in space (Illingworth et al., 2018). However, signal attenuation by hydrometeors and the presence of multiple scatters are expected to limit the ability of the EarthCARE CPR to study deep convective clouds (Kollias et al., 2018). Furthermore, the Doppler velocity measurements in large-scale precipitation regimes will be considerably impacted by the platform motion (Kollias et al., 2014).

Post-processing and spatial averaging of the EarthCARE CPR raw Doppler velocity observations are expected to reduce the uncertainty in the Doppler velocity measurements (Kollias et al., 2014). However, a different observing platform is required to address the remaining gap in convective dynamics and to provide even higher quality Doppler velocity measurements in shallow clouds and large-scale cloud and precipitation systems. These critical measurements gaps were acknowledged in the latest NASA Earth Science Decadal Survey Report (National Academies of Sciences, Engineering, and Medicine, 2018). NASA recently completed a study, known as Aerosols, Clouds, Convection, and Precipitation (ACCP), to identify candidate spaceborne architectures to pursue coupled aerosol-cloud-precipitation science in the next decade. The recommended architecture is currently being evaluated as part of NASA’s Earth System Observatory (https://science.nasa.gov/earth-science/earth-system-observatory) and is named as the Atmosphere Observing System (AOS). The need for multi-frequency Doppler radar measurements were deemed critical to capturing all types of cloud and precipitation systems. Other space agencies such as JAXA and ESA are looking for future spaceborne Doppler radar missions. JAXA is currently evaluating different options for a follow-up to the NASA/JAXA Global Precipitation Measurement (GPM) Mission Dual-frequency Precipitation Radar (DPR) with a 13-GHz radar with Doppler capability and ESA recently selected WInd VElocity Radar Nephoscope (WIVERN, Illingworth et al., 2018), a 94-GHz conically scanning Doppler radar for additional study as part of ESA’s Earth Explorer program. Finally, the explosive growth in the use of CubeSats in Earth Sciences offers ample opportunities for creative approaches on how to best monitor and investigate cloud and precipitation processes (Stephens et al., 2020).

Here, the third part of the “Mind the Gap” article series is presented. The Mind the Gap articles highlight existing gaps in satellite-based radar measurements of cloud and precipitation systems and suggest future improvements. The first Mind the Gap study (Lamer et al., 2020) focused on the challenge of detecting hydrometeors in the lowest km of the atmosphere detection due to the Earth’s surface return. The Lamer et al. (2020) study highlighted the advantages of a short-pulse radar (Kollias, 2007). The second Mind the Gap study (Battaglia et al., 2020a) focused on the biases in liquid water path (LWP) estimates due to the large radar footprint and the limited sensitivity in small LWP amounts using Path Integrated Attenuation (PIA) techniques. The added value of brightness temperature (T_B) derived by adopting radiometric radar modes was investigated. The third Mind the Gap article focuses on the third large spaceborne radar measurement gap: Doppler velocity. High resolution model output and a comprehensive forward and inverse spaceborne Doppler radar simulator is used to characterize the impact of the sampling volume on the characterization of updraft and downdraft properties. Furthermore, the impact of the uncertainty in the Doppler velocity measurements on the estimation of hydrometeor mean size and density is presented. The performance of different planned spaceborne Doppler radar systems against these requirements is analyzed using state-of-the-art forward and inverse simulations. The spaceborne Doppler radar systems considered in this study operate at three different frequencies: 94, 35, and 13 GHz, thus, covering the frequency range of existing and planned spaceborne radar systems. The radar systems are also separated into two categories based on the technique they used to acquire Doppler velocity measurements from space. Three systems that employ the displaced phase center antenna (DPCA) technique that rely on two antennas strategically deployed such that their combined measurements can effectively remove the satellite motion effects on the Doppler velocity measurements are evaluated (Tanelli et al., 2002; Durden et al., 2007; Tanelli et al., 2016). These systems resemble those considered during the ACCP study. Three additional radars that utilize a single antenna are also considered. One of them is the EarthCARE CPR and the other two are large antenna 13-GHz radar systems that resemble spaceborne radar concepts considered by space agencies. The trade-offs between the selected radar frequency, footprint, and the technology used for the Doppler velocity estimation are presented

2 Datasets and Methods

2.1 Observations

In this study, a dataset of over 20,000 5 min averaged raindrop spectra from two-dimensional video disdrometers (2DVDs) is used to estimate the impact of mean Doppler velocity accuracy on the characterization of hydrometeor diameter. The 2DVD dataset is described in Williams et al. (2014). For the forward calculations, the raindrops are simulated as oblate spheroids (Brandes et al., 2002), with a terminal velocity described in Lhermitte (2002) and the T-matrix scattering theory (Waterman, 1965) is used for the radar reflectivity estimation.

2.2 Numerical Model Simulations

Numerical simulations obtained from high spatial resolution (<250 m) conducted under the scope of NASA ACCP study complement the sparse observational datasets of convective cloud properties. ACCP relied on an array of models that proved accurate at simulating different cloud systems ranging from shallow to deep convection including warm, mixed-phase, and ice clouds. The following numerical model simulations are analyzed in the current study:

- A Weather Research and Forecasting (WRF, Model V3.8.; Skamarock et al., 2008; Skamarock, 2008; Varble et al., 2020) simulation on the 20 May 2011 squall-line event that took place during the Mid-Latitude Continental Convective Clouds Experiment (MC3E; Jensen et al., 2016) in Oklahoma. A horizontal cross section through the MC3E simulation taken at 12-km height allows us to appreciate the inhomogeneity of this convective storm that presented vigorous updrafts within only a few hundred meters of downdrafts (Figure 1A).

- A Regional Atmospheric Modeling System (RAMS, v6.2.05; Cotton et al., 2003; Storer and Posselt, 2019) simulation of the deep convection cases of 11^th and 17^th August 1999, that took place during the Kwajalein Experiment (KWAJEX, Yuter et al., 2005) and of the weakly organized oceanic convection case of 3 February 1999, that took place during the Tropical Rainfall Measuring Mission—Large Scale Biosphere-Atmosphere Experiment (TRMM-LBA, Silva Dias et al., 2002). A horizontal cross section through the TRMM-LBA simulation taken at 10 km height allows us to appreciate the inhomogeneity of individual coherent updraft structures that formed in this storm (Figure 1B).

- A System for Atmospheric Modeling (SAM, V6.11.2; Khairoutdinov and Randall 2003) is simulation of the strong tropical oceanic convection cases that occurred during the Global Atmospheric Research Program’s Atlantic Tropical Experiment (GATE, Zipser and Gautier, 1978; Xu and Randall, 2001) and of the shallow convective cumulus case that took place during the Rain in Cumulus over the Ocean experiment (RICO, Rauber et al., 2007). A horizontal cross section through the RICO simulation taken at 1 km height allows us to appreciate the weak (vertical air motion +2–6 m s⁻¹) and sub-kilometer horizontal scale coherent updrafts that are frequent features of this shallow convective cloud regime (Figure 1C).

FIGURE 1

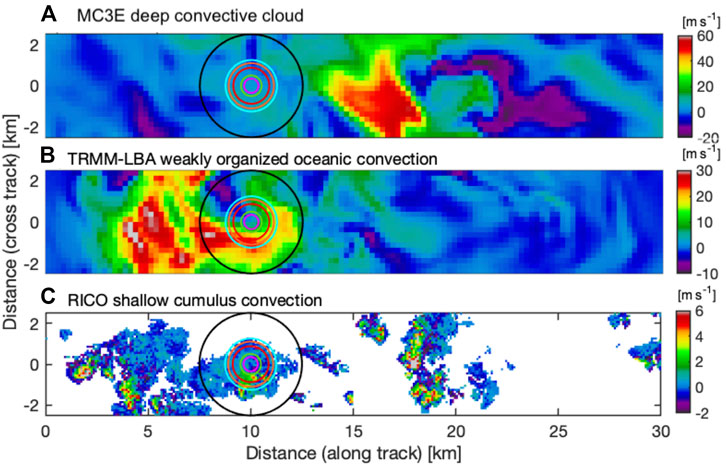
FIGURE 1. Horizontal cross-section showing vertical air motion (V_AIR in ms⁻¹; positive indicates upward motion) from three different model simulations: (A) MC3E at 12 km height, (B) TRMM-LBA at 10 km height, and (C) RICO at 1 km height. Overlaid circles represent the instantaneous field of view (IFOV) of the six radars under consideration (color coded as in Table 1).

In the current study, these numerical simulation results are directly used to quantify the individual impacts of signal penetration, instantaneous field of view, and platform motion on the characterization of convective updrafts (results in Section 3) and are input to a spaceborne radar forward simulator to emulate the performance of six spaceborne Doppler radar systems, whose specifications are listed in Table 1 (results in Section 4).

TABLE 1

TABLE 1. Technical specifications for the six spaceborne radar architectures under consideration.

2.3 Spaceborne Doppler Radar Forward Simulator

The forward simulator used in the current study was designed to forward-simulate attenuated radar reflectivity factor and mean Doppler velocity (MDV, the sum of the vertical air motion and reflectivity-weighted hydrometeor sedimentation velocity) considering known instrument sampling limitations. It uses scattering calculations to estimate the radar reflectivity factor and the gas and liquid attenuation at the model native resolution following T-matrix for cloud, drizzle, and rain hydrometeor species; the Self-Similar Rayleigh-Gans Approximation (SSRGA, Hogan and Westbrook, 2014) for ice and snow particles; and Mie for hail and graupel particles, that are assumed to have a spherical shape with different densities (0.9 and 0.4 g cm⁻³, respectively). This information is also combined to produce estimates of attenuated radar reflectivity, MDV, and spectrum width. A realistic Earth’s surface echo is added to the first model level as in Burns et al. (2016). The addition of a surface echo produces a more realistic radar performance in the lowest 1 km of the atmosphere (see Lamer et al., 2020 for more details). An instrument forward-simulator is then used to emulate effects caused by an array of radar specifications:

- Sampling geometry parameters including antenna beamwidth, pulse length, and satellite orbit as in the work of Kollias et al. (2014)

- Along-track integration as in the work of Kollias et al. (2014)

- Sampling rate (i.e., pulse repetition frequency) as in the work of Kollias et al. (2014)

- Platform motion as in the work of Kollias et al. (2014)

- Radar receiver noise in the raw I/Q radar signals, which dictates the signal-to-noise (SNR) ratio

- Doppler estimation technique including Pulse-pair or Doppler spectra-based moment estimation as in the work of Kollias et al. (2014)

- Off-nadir operation as in the work of Battaglia et al. (2020a)

The forward-simulated radar observables at the radar resolution are finally used as inputs in a retrieval algorithm to produce “best-estimate” radar observables (i.e., data products) for a complete end-to-end process. Those include the following: a feature mask (location of detected meteorological observations), as well as an MDV field corrected for velocity aliasing as in the work of Kollias et al. (2014).

3 Radar Sampling Parameters and Their Individual Impact on Retrieved Cloud Properties

In this section, we describe key radar sampling parameters and the radar specifications that influence them. Then, through comparison with observed and simulated benchmarks, we estimate their impact on retrieved cloud properties.

3.1 Signal Penetration

Radar signal penetration is affected by attenuation caused by gases and hydrometeors, which is wavelength specific, and has multiple scattering, which depends on the radar IFOV and the type of hydrometeor present in the radar sampling volume (Battaglia et al., 2016).

3.1.1 The Impact of Signal Penetration on Retrieving Convective Updraft Mass Flux

Determining signal penetration depth is important to determine the ability of a spaceborne Doppler radar system to detect the portions of convective storms where most of the convective transport occurs. Here we will focus on quantifying the impact of signal penetration on the characterization of updraft mass flux (M_F), which is central to cumulus parameterization schemes in large-scale models (e.g., Arakawa and Schubert, 1974; Tiedtke, 1989).

The observational record of convective updraft properties is sparse. Under shallow convective cloud conditions, vertically pointing lidar, and radar systems have been used to characterize the sub-cloud and cloud layer dynamics (Lamer et al., 2015; Lamer and Kolias, 2015; Lareau et al., 2018; Endo et al., 2019). Only recently has the information from both these been merged to provide a comprehensive view of the dynamical field in and around shallow convective cloud systems (Zhu et al., 2021). In deep convection, limited aircraft observations and profiling radar techniques are available (e.g., LeMone and Zipser, 1980; Heymsfield et al., 2010; Williams, 2012; Heymsfield et al., 2013; Kumar et al., 2015; Wang et al., 2020). Based on the airborne Doppler radar observations, the peak updraft values are often above 10-km altitude (Heymsfield et al., 2010; Heymsfield et al., 2013). Here, direct sampling of the numerical simulations is used to construct a more comprehensive benchmark of convective updraft properties. A conservative threshold of 2 m s⁻¹ is used to identify a model grid point that contains convective updrafts (Houze, 1997). We track information about the fractional area coverage in the entire domain of the simulation (${\alpha }_U$) and the mean air velocity ($V_U$) of these convective updrafts at each height through the atmospheric column and compute the mass flux ($M_F$) as

$M_F\left(Z\right)=\rho \cdot {\alpha }_U\cdot V_U(1)$

where $\rho$ is the air density in kg m⁻³ and Z is the model grid level (i.e., height).

The corresponding profiles for the different convective cases are shown in Figure 2. Figure 2C indicates that mass flux through the simulated cloud systems generally peaks at or above 6–8 km height except for the RICO shallow convection case which is confined below 4 km, and the KWAJEX case that peaks at 3 km but exhibits a secondary maximum at 11 km. Thus, a spaceborne Doppler radar should be able to penetrate down to ∼6 km above the surface to capture most of the shape and the peak of the convective mass flux profile in deep convective systems.

FIGURE 2

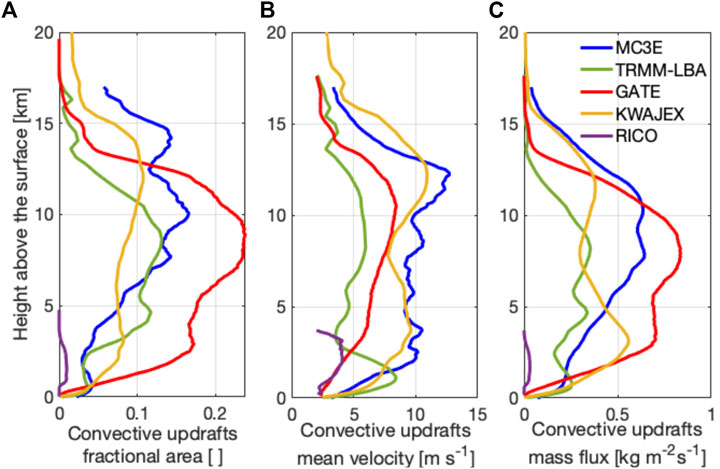
FIGURE 2. Profiles of storm-averaged convective updraft (A) fractional area, (B) mean velocity, and (C) mass flux estimated directly from the numerical model simulations. Results are shown for the different cloud types under study (MC3E: blue, GATE: red, KWAJEX: yellow, TRMM-LBA: green, RICO: purple).

Using the radar forward simulator, we further evaluate the impact of signal penetration on the characterization of convective updraft mass flux. Since the radar simulator used in this study accounts for frequency but lacks representation for multiple scattering effects (Battaglia et al., 2011; Battaglia et al., 2015), a conservative criterion based on signal-to-noise ratio (SNR) is used to estimate the penetration depth of the radar signal under different atmospheric conditions. Figures 3A,B, respectively, show the fraction of convective updrafts (V_AIR >2 ms⁻¹) with SNR > +5 dB as seen by a 35 and 94 GHz radar as a function of height. Starting at 14 km, both radar systems detect 100% of the scenes for all simulations. Moving downwards to ∼12 km, the intense MC3E and KWAJEX deep convective cases produce strong signal attenuation at 94 GHz and, as a result, a decrease in the fraction of updrafts is detected. The 35-GHz system is more resilient and only begins being affected by signal attenuation in these storms at ∼9 km. Due to signal attenuation which is generally strongest in the convective core, which is responsible for the bulk of the vertical transport of energy and moisture, even a small loss in the fraction of echoes detected could induce a large underestimation of the mass flux. Assuming that detection of 80% of convective updrafts is sufficient to capture the bulk of the mass flux occurring at each height, we estimate that a 94 GHz radar could be used to characterize the mass flux profile of deep convective systems from cloud top through ∼11 km and of weaker convective storms from cloud top through 7 km. Since this height is generally higher than the location of the mass flux peak, we conclude that a 94 GHz radar system alone would not be appropriate to monitor the mass flux of deep convective cloud systems. As for a 35 GHz radar, the intense continental convection (MC3E) case limits its “effective penetration” to 9 km height above the ground. In all other cases, the 35 GHz radar will be able to capture the peak of the convective mass flux and, in the case of weaker convective storms, penetrate much lower. Thus, a 35 GHz radar would be appropriate to monitor the mass flux peak in all, but the strongest deep convective systems.

FIGURE 3

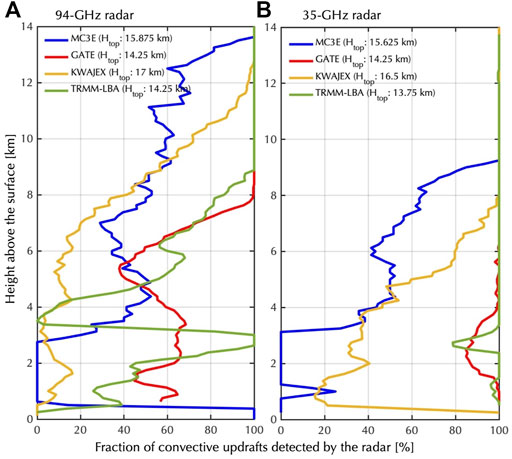
FIGURE 3. Fraction of convective updraft (V_AIR >2 ms⁻¹) detected by the (A) 94 GHz and (B) 35 GHz radars as a function of height. An estimate of cloud height (H_top) for the various cloud types simulated is given in the legend. Results are shown for the different cloud types under study (colors as in Figure 2).

3.2 Instantaneous Field of View

3.2.1 Factor Impacting Instantaneous Field of View

The IFOV of spaceborne radars is effectively the projection of the radar sampling volume on Earth’s surface. IFOV is modulated by four main factors: 1) frequency (f), which inversely correlates with IFOV (ceteris paribus), 2) antenna size (D) which directly acts to increase IFOV, 3) number of antennas used for the Doppler velocity estimation, which indirectly acts to increase IFOV by decreasing antenna sizes, and 4) distance from the Earth (H_SAT), which directly acts to increase IFOV. A commonly used approximate relationship for the radar IFOV is

$IFOV\cong 0.369\frac{H_{SAT} \left[km\right]}{D \left[m\right]\cdot f\left[GHz\right]}(2)$

The IFOVs for six spaceborne Doppler radar architectures considered in this study are listed in Table 1. The average orbit height is the same (H_SAT = 400 km) for all the architectures. This results in the 94 GHz radars having an overall smaller IFOV. Number of antennas comes next, with non-DPCA systems having overall smaller IFOV than DPCA systems.

3.2.2 The Impact of Instantaneous Field of View on Retrieving Convective Updraft Mass Flux

The relationship between the updraft chord length (UCL) and the spaceborne radar IFOV is very important to determine the ability of a spaceborne Doppler radar system to resolve, and thus characterize, convective updraft properties. The spaceborne Doppler radar MDV measurements are the result of the convolution of true updraft properties with the IFOV. In the case of under sampling (IFOV > UCL), the estimated MDV is expected to underestimate the updraft magnitude and overestimate the updraft size. In previous studies, the impact of the radar range resolution and IFOV on shallow cloud properties (vertical and horizontal coverage and LWP) was demonstrated (e.g., Battaglia et al., 2020b; Lamer et al., 2020). Here we will assess the impact of sampling geometry on our ability to characterize updraft mass flux (M_F) and its components.

The observational record of convective updraft chord UCLs is sparse and measurements from limited aircraft observations and profiling radar techniques (e.g., LeMone and Zipser, 1980; Williams, 2012; Kumar et al., 2015; Lamer et al., 2015; Wang et al., 2020) are challenging to consolidate due to their limited sampling of individual storms and the strong dependency of their results on the instrument/platform sampling geometry and strategy used. Nevertheless, most reports of deep convective updraft cores document them as being less than 5 km, with their distribution peaking around 2–3 km (Wang et al., 2020) while shallow convective updraft cores were reported to be 100–500 m wide (Lamer et al., 2015).

Once again, direct sampling of the high-resolution model outputs is used to derive additional statistics of the properties of the convective updrafts. Spatially coherent convective updrafts are identified as contiguous updraft regions with air motion larger than 2 m s⁻¹. We track information about the fractional area coverage (${\alpha }_U$) and the mean air velocity ($V_U$) of convective updrafts of different chord lengths and compute their mass flux ($M_F$) as

$M_F\left(UCL\right)=\rho \cdot {\alpha }_U\cdot V_U(3)$

The distribution of ${\alpha }_U$, $V_U$, and $M_F$ as a function of the UCL and the cumulative distribution of the contribution of updrafts with different UCL to the total M_F are shown in Figure 4. The UCL bins are 0.25 km wide, with center values from 0.25 to 10 km. Shallow convection is characterized by the narrowest UCL’s with only a small fraction of them exceeding 500 m. Deep convection simulations exhibit a broader distribution of UCLs especially for the more intense cases (MC3E, KWAJEX, Figure 4A). The mean V_U increases with the UCL, suggesting that broader updrafts are also characterized by stronger updraft magnitudes. This relationship between UCL and V_U can explain the contribution to the total M_F by updrafts with different UCL. Updrafts with UCL larger than 1.5 km equally contribute to the total updraft mass flux occurring in deep convective storms (Figure 4C). In weaker convective systems like TRMM-LBA and RICO, smaller convective updrafts (1.8 and 0.5 km UCL, respectively) are seen to be responsible for the bulk of the transport since larger updrafts do not seem to be systematically exhibiting stronger velocities.

FIGURE 4

FIGURE 4. As a function of convective updraft chord length (A) fraction area, (B) mean updraft velocity, (C) contribution to the total convective updraft mass flux, and (D) cumulative fraction of the total convective updraft mass flux starting from the largest updrafts. Results are shown for the different cloud types under study (colors as in Figure 2). Note that the purple line in “d” is not visible as it runs along the y-axis.

The cumulative fraction of $M_F\left(UCL\right)$ allows us to determine which updraft sizes together contribute to 50% of the convective updraft mass flux. In the intense deep convective systems, that would be updrafts larger than ∼6 km; in weakly organized oceanic deep convective systems, that would be updrafts larger than ∼3 km; in shallow convective cloud systems, that would be updrafts <375 m. This behavior drives a need to design radar architectures that have an IFOV $\le$ 3 km to monitor the bulk of the mass flux in deep convective systems.

Figure 1 allows us to visualize the IFOV achieved by the 6 radar architectures relative to the simulated cloud scenes noting that none of these architectures meet the criteria established for monitoring the mass flux of shallow convective clouds. On the other hand, five of the radar architectures meet the criteria established for monitoring the mass flux of deep convective clouds (radar 1, 2, 3, 5, and 6) except for when significant attenuation occurs.

To further evaluate the impact of IFOV on the characterization of convective updraft mass flux, we perform forward simulations where only the sampling geometry is considered. In effect, we turn on the radar instrument model and estimate the resulting vertical air motion. From those motions, at each radar height, the area fraction, the magnitude of updrafts of velocity >2 m s⁻¹, and their mass flux are computed. Using the same model swaths, the same convective updraft parameters are estimated at each model height using direct sampling at the native model resolution. The differences of these updraft properties as derived by the radar IFOV and the direct model sampling at each height are normalized by the model direct sampling value (i.e., relative errors). The relative errors in the updraft properties from all heights are used to compile the relative error distributions for different convective scenes and radar systems (Figure 5). As expected, the 1.0 km IFOV provides the best agreement between the model output and the forward-simulated radar observations for all three convective updraft parameters with most of the relative error values within ±20%. A 2.5-km IFOV results in broader relative error distributions in ${\alpha }_U$ and $V_U$ (±35%). The M_F relative error distribution is centered around zero; however, in some cases, relative errors up to 50% in the M_F are estimated. The impact of the radar sampling volume on the convective updraft parameters is more drastic at 5 km IFOV with errors up to 100%.

FIGURE 5

FIGURE 5. Normalized distribution of the relative error $\left(\frac{model-radar}{model}\cdot 100\%\right)$ in the (A) convective updraft fraction, (B) mean convective updraft velocity, and (C) convective updraft mass flux. Results are shown for three different instantaneous radar field of views close to that of radar 1 (1.0 km; green), radar 5 (2.5 km; cyan), radar 4 (5.0 km; black).

In all cases, non-uniform beam filling (under sampling of the model dynamics) is responsible for the observed errors. Updraft features smaller than the IFOV presenting weak radar reflectivity go undetected (thus causing a negative ${\alpha }_U$ error) while those presenting large radar reflectivity appear horizontally smoothed (thus causing a positive ${\alpha }_U$ error). Beyond distorting the fractional area of convective updrafts, non-uniform beam filling also tends to cause an underestimation of the velocity of small convective updraft features surrounded by most downdrafts or clear air (thus causing a negative $V_U$ bias). Due to the way we defined convective updrafts (i.e., MDV >2 ms⁻¹) this negative $V_U$ bias may lead to convective updrafts being misclassified as non-convective (weak) updraft, thus taking only the strongest convective updrafts into consideration and yielding an overall positive error in the distribution of $V_U$ and M_F. It is important to note that these results are based only on a small number of simulated cases and that the relative error magnitude depends on the convection type. Exploring these convective type-based errors should be the focus of future studies.

3.3 Platform Motion

Radar mean Doppler velocity (MDV) is the reflectivity-weighted average line of sight motion of the targets present within the radar IFOV relative to the radar frame of reference. The radar own motion will contribute to the Doppler signal and its effect can be cancelled out by subtracting the contribution due to the projection of the satellite velocity along the antenna boresight. There is, however, an additional effect to be accounted for. Due to the large velocity of LEO satellites, the projection of the velocity along different lines of sight within the IFOV will differ significantly from the boresight projection; correspondingly, the radiation backscattered from the forward/backward (with respect to the satellite motion) part of the IFOV will be phase shifted when backscattered from a target receding/approaching the radar. In perfectly homogeneous atmospheric conditions (i.e., where the reflectivity field is the same throughout the IFOV), the reflectivity contributions of the perceived “away” and “towards” motions are perfectly balanced such that the recorded MDV is solely influenced by hydrometeor sedimentation velocity (V_SED) and air motion ($V_{AIR}$). In inhomogeneous atmospheric conditions, however, the reflectivity contributions of the perceived “away” and “towards” motions are out of balance, thus introducing a bias to the MDV that, to first approximation, is proportional to the radar reflectivity gradient within the IFOV and proportional to IFOV² (details are given in the work of Battaglia et al., 2020a).

To alleviate this bias, displaced phase center antenna (DPCA) systems rely on two antennas strategically deployed such that their combined measurements can provide an unbiased MDV estimate (Tanelli et al., 2002; Durden et al., 2007; Sy et al., 2014; Tanelli et al., 2016).

3.3.1 The Impact of Platform Motion on Identifying Convective Updrafts

To quantify the impact of platform motion on the MDV measured by spaceborne radars, we performed forward simulations of the weakly organized convective cloud scene of TRMM-LBA, setting $V_{AIR}$ and V_SED to 0 m s⁻¹. Figure 6 shows results for radar 5, which is a non-DPCA 13-GHz system with a 4 m antenna. Similar results are obtained from forward-simulations of the other two non-DCPA systems (radar 2 and radar 6; not shown). As highlighted by Figure 6B, platform motion alone can introduce MDV biases on the order of 30 m s⁻¹ in this highly heterogenous cloud scene. The MDV biases due to non-uniform beam filling (NUBF) will occur at the edges of every convective cloud (where large horizontal gradients of radar reflectivity occur) and within the periphery of all convective cores since a vertically oriented area of high radar reflectivity is one of their characteristic radar features. Although the use of the along-track radar reflectivity gradient can be used to correct for most of the NUBF-induced velocity bias, considerable residual errors from the application of an imperfect correction could complicate the detection of convective updrafts and could lead to false detections. Considering that this bias is nearly double the magnitude of the strongest dynamical features simulated by the model and the proximity to the location of the actual convective updrafts, we suggest that a non-DPCA system would be difficult to use for dynamical studies in such complex cloud scenes.

FIGURE 6

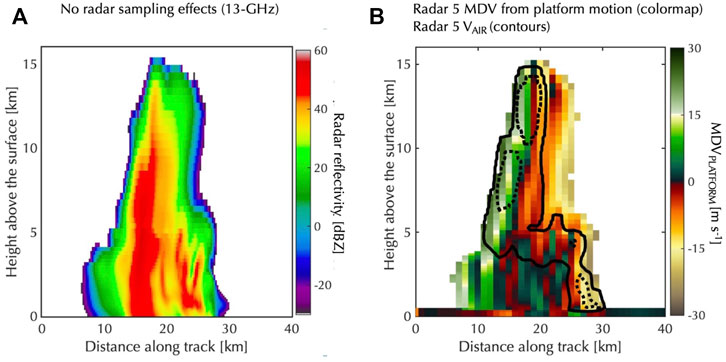
FIGURE 6. Forward simulation of TRMM-LBA weakly organized convection: (A) radar reflectivity at 13 GHz without radar sampling effects and (B) apparent MDV induced strictly from platform motion and NUBF conditions for radar 5 (i.e., air motion and particle sedimentation set to 0 m s^-1). Overlaid on “b” are V_AIR contours drawn from forward-simulations with no platform motion effects (2 m s⁻¹: solid and 8 m s⁻¹: dotted).

3.4 Mean Doppler Velocity Uncertainty

3.4.1 Factors Impacting Mean Doppler Velocity Uncertainty

The total MDV error budget $\left({\sigma }_{MDV}\right)$ for a spaceborne Doppler radar is affected by three main factors 1) intrinsic noise (spectral broadening) introduced by the platform motion (${\sigma }_B)$, 2) outstanding error in correcting MDV biases caused by non-uniform beam filling (${\sigma }_{NUBF})$, and 3) outstanding error due to uncertainty in the antenna pointing characterization or alternatively error in the estimation of the horizontal wind when off-nadir pointing is needed. The MDV total error budget is given by the following expression:

${\sigma }_{MDV}=\sqrt{{\sigma }_B^2+{\sigma }_{NUBF}^2+{\sigma }_P^2}(4)$

Figure 7 shows the individual contribution of these factors in the 6 radar architectures under consideration in the current study. The relationship of ${\sigma }_B$ with signal-to-noise ratio (SNR) becomes evident (Figure 7A); for any of the radar configurations ${\sigma }_B$ is systematically lower for atmospheric features of higher radar reflectivity. The dependency of the MDV uncertainty with SNR is inherent to all the radar architectures; however, the DPCA radar architectures (1, 3, and 4) have negligible ${\sigma }_B$ errors, as with any radar on a non-moving platform. On the other hand, the non-DPCA radars (2, 5, and 6) have much higher ${\sigma }_B$ errors. This is clearly illustrated in the comparison of the two 94-GHz radar system. Despite its larger antenna and higher sensitivity, the EarthCARE CPR (radar 2) has a much higher ${\sigma }_B$ contribution to the overall MDV error budget than the smaller antenna, which is a less sensitive DPCA 94-GHz radar.

FIGURE 7

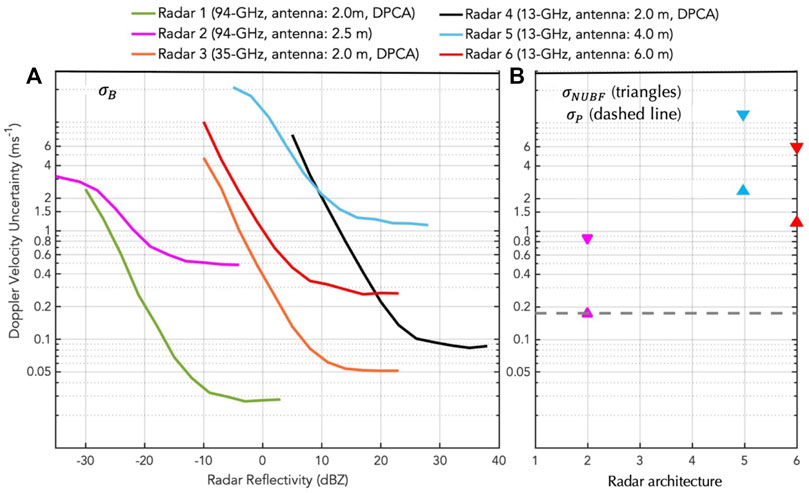
FIGURE 7. Doppler velocity uncertainty from (A) spectral broadening (${\sigma }_B$) and (B) non-uniform beam filling (${\sigma }_{NUBF}$; triangles), and mis-pointing (${\sigma }_P$; dashed line). Results are shown for the 6 radars under consideration (color coded as in Table 1).

In addition to SNR, the ${\sigma }_B$ for the non-DPCA radar architectures depends on the normalized spectrum width (Kollias et al., 2014). This explains the difference in their curves. Noticeably, for the same radar frequency, ${\sigma }_B$ is lower for the radar with larger antenna. This is illustrated in the case of two of the 13-GHz radars (5 and 6). For a 20 dBZ echo, the ${\sigma }_B$ is 1.2 and 0.28 ms⁻¹ for radars 5 and 6, respectively. In addition to having a negligible ${\sigma }_B$, the use of a pair of antennas by the DPCA radars allows them to avoid the non-uniform beam filling MDV biases, something that is not the case for the non-DPCA radars. The along-track gradient of the radar reflectivity has been suggested to correct the NUBF velocity bias; however, the correction depends on the detailed distribution of the radar reflectivity within the radar sampling volume that is not known (Sy et al., 2014; Kollias et al., 2018). Thus, there is a residual, unbiased velocity error from the NUBF correction $\left({\sigma }_{NUBF}\right)$ that increases the total MDV error budget $\left({\sigma }_{MDV}\right)$. The residual error from the NUBF correction is proportional to the square of the radar IFOV $\left({\sigma }_{NUBF}\propto IFO{V}^2\right)$. In Battaglia et al. (2020b), an estimate for ${\sigma }_{NUBF}$ was provided for a gentle along-track radar reflectivity gradients of 3 dBZkm⁻¹ (non-convective conditions, Kollias et al., 2014). These estimates should be considered as a lower bound ${\sigma }_{NUBF}$ estimate. An along-track radar reflectivity gradient of 15 dBZkm^-1 (convective conditions) is used to provide an upper bound ${\sigma }_{NUBF}$ estimate. The upper and the lower bound ${\sigma }_{NUBF}$ estimates are shown in Figure 7B. For the EarthCARE CPR, sampling convection is expected to be very challenging, thus, the lower bound ${\sigma }_{NUBF}$ estimate is more relevant (Kollias et al., 2018). Due to its very narrow IFOV, the ${\sigma }_{NUBF}$ is small compared to the ${\sigma }_{B }$ term. On the other hand, the ${\sigma }_{NUBF}$ term dominates the MDV error budget ${\sigma }_{MDV}$ for the two non-DPCA 13-GHz radars (5 and 6). The ${\sigma }_{NUBF}$ term is the dominant term in the ${\sigma }_{MDV}$ budget even for a 6.0-m antenna size.

Finally, the ${\sigma }_P$ term represents uncertainty in the MDV introduced by antenna pointing uncertainties related to thermal distortions and vibrations of the antenna structure and/or uncertainty in the estimation of the horizontal wind when off-nadir pointing is needed. An uncertainty of 10–15 μrad in the knowledge of the spaceborne radar antenna pointing at an altitude of 400 km corresponds to an MDV uncertainty of 0.08–0.11 ms⁻¹ (Battaglia and Kollias, 2015). For the DPCA radar architectures studied here, a 2 off-nadir forward (along-track) pointing is required to minimize the vertical extend of the surface echo (Beauchamp et al., 2021). In this case, a 5 ms⁻¹ uncertainty in the knowledge of the horizontal wind will introduce ∼0.2 ms⁻¹ uncertainty in the MDV estimate (grey dashed line in Figure 7).

Summing these error sources allows us to conclude that DPCA radar configurations are overall more accurate (in terms of MDV) than non-DPCA systems especially in highly heterogenous conditions. It is worth noting that the MDV uncertainty depicted in Figure 7 estimates for “best-estimate” MDV produced at the highest resolution available. For relatively homogeneous scenes such as stratiform cloud conditions, it may be acceptable to perform additional along-track averaging (Kollias et al., 2014), apply noise-filtering techniques (Sy et al., 2014) or rely on conditional sampling (Protat and Williams, 2011) to produce a coarser but high precision MDV “best-estimate”. These techniques have been shown to lead to reduction of the MDV uncertainty by as much as a factor of 2 In forward simulations of the EarthCARE satellite (here radar 2).

3.4.2 The Impact of Mean Doppler Velocity Uncertainty on Retrieving Particle Diameter and Rime Fraction in Weak Air Motion Regimes

The MDV measured by a nadir-looking spaceborne Doppler radar represents the sum of vertical air motion (${\text{V}}_{\text{AIR}})$ and the reflectivity-weighted hydrometeor sedimentation velocity (V_SED):

$MDV= V_{SED}+V_{AIR}(5)$

Separating the contributions of these two terms is a necessary step for using MDV for dynamical studies which are associated with ${\text{V}}_{\text{AIR}}$ and microphysical studies which are associated with hydrometeor properties that impact V_SED (e.g., Kollias et al., 2002; Zhu et al., 2021). The condition $\left|V_{air}\right|<2 m{s}^{-1}$ is often used to separate stratiform and convective cloud conditions (Houze, 1997). In stratiform clouds, (e.g., frontal stratiform precipitation, stratiform regions of convective systems, ice clouds), the horizontal microphysical variability is moderate, and the vertical air velocity is much smaller than the hydrometeor sedimentation velocity. When these conditions are satisfied, the MDV can be related to the shape of the particle size distribution (PSD), to relevant moments (e.g., rainfall rate), and, under certain conditions, allow us to study the microphysical processes that influence their evolution (e.g., Protat and Williams, 2011; Kalesse and Kollias, 2013). The extent to which such inferences can be made with reasonable uncertainty, depends on the magnitude of ${\sigma }_{MDV}$.

A combination of experimental and theoretical relationships between MDV and microphysical variables are presented here to illustrate the impact of the MDV uncertainty on microphysical variables in stratiform conditions. The formulation of analytical relationships between radar observables and microphysical variables requires a mathematical representation for the particle size distribution (PSD). The gamma distribution first introduced by Ulbrich (1983) and Willis (1984), and its normalization introduced by Testud et al. (2001) has been widely used to describe the PSD:

$\mathbf{N}\left({\mathbf{N}}_0^{\ast },{\mathbf{D}}_{\mathbf{m}},\mathbf{\mu }\right)\mathbf{=}{\mathbf{N}}_{\mathbf{0}}^{\mathbf{\ast }}\mathbf{f}\left(\mathbf{\mu }\right){\left(\frac{\mathbf{D}}{{\mathbf{D}}_{\mathbf{m}}}\right)}^{\mathbf{\mu }}\mathbf{}\mathbf{exp}\left(-\left(4+\mathbf{\mu }\right)\frac{\mathbf{D}}{{\mathbf{D}}_{\mathbf{m}}}\right)(6)$

where

$f\left(\mu \right)=\frac{\Gamma \left(4\right){\left(4+\mu \right)}^{4+\mu }}{4^4\Gamma \left(4+\mu \right)}$

The three parameters $\left(N_0^{\ast },D_m,\mu \right)$ have the following meanings: D_m is the volume-weighted mean diameter (defined as the ratio of the 4th to the 3rd moment of the PSD), $N_0^{\ast }$ is the intercept parameter of the exponential distribution that has the same water content as D_m, and $\mu$ describes the PSD shape. The MDV is independent of $N_0^{\ast }$ and for liquid phase hydrometeors (drizzle and raindrops), is a function of only D_m and $\mu$ In addition, the MDV is the reflectivity-weighted PSD sedimentation velocity; thus, the relationship between MDV and (D_m, $\mu$) depends also on the selected radar frequency. The relationship between MDV and D_m is shown in Figure 8 for four different $\mu$ values (−2, 0, 3, and 12) at 94 GHz radar (A), 35 GHz (B), and 13 GHz (C). Plotted under these analytical relationships are MDV and D_m estimates from the two-dimensional video disdrometer (2DVDs) observations (analysis details described in Section 2.1). Overall, the experimental data and the theoretical relationships agree and two distinct regimes emerge for each radar frequency.

FIGURE 8

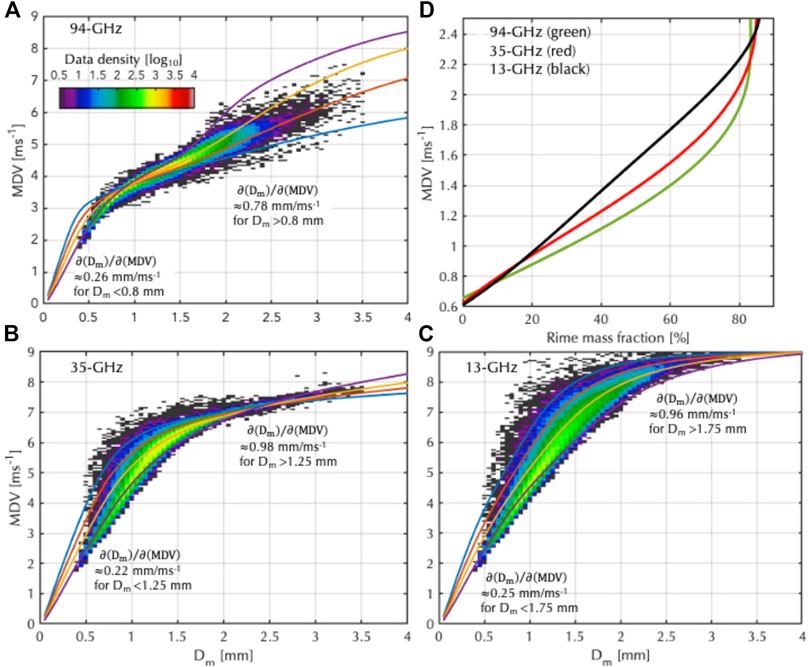
FIGURE 8. (A) For a 94-GHz radar, relationships between raindrop particle size distribution (PSD’s) mean volume-weighted diameter (D_m) and mean Doppler velocity (MDV) from ground-based measurements (colormap) and from different MDV-D_m relationships derived for a gamma distribution for different shape parameter (μ) values (colored lines). (B) Same as “a” for a 35-GHz radar. (C) Same as “a” for a 13-GHz radar. (D) relationship between rime mass fraction and mean Doppler velocity (MDV) from literature based on studies performed with a 94 GHz (green), 35 GHz (red) and 13 GHz radar (black).

The D_m estimation is often based on a combination of radar observables, however, here, we assume that MDV is the only available radar measurement. Under this assumption, the error in the D_m estimation is controlled by the rate of change of D_m with MDV and the MDV measurement error:

$\delta \left(D_m\right)\approx \frac{\partial \left(D_m\right)}{\partial \left(MDV\right)}\delta \left(MDV\right)(7)$

At W-band, two different $\partial \left(D_m\right)/\partial \left(MDV\right)$ regimes are present with very different slope values, one for D_m values lower than 0.8 mm where $\partial \left(D_m\right)/\partial \left(MDV\right)\approx 0.26 mm/m{s}^{-1}$ and another one for D_m values higher than 0.8 mm where $\partial \left(D_m\right)/\partial \left(MDV\right)\approx 0.78 mm/m{s}^{-1}$. The lower the $\partial \left(D_m\right)/\partial \left(MDV\right)$ value, lower the uncertainty in the D_m retrieval for a set MDV uncertainty. For example, an MDV uncertainty of 0.2 ms⁻¹ translates to an error of 0.05 and 0.15 mm, respectively, for D_m values less 0.8 than and greater than 0.8 mm. The range of D_m values where the slope $\partial \left(D_m\right)/\partial \left(MDV\right)$ is low increases at lower radar frequencies, suggesting that lower frequency radars are preferred for retrieving D_m from MDV measurements. On the other hand, at high D_m values (>1.75 mm) the slope $\partial \left(D_m\right)/\partial \left(MDV\right)$ at 94-GHz smaller thus suggesting that the 94-GHz MDV measurements will exhibit larger dynamic (sensitivity) range to D_m changes in high-D_m regimes. These differences are due to differences in the scattering by raindrops at the different radar frequencies (Kollias et al., 2002; Kollias et al., 2016). The complimentary use of MDV estimates at different radar frequencies can provide a strong constraint for D_m estimation (Giangrande et al., 2012; Matrosov, 2017).

The determination of the rime fraction in ice particles is another example where the use of the MDV can provide a strong constraint (Mason et al., 2018; Oue et al., 2021). In a recent study, Kneifel and Moisseev (2020) analyzed a large dataset of surface-based radar and in-situ observations and derived an experimental relationship between MDV and rime mass fraction (FR). The average relationship between MDV and RF for three radar frequencies (94-GHz, 35-GHz, and 13-GHz) is shown in Figure 8D. Although there is a considerable spread, the experimentally derived relationships offer a first order relationship for converting MDV errors to FR errors. If we focus on the FR range of 20–80%, an MDV uncertainty of 0.2 ms⁻¹ translates to an error of 14, 12, and 10% in FR at 94-, 35-, and 13 GHz respectively. This assessment ignores the fact that the shape of the particle size distribution (D_m) will also affect the MDV magnitude; thus, here it is assumed that this information is provided by other measurements (e.g., dual-wavelength radar measurements, Pfitzenmaier et al., 2019).

4 Spaceborne Doppler Radar Performance in Convection

Six spaceborne Doppler radar systems, whose specifications can be found in Table 1, are being forward simulated in this study; these systems resemble those under consideration by NASA’s AOS mission, other space agencies, as well as the JAXA/ESA EarthCARE CPR.

4.1 Deep Convective Clouds

A vertical cross section of the 13 GHz radar reflectivity and MDV from the MC3E continental squall line case at the model resolution is shown in Figure 9 (panels a and b, respectively). The simulation includes a deep convective core with radar reflectivity values between 40 and 55 dBZ and a cloud top above 15 km height trailed by stratiform precipitation. The convective core includes a tilted, coherent updraft structure with V_AIR values of more than 30–40 ms⁻¹. In addition, the spaceborne Doppler radar raw, uncorrected MDV simulations of the same event for the 3 DPCA architectures examined here (radars 1, 3, and 4) are shown in Figure 9. This comparison highlights tradeoffs between radar frequency, and IFOV choices in observing deep convective cloud dynamics from space.

FIGURE 9

FIGURE 9. Forward simulation of MC3E deep convection (A) radar reflectivity at 13 GHz without radar sampling effects (B) mean Doppler velocity at 13 GHz without radar sampling effects (i.e., truth) as well as mean Doppler velocity for (C) radar 4, (D) radar 3, and (E) radar 1.

Of the proposed DPCA radar architectures, radar 4 with its 13 GHz frequency experiences the least amount of attenuation compared to the 35 and 94 GHz radar architectures. Radar 4 can penetrate the entire depth of the convective cloud and its “best-estimate” MDV captures many of the key dynamical features of the squall line. It resolves the main updraft structure, especially above 3–4 km height. A drawback of this system is that its larger IFOV (5.06 km) causes a visible broadening of the high reflectivity updrafts and a misdetection of low reflectivity downdraft structures. The large radar IFOV also modulates the magnitude of the detected updrafts and downdrafts. In addition to the convective core, the 13 GHz MDV can capture well the transition from frozen to melted hydrometeors and some of the broad, weak dynamical structures.

The 35 GHz radar signal experiences considerable attenuation in the convective core, where the radar signal penetrates to an altitude of 9–10 km, thus capturing the upper 5 km of the convective cloud dynamical structure. However, its superior resolution (IFOV 2.44 km) results in an improved representation of the updraft and downdraft coherent structures, both in terms of their true size and true velocity in the upper 5 km of the squall line.

Finally, the 94 GHz radar penetrates only the upper most 2 km from the convective cloud top, thus, providing limited information about the main convective updraft properties. On the other hand, the superior resolution of the 94 GHz radar (IFOV 1 km) allows it to retrieve several weak dynamical structures resolved in the deep convective cloud simulations.

Together, the three simulated MDV fields provide complimentary information. The 13 GHz radar provides a complete view of the storm’s main dynamical features from the lower levels to the cloud top. On the other hand, the 35 GHz radar can provide higher resolution V_AIR and UCL information in the upper 5 km of the convective core; and the 94 GHz radar can add dynamical information outside of the deep convective core. These confirm previous findings based on airborne observations (Battaglia et al., 2016). Differences in MDVs observed by the different frequency radars resulting from non-Rayleigh scattering can also be exploited (Mroz et al., 2021).

4.2 Weakly Organized Oceanic Convection

A vertical cross section of the 13 GHz radar MDV from the TRMM-LBA weakly organized oceanic convection at the model resolution is shown in Figure 10A. In addition, the spaceborne Doppler radar raw uncorrected MDV simulations of the same event for the radar architectures (3, 4, and 5) are shown in Figure 10. Note here that “raw” MDV is shown since current techniques to correct for NUBF are too uncertain in this highly heterogeneous case (Section 3.3). Comparing the two 13 GHz radar systems highlighting the tradeoff between using 1) a DPCA system that requires two antennas and as such achieves a larger IFOV (radar 4) and 2) one antenna system that can achieve a smaller IFOV (radar 5). For completeness, the performance of the 35-GHz DPCA system (radar 3) is also presented.

FIGURE 10

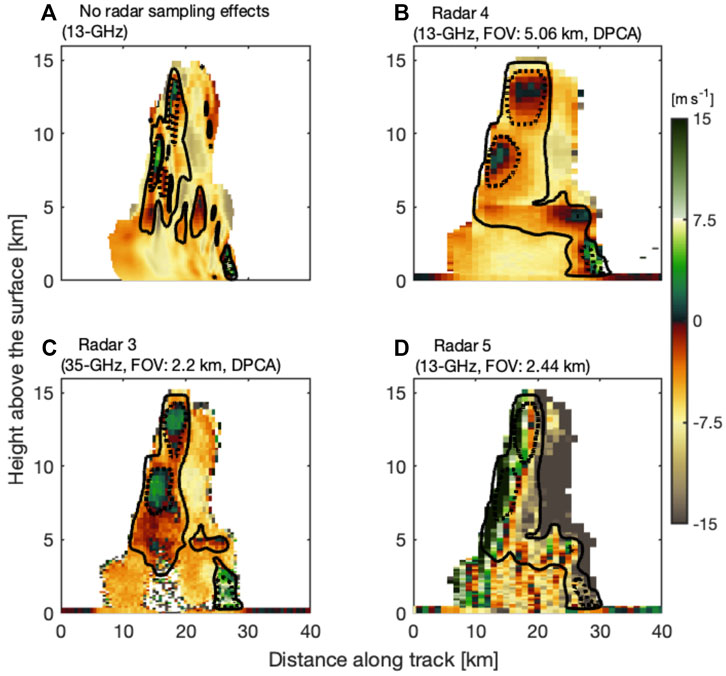
FIGURE 10. Forward simulation of TRMM-LBA weakly organized convection (A) mean Doppler velocity at 13 GHz without radar sampling effects (i.e., truth) as well as mean Doppler velocity for (B) radar 4, (C) radar 3, and (D) radar 5. Overlaid on each plot are air motion contours drawn from forward-simulations with no platform motion effects (2 m s⁻¹: solid and 8 m s⁻¹: dotted). Radar reflectivity was presented in Figure 6.

Although radar 5 has a smaller IFOV (2.44 km) and is better positioned to resolve narrow dynamical features, this advantage is lessened by the high MDV bias and uncertainty this non-DPCA system experiences. As illustrated in Figure 10D, the “raw” MDV from radar 5 looks widely different from the model “truth.”

In contrast, it is evident that radar 4 cannot precisely observe the boundaries of the narrow storm and of its narrow updrafts and downdrafts because of its larger IFOV (5.06 km); however, we would argue that it does reasonably well at locating the center location of the strongest dynamical features of the storm (comparing the location of the velocity isocontours in a and b). In addition, the “raw” MDV that this DPCA system measures is undeniably closer in magnitude to the model truth than that measured by the non-DPCA system.

As for the 35-GHz DPCA radar system (radar 3), we see better penetration in this weaker deep convective storm, only missing the lower 3 km of the storm below the updraft core. The small IFOV of this system (2.2 km) also allows it to better resolve the storm boundaries as well as the boundaries and magnitude of its dynamical features.

This comparison again suggests that 35 GHz and 13 GHz offer complementary information and that the use of DPCA is paramount when it comes to measuring weakly organized convective cloud dynamics.

4.3 Shallow Oceanic Convection

A vertical cross section of the 94 GHz radar reflectivity and MDV from the RICO shallow oceanic convection case at the model resolution is shown in Figure 11 (panels a and b, respectively). In addition, the spaceborne Doppler radar raw, uncorrected MDV simulations of the same event for the 3 DPCA architectures examined here (radars 1, 3, 4) are shown in Figure 11. This comparison highlights the impact of IFOV choice in observing shallow convection from space (Battaglia et al., 2020a; Lamer et al., 2020).

FIGURE 11

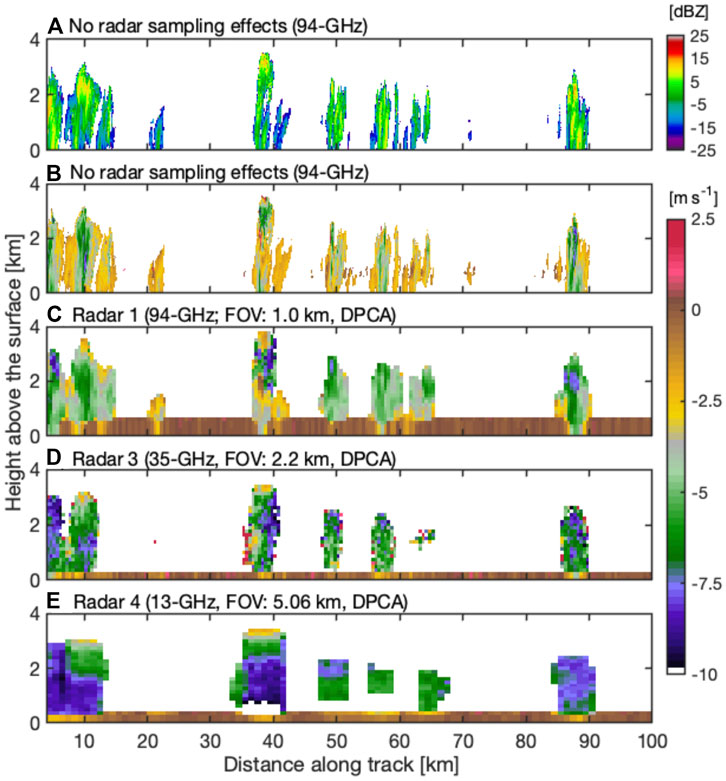
FIGURE 11. Forward simulation of RICO shallow oceanic convection (A) radar reflectivity at 94 GHz without radar sampling effects (B) mean Doppler velocity at 94 GHz without radar sampling effects (i.e., truth) as well as mean Doppler velocity for (C) radar 1, (D) radar 3, and (E) radar 4.

In contrast to the MC3E and TRMM-LBA deep convection cases, the location of the convective updrafts is difficult to determine just from the MDV simulations. The main reason is the weak V_AIR magnitude (2–6 ms⁻¹) that is often lower than the sedimentation velocity V_SED, thus, resulting in an overall negative MDV value. Due to its narrow IFOV, the 94 GHz DPCA radar is capable of documenting most of the cloud-scale MDV features, especially in the most developed clouds (Figure 11C). This is not the case for shallower cloud (Figure 11C, 50–70 km along track). These results suggest that the 94 GHz MDV observations will be conditionally useful for documenting the V_AIR and V_SED using an appropriate inversion technique that will be able to separate their contributions to the observed MDV. At 35 GHz and 13 GHz, the IFOV is 2.5 and 5 km, respectively, and the considerable impact of the radar sampling volume is obvious (Figures 11D,E). These findings are in line with those discussed in Lamer et al. (2020) and Battaglia et al. (2013) indicating that this cloud type requires the deployment of spaceborne radar with sub-kilometer IFOV, short pulse and high sensitivity.

5 Summary

The estimation of the Doppler velocity from a spaceborne platform with sufficient accuracy (2–3 ms⁻¹) and resolution in deep convection and 0.2–0.3 ms⁻¹ in large particle sedimentation regimes (e.g., weak dynamics regimes such as mid- and high-latitude frontal systems) from low Earth orbiting (∼400 km altitude) satellite platforms that move at 7,600 ms⁻¹ is a daunting task.

Using an array of numerical simulation examined within the context of the NASA Aerosols, Clouds, Convection, and Precipitation Decadal Survey study and surveying past airborne Doppler radar observations we established that convective updraft mass flux peaks above 6–8 km. This finding drives a need to rely on radar frequencies that can achieve significant penetration to this depth. Using forward simulations, it was determined that both a 35 GHz radar and 13 GHz radar could achieve such penetration in deep convective cloud systems. It was further established that updrafts larger than 3 km are responsible for the bulk of the updraft mass flux through these storms, thus driving a need to deploy radars with IFOV smaller than 3 km.

Platform motion was showed to significantly impact the mean Doppler velocity (MDV) measured by traditional single-antenna radars. Biases on the order of 30 m s⁻¹ were estimated for the simulated convective clouds. This finding strongly discourages the use of traditional systems for deep convective cloud dynamical studies and favors the use of displaced phase center antenna (DPCA) systems, which are designed to compensate for non-uniform beam filling effects on MDV. A combination of analytical and observed relationships allow us to estimate that outstanding sources of MDV uncertainties would lead to retrieval errors on the order of 0.05–0.15 mm for D_m and 25% for rime fraction (for −10 dBZ echo observed by a 94-GHz DPCA).

Comprehensive forward simulations allow us to appreciate the advantages and drawbacks of each of the six radar architectures currently under consideration by the mission that arose from the ACCP study. We find that the MDV collected by the 94 , 35 , and 13 GHz system provide complementary information. The 13 GHz radar provides a complete view of the storm’s main dynamical features from the lower levels to the cloud top. On the other hand, the 35 GHz radar can provide higher spatial resolution air motion and updraft chord length information in the upper 5 km of the convective cores while the 94 GHz radar can provide additional dynamical information outside of the deep convective cores. Furthermore, differences in MDV observed between the different frequency radars results from non-Rayleigh scattering can also be exploited. When it comes to the shallow convective cloud regime, the findings of our analysis are in line with those discussed in the work of Lamer et al. (2020) and Battaglia et al. (2013) indicating that this cloud type requires the deployment of spaceborne radar with sub-kilometer IFOV, short pulse, and high sensitivity.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

PK led the analysis and writing of this article. AB and KL contributed to the writing. BT and SB contributed to the analysis and interpretation.

Funding

PK’s contributions were performed within the ACCP (now AOS) Decadal Survey Study Team supported by NASA (contract no. 80NSSC19K0923). AB and BT’s contributions were supported by the European Space Agency under the “Raincast” activity (contract no. 4000125959/18/NL/NA). KL’s contributions were supported by the US Department of Energy (DOE) Atmospheric System Research Program under contract DE-SC0012704. SB’s contributions were performed within the ACCP (now AOS) Decadal Survey Study Team supported by NASA. SB’s contributions were supported by the ACCP study.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The numerical model simulations used in the current study are freely available online through the links provided in their introductory publications given in Section 2.2 of this article.

References

Arakawa, A., and Schubert, W. H. (1974). Interaction of a Cumulus Cloud Ensemble with the Large-Scale Environment, Part I. J. Atmos. Sci. 31, 674–701. doi:10.1175/1520-0469(1974)031<0674:ioacce>2.0.co;2

CrossRef Full Text | Google Scholar

Battaglia, A., Kollias, P., Dhillon, R., Roy, R., Tanelli, S., Lamer, K., et al. (2020a). Spaceborne Cloud and Precipitation Radars: Status, Challenges, and Ways Forward. Rev. Geophys. 58 (No. 3), e2019RG000686–9208. doi:10.1029/2019RG000686

PubMed Abstract | CrossRef Full Text | Google Scholar

Battaglia, A., Kollias, P., Dhillon, R., Lamer, K., Khairoutdinov, M., and Watters, D. (2020b). Mind the gap - Part 2: Improving Quantitative Estimates of Cloud and Rain Water Path in Oceanic Warm Rain Using Spaceborne Radars. Atmos. Meas. Tech. 13, 4865–4883. doi:10.5194/amt-13-4865-2020

CrossRef Full Text | Google Scholar

Battaglia, A., Augustynek, T., Tanelli, S., and Kollias, P. (2011). Multiple Scattering Identification in Spaceborne W-Band Radar Measurements of Deep Convective Cores. J. Geophys. Res. 116, D19201. doi:10.1029/2011JD016142

CrossRef Full Text | Google Scholar

Battaglia, A., and Kollias, P. (2015). Using Ice Clouds for Mitigating the EarthCARE Doppler Radar Mispointing. IEEE Trans. Geosci. Remote Sensing 53 (4), 2079–2085. doi:10.1109/TGRS.2014.2353219

CrossRef Full Text | Google Scholar

Battaglia, A., Mroz, K., Lang, T., Tridon, F., Tanelli, S., Tian, L., et al. (2016). Using a Multiwavelength Suite of Microwave Instruments to Investigate the Microphysical Structure of Deep Convective Cores. J. Geophys. Res. Atmos. 121, 9356–9381. doi:10.1002/2016JD025269

PubMed Abstract | CrossRef Full Text | Google Scholar

Battaglia, A., Tanelli, S., and Kollias, P. (2013). Polarization Diversity for Millimeter Spaceborne Doppler Radars: An Answer for Observing Deep Convection? J. Atmos. Oceanic Technology 30 (12), 2768–2787. doi:10.1175/jtech-d-13-00085.1

CrossRef Full Text | Google Scholar

Battaglia, A., Tanelli, S., Mroz, K., and Tridon, F. (2015). Multiple Scattering in Observations of the GPM Dual-Frequency Precipitation Radar: Evidence and Impact on Retrievals. J. Geophys. Res. Atmos. 120, 4090–4101. doi:10.1002/2014JD022866

PubMed Abstract | CrossRef Full Text | Google Scholar

Beauchamp, R. M., Tanelli, S., and Sy, O. O. (2021). Observations and Design Considerations for Spaceborne Pulse Compression Weather Radar. IEEE Trans. Geosci. Remote Sensing 59 (6), 4535–4546. doi:10.1109/TGRS.2020.3013164

CrossRef Full Text | Google Scholar

Brandes, E. A., Zhang, G., and Vivekanandan, J. (2002). Experiments in Rainfall Estimation with a Polarimetric Radar in a Subtropical Environment. J. Appl. Meteorol. 41, 674–685. doi:10.1175/1520-0450(2002)041<0674:eirewa>2.0.co;2

CrossRef Full Text | Google Scholar

Burns, D., Kollias, P., Tatarevic, A., Battaglia, A., and Tanelli, S. (2016). The Performance of the EarthCARE Cloud Profiling Radar in marine Stratiform Clouds. J. Geophys. Res. Atmos. 121, 525–614. doi:10.1002/2016JD025090

CrossRef Full Text | Google Scholar

Cotton, W. R., Pielke Sr., R. A., Walko, R. L., Liston, G. E., Tremback, C. J., Jiang, H., et al. (2003). RAMS 2001: Current Status and Future Directions. Meteorology Atmos. Phys. 82, 5–29. doi:10.1007/s00703-001-0584-9

CrossRef Full Text | Google Scholar

Durden, S. L., Siqueira, P. R., and Tanelli, S. (2007). On the Use of Multi-Antenna Radars for Spaceborne Doppler Precipitation Measurements. Ieee Geosci. Remote Sensing Lett. 1064, 181. doi:10.1109/lgrs.2006.887136

CrossRef Full Text | Google Scholar

Endo, S., Zhang, D., Vogelmann, A. M., Kollias, P., Lamer, K., Oue, M., et al. (2019). Reconciling Differences Between Large‐Eddy Simulations and Doppler Lidar Observations of Continental Shallow Cumulus Cloud‐Base Vertical Velocity. Geophys. Res. Lett. 46, 11539–11547. doi:10.1029/2019gl084893

CrossRef Full Text | Google Scholar

Gasparini, B., Rasch, P. J., Hartmann, D. L., Wall, C. J., and Dütsch, M. (2021). A Lagrangian Perspective on Tropical Anvil Cloud Lifecycle in Present and Future Climate. J. Geophys. Res. Atmospheres 126, e2020JD033487. doi:10.1029/2020jd033487

CrossRef Full Text | Google Scholar

Giangrande, S. E., Luke, E. P., and Kollias, P. (2012). Characterization of Vertical Velocity and Drop Size Distribution Parameters in Widespread Precipitation at ARM Facilities. J. Appl. Meteorol. Climatol. 51, 380–391. doi:10.1175/JAMC-D-10-05000.1

CrossRef Full Text | Google Scholar

Hartmann, D. L., Gasparini, B., Berry, S. E., and Blossey, P. N. (2018). The Life Cycle and Net Radiative Effect of Tropical Anvil Clouds. J. Adv. Model. Earth Syst. 10, 3012–3029. doi:10.1029/2018ms001484

CrossRef Full Text | Google Scholar

Heymsfield, G. M., Tian, L., Heymsfield, A. J., Li, L., and Guimond, S. (2010). Characteristics of Deep Tropical and Subtropical Convection from Nadir-Viewing High-Altitude Airborne Doppler Radar. J. Atmos. Sci. 67 (2), 285–308. doi:10.1175/2009jas3132.1

CrossRef Full Text | Google Scholar

Heymsfield, G. M., Tian, L., Li, L., McLinden, M., and Cervantes, J. I. (2013). Airborne Radar Observations of Severe Hailstorms: Implications for Future Spaceborne Radar. J. Appl. Meteorology Climatology 52 (8), 1851–1867. doi:10.1175/jamc-d-12-0144.1

CrossRef Full Text | Google Scholar

Hogan, R. J., and Westbrook, C. D. (2014). Equation for the Microwave Backscatter Cross Section of Aggregate Snowflakes Using the Self-Similar Rayleigh-Gans Approximation. J. Atmos. Sci. 71 (9), 3292–3301. doi:10.1175/jas-d-13-0347.1

CrossRef Full Text | Google Scholar

Houze, R. A. (1997). Stratiform Precipitation in Regions of Convection: A Meteorological Paradox? Bull. Amer. Meteorol. Soc. 78 (10), 2179–2196. doi:10.1175/1520-0477(1997)078<2179:spiroc>2.0.co;2

CrossRef Full Text | Google Scholar

Illingworth, A. J., Battaglia, A., Bradford, J., Forsythe, M., Joe, P., Kollias, P., et al. (2018). WIVERN: A New Satellite Concept to Provide Global In-Cloud Winds, Precipitation, and Cloud Properties. Bull. Am. Meteorol. Soc. 99 (8), 1669–1687. doi:10.1175/bams-d-16-0047.1

CrossRef Full Text | Google Scholar

Jensen, M. P., Petersen, W. A., Bansemer, A., Bharadwaj, N., Carey, L. D., Cecil, D. J., et al. (2016). The Midlatitude Continental Convective Clouds Experiment (MC3E). Bull. Amer. Meteorol. Soc 97, 1667–1686. doi:10.1175/bams-d-14-00228.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalesse, H., and Kollias, P. (2013). Climatology of High Cloud Dynamics Using Profiling ARM Doppler Radar Observations. J. Clim. 26 (17), 6340–6359. doi:10.1175/jcli-d-12-00695.1

CrossRef Full Text | Google Scholar

Khairoutdinov, M. F., and Randall, D. A. (2003). Cloud Resolving Modeling of the ARM Summer 1997 IOP: Model Formulation, Results, Uncertainties, and Sensitivities. J. Atmos. Sci. 60, 607–625. doi:10.1175/1520-0469(2003)060<0607:crmota>2.0.co;2

CrossRef Full Text | Google Scholar

Kneifel, S., and Moisseev, D. (2020). Long-Term Statistics of Riming in Nonconvective Clouds Derived from Ground-Based Doppler Cloud Radar Observations. J. Atmos. Sci. 77, 3495–3508. doi:10.1175/JAS-D-20-0007.1

CrossRef Full Text | Google Scholar

Kollias, P., Albrecht, B. A., and Marks, F. (2002). Why Mie? Bull. Am. Meteorol. Soc. 83 (10), 1471–1483. doi:10.1175/bams-83-10-1471(2002)083<1471:wm>2.3.co;2

CrossRef Full Text | Google Scholar

Kollias, P., Battaglia, A., Tatarevic, A., Lamer, K., Tridon, F., and Pfitzenmaier, L. (2018). “The EarthCARE Cloud Profiling Radar (CPR) Doppler Measurements in Deep Convection: Challenges, Post-Processing, and Science Applications,” in Proc. SPIE 10776, Remote Sensing of the Atmosphere, Clouds and Precipitation VIII, Honolulu, HI, October 22, 2018, 107760R. doi:10.1117/12.2324321

CrossRef Full Text | Google Scholar

Kollias, P., Clothiaux, E. E., Ackerman, T. P., Albrecht, B. A., Widener, K. B., Moran, K. P., et al. (2016). Development and Applications of ARM Millimeter-Wavelength Cloud Radars. Meteorol. Monogr. 57 (1), 170065–179401. doi:10.1175/amsmonographs-d-15-0037.1

CrossRef Full Text | Google Scholar

Kollias, P. (2007). Considerations for Spaceborne 94 GHz Radar Observations of Precipitation. Geophys. Res. Lett. doi:10.1029/2007gl031536

CrossRef Full Text | Google Scholar

Kollias, P., Tanelli, S., Battaglia, A., and Tatarevic, A. (2014). Evaluation of EarthCARE Cloud Profiling Radar Doppler Velocity Measurements in Particle Sedimentation Regimes. J. Atmos. Oceanic Technol. 31 (2), 366–386. doi:10.1175/jtech-d-11-00202.1

CrossRef Full Text | Google Scholar

Kumar, V. V., Jakob, C., Protat, A., Williams, C. R., and May, P. T. (2015). Mass-flux Characteristics of Tropical Cumulus Clouds from Wind Profiler Observations at Darwin, Australia. J. Atmos. Sci. 72, 1837–1855. doi:10.1175/jas-d-14-0259.1

CrossRef Full Text | Google Scholar

Lamer, K., Kollias, P., Battaglia, A., and Preval, S. (2020). Mind the gap - Part 1: Accurately Locating Warm marine Boundary Layer Clouds and Precipitation Using Spaceborne Radars. Atmos. Meas. Tech. 13, 2363–2379. doi:10.5194/amt-13-2363-2020

CrossRef Full Text | Google Scholar

Lamer, K., Kollias, P., and Nuijens, L. (2015). Observations of the Variability of Shallow Trade Wind Cumulus Cloudiness and Mass Flux. J. Geophys. Res. Atmos.J. Geophys. Res. Atmos. 120, 6161–6178. doi:10.1002/2014jd022950

CrossRef Full Text | Google Scholar

Lamer, K., and Kollias, P. (2015). Observations of Fair-Weather Cumuli over Land: Dynamical Factors Controlling Cloud Size and Cover. Geophys. Res. Lett. 42, 8693–8701. doi:10.1002/2015gl064534

CrossRef Full Text | Google Scholar

Lareau, N. P., Zhang, Y., and Klein, S. A. (2018). Observed Boundary Layer Controls on Shallow Cumulus at the ARM Southern Great Plains Site. J. Atmos. Sci. 75, 2235–2255. doi:10.1175/jas-d-17-0244.1

CrossRef Full Text | Google Scholar

LeMone, M. A., and Zipser, E. J. (1980). Cumulonimbus Vertical Velocity Events in GATE. Part I: Diameter, Intensity and Mass Flux. J. Atmos. Sci. 37, 2444–2457. doi:10.1175/1520-0469(1980)037<2444:cvveig>2.0.co;2

CrossRef Full Text | Google Scholar

Lhermitte, R. (2002). Centimeter & Millimeter Wavelength Radars in Meteorology. Miami, FL: Lhermitte Publications.

Google Scholar

Mason, S. L., Chiu, C. J., Hogan, R. J., Moisseev, D., and Kneifel, S. (2018). Retrievals of Riming and Snow Density from Vertically Pointing Doppler Radars. J. Geophys. Res. Atmos. 123, 13807. doi:10.1029/2018jd028603

CrossRef Full Text | Google Scholar

Matrosov, S. Y. (2017). Characteristic Raindrop Size Retrievals from Measurements of Differences in Vertical Doppler Velocities at Ka- and W-Band Radar Frequencies. J. Atmos. Oceanic Technology 34 (1), 65–71. doi:10.1175/jtech-d-16-0181.1

CrossRef Full Text | Google Scholar

Mitchell, D. L., and Finnegan, W. (2009). Modification of Cirrus Clouds to Reduce Global Warming. Environ. Res. Lett. 4, 0445102.

CrossRef Full Text | Google Scholar

Mroz, K., Battaglia, A., Nguyen, C., Heymsfield, A., Protat, A., and Wolde, M. (2021). Triple-frequency Radar Retrieval of Microphysical Properties of Snow. Atmos. Meas. Tech. 14, 7243–7254. doi:10.5194/amt-14-7243-2021

CrossRef Full Text | Google Scholar

National Academies of Sciences, Engineering, and Medicine (2018). Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space. Washington, DC: The National Academies Press. doi:10.17226/24938

CrossRef Full Text | Google Scholar

Oue, M., Kollias, P., Matrosov, S. Y., Battaglia, A., and Ryzhkov, A. V. (2021). Analysis of the Microphysical Properties of Snowfall Using Scanning Polarimetric and Vertically Pointing Multi-Frequency Doppler Radars. Atmos. Meas. Tech. 14, 4893–4913. doi:10.5194/amt-14-4893-2021

CrossRef Full Text | Google Scholar

Pfitzenmaier, L., Battaglia, A., and Kollias, P. (2019). The Impact of the Radar-Sampling Volume on Multiwavelength Spaceborne Radar Measurements Using Airborne Radar Observations. Remote Sensing 11, 2263. doi:10.3390/rs11192263

CrossRef Full Text | Google Scholar

Protat, A., and Williams, C. R. (2011). The Accuracy of Radar Estimates of Ice Terminal Fall Speed from Vertically Pointing Doppler Radar Measurements. J. Appl. Meteorology Climatology 50 (10), 2120–2138. doi:10.1175/jamc-d-10-05031.1

CrossRef Full Text | Google Scholar

Rauber, R. M., Stevens, B., Ochs, H. T., Knight, C., Albrecht, B. A., Blyth, A. M., et al. (2007). Rain in Shallow Cumulus over the Ocean: The RICO Campaign. B. Am. Meteorol. Soc. 88, 1912–1928. doi:10.1175/bams-88-12-1912

CrossRef Full Text | Google Scholar

Sanderson, B. M., Piani, C., Ingram, W. J., Stone, D. A., and Allen, M. R. (2008). Towards Constraining Climate Sensitivity by Linear Analysis of Feedback Patterns in Thousands of Perturbed-Physics GCM Simulations. Clim. Dyn. 30, 175–190. doi:10.1007/s00382-007-0280-7

CrossRef Full Text | Google Scholar

Satoh, M., Noda, A. T., Seiki, T., Chen, Y.-W., Kodama, C., Yamada, Y., et al. (2018). Toward Reduction of the Uncertainties in Climate Sensitivity Due to Cloud Processes Using a Global Non-hydrostatic Atmospheric Model. Prog. Earth Planet. Sci. 5, 67. doi:10.1186/s40645-018-0226-1

CrossRef Full Text | Google Scholar

Schutgens, N. A. J. (2008). Simulated Doppler Radar Observations of Inhomogeneous Clouds: Application to the EarthCARE Space mission. J. Atmos. oceanic Technol. 25 (1), 26–42. doi:10.1175/2007jtecha956.1

CrossRef Full Text | Google Scholar

Silva Dias, M. A. F., Rutledge, S., Kabat, P., Silva Dias, P. L., Nobre, C., Fisch, G., et al. (2002). Cloud and Rain Processes in a Biosphere-Atmosphere Interaction Context in the Amazon Region. J. Geophys. Res. 107 (D20), 8072. doi:10.1029/2001JD000335

CrossRef Full Text | Google Scholar

Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Barker, D., Duda, M. G., et al. (2008). A Description of the Advanced Research WRF Version 3. Boulder, CO: University Corporation for Atmospheric Research, NCAR/TN-475+STR. doi:10.5065/D68S4MVH

CrossRef Full Text | Google Scholar

Stephens, G. L., van den Heever, S. C., Haddad, Z. S., Posselt, D. J., Storer, R. L., Grant, L. D., et al. (2020). A Distributed Small Satellite Approach for Measuring Convective Transports in the Earth's Atmosphere. IEEE Trans. Geosci. Remote Sensing 58, 4–13. doi:10.1109/TGRS.2019.2918090

CrossRef Full Text | Google Scholar

Storer, R. L., and Posselt, D. J. (2019). Environmental Impacts on the Flux of Mass through Deep Convection. Q.J.R. Meteorol. Soc. 145, 3832–3845. doi:10.1002/qj.3669

CrossRef Full Text | Google Scholar

Sy, O. O., Tanelli, S., Takahashi, N., Ohno, Y., Horie, H., and Kollias, P. (2014). Simulation of EarthCARE Spaceborne Doppler Radar Products Using Ground-Based and Airborne Data: Effects of Aliasing and Nonuniform Beam-Filling. IEEE Trans. Geosci. Remote Sensing 52 (2), 1463–1479. doi:10.1109/TGRS.2013.2251639

CrossRef Full Text | Google Scholar

Tanelli, S., Durden, S. L., and Johnson, M. P. (2016). Airborne Demonstration of DPCA for Velocity Measurements of Distributed Targets. IEEE Geosci. Remote Sensing Lett. 13, 1415–1419. doi:10.1109/lgrs.2016.2581174

CrossRef Full Text | Google Scholar

Tanelli, S., Im, E., Durden, S. L., Facheris, L., and Giuli, D. (2002). The Effects of Nonuniform Beam Filling on Vertical Rainfall Velocity Measurements with a Spaceborne Doppler Radar. J. Atmos. Oceanic Technol. 19 (7), 1019–1034. doi:10.1175/1520-0426(2002)019<1019:teonbf>2.0.co;2

CrossRef Full Text | Google Scholar

Testud, J., Oury, S., Black, R. A., Amayenc, P., and Dou, X. (2001). The Concept of "Normalized" Distribution to Describe Raindrop Spectra: A Tool for Cloud Physics and Cloud Remote Sensing. J. Appl. Meteorol. 40, 1118–1140. doi:10.1175/1520-0450(2001)040<1118:tcondt>2.0.co;2

CrossRef Full Text | Google Scholar

Tiedtke, M. (1989). A Comprehensive Mass Flux Scheme for Cumulus Parameterization in Large-Scale Models. Mon. Wea. Rev. 117, 1779–1800. doi:10.1175/1520-0493(1989)117<1779:acmfsf>2.0.co;2

CrossRef Full Text | Google Scholar

Ulbrich, C. W. (1983). Natural Variations in the Analytical Form of the Raindrop Size Distribution. J. Clim. Appl. Meteorol. 22, 1764–1775. doi:10.1175/1520-0450(1983)022<1764:nvitaf>2.0.co;2

CrossRef Full Text | Google Scholar

vanZanten, M. C., Stevens, B., Nuijens, L., Siebesma, A. P., Ackerman, A. S., Burnet, F., et al. (2011). Controls on Precipitation and Cloudiness in Simulations of Trade-Wind Cumulus as Observed during RICO. J. Adv. Model. Earth Syst. 3, a–n. doi:10.1029/2011MS000056

CrossRef Full Text | Google Scholar

Varble, A., Morrison, H., and Zipser, E. (2020). Effects of Under-resolved Convective Dynamics on the Evolution of a Squall Line. Monthly Weather Rev. 148 (1), 289–311. doi:10.1175/mwr-d-19-0187.1

CrossRef Full Text | Google Scholar

Wang, D., Giangrande, S. E., Feng, Z., Hardin, J. C., and Prein, A. F. (2020). Updraft and Downdraft Core Size and Intensity as Revealed by Radar Wind Profilers: MCS Observations and Idealized Model Comparisons. J. Geophys. Res. Atmos. 125, e2019JD031774. doi:10.1029/2019jd031774

CrossRef Full Text | Google Scholar

Waterman, P. C. (1965). Matrix Formulation of Electromagnetic Scattering. Proc. IEEE 53 (8), 805–812. doi:10.1109/proc.1965.4058

CrossRef Full Text | Google Scholar

Williams, C. R., Carey, L. D., Chandrasekar, V., Gatlin, P. N., Haddad, Z. S., Meneghini, R., et al. (2014). Describing the Shape of Raindrop Size Distributions Using Uncorrelated Raindrop Mass Spectrum Parameters. J. Appl. Meteorol. Climatol. 53, 1282–1296. doi:10.1175/JAMC-D-13-076.1

CrossRef Full Text | Google Scholar

Williams, C. R. (2012). Vertical Air Motion Retrieved from Dual-Frequency Profiler Observations. J. Atmos. Ocean. Tech. 29, 1471–1480. doi:10.1175/JTECH-D-11-00176.1

CrossRef Full Text | Google Scholar

Willis, P. T. (1984). Functional Fits to Some Observed Drop Size Distributions and Parameterization of Rain. J. Atmos. Sci. 41, 1648–1661. doi:10.1175/1520-0469(1984)041<1648:fftsod>2.0.co;2

CrossRef Full Text | Google Scholar

Xu, K.-M., and Randall, D. A. (2001). Explicit Simulation of Cumulus Ensembles with the GATE Phase III Data: Budgets of a Composite Easterly Wave. Q.J R. Met. Soc. 127 (575), 1571–1591. doi:10.1002/qj.49712757506

CrossRef Full Text | Google Scholar

Yuter, S. E., Houze, R. A., Smith, E. A., Wilheit, T. T., and Zipser, E. (2005). Physical Characterization of Tropical Oceanic Convection Observed in KWAJEX. J. Appl. Meteorology 44, 385–415. doi:10.1175/jam2206.1

CrossRef Full Text | Google Scholar

Zelinka, M. D., Randall, D. A., Webb, M. J., and Klein, S. A. (2017). Clearing Clouds of Uncertainty. Nat. Clim Change 7, 674–678. doi:10.1038/nclimate3402

CrossRef Full Text | Google Scholar

Zhu, Z., Kollias, P., Yang, F., and Luke, E. (2021). On the Estimation of In-Cloud Vertical Air Motion Using Radar Doppler Spectra. Geophys. Res. Lett. 48, e2020GL090682. doi:10.1029/2020gl090682

CrossRef Full Text | Google Scholar

Zipser, E. J., and Gautier, C. (1978). Mesoscale Events within a GATE Tropical Depression. Mon. Wea. Rev. 106, 789–805. doi:10.1175/1520-0493(1978)106<0789:mewagt>2.0.co;2

CrossRef Full Text | Google Scholar