Uncertainty is not sufficient for identifying noisy labels in training data for binary segmentation of building footprints

Obtaining high quality labels is a major challenge for the application of deep neural networks in the remote sensing domain. A common way of acquiring labels is the usage of crowd sourcing which can provide much needed training data sets but also often contains incorrect labels which can affect the training process of a deep neural network significantly. In this paper, we exploit uncertainty to identify a certain type of label noise for semantic segmentation of buildings in satellite imagery. That type of label noise is known as “omission noise,” i.e., missing labels for whole buildings which still appear in the satellite image. Following the literature, uncertainty during training can help in identifying the “sweet spot” between generalizing well and overfitting to label noise, which is further used to differentiate between noisy and clean labels. The differentiation between clean and noisy labels is based on pixel-wise uncertainty estimation and beta distribution fitting to the uncertainty estimates. For our study, we create a data set for building segmentation with different levels of omission noise to evaluate the impact of the noise level on the performance of the deep neural network during training. In doing so, we show that established uncertainty-based methods to identify noisy labels are in general not sufficient enough for our kind of remote sensing data. On the other hand, for some noise levels, we observe some promising differences between noisy and clean data which opens the possibility to refine the state-of-the-art methods further.

1 Introduction

Deep neural networks (DNNs) have produced state-of-the-art results on a wide variety of classification and segmentation tasks, including semantic segmentation of remote sensing imagery (Kemker et al., 2018). However, label noise in training data can potentially impair the performance of DNNs by damaging a network’s generalization ability, as it was empirically shown that DNNs are able to overfit to completely random noise (Zhang et al., 2021). In general, the effect that label noise has on the training of DNNs is not well understood: In practice, models often generalize reasonably well even in high-noise environments (Rolnick et al., 2018; Wang et al., 2018), but in other cases label noise is known for affecting model training in segmentation substantially (Rahaman et al., 2022).

Label noise can appear during any part of data collection, processing, or analysis, for a wide variety of reasons. Researchers often rely on less accurate automated processes to label large amounts of data cheaply, but even expert opinions can disagree on the same segmentation task (Redekop and Chernyavskiy, 2021). In semantic segmentation, it is practically impossible for annotators to accurately label images pixel-by-pixel, leading to unavoidable noise along segmentation boundaries (Collier et al., 2020). In (Mnih and Hinton, 2012) the authors refer to this phenomenon as “registration noise.” Registration noise can appear in the form of shifts, rotations or inaccuracies of boundary geometries. Remote sensing datasets may also be incomplete or out-of-date; thus building labels do not match the architecture in the corresponding satellite image. The case where a label is missing for a building that appears in the satellite image is referred to as “omission noise”.

There are many approaches for dealing with label noise in Deep Learning. The authors of (Algan and Ulusoy, 2021) organize these into “noise model based” and “noise model free” categories. “Noise model based” approaches seek to estimate underlying noise structures in order to de-emphasize, relabel, or remove noisy labels so that the model does not learn from them, while “noise model free” approaches exploit noisy labels to improve robustness, for example, to speed up gradient descent through hard example mining or to avoid overfitting (Chang et al., 2017). There exist many different model architectures and loss functions for dealing with noisy labels across these categories (Mnih and Hinton, 2012; Fobi et al., 2020; Kang et al., 2020; Kang et al., 2021). This paper falls into the “noise model based” category, aiming to identify a noisy label distribution for potential relabeling.At the same time, as interpretability becomes a major focus in the field of Deep Learning, research on predictive uncertainty is on the rise, since critical applications of deep learning models require uncertainty measures such as confidence estimates to interpret and trust model predictions (Henne et al., 2020). Ensemble learning and Monte-Carlo dropout, two of the most popular techniques for obtaining confidence measures, estimate predictive uncertainty by evaluating the same predictions across multiple models or on the same model with slightly different parameters. There also exists an expanding amount of literature on interpreting uncertainty in Deep Learning, as uncertainty estimates likely contain useful information about the data and the network itself (Abdar et al., 2021). The field of remote sensing notably lacks meaningful exploration of uncertainty; Haas and Rabus (2021) address this open question, but they do not include label noise in their research.

Since label noise is detrimental to the practical utility of DNNs, it is important to gain a more thorough understanding of how networks learn in the face of this issue. Intuitively, it makes sense that label noise can influence the uncertainty of a model: If the labeling pattern of some samples (noisy) deviates from the labeling pattern of the majority (clean), this might cause the model to be more uncertain on the deviating ones. Both, Köhler et al. (2019) and Redekop and Chernyavskiy (2021), study the relationship between label noise and predictive uncertainty, in the fields of image classification and medical image segmentation, respectively. Specifically, they use observed patterns in uncertainty throughout CNN training to choose the ideal epoch at which to separate clean from noisy labels based on the unique distributions of their respective uncertainties. Our goal is to find out if similar methods can be used successfully for remote sensing data. The method in Arazo et al. (2019) uses a similar approach by fitting a beta mixture to clean and noisy label distributions, but they use the loss function rather than uncertainty for the task of finding the optimal epoch for differentiation between clean and noisy labels.

In this work, we assess the suitability of those methods on remote sensing imagery. To this end, we introduce noise in the labels of a dataset on building footprints and evaluate if those methods are able to successfully identify the added noise. We use the heuristics suggested by Köhler et al. (2019) and Redekop and Chernyavskiy (2021) to choose the ideal epoch to find label noise. Next, we fit a mixed beta distribution to the uncertainty values of the chosen epoch in order to separate the clean and noisy label components. Finally, we use the fitted distribution to classify each pixel as either clean or noisy, and report several performance metrics.

2 Methods

The approach described by Köhler et al. (2019) and Redekop and Chernyavskiy (2021) works as follows: It is assumed that during training a DNN, there is a point in time when the model has already learned to recognize the important patterns, but has not yet learned to overfit on the noise in the training data. This is a reasonable assumption since it was empirically shown by Arpit et al. (2017) and Arazo et al. (2019) that DNNs usually start overfitting to noise only in the later epochs. It is further assumed that the predictive uncertainty at such a point is noticeably different on noisy than on clean samples.

Each, Köhler et al. (2019) and Redekop and Chernyavskiy (2021), recommend empirically promising heuristics for choosing an epoch at which the predictive uncertainty can be used to correctly distinguish between noisy and clean labels without knowledge of the underlying noise distribution. In both cases, these heuristics are an observed local minimum of an uncertainty measure at a specific epoch that coincides with the global maximum of test accuracy. The authors conclude that this observed local minimum can therefore be used as an indicator for the epoch of highest test accuracy, which is equivalent to the abovementioned point in time. Neither paper provides a theoretical explanation nor robust testing of these heuristics. Still, in the absence of alternative indicators, we also use these heuristics to choose an appropriate epoch. At the chosen epoch, the predictive uncertainties are calculated for each training sample, and two unimodal distributions are then fitted to the histogram of the uncertainties. Those two distributions should, ideally, represent the uncertainty distribution of the clean and noisy samples, respectively. Those two distributions can subsequently be used to classify the training samples as clean or noisy. Our contribution consists of applying the methods presented by Köhler et al. (2019) and Redekop and Chernyavskiy (2021) on a remote sensing dataset with several different levels of label noise and evaluating the performance of those methods to determine whether the proposed methods can successfully be utilized in the remote sensing domain.We use a DeepLabV3+ model (Chen et al., 2018) with dropout (rate = .1), a binary crossentropy loss, the Adam optimizer (Kingma and Ba, 2014), and an initial learning rate of 10^–4 with exponential decay for the semantic segmentation of building footprints on a satellite imagery dataset of the city of Rotterdam (Shermeyer et al., 2020). From this dataset, only images that contained at least 30% buildings were selected for training and validation to reduce the effect of class imbalances. We train the model for 100 epochs with a batch size of 8, using 2,574 and 643 RGB images for training and validation, respectively (80%/20% split). Each image has 256 × 256 pixels. To obtain uncertainty estimates, the model predicts on the training data at the end of each epoch, using MC Dropout (Gal and Ghahramani, 2016) with 20 forward passes to output a vector of softmax predictions for each pixel.

In our analysis, we focus on omission noise, which appears when objects that are visible in the image are missing in the label mask (Mnih and Hinton, 2012). This is a very common noise type in remote sensing imagery that can stem from out-of-date or incomplete reference data. To evaluate how well the method is capable of identifying omission noise, we created 11 different versions of the initial dataset, each version containing the same images but a different amount of omission noise in the labels. We subsequently train a model on each of the 11 versions, using the original (0% noise) validation labels for all trials. Our 11 datasets cover the noise levels between 0% and 100% in intervals of 10 percentage points. The percentage of noise refers here to the fraction of true building pixels that are converted to background pixels, meaning that in a dataset with 10% omission noise, roughly 10% of the true building pixels in each image have been converted to background pixels. Since we only convert whole building geometries, the exact noise level in an image can vary to some degree.

For calculating the predictive uncertainties for each training pixel x, we perform T ≔ 20 forward passes with dropout (Gal and Ghahramani, 2016) at the end of each epoch to obtain a sequence of one-hot encoded softmax vectors ${(g^t(x))}_{t=\mathrm{1,2},\dots T}$ with $g^t(x)={(g_c^t(x))}_{c=1,\dots ,C}\in {\mathbb{R}}^C$, where C = 2 is the number of classes. The class index c = 0 stands for the building class and c = 1 for the background class. We track three uncertainty measures during training:

1. The average softmax value of the predicted class:

$\mu ≔\frac{1}{T}\sum _{t=1}^T{\max }_{c\in \left\{\mathrm{0,1}\right\}}{g}_c^t\left(x\right)(1)$

2. The standard deviation of the softmax scores for the building class, as proposed by (Köhler et al., 2019):

${\sigma }_0≔\sqrt{\sum _{t=1}^T{\left(g_0^t\left(x\right)-{\mu }_0\right)}^2}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}with\hspace{0.17em}}{\mu }_0≔\frac{1}{T}\sum _{t=1}^T{g}_0^t\left(x\right).(2)$

3. A measure used by (Redekop and Chernyavskiy, 2021) and defined by (Kwon et al., 2020) which is designed to capture the aleatoric part of a model output’s variance¹. We will refer to it as Var_al in the remainder of this paper:

$Va{r}_{al}≔\frac{1}{T}\sum _{t=1}^T{g}_0^t\left(x\right)\cdot \left(1-g_0^t\left(x\right)\right)(3)$

In our experiments, the standard deviation of the model predictions as proposed by Köhler et al. (2019) turned out to be most successful uncertainty measure for identifying an optimal epoch, to the effect that the observed local minimum in this uncertainty measure was most clearly visible qualitatively. Following the recommendation by Köhler et al. (2019), we fit a mixed beta distribution to the histogram of predictive uncertainty values at the chosen epoch to extract “noisy” and “clean” components. We use the betamix algorithm and code implementation² from Schröder and Rahmann (2017), since the predictive uncertainties include 0 and 1 values, which hinder performance of the traditional MLE-based EM algorithm (Schröder and Rahmann, 2017; Arazo et al., 2019). The algorithm assigns each uncertainty value in the histogram to one of the two components based on a posterior likelihood distribution. We compare how accurately the pixels assigned to the “noisy” component match the actual known omission noise, or building pixels removed from the training labels. The percentage of total pixels assigned to the “noisy” component by the betamix algorithm should ideally match the known omission noise level, or percentage of building pixels removed. The labels in the “noisy” distribution are then used to calculate pixel-wise accuracy metrics against the actual (known) omission noise.

3 Results

We will first touch on the process of selecting a suitable epoch for extracting uncertainty values: Figure 1 shows the development of the standard deviation of the softmax scores for the building class σ₀ during training, computed over the full training set and all forward passes, for each of the noisy datasets. Predictive uncertainty measures seem to adhere to specific patterns throughout model training, especially at low-to-medium omission noise levels. When training with omission noise levels above 0%, the average standard deviation of the softmax values first decreases before reaching a minimum sometime within the first half of training and increasing again. This result mirrors the observation by (Köhler et al., 2019) of an early minimum in the network’s standard deviation during training, allowing us to use the epoch of this minimum for separating between clean and noisy labels by fitting a mixed beta distribution. Interestingly, this pattern does not appear at the 0% omission noise level; in that case, the standard deviation steadily decreases throughout the entire training process. However, at noise levels equal and above 50%, the heuristic seems to be less helpful, as the magnitude of uncertainty is smaller overall and there seems to be more randomness in the uncertainty values throughout training. For reasons of brevity, we do not show the other uncertainty measures explained in Section 2, though they also show similar behaviours in that for datasets with existing but not extremely high noise levels, the uncertainty first decreases before starting to increase again. For each noise level we choose the epoch at the first local minimum in predictive uncertainty for further analysis, if such a minimum exists. The extracted epochs are shown in Table 1.

FIGURE 1

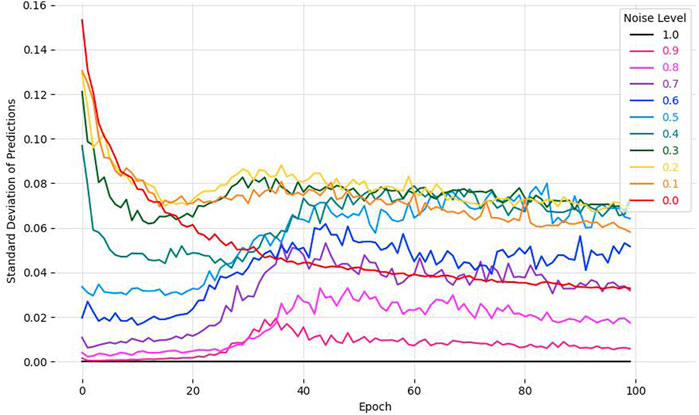
FIGURE 1. Standard deviation of the softmax values of the building class σ₀ across 100 training epochs for different noise levels in training data.

TABLE 1

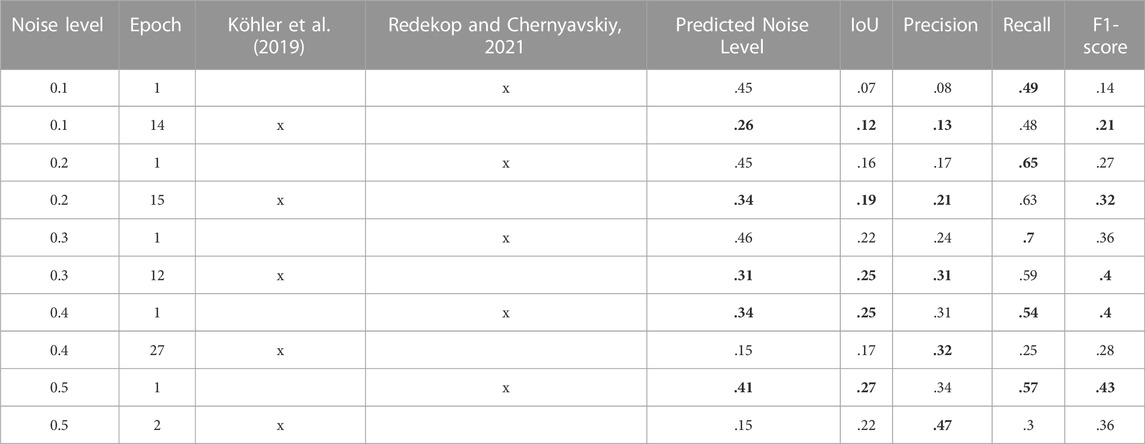
TABLE 1. Table of pixel-wise accuracy metrics for pixels classified as “noisy” by the betamix algorithm versus known omission noise. The method proposed by Köhler et al. (2019) uses the standard deviation of softmax values of the building class σ₀ to select an epoch, and the mean softmax values of the predicted class μ, within the chosen epoch to identify noisy samples. The method proposed by Redekop and Chernyavskiy, 2021 uses the difference in Var_al for epoch selection and Var_al for identification. Bold values show the best result for each noise level between the two heuristics.

Next, we fit a mixed beta distribution onto the uncertainty values from the chosen epochs. Figures 2A, B show the uncertainty histograms of the training sets with 20% and 30% noise respectively at the epochs chosen by the heuristic described above, as well as the two components of the mixed beta distribution that were fitted by the betamix algorithm onto the data. The uncertainty measure used here is the average softmax value of the predicted class μ, which is more interpretable as a confidence score. Note that this is a different measure than the one used for identifying the epoch in the first place. We chose a different measure here since it became apparent qualitatively that histograms generated by this measure had more distinct modes than the ones generated with the standard deviation of the building class. The histograms show that the majority of samples is assigned a very high confidence near 1.0 for both of the noise levels. However there is also a local maximum between .6 and .7. Based on the works of Köhler et al. (2019) and Redekop and Chernyavskiy (2021), we assume the component comprised of lower uncertainty values is “clean,” and the component of higher uncertainty “noisy.” For reasons of brevity, we only show the distributions for the those two noise levels, where the distinction into two modes is most visible. At the higher noise levels and especially above 50%, the smaller local maximum vanishes again, and the betamix algorithm is only able to fit a single component, in other words failing to identify any label noise. The likely reason for this is that for too high noise levels, the network is not able to distinguish between clean and noisy labels anymore.

FIGURE 2

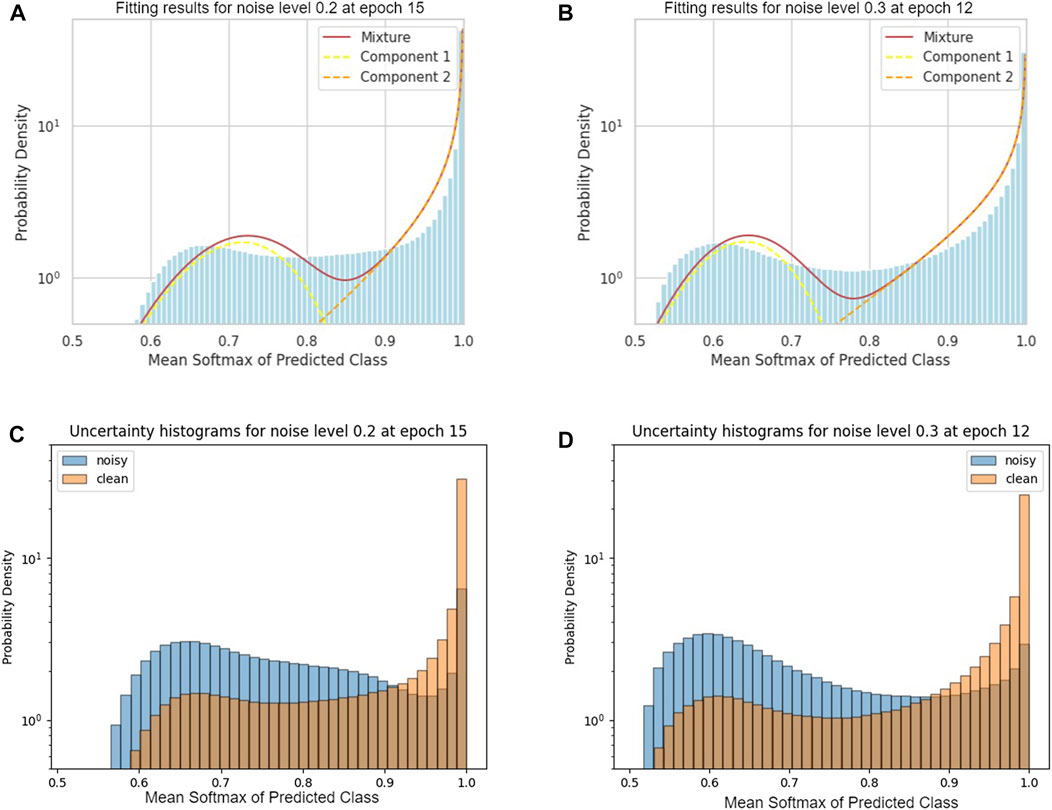
FIGURE 2. Mixed beta distributions fit and uncertainty histograms of clean and noisy samples. (A) Mixed beta distributions fit by the betamix algorithm for training data with 20% noise (B) Mixed beta distributions fit by the betamix algorithm for training data with 30% noise (C) Uncertainty histograms of clean and noisy samples for training data with 20% noise (D) Uncertainty histograms of clean and noisy samples for training data with 30% noise. Uncertainties were computed by taking the mean softmax value of the predicted class μ.

Since in our experimental setup we have complete information on the noise in the data, we can check if the distributions found by the betamix algorithm actually correspond with the distributions of the noisy and clean samples. Figures 2C, D show the histograms of the actual clean and noisy samples in the training sets with 20% and 30% label noise, respectively. What can be seen is that the clean labels are indeed concentrated on the very high confidence scores, however the distinction at the lower confidence scores is not so clear, since similar amounts of clean and noisy samples can be found there. Furthermore, there is a noticeable difference between noise levels: The histograms of the training sets with 20% and 30% label noise allow a much better distinction between clean and noisy samples than the ones for the other training sets. For reasons of brevity, we only show the histograms of the two noise levels where the distinction between clean and noisy samples works best.

Another interesting observation is how the different uncertainties are distributed spatially. As can be seen in Figure 3, predictive uncertainty seems to be largely concentrated along the borders of buildings, based on heatmaps of all four uncertainty measures.

FIGURE 3

FIGURE 3. Heatmaps of predictive uncertainty during training with 0% omission noise in the top row and 20% omission noise in the bottom row at epoch 15. (A) Satellite image (B) training label (C) average softmax of predicted class (D) standard deviation (E) Var_al. All uncertainty values are scaled for better visibility.

Accuracy metrics for the task of identifying noisy samples are shown in Table 1 for the different noise levels, for both the approach described by Köhler et al. (2019) and the approach described by Redekop and Chernyavskiy (2021). The main difference between the two approaches are the uncertainty measures used: The former use the standard deviation of the softmax values of the building class σ₀ for epoch selection and the mean softmax value of the predicted class μ for noisy sample identification. The latter use the change in Var_al between subsequent epochs for epoch selection and Var_al for noisy sample identification. The accuracy metrics indicate that both methods do a poor job at accurately detecting the noisy pixels. The maximum IoU score achieved for any noise level or heuristic is .27 (50% noise; epoch 1; Redekop’s approach), much lower than the usual threshold of .5 needed to be considered successful. In general, using the approach from (Redekop and Chernyavskiy, 2021) results in a greater predicted noise level, likely because it usually selects an earlier epoch at which to fit the distribution, so that there is more uncertainty in the model’s predictions and therefore more pixels are classified as noisy. For the same reason, this heuristic leads to lower Precision and higher Recall scores, as there are more predicted noisy (positive) pixels overall, and therefore more false positives and fewer false negatives. Above the noise level of .5 it was mostly not possible anymore to fit two beta distributions onto the histograms, therefore there are no results reported for the higher noise levels.

4 Discussion

The results in Figure 1 clearly indicate that the existence of label noise does affect the uncertainty of the model during training. In accordance with the observations of Köhler et al. (2019) and Redekop and Chernyavskiy (2021), label noise causes the training uncertainty first to decrease before increasing again. The fact that this behaviour is not visible in the upper noise levels is also to be expected: In the extreme case of 100% label noise, the training labels consists solely of background and therefore the model cannot learn any patterns, but will instead predict the background class every single time, resulting in maximum confidence. This implies that if a model’s uncertainty during training can be used for identifying noisy labels, it would only possible for noise levels below a certain threshold.Furthermore, we see from the comparison in Figures 2A, B with Figures 2C, D that the uncertainty distributions of clean and noisy samples overlap strongly and therefore are not accurately captured by the betamix algorithm. Finetuning or replacing the algorithm so that the two distributions are found more reliably could be a next step in future attempts to utilize uncertainty for noisy label detection, even though reliable noisy label identification based on uncertainty alone would still not be possible because of the large overlap between the two distributions.

The results that we have shown here are not as good as the ones reported by Köhler et al. (2019) and Redekop and Chernyavskiy (2021) on their respective datasets, which brings up the question why the methods seem to work better on natural and medical images than on remote sensing imagery. One possibility could be the higher fraction of boundaries between background and target class. We observed that boundary pixels have much larger uncertainties than the average. A similar observation based on Var_al is made in Kwon et al. (2020). (Collier et al. (2020) gives a potential reason for this phenomenon:

“Image segmentation datasets have naturally occurring heteroscedastic uncertainty. A single 512 × 512 image has 262,144 pixels, so, in practice human annotators cannot label pixels individually but label collections of pixels at a time. As a result annotations tend to be noisy at the boundaries of objects.”

Since ground-truth building annotations do not perfectly align with building pixels in the satellite imagery data, there is naturally occurring boundary noise in the semantic segmentation task. Therefore, the model may correctly pick up on boundary noise and be more uncertain on those pixels during training; however, this could make it difficult to track uncertainty on other kinds of noise, even when it is manually added and known to the researcher. We attempted to account for this property by masking out the boundary pixels during the fitting of the beta distributions. Alternatively, we also used a loss function specifically designed to reduce the uncertainty on boundaries (Bokhovkin and Burnaev, 2019). Both times however, the results looked still similar to the ones shown above, indicating that boundaries are not the only source of the discrepancy.

As Table 1 shows, the above mentioned overlap between uncertainty distributions of clean and noisy samples leads to overall poor results of the methods for identifying noisy samples. The performance metrics indicate that predictive uncertainty is a poor indicator of omission noise alone, especially when more than 50% of building labels have been removed before network training.

In summary, the initial goal of identifying noisy labels based on uncertainty could not be achieved to a satisfying degree. Still, a promising difference in uncertainty distributions between clean and noisy labels can be noticed at least for some of the noise levels. Refining the methods used in this work to more accurately capture the true distributions of clean and noisy labels could still be of use for label cleaning purposes, e.g., for obtaining a prior probability on potentially noisy samples or for establishing a subset of most trustworthy samples.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://zenodo.org/record/6651463#.Y1vdcErP1FE.

Author contributions

HU carried out all the experiments, performed literature research, processed the results and wrote the bigger part of the introduction, methods and results sections. JG had the initial idea for the paper, provided code for parts of the experiments, supervised and guided the experiments and formulated the bigger part of the discussion section. JN gave advice on how to structure the experiments, formulated parts of the paper and supported the overall writing process.

Funding

This research was conducted at the German Aerospace Center (DLR), within the scope of a collaboration with Princeton University’s Summer Work Program supported by the Helmholtz Information and Data Science Academy (HIDA).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://github.com/ykwon0407/UQ_BNN/blob/master/retina/utils.py

²https://bitbucket.org/genomeinformatics/betamix/src/master/

References

Abdar, M., Pourpanah, F., Hussain, S., Rezazadegan, D., Liu, L., Ghavamzadeh, M., et al. (2021). A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Inf. Fusion 76, 243–297. doi:10.1016/j.inffus.2021.05.008

CrossRef Full Text | Google Scholar

Algan, G., and Ulusoy, I. (2021). Image classification with deep learning in the presence of noisy labels: A survey. Knowledge-Based Syst. 215, 106771. doi:10.1016/j.knosys.2021.106771

CrossRef Full Text | Google Scholar

Arazo, E., Ortego, D., Albert, P., O’Connor, N., and McGuinness, K. (2019). “Unsupervised label noise modeling and loss correction,” in International conference on machine learning (PMLR), 312–321.

Google Scholar

Arpit, D., Jastrzkebski, S., Ballas, N., Krueger, D., Bengio, E., Kanwal, M. S., et al. (2017). A closer look at memorization in deep networks. Int. Conf. Mach. Learn., Sydney, Australia.

Google Scholar

Bokhovkin, A., and Burnaev, E. (2019). “Boundary loss for remote sensing imagery semantic segmentation,” in International symposium on neural networks (Springer), 388–401.

CrossRef Full Text | Google Scholar

Chang, H.-S., Learned-Miller, E., and McCallum, A. (2017). Active bias: Training more accurate neural networks by emphasizing high variance samples. Adv. Neural Inf. Process. Syst. 30.

Google Scholar

Chen, L.-C., Zhu, Y., Papandreou, G., Schroff, F., and Adam, H. (2018). “Encoder-decoder with atrous separable convolution for semantic image segmentation,” in Proceedings of the European conference on computer vision (ECCV), 801.

CrossRef Full Text | Google Scholar

Collier, M., Mustafa, B., Kokiopoulou, E., Jenatton, R., and Berent, J. (2020). A simple probabilistic method for deep classification under input-dependent label noise. arXiv preprint arXiv:2003.06778.

Google Scholar

Fobi, S., Conlon, T., Taneja, J., and Modi, V. (2020). “Learning to segment from misaligned and partial labels,” in Proceedings of the 3rd ACM SIGCAS conference on computing and sustainable societies, 286–290.

CrossRef Full Text | Google Scholar

Gal, Y., and Ghahramani, Z. (2016). “Dropout as a bayesian approximation: Representing model uncertainty in deep learning,” in International conference on machine learning (PMLR).

Google Scholar

Gütter, J. A., Kruspe, A., Zhu, X. X., and Niebling, J. (2022). Impact of training set size on the ability of deep neural networks to deal with omission noise. Front. Remote Sens. 3, 2431. doi:10.3389/frsen.2022.932431

CrossRef Full Text | Google Scholar

Haas, J., and Rabus, B. (2021). Uncertainty estimation for deep learning-based segmentation of roads in synthetic aperture radar imagery. Remote Sens. 13, 1472. doi:10.3390/rs13081472

CrossRef Full Text | Google Scholar

Henne, M., Schwaiger, A., Roscher, K., and Weiss, G. (2020). Benchmarking uncertainty estimation methods for deep learning with safety-related metrics, 83–90. SafeAI@ AAAI.

Google Scholar

Kang, J., Fernandez-Beltran, R., Duan, P., Kang, X., and Plaza, A. J. (2020). Robust normalized softmax loss for deep metric learning-based characterization of remote sensing images with label noise. IEEE Trans. Geoscience Remote Sens. 59, 8798–8811. doi:10.1109/tgrs.2020.3042607

CrossRef Full Text | Google Scholar

Kang, J., Fernandez-Beltran, R., Sun, X., Ni, J., and Plaza, A. (2021). Deep learning-based building footprint extraction with missing annotations. IEEE Geoscience Remote Sens. Lett. 19, 1–5. doi:10.1109/lgrs.2021.3072589

CrossRef Full Text | Google Scholar

Kemker, R., Salvaggio, C., and Kanan, C. (2018). Algorithms for semantic segmentation of multispectral remote sensing imagery using deep learning. ISPRS J. photogrammetry remote Sens. 145, 60–77. doi:10.1016/j.isprsjprs.2018.04.014

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980

Google Scholar

Köhler, J. M., Autenrieth, M., and Beluch, W. H. (2019). Uncertainty based detection and relabeling of noisy image labels. CVPR Work shops, 33–37.

Google Scholar

Kwon, Y., Won, J.-H., Kim, B. J., and Paik, M. C. (2020). Uncertainty quantification using bayesian neural networks in classification: Application to biomedical image segmentation. Comput. Statistics Data Analysis 142, 106816. doi:10.1016/j.csda.2019.106816

CrossRef Full Text | Google Scholar

Mnih, V., and Hinton, G. E. (2012). “Learning to label aerial images from noisy data,” in Proceedings of the 29th International conference on machine learning (ICML-12), 567–574.

Google Scholar

Rahaman, M., Hillas, M. M., Tuba, J., Ruma, J. F., Ahmed, N., and Rahman, R. M. (2022). Effects of label noise on performance of remote sensing and deep learning-based water body segmentation models. Cybern. Syst. 53, 581–606. doi:10.1080/01969722.2021.1989171

CrossRef Full Text | Google Scholar

Redekop, E., and Chernyavskiy, A. (2021). “Uncertainty-based method for improving poorly labeled segmentation datasets,” in 2021 IEEE 18th international symposium on biomedical imaging (ISBI) (IEEE), 1831.

CrossRef Full Text | Google Scholar

Rolnick, D., Veit, A., Belongie, S., and Shavit, N. (2018). Deep learning is robust to massive label noise. arXiv preprint arXiv:1705.10694.

Google Scholar

Schröder, C., and Rahmann, S. (2017). A hybrid parameter estimation algorithm for beta mixtures and applications to methylation state classification. Algorithms Mol. Biol. 12, 21–12. doi:10.1186/s13015-017-0112-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Shermeyer, J., Hogan, D., Brown, J., Van Etten, A., Weir, N., Pacifici, F., et al. (2020). “Spacenet 6: Multi-sensor all weather mapping dataset,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition workshops, 196.

CrossRef Full Text | Google Scholar

Wang, F., Chen, L., Li, C., Huang, S., Chen, Y., Qian, C., et al. (2018). “The devil of face recognition is in the noise,” in Proceedings of the European conference on computer vision (ECCV), 765.

CrossRef Full Text | Google Scholar

Zhang, C., Bengio, S., Hardt, M., Recht, B., and Vinyals, O. (2021). Understanding deep learning (still) requires rethinking generalization. Commun. ACM 64, 107–115. doi:10.1145/3446776

CrossRef Full Text | Google Scholar