The Degree of Linear Polarization for Suspended Particle Fields from Diverse Natural Waters

The Degree of Linear Polarization (DoLP) for unperturbed particle fields in waters from six diverse regions around the globe was measured with the custom Multi-Angle Scattering Optical Tool (MASCOT). DoLP here is defined as the ratio of two elements of Mueller scattering matrix, i.e., -$M_{12}/M_{11}$. Field sites covered inland waters, coastal oceans and open oceans, including both ocean color Case I and II water types. The angular shape of the measured particulate DoLP was analyzed in detail for each field site and for the ensemble average. Three parameters used to quantitatively characterize DoLP shape were the symmetry with respect to 90°, peak magnitude, and peak angle of measured DoLP angular curve. Vertical profiles of particulate DoLP were analyzed with maximum recorded depth of 111 m. Converse to Rayleigh scatterers, we found measured particulate DoLPs were not symmetric with respect to 90°. On average, DoLP peaks were shifted slightly toward larger angles, with most falling between estimated values of 90° and 95°. All particulate DoLP peak magnitudes generally varied within [0.6, 0.9]. Lorenz-Mie (homogeneous sphere) light scattering theory was used to construct a new inversion for bulk particulate refractive index from a lookup table based on DoLP and spectral attenuation measurements. We compared the Mie-DoLP-based particulate refractive index retrieval with the backscattering-based model from (Twardowski et al., J. Geophys. Res., 2001, 106(C7), 14,129–14,142). Particulate refractive index retrieved with the two models were in some cases comparable. At two of the six field sites we saw good agreement between the two models, whereas at another two field sites we observed large discrepancies between the two models. Further investigation on the choice of the modeled particle shapes and compositions may improve this retrieval approach. Results are compatible with previous studies on DoLPs in natural waters and comprehensive observations are provided on the particulate DoLP angular shape, vertical profile and global distributions that are important for future vector radiative transfer simulations. This study is relevant to future PACE polarimeters and associated remote retrieval of oceanic particle composition using polarimetry.

Introduction

Light scattering measurements of ocean waters have been used to infer the marine biological states and the microphysical properties of marine particulates (Brown and Gordon 1973; Gordon 1988; Zaneveld 1995; Subramaniam et al., 2001; Twardowski et al., 2001; Lee et al., 2002; Maritorena et al., 2002; Behrenfeld et al., 2005; Kostadinov et al., 2009). Elastic light scattering of a waterbody is described by its Mueller matrix (Mishchenko et al., 2002; Jonasz and Fournier 2007). The Mueller matrix (a 4-by-4 matrix) linearly transforms the incident Stokes vector (a 4-element array) to the scattered Stokes vector. The first element in the Mueller matrix is proportional to the Volume Scattering Function (VSF) in ocean optics. The VSF describes the angular distribution of unpolarized scattered radiation by a volume element of water. The VSF itself and its various derived quantities such as the scattering coefficient ($b$), backscattering coefficient ($b_b$), and backscattering ratio ($b_b/b$), have been increasingly studied and utilized in marine optical sensing (Twardowski et al., 2001; Lee et al., 2002; Maritorena et al., 2002; Boss et al., 2004; Sullivan et al., 2005; Loisel et al., 2007; Twardowski et al., 2007; Kostadinov et al., 2009; Zhang et al., 2011; Twardowski and Tonizzo 2018; Zhai et al., 2020). There have been scarce studies on optical inversions for ocean particles that use linear polarization properties of the scattered light (Chami and McKee 2007; Tonizzo et al., 2009; Lotsberg and Stamnes 2010; Tonizzo et al., 2011; Koestner et al., 2018; Koestner et al., 2020).

The $-\frac{M_{12}}{M_{11}}$ element of the Mueller matrix is equivalent to the Degree of Linear Polarization (DoLP) for unpolarized incident light and when $M_{13}$ element is zero (see detailed disscussion in Theoretical Background). There is very limited information on the in-water particulate Mueller matrix. Few studies have been carried out to directly measure the DoLP element in natural waters (Kadyshevich and Lyubovtseva 1976; Voss and Fry 1984; Koestner et al., 2020). Measurements for all these studies were collected with discretely collected, and thus perturbed, samples. Voss and Fry (Voss and Fry 1984) provided a Mueller matrix for an “average ocean” based on samples collected from the Atlantic and Pacific oceans, but with limited assessment of variability in DoLP and no measurements in coastal and inland waters.

Accurate and meaningful simulations of the full Mueller matrix for marine particulates have also progressed slowly due to the large size and complex shape and composition of marine particulates (Zhai et al., 2013; Bi and Yang 2015; Sun et al., 2016; Xu et al., 2017; Stegmann et al., 2019; Zhai et al., 2020). An associated challenge is vector radiative transfer simulations for the entire ocean and atmospheric system (Zhai et al., 2010; Xu et al., 2016; Stamnes et al., 2018; Chowdhary et al., 2019; Ding et al., 2019). The computational speed of such simulations is relatively slower than the scalar versions. As one important element in the Mueller matrix for marine particles, DoLP affects the accuracy of vector Radiative Transfer (vRT) computations of the polarized radiance field under and above water. The term “vector” comes from the inclusion of the full Stokes vector and the entire 4-by-4 Mueller matrix in the RT code instead of just the first element of the Stokes vector. The treatment of the marine particulate Mueller matrix in vRT models generally fall into two categories: 1) based on in situ measurements (Kokhanovsky 2003; Zhai et al., 2010; You et al., 2011a, 2011b; Xu et al., 2016); and 2) numerically constructed with Lorenz-Mie or non-spherical particle single scattering models (Chowdhary et al., 2012; Ibrahim et al., 2012; Stegmann et al., 2019). As mentioned, in situ measurements are scarce and the Voss and Fry “ocean average” matrix (Voss and Fry 1984) has been typically employed (Kokhanovsky 2003; Zhai et al., 2010; Xu et al., 2016). Because of these challenges, DoLP has seen limited use in ocean optics and remote sensing applications specifically. Accuracy of the underwater Mueller matrix elements in vRT models are key to the success of future remote retrieval approaches based on either passive or active sensors (Chowdhary et al., 2019; Jamet et al., 2019).

The NASA PACE satellite mission will have two polarimeters, HARP and SPEXone (Chowdhary et al., 2019). Our understanding of particulate DoLP in the ocean is not sufficient to start formulating inversion algorithms to interpret the polarized water-leaving radiance from these polarimeters. Lidar is also an emerging tool in satellite remote sensing, with the recent CALIPSO mission demonstrating the potential of using remote lidar for particle characterizations (Hostetler et al., 2018). Jamet et al. (2019) discussed the potential applications of new remote lidar measurements for ocean science. A better understanding of polarized scattering by underwater particles is necessary to interpret and apply these emerging remote sensing techniques and the novel measurements they will provide.

In this study, we analyzed the in situ measured underwater particulate DoLP from six diverse regions around the globe. The field sites cover inland lakes, coastal oceans and open oceans. Both ocean color case I and case II waters were encountered during measurements. The angular shapes of the measured DoLPs of these waters were assessed in detail. We quantify the symmetry, peak magnitude and peak angle of the measured DoLPs. Vertical variations of DoLP at each location and for the ensemble average were analyzed. Numerical simulations of the particulate DoLP with homogeneous sphere and asymmetric hexahedral particle light scattering models were conducted with lookup tables containing particle refractive indices and size distributions. By matching the simulated and measured DoLP, we were able to retrieve particulate refractive index, which is an important particle composition parameter closely related to particle density (Aas 1996). The retrieved refractive indices were compared against values retrieved with another independent method.

Theoretical Background

The 4-by-4 Mueller matrix $\mathit{M}$ is the linear transformation between incident and scattered light:

$\left(\begin{array}{c}{I}_{sca}\\ Q_{sca}\\ \begin{array}{c}{U}_{sca}\\ V_{sca}\end{array}\end{array}\right)=\frac{1}{{\left(kR\right)}^2}\mathit{M}\left(\begin{array}{c}{I}_{inc}\\ Q_{inc}\\ \begin{array}{c}{U}_{inc}\\ V_{inc}\end{array}\end{array}\right),(1)$

where ${(I Q U V)}^T$ is the Stokes vector and subscripts indicate incident (inc.) and scattered (sca) light. $k$ is the wavenumber in medium and R is the distance to the observation point. Typically, the underwater particles are assumed to be randomly positioned and randomly oriented due to turbulence. In addition, with the assumption that each particle in the volume element has its mirror counterpart with respect to the scattering plane (the plane containing the directions of incident and scattered light), and/or a more strict assumption that each particle itself has a plane of symmetry, $\mathit{M}$ can be reduced to (van de Hulst 1957; Mishchenko and Yurkin 2017),

$\mathit{M}=\left(\begin{array}{c}{M}_{11}\left(\psi \right)\\ M_{12}\left(\psi \right)\\ \begin{array}{c}0\\ 0\end{array}\end{array}\begin{array}{c}{M}_{12}\left(\psi \right)\\ M_{22}\left(\psi \right)\\ \begin{array}{c}0\\ 0\end{array}\end{array}\begin{array}{c}0\\ 0\\ \begin{array}{c}{M}_{33}\left(\psi \right)\\ -M_{34}\left(\psi \right)\end{array}\end{array}\begin{array}{c}0\\ 0\\ \begin{array}{c}{M}_{34}\left(\psi \right)\\ M_{44}\left(\psi \right)\end{array}\end{array}\right)(2)$

The scattering angle $\psi$ ranges from 0° to 180°. The two assumptions may often hold true in the ocean surface mixing layer (Basterretxea et al., 2020), however, they can be violated in certain situations such as in the presence of assemblages of elongated diatoms in laminar flow (Nayak et al., 2018; McFarland et al., 2020). Nonetheless, previous measurements showed the average ocean water Mueller matrix generally obeys the symmetric and sparse form in Eq. 2 (Kadyshevich and Lyubovtseva 1976; Voss and Fry 1984; Fry and Voss 1985), although these measurements were carried out on discretely collected samples and thus not in their natural unperturbed environment. Measurements on lab samples of phytoplankton and silt also confirmed that $M_{14}$ = 0 and it is acceptable to set $M_{13}$ = 0 for most plankton (Volten et al., 1998). The Degree of Linear Polarization (DoLP) is defined as,

$DoLP=\frac{\sqrt{Q_{sca}^2+U_{sca}^2}}{I_{sca}}.(3)$

For unpolarized incident light ($\begin{array}{cc}{I}_{inc}& \begin{array}{cc}0& \begin{array}{cc}0& 0\end{array}\end{array}\end{array}$), DoLP can be reduced to (from Eqs. 1, 2):

$DoLP=\frac{Q_{sca}}{I_{sca}}=-\frac{M_{12}}{M_{11}}.(4)$

The minus sign in Eq. 4 is a choice made to indicate that positive values of DoLP refer to polarization directions that are perpendicular to scattering plane, as indicated in Eq. 7. In the case of vertically polarized (perpendicular to the scattering plane) incident light ($\begin{array}{cc}{I}_{inc}& \begin{array}{cc}-I_{inc}& \begin{array}{cc}0& 0\end{array}\end{array}\end{array}$), from Eqs 1, 2, we have,

$I_{v,sca}=I_{inc}\left(M_{11}-M_{12}\right).(5)$

In the case of horizontally polarized (parallel to the scattering plane) incident light ($\begin{array}{cc}{I}_{inc}& \begin{array}{cc}{I}_{inc}& \begin{array}{cc}0& 0\end{array}\end{array}\end{array}$), from Eqs 1, 2, we have,

$I_{h, sca}=I_{inc}\left(M_{11}+M_{12}\right).(6)$

Solving for $M_{12}$ and $M_{11}$ from Eqs 5, 6, we have $M_{12}=0.5(\frac{I_{h,sca}}{I_{inc}}-\frac{I_{v,sca}}{I_{inc}})$ and $M_{11}=0.5(\frac{I_{h,sca}}{I_{inc}}+\frac{I_{v,sca}}{I_{inc}})$. By definition, the normalized scattered intensities $\frac{I_{v,sca}}{I_{inc}},\frac{I_{h,sca}}{I_{inc}}$ are proportional to the respective volume scattering functions ${\beta }_v,{\beta }_h$ by the same constant. For the volume element of water, DoLP can be given in terms of ${\beta }_v,{\beta }_h$:

$DoLP=-\frac{M_{12}}{M_{11}}=\frac{\frac{I_{v, sca}}{I_{inc}}-\frac{I_{h, sca}}{I_{inc}}}{\frac{I_{v, sca}}{I_{inc}}+\frac{I_{h, sca}}{I_{inc}}}=\frac{{\beta }_v-{\beta }_h}{{\beta }_v+{\beta }_h}.(7)$

The particulate DoLP ($DoL{P}_p$) is obtained by subtracting the pure seawater volume scattering functions ${\beta }_{v,sw}$ and ${\beta }_{h,sw}$, denoted with the subscript “sw”,

$DoL{P}_p=\frac{{\beta }_{v,p}-{\beta }_{h,p}}{{\beta }_{v,p}+{\beta }_{h,p}}=\frac{\left({\beta }_v-{\beta }_{v,sw}\right)-\left({\beta }_h-{\beta }_{h,sw}\right)}{\left({\beta }_v-{\beta }_{v,sw}\right)+\left({\beta }_h-{\beta }_{h,sw}\right)}.(8)$

The pure seawater volume scattering functions with respect to vertical and horizontal incident light, ${\beta }_{v,sw}$ and ${\beta }_{h,sw}$, are given by,

${\beta }_{v,sw}\left(\psi ,\text{δ}\right)={\beta }_{sw}\left({90}^o,\text{δ}\right)\frac{1}{1+\text{δ}},(\mathrm{9a})$

${\beta }_{h,sw}\left(\psi ,\text{δ}\right)=0.5{\beta }_{sw}\left({90}^o,\text{δ}\right)\left(1+\frac{1-\text{δ}}{1+\text{δ}}cos2\psi \right),(\mathrm{9b})$

where $\text{δ}$ is the depolarization ratio of pure seawater and ${\beta }_{sw}\left({90}^o,\text{δ}\right)$ is the unpolarized pure seawater VSF at 90°. In this study,$\text{ δ}$ is set equal to 0.039 as suggested by various studies (Farinato and Rowell 1976; Jonasz and Fournier 2007; Werdell et al., 2018; Zhang et al., 2019), and ${\beta }_{sw}\left({90}^o,\text{δ}\right)$ was computed according to (Zhang et al., 2009).

Methods

Measurements

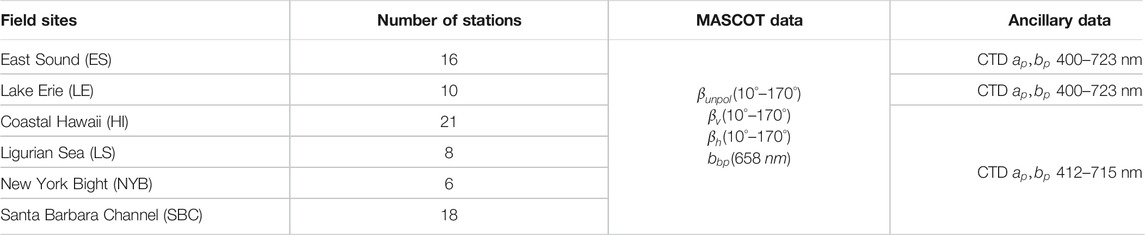
Underwater DoLP was measured with the Multi-Angle Scattering Optical Tool (MASCOT) (Twardowski et al., 2012; Sullivan et al., 2013). It has an array of 17 silicon diode detectors covering 10°–170° scattering angles (source-sample-detector angle) in 10° increments. Incident light source is a 30 mW 658 nm laser diode passing through a wedge depolarizer to provide unpolarized incident radiation. The sampling rate is 20 Hz. Full angles of the Detector field of views (FOVs) are 0.8°, 2°, 3°, and 4° for the 10°, 20°, 30°, and 40° detectors, respectively. FOV is 5° for the rest of the detectors. MASCOT covers a large scattering angle range, enabling accurate measurement of VSF at mid- and back-scatter angles. The MASCOT was designed with minimal form factors and structural elements (moving parts, sample holder, etc.) to minimize stray light contamination. It is an in situ device designed for direct measurement in nominally unperturbed waters. A filter wheel mounted in front of the source window can generate unpolarized (empty space on wheel), horizontally or vertically polarized incident light, or a dark blank (opaque location on wheel). The wheel continually spins at a rate that allows each location on the wheel to be sampled for 1 s. Particulate DoLP for unpolarized light was computed with Eq. 8. Accurate measurements of polarization elements have been verified with Lorenz-Mie theory for microspherical beads. For details on the instrument calibration and correction procedures in VSF measurement of MASCOT see (Twardowski et al., 2012). The MASCOT has been deployed extensively since 2006 (Sullivan and Twardowski 2009; You et al., 2011b; Gleason et al., 2012; Twardowski et al., 2012; Sullivan et al., 2013; Moore et al., 2017). Table 1 lists the field sites and measurements relevant in this study. Locations cover inland lakes, coastal oceans and open oceans. Relevant particulate inherent optical properties (IOPs) were also measured. Particulate absorption coefficient $a_p\left[m^{-1}\right]$ and scattering coefficient $b_p\left[m^{-1}\right]$ were derived from measurements of non-water absorption $a_{nw}$, non-water attenuation $c_{nw}$, and absorption in the dissolved fraction $a_{CDOM}$ with a 25-cm flow cell WET Labs ACS or AC9 device following the protocol in Twardowski et al. (1999). Backscattering coefficient $b_{bp}\left[m^{-1}\right]$ was derived from MASCOT unpolarized VSF measurements. The particulate backscattering coefficient is,

$b_{bp}=2\pi \underset{{90}^o}{\overset{{180}^o}{{\displaystyle \int }}}{\beta }_{unpol,p}\left(\psi \right)\sin \left(\psi \right)d\psi ,(10)$

where ${\beta }_{unpol,p}$ is the interpolated unpolarized particulate VSF measured with MASCOT. ${\beta }_{unpol,p}(180˚)$ = ${\beta }_{unpol,p}(170˚)$ is assumed in Eq.10. Since the $\sin \left(\psi \right)$weighting in the integral approaches 0 at 180°, precise accuracy near 180° is not critical. The particulate scattering coefficient $b_p$ measured with ACS or AC9 at 657 nm was used to compute the backscattering ratio $b_{bp}/b_p$. At each field site, measurements were collected at over a dozen stations spanning the region. For each station, all measurements were averaged to 1-m depth bins ranging from the surface down to the maximum measurement depth.

TABLE 1

TABLE 1. Field sites and data collected with the MASCOT device and ancillary instrumentation.

To prepare the DoLP angular curve for parameterization, the MATLAB Piecewise Cubic Hermite Interpolating Polynomial (PCHIP) function was used to interpolate the measured 17-angle DoLP angular curve (10°–170° in 10° increment) to a 161-angle DoLP curve (10°–170° in 1° increment). Three parameters were then used to quantify the DoLP shape: the asymmetry parameter, the peak magnitude and the peak angle. The asymmetry parameter $g$ is defined as,

$g=-\underset{{10}^o}{\overset{{170}^o}{{\displaystyle \int }}}{P}_0\left(\psi \right)\cos \left(\psi \right)\sin \left(\psi \right)d\psi ,(11)$

where $P_0\left(\psi \right)$ is the interpolated DoLP. When $g$ = 0, the DoLP shape is symmetrical with respect to 90° and $g$>0 and g < 0 indicate that the DoLP shape is shifted towards the backward or forward direction, respectively. Parameter $g$ can be computed for DoLP generated either by measurements or numerical simulations.

The peak magnitude $DoL{P}_{max}$ is simply the magnitude of the DoLP peak. For the measured 17-angle DoLP, the peak angle falls on the detector angles such as 80°, 90°, 100°, etc. The MATLAB PCHIP interpolation retains the local maximum and minimum of the 17-angle DoLP so the peak angle of the 161-angle DoLP remains the same. To obtain higher angle precision than 10°, ${\psi }_{max}$ was obtained by fitting a skewed Rayleigh DoLP to the 161-angle DoLP. Following (Kokhanovsky 2003), the skewed Rayleigh DoLP is given in this study as:

$P\left(\psi \right)=\frac{DoL{P}_{max}\cdot si{n}^2\left(\psi -{\psi }_{max}+\frac{\pi }{2}\right)}{1+DoL{P}_{max}\cdot co{s}^2\left(\psi -{\psi }_{max}+\frac{\pi }{2}\right)}.(12)$

With $DoL{P}_{max}$ already obtained, ${\psi }_{max}$ is determined by minimizing the RMSE between $P\left(\psi \right)$ and the measured 161-angle DoLP ($P_0\left(\psi \right)$). Graphically, this means horizontally shifting $P\left(\psi \right)$ to fit the measured DoLP. The RMSE ($\epsilon$) is defined as,

$\epsilon =\sqrt{\frac{{{\displaystyle \sum }}_{\theta =10}^{\theta =170}{(P\left(\psi \right)-P_0\left(\psi \right))}^2}{161}}.(13)$

The use of this method is justified by the overall small RMSE between measurements and Eq. 12, and small deviation of ${\psi }_{max}$ from 90° (see Measured Particulate DoLP Angular Shape second paragraph). For DoLPs with high enough angular resolution such as those generated by numerical simulations, there is no need to apply this method.

Modeling

Light scattering simulations with homogeneous spheres were performed to help interpret observations. Also, we attempt to retrieve the particulate refractive index by fitting simulated DoLP to measurements, i.e., through inversion. In modelling, The bulk particulate DoLP is given by,

$DoL{P}_{p,model}\left(\psi ,n_p,\xi \right)=-\frac{M_{12}\left(\psi ,n_p,\xi \right)}{M_{11}\left(\psi ,n_p,\xi \right)},(14)$

where the bulk $M_{12}$ and $M_{11}$ are computed for Junge type particle size distribution as,

$M_{12}\left(\psi ,n_p,\xi \right)=\underset{D_{min}}{\overset{D_{max}}{{\displaystyle \int }}}{S}_{12}\left(\psi ,n_p,D\right)D^{-\xi }dD,(\mathrm{15a})$

$M_{11}\left(\psi ,n_p,\xi \right)=\underset{D_{min}}{\overset{D_{max}}{{\displaystyle \int }}}{S}_{11}\left(\psi ,n_p,D\right)D^{-\xi }dD.(\mathrm{15b})$

where $n_p$ is the particulate refractive index relative to water, $n_p=n+i{n}^{\prime }$, $n$ and $n^{\prime }$ are the real and imaginary parts. D is the particle diameter, $\xi$ is the slope of the Junge-type particle size distribution. The size averaging was computed in a diameter range from $0.01\mu m$ to $163\mu m$ with 195 logarithmically spaced abscissae. Range of $\xi$ was [2,4] in 0.1 increments. Scattering angle $\psi$ range was [0°,180°] in 0.25° increments. In this study, the incident wavelength is 658 nm in vacuum (MASCOT detection wavelength (Twardowski et al., 2012)), that is around 495 nm in water. $S_{12}$ and $S_{11}$ are outputs from the single scattering models. For the homogeneous spheres, the Lorenz Mie computational program adapted from the Bohren and Huffman formulation (Bohren and Huffman 1998; Twardowski et al., 2001) was used. A Lookup Table (LUT) was constructed with $n$ in the range [1.001,1.3] in 0.002 increments, and $n^{\prime }$ fixed at 0.005 (relative to water).

Figure 1 shows the simulated DoLP angular functions of the homogeneous sphere model for different $\xi$ and $n$. Figure 2 shows variation of the particle refractive index $n$ with the three shape parameters (peak magnitude $DoL{P}_{max}$, peak angle ${\psi }_{max}$ , asymmetry parameter $g$) of the simulated DoLPs. The overall trend in $\xi$ between 2.8 and 4 is that the DoLP peak decreases and the DoLP shape shifts to large scattering angles (towards $\psi \in$[90°,180°]) with increasing particulate refractive index. Negative branches in DoLP can be spotted near 180° in Figure 1.

FIGURE 1

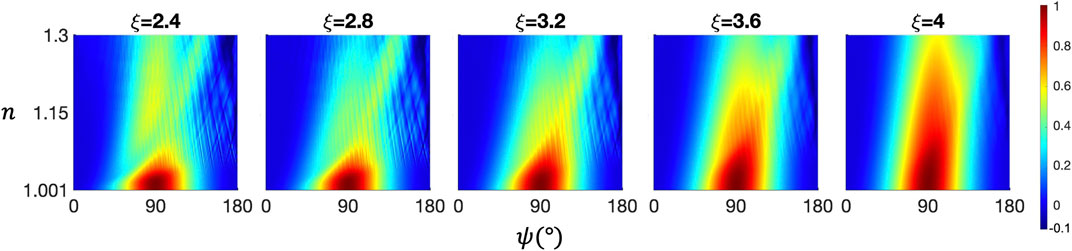
FIGURE 1. Surface plots of the DoLP angular shape modeled with the Lorenz-Mie light scattering model. X-axes are the scattering angle $\psi$, y-axes are the particulate refractive indices $n$. The PSD slope $\xi$ is fixed for each panel. Color indicates magnitude of the DoLP angular curve.

FIGURE 2

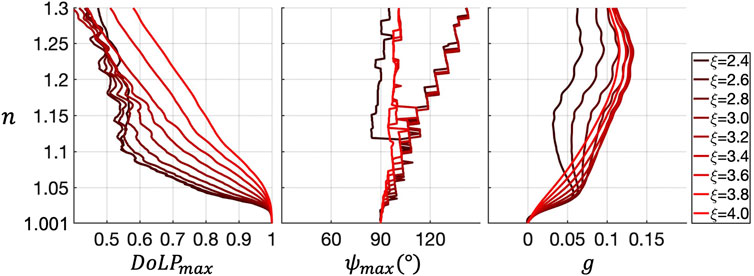
FIGURE 2. Particulate refractive index $n$ plotted against peak magnitude $DoL{P}_{max}$, peak angle ${\psi }_{max}$ and asymmetry parameter $g$ of the Lorenz-Mie DoLPs (Figure 1) for different PSD slopes $\xi$.

Another light scattering model, the asymmetric hexahedral particle scattering model was examined in this study. Originally, the Volume Scattering Function (VSF) from the asymmetric hexahedral model dataset was used in another study to retrieve particle size distributions (Twardowski et al., 2012). In this study, we examine its DoLP element. In the asymmetric hexahedral model, at each particle size, the scattering properties of an ensemble of randomly distorted hexahedra were computed with the Discrete Dipole Approximation (DDA) method (Yurkin and Hoekstra 2007) and the Improved Geometric Optics Method (IGOM) (Yang and Liou 1996). After ensemble averaging at each particle size and a subsequent size averaging, the scattering properties for a polydispersion of particles were obtained. The particulate refractive index range was [1.02,1.2] in 0.02 increments, with the imaginary part fixed at 0.002. The equivalent sphere diameter increased exponentially from 0.01 to 163 μm. Incident wavelength was 658 nm in vacuum ($\approx$ 495 nm in water).

Figure 3 panels show the simulated DoLP angular functions of the asymmetric hexahedron model for different $\xi$ and $n_p$. Figure 4 panels show variation of the particle refractive index $n$ with the three shape parameters (peak magnitude $DoL{P}_{max}$, peak angle ${\psi }_{max}$ , asymmetry parameter $g$) of the simulated DoLPs. In contrast to the sphere model, there is little variation of the DoLP shape with the refractive index for $\xi$ values of 3.6 and 4 (Figure 3). At $\xi$ = 4, the DoLP shape does not vary with refractive index, the peak magnitude stays at 1, and the DoLP shape stays symmetrical with respect to 90° throughout the [1.02,1.2] refractive index range. Figure 4 panels show that for $\xi \ge$3.6, there is little variation of $DoL{P}_{max}$, ${\psi }_{max}$ and $g$ with refractive index. For $\xi \ge$3.6, the asymmetric hexahedra model cannot be used effectively for retrieval of the refractive index. For $\xi$ < 3.6, the hexahedral DoLPs is problematic as well, as there are multiple solutions in some cases. This is in contrast to Figures 1, 2 of the sphere model, where variations in DoLP shape with refractive index are more monotonic and unique. Due to these properties with the hexahedral model, we did not use it for the retrieval part of our study. Nonetheless, the comparison between the DoLPs of the homogeneous sphere and the asymmetric hexahedron model showed the DoLP shape is very sensitive to particle shapes. Thus, for simulation purposes, this brings the question of which particle shape may be the most suitable for reproducing the measured DoLPs in the field. We will discuss this further below.

FIGURE 3

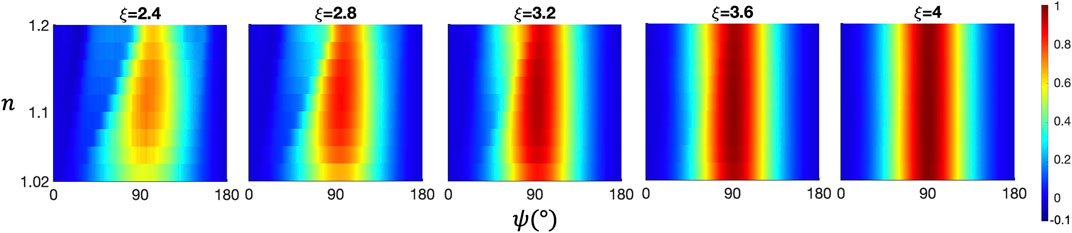
FIGURE 3. Surface plots of the DoLP angular shape modeled with the asymmetric hexahedral particle light scattering model, same as Figure 1.

FIGURE 4

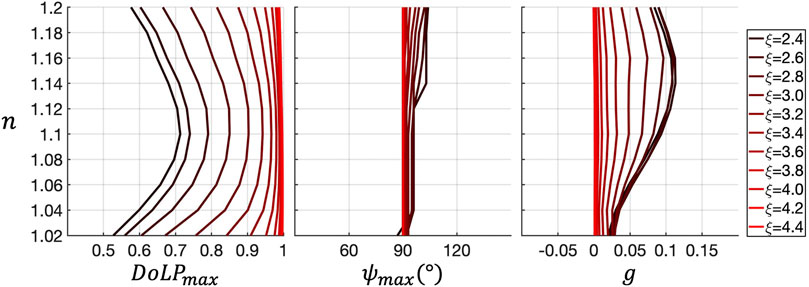
FIGURE 4. Particulate refractive index $n$ plotted against the three DoLP shape parameters of the asymmetric hexahedral DoLPs, same as Figure 2.

Results and Discussion

Measured Particulate DoLP Angular Shape

Figure 5A panels show measured particulate DoLP at each field site. A considerable number of DoLP curves exhibited large, highly intermittent spikes at 30°, 40°, 140°, 150°, and 160°. These isolated spikes at specific angles are generated by particulates such as large organisms and aggregates drifting into the sample volume, and isolated light paths for individual detectors. At those angles, spikes with magnitudes larger than 0.2 were flagged and these DoLPs were removed from the analysis. After that screening, at each field site, outliers with magnitude falling out of the [15%, 85%] inter-percentile range at any one of the 17 scattering angles were removed. This percentile range eliminated DoLPs with potentially high uncertainty and maintained enough DoLP samples for each field sites. The HI data also showed more variability in the backward direction due to the very low measured scattering signals in this clear water; this was from a higher contribution from MASCOT instrument noise. Remaining fluctuations in the DoLP angular curves are from small scale environmental variability in particle fields; note measurements of vertical and horizontal polarized scattering in the sample volume were not made exactly simultaneously.

FIGURE 5

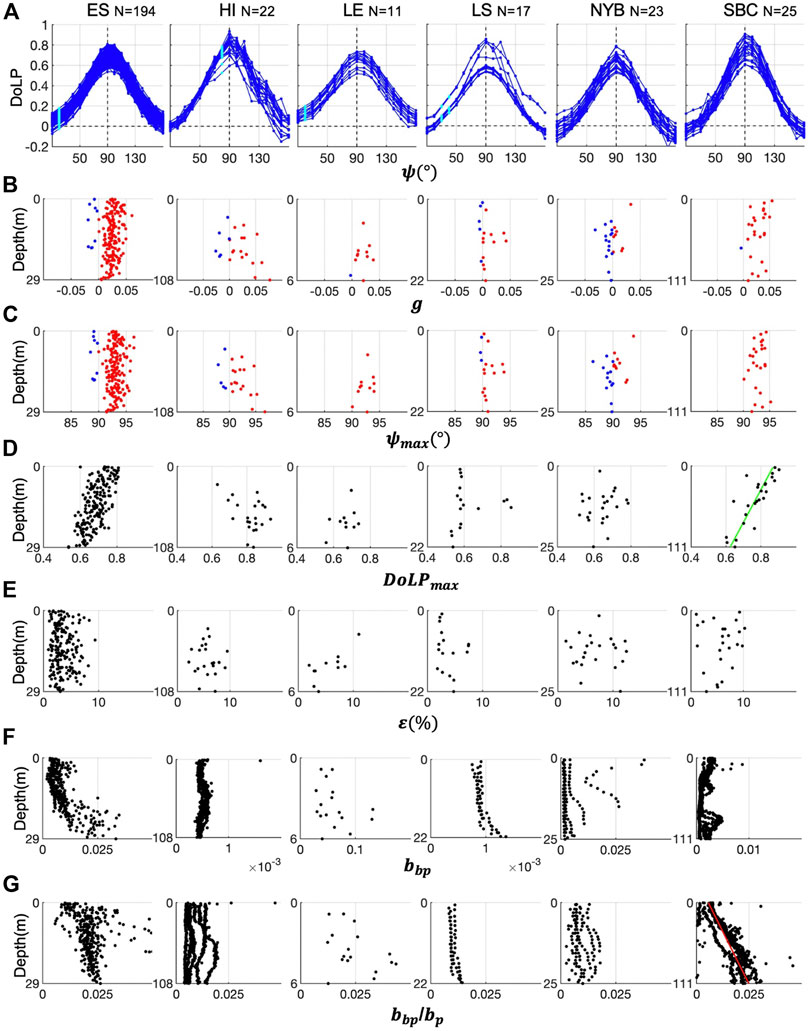
FIGURE 5. (A) Measured particulate DoLPs plotted against scattering angle $\psi$. Titles are abbreviations of the field sites names (see Table 1). “N” indicates number of samples. Field sites are listed from left to right in alphabetical order. Cyan dots indicate NaN values that are linearly connected to adjacent data points. (B) Vertical profiles of the asymmetry parameter $g$ of DoLPs of each field site. Blue dots indicate negative $g$ and red dots indicate positive $g$. (C) Vertical profiles of the peak angle ${\psi }_{max}$ of DoLPs of each field site. Blue dots correspond to ${\psi }_{max}$<90° and red dots correspond to ${\psi }_{max}$>90°. (D) Vertical profiles of the peak magnitude $DoL{P}_{max}$ of DoLPs of each field site. (E) Vertical profiles of the RMSE $\epsilon$ (Eq. 13) between the measured DoLPs and their best-fit skewed Rayleigh DoLPs (Eq. 12) of each field site. (F) Vertical profiles of the particulate backscattering coefficient $b_{bp}$ of each field site. (G) Vertical profiles of the particulate backscattering ratio $b_{bp}/b_p$ of each field site. Linear least squares fit to the vertical profiles are overlaid where significant (where the coefficient of determination $R^2$>0.5). Red lines indicate positive correlation between the quantity and depth, green lines indicate negative correlation.

Figures 5B–G panels show vertical profiles of the three shape parameters, percent RMSE and backscattering parameters at each field site. Linear least-squares fit to the vertical profiles in Figures 5B–G panels are displayed if the coefficient of determination $R^2$>0.5. Note that Eq. 12 is introduced to deal with the lower angular resolution of the instrument and to estimate a proper ${\psi }_{max}$ for each measured DoLP as accurately as possible. Horizontally shifting the standard Rayleigh DoLP can bring non-zero values at 0° and 180°. Nonetheless, the RMSEs are generally small (<10%) between measurement and Eq. 12 (see Figure 5E panels), and the obtained ${\psi }_{max}$ typically show small deviation from 90° (within 5°), justifying the use of Eqs 12, 13 to treat this special situation. The peak angle ${\psi }_{max}$ and the asymmetry parameter $g$ will complement each other in the task of quantifying the relative asymmetry of measured DoLP with respect to 90°.

In Figure 5B panels, a relatively high proportion of $g$ are positive among the six field sites. Correspondingly, Figure 5C panels also show a high proportion of ${\psi }_{max}$ that are greater than 90°. This means the measured particulate DoLPs of the six field sites are not symmetric to 90° and generally shift to angular range greater than 90°. This observation agrees with previous measurements (Voss and Fry 1984; Koestner et al., 2020). In Koestner et al. (2020), from the analysis of ocean water samples in the San Diego area, ${\psi }_{max}$ ranged from 91° to 98° with a mean value of 94°. The right-shifted tendency in DoLP is also observed in the simulated DoLP in Modeling, and in other single scattering simulations of the DoLP of marine-like particulates (Lotsberg and Stamnes 2010; Xu et al., 2017; Stegmann et al., 2019). At field sites ES and SBC, $DoL{P}_{max}$ decreases with increasing depth.

Figure 6 shows the box-whisker plots of $DoL{P}_{max}$, ${\psi }_{max}$ and $g$ of the six field sites. For the six field sites, $g$ generally fell in the range [0,0.04], ${\psi }_{max}$ in the range [90°,95°], with a ensemble-averaged mean of around 92°. $DoL{P}_{max}$ were in the range [0.6,0.9] with a ensemble-averaged mean around 0.7. LE, LS and NYB show very low $DoL{P}_{max}$, with the minimum at the three sites approaching 0.5. Simulations have shown low DoLP peaks are usually associated with particles with high bulk refractive index, as shown in Figures 1, 2. However, in Zhai et al. (2020), we also showed that a densely-packed aggregate of cyanobacteria cells (with low refractive index) can also have a very low DoLP peak (<0.5) due to the colony structure. The Lake Erie measurements were made when the lake was in a state of cyanobacteria (mainly Microcystis) bloom (Moore et al., 2017). The origin of the low $DoL{P}_{max}$ values for LS and NYB are more difficult to interpret relative to the simulations, as the backscattering ratios at LS and NYB were relatively low (see Figure 5G). A possible explanation could be the complication of having a mixture of multiple particle types contributing to polarized scattering; further investigation is needed to better understand the relative contributions of both high refractive index suspended sediments and low refractive index biological material in the manifestation of DoLP for complex particle mixtures, and some contribution from bubbles may possibly play a role.

FIGURE 6

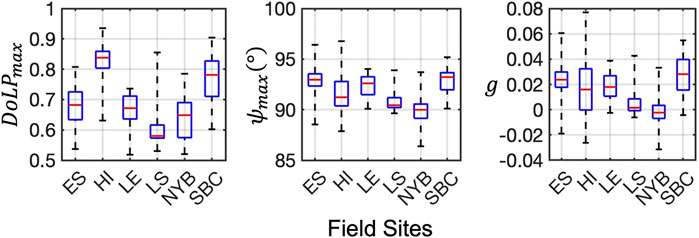
FIGURE 6. From left to right panel: Box-whisker plots of the peak magnitude $DoL{P}_{max}$, peak angle ${\psi }_{max}$ and asymmetry parameter $g$ of the measured DoLPs at the six field sites. Blue box top and bottom bars are the 75^th and 25^th percentile. Red bar is the median. Top and bottom whiskers indicate maximum and minimum.

DoLPs from all field sites in Figure 5A were averaged into 1 m depth bins and sorted according to their measurement depth to obtain a ensemble averaged DoLP in Figure 7. Figure 7 shows the ensemble averaged particulate DoLP along with the vertical profiles of $g$, ${\psi }_{max}$ and $DoL{P}_{max}$. Ensemble average DoLPs mostly exhibited positive asymmetry parameters and peak angles greater than 90°, meaning the DoLPs were generally right shifted. The vertical profile of $P_{max}$ shows a discontinuity at around 30 m depth; this jump is an artefact since the water depth at several field sites end at 30 m. Within the depth range [0 m,30 m], $DoL{P}_{max}$ showed decreasing trends with increasing depth.

FIGURE 7

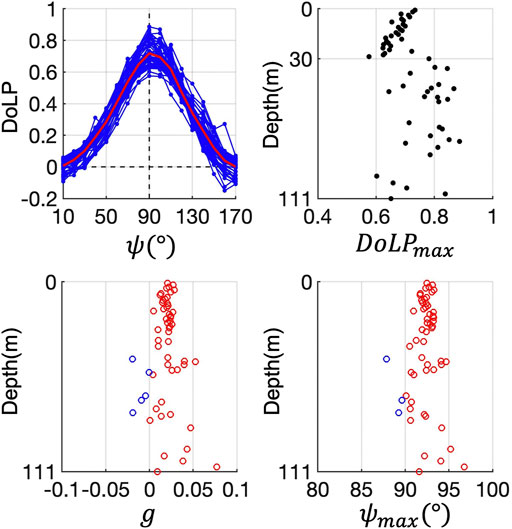
FIGURE 7. Ensemble averaged particulate DoLP. Measured DoLPs from all field sites are grouped together and then averaged into 1-m depth bins. The mean is overlaid as the red curve. Vertical profiles of the peak magnitude $DoL{P}_{max}$, asymmetry parameter $g$ and peak angle ${\psi }_{max}$ are displayed. $g$>0 data points are indicated with red circle; $g$<0 data points are indicated with blue circle. ${\psi }_{max}$>90° data points are indicated with red circle; ${\psi }_{max}$<90° data points are indicated with blue circle.

Figure 8 compares the ensemble averaged DoLP in this study with the Voss and Fry global mean DoLP (Voss and Fry 1984). Figure 8 left panel shows the ensemble averaged particulate DoLP of this study and the seawater DoLP computed with Eqs. 9a–b at a temperature of 20°C and a salinity of 35 ppt. Figure 8 right panel shows the ensemble averaged total (seawater plus particulates) DoLP, Voss and Fry DoLP and seawater DoLP. The red error bars and the grey area indicate standard deviation of our DoLP and the Voss and Fry DoLP, respectively. The pure seawater DoLP has a peak of around 0.92, the total DoLP has a higher peak (0.74) than the particulate DoLP (0.72), but they are both higher than the peak of the Voss and Fry DoLP (0.66). The Voss and Fry DoLP and our total and particulate DoLPs all have highest variability around 90°. Note Voss and Fry DoLP did not converge to zero in far backward angles (beyond about 140°); this may be due to reflection errors related to the cuvette in the bench top apparatus that was used.

FIGURE 8

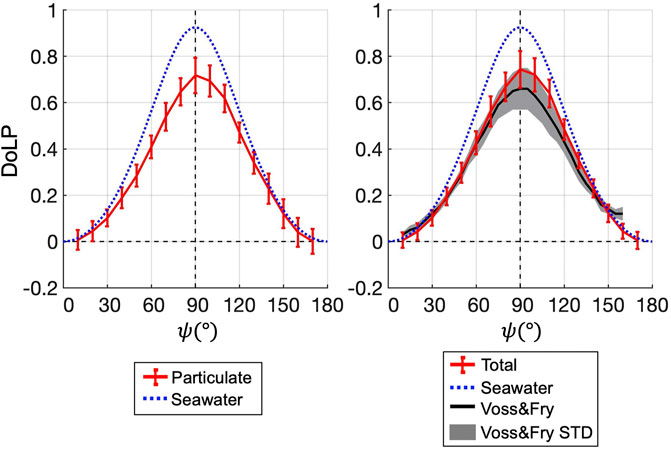
FIGURE 8. Left: The ensemble average particulate DoLP from Figure 7 is plotted as the red curve with error bars indicating standard deviation at 17 angles. Seawater DoLP at 20°C and a salinity of 35 ppt is the blue dotted curve. Right: Same as left panel, except that the particulate DoLP is replaced with total DoLP (particulate plus seawater) from this study. The global mean total DoLP from the Voss and Fry study is overlaid as the black curve. Grey area is the standard deviation of the Voss and Fry DoLP.

Retrieving Particulate Refractive Index With DoLP

As mentioned in Modeling, there is potential with using a DoLP LUT to retrieve the particulate refractive index through inversion. For a measured DoLP with a corresponding PSD slope value, a bulk particulate refractive index can be retrieved by finding a best-fit to the measurement from the simulated DoLP LUT. We attempt to retrieve particulate refractive index with this approach. With the co-located backscattering ratio measurements, another bulk particulate refractive index retrieval approach (Twardowski et al., 2001) (referred to as “the Twardowski model” in texts and figures below) was used for comparison.

At each measured DoLP depth, the Junge-type PSD slope ($\xi$) is estimated from the particulate attenuation ($c_p$) spectral curve following (Boss et al., 2001). The measured $c_p$ spectrum in the range 440–712 nm can be parameterized by a power-law relationship with a beam attenuation slope $\gamma$,

$c_p=c_p\left(440\right){\left(\frac{\lambda }{440}\right)}^{-\gamma }.(16)$

The PSD slope $\xi$ is related to $\gamma$ by (Boss et al., 2001),

$\xi =\gamma +3-0.5\text{exp}(-6\gamma ).(17)$

The Twardowski et al. model relates $\xi$ and backscattering ratio (denoted as $\widetilde{b_{bp}}$ here) to the bulk particulate refractive index $n$ (Twardowski et al., 2001),

$n=1+{\widetilde{b_{bp}}}^{0.5377+0.4867{(\xi -3)}^2}\left[1.4676+2.2950{\left(\xi -3\right)}^2+2.3113{\left(\xi -3\right)}^4\right].(18)$

Figure 9 shows the results of refractive index retrieval at field site East Sound (ES). In Figure 9B, The second panel shows relative errors of the decimal part of the refractive indices retrieved with the two models,

${\epsilon }_{n_p}=100\left(\frac{n_{DoLP}-n_{Twardowski}}{n_{Twardowski}-1}\right).(19)$

Figures 10–14 show the same contents for the other field sites, HI (Hawaii), LE (Lake Erie), Ligurian Sea (LS), NYB (New York Bight) and SBC (Santa Barbara Channel). Overall, at ES, HI, LE and SBC, refractive indices retrieved with the DoLP model and the Twardowski model were roughly comparable. At ES (Figure 9), $n$ retrieved with the DoLP model are mostly lower than the $n$ retrieved with the Twardowski model. The combination of relatively high $b_b/b$ and relatively low PSD slope $\xi$ resulted in lower $n$ from the DoLP model compared to the Twardowski model. Moderate to low PSD slope means that larger particles take up relatively more proportion in the particle assemblage. In terms of the quality of the fitting between measured and simulated DoLP in Figure 9A, we see that a lot of the measured DoLPs possess negative branches near 10° and 170°, and the simulated DoLPs generally do not have this feature around the same scattering angles. Simulated DoLPs generally have higher peak angle ${\psi }_{max}$ and higher peaks. At the other field sites, we saw a similar pattern.

FIGURE 9

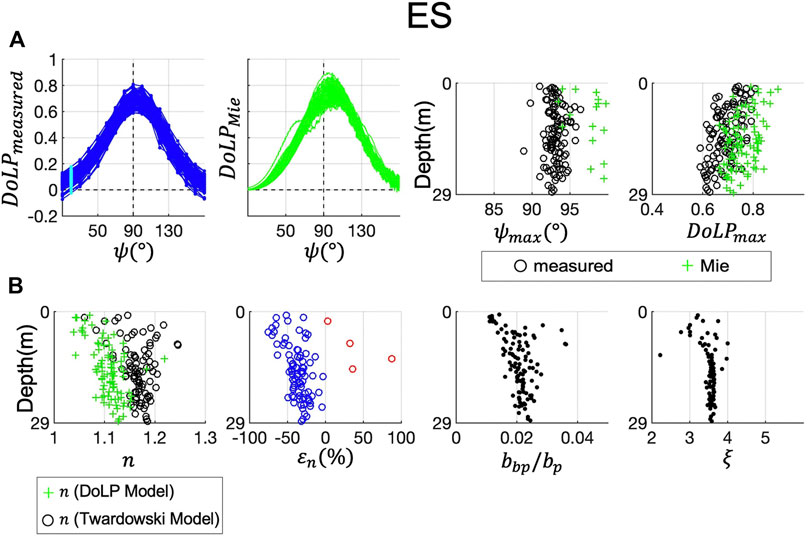
FIGURE 9. Particulate refractive index retrieval at field site ES (East Sound). (A) From left to right: Measured particulate DoLP ($DoL{P}_{measured}$). The best fit simulated DoLP ($DoL{P}_{Mie}$) corresponding to each measured DoLP. Comparison of ${\psi }_{max}$ and $DoL{P}_{max}$ of the measured and simulated DoLP. (B) From left to right: Retrieved refractive indices of the Twardowski model and the DoLP model. Relative error (${\epsilon }_n$) of the decimal parts of the two refractive indices. Backscattering ratio $b_{bp}/b_p$ used in the Twardowski model. PSD slope $\xi$ used in both models.

FIGURE 10

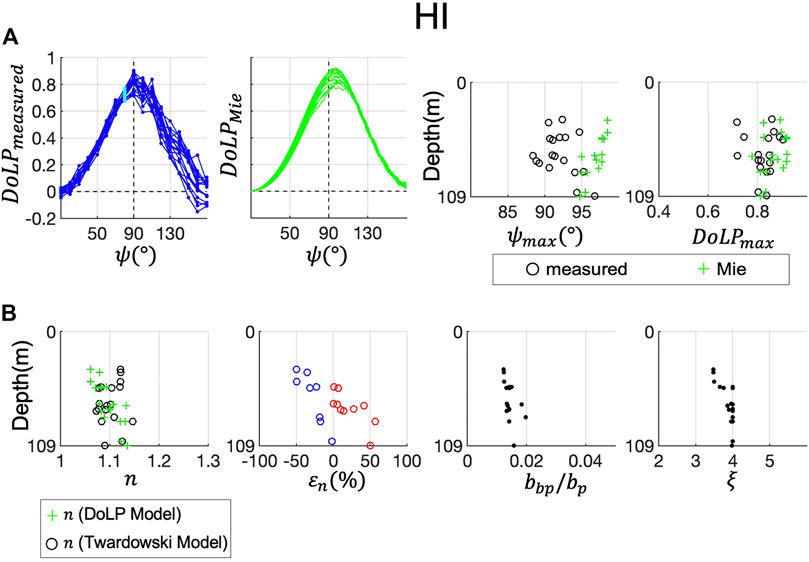
FIGURE 10. Refractive index retrieval at field site HI (Hawaii). Same as Figure 9.

FIGURE 11

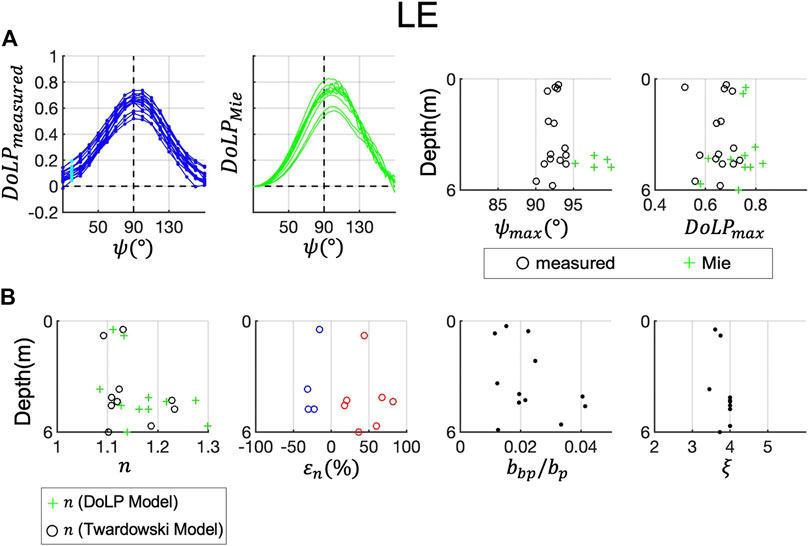
FIGURE 11. Refractive index retrieval at field site LE (Lake Erie). Same as Figure 9.

FIGURE 12

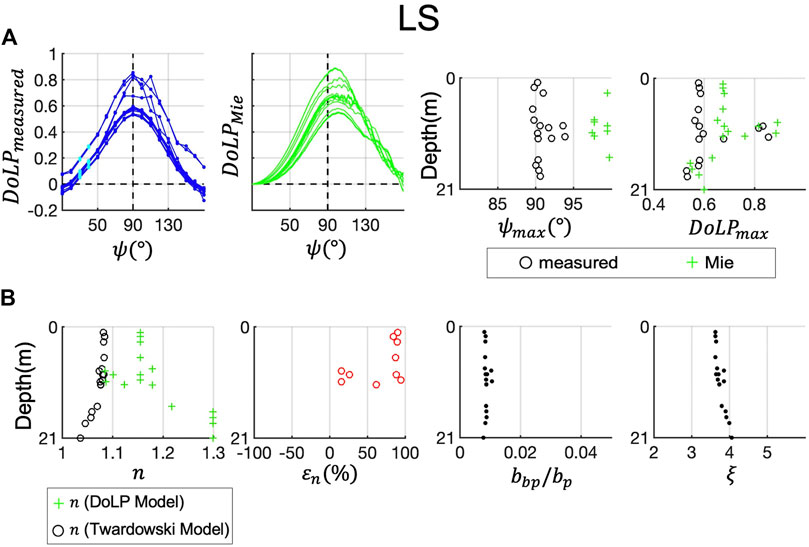
FIGURE 12. Refractive index retrieval at field site LS (Ligurian Sea). Same as Figure 9.

FIGURE 13

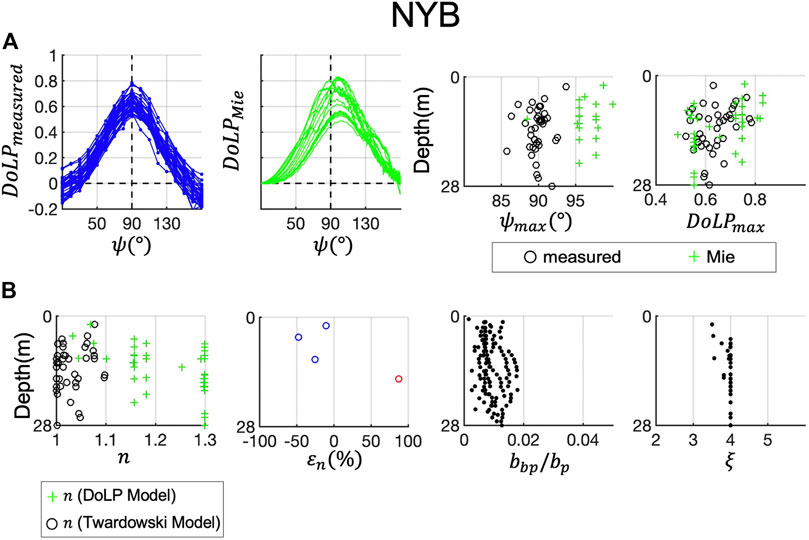
FIGURE 13. Refractive index retrieval at field site NYB (New York Bight). Same as Figure 9.

FIGURE 14

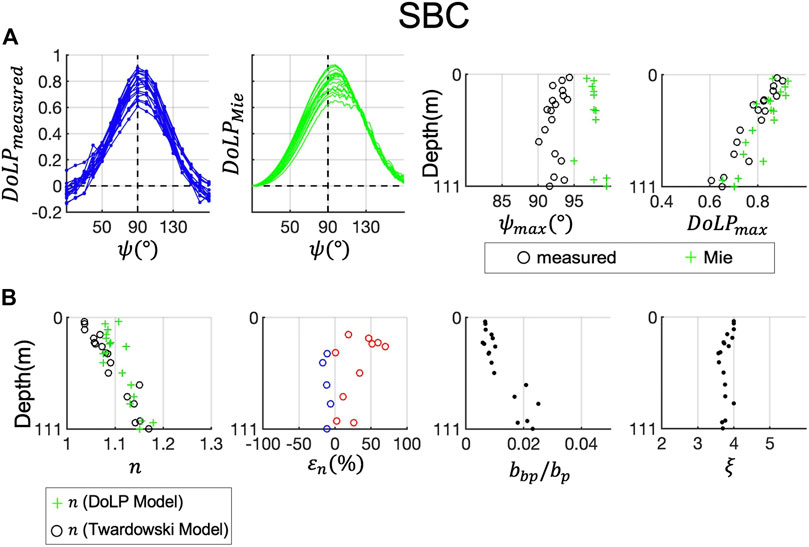
FIGURE 14. Refractive index retrieval at field site SBC (Santa Barbara Channel). Same as Figure 9.

At HI, LE and SBC, refractive indices retrieved with the DoLP model and the Twardowski model were comparable. We capped the PSD slope values at 4 for these retrievals because oceanic PSD slope values do not typically exceed 4 in natural waters (Reynolds et al., 2010; their Figure 11), thus removing some potential uncertainty in the derivation of $\xi$ from $\gamma$. Among the six field sites, HI and SBC exhibited strongest agreement between the refractive indices retrieved with the two models. One reason for this is the DoLP peaks were generally high (0.7–0.8) at the two sites; another reason is the $b_b/b$ and $\xi$ values were in copacetic ranges.

At LE, the DoLP peaks are low, with extreme values approaching 0.5. Thus, the DoLP model returns high refractive indices. Values of $b_b/b$ at LE are the highest among the six field sites, so the Twardowski model also returns high refractive indices similar to the DoLP model. At LS and NYB, the situation is in contrast to the aforementioned sites. On one hand, $b_b/b$ at LS and NYB are generally lower compared to the other sites, resulting in low refractive indices (<1.1) retrieved from the Twardowski model. On the other hand, a considerable amount of DoLPs possess peaks around 0.6, leading to retrieved $n$ values around 1.15–1.3 for the DoLP model. The extreme value of 1.3 returned by the DoLP model at LS and NYB is due to the combination of high $\xi$ (approaching 4) and low DoLP peak (∼0.6). In Figure 2 first panel, for the $\xi$ = 4 curve, if $DoL{P}_{max}$ is lower than 0.6, the corresponding $n$ approaches 1.3.

Inconsistencies in the models for LS and NYB could be due to several factors not accounted for that may affect the two models differently, including complex particle mixtures (i.e., broad n_p distributions), complex particle shapes, aggregations and bubbles. Further work is needed to interpret the influence of these factors. The Twardowski model and the DoLP model here are both based on the Lorenz-Mie (homogeneous sphere) model, although the key scattering parameters of the two models, DoLP and $b_b/b$, might have different sensitivity to changes in the particle size, shape and refractive index. Systematic study is needed to investigate the feasibility of using non-spherical and inhomogeneous particle shapes such as coated spheres, spheroids, coated spheroids, etc. in DoLP simulations. In Zhai et al. (2020), for cellular contents with very low particle refractive index ($n$=0.75 for gas vacuole, $n$ = 1.035 for cytoplasm, $n$ = 1.05 for cell wall), we observed significant decreases in DoLP with increasing aggregate size for densely packed aggregates of layered spheres. At large aggregate sizes (diameter ∼24 $\mu m$), simulated DoLP peaks decrease to values below 0.5. This aggregate model produces very high backscattering ratios, consistent with the values observed for LE (see Figure 11), and is an example of how accounting for complex particle mixtures and aggregation can significantly affect scattering parameters. Besides modeling issues, the negative branches in measured DoLP curve at around 10° and 170° were the most prominent at NYB among all field sites (see Figure 13A first panel). This feature helped in forming very low DoLP peaks in the simulated DoLPs (see Figure 13A second panel). Negative branches are more prominent at NYB, LS, HI and SBC (see Figure 5A); these locations have clear ocean waters compared to ES and LE. This indicates that in clear waters, MASCOT instrument noise or calibration error could be magnified around 10° and 170°.

Although model discrepancies here require further work to elucidate impacts of these complicating factors, the DoLP model provides another tool to assess oceanic particle composition that may help constrain bulk refractive index estimates. It is also progress toward operational application of remote polarimetry data in determining bulk refractive index and closely related particle density. Particle density is essential for determinations of particle sinking rates (Briggs et al., 2020; Nayak and Twardowski 2020; Omand et al., 2020) and relationships between particulate organic carbon and chlorophyll concentrations (Loisel et al., 2007), and is currently not a parameter that can be derived remotely.

Conclusion

In this study, we analyzed the angular shape of the particulate Degree of Linear Polarization (DoLP) measured at six locations around the globe. The measured DoLP shapes were quantified with three parameters: the peak magnitude $DoL{P}_{max}$, peak angle ${\psi }_{max}$ and asymmetry parameter $g$. Compared to the perfect symmetry with respect to 90° of the DoLP of a Rayleigh scatterer ($g$=0), the measured DoLPs deviate from symmetry with slight shift to the >90° angular range ($g$>0). Peak angle ${\psi }_{max}$ of measured DoLPs were generally within 90° and 95°, with a global mean of around 92°. This reaffirms the right-shifting characteristic observed in previous studies for a wide range of water types. $DoL{P}_{max}$ generally varied within [0.6, 0.9] with a global mean of around 0.7. Overall, these observations are consistent with results from previous measurement on ocean waters (Voss and Fry 1984; Koestner et al., 2020) and plankton cultures (Fry and Voss 1985; Quinby-Hunt et al., 1989; Volten et al., 1998; Witkowski et al., 1998).

An inversion model was developed to retrieve bulk particulate refractive index by finding a best fit to each measured particulate DoLP from a simulated DoLP dataset (the DoLP model). Lorenz-Mie theory for scattering by homogeneous spheres was used in the simulations. An independent retrieval model based on backscattering ratio was used (the Twardowski model) for comparison. The retrievals were performed at all six field sites. The particulate refractive index retrieved with the DoLP model and the Twardowski model were comparable at the six field sites. At ES, the DoLP model underestimated the refractive index compared to the Twardowski model due to low PSD slope values. At HI and SBC, the DoLP model and the Twardowski model produced refractive index values that are close throughtout the measurement depth. At LE, refractive indices retrieved by the two models were roughly comparable. At LS and NYB, the combination of high PSD slope values and low DoLP peaks resulted in very high refractive indices (1.25–1.3) retrieved with the DoLP model, while low backscattering ratios resulted in low refractive indices (<1.1) retrieved with the Twardowski model. Mixture of particles with a broad range of shape and composition at the two sites might be the cause for relatively large model discrepancies.

In future studies, modeling work with various particle shapes and compositions is needed to investigate the sensitivity of DoLP to these particle features. As shown in Modeling, the simulated DoLPs of Lorenz-Mie and asymmetric hexahedral model showed different variations with changing refractive index. Possible candidate particle models include coated sphere, spheroid and coated spheroid. These shapes were used in simulating marine particulate inherent optical properties (Clavano et al., 2007; Xu et al., 2017; Organelli et al., 2018; Duforêt-Gaurier et al., 2018), although the focus of those studies were not on the linear polarization element. In addition, more work is needed to better understand and validate relationships between DoLP and other IOPs such as backscattering ratio, particulate albedo, and size distributions.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

MT collected the field data and carried out Lorenz-Mie modeling work. SZ analyzed the data, performed the simulations and wrote the paper. MT edited the paper.

Funding

Funding for MT and SZ was provided by the NASA PACE program (80NSSC20M0225), the NASA US Investigator program (80NSSC19K1195) and the Harbor Branch Oceanographic Institute Foundation. Additional support for MT was provided by Belgian Science Policy Office Research Programme for Earth Observation STEREO III (STEREO/00/374).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with one of the authors (MT).

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We are indebted to those that participated in the development of MASCOT, including Alex Derr, Wes Strubhar, and Dave Romanko. We are also indebted to those who helped collect and process data from MASCOT and other sensors for the various field sites, including Scott Freeman, Nicole Stockley, Heather Groundwater, and Matt Slivkoff.

References

Aas, E. (1996). Refractive index of Phytoplankton Derived from its Metabolite Composition. J. Plankton Res. 18 (12), 2223–2249. doi:10.1093/plankt/18.12.2223

CrossRef Full Text | Google Scholar

Basterretxea, G., Font-Muñoz, J. S., and Tuval, I. (2020). Phytoplankton Orientation in a Turbulent Ocean: A Microscale Perspective. Front. Mar. Sci. 7 (March), 185. doi:10.3389/fmars.2020.00185

CrossRef Full Text | Google Scholar

Behrenfeld, M. J., Boss, E., Siegel, D. A., and Shea, D. M. (2005). Carbon-Based Ocean Productivity and Phytoplankton Physiology from Space. Glob. Biogeochem. Cycles 19 (1), 1–14. doi:10.1029/2004GB002299

CrossRef Full Text | Google Scholar

Bi, L., and Yang, P. (2015). Impact of Calcification State on the Inherent Optical Properties of Emiliania Huxleyi Coccoliths and Coccolithophores. J. Quantitative Spectrosc. Radiative Transfer 155 (April), 10–21. doi:10.1016/j.jqsrt.2014.12.017

CrossRef Full Text | Google Scholar

Bohren, C. F., and Huffman, D. R. (1998). Absorption and Scattering of Light by Small Particles. Wiley.

Boss, E., Pegau, W. S., Lee, M., Twardowski, M., Shybanov, E., Korotaev, G., et al. (2004). Particulate Backscattering Ratio at LEO 15 and its Use to Study Particle Composition and Distribution. J. Geophys. Res. 109 (1), 1014. doi:10.1029/2002jc001514

CrossRef Full Text | Google Scholar

Boss, E., Twardowski, M. S., and Herring, S. (2001). Shape of the Particulate Beam Attenuation Spectrum and its Inversion to Obtain the Shape of the Particulate Size Distribution. Appl. Opt. 40 (27), 4885. doi:10.1364/ao.40.004885

PubMed Abstract | CrossRef Full Text | Google Scholar

Briggs, N., Dall’Olmo, G., and Claustre, H. (2020). Major Role of Particle Fragmentation in Regulating Biological Sequestration of CO2 by the Oceans. Science 367 (6479), 791–793. doi:10.1126/science.aay1790

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, O. B., and Gordon, H. R. (1973). Two Component Mie Scattering Models of Sargasso Sea Particles. Appl. Opt. 12 (10), 2461. doi:10.1364/ao.12.002461

PubMed Abstract | CrossRef Full Text | Google Scholar

Chami, M., and McKee, D. (2007). Determination of Biogeochemical Properties of Marine Particles Using above Water Measurements of the Degree of Polarization at the Brewster Angle. Opt. Express 15 (15), 9494. doi:10.1364/oe.15.009494

PubMed Abstract | CrossRef Full Text | Google Scholar

Chowdhary, J., Cairns, B., Waquet, F., Knobelspiesse, K., Ottaviani, M., Redemann, J., et al. (2012). Sensitivity of Multiangle, Multispectral Polarimetric Remote Sensing over Open Oceans to Water-Leaving Radiance: Analyses of RSP Data Acquired during the MILAGRO Campaign. Remote Sensing Environ. 118 (March), 284–308. doi:10.1016/j.rse.2011.11.003

CrossRef Full Text | Google Scholar

Chowdhary, J., Zhai, P.-W., Boss, E., Dierssen, H., Frouin, R., Ibrahim, A., et al. (2019). Modeling Atmosphere-Ocean Radiative Transfer: A PACE Mission Perspective. Front. Earth Sci. 7 (June), 100. doi:10.3389/feart.2019.00100

CrossRef Full Text | Google Scholar

Clavano, W., Boss, E., and Karp-Boss, L. (2007). Inherent Optical Properties of Non-spherical Marine-Like Particles, Äî from Theory to Observation. Oceanography Mar. Biol. 38, 1–38. doi:10.1201/9781420050943.ch1

CrossRef Full Text | Google Scholar

Ding, J., Yang, P., King, M. D., Platnick, S., Liu, X., Meyer, K. G., et al. (2019). A Fast Vector Radiative Transfer Model for the Atmosphere-Ocean Coupled System. J. Quantitative Spectrosc. Radiative Transfer 239 (December), 106667. doi:10.1016/j.jqsrt.2019.106667

CrossRef Full Text | Google Scholar

Duforêt-Gaurier, L., Dessailly, D., Moutier, W., and Loisel, H. (2018). Assessing the Impact of a Two-Layered Spherical Geometry of Phytoplankton Cells on the Bulk Backscattering Ratio of Marine Particulate Matter. Appl. Sci. 8 (12), 2689. doi:10.3390/app8122689

CrossRef Full Text | Google Scholar

Farinato, R. S., and Rowell, R. L. (1976). New Values of the Light Scattering Depolarization and Anisotropy of Water. J. Chem. Phys. 65 (2), 593–595. doi:10.1063/1.433115

CrossRef Full Text | Google Scholar

Fry, E. S., and Voss, K. J. (1985). Measurement of the Mueller Matrix for Phytoplankton1. Limnol. Oceanogr. 30 (6), 1322–1326. doi:10.4319/lo.1985.30.6.1322

CrossRef Full Text | Google Scholar

Gleason, A. C. R., Voss, K. J., Gordon, H. R., Twardowski, M., Sullivan, J., Trees, C., et al. (2012). Detailed Validation of the Bidirectional Effect in Various Case I and Case II Waters. Opt. Express 20 (7), 7630. doi:10.1364/oe.20.007630

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordon, H. R., Brown, O. B., Evans, R. H., Brown, J. W., Smith, R. C., Baker, K. S., et al. (1988). A Semianalytic Radiance Model of Ocean Color. J. Geophys. Res. 93 (D9), 10909–10924. doi:10.1029/JD093iD09p10909

CrossRef Full Text | Google Scholar

Hostetler, C. A., Behrenfeld, M. J., Hu, Y., Hair, J. W., and Schulien, J. A. (2018). Spaceborne Lidar in the Study of Marine Systems. Annu. Rev. Mar. Sci. 10 (1), 121–147. doi:10.1146/annurev-marine-121916-063335

PubMed Abstract | CrossRef Full Text | Google Scholar

Ibrahim, A., Gilerson, A., Harmel, T., Tonizzo, A., Chowdhary, J., and Ahmed, S. (2012). The Relationship between Upwelling Underwater Polarization and Attenuation/Absorption Ratio. Opt. Express 20 (23), 25662. doi:10.1364/oe.20.025662

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamet, C., Ibrahim, A., Ahmad, Z., Angelini, F., Babin, M., Behrenfeld, M. J., et al. (2019). Going beyond Standard Ocean Color Observations: Lidar and Polarimetry. Front. Mar. Sci. 6 (May), 251. doi:10.3389/fmars.2019.00251

CrossRef Full Text | Google Scholar

Jonasz, M., and Fournier, G. (2007). Light Scattering by Particles in Water: Theoretical and Experimental Foundations. Elsevier.

Kadyshevich, E., and Lyubovtseva, Y. S. (1976). Light-Scattering Matrices of Pacific and Atlantic Ocean Waters. Izvestiya Atmos. Oceanic Phys. 12 (2), 106–111.

Google Scholar

Koestner, D., Stramski, D., and Reynolds, R. A. (2020). Polarized Light Scattering Measurements as a Means to Characterize Particle Size and Composition of Natural Assemblages of Marine Particles. Appl. Opt. 59 (27), 8314. doi:10.1364/ao.396709

PubMed Abstract | CrossRef Full Text | Google Scholar

Koestner, D., Stramski, D., and Reynolds, R. (2018). Measurements of the Volume Scattering Function and the Degree of Linear Polarization of Light Scattered by Contrasting Natural Assemblages of Marine Particles. Appl. Sci. 8 (12), 2690. doi:10.3390/app8122690

CrossRef Full Text | Google Scholar

Kokhanovsky, A. A. (2003). Parameterization of the Mueller Matrix of Oceanic Waters. J. Geophys. Res. 108 (6), 3175. doi:10.1029/2001jc001222

CrossRef Full Text | Google Scholar

Kostadinov, T. S., Siegel, D. A., and Maritorena, S. (2009). Retrieval of the Particle Size Distribution from Satellite Ocean Color Observations. J. Geophys. Res. 114 (9), 9015. doi:10.1029/2009JC005303

CrossRef Full Text | Google Scholar

Lee, Z., Carder, K. L., and Arnone, R. A. (2002). Deriving Inherent Optical Properties from Water Color: A Multiband Quasi-Analytical Algorithm for Optically Deep Waters. Appl. Opt. 41 (27), 5755. doi:10.1364/ao.41.005755

PubMed Abstract | CrossRef Full Text | Google Scholar

Loisel, H., Mériaux, X., Berthon, J.-F., and Poteau, A. (2007). Investigation of the Optical Backscattering to Scattering Ratio of Marine Particles in Relation to Their Biogeochemical Composition in the Eastern English Channel and Southern North Sea. Limnol. Oceanogr. 52 (2), 739–752. doi:10.4319/lo.2007.52.2.0739

CrossRef Full Text | Google Scholar

Lotsberg, J. K., and Stamnes, J. J. (2010). Impact of Particulate Oceanic Composition on the Radiance and Polarization of Underwater and Backscattered Light. Opt. Express 18 (10), 10432. doi:10.1364/oe.18.010432

PubMed Abstract | CrossRef Full Text | Google Scholar

Maritorena, S., Siegel, D. A., and Peterson, A. R. (2002). Optimization of a Semianalytical Ocean Color Model for Global-Scale Applications. Appl. Opt. 41 (15), 2705. doi:10.1364/ao.41.002705

PubMed Abstract | CrossRef Full Text | Google Scholar

McFarland, M., Nayak, A. R., Stockley, N., Twardowski, M., and Sullivan, J. (2020). Enhanced Light Absorption by Horizontally Oriented Diatom Colonies. Front. Mar. Sci. 7 (July), 494. doi:10.3389/fmars.2020.00494

CrossRef Full Text | Google Scholar

Mishchenko, M. I., Travis, L. D., and Lacis, A. A. (2002). Scattering, Absorption, and Emission of Light by Small Particles. Cambridge University Press.

Mishchenko, M. I., and Yurkin, M. A. (2017). On the Concept of Random Orientation in Far-Field Electromagnetic Scattering by Nonspherical Particles. Opt. Lett. 42 (3), 494. doi:10.1364/ol.42.000494

PubMed Abstract | CrossRef Full Text | Google Scholar

Moore, T. S., Mouw, C. B., Sullivan, J. M., Twardowski, M. S., Burtner, A. M., Ciochetto, A. B., et al. (2017). Bio-Optical Properties of Cyanobacteria Blooms in Western Lake Erie. Front. Mar. Sci. 4 (SEP), 300. doi:10.3389/fmars.2017.00300

CrossRef Full Text | Google Scholar

Nayak, A. R., McFarland, M. N., Sullivan, J. M., and Twardowski, M. S. (2018). Evidence for Ubiquitous Preferential Particle Orientation in Representative Oceanic Shear Flows. Limnol. Oceanogr. 63 (1), 122–143. doi:10.1002/lno.10618

PubMed Abstract | CrossRef Full Text | Google Scholar

Nayak, A. R., and Twardowski, M. S. (2020). "Breaking" News for the Ocean's Carbon Budget. Science 367 (6479), 738–739. doi:10.1126/science.aba7109

PubMed Abstract | CrossRef Full Text | Google Scholar

Omand, M. M., Govindarajan, R., He, J., and Mahadevan, A. (2020). Sinking Flux of Particulate Organic Matter in the Oceans: Sensitivity to Particle Characteristics. Sci. Rep. 10 (1), 1–16. doi:10.1038/s41598-020-60424-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Organelli, E., Dall’Olmo, G., Brewin, R. J. W., Tarran, G. A., Boss, E., and Bricaud, A. (2018). The Open-Ocean Missing Backscattering Is in the Structural Complexity of Particles. Nat. Commun. 9 (1), 5439. doi:10.1038/s41467-018-07814-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Quinby-Hunt, M. S., Hunt, A. J., Lofftus, K., and Shapiro, D. (1989). Polarized-light Scattering Studies of marine Chlorella. Limnol. Oceanogr. 34 (8), 1587–1600. doi:10.4319/lo.1989.34.8.1587

CrossRef Full Text | Google Scholar

Reynolds, R. A., Stramski, D., Wright, V. M., and Woźniak, S. B. (2010). Measurements and Characterization of Particle Size Distributions in Coastal Waters. J. Geophys. Res. 115 (8), 8024. doi:10.1029/2009JC005930

CrossRef Full Text | Google Scholar

Stamnes, S., Hostetler, C., Ferrare, R., Burton, S., Liu, X., Hair, J., et al. (2018). Simultaneous Polarimeter Retrievals of Microphysical Aerosol and Ocean Color Parameters from the "MAPP" Algorithm with Comparison to High-Spectral-Resolution Lidar Aerosol and Ocean Products. Appl. Opt. 57 (10), 2394. doi:10.1364/ao.57.002394

PubMed Abstract | CrossRef Full Text | Google Scholar

Stegmann, P. G., Sun, B., Ding, J., Yang, P., and Zhang, X. (2019). Study of the Effects of Phytoplankton Morphology and Vertical Profile on Lidar Attenuated Backscatter and Depolarization Ratio. J. Quantitative Spectrosc. Radiative Transfer 225 (March), 1–15. doi:10.1016/j.jqsrt.2018.12.009

CrossRef Full Text | Google Scholar

Subramaniam, A., Christopher, W. B., Hood, R., Carpenter, E. J., and Capone, D. G. (2001). Detecting Trichodesmium Blooms in SeaWiFS Imagery. Deep-Sea Res. Part Topical Stud. Oceanography 49 (1–3), 107–121. doi:10.1016/S0967-0645(01)00096-0

CrossRef Full Text | Google Scholar

Sullivan, J. M., and Twardowski, M. S. (2009). Angular Shape of the Oceanic Particulate Volume Scattering Function in the Backward Direction. Appl. Opt. 48 (35), 6811–6819. doi:10.1364/AO.48.006811

PubMed Abstract | CrossRef Full Text | Google Scholar

Sullivan, J. M., Twardowski, M. S., Donaghay, P. L., and Freeman, S. A. (2005). Use of Optical Scattering to Discriminate Particle Types in Coastal Waters. Appl. Opt. 44 (9), 1667–1680. doi:10.1364/AO.44.001667

PubMed Abstract | CrossRef Full Text | Google Scholar

Sullivan, J. M., Twardowski, M. S., Ronald, J., Zaneveld, V., and Moore, C. C. (2013). “Measuring Optical Backscattering in Water,” in Light Scattering Reviews 7: Radiative Transfer and Optical Properties of Atmosphere and Underlying Surface, 189–224. doi:10.1007/978-3-642-21907-8_6

CrossRef Full Text | Google Scholar

Sun, B., Kattawar, G. W., Yang, P., Twardowski, M. S., and Sullivan, J. M. (2016). Simulation of the Scattering Properties of a Chain-Forming Triangular Prism Oceanic Diatom. J. Quantitative Spectrosc. Radiative Transfer 178 (July), 390–399. doi:10.1016/j.jqsrt.2016.02.035

CrossRef Full Text | Google Scholar

Tonizzo, A., Gilerson, A., Harmel, T., Ibrahim, A., Chowdhary, J., Gross, B., et al. (2011). Estimating Particle Composition and Size Distribution from Polarized Water-Leaving Radiance. Appl. Opt. 50 (25), 5047–5058. doi:10.1364/AO.50.005047

CrossRef Full Text | Google Scholar

Tonizzo, A., Zhou, J., Gilerson, A., Twardowski, M. S., Gray, D. J., Arnone, R. A., et al. (2009). Polarized Light in Coastal Waters: Hyperspectral and Multiangular Analysis. Opt. Express 17 (7), 5666. doi:10.1364/oe.17.005666

PubMed Abstract | CrossRef Full Text | Google Scholar

Twardowski, M. S., Boss, E., Macdonald, J. B., Pegau, W. S., Barnard, A. H., and Zaneveld, J. R. V. (2001). A Model for Estimating Bulk Refractive Index from the Optical Backscattering Ratio and the Implications for Understanding Particle Composition in Case I and Case II Waters. J. Geophys. Res. 106 (C7), 14129–14142. doi:10.1029/2000JC000404

CrossRef Full Text | Google Scholar

Twardowski, M. S., Claustre, H., Freeman, S. A., Stramski, D., and Huot, Y. (2007). Optical Backscattering Properties of the "clearest" Natural Waters. Biogeosciences 4 (6), 1041–1058. doi:10.5194/bg-4-1041-2007

CrossRef Full Text | Google Scholar

Twardowski, M. S., Sullivan, J. M., Donaghay, P. L., and Zaneveld, J. R. V. (1999). Microscale Quantification of the Absorption by Dissolved and Particulate Material in Coastal Waters with an Ac-9. J. Atmos. Oceanic Technol. 16 (6), 691–707. doi:10.1175/1520-0426(1999)016<0691:mqotab>2.0.co;2

CrossRef Full Text | Google Scholar

Twardowski, M., and Tonizzo, A. (2018). Ocean Color Analytical Model Explicitly Dependent on the Volume Scattering Function. Appl. Sci. 8 (12), 2684. doi:10.3390/app8122684

CrossRef Full Text | Google Scholar

Twardowski, M., Zhang, X., Vagle, S., Sullivan, J., Freeman, S., Czerski, H., et al. (2012). The Optical Volume Scattering Function in a Surf Zone Inverted to Derive Sediment and Bubble Particle Subpopulations. J. Geophys. Res. 117 (2), a–n. doi:10.1029/2011JC007347

CrossRef Full Text | Google Scholar

van de Hulst, H. C. (1957). Light Scattering by Small Particles. New York: John Wiley & Sons.

Volten, H., De Haan, J. F., Hovenier, J. W., Schreurs, R., Vassen, W., Dekker, A. G., et al. (1998). Laboratory Measurements of Angular Distributions of Light Scattered by Phytoplankton and Silt. Limnol. Oceanogr. 43 (6), 1180–1197. doi:10.4319/lo.1998.43.6.1180

CrossRef Full Text | Google Scholar

Voss, K. J., and Fry, E. S. (1984). Measurement of the Mueller Matrix for Ocean Water. Appl. Opt. 23 (23), 4427. doi:10.1364/ao.23.004427

PubMed Abstract | CrossRef Full Text | Google Scholar

Werdell, P. J., McKinna, L. I. W., Boss, E., Ackleson, S. G., Craig, S. E., Gregg, W. W., et al. (2018). An Overview of Approaches and Challenges for Retrieving Marine Inherent Optical Properties from Ocean Color Remote Sensing, Prog. Oceanography, 160, 186, 212. doi:10.1016/j.pocean.2018.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Witkowski, K., Król, T., Zielirińki, A., and Kuteń, E. (1998). A Light-Scattering Matrix for Unicellular Marine Phytoplankton. Limnol. Oceanogr. 43 (5), 859–869. doi:10.4319/lo.1998.43.5.0859

CrossRef Full Text | Google Scholar

Xu, F., Dubovik, O., Zhai, P.-W., Diner, D. J., Kalashnikova, O. V., Seidel, F. C., et al. (2016). Joint Retrieval of Aerosol and Water-Leaving Radiance from Multispectral, Multiangular and Polarimetric Measurements over Ocean. Atmos. Meas. Tech. 9 (7), 2877–2907. doi:10.5194/amt-9-2877-2016

CrossRef Full Text | Google Scholar

Xu, G., Sun, B., Brooks, S. D., Yang, P., Kattawar, G. W., and Zhang, X. (2017). Modeling the Inherent Optical Properties of Aquatic Particles Using an Irregular Hexahedral Ensemble. J. Quantitative Spectrosc. Radiative Transfer 191 (April), 30–39. doi:10.1016/j.jqsrt.2017.01.020

CrossRef Full Text | Google Scholar

Yang, P., and Liou, K. N. (1996). Geometric-optics-integral-equation Method for Light Scattering by Nonspherical Ice Crystals. Appl. Opt. 35 (33), 6568. doi:10.1364/ao.35.006568

PubMed Abstract | CrossRef Full Text | Google Scholar

You, Y., Kattawar, G. W., Voss, K. J., Bhandari, P., Wei, J., Lewis, M., et al. (2011a). Polarized Light Field under Dynamic Ocean Surfaces: Numerical Modeling Compared with Measurements. J. Geophys. Res. 116 (10), C00H05. doi:10.1029/2011JC007278

CrossRef Full Text | Google Scholar

You, Y., Tonizzo, A., Gilerson, A. A., Cummings, M. E., Brady, P., Sullivan, J. M., et al. (2011b). Measurements and Simulations of Polarization States of Underwater Light in Clear Oceanic Waters. Appl. Opt. 50 (24), 4873–4893. doi:10.1364/AO.50.004873

PubMed Abstract | CrossRef Full Text | Google Scholar

Yurkin, M. A., and Hoekstra, A. G. (2007). The Discrete Dipole Approximation: An Overview and Recent Developments. J. Quantitative Spectrosc. Radiative Transfer 106 (1–3), 558–589. doi:10.1016/j.jqsrt.2007.01.034

CrossRef Full Text | Google Scholar

Zaneveld, J. R. V. (1995). A Theoretical Derivation of the Dependence of the Remotely Sensed Reflectance of the Ocean on the Inherent Optical Properties. J. Geophys. Res. 100 (C7), 13135–13142. doi:10.1029/95jc00453

CrossRef Full Text | Google Scholar

Zhai, P.-W., Hu, Y., Chowdhary, J., Trepte, C. R., Lucker, P. L., and Josset, D. B. (2010). A Vector Radiative Transfer Model for Coupled Atmosphere and Ocean Systems with a Rough Interface. J. Quantitative Spectrosc. Radiative Transfer 111 (7–8), 1025–1040. doi:10.1016/j.jqsrt.2009.12.005

CrossRef Full Text | Google Scholar

Zhai, P.-W., Hu, Y., Trepte, C. R., Winker, D. M., Josset, D. B., Lucker, P. L., et al. (2013). Inherent Optical Properties of the Coccolithophore: Emiliania Huxleyi. Opt. Express 21 (15), 17625. doi:10.1364/oe.21.017625

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhai, S., Twardowski, M., Hedley, J. D., McFarland, M., Nayak, A. R., and Moore, T. (2020). Optical Backscattering and Linear Polarization Properties of the Colony Forming Cyanobacterium Microcystis. Opt. Express 28 (25), 37149. doi:10.1364/oe.405871

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Hu, L., and He, M.-X. (2009). Scattering by Pure Seawater: Effect of Salinity. Opt. Express 17 (7), 5698. doi:10.1364/oe.17.005698

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Stramski, D., Reynolds, R. A., and Blocker, E. R. (2019). Light Scattering by Pure Water and Seawater: The Depolarization Ratio and its Variation with Salinity. Appl. Opt. 58 (4), 991. doi:10.1364/ao.58.000991

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Twardowski, M., and Lewis, M. (2011). Retrieving Composition and Sizes of Oceanic Particle Subpopulations from the Volume Scattering Function. Appl. Opt. 50 (9), 1240–1259. doi:10.1364/AO.50.001240

PubMed Abstract | CrossRef Full Text | Google Scholar