Transportable optical cavity systems for terrestrial and space-borne portable optical atomic clocks

High finesse optical cavities have been the backbone of realizing narrow linewidth lasers to drive coherent excitations on dipole-forbidden transitions in atoms and ions for applications in atomic frequency standards. Over the past decade, increasing efforts have been made to develop technologies that enable the operation of all-optical atomic clocks in a portable form factor outside laboratory environments relying on transportable high-finesse optical cavities for field applications in positioning, navigation, timing (PNT) and communication. However, the compactness of such systems makes them more susceptible to environmental noises that limit their performance and stability. This review aims to address the underlying physics behind high-finesse optical cavities, cavity-based laser frequency stabilization schemes and various sources of noise arising from thermal, vibrational, acoustic, power and polarization fluctuations that impede the stability of portable optical cavities, as well as outline the strategies for minimizing their influences. We also discuss about the minimization of the residual amplitude modulation (RAM) noise that degrades the laser linewidth. In addition, our study encompasses a comparative analysis of various transportable, high-finesse optical cavity systems that are currently accessible for terrestrial and space-based metrology applications, as well as an exploration of the potential applications that these cavities can facilitate. We also review recent advancements in designing such systems and highlight their efforts for constructing ultra-stable, compact, high-finesse cavities for terrestrial and space-borne transportable all-optical atomic clocks.

1 Introduction

Atomic clocks have facilitated exceptional precision in timekeeping, a crucial requirement for global positioning system (GPS) and navigation systems (Boldbaatar et al., 2023), telecommunications and timestamping of financial transactions (Marlow and Scherer, 2021), and strategic applications (Vig, 1993). The unprecedented accuracy in time and frequency metrology offered by next-generation optical atomic clocks has ushered in a new experimental epoch in search for the physics beyond the standard model (BSM) (DeMille et al., 2017), investigating the temporal variation of the fundamental physical constants, search for the dark matter (DM) (Safronova et al., 2018), advancement in geodetic measurements (Mehlstäubler et al., 2018). These scientific endeavours depend on the extremely high accuracy and low instability offered by optical atomic clocks.

Enhanced precision in time measurement aided by narrow linewidth lasers stabilized to high-finesse optical cavities have ushered in a new era in frequency metrology. This has led to integrating such portable, ultra-stable cavities as payloads in satellites. Such payloads have enabled tracking of distances between two satellites in highly successful space missions like GRACE-FO¹. The GRACE-FO mission has revealed interesting information by mapping the Earth’s gravitational field, measuring water and ice distribution over the Earth’s surface, and contributing the studies in geodesy and climate changes (Landerer et al., 2020; Tapley et al., 2019). The importance of such missions was appreciated and promoted further through future missions like NGGM² (Nicklaus et al., 2017). The theory of general relativity (Misner et al., 2017), which is based on principles like local Lorentz invariance (LLI), Einstein’s equivalence principle, etc. (Rodrigues and Oliveira, 2016), can be tested by measuring the gravitational redshift using precision optical clocks in space owing to longer interrogation times in unperturbed space environments (Gill et al., 2008). Several space missions have been proposed for similar measurements, like STAR³ (Braxmaier et al., 2010), BOOST⁴ (Sanjuan et al., 2019), STE-QUEST⁵ (Altschul et al., 2015), SOC⁶ (Bongs et al., 2015), etc.

Lab-based lasers designed for coherently addressing the clock transition in stationary optical clocks outperform their counterparts made for portable clocks. For example, notable stationary clock laser systems developed by (Bothwell et al., 2019; Schwarz et al., 2020) demonstrate instability levels of approximately $5\times 10^{-17}/\sqrt{\tau }$ ($\tau$ refers to total averaging time) as compared to the portable clock laser system from (Herbers et al., 2022) exhibiting a stability around $1.6\times 10^{-16}/\sqrt{\tau }$. The three-fold better stability of lab-based clock laser systems arises largely from the well-controlled and isolated lab environments from which they operate. Despite their potential use in various applications, the large size of lab-based clocks renders them impractical for field operations and makes them vulnerable to external disturbances. This leads to the development of portable clocks for out-of-lab applications. Developing portable optical atomic clocks would bridge the technology gap to build a more resilient PNT (Positioning, Navigation and Timing) system (Hollberg, 2020; Bondarescu et al., 2015; Roslund et al., 2024), facilitate deep space missions (Georgescu, 2019), and perform geodetic measurements (Grotti et al., 2018) as well as fundamental physics experiments (Tsai et al., 2023; Derevianko et al., 2022; Takamoto et al., 2020).

The superior stability of lab-based optical clocks is attributed to the laser frequency stability that interrogates the clock transition. Such a laser is more stable than those in portable clocks as they leverage the advantage of being decoupled from the environment. Measurement of stability of a frequency standard is quantified by Allan deviation expressed as follows (Itano et al., 1993):

${\sigma }_y\left(\tau \right)\approx \frac{\mathrm{\Delta }{v}_0}{v_0\sqrt{N}}\sqrt{\left(\frac{T_c}{\tau }\right)}=\frac{1}{Q\sqrt{N}}\sqrt{\left(\frac{T_c}{\tau }\right)},(1)$

where $v_0$ and $\mathrm{\Delta }{v}_0$ are the resonance frequency and linewidth of the clock transition, respectively. $Q(=\frac{v_0}{\mathrm{\Delta }{v}_0})$ is known as the quality factor for an atomic transition. $N$ refers to the number of atoms (or ions) under interrogation. $T_c$ and $\tau$ are the interrogation time for one complete cycle and total averaging time, respectively. Equation 1 indicates that lower linewidth ensures better stability. Atoms possessing dipole-forbidden transitions exhibit significantly narrower linewidths compared to those with dipole-allowed transitions. Consequently, these atoms are favoured as suitable candidates for atomic clocks.

Laser frequencies are susceptible to drifts due to various environmental and operational factors like air pressure, humidity, temperature, acoustic noises, laser diode current, grating position, etc. As a result, the primary experimental challenge lies in developing robust control and feedback systems for these lasers to mitigate such environmental and technical disturbances and achieve a narrow linewidth with a low drift in frequency. This necessitates the requirement that lasers must be stabilised to highly stable references that surpass the intrinsic frequency stability of the laser itself (Fox et al., 2003). The chosen reference must be able to detect continuous changes in the quantity we aim to stabilize, such as frequency, phase, and polarization. Examples of references include atomic or molecular transitions (dipole-forbidden), frequency combs, optical cavities, etc. Clock transitions characterized by extremely narrow linewidth ($\lesssim$1 Hz) require employing ultra-high finesse cavities to ensure stability for the clock laser. This is attributed to the ability of the highly reflective mirrors of an optical cavity to produce sharp and extremely narrow transmission peaks at specific frequency intervals, which can be utilized to reference the laser frequency. Additionally, the laser frequency needs to be referenced for stabilisation, for which we shall revisit the popular and widely adopted laser stabilization technique known as the Pound-Drever-Hall (PDH) method.

To realize a laser with frequency stability of about $10^{-15}$, the normalized length variation $(\mathrm{\Delta }L/L)$ of the cavity should be restricted to a value which is about one-tenth of the proton radius (Alnis et al., 2008). Designing such an ultra-stable high-finesse cavity presents a formidable challenge due to fundamental limitations of thermal noise floor and external perturbations, such as mechanical or thermal noise that affect the stability of the cavity. The fundamental thermal noise floor sets the ultimate lower limit on length stability, which depends on the material properties used for the cavity spacer, mirror substrate, and coating (Numata et al., 2004). Since the thermal noise floor is inversely proportional to the cavity length, it is advantageous to use longer optical resonators to achieve a lower thermal limit (Swallows et al., 2012; Häfner et al., 2015).

However, operating a cavity with a longer length for transportable clock purposes poses a significant challenge in mitigating mechanical and other vibrational noises. For portable clocks, there is a necessary trade-off between optimizing cavity length to reduce the thermal noise floor and managing the practical challenges of transporting such systems. This trade-off limits the stability of portable optical clocks compared to state-of-the-art, lab-based systems. Furthermore, external temperature fluctuations influence the cavity length arising from thermal expansion. Local heating of the cavity surface due to thermal radiation emitted by the cavity housing also affects the optical path length (Dai et al., 2015). While these issues are better addressed in stationary cavities placed in well-controlled lab environments, significant challenges emerge when attempting to make these cavities transportable. Mitigating these challenges requires robust active temperature control systems which can withstand harsh operating environments.

The mechanical stability of the cavity is significantly affected by vibrational noise arising out of environmental and mechanical disturbances in the structure and mounting. Compared to stationary lab-based cavities (Millo et al., 2009), transportable cavities require a robust, rigid mounting structure to withstand rapid movements and acceleration during transport, which can introduce greater stress on the cavity and potentially result in changes in its length. This requirement also presents considerable challenges in mitigating vibrational noise (Häfner et al., 2020; Zhao et al., 2022). Therefore, careful considerations in designing control systems and robust housing are crucial for ensuring mechanical stability and operating portable cavities at room temperature. Subtle choices of cavity spacer material, mirror substrate, mirror coatings, and mounting material, in conjunction with excellent thermal and mechanical stability, become essential in developing a robust portable cavity that can only be limited by the thermal noise floor.

In addition to the above-mentioned issues, optical cavities meant for space-based missions need to meet more robust and rugged requirements, given the harsh outer space environment. Cavities onboard spacecraft would experience large accelerations and shocks during launch, requiring more rigorous mounting strategies (Tao and Chen, 2018; He et al., 2021). The size, weight, and power (SWaP) of the assembly are major factors that constitute the payload and directly affect the overall project cost. Compact breadboards must be integrated carefully for space optimization with rigidly attached optical components, demanding the miniaturization of optics. The space radiation in and around the Earth’s atmosphere can severely damage the electronic components and optics of the satellite onboard lasers. This radiation originates from various sources such as solar flares consisting of charged particles, high energy cosmic and gamma rays, and particles losing energy in the form of Bremsstrahlung or secondary X-rays⁷. The mirror coatings are also prone to space radiation, affecting the thermal noise floor and finesse of the cavity. To avoid radiation damage, sensitive optics (such as mirror coatings) and electronic components necessitate conducting radiation-hardened tests (Cole et al., 2024). In addition to all this, automation of electronics is required for space-borne optical cavities, which can be operated without human intervention for years.

This review article explores the challenges, obstacles, and strategies involved in the design and construction of high-finesse, ultra-stable, portable optical cavity systems. We also outline the significant developments in portable cavities over the past 2 decades. Such details are critical and essential for the development of portable optical clocks. A number of review articles and technical reports on optical clocks for both introductory and expert levels have been published erstwhile (Gill, 2005; Margolis, 2009; Riehle, 2015; Ludlow et al., 2015; Abdel-Hafiz et al., 2019). Recently (Boyd and Lahaye, 2024), published a pedagogical article on development of ultra-stable lasers.

We shall initiate a discussion on the basic principles of the cavity and delineate the geometrical criteria that such cavities must fulfil for achieving laser beam stability in Section 2. We shall follow it up with a brief discussion on the evolution of laser stabilization techniques for cavities in Section 3, subsequently exploring the theory of the PDH method, which is one of the most effective techniques. Thereafter, we delve into Section 4, where we discuss about different noise sources and their impact on cavity stability. We also outline the strategies to alleviate these noises and provide guidelines to develop an ultra-stable, high-finesse portable optical cavity. Since residual amplitude modulation (RAM) is a conglomeration of many effects, mainly arising due to the use of an electro-optic modulator (EOM) and is a major experimental hurdle in achieving stability below $10^{-15}-10^{-16}$, we dedicate Section 4-3 to it. We conclude this article by reviewing some notable cases of portable prototypes and ready-to-deploy cavities that can be used for terrestrial and space-borne applications cavities (Section 5).

2 Fabry-Pérot cavity

2.1 Introduction

An optical Fabry-Pérot (FP) resonator consists of two parallel mirrors separated by a distance that sustains standing waves determined by the cavity length. We discuss here only the important results and formulas. Detailed discussions can be found on cavities elsewhere (Silfvast, 2004; Milonni and Eberly, 2010). Figure 1 illustrates the schematic of the FP cavity with two nearly flat mirrors (${\mathrm{M}}_{\mathrm{1}}$ and ${\mathrm{M}}_{\mathrm{2}}$) positioned at a distance of $L$ and possessing equal transmission $(t)$ and reflection $(r)$ coefficients. These coefficients correspond to transmissivity $(T)$ and reflectivity $(R)$ as $T=|t{|}^2$ and $R=|r{|}^2$, respectively. For an incident beam of field amplitude $E_0$, part of it will be transmitted $(E_t)$ through ${\mathrm{M}}_{\mathrm{2}}$, and part will be reflected $(E_{\text{ref}})$ from ${\mathrm{M}}_{\mathrm{1}}$. The intensity of transmitted light $(I_t=|E_t{|}^2)$ for an incident beam $(I_0=|E_0{|}^2)$ at the input mirror is given by:

$\frac{I_{\text{t}}}{I_0}=\frac{1}{1+\frac{4r^2}{{\left(1-r^2\right)}^2}{\sin }^2\left(\frac{\varphi }{2}\right)},(2)$

Figure 1

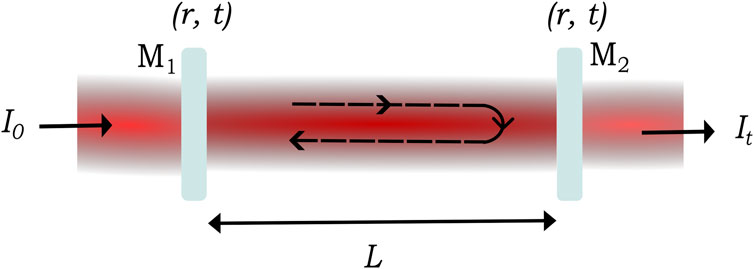
Figure 1. A plane parallel mirror (${\text{M}}_1$ and ${\text{M}}_2$) cavity of length $L$ with equal mirror transmission (t) and reflection (r) coefficients. The darker colour inside the cavity shows its ability to store light as it circulates due to the interference of resonant wavelengths.

The phase factor $\varphi$ accounts for the phase difference accumulated as light travels between the mirrors of the FP cavity. For normal incidence, $\varphi =2\frac{2\pi }{\lambda }L$, where $\lambda$ is the wavelength. Constructive interference happens when the optical path length difference becomes equal to an integral multiple of the wavelength, leading to interference maxima when $\varphi =2m\pi$ (with $m$ as the interference order). The resonance condition for sustaining standing waves is $2L=m\lambda$, allowing only specific wavelengths to resonate (Figure 2). The separation between neighbouring transmission peaks in wavelength space is known as the free spectral range (FSR), denoted as:

$\mathrm{F}\mathrm{S}\mathrm{R}=\frac{c}{2L_{\text{opt}}}=\frac{1}{t_{\text{rp}}}.(3)$

Figure 2

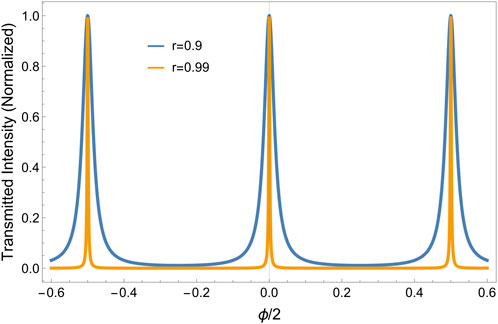
Figure 2. Transmitted intensity pattern showing the periodic occurrence of intensity maxima for resonant wavelengths (using Equation 2) for two different values of $r$ (reflection coefficient).

Here $c$ represents the speed of light, $L_{\text{opt}}=nL$, denotes optical path length within cavity (where $n=$refractive index of the cavity bore medium), and $t_{\text{rp}}$ refers to the photon round-trip time. The full width at half maxima (FWHM) of the transmission peaks is expressed as:

$\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}=\frac{c\left(1-r^2\right)}{2\pi r{L}_{\text{opt}}}.(4)$

Another significant metric used to evaluate the quality of an optical cavity is finesse, defined as the ratio of FSR (Equation 3) to FWHM (Equation 4):

$\mathrm{F}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{e}=\mathcal{F}=\frac{\mathrm{F}\mathrm{S}\mathrm{R}}{\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}}=\frac{\pi r}{1-r^2}.(5)$

Equation 4 indicates that selecting mirrors with higher reflectivity leads to narrower transmission peaks. Conversely, Equation 5 shows that to observe very narrow linewidth peaks, one would need a cavity with very high finesse. We highlight the linewidth (FWHM) and finesse for different values of reflection coefficient $(r)$ for a cavity of length $10\mathrm{c}\mathrm{m}$ in Figure 2 (for $r=0.9$, FWHM $\sim 100\mathrm{M}\mathrm{H}\mathrm{z}$ and $\mathcal{F}\sim 15$; for $r=0.99$, FWHM $\sim 10\mathrm{M}\mathrm{H}\mathrm{z}$ and $\mathcal{F}\sim 160$). Intriguingly, $r\sim 1$ would mean near infinite finesse, implying that the photons will perpetually bounce in the cavity forever without decaying or escaping.

Equation 5 holds when the cavity is lossless. In a realistic cavity, the coefficients of reflection of both mirrors differ $(r_1\ne r_2)$, and finite losses exist inside the cavity, necessitating a more generalized expression of finesse:

$\mathcal{F}=\frac{\pi \sqrt{r_1{r}_{2}l}}{1-r_1{r}_{2}l}.(6)$

In Equation 6, the factor $l$ is responsible for accounting for the losses that occur due to absorption and scattering of photons inside the cavity.

2.2 Cavity linewidth

The linewidth of a laser operating in a single transverse mode may be reduced (narrowed down) by stabilising it to the peak transmission of an ultra-high finesse cavity resonance. However, there is an ultimate lower limit on the laser linewidth that may be achieved in this manner. Since it is virtually impossible to distinguish spontaneously emitted photons from those emitted due to stimulated radiation, the phase of the laser light evolves randomly, putting a lower limit on the laser linewidth. Spontaneous emission introduces quantum noise due to the intrinsic random nature of the emission process itself, affecting the ultimate coherence and stability of laser light. These factors lead to the Schawlow-Townes linewidth, representing the fundamental limit to the linewidth of a laser (Hooker and Webb, 2010):

$\mathrm{\Delta }{\nu }_{\text{ST}}=\pi h{\nu }_0\frac{{\left(\mathrm{\Delta }{\nu }_c\right)}^2}{P},(7)$

where ${\nu }_0$ is laser frequency, $\mathrm{\Delta }{\nu }_c$ is the cavity resonance width and $P$ is the output laser power. To illustrate the above discussion with an example, we may consider a diode laser operating at $10\mathrm{\mu }\mathrm{W}$ power is probing the clock transition on ⁴⁰$C{a}^{+}$ ion (at $729\mathrm{n}\mathrm{m}$ with natural linewidth of $130\mathrm{m}\mathrm{H}\mathrm{z}$) with a high-finesse cavity of length $10\mathrm{c}\mathrm{m}$ with mirror reflectivity of $99.99\%$, the Schawlow-Townes linewidth (Equation 7) is $\mathrm{\Delta }{\nu }_{\text{ST}}\sim 0.8\mathrm{m}\mathrm{H}\mathrm{z}$. The desired linewidth is more than 150 times higher than the ultimate limit, and therefore, it is possible to achieve it by stabilising the laser at a sufficiently high finesse optical cavity.

Just as the linewidth of the laser is constrained by phase noise, shot noise limits the precision with which we can measure its amplitude or intensity. At low powers, small intensity fluctuations in the laser become visible owing to the quantum nature of photons which imposes limits on the detection efficiency of the signal. The randomness is due to Poissonian statistics followed by photons and is limited by the quantum uncertainty principle (Yariv, 1989). Section 3.2 on the PDH method provides an example of evaluating shot noise.

2.3 Beam stability

Optical cavities exhibit two types of modes: longitudinal and transverse. While longitudinal modes depend on cavity length (quantified by the integer the $m$ defined as before), the transverse modes represent the spatial extent of the electromagnetic field with a Gaussian intensity profile. Transverse modes are described by integer values $p$ and $q$, and both numbers are responsible for different mode shapes in the radial and azimuthal directions, respectively, in a plane perpendicular to the length of the cavity axis. The resonant frequency for a cavity mode $(m,p,q)$ combines both longitudinal and transverse modes given as:

${\nu }_{m,p,q}=\mathrm{F}\mathrm{S}\mathrm{R}\left[m+\frac{p+q+1}{\pi }\arccos \left(\sqrt{g_1{g}_2}\right)\right],(8)$

where $g_1,g_2$ are related to mirror geometry, which are defined in Equation 9.

Usually the fundamental mode is made to couple to the cavity by designing it such that transverse modes lie quite far away from longitudinal resonances to avoid higher-order mode (HOM) degeneracy (Álvarez, 2019). HOMs become co-resonant with other fundamental modes when the ratio of longitudinal mode FSR to transverse mode FSR becomes an integer. Therefore, the ratio of $R$ and $L$ should be chosen quite large so that the second term in Equation 8 becomes large enough to increase transverse FSR and prevent the coupling of HOMs.

The survival of cavity modes is also influenced by mirror geometry, which can be planar, spherical, or a combination of both. Plano-concave mirrors are commonly preferred for easier alignment and better modal confinement. For stability, specific values of the radii of curvature ($R_1$, $R_2$) and cavity length $(L)$ are required, ensuring the intracavity beam periodically reproduces its shape and enhances eigenmodes (Siegman, 1986). In unstable configurations, the beam size grows until it exceeds the mirror size, rendering the cavity unusable. However, such setups are beneficial in gravitational wave detection, as larger beams reduce Brownian noise (Wang et al., 2018), also refer to Section 4.1. Using the ray transfer matrix scheme, the stability condition for the FP cavity follows the inequality:

$\begin{array}{c}0\le \left(1-\frac{L}{R_1}\right)\left(1-\frac{L}{R_2}\right)\le 1,\\ 0\le g_1{g}_2\le 1,g_i=\left(1-\frac{L}{R_i}\right).\end{array}(9)$

The above equation is a set of hyperbolas dictating the allowed region for stable cavity configuration shown in Figure 3. Magnification in beam size after a round trip inside a cavity is provided by Equation 10:

$g=g_1{g}_2.(10)$

Figure 3

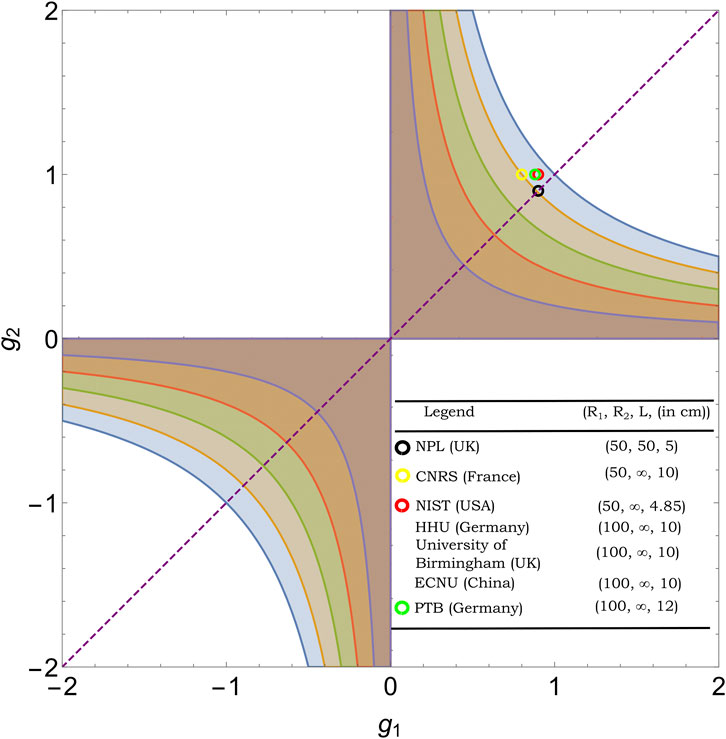
Figure 3. Stability diagram for an optical resonator. Circles show mirror configurations chosen by groups listed in Section 5. The purple-coloured dashed line across the plot shows the symmetric region where both mirror sizes have equal radii of curvatures. Notably, all groups have chosen to design their portable cavities near the edge of the stability region to achieve larger mode sizes at mirrors.

This indicates the need to design the cavity in the geometrical stability region to maintain a finite beam size. There are several cavity configurations listed below that fall under the stability region:

$\begin{array}{c}{R}_1=R_2=L\left(\text{confocal}\right),\\ R_1=R_2=\frac{L}{2}\left(\text{concentric}\right),\\ R_1=R_2=\infty \left(\text{Plane\hspace{0.17em}Parallel}\right),\\ R_1=L,R_2=\infty \text{or}{R}_1=2L,R_2=\infty \left(\text{Hemispherical}\right).\end{array}$

Mode size (beam transverse dimension) at the cavity mirror (subscripts stand for first and second mirror) is given by:

$w_{\mathrm{1,2}}=\sqrt{\frac{L\lambda }{\pi }}{\left[\frac{g_{\mathrm{2,1}}}{g_{\mathrm{1,2}}\left(1-g_1{g}_2\right)}\right]}^{\mathrm{1/4}}.(11)$

Where as the beam waist (minimum transverse dimension) inside cavity is given by:

$w_0=\sqrt{\frac{L\lambda }{\pi }}{\left[\frac{g_1{g}_2\left(1-g_1{g}_2\right)}{{\left(g_1+g_2-2g_1{g}_2\right)}^2}\right]}^{\mathrm{1/4}}.(12)$

Since laser beam intensity follows a Gaussian profile along the transverse direction, Equations 11, 12 become useful in evaluating radii of mirror curvatures and length of the cavity by measuring the mode size on a camera.

A larger spot (mode) size is desirable for a lower thermal noise floor (discussed in Section 4.1). From Figure 4A, we observe that larger mode sizes are achievable by arranging the cavity in a concentric configuration, which is in proximity to the edge of the stability diagram. For the plano-concave cavity (Figure 4B), the largest mode sizes at mirrors are achieved near $R=L$ (hemispherical configuration). However, this is a highly unstable arrangement, being on the edge of the stability diagram ($g_1=0$, $g_2\approx 1$). Instead, a near-hemispherical scheme $(R>L)$ is employed in plano-concave cavities so that $g_2$ stays inside the stability region. Consequently, many research groups opt for a hemispherical or nearly hemispherical configuration when constructing ultra-stable optical cavities (see Figure 3). This configuration ensures geometric stability and facilitates the attainment of the required beam radius at the cavity mirrors.

Figure 4

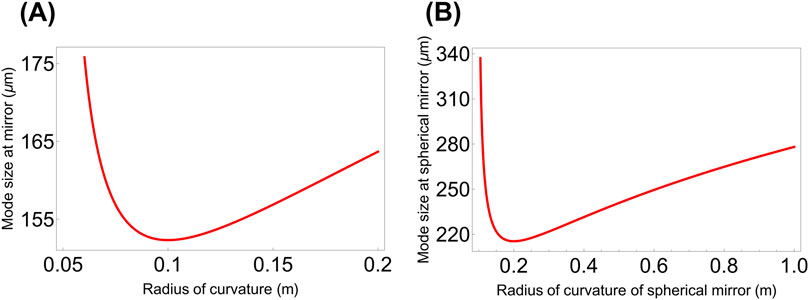
Figure 4. Plot of mode size (Equation 11) at mirror with variation in radii of curvature (A) for $R_1=R_2$(B) for a plano-concave cavity. Parameters used to generate these plots: $\lambda =729\mathrm{n}\mathrm{m}$ (clock transition for ⁴⁰${Ca}^{+}$ ion) and $L=10\mathrm{c}\mathrm{m}$.

3 Laser stabilization

Laser frequency stabilisation is an essential need in a plethora of applications, such as atomic clocks (Jiang et al., 2011), low-phase-noise microwave generation (Liu et al., 2024), gravitational wave detection (Meylahn et al., 2022), precision spectroscopy (Döringshoff et al., 2019), and other fields. The frequency stability of a diode laser deteriorates due to various noises arising out of mechanical vibrations, temperature fluctuations or noise from the laser current source. Such noise sources impact the stability of the laser frequency over different timescales. Slower or long-term drifts in laser frequency occur due to thermal effects over prolonged periods, ranging from a few hours or weeks to well over a few months. In contrast, faster or short-term fluctuations arising from technical noises affect the laser over much smaller time intervals, spanning from a microsecond to a few seconds (Boyd and Lahaye, 2024).

Various methods for laser frequency stabilization have been employed, utilizing cavity resonance or atomic transitions. The usual approach is to send a part of the unstabilized laser light towards a reference atomic transition or a cavity resonance and compare the output (and/or reflected) light with the remaining portion. One may choose a set point or reference point anywhere on the resulting atomic/cavity resonance lineshape. The set point can be selected either on the side of the transition/transmission lineshape (hence called side-of-fringe frequency stabilization) or at the top of the cavity/atomic resonance (top-of-fringe frequency stabilization), as depicted in Figure 5. An error signal, which is derived as a difference between the set point and actual frequency, is used to evaluate the laser frequency drift relative to the set point. It helps to provide feedback, which then corrects the laser frequency by modulating diode current or piezo voltage or a suitable combination of both using a control loop response (PID - Proportional, Integral and Derivative) system.

Figure 5

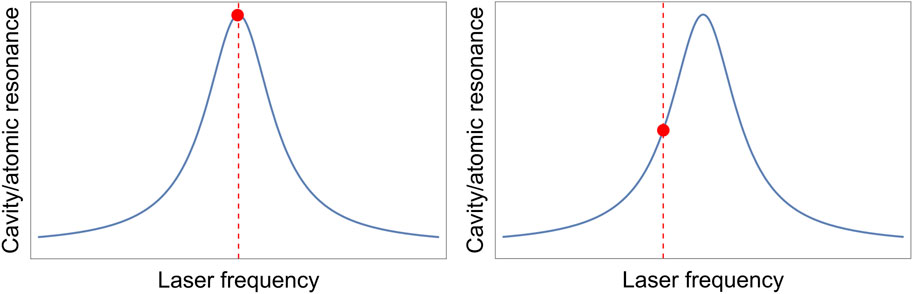
Figure 5. Laser frequency stabilization by choosing the set point at the top (left) or at the side (right) of the cavity transmission/reflection signal or atomic lineshape.

In the case of a side-of-fringe-based technique of laser frequency stabilization, the error signal becomes positive if the laser has drifted to a higher frequency and negative if it drifts to a lower frequency with respect to the set point identified on the transmission curve. While this error signal is just a constant offset, it has several practical disadvantages. The error signal amplitude is proportional to the drift in the actual laser frequency to the set point. Hence, it would be difficult to determine whether the changes in error signal amplitude stem from fluctuations in laser intensity or frequency. Consequently, any amplitude noise arising in the laser frequency can cause ambiguity in the error signal determination and impact the fidelity of stabilized laser frequency (Black, 2001). Moreover, due to the symmetry of cavity transmission or atomic lineshape profile, any significant frequency drift will result in overshooting of the corresponding set point position on the opposite side of the resonance. This leads to a negative error signal, compelling the feedback loop to adjust the frequency in the same direction, causing a runaway effect.

Alternatively, the top-of-fringe method can be used to set the reference point at the center of the cavity resonance peak. In this method, low-frequency modulation on the laser light is used to obtain the derivative of the cavity transmission signal, producing an asymmetric signal. Consequently, the sign of error signal varies with the laser frequency drift relative to the center point, effectively addressing the symmetry issue in the lineshape profile faced by the side-of-fringe laser stabilization method. However, environmental vibrations causing frequency drifts larger than the profile linewidth can quickly disengage the laser from the set point (Drever et al., 1983). Additionally, in the case of a cavity-based stabilization technique, any amplitude-modulated noise present in light, whose response is faster than the photon lifetime, cannot be detected through the cavity transmission signal. This limitation significantly affects the resolution of the laser stabilization mechanism.

(Hansch and Couillaud, 1980) proposed a simple yet elegant approach for laser frequency stabilization exploiting polarization of light. Their approach requires one to split a plane-polarized laser beam into two orthogonal polarizations by inserting a polarizer in the cavity axis. One polarization is reflected directly off the first mirror of the FP cavity, while the other passes through for a round trip, eventually returning to the first mirror. The error signal arises from the phase difference between these two polarizations. This method eliminates the need for external modulation, unlike the Pound-Drever-Hall (PDH) technique (discussed later). However, the error signal is a constant offset signal, making it susceptible to low-frequency laser technical noises.

(Bjorklund, 1980) introduced a laser frequency stabilization technique that references the laser to a Doppler-free saturated absorption line in a gas cell. In this method, the laser light is phase-modulated using an EOM, creating sidebands around the carrier frequency. When the phase-modulated laser interacts with the absorption line, it causes differential attenuation and phase shifts between the carrier and sidebands. A photodetector records the modulated light, and the signal is mixed with the original modulation frequency using a phase-sensitive detector, e.g., a lock-in amplifier, generating an error signal that indicates the deviation in laser frequency from the absorption line center. However, the effectiveness of this technique depends on the precision of the laser’s alignment to the absorption line center, as offsets can degrade the error signal quality. A significant limitation is RAM, which adds unwanted noises to the sidebands, increasing noise in the detected error signal and reducing frequency lock accuracy and stability.

(Shirley, 1982) introduced modulation transfer spectroscopy (MTS). In this method, near atomic resonance, an amplitude- or phase-modulated pump beam is made to coincide with an unmodulated counter-propagating beam, resulting in the transfer of modulation to the originally unmodulated beam. This process resembles a form of four-wave mixing. It creates a non-linear interaction near the absorption feature, generating a modulation sideband on the counter-propagating beam. The error signal used for laser stabilization is derived from this modulated absorption and dispersion line. Since MTS operates in a non-linear regime near resonance, it is less prone to background noise and baseline fluctuations that could shift the locking point of the laser. However, MTS has limitations due to the inherently weak signals generated through non-linear processes, requiring careful optimization to maximize the error signal slope for effective stabilization.

(Corwin et al., 1998) implemented the dichroic atomic vapor laser lock (DAVLL) method for laser stabilization. In this technique, a known magnetic field applied on the atomic vapor cell splits the Doppler-broadened absorption signal. The process involves converting the laser light to linearly polarized light, decomposing it into orthogonal circular polarizations (to probe the Zeeman split energy levels), and then detecting the absorption signals with balanced photodetectors. The error signal is generated based on the difference between the Doppler broadened absorption of two orthogonal circular polarizations. Since no external modulations are required, it is useful in the development of compact devices given the lower amount of resources (fewer optical and electronic components). However, DAVLL sensitivity is prone to shortcomings, such as small slope error signals and inaccurate frequency referencing points and is susceptible to environmental variations. The PDH technique provides a much larger slope in error signals, providing more precise frequency stabilization and avoiding the Doppler background issues present in DAVLL. Additionally, PDH is less affected by environmental factors, making it a more robust method of laser stabilization when frequency stabilization is required on the Hz or sub- Hz levels.

T.W. Hansch and J.L. Hall developed the optical frequency comb (OFC) technique, revolutionizing the precise measurement of optical frequencies. This groundbreaking achievement was recognized with the Nobel Prize in Physics in 2005 (Hänsch, 2006; Hall, 2006). To stabilize a laser using an OFC, the laser is referenced to one of the comb teeth. The evenly spaced frequency teeth are generated using mode-locked lasers. Frequency of the ${\mathrm{n}}^{\text{th\hspace{0.17em}}}$ tooth of comb is given by $f_n=n{f}_{\text{rep\hspace{0.17em}}}+f_{\text{off\hspace{0.17em}}}$, where $f_{\text{rep\hspace{0.17em}}}$ is the repetition frequency (spacing between comb teeth), $f_{\text{off\hspace{0.17em}}}$ is offset frequency. $f_{\text{rep\hspace{0.17em}}}$ is determined by stabilizing the OFC to a stable reference frequency, allowing precise control of the offset frequency and $f_{\text{off\hspace{0.17em}}}$ is detected via a self-reference locking method. The generation of the error signal occurs through the phase-locked loop (PLL) technology. One of the biggest advantages of this method is that multiple lasers can be stabilized simultaneously, referencing them to different comb teeth. In contrast, OFC-based stabilization is highly precise but expensive, complex, and requires large setups, limiting its practical use in many environments.

Another recently developed approach to stabilize the laser frequency leverages spectral hole burning in rare-earth-ion-doped crystals (Wu et al., 2021; Julsgaard et al., 2007). At cryogenic temperatures, these crystals exhibit an exceptionally narrow and stable lineshape profile with extended coherence times, providing a reliable frequency reference (Cone et al., 2013; Thorpe et al., 2013). The laser is stabilized by referencing its frequency at the center of the hole-burning profile. The error signal generated here uses a method similar to the Pound-Drever-Hall (PDH) technique. The key difference is that the optical cavity is replaced by a spectral hole-burning lineshape in this method. This approach offers advantages such as compactness, vibration resistance, making the system suitable for miniaturization and portability. However, a key limitation is that the crystals require a low-temperature environment facilitated only through cryogenic systems, which pose significant challenges for field operations. Also, as a precursor to stabilize the laser through the hole-burning effect, it is essential to enable a pre-stabilisation of the target laser.

The PDH laser stabilization method addresses most of the aforementioned limitations by introducing fast phase modulation of laser light (modulating frequency much larger than the cavity’s linewidth). It results in sidebands on both sides of the laser frequency (carrier), providing a large capture range. Consequently, an error signal can be detected at high frequencies where most laser noises become weak, resulting in a high SNR ratio (Fox et al., 2003). The error signal is antisymmetric as it is a derivative of reflected light. Therefore, PDH method can be called a modified version of conventional cavity or atomic resonance-based top-of-fringe stabilization, using reflected light at higher modulation frequencies.

3.1 Pound-Drever-Hall (PDH) technique

A simple schematic for the Pound-Drever-Hall (PDH) method of laser frequency stabilization method is shown in Figure 6. The laser light is initially passed through a Faraday isolator, a key component designed to prevent any reflected light from other surfaces from disrupting the laser’s output. Next, the light goes through a polarizing beam splitter (PBS), which separates it into two parts. One part is sent to the experimental setup, while the other is directed towards the PDH setup. In the PDH setup, the light travels through an EOM, driven by a radio-frequency (RF) signal. This RF signal changes the refractive index of the medium, leading to phase modulation of the incoming light and generating a pair of sidebands on either side of the original laser frequency (the carrier). After the EOM, the light enters a high-finesse optical cavity via another PBS. When the light reflects off the high-finesse cavity, both the carrier and the sidebands are detected by a photodiode, which converts the optical signal into an electrical one containing phase information. This electrical signal is mixed with another RF signal at the modulation frequency, creating a beat signal. A low-pass filter removes the higher frequency components, isolating the DC portion, which contains information about the phase of the laser light. This phase information detects frequency deviations and is fed into a feedback loop to correct and stabilize the laser’s frequency.

Figure 6

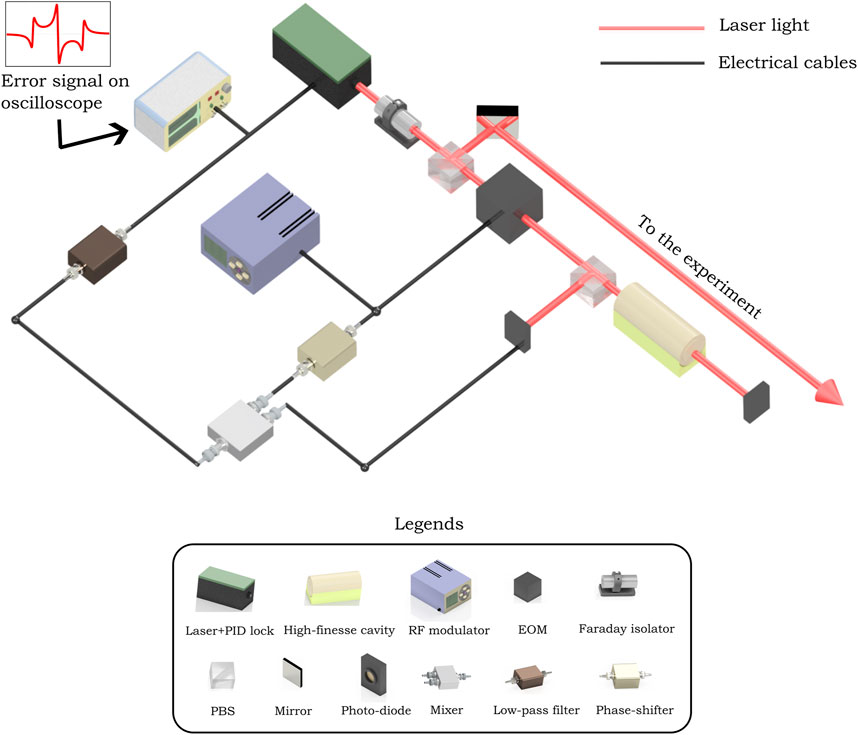
Figure 6. Schematic for PDH laser frequency stabilization method, which uses phase modulation of laser light. A polarizing beam splitter (PBS) is usually placed after a half-wave plate (not shown here) to control the intensity of light going along two polarizations.

Let us consider the laser’s electric field as $E=E_0{e}^{i\omega t}$, $E_0$ being the complex amplitude, $\omega$ is frequency and $t$ is time. After passing through EOM, it takes the form $E=E_0{e}^{i(\omega t+\beta \sin \mathrm{\Omega }t)}$, where $\mathrm{\Omega }$ and $\beta$ denote RF-modulation frequency and modulation depth, respectively. The Jacobi-Anger relation (Andrews et al., 1999) is used here to simplify the exponential by expressing in terms of Bessel functions of the first kind $J_n$, where n is integer order:

$e^{i\beta \sin \mathrm{\Omega }t}=J_0\left(\beta \right)+2{\displaystyle \sum _{n=1}^{\infty }}{J}_{2n}\left(\beta \right)\cos \left(2n\mathrm{\Omega }t\right)+2i{\displaystyle \sum _{n=0}^{\infty }}{J}_{2n+1}\left(\beta \right)\sin \left(\left(2n+1\right)\mathrm{\Omega }t\right).(13)$

For sufficiently low modulation depth, only first-order terms can be retained, and the expression in Equation 13 reduces to $e^{i\beta \sin \mathrm{\Omega }t}\approx J_0(\beta )+2i{J}_1(\beta )\sin \mathrm{\Omega }t$. Writing sine term in exponentials reveals that the light breaks out in three independent signals, one being the carrier and two sidebands with frequency $\omega \pm \mathrm{\Omega }$:

$E\approx E_0\left\{J_0\left(\beta \right)e^{i\omega t}+J_1\left(\beta \right)e^{i\left(\omega +\mathrm{\Omega }\right)t}-J_1\left(\beta \right)e^{i\left(\omega -\mathrm{\Omega }\right)t}\right\}.(14)$

Under this approximation, almost all power is divided among three components. If the incident power on the EOM is $P_0=|E_0{|}^2$, then $P_0=P_c+2P_s$, where $P_c=P_0{J}_0^2(\beta )$ is carrier power and $P_s=P_0{J}_1^2(\beta )$ is power among each of sidebands.

The above light signal containing sidebands impinges on the cavity, further breaking in reflected and transmitted parts. Following the argument given by (Black, 2001), two components make the total reflected light: one is the promptly reflected light, bouncing right away from the first mirror, and the other is the leakage light which enters the cavity and meets the promptly reflected light after making the round trip. The phase difference acquired by the leakage light decides the coherent sum of two parts. When the wavelength is near the resonance condition of the resonator, the total reflected light is given as:

$E_{\text{ref}}=E_{0}r\frac{e^{i\delta }-1}{1-r^2{e}^{i\delta }}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\delta =\frac{\omega }{\mathrm{F}\mathrm{S}\mathrm{R}}=2\frac{2\pi }{\lambda }L.(15)$

Thus, the reflection amplitude $R(\omega )$ is defined as:

$R\left(\omega \right)=\frac{E_{\text{ref}}}{E_0}=r\frac{e^{i\delta }-1}{1-r^2{e}^{i\delta }},(16)$

where $\delta$ is the phase difference associated with the round-trip path covered by the light field.

Due to the reflection of the carrier and the sidebands, each component (Equation 15) has its own reflection coefficients $\left(R(\omega )\right.$ and $R(\omega \pm \mathrm{\Omega })$, according to Equation 16). The total reflected electric field then given by Equation 17:

$E_{\text{ref}}=E_0\left\{R\left(\omega \right)J_0\left(\beta \right)e^{i\omega t}+R\left(\omega +\mathrm{\Omega }\right)J_1\left(\beta \right)e^{i\left(\omega +\mathrm{\Omega }\right)t}-R\left(\omega -\mathrm{\Omega }\right)J_1\left(\beta \right)e^{i\left(\omega -\mathrm{\Omega }\right)t}\right\}.(17)$

The photodetector will read the reflected power:

$\begin{array}{cc}\hfill P_{\text{ref}}=E_{\text{ref}}^{*}{E}_{\text{ref}}=& |E_0{|}^2\left\{|R\left(\omega \right){|}^2{J}_0^2\left(\beta \right)+|R\left(\omega +\mathrm{\Omega }\right){|}^2{J}_1^2\left(\beta \right)+|R\left(\omega -\mathrm{\Omega }\right){|}^2{J}_1^2\left(\beta \right)\right.\hfill \\ \hfill & +J_0\left(\beta \right)J_1\left(\beta \right)\left[R^{*}\left(\omega \right)R\left(\omega +\mathrm{\Omega }\right)e^{i\mathrm{\Omega }t}-R^{*}\left(\omega \right)R\left(\omega -\mathrm{\Omega }\right)e^{-i\mathrm{\Omega }t}\right.\hfill \\ \hfill & +R\left(\omega \right)R^{*}\left(\omega +\mathrm{\Omega }\right)\left.e^{-i\mathrm{\Omega }t}-R\left(\omega \right)R^{*}\left(\omega -\mathrm{\Omega }\right)e^{i\mathrm{\Omega }t}\right]\hfill \\ \hfill & -\left.J_1^2\left(\beta \right)\left[R^{*}\left(\omega +\mathrm{\Omega }\right)R\left(\omega -\mathrm{\Omega }\right)e^{-2i\mathrm{\Omega }t}+R^{*}\left(\omega -\mathrm{\Omega }\right)R\left(\omega +\mathrm{\Omega }\right)e^{2i\mathrm{\Omega }t}\right]\right\},\hfill \end{array}(18)$

or

$\begin{array}{cc}\hfill P_{\text{ref}}=|E_{\text{ref}}{|}^2=& P_0\left[|R\left(\omega \right){|}^2{J}_0^2\left(\beta \right)+|R\left(\omega +\mathrm{\Omega }\right){|}^2{J}_1^2\left(\beta \right)+|R\left(\omega -\mathrm{\Omega }\right){|}^2{J}_1^2\left(\beta \right)\right.\hfill \\ \hfill & +2J_0\left(\beta \right)J_1\left(\beta \right)\cos \mathrm{\Omega }t\text{\hspace{0.17em}Re}\left\{R\left(\omega \right)R^{*}\left(\omega +\mathrm{\Omega }\right)-R^{*}\left(\omega \right)R\left(\omega -\mathrm{\Omega }\right)\right\}\hfill \\ \hfill & +2J_0\left(\beta \right)J_1\left(\beta \right)\sin \mathrm{\Omega }t\text{\hspace{0.17em}Im}\left\{R\left(\omega \right)R^{*}\left(\omega +\mathrm{\Omega }\right)-R^{*}\left(\omega \right)R\left(\omega -\mathrm{\Omega }\right)\right\}\hfill \\ \hfill & -\left.J_1^2\left(\beta \right)\left\{\cos 2\mathrm{\Omega }t\text{\hspace{0.17em}Re}\left\{R^{*}\left(\omega +\mathrm{\Omega }\right)R\left(\omega -\mathrm{\Omega }\right)\right\}-\sin 2\mathrm{\Omega }t\text{\hspace{0.17em}Im}\left\{\left(R\left(\omega +\mathrm{\Omega }\right)\right)R^{*}\left(\omega -\mathrm{\Omega }\right)\right\}\right\}\right].\hfill \end{array}(19)$

Equation 18 or Equation 19 contains constant and oscillating terms (with frequencies $\mathrm{\Omega }$ and $2\mathrm{\Omega }$). The subsequent treatment chosen for this signal profoundly influences the performance of the servo-lock, as the essence of the PDH technique lies in it. It must be noted that, $\sin \mathrm{\Omega }t$ and $\cos \mathrm{\Omega }t$ are the only useful terms as they contain the phase of the carrier signal. Let us define the phase information term as:

$E\left(\omega ,\mathrm{\Omega }\right)=R\left(\omega \right)R^{*}\left(\omega +\mathrm{\Omega }\right)-R^{*}\left(\omega \right)R\left(\omega -\mathrm{\Omega }\right).(20)$

This expression is plotted for two different values of $\mathrm{\Omega }$ in Figure 7. Notably, the plot depicts a steep slope on both sides of the carrier frequency with a change in sign as frequency wanders towards the lower or higher side of the resonance. The reflected signal (power read by photo-diode as expressed in Equation 19) is mixed with a signal $\sin \mathrm{\Omega }t$ generated by the RF modulator (after adding a phase $\varphi$) to finally extract $E(\omega ,\mathrm{\Omega })$. The inclusion of extra phase $\varphi$ compensates for the practical path delays encountered by the reflected signal from the photodiode along the electrical lines. Subsequently, the signal undergoes through a low-pass filter, facilitating the extraction of phase information of the carrier. Prior to analyzing the filtered signal, it is relevant to discuss the effect of two extremes of modulation frequency $\mathrm{\Omega }$ that dictates the behaviour of $E(\omega ,\mathrm{\Omega })$.

Figure 7

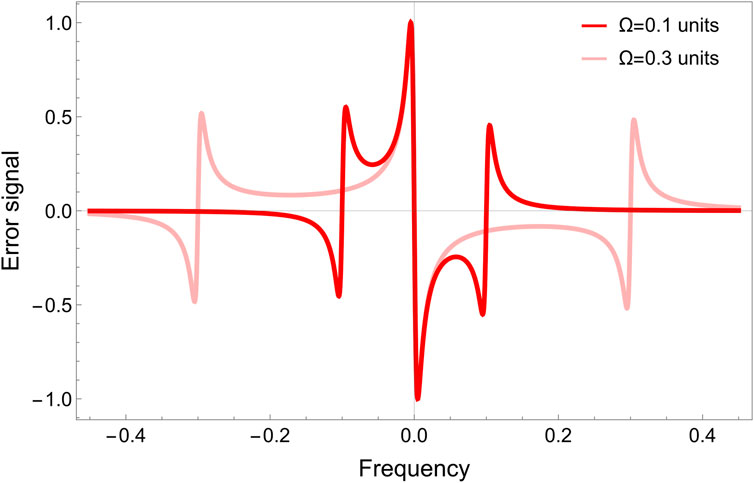
Figure 7. Plot of $E(\omega ,\mathrm{\Omega })$ for two different modulation frequencies showing the effect of capture range on frequency stabilization. Frequencies of laser light and RF modulation are in arbitrary units. Other parameters used: FSR = 1.5 units and r = 99.99%.

3.1.1 Low modulation frequency regime

Here, we will examine the effect of very low modulation frequency, i.e., $\mathrm{\Omega }\gg \mathrm{FWHM}$. In this case, the sideband reflection coefficients can be expressed as given in Equation 21:

$R\left(\omega \pm \mathrm{\Omega }\right)\approx R\left(\omega \right)\pm \frac{dR\left(\omega \right)}{d\omega }\mathrm{\Omega }\left({\text{Taylor}}^{\prime }\text{s\hspace{0.17em}expansion}\right),(21)$

so that the phase term (Equation 20) can be written as:

$E\left(\omega ,\mathrm{\Omega }\right)\approx 2\mathrm{\Omega }\text{\hspace{0.17em}Re}\left[R\left(\omega \right)\frac{d{R}^{*}\left(\omega \right)}{d\omega }\right]=\mathrm{\Omega }\text{\hspace{0.17em}Re}\left[\frac{d|R\left(\omega \right){|}^2}{d\omega }\right],(22)$

and only the cosine terms survive in Equation 19. Then, the mixer will multiply the expression in Equation 22 with the RF signal (see Figure 6):

$\sin \left(\mathrm{\Omega }t+\varphi \right)\times 2J_0\left(\beta \right)J_1\left(\beta \right)\cos \mathrm{\Omega }t\text{\hspace{0.17em}Re}\left[\frac{d|R\left(\omega \right){|}^2}{d\omega }\right]\mathrm{\Omega }.(23)$

The signal in Equation 23 is passed through the low pass filter to yield the PDH error signal, which can be observed on an oscilloscope:

$ϵ=2P_0{J}_0\left(\beta \right)J_1\left(\beta \right)\mathrm{\Omega }\sin \varphi \frac{d|R\left(\omega \right){|}^2}{d\omega }.(24)$

The importance of phase delay $\varphi$ becomes clear now as it can be adjusted to obtain the low-frequency error signal (in Figure 6). At $\varphi =\pi /2$, Equation 24 simplifies to:

$ϵ=2\sqrt{P_c{P}_s}\mathrm{\Omega }\frac{d|R\left(\omega \right){|}^2}{d\omega }.(25)$

The PDH error signal in Equation 25 is plotted in Figure 8. It demonstrates that the PDH error signal has a smaller acquisition range at lower modulation frequencies, thereby limiting its utility. Subsequent analysis will showcase that PDH serves best at higher modulation frequencies.

Figure 8

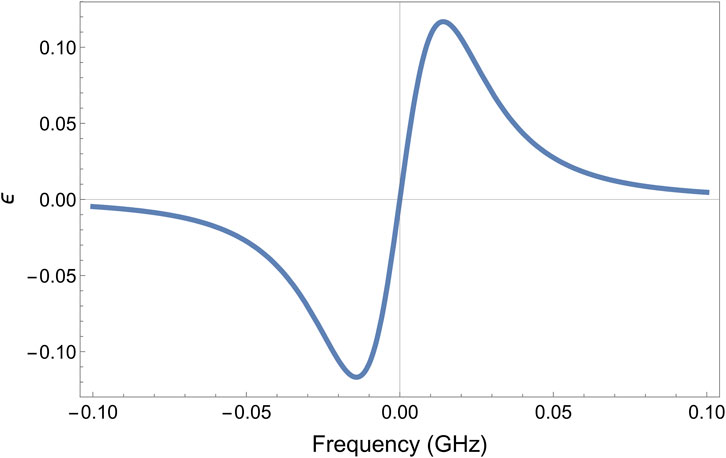
Figure 8. Error signal at very low modulation frequency. Parameters used are: $P_0=50\mathrm{\mu }$W, $\beta =1,\mathrm{\Omega }=1$ MHz and FWHM = 49 MHz.

3.1.2 High modulation frequency regime

In the regime $\mathrm{\Omega }\gg \mathrm{FWHM}$, sidebands would be located quite far from the transmission peaks (or the carrier frequency), and they will be completely reflected, i.e., $R(\omega \pm \mathrm{\Omega })=-1$ Therefore, Equation 20 will take the form:

$E\left(\omega ,\mathrm{\Omega }\right)=-1\left[R\left(\omega \right)-R^{*}\left(\omega \right)\right]=-2i\text{\hspace{0.17em}Im}\left[R\left(\omega \right)\right].(26)$

This time, sine term survives in Equation 19, so that mixer multiplies the expression in Equation 26 with RF signal:

$\sin \left(\mathrm{\Omega }t+\varphi \right)\times 2J_0\left(\beta \right)J_1\left(\beta \right)\sin \mathrm{\Omega }t\left(-2i\right)\text{Im}\left[R\left(\omega \right)\right].(27)$

In this case, the expression in Equation 27 with yield a low pass signal (after adjusting phase $\varphi =0$):

$ϵ=-4i{P}_0{J}_0\left(\beta \right)J_1\left(\beta \right)\text{Im}\left[R\left(\omega \right)\right].(28)$

The expression in Equation 28 can be simplified using the following approximations to see the significance of high-frequency modulation. If the laser frequency drifts by a very small amount from the resonance $(\mathrm{\Delta }\omega \ll {\omega }_0)$, the phase in $R(\omega )$ changes as (Equation 16; Equation 8):

$\delta =\frac{{\omega }_0+\mathrm{\Delta }\omega }{\mathrm{F}\mathrm{S}\mathrm{R}}=2\pi N+\frac{\mathrm{\Delta }\omega }{\mathrm{F}\mathrm{S}\mathrm{R}}\left(\text{N\hspace{0.17em}being\hspace{0.17em}integer}\right).$

These small changes would be incorporated in the reflected carrier signal as:

$R\left(\omega +\mathrm{\Delta }\omega \right)=r\frac{e^{i\left(2\pi N+\frac{\mathrm{\Delta }\omega }{\mathrm{F}\mathrm{S}\mathrm{R}}\right)}-1}{1-r^2{e}^{i\left(2\pi N+\frac{\mathrm{\Delta }\omega }{\mathrm{F}\mathrm{S}\mathrm{R}}\right)}}\approx r\frac{i\frac{\mathrm{\Delta }\omega }{\mathrm{F}\mathrm{S}\mathrm{R}}}{1-r^2}.$

Making use of $\mathrm{\Delta }\omega =2\pi \mathrm{\Delta }\nu$ and recalling finesse (Equation 5), $\mathcal{F}=\frac{\pi r}{1-r^2}=\frac{\mathrm{F}\mathrm{S}\mathrm{R}}{{\nu }_{1/2}}$,

$R\left(\nu +\mathrm{\Delta }\nu \right)=2i\frac{\mathrm{\Delta }\nu }{{\nu }_{1/2}}.$

Then the PDH error signal for high modulation can be expressed as:

$ϵ=-4i{P}_0{J}_0\left(\beta \right)J_1\left(\beta \right)\left[2i\frac{\mathrm{\Delta }\nu }{{\nu }_{1/2}}\right]=8\sqrt{P_c{P}_s}\frac{\mathrm{\Delta }\nu }{{\nu }_{1/2}}.(29)$

This error signal responds directly to any linear drift in the laser frequency $(\mathrm{\Delta }\nu )$ and thus makes the feedback loop highly sensitive to frequency fluctuations. It is valid for larger frequency excursions that are much larger than the resonance linewidth, making the PDH technique not limited to the linewidth features only. Therefore, the high modulation frequency region exploits the PDH technique to its fullest potential.

However, it is crucial to note that the PDH error signal is unable to distinguish between variations in laser frequency and changes in cavity length. This means that any change in the cavity length, while the laser output remains unchanged, will manifest as a shift in the laser’s frequency. This may happen because the cavity itself is influenced by various noise sources, as elaborated in the Section 4. Therefore, a more general expression for the error signal, containing both kinds of fluctuations, is given as:

${ϵ}_{\text{PDH}}=\frac{8\sqrt{{\mathrm{P}}_{\mathrm{c}}{\mathrm{P}}_{\mathrm{s}}}\nu }{{\nu }_{1/2}}\left[\frac{\mathrm{\Delta }v}{\nu }+\frac{\mathrm{\Delta }L}{L}\right].(30)$

3.1.3 Dependence of error signal on modulation depth

To achieve a substantial feedback signal, a considerably steeper error signal is required. Equation 29 suggests that $ϵ$ can be maximized either by reducing the linewidth of the resonance peaks (for which higher finesse is required) or by increasing the term $\sqrt{P_c{P}_s}$, which depends on the modulation depth $\beta$. Determining optimum modulation depth involves finding the maximum of $ϵ$ by writing it in terms of Bessel functions:

$\frac{dϵ}{d\beta }=\frac{1}{2}{J}_0^2\left(x\right)-J_1^2\left(x\right)-\frac{1}{2}{J}_0\left(x\right)J_1\left(x\right)=0,(31)$

Solving Equation 31 yields the first zero at $\beta =1.08$ (also mentioned in (Black, 2001)). However, this contradicts the approximation used in obtaining Equation 14, which neglects the higher-order terms. Considering a large value of $\beta$, second-order sidebands grow significantly in the output beam of EOM, and the electric field expression in Equation 14 modifies to:

$E\approx E_0\left\{J_0\left(\beta \right)e^{i\omega t}+J_1\left(\beta \right)\left(e^{i\left(\omega +\mathrm{\Omega }\right)t}-e^{i\left(\omega -\mathrm{\Omega }\right)t}\right)+J_2\left(\beta \right)\left(e^{i\left(\omega +2\mathrm{\Omega }\right)t}+e^{i\left(\omega -2\mathrm{\Omega }\right)t}\right)\right\}.(32)$

Again, following the same procedure on Equation 32 to find the error signal, the useful expression after filtering out all AC terms reduces to:

$ϵ=\sqrt{P_c{P}_{s_1}}\mathrm{I}\mathrm{m}\left\{E\left(\omega ,\mathrm{\Omega }\right)\right\}+\sqrt{P_c{P}_{s_2}}\mathrm{I}\mathrm{m}\left\{E\left(\omega ,2\mathrm{\Omega }\right)\right\},(33)$

where $E(\omega ,\mathrm{\Omega })=R(\omega )R^{*}(\omega +\mathrm{\Omega })-R^{*}(\omega )R(\omega -\mathrm{\Omega })$ and $E(\omega ,2\mathrm{\Omega })=R(\omega +\mathrm{\Omega })R^{*}(\omega +2\mathrm{\Omega })-R(\omega -\mathrm{\Omega })R^{*}(\omega -2\mathrm{\Omega })$. $P_{s_1}$ and $P_{s_2}$ denote the power in first order and second order sidebands, respectively. The error signal in Equation 33 is plotted in Figure 9 for $1\%$ of input power fed to second-order sidebands. It is evident that including second-order sidebands doesn’t affect the error signal over the effective capture range. Therefore, it is safe to choose a value of modulation depth $\beta$ close to unity for a higher slope of the error signal $ϵ$.

Figure 9

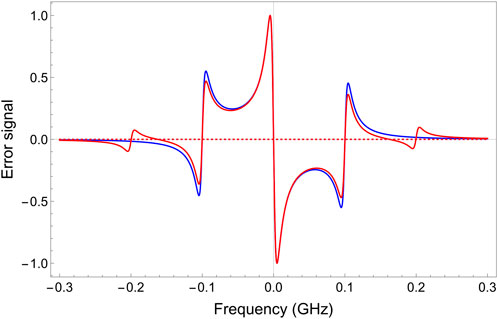
Figure 9. Effect of second order sidebands on the error signal. The blue curve is the error signal with first-order sidebands only (Equation 20), and the red curve contains both first and second-order sidebands (Equation 33). P_s1 and P_s2 are considered 1% and 33% of P₀, respectively. Other parameters used: Ω = 100 MHz and FWHM = 10 MHz.

3.2 Shot noise limit

Laser stabilisation using the PDH technique is fundamentally restricted by the shot noise. Shot noise occurs because of the quantum nature of light (photon) itself. At very low laser powers, individual photons arrive randomly at the detector and produce larger fluctuations than the average signal. Black (2001) estimated shot noise in PDH error signal due to randomly approaching photons on the photodiode. On resonance, since there is no reflected carrier power, the detected power is approximate $P_{\text{ref}}=2P_s$ and shot noise spectral density is given as,

$S=\sqrt{2\frac{hc}{\lambda }2P_s}.(34)$

Scaling this noise spectrum to yield equivalent noise sensitivity in the optical length of the cavity (dividing Equation 34 by proportional constant term $\frac{8\sqrt{P_c{P}_s}}{{\nu }_{1/2}}$ in the error signal (Equation 29)):

$S_L=\frac{\sqrt{hc}}{8}\frac{\sqrt{\lambda }}{\mathcal{F}\sqrt{P_c}},(35)$

Equation 35 can be expressed in terms of frequency noise,

$S_v=\frac{v}{L}{S}_L=\frac{\sqrt{h{c}^3}}{8}\frac{1}{\mathcal{F}L\sqrt{\lambda P_c}}.(36)$

For a laser at $729\mathrm{n}\mathrm{m}$ at input power of $10\mathrm{\mu }\mathrm{W}$ locked to an ultra-stable cavity of length $10\mathrm{c}\mathrm{m}$ with finesse 400000, Equation 36 gives $S_L\sim 3.8\times 10^{-20}\frac{\mathrm{m}}{\sqrt{\mathrm{H}\mathrm{z}}}$ which is at significantly lower level with respect to typical fundamental thermal noise floor found in most exceptional optical resonators $(10^{-16})$.

4 Noises limiting the stability of cavity

4.1 Fundamental thermal noise floor

The stability of an ultra-stable cavity is ultimately constrained due to fundamental thermal noise. It emanates due to the material properties of cavity components (mirror substrates, mirror coatings, and cavity spacer), leading to instability in the optical length of the cavity. Frequency of ${\mathrm{m}}^{\text{th}}$ longitudinal mode of the cavity is given by:

$v_m=m\frac{c}{2nL}.(37)$

In Equation 37 $n$ represents the refractive index of the medium within the cavity bore. Upon differentiation,

$\frac{\mathrm{\Delta }v}{v}=-\frac{\mathrm{\Delta }L}{L}.(38)$

Equation 38 indicates that the stability in the cavity’s optical length governs the frequency stability of laser.

Levin formulated inherent thermal noise (Levin, 1998), based upon an earlier calculation reported for LIGO’s mirrors (González and Saulson, 1994) using fluctuation-dissipation theorem (Callen and Welton, 1951). Power spectral density due to thermal fluctuation noise at a particular frequency $f$, in length, is given by:

$S_L\left(f\right)=\frac{2K_{B}T}{{\left(\pi f\right)}^2}\frac{W_{\text{diss}}}{F_0^2}.(39)$

Here, $T$ and $K_B$ represent operating temperature (in Kelvin) and Boltzmann’s constant, respectively. A periodic force of amplitude $F_0$ (e.g., the radiation pressure force of laser) was supposed to act on the cavity mirrors while deriving these results. $W_{\text{diss}}$ denotes the time-averaged power dissipation inside the test mass (cavity component) subjected to $F_0$:

$W_{\text{diss\hspace{0.17em}}}=2\pi fU\alpha .(40)$

Here, $U$ represents the elastic strain energy corresponding to the maximum deformation of test mass and $\alpha$ denotes the mechanical loss angle of material. The latter is a measure of energy dissipation within a medium subjected to periodic stress, resulting in heat generation and contributing to the thermal noise. The above equations elucidate Brownian noise’s dependence on the material’s mechanical properties. Generally, the deformation of the cavity shape results from different combinations of loss angles and the coefficient of thermal expansion (CTE) of the component materials (Legero et al., 2010).

Therefore, identifying suitable materials for mirror substrate, mirror coating, and spacer is crucial for reducing the fundamental thermal noise (Harry et al., 2012). Fused silica (FS), ultra-low-expansion (ULE) glass, zerodur, silicon, and some glass ceramics are popular choices for spacers and substrates because of their extremely low CTEs and lower loss angles. Table 1 lists some of the properties of these materials. At cryogenic temperature ($\le 1.5$ K), a spacer made from a single silicon crystal demonstrated a thermal noise floor of order $10^{-17}$, as the pure crystalline structure of the spacer has negligible aging (lower long-term drift) (Wiens et al., 2014). The loss angle of mirror coatings generally limits the thermal noise compared to that of substrate and spacer materials. Several groups reported different material choices for mirror coatings to reduce the thermal noise floor. ${\mathrm{S}\mathrm{i}\mathrm{O}}_2/{\mathrm{T}\mathrm{a}}_2{\mathrm{O}}_5$ dielectric coating is usually chosen by most groups, but it significantly limits noise in mixed material (i.e., spacer and substrate are made from distinct materials) cavities (Kessler et al., 2012). Crystalline coatings (e.g., $\mathrm{G}\mathrm{a}\mathrm{A}\mathrm{s}/\mathrm{A}\mathrm{l}\mathrm{G}\mathrm{a}\mathrm{A}\mathrm{s}$, $\mathrm{T}\mathrm{i}{\mathrm{O}}_{\mathrm{2}}:\mathrm{G}\mathrm{e}{\mathrm{O}}_{\mathrm{2}}$) with lower loss angles have reduced thermal noise significantly (Cole et al., 2013; Chalermsongsak et al., 2016). In gravitational wave detectors (Vajente et al., 2021), demonstrated a two-fold improvement in thermal noise when mirrors were coated with a mixture of Titanium Dioxide $\left({\mathrm{T}\mathrm{i}\mathrm{O}}_2,44\%\right)$ and Germanium-Di-oxide $\left({\mathrm{G}\mathrm{e}\mathrm{O}}_2,56\%\right)$.

Table 1

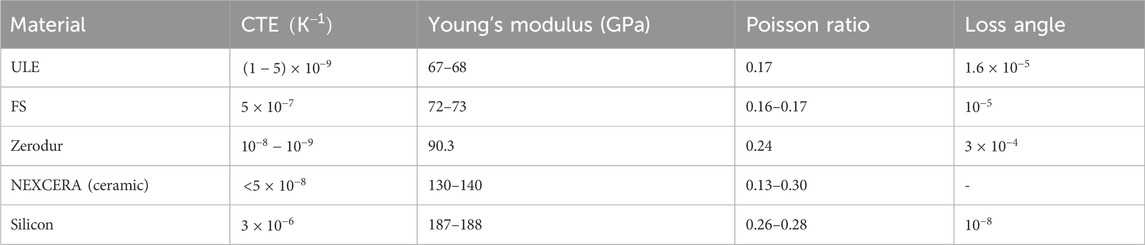
Table 1. Widely used materials for spacer and mirror substrate. CTEs are mentioned around room temperature.

Equation 39 can be further extended to describe the length fluctuations in the form of power spectral density due to all components of the cavity as:

$S_L\left(f\right)=\frac{4K_{B}T}{\pi f{F}_0^2}\left(U_{\text{SP}}{\alpha }_{\text{SP}}+U_{\text{IMS}}{\alpha }_{\text{IMS}}+U_{\text{EMS}}{\alpha }_{\text{EMS}}+U_{\text{IMC}}{\alpha }_{\text{IMC}}+U_{\text{EMC}}{\alpha }_{\text{EMC}}\right),(41)$

where $U$ and $\alpha$ are the same quantities defined in Equation 40. If mirror substrates and coatings are identical (that is, $\mathrm{I}\mathrm{M}\mathrm{C}=\mathrm{E}\mathrm{M}\mathrm{C}=\mathrm{M}\mathrm{C}$ and $\mathrm{I}\mathrm{M}\mathrm{S}=\mathrm{E}\mathrm{M}\mathrm{S}=\mathrm{M}\mathrm{S}$),

$S_L\left(f\right)=\frac{4K_{B}T}{\pi f{F}_0^2}\left(U_{\text{SP}}{\alpha }_{\text{SP}}+2U_{\text{MS}}{\alpha }_{\text{MS}}+2U_{\text{MC}}{\alpha }_{\text{MC}}\right),(42)$

where the abbreviations used in Equations 41, 42 read as:

Kessler et al. (2012) built upon earlier put theoretical work on thermal noises and presented simplified formulas for quantifying substrate and coating contribution to noise:

$\begin{array}{cc}\hfill & S_{\text{MS}}=\frac{4K_{B}T}{2\pi f}\frac{1-{\sigma }_{\text{MS}}^2}{\sqrt{\pi }{Y}_{\text{MS}}\omega }{\alpha }_{\text{MS}}\hfill \\ \hfill & S_{\text{MC}}=\frac{4K_{B}T}{2\pi f}\frac{2\left(1+{\sigma }_{\text{MS}}\right)\left(1-2{\sigma }_{\text{MS}}\right)d_{\text{MC}}}{\pi Y_{\text{MS}}{\omega }^2}{\alpha }_{\text{MC}}.\hfill \end{array}(43)$

It is important to note here that the mirrors were treated as infinite half-space in deriving these equations, that is, beam size was considered quite small relative to the mirror dimensions. Here, ${\sigma }_{\text{MS}}$ and ${\mathrm{Y}}_{\text{MS}}$ represent the Poisson’s ratio and Young’s modulus of the mirror substrate, $d_{\text{MC}}$ is the thickness of mirror coating, ${\alpha }_{\text{MS}}$ and ${\alpha }_{\text{MC}}$ denotes loss angle of the mirror substrate and mirror coating. $\omega$ represents the beam waist here. Contribution from cavity spacer to the thermal noise was also improved upon the earlier work reported by (Numata et al., 2004) by reducing the effective face area of the cylindrical spacer (subtracting the face area of the central bore):

$U_{\text{SP}}=\frac{L}{2Y_{\text{SP}}{A}_{\text{SP}}}{F}_0^2=\frac{L}{2\pi Y_{\text{SP}}\left(R_{\text{SP}}^2-r_{\text{SP}}^2\right)}{F}_0^2,(44)$

where $r_{\text{SP}}$ and $R_{\text{SP}}$ in Equation 44 denote the inner and outer (bore) radius of a cylindrical spacer of average length $L$, respectively. Thermal fluctuation noise spectral density in length due to cavity spacer then reduces to:

$S_{\text{SP}}\left(f\right)=\frac{4K_{B}T}{\pi f}\frac{L}{2\pi Y_{\text{SP}}\left(R_{\text{SP}}^2-r_{\text{SP}}^2\right)}{\alpha }_{\text{SP}}.(45)$

The resulting fractional frequency $\left(y=\frac{\mathrm{\Delta }v}{v}\right)$ instability due to thermal fluctuations in length can be related as $S_y(f)\equiv \frac{S_v(f)}{v^2}=\frac{S_L(f)}{L^2}$. In time domain, instability of fractional frequency is represented by Allan deviation, ${\sigma }_y(\tau )$. Since the thermal noise in Equation 43 and Equation 45 from all three contributions behaves as $1/f$, the resulting Allan deviation for $1/f$ noise (or flicker frequency) noise will be constant in time:

${\sigma }_y\left(\tau \right)={\sigma }_y=\sqrt{2\ln \left(2\right)S_y\left(f\right)f}.(46)$

Generally, mirror coatings significantly contribute to fundamental thermal noise floor due to their higher loss angle (Amairi et al., 2013), while the noise due to the spacer has little effect on the overall fractional frequency instability.

From Equation 43, it is evident that the noise contribution due to mirror substrate and mirror coating scales as ${\omega }^{-1}$ and ${\omega }^{-2}$ respectively. This suggests using a larger beam diameter and choosing a hemispherical or near hemispherical cavity configuration rather than a concentric or confocal configuration for better stability (Figure 10). Equation 46 implies that the fractional frequency instability due to spacer contribution scales as $\frac{1}{\sqrt{L}}$, which advocates for utilizing longer cavity spacers for lower thermal noise. However, it compromises with the vibrational stability. In comparison to lab-based longer cavities, the choice of a smaller length for the spacer puts a significant restriction on the stability of portable cavities to attain the fundamental thermal noise level below $10^{-16}$, as shown in Figure 11. Utilizing a smaller bore radius is also preferable due to the inverse dependence of the noise spectral density on the cavity spacer face area (see Equation 45). While all this analysis has been conducted for Gaussian beams and optimizing cavity parameters, alternative approaches suggesting different beam and mirror shapes can be considered to lower the thermal noise floor by introducing entirely new cavity designs (Bondarescu et al., 2008).

Figure 10

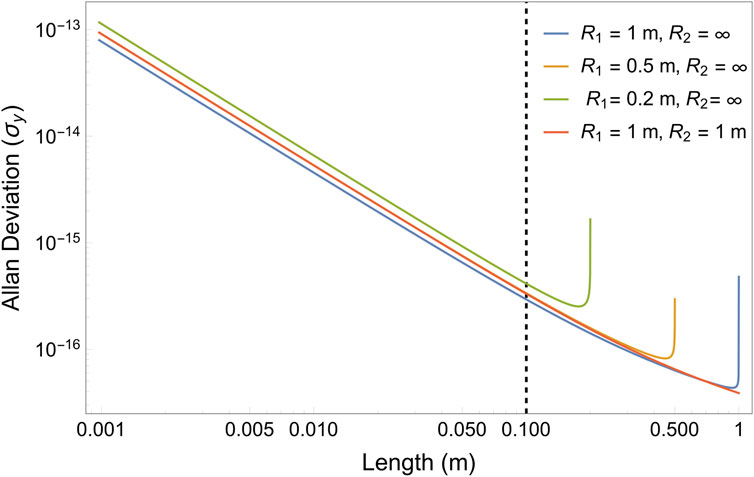
Figure 10. Variation in Allan deviation (thermal noise) with respect to cavity length for different combinations of mirror curvatures. For example, the near-planar geometry $({\mathrm{R}}_{\mathrm{1}}=1\mathrm{m},{\mathrm{R}}_{\mathrm{2}}=\infty )$ is the optimum choice for a short $10\mathrm{c}\mathrm{m}$ cavity (shown by dashed line).

Figure 11

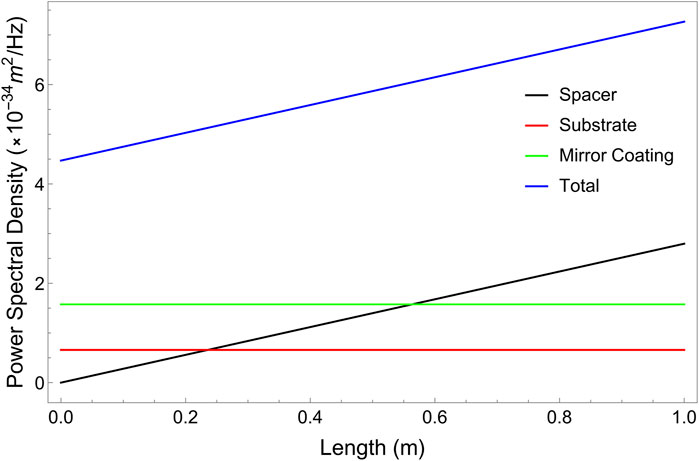
Figure 11. Plot of noise contribution from different parts of the optical cavity in the fundamental thermal noise floor with variation in length. Mirrors of fused silica and cavity spacer of ULE glass are considered here (see Equation 43; Equation 45). $\omega$ (beam waist) was considered constant here.

4.2 External perturbations affecting the stability of cavity

4.2.1 Temperature fluctuation noise

Fluctuations in the ambient temperature cause cavity components to thermally expand (or compress), affecting the optical length along its axis. According to the law of thermal expansion, for a change of $\mathrm{\Delta }T$ in temperature, a rod of length $L$ with CTE equals to $\alpha (T)$ experiences a change in length for a change $\mathrm{\Delta }T$ in temperature:

$\mathrm{\Delta }L=\alpha \left(T\right)L\mathrm{\Delta }T.(47)$

Using the above equation and Equation 38, a change in laser frequency can be estimated arising out of temperature-induced changes in the cavity dimensions. To illustrate the severe impact of temperature fluctuations, let us consider the following example. For addressing the $729\mathrm{n}\mathrm{m}$ clock transition in ⁴⁰Ca⁺ ion with a linewidth around $130\mathrm{m}\mathrm{H}\mathrm{z}$, let us consider a ULE cavity (see Table 1) of length $L=10\mathrm{c}\mathrm{m}$ operating under vacuum. Let us consider the refractive index of the cavity bore to be 1. If we consider $1\mathrm{m}\mathrm{K}$ change in temperature, it would yield a frequency drift of $\mathrm{\Delta }\nu \sim 4\mathrm{k}\mathrm{H}\mathrm{z}$, highlighting the challenge of achieving sub-Hz level frequency stabilisation.

If the temperature is stabilised at $\mathrm{m}\mathrm{K}$ level, then minor variations in $\alpha (T)$ should be considered and temperature sensitivity of resonant frequency could be given by Equation 48:

$\frac{\mathrm{\Delta }v}{v}={\int }_T^{T+\delta T}\alpha \left(T\right)dT.(48)$

As most materials used in optical cavities have a turn-around temperature, i.e., at which the first-order linear expansion coefficient vanishes, it is written more generally as:

$\alpha \left(T\right)=a\left(T-T_0\right)+b{\left(T-T_0\right)}^2+\mathcal{O}\left(\delta T^3\right),(49)$

where, $a$ and $b$ are expansion coefficients, in units ${\text{K}}^{-2}$ and ${\text{K}}^{-3}$, respectively. $\mathcal{O}$($\delta T^3$) is third order term and $T_0$ is called CTE-null temperature. The widespread use of ULE glass as a choice for spacer is also reinforced by the fact that it exhibits a CTE-null point around room temperature (though higher CTE-null is favoured during manufacturing so that heating only is required for thermal stabilization). Because of extremely low CTE null temperature, cavities constructed using a single silicon crystal operate at cryogenic temperature (whereas sapphire doesn’t have a CTE null, but it is nearly zero at cryogenic temperatures). Equation 49 indicates that if the cavity is operated in the vicinity of $T_0$, then the linear term vanishes, and the quadratic term becomes significant. For instance, the value of $b$ for ULE is around $10^{-11}/K^3$, and if temperature fluctuations are controlled at mK level, then $\alpha (T)$ is on order $10^{-17}$, indicating a significant reduction in sensitivity to the temperature fluctuations.

As highlighted in Section 4.1, additional complications arise when cavities are made from different materials for spacer and substrate. A mismatch in the CTE of the spacer and substrate tends to deform the cavity (by bending the mirrors) and hence change the effective optical length. The effective CTE in this case was given by (Notcutt et al., 1995):

${\alpha }_{\text{eff}}={\alpha }_{\text{spacer}}+2\gamma \frac{R}{L}\left({\alpha }_{\text{substrate}}-{\alpha }_{\text{spacer}}\right)+\mathrm{\Gamma },(50)$

where $\gamma$ is the thermo-mechanical stress coupling coefficient between the radial expansion of mirrors and the linear expansion of the spacer. $\mathrm{\Gamma }$ represents the contribution from the rest of the factors that make the cavity non-ideal, including the temperature-dependent thickness of coatings and non-resonant phase shift of light upon reflections, ultimately leading to alterations in the cavity length (Fox, 2009).

Let us consider the widespread case of ULE glass and FS as spacer and substrate, respectively. Since ${\alpha }_{\text{FS}}>{\alpha }_{\text{ULE}}$, ${\alpha }_{\text{eff}}$ becomes positive (Equation 50), leading to a complicated non-linear expansion of cavity. The magnitude of ${\alpha }_{\text{eff}}$ will be further enhanced due to the ratio $(\frac{R}{L})$, which is desired to be large for the geometrical stability of the beam. Therefore, it is more beneficial to work on reducing the coupling coefficient to minimize the final CTE of the cavity (Legero et al., 2010). The same authors devised an ingenious solution of attaching a ULE ring at the backside of FS mirrors, offering the freedom of engineering $T_0$ by studying the ring parameters.

From an experimental perspective, temperature-induced drifts are minimized by housing the cavity inside a vacuum chamber while ensuring mechanical decoupling between them. This arrangement prevents ambient temperature changes from affecting the cavity surface’s local temperature. Multiple heat shields made of aluminium or titanium are used for this purpose. These shields are positioned between the cavity and vacuum chamber to efficiently block heat exchange due to convection and radiation, as illustrated in Figure 12A. The surfaces of heat shields are highly polished to reduce thermal radiation (a smooth surface ensures low emissivity), thereby significantly increasing the heat exchange time constant between the shields and cavity (Amairi, 2014). Radiative heat transfer can be minimized by actively controlling the temperature of the entire system, which can be accomplished through the use of active Peltier coolers and resistive heaters. This approach helps to suppress the temperature fluctuations and maintain the temperature around zero crossing of the spacer material (Figure 12B).

Figure 12

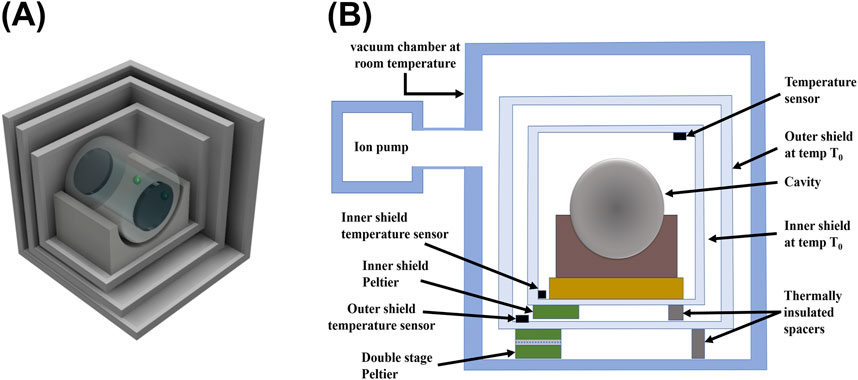
Figure 12. A general schematic diagram showing thermal isolation of cavity. (A) Multiple highly polished heat shields are placed around the cavity to reduce heat transfer between the cavity and the outer environment. (B) Cavity placed inside heat shields and vacuum chamber. Temperature is monitored using sensors placed at several locations and stabilised through Peltier coolers.

It is also worthwhile to note the cavity creep rate, which is a gradual long-term alteration in the dimension of the cavity. ULE material exhibits a creep rate of approximately one-tenth that of Zerodur. Moreover, ULE demonstrates adiabatic variation, whereas Zerodur experiences random step changes in length, proving ULE glass to be a better choice for cavity spacers (Roberts et al., 1999).

4.2.2 Vibrational noise

Low-frequency vibrational noises, spanning from 0.1 Hz to 100 Hz, such as seismic vibrations, pressure fluctuations in the atmosphere and other infrasonic acoustic noises, severely affect the stabilization of laser linewidth in sub-hertz level by exciting the vibrational eigenmodes of cavity (Nazarova et al., 2006). The extent to which these vibrations affect the cavity is influenced by its shape and the points at which it is mounted. Mounting the cavity vertically by fixing it at the midplane offers the advantage of ensuring that upper and lower halves undergo equal and opposite length changes, effectively nullifying the total effect and maintaining a constant length. Conversely, horizontal mounting configurations can also offer advantages, particularly because most vibrations are typically vertical, and Poisson’s ratio scales these vibrations down along the optical length. Additionally, various symmetrical configurations, such as cylindrical, cubic, spherical, and triangular shapes have been explored. However, the existence of complex material properties may lead to imperfections in symmetry. Therefore, finite element analysis (FEA) should be utilized to determine the most optimal mounting strategy and positions for the cavity (Banerjee et al., 2023). This approach aims to minimize sensitivity to mounting forces and external vibrations. Cylindrical and cubical designs are often preferred for their reduced volume and design simplicity. Notably, while a smaller cavity has a higher thermal noise floor, it simultaneously exhibits reduced susceptibility to external vibrational noise.

According to Hooke’s law, low acceleration force (such as self-weight due to gravity) can cause structural deformation of the cavity spacer. This is mainly attributed to two factors, the Poisson’s effect and mirror tilt (Álvarez, 2019). When subjected to a small acceleration $a_i$ in the ${\mathrm{i}}^{\text{th\hspace{0.17em}}}$ direction, the relative change in optical path length can be approximated as a linear function (Amairi et al., 2013):

$\frac{\mathrm{\Delta }L}{L}=-\frac{\mathrm{\Delta }\nu }{\nu }={\displaystyle \sum _{i=x,y,z}}{a}_i{k}_i+{\displaystyle \sum _{i=x,y,z}}{a}_i{\beta }_i\mathrm{\Delta }r.(51)$

On the right-hand side of Equation 51, first term represents the relative change in length caused by minor external acceleration forces, with $k_i$ as the sensitivity coefficient. The second term indicates displacement of optical mode from the cavity’s symmetry axis due to mirror tilt by $\mathrm{\Delta }r$, with a coefficient ${\beta }_i$. Ideally, $\mathrm{\Delta }r$ should be zero, but achieving absolute parallelism poses a challenge experimentally. To minimize $\mathrm{\Delta }r$ and the deformation from self-weight, a portable cavity should be rigidly mounted at the Airy points (specific locations on the cavity spacer where optical path length deformation is minimal due to gravity). These points can be identified using finite element analysis (FEA) (Chen et al., 2006). An acceleration sensitivity of order $10^{-11}/\mathrm{g}$ (where $\mathrm{g}=9.8\mathrm{m}.{\mathrm{s}}^{-\mathrm{2}}$, is the acceleration due to gravity) is attainable by proper mounting of the cavity at the Airy points (Leibrandt et al., 2013; Webster and Gill, 2011).

For further reduction of fractional frequency instability, the entire cavity setup must be positioned on a passive or active vibration isolation (AVI) platform to sufficiently mitigate the vibrational noise and reach below the fundamental thermal noise. Although the air-suspended optical tables effectively attenuate vibrational noise above their resonance frequency (scaling as $f^{-2}$), they fall short in controlling low-frequency disturbances (below $10\mathrm{H}\mathrm{z}$). The AVI platforms, equipped with sensors and actuators, offer feedback and feed-forward control, providing superior isolation from extremely low-frequency vibrations. This is particularly advantageous compared to passive systems, which can amplify vibrations at low frequencies.

4.2.3 Pressure fluctuations

Pressure fluctuations inside the cavity bore cause variations in the refractive index, thereby impacting the optical path length. The change in pressure occurs mainly due to temperature shifts and statistical fluctuations in the number of gas molecules present inside the cavity bore. However, frequency drift induced by pressure changes is less significant than that caused by the direct temperature fluctuations (Equation 47). The effect of change in pressure on the optical path length $\left(nL,n\right.$ denotes refractive index of medium within bore) can be quantified as given in Equation 52 (Roberts et al., 1999):

$\frac{d\left(nL\right)}{dP}=L\frac{dn}{dP},(52)$

which couples with the cavity length instability to yield Equation 53:

$\frac{\mathrm{\Delta }L}{L}=\frac{dn}{dP}\mathrm{\Delta }P.(53)$

At room temperature, $\frac{dn}{dP}$ for dry air is approximately equal to $3\times 10^{-7}{\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}}^{-1}$. This suggests that to reduce pressure effects below the thermal noise floor and stabilise relative length fluctuations up to $10^{-16}$ order, it is necessary to maintain a stable vacuum level of order $10^{-9}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$. Care should be taken while choosing vacuum pumps, as pumps with moving parts can result in vibrations. Ion pumps can be used alternatively, achieving $10^{-7}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$ pressure level without baking the system.

4.2.4 Cavity power fluctuations

In high finesse optical cavities (Finesse $\ge 100000$), power fluctuations become a serious concern due to the radiation pressure produced by a highly intense beam inside the cavity. This radiation pressure directly affects the mirror curvature, causing it to bend and lengthen the cavity. For an input power $P$, if the force exerted on cavity mirrors is $F$, the bending $(\kappa )$ of a mirror could be estimated from the following equation (assuming mirror size is significantly larger than the beam waist) (Bergquist et al., 1992):

$\kappa =3F\frac{r^2\left(1-{\sigma }_{\text{MS}}^2\right)}{4\pi Y_{\text{MS}}{t}^3},(54)$

where $r$ is the distance between the center and clamped edge of the mirror, and $t$ is the thickness of the mirrors (Equation 54). Therefore, fractional length change due to the bending of mirrors could be estimated by $\frac{2\kappa }{L}$. The strain $(\frac{\mathrm{\Delta }L}{L})$ induced in the spacer by power fluctuations can also be modelled similarly to a mechanical bar. The force acting on the cross-sectional area $A$ of the mirrors (which can be thought of end of the bar) produces strain:

$\frac{\mathrm{\Delta }L}{L}=\frac{F}{A{Y}_{\text{spacer}}},(55)$

where $Y_{\text{spacer}}$ is Young’s modulus of spacer in Equation 55.

The power circulating within the cavity is significantly higher than the input power $(I_{\text{cavity}}\approx I_{\text{in}}\frac{F}{\pi })$ (Boyd and Lahaye, 2024), leading to local heating of the mirror coatings. Initial layers of coating absorb most of the power, thereby causing a transient response in the optical path length, resulting in frequency instability.

(Keller et al., 2014) observed that a change of $\pm 5\mathrm{\mu }\mathrm{W}$ in input power resulted in a frequency fluctuation sensitivity of $2\times 10^{-13}{\mathrm{W}}^{-1}$ for a cylindrical cavity (length$=12\mathrm{c}\mathrm{m}$, finesse $\approx 280000$). To maintain power fluctuations below thermal noise floor $\left(10^{-16}\right)$, a fractional intensity instability of order $10^{-4}$ is necessary. Active power stabilization is employed to mitigate these fluctuations, where an AOM is placed between the laser and cavity, allowing its zeroth order to enter the cavity. An error signal is generated after comparing the transmitted power from the cavity and reference voltage. This error signal controls the RF power driving the AOM, regulating power among different orders such that zeroth-order power remains constant (Tricot et al., 2018). demonstrated a similar scheme of active power stabilization of laser using AOM, showing the efficiency of the approach.

4.3 Minimization of residual amplitude modulation (RAM)

EOMs used for phase modulation consist of birefringent crystals like lithium niobate $({\text{LiNbO}}_3)$ whose refractive index (both for ordinary and extraordinary rays) is linearly dependent upon the applied electric field. An EOM’s working principle can be considered as a variable waveplate whose polarization depends upon the applied electric field. These crystals also possess natural birefringence even in absence of electric field which depends upon the temperature of the environment. This natural birefringence is one of the major sources of RAM during the phase modulation of input light in the PDH technique.

There is an additional photocurrent that contributes to the RAM noise due to thermal causes and other sources like the etalon effect (causes parasitic interference), misalignment of the crystal’s principal axis with the incident beam, inhomogeneity or defect in crystal, vibration instability, RF input signal fluctuation, non-uniformity of the modulating electric field, and photorefractive effect on the crystal (Domínguez et al., 2021) sets an offset to the PDH error signal (Herbers, 2021):

${ϵ}_{\text{tot}}={ϵ}_{\text{PDH}}+\mathrm{\Delta }{ϵ}_{\text{RAM}}.$

If the amplitude of the RAM remains constant, it only introduces a constant frequency offset denoted as $\mathrm{\Delta }{v}_{\text{RAM\hspace{0.17em}}}$, which does not impact the laser stability. However, in a practical scenario, RAM amplitude fluctuates and as a result, the laser stabilization set point also fluctuates. Since ${ϵ}_{\text{PDH}}$ is inversely proportional to $L$ (Equation 30), longer cavities are less affected by RAM noise. But, in the case of portable clock lasers, due to the smaller length of the cavity, they are more susceptible to RAM. After amplitude modulation with the RF frequency $\mathrm{\Omega }$ the output photocurrent is given as (Wong and Hall, 1985; Herbers, 2021):

$I\left(\mathrm{\Omega }\right)=-\sin \left(2{\theta }_p\right)\sin \left(2{\theta }_a\right){\left|E_{0,x}\right|}^2{J}_1\left(\beta \right)\sin \left(2\pi \mathrm{\Omega }t\right)\sin \left(\mathrm{\Delta }{\varphi }_{e,o}\right),(56)$

or

$I\left(\mathrm{\Omega }\right)=I_0\sin \left(2\pi \mathrm{\Omega }t\right),(57)$

where,

$J_1\left(\beta \right)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{e}^{i\left[\beta \sin \left(\varphi \right)-\varphi \right]}d\varphi ,(58)$

and

$I_0=-\sin \left(2{\theta }_p\right)\sin \left(2{\theta }_a\right){\left|E_{0,x}\right|}^2{J}_1\left(\beta \right)\sin \left(\mathrm{\Delta }{\varphi }_{e,o}\right).(59)$

In Equation 56–59, $E_{0,x}$ is the amplitude of incident light along the x-axis, $J_1(\beta )$ is first order Bessel function with $\beta$ as the modulation depth and $\mathrm{\Delta }{\varphi }_{e,o}$ is the phase difference between e-ray and o-ray. To stabilize and lock the laser, which will not degrade over time, the amplitude ${\mathrm{I}}_0$ needs to be constant and as well as small. This implies the necessity to ensure that parameters such as ${\theta }_p,{\theta }_a,E_{0,x}$, and $\mathrm{\Delta }{\varphi }_{e,o}$ should not fluctuate over time. This can be achieved through controlling and stabilizing various factors, including vibrational noise, scattering, laser power, applied radio frequency, modulation field power, and most significantly, surrounding temperature.

Two primary approaches are utilized to minimize RAM noise. The first involves passive RAM noise reduction, achieved by tilting the parallel surfaces to eliminate parasitic interference resulting from the etalon effect. Additionally, carefully aligning the polarizing angles helps to reduce polarization noise. Active temperature stabilization of the EOM should also be implemented to prevent RAM generation resulting from fluctuations in natural birefringence and crystal deformation (Zhang et al., 2014). Moreover, during the selection of EOM crystals, it is better to consider crystals having low thermal dependence (Jin, 2021). Additionally, incorporating a special type of crystal before EOM to separate the e-ray and o-ray can help to reduce polarization noise (Figure 13).

Figure 13

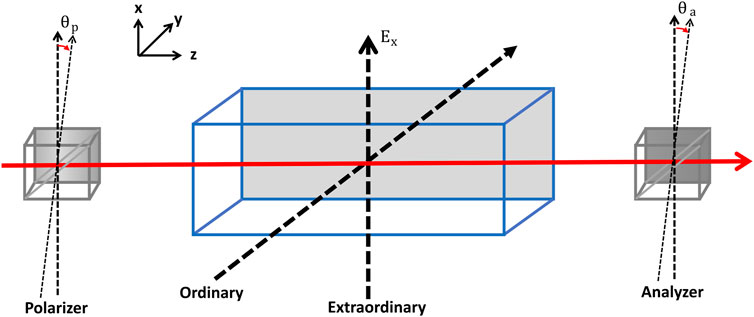
Figure 13. EOM crystal with ordinary and extraordinary axis where latter is aligned along the applied field direction. If the polarizer and analyzer axis are perfectly aligned with extraordinary axis, ${\theta }_p$ and ${\theta }_a$ become zero.

RAM noise can be further suppressed by active control method, as illustrated in Figure 14. This method involves the use of two polarizing beam splitters to decrease the effective optical path length, thereby minimizing RAM. Additionally, spatial filtering is implemented using optical fibre. In the active control method, one part of light before the cavity is picked using a beam splitter and sent to a photodiode, whose signal is also modulated in the same way as the PDH signal. As a result, RAM, which is in phase with the PDH signal, can be detected, and a correction DC signal using bias tee can be applied to EOM. This additional DC signal can impact the phase difference between the e-ray and o-ray $\left(\mathrm{\Delta }{\varphi }_{e,o}\right)$, effectively adjusting $\left(\mathrm{\Delta }{\varphi }_{e,o}\right)$ to zero (Wong and Hall, 1985). Zhang et al. (2014) also demonstrated that it is essential to manage both the quadrature and phase components of RAM for enhanced long-term stability. By implanting an active servo loop containing both DC voltage and temperature control system on the EOM, they achieved RAM noise suppression at the level of $10^{-6}$ order.

Figure 14

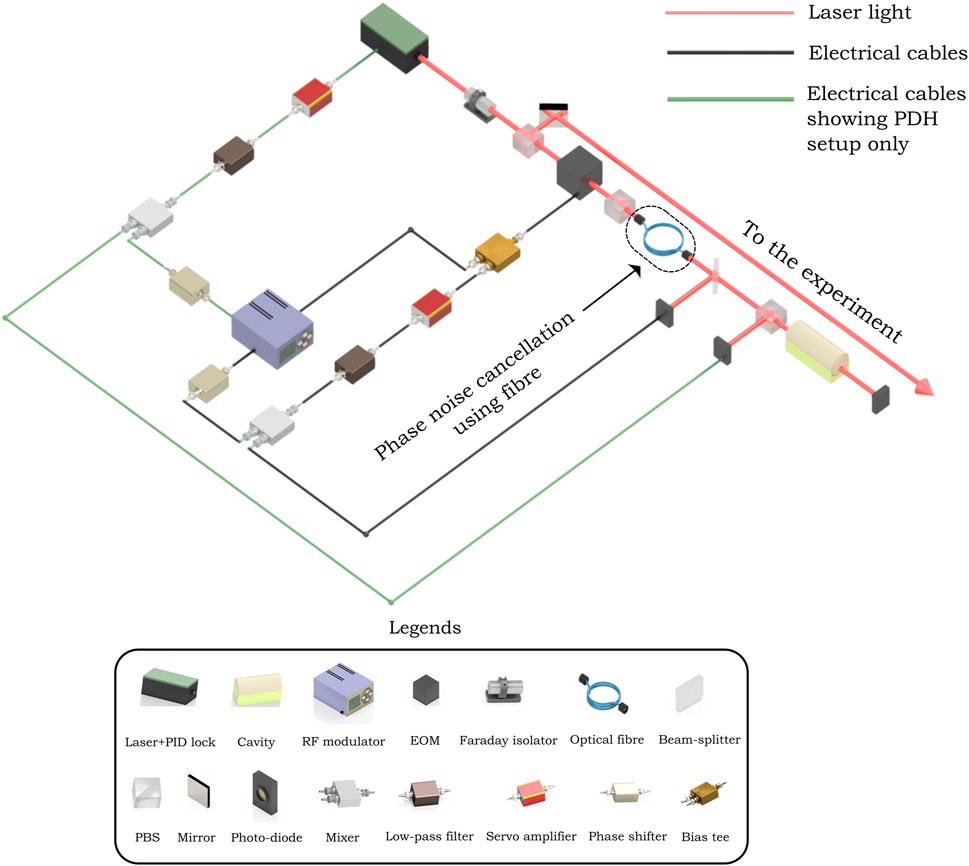
Figure 14. Schematic diagram of active stabilization of RAM noise. The PDH setup (Figure 6) is highlighted using green cables, which is surrounded by the RAM compensation setup. PBS is generally used with half-wave plates (not shown here) to distribute the intensity among two directions of polarization (except the PBS between EOM and fibre).

5 Case studies

Here, we mention a few noteworthy transportable cavities in detail. These designs emerged as paradigms due to their unique geometries, optimum mixed-material properties and mounting strategies. These optical cavities have made significant advancements in thermal and vibrational isolation, rendering them suitable for use in challenging environments like spacecraft, satellites, and terrestrial vehicles. They have also set a benchmark, inspiring research groups worldwide to confidently explore similar geometries. All of these cavities are made from ULE glass as the spacer material and FS as the mirror substrate material.

5.1 Cubical cavities

5.1.1 5 $\mathrm{c}\mathrm{m}$ cubic cavity (NPL, United Kingdom)

A cubic spacer of ULE ($5\mathrm{c}\mathrm{m}$ side length) was designed to be length-insensitive to mounting forces by holding the cube in a tetrahedron geometry (Webster and Gill, 2011). Four truncated vertices were found to be appropriate positions for mounting the cavity such that optical length becomes insensitive to compressive and inertial forces when held at a particular cut depth. This mounting design uses the highest symmetry to the optical axis. A Nd:YAG laser is employed to record a beat note with another stable laser, revealing acceleration sensitivities of $2.45(3)$, $0.21(4)$ and $0.01(1)\times 10^{-11}/g$ along the optical axis and two transverse directions, respectively. These values remain the least sensitive reported by various groups over the last decade. The worst-case acceleration sensitivity for this cavity is $2.5\times 10^{-11}/g$.

NPL recently reported (Hill et al., 2021) a dual-optical axis cubic cavity based on a similar design for multiple laser stabilisation. This cavity had three bores drilled on parallel faces, and two of them were used as optical cavities with ULE rings attached on the backside of mirrors for thermal compensation. The cavity is mounted within a single aluminium thermal shield with highly polished walls, situated inside an aluminium vacuum chamber operated at less than $<1\times 10^{-7}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$. The thermal time constant of the cavity turns out to be 8.5 h when a minor temperature step is applied. The chamber is operated at $25°\mathrm{C}$, near to CTE null temperatures of two cavities ($24°\mathrm{C}$ and $26°\mathrm{C}$) with a few $\mathrm{m}\mathrm{K}$ stability. The observed difference in zero CTEs of $2\mathrm{K}$ along both cavities is suspected to have originated from anisotropy in ULE material along the two directions. It is conjectured that drilling two cavities on a single spacer caused this asymmetry, leading to different frequency drift rates for the same $698\mathrm{n}\mathrm{m}$ laser locked to them. The authors hope that choosing cavities perpendicular to the growth axis could mitigate these issues. Acceleration sensitivity is $\mathrm{1}-\mathrm{2}$ orders lesser than the original cavity mentioned above. The mirror coating was tested by proton beam irradiance of $36\mathrm{M}\mathrm{e}\mathrm{V}$ while it was housed in the chamber, but no degradation in performance was recorded. By performing noise calculations on the clock laser cavity, authors estimate the thermal noise limits of $1\times 10^{-15}$ and $<5\times 10^{-16}$ for dielectric mirror coatings and crystalline coatings, respectively. This cavity is a subject candidate for the laser interferometer space antenna (LISA) mission, and further progress was reported in the conference article (Stacey et al., 2023).

A recent collaboration between academia and various industries (Cole et al., 2024) lately published an article on a space-deployable cubic cavity at the technology readiness level (TRL) 6. Crystalline coating of $\mathrm{G}\mathrm{a}\mathrm{A}\mathrm{s}/\mathrm{A}\mathrm{l}\mathrm{G}\mathrm{a}\mathrm{A}\mathrm{s}$ are used here for lower thermal (Brownian) noise. Theoretical fractional frequency instability limited by thermal noise is computed as $3\times 10^{-16}$. This cavity is mounted in a titanium frame, which is then enclosed within gold-coated, highly polished thermal shields for both lower thermal emissivity and thermal isolation. This entire assembly is installed in a vacuum chamber operating at $1\times 10^{-7}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$. An automatic re-lock method has been devised using field programmable gate array (FPGA) to eliminate the need for human monitoring of control electronics. This method activates when coupled laser light to the cavity is lost for a certain duration. The vacuum chamber is monitored and operated near the CTE null temperature $(32.1(1)°\mathrm{C})$ to compensate for thermal changes. The thermal time constant of the system measured out to be 16 h. Performance of this cavity is moderate regarding acceleration sensitivity, with values of $(0.2-8)\times 10^{-11}/g$ perpendicular to cube faces. The authors attributed the reduced sensitivity to the support screws used to secure the cavity within the titanium cage, suggesting that the screws may not have been adequately tightened. Rigorous tests for cavity finesse were performed pre and post-high energy proton beam radiation exposure to the cavity to check the resilience of crystalline coatings. Cavity ring-down spectroscopy (CRDS) measurements yield almost the same results in both cases and show the robustness of crystalline coatings against possible space radiation. The cavity was additionally subjected to large vibrational shocks (up to $360\mathrm{g}$) and huge temperature variations ($-40°$ to $+60°$), and the system showed no significant difference in performance.

5.1.2 Dual-axis $10\mathrm{c}\mathrm{m}$ cubic cavity (ECNU, China)

A ULE glass cubic block of $10\mathrm{c}\mathrm{m}$ side length is used as a spacer where three orthogonal cylindrical holes of diameter $10\mathrm{m}\mathrm{m}$ are carved out (Chen et al., 2020). Two of these bores are used as optical cavities, while the third bore is utilised for vacuum purposes. The corners of the cube are truncated, and conical holes are made where Viton balls sit to support the aluminium cage, which holds the cube rigidly. Tetrahedral configuration is chosen for mounting the cavity for symmetry reasons. An additional ULE annulus is optically contacted to the backside of FS mirrors for thermal compensation. The cavity is estimated to be insensitive to vibrations applied along the cavity length if the laser spot is located on the mirror center. Acceleration sensitivities to the cavity length are measured out to be in the range $(0.9-2)\times 10^{-10}/g$ in all three directions. The aluminium cage holding the cube is sealed with gold-coated copper plates to reduce the effect of environmental thermal radiation. A similar shield surrounds the first shield, and this assembly is placed inside a vacuum chamber operating at $<7\times 10^{-8}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$. Two $1064\mathrm{n}\mathrm{m}$ lasers are stabilized to the cavity, and their instabilities measured out to be $5.6\times 10^{-16}$ and $6.8\times 10^{-16}$ at $1\mathrm{s}$, which are close to fundamental noise-limited laser instability of $4.3\times 10^{-16}$. The authors intend to use this transportable cavity to measure the frequency ratio among atomic clocks and detect gravitational waves.

5.2 Spherical cavity (NIST, United States)

A spherical cavity spacer (Leibrandt et al., 2011b) is designed for ultra-stable frequency control in outside laboratory environments by holding the spherical spacer at a “squeeze insensitive angle” (this angle refers to points on the spacer where changes in mounting force have little effect on cavity length). The authors also highlight the benefit of carving out multiple cavities in the sphere as long as mounting forces act on a diameter only. The spacer is $50.8\mathrm{m}\mathrm{m}$ in diameter to which FS mirrors are bonded by polishing the ends flat (cavity length$=48.5\mathrm{m}\mathrm{m}$ and $12.7\mathrm{m}\mathrm{m}$ diameter). Invar mounts hold the cavity with Viton o-rings serving as a contact between the mount and spacer. For this configuration, the Allan deviation limit due to thermal noise is calculated to be $6.5\times 10^{-16}$. Measured acceleration sensitivities in three perpendicular directions fall in the range of $0.4-3.2\times 10^{-10}/g$. The laser stabilized to the cavity shows a fractional frequency stability of $1.2\times 10^{-15}$ between 0.4 and $13\mathrm{s}$. With active feed-forward, acceleration sensitivity was further reduced to $(0.1-0.6)\times 10^{-10}/g$ while testing this cavity on a vehicle (Leibrandt et al., 2011a).

A significant improvement in the same cavity was published 2 years later, showcasing better acceleration sensitivity and thermal stabilisation by performing real-time feed-forward correction (Leibrandt et al., 2013). The cavity mounting scheme underwent significant changes, holding it by stainless steel flexure springs along a direction perpendicular to the optical axis in a cubic cage. Torlon balls are the contact between the spacer and springs and bear a load of $100\mathrm{N}$ compressive force. This stiffer mounting yields a worst linear acceleration sensitivity of $2(1)\times 10^{-11}/g$ over $0-50\mathrm{H}\mathrm{z}$, which makes it a robust candidate for non-laboratory applications.

5.3 Cylindrical cavities

5.3.1 $10\mathrm{c}\mathrm{m}$ cylindrical cavity (LNE-SYRTE, France)

A cavity of length $10\mathrm{c}\mathrm{m}$ (diameter $110\mathrm{m}\mathrm{m}$) was mounted vertically and fixed rigidly at its midplane to resonate at telecommunication wavelength of $1.542\mu \mathrm{m}$ (Argence et al., 2012). Mirror geometry is plano-concave (radius of curvature equal to $500\mathrm{m}\mathrm{m}$). These dimensions, along with the position of venting holes and the central ring, were chosen after intensive finite element method (FEM) simulations to find minimum transverse vibration sensitivity. The assembly can withstand $\sim 6\mathrm{g}$ and over $20\mathrm{g}$ of quasi-static acceleration along transverse and axial directions, respectively. The cavity is enclosed with two gold-coated, highly polished aluminium shields inside a stainless steel vacuum chamber; all are rigidly bolted to each other through titanium standoffs (for thermal resistance). The overall thermal time constant of the assembly was $\sim 1.7$ days, which is in good agreement with modelling ($\sim 1.5$ days). The assembly has a total mass of $40\mathrm{k}\mathrm{g}$, most of which is attributed to the vacuum chamber alone $(\sim 20\mathrm{k}\mathrm{g})$. Authors have suggested using titanium in place of steel for the vacuum chamber as it has similar thermo-mechanical properties but $40\%$ lower mass density and lower outgassing rate of ${\mathrm{H}}_{\mathrm{2}}$ at the operated vacuum level of $<10^{-6}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$. Along the axis of the cavity, vibration sensitivity is measured out to be $(4\pm 0.5)\times 10^{-11}/\mathrm{m}.{\mathrm{s}}^{-\mathrm{2}}$, which turns out to be an order of magnitude higher than the FEM simulations. Authors have suspected that complex housing of the cavity may be the reason for this degradation. The fractional frequency instability of laser locked to the cavity is $5-6\times 10^{-16}$ at $1\mathrm{s}$, which is remarkably close to the fundamental limit $(\approx 4\times 10^{-16})$.

5.3.2 $10\mathrm{c}\mathrm{m}$ near-cylindrical cavity (HHU, Germany)

This cavity was designed to be a subsystem for the cold Caesium atomic clock onboard a satellite to test Einstein’s Equivalence principle (Chen et al., 2014). A frequency comb will convert ultra-stable optical frequency at $1064\mathrm{n}\mathrm{m}$ to provide an ultra-stable microwave signal. The cavity spacer is $100\mathrm{m}\mathrm{m}$ long with a diameter of $60\mathrm{m}\mathrm{m}$. ULE rings are bonded on the rear side of the FS mirrors to compensate for FS’s higher thermal expansion than ULE. The cavity is rigidly mounted in a frame, secured by several short posts passing through protruding edges on surfaces parallel to the cavity axis. This setup serves to decouple accelerations in different directions. The same frame serves as an inner thermal shield by enclosing it with polished aluminium plates. This inner thermal shield is then enclosed by a second aluminium heat shield. The whole system is placed rigidly inside an evacuated chamber operating at $1\times 10^{-7}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$. The cavity with housing and chamber is considerably light as it only weighs $10\mathrm{k}\mathrm{g}$. It was shaken with bare hands to measure an axial vibration sensitivity of $3.9\times 10^{-10}/g$. The whole system was subjected to large temperature variation of $-30°$ to $+50°$, and laser light coupling fluctuated from $40\%$ to $15\%$, which proves the credibility of the setup for space and terrestrial applications. The cavity achieves a fractional instability of $1\times 10^{-15}$ at $1-10\mathrm{s}$, which it is quite far from the calculated thermal limit, $4\times 10^{-16}$.

5.3.3 $10\mathrm{c}\mathrm{m}$ cylindrical cavity (University of Birmingham, United Kingdom)

(Świerad et al., 2016) proposed a space-grade laser system for the Strontium (Sr) optical lattice clock (SOC2) project by the European space agency (ESA). The clock transition (¹S₀-³P₀) in the Sr atom has a frequency of $429\mathrm{T}\mathrm{H}\mathrm{z}$ with natural linewidth of $1.2\mathrm{m}\mathrm{H}\mathrm{z}$. The cylindrical spacer measures $100\mathrm{m}\mathrm{m}$ in length and $110\mathrm{m}\mathrm{m}$ in diameter with dielectric coatings on mirrors. ULE annulus is bonded to the mirror substrates to limit the thermal expansion. This configuration has an estimated flicker thermal limit of $5\times 10^{-16}$. The cavity is mounted vertically and rigidly held to the inner heat shield by a cylindrical rim around the mid-plane of the cavity orthogonal to the optical axis. This inner shield is surrounded by a similar outer heat shield, both made of gold-coated aluminium and enclosed in gold-coated aluminium vacuum chamber (operated at $2.5\times 10^{-6}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$). Acceleration sensitivity along the axis is $3.6\times 10^{-10}/g$. The cavity achieves the best fractional instability of $7.9\times 10^{-16}$ at an averaging time of $300\mathrm{m}\mathrm{s}$. However, it increases to $2.5\times 10^{-15}$ at $1\mathrm{s}$, for which the authors suspect that pressure fluctuations or spurious intensity fluctuations in the beam between the cavity and error-signal photodiode might be the reasons for the degradation.

5.3.4 $12\mathrm{c}\mathrm{m}$ cylindrical cavity (PTB, Germany)

A field-deployable cylindrical cavity is made to sustain shocks up to $50\mathrm{g}$ (Häfner et al., 2020). The spacer is $120\mathrm{m}\mathrm{m}$ long and $60.8\mathrm{m}\mathrm{m}$ in diameter with $10\mathrm{m}\mathrm{m}$ bore diameter. Mirrors are coated with dielectric $(\mathrm{T}{\mathrm{a}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}/\mathrm{S}\mathrm{i}{\mathrm{O}}_{\mathrm{2}})$ high reflectivity coatings. Additional ULE rings are bonded to the backside of mirrors to reduce their thermal expansion. The fundamental noise limit was obtained to be $2.8\times 10^{-16}$. The cavity is rigidly mounted to an inner gold-plated aluminium heat shield with a cage of flexible wires and bars working as a holding frame. This unique design was simulated to make the cavity robust to accelerations and to avoid overdetermining degrees of freedom (mounting points). Vibration sensitivity in three orthogonal directions falls in $(0.7-12.3)\times 10^{-10}/g$. The cavity is thermally stabilized actively by monitoring the inner shield and adjusting the temperature of the outer shield. The complete assembly is kept in a chamber operating at $3\times 10^{-8}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$. This cavity shows an instability of approximately $3\times 10^{-16}$ between $0.5-10\mathrm{s}$.

Two years later, the same group reported a new and improved transportable cavity system (Herbers et al., 2022) with the highest instability reported till date ($1.6\times 10^{-16}$ against the calculated fundamental noise limit of $0.7\times 10^{-16}$). The major breakthrough is accounted for by the newly discovered crystalline coatings $\mathrm{A}{\mathrm{l}}_{\mathrm{0.92}}\mathrm{G}{\mathrm{a}}_{\mathrm{0.08}}\mathrm{A}\mathrm{s}/\mathrm{G}\mathrm{a}\mathrm{A}\mathrm{s}$ for which mechanical loss is significantly lesser than amorphous or dielectric coatings. The pressure fluctuations have been reduced, too, as the evacuated chamber is operated at $10^{-9}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$ level. The worst case acceleration sensitivity for this cavity is $0.6\times 10^{-11}/\mathrm{m}.{\mathrm{s}}^{-\mathrm{2}}$.

To conclude, we compare various parameters and features of transportable cavities covered in this section, summarised in the Table 2. Identifying force-insensitive geometry and mounting strategies is the first step in designing a cavity. A symmetric cavity (cubical, spherical and cylindrical) can readily distribute the load evenly throughout the body. At the same time, mounting methodology recognizes the points where the effect of compressive forces is minimal on the cavity. Consequently, the cavities in Section 5.1.1 and Section 5.2 offer more ruggedness towards vibrational noise and hence show a lower Allan deviation noise limit. Thereafter, it comes down to selecting the suitable material for the cavity, where all groups have chosen similar materials for the spacer and substrate. ULE glass has more resistance to thermal expansion while FS have a smaller loss angle, which makes a good pair in terms of thermal stability and lower fundamental noise floor. However, a difference in the CTE null temperature of constituting materials leads to a decrease in the combined CTE null, which is favourable in some of the cases, as it falls in a range near room temperature. The development of crystalline mirror coatings has significantly improved the thermal noise limit, as in cases given in Section 5.1.1 and Section 5.3.4. Noise contribution due to mirror coatings is still the biggest hurdle to improving the fundamental Allan deviation limit, and researchers are doing intensive studies to find alternatives. Further, acceleration sensitivity is a direct measure of the robustness of transportable systems under external vibrations. As rigid mounting is necessary to secure the cavity under rugged operations outside lab environments, the above-listed groups have shown profound progress in mounting strategies to decouple vibrational noise. Thermal fluctuations caused by any small variations in the cavity environment are minimized by multiple well-polished heat shields coated with low-emissivity materials. However, system weight should be controlled for transportability purposes by carefully choosing the housing materials. Vacuum levels of $10^{-9}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$ are enough to control small effects of pressure variations, as seen in the last case, but the presence of large pumping stations may compromise the system’s compactness. Budget-friendly compact pumping solutions need to be carefully considered for portable applications.

Table 2

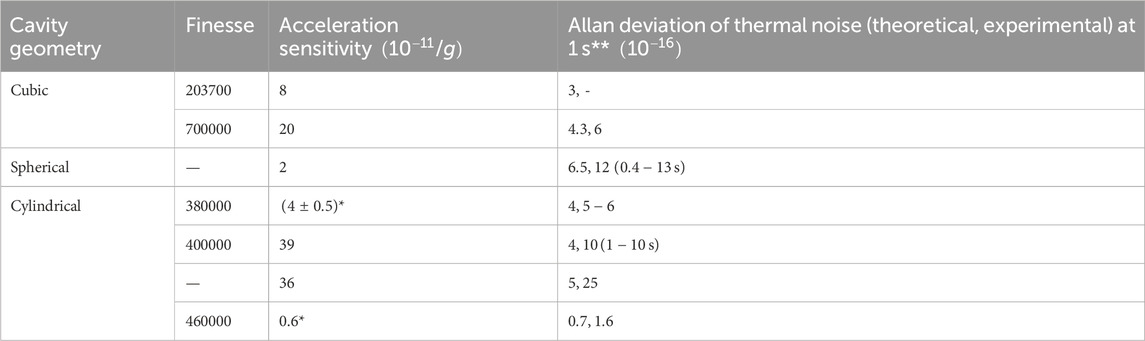
Table 2. Comparison among the various cavities mentioned here. Acceleration sensitivity is reported for the worst cases (highest value along one of the orientations). *These values are originally reported in unit of $10^{-11}{({\mathrm{m}.\mathrm{s}}^{-\mathrm{2}})}^{-1}$ **Interval reported other than $1\mathrm{s}$ is mentioned in brackets.

6 Summary and outlook

This article is dedicated to developing and understanding transportable high-finesse, ultra-stable optical cavities, which have emerged as critical tools to stabilize frequencies for portable optical clocks, enable out-of-lab high-precision experiments and generation of highly stable microwave signals, etc. The article begins with discussions on geometrical considerations for a high-finesse, ultra-stable optical cavity and highlights that high-quality mirrors with reflection coefficient $r>99.9995\%$ are required to exhibit very narrow transmission peaks. This also ensures an increased lifetime of radiation inside the cavity. We reviewed the widely adopted PDH method for laser frequency stabilization and provided a detailed discussion of the methodology. This highly sensitive technique helps in achieving a highly stable and narrow linewidth laser owing to its non-dependence on cavity transmission. We further delved into different noise sources that affect the length stability of the FP cavity, with the lower limit being determined by fundamental noise primarily arising from the material properties of the spacer, mirrors and coatings. Notably, Brownian noise contribution from mirror coating dominates the thermal noise floor, highlighting the potential for improvement by adopting alternative coating materials with lower loss angles. A longer cavity spacer with a large beam diameter is advised to reduce the fundamental noises arising from mirror substrate and coatings because of their $1/\omega$ and $1/{\omega }^2$ dependence, respectively (Equation 43). Consequently, for the case of portable small cavities, mirror curvatures should be chosen to ensure the cavity operates around hemispherical or near-hemispherical configurations $(R>L)$, yielding large $\omega$. Cavity components with higher Young’s modulus, Poisson’s ratio, and lower loss angles are preferable for lowering the thermal noise floor. Table 1 highlights the materials widely used in the construction of cavities due to their excellent values of aforementioned quantities.

Furthermore, this article also discusses different sources of external noise, such as vibrations, temperature fluctuations, acoustic noise, pressure fluctuations inside the cavity, and input beam power fluctuations that can compromise the laser frequency stability, and reviews strategies to mitigate them. To diminish the effect of deformation in length due to self-weight and mirror tilt in portable cavities, rigidly mounting the cavity on its Airy points effectively minimizes the effects of compressive forces on optical length which also helps in achieving acceleration sensitivity at $10^{-11}/g-10^{-12}/g$ level. The cavity system should be mounted on an AVI platform to attenuate vibrations at smaller frequencies (less than 100 Hz). External temperature fluctuations pose severe issues in frequency stabilization, underscoring the importance of meticulously selecting materials for cavity spacer and substrate with lower CTEs and around room-temperature CTE null points. Currently, the effective CTE of the cavity is restricted due to using FS as mirror substrates. There is a need to develop better candidates than FS, which possess lower CTE and loss angle than ULE spacers. Further, the cavity must be operated under vacuum conditions around CTE null point to minimize possible temperature changes from radiative and convective heat transfer. Using multiple highly polished heat shields (with low thermal emissivity, $<0.05$) blocks heat transfer via radiation very well. We also discussed the pressure fluctuations inside the cavity bore and inferred that a stable vacuum level of order $10^{-9}\mathrm{m}\mathrm{b}\mathrm{a}\mathrm{r}$ would be sufficient to reach the stability of order $10^{-16}$. Input power fluctuation also creates instability in the cavity length, giving rise to frequency instability. As a result, it should be stabilised at $\mu$W level by analysing the transmitted intensity recorded on the photodiode. Parasitic etalon effects caused by RAM should be minimized to reach the fundamental thermal noise limit.

We have also discussed a few significant case studies reported by various research groups over the past 15 years. Figure 15 shows a growing interest in transportable optical cavities in recent years worldwide. These case studies offer guidance and advice to anyone aiming to design and develop such transportable optical cavity systems. This review offers critical insight and encourages meticulous considerations in material selection and notes the importance of prior simulations to overcome various noises and possible deformations. With all the parameters studied well and controlled carefully, it is feasible to construct portable cavities at stability levels compared to stationary cavities in laboratories. Future developments are eagerly awaited for coating materials to surpass the fundamental thermal noise limit beyond $10^{-16}$ levels of stability. More efforts must be made in thermal and vibrational isolation to prepare these cavities for non-laboratory experiments such as space exploratory missions or outdoor precision measurements.

Figure 15

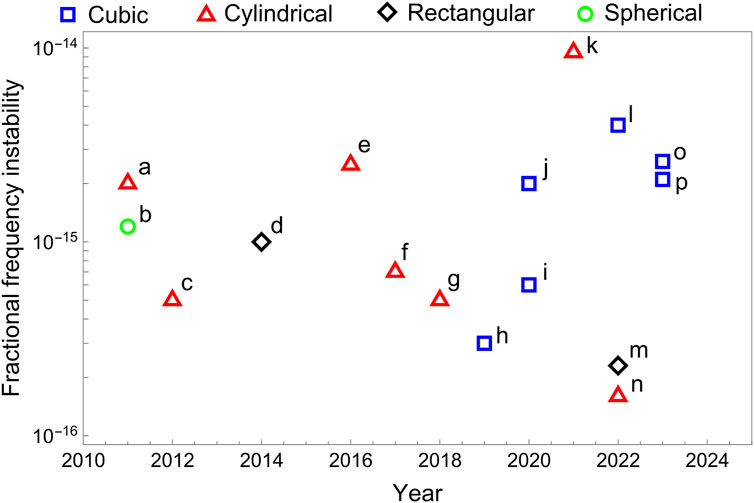
Figure 15. Progress of various terrestrial and space-borne (transportable) cavities over the past 15 years. Source of data: (A) (Vogt et al., 2011), (B) (Leibrandt et al., 2011b), (C) (Argence et al., 2012), (D) (Chen et al., 2014), (E) (Świerad et al., 2016), (F) (Tai et al., 2017), (G) (Tao and Chen, 2018), (H) (Sanjuan et al., 2019), (I) (Chen et al., 2020), (J) (Wang et al., 2020) (K) (Xu et al., 2021), (L) (Stacey et al., 2023), (M) (Xiao et al., 2022), (N) (Herbers et al., 2022), (O) (Jiao et al., 2023), (P) (Zhao et al., 2023).

Author contributions

RP: Writing–original draft, Writing–review and editing. VY: Writing–original draft, Writing–review and editing. AS: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. RP gratefully acknowledges financial support from the University Grants Commission (UGC) through the Junior Research Fellowship (JRF) (NTA Ref. No.: 231610201995). VY expresses gratitude for the financial support he received from the Prime Minister’s Research Fellowship (PMRF). AS acknowledges funding received from IIT Tirupati Navavishkar I-Hub Foundation (iNiF) through the grant number PHY2324010NHUBARIJ.

Acknowledgments

We thank Ashok Chilukoti and Sumit Achar for meticulously reviewing the manuscript. We acknowledge Gyanendra Pratap Roy and Poorvisha C for their valuable assistance with figures and 3D diagrams. We sincerely thank Sumit Achar, Abhijit Kundu and Himanshu Miriyala for sharing their insightful suggestions while preparing the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Gravity Recovery and Climate Experiment Follow-on or GRACE-FO, in short, is a successor mission of GRACE (which was operational between 2002-2017). It is a joint mission between NASA, United States and GFZ, Germany, launched in 2018.

²Next-Generation Gravity Mission (NGGM) is a proposed space mission between European Space Agency (ESA) and NASA, United States.

³Space-Time Asymmetry Research (STAR) is a proposed future mission by NASA, United States, involving people from Germany, Britain, and Saudi Arabia. It aims to study special and general relativity with better precision.

⁴BOOST (BOOst Symmetry Test) is a proposed space mission by DLR, Germany, to study Lorentz invariance violations.

⁵Space–Time Explorer and Quantum Equivalence Space Test (STE-QUEST) was a proposed mission not selected for ESA’s cosmic vision M3, but it is noteworthy to mention because it proposed optical atomic clocks will be deployed in space to test Einstein’s equivalence principle.

⁶Space Optical Clocks (SOC) is ESA’s planned mission to place optical clocks and frequency comb on the International Space Station (ISS) for improving the microwave link between Earth and ISS.

⁷https://llis.nasa.gov/lesson/824

References

Abdel-Hafiz, M., Ablewski, P., Al-Masoudi, A., Martínez, H., Balling, P., Barwood, G., et al. (2019). Guidelines for developing optical clocks with fractional frequency uncertainty. Tech. Rep. Leibniz Univ. Hann. Ger. doi:10.15488/5553

CrossRef Full Text | Google Scholar

Alnis, J., Matveev, A., Wilken, T., Kolachevsky, N., Udem, T., and Hänsch, T. (2008). Subhertz linewidth diode lasers by stabilization to vibrationally and thermally compensated ultralow-expansion glass Fabry-Pérot cavities. Phys. Rev. A 77, 053809. doi:10.1103/PhysRevA.77.053809

CrossRef Full Text | Google Scholar

Altschul, B., Bailey, Q., Blanchet, L., Bongs, K., Bouyer, P., Cacciapuoti, L., et al. (2015). Quantum tests of the Einstein equivalence principle with the STE–QUEST space mission. Adv. Space Res. 55, 501–524. doi:10.1016/j.asr.2014.07.014

CrossRef Full Text | Google Scholar

Álvarez, M. (2019). Optical cavities for optical atomic clocks, atom interferometry and gravitational-wave detection. (UK): School of Physics and Astronomy, University of Birmingham. Ph.D. thesis. doi:10.1007/978-3-030-20863-9

CrossRef Full Text | Google Scholar

Amairi, S. (2014). A long optical cavity for sub-Hertz laser spectroscopy. Gottfried Wilhelm Leibniz Universität Hannover. Ph.D. thesis.

Google Scholar

Amairi, S., Legero, T., Kessler, T., Sterr, U., Wübbena, J., Mandel, O., et al. (2013). Reducing the effect of thermal noise in optical cavities. Appl. Phys. B 113, 233–242. doi:10.1007/s00340-013-5464-8

CrossRef Full Text | Google Scholar

Andrews, G., Askey, R., and Roy, R. (1999). Special functions. Cambridge University Press.

Google Scholar

Argence, B., Prevost, E., Lévèque, T., Goff, R., Bize, S., Lemonde, P., et al. (2012). Prototype of an ultra-stable optical cavity for space applications. Opt. Express 20, 25409–25420. doi:10.1364/OE.20.025409

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, S., Johnson, S., Vaghasia, Y., Palodhi, K., Haldar, S., and De, S. (2023). Modelling and design of ultra-high stable Fabry–Pérot cavity. Int. J. Mech. Sci. 250, 108299. doi:10.1016/j.ijmecsci.2023.108299

CrossRef Full Text | Google Scholar

Bergquist, J., Itano, W., and Wineland, D. (1992). Laser stabilization to a single ion. Front. Laser Spectrosc. Proc. Int. Sch. Phys. “Enrico Fermi 120, 359–376.

Google Scholar

Bjorklund, G. (1980). Frequency-modulation spectroscopy: a new method for measuring weak absorptions and dispersions. Opt. Lett. 5, 15–17. doi:10.1364/OL.5.000015

PubMed Abstract | CrossRef Full Text | Google Scholar

Black, E. (2001). An introduction to Pound–Drever–Hall laser frequency stabilization. Am. J. Phys. 69, 79–87. doi:10.1119/1.1286663

CrossRef Full Text | Google Scholar

Boldbaatar, E., Grant, D., Choy, S., Zaminpardaz, S., and Holden, L. (2023). Evaluating optical clock performance for GNSS positioning. Sensors 23, 5998. doi:10.3390/s23135998

PubMed Abstract | CrossRef Full Text | Google Scholar

Bondarescu, M., Kogan, O., and Chen, Y. (2008). Optimal light beams and mirror shapes for future LIGO interferometers. Phys. Rev. D. 78, 082002. doi:10.1103/PhysRevD.78.082002

CrossRef Full Text | Google Scholar

Bondarescu, R., Schärer, A., Lundgren, A., Hetényi, G., Houlié, N., Jetzer, P., et al. (2015). Ground-based optical atomic clocks as a tool to monitor vertical surface motion. Geophys. J. Int. 202, 1770–1774. doi:10.1093/gji/ggv246

CrossRef Full Text | Google Scholar

Bongs, K., Singh, Y., Smith, L., He, W., Kock, O., Świerad, D., et al. (2015). Development of a strontium optical lattice clock for the SOC mission on the ISS. Proc. Phys. 16, 553–564. doi:10.1016/j.crhy.2015.03.009

CrossRef Full Text | Google Scholar

Bothwell, T., Kedar, D., Oelker, E., Robinson, J., Bromley, S., Tew, W., et al. (2019). JILA SrI optical lattice clock with uncertainty of 2.0 × 10⁻¹⁸. Metrologia 56, 065004. doi:10.1088/1681-7575/ab4089

CrossRef Full Text | Google Scholar

Boyd, J., and Lahaye, T. (2024). A basic introduction to ultrastable optical cavities for laser stabilization. Am. J. Phys. 92, 50–58. doi:10.1119/5.0161369

CrossRef Full Text | Google Scholar

Braxmaier, C., Schuldt, T., Allab, M., van Zoest, T., Theil, S., Pelivan, I., et al. (2010). “The space-time asymmetry research (STAR) program,” in Eftf, 1–8. doi:10.1109/EFTF.2010.6533664

CrossRef Full Text | Google Scholar

Callen, H., and Welton, T. (1951). Irreversibility and generalized noise. Phys. Rev. 83, 34–40. doi:10.1103/PhysRev.83.34

CrossRef Full Text | Google Scholar

Chalermsongsak, T., Hall, E., Cole, G., Follman, D., Seifert, F., Arai, K., et al. (2016). Coherent cancellation of photothermal noise in GaAs/Al_0.92Ga_0.08 Bragg mirrors. Metrologia 53, 860–868. doi:10.1088/0026-1394/53/2/860

CrossRef Full Text | Google Scholar

Chen, L., Hall, J., Ye, J., Yang, T., Zang, E., and Li, T. (2006). Vibration-induced elastic deformation of Fabry-Pérot cavities. Phys. Rev. A 74, 053801. doi:10.1103/PhysRevA.74.053801

CrossRef Full Text | Google Scholar

Chen, Q., Nevsky, A., Cardace, M., Schiller, S., Legero, T., Häfner, S., et al. (2014). A compact, robust, and transportable ultra-stable laser with a fractional frequency instability of 1 × 10⁻¹⁵. Rev. Sci. Instrum. 85, 113107. doi:10.1063/1.4898334

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Jiang, Y., Li, B., Yu, H., Jiang, H., Wang, T., et al. (2020). Laser frequency instability of 6 × 10⁻¹⁶ using 10-cm-long cavities on a cubic spacer. Chin. Opt. Lett. 18, 030201. doi:10.3788/col202018.030201

CrossRef Full Text | Google Scholar

Cole, G., Koller, S., Greve, C., Barwood, G., Deutsch, C., Gaynor, P., et al. (2024). Towards space-deployable laser stabilization systems based on vibration-insensitive cubic cavities with crystalline coatings. Opt. Express 32, 5380–5396. doi:10.1364/OE.506833

PubMed Abstract | CrossRef Full Text | Google Scholar

Cole, G., Zhang, W., Martin, M., Ye, J., and Aspelmeyer, M. (2013). Tenfold reduction of Brownian noise in high-reflectivity optical coatings. Nat. Photonics 7, 644–650. doi:10.1038/nphoton.2013.174

CrossRef Full Text | Google Scholar

Cone, R., Thiel, C., Sun, Y., Böttger, T., and Macfarlane, R. (2013). “Quantum information, laser frequency stabilization, and optical signal processing with rare-earth doped materials,” in Frontiers in optics 2013 (Washington, DC: Optica Publishing Group). LTu1G.3. doi:10.1364/LS.2013.LTu1G.3

CrossRef Full Text | Google Scholar

Corwin, K., Lu, Z.-T., Hand, C., Epstein, R., and Wieman, C. (1998). Frequency-stabilized diode laser with the zeeman shift in an atomic vapor. Appl. Opt. 37, 3295–3298. doi:10.1364/AO.37.003295

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, X., Jiang, Y., Hang, C., Bi, Z., and Ma, L. (2015). Thermal analysis of optical reference cavities for low sensitivity to environmental temperature fluctuations. Opt. Express 23, 5134–5146. doi:10.1364/OE.23.005134

PubMed Abstract | CrossRef Full Text | Google Scholar

DeMille, D., Doyle, J., and Sushkov, A. (2017). Probing the frontiers of particle physics with tabletop-scale experiments. Science 357, 990–994. doi:10.1126/science.aal3003

PubMed Abstract | CrossRef Full Text | Google Scholar

Derevianko, A., Gibble, K., Hollberg, L., Newbury, N., Oates, C., Safronova, M., et al. (2022). Fundamental physics with a state-of-the-art optical clock in space. Quantum Sci. Technol. 7, 044002. doi:10.1088/2058-9565/ac7df9

CrossRef Full Text | Google Scholar

Domínguez, A., Larcher, W., and Kozameh, C. (2021). Fundamental residual amplitude modulation in electro-optic modulators. arXiv. doi:10.48550/arXiv.1710.10719

CrossRef Full Text | Google Scholar

Döringshoff, K., Gutsch, F., Schkolnik, V., Kürbis, C., Oswald, M., Pröbster, B., et al. (2019). Iodine frequency reference on a sounding rocket. Phys. Rev. Appl. 11, 054068. doi:10.1103/PhysRevApplied.11.054068

CrossRef Full Text | Google Scholar

Drever, R., Hall, J., Kowalski, F., Hough, J., Ford, G., Munley, A., et al. (1983). Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 31, 97–105. doi:10.1007/BF00702605

CrossRef Full Text | Google Scholar

Fox, R. (2009). Temperature analysis of low-expansion Fabry-Pérot cavities. Opt. Express 17, 15023–15031. doi:10.1364/OE.17.015023

PubMed Abstract | CrossRef Full Text | Google Scholar

Fox, R., Oates, C., and Hollberg, L. (2003). 1. Stabilizing diode lasers to high-finesse cavities. Cavity-Enhanced Spectrosc. 40, 1–46. doi:10.1016/S1079-4042(03)80017-6

CrossRef Full Text | Google Scholar

Georgescu, I. (2019). A space chronometer. Nat. Rev. Phys. 1, 421. doi:10.1038/s42254-019-0084-9

CrossRef Full Text | Google Scholar

Gill, P. (2005). Optical frequency standards. Metrologia 42, S125–S137. doi:10.1088/0026-1394/42/3/S13

CrossRef Full Text | Google Scholar

Gill, P., Margolis, H., Curtis, A., Klein, H., Lea, S., Webster, S., et al. (2008). “Optical atomic clocks for space,” in Tech. rep. Teddington (UK): National Physical Laboratory.

Google Scholar

González, G., and Saulson, P. (1994). Brownian motion of a mass suspended by an anelastic wire. J. Acoust. Soc. Am. 96, 207–212. doi:10.1121/1.410467

CrossRef Full Text | Google Scholar

Grotti, J., Koller, S., Vogt, S., Häfner, S., Sterr, U., Lisdat, C., et al. (2018). Geodesy and metrology with a transportable optical clock. Nat. Phys. 14, 437–441. doi:10.1038/s41567-017-0042-3

CrossRef Full Text | Google Scholar

Häfner, S., Falke, S., Grebing, C., Vogt, S., Legero, T., Merimaa, M., et al. (2015). 8 × 10⁻¹⁷ fractional laser frequency instability with a long room-temperature cavity. Opt. Lett. 40, 2112–2115. doi:10.1364/OL.40.002112

PubMed Abstract | CrossRef Full Text | Google Scholar

Häfner, S., Herbers, S., Vogt, S., Lisdat, C., and Sterr, U. (2020). Transportable interrogation laser system with an instability of mod 3 × 10⁻¹⁶. Opt. Express 28, 16407–16416. doi:10.1364/OE.390105

PubMed Abstract | CrossRef Full Text | Google Scholar

Hall, J. (2006). Nobel lecture: defining and measuring optical frequencies. Rev. Mod. Phys. 78, 1279–1295. doi:10.1103/RevModPhys.78.1279

PubMed Abstract | CrossRef Full Text | Google Scholar

Hänsch, T. (2006). Nobel lecture: passion for precision. Rev. Mod. Phys. 78, 1297–1309. doi:10.1103/RevModPhys.78.1297

CrossRef Full Text | Google Scholar

Hansch, T., and Couillaud, B. (1980). Laser frequency stabilization by polarization spectroscopy of a reflecting reference cavity. Opt. Commun. 35, 441–444. doi:10.1016/0030-4018(80)90069-3

CrossRef Full Text | Google Scholar

G. Harry, T. Bodiya, and R. DeSalvo (2012). Optical coatings and thermal noise in precision measurement (Cambridge University Press).

Google Scholar

He, K., Li, Q., Liu, L., and Yang, H. (2021). Active vibration isolation of ultra-stable optical reference cavity of space optical clock. Aerosp. Sci. Technol. 112, 106633. doi:10.1016/j.ast.2021.106633

CrossRef Full Text | Google Scholar

Herbers, S. (2021). Transportable ultra-stable laser system with an instability down to 10⁻¹⁶. Gottfried Wilhelm Leibniz Univ. Hann. Ger. Ph.D. thesis. doi:10.15488/11624

CrossRef Full Text | Google Scholar

Herbers, S., Häfner, S., Dörscher, S., Lücke, T., Sterr, U., and Lisdat, C. (2022). Transportable clock laser system with an instability of 10⁻¹⁶. Opt. Lett. 47, 5441–5444. doi:10.1364/OL.470984

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill, I., Hendricks, R., Donnellan, S., Gaynor, P., Allen, B., Barwood, G., et al. (2021). Dual-axis cubic cavity for drift-compensated multi-wavelength laser stabilisation. Opt. Express 29, 36758–36768. doi:10.1364/OE.436019

PubMed Abstract | CrossRef Full Text | Google Scholar

Hollberg, L. (2020). “Atomic clocks for GNSS,”, 47. John Wiley and Sons, Ltd, 1497–1519. doi:10.1002/9781119458555.ch47

PubMed Abstract | CrossRef Full Text | Google Scholar

Hooker, S., and Webb, C. (2010). Laser physics. Oxford University Press.

Google Scholar

Itano, W., Bergquist, J., Bollinger, J., Gilligan, J., Heinzen, D., Moore, F., et al. (1993). Quantum projection noise: population fluctuations in two-level systems. Phys. Rev. A 47, 3554–3570. doi:10.1103/PhysRevA.47.3554

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, Y., Ludlow, A., Lemke, N., Fox, R., Sherman, J., Ma, L., et al. (2011). Making optical atomic clocks more stable with 10⁻¹⁶-level laser stabilization. Nat. Photonics 5, 158–161. doi:10.1038/nphoton.2010.313

CrossRef Full Text | Google Scholar

Jiao, D., Deng, X., Gao, J., Zhang, L., Xu, G., Liu, T., et al. (2023). Highly vibration-resistant sub-hertz ultra-stable laser passing over 1700 km transport test. Infrared Phys. Technol. 130, 104608. doi:10.1016/j.infrared.2023.104608

CrossRef Full Text | Google Scholar

Jin, L. (2021). Suppression of residual amplitude modulation of ADP electro-optical modulator in Pound-Drever-Hall laser frequency stabilization. Opt. Laser. Technol. 136, 106758. doi:10.1016/j.optlastec.2020.106758

CrossRef Full Text | Google Scholar

Julsgaard, B., Walther, A., Kröll, S., and Rippe, L. (2007). Understanding laser stabilization using spectral hole burning. Opt. Express 15, 11444–11465. doi:10.1364/OE.15.011444

PubMed Abstract | CrossRef Full Text | Google Scholar

Keller, J., Ignatovich, S., Webster, S., and Mehlstäubler, T. (2014). Simple vibration-insensitive cavity for laser stabilization at the 10⁻¹⁶ level. Appl. Phys. B 116, 203–210. doi:10.1007/s00340-013-5676-y

CrossRef Full Text | Google Scholar

Kessler, T., Legero, T., and Sterr, U. (2012). Thermal noise in optical cavities revisited. J. Opt. Soc. Am. B 29, 178–184. doi:10.1364/JOSAB.29.000178

CrossRef Full Text | Google Scholar

Landerer, F., Flechtner, F., Save, H., Webb, F., Bandikova, T., Bertiger, W., et al. (2020). Extending the global mass change data record: GRACE follow-on instrument and science data performance. Geophys. Res. Lett. 47, e2020GL088306. doi:10.1029/2020GL088306

CrossRef Full Text | Google Scholar

Legero, T., Kessler, T., and Sterr, U. (2010). Tuning the thermal expansion properties of optical reference cavities with Fused Silica mirrors. J. Opt. Soc. Am. B 27, 914–919. doi:10.1364/JOSAB.27.000914

CrossRef Full Text | Google Scholar

Leibrandt, D., Bergquist, J., and Rosenband, T. (2013). Cavity-stabilized laser with acceleration sensitivity below 10⁻¹² g⁻¹. Phys. Rev. A 87, 023829. doi:10.1103/PhysRevA.87.023829

CrossRef Full Text | Google Scholar

Leibrandt, D., Thorpe, M., Bergquist, J., and Rosenband, T. (2011a). Field-test of a robust, portable, frequency-stable laser. Opt. Express 19, 10278–10286. doi:10.1364/OE.19.010278

PubMed Abstract | CrossRef Full Text | Google Scholar

Leibrandt, D., Thorpe, M., Notcutt, M., Drullinger, R., Rosenband, T., and Bergquist, J. (2011b). Spherical reference cavities for frequency stabilization of lasers in non-laboratory environments. Opt. Express 19, 3471–3482. doi:10.1364/OE.19.003471

PubMed Abstract | CrossRef Full Text | Google Scholar

Levin, Y. (1998). Internal thermal noise in the ligo test masses: a direct approach. Phys. Rev. D. 57, 659–663. doi:10.1103/PhysRevD.57.659

CrossRef Full Text | Google Scholar

Liu, Y., Lee, D., Nakamura, T., Jin, N., Cheng, H., Kelleher, M., et al. (2024). Low-noise microwave generation with an air-gap optical reference cavity. Apl. Photonics 9, 010806. doi:10.1063/5.0174544

CrossRef Full Text | Google Scholar

Ludlow, A., Boyd, M., Ye, J., Peik, E., and Schmidt, P. (2015). Optical atomic clocks. Rev. Mod. Phys. 87, 637–701. doi:10.1103/RevModPhys.87.637

CrossRef Full Text | Google Scholar

Margolis, H. (2009). Frequency metrology and clocks. J. Phys. B At. Mol. Opt. Phys. 42, 154017. doi:10.1088/0953-4075/42/15/154017

CrossRef Full Text | Google Scholar

Marlow, B., and Scherer, D. (2021). A review of commercial and emerging atomic frequency standards. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 68, 2007–2022. doi:10.1109/TUFFC.2021.3049713

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehlstäubler, T., Grosche, G., Lisdat, C., Schmidt, P., and Denker, H. (2018). Atomic clocks for geodesy. Rep. Prog. Phys. 81, 064401. doi:10.1088/1361-6633/aab409

PubMed Abstract | CrossRef Full Text | Google Scholar

Meylahn, F., Knust, N., and Willke, B. (2022). Stabilized laser system at 1550 nm wavelength for future gravitational-wave detectors. Phys. Rev. D. 105, 122004. doi:10.1103/PhysRevD.105.122004

CrossRef Full Text | Google Scholar

Millo, J., Magalhães, D., Mandache, C., Le Coq, Y., English, E., Westergaard, P., et al. (2009). Ultrastable lasers based on vibration insensitive cavities. Phys. Rev. A 79, 053829. doi:10.1103/PhysRevA.79.053829

CrossRef Full Text | Google Scholar

Milonni, P., and Eberly, J. (2010). Laser oscillation: power and frequency. John Wiley and Sons, Ltd, 175–228. chap. 5.

Google Scholar

Misner, C., Thorne, K., and Wheeler, J. (2017). Gravitation. Princeton University Press.

Google Scholar

Nazarova, T., Riehle, F., and Sterr, U. (2006). Vibration-insensitive reference cavity for an ultra-narrow-linewidth laser. Appl. Phys. B 83, 531–536. doi:10.1007/s00340-006-2225-y

CrossRef Full Text | Google Scholar

Nicklaus, K., Herding, M., Wang, X., Beller, N., Fitzau, O., Giesberts, M., et al. (2017). “High stability laser for next generation gravity missions,” in Proc. SPIE. Editors Z. Sodnik, B. Cugny, and N. Karafolas Bellingham, WA: International Society for Optics and Photonics SPIE, 10563. doi:10.1117/12.2304161

CrossRef Full Text | Google Scholar

Notcutt, M., Taylor, C., Mann, A., and Blair, D. (1995). Temperature compensation for cryogenic cavity stabilized lasers. J. Phys. D. Appl. Phys. 28, 1807–1810. doi:10.1088/0022-3727/28/9/008

CrossRef Full Text | Google Scholar

Numata, K., Kemery, A., and Camp, J. (2004). Thermal-noise limit in the frequency stabilization of lasers with rigid cavities. Phys. Rev. Lett. 93, 250602. doi:10.1103/PhysRevLett.93.250602

PubMed Abstract | CrossRef Full Text | Google Scholar

Riehle, F. (2015). Towards a redefinition of the second based on optical atomic clocks. C. R. Phys. 16, 506–515. doi:10.1016/j.crhy.2015.03.012

CrossRef Full Text | Google Scholar

Roberts, M., Taylor, P., and Gill, P. (1999). Laser linewidth at the sub-Hertz level. Tech. Rep. Available at: https://eprintspublications.npl.co.uk/1250/

Google Scholar

Rodrigues, W., and Oliveira, E. (2016). The many faces of maxwell, Dirac and Einstein equations. 2 edn. Cham: Springer.

Google Scholar

Roslund, J., Cingöz, A., Lunden, W., Partridge, G., Kowligy, A., Roller, F., et al. (2024). Optical clocks at sea. Nature 628, 736–740. doi:10.1038/s41586-024-07225-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Safronova, M., Budker, D., DeMille, D., Kimball, D., Derevianko, A., and Clark, C. (2018). Search for new Physics with atoms and molecules. Rev. Mod. Phys. 90, 025008. doi:10.1103/RevModPhys.90.025008

CrossRef Full Text | Google Scholar

Sanjuan, J., Abich, K., Gohlke, M., Resch, A., Schuldt, T., Wegehaupt, T., et al. (2019). Long-term stable optical cavity for special relativity tests in space. Opt. Express 27, 36206–36220. doi:10.1364/OE.27.036206

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwarz, R., Dörscher, S., Al-Masoudi, A., Benkler, E., Legero, T., Sterr, U., et al. (2020). Long term measurement of the ⁸⁷Sr clock frequency at the limit of primary Cs clocks. Phys. Rev. Res. 2, 033242. doi:10.1103/PhysRevResearch.2.033242

CrossRef Full Text | Google Scholar

Shirley, J. (1982). Modulation transfer processes in optical heterodyne saturation spectroscopy. Opt. Lett. 7, 537–539. doi:10.1364/OL.7.000537

PubMed Abstract | CrossRef Full Text | Google Scholar

Siegman, A. (1986). Lasers. Melville, NY: University Science Books. Available at: https://uscibooks.aip.org/books/lasers/

Google Scholar

Silfvast, W. (2004). Laser fundamentals. 2 edn. Cambridge University Press.

Google Scholar

Stacey, J., Barwood, G., Spampinato, A., Tsoulos, P., Robinson, C., Gaynor, P., et al. (2023). “Laser frequency stabilisation for the LISA mission using a cubic cavity,” in Proc. SPIE. Editors K. Minoglou, N. Karafolas, and B. Cugny, 12777. doi:10.1117/12.2691441266

CrossRef Full Text | Google Scholar

Swallows, M., Martin, M., Bishof, M., Benko, C., Lin, Y., Blatt, S., et al. (2012). Operating a ⁸⁷ Sr optical lattice clock with high precision and at high density. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 59, 416–425. doi:10.1109/TUFFC.2012.2210

PubMed Abstract | CrossRef Full Text | Google Scholar

Świerad, D., Häfner, S., Vogt, S., Venon, B., Holleville, D., Bize, S., et al. (2016). Ultra-stable clock laser system development towards space applications. Sci. Rep. 6, 33973. doi:10.1038/srep33973

PubMed Abstract | CrossRef Full Text | Google Scholar

Tai, Z.-Y., Yan, L.-L., Zhang, Y.-Y., Zhang, X.-F., Guo, W.-G., Zhang, S.-G., et al. (2017). Transportable 1555-nm ultra-stable laser with sub-0.185-Hz linewidth. Chin. Phys. Lett. 34, 090602. doi:10.1088/0256-307X/34/9/090602

CrossRef Full Text | Google Scholar

Takamoto, M., Ushijima, I., Ohmae, N., Yahagi, T., Kokado, K., Shinkai, H., et al. (2020). Test of general relativity by a pair of transportable optical lattice clocks. Nat. Photonics 14, 411–415. doi:10.1038/s41566-020-0619-8

CrossRef Full Text | Google Scholar

Tao, B.-K., and Chen, Q.-F. (2018). A vibration-insensitive-cavity design holds impact of higher than $$100g$$ 100 g. Appl. Phys. B 124, 228. doi:10.1007/s00340-018-7096-5

CrossRef Full Text | Google Scholar

Tapley, B., Watkins, M., Flechtner, F., Reigber, C., Bettadpur, S., Rodell, M., et al. (2019). Contributions of GRACE to understanding climate change. Nat. Clim. Change 9, 358–369. doi:10.1038/s41558-019-0456-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorpe, M., Leibrandt, D., and Rosenband, T. (2013). Shifts of optical frequency references based on spectral-hole burning in Eu³⁺: Y₂SiO₅. New J. Phys. 15, 033006. doi:10.1088/1367-2630/15/3/033006

CrossRef Full Text | Google Scholar

Tricot, F., Phung, D., Lours, M., Guérandel, S., and de Clercq, E. (2018). Power stabilization of a diode laser with an acousto-optic modulator. Rev. Sci. Instrum. 89, 113112. doi:10.1063/1.5046852

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, Y., Eby, J., and Safronova, M. (2023). Direct detection of ultralight dark matter bound to the sun with space quantum sensors. Nat. Astron. 7, 113–121. doi:10.1038/s41550-022-01833-6

CrossRef Full Text | Google Scholar

Vajente, G., Yang, L., Davenport, A., Fazio, M., Ananyeva, A., Zhang, L., et al. (2021). Low mechanical loss TiO₂: GeO₂ coatings for reduced thermal noise in gravitational wave interferometers. Phys. Rev. Lett. 127, 071101. doi:10.1103/PhysRevLett.127.071101

PubMed Abstract | CrossRef Full Text | Google Scholar

Vig, J. (1993). Military applications of high accuracy frequency standards and clocks. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 40, 522–527. doi:10.1109/58.238104

PubMed Abstract | CrossRef Full Text | Google Scholar

Vogt, S., Lisdat, C., Legero, T., Sterr, U., Ernsting, I., Nevsky, A., et al. (2011). Demonstration of a transportable 1 Hz-linewidth laser. Appl. Phys. B 104, 741–745. doi:10.1007/s00340-011-4652-7

CrossRef Full Text | Google Scholar

Wang, H., Álvarez, M., Collins, C., Brown, D., Wang, M., Mow-Lowry, C., et al. (2018). Feasibility of near-unstable cavities for future gravitational wave detectors. Phys. Rev. D. 97, 022001. doi:10.1103/PhysRevD.97.022001

CrossRef Full Text | Google Scholar

Wang, S., Cao, J., Yuan, J., Liu, D., Shu, H., and Huang, X. (2020). Integrated multiple wavelength stabilization on a multi-channel cavity for a transportable optical clock. Opt. Express 28, 11852–11860. doi:10.1364/OE.383115

PubMed Abstract | CrossRef Full Text | Google Scholar

Webster, S., and Gill, P. (2011). Force-insensitive optical cavity. Opt. Lett. 36, 3572–3574. doi:10.1364/OL.36.003572

PubMed Abstract | CrossRef Full Text | Google Scholar

Wiens, E., Chen, Q., Ernsting, I., Luckmann, H., Rosowski, U., Nevsky, A., et al. (2014). Silicon single-crystal cryogenic optical resonator. Opt. Lett. 39, 3242–3245. doi:10.1364/OL.39.003242

PubMed Abstract | CrossRef Full Text | Google Scholar

Wong, N., and Hall, J. (1985). Servo control of amplitude modulation in frequency-modulation spectroscopy: demonstration of shot-noise-limited detection. J. Opt. Soc. Am. B 2, 1527–1533. doi:10.1364/JOSAB.2.001527

CrossRef Full Text | Google Scholar

Wu, Y., Sun, B., and Li, X. (2021). Semiconductor laser active frequency stabilization technologies: a review. J. Korean Phys. Soc. 79, 795–809. doi:10.1007/s40042-021-00308-7

CrossRef Full Text | Google Scholar

Xiao, R., Xu, Y., Wang, Y., Sun, H., and Chen, Q. (2022). Transportable 30 cm optical cavity based ultrastable lasers with beating instability of 2 × 10⁻¹⁶. Appl. Phys. B 128, 220. doi:10.1007/s00340-022-07938-0

CrossRef Full Text | Google Scholar

Xu, G., Jiao, D., Chen, L., Zhang, L., Dong, R., Liu, T., et al. (2021). Vibration modes of a transportable optical cavity. Opt. Express 29, 24264–24277. doi:10.1364/OE.422182

PubMed Abstract | CrossRef Full Text | Google Scholar

Yariv, A. (1989). Quantum electronics. John Wiley and Sons.

Google Scholar

Zhang, W., Martin, M., Benko, C., Hall, J., Ye, J., Hagemann, C., et al. (2014). Reduction of residual amplitude modulation to 1 × 10⁻⁶ for frequency modulation and laser stabilization. Opt. Lett. 39, 1980–1983. doi:10.1364/OL.39.001980

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, P., Deng, J., Xing, C., Meng, F., Meng, L., Xie, Y., et al. (2022). A spaceborne mounting method for fixing a cubic Fabry-Pérot cavity in ultra-stable lasers. Appl. Sci. 12, 12763. doi:10.3390/app122412763

CrossRef Full Text | Google Scholar

Zhao, W., Yang, H., Wu, H., Fu, Y., Ge, J., and Zhang, S. (2023). All-fiber-device-coupled compact, transportable ultra-stable laser. Rev. Sci. Instrum. 94, 033002. doi:10.1063/5.0136173

PubMed Abstract | CrossRef Full Text | Google Scholar