- 1Department of Physics, Holon Institute of Technology, Holon, Israel
- 2Institute for Theoretical Physics, Leibniz University Hanover, Hanover, Germany
This study investigates the possibility of achieving a slow signal field at the level of single photons inside nanofibers by exploiting stimulated Brillouin scattering, which involves a strong pump field and the vibrational modes of the waveguide. The slow signal is significantly amplified for a pump field, with a frequency higher than that of the signal and attenuated for a lower pump frequency. We introduce a configuration for obtaining a propagating slow signal without gain or loss and with a relatively wide bandwidth. This process involves two strong pump fields with frequencies both higher and lower than that of the signal where the effects of signal amplification and attenuation compensate each other. We account for thermal fluctuations due to the scattering of thermal phonons and identify conditions under which thermal contributions to the signal field are negligible. The slowing of light through Brillouin optomechanics may serve as a vital tool for optical quantum information processing and quantum communications within nanophotonic structures.
1 Introduction
Significant progress has been achieved in recent years in fabricating waveguides with cross-sections nearing nanoscale dimensions (Safavi-Naeini et al., 2019), opening new horizons for stimulated Brillouin scattering (SBS). A pivotal advance in SBS emerged with the identification of a dominant mechanism induced by radiation pressure, as has been theoretically predicted (Rakich et al., 2012; Van-Laer et al., 2016; Zoubi and Hammerer, 2016; Rakich and Marquardt, 2018) and experimentally realized (Shin et al., 2013; Beugnot et al., 2014; Van-Laer et al., 2015a; Van-Laer et al., 2015b; Kittlaus et al., 2016; Kittlaus et al., 2017). SBS in waveguides has found application across a broad spectrum of communication and information processing technologies. The substantial enhancement of SBS in waveguides facilitates the amplification of the Stokes field (Kittlaus et al., 2016; Kittlaus et al., 2017; Otterstrom et al., 2019), paving the path towards a Brillouin laser (Otterstrom et al., 2018a; Gundavarapu et al., 2019; Chauhan et al., 2021) and light storage (Zhu et al., 2007; Merklein et al., 2017). Various proposals for nanoscale waveguides (Safavi-Naeini et al., 2019) have emerged in the literature, where a waveguide’s mechanical quality factor—determining the sound wave lifetime (Eggleton et al., 2013)—significantly impacts the efficiency of each proposed device. Moreover, thermal phonons pose major challenges to efficient photon and phonon processes within waveguides (Kharel et al., 2016; Van-Laer et al., 2017; Behunin et al., 2018; Dallyn et al., 2022). To address these challenges, optomechanical cooling via sideband cooling in a continuous system has been demonstrated, using SBS to cool a continuum of traveling wave phonons in a waveguide by tens of kelvins (Otterstrom et al., 2018b). These achievements open the possibility of developing versatile light–matter interfaces (Hammerer et al., 2010) based on SBS achieving, for example, optomechanical entanglement (Zhu et al., 2024) or nonlinear photon interactions (Zoubi and Hammerer, 2017).
This study introduces a configuration to achieve slow photons using SBS within waveguides. By coupling a signal field to classical pump fields through Brillouin scattering mediated by acoustic waves, it is possible to achieve a low effective group velocity; however, the signal’s amplitude is significantly amplified when the pump frequency exceeds that of the signal and is considerably attenuated when the pump frequency is lower (Thevenaz, 2008). A stable signal amplitude can be maintained by employing two simultaneous pump fields with frequencies both above and below that of the signal. The Brillouin scattering from the higher pump field into the signal is balanced by the scattering from the signal field into the lower pump field. We account for the impact of thermal phonons in the waveguide medium and identify conditions under which thermal contributions to the signal amplitude are negligible. The real-space quantum Langevin equations of motion for the signal field are solved by assuming classical pump fields and adiabatically eliminating the phonon components. As a result, the signal field propagates through the waveguide without any gain or loss, with an effective group velocity significantly more reduced than the group velocity of light.
The ability to control the group velocity of light within waveguides opens new avenues for enhancing light–matter interactions, which are crucial for optical quantum information processing (O’Brien, 2007). Slowing the photons extends their interaction time with the medium, potentially increasing the efficiency of quantum gates and other processing elements (Zoubi and Hammerer, 2017; Zoubi, 2021; Zoubi, 2023). Furthermore, the stable propagation of slow light without gain or loss is essential for maintaining the coherence of quantum states necessary for quantum communication and computing.
The paper is structured as follows. Section 2 introduces a coupled system of photons and phonons via SBS within a waveguide. Section 3 describes two methodologies to achieve a slow propagating signal field utilizing SBS and a strong classical pump field. The first method employs a pump field with a frequency higher than that of the signal, leading to significant signal amplification. The second method utilizes a pump field with a frequency lower than the signal’s, resulting in considerable signal attenuation. The impact of thermal fluctuations is analyzed in both scenarios. Section 4 discusses the achievement of a slow signal at the single-photon level without gain or loss by implementing two pump fields with frequencies both above and below that of the signal while minimizing thermal contributions. Section 5 feature a discussion and conclusions. Detailed derivations of the equations of motion and their solutions are presented in the appendices.
2 Continuum quantum optomechanics in nanophotonic wires
We start by presenting a system of interacting light and sound waves within nanoscale waveguides via Brillouin scattering. The system consists of a waveguide composed of dielectric material placed in free space, characterized by a refractive index
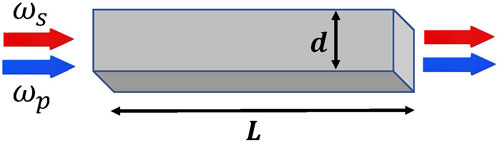
Figure 1. Schematic diagram of a waveguide of length
The Hamiltonian for propagating photons within a waveguide is described by
where
where
where
In Zoubi and Hammerer (2016), we solved the equations of motion for the electromagnetic field and mechanical excitation to derive the photon and phonon dispersions analytically for the specific case of a cylindrical waveguide, obtaining the frequencies
and its inverse transformation by
Translational symmetry ensures the identities
This formulation allows for a nuanced treatment of the propagation dynamics of light pulses within the waveguide, encapsulating the effects of group velocity and phase shifts in real space.
Similarly, we define the mechanical excitation field operator as
and its inverse transformation by
which satisfy the commutation relation
The real-space photon and phonon field operators, having a dimension of
The coupling parameter for photon–phonon interaction,
This formulation provides a compact description of the interaction between photons and phonons in the real-space framework, accommodating the direct and inverse scattering processes.
3 Slow light in Brillouin quantum optomechanics
We proceed on this basis to describe the phenomena of signal field amplification and attenuation by exploiting stimulated inter-modal Brillouin scattering of co-propagating photons that belong to distinct spatial optical modes (Kittlaus et al., 2017). We assume a signal field in branch
Both the signal and pump fields are assumed to propagate in the rightward direction. The rate of photon damping is considered negligible during their transit along the waveguide’s length
with
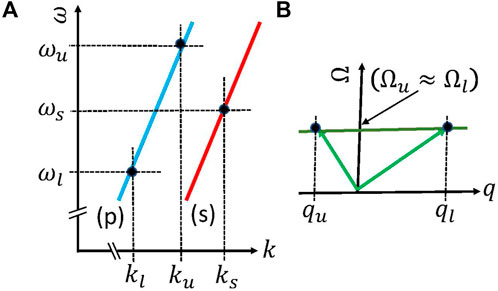
Figure 2. (A) The photonic branches
In our analysis, we explore two distinct scenarios based on the relationship between the pump and signal frequencies: 1) the pump frequency is higher than that of the signal, denoted as
3.1 Slow light with signal amplification
In the scenario where
The interaction Hamiltonian between photons and phonons is given by
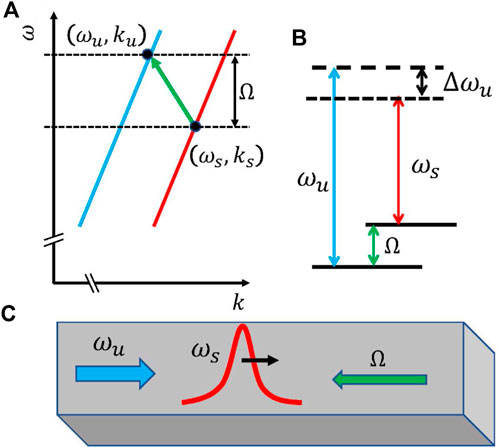
Figure 3. (A) A pump field
The Heisenberg–Langevin equations of motion for the photon and phonon field operators are formulated as
The resulting signal field operator is (see appendix A for details):
where
and the shift in wavenumber is given by
with
Using the relations (12), the average number of photons per unit length, or photon density, is calculated as
where
In this formulation, correlations between the Langevin force operators and the initial signal operator are disregarded. This approach focuses on the significant impact of the gain and thermal noise on the evolution of the photon density within the medium, illustrating how amplification and thermal effects contribute to the overall behavior of the signal.
The effective group velocity is defined by
We obtain
The rate of change of the gain
Our primary goal is to achieve a slow propagating signal, aiming for
For the case of
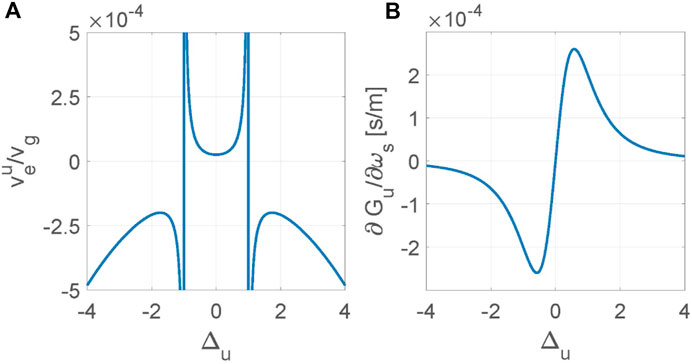
Figure 5. (A) The relative effective group velocity
3.2 Slow light with signal attenuation
For the scenario where
Furthermore, the interaction Hamiltonian between photons and phonons is described by
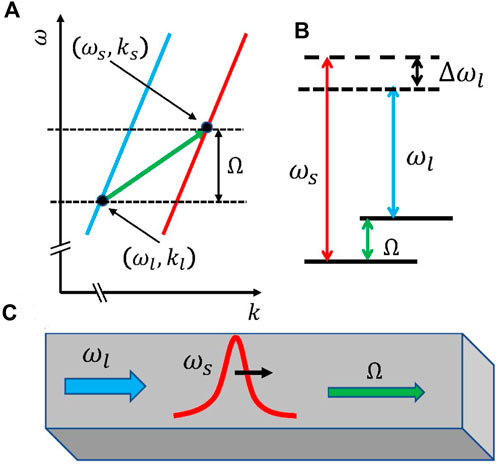
Figure 6. (A) A signal field
The Heisenberg–Langevin equations of motion for the photon and phonon field operators are given by
The solution to the equations of motion, as provided in Appendix B, yields
with the detuning frequency defined as
and the wavenumber shift is
where
The photon density, using relations (12), is given by
where the thermal contribution is defined by
The effective group velocity is given by
This leads to
The rate of change of the gain with respect to the signal frequency is calculated as
Our main goal is to achieve a slow propagating signal, aiming for
In Figure 4, we plot the gain factor
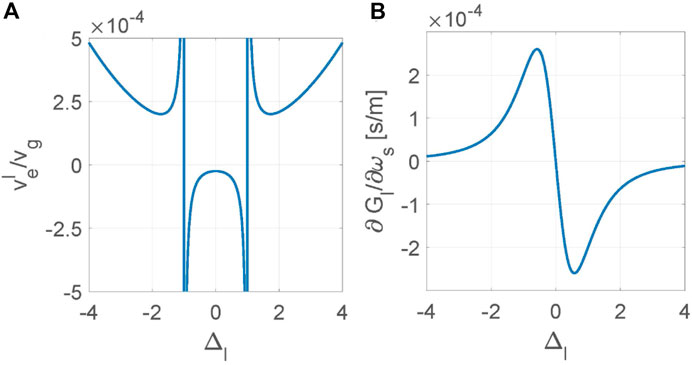
Figure 7. (A) The relative effective group velocity
4 Slow light without gain and loss
Based on this discussion, we conclude that achieving a slow signal within a waveguide while maintaining a constant signal amplitude using SBS with a single pump field is unattainable. Our primary interest lies in slowing down the signal field to the level of single photons. Our objective is to attain a propagating signal with an effective group velocity significantly lower than that in free space while also ensuring a constant average number of quanta. Additionally, it is crucial to minimize the impact of thermal fluctuations, preventing them from significantly affecting the propagating signal. Therefore, our goal is to introduce a configuration that enables the realization of slow signals at the single-photon level without inducing gain or loss.
To address the challenges previously discussed, we propose a unique configuration in which the signal field is coupled through SBS to two pump fields, involving a dispersion-less vibration mode. This approach aims to demonstrate that by merging the two above scenarios, a slow signal can be achieved without gain or loss, where the processes of signal amplification and attenuation counterbalance each other. Specifically, a signal with frequency
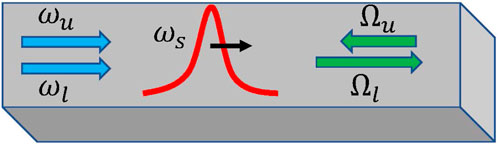
Figure 8. A signal field of frequency
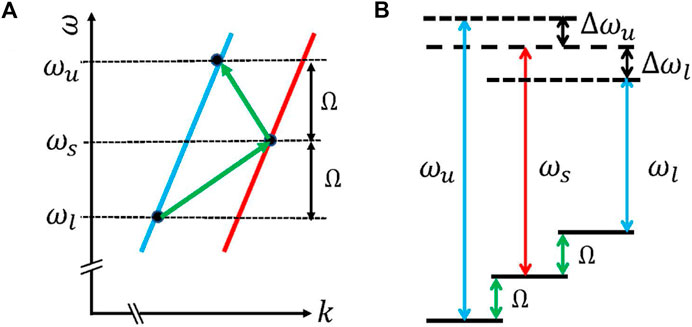
Figure 9. (A) A pump field
The photon Hamiltonian is specified in (11), and the phonon Hamiltonian combines both upper and lower phonon contributions,
In the interaction picture, the equation of motion for the photon operator is expressed as
and the phonon equations of motion follow from Equations 15 and 26. Adopting a similar approach to that in Appendices A and B for solving these equations, we arrive at
where
and
The key control parameters remain the scaled detunings
For the photon density, we obtain
where the thermal fluctuation contribution is given by
Utilizing relations (12) for both the upper and lower processes, correlations among the Langevin force operators corresponding to the upper and lower processes are neglected.
The effective group velocity is defined by
We have
The rate of change of gain with respect to the signal frequency is expressed as
The objective is to achieve a slow propagating signal, where
We aim to achieve the propagation of light without gain or loss, which is possible when
Additionally, the thermal fluctuation contribution to the signal needs to be significantly less than 1. At the waveguide output, at
The contribution of thermal fluctuations to the average number of signal photons at the waveguide output should also be much smaller than 1:
For further analysis of the result, we define the ratios
For the case of zero gain
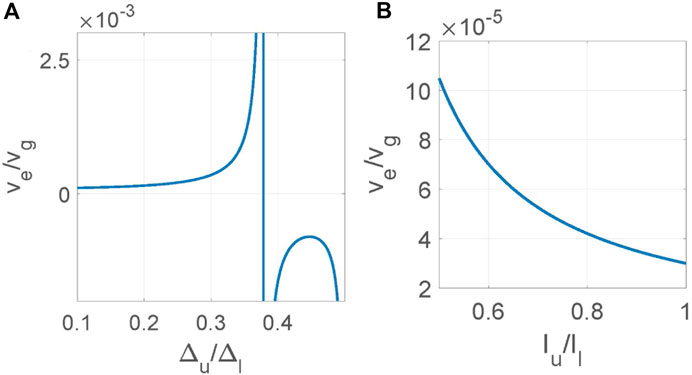
Figure 10. (A) Relative effective group velocity
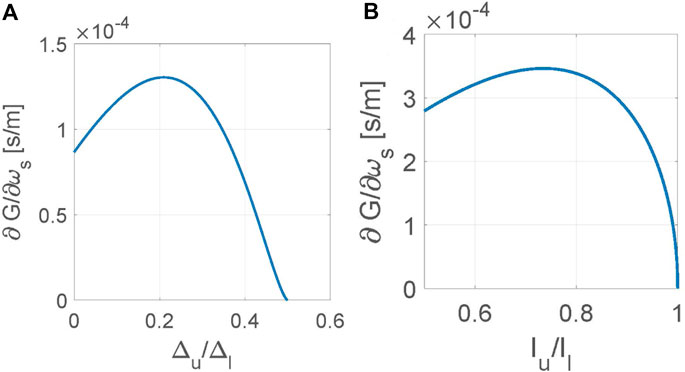
Figure 11. (A) Rate of change of the gain factor with respect to the signal frequency
5 Discussion and conclusion
Optical quantum information processing is currently a leading candidate for the development of quantum computers. Generally, the components used in quantum information processing differ from those used in communication, which implies a need for interfaces between devices with varying physical properties. Such interfacing can significantly affect the coherence of quantum information. Nanophotonic structures involving photons can serve purposes in both quantum communication and quantum computing. This setup marks a crucial step toward an all-optical on-chip platform, using the same photons for quantum communication and computing, thereby avoiding the decoherence effects associated with interfacing. Interactions among photons are critical for developing optical quantum logic gates. One of the primary obstacles to fabricating efficient photon-based quantum logic gates is the rapid propagation of optical fields within extensive nanophotonic structures. The high speed of light in these structures limits the accumulation of the nonlinear phases necessary for operating quantum logic gates.
In this study, we introduce a configuration that enables slow signal propagation at the single-photon level by exploiting stimulated Brillouin scattering (SBS) within waveguides. The signal field can be significantly slowed via Brillouin scattering, which involves a classical pump field and propagating phonons. When the pump frequency exceeds that of the signal, it results in a substantial amplification of the signal amplitude; conversely, a pump frequency lower than that of the signal causes notable attenuation. To achieve a slow signal field without gain or loss, we propose a novel configuration that utilizes two pump fields with frequencies both above and below that of the signal. This arrangement allows the effects of amplification and attenuation to counterbalance each other, thus enabling the signal to propagate at a constant amplitude with an effective group velocity significantly more reduced than that in free space. Additionally, this configuration can accommodate slow signals over wide bandwidths, extending up to tens of megahertz. We also consider the effects of thermal fluctuations by calculating the scattering of the pump fields off thermal phonons into and out of the signal field and establish conditions under which thermal contributions are negligible.
Slow light has been realized in a free-space medium containing an atomic ensemble (Tey et al., 2008; Hammerer et al., 2010). The control over light propagation in an optical medium can be achieved through electromagnetic induced transparency (EIT), which enables the generation of both fast and slow light. In this process, coherent destructive interference prevents excitation within the optical medium (Lukin et al., 2001; Fleischhauer et al., 2005; Chang et al., 2014). EIT inherently satisfies the phase-matching requirement due to the presence of atomic components. To illustrate EIT, we examine a three-level atom configured in a lambda scheme with two lower metastable states,
EIT has been demonstrated in cavity optomechanics via coupling between vibrational modes and photon modes through radiation pressure (Safavi-Naeini et al., 2011), where photons and phonons are localized within the resonator and phase-matching occurs naturally (Weis et al., 2010). Brillouin scattering induced transparency was shown by utilizing long-lived propagating light and phonons in a silica resonator under the required phase-matching conditions (Kim et al., 2015). Moreover, higher-order side-band induced transparency in optomechanical systems (Xiong et al., 2012), and optomechanical group delays in spinning resonator (Zhang and Shen, 2024) have been demonstrated. The approach introduced in the current paper allows for the propagation of signals across a broader bandwidth than achievable with the EIT scheme. Here, the phonon component serves a role analogous to the atomic component in EIT, ensuring phase-matching for the Brillouin scattering between the signal and pump fields.
The generation of slow photons is important for fundamental physics, such as for quantum nonlinear optics at the level of single photons, which rely on the derivation of effective photon–photon interactions (Zoubi and Hammerer, 2017). Additionally, the formation of photon bound states has been explored (Zoubi, 2021). Slow photons in waveguides provide a test system for studying quantum phases of a gas of interacting photons. Moreover, slow photons have practical applications in nanophotonics for physical implementation in quantum information and quantum communication. The time delay achieved by slowing photons inside waveguides can serve as a memory device, a critical component for quantum computing with photons. A time delay in the order of microseconds can be achieved once the effective group velocity approaches the velocity of sound waves inside a waveguide.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
HZ: Writing–review and editing, Writing–original draft. KH: Writing–review and editing, Writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. KH got a funding from: Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through Project-ID 390837967.
Acknowledgments
KH acknowledges support through Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through Project-ID 390837967 - EXC 2123.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frqst.2024.1437933/full#supplementary-material
References
Aspelmeyer, M., Kippenberg, T. J., and Marquardt, F. (2014). Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452. doi:10.1103/revmodphys.86.1391
Behunin, R. O., Otterstrom, N. T., Rakich, P. T., Gundavarapu, S., and Blumenthal, D. J. (2018). Fundamental noise dynamics in cascaded-order Brillouin lasers. Phys. Rev. A 98, 023832. doi:10.1103/physreva.98.023832
Beugnot, J.-C., Lebrun, S., Pauliat, G., Maillotte, H., Laude, V., and Sylvestre, T. (2014). Brillouin light scattering from surface acoustic waves in a subwavelength-diameter optical fibre. Nat. Commun. 5, 5242. doi:10.1038/ncomms6242
Chang, D. E., Vuletic, V., and Lukin, M. D. (2014). Quantum nonlinear optics - photon by photon. Nat. Photonics 8, 685–694. doi:10.1038/nphoton.2014.192
Chauhan, N., Isichenko, A., Liu, K., Wang, J., Zhao, Q., Behunin, R. O., et al. (2021). Visible light photonic integrated Brillouin laser. Nat. Commun. 12, 4685. doi:10.1038/s41467-021-24926-8
Dallyn, J. H., Liu, K., Harrington, M. W., Brodnik, G. M., Rakich, P. T., Blumenthal, D. J., et al. (2022). Thermal and driven noise in Brillouin lasers. Phys. Rev. A 105, 043506. doi:10.1103/physreva.105.043506
Eggleton, B. J., Poulton, C. G., and Pant, R. (2013). Inducing and harnessing stimulated Brillouin scattering in photonic integrated circuits. Adv. Opt. Phot. 5, 536. doi:10.1364/aop.5.000536
Fleischhauer, M., Imamoglu, A., and Marangos, J. P. (2005). Electromagnetically induced transparency: optics in coherent media. Rev. Mod. Phys. 77, 633–673. doi:10.1103/revmodphys.77.633
Gundavarapu, S., Brodnik, G. M., Puckett, M., Huffman, T., Bose, D., Behunin, R., et al. (2019). Sub-hertz fundamental linewidth photonic integrated Brillouin laser. Nat. Photonics 13, 60–67. doi:10.1038/s41566-018-0313-2
Hammerer, K., Sorensen, A. S., and Polzik, E. S. (2010). Quantum interface between light and atomic ensembles. Rev. Mod. Phys. 82, 1041–1093. doi:10.1103/revmodphys.82.1041
Kharel, P., Behunin, R. O., Renninger, W. H., and Rakich, P. T. (2016). Noise and dynamics in forward Brillouin interactions. Phys. Rev. A 93, 063806. doi:10.1103/physreva.93.063806
Kim, J., Kuzyk, M. C., Han, K., Wang, H., and Bahl, G. (2015). Non-reciprocal Brillouin scattering induced transparency. Nat. Phys. 11, 275–280. doi:10.1038/nphys3236
Kittlaus, E. A., Otterstorm, N. T., and Rakich, P. T. (2017). On-chip inter-modal Brillouin scattering. Nat. Commun. 8, 15819. doi:10.1038/ncomms15819
Kittlaus, E. A., Shin, H., and Rakich, P. T. (2016). Large Brillouin amplification in silicon. Nat. Photonics 10, 463–467. doi:10.1038/nphoton.2016.112
Lukin, M. D., Fleischhauer, M., Cote, R., Duan, L. M., Jaksch, D., Cirac, J. I., et al. (2001). Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 87, 037901. doi:10.1103/physrevlett.87.037901
Merklein, M., Stiller, B., Vu, K., Madden, S. J., and Eggleton, B. J. (2017). A chip-integrated coherent photonic-phononic memory. Nat. Commun. 8, 574. doi:10.1038/s41467-017-00717-y
O’Brien, J. L. (2007). Optical quantum computing. Science 318, 1567–1570. doi:10.1126/science.1142892
Otterstrom, N. T., Behunin, R. O., Kittlaus, E. A., and Rakich, P. T. (2018b). Optomechanical cooling in a continuous system. Phys. Rev. X 8, 041034. doi:10.1103/physrevx.8.041034
Otterstrom, N. T., Behunin, R. O., Kittlaus, E. A., Wang, Z., and Rakich, P. T. (2018a). A silicon Brillouin laser. Science 360, 1113–1116. doi:10.1126/science.aar6113
Otterstrom, N. T., Kittlaus, E. A., Gertler, S., Behunin, R. O., Lentine, A. L., and Rakich, P. T. (2019). Resonantly enhanced nonreciprocal silicon Brillouin amplifier. Optica 6, 1117. doi:10.1364/optica.6.001117
Rakich, P., and Marquardt, F. (2018). Quantum theory of continuum optomechanics. New J. Phys. 20, 045005. doi:10.1088/1367-2630/aaac4f
Rakich, P. T., Reinke, C., Camacho, R., Davids, P., and Wang, Z. (2012). Giant enhancement of stimulated Brillouin scattering in the subwavelength limit. Phys. Rev. X 2, 011008. doi:10.1103/physrevx.2.011008
Safavi-Naeini, A. H., Alegre, T. P. M., Chan, J., Eichenfield, M., Winger, M., Lin, Q., et al. (2011). Electromagnetically induced transparency and slow light with optomechanics. Nature 472, 69–73. doi:10.1038/nature09933
Safavi-Naeini, A. H., Van-Thourhout, D., Baets, R., and Van-Laer, R. (2019). Controlling phonons and photons at the wavelength scale: integrated photonics meets integrated phononics. Optica 6, 213. doi:10.1364/OPTICA.6.000213
Shin, H., Qiu, W., Jarecki, R., Cox, J. A., Olsson, R. H., Starbuck, A., et al. (2013). Tailorable stimulated Brillouin scattering in nanoscale silicon waveguides. Nat. Commun. 4, 1944. doi:10.1038/ncomms2943
Tey, M. K., Chen, Z., Aljunid, S. A., Chng, B., Huber, F., Maslennikov, G., et al. (2008). Strong interaction between light and a single trapped atom without the need for a cavity. Nat. Phys. 4, 924–927. doi:10.1038/nphys1096
Thevenaz, L. (2008). Slow and fast light in optical fibres. Nat. Photonics 2, 474–481. doi:10.1038/nphoton.2008.147
Van-Laer, R., Baets, R., and Van-Thourhout, D. (2016). Unifying Brillouin scattering and cavity optomechanics. Phys. Rev. A 93, 053828. doi:10.1103/physreva.93.053828
Van-Laer, R., Bazin, A., Kuyken, B., Baets, R., and Van-Thourhout, D. (2015b). Net on-chip Brillouin gain based on suspended silicon nanowires. New J. Phys. 17, 115005. doi:10.1088/1367-2630/17/11/115005
Van-Laer, R., Kuyken, B., Van-Thourhout, D., and Baets, R. (2015a). Interaction between light and highly confined hypersound in a silicon photonic nanowire. Nat. Photonics 9, 199–203. doi:10.1038/nphoton.2015.11
Van-Laer, R., Sarabalis, C. J., Baets, R., Van-Thourhout, D., and Safavi-Naeini, A. H. (2017). Thermal Brillouin noise observed in silicon optomechanical waveguide. J. Opt. 19, 044002. doi:10.1088/2040-8986/aa600d
Weis, S., Riviere, R., Deleglise, S., Gavartin, E., Arcizet, O., Schliesser, A., et al. (2010). Optomechanically induced transparency. Science 330, 1520–1523. doi:10.1126/science.1195596
Xiong, H., Si, L.-G., Zheng, A.-S., Yang, X., and Wu, Y. (2012). Higher-order sidebands in optomechanically induced transparency. Phys. Rev. A 86, 013815. doi:10.1103/physreva.86.013815
Zhang, W., and Shen, H. Z. (2024). Optomechanical second-order sidebands and group delays in a spinning resonator with a parametric amplifier and non-markovian effects. Phys. Rev. A 109, 033701. doi:10.1103/physreva.109.033701
Zhu, C., Genes, C., and Stiller, B. (2024). Optoacoustic entanglement in a continuous Brillouin-active solid state system. arXiv:2401.10665.
Zhu, Z., Gauthier, D. J., and Boyd, R. W. (2007). Stored light in an optical fiber via stimulated Brillouin scattering. Science 318, 1748–1750. doi:10.1126/science.1149066
Zoubi, H. (2021). Formation of photon molecules in nanoscale waveguides. Phys. Rev. A 104, 063510. doi:10.1103/physreva.104.063510
Zoubi, H. (2023). Collective states of photons and phonons via inter-modal Brillouin scattering. Eur. Phys. J. D 77, 171. doi:10.1140/epjd/s10053-023-00753-y
Zoubi, H., and Hammerer, K. (2016). Optomechanical multimode Hamiltonian for nanophotonic waveguides. Phys. Rev. A 94, 053827. doi:10.1103/physreva.94.053827
Keywords: slow light, stimulated Brillouin scattering, quantum optomechanics, photon-phonon interaction, nanowires, nanophotonics
Citation: Zoubi H and Hammerer K (2024) Slow light through Brillouin scattering in continuum quantum optomechanics. Front. Quantum Sci. Technol. 3:1437933. doi: 10.3389/frqst.2024.1437933
Received: 24 May 2024; Accepted: 20 June 2024;
Published: 29 July 2024.
Edited by:
Sankar Davuluri, Birla Institute of Technology and Science, IndiaReviewed by:
Nitesh Chauhan, University of Colorado Boulder, United StatesH. Z. Shen, Northeast Normal University, China
Copyright © 2024 Zoubi and Hammerer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hashem Zoubi, aGFzaGVtekBoaXQuYWMuaWw=
 Hashem Zoubi
Hashem Zoubi Klemens Hammerer
Klemens Hammerer