
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
MINI REVIEW article
Front. Quantum Sci. Technol., 12 July 2024
Sec. Quantum Optics
Volume 3 - 2024 | https://doi.org/10.3389/frqst.2024.1426216
This article is part of the Research TopicPrecision Measurements and Quantum Technologies Utilizing OpticsView all 5 articles
Rydberg atoms have highly controllable exotic properties such as strong inter-atomic interaction, high polarizability, and long lifetimes which enabled unprecedented progress in Rydberg atom-based quantum Technologies. We present a brief review of recent progress in the development of quantum technologies using Rydberg atoms. We highlight the recent advances in the various regimes of quantum technologies such as quantum Information processing, quantum sensing, quantum simulation of many-body physics and single-photon sources for quantum communications.
Rydberg atoms have the outer electron excited to a high-lying energy level imparting exaggerated properties to the Rydberg atoms such as large interatomic interaction such as Van der Waals and dipole-dipole interaction, large polarisabilities and long lifetimes. These exotic properties of Rydberg atoms are highly controllable and make Rydberg atoms a versatile platform for a wide range of quantum technology applications Adams et al. (2019) such as quantum information processing Saffman et al. (2010), quantum sensing Buhmann et al. (2021), Meyer et al. (2021), quantum simulation of many-body physics Scholl et al. (2021) and single-photon sources for quantum communication Ripka et al. (2018), Müller et al. (2013).
Quantum Information processing is a complex phenomena which involves both quantum computing and quantum simulation that focuses on solving various difficult problems like simulating many body systems, factorization of large numbers, and understanding condensed matter systems which are impossible for today’s classical computers Wu et al. (2021). Control and manipulation of ultra-cold Rydberg atoms offer a promising avenue for quantum information processing Saffman et al. (2010). Quantum computing is performed via quantum gate operations. The fundamental requirement for such quantum gate operations is to develop the platform of scalable and high-fidelity qubit system which can perform long algorithms operations efficiently as per DiVincenzo criteria DiVincenzo (2000).
Rydberg atoms with high principal quantum numbers n have extraordinary properties such as long-range dipole-dipole interactions scaling as
Quantum Entanglement is an important phenomenon in quantum mechanics in which two or more particles are generated or interact in such a way that their quantum states are correlated and cannot be described independently even though the individual particles may be separated spatially. The correlations exhibited by entangled states have no classical analogue. Quantum entanglement has important applications in emerging quantum technologies such as quantum information Processing Isenhower et al. (2010), quantum cryptography and teleportation.
Atoms in highly excited Rydberg states with large principal quantum numbers Silpa et al. (2022) exhibit interesting characteristic features such as large dipole moments. This makes the Rydberg atoms highly polarisable with static polarisability scaling as
The generation of entanglement between Rydberg atoms can be done using the mechanism of Rydberg blockade as shown in Figure 1. To understand the mechanism of the Rydberg blockade, let us consider two atoms
When the two atoms are excited by the same laser field, then as a consequence of the Rydberg blockade, the two-atom system is prepared in a superposition of having one atom or the other atom in the excited Rydberg state resulting in an entangled state given by:
Entanglement between two individual atoms was obtained using Rydberg blockade in Wilk et al. (2010). Demonstration of CNOT gate between two individually addressed neutral atoms Knoernschild et al. (2010) using Rydberg blockade was reported in Isenhower et al. (2010).
Individual Rydberg atoms in arrays of optical tweezers have become a powerful platform for scalable quantum computing Saffman (2016) with Rydberg atomic qubits. Atom by atom assembly in a 3D atomic structure is reported in Barredo et al. (2018). A 51 atom quantum simulator in an array of Rydberg atoms was demonstrated in Bernien et al. (2017). A photon-photon quantum gate was reported in Tiarks et al. (2019). Schrodinger cat states were generated using Rydberg atom arrays in Omran et al. (2019). A 256-atom programmable quantum simulator was demonstrated in Ebadi et al. (2021). A quantum processor based on coherent transport of entangled atom arrays was reported in Bluvstein et al. (2022). Multi-qubit entanglement and algorithms on a Rydberg atom quantum computer were demonstrated in Graham et al. (2022). Quantum optimization of maximum independent sets using Rydberg atom arrays was presented in Ebadi et al. (2021). High-fidelity parallel entangling gates on a Rydberg atom quantum computer was demonstrated in Evered et al. (2023). Hardware-Efficient, Fault-Tolerant quantum Computation with Rydberg Atoms was presented in Cong et al. (2022).
Quantum sensing Degen et al. (2017) stands at the forefront of precision measurement, offering unparalleled sensitivity and accuracy across diverse fields. From atomic-scale sensors to solid-state systems, quantum sensing techniques promise transformative applications in science and technology. Examples include quantum magnetometers for precise magnetic field detection, quantum gyroscopes enabling accurate navigation, and quantum gravimeters for high-precision gravity measurements Adams et al. (2019), Degen et al. (2017).
Among the myriad approaches to quantum sensing, the utilization of Rydberg atoms presents unique opportunities. Rydberg atoms possess high dipole moments
Recent advances have enabled hot-atom vapour cell systems to sense microwave (MW) fields with exceptional sensitivity in Rydberg atoms. Initially, sensors split an electromagnetically induced transparency (EIT) line due to the MW-induced Autler-Townes (A-T) effect, lacking phase information. Treating atoms as a MW mixer Simons et al. (2019) with optical output significantly enhanced sensitivity, eliminating the need for a MW local oscillator (LO) and making the receiver entirely optical. This optical-bias detection method offers advantages like stealthy electric field measurement and improved sensitivity. With phase-stable laser fields and optimized setups, further enhancements in sensitivity and spectral resolution are achievable, enabling tunable detection of a wide bandwidth of MW and mm-wave frequencies Borówka et al. (2024). Cold atom quantum sensing, particularly utilizing Rydberg atoms, marks a significant leap in precision measurement capabilities. By leveraging techniques such as Magneto-Optical Traps and polarization gradient cooling, researchers can capture and cool Rubidium atoms to ultra-low temperatures, approaching absolute zero. Advanced data acquisition techniques, including multi-carrier modulation and frequency detuning, can be applicable in cold atoms as well, These developments open new avenues for quantum sensing and metrology, promising breakthroughs in fundamental research and practical applications alike.
Optical tweezers provide precise control over the position and motion of individual atoms, allowing for highly localized sensing. This enables sensitive detection of weak microwave signals with improved signal-to-noise ratios. By confining atoms in optical tweezers as shown in Figure 2, they are effectively shielded from external disturbances, such as stray electromagnetic fields or thermal fluctuations. This isolation enhances the stability and reliability of microwave sensing measurements. Quantum sensing with single atoms enables unprecedented precision in detecting and characterizing microwave fields Facon et al. (2016). This level of resolution is particularly valuable for probing localized microwave phenomena or studying quantum effects at the single-atom level. Circular states, such as circular Rydberg states, indeed have unique properties that can make them advantageous for certain quantum sensing applications compared to non-circular states. Circular Rydberg states are characterized by their high angular momentum and unique geometric properties, which can lead to enhanced sensitivity to external fields. One advantage of circular Rydberg states is their long lifetime, which is often orders of magnitude longer than non-circular states. This longer lifetime can result in increased coherence time, allowing for more precise measurements and reducing decoherence effects.
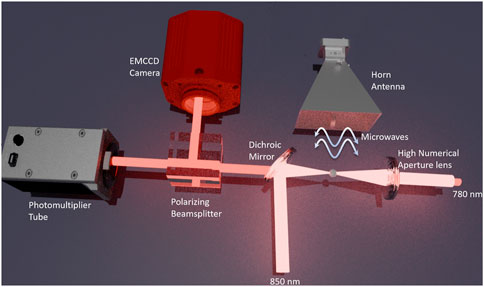
Figure 2. Schematic of the optical tweezer setup for trapping single atom. The wavelength of the tweezer is 850 nm and the probe is 780 nm for trapping 87Rb with a horn antenna placed in the far-field limit.
Additionally, circular Rydberg states have strong electric dipole moments, making them highly sensitive to electric fields. This sensitivity can be leveraged in electric field sensing applications, where even weak electric fields can induce measurable changes in the state of the atom. The utilization of Rydberg atoms in quantum sensing represents a significant advancement, offering unparalleled sensitivity and resolution across a broad range of frequencies. From room temperature vapour cell sensors to cold atom platforms, Rydberg atom-based sensing techniques continue to push the boundaries of quantum metrology. By leveraging the unique properties of Rydberg atoms and incorporating advanced measurement techniques, researchers are poised to unlock new frontiers in quantum sensing with profound implications for science and technology.
Many-body physics explores the quantum behaviour of systems composed of many interacting particles, revealing emergent phenomena such as superconductivity and magnetism. It delves into the complex interplay of quantum mechanics, statistical mechanics, and computational methods to understand how these systems behave collectively.
Due to the extended lifetime of Rydberg states, which scales in the
Emerging more recently, this approach traps single laser-cooled atoms in tightly focused dipole traps or optical tweezers. It offers a bottom-up method for creating arrays of individual atoms, providing unique opportunities for controlled manipulation and study Browaeys and Lahaye (2020). An optical dipole trap with a tight focus of about 1
The next step involves creating arrays of microtraps. One method utilizes a spatial light modulator (SLM) to imprint an appropriate phase pattern on the trapping beam before focusing, allowing for the realization of almost arbitrary arrays of traps in the focal plane of the objective. Alternatively, arrays of microlenses or interference techniques can be employed. However, stochastic loading of microtraps initially limited the platform to a few atoms due to the probability of having all
In optical lattices with large spacing between sites, Rydberg atoms exhibit strong dipole-dipole interactions, even over micrometer distances. These interactions give rise to energy shifts in the pair states, akin to van der Waals forces. By mapping ground and Rydberg states onto a spin-1/2 model, researchers construct Hamiltonians describing ensembles of atoms prepared in the same state and driven by coherent lasers
for dipole coupled states
One method involves suddenly changing a parameter in the Hamiltonian and observing the resulting dynamics of the closed many-body system. Another approach is to prepare the ground state by adiabatically varying the parameters of the Hamiltonian and studying its properties. Experiments in the Ising model regime have utilized both approaches. The generic phase diagram of the quantum Ising model, particular attention is given to the case of nearest-neighbor couplings and the emergence of paramagnetic and antiferromagnetic phases. By controlling parameters like detuning and Rabi frequency, researchers can explore the phase diagram of this model. Experimental implementations involve quenching, where the Rydberg excitation laser is suddenly applied after preparing the atoms in their ground state and measuring relevant quantities such as average magnetization and spin-spin correlation function. Adiabatic ground state preparation, initially demonstrated in specific regimes, allows controlled excitations separated by specific distances in one and two dimensions the study of quantum phase transitions, and the investigation of revivals in system dynamics, offering insights into the behavior of many-body systems. The potential of Rydberg dressing in observing interaction-driven dynamics is also demonstrated, although challenges remain in scaling up the system size.
Quantum simulation of 2D Ferromagnets with hundreds of Rydberg atoms was demonstrated in Scholl et al. (2021). Quantum many-body dynamics in driven Rydberg array was demonstrated in Bluvstein et al. (2021). Continuous symmetry breaking in a two-dimensional Rydberg array was reported in Chen et al. (2023). Hardware-Efficient, Fault-Tolerant quantum computation with Rydberg Atoms was demonstrated in Cong et al. (2022).
In Quantum communication, it is important to securely and efficiently send as well as receive signals with minimum losses. Rydberg atoms with their highly controllable dipolar interactions can be used as a highly efficient and deterministic single-photon source for quantum communications. In the presence of strong dipole-dipole interaction between Rydberg atoms, an atomic ensemble behaves like a single superatom with collective photon coupling. A cavity-enhanced deterministic single-photon source using such Rydberg superatom was demonstrated in Sun et al. (2022). An efficient approach was demonstrated for multi-photon generation via a Rydberg superatom using Rydberg blockade in Yang et al. (2022). A room-temperature on-demand single photon source via four-wave mixing was demonstrated in Ripka et al. (2018). Deterministic time-Bin entanglement between a single Photon and a Rydberg atomic Ensemble was reported in Sun et al. (2022).
Ultra-cold individual Rydberg atoms trapped in arrays of optical tweezers have recently been established as one of the most promising and versatile candidates which can serve as the fundamental building blocks for emerging quantum technologies. The high degree of controllability in cold Rydberg atomic systems such as inter-atomic interaction, spin-states, temperatures and dimensionality combined with the availability of appropriate lasers for excitation to highly excited Rydberg states makes cold Rydberg atoms a versatile system for exploring various regimes of quantum technologies. The unique and exotic properties of Rydberg atoms such as strong long-ranged inter-atomic interaction, large dipole moments and long lifetimes make Rydberg atoms ideally suited for scalable quantum information processing, quantum sensing, quantum simulation of many-body physics and single-photon sources for quantum communications due to its high degree of controllability.
SB: Writing–original draft, Writing–review and editing, AT: Writing–original draft, Writing–review and editing, YJ: Writing–original draft, Writing–review and editing, SB: Writing–original draft, Writing–review and editing, SR: Writing–original draft, Writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
SR acknowledges funding from the Department of Science and Technology, India, via the WOS-A project Grant Nos. SR/WOS-A/PM-59/2019. S.K.B. acknowledges the funding from the I-HUB Quantum Technology Foundation via the SPIKE Project Grant Nos. I-HUB/SPIKE/2023-24/004.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Adams, C. S., Pritchard, J. D., and Shaffer, J. P. (2019). Rydberg atom quantum technologies. J. Phys. B Atomic Mol. Opt. Phys. 53, 012002. doi:10.1088/1361-6455/ab52ef
Barredo, D., Lienhard, V., de Léséleuc, S., Lahaye, T., and Browaeys, A. (2018). Synthetic three-dimensional atomic structures assembled atom by atom. Nature 561, 79–82. doi:10.1038/s41586-018-0450-2
Bernien, H., Schwartz, S., Keesling, A., Levine, H., Omran, A., Pichler, H., et al. (2017). Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584. doi:10.1038/nature24622
Bluvstein, D., Levine, H., Semeghini, G., Wang, T. T., Ebadi, S., Kalinowski, M., et al. (2022). A quantum processor based on coherent transport of entangled atom arrays. Nature 604, 451–456. doi:10.1038/s41586-022-04592-6
Bluvstein, D., Omran, A., Levine, H., Keesling, A., Semeghini, G., Ebadi, S., et al. (2021). Controlling quantum many-body dynamics in driven rydberg atom arrays. Science 371, 1355–1359. doi:10.1126/science.abg2530
Borówka, S., Mazelanik, M., Wasilewski, W., and Parniak, M. (2024). Optically-biased rydberg microwave receiver enabled by hybrid nonlinear interferometry. doi:10.48550/arXiv.2403.05310
Browaeys, A., and Lahaye, T. (2020). Many-body physics with individually controlled rydberg atoms. Nat. Phys. 16, 132–142. doi:10.1038/s41567-019-0733-z
Buhmann, S. Y., Giesen, S. M., Diekmann, M., Berger, R., Aull, S., Zahariev, P., et al. (2021). Quantum sensing protocol for motionally chiral Rydberg atoms. New J. Phys. 23, 083040. doi:10.1088/1367-2630/ac1af7
Chen, C., Bornet, G., Bintz, M., Emperauger, G., Leclerc, L., Liu, V. S., et al. (2023). Continuous symmetry breaking in a two-dimensional rydberg array. Nature 616, 691–695. doi:10.1038/s41586-023-05859-2
Cong, I., Levine, H., Keesling, A., Bluvstein, D., Wang, S.-T., and Lukin, M. D. (2022). Hardware-efficient, fault-tolerant quantum computation with rydberg atoms. Phys. Rev. X 12, 021049. doi:10.1103/PhysRevX.12.021049
Degen, C. L., Reinhard, F., and Cappellaro, P. (2017). Quantum sensing. Rev. Mod. Phys. 89, 035002. doi:10.1103/RevModPhys.89.035002
DiVincenzo, D. P. (2000). The physical implementation of quantum computation. Fortschritte der Physik 48, 771–783. doi:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E
Ebadi, S., Wang, T. T., Levine, H., Keesling, A., Semeghini, G., Omran, A., et al. (2021). Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 595, 227–232. doi:10.1038/s41586-021-03582-4
Evered, S. J., Bluvstein, D., Kalinowski, M., Ebadi, S., Manovitz, T., Zhou, H., et al. (2023). High-fidelity parallel entangling gates on a neutral-atom quantum computer. Nature 622, 268–272. doi:10.1038/s41586-023-06481-y
Facon, A., Dietsche, E.-K., Grosso, D., Haroche, S., Raimond, J.-M., Brune, M., et al. (2016). A sensitive electrometer based on a rydberg atom in a Schrödinger-cat state. Nature 535, 262–265. doi:10.1038/nature18327
Gallagher, T. (1994). Rydberg atoms. Cambridge monographs on atomic, molecular and chemical physics. Cambridge University Press.
Graham, T. M., Song, Y., Scott, J., Poole, C., Phuttitarn, L., Jooya, K., et al. (2022). Multi-qubit entanglement and algorithms on a neutral-atom quantum computer. Nature 604, 457–462. doi:10.1038/s41586-022-04603-6
Isenhower, L., Urban, E., Zhang, X. L., Gill, A. T., Henage, T., Johnson, T. A., et al. (2010). Demonstration of a neutral atom controlled-not quantum gate. Phys. Rev. Lett. 104, 010503. doi:10.1103/PhysRevLett.104.010503
Jaksch, D., Cirac, J. I., Zoller, P., Rolston, S. L., Côté, R., and Lukin, M. D. (2000). Fast quantum gates for neutral atoms. Phys. Rev. Lett. 85, 2208–2211. doi:10.1103/PhysRevLett.85.2208
Knoernschild, C., Zhang, X. L., Isenhower, L., Gill, A. T., Lu, F. P., Saffman, M., et al. (2010). Independent individual addressing of multiple neutral atom qubits with a micromirror-based beam steering system. Appl. Phys. Lett. 97, 134101. doi:10.1063/1.3494526
Meyer, D. H., O’Brien, C., Fahey, D. P., Cox, K. C., and Kunz, P. D. (2021). Optimal atomic quantum sensing using electromagnetically-induced-transparency readout. Phys. Rev. A 104, 043103. doi:10.1103/PhysRevA.104.043103
Müller, M. M., Kölle, A., Löw, R., Pfau, T., Calarco, T., and Montangero, S. (2013). Room-temperature Rydberg single-photon source. Phys. Rev. A 87, 053412. doi:10.1103/PhysRevA.87.053412
Omran, A., Levine, H., Keesling, A., Semeghini, G., Wang, T. T., Ebadi, S., et al. (2019). Generation and manipulation of Schrödinger cat states in rydberg atom arrays. Science 365, 570–574. doi:10.1126/science.aax9743
Ripka, F., Kübler, H., Löw, R., and Pfau, T. (2018). A room-temperature single-photon source based on strongly interacting Rydberg atoms. Science 362, 446–449. doi:10.1126/science.aau1949
Saffman, M. (2016). Quantum computing with atomic qubits and rydberg interactions: progress and challenges. J. Phys. B Atomic, Mol. Opt. Phys. 49, 202001. doi:10.1088/0953-4075/49/20/202001
Saffman, M., Walker, T. G., and Mølmer, K. (2010). Quantum information with Rydberg atoms. Rev. Mod. Phys. 82, 2313–2363. doi:10.1103/RevModPhys.82.2313
Scholl, P., Schuler, M., Williams, H. J., Eberharter, A. A., Barredo, D., Schymik, K.-N., et al. (2021). Quantum simulation of 2D antiferromagnets with hundreds of Rydberg atoms. Nature 595, 233–238. doi:10.1038/s41586-021-03585-1
Silpa, B S, Barik, S. K., Chaudhuri, S., and Roy, S. (2022). Transition frequency measurement of highly excited rydberg states of 87rb for a wide range of principal quantum numbers. Opt. Continuum 1, 1176–1192. doi:10.1364/OPTCON.458153
Simons, M. T., Haddab, A. H., Gordon, J. A., and Holloway, C. L. (2019). A Rydberg atom-based mixer: measuring the phase of a radio frequency wave. Appl. Phys. Lett. 114, 114101. doi:10.1063/1.5088821
Sun, P.-F., Yu, Y., An, Z.-Y., Li, J., Yang, C.-W., Bao, X.-H., et al. (2022). Deterministic time-bin entanglement between a single photon and an atomic ensemble. Phys. Rev. Lett. 128, 060502. doi:10.1103/PhysRevLett.128.060502
Tiarks, D., Schmidt-Eberle, S., Stolz, T., Rempe, G., and Dürr, S. (2019). A photon–photon quantum gate based on Rydberg interactions. Nat. Phys. 15, 124–126. doi:10.1038/s41567-018-0313-7
Wilk, T., Gaëtan, A., Evellin, C., Wolters, J., Miroshnychenko, Y., Grangier, P., et al. (2010). Entanglement of two individual neutral atoms using rydberg blockade. Phys. Rev. Lett. 104, 010502. doi:10.1103/PhysRevLett.104.010502
Wu, X., Liang, X., Tian, Y., Yang, F., Chen, C., Liu, Y.-C., et al. (2021). A concise review of rydberg atom based quantum computation and quantum simulation. Chin. Phys. B 30, 020305. doi:10.1088/1674-1056/abd76f
Keywords: quantum technology, quantum sensing, quantum computation and information, quantum simulation, quantum communication (QC)
Citation: Barik SK, Thakur A, Jindal Y, S SB and Roy S (2024) Quantum technologies with Rydberg atoms. Front. Quantum Sci. Technol. 3:1426216. doi: 10.3389/frqst.2024.1426216
Received: 30 April 2024; Accepted: 26 June 2024;
Published: 12 July 2024.
Edited by:
Sankar Davuluri, Birla Institute of Technology and Science, IndiaReviewed by:
Ashok Vudayagiri, University of Hyderabad, IndiaCopyright © 2024 Barik, Thakur, Jindal, S and Roy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sanjukta Roy, c2FuanVrdGFAcnJpLnJlcy5pbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.