Lying particles

The common feature of several experiments, performed and proposed, in which particles provide misleading evidence about where they have been, is identified and discussed. It is argued that the experimental results provide a consistent picture when interference amplification effects are taken into account.

1 Introduction

Perhaps the most significant difference between classical and quantum physics is that quantum particles do not have well-defined trajectories [unless we accept the Bohmian interpretation, Bohm (1952)]. Standard quantum mechanics does not have a clear concept of the location of a particle. There is no answer to the question: Through which slit did the particle pass in a two-slit interference experiment? Still, there is a growing interest in discussing which-path questions for particles passing through interferometers, notably following Wheeler’s controversial proposal, Wheeler (1978).

Wheeler suggested assigning a well-defined path to the particle in the interference experiment of the wave packets when only one wave packet had a continuous trajectory from the source to the detector. I proposed an alternative approach, Vaidman (2013a), in which the particle was present at the locations where it left a significant trace in the environment. According to my definition, a pre and postselected particle can be in several places simultaneously, and, moreover, the particle might have disconnected regions of presence. My proposal created a significant controversy, (Li et al., 2013; Vaidman, 2013b; Griffiths, 2016; Vaidman, 2017a; Salih, 2018; Hashmi et al., 2016; Vaidman, 2018; Hashmi et al., 2018; Paneru and Cohen, 2017; Duprey and Matzkin, 2017; Aharonov et al., 2017; Aharonov et al., 2018; Hance et al., 2023b; Vaidman, 2023; Hance et al., 2023a).

To demonstrate the usefulness of my definition, I led an experiment, Danan et al. (2013), in which the photons themselves told us where they had been inside an interferometer, which only increased the controversy, (Englert et al., 2017; Peleg and Vaidman, 2019; Englert et al., 2019; Zhou et al., 2017; Geppert-Kleinrath et al., 2018; Vaidman, 2020; Bartkiewicz et al., 2015; Vaidman, 2016a; Potoček and Ferenczi, 2015; Vaidman, 2016b; Li et al., 2015; Ben-Israel et al., 2017; Sokolovski, 2017; Vaidman, 2017b; Salih, 2015; Vaidman et al., 2015). Although the experiment was supposed to demonstrate the local trace left by photons in different locations, because of the difficulty of performing conditional counting, the measurement pointer was the photon itself: the photon’s degree of freedom of transversal motion affected by the local interaction with the environment. The justification for this modification in the experiment of Danan et al. (2013) was the fact that the record in this degree of freedom of the photon was not distorted during the time the photon wave packet was moving toward the detector.

I also argued that there was another way to interpret this experiment as a demonstration of the presence of the particle in various interferometer paths. All interactions are local. If the pre and postselected photons bring information about a disturbance which was solely introduced in one location, then the photon tells us that it was there. This sounds like a very strong argument, but it turned out to be a subtle issue. This is what I analyze in this report. The analysis demonstrates the core of the resolution of the debates (Vaidman, 2017c, Alonso and Jordan, 2015 and Vaidman and Tsutsui, 2018; Nikolaev, 2017, Bhati and Arvind, 2022 and Reznik et al., 2023, Yuan and Feng, 2023 and Reznik et al., 2024).

2 The general setup

We consider a particle entering an interferometer with multiple paths in a particular input state that reaches a particular output port. The interferometer has mirrors and beam splitters that cause a well-defined unitary evolution of the degree of freedom of the path of the particle. In addition, the particle has another degree of freedom with a specified state |Φ⟩ at the input port which is observed at the output port. For my analysis, I assume that if the interferometer is undisturbed, the state of this degree of freedom remains unchanged everywhere inside the interferometer. The presence of the pre and postselected particle in a particular path of the interferometer is then characterized by the effect of the local disturbance in this path on the state of the particle at the output port. Any small disturbance of the non-path degree of freedom in a particular path can always be expressed as

$|\mathrm{\Phi }\rangle \to \mathcal{N}\left(|\mathrm{\Phi }\rangle +ϵ|{\mathrm{\Phi }}_{\perp }\rangle \right),ϵ\ll 1,(1)$

where ⟨Φ|Φ_⊥⟩ = 0. The non-path degree of freedom of the state in the output port is:

$|{\mathrm{\Phi }\rangle }_{\mathit{out}}=\mathcal{N}\left(|\mathrm{\Phi }\rangle +\alpha ϵ|{\mathrm{\Phi }}_{\perp }\rangle \right).(2)$

The parameter α characterizes the modification of the effect of the interaction and thus the amount of presence of the particle in the respective path.

As expected, the one-path “interfereometer” has a measure of presence in the path α = 1, Figure 1A. If we add a beamsplitter, Figures 1B–D, but consider the particle which reaches the detector, then the particle has presence

${\alpha }_{\text{IN}}={\alpha }_{\text{OUT}}=1,{\alpha }_{\text{REF}}=0.(3)$

Figure 1

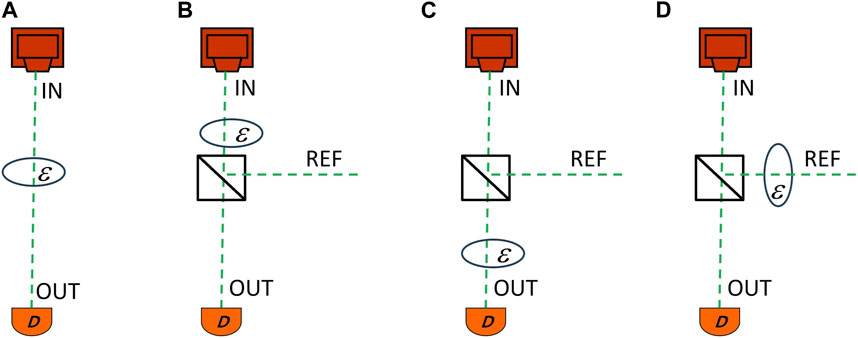
Figure 1. A particle tells us about its presence. (A) Reference signal from the path certainly taken by the particle. (B–D) Obtaining the signal of presence of the particle (modification of the state reaching the detector) in different paths of pre and postselected particle when a beam splitter is added. The ellipse with ϵ indicates the location where the disturbance is introduced to test for the presence of the particle.

If we consider a balanced Mach-Zehnder interferometer (MZI) Figure 2A, tuned to constructive interference, then we are not surprised to obtain

${\alpha }_{\text{IN}}={\alpha }_{\text{OUT}}=1,{\alpha }_A={\alpha }_B=\frac{1}{2}.(4)$

Figure 2

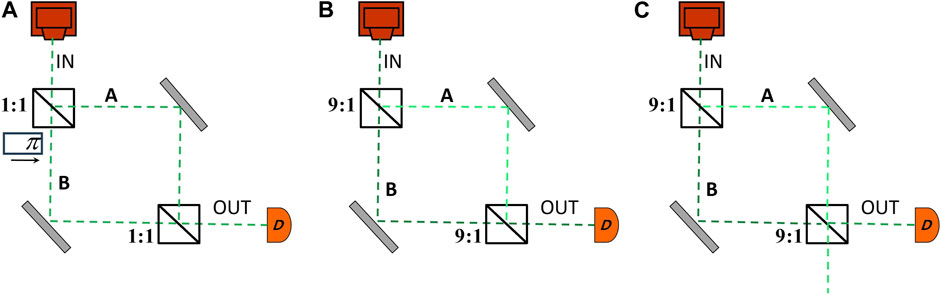
Figure 2. A Mach-Zehnder interferometer. (A) Balanced MZI tuned to constructive interference towards port OUT. (In Section 3 it will be explained how a device in arm B introducing relative phase π in the non-path degree of freedom makes the particles lie about its presence in the input channel IN.). (B) Unbalanced MZI tuned to constructive interference towards port OUT. (C) Unbalanced MZI tuned to maximally destructive interference towards port OUT. The effect of disturbance in various paths on the signal observed by the position-resolving detector at port OUT characterises the presence of the particle in these paths.

If MZI has beam splitters reflecting 90%, which is also tuned to constructive interference, Figure 2B, we obtain

${\alpha }_{\text{IN}}={\alpha }_{\text{OUT}}=1,{\alpha }_A=0.9,{\alpha }_B=0.1.(5)$

If we tune this interferometer to the minimum intensity at the detector, Figure 2C, then the experiment shows marks of the presence in the arms of the interferometer which are less intuitive

${\alpha }_{\text{IN}}={\alpha }_{\text{OUT}}=1,{\alpha }_A=\frac{9}{8},{\alpha }_B=-\frac{1}{8}.(6)$

However, I do not consider these results to be incorrect. They provide the same characterizations of the presence of a pre and postselected particle at particular locations as given by the weak value of the projection on these locations. They describe the universal property of modifications of all weak couplings at these locations, Dziewior et al. (2019). The particles do not lie about their presence (in the above sense), which can be larger than one or negative, or even corresponding to a complex number. The presence can be anomalously large; the only constraint is that at any moment of time one particle should have a total presence in all paths of an interferometer equal to 1.

Particles also do not lie when they tell us about a surprising picture of presence in nested MZI, (Vaidman, 2013a; Danan et al., 2013), see Figure 3A.

${\alpha }_{\text{IN}}={\alpha }_{\text{OUT}}=1,{\alpha }_C=1,{\alpha }_E={\alpha }_F=0,{\alpha }_A=1,{\alpha }_B=-1.(7)$

I consider these results to be a correct demonstration of the presence of the particle in the interferometer, since it faithfully represents the trace left on the paths by the particle. Every mirror in the path gets a kick equal to $\alpha \sqrt{2}p$ where p is the momentum of the particle. (Note that in experiment Danan et al. (2013) a special arrangement with disturbances with different frequencies was implemented. This allowed the measurement of the presence in all paths simultaneously, but instead of α, only the absolute value of the signal |α| was observed. Indeed, in Figure 3A we see essentially equal signals from A, B, and C and no signals from E and F.)

Figure 3

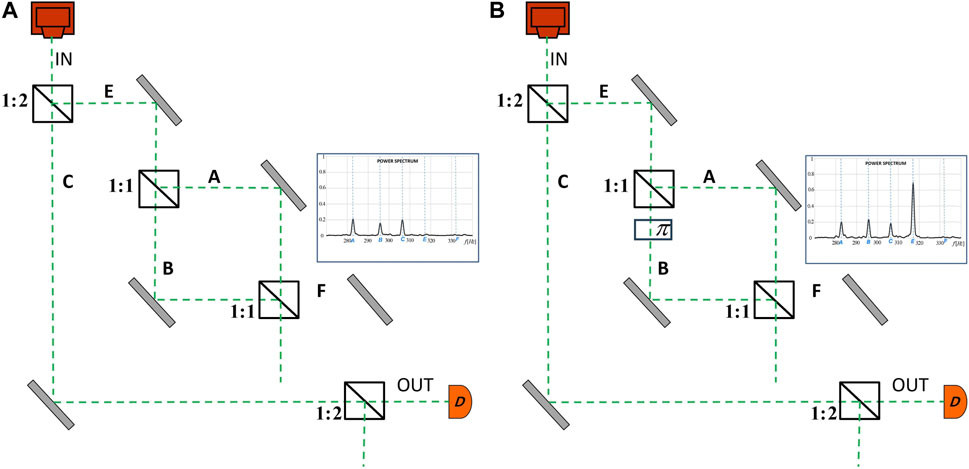
Figure 3. Nested Mach-Zehnder interferometer. (A) The interferometer with a particle present in a disconnected region, cf. Figure 2B of Danan et al. (2013). Position-resolving detector D shows the presence at different arms by identifying frequencies of disturbances at various arms. (B) The same interferometer with a device introduced in path B which affects the non-path degree of freedom of the particle making it to lie about where it has been. The traces left by the particle on the parts of the interferometer are essentially the same in the two cases. The power spectrum graph in (A) shows actual experimental results of Danan et al. experiment testing presence in various paths, while (B) shows predicted (by Alonso and Jordan (2015)) results of the same experiment with the π phase shifter in arm B.

3 Interferometers with particles lying about where they have been

Let us now consider cases where particles lie about their presence in a particular path of the interferometer. Our setup is the same as above, but we add in one of the paths a device which affects the non-path degree of freedom in the following way. It adds the relative phase π to the component |Φ_⊥⟩ which is created by the disturbance (1):

$a|\mathrm{\Phi }\rangle +b|{\mathrm{\Phi }}_{\perp }\rangle \to a|\mathrm{\Phi }\rangle -b|{\mathrm{\Phi }}_{\perp }\rangle .(8)$

This corresponds to a modification of the experiment of Danan et al. (2013) proposed by Alonso and Jordan (2015). They inserted a Dove prism inside an interferometer. The non-path degree of freedom of the particle was its transversal motion. The disturbance was a transversal shift. The shift of a well-aligned Gaussian profile created an orthogonal component which was an odd function in the transverse direction. The action of the Dove prism on such a component is to flip its sign, i.e., to add phase π. The other proposals (Nikolaev, 2017; Bhati and Arvind, 2022; Yuan and Feng, 2023) have an equivalent mathematical structure.

Introducing the relative phase to the component that is not present changes nothing, so placing the device makes no effect if the interferometer is not disturbed, but it causes the particles to lie (in some cases) about where they have been by spoiling the mathematical equivalence between the local trace on the environment and the observed trace on the non-path degree of freedom of the particle. The records created locally on the particle are distorted during the passage of the particle to the output port. I will show two examples of how it happens.

Let us add this device at the beginning of the path B of the balanced MZI described in Figure 2A. Then, our method of characterization of the presence of the particle by observing the effect of introducing the disturbance (1) in different paths on the non-path degree of freedom at the output port will lead, instead of (4) to

${\alpha }_{\text{IN}}=0,{\alpha }_{\text{OUT}}=1,{\alpha }_A={\alpha }_B=\frac{1}{2}.(9)$

Clearly, this description does not make sense. We know that the particle entered the interferometer. The method itself tells us that it left the interferometer, but the method also tells us that the particle was not present at the input port. The malfunction of the method is transparent: the orthogonal component created at the input port splits into a superposition in the arms A and B and the phase device in the arm B causes destructive interference in the output port. The absence of the signal from the input port does not ensure that the particle was not there.

The second example is a nested interferometer of Danan et al. (2013), which has already been a subject of great controversy. Figure 3B shows explicitly the phase π device added in the arm B. Then, our method of characterization of presence by observing the effect leads instead of (7) to

${\alpha }_{\text{IN}}=3,{\alpha }_{\text{OUT}}=1,{\alpha }_C=1,{\alpha }_E=2,{\alpha }_F=0,{\alpha }_A=1,{\alpha }_B=-1.(10)$

These results are neither present a sensible classical picture, nor describe faithfully a modification of the weak couplings of the particle with the environment which are, in fact, not affected by the phase shifting device and remain to be described correctly by (7).

4 Discussion

In Figure 3B I show an experiment with nested interferometer in which we get a signal from the path E, but I claim that it was not there. How can the particle bring a signal from the place where the particle has not been? It contradicts the idea of causality and locality of all interactions.

The answer to this question is not simple. In fact, there is some kind of particle presence in E, also in the interferometer described in Figure 3A without the π shifter, which I named “secondary” presence, Vaidman (2014). The main property of the secondary presence is that although there is no trace of the first order (in ϵ) in E, blocking E affects the first-order traces elsewhere (in A and B). Also, when the interferometer is not ideal (and there are no ideal interferometers) there will be a higher order trace in E.

The question to be answered is how the phase shifter causes particles to lie about their presence showing a strong signal in E that looks like a signal of ordinary presence. This is due to the anomalous sensitivity to the presence in E when the π phase device is inserted. If we add a nondemolition measurement of the presence in E and condition our observation of the signal on finding the particle in E, our signal instead of α_E = 2 will be α_{E [conditioned on presence in E]} → ∞. This follows from the definition of α in (2), since the state at the output port is |Φ_⊥⟩.

The locality of interaction tells us that if the particle brings a signal from a particular location, the particle must have some presence there, but the “amount of presence” is not characterized directly by this signal. It is characterized by the ratio between the obtained signal and the reference signal that would be obtained if the particle were localized there. Since in the nested interferometer with the phase shifter the signal is finite, but the localized particle in this experiment leads to an unbounded signal, the ratio is zero. The method tells us that the particle was not present there. See the analysis of a realistic experiment in Yuan and Feng (2023); Reznik et al. (2024).

I suggest adopting the definition according to which the particle passing through an interferometer was in a particular path if a local disturbance in this path (if it was performed) can be observed in the output state of the particle. Every path which fulfills this criterion is the path where, by this definition, the particle was. In many cases, then, the particle is present in more than one path simultaneously. This definition contradicts the fact that a single particle is never found in two places simultaneously. The setup I proposed cannot demonstrate this contradiction, because the proposal introduces disturbances in the paths one by one and not simultaneously together. Let us see what happens if we introduce disturbances in two places simultaneously.

We consider a particle passing MZI described in Figure 2A and try to observe its presence in arms A and B. To obtain evidence that it is present simultaneously in two places, we need that the particle will have two non-path degrees of freedom |Φ_A⟩ and |Φ_B⟩ affected by the disturbances in the two paths. Then, the non-path degree of freedom state of the particle will be

$|{\mathrm{\Phi }}_A\rangle |{\mathrm{\Phi }}_B\rangle \to \mathcal{N}\left(|{\mathrm{\Phi }}_A\rangle |{\mathrm{\Phi }}_B\rangle +\frac{ϵ}{2}|{\mathrm{\Phi }}_{A\perp }\rangle |{\mathrm{\Phi }}_B\rangle +\frac{ϵ}{2}|{\mathrm{\Phi }}_A\rangle |{\mathrm{\Phi }}_{B\perp }\rangle \right).(11)$

There is a first-order signal both from path A and from path B, so at this stage, by definition, the particle was in two places. However, we will never be able to find one particular particle in two places simultaneously. Performing analysis of this state on an ensemble of particles starting at the source and ending up at the output port we will observe these first-order traces, so we will be able to use the definition. This, however, does not provide direct information about every particle in the ensemble. A particular measurement which occasionally (with probability larger than 0) finds state |Φ_A⊥⟩ tells us that the particle was in the path A and finding |Φ_B⊥⟩ tells us that another particle was in path B. The corresponding degrees of freedom in state (11) are entangled, and the term |Φ_A⊥⟩|Φ_B⊥⟩ is not present.

We do not have to adopt the many-world interpretation Vaidman (2002) to appreciate the result of this paper, but it seems to me that this interpretation provides the most satisfactory resolution of the apparent paradox of claiming that the particle in some sense is in two places simultaneously, in spite of the fact that we are not able to find the particle simultaneously in two places. In a world the particle passes through the interferometer, it has “memory” of order ϵ of being both in A and in B. However, at the moment when a measurement verifying the presence of |Φ_A⊥⟩ is performed, the world splits into two, one in which we know that it was in A and one in which we have no decisive information. Due to the entanglement of degrees of freedom, in the world we know about the presence in the path A the component of order ϵ signifying the presence in the path B is erased. This is why we never find definite evidence of simultaneous presence in the two arms of the interferometer.

How can I accuse photons that they are “lying” about where they have been when standard quantum mechanics does not provide a definition for locations of particles inside interferometers? It is known that in some cases observations do not show Bohmian positions of particles (Aharonov and Vaidman, 1996), and in any case I do not adopt here the Bohmian definition. However, results of experiments, like those presented in Figure 3B strongly suggest that the photons have been in the path E since they show a signal originated there. I claim that they lye about presence in E because they were not there according to the definition that the particle was present in the location where it left a trace. The trace in E is negligible compared to the trace in locations (like C) where the photon clearly has been. And it is not that the naive definition about presence in the location about which the particle brings information has to be abandoned; we just have to listen to photons carefully, by comparing the strength of the signal to the reference signal from locations in which the particle definitely was present.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LV: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work has been supported in part by the U.S.-Israel Binational Science Foundation Grant No. 735/18 and by the Israel Science Foundation Grant No. 2064/19.

Acknowledgments

I thank Jan Dziewior and Gregory Reznik for very helpful discussions.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aharonov, Y., Cohen, E., Landau, A., and Elitzur, A. C. (2017). The case of the disappearing (and re-appearing) particle. Sci. Rep. 7, 531. doi:10.1038/s41598-017-00274-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Aharonov, Y., Cohen, E., Waegell, M., and Elitzur, A. C. (2018). The weak reality that makes quantum phenomena more natural: novel insights and experiments. Entropy 20, 854. doi:10.3390/e20110854

PubMed Abstract | CrossRef Full Text | Google Scholar

Aharonov, Y., and Vaidman, L. (1996). About position measurements which do not show the Bohmian particle position. Bohmian Mech. Quantum Theory Apprais., 141–154. doi:10.1007/978-94-015-8715-0_10

CrossRef Full Text | Google Scholar

Alonso, M. A., and Jordan, A. N. (2015). Can a Dove prism change the past of a single photon? Quantum Stud. Math. Found. 2, 255–261. doi:10.1007/s40509-015-0044-8

CrossRef Full Text | Google Scholar

Bartkiewicz, K., Černoch, A., Javůrek, D., Lemr, K., Soubusta, J., and Svozilík, J. (2015). One-state vector formalism for the evolution of a quantum state through nested mach-zehnder interferometers. Phys. Rev. A 91, 012103. doi:10.1103/PhysRevA.91.012103

CrossRef Full Text | Google Scholar

Ben-Israel, A., Knips, L., Dziewior, J., Meinecke, J., Danan, A., and Weinfurter, H. (2017). An improved experiment to determine the ‘past of a particle’ in the nested mach-zehnder interferometer. Chin. Phys. Lett. 34, 020301. doi:10.1088/0256-307x/34/2/020301

CrossRef Full Text | Google Scholar

Bhati, R. S., and Arvind, H. (2022). Do weak values capture the complete truth about the past of a quantum particle? Phys. Lett. A 429, 127955. doi:10.1016/j.physleta.2022.127955

CrossRef Full Text | Google Scholar

Bohm, D. (1952). A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Phys. Rev. 85, 166–179. doi:10.1103/physrev.85.166

CrossRef Full Text | Google Scholar

Danan, A., Farfurnik, D., Bar-Ad, S., and Vaidman, L. (2013). Asking photons where they have been. Phys. Rev. Lett. 111, 240402. doi:10.1103/PhysRevLett.111.240402

PubMed Abstract | CrossRef Full Text | Google Scholar

Duprey, Q., and Matzkin, A. (2017). Null weak values and the past of a quantum particle. Phys. Rev. A 95, 032110. doi:10.1103/PhysRevA.95.032110

CrossRef Full Text | Google Scholar

Dziewior, J., Knips, L., Farfurnik, D., Senkalla, K., Benshalom, N., Efroni, J., et al. (2019). Universality of local weak interactions and its application for interferometric alignment. Proc. Natl. Acad. Sci. U. S. A. 116, 2881–2890. doi:10.1073/pnas.1812970116

PubMed Abstract | CrossRef Full Text | Google Scholar

Englert, B.-G., Horia, K., Dai, J., Len, Y. L., and Ng, H. K. (2017). Past of a quantum particle revisited. Phys. Rev. A 96, 022126. doi:10.1103/PhysRevA.96.022126

CrossRef Full Text | Google Scholar

Englert, B.-G., Horia, K., Dai, J., Len, Y. L., and Ng, H. K. (2019). Reply to “Comment on ‘Past of a quantum particle revisited’ ”. Phys. Rev. A 99, 026104. doi:10.1103/PhysRevA.99.026104

CrossRef Full Text | Google Scholar

Geppert-Kleinrath, H., Denkmayr, T., Sponar, S., Lemmel, H., Jenke, T., and Hasegawa, Y. (2018). Multifold paths of neutrons in the three-beam interferometer detected by a tiny energy kick. Phys. Rev. A 97, 052111. doi:10.1103/PhysRevA.97.052111

CrossRef Full Text | Google Scholar

Griffiths, R. B. (2016). Particle path through a nested Mach-Zehnder interferometer. Phys. Rev. A 94, 032115. doi:10.1103/PhysRevA.94.032115

CrossRef Full Text | Google Scholar

Hance, J. R., Rarity, J., and Ladyman, J. (2023a). Reply to “Comment on weak values and the past of a quantum particle”. Phys. Rev. Res. 5, 048002. doi:10.1103/physrevresearch.5.048002

CrossRef Full Text | Google Scholar

Hance, J. R., Rarity, J., and Ladyman, J. (2023b). Weak values and the past of a quantum particle. Phys. Rev. Res. 5, 023048. doi:10.1103/physrevresearch.5.023048

CrossRef Full Text | Google Scholar

Hashmi, F. A., Li, F., Zhu, S.-Y., and Zubairy, M. S. (2016). Two-state vector formalism and quantum interference. J. Phys. A Math. Theor. 49, 345302. doi:10.1088/1751-8113/49/34/345302

CrossRef Full Text | Google Scholar

Hashmi, F. A., Li, F., Zhu, S.-Y., and Zubairy, M. S. (2018). Reply to the Comment on ‘Two-state vector formalism and quantum interference’. J. Phys. A Math. Theor. 51, 068001. doi:10.1088/1751-8121/aa8d23

CrossRef Full Text | Google Scholar

Li, F., Hashmi, F. A., Zhang, J.-X., and Zhu, S.-Y. (2015). An ideal experiment to determine the ‘past of a particle’ in the nested Mach-Zehnder interferometer. Chin. Phys. Lett. 32, 050303. doi:10.1088/0256-307X/32/5/050303

CrossRef Full Text | Google Scholar

Li, Z.-H., Al-Amri, M., and Zubairy, M. S. (2013). Comment on “Past of a quantum particle”. Phys. Rev. A 88, 046102. doi:10.1103/PhysRevA.88.046102

CrossRef Full Text | Google Scholar

Nikolaev, G. N. (2017). Paradox of photons disconnected trajectories being located by means of “weak measurements” in the nested mach–zehnder interferometer. JETP Lett. 105, 152–157. doi:10.1134/S0021364017030110

CrossRef Full Text | Google Scholar

Paneru, D., and Cohen, E. (2017). Past of a particle in an entangled state. Int. J. Quan. Inf. 15, 1740019. doi:10.1142/S0219749917400196

CrossRef Full Text | Google Scholar

Peleg, U., and Vaidman, L. (2019). Comment on “Past of a quantum particle revisited”. Phys. Rev. A 99, 026103. doi:10.1103/PhysRevA.99.026103

CrossRef Full Text | Google Scholar

Potoček, V., and Ferenczi, G. (2015). Which-way information in a nested Mach-Zehnder interferometer. Phys. Rev. A 92, 023829. doi:10.1103/PhysRevA.92.023829

CrossRef Full Text | Google Scholar

Reznik, G., Versmold, C., Dziewior, J., Huber, F., Bagchi, S., Weinfurter, H., et al. (2023). Photons are lying about where they have been, again. Phys. Lett. A 470, 128782. doi:10.1016/j.physleta.2023.128782

CrossRef Full Text | Google Scholar

Reznik, G., Versmold, C., Dziewior, J., Huber, F., Weinfurter, H., Dressel, J., et al. (2024). Comment on Photons can Tell’Contradictory’answer about where they have been. Eur. Phys. J. Plus 139, 181. doi:10.1140/epjp/s13360-023-04818-0

CrossRef Full Text | Google Scholar

Salih, H. (2015). Commentary: “Asking photons where they have been” - without telling them what to say. Front. Phys. 3, 47. doi:10.3389/fphy.2015.00047

CrossRef Full Text | Google Scholar

Salih, H. (2018). Comment on “Particle path through a nested Mach-Zehnder interferometer”. Phys. Rev. A 97, 026101. doi:10.1103/PhysRevA.97.026101

CrossRef Full Text | Google Scholar

Sokolovski, D. (2017). Asking photons where they have been in plain language. Phys. Lett. A 381, 227–232. doi:10.1016/j.physleta.2016.11.010

CrossRef Full Text | Google Scholar

Vaidman, L. (2002). “Many-worlds interpretation of quantum mechanics,” in The stanford encyclopedia of philosophy. Editor E. N. Zalta (USA: Metaphysics Research Lab, Stanford University).

Google Scholar

Vaidman, L. (2013a). Past of a quantum particle. Phys. Rev. A 87, 052104. doi:10.1103/physreva.87.052104

CrossRef Full Text | Google Scholar

Vaidman, L. (2013b). Reply to “Comment on ‘past of a quantum particle’ ”. Phys. Rev. A 88, 046103. doi:10.1103/PhysRevA.88.046103

CrossRef Full Text | Google Scholar

Vaidman, L. (2014). Tracing the past of a quantum particle. Phys. Rev. A 89, 024102. doi:10.1103/PhysRevA.89.024102

CrossRef Full Text | Google Scholar

Vaidman, L. (2016a). Comment on “One-state vector formalism for the evolution of a quantum state through nested mach-zehnder interferometers”. Phys. Rev. A 93, 036103. doi:10.1103/PhysRevA.93.036103

CrossRef Full Text | Google Scholar

Vaidman, L. (2016b). Comment on “Which-way information in a nested mach-zehnder interferometer”. Phys. Rev. A 93, 017801. doi:10.1103/PhysRevA.93.017801

CrossRef Full Text | Google Scholar

Vaidman, L. (2017a). Comment on “Particle path through a nested Mach-Zehnder interferometer”. Phys. Rev. A 95, 066101. doi:10.1103/PhysRevA.95.066101

CrossRef Full Text | Google Scholar

Vaidman, L. (2017b). A comment on “Asking photons where they have been in plain language”. Available at: https://arxiv.org/abs/1703.03615v1.

Google Scholar

Vaidman, L. (2017c). Comment on “Paradox of photons disconnected trajectories being located by means of ‘weak measurements’ in the nested Mach–Zehnder interferometer” (JETP Letters 105, 152 (2017)). JETP Lett. 105, 473–474. doi:10.1134/S0021364017070037

CrossRef Full Text | Google Scholar

Vaidman, L. (2018). Comment on “Two-state vector formalism and quantum interference”. J. Phys. A Math. Theor. 51, 068002. doi:10.1088/1751-8121/aa8d24

CrossRef Full Text | Google Scholar

Vaidman, L. (2020). Neutrons and photons inside a nested Mach-Zehnder interferometer. Phys. Rev. A 101, 052119. doi:10.1103/PhysRevA.101.052119

CrossRef Full Text | Google Scholar

Vaidman, L. (2023). Comment on “Weak values and the past of a quantum particle”. Phys. Rev. Res. 5, 048001. doi:10.1103/PhysRevResearch.5.048001

CrossRef Full Text | Google Scholar

Vaidman, L., Danan, A., Farfurnik, D., and Bar-Ad, S. (2015). Response: commentary: “Asking photons where they have been” - without telling them what to say. Front. Phys. 3, 47. doi:10.3389/fphy.2015.00048

CrossRef Full Text | Google Scholar

Vaidman, L., and Tsutsui, I. (2018). When photons are lying about where they have been. Entropy 20, 538. doi:10.3390/e20070538

PubMed Abstract | CrossRef Full Text | Google Scholar

Wheeler, J. (1978). “The “past” and the “delayed-choice” double-slit experiment,” in Mathematical foundations of quantum theory (Germany: Elsevier), 9–48. doi:10.1016/B978-0-12-473250-6.50006-6

CrossRef Full Text | Google Scholar

Yuan, Q., and Feng, X. (2023). Photons can tell “contradictory” answer about where they have been. Eur. Phys. J. Plus 138, 70. doi:10.1140/epjp/s13360-023-03677-z

CrossRef Full Text | Google Scholar

Zhou, Z.-Q., Liu, X., Kedem, Y., Cui, J.-M., Li, Z.-F., Hua, Y.-L., et al. (2017). Experimental observation of anomalous trajectories of single photons. Phys. Rev. A 95, 042121. doi:10.1103/PhysRevA.95.042121

CrossRef Full Text | Google Scholar