Continuous dynamical decoupling of optical 171Yb+ qudits with radiofrequency fields

The use of multilevel quantum information carriers, also known as qudits, has attracted significant interest as a way of further scaling quantum computing devices. However, such multilevel systems usually express shorter coherence time than their two-level counterparts, which limits their computational potential. We thus propose and experimentally demonstrate two approaches for realizing the continuous dynamical decoupling of magnetic-sensitive states with m_F = ±1 for qudits encoded in optical transition of trapped ¹⁷¹Yb⁺ ions. We improve the coherence time of qudit levels by an order of magnitude (more than 9 ms) without any magnetic shielding, revealing the potential advantage of the symmetry of the ¹⁷¹Yb⁺ ion energy structure for counteracting magnetic field noise. Our results are a step toward realizing qudit-based algorithms using trapped ions.

1 Introduction

The development of quantum computers is stimulated by the idea of achieving significantly higher speeds than machines based on classical principles for solving computational tasks and is related to issues such as cryptography (Shor, 1994), searching (Grover, 1996), optimization (Farhi et al., 2014), simulation of quantum systems (Lloyd, 1996), and solving large systems of linear equations (Harrow et al., 2009). Existing prototypes of quantum computing devices use various physical platforms, such as superconducting circuits (Arute et al., 2019; Wu et al., 2021), semiconductor quantum dots (Xue et al., 2022; Madzik et al., 2022; Noiri et al., 2022), optical systems (Zhong et al., 2020; Madsen et al., 2022), neutral atoms (Ebadi et al., 2021; Scholl et al., 2021; Henriet et al., 2020; Graham et al., 2022), and trapped ions (Zhang et al., 2017; Blatt and Roos, 2012; Hempel et al., 2018) to implement quantum computing protocols. Although several experiments have reported achieving quantum advantage in solving sampling problems (Arute et al., 2019; Wu et al., 2021; Zhong et al., 2020), the computational power of the existing generation of quantum computers is limited. These limitations are related to the fact that, in order to solve a practically relevant computational problem, scalability of the devices with respect to the number of information carriers used (for example, qubits, which are quantum counterparts of classical bits) must be combined with a high degree of quality of operations on the information carriers. The combination of the quantitative and qualitative characteristics of quantum computing devices underlies the idea of quantum volume (QV) (Cross et al., 2019), which is one of the metrics for quantum computing power. Trapped ions are one the first systems proposed for quantum computing (Cirac and Zoller, 1995; Monroe et al., 1995), which currently demonstrates the highest QV of 2¹⁵ = 32768 (Qua, 2023). The reasons behind these results are the demonstration of high-fidelity operations between the qubits (Gaebler et al., 2016) and long coherence times (Wang et al., 2021), which also allow one to prototype quantum error correction techniques (Chiaverini et al., 2004; Schindler et al., 2011; Stricker et al., 2020; Egan et al., 2021; Erhard et al., 2021; Postler et al., 2022; Ryan-Anderson et al., 2022). However, for trapped ions, as for other platforms for quantum computing, the problem of scaling the system to a large number of qubits and preserving a high-enough fidelity of quantum gates is a challenge still outstanding (Bruzewicz et al., 2019; Fedorov et al., 2022). In particular for trapped-ion-based systems, the number of controlled information carriers within a single trap is approximately 20–30. Various techniques have been considered to further increase the number of controlled ions (Bruzewicz et al., 2019; Monroe and Kim, 2013).

The structure of information carriers in quantum domains is typically much more complex and is artificially restricted to fit the conventional binary paradigm. In particular, the structure of the Hilbert space of trapped ions (Low et al., 2020a; Ringbauer et al., 2021; Aksenov et al., 2022), neutral atoms (Weggemans et al., 2022), photonic systems (Lanyon et al., 2009; Kues et al., 2017; Chi et al., 2022a), and superconducting circuits (Neeley et al., 2009; Fedorov et al., 2012; Peterer et al., 2015; Svetitsky et al., 2014; Braumüller et al., 2015; Hill et al., 2021) that are used in quantum information processing admits much more complex quantum information encoding (for a review, see Wang et al. (2020)), which is the essence of qudit-based quantum computing (Farhi and Gutmann, 1998; Kessel’ and Ermakov, 1999, Kessel’ and Ermakov, 2000; Kessel and Yakovleva, 2002; Muthukrishnan and Stroud, 2000; Nielsen et al., 2002; Wang et al., 2003; Klimov et al., 2003; Bagan et al., 2003; Vlasov, 2003; Greentree et al., 2004; O’Leary et al., 2006; Ralph et al., 2007; Lanyon et al., 2008; Ionicioiu et al., 2009; Ivanov et al., 2012; Li et al., 2013; Kiktenko et al., 2015b,a; Song et al., 2016; Frydryszak et al., 2017; Bocharov et al., 2017; Gokhale et al., 2019; Luo et al., 2019; Low et al., 2020b; Jin et al., 2021; Neeley et al., 2009; Lanyon et al., 2009; Fedorov et al., 2012; Mischuck et al., 2012; Peterer et al., 2015; Svetitsky et al., 2014; Braumüller et al., 2015; Kues et al., 2017; Godfrin et al., 2017; Low et al., 2020b; Sawant et al., 2020; Low et al., 2020a; Pavlidis and Floratos, 2021; Rambow and Tian, 2021; Chi et al., 2022b; Nikolaeva et al., 2022; Zhou et al., 2023). In recent years, multiqudit quantum processors (Hill et al., 2021; Ringbauer et al., 2021; Chi et al., 2022b; Aksenov et al., 2022), including systems based on ⁴⁰Ca⁺ (Ringbauer et al., 2021) and ¹⁷¹Yb⁺ (Aksenov et al., 2022) qudits, have been demonstrated. The use of qudits potentially allows quantum algorithms to be realized more efficiently (Nikolaeva et al., 2021). This is possible, first, because several qubits can be encoded into one (Kessel’ and Ermakov, 1999; Kessel’ and Ermakov, 2000; Kessel and Yakovleva, 2002; Kiktenko et al., 2015b,a); for example, a ququart processor is formally equivalent to a two-qubit processor, but the quality of operations within a single trapped ion in the ququart case may be higher rather than a two-qubit gate involving physical interaction between two ions. Second, the use of additional qudit levels can substitute ancilla qubits in multiqubit gate decompositions (Barenco et al., 1995)—for example, for the Toffoli gate (Ralph et al., 2007; Lanyon et al., 2009; Ionicioiu et al., 2009; Fedorov et al., 2012; Liu et al., 2020; Baker et al., 2020; Kiktenko et al., 2020; Liu et al., 2022; Galda et al., 2021; Gu et al., 2021). It is interesting that the first realization of two-qubit gates used two qubits stored in a single trapped ion in the qudit setup (Monroe et al., 1995). Thus, qudit-based quantum information processing can be considered a useful paradigm for increasing the power of quantum computing devices.

From an experimental point of view, switching from qubit to qudit logic does not significantly change the methods used. Any algorithm is divided into a sequence of single- and multiqudit quantum gates, which must constitute a universal set. The design process of the algorithms, however, changes drastically. Algorithm design where additional levels are used as ancillas or where, for example, a ternary logic is intrinsically used requires a whole new set of approaches (Nikolaeva et al., 2023; Kiktenko et al., 2020; Galda et al., 2021). If additional levels are used just to encode more qubits in one particle, the situation is somewhat easier, as conventional qubit algorithms can be straightforwardly mapped onto native qudit gates and optimized afterward. However, to fully harness the potential of the qudit encoding, it is advantageous to keep in mind the structure of the native qudit gates already on the transpiling stage of the algorithm preparation.

The serious challenge is, however, to ensure long coherence times for the qudit states. For example, in the experimental demonstration of trapped-ion-based qudits on ⁴⁰Ca⁺ (Ringbauer et al., 2021) with control up to seven levels, magnetic shielding is proposed as a solution to this problem. Our previous experimental setup has been based on optical qudits encoded in a quadrupole transition at 435 nm in ¹⁷¹Yb⁺ (Aksenov et al., 2022) with the use of the magnetic-sensitive Zeeman sublevels of the upper level. We note that this transition is typically used in quantum metrology (Tamm et al., 2000; Lacroûte et al., 2016; Leute et al., 2016; Semerikov et al., 2018), and it has been used as per qubit encoding with ytterbium ions (Zalivako et al., 2021). However, such a qudit structure has led to relatively short coherence times, which limits the realization of quantum algorithms (Aksenov et al., 2022).

In this work, we demonstrate two approaches for the realization of continuous dynamical decoupling of magnetic-sensitive states with m_F = ±1 for qudits encoded in ¹⁷¹Yb⁺ trapped ions. The simplicity of the techniques presented is due to the symmetry of the ¹⁷¹Yb⁺ ion energy structure for counteracting the magnetic field noise and a large quadratic Zeeman shift lifting degeneracy of the transitions between neighboring Zeeman sublevels. We achieve qudit level coherence time of more than 9 ms without any magnetic shielding. Our results indicate the potential advantages of ytterbium-ion-based qudits and open the way to the realization of qudit-based algorithms.

Our work is organized as follows: in Section 2, we describe the basics of continuous dynamical decoupling for ytterbium-based qudits. We also present the method for radiofrequency dressing of ²D_3/2 manifold qudit states. Section 3 describes dynamical decoupling schemes we propose to use for prolonging the coherence time of qudit sublevels. In Section 4, we describe the realization of operations with qudits. In Section 5, we provide the results of the experimental implementation of two dynamical decoupling schemes. In Section 6 we discuss and compare proposed methods with each other and with approaches used with other ion species. We conclude in Section 7.

2 Continuous dynamical decoupling of ¹⁷¹Yb⁺ optical qudit

2.1 Basic principles of continuous dynamical decoupling

Dynamical decoupling is a well-known technique for suppressing decoherence (Viola and Lloyd, 1998; Viola et al., 1999; Viola and Knill, 2003). The detailed description and the comparison of different dynamical decoupling methods with the focus on trapped ions can be found, for example, in Valahu et al. (2022). Here, we only summarize basic principles of continuous dynamical decoupling (CDD) and multilevel continuous dynamical decoupling (MCDD). Let us consider a pair of Zeeman components with opposite magnetic quantum numbers. For simplicity, we consider levels | − 1⟩ and |1⟩ with m_F = −1 and m_F = 1, respectively. The action of magnetic field fluctuations on this two-level system in the first order can be described by the following Hamiltonian:

$H_B=-g_F{\mu }_B\delta B\left(t\right){\sigma }_z,(1)$

where g_F is the g-factor for the total angular momentum F, μ_B is the Bohr magneton, $\delta B\left(t\right)$ is the magnetic field fluctuations, and σ_z is the Pauli matrix. Thus, as the eigenenergies of these levels linearly depend on the magnetic field, their phases rapidly decohere in the noisy environment, which in turn limits their application in quantum information processing and prevents their use as qudit states.

In order to suppress dephasing due to magnetic field fluctuations, we need to find or engineer states with energies which are weakly dependent on the field magnitude. Part of the solution seems to be the storage information in superposition states:

$\begin{array}{c}\hfill |+⟩=\frac{1}{\sqrt{2}}\left(|1⟩+|-1⟩\right),\\ \hfill |-⟩=\frac{1}{\sqrt{2}}\left(|1⟩-|-1⟩\right),\end{array}(2)$

as, due to the symmetric influence of the Zeeman shift on both |1⟩ and | − 1⟩ in their basis, H_B takes the form of

$H_{B\pm }=-g_F{\mu }_B\delta B\left(t\right)\left(|+\rangle \langle -|+|-\rangle \langle +|\right).(3)$

Here, we see that the magnetic field noise does not change the mean energies of these states, so they do not dephase in the interaction picture. However, fluctuations in this basis couple $|+⟩$ and $|-⟩$ states, causing the population transfer between them. This noise-induced population transfer has a resonant nature, which is mostly caused by the Fourier component noise at frequencies close to the energy difference between | − ⟩ and | + ⟩ states—zero in our case. Thus, constant field shifts and low-frequency noise components mostly contribute to this effect. This is especially inconvenient as, in experiment low-frequency noise and particularly in the harmonics of mains power supply, a frequency of (50 Hz) dominates the noise spectrum.

The idea behind the CDD approach is to lift these states of degeneracy by applying the dressing electromagnetic field, coupling levels $|1⟩$, and $|-1⟩$. States $|+⟩$ and $|-⟩$ diagonalize the resulting Hamiltonian, but this time their eigenenergies differ by a Rabi frequency Ω of the dressing field. In this case, low-frequency noise cannot cause the population transfer between these states anymore as it is off-resonant. More precisely, to excite transitions between $|+⟩$ and $|-⟩$, the noise frequency should be close to Ω, or its magnitude must be large enough to broaden this transition. These conditions can be written thus:

$\frac{\left|g_F{\mu }_B\widetilde{\delta B}\left(\omega \right)\right|}{\hslash \left|\omega -\mathrm{\Omega }\right|}\ge 1,(4)$

where $\widetilde{\delta B}\left(\omega \right)$ is the Fourier amplitude of the noise. Thus, if the dressing field Rabi frequency Ω is larger than the bandwidth of the noise and the Larmor precession frequency of the state under influence of the noise, then the noise effect on the states is suppressed. This technique is known as the CDD approach. Although decoupling from magnetic field fluctuations monotonically improves with increase of Ω, other factors cause degradation of the method’s performance if Ω is too large, which determines the existence of an optimal value. These factors include increasing dephasing due to the dressing field amplitude fluctuations and off-resonant coupling to other states.

We note that there are more sophisticated techniques to decouple these sources of errors, such as using concatenated (Cai et al., 2012) or modulated (Farfurnik et al., 2017) dressing fields; however, these are beyond the scope of the present work. We considered only a two-level system, but this method can be generalized to multiple states becoming MCDD.

2.2 Radiofrequency dressing of ²D_3/2 manifold qudit states

In this paper, we focus on decoupling ²D_3/2 (F = 2, m_F = ±1) states (| − 1⟩ and |1⟩, respectively) of the ²D_3/2 manifold from the magnetic noise using radiofrequency fields (Figure 1). These states, along with |0⟩ = ²D_3/2 (F = 2, m_F = 0), and |g⟩ = ²S_1/2 (F = 0, m_F = 0), form a ququart, which is a qudit with four states for information encoding. We note that two other Zeeman sublevels with m_F = ±2 can be also employed for information encoding, although in this paper we do not use them for this purpose. This is because, from a quantum information processing prospective, an ion string consisting of N 4-level systems can easily be mapped and interpreted as a 2N qubit processor. In addition, using these states would require more sophisticated decoupling schemes to protect them from magnetic field fluctuations. We note, however, that we still tracked their populations in our experiments to detect leakages from the qudit subspace during experiments.

FIGURE 1

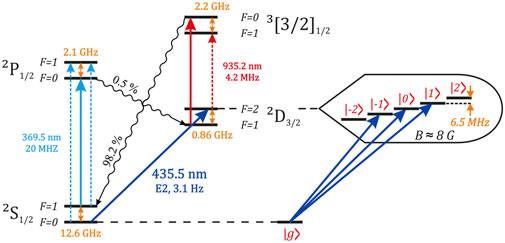
FIGURE 1. ¹⁷¹Yb⁺ level structure used for qudit manipulations. Solid lines show laser fields used for laser cooling, state initialization, manipulation, and readout. Dotted lines correspond to modulation sidebands obtained with electro-optical modulators and preventing population trapping in metastable hyperfine sublevels.

As follows from the previous subsection, protecting a pair of magnetic sublevels from noise requires their coupling with an electromagnetic field. However, the selection rules prevent the direct coupling of | − 1⟩ and |1⟩ states with a magnetic-dipole radiofrequency field, so a |0⟩ state is used for that as a mediator.

Let us the consider a four-level system of states |g⟩, | − 1⟩, |0⟩, |1⟩ (Figure 2A) with the corresponding Hamiltonian of the following form:

$\begin{array}{l}\hfill H_0=\hslash \left(\begin{array}{cccc}\hfill -{\omega }_{\mathit{opt}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_1\hfill \end{array}\right).\end{array}(5)$

FIGURE 2

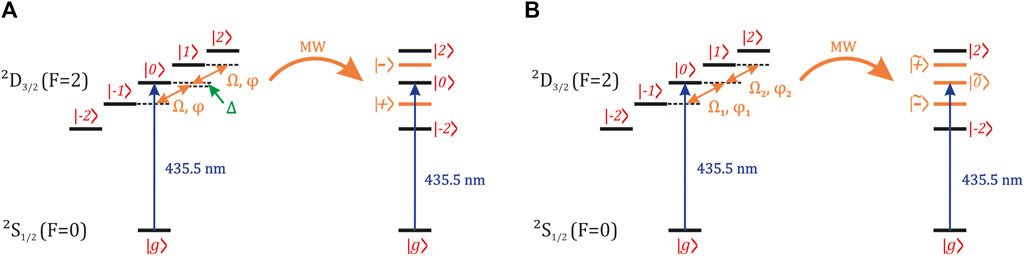
FIGURE 2. Dynamical decoupling schemes under consideration. Orange arrows on the left side of the pictures show decoupling fields with corresponding Rabi frequencies and phases. Right side shows eigenstates of the dressed ion. Black lines show states unaffected by the dressing, while orange corresponds to superposition eigenstates determined by the interaction with the dressing fields. (A) Monochromatic radiofrequency dressing. (B) Bichromatic radiofrequency dressing.

Here, ${\omega }_{\mathit{opt}}=2\pi \times \frac{c}{435.5\mathrm{n}\mathrm{m}}$ — frequency difference between |g⟩ and ²D_3/2(F = 2) manifold. We note that, due to the quadratic Zeeman shift, $\left|{\omega }_{-1}\right|\ne {|\omega }_1|$. We then add dressing radiofrequency fields with Rabi frequencies, field frequencies, and phases Ω₁, ω_D1, ϕ₁ and Ω₂, ω_D2, ϕ₂, which couple | − 1⟩ with |0⟩ and |0⟩ with |1⟩, respectively. We also place the constraint on field frequencies, such that ω_D1 + ω_D2 = ω₁ − ω₋₁. This means that a sum frequency of dressing fields is equal to the spacing between | − 1⟩ and |1⟩ states. That enables us to parametrize frequencies by a single detuning Δ = ω_D2 − ω₁ (Figure 2A). Therefore, our consideration reduces it to the classical problem of a V-system. The interaction with dressing fields is described by the following Hamiltonian:

$\begin{array}{ll}\hfill H_D& =\frac{\hslash {\mathrm{\Omega }}_1}{2}{e}^{-i{\omega }_{D1}t-i{\varphi }_1}|0⟩⟨-1|\hfill \\ \hfill & +\frac{\hslash {\mathrm{\Omega }}_2}{2}{e}^{-i{\omega }_{D2}t-i{\varphi }_2}|1⟩⟨0|+h.c.\hfill \\ \hfill & =\frac{\hslash {\mathrm{\Omega }}_1}{2}{e}^{i\left({\omega }_{-1}+\mathrm{\Delta }\right)t-i{\varphi }_1}|0⟩⟨-1|\hfill \\ \hfill & +\frac{\hslash {\mathrm{\Omega }}_2}{2}{e}^{-i\left({\omega }_1+\mathrm{\Delta }\right)t-i{\varphi }_2}|1⟩⟨0|+h.c.\hfill \end{array}(6)$

Moving to the rotation frame determined by the dressing fields (H_rot = e^iAt(H₀ + H_D − A)e^−iAt, where A = diag(−ω_opt, ω₋₁ + Δ, 0, ω₁ + Δ)), and applying the rotating wave approximation gives us the total system Hamiltonian of the form:

$H_{\text{RWA}}=\frac{\hslash }{2}\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -2\mathrm{\Delta }\hfill & \hfill {\mathrm{\Omega }}_1{e}^{i{\varphi }_1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {{\mathrm{\Omega }}_{1}e}^{-i{\varphi }_1}\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_2{e}^{i{\varphi }_2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_2{e}^{-i{\varphi }_2}\hfill & \hfill -2\mathrm{\Delta }\hfill \end{array}\right).(7)$

Exact expressions for eigenstates and eigenvalues of this Hamiltonian are rather bulky, so we do not provide them here explicitly. Two particular cases are considered in the following section in detail.

3 Decoupling schemes

3.1 Monochromatic decoupling scheme

In this first scheme, we consider the case of the use of a single dressing field, which couples states | − 1⟩ and |1⟩ via Raman two-photon transition. In this case, $\mathrm{\Delta }=-\frac{{\omega }_1+{\omega }_{-1}}{2}$, ϕ₁ = ϕ₂ = ϕ, and Ω₁ = Ω₂ = Ω ≪Δ (Figure 2A). The scheme is equivalent to the classic two-level CDD scheme, but the two-photon process helps avoid the selection rules problem. If we put ϕ = 0 (only relative phases in the system make any difference, so this does not reduce generality), the eigenstates for this case are {|g⟩, |0⟩, | + ⟩, | − ⟩} and their eigenenergies are E = {0, Ω²/(2Δ), − Δ − Ω²/(2Δ), − Δ}, respectively. Here, one can note that the degeneracy of | + ⟩ and | − ⟩ states is lifted by the value of the effective Raman Rabi frequency ${\mathrm{\Omega }}_e=\frac{{\mathrm{\Omega }}^2}{2\mathrm{\Delta }}$. At the same time, the |0⟩ state experiences the Stark shift by the same value.

Such a scheme has its own advantages and disadvantages. As discussed in the previous section, lifting the degeneracy of | + ⟩ and | − ⟩ states allows the protection of them from magnetic field noise with frequency and effective amplitude below Ω_e. At the same time, this scheme affects only states | − 1⟩ and |1⟩ and leaves all others unperturbed (except the Stark shift on the |0⟩). Thus, all quantum control techniques involving other states can be used without any changes. For example, a two-qudit Mølmer-Sørensen gate (MS) (Schmidt-Kaler et al., 2003; Mølmer and Sørensen, 1999; Sørensen and Mølmer, 1999, 2000) with states |g⟩ and |0⟩ can be performed exactly as for the qubit case. Furthermore, as shown in the following section, such qudit states can be rapidly and efficiently controlled with bichromatic laser fields, which is not a significant complication of the setup: bichromatic fields are also necessary for MS gates, so their support is routinely embedded in the experimental setups. On the other hand, the noise bandwidth, which can be suppressed by this method, is significantly limited by the difference in the transition frequencies between the Zeeman components, as

${\mathrm{\Omega }}_e\ll \mathrm{\Omega }\ll \mathrm{\Delta }=-\frac{{\omega }_1+{\omega }_{-1}}{2}.(8)$

Thus, for example, for the value of the magnetic field B ≈ 8 G, only noise of a value well below approximately 1 kHz can be suppressed. We note that, in low-noise or high-bias-field applications, this method appears to be the most convenient.

3.2 Bichromatic decoupling scheme

The aforementioned scheme is based on the fact that the radiofrequency field is relatively far-detuned from $\left|-1\right.⟩\to |0\rangle$ and $\left|0\right.⟩\to |1\rangle$ transitions; therefore, the population in |0⟩ decouples from $\left|-1\right.⟩$ and |1⟩ states. Alternatively, one can use a pair of radiofrequency fields resonant to $\left|-1\right.⟩\to |0\rangle$ and $\left|0\right.⟩\to |1\rangle$ transitions (Figure 2B). This corresponds to the case of Δ = 0. Let us also assume that Ω₁ = Ω₂ = Ω, ϕ₁ = 0, and ϕ₂ = ϕ (as already mentioned, only relative phases are relevant). Eigenstates for such a system are as follows:

$\begin{array}{cc}\hfill & \left|g\right.⟩=\left|g\right.⟩,\hfill \\ \hfill & \left|\widetilde{+}\right.⟩=\frac{1}{2}\left(e^{i\varphi }|-1\rangle +|1\rangle +\sqrt{2}{e}^{i\varphi }|0\rangle \right),\hfill \\ \hfill & \left|\widetilde{-}\right.⟩=\frac{1}{2}\left(e^{i\varphi }|-1\rangle +|1\rangle -\sqrt{2}{e}^{i\varphi }|0\rangle \right),\hfill \\ \hfill & \left|\tilde{0}\right.⟩=\frac{1}{\sqrt{2}}\left(-e^{i\varphi }|-1\rangle +|1\rangle \right).\hfill \end{array}(9)$

Corresponding eigenenergies are $E=\{0,\frac{\mathrm{\Omega }}{\sqrt{2}},-\frac{\mathrm{\Omega }}{\sqrt{2}},0\}$. This is a particular case of the MCDD approach.

It is important to note that state $\left|\tilde{0}\right.⟩$ eigenenergy does not depend on either magnetic field magnitude or on the dressing Rabi frequency Ω; therefore, it is protected from the fluctuations of both of these values. In turn, states $\left|\widetilde{+}\right.⟩$ and $\left|\widetilde{-}\right.⟩$ are protected from magnetic field fluctuations, but they are still susceptible to Rabi frequency noise.

This scheme has an advantage of higher decoupling Rabi frequency, as only condition $\mathrm{\Omega }\ll -\left({\omega }_1+{\omega }_{-1}\right)$ must be satisfied, which is more relaxed than for a monochromatic case. Thus, faster and larger magnetic field fluctuations can be suppressed. On the other hand, this encoding scheme resonantly involves state |0⟩, which can no longer be used for information storage independently from $\left|-1\right.⟩$ and $\left|1\right.⟩$.

4 Qudit manipulation

To use qudits for quantum computing not only requires sufficiently long coherence time but also allows one to implement fast and efficient control for single- and two-qudit operations. Here, we discuss how gates can be performed with the dressed qudits described previously.

4.1 Single-qudit operations

In case of a conventional ion-based qubit setup, single-qubit operations are usually performed by applying a resonant electromagnetic field to the qubit transition, which causes a state vector rotation on the Bloch sphere around some axis in the equatorial plane (Häffner et al., 2008). The rotation axis is determined by the relative field phase ϕ_S with respect to the qubit phase. The Hamiltonian generating such an operation in the interaction picture is given by

$H_{sq}=\frac{\hslash {\mathrm{\Omega }}_S}{2}\left(e^{-i{\varphi }_S}{\sigma }^{+}+e^{i{\varphi }_S}{\sigma }^{-}\right).(10)$

Here, Ω_S is the Rabi frequency of the field, ϕ_S is the field phase determining rotation axis, and σ^± are Pauli operators.

With undressed qudits, we could use the same approach connecting state |g⟩ with all other qudit states with a laser beam. As can be shown explicitly (Aksenov et al., 2022; Pogorelov et al., 2021), such operations constitute a universal single-qudit gate set. We can thus derive the control field configurations required to generate an analogous single-qudit gate set for dressed qudits case. In order to do so, we first write down a required gate Hamiltonian $H_{\text{sq}}^D$ in the dressed basis and interaction picture similar to the expression (10). Transforming it into an original basis of Zeeman sublevels using a relation $H_{\text{sq}}=e^{-iAt}{e}^{-i{H}_{\text{RWA}}t/\hslash }{H}_{\text{sq}}^D{e}^{i{H}_{\text{RWA}}t/\hslash }{e}^{iAt}$ gives us a required field configuration. We note that transferring back to a bare basis causes the appearance of oscillating terms, reflecting dressed states energy shifts.

For the monochromatic case, we have:

$\begin{array}{ll}\hfill H_{\text{sq}}^{g+}& =\frac{\hslash {\mathrm{\Omega }}_S}{2}\left(e^{-i{\varphi }_S}|+\rangle \langle g|+h.c.\right)\hfill \\ \hfill & \to \frac{\hslash {\mathrm{\Omega }}_S}{2\sqrt{2}}\left[e^{-i{\varphi }_S-i{\omega }_{\text{opt}}t+i{\mathrm{\Omega }}_{e}t}\left(e^{-i{\omega }_{1}t}|1\rangle +e^{-i{\omega }_{-1}t}|-1\rangle \right)\langle g|+h.c.\right],\hfill \end{array}(11)$

$\begin{array}{ll}\hfill H_{\text{sq}}^{g-}& =\frac{\hslash {\mathrm{\Omega }}_S}{2}\left(e^{-i{\varphi }_S}|-\rangle \langle g|+h.c.\right)\hfill \\ \hfill & \to \frac{\hslash {\mathrm{\Omega }}_S}{2\sqrt{2}}\left[e^{-i{\varphi }_S-i{\omega }_{\text{opt}}t}\left(e^{-i{\omega }_{1}t}|1\rangle -e^{-i{\omega }_{-1}t}|-1\rangle \right)\langle g|+h.c.\right].\hfill \end{array}(12)$

Therefore, corresponding single-qudit operations for monochromatically dressed qudits can be performed with a bichromatic laser field (Figure 3A). Its components are resonant (in the case of |g⟩ → | − ⟩ transition) or detuned by −Ω_e (for |g⟩ → | +⟩) from transitions between |g⟩ and states | − 1⟩ and |1⟩. The asymmetry between these states is caused by the Stark shift. The relative phase between Fourier components in this beam determine which single-qudit operations is performed (between |g⟩ and | + ⟩ or |g⟩ and | − ⟩). As with the qubit case, the common phase ϕ_S of the beam components determines the axis of the state vector rotation, and the effective Rabi frequency of such an operation is $\sqrt{2}$ larger than a Rabi frequency of each frequency component.

FIGURE 3

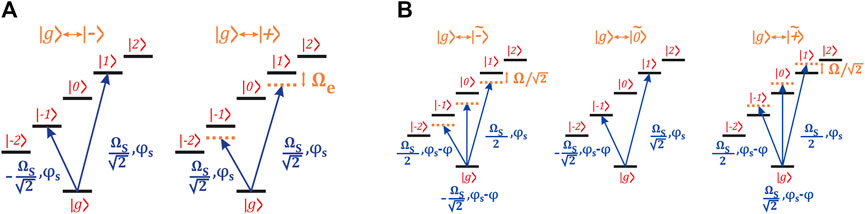
FIGURE 3. Configurations of the laser fields required to perform single-qudit operations for both decoupling schemes. (A) Monochromatic CDD scheme. (B) Bichromatic MCDD scheme.

We note that, using this technique, we can engineer a Hamiltonian, which couples |g⟩ with only one particular excited qudit state; the duration of the operation is thus not limited by the necessity of spectroscopically resolving each of the |g⟩ → |±⟩ transitions (Webster et al., 2013; Martínez-Lahuerta et al., 2023). At the same time, from an experimental point of view, bichromatic addressing fields do not introduce significant additional complications as their support is required anyway to implement two-qubit gates, such as the MS gate.

Similarly, we can obtain field configuration for a case of bichromatic dressing, where the required fields become more complicated:

$\begin{array}{ll}\hfill H_{\text{sq}}^{g\widetilde{+}}& =\frac{\hslash {\mathrm{\Omega }}_S}{2}\left(e^{-i{\varphi }_S}|\widetilde{+}\rangle \langle g|+h.c.\right)\hfill \\ \hfill & \to \frac{\hslash {\mathrm{\Omega }}_S}{4}\left[e^{-i{\varphi }_S-i{\omega }_{\text{opt}}t-i\mathrm{\Omega }t/\sqrt{2}}\left(e^{i\varphi -i{\omega }_{-1}t}|-1\rangle +e^{-i{\omega }_{1}t}|1\rangle +\sqrt{2}{e}^{i\varphi }|0\rangle \right)\langle g|+h.c.\right],\hfill \end{array}(13)$

$\begin{array}{ll}\hfill H_{\text{sq}}^{g\widetilde{-}}& =\frac{\hslash {\mathrm{\Omega }}_S}{2}\left(e^{-i{\varphi }_S}|\widetilde{-}\rangle \langle g|+h.c.\right)\hfill \\ \hfill & \to \frac{\hslash {\mathrm{\Omega }}_S}{4}\left[e^{-i{\varphi }_S-i{\omega }_{\text{opt}}t+i\mathrm{\Omega }t/\sqrt{2}}\left(e^{i\varphi -i{\omega }_{-1}t}|-1\rangle +e^{-i{\omega }_{1}t}|1\rangle -\sqrt{2}{e}^{i\varphi }|0\rangle \right)\langle g|+h.c.\right],\hfill \end{array}(14)$

$\begin{array}{ll}\hfill H_{\text{sq}}^{g\tilde{0}}& =\frac{\hslash {\mathrm{\Omega }}_S}{2}\left(e^{-i{\varphi }_S}|\tilde{0}\rangle \langle g|+h.c.\right)\hfill \\ \hfill & \to \frac{\hslash {\mathrm{\Omega }}_S}{2\sqrt{2}}\left[e^{-i{\varphi }_S-i{\omega }_{\text{opt}}t}\left(-e^{i\varphi -i{\omega }_{-1}t}|-1\rangle +e^{-i{\omega }_{1}t}|1\rangle \right)\langle g|+h.c.\right].\hfill \end{array}(15)$

Thus, to excite $|\tilde{\pm }\rangle$ states, one needs to use trichromatic laser beams, while for the $|\tilde{0}\rangle$ state, a bichromatic field is sufficient (Figure 3B).

4.2 Two-qudit operations

In the ququart case, a single two-qudit MS-type gate on any transition is sufficient to finish a universal multiqudit gate set (Aksenov et al., 2022; Pogorelov et al., 2021). Therefore, a monochromatic decoupling scheme requires no changes in ion entanglement procedure because states |g⟩ and |0⟩ are ideally suited for such gates and are not coupled to any others by the dressing fields. This is not the case for bichromatic decoupling, so the entanglement procedure must be modified accordingly.

The protocol for such a gate can be derived as for single-qudit operations. As dressing involves only internal degrees of freedom of ions and commutation relations of the operators $|\tilde{0}\rangle \langle g|$, $|g\rangle \langle \tilde{0}|$, |g⟩⟨g|, $|\tilde{0}\rangle \langle \tilde{0}|$ are the same as for |0⟩⟨g|, |g⟩⟨0|, |g⟩⟨g|, |0⟩⟨0|, all results for the conventional MS gate dynamics stay the same if we replace |0⟩ in all operators with $|\tilde{0}\rangle$. Therefore, in this case, to perform a MS gate we need not a bichromatic laser field as usual for a MS gate but a field with four spectral components, which are slightly detuned from the red and blue secular sidebands of |g⟩ → | − 1⟩ and |g⟩ → |1⟩ transitions. Such fields can be readily generated using arbitrary-waveform generator feeding signal to acousto-optical modulators.

5 Experimental results

5.1 Setup

Ytterbium ions were stored in a linear Pauli trap with single-particle secular frequencies of $\left\{{\omega }_x,{\omega }_y,{\omega }_z\right\}=2\pi \times \left\{3.88,3.95,0.16\right\}$ MHz, where z is directed along the trap axis. The trap is installed inside a vacuum chamber with residual pressure below 10^–10 mbar. All experiments were performed with an ion chain of 5 ions, which allowed efficient and single-shot readouts of all Zeeman sublevels of the ²D_3/2 (F = 2) manifold. Three orthogonal pairs of coils provided a magnetic field of 7.7 G, directed orthogonally to the trap axis. At this field, transition frequencies between Zeeman components of the ²D_3/2 manifold are as follows: ${\omega }_{m_i,m_i+1}\approx 2\pi \times \left[6465-11m_i\right]$ kHz, where m_i is a magnetic quantum number of the level; thus, ω_−1,0 − ω_0,1 ≈ 2π × 11 kHz. We do not use magnetic shielding in this setup except that synchronizing experiments start with a mains supply line signal.

Each experiment began with the Doppler cooling procedure with duration of 6 ms. The cooling process was carried out with a laser beam at 369 nm which was red-detuned from the ²S_1/2 (F = 1) →²P_1/2 (F = 0) quasi-cyclic transition (Zalivako et al., 2020). The beam was aligned at an angle to all principal axes of the trap, which provided cooling along all three of them. Another cooling beam along the trap axis assisted ion recrystallization in the case of crystal melting. Population trapping in ²S_1/2 (F = 0) was avoided by the beam phase-modulation at 14.7 GHz with an electro-optical modulator (EOM), while the population leakage to ²D_3/2 due to spontaneous decay from the ²P_1/2 state was circumvented with the repumping laser at 935 nm. The latter is also phase-modulated at 3.07 GHz to remove population from both hyperfine components. Coherent population trapping, which could arise due to smaller total angular momentum of the ²P_1/2 (F = 0) level with respect to the ²S_1/2 (F = 1) state, was prevented by applying a rather strong bias magnetic field and by the optimization of the beam polarizations (Berkeland and Boshier, 2002; Ejtemaee et al., 2010). After the cooling procedure, ions were optically pumped into the ²S_1/2 (F = 0, m_F = 0) state by turning off EOM at 14.7 GHz and turning on another EOM in this beam at 2.1 GHz. The process takes 10 μs, which is followed by blocking the cooling and repumping beams.

Optical qudit manipulations are performed with laser pulses at 435.5 nm. The fundamental harmonic of the external-cavity diode laser at 871 nm is frequency stabilized to the high-finesse optical ULE cavity. Details on the laser stabilization subsystem can be found in Zalivako et al. (2020). Laser emission is then passed through the tapered amplifier and the bow-tie cavity second-harmonic generator. The beam at 435 nm is passed through an acousto-optical modulator (AOM) for frequency, amplitude, and phase control and through an acousto-optical deflector providing the spatial steering of the beam and, therefore, the choice of the ion to be controlled. Then, the beam is focused on the ions with a system of telescopes and an in-vacuum high-aperture lens. The system provides individual ion addressing with cross-talk of 3%–10%, depending on the ion. Signals for AOM and AOD are derived from several phase-coherent direct digital synthesizers (DDS). To generate multichromatic laser beams—required to control decoupled qudits—three DDS channels are combined before AOM. Radiofrequency dressing fields are applied to one of the trap compensation electrodes. These are generated by another combined pair of DDS channels. After combining, the dressing signal is power amplified. These DDS channels are also phase-coherent with those used for AOM driving. Thus, the setup enables one to control the relative phases and amplitudes of all signals.

After required quantum operations are performed on all five ions, qudit state populations are detected via electron shelving (Semenin et al., 2021). In order to implement such a procedure, cooling and repumper beams are turned on again, but EOM at 3.07 GHz in the repumping beam is disabled, preventing population pumping from the ²D_3/2 (F = 2) manifold to the ²S_1/2 — ²P_1/2 subspace. In the case of an ion being projected into |g⟩ state, a strong fluorescence signal occurs, which is collected with a high-aperture lens onto a multi-channel PMT detector; in all other qudit states, the fluorescence is suppressed. If the number of registered photons from a particular ion appears to be above some threshold, then the qudit is considered to be in state |g⟩ and in a certain other state otherwise. To measure the populations of all qudit states at the end of the experiment, we apply an additional π-pulse resonant to the |g⟩ → |k − 3⟩ transition to each of the ions before the readout occurs, where k = {1, …, 5} is the number of the particular ion. Thus, the probability of finding kth ion fluorescing is equal to the population of state |k − 3⟩ at the end of the experiment. The population of the last state |g⟩ can be determined by the normalization condition.

5.2 Dressed states manipulation and coherence

Dressing field frequencies and amplitudes were calibrated by observing Rabi-floppings between different Zeeman sublevels of the ²D_3/2 manifold. The effective Rabi frequency for monochromatic dressing was set to Ω_e = 2π × 1.5 kHz, and Rabi frequencies in bichromatic dressing to Ω₁ = Ω₂ = Ω = 2π × 3.3 kHz.

The relative phases and amplitudes of Fourier components in multichromatic addressing laser beams—required to interact with each particular dressed qudit state—were found spectroscopically to compensate for possible delays and losses in cables and signal combiners. To do so, parameters are initially set in according to the theory given in the previous section. The spectroscopy of all transitions between |g⟩ and upper dressed qudit states was then performed using weak and long laser pulses to resolve all transitions. Afterward, the relative amplitudes and phases were optimized to suppress excitation of any other transitions except that targeted. Spectroscopy results after addressing field optimization are shown in Figure 4.

FIGURE 4

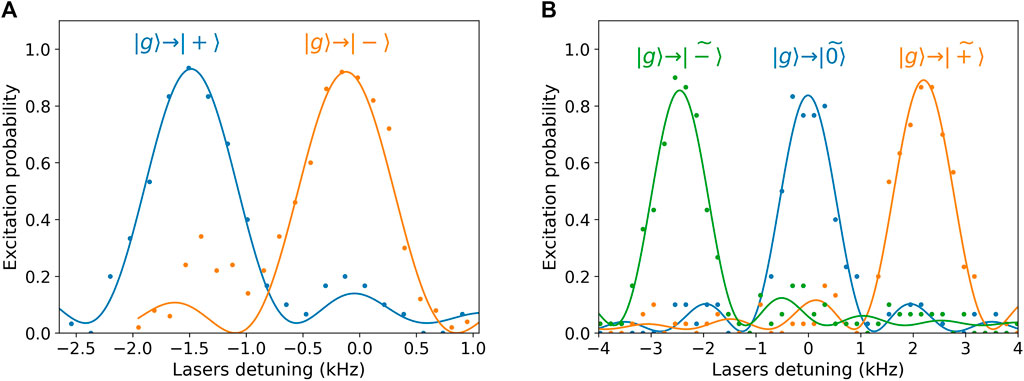
FIGURE 4. Spectroscopy of the dressed states after optimization of the addressing laser fields. Different colors correspond to laser beam configurations engineered to address only a particular dressed state. Points show experimental data, while solid lines represent fit by the theoretical curve. (A) Monochromatic CDD scheme. (B) Bichromatic MCDD scheme.

In the monochromatic case, one can see that parasitic dressed state excitations are not fully suppressed because of decoherence occurring due to magnetic field fluctuations. The dressing Rabi frequency is evidently not sufficient in this case to protect the states from all fluctuations. Its increase, however, would cause a too strong non-resonant excitation of |0⟩ state. On the other hand, the bichromatic decoupling scheme enables one to apply stronger dressing fields and, thus, better decouple states from magnetic field fluctuations.

The comparison of Ramsey contrast decay for different dynamical decoupling schemes and different states is presented in Figure 5. In this measurement, two π/2-pulses designed to excite the state under consideration were applied to the ion separated by a varying delay time. A common frequency shift was added to all addressing laser fields and its scanning gave rise to Ramsey fringes in excitation probability dependence. Each data point in fringes is a result of the averaging of 300 measurements (except MCDD, where only 100 measurements per point were taken). Ramsey fringes were first fitted by the theoretical curve (Riehle, 2003) and contrast was extracted from the fit data. The dependence of the contrast on the delay between pulses was fitted with expression f(t) = a exp(−t/τ), where τ is a coherence time $(T_2^{*})$ and t is a delay between pulses. The duration of the pulses is approximately 6 μs, similar to those used in quantum computing experiments for single-qubit operations. This thus proves the feasibility of dressed states manipulation at such rates.

FIGURE 5

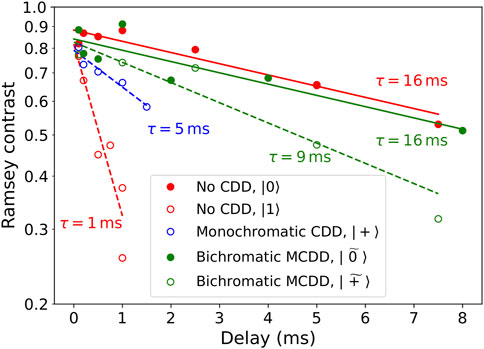
FIGURE 5. Dependence of the Ramsey fringes contrast on the delay between π/2 pulses. Different colors correspond to different decoupling schemes. For each scheme (except monochromatic), coherence time for several qudit states is measured. Data for fully decoupled states (|0⟩ and $|\tilde{0}\rangle$) are shown in filled circles, while unprotected (|1⟩) or decoupling field amplitude sensitive states (| + ⟩ and $|\widetilde{+}\rangle$) are drawn with empty circles. One can see that, without CDD coherence, time for |1⟩ is drastically shorter than that for |0⟩, while bichromatic MCDD ensures that all qudit states preserve coherence by an order of magnitude longer than the bare |1⟩ state. The monochromatic CDD scheme shows intermediate results between bare states and bichromatic MCDD.

As is evident from Figure 5, in the absence of dynamical decoupling, |0⟩ state demonstrates relatively long coherence times of $T_2^{*}=16$ ms. This value is limited not by magnetic field fluctuations but by the addressing laser frequency stability, which was confirmed by both laser stability comparison with other references and by repeating Ramsey measurements at different bias magnetic fields affecting the energy level sensitivity to the fluctuations. The coherence time of the magnetically sensitive |1⟩ state, on the other hand, is only in the order of 1 ms, which limits its application to quantum computing.

When the monochromatic dynamic decoupling scheme is applied, the coherence time of dressed | + ⟩ and | − ⟩ states increases to 5 ms. However, as already mentioned, the used efficient Rabi frequency appears to be insufficient to suppress all noise, so this value is still lower than that for bare |0⟩. The bichromatic dressing scheme in this case demonstrates better results: dressed state $|\tilde{0}\rangle$ shows the same coherence time as |0⟩, while $T_2^{*}$ for $\left|\widetilde{+}\right.⟩$ and $\left|\widetilde{-}\right.⟩$ reaches 9 ms—an order of magnitude longer than initial values without dynamical decoupling. Thus, our results indicate the achievement of qudit level coherence time of more than 9 ms without any magnetic shielding, which is an order of magnitude longer than the usual time for single-qudit operations and is sufficient for several dozen two-qudit operations. This result can be further improved by applying stronger bias magnetic field and techniques to suppress dressing field fluctuations. Thus, our results reveal the potential advantage of the symmetry of the ¹⁷¹Yb⁺ ion energy structure to counteract magnetic field noise.

6 Discussion

As can be seen from the experimental results, both schemes presented have advantages and disadvantages. The monochromatic CDD method is easier to experimentally implement as it does not require more than two spectral components in addressing beams and MS entangling operations and also needs no modification with respect to undressed qudits or qubits. Thus, this method enables ready upgrade of a conventional ytterbium optical qubit quantum processor to a qudit setup and realizing qudit quantum algorithms. At the same time, the bichromatic scheme can suppress faster and larger magnetic field fluctuations—clearly seen from the experimental data which results in longer coherence time. The price to pay is the necessity of using control fields with three spectral components for single-qudit operations and four components for two-qudit gates, which still can be carried out with arbitrary waveform generators.

The calcium ion is another well-known work-horse in the field of ion quantum computing and is also being actively studied as a platform for qudit implementation (Pogorelov et al., 2021). Here, we would like to point out that, although it is possible to achieve a CDD with this ion (Martínez-Lahuerta et al., 2023), this is more complicated and less flexible than for ytterbium. First, in case of ytterbium, only dressing of the upper levels is required as |g⟩ is intrinsically magnetically insensitive. In case of calcium, both upper and lower manifolds must be dressed. Second, as ⁴⁰Ca⁺ has a very small quadratic Zeeman shift and all transitions between neighboring sublevels are degenerate, radiofrequency dressing fields always mix all sublevels in the upper manifold. Both these factors significantly complicate the structure of the dressed states and manipulation process of such qudits. That inevitably increases the contribution of the addressing errors to the gate fidelities. At the same time, as shown in this paper, ytterbium's symmetric energy structure and large quadratic Zeeman shift enables one to engineer simple and flexible decoupling schemes involving only states of interest and keeps the addressing system rather simple.

7 Conclusion

Limitations related to short coherence times are important for realizing quantum information processing. In this work, we address this problem by demonstrating two approaches to the realization of continuous dynamical decoupling of magnetic-sensitive states with m_F = ±1 for qudits encoded in ¹⁷¹Yb⁺ trapped ions. We show that qudit level coherence time of more than 9 ms can be achieved without any magnetic shielding. The key ingredient of the proposed schemes is the use of the symmetry of the ¹⁷¹Yb⁺ ion energy structure to counteract the magnetic field noise. Our results are important for realizing qudit-based algorithms with trapped ions.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

IZ, AB, and IS developed the conception and design of the study. IZ performed theoretical analysis. AB, AK, PS, KG, and VS contributed to setting up the experiment. AB, IZ, PL, and KG carried out the experiments. IZ, AF, and NS performed data analysis. IZ, AF, KK, and NK wrote sections of the manuscript. NK supervised the project. All authors contributed to the article and approved the submitted version.

Funding

The experimental work supported by the Russian Roadmap on Quantum Computing (Contract No. 868-1.3-15/15-2021, 5 October 2021).

Acknowledgments

The authors thank A. S. Nikolaeva and E. O. Kiktenko for fruitful discussion and useful comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aksenov, M. A., Zalivako, I. V., Semerikov, I. A., Borisenko, A. S., Semenin, N. V., Sidorov, P. L., et al. (2022). Realizing quantum gates with optically-addressable ¹⁷¹yb⁺ ion qudits. Quantum Phys. doi:10.48550/ARXIV.2210.09121

CrossRef Full Text | Google Scholar

Arute, F., Arya, K., Babbush, R., Bacon, D., Bardin, J. C., Barends, R., et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510. doi:10.1038/s41586-019-1666-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Bagan, E., Baig, M., and Muñoz Tapia, R. (2003). Minimal measurements of the gate fidelity of a qudit map. Phys. Rev. A 67, 014303. doi:10.1103/PhysRevA.67.014303

CrossRef Full Text | Google Scholar

Baker, J. M., Duckering, C., and Chong, F. T. (2020). “Efficient quantum circuit decompositions via intermediate qudits,” in 2020 IEEE 50th International Symposium on Multiple-Valued Logic, Miyazaki, Japan, November 9-11, 2020 (New York, NY: ISMVL), 303–308.

CrossRef Full Text | Google Scholar

Barenco, A., Bennett, C. H., Cleve, R., DiVincenzo, D. P., Margolus, N., Shor, P., et al. (1995). Elementary gates for quantum computation. Phys. Rev. A 52, 3457–3467. doi:10.1103/PhysRevA.52.3457

PubMed Abstract | CrossRef Full Text | Google Scholar

Berkeland, D. J., and Boshier, M. G. (2002). Destabilization of dark states and optical spectroscopy in zeeman-degenerate atomic systems. Phys. Rev. A 65, 033413. doi:10.1103/PhysRevA.65.033413

CrossRef Full Text | Google Scholar

Blatt, R., and Roos, C. F. (2012). Quantum simulations with trapped ions. Nat. Phys. 8, 277–284. doi:10.1038/nphys2252

CrossRef Full Text | Google Scholar

Bocharov, A., Roetteler, M., and Svore, K. M. (2017). Factoring with qutrits: Shor’s algorithm on ternary and metaplectic quantum architectures. Phys. Rev. A 96, 012306. doi:10.1103/PhysRevA.96.012306

CrossRef Full Text | Google Scholar

Braumüller, J., Cramer, J., Schlör, S., Rotzinger, H., Radtke, L., Lukashenko, A., et al. (2015). Multiphoton dressing of an anharmonic superconducting many-level quantum circuit. Phys. Rev. B 91, 054523. doi:10.1103/PhysRevB.91.054523

CrossRef Full Text | Google Scholar

Bruzewicz, C. D., Chiaverini, J., McConnell, R., and Sage, J. M. (2019). Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 6, 021314. doi:10.1063/1.5088164

CrossRef Full Text | Google Scholar

Cai, J.-M., Naydenov, B., Pfeiffer, R., McGuinness, L. P., Jahnke, K. D., Jelezko, F., et al. (2012). Robust dynamical decoupling with concatenated continuous driving. New J. Phys. 14, 113023. doi:10.1088/1367-2630/14/11/113023

CrossRef Full Text | Google Scholar

Chi, Y., Huang, J., Zhang, Z., Mao, J., Zhou, Z., Chen, X., et al. (2022b). A programmable qudit-based quantum processor. Nat. Commun. 13, 1166. doi:10.1038/s41467-022-28767-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chi, Y., Huang, J., Zhang, Z., Mao, J., Zhou, Z., Chen, X., et al. (2022a). A programmable qudit-based quantum processor. Nat. Commun. 13, 1166. doi:10.1038/s41467-022-28767-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiaverini, J., Leibfried, D., Schaetz, T., Barrett, M. D., Blakestad, R. B., Britton, J., et al. (2004). Realization of quantum error correction. Nature 432, 602–605. doi:10.1038/nature03074

PubMed Abstract | CrossRef Full Text | Google Scholar

Cirac, J. I., and Zoller, P. (1995). Quantum computations with cold trapped ions. Phys. Rev. Lett. 74, 4091–4094. doi:10.1103/PhysRevLett.74.4091

PubMed Abstract | CrossRef Full Text | Google Scholar

Cross, A. W., Bishop, L. S., Sheldon, S., Nation, P. D., and Gambetta, J. M. (2019). Validating quantum computers using randomized model circuits. Phys. Rev. A 100, 032328. doi:10.1103/PhysRevA.100.032328

CrossRef Full Text | Google Scholar

Ebadi, S., Wang, T. T., Levine, H., Keesling, A., Semeghini, G., Omran, A., et al. (2021). Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 595, 227–232. doi:10.1038/s41586-021-03582-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Egan, L., Debroy, D. M., Noel, C., Risinger, A., Zhu, D., Biswas, D., et al. (2021). Fault-tolerant control of an error-corrected qubit. Nature 598, 281–286. doi:10.1038/s41586-021-03928-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ejtemaee, S., Thomas, R., and Haljan, P. C. (2010). Optimization of yb⁺ fluorescence and hyperfine-qubit detection. Phys. Rev. A 82, 063419. doi:10.1103/PhysRevA.82.063419

CrossRef Full Text | Google Scholar

Erhard, A., Poulsen Nautrup, H., Meth, M., Postler, L., Stricker, R., Stadler, M., et al. (2021). Entangling logical qubits with lattice surgery. Nature 589, 220–224. doi:10.1038/s41586-020-03079-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Farfurnik, D., Aharon, N., Cohen, I., Hovav, Y., Retzker, A., and Bar-Gill, N. (2017). Experimental realization of time-dependent phase-modulated continuous dynamical decoupling. Phys. Rev. A 96, 013850. doi:10.1103/PhysRevA.96.013850

CrossRef Full Text | Google Scholar

Farhi, E., Goldstone, J., and Gutmann, S. (2014). A quantum approximate optimization algorithm. Available at: https://arxiv.org/abs/1411.4028.

Google Scholar

Farhi, E., and Gutmann, S. (1998). Analog analogue of a digital quantum computation. Phys. Rev. A 57, 2403–2406. doi:10.1103/PhysRevA.57.2403

CrossRef Full Text | Google Scholar

Fedorov, A., Steffen, L., Baur, M., da Silva, M. P., and Wallraff, A. (2012). Implementation of a toffoli gate with superconducting circuits. Nature 481, 170–172. doi:10.1038/nature10713

PubMed Abstract | CrossRef Full Text | Google Scholar

Fedorov, A. K., Gisin, N., Beloussov, S. M., and Lvovsky, A. I. (2022). Quantum computing at the quantum advantage threshold: A down-to-business review. Quantum Phys. doi:10.48550/ARXIV.2203.17181

CrossRef Full Text | Google Scholar

Frydryszak, A., Jakóbczyk, L., and Ługiewicz, P. (2017). Determining quantum correlations in bipartite systems - from qubit to qutrit and beyond. J. Phys. Conf. Ser. 804, 012016. doi:10.1088/1742-6596/804/1/012016

CrossRef Full Text | Google Scholar

Gaebler, J. P., Tan, T. R., Lin, Y., Wan, Y., Bowler, R., Keith, A. C., et al. (2016). High-fidelity universal gate set for ${^{9}\mathrm{Be}}^{+}$ ion qubits. Phys. Rev. Lett. 117, 060505. doi:10.1103/PhysRevLett.117.060505

PubMed Abstract | CrossRef Full Text | Google Scholar

Galda, A., Cubeddu, M., Kanazawa, N., Narang, P., and Earnest-Noble, N. (2021). Implementing a ternary decomposition of the toffoli gate on fixed-frequency transmon qutrits. Available at: https://arxiv.org/pdf/2109.00558.pdf (ARXIV:2109.00558.

Google Scholar

Godfrin, C., Ferhat, A., Ballou, R., Klyatskaya, S., Ruben, M., Wernsdorfer, W., et al. (2017). Operating quantum states in single magnetic molecules: Implementation of grover’s quantum algorithm. Phys. Rev. Lett. 119, 187702. doi:10.1103/PhysRevLett.119.187702

PubMed Abstract | CrossRef Full Text | Google Scholar

Gokhale, P., Baker, J. M., Duckering, C., Brown, N. C., Brown, K. R., and Chong, F. T. (2019). “Asymptotic improvements to quantum circuits via qutrits,” in Proceedings of the 46th International Symposium on Computer Architecture (New York, NY, USA: Association for Computing Machinery), ISCA ’19, New York, USA, June 18 - 22, 2022, 554–566.

CrossRef Full Text | Google Scholar

Graham, T. M., Song, Y., Scott, J., Poole, C., Phuttitarn, L., Jooya, K., et al. (2022). Multi-qubit entanglement and algorithms on a neutral-atom quantum computer. Nature 604, 457–462. doi:10.1038/s41586-022-04603-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Greentree, A. D., Schirmer, S. G., Green, F., Hollenberg, L. C. L., Hamilton, A. R., and Clark, R. G. (2004). Maximizing the hilbert space for a finite number of distinguishable quantum states. Phys. Rev. Lett. 92, 097901. doi:10.1103/PhysRevLett.92.097901

PubMed Abstract | CrossRef Full Text | Google Scholar

Grover, L. K. (1996). “A fast quantum mechanical algorithm for database search,” in Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing (New York, NY, USA: Association for Computing Machinery), STOC ’96, Pennsylvania, USA, May 22 - 24, 1996, 212–219.

CrossRef Full Text | Google Scholar

Gu, X., Allcock, J., An, S., and Liu, Y.-x. (2021). Efficient multi-qubit subspace rotations via topological quantum walks. Quantum Phys. doi:10.48550/ARXIV.2111.06534

CrossRef Full Text | Google Scholar

Häffner, H., Roos, C. F., and Blatt, R. (2008). Quantum computing with trapped ions. Phys. Rep. 469, 155–203. doi:10.1016/j.physrep.2008.09.003

CrossRef Full Text | Google Scholar

Harrow, A. W., Hassidim, A., and Lloyd, S. (2009). Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 103, 150502. doi:10.1103/PhysRevLett.103.150502

PubMed Abstract | CrossRef Full Text | Google Scholar

Hempel, C., Maier, C., Romero, J., McClean, J., Monz, T., Shen, H., et al. (2018). Quantum chemistry calculations on a trapped-ion quantum simulator. Phys. Rev. X 8, 031022. doi:10.1103/PhysRevX.8.031022

CrossRef Full Text | Google Scholar

Henriet, L., Beguin, L., Signoles, A., Lahaye, T., Browaeys, A., Reymond, G.-O., et al. (2020). Quantum computing with neutral atoms. Quantum 4, 327. doi:10.22331/q-2020-09-21-327

CrossRef Full Text | Google Scholar

Hill, A. D., Hodson, M. J., Didier, N., and Reagor, M. J. (2021). Realization of arbitrary doubly-controlled quantum phase gates. Quantum Phys. doi:10.48550/ARXIV.2108.01652

CrossRef Full Text | Google Scholar

Ionicioiu, R., Spiller, T. P., and Munro, W. J. (2009). Generalized toffoli gates using qudit catalysis. Phys. Rev. A 80, 012312. doi:10.1103/PhysRevA.80.012312

CrossRef Full Text | Google Scholar

Ivanov, S. S., Tonchev, H. S., and Vitanov, N. V. (2012). Time-efficient implementation of quantum search with qudits. Phys. Rev. A 85, 062321. doi:10.1103/PhysRevA.85.062321

CrossRef Full Text | Google Scholar

Jin, Z., Gong, W.-J., Zhu, A.-D., Zhang, S., Qi, Y., and Su, S.-L. (2021). Dissipative preparation of qutrit entanglement via periodically modulated rydberg double antiblockade. Opt. Express 29, 10117–10133. doi:10.1364/OE.419568

PubMed Abstract | CrossRef Full Text | Google Scholar

Kessel’, A. R., and Ermakov, V. L. (1999). Multiqubit spin. J. Exp. Theor. Phys. Lett. 70, 61–65. doi:10.1134/1.568130

CrossRef Full Text | Google Scholar

Kessel’, A. R., and Ermakov, V. L. (2000). Physical implementation of three-qubit gates on a separate quantum particle. J. Exp. Theor. Phys. Lett. 71, 307–309. doi:10.1134/1.568340

CrossRef Full Text | Google Scholar

Kessel, A. R., and Yakovleva, N. M. (2002). Implementation schemes in nmr of quantum processors and the deutsch-jozsa algorithm by using virtual spin representation. Phys. Rev. A 66, 062322. doi:10.1103/PhysRevA.66.062322

CrossRef Full Text | Google Scholar

Kiktenko, E., Fedorov, A., Strakhov, A., and Man’ko, V. (2015a). Single qudit realization of the deutsch algorithm using superconducting many-level quantum circuits. Phys. Lett. A 379, 1409–1413. doi:10.1016/j.physleta.2015.03.023

CrossRef Full Text | Google Scholar

Kiktenko, E. O., Fedorov, A. K., Man’ko, O. V., and Man’ko, V. I. (2015b). Multilevel superconducting circuits as two-qubit systems: Operations, state preparation, and entropic inequalities. Phys. Rev. A 91, 042312. doi:10.1103/PhysRevA.91.042312

CrossRef Full Text | Google Scholar

Kiktenko, E. O., Nikolaeva, A. S., Xu, P., Shlyapnikov, G. V., and Fedorov, A. K. (2020). Scalable quantum computing with qudits on a graph. Phys. Rev. A 101, 022304. doi:10.1103/PhysRevA.101.022304

CrossRef Full Text | Google Scholar

Klimov, A. B., Guzmán, R., Retamal, J. C., and Saavedra, C. (2003). Qutrit quantum computer with trapped ions. Phys. Rev. A 67, 062313. doi:10.1103/PhysRevA.67.062313

CrossRef Full Text | Google Scholar

Kues, M., Reimer, C., Roztocki, P., Cortés, L. R., Sciara, S., Wetzel, B., et al. (2017). On-chip generation of high-dimensional entangled quantum states and their coherent control. Nature 546, 622–626. doi:10.1038/nature22986

PubMed Abstract | CrossRef Full Text | Google Scholar

Lacroûte, C., Souidi, M., Bourgeois, P.-Y., Millo, J., Saleh, K., Bigler, E., et al. (2016). Compact Yb⁺optical atomic clock project: Design principle and current status. J. Phys. Conf. Ser. 723, 012025. doi:10.1088/1742-6596/723/1/012025

CrossRef Full Text | Google Scholar

Lanyon, B. P., Barbieri, M., Almeida, M. P., Jennewein, T., Ralph, T. C., Resch, K. J., et al. (2009). Simplifying quantum logic using higher-dimensional hilbert spaces. Nat. Phys. 5, 134–140. doi:10.1038/nphys1150

CrossRef Full Text | Google Scholar

Lanyon, B. P., Weinhold, T. J., Langford, N. K., O’Brien, J. L., Resch, K. J., Gilchrist, A., et al. (2008). Manipulating biphotonic qutrits. Phys. Rev. Lett. 100, 060504. doi:10.1103/PhysRevLett.100.060504

PubMed Abstract | CrossRef Full Text | Google Scholar

Leute, J., Huntemann, N., Lipphardt, B., Tamm, C., Nisbet-Jones, P. B. R., King, S. A., et al. (2016). Frequency comparison of ¹⁷¹yb⁺ ion optical clocks at ptb and npl via gps ppp. IEEE Trans. Ultrasonics, Ferroelectr. Freq. Control 63, 981–985. doi:10.1109/TUFFC.2016.2524988

CrossRef Full Text | Google Scholar

Li, B., Yu, Z.-H., and Fei, S.-M. (2013). Geometry of quantum computation with qutrits. Sci. Rep. 3, 2594. doi:10.1038/srep02594

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W.-Q., Wei, H.-R., and Kwek, L.-C. (2020). Low-cost fredkin gate with auxiliary space. Phys. Rev. Appl. 14, 054057. doi:10.1103/PhysRevApplied.14.054057

CrossRef Full Text | Google Scholar

Liu, W.-Q., Wei, H.-R., and Kwek, L.-C. (2022). Universal quantum multi-qubit entangling gates with auxiliary spaces. New Jersey, United States: Advanced Quantum Technologies. 2100136. doi:10.1002/qute.202100136

CrossRef Full Text | Google Scholar

Lloyd, S. (1996). Universal quantum simulators. Science 273, 1073–1078. doi:10.1126/science.273.5278.1073

PubMed Abstract | CrossRef Full Text | Google Scholar

Low, P. J., White, B. M., Cox, A. A., Day, M. L., and Senko, C. (2020a). Practical trapped-ion protocols for universal qudit-based quantum computing. Phys. Rev. Res. 2, 033128. doi:10.1103/PhysRevResearch.2.033128

CrossRef Full Text | Google Scholar

Low, P. J., White, B. M., Cox, A. A., Day, M. L., and Senko, C. (2020b). Practical trapped-ion protocols for universal qudit-based quantum computing. Phys. Rev. Res. 2, 033128. doi:10.1103/PhysRevResearch.2.033128

CrossRef Full Text | Google Scholar

Luo, Y.-H., Zhong, H.-S., Erhard, M., Wang, X.-L., Peng, L.-C., Krenn, M., et al. (2019). Quantum teleportation in high dimensions. Phys. Rev. Lett. 123, 070505. doi:10.1103/PhysRevLett.123.070505

PubMed Abstract | CrossRef Full Text | Google Scholar

Madsen, L. S., Laudenbach, F., Askarani, M. F., Rortais, F., Vincent, T., Bulmer, J. F. F., et al. (2022). Quantum computational advantage with a programmable photonic processor. Nature 606, 75–81. doi:10.1038/s41586-022-04725-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Madzik, M. T., Asaad, S., Youssry, A., Joecker, B., Rudinger, K. M., Nielsen, E., et al. (2022). Precision tomography of a three-qubit donor quantum processor in silicon. Nature 601, 348–353. doi:10.1038/s41586-021-04292-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez-Lahuerta, V. J., Pelzer, L., Dietze, K., Krinner, L., Schmidt, P. O., and Hammerer, K. (2023). Quadrupole transitions and quantum gates protected by continuous dynamic decoupling. Quantum Phys. doi:10.48550/arXiv.2301.07974

CrossRef Full Text | Google Scholar

Mischuck, B. E., Merkel, S. T., and Deutsch, I. H. (2012). Control of inhomogeneous atomic ensembles of hyperfine qudits. Phys. Rev. A 85, 022302. doi:10.1103/PhysRevA.85.022302

CrossRef Full Text | Google Scholar

Mølmer, K., and Sørensen, A. (1999). Multiparticle entanglement of hot trapped ions. Phys. Rev. Lett. 82, 1835–1838. doi:10.1103/PhysRevLett.82.1835

CrossRef Full Text | Google Scholar

Monroe, C., and Kim, J. (2013). Scaling the ion trap quantum processor. Science 339, 1164–1169. doi:10.1126/science.1231298

PubMed Abstract | CrossRef Full Text | Google Scholar

Monroe, C., Meekhof, D. M., King, B. E., Itano, W. M., and Wineland, D. J. (1995). Demonstration of a fundamental quantum logic gate. Phys. Rev. Lett. 75, 4714–4717. doi:10.1103/PhysRevLett.75.4714

PubMed Abstract | CrossRef Full Text | Google Scholar

Muthukrishnan, A., and Stroud, C. R. (2000). Multivalued logic gates for quantum computation. Phys. Rev. A 62, 052309. doi:10.1103/PhysRevA.62.052309

CrossRef Full Text | Google Scholar

Neeley, M., Ansmann, M., Bialczak, R. C., Hofheinz, M., Lucero, E., O’Connell, A. D., et al. (2009). Emulation of a quantum spin with a superconducting phase qudit. Science 325, 722–725. doi:10.1126/science.1173440

PubMed Abstract | CrossRef Full Text | Google Scholar

Nielsen, M. A., Bremner, M. J., Dodd, J. L., Childs, A. M., and Dawson, C. M. (2002). Universal simulation of Hamiltonian dynamics for quantum systems with finite-dimensional state spaces. Phys. Rev. A 66, 022317. doi:10.1103/PhysRevA.66.022317

CrossRef Full Text | Google Scholar

Nikolaeva, A. S., Kiktenko, E. O., and Fedorov, A. K. (2021). Efficient realization of quantum algorithms with qudits. Quantum Phys. doi:10.48550/ARXIV.2111.04384

CrossRef Full Text | Google Scholar

Nikolaeva, A. S., Kiktenko, E. O., and Fedorov, A. K. (2022). Decomposing the generalized toffoli gate with qutrits. Phys. Rev. A 105, 032621. doi:10.1103/PhysRevA.105.032621

CrossRef Full Text | Google Scholar

Nikolaeva, A. S., Kiktenko, E. O., and Fedorov, A. K. (2023). Generalized toffoli gate decomposition using ququints: Towards realizing grover’s algorithm with qudits. Entropy 25, 387. doi:10.3390/e25020387

PubMed Abstract | CrossRef Full Text | Google Scholar

Noiri, A., Takeda, K., Nakajima, T., Kobayashi, T., Sammak, A., Scappucci, G., et al. (2022). Fast universal quantum gate above the fault-tolerance threshold in silicon. Nature 601, 338–342. doi:10.1038/s41586-021-04182-y

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Leary, D. P., Brennen, G. K., and Bullock, S. S. (2006). Parallelism for quantum computation with qudits. Phys. Rev. A 74, 032334. doi:10.1103/PhysRevA.74.032334

CrossRef Full Text | Google Scholar

Pavlidis, A., and Floratos, E. (2021). Quantum-fourier-transform-based quantum arithmetic with qudits. Phys. Rev. A 103, 032417. doi:10.1103/PhysRevA.103.032417

CrossRef Full Text | Google Scholar

Peterer, M. J., Bader, S. J., Jin, X., Yan, F., Kamal, A., Gudmundsen, T. J., et al. (2015). Coherence and decay of higher energy levels of a superconducting transmon qubit. Phys. Rev. Lett. 114, 010501. doi:10.1103/PhysRevLett.114.010501

PubMed Abstract | CrossRef Full Text | Google Scholar

Pogorelov, I., Feldker, T., Marciniak, C. D., Postler, L., Jacob, G., Krieglsteiner, O., et al. (2021). Compact ion-trap quantum computing demonstrator. PRX Quantum 2, 020343. doi:10.1103/PRXQuantum.2.020343

CrossRef Full Text | Google Scholar

Postler, L., Heuen, S., Pogorelov, I., Rispler, M., Feldker, T., Meth, M., et al. (2022). Demonstration of fault-tolerant universal quantum gate operations. Nature 605, 675–680. doi:10.1038/s41586-022-04721-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Qua (2023). Quantum volume reaches 5 digits for the first time: 5 perspectives on what it means for quantum computing. Available at: https://www.quantinuum.com/news/quantum-volume-reaches-5-digits-for-the-first-time-5-perspectives-on-what-it-means-for-quantum-computing.

Google Scholar

Ralph, T. C., Resch, K. J., and Gilchrist, A. (2007). Efficient toffoli gates using qudits. Phys. Rev. A 75, 022313. doi:10.1103/PhysRevA.75.022313

CrossRef Full Text | Google Scholar

Rambow, P., and Tian, M. (2021). Reduction of circuit depth by mapping qubit-based quantum gates to a qudit basis. Quantum Phys. doi:10.48550/ARXIV.2109.09902

CrossRef Full Text | Google Scholar

Riehle, F. (2003). Frequency standards. New Jersey, United States: John Wiley and Sons, Ltd. doi:10.1002/3527605991

CrossRef Full Text | Google Scholar

Ringbauer, M., Meth, M., Postler, L., Stricker, R., Blatt, R., Schindler, P., et al. (2021). A universal qudit quantum processor with trapped ions. Nat. Phys. 18, 1053–1057. doi:10.1038/s41567-022-01658-0

CrossRef Full Text | Google Scholar

Ryan-Anderson, C., Brown, N. C., Allman, M. S., Arkin, B., Asa-Attuah, G., Baldwin, C., et al. (2022). Implementing fault-tolerant entangling gates on the five-qubit code and the color code. Quantum Phys. doi:10.48550/ARXIV.2208.01863

CrossRef Full Text | Google Scholar

Sawant, R., Blackmore, J. A., Gregory, P. D., Mur-Petit, J., Jaksch, D., Aldegunde, J., et al. (2020). Ultracold polar molecules as qudits. New J. Phys. 22, 013027. doi:10.1088/1367-2630/ab60f4

CrossRef Full Text | Google Scholar

Schindler, P., Barreiro, J. T., Monz, T., Nebendahl, V., Nigg, D., Chwalla, M., et al. (2011). Experimental repetitive quantum error correction. Science 332, 1059–1061. doi:10.1126/science.1203329

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt-Kaler, F., Häffner, H., Riebe, M., Gulde, S., Lancaster, G. P. T., Deuschle, T., et al. (2003). Realization of the cirac–zoller controlled-not quantum gate. Nature 422, 408–411. doi:10.1038/nature01494

PubMed Abstract | CrossRef Full Text | Google Scholar

Scholl, P., Schuler, M., Williams, H. J., Eberharter, A. A., Barredo, D., Schymik, K.-N., et al. (2021). Quantum simulation of 2d antiferromagnets with hundreds of rydberg atoms. Nature 595, 233–238. doi:10.1038/s41586-021-03585-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Semenin, N. V., Borisenko, A. S., Zalivako, I. V., Semerikov, I. A., Khabarova, K. Y., and Kolachevsky, N. N. (2021). Optimization of the readout fidelity of the quantum state of an optical qubit in the 171yb+ ion. JETP Lett. 114, 486–492. doi:10.1134/s0021364021200108

CrossRef Full Text | Google Scholar

Semerikov, I. A., Khabarova, K. Y., Zalivako, I. V., Borisenko, A. S., and Kolachevsky, N. N. (2018). Compact transportable optical standard based on a single 171yb+ ion (“ybis”project). Bull. Lebedev Phys. Inst. 45, 337–340. doi:10.3103/S1068335618110039

CrossRef Full Text | Google Scholar

Shor, P. (1994). “Algorithms for quantum computation: Discrete logarithms and factoring,” in Proceedings 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, United States, November 20 - 22, 1994, 124–134.

Google Scholar

Song, C., Su, S.-L., Wu, J.-L., Wang, D.-Y., Ji, X., and Zhang, S. (2016). Generation of tree-type three-dimensional entangled states via adiabatic passage. Phys. Rev. A 93, 062321. doi:10.1103/PhysRevA.93.062321

CrossRef Full Text | Google Scholar

Sørensen, A., and Mølmer, K. (2000). Entanglement and quantum computation with ions in thermal motion. Phys. Rev. A 62, 022311. doi:10.1103/PhysRevA.62.022311

CrossRef Full Text | Google Scholar

Sørensen, A., and Mølmer, K. (1999). Quantum computation with ions in thermal motion. Phys. Rev. Lett. 82, 1971–1974. doi:10.1103/PhysRevLett.82.1971

CrossRef Full Text | Google Scholar

Stricker, R., Vodola, D., Erhard, A., Postler, L., Meth, M., Ringbauer, M., et al. (2020). Experimental deterministic correction of qubit loss. Nature 585, 207–210. doi:10.1038/s41586-020-2667-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Svetitsky, E., Suchowski, H., Resh, R., Shalibo, Y., Martinis, J. M., and Katz, N. (2014). Hidden two-qubit dynamics of a four-level josephson circuit. Nat. Commun. 5, 5617. doi:10.1038/ncomms6617

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamm, C., Engelke, D., and Bühner, V. (2000). Spectroscopy of the electric-quadrupole transition ²S_1/2(f = 0)−−²D_3/2(f = 2) in trapped ¹⁷¹yb⁺. Phys. Rev. A 61, 053405. doi:10.1103/PhysRevA.61.053405

CrossRef Full Text | Google Scholar

Valahu, C. H., Apostolatos, I., Weidt, S., and Hensinger, W. K. (2022). Quantum control methods for robust entanglement of trapped ions. J. Phys. B Atomic, Mol. Opt. Phys. 55, 204003. doi:10.1088/1361-6455/ac8eff

CrossRef Full Text | Google Scholar

Viola, L., Knill, E., and Lloyd, S. (1999). Dynamical decoupling of open quantum systems. Phys. Rev. Lett. 82, 2417–2421. doi:10.1103/PhysRevLett.82.2417

CrossRef Full Text | Google Scholar

Viola, L., and Knill, E. (2003). Robust dynamical decoupling of quantum systems with bounded controls. Phys. Rev. Lett. 90, 037901. doi:10.1103/PhysRevLett.90.037901

PubMed Abstract | CrossRef Full Text | Google Scholar

Viola, L., and Lloyd, S. (1998). Dynamical suppression of decoherence in two-state quantum systems. Phys. Rev. A 58, 2733–2744. doi:10.1103/PhysRevA.58.2733

CrossRef Full Text | Google Scholar

Vlasov, A. Y. (2003). “Algebra of quantum computations with higher dimensional systems,” in First international symposium on quantum informatics. Editor Y. I. Ozhigov (Bellingham, Washington: International Society for Optics and Photonics SPIE), 5128, 29–36. doi:10.1117/12.517863

CrossRef Full Text | Google Scholar

Wang, P., Luan, C.-Y., Qiao, M., Um, M., Zhang, J., Wang, Y., et al. (2021). Single ion qubit with estimated coherence time exceeding one hour. Nat. Commun. 12, 233. doi:10.1038/s41467-020-20330-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Sanders, B. C., and Berry, D. W. (2003). Entangling power and operator entanglement in qudit systems. Phys. Rev. A 67, 042323. doi:10.1103/PhysRevA.67.042323

CrossRef Full Text | Google Scholar

Wang, Y., Hu, Z., Sanders, B. C., and Kais, S. (2020). Qudits and high-dimensional quantum computing. Front. Phys. 8. doi:10.3389/fphy.2020.589504

CrossRef Full Text | Google Scholar

Webster, S. C., Weidt, S., Lake, K., McLoughlin, J. J., and Hensinger, W. K. (2013). Simple manipulation of a microwave dressed-state ion qubit. Phys. Rev. Lett. 111, 140501. doi:10.1103/PhysRevLett.111.140501

PubMed Abstract | CrossRef Full Text | Google Scholar

Weggemans, J. R., Urech, A., Rausch, A., Spreeuw, R., Boucherie, R., Schreck, F., et al. (2022). Solving correlation clustering with QAOA and a rydberg qudit system: A full-stack approach. Quantum 6, 687. doi:10.22331/q-2022-04-13-687

CrossRef Full Text | Google Scholar

Wu, Y., Bao, W.-S., Cao, S., Chen, F., Chen, M.-C., Chen, X., et al. (2021). Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett. 127, 180501. doi:10.1103/PhysRevLett.127.180501

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, X., Russ, M., Samkharadze, N., Undseth, B., Sammak, A., Scappucci, G., et al. (2022). Quantum logic with spin qubits crossing the surface code threshold. Nature 601, 343–347. doi:10.1038/s41586-021-04273-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Zalivako, I., Semerikov, I., Borisenko, A., Aksenov, M., Vishnyakov, P., Sidorov, P., et al. (2020). Compact ultrastable laser system for spectroscopy of 2s1/2 → 2d3/2 quadrupole transition in 171yb+ ion. Quantum Electron. 50, 850–854. doi:10.1070/QEL17373

CrossRef Full Text | Google Scholar

Zalivako, I. V., Semerikov, I. A., Borisenko, A. S., Aksenov, M. D., Khabarova, K. Y., and Kolachevsky, N. N. (2021). Experimental study of the optical qubit on the 435-nm quadrupole transition in the 171yb+ ion. JETP Lett. 114, 59–64. doi:10.1134/S0021364021140113

CrossRef Full Text | Google Scholar

Zhang, J., Pagano, G., Hess, P. W., Kyprianidis, A., Becker, P., Kaplan, H., et al. (2017). Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator. Nature 551, 601–604. doi:10.1038/nature24654

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhong, H.-S., Wang, H., Deng, Y.-H., Chen, M.-C., Peng, L.-C., Luo, Y.-H., et al. (2020). Quantum computational advantage using photons. Science 370, 1460–1463. doi:10.1126/science.abe8770

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, H., Gao, H., Leitao, N. T., Makarova, O., Cong, I., Douglas, A. M., et al. (2023). Robust Hamiltonian engineering for interacting qudit systems. Quantum Phys. doi:10.48550/arXiv.2305.09757

CrossRef Full Text | Google Scholar