Self-assisted deterministic hyperentangled-Bell-state analysis for polarization and double longitudinal momentum degrees of freedom of photon system

Hyperentangled state analysis is an important module in high-capacity quantum communication. We present a self-assisted deterministic hyperentangled-Bell-state analysis (HBSA) scheme for photon system entangled in three degrees of freedom (DOFs), where 64 polarization-double longitudinal momentum hyperentangled Bell states are completely distinguished. In this HBSA scheme, the four first longitudinal momentum Bell states are distinguished determinately by nondestructive first longitudinal momentum Bell state analyzer, which is constructed with cross-Kerr nonlinearity medium. The 16 second longitudinal momentum-polarization hyperentangled Bell states are distinguished determinately by self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer using linear optical elements, where the first longitudinal momentum Bell state and time-bin entangled state are used as auxiliary. Using this self-assisted method, the application of nonlinear optical resource in HBSA scheme has been largely reduced, which makes this self-assisted deterministic HBSA scheme has potential application prospects in high-capacity quantum communication.

1 Introduction

Entangled photon system is an important quantum resource in quantum information protocol, and it has important applications in quantum communication (Sidhu et al., 2021), such as quantum dense coding (Bennett and Wiesner, 1992; Liu et al., 2002), quantum teleportation (Bennett et al., 1993; Graham et al., 2015; Yang et al., 2020), quantum secret sharing (Hillery et al., 1999; Karlsson et al., 1999; Xiao et al., 2004; Luo et al., 2019; Gu et al., 2021), quantum key distribution (Bennett et al., 1992; Shang et al., 2020; Chai et al., 2020; Xu et al., 2020; Pittaluga et al., 2021; Chen et al., 2021; Liu H et al., 2021; Liu W.-B et al., 2021; Woodward et al., 2021; Kwek et al., 2021; Wang et al., 2022; Xie et al., 2022), quantum secure direct communication (Long and Liu, 2002; Deng et al., 2003; Deng and Long, 2004; Zhang et al., 2017; Zhou et al., 2020; Zhang et al., 2022), quantum digital signatures (Lu et al., 2021) and so on. In the quantum communication protocols, the entangled state analysis is a crucial step to read out quantum information. Using only linear optical elements, the success rate of Bell state analysis (BSA) is 50% in theory and experiment (Mattle et al., 1996; Lütkenhaus et al., 1999; Vaidman and Yoran, 1999; Calsamiglia, 2002; Ursin et al., 2004; Van Houwelingen et al., 2006). If nonlinear optical elements are introduced in BSA, the success rate of BSA can be increased to 100% (Lin et al., 2009; Bonato et al., 2010).

Photon system has multiple DOFs, such as polarization, momentum (spatial), temporal, frequency and so on. The entanglement can be existed in multiple DOFs of photon system simultaneously, which is called hyperentanglement (Kwiat and Weinfurter, 1998), and the hyperentangled photon states have been prepared in many types, such as polarization-frequency hyperentanglement (Yabushita and Kobayashi, 2004), polarization-temporal hyperentanglement (Schuck et al., 2006), polarization-momentum hyperentanglement (Barbieri et al., 2005; Barbieri et al., 2007; Vallone et al., 2009), polarization-momentum-temporal hyperentanglement (Barreiro et al., 2005) and polarization-orbital-angular-momentum hyperentanglement (Barreiro et al., 2008). Hyperentanglment has important applications in quantum error-correcting (Wilde and Uskov, 2009; Li et al., 2016), quantum cryptography (Bruss and Macchiavello, 2002; Cerf et al., 2002), quantum repeater (Wang et al., 2012), entanglement purification (Simon and Pan, 2002; Li, 2010; Sheng and Deng, 2010a; 2010b), and BSA (Walborn et al., 2003; Schuck et al., 2006; Barbieri et al., 2007; Williams et al., 2017), where entanglement in the additional DOF is used as auxiliary.

Hyperentanglement can be used to enhance the channel capacity of quantum communication, such as hyperdense coding (Barreiro et al., 2008), quantum hyperteleportation (Sheng et al., 2010; Wang X.-L. et al., 2015), hyperentanglement swapping (Sheng et al., 2010; Ren et al., 2012), hyperentanglement purification (Ren et al., 2014; Wang T.-J. et al., 2015; Wang et al., 2016b), and hyperentanglement concentration (Ren et al., 2013; Li and Ghose, 2015). In the high-capacity quantum communication, HBSA is crucial step to read out the quantum information (Cui et al., 2019; Zou et al., 2020). Using only linear optical elements, the 16 polarization-momentum hyperentangled Bell states can be divided to seven groups (Wei et al., 2007), and the differentiable groups can be increased by using entangled states of additional DOFs as auxiliary (Li and Ghose, 2017). Especially, the 16 polarization-momentum hyperentangled Bell states can be completely distinguished via linear optics, assisted by time bin and an auxiliary fixed Bell state of another momentum DOF (Gao et al., 2019).

The success rate of HBSA can also be increased by using nonlinear optical elements. In 2010, Sheng et al. (2010) gave the first scheme for the complete HBSA with the help of cross-Kerr nonlinearity, which can completely distinguish the 16 polarization-spatial hyperentangled Bell states. Subsequently, the complete HBSA schemes have been investigated using one-sided quantum-dot-cavity system (Ren et al., 2012) and double-sided quantum-dot-cavity system (Wang et al., 2016a). In 2016, the self-assisted complete HBSA scheme has been presented using cross-Kerr nonlinearity, which can reduce the nonlinear optical resource used in complete HBSA (Li and Ghose, 2016). Recently, the HBSA for six-qubit three DOFs of photon system has attracted much attention, and the nondestructive HBSA scheme (Liu et al., 2016) for polarization-double longitudinal momentum DOFs and deterministic HBSA schemes for polarization-spatial-time-bin DOFs have been proposed with cross-Kerr nonlinearity (Wang et al., 2018; Zhang et al., 2021).

In this article, we propose a self-assisted deterministic HBSA scheme for polarization-double longitudinal momentum DOFs of photon system. First, we construct a nondestructive first longitudinal momentum Bell state analyzer to completely distinguish the four first longitudinal momentum Bell states without destructing the hyperentangled Bell state. Then we use the self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer to completely distinguish the 16 second longitudinal momentum-polarization hyperentangled Bell states, where the first longitudinal momentum Bell state and time-bin entangled state are used as auxiliary. In this scheme, only the nondestructive first longitudinal momentum Bell state analyzer is constructed with cross-Kerr nonlinearity medium, and the self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer is constructed with linear optical elements, which has largely reduced the application of nonlinear optical resource in HBSA scheme. With these amazing results, this self-assisted deterministic HBSA scheme has potential application prospects in high-capacity quantum communication.

2 Self-assisted deterministic hyperentangled-Bell-state analysis

In this section, we will introduce the self-assisted deterministic HBSA for polarization and double longitudinal momentum DOFs of photon system, assisted by cross-Kerr nonlinearity medium and time-bin DOF. The hyperentangled Bell state can be described as

$|\mathrm{\Psi }\left(t\right){\rangle }_{AB}=|{\phi }_F\rangle \otimes |{\phi }_S\rangle \otimes |{\phi }_P\rangle \otimes |\phi \left(t\right)\rangle .(1)$

|φ_F⟩ represents one of four first longitudinal momentum Bell states, which are described as

$|{{\varphi }_F^{\pm }\rangle }_{AB}=\frac{1}{\sqrt{2}}{\left(|rr\rangle \pm |ll\rangle \right)}_{AB},|{{\psi }_F^{\pm }\rangle }_{AB}=\frac{1}{\sqrt{2}}{\left(|rl\rangle \pm |lr\rangle \right)}_{AB}.(2)$

|φ_S⟩ represents one of 4 second longitudinal momentum Bell states, which are described as

$|{{\varphi }_S\rangle }_{AB}^{\pm }=\frac{1}{\sqrt{2}}{\left(|EE\rangle \pm |II\rangle \right)}_{AB},|{{\psi }_S\rangle }_{AB}^{\pm }=\frac{1}{\sqrt{2}}{\left(|EI\rangle \pm |IE\rangle \right)}_{AB}.(3)$

|φ_P⟩ represents one of four polarization Bell states, which are described as

$|{{\varphi }_P\rangle }_{AB}^{\pm }=\frac{1}{\sqrt{2}}{\left(|HH\rangle \pm |VV\rangle \right)}_{AB},|{{\psi }_P\rangle }_{AB}^{\pm }=\frac{1}{\sqrt{2}}{\left(|HV\rangle \pm |VH\rangle \right)}_{AB}.(4)$

Here the subscripts A and B denote the two hyperentangled photons. The subscripts F, S and p denote the first longitudinal momentum DOF, second longitudinal momentum DOF, and polarization DOF. r and l represent the right and left modes of the first longitudinal momentum DOF $\vec{c}$. E and I denote the external and internal modes of the second longitudinal momentum DOF $\vec{k}$. The Bell states of the first longitudinal momentum DOF $\vec{c}$ and the second longitudinal momentum DOF $\vec{k}$ have been generated in experiment by using a two-crystal system constituted of two type I β barium borate BBO crystal slabs, where the two crystal slabs are aligned one behind the other (Vallone et al., 2009). H and V represent the horizontal and the vertical polarizations of photon. |φ(t)⟩ represents the entangled state of time-bin qudits of infinite dimension, where t is the time since photon pair creation and ${\int }_{-\infty }^{+\infty }⟨\phi (t)|\phi (t)⟩=1$ (Williams et al., 2017). The 64 polarization-double longitudinal momentum hyperentangled Bell states are determinately discriminated with two steps. The first step is implemented by nondestructive first longitudinal momentum Bell state analyzer, and the second step is implemented by self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer.

2.1 Nondestructive first longitudinal momentum Bell state analyzer

The nondestructive first longitudinal momentum Bell state analyzer consists of two quantum nondemolition detectors (QNDs), which are constructed by cross-Kerr nonlinearity medium. The Hamiltonian of a cross-Kerr nonlinearity interaction is $H=\hslash \chi a_s^{†}{a}_s{a}_p^{†}{a}_p$, where $a_s^{†}$ $(a_p^{†})$ and a_s (a_p) represent the creation and annihilation operators of the signal (probe) state. ℏχ is the coupling strength of the cross-Kerr nonlinearity, and it is related to the material. If the signal state interacts with the probe state in the medium, the probe state will obtain a phase shift. For example, if the signal state is |ψ⟩_s = a|0⟩_s + b|1⟩_s and the probe state is the coherent state |α⟩_p, the effect of cross-Kerr nonlinearity can be expressed as

$U|\psi {\rangle }_s|\alpha {\rangle }_p=e^{\mathit{iHt∕\hslash }}\left(a|0{\rangle }_s+b|1{\rangle }_s\right)|\alpha {\rangle }_p=a|0{\rangle }_s|\alpha {\rangle }_p+b|1{\rangle }_s|\alpha e^{i\theta }{\rangle }_p.(5)$

where 0 and 1 represent the photon number of signal state and θ = ℏχt.

The first QND (QND₁) is constructed by four cross-Kerr nonlinearity mediums. After the signal state (hyperentangled state of photons AB) interacts with the probe state (coherent state) in cross-Kerr nonlinearity mediums as shown in Figure 1, the signal state and probe state will be evolved as

$\begin{array}{l}\hfill \begin{array}{cc}\hfill |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\varphi }_F^{\pm }\rangle |{\alpha }_1\rangle & \to \frac{1}{\sqrt{2}}|{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle \left(|l{\rangle }_A|l{\rangle }_B\pm |r{\rangle }_A|r{\rangle }_B\right)|{\alpha }_1\rangle ,\hfill \\ \hfill |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\psi }_F^{\pm }\rangle |{\alpha }_1\rangle & \to \frac{1}{\sqrt{2}}|{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle \left(|l{\rangle }_A|r{\rangle }_B|{\alpha }_1{e}^{-i\beta }\rangle \pm |r{\rangle }_A|l{\rangle }_B|{\alpha }_1{e}^{i\beta }\rangle \right).\hfill \end{array}\end{array}(6)$

FIGURE 1

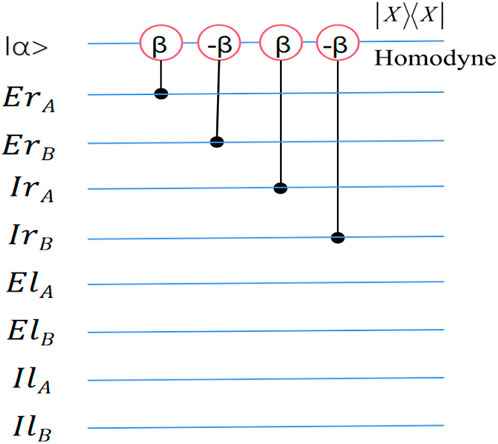
FIGURE 1. The circuit diagram of QND₁ in nondestructive first longitudinal momentum Bell state analyzer. When a photon passes through cross-Kerr nonlinearity medium, the coherent state will obtain a phase shift + β or − β. Homodyne measurement is used to distinguish the different phase shifts of coherent state.

Then the probe state (coherent state) is measured using the X-quadrature measurement, where phase shifts differing in sign “±” can’t be distinguished in X-quadrature measurement. If the coherent state has no phase shift, the first longitudinal momentum DOF of two-photon system is in one of the even parity states $|{\varphi }_F^{\pm }\rangle$. If the coherent state has a phase shift + β (−β), the first longitudinal momentum DOF of two-photon system is in one of the odd parity states $|{\psi }_F^{\pm }\rangle$. Therefore, the even parity states $|{\varphi }_F^{\pm }\rangle$ and odd parity states $|{\psi }_F^{\pm }\rangle$ of the first longitudinal momentum DOF can be divided into two groups with QND₁.

Subsequently, the two photons pass through the 50:50 beam splitters (BSs) as shown in Figure 2, which have the evolutions as

$\begin{array}{l}\hfill \begin{array}{c}|{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\varphi }_F^{+}\rangle \to |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\varphi }_F^{+}\rangle ,\hfill \\ |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\varphi }_F^{-}\rangle \to |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\psi }_F^{+}\rangle ,\\ |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\psi }_F^{+}\rangle \to |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\varphi }_F^{-}\rangle ,\hfill \\ |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\psi }_F^{-}\rangle \to |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\psi }_F^{-}\rangle .\end{array}\end{array}(7)$

FIGURE 2

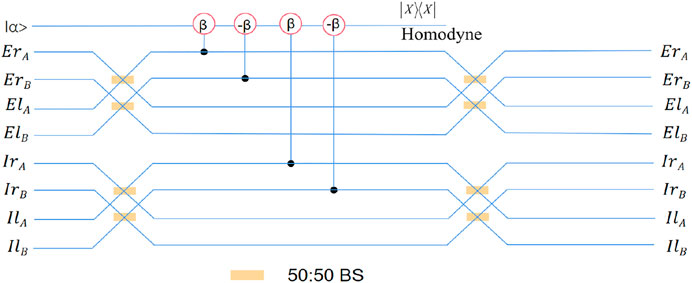
FIGURE 2. The circuit diagram of the rest part of nondestructive first longitudinal momentum Bell state analyzer, which consists of QND₂ and 50:50 BSs. BS (beam splitter) acts a Hadamard operation on first longitudinal momentum DOF.

Then the two photons pass through the second QND (QND₂), which has the same construction as QND₁, and the signal state and probe state will be evolved as

$\begin{array}{l}\hfill \begin{array}{cc}\hfill & |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\varphi }_F^{\pm }\rangle |{\alpha }_2\rangle \to \frac{1}{\sqrt{2}}|{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle \left(|l{\rangle }_A|l{\rangle }_B\pm |r{\rangle }_A|r{\rangle }_B\right)|{\alpha }_2\rangle ,\hfill \\ \hfill & |{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle |{\psi }_F^{\pm }\rangle |{\alpha }_2\rangle \to \frac{1}{\sqrt{2}}|{\phi }_P\rangle |{\phi }_S\rangle |\phi \left(t\right)\rangle \left(|l{\rangle }_A|r{\rangle }_B|{\alpha }_2{e}^{-i\beta }\rangle \pm |r{\rangle }_A|l{\rangle }_B|{\alpha }_2{e}^{i\beta }\rangle \right).\hfill \end{array}\end{array}(8)$

The probe state (coherent state) of QND₂ is measured using the X-quadrature measurement. If the coherent state has no phase shift, the first longitudinal momentum DOF of two-photon system is in one of the even parity states $|{\varphi }_F^{\pm }\rangle$ (the original states are $|{\varphi }_F^{+}\rangle$ and $|{\psi }_F^{+}\rangle$). If the coherent state has a phase shift + β (−β), the first longitudinal momentum DOF of two-photon system is in one of the odd parity states $|{\psi }_F^{\pm }\rangle$ (the original states are $|{\varphi }_F^{-}\rangle$ and $|{\psi }_F^{-}\rangle$). Now, we can see that the four first longitudinal momentum Bell states can be completely distinguished by QND₁ and QND₂ (shown in Table 1). The 50:50 BSs after QND₂ are used to recover the first longitudinal momentum states to the original one.

TABLE 1

TABLE 1. The relationship between four first longitudinal momentum Bell states and the measurement results of QND₁ and QND₂.

2.2 Self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer

In the self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer, the 16 second longitudinal momentum-polarization hyperentangled Bell states can be completely distinguished using linear optics, where the first longitudinal momentum Bell state and time-bin entangled state are used as auxiliary. As there are four first longitudinal momentum Bell states, which have been distinguished by the nondestructive first longitudinal momentum Bell state analyzer, we use the auxiliary first longitudinal momentum Bell state |ϕ⁻⟩_F as an example to illustrate the auxiliary function of first longitudinal momentum Bell state.

The initial state of self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer can be expressed as

$|Z\left(t\right){\rangle }_{AB}=|{\varphi }^{-}{\rangle }_F\otimes |{\phi }_S\rangle \otimes |{\phi }_P\rangle \otimes |\phi \left(t\right)\rangle .(9)$

where |φ_S⟩⊗|φ_P⟩ represents one of 16 second longitudinal momentum-polarization hyperentangled Bell states. The quantum circuit of self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer is shown in Figure 3 and Figure 4. Here we take the hyperentangled state $|Z(t){\rangle }_{AB}^0$ as an example to describe the procedure of self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer in detail, where

$|Z{\left(t\right)\rangle }_{AB}^0=\frac{1}{2\sqrt{2}}\left(|HV\rangle +|VH\rangle \right)\otimes \left(|II\rangle +|EE\rangle \right)\otimes \left(|ll\rangle -|rr\rangle \right)\otimes |\phi \left(t\right)\rangle .(10)$

FIGURE 3

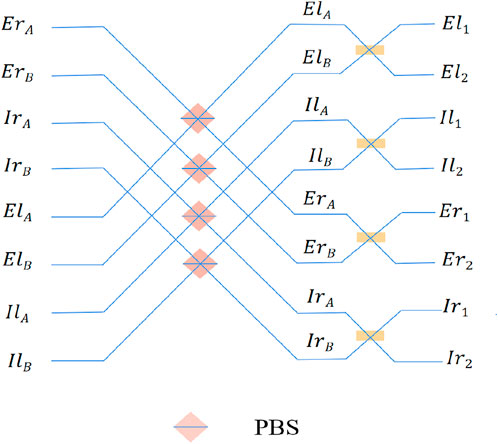
FIGURE 3. The circuit diagram of the first part of self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer. PBS represents a polarizing beam splitter, which transmits horizontal polarization state |H⟩ and reflects vertical polarization state |V⟩.

FIGURE 4

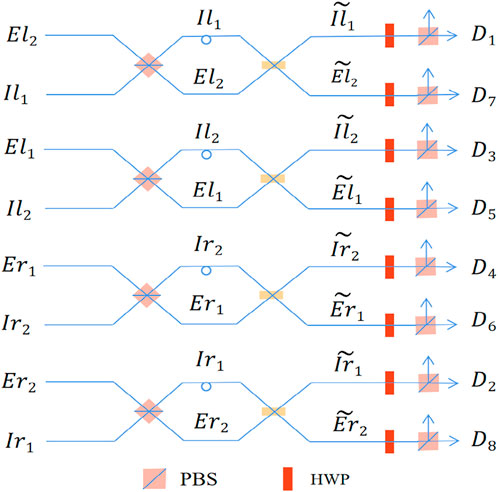
FIGURE 4. The circuit diagram of the second part of self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer. HWP represents a half-wave plate, which can perform the Hadamard operation on the polarization DOF of a photon. The optical loop on the path denotes an optical time delay Δt.

First, the two photons A and B pass through PBSs (polarzing beam splitter) and BSs shown in Figure 3. The function of PBS is transmitting horizontal polarization state |H⟩ and reflecting vertical polarization state |V⟩, where the spatial mode of photon is changed (invariant) for the reflecting (transmitting) case. The functions of PBSs are expressed as

$X_{Hr}^{†}\to X_{Hr}^{†},X_{Vr}^{†}\to X_{Vl}^{†},X_{Hl}^{†}\to X_{Hl}^{†},X_{Vl}^{†}\to X_{Vr}^{†},(11)$

where X represents one of symbols E_A, E_B, I_A and I_B. The functions of 50:50 BSs in Figure 3 are expressed as

$\begin{array}{l}\hfill \begin{array}{cc}\hfill Y_{AH}^{†}\to \frac{1}{\sqrt{2}}\left(Y_{1H}^{†}+Y_{2H}^{†}\right),& Y_{AV}^{†}\to \frac{1}{\sqrt{2}}\left(Y_{1V}^{†}+Y_{2V}^{†}\right),\hfill \\ \hfill Y_{BH}^{†}\to \frac{1}{\sqrt{2}}\left(Y_{1H}^{†}-Y_{2H}^{†}\right),& Y_{BV}^{†}\to \frac{1}{\sqrt{2}}\left(Y_{1V}^{†}-Y_{2V}^{†}\right),\hfill \end{array}\end{array}(12)$

where Y represents one of the symbols Il, Ir, El and Er. After the two photons pass through PBSs and BSs, the hyperentangled state $|Z(t){\rangle }_{AB}^0$ is transferred to

$\begin{array}{ll}\hfill |Z\left(t\right){\rangle }_{AB}^1& =\frac{1}{2\sqrt{2}}\left(I{l}_{1H}^{†}I{r}_{1V}^{†}-I{l}_{2H}^{†}I{r}_{2V}^{†}+E{l}_{1H}^{†}E{r}_{1V}^{†}-E{l}_{2H}^{†}E{r}_{2V}^{†}-I{r}_{1H}^{†}I{l}_{1V}^{†}+I{r}_{2H}^{†}I{l}_{2V}^{†}-E{r}_{1H}^{†}E{l}_{1V}^{†}+E{r}_{2H}^{†}E{l}_{2V}^{†}\right)\hfill \\ \hfill & |0\rangle \otimes |\phi \left(t\right)\rangle .\hfill \end{array}(13)$

Subsequently, the two photons pass through PBSs and BSs shown in Figure 4, where the time delay Δt is introduced between the PBSs and BSs. The functions of PBSs in Figure 4 are expressed as

$\begin{array}{l}\hfill \begin{array}{cc}\hfill & W_{\mathit{HE1}}^{†}\to W_{\mathit{HE1}}^{†},W_{\mathit{V\; E1}}^{†}\to W_{\mathit{V\; I2}}^{†},W_{\mathit{HI1}}^{†}\to W_{\mathit{HI1}}^{†},W_{\mathit{V\; I1}}^{†}\to W_{\mathit{V\; E2}}^{†},\hfill \\ \hfill & W_{\mathit{HE2}}^{†}\to W_{\mathit{HE2}}^{†},W_{\mathit{V\; E2}}^{†}\to W_{\mathit{V\; I1}}^{†},W_{\mathit{HI2}}^{†}\to W_{\mathit{HI2}}^{†},W_{\mathit{V\; I2}}^{†}\to W_{\mathit{V\; E1}}^{†},\hfill \end{array}\end{array}(14)$

where W represents one of symbols l and r. The functions of 50:50 BSs in Figure 4 are expressed as

$\begin{array}{l}\hfill \begin{array}{cc}\hfill I_1^{†}\to \frac{1}{\sqrt{2}}\left({{\tilde{I}}_1}^{†}+{\tilde{E}}_2^{†}\right),& I_2^{†}\to \frac{1}{\sqrt{2}}\left({{\tilde{I}}_2}^{†}+{\tilde{E}}_1^{†}\right),\hfill \\ \hfill E_1^{†}\to \frac{1}{\sqrt{2}}\left({{\tilde{I}}_2}^{†}-{{\tilde{E}}_1}^{†}\right),& E_2^{†}\to \frac{1}{\sqrt{2}}\left({{\tilde{I}}_1}^{†}-{{\tilde{E}}_2}^{†}\right),\hfill \end{array}\end{array}(15)$

where the symbols of first longitudinal momentum DOF are ignored for simplicity. After the two photons pass through PBSs and BSs, the hyperentangled state $|Z(t){\rangle }_{AB}^1$ is transferred to

$\begin{array}{ll}\hfill |Z{\left(t\right)\rangle }_{AB}^2& =\frac{1}{4\sqrt{2}}\left(+{\widetilde{Il}}_{1H^{\prime }}^{†}{\widetilde{Ir}}_{1V}^{†}+{\widetilde{El}}_{2H^{\prime }}^{†}{\widetilde{Ir}}_{1V}^{†}-{\widetilde{Il}}_{1H^{\prime }}^{†}{\widetilde{Er}}_{2V}^{†}-{\widetilde{El}}_{2H^{\prime }}^{†}{\widetilde{Er}}_{2V}^{†}-{\widetilde{Il}}_{2H^{\prime }}^{†}{\widetilde{Ir}}_{2V}^{†}+{\widetilde{El}}_{1H^{\prime }}^{†}{\widetilde{Ir}}_{2V}^{†}\right.\hfill \\ \hfill & -{\widetilde{Il}}_{2H^{\prime }}^{†}{\widetilde{Er}}_{1V}^{†}-{\widetilde{El}}_{1H^{\prime }}^{†}{\widetilde{Er}}_{1V}^{†}+{\widetilde{Il}}_{2H}^{†}{\widetilde{Ir}}_{2V^{\prime }}^{†}+{\widetilde{El}}_{1H}^{†}{\widetilde{Ir}}_{2V^{\prime }}^{†}-{\widetilde{Il}}_{2H}^{†}{\widetilde{Er}}_{1V^{\prime }}^{†}-{\widetilde{El}}_{1H}^{†}{\widetilde{Er}}_{1V^{\prime }}^{†}\hfill \\ \hfill & -{\widetilde{Il}}_{1H}^{†}{\widetilde{Ir}}_{1V^{\prime }}^{†}+{\widetilde{El}}_{2H}^{†}{\widetilde{Ir}}_{1V^{\prime }}^{†}-{\widetilde{Il}}_{1H}^{†}{\widetilde{Er}}_{2V^{\prime }}^{†}-{\widetilde{El}}_{2H}^{†}{\widetilde{Er}}_{2V^{\prime }}^{†}-{\widetilde{Ir}}_{1H^{\prime }}^{†}{\widetilde{Il}}_{1V}^{†}+{\widetilde{Er}}_{2H^{\prime }}^{†}{\widetilde{Il}}_{1V}^{†}\hfill \\ \hfill & -{\widetilde{Ir}}_{1H^{\prime }}^{†}{\widetilde{El}}_{2V}^{†}-{\widetilde{Er}}_{2H^{\prime }}^{†}{\widetilde{El}}_{2V}^{†}+{\widetilde{Ir}}_{2H^{\prime }}^{†}{\widetilde{Il}}_{2V}^{†}+{\widetilde{Er}}_{1H^{\prime }}^{†}{\widetilde{Il}}_{2V}^{†}-{\widetilde{Ir}}_{2H^{\prime }}^{†}{\widetilde{El}}_{1V}^{†}-{\widetilde{Er}}_{1H^{\prime }}^{†}{\widetilde{El}}_{1V}^{†}\hfill \\ \hfill & -{\widetilde{Ir}}_{2H}^{†}{\widetilde{Il}}_{2V^{\prime }}^{†}+{\widetilde{Er}}_{1H}^{†}{\widetilde{Il}}_{2V^{\prime }}^{†}-{\widetilde{Ir}}_{2H}^{†}{\widetilde{El}}_{1V^{\prime }}^{†}-{\widetilde{Er}}_{1H}^{†}{\widetilde{El}}_{1V^{\prime }}^{†}+{\widetilde{Ir}}_{1H}^{†}{\widetilde{Il}}_{1V^{\prime }}^{†}\hfill \\ \hfill & +\left.{\widetilde{Er}}_{2H}^{†}{\widetilde{Il}}_{1V^{\prime }}^{†}-{\widetilde{Ir}}_{1H}^{†}{\widetilde{El}}_{2V^{\prime }}^{†}-{\widetilde{Er}}_{2H}^{†}{\widetilde{El}}_{2V^{\prime }}^{†}\right)|0\rangle .\hfill \end{array}(16)$

Here H′ (V′) represents the component that experiences a time delay Δt.

At last, the two photons pass through HWPs as shown in Figure 4, whose function are $|H\rangle \to \frac{1}{\sqrt{2}}(|H\rangle +|V\rangle )$ and $|V\rangle \to \frac{1}{\sqrt{2}}(|H\rangle -|V\rangle )$. After passing through the HWPs, the state of two photons becomes:

$\begin{array}{ll}\hfill |Z{\left(t\right)\rangle }_{AB}^3& =\frac{1}{4}\left({\widetilde{Il}}_{1H^{\prime }}^{†}{\widetilde{Ir}}_{1H}^{†}-{\widetilde{Il}}_{1V^{\prime }}^{†}{\widetilde{Ir}}_{1V}^{†}+{\widetilde{El}}_{2H^{\prime }}^{†}{\widetilde{Ir}}_{1H}^{†}-{\widetilde{El}}_{2V^{\prime }}^{†}{\widetilde{Er}}_{1V}^{†}\right.\hfill \\ \hfill & -{\widetilde{Il}}_{1H^{\prime }}^{†}{\widetilde{Er}}_{2H}^{†}+{\widetilde{Il}}_{1V^{\prime }}^{†}{\widetilde{Er}}_{2V}^{†}-{\widetilde{El}}_{2H^{\prime }}^{†}{\widetilde{Er}}_{2H}^{†}+{\widetilde{El}}_{2V^{\prime }}^{†}{\widetilde{Er}}_{2V}^{†}\hfill \\ \hfill & -{\widetilde{Il}}_{2H^{\prime }}^{†}{\widetilde{Ir}}_{2H}^{†}+{\widetilde{Il}}_{2V^{\prime }}^{†}{\widetilde{Ir}}_{2V}^{†}+{\widetilde{El}}_{1H^{\prime }}^{†}{\widetilde{Ir}}_{2H}^{†}+{\widetilde{El}}_{1V^{\prime }}^{†}{\widetilde{Ir}}_{2H}^{†}\hfill \\ \hfill & \left.+{\widetilde{Il}}_{2H^{\prime }}^{†}{\widetilde{Er}}_{1H}^{†}-{\widetilde{Il}}_{2V^{\prime }}^{†}{\widetilde{Er}}_{1V}^{†}+{\widetilde{El}}_{1H^{\prime }}^{†}{\widetilde{Er}}_{1H}^{†}+{\widetilde{El}}_{1V^{\prime }}^{†}{\widetilde{Er}}_{1V}^{†}\right)|0\rangle .\hfill \end{array}(17)$

Then the two photons pass through PBSs and they are detected at the output ports. The detection result is one of the 16 conditions $D_1^{\pm }{D}_2^{\pm }$, $D_2^{\pm }{D}_7^{\pm }$, $D_1^{\pm }{D}_8^{\pm }$, $D_7^{\pm }{D}_8^{\pm }$, $D_3^{\pm }{D}_4^{\pm }$, $D_4^{\pm }{D}_5^{\pm }$, $D_3^{\pm }{D}_6^{\pm }$ and $D_5^{\pm }{D}_6^{\pm }$, and the two detectors are triggered with a time interval Δt. Here, the superscript “+” represents that detector is in the H port of PBS, and the superscript “-” represents that the detector is in the V port of PBS.

The other 15 second longitudinal momentum-polarization hyperentangled Bell states also can be distinguished by the quantum circuits shown in Figures 3, 4 using the first longitudinal momentum Bell state |ϕ⁻⟩_F as auxiliary. The detection results of 16 second longitudinal momentum-polarization hyperentangled Bell states assisted by the first longitudinal momentum Bell state |ϕ⁻⟩_F are shown in Table 2. If the first longitudinal momentum DOF of two-photon system is in one of other three Bell states, the 16 second longitudinal momentum-polarization hyperentangled Bell states also can be distinguished by the quantum circuits shown in Figure 3 and Figure 4 using the first longitudinal momentum Bell state as auxiliary. The detection results of 16 s longitudinal momentum-polarization hyperentangled Bell states assisted by the other three first longitudinal momentum Bell states are shown in Tables 3–5. Now, it is obvious that the 64 polarization-double longitudinal momentum hyperentangled Bell states are determinately discriminated with the two steps shown in Figures 1–4.

TABLE 2

TABLE 2. The relationship of the 16 second longitudinal momentum-polarization hyperentangled Bell states, the detection results and the time interval of two triggered photon detectors. The auxiliary first longitudinal momentum Bell state is |ϕ⁻⟩_F.

TABLE 3

TABLE 3. The relationship of the 16 second longitudinal momentum-polarization hyperentangled Bell states, the detection results and the time interval of two triggered photon detectors. The auxiliary first longitudinal momentum Bell state is |ϕ⁺⟩_F.

TABLE 4

TABLE 4. The relationship of the 16 second longitudinal momentum-polarization hyperentangled Bell states, the detection results and the time interval of two triggered photon detectors. The auxiliary first longitudinal momentum Bell state is |ψ⁺⟩_F.

TABLE 5

TABLE 5. The relationship of the 16 second longitudinal momentum-polarization hyperentangled Bell states, the detection results and the time interval of two triggered photon detectors. The auxiliary first longitudinal momentum Bell state is |ψ⁻⟩_F.

3 Discussion and summary

We have presented a self-assisted deterministic HBSA protocol for 64 two-photon hyperentangled Bell states in polarization and double longitudinal momentum DOFs. The self-assisted deterministic HBSA protocol is implemented with two steps. In the first step, the nondestructive first longitudinal momentum Bell-state analyzer is constructed for distinguishing the four first longitudinal momentum Bell states nondestructively, which consists of two QNDs using cross-Kerr nonlinearity medium. In the second step, the self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer is constructed for distinguishing 16 second longitudinal momentum-polarization hyperentangled Bell states using linear optics, where the first longitudinal momentum Bell state and time-bin entangled state are used as auxiliary. With the detection results of QNDs and photon detectors, the 64 two-photon hyperentangled Bell states can be determinately read out as shown in Tables 1–5.

The cross-Kerr nonlinear medium is important for distinguishing the four Bell states of first longitudinal momentum DOF, which needs to distinguish the phase shift ± β of the coherent state from the phase shift 0, so the phase shift generated by the interaction between photons and coherent light directly affects the efficiency of nondestructive first longitudinal momentum Bell-state analyzer. In the past few years, great progresses have been made in the Kerr nonlinearity. In 2011, He et al. (2011) showed that the effects due to the transverse DOFs significantly affect the cross-phase modulation process, which made the single-photon-coherent-state interaction easier to be realized. But the inclusion of loss (nonunitary dynamics), noninstantaneous interactions (and the associated noise), and the effect of the forces due to the interaction on the motion of the pulses affect the interaction of photons with coherent light. In the work proposed by Hoi et al. (2013), the average cross-Kerr phase shift was demonstrated up to 20° per photon with both coherent microwave fields at the single-photon level. In this work, to achieve quantum nondemolition requires a higher signal-to-noise (SNR) ratio (e.g., SNR ≥0.6 under very general assumptions), while the SNR measured in experiment is only 0.38. Vinu and Roy, (2020) explored cross-Kerr nolinearity by a three-level emitter (3LE) embedded in a waveguide and driven by two light beams, where the values of the cross-Kerr phase shift for a ladder system with both the probe and drive fields at the single-photon level are similar to the experimentally observed value of approximately 10°. This interaction is weak as the resulting phase shift needs to be amplified in the measurement process. At present, the phase shift generated by the interaction between photons and coherent light in cross-Kerr medium is small and unstable in actual operation, and it is difficult to generate a corresponding phase shift every time, which is hard to achieve the requirement of QND. As QND constructed by cross-Kerr nonlinear medium is the essential device of BSA for first longitudinal momentum DOF, the efficiency of BSA for first longitudinal momentum DOF will be reduced by the weak interaction of photons and coherent light in cross-Kerr medium. Therefore, the strong interaction of photons and coherent light in cross-Kerr medium could improve the efficiency of BSA for first longitudinal momentum DOF.

In the self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer, the time intervals 0 and Δt have divided the 16 hyperentangled Bell states into two groups, which is an important procedure for completely distinguishing 16 hyperentangled Bell states. The time delay Δt in Figure 4 is caused by the different lengths of the two spatial modes between the PBSs and BSs, which is longer than the resolution time of the photon detector in the nanometer scale. Moreover, time delay Δt needs to satisfy “ωΔt = 2mπ” (m is an integer) to ensure the constructive interference or destructive interference, i.e. the components of photons in the same polarization and longitudinal momentum modes with a time delay Δt can be interfering constructively or destructively, such as

$\begin{array}{l}\hfill \begin{array}{cc}\hfill {Il}_{2H^{\prime }}^{†}{\widetilde{Ir}}_{2V^{\prime }}^{†}+{Il}_{2H}^{†}{\widetilde{Ir}}_{2V}^{†}& =2{Il}_{2H}^{†}{\widetilde{Ir}}_{2V}^{†},\hfill \\ \hfill {Il}_{2H^{\prime }}^{†}{\widetilde{Ir}}_{2V^{\prime }}^{†}-{Il}_{2H}^{†}{\widetilde{Ir}}_{2V}^{†}& =0.\hfill \end{array}\end{array}(18)$

Williams et al. (Williams et al., 2017) have experimentally demonstrated the time delay Δt = 5 ns (Δt = 10 ns) by setting the fiber lengths of the short and long arms of the interferometer to 1 and 2 m (2 and 4 m), and the resolution time of photon detector in their experiment is 4 ns.

In summary, we have presented a self-assisted deterministic HBSA protocol for photon systems entangled in polarization and double longitudinal momentum DOFs. The four first longitudinal momentum Bell states are distinguished by the nondestructive first longitudinal momentum Bell-state analyzer with cross-Kerr nonlinearity medium, and the 16 second longitudinal momentum-polarization hyperentangled Bell states are distinguished by the self-assisted second longitudinal momentum-polarization hyperentangled Bell state analyzer with the first longitudinal momentum Bell state and time-bin entangled state as auxiliary. By using self-assisted method, the application of cross-Kerr nonlinearity resource has been largely reduced in HBSA scheme for three DOFs of photon system, which makes this self-assisted deterministic HBSA scheme has potential application prospects in high-capacity quantum communication.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

BR contributed to conception and design of the study. CY and ZZ performed the statistical analysis. CY and JQ organized the figures and tables. CY wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China under Grant No. 11604226, and the Program of Beijing Municipal Commission of Education of China under Grant No. CIT&TCD201904080.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frqst.2022.985130/full#supplementary-material

References

Barbieri, M., Cinelli, C., Mataloni, P., and De Martini, F. (2005). Polarization-momentum hyperentangled states: Realization and characterization. Phys. Rev. A . Coll. Park. 72, 052110. doi:10.1103/physreva.72.052110

CrossRef Full Text | Google Scholar

Barbieri, M., Vallone, G., Mataloni, P., and De Martini, F. (2007). Complete and deterministic discrimination of polarization bell states assisted by momentum entanglement. Phys. Rev. A . Coll. Park. 75, 042317. doi:10.1103/physreva.75.042317

CrossRef Full Text | Google Scholar

Barreiro, J. T., Langford, N. K., Peters, N. A., and Kwiat, P. G. (2005). Generation of hyperentangled photon pairs. Phys. Rev. Lett. 95, 260501. doi:10.1103/physrevlett.95.260501

PubMed Abstract | CrossRef Full Text | Google Scholar

Barreiro, J. T., Wei, T.-C., and Kwiat, P. G. (2008). Beating the channel capacity limit for linear photonic superdense coding. Nat. Phys. 4, 282–286. doi:10.1038/nphys919

CrossRef Full Text | Google Scholar

Bennett, C. H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., and Wootters, W. K. (1993). Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels. Phys. Rev. Lett. 70, 1895–1899. doi:10.1103/physrevlett.70.1895

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, C. H., Brassard, G., and Mermin, N. D. (1992). Quantum cryptography without bell’s theorem. Phys. Rev. Lett. 68, 557–559. doi:10.1103/physrevlett.68.557

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, C. H., and Wiesner, S. J. (1992). Communication via one-and two-particle operators on einstein-podolsky-rosen states. Phys. Rev. Lett. 69, 2881–2884. doi:10.1103/physrevlett.69.2881

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonato, C., Haupt, F., Oemrawsingh, S. S., Gudat, J., Ding, D., van Exter, M. P., et al. (2010). Cnot and bell-state analysis in the weak-coupling cavity qed regime. Phys. Rev. Lett. 104, 160503. doi:10.1103/physrevlett.104.160503

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruss, D., and Macchiavello, C. (2002). Optimal eavesdropping in cryptography with three-dimensional quantum states. Phys. Rev. Lett. 88, 127901. doi:10.1103/physrevlett.88.127901

PubMed Abstract | CrossRef Full Text | Google Scholar

Calsamiglia, J. (2002). Generalized measurements by linear elements. Phys. Rev. A. Coll. Park. 65, 030301. doi:10.1103/physreva.65.030301

CrossRef Full Text | Google Scholar

Cerf, N. J., Bourennane, M., Karlsson, A., and Gisin, N. (2002). Security of quantum key distribution usingd-level systems. Phys. Rev. Lett. 88, 127902. doi:10.1103/physrevlett.88.127902

PubMed Abstract | CrossRef Full Text | Google Scholar

Chai, G., Li, D., Cao, Z., Zhang, M., Huang, P., and Zeng, G. (2020). Blind channel estimation for continuous-variable quantum key distribution. Quantum Eng. 2, e37. doi:10.1002/que2.46

CrossRef Full Text | Google Scholar

Chen, J.-P., Zhang, C., Liu, Y., Jiang, C., Zhang, W.-J., Han, Z.-Y., et al. (2021). Twin-field quantum key distribution over a 511 km optical fibre linking two distant metropolitan areas. Nat. Photonics 15, 570–575. doi:10.1038/s41566-021-00828-5

CrossRef Full Text | Google Scholar

Cui, Z.-X., Zhong, W., Zhou, L., and Sheng, Y.-B. (2019). Measurement-device-independent quantum key distribution with hyper-encoding. Sci. China Phys. Mech. Astron. 62, 1–10. doi:10.1007/s11433-019-1438-6

CrossRef Full Text | Google Scholar

Deng, F.-G., Long, G. L., and Liu, X.-S. (2003). Two-step quantum direct communication protocol using the einstein-podolsky-rosen pair block. Phys. Rev. A . Coll. Park. 68, 042317. doi:10.1103/physreva.68.042317

CrossRef Full Text | Google Scholar

Deng, F.-G., and Long, G. L. (2004). Secure direct communication with a quantum one-time pad. Phys. Rev. A . Coll. Park. 69, 052319. doi:10.1103/physreva.69.052319

CrossRef Full Text | Google Scholar

Gao, C.-Y., Ren, B.-C., Zhang, Y.-X., Ai, Q., and Deng, F.-G. (2019). The linear optical unambiguous discrimination of hyperentangled bell states assisted by time bin. Ann. Phys. 531, 1900201. doi:10.1002/andp.201900201

CrossRef Full Text | Google Scholar

Graham, T., Zeitler, C., Bernstein, H., Javadi, H., and Kwiat, P. G. (2015). “Towards space-to-ground superdense teleportation,” in Frontiers in Optics 2015, OSA Technical Digest (Optica Publishing Group). doi:10.1364/FIO.2015.FTh2D.3

CrossRef Full Text | Google Scholar

Gu, J., Cao, X.-Y., Yin, H.-L., and Chen, Z.-B. (2021). Differential phase shift quantum secret sharing using a twin field. Opt. Express 29, 9165–9173. doi:10.1364/oe.417856

PubMed Abstract | CrossRef Full Text | Google Scholar

He, B., Lin, Q., and Simon, C. (2011). Cross-kerr nonlinearity between continuous-mode coherent states and single photons. Phys. Rev. A . Coll. Park. 83, 053826. doi:10.1103/physreva.83.053826

CrossRef Full Text | Google Scholar

Hillery, M., Bužek, V., and Berthiaume, A. (1999). Quantum secret sharing. Phys. Rev. A . Coll. Park. 59, 1829–1834. doi:10.1103/physreva.59.1829

CrossRef Full Text | Google Scholar

Hoi, I.-C., Kockum, A. F., Palomaki, T., Stace, T. M., Fan, B., Tornberg, L., et al. (2013). Giant cross–kerr effect for propagating microwaves induced by an artificial atom. Phys. Rev. Lett. 111, 053601. doi:10.1103/physrevlett.111.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

Karlsson, A., Koashi, M., and Imoto, N. (1999). Quantum entanglement for secret sharing and secret splitting. Phys. Rev. A . Coll. Park. 59, 162–168. doi:10.1103/physreva.59.162

CrossRef Full Text | Google Scholar

Kwek, L.-C., Cao, L., Luo, W., Wang, Y., Sun, S., Wang, X., et al. (2021). Chip-based quantum key distribution. AAPPS Bull. 31, 15–18. doi:10.1007/s43673-021-00017-0

CrossRef Full Text | Google Scholar

Kwiat, P. G., and Weinfurter, H. (1998). Embedded bell-state analysis. Phys. Rev. A . Coll. Park. 58, R2623–R2626. doi:10.1103/physreva.58.r2623

CrossRef Full Text | Google Scholar

Li, T., Wang, G.-Y., Deng, F.-G., and Long, G.-L. (2016). Deterministic error correction for nonlocal spatial-polarization hyperentanglement. Sci. Rep. 6, 20677–20678. doi:10.1038/srep20677

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X.-H. (2010). Deterministic polarization-entanglement purification using spatial entanglement. Phys. Rev. A . Coll. Park. 82, 044304. doi:10.1103/physreva.82.044304

CrossRef Full Text | Google Scholar

Li, X.-H., and Ghose, S. (2017). Hyperentangled bell-state analysis and hyperdense coding assisted by auxiliary entanglement. Phys. Rev. A . Coll. Park. 96, 020303. doi:10.1103/physreva.96.020303

CrossRef Full Text | Google Scholar

Li, X.-H., and Ghose, S. (2015). Hyperentanglement concentration for time-bin and polarization hyperentangled photons. Phys. Rev. A . Coll. Park. 91, 062302. doi:10.1103/physreva.91.062302

CrossRef Full Text | Google Scholar

Li, X.-H., and Ghose, S. (2016). Self-assisted complete maximally hyperentangled state analysis via the cross-kerr nonlinearity. Phys. Rev. A . Coll. Park. 93, 022302. doi:10.1103/physreva.93.022302

CrossRef Full Text | Google Scholar

Lin, X.-M., Chen, Z.-H., Lin, G.-W., Chen, X.-D., and Ni, B.-B. (2009). Optical bell state and greenberger–horne–zeilinger-state analyzers through the cavity input–output process. Opt. Commun. 282, 3371–3374. doi:10.1016/j.optcom.2009.04.065

CrossRef Full Text | Google Scholar

Liu, H., Jiang, C., Zhu, H.-T., Zou, M., Yu, Z.-W., Hu, X.-L., et al. (2021). Field test of twin-field quantum key distribution through sending-or-not-sending over 428 km. Phys. Rev. Lett. 126, 250502. doi:10.1103/physrevlett.126.250502

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W.-B., Li, C.-L., Xie, Y.-M., Weng, C.-X., Gu, J., Cao, X.-Y., et al. (2021). Homodyne detection quadrature phase shift keying continuous-variable quantum key distribution with high excess noise tolerance. PRX Quantum 2, 040334. doi:10.1103/prxquantum.2.040334

CrossRef Full Text | Google Scholar

Liu, Q., Wang, G.-Y., Ai, Q., Zhang, M., and Deng, F.-G. (2016). Complete nondestructive analysis of two-photon six-qubit hyperentangled bell states assisted by cross-kerr nonlinearity. Sci. Rep. 6, 22016–22110. doi:10.1038/srep22016

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X. S., Long, G. L., Tong, D. M., and Li, F. (2002). General scheme for superdense coding between multiparties. Phys. Rev. A . Coll. Park. 65, 022304. doi:10.1103/physreva.65.022304

CrossRef Full Text | Google Scholar

Long, G.-L., and Liu, X.-S. (2002). Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. A . Coll. Park. 65, 032302. doi:10.1103/physreva.65.032302

CrossRef Full Text | Google Scholar

Lu, Y.-S., Cao, X.-Y., Weng, C.-X., Gu, J., Xie, Y.-M., Zhou, M.-G., et al. (2021). Efficient quantum digital signatures without symmetrization step. Opt. Express 29, 10162–10171. doi:10.1364/oe.420667

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, G.-F., Zhou, R.-G., and Hu, W.-W. (2019). Novel quantum secret image-sharing scheme. Chin. Phys. B 28, 040302. doi:10.1088/1674-1056/28/4/040302

CrossRef Full Text | Google Scholar

Lütkenhaus, N., Calsamiglia, J., and Suominen, K.-A. (1999). Bell measurements for teleportation. Phys. Rev. A . Coll. Park. 59, 3295–3300. doi:10.1103/physreva.59.3295

CrossRef Full Text | Google Scholar

Mattle, K., Weinfurter, H., Kwiat, P. G., and Zeilinger, A. (1996). Dense coding in experimental quantum communication. Phys. Rev. Lett. 76, 4656–4659. doi:10.1103/physrevlett.76.4656

PubMed Abstract | CrossRef Full Text | Google Scholar

Pittaluga, M., Minder, M., Lucamarini, M., Sanzaro, M., Woodward, R. I., Li, M.-J., et al. (2021). 600-km repeater-like quantum communications with dual-band stabilization. Nat. Photonics 15, 530–535. doi:10.1038/s41566-021-00811-0

CrossRef Full Text | Google Scholar

Ren, B.-C., Du, F.-F., and Deng, F.-G. (2013). Hyperentanglement concentration for two-photon four-qubit systems with linear optics. Phys. Rev. A . Coll. Park. 88, 012302. doi:10.1103/physreva.88.012302

CrossRef Full Text | Google Scholar

Ren, B.-C., Du, F.-F., and Deng, F.-G. (2014). Two-step hyperentanglement purification with the quantum-state-joining method. Phys. Rev. A . Coll. Park. 90, 052309. doi:10.1103/physreva.90.052309

CrossRef Full Text | Google Scholar

Ren, B.-C., Wei, H.-R., Hua, M., Li, T., and Deng, F.-G. (2012). Complete hyperentangled-bell-state analysis for photon systems assisted by quantum-dot spins in optical microcavities. Opt. Express 20, 24664–24677. doi:10.1364/oe.20.024664

PubMed Abstract | CrossRef Full Text | Google Scholar

Schuck, C., Huber, G., Kurtsiefer, C., and Weinfurter, H. (2006). Complete deterministic linear optics bell state analysis. Phys. Rev. Lett. 96, 190501. doi:10.1103/physrevlett.96.190501

PubMed Abstract | CrossRef Full Text | Google Scholar

Shang, T., Tang, Y., Chen, R., and Liu, J. (2020). Full quantum one-way function for quantum cryptography. Quantum Eng. 2, e32. doi:10.1002/que2.33

CrossRef Full Text | Google Scholar

Sheng, Y.-B., and Deng, F.-G. (2010a). One-step deterministic polarization-entanglement purification using spatial entanglement. Phys. Rev. A . Coll. Park. 82, 044305. doi:10.1103/physreva.82.044305

CrossRef Full Text | Google Scholar

Sheng, Y.-B., and Deng, F.-B. (2010b). Deterministic entanglement purification and complete nonlocal bell-state analysis with hyperentanglement. Phys. Rev. A . Coll. Park. 81, 032307. doi:10.1103/physreva.81.032307

CrossRef Full Text | Google Scholar

Sheng, Y.-B., Deng, F.-G., and Long, G. L. (2010). Complete hyperentangled-bell-state analysis for quantum communication. Phys. Rev. A . Coll. Park. 82, 032318. doi:10.1103/physreva.82.032318

CrossRef Full Text | Google Scholar

Sidhu, J. S., Joshi, S. K., Gündoğan, M., Brougham, T., Lowndes, D., Mazzarella, L., et al. (2021). Advances in space quantum communications. IET Quantum Commun. 2, 182–217. doi:10.1049/qtc2.12015

CrossRef Full Text | Google Scholar

Simon, C., and Pan, J.-W. (2002). Polarization entanglement purification using spatial entanglement. Phys. Rev. Lett. 89, 257901. doi:10.1103/physrevlett.89.257901

PubMed Abstract | CrossRef Full Text | Google Scholar

Ursin, R., Jennewein, T., Aspelmeyer, M., Kaltenbaek, R., Lindenthal, M., Walther, P., et al. (2004). Quantum teleportation across the danube. Nature 430, 849. doi:10.1038/430849a

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaidman, L., and Yoran, N. (1999). Methods for reliable teleportation. Phys. Rev. A . Coll. Park. 59, 116–125. doi:10.1103/physreva.59.116

CrossRef Full Text | Google Scholar

Vallone, G., Ceccarelli, R., De Martini, F., and Mataloni, P. (2009). Hyperentanglement of two photons in three degrees of freedom. Phys. Rev. A . Coll. Park. 79, 030301. doi:10.1103/physreva.79.030301

CrossRef Full Text | Google Scholar

Van Houwelingen, J., Brunner, N., Beveratos, A., Zbinden, H., and Gisin, N. (2006). Quantum teleportation with a three-bell-state analyzer. Phys. Rev. Lett. 96, 130502. doi:10.1103/physrevlett.96.130502

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinu, A., and Roy, D. (2020). Amplification and cross-kerr nonlinearity in waveguide quantum electrodynamics. Phys. Rev. A . Coll. Park. 101, 053812. doi:10.1103/physreva.101.053812

CrossRef Full Text | Google Scholar

Walborn, S., Pádua, S., and Monken, C. (2003). Hyperentanglement-assisted bell-state analysis. Phys. Rev. A . Coll. Park. 68, 042313. doi:10.1103/physreva.68.042313

CrossRef Full Text | Google Scholar

Wang, G.-Y., Ai, Q., Ren, B.-C., Li, T., and Deng, F.-G. (2016a). Error-detected generation and complete analysis of hyperentangled bell states for photons assisted by quantum-dot spins in double-sided optical microcavities. Opt. Express 24, 28444–28458. doi:10.1364/oe.24.028444

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, G.-Y., Liu, Q., and Deng, F.-G. (2016b). Hyperentanglement purification for two-photon six-qubit quantum systems. Phys. Rev. A . Coll. Park. 94, 032319. doi:10.1103/physreva.94.032319

CrossRef Full Text | Google Scholar

Wang, M., Yan, F., and Gao, T. (2018). Deterministic state analysis for polarization-spatial-time-bin hyperentanglement with nonlinear optics. Laser Phys. Lett. 15, 125206. doi:10.1088/1612-202x/aaea73

CrossRef Full Text | Google Scholar

Wang, S., Yin, Z.-Q., He, D.-Y., Chen, W., Wang, R.-Q., Ye, P., et al. (2022). Twin-field quantum key distribution over 830-km fibre. Nat. Photonics 16, 154–161. doi:10.1038/s41566-021-00928-2

CrossRef Full Text | Google Scholar

Wang, T.-J., Liu, L.-L., Zhang, R., Cao, C., and Wang, C. (2015). One-step hyperentanglement purification and hyperdistillation with linear optics. Opt. Express 23, 9284–9294. doi:10.1364/oe.23.009284

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X.-L., Cai, X.-D., Su, Z.-E., Chen, M.-C., Wu, D., Li, L., et al. (2015). Quantum teleportation of multiple degrees of freedom of a single photon. Nature 518, 516–519. doi:10.1038/nature14246

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, T.-J., Song, S.-Y., and Long, G. L. (2012). Quantum repeater based on spatial entanglement of photons and quantum-dot spins in optical microcavities. Phys. Rev. A . Coll. Park. 85, 062311. doi:10.1103/physreva.85.062311

CrossRef Full Text | Google Scholar

Wei, T.-C., Barreiro, J. T., and Kwiat, P. G. (2007). Hyperentangled bell-state analysis. Phys. Rev. A . Coll. Park. 75, 060305. doi:10.1103/physreva.75.060305

CrossRef Full Text | Google Scholar

Wilde, M. M., and Uskov, D. B. (2009). Linear-optical hyperentanglement-assisted quantum error-correcting code. Phys. Rev. A 79, 022305. doi:10.1103/physreva.79.022305

CrossRef Full Text | Google Scholar

Williams, B. P., Sadlier, R. J., and Humble, T. S. (2017). Superdense coding over optical fiber links with complete bell-state measurements. Phys. Rev. Lett. 118, 050501. doi:10.1103/physrevlett.118.050501

PubMed Abstract | CrossRef Full Text | Google Scholar

Woodward, R. I., Lo, Y., Pittaluga, M., Minder, M., Paraïso, T., Lucamarini, M., et al. (2021). Gigahertz measurement-device-independent quantum key distribution using directly modulated lasers. npj Quantum Inf. 7, 58–66. doi:10.1038/s41534-021-00394-2

CrossRef Full Text | Google Scholar

Xiao, L., Long, G. L., Deng, F.-G., and Pan, J.-W. (2004). Efficient multiparty quantum-secret-sharing schemes. Phys. Rev. A . Coll. Park. 69, 052307. doi:10.1103/physreva.69.052307

CrossRef Full Text | Google Scholar

Xie, Y.-M., Lu, Y.-S., Weng, C.-X., Cao, X.-Y., Jia, Z.-Y., Bao, Y., et al. (2022). Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference. PRX Quantum 3, 020315. doi:10.1103/prxquantum.3.020315

CrossRef Full Text | Google Scholar

Xu, F., Ma, X., Zhang, Q., Lo, H.-K., and Pan, J.-W. (2020). Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 92, 025002. doi:10.1103/revmodphys.92.025002

CrossRef Full Text | Google Scholar

Yabushita, A., and Kobayashi, T. (2004). Spectroscopy by frequency-entangled photon pairs. Phys. Rev. A . Coll. Park. 69, 013806. doi:10.1103/physreva.69.013806

CrossRef Full Text | Google Scholar

Yang, L., Liu, Y.-C., and Li, Y.-S. (2020). Quantum teleportation of particles in an environment. Chin. Phys. B 29, 060301. doi:10.1088/1674-1056/ab84de

CrossRef Full Text | Google Scholar

Zhang, H.-R., Wang, P., Yu, C.-Q., and Ren, B.-C. (2021). Deterministic nondestructive state analysis for polarization-spatial-time-bin hyperentanglement with cross-kerr nonlinearity. Chin. Phys. B 30, 030304. doi:10.1088/1674-1056/abd7d5

CrossRef Full Text | Google Scholar

Zhang, H., Sun, Z., Qi, R., Yin, L., Long, G.-L., and Lu, J. (2022). Realization of quantum secure direct communication over 100 km fiber with time-bin and phase quantum states. Light. Sci. Appl. 11, 83–89. doi:10.1038/s41377-022-00769-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, W., Ding, D.-S., Sheng, Y.-B., Zhou, L., Shi, B.-S., and Guo, G.-C. (2017). Quantum secure direct communication with quantum memory. Phys. Rev. Lett. 64, 220501. doi:10.1103/physrevlett.118.220501

CrossRef Full Text | Google Scholar

Zhou, Z., Sheng, Y., Niu, P., Yin, L., Long, G., and Hanzo, L. (2020). Measurement-device-independent quantum secure direct communication. Sci. China Phys. Mech. Astron. 63, 230362–230366. doi:10.1007/s11433-019-1450-8

CrossRef Full Text | Google Scholar

Zou, Z.-K., Zhou, L., Zhong, W., and Sheng, Y.-B. (2020). Measurement-device–independent quantum secure direct communication of multiple degrees of freedom of a single photon. EPL Europhys. Lett. 131, 40005–40010. doi:10.1209/0295-5075/131/40005

CrossRef Full Text | Google Scholar