Is olive crop modelling ready to assess the impacts of global change?

Olive trees, alongside grapevines, dominate the Mediterranean tree crop landscape. However, as climate change intensifies, the Mediterranean region, which encompasses 95% of the global olive cultivation area, faces significant challenges. Rising carbon dioxide (CO₂) levels, increasing temperatures, and declining precipitation pose substantial threats to olive tree performance. Photosynthesis, respiration, phenology, water use and ultimately yield are possibly the main factors affected. To address this future scenario, it is crucial to develop adaptation and mitigation strategies. Nevertheless, breeding programs and field management practice testing for tree crops are time-consuming endeavors. Fortunately, models can accelerate the evaluation of tailored solutions. In this review, we critically examine the current state of olive tree modeling and highlight key areas requiring improvement. Given the expected impact of climate change, prioritizing research on phenology, particularly regarding bloom and pollination, is essential. Simulations of biomass should incorporate approaches that account for the interactive effects of CO₂ and temperature on photosynthesis and respiration. Furthermore, accurately simulating the influence of water stress on yield necessitates the development of models that integrate canopy behavior with root performance under conditions of water scarcity. By addressing these critical aspects, olive tree models can enhance our understanding of climate change impacts and inform sustainable agricultural practices.

1 Introduction

The cultivation of olive (Olea europaea L.) trees started somewhere in the eastern Mediterranean area long before the Greek and Roman civilizations, at around 4000 BC (Kostelenos and Kiritsakis, 2017). As an appreciated source of food and oil, olive trees then spread over centuries around southern Europe and northern Africa. Only recently, olive growing has been introduced to other areas of the world, but more than 95% of the 10 Mha covered by olive orchards is still concentrated in Mediterranean basin countries (FAOSTAT, 2023). Historically a low input crop grown on rolling landscapes with shallow soils, olive trees withstand the harsh drought-prone conditions prevailing in most olive growing regions. The capacity of olive cropping systems to grow and yield even under these unfavorable conditions is related both to several physiological traits of this species and to appropriate management schemes (Connor, 2005), and it has been key for the wide expansion of the crop in regions with a Mediterranean climate.

Traditional techniques of olive production, established by trial and error in the absence of thorough scientific understanding, have persisted for centuries. Since water deficit is the main factor limiting yield expression, critical aspects of management target the control of tree transpiration and non-consumptive water losses. As a result, traditional rainfed olive orchards exhibit low planting densities (usually below 160 trees ha^-1) and small canopy size, with soil management oriented to minimizing water use by the understory through tillage, mowing, grazing or herbicides. New, more productive, olive cropping systems have appeared in the last decades due to the introduction of irrigation and technological innovations. They are characterized by narrower tree spacings (even >1500 trees ha^-1 for hedgerow orchards) and higher use of inputs (water, fertilizers, pesticides), being suitable for mechanical pruning and harvesting in many cases.

Olive has special features that make it especially hard to analyze in terms of response to climate change and adaptation. First, most olive orchards concentrate around the Mediterranean basin, where changes in rainfall and temperature are expected to be more dramatic than in other areas (Simolo et al., 2014; IPCC, 2021). Forecasts for the worst scenarios show an increase in average temperatures from 2 to 5 °C and precipitations reduced by 10-30% by the end of the century in many Mediterranean olive growing areas. Second, being a perennial tree there are aspects of its physiology that may require new models (e.g. use of reserves, mortality). Gaps in knowledge are wider in trees in general and in olives in particular due to limited research funding. In addition to that, the time scale is much longer than in annual crops, breeding programs are slower, and management decisions take years to have an effect and have to consider the expected conditions of the next 10 to 20 years.

In this review, we want to analyze if available modelling tools are adequate for evaluating the effect of global change on olive production. Models must be suitable for this task if they are to be applied to address questions related to climate change adaptation and/or mitigation. We will deal only with dynamic crop models which should include at least the simulation of phenology, growth and yield. Published models targeting the simulation of specific processes are also considered when they are mechanistic and present the potential to be used as components of full olive orchard models. This implies that empirical models are excluded from the review, even if they have been more common (e.g. Moriondo et al., 2015). We have structured the review in two main parts, the first related to the processes taken into account for the simulation of olive performance, i.e. the submodels, and the second to complete crop models of olive orchards. Both topics are preceded by a short introductory section on the most relevant uses of crop simulation models.

2 Utility of crop models for olive growing

2.1 Yield forecast

Forecasts of crop production provide independent and timely information to support policy making regarding agricultural markets. Crop models have frequently been the central elements of yield forecasting systems (e.g. Van der Velde et al., 2019). Indeed, the development of crop models started for meeting the demand for yield forecasts for the US as a strategic tool (Jones et al., 2017). Although crop models have been refined and improved in robustness over time, their direct application in yield forecasting is still limited by the lack of data and limitations of models (Basso and Liu, 2019). This has led to the application of alternative, empirical models, with wide adoption of deep learning techniques (Van Klompenburg et al., 2020), which are outside the scope of this review and are probably not efficient for the task (Morales and Villalobos, 2023).

2.2 Plant breeding programs

Crop models have been a great asset for understanding genotype-environment interactions and for designing ideotypes in silico for annual species. For instance, Agüera et al. (1997) used the OilcropSun model (Villalobos et al., 1996) to show the gains in sunflower yield associated with high early vigor genotypes. This use of crop models should be more powerful for perennials as breeding programs are slower and experiments more costly. In olives, the juvenile period, i.e. the time from germination to first flower, is typically 3 years or more (e.g. Hammami et al., 2021) which slows down the selection process. On the other hand, the productivity of new olive genotypes should be evaluated at least until maximum productivity is achieved, which takes 6-7 years in modern superintensive orchards and much longer in other orchard types (León et al., 2007). Therefore, experimental evaluation of new cultivars is time consuming and requires large dedicated plots to ensure homogeneous conditions. Crop models may incorporate parameters that can be measured rapidly in single plants, which makes the whole process much faster and cheaper than a purely experimental approach.

2.3 Hydrology

As olive orchards are important components of agroecosystems around the Mediterranean they have attracted attention in terms of hydrology and management to control soil erosion (Vanwalleghem et al., 2011). These problems occur at rather long-time scales so we need to resort to models. Furthermore, models are required also for calculating irrigation requirements in olive orchards (Testi et al., 2006). Water balance models of olive orchards have been proposed with different approaches, from very simple to quite complex. For instance, Abazi et al. (2013) used crop coefficients to calculate olive transpiration, while Garcia-Tejera et al. (2017) developed a full-fledged model based on the Soil-Plant-Atmosphere-Continuum (SPAC). The limitations of the crop coefficient approach have been shown for fruit trees in general by Villalobos et al. (2013), including its expected change as atmospheric CO₂ concentrations increase.

2.4 Carbon balance and mitigation capacity of olive orchards

Society is encouraging farmers to reduce CO₂ emissions associated with crop production. For instance, the green objectives in the new Common Agricultural Policy of the European Union will drive important changes in olive growing, like the adoption of protective cover crops during winter. On the other hand, carbon credit markets are emerging as a new opportunity for income for farmers in exchange for capturing C (Northrup et al., 2021). If we consider the soil, C capture is a slow process so soil organic matter changes may take many years before they can be detected (Fowler et al., 2023). Because of the possibility of performing simulations of decades or centuries, some models represent an invaluable asset to evaluate long-temporal trends in soil C stocks for specific environmental conditions and cropping systems (Mairech et al., 2020). Accumulation of C in standing trees may be quite variable as it depends among other factors on water and nutrient availability (Nardino et al., 2013). Therefore, carbon capture cannot be quantified solely by measurements but requires models that integrate all aspects of the carbon balance (tree photosynthesis and respiration, heterotrophic respiration, understory (if any) photosynthesis and respiration) in response to environmental (radiation, temperature, water availability) and management (pruning, tillage) factors (López-Bernal et al., 2023).

2.5 Impacts of global change

Fruit tree plantations are long-term projects designed to last more than 15-20 years. Therefore, expected environmental changes will have an effect on the overall performance of the plantation. The analysis of the expected effects of global change on crop production has been mostly devoted to annuals (White et al., 2011). For fruit trees and vines, the analyses of productivity under climate change have been mostly qualitative (e.g. Keller, 2010). Most attention has been directed at phenological development as warming may threaten the accumulation of enough chilling during winter (De Melo-Abreu et al., 2004), while only a few studies have quantified changes in olive productivity (Mairech et al., 2021; López-Bernal et al., 2023). In addition, physiologically based demographic modelling (PBDM) approaches have been used for evaluating how yield losses due to the olive fruit fly pest may change under climate change scenarios for different regions (e.g. Gutierrez et al., 2009; Ponti et al., 2014).

3 Olive models and submodels

3.1 Phenological development

Predicting phase development of olive trees has emerged in the last 20 years as an important topic for researchers due to its potential to address many practical questions related to the thermal adaptation of this species under new environments or future climate scenarios. So far, most studies on olive phenology have focused on the timing of flowering while other stages of the reproductive and vegetative cycle have barely received attention.

Olive blossoms in late spring in Mediterranean regions. Inflorescence formation requires low temperatures, their initiation taking place at the end of winter on 1-year axillary buds upon exposure to chilling for a long enough period (Haberman et al., 2017). Incomplete chilling delays the release of floral bud dormancy and reduces inflorescence and fruit production (Engelen et al., 2023), and it can result in asynchronous bud break and flowering (Medina-Alonso et al., 2020) or even suppress the production of reproductive structures under very warm environments (Hartmann, 1953). After dormancy release, warm temperatures contribute to accelerating development (Ramos et al., 2018; Di Paola et al., 2021).

The mathematical description of flowering time in olive has often capitalized on existing models of spring phenology developed for temperate trees. Purely thermal time models are based on heat accumulation after a fixed date, and they provide the simplest alternative for predicting flowering time. Model accuracy can be quite high for local conditions if thermal time requirements are properly calibrated (e.g. Model 3 in De Melo-Abreu et al., 2004). On the contrary, in fixing the date at which thermal time summation starts (e.g. February 1^st in the Northern hemisphere) some empiricism is introduced, as it is implicitly independent of the time at which dormancy is actually released. This issue may not be a big deal in regions with cold winters, where average temperatures are close to or lower than the base temperature, so heat accumulation is negligible until late winter. Nevertheless, it makes this type of model inappropriate for warm locations and climate change studies.

Sequential models offer a more comprehensive simulation of the processes leading to flowering, which are divided into two stages. The first accounts for dormancy release as a function of chilling accumulation. After enough chilling has been accumulated (i.e. ‘chilling requirement’), the forcing phase starts, which simulates the developmental rate as a function of heat accumulation. A number of sequential models have been developed and/or calibrated for olive orchards in the last decades (Table 1), each one characterized by a particular combination of approaches for computing chill and heat accumulation. Inspired by the Utah model used in other temperate species (Richardson et al., 1974), piecewise approximations are typically applied for estimating the increment of chilling as a function of hourly or daily temperature (e.g. De Melo-Abreu et al., 2004). Reversal of chilling due to high temperatures may be considered as well. On the other hand, heat accumulation may be simulated from the difference between mean daily temperature and base temperature or use more complex, sometimes non-linear, temperature response functions at the hourly scale (e.g. Marra et al., 2018).

TABLE 1

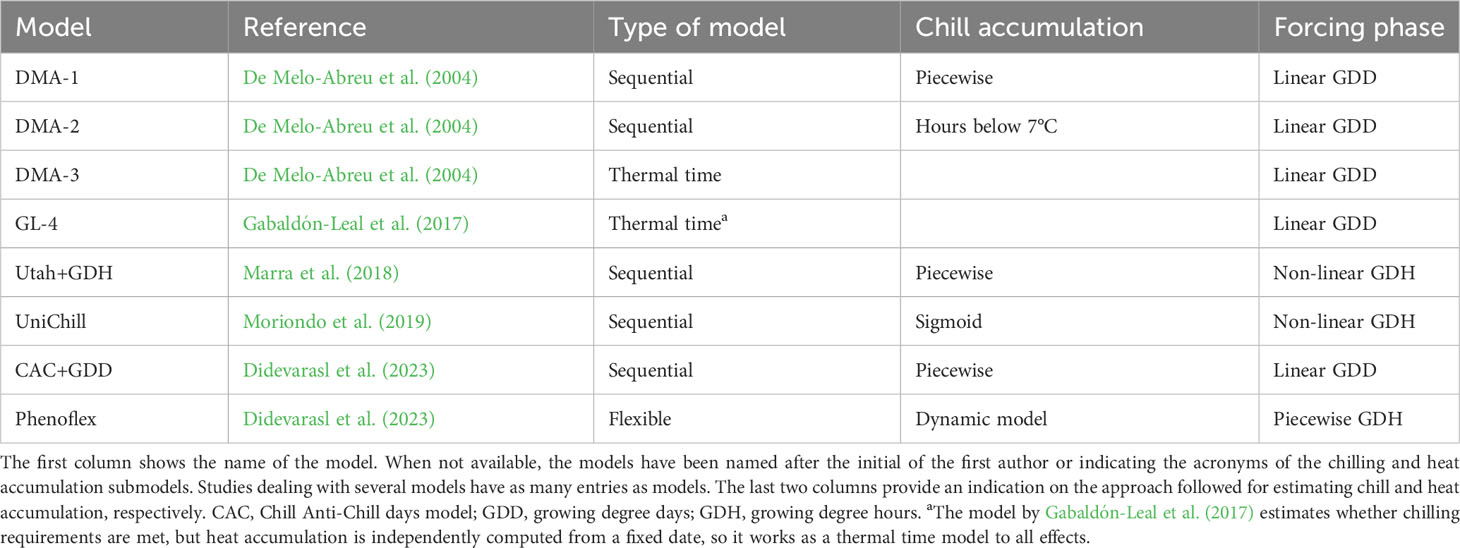
Table 1 Types of spring phenology models specifically developed or calibrated for predicting full flowering in olive trees.

The main problem with sequential models is related to the lack of empirical records delineating chilling requirements for olive trees. Indeed, values for different cultivars have been estimated by fitting model parameters against flowering date records (De Melo-Abreu et al., 2004). To some extent, this is undesirable because chilling and heat requirements are calibrated together, which challenges their accurate determination. Besides, the flowering response to chilling is not a Boolean function, so flowering may proceed following a rather warm winter even if chilling accumulation is not enough to meet the estimated requirements. This seems to be the case in warm olive growing areas (e.g. Medina-Alonso et al., 2020). This phenomenon also casts doubt on how well existing chilling sub-models mimic tree responses to temperature during dormancy.

Parallel and alternating models are more complex process-based models accounting for possible compensation between chill and heat accumulation, which implies that some chill beyond the minimum requirement reduces the amount of heat necessary for flowering, as observed for some temperate trees (Pope et al., 2014). Both modelling frameworks present a large number of parameters so extensive calibration datasets are required to avoid overfitting. To the best of our knowledge, neither parallel nor alternating models have been tested for olive so far, but a recent study (Didevarasl et al., 2023) has used a modelling framework with a flexible overlap of chill and heat accumulation. The so call Phenoflex model (Luedeling et al., 2021) couples the dynamic model for chill accumulation (Fishman et al., 1987a; Fishman et al., 1987b) with a sigmoidal growing degree hour sub-model (Anderson et al., 1986) and it includes 12 parameters. However, the higher complexity of Phenoflex does not necessarily translate into a substantial improvement in the prediction of flowering time with respect to sequential models (Didevarasl et al., 2023).

The simulation of other events of the reproductive cycle has received less attention. Sequential models are appropriate for predicting bud break dates (Cesaraccio et al., 2004), although Phenoflex has also been used (Didevarasl et al., 2023). Fruit development seems to be affected by exogenous (environmental conditions) and endogenous (crop load) factors (Beltrán et al., 2017). Thermal time approaches have led to satisfactory results in some cases (Trentacoste et al., 2012; Didevarasl et al., 2023), but they are often unable to match the length of fruit developmental phases (Di Paola et al., 2021).

With regard to vegetative development, trees stop growing in late fall and growth is resumed whenever favorable temperature conditions return in early spring. As this winter rest stage seems to be controlled by temperature, López-Bernal et al. (2020a) proposed two simple chilling accumulation models for estimating the date of the onset of vegetative dormancy. Vegetative bud break has been simulated by simple empirical rules so far. For instance, OliveCan, a full model of the development, growth and yield of olive orchards (López-Bernal et al., 2018), counts the days with a mean temperature above a threshold after the winter solstice and sets the end of the rest period after a certain number have been reached. Likewise, Moriondo et al. (2019) used a thermal time approach for the task, with heat accumulation starting on a fixed date (January 1^st).

3.2 Water balance

The different components of the water balance of olive orchards have drawn the attention of numerous researchers, who have developed specific submodels. Evaporation from the soil surface below the trees may be evaluated using the equation of Bonachela et al. (1999), who also proposed a method for including evaporation from wet bulbs under drip irrigation (Bonachela et al., 2001). Models of olive transpiration have followed different approaches, from the simple use of a transpiration coefficient (Orgaz et al., 2006) to the coupling of conductance, photosynthesis and water potential (Garcia-Tejera et al., 2017; see 3.3.4). Villalobos et al. (2013) proposed a simple mechanistic-based equation for the calculation of transpiration of fruit trees and calibrated it for olive and other fruit species.

Rainfall interception in olive canopies was modeled by Gómez et al. (2001). Additional studies of infiltration in olive orchards led to a method for determining the curve number of olive orchards (Romero et al., 2007) which is used for calculating surface runoff with the Soil Conservation Service method (Boughton, 1989).

Direct evaporation from wet olive trees may be calculated using the Penman-Monteith equation for zero canopy resistance until all intercepted rainfall is evaporated (López-Bernal et al., 2018). The required aerodynamic resistance is deduced from the model proposed by Raupach (1994). The transpiration of the cover crop below olive orchards may be calculated as a function of intercepted radiation (López-Bernal et al., 2023) following the general procedure of Ceres models (Garrison et al., 1999).

3.3 Biomass accumulation and partitioning

3.3.1 Simple models

Crop growth may be simulated using a photosynthesis model (see 3.3.2) or following a simple model based on resource use. Monteith (1977) showed that the biomass accumulation (ΔB) of crops is linearly related to intercepted radiation. Therefore, for a period of duration t:

$\begin{array}{ll}\Delta B=\text{RUE} {\sum }_1^t{f}_{\text{i}} R_{\text{spi}} & (1)\end{array}$

Where RUE is the Radiation-Use Efficiency (g dry matter (MJ PAR)^-1), R_spi is incoming Photosynthetically-Active Radiation (PAR, MJ m^-2) and f_i is the fraction of PAR intercepted on day ‘i’. Mariscal et al. (2000a) were the first to measure the RUE of olive trees and Mariscal et al. (2000b) proposed a model of radiation interception for olive canopies which is currently used in OliveCan.

Alternatively, some crop models like Cropsyst (Stöckle et al., 2003) have adopted water use as the basis for estimating biomass accumulation. The idea was originally developed by Tanner and Sinclair (1983), who showed that the Water-Use Efficiency (WUE), the amount of dry matter produced per unit of water transpired, is inversely proportional to Vapor Pressure Deficit (VPD). This idea has been applied to quantifying tree photosynthesis in olive orchards (López-Bernal et al., 2015a) as a function of transpiration. However, because of the response of photosynthesis to internal CO₂ (see 3.3.3), WUE will increase in proportion to stomatal resistance (Brodribb, 1996). This problem is common to both WUE and RUE simple approaches.

3.3.2 Photosynthesis and respiration

Early models of crop photosynthesis used empirical relationships between leaf CO₂ uptake and irradiance which could be integrated for the whole canopy (De Wit, 1965). This approach was incorporated into the olive model of Abdel-Razik (1989). Mechanistic models of photosynthesis arrived much later with the work of Farquhar et al. (1980), who provided equations for predicting the effects of temperature, radiation and internal CO₂ concentration on leaf photosynthesis. The parameters of this model were measured for olive by Diaz-Espejo et al. (2006) and later included in OliveCan and the model of Morales et al. (2016).

Scaling up of leaf to tree photosynthesis requires a distribution of radiation among leaves in the canopy. Morales et al. (2016) used the approach of Maespa, which calculates radiation at a set of points within the crown. Calculation of photosynthesis is then performed at each point and the values are integrated. On the other hand, in OliveCan we followed the method of Mariscal et al. (2000a) that performs the calculation only at the soil level, then deduces intercepted radiation and sunlit leaf area and calculates photosynthesis for the two classes (sunlit and shaded leaves) following De Pury and Farquhar (1997).

The model of Farquhar assumes steady-state conditions so it ignores rapid fluctuations in light and temperature that occur within the canopy. To address that situation, a dynamic photosynthesis model is required (e.g. Morales et al., 2018) although it has not been tested in fruit trees so far.

Respiration models still follow the division into maintenance (proportional to biomass) and growth (proportional to photosynthesis) components proposed by McCree (1970). That idea was later completed with the works of Penning de Vries (De Vries et al., 1974; De Vries, 1975), which provided a mechanistic biochemical basis for the simulation of the two components. Pérez-Priego et al. (2014) calibrated the maintenance respiration parameters of the different organs of olives (stems, leaves, fruits) and measured their response to temperature. Mariscal et al. (2000a) determined the coefficients of growth respiration for olives. McCree and De Vries approaches have been incorporated into the olive models of Morales et al. (2016) and OliveCan (López-Bernal et al., 2018).

The response of photosynthesis to increased CO₂ concentration seems to be limited by the inability of plants to use the excess C (downregulation of photosynthesis by sink limitation) (Ainsworth et al., 2004). However, the existing evidence in olive trees (Tognetti et al., 2001) shows almost no downregulation, although some differences may exist among cultivars. A lack of downregulation has been observed in many other tree species (Herrick and Thomas, 2001; Davey et al., 2006). Besides, evidences of downregulation in some forest trees under enriched CO₂ seems to be the result of reductions in leaf N concentration (Medlyn et al., 1999). Therefore, N availability may limit the response of olive trees to higher CO₂ and deserves specific research.

3.3.3 Conductance and transpiration

The model of photosynthesis of Farquhar sets a biochemical limit for CO₂ uptake by the leaf (demand) but does not yield directly the actual photosynthesis. The latter is the result of an equilibrium between the calculated CO₂ demand and the supply, which is the flux of CO₂ entering via stomata, i.e. the product of stomatal conductance and difference in CO₂ concentration between the atmosphere and the leaf mesophyll (Leuning, 1995). Stomatal conductance is proportional to CO₂ concentration and air humidity. The first to propose such a model were Ball et al. (1987), who used CO₂ concentration at the leaf surface and relative humidity. Later, Leuning (1995) modified it to consider internal CO₂ concentration and VPD. Moriana et al. (2002) calibrated the model of Leuning for olives and showed its advantage over previous empirical models like that of Stewart (1988), which had been used by Villalobos et al. (2000) for that species. The model of Leuning has been used in Maespa (Duursma and Medlyn, 2012) which serves for different tree species and was adapted for olives by Morales et al. (2016). Both, Leuning (1995) and Ball et al. (1987) used net photosynthesis as a driver for stomatal conductance.

Dewar (2002) opted for gross (instead of net) photosynthesis as the driving variable of conductance, so minimum (nighttime) conductance occurs when gross photosynthesis is zero. Tuzet et al. (2003) incorporated the role of leaf water potential in stomatal closure, which superseded the role of air humidity. However, in Tuzet’s approach, the calculation of conductance requires the simultaneous determination of leaf water potential (see 3.3.4). Fortunately, the high atmospheric coupling of olive trees (Villalobos et al., 2000) simplifies the solution, as boundary layer resistance does not need to be considered. This approach was adopted by López-Bernal et al. (2018) for the calculation of photosynthesis in OliveCan.

3.3.4 Water uptake

Two distinct approaches have been employed to model water uptake: macroscopic and microscopic. The macroscopic approach describes root system water uptake using empirical functions that respond to water potential (Feddes and Raats, 2004). Such models have been extensively employed by soil hydrologists to calculate the sink term in Richard’s equation (e.g. Hydrus model, Šimunek et al., 2012). Conversely, the microscopic approach involves upscaling water uptake from a single root to the entire root system. Most models used for calculating water uptake by individual roots employ the analytical solution proposed by Gardner (1960), which calculates the water uptake of a single root by considering the water potential difference between the midpoint of two consecutive roots and the root surface, divided by the soil hydraulic resistance.

Since Gardner’s groundbreaking solution, research on soil-root interactions has incorporated additional factors that affect water flow paths. Herkelrath et al. (1977) included the effect of root contact, while Bristow et al. (1984) explored the interaction between soil texture and rhizosphere resistance. Later on, other researchers kept exploring drought effects on roots. North and Nobel (1997) and Stirzaker and Passioura (1996) delved into the impact of dryness on the contact between roots and soil and proposed conceptual models. North and Nobel (1992) investigated the effects of dry conditions on root morphology, such as suberification and collapse of the root cortex. They demonstrated the decay and recovery of root radial hydraulic resistance during dry and wetting cycles. Finally, Steudle and Peterson (1998) provided a more detailed description of water flow paths through the root, introducing the concept of ‘composite transport’. The composite transport model distinguishes three water paths in roots: the symplastic path (across cell walls), the apoplastic path (around cells), and the transcellular path (through cells). This model acknowledges the roles of hydraulic and osmotic forces in water uptake.

Recent advances in root water uptake modelling are linked to the explicit representation of the root hydraulic architecture (RHA), (like R-SWMS) (Lobet et al., 2014). These models represent a significant step towards a more comprehensive understanding of root water dynamics. The RHA models combine a three-dimensional (3D) representation of the root system with transport equations for individual roots (Doussan et al., 1998). This approach allows for capturing the uneven distribution of roots in the soil and the variation in water uptake rates. This becomes particularly important in scenarios involving drip or micro sprinkler irrigation, where contrasting soil moisture conditions and root densities are generated (Fernández et al., 1991; Fernandes et al., 2021). While most of the developments in RHA models have focused on annual crops (primarily maize), efforts have also been made in the context of trees. For instance, Vercambre et al. (2003) developed a 3D representation of plum root architecture to investigate water and nutrient uptake. In the case of olive trees, Sorgonà et al. (2018) described coarse root architecture on a high-density orchard.

The modeling of water uptake in olive trees is still in its early stages. Garcia-Tejera et al. (2016) and López-Bernal et al. (2020b) have conducted studies demonstrating that olive tree root radial hydraulic resistance varies with temperature, which is the primary cause of low water potentials during winter in Mediterranean climates (López-Bernal et al., 2015b). Garcia-Tejera et al. (2016) proposed an empirical model to account for such variation. To capture the effects of root system distribution on olive tree behavior under deficit conditions, Garcia-Tejera et al. (2017) developed a SPAC model, which incorporates a soil multicompartment solution (see Figure 1). This model lies between simple 1D models and a more detailed 3D representation of the root system. It divides the soil into two horizontal compartments and several vertical layers, allowing for the accommodation of differential soil wetted fractions induced by drip irrigation systems. The SPAC model has been integrated into OliveCan to simulate the effects of water stress under localized irrigation.

FIGURE 1

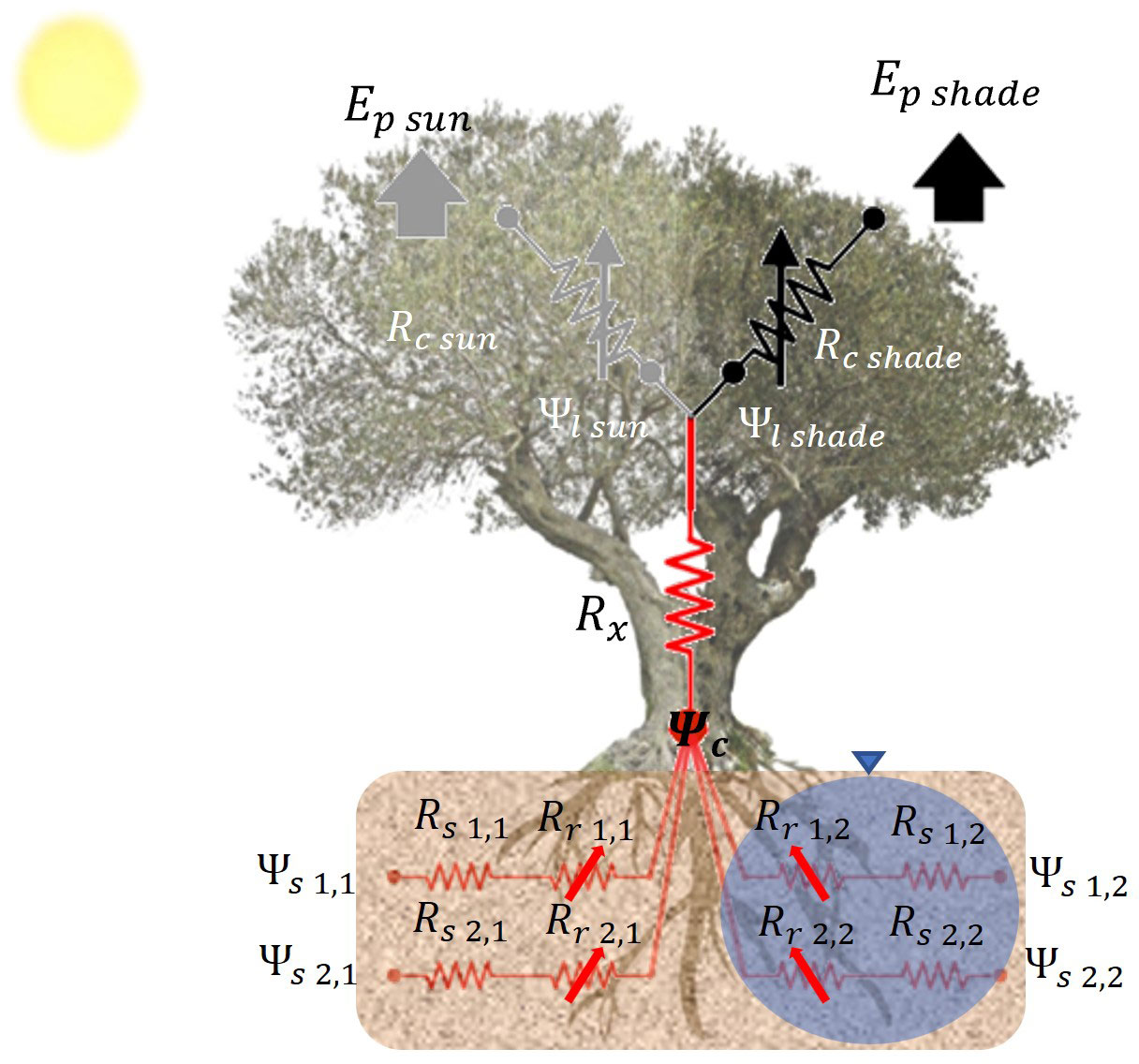
Figure 1 Schematic representation of the SPAC model with a soil multicompartment solution. The diagram represents the transport for water from the two soil compartments (irrigated and non-irrigated soil fractions) to the atmosphere. Symbols in the diagram are the soil (R_s), root (R_r) and xylem (R_x) resistances, the soil (Ψ_s), collar (Ψ_c) and leaf (Ψ_l) water potentials, and the stomatal resistance (R_c) and transpiration (E_p) for sunlit and shaded canopy fractions. Numbers indicate the soil layer and the soil compartment. Arrows indicate that the resistance is variable.

3.4 Yield

3.4.1 Harvest index

Yield may be calculated as the product of biomass and Harvest Index (HI) (Donald, 1962). The value of HI may be taken as constant or alternatively assuming a linear increase with time since flowering (Bindi et al., 1999). The former approach was included in the olive model proposed by Moriondo et al. (2019), while the last one has not been tried in trees. A more elaborate approach is using partitioning coefficients, so biomass of the harvestable organ receives a fraction of available carbohydrates during a given period as in the model of Morales et al. (2016).

An even simpler approach for calculating olive yield is based on the concept of RUE for oil production (Villalobos et al., 2006), i.e. the amount of oil produced per unit intercepted PAR, which lies between 0.17 g oil (MJ PAR)^-1 in intensive orchards (Iniesta et al., 2009) and 0.12 g oil (MJ PAR)^-1 in hedgerow olive groves (Connor et al., 2016).

3.4.2 Number of fruits

Olive and many other tree species for which there is no direct manipulation of fruit load (i.e. fruit thinning) exhibit alternate bearing i.e. years with high yields are followed by years with low yields, which is associated with changes in the number of flowers (Monselise and Goldschmidt, 1982). Olive fruits appear on inflorescences originating on shoots grown in the previous season. The experiment of Stutte and Martin (1986) showed that manipulation of the number of fruits at the start of the summer affects flowering in the next season. This led to the idea of a so-called “floral induction” in summer which has been challenged since the work of Dag et al. (2010). This is so because new lateral buds are being formed until mid-autumn and they can potentially bear inflorescences in the next spring. Nevertheless, all of the buds on well-lignified parts of the shoot can potentially differentiate to form inflorescences (Lavee, 2015).

As new inflorescences appear on previous years’ generated buds the availability of carbon for new shoot growth limits the potential number of inflorescences that can be formed for the next season. Heavy fruit load implies reduced shoot growth which will be ultimately the reason for alternate bearing (Connor and Fereres, 2005). The equilibrium between vegetative and reproductive growth of the tree may be broken by any factor leading to low fruit numbers such as extreme water deficit around flowering (Rapoport et al., 2012) or lack of winter chilling (Hartmann, 1953; De Melo-Abreu et al., 2004). Other possible causes are poor pollination and reduced fruit setting due to heat (Koubouris et al., 2015), or fruit drop in later stages e.g. by pest attacks (Perdikis et al., 2009). All in all, any imbalance between vegetative and reproductive growth will mark the start of oscillations in fruit number and thus, yield.

To analyze the interaction between tree growth and the number of fruits we can use a conceptual model as follows. Yield (Y, g m^-2) is the product of mean fruit weight (w, g glucose/fruit) and the number of fruits (N_f, m^-2), which may be calculated as a function of the number of positions (leaf axils) (N_p, m^-2):

$\begin{array}{ll}Y=N_{\text{p}} \alpha \beta w & (2)\end{array}$

where α is the ratio number of inflorescences per position (dimensionless) and β is the number of fruits per inflorescence (dimensionless).

A fraction (f_s) of tree photosynthesis (P, g glucose m^-2) is directed to shoot (including fruit) growth. The production of each new leaf position requires an amount of glucose γ (g). Therefore, the number of positions generated in a given year may be calculated as a function of the number of positions in the previous season (N_p’), the fraction (f_s) of P directed to the shoot and γ:

$\begin{array}{ll}{N}_{\text{p}}=\frac{f_{\text{s}}P-N_{\text{p}}^{\text{'}} \alpha \beta w}{\gamma } & (3)\end{array}$

By combining equations 2 and 3, yield may be expressed as a function of the previous year’s yield (Y’):

$\begin{array}{ll}Y=\frac{ \alpha \beta w}{\gamma }(f_{\text{s}}P-Y\text{'})& (4)\end{array}$

This recurrence equation provides a theoretical framework for understanding productivity in olive orchards. Mathematically, oscillations in yield dampen gradually if α·β·w/γ is lower than 1 and that must be the case in nature. Departures from equilibrium may occur due to exogenous events (e.g. lack of chilling, extreme weather events affecting fruit set), leading to oscillations that will tend to disappear over time until any further departure occurs (Figure 2)). The equilibrium yield (Y_eq) is obtained when Y and Y’ are equal so:

FIGURE 2

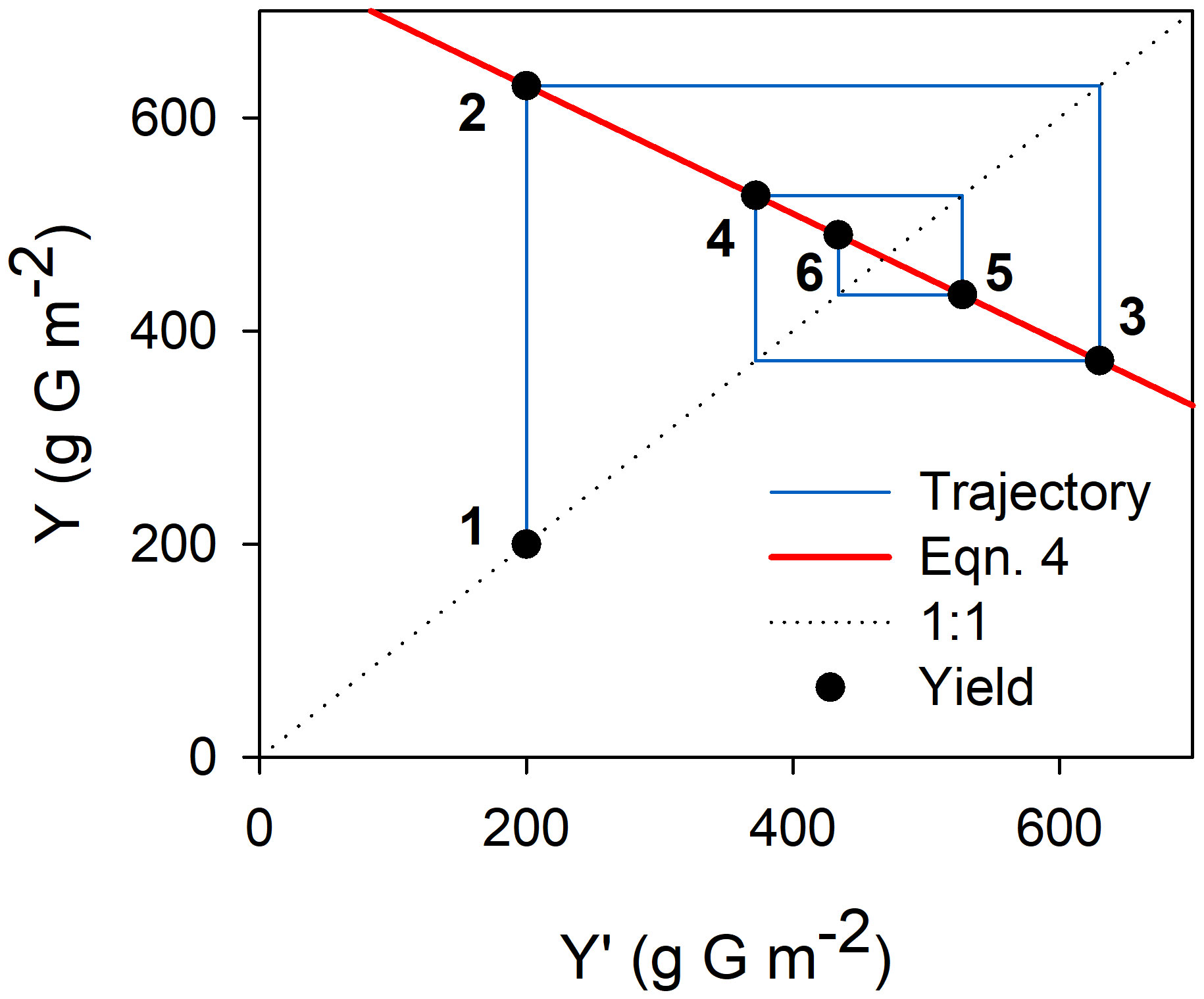
Figure 2 Graphical representation of the dampening of yield oscillations following a year of low yield due to an adverse exogenous event (e.g. severe water deficit during flowering leading to low fruit set and yield). Yield in successive years (solid circles numbered from 1-6) is calculated from Equation 4 (red line). ‘G’ in the axis titles stands for glucose. Parameter values for this example were α=0.5 inflorescences node^-1, β=2.0 fruits inflorescence^-1, w=1.5 g glucose fruit^-1, γ=2.5 g glucose node^-1, f_s=0.5, P=2500 g glucose m^-2. Initial yield was set as 200 g glucose m^-2.

$\begin{array}{ll}{Y}_{\text{eq}}=\frac{f_{\text{s}}P}{1+\frac{\gamma }{\alpha \beta w}}& (5)\end{array}$

And equilibrium Harvest Index may be calculated as:

$\begin{array}{ll}H{I}_{\text{eq}}=\frac{1}{1+\frac{\gamma }{\alpha \beta w}}& (6)\end{array}$

Note that the definition of HI in trees has to be different from the classic one that we use in annual plants (ratio yield/shoot biomass) (Donald, 1962). For a perennial, HI may be defined as the ratio of yield and annual shoot growth.

Events reducing the number of fruits (e.g. heatwaves or drought at some stages) are likely to become more frequent in the future so departures from equilibrium yield and HI will be the rule. Specific submodels of fruit number will thus be required in olive crop models, while the use of HI or fixed partitioning coefficients to fruit (Morales et al., 2016) should be avoided unless the analysis goes beyond a single season (i.e. for the calculation of long-term average productivity).

The model encapsulated in eq. 4 shows that olive yield depends on tree photosynthesis (see section 3.3.2) and 5 parameters, namely:

- f_s (fraction of carbohydrates invested in the aerial part, i.e. not used in root growth): until now, the partitioning coefficients (PC) to coarse and fine roots have been taken as constants (Morales et al., 2016; López-Bernal et al., 2018). However, fine root turnover makes it difficult to accurately measure its PC (Soda et al., 2017). Furthermore, the root PC of trees increases in response to water stress (Ledo et al., 2018).

- α (number of inflorescences per position): its variation may be due to lack of chilling (Hackett and Hartmann, 1964; Malik and Bradford, 2005) or late harvest (Lavee, 2007) in “on” years. The chilling requirement for setting inflorescences is variable among cultivars (Hartmann and Porlingis, 1957).

- β (number of fruits per inflorescence): apart from clear genotypic differences (Lavee et al., 1996), the efficiency of flowering in olives may be reduced by poor pollination, fruit abortion or fruit drop. The first and second may be caused by water stress or heat stress during flowering (Koubouris et al., 2009; Fernandez, 2014). Pollination may be also prevented by a lack of compatible pollen (Sánchez-Estrada and Cuevas, 2018), which may occur in isolated monovarietal plantations or when rainy weather prevents airborne pollen transport (Rojo et al., 2015). After a few weeks from bloom, fruit drop will only occur under extreme water stress (Lavee et al., 1990).

- w: The average mass per fruit is, first of all, a cultivar characteristic that depends on cell number (Hammami et al., 2011). Fruit number will also affect final fruit size due to competition for available carbohydrates (Trentacoste et al., 2010). This effect would tend to reduce oscillations in yield. Nevertheless, it is clear that modelling olive yield in specific seasons requires both knowing fruit number and tree photosynthesis, i.e. we may be source or sink-limited.

- γ: the amount of glucose per leaf axil (position) is related to internode length, which may be variable among cultivars and depends on fruit load (Rosati et al., 2018), being higher in “off” years. This effect would also reduce oscillations in fruit numbers.

As a final remark, some authors have shown reductions in olive tree transpiration when fruit numbers are low (Bustan et al., 2016; Miserere et al., 2019), but the effect on tree photosynthesis is still unknown.

3.4.3 Oil accumulation

Several studies have shown the typical patterns of oil accumulation for the main olive cultivars (Trentacoste et al., 2010; Navas-Lopez et al., 2019), finding a general negative effect of high temperature on oil concentration. The quality of olive oil is partly dependent on fatty acid composition which has been characterized by Rondanini et al. (2014) or Dag et al. (2011), who have shown a strong effect of harvest date and cultivars. However, despite the importance of oil concentration and quality on marketable price (Finotti et al., 2007), they have not been incorporated into existing olive crop models.

3.5 Soil carbon

Inputs of carbon to the soil include tree residues from senescence (leaves and roots) and pruning and the remains of cover crops (shoots and roots). In OliveCan, the heterotrophic respiration is calculated following Huang et al. (2009), including the effect of soil water content on decomposition (Verstraeten et al., 2006). Other soil carbon models are available but have not been incorporated to olive crop models. For instance, Nieto et al. (2019) applied RothC to evaluate the impact of changes in olive residue management.

3.6 Impacts of pests and diseases

Plant pathogens and crop-feeding arthropods are key components of agroecosystems. Simulating yield losses associated to these biotic factors requires a deep understanding of the complex interactions between the crop and its natural enemies, which are modulated by environmental conditions and management. As a result, the development of process-based models predicting the impacts of pests and diseases is still a major scientific challenge even for some of the most important crops (Donatelli et al., 2017). In olive trees, a PBDM approach has been proposed for simulating yield losses caused by the olive fruit fly (Gutierrez et al., 2009; Ponti et al., 2013; see below for more details).

3.7 Full models

A crop simulation model aiming to simulate the impacts of global changes should at least include submodels for phenological development, growth and yield. We will thus leave out the models proposed by Abdel-Razik (1989) and Viola et al. (2012) as well as AdaptaOlive (Lorite et al., 2018). The former two do not simulate phenology while the latter lacks a ‘growth’ model component.

Gutierrez et al. (2009) presented a PBDM approach for simulating the impacts of olive fruit fly on olive yield. In the model, fruit mortality due to fly attack is computed by considering fruit age and availability, so, although the emphasis is on the interactions between the olive trees and fruit fly populations, the model also includes components simulating flowering date and age-structured growth and yield of the trees. The effect of temperature on olive fly’s vital rates is also accounted for. This model has been subsequently refined by including a module of the water balance that accounts for the impacts of water deficit on photosynthesis rates (Ponti et al., 2013).

Morales et al. (2016) presented a model of olive orchards based on Maespa (Duursma and Medlyn, 2012), which in turn is an evolution of Maestra (Medlyn, 2004). It was designed for simulating potential growth and includes a joint photosynthesis-conductance model (FBBL type) and the phenology model of De Melo-Abreu et al. (2004). It uses fixed partitioning coefficients including one for fruits, that will determine yield unless flowering fails in case of insufficient chilling in winter.

López-Bernal et al. (2018) developed OliveCan, which includes the model of Mariscal et al. (2000b) for radiation interception and the model of De Melo-Abreu et al. (2004) for phenology. It combines an FBBL with the model of Tuzet et al. (2003) which is based on leaf water potential. The latter is simulated by solving the SPAC model proposed by Garcia-Tejera et al. (2017), driven by a full water balance submodel. It is thus the only mechanistic model of olive orchards in terms of response to water deficits. Furthermore, the model incorporates a submodel of the carbon and water balance of cover crops (López-Bernal et al., 2023).

Finally, Moriondo et al. (2019) introduced a much simpler olive model than the aforementioned. It uses the UniChill model (Chuine, 2000) for phenology, while biomass accumulation is simulated through a simple radiation-use efficiency approach. Yield is deduced by applying a HI value that can be reduced by various abiotic stresses.

4 Discussion

Crop models designed to cope with global change effects require a mechanistic and accurate description of tree responses to the increases in temperature and CO₂ concentration. Furthermore, projections show also reduced rainfall around the Mediterranean (Longobardi and Villani, 2010), where most olive growing occurs, and an increase in climatic extremes (Diffenbaugh et al., 2007). However, the reported increase in extreme heat events seems to be the result of a shift in the mean value, and not in the variance (Simolo et al., 2014).

Many important processes are affected by temperature, including phenological development, respiration, photosynthesis, growth and senescence. The most dramatic effects of gradual temperature changes will be the change in flowering date and the possible lack of winter chilling. Episodic heat events may reduce pollination and fruit set. In any case, the need for accurate submodels of phenology and fruit number cannot be underrated as opposed to using HI, which can only be applied to gross long-term evaluations of productivity.

On the other hand, CO₂ concentration affects photosynthesis and stomatal conductance. Higher CO₂ improves potential photosynthesis but promotes some stomatal closure. The overall effect on tree carbon accumulation would depend also on the expected increase in respiration rate (due to higher temperature). Therefore, the efficiency parameters normally used to estimate biomass accumulation (RUE or WUE) will inevitably change in parallel to the atmospheric CO₂ concentration, which forces the adoption of a photosynthesis/conductance model.

Available olive crop models have already incorporated satisfactory solutions for tree photosynthesis and conductance but there is still room for improvement. First, calibration of the parameters of the model of Farquhar et al. (1980) should be performed for the main olive cultivars and their dependence on leaf N concentration should be quantified. Second, inhibition of carboxylation by combined water and heat stress should also be considered. Third, the interactions of stomatal conductance, transpiration and water potential are still a work in progress. A more mechanistic approach to this problem requires a detailed model of the stomatal functioning in response to water potential in guard and accompanying cells (Buckley, 2017). Moreover, the inclusion of more mechanistic functions to simulate root water uptake under deficit conditions is a must if we aim to properly model olive behavior under the water stress conditions that the overwhelming majority of olive groves endure every summer. At moderate soil water deficits, stomatal closure is not driven by xylem cavitation but by the declines in soil water potential (Carminati and Javaux, 2020; Corso et al., 2020). Dietrich et al. (2018), demonstrated that cutting half of the tree sapwood had no effect on water potential nor in transpiration. In olive cultivar ‘Kalamata’, Rodriguez-Dominguez and Brodribb (2020) showed that 81% of the whole hydraulic plant resistance under non-stressed conditions belongs to root radial hydraulic resistance, and the value increases up to 95% under moderate water stress. Thus, efforts should concentrate on disentangling root water uptake response under water deficit. In maize, circadian oscillation in root radial hydraulic resistance has been observed, being proportional to previous water stress conditions (Caldeira et al, 2014). Does olive roots respond in the same way? The answer could reveal novel approaches to improve olive performance under water scarcity scenarios. For instance, simulations have shown that changes in root morphology could enhance water use efficiency in olives under deficit irrigation by developing rootstocks with more active root growth in the wet bulb (Garcia-Tejera et al., 2018). It is, therefore, crucial to advance in the development of more comprehensive models that link the water demand (canopy) and supply (roots) functions.

In terms of carbon allocation, available models incorporate partitioning coefficients that have only been measured in large trees (Villalobos et al., 2006) for the cultivar ‘Arbequina’. Apart from expanding the calibration to other cultivars with contrasting growth habits (e.g. ‘Frantoio’), we need to understand how water stress changes the partitioning of assimilates, with special emphasis on root/shoot C distribution, a delicate variable that may lead to significant errors over multiannual simulations. On the other hand, the modelling of reserve dynamics is still very simplistic in the main existing models, serving mainly as a pool for carbon not used in the growth of other organs. However, the work of Bustan et al. (2011) showed that reserves in olive trees act as a separate sink, i.e. some C is partitioned to reserves even when C supply is limited. More studies focused on the way olives distribute their assimilates in response to the environment are paramount to improve models, in particular their ability to simulate extreme conditions and multi-annual effects on growth.

Olive spring phenology models have been tested successfully for predicting flowering dates in traditional growing areas (De Melo-Abreu et al., 2004), where chilling requirements are always satisfied, but more complex approaches may be required in new environments of the Southern Hemisphere with warmer winters (Torres et al., 2017) and for the future projected climate around the Mediterranean. In any case, a better understanding of the requirements and responses to chilling is of the utmost importance to improve the robustness of existing and new models in the context of climate change studies.

The requirement of a submodel for fruit number in olive trees is amplified by the expected effects of warming, caused by the lack of winter chilling and/or by heat events during flowering. On the other hand, oil accumulation may be compromised by higher temperatures. The effects of C supply and temperature and their interactions on oil quantity and quality (fatty acid composition and organoleptic or stability compounds) should be incorporated into olive crop models if we want to evaluate the economic sustainability of orchards.

Finally, olive crop models will need to include an N balance submodel to improve the simulation of photosynthesis and the dynamics of organic dry matter, which determines the capacity for CO₂ capture in the soil. Although Abdel-Razik (1989) introduced simple fertilization effects on growth, mechanistic models have overlooked olive N balance. A reason for this may be that N has rarely represented a concern in olive, due to the extensive management and the relatively low requirements of the traditional growing systems. Nevertheless, the new intensive and superintensive olive farming set a new scenario where N supply becomes quickly a relevant limitation to growth, and it is sometimes purposely part of the growth regulation techniques to extend the orchard lifespan. Assuming permanent N sufficiency in high demand systems may lead to significant mismatching in the calculation of growth and yield, both in long- and short-term simulations. The inclusion in the modern process-based models of a sound N uptake and distribution submodel -including N fate in soil organic matter- is paramount to correctly simulate olive growth and, especially, the increased photosynthesis rates expected under the future atmospheric CO₂ levels.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was funded by “Ministerio de Ciencia e Innovación” (MCIN/AEI/10.13039/501100011033) through projects TED2021-132217A-I00 and PID2019-110575RB-I00. The former was also supported by the European Union “NextGenerationUE”/Recovery and Resilience Facility. We also acknowledge financial support from “Ministerio de Ciencia, Innovación y Universidades”, through the Severo Ochoa and María de Maeztu Program for Centers and Units of Excellence in R&D (grant number CEX2019-000968-M). Postdoctoral fellowships were granted to the second and third authors by “Consejería de Transformación Económica, Industria, Conocimiento y Universidades” (“Junta de Andalucía”, Spain, grant number POSTDOC-21-00381) and “Ministerio de Universidades (‘María Zambrano’ scholarship, grant number 2021/86493), respectively.

Acknowledgments

The help of Dr. Alejandro Morales and Dr. Jose Paulo Melo e Abreu in developing the different submodels of olive orchards is greatly appreciated. The authors also thank the constructive suggestions from two reviewers which enabled us to improve the final version of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abazi, U., Lorite, I. J., Cárceles, B., Raya, A. M., Durán, V. H., Francia, J. R., et al. (2013). WABOL: A conceptual water balance model for analyzing rainfall water use in olive orchards under different soil and cover crop management strategies. Comput. Electron. Agr. 91, 35–48. doi: 10.1016/j.compag.2012.11.010

CrossRef Full Text | Google Scholar

Abdel-Razik, M. (1989). A model of the productivity of olive trees under optional water and nutrient supply in desert conditions. Ecol. Model. 45 (3), 179–204. doi: 10.1016/0304-3800(89)90081-1

CrossRef Full Text | Google Scholar

Agüera, F., Villalobos, F. J., Orgaz, F. (1997). Evaluation of sunflower (Helianthus annuus, L.) genotypes differing in early vigour using a simulation model. Developments Crop Sci. 25, 145–154. doi: 10.1016/S0378-519X(97)80016-5

CrossRef Full Text | Google Scholar

Ainsworth, E. A., Rogers, A., Nelson, R., Long, S. P. (2004). Testing the “source–sink” hypothesis of down-regulation of photosynthesis in elevated [CO₂] in the field with single gene substitutions in Glycine max. Agric. For. Meteorol. 122 (1-2), 85–94. doi: 10.1016/j.agrformet.2003.09.002

CrossRef Full Text | Google Scholar

Anderson, J. L., Kesner, C. D., Richardson, E. A. (1986). Validation of chill unit and flower bud phenology models for ‘Montmorency’ sour cherry. Acta Hortic. 184, 71–78. doi: 10.17660/ActaHortic.1986.184.7

CrossRef Full Text | Google Scholar

Ball, J. T., Woodrow, I. E., Berry, J. A. (1987). “A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions,” in Progress in Photosynthesis Research. Ed. Biggins, J. (Dordrecht, The Netherlands: Springer), 221–224. doi: 10.1007/978-94-017-0519-6_48

CrossRef Full Text | Google Scholar

Basso, B., Liu, L. (2019). Seasonal crop yield forecast: Methods, applications, and accuracies. Adv. Agron. 154, 201–255. doi: 10.1016/bs.agron.2018.11.002

CrossRef Full Text | Google Scholar

Beltrán, G., Uceda, M., Hermoso, M., Frías, L. (2017). “Maduración,” in El cultivo del Olivo. Eds. Barranco, D., Fernández-Escobar, R., Rallo, L. (Madrid, Spain: Mundi-Prensa), 187–212.

Google Scholar

Bindi, M., Sinclair, T. R., Harrison, J. (1999). Analysis of seed growth by linear increase in harvest index. Crop Sci. 39 (2), 486–493. doi: 10.2135/cropsci1999.0011183X0039000200031x

CrossRef Full Text | Google Scholar

Bonachela, S., Orgaz, F., Villalobos, F. J., Fereres, E. (1999). Measurement and simulation of evaporation from soil in olive orchards. Irrig. Sci. 18, 205–211. doi: 10.1007/s002710050064

CrossRef Full Text | Google Scholar

Bonachela, S., Orgaz, F., Villalobos, F. J., Fereres, E. (2001). Soil evaporation from drip-irrigated olive orchards. Irrig. Sci. 20, 65–71. doi: 10.1007/s002710000030

CrossRef Full Text | Google Scholar

Boughton, W. C. (1989). A review of the USDA SCS curve number method. Soil Res. 27 (3), 511–523. doi: 10.1071/SR9890511

CrossRef Full Text | Google Scholar

Bristow, K. L., Campbell, G. S., Calissendorff, C. (1984). The effects of texture on the resistance to water movement within the rhizosphere. Soil Sci. Soc Am. J. 48 (2), 266–270. doi: 10.2136/sssaj1984.03615995004800020007x

CrossRef Full Text | Google Scholar

Brodribb, T. (1996). Dynamics of changing intercellular CO₂ concentration (c_i) during drought and determination of minimum functional c_i. Plant Physiol. 111 (1), 179–185. doi: 10.1104/pp.111.1.179

PubMed Abstract | CrossRef Full Text | Google Scholar

Buckley, T. N. (2017). Modeling stomatal conductance. Plant Physiol. 174 (2), 572–582. doi: 10.1104/pp.16.01772

PubMed Abstract | CrossRef Full Text | Google Scholar

Bustan, A., Avni, A., Lavee, S., Zipori, I., Yeselson, Y., Schaffer, A. A., et al. (2011). Role of carbohydrate reserves in yield production of intensively cultivated oil olive (Olea europaea L.) trees. Tree Physiol. 31 (5), 519–530. doi: 10.1093/treephys/tpr036

PubMed Abstract | CrossRef Full Text | Google Scholar

Bustan, A., Dag, A., Yermiyahu, U., Erel, R., Presnov, E., Agam, N., et al. (2016). Fruit load governs transpiration of olive trees. Tree Physiol. 36 (3), 380–391. doi: 10.1093/treephys/tpv138

PubMed Abstract | CrossRef Full Text | Google Scholar

Caldeira, C. F., Jeanguenin, L., Chaumont, F., Tardieu, F. (2014). Circadian rhythms of hydraulic conductance and growth are enhanced by drought and improve plant performance. Nat. Commun. 5 (1), 5365. doi: 10.1038/ncomms6365

PubMed Abstract | CrossRef Full Text | Google Scholar

Carminati, A., Javaux, M. (2020). Soil rather than xylem vulnerability controls stomatal response to drought. Trends Plant Sci. 25 (9), 868–880. doi: 10.1016/j.tplants.2020.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Cesaraccio, C., Spano, D., Snyder, R. L., Duce, P. (2004). Chilling and forcing model to predict bud-burst of crop and forest species. Agric. For. Meteorol. 126, 1–13. doi: 10.1016/j.agrformet.2004.03.002

CrossRef Full Text | Google Scholar

Chuine, I. (2000). A unified model for budburst of trees. J. Theor. Biol. 207, 337–347. doi: 10.1006/jtbi.2000.2178

PubMed Abstract | CrossRef Full Text | Google Scholar

Connor, D. J. (2005). Adaptation of olive (Olea europaea L.) to water-limited environments. Aust. J. Agric. Res. 56, 1181–1189. doi: 10.1071/AR05169

CrossRef Full Text | Google Scholar

Connor, D. J., Fereres, E. (2005). The physiology and adaptation of yield expression in olive. Hortic. Rev. 31, 155–229. doi: 10.1002/9780470650882.ch4

CrossRef Full Text | Google Scholar

Connor, D. J., Gómez-del-Campo, M., Trentacoste, E. R. (2016). Relationships between olive yield components and simulated irradiance within hedgerows of various row orientations and spacings. Sci. Hortic. 198, 12–20. doi: 10.1016/j.scienta.2015.11.009

CrossRef Full Text | Google Scholar

Corso, D., Delzon, S., Lamarque, L., Cochard, H., Torres-Ruiz, J., King, A., et al. (2020). Neither xylem collapse, cavitation, or changing leaf conductance drive stomatal closure in wheat. Plant Cell Environ. 43 (4), 854–865. doi: 10.1111/pce.13722

PubMed Abstract | CrossRef Full Text | Google Scholar

Dag, A., Bustan, A., Avni, A., Tzipori, I., Lavee, S., Riov, J. (2010). Timing of fruit removal affects concurrent vegetative growth and subsequent return bloom and yield in olive (Olea europaea L.). Sci. Hortic. 123 (4), 469–472. doi: 10.1016/j.scienta.2009.11.014

CrossRef Full Text | Google Scholar

Dag, A., Kerem, Z., Yogev, N., Zipori, I., Lavee, S., Ben-David, E. (2011). Influence of time of harvest and maturity index on olive oil yield and quality. Sci. Hortic. 127 (3), 358–366. doi: 10.1016/j.scienta.2010.11.008

CrossRef Full Text | Google Scholar

Davey, P. A., Olcer, H., Zakhleniuk, O., Bernacchi, C. J., Calfapietra, C., Long, S. P., et al. (2006). Can fast-growing plantation trees escape biochemical down-regulation of photosynthesis when grown throughout their complete production cycle in the open air under elevated carbon dioxide? Plant Cell Environ. 29 (7), 1235–1244. doi: 10.1111/j.1365-3040.2006.01503.x

PubMed Abstract | CrossRef Full Text | Google Scholar

De Melo-Abreu, J. P., Barranco, D., Cordeiro, A. M., Tous, J., Rogado, B. M., Villalobos, F. J. (2004). Modelling olive flowering date using chilling for dormancy release and thermal time. Agric. For. Meteorol. 125, 117–127. doi: 10.1016/j.agrformet.2004.02.009

CrossRef Full Text | Google Scholar

De Pury, D. G. G., Farquhar, G. D. (1997). Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant Cell Environ. 20 (5), 537–557. doi: 10.1111/j.1365-3040.1997.00094.x

CrossRef Full Text | Google Scholar

De Vries, F. P. (1975). The cost of maintenance processes in plant cells. Ann. Bot. 39 (1), 77–92. doi: 10.1093/oxfordjournals.aob.a084919

CrossRef Full Text | Google Scholar

De Vries, F. P., Brunsting, A. H. M., Van Laar, H. H. (1974). Products, requirements and efficiency of biosynthesis a quantitative approach. J. Theor. Biol. 45 (2), 339–377. doi: 10.1016/0022-5193(74)90119-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Dewar, R. C. (2002). The Ball–Berry–Leuning and Tardieu–Davies stomatal models: synthesis and extension within a spatially aggregated picture of guard cell function. Plant Cell Environ. 25 (11), 1383–1398. doi: 10.1046/j.1365-3040.2002.00909.x

CrossRef Full Text | Google Scholar

De Wit, C. T. (1965). Photosynthesis of leaf canopies. Pudoc. 663.

Google Scholar

Diaz-Espejo, A., Walcroft, A. S., Fernández, J. E., Hafidi, B., Palomo, M. J., Girón, I. F. (2006). Modeling photosynthesis in olive leaves under drought conditions. Tree Physiol. 26 (11), 1445–1456. doi: 10.1093/treephys/26.11.1445

PubMed Abstract | CrossRef Full Text | Google Scholar

Didevarasl, A., Costa Saura, J. M., Spano, D., Deiana, P., Snyder, R., Mulas, M., et al. (2023). Modelling phenological phases across olive cultivars in the Mediterranean. Plants 12 (18), 3181. doi: 10.3390/plants12183181

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietrich, L., Hoch, G., Kahmen, A., Korner, C. (2018). Losing half the conductive area hardly impacts the water status of mature trees. Sci. Rep. 8, 15006. doi: 10.1038/s41598-018-33465-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Diffenbaugh, N. S., Pal, J. S., Giorgi, F., Gao, X. (2007). Heat stress intensification in the Mediterranean climate change hotspot. Geophys. Res. Lett. 34 (11). doi: 10.1029/2007GL030000

CrossRef Full Text | Google Scholar

Di Paola, A., Chiriacò, M. V., Di Paola, F., Nieddu, G. (2021). A phenological model for olive (Olea europaea L. var. europaea) growing in Italy. Plants 10, 1115. doi: 10.3390/plants10061115

PubMed Abstract | CrossRef Full Text | Google Scholar

Donald, C. M. (1962). In search of yield. J. Aust. Inst. Agric. Sci. 28, 171–178.

Google Scholar

Donatelli, M., Magarey, R. D., Bregaglio, S., Willocquet, L., Whish, J. P. M., Savary, S. (2017). Modelling the impacts of pests and diseases on agricultural systems. Agric. Syst. 155, 213–224. doi: 10.1016/j.agsy.2017.01.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Doussan, C., Vercambre, G., Pagés, L. (1998). Modelling of the hydraulic architecture of root systems: An integrated approach to water absorption—Distribution of axial and radial conductances in maize. Ann. Bot. 81 (2), 225–232. doi: 10.1006/anbo.1997.0541

CrossRef Full Text | Google Scholar

Duursma, R. A., Medlyn, B. E. (2012). MAESPA: a model to study interactions between water limitation, environmental drivers and vegetation function at tree and stand levels, with an example application to [CO₂]×drought interactions. Geosci. Model. Dev. 5 (4), 919–940. doi: 10.5194/gmd-5-919-2012

CrossRef Full Text | Google Scholar

Engelen, C., Wechsler, T., Bakhshian, O., Smoly, I., Flaks, I., Friedlander, T., et al. (2023). Studying parameters affecting accumulation of chilling units required for olive winter flower induction. Plants 12, 1714. doi: 10.3390/plants12081714

PubMed Abstract | CrossRef Full Text | Google Scholar

FAOSTAT (2023). Available at: https://www.fao.org/faostat/en/#data/QCL (Accessed June 23, 2023).

Google Scholar

Farquhar, G. D., von Caemmerer, S. V., Berry, J. A. (1980). A biochemical model of photosynthetic CO₂ assimilation in leaves of C3 species. Planta 149, 78–90. doi: 10.1007/BF00386231

PubMed Abstract | CrossRef Full Text | Google Scholar

Feddes, R. A., Raats, P. A. C. (2004). “Parameterizing the soil–water–plant root system,” in Unsaturated-zone modeling: progress, challenges and applications. Eds. Feddes, R. A., De Rooij, G. H., Van Dam, J. C. (Dordrecht, The Netherlands: Kluwer Academic Publishers), 95–141. Available at: https://edepot.wur.nl/35358.

Google Scholar

Fernandes, R. D., Egea, G., Hernandez-Santana, V., Diaz-Espejo, A., Fernandez, J. E., Perez-Martin, A., et al. (2021). Response of vegetative and fruit growth to the soil volume wetted by irrigation in a super-high-density olive orchard. Agric. Water Manage. 258, 107197. doi: 10.1016/j.agwat.2021.107197

CrossRef Full Text | Google Scholar

Fernandez, J. E. (2014). Understanding olive adaptation to abiotic stresses as a tool to increase crop performance. Env. Exp. Bot. 103, 158–179. doi: 10.1016/j.envexpbot.2013.12.003

CrossRef Full Text | Google Scholar

Fernández, J. E., Moreno, F., Cabrera, F., Arrue, J. L., Martín-Aranda, J. (1991). Drip irrigation, soil characteristics and the root distribution and root activity of olive trees. Plant Soil 133, 239–251. doi: 10.1007/BF00009196

CrossRef Full Text | Google Scholar

Finotti, E., Bersani, A. M., Bersani, E. (2007). Total quality indexes for extra-virgin olive oils. J. Food Qual. 30 (6), 911–931. doi: 10.1111/j.1745-4557.2007.00159.x

CrossRef Full Text | Google Scholar

Fishman, S., Erez, A., Couvillon, G. A. (1987a). The temperature dependence of dormancy breaking in plants: Mathematical analysis of a two-step model involving a cooperative transition. J. Theor. Biol. 124, 473–483. doi: 10.1016/S0022-5193(87)80221-7

CrossRef Full Text | Google Scholar

Fishman, S., Erez, A., Couvillon, G. A. (1987b). The temperature dependence of dormancy breaking in plants: Computer simulation of processes studied under controlled temperatures. J. Theor. Biol. 126, 309–321. doi: 10.1016/S0022-5193(87)80237-0

CrossRef Full Text | Google Scholar

Fowler, A. F., Basso, B., Millar, N., Brinton, W. F. (2023). A simple soil mass correction for a more accurate determination of soil carbon stock changes. Sci. Rep. 13 (1), 2242. doi: 10.1038/s41598-023-29289-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Gabaldón-Leal, C., Ruiz-Ramos, M., de la Rosa, R., León, L., Belaj, A., Rodríguez, A., et al. (2017). Impact of changes in mean and extreme temperaturas caused by climate change on olive flowering in southern Spain. Int. J. Climatol. 37, 940–957. doi: 10.1002/joc.5048

CrossRef Full Text | Google Scholar

Garcia-Tejera, O., López-Bernal, Á., Orgaz, F., Testi, L., Villalobos, F. J. (2017). Analysing the combined effect of wetted area and irrigation volume on olive tree transpiration using a SPAC model with a multi-compartment soil solution. Irrig. Sci. 35, 409–423. doi: 10.1007/s00271-017-0549-5

CrossRef Full Text | Google Scholar

Garcia-Tejera, O., López-Bernal, Á., Orgaz, F., Testi, L., Villalobos, F. J. (2018). Are olive root systems optimal for deficit irrigation? Eur. J. Agron. 99, 72–79. doi: 10.1016/j.eja.2018.06.012

CrossRef Full Text | Google Scholar

Garcia-Tejera, O., López-Bernal, Á., Villalobos, F. J., Orgaz, F., Testi, L. (2016). Effect of soil temperature on root resistance: implications for different trees under Mediterranean conditions. Tree Physiol. 36 (4), 469–478. doi: 10.1093/treephys/tpv126

PubMed Abstract | CrossRef Full Text | Google Scholar

Gardner, W. R. (1960). Dynamic aspects of water availability to plants. Soil Sci. 89 (2), 63–73. doi: 10.1097/00010694-196002000-00001

CrossRef Full Text | Google Scholar

Garrison, M. V., Batchelor, W. D., Kanwar, R. S., Ritchie, J. T. (1999). Evaluation of the CERES-Maize water and nitrogen balances under tile-drained conditions. Agr. Syst. 62 (3), 189–200. doi: 10.1016/S0308-521X(99)00064-5

CrossRef Full Text | Google Scholar

Gómez, J. A., Giráldez, J. V., Fereres, E. (2001). Rainfall interception by olive trees in relation to leaf area. Agric. Water Manage. 49 (1), 65–76. doi: 10.1016/S0378-3774(00)00116-5

CrossRef Full Text | Google Scholar

Gutierrez, A. P., Ponti, L., Cossu, Q. A. (2009). Effects of climate warming on Olive and olive fly (Bactrocera oleae (Gmelin)) in California and Italy. Climatic Change 95, 195–217. doi: 10.1007/s10584-008-9528-4

CrossRef Full Text | Google Scholar

Haberman, A., Bakhshian, O., Cerezo-Medina, S., Paltiel, J., Adler, C., Ben Ari, G., et al. (2017). A possible role for FT-encoding genes in interpreting environmental and internal cues affecting olive (Olea europaea L.) flower induction. Plant Cell Environ. 40, 1263–1280. doi: 10.1111/pce.12922

PubMed Abstract | CrossRef Full Text | Google Scholar

Hackett, W. P., Hartmann, H. T. (1964). Inflorescence formation in olive as influenced by low temperature, photoperiod, and leaf area. Bot. Gaz. 125 (1), 65–72. doi: 10.1086/336247

CrossRef Full Text | Google Scholar

Hammami, S. B., León, L., Rapoport, H. F., de la Rosa, R. (2021). A new approach for early selection of short juvenile period in olive progenies. Sci. Hortic. 281, 109993. doi: 10.1016/j.scienta.2021.109993

CrossRef Full Text | Google Scholar

Hammami, S. B., Manrique, T., Rapoport, H. F. (2011). Cultivar-based fruit size in olive depends on different tissue and cellular processes throughout growth. Sci. Hortic. 130 (2), 445–451. doi: 10.1016/j.scienta.2011.07.018

CrossRef Full Text | Google Scholar

Hartmann, H. (1953). Effect of winter chilling on fruitfulness and vegetative growth in the olive. Proc. Am. Soc Hortic. Sci. 62, 184–190.

Google Scholar

Hartmann, H. T., Porlingis, I. (1957). Effect of different amounts of winter chilling on fruitfulness of several olive varieties. Bot. Gaz. 119 (2), 102–104. doi: 10.1086/335969

CrossRef Full Text | Google Scholar

Herkelrath, W. N., Miller, E. E., Gardner, W. R. (1977). Water uptake by plants: II. The root contact model. Soil Sci. Soc. Am. J. 41 (6), 1039–1043. doi: 10.2136/sssaj1977.03615995004100060004x

CrossRef Full Text | Google Scholar

Herrick, J. D., Thomas, R. B. (2001). No photosynthetic down-regulation in sweetgum trees (Liquidambar styraciflua L.) after three years of CO₂ enrichment at the Duke Forest FACE experiment. Plant Cell Environ. 24 (1), 53–64. doi: 10.1046/j.1365-3040.2001.00652.x

CrossRef Full Text | Google Scholar

Huang, Y., Yu, Y., Zhang, W., Sun, W., Liu, S., Jiang, J., et al. (2009). Agro-C: a biogeophysical model for simulating the carbon budget of agroecosystems. Agric. For. Meteorol. 149 (1), 106–129. doi: 10.1016/j.agrformet.2008.07.013

CrossRef Full Text | Google Scholar

Iniesta, F., Testi, L., Orgaz, F., Villalobos, F. J. (2009). The effects of regulated and continuous deficit irrigation on the water use, growth and yield of olive trees. Eur. J. Agron. 30, 258–265. doi: 10.1016/j.eja.2008.12.004

CrossRef Full Text | Google Scholar

IPCC (2021). Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. Eds. Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S. L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M. I., Huang, M., Leitzell, K., Lonnoy, E., Matthews, J. B. R., Maycock, T. K., Waterfield, T., Yelekçi, O., Yu, R., Zhou, B. (Cambridge, UK and New York, USA: Cambridge University Press). doi: 10.1017/9781009157896

CrossRef Full Text | Google Scholar

Jones, J. W., Antle, J. M., Basso, B., Boote, K. J., Conant, R. T., Foster, I., et al. (2017). Brief history of agricultural systems modeling. Agr. Syst. 155, 240–254. doi: 10.1016/j.agsy.2016.05.014

CrossRef Full Text | Google Scholar

Keller, M. (2010). Managing grapevines to optimise fruit development in a challenging environment: a climate change primer for viticulturists. Aust. J. Grape. Wine R. 16, 56–69. doi: 10.1111/j.1755-0238.2009.00077.x

CrossRef Full Text | Google Scholar

Kostelenos, G., Kiritsakis, A. (2017). “Olive tree history and evolution,” in Olives and Olive Oil as Functional Foods: Bioactivity, Chemistry and Processing. Eds. Shahidi, F., Kiritsakis, A. (New Dehli, India: Wiley), 1–12. doi: 10.1002/9781119135340.ch1

CrossRef Full Text | Google Scholar

Koubouris, G. C., Kavroulakis, N., Metzidakis, I. T., Vasilakakis, M. D., Sofo, A. (2015). Ultraviolet-B radiation or heat cause changes in photosynthesis, antioxidant enzyme activities and pollen performance in olive tree. Photosynthetica 53, 279–287. doi: 10.1007/s11099-015-0102-9

CrossRef Full Text | Google Scholar

Koubouris, G. C., Metzidakis, I. T., Vasilakakis, M. D. (2009). Impact of temperature on olive (Olea europaea L.) pollen performance in relation to relative humidity and genotype. Env. Exp. Bot. 67, 209–214. doi: 10.1016/j.envexpbot.2009.06.002

CrossRef Full Text | Google Scholar

Lavee, S. (2007). Biennial bearing in olive (Olea europaea). Annales. Ser. Hist. Naturalis 17 (1), 101–112.

Google Scholar

Lavee, S. (2015). Alternate bearing in olive initiated by abiotic induction leading to biotic responses. Adv. Hortic. Sci. 29 (4), 213–220. doi: 10.13128/ahs-22742

CrossRef Full Text | Google Scholar

Lavee, S., Nashef, M., Wodner, M., Harshemesh, H. (1990). The effect of complementary irrigation added to old olive trees (Olea europaea L.) cv. Souri on fruit characteristics, yield and oil production. Adv. Hortic. Sci. 4, 135–138.

Google Scholar

Lavee, S., Rallo, L., Rapoport, H. F., Troncoso, A. (1996). The floral biology of the olive: effect of flower number, type and distribution on fruitset. Sci. Hortic. 66 (3-4), 149–158. doi: 10.1016/S0304-4238(96)00941-7

CrossRef Full Text | Google Scholar

Ledo, A., Paul, K. I., Burslem, D. F., Ewel, J. J., Barton, C., Battaglia, M., et al. (2018). Tree size and climatic water deficit control root to shoot ratio in individual trees globally. New Phytol. 217 (1), 8–11. doi: 10.1111/nph.14863

PubMed Abstract | CrossRef Full Text | Google Scholar

León, L., de la Rosa, R., Barranco, D., Rallo, L. (2007). Breeding for early bearing in olive. HortScience 42 (3), 499–502. doi: 10.21273/HORTSCI.42.3.499

CrossRef Full Text | Google Scholar

Leuning, R. (1995). A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant Cell Environ. 18 (4), 339–355. doi: 10.1111/j.1365-3040.1995.tb00370.x

CrossRef Full Text | Google Scholar

Lobet, G., Couvreur, V., Meunier, F., Javaux, M., Draye, X. (2014). Plant water uptake in drying soils. Plant Physiol. 164 (4), 1619–1627. doi: 10.1104/pp.113.233486

PubMed Abstract | CrossRef Full Text | Google Scholar

Longobardi, A., Villani, P. (2010). Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 30 (10), 1538–1546. doi: 10.1002/joc.2001

CrossRef Full Text | Google Scholar

López-Bernal, Á., García-Tejera, O., Testi, L., Orgaz, F., Villalobos, F. J. (2015b). Low winter temperatures induce a disturbance of water relations in field olive trees. Trees 29, 1247–1257. doi: 10.1007/s00468-015-1204-5

CrossRef Full Text | Google Scholar

López-Bernal, Á., Garcia-Tejera, O., Testi, L., Orgaz, F., Villalobos, F. J. (2020a). Studying and modelling winter dormancy in olive trees. Agric. For. Meteorol. 280, 107776. doi: 10.1016/j.agrformet.2019.107776

CrossRef Full Text | Google Scholar

López-Bernal, Á., Garcia-Tejera, O., Testi, L., Villalobos, F. J. (2020b). Genotypic variability in radial resistance to water flow in olive roots and its response to temperature variations. Tree Physiol. 40 (4), 445–453. doi: 10.1093/treephys/tpaa010

PubMed Abstract | CrossRef Full Text | Google Scholar

López-Bernal, Á., Garcia-Tejera, O., Testi, L., Villalobos, F. J. (2023). Modelling the impacts of cover crop management strategies on the water use, carbon exchange and yield of olive orchards. J. Forestry Res. 34, 283–295. doi: 10.1007/s11676-022-01570-6

CrossRef Full Text | Google Scholar

López-Bernal, Á., Garcia-Tejera, O., Vega, V. A., Hidalgo, J. C., Testi, L., Orgaz, F., et al. (2015a). Using sap flow measurements to estimate net assimilation in olive trees under different irrigation regimes. Irrig. Sci. 33, 357–366. doi: 10.1007/s00271-015-0471-7

CrossRef Full Text | Google Scholar

López-Bernal, Á., Morales, A., Garcia-Tejera, O., Testi, L., Orgaz, F., De Melo-Abreu, J. P., et al. (2018). OliveCan: a process-based model of development, growth and yield of olive orchards. Front. Plant Sci. 9. doi: 10.3389/fpls.2018.00632

PubMed Abstract | CrossRef Full Text | Google Scholar

Lorite, I. J., Gabaldon-Leal, C., Ruiz-Ramos, M., Belaj, A., de la Rosa, R., Leon, L., et al. (2018). Evaluation of olive response and adaptation strategies to climate change under semi-arid conditions. Agric. Water Manage. 204, 247–261. doi: 10.1016/j.agwat.2018.04.008

CrossRef Full Text | Google Scholar

Luedeling, E., Schiffers, K., Fohrmann, T., Urbach, C. (2021). PhenoFlex - an integrated model to predict spring phenology in temperate fruit trees. Agric. For. Meteorol. 307, 108491. doi: 10.1016/j.agrformet.2021.108491

CrossRef Full Text | Google Scholar

Mairech, H., López-Bernal, Á., Moriondo, M., Dibari, C., Regni, L., Proietti, P., et al. (2020). Is new olive farming sustainable? A spatial comparison of productive and environmental performances between traditional and new olive orchards with the model OliveCan. Agric. Syst. 181, 102816. doi: 10.1016/j.agsy.2020.102816

CrossRef Full Text | Google Scholar

Mairech, H., López-Bernal, Á., Moriondo, M., Dibari, C., Regni, L., Proietti, P., et al. (2021). Sustainability of olive growing in the Mediterranean area under future climate scenarios: Exploring the effects of intensification and deficit irrigation. Eur. J. Agron. 129, 126319. doi: 10.1016/j.eja.2021.126319

CrossRef Full Text | Google Scholar

Malik, N. S., Bradford, J. M. (2005). Flowering and fruiting in ‘Arbequina’ olives in subtropical climates where olives normally remain vegetative. Int. J. Fruit Sci. 5 (4), 47–56. doi: 10.1300/J492v05n04_06

CrossRef Full Text | Google Scholar

Mariscal, M. J., Orgaz, F., Villalobos, F. J. (2000a). Radiation-use efficiency and dry matter partitioning of a young olive (Olea europaea) orchard. Tree Physiol. 20, 65–72. doi: 10.1093/treephys/20.1.65

PubMed Abstract | CrossRef Full Text | Google Scholar

Mariscal, M. J., Orgaz, F., Villalobos, F. J. (2000b). Modelling and measurement of radiation interception by olive canopies. Agric. For. Meteorol. 100 (2-3), 183–197. doi: 10.1016/S0168-1923(99)00137-9

CrossRef Full Text | Google Scholar

Marra, F. P., Macaluso, L., Marino, G., Caruso, T. (2018). Predicting olive flowering phenology with phenoclimatic models. Acta Hortic. 1229, 189–194. doi: 10.17660/ActaHortic.2018.1229.29

CrossRef Full Text | Google Scholar

McCree, K. (1970). “An equation for the rate of respiration of white clover plants grown under controlled conditions,” in Prediction and measurement of photosynthetic productivity. Ed. Setlik, I. (Wageningen, The Netherlands: Pudoc), 221–229.

Google Scholar

Medina-Alonso, M. G., Navas, J. F., Cabezas, J. M., Weiland, C. M., Ríos-Mesa, D., Lorite, I. J., et al. (2020). Differences on flowering phenology under Mediterranean and Subtropical environments for two representative olive cultivars. Env. Exp. Bot. 180, 104239. doi: 10.1016/j.envexpbot.2020.104239

CrossRef Full Text | Google Scholar

Medlyn, B. E. (2004). “A MAESTRO retrospective,” in Forests at the Land–Atmosphere Interface. Eds. Mencuccini, M., Grace, J., Moncrieff, J., McNaughton, K. G. (Wallingford, UK: CAB International), 105–121. doi: 10.1079/9780851996776.0105

CrossRef Full Text | Google Scholar

Medlyn, B. E., Badeck, F. W., De Pury, D. G. G., Barton, C. V. M., Broadmeadow, M., Ceulemans, R., et al. (1999). Effects of elevated [CO₂] on photosynthesis in European forest species: a meta-analysis of model parameters. Plant Cell Environ. 22 (12), 1475–1495. doi: 10.1046/j.1365-3040.1999.00523.x

CrossRef Full Text | Google Scholar

Miserere, A., Searles, P. S., Manchó, G., Maseda, P. H., Rousseaux, M. C. (2019). Sap flow responses to warming and fruit load in young olive trees. Front. Plant Sci. 10. doi: 10.3389/fpls.2019.01199

PubMed Abstract | CrossRef Full Text | Google Scholar

Monselise, P. S., Goldschmidt, E. E. (1982). Alternate bearing in fruit trees. Hortic. Rev. 4, 128–173. doi: 10.1002/9781118060773.ch5

CrossRef Full Text | Google Scholar

Monteith, J. L. (1977). Climate and the efficiency of crop production in Britain. Philos. T. R. Soc B. 281 (980), 277–294. doi: 10.1098/rstb.1977.0140

CrossRef Full Text | Google Scholar

Morales, A., Kaiser, E., Yin, X., Harbinson, J., Molenaar, J., Driever, S. M., et al. (2018). Dynamic modelling of limitations on improving leaf CO₂ assimilation under fluctuating irradiance. Plant Cell Environ. 41 (3), 589–604. doi: 10.1111/pce.13119

PubMed Abstract | CrossRef Full Text | Google Scholar

Morales, A., Leffelaar, P. A., Testi, L., Orgaz, F., Villalobos, F. J. (2016). A dynamic model of potential growth of olive (Olea europaea L.) orchards. Eur. J. Agron. 74, 93–102. doi: 10.1016/j.eja.2015.12.006

CrossRef Full Text | Google Scholar

Morales, A., Villalobos, F. J. (2023). Using machine learning for crop yield prediction in the past or the future. Front. Plant Sci. 14. doi: 10.3389/fpls.2023.1128388

PubMed Abstract | CrossRef Full Text | Google Scholar

Moriana, A., Villalobos, F. J., Fereres, E. (2002). Stomatal and photosynthetic responses of olive (Olea europaea L.) leaves to water deficits. Plant Cell Environ. 25 (3), 395–405. doi: 10.1046/j.0016-8025.2001.00822.x

CrossRef Full Text | Google Scholar

Moriondo, M., Ferrise, R., Trombi, G., Brilli, L., Dibari, C., Bindi, M. (2015). Modelling olive trees and grapevines in a changing climate. Environ. Modell. Soft. 72, 387–401. doi: 10.1016/j.envsoft.2014.12.016

CrossRef Full Text | Google Scholar

Moriondo, M., Leolini, L., Brilli, L., Dibari, C., Tognetti, R., Giovannelli, A., et al. (2019). A simple model simulating development and growth of an olive grove. Eur. J. Agron. 105, 29–145. doi: 10.1016/j.eja.2019.02.002

CrossRef Full Text | Google Scholar

Nardino, M., Pernice, F., Rossi, F., Georgiadis, T., Facini, O., Motisi, A., et al. (2013). Annual and monthly carbon balance in an intensively managed Mediterranean olive orchard. Photosynthetica 51, 63–74. doi: 10.1007/s11099-012-0079-6

CrossRef Full Text | Google Scholar

Navas-Lopez, J. F., León, L., Trentacoste, E. R., de la Rosa, R. (2019). Multi-environment evaluation of oil accumulation pattern parameters in olive. Plant Physiol. Bioch. 139, 485–494. doi: 10.1016/j.plaphy.2019.04.016

CrossRef Full Text | Google Scholar

Nieto, O. M., Castro, J., Fernández, E., Smith, P. (2010). Simulation of soil organic carbon stocks in a Mediterranean olive grove under different soil-management systems using the RothC model. Soil Use Manage. 26 (2), 118–125. doi: 10.1111/j.1475-2743.2010.00265.x

CrossRef Full Text | Google Scholar

North, G. B., Nobel, P. S. (1992). Drought-induced changes in hydraulic conductivity and structure in roots of Ferocactus acanthodes and Opuntia ficus-indica. New Phytol. 120 (1), 9–19. doi: 10.1111/j.1469-8137.1992.tb01053.x

CrossRef Full Text | Google Scholar

North, G. B., Nobel, P. S. (1997). Root-soil contact for the desert succulent Agave deserti in wet and drying soil. New Phytol. 135 (1), 21–29. doi: 10.1046/j.1469-8137.1997.00620.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Northrup, D. L., Basso, B., Wang, M. Q., Morgan, C. L., Benfey, P. N. (2021). Novel technologies for emission reduction complement conservation agriculture to achieve negative emissions from row-crop production. P. Natl. Acad. Sci. 118 (28), e2022666118. doi: 10.1073/pnas.2022666118

CrossRef Full Text | Google Scholar

Orgaz, F., Testi, L., Villalobos, F. J., Fereres, E. (2006). Water requirements of olive orchards–II: determination of crop coefficients for irrigation scheduling. Irrig. Sci. 24, 77–84. doi: 10.1007/s00271-005-0012-x

CrossRef Full Text | Google Scholar

Perdikis, D., Garantonakis, N., Giatropoulos, A., Paraskevopoulos, A., Lykouressis, D., Kitsis, P. (2009). Damage evaluation of Rhynchites cribripennis (Col., Attelabidae) in olive fruits. J. Appl. Entomol. 133 (7), 512–517. doi: 10.1111/j.1439-0418.2009.01394.x

CrossRef Full Text | Google Scholar

Pérez-Priego, O., Testi, L., Kowalski, A. S., Villalobos, F. J., Orgaz, F. (2014). Aboveground respiratory CO₂ effluxes from olive trees (Olea europaea L.). Agrofor. Syst. 88, 245–255. doi: 10.1007/s10457-014-9672-y

CrossRef Full Text | Google Scholar

Ponti, L., Gutierrez, A. P., Basso, B., Neteler, M., Ruti, P. M., Dell’Aquila, A., et al. (2013). Olive agroecosystems in the mediterranean basin: multitrophic analysis of climate effects with process-based representation of soil water balance. Proc. Environ. Sci. 19, 122–131. doi: 10.1016/j.proenv.2013.06.014

CrossRef Full Text | Google Scholar

Ponti, L., Gutierrez, A. P., Ruti, P. M., Dell’Aquila, A. (2014). Fine-scale ecological and economic assessment of climate change on olive in the Mediterranean Basin reveals winners and losers. P. Natl. Acad. Sci. 111, 5598–5603. doi: 10.1073/pnas.1314437111

CrossRef Full Text | Google Scholar

Pope, K. S., Da Silva, D., Brown, P. H., DeJong, T. M. (2014). A biologically based approach to modeling spring phenology in temperate deciduous trees. Agric. For. Meteorol. 198, 15–23. doi: 10.1016/j.agrformet.2014.07.009

CrossRef Full Text | Google Scholar

Ramos, A., Rapoport, H. F., Cabello, D., Rallo, L. (2018). Chilling accumulation, dormancy release temperature, and the role of leaves in olive reproductive budburst: Evaluation using shoot explants. Sci. Hortic. 231, 241–252. doi: 10.1016/j.scienta.2017.11.003

CrossRef Full Text | Google Scholar

Rapoport, H. F., Hammami, S. B., Martins, P., Pérez-Priego, O., Orgaz, F. (2012). Influence of water deficits at different times during olive tree inflorescence and flower development. Environ. Exp. Bot. 77, 227–233. doi: 10.1016/j.envexpbot.2011.11.021

CrossRef Full Text | Google Scholar

Raupach, M. R. (1994). Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Bound. Layer Meteorol. 71, 211–216. doi: 10.1007/BF00709229

CrossRef Full Text | Google Scholar

Richardson, E. A., Seeley, S. D., Walker, D. R. (1974). A model for estimating the completion of rest for ‘Red haven’ and ‘Elberta’ peach trees. HortScience 9 (4), 331–332. doi: 10.21273/HORTSCI.9.4.331

CrossRef Full Text | Google Scholar

Rodriguez-Dominguez, C. M., Brodribb, T. J. (2020). Declining root water transport drives stomatal closure in olive under moderate water stress. New Phytol. 225 (1), 126–134. doi: 10.1111/nph.16177

PubMed Abstract | CrossRef Full Text | Google Scholar

Rojo, J., Rapp, A., Lara, B., Fernández-González, F., Pérez-Badia, R. (2015). Effect of land uses and wind direction on the contribution of local sources to airborne pollen. Sci. Total Environ. 538, 672–682. doi: 10.1016/j.scitotenv.2015.08.074

PubMed Abstract | CrossRef Full Text | Google Scholar

Romero, P., Castro, G., Gómez, J. A., Fereres, E. (2007). Curve number values for olive orchards under different soil management. Soil Sci. Soc Am. J. 71 (6), 1758–1769. doi: 10.2136/sssaj2007.0034

CrossRef Full Text | Google Scholar

Rondanini, D. P., Castro, D. N., Searles, P. S., Rousseaux, M. C. (2014). Contrasting patterns of fatty acid composition and oil accumulation during fruit growth in several olive varieties and locations in a non-Mediterranean region. Eur. J. Agron. 52, 237–246. doi: 10.1016/j.eja.2013.09.002

CrossRef Full Text | Google Scholar

Rosati, A., Paoletti, A., Al Hariri, R., Famiani, F. (2018). Fruit production and branching density affect shoot and whole-tree wood to leaf biomass ratio in olive. Tree Physiol. 38 (9), 1278–1285. doi: 10.1093/treephys/tpy009

PubMed Abstract | CrossRef Full Text | Google Scholar

Sánchez-Estrada, A., Cuevas, J. (2018). ‘Arbequina’ olive is self-incompatible. Sci. Hortic. 230, 50–55. doi: 10.1016/j.scienta.2017.11.018

CrossRef Full Text | Google Scholar

Simolo, C., Brunetti, M., Maugeri, M., Nanni, T. (2014). Increasingly warm summers in the Euro–Mediterranean zone: mean temperatures and extremes. Reg. Environ. Change 14, 1825–1832. doi: 10.1007/s10113-012-0373-7

CrossRef Full Text | Google Scholar

Šimunek, J., Van Genuchten, M. T., Šejna, M. (2012). HYDRUS: Model use, calibration, and validation. Transac ASABE 55 (4), 1263–1274. doi: 10.13031/2013.42239

CrossRef Full Text | Google Scholar

Soda, N., Ephrath, J. E., Dag, A., Beiersdorf, I., Presnov, E., Yermiyahu, U., et al. (2017). Root growth dynamics of olive (Olea europaea L.) affected by irrigation induced salinity. Plant Soil 411, 305–318. doi: 10.1007/s11104-016-3032-9

CrossRef Full Text | Google Scholar

Sorgonà, A., Proto, A. R., Abenavoli, L. M., Di Iorio, A. (2018). Spatial distribution of coarse root biomass and carbon in a high-density olive orchard: effects of mechanical harvesting methods. Trees 32, 919–931. doi: 10.1007/s00468-018-1686-z

CrossRef Full Text | Google Scholar

Steudle, E., Peterson, C. A. (1998). How does water get through roots? J. Exp. Bot. 49 (322), 775–788. doi: 10.1093/jxb/49.322.775

CrossRef Full Text | Google Scholar

Stewart, J. B. (1988). Modelling surface conductance of pine forest. Agric. For. Meteorol. 43 (1), 19–35. doi: 10.1016/0168-1923(88)90003-2

CrossRef Full Text | Google Scholar

Stirzaker, R. J., Passioura, J. B. (1996). The water relations of the root-soil interface. Plant Cell Environ. 19 (2), 201–208. doi: 10.1111/j.1365-3040.1996.tb00241.x

CrossRef Full Text | Google Scholar

Stöckle, C. O., Donatelli, M., Nelson, R. (2003). CropSyst, a cropping systems simulation model. Eur. J. Agron. 18 (3-4), 289–307. doi: 10.1016/S1161-0301(02)00109-0

CrossRef Full Text | Google Scholar

Stutte, W., Martin, G. C. (1986). Effect of killing the seed on return to bloom of olive. Sci. Hortic. 29, 107–113. doi: 10.1016/0304-4238(86)90036-1

CrossRef Full Text | Google Scholar

Tanner, C. B., Sinclair, T. R. (1983). “Efficient water use in crop production: research or re-search?,” in Limitations to Efficient Water Use in Crop Production. Eds. Taylor, H. M., Jordan, W. R., Sinclair, T. R. (Madison, WI, USA: American Society of Agronomy), 1–27. doi: 10.2134/1983.limitationstoefficientwateruse.c1

CrossRef Full Text | Google Scholar

Testi, L., Villalobos, F. J., Orgaz, F., Fereres, E. (2006). Water requirements of olive orchards: I simulation of daily evapotranspiration for scenario analysis. Irrig. Sci. 24, 69–76. doi: 10.1007/s00271-005-0011-y

CrossRef Full Text | Google Scholar

Tognetti, R., Sebastiani, L., Vitagliano, C., Raschi, A., Minnocci, A. (2001). Responses of two olive tree (Olea europaea L.) cultivars to elevated CO₂ concentration in the field. Photosynthetica 39, 403–410. doi: 10.1023/A:1015186411662

CrossRef Full Text | Google Scholar

Torres, M., Pierantozzi, P., Searles, P., Rousseaux, M. C., Garcia-Inza, G., Miserere, A., et al. (2017). Olive cultivation in the southern hemisphere: flowering, water requirements and oil quality responses to new crop environments. Front. Plant Sci. 8. doi: 10.3389/fpls.2017.01830

PubMed Abstract | CrossRef Full Text | Google Scholar

Trentacoste, E. R., Puertas, C. M., Sadras, V. O. (2010). Effect of fruit load on oil yield components and dynamics of fruit growth and oil accumulation in olive (Olea europaea L.). Eur. J. Agron. 32 (4), 249–254. doi: 10.1016/j.eja.2010.01.002

CrossRef Full Text | Google Scholar

Trentacoste, E. R., Puertas, C. M., Sadras, V. O. (2012). Modelling the intraspecific variation in the dynamics of fruit growth, oil and water concentration in olive (Olea europaea L.). Eur. J. Agron. 38, 83–93. doi: 10.1016/j.eja.2012.01.001

CrossRef Full Text | Google Scholar

Tuzet, A., Perrier, A., Leuning, R. (2003). A coupled model of stomatal conductance, photosynthesis and transpiration. Plant Cell Environ. 26 (7), 1097–1116. doi: 10.1046/j.1365-3040.2003.01035.x

CrossRef Full Text | Google Scholar

Van der Velde, M., van Diepen, C. A., Baruth, B. (2019). The European crop monitoring and yield forecasting system: Celebrating 25 years of JRC MARS Bulletins. Agric. Syst. 168, 56–57. doi: 10.1016/j.agsy.2018.10.003

CrossRef Full Text | Google Scholar

Van Klompenburg, T., Kassahun, A., Catal, C. (2020). Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agr. 177, 105709. doi: 10.1016/j.compag.2020.105709

CrossRef Full Text | Google Scholar

Vanwalleghem, T., Amate, J. I., de Molina, M. G., Fernández, D. S., Gómez, J. A. (2011). Quantifying the effect of historical soil management on soil erosion rates in Mediterranean olive orchards. Agric. Ecosyst. Environ. 142 (3-4), 341–351. doi: 10.1016/j.agee.2011.06.003

CrossRef Full Text | Google Scholar

Vercambre, G., Pagès, L., Doussan, C., Habib, R. (2003). Architectural analysis and synthesis of the plum tree root system in an orchard using a quantitative modelling approach. Plant Soil 251 (1), 1–11. doi: 10.1023/A:1022961513239

CrossRef Full Text | Google Scholar

Verstraeten, W. W., Veroustraete, F., Feyen, J. (2006). On temperature and water limitation of net ecosystem productivity: Implementation in the C-Fix model. Ecol. Model. 199 (1), 4–22. doi: 10.1016/j.ecolmodel.2006.06.008

CrossRef Full Text | Google Scholar

Villalobos, F. J., Hall, A. J., Ritchie, J. T., Orgaz, F. (1996). OILCROP-SUN: A development, growth, and yield model of the sunflower crop. Agron. J. 88 (3), 403–415. doi: 10.2134/agronj1996.00021962008800030008x

CrossRef Full Text | Google Scholar

Villalobos, F. J., Orgaz, F., Testi, L., Fereres, E. (2000). Measurement and modeling of evapotranspiration of olive (Olea europaea L.) orchards. Eur. J. Agron. 13 (2-3), 155–163. doi: 10.1016/S1161-0301(00)00071-X

CrossRef Full Text | Google Scholar

Villalobos, F. J., Testi, L., Hidalgo, J., Pastor, M., Orgaz, F. (2006). Modelling potential growth and yield of olive (Olea europaea L.) canopies. Eur. J. Agron. 24 (4), 296–303. doi: 10.1016/j.eja.2005.10.008

CrossRef Full Text | Google Scholar

Villalobos, F. J., Testi, L., Orgaz, F., Garcia-Tejera, O., López-Bernal, Á., González-Dugo, M. V., et al. (2013). Modelling canopy conductance and transpiration of fruit trees in Mediterranean areas: a simplified approach. Agric. For. Meteorol. 171, 93–103. doi: 10.1016/j.agrformet.2012.11.010

CrossRef Full Text | Google Scholar

Viola, F., Noto, L. V., Cannarozzo, M., La Loggia, G., Porporato, A. (2012). Olive yield as a function of soil moisture dynamics. Ecohydrology 5, 99–107. doi: 10.1002/eco.208

CrossRef Full Text | Google Scholar

White, J. W., Hoogenboom, G., Kimball, B. A., Wall, G. W. (2011). Methodologies for simulating impacts of climate change on crop production. Field Crop Res. 124 (3), 357–368. doi: 10.1016/j.fcr.2011.07.001

CrossRef Full Text | Google Scholar