An efficient genomic prediction method without the direct inverse of the genomic relationship matrix

GBLUP, the most widely used genomic prediction (GP) method, consumes large and increasing amounts of computational resources as the training population size increases due to the inverse of the genomic relationship matrix (GRM). Therefore, in this study, we developed a new genomic prediction method (RHEPCG) that avoids the direct inverse of the GRM by combining randomized Haseman–Elston (HE) regression (RHE-reg) and a preconditioned conjugate gradient (PCG). The simulation results demonstrate that RHEPCG, in most cases, not only achieves similar predictive accuracy with GBLUP but also significantly reduces computational time. As for the real data, RHEPCG shows similar or better predictive accuracy for seven traits of the Arabidopsis thaliana F2 population and four traits of the Sorghum bicolor RIL population compared with GBLUP. This indicates that RHEPCG is a practical alternative to GBLUP and has better computational efficiency.

Introduction

Currently, genomic prediction (GP) has been widely applied to many species, such as dairy cattle, dairy sheep, maize, and wheat (Pszczola et al., 2011; Duchemin et al., 2012; Crossa et al., 2014). For example, significant achievements have been made in the genetic improvement of dairy cattle via GP in many countries, such as the United States, Australia, Canada, New Zealand, and France (Hayes et al., 2009; Winkelman et al., 2015; García-Ruiz et al., 2016; Weller et al., 2017). Moreover, GP helps to optimize the breeding procedure when used with many other breeding technologies. For example, it can accelerate the selection of superior pure lines from the large numbers of those generated by doubled haploid (DH) technology, which is otherwise a significant problem in terms of the consumption of time and money (Wang et al., 2020). Additionally, GP can rapidly increase the frequencies of favorable alleles when combined with genome editing (GE) (Jenko et al., 2015; Bastiaansen et al., 2018).

Many computational methods of GP have been proposed and GBLUP is the most widely used (Meuwissen et al., 2001; Daetwyler et al., 2013; Mouresan et al., 2019). For conventional GBLUP, restricted maximum likelihood (REML) is often used to estimate heritability, and its computational complexity is cubic of the training population size (Xu et al., 2014). The fact that the inverse of the genomic relationship matrix (GRM) is essential when estimating the heritability in REML and calculating the best linear unbiased prediction (BLUP) contributes to the decrease of the computational efficiency of GBLUP when the size of the training population increases. To improve computational efficiency, methods such as IBS-based HE regression, algorithm for proven and young (APY), updating the inverse, recursive algorithm, spectral decomposition, and the preconditioned conjugate gradient (PCG) algorithm are employed (Kang et al., 2008; Legarra and Misztal, 2008; Misztal et al., 2009; Endelman, 2011; Faux et al., 2012; Meyer et al., 2013; Chen, 2014; Misztal, 2016; Liu and Chen, 2017; Masuda et al., 2017; Vandenplas et al., 2018; Vandenplas et al., 2020). In particular, PCG solves mixed model equations (MMEs) via iteration instead of by directly inversing the GRM. Recently, we proposed a fast GP method (SHEAPY) combining randomized Haseman–Elston regression (RHE-reg) and a modified APY (Liu and Chen, 2022). In the SHEAPY, RHE-reg is used to estimate heritability because of its high computational speed. In this study, we continue to combine it with PCG, calculating marker values to develop a new GP method (RHEPCG), which can significantly improve computational efficiency without the direct inverse of GRM.

Materials and methods

Genetic model and the linear system of MMEs

Herein, we only focus on additive effects, and the basic model is described as:

$\begin{array}{ll}\mathbf{y}=X\theta +Zu+e& \text{, (1)}\end{array}$

in which  y is the n×1 vector of the standardized phenotypic values; θ is a fixed effect; X is the n×1 vector of the incidence; Z is the n×m matrix of the standardized genotypic values; u is the m×1 vector of SNP marker effects; and e is the n × 1 vector of the residual error.

On the basis of the above genetic model of additive effect, the linear system of MMEs was as follows:

$\begin{array}{ll}\mathbf{\left[}\begin{array}{cc}{X}^{T}X& X^{T}Z\\ Z^{T}X& Z^{T}Z+I\frac{{\sigma }_e^2}{{\sigma }_g^2}\end{array}\mathbf{\right]}\mathbf{\left[}\begin{array}{c}\widehat{\theta }\\ \widehat{u}\end{array}\mathbf{\right]}=\mathbf{\left[}\begin{array}{c}{X}^{T}y\\ Z^{T}y\end{array}\mathbf{\right]}& \text{, (2)}\end{array}$

in which I is the identity matrix, ${\sigma }_g^2$ is the variance of SNP marker effects, and ${\sigma }_e^2$ is the residual variance.

To solve MMEs, randomized HE-reg based on IBS was used to estimate heritability, which was then introduced into Equation 2 with residual variance. Then, PCG was used to solve Equation 2 to obtain marker values.

Estimating heritability via randomized HE-reg based on IBS

IBS-based RHE regression is a method of moment that can reduce computational time and memory to $\mathcal{O}\left(\frac{nmk}{\max \left(lo{g}_3^{\left(n\right)}lo{g}_3^{\left(m\right)}\right)}+nm\right)$ and O(nm) , respectively ( n , m , and k represent the number of samples, the number of markers, and the length of random vector, respectively) (Wu and Sankararaman, 2018; Liu and Chen, 2022). Here, it was used to estimate the heritability:

$\begin{array}{ll}{y}_i{y}_i=b_0+b_1{\omega }_{ij}+e& (3)\end{array}$

in which y_i and y_j represent the phenotypic values of individuals i and. from the training population; b₀ is the intercept; b₁ is the regression coefficient; is the genetic relatedness (${\omega }_{ij}=\frac{\text{ZiZj}"}{\text{m}}$) between a pair of individuals i and j; z_i and z_j are the genotype vector of individuals i and j; and is residual error. For a trait, its phenotypic variance is ${\widehat{\sigma }}_y^2=\frac{{\sum }_{i=1}^n{y}_i^2-n{\overline{y}}^2}{n-1}$, its additive genetic variance is ${\widehat{\sigma }}_g^2={\widehat{b}}_1$, and its error variance is ${\widehat{\sigma }}_e^2={\widehat{\sigma }}_y^2-{\widehat{\sigma }}_g^2$. The computational equation of ${\widehat{\sigma }}_g^2$ and ${\widehat{\sigma }}_e^2$ is described as:

$\begin{array}{ll}\left[\begin{array}{cc}tr\left[{\mathbf{\omega }}^2\right]& tr\left[\mathbf{\omega }\right]\\ tr\left[\mathbf{\omega }\right]& n\end{array}\right]\left[\begin{array}{c}{\widehat{\sigma }}_g^2\\ {\widehat{\sigma }}_e^2\end{array}\right]=\left[\begin{array}{c}{y}^{\text{T}}\mathbf{\omega }y\\ y^{\text{T}}y\end{array}\right],& (4)\end{array}$

in which $\omega =\frac{Z{Z}^{\prime }}{m}$ corresponds to the genomic related matrix between individuals and $\widehat{tr\left[\omega \right]}=n$. To accelerate computational efficiency, $\widehat{tr\left[{\omega }^2\right]}$ was calculated via a randomized estimation. The equation is as below:

$\begin{array}{ll}\widehat{tr\left[{\mathbf{\omega }}^2\right]}=\frac{1}{s}\frac{1}{m^2}\sum _{s=1}^S({\mathbf{w}}_{\mathbf{s}}^{\text{'}}\mathbf{Z}{\mathbf{Z}}^T)\left(\mathbf{Z}{\mathbf{Z}}^T{\mathbf{w}}_{\mathbf{s}}\right).& (5)\end{array}$

In the equation, S represents the rounds of randomization implemented, and was set as 5 throughout the study; each entry of w_s comes from a standard normal distribution N (0,1).

Preconditioned conjugate gradient (PCG) algorithm

When the MMEs are described as Ax = b, in which A is the coefficient matrix, x is the vector of solutions, and b is the right-hand side, the PCG is used to solve the linear system of MMEs and compute marker effects. As it does not need to invert GRM like conventional methods, a much higher efficiency can be achieved (Vandenplas et al., 2019). Its code is as follows (Tsuruta et al., 2001; Vandenplas et al., 2018):

When n = 0,

x₀=1 ; e₀=0 ;  α₀=1 ( 1 is a vector of containing 1.);

$\begin{array}{ll}{r}_0=b-A{x}_0& \text{;}\end{array}$

$\begin{array}{ll}{p}_0=M^{-1}{r}_0& \text{;}\end{array}$

When n=1, 2…..,

$\begin{array}{ll}{w}_n=M^{-1}{p}_{n-1}& \text{;}\end{array}$

$\begin{array}{ll}{\alpha }_n=p_{n-1}^{\text{'}}{w}_n& \text{;}\end{array}$

$\begin{array}{ll}{\beta }_n=\raisebox{1ex}{${\alpha }_n$}\!\left/ \!\raisebox{-1ex}{${\alpha }_{n-1}$}\right.& \text{;}\end{array}$

$\begin{array}{ll}{\alpha }_{n-1}={\alpha }_n& \text{;}\end{array}$

$\begin{array}{ll}{e}_n=w_n+e_{n-1}{\beta }_n& \text{;}\end{array}$

$\begin{array}{ll}{q}_n=A{e}_n& \text{;}\end{array}$

$\begin{array}{ll}{ϵ}_n=\raisebox{1ex}{$p_{n-1}^{\text{'}}{w}_n$}\!\left/ \!\raisebox{-1ex}{$e_n^{\text{'}}{q}_n$}\right.& \text{;}\end{array}$

$\begin{array}{ll}{x}_n=x_{n-1}+e_n{ϵ}_n& \text{;}\end{array}$

$\begin{array}{ll}{r}_n=r_{n-1}-{ϵ}_n{q}_n& (\mathrm{})\end{array}$

Until convergence.

End.

Here, $A=\left[\begin{array}{cc}{X}^{T}X& X^{T}Z\\ Z^{T}X& Z^{T}Z+I\frac{{\sigma }_e^2}{{\sigma }_g^2}\end{array}\right]$, M is the preconditioner matrix, and M = diag(A); r , p , and w are vectors, $\text{x}=\left[\begin{array}{c}\widehat{\theta }\\ \widehat{u}\end{array}\right]$, and $b=\left[\begin{array}{c}{X}^{T}y\\ Z^{T}y\end{array}\right]$. To solve MMEs, ${\widehat{\sigma }}_g^2$ via RHE regression based on IBS and ${\widehat{\sigma }}_e^2$ are introduced into A matrix.

Simulated data

The F2 population was simulated to evaluate the performance and cost time of GBLUP and RHEPCG. We simulated a chromosome with a length of 2,000 cM (the recombination rate was c between the i^th and (i+1)^th markers), and all markers in this chromosome were defined as QTL, the effects of which followed a standard normal distribution. A series of different training population sizes (1,000, 1,200, 2,000, 6,000, 10,000, 15,000, and 20,000), candidate population sizes (100, 200, 300, and 400), and heritability (0.2, 0.4, 0.6, 0.65, and 0.8) were simulated. Each simulation scenario included 10 replications.

Real data

Two sets of data (Arabidopsis thaliana and Sorghum bicolor) were used to evaluate the predictive accuracy of GBLUP and RHEPCG. (1) An A. thaliana F2 population (P15) with 434 individuals derived from a cross between Br-0 and C24 was obtained from the study by Salomé et al. It consisted of a total of 233 SNP markers and seven traits, including DTF1 (days until visible flower buds in the center of the rosette), DTF2 (days until inflorescence stem reached 1 cm in height), DTF3 (days until first open flower), RLN (rosette leaf number), CLN (cauline leaf number), TLN (total leaf number: sum of RLN and CLN), and LIR1 (leaf initiation rate [RLN/DTF1]) (Salomé et al., 2011). (2) A S. bicolor RIL population with 399 individuals derived from a cross between S. bicolor BTx623 and S. bicolor IS3620C was obtained from the study by Kong et al. It consisted of a total of 381 bins and five traits, including PH (plant height), BTF (base to flag length), FTR (flag to rachis length), ND (number of nodes), and FL (days to flowering). The phenotype data were obtained from the University of Georgia Plant Science Farm, Watkinsville, GA, USA on May 10, 2011 (Kong et al., 2018).

Implementation and computations

The GBLUP and RHEPCG were written in R language (R Core Team, 2017) and run on a server of the CentOS Linux operating system (Intel (R) Xeon (R) CPU E7-4870 @2.40GHz) with 80 CPUs and 755G memory. The RHEPCG program is available from the authors. The squared correlation coefficient (r²) between the phenotypes and the predicted genotypic values were defined as the prediction accuracy.

Results and discussion

Comparison of GBLUP and RHEPCG in simulated F2 population studies

A series of simulations of the F2 population at different levels of parameters, including training population size, candidate population size, and heritability were used to assess the estimated heritability, predictive accuracy, and consumption time of GBLUP and RHEPCG.

Table 1 shows the predictive accuracy and computational time of the GBLUP and RHEPCG at different training population sizes (1,000, 2,000, 6,000, 10,000, 15,000, and 20,000). As the training population size increased, both methods demonstrated an obvious uptrend of predictive accuracy. When the training population size was 1,000, RHEPCG was slightly better than GBLUP in predictive accuracy ( $r_{RHEPCG}^2=0.597\pm 0.007$ vs $r_{GBLUP}^2=0.541\pm 0.027$), but when the training population size was 10,000, an opposite result was achieved ($r_{GBLUP}^2=0.640\pm 0.014$ vs $r_{RHEPCG}^2=0.607\pm 0.023$). In other conditions, both methods performed similarly (for example, when a training population size was 20,000 $r_{GBLUP}^2=0.653\pm 0.017$ vs. $r_{RHEPCG}^2=0.648\pm 0.021$). With the enlargement of the training population, the predictive accuracy approximated the true heritability, which as some studies have demonstrated, is the upper bound of predictive accuracy (de los Campos et al., 2013; Liu and Chen, 2018). Meanwhile, RHEPCG was significantly faster than GBLUP (for example, when a training population size was 20,000 T_GBLUP=53666s vs T_RHEPCG=1237s ). When the training population size was 1,000, 2,000, 6,000, 10,000, 15,000, and 20,000, the computational time of GBLUP was 4, 8, 9, 15, 28, and 43 times that of RHEPCG, respectively. In other words, the larger the training population size, the more obvious the advantage of the computational efficiency of RHEPCG becomes.

TABLE 1

Table 1 Comparison of the estimated heritability, predictive accuracy, and computational time of GBLUP and RHEPCG at the different training population sizes based on 10 simulations in the Arabidopsis thaliana F2 population.

In Table 2, the predictive accuracy of both methods was similar at different candidate population sizes (100, 200, 300, and 400), which means the latter has no significant impact on the former. Table 3 shows that the predictive accuracy of GBLUP and RHEPCG increased when heritability varied from 0.2 to 0.4, 0.6, and 0.8. According to further analysis, the correlation between the estimated heritability and the predictive accuracy was 0.999 for both GBLUP and RHEPCG (P_Two−tailed=0.001 ), and our results are consistent with Daetwyler et al. (2008) in that heritability can significantly influence predictive accuracy.

TABLE 2

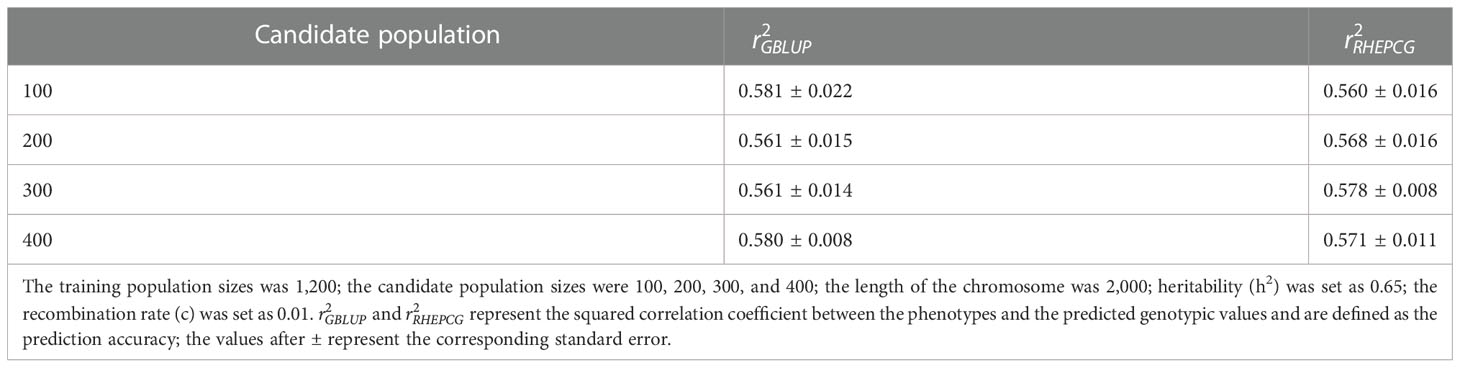
Table 2 Comparison of the predictive accuracy of GBLUP and RHEPCG at the different candidate population sizes based on 10 simulations in the Arabidopsis thaliana F2 population.

TABLE 3

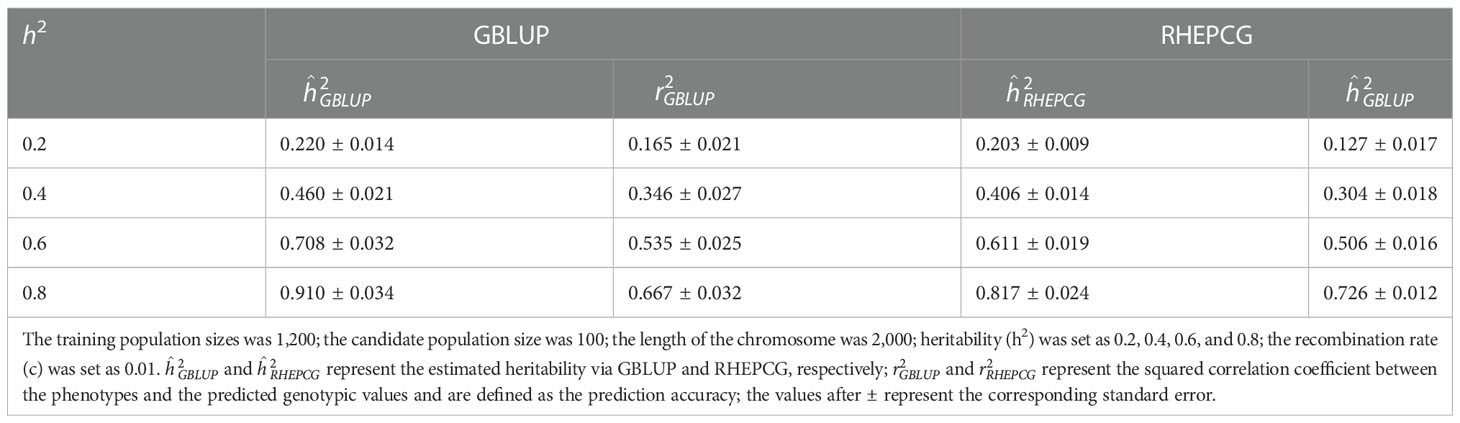
Table 3 Comparison of the estimated heritability and predictive accuracy of GBLUP and RHEPCG at different levels of heritability based on 10 simulations in the Arabidopsis thaliana F2 population.

Currently, IBS-based RHE regression is used to estimate gene-environmental heritability and multi-trait genetic correlation (Kerin and Marchini, 2020; Wu et al., 2022). Therefore, RHEPCG can also be applied to such data via the incorporation of these effects into the model in the future.

Comparison of GBLUP and RHEPCG in studies of the A. thaliana F2 and S. bicolor RIL populations

A comparison of GBLUP and RHEPCG based on seven traits of the A. thaliana F2 population was performed in this study. Table 4 shows a significant difference between the estimated heritability via GBLUP and that via RHEPCG in seven traits of A. thaliana F2 (P15). Meanwhile, the seven traits were used to evaluate the predictive accuracy of GBLUP and RHEPCG (Table 4). The two methods showed similar predictive accuracy in six traits: DTF1, DTF2, DTF3, CLN, TLN and LIR1 (for example, the predictive accuracies of DTF1 were $r_{GBLUP}^2=0.383\pm 0.017$ and $r_{RHEPCG}^2=0.368\pm 0.024$). RHEPCG was significantly better than GBLUP for RLN (the predictive accuracies of RLN were $r_{GBLUP}^2=0.555\pm 0.046$ and $r_{RHEPCG}^2=0.640\pm 0.015$).

TABLE 4

Table 4 Comparison of the predictive accuracy between GBLUP and RHEPCG in seven traits from the Arabidopsis thaliana F2 (P15) population based on 10 simulations.

In addition, the predictive accuracy of GBLUP and RHEPCG was evaluated based on five traits of the S. bicolor RIL population (Table 5). The estimated heritability of PH, BTF, FTR, and ND via GBLUP differed significantly from that via RHEPCG, and the two methods had similar predictive accuracy for PH, BTF, FTR, and FL (for example, the predictive accuracies of PH were $r_{GBLUP}^2=0.289\pm 0.011$ and $r_{RHEPCG}^2=0.257\pm 0.016$), and the predictive accuracy of GBLUP was significantly superior to that of RHEPCG for ND (the predictive accuracies of ND were $r_{GBLUP}^2=0.306\pm 0.015$ and $r_{RHEPCG}^2=0.197\pm 0.039$).

TABLE 5

Table 5 Comparison of the predictive accuracy between GBLUP and RHEPCG in five traits from the Sorghum bicolor RIL population based on 10 simulations.

These results show that GBLUP and RHEPCG have different estimated heritability in some traits of A. thaliana and S. bicolor. According to Chen (2016), strong selection can lead to differences in the estimated heritability via LMM and HE, and therefore, these traits are very likely to have undergone strong selection. In the future, we will investigate the influence of strong selection on predictive accuracy.

Conclusion

We present a new computing method of genomic prediction (RHEPCG) that does not require direct inversion of the GRM. Compared with GBLUP, it can significantly reduce computational time while maintaining predictive accuracy.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

HLL conceived and performed the study, interpreted the results, and wrote the manuscript. HL and CX interpreted the results and wrote the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the National Natural Science Foundation of China (32271984).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bastiaansen, J. W. M., Bovenhuis, H., Groenen, M. A. M., Megens, H. J., Mulder, H. A. (2018). The impact of genome editing on the introduction of monogenic traits in livestock. Genet. Selection Evol. 50, 18. doi: 10.1186/s12711-018-0389-7

CrossRef Full Text | Google Scholar

Chen, G. B. (2014). Estimating heritability of complex traits from genome-wide association studies using IBS-based haseman-elston regression. Front. Genet. 5. doi: 10.3389/fgene.2014.00107

CrossRef Full Text | Google Scholar

Chen, G. B. (2016). On the reconciliation of missing heritability for genome-wide association studies. Eur. J. Hum. Genet. 24, 1810–1816. doi: 10.1038/ejhg.2016.89

PubMed Abstract | CrossRef Full Text | Google Scholar

Crossa, J., Pérez, P., Hickey, J., Burgueño, J., Ornella, L., Cerón-Rojas, J., et al. (2014). Genomic prediction in CIMMYT maize and wheat breeding programs. Heredity 112, 48–60. doi: 10.1038/hdy.2013.16

PubMed Abstract | CrossRef Full Text | Google Scholar

Daetwyler, H. D., Calus, M. P. L., Pong-Wong, R., de los Campos, G., Hickey, J. M. (2013). Genomic prediction in animals and plants: simulation of data, validation, reporting, and benchmarking. Genetics 193, 347–365. doi: 10.1534/genetics.112.147983

PubMed Abstract | CrossRef Full Text | Google Scholar

Daetwyler, H. D., Villanueva, B., Woolliams, J. A. (2008). Accuracy of predicting the genetic risk of disease using a genome-wide approach. PLos One 3, e3395. doi: 10.1371/journal.pone.0003395

PubMed Abstract | CrossRef Full Text | Google Scholar

de los Campos, G., Vazquez, A. I., Fernando, R., Klimentidis, Y. C., Sorensen, D. (2013). Prediction of complex human traits using the genomic best linear unbiased predictor. PLos Genet. 9, e1003608. doi: 10.1371/journal.pgen.1003608

PubMed Abstract | CrossRef Full Text | Google Scholar

Duchemin, S. I., Colombani, C., Legarra, A., Baloche, G., Larroque, H., Astruc, J. M., et al. (2012). Genomic selection in the French lacaune dairy sheep breed. J. Dairy Sci. 95, 2723–2733. doi: 10.3168/jds.2011-4980

PubMed Abstract | CrossRef Full Text | Google Scholar

Endelman, J. B. (2011). Ridge regression and other kernels for genomic selection with r package rrBLUP. Plant Genome 4, 250–255. doi: 10.3835/plantgenome2011.08.0024

CrossRef Full Text | Google Scholar

Faux, P., Gengler, N., Misztal, I. (2012). A recursive algorithm for decomposition and creation of the inverse of the genomic relationship matrix. J. Dairy Sci. 95, 6093–6102. doi: 10.3168/jds.2011-5249

PubMed Abstract | CrossRef Full Text | Google Scholar

García-Ruiz, A., Cole, J. B., VanRaden, P. M., Wiggans, G. R., Ruiz-López, F. J., van Tassell, C. P. (2016). Changes in genetic selection differentials and generation intervals in US Holstein dairy cattle as a result of genomic selection. Proc. Natl. Acad. Sci. U.S.A. 113, E3995–E4004. doi: 10.1073/pnas.1519061113

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayes, B. J., Bowman, P. J., Chamberlain, A. J., Goddard, M. E. (2009). Invited review: Genomic selection in dairy cattle: Progress and challenges. J. Dairy Sci. 92, 433–443. doi: 10.3168/jds.2008-1646

PubMed Abstract | CrossRef Full Text | Google Scholar

Jenko, J., Gorjanc, G., Cleveland, M. A., Varshney, R. K., Whitelaw, C. B. A., Woolliams, J. A., et al. (2015). Potential of promotion of alleles by genome editing to improve quantitative traits in livestock breeding programs. Genet. Selection Evol. 47, 55. doi: 10.1186/s12711-015-0135-3

CrossRef Full Text | Google Scholar

Kang, H. M., Zaitlen, N. A., Wade, C. M., Kirby, A., Heckerman, D., Daly, M. J., et al. (2008). Efficient control of population structure in model organism association mapping. Genetics 178, 1709–1723. doi: 10.1534/genetics.107.080101

PubMed Abstract | CrossRef Full Text | Google Scholar

Kerin, M., Marchini, J. (2020). A non-linear regression method for estimation of gene–environment heritability. Bioinformatics 36, 5632–5639. doi: 10.1093/bioinformatics/btaa1079

PubMed Abstract | CrossRef Full Text | Google Scholar

Kong, W., Kim, C., Zhang, D., Guo, H., Tan, X., Jin, H., et al. (2018). Genotyping by sequencing of 393 Sorghum bicolor BTx6233×IS3620C recombinant inbred lines improves sensitivity and resolution of QTL detection. G3 Genes|Genomes|Genetics 8, 2563–2572. doi: 10.1534/g3.118.200173

CrossRef Full Text | Google Scholar

Legarra, A., Misztal, I. (2008). Technical note: Computing strategies in genome-wide selection. J. Dairy Sci. 91, 360–366. doi: 10.3168/jds.2007-0403

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H., Chen, G. B. (2017). A fast genomic selection approach for large genomic data. Theor. Appl. Genet. 130, 1277–1284. doi: 10.1007/s00122-017-2887-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H., Chen, G. B. (2018). A new genomic prediction method with additive-dominance effects in the least-squares framework. Heredity 121, 196–204. doi: 10.1038/s41437-018-0099-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H., Chen, G. B. (2022). A novel genomic prediction method combining randomized haseman-elston regression with a modified algorithm for proven and young for large genomic data. Crop J. 10, 550–554. doi: 10.1016/j.cj.2021.09.001

CrossRef Full Text | Google Scholar

Masuda, Y., Misztal, I., Legarra, A., Tsuruta, S., Lourenco, D. A. L., Fragomeni, B. O., et al. (2017). Technical note: Avoiding the direct inversion of the numerator relationship matrix for genotyped animals in single-step genomic best linear unbiased prediction solved with the preconditioned conjugate gradient. J. Anim. Sci. 95, 49–52. doi: 10.2527/jas.2016.0699

PubMed Abstract | CrossRef Full Text | Google Scholar

Meuwissen, T. H., Hayes, B. J., Goddard, M. E. (2001). Prediction of total genetic value using genome-wide dense marker maps. Genetics 157, 1819–1829. doi: 10.1093/genetics/157.4.1819

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, K., Tier, B., Graser, H. U. (2013). Technical note: updating the inverse of the genomic relationship matrix. J. Anim. Sci. 91, 2583–2586. doi: 10.2527/jas.2012-6056

PubMed Abstract | CrossRef Full Text | Google Scholar

Misztal, I. (2016). Inexpensive computation of the inverse of the genomic relationship matrix in populations with small effective population size. Genetics 202, 401–409. doi: 10.1534/genetics.115.182089

PubMed Abstract | CrossRef Full Text | Google Scholar

Misztal, I., Legarra, A., Aguilar, I. (2009). Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J. Dairy Sci. 92, 4648–4655. doi: 10.3168/jds.2009-2064

PubMed Abstract | CrossRef Full Text | Google Scholar

Mouresan, E. F., Selle, M., Rönnegård, L. (2019). Genomic prediction including SNP-specific variance predictors. G3 Genes|Genomes|Genetics 9, 3333–3343. doi: 10.1534/g3.119.400381

CrossRef Full Text | Google Scholar

Pszczola, M., Mulder, H. A., Calus, M. P. L. (2011). Effect of enlarging the reference population with (un)genotyped animals on the accuracy of genomic selection in dairy cattle. J. Dairy Sci. 94, 431–441. doi: 10.3168/jds.2009-2840

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team (2017). R: A language and environment for statistical computing (Vienna, Austria: R Foundation for Statistical Computing).

Google Scholar

Salomé, P. A., Bomblies, K., Laitinen, R. A. E., Yant, L., Mott, R., Weigel, D. (2011). Genetic architecture of flowering-time variation in arabidopsis thaliana. Genetics 188, 421–433. doi: 10.1534/genetics.111.126607

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsuruta, S., Misztal, I., Strandén, I. (2001). Use of preconditioned conjugate gradient algorithm as a generic solver for mixed-model equations in animal breeding applications. J. Anim. Sci. 79, 1166–1172. doi: 10.2527/2001.7951166x

PubMed Abstract | CrossRef Full Text | Google Scholar

Vandenplas, J., Calus, M. P. L., Eding, H., Vuik, C. (2019). A second-level diagonal preconditioner for single-step SNPBLUP. Genet. Selection Evol. 51, 30. doi: 10.1186/s12711-019-0472-8

CrossRef Full Text | Google Scholar

Vandenplas, J., Eding, H., Bosmans, M., Calus, M. P. L. (2020). Computational strategies for the preconditioned conjugate gradient method applied to ssSNPBLUP, with an application to a multivariate maternal model. Genet. Selection Evol. 52, 24. doi: 10.1186/s12711-020-00543-9

CrossRef Full Text | Google Scholar

Vandenplas, J., Eding, H., Calus, M. P. L., Vuik, C. (2018). Deflated preconditioned conjugate gradient method for solving single-step BLUP models efficiently. Genet. Selection Evol. 50, 51. doi: 10.1186/s12711-018-0429-3

CrossRef Full Text | Google Scholar

Wang, N., Wang, H., Zhang, A., Liu, Y., Yu, D., Hao, Z., et al. (2020). Genomic prediction across years in a maize doubled haploid breeding program to accelerate early-stage testcross testing. Theor. Appl. Genet. 133, 2869–2879. doi: 10.1007/s00122-020-03638-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Weller, J. I., Ezra, E., Ron, M. (2017). Invited review: A perspective on the future of genomic selection in dairy cattle. J. Dairy Sci. 100, 8633–8644. doi: 10.3168/jds.2017-12879

PubMed Abstract | CrossRef Full Text | Google Scholar

Winkelman, A. M., Johnson, D. L., Harris, B. L. (2015). Application of genomic evaluation to dairy cattle in new Zealand. J. Dairy Sci. 98, 659–675. doi: 10.3168/jds.2014-8560

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Burch, K. S., Ganna, A., Pajukanta, P., Pasaniuc, B., Sankararaman, S. (2022). Fast estimation of genetic correlation for biobank-scale data. Am. J. Hum. Genet. 109, 24–32. doi: 10.1016/j.ajhg.2021.11.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Sankararaman, S. (2018). A scalable estimator of SNP heritability for biobank-scale data. Bioinformatics 34, i187–i194. doi: 10.1093/bioinformatics/bty253

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, S., Zhu, D., Zhang, Q. (2014). Predicting hybrid performance in rice using genomic best linear unbiased prediction. Proc. Natl. Acad. Sci. U.S.A. 111, 12456–12461. doi: 10.1073/pnas.1413750111

PubMed Abstract | CrossRef Full Text | Google Scholar