- 1Department of Agronomy, Purdue University, West Lafayette, IN, United States
- 2Department of Animal Sciences, Purdue University, West Lafayette, IN, United States
The rapid development of remote sensing in agronomic research allows the dynamic nature of longitudinal traits to be adequately described, which may enhance the genetic improvement of crop efficiency. For traits such as light interception, biomass accumulation, and responses to stressors, the data generated by the various high-throughput phenotyping (HTP) methods requires adequate statistical techniques to evaluate phenotypic records throughout time. As a consequence, information about plant functioning and activation of genes, as well as the interaction of gene networks at different stages of plant development and in response to environmental stimulus can be exploited. In this review, we outline the current analytical approaches in quantitative genetics that are applied to longitudinal traits in crops throughout development, describe the advantages and pitfalls of each approach, and indicate future research directions and opportunities.
Introduction
Enhancing agricultural production efficiency by reducing yield gaps while also breeding more stress-resilient cultivars is the next challenge for plant breeders (Godfray et al., 2010; Foley et al., 2011; Ray et al., 2013; Challinor et al., 2014; Tai et al., 2014). The most feasible solutions are developing innovative approaches to speed up the genetic improvement of economically important traits and characterizing novel traits and incorporating them into breeding programs (Duvick, 2005; Lange and Federizzi, 2009; Fischer and Edmeades, 2010; Nolan and Santos, 2012; Rogers et al., 2015).
Plant breeding was established as a science in the beginning of the 20th century, when new insights about the genetic basis of phenotypic variation for quantitative traits were integrated with the foundational theories of inheritance mechanisms and crop hybridization elucidated by Mendel and Darwin, respectively (Johannsen, 1909, 1911; East, 1911; Bradshaw, 2017). Since then, plant breeders have improved crop productivity by selecting for numerous traits. Breeding objectives are constantly refined to address new challenges, including adaptation to new production areas, addressing emerging pests and diseases, various end uses, advanced farming technologies, and climate change (Toenniessen, 2002; Baenziger et al., 2006; Tester and Langridge, 2010; Gilliham et al., 2017). For instance, in 1955 the focus of soybean breeding was to increase seed oil content, canopy ground cover, and ripening uniformity. Ten years later the focus shifted to reducing pod shattering and lodging, and then it changed again over the years to include quality and value-added traits (Baenziger et al., 2006). Similar shifts in breeding goals and phenotyping technologies have also occurred in animal breeding (Henryon et al., 2014; Miglior et al., 2017). However, throughout history, improving traits of interest depends on the ability to quantify phenotypes across genotypes replicated over multiple environments (Stoskopf et al., 1994). Therefore, potentially valuable traits may have been neglected due to costly phenotyping and technological limitations.
Plant phenotyping has always been paramount for genetic improvement. Recent advances in proximal remote sensing, paired with new sensors and computer science applications, has enabled cost-effective high-throughput phenotyping (HTP) and dissection of novel traits (Montes et al., 2007; Furbank and Tester, 2011; Fiorani and Schurr, 2013; Araus and Cairns, 2014; Coppens et al., 2017). HTP provides time-series measurements that track the development of a crop through its life stages and as it responds to the environment. Information on gene function, the activation of genes, interaction of genes networks at different stages of plant development and in response to environmental stimulus can now be exploited (Wu and Lin, 2006; Montes et al., 2007). It is increasingly possible for plant breeders to consider light interception, biomass accumulation, and response to drought stress as dynamic traits, rather than static points in time (Montes et al., 2007). This analytical framework enhances our understanding of crop development and bridges gaps in understanding the relationship between genotype and phenotype (Granier and Vile, 2014; Araus et al., 2018).
Traits that are expressed repeatedly or continuously over the lifetime of an individual can be defined as longitudinal traits (Yang et al., 2006; Oliveira et al., 2019a), infinite-dimensional traits (Kirkpatrick and Heckman, 1989), or function-valued traits (Promislow et al., 1996). The study of longitudinal traits can provide important insights into the genetic mechanisms underlying physiological responses to environmental stresses and developmental processes. This information can be used to improve predictive ability for complex polygenic traits under multivariate settings, and contribute to identifying overall (e.g., soybean yield) or time specific Quantitative Trait Loci (QTL) (Fahlgren et al., 2015; Campbell et al., 2017; Sun et al., 2017). Such analysis enables assessment of the statistical association of genetic and environmental factors, such as the relationship between molecular markers and response to abiotic stress at different developmental stages (Langridge and Fleury, 2011). In this context, phenotypic data describes a function changing continuously in response to other variables (Stinchcombe and Kirkpatrick, 2012; Granier and Vile, 2014). These approaches generate a vast amount of data, which requires advanced statistical approaches to enable evaluation of the phenotypic data as a function of time. In this literature review, we will outline the current analytical approaches in quantitative genetics and genomics that can be applied to HTP quantified over time (Figure 1). In addition, we describe the advantages and pitfalls of each method and explore directions and opportunities for future research.
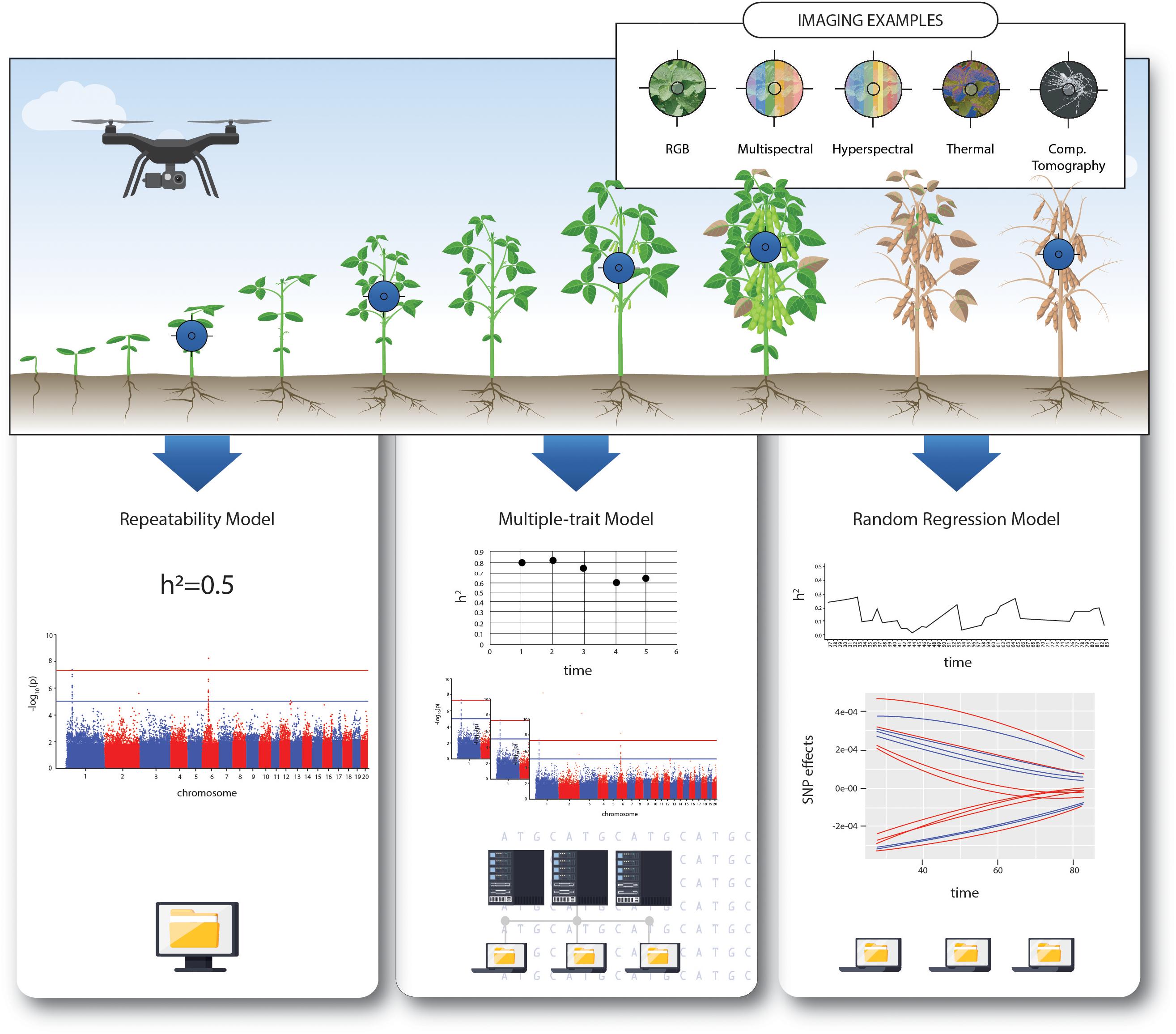
Figure 1. Schematic workflow of longitudinal data analyses. Different remote-sensing tools most commonly used for high-throughput phenotyping monitoring crop growth and development. Comparative overview of the potential models for genomic analysis, together with examples of outputs and computational demand.
Phenotyping Longitudinal Traits
Current HTP platforms, also referred to as “phenomic” tools, include a variety of methodologies that use remote sensing to obtain non-destructive phenotypic measurements, either in controlled environments or in the field (Pauli et al., 2016b). The most common types of sensors for crop phenotyping include red-green-blue (RGB; Xavier et al., 2017), multispectral (Xu et al., 2019), hyperspectral (Bodner et al., 2018), fluorescence (Pérez-Bueno et al., 2016), thermal (Sagan et al., 2019), three-dimensional (3D; Topp et al., 2013), and laser-imaging detection and ranging (LiDAR) (Sun et al., 2018) devices. In general, these sensors rely on the interaction between electromagnetic radiation and plants (reflecting, absorbing, or transmitting photons), which is captured by the sensor as reflected radiation (Fiorani et al., 2012; Li et al., 2014). Thus, the sensors interpret the plants as optical objects, with each component of the plant displaying a characteristic spectral signature arising from wavelength-specific properties of absorbance, reflectance, and transmittance from the vegetation surface (Schowengerdt, 2012; Li et al., 2014).
The spectral signatures of plants change during the life cycle, giving rise to genotype-time-specific phenotypes. For instance, during senescence, there is an increase of reflectance in the red region caused by a loss of chlorophyll (Schowengerdt, 2012). For field-based phenotyping, these sensing tools are usually integrated into ground or aerial vehicles (Araus et al., 2018). Most HTP platforms have the spatial and temporal resolution needed to capture longitudinal traits. However, the needs and resources of the specific experiment should drive the choice of platform and sensor, as these choices directly impact the scale and type of research (Pauli et al., 2016b). Several reviews have focused on HTP and its nuances, such as data collection, data processing and types of sensors (Fahlgren et al., 2015; Rahaman et al., 2015; Singh et al., 2016; Tardieu et al., 2017; Yang et al., 2017; Zhao et al., 2019; Reynolds et al., 2020).
The genetic control of longitudinal traits captured with HTP was recently reported for different crops. In a greenhouse, Neilson et al. (2015) investigated the growth and dynamic phenotypic responses of sorghum to water-limited conditions and various levels of fertilizer over time. They defined and measured several traits, including leaf area, shoot biomass, height, tiller number, and leaf greenness using laser scanning, RGB, and near-infrared (NIR) cameras. In barley, multiple sensors captured daily images in a greenhouse over 58 days measuring the spectrum of visible light, fluorescence, and NIR in order to dissect phenotypic components of drought responses (Chen et al., 2014). Tiller growth in rice was examined using more than 700 traits extracted from an imaging system combining computed tomography (CT) and RGB imaging during the tillering process (Wu et al., 2019).
In the field, Sun et al. (2018) used LiDAR mounted on a tractor to quantify leaf area, stem height, and plant volume in cotton in the field from 43 to 109 days after planting. From these measurements, they generated genotype-specific growth curves and assessed variability in traits and their genetic correlation to yield over time. In soybean, an unmanned aerial vehicle (UAV, aka drone) with an RGB camera measured canopy coverage in the field across several days after planting for genome-wide association analysis and genomic selection (Xavier et al., 2017; Hearst, 2019; Moreira et al., 2019). Blancon et al. (2019) characterized the dynamics of the green-leaf-area index in a diversity panel of maize under well-watered and water-deficient treatments using multispectral imagery acquired from a UAV throughout the growth cycle. Thermal and hyperspectral sensors mounted to a manned aircraft were used to extract canopy temperature and vegetation indexes of more than 500 lines of wheat in five field environments over a range of dates (Rutkoski et al., 2016).
Field-based HTP for roots has seen less progress than HTP of above-ground traits due to the difficulty of below-ground imaging (Atkinson et al., 2019). Shovelomics is a high-throughput method for root phenotyping and that has been used for crops, such as maize, common bean, cowpea, and wheat (Trachsel et al., 2011; Burridge et al., 2016; York et al., 2018). It consists of extracting several traits from images. However, it is destructive and labor-intensive, requiring manual root excavation, which limits its ability to capture repeated records over time. Recently, geophysical techniques, including electrical resistance tomography, electromagnetic inductance, and ground-penetrating radar have contributed to identify and quantify roots in the field in a non-destructive manner (Shanahan et al., 2015; Whalley et al., 2017; Liu et al., 2018a; Atkinson et al., 2019). Nevertheless, HTP root phenotyping is more commonly performed in controlled environments that allow the use of alternative growth systems that enable root imaging, such as rhizotrons, growth pouches and transparent artificial growth media (Atkinson et al., 2019; Ma et al., 2019). To model the growth dynamics of maize, Hund et al. (2009) performed daily scans of root systems grown over blotting paper. Topp et al. (2013) used 3D imaging phenotyping of rice root architecture in a gellan gum medium on various days of growth to perform QTL detection analysis. Recent advances in the use of X-ray CT and magnetic resonance imaging in plant sciences have enabled monitoring of root system architecture and dynamic growth over time in soil (Metzner et al., 2015; Pfeifer et al., 2015; van Dusschoten et al., 2016; Pflugfelder et al., 2017; Gao et al., 2019). More details and additional techniques for root phenotyping are presented in Atkinson et al. (2019).
Modeling Longitudinal Traits
Plant growth and development are characterized by several phenotypic changes, which can only be studied by monitoring repeated phenotypes over time (Li and Sillanpää, 2015). HTP platforms allow tracking of traits with a high temporal resolution, whether continuously over time or in discrete intervals (Furbank and Tester, 2011). Traditionally, mathematical functions are used to describe temporal trajectories of traits during the plant’s life cycle (Paine et al., 2012). Analysis of longitudinal traits usually employs one of the following two techniques (Li and Sillanpää, 2013): (1) smooth functions (such as splines; e.g., van Eeuwijk et al., 2018; Oliveira et al., 2019a) or parametric functions (such as growth models; e.g., Paine et al., 2012) to fit the phenotypic records over time, providing interpolated values for all time points; or (2) the data is reparameterized by estimating the function’s coefficients, which are then used in the analysis to represent the trait over time. Either way, it is necessary to select the function that best fits the shape of the trajectory of the trait to accurately estimate the curve parameters and results. Paine et al. (2012) provide a detailed review about growth models, highlighting basic functional forms, advantages and disadvantages. In this section, we will describe the main functions that have been successfully used to fit a variety of traits for the purposes of crop improvement.
Many of the complexities of plant growth are commonly represented using non-linear growth models that account for temporal variation in growth, capturing age and size-dependent growth (Paine et al., 2012). Usually, the growth pattern within a plant life cycle follows a sigmoid curve (S-shaped) characterized by an initial slow growth that then increases rapidly, approaching an exponential growth rate, and finally slows when it reaches a saturation phase (Yin et al., 2003). The S-shaped curve can be described by sigmoidal functions such as the logistic, Gompertz, Richards or β functions (Gompertz, 1815; Richards, 1959; Yin et al., 2003; Poorter et al., 2013). In this case, the Gompertz function is a special case of the Richard function; which is one of the oldest growth models frequently used to fit various biological processes across species (Tjørve and Tjørve, 2017). The Gompertz function has been used to describe biomass accumulation in maize kernels (Meade et al., 2013), barley biomass (Chen et al., 2014), and various longitudinal traits in wheat (Camargo et al., 2018) and sorghum (Neilson et al., 2015). The Logistic function is more commonly used in its asymptotic form to describe the time dependence of biological growth processes for traits such as biomass, canopy coverage, canopy size, volume, length, and area (Thornley et al., 2005; Paine et al., 2012). The Logistic function can have one, two, three, four, or five-parameters (Tessmer et al., 2013). One- and two-parameter logistic models are simplistic and frequently do not fit the data well, but are still used in several studies (e.g., Paine et al., 2012; Tessmer et al., 2013). The three-parameter logistic function (3PL; also known as a Verhulst or autocatalytic growth function) is perhaps the most popular model for plant growth analysis. In a water-limitation experiment in sorghum, a 3PL model had the best performance of a variety of sigmoidal models to fit the projected leaf area (Neilson et al., 2015). Sun et al. (2018) used a 3PL model to fit growth curves for canopy height, projected canopy area, and plant volume obtained from HTP in cotton. In wheat, Baillot et al. (2018) estimated various grain-filling parameters by fitting a 3PL model. The four-parameter logistic (4PL) model is more flexible than the 3PL as it has fewer constraints (Pinheiro and Bates, 2000). Camargo et al. (2018) phenotyped the average of area, height, and senescence in wheat throughout its lifecycle and found that 4PL models best fit the longitudinal data. The five-parameter version (5PL) provides maximum flexibility and accommodates asymmetry (Gottschalk and Dunn, 2005), despite its higher complexity compared to the lower number of parameters.
Many biological curves cannot be described by sigmoidal functions. A Power Law (also known as allometry) function is a type of non-asymptotic, non-linear growth model that does not produce an S-shaped curve (Marquet et al., 2005). They are often used in ecology to predict relationships in plant communities (Chen and Shiyomi, 2019). It effectively captures temporal variation in growth as it allows the relative growth rate to slow down over time and with an increase in biomass (Paine et al., 2012). A Power Law function was used to fit projected leaf area data in sorghum receiving various levels of nitrogen (Neilson et al., 2015), as well as leaf length and rosette area in Arabidopsis thaliana (An et al., 2016).
Linear models, such as orthogonal polynomials and spline functions, are also used to fit longitudinal traits (Oliveira et al., 2019a). The use of polynomials in crop growth models started in the 1960s as a functional approach to fit growth data and provide a clear picture of ontogenetic drift (Vernon and Allison, 1963; Hughes and Freeman, 1967; Poorter, 1989). One of the advantages of these functions is that they do not require prior knowledge of the longitudinal shape of the phenotype. Therefore, they are useful for fitting biological data of any shape simply by choosing different orders of the polynomials. Although they are not linear in time, polynomial functions are linear in their parameters, and consequently, can take advantage of the inference methods available for linear models (Yang et al., 2006). For instance, cubic polynomial functions have been used to describe grain growth in crops such as rice (Jones et al., 1979; Shi et al., 2015), wheat (Gebeyehou et al., 1982), barley (Leon and Geisler, 1994), and safflower (Koutroubas and Papakosta, 2010). One of the main difficulties with this approach is choosing the appropriate degree of polynomial to fit the data while avoiding spurious upward or downward trends or overfitting or underfitting the data (Paine et al., 2012).
Orthogonal polynomials are particularly popular for fitting biological curves because they have much lower correlations among their coefficients and provide estimates of the covariance matrices that tend to be more robust over a variety of data sets (Schaeffer, 2004). Legendre polynomials represent simple orthogonal polynomials and have been used successfully to fit longitudinal traits in livestock breeding programs (e.g., Albuquerque and Meyer, 2001; Oliveira et al., 2017, 2019b; Brito et al., 2017) and for plant research (e.g., Yang et al., 2006; Yang and Xu, 2007; Campbell et al., 2018; Momen et al., 2019).
Spline functions offer a more flexible alternative for modeling longitudinal traits compared to orthogonal polynomials (van Eeuwijk et al., 2018). Splines are piecewise polynomial functions, linked at specific points called knots (de Boor, 1980). For longitudinal data, these knots represent time points within the data collection interval (Li and Sillanpää, 2015). The greater flexibility of splines is due to the independence of each segment, which can have the same or different polynomial degrees, accommodating abrupt changes in the trajectory (Meyer, 2005b). A particular type of spline function is the basis spline, or B-spline (de Boor, 1980), extensively deployed in animal breeding (Meyer, 2005b; Oliveira et al., 2019a). Another version of spline is P-spline, which combines B-splines with different penalties on the coefficients of adjacent B-splines, resulting in smoother curves (Eilers and Marx, 1996; Meyer, 2005b).
Spline functions have recently been used to model longitudinal traits in crops. For instance, haulm senescence was assessed at several points during the growing season in a diploid potato mapping population and fitted using P-splines (Hurtado et al., 2012). Montesinos-López et al. (2017) used a B-spline function to fit wheat canopy hyperspectral bands in a yield prediction model. B-splines have also modeled rice temporal shoot biomass in a water-limited environment (Momen et al., 2019).
Statistical Genetic Models
Plant breeding is mostly based on the selection of new genetically superior cultivars from a large set of candidates. Simple arithmetic means of the phenotypic values, or Best Linear Unbiased Estimation (BLUE, treating genotypes as fixed effects), were used for selection prior to the development of Best Linear Unbiased Prediction (BLUP; Henderson, 1974). BLUPs are based on a mixed linear model and are now the most commonly used method for genetic evaluation of plant and livestock species (Piepho et al., 2008; Mrode, 2014). In the mixed-model framework, the genotypes are fitted as random and the genotypic effects are estimated by BLUP. The main advantage of BLUP over previous methods is its increased prediction accuracy for genetic effects. This is due to the shrinkage toward the mean that depends on the amount of information available (from the individual and/or its relatives), which will adjust extreme high and low performance toward the overall mean, and also to the incorporation of the genetic correlation between related genotypes from pedigree or genomic information (Piepho et al., 2008). The latter is not a requirement for the model, so the simplest case of BLUP uses no relationship matrix and the genotypes are considered to be independent random variables (Yan and Rajcan, 2003; Cullis et al., 2006). Piepho et al. (2008) present several examples of BLUP analyses in plant breeding.
Although rarely used, pedigree data is an easy and inexpensive source of information for plant breeders to leverage the relationship between individuals for a more accurate estimation of breeding values. Pedigree-based BLUPs have been successfully used in various crops (Bromley et al., 2000; Rutkoski et al., 2016; Basnet et al., 2019; Moreira et al., 2019), and have contributed to major advancements in the rates of genetic progress.
The inclusion of genomic information provides more accurate estimates of genetic relatedness among genotypes, especially with regards to the Mendelian sampling effects (Habier et al., 2007). Genomic information traces allele inheritance, capturing small segments of the genome shared among individuals, even when they are apparently unrelated through pedigree (Velazco et al., 2019). Plant breeders have widely adopted genomic-based BLUPs (GBLUP) for genomic selection (Auinger et al., 2016; Crossa et al., 2017; Schrag et al., 2019). Although genomic information is promising, in practice high-density genotyping is not always feasible for all genotypes within a breeding program due to genotyping costs, logistics, or both (Habier et al., 2009). An alternative is to construct a joint relationship matrix based on pedigree and genomic relationships to predict BLUPs for genotyped and non-genotyped material, which is called single-step GBLUP (ssGBLUP; Misztal et al., 2009; Aguilar et al., 2010; Christensen and Lund, 2010). This approach integrates both relationship matrices, connecting their different yet complementary information on genetic relatedness, and provides more reliable and accurate estimates of genetic similarities between genotypes. Genomic breeding values based on the ssGBLUP approach are commonly used in animal breeding (Aguilar et al., 2010; Legarra et al., 2014; Meuwissen et al., 2015; Guarini et al., 2019a, b; Oliveira et al., 2019c), and their use has started to become popular in plant breeding as well (Ashraf et al., 2016; Cappa et al., 2019; Velazco et al., 2019). In sorghum, Velazco et al. (2019) demonstrated that this methodology improves the predictive ability for complex traits, especially for traits with low heritability estimates, measured late in the development stage, or those that are difficult or expensive to measure.
For longitudinal traits, one can calculate BLUPs for each time point separately as individual traits with unique phenotypes; however, these approaches do not directly investigate and compare trends over time (Littell et al., 1998). This makes it difficult to consider a large number of time points and inhibit data comparison when BLUPs shrink differently due to discrepancies in heritability estimates. The main goal of fitting curves and patterns for longitudinal traits is to consider variability in the developmental process across many points in time (e.g., growth). Analytical methods have been developed to better evaluate longitudinal traits using the BLUP context, a simple analysis of variance, or both (Littell, 1990; Meyer and Kirkpatrick, 2005; Mrode, 2014). We will discuss the main methods in this review.
Repeatability Model
Individual measurements recorded over time can be treated as repeated records of the same trait. This is known as the repeatability model. There are two critical assumptions implicit in this method: (1) the variances of different measurements within the same genotype (or individual) are always equal, regardless of the time interval between records; and (2) the genetic correlations between all measurements are equal to one, i.e., measurements at different time points are all influenced by the same genes (Falconer and Mackay, 1996; Meyer and Hill, 1997; Littell et al., 1998). In this scenario, simple repeatability models are the standard approach.
One of the simplest methods is the repeated-measurements analysis of variance (ANOVA) using a split-plot in time design, which treats the genotypes as a whole-plot unit and genotypes at particular times as a sub-plot unit (Rowell and Walters, 1976; Littell, 1990). It is important to mention that as time is a factor in the experiment that cannot be randomized, this is not a true split-plot design. Also, this method assumes the data have equal variances (homoscedasticity) in all repeated measurements and that all pairs of measurements will have the same correlation (i.e., compound symmetry), which are unrealistic assumptions for most crop datasets. However, Huynh and Feldt (1970) showed that the equality of the variances of differences between any two treatment measurements assumed to be correlated was sufficient to perform a split-plot ANOVA. In this case, if the data violate the Huynh and Feldt condition, the F-statistics for the sub-plot unit and their interaction will be inflated. Thus, this method is prone to high Type I error rates, leading to conclusions that effects are statistically significant when they are not (Scheiner and Gurevitch, 2001; Fernandez, 2019).
In the context of mixed models, specifying the random and fixed effects in the model will depend on the study objectives, data structure, and the assumptions that can be made. Usually, time is considered as a fixed effect because it is not randomized in an experiment. Simple repeatability models have been used to calculate BLUPs and BLUEs of longitudinal traits derived from HTP for genomic prediction, such as in wheat (Rutkoski et al., 2016; Sun et al., 2017).
Multiple-Trait Model
Often, HTP platforms are used to generate phenotypes of plants in different “ages” or development stages, with the mean and variance of the phenotypes between measurements/assay dates changing over time. Thus, the assumption is that the genetic control of longitudinal traits will be different over time, characterizing the longitudinal records/phenotypes as different traits. A common approach to analyze longitudinal traits in this scenario is a multi-trait analysis that considers each time point as a different dependent variable (Sun et al., 2017).
Multivariate analysis of variance (MANOVA) is an extension of ANOVA, mentioned earlier, that avoids the covariance structure problems raised in repeated-measures ANOVA. However, it still requires equality in covariance among the groups being compared and balanced data over time. In addition, MANOVA assumes a multivariate normal distribution. Alternative methods have been proposed to overcome these restrictions (Krishnamoorthy and Lu, 2010; Krishnamoorthy and Yu, 2012; Konietschke et al., 2015), but MANOVA still has limited use in practice.
In the BLUP context, multiple-trait mixed models were first implemented by Henderson and Quaas (1976) to analyze two or more correlated traits making use of genetic and residual covariances among the traits (Speidel, 2011). Using this method, one can directly model the covariance structure of multiple dependent variables and efficiently handle missing data (Mrode, 2014). The main advantage of using a multiple-trait model (MTM) over a single-trait repeatability model is the improved evaluation accuracy for each trait arising from better connections in the data between the genetic and residual covariance (Colleau et al., 1999; Mrode, 2014). This data structure will benefit the prediction of traits with lower heritabilities when combined with highly heritable traits and genotypes with missing records for one or more traits (Mrode, 2014). In wheat, MTM was used to predict BLUPs for canopy temperature and normalized difference vegetation index (NDVI; Sun et al., 2017), and BLUEs for green NDVI (Juliana et al., 2018).
There are some disadvantages of multiple-trait mixed models. For instance, high-dimensional longitudinal data (e.g., traits recorded multiple times over a long period) can lead to over-parameterized models with high computational requirements (Speidel, 2011). There is also the potential for high correlations between consecutive measurements, which can reduce the power of the tests of significance (Foster et al., 2006). There are approaches to reduce the dimensionality of the MTM, which we are discussed below. It is worth noting that, when applying these approaches, the appropriate models should still be adequate to describe the data, accounting for the changes of mean and covariance over time, and estimate the necessary genetic parameters (Mrode, 2014).
Canonical transformation of phenotypic records is a common procedure to eliminate autocorrelation among traits through eigenvalue decomposition (Meyer and Hill, 1997). A set of highly correlated measures will provide eigenvalues close to zero. Under the framework of canonical transformed phenotypes, the original observations are transformed into a new set of response variables and the ones with the highest eigenvalues are selected to compose the new combination of traits. After fitting the MTM with the new values, the results are transformed back to the original scale (Mrode, 2014). Grosu et al. (2013) highlighted that canonical transformation can only be used if all individuals are recorded for all the traits and that the model needs to be the same for each trait, accommodating only two random effects: residual and genetic. Another strategy to fit MTM is referred to as “bending” (Thompson and Meyer, 1986; Meyer, 2019). It does not require all traits to be measured in all individuals. This procedure forces a decreased autocorrelation among traits by shrinking the covariance among traits by a bending factor, which creates a positive-definite covariance matrix.
The principal component analysis (PCA) and factor analysis (FA) methods are often more appropriate to reduce dimensionality for a large number of traits. FA identifies common factors, called latent variables, associated with the correlations between variables (Mrode, 2014). On the other hand, the PCA approach aims to create independent variables (principal components) that explain the maximum amount of variation in the dataset (Mrode, 2014). Thereafter, the principal components or latent variables become the new dependent variables in the MTM. Both methods have been used to reduce the dimensionality of longitudinal trait analysis in animals (Macciotta et al., 2017; Durón-Benítez et al., 2018; Vargas et al., 2018), and plants (Kwak et al., 2016; Yano et al., 2019).
As longitudinal traits are, by definition, taken along a time trajectory, the whole data set can be represented by parameters describing the shape of the trajectory curve (e.g., growth curve). These parameters can become the new dependent variables or integrated covariance structures in MTM (Speidel, 2011; Oliveira et al., 2019a); however, none of the approaches to analyze longitudinal data that we have discussed so far have considered that the genetic and environmental variances may change over time (Meyer, 1998, 2005a; Oliveira et al., 2019a). In addition, these approaches are limited to the time points at which traits were measured. Random regression models (RRMs) provide a way to overcome these limitations (Schaeffer, 2004).
Random Regression Model
A common property of longitudinal traits is that the covariance between repeated measures depends on the interval of time between them. In other words, measurements collected closer in time will be more correlated than measures collected farther apart. Kirkpatrick et al. (1990) presented the concept of analyzing longitudinal data using covariance functions by describing the covariance structure of the traits as a function of time. In essence, this approach fits a set of orthogonal functions to a given covariance matrix for the records taken over time (Meyer and Hill, 1997).
First-order autoregressive analysis (AR-1) is an appealing method for modeling covariance structure for phenotypes measured over time (Apiolaza and Garrick, 2001; Yang et al., 2006; Vanhatalo et al., 2019). It assumes homogenous variances and correlations that decline exponentially as measurements are separated by greater time intervals. Thus, two measurements collected closer in time will be more correlated than those further apart (Wade et al., 1993; Littell et al., 2000; Piepho et al., 2004). The AR-1 structure is only applicable for measurements taken at equally spaced time points (Wang and Goonewardene, 2004). Though this is a difficult requirement to meet in agricultural research, especially in field trials, modeling the longitudinal trait as described in the previous section would make the data evenly spaced over time and validate the AR-1 method. An alternative is to use a spatial power covariance structure that allows for unequal intervals between time points (Wang and Goonewardene, 2004).
Note that so far, we are assuming homogenous variance over time. There are also covariance structures to handle heterogeneous variance, such as the first-order ante-dependence structure (Wolfinger, 1996). Thus, Legendre orthogonal polynomials and splines are more attractive covariance functions as they produce relatively small correlations among the regression parameters and adjust flexibly to the shape of the trajectory curve (Schaeffer, 2004; Meyer, 2005a, b; Bohmanova et al., 2008; Pereira et al., 2013; Brito et al., 2018). In plants, different covariance structures have been assessed for a variety of traits (Apiolaza et al., 2011; Sun et al., 2017; Campbell et al., 2019).
Meyer and Hill (1997) showed that covariance functions are equivalent to RRMs. Schaeffer (2016) reported that covariance functions help to predict the change in variation over time, while RRMs are a way to estimate covariance functions and determine individual differences in trajectories. RRMs provide a robust framework for modeling trait trajectories using covariance at or between each time point with no assumptions of constant variances or correlations. RRMs provide insights about the temporal genetic variation of developmental behavior underlying the studied traits (Oliveira et al., 2019a). Despite the increased computational cost, RRMs result in more accurate breeding values compared to other methods (Sun et al., 2017; Oliveira et al., 2019a).
The RRMs were first introduced in animal breeding to overcome over-parameterized models in MTM and they have been used extensively since then (Jamrozik and Schaeffer, 1997; Schaeffer, 2004; van Pelt et al., 2015; Englishby et al., 2016; Oliveira et al., 2019a). In summary, RRMs set the parameters of the function describing the trajectory of the trait as fixed and random effects in the model, resulting in fewer parameters than MTM (Schaeffer, 2016; Oliveira et al., 2019a). Consequently, in RRMs the random parameters do not correspond directly to the individuals’ genetic value for the longitudinal trait. Rather, they correspond to the genetic values of sets of regression coefficients that represent the time trajectory of the longitudinal trait for each genotype (Turra et al., 2012). Estimates of genetic parameters and breeding values can be obtained for all time points within the interval analyzed from the genetic (co)variance matrices for the regression coefficients and the matrix of independent covariates for all time points associated with the function used (Oliveira et al., 2019a). When the same fixed effects are used in all models, it is appropriate to examine different covariance structures using real data and select the one that best fits the model based on a statistical methods, such as the Akaike Information Criterion (AIC, Wang and Goonewardene, 2004) or Bayesian Information Criterion (BIC, Neath and Cavanaugh, 2012). Finally, estimate the effects of interest using the selected covariance structure. In a general form, RRM can be described as follows (Oliveira et al., 2019a):
where ygij is the jth repeated record of genotype i (e.g., canopy coverage at different days after planting); bqg is the qth fixed regression coefficient for the gth group; ari is the rth random regression coefficient for the additive genetic effect of the ith genotype; psi is the sth random regression coefficient for permanent environmental effect of the ith genotype; egij is the residual effect; and zqg, zri and zsi are the covariates related to the function used to describe time (e.g., days after planting), assuming the same function (e.g., Legendre polynomial) with possible different orders Q, R, and S (e.g., linear, quadratic, cubic) (Oliveira et al., 2019a).
Random regression models have been shown to be the most effective choice to genetically evaluate longitudinal traits in numerous livestock breeding programs (as reviewed by Oliveira et al., 2019a), but there are only a few examples of the applications of RRMs in plant breeding, especially when incorporating genomic information. Sun et al. (2017) captured the change of HTP traits continually over wheat growth stages using RRMs. Campbell et al. (2018) used RRMs to predict shoot growth trajectories in a rice diversity panel and demonstrated an improvement in prediction accuracy compared to a single-time-point model. Based on the same rice dataset, Campbell et al. (2019) used RRMs to identify QTL with time-specific effects. Multiple-trait RRMs are also feasible and have been implemented in several settings in animal breeding programs (Nobre et al., 2003; Muir et al., 2007; Oliveira et al., 2019b, c).
Implementation of Genomic Selection for Longitudinal Traits
Meuwissen et al. (2001) introduced the concept of genomic selection (GS) based on the idea that markers from dense genome-wide genotyping will be in linkage disequilibrium with QTLs that have an effect on the quantitative trait of interest. Thus, they can be used for selection without identifying the QTL or the functional polymorphism. This increased understanding of GS arose as it became known that markers would carry relationship information in addition to the signal captured by the linkage disequilibrium between markers and QTL (Habier et al., 2007; Meuwissen, 2009).
In GS, genomic and phenotypic data are combined in a training population to enable the development of prediction equations that can be used in a testing (or target) population of selection candidates consisting of individuals that were genotyped but not phenotyped (Crossa et al., 2017). Therefore, GS enables a more accurate selection of individuals at an early age (with no measurements). This increases the rate of genetic gain by reducing the time required for the variety development and the cost per cycle. HTP is able to generate high-quality quantitative data and effectively characterizes large training populations during the growing season. The combination of GS and HTP has the potential to increase precision and efficiency while lowering costs and minimizing labor (Araus et al., 2018).
Under the longitudinal framework of GS, the prediction of temporal breeding values enables targeted selection on specific periods in the growing season or selection of individuals that exhibit desirable trait trajectories. In addition, the longitudinal trait can be used as secondary traits to improve the genomic selection of economic endpoint traits such as yields (Sun et al., 2017). Campbell et al. (2018) used RRMs with a second-order Legendre polynomial to perform pedigree and genomic predictions of shoot growth trajectories in a rice diversity panel. They demonstrated an improvement in prediction accuracy using the RRM compared to a single-time-point model. Furthermore, the authors reported that genomic RRMs were useful in predicting future phenotypes using a subset of early measurements. Another study in rice used RRMs to predict projected shoot area in controlled and water-limited conditions using Legendre polynomials and B-spline basis functions (Momen et al., 2019). Before fitting both functions, they adjusted raw phenotypic measurements to obtain BLUEs for downstream genetic analysis. Overall, RRMs produced higher prediction accuracy compared to the baseline multiple-trait model. In addition, B-splines performed slightly better than Legendre polynomials (Momen et al., 2019).
Currently, statistical models used in GS for plant breeding are most often single-trait (univariate) and do not take advantage of genetic covariance among traits or phenotypic records collected at different time points (Jia et al., 2012). However, MTM for GS was shown to outperform single-trait models by accounting for correlation among traits, thereby increasing prediction accuracy, statistical power, parameter estimation accuracy, and reducing trait selection bias (Jia et al., 2012; Guo G. et al., 2014; Montesinos-López et al., 2016, 2019). These advantages are even more obvious for low-heritability traits, such as yield, that are genetically correlated with highly heritable traits (Guo G. et al., 2014; Jiang et al., 2015). Recently, studies in the CIMMYT (2019) wheat breeding program1 have shown that the accuracy of GS is greatly improved by incorporating HTP longitudinal data from the so-called secondary traits measured with UAV (Rutkoski et al., 2016; Montesinos-López et al., 2017; Sun et al., 2017, 2019), an approach that is relatively inexpensive to implement as HTP and genotyping have become more accessible (e.g., targeted genotyping-by-sequencing approach; Pembleton et al., 2016). In addition, secondary traits are also useful to predict the primary trait at early growth stages, since they can often be phenotyped ahead of a primary trait like grain yield (Sun et al., 2017). Therefore, longitudinal traits can be used as secondary traits to improve the accuracy of GS and contribute to a better understanding of the biological mechanisms underlying stress responses and development. As described in the previous section, there are various ways to extract the genetic information from longitudinal traits and the methods employed will determine how they can be used in GS.
Rutkoski et al. (2016) used HTP canopy temperature (CT), green normalized difference vegetation index (GNDVI), and red normalized difference vegetation index (RNDVI) taken over time as secondary traits in GS for yield in wheat. First, they estimated BLUEs for the longitudinal traits using the repeatability model and used them in an MTM with yield, for pedigree and genomic predictions. They found that multiple-trait modeling with secondary traits increased accuracies for grain yield using both pedigree and genomic information, compared to the single-trait models. In another study, CT and NDVI also improved the ability to predict grain yield in wheat (Sun et al., 2017). However, in addition to a repeatability model, the authors also used MTM and RRMs to calculate BLUPs for the secondary traits in order to compare their efficiency. The predictive ability improved by 70%, on average, when including secondary traits, and the predictive ability of RRM and MTM were superior to the repeatability model. Also in wheat, Juliana et al. (2018) performed pedigree and genomic multi-trait prediction models using BLUEs of yield and GNDVI measured at different dates. They found that including GNDVI increased prediction accuracies. Sun et al. (2019) used an RRM with a cubic smoothing spline to predict BLUPs for CT and GNDVI in wheat. In a second step, they used BLUPs for secondary traits and grain yield as the dependent variables in GS. The prediction accuracy using the secondary traits increased by an average of 146% for grain yield across cycles and the secondary traits measured in the early stages were optimal for enhancing the prediction accuracy. Montesinos-López et al. (2017) and Crain et al. (2018) obtained similar results in wheat. Howard and Jarquin (2019) modeled the genetic covariance between canopy coverage and yield using the SoyNAM dataset (Song et al., 2017; Diers et al., 2018) and demonstrated that, based on different cross-validation schemes, the predictive ability was the highest when both canopy and marker information were included in the model. Two other papers reported similar improvements with the same dataset (Xavier et al., 2017; Jarquin et al., 2018).
Given the capability of HTP to collect multiple temporal traits at the same time, multiple-trait RRMs (MTRRMs) can be powerful tools for joint genomic prediction of several longitudinal traits (Oliveira et al., 2016). In addition, MTRRMs can incorporate different functions to describe different traits in the same model and estimate genetic correlations between different traits over time (Oliveira et al., 2016). In animals, MTRRMs are a plausible alternative for joint genetic prediction of milk yield and milk constituents in goats (Oliveira et al., 2016), cattle (Oliveira et al., 2019c), and buffaloes (Borquis et al., 2013). Recently, MTRRMs for projected shoot area and water-use recorded daily over a period of 20 days showed better predictive abilities compared to single-trait RRMs (Baba et al., 2020).
In animal breeding and multiple-stage plant breeding analysis, it is common to use deregressed genetic values as the pseudo-phenotypes for genomic predictions. Oliveira et al. (2018) compared different deregression methods for longitudinal traits. However, this multiple-step approach may result in lower accuracies, bias, and loss of information (Legarra et al., 2009; Kang et al., 2017). Considering the advantages of ssGBLUP and RRMs in genetic evaluation, integrating both approaches is an effective strategy to enhance the genomic prediction of longitudinal traits (Kang et al., 2017). Koivula et al. (2015) reported higher accuracy and less bias in the prediction of Nordic Red Dairy cows for milking performance using a ssGBLUP RRM compared to the traditional pedigree-based RRM. Kang et al. (2017) showed that ssGBLUP RRMs achieved the highest accuracy and least bias under a variety of scenarios, including persistency of accuracy over generations, compared to other models. In summary, the use of ssGBLUP based on RRMs can increase the reliability of genomic predictions for test-day traits in dairy cattle (Koivula et al., 2015; Kang et al., 2018; Oliveira et al., 2019c), and possibly in crops.
Detecting QTL and Causal Variants Associated With Longitudinal Traits
One of the main goals in genomic research is to predict the phenotypic variation using genotypes, by identifying genetic variants. The development of an organism is the result of an interacting network of genes and environmental factors (Wu and Lin, 2006). Unlike single-time-point measurements, studying longitudinal traits as a function of time allows the comprehensive assessment of crop growth and development (e.g., age metabolic rate; Ma et al., 2002). However, in plants, the detection of QTL analysis or genome-wide association studies (GWAS) for longitudinal traits are still performed at each time point independently. For instance, Würschum et al. (2014) used linkage mapping at discrete time points separately to identify time-specific QTLs associated with plant height in triticale. In cotton, canopy-related traits were used separately for each of the several studied days to map additive QTL effects and their interaction with the environment (Pauli et al., 2016a). In soybeans, a GWAS was used to identify QTL for each individual canopy coverage measurement spanning 14–56 days after planting (Xavier et al., 2017). Zhang et al. (2017) performed QTL mapping for several growth-related traits at 16 time points separately in maize. Also in maize, analysis of individual time points found different and simultaneous QTLs controlling plant height at different growth stages (Wang et al., 2019). Using time point growth-related traits, Knoch et al. (2020) found evidence of temporal QTLs in canola. Although useful, these static examinations provide a simplified view of genetic control, neglecting temporal changes and developmental features of trait formation (Wu and Lin, 2006). In addition, in animals, it has been shown that neither the phenotypic nor additive polygenic effects of longitudinal traits are constant throughout the entire phenotypic expression (Szyda et al., 2014; Brito et al., 2018; Oliveira et al., 2019a).
As an alternative, Ma et al. (2002) proposed a dynamic model, called functional mapping, to map QTLs associated with the whole developmental process of longitudinal traits. As mentioned earlier, longitudinal traits can be represented as curves, described by a few parameters from a linear or non-linear function over a given time. The idea behind functional mapping is that the difference in curve parameters among genotypes may suggest temporal patterns of genetic control over the phenotypic trajectory (Ma et al., 2002). Thus, functional mapping allows testing of timing and the duration of QTL expression (Wu et al., 2004). Several modeling strategies for functional mapping have been proposed and have been reviewed by Li and Sillanpää (2015). One of the approaches (the two-stage method) consists of modeling the whole phenotypic trajectory using linear and non-linear models and using these parameters as latent-trait phenotypes for QTL detection (Li and Sillanpää, 2015). Often, researchers perform analyses for individual time points followed by this two-stage method to derive the curve parameters. Busemeyer et al. (2013) used a logistic function to fit high-throughput-derived biomass from different development stages of a large mapping population of 647 double-haploid triticale lines. In addition to GWAS for the individual days, they performed a multiple-trait functional GWAS using the parameters from the logistic curve to reveal temporal genetic patterns of biomass regulation. A similar approach was used to assess image-derived biovolume in maize lines (Muraya et al., 2017); digital biomass accumulation in spring barley (Neumann et al., 2017); and area, height, and senescence in wheat (Camargo et al., 2018). Campbell et al. (2017) calculated the projected shoot area in 360 rice accessions from 19 to 41 days after transplanting. They modeled the longitudinal phenotypes using a power function (Paine et al., 2012) and used the parameters as the pseudo-phenotypes in a multiple-trait GWAS. In order to reveal the temporal dynamics of senescence in potato, Hurtado et al. (2012) employed P-splines as a smoothing curve and used the curve parameters for identifying QTLs.
Kwak et al. (2014) proposed two simple regression-based methods to map QTL by analyzing each time point separately and then combining test statistics across time points to determine the overall significance. Later, Kwak et al. (2016) proposed an improved approach where the observed longitudinal traits were replaced by a smoothing approximation, followed by dimensional reduction via PCA. Multiple-trait QTL analysis was then performed on the reduced data (using principal components). Muraya et al. (2017) implemented the approach suggested by Kwak et al. (2016). They used B-splines to smooth the phenotype followed by PCA for variable reduction and performed a multiple−QTL analysis following the methods of Kwak et al. (2014) to reveal the underlying genetic variation of growth dynamics in maize. Temporal height QTLs in the model C4 grass Setaria were also revealed using this approach (Feldman et al., 2017). Animal breeders have been using PCA for longitudinal trait analysis for a long time to synthesize complex patterns and reduce computationally demanding multiple-trait QTL detection (Macciotta et al., 2006, 2015, 2017; Zhang et al., 2018).
RRMs offer a better option to fit longitudinal traits and have been widely used in genetic evaluation of animals (Ning et al., 2017; Oliveira et al., 2019a). The random regression approach uncovers SNP effects over time because it is able to identify persistent and time-specific transient QTLs. Moreover, RRMs have increased statistical power to detect QTLs over other approaches because they leverage the full set of raw longitudinal phenotypes (Ning et al., 2017) and can capture QTLs with significant effects in specific regions of the development curve, though the effects of these QTLs may be small overall. RRMs are also useful for detecting QTL in gene-by-environment interactions (Lillehammer et al., 2007; Carvalheiro et al., 2019).
Das et al. (2011) proposed a method called functional GWAS (fGWAS), based on RRMs, which integrates GWAS and mathematical models describing biological processes. In summary, fGWAS estimates the mean for different SNP effects for each genotype and time point and then performs hypothesis testing to determine whether the SNP has any additive or dominant effect during the time course. The main drawback of this method is that it only performs a single-locus analysis. Later, Ning et al. (2017) proposed a modification of fGWAS by estimating the time-dependent population mean and the SNP effects separately, instead of fitting them directly. They also extended the model to capture the time-varying polygenic effect of complex traits by treating SNPs as covariates (fGWAS-C) or factors (fGWAS-F). However, their method was shown to be computationally inefficient due to the high dimensionality of the mixed model equations compared to other models. Subsequently, Ning et al. (2018) proposed a rapid longitudinal GWAS method, transforming the covariance matrices to diagonal matrices using eigen-decomposition. This way the model can be solved by a weighted least squares model for each SNP test.
To the best of our knowledge, Campbell et al. (2019) were the first to use RRM GWAS in a major row crop. They took the genomic breeding values derived from RRMs using Legendre orthogonal polynomials to assess the genetic architecture of rice shoot growth over a period of 20 days during early vegetative growth. They found both transient and persistent effects associated with shoot growth and more associations with the RRM when compared to single-time-point analysis.
Challenges and Future Developments
To capitalize on advances in phenotyping and molecular technologies, greater progress is needed in developing ways in which breeders can manipulate systems to understand the relationships between genotype and phenotype. The underlying biological changes due to environmental systems and/or over time can be captured with longitudinal data. The major challenge is synthesizing the various layers of information together in a meaningful manner to understand the downstream effects of developmental stress and implications for breeding (Harfouche et al., 2019).
Non-Additive Effects and GxE
Non-additive genetic effects may significantly contribute to the total genetic variation of complex traits. Prediction models that include dominance effects represent an important component of breeding programs that focus on crossbred populations, hybrid production, and vegetatively-propagated species (de Almeida Filho et al., 2019). There is also ample evidence of the importance of epistasis in the genetic architecture of complex traits in various crops (Guo T. et al., 2014; Monir and Zhu, 2018). Integrating non-additive effects into statistical models may improve prediction accuracy and detect more QTLs than simple additive models, especially when the non-additive variance contributes to a large proportion of the genetic variance (Bouvet et al., 2016; Bonnafous et al., 2018; Liu et al., 2018b, 2019; Monir and Zhu, 2018; Varona et al., 2018). However, these studies are restricted to single-time-point traits. For longitudinal traits, it may be challenging to have a full genetic model (including both additive and non-additive effects), requiring dense marker panels to estimate the time-dependent (co)variances, as well as partitioning of the genetic variance components. Nevertheless, full genetic models of longitudinal traits may have the potential to impact future design and implementation of breeding strategies.
The temporal dynamics of longitudinal traits lead to interactions that change the phenotype over time. This may be because the gene-gene and gene-environment interactions (GxE) are time- or age-dependent and need to be properly modeled (Fan et al., 2012). In this case, environmental descriptors should be measured several times as the trait phenotypes. The resulting model is a multiple-trait, multiple-environment model with a variety of interactions, in which computational issues may arise due to the increase in the number of parameters being estimated. It has been shown that RRMs can account simultaneously for the additive genetic effect and some degree of GxE in longitudinal traits in animal breeding by allowing for the estimation of genetic (co)variance components and breeding values over the whole trajectory of a time-dependent trait and environment-dependent covariate (Brügemann et al., 2011; Santana et al., 2016; Bohlouli et al., 2019). In plant breeding, therefore, this model may provide considerable biological insights into the mechanisms determining performance in specific environments, making it a worthwhile method for study in future research.
Complementary “-Omics” Technologies
The rapid advances in “-omics” technologies enable the generation of large-scale “-omics” datasets for many crop species, providing new opportunities to investigate and improve complex traits. The different approaches described in this review offer valuable tools to combine phenomics and genomics data to reveal the underlying genetic basis of longitudinal traits. However, one current challenge is integrating additional “-omics” technologies (e.g., transcriptomics, metagenomics, proteomics, metabolomics, epigenomics) to provide a holistic multi-omics approach to study biological mechanisms and their response to environmental stresses for important agronomic traits.
Recently, methods that combine “-omics” information have been used in some crops to study phenotypic networks for single-point traits, for example, to pinpoint candidate genes and/or loci and predict phenotypic variation (Acharjee et al., 2016; Li et al., 2016; Das et al., 2017; Sheng et al., 2017; Pandey et al., 2018; Jiang et al., 2019). A meta-analysis of the detailed “-omics” datasets regarding longitudinal traits in crops has been limited so far. Baker et al. (2019) characterized the mechanistic connections between the genomic architecture, transcriptomic expression networks, and phenotypic variation of growth curves that underlie the developmental dynamics of plant height in Brassica rapa. The combination of multi-omics approaches also seems promising to elucidate senescence processes in model and crop plants (Großkinsky et al., 2018). When joint modeling longitudinal “-omics” data (one or more type of “-omics” data measured over time) the statistical analysis becomes more challenging. Some key points can be found in Sperisen et al. (2015). In general, there is a need to adapt methodologies and experimental designs to explore processes related to the global evolution of biological processes such as growth and development. Despite all these challenges, integrative methods can increase analysis power to find true causal variants, regulatory networks, and pathways. These, in turn, could be incorporated into GS and breeding programs to speed up genetic gains (Suravajhala et al., 2016).
Deep Learning
Deep learning (DL) is a powerful and highly flexible class of machine learning algorithms based on representation-learning methods that incorporates multiple levels in a non-linear hierarchical learner (Lecun et al., 2015). Essentially, DL is an advanced version of artificial neural networks (ANN) with multiple hidden layers that aims to mimic the human brain functioning (Patterson and Gibson, 2017).
Deep learning has demonstrated its utility in different fields of biological sciences, such as disease diagnosis (Gao et al., 2018), multi-omics data integration (Chaudhary et al., 2018), predicting DNA- and RNA-binding specificity (Trabelsi et al., 2019), and, recently, in plant breeding genomic prediction (Ma et al., 2018; Montesinos-López A. et al., 2018; Montesinos-López O. A. et al., 2018; Montesinos-López et al., 2019). Zou et al. (2019) and Pérez-Enciso and Zingaretti (2019) provide a primer on DL in genomics. The growing interest in DL methods in plant breeding, especially for prediction, may arise from its powerful capability of learning complex non-linear relationships between predictors and responses hidden in big data, usually resulting in higher accuracy when compared with other methods (Montesinos-López A. et al., 2018; Pérez-Enciso and Zingaretti, 2019; Zou et al., 2019). It is important to point out that even though DL can deal with complex scenarios and achieve state-of-the-art accuracy, it requires domain knowledge and large-scale datasets, while the interpretation of the underlying biology is more challenging than for standard statistical models (Zou et al., 2019).
Within the classes of DL, recurrent neural networks (RNN) are designed for sequential or time-series data (Lecun et al., 2015) and may be the most appropriate architecture to model longitudinal traits. An RNN can be thought of as a memory state that retains information on previous data the network has seen and updates its predictions in the light of new information. Thus, besides prediction, RNN has the ability to capture long-term temporal dependencies (Che et al., 2018). Recently, RNNs have achieved astonishing results in many applications with time series or sequential data, particularly in human sciences (Azizi et al., 2018; Che et al., 2018; Lee et al., 2019; Sung et al., 2019; Zhong et al., 2019). Despite its advantages, to our best knowledge RNNs have not been employed in genomic prediction or mapping QTL for longitudinal traits in plant breeding. In the context, versatile DL models for multiple-trait analysis (Montesinos-López O. A. et al., 2018), multiple-environment analysis (Montesinos-López O. A. et al., 2018), and performing simultaneous predictions of mixed phenotypes (binary, ordinal and continuous; Montesinos-López et al., 2019) have been successfully implemented. Such cases are not only encouraging but may lead to future integration of DL and RNNs into the analysis of longitudinal traits in crops. DL is a powerful approach and is likely to transform many domains in plant breeding because it has the potential to handle all the complexities highlighted in this review. Needless to say, further innovation and technology assessment are required to fully enable DL to deal with the unique properties of planting breeding data.
Author Contributions
FM, KR, and LB conceptualized the manuscript. FM wrote the manuscript. HO, LB, and KR critically revised and improved the manuscript. JV edited section 3 “Modeling Longitudinal Traits.” All authors read and approved the manuscript.
Funding
Funding support for this review was provided by Purdue University “2019 Elevating the Visibility of Agricultural Research: 150th Anniversary Review Manuscripts.”
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Purdue University “2019 Elevating the Visibility of Agricultural Research: 150th Anniversary Review Papers.” Dr. Alencar Xavier is also acknowledged for reviewing the manuscript and providing valuable suggestions.
Abbreviations
3D, three-dimensional; 3PL, three-parameter logistic; 4PL, four-parameter logistic; 5PL, five-parameter logistic; ANOVA, analysis of variance; AR-1, first-order autoregressive analysis; BIC, Bayesian information criterion; BLUE, Best Linear Unbiased Estimation; BLUP, Best Linear Unbiased Prediction; CIMMYT, International Maize and Wheat Improvement Center; CT, canopy temperature; CT, computed tomography; DL, deep learning; FA, factor analysis; GWAS, genome-wide association studies; GS, genomic selection; GBLUP, genomic-based BLUP; GNDVI, green normalized difference vegetation index; HTP, high-throughput phenotyping; LiDAR, laser-imaging detection and ranging; MTM, multiple-trait model; MTRRM, multiple-trait random regression model; MANOVA, multivariate analysis of variance; NIR, near-infrared; NDVI, normalized difference vegetation index; PCA, principal component analysis; QTL, quantitative trait loci; RRM, random regression model; RNN, recurrent neural networks; RNDVI, red normalized difference vegetation index; RGB, red-green-blue; ssGBLUP, single-step GBLUP; AIC, Akaike information criterion; UAV, unmanned aerial vehicle.
Footnotes
References
Acharjee, A., Kloosterman, B., Visser, R. G. F., and Maliepaard, C. (2016). Integration of multi-omics data for prediction of phenotypic traits using random forest. BMC Bioinformatics 17:180. doi: 10.1186/s12859-016-1043-4
Aguilar, I., Misztal, I., Johnson, D. L., Legarra, A., Tsuruta, S., and Lawlor, T. J. (2010). Hot topic: a unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 93, 743–752. doi: 10.3168/jds.2009-2730
Albuquerque, L. G., and Meyer, K. (2001). Estimates of covariance functions for growth from birth to 630 days of age in Nelore cattle. J. Anim. Sci. 79, 2776–2789. doi: 10.2527/2001.79112776x
An, N., Palmer, C. M., Baker, R. L., Markelz, R. J. C., Ta, J., Covington, M. F., et al. (2016). Plant high-throughput phenotyping using photogrammetry and imaging techniques to measure leaf length and rosette area. Comput. Electron. Agric. 127, 376–394. doi: 10.1016/J.COMPAG.2016.04.002
Apiolaza, L. A., and Garrick, D. J. (2001). Analysis of Longitudinal Data from Progeny Tests: Some Multivariate Approaches. Available at: https://academic.oup.com/forestscience/article-abstract/47/2/129/4617386 (accessed June 4, 2019).
Apiolaza, L. A., Gilmour, A. R., and Garrick, D. J. (2011). Variance modelling of longitudinal height data from a Pinus radiata progeny test. Can. J. For. Res. 30, 645–654. doi: 10.1139/x99-246
Araus, J. L., and Cairns, J. E. (2014). Field high-throughput phenotyping: the new crop breeding frontier. Trends Plant Sci. 19, 52–61. doi: 10.1016/j.tplants.2013.09.008
Araus, J. L., Kefauver, S. C., Zaman-Allah, M., Olsen, M. S., and Cairns, J. E. (2018). Translating High-Throughput Phenotyping into Genetic Gain. Amsterdam: Elsevier, doi: 10.1016/j.tplants.2018.02.001
Ashraf, B., Edriss, V., Akdemir, D., Autrique, E., Bonnett, D., Crossa, J., et al. (2016). Genomic prediction using phenotypes from pedigreed lines with no marker data. Crop Sci. 56, 957–964. doi: 10.2135/cropsci2015.02.0111
Atkinson, J. A., Pound, M. P., Bennett, M. J., and Wells, D. M. (2019). Uncovering the hidden half of plants using new advances in root phenotyping. Curr. Opin. Biotechnol. 55, 1–8. doi: 10.1016/j.copbio.2018.06.002
Auinger, H. J., Schönleben, M., Lehermeier, C., Schmidt, M., Korzun, V., Geiger, H. H., et al. (2016). Model training across multiple breeding cycles significantly improves genomic prediction accuracy in rye (Secale cereale L.). Theor. Appl. Genet. 129, 2043–2053. doi: 10.1007/s00122-016-2756-5
Azizi, S., Bayat, S., Yan, P., Tahmasebi, A., Kwak, J. T., Xu, S., et al. (2018). Deep recurrent neural networks for prostate cancer detection: analysis of temporal enhanced ultrasound. IEEE Trans. Med. Imaging 37, 2695–2703. doi: 10.1109/TMI.2018.2849959
Baba, T., Momen, M., Campbell, M. T., Walia, H., and Morota, G. (2020). Multi-trait random regression models increase genomic prediction accuracy for a temporal physiological trait derived from high-throughput phenotyping. PLoS ONE 15:e0228118. doi: 10.1371/journal.pone.0228118
Baenziger, P. S., Russell, W. K., Graef, G. L., and Campbell, B. T. (2006). Improving lives: 50 Years of crop breeding, genetics, and cytology (C-1). Crop Sci. 2013, 2230–2244. doi: 10.2135/cropsci2005.11.0404gas
Baillot, N., Girousse, C., Allard, V., Piquet-Pissaloux, A., and Le Gouis, J. (2018). Different grain-filling rates explain grain-weight differences along the wheat ear. PLoS ONE 13:e0209597. doi: 10.1371/journal.pone.0209597
Baker, R. L., Leong, W. F., Brock, M. T., Rubin, M. J., Markelz, R. J. C., Welch, S., et al. (2019). Integrating transcriptomic network reconstruction and eQTL analyses reveals mechanistic connections between genomic architecture and Brassica rapa development. PLoS Genet. 15:e1008367. doi: 10.1371/journal.pgen.1008367
Basnet, B. R., Crossa, J., Dreisigacker, S., Pérez-Rodríguez, P., Manes, Y., Singh, R. P., et al. (2019). Hybrid wheat prediction using genomic, pedigree, and environmental covariables interaction models. Plant Genome 12, 1–13. doi: 10.3835/plantgenome2018.07.0051
Blancon, J., Dutartre, D., Tixier, M.-H., Weiss, M., Comar, A., Praud, S., et al. (2019). A high-throughput model-assisted method for phenotyping maize green leaf area index dynamics using unmanned aerial vehicle imagery. Front. Plant Sci. 10:685. doi: 10.3389/fpls.2019.00685
Bodner, G., Nakhforoosh, A., Arnold, T., and Leitner, D. (2018). Hyperspectral imaging: a novel approach for plant root phenotyping. Plant Methods 14:84. doi: 10.1186/s13007-018-0352-1
Bohlouli, M., Alijani, S., Naderi, S., Yin, T., and König, S. (2019). Prediction accuracies and genetic parameters for test-day traits from genomic and pedigree-based random regression models with or without heat stress interactions. J. Dairy Sci. 102, 488–502. doi: 10.3168/jds.2018-15329
Bohmanova, J., Miglior, F., Jamrozik, J., Misztal, I., and Sullivan, P. G. (2008). Comparison of random regression models with legendre polynomials and linear splines for production traits and somatic cell score of canadian holstein cows. J. Dairy Sci. 91, 3627–3638. doi: 10.3168/jds.2007-0945
Bonnafous, F., Fievet, G., Blanchet, N., Boniface, M.-C. C., Carrère, S., Gouzy, J., et al. (2018). Comparison of GWAS models to identify non-additive genetic control of flowering time in sunflower hybrids. Theor. Appl. Genet. 131, 319–332. doi: 10.1007/s00122-017-3003-4
Borquis, R. R. A., Neto, F. R., de, A., Baldi, F., Hurtado-Lugo, N., de Camargo, G. M. F., et al. (2013). Multiple-trait random regression models for the estimation of genetic parameters for milk, fat, and protein yield in buffaloes. J. Dairy Sci. 96, 5923–5932. doi: 10.3168/JDS.2012-6023
Bouvet, J. M., Makouanzi, G., Cros, D., and Vigneron, P. (2016). Modeling additive and non-additive effects in a hybrid population using genome-wide genotyping: prediction accuracy implications. Heredity (Edinb) 116, 146–157. doi: 10.1038/hdy.2015.78
Bradshaw, J. E. (2017). Plant Breeding: Past, Present and Future. Dordrecht: Springer, doi: 10.1007/978-3-319-23285-0
Brito, L. F., Silva, F. G., Oliveira, H. R., Souza, N. O., Caetano, G. C., Costa, E. V., et al. (2017). Modelling lactation curves of dairy goats by fitting random regression models using Legendre polynomials or B-splines. Can. J. Anim. Sci. 98, 73–83. doi: 10.1139/cjas-2017-0019
Brito, L. F., Silva, F. G., Oliveira, H. R., Souza, N. O., Caetano, G. C., Costa, E. V., et al. (2018). Modelling lactation curves of dairy goats by fitting random regression models using Legendre polynomials or B-splines. Can. J. Anim. Sci. 98, 73–83. doi: 10.1139/cjas-2017-0019
Bromley, C. M., Van Vleck, L. D., Johnson, B. E., and Smith, O. S. (2000). Estimation of genetic variance in corn from F1 performance with and without pedigree relationships among inbred lines. Crop Sci. 40, 651–655. doi: 10.2135/cropsci2000.403651x
Brügemann, K., Gernand, E., von Borstel, U. U., and König, S. (2011). Genetic analyses of protein yield in dairy cows applying random regression models with time-dependent and temperature x humidity-dependent covariates. J. Dairy Sci. 94, 4129–4139. doi: 10.3168/jds.2010-4063
Burridge, J., Jochua, C. N., Bucksch, A., and Lynch, J. P. (2016). Legume shovelomics: high-throughput phenotyping of common bean (Phaseolus vulgaris L.) and cowpea (Vigna unguiculata subsp, unguiculata) root architecture in the field. F. Crop. Res. 192, 21–32. doi: 10.1016/j.fcr.2016.04.008
Busemeyer, L., Ruckelshausen, A., Möller, K., Melchinger, A. E., Alheit, K. V., Maurer, H. P., et al. (2013). Precision phenotyping of biomass accumulation in triticale reveals temporal genetic patterns of regulation. Sci. Rep. 3:2442. doi: 10.1038/srep02442
Camargo, A. V., Mackay, I., Mott, R., Han, J., Doonan, J. H., Askew, K., et al. (2018). Functional mapping of quantitative trait loci (QTLs) associated with plant performance in a wheat MAGIC mapping population. Front. Plant Sci. 9:887. doi: 10.3389/fpls.2018.00887
Campbell, M., Momen, M., Walia, H., and Morota, G. (2019). Leveraging breeding values obtained from random regression models for genetic inference of longitudinal traits. Plant Genome 12:435685. doi: 10.3835/plantgenome2018.10.0075
Campbell, M., Walia, H., and Morota, G. (2018). Utilizing random regression models for genomic prediction of a longitudinal trait derived from high-throughput phenotyping. Plant Direct 2:e00080. doi: 10.1002/pld3.80
Campbell, M. T., Du, Q., Liu, K., Brien, C. J., Berger, B., Zhang, C., et al. (2017). A comprehensive image-based phenomic analysis reveals the complex genetic architecture of shoot growth dynamics in rice (Oryza sativa). Plant Genome 10, 1–14. doi: 10.3835/plantgenome2016.07.0064
Cappa, E. P., de Lima, B. M., da Silva-Junior, O. B., Garcia, C. C., Mansfield, S. D., and Grattapaglia, D. (2019). Improving genomic prediction of growth and wood traits in Eucalyptus using phenotypes from non-genotyped trees by single-step GBLUP. Plant Sci. 284, 9–15. doi: 10.1016/j.plantsci.2019.03.017
Carvalheiro, R., Costilla, R., Neves, H. H. R., Albuquerque, L. G., Moore, S., and Hayes, B. J. (2019). Unraveling genetic sensitivity of beef cattle to environmental variation under tropical conditions. Genet. Sel. Evol. 51:29. doi: 10.1186/s12711-019-0470-x
Challinor, A. J., Watson, J., Lobell, D. B., Howden, S. M., Smith, D. R., and Chhetri, N. (2014). A meta-analysis of crop yield under climate change and adaptation. Nat. Clim. Change 4, 287–291. doi: 10.1038/nclimate2153
Chaudhary, K., Poirion, O. B., Lu, L., and Garmire, L. X. (2018). Deep learning–based multi-omics integration robustly predicts survival in liver cancer. Clin. Cancer Res. 24, 1248–1259. doi: 10.1158/1078-0432.CCR-17-0853
Che, Z., Purushotham, S., Cho, K., Sontag, D., and Liu, Y. (2018). Recurrent neural networks for multivariate time series with missing values. Sci. Rep. 8:6085. doi: 10.1038/s41598-018-24271-9
Chen, D., Neumann, K., Friedel, S., Kilian, B., Chen, M., Altmann, T., et al. (2014). Dissecting the phenotypic components of crop plant growth and drought responses based on high-throughput image analysis. Plant Cell 26, 4636–4655. doi: 10.1105/tpc.114.129601
Chen, J., and Shiyomi, M. (2019). A power law model for analyzing spatial patterns of vegetation abundance in terms of cover, biomass, density, and occurrence: derivation of a common rule. J. Plant Res. 132, 481–497. doi: 10.1007/s10265-019-01116-8
Christensen, O. F., and Lund, M. S. (2010). Genomic prediction when some animals are not genotyped. Genet. Sel. Evol. 42:2. doi: 10.1186/1297-9686-42-2
CIMMYT (2019). CIMMYT: International Maize and Wheat Improvement Center. Available at: https://www.cimmyt.org/ [Accessed October 1, 2019]
Colleau, J. J., Ducrocq, V., Boichard, D., and Larroque, H. (1999). Approximate Multitrait BLUP Evaluation to Combine Functional Traits Information. Available at: file: C:/Users/Fabiana/OneDrive-purdue.edu/PhD/Reviewpaper/393-784-1-SM.pdf (accessed June 3, 2019).
Coppens, F., Wuyts, N., Inzé, D., and Dhondt, S. (2017). Unlocking the potential of plant phenotyping data through integration and data-driven approaches. Curr. Opin. Syst. Biol. 4, 58–63. doi: 10.1016/j.coisb.2017.07.002
Crain, J., Mondal, S., Rutkoski, J., Singh, R. P., and Poland, J. (2018). Combining high-throughput phenotyping and genomic information to increase prediction and selection accuracy in wheat breeding. Plant Genome 11, 1–14. doi: 10.3835/plantgenome2017.05.0043
Crossa, J., Pérez-Rodríguez, P., Cuevas, J., Montesinos-López, O., Jarquín, D., de Los Campos, G., et al. (2017). Genomic selection in plant breeding: methods, models, and perspectives. Trends Plant Sci. 22, 961–975. doi: 10.1016/j.tplants.2017.08.011
Cullis, B. R., Smith, A. B., and Coombes, N. E. (2006). On the design of early generation variety trials with correlated data. J. Agric. Biol. Environ. Stat. 11, 381–393. doi: 10.1198/108571106X154443
Das, A., Rushton, P. J., and Rohila, J. S. (2017). Metabolomic profiling of soybeans (Glycine max L.) reveals the importance of sugar and nitrogen metabolism under drought and heat stress. Plants 6, 199–208. doi: 10.3390/plants6020021
Das, K., Li, J., Wang, Z., Tong, C., Fu, G., Li, Y., et al. (2011). A dynamic model for genome-wide association studies. Hum. Genet. 129, 629–639. doi: 10.1007/s00439-011-0960-6
de Almeida Filho, J. E., Guimarães, J. F. R., Fonsceca e Silva, F., Vilela de Resende, M. D., Muñoz, P., Kirst, M., et al. (2019). Genomic prediction of additive and non-additive effects using genetic markers and pedigrees. G3 9, 2739–2748. doi: 10.1534/g3.119.201004
Diers, B. W., Specht, J., Rainey, K. M., Cregan, P., Song, Q., Ramasubramanian, V., et al. (2018). Genetic architecture of soybean yield and agronomic traits. G3 (Bethesda) 8, 3367–3375. doi: 10.1534/g3.118.200332
Durón-Benítez, A.-A., Weller, J. I., and Ezra, E. (2018). Using geometric morphometrics for the genetics analysis of shape and size of lactation curves in Israeli first-parity Holstein cattle. J. Dairy Sci. 101, 11132–11142. doi: 10.3168/jds.2018-15209
Duvick, D. N. (2005). Genetic progress in yield of United States maize (Zea mays L.). Maydica 50, 193–202.
East, E. M. (1911). The genotype hypothesis and hybridization. Am. Nat. 45, 160–174. doi: 10.1086/279203
Eilers, P. H. C., and Marx, B. D. (1996). Flexible Smoothing with B-splines and Penalties. Available at: https://projecteuclid.org/download/pdf_1/euclid.ss/1038425655 (accessed May 24, 2019).
Englishby, T. M., Banos, G., Moore, K. L., Coffey, M. P., Evans, R. D., and Berry, D. P. (2016). Genetic analysis of carcass traits in beef cattle using random regression models. J. Anim. Sci. 94, 1354–1364. doi: 10.2527/jas.2015-0246
Fahlgren, N., Gehan, M. A., and Baxter, I. (2015). Lights, camera, action: high-throughput plant phenotyping is ready for a close-up. Curr. Opin. Plant Biol. 24, 93–99. doi: 10.1016/J.PBI.2015.02.006
Falconer, D. S., and Mackay, T. F. C. (1996). Introduction to Quantitative Genetics, 4th Edn. Burnt Mill: Longman.
Fan, R., Albert, P. S., and Schisterman, E. F. (2012). A discussion of gene-gene and gene-environment interactions and longitudinal genetic analysis of complex traits. Stat. Med. 31, 2565–2568. doi: 10.1002/sim.5495
Feldman, M. J., Paul, R. E., Banan, D., Barrett, J. F., Sebastian, J., Yee, M. C., et al. (2017). Time dependent genetic analysis links field and controlled environment phenotypes in the model C4grass Setaria. PLoS Genet. 13:e1006841. doi: 10.1371/journal.pgen.1006841
Fernandez, G. C. J. (2019). Repeated measure analysis of line-source sprinkler experiments. HortScience 26, 339–342. doi: 10.21273/hortsci.26.4.339
Fiorani, F., Rascher, U., Jahnke, S., and Schurr, U. (2012). Imaging plants dynamics in heterogenic environments. Curr. Opin. Biotechnol. 23, 227–235. doi: 10.1016/j.copbio.2011.12.010
Fiorani, F., and Schurr, U. (2013). Future scenarios for plant phenotyping. Annu. Rev. Plant Biol. 64, 267–291. doi: 10.1146/annurev-arplant-050312-120137
Fischer, R. A., and Edmeades, G. O. (2010). Breeding and cereal yield progress. Crop Sci. 50, S-85–S-98. doi: 10.2135/cropsci2009.10.0564
Foley, J. A., Ramankutty, N., Brauman, K. A., Cassidy, E. S., Gerber, J. S., Johnston, M., et al. (2011). Solutions for a cultivated planet. Nature 478, 337–342. doi: 10.1038/nature10452
Foster, J. J., Barkus, E., and Yavorsky, C. (2006). Understanding and using advanced statistics. Choice Rev. 43, 43-5938–43-5938. doi: 10.5860/choice.43-5938
Furbank, R. T., and Tester, M. (2011). Phenomics - technologies to relieve the phenotyping bottleneck. Trends Plant Sci. 16, 635–644. doi: 10.1016/j.tplants.2011.09.005
Gao, A. W., Schlüter, S., Blaser, S. R. G. A., Shen, J., and Vetterlein, D. (2019). A shape-based method for automatic and rapid segmentation of roots in soil from X-ray computed tomography images: rootine. Plant Soil 441, 1–13. doi: 10.1007/s11104-019-04053-6
Gao, L., Pan, H., Liu, F., Xie, X., Zhang, Z., and Han, J. (2018). “Brain disease diagnosis using deep learning features from longitudinal MR images,” in Lecture Notes in Computer Science (Including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), eds R. Goebel, Y. Tanaka, and W. Wahlster, (Cham: Springer), 327–339. doi: 10.1007/978-3-319-96890-2_27
Gebeyehou, G., Knott, D. R., and Baker, R. J. (1982). Rate and duration of grain filling in durum wheat cultivars1. Crop Sci. 22:337. doi: 10.2135/cropsci1982.0011183X002200020033x
Gilliham, M., Able, J. A., and Roy, S. J. (2017). Translating knowledge about abiotic stress tolerance to breeding programmes. Plant J. 90, 898–917. doi: 10.1111/tpj.13456
Godfray, H. C. J., Beddington, J. R., Crute, I. R., Haddad, L., Lawrence, D., Muir, J. F., et al. (2010). Food security: the challenge of feeding 9 billion people. Science (80-) 327, 812–818. doi: 10.1126/science.1185383
Gompertz, B. (1815). On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Proc. R. Soc. Lond. 2, 252–253. doi: 10.1098/rspl.1815.0271
Gottschalk, P. G., and Dunn, J. R. (2005). The five-parameter logistic: a characterization and comparison with the four-parameter logistic. Anal. Biochem. 343, 54–65. doi: 10.1016/j.ab.2005.04.035
Granier, C., and Vile, D. (2014). Phenotyping and beyond: modelling the relationships between traits. Curr. Opin. Plant Biol. 18, 96–102. doi: 10.1016/j.pbi.2014.02.009
Grosu, H., Schaeffer, L., Oltenacu, P. A., Norman, D., Powell, R. L., Kremer, V., et al. (2013). History of Genetic Evaluation Methods in Dairy Cattle. Available at: https://books.google.com/books/about/History_of_Genetic_Evaluation_Methods_in.html?id=dNbsoQEACAAJ (accessed June 6, 2019).
Großkinsky, D. K., Jaya Syaifullah, S., Roitsch, T., Lim, P., Syaifullah, S. J., and Roitsch, T. (2018). Integration of multi-omics techniques and physiological phenotyping within a holistic phenomics approach to study senescence in model and crop plants. J. Exp. Bot. 69, 825–844. doi: 10.1093/jxb/erx333
Guarini, A. R., Lourenco, D. A. L., Brito, L. F., Sargolzaei, M., Baes, C. F., Miglior, F., et al. (2019a). Genetics and genomics of reproductive disorders in canadian holstein cattle. J. Dairy Sci. 102, 1341–1353. doi: 10.3168/jds.2018-15038
Guarini, A. R., Lourenco, D. A. L., Brito, L. F., Sargolzaei, M., Baes, C. F., Miglior, F., et al. (2019b). Use of a single-step approach for integrating foreign information into national genomic evaluation in Holstein cattle. J. Dairy Sci. 102, 8175–8183. doi: 10.3168/jds.2018-15819
Guo, G., Zhao, F., Wang, Y., Zhang, Y., Du, L., and Su, G. (2014). Comparison of single-trait and multiple-trait genomic prediction models. BMC Genet. 15:30. doi: 10.1186/1471-2156-15-30
Guo, T., Yang, N., Tong, H., Pan, Q., Yang, X., Tang, J., et al. (2014). Genetic basis of grain yield heterosis in an “immortalized F2” maize population. Theor. Appl. Genet. 127, 2149–2158. doi: 10.1007/s00122-014-2368-x
Habier, D., Fernando, R. L., and Dekkers, J. C. M. (2007). The impact of genetic relationship information on genome-assisted breeding values. Genetics 177, 2389–2397. doi: 10.1534/genetics.107.081190
Habier, D., Fernando, R. L., and Dekkers, J. C. M. (2009). Genomic selection using low-density marker panels. Genetics 182, 343–353. doi: 10.1534/genetics.108.100289
Harfouche, A. L., Jacobson, D. A., Kainer, D., Romero, J. C., Harfouche, A. H., Scarascia Mugnozza, G., et al. (2019). Accelerating climate resilient plant breeding by applying next-generation artificial intelligence. Trends Biotechnol. 37, 1217–1235. doi: 10.1016/j.tibtech.2019.05.007
Hearst, A. A. (2019). Remote Sensing of Soybean Canopy Cover, Color, and Visible Indicators of Moisture Stress Using Imagery from Unmanned Aircraft Systems, PhD., West Lafayette: Agricultural and Biological Engineering.
Henderson, C. R. (1974). General flexibility of linear model techniques for sire evaluation. J. Dairy Sci. 57, 963–972. doi: 10.3168/jds.s0022-0302(74)84993-3
Henderson, C. R., and Quaas, R. L. (1976). Multiple trait evaluation using relatives’, records J. Anim. Sci. 43, 1188–1197. doi: 10.2527/jas1976.4361188x
Henryon, M., Berg, P., and Sørensen, A. C. (2014). Invited review: animal-breeding schemes using genomic information need breeding plans designed to maximise long-term genetic gains. Livest. Sci. 166, 38–47. doi: 10.1016/j.livsci.2014.06.016
Howard, R., and Jarquin, D. (2019). Genomic prediction using canopy coverage image and genotypic information in soybean via a hybrid model. Evol. Bioinform. 15:117693431984002. doi: 10.1177/1176934319840026
Hughes, A. P., and Freeman, P. R. (1967). Growth analysis using frequent small harvests. J. Appl. Ecol. 4:553. doi: 10.2307/2401356
Hund, A., Trachsel, S., and Stamp, P. (2009). Growth of axile and lateral roots of maize: I development of a phenotying platform. Plant Soil 325, 335–349. doi: 10.1007/s11104-009-9984-2
Hurtado, P. X., Schnabel, S. K., Zaban, A., Veteläinen, M., Virtanen, E., Eilers, P. H. C., et al. (2012). Dynamics of senescence-related QTLs in potato. Euphytica 183, 289–302. doi: 10.1007/s10681-011-0464-4
Huynh, H., and Feldt, L. S. (1970). Conditions under which mean square ratios in repeated measurements designs have exact F-distributions. J. Am. Stat. Assoc. 65, 1582–1589. doi: 10.1080/01621459.1970.10481187
Jamrozik, J., and Schaeffer, L. R. (1997). Estimates of genetic parameters for a test day model with random regressions for yield traits of first lactation holsteins. J. Dairy Sci. 80, 762–770. doi: 10.3168/jds.S0022-0302(97)75996-4
Jarquin, D., Howard, R., Xavier, A., and Das Choudhury, S. (2018). Increasing predictive ability by modeling interactions between environments, genotype and canopy coverage image data for soybeans. Agronomy 8:51. doi: 10.3390/agronomy8040051
Jia, Y., Jannink, J.-L. L., and Goddard, M. E. (2012). Multiple-trait genomic selection methods increase genetic value prediction accuracy. Genetics 192, 1513–1522. doi: 10.1534/genetics.112.144246
Jiang, J., Xing, F., Wang, C., Zeng, X., and Zou, Q. (2019). Investigation and development of maize fused network analysis with multi-omics. Plant Physiol. Biochem. 141, 380–387. doi: 10.1016/j.plaphy.2019.06.016
Jiang, J., Zhang, Q., Ma, L., Li, J., Wang, Z., and Liu, J. F. (2015). Joint prediction of multiple quantitative traits using a Bayesian multivariate antedependence model. Heredity (Edinb) 115, 29–36. doi: 10.1038/hdy.2015.9
Johannsen, W. (1909). Elemente der Exakten Erblichkeitslehre. [Elements of the Exact Theory of Inheritance]. Jena: G. Fischer, doi: 10.5962/bhl.title.94247
Johannsen, W. (1911). The genotype conception of heredity. Am. Nat. 45, 129–159. doi: 10.1086/279202
Jones, D. B., Peterson, M. L., and Geng, S. (1979). Association between grain filling rate and duration and yield components in rice. Crop Sci. 19:641. doi: 10.2135/cropsci1979.0011183x001900050023x
Juliana, P., Montesinos-López, O. A., Crossa, J., Mondal, S., González Pérez, L., Poland, J., et al. (2018). Integrating genomic-enabled prediction and high-throughput phenotyping in breeding for climate-resilient bread wheat. Theor. Appl. Genet. 132, 177–194. doi: 10.1007/s00122-018-3206-3
Kang, H., Ning, C., Zhou, L., Zhang, S., Yan, Q., and Liu, J. F. (2018). Short communication: single-step genomic evaluation of milk production traits using multiple-trait random regression model in Chinese Holsteins. J. Dairy Sci. 101, 11143–11149. doi: 10.3168/jds.2018-15090
Kang, H., Zhou, L., Mrode, R., Zhang, Q., and Liu, J. F. (2017). Incorporating the single-step strategy into a random regression model to enhance genomic prediction of longitudinal traits. Heredity (Edinb) 119, 459–467. doi: 10.1038/hdy.2016.91
Kirkpatrick, M., and Heckman, N. (1989). A quantitative genetic model for growth, shape, reaction norms, and other infinite-dimensional characters. J. Math. Biol. 27, 429–450. doi: 10.1007/BF00290638
Kirkpatrick, M., Lofsvold, D., and Bulmer, M. (1990). Analysis of the inheritance, selection and evolution of growth trajectories. Genetics 124, 979–993.
Knoch, D., Abbadi, A., Grandke, F., Meyer, R. C., Samans, B., Werner, C. R., et al. (2020). Strong temporal dynamics of QTL action on plant growth progression revealed through high-throughput phenotyping in canola. Plant Biotechnol. J. 18, 68–82. doi: 10.1111/pbi.13171
Koivula, M., Strandén, I., Pösö, J., Aamand, G. P., and Mäntysaari, E. A. (2015). Single-step genomic evaluation using multitrait random regression model and test-day data. J. Dairy Sci. 98, 2775–2784. doi: 10.3168/jds.2014-8975
Konietschke, F., Bathke, A. C., Harrar, S. W., and Pauly, M. (2015). Parametric and nonparametric bootstrap methods for general MANOVA. J. Multivar. Anal. 140, 291–301. doi: 10.1016/j.jmva.2015.05.001
Koutroubas, S. D., and Papakosta, D. K. (2010). Seed filling patterns of safflower: genotypic and seasonal variations and association with other agronomic traits. Ind. Crops Prod. 31, 71–76. doi: 10.1016/J.INDCROP.2009.09.014
Krishnamoorthy, K., and Lu, F. (2010). A parametric bootstrap solution to the MANOVA under heteroscedasticity. J. Stat. Comput. Simul. 80, 873–887. doi: 10.1080/00949650902822564
Krishnamoorthy, K., and Yu, J. (2012). Multivariate Behrens-Fisher problem with missing data. J. Multivar. Anal. 105, 141–150. doi: 10.1016/j.jmva.2011.08.019
Kwak, I.-Y., Moore, C. R., Spalding, E. P., and Broman, K. W. (2016). Mapping quantitative trait loci underlying function-valued traits using functional principal component analysis and multi-trait mapping. G3 6, 79–86. doi: 10.1534/G3.115.024133
Kwak, I.-Y. Y., Moore, C. R., Spalding, E. P., and Broman, K. W. (2014). A simple regression-based method to map quantitative trait loci underlying function-valued phenotypes. Genetics 197, 1409–1416. doi: 10.1534/genetics.114.166306
Lange, C. E., and Federizzi, L. C. (2009). Estimation of soybean genetic progress in the South of Brazil using multi-environmental yield trials. Sci. Agric. 66, 309–316. doi: 10.1590/s0103-90162009000300005
Langridge, P., and Fleury, D. (2011). Making the most of “omics” for crop breeding. Trends Biotechnol. 29, 33–40. doi: 10.1016/j.tibtech.2010.09.006
Lecun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521, 436–444. doi: 10.1038/nature14539
Lee, G., Nho, K., Kang, B., Sohn, K. A., Kim, D., Weiner, M. W., et al. (2019). Predicting Alzheimer’s disease progression using multi-modal deep learning approach. Sci. Rep. 9:1952. doi: 10.1038/s41598-018-37769-z
Legarra, A., Aguilar, I., and Misztal, I. (2009). A relationship matrix including full pedigree and genomic information. J. Dairy Sci. 92, 4656–4663. doi: 10.3168/jds.2009-2061
Legarra, A., Christensen, O. F., Aguilar, I., and Misztal, I. (2014). Single step, a general approach for genomic selection. Livest. Sci. 166, 54–65. doi: 10.1016/j.livsci.2014.04.029
Leon, J., and Geisler, G. (1994). Variation in rate and duration of growth among spring barley cultivars1. Plant Breed. 112, 199–208. doi: 10.1111/j.1439-0523.1994.tb00671.x
Li, D., Huang, Z., Song, S., Xin, Y., Mao, D., Lv, Q., et al. (2016). Integrated analysis of phenome, genome, and transcriptome of hybrid rice uncovered multiple heterosis-related loci for yield increase. Proc. Natl. Acad. Sci. U.S.A. 113, E6026–E6035. doi: 10.1073/pnas.1610115113
Li, L., Zhang, Q., and Huang, D. (2014). A review of imaging techniques for plant phenotyping. Sensors (Switzerland) 14, 20078–20111. doi: 10.3390/s141120078
Li, Z., and Sillanpää, M. J. (2013). A bayesian nonparametric approach for mapping dynamic quantitative traits. Genetics 194, 997–1016. doi: 10.1534/genetics.113.152736
Li, Z., and Sillanpää, M. J. (2015). Dynamic quantitative trait locus analysis of plant phenomic data. 20, 822–833. doi: 10.1016/j.tplants.2015.08.012
Lillehammer, M., Ødegård, J., and Meuwissen, T. H. (2007). Random regression models for detection of gene by environment interaction. Genet. Sel. Evol. 39:105. doi: 10.1186/1297-9686-39-2-105
Littell, R. C. (1990). “Analysis of repeated measures data,” in Conference on Applied Statistic in Agriculture, Gainesville, FL, doi: 10.1007/978-981-10-3794-8
Littell, R. C., Henry, P. R., and Ammerman, C. B. (1998). Statistical analysis of repeated measures data using SAS procedures. J. Anim. Sci. 76, 1216-1231. doi: 10.2527/1998.7641216x
Littell, R. C., Pendergast, J., and Natarajan, R. (2000). Tutorial in Biostatics: modelling covariance structure in the analysis of repeated measures data. Stat. Med. 19, 1793–1819. doi: 10.1002/1097-0258(20000715)19:13<1793::aid-sim482>3.0.co;2-q
Liu, X., Dong, X., Xue, Q., Leskovar, D. I., Jifon, J., Butnor, J. R., et al. (2018a). Ground penetrating radar (GPR) detects fine roots of agricultural crops in the field. Plant Soil 423, 517–531. doi: 10.1007/s11104-017-3531-3
Liu, X., Wang, H., Wang, H., Guo, Z., Xu, X., Liu, J., et al. (2018b). Factors affecting genomic selection revealed by empirical evidence in maize. Crop J. 6, 341–352. doi: 10.1016/j.cj.2018.03.005
Liu, X., Wang, H., Hu, X., Li, K., Liu, Z., Wu, Y., et al. (2019). Improving genomic selection with quantitative trait loci and nonadditive effects revealed by empirical evidence in maize. Front. Plant Sci. 10:1129. doi: 10.3389/fpls.2019.01129
Ma, C. X., Casella, G., and Wu, R. (2002). Functional mapping of quantitative trait loci underlying the character process: a theoretical framework. Genetics 161, 1751–1762.
Ma, L., Shi, Y., Siemianowski, O., Yuan, B., Egner, T. K., Mirnezami, S. V., et al. (2019). Hydrogel-based transparent soils for root phenotyping in vivo. Proc. Natl. Acad. Sci. U.S.A. 166, 11063–11068. doi: 10.1073/pnas.1820334116
Ma, W., Qiu, Z., Song, J., Li, J., Cheng, Q., Zhai, J., et al. (2018). A deep convolutional neural network approach for predicting phenotypes from genotypes. Planta 248, 1307–1318. doi: 10.1007/s00425-018-2976-9
Macciotta, N. P. P., Biffani, S., Bernabucci, U., Lacetera, N., Vitali, A., Ajmone-Marsan, P., et al. (2017). Derivation and genome-wide association study of a principal component-based measure of heat tolerance in dairy cattle. J. Dairy Sci. 100, 4683–4697. doi: 10.3168/jds.2016-12249
Macciotta, N. P. P., Gaspa, G., Bomba, L., Vicario, D., Dimauro, C., Cellesi, M., et al. (2015). Genome-wide association analysis in Italian simmental cows for lactation curve traits using a low-density (7K) SNP panel. J. Dairy Sci. 98, 8175–8185. doi: 10.3168/jds.2015-9500
Macciotta, N. P. P., Vicario, D., and Cappio-Borlino, A. (2006). Use of multivariate analysis to extract latent variables related to level of production and lactation persistency in dairy cattle. J. Dairy Sci. 89, 3188–3194. doi: 10.3168/jds.S0022-0302(06)72593-0
Marquet, P. A., Quiñones, R. A., Abades, S., Labra, F., Tognelli, M., Arim, M., et al. (2005). Scaling and power-laws in ecological systems. J. Exp. Biol. 208, 1749–1769. doi: 10.1242/jeb.01588
Meade, K. A., Cooper, M., and Beavis, W. D. (2013). Modeling biomass accumulation in maize kernels. F. Crop. Res. 151, 92–100. doi: 10.1016/j.fcr.2013.07.014
Metzner, R., Eggert, A., van Dusschoten, D., Pflugfelder, D., Gerth, S., Schurr, U., et al. (2015). Direct comparison of MRI and X-ray CT technologies for 3D imaging of root systems in soil: potential and challenges for root trait quantification. Plant Methods 11:17. doi: 10.1186/s13007-015-0060-z
Meuwissen, T. H. (2009). Accuracy of breeding values of “unrelated” individuals predicted by dense SNP genotyping. Genet. Sel. Evol. 41:35. doi: 10.1186/1297-9686-41-35
Meuwissen, T. H. E., Hayes, B. J., and Goddard, M. E. (2001). Prediction of total genetic value using genome-wide dense marker maps. Genetics 157, 1819–1829.
Meuwissen, T. H. E., Svendsen, M., Solberg, T., and Ødegård, J. (2015). Genomic predictions based on animal models using genotype imputation on a national scale in Norwegian Red cattle. Genet. Sel. Evol. 47:79. doi: 10.1186/s12711-015-0159-8
Meyer, K. (1998). Estimating covariance functions for longitudinal data using a random regression model. Genet. Sel. Evol. 30, 221–240. doi: 10.1186/1297-9686-30-3-221
Meyer, K. (2005a). Advances in methodology for random regression analyses. Austr. J. Exp. Agric. 45, 847–858. doi: 10.1071/EA05040
Meyer, K. (2005b). Random regression analyses using B-splines to model growth of Australian Angus cattle. Genet. Sel. Evol. 37:473. doi: 10.1186/1297-9686-37-6-473
Meyer, K. (2019). “Bending” and beyond: better estimates of quantitative genetic parameters? J. Anim. Breed. Genet. 136, 243–251. doi: 10.1111/jbg.12386
Meyer, K., and Hill, W. G. (1997). Estimation of genetic and phenotypic covariance functions for longitudinal or “repeated” records by restricted maximum likelihood. Livest. Prod. Sci. 47, 185–200. doi: 10.1016/S0301-6226(96)01414-5
Meyer, K., and Kirkpatrick, M. (2005). Up hill, down dale: quantitative genetics of curvaceous traits. Philos. Trans. R. Soc. B Biol. Sci. 360, 1443–1455. doi: 10.1098/rstb.2005.1681
Miglior, F., Fleming, A., Malchiodi, F., Brito, L. F., Martin, P., and Baes, C. F. (2017). A 100-Year review: identification and genetic selection of economically important traits in dairy cattle. J. Dairy Sci. 100, 10251–10271. doi: 10.3168/jds.2017-12968
Misztal, I., Legarra, A., and Aguilar, I. (2009). Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J. Dairy Sci. 92, 4648–4655. doi: 10.3168/JDS.2009-2064
Momen, M., Campbell, M. T., Walia, H., and Morota, G. (2019). Predicting longitudinal traits derived from high-throughput phenomics in contrasting environments using genomic legendre polynomials and B-splines. G3 (Bethesda) 9, 3369–3380. doi: 10.1534/g3.119.400346
Monir, M. M., and Zhu, J. (2018). Dominance and epistasis interactions revealed as important variants for leaf traits of maize NAM population. Front. Plant Sci. 9:627. doi: 10.3389/fpls.2018.00627
Montes, J. M., Melchinger, A. E., and Reif, J. C. (2007). Novel throughput phenotyping platforms in plant genetic studies. Trends Plant Sci. 12, 433–436. doi: 10.1016/j.tplants.2007.08.006
Montesinos-López, A., Montesinos-López, O. A., Gianola, D., Crossa, J., and Hernández-Suárez, C. M. (2018). Multi-environment genomic prediction of plant traits using deep learners with dense architecture. G3 8, 3813–3828. doi: 10.1534/g3.118.200740
Montesinos-López, O. A., Montesinos-López, A., Crossa, J., Gianola, D., Hernández-Suárez, C. M., and Martín-Vallejo, J. (2018). Multi-trait, multi-environment deep learning modeling for genomic-enabled prediction of plant traits. G3 8, 3829–3840. doi: 10.1534/g3.118.200728
Montesinos-López, O. A., Martín-Vallejo, J., Crossa, J., Gianola, D., Hernández-Suárez, C. M., Montesinos-López, A., et al. (2019). New deep learning genomic-based prediction model for multiple traits with binary, ordinal, and continuous phenotypes. G3 (Bethesda) 9, 1545–1556. doi: 10.1534/g3.119.300585
Montesinos-López, O. A., Montesinos-López, A., Crossa, J., los Campos, G., Alvarado, G., Suchismita, M., et al. (2017). Predicting grain yield using canopy hyperspectral reflectance in wheat breeding data. Plant Methods 13:4. doi: 10.1186/s13007-016-0154-2
Montesinos-López, O. A., Montesinos-López, A., Crossa, J., Toledo, F. H., Pérez-Hernández, O., Eskridge, K. M., et al. (2016). A genomic bayesian multi-trait and multi-environment model. G3 (Bethesda) 6, 2725–2744. doi: 10.1534/g3.116.032359
Moreira, F. F., Hearst, A. A., Cherkauer, K. A., and Rainey, K. M. (2019). Improving the efficiency of soybean breeding with high-throughput canopy phenotyping. Plant Methods 15:139. doi: 10.1186/s13007-019-0519-4
Mrode, R. (2014). Linear Models for the Prediction of Animal Breeding Values, ed. R. Mrode. Wallingford: CABI, doi: 10.1079/9781780643915.0000
Muir, B. L., Kistemaker, G., Jamrozik, J., and Canavesi, F. (2007). Genetic parameters for a multiple-trait multiple-lactation random regression test-day model in italian holsteins. J. Dairy Sci. 90, 1564–1574. doi: 10.3168/jds.S0022-0302(07)71642-9
Muraya, M. M., Chu, J., Zhao, Y., Junker, A., Klukas, C., Reif, J. C., et al. (2017). Genetic variation of growth dynamics in maize (Zea mays L.) revealed through automated non-invasive phenotyping. Plant J. 89, 366–380. doi: 10.1111/tpj.13390
Neath, A. A., and Cavanaugh, J. E. (2012). The bayesian information criterion: background, derivation, and applications. Wiley Interdiscip. Rev. Comput. Stat. 4, 199–203. doi: 10.1002/wics.199
Neilson, E. H., Edwards, A. M., Blomstedt, C. K., Berger, B., Møller, B. L., and Gleadow, R. M. (2015). Utilization of a high-throughput shoot imaging system to examine the dynamic phenotypic responses of a C4 cereal crop plant to nitrogen and water deficiency over time. J. Exp. Bot. 66, 1817–1832. doi: 10.1093/jxb/eru526
Neumann, K., Zhao, Y., Chu, J., Keilwagen, J., Reif, J. C., Kilian, B., et al. (2017). Genetic architecture and temporal patterns of biomass accumulation in spring barley revealed by image analysis. BMC Plant Biol. 17:137. doi: 10.1186/s12870-017-1085-4
Ning, C., Kang, H., Zhou, L., Wang, D., Wang, H., Wang, A., et al. (2017). Performance gains in genome-wide association studies for longitudinal traits via modeling time-varied effects. Sci. Rep. 7:590. doi: 10.1038/s41598-017-00638-2
Ning, C., Wang, D., Zheng, X., Zhang, Q., Zhang, S., Mrode, R., et al. (2018). Eigen decomposition expedites longitudinal genome-wide association studies for milk production traits in Chinese Holstein. Genet. Sel. Evol. 50:12. doi: 10.1186/s12711-018-0383-0
Nobre, P. R. C., Misztal, I., Tsuruta, S., Bertrand, J. K., Silva, L. O. C., and Lopes, P. S. (2003). Analyses of growth curves of Nellore cattle by multiple-trait and random regression models. J. Anim. Sci. 81, 918–926. doi: 10.2527/2003.814918x
Nolan, E., and Santos, P. (2012). The contribution of genetic modification to changes in corn yield in the United States. Am. J. Agric. Econ. 94, 1171–1188. doi: 10.1093/ajae/aas069
Oliveira, H. R., Brito, L. F., Lourenco, D. A. L., Silva, F. F., Jamrozik, J., Schaeffer, L. R., et al. (2019a). Invited review: advances and applications of random regression models: from quantitative genetics to genomics. J. Dairy Sci. 102, 7664–7683. doi: 10.3168/jds.2019-16265
Oliveira, H. R., Brito, L. F., Silva, F. F., Lourenco, D. A. L., Jamrozik, J., and Schenkel, F. S. (2019b). Genomic prediction of lactation curves for milk, fat, protein, and somatic cell score in Holstein cattle. J. Dairy Sci. 102, 452–463. doi: 10.3168/jds.2018-15159
Oliveira, H. R., e Silva, F. F., Barbosa da Silva, M. V. G., Barbosa Dias de Siqueira, O. H. G., Machado, M. A., and do Carmo Panetto, J. C. (2017). Bayesian models combining legendre and b-spline polynomials for genetic analysis of multiple lactations in Gyr cattle. Livest. Sci. 201, 78–84. doi: 10.1016/j.livsci.2017.05.007
Oliveira, H. R., Silva, F. F., Brito, L. F., Guarini, A. R., Jamrozik, J., and Schenkel, F. S. (2018). Comparing deregression methods for genomic prediction of test-day traits in dairy cattle. J. Anim. Breed. Genet. 135, 97–106. doi: 10.1111/jbg.12317
Oliveira, H. R. R., Lourenco, D. A. L. A. L., Masuda, Y., Misztal, I., Tsuruta, S., Jamrozik, J., et al. (2019c). Application of single-step genomic evaluation using multiple-trait random regression test-day models in dairy cattle. J. Dairy Sci. 102, 2365–2377. doi: 10.3168/jds.2018-15466
Oliveira, H. R., Silva, F. F., Siqueira, O. H., Souza, N. O., Junqueira, V. S., Resende, M. D. V. V., et al. (2016). Combining different functions to describe milk, fat, and protein yield in goats using Bayesian multiple-trait random regression models. J. Anim. Sci. 94, 1865–1874. doi: 10.2527/jas.2015-0150
Paine, C. E. T. T., Marthews, T. R., Vogt, D. R., Purves, D., Rees, M., Hector, A., et al. (2012). How to fit nonlinear plant growth models and calculate growth rates: an update for ecologists. Methods Ecol. Evol. 3, 245–256. doi: 10.1111/j.2041-210X.2011.00155.x
Pandey, V., Singh, M., Pandey, D., and Kumar, A. (2018). Integrated proteomics, genomics, metabolomics approaches reveal oxalic acid as pathogenicity factor in Tilletia indica inciting Karnal bunt disease of wheat. Sci. Rep. 8:7826. doi: 10.1038/s41598-018-26257-z
Patterson, J., and Gibson, A. (2017). Deep Learning: A Practitioner’s Approach. Sebastopol, CA: O’Reilly Media.
Pauli, D., Andrade-Sanchez, P., Carmo-Silva, A. E., Gazave, E., French, A. N., Heun, J., et al. (2016a). Field-based high-throughput plant phenotyping reveals the temporal patterns of quantitative trait loci associated with stress-responsive traits in cotton. G3 6:865. doi: 10.1534/G3.115.023515
Pauli, D., Chapman, S. C., Bart, R., Topp, C. N., Lawrence-Dill, C. J., Poland, J., et al. (2016b). The quest for understanding phenotypic variation via integrated approaches in the field environment. Plant Physiol. 172, 00592.2016. doi: 10.1104/pp.16.00592
Pembleton, L. W., Drayton, M. C., Bain, M., Baillie, R. C., Inch, C., Spangenberg, G. C., et al. (2016). Targeted genotyping-by-sequencing permits cost-effective identification and discrimination of pasture grass species and cultivars. Theor. Appl. Genet. 129, 991–1005. doi: 10.1007/s00122-016-2678-2
Pereira, R. J., Bignardi, A. B., El Faro, L., Verneque, R. S., Vercesi Filho, A. E., and Albuquerque, L. G. (2013). Random regression models using legendre polynomials or linear splines for test-day milk yield of dairy Gyr (Bos indicus) cattle. J. Dairy Sci. 96, 565–574. doi: 10.3168/JDS.2011-5051
Pérez-Bueno, M. L., Pineda, M., Cabeza, F. M., and Barón, M. (2016). Multicolor fluorescence imaging as a candidate for disease detection in plant phenotyping. Front. Plant Sci. 7:1790. doi: 10.3389/fpls.2016.01790
Pérez-Enciso, M., and Zingaretti, L. M. (2019). A guide for using deep learning for complex trait genomic prediction. Genes (Basel) 10:E553. doi: 10.3390/genes10070553
Pfeifer, J., Kirchgessner, N., Colombi, T., and Walter, A. (2015). Rapid phenotyping of crop root systems in undisturbed field soils using X-ray computed tomography. Plant Methods 11:41. doi: 10.1186/s13007-015-0084-4
Pflugfelder, D., Metzner, R., Dusschoten, D., Reichel, R., Jahnke, S., and Koller, R. (2017). Non-invasive imaging of plant roots in different soils using magnetic resonance imaging (MRI). Plant Methods 13:102. doi: 10.1186/s13007-017-0252-9
Piepho, H. P., Büchse, A. B., Richter, C., Büchse, D. A. B., Büchse, A., and Richter, C. (2004). A mixed modelling aproach for randomized experiments with repeated measures. J. Agron. Crop Sci. 190, 230–247. doi: 10.1111/j.1439-037X.2004.00097.x
Piepho, H. P., Möhring, J., Melchinger, A. E., and Büchse, A. (2008). BLUP for phenotypic selection in plant breeding and variety testing. Euphytica 161, 209–228. doi: 10.1007/s10681-007-9449-8
Pinheiro, J., and Bates, D. (2000). Mixed-Effects Models in S and S-PLUS. New York, NY: Springer-Verlag, doi: 10.1007/b98882
Poorter, H. (1989). Plant growth analysis: towards a synthesis of the classical and the functional approach. Physiol. Plant. 75, 237–244. doi: 10.1111/j.1399-3054.1989.tb06175.x
Poorter, H., Anten, N. P. R., and Marcelis, L. F. M. (2013). Physiological mechanisms in plant growth models: do we need a supra-cellular systems biology approach? Plant Cell Environ. 36, 1673–1690. doi: 10.1111/pce.12123
Promislow, D. E. L., Tatar, M., Khazaeli, A. A., and Curtsinger, J. W. (1996). Age-specific patterns of genetic variance in Drosophila melanogaster. I. mortality. Genetics 143, 839–848.
Rahaman, M. M., Chen, D., Gillani, Z., Klukas, C., and Chen, M. (2015). Advanced phenotyping and phenotype data analysis for the study of plant growth and development. Front. Plant Sci. 6:619. doi: 10.3389/fpls.2015.00619
Ray, D. K., Mueller, N. D., West, P. C., and Foley, J. A. (2013). Yield trends are insufficient to double global crop production by 2050. PLoS ONE 8:e66428. doi: 10.1371/journal.pone.0066428
Reynolds, M., Chapman, S., Crespo-Herrera, L., Molero, G., Mondal, S., Pequeno, D. N. L., et al. (2020). Breeder friendly phenotyping. Plant Sci. doi: 10.1016/j.plantsci.2019.110396
Richards, F. J. (1959). A flexible growth function for empirical use. J. Exp. Bot. 10, 290–301. doi: 10.1093/jxb/10.2.290
Rogers, J., Chen, P., Shi, A., Zhang, B., Scaboo, A., Smith, S. F., et al. (2015). Agronomic performance and genetic progress of selected historical soybean varieties in the southern USA. Plant Breed. 134, 85–93. doi: 10.1111/pbr.12222
Rowell, J. G., and Walters, D. E. (1976). Analysing data with repeated observations on each experimental unit. J. Agric. Sci. 87, 423–432. doi: 10.1017/S0021859600027763
Rutkoski, J., Poland, J., Mondal, S., Autrique, E., Pérez, L. G., Crossa, J., et al. (2016). Canopy temperature and vegetation indices from high-throughput phenotyping improve accuracy of pedigree and genomic selection for grain yield in wheat. G3 6, 2799–2808. doi: 10.1534/g3.116.032888
Sagan, V., Maimaitijiang, M., Sidike, P., Eblimit, K., Peterson, K. T., Hartling, S., et al. (2019). UAV-based high resolution thermal imaging for vegetation monitoring, and plant phenotyping using ICI 8640 P, FLIR Vue Pro R 640, and thermomap cameras. Remote Sens. 11:330. doi: 10.3390/rs11030330
Santana, M. L., Bignardi, A. B., Pereira, R. J., Menéndez-Buxadera, A., and El Faro, L. (2016). Random regression models to account for the effect of genotype by environment interaction due to heat stress on the milk yield of Holstein cows under tropical conditions. J. Appl. Genet. 57, 119–127. doi: 10.1007/s13353-015-0301-x
Schaeffer, L. R. (2004). Application of random regression models in animal breeding. Livest. Prod. Sci. 86, 35–45. doi: 10.1016/S0301-6226(03)00151-9
Schaeffer, L. R. (2016). Random Regression Models. Available online at: https://www.luke.fi/wp-content/uploads/2018/01/Random-regression-model.pdf (accessed June 3, 2019).
Scheiner, S. M., and Gurevitch, J. (2001). Design and Analysis of Ecological Experiments. Oxford: Oxford University Press.
Schowengerdt, R. A. (2012). Remote Sensing: Models and Methods for Image Processing. Amsterdam: Elsevier, doi: 10.1016/j.jenvman.2011.10.007
Schrag, T. A., Schipprack, W., and Melchinger, A. E. (2019). Across-years prediction of hybrid performance in maize using genomics. Theor. Appl. Genet. 132, 933–946. doi: 10.1007/s00122-018-3249-5
Shanahan, P. W., Binley, A., Whalley, W. R., and Watts, C. W. (2015). The use of electromagnetic induction to monitor changes in soil moisture profiles beneath different wheat genotypes. Soil Sci. Soc. Am. J. 79:459. doi: 10.2136/sssaj2014.09.0360
Sheng, J., Zheng, X., Wang, J., Zeng, X., Zhou, F., Jin, S., et al. (2017). Transcriptomics and proteomics reveal genetic and biological basis of superior biomass crop Miscanthus. Sci. Rep. 7:13777. doi: 10.1038/s41598-017-14151-z
Shi, P., Tang, L., Lin, C., Liu, L., Wang, H., Cao, W., et al. (2015). Modeling the effects of post-anthesis heat stress on rice phenology. F. Crop. Res. 177, 26–36. doi: 10.1016/j.fcr.2015.02.023
Singh, A., Ganapathysubramanian, B., Singh, A. K. A., and Sarkar, S. (2016). Machine learning for high-throughput stress phenotyping in plants. Trends Plant Sci. 21, 110–124. doi: 10.1016/J.TPLANTS.2015.10.015
Song, Q., Yan, L., Quigley, C., Jordan, B. D., Fickus, E., Schroeder, S., et al. (2017). Genetic characterization of the soybean nested association mapping population. Plant Genome 10, 1–14. doi: 10.3835/plantgenome2016.10.0109
Speidel, S. E. (2011). Random Regression Models for the Prediction of Days to Finish in Beef Cattle. Available at: https://mountainscholar.org/bitstream/handle/10217/69294/Speidel_colostate_0053A_10777.pdf?sequence=1 (accessed July 8, 2019).
Sperisen, P., Cominetti, O., and Martin, F. P. J. (2015). Longitudinal omics modeling and integration in clinical metabonomics research: challenges in childhood metabolic health research. Front. Mol. Biosci. 2:44. doi: 10.3389/fmolb.2015.00044
Stinchcombe, J. R., and Kirkpatrick, M. (2012). Genetics and evolution of function-valued traits: understanding environmentally responsive phenotypes. Trends Ecol. Evol. 27, 637–647. doi: 10.1016/j.tree.2012.07.002
Stoskopf, N. C., Tomes, D. T., and Christie, B. R. (1994). Plant breeding: theory and practice. Choice Rev. 32, 32-0301–32-0301. doi: 10.5860/choice.32-0301
Sun, J., Poland, J. A., Mondal, S., Crossa, J., Juliana, P., Singh, R. P., et al. (2019). High-throughput phenotyping platforms enhance genomic selection for wheat grain yield across populations and cycles in early stage. Theor. Appl. Genet. 132, 1705–1720. doi: 10.1007/s00122-019-03309-0
Sun, J., Rutkoski, J. E., Poland, J. A., Crossa, J., Jannink, J.-L., and Sorrells, M. E. (2017). Multitrait, random regression, or simple repeatability model in high-throughput phenotyping data improve genomic prediction for wheat grain yield. Plant Genome 10, 1–15. doi: 10.3835/plantgenome2016.11.0111
Sun, S., Li, C., Paterson, A. H., Jiang, Y., Xu, R., Robertson, J. S., et al. (2018). In-field high throughput phenotyping and cotton plant growth analysis using LiDAR. Front. Plant Sci. 9:16. doi: 10.3389/fpls.2018.00016
Sung, J. M., Cho, I.-J., Sung, D., Kim, S., Kim, H. C., Chae, M.-H., et al. (2019). Development and verification of prediction models for preventing cardiovascular diseases. PLoS ONE 14:e0222809. doi: 10.1371/journal.pone.0222809
Suravajhala, P., Kogelman, L. J. A., and Kadarmideen, H. N. (2016). Multi-omic data integration and analysis using systems genomics approaches: methods and applications In animal production, health and welfare. Genet. Sel. Evol. 48:38. doi: 10.1186/s12711-016-0217-x
Szyda, J., Komisarek, J., and Antkowiak, I. (2014). Modelling effects of candidate genes on complex traits as variables over time. Anim. Genet. 45, 322–328. doi: 10.1111/age.12144
Tai, A. P. K., Martin, M. V., and Heald, C. L. (2014). Threat to future global food security from climate change and ozone air pollution. Nat. Clim. Change 4, 817–821. doi: 10.1038/nclimate2317
Tardieu, F., Cabrera-Bosquet, L., Pridmore, T., and Bennett, M. (2017). Plant phenomics, from sensors to knowledge. Curr. Biol. 27, R770–R783. doi: 10.1016/j.cub.2017.05.055
Tessmer, O. L., Jiao, Y., Cruz, J. A., Kramer, D. M., and Chen, J. (2013). Functional approach to high-throughput plant growth analysis. BMC Syst. Biol. 7:S17. doi: 10.1186/1752-0509-7-S6-S17
Tester, M., and Langridge, P. (2010). Breeding technologies to increase crop production in a changing world. Science (80-) 327, 818–822. doi: 10.1126/science.1183700
Thompson, R., and Meyer, K. (1986). A review of theoretical aspects in the estimation of breeding values for multi-trait selection. Livest. Prod. Sci. 15, 299–313. doi: 10.1016/0301-6226(86)90071-0
Thornley, J. H. M., France, J., and Cannell, M. G. R. (2005). An open-ended logistic-based growth function. Ecol. Modell. 184, 257–261. doi: 10.1016/j.ecolmodel.2004.10.007
Tjørve, K. M. C., and Tjørve, E. (2017). The use of gompertz models in growth analyses, and new gompertz-model approach: an addition to the unified-richards family. PLoS ONE 12:e0178691. doi: 10.1371/journal.pone.0178691
Toenniessen, G. H. (2002). Crop genetic improvement for enhanced human nutrition. J. Nutr. 132, 2943S–2946S. doi: 10.1093/jn/132.9.2943s
Topp, C. N., Iyer-Pascuzzi, A. S., Anderson, J. T., Lee, C.-R., Zurek, P. R., Symonova, O., et al. (2013). 3D phenotyping and quantitative trait locus mapping identify core regions of the rice genome controlling root architecture. Proc. Natl. Acad. Sci. U.S.A. 110, E1695–E1704. doi: 10.1073/pnas.1304354110
Trabelsi, A., Chaabane, M., and Ben-Hur, A. (2019). Comprehensive evaluation of deep learning architectures for prediction of DNA/RNA sequence binding specificities. Bioinformatics (Narnia) 35, i269–i277. doi: 10.1093/bioinformatics/btz339
Trachsel, S., Kaeppler, S. M., Brown, K. M., and Lynch, J. P. (2011). Shovelomics: high throughput phenotyping of maize (Zea mays L.) root architecture in the field. Plant Soil 341, 75–87. doi: 10.1007/s11104-010-0623-8
Turra, E. M., de Oliveira, D. A. A., Valente, B. D., Teixeira, E., de, A., Prado, S., et al. (2012). Estimation of genetic parameters for body weights of Nile tilapia Oreochromis niloticus using random regression models. Aquaculture 354–355, 31–37. doi: 10.1016/j.aquaculture.2012.04.035
van Dusschoten, D., Metzner, R., Kochs, J., Postma, J. A., Pflugfelder, D., Buehler, J., et al. (2016). Quantitative 3D analysis of plant roots growing in soil using magnetic resonance imaging. Plant Physiol. 170, 01388.2015. doi: 10.1104/pp.15.01388
van Eeuwijk, F. A., Bustos-Korts, D., Millet, E. J., Boer, M. P., Kruijer, W., Thompson, A., et al. (2018). Modelling strategies for assessing and increasing the effectiveness of new phenotyping techniques in plant breeding. Plant Sci. 282, 23–39. doi: 10.1016/j.plantsci.2018.06.018
van Pelt, M. L., Meuwissen, T. H. E., de Jong, G., and Veerkamp, R. F. (2015). Genetic analysis of longevity in Dutch dairy cattle using random regression. J. Dairy Sci. 98, 4117–4130. doi: 10.3168/jds.2014-9090
Vanhatalo, J., Li, Z., and Sillanpää, M. J. (2019). A Gaussian process model and bayesian variable selection for mapping function-valued quantitative traits with incomplete phenotypic data. Bioinformatics 35, 3684–3692. doi: 10.1093/bioinformatics/btz164
Vargas, G., Schenkel, F. S., Brito, L. F., Neves, H. H., de, R., Munari, D. P., et al. (2018). Unravelling biological biotypes for growth, visual score and reproductive traits in Nellore cattle via principal component analysis. Livest. Sci. 217, 37–43. doi: 10.1016/j.livsci.2018.09.010
Varona, L., Legarra, A., Toro, M. A., and Vitezica, Z. G. (2018). Non-additive effects in genomic selection. Front. Genet. 9:78. doi: 10.3389/fgene.2018.00078
Velazco, J. G., Malosetti, M., Hunt, C. H., Mace, E. S., Jordan, D. R., and van Eeuwijk, F. A. (2019). Combining pedigree and genomic information to improve prediction quality: an example in sorghum. Theor. Appl. Genet. 132, 2055–2067. doi: 10.1007/s00122-019-03337-w
Vernon, A. J., and Allison, J. C. S. (1963). A method of calculating net assimilation rate. Nature 200:814. doi: 10.1038/200814a0
Wade, K. M., Quaas, R. L., and Van Vleck, L. D. (1993). Estimation of the parameters involved in a first-order autoregressive process for contemporary groups. J. Dairy Sci. 76, 3033–3040. doi: 10.3168/JDS.S0022-0302(93)77643-2
Wang, L. A., and Goonewardene, Z. (2004). The use of MIXED models in the analysis of animal experiments with repeated measures data. Can. J. Anim. Sci. 84, 1–11. doi: 10.4141/a03-123
Wang, X., Zhang, R., Song, W., Han, L., Liu, X., Sun, X., et al. (2019). Dynamic plant height QTL revealed in maize through remote sensing phenotyping using a high-throughput unmanned aerial vehicle (UAV). Sci. Rep. 9:3458. doi: 10.1038/s41598-019-39448-z
Whalley, W. R., Binley, A., Watts, C. W., Shanahan, P., Dodd, I. C., Ober, E. S., et al. (2017). Methods to estimate changes in soil water for phenotyping root activity in the field. Plant Soil 415, 407–422. doi: 10.1007/s11104-016-3161-1
Wolfinger, R. D. (1996). Heterogeneous variance-covariance structures for repeated measures. J. Agric. Biol. Environ. Stat. 1, 205–230.
Wu, D., Guo, Z., Ye, J., Feng, H., Liu, J., Chen, G., et al. (2019). Combining high-throughput micro-CT-RGB phenotyping and genome-wide association study to dissect the genetic architecture of tiller growth in rice. J. Exp. Bot. 70, 545–561. doi: 10.1093/jxb/ery373
Wu, R., Ma, C. X., Lin, M., Wang, Z., and Casella, G. (2004). Functional mapping of quantitative trait loci underlying growth trajectories using a transform-both-sides logistic model. Biometrics 60, 729–738. doi: 10.1111/j.0006-341X.2004.00223.x
Wu, R. L., and Lin, M. (2006). Functional mapping – How to map and study the genetic architecture of dynamic complex traits. Nat. Rev. Genet. 7, 229–237. doi: 10.1038/nrg1804
Würschum, T., Liu, W., Busemeyer, L., Tucker, M. R., Reif, J. C., Weissmann, E. A., et al. (2014). Mapping dynamic QTL for plant height in triticale. BMC Genet. 15:59. doi: 10.1186/1471-2156-15-59
Xavier, A., Hall, B., Hearst, A. A., Cherkauer, K. A., and Rainey, K. M. (2017). Genetic architecture of phenomic-enabled canopy coverage in Glycine max. Genetics 206, 1081–1089. doi: 10.1534/genetics.116.198713
Xu, R., Li, C., and Paterson, A. H. (2019). Multispectral imaging and unmanned aerial systems for cotton plant phenotyping. PLoS ONE 14:e0205083. doi: 10.1371/journal.pone.0205083
Yan, W., and Rajcan, I. (2003). Prediction of cultivar performance based on single- versus multiple-year tests in soybean. Crop Sci. 43, 549–555. doi: 10.2135/CROPSCI2003.5490
Yang, G., Liu, J., Zhao, C., Li, Z. Z., Huang, Y., Yu, H., et al. (2017). Unmanned aerial vehicle remote sensing for field-based crop phenotyping: current status and perspectives. Front. Plant Sci. 8:1111. doi: 10.3389/fpls.2017.01111
Yang, R., Tian, Q., and Xu, S. (2006). Mapping quantitative trait loci for longitudinal traits in line crosses. Genetics 173, 2339–2356. doi: 10.1534/genetics.105.054775
Yang, R., and Xu, S. (2007). Bayesian shrinkage analysis of quantitative trait Loci for dynamic traits. Genetics 176, 1169–1185. doi: 10.1534/genetics.106.064279
Yano, K., Morinaka, Y., Wang, F., Huang, P., Takehara, S., Hirai, T., et al. (2019). GWAS with principal component analysis identifies a gene comprehensively controlling rice architecture. Proc. Natl. Acad. Sci. U.S.A. 116:201904964. doi: 10.1073/pnas.1904964116
Yin, X., Goudriaan, J., Lantinga, E. A., Vos, J., and Spiertz, H. J. (2003). A flexible sigmoid function of determinate growth. Ann. Bot. 91, 361–371. doi: 10.1093/aob/mcg029
York, L. M., Slack, S., Bennett, M. J., and Foulkes, M. J. (2018). Wheat shovelomics I: a field phenotyping approach for characterising the structure and function of root systems in tillering species. bioRxiv [preprint] doi: 10.1101/280875
Zhang, W., Gao, X., Shi, X., Zhu, B., Wang, Z., Gao, H., et al. (2018). PCA-based multiple-trait GWAS analysis: a powerful model for exploring pleiotropy. Animals (Basel) 8:239. doi: 10.3390/ani8120239
Zhang, X., Huang, C., Wu, D., Qiao, F., Li, W., Duan, L., et al. (2017). High-throughput phenotyping and QTL mapping reveals the genetic architecture of maize plant growth. Plant Physiol. 173, 1554–1564. doi: 10.1104/pp.16.01516
Zhao, C., Zhang, Y., Du, J., Guo, X., Wen, W., Gu, S., et al. (2019). Crop phenomics: current status and perspectives. Front. Plant Sci. 10:714. doi: 10.3389/fpls.2019.00714
Zhong, Z., Sun, A. Y., Yang, Q., and Ouyang, Q. (2019). A deep learning approach to anomaly detection in geological carbon sequestration sites using pressure measurements. J. Hydrol. 573, 885–894. doi: 10.1016/j.jhydrol.2019.04.015
Keywords: digital agriculture, genomic estimated breeding values, genomic selection, plant breeding, repeated record, time-dependent trait
Citation: Moreira FF, Oliveira HR, Volenec JJ, Rainey KM and Brito LF (2020) Integrating High-Throughput Phenotyping and Statistical Genomic Methods to Genetically Improve Longitudinal Traits in Crops. Front. Plant Sci. 11:681. doi: 10.3389/fpls.2020.00681
Received: 26 February 2020; Accepted: 30 April 2020;
Published: 26 May 2020.
Edited by:
Luisa M. Trindade, Wageningen University and Research, NetherlandsReviewed by:
Oene Dolstra, Wageningen University and Research, NetherlandsShouvik Das, Indian Agricultural Research Institute (ICAR), India
Copyright © 2020 Moreira, Oliveira, Volenec, Rainey and Brito. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Luiz F. Brito, YnJpdG9sQHB1cmR1ZS5lZHU=
 Fabiana F. Moreira
Fabiana F. Moreira Hinayah R. Oliveira
Hinayah R. Oliveira Jeffrey J. Volenec
Jeffrey J. Volenec Katy M. Rainey
Katy M. Rainey Luiz F. Brito
Luiz F. Brito