Phosphate rebinding induces force reversal via slow backward cycling of cross-bridges

Objective: Previous studies on muscle fibers, myofibrils, and myosin revealed that the release of inorganic phosphate (P_i) and the force-generating step(s) are reversible, with cross-bridges also cycling backward through these steps by reversing force-generating steps and rebinding P_i. The aim was to explore the significance of force redevelopment kinetics (rate constant k_TR) in cardiac myofibrils for the coupling between the P_i binding induced force reversal and the rate-limiting transition f^– for backward cycling of cross-bridges from force-generating to non-force-generating states.

Methods: k_TR and force generation of cardiac myofibrils from guinea pigs were investigated at 0.015–20 mM P_i. The observed force-[P_i], force-log [P_i], k_TR-[P_i], and k_TR-force relations were assessed with various single-pathway models of the cross-bridge cycle that differed in sequence and kinetics of reversible P_i release, reversible force-generating step and reversible rate-limiting transition. Based on the interpretation that k_TR reflects the sum of rate-limiting transitions in the cross-bridge cycle, an indicator, the coupling strength, was defined to quantify the contribution of P_i binding induced force reversal to the rate-limiting transition f^– from the [P_i]-modulated k_TR-force relation.

Results: Increasing [P_i] decreased force by a bi-linear force-log [P_i] relation, increased k_TR in a slightly downward curved dependence with [P_i], and altered k_TR almost reciprocally to force reflected by the k_TR-force relation. Force-[P_i] and force-log [P_i] relations provided less selectivity for the exclusion of models than the k_TR-[P_i] and k_TR-force relations. The k_TR-force relation observed in experiments with cardiac myofibrils yielded the coupling strength +0.84 ± 0.08 close to 1, the maximum coupling strength expected for the reciprocal k_TR–force relationship. Single pathway models consisting of fast reversible force generation before or after rapid reversible P_i release failed to describe the observed k_TR–force relation. Single pathway models consistent with the observed k_TR-force relation had either slow P_i binding or slow force reversal, i.e., in the consistent single pathway models, f^– was assigned to the rate of either P_i binding or force reversal.

Conclusion: Backward flux of cross-bridges from force-generating to non-force-generating states is limited by the rates of P_i binding or force reversal ruling out other rate-limiting steps uncoupled from P_i binding induced force reversal.

1 Introduction

Muscle generates force through the cross-bridge ATPase cycle, during which the cross-bridges pass through various chemical and structural states, which are grouped into non-force-generating and force-generating states. The forward transition from non-force-generating to force-generating states is associated with the release of inorganic phosphate (P_i) and the force-generating step, also called the power stroke when referring to the individual myosin motor. Studies on muscle fibers and myosin working under load indicate that P_i release is reversible, allowing cross-bridges to rebind P_i and reverse force generation, i.e., the force produced by cross-bridges, by cycling backward from force-generating to non-force-generating states (Mannherz, 1970; Ulbrich and Ruegg, 1971; Hibberd et al., 1985a; Hibberd et al., 1985b; Webb et al., 1986). However, models of the cross-bridge ATPase cycle differ with respect to the sequence of P_i release and the power stroke. The original model, which proposed that the force-generating step occurs concurrently with P_i release (Eisenberg et al., 1980), has undergone continuous refinement. Many studies support models where the power stroke precedes P_i release (Millar and Homsher, 1990; Kawai and Halvorson, 1991; Dantzig et al., 1992; Ranatunga, 1999; Muretta et al., 2015; Woody et al., 2019; Matusovsky et al., 2021; Scott et al., 2021), whereas others support the opposite sequence (Davis and Rodgers, 1995; Smith, 2014; Llinas et al., 2015; Rahman et al., 2018; Offer and Ranatunga, 2020; Hwang et al., 2021; Moretto et al., 2022). Further complexity arises because of the need for at least one additional power stroke (Capitanio et al., 2006; Hwang et al., 2021; Matusovsky et al., 2021) and recent evidence from kinetics of single molecule fluorescence and molecular modelling that P_i release from muscle myosin (myosin II) occurs in multiple step (Moretto et al., 2022). Earlier evidence for a stepwise mechanism of P_i release has been given by studies of crystal structures of myosin VI (Llinas et al., 2015; Robert-Paganin et al., 2020). Moreover, the correlation between mechanical and energetic quantities led to the concept that the myosin power stroke is weakly coupled to its ATPase cycle (Yanagida et al., 1985; Ishijima et al., 1998) or more concretely to models in which cross-bridges can cycle through additional pathways, enabling some uncoupling (Linari et al., 2010; Debold et al., 2013; Scott et al., 2021), or loosening of the coupling (Caremani et al., 2013; Governali et al., 2020) between force generation and P_i release. Additional pathways include the detachment of myosin from actin before releasing P_i (Linari et al., 2010), P_i release from one pre-power stroke state and three post-power stroke states (Caremani et al., 2013; Governali et al., 2020), and detachment of myosin upon rebinding of P_i to the pre-power stroke (Debold et al., 2013) or to the post-power stroke state (Scott et al., 2021). The advantages and disadvantages of the different models are discussed in details (Debold, 2021; Mansson et al., 2023; Rassier and Mansson, 2025); however, arriving at a consensus remains challenging to date.

Understanding the mechanisms of P_i release and force generation is linked to their relation to the transitions limiting the rates of cross-bridge cycling. Although these rate-limiting transitions have been explored in many studies discussed by Gordon et al. (2000), Takagi et al. (2004), Geeves and Holmes (2005), Mansson et al. (2015), Stehle and Tesi (2017), Rahman et al. (2018), their nature remains controversial. Elucidating the relationship between these rate-limiting transitions and reversible P_i release and force generation is important for developing targeted strategies to modulate the rate of muscle contraction reviewed by Gordon et al. (2000), Takagi et al., (2004), Hinken and Solaro (2007), Stehle and Iorga (2010), Mansson et al. (2015), Geeves (2016), Houdusse and Sweeney (2016), Stehle and Tesi (2017). This study aims to explore the coupling between the process of P_i release-associated force generation and rate-limiting transitions. This coupling is still poorly understood, even for the main pathway. Because of the open questions regarding the sequence of P_i release and force generation and the increasing difficulty to identify specific rate-limiting transitions in multi-step and multi-pathway model, the strategy for defining the constraints for the rate-limiting step in this study was to analyze simple, single-pathway models with various sequence and kinetics of the P_i release and the force-generating step.

A measurement of the rates limiting the transition between non-force-generating and force-generating states is the kinetics of mechanically-induced force redevelopment induced by rapidly switching from a transient period of active unloaded shortening to active isometric contraction (Brenner, 1988). The rate constant k_TR of this force redevelopment represents the sum of apparent rate constants in the cross-bridge ATPase cycle limiting the transitions of cross-bridges between non-force-generating and force-generating states (Brenner, 1988), reviewed in Gordon et al. (2000). The addition of P_i increases k_TR and decreases force in skeletal and cardiac muscle (Millar and Homsher, 1990; Regnier et al., 1995; Araujo and Walker, 1996; Wahr et al., 1997; Regnier and Homsher, 1998; Tesi et al., 2000; Stehle et al., 2002a; Tesi et al., 2002; Hinken and McDonald, 2004; Edes et al., 2007; Papp et al., 2014; Stehle, 2017; Stehle and Tesi, 2017; Governali et al., 2020). The opposing effects of [P_i] on k_TR and force provide evidence for P_i shifting of cross-bridges backward from force-generating to non-force-generating states (Hibberd et al., 1985a; Hibberd et al., 1985b; Webb et al., 1986; Kawai and Halvorson, 1991; Dantzig et al., 1992; Ranatunga, 1999; Mansfield et al., 2012; Woodward and Debold, 2018). Without P_i, redistribution is solely determined by the rate-limiting forward transitions f and g in the ATPase cycle, and k_TR = f + g, with f denoting the apparent rate constant of the transition to force-generating states and g the apparent rate constant of the transition to non-force-generating states. Increasing [P_i] promotes the rebinding of P_i and facilitates the backward transition to non-force states, characterized by the apparent rate constant f^– which contributes to k_TR by k_TR = f + g + f^–, where f^– is a function of [P_i.] (Palmer and Kentish, 1998; Stehle et al., 2002a; Stehle and Tesi, 2017). Recently, the reversibility of force generation was demonstrated at the molecular level by identifying elementary reverse strokes of force measurements on single cardiac myosin heads and filaments (Woody et al., 2019; Hwang et al., 2021). The step size of the two reverse strokes quantified in the experiments with single cardiac myosin were −6 nm and −3 nm and of similar magnitude as the two forward strokes of +6 nm and +3 nm (Hwang et al., 2021). Importantly, reverse strokes were confirmed by their experiments with single cardiac myosin filaments also to occur at high physiological [ATP].

The present study explored the effects of [P_i] on k_TR and force in cardiac myofibrils of guinea pigs on the kinetic coupling of P_i binding induced force reversal and f^–. The interrelation between k_TR and force at various [P_i], i.e., the P_i-modulated k_TR-force relation is demonstrated to provide a basis for probing the strength of this coupling. The coupling strength (CS) derived from this interrelation reaches its theoretical maximum when P_i binding and the reversal of the force-generating step are combined with f^– into a slow single step, according to the limiting case of a two-state cross-bridge model in which P_i alters k_TR and force in a simple reciprocal manner, such that, k_TR changes in proportion to 1/force, i.e., delta k_TR = 1/delta F. Based on this limiting case, an empirical equation was developed to define CS on a scale of +1 for maximum coupling and 0 for the case when k_TR becomes independent of [P_i]. The P_i-modulated k_TR-force relation of the cardiac myofibrils from guinea pigs yielded a high CS of +0.84 ± 0.08. Testing different models revealed that either P_i binding or force reversal, or both, must be connected to f^– to yield the high CS observed in the experiments.

2 Materials and methods

2.1 Myofibrillar preparation and solutions

Dunkin-Hartley guinea pigs weighing 450–750 g were anesthetized with 5 vol% isoflurane and euthanized by decapitation. The use of animals and procedures in this study complied with the law for animal protection (TierSchG) transferred from the EU guidelines and was reviewed and approved by the Official Animal Care and Use Committee (LANUV NRW, Az 84-02.05.20.13.080 and 84-02.05.50.15.029). After exsanguination of the animal body, the heart was excised, and skinned strips from the trabeculae were prepared as described previously (Linke et al., 1993). First, the blood was removed from the heart by a brief (2–3 min) retrograde perfusion through the aorta at 37°C using a perfusion solution containing 132 mM NaCl, 5 mM KCl, 1 mM MgCl₂, 10 mM TRIS, 5 mM EGTA, 1 mM sodium azide, 7 mM glucose, and 2 mM DTT, adjusted to pH 7.1. The heart was then transferred into an ice-cold perfusion solution without glucose, and the left ventricular cavity was opened by cutting in the axial direction. Thin strips with diameters of 0.3–0.4 mm were dissected from the endocardial trabeculae carneae under observation through a Olympus SZ51 stereomicroscope (Olympus, Hamburg, Germany) at about 20-fold magnification using a Vannas spring Scissors and a Dumont#5SF forceps (Fine Science Tools, Heidelberg, Germany) and pinned with microneedles on the Sylgard surface (Sylgard 184 Elastomer Kit, Dow Corporate, Mat. No. 4019862) in a chamber containing ice-cold skinning solution comprising 1% v/v Triton-X-100, 5 mM K-phosphate, 5 mM Na-azide, 3 mM Mg-acetate, 5 mM K₂EGTA, 3 mM Na₂ATP (including 3 mM MgCl₂ and 6 mM KOH), 47 mM Na₂CrP, 2 mM DTT, 0.5 mM 4-(2-aminoethyl) benzenesulfonylfluoride HCl, 10 μM leupeptin, 10 μM antipaine, 5 mg/mL aprotinine (adjusted to pH 7 at 0°C). EGTA (324,626) was from Merck Millipore. Triton X-100 (T8787), Na₂ATP (A2383), Na₂CrP (2,380) and protease inhibitors were from Merck Sigma Aldrich in high purity grade. The pinned strips were incubated in the skinning solution at 0°C for 4 h, and the skinning solution was replaced by storage solution (same composition as the skinning solution but without triton), in which the skinned strips were stored at 4°C for up to 3 days. Myofibrils were prepared on the day of the mechanical experiment by homogenizing the skinned strips at 0°C for 4–6 s at maximum speed using a blender (T10 Ultra-Turrax, IKA, Stauffen, Germany). The homogenate was then filtered through polypropylene meshes with 22 µm pore openings.

The standard activating buffer (pCa 4.5) used for mechanical experiments contained 10 mM imidazole, 3 mM CaCl₂K₄EGTA, 1 mM Na₂MgATP, 3 mM MgCl₂, 47.7 mM Na₂CrP, 2 mM DTT, and different [P_i] with a pH of 7.0 at 10°C, and µ = 0.178 M. The standard relaxation buffer (pCa 7) contained 3 mM K₄Cl₂EGTA, instead of 3 mM CaCl₂K₄EGTA. Submaximal activating buffers, pCa (5.88–5.03), were prepared by mixing the standard activating and relaxing buffers in different ratios. Free calcium concentration [Ca²⁺] and pCa = -log [Ca²⁺]/M were calculated using a computer program (Fabiato and Fabiato, 1979). The [P_i] in the buffers was measured using a phosphate assay kit (E−6646; Molecular Probes, Eugene, OR). P_i contamination in the standard activating buffer was 170 ± 20 µM (mean ± SD). Activating and relaxing buffers of lower [P_i] (15 ± 5 µM P_i) were produced by adding 1 mM methylguanosine and 0.5 units/mL purine nucleotide phosphorylase (PNP). Activating and relaxing buffers with higher [P_i] were produced by adding phosphate buffer (30% NaH₂PO₄⁻ 70% Na₂HPO₄^2-, pH 6.85). To maintain constant ionic strength, [Na₂CrP] was reduced by 0.67 mM per 1 mM increase of [P_i]. All activating and relaxing buffers of different [P_i] were adjusted to a final pH 7.0 at 10°C.

2.2 Apparatus and technique to measure myofibril force redevelopment

The mechanical setup consisted of an Olympus IX-70 microscope with a self-built rigid stage on top to which all manipulators for positioning of the chamber, the solution flow, the micro-needles and the atomic force cantilever were mounted. The micro-flow for the rapid solution change and the optics for force detection by the principle of atomic force microscopy has been described previously (Stehle et al., 2002a; Stehle et al., 2002b). A droplet of myofibrils suspended in the storage solution was added to the thermostatically controlled (10°C) chamber filled with relaxing solution. After sedimentation, a thin myofibril bundle was picked up from the bottom of the chamber at one of its ends using a tungsten micro-needle (# 5,775, A-M Systems, Inc., Carlsborg, WA) connected via a piezo actuator (P602.1SL, Physik Instr.) to a micromanipulator. The bundle was then moved with the micromanipulator to position its other, free end close to the tip of the atomic force cantilever (Nanoprobe^© FESP type, compliance: 0.2–0.4 μm/μN), which was coated with a mixture (2:3 v/v) of 4% nitrocellulose in amyl-acetate and silicon adhesive (3140 RTV Coating, Dow Corning, Midland, United States). To fix the free end of the bundle at the surface of the coating, the bundle was pressed against the coating using a microneedle installed on a separate manipulator.

Dimensions and sarcomere length (SL) of myofibrils were determined under phase contrast microscopy using the 60x/0.70 Ph2 LCPlanFl objective and the 1.5 magnification lens built in the IX-70 microscope imaged to an ORCA-ER camera (Hamamatsu Photonics, Japan). The bundles used in the experiments had diameters ranging from 1.0 to 3.2 µm and slack lengths of 31–66 µm. The mean slack sarcomere length was 2.02 ± 0.11 µm (mean ± SD). Prior to activation, the bundles were stretched to a 2.4 µm SL. Signal conditioning for movement of actuators and acquisition of force and length signals was performed using a PCI6110-E device under self-written programs in LabView 4.0 (National Instruments, Austin, TX). During force recording, the myofibrils were exposed to one of two laminar streams of solutions produced by a double-channel theta-style capillary (TGC150-15, Clark Electromed. Instr., UK) and driven by gravitational pressure (30–35 cm H₂O). Rapid Ca²⁺ activation and relaxation were induced by rapid solution changes (Colomo et al., 1998). The position of the flow was altered by the rapid lateral movement of the capillary, controlled by a piezo actuator (P289.40, Physik Instrumente, Karlsruhe, Germany), which effectively changed the solution at the bundle within 5–15 ms. Force redevelopment (k_TR-measurement) was induced during Ca²⁺ activation. Rapid length changes were applied to the bundle via the microneedle using a piezo actuator (P602.1SL, Physik Instrumente). To determine the rate constant k_TR for force redevelopment, a single exponential function was fitted to the force transients using the LabView program.

2.3 Coupling strength (CS) and model simulation

An indicator, the coupling strength (CS) was defined to quantify the coupling between P_i binding induced force reduction and the rate-limiting backward transition f^– in the cross-bridge ATPase cycle. CS was scaled to 0 for no coupling, to +1 for maximum coupling, and to approach the limit value of −1 for maximum inverse coupling.

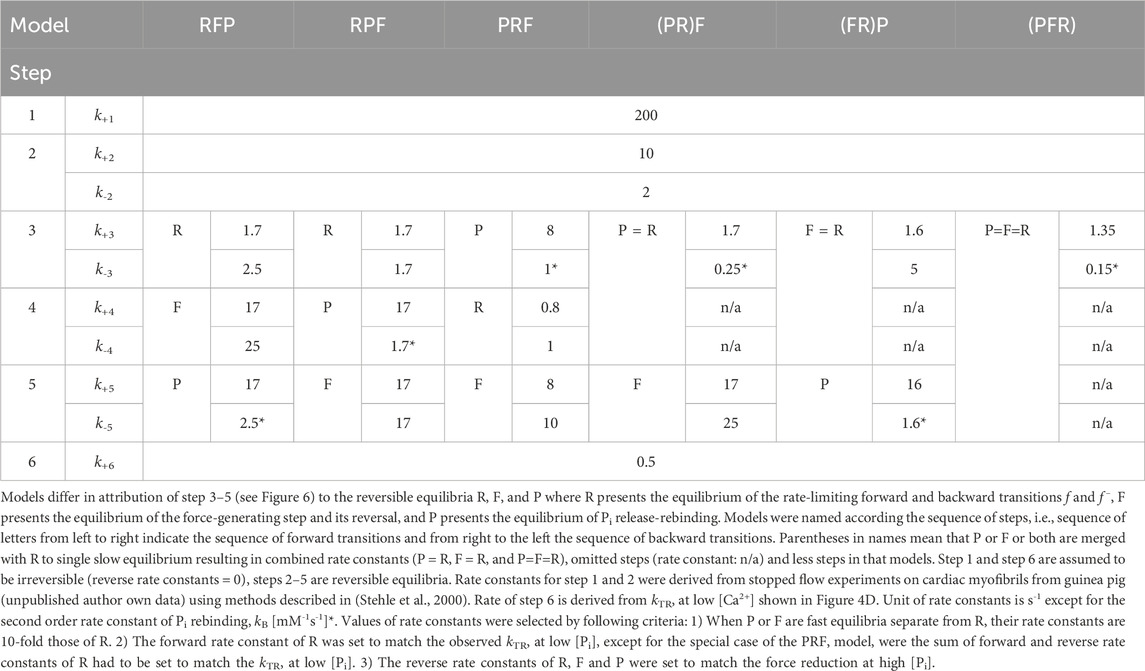
The maximum positive coupling exists when P_i rebinding, the reverse of the force-generating step, and the rate-limiting step for the backward transition of cross-bridges from force-generating states to non-force-generating states all represent the same step, with no other steps contributing to the backward cycling of cross-bridges. This scenario corresponds to the two-state model (Figure 1), involving the forward rates f and g and the reverse rate f^–, where f represents the P_i release-coupled force generation and f^– the P_i binding-coupled reverse of force generation. In this model, the force (F) is proportional to the fraction of attached motors f/(f + g + f ^–), and the rate constant of tension redevelopment k_TR is equal to the sum of the rate constants: k_TR = f + g + f ^– (Huxley, 1957; Brenner, 1988; Stehle et al., 2002a). For different [P_i], the statement is correct under the condition that the force per motor remains the same when changing [P_i]. The latter is supported by several studies on slow (Governali et al., 2020; Smith et al., 2020), fast skeletal (Caremani et al., 2008), and cardiac muscle preparations (Ebus et al., 1994; Zhao and Kawai, 1996).

Figure 1

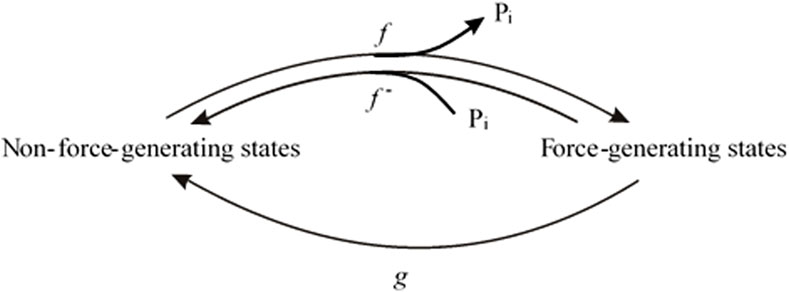
Figure 1. Two-state model in which P_i release step, force-generating step and the rate-limiting step for entering force-generating states are merged to single, fully reversible equilibrium.

To implement the [P_i] dependence of the force and k_TR associated with P_i binding in this model, the (fixed) rate constant f^– was replaced by an apparent rate constant f^–_app defined by Equation 1:

$f^{–}\text{app}=f^{–}0+f^{–}+\text{Pi}(1)$

where f ^–₀ is the value of f^–_app at standard [P_i], i.e., the [P_i] in the standard activating solution, and f ^–_+Pi is an arbitrary function of [P_i] describing the change in f^–_app from standard [P_i] to a given [P_i].

Then, at standard [P_i]:

$F_0\propto f/\left(f+g+f^{–}0\right)(\mathrm{2a})$

$k_{\text{TR},0}=f+g+f^{–}0(\mathrm{2b})$

where F₀ is F and k_TR,0 is k_TR at the standard [P_i].

At any given [P_i]:

$F_{+\text{Pi}}\propto f/\left(f+g+f^{–}0+f^{–}+\text{Pi}\right)(\mathrm{3a})$

$k_{\text{TR},+\text{Pi}}=f+g+f^{–}0+f^{–}+\text{Pi}(\mathrm{3b})$

where F_+Pi is F, and k_TR,+Pi is k_TR at the given [P_i], respectively.

Inserting Equation 2b in Equation 2a yields

$F_0\propto f/k_{\text{TR},0}(\mathrm{4a})$

Inserting Equation 3b in Equation 3a yields

$F_{+\text{Pi}}\propto f/k_{\text{TR},+\text{Pi}}(\mathrm{4b})$

Dividing Equation 4b by Equation 4a results in

$F_{+\text{Pi}}/F_0\propto \left(f/k_{\text{TR},+\text{Pi}}\right)/\left(f/k_{\text{TR},0}\right)=k_{\text{TR},0}/k_{\text{TR},+\text{Pi}}(5)$

Equation 5 demonstrates that the force at the respective [P_i] normalized to the force at the standard [P_i] is reciprocally related to k_TR at the respective [P_i] normalized to k_TR at the standard [P_i]. Therefore, changes in [P_i] result in reciprocal alterations in force and k_TR.

Equation 5 can be expressed as

$k_{\text{TR},\text{Pi}}=k_{\text{TR},0}{F}_0/F_{\text{Pi}}(6)$

where k_TR,Pi is k_TR and F_Pi, is the force at a given [P_i]. k_TR,0 is k_TR and F₀ is the force at basal [P_i].

The CS is defined as 0 when P_i alters the force without changing k_TR (k_TR = constant) and is defined as 1 for maximum coupling as described in Equation 6.

Based on the two edge cases for CS = 0, k_TR,Pi = k_TR,0, and CS = +1, k_TR,Pi = k_TR,0F₀/F_Pi (Equation 6), an empirical equation was formulated to describe the intermediate shapes of the P_i-modulated k_TR-force relation in terms of a linear scale for CS within the interval [0, +1]:

${\mathrm{k}}_{\text{TR},\text{Pi}}=k_{\text{TR},0}\left(\mathit{\text{CS}}\left({\mathit{F}}_0/{\mathit{F}}_{\text{Pi}}-1\right)+1\right)=k_{\text{TR},0}\left(1-\mathit{\text{CS}}+\mathit{\text{CS\hspace{0.17em}}}{\mathit{F}}_0/{\mathit{F}}_{\text{Pi}}\right)(7)$

CS can be negative, i.e., k_TR,Pi can decrease with decreasing F_Pi if rate-limiting transitions f and f^– occur after rapid P_i release-rebinding. In this case, increasing [P_i] further reduces the force by shifting the cross-bridges back to non-force-generating states via P_i binding. However, k_TR,Pi decreases because the starting state of the rate-limiting forward transition f to force-generating states is the post-P_i release state, which is also the P_i-rebinding state. Increasing [P_i] lowers the occupancy of this state via P_i rebinding and therefore the contribution of f for rate modulating k_TR. Consequently, k_TR decreases from f + f^– + g at low [P_i] to f^– + g at high [P_i]. The empirical equation describing the relation between k_obs and force due to decreasing f (Poggesi et al., 2005) was transformed to describe k_TR-force relations with a negative CS in the interval (−1, 0], i.e., for CS > −1 and ≤0.

$k_{\text{TR},\text{Pi}}=k_{\text{TR},0}\left(1+CS\right)/\left(1+CS{F}_{\text{Pi}}/F_0\right)(8)$

The assumption for deriving (Equation 8) is that basal [P_i] is zero. This assumption is not required to derive Equation 7, for which any standard [P_i] can be defined as the basal [P_i].

To illustrate the dependence of k_TR-force relations on CS, the normalized k_TR (y = k_TR,Pi/k_TR,0) is plotted versus the normalized force (x = F_Pi/F₀) for increasing CS from 0 to 1 in increments of 0.1, as calculated using Equation 7 (Figure 2A) and for decreasing CS from 0 to −0.9 in increments of −0.1 using Equation 8 (Figure 2B). Starting from a flat, linear relation for zero CS, k_TR increases with force reduction by P_i; CS becomes positive. Conversely, the more k_TR decreases with force reduction, the more CS becomes negative. The magnitude of change in k_TR and the curvature of the k_TR-force relation increase with the absolute value of CS.

Figure 2

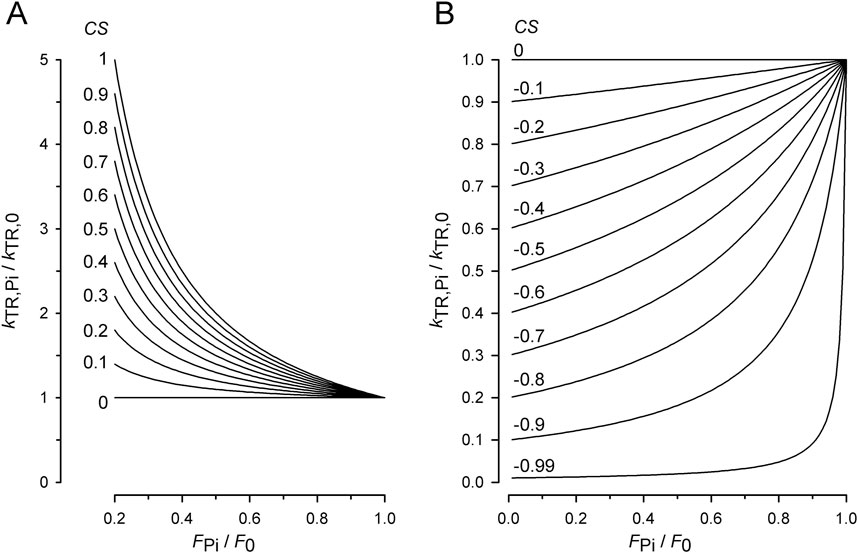
Figure 2. Effect of coupling strength (CS) on normalized k_TR–force relations. (A) Relations for positive CS calculated by Equation 7. Increasing the CS by constant step sizes from 0 to 1 results in equidistant series of relations. For CS = 1, Equation 7 becomes equivalent to Equation 6 and y = 1/x. (B) Relations for negative CS calculated by Equation 8. Decreasing the CS by constant step sizes results in equidistant decreases of k_TR,Pi-values at the ordinate. Note that for zero CS, k_TR,Pi = k_TR,0 and y = 1 for Equation 7 as well as for Equation 8.

Equation 7 and Equation 8 can be used to fit the k_TR-force data of muscle preparations obtained at various [P_i] to derive the CS from the experimental data or data obtained by model simulations.

Model simulations were performed using the Berkeley Madonna 8.3.18 differential equation solver. Graphs and fits of experimental and model data were produced by SigmaPlot 8.0. Statistic F-test was performed under GraphPad Prism 4.

3 Results

3.1 Characteristics of force redevelopment at different [P_i]

Figure 3 shows the force transients of the guinea pig cardiac myofibrils at 10°C, pCa 4.5, and different [P_i]. The force recordings in Figure 3A illustrate the experimental protocol. The myofibril bundle was exposed to the flow of the relaxing solution (pCa 8), and calcium-induced force development was initiated by rapidly switching to the flow of the activating solution (pCa 4.5), consisting of the same [P_i] as the relaxing solution. To measure k_TR during steady-state Ca²⁺ activation, the kinetics of force redevelopment following a transient period of active unloaded shortening was induced (Brenner, 1988). This was performed by applying a slack and re-stretch maneuver to the myofibril bundle consisting of a fast release by 15% of myofibril length to induce unloaded shortening for 50 ms and then a rapid stretch to the original length. After the redevelopment of the force, the bundle was relaxed by switching back from the activating to the relaxing solution. Subsequently, the next activation-k_TR-measurement-relaxation cycle is performed at the next [P_i].

Figure 3

Figure 3. Experimental protocol and force redevelopment at different [P_i] at 10°C. (A) Typical full force transients obtained from a myofibril bundle (2.3 µm diameter, 66 µm length) at 0.17 ± 0.04 mM P_i (contaminant [P_i] in standard buffer, black transient) and 20 mM P_i (pink transient). At t = 0.5 s, the bundle was activated by switching from relaxing solution (pCa 8) to activating solution (pCa 4.5). At t = 4.5 s, the bundle was slackened for 100 ms by 15% of its length and then re-stretched to the original length to induce force redevelopment. At t = 8.5 s, the bundle was relaxed by switching back to relaxing solution. Force redevelopment after re-stretch mostly starts from a higher level than slack force like in this example. (B) Force redevelopment transients from a myofibril bundle (3.2 µm diameter, 47 µm length) at 1 mM P_i (black), 2.5 mM P_i (blue), 10 mM P_i (grey), and 20 mM P_i (green). Red lines are single exponentials fitted to transients yielding values for k_TR of 1.4 s⁻¹ (1 mM P_i), 1.7 s⁻¹ (2.5 mM P_i), 1.9 s⁻¹ (10 mM P_i), and 2.9 s⁻¹ (20 mM P_i). In this experiment, force redevelopments started close to slack force enabling the comparison of their initial force rises that exhibit similar slopes as shown in (C).

Increasing [P_i] reduced the isometric force and the time required to reach the force plateau (Figures 3A, B). Force transients were fitted using single exponential functions (red lines in Figures 3B, C) to determine the rate constant of tension redevelopment, k_TR. Increasing [P_i] from 1 mM up to 20 mM decreased force by approximately 50% and increased k_TR by approximately 2.1-fold (Figure 3B), while the initial slope of the force redevelopment remained relatively constant (less than 15% change, Figure 3C). The constant initial slope is expected when the rate constant of an exponential function changes reciprocally with its amplitude, indicating the maximum possible rate modulation of k_TR (Equation 6).

3.2 Dependence of force and k_TR on the [P_i]

To exploit the force reduction and rate modulation of k_TR over a broad range of [P_i], force redevelopment transients were recorded from 19 myofibril bundles at variable [P_i] ranging from 0.015 mM to 20 mM. The force values of the transients were then normalized to the mean force produced by the myofibril bundle in the standard activating solution containing a contaminant [P_i] of 0.17 mM. Figure 4A illustrates the relationship between the normalized active force and [P_i]. Force reduction was already observed at low, sub-millimolar [P_i] levels. Fitting the force-[P_i] relation using a hyperbolic function yields three parameters: the fit value at zero [P_i] (F_0Pi), [P_i] for half-maximum hyperbolic change (P_i50), and the final value at infinity [P_i] (F_∞Pi). The fitted F_∞Pi (0.13 ± 0.09) suggests an active force component that cannot be inhibited by P_i. Plotting force on a logarithmic scale of [P_i] revealed a bilinear relationship with a 6-fold less steep decrease in force per decade increase of [P_i] for data with ≤1 mM P_i than for the data with ≥2.5 mM P_i (Figure 4B).

Figure 4

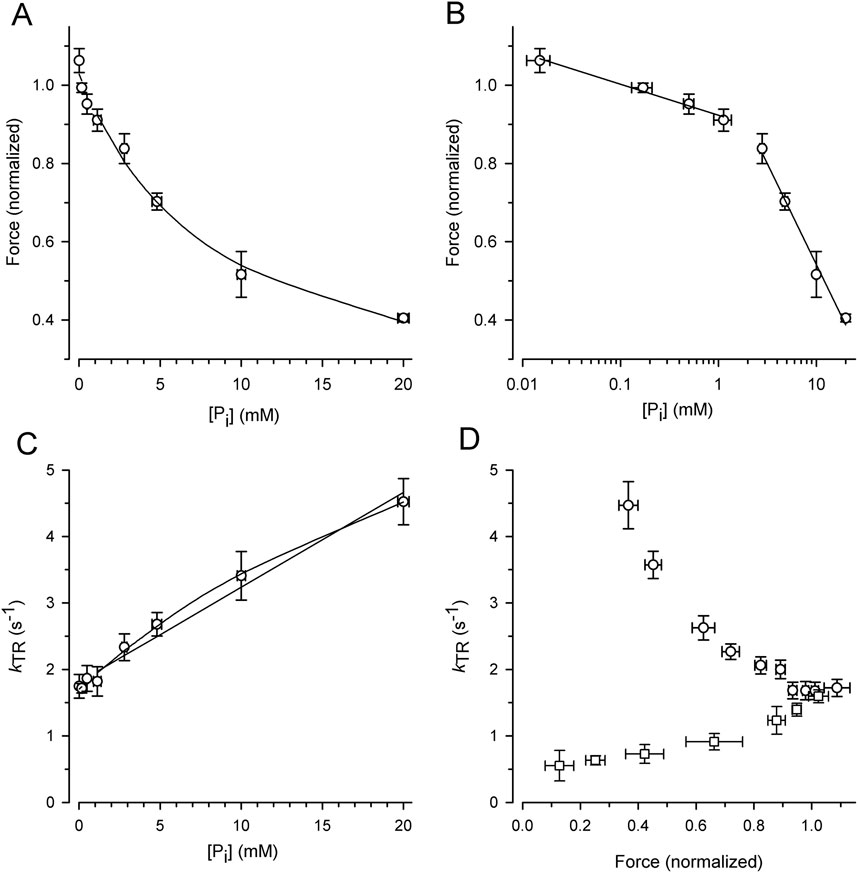
Figure 4. Alteration of force and k_TR by [P_i] and comparison of k_TR-force relations resulting from varying [P_i] and [Ca²⁺] at 10°C. For each myofibril, force data was normalized to force measured in standard activating solution (0.17 mM P_i, pCa 4.5). (A) Force-[P_i] relation. The line present the hyperbolic function fitted to the data yielding F_0Pi = 1.03 ± 0.02, P_i50 = 8.4 ± 2.1 mM and F_∞Pi = 0.13 ± 0.09. (B) Force-log [P_i] relation. Lines indicate linear regression lines with slopes of −0.08 per decade increase of [P_i] at low [P_i] (≤1 mM P_i) and −0.51 at high [P_i] (≥2.5 mM P_i). (C) k_TR-[P_i] relation and analysis of its curvature. The lines present linear (k_0Pi = 1.81 ± 0.07 s^-1, slope = 0.143 ± 0.008 s^-1/mM P_i) or hyperbolic fit functions (k_0Pi = 1.70 ± 0.04 s⁻¹, P_i50 = 33 ± 9 mM and k_∞Pi = 9.2 ± 1.3 s⁻¹) to the data. (D) Relations of k_TR versus force altered either by changing the [P_i] between 0.015 mM and 20 mM (circles) at full Ca²⁺ activation (pCa 4.5) or by changing the pCa between 4.5 and 5.88 (squares) at constant [P_i] of 0.17 mM. Data was sorted for increasing normalized force values, subdivided in similar groups of n = 14–15 and plotted as mean ± s.d. For force and mean ± SEM for k_TR.

Figure 4C illustrates the increase in the k_TR-data with the [P_i], which can be fitted with a linear and hyperbolic function. If a process other than P_i binding limits the backward transition from force-generating to non-force-generating states (f^–), k_TR saturates at high [P_i], resulting in a hyperbolic k_TR-[P_i] relation. In contrast, if f^– refers to the rate constant of P_i binding, a linear increase in k_TR with [P_i] is expected. A weak curvature in the k_TR-[P_i] relation was observed, and the hyperbola fits the data significantly better (p = 0.0052 yielded by F-test) than the linear curve (lines in Figure 4C).

The effects of [P_i] on k_TR and force were analyzed by plotting the k_TR-force relation, i.e., by pairing the k_TR values with the corresponding relative force from the same transient (Figure 4D, circles). Because force decreases with increasing k_TR, the k_TR-force relation exhibits a negative slope that becomes steeper at low forces. To determine whether k_TR simply increased owing to the lower isometric force, the force was reduced by reducing [Ca²⁺] in the standard activating solution without adding P_i. Force transients from eight myofibrils were recorded at both full and partial Ca²⁺ activation. The force of each transient was normalized to the force at full Ca²⁺ activation (pCa 4.5, 0.17 mM P_i), and the k_TR value was paired with the normalized force from the same transient and plotted in Figure 4D (square symbols). Consistent with previous studies, Ca²⁺ modulates k_TR in the same direction as the force (Brenner, 1988; Sweeney and Stull, 1990; Regnier et al., 1995; Wolff et al., 1995; Edes et al., 2007; Norman et al., 2007; Kreutziger et al., 2008; Papp et al., 2014), which is opposite to the P_i-modulated k_TR-force relation.

3.3 Quantification of coupling strength from [P_i]-modulated k_TR-force data

To quantify the CS from the experiments with varying [P_i], each individual k_TR value obtained from each transient was paired with the normalized force value from the same transient, and these data pairs were plotted in the k_TR,Pi-force relation shown in Figure 5. The symbols represent the values of 144 force transients obtained from 19 myofibrils at different [P_i] (indicated by different symbols or colors in the online version). The line represents the best fit of Equation 7 to the data, yielding a CS of 0.84 ± 0.08 and k_TR,0 of 1.73 ± 0.07 s^-1. The latter reflects the k_TR-value of the fit curve at unity force in the standard solution, which is 0.17 mM P_i.

Figure 5

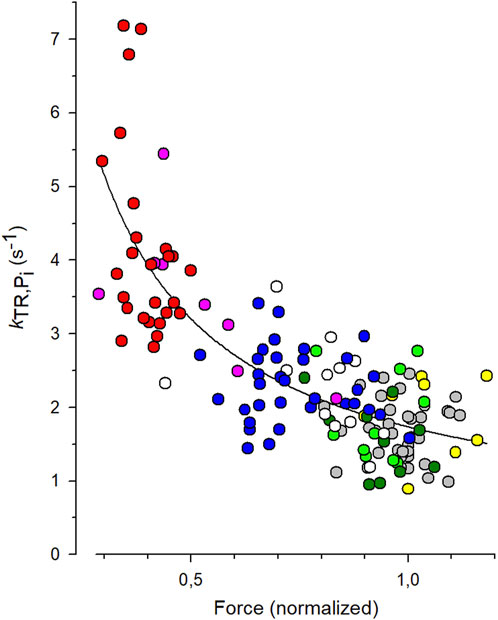
Figure 5. Fit of coupling strength (CS) function (Equation 7) to k_TR-force data. All force data is normalized to mean force of each myofibril at 0.17 mM P_i that was the contaminant [P_i] in standard solution. Grey symbols: data obtained at 0.17 mM P_i (36 transients), green: 0.5 mM P_i (10 transients), dark green: 1 mM P_i (10 transients), white: 2.5 mM P_i (12 transients), blue: 5 mM P_i (33 transients), pink: 10 mM P_i (8 transients), red: 20 mM P_i (26 transients). In three myofibrils, [P_i] was further reduced by the P_i scavenger PNP resulting in a [P_i] of 0.015 mM (yellow, data of 9 transients). The best fit of Equation 7 (line) to the pooled k_TR-force data yields the fit coefficients CS = 0.84 ± 0.08 and k_TR,0 = 1.73 ± 0.07 s⁻¹ (mean ± s.d).

3.4 Rate modulation of k_TR by [P_i] and coupling strength depend on the model

To assess the compatibility of the high CS obtained in the myofibril experiments with cross-bridge cycle models, various models with different sequences and kinetics for three critical events determining the reversible transition into force-generating states were tested for their [P_i]-dependent modulation of force and k_TR. Three critical events were defined as reversible equilibria: an equilibrium abbreviated as R for the rate-limiting forward and backward transitions (f and f^–), an equilibrium abbreviated as F for the force-generating step and its reversal, and an equilibrium abbreviated as P for P_i release-rebinding. The equilibria R, F, and P were incorporated into various models of the cross-bridge cycle using the same rate constants for ATP binding (step 1), ATP hydrolysis (step 2), and load-dependent ADP release (step 6), but with different sequences of R, F, and P (steps 3–5) and different associations of P or F with R. Models were named by the letters from left to right according their sequence in forward direction of the cycle indicating the sequence of steps for forward transitions. The sequence of steps for backwards transitions results from reading the letters of model names from right to left. Parentheses in names mean that P or F or both are merged with R to single slow equilibrium resulting in combined rate constants (P = R, F = R, and P = F = R), To simulate scenarios where F or P, or both, act as the rate-limiting forward-backward transition, they were combined with R into a single equilibrium, indicated by enclosing either F or P or both with R by a parenthesis in the model name. The different models and their corresponding rate constants are described in Table 1, their schemes are illustrated in Figure 6.

Table 1

Table 1. Rate constants for simulations of 6 different models of the cross-bridge cycle.

Figure 6

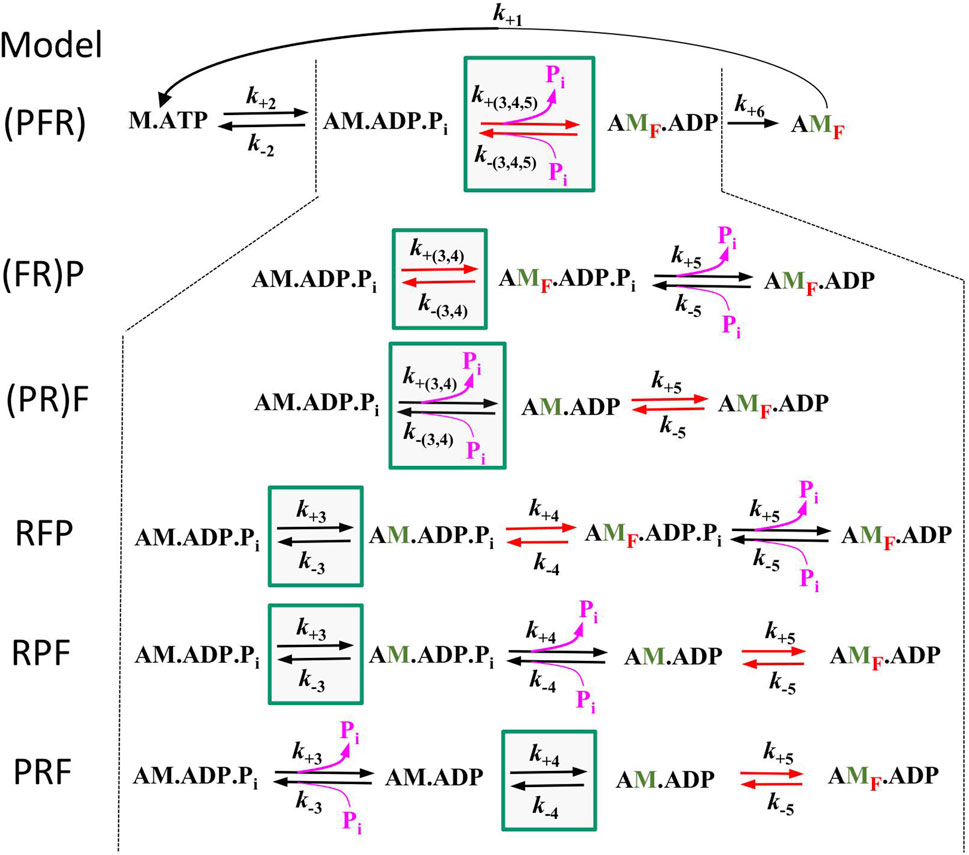
Figure 6. Schemes of the 6 different models tested in this study. All models are equal in step 1 (ATP binding), step 2 (ATP hydrolysis), and step 6 (load dependent forward transition, g) but differ in step 3–5. Green boxes mark the equilibrium for rate-limiting forward and backward transitions f and f ^–(equilibrium R), red arrows mark the equilibrium of the force-generating step and its reversal (equilibrium F) and pink arrows the equilibrium of P_i release-rebinding (equilibrium P). Lettering of models from left to right indicate the sequence of equilibria in forward direction, brackets indicate inclusion of F or P or both with R. Green labelled ‘M′ indicate strongly bound myosin states that have undergone the rate limiting transition, red subscript ‘F′ in states indicate force-producing myosin states.

To determine k_TR-values and force for each model, force redevelopment transients were simulated for each model and [P_i]. This involved the calculation of the steady-state distribution of states during unloaded shortening (with the forward rate constant of step 6 set to k’₊₆ = 50 s^-1) and then switching it at t = 0 to a low value for isometric contraction (k₊₆ = 0.5 s^-1). The simulated transients were then fitted using the same type of single exponential function that was used to fit the transients from the myofibril experiments.

The force amplitude for each model was normalized to the force amplitude at 0.17 mM P_i, and the normalized force was plotted against either the [P_i] (Figure 7A) or the log [P_i] (Figure 7B) together with the relations obtained from the myofibril experiments. The curvature of the myofibril force-[P_i] relation can be largely described by the (PFR) and (PR)F models, where P_i release/rebinding limits the forward/backward transition into/from force-generating states; however, both models overestimate the observed force reduction at the highest [P_i] of 20 mM P_i. A similar curvature of the force-[P_i] relation was predicted by the RPF model, with the sequence of the rate-limiting transition controlling rapid P_i release, triggering fast force generation. Models in which force generation precedes rapid P_i release predict increased curvatures, regardless of whether F is coupled to R in the (FR)P model or whether F is a fast step following R in the RFP model. The PRF model, in which rapid P_i release precedes the rate-limiting transition, yields the lowest curvature. Nevertheless, all the models recapitulate the basic feature of force reduction over a large range of [P_i], making it difficult to exclude certain models based on the force-[P_i] and force-log [P_i] relations.

Figure 7

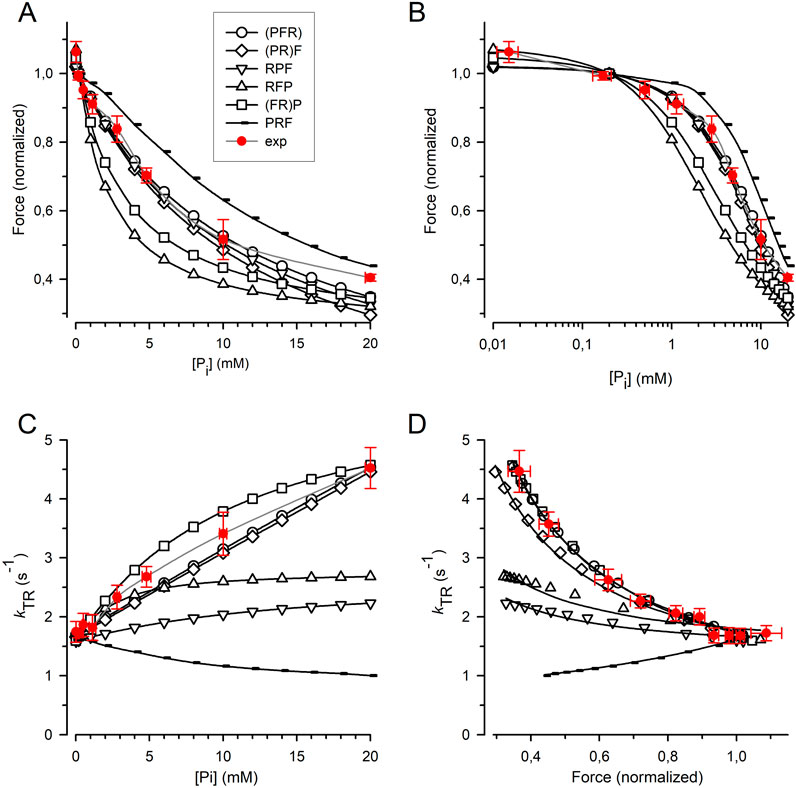
Figure 7. Relation of force and k_TR on [P_i] predicted by cross-bridge models differing in sequence and kinetics of reversible equilibria for P_i release and force-generating step. (A) Force-[P_i] relations. (B) Force-log [P_i] relations. (C) k_TR-[P_i] relations. (D) k_TR-force relations. Filled red circles and error bars represent the experimental data replotted from Figure 5. Black symbols indicate relations calculated for the different models: Open circles refer to the (PFR) model in which P_i release, force-generating step and rate-limiting transition f are merged to a single slow step. Squares refer to the (FR)P model in which the force-generating step presents the rate-limiting transition f followed by faster P_i release. Diamonds refer to the (PR)F model in which the P_i release presents the rate-limiting transition f followed by a faster force-generating step. Tip-up triangles refer to the RFP-model with the sequence: 1. Rate-limiting transition f, 2. Fast force-generating step, 3. Rapid P_i release. Tip-down triangles refer to the RPF model with the sequence: 1. Rate-limiting transition f, 2. Rapid P_i release, 3. Fast force-generating step. Small symbols present the PRF model with the sequence: 1. Rapid P_i release, 2. Rate-limiting transition f, 3. Fast force-generating step. Lines in subfigures (A–C) are spline curves. Lines in (D) represent best fits of Equation 7 to each model except for the RPF model fitted by Equation 8. Model-dependent CS: 0.86 ± 0.02 for (PFR), 0.90 ± 0.02 for (FR)P, 0.67 ± 0.02 for (PR)F, 0.26 ± 0.03 for RFP, 0.19 ± 0.03 for RPF, and −0.52 ± 0.01 for PRF. The CS of experimental data (red) is 0.84 ± 0.08.

Figure 7C shows that the k_TR-[P_i] relation strongly depends on the type of cross-bridge model used. In the (PFR) and (PR)F models, where the backward transition f^– is directly limited by P_i rebinding, k_TR increases steeply and linearly with [P_i]. In addition, a steep but curved increase in k_TR with [P_i] was observed when force generation and its reversal were coupled to rate-limiting transitions prior to rapid P_i release-rebinding, as in the (FR)P model. The k_TR-[P_i] relation for cardiac myofibril falls between the linear relations predicted by the (PFR) and (PR)F models and the curved relation predicted by the (FR)P model, which is consistent with these three models. In contrast, the RFP and RPF models in which F and P are fast, reversible equilibria produce less steep k_TR-[P_i] relations than those observed in the experiments. Notably, the PRF model, in which rapid P_i release-rebinding occurs before the rate-limiting transitions f and f⁻ predicts a declining k_TR-[P_i] relation.

To determine the CS, Equation 7 (see Methods) was fitted to the k_TR-force data simulated for each model (Figure 7D). Sequential models in which P_i release and rebinding were integrated with rate-limiting transitions yielded a high CS of 0.86 for the (PFR) model and 0.90 for the (PR)F model) (Figure 7D). The CS of these models does not reach the maximum value of 1.0 observed in a two-state model because the ATP cleavage step also participates slightly in limiting the redistribution of cross-bridges between the non-force and force-generating states. The CS of both models was in agreement with the CS of 0.84 ± 0.08 obtained in the real experiments (Figure 5). A reasonably high CS of 0.67 is also observed in the (FR)P model, where fast P_i release-rebinding occurred after rate-limiting, reversible force generation. However, when both the force-generating step and P_i release are fast, reversible equilibria separate from the rate-limiting transitions f and f^–, the CS becomes low, regardless of whether the force-generating step occurs before (RFP model, CS = 0.26) or after P_i release (RPF model, CS = 0.19). The prerequisites for significant rate-modulation of k_TR and high CS is less the sequence of F and P than their kinetics. Finally, inverted rate modulation of k_TR occurs when reversible P_i release precedes the reversible rate-limiting transition as in the PRF model which results in a negative CS of −0.51.

4 Discussion

4.1 Implications of force-[P_i] and force-log [P_i] relations for the mechanism of force generation

The asymptote of the hyperbolic fit to the force-[P_i] relation provides an estimate of the relative active force remaining at infinite [P_i] (F_∞Pi). F_∞Pi value <0 indicates that saturating [P_i] cannot fully reverse the active force, possibly due to the presence of force-producing AM.ADP.P_i states (Kawai and Halvorson, 1991; Millar and Homsher, 1992; Tesi et al., 2002) or due to limited reversibility of the process of P_i release-associated force generation, i.e., energy dissipation during this process preventing complete reversal of active force. Energy dissipation is usually not reflected by models because they treat cross-bridges as closed system. Because also all the models in this study simulated in Figure 7 assume that the P_i release per se and force generation is fully reversible, only the force-[P_i] relations of the RFP and (FR)P models, in which force is generated before P_i release, do not approach zero force at infinite [P_i] (Figure 7A). In all other models, F_∞Pi = 0. Notably, studies on fast skeletal muscles, such as those performed on skinned fibers (Millar and Homsher, 1990; Pate et al., 1993; Wahr et al., 1997; Wang et al., 2015), exhibited higher asymptote values than those performed on myofibrils (Tesi et al., 2000; Tesi et al., 2002). This discrepancy is attributed to P_i accumulation and gradients in fibers, which lead to an underestimation of force modulation by P_i (Cooke and Pate, 1985; Cooke et al., 1988), particularly in thicker fiber preparations with high ATPase activity as fast skeletal fibers (Kentish, 1986), emphasizing the need to evaluate F_∞Pi with cardiac myofibrils.

The value of F_∞Pi = 0.13 ± 0.09 obtained in this study is consistent with those obtained using fibers (Kentish, 1986), myocytes (Araujo and Walker, 1996; Hinken and McDonald, 2004), and myofibrils (Stehle, 2017) from the cardiac muscle. Interestingly, Tesi et al. explored the force-[P_i] relation of rabbit psoas and of rabbit soleus myofibrils up to 70 mM P_i reporting a similar low asymptote value of 0.07 ± 0.02 for the myofibrils from the fast but a much higher value of 0.44 ± 0.06 for those of the slow muscle which they attributed to a highly occupied force-producing AM.ADP.P_i state in slow skeletal muscle (Tesi et al., 2000; Tesi et al., 2002). Also direct comparisons between slow and fast skeletal muscle fibers revealed that slow rabbit soleus fibers exhibit less efficient force reduction than fast rabbit psoas muscle fibers (Millar and Homsher, 1992; Potma et al., 1995; Wahr et al., 1997). Given the low F_∞Pi, the force-[P_i] relations of myofibrils observed in cardiac and fast skeletal muscles suggest minimal contributions from force-producing AM.ADP.P_i state(s) in these muscles. However, due to the limited [P_i] range of the relations such states cannot be completely excluded. Possible explanations include lower reversibility of the process of P_i release-associated force generation or a higher occupancy of the force-producing AM.ADP.P_i state in slow skeletal than in fast skeletal or cardiac muscle. This is not simply related to the myosin heavy chain (MHC) isoform since rabbit soleus myofibrils (Tesi et al., 2002) and guinea pig cardiac myofibrils investigated in this study both contain slow β−MHC (Reiser and Kline, 1998). However, it has been recently shown for human β-MHC that differences in the isoform of myosin light chain 1 (MLC1) in slow skeletal and cardiac muscle account for 3-fold lower detachment rates and velocities of actin sliding for slow skeletal compared to cardiac myosin (Osten et al., 2022; Wang et al., 2022). Thus, despite of the same β-MHC, slow skeletal myosin appears to have 3-fold longer attachment times of post-power stroke states than cardiac myosin. Whether this prolonged attachment can result in reduced reversibility of the process of P_i release-associated force generation explaining the high residual active force of slow skeletal muscle remains to be tested. Limited reversibility linked to longer attachment times could also provide a protective mechanism for preserving force even at high [P_i], low pH and elevated [ADP] during muscle fatigue in this muscle type (Karatzaferi et al., 2017; Moretto et al., 2022).

The shape of the force-log [P_i] relation in skeletal and cardiac muscle preparations and its significance for the force-generating mechanism have been previously described (Pate and Cooke, 1989; Araujo and Walker, 1996; Tesi et al., 2000; Tesi et al., 2002). Based on reduced models consisting of reversible equilibria for the force-generating step and P_i release not implemented in a full cross-bridge cycle, a nearly mono-linear force-log [P_i] relation is expected for the one-step model when force generation and P_i release occur simultaneously (Pate and Cooke, 1989), whereas a sigmoidal relation is expected for two-step models, e.g., when force generation precedes or occurs after P_i release (Tesi et al., 2000; Tesi et al., 2002). In a previous study on cardiac muscles, mono-linear and sigmoid functions were fitted to force-log [P_i] data obtained from skinned rat myocytes (Araujo and Walker, 1996). Neither fit accurately matched the experimental data, suggesting that a bilinear fit may provide a better fit to the data of Araujo and Walker. Tesi et al. were the first to use a bi-linear function to analyze their data from rabbit psoas myofibrils at 5°C (Tesi et al., 2000). The slopes of the two lines in their study were −0.07 and −0.40, which are comparable to the −0.08 and −0.51 observed in this study (Figure 4B), indicating a close similarity between force-log [P_i] relations in fast skeletal and cardiac myofibrils. The force-log [P_i] relation obtained for skinned rat myocytes was interpreted to have no evidence for the two-step model (Araujo and Walker, 1996) while an earlier report on rat ventricular trabeculae (Kentish, 1986) and the myofibril data from fast skeletal muscle were interpreted to be in rough agreement with the two-step model (Tesi et al., 2000). Force-log [P_i] relations reported for skinned fibers from rabbit soleus and rabbit psoas muscle were mono-linear with higher slope for the slow soleus muscle (Millar and Homsher, 1992). However, only myofibrils enable the exploration of the force-log [P_i] relation in the sub-millimolar range because the ATPase activity and long lateral diffusion distance of skinned fibers result in lateral [P_i] gradients of 1–2 mM P_i in skinned fibers (Cooke and Pate, 1985). The slopes of the first line at low [P_i], up to 1 mM P_i for fast skeletal myofibrils (Tesi et al., 2000) and cardiac myofibrils (Figure 4B) are higher than the slope of the sigmoidal relation for a simple two-step model. However, a larger strain distribution of force-generating cross-bridges also increases the slope in this [P_i] range (Pate et al., 1998). Given the similarity of the force-log [P_i] relations in fast skeletal and cardiac myofibrils and the different interpretations of force-log [P_i] relations in previous studies of the two muscle types (Araujo and Walker, 1996; Tesi et al., 2000), the force-log [P_i] relation alone cannot definitively distinguish between the one-step and two-step models.

Compared with previous studies on force-log [P_i] relations (Kawai and Halvorson, 1991; Millar and Homsher, 1992; Wahr et al., 1997; Tesi et al., 2002), the use of various full cross-bridge cycle models in this study instead of isolated one- or two-step models without integration in a cycle is a major advancement. Interestingly, regarded over the full [P_i] range, force-[P_i], and force-log [P_i] relations simulated for various full cycle models were comparable (Figures 7A, B). At low [P_i], the results from the full cycle models in this study were opposite to predictions made by the “isolated step” models (Pate and Cooke, 1989; Tesi et al., 2000). While isolated one-step models predict overall mono-linear force-log [P_i] relation with higher slopes at low [P_i] than isolated two-step models (Pate and Cooke, 1989; Tesi et al., 2000), in this study, the (PFR) model which integrates the one-step model in the cycle even yields a flatter force-log [P_i] relation than the RFP model which integrates the two-step model. None of the models explored in this study exhibited a monophasic relation expected from isolated one-step models of P_i release-associated force generation. Overall, the simulations with various full-cycle models suggests that the overall shape of the force-log [P_i] relation is rather insensitive to the specific coupling mechanism between force generation and P_i release. Instead, the slope of the force-log [P_i] relation at low [P_i] is influenced by the coupling mechanism in a more complex manner than previously understood.

4.2 Implications of the k_TR-[P_i] relation for the mechanism of force-generation

The addition of 10 mM P_i increases k_TR 2.4-fold in skinned cardiac myocytes from human donor hearts (Papp et al., 2014), which is comparable to the 2.0-fold increase in k_TR by 10 mM P_i observed in cardiac myofibrils from guinea pigs in this study. In rat skinned cardiac myocytes, the addition of 10 mM P_i increased k_TR by 3.8-fold (Hinken and McDonald, 2004), whereas in cardiomyocytes from humans, pigs, and mice, the increases are 1.5-fold, 1,6-fold and 2.9-fold, respectively (Edes et al., 2007). The stronger P_i effects in mice and rats compared to those in human, pig, and guinea pig hearts may be partly related to the fast α-MHC isoform present in murine and rat ventricles compared to the slow β-MHC isoform expressed in humans, pigs, and guinea pigs (Reiser and Kline, 1998). However, MHC isoform differences are not the only determinant of the k_TR-[P_i] relation, since myofibril and fiber preparations from slow skeletal muscle exhibit no change in k_TR (Wahr et al., 1997; Tesi et al., 2000; Tesi et al., 2002), with one exception where force development kinetics was induced by T-jumps (Governali et al., 2020). In most studies on slow skeletal muscle preparations, the insensitivity of k_TR to P_i could indicate incomplete reversibility within the process of P_i release-associated force generation or different force-generating mechanisms in this muscle type (Stehle and Tesi, 2017).

The model simulations in this study revealed that the slope and curvature of the k_TR-[P_i] relation are sensitive to the force-generating mechanism. The slope is strongly positive for models in which P_i binding induced force reversal is slow and limits f^–. In contrast, the slope is flat for models in which P_i binding induced force reversal is a fast process. The slope becomes negative for models in which P_i release-rebinding is a fast equilibrium before the rate-limiting transitions f and f^– in the cycle. The k_TR-[P_i] relation is linear when P_i rebinding directly limits the backwards transition of cross-bridges from force-generating to non-force-generating states, and the relation curves downward when P_i rebinding is fast; therefore, another process becomes rate-limiting for this transition at high [P_i]. Despite the clear prediction of the mechanism, the curvature of the k_TR–[P_i] relations reported in the literature does not provide a unique picture of the force-generating mechanism. Downward-curved k_TR-[P_i] relations were reported for skinned fast (Regnier et al., 1995; Wahr et al., 1997) and slow (Wahr et al., 1997; Governali et al., 2020) muscle fibers, a slightly downward-curved relation for myofibrils from rabbit psoas (Tesi et al., 2000), apparently linear k_TR-[P_i] relation in a previous study of cardiac myofibrils from guinea pig (Stehle, 2017), and even an upward curvature for skinned rat cardiac myocytes (Hinken and McDonald, 2004). The slightly downward curved k_TR-[P_i] relation obtained for cardiac myofibrils in this study can better fitted by a hyperbola than by a linear function (Figure 4C) suggesting that another process than P_i rebinding limits f^– at infinite [P_i]. However, the low curvature represented by the high P_i50 = 33 ± 9 mM indicates that at physiological [P_i], i.e., at [P_i] up to 30 mM (Cady et al., 1989), the rate of P_i rebinding limits f^–. The high P_i50–value and the variability of curvatures of k_TR-[P_i] relations in literature corroborate the difficulty in determining the force-generating mechanism from the shape of this relation. Therefore, an alternative criterion was explored in this study: the combined modulation of k_TR and force by [P_i], i.e., the k_TR-force relation was described in terms of the CS.

4.3 Implications of the k_TR-force relation for the mechanism of force generation

Early models of the cross-bridge cycle implied that the P_i release step is connected to steps that limit the transition of cross-bridges from non-force-generating to force-generating states (Huxley, 1957; Lymn and Taylor, 1971; Eisenberg et al., 1980). In contrast, newer models propose that P_i release occurs rapidly, independent of slower step(s) in the ATPase cycle (Millar and Homsher, 1990; Kawai and Halvorson, 1991; Dantzig et al., 1992; Ranatunga, 1999). The latest models involve branched pathways and multiple steps of force generation and P_i release (introduction and reviews (Debold, 2021; Mansson et al., 2023)), making it increasingly difficult to identify specific rate-limiting transitions to certain steps in the cycle. Novel insights into the structural cycle of myosin (Muretta et al., 2015; Houdusse and Sweeney, 2016; Irving, 2017; Robert-Paganin et al., 2020; Matusovsky et al., 2021), highly time-resolved force measurements of single myosin (Woody et al., 2019; Scott et al., 2021), and load-dependent, organized conformational changes of the cross-bridge ensemble on the thick filament (Linari et al., 2015; Irving, 2017; Brunello et al., 2020; Park-Holohan et al., 2021) further revive the question of which steps limit forward and backward cycling between non-force-generating and force-generating states.

The first attempt to distinguish P_i release-associated force generation from the rate-limiting transition in the traditional, sequential pathway of the cross-bridge cycle was based on classical experiments using caged-P_i. The rapid increase in [P_i] produced by the flash photolysis of caged-P_i in muscle fibers induces a fast force decay with a rate constant k_Pi considerably higher than k_TR (Millar and Homsher, 1990; Dantzig et al., 1992). The dependence of k_Pi on [P_i] was interpreted as fast reversible force generation followed by rapid reversible P_i release (Millar and Homsher, 1990; Dantzig et al., 1992) reviewed in Takagi et al. (2004): Rapid P_i binding and fast force reversal determine the high k_Pi, while slower transitions limit redistribution among force-generating and non-force-generating states and determine the low k_TR. However, this scenario has been questioned by studies exploring the force kinetics upon rapid changes in [P_i] in myofibrils (Tesi et al., 2000; Stehle, 2017) reviewed in Stehle and Tesi (2017). Thin myofibril bundles are ideal for studying the force kinetics induced by rapid switching between two solutions of different [P_i], enabling a change in [P_i] in both directions, e.g., from initial low [P_i] or initial high [P_i] to the same final [P_i]. Notably, this was first reported for myofibrils from fast skeletal muscle (Tesi et al., 2000) and later for cardiac myofibrils (Stehle, 2017), the force kinetics at the same final [P_i] are strikingly different depending on the direction of [P_i] change. Rapid increases in [P_i] induce fast force decay, as in fibers, whereas rapid decreases in [P_i] induce slow force rises with k_-Pi similar to k_TR. Furthermore, in cardiac myofibrils, the fast kinetics of force decay with a rapid increase in [P_i] was attributed to the sequential “give” of sarcomeres (Stehle, 2017), a phenomenon also observed during fast muscle relaxation (Huxley and Simmons, 1970; Flitney and Hirst, 1978; Stehle et al., 2002a). The rapid decrease in [P_i] to a low final [P_i], i.e., the rapid prevention of backward cycling via P_i rebinding, induces forward kinetics limited by the same transition limiting force redevelopment, implying that P_i release coupled force generation in the forward direction is linked to the rate-limiting transition f (Stehle and Tesi, 2017).

This study was the first to analyze the CS between the processes of P_i binding induced force reversal and transition limiting backward cycling, represented by the rate constant f^–. Empirical equations were developed to derive this CS from k_TR-force relations. The major assumption for deriving Equations 7, 8 for describing CS is that the rate constant of force redevelopment represents the sum of the rate constants limiting redistribution between the non-force- and force-generating states. However, this assumption has been challenged by Kawai, who argued that cross-bridges must complete multiple cycles because their step size is much smaller than the distance of the filament sliding during force redevelopment (Wang and Kawai, 2013). A prediction of Kawai’s model (Wang and Kawai, 2013) is that k_TR is inversely related to the tension cost, defined as the ratio of isometric tension to ATPase. Tension cost is independent of Ca²⁺ activation (Brenner, 1988) and increases approximately 2-fold with increasing [P_i] to 30 mM in fast skeletal and cardiac muscle (Ebus et al., 1994; Potma et al., 1995; Potma and Stienen, 1996; Governali et al., 2020). However, this 2-fold change in tension cost is insufficient to explain the 10-fold or 15-fold difference observed in k_TR when the force was reduced by altering Ca²⁺ and Pi in cardiac myofibrils (Figure 2D) or fast skeletal muscle fibers (Regnier et al., 1995), respectively. The classical interpretation of k_TR provides a simple explanation for these substantial differences and opposing changes in k_TR resulting from force reduction via Ca²⁺ and P_i by decreasing f and increasing f ^–, respectively (reviewed in (Stehle and Tesi, 2017).

Model simulations reveal that CS is high when either the reversible equilibrium for P_i release P, the reversible equilibrium for force generation F, or both equilibria are connected to the rate-limiting forward-backward transition between non-force-generating and force-generating states R, as observed in the (PR)F, (FR)P, and (PFR) models. Conversely, CS decreases when both F and P are separated from R, as in the RFP and RPF models (Figure 7D). On a scale from +1 for maximum positive over zero for no coupling to −1 for maximum inverse coupling, the k_TR-force relation in cardiac myofibrils yielded a high CS of 0.84 close to 1, which is consistent with the (PR)F, (FR)P, and (PFR) models, but not with the RFP and RPF models.

Owing to the linear scaling of the positive CS defined by Equation 7 (illustrated in Figure 2A), positive CS reflects the ratio of the relative increase in k_TR to the relative decrease in the force induced by a certain increase in [P_i]. Therefore, the CS of 0.84 in this study indicates that, on average, k_TR increases by 0.84 times the reduction in force; for example, k_TR increases 0.84 × 2-fold = 1.68-fold when force is reduced 2-fold to half of its initial value. To the author´s knowledge, no previous study has considered this ratio, while numerous studies on several muscle types have reported k_TR and force values that contain this information. In skinned rat cardiac myocytes, the addition of 10 mM P_i increased k_TR by 3.8-fold, whereas it reduced the force by 3-fold (Hinken and McDonald, 2004). Similarly, in skinned cardiac myocytes from human donor hearts, the addition of 10 mM P_i resulted in a 2.4-fold increase in k_TR and a 2.5-fold reduction in force (Papp et al., 2014). These changes in k_TR and force are comparable to the 2.0-fold increase in k_TR and 2.0-fold reduction in force observed in cardiac myofibrils from guinea pigs, likely because of the similar β-MHC isoform present in guinea pigs and human hearts. However, in all these studies, including those on fast skeletal muscle, k_TR changes almost reciprocally with force. In fast muscle fibers, the addition of ≥10 mM P_i reduced the force by half and doubled k_TR (Wahr et al., 1997; Linari et al., 2010), whereas the addition of 5 mM P_i was sufficient to halve the force and double k_TR in myofibrils of this muscle type (Tesi et al., 2000; Tesi et al., 2002). Notably, theoretical modeling of [P_i]-dependent changes in k_TR and force in fast muscles also displayed sensitive, reciprocal changes in k_TR and force (Linari et al., 2010). In the model of Linari et al., the formation of strongly bound cross-bridges and force generation were combined with the kinetics of a slow process analogous to the (FR)P model simulated here. Therefore, both experimental and theoretical data from cardiac and fast skeletal muscles support the view that CS is high, close to one. However, the CS of the slow skeletal muscles remains unclear. The insensitivity of k_TR to [P_i] reported for fibers (Wahr et al., 1997) and myofibrils (Tesi et al., 2002) from slow rabbit soleus muscle indicated a low CS, even when considering the lower effects of P_i on force in slow skeletal muscle than in fast skeletal muscle. However, a recent study on slow rabbit soleus muscle fibers reported sensitive changes in the rate constant of force development kinetics following T-jumps and force by [P_i] (Governali et al., 2020). Assuming that the latter rate constant reports the same transitions in the cross-bridge cycle as k_TR, the experiments of Governali et al. on slow muscle indicate a high CS similar to that observed in fast skeletal and cardiac muscle.

The high CS observed in fast skeletal and cardiac muscle may be due to either slow rebinding of P_i, i.e., low k_B as in (PFR) and (PR)F models, or slow reversal of the power stroke, as in (RFP) and (FR)P models. A low k_B does not necessarily contradict the classical prediction of ultra-rapid rate constants from diffusion-limited reactions because P_i is released and potentially rebounds through so-called backdoor mechanisms, which may limit the rate of P_i release and rebinding (Yount et al., 1995; Cecchini et al., 2010; Houdusse and Sweeney, 2016; Moretto et al., 2022). However, model simulations also revealed a high CS for the (FR)P model, in which force generation is coupled to rate-limiting transitions prior to rapid reversible P_i release; i.e., a high CS per se does not exclude rapid P_i rebinding. In the (FR)P model, the rate-limiting backward transition to non-force-generating states, represented by f^– is limited by the reversal of the force-generating steps. Force-reverse steps have been detected and quantified using the laser trap technique for single cardiac myosin and cardiac myosin filaments (Woody et al., 2019; Hwang et al., 2021). In the single myosin force experiments conducted by Hwang, two reverse steps were identified in the presence of ADP and P_i but in the absence of ATP. The authors, therefore, attributed these two reverse strokes in their model analysis to different actin-bound myosin.ADP states occurring after P_i release. However, simply assigning a sequence of reversible power strokes, i.e., forward steps in total to f and reverse steps in total to f^– after rapid P_i release-rebinding in a sequential model would yield a negative CS similar to the PRF model. Whenever the post-P_i release state precedes the rate-limiting transition into force-generating states, the occupancy of this post-P_i release state decreases with increasing [P_i], whereby k_TR no longer increases but decreases with [P_i], i.e., leading to an inverse rate modulation of k_TR by P_i. Therefore, to implement a sequence of rate-limiting reverse steps in the full ATPase cross-bridge cycle with a high positive CS and rate modulation of k_TR, they must be closely assigned either along or before P_i release-rebinding, as seen in the (PFR) or (FR)P models. The scenario involving rapid reversible power strokes before fast reversible P_i release aligns with the proposal of Woody et al. (2019). However, the coupling of the power stroke to the rate-limiting transition remains unsolved.

The observed high CS contradicts the classical two-step mechanisms of force generation. Traditional sequential pathways involve an intermediate fast reversible force-generating step followed by rapid reversible P_i release, with a slower process that rate limits forward and backward fluxes of cross-bridges, i.e., f and f^– independent of the force-generating step in the cycle (Millar and Homsher, 1990; Kawai and Halvorson, 1991; Dantzig et al., 1992; Ranatunga, 1999; Takagi et al., 2004). This scenario is reflected by the RFP model, which yields a CS of 0.26, significantly lower than the CS of 0.84 observed in the cardiac myofibril experiments (Figure 7D). Using the rate constants from classical studies favoring the RFP model for rabbit psoas muscle at 10°C (Millar and Homsher, 1990; Dantzig et al., 1992) resulted in a low CS of 0.28 (Figure 8). CS further decreased to 0.19, when the sequence of the two fast reversible equilibria was permuted and force generation occurred after P_i release, as shown by the RPF model in Figure 7D.

Figure 8

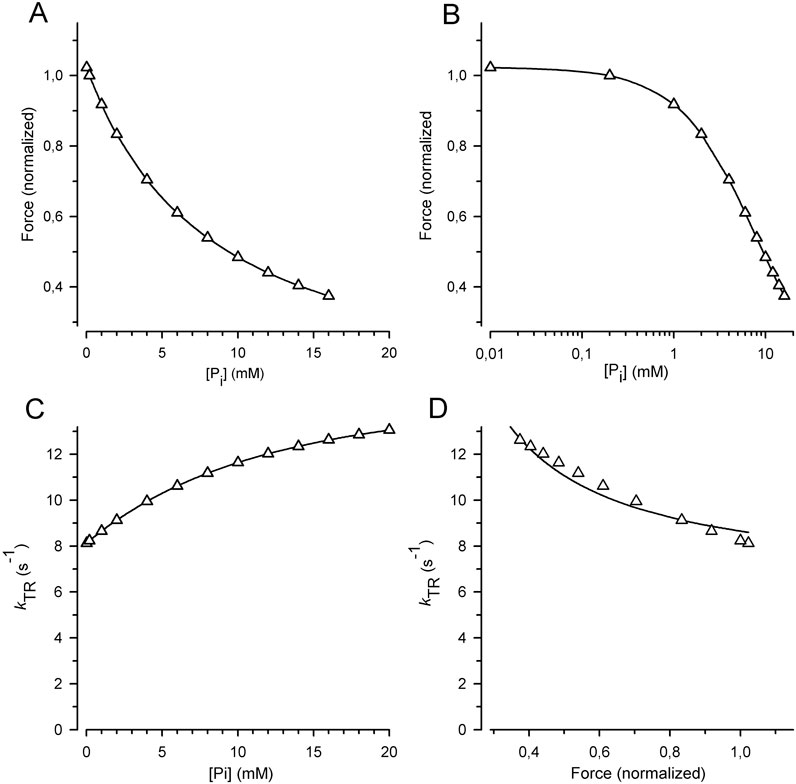
Figure 8. Relation of force and k_TR on [P_i] predicted for the classical two-step mechanism of fast force generation followed by rapid P_i release in rabbit psoas muscle fibers at 10°C (Millar and Homsher, 1990; Dantzig et al., 1992). (A) Force-[P_i] relations. (B) Force-log [P_i] relations. (C) k_TR-[P_i] relations. (D) k_TR-force relations. Relations were calculated using the six-state RFP-type model in which the reversible rate-limiting transition into force-generating states (step 3) controls fast reversible force generation (step 4) that triggers rapid reversible P_i release (step 5). Step 1 = ATP binding, step 2 = reversible ATP hydrolysis and step 6 = rate-limiting forward transition for leaving force-generating states (slow isomerization and ADP release). Rate constants of step 1 (k₊₁ = 250 s⁻¹), and step 2 (k₊₂ = 20 s⁻¹, k_-2 = 3 s⁻¹) were derived from stopped flow experiments with rabbit psoas myofibrils (Herrmann et al., 1992; Stehle et al., 2000). Rate constants of step 3 (k ₊₃ = 10 s⁻¹, k_-3 = 10 s⁻¹) and step 6 (k₊₆ = 2 s⁻¹) were derived from values in the literature for k_TR (Tesi et al., 2000) and ATPase (Potma et al., 1995). Rate constants of step 4 (k₊₄ = 21 s⁻¹, k_-4 = 100 s⁻¹) and step 5 (k₊₅ = 500 s⁻¹, k_-5 = 8 s⁻¹) are from caged-P_i experiments (Dantzig et al., 1992). Lines in subfigures (A–C) are spline curves. Lines in (D) represent the best fit of Equation 7 to the model data yielding CS = 0.28 ± 0.02 (compared to the CS obtained by the experiments in this study of 0.84 ± 0.08).

High CS can be obtained by increasing the rate constants of P_i release and force generation in the forward direction, but not in the backward direction. For example, P_i release can be made fast in the RFP model (high k_P) when P_i binding is slow; i.e., the low k_B limits the rate of f ^–. The loss of force modulation by [P_i] resulting from the high k_P/k_B ratio, i.e., the higher equilibrium constant of the reversible P_i release (K_P), must be compensated by lowering the equilibrium constant of the preceding fast reversible force-generating step (K_F). Thereby, it is possible to obtain the rate modulation of k_TR by [P_i] by slow rate constant for P_i rebinding even for high rate constants of P_i release. The combination of low K_F and high K_P results in a low occupancy of the post-power-stroke, force-producing AM_F.ADP.P_i state. Because this state is the initial state of P_i release, its low occupancy limits the rate of P_i release, even though k_P is high. Thereby, flux to force-generating states is still limited by transition through the P_i release-rebinding equilibrium. Nevertheless, to obtain a high CS, it is essential to keep either the kinetics of P_i rebinding or force reversal slow and coupled to f^–.

The above combination of low K_F and high K_P in the RFP model would result in high free energy for the force-producing AM_F.ADP.P_i state with a large drop in free energy during P_i release and high energy barrier for P_i rebinding. This could be a problem for efficiency and reversibility of P_i release-associated force generation. Given that P_i release and rebinding are multiple equilibria (Llinas et al., 2015; Moretto et al., 2022), the energy associated with P_i release can be partitioned to more than one step, facilitating P_i rebinding and its modulation by pH during muscle fatigue (Moretto et al., 2022). During the multistep P_i release reported by Muretto et al., the power stroke occurs in different myosin states after the P_i release from the active site. It occurs either while P_i is bound to the secondary P_i binding site, bound to the surface of myosin or already released free in solution. Whether in such scenario the different rates of P_i rebinding could be directly involved in limiting the backward flux of cross-bridges from force-generating states to non-force-generating states needs to be tested. As discussed in 4.2., P_i binding limiting f^–would manifest in linear k_TR–[P_i] relations as observed in the (PFR) and (PR)F models, and literature reports varying curvatures in k_TR–[P_i] relations, generally exhibiting slightly downward curvatures, but without evidence of k_TR approaching a maximum, [P_i]-independent value at high [P_i]. Therefore, it is likely that the rate of backward cycling of cross bridges is substantially limited by the rate of P_i rebinding, which has not yet been directly measured.

A major limitation of the current model analysis was the simplification to a single sequential pathway. The aim was to outline the primary pathway by comparing various scenarios, rather than increasing the level of complexity or refining a certain model. Owing to the single pathway and full reversibility of the steps in all models, each model predicts a parallel decrease in force and ATPase by P_i, i.e., [P_i]-independent ATPase/force ratios, called the tension cost, and cannot account for the well-known observed increase in tension cost with increasing [P_i]. Studies on skinned cardiac trabecular fibers from swine containing also the slow β-MHC as expressed in the guinea pig indicate that 20 mM P_i doubles the tension cost (Herzig et al., 1981; Strauss et al., 1994). Similar increase in tension cost have been found in fast (Potma and Stienen, 1996) and slow skeletal muscle fibers (Governali et al., 2020) leading to models with side pathways to uncouple (Linari et al., 2010) or loosely couple (Caremani et al., 2013; Governali et al., 2020) P_i release and force generation. As shown in Figure 1 of Linari et al.’s Study (Linari et al., 2010), adding a non-force-producing side pathway for the uncoupling of ATPase activity from force generation results in a substantial reduction in the [P_i]-dependence of ATPase by approximately 3-fold. However, this modification produced only minor changes of 15% in the [P_i] dependences of force and k_TR, with these changes occurring almost reciprocally, indicating that adding a non-force-producing pathway does not significantly alter CS. However, cross-bridge models with multiple reversible force-generating steps and loose coupling to P_i release (Caremani et al., 2013; Governali et al., 2020) can predict high CS even for rapid P_i release-rebinding kinetics when the total flux through these steps passes over the P_i release-rebinding step and participates in the rate-limiting f and f^–. This is evident from the [P_i]-dependent reciprocal changes in force and k_TR simulated for the loose coupling model depicted in Figure 4 of Governali et al. (2020) that yielded a high CS close to 1.

The ultrafast, high-sensitive force recordings of a single myosin indicate that myosin generates a power stroke within less than 1 ms upon strong binding to the actin filament (Capitanio et al., 2012). Recent studies using the same technique (Woody et al., 2019; Scott et al., 2021) detected no effects of P_i on the attachment time of heads prior to execution or on the size or rate of the initial power stroke. Rapid reversible P_i release-rebinding was attributed to the post-power-stroke state, as reflected by a load and [P_i]-dependent drop in force manifested in the averaged single myosin force transients (Woody et al., 2019). Recent time- and structurally resolved measurements that classify attachment-detachment events in HMM in combination with myosin lever arm orientation also detected no effect of P_i on the lifetime between the attachment of the myosin head to actin and the power stroke (Matusovsky et al., 2021). Thus, time-resolved single myosin force and structure studies indicate that P_i does not affect the lifetime of the pre-force-generating state. These findings have been interpreted to indicate that strong myosin attachment triggers the power stroke before P_i release (Woody et al., 2019; Matusovsky et al., 2021; Scott et al., 2021). However, this interpretation has been challenged by the finding of a secondary P_i binding site outside of the active site and the successful modelling of both the [P_i]-insensitivity of single myosin force transients and the [P_i]-sensitivity of muscle force transients by a model in which the power stroke occurs after P_i release from the active site (Moretto et al., 2022) using multi-scale model simulations (Rahman et al., 2018). Furthermore, there is dissent about the interpretation of the increased amount of short-lived attachments of single cardiac myosin found at high [P_i] (Woody et al., 2019) which could be also interpreted as increased non-force-producing attachments due to rapid, fully reversible P_i release occurring before the power stroke (Robert-Paganin et al., 2020; Debold, 2021). In such a model, P_i rebinding decreases the probability of power strokes from the attached pre-force AM.ADP state rather than the lifetime of pre-power-stroke attachments or the size of the power stroke. Whether P_i is released before or after the power stroke, the observation of rapid power stroke upon strong attachment of myosin to actin implies that they are closely coupled fast equilibria, and the question is restricted to how the preceding strong binding of myosin to actin limits the first event. The sequential models analyzed in this study for CS did not involve the kinetics of myosin binding to actin. Time-resolved X-ray diffraction studies of contracting muscles have identified that the attachment of myosin heads to actin in the same type of conformation as that found during steady-state isometric contraction is the rate-limiting structural change for force development upon electrically stimulating intact muscle fibers (Reconditi et al., 2011). Both the pre-P_i release power stroke and the pre-power stroke P_i release scenario can result in high CS, provided that the reversible power stroke in the pre-P_i or the reversible P_i release in the pre-power stroke P_i release is strongly dependent on the preceding, rate-limiting, strong binding of myosin to actin.

In summary, the findings in this study demonstrate that the [P_i]-modulated k_TR-force relation is a sensitive probe of the coupling between the P_i binding step, reversal of the force-generating step, and transition limiting backward flux of cross-bridges from force-generating to non-force-generating states expressed by the rate constant f^–. The high CS observed in cardiac myofibrils, in combination with the simulations of k_TR-force relations using various sequential models, indicates that P_i binding induced force reversal is strongly coupled to f^–. Additionally, previous studies on myofibrils have shown that a rapid decrease in [P_i] to a low final [P_i] induces a slow increase in force with a rate constant k_–Pi similar to k_TR indicating that P_i release coupled with force generation in the forward direction is strongly coupled to the rate-limiting transition f (Tesi et al., 2000; Stehle, 2017; Stehle and Tesi, 2017). Taken together, these findings indicate that the reversible force generation associated with P_i release cannot be decoupled from either the rate-limiting forward transition f or from the rate-limiting backward transition f^–. Consequently, this substantially limits models by excluding the potential contributions of other rate-limiting processes uncoupled from either reversible P_i release or force generation. Further research is needed to better define these rate-limiting transitions in the context of structural and chemical aspects of the myosin motor ATPase cycles.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The animal study was approved by Landesamt für Natur, Umwelt und Verbraucherschutz Nordrhein-Westfalen (LANUV NRW Leibnizstrasse 10 D-45659, Recklinghausen Germany). The study was conducted in accordance with the local legislation and institutional requirements.

Author contributions

RS: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing–original draft, Writing–review and editing, Project administration, Supervision.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by a grant from the Köln Fortune program (Faculty of Medicine, University of Cologne) to RS.

Acknowledgments

The author is grateful to Stefan Zittrich for his help with the preparations of buffers and myofibrils.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Araujo A., Walker J. W. (1996). Phosphate release and force generation in cardiac myocytes investigated with caged phosphate and caged calcium. Biophys. J. 70, 2316–2326. doi:10.1016/S0006-3495(96)79797-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Brenner B. (1988). Effect of Ca²⁺ on cross-bridge turnover kinetics in skinned single rabbit psoas fibers: implications for regulation of muscle contraction. Proc. Natl. Acad. Sci. U. S. A. 85, 3265–3269. doi:10.1073/pnas.85.9.3265

PubMed Abstract | CrossRef Full Text | Google Scholar

Brunello E., Fusi L., Ghisleni A., Park-Holohan S. J., Ovejero J. G., Narayanan T., et al. (2020). Myosin filament-based regulation of the dynamics of contraction in heart muscle. Proc. Natl. Acad. Sci. U. S. A. 117, 8177–8186. doi:10.1073/pnas.1920632117

PubMed Abstract | CrossRef Full Text | Google Scholar

Cady E. B., Jones D. A., Lynn J., Newham D. J. (1989). Changes in force and intracellular metabolites during fatigue of human skeletal muscle. J. Physiol. 418, 311–325. doi:10.1113/jphysiol.1989.sp017842

PubMed Abstract | CrossRef Full Text | Google Scholar

Capitanio M., Canepari M., Cacciafesta P., Lombardi V., Cicchi R., Maffei M., et al. (2006). Two independent mechanical events in the interaction cycle of skeletal muscle myosin with actin. Proc. Natl. Acad. Sci. U. S. A. 103, 87–92. doi:10.1073/pnas.0506830102

PubMed Abstract | CrossRef Full Text | Google Scholar

Capitanio M., Canepari M., Maffei M., Beneventi D., Monico C., Vanzi F., et al. (2012). Ultrafast force-clamp spectroscopy of single molecules reveals load dependence of myosin working stroke. Nat. Methods 9, 1013–1019. doi:10.1038/nmeth.2152

PubMed Abstract | CrossRef Full Text | Google Scholar

Caremani M., Dantzig J., Goldman Y. E., Lombardi V., Linari M. (2008). Effect of inorganic phosphate on the force and number of myosin cross-bridges during the isometric contraction of permeabilized muscle fibers from rabbit psoas. Biophys. J. 95, 5798–5808. doi:10.1529/biophysj.108.130435

PubMed Abstract | CrossRef Full Text | Google Scholar

Caremani M., Melli L., Dolfi M., Lombardi V., Linari M. (2013). The working stroke of the myosin II motor in muscle is not tightly coupled to release of orthophosphate from its active site. J. Physiol. 591, 5187–5205. doi:10.1113/jphysiol.2013.257410

PubMed Abstract | CrossRef Full Text | Google Scholar

Cecchini M., Alexeev Y., Karplus M. (2010). Pi release from myosin: a simulation analysis of possible pathways. Struct. Lond. Engl. 1993 18, 458–470. doi:10.1016/j.str.2010.01.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Colomo F., Nencini S., Piroddi N., Poggesi C., Tesi C. (1998). Calcium dependence of the apparent rate of force generation in single striated muscle myofibrils activated by rapid solution changes. Adv. Exp. Med. Biol. 453, 373–381. doi:10.1007/978-1-4684-6039-1_42

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooke R., Franks K., Luciani G. B., Pate E. (1988). The inhibition of rabbit skeletal muscle contraction by hydrogen ions and phosphate. J. Physiol. 395, 77–97. doi:10.1113/jphysiol.1988.sp016909

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooke R., Pate E. (1985). The effects of ADP and phosphate on the contraction of muscle fibers. Biophys. J. 48, 789–798. doi:10.1016/S0006-3495(85)83837-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Dantzig J. A., Goldman Y. E., Millar N. C., Lacktis J., Homsher E. (1992). Reversal of the cross-bridge force-generating transition by photogeneration of phosphate in rabbit psoas muscle fibres. J. Physiol. 451, 247–278. doi:10.1113/jphysiol.1992.sp019163

PubMed Abstract | CrossRef Full Text | Google Scholar

Davis J. S., Rodgers M. E. (1995). Indirect coupling of phosphate release to de novo tension generation during muscle contraction. Proc. Natl. Acad. Sci. U. S. A. 92, 10482–10486. doi:10.1073/pnas.92.23.10482

PubMed Abstract | CrossRef Full Text | Google Scholar

Debold E. P. (2021). Recent insights into the relative timing of myosin's powerstroke and release of phosphate. Cytoskelet. Hob. 78, 448–458. doi:10.1002/cm.21695

PubMed Abstract | CrossRef Full Text | Google Scholar

Debold E. P., Walcott S., Woodward M., Turner M. A. (2013). Direct observation of phosphate inhibiting the force-generating capacity of a miniensemble of Myosin molecules. Biophys. J. 105, 2374–2384. doi:10.1016/j.bpj.2013.09.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebus J. P., Stienen G. J., Elzinga G. (1994). Influence of phosphate and pH on myofibrillar ATPase activity and force in skinned cardiac trabeculae from rat. J. physiology 476, 501–516. doi:10.1113/jphysiol.1994.sp020150

PubMed Abstract | CrossRef Full Text | Google Scholar

Edes I. F., Czuriga D., Csanyi G., Chlopicki S., Recchia F. A., Borbely A., et al. (2007). Rate of tension redevelopment is not modulated by sarcomere length in permeabilized human, murine, and porcine cardiomyocytes. Am. J. Physiol. Regul. Integr. Comp. Physiol. 293, R20–R29. doi:10.1152/ajpregu.00537.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Eisenberg E., Hill T. L., Chen Y. (1980). Cross-bridge model of muscle contraction. Quantitative analysis. Biophys. J. 29, 195–227. doi:10.1016/S0006-3495(80)85126-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Fabiato A., Fabiato F. (1979). Calculator programs for computing the composition of the solutions containing multiple metals and ligands used for experiments in skinned muscle cells. J. de physiologie 75, 463–505.

PubMed Abstract | Google Scholar

Flitney F. W., Hirst D. G. (1978). Cross-bridge detachment and sarcomere 'give' during stretch of active frog's muscle. J. Physiol. 276, 449–465. doi:10.1113/jphysiol.1978.sp012246

PubMed Abstract | CrossRef Full Text | Google Scholar

Geeves M. A. (2016). Review: the ATPase mechanism of myosin and actomyosin. Biopolymers 105, 483–491. doi:10.1002/bip.22853

PubMed Abstract | CrossRef Full Text | Google Scholar

Geeves M. A., Holmes K. C. (2005). The molecular mechanism of muscle contraction. Adv. Protein Chem. 71, 161–193. doi:10.1016/S0065-3233(04)71005-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordon A. M., Homsher E., Regnier M. (2000). Regulation of contraction in striated muscle. Physiol. Rev. 80, 853–924. doi:10.1152/physrev.2000.80.2.853

PubMed Abstract | CrossRef Full Text | Google Scholar

Governali S., Caremani M., Gallart C., Pertici I., Stienen G., Piazzesi G., et al. (2020). Orthophosphate increases the efficiency of slow muscle-myosin isoform in the presence of omecamtiv mecarbil. Nat. Commun. 11, 3405. doi:10.1038/s41467-020-17143-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Herrmann C., Houadjeto M., Travers F., Barman T. (1992). Early steps of the Mg²⁺-ATPase of relaxed myofibrils. A comparison with Ca²⁺-activated myofibrils and myosin subfragment 1. Biochemistry 31, 8036–8042. doi:10.1021/bi00149a038

PubMed Abstract | CrossRef Full Text | Google Scholar

Herzig J. W., Peterson J. W., Ruegg J. C., Solaro R. J. (1981). Vanadate and phosphate ions reduce tension and increase cross-bridge kinetics in chemically skinned heart muscle. Biochim. Biophys. Acta 672, 191–196. doi:10.1016/0304-4165(81)90392-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Hibberd M. G., Dantzig J. A., Trentham D. R., Goldman Y. E. (1985a). Phosphate release and force generation in skeletal muscle fibers. Science 228, 1317–1319. doi:10.1126/science.3159090

PubMed Abstract | CrossRef Full Text | Google Scholar

Hibberd M. G., Webb M. R., Goldman Y. E., Trentham D. R. (1985b). Oxygen exchange between phosphate and water accompanies calcium-regulated ATPase activity of skinned fibers from rabbit skeletal muscle. J. Biol. Chem. 260, 3496–3500. doi:10.1016/s0021-9258(19)83649-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Hinken A. C., McDonald K. S. (2004). Inorganic phosphate speeds loaded shortening in rat skinned cardiac myocytes. Am. J. physiology Cell. physiology 287, C500–C507. doi:10.1152/ajpcell.00049.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Hinken A. C., Solaro R. J. (2007). A dominant role of cardiac molecular motors in the intrinsic regulation of ventricular ejection and relaxation. Physiol. (Bethesda) 22, 73–80. doi:10.1152/physiol.00043.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Houdusse A., Sweeney H. L. (2016). How myosin generates force on actin filaments. Trends Biochem. Sci. 41, 989–997. doi:10.1016/j.tibs.2016.09.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Huxley A. F. (1957). Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 7, 255–318. doi:10.1016/s0096-4174(18)30128-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Huxley A. F., Simmons R. M. (1970). Rapid 'give' and the tension 'shoulder' in the relaxation of frog muscle fibres. J. Physiol. 210, 32P–33P.

PubMed Abstract | Google Scholar

Hwang Y., Washio T., Hisada T., Higuchi H., Kaya M. (2021). A reverse stroke characterizes the force generation of cardiac myofilaments, leading to an understanding of heart function. Proc. Natl. Acad. Sci. U. S. A. 118, e2011659118. doi:10.1073/pnas.2011659118

PubMed Abstract | CrossRef Full Text | Google Scholar

Irving M. (2017). Regulation of contraction by the thick filaments inSkeletal muscle. Biophys. J. 113, 2579–2594. doi:10.1016/j.bpj.2017.09.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishijima A., Kojima H., Funatsu T., Tokunaga M., Higuchi H., Tanaka H., et al. (1998). Simultaneous observation of individual ATPase and mechanical events by a single myosin molecule during interaction with actin. Cell. 92, 161–171. doi:10.1016/s0092-8674(00)80911-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Karatzaferi C., Adamek N., Geeves M. A. (2017). Modulators of actin-myosin dissociation: basis for muscle type functional differences during fatigue. Am. J. Physiol. Cell. Physiol. 313, C644-C654–C654. doi:10.1152/ajpcell.00023.2017

PubMed Abstract | CrossRef Full Text | Google Scholar

Kawai M., Halvorson H. R. (1991). Two step mechanism of phosphate release and the mechanism of force generation in chemically skinned fibers of rabbit psoas muscle. Biophys. J. 59, 329–342. doi:10.1016/S0006-3495(91)82227-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Kentish J. C. (1986). The effects of inorganic phosphate and creatine phosphate on force production in skinned muscles from rat ventricle. J. physiology 370, 585–604. doi:10.1113/jphysiol.1986.sp015952

PubMed Abstract | CrossRef Full Text | Google Scholar

Kreutziger K. L., Piroddi N., Scellini B., Tesi C., Poggesi C., Regnier M. (2008). Thin filament Ca2+ binding properties and regulatory unit interactions alter kinetics of tension development and relaxation in rabbit skeletal muscle. J. physiology 586, 3683–3700. doi:10.1113/jphysiol.2008.152181

PubMed Abstract | CrossRef Full Text | Google Scholar

Linari M., Brunello E., Reconditi M., Fusi L., Caremani M., Narayanan T., et al. (2015). Force generation by skeletal muscle is controlled by mechanosensing in myosin filaments. Nature 528, 276–279. doi:10.1038/nature15727

PubMed Abstract | CrossRef Full Text | Google Scholar

Linari M., Caremani M., Lombardi V. (2010). A kinetic model that explains the effect of inorganic phosphate on the mechanics and energetics of isometric contraction of fast skeletal muscle. Proc. Biol. Sci. 277, 19–27. doi:10.1098/rspb.2009.1498

PubMed Abstract | CrossRef Full Text | Google Scholar

Linke W. A., Bartoo M. L., Pollack G. H. (1993). Spontaneous sarcomeric oscillations at intermediate activation levels in single isolated cardiac myofibrils. Circ. Res. 73, 724–734. doi:10.1161/01.res.73.4.724

PubMed Abstract | CrossRef Full Text | Google Scholar

Llinas P., Isabet T., Song L., Ropars V., Zong B., Benisty H., et al. (2015). How actin initiates the motor activity of Myosin. Dev. Cell. 33, 401–412. doi:10.1016/j.devcel.2015.03.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Lymn R. W., Taylor E. W. (1971). Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry 10, 4617–4624. doi:10.1021/bi00801a004

PubMed Abstract | CrossRef Full Text | Google Scholar

Mannherz H. G. (1970). On the reversibility of the biochemical reactions of muscular contraction during the absorption of negative work. FEBS Lett. 10, 233–236. doi:10.1016/0014-5793(70)80636-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Mansfield C., West T. G., Curtin N. A., Ferenczi M. A. (2012). Stretch of contracting cardiac muscle abruptly decreases the rate of phosphate release at high and low calcium. J. Biol. Chem. 287, 25696–25705. doi:10.1074/jbc.M112.373498

PubMed Abstract | CrossRef Full Text | Google Scholar

Mansson A., Rassier D., Tsiavaliaris G. (2015). Poorly understood aspects of striated muscle contraction. Biomed. Res. Int. 2015, 245154. doi:10.1155/2015/245154

PubMed Abstract | CrossRef Full Text | Google Scholar

Mansson A., Usaj M., Moretto L., Matusovsky O., Velayuthan L. P., Friedman R., et al. (2023). New paradigms in actomyosin energy transduction: critical evaluation of non-traditional models for orthophosphate release. Bioessays 45, e2300040. doi:10.1002/bies.202300040

PubMed Abstract | CrossRef Full Text | Google Scholar

Matusovsky O. S., Kodera N., MacEachen C., Ando T., Cheng Y. S., Rassier D. E. (2021). Millisecond conformational dynamics of skeletal myosin II power stroke studied by high-speed atomic force microscopy. ACS Nano 15, 2229–2239. doi:10.1021/acsnano.0c06820

PubMed Abstract | CrossRef Full Text | Google Scholar

Millar N. C., Homsher E. (1990). The effect of phosphate and calcium on force generation in glycerinated rabbit skeletal muscle fibers. A steady-state and transient kinetic study. J. Biol. Chem. 265, 20234–20240. doi:10.1016/s0021-9258(17)30494-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Millar N. C., Homsher E. (1992). Kinetics of force generation and phosphate release in skinned rabbit soleus muscle fibers. Am. J. Physiol. 262, C1239–C1245. doi:10.1152/ajpcell.1992.262.5.C1239

PubMed Abstract | CrossRef Full Text | Google Scholar

Moretto L., Usaj M., Matusovsky O., Rassier D. E., Friedman R., Mansson A. (2022). Multistep orthophosphate release tunes actomyosin energy transduction. Nat. Commun. 13, 4575. doi:10.1038/s41467-022-32110-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Muretta J. M., Rohde J. A., Johnsrud D. O., Cornea S., Thomas D. D. (2015). Direct real-time detection of the structural and biochemical events in the myosin power stroke. Proc. Natl. Acad. Sci. U. S. A. 112, 14272–14277. doi:10.1073/pnas.1514859112

PubMed Abstract | CrossRef Full Text | Google Scholar

Norman C., Rall J. A., Tikunova S. B., Davis J. P. (2007). Modulation of the rate of cardiac muscle contraction by troponin C constructs with various calcium binding affinities. Am. J. physiology Heart circulatory physiology 293, H2580–H2587. doi:10.1152/ajpheart.00039.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Offer G., Ranatunga K. W. (2020). The location and rate of the phosphate release step in the muscle cross-bridge cycle. Biophys. J. 119, 1501–1512. doi:10.1016/j.bpj.2020.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Osten J., Mohebbi M., Uta P., Matinmehr F., Wang T., Kraft T., et al. (2022). Myosin essential light chain 1sa decelerates actin and thin filament gliding on β-myosin molecules. J. Gen. Physiol. 154, e202213149. doi:10.1085/jgp.202213149

PubMed Abstract | CrossRef Full Text | Google Scholar

Palmer S., Kentish J. C. (1998). Roles of Ca2+ and crossbridge kinetics in determining the maximum rates of Ca2+ activation and relaxation in rat and Guinea pig skinned trabeculae. Circ. Res. 83, 179–186. doi:10.1161/01.res.83.2.179

PubMed Abstract | CrossRef Full Text | Google Scholar

Papp Z., van der Velden J., Borbely A., Edes I., Stienen G. J. M. (2014). Altered myocardial force generation in end-stage human heart failure. Esc. Heart Fail 1, 160–165. doi:10.1002/ehf2.12020

PubMed Abstract | CrossRef Full Text | Google Scholar

Park-Holohan S. J., Brunello E., Kampourakis T., Rees M., Irving M., Fusi L. (2021). Stress-dependent activation of myosin in the heart requires thin filament activation and thick filament mechanosensing. Proc. Natl. Acad. Sci. U. S. A. 118, e2023706118. doi:10.1073/pnas.2023706118

PubMed Abstract | CrossRef Full Text | Google Scholar

Pate E., Cooke R. (1989). A model of crossbridge action: the effects of ATP, ADP and Pi. J. Muscle Res. Cell. Motil. 10, 181–196. doi:10.1007/BF01739809

PubMed Abstract | CrossRef Full Text | Google Scholar

Pate E., Franks-Skiba K., Cooke R. (1998). Depletion of phosphate in active muscle fibers probes actomyosin states within the powerstroke. Biophys. J. 74, 369–380. doi:10.1016/S0006-3495(98)77794-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Pate E., Franks-Skiba K., White H. D., Cooke R. (1993). The use of differing nucleotides to investigate cross-bridge kinetics. J. Biol. Chem. 268, 10046–10053. doi:10.1016/s0021-9258(18)82170-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Poggesi C., Tesi C., Stehle R. (2005). Sarcomeric determinants of striated muscle relaxation kinetics. Pflugers Arch. 449, 505–517. doi:10.1007/s00424-004-1363-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Potma E. J., Stienen G. J. (1996). Increase in ATP consumption during shortening in skinned fibres from rabbit psoas muscle: effects of inorganic phosphate. J. physiology 496 (Pt 1), 1–12. doi:10.1113/jphysiol.1996.sp021660

PubMed Abstract | CrossRef Full Text | Google Scholar

Potma E. J., van Graas I. A., Stienen G. J. (1995). Influence of inorganic phosphate and pH on ATP utilization in fast and slow skeletal muscle fibers. Biophys. J. 69, 2580–2589. doi:10.1016/S0006-3495(95)80129-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahman M. A., Usaj M., Rassier D. E., Mansson A. (2018). Blebbistatin effects expose hidden secrets in the force-generating cycle of actin and myosin. Biophys. J. 115, 386–397. doi:10.1016/j.bpj.2018.05.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Ranatunga K. W. (1999). Effects of inorganic phosphate on endothermic force generation in muscle. Proc. Biol. Sci. 266, 1381–1385. doi:10.1098/rspb.1999.0791

PubMed Abstract | CrossRef Full Text | Google Scholar

Rassier D. E., Mansson A. (2025). Mechanisms of myosin II force generation: insights from novel experimental techniques and approaches. Physiol. Rev. 105, 1–93. doi:10.1152/physrev.00014.2023

PubMed Abstract | CrossRef Full Text | Google Scholar

Reconditi M., Brunello E., Linari M., Bianco P., Narayanan T., Panine P., et al. (2011). Motion of myosin head domains during activation and force development in skeletal muscle. Proc. Natl. Acad. Sci. U. S. A. 108, 7236–7240. doi:10.1073/pnas.1018330108

PubMed Abstract | CrossRef Full Text | Google Scholar

Regnier M., Homsher E. (1998). The effect of ATP analogs on posthydrolytic and force development steps in skinned skeletal muscle fibers. Biophys. J. 74, 3059–3071. doi:10.1016/S0006-3495(98)78013-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Regnier M., Morris C., Homsher E. (1995). Regulation of the cross-bridge transition from a weakly to strongly bound state in skinned rabbit muscle fibers. Am. J. Physiol. 269, C1532–C1539. doi:10.1152/ajpcell.1995.269.6.C1532

PubMed Abstract | CrossRef Full Text | Google Scholar

Reiser P. J., Kline W. O. (1998). Electrophoretic separation and quantitation of cardiac myosin heavy chain isoforms in eight mammalian species. Am. J. Physiol. 274, H1048–H1053. doi:10.1152/ajpheart.1998.274.3.H1048

PubMed Abstract | CrossRef Full Text | Google Scholar

Robert-Paganin J., Pylypenko O., Kikuti C., Sweeney H. L., Houdusse A. (2020). Force generation by myosin motors: a structural perspective. Chem. Rev. 120, 5–35. doi:10.1021/acs.chemrev.9b00264

PubMed Abstract | CrossRef Full Text | Google Scholar

Scott B., Marang C., Woodward M., Debold E. P. (2021). Myosin's powerstroke occurs prior to the release of phosphate from the active site. Cytoskelet. Hob. 78, 185–198. doi:10.1002/cm.21682

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith D. A. (2014). A new mechanokinetic model for muscle contraction, where force and movement are triggered by phosphate release. J. Muscle Res. Cell. Motil. 35, 295–306. doi:10.1007/s10974-014-9391-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith I. C., Collao N., Herzog W. (2020). The effects of inorganic phosphate on contractile function of slow skeletal muscle fibres are length-dependent. Biochem. Biophys. Res. Commun. 533, 818–823. doi:10.1016/j.bbrc.2020.09.092

PubMed Abstract | CrossRef Full Text | Google Scholar

Stehle R. (2017). Force responses and sarcomere dynamics of cardiac myofibrils induced by rapid changes in [P_i]. Biophys. J. 112, 356–367. doi:10.1016/j.bpj.2016.11.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Stehle R., Iorga B. (2010). Kinetics of cardiac sarcomeric processes and rate-limiting steps in contraction and relaxation. J. Mol. Cell. Cardiol. 48, 843–850. doi:10.1016/j.yjmcc.2009.12.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Stehle R., Kruger M., Pfitzer G. (2002a). Force kinetics and individual sarcomere dynamics in cardiac myofibrils after rapid Ca²⁺ changes. Biophys. J. 83, 2152–2161. doi:10.1016/S0006-3495(02)73975-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Stehle R., Kruger M., Scherer P., Brixius K., Schwinger R. H., Pfitzer G. (2002b). Isometric force kinetics upon rapid activation and relaxation of mouse, Guinea pig and human heart muscle studied on the subcellular myofibrillar level. Basic Res. Cardiol. 97 (Suppl. 1), I127–I135. doi:10.1007/s003950200041

PubMed Abstract | CrossRef Full Text | Google Scholar

Stehle R., Lionne C., Travers F., Barman T. (2000). Kinetics of the initial steps of rabbit psoas myofibrillar ATPases studied by tryptophan and pyrene fluorescence stopped-flow and rapid flow-quench. Evidence that cross-bridge detachment is slower than ATP binding. Biochemistry 39, 7508–7520. doi:10.1021/bi0004753

PubMed Abstract | CrossRef Full Text | Google Scholar

Stehle R., Tesi C. (2017). Kinetic coupling of phosphate release, force generation and rate-limiting steps in the cross-bridge cycle. J. Muscle Res. Cell. Motil. 38, 275–289. doi:10.1007/s10974-017-9482-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Strauss J. D., Bletz C., Ruegg J. C. (1994). The calcium sensitizer EMD 53998 antagonizes phosphate-induced increases in energy cost of isometric tension in cardiac skinned fibres. Eur. J. Pharmacol. 252, 219–224. doi:10.1016/0014-2999(94)90600-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Sweeney H. L., Stull J. T. (1990). Alteration of cross-bridge kinetics by myosin light chain phosphorylation in rabbit skeletal muscle: implications for regulation of actin-myosin interaction. Proc. Natl. Acad. Sci. U. S. A. 87, 414–418. doi:10.1073/pnas.87.1.414

PubMed Abstract | CrossRef Full Text | Google Scholar

Takagi Y., Shuman H., Goldman Y. E. (2004). Coupling between phosphate release and force generation in muscle actomyosin. Philos. Trans. R. Soc. Lond B Biol. Sci. 359, 1913–1920. doi:10.1098/rstb.2004.1561

PubMed Abstract | CrossRef Full Text | Google Scholar

Tesi C., Colomo F., Nencini S., Piroddi N., Poggesi C. (2000). The effect of inorganic phosphate on force generation in single myofibrils from rabbit skeletal muscle. Biophys. J. 78, 3081–3092. doi:10.1016/S0006-3495(00)76845-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Tesi C., Colomo F., Piroddi N., Poggesi C. (2002). Characterization of the cross-bridge force-generating step using inorganic phosphate and BDM in myofibrils from rabbit skeletal muscles. J. Physiol. 541, 187–199. doi:10.1113/jphysiol.2001.013418

PubMed Abstract | CrossRef Full Text | Google Scholar

Ulbrich M., Ruegg J. C. (1971). Stretch induced formation of ATP-32P in glycerinated fibres of insect flight muscle. Experientia 27, 45–46. doi:10.1007/BF02137732

PubMed Abstract | CrossRef Full Text | Google Scholar

Wahr P. A., Cantor H. C., Metzger J. M. (1997). Nucleotide-dependent contractile properties of Ca²⁺-activated fast and slow skeletal muscle fibers. Biophys. J. 72, 822–834. doi:10.1016/s0006-3495(97)78716-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang L., Bahadir A., Kawai M. (2015). High ionic strength depresses muscle contractility by decreasing both force per cross-bridge and the number of strongly attached cross-bridges. J. Muscle Res. Cell. Motil. 36, 227–241. doi:10.1007/s10974-015-9412-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang L., Kawai M. (2013). A re-interpretation of the rate of tension redevelopment (k_TR) in active muscle. J. Muscle Res. Cell. Motil. 34, 407–415. doi:10.1007/s10974-013-9366-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang T., Spahiu E., Osten J., Behrens F., Grunhagen F., Scholz T., et al. (2022). Cardiac ventricular myosin and slow skeletal myosin exhibit dissimilar chemomechanical properties despite bearing the same myosin heavy chain isoform. J. Biol. Chem. 298, 102070. doi:10.1016/j.jbc.2022.102070

PubMed Abstract | CrossRef Full Text | Google Scholar

Webb M. R., Hibberd M. G., Goldman Y. E., Trentham D. R. (1986). Oxygen exchange between Pi in the medium and water during ATP hydrolysis mediated by skinned fibers from rabbit skeletal muscle. Evidence for Pi binding to a force-generating state. J. Biol. Chem. 261, 15557–15564. doi:10.1016/s0021-9258(18)66750-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolff M. R., McDonald K. S., Moss R. L. (1995). Rate of tension development in cardiac muscle varies with level of activator calcium. Circulation Res. 76, 154–160. doi:10.1161/01.res.76.1.154

PubMed Abstract | CrossRef Full Text | Google Scholar

Woodward M., Debold E. P. (2018). Acidosis and phosphate directly reduce myosin's force-generating capacity through distinct molecular mechanisms. Front. physiology 9, 862. doi:10.3389/fphys.2018.00862

PubMed Abstract | CrossRef Full Text | Google Scholar

Woody M. S., Winkelmann D. A., Capitanio M., Ostap E. M., Goldman Y. E. (2019). Single molecule mechanics resolves the earliest events in force generation by cardiac myosin. Elife 8, e49266. doi:10.7554/eLife.49266

PubMed Abstract | CrossRef Full Text | Google Scholar

Yanagida T., Arata T., Oosawa F. (1985). Sliding distance of actin filament induced by a myosin crossbridge during one ATP hydrolysis cycle. Nature 316, 366–369. doi:10.1038/316366a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Yount R. G., Lawson D., Rayment I. (1995). Is myosin a “back door” enzyme? Biophys. J. 68, 44S–49S. ; discussion 47S-49S.

PubMed Abstract | Google Scholar

Zhao Y., Kawai M. (1996). Inotropic agent EMD-53998 weakens nucleotide and phosphate binding to cross-bridges in porcine myocardium. Am. J. Physiol. 271, H1394–H1406. doi:10.1152/ajpheart.1996.271.4.H1394

PubMed Abstract | CrossRef Full Text | Google Scholar