Methods for assessing cardiac myofilament calcium sensitivity

Myofilament calcium (Ca²⁺) sensitivity is one of several mechanisms by which force production of cardiac muscle is modulated to meet the ever-changing demands placed on the heart. Compromised Ca²⁺ sensitivity is associated with pathologies, which makes it a parameter of interest for researchers. Ca²⁺ Sensitivity is the ratio of the association and dissociation rates between troponin C (TnC) and Ca²⁺. As it is not currently possible to measure these rates in tissue preparations directly, methods have been developed to infer myofilament sensitivity, typically using some combination of force and Ca²⁺ measurements. The current gold-standard approach constructs a steady-state force-Ca²⁺ relation by exposing permeabilised muscle samples to a range of Ca²⁺ concentrations and uses the half-maximal concentration as a proxy for sensitivity. While a valuable method for steady-state investigations, the permeabilisation process makes the method unsuitable when examining dynamic, i.e., twitch-to-twitch, changes in myofilament sensitivity. The ability of the heart to transiently adapt to changes in load is an important consideration when evaluating the impact of disease states. Alternative methods have been proffered, including force-Ca²⁺ phase loops, potassium contracture, hybrid experimental-modelling and conformation-based fluorophore approaches. This review provides an overview of the mechanisms underlying myofilament Ca²⁺ sensitivity, summarises existing methods, and explores, with modelling, whether any of them are suited to investigating dynamic changes in sensitivity. We conclude that a method that equips researchers to investigate the transient change of myofilament Ca²⁺ sensitivity is still needed. We propose that such a method will involve simultaneous measurements of cytosolic Ca²⁺ and TnC activation in actively twitching muscle and a biophysical model to interpret these data.

1 Introduction

Calcium (Ca²⁺) sensitivity is a critical mechanism by which force production of cardiac muscle is modulated to meet the ever-changing demands placed on the heart. As the ventricles of the heart form an electrical syncytium (i.e., the entire ventricle contracts with each beat), the work performed by cardiac muscle cannot be regulated through mechanisms like recruitment, as is the case in skeletal muscle. Instead, changes in frequency, stroke volume, and contractility represent the cornerstones of cardiac output regulation. Ca²⁺ sensitivity falls under the umbrella of mechanisms that modulate contractility.

Due to the functional importance of Ca²⁺ sensitivity and its disruption in pathologies, particularly in diabetic cardiomyopathy (Bielefeld et al., 1983), dilated cardiomyopathy (Wolff et al., 1996), and hypertrophic cardiomyopathy (Frey et al., 2012), the scientific community has developed several methods for assessing sensitivity. Generally, those methods require simultaneous measurements of cytosolic Ca²⁺ concentration (hereon [Ca²⁺]_i) and one of length or force. To our knowledge, the earliest force-Ca²⁺ curve of cardiac muscle was obtained from skinned muscles by the seminal study of Fabiato and Fabiato (1975), following a demonstration of the force-Ca²⁺ curve obtained from glycerated ventricular rings (Bozler, 1968) and curvature relations between ATPase activity and Ca²⁺ in cardiac myosin by Katz and colleagues in the 1960s (Katz and Repke, 1966; Katz, 1967). Since then, methods have been developed to accommodate intact muscle preparations from animals of varying sizes (e.g., mouse (McDonald et al., 1995; Rajan et al., 2007) to human (Van der Velden et al., 2000; Gomes et al., 2005)), which are more physiologically appropriate than their permeabilised counterparts.

This review focuses on ex-vivo methods used by the scientific community to assess cardiac myofilament Ca²⁺ sensitivity. We first summarise the knowledge and concepts that underpin myofilament calcium sensitivity before examining the various measurement methods that have been used to probe this characteristic in ex-vivo heart tissue. These include identification techniques using chemical and electrical stimuli, mathematical model-based analyses, and recently developed fluorescent probes. We outline necessary considerations for each of the methods and speculate on the future direction of ex-vivo methods for assessing myofilament Ca²⁺ sensitivity.

2 Subcellular basis of cardiac myofilament Ca²⁺ sensitivity

An in-depth description of the modulatory mechanisms of Ca²⁺ sensitivity has been provided in existing reviews (Allen and Kentish, 1985; Chung et al., 2016). We, thus, provide a brief overview of the key proteins involved in the Ca²⁺-based regulation of cardiac myofilament interaction to define the nomenclature used throughout the review.

We start with the structures involved in force production and Ca²⁺-based regulation. “Myofilaments” refers to strand-like protein complexes whose interaction results in force production. In a reductive sense, there are two types of myofilaments: the thin filament, which consists of actin, the troponin complex, and tropomyosin, and the thick filament, which consists of mainly myosin molecules (De Tombe, 2003). Another important protein in force regulation is myosin-binding protein C, which regulates the structural arrangement of the lattice (Knöll, 2012). In cardiac muscle, force production occurs from crossbridge cycling–a process whereby myosin heads of the thick filament cyclically interact with actin molecules of the thin filament. At low [Ca²⁺]_i, troponin and tropomyosin prevent actin and myosin from interacting (Tobacman, 2021). The troponin complex comprises three subunits: troponin C (TnC), troponin I (TnI), and troponin T (TnT). The arrival of an action potential induces [Ca²⁺]_i to increase due to extracellular and intracellular Ca²⁺ fluxes. Ca²⁺ binding to TnC causes a conformational change in the thin filament, removing the steric hindrance and enabling strong myosin-actin binding.

3 Sensitivity versus responsiveness

Augmented Ca²⁺ sensitivity has, at times, been misrepresented as greater force production for a given [Ca²⁺]_i (Bers, 2002). The authors of this review would like to demarcate myofilament-centric Ca²⁺ sensitivity from cross-bridge-centric responsiveness, as was the historical definition (Marban and Kusuoka, 1987). TnC-Ca²⁺ binding affinity, or the ratio of Ca²⁺ attachment and detachment rates, is Ca²⁺ sensitivity, which can be modulated through post-translational modifications like the phosphorylation of TnI (Salhi et al., 2016; Bowman et al., 2019). In contrast, cross-bridge-centric mechanisms, such as the number of available cross-bridges and unitary force (force generated per cross-bridge (De Tombe and Ter Keurs, 2016)), are mechanisms of “responsiveness”. Cooperativity represents a grey area of cross-bridge- and myofilament-centric mechanisms, where bound cross-bridges increase the Ca²⁺ binding affinity of proximal TnC sub-units. Hopefully, the issue with the pervasive definition of Ca²⁺ sensitivity is now apparent; it conflates responsiveness, cooperativity, and sensitivity.

This conflation has likely arisen partly because of the challenges associated with inferring sensitivity from force and Ca²⁺ measurements, as most of the methods discussed in this review have done. Let us consider the reaction states of a myofilament in a three-state representation (Figure 1): A, no Ca²⁺ is bound to TnC, so myosin and actin are unable to bind to form a cross-bridge; B, Ca²⁺ is bound to TnC and the tropomyosin-troponin complex has undergone a conformational change, but myosin and actin have not yet bound; and C, myosin and actin are strongly bound. When measuring the effect of Ca²⁺ on force, the only state we can measure is State C, which manifests, indirectly and macroscopically, as force production. Hence, we cannot differentiate between the changes in sensitivity that are driven by myofilament-centric processes (between States A and B) and those driven by cross-bridge-centric processes (between States B and C).

FIGURE 1

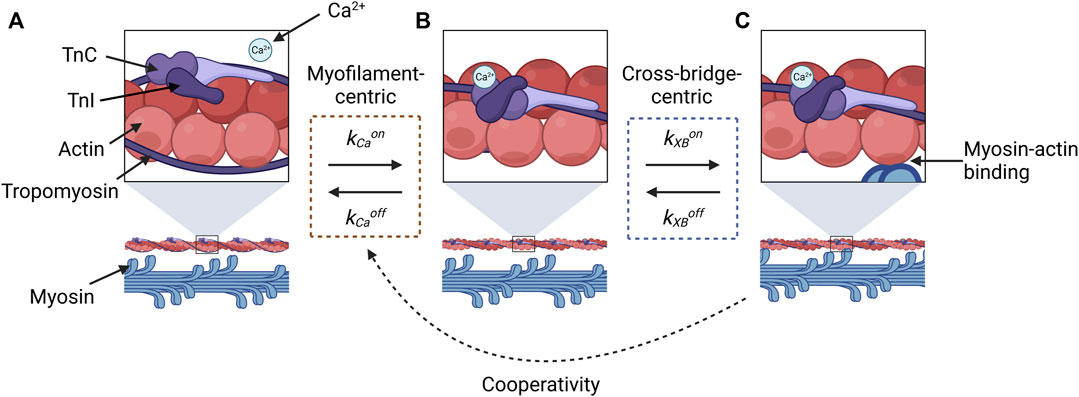
FIGURE 1. Illustration of reaction states for cross-bridge formation that are relevant for evaluating the constituent components of force-Ca²⁺ dynamics. State (A) represents the absence of Ca²⁺, and the myosin-binding sites of actin molecules (top panel) are sterically inhibited by tropomyosin and the troponin complex, so myosin-actin binding does not occur (lower panel). Once Ca²⁺ binds to TnC, a conformational change in tropomyosin and troponin removes the steric hindrance (B), which makes actin-myosin binding possible (C). The transition between (A) and (B) is described by the kinetic rates for the association (k_Ca^on) and dissociation (k_Ca^off) of Ca²⁺ to and from TnC, respectively (orange dashed box). The transition between States (B) and (C) is described by the kinetic rates associated with the attachment (k_XB^on) and detachment (k_XB^off) of cross-bridges (blue dashed box). Force-dependent cooperativity is indicated by the dotted black arrow, where the force by crossbridges modulates Ca²⁺-TnC binding affinity. This figure was created with BioRender.com.

In addition, there is a temporal delay between any change in [Ca²⁺]_i and the number of strongly bound cross bridges, as the transition from State A to State B and State B to State C is not instantaneous. To infer the ratio of k_Ca^on and k_Ca^off (sensitivity) using force information alone requires both reactions to be in equilibrium. If not, the number of bound cross-bridges will be rate-limited by time dynamics and will not reflect the underlying binding affinities. The notion of equilibrium and steady state is essential for the sensitivity assessment methods discussed below.

4 Steady-state force-Ca²⁺ relation

The most used method for inferring myofilament Ca²⁺ sensitivity utilises the steady-state force-Ca²⁺ relation. This relation is constructed by measuring the steady-state force production of a muscle sample over a range of prescribed or measured Ca²⁺ concentrations, typically expressed as pCa (Figure 2). Such an experiment can be conducted under a range of temperatures and sarcomere lengths (Kentish et al., 1983; Harrison and Bers, 1989). These data are typically fitted to a Hill equation, where EC₅₀ (also k_d) is defined as the Ca²⁺ concentration associated with half-maximal force production and n is the Hill coefficient, a measure of the steepness, or cooperativity, of the relation (e.g., Equation 1). The force produced is normalised to the peak value (F_max) obtained under the highest concentration of Ca²⁺. A lower EC₅₀ represents an increased Ca²⁺ sensitivity, as a lesser Ca²⁺ concentration is required for the sample to reach half-maximal force production (Figure 2A). This technique has been performed using permeabilised (Fabiato and Fabiato, 1975; Wolff et al., 1996) and intact (Gao et al., 1994; Varian et al., 2006) muscle preparations.

$\mathit{F}=\frac{{\mathit{F}}_{\mathit{max}}\times {\left({\left[\mathbf{C}{\mathbf{a}}^{\mathbf{2}+}\right]}_{\mathbf{i}}\right)}^{\mathit{n}}}{{\left({\left[\mathbf{C}{\mathbf{a}}^{\mathbf{2}+}\right]}_{\mathbf{i}}\right)}^{\mathit{n}}+{\left(\mathbf{E}{\mathbf{C}}_{\mathbf{50}}\right)}^{\mathit{n}}}(1)$

FIGURE 2

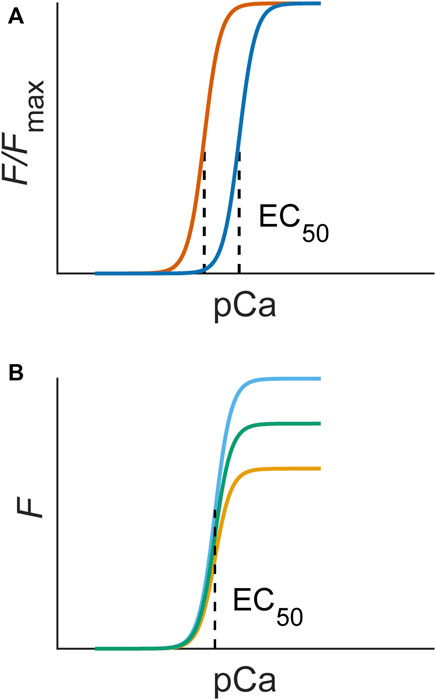
FIGURE 2. (A) An increase in myofilament sensitivity is associated with a left shift of the force-Ca²⁺ curve (blue to orange), quantifiable as EC₅₀. (B) A change in responsiveness alone would not change sensitivity and, hence, would not change the EC₅₀ of steady-state force-Ca²⁺ curves. The Hill equation (Eq. 1) used to fit experimental data contains these parameters: F_max is the maximum force, n is the Hill coefficient, which indicates the steepness, or cooperativity, of the relation, and EC₅₀ is the concentration of Ca²⁺ associated with half-maximal force production (dotted line).

As mentioned in the introduction, Fabiato and Fabiato (1975) performed the first example of this method using skinned (or permeabilised) samples. The skinning process removes all sarcolemmal structures by chemical (e.g., triton or saponin) or mechanical means, exposing the contractile myofilament proteins to the bathing solution. In this way, skinning can be thought of as a means of homogenising the extracellular and intracellular compartments. Permeabilisation is known to increase myofilament lattice spacing (Matsubara, 1980), which is thought to decrease the probability of cross-bridge formation (McDonald and Moss, 1995). This concern is mitigated by the use of a high-molecular-weight polymer, such as dextran (2%–3%), to compress the myofilament lattice back to near physiological levels (Irving et al., 2000). After skinning, permeabilised muscles are no longer capable of producing a force twitch. Instead, these samples produce a sustained contracture force in response to the presented Ca²⁺ concentration in the bathing solution. A secondary benefit of leveraging permeabilised samples is the ability to use frozen samples with minimal impact on the apparent myofilament Ca²⁺ sensitivity (Milburn et al., 2022), which enables the use of human samples from existing tissue banks. Steady-state length-Ca²⁺ relations have also been used to assess myofilament Ca²⁺ sensitivity in skinned cardiac myocytes (Siri et al., 1991; Lim et al., 2001), though this is uncommon. Achieving the low Ca²⁺ concentration needed to assess the entire relation (∼1 nM) necessitates the use of a chelating agent, such as EGTA or BAPTA (Bers et al., 2010). Free [Ca²⁺] is estimated using specialist software, which account for variables like pH, ionic strength, and temperature (Brooks and Storey, 1992; Dweck et al., 2005). For each [Ca²⁺], the permeabilised sample is left in the Ca²⁺ solution until a steady-state force (or length) is reached, which is to say that the relation is the direct result of binding kinetics instead of a conflation of rate-limited reactions.

In an intact muscle, where the sarcolemma is maintained, intracellular and extracellular Ca²⁺ concentrations are not equivalent. As a result, [Ca²⁺]_i concentration must be measured using a fluorescent indicator (e.g., Fura-2 (Grynkiewicz et al., 1985)). The bathing solution used for these studies also commonly contains caffeine or ryanodine, which enables tetanic contractions by limiting the sequestering of Ca²⁺ from the cytosolic space (Allen and Westerblad, 1995). Ryanodine has been shown to have no effect on myofilament Ca²⁺ sensitivity (Fabiato, 1985), but caffeine increases myofilament Ca²⁺ sensitivity (Wendt and Stephenson, 1983). Hence, when using tetani-based contracture to assess the steady-state force-Ca²⁺ relation, ryanodine should be used to inhibit the sequestering of Ca²⁺ within the SR. As in skinned experiments, force and intracellular Ca²⁺ are measured simultaneously during tetani over a range of extracellular Ca²⁺ concentrations. The extent of shortening of intact cells undergoing a tetanic contraction has also been used to assess sensitivity (Hongo et al., 1998).

The steady-state force-Ca²⁺ relations and, therefore, myofilament sensitivity, measured using intact and skinned samples are not equivalent, with intact samples appearing to have a greater Ca²⁺ sensitivity (Gao et al., 1994; Varian et al., 2006). However, skinning does not appear to negatively affect the maximum force production of cardiac muscle (Choi et al., 2020). The discrepancy in Ca²⁺ sensitivity has instead been speculatively attributed to a loss of post-translational modifications caused by the permeabilisation process (Chung et al., 2016). Hence, intact assessment of myofilament Ca²⁺ sensitivity appears preferable for steady-state sensitivity measurements.

5 Potassium contracture

The potassium (K⁺) contracture technique was developed by Varian et al. (2006) to measure steady-state myofilament Ca²⁺ sensitivity using intact muscle preparations (Figure 3A). The protocol involves switching the superfusate buffer to a modified composition with elevated KCl concentration (100 mM–150 mM). The high level of extracellular K⁺ evokes muscle contracture by depolarization of the cell membrane (Niedergerke, 1956); the force of contracture is proportional to the ratio of [Ca²⁺] to the square of [Na⁺] in the superfusate (Lüttgau and Niedergerke, 1958). Thus, the modified superfusate contains an increased concentration of CaCl₂ (around 5 mM) and a reduced concentration of NaCl (around 40 mM). The contracture ceases upon return to normal superfusate solution. The contracture takes about 5 min to complete.

FIGURE 3

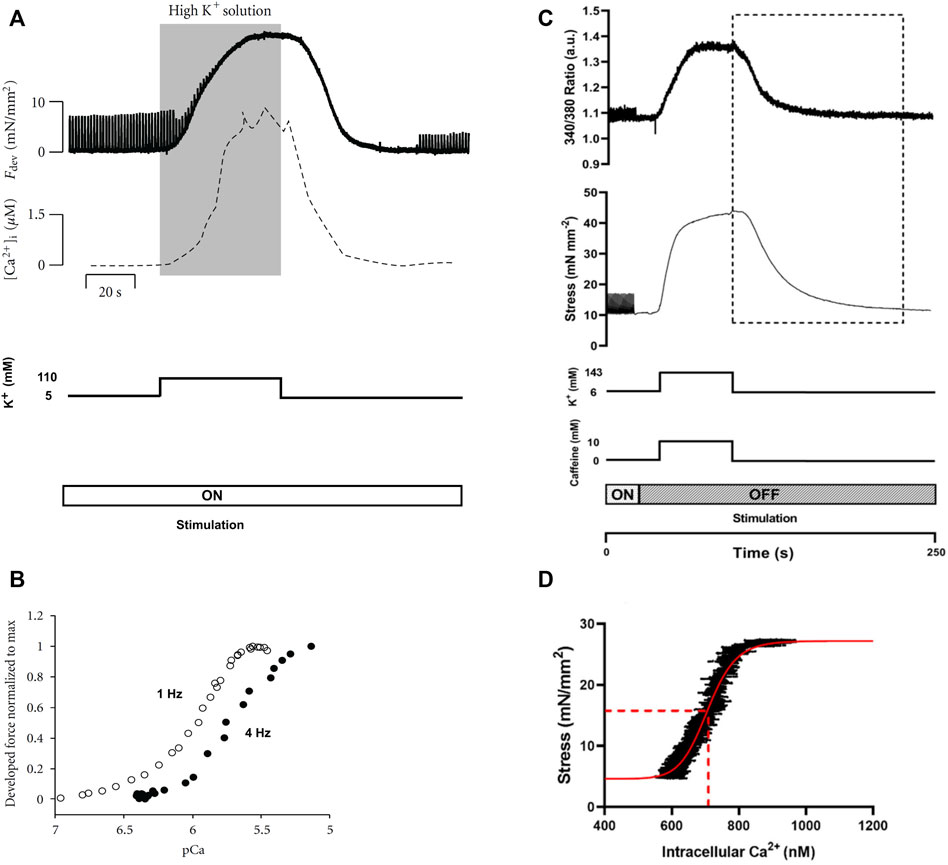
FIGURE 3. Potassium contracture techniques. Panels (A) and (B) are replicated from Varian et al. (2012). Panels (C) and (D) are reproduced from Jones et al. (2023). (A) The contracture protocol of Varian et al. exposes muscle to a high K⁺ superfusate solution (shaded region), with the electrical stimulation (at 1 Hz) remains on (Varian et al., 2012). Force twitches diminish upon contracture and re-develop upon washout of the high K⁺ superfusate. (B) Force-[Ca²⁺]_i data were obtained from the rising (upstroke) phase of the contracture (shaded region in panel (A). The 4 Hz data were positioned left to that of the 1 Hz, which was interpreted by Varian et al. as reduced myofilament Ca²⁺ sensitivity (i.e., frequency-dependent myofilament desensitization). (C) The high-K⁺ contracture protocol of the Ward lab (Jones et al., 2023) includes high caffeine with the electrical stimulation halted. (D) Force-[Ca²⁺]_i data were taken from the downstroke phase of the contracture (indicated by the dotted rectangle in panel (C) for curve fitting (red line) for the estimation of EC₅₀ (dotted red line).

Varian et al. (2006) simultaneously measured [Ca²⁺]_i and showed comparable up and down strokes of Ca²⁺ to that of the contracture force. As quoted from the authors, both [Ca²⁺]_i and force ‘rise and fall at nearly the same rate’ (Figure 3A). However, only the rising phase up to the maximum force of contracture (i.e., upstroke) has been used to estimate myofilament Ca²⁺ sensitivity from the resulting sigmoidal curve (Figure 3B). The sigmoidal force-Ca²⁺ curves from the upstroke and downstroke have not been compared, so it remains to be seen if they are equivalent.

Pulsatile electrical stimulation remains throughout the contracture, such that the muscle can be paced at various stimulation frequencies. This stimulation protocol allowed Varian et al. to conclude that myofilament Ca²⁺ sensitivity decreases with increasing frequency (i.e., a rightward shift of the force-[Ca²⁺]_i curve; Figure 3B) (Varian and Janssen, 2007). Such a modulatory role of frequency-dependent myofilament desensitization was found to be mediated through a kinase-specific pathway involving phosphorylation of myofilament proteins (Varian et al., 2012), and to be impaired in ventricular hypertrophy (Varian et al., 2009).

Although potassium contracture was developed almost two decades ago, it has not gained widespread popularity within the scientific community. Only one other research group has since adopted the technique (Kaur et al., 2016; Jones et al., 2023), albeit with three adjustments (Figure 3C). First, the elevated KCl in the superfusate is supplemented with caffeine (10 mM) to increase [Ca²⁺]_i through induced release of Ca²⁺ from the SR. Note that caffeine changes myofilament sensitivity (Wendt and Stephenson, 1983). Second, stimulation is halted throughout the contracture. Third, the downstroke of the contracture is used instead for constructing the force-Ca²⁺ curve (Figure 3D).

The K⁺ contracture protocol has been performed with variations that are specific to the study aim. Varian et al. aimed to assess the frequency-dependence of myofilament Ca²⁺ sensitivity and, hence, required stimulation and the upstroke of the K⁺ contracture was used. In contrast, Ward et al. focused on Ca²⁺ handling; hence, caffeine was added, and the downstroke of the K⁺ contracture was used. A consideration for future use of the K⁺ contracture technique will include whether the upstroke and downstroke produce the same force-Ca²⁺ curve, given the knowledge that the upstroke positively correlates with the prior stimulation frequency (Niedergerke, 1956; Gibbons and Fozzard, 1971).

It is not immediately clear as to why this method has not gained widespread popularity. Monasky et al. (2010), from the Janssen lab that pioneered this technique, commented that ‘the potassium contracture based assessment of calcium sensitivity is more technically challenging [than permeabilised steady-state analysis] and has a lower experimental success rate’. We speculate that these factors, combined with the relative ease with which force-Ca²⁺ phase-plane loop analysis can be performed (often with an insufficient appreciation of their limitations; see “Twitch-Based Methods”), have contributed to the poor uptake of potassium contracture as a method for evaluating myofilament Ca²⁺ sensitivity.

6 Twitch-based methods

With the advent of fluorescent indicators, initially aequorin (Shimomura, 1995), then Fura−2 (Grynkiewicz et al., 1985), investigators sought to leverage the new capability of simultaneous force (or length) and intracellular Ca²⁺ measurements to assess Ca²⁺-based contractile regulation. These techniques use force and Ca²⁺ measurements recorded in twitching intact muscle tissue (e.g., papillary muscles or trabeculae) or single-cell preparations. Each technique described in this section can be applied to a single twitch.

6.1 Using a single data point

For a time, twitch-based methods used relations derived from single time points of Ca²⁺ and contractile (i.e., force or length) traces to infer sensitivity. Early work by Blinks and colleagues hypothesised that the peak of a Ca²⁺ transient and associated twitch force amplitude, while dissociated in time, corresponded closely to the steady-state force-Ca²⁺ relation (Endoh and Blinks, 1988; Blinks, 1993). Backx et al. (1995) subsequently disproved this hypothesis by plotting the peak-force-Ca²⁺ relation on the same axis as tetanic (ryanodine) force-Ca²⁺ and illustrating that they were quite different (Figure 4A). In fact, empirical findings indicate that any shift in the peak Ca²⁺-force relation results from a modulation in the time course of the Ca²⁺ and force twitch rather than a change of myofilament Ca²⁺ sensitivity (Hajjar et al., 1992).

FIGURE 4

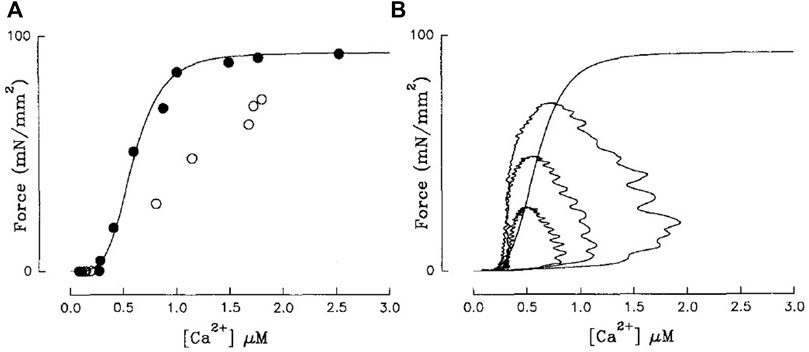
FIGURE 4. (A) Steady-state force-Ca²⁺ (black) and peak-force-Ca²⁺ relations (white) are not equivalent. (B) Isometric force-Ca²⁺ phase-plane loops at three different [Ca²⁺]_o are also not equivalent to the steady-state relation (sigmoid). Steady-state force-Ca²⁺ relation was measured using ryanodine-induced tetani. Reproduced from Backx et al. (1995).

As with steady-state relations, researchers have also considered Ca²⁺-length relations with single data point approaches. Siri et al. (1991) plotted sarcomere length measured in isolated cells not loaded with Fura-2 against [Ca²⁺]_i measured in other cells from the same heart paced at the same stimulation frequency. They plotted two collections of data points per group, one between diastolic sarcomere length and Ca²⁺ and the other between systolic sarcomere length and peak Ca²⁺. The range of [Ca²⁺]_i over which relations were plotted was achieved by leveraging the frequency dependency of Ca²⁺ transient amplitude. It should be noted that TnI phosphorylation, and therefore myofilament Ca²⁺ sensitivity, has since been shown to be frequency dependent (Varian and Janssen, 2007). When comparing controls and an animal model of congestive heart failure (aortic-banded guinea pigs), they observed that the Ca²⁺-sarcomere length relations for each group overlayed, indicating no sensitivity shift (Siri et al., 1991). Besides the challenge of collecting sarcomere length and [Ca²⁺]_i information from different cells, a temporal offset between peak Ca²⁺ and systolic length is also present, leading to the same issue as in the force-equivalent method.

6.2 Phase-plane loops

Phase-plane loops are generated by parametrically plotting either force or length against [Ca²⁺]_i (Figure 4B). A component of the phase-plane loop, typically the relaxation phase, is used to indicate myofilament Ca²⁺ sensitivity. The linear gradient (Ward et al., 2010), EC₅₀ (Gao et al., 1998; Jones et al., 2023), and qualitative assessment of the trajectory of the relaxation phase (Kentish and Wrzosek, 1998; Zhao et al., 2016) have all been considered as sensitivity indicators. The relaxation phase is the predominant focus for this technique because this is the part of the twitch with the slowest rate of change of Ca²⁺, suggesting it has the greatest chance of achieving force-Ca²⁺ equilibrium. However, the non-linear nature of the relaxation phase means the linear gradient is sensitive to the position along the relaxation phase where it is measured. Further, EC₅₀ conflates Ca²⁺ handling with myofilament and crossbridge effects (i.e., a large change in diastolic Ca²⁺ or Ca²⁺ amplitude would be interpreted as a change of sensitivity regardless of TnC-Ca²⁺ binding affinity).

In fact, cynicism has plagued the acceptability of these methods since their inception, with numerous studies speculating that force and Ca²⁺ are not in equilibrium throughout the loop (Yue et al., 1986; Yue, 1987; Endoh and Blinks, 1988; McIvor et al., 1988). Subsequent studies affirmed these suspicions by demonstrating that mechanical loading decouples the force and Ca²⁺ signals in the time domain (Peterson et al., 1988; Brutseart and Sys, 1989; Spurgeon et al., 1992). Spurgeon et al. (1992) suggested that, under isometric conditions, equilibrium between force and Ca²⁺ is reached only at the end of diastole. As expected, force-Ca²⁺ phase-plane loops sit on a different relation from that of steady-state (Figure 4B; (Backx et al., 1995)). Substantially slowing the sequestering of Ca²⁺ and the downstroke of the Ca²⁺ transient, using cyclopiazonic acid (SERCA inhibitor) brought the two relations into alignment (Backx et al., 1995), reinforcing the lack of equilibrium under physiological conditions. Despite these criticisms, force-Ca²⁺ phase-plane loops are still used to infer myofilament sensitivity (Kentish and Wrzosek, 1998; Han et al., 2010; Ward, 2014; Jones et al., 2023), given the conjecture that this approach can predict sensitivity under conditions known to modify sensitivity (Ward, 2014; Jones et al., 2023). This technique is better used to qualitatively assess disruptions to the time course of Ca²⁺ cycling (Pérez et al., 1999).

To emphasise the fallibility of force-Ca²⁺ phase-plane loops as an indicator of myofilament Ca²⁺ sensitivity, we have included in silico analyses focusing on conditions that modify phase-plane loop morphology in the absence of a change in myofilament Ca²⁺ sensitivity. Using a detailed mathematical model of Ca²⁺-force dynamics (Rice et al., 2008), we show that phase-loop morphology is influenced when only Ca²⁺ handling changes (Figures 5A,B). As temperature increases, the relaxation phase gradient approaches that of the steady-state relation, though Ca²⁺ amplitude remains influential. EC₅₀ is also an inappropriate indicator of myofilament sensitivity because of the undue influence of Ca²⁺ transient amplitude. Further, an equal change to TnC-Ca²⁺ binding rates (i.e., modifying association and dissociation rates change by the same factor) is not associated with a change of myofilament Ca²⁺ sensitivity but manifests as a change of phase-plane loop morphology (Figures 5C,D). While changes in Ca²⁺ sensitivity would also lead to a change in phase-plane loop morphology, it is uncertain which aspect of the loop should be considered as an indicator due to the conflation of many other factors. Despite their convenience, phase-plane loops are unsuitable for quantifying myofilament Ca²⁺ sensitivity.

FIGURE 5

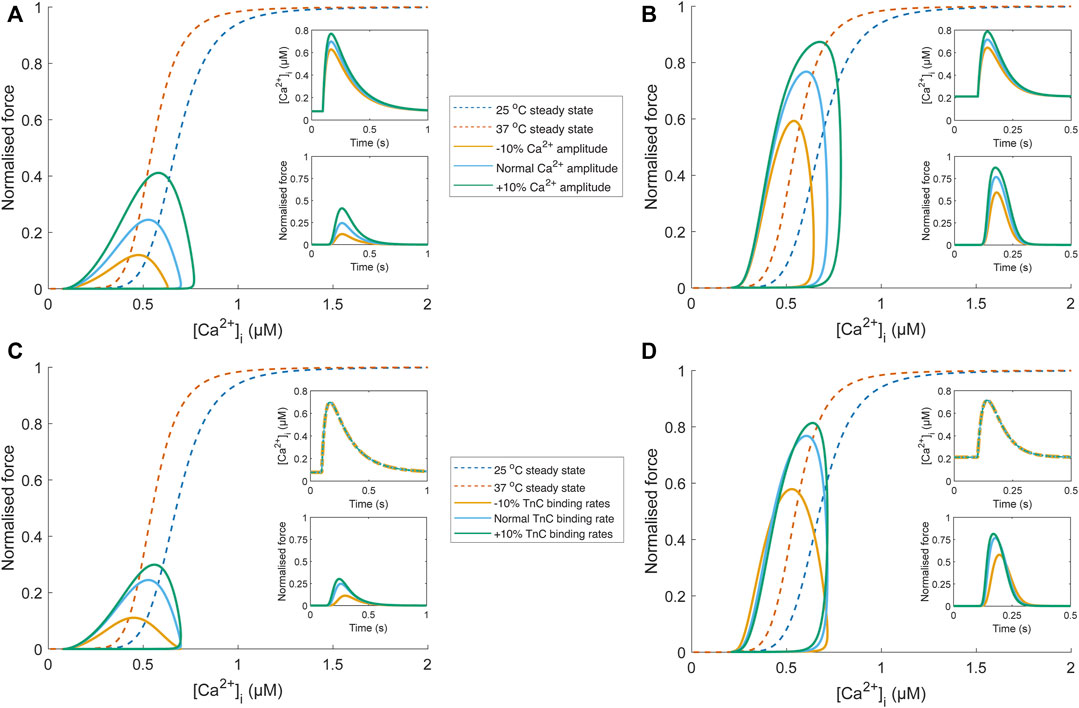
FIGURE 5. Comparison of phase-plane loop morphology under conditions where Ca²⁺ sensitivity is unchanged using a biophysical model (Rice et al., 2008). Temperature-dependent Ca²⁺ transients (25°C and 37°C) were obtained from Chung and Campbell (2013), scaled to align with the force-Ca²⁺ relation of the biophysical model (blue (25°C) and orange (37°C) dashed lines), and fit with a Ca²⁺ transient function, defined by two decaying exponentials with parameters τ₁, τ₂, Ca_dias, Ca_amp, and t_start (see Appendix of Rice et al. (2008)). The parameter set for the “normal” Ca²⁺ transient at each temperature was τ₁ = 34.9 ms, τ₂ = 183.3 ms, Ca_dias = 0.078 µM, Ca_amp = 0.70 µM, and t_start = 96.4 ms (25°C Ca²⁺ transient); τ₁ = 54.4 ms, τ₂ = 31.8 ms, Ca_dias = 0.21 µM, Ca_amp = 0.72 µM, and t_start = 100 ms (37°C Ca²⁺ transient). The influence of Ca²⁺ handling on phase-plane loop morphology is illustrated in panels (A) and (B), where the amplitude of the “normal” temperature-dependent Ca²⁺ transient (blue) was increased (green) and decreased (yellow) by 10% by changing the Ca_amp parameter. These Ca²⁺ transients were then provided as an input to the biophysical model (upper insets; (A) and (B). The resultant force output of the model (lower insets; (A) and (B) was plotted against the Ca²⁺ transient, and despite no change to myofilament sensitivity, modulation of Ca²⁺ transient amplitude results in different phase-plane loop morphologies (EC₅₀ and relaxation phase gradient) at 25°C (A) and 37°C (B). Concomitant changes (i.e., all changed by the same factor) of TnC-Ca²⁺ binding rates in the biophysical model (k_on, k_offHT, and k_offLT) also influence the phase-plane loop morphology at 25°C (C) and 37°C (D) when the same temperature-dependent Ca²⁺ transient is provided as input (upper insets; C and D).

In light of the foibles of force-Ca²⁺ phase-plane loops, Spurgeon et al. (1992) hypothesised that single cells undergoing unloaded shortening would be under equilibrium throughout the entire re-lengthening phase. This technique uses single-cell preparations, and unloaded shortening is plotted against Ca²⁺ (Graham et al., 2005; Zhao et al., 2016). As with the force-Ca²⁺ phase plane loops, EC₅₀ (Zhao et al., 2016), linear gradient (of the final linear region) (Graham et al., 2005), and qualitative assessment of the trajectory (Spurgeon et al., 1992) have been used to infer myofilament sensitivity. Zhao et al. (2016) removed the diastolic length and Ca²⁺ effects by translating the bottom-left data point of their signals to the origin (i.e., minimum sarcomere length and Fura-2 fluorescence set to zero). However, Ca²⁺ transient amplitude would still have too large an influence on EC₅₀ for this to be a consistently useful indicator. Of course, the length dependency of sensitivity (De Tombe et al., 2010) presents an additional challenge.

7 Model-based assessment

A modelling-based approach to infer myofilament Ca²⁺ sensitivity would involve fitting experimental data with a biophysical cardiac model and calculating the TnC-Ca²⁺ binding rates. Biophysical cardiac models represent Ca²⁺ and myofilament dynamics as biochemical reactions with mass action kinetics, where the kinetic rate of a reaction is proportional to the concentration of the reactants. Mass action kinetics are used to model the binding interactions between Ca²⁺, TnC, and myosin and the transition of tropomyosin and the troponin complex between different configurations or states. These states evolve dynamically and are described by a set of ordinary differential equations, which are solved to predict the behaviour of the system over time. Each state represents a fractional occupancy of TnC in a given configuration; the states sum to one because TnC is conserved in the system. The transition between states is governed by two kinetic rates: one in the forward direction and one in the reverse direction. The ratio between the forward and reverse rates determines the steady-state ratio between two states.

The complexity of a model depends on the number of states and the formulation of the kinetic rates. The ability to uniquely identify model parameters from experimental data depends on the model complexity and the information content of the data (Shames et al., 1996). For an inotropic response where the input Ca²⁺ transient is unchanged, the increase in force/pressure can be due to either an increase in Ca²⁺ affinity for TnC (sensitivity) or an increase in the rate of cross-bridge formation (responsiveness). A Ca²⁺-myofilament model that is considered identifiable would be able to distinguish between these two effects. For a given data set, the higher the complexity, the greater the number of parameters, and the less identifiable the model becomes.

One study has proposed a model-based framework explicitly for assessing myofilament Ca²⁺ sensitivity using a simple two-state, seven-parameter model (Op Den Buijs et al., 2008). This model is highly simplified compared to others in the literature (Rice et al., 2008) in an effort to improve identifiability. Here, we want to determine whether such a model is identifiable given simulated data sets consisting of Ca²⁺ transients as inputs and force/pressure responses as outputs. We first used an input Ca²⁺ transient (Figure 6A) to simulate a control pressure response (Figure 6B; blue line). Model parameters are from Table 2 of Op Den Buijs et al. (2008). We then simulated two sets of inotropic responses by increasing the parameter governing the Ca²⁺ affinity for TnC (k₁) by 25% or 50%, which elicited greater pressure responses (Figure 6B; orange and green open circles). These simulated responses were driven solely by increased Ca²⁺ sensitivity with no contribution from cross-bridge responsiveness. To test the identifiability of this simple model, we sought to find a new set of parameters that could fit these simulated responses where only the parameters governing cross-bridge responsiveness were allowed to be modified (α, β, and k_d); all other parameters were kept at control values. Using Matlab’s particle swarm optimizer, we found new parameter sets that could fit these sets of simulated responses to within 0.4% NRMSE (Figure 6B; orange and green lines). These parameter sets were identical to the control parameters except for increases in the values associated with the cross-bridge responsiveness parameters. We, therefore, have a model that can achieve similar fits to inotropic responses by increasing either the Ca²⁺ sensitivity or the cross-bridge responsiveness parameters. Hence, a simple model of Ca²⁺-myofilament dynamics is not identifiable for a data set that consists of Ca²⁺ inputs and force/pressure responses.

FIGURE 6

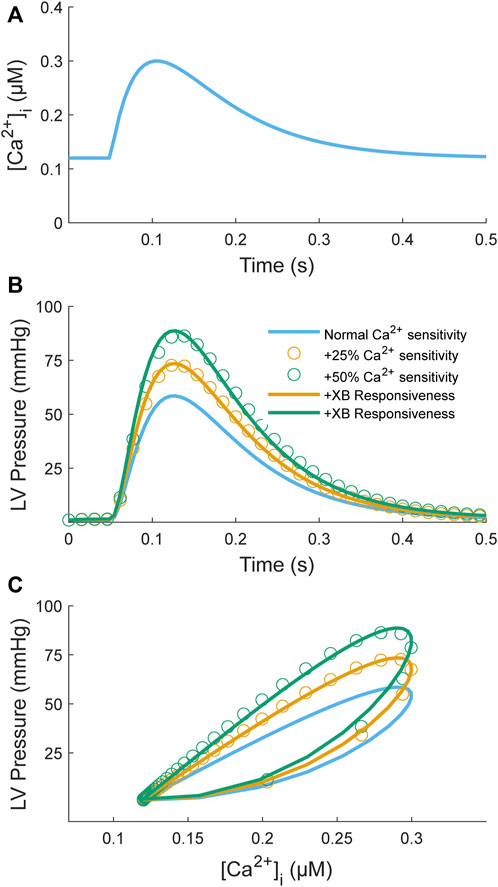
FIGURE 6. Model simulation of an increase in Ca²⁺ myofilament sensitivity to test identifiability. The myofilament model (Op Den Buijs et al., 2008) takes a Ca²⁺ transient (A) as input and produces an LV pressure transient (B) as output; a parametric plot of these two variables produces a phase-loop (C). The Ca²⁺ transient function is defined by two decaying exponentials with parameters τ₁ = 80 ms, τ₂ = 40 ms, Ca_dias = 0.12 µM, Ca_amp = 0.3 µM, and t_start = 50 ms (see Appendix of Rice et al. (2008)). The myofilament model was used to simulate two sets of positive inotropic responses corresponding to an increase in the Ca²⁺ binding affinity by 25% (orange open circles) or 50% (green open circles) relative to control (blue line). The model parameters for the control model were taken from Table 2 of Op Den Buijs et al. (2008): k₁ = 38 s⁻¹, k₃ = 361 s⁻¹, α = 0.29 nM⁻²s⁻¹, β = 658, k_d = 212 s⁻¹, and Ca_t = 117 nM. For generation of the simulation data, all parameters were kept the same except for k₁, which was increased by either 25% or 50%. The model was then fitted individually to these two data sets by constraining the Ca²⁺ parameters (k₁, k₃, Ca_t) to be unchanged from control and allowing only the cross-bridge parameters to be modified (α, β, k_d). The resulting fitted curves are illustrated as orange or green lines, respectively. The objective was to assess whether the inotropic response induced by increasing Ca²⁺ binding affinity can be replicated by only a change in cross-bridge kinetics. For both cases, parameter sets were found where the NRMSEs were below 0.4%. The parameter values were α = 0.82 nM⁻²s⁻¹, β = 1,505, k_d = 390 s⁻¹ (orange line) and α = 1.45 nM⁻²s⁻¹, β = 3,280, k_d = 703 s⁻¹ (green line) for a 25% and 50% increase in k₁, respectively.

8 TnC conformation-based fluorophores

When Ca²⁺ binds to TnC, there are concomitant conformational changes to the proteins associated with the ‘activation’ of the thin filament (Gordon et al., 2000). Several groups have leveraged this phenomenon using targeted fluorescence probes to infer myofilament activation status (Hannon et al., 1992; Davis et al., 2007; Badr et al., 2016).

One such probe is 2-(4′-iodacetamidoanilino)naphthalene-6-sulfonic acid (IAANS; λ_ex 328 nm, λ_em 445 nm), which has a fluorescent intensity sensitive to the hydrophobicity of its local environment (Hannon et al., 1992). Ca²⁺ binding to TnC induces a conformational change that exposes a hydrophobic patch located in the B helix of TnC (Dong et al., 1999). Hence, an increase in fluorescent intensity should reflect the activation state of the thin filament. IAANS is introduced to permeabilised preparations by first removing the native TnC and reconstituting TnC labelled with IAANS (Johnson et al., 1980; Hannon et al., 1992). IAANS binds to wild-type TnC at Cys-35 and Cys-84, which are on opposite sides of the low-affinity regulatory Ca²⁺ binding site (Putkey et al., 1997). Due to possible modifications of TnC function caused by these binding locations (Putkey et al., 1997; Davis et al., 2007), Davis et al. (2007) developed a novel fluorescent TnC, where Thr-53 was mutated to Cys-53, which enabled accurate measurements of the rate of Ca²⁺ dissociation from the regulatory domain of TnC. However, IAANS-labelled TnC is currently limited to permeabilised samples.

Another recently developed conformation-based fluorophore uses fluorescence (or Förster) resonance energy transfer (FRET). FRET uses energy transfer between pairs of chromophores to measure intermolecular distance (Clegg, 1995). In cardiac applications, FRET-based sensors leverage the conformational change of TnC that occurs upon the binding of Mg²⁺ or Ca²⁺ to infer the extent of activation (Sevrieva et al., 2014; Badr et al., 2016). As with IAANS, FRET-based sensors require the replacement of endogenous TnC with a modified TnC that includes a pair of fluorophores. Initially, endogenous TnC was replaced in permeabilised samples (Badr et al., 2016), but a recent study replaced endogenous TnC in intact twitching cardiac preparations using a transgenic mouse model (Vetter et al., 2020). In each case, the modified cardiac preparations exhibited a reduced Ca²⁺ sensitivity (Badr et al., 2016; Vetter et al., 2020). There must also be concerns that, in a disease model, post-translational modifications arising from disease progression may differentially affect the modified and endogenous TnC proteins.

Though Vetter et al. (2020) mentions loading preparations with Fura-2 for Ca²⁺ measurement, the excitation and emission wavelengths of the donor fluorophore in the FRET pair (Clover; λ_ex 505 nm, λ_em 515 nm) are incompatible with this Ca²⁺-sensitive fluorophore (Fura-2; λ_ex 360 nm/380 nm, λ_em 510 nm). Using an alternative Ca²⁺ sensitive dyes that has an emission peak at shorter wavelengths, such as Indo−1 (λ_ex 335 nm, λ_em 405 nm/485 nm), or developing a FRET pair with a donor fluorophore operating at a longer wavelength may enable the simultaneous measurement of Ca²⁺ and TnC activation in intact cardiac preparations.

9 Closing remarks

In vivo, the heart is exposed to ever-changing conditions and demands. However, despite the number of methods discussed, there remains none capable of assessing the time course of sensitivity changes following a sudden change of conditions, for example, under post-rest potentiation with a sudden change of stimulus frequency (Bers et al., 1993) or in eliciting the slow force response with a sudden change of muscle length (Dowrick et al., 2019). The time course of myofilament Ca²⁺ sensitivity adaption presents a potential dimension to consider the deleterious impacts of cardiomyopathies. The limitations with existing methods for assessing transient sensitivity are derived from a need for more information on the distribution of reaction states. Force and Ca²⁺ measurements alone require a steady state in two different reactions (i.e., Ca²⁺-TnC and actin-myosin binding) to provide an insight into the sensitivity of cardiac muscle, which is not possible from physiologically twitching samples (Spurgeon et al., 1992). For sensitivity inference through a hybrid experimentation-modelling approach to become a valid approach, additional simultaneous state information is required. FRET-based TnC biosensors (Badr et al., 2016; Vetter et al., 2020) represent a step in this direction by providing a measure of the activation state of the thin filament, but they have yet to be used in conjunction with a cytosolic Ca²⁺ sensor, and they may overlook the contributions of post-translational modifications to the replaced myofilament proteins. The field is currently not equipped to assess transient myofilament Ca²⁺ sensitivity, but we propose that such a method will involve the use of simultaneously measured cytosolic Ca²⁺ and TnC activation in actively-twitching cardiac muscle preparations to identifiably parameterise a biophysical model.

Author contributions

JD: Conceptualization, Formal Analysis, Visualization, Writing–original draft, Writing–review and editing. AT: Conceptualization, Supervision, Writing–review and editing, Writing–original draft. J-CH: Conceptualization, Supervision, Visualization, Writing–original draft, Writing–review and editing. KT: Conceptualization, Formal Analysis, Supervision, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The study was supported by the Health Research Council of New Zealand through Sir Charles Hercus Health Research Fellowship Grants (20/011 and 21/116; awarded to J-CH, KT, respectively) and an Explorer Grant (21/758, awarded to J-CH), the University of Auckland through a Doctoral Scholarship (awarded to JD), the Royal Society of New Zealand through a Marsden Project Grant (MFP-UOA2206, awarded to J-CH) and a James Cook Research Fellowship (awarded to AT), and the Heart Foundation of New Zealand through a Project Grant (1929, awarded to J-CH).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen D., Westerblad H. (1995). The effects of caffeine on intracellular calcium, force and the rate of relaxation of mouse skeletal muscle. J. Physiol. 487, 331–342. doi:10.1113/jphysiol.1995.sp020883

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen D. G., Kentish J. C. (1985). The cellular basis of the length-tension relation in cardiac muscle. J. Mol. Cell. Cardiol. 17, 821–840. doi:10.1016/s0022-2828(85)80097-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Backx P. H., Gao W.-D., Azan-Backx M. D., Marban E. (1995). The relationship between contractile force and intracellular [Ca²⁺] in intact rat cardiac trabeculae. J. Gen. Physiol. 105, 1–19. doi:10.1085/jgp.105.1.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Badr M. A., Pinto J. R., Davidson M. W., Chase P. B. (2016). Fluorescent protein-based Ca²⁺ sensor reveals global, divalent cation-dependent conformational changes in cardiac troponin C. PloS One 11, e0164222. doi:10.1371/journal.pone.0164222

PubMed Abstract | CrossRef Full Text | Google Scholar

Bers D., Bassani R., Bassani J., Baudet S., Hryshko L. (1993). Paradoxical twitch potentiation after rest in cardiac muscle: increased fractional release of SR calcium. J. Mol. Cell. Cardiol. 25, 1047–1057. doi:10.1006/jmcc.1993.1117

PubMed Abstract | CrossRef Full Text | Google Scholar

Bers D. M. (2002). Cardiac excitation-contraction coupling. Nature 415, 198–205. doi:10.1038/415198a

PubMed Abstract | CrossRef Full Text | Google Scholar

Bers D. M., Patton C. W., Nuccitelli R. (2010). A practical guide to the preparation of Ca2+ buffers. Cambridge, Massachusetts: Academic Press.

Google Scholar

Bielefeld D. R., Pace C. S., Boshell B. R. (1983). Altered sensitivity of chronic diabetic rat heart to calcium. Am. J. Physiol.-Endocrinol. Metab. 8. doi:10.1152/ajpendo.1983.245.6.E560

PubMed Abstract | CrossRef Full Text | Google Scholar

Blinks J. (1993). “Analysis of the effect of drugs on myofibrillar Ca²⁺ sensitivity in intact cardiac muscle,” in Modulation of cardiac calcium sensitivity: a new approach to increasing the strength of the heart. Editors J. A. Lee, and D. G. Allen (New York, NY: Oxford Academic), 242–282.

CrossRef Full Text | Google Scholar

Bowman J. D., Coldren W. H., Lindert S. (2019). Mechanism of cardiac troponin C calcium sensitivity modulation by small molecules illuminated by umbrella sampling simulations. J. Chem. Inf. Model. 59, 2964–2972. doi:10.1021/acs.jcim.9b00256

PubMed Abstract | CrossRef Full Text | Google Scholar

Bozler E. (1968). Control of the contractile mechanism of smooth and cardiac muscle. Am. J. Physiol. 215, 509–512. doi:10.1152/ajplegacy.1968.215.2.509

PubMed Abstract | CrossRef Full Text | Google Scholar

Brooks S. P. J. J., Storey K. B. (1992). Bound and determined: a computer program for making buffers of defined ion concentrations. Anal. Biochem. 201, 119–126. doi:10.1016/0003-2697(92)90183-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Brutseart D. L., Sys S. U. (1989). Relaxation and diastole of the heart. Physiol. Rev. 69, 1228–1315. doi:10.1152/physrev.1989.69.4.1228

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi D. H., Pham T., Loiselle D. S., Taberner A. J., Han J.-C., Tran K. (2020). The inverse relationship between cardiac muscle stress and cross-sectional area is preserved in Ba²⁺ contracture and in chemically-permeabilised Ca²⁺ contracture. Exp. Mech. 61, 107–117. doi:10.1007/s11340-020-00652-y

CrossRef Full Text | Google Scholar

Chung C. S., Campbell K. S. (2013). Temperature and transmural region influence functional measurements in unloaded left ventricular cardiomyocytes. Physiol. Rep. 1, e00158. doi:10.1002/phy2.158

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung J.-H., Biesiadecki B. J., Ziolo M. T., Davis J. P., Janssen P. M. (2016). Myofilament calcium sensitivity: role in regulation of in vivo cardiac contraction and relaxation. Front. Physiol. 7, 562. doi:10.3389/fphys.2016.00562

PubMed Abstract | CrossRef Full Text | Google Scholar

Clegg R. M. (1995). Fluorescence resonance energy transfer. Curr. Opin. Biotechnol. 6, 103–110. doi:10.1016/0958-1669(95)80016-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Davis J. P., Norman C., Kobayashi T., Solaro R. J., Swartz D. R., Tikunova S. B. (2007). Effects of thin and thick filament proteins on calcium binding and exchange with cardiac troponin C. Biophys. J. 92, 3195–3206. doi:10.1529/biophysj.106.095406

PubMed Abstract | CrossRef Full Text | Google Scholar

De Tombe P. P. (2003). Cardiac myofilaments: mechanics and regulation. J. Biomech. 36, 721–730. doi:10.1016/s0021-9290(02)00450-5

PubMed Abstract | CrossRef Full Text | Google Scholar

De Tombe P. P., Mateja R. D., Tachampa K., Mou Y. A., Farman G. P., Irving T. C. (2010). Myofilament length dependent activation. J. Mol. Cell. Cardiol. 48, 851–858. doi:10.1016/j.yjmcc.2009.12.017

PubMed Abstract | CrossRef Full Text | Google Scholar

De Tombe P. P., Ter Keurs H. E. (2016). Cardiac muscle mechanics: sarcomere length matters. J. Mol. Cell. Cardiol. 91, 148–150. doi:10.1016/j.yjmcc.2015.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong W.-J., Xing J., Villain M., Hellinger M., Robinson J. M., Chandra M., et al. (1999). Conformation of the regulatory domain of cardiac muscle troponin C in its complex with cardiac troponin I. J. Biol. Chem. 274, 31382–31390. doi:10.1074/jbc.274.44.31382

PubMed Abstract | CrossRef Full Text | Google Scholar

Dowrick J. M., Tran K., Loiselle D. S., Nielsen P. M. F., Taberner A. J., Han J.-C., et al. (2019). The slow force response to stretch: controversy and contradictions. Acta Physiol. 226, e13250. doi:10.1111/apha.13250

PubMed Abstract | CrossRef Full Text | Google Scholar

Dweck D., Reyes-Alfonso A., Potter J. D. (2005). Expanding the range of free calcium regulation in biological solutions. Anal. Biochem. 347, 303–315. doi:10.1016/j.ab.2005.09.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Endoh M., Blinks J. R. (1988). Actions of sympathomimetic amines on the Ca²⁺ transients and contractions of rabbit myocardium: reciprocal changes in myofibrillar responsiveness to Ca²⁺ mediated through alpha-and beta-adrenoceptors. Circ. Res. 62, 247–265. doi:10.1161/01.res.62.2.247

PubMed Abstract | CrossRef Full Text | Google Scholar

Fabiato A. (1985). Effects of ryanodine in skinned cardiac cells. Fed. Proc. 44, 2970–2976.

PubMed Abstract | Google Scholar

Fabiato A., Fabiato F. (1975). Contractions induced by a calcium-triggered release of calcium from the sarcoplasmic reticulum of single skinned cardiac cells. J. Physiol. 249, 469–495. doi:10.1113/jphysiol.1975.sp011026

PubMed Abstract | CrossRef Full Text | Google Scholar

Frey N., Luedde M., Katus H. A. (2012). Mechanisms of disease: hypertrophic cardiomyopathy. Nat. Rev. Cardiol. 9, 91–100. doi:10.1038/nrcardio.2011.159

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao W. D., Backx P. H., Azan-Backx M., Marban E., Hopkins J. (1994). Myofilament Ca²⁺ sensitivity in intact versus skinned rat ventricular muscle. Circ. Res. 74, 408–415. doi:10.1161/01.res.74.3.408

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao W. D., Perez N. G., Marban E. (1998). Calcium cycling and contractile activation in intact mouse cardiac muscle. J. Physiol. 507, 175–184. doi:10.1111/j.1469-7793.1998.175bu.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibbons W., Fozzard H. (1971). High potassium and low sodium contractures in sheep cardiac muscle. J. Gen. Physiol. 58, 483–510. doi:10.1085/jgp.58.5.483

PubMed Abstract | CrossRef Full Text | Google Scholar

Gomes A. V., Liang J., Potter J. D. (2005). Mutations in human cardiac troponin I that are associated with restrictive cardiomyopathy affect basal ATPase activity and the calcium sensitivity of force development. J. Biol. Chem. 280, 30909–30915. doi:10.1074/jbc.M500287200

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordon A. M., Homsher E., Regnier M. (2000). Regulation of contraction in striated muscle. Physiol. Rev. 80, 853–924. doi:10.1152/physrev.2000.80.2.853

PubMed Abstract | CrossRef Full Text | Google Scholar

Graham M., Bru-Mercier G., Hopkins P., Harrison S. (2005). Transient and sustained changes in myofilament sensitivity to Ca²⁺ contribute to the inotropic effects of sevoflurane in rat ventricle. Br. J. Anaesth. 94, 279–286. doi:10.1093/bja/aei053

PubMed Abstract | CrossRef Full Text | Google Scholar

Grynkiewicz G., Poenie M., Tsien R. Y. (1985). A new generation of Ca²⁺ indicators with greatly improved fluorescence properties. J. Biol. Chem. 260, 3440–3450. doi:10.1016/s0021-9258(19)83641-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Hajjar R. J., Grossman W., Gwathmey J. K. (1992). Responsiveness of the myofilaments to Ca²⁺ in human heart failure: implications for Ca²⁺ and force regulation. Basic Res. Cardiol. 87, 143–159. doi:10.1007/978-3-642-72474-9_12

PubMed Abstract | CrossRef Full Text | Google Scholar

Han J.-C., Taberner A. J., Nielsen P. M. F., Kirton R. S., Ward M.-L., Loiselle D. S. (2010). Energetics of stress production in isolated cardiac trabeculae from the rat. Am. J. Physiol.-Heart Circ. Physiol. 299, H1382–H1394. doi:10.1152/ajpheart.00454.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Hannon J. D., Martyn D. A., Gordon A. M. (1992). Effects of cycling and rigor crossbridges on the conformation of cardiac troponin C. Circ. Res. 71, 984–991. doi:10.1161/01.res.71.4.984

PubMed Abstract | CrossRef Full Text | Google Scholar

Harrison S. M., Bers D. M. (1989). Influence of temperature on the calcium sensitivity of the myofilaments of skinned ventricular muscle from the rabbit. J. Gen. Physiol. 93, 411–428. doi:10.1085/jgp.93.3.411

PubMed Abstract | CrossRef Full Text | Google Scholar

Hongo K., Kusakari Y., Konishi M., Kurihara S., Mochizuki S. (1998). Estimation of myofibrillar responsiveness to Ca²⁺ in isolated rat ventricular myocytes. Pflügers Arch. 436, 639–645. doi:10.1007/s004240050683

PubMed Abstract | CrossRef Full Text | Google Scholar

Irving T. C., Konhilas J., Perry D., Fischetti R., De Tombe P. P. (2000). Myofilament lattice spacing as a function of sarcomere length in isolated rat myocardium. Am. J. Physiol.-Heart Circ. Physiol. 279, H2568–H2573. doi:10.1152/ajpheart.2000.279.5.H2568

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson J. D., Collins J. H., Robertson S. P., Potter J. D. (1980). A fluorescent probe study of Ca²⁺ binding to the Ca²⁺-specific sites of cardiac troponin and troponin C. J. Biol. Chem. 255, 9635–9640. doi:10.1016/s0021-9258(18)43439-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones T. L., Kaur S., Kang N., Ruygrok P. N., Ward M. L. (2023). Impaired calcium handling mechanisms in atrial trabeculae of diabetic patients. Physiol. Rep. 11, e15599. doi:10.14814/phy2.15599

PubMed Abstract | CrossRef Full Text | Google Scholar

Katz A. M. (1967). Regulation of cardiac muscle contractility. J. Gen. Physiol. 50, 185–196. doi:10.1085/jgp.50.6.185

PubMed Abstract | CrossRef Full Text | Google Scholar

Katz A. M., Repke D. I. (1966). Control of myocardial contraction: the sensitivity of cardiac actomyosin to calcium ion. Science 152, 1242–1243. doi:10.1126/science.152.3726.1242

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaur S., Kong C. H., Cannell M. B., Ward M. L. (2016). Depotentiation of intact rat cardiac muscle unmasks an Epac-dependent increase in myofilament Ca²⁺ sensitivity. Clin. Exp. Pharmacol. Physiol. 43, 88–94. doi:10.1111/1440-1681.12504

PubMed Abstract | CrossRef Full Text | Google Scholar

Kentish J. C., Terkeurs H. E. D. J., Noble M. I. M., Ricciardi L., Schouten V. J. A. (1983). The relationships between force, [Ca²⁺] and sarcomere length in skinned trabeculae from rat ventricle. J. Physiol. 345, 24P.

Google Scholar

Kentish J. C., Wrzosek A. (1998). Changes in force and cytosolic Ca²⁺ concentration after length changes in isolated rat. J. Physiol. 506, 431–444. doi:10.1111/j.1469-7793.1998.431bw.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Knöll R. (2012). Myosin binding protein C: implications for signal-transduction. J. Muscle Res. Cell. Motil. 33, 31–42. doi:10.1007/s10974-011-9281-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Lim C. C., Helmes M. H., Sawyer D. B., Jain M., Liao R. (2001). High-throughput assessment of calcium sensitivity in skinned cardiac myocytes. Am. J. Physiol.-Heart Circ. Physiol. 281, H969–H974. doi:10.1152/ajpheart.2001.281.2.H969

PubMed Abstract | CrossRef Full Text | Google Scholar

Lüttgau H.-C., Niedergerke R. (1958). The antagonism between Ca and Na ions on the frog's heart. J. Physiol. 143, 486–505. doi:10.1113/jphysiol.1958.sp006073

PubMed Abstract | CrossRef Full Text | Google Scholar

Marban E., Kusuoka H. (1987). Maximal Ca²⁺-activated force and myofilament Ca²⁺ sensitivity in intact mammalian hearts Differential effects of inorganic phosphate and hydrogen ions. J. Gen. Physiol. 90, 609–623. doi:10.1085/jgp.90.5.609

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsubara I. (1980). X-ray diffraction studies of the heart. Annu. Rev. Biophys. Bioeng. 9, 81–105. doi:10.1146/annurev.bb.09.060180.000501

PubMed Abstract | CrossRef Full Text | Google Scholar

McDonald K., Field L., Parmacek M., Soonpaa M., Leiden J., Moss R. (1995). Length dependence of Ca²⁺ sensitivity of tension in mouse cardiac myocytes expressing skeletal troponin C. J. Physiol. 483, 131–139. doi:10.1113/jphysiol.1995.sp020573

PubMed Abstract | CrossRef Full Text | Google Scholar

McDonald K. S., Moss R. L. (1995). Osmotic compression of single cardiac myocytes eliminates the reduction in Ca²⁺ sensitivity of tension at short sarcomere length. Circ. Res. 77, 199–205. doi:10.1161/01.res.77.1.199

PubMed Abstract | CrossRef Full Text | Google Scholar

McIvor M. E., Orchard C. H., Lakatta E. (1988). Dissociation of changes in apparent myofibrillar Ca²⁺ sensitivity and twitch relaxation induced by adrenergic and cholinergic stimulation in isolated ferret cardiac muscle. J. Gen. Physiol. 92, 509–529. doi:10.1085/jgp.92.4.509

PubMed Abstract | CrossRef Full Text | Google Scholar

Milburn G., Moonschi F. H., White A. M., Thompson M., Birks E. J., Campbell K. S. (2022). Prior freezing has minimal impact on the contractile properties of permeabilized human myocardium. Biophys. J. 121, 109a. doi:10.1016/j.bpj.2021.11.2191

CrossRef Full Text | Google Scholar

Monasky M. M., Biesiadecki B. J., Janssen P. M. L. (2010). Increased phosphorylation of tropomyosin, troponin I, and myosin light chain-2 after stretch in rabbit ventricular myocardium under physiological conditions. J. Mol. Cell. Cardiol. 48, 1023–1028. doi:10.1016/j.yjmcc.2010.03.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Niedergerke R. (1956). The potassium chloride contracture of the heart and its modification by calcium. J. Physiol. 134, 584–599. doi:10.1113/jphysiol.1956.sp005667

PubMed Abstract | CrossRef Full Text | Google Scholar

Op Den Buijs J., Ligeti L., Ivanics T., Miklós Z., Van Der Vusse G., Van Riel N. (2008). Mathematical modelling of the calcium–left ventricular pressure relationship in the intact diabetic rat heart. Acta Physiol. 193, 205–217. doi:10.1111/j.1748-1716.2008.01831.x

CrossRef Full Text | Google Scholar

Pérez N. G., Hashimoto K., McCune S., Altschuld R. A., Marbán E. (1999). Origin of contractile dysfunction in heart failure: calcium cycling versus myofilaments. Circulation 99, 1077–1083. doi:10.1161/01.cir.99.8.1077

PubMed Abstract | CrossRef Full Text | Google Scholar

Peterson J. N., Berman M. R., Hunter W. C. (1988). Mechanical assay of role of calcium during isometric relaxation. Biophys. J. 53, 20814–23998.

Google Scholar

Putkey J. A., Liu W., Lin X., Ahmed S., Zhang M., Potter J. D., et al. (1997). Fluorescent probes attached to Cys 35 or Cys 84 in cardiac troponin C are differentially sensitive to Ca²⁺-dependent events in vitro and in situ. Biochemistry 36, 970–978. doi:10.1021/bi9617466

PubMed Abstract | CrossRef Full Text | Google Scholar

Rajan S., Ahmed R. P., Jagatheesan G., Petrashevskaya N., Boivin G. P., Urboniene D., et al. (2007). Dilated cardiomyopathy mutant tropomyosin mice develop cardiac dysfunction with significantly decreased fractional shortening and myofilament calcium sensitivity. Circ. Res. 101, 205–214. doi:10.1161/CIRCRESAHA.107.148379

PubMed Abstract | CrossRef Full Text | Google Scholar

Rice J. J., Wang F., Bers D. M., De Tombe P. P. (2008). Approximate model of cooperative activation and crossbridge cycling in cardiac muscle using ordinary differential equations. Biophys. J. 95, 2368–2390. doi:10.1529/biophysj.107.119487

PubMed Abstract | CrossRef Full Text | Google Scholar

Salhi H. E., Hassel N. C., Siddiqui J. K., Brundage E. A., Ziolo M. T., Janssen P. M. L., et al. (2016). Myofilament calcium sensitivity: mechanistic insight into TnI Ser-23/24 and Ser-150 phosphorylation integration. Front. Physiol. 7, 567. doi:10.3389/fphys.2016.00567

PubMed Abstract | CrossRef Full Text | Google Scholar

Sevrieva I., Knowles A. C., Kampourakis T., Sun Y.-B. (2014). Regulatory domain of troponin moves dynamically during activation of cardiac muscle. J. Mol. Cell. Cardiol. 75, 181–187. doi:10.1016/j.yjmcc.2014.07.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Shames D. M., Baker A. J., Weiner M. W., Camacho S. A. (1996). Ca(2+)-force relationship of frog skeletal muscle: a dynamic model for parameter estimation. Am. J. Physiol.-Cell. Physiol. 271, C2062–C2071. doi:10.1152/ajpcell.1996.271.6.C2062

PubMed Abstract | CrossRef Full Text | Google Scholar

Shimomura O. (1995). A short story of aequorin. Biol. Bull. 189, 1–5. doi:10.2307/1542194

PubMed Abstract | CrossRef Full Text | Google Scholar

Siri F. M., Krueger J., Nordin C., Ming Z., Aronson R. S. (1991). Depressed intracellular calcium transients and contraction in myocytes from hypertrophied and failing Guinea pig hearts. Am. J. Physiol.-Heart Circ. Physiol. 261, H514–H530. doi:10.1152/ajpheart.1991.261.2.H514

PubMed Abstract | CrossRef Full Text | Google Scholar

Spurgeon H. A., DuBell W. H., Stern M. D., Sollott S. J., Ziman B. D., Silverman H. S., et al. (1992). Cytosolic calcium and myofilaments in single rat cardiac myocytes achieve a dynamic equilibrium during twitch relaxation. J. Physiol. 447, 83–102. doi:10.1113/jphysiol.1992.sp018992

PubMed Abstract | CrossRef Full Text | Google Scholar

Tobacman L. S. (2021). Troponin revealed: uncovering the structure of the thin filament on-off switch in striated muscle. Biophys. J. 120, 1–9. doi:10.1016/j.bpj.2020.11.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Van der Velden J., De Jong J. W., Owen V., Burton P., Stienen G. (2000). Effect of protein kinase A on calcium sensitivity of force and its sarcomere length dependence in human cardiomyocytes. Cardiovasc. Res. 46, 487–495. doi:10.1016/s0008-6363(00)00050-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Varian K. D., Biesiadecki B. J., Ziolo M. T., Davis J. P., Janssen P. M. (2012). Staurosporine inhibits frequency-dependent myofilament desensitization in intact rabbit cardiac trabeculae. Biochem. Res. Int. 2012, 290971. doi:10.1155/2012/290971

PubMed Abstract | CrossRef Full Text | Google Scholar

Varian K. D., Janssen P. M. L. (2007). Frequency-dependent acceleration of relaxation involves decreased myofilament calcium sensitivity. Am. J. Physiol.-Heart Circ. Physiol. 292, H2212–H2219. doi:10.1152/ajpheart.00778.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Varian K. D., Raman S., Janssen P. M. (2006). Measurement of myofilament calcium sensitivity at physiological temperature in intact cardiac trabeculae. Am. J. Physiol.-Heart Circ. Physiol. 290, H2092–H2097. doi:10.1152/ajpheart.01241.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Varian K. D., Xu Y., Torres C. A. A., Monasky M. M., Janssen P. M. L. (2009). A random cycle length approach for assessment of myocardial contraction in isolated rabbit myocardium. Am. J. Physiol.-Heart Circ. Physiol. 297, H1940–H1948. doi:10.1152/ajpheart.01289.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Vetter A. D., Martin A. A., Thompson B. R., Thomas D. D., Metzger J. M. (2020). Sarcomere integrated biosensor detects myofilament-activating ligands in real time during twitch contractions in live cardiac muscle. J. Mol. Cell. Cardiol. 147, 49–61. doi:10.1016/j.yjmcc.2020.07.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Ward M.-L., Crossman D. J. (2014). Mechanisms underlying the impaired contractility of diabetic cardiomyopathy. World. J. Cardiol. 6, 577–584. doi:10.4330/wjc.v6.i7.577

PubMed Abstract | CrossRef Full Text | Google Scholar

Ward M.-L., Crossman D. J., Loiselle D. S., Cannell M. B. (2010). Non-steady-state calcium handling in failing hearts from the spontaneously hypertensive rat. Pflügers Arch. 460, 991–1001. doi:10.1007/s00424-010-0876-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Wendt I., Stephenson D. (1983). Effects of caffeine on Ca-activated force production in skinned cardiac and skeletal muscle fibres of the rat. Pflügers Arch. 398, 210–216. doi:10.1007/BF00657153

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolff M. R., Buck S. H., Stoker S. W., Greaser M. L., Mentzer R. M. (1996). Myofibrillar calcium sensitivity of isometric tension is increased in human dilated cardiomyopathies: role of altered beta-adrenergically mediated protein phosphorylation. J. Clin. Invest. 98, 167–176. doi:10.1172/JCI118762

PubMed Abstract | CrossRef Full Text | Google Scholar

Yue D. T. (1987). Intracellular [Ca²⁺] related to rate of force development in twitch contraction of heart. Am. J. Physiol.-Heart Circ. Physiol. 252, H760–H770. doi:10.1152/ajpheart.1987.252.4.H760

PubMed Abstract | CrossRef Full Text | Google Scholar

Yue D. T., Marban E., Wier W. G. (1986). Relationship between force and intracellular [Ca²⁺] in tetanized mammalian heart muscle. J. Gen. Physiol. 87, 223–242. doi:10.1085/jgp.87.2.223

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao Z. H., Jin C. L., Jang J. H., Wu Y. N., Kim S. J., Jin H. H., et al. (2016). Assessment of myofilament Ca²⁺ sensitivity underlying cardiac excitation-contraction coupling. J. Vis. Exp. 114, e54057. doi:10.3791/54057

CrossRef Full Text | Google Scholar