Bound Ca2+ moves faster and farther from single open channels than free Ca2+

A concept of Ca²⁺ nanodomains established in the cytoplasm after opening single-calcium channels helps mechanistically understand the physiological mechanisms of Ca²⁺ signaling. It predicts standing gradients of cytoplasmic free Ca²⁺ around single channels in the plasma membrane. The fate of bound Ca²⁺ attracted much less attention. This study aimed to examine the profiles of Ca²⁺ bound to low-mobility buffers such as bulky Ca²⁺-binding proteins. The solution of non-linear PDEs for an immobile buffer predicts fast decay of free [Ca²⁺] from the channel lumen and the traveling wave for bound Ca²⁺. For low-mobility buffers like calmodulin, the calculated profiles of free and bound Ca²⁺ are similar. Theoretical predictions are tested by imaging 1D profiles of Ca²⁺ bound to low-mobility fluo-4-dextran. The traveling waves of bound Ca²⁺ are observed that develop during the opening of single channels. The findings tempt to propose that Ca²⁺ signaling may not be solely related by the absolute free [Ca²⁺] at the sensor location, which is extremely localized, but determined by the time when a wave of bound Ca²⁺ reaches a threshold needed for sensor activation.

1 Introduction

Many fundamental physiological Ca²⁺-dependent processes are initiated by local [Ca²⁺] increases generated in the vicinity of the Ca²⁺ entry into the cell and dubbed as Ca²⁺ nanodomains (Eisner et al., 2023; Augustine et al., 2003; Eggermann et al., 2011). The processes attracted much attention from researchers, but their theoretical description is yet far from complete. The first important result was obtained by Neher (1986), who considered steady-state Ca²⁺ distributions in excess buffer approximation, EBA.

The EBA formalism has been developed to explain the different effects of the Ca²⁺ buffers BAPTA and EGTA in modulating the activity of nearby Ca²⁺-dependent K⁺-channels (blocking vs non-blocking actions, respectively). For channel activation, Ca²⁺ entering into the cytoplasm must reach the neighboring K⁺ channel. The distance between Ca²⁺ and K⁺ channels then should be smaller than the width of free [Ca²⁺] transient. BAPTA and EGTA produce Ca²⁺ nanodomains with different widths because EGTA captures Ca²⁺ apparently slower than BAPTA. The on-rate constant for Ca²⁺ binding by EGTA is assumed to be 100-fold lower than that for BAPTA and corresponds to a 10-fold bigger intrinsic space constant r_o (Table 1). The smaller width of Ca²⁺ nanodomains in BAPTA explains why this buffer abolishes the coupling between Ca²⁺ and Ca²⁺-dependent K-channels, whereas EGTA has virtually no influence.

TABLE 1

TABLE 1. Basic definitions and model parameters.

The seemingly slow calcium binding by EGTA has been previously explained (Mironova and Mironov, 2008; Mironov, 2019). Briefly, by dissolution, EGTA forms five species at different proportions in the absence of Ca²⁺. A doubly protonated EGTA (H₂EGTA^2-) is dominant at physiological pH. It cannot bind Ca²⁺ efficiently because K_d = 4 M (Smith et al., 1984) indicates extremely low affinity to Ca²⁺. Another form, HEGTA^3-, has K_d = 5 µM and thus has high affinity, but in 10 mM EGTA at normal pH, [HEGTA^3-] = 0.1 mM, i.e., 100 times smaller than nominal EGTA. A calcium ion is captured by the first buffer molecule it meets in the cytoplasm, with the on-rate close to the diffusion limit, k_on ≈ 10⁸ M^-1s^-1. Because the rate of Ca²⁺ binding is k_on [Buffer], an apparent 100-fold difference in k_on values for BAPTA and EGTA simply reflects the ratio [BAPTA]/[HEGTA^3-] = 100. EGTA has the important property of slowly accommodating Ca²⁺ after exchanging it for protons. The equilibrium between different EGTA forms is established slowly. This explains why EGTA minimally disturbs fast local calcium transients but, at the same time, is effective in preventing calcium overload, e.g., in whole-cell recordings. On a longer time scale, EGTA virtually eliminates deleterious long-lasting increases in cytoplasmic calcium. The same considerations may be applied to another “slow” Ca²⁺ buffer, parvalbumin, which also has to free the binding sites from Mg before capturing Ca²⁺.

Ca²⁺ unbinding from the buffer is neglected in EBA because the reverse reaction is very slow. Therefore, Ca²⁺ nanodomains established during channel opening quickly disappear after channel closure. The measurements of local Ca²⁺ increases generated by single Ca²⁺ channels in the oocytes, dubbed as sparklets (Demuro and Parker, 2006), underline this notion. Despite the undisputed importance in presenting Ca²⁺ profiles around single channels, the EBA model is oversimplified.

Another limiting concept in describing Ca²⁺ behavior in the cytoplasm is rapid buffer approximation (RBA). It presumes fast equilibration between Ca²⁺ and the buffer (Neher and Augustine, 1992; Wagner and Keizer, 1994; Pape et al., 1995; Naraghi and Neher, 1997; Smith et al., 2001; Mironova and Mironov, 2008; Mironov, 2019). The corresponding equations have been known for decades (Crank, 1979) and have been successfully applied to describing global Ca²⁺ transients in bulk cytoplasm. The basic parameters in RBA are the cytoplasmic Ca²⁺-buffering capacity and apparent Ca²⁺ diffusion coefficient. The former depends on the free [Ca²⁺] level, buffer concentration, and affinity to Ca, and the latter also includes the buffer diffusion coefficient (Neher and Augustine, 1992; Wagner and Keizer, 1994; Pape et al., 1995; Naraghi and Neher, 1997; Smith et al., 2001). The current status of RBA and EBA, with numerous examples of applications in physiology, was recently surveyed in a comprehensive review (Eisner et al., 2023).

In EBA, the diffusion of the buffer is completely neglected (the steady-state Ca²⁺ gradients are dependent only on D_Ca through r_o). In RBA, the buffer diffusion coefficient D_b is treated implicitly and included in the apparent Ca²⁺ diffusion coefficient. It is still imperative to better understand the role of buffer motility because the imaging of Ca²⁺ with common organic indicator dyes may not correctly deliver actual changes in cytoplasmic [Ca²⁺] needed to understand fundamental physiological events. Ca²⁺ signaling is mostly examined using synthetic buffers and indicators (EGTA, BAPTA, fluo-X, etc.). They all have diffusion coefficients compatible with that of Ca²⁺, justifying the application of EBA. In physiology, putative Ca²⁺-binding proteins have order of magnitude smaller diffusion coefficients (Sanabria et al., 2008; Schwaller, 2010; Matthews and Dietrich, 2015). In order to reproduce the in vivo situations, it is more consistent to employ genetically encoded sensors that are also bulky proteins (Mironov et al., 2009; Lin and Schnitzer, 2016). The changes in their fluorescence can be expected to depict physiologically relevant cytoplasmic Ca²⁺ signals better. However, care should be taken in choosing a probe with proper fast reaction time as the changes in fluorescence may reflect conformational kinetics to achieve the fluorescent state of the protein and may not reflect the “true” kinetics of local Ca²⁺ increase (Lock et al., 2015).

The actual free Ca²⁺ levels around a single channel are of extreme importance but not yet directly measured. The problem is that when free [Ca²⁺] is smaller than the concentration of cytoplasmic buffers and/or their affinity, the assumptions of both EBA and RBA are correct. However, the theoretical estimates (Mironov, 1990; Mironov, 2019) and experiments (Tay et al., 2012; Tadross et al., 2013) indicate too high calcium levels at the channel lumen. The local [Ca²⁺] may be around 1 mM, which obviously exceeds the buffer concentration (0.2 mM is a typical value). The considerations are substantiated by a current look at synaptic transmission. This process is triggered by Ca²⁺ binding to the synaptotagmin sensor (Syt). The Ca²⁺–Syt dissociation constant is in the range of K_Syt = 40–100 μM, as compiled from different studies (Bornschein and Schmidt, 2019). Half-activation of the sensor occurs at [Ca²⁺] = K_Syt, and 90% activation is required to make synaptic transmission reliable. This is achieved at 10 K_Syt, from which one can deduce that the local [Ca²⁺] at the secretion site should be in the range of 0.4–1 mM. This is within the aforementioned theoretical and experimental estimates.

All these considerations prompt examination of the time and concentration dependence of Ca²⁺ nanodomains in the vicinity of single channels, with a closer look at the effects of buffer diffusion. In the following section, I focus on slow diffusion of buffers, keeping in mind that putative Ca²⁺-binding proteins (and Ca²⁺-sensors) diffuse much slower than Ca²⁺. The analysis starts from the time-dependent RD problem for the immobile buffer, which has an analytical solution. It predicts that Ca²⁺ gradients build up relatively fast around a single channel, and the profile of the Ca²⁺-bound buffer corresponds to the traveling wave. Within a few milliseconds, such waves can propagate over 1 μm, a typical dimension for central synapses. The case is then extended to introduce the slow motility of the buffer (D_b << D_Ca) to reproduce the situation in vivo. For low-mobility buffers, the patterns of bound Ca²⁺ are found to be similar to those of immobile buffers. To test theoretical predictions, the 1D-distributions of Ca²⁺ in thin pipettes were examined. Ca²⁺ influx was induced by a single α-synuclein channel in inside-out patches from hippocampal neurons. Incoming Ca²⁺ was captured by a low-mobility buffer (fluo-4-dextran). 1D distributions of bound Ca²⁺ agreed well with theoretical predictions. The main conclusion of the study is that although free Ca²⁺ profiles are well-localized to the lumen of single Ca²⁺ channels, the bound species may spread out, delivering message(s) to activate distant targets.

2 Methods

2.1 Ethical approval

All mouse experiments were approved and performed in accordance with the guidelines and regulations by the local authority, the Lower Saxony State Office for Consumer Protection and Food Safety (Niedersächsisches Landesamt für Verbraucherschutz und Lebensmittelsicherheit), and executed at the Georg August University, Göttingen. Briefly, all animals had free access to the shelter and to water and food, and every effort was made to minimize animal suffering and the number of animals used. For removal of tissues, the animals were deeply anesthetized by CO₂ inhalation at a fixed concentration and rapidly killed by cervical dislocation.

2.2 Cell preparations and solutions

Cultured hippocampal neurons were obtained from neonatal mice (NMRI, P3–P6), as described previously (Mironov, 2015). During the experiments, the coverslips with cells were mounted in a recording chamber that was continuously superfused at 34°C.

2.3 Patch-clamp and imaging

The electrophysiology and imaging in cultured hippocampal neurons are performed as described previously (Mironov, 2015; Mironov, 2019). Bath and pipette solutions contain 30 mM Tris buffer (pH 7.4) and 154 mM NaCl or 88 mM CaCl₂. The solutions have an osmolality of 305–315 mosmol/l. Fluo-4 and Fluo-4 dextran (M.W. 30 kDa) were obtained from Thermo Fisher (Osterode, Germany). Both dyes were used at a concentration of 0.3 mM. Fluo-4 dextran was dissolved at 1% concentration. Dextran (10 kDa) has a diffusion coefficient of D = 15 μm²/s (Shuai and Parker, 2005), which is close to the measured value for calmodulin, D = 10 μm²/s (Sanabria et al., 2008). Given D_Ca = 200 μm²/s, both values are close to the relative diffusion coefficients d = 0.03 (Mironova and Mironov, 2008) used in this study (Table 1).

Patch electrodes were pulled from borosilicate glass (1.4 mm o. d., WPI, Berlin, Germany). The pipettes have a small bore (<0.1 µm) and a long shank (≈5 mm), with a resistance of ≈40 MOhm. Coverslips with the hippocampal neurons are placed on the microscope stage. The cells are patched, inside-out patches are excised, and synuclein (α-Syn) channels are forced to incorporate into the membrane (Mironov, 2015). The horizontally oriented pipette is then lowered to the bottom to enter the TIRF illumination layer (≈200 nm above the coverslip).

For imaging, an upright microscope (Axioscope 2, Zeiss) is used with a ×63 objective lens (N. A. 1.4). The fluorescence is excited by 488 nm light from an SLM Diodenlaser (Soliton, Gilching, Germany). The laser beam is delivered from below through a prism (TIRF Labs, Inc. Cary NC) at an angle appropriate to evoke TIRF. The emission (525 nm) passes through a dichroic mirror filter at 535 nm. The images are captured by using a cooled CCD camera, iXON Ultra 888 EMCCD (ANDOR, Oxford Instruments), operated under ANDOR software. The line-scan mode (512 × 2 pixels at 12-bit resolution) has an acquisition time of 0.1 ms. Because the fluorescence of fluo-4 increases >10-fold after Ca²⁺ binding, this minimizes out-of-focus effects that appear in imaging of living cells. The cell-free experimental configuration also provides good control of the solutions bathing the patch.

Single-channel events were recorded in 12 patches obtained from different neurons with the pipettes filled with Fluo-4-dextran solution. Eight patches with synuclein channels were recorded with Fluo-4 in the pipette. The episodes of channel opening were collected at different holding potentials. They were analyzed offline to examine the dependence of bound Ca²⁺ distributions upon single-channel Ca²⁺ flux and its duration.

2.4 Basics of the reaction–diffusion equation

To start with, consider Ca²⁺ diffusion from a single channel in the presence of a single buffer as a system of two partial differential equations (PDE)

$\begin{array}{c}\partial \left[{\text{Ca}}^{2+}\right]/\partial t=D_{Ca}\Delta \left[{\text{Ca}}^{2+}\right]–k_{on}\left[{\text{Ca}}^{2+}\right]\left[F\right]+k_{off}\left[B\right],\\ \partial \left[F\right]/\partial t=D_b\Delta \left[F\right]–kon\left[{\text{Ca}}^{2+}\right]\left[F\right]+k_{off}\left[B\right].\end{array}(1)$

Here, Δ stands for the Laplacian; [Ca²⁺], [F], and [B] are the concentrations of calcium and buffer in free and Ca²⁺-bound forms, respectively; k_on and k_off are the rate constants of calcium-binding to and dissociation from the buffer. The ratio k_off/k_on = K_d is the dissociation constant of the buffer and measures its affinity to calcium. D_Ca and D_b are the diffusion coefficients for calcium and buffer, respectively. For simplicity, the equations are set for a single buffer, but generalization for multiple buffers is straightforward, as discussed below. The definitions and typical parameters are summarized in Table 1.

In the following derivations, all concentrations are normalized by dividing by the total buffer concentration B_o. Equation 1 is then written as

$c_t=\Delta c–cf+\mathrm{\gamma }\left(1-f\right),(\mathrm{2a})$

$f_t=d\Delta f-cf+\gamma \left(1–f\right),(\mathrm{2b})$

where the subscript denotes the time derivative, c = [Ca²⁺]/B_o and f = [F]/B_o are the normalized concentrations of free calcium and free buffer, respectively; d = D_b/D_Ca is the relative diffusion coefficient, and γ = k_off/k_onB_o = K_d/B_o = 0.002 is the normalized dissociation constant. The last term on the right-hand side in Eq. 2a describes Ca²⁺ dissociation, and b = 1–f is the normalized concentration of the Ca²⁺-bound buffer. The dimensionless times and distances are defined as τ = 1/k_onB_o = 50 μs and r_o = √D_Ca/B_ok_on = 0.1 μm, respectively. These intrinsic constants of Ca²⁺-buffering (Table 1) are calculated for diffusion-limited k_on = 10⁸ M^-1s^-1 and B_o = 0.2 mM, typical values for cytoplasmic calcium-binding proteins, and D_Ca = 200 μm²/s.

The boundary condition is specified by assuming the constant flux through the open channel

$c_r=-i/2\pi z{R}^2{D}_{Ca}F,(3)$

where i is a single-channel current, F is the Faraday constant, and R is the exit radius (R = 0.5 nm, (Malasics et al., 2009)). For radial diffusion, it is useful to transform c = u/r, which replaces the Laplacian Δ = 1/r²d (r²dc/dr) with the second derivative Δ = d²u/dr². The boundary condition transforms into

$R{u}_r–u\approx -u=-AR,(4)$

where A is the Ca²⁺ concentration at the channel lumen. Because R is very small, the first term can be neglected. For i = 0.1 pA, the constant is A = 0.7 mM.

The linearized version (EBA) assumes a fast irreversible binding of Ca²⁺ to buffer. This sets f = 1 and γ = 0 in Eq. 2a and leads to a simple ordinary differential equation (ODE) of the second order

$\Delta c=c,(5)$

which has an exponential–hyperbolic solution

$c=\left(A/r\right)\exp \left(-r/r_o\right),(6)$

The solution of the transcendental Equation 6 is given by the Lambert function defined as W = exp (-W) (Olver et al., 2011). The reference point may be r = 0.57 r_o for c = A. In the 1D case, the 1/r factor is absent, and r = 0.37r_o.

2.5 Numerical solution of reaction–diffusion equations

The PDEs derived in the text below are solved with Du Fort–Frankel numerical integration (Du Fort and Frankel, 1953). Its performance is better than that of the Crank–Nicolson algorithm and unconditionally stable. For discretization of diffusion equation c_t = Dc_xx, the concentrations at times t_n = nΔt and space points x_m = mΔx are needed. The following parameters are calculated

$d_1=\left(1-\alpha \right)/\left(1+\alpha \right),d_2=\alpha /\left(1+\alpha \right),\text{with\hspace{0.17em}}\alpha =2D\Delta t/\Delta x^2,(7)$

and the reaction–diffusion (RD) equation is then solved explicitly at each mesh point as

$c_m^{n+1}=d_1{c}_m^{n-1}+d_2\left(c_{m+1}^n+c_{m-1}^n\right)-\Delta t{c}_m^n{f}_m^n.(8)$

The last term is the reaction term (-cf) specified by respective terms in the PDEs derived below.

3 Results

3.1 Immobile buffer

Ca²⁺ diffusion in the presence of a single immobile buffer is described by the PDE system as

$c_t=\Delta c–cf,(\mathrm{9a})$

$f_t=-cf.(\mathrm{9b})$

For the initial concentration of free buffer f_o = 1, integration of the second equation gives

$f=f_o{e}^{-y},(10)$

where a new variable,

$y={\displaystyle \int }cdt,(11)$

the integral of Ca²⁺ concentration, is introduced. Integration of Eq. 9a then gives a non-linear PDE

$y_t=\Delta y-\mathit{1}+e^{-y},(12)$

with the boundary condition y_R= tc_R. Equation 12 has no general solution even in the 1D case except a self-similar particular solution in moving coordinates z = ax–bt (Polyanin and Zaitsev, 2004).

Eq. 12 (Smith et al., 2001) was solved numerically using the Du Fort–Frankel algorithm described in above. Figure 1 shows the calculated radial (3D) and 1D profiles for free Ca²⁺ and Ca²⁺-bound buffers for different Ca²⁺ fluxes. They are coded as relative Ca²⁺ levels at channel lumen A = [Ca²⁺]/B_o. It is seen that [Ca²⁺] decays rapidly from the entry site. In the 3D case, [Ca²⁺] is very big due to the hyperbolic factor 1/r, intrinsic in radial symmetry, Eq. 6 (Mironov, 2019). Large free Ca²⁺ values strongly violate the EBA assumption that [Ca²⁺]<<B_o. The spatial profiles of the Ca²⁺-bound buffer expand with time as traveling waves. They appear already for a very small relative Ca²⁺ flux A = 0.01 and widen with increasing A (Figure 1). The increment between subsequent curves decreases with time, indicating a decrease in wave speed.

FIGURE 1

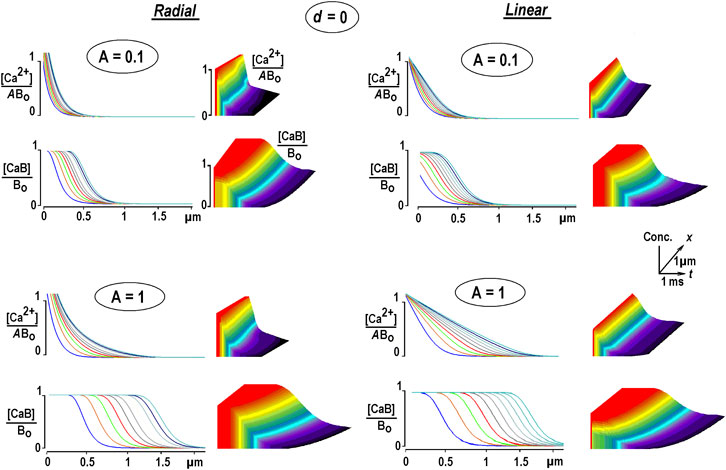
FIGURE 1. Changes in free and bound Ca²⁺ in the presence of an immobile buffer. The solutions are obtained from Eq. 12. Differently colored curves are 0.25 ms apart. Time and space scales are the same in all panels. The concentrations of free and bound Ca²⁺ [CaB] are normalized to the total buffer concentration, B_o. To compare the waveforms of transients of free [Ca²⁺], it is additionally divided by the concentration of Ca²⁺ at the channel lumen (A). Radial Ca²⁺ increases near the channel are cut from above because they are too big due to the hyperbolical factor 1/r that appears in radial diffusion, Eq. 6. At constant Ca²⁺ influx, the Ca-bound buffer spreads out, which mirrors a depletion of the free buffer. The waves have a tahn-like form, a hallmark of many RD systems (Polyanin and Zaitsev, 2004). The increment between the curves decreases with time, indicating a decrease in instantaneous velocity. Each panel is complemented with 3D plots on the right, with the axes defining time, space, and relative concentrations, respectively (the scaling is indicated in the inset in the middle). The concentrations in the panels are plotted on the z-axis, and increases are represented by warmer colors, with time running from left to right along the x-axis.

A simple analytical argument helps understand the appearance of traveling waves. Free Ca²⁺ approach fast exponential–hyperbolic steady-state solution given by Eq. 4 in EBA. Under such conditions, the bound Ca²⁺ is obtained from Eq. 9b as

$\left[{\text{Ca}}^{2+}-bound\right]=b=\mathit{1}-f=1-\mathit{exp}\left[-At/r_o^{.}\mathit{exp}\left(-r/r_o\right)\right].(13)$

The expression describes the traveling wave spreading out according to the time constant proportional to the Ca²⁺ level at channel lumen, A.

Another interesting feature emerges when we identify, for a moment, the bound buffer with an immobile Ca²⁺-sensor (McMahon and Jackson, 2018). The temporal and spatial patterns of sensor activation should then be given by the profiles for the Ca²⁺-bound buffer, as shown in Figure 1. From this, one may deduce that a crucial factor in the Ca²⁺-mediated functional response may be the time when a sensor at a given location is saturated with Ca²⁺. A suggestion with such a role of bound Ca²⁺ underlines a statement that “messages diffuse faster than messengers” (Pando et al., 2006) coined by simulating the diffusion of particles in the presence of traps as applied for GFP-tagged glucocorticoid receptors in the nuclei of mouse adenocarcinoma cells. The mathematical formulation of the problem resembles that considered in this study.

Both the 3D and 1D cases of Ca²⁺ diffusion are physiologically relevant because they present Ca²⁺ diffusion defined by specific geometric constraints. For radial diffusion, Ca²⁺ spreads out in a semi-infinite cytoplasm free from intracellular organelles of macromolecular aggregates that may hinder diffusion. 1D diffusion may imitate Ca²⁺ diffusion through a tortuous pathway that extends from the point of Ca²⁺ entry to the sensor. A well-known 1D example is the Ca²⁺ waves in neuronal dendrites (Augustine et al., 2003; Mironov, 2008). Of note, in linear models, the 3D and 1D solutions are related: the former is obtained from the latter by simple division of the solution by the distance from the channel lumen. The application of such transformation is shown in Supplementary Figure SB.

A general conclusion from this section is that bound Ca²⁺ distribution in the presence of an immobile buffer is dynamic rather than static. A simple time-dependent model shows inherent contradictions with the linear EBA model: (i) free buffer is not in excess even for small Ca²⁺ fluxes (i < 0.1 pA), (ii) not constant, and (iii) shows the time- and space-dependent changes in bound Ca²⁺ that mirror buffer depletion. The conclusions are also valid for low-mobility buffers, as examined in the following section.

3.2 Slowly moving buffer

The results in the previous section are extended below to the case of a slowly moving buffer. Eq. (2) is now given as

$\begin{array}{l}{c}_t=\Delta c–cf,\\ f_t=d^{.}\Delta f-cf.\end{array}(14)$

The system was solved in Supplementary Appendix SA1. The calculations presented in Figure 2 were made for calmodulin, the relative diffusion coefficient of which is set to d = 0.03. This is compatible with a relative diffusion coefficient d = 0.07 for an endogenous “immobile” buffer in chromaffin cells (Neher and Augustine, 1992). The radial and linear Ca²⁺ profiles resemble the data obtained for the immobile buffer (the dots in Figure 2). A close relationship validates expansion on a small parameter d applied in deriving the solution of Eq. B1 in Supplementary Appendix SA1. It also indicates that immobile buffer approximation serves as a good approximation for slowly moving buffer.

FIGURE 2

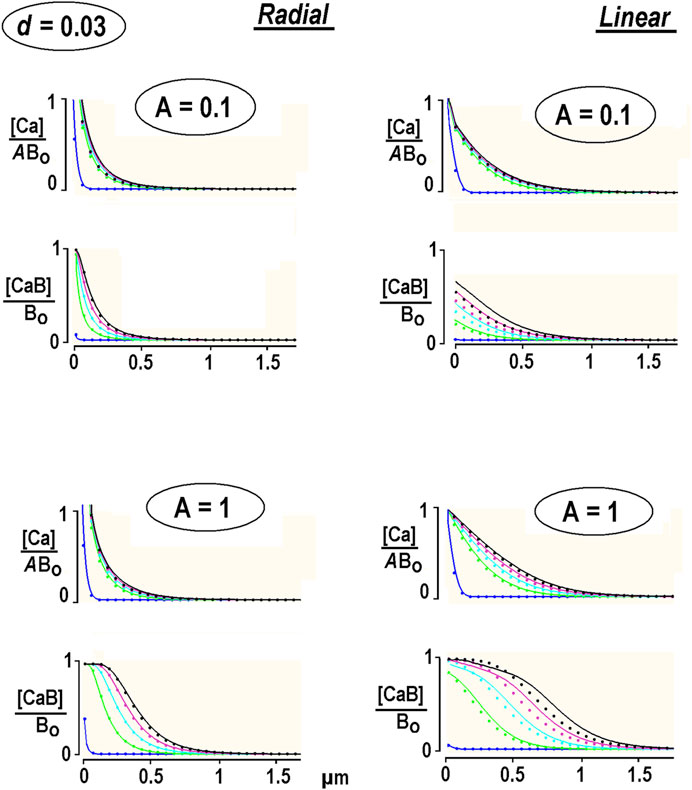
FIGURE 2. Diffusion of free and bound Ca²⁺ in the presence of a low-mobility buffer. The concentration profiles are obtained from the non-linear PDEs for low-mobility buffer (smooth curves, Supplementary Appendix SA1) and immobile buffer [dots, Eq. 12]. The first curve is taken at 0.1 ms, and the interval between the following curves is 0.25 ms. Each panel presents the results for different relative Ca²⁺ concentrations at the channel lumen, A = [Ca²⁺]/B_o. Free [Ca²⁺] is also divided by A to compare the waveforms.

Free Ca²⁺ approached the steady state quickly, but the bound Ca²⁺ was never stationary. [CaB] waves became denser with time. The speed of changes in free and bound Ca²⁺ changes with time and can be characterized by the instantaneous velocity. This was estimated as the x-distance between the half-amplitude points divided by the time increment between the respective curves. For linear diffusion with small Ca²⁺ flux (A = 0.1, the right panels in Figure 2), it subsided from 56 to 3 μm/s, as estimated at 0.1 and 5 ms after the pulse. The velocity changed at the same time points from 78 to 18 μm/s for bigger Ca²⁺ fluxes (A = 1). In contrast, the bound Ca²⁺ “moved” much faster. For A = 0.1, the velocities at 0.1 and 5 ms after beginning the pulse were 84 and 46 μm/s, and for A = 1, they were 107 and 85 μm/s, respectively. For the radial diffusion (Figure 2, the left panels), the values are around 40% smaller. This can be explained by the role of the damping hyperbolic factor (1/r). The 1D values are in the range for Ca²⁺ waves measured in neuronal dendrites (Augustine et al., 2003; Mironov, 2008). The data thus demonstrate that the bound Ca²⁺ apparently “moves” much faster than free Ca²⁺ and overtakes it within a few milliseconds after switching on Ca²⁺ influx.

3.3 Patch-clamp and imaging

In order to test theoretical predictions, I sought for experimental proof-of-principle and aimed to obtain the 1D profiles of the Ca²⁺-bound buffer. They were imaged after opening of single channels, and bound Ca²⁺ was monitored within a thin pipette filled with fluo-4(X) indicator dyes (inset in Figure 3A). α-Synuclein forms in the plasma membrane of hippocampal neurons’ Ca²⁺-permeable channels (Mironov, 2015). A single channel in the inside-out patch influx was used to generate controllable “outward” Ca²⁺ influx into the patch pipette. The data shown are representative of recordings made in 12 patches for fluo-4-dextran and in eight patches for fluo-4.

FIGURE 3

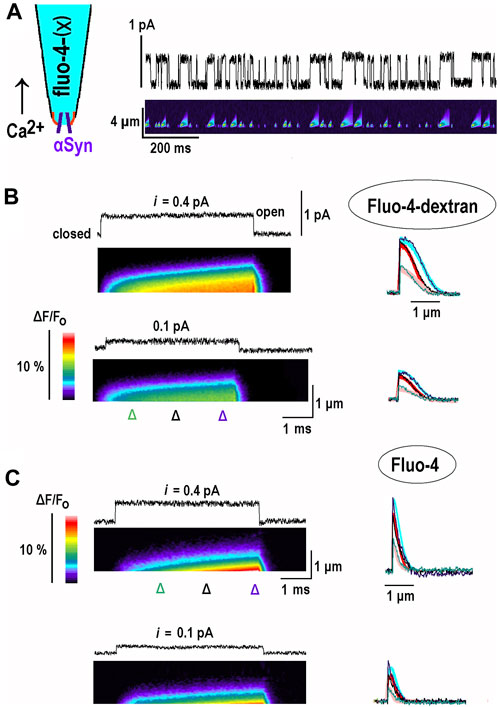
FIGURE 3. Changes in fluorescence of Ca²⁺-bound buffer due to opening of single α-synuclein channels in inside-out patches. α-Synuclein (α-Syn) channels are incorporated into inside-out patches excised from cultured hippocampal neurons (see Methods and Mironov (2015); Mironov (2019)). The pipette solution contained fluo-4-dextran (B) or fluo-4 (C) in 154 mM NaCl, and the bathing solution contained 88 mM CaCl₂. Opening of channels in this configuration (the inset in the left upper corner in (A) induced “outward” Ca²⁺ current and local increases of Ca²⁺ bound to indicator dyes. During 1-s long pulses, at different potentials from 10 to 20 openings were observed. The patterns of CaB fluorescence were stereotypic and scaled by duration of opening, which ranges from 3 to 20 ms, and the single channel current. Following the return to the closed state, the fluorescence decreased fast due to Ca²⁺ diffusion and reaction with remaining free buffer molecules. (A). Experimental configuration and simultaneous recording of channel activity at +80 mV (upper trace) and fluorescence of Ca²⁺ bound to fluo-4-dextran (lower kymograph). The record is a sample episode of 1-s-long excursions from 0 mV. (B). Each panel shows a single-channel current and the fluorescence of Ca²⁺ bound to Fluo-4 dextran (kymographs). They present relative changes in fluorescence (background subtracted, calibration bar on the left). The panels depict fluorescence measured along a line on the line-scan of the y-axis (distance from the tip), with time running from left to right along the x-axis. Increased normalized fluorescence (F/F_o) corresponded to an increase in bound Ca²⁺ (warmer colors). The line scans made at time points are indicated by triangles below the kymograph. They are presented on the right and indicate a spread out of bound Ca²⁺. Experimental traces are overlaid upon the thick theoretical curves, which were calculated as described in the Results section and show good agreement. (C). The same protocols were repeated with Fluo-4 in the pipette. Note that in the case of the high-mobility buffer both free and bound [Ca²⁺] built up the stationary gradients fast.

This 1D experimental system for examination of CaB waves has several advantages: (i) the number of pixels to collect is equal to N, not to N³ as in the 3D case, which allows faster measurements; (ii) 1D profiles are more extended because they do not include a “hyperbolic factor”, 1/r, a distance from the source (Figures 1, 2); (iii) the openings are longer than generated by voltage-dependent Ca²⁺ channels, which open normally less than for a couple of milliseconds, which allows more room for the waves to develop.

The channels in the inside-out patch show stable activity for about 20 min. The patch was held at 0 mV, where the current was 0, and the potential was periodically shifted for 1 s. Between 10 and 20 openings are observed during the pulse (Figure 3A). Changes in fluorescence in response to channel opening were stereotypic and depended only on opening duration and single-channel current. The distribution of bound Ca²⁺ expanded with time and formed a traveling wave (Figure 3B). After returning to the closed state, the fluorescence decreased fast due to Ca²⁺ diffusion and reaction with free buffer molecules. In the 1D case, the diffusional time constant can be estimated as x²/2D_Ca = 1 μm²/(2.200 μm²/s) = 2.5 ms. When only 10% free buffer is available, the reaction time constant is small, 1/k_onB_o = 1/(2 × 10^−5 M) (10⁸ M^-1s^-1) = 0.5 ms, which promotes fast decay of bound [Ca²⁺]. The vertical cross-sections of the kymograph in the rightmost panel in Figure 3B show the relative fluorescence in time and space and indicate a spread out of bound Ca²⁺. Experimental traces are overlaid upon thick theoretical curves calculated using the model described above and plotted in Figure 2. Both sets of data show a good agreement.

The experiments were also carried out with Fluo-4-filled pipettes. The distribution of bound Ca²⁺ was narrower and quickly attained the steady state. This is expected as Fluo-4 has a diffusion coefficient of approximately 100 μm²/s (Mironov, 2019), which is close to that of Ca²⁺. These experiments may be treated within the EBA framework by setting the relative diffusion coefficient in Eq. (2) to d = 1. The solution is obtained in Supplementary Appendix SB1 and used to plot the thick traces in Figure 3C. The theoretical predictions show good correspondence with experimental traces.

4 Discussion

Ca²⁺ nanodomains established in the cytoplasm in the vicinity of a single calcium channel represent an accepted paradigm to explain secretion during synaptic transmission (Eisner et al., 2023; Augustine et al., 2003; Eggermann et al., 2011; Südhof, 2017). As discussed in the Introduction, the existence of local Ca²⁺ gradients is based upon the simplest (and widely used) linearized model, which uses the excessive buffer approximation, EBA (Neher, 1986). It assumes irreversible Ca²⁺ binding and a constant buffer concentration and does not consider buffer diffusion (or implicitly assumes that the buffer mobility is similar to that of Ca²⁺). The neglect of possible saturation, and thus depletion of free buffer, may yet invalidate a simple linearized model.

The aim of the study is to examine the time-dependent Ca²⁺ changes around an open Ca²⁺ channel. The non-linear RD problem of Ca²⁺ diffusion in the presence of a low-mobility buffer has the rationale that putative Ca²⁺-binding species are bulky proteins whose diffusion coefficients are smaller than D_Ca by an order of magnitude. The analysis starts with the case of an immobile buffer. The solution of the non-linear Eq. (9) shows that [Ca²⁺] transients decay and stay localized to the open channel, similar as in EBA. More intriguing are the profiles of bound Ca²⁺, which forms the traveling waves (Figure 1). This result follows directly from EBA, as given by Eq. (9). This obviously contradicts the assumption about the constant concentration of free buffer that should mirror the profile of bound Ca²⁺. The traveling waves of the Ca²⁺-bound buffer appear already for small Ca²⁺ fluxes. Their speed ranges from 20 to 120 μm/s, and they are faster for 1D diffusion. The velocity is high enough to reliably deliver Ca²⁺-mediated changes along submicron distances within a few milliseconds. The scales are compatible with the size of both post- and pre-synaptic endings and the duration of fast synaptic events.

The low-mobility buffer only slightly modifies the waveform of waves of bound Ca²⁺ (Figure 2). We may also consider a Ca²⁺-bound buffer as a Ca²⁺-sensor (McMahon and Jackson, 2018). Indeed, if the buffer and sensor have identical binding and diffusion characteristics, their concentration changes should be identical. EBA treats the width of Ca²⁺ nanodomains as a major determinant of Ca²⁺-mediated signals. The situation is yet dynamic, not static, and the distribution of Ca²⁺-bound species is extended in time and space. This may be crucial in Ca²⁺ signaling, in which the onset of related events may be determined by the time needed for the Ca²⁺-bound sensor at a given location to reach a threshold for activation. Of course, further reaction steps may follow Ca²⁺ binding that would expand the activation zone in time and space and correspondingly delay a physiological event. The inclusion of subsequent reaction steps in sensor activation would be possible.

The main advantage of the model is the possibility to obtain the analytical solution and predict novel buffer-mediated effects. Of course, it is still oversimplified and has several limitations worth mentioning: (a) it operates on a fast time scale (<10 ms) and neglects Ca²⁺ dissociation from the buffer, (b) it skips the effects of buffer saturation, which were examined in Mironov (2019), and (c) it considers only a single Ca²⁺ buffer. A careful analysis of the effects needs further work, but it may change the quantitative, not the qualitative, outcome of the study.

For example, the cytoplasm contains multiple buffers with different properties, and the case of a single buffer is readily extended to such situations. When Ca²⁺ unbinding is neglected, the characteristic temporal and spatial scales (Table 1) can be defined through the apparent rate constant k = ∑k_on,nB_o,n, which is a sum of all buffers present. A good guess is to assume approximately the same k_on,n, close to the diffusion limit k = k_on,dl. Then, the introduction of apparent k = k_on,dl ∑B_o is equivalent to the consideration of a single buffer with concentration ∑B_o, as treated in the report. “Slow” buffers like EGTA and parvalbumin can also be included. As discussed in the Introduction, their slow Ca²⁺ binding is only apparent. This is due to the small amount of available Ca²⁺-binding sites, as the others are already occupied by protons (EGTA) and Mg²⁺ (parvalbumin). A diffusional correction (Supplementary Appendix SA1) is also linear and represented by a sum of contributions from all buffers taken with appropriate weights, i.e., the relative concentrations.

Ca²⁺-unbinding may become important for bigger k_off > 1,000 s^-1 corresponding to τ_off < 1 ms, which becomes compatible with the channel open and closed times. The case is relevant for small organic Ca²⁺-binding species, such as citrate, lactate, and oxalate Their effects on local Ca²⁺ transients are not examined yet, but in such studies, at least two side effects should be considered. The low-affinity buffers are weak electrolytes equilibrated with neutral forms, which are membrane-permeable. Penetration into intracellular organelles such as mitochondria may influence physiological responses. Ca²⁺-binding will also displace protons from the binding sites of low-affinity buffers, resulting in fast changes in the cytoplasmic pH, which may invoke specific effects.

In summary, theoretical treatment and experimental data of Ca²⁺ diffusion in the presence of a slowly moving buffer show the spread out of bound Ca, which may play an important role in physiological events. In particular, Ca²⁺-mediated signaling may be determined by the time when a threshold level of sensor activation is reached by a wave-transported Ca²⁺-bound species.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SM: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, software, validation, writing–original draft, and writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The work was supported by DFG grant MI 685/2-1 and funded by Deutsche Forschungsgemeinschaft through the DFG Research Center for Molecular Physiology of the Brain.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2023.1266120/full#supplementary-material

References

Augustine G. J., Santamaria F., Tanaka K. (2003). Local calcium signaling in neurons. Neuron 40, 331–346. doi:10.1016/s0896-6273(03)00639-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bornschein G., Schmidt H. (2019). Synaptotagmin Ca²⁺ sensors and their spatial coupling to presynaptic ca_v channels in central cortical synapses. Front. Mol. Neurosci. 11, 494. doi:10.3389/fnmol.2018.00494

PubMed Abstract | CrossRef Full Text | Google Scholar

Crank J. (1979). The mathematics of diffusion. Oxford: Oxford University Press.

Google Scholar

Demuro A., Parker I. (2006). Imaging single-channel calcium microdomains. Cell Calcium 40, 413–422. doi:10.1016/j.ceca.2006.08.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Du Fort E. G., Frankel E. G. (1953). Stability conditions in the numerical treatment on parabolic differential equations. Math. Tables Other Aids Comput. 17, 135–152.

CrossRef Full Text | Google Scholar

Eggermann E., Bucurenciu I., Goswami S. P., Jonas P. (2011). Nanodomain coupling between Ca²⁺ channels and sensors of exocytosis at fast mammalian synapses. Nat. Rev. Neurosci. 13, 7–21. doi:10.1038/nrn3125

PubMed Abstract | CrossRef Full Text | Google Scholar

Eisner D., Neher E., Taschenberger H., Smith G. (2023). Physiology of intracellular calcium buffering. Physiol. Rev. 103, 2767–2845. doi:10.1152/physrev.00042.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin M. Z., Schnitzer M. J. (2016). Genetically encoded indicators of neuronal activity. Nat. Neurosci. 19, 1142–1153. doi:10.1038/nn.4359

PubMed Abstract | CrossRef Full Text | Google Scholar

Lock J. T., Parker I., Smith I. F. (2015). A comparison of fluorescent Ca²⁺ indicators for imaging local Ca²⁺ signals in cultured cells. Cell calcium 58, 638–648. doi:10.1016/j.ceca.2015.10.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Malasics A., Gillespie D., Nonner W., Henderson D., Eisenberg B., Boda D. (2009). Protein structure and ionic selectivity in calcium channels: selectivity filter size, not shape, matters. Biochim. Biophys. Acta. 1788, 2471–2480. doi:10.1016/j.bbamem.2009.09.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Matthews E. A., Dietrich D. (2015). Buffer mobility and the regulation of neuronal calcium domains. Front. Cell Neurosci. 9, 48. doi:10.3389/fncel.2015.00048

PubMed Abstract | CrossRef Full Text | Google Scholar

McMahon S. M., Jackson M. B. (2018). An inconvenient truth: calcium sensors are calcium buffers. Trends Neurosci. 41, 880–884. doi:10.1016/j.tins.2018.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Mironov S. L. (1990). Theoretical analysis of Ca wave propagation along the surface of intracellular stores. J. Theor. Biol. 146, 87–97. doi:10.1016/s0022-5193(05)80045-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Mironov S. L. (2008). Metabotropic glutamate receptors activate dendritic calcium waves and TRPM channels which drive rhythmic respiratory patterns in mice. J. Physiol. 586, 2277–2291. doi:10.1113/jphysiol.2007.149021

PubMed Abstract | CrossRef Full Text | Google Scholar

Mironov S. L. (2015). α-Synuclein forms non-selective cation channels and stimulates ATP-sensitive potassium channels in hippocampal neurons. J. Physiol. 593, 145–159. doi:10.1113/jphysiol.2014.280974

PubMed Abstract | CrossRef Full Text | Google Scholar

Mironov S. L. (2019). Rethinking calcium profiles around single channels: the exponential and periodic calcium nanodomains. Sci. Rep. 9, 17196. doi:10.1038/s41598-019-53095-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Mironov S. L., Skorova E., Hartelt N., Mironova L. A., Kügler S., Kügler S. (2009). Remodelling of the respiratory network in a mouse model of Rett syndrome depends on brain-derived neurotrophic factor regulated slow calcium buffering. J. Physiol. 587, 2473–2485. doi:10.1113/jphysiol.2009.169805

PubMed Abstract | CrossRef Full Text | Google Scholar

Mironova L. A., Mironov S. L. (2008). Approximate analytical time-dependent solutions to describe large-amplitude local calcium transients in the presence of buffers. Biophys. J. 94, 349–358. doi:10.1529/biophysj.107.113340

PubMed Abstract | CrossRef Full Text | Google Scholar

Naraghi M., Neher E. (1997). Linearized buffered Ca²⁺ diffusion in microdomains and its implications for calculation of [Ca²⁺] at the mouth of a calcium channel. J. Neurosci. 17, 6961–6973. doi:10.1523/JNEUROSCI.17-18-06961.1997

PubMed Abstract | CrossRef Full Text | Google Scholar

Neher E. (1986). Concentration profiles of intracellular Ca²⁺ in the presence of diffusible chelator. Exp. Brain Res. 14, 80–96.

CrossRef Full Text | Google Scholar

Neher E., Augustine G. J. (1992). Calcium gradients and buffers in bovine chromaffin cells. J. Physiol. 450, 273–301. doi:10.1113/jphysiol.1992.sp019127

PubMed Abstract | CrossRef Full Text | Google Scholar

Olver F. W., Lozier D. W., Boisvert R., Clark C. W. (2011). The NIST handbook of mathematical functions. New York, NY: Cambridge University Press.

Google Scholar

Pando B., Ponce Dawson S., Mak D. O., Pearson J. E. (2006). Messages diffuse faster than messengers. PNAS 103, 5338–5342. doi:10.1073/pnas.0509576103

PubMed Abstract | CrossRef Full Text | Google Scholar

Pape P. C., Jong D. C., Chandler W. K. (1995). Calcium release and its voltage dependence in frog cut muscle fibers equilibrated with 20 mM EGTA. J. Gen. Physiol. 106, 259–336. doi:10.1085/jgp.106.2.259

PubMed Abstract | CrossRef Full Text | Google Scholar

Polyanin A. D., Zaitsev V. F. (2004). Handbook of nonlinear partial differential equations. Boca Raton: Chapman and Hall/CRC Press.

Google Scholar

Prudnikov A. P., Brychkov Yu. A., Marichev O. I. (1992). Integrals and series: inverse Laplace transforms. New York: Gordon and Breach Science Publishers.

Google Scholar

Sanabria H., Digman M. A., Gratton E. A., Waxham M. N. (2008). Spatial diffusivity and availability of intracellular calmodulin. Biophys. J. 95, 6002–6015. doi:10.1529/biophysj.108.138974

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwaller B. (2010). Cytosolic Ca²⁺ buffers. Cold Spring Harb. Perspect. Biol. 2, a004051. doi:10.1101/cshperspect.a004051

PubMed Abstract | CrossRef Full Text | Google Scholar

Shuai J., Parker I. (2005). Optical single-channel recording by imaging Ca2+ flux through individual ion channels: theoretical considerations and limits to resolution. Cell Calcium 37, 283–299. doi:10.1016/j.ceca.2004.10.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith G. D., Dai L., Miura R., Sherman A. (2001). Asymptotic analysis of buffered calcium diffusion near a point source. SIAM J. Appl. Math. 61, 1816–1838. doi:10.1137/s0036139900368996

CrossRef Full Text | Google Scholar

Smith P. D., Liesegang G. W., Berger R. L., Czerlinski G., Podolsky R. J. (1984). A stopped-flow investigation of calcium ion binding by ethylene glycol bis(beta-aminoethyl ether)-N,N'-tetraacetic acid. Anal. Biochem. 143, 188–195. doi:10.1016/0003-2697(84)90575-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Südhof T. C. (2017). Molecular neuroscience in the 21st century: a personal perspective. Neuron 96, 536–541. doi:10.1016/j.neuron.2017.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Tadross M. R., Tsien R. W., Yue D. T. (2013). Ca2+ channel nanodomains boost local Ca2+ amplitude. Proc. Natl. Acad. Sci. U. S. A. 110, 15794–15799. doi:10.1073/pnas.1313898110

PubMed Abstract | CrossRef Full Text | Google Scholar

Tay L. H., Dick I. E., Yang W., Mank M., Griesbeck O., Yue D. T. (2012). Nanodomain Ca²⁺ of Ca²⁺ channels detected by a tethered genetically encoded Ca²⁺ sensor. Nat. Commun. 3, 778. doi:10.1038/ncomms1777

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagner J., Keizer J. (1994). Effects of rapid buffers on Ca²⁺ diffusion and Ca oscillations. Biophys. J. 67, 447–456. doi:10.1016/S0006-3495(94)80500-4

PubMed Abstract | CrossRef Full Text | Google Scholar