Linking cortex and contraction—Integrating models along the corticomuscular pathway

Computational models of the neuromusculoskeletal system provide a deterministic approach to investigate input-output relationships in the human motor system. Neuromusculoskeletal models are typically used to estimate muscle activations and forces that are consistent with observed motion under healthy and pathological conditions. However, many movement pathologies originate in the brain, including stroke, cerebral palsy, and Parkinson’s disease, while most neuromusculoskeletal models deal exclusively with the peripheral nervous system and do not incorporate models of the motor cortex, cerebellum, or spinal cord. An integrated understanding of motor control is necessary to reveal underlying neural-input and motor-output relationships. To facilitate the development of integrated corticomuscular motor pathway models, we provide an overview of the neuromusculoskeletal modelling landscape with a focus on integrating computational models of the motor cortex, spinal cord circuitry, α-motoneurons  and skeletal muscle in regard to their role in generating voluntary muscle contraction. Further, we highlight the challenges and opportunities associated with an integrated corticomuscular pathway model, such as challenges in defining neuron connectivities, modelling standardisation, and opportunities in applying models to study emergent behaviour. Integrated corticomuscular pathway models have applications in brain-machine-interaction, education, and our understanding of neurological disease.

1 Introduction

From everyday tasks to highly-skilled athletic performance, movement is the result of a complex interaction between the central and peripheral nervous systems and muscle-tendon actuators. Neural circuits recruit skeletal muscle in a coordinated manner to produce movement and are connected through various feedback loops in the brain and spinal cord. Control of voluntary movement involves the interaction of multiple structures including the motor cortex, spinal cord circuits, skeletal muscles, and sensory organs. Signals from the motor cortex are carried via neurons of the corticospinal tract, and are integrated within spinal cord circuits, which in turn interact with skeletal muscles via α-motoneurons. Corticomotoneuronal cells (CM) of the motor cortex also make direct connections with α-motoneurons, particularly in the distal muscles of the upper limb (Lemon, 2008; Rathelot and Strick, 2009; Yeo et al., 2013). Sensory organs within the muscle and tendon provide the nervous system with information on the current state of the muscles, including their force, length, and contraction velocity, which modulates the descending drive from the cortex.

A mechanistic understanding of motor pathways, originating from the motor cortex, can lead to more effective diagnoses and personalised interventions to treat neuromuscular disorders. Neuromuscular pathologies may affect any and all parts of the motor pathway, impairing movement control and reducing quality of life. Degenerative disorders originating from supraspinal circuits, for example, impact the descending drive and can lead to ataxia (lack of coordination), dystonia (involuntary muscle spasms), and spasticity (stiffness, tightness of muscles) (Mukherjee and Chakravarty, 2010; Ganguly et al., 2021). Given the highly integrated and intricate nature of the motor pathway, the effects of neuromuscular disorders often spread beyond the afflicted region. For example, disorders such as amyotrophic and primary lateral scleroses affect “lower” and “upper” motoneurons, leading to the degeneration of muscle and muscle weakness, respectively (Tawil and Venance, 2011; Larsson et al., 2018). More generally, motoneuron atrophy also alters a muscle’s fibre composition during ageing (sarcopenia) (Larsson et al., 2018). Many other diseases also originate from the brain and have a downstream effect on muscle contraction including cerebral palsy, stroke, Parkinson’s, and Huntington’s disease. These are a few illustrative examples of movement disorders involving the motor pathway.

Experimental techniques capture essential data to investigate the properties and function of various components in healthy and diseased states, which provides valuable insight to understand the motor pathway. However, given the complexity and interdependency of the motor pathway, combined with technical and ethical limitations, experiments on isolated parts of the pathway leave many unanswered questions regarding the input/output relationships of the system. For example, transcranial magnetic stimulation (TMS) has been successfully used as a measure of cortical excitability to assess patients with stroke and epilepsy, but its limited ability to only impact the cortical level and the large variability in responses is a major limitation in exploring the role of subcortical components in the motor pathway (Blicher et al., 2009; Badawy et al., 2014). Neuromuscular activity and architecture can be characterised by various means such as: electrophysiological techniques for muscle activity, motor unit number, and spike train estimates, medical imaging for motor unit anatomy, intramuscular pressure for muscle activity, and joint force estimation for determining motor unit twitch properties (Troiani et al., 1999; Holobar et al., 2010; Csapo et al., 2015; Ateş et al., 2018; Lapatki et al., 2019; Rohlén et al., 2020). Each experimental technique is accompanied by certain drawbacks; for example, electrophysiological techniques only capture a fraction of active motor units, are prone to cross-talk, and are sensitive to movement artefacts (Negro et al., 2016a; Yavuz et al., 2018; Lapatki et al., 2019; Mesin, 2020), and medical imaging techniques are typically constrained to low contraction levels or non-functional poses (Csapo et al., 2015; Rohlén et al., 2020). These limitations highlight a need for a computational approach, which incorporates experimental data to understand the motor pathway.

Mathematical and computational models provide an alternative means to investigate the motor pathway. The process of describing physiological systems as mathematical models requires systematic and detailed analyses of the system and the identification of relevant inputs, outputs and “physiological parameters”. The advantage of mathematical models is the ability to perform in silico experiments to test hypotheses, which is especially beneficial to intricately connected systems such as the motor pathway. However, integrating the various components of the motor pathway remains a challenge, and most approaches only consider a limited number of parts or combinations of the physiological components involved in movement generation. A common example is to include α-motoneuron pools in skeletal muscle models to predict force generation as a function of α-motoneuron firing times or neural input (e.g., Röhrle et al., 2008; Farina et al., 2017; Sartori et al., 2017; Volk et al., 2021). Integrating afferent feedback from proprioceptive sensory organs within spinal cord neuronal circuits is another example of combining different components of the motor pathway to understand inherent behaviour, such as the relationship between spinal circuit connectivity and postural control (e.g., Stienen et al., 2007; Raphael et al., 2010; Elias et al., 2014; Dideriksen et al., 2015; Sreenivasa et al., 2015; Moraud et al., 2016; Aoyama and Kohno, 2022; Kapardi et al., 2022). By beginning to incorporate more physiologically realistic circuits further upstream to muscle, neuromusculoskeletal models can become more useful in answering questions about motor pathologies and motor control.

Our aim is to facilitate the development of a generalised, integrated model of the motor pathway from motor cortex to muscle for the voluntary control of movement, i.e., the corticomuscular pathway, by building on existing models. Holistic corticomuscular pathway models, which aim to represent the interconnections within the pathway rather than isolated parts, could provide distinct insights. For example, investigating the contribution of the cortex to long-latency responses of reflexes could help to distinguish spinal and cortical contributions to reflexes (Matthews, 1991; Reschechtko and Pruszynski, 2020). Elucidating relationships between motor cortex excitability and motor output can provide a more mechanistic understanding of underlying clinical presentations enabling design of more effective rehabilitation protocols (Derosiere et al., 2020). Clinically, modelling of neurosurgical procedures could help guide treatments, such as selective dorsal rhizotomy, which involves the cutting of dorsal roots to mitigate spasticity in patients with cerebral palsy by reducing sensory feedback (Enslin et al., 2019). Furthermore, the relationship between cortical activity and muscle activity, and ultimately the role of the motor cortex in the generation of movement can be investigated (Scott, 2008). This, certainly incomplete, list of research questions reveals the potential of a holistic approach to modelling the corticomuscular pathway.

Despite advances towards integrated modelling of the neuromuscular system, the contribution of the central nervous system (CNS), or any supraspinal input, is rarely considered. Recently, attempts have been made towards modelling more complex representations of the corticomuscular pathway (Teka et al., 2017; James et al., 2018; Pérez Fernández et al., 2021). These models are important milestones towards a holistic approach of motor pathway modelling but are limited in scope since they either consider very specialised pathways, such as the control of eye movement (James et al., 2018; Pérez Fernández et al., 2021), or use simplified model components (Teka et al., 2017). Thus, these modelling frameworks are not suited to investigate the complex interplays within the corticomuscular pathway and related pathologies, highlighting the need for an integrated model.

This work provides an overview of the modelling landscape of components that make up the pathway from cortex to muscle, namely, the motor cortex, spinal circuits, skeletal muscle, and proprioceptive sensory organs. Section 2 provides the physiological background for each component. Section 3 addresses the mathematical modelling of the corticomuscular pathway. Here, each subsection synthesises typical modelling approaches and provides exemplary model equations, together with relevant parameterisation and proposals for input-output parameters to adjacent component models. Section 4 concludes with a discussion on model implementation, validation, and future opportunities.

2 Physiological background of the corticomuscular pathway

The motor cortex issues volitional movement commands as a result of intricate interactions involving internal network dynamics and connections with other brain areas (Sauerbrei et al., 2020; Logiaco et al., 2021). These movement commands, in the form of action potentials, travel down the spinal cord and synapse with a variety of spinal interneurons as well as α-motoneurons (Lemon, 2008; Baldissera et al., 2011). A number of descending pathways, such as the reticulospinal pathway, progress via brainstem nuclei, and while these are clearly important for motor control (Sheean, 2002; Li et al., 2019), they are beyond further scope of this text. Each α-motoneuron innervates a specific set of muscle fibres (forming the motor unit), thus controlling muscle contraction. The state of the musculoskeletal system is monitored by a number of sensory organs in muscle and tendon, which send signals back to the central nervous system where this afferent information is used to adapt the movement commands. This work focuses on the feedback pathways within the spinal cord circuits; for models of feedback in motor control involving supraspinal circuits see Scott (2016). Figure 1 shows the overview of the components in the motor pathway considered. In the following section, an overview of the relevant physiology of components making up the corticomuscular pathway is given. A more detailed anatomical and physiological description of the components of the neuromuscular system and movement control can be found in Kandel et al. (2021).

FIGURE 1

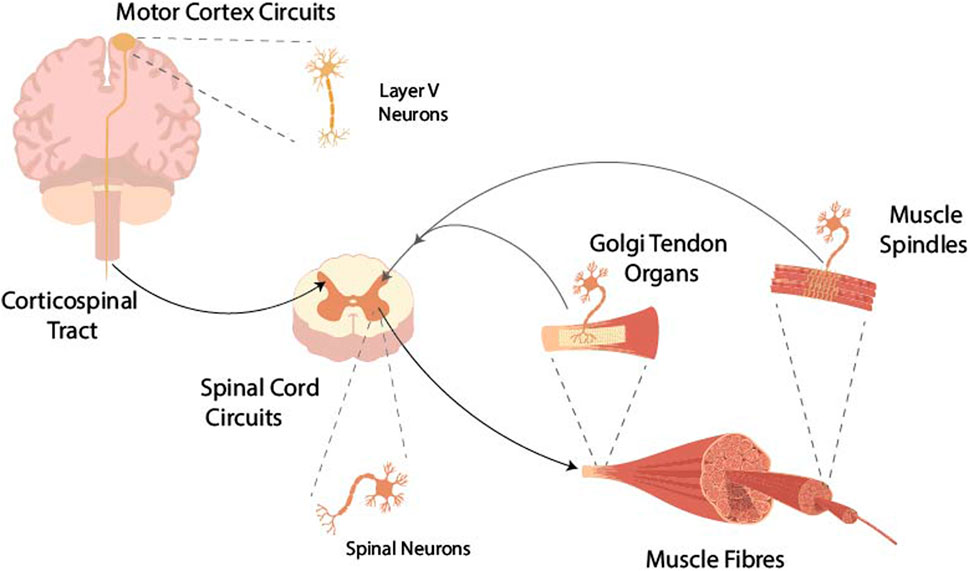
FIGURE 1. Intentional movement commands from the motor cortex are transferred via the axons of layer V pyramidal neurons, which make up the corticospinal tract, to the neurons of the spinal cord. From these, the α-motoneurons finally activate muscle fibres. Muscle contraction is monitored by Golgi tendon organs and muscle spindles and sensory information is fed back to the spinal circuits modulating the activity of the neurons in the spinal cord.

2.1 Motor cortex

The motor cortex is directly involved in the generation of muscle contraction. The experiments of Fritsch and Hitzig in the mid-19th century established that electrically stimulating the frontal regions of the cortex elicits movement, mainly in the contralateral side of the body (Gross, 2007; Hagner, 2012). By the 1930s, mapping of body representations in the motor and sensory areas was carried out through electrical stimulation applied to the exposed cortical surface of epileptic patients in surgery (Penfield and Boldrey, 1937). Presently, studies using non-invasive methods, including TMS, link the stimulation of neurons in the motor cortex to evoked responses in the peripheral muscle (Badawy et al., 2014; Volz et al., 2015). Neurons in the motor cortex make up a significant proportion of the corticospinal tract (CST), which is one of the primary motor pathways involved in voluntary movement of humans (Lemon, 2008). CST neurons then connect to spinal interneurons and α-motoneurons and then on to muscle, resulting in movement.

Neurons of the central and peripheral nervous system send and receive information through electrochemical signalling. The membrane of a neuron acts to separate charges between the inside and outside of the cell. It also contains channels which control ion flow and pumps that maintain concentrations of ions inside and outside of the cell. At rest, there is typically a high concentration of extracellular Na⁺ and Cl⁻ and intracellularly a high concentration of K⁺. This difference in ion concentrations creates an electrical potential. When the electrical potential of the neuron reaches a certain threshold a sudden and transient depolarisation of the cell occurs, known as an action potential or ‘spike’. When a pre-synaptic neuron fires an action potential, it travels down the axon and crosses the synapse with post-synaptic neurons resulting in a post-synaptic potential, either increasing or decreasing the membrane potential of the post-synaptic neurons. The membrane potential ranges from approximately −90 mV when it is at rest, to approximately 50 mV during an action potential. The threshold is approximately −60 mV, though these values depend on species and cell type (Dayan and Abbott, 2001). A typical representation of an action potential is shown in Figure 2, note that the shape of an action potential can vary widely (Krutki et al., 2022).

FIGURE 2

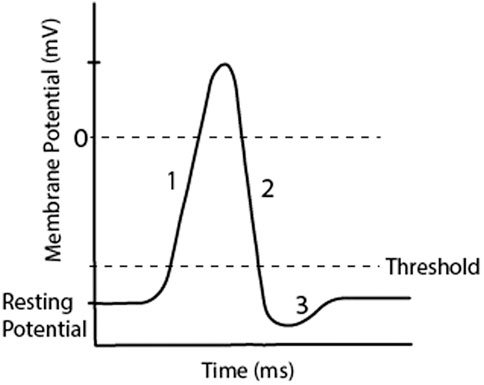
FIGURE 2. A representation of an action potential in a neuron, which occurs when the membrane reaches threshold from accumulated post-synaptic potentials. Regions of the graph show 1) Depolarisation, 2) Repolarisation, 3) Hyperpolarisation. This transient increase in membrane potential occurs over less than 3 ms.

In 1 mm² of surface area in the motor cortex there are approximately 50,000–90,000 neurons (Young et al., 2013; Collins et al., 2016). Neurons in the cortex have a diverse range of morphologies and electrophysiological behaviour. Neurons can be categorised by their connectivity: those that are connected within the cortex are refered to as corticocortical neurons and those that make connections outside the cortex include corticothalamic, corticospinal or corticomotor neurons (Oswald et al., 2013). Neurons can also be distinguished by their effect on post-synaptic ion channels resulting from neurotransmitter release. Excitatory neurotransmitters such as glutamate increase a cell’s likelihood to fire an action potential, whereas inhibitory neurotransmitters decrease a cell’s likelihood to fire an action potential. Excitatory and inhibitory post-synaptic potentials are received and integrated mostly in the dendrites of a post-synaptic neuron which, if it reaches threshold, triggers an action potential to propagate along the post-synaptic neuron’s axon. Therefore, the connectivity of neurons can play a significant role in the propagation of action potentials and information in the neuronal circuits involving movement (Udvary et al., 2022). For more information on neuron behaviour and circuits, see Dayan and Abbott (2001).

Experiments involving microstimulation or tracer injections have uncovered a somatotopic organisation of the motor cortex with areas effecting the lower limb located more medially and the areas controlling the trunk, upper limb, face and hands extending distally [(He et al., 1995; Mitz and Wise, 1997; Park et al., 2001), but very recently revised by (Gordon et al., 2022)]. The face and hands, which have finer motor control, are represented by larger surface areas of the cortex (Schieber, 2001). Recent research has also showed distributed and overlapping representations of muscles and body parts in specific regions, for example, in the upper limb region, digit, wrist, elbow and shoulder areas show patchy (0.25–1.0 mm radius) connectivity patterns (Schieber, 2001; Rathelot and Strick, 2009; Hatsopoulos, 2010; Card and Gharbawie, 2020). This suggests that the intrinsic networks may be functionally connected according to end-effectors (i.e., muscles) within the somatotopic organisation of the motor cortex (Card and Gharbawie, 2020).

Evidence of the cortex having a layered structure dates back to histological staining carried out by Broadmann and Cajal who delineated the cortex into six layers differing in populations of cell bodies and cell types (Castro-Alamancos, 2013). In the motor cortex, layer V is the most prominent and contains the bodies of large pyramidal cells which serves as the main ‘output’ layer to other movement areas in the brainstem and spinal cord (Li N. et al., 2015) (for review of descending tracts see Lemon, 2008). Layer I mainly contains projections and no cell bodies. Thalamic input projections to the motor cortex occur across all layers, densely to layer III–V and less densely to layer VI (Tanaka, 2016). Experimental evidence has also suggested the idea of vertical columns in the cortex but the functional properties of this spatial structure have not been determined (Horton and Adams, 2005; Georgopoulos et al., 2007).

The motor cortex instigates voluntary muscle contraction of the body mainly thorough direct corticomotor (CM) connections to α-motoneurons and the corticospinal tract (CST) via spinal interneuron circuits (Lemon, 2008; Fregosi et al., 2019). The CST is the major anatomical pathway for transmitting movement related information from the brain to the spinal cord (Figure 1). Only approximately 0.05% of cells in the motor cortex contribute to the CST (Keller, 1993). However, projections from the motor cortex are the largest contributor to the CST, making up 30%–50% of the descending pathway, which contains approximately 1 million myelinated axons (Keller, 1993; Saliani et al., 2017). Other contributions to the CST come from secondary motor areas including the premotor and supplementary motor areas, as well as the somatosensory cortex (Dum and Strick, 2005; Lemon, 2008). Approximately 90% of neurons of the CST decussate in the brain stem, resulting in contralateral control (Lacroix et al., 2004; Natali et al., 2022). CST axons project to the grey matter of the ventral horn of the spinal cord forming synapses with interneurons and α-motoneurons along multiple levels of the spinal column and multiple α-motoneuron pools within levels.

2.2 Spinal circuitry

In the spinal circuits, signals from motor areas in the brain as well as from peripheral sensory organs are integrated and processed (Kandel et al., 2021). The α-motoneurons located in the ventral horn of the spinal cord, receive these signals and activate muscle contraction (Figure 1). Some afferent nerves, originating from peripheral sensory organs in muscles, form direct (i.e., monosynaptic) connections to the α-motoneurons. However, most afferent nerves terminate on interneurons which then connect, directly or indirectly via several other interneurons to α-motoneurons, creating polysynaptic pathways. These pathways excite or inhibit α-motoneurons, depending on the type of sensory organ and the muscle it is located in (Baldissera et al., 2011). Thereby, interneurons are themselves regulated by supraspinal inputs (Baldissera et al., 2011). In addition, signal transmission from central as well as peripheral pathways differs between flexor and extensor muscles (Yavuz et al., 2018; Castle-Kirszbaum and Goldschlager, 2021). Further, Renshaw cells deliver direct recurrent inhibition to α-motoneurons (Windhorst, 1990). The totality of these pathways determines the generation of action potentials along the motor axon to initiate contraction in the muscle fibres. Spinal circuits also potentially contribute to the recruitment of muscle synergies, i.e., groups of multiple muscles activated concurrently, and in central pattern generators, particularly in locomotion (Duysens and de Crommert, 1998; Tresch and Bizzi, 1999; Dietz, 2003).

Each α-motoneuron innervates a specific set of muscle fibres, which is called a motor unit (MU) (Section 2.3). The number of innervated muscle fibres is proportional to the size of the neuron, resulting in different sized motor units (Heckman and Enoka, 2012). A pool of α-motoneurons, which consists of all the motoneurons that innervate a single muscle, typically contains a larger number of smaller neurons (Gustafsson and Pinter, 1984; Powers and Binder, 1985). The central nervous system uses two strategies to modulate the force that is produced by a specific muscle: recruitment increases the number of active MUs and rate coding increases the activity of a specific MU. With increasing excitatory synaptic input into a pool of α-motoneurons, motor units are usually recruited in an ordered manner, from smallest (low-threshold) to largest (high-threshold), following Henneman’s size principle (Henneman et al., 1965). At the same time, increasing synaptic input leads to an increase in the frequency of action potentials generated by a specific neuron. Small neurons, which are recruited earlier, usually fire action potentials at higher rates compared to large motoneurons. This is known as the onion skin principle (De Luca and Hostage, 2010). The size and onion skin principle are illustrated in Figure 3. Note that recent evidence suggests that Henneman’s size principle might be a simplification, and that more complex patterns of motor unit recruitment are possible (Marshall et al., 2022). Further, it is widely accepted that motoneurons innervating one and the same muscle share most of the inputs (Negro et al., 2016b; Del Vecchio et al., 2022). Interestingly, recent research suggests that this approach should be redefined to functional groups of motor units spanning more than one muscle (Hug et al., 2023).

FIGURE 3

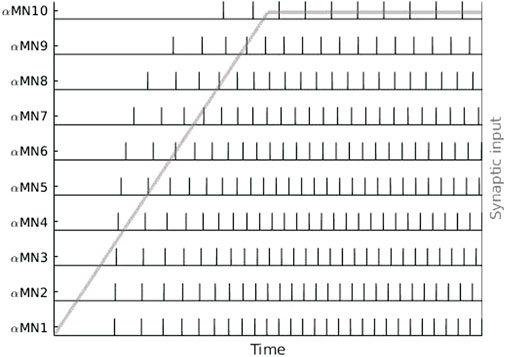
FIGURE 3. Sequence of action potentials of ten α-motoneurons (αMN) in response to a ramp-and-hold type of synaptic input (grey). Cell size and recruitment threshold increase exponentially from αMN1 to αMN10. The number of recruited α-motoneurons and their respective firing rates increase with increasing synaptic input, illustrating the size principle and onion skin firing scheme.

More detailed information on motor units can be found in Heckman and Enoka (2012) and for an elaborate review of the neural circuits within the spinal cord see Baldissera et al. (2011).

2.3 Skeletal muscle

Skeletal muscle can rapidly contract and generate force in response to recruitment via the central and peripheral nervous systems (Figure 1). The tremendous range of movements that the human body is capable of is partly made possible by the variety of muscle shapes and architecture. For example, the soleus of the lower legs may be thousands of times larger than the lumbricals of the hand. Despite this variety, individual muscles and tendons (musculotendon complex) share commonalities that are adapted to each individual joint. Skeletal muscle is a hierarchical structure of repeating units—these are, from the largest (at the centimeter range) to the smallest (at the micrometer range): muscle fascicles, fibres, myofibrils, and sarcomeres. The contractile elements are surrounded by connective tissues: the epimysium, perimysium, and endomysium, which surround the muscle, fascicles, and fibres, respectively. Connective tissues are the primary means of force transmission, both laterally within the muscle and longitudinally towards the tendons (Purslow, 2010; Turrina et al., 2013).

Muscle fibres can be separated by histochemical staining intensities, which generally correspond to their rate of contraction and fatiguability. Commonly, three classifications are used, type-I, -IIA, and -IIB, but there may be up to seven, with each classification increasing in contractile speed and fatiguability (Scott et al., 2001). A single α-motoneuron typically innervates multiple muscle fibres. The neuron and its fibres are referred to as a motor unit. Muscles have varying numbers of motor units (equalling the number of α-motoneuron axons per muscle), e.g., ranging from five in the rectus lateralis to approximately 1750 in the gastrocnemius. Furthermore, motor units within a muscle vary in size according to the number of muscle fibres they contain, termed as a motor unit’s innervation ratio. The largest motor unit in a muscle may contain up to eighty times the fibres of the smallest one. The remaining motor units typically follow an exponential distribution between these extremes (Heckman and Enoka, 2012, and references therein). Furthermore, the contractile properties of motor units varies due to their fibre type composition. The three-fold classification of muscle fibres is thus commonly applied to motor units also, with type-I, IIA, and IIB fibres comprising type S, FR, and FF motor units, respectively. The variability in contraction dynamics and fatigability means that certain motor units are better suited for certain tasks, e.g., type S, FR, and FF motor units for posture maintenance, walking and running (Henning and Lomo, 1985).

The distribution of a motor unit’s fibres (or motor unit anatomy) is typically not uniform within the muscle but rather limited to a fraction of the muscle. Motor unit anatomy can be altered due to factors, such as age, pathological conditions, and level of physical (in) activity (e.g., Lexell and Downham, 1991; Messi et al., 2016). Despite this large degree of variation, motor unit anatomy can be generalised as locally confined to a region of the muscle, overlapping with multiple other territories, irregularly shaped, and as having varying degrees of fibre-type clustering (e.g., Bodine-Fowler et al., 1990; Lexell and Downham, 1991; van Dijk et al., 2016). Muscle force production is a complex interplay between various factors, including its geometry, material properties, fibre-arrangement, and motor unit recruitment and anatomy.

The neural system does not recruit individual muscle fibres but rather groups of fibres simultaneously, i.e., via recruitment of motor units. An action potential from the α-motoneuron arrives at the neuromuscular junctions of all fibres that it innervates. When recruited, excitation-contraction coupling initiates at the muscle fibre’s neuromuscular junction, leading to (local) depolarisation of the muscle fibre. Sarcomeres are composed of thin (myosin) and thick (actin) filaments, and is the site at which chemical energy is converted into mechanical force. This process is referred to as cross bridge cycling, and is initiated by changes in ion concentrations within the cell as a result of muscle (fibre) recruitment via the α-motoneurons. The amount of force produced within the sarcomere depends in part on the degree of overlap between the thick- and thin-filaments and the rate of contraction. Briefly, as sarcomeres lengthen or shorten beyond their optimal length, filament overlap decreases and fewer cross bridges can be formed, leading to lower force production (Ramsey and Street, 1940; Gordon et al., 1966). Furthermore, as the rate of contraction increases, myosin heads may no longer find actin attachment sites and a lower force is produced (Hill, 1938). The action potential propagates outwards towards the fibre’s distal ends. In the wake of the action potential, an increase in Ca²⁺ concentration occurs in the sarcoplasm, leading to cross bridge cycling in muscle fibres.

2.4 Proprioceptive feedback

The ability to perform coordinated movements is closely linked to the ability to sense position. The term proprioception is commonly used to describe the awareness of limb position and movement, force, effort and balance (Proske and Gandevia, 2012). Several sensory organs provide the central nervous system with proprioceptive information. In particular, muscle spindles and Golgi tendon organs (GTOs) (Figure 1) play an important role in motion control, since their activity is closely related to muscle activity.

Muscle spindles can be found in almost all skeletal muscles and make the biggest contribution to proprioception (Macefield and Knellwolf, 2018). They are sensitive to length changes of their parent muscle, i.e., muscle fibre stretch. The number of muscle spindles in human muscles can vary between less than ten and more than 1,000, depending on muscle size and function (Banks, 2006). Anatomically, muscle spindles are arranged in parallel to and embedded within the main, or extrafusal, muscle fibres. Three different types of intrafusal fibres experience length changes whenever their parent muscle changes in length. The different types of fibres have different viscoelastic properties that make them differently sensitive to muscle length and velocity. The sensory information is transferred to the neural circuits in the spinal cord via two types of afferent nerves, Ia (primary) and II (secondary) afferents. Thereby, Ia afferents are unique in that they form monosynaptic connections to α-motoneurons of the same (homonymous) muscle (Stauffer et al., 1976; Watt et al., 1976). Further, Ia and II afferents connect di- and polysynaptically to the homonymous as well as to other (heteronymous) muscles, i.e., synergists and antagonists (Scott and Mendell, 1976; Watt et al., 1976). In general, muscle spindles excite homonymous and synergistic muscles and inhibit antagonists (Scott and Mendell, 1976; Watt et al., 1976). In particular, the excitatory Ia input to motoneurons contributes to a considerable extent to muscle activation (Gandevia et al., 1990; Hiebert and Pearson, 1999). Muscle spindle activity is modulated by the fusimotor system, which comprises two types of spinal neurons, namely, static and dynamic γ-motoneurons (Matthews, 1962). By activating muscle spindles, γ-motoneurons modulate the spindles’ sensitivity and, importantly, ensure that spindles remain responsive during muscle contraction (Macefield and Knellwolf, 2018).

Golgi tendon organs are located at the musculotendinous interface and each GTO lies in series with a number of muscle fibres (Schoultz and Swett, 1972). GTOs are sensitive to the force produced by these muscle fibres (Anderson, 1974). Thereby, each GTO is sensitive to contractions of several motor units and each motor unit is monitored by several GTOs (Jami, 1992). Each tendon organ is usually innervated by a single afferent nerve fibre, a Ib afferent (Schoultz and Swett, 1972). Ib afferents form di- or trisynaptic inhibitory connections to the α-motoneuron pool of the homonymous muscle (Jami, 1992). The number of GTOs per muscle is in general smaller than the number of spindles, with approximately 0.7 GTOs per muscle spindle (Jami, 1992). For information beyond this short summary the reader is referred to Proske and Gandevia (2012) and Kandel et al. (2021).

3 Mathematical modelling of the corticomuscular pathway

This work aims to describe how state-of-the-art models of the motor cortex, spinal circuits, skeletal muscle, and proprioceptive sensory organs can be integrated to form a model of the corticomuscular pathway. Figure 4 provides an overview of the model components and illustrates the relevant interfaces. We consider the voluntary and sensory control of an antagonistic muscle pair. Therefore, neither synergistic muscle activity nor rhythmic muscle activity (i.e., emerging from central pattern generators) is considered. Additionally, proprioceptive feedback is considered on the spinal cord level only, i.e., spinal-cortical pathways are beyond the scope of this work.

FIGURE 4

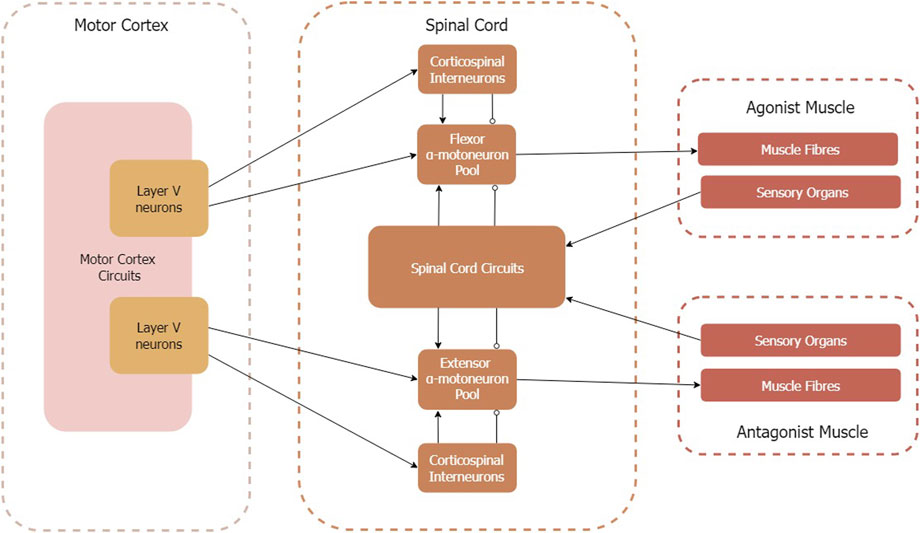
FIGURE 4. Circuit diagram of corticomuscular pathway model components. Arrows indicate excitatory connections, circles indicate inhibitory connections. Note that the spinal circuits transmit sensory organ signals differently to flexor and extensor α-motoneuron pools (for details see Section 2.4).

We define mathematical models as both stochastic and deterministic models as opposed to experimental or animal models. Modelling approaches to physiological systems can be classified broadly into two categories: phenomenological and biophysical. Phenomenological models aim to describe and relate input/output variables to match experimental data, irrespective of the underlying mechanism, i.e., a “black-box” approach. In contrast, biophysical models use relevant physiological knowledge to describe the underlying mechanism(s). Phenomenological models may be useful for model reduction, and may be the only viable choice when computational costs are a factor. On the other hand, mechanistic physiological representations may be paramount to understand emergent behaviour in integrated, complex systems.

This section is structured as follows; first motor cortex modelling is covered, including isolated neuron models, approaches to form neural networks, and the corticospinal pathway (Section 3.1). Second, spinal circuitry models are described, with a focus on spinal neurons and pathways (Section 3.2). Thirdly, an overview of skeletal muscle modelling is provided, with a focus on contractile behaviour and the integration of sensory fibres (Section 3.3). Lastly, proprioceptive feedback modelling is described, closing the loop between the skeletal muscle and spinal circuit models (Section 3.4). This paper by no means aims to include a detailed description of all models, but to provide an overview of the modelling approaches taken in representing each component and how they can be connected.

3.1 Motor cortex models

The role of the motor cortex in the generation of movement, functionally and computationally, has not been resolved (Scott, 2008; Tanaka, 2016). Electrophysiological studies have provided insights into mapping the physiological structure of the motor cortex, but have not yet been able to provide a cohesive understanding of how the neural activity in the motor cortex is involved in producing muscle contraction. There have been two main theories about how neurons in the motor cortex relate to and produce movement. The previously held representational view sought to relate the firing of pyramidal neurons in the motor cortex to movement parameters such as muscle tension, direction and velocity of movement, joint angle, or EMG (Georgopoulos et al., 1986; Sergio and Kalaska, 1997; Reina et al., 2001; Cherian et al., 2011). Phenomenological approaches to modelling cortical activity in movement have therefore used kinematic variables, such as movement direction, as an input to describe the firing rates of upper motoneurons (Mussa-Ivaldi, 1988; Todorov, 2000). This approach is described in Section 3.1.2.

More recently, the dynamical systems perspective argues that individual neurons cannot code for movement parameters, but there may be patterns generated by the activity of populations of neurons which determine the motor output. For a summary on dynamical systems in modelling movements see Shenoy et al. (2013). Neuron activity has been modelled at different levels, from individual cells using biophysically-based models of neurons model action potentials (further described in section 3.1.1) to populations of neurons connected in networks (Wilson and Cowan, 1972; Brette and Gerstner, 2005; Jolivet et al., 2008; Abbott et al., 2016; Vyas et al., 2020). Recently, artificial neural network models have been used to model the complex dynamics found in cortical activity. Some of these are phenomenological in their representation of the motor cortex while others reconstruct detailed physiological structures (Hill and Tononi, 2004; Esser et al., 2005; Potjans and Diesmann, 2014; Michaels et al., 2020; Dura-Bernal et al., 2022). Neural network models are able to replicate the firing dynamics of the cortex during rest and movement. Firing rates of neurons in the cortex, even at rest, are highly irregular and asynchronous with long tailed distributions of interspike intervals (Churchland and Shenoy, 2007; Kumar et al., 2008; Tomov et al., 2014; Borges et al., 2020; Dabrowska et al., 2021) and these properties are thought to arise from, or be influenced by the properties of the neural network (Destexhe, 2011; Chen and Gong, 2019).

3.1.1 Individual neurons

The initiation and propagation of action potentials in neurons were first quantitatively modelled by Hodgkin and Huxley in 1952 (Hodgkin and Huxley, 1952). Their model incorporated the sum of three currents (K⁺, Na⁺ and leak) to describe the membrane current (Eq. 1). The rapid, transient Na⁺ current is responsible for the ‘spike’ of the action potential and the K⁺ current is responsible for repolarising the neuron back to resting potential or a hyperpolarised, refractory state after an action potential. The proportion of ion-channels available as a proportion of the maximum conductance is described by three voltage and time dependent variables m, n and h in Eq. 1:

$C_{\text{m}}\frac{dV}{dt}=I\left(t\right)-g_{\text{K}}{n}^4\left(V\left(t\right)-E_{\text{K}}\right)-g_{\text{Na}}{m}^{3}h\left(V\left(t\right)-E_{\text{Na}}\right)-g_{\text{L}}\left(V\left(t\right)-E_{\text{L}}\right).(1)$

Therein, C_m is the membrane capacitance, V is the membrane potential of the neuron, I is an applied membrane current, g is the conductance of the membrane (subscript denotes ion channel) and E is the equilibrium potential of the respective channels (denoted by subscripts).

In models with many neurons, Hodgkin-Huxley equations may be computationally expensive, and so simplified neuron models such as Izhikevich neurons, Fitz-Hugh Nagamo and leaky integrate-and-fire (LIF) neurons are used to reduce computational burden (Izhikevich, 2003; Yamazaki et al., 2022). These simplified neuron models neglect detailed ion-channel dynamics but are still able to describe the basic shape and timings of neuronal action potentials (Trappenberg, 2002). The leaky integrate-and-fire neuron takes the form:

${\tau }_{\text{m}}\frac{dV\left(t\right)}{dt}=-\left(V\left(t\right)-V_{\text{r}}\right)+\frac{I\left(t\right)}{C_{\text{m}}},(2)$

where V is the membrane potential, V_r is the value to which the membrane potential is reset after firing an action potential, τ_m is the time constant and C_m is the capacitance of the membrane. I represents the currents in and out of the cell due to post-synaptic potentials from other neurons or external microelectrodes (Dayan and Abbott, 2001; Gerstner et al., 2014) (Eq. 2).

3.1.2 Representational approach

Motor cortex neurons have been found to be most ‘active’ for certain directions, exhibiting tuning curves of preferred directions (Georgopoulos et al., 1986). By representing the firing of individual neurons as vectors and then using a weighted vector sum, Georgopoulos et al. (1986) found that the resulting population vector was in a direction congruent with the direction of hand movement. The firing rate of neurons using their ‘preferred direction’ can be characterised by the following cosine tuning equation, where fr(i, t) is activity of neuron i at time t, d(t) is intended movement direction, d_pref(i) is the preferred direction of the neuron, fr₀ is the baseline firing rate and g_neuron(i) is the gain of the neuron, i.e., a scaling factor representing the neuron’s sensitivity to input (Eq. 3):

$fr\left(i,t\right)=f{r}_{\text{0}}+g_{\text{neuron}}\left(i\right)\cos \left[d\left(t\right)-d_{\text{pref}}\left(i\right)\right].(3)$

It has been suggested that the preferred direction of neurons is determined by the musculoskeletal system’s biomechanical properties (Hirashima and Nozaki, 2012; Lillicrap and Scott, 2013; Suminski et al., 2015). Neural activity in the motor cortex has been phenomenologically described in motor control models based on the assumption that neuronal firing rates are reflective of properties such as end effector position and velocity, joint torque or muscle-length (Mussa-Ivaldi, 1988; Todorov, 2000; Ajemian et al., 2008). Models by Mussa-Ivaldi (1988) and Todorov (2000) have demonstrated that neuron firing can also be described using functions of muscle length, shortening velocity, acceleration and force.

The general equation of phenomenological models of neuron firing rates is:

$fr\left(i,t-\varphi \left(i\right)\right)=f_i\left(p_1\left(t\right),p_2\left(t\right),\dots ,p_N\left(t\right)\right),(4)$

where fr(i) is neuron activity, ϕ(i) is the neuron specific latency between cortex and muscle, f_i is a neuron specific input-output function, and p_i are movement parameters (Wang et al., 2022) (Eq. 4). These models have been able to reproduce the directional tuning curve of activity from recorded neuron populations but the correlations to kinematics and biomechanical properties may be epiphenomenal and do not capture the nuances in the wide range of individual neuron activity or represent the physiological connections of supraspinal circuits (Scott, 2000).

Modelling approaches using traditional recurrent neural networks (RNNs) to generate neural activity at the population level based on muscle activity, have also been implemented to capture both directional tuning properties and underlying rotational dynamics observed in neural firing data (Michaels et al., 2016; 2020; Sussillo et al., 2016). Rotational trajectories in neural firing data have been observed in the primate motor cortex during arm reaches following the application of a dimensionality reduction method, jPCA. When the first two principal components are plotted against each other, they show rotational trajectories which are thought to represent oscillatory or rhythmic patterns of activity in the brain. The criticisms of this approach is that rotational dynamics are not linked to physiological structure, mechanisms or behaviour and so lacks explanatory power (Lebedev et al., 2019). Traditional RNNs also use non-biophysically based models of ‘neurons’ and continuous values of activation rather than capturing the dynamics of physiological action potentials.

3.1.3 Spiking neural networks

A neural network refers to a population of neurons as well as the synapses and connections between them. Spiking neural networks are artificial neural networks based on biologically-realistic models of neuron action potentials (described in the previous Section 3.1.1), which encode information in the coordinated timing of action potentials or ‘spikes’. Synaptic current models are used to represent the dynamics of the receptors or rate of ion flows in the pre- and/or post-synaptic neuron. Inhibitory synapses typically are stronger than excitatory synapses by two to six times (Alvarez and Destexhe, 2004; Xue et al., 2014; Gao et al., 2017).

The single exponential model of a post-synaptic current (I_syn) acting on the membrane potential takes the general form of an exponential decay function with time constant τ_syn (Eq. 5):

$\frac{d{I}_{\text{syn}}\left(t\right)}{dt}=-\frac{I_{\text{syn}}\left(t\right)}{{\tau }_{\text{syn}}}.(5)$

The connectivity, or topology, of neural networks and its influence on firing dynamics is a rich area of research (Larremore et al., 2011; Litwin-Kumar and Doiron, 2012; Bennett and White, 2021). Neurons in the brain exhibit local connectivity, but also have long range connections between areas. Small world or patchy network topologies where the distribution of connections are unevenly distributed or spatially defined may be more physiologically representative than a model with random connectivity (Wang and Chen, 2003; She et al., 2016; Card and Gharbawie, 2020). In the motor cortex there is broader intralayer connectivity with narrower, columnar interlayer connectivity and recurrent connections between layers, with a large number of connections from superficial layers to deep layers (Weiler et al., 2008; Hooks et al., 2013). The connectivity of a neural network model can have an architecture based on these connectivity principles, and experimental data from physiological experiments can also be used to inform and tune these connectivity parameters.

Potjans and Diesmann (2014) used previous experimental data to create a cortex model with complex connectivity within and between cortical layers which was able to capture the asynchronous, irregular spiking behaviour in larger, more realistic numbers of neurons and synapses (i.e., tens-of-thousands and millions respectively). Large-scale biologically-inspired spiking neural networks, containing populations of hundreds to tens-of-thousands of excitatory and inhibitory leaky integrate-and-fire neurons, have recently been used in models of motor cortical activity (Esser et al., 2005; Farokhniaee and Lowery, 2019; Rostami et al., 2020). These models have been able to replicate the spontaneous firing activity in the laminar structure of the cortex, the oscillatory rhythm in the condition of Parkinson’s disease and neural states involving movement (Farokhniaee and Lowery, 2019; Rostami et al., 2020). Spiking neural networks are more biologically realistic than traditional RNNs and so can provide a more mechanistic understanding about how cortical activity is generated. However, previous cortical models have not been linked with models of muscle contraction and feedback circuits in the spinal cord to represent the corticomuscular pathway.

3.1.4 Corticospinal pathway

The descending activity from the motor cortex to neuron pools in the spinal cord has typically been modelled as direct inputs of firing rates or currents which represent the cumulative descending drive of the corticospinal tract and brain (Stienen et al., 2007; Sreenivasa et al., 2015; Mascaro et al., 2020; Volk et al., 2021). This is supported by experimental and simulation studies which suggest that the majority of the input to α-motoneurons are common to the pool (Negro et al., 2016b; Del Vecchio et al., 2022). However, recent work by Marshall et al. (2022), showed that motor units might be flexibly recruited according to task demands and suggested that the descending drive from the cortex may play a role in this ability. Previous models that have linked motor cortex or brain activity to spinal cord and muscle models have used the output of individual neurons or neuron groups to drive individual muscles (Teka et al., 2017; Mascaro et al., 2020; Pérez Fernández et al., 2021). Teka et al. (2017) used six neurons corresponding to each muscle in the upper limb arm model to directly control the spinal motoneurons. Pérez Fernández et al. (2021) used a more complex neural model of three layers representing the sensory input, interneurons and α-motoneurons, respectively, with 48 neurons in each layer. These models, however, do not capture the complex dynamics of firing in the motor cortex nor take into account any recurrent connections which are prevalent in the circuitry and subsequently play a role in α-motoneuron recruitment.

The previous subsections described approaches to modelling the upstream neural activity of the motor cortex. Here we provide an example of a motor cortex model using a spiking neural network that can provide the descending drive of the corticospinal tract and be integrated with downstream spinal cord and muscle models discussed in Section 2.3 and Section 3.4, paving the way towards modelling the connection from cortex to muscle. A more detailed description of this motor cortex model can be found in Haggie et al. (2022).

The cortex can be represented by a spiking neural network with populations arranged in a laminar structure. The connectivity within and between cortical layers is adapted from previous cortical models notably Esser et al. (2005) and Potjans and Diesmann (2014), which were based on experimental evidence. Individual neuron activity is described by a leaky integrate-and-fire (Eq. 2), to reduce computational expense allowing for more realistic numbers of neurons in networks, i.e., tens of thousands, and degrees of synaptic connections of each neuron, i.e., thousands, to be modelled. Parameters are described in Table 1.

TABLE 1

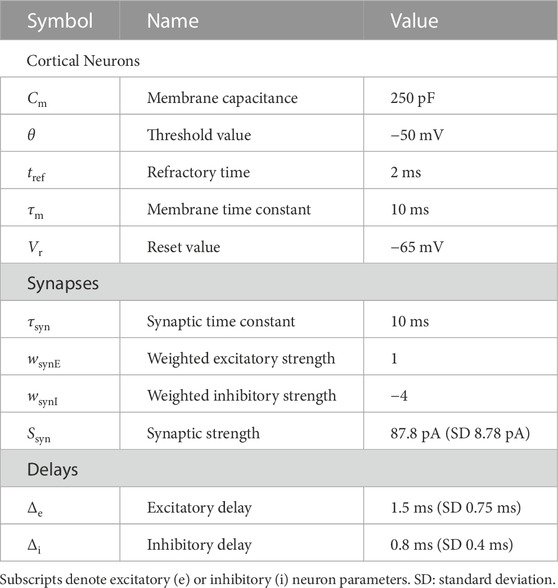
TABLE 1. Table of example parameters for a spiking neural network model of motor cortex (taken from Potjans and Diesmann, 2014).

When the neuron membrane potential reaches threshold θ, the neuron fires an action potential. On the firing of an action potential in a pre-synaptic neuron, the post-synaptic neuron receives a change in synaptic current, $I_{\text{syn}}^{\text{post}}$, of the synaptic strength value, S_syn, scaled by a relative weighting value, w_syn (Eq. 6). The synaptic strength and the synaptic weight both contribute to the change in conductivity which influences the response of the post-synaptic membrane potential in response to the pre-synaptic action potential. The synaptic weight specifically represents the potential modulation of the post-synaptic transmission. This occurs after a delay Δ which accounts for the time it takes for the action potential to propagate down the axon. The value of $I_{\text{syn}}^{\text{post}}$ is described by a single exponential model in Eq. 5. After a neuron fires an action potential, its membrane potential is reset to V_r. A neuron cannot fire an action potential to other neurons when it is within the time of the refractory period (t_ref) since its previous action potential.

$\begin{array}{ll}\hfill I_{\text{syn}}^{\text{post}}\left(t\right)& =I_{\text{syn}}^{\text{post}}\left(t\right)+S_{\text{syn}}{w}_{\text{syn}},\hfill \\ \hfill & \text{when\hspace{0.17em}pre-synaptic\hspace{0.17em}neuron\hspace{0.17em}}V\left(t\right)\ge \theta .\hfill \end{array}(6)$

The firing frequency of a neuron is the number of times the neuron reaches the threshold over a timestep. The firing activity of a proportion of the layer V motor cortex neurons in this spiking neural network can then be used to represent the descending corticospinal tracts which synapse onto spinal interneurons and α-motoneurons in the spinal cord. Because the specific connectivity of the corticospinal tract to the spinal cord neurons is still unknown, this could be a probabilistic parameter based on spatial distances or tuned to experimental data of the input to α-motoneurons.

Model inputs and outputs: The model receives input from a Poisson distribution to maintain spontaneous activity during resting state, and an external stimulation or extrinsic currents can be applied to increase firing frequencies and produce the patterns of increased firing related to motor output depending on the research question. The output of this model would be the firing times of a subset of the group representing layer V excitatory pyramidal neurons which make up part of the axons in the corticospinal tract connecting the cortex to spinal circuitry.

3.2 Spinal circuitry models

In the spinal cord, descending motor commands, for example, from the motor cortex, as well as signals from peripheral sensory organs are integrated and processed by interneurons, Renshaw-cells and α-motoneurons, which subsequently activate muscle fibres (Section 2.2). To represent the spinal circuitry, populations of neurons and their connections within the spinal cord as well as to the periphery need to be defined according to the physiological pathways. Different modelling strategies for neurons are extensively discussed in Section 3.1 and so this section will focus on the specific neuron characteristics that need to be considered in the spinal cord.

3.2.1 Spinal neurons

Models of neurons in spinal circuits mainly use two approaches to describe neuron behaviour. Transfer functions can be used to describe the input-output behaviour of neuron populations, following a phenomenological approach. For example, the relation between input, α_in(t) ∈ [−1, 1], and the activity of a neuron population, α_out(t) ∈ [0, 1], is typically described by a sigmoidal function (e.g., Raphael et al., 2010):

${\alpha }_{\text{out}}\left(t\right)={\left[1+\exp \left(-a\left[{\alpha }_{\text{in}}\left(t\right)-b\right]\right)\right]}^{-1},(7)$

where, a and b are parameters that are tuned to represent experimentally determined input-output behaviour (Eq. 7). Due to their low computational cost, transfer functions are well suited to investigate the interplay within large networks of neuron populations; however, transfer functions cannot adequately represent the spiking activity of single α-motoneurons (e.g., Raphael et al., 2010; Li S. et al., 2015; Teka et al., 2017; Parziale et al., 2020).

The second approach employs biophysical neuron models, which explicitly model the membrane dynamics of individual neurons in response to synaptic inputs (Section 3.1.1). Cisi and Kohn (2008) used the Hodgkin-Huxley formalism to describe α-motoneurons, interneurons and Renshaw-cells by a compartmental model considering the activity of a number of ion channels. Their model has been integrated in several models of spinal cord circuitry, e.g., by Dideriksen et al. (2015) and Elias et al. (2014). Variations of the standard integrate-and-fire model (Section 3.1.1) were employed by Sreenivasa et al. (2015), Stienen et al. (2007) and York et al. (2022), which is a common way to reduce the computational cost of modelling neuron populations. In the biophysical modelling approach, each neuron is modelled individually and governed by one set of equations. Neuron populations can be obtained by replicating the models according to the desired pool size. α-motoneurons that innervate the same muscle differ significantly from each other with respect to their properties and behaviour (Section 2.2). The model parameters for a pool of α-motoneurons can be obtained from an exponential distribution where the value of a parameter p_i of the i-th neuron of a pool of N_MN α-motoneurons is calculated from the equation:

$p_i=p_{\text{low}}+\frac{p_{\text{up}}-p_{\text{low}}}{100}\exp \left(\ln \left(100\right)\frac{i}{N_{\text{MN}}}\right),(8)$

where p_low and p_up are the lower and upper extremes of the parameter’s value range, respectively (Fuglevand et al., 1993; Negro and Farina, 2011) (Eq. 8). α-motoneuron pools that follow the approach described above inherently account for physiological principles like the orderly recruitment following the size principle. Populations of interneurons and Renshaw-cells are usually described with a constant set of parameters (e.g., Cisi and Kohn, 2008; Sreenivasa et al., 2015). In Table 2 we provide an exemplary set of parameters for α-motoneurons and interneurons following the integrate-and-fire approach (Eq. 2).

TABLE 2

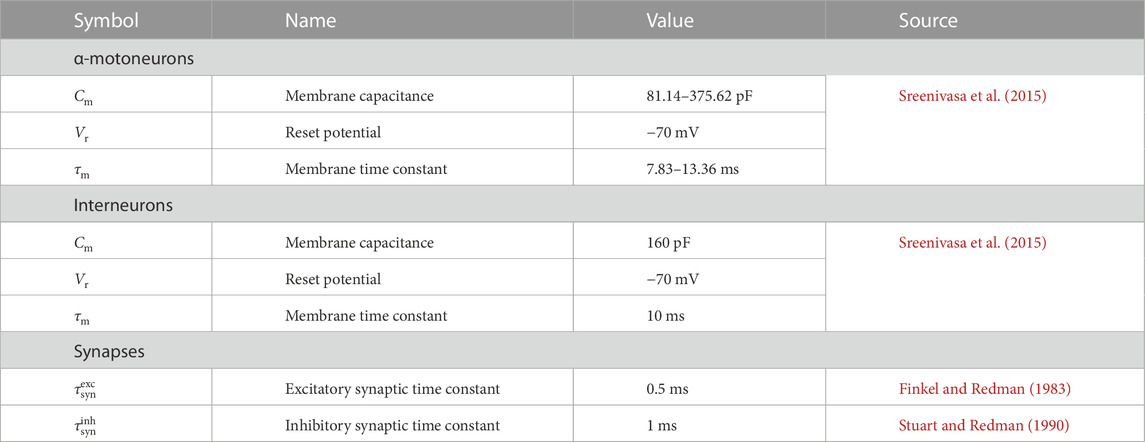
TABLE 2. Example parameters for spinal cord neurons and synapses according to the standard leaky-integrate-and-fire modelling approach.

3.2.2 Spinal pathways

The neurons in the spinal cord receive inputs from different sources and are connected to each other via synapses, creating spinal pathways. Due to the large number of, partly still unknown, interactions between the neurons of the spinal cord, modellers must make a decision on which pathways shall be considered. Focusing on a single pathway such as the monosynaptic stretch reflex, which is based on the monosynaptic connection of muscle spindle Ia afferents and α-motoneurons, enables the investigation of pathways in isolation, but possible interactions are neglected (e.g., Schuurmans et al., 2009). Often, a system with two muscles, acting as agonist and antagonist, and their respective motoneuron pools and sensory organs are considered. Thereby, muscle spindles provide feedback to the neuron pools of both muscles, i.e., both the excitatory homonymous input to the agonist muscle and the reciprocal inhibition of the antagonist, enabling the coordination of behaviour based on sensory information (e.g., Sreenivasa et al., 2015). Considering further pathways, for example, the secondary afferents of muscle spindles or Ib afferents from Golgi tendon organs, can provide additional sources of sensory information. For those specific afferents, often only the connections to the homonymous muscle are considered (e.g., Elias et al., 2014; Dideriksen et al., 2015; Moraud et al., 2016; York et al., 2022). By implementing both mechanical and neural interactions between the simulated muscles, these approaches are suited to improving our understanding of strategies the central neural system could use to control the neuromuscular system. To investigate the spinal circuity in more detail, modellers could also consider the influences of Renshaw-cells, sensory pathways involving more than one interneuron (e.g., Stienen et al., 2007; Raphael et al., 2010; Buhrmann and Di Paolo, 2014; Parziale et al., 2020) and γ-motoneurons, which innervate muscle spindles (Li S. et al., 2015). These models can help researchers to understand how certain connectivity rules and their modulation enable the central nervous system to perform numerous different tasks with one anatomical kind of neuronal network.

In the spinal cord, information is exchanged between the cells via synapses. Physiologically, every spike of a pre-synaptic cell induces a local change of the membrane potential in the post-synaptic cell. The configuration of synapses in the model ultimately depends on the neuron model. Using the leaky integrate-and-fire approach, synapses can be defined as described in Section 3.1.4, Eqs 5, 6, where the time constant can be chosen according to experimental observations (Table 2). The synaptic strength in combination with the synaptic weight, previously defined in Section 3.1.4, defines the potency of the interaction, which can vary between pathways and movement tasks (Bawa and Sinkjaer, 1999; Baudry and Enoka, 2009; Yavuz et al., 2018). Thus, these parameters need to be adjusted to the applied scenario. The weights can be tuned empirically to obtain some desired motor output (Teka et al., 2017; Kapardi et al., 2022) or by employing an optimisation algorithm (Raphael et al., 2010). When considering populations of neurons, the connectivity rules can be based on the distance of the neurons to each other (e.g., Sreenivasa et al., 2015) or on stochastic distributions (e.g., Dideriksen et al., 2015).

Neural signals (action potentials) require a finite amount of time to travel from the sensory organs to their respective target neurons in the spinal cord. This means that sensory information is not provided to the neural system instantaneously. The delay in the transmission of action potentials is determined by the conduction velocity of the respective nerve and the anatomical distance between the muscle and the location of the neuron pool in the spinal cord. Conduction velocities for the nerve types named within this document can be found in Table 3.

TABLE 3

TABLE 3. Conduction velocities for different types of nerves and their distribution within populations.

Model inputs and outputs: The signals emerging from supraspinal centres as well as sensory organs serve as inputs to a spinal circuit model. For each arriving spike from pre-synaptic neurons, the target neurons receive a post-synaptic potential, i.e., current is injected into these neurons. The final output variables of this model component would be the firing rates $f{r}_i^{\text{MN}},\; wherei=1,\dots ,N_{\text{MN}}$, of the α-motoneurons, each innervating a specific set of muscle fibres.

3.3 Skeletal muscle models

In skeletal muscles, α-motoneuron axons synapse with muscle fibres at their neuromuscular junction and initiate excitation-contraction coupling. This leads, ultimately, to force generation that is transmitted to the skeleton via the connective tissues. There are a multitude of methods to model skeletal muscle. The following presents only a brief description of the modelling landscape, with a particular focus on muscle’s contractile behaviour. First, a general overview of muscle modelling is given followed by an exemplary model to demonstrate integration of sensory fibres.

Muscle models can be broadly classified as either phenomenological or biophysical, stemming from pioneering works of Hill (1938) and Huxley (1957), respectively. Phenomenological models are a superposition of lumped parameter functions that describe various muscle behaviours as black boxes at the macroscopic level and are typically based on Hill’s experimental observations (Section 3.3.2). Biophysical models consider the micromechanics and energetics of the interactions within the cross bridges and are typically based on Huxley’s sliding filament theory (Section 3.3.3). While the later models capture muscle behaviours such as the force-length in an emergent sense, i.e., based on micromechanical interactions, they are typically too cumbersome and computationally expensive to describe whole muscle behaviour. This has favoured the popularity of phenomenological models, especially in the simulation of limb or whole body movement.

For further reading on muscle modelling, see Dao and Tho (2018) or Röhrle et al. (2019) for 3D models (the latter including multiscale models), and Rockenfeller and Günther (2017b); Scovil and Ronsky (2006); Schmitt et al. (2019) for 1D models.

3.3.1 Spatial modelling of skeletal muscles

Independent of the approach used to describe muscle behaviour, a muscle model usually requires a spatial component to predict movement, i.e., muscle forces must be directed and transmitted towards the skeleton to generate joint torques and limb movement. Muscles are typically modelled either as line-segments (1D models) or as volumes (3D models). One-dimensional models assume that force transmission within the muscle is solely characterized by the attachment points of the musculotendon complex. That is, a single force vector between attachment points describes whole muscle behaviour (e.g., Delp et al., 2007; Wu et al., 2016; Wochner et al., 2020). This idealisation of muscles provides a straightforward and computationally inexpensive method to model muscles, but comes at the cost of physiological accuracy.

On the other hand, 3D models treat the muscle as a volumetric solid and are able to capture varying fibre architecture and force transmission to the skeleton via attachment areas (rather than points) (e.g., Johansson et al., 2000; Blemker et al., 2005; Röhrle et al., 2017). While being more computationally expensive and often difficult to characterise, 3D models can reveal subtleties in muscle deformation not possible via 1D models, e.g., varying line-of-action, non-uniform muscle strains, contact with surrounding tissue, and surface deformations (e.g., Blemker et al., 2005; Wu et al., 2014; Röhrle et al., 2017; Weickenmeier et al., 2017; Ramasamy et al., 2018; Péan et al., 2019).

3.3.2 Phenomenological approach: Hill-type models

Phenomenological models stem from the pioneering work of Hill (1938), who investigated the relationship between force production and contraction velocity. These models describe whole muscle behaviour and are typically composed of three elements: contractile element (CE), passive element (PE) and series elastic element (SEE), with the relationship (e.g., Zajac, 1989):

$F_{\text{CE}}\left(t\right)+F_{\text{PE}}\left(t\right)=F_{\text{SEE}}\left(t\right).(9)$

where F_CE(t) is the contractile element and represents the muscle active or contractile force, and F_PE(t) and F_SEE(t) are the parallel elastic and serial elastic elements and typically represent the connective tissues in the muscle and tendons, respectively (Eq. 9). Here, we focus on muscle’s active force and thus only consider the F_CE in the following (Eq. 10). The CE accounts for the hallmark behaviours of muscle contraction such as the force-velocity f_vel(t) ∈ [0, 1] and force-length f_len(t) ∈ [0, 1] relationships via superposition, (e.g., Gordon et al., 1966; Lloyd and Besier, 2003):

$F_{\text{CE}}\left(t\right)={\alpha }_{\text{musc}}\left(t\right)F_{\text{max}}\cos \left({\varphi }_{\text{penn}}\right)f_{\text{len}}\left(L\left(t\right)\right)f_{\text{vel}}\left(\dot{L}\left(t\right)\right).(10)$

Here, L(t) and $\dot{L}(t)=dL(t)/dt$ are muscle length and velocity, respectively, F_max is the maximum isometric force and ϕ_penn is the pennation angle. Lastly, α_musc(t) ∈ [0, 1] is the muscle activity, which describes the average degree of muscle activation, with α_musc(t) = 1 for full activation.

Eq. 10 assumes that the muscle properties, deformation, and activation are constant over the muscle. Therefore, such models lend themselves to a 1D representation of muscles, i.e., as line segments between attachment points. The low computational cost and simplicity of these models have led to their prevalence in the musculoskeletal biomechanical modelling community (e.g., Hatze, 1981; Zajac, 1989; Cheng et al., 2000; Scovil and Ronsky, 2006; Delp et al., 2007; Wu et al., 2016; Seth et al., 2018; Wochner et al., 2020).

Despite their prevalence, 1D muscle models are not without limitations. For example, it is not straight-forward to capture complex muscle architecture, model contact with surrounding tissues, or to consider the distributions of connective tissue and shearing within the muscle.

To overcome these limitations, the phenomenological approach has also been utilized with 3D geometries (e.g., Blemker et al., 2005; Wu et al., 2014; Röhrle et al., 2017; Weickenmeier et al., 2017; Péan et al., 2019). Here, local contractile stresses rather than total muscle force are considered. Then, Eq. 10 can be reformulated as (e.g., Johansson et al., 2000):

${\mathit{S}}_{\text{CE}}\left(t,\mathit{X}\right)={\alpha }_{\text{musc}}\left(t\right)S_{\text{max}}{f}_{\text{len}}\left({\lambda }_{\text{f}}\left(t,\mathit{X}\right)\right)f_{\text{vel}}\left(\dot{{\lambda }_{\text{f}}}\left(t,\mathit{X}\right)\right)\mathit{M},(11)$

where λ_f = L(X)/L₀(X) is the normalised fibre length or fibre stretch at position X, and is the square of the invariant I₄ of the Cauch-Green deformation tensor (Eq. 11). For the 1D case, the geometric line segment acts to direct F_CE(t) towards the attachment points, whereas in the 3D case, muscle stress is directed along the local muscle fibre direction a(X) and is accounted for by the structural tensor M = a ⊗a. An exemplary force-length relationship (Röhrle et al., 2017) is given as;

$f_{\text{len}}\left({\lambda }_{\text{f}}\right)=\exp \left(-{\left|\frac{\frac{{\lambda }_{\text{f}}}{{\lambda }_{\text{f}}^{\text{opt}}}-1}{w_i}\right|}^{r_i}\right),(12)$

where ${\lambda }_{\text{f}}^{\text{opt}}$ is the optimal fibre length, w_i and r_i govern shape of the force-length relationship, where i = asc when ${\lambda }_{\text{f}}<{\lambda }_{\text{f}}^{\text{opt}}$ and i = dsc when ${\lambda }_{\text{f}}>{\lambda }_{\text{f}}^{\text{opt}}$ corresponding to the ascending and descending legs, respectively. Additionally, an exemplary force-velocity relation (van Leeuwen, 1991; Böl and Reese, 2008) is given as;

$f_{\text{vel}}\left({\dot{\lambda }}_{\text{f}}\right)=\left\{\begin{array}{cc}\frac{1-{\dot{\stackrel{̄}{\lambda }}}_{\text{f}}}{1+q_{\text{c}}{\dot{\stackrel{̄}{\lambda }}}_{\text{f}}}\hfill & \text{if\hspace{0.17em}}{\dot{\lambda }}_{\text{f}}\le 0,\hfill \\ d_{\text{v}}-\left(d_{\text{v}}-1\right)\frac{1+{\dot{\stackrel{̄}{\lambda }}}_{\text{f}}}{1-q_{\text{c}}{q}_{\text{e}}{\dot{\stackrel{̄}{\lambda }}}_{\text{f}}}\hfill & \text{if\hspace{0.17em}}{\dot{\lambda }}_{\text{f}}>0,\hfill \end{array}\right.(13)$

where ${\dot{\stackrel{̄}{\lambda }}}_{\text{f}}={\dot{\lambda }}_{\text{f}}/{\dot{\lambda }}_{\text{f}}^{\text{min}}$ is the stretch rate normalised to the minimum fibre stretch rate, and q_c and q_e are dimensionless characterisation parameters for the concentric and eccentric parts, respectively. Lastly, d_v is the degree of force enhancement during eccentric contractions. Exemplary material parameters for Eqs 12, 13 are given in Table 4.

TABLE 4

TABLE 4. Material properties for the muscle contractile stress.

Typically, muscle activation (α_musc(t); Eqs 10, 11) is treated at the whole muscle level, i.e., α_musc scales whole muscle activity—regardless of the dimensionality of the muscle model, i.e., 1D or 3D (e.g., Blemker et al., 2005; Delp et al., 2007; Péan et al., 2019; Wochner et al., 2020). A common approach to characterize α_musc is via a muscle’s electrophysiological signals. Here, electromyography (EMG) signals are rectified and smoothed and serve as a basis for muscle activity. However, since the EMG-to-force relationship is non-linear, a further mapping is used and is usually termed “activation dynamics,” i.e.,

${\alpha }_{\text{musc}}\left(t\right)=f\left(EMG\left(t\right)\right),(14)$

where EMG(t) is the rectified and smoothed EMG signal. While this is common place in 1D models (e.g., Hatze, 1981; Lloyd and Besier, 2003; Rockenfeller and Günther, 2017a; Walter et al., 2020), 3D models typically apply inverse dynamics to compute α_musc(t) or impose it directly (e.g., Röhrle and Pullan, 2007; Péan et al., 2019).

While 3D models theoretically allow for spatial heterogeneity of muscle properties and activation, this is often overlooked. This means that the muscle volume is activated simultaneously (e.g., via Eq. 14), and no distinction is made between different fibre types. Recently, 3D models have included the spatial distribution of motor units by treating them in a volumetric sense, i.e., VF_i(X) represents the volume fraction of motor unit i at position X in the muscle. Then, muscle activity may be computed by (e.g., Röhrle et al., 2019; Saini and Röhrle, 2023),

${\alpha }_{\text{musc}}\left(t,\mathit{X}\right)=\sum _i^{N_{\text{MN}}}{\alpha }_i\left(t\right){\text{VF}}_i\left(\mathit{X}\right),(15)$

where α_i(t) is the activity of motor unit i. Heterogeneous contractile properties can analogously be defined in relation to VF_i(X). For example, the peak isometric stress (S_max, Eq. 11), which is typically spatially constant, may be defined by

$S_{\text{max}}\left(\mathit{X}\right)=\sum _i^{N_{\text{MN}}}{S}_{\text{max},i}{\text{VF}}_i\left(\mathit{X}\right),(16)$

where S_max,i is the peak isometric stress of motor unit i.

Note that Eq. 11 additively splits passive and active muscle behaviours and can be considered as a generalisation of the Hill-type model (Eq. 10). Alternatively, passive and active contributions can be multiplicatively split (at the level of the deformation gradient). For detailed discussion of the differences between the approaches, and a further development of hybrid approaches, see Klotz et al. (2021).

3.3.3 Biophysical approach: Sliding filament models

Rather than taking a black box approach to muscle contraction, biophysical models simulate contractile mechanisms at the microscale. These models are primarily based on the sliding filament theory pioneered by A. F. Huxley (Huxley, 1957). Briefly, the starting point of the model is a fraction of attached cross bridges n_XB (u_XB, t), where u_XB is the cross bridge displacement from the equilibrium (null force) position (along direction x). The conservation of cross bridges over an arbritary distance yields (e.g., Keener and Sneyd, 2009):

$\frac{\partial n_{\text{XB}}}{\partial t}=\left(1-n_{\text{XB}}\right)f_{\text{atc}}\left(u_{\text{XB}}\right)-n_{\text{XB}}{g}_{\text{dtc}}\left(u_{\text{XB}}\right)+v\left(t\right)\frac{\partial n_{\text{XB}}}{\partial x}.(17)$

That is, the rate of change of cross bridges ${\dot{n}}_{\text{XB}}$ is the difference between attachment (1 − n_XB) f_atc(u_XB) and detachment n_XB g_dtc(u_XB) plus the “inflow” of n_XB over u_XB with velocity v (where v > 0 is contraction). By assuming that a bound cross bridge acts as a linear spring with stiffness κ, total contractile muscle force can be computed by:

$F_{\text{CE}}\left(t\right)={\alpha }_{\text{musc}}\left(t\right){\rho }_{\text{XB}}\kappa {\int }_{\infty }^{-\infty }{u}_{\text{XB}}{n}_{\text{XB}}\left(u_{\text{XB}},t\right)dx,(18)$

where ρ_XB is the total number of cross bridges with displacement u_XB. Force production occurs via the molecular motor myosin, which interacts with actin and converts chemical energy into mechanical energy. Such models have been typically been used to study micromechanical contraction dynamics, as they become too cumbersome and computationally expensive at the whole muscle scale. Attempts have been made to simplify the partial differential equations in the Huxley type models to ordinary differential equations (e.g., Zahalak, 1981; Razumova et al., 1999). These models make certain a priori assumptions on the distribution of cross bridges n(x, t) and have been used at the whole muscle scale for 1D and 3D models (e.g., Gielen et al., 2000; Oomens et al., 2003; Hayashibe and Guiraud, 2013). In such models, muscle activity is typically a function of α-motoneuron firing times ($f{r}_i^{\text{MN}}(t)$, for α-motoneuron i) that control Ca²⁺ concentration, leading subsequently to cross bridge cycling (e.g., Razumova et al., 1999; Shorten et al., 2007). This can be broadly formulated as (c.f. Eq. 14)

${\alpha }_{\text{musc}}\left(t\right)=f\left(f{r}_i^{\text{MN}}\left(t\right)\right)i=1,\dots ,N_{\text{MN}},(19)$

where N_MN is the total number of α-motoneurons. Note that the phenomenological approach can also be applied to compute muscle activity on the basis of individual motor unit activity (e.g., Fuglevand et al., 1993; Raikova et al., 2018).

The muscle models presented thus far do not consider action potential propagation along muscle fibres. This can be justified by assuming instantaneous propagation of the action potential, which has been shown to have a negligible effect on musculotendon force, when behaviour in the range of seconds is of interest (Schmid et al., 2019; Saini et al., 2022). However, action potential propagation must be modelled when sub-millisecond contractile behaviour is of interest or when electrophysiological modelling is required (e.g., Mordhorst et al., 2015; Klotz et al., 2022). The latter requires multi-physics modelling to compute potential fields at the macroscopic scale (e.g., Fernandez et al., 2005; Böl et al., 2011; Klotz et al., 2022) or within individual muscle fibres via multiscale modelling (e.g., Heidlauf and Röhrle, 2014; Mordhorst et al., 2015; Schmid et al., 2019). Multi-physics muscle models simulate action potential propagation via Hodgkin-Huxley type models (Hodgkin and Huxley, 1952). In multiscale models, muscle activity is a function of the local (half) sarcomere stress γ_sarc, which itself is dependent on the percentage of cross bridges in the post-stroke state ${\bar{A}}_2(t)$, and the rate of shortening ${\dot{\lambda }}_{\text{f}}$ along the fibre, parameterised by s, i.e., (c.f. Eq. 15),

${\alpha }_{\text{musc}}\left(t,\mathit{X}\right)=f\left({\gamma }_{\text{sarc}}\left({\bar{A}}_2\left(t\right),{\dot{\lambda }}_{\text{f}}\left(s\right),\mathit{X}\right)\right).(20)$

3.3.4 Integrating proprioceptive feedback

Mechanical quantities such as muscle stretch, rates of stretch, pressure, and tension throughout the musculotendon complex are sensed by proprioceptive sensory organs, which interact with the neural system, completing the feedback loop (Section 3.4). From a modelling perspective, these mechanical quantities are readily available from the muscle models.

Within the 3D framework, a distribution of muscle spindles can be defined within the muscle at locations ${\mathit{X}}_k^{\text{spindle}},k=1,\dots ,N_{\text{spindle}}$. Experimental data on the exact locations of muscle spindles is sparse; assuming a uniform distribution seems reasonable to ensure a good sensory coverage of the muscle. On the other hand, Golgi tendon organs (GTOs) are confined to regions adjacent to the myotendinous junctions and each GTO lies in series within a specific set of muscle fibres (Schoultz and Swett, 1972), i.e., at locations ${\mathit{X}}_j^{\text{GTO}},j=1,\dots ,N_{\text{GTO}}$ confined to the myotendinous region. These locations are associated with a set of fibres for 3D multiscale models and with a given volume (with fibre orientation) for 3D macroscopic models. The mechanical variable of interest can be extracted in a straightforward manner at these locations at any given time, e.g., stretch and rate of stretch may be used for the muscle spindles, i.e., ${\lambda }_{\text{f}}({\mathit{X}}_k^{\text{spindle}},t),{\dot{\lambda }}_{\text{f}}({\mathit{X}}_k^{\text{spindle}},t)$, or fibre tensile stress for Golgi tendon organs, i.e., $\mathit{S}({\mathit{X}}_j^{\text{GTO}},t)$. Note that λ_f does not require the modelling of individual fibres (i.e., multiscale model), and can be approximated by local deformation in continuum mechanical models, or by whole muscle deformation in 1D models (see below). Furthermore, since many Golgi tendon organ models take total muscle force as input (Section 3.4.2), the local stresses need to be converted to a singular force value that represents total muscle force. This may be achieved by defining a surface over the myotendinous junctions and calculating the total force from the local stresses and the plane’s cross-sectional area, i.e., F_musc = ∫_SS(X^GTO)dS.

In 1D models, the entire muscle experiences the same deformation and thus only an averaged sense of muscle stretch can be obtained, i.e., λ_f(t) = f(L(t)/L₀(t)), where L₀ and L are the resting and current muscle lengths, respectively. That is, all muscle spindles experience the same deformation. Computing GTO activity is similarly straightforward given that force at the myotendinous junction must equal total muscle force (at static equilibrium) since the musculotendon-complex is modelled as a 1D force vector.

Model inputs and outputs: Typical inputs to muscle models are spike trains of the α-motoneuron pool. Typical outputs of the muscle models are contractile forces and length changes (for non-isometric contractions). Muscle models may either be biophysical or phenomenological or a combination of the two (i.e., multiscale models), and either 1D or 3D.

3.4 Proprioceptive feedback models

The preceding sections dealt with efferent activity in the descending corticomuscular pathway, through which signals from the motor cortex are propagated through the spinal circuitry and culminate in muscle contraction. The afferent or ascending pathway proceeds in the opposite direction, where proprioceptive information from sensory organs embedded in the musculotendon complex are carried “upstream” towards the spinal cord and motor cortex. Muscle spindles and Golgi tendon organs are the major sources of proprioceptive feedback directly modulating muscle activity. Thereby, muscle spindle activity excites and GTO activity inhibits the α-motoneurons of the parent muscle (Section 2.4). This section will describe the contributions of these two types of sensory organs to the corticomuscular pathway and the most frequently used modelling approaches.

3.4.1 Muscle spindles

Muscle spindles are specialised organs that sense muscle stretch and stretch velocity. There exists a range of phenomenological models that provide mathematical functions to describe the experimentally derived relationship between muscle stretch and the resulting change in afferent firing rate (Prochazka and Gorassini (1998) and references therein). Prochazka and Gorassini (1998) provides a generalised model for the muscle spindle Ia firing rate fr_Ia(t):

$f{r}_{\text{Ia}}\left(t\right)=4.3v_{\text{fib}}{\left(t\right)}^{0.6}+u_{\text{fib}}\left(t\right)+{\overline{fr}}_{\text{Ia}},(21)$

where the firing rate depends on the muscle fibre displacement u_fib(t), muscle fibre velocity v_fib(t) and the mean firing rate ${\overline{fr}}_{\text{Ia}}$. Fibre deformation information may be derived via a muscle biomechanical model (i.e., Section 3.3.4). This model has been able to replicate experimentally recorded muscle spindle firing rates for a range of stretch velocities, however, it ignores the modulation of spindle sensitivity by the fusimotor system.

Maltenfort and Burke (2003) and Schmid et al. (2022) proposed another phenomenological model, which calculates the Ia afferent firing rate not only in response to muscle stretch, but also in response to fusimotor activation. Therefore, separate Ia firing rates in response to passive stretch, and static and dynamic fusimotor input are calculated, then the contributions in response to fusimotor drive are summed such that the higher rate partially suppresses the lower rate before being added to the passive contribution.

Mileusnic et al. (2006) and Lin and Crago (2002b) both created so called semi-physiological models, by explicitly modelling the anatomical structure of the spindle, i.e., the three intrafusal fibre types and their contributions to Ia and II afferent firing rates as well as their sensitivity to fusimotor input. In the physiological spindle, the contributions of each of the intrafusal fibres to the overall firing rate are summed non-linearly, meaning that the lower firing rates are partially suppressed by the higher rates, which is known as occlusion (Schäfer, 1974; Banks, 1994). The model by Mileusnic et al. (2006) considers this appropriately, while in comparison the larger rate in the model by Lin and Crago (2002b) completely suppresses the lower rate. Recently, Blum et al. (2020) published a sophisticated muscle spindle model, based on the contraction mechanism of the intrafusal fibres and their interaction with the muscle-tendon complex. The model is able to predict many experimentally observed activation- and history-dependent patterns of Ia afferent firing without explicitly modelling them. However, due to its complexity, it is expected to exceed the requirements for a muscle spindle model in a framework focusing mainly on the corticomuscular pathway from cortex to contraction.

Commonly, muscle spindle models represent the afferent firing rates as continuous frequency values. However, for the integration in spike-based spinal circuitry models, the signals have to be converted into spike trains. A Poisson process such as that described by Vannucci et al. (2017) or alternatively a renewal process (Gerstner et al., 2014; Ross, 2014) can be used. This means that the variability of the inter-spike intervals of individual spindles can also be considered (e.g., Burke et al., 1979; Nordh et al., 1983). It must be noted that the described muscle spindle models are parameterised with experimental data of muscle spindle firing rates recorded from cats. To represent human muscle spindle firing, which is slower than in cats, the frequency can be scaled (e.g., Dimitriou and Edin, 2008; Grandjean and Maier, 2014).

Model inputs and outputs: The choice of the muscle spindle model is coupled to the types of pathways that shall be considered within the spinal circuitry model. Depending on the model, muscle fibre stretch, its first and second time derivatives as well as activity of static and dynamic γ-motoneurons modulate the firing rates of the muscle spindle’s Ia and II afferents. It might be necessary to convert the firing rates into spike trains to pass the information to respective target neurons in the spinal cord.

3.4.2 Golgi tendon organs

Golgi tendon organs (GTO) are located at the muscle-tendon interface and sense the force produced by the muscle fibres to which they are connected (Section 2.4). To our knowledge the only biophysically representative GTO model that relates single GTO activity to the contraction of specific muscle fibres was presented by Mileusnic and Loeb (2006). The integration of this model in the corticomuscular pathway, requires the muscle model to provide the tension in single muscle fibres and their assignment to specific motor units.

According to Al-Falahe et al. (1990), the ensemble firing rate of all GTOs in a muscle is a better representation of muscle force than the activity of single GTOs. Thus, several so called ensemble or population models have been proposed (e.g., Lin and Crago, 2002a; Mileusnic and Loeb, 2009; Crago, 2018) that relate total muscle force to the summed, or alternatively averaged, Ib afferent firing rate. The model by Lin and Crago (2002a), which is based on a three step filtering process, is the only one which considers the effect of muscle tension history. However, if this is not relevant for the intended modelling approach, a computationally more efficient approach such as a polynomial function can be used. A saturating function (Eq. 22) as proposed by Mileusnic and Loeb (2009) and Crago (2018) is able to predict the relation between total muscle force F_musc(t) and (total or mean) Ib afferent firing rate fr_Ib(t), wherein, F_max denotes the maximum voluntary muscle force:

$f{r}_{\text{Ib}}\left(t\right)=a{\left(\frac{F_{\text{musc}}\left(t\right)}{F_{\text{max}}}\right)}^b+c.(22)$

The parameter b determines the steepness of the function and takes on values between 0.2 and 0.26 (Mileusnic and Loeb, 2009; Crago, 2018), and the parameters a and c determine the lower threshold for sustained firing and the maximum rate at maximum muscle force. Muscle force may be derived via a muscle biomechanical model (i.e., Section 3.3.4). These parameters can be tuned to correspond to the range of frequencies recorded in human subjects (e.g., Dimitriou and Edin, 2008).

Note that, to convert the Ib afferent frequency values into a spike train, a Poisson or renewal process can be employed, similar to the muscle spindle models (Section 3.4.1).

Model inputs and outputs: The Golgi tendon organ model calculates the firing times of Ib afferents with reference to the total (or alternatively local) muscle force. Similar to muscle spindle afferents, it might be necessary to convert the firing rates into spike trains to pass the information to the respective target neurons in the spinal cord.

4 Discussion

In the preceding sections, we presented the modelling landscape of the corticomuscular motor pathway: the motor cortex, the spinal cord circuits, skeletal muscles and proprioceptive feedback systems, with a particular focus on their integration. System level models are important, particularly in the fields of motor control and biomechanics, because studying complex physiological behaviour such as movement involves many elaborate, complex, and hierarchical interactions and mechanisms. Individual components have usually been modelled in isolation by phenomenological and biophysical descriptions. However, there are very few studies which have taken a holistic approach to corticomuscular pathway modelling, i.e., between cortex and contraction.

Existing models of the corticomuscular pathway, which have considered the motor cortex and spinal network in conjunction with biomechanical models of muscle have typically used individual neurons or motor units to control each muscle separately. Simplified circuits of the spinal cord and connectivity from the cortex are used, which is understandable given that these connections are intricate and challenging to define. However, building on state-of-the art models of each component along the corticomuscular pathway and integrating them will result in a more realistic model to explore motor control.

Simplifying components of the corticomuscular pathway such as descending drive or motor unit recruitment can result in specific nuanced behaviour being missed. For example, the use of single α-motoneurons and motoneuron pools to represent an entire muscle means that questions regarding how recruitment might change within the MN pool, which occurs in fatigue, ageing and disease states, cannot be answered. Increasing the complexity of previous models, such as that by Teka et al. (2017), which used simplified single neuron models to represent descending drive and simplified motor unit pools to model contraction of individual Hill-type muscle models in the arm with an integrated spinal network, means that more complex behaviours and strategies used by the human motor control system can be explored. A key suggestion from the work by Teka et al. (2017) was that the afferent feedback from spinal networks played a significant role in the directional firing of motor cortex neurons, which highlights the potential interaction of subsystems in emergent phenomena. However, ignoring the behaviour of populations or networks of neurons by only having simplified, single neuron representations makes it difficult to address questions about the role of motor cortex.

A more realistic model of the corticomuscular pathway is needed to provide a mechanistic understanding of the entire system. Recent studies have discussed “closing the loop” between the computations of the brain and biomechanical representations of body (James et al., 2018; Mascaro et al., 2020; Pérez Fernández et al., 2021). James et al. (2018) integrated detailed brain circuits and biomechanical models in saccadic eye movements and Pérez Fernández et al. (2021) addressed the vestibular-ocular reflex. However, extraocular motor units use unique recruitment and contractile characteristics and are hard to compare to generalised limb movements (Shall and Goldberg, 1992). A more generalisable model which incorporates typical corticospinal and proprioceptive circuits of limb muscles would be more useful in applying the model to understanding neuromuscular diseases involving the corticomuscular pathway.

Mascaro et al. (2020) described a methodological framework in which combining experimental data with computational models can be used to construct and update model parameters, as well as drive experimental design. The framework by Mascaro et al. (2020) used experimental data from calcium imaging and electrophysiological recordings to drive and tune a mouse model which combined a spinal cord and biomechanical model of the upper limb, but did not yet include the motor cortex. Including the motor cortex would be a step further in modelling the entire corticomuscular pathway. In a similar framework with a human model, experimental data for model tuning and testing could be derived from non-invasive means such as TMS, functional near-infrared spectroscopy (fNIRS), electroencephalography (EEG), and EMG, as well as available invasive electrophysiological recordings such as that taken from micro-electrocorticography (μECoG) of epilepsy patients. The characterisation and validation of an integrated corticomuscular pathway model poses a major challenge, this will be further discussed in Section 4.2.

The work outlined here lays out the beginning of a framework for integrating the motor areas upstream from the spinal cord in biomechanical models and reinforces the constructive synergy of experimental and modelling research. An important consideration to build and run these models is a suitable implementation environment. An overview of existing platforms is outlined in Section 4.1. The integration of complex, physiologically based models of the motor cortex, spinal cord, muscle and sensory feedback organs can build understanding about the corticomuscular pathway at the biophysical level with the continued use of experimental data and testing (Section 4.2).

4.1 Implementation

There are a plethora of model implementations, software packages, and programs for each of the corticomuscular pathway components, available both in the literature and commercially. The selection of a particular modelling tool is challenging and is often guided by a mixture of practical (e.g., cost and availability) and research considerations. The wide range of available options hinders collaboration within the modelling community as modelling tools typically remain isolated, leading to model duplication and impeding validation and verification. Compounding this issue is a poor uptake of strong open-source policies by journals and research groups regarding the availability of the modelling outputs. Therefore, most models are implemented and kept in-house, using general purpose programming languages such as Fortran, C++, Matlab, or Python.

Despite this, certain software tools have gained prominence within the neuromuscular modelling community. For example, modelling the brain with neural network packages such as NEURON (Hines and Carnevale, 2001), NEST (Diesmann and Gewaltig, 2001), BRIAN2 (Stimberg et al., 2019), or MIIND (Osborne et al., 2021); or modelling musculoskeletal mechanics with OpenSim (Delp et al., 2007), or AnyBody Modelling System (AnyBody, Aalborg, Denmark) for 1D muscle models; or FEBio (Maas et al., 2012) or OpenCMISS (Bradley et al., 2011) for 3D models. An overview of software tools is provided in Table 5. In addition to these tools, databases provide important steps towards model unification and data sharing at the level of the individual motor pathway components. For example, the Musculoskeletal Atlas Project (MAP) (Zhang et al., 2014) aims to standardise musculoskeletal geometries and ModelDB provides a model exchange platform for computational neuroscience (McDougal et al., 2017). Also, The Allen Institue (Brain Map and Neurodata Without Borders) (Oh et al., 2014) and eBrains (Human Brain Project) (Schirner et al., 2022) provide a wide range of data and tools for brain-based research and technology development. BioModels hosts a broad collection of mathematical models of biological systems (Malik-Sheriff et al., 2020).

TABLE 5

TABLE 5. A list of selected software tool for the implementation of the corticomuscular motor pathway.

Although most modelling tools can interface with others via application programming interfaces (APIs), this often comes with modelling limitations, or involves added model configuration effort and computational costs. Here, standardisation of models and their inputs and outputs is key to unifying motor pathway models and fostering exchange and communication within the modelling community. For example, the Human Physiome project (Nickerson et al., 2016) seeks to standardise computer models across physiological systems (including the neural, spinal and musculoskeletal systems) and across scales. The Physiome Model Repository (PMR) (Yu et al., 2011) provides a platform to supply standardised modelling components for the motor pathway. Beyond that, the Physiome journal offers a means to publish mathematical models of physiologial components in a peer-reviewed journal, thereby ensuring model availability and reproducibility. Additionally, projects such as SimTK (National Institutes of Health, United States) provide a platform to share software, data, and models for the biomedical modelling community. Recently developed modelling tools enable the modelling of the integrated motor pathway in a single environment (e.g., Iyengar et al., 2019; Maier et al., 2019). While these tools currently exclude cortex modelling, they take steps towards a fully integrated motor pathway modelling environment.

In neuroscience, there have been recent advances in capturing and processing large sets of neural data recorded from microelectrode arrays, even in real time (Franke et al., 2012; Robinson et al., 2013). Newman et al. (2012) developed the NeuroRighter API which can be used to carry out ‘closed-loop’ experiments in which dynamic, real-world behaviour can be linked to electrophysiological measurements of brain activity. Taking a “Model-in-the-loop” approach (Potter et al., 2014) to combine model building with experiments is necessary for hypothesis testing and generation, data collection, and model validation.

4.2 Model validation

It is important to validate physiological models by comparing output variables or behaviours to experimental data. This poses a challenge in validating corticomuscular pathway modelling methods since the neuromuscular system remains relatively inaccessible to non-invasive methods. However, this lack of experimental data provides an opportunity to use modelling to inform and guide experimental studies and to increase our understanding of the corticomuscular pathway in an iterative fashion, i.e., formulating theories, building models, and conducting experiments, the findings of which can refine theories.

Motor pathway components have largely been validated in isolation. At the system or corticomuscular pathway level, however, what remains a challenge is the validation of the interactions and overall behaviour. Coupling previously validated models of individual components means that new parameters of connectivity will arise. This can result in new emergent behaviours and interactions, resulting in behaviours or outputs which need to be systematically validated. The modelling frameworks that combine spinal circuits, muscles and sensory organs already provide various coupling strategies and can be referred to for respective validation data (e.g., Stienen et al., 2007; Raphael et al., 2010; Dideriksen et al., 2015; Sreenivasa et al., 2015; Moraud et al., 2016; Kapardi et al., 2022).

This leaves two challenges for the validation of a model of the corticomuscular pathway. First, experimental studies which guide the coupling of the motor cortex and the spinal circuits have to be identified. Second, the overall system behaviour, ideally involving the action of all model components, has to be validated by comparing the simulated motor output to those of appropriate experimental studies.

There are many techniques used in the field of connectomics such as anterograde and viral tracers which are used to map the connections of neurons (Rathelot and Strick, 2009; Saleeba et al., 2019). However, only in simpler organisms such as a roundworm, C. Elegans (Varshney et al., 2011), has the full connectivity of neurons been mapped; the mouse brain has also been a recent focus of large-scale research projects (Oh et al., 2014; Erö et al., 2018). The sheer scale and complexity of mapping the human nervous system proves to be a challenge, though methods in electron microscopy and immunohistochemistry can be useful in determining synaptic pathways in the cortex and spinal cord (Saleeba et al., 2019 for a review on these methods). Invasive techniques for measuring data from neuron activity such as electrode arrays and calcium imaging (Trautmann et al., 2021) can be used, as well as intramuscular and intracellular electrodes (e.g., Powers and Binder, 1985; Zaback et al., 2022). Perturbations through pharmacological blockades, optogenetics, or localised lesions in animal models can also provide experimental evidence to test disruptions and resulting behaviour in the corticomuscular pathway model (Ziemann, 2013; Watanabe et al., 2020).

Non-invasive brain stimulation techniques such as transcranical direct current stimulation (tDCS), TMS and transcranial alternating current stimulation (tACS) can be used to stimulate activity in the motor cortex and investigate the downstream effects. For example, different protocols of strength and timings of TMS experiments can have facilitatory or inhibitory effects on the size of the motor evoked potentials (MEP) recorded by electromyography (EMG) (Ni et al., 2011; Volz et al., 2015). This can be combined with other experimental manipulations of excitation or inhibition, for example, through pharmacological blockades, to develop and test theories about circuits in the corticomuscular pathway (Ziemann, 2013). In addition, peripheral nerves can also be strategically stimulated with direct current stimulation to modulate spinal circuitry (e.g., Pierrot-Deseilligny, 2002) and high-density EMG can be utilised to analyse the activity of motor units (e.g., Yavuz et al., 2018). These experimental methods can be used in the model development loop to validate and fine tune the parameters in building the corticomuscular pathway circuitry.

4.3 Opportunities

Integrating existing knowledge about the motor system in a single system model means that we can potentially explain many phenomena involving different types of human movements and movement pathologies. A model encompassing the corticomuscular motor pathway will be able to contribute to explaining a wide range of electrophysiological findings related to health and disease, such as the task-dependent alteration of the motor unit recruitment order (e.g., Desnedt and Gidaux, 1981; Formento et al., 2021). Furthermore, it can also be of great benefit to provide a model of neurosurgical procedures, for example, selective dorsal rhizotomy for the reduction of spasticity in cerebral palsy patients by selectively cutting dorsal afferent fibres carrying sensory feedback to the spinal cord, or for the investigation of other “upper” or “lower” motoneuron diseases to compare and understand the causes of spasticity and flaccidity. Models may also help with the interpretation of responses to brain stimulation such as the effect of TMS protocols on motor evoked potentials as well as shed light onto the significance of direct, corticomotoneuronal connections on motor control, a characteristic unique to humans as well as higher primates (Lemon, 2008). An integrated modelling framework can also be used to investigate the effect of traumatic events on the corticomuscular pathway such as spinal cord injury or ischemic stroke. Continued development and improvement of the modelling frameworks, for example, by extending sensory feedback loops to the cortex, can also enable the investigation of the contribution of the cortex to long-latency responses of reflexes (Matthews, 1991; Reschechtko and Pruszynski, 2020).

A model of the corticomuscular motor pathway combines the fields of computational neuroscience and biomechanics. To continue the development of integrated models in motor control, experts from experimental neuroscience, connectomics, computer science, electrical engineering and mathematics will need to collaborate, providing an opportunity to open up new fields of research. Including clinicians in the model development process is an opportunity to guide clinically relevant questions, experiments and applications and can promote use in relevant cases. Models such as the one proposed in this text, which combine multiple subsystems from the brain to the muscle, can direct experiments, allow us to test theories and thereby develop new concepts and hypotheses of human motor control.

5 Conclusion

The motor pathway is composed of multiple interrelated and intricately connected subsystems. Therefore, knowledge of individual components cannot illuminate properties of the entire system since the interrelations themselves are responsible for emergent behaviours. So far, the field of computational biomechanics has tended to focus on motor output, i.e., the properties of muscle and the peripheral nervous system, while the field of computational neuroscience has tended towards the central nervous system, brain regions, and the properties of neural networks.

Modelling the corticomuscular motor pathway from motor cortex to muscle contraction is the next step in integrating neuroscience models of neurons and brain activity with biomechanical models of muscles in the body. This allows microscale models of cells to be expanded upon to allow for the exploration of larger meso- and macroscale systems. For each component in the corticomuscular motor pathway, the motor cortex, the spinal cord, the muscle, and its proprioceptors, a variety of modelling approaches already exists. Choosing the type and complexity of the model and components will depend on the scientific questions asked or the application in which it is to be used.

A major challenge which remains in modelling the corticomuscular pathway is being able to characterise the connectivity between the parts and so the gathering of additional experimental evidence will be vital to provide plausible parameters and validation. This endeavour requires a team of interdisciplinary experts to direct and test new theories. Creating integrated models means that how each of these different components interact and contribute to complex behaviours can be explored which will develop our understanding of motor pathologies and the human motor system.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization: TB, LH, AM, and HS. Funding acquisition: TB, AM and OR. Methodology: LH, HS and LS. Supervision: TB, AM and OR. Visualization: LH and LS. Writing—original draft: LH, HS and LS. Writing—review and editing: All. All authors contributed to the article and approved the submitted version.

Funding

This research was partially funded by the New Zealand Ministry of Business, Innovation and Employment’s (MBIE) Catalyst Strategic Fund (project “12 Labours”) and partially by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC 2075—390740016 and projects “Priority Program 2311” (ID 465243391) and “Soft Tissue Robotics” (ID GRK2198). Additional funding was also provided by Callaghan Innovation, New Zealand’s innovation agency (ID SMACH1801), the Li Ka Shing Foundation, the Friedlander Foundation and the University of Auckland.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbott, L. F., DePasquale, B., and Memmesheimer, R. M. (2016). Building functional networks of spiking model neurons. Nat. Neurosci. 19, 350–355. doi:10.1038/nn.4241

PubMed Abstract | CrossRef Full Text | Google Scholar

Ajemian, R., Green, A., Bullock, D., Sergio, L., Kalaska, J., and Grossberg, S. (2008). Assessing the function of motor cortex: Single-neuron models of how neural response is modulated by limb biomechanics. Neuron 58, 414–428. doi:10.1016/j.neuron.2008.02.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Al-Falahe, N. A., Nagaoka, M., and Vallbo, A. B. (1990). Response profiles of human muscle: Afferents during active finger movements. Brain 113, 325–346. doi:10.1093/brain/113.2.325

PubMed Abstract | CrossRef Full Text | Google Scholar

Alvarez, F. P., and Destexhe, A. (2004). Simulating cortical network activity states constrained by intracellular recordings. Neurocomputing 58-60, 285–290. doi:10.1016/j.neucom.2004.01.057

CrossRef Full Text | Google Scholar

Anderson, J. H. (1974). Dynamic characteristics of golgi tendon organs. Brain Res. 67, 531–537. doi:10.1016/0006-8993(74)90501-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Aoyama, T., and Kohno, Y. (2022). Differences in motor unit firing properties of the vastus lateralis muscle during postural and voluntary tasks. Front. Physiology 13, 955912. doi:10.3389/fphys.2022.955912

CrossRef Full Text | Google Scholar

Ateş, F., Davies, B. L., Chopra, S., Coleman-Wood, K., Litchy, W. J., and Kaufman, K. R. (2018). Intramuscular pressure of tibialis anterior reflects ankle torque but does not follow joint angle-torque relationship. Front. Physiology 9, 22. doi:10.3389/fphys.2018.00022

CrossRef Full Text | Google Scholar

Badawy, R. A., Strigaro, G., and Cantello, R. (2014). Tms, cortical excitability and epilepsy: The clinical impact. Epilepsy Res. 108, 153–161. doi:10.1016/j.eplepsyres.2013.11.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Baldissera, F., Hultborn, H., and Illert, M. (2011). Integration in spinal neuronal systems. John Wiley & Sons, Ltd, 509–595. doi:10.1002/cphy.cp010212

CrossRef Full Text | Google Scholar

Banks, R. (2006). An allometric analysis of the number of muscle spindles in mammalian skeletal muscles. J. Anat. 208, 753–768. doi:10.1111/j.1469-7580.2006.00558.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Banks, R. (1994). The motor innervation of mammalian muscle spindles. Prog. Neurobiol. 43, 323–362. doi:10.1016/0301-0082(94)90059-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Baudry, S., and Enoka, R. M. (2009). Influence of load type on presynaptic modulation of Ia afferent input onto two synergist muscles. Exp. Brain Res. 199, 83–88. doi:10.1007/s00221-009-1951-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Bawa, P., and Sinkjaer, T. (1999). Reduced short and long latency reflexes during voluntary tracking movement of the human wrist joint. Acta physiol. Scand. 167, 241–246. doi:10.1046/j.1365-201x.1999.00608.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, A., and White, A. (2021). Dynamical properties of spiking neural networks with small world topologies. Procedia Comput. Sci. 190, 71–81. doi:10.1016/j.procs.2021.06.009

CrossRef Full Text | Google Scholar

Blemker, S. S., Pinsky, P. M., and Delp, S. L. (2005). A 3D model of muscle reveals the causes of nonuniform strains in the biceps brachii. J. Biomechanics 38, 657–665. doi:10.1016/j.jbiomech.2004.04.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Blicher, J. U., Jakobsen, J., Andersen, G., and Nielsen, J. F. (2009). Cortical excitability in chronic stroke and modulation by training: A TMS study. Neurorehabilitation Neural Repair 23, 486–493. doi:10.1177/1545968308328730

PubMed Abstract | CrossRef Full Text | Google Scholar

Blum, K. P., Campbell, K. S., Horslen, B. C., Nardelli, P., Housley, S. N., Cope, T. C., et al. (2020). Diverse and complex muscle spindle afferent firing properties emerge from multiscale muscle mechanics. Elife 9, e55177. doi:10.7554/eLife.55177

PubMed Abstract | CrossRef Full Text | Google Scholar

Bodine-Fowler, S. C., Garfinkel, A., Roy, R. R., and Edgerton, V. R. (1990). Spatial distribution of muscle fibers within the territory of a motor unit. Muscle & Nerve 13, 1133–1145. doi:10.1002/mus.880131208

PubMed Abstract | CrossRef Full Text | Google Scholar

Böl, M., and Reese, S. (2008). Micromechanical modelling of skeletal muscles based on the finite element method. Comput. Methods Biomechanics Biomed. Eng. 11, 489–504. doi:10.1080/10255840701771750

CrossRef Full Text | Google Scholar

Böl, M., Weikert, R., and Weichert, C. (2011). A coupled electromechanical model for the excitation-dependent contraction of skeletal muscle. J. Mech. Behav. Biomed. Mater. 4, 1299–1310. doi:10.1016/j.jmbbm.2011.04.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Borges, F. S., Protachevicz, P. R., Pena, R. F., Lameu, E. L., Higa, G. S., Kihara, A. H., et al. (2020). Self-sustained activity of low firing rate in balanced networks. Phys. A Stat. Mech. its Appl. 537, 122671. doi:10.1016/j.physa.2019.122671

CrossRef Full Text | Google Scholar

Boyd, I. t., and Kalu, K. (1979). Scaling factor relating conduction velocity and diameter for myelinated afferent nerve fibres in the cat hind limb. J. physiology 289, 277–297. doi:10.1113/jphysiol.1979.sp012737

PubMed Abstract | CrossRef Full Text | Google Scholar

Bradley, C., Bowery, A., Britten, R., Budelmann, V., Camara, O., Christie, R., et al. (2011). OpenCMISS: A multi-physics & multi-scale computational infrastructure for the VPH/Physiome project. Prog. Biophysics Mol. Biol. 107, 32–47. doi:10.1016/j.pbiomolbio.2011.06.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Brette, R., and Gerstner, W. (2005). Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiology 94, 3637–3642. doi:10.1152/jn.00686.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Buhrmann, T., and Di Paolo, E. A. (2014). Spinal circuits can accommodate interaction torques during multijoint limb movements. Front. Comput. Neurosci. 8, 144. doi:10.3389/fncom.2014.00144

PubMed Abstract | CrossRef Full Text | Google Scholar

Burke, D., Skuse, N., and Stuart, D. (1979). The regularity of muscle spindle discharge in man. J. physiology 291, 277–290. doi:10.1113/jphysiol.1979.sp012812

PubMed Abstract | CrossRef Full Text | Google Scholar

Card, N. S., and Gharbawie, O. A. (2020). Principles of intrinsic motor cortex connectivity in primates. J. Neurosci. 40, 4348–4362. doi:10.1523/JNEUROSCI.0003-20.2020

PubMed Abstract | CrossRef Full Text | Google Scholar

Castle-Kirszbaum, M., and Goldschlager, T. (2021). Pyramidal weakness: Is it time to retire the term? Clin. Anat. 34, 478–482. doi:10.1002/ca.23715

PubMed Abstract | CrossRef Full Text | Google Scholar

Castro-Alamancos, M. A. (2013). The motor cortex: A network tuned to 7-14 hz. Front. Neural Circuits 7, 21. doi:10.3389/fncir.2013.00021

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, G., and Gong, P. (2019). Computing by modulating spontaneous cortical activity patterns as a mechanism of active visual processing. Nat. Commun. 10, 4915. doi:10.1038/s41467-019-12918-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, E. J., Brown, I. E., and Loeb, G. E. (2000). Virtual muscle: A computational approach to understanding the effects of muscle properties on motor control. J. Neurosci. Methods 101, 117–130. doi:10.1016/s0165-0270(00)00258-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Cherian, A., Krucoff, M. O., and Miller, L. E. (2011). Motor cortical prediction of emg: Evidence that a kinetic brain-machine interface may be robust across altered movement dynamics. J. Neurophysiology 106, 564–575. doi:10.1152/jn.00553.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Churchland, M. M., and Shenoy, K. V. (2007). Temporal complexity and heterogeneity of single-neuron activity in premotor and motor cortex. J. Neurophysiology 97, 4235–4257. doi:10.1152/jn.00095.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Cisi, R. R., and Kohn, A. F. (2008). Simulation system of spinal cord motor nuclei and associated nerves and muscles, in a web-based architecture. J. Comput. Neurosci. 25, 520–542. doi:10.1007/s10827-008-0092-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Collins, C. E., Turner, E. C., Sawyer, E. K., Reed, J. L., Young, N. A., Flaherty, D. K., et al. (2016). Cortical cell and neuron density estimates in one chimpanzee hemisphere. Proc. Natl. Acad. Sci. U. S. A. 113, 740–745. doi:10.1073/pnas.1524208113

PubMed Abstract | CrossRef Full Text | Google Scholar

Crago, P. E. (2018). Neuromodulation by combined sensory and motor stimulation in the peripheral nerve: Tendon organ afferent activity. J. Neural Eng. 16, 016015. doi:10.1088/1741-2552/aaeaa9

PubMed Abstract | CrossRef Full Text | Google Scholar

Csapo, R., Malis, V., Sinha, U., and Sinha, S. (2015). Mapping of spatial and temporal heterogeneity of plantar flexor muscle activity during isometric contraction: Correlation of velocity-encoded MRI with EMG. J. Appl. Physiology 119, 558–568. doi:10.1152/japplphysiol.00275.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Dabrowska, P. A., Voges, N., von Papen, M., Ito, J., Dahmen, D., Riehle, A., et al. (2021). On the complexity of resting state spiking activity in monkey motor cortex. Cereb. Cortex Commun. 2, tgab033. doi:10.1093/texcom/tgab033

PubMed Abstract | CrossRef Full Text | Google Scholar

Dao, T. T., and Tho, M.-C. H. B. (2018). A systematic review of continuum modeling of skeletal muscles: Current trends, limitations, and recommendations. Appl. Bionics Biomechanics 2018. doi:10.1155/2018/7631818

CrossRef Full Text | Google Scholar

Dayan, P., and Abbott, L. F. (2001). Theoretical neuroscience: Computational and mathematical modeling of neural systems. The MIT Press.

Google Scholar

De Luca, C. J., and Hostage, E. C. (2010). Relationship between firing rate and recruitment threshold of motoneurons in voluntary isometric contractions. J. neurophysiology 104, 1034–1046. doi:10.1152/jn.01018.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Del Vecchio, A., Jones, R. H., Schofield, I. S., Kinfe, T. M., Ibáñez, J., Farina, D., et al. (2022). Interfacing motor units in non-human primates identifies a principal neural component for force control constrained by the size principle. J. Neurosci. 42, 7386–7399. doi:10.1523/JNEUROSCI.0649-22.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

Delp, S. L., Anderson, F. C., Arnold, A. S., Loan, P., Habib, A., John, C. T., et al. (2007). OpenSim: Open-Source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 54, 1940–1950. doi:10.1109/TBME.2007.901024

PubMed Abstract | CrossRef Full Text | Google Scholar

Derosiere, G., Vassiliadis, P., and Duque, J. (2020). Advanced tms approaches to probe corticospinal excitability during action preparation. NeuroImage 213, 116746. doi:10.1016/j.neuroimage.2020.116746

PubMed Abstract | CrossRef Full Text | Google Scholar

Desnedt, J. E., and Gidaux, E. (1981). Spinal motoneuron recruitment in man: Rank deordering with direction but not with speed of voluntary movement. Science 214, 933–936. doi:10.1126/science.7302570

PubMed Abstract | CrossRef Full Text | Google Scholar

Destexhe, A. (2011). Intracellular and computational evidence for a dominant role of internal network activity in cortical computations. Curr. Opin. Neurobiol. 21, 717–725. doi:10.1016/j.conb.2011.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Dideriksen, J. L., Negro, F., and Farina, D. (2015). The optimal neural strategy for a stable motor task requires a compromise between level of muscle cocontraction and synaptic gain of afferent feedback. J. Neurophysiology 114, 1895–1911. doi:10.1152/jn.00247.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Diesmann, M., and Gewaltig, M.-O. (2001). Nest: An environment for neural systems simulations. Forsch. wisschenschaftliches Rechn. Beiträge zum Heinz-Billing-Preis 58, 43–70.

Google Scholar

Dietz, V. (2003). Spinal cord pattern generators for locomotion. Clin. Neurophysiol. 114, 1379–1389. doi:10.1016/S1388-2457(03)00120-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Dimitriou, M., and Edin, B. B. (2008). Discharges in human muscle receptor afferents during block grasping. J. Neurosci. 28, 12632–12642. doi:10.1523/JNEUROSCI.3357-08.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Dum, R. P., and Strick, P. L. (2005). Frontal lobe inputs to the digit representations of the motor areas on the lateral surface of the hemisphere. J. Neurosci. 25, 1375–1386. doi:10.1523/JNEUROSCI.3902-04.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Dura-Bernal, S., Neymotin, S. A., Suter, B. A., Dacre, J., Schiemann, J., Duguid, I., et al. (2022). Multiscale model of primary motor cortex circuits reproduces in vivo cell type-specific dynamics associated with behavior. biorxiv. doi:10.1101/2022.02.03.479040

CrossRef Full Text | Google Scholar

Duysens, J., and de Crommert, H. W. V. (1998). Neural control of locomotion; part 1: The central pattern generator from cats to humans. Gait Posture 7, 131–141. doi:10.1016/S0966-6362(97)00042-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Elias, L. A., Watanabe, R. N., and Kohn, A. F. (2014). Spinal mechanisms may provide a combination of intermittent and continuous control of human posture: Predictions from a biologically based neuromusculoskeletal model. PLoS Comput. Biol. 10, e1003944. doi:10.1371/journal.pcbi.1003944

PubMed Abstract | CrossRef Full Text | Google Scholar

Enslin, J. M. N., Langerak, N. G., and Fieggen, A. G. (2019). The evolution of selective dorsal rhizotomy for the management of spasticity. Neurotherapeutics 16, 3–8. doi:10.1007/s13311-018-00690-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Erö, C., Gewaltig, M. O., Keller, D., and Markram, H. (2018). A cell atlas for the mouse brain. Front. Neuroinformatics 12, 84. doi:10.3389/fninf.2018.00084

CrossRef Full Text | Google Scholar

Esser, S., S, L. H., and Tononi, G. (2005). Modeling the effects of transcranial magnetic stimulation on cortical circuits. J. Neurophysiology 94, 622–639. doi:10.1152/jn.01230.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Farina, D., Vujaklija, I., Sartori, M., Kapelner, T., Negro, F., Jiang, N., et al. (2017). Man/machine interface based on the discharge timings of spinal motor neurons after targeted muscle reinnervation. Nat. Biomed. Eng. 1, 0025. doi:10.1038/s41551-016-0025

CrossRef Full Text | Google Scholar

Farokhniaee, A., and Lowery, M. M. (2019). “A thalamo-cortex microcircuit model of beta oscillations in the parkinsonian motor cortex,” in 2019 41st annual international conference of the IEEE engineering in medicine and biology society (EMBC), Berlin, Germany (Institute of Electrical and Electronics Engineers Inc.), 2145–2148. doi:10.1109/EMBC.2019.8857790

CrossRef Full Text | Google Scholar

Fernandez, J. W., Buist, M. L., Nickerson, D. P., and Hunter, P. J. (2005). Modelling the passive and nerve activated response of the rectus femoris muscle to a flexion loading: A finite element framework. Med. Eng. Phys. 27, 862–870. doi:10.1016/j.medengphy.2005.03.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Finkel, A. S., and Redman, S. J. (1983). The synaptic current evoked in cat spinal motoneurones by impulses in single group 1a axons. J. Physiology 342, 615–632. doi:10.1113/jphysiol.1983.sp014872

PubMed Abstract | CrossRef Full Text | Google Scholar

Firmin, L., Field, P., Maier, M. A., Kraskov, A., Kirkwood, P. A., Nakajima, K., et al. (2014). Axon diameters and conduction velocities in the macaque pyramidal tract. J. Neurophysiology 112, 1229–1240. doi:10.1152/jn.00720.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Formento, E., Botros, P., and Carmena, J. M. (2021). Skilled independent control of individual motor units via a non-invasive neuromuscular–machine interface. J. Neural Eng. 18, 066019. doi:10.1088/1741-2552/ac35ac

CrossRef Full Text | Google Scholar

Franke, F., Jäckel, D., Dragas, J., Müller, J., Radivojevic, M., Bakkum, D., et al. (2012). High-density microelectrode array recordings and real-time spike sorting for closed-loop experiments: An emerging technology to study neural plasticity. Front. Neural Circuits 6, 105. doi:10.3389/fncir.2012.00105

PubMed Abstract | CrossRef Full Text | Google Scholar

Fregosi, M., Contestabile, A., Badoud, S., Borgognon, S., Cottet, J., Brunet, J. F., et al. (2019). Corticotectal projections from the premotor or primary motor cortex after cortical lesion or parkinsonian symptoms in adult macaque monkeys: A pilot tracing study. Front. Neuroanat. 13, 50. doi:10.3389/fnana.2019.00050

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuglevand, A. J., Winter, D. A., and Patla, A. E. (1993). Models of recruitment and rate coding organization in motor-unit pools. J. neurophysiology 70, 2470–2488. doi:10.1152/jn.1993.70.6.2470

PubMed Abstract | CrossRef Full Text | Google Scholar

Gandevia, S., Macefield, G., Burke, D., and McKenzie, D. (1990). Voluntary activation of human motor axons in the absence of muscle afferent feedback: The control of the deafferented hand. Brain 113, 1563–1581. doi:10.1093/brain/113.5.1563

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganguly, J., Kulshreshtha, D., Almotiri, M., and Jog, M. (2021). Muscle tone physiology and abnormalities. Toxins 13, 282. doi:10.3390/TOXINS13040282

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, R., Peterson, E. J., and Voytek, B. (2017). Inferring synaptic excitation/inhibition balance from field potentials. NeuroImage 158, 70–78. doi:10.1016/j.neuroimage.2017.06.078

PubMed Abstract | CrossRef Full Text | Google Scholar

Garny, A., and Hunter, P. J. (2015). OpenCOR: A modular and interoperable approach to computational biology. Front. Physiology 6, 26. doi:10.3389/fphys.2015.00026

PubMed Abstract | CrossRef Full Text | Google Scholar

Georgopoulos, A. P., Merchant, H., Naselaris, T., and Amirikian, B. (2007). Mapping of the preferred direction in the motor cortex. Proc. Natl. Acad. Sci. U. S. A. 104, 11068–11072. doi:10.1073/pnas.0611597104

PubMed Abstract | CrossRef Full Text | Google Scholar

Georgopoulos, A. P., Schwartz, A. B., and Kettner, R. E. (1986). Neuronal population coding of movement direction. Sci. New Ser. 233, 1416–1419. doi:10.1126/science.3749885

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerstner, W., Kistler, W. M., Naud, R., and Paninski, L. (2014). Neuronal dynamics: From single neurons to networks and models of cognition. Cambridge University Press.

Google Scholar

Gielen, A. W. J., Oomens, C. W. J., Bovendeerd, P. H. M., Arts, T., and Janssen, J. D. (2000). A finite element approach for skeletal muscle using a distributed moment model of contraction. Comput. Methods Biomechanics Biomed. Eng. 3, 231–244. doi:10.1080/10255840008915267

CrossRef Full Text | Google Scholar

Gordon, A. M., Huxley, A. F., and Julian, F. J. (1966). The variation in isometric tension with sarcomere length in vertebrate muscle fibres. J. Physiology 184, 170–192. doi:10.1113/jphysiol.1966.sp007909

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordon, E. M., Chauvin, R. J., Van, A. N., Rajesh, A., Nielsen, A., Newbold, D. J., et al. (2022). A mind-body interface alternates with effector-specific regions in motor cortex. bioRxiv Prepr. doi:10.1101/2022.10.26.513940

CrossRef Full Text | Google Scholar

Grandjean, B., and Maier, M. A. (2014). Model-based prediction of fusimotor activity and its effect on muscle spindle activity during voluntary wrist movements. J. Comput. Neurosci. 37, 49–63. doi:10.1007/s10827-013-0491-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Gross, C. G. (2007). The discovery of motor cortex and its background. J. Hist. Neurosci. 16, 320–331. doi:10.1080/09647040600630160

PubMed Abstract | CrossRef Full Text | Google Scholar

Gustafsson, B., and Pinter, M. (1984). An investigation of threshold properties among cat spinal alpha-motoneurones. J. physiology 357, 453–483. doi:10.1113/jphysiol.1984.sp015511

PubMed Abstract | CrossRef Full Text | Google Scholar

Haggie, L., Besier, T., and McMorland, A. (2022). Modelling spontaneous firing activity of the motor cortex in a spiking neural network with random and local connectivity. biorxiv Prepr. doi:10.1101/2022.12.12.520017

CrossRef Full Text | Google Scholar

Hagner, M. (2012). The electrical excitability of the brain: Toward the emergence of an experiment. J. Hist. Neurosci. 21, 237–249. doi:10.1080/0964704X.2011.595634

PubMed Abstract | CrossRef Full Text | Google Scholar

Hatsopoulos, N. G. (2010). Columnar organization in the motor cortex. Cortex 46, 270–271. doi:10.1016/j.cortex.2008.07.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Hatze, H. (1981). Estimation of myodynamic parameter values from observations on isometrically contracting muscle groups. Eur. J. Appl. Physiology Occup. Physiology 46, 325–338. doi:10.1007/BF00422120

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayashibe, M., and Guiraud, D. (2013). Voluntary EMG-to-force estimation with a multi-scale physiological muscle model. Biomed. Eng. OnLine 12, 86. doi:10.1186/1475-925X-12-86

PubMed Abstract | CrossRef Full Text | Google Scholar

He, S.-Q., Dum, R. P., and Strick, P. L. (1995). Topographic organization of corticospinal projections from the frontal lobe: Motor areas on the medial surface of the hemisphere. J. Neurosci. 15, 3284–3306. doi:10.1523/JNEUROSCI.15-05-03284.1995

PubMed Abstract | CrossRef Full Text | Google Scholar

Heckman, C., and Binder, M. D. (1988). Analysis of effective synaptic currents generated by homonymous ia afferent fibers in motoneurons of the cat. J. Neurophysiology 60, 1946–1966. doi:10.1152/jn.1988.60.6.1946

PubMed Abstract | CrossRef Full Text | Google Scholar

Heckman, C., and Enoka, R. M. (2012). “Motor unit,” in Comprehensive physiology (John Wiley & Sons, Ltd), 2629–2682. doi:10.1002/cphy.c100087

PubMed Abstract | CrossRef Full Text | Google Scholar

Heidlauf, T., and Röhrle, O. (2014). A multiscale chemo-electro-mechanical skeletal muscle model to analyze muscle contraction and force generation for different muscle fiber arrangements. Front. Physiology 5, 498. doi:10.3389/fphys.2014.00498

PubMed Abstract | CrossRef Full Text | Google Scholar

Henneman, E., Somjen, G., and Carpenter, D. O. (1965). Functional significance of cell size in spinal motoneurons. J. neurophysiology 28, 560–580. doi:10.1152/jn.1965.28.3.560

PubMed Abstract | CrossRef Full Text | Google Scholar

Henning, R., and Lomo, T. (1985). Firing patterns of motor units in normal rats. Nature 314, 164–166. doi:10.1038/314164a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Hiebert, G. W., and Pearson, K. G. (1999). Contribution of sensory feedback to the generation of extensor activity during walking in the decerebrate cat. J. neurophysiology 81, 758–770. doi:10.1152/jn.1999.81.2.758

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill, A. V. (1938). The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. B - Biol. Sci. 126, 136–195. doi:10.1098/rspb.1938.0050

CrossRef Full Text | Google Scholar

Hill, S., and Tononi, G. (2004). Modeling sleep and wakefulness in the thalamocortical system. J. Neurophysiology 93, 1671–1698. doi:10.1152/jn.00915.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Hines, M. L., and Carnevale, N. T. (2001). Neuron: A tool for neuroscientists. Neurosci. 7, 123–135. doi:10.1177/107385840100700207

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirashima, M., and Nozaki, D. (2012). Learning with slight forgetting optimizes sensorimotor transformation in redundant motor systems. PLoS Comput. Biol. 8, e1002590. doi:10.1371/journal.pcbi.1002590

PubMed Abstract | CrossRef Full Text | Google Scholar

Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiology 117, 500–544. doi:10.1113/jphysiol.1952.sp004764

PubMed Abstract | CrossRef Full Text | Google Scholar

Holobar, A., Minetto, M. A., Botter, A., Negro, F., and Farina, D. (2010). Experimental analysis of accuracy in the identification of motor unit spike trains from high-density surface EMG. IEEE Trans. Neural Syst. Rehabilitation Eng. 18, 221–229. doi:10.1109/TNSRE.2010.2041593

PubMed Abstract | CrossRef Full Text | Google Scholar

Hooks, B. M., Mao, T., Gutnisky, D. A., Yamawaki, N., Svoboda, K., and Shepherd, G. M. (2013). Organization of cortical and thalamic input to pyramidal neurons in mouse motor cortex. J. Neurosci. 33, 748–760. doi:10.1523/JNEUROSCI.4338-12.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Horton, J. G., and Adams, D. L. (2005). The cortical column: A structure without a function. Philosophical Trans. R. Soc. B Biol. Sci. 360, 837–862. doi:10.1098/rstb.2005.1623

PubMed Abstract | CrossRef Full Text | Google Scholar

Hug, F., Avrillon, S., Ibáñez, J., and Farina, D. (2023). Common synaptic input, synergies and size principle: Control of spinal motor neurons for movement generation. J. Physiology 601, 11–20. doi:10.1113/JP283698

CrossRef Full Text | Google Scholar

Huxley, A. F. (1957). Muscle structure and theories of contraction. Prog. Biophysics Biophysical Chem. 7, 255–318. doi:10.1016/S0096-4174(18)30128-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Iyengar, R. S., Pithapuram, M. V., Singh, A. K., and Raghavan, M. (2019). Curated model development using NEUROiD: A web-based NEUROmotor integration and design platform. Front. Neuroinformatics 13, 56. doi:10.3389/fninf.2019.00056

PubMed Abstract | CrossRef Full Text | Google Scholar

Izhikevich, E. M. (2003). Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569–1572. doi:10.1109/TNN.2003.820440

PubMed Abstract | CrossRef Full Text | Google Scholar

James, S. S., Papapavlou, C., Blenkinsop, A., Cope, A. J., Anderson, S. R., Moustakas, K., et al. (2018). Integrating brain and biomechanical models—a new paradigm for understanding neuro-muscular control. Front. Neurosci. 12, 39. doi:10.3389/fnins.2018.00039

PubMed Abstract | CrossRef Full Text | Google Scholar

Jami, L. (1992). Golgi tendon organs in mammalian skeletal muscle: Functional properties and central actions. Physiol. Rev. 72, 623–666. doi:10.1152/physrev.1992.72.3.623

PubMed Abstract | CrossRef Full Text | Google Scholar

Johansson, T., Meier, P., and Blickhan, R. (2000). A finite-element model for the mechanical analysis of skeletal muscles. J. Theor. Biol. 206, 131–149. doi:10.1006/jtbi.2000.2109

PubMed Abstract | CrossRef Full Text | Google Scholar

Jolivet, R., Kobayashi, R., Rauch, A., Naud, R., Shinomoto, S., and Gerstner, W. (2008). A benchmark test for a quantitative assessment of simple neuron models. J. Neurosci. Methods 169, 417–424. doi:10.1016/j.jneumeth.2007.11.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Kandel, E., Koester, J. D., Mack, S. H., and Siegelbaum, S. (2021). Principles of neural science. Sixth Edition6th edition edn. New York, NY: McGraw Hill/Medical.

Google Scholar

Kapardi, M., Pithapuram, M. V., Rangayyan, Y. M., Iyengar, R. S., Singh, A. K., Sripada, S., et al. (2022). In-silico neuro musculoskeletal model reproduces the movement types obtained by spinal micro stimulation. Comput. Methods Programs Biomed. 220, 106804. doi:10.1016/j.cmpb.2022.106804

PubMed Abstract | CrossRef Full Text | Google Scholar

Keener, J., and Sneyd, J. (2009). Mathematical physiology: II: Systems physiology. Interdisciplinary applied mathematics. second edn. New York: Springer-Verlag. doi:10.1007/978-0-387-79388-7

CrossRef Full Text | Google Scholar

Keller, A. (1993). Intrinsic synaptic organization of the motor cortex. Cereb. Cortex 3, 430–441. doi:10.1093/cercor/3.5.430

PubMed Abstract | CrossRef Full Text | Google Scholar

Kent-Braun, J. A., and Ng, A. V. (1999). Specific strength and voluntary muscle activation in young and elderly women and men. J. Appl. Physiology 87, 22–29. doi:10.1152/jappl.1999.87.1.22

PubMed Abstract | CrossRef Full Text | Google Scholar

Klotz, T., Bleiler, C., and Röhrle, O. (2021). A physiology-guided classification of active-stress and active-strain approaches for continuum-mechanical modeling of skeletal muscle tissue. Front. Physiology 12, 685531. doi:10.3389/fphys.2021.685531

CrossRef Full Text | Google Scholar

Klotz, T., Gizzi, L., and Röhrle, O. (2022). Investigating the spatial resolution of EMG and MMG based on a systemic multi-scale model. Biomechanics Model. Mechanobiol. 21, 983–997. doi:10.1007/s10237-022-01572-7

CrossRef Full Text | Google Scholar

Krutki, P., Mrowczynski, W., Celichowski, J., and Baczyk, M. (2022). Ia epsps in rat spinal motoneurons are potentiated after a 5-week whole body vibration. J. Appl. Physiology 132, 178–186. doi:10.1152/japplphysiol.00519.2021

CrossRef Full Text | Google Scholar

Kumar, A., Rotter, S., and Aertsen, A. (2008). Conditions for propagating synchronous spiking and asynchronous firing rates in a cortical network model. J. Neurosci. 28, 5268–5280. doi:10.1523/JNEUROSCI.2542-07.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Lacroix, S., Havton, L. A., McKay, H., Yang, H., Brant, A., Roberts, J., et al. (2004). Bilateral corticospinal projections arise from each motor cortex in the macaque monkey: A quantitative study. J. Comp. Neurology 473, 147–161. doi:10.1002/cne.20051

PubMed Abstract | CrossRef Full Text | Google Scholar

Lapatki, B. G., Eiglsperger, U., Schindler, H. J., Radeke, J., Holobar, A., and van Dijk, J. P. (2019). Three-dimensional amplitude characteristics of masseter motor units and representativeness of extracted motor unit samples. Clin. Neurophysiol. 130, 388–395. doi:10.1016/j.clinph.2018.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Larremore, D. B., Shew, W. L., Ott, E., and Restrepo, J. G. (2011). Effects of network topology, transmission delays, and refractoriness on the response of coupled excitable systems to a stochastic stimulus. Chaos 21, 025117. doi:10.1063/1.3600760

PubMed Abstract | CrossRef Full Text | Google Scholar

Larsson, L., Degens, H., Li, M., Salviati, L., il Lee, Y., Thompson, W., et al. (2018). Sarcopenia: Aging-Related loss of muscle mass and function. Physiol. Rev. 99, 427–511. doi:10.1152/physrev.00061.2017

PubMed Abstract | CrossRef Full Text | Google Scholar

Lebedev, M. A., Ossadtchi, A., Mill, N. A., Urpí, N. A., Cervera, M. R., and Nicolelis, M. A. (2019). Analysis of neuronal ensemble activity reveals the pitfalls and shortcomings of rotation dynamics. Sci. Rep. 9, 18978. doi:10.1038/s41598-019-54760-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemon, R. N. (2008). Descending pathways in motor control. Annu. Rev. Neurosci. 31, 195–218. doi:10.1146/annurev.neuro.31.060407.125547

PubMed Abstract | CrossRef Full Text | Google Scholar

Lexell, J., and Downham, D. Y. (1991). The occurrence of fibre-type grouping in healthy human muscle: A quantitative study of cross-sections of whole vastus lateralis from men between 15 and 83 years. Acta Neuropathol. 81, 377–381. doi:10.1007/BF00293457

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, N., Chen, T. W., Guo, Z. V., Gerfen, C. R., and Svoboda, K. (2015a). A motor cortex circuit for motor planning and movement. Nature 519, 51–56. doi:10.1038/nature14178

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Chen, Y. T., Francisco, G. E., Zhou, P., and Rymer, W. Z. (2019). A unifying pathophysiological account for post-stroke spasticity and disordered motor control. Front. Neurology 10, 468. doi:10.3389/fneur.2019.00468

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Zhuang, C., Hao, M., He, X., Marquez, J. C., Niu, C. M., et al. (2015b). Coordinated alpha and gamma control of muscles and spindles in movement and posture. Front. Comput. Neurosci. 9, 122. doi:10.3389/fncom.2015.00122

PubMed Abstract | CrossRef Full Text | Google Scholar

Lillicrap, T. P., and Scott, S. H. (2013). Preference distributions of primary motor cortex neurons reflect control solutions optimized for limb biomechanics. Neuron 77, 168–179. doi:10.1016/j.neuron.2012.10.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, C.-C. K., and Crago, P. E. (2002a). Neural and mechanical contributions to the stretch reflex: A model synthesis. Ann. Biomed. Eng. 30, 54–67. doi:10.1114/1.1432692

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, C.-C. K., and Crago, P. E. (2002b). Structural model of the muscle spindle. Ann. Biomed. Eng. 30, 68–83. doi:10.1114/1.1433488

PubMed Abstract | CrossRef Full Text | Google Scholar

Litwin-Kumar, A., and Doiron, B. (2012). Slow dynamics and high variability in balanced cortical networks with clustered connections. Nat. Neurosci. 15, 1498–1505. doi:10.1038/nn.3220

PubMed Abstract | CrossRef Full Text | Google Scholar

Lloyd, D. G., and Besier, T. F. (2003). An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J. Biomechanics 36, 765–776. doi:10.1016/S0021-9290(03)00010-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Logiaco, L., Abbott, L. F., and Escola, S. (2021). Thalamic control of cortical dynamics in a model of flexible motor sequencing. Cell. Rep. 35, 109090. doi:10.1016/j.celrep.2021.109090

PubMed Abstract | CrossRef Full Text | Google Scholar

Maas, S. A., Ellis, B. J., Ateshian, G. A., and Weiss, J. A. (2012). FEBio: Finite elements for biomechanics. J. Biomechanical Eng. 134, 011005. doi:10.1115/1.4005694

PubMed Abstract | CrossRef Full Text | Google Scholar

Macefield, V. G., and Knellwolf, T. P. (2018). Functional properties of human muscle spindles. J. neurophysiology 120, 452–467. doi:10.1152/jn.00071.2018

PubMed Abstract | CrossRef Full Text | Google Scholar

Maier, B., Emamy, N., Krämer, A., and Mehl, M. (2019). “Highly parallel multi-physics simulation of muscular activation and EMG,” in Coupled VIII: Proceedings of the VIII international conference on computational methods for coupled problems in science and engineering, Sitges, Spain (CIMNE), 610–621.

Google Scholar

Malik-Sheriff, R. S., Glont, M., Nguyen, T. V. N., Tiwari, K., Roberts, M. G., Xavier, A., et al. (2020). BioModels — 15 years of sharing computational models in life science. Nucleic Acids Res. 48, D407-D415–D415. doi:10.1093/nar/gkz1055

PubMed Abstract | CrossRef Full Text | Google Scholar

Maltenfort, M. G., and Burke, R. (2003). Spindle model responsive to mixed fusimotor inputs and testable predictions of β feedback effects. J. neurophysiology 89, 2797–2809. doi:10.1152/jn.00942.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

Marshall, N. J., Glaser, J. I., Trautmann, E. M., Amematsro, E. A., Perkins, S. M., Shadlen, M. N., et al. (2022). Flexible neural control of motor units. Nat. Neurosci. 25, 1492–1504. doi:10.1038/s41593-022-01165-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Mascaro, A. L. A., Falotico, E., Petkoski, S., Pasquini, M., Vannucci, L., Tort-Colet, N., et al. (2020). Experimental and computational study on motor control and recovery after stroke: Toward a constructive loop between experimental and virtual embodied neuroscience. Front. Syst. Neurosci. 14, 31. doi:10.3389/fnsys.2020.00031

PubMed Abstract | CrossRef Full Text | Google Scholar

Matthews, P. B. (1991). The human stretch reflex and the motor cortex. Trends Neurosci. 14, 87–91. doi:10.1016/0166-2236(91)90064-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Matthews, P. (1962). The differentiation of two types of fusimotor fibre by their effects on the dynamic response of muscle spindle primary endings. Q. J. Exp. Physiology Cogn. Med. Sci. Transl. Integration 47, 324–333. doi:10.1113/expphysiol.1962.sp001616

PubMed Abstract | CrossRef Full Text | Google Scholar

Maughan, R. J., Watson, J. S., and Weir, J. (1983). Strength and cross-sectional area of human skeletal muscle. J. Physiology 338, 37–49. doi:10.1113/jphysiol.1983.sp014658

PubMed Abstract | CrossRef Full Text | Google Scholar

McDougal, R. A., Morse, T. M., Carnevale, T., Marenco, L., Wang, R., Migliore, M., et al. (2017). Twenty years of modeldb and beyond: Building essential modeling tools for the future of neuroscience. J. Comput. Neurosci. 42, 1–10. doi:10.1007/s10827-016-0623-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Mesin, L. (2020). Crosstalk in surface electromyogram: Literature review and some insights. Phys. Eng. Sci. Med. 43, 481–492. doi:10.1007/s13246-020-00868-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Messi, M. L., Li, T., Wang, Z.-M., Marsh, A. P., Nicklas, B., and Delbono, O. (2016). Resistance training enhances skeletal muscle innervation without modifying the number of satellite cells or their myofiber association in obese older adults. Journals Gerontology Ser. A 71, 1273–1280. doi:10.1093/gerona/glv176

CrossRef Full Text | Google Scholar

Michaels, J. A., Dann, B., and Scherberger, H. (2016). Neural population dynamics during reaching are better explained by a dynamical system than representational tuning. PLoS Comput. Biol. 12, e1005175. doi:10.1371/journal.pcbi.1005175

PubMed Abstract | CrossRef Full Text | Google Scholar

Michaels, J. A., Schaffelhofer, S., Agudelo-Toro, A., and Scherberger, H. (2020). A goal-driven modular neural network predicts parietofrontal neural dynamics during grasping. Proc. Natl. Acad. Sci. U. S. A. 117, 32124–32135. doi:10.1073/pnas.2005087117

PubMed Abstract | CrossRef Full Text | Google Scholar

Mileusnic, M., and Loeb, G. (2009). Force estimation from ensembles of golgi tendon organs. J. neural Eng. 6, 036001. doi:10.1088/1741-2560/6/3/036001

PubMed Abstract | CrossRef Full Text | Google Scholar

Mileusnic, M. P., Brown, I. E., Lan, N., and Loeb, G. E. (2006). Mathematical models of proprioceptors. I. control and transduction in the muscle spindle. J. neurophysiology 96, 1772–1788. doi:10.1152/jn.00868.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Mileusnic, M. P., and Loeb, G. E. (2006). Mathematical models of proprioceptors. II. structure and function of the golgi tendon organ. J. neurophysiology 96, 1789–1802. doi:10.1152/jn.00869.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitz, A. R., and Wise, S. P. (1997). The somatotopic organization of the supplementary motor area: Intracortical microstimulation mapping. J. Neurosci. 7, 1010–1021. doi:10.1523/JNEUROSCI.07-04-01010.1987

PubMed Abstract | CrossRef Full Text | Google Scholar

Moraud, E. M., Capogrosso, M., Formento, E., Wenger, N., DiGiovanna, J., Courtine, G., et al. (2016). Mechanisms underlying the neuromodulation of spinal circuits for correcting gait and balance deficits after spinal cord injury. Neuron 89, 814–828. doi:10.1016/j.neuron.2016.01.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Mordhorst, M., Heidlauf, T., and Röhrle, O. (2015). Predicting electromyographic signals under realistic conditions using a multiscale chemo–electro–mechanical finite element model. Interface Focus 5, 20140076. doi:10.1098/rsfs.2014.0076

PubMed Abstract | CrossRef Full Text | Google Scholar

Mukherjee, A., and Chakravarty, A. (2010). Spasticity mechanisms - for the clinician. Front. Neurology 1, 149. doi:10.3389/fneur.2010.00149

PubMed Abstract | CrossRef Full Text | Google Scholar

Mussa-Ivaldi, F. A. (1988). Do neurons in the motor cortex encode movement direction? An alternative hypothesis. Neurosci. Lett. 91, 106–111. doi:10.1016/0304-3940(88)90257-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Natali, A., Reddy, V., and Bordoni, B. (2022). Neuroanatomy, corticospinal cord tract. Treasure Island, FL: StatPearls Publishing.

Google Scholar

Negro, F., and Farina, D. (2011). Decorrelation of cortical inputs and motoneuron output. J. neurophysiology 106, 2688–2697. doi:10.1152/jn.00336.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Negro, F., Muceli, S., Castronovo, A. M., Holobar, A., and Farina, D. (2016a). Multi-channel intramuscular and surface EMG decomposition by convolutive blind source separation. J. neural Eng. 13, 026027. doi:10.1088/1741-2560/13/2/026027

PubMed Abstract | CrossRef Full Text | Google Scholar

Negro, F., Yavuz, U. Ş., and Farina, D. (2016b). The human motor neuron pools receive a dominant slow-varying common synaptic input. J. physiology 594, 5491–5505. doi:10.1113/JP271748

PubMed Abstract | CrossRef Full Text | Google Scholar

Newman, J. P., Zeller-Townson, R., Fong, M. F., Desai, S. A., Gross, R. E., and Potter, S. M. (2012). Closed-loop, multichannel experimentation using the open-source NeuroRighter electrophysiology platform. Front. Neural Circuits 6, 98. doi:10.3389/fncir.2012.00098

PubMed Abstract | CrossRef Full Text | Google Scholar

Ni, Z., Müller-Dahlhaus, F., Chen, R., and Ziemann, U. (2011). Triple-pulse TMS to study interactions between neural circuits in human cortex. Brain Stimul. 4, 281–293. doi:10.1016/j.brs.2011.01.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Nickerson, D., Atalag, K., de Bono, B., Geiger, J., Goble, C., Hollmann, S., et al. (2016). The Human Physiome: How standards, software and innovative service infrastructures are providing the building blocks to make it achievable. Interface Focus 6, 20150103. doi:10.1098/rsfs.2015.0103

PubMed Abstract | CrossRef Full Text | Google Scholar

Nordh, E., Hilliger, M., and Vallbo, Å. (1983). The variability of inter-spike intervals of human spindle afferents in relaxed muscles. Brain Res. 271, 89–99. doi:10.1016/0006-8993(83)91367-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Oh, S. W., Harris, J. A., Ng, L., Winslow, B., Cain, N., Mihalas, S., et al. (2014). A mesoscale connectome of the mouse brain. Nature 508, 207–214. doi:10.1038/nature13186

PubMed Abstract | CrossRef Full Text | Google Scholar

Oomens, C. W. J., Maenhout, M., van Oijen, C. H., Drost, M. R., and Baaijens, F. P. (2003). Finite element modelling of contracting skeletal muscle. Philosophical Trans. R. Soc. B Biol. Sci. 358, 1453–1460. doi:10.1098/rstb.2003.1345

PubMed Abstract | CrossRef Full Text | Google Scholar

Osborne, H., Lai, Y. M., Lepperød, M. E., Sichau, D., Deutz, L., and De Kamps, M. (2021). Miind: A model-agnostic simulator of neural populations. Front. Neuroinformatics 15, 614881. doi:10.3389/fninf.2021.614881

CrossRef Full Text | Google Scholar

Oswald, M., Tantirigama, M., Sonntag, I., Hughes, S., and Empson, R. (2013). Diversity of layer 5 projection neurons in the mouse motorcortex. Front. Cell. Neurosci. 7, 174. doi:10.3389/fncel.2013.00174

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, M. C., Belhaj-Saïf, A., Gordon, M., and Cheney, P. D. (2001). Consistent features in the forelimb representation of primary motor cortex in rhesus macaques. J. Neurosci. 21, 2784–2792. doi:10.1523/jneurosci.21-08-02784.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Parziale, A., Senatore, R., and Marcelli, A. (2020). Exploring speed–accuracy tradeoff in reaching movements: A neurocomputational model. Neural Comput. Appl. 32, 13377–13403. doi:10.1007/s00521-019-04690-z

CrossRef Full Text | Google Scholar

Péan, F., Tanner, C., Gerber, C., Fürnstahl, P., and Goksel, O. (2019). A comprehensive and volumetric musculoskeletal model for the dynamic simulation of the shoulder function. Comput. Methods Biomechanics Biomed. Eng. 22, 740–751. doi:10.1080/10255842.2019.1588963

CrossRef Full Text | Google Scholar

Penfield, W., and Boldrey, E. (1937). Somatic motor and sensory representation in the cerebral cortex of man as studied by electrical stimulation. Brain A J. Neurology 60, 389–443. doi:10.1093/brain/60.4.389

CrossRef Full Text | Google Scholar

Pérez Fernández, J., Alcázar Vargas, M., Velasco García, J. M., Cabrera Carrillo, J. A., and Castillo Aguilar, J. J. (2021). A biological-like controller using improved spiking neural networks. Neurocomputing 463, 237–250. doi:10.1016/j.neucom.2021.08.005

CrossRef Full Text | Google Scholar

Pierrot-Deseilligny, E. (2002). Propriospinal transmission of part of the corticospinal excitation in humans. Muscle Nerve 26, 155–172. doi:10.1002/mus.1240

PubMed Abstract | CrossRef Full Text | Google Scholar

Potjans, T. C., and Diesmann, M. (2014). The cell-type specific cortical microcircuit: Relating structure and activity in a full-scale spiking network model. Cereb. Cortex 24, 785–806. doi:10.1093/cercor/bhs358

PubMed Abstract | CrossRef Full Text | Google Scholar

Potter, S. M., El Hady, A., and Fetz, E. E. (2014). Closed-loop neuroscience and neuroengineering. Front. Neural Circuits 8, 115. doi:10.3389/fncir.2014.00115

PubMed Abstract | CrossRef Full Text | Google Scholar

Powers, R. K., and Binder, M. D. (1985). Distribution of oligosynaptic group i input to the cat medial gastrocnemius motoneuron pool. J. neurophysiology 53, 497–517. doi:10.1152/jn.1985.53.2.497

PubMed Abstract | CrossRef Full Text | Google Scholar

Prochazka, A., and Gorassini, M. (1998). Models of ensemble firing of muscle spindle afferents recorded during normal locomotion in cats. J. physiology 507, 277–291. doi:10.1111/j.1469-7793.1998.277bu.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Proske, U., and Gandevia, S. C. (2012). The proprioceptive senses: Their roles in signaling body shape, body position and movement, and muscle force. Physiol. Rev. 92, 1651–1697. doi:10.1152/physrev.00048.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Purslow, P. P. (2010). Muscle fascia and force transmission. J. Bodyw. Mov. Ther. 14, 411–417. doi:10.1016/j.jbmt.2010.01.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Raikova, R., Celichowski, J., Angelova, S., and Krutki, P. (2018). A model of the rat medial gastrocnemius muscle based on inputs to motoneurons and on an algorithm for prediction of the motor unit force. J. Neurophysiology 120, 1973–1987. doi:10.1152/jn.00041.2018

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramasamy, E., Avci, O., Dorow, B., Chong, S.-Y., Gizzi, L., Steidle, G., et al. (2018). An efficient modelling-simulation-analysis workflow to investigate stump-socket interaction using patient-specific, three-dimensional, continuum-mechanical, finite element residual limb models. Front. Bioeng. Biotechnol. 6, 126. doi:10.3389/fbioe.2018.00126

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramsey, R. W., and Street, S. F. (1940). The isometric length-tension diagram of isolated skeletal muscle fibers of the frog. J. Cell. Comp. Physiology 15, 11–34. doi:10.1002/jcp.1030150103

CrossRef Full Text | Google Scholar

Raphael, G., Tsianos, G. A., and Loeb, G. E. (2010). Spinal-like regulator facilitates control of a two-degree-of-freedom wrist. J. Neurosci. 30, 9431–9444. doi:10.1523/JNEUROSCI.5537-09.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Rathelot, J.-A., and Strick, P. L. (2009). Subdivisions of primary motor cortex based on cortico-motoneuronal cells. Proc. Natl. Acad. Sci. 106, 918–923. doi:10.1073/pnas.0808362106

PubMed Abstract | CrossRef Full Text | Google Scholar

Razumova, M. V., Bukatina, A. E., and Campbell, K. B. (1999). Stiffness-distortion sarcomere model for muscle simulation. J. Appl. Physiology 87, 1861–1876. doi:10.1152/jappl.1999.87.5.1861

PubMed Abstract | CrossRef Full Text | Google Scholar

Reina, G. A., Moran, D. W., Schwartz, A. B., and Anthony, G. (2001). On the relationship between joint angular velocity and motor cortical discharge during reaching. Am. Physiological Soc. 85, 2576–2589. doi:10.1152/jn.2001.85.6.2576

PubMed Abstract | CrossRef Full Text | Google Scholar

Reschechtko, S., and Pruszynski, J. (2020). Stretch reflexes, 30. Cambridge, MA: Cell Press, 1025–1030. doi:10.1016/j.cub.2020.07.092

CrossRef Full Text | Google Scholar

Robinson, J. T., Jorgolli, M., and Park, H. (2013). Nanowire electrodes for high-density stimulation and measurement of neural circuits. Front. Neural Circuits 7, 38. doi:10.3389/fncir.2013.00038

PubMed Abstract | CrossRef Full Text | Google Scholar

Rockenfeller, R., and Günther, M. (2017a). Hill equation and Hatze’s muscle activation dynamics complement each other: Enhanced pharmacological and physiological interpretability of modelled activity-pCa curves. J. Theor. Biol. 431, 11–24. doi:10.1016/j.jtbi.2017.07.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Rockenfeller, R., and Günther, M. (2017b). How to model a muscle’s active force–length relation: A comparative study. Comput. Methods Appl. Mech. Eng. 313, 321–336. doi:10.1016/j.cma.2016.10.003

CrossRef Full Text | Google Scholar

Rohlén, R., Stålberg, E., Stöverud, K.-H., Yu, J., and Grönlund, C. (2020). A method for identification of mechanical response of motor units in skeletal muscle voluntary contractions using ultrafast ultrasound imaging—simulations and experimental tests. IEEE Access 8, 50299–50311. doi:10.1109/ACCESS.2020.2980053

CrossRef Full Text | Google Scholar

Röhrle, O., Davidson, J. B., and Pullan, A. J. (2008). Bridging scales: A three-dimensional electromechanical finite element model of skeletal muscle. SIAM J. Sci. Comput. 30, 2882–2904. doi:10.1137/070691504

CrossRef Full Text | Google Scholar

Röhrle, O., and Pullan, A. J. (2007). Three-dimensional finite element modelling of muscle forces during mastication. J. Biomechanics 40, 3363–3372. doi:10.1016/j.jbiomech.2007.05.011

CrossRef Full Text | Google Scholar

Röhrle, O., Sprenger, M., and Schmitt, S. (2017). A two-muscle, continuum-mechanical forward simulation of the upper limb. Biomechanics Model. Mechanobiol. 16, 743–762. doi:10.1007/s10237-016-0850-x

CrossRef Full Text | Google Scholar

Röhrle, O., Yavuz, U. Ş., Klotz, T., Negro, F., and Heidlauf, T. (2019). Multiscale modeling of the neuromuscular system: Coupling neurophysiology and skeletal muscle mechanics. Wiley Interdiscip. Rev. Syst. Biol. Med. 11, e1457. doi:10.1002/wsbm.1457

PubMed Abstract | CrossRef Full Text | Google Scholar

Ross, S. M. (2014). Introduction to probability models. Academic Press.

Google Scholar

Rostami, V., Rost, T., Riehle, A., van Albada, S. J., and Nawrot, M. P. (2020). Spiking neural network model of motor cortex with joint excitatory and inhibitory clusters reflects task uncertainty, reaction times, and variability dynamics. bioRxiv. doi:10.1101/2020.02.27.968339

CrossRef Full Text | Google Scholar

Saini, H., Klotz, T., and Röhrle, O. (2022). Modelling motor units in 3D: Influence on muscle contraction and joint force via a proof of concept simulation. Res. Square Prepr. doi:10.21203/rs.3.rs-1867821/v1

CrossRef Full Text | Google Scholar

Saini, H., and Röhrle, O. (2022). A biophysically guided constitutive law of the musculotendon-complex: Modelling and numerical implementation in Abaqus. Comput. Methods Programs Biomed. 107152doi, 107152. doi:10.1016/j.cmpb.2022.107152

PubMed Abstract | CrossRef Full Text | Google Scholar

Saini, H., and Röhrle, O. (2023). “Simulation study to investigate the accuracy of in vivo motor-unit twitch force measurements,” in Computer methods, imaging and visualization in biomechanics and biomedical engineering II (Springer International Publishing), 234–243. doi:10.1007/978-3-031-10015-4_20

CrossRef Full Text | Google Scholar

Saleeba, C., Dempsey, B., Le, S., Goodchild, A., and McMullan, S. (2019). A student’s guide to neural circuit tracing. Front. Neurosci. 13, 897. doi:10.3389/fnins.2019.00897

PubMed Abstract | CrossRef Full Text | Google Scholar

Saliani, A., Perraud, B., Duval, T., Stikov, N., Rossignol, S., and Cohen-Adad, J. (2017). Axon and myelin morphology in animal and human spinal cord. Front. Neuroanat. 11, 129. doi:10.3389/fnana.2017.00129

PubMed Abstract | CrossRef Full Text | Google Scholar

Sartori, M., Yavuz, U. Ş., and Farina, D. (2017). In vivo neuromechanics: Decoding causal motor neuron behavior with resulting musculoskeletal function. Sci. Rep. 7, 13465. doi:10.1038/s41598-017-13766-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Sauerbrei, B. A., Guo, J. Z., Cohen, J. D., Mischiati, M., Guo, W., Kabra, M., et al. (2020). Cortical pattern generation during dexterous movement is input-driven. Nature 577, 386–391. doi:10.1038/s41586-019-1869-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Schäfer, S. (1974). The discharge frequencies of primary muscle spindle endings during simultaneous stimulation of two fusimotor filaments. Pflügers Arch. 350, 359–372. doi:10.1007/BF00592644

CrossRef Full Text | Google Scholar

Schieber, M. H. (2001). Constraints on somatotopic organization in the primary motor cortex. J. Neurophysiology 86, 2125–2143. doi:10.1152/jn.2001.86.5.2125

PubMed Abstract | CrossRef Full Text | Google Scholar

Schirner, M., Domide, L., Perdikis, D., Triebkorn, P., Stefanovski, L., Pai, R., et al. (2022). Brain simulation as a cloud service: The Virtual Brain on EBRAINS. NeuroImage 251, 118973. doi:10.1016/j.neuroimage.2022.118973

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmid, L., Klotz, T., Siebert, T., and Röhrle, O. (2019). Characterization of electromechanical delay based on a biophysical multi-scale skeletal muscle model. Front. Physiology 10, 1270. doi:10.3389/fphys.2019.01270

CrossRef Full Text | Google Scholar

Schmid, L., Klotz, T., Yavuz, U. Ş., Maltenfort, M., and Röhrle, O. (2022). Spindle model responsive to mixed fusimotor inputs: An updated version of the maltenfort and Burke (2003) model. Physiome. doi:10.36903/physiome.19070171.v2

CrossRef Full Text | Google Scholar

Schmitt, S., Günther, M., and Häufle, D. F. B. (2019). The dynamics of the skeletal muscle: A systems biophysics perspective on muscle modeling with the focus on hill-type muscle models. Mittl. 42. doi:10.1002/gamm.201900013

CrossRef Full Text | Google Scholar

Schoultz, T. W., and Swett, J. E. (1972). The fine structure of the golgi tendon organ. J. Neurocytol. 1, 1–26. doi:10.1007/BF01098642

PubMed Abstract | CrossRef Full Text | Google Scholar

Schuurmans, J., de Vlugt, E., Schouten, A. C., Meskers, C. G., de Groot, J. H., and van der Helm, F. C. (2009). The monosynaptic Ia afferent pathway can largely explain the stretch duration effect of the long latency M2 response. Exp. Brain Res. 193, 491–500. doi:10.1007/s00221-008-1647-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Scott, J. G., and Mendell, L. M. (1976). Individual EPSPs produced by single triceps surae Ia afferent fibers in homonymous and heteronymous motoneurons. J. Neurophysiology 39, 679–692. doi:10.1152/jn.1976.39.4.679

PubMed Abstract | CrossRef Full Text | Google Scholar

Scott, S. H. (2016). A functional taxonomy of bottom-up sensory feedback processing for motor actions. Trends Neurosci. 39, 512–526. doi:10.1016/j.tins.2016.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Scott, S. H. (2008). Inconvenient Truths about neural processing in primary motor cortex. J. Physiology 586, 1217–1224. doi:10.1113/jphysiol.2007.146068

PubMed Abstract | CrossRef Full Text | Google Scholar

Scott, S. H. (2000). Population vectors and motor cortex: Neural coding or epiphenomenon? Nat. Neurosci. 3, 307–308. doi:10.1038/73859

PubMed Abstract | CrossRef Full Text | Google Scholar

Scott, W., Stevens, J., and Binder–Macleod, S. A. (2001). Human skeletal muscle fiber type classifications. Phys. Ther. 81, 1810–1816. doi:10.1093/ptj/81.11.1810

PubMed Abstract | CrossRef Full Text | Google Scholar

Scovil, C. Y., and Ronsky, J. L. (2006). Sensitivity of a Hill-based muscle model to perturbations in model parameters. J. Biomechanics 39, 2055–2063. doi:10.1016/j.jbiomech.2005.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Sergio, L. E., and Kalaska, J. F. (1997). Systematic changes in directional tuning of motor cortex cell activity with hand location in the workspace during generation of static isometric forces in constant spatial directions. J. Neurophysiology 78, 1170–1174. doi:10.1152/jn.1997.78.2.1170

PubMed Abstract | CrossRef Full Text | Google Scholar

Seth, A., Hicks, J. L., Uchida, T. K., Habib, A., Dembia, C. L., Dunne, J. J., et al. (2018). OpenSim: Simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLOS Comput. Biol. 14, e1006223. doi:10.1371/journal.pcbi.1006223

PubMed Abstract | CrossRef Full Text | Google Scholar

Shall, M. S., and Goldberg, S. J. (1992). Extraocular motor units: Type classification and motoneuron stimulation frequency-muscle unit force relationships. Brain Res. 587, 291–300. doi:10.1016/0006-8993(92)91010-C

PubMed Abstract | CrossRef Full Text | Google Scholar

She, Q., Chen, G., and Chan, R. H. (2016). Evaluating the small-world-ness of a sampled network: Functional connectivity of entorhinal-hippocampal circuitry. Sci. Rep. 6, 21468. doi:10.1038/srep21468

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheean, G. (2002). The pathophysiology of spasticity. Eur. J. Neurology 9, 3–9. doi:10.1046/j.1468-1331.2002.0090s1003.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Shenoy, K. V., Sahani, M., and Churchland, M. M. (2013). Cortical control of arm movements: A dynamical systems perspective. Annu. Rev. Neurosci. 36, 337–359. doi:10.1146/annurev-neuro-062111-150509

PubMed Abstract | CrossRef Full Text | Google Scholar

Shorten, P. R., O’Callaghan, P., Davidson, J. B., and Soboleva, T. K. (2007). A mathematical model of fatigue in skeletal muscle force contraction. J. Muscle Res. Cell. Motil. 28, 293–313. doi:10.1007/s10974-007-9125-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Sreenivasa, M., Ayusawa, K., and Nakamura, Y. (2015). Modeling and identification of a realistic spiking neural network and musculoskeletal model of the human arm, and an application to the stretch reflex. IEEE Trans. Neural Syst. Rehabilitation Eng. 24, 591–602. doi:10.1109/TNSRE.2015.2478858

PubMed Abstract | CrossRef Full Text | Google Scholar

Stauffer, E. K., Watt, D., Taylor, A., Reinking, R. M., and Stuart, D. G. (1976). Analysis of muscle receptor connections by spike-triggered averaging. 2. spindle group ii afferents. J. Neurophysiology 39, 1393–1402. doi:10.1152/jn.1976.39.6.1393

PubMed Abstract | CrossRef Full Text | Google Scholar

Stienen, A. H., Schouten, A. C., Schuurmans, J., and Van Der Helm, F. C. (2007). Analysis of reflex modulation with a biologically realistic neural network. J. Comput. Neurosci. 23, 333–348. doi:10.1007/s10827-007-0037-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Stimberg, M., Brette, R., and Goodman, D. (2019). Brian 2, an intuitive and efficient neural simulator. eLIFE 8, e47314–e47341. doi:10.7554/eLife.47314

PubMed Abstract | CrossRef Full Text | Google Scholar

Stuart, G., and Redman, S. (1990). Voltage dependence of Ia reciprocal inhibitory currents in cat spinal motoneurones. J. physiology 420, 111–125. doi:10.1113/jphysiol.1990.sp017903

PubMed Abstract | CrossRef Full Text | Google Scholar

Suminski, A. J., Mardoum, P., Lillicrap, T. P., and Hatsopoulos, N. G. (2015). Temporal evolution of both premotor and motor cortical tuning properties reflect changes in limb biomechanics. J. Neurophysiology 113, 2812–2823. doi:10.1152/jn.00486.2014

PubMed Abstract | CrossRef Full Text | Google Scholar

Sussillo, D., Churchland, M., Kaufman, M., and Shenoy, K. (2016). A neural network that finds a naturalistic solution for the production of muscle activity. Nat. Neurosci. 18, 1025–1033. doi:10.1038/nn.4042

PubMed Abstract | CrossRef Full Text | Google Scholar

Tanaka, H. (2016). Modeling the motor cortex: Optimality, recurrent neural networks, and spatial dynamics. Neurosci. Res. 104, 64–71. doi:10.1016/j.neures.2015.10.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Tawil, R., and Venance, S. (2011). Neuromuscular disorders. John Wiley & Sons.

Google Scholar

Teka, W. W., Hamade, K. C., Barnett, W. H., Kim, T., Markin, S. N., Rybak, I. A., et al. (2017). From the motor cortex to the movement and back again. PloS one 12, e0179288. doi:10.1371/journal.pone.0179288

PubMed Abstract | CrossRef Full Text | Google Scholar

Todorov, E. (2000). Direct cortical control of muscle activation in voluntary arm movements: A model. Nat. Neurosci. 3, 391–398. doi:10.1038/73964

PubMed Abstract | CrossRef Full Text | Google Scholar

Tomov, P., Pena, R. F., Zaks, M. A., and Roque, A. C. (2014). Sustained oscillations, irregular firing, and chaotic dynamics in hierarchical modular networks with mixtures of electrophysiological cell types. Front. Comput. Neurosci. 8, 103. doi:10.3389/fncom.2014.00103

PubMed Abstract | CrossRef Full Text | Google Scholar

Trappenberg, T. (2002). Fundamentals of computational neuroscience. Oxford University Press UK.

Google Scholar

Trautmann, E. M., O’Shea, D. J., Sun, X., Marshel, J. H., Crow, A., Hsueh, B., et al. (2021). Dendritic calcium signals in rhesus macaque motor cortex drive an optical brain-computer interface. Nat. Commun. 12, 3689. doi:10.1038/s41467-021-23884-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Tresch, M. C., and Bizzi, E. (1999). Responses to spinal microstimulation in the chronically spinalized rat and their relationship to spinal systems activated by low threshold cutaneous stimulation. Exp. Brain Res. 129, 401–416. doi:10.1007/s002210050908

PubMed Abstract | CrossRef Full Text | Google Scholar

Troiani, D., Filippi, G. M., and Bassi, F. A. (1999). Nonlinear tension summation of different combinations of motor units in the anesthetized cat peroneus longus muscle. J. Neurophysiology 81, 771–780. doi:10.1152/jn.1999.81.2.771

PubMed Abstract | CrossRef Full Text | Google Scholar

Turrina, A., Martínez-González, M. A., and Stecco, C. (2013). The muscular force transmission system: Role of the intramuscular connective tissue. J. Bodyw. Mov. Ther. 17, 95–102. doi:10.1016/j.jbmt.2012.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Udvary, D., Harth, P., Macke, J. H., Hege, H. C., de Kock, C. P., Sakmann, B., et al. (2022). The impact of neuron morphology on cortical network architecture. Cell. Rep. 39, 110677. doi:10.1016/j.celrep.2022.110677

PubMed Abstract | CrossRef Full Text | Google Scholar

van Dijk, J. P., Eiglsperger, U., Hellmann, D., Giannakopoulos, N. N., McGill, K. C., Schindler, H. J., et al. (2016). Motor unit activity within the depth of the masseter characterized by an adapted scanning EMG technique. Clin. Neurophysiol. 127, 3198–3204. doi:10.1016/j.clinph.2016.05.186

PubMed Abstract | CrossRef Full Text | Google Scholar

van Leeuwen, J. L. (1991). Optimum power output and structural design of sarcomeres. J. Theor. Biol. 149, 229–256. doi:10.1016/S0022-5193(05)80279-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Vannucci, L., Falotico, E., and Laschi, C. (2017). Proprioceptive feedback through a neuromorphic muscle spindle model. Front. Neurosci. 11, 341. doi:10.3389/fnins.2017.00341

PubMed Abstract | CrossRef Full Text | Google Scholar

Varshney, L. R., Chen, B. L., Paniagua, E., Hall, D. H., and Chklovskii, D. B. (2011). Structural properties of the caenorhabditis elegans neuronal network. PLoS Comput. Biol. 7, e1001066. doi:10.1371/journal.pcbi.1001066

PubMed Abstract | CrossRef Full Text | Google Scholar

Volk, V. L., Hamilton, L. D., Hume, D. R., Shelburne, K. B., and Fitzpatrick, C. K. (2021). Integration of neural architecture within a finite element framework for improved neuromusculoskeletal modeling. Sci. Rep. 11, 22983. doi:10.1038/s41598-021-02298-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Volz, L., Hamada, M., Rothwell, J., and Grefkes, C. (2015). What makes the muscle twitch: Motor system connectivity and TMS-induced activity. Cereb. Cortex 25, 2346–2353. doi:10.1093/cercor/bhu032

PubMed Abstract | CrossRef Full Text | Google Scholar

Vyas, S., Golub, M. D., Sussillo, D., and Shenoy, K. V. (2020). Computation through neural population dynamics. Annu. Rev. Neurosci. 43, 249–275. doi:10.1146/annurev-neuro-092619-094115

PubMed Abstract | CrossRef Full Text | Google Scholar

Walter, J. R., Saini, H., Maier, B., Mostashiri, N., Aguayo, J. L., Zarshenas, H., et al. (2020). “Comparative study of a biomechanical model-based and black-box approach for subject-specific movement prediction,” in International conference of the IEEE engineering in medicine & biology (society (EMBC), IEEE, 4775–4778. doi:10.1109/EMBC44109.2020.9176600

CrossRef Full Text | Google Scholar

Wang, T., Chen, Y., and Cui, H. (2022). From parametric representation to dynamical system: Shifting views of the motor cortex in motor control. doi:10.1007/s12264-022-00832-x

CrossRef Full Text | Google Scholar

Wang, X. F., and Chen, G. (2003). Complex networks: Small-world, scale-free and beyond. IEEE Circuits Syst. Mag. 3, 6–20. doi:10.1109/MCAS.2003.1228503

CrossRef Full Text | Google Scholar

Watanabe, H., Sano, H., Chiken, S., Kobayashi, K., Fukata, Y., Fukata, M., et al. (2020). Forelimb movements evoked by optogenetic stimulation of the macaque motor cortex. Nat. Commun. 11, 3253. doi:10.1038/s41467-020-16883-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Watt, D., Stauffer, E. K., Taylor, A., Reinking, R. M., and Stuart, D. G. (1976). Analysis of muscle receptor connections by spike-triggered averaging. 1. spindle primary and tendon organ afferents. J. neurophysiology 39, 1375–1392. doi:10.1152/jn.1976.39.6.1375

PubMed Abstract | CrossRef Full Text | Google Scholar

Weickenmeier, J., Jabareen, M., Le Révérend, B. J. D., Ramaioli, M., and Mazza, E. (2017). Experimental and numerical characterization of the mechanical masseter muscle response during biting. J. Biomechanical Eng. 139, 121007. doi:10.1115/1.4037592

CrossRef Full Text | Google Scholar

Weiler, N., Wood, L., Yu, J., Solla, S., and Shepherd, G. M. (2008). Top-down laminar organization of the excitatory network in motor cortex. Nat. Neurosci. 11, 360–366. doi:10.1038/nn2049

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, H. R., and Cowan, J. D. (1972). Excitatory and inhibitory interactions in localized populations of model neurons. Biophysical J. 12, 1–24. doi:10.1016/S0006-3495(72)86068-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Windhorst, U. (1990). Activation of renshaw cells. Prog. Neurobiol. 35, 135–179. doi:10.1016/0301-0082(90)90020-H

PubMed Abstract | CrossRef Full Text | Google Scholar

Wochner, I., Driess, D., Zimmermann, H., Haeufle, D. F. B., Toussaint, M., and Schmitt, S. (2020). Optimality principles in human point-to-manifold reaching accounting for muscle dynamics. Front. Comput. Neurosci. 14, 38. doi:10.3389/fncom.2020.00038

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, T., Hung, A., and Mithraratne, K. (2014). Generating facial expressions using an anatomically accurate biomechanical model. IEEE Trans. Vis. Comput. Graph. 20, 1519–1529. doi:10.1109/TVCG.2014.2339835

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, W., Lee, P. V. S., Bryant, A. L., Galea, M., and Ackland, D. C. (2016). Subject-specific musculoskeletal modeling in the evaluation of shoulder muscle and joint function. J. Biomechanics 49, 3626–3634. doi:10.1016/j.jbiomech.2016.09.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, M., Atallah, B. V., and Scanziani, M. (2014). Equalizing excitation-inhibition ratios across visual cortical neurons. Nature 511, 596–600. doi:10.1038/nature13321

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamazaki, K., Vo-Ho, V. K., Bulsara, D., and Le, N. (2022). Spiking neural networks and their applications: A review. Brain Sci. 12, 863. doi:10.3390/brainsci12070863

PubMed Abstract | CrossRef Full Text | Google Scholar

Yavuz, U. Ş., Negro, F., Diedrichs, R., and Farina, D. (2018). Reciprocal inhibition between motor neurons of the tibialis anterior and triceps surae in humans. J. neurophysiology 119, 1699–1706. doi:10.1152/jn.00424.2017

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeo, S. S., Chang, P.-H., and Jang, S. H. (2013). The cortical activation differences between proximal and distal joint movements of the upper extremities: A functional nirs study. NeuroRehabilitation 32, 861–866. doi:10.3233/NRE-130910

PubMed Abstract | CrossRef Full Text | Google Scholar

York, G., Osborne, H., Sriya, P., Astill, S., de Kamps, M., and Chakrabarty, S. (2022). The effect of limb position on a static knee extension task can be explained with a simple spinal cord circuit model. J. Neurophysiology 127, 173–187. doi:10.1152/jn.00208.2021

PubMed Abstract | CrossRef Full Text | Google Scholar

Young, N., Collins, C., and Kaas, J. (2013). Cell and neuron densities in the primary motor cortex of primates. Front. Neural Circuits 7, 30–11. doi:10.3389/fncir.2013.00030

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, T., Lloyd, C. M., Nickerson, D. P., Cooling, M. T., Miller, A. K., Garny, A., et al. (2011). The Physiome model repository 2. Bioinformatics 27, 743–744. doi:10.1093/bioinformatics/btq723

PubMed Abstract | CrossRef Full Text | Google Scholar

Zaback, M., Tiwari, E., Krupka, A. J., Marchionne, F., Negro, F., Lemay, M. A., et al. (2022). Toward assessing the functional connectivity of spinal neurons. Front. Neural Circuits 16, 839521. doi:10.3389/fncir.2022.839521

PubMed Abstract | CrossRef Full Text | Google Scholar

Zahalak, G. I. (1981). A distribution-moment approximation for kinetic theories of muscular contraction. Math. Biosci. 55, 89–114. doi:10.1016/0025-5564(81)90014-6

CrossRef Full Text | Google Scholar

Zajac, F. E. (1989). Muscle and tendon: Properties, models, scaling, and application to biomechanics and motor control. Crit. Rev. Biomed. Eng. 17, 359–411.

PubMed Abstract | Google Scholar

Zengel, J. E., Reid, S. A., Sypert, G. W., and Munson, J. B. (1985). Membrane electrical properties and prediction of motor-unit type of medial gastrocnemius motoneurons in the cat. J. neurophysiology 53, 1323–1344. doi:10.1152/jn.1985.53.5.1323

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Sorby, H., Clement, J., Thomas, C. D. L., Hunter, P., Nielsen, P., et al. (2014). “The MAP client: User-friendly musculoskeletal modelling workflows,” in Biomedical simulation. Lecture notes in computer science. Editors F. Bello, and S. Cotin (Cham: Springer International Publishing), 182–192. doi:10.1007/978-3-319-12057-7_21

CrossRef Full Text | Google Scholar

Ziemann, U. (2013). Pharmaco-transcranial magnetic stimulation studies of motor excitability. Handb. Clin. Neurology 116, 387–397. doi:10.1016/B978-0-444-53497-2.00032-2

PubMed Abstract | CrossRef Full Text | Google Scholar