A glucose-insulin-glucagon coupled model of the isoglycemic intravenous glucose infusion experiment

Type 2 diabetes (T2D) is a pathophysiology that is characterized by insulin resistance, beta- and alpha-cell dysfunction. Mathematical models of various glucose challenge experiments have been developed to quantify the contribution of insulin and beta-cell dysfunction to the pathophysiology of T2D. There is a need for effective extended models that also capture the impact of alpha-cell dysregulation on T2D. In this paper a delay differential equation-based model is developed to describe the coupled glucose-insulin-glucagon dynamics in the isoglycemic intravenous glucose infusion (IIGI) experiment. As the glucose profile in IIGI is tailored to match that of a corresponding oral glucose tolerance test (OGTT), it provides a perfect method for studying hormone responses that are in the normal physiological domain and without the confounding effect of incretins and other gut mediated factors. The model was fit to IIGI data from individuals with and without T2D. Parameters related to glucagon action, suppression, and secretion as well as measures of insulin sensitivity, and glucose stimulated response were determined simultaneously. Significant impairment in glucose dependent glucagon suppression was observed in patients with T2D (duration of T2D: 8 (6–36) months) relative to weight matched control subjects (CS) without diabetes (k₁ (mM)⁻¹: 0.16 ± 0.015 (T2D, n = 7); 0.26 ± 0.047 (CS, n = 7)). Insulin action was significantly lower in patients with T2D (a₁ (10 pM min)⁻¹: 0.000084 ± 0.0000075 (T2D); 0.00052 ± 0.00015 (CS)) and the Hill coefficient in the equation for glucose dependent insulin response was found to be significantly different in T2D patients relative to CS (h: 1.4 ± 0.15; 1.9 ± 0.14). Trends in parameters with respect to fasting plasma glucose, HbA1c and 2-h glucose values are also presented. Significantly, a negative linear relationship is observed between the glucagon suppression parameter, k₁, and the three markers for diabetes and is thus indicative of the role of glucagon in exacerbating the pathophysiology of diabetes (Spearman Rank Correlation: (n = 12; (−0.79, 0.002), (−0.73,.007), (−0.86,.0003)) respectively).

1 Introduction

Glucose homeostasis is maintained primarily by the action of the two pancreatic hormones, insulin and glucagon, in conjunction with a host of other modulators. (Röder et al., 2016). Beta- and alpha-cell dysfunction both contribute to the pathophysiology of type 2 diabetes (T2D). (Burcelin et al., 2008; Ashcroft and Rorsman, 2012; Cryer, 2012; Cerf, 2013; Godoy-Matos, 2014; Moon and Won, 2015; Eizirik et al., 2020). Reduced insulin secretion from the pancreatic beta-cells and reduced insulin sensitivity in various tissues in the body lead to high postprandial glucose excursions. (DeFronzo and Tripathy, 2009; Montanya, 2014; Titchenell et al., 2016; Santoleri and Titchenell, 2019). In addition, higher basal levels of glucagon and impaired suppression of glucagon secretion is implicated in elevated fasting and post-prandial glucose levels in individuals with T2D. (Unger and Orci, 1975; Gerich, 1988; Dunning and Gerich, 2007; Lee et al., 2011). Theoretical models of glucose, insulin and glucagon dynamics can be used to quantify the extent of dysregulation in hormonal control of glucose homeostasis in T2D by fitting the models to data from various glucose challenge experiments. (Bergman et al., 1979; Bergman et al., 1981; Mari et al., 2002a; Dalla Man et al., 2002; Ferrannini et al., 2005; Dalla Man et al., 2006; Panunzi et al., 2007; Palumbo et al., 2013; Kelly et al., 2019; Bergman, 2021; Morettini et al., 2021).

The oral glucose tolerance test (OGTT) and the intravenous glucose tolerance test (IVGTT) have been used to quantify different aspects of plasma glucose regulation. (Panunzi et al., 2007; Cobelli et al., 2014; Bergman, 2021). The advantage of the OGTT is that it represents a physiological response to oral ingestion of nutrients. The challenge from a mathematical modeling point of view is that stimulation of the gut results not only in glucose dependent insulin secretion but also numerous confounding factors, e.g., the incretin effect. (Nauck et al., 1986; Knop et al., 2007; Nauck and Meier, 2016). Gut mediated effects do not come into play when glucose is administered intravenously. In a typical IVGTT, both first phase and second phase insulin secretion are observed in response to glucose challenge. (Bergman et al., 1981; Caumo and Luzi, 2004). Another method for studying glucose-insulin-glucagon dynamics is the isoglycemic intravenous glucose infusion (IIGI), which matches the glucose excursion observed during an OGTT but does not stimulate incretin secretion. (Bagger et al., 2011; Bagger et al., 2014; Nauck and Meier, 2016). Historically, IIGI has been used to obtain a quantitative measure of the incretin effect based on the differential insulin response observed in the OGTT and the corresponding IIGI experiment. In an IIGI, the typical first phase insulin response followed by the slower second phase of the bolus IVGTT is not observed. Instead, a single phase that tracks glucose concentration is observed. The shape of the insulin response is closer to that observed during oral ingestion because the delivery of glucose to the beta cells mimics normal physiological graded delivery from oral glucose administration. (Caumo and Luzi, 2004). Thus, the data from such experiments can be used to estimate parameters of glucose dependent insulin response in addition to insulin sensitivity by fitting a suitable minimal model of glucose regulation without confounding factors from the gut.

While the role of insulin mediated regulation of glucose homeostasis is well established and the contribution to the pathophysiology of T2D has been extensively quantified (Mari et al., 2002b; Panunzi et al., 2007; Cobelli et al., 2009; Cobelli et al., 2014; Bergman, 2021), the role of glucagon and alpha-cell dysregulation is less well studied from a computational perspective. Models have been developed to study glucagon secretion from the alpha cells or pancreatic islets addressing glucose dependent intrinsic and paracrine regulation. (Diderichsen and Göpel, 2006; Fridlyand and Philipson, 2012; Watts and Sherman, 2014; Briant et al., 2016; Watts et al., 2016; Briant et al., 2018; Zmazek et al., 2021). At the whole-body systems level, glucagon dynamics has been included in complex models that describe regulation of glucose homeostasis by the interplay between different organ systems. (Cobelli et al., 1982; Sulston et al., 2006; Kim et al., 2007; De Gaetano and Hardy, 2019). These models included many coupled differential equations and large number of parameters which make them less amenable to validation based on data from glucose challenge experiments for example. On the other hand, minimal models such as those developed for assessing insulin sensitivity and beta cell function are particularly useful in highlighting the contribution of specific impairments to the pathophysiology of diabetes and are more easily validated with data. (Bergman et al., 1979; Mari et al., 2002a; Dalla Man et al., 2002; Ferrannini et al., 2005; Panunzi et al., 2007; Bergman, 2021). The drawback with the glucose-insulin models is that they do not include the dynamics of the counter-regulator glucagon in establishing glucose homeostasis. A more complete minimal model which includes glucagon dynamics coupled to insulin and glucose dynamics would be self-consistent and yield information on glucagon action, secretion and suppression in addition to insulin related parameters. A few minimal models have included glucagon dynamics during IVGTT and OGTT respectively. (Kelly et al., 2019; Morettini et al., 2021). Glucagon dynamics has been described differently in each of the previous models (complex and minimal) particularly with respect to the regulation of glucagon secretion and suppression. In the paper by Morettini et al. (2021), a glucagon-c-peptide coupled model which did not include glucose dynamics was developed to describe suppression of glucagon secretion during OGTT. As the model did not include glucose dynamics, parameters related to glucagon action and secretion, insulin sensitivity, and secretion could not be determined simultaneously. In the IVGTT minimal model, (Kelly et al., 2019), the dynamics of glucose, insulin and glucagon were all included. In the description of glucagon dynamics, glucagon suppression is assumed to be linearly dependent on plasma insulin concentration and glucagon secretion occurs only when glucose levels drop below baseline. Experimental evidence from human islet level studies indicates that glucagon suppression at low glucose is controlled primarily through intrinsic regulation by glucose. (Tian et al., 2011; Walker et al., 2011; Yu et al., 2019). At high glucose, the intrinsic regulation is modulated by glucose dependent paracrine effects mediated by somatostatin. (Briant et al., 2016; Briant et al., 2018). In the paper by Elliot et al., (Elliott et al., 2015), insulin and somatostatin have been shown to act synergistically in regulating glucagon concentrations at high glucose in human islets. In the hypoglycemic range Bolli et al. (1984) have shown that glucagon secretion is regulated exclusively by glucose. Though the nature of paracrine regulation and the factors that mediate it are uncertain there is consensus on the observation that it occurs in a glucose dependent manner. In the OGTT model, (Morettini et al., 2021), glucagon suppression is attributed exclusively to insulin, ignoring intrinsic regulation by glucose. In the IVGTT minimal model, (Kelly et al., 2019), glucagon suppression is again attributed to insulin at glucose levels above baseline. In the comprehensive models, insulin dependent hyperbolic tangent functions, (Cobelli et al., 1982), quadratic functions, (Kim et al., 2007), and inverse functions (Sulston et al., 2006) have been used to describe glucagon suppression but it is unclear why the particular forms were chosen.

In this paper, a parsimonious model based on delay differential equations, that extends previous insulin-glucose models (Panunzi et al., 2007) was developed to include glucagon dynamics. The coupled model allows for the determination of parameters related to both insulin and glucagon regulation of glucose homeostasis in one step. Glucagon and insulin response to glucose are modeled on dose response data from human islet level studies of alpha and beta cell secretion in contrast to previous models. (Walker et al., 2011). The glucagon dynamics is described by a phenomenological model based on the data from IIGI experiments. Glucagon secretion and suppression are shown to be regulated by glucose as in reference (Walker et al., 2011; De Gaetano and Hardy, 2019) but the magnitude of the suppression is varied during the course of the dynamics. This allows for the description of the prolonged suppression of glucagon secretion and resulting delayed recovery to baseline as observed in the data which is likely due to paracrine effects. The model thus incorporates intrinsic and possible paracrine regulation in a glucose dependent manner and is described in detail in the methods section.

The model developed is fit simultaneously to glucose, insulin and glucagon data from IIGI experiments on individuals with T2D and without diabetes (CS) previously published in the papers by Bagger et al. among others. (Bagger et al., 2011; Mari et al., 2013; Bagger et al., 2014; Alskär et al., 2016; Guiastrennec et al., 2016; Røge et al., 2017; Tura et al., 2017). There are significant advantages of fitting IIGI over OGTT data namely: 1) there are fewer parameters in the model as exogenous glucose arrival is a known quantity unlike in an OGTT; 2) hormone secretory and suppression parameters determined are free of gut mediated effects; 3) parameters that could not be estimated from fitting OGTT data, because of gut stimulation can be determined from IIGI, such as the Hill coefficient in the glucose dependent insulin response; 4) the data from the IIGI experiments also reveal unusual behavior in the insulin response in T2D patients such as significant time delays in insulin secretion, quantification of which would give another tool to distinguish between T2D and control subjects (CS); and 5) there have also been questions regarding insulin response contributing to post prandial glucose lowering below baseline, a phenomenon observed particularly when exogenous glucose loads are high. (Saha, 2006; Parekh et al., 2014). A related pathophysiology is reactive hypoglycemia where glucose levels drop well below baseline and patients present with the Whipple’s triad. (Ahmadpour and Kabadi, 1997; Brun et al., 2000; Suzuki et al., 2016). If there is a lag in insulin return to baseline, i.e., if high levels of insulin secretion persist after plasma glucose levels start dropping, then it would explain postprandial glucose lowering. Modeling the glucose dependent insulin response using a hysteresis model should reveal if a lag in insulin recovery to baseline levels exists and causes postprandial hypoglycemia.

In this paper, the role of alpha- and beta-cell dysfunction in T2D is quantified and highlighted. The question of whether hysteresis in insulin secretion plays a role in postprandial hypoglycemia is also addressed. In addition, correlations between the parameters determined and the hallmarks of T2D, fasting plasma glucose (FPG), hemoglobin A1c (HbA1c) and 2-h plasma glucose (2 h PG) values are presented and highlighted.

2 Modeling and data analysis

2.1 Glucose-insulin-glucagon model

In this paper, a parsimonious model that includes glucagon dynamics was developed to describe the coupled glucose-insulin-glucagon system and is presented in Eqs 1–3. The model is an extension of the delay differential equation model of Panunzi et al. (Panunzi et al., 2007; De Gaetano et al., 2008). Equation 1 describes glucose dynamics. The rate of change of glucose is given by a source term depending on glucagon and the exogenous glucose infused during the IIGI experiment and clearance terms depending on glucose and insulin. The first term in Eq. 1 represents glucose dependent glucose clearance as in the Bergman model (Bergman et al., 1979) and is first order in glucose with rate constant S_G. The second term represents insulin dependent glucose clearance and is first order in insulin and glucose. The rate constant a₁ gives a measure of insulin sensitivity; it is analogous to the parameter S_I in the Bergman minimal model and K_xgI in the paper by Panunzi et al. Hepatic glucose production is assumed to be driven primarily by glucagon and is given by the third term in Eq. 1. It is first order in glucagon concentration and the rate constant a₂ gives a measure of glucagon action in the liver. Hepatic glucose production would likely also depend on other substrates such as glycogen in glycogenolysis, but they are assumed to be in excess and the pseudo first order (Keeler et al., 2018) dependence on glucagon used should be sufficient. In the model of De Gaetano et al., (De Gaetano and Hardy, 2019), glucagon is included in the fast dynamics, but they use saturation kinetics to describe glucagon-dependent hepatic glucose production while a first order dependence is used in the paper by Kelly et al. (2019) As the extent of insulin dependent suppression of hepatic glucose production is uncertain, it was not included in this model (Gastaldelli et al., 2001; Adkins et al., 2003; Kaplan et al., 2008). The rate of glucose arrival in the plasma, R_IIGI, is determined from the glucose infusion rate, G_infusion, during the IIGI as shown in Eq. 6. In the underlying experiments, the glucose infusion was manually adjusted in the IIGI protocol to match the OGTT profile. The average amount of glucose infused every 15 min was used to approximate the actual glucose infusion rate which involved adjustments every 5 min.

In Eq. 2 describing insulin dynamics, n₁ is the insulin degradation constant, γ₁ is a measure of insulin secretion and ψ(G[t]) is the dose-response relationship for glucose-dependent insulin secretion. Two models were used to describe insulin dynamics. The dose-response function, ψ(G[t]), is represented by a Hill function, Eq. 4a, in Model 1. While the Hill function has been used by other researchers, (Panunzi et al., 2007), the parameter K in Eq. 4 in this paper is fixed at the value obtained by fitting dose-response data from in vitro human pancreatic islet level studies (Walker et al., 2011) and is set at 17 mM.

As some researchers (Mari et al., 2002a; Keenan et al., 2012; Parekh et al., 2014) have raised the possibility of hysteresis-like behavior in insulin secretion in response to exogenous glucose influx, in Model 2, Eq. 4b was used to fit the IIGI data. In the hysteresis model, insulin secretory response to glucose depends on whether glucose levels are increasing or decreasing. The Hill coefficient h₁ controls the response when glucose levels are increasing and h₂ describes the secretory response when glucose levels are decreasing. C₁ is an adjustment constant determined to make the two curves meet at the hysteresis point, (G_hyst, t_hyst). A sample plot showing hysteretic dose-response is shown in Figure 1. Here h₁ is set to be lower than h₂. Two Hill equations are used here as studies at the islet level indicate that the physiological dose-response shows this behavior. Logistic functions have been used in the paper by Keenan et al. to model hysteresis in c-peptide secretion. (Keenan et al., 2012). Changes in insulin secretory patterns with time have also been modeled using different potentiation factors as in the work by Mari et al. which is in turn derived from deconvolution of c-peptide kinetics. (Mari et al., 2002a).

FIGURE 1

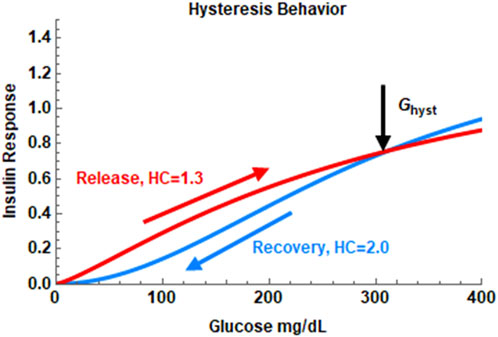
FIGURE 1. The hysteresis behavior of the insulin dose-response in Model 2. In this example, the Hill coefficient, h, is set at 1.3 during the insulin release phase and set at 2.0 during the recovery phase. The hysteresis turning point is set at the maximum of the glucose profile in the IIGI experiment.

Glucagon dynamics is described by Eq. 3 and is the sum of two terms, a clearance term, and a glucose dependent response term. Glucagon degradation or clearance is assumed to be first order in glucagon with degradation constant, n_2, which was obtained from the literature. (Alford et al., 1976). The second term describes the response to glucose. Islet level (Walker et al., 2011) and other studies (De Gaetano and Hardy, 2019) indicate that glucagon levels decrease exponentially as a function of glucose elevation. Preliminary investigations while modeling OGTT experiments showed that the glucagon dynamics shows hysteresis like behavior in response to glucose challenge. The suppression of glucagon in response to glucose challenge follows a different glucose dependence than the recovery after the plasma glucose level reaches a maximum. Thus, the glucagon dose-response is given by two different exponential terms (Eq. 5), one when glucose level is rising and a different one when glucose level is falling. The change in behavior is assumed to occur at the maximum of the glucose curve occurring at glucose concentration G_hyst, and time t_hyst. G_hyst is determined by finding the maximum of the plasma glucose profile, ie., the IIGI data, numerically and t_hyst is the time at which the maximum occurs (Wolfram Research, Inc, 2019). The reason for this slow recovery of glucagon levels post glucose influx is uncertain but likely due to paracrine modulation of glucagon secretion while the early suppression is likely due to intrinsic regulation by glucose. As both paracrine regulators, insulin and somatostatin, are secreted in a glucose dependent manner, here the paracrine modulation is also assumed to occur in a glucose dependent manner without explicit dependence on insulin or somatostatin concentration. The two exponential glucose dependent response terms were able to capture glucagon dynamics reasonably well during the 240 min duration of the IIGI experiment as shown in the results section. This persistent suppression of glucagon was also observed by Gerich (Mitrakou et al., 1990; Gerich, 1993) and in a larger study by Faerch et al. (Færch et al., 2016) The suppression and recovery constants are k₁ and k₂ respectively. The rate constant γ₂ is a measure of glucagon secretion. The parameters τ, τ₁ and τ₂ represent possible time delays in glucose distribution, insulin secretion and glucagon suppression respectively.

$\frac{\mathit{d}\mathit{G}\left[\mathit{t}\right]}{\mathit{d}\mathit{t}}=-\left({\mathbf{S}}_{\mathbf{G}}+{\mathbf{a}}_1\mathbf{I}\left[\mathbf{t}\right]\right)\mathbf{G}\left[\mathbf{t}\right]+{\mathbf{a}}_2\mathbf{A}\left[\mathbf{t}\right]+{\mathbf{R}}_{\mathbf{I}\mathbf{I}\mathbf{G}\mathbf{I}}\left[\mathbf{t}-\mathbf{\tau }\right]/\mathbf{V} (1)$

$\frac{\mathit{d}\mathit{I}\left[\mathit{t}\right]}{\mathit{d}\mathit{t}}=-{\mathit{n}}_1\mathit{I}\left(\mathit{t}\right)+{\mathbf{\gamma }}_1\mathbf{\psi }\left(\mathbf{G}\left[\mathbf{t}-{\mathbf{\tau }}_1\right]\right)(2)$

$\frac{\mathit{d}\mathit{A}\left[\mathit{t}\right]}{\mathit{d}\mathit{t}}=-{\mathit{n}}_2\mathit{A}\left(\mathit{t}\right)+{\mathbf{\gamma }}_2\mathbf{\varphi }\left(\mathbf{G}\left[\mathbf{t}-{\mathbf{\tau }}_2\right]\right)(3)$

${\mathit{\psi }}_{\mathit{H}\mathit{i}\mathit{l}\mathit{l}}=\frac{1.5\mathit{G}{\left[\mathit{t}\right]}^{\mathit{h}}}{{\mathit{K}}^{\mathit{h}}+\mathit{G}{\left[\mathit{t}\right]}^{\mathit{h}}}\mathit{(a)}$

${\mathit{\psi }}_{\mathit{H}\mathit{y}\mathit{s}\mathit{t}\mathit{e}\mathit{r}\mathit{e}\mathit{s}\mathit{i}\mathit{s}}=\{\begin{array}{c}\frac{1.5\mathit{G}{\left[\mathit{t}\right]}^{{\mathit{h}}_1}}{{\mathit{K}}^{{\mathit{h}}_1}+\mathit{G}{\left[\mathit{t}\right]}^{{\mathit{h}}_1}},\mathit{t}<{\mathit{t}}_{\mathit{h}\mathit{y}\mathit{s}\mathit{t}}\\ \frac{{\mathit{C}}_1\mathit{G}{\left[\mathit{t}\right]}^{{\mathit{h}}_2}}{{\mathit{K}}^{{\mathit{h}}_2}+\mathit{G}{\left[\mathit{t}\right]}^{{\mathit{h}}_2}},\mathit{t}\ge {\mathit{t}}_{\mathit{h}\mathit{y}\mathit{s}\mathit{t}}\end{array}\mathit{(b)}(4)$

$\mathbf{\varphi }\left(\mathbf{G}\left[\mathbf{t}-{\mathbf{\tau }}_2\right]\right)=\{\begin{array}{c}{\mathit{e}}^{-{\mathit{k}}_1\mathit{G}\left[\mathit{t}-{\mathit{t}}_2\right]},\mathit{t}<{\mathit{t}}_{\mathit{h}\mathit{y}\mathit{s}\mathit{t}}\\ {\mathit{e}}^{-{\mathit{k}}_2\mathit{G}\left[\mathit{t}-{\mathit{t}}_2\right]}+\mathit{y}\mathit{s}\mathit{h}\mathit{i}\mathit{f}\mathit{t},\mathit{t}\ge {\mathit{t}}_{\mathit{h}\mathit{y}\mathit{s}\mathit{t}}\end{array}(5)$

$\mathit{yshift}={\mathit{e}}^{-{\mathit{k}}_{\mathbf{1}}{\mathit{G}}_{\mathit{hyst}}}$

${\mathit{R}}_{\mathit{I}\mathit{I}\mathit{G}\mathit{I}}\mathit{m}\mathit{g}{\left(\mathit{k}\mathit{g} \mathit{min}\right)}^{-\mathbf{1}}={\mathit{G}}_{\mathit{I}\mathit{n}\mathit{f}\mathit{u}\mathit{s}\mathit{i}\mathit{o}\mathit{n}}\left(\mathit{g}\right)/\mathbf{15}\left(\mathit{min}\right)\times \frac{\mathbf{1000}}{(\mathit{s}\mathit{u}\mathit{b}\mathit{j}\mathit{e}\mathit{c}\mathit{t} \mathit{w}\mathit{e}\mathit{i}\mathit{g}\mathit{h}\mathit{t} \left(\mathit{k}\mathit{g}\right))}(6)$

2.2 Parameter estimation and statistics

Models 1 and 2 were simultaneously fit to glucose, insulin and glucagon data from IIGI tests on eight patients with diabetes (T2D) and eight weight matched control subjects (CS) without diabetes. (Bagger et al., 2011; Bagger et al., 2014). The glucose infusion in IIGI was manually adjusted to obtain a glucose profile that matches the OGTT glucose profile. The data available from the glucose infusion was the total amount of glucose infused in 15-min blocks for a total of 240 min. A uniform glucose infusion rate was thus used for every 15-min block of the infusion experiment as described in Eq. 6. This approximates the actual infusion rate which was adjusted every 5 min. As this approximation was applied across all patients, trends in estimated parameters within groups and between groups should likely be unaffected.

The parameters that were determined from the fit are glucagon action a₂, secretion γ₂ and suppression k₁, insulin action a₁, secretion γ₁ and the Hill coefficients h, or h₁ and h₂ depending on the model used. As the exogenous glucose arrival, R_IIGI is continuous but not smooth, the time delay terms could not be estimated using the Levenberg-Marquardt algorithm in all subjects. The times delays, τ, τ₁, τ₂, were therefore adjusted manually. The glucagon recovery parameter k₂ was also adjusted manually. These parameters were adjusted to obtain a reasonable visual fit before running the Levenberg-Marquardt algorithm to estimate the other parameters. The time delays as well as k₂ were easy to set manually as good visual fits were obtained over a relatively narrow range of parameter values. No constraints were set on the values. The parameters n₁, n₂ and S_G were obtained from the literature and set at 0.14 min⁻¹, (Duckworth et al., 1998), 0.08 min⁻¹, (Alford et al., 1976; De Gaetano and Hardy, 2019; Grøndahl et al., 2021), and 0.014 min⁻¹ (Dalla Man et al., 2002) respectively. V was fixed at 1.35 dL/kg. (Man et al., 2005).

The fitting was done using the nonlinear regression package NonLinearModelFit in Wolfram Mathematica, Version 12.0. (Wolfram Research, Inc, 2019). The Levenberg-Marquardt algorithm was used for the least-squares minimization. This package also provides all the statistics related to the fits.

A weighted least-squares regression was used for some of the subjects to improve the fits. The weights were determined using the coefficient of variation (CV) for glucose, insulin, and glucagon concentrations. The CVs used were 2%, 3% and 5.5% for glucose, insulin, and glucagon respectively. The caveat with using a constant CV in least squares fitting is that the fit is skewed heavily towards lower data values.

Significance of differences in parameters between groups (T2D vs. CS) was tested using the non-parametric Mann-Whitney U test. (MannWhitneyTest. Wolfram Research, 2010). The p values <0 .05 indicated significant differences between groups based on the null hypothesis that the median difference is zero. Correlations between parameters were determined using the nonparametric Spearman Rank Test. Comparison of Model 1 and Model 2 was done based on the Akaike Information Criterion corrected for small sample size (AICc). (Akaike, 1974; Portet, 2020).

Identifiability of parameters determined was checked using publicly available software, STRIKE-GOLDD Version 3.0. (Villaverde et al., 2016; Villaverde et al., 2019). All parameters in the model that were estimated using the least-squares fitting were assessed to be locally structurally identifiable.

Model validation (Hasdemir et al., 2015) was carried out by simulating data from IIGI experiments that matched OGTT glucose profiles with varying glucose loads (Bagger et al., 2014) on the same set of patients with T2D and CS as in this study. The results are presented in the supplementary section.

3 Experimental methods

The experimental methods are discussed in detail in the paper by Bagger et al. (Bagger et al., 2011; Bagger et al., 2014) A brief overview of the individuals and methods used is presented here.

3.1 Subjects

Eight patients (3 male) with T2D [mean age, 57 (range 40–75) years.; body mass index (BMI), 29 (25–34) kg/m²; duration of diabetes, 8 (6–36) months] and eight gender-, age-, and BMI-matched healthy control individuals [age, 57 (38–74) years.; BMI, 29 (26–33) kg/m²] were studied. All patients with T2D were diagnosed based on the criteria of the World Health Organization. (Expert Committee on the Diagnosis, 2003).

3.2 Experimental design

Participants were subject to OGTT followed by IIGI on a subsequent day. The subjects were studied in the morning in a recumbent position after an overnight fast (10 h) fast. On OGTT days, the participants ingested 75 g glucose dissolved in 300 g water. Blood samples were drawn 15, 10, 0 before and 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, 70, 90, 120, 150, 180, 240 min after ingestion of glucose. IIGI was performed using a sterile 20% wt/vol glucose infusion. The infusion rate was adjusted aiming at duplication of the plasma glucose profiles determined on the corresponding OGTT day. Blood was sampled as on the OGTT days. Analytical methods used to determine glucose, insulin and glucagon concentrations are described in Bagger et al. (Bagger et al., 2014).

4 Results

In the first and second subsections, the fits obtained using Model 1 for CS are discussed first, followed by the fits for patients with T2D, and trends within groups presented. In the third subsection, the parameters obtained for CS and patients with T2D are compared. In the fourth subsection correlations with hemoglobin A1c (HbA1c), fasting plasma glucose (FPG) and 2-h plasma glucose (2 h PG) will be presented and implications for categorizing patients with T2D in terms of impaired glucagon suppression in addition to insulin sensitivity will be discussed. In the fourth subsection the question of possible hysteresis behavior in glucose dependent insulin secretion will be explored by comparing Models 1 and 2 of insulin secretion. The implications with respect to postprandial glucose lowering will be discussed.

4.1 Control subjects

The glucose infusion data was first converted to a plasma glucose arrival profile using Eq. 6. The glucose arrival rate profile in four CS subjects is plotted in Figure 2, panel A. This figure highlights the significant variation in glucose arrival profiles between the different subjects that could have an impact on extent of glucose excursions post glucose infusion. In addition, the shape of the plasma glucose profile in IIGI is also dictated by the shape of the exogenous glucose input, which in turn depends on the glucose excursions during the prior OGTTs.

FIGURE 2

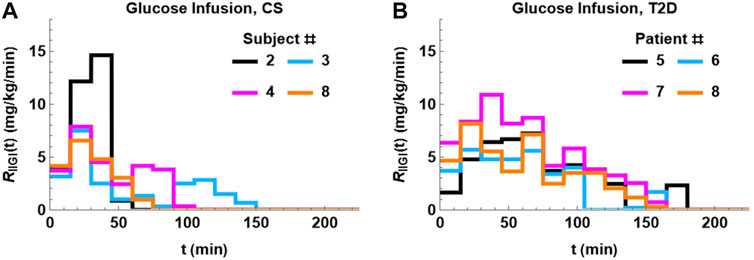
FIGURE 2. Glucose arrival profiles, R_IIGI, determined using Eq. 6. There is significant difference between the profiles both within groups and between groups. The profiles tend be more bimodal in CS subjects (A). The glucose arrival profile for T2D (B) is unimodal and more prolonged relative to CS.

The coupled Eqs 1–3 with insulin response given by Eq. 4a) were then fit to the data. A reasonable fit with low standard errors was not obtained for CS 6. The IIGI experiments involve manual adjustment of glucose infusion rates to obtain glucose profiles that match the OGTT profiles which sometimes result in overshoot in plasma glucose values that may trigger first phase insulin secretion which is likely what happened in CS 6 and could not be fit with this model. This subject was excluded from further study. The fits obtained for the remaining seven CS subjects are presented in Figure 3 and the estimated and manually adjusted parameters in Table 1. The fits were uniformly good for CS subjects with high coefficient of determination (adjusted R²) values >0 .97. The standard errors in all the estimated parameters were low and the p-values for all the parameters <0.05 except for a₁ of patient 2. The average values, standard errors of the mean and ranges of the parameters are presented in Table 3.

FIGURE 3

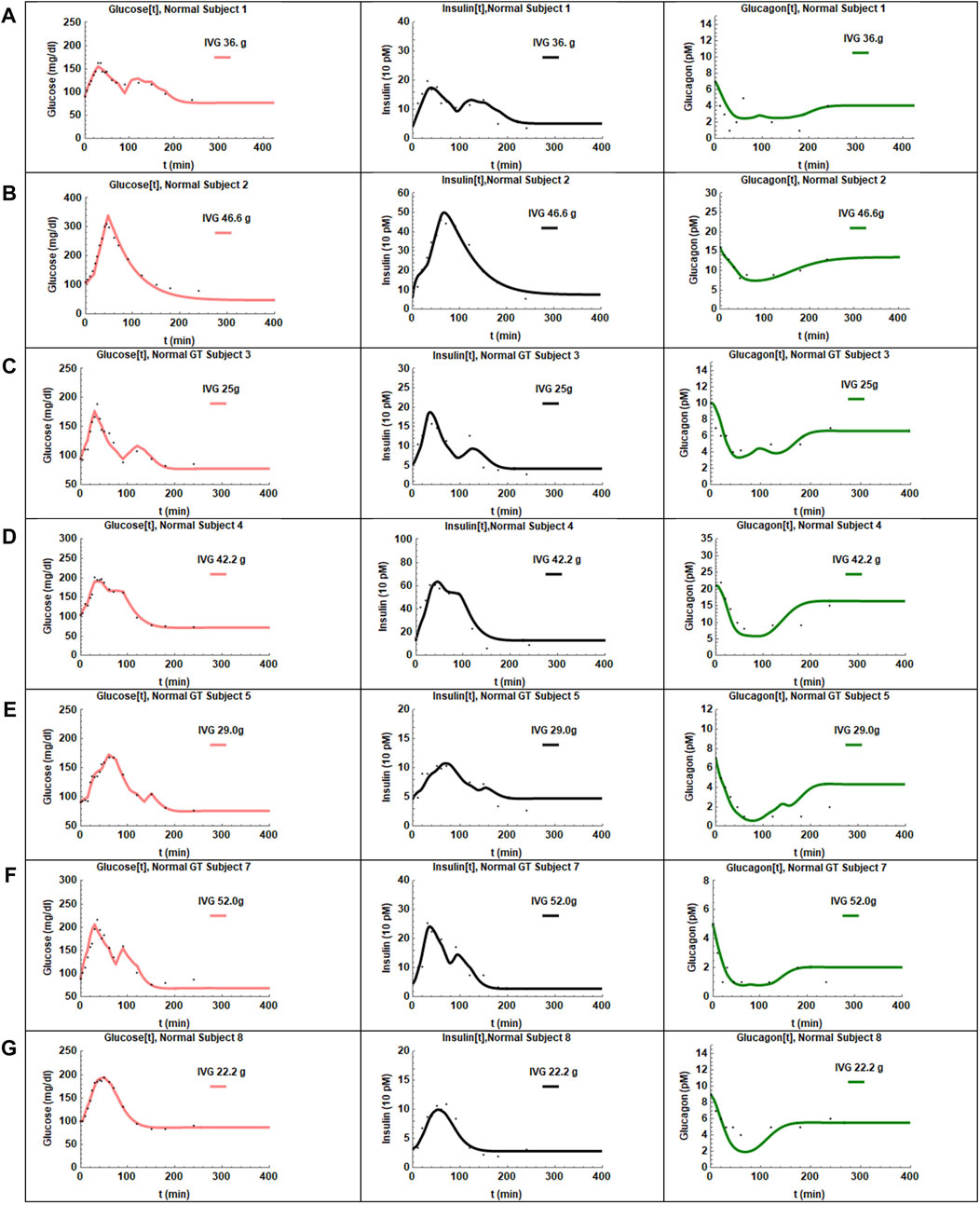
FIGURE 3. The fits obtained for the seven CS subjects are presented in panels (A–G). The adjusted R² values were >0.97 for all the fits. The glucose profiles were fit the best by the model. In some cases, the insulin recovery was not captured perfectly (D,E). Glucagon shows very slow recovery and is captured reasonably well by the hysteresis model except for one subject (E).

TABLE 1

TABLE 1. Parameters obtained from fitting the coupled Model 1 to the seven CS subjects.

The CS subjects showed a wide range of insulin sensitivities, a₁, 0.000055–0.0012. Subjects two and four showed lower insulin sensitivity relative to other CS subjects. The range in insulin sensitivities can be attributed to the fact that the CS subjects were weight matched to the T2D group (average BMI $=$ 29). The glucose dependent insulin secretion parameter γ₁ showed modest variation with one outlier, CS subject 4. The Hill coefficient, h, was divided into two groups, one centered around h $=$ 2.0 and another around h $=$ 1.35. Subjects with higher values of h have a steeper insulin dose-response to glucose. In general, there were no time delays in the CS subjects with respect to insulin secretion or action except for a 12-min delay in insulin secretion in CS 2 who also had the lowest insulin sensitivity.

The glucagon suppression parameter k₁ in CS subjects was clustered around 0.26, close to the value of 0.25 determined from human islet level studies. Only one subject, CS 2, had anomalously low glucagon suppression. The average glucagon recovery parameter k₂ was 0.50 and shows that glucagon recovery is much slower than suppression in CS subjects. The glucagon action parameter, a₂, which is a measure of glucagon effectiveness in glucose release appeared to be significantly attenuated in CS 2 and 4 relative to the others; the average value was determined to be 0.25. The glucagon secretion parameter γ₂ in normal subjects did not show a huge spread except for CS 4 who had a much higher value relative to others. No time delays, τ₂, were observed in glucagon suppression.

There was also a short time delay, τ, in R_IIGI in CS subjects two and three of 3 and 5 min respectively. This behavior was observed in most patients with T2D.

4.2 Patients with T2D

The coupled Eqs. 1– 3 with the plasma glucose arrival profile determined using Eq. 6 were fit to the data. The fits for the patients with T2D are shown in Figure 4 and the estimated parameters in Table 2. The adjusted R² values for the fit were high for all patients (>0.98). The SE values were low and p values were <0.05 for all parameters except for the insulin sensitivity parameter a₁ in three patients. The fits for those three patients were particularly sensitive to initial guess values for the nonlinear least-squares regression. Possible reasons for the difficulty in fitting these patients might be: 1) The baseline glucagon data for subjects one and two did not match the values on OGTT day indicating greater uncertainty in glucagon data points. 2) T2D subject three had multiple data values near the detection limit of glucagon. The average values, standard errors of the mean and ranges of the parameters are presented in Table 3. Of the eight patients studied patient four could not be fit, likely due to the overshoot in infused glucose as described previously and was excluded from further study.

FIGURE 4

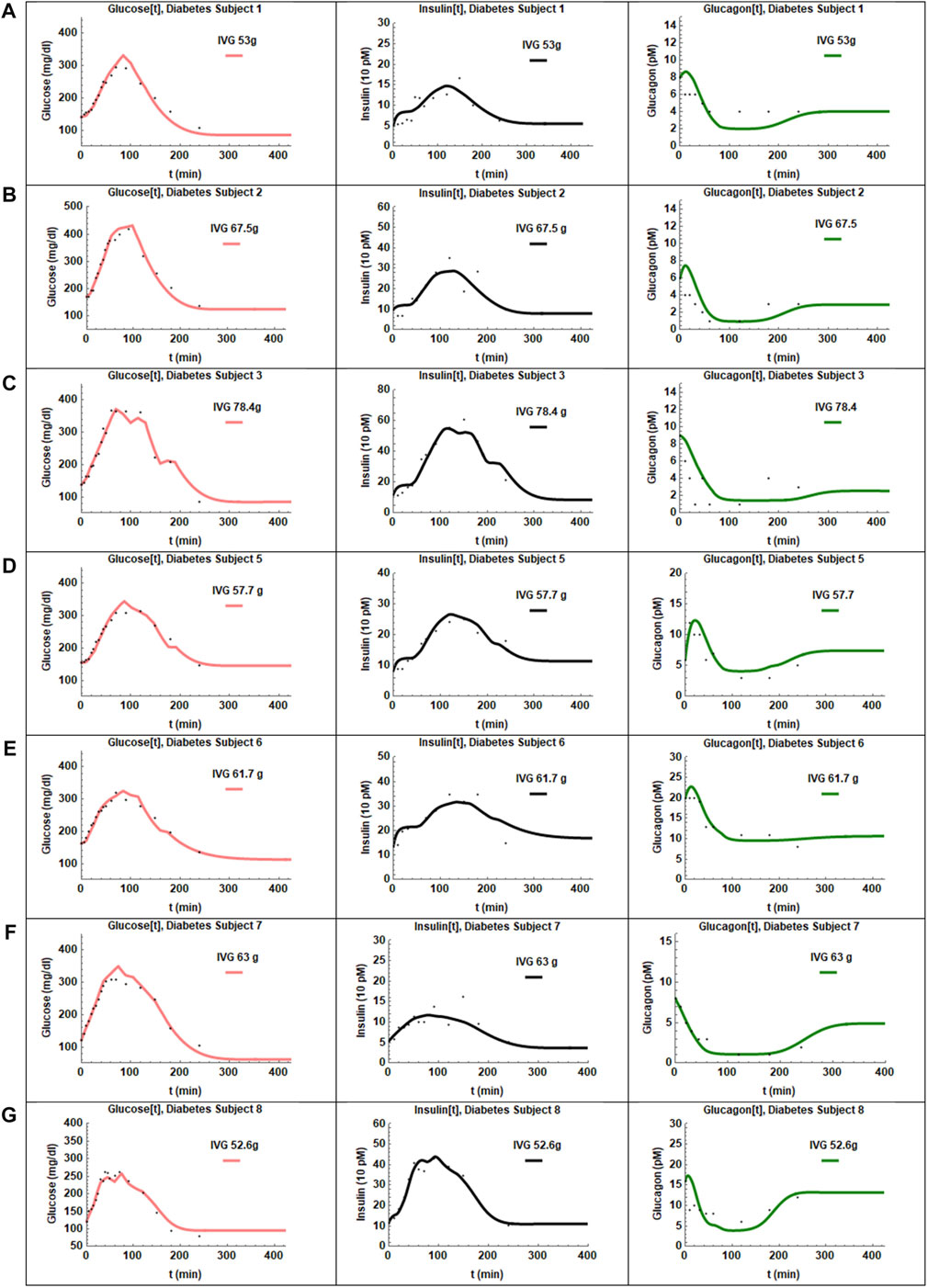
FIGURE 4. The fits obtained for the seven patients with T2D are presented in panels (A–G). The adjusted R² values were >0.98 for all subjects. The glucose and insulin profiles were fit best by the model. Glucagon recovery is slow as seen in panels (A–G) and again described reasonably well by the hysteresis model.

TABLE 2

TABLE 2. Parameters obtained from fitting the coupled Model 1 to patients with T2D.

TABLE 3

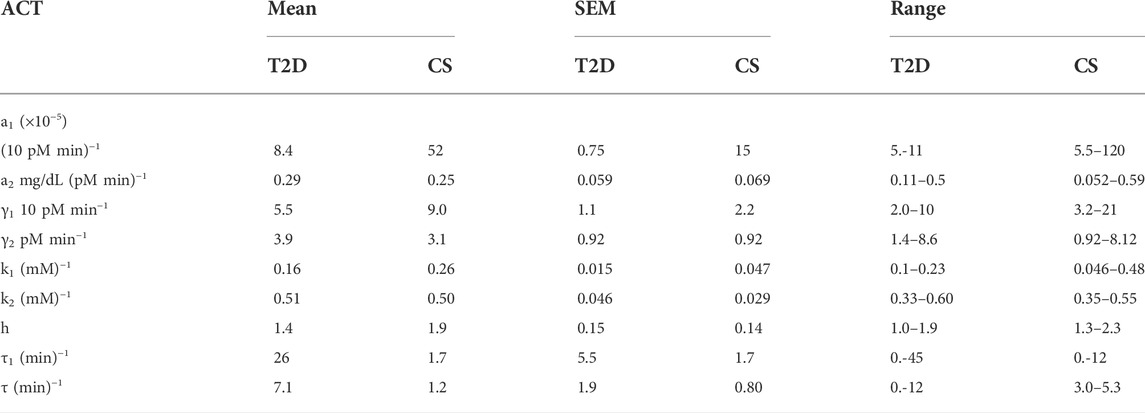
TABLE 3. Average values, standard errors, and ranges of the parameters in patients with T2D and CS subjects.

Patients with T2D showed a large delay in insulin secretion, τ₁, with a mean value of 26 min. The insulin sensitivities, a₁, in patients with T2D were narrowly distributed around the mean value of 0.000084. The insulin secretion parameter, γ₁, had an average of value of 5.5 and a narrow spread of 1.1. The Hill coefficient clustered around two values, four patients around h $=$ 1.75 and three patients around h $=$ 1.0.

The glucagon suppression parameter in patients with T2D was below 0.2 for all subjects except subject 8. Values of glucagon action, a₂, were mixed with four subjects showing significantly higher values than the other three. The glucagon secretion parameters, γ₂, were evenly distributed about the mean except for subject 8. A time delay, τ₂, of 5 minutes was observed in one patient.

The glucose arrival rate R_IIGI profile in four patients with T2D is plotted in Figure 2, panel B. The infusion profiles are unimodal and prolonged, extending to 180 min in some subjects. The infusion profiles in T2D show less variability than the CS subjects. Remarkably, a time delay, τ, had to be introduced in R_IIGI and had an average of 7 min with 12 min being the longest delay.

4.3 Comparison of patients with T2D and CS subjects

Mean values and ranges of the parameters for patients with T2D and CS subjects are presented in Table 3. The Mann-Whitney U test was used to compare the median differences between T2D and CS parameters. The results of the comparison test are presented in Table 4. There are significant differences (p-value<0.05) between five of the T2D and CS parameters, namely: the insulin sensitivity parameter, a₁, the glucagon suppression parameter k₁, the Hill coefficient, h, in the insulin dose-response curve and the time delays in insulin secretion and exogenous glucose arrival.

TABLE 4

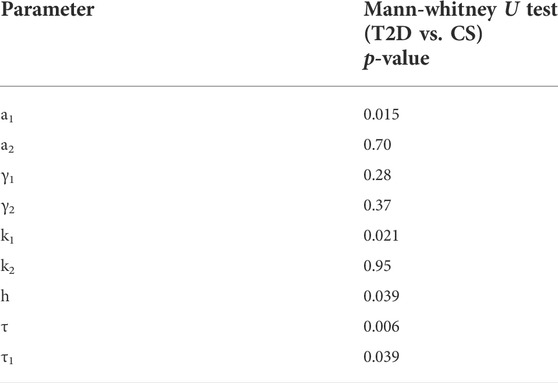
TABLE 4. Results of the Mann-Whitney U test. The insulin sensitivity parameter, a₁, the glucagon suppression parameter k₁, the Hill coefficient h, the insulin secretion time delay τ₁ and the infused glucose R_IIGI time delay τ, are found to be significantly different between the T2D and CS groups.

Insulin sensitivity, a₁, is much lower in patients with T2D than CS subjects except for two outliers CS 2 and four who had insulin sensitivities on par with patients with T2D. Homa-IR (84) is a method of estimating insulin resistance from fasting glucose and insulin levels. The insulin sensitivity parameters determined using Model 1 showed a positive correlation with 1/HomaIR (n $=$ 14 (CS and T2D patients), Spearman Rank Test correlation $=$ 0.70, p value $=$.0056). The Hill coefficient, h, which is a measure of the rapidity of the insulin response to glucose elevation, is higher in CS subjects than T2D subjects. Insulin secretion is delayed on average by 26 min in patients with T2D. In addition, there was delay of ∼10 min in R_IIGI circulation in patients with T2D.

The glucagon suppression constant k₁ is significantly lower in patients with T2D relative to CS. Glucagon action in the liver is not significantly different between CS and T2D though there is significant variation within groups. The glucagon secretion parameter is not significantly different between T2D and CS groups in this study.

The glucose infusion profiles are also different between the two groups. The infusion profiles of the CS subjects are bimodal (two peaks), shorter, and show more variability relative to patients with T2D. The infusion profile in patients with T2D is unimodal and more prolonged lasting up to 180 min in some cases.

4.3.1 Trends in parameters

Fasting plasma glucose (FPG), HbA1c and 2 h OGTT plasma glucose levels are all used to diagnose diabetes. (Diabetes Association, 2022). The parameters obtained from the fits were plotted against FPG, HbA1c and 2 h PG (which is approximately matched to 2 h OGTT glucose) to see which parameters correlated with these determinants of diabetes. The contribution of parameters related to glucagon dynamics to impaired FPG, HbA1c and 2 h PG levels is established. As this model differs significantly from previously established models, parameters related to insulin sensitivity and dose-response are classified based on correlations with FPG, HbA1c and 2 h PG. As the sample size is small, the cut-off valus separating T2D and CS are tentatively assigned by visual inspection of Figure 5 and not through statistical tools such as receiver operating characteristic (ROC) curves.

FIGURE 5

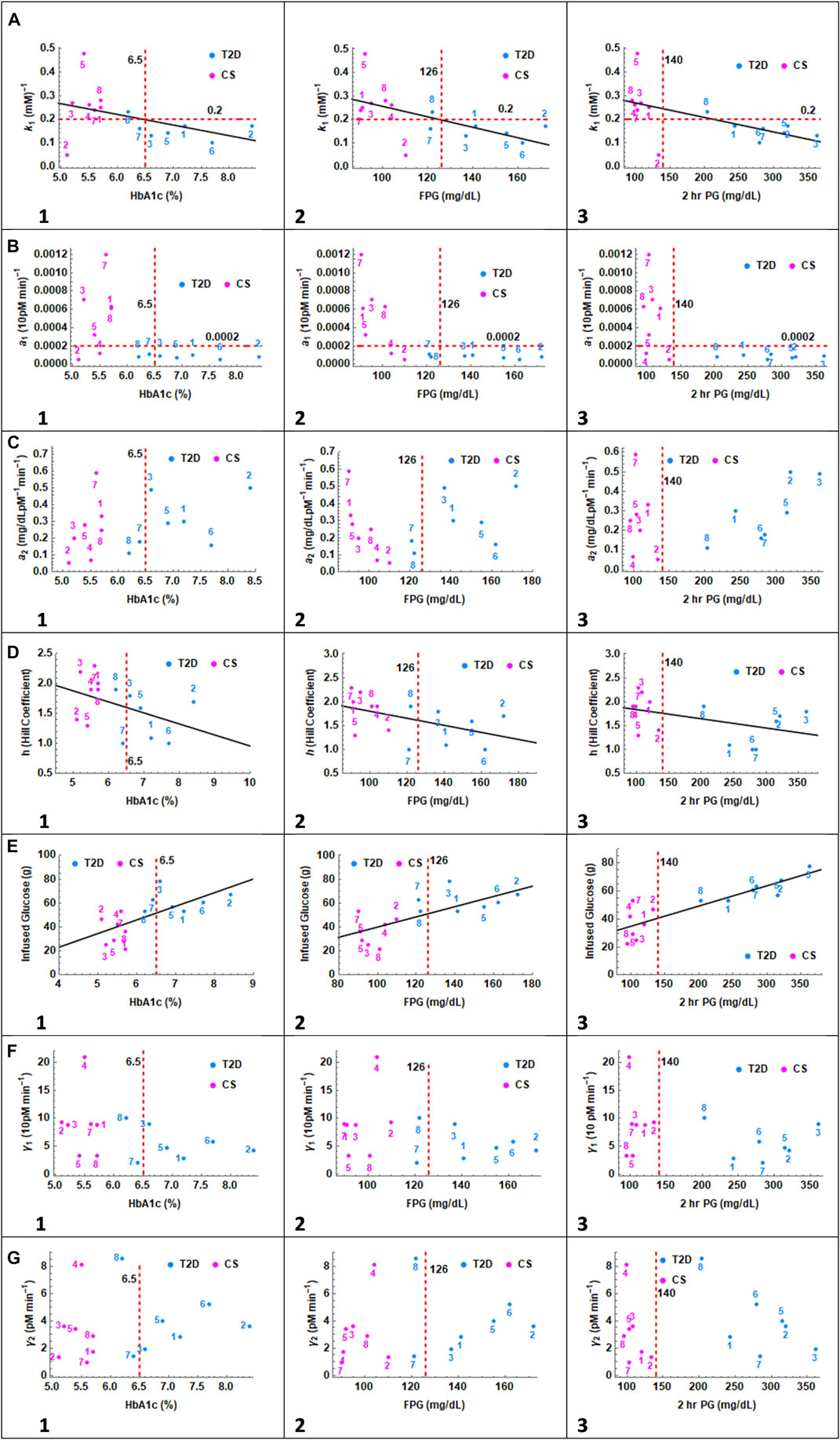
FIGURE 5. In the series of panels (A) through (G), the parameters related to glucagon suppression k₁, insulin action a₁, glucagon action a₂, Hill coefficient h, infused glucose, insulin secretion γ₁ and glucagon secretion γ₂ are plotted as a function of HbA1c, FPG and 2 h PG values. In panel (A) 1, 2, and 3, CS and T2D subjects partition into distinct quadrants except for one CS subject. A linear relationship is observed between glucagon suppression and HbA1c, FPG, and 2 h PG. The cutoff value separating patients with T2D, and CS subjects is set at 0.2. In Panel (B), the correlation with insulin sensitivity parameter a₁ is presented. CS subjects and patients with T2D again partition into two distinct quadrants except for CS 2 and 4. The cutoff value separating patients with T2D, and CS subjects is 0.0002. In panel (C) no clear distinction between patients with T2D and CS subjects is observed with respect to glucagon action parameter a₂. In Panel (D), the Hill coefficient, h, is trending higher in CS subjects toward h $=$ two and in patients with T2D towards h $=$ 1. In Panel (E), infused glucose, an indicator of the incretin effect, shows a linear trend with respect to HbA1C, FPG and 2 h PG, particularly in patients with T2D. In panel (F), no difference in insulin secretion parameter, γ₁, between CS and T2D is observed. In panel (G), patients with T2D show a weak linear trend towards higher HbA1c and FPG values with increasing glucagon secretion parameter.

In panel A, the glucagon suppression parameter, k₁, is plotted against HbA1c, FPG and 2 h PG. A linear trend was observed in all three cases with glucose dependent glucagon suppression constant decreasing with increasing A1c, FG and 2 h PG. Two outliers are observed, CS subject 5 with very high suppression and CS subject 2 with very low suppression. The patients with T2D and CS subjects separate into two distinct non-overlapping quadrants, particularly when plotted against 2 h PG. The k₁ value of 0.2 serves as the demarcation between CS and T2D groups. The Spearman Rank Correlation Coefficient and the p-value between k₁ and HbA1c, FPG, and 2 h PG with and without the two outliers are: (n = 14; (−0.46,0.1), (−0.67,.009), (−0.75, 0.002)), and (n = 12; (−0.79, 0.002), (−0.73,.007), (−0.86,.0003)) respectively.

In panel B, the insulin sensitivity parameter, a_1, is plotted against HbA1c, FPG and 2 h PG. All patients with T2D show uniformly low values of insulin sensitivity and again fall into a separate quadrant. Two CS subjects overlap with patients with T2D with respect to a₁. The demarcation for a₁ values between T2D and CS is set at 0.0002 which would place CS 2 and 4 in the diabetes group.

In panel C the glucagon action parameter, a_2, is plotted against HbA1c, FPG and 2 h PG. The action parameter is a measure of glucagon dependent glucose release from the liver. The glucagon action parameter is not significantly different between the two groups. There are no clear trends with respect to a₂ though within the T2D group, 2 h PG values increase linearly with increasing a₂.

In panel D the Hill coefficient which describes the steepness of the glucose dependent insulin response is plotted against HbA1c, FPG and 2 h PG. The Hill coefficient decreases with increasing HbA1c and FPG levels. A value of h $=$ 2 appears to be closer to normal secretory response and h $=$ 1 appears to be the low end of the response.

In Panel E, the total glucose infused in the IIGI experiment is plotted against HbA1c, FPG and 2 h PG. The premise of the IIGI experiment is that if the insulin response to glucose challenge is entirely glucose dependent, with no incretin effect, then the amount of glucose infused will be identical to that of the OGTT glucose challenge experiment. In this case it would be 75 g glucose as in the matching OGTT. The lower the amount of glucose required, the greater the incretin effect. (Nauck et al., 1986). A strong linear relationship is seen with 2 h PG levels particularly within the T2D group. The T2D patient three who showed no incretin effect, had the highest 2 h PG level. The Spearman Rank Correlation Coefficient and the p-value between Glucose_Infused and HbA1c, FPG, and 2 h PG are (0.74,.0025), (0.72,.0035), and (0.88,.000039) respectively.

In Panel F insulin secretion parameter γ₁ is presented. There is no difference between the insulin secretion parameter between the T2D and CS groups and no trends with respect to HbA1c, FPG or 2 h PG. This implies that incretin effects are primarily responsible for differences in insulin secretion between the two groups under OGTT conditions.

In Panel G, the glucagon secretion parameter γ₂ is plotted as a function of HbA1C, FPG and 2 h PG. There is trend towards increasing HbA1c and fasting glucose with increasing glucagon secretion within the T2D group. No pattern was seen with respect to 2 h glucose.

4.4 Hysteresis in insulin secretion

To assess the role of hysteresis in glucose dependent insulin secretion, Model 1 without hysteresis, Eq. 4a was compared with Model 2, where insulin secretion is described by Eq. 4b. In Model 1, the insulin secretion is described by a single Hill function with coefficient h. In the hysteresis model, insulin secretion is described by two Hill functions with coefficients h₁ and h₂. The Hill coefficients h₁ and h₂ are varied between the rising and recovery phases of insulin secretion, but the parameter K is assumed to be constant and same in both models.

The results in Section 4, describe the fits obtained with Model 1 for CS and T2D subjects. The parameters obtained using the hysteresis Model 2 are presented in Tables 5, 6. The fits are presented in Supplementary Figures S3, 4. Visually the fits for the different subjects are not very different for Model 1 and Model 2. In Model 2, the Hill coefficients h₂ is greater than h₁ for all CS subjects. Thus, insulin levels fall more steeply when glucose is declining. In the patients with T2D h₁ $\sim$ h₂ indicating there is no hysteresis and the results are essentially equivalent to the Model 1. The values of h in Model 1 were comparable to h₂ in Model 2 in CS subjects. In patients with T2D, h was comparable to h₁ and h₂, in other words, a single Hill equation is sufficient to describe insulin dose-response.

TABLE 5

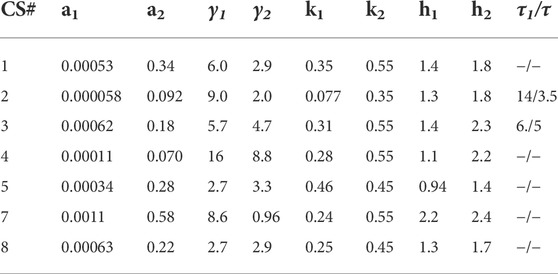
TABLE 5. Parameters determined from fitting the hysteresis Model 2 to data from CS subjects. The parameters obtained are similar to that for Hill Model 1. The values of h₁ are lower than h₂ in all subjects implying a steeper glucose dependent dose-response during the insulin recovery phase.

TABLE 6

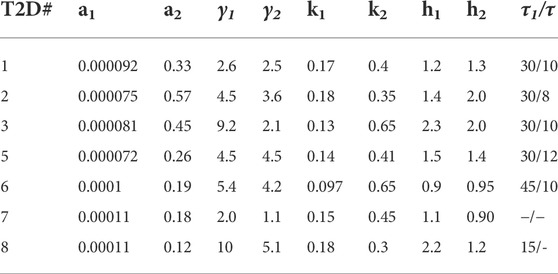
TABLE 6. Parameters determined from fitting the hysteresis Model 2 to data from patients with T2D. The parameters a₁-k₂ are comparable to that for Hill Model 1. The value of h₁ is approximately equal to h₂ in all subjects implying there is no hysteresis in diabetic subjects. Only subject eight showed a significant drop in h₂ compared to h₁.

In Model 1, h was significantly higher in CS subjects compared to patients with T2D. In Model 2, h₂ is significantly higher in CS subjects relative to patients with T2D. So, both models show a change in behaviour in patients with T2D.

Model comparison is made based on the Akaike Information Criterion with small sample correction (AICc). (Akaike, 1974). This criterion gives an estimate of whether the model with more parameters reduces the error sufficiently to justify the increase in complexity. The Akaike criterion can only be used to compare models using the same data set, so the AICc values are presented in Tables 7, 8 for individual CS and T2D subjects respectively. The lower the AICc value, the better the fit. The differences in AICc values are given in column 4. The AICc differences were variable with some subjects fit better by Model 1 and others by Model 2. The criterion cannot therefore be used to pick one model over the other.

TABLE 7

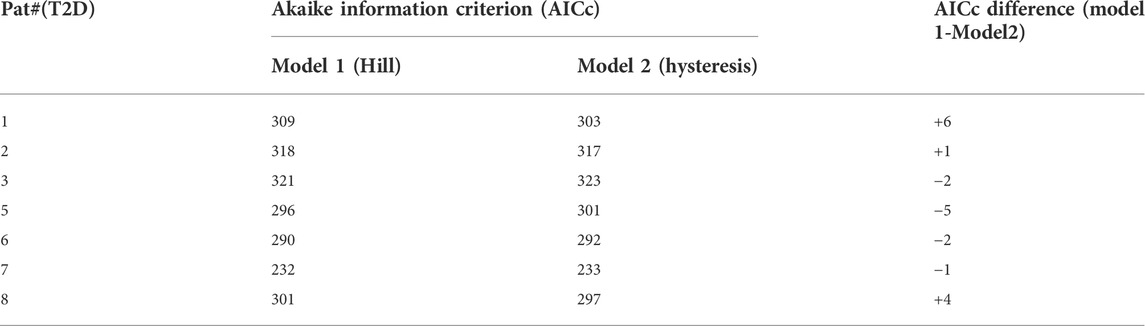
TABLE 7. Values of the Akaike Information Criterion corrected for small sample size (AICc) is presented for patients with T2D. Smaller AICc values indicate a better fit. The AICc values are not uniformly less for one model over the other in all patients.

TABLE 8

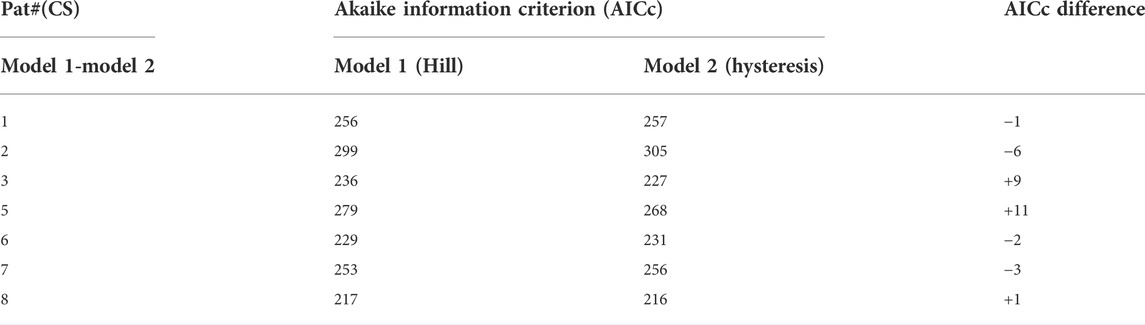
TABLE 8. Values of the Akaike Information Criterion corrected for small sample size (AICc) is presented for CS subjects. Smaller AICc values indicate a better fit. The AICc values are not uniformly less for one model over the other.

5 Discussion

T2D is a disease that is manifested when insulin resistance and beta- and alpha-cell dysfunction occur. (Topp et al., 2000; Topp et al., 2007; Burcelin et al., 2008; Ashcroft and Rorsman, 2012; Ha et al., 2016). As these three determinants of diabetes are intrinsically coupled, it is important to quantify parameters related to them in a self-consistent manner without splitting the coupled dynamics into separate subsystems. The parsimonious coupled system of delay differential equations used in this paper allow for estimation of all parameters in a single step. The coupled glucose-insulin-glucagon model was used to fit data from IIGI experiments to quantify glucagon action, suppression, and secretion as well as insulin resistance and secretion, without the confounding influence of incretins and other gut mediated factors. The results presented in Section 4 show that the model captures the coupled dynamics correctly and yields parameters related to both alpha and beta cell dysfunction and insulin resistance in one step. As this is a new extended model based on delay differential equations, some comparisons will be made with parameters related to insulin resistance and secretion from the single delay differential model of De Gaetano et al., where the coupled insulin-glucose dynamics was studied. (Panunzi et al., 2007; De Gaetano and Hardy, 2019).

Alpha cell dysfunction is known to contribute to both fasting and postprandial hyperglycemia in T2D. (Dunning and Gerich, 2007; Burcelin et al., 2008; Lund et al., 2014). Increased glucagon secretion, lowered glucagon suppression and differences in glucagon action could contribute to elevated fasting glucose levels and continued glucose production in the post prandial state. In this study, the glucagon suppression parameter, k₁, was found to be significantly lower in patients with T2D relative to CS. The parameter also showed clear linear relationship with respect to HbA1c, FPG and 2 h PG values. There was strong negative correlation with all three indicators of diabetes. HbA1c levels have been shown to correlate better with post-prandial glucose levels and less with fasting glucose levels. (Landgraf, 2004; Hershon et al., 2019). Two hr PG values are reflective of postprandial glucose excursions. This shows that glucagon suppression is impaired in T2D and has an impact on both fasting and postprandial glucose levels and likely exacerbates hyperglycemia in patients with T2D.

The glucagon secretion parameter γ₂ was not significantly different between CS and patients with T2D in this study. In the paper by Unger et al. (1970) similarly, statistically significant differences were not observed in fasting glucagon levels between CS and T2D subjects but when hyperglycemia was induced by glucose infusion in the CS so as to simulate the fasting hyperglycemia of T2D patients, mean glucagon fell significantly below the T2D mean, indicating the level of glucagonemia is high for the prevailing glycemia in T2D. This is also in line with former observations measuring hepatic glucose output using radiolabeled isotopes showing a clear positive correlation between baseline glucose and hepatic glucose output. (Baron et al., 1987). Even with great basal variation in basal glucagon the hepatic glucose output was suppressible by suppressing glucagon alone in pancreatic clamp (using somatostatin and basal insulin infusion). (Baron et al., 1987).

The glucagon action parameter, a₂, which is a measure of how effective it is in hepatic glucose production, is not significantly different between the CS and T2D subjects and is thus not the likely cause of elevated fasting and post prandial plasma glucose levels.

Modeling IIGI gives information regarding glucose stimulated insulin secretion. In model 1, there are three parameters describing insulin secretion: 1) a measure of the magnitude of insulin secretion, γ₁. 2) the steepness of the response based on the Hill coefficient, h, in the dose-response expression, ψ and 3) the time delay in insulin response, τ₁. A point to note is that differences in hepatic insulin extraction (HPE) may exist between subjects and the insulin secretion parameters determined are reflective of post HPE plasma insulin levels. The differences in HPE could also account for the some of the variation in plasma insulin levels between subjects but is not considered here. (Bojsen-Møller et al., 2018; Santoleri and Titchenell, 2019; Piccinini and Bergman, 2020).

The parameter γ₁ which is a measure of glucose dependent insulin secretion was not significantly different between T2D and CS subjects. There may be multiple reasons for this observation. The patients with T2D in this study were newly diagnosed and thus in the early stages of disease progression. This result is also consistent with the estimation of the incretin effects from the IIGI experiments in this study which showed that the incretin dependent insulin response is the dominant factor in differentiating between the levels of insulin secretion in CS and T2D subjects. The incretin dependent insulin secretion was found to be significantly impaired in patients with T2D. (Bagger et al., 2011).

Though the insulin secretion parameter was not significantly different, the steepness of the insulin response as reflected by the Hill coefficient, h, is significantly different between the two groups. A value of h $=$ 2 appears to be closer to normal secretory response, observed in CS subjects with higher insulin sensitivity and h $=$ 1 appears to be the low end of the response observed in T2D subjects who have much lower insulin sensitivity. A point of note is that the CS subjects in this study were weight matched to the patients with T2D and the T2D patients were newly diagnosed. It is possible that a clearer demarcation between CS and T2D groups with respect to the Hill coefficient might become evident when studying a wider spectrum of T2D and CS subjects. In the paper by De Gaetano et al., the average estimated value for the Hill coefficient in normal individuals was 2.4.

Significant differences in time delay in glucose stimulated insulin secretion, τ₁, was observed between CS and T2D subjects. There was a significant time delay in only one CS subject who also had low insulin sensitivity whereas most T2D had large time delays in insulin secretion. The reason for the delay in insulin secretion is unclear but might be partly related to the delay in exogenous glucose (R_IIVG) arrival observed in the patients with T2D. In the paper by De Gaetano where they fit data from IVGTT on normal subjects, a delay in the insulin secretion term had to be introduced to produce the characteristic second phase insulin secretion profile. This result is very different from that observed in this IIGI study where no significant delays were observed in glucose stimulated insulin secretion in the CS subjects.

The insulin sensitivity parameter showed significant differences between T2D and CS subjects following established trends. The magnitude of the average insulin sensitivity of 0.0005 (10 pM min)⁻¹ in CS subjects is near the lower end of the glucose sensitivity parameter estimates in normal subjects in the paper by De Gaetano et al. In addition, two CS subjects had insulin sensitivities that were on par with T2D patients. This is likely because the CS group was weight matched to the patients with T2D in this study. In fact, some CS subjects showed very high levels of insulin secretion indicative of the compensatory phase in response to falling insulin sensitivities. A cut-off value of 0.0002 (10 pM min)⁻¹ separating T2D and CS was tentatively assigned though a much larger study would be required to correctly identify the cut-off based on ROC curves for example. The insulin sensitivity measures determined in this study correlated well with HOMA-IR values. Though HOMA-IR is considered to be a measure of hepatic insulin resistance it has been found to correlate well with insulin sensitivity measures from the hyperinsulinemic-euglycemic clamp, for example. (Matthews et al., 1985).

As seen in Figure 2, the exogenous glucose that is infused has distinct profiles for the different subjects that is particularly apparent in CS patients. To delineate the influence of infused glucose on post infusion glucose profiles, the effect of substituting R_IIGI of one patient with that of another was studied. In order to make a meaningful inference, two CS subjects, 2 and 4, who had similar parameters including similar amounts of total glucose infused (Table 1; Figure 3 Panel B and D), but showed very different post infusion glucose profiles were chosen for the simulations. In Figure 6A, the fit obtained for CS 4 (light blue solid line) as well as the glucose data for CS 2 and CS 4 are shown. In the second simulation (Figure 6B), all parameters of the CS 4 fit were retained but the exogenous glucose infusion R_IIGI of CS 2 was substituted. This causes the CS 4 glucose profile to spike very much like that seen in CS 2. In Panel C, 4 parameters of CS 2 were substituted retaining only insulin secretion and glucagon action parameters. It is shown that patient four transitions to patient two completely. The effect of the exogenous glucose profile is dramatic in this case. This result indicates that rate of glucose arrival could have a big impact on glucose dynamics. As IIGI is isoglycemic with the corresponding OGTT this suggests that rate of glucose arrival from the gut could play a role in glucose dynamics post oral ingestion as well and account in part for the differences in glucose excursions between subjects. The role of gastric emptying in glucose homeostasis has been studied by several researchers where this effect has been observed, eg., Holst et al. and references therein. (Brener et al., 1983; Horowitz et al., 1993; Holst et al., 2016). This possibility has been suggested in the paper by Fiorentino et al. where the role of sodium-glucose co-transporters is investigated. (Fiorentino et al., 2017). This result may also have direct relevance to the findings in the paper by Utzschneider et al. where they made an association between plasma glucose profile shape and beta cell function in newly diagnosed T2D patients. (Utzschneider et al., 2021).

FIGURE 6

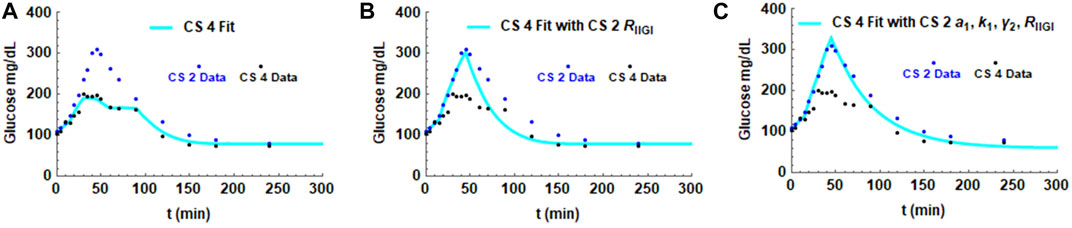
FIGURE 6. Simulations showing the effect of the exogenous glucose arrival R_IIGI on the glucose profile. Parameters in the fit for CS 4 were substituted with the values obtained from the CS 2 fit. Panel (A) shows the fit with all CS 4 parameters. Panel (B) shows the effect of substituting CS 2 glucose infusion, R_IIGI, in the simulation. Panel (C) shows the impact of substituting CS 2 insulin sensitivity parameter a₁, glucagon secretion parameter k₁ and glucagon secretion parameter γ₂ in addition to R_IIGI on the CS 4 fit.

A consequence of ingesting large glucose loads is often a lowering of glucose to values below baseline levels or postprandial hypoglycemia. (Saha, 2006; Parekh et al., 2014). This phenomenon is seen in most of the subjects in this study, particularly the CS subjects. One explanation could be that delayed recovery of glucagon to baseline levels causes the glucose levels in turn to fall below baseline. In the paper by Wang, G., (Wang, 2014)., hysteresis in insulin action is hypothesized to cause postprandial hypoglycemia. As modeling in this study with constant insulin action, a₁, was able to reproduce the plasma glucose profiles correctly, including the postprandial dip, hysteresis behaviour in insulin secretion was considered a possibility instead. If insulin secretion falls off more slowly after glucose levels start falling, it could contribute to post-prandial lowering of glucose below baseline. The fits of the hysteresis model 2, showing h₁<h₂ in CS subjects, on the contrary, predict insulin levels returning to baseline levels more sharply than the rise. The hysteresis model of glucose dependent insulin secretion thus does not appear to explain post-prandial hypoglycemia. Secondly, the hysteresis model 2, with one extra parameter, did not provide a significantly improved description of the dynamics relative to the Hill model 1 as indicated by the AICc criterion.

Modeling IIGI is shown to reveal different levels of impairment in alpha- and beta-cell function and insulin action in T2D. The contribution of various parameters to glucose homeostasis, particularly those related to glucagon dynamics have been estimated. Quantification of the significant impairment in glucagon suppression in patients with T2D should help in classifying patients based on alpha-cell dysregulation. Changes in insulin dose-response parameters in T2D without the confounding influence of incretins and other gut mediated factors as well as first phase insulin release have been determined. The importance of considering exogenous glucose arrival on exacerbating postprandial glucose excursions is highlighted using model simulations. In addition to T2D, the model developed was also used to explore the role of hysteresis in insulin secretion in explaining phenomena such as post prandial glucose lowering and a related pathophysiology reactive hypoglycemia. Results from this study show that hysteresis in insulin secretion is not the likely cause of postprandial glucose lowering. While the model developed is shown to be very effective in determining parameters related to the coupled dynamics from IIGI data, shortcomings of fitting IIGI data are that some of the parameters had to be adjusted manually. Future work would include fitting the model to larger sets of data which would allow for classification of patients based on cut-off values of parameters related to both alpha- and beta-cell impairment determined from ROC curves.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Ethics statement

The studies involving human participants were reviewed and approved by the Scientific-Ethical Committee of the Capital Region of Denmark (registration no. H-A-2007-0048), the Danish Data Protection Agency (registration j. nr. 2007- 41-1058) and at www.ClinicalTrials.gov (ID NCT00529048). The study was conducted according to the principles of the Helsinki Declaration II. The patients/participants provided their written informed consent to participate in this study.

Author contributions

VS: Development of computational model, Fitting model to data, Analysis of results, and Manuscript preparation. JB: Conduction of experimental procedures and collection of samples, Delivery of raw data, Interpretation of results, and Manuscript preparation. JH: Biochemical analysis of glucagon, Interpretation of results, and Manuscript review. FK: Conductor of experimental protocol, Interpretation of results, and Manuscript review. TV: Principal Investigator and Conductor of experimental protocol, Interpretation of results, and Manuscript review.

Funding

(VS) This work was facilitated by financial and institutional support from the Whiting School of Engineering, JH University. The research and open access publication charges were partially funded by the NIH K25 grant number DK131328. (JB) Original work was funded by an unrestricted research grant (no. 34851) from the Investigator Initiated Studies Program of Merck&Co.

Acknowledgments

(VS) Many useful discussions with Professor Patrik Rorsman are gratefully acknowledged. A special thank you to Dr Arthur Sherman for many useful discussions and editing the manuscript. Thanks also to Dr Shankar Subramaniam for useful discussions regarding glucose homeostasis. Thanks to Vinayak Harihar for editing the manuscript and many useful suggestions. Thanks to the reviewers for helpful critiques and suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2022.911616/full#supplementary-material

References

Adkins A., Basu R., Persson M., Dicke B., Shah P., Vella A., et al. (2003). Higher insulin concentrations are required to suppress gluconeogenesis than glycogenolysis in nondiabetic humans. Diabetes 52 (9), 2213–2220. doi:10.2337/diabetes.52.9.2213

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmadpour S., Kabadi U. M. (1997). Pancreatic α-cell function in idiopathic reactive hypoglycemia. Metabolism. 46 (6), 639–643. doi:10.1016/s0026-0495(97)90006-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Akaike H. (1974). A new look at the statistical model identification. IEEE Trans. Autom. Contr. 19 (6), 716–723. doi:10.1109/tac.1974.1100705

CrossRef Full Text | Google Scholar

Alford F. P., Bloom S. R., Nabarro J. D. N. (1976). Glucagon metabolism in man. Studies on the metabolic clearance rate and the plasma acute disappearance time of glucagon in normal and diabetic subjects. J. Clin. Endocrinol. Metab 42(5):830–838. doi:10.1210/jcem-42-5-830

PubMed Abstract | CrossRef Full Text | Google Scholar

Alskär O., Bagger J. I., Røge R. M., Knop F. K., Karlsson M. O., Vilsbøll T., et al. (2016). Semimechanistic model describing gastric emptying and glucose absorption in healthy subjects and patients with type 2 diabetes. J. Clin. Pharmacol. 56 (3), 340–348. doi:10.1002/jcph.602

PubMed Abstract | CrossRef Full Text | Google Scholar

Diabetes Association American (2022). Classification and Diagnosis of Diabetes : Standards of Medical Care in Diabetes — 2022, 17–38.

Google Scholar

Ashcroft F. M., Rorsman P. (2012). Diabetes mellitus and the β -cell : The last ten years. Cell. 148 (6), 1160–1171. doi:10.1016/j.cell.2012.02.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Bagger J. I., Knop F. K., Lund A., Holst J. J., Vilsbøll T. (2014). Glucagon responses to increasing oral loads of glucose and corresponding isoglycaemic intravenous glucose infusions in patients with type 2 diabetes and healthy individuals. Diabetologia 57 (8), 1720–1725. doi:10.1007/s00125-014-3264-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Bagger J. I., Knop F. K., Lund A., Vestergaard H., Holst J. J., Vilsbøll T. (2011). Impaired regulation of the incretin effect in patients with type 2 diabetes. J. Clin. Endocrinol. Metab. 96 (3), 737–745. doi:10.1210/jc.2010-2435

PubMed Abstract | CrossRef Full Text | Google Scholar

Baron A. D., Schaeffer L., Shragg P., Kolterman O. G. (1987). Role of hyperglucagonemia in maintenance of increased rates of hepatic glucose output in type II diabetics. Diabetes 36 (3), 274–283. doi:10.2337/diab.36.3.274

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergman R. N., Ider Y. Z., Bowden C. R., Cobelli C. (1979). Quantitative estimation of insulin sensitivity. Am. J. Physiol. 5 (6), E667–E677. doi:10.1152/ajpendo.1979.236.6.E667

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergman R. N. (2021). Origins and history of the minimal model of glucose regulation. Front. Endocrinol. 11, 583016. doi:10.3389/fendo.2020.583016

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergman R. N., Phillips L. S., Cobelli C. (1981). Physiologic evaluation of factors controlling glucose tolerance in man. Measurement of insulin sensitivity and β-cell glucose sensitivity from the response to intravenous glucose. J. Clin. Investig. 68 (6), 1456–1467. doi:10.1172/jci110398

PubMed Abstract | CrossRef Full Text | Google Scholar

Bojsen-Møller K. N., Lundsgaard A. M., Madsbad S., Kiens B., Holst J. J. (2018). Hepatic insulin clearance in regulation of systemic insulin concentrations-role of carbohydrate and energy availability. Diabetes 67 (11), 2129–2136. doi:10.2337/db18-0539

PubMed Abstract | CrossRef Full Text | Google Scholar

Bolli G., de Feo P., Perriello G., De Cosmo S., Compagnucci P., Santeusanio F., et al. (1984). Mechanisms of glucagon secretion during insulin-induced hypoglycemia in man Role of the beta cell and arterial hyperinsulinemia. J. Clin. Investig. 73 (4), 917–922. doi:10.1172/JCI111315

PubMed Abstract | CrossRef Full Text | Google Scholar

Brener W., Hendrix T. R. M. P., McHugh P. R. (1983). Regulation of the gastric emptying of glucose. Gastroenterology 85 (1), 76–82. doi:10.1016/s0016-5085(83)80232-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Briant L., Salehi A., Vergari E., Zhang Q., Rorsman P. (2016). Glucagon secretion from pancreatic α-cells. Ups. J. Med. Sci. 121 (2), 113–119. doi:10.3109/03009734.2016.1156789

PubMed Abstract | CrossRef Full Text | Google Scholar

Briant L. J. B., Reinbothe T. M., Spiliotis I., Miranda C., Rodriguez B., Rorsman P. (2018). δ-cells and β-cells are electrically coupled and regulate α-cell activity via somatostatin. J. Physiol. 596 (2), 197–215. doi:10.1113/JP274581

PubMed Abstract | CrossRef Full Text | Google Scholar

Brun J. F., Fedou C., Mercier J. (2000). Postprandial reactive hypoglycemia. Diabetes Metab. 26 (5), 337–351.

PubMed Abstract | Google Scholar

Burcelin R., Knauf C., Cani P. D. (2008). Pancreatic alpha-cell dysfunction in diabetes. Diabetes Metab. 34, S49–S55. doi:10.1016/S1262-3636(08)73395-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Caumo A., Luzi L. (2004). First-phase insulin secretion: Does it exist in real life? Considerations on shape and function. Am. J. Physiol. Endocrinol. Metab. 287 (3 50-3), 371–385. doi:10.1152/ajpendo.00139.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Cerf M. E. (2013). Beta cell dysfunction and insulin resistance. Front. Endocrinol. (Lausanne). 4 (MAR), 1–12. doi:10.3389/fendo.2013.00037

PubMed Abstract | CrossRef Full Text | Google Scholar

Cobelli C., Federspil G., Pacini G., Salvan A., Scandellari C. (1982). An integrated mathematical model of the dynamics of blood glucose and its hormonal control. Math. Biosci. 58 (1), 27–60. doi:10.1016/0025-5564(82)90050-5

CrossRef Full Text | Google Scholar

Cobelli C., Man C. D., Sparacino G., Magni L., Nicolao G. De, Kovatchev B. P. (2009). Diabetes: Models, signals, and control. IEEE Rev. Biomed. Eng. 2, 54–96. doi:10.1109/RBME.2009.2036073

PubMed Abstract | CrossRef Full Text | Google Scholar

Cobelli C., Man C. D., Toffolo G., Basu R., Vella A., Rizza R. (2014). The oral minimal model method. Diabetes 63 (4), 1203–1213. doi:10.2337/db13-1198

PubMed Abstract | CrossRef Full Text | Google Scholar

Cryer P. E. (2012). Minireview: Glucagon in the pathogenesis of hypoglycemia and hyperglycemia in diabetes. Endocrinology 153 (3), 1039–1048. doi:10.1210/en.2011-1499

PubMed Abstract | CrossRef Full Text | Google Scholar

Dalla Man C., Camilleri M., Cobelli C. (2006). A system model of oral glucose absorption: Validation on gold standard data. IEEE Trans. Biomed. Eng. 53 (12), 2472–2478. doi:10.1109/TBME.2006.883792

PubMed Abstract | CrossRef Full Text | Google Scholar

Dalla Man C., Caumo A., Cobelli C. (2002). The oral glucose minimal model: Estimation of insulin sensitivity from a meal test. IEEE Trans. Biomed. Eng. 49 (5), 419–429. doi:10.1109/10.995680

PubMed Abstract | CrossRef Full Text | Google Scholar

De Gaetano A., Hardy T. A. (2019). A novel fast-slow model of diabetes progression: Insights into mechanisms of response to the interventions in the Diabetes Prevention Program. PLoS One 14 (10), e0222833–39. doi:10.1371/journal.pone.0222833

PubMed Abstract | CrossRef Full Text | Google Scholar

De Gaetano A., Hardy T., Beck B., Abu-raddad E., Palumbo P., Bue-valleskey J., et al. (2008). Mathematical models of diabetes progression. Am. J. Physiol. 295 (6). doi:10.1152/ajpendo.90444.2008

CrossRef Full Text | Google Scholar

DeFronzo R. A., Tripathy D. (2009). Skeletal muscle insulin resistance is the primary defect in type 2 diabetes. Diabetes Care 32 (2), S157–S163. doi:10.2337/dc09-S302

PubMed Abstract | CrossRef Full Text | Google Scholar

Diderichsen P. M., Göpel S. O. (2006). Modelling the electrical activity of pancreatic α-cells based on experimental data from intact mouse islets. J. Biol. Phys. 32 (3–4), 209–229. doi:10.1007/s10867-006-9013-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Duckworth W. C., Bennett R. G., Hamel F. G. (1998). Insulin degradation: Progress and potential. Endocr. Rev. 19 (5), 608–624. doi:10.1210/edrv.19.5.0349

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunning B. E., Gerich J. E. (2007). The role of α-cell dysregulation in fasting and postprandial hyperglycemia in type 2 diabetes and therapeutic implications. Endocr. Rev. 28 (3), 253–283. doi:10.1210/er.2006-0026

PubMed Abstract | CrossRef Full Text | Google Scholar

Eizirik D. L., Pasquali L., Cnop M. (2020). Pancreatic β-cells in type 1 and type 2 diabetes mellitus: Different pathways to failure. Nat. Rev. Endocrinol. 16 (7), 349–362. doi:10.1038/s41574-020-0355-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Elliott A. D., Ustione A., Piston D. W. (2015). Somatostatin and insulin mediate glucose-inhibited glucagon secretion in the pancreatic alpha-cell by lowering cAMP. Am. J. Physiol. Endocrinol. Metab. 308, E130–E143. doi:10.1152/ajpendo.00344.2014

PubMed Abstract | CrossRef Full Text | Google Scholar

Expert committee on the Diagnosis and classification of diabetes mellitus. Diabetes Care. 2003;26(1):S5–S20.

PubMed Abstract | CrossRef Full Text | Google Scholar

Færch K., Vistisen D., Pacini G., Torekov S. S., Johansen N. B., Witte D. R., et al. (2016). Insulin resistance is accompanied by increased fasting glucagon and delayed glucagon suppression in individuals with normal and impaired glucose regulation. Diabetes 65 (11), 3473–3481. doi:10.2337/db16-0240

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferrannini E., Gastaldelli A., Miyazaki Y., Matsuda M., Mari A., DeFronzo R. A. (2005). beta-Cell function in subjects spanning the range from normal glucose tolerance to overt diabetes: a new analysis. J. Clin. Endocrinol. Metab. 90 (1), 493–500. doi:10.1210/jc.2004-1133

PubMed Abstract | CrossRef Full Text | Google Scholar

Fiorentino T. V., Suraci E., Arcidiacono G. P., Cimellaro A., Mignogna C., Presta I., et al. (2017). Duodenal sodium/glucose cotransporter 1 expression under fasting conditions is associated with postload hyperglycemia. J. Clin. Endocrinol. Metab. 102 (11), 3979–3989. doi:10.1210/jc.2017-00348

PubMed Abstract | CrossRef Full Text | Google Scholar

Fridlyand L. E., Philipson L. H. (2012). A computational systems analysis of factors regulating α cell glucagon secretion. Islets 4 (4), 262–283. doi:10.4161/isl.22193

PubMed Abstract | CrossRef Full Text | Google Scholar

Gastaldelli A., Toschi E., Pettiti M., Frascerra S., Quin A., Sironi A. M., et al. (2001). Effect of physiological hyperinsulinemia on gluconeogenesis in nondiabetic subjects and in type 2 diabetic patients. Diabetes 50 (8), 1807–1812. doi:10.2337/diabetes.50.8.1807

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerich J. E. (1993). Control of glycaemia. Baillieres Clin. Endocrinol. Metab. 7, 551–586. doi:10.1016/s0950-351x(05)80207-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerich J. E. (1988). Lilly lecture 1988. Glucose counterregulation and its impact on diabetes mellitus. Diabetes 37 (12), 1608–1617. doi:10.2337/diab.37.12.1608

PubMed Abstract | CrossRef Full Text | Google Scholar

Godoy-Matos A. F. (2014). The role of glucagon on type 2 diabetes at a glance. Diabetol. Metab. Syndr. 6, 91. doi:10.1186/1758-5996-6-91

PubMed Abstract | CrossRef Full Text | Google Scholar

Grøndahl M. F. G., Lund A. B., Bagger J. I., Petersen T. S., Wewer Albrechtsen N. J., Holst J. J., et al. Glucagon clearance is preserved in type 2 diabetes. , . 2021;71(1):73–82. doi:10.2337/db21-0024

CrossRef Full Text | Google Scholar

Guiastrennec B., Sonne D. P., Hansen M., Bagger J. I., Lund A., Rehfeld J. F., et al. (2016). Mechanism-based modeling of gastric emptying rate and gallbladder emptying in response to caloric intake. CPT. Pharmacometrics Syst. Pharmacol. 5 (12), 692–700. doi:10.1002/psp4.12152

PubMed Abstract | CrossRef Full Text | Google Scholar

Ha J., Satin L. S., Sherman A. S. (2016). A mathematical model of the pathogenesis, prevention, and reversal of type 2 diabetes. Endocrinology 157 (2), 624–635. doi:10.1210/en.2015-1564

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasdemir D., Hoefsloot H. C. J., Smilde A. K. (2015). Validation and selection of ODE based systems biology models: How to arrive at more reliable decisions. BMC Syst. Biol. 9 (1), 32–19. doi:10.1186/s12918-015-0180-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Hershon K. S., Hirsch B. R., Odugbesan O. (2019). Importance of postprandial glucose in relation to A1C and cardiovascular disease. Clin. Diabetes 37 (3), 250–259. doi:10.2337/cd18-0040

PubMed Abstract | CrossRef Full Text | Google Scholar

Holst J. J., Gribble F., Horowitz M., Rayner C. K. (2016). Roles of the gut in glucose homeostasis. Diabetes Care 39 (6), 884–892. doi:10.2337/dc16-0351

PubMed Abstract | CrossRef Full Text | Google Scholar

Horowitz M., Edelbroek M. A. L., Wishart J. M., Straathof J. W. (1993). Relationship between oral glucose tolerance and gastric emptying in normal healthy subjects. Diabetologia 36 (9), 857–862. doi:10.1007/BF00400362

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaplan W., Sunehag A. L., Dao H., Haymond M. W. (2008). Short-term effects of recombinant human growth hormone and feeding on gluconeogenesis in humans. Metabolism. 57 (6), 725–732. doi:10.1016/j.metabol.2008.01.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Keeler J., de Paula J., Atkins P. (2018). Atkins’ physical chemistry. 11th ed., 1. Oxford University Press.

Google Scholar

Keenan D. M., Basu R., Liu Y., Basu A., Bock G., Veldhuis J. D. (2012). Logistic model of glucose-regulated C-peptide secretion: Hysteresis pathway disruption in impaired fasting glycemia. Am. J. Physiol. Endocrinol. Metab. 303 (3), E397–E409. doi:10.1152/ajpendo.00494.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Kelly R. A., Fitches M. J., Webb S. D., Pop S. R., Chidlow S. J., Sotsky M. J., et al. (2019). Modelling the effects of glucagon during glucose tolerance testing. Theor. Biol. Med. Model. 16 (1), 21–17. doi:10.1186/s12976-019-0115-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim J., Saidel G. M., Cabrera M. E. (2007). Multi-scale computational model of fuel homeostasis during exercise: Effect of hormonal control. Ann. Biomed. Eng. 35 (1), 69–90. doi:10.1007/s10439-006-9201-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Knop F. K., Vilsbøll T., Højberg P. V., Larsen S., Madsbad S., Vølund A., et al. (2007). Reduced incretin effect in type 2 diabetes. Diabetes 56, 1951–1959. doi:10.2337/db07-0100

PubMed Abstract | CrossRef Full Text | Google Scholar

Landgraf R. (2004). The relationship of postprandial glucose to HbA1c. Diabetes. Metab. Res. Rev. 20 (2), S9–S12. doi:10.1002/dmrr.517

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee Y., Wang M. Y., Du X. Q., Charron M. J., Unger R. H. (2011). Glucagon receptor knockout prevents insulin-deficient type 1 diabetes in mice. Diabetes 60 (2), 391–397. doi:10.2337/db10-0426

PubMed Abstract | CrossRef Full Text | Google Scholar

Lund A., Bagger J. I., Christensen M., Knop F. K., Vilsbøll T. (2014). Glucagon and type 2 diabetes: The return of the alpha cell. Curr. Diab. Rep. 14 (12), 555–557. doi:10.1007/s11892-014-0555-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Man C. D., Yarasheski K. E., Caumo A., Robertson H., Toffolo G., Polonsky K. S., et al. (2005). Insulin sensitivity by oral glucose minimal models: Validation against clamp. Am. J. Physiol. Endocrinol. Metab. 289 (6), 954–959. doi:10.1152/ajpendo.00076.2005

CrossRef Full Text | Google Scholar

MannWhitneyTest. Wolfram Research (2010). Wolfram lang funct.

Google Scholar

Mari A., Bagger J. I., Ferrannini E., Holst J. J., Knop F. K., Vilsbøll T. (2013). Mechanisms of the incretin effect in subjects with normal glucose tolerance and patients with type 2 diabetes. PLoS One 8 (9), e73154. doi:10.1371/journal.pone.0073154

PubMed Abstract | CrossRef Full Text | Google Scholar

Mari A., Schmitz O., Gastaldelli A., Oestergaard T., Nyholm B., Ferrannini E. (2002). Meal and oral glucose tests for assessment of β-cell function: Modeling analysis in normal subjects. Am. J. Physiol. Endocrinol. Metab. 283 (6 46-6), 1159–1166. doi:10.1152/ajpendo.00093.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

Mari A., Tura A., Gastaldelli A., Ferrannini E. (2002). Assessing insulin secretion by modeling in multiple-meal tests: Role of potentiation. Diabetes 51 (L), S221–S226. doi:10.2337/diabetes.51.2007.s221

PubMed Abstract | CrossRef Full Text | Google Scholar

Matthews D. R., Hosker J. P., Rudenski A. S., Naylor B. A., Treacher D. F., Turner R. C. (1985). Homeostasis model assessment: Insulin resistance and β-cell function from fasting plasma glucose and insulin concentrations in man. Diabetologia 28 (7), 412–419. doi:10.1007/BF00280883

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitrakou A., Kelley D., Veneman T., Jenssen T., Pangburn T., Reilly J., et al. (1990). Contribution of abnormal muscle and liver glucose metabolism to postprandial hyperglycemia in NIDDM. Diabetes 39 (11), 1381–1390. doi:10.2337/diab.39.11.1381

PubMed Abstract | CrossRef Full Text | Google Scholar

Montanya E. (2014). Insulin resistance compensation: not just a matter of β-cells?, 63. Diabetes, 832–834.

CrossRef Full Text | Google Scholar

Moon J. S., Won K. C. (2015). Pancreatic α-cell dysfunction in type 2 diabetes: Old kids on the block 39(1):1. 9. doi:10.4093/dmj.2015.39.1.1

CrossRef Full Text | Google Scholar

Morettini M., Burattini L., Göbl C., Pacini G., Ahrén B., Tura A. (2021). Mathematical model of glucagon kinetics for the assessment of insulin-mediated glucagon inhibition during an oral glucose tolerance test. Front. Endocrinol. 12, 611147. doi:10.3389/fendo.2021.611147

CrossRef Full Text | Google Scholar

Nauck M., Stöckmann F., Ebert R., Creutzfeldt W. (1986). Reduced incretin effect in Type 2 (non-insulin-dependent) diabetes. Diabetologia 29 (1), 46–52. doi:10.1007/BF02427280

PubMed Abstract | CrossRef Full Text | Google Scholar

Nauck M. A., Meier J. J. (2016). The incretin effect in healthy individuals and those with type 2 diabetes: Physiology, pathophysiology, and response to therapeutic interventions. Lancet. Diabetes Endocrinol. 4 (6), 525–536. doi:10.1016/S2213-8587(15)00482-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Palumbo P., Ditlevsen S., Bertuzzi A., Gaetano A. De (2013). Mathematical modeling of the glucose – insulin system : A review. Math. Biosci. 244 (2), 69–81. doi:10.1016/j.mbs.2013.05.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Panunzi S., Palumbo P., De Gaetano A. (2007). A discrete single delay model for the intra-venous glucose tolerance test. Theor. Biol. Med. Model. 4, 35–16. doi:10.1186/1742-4682-4-35

PubMed Abstract | CrossRef Full Text | Google Scholar

Parekh S., Bodicoat D. H., Brady E., Webb D., Mani H., MoStafa S., et al. (2014). Clinical characteristics of people experiencing biochemical hypoglycaemia during an oral glucose tolerance test : Cross-sectional analyses from a UK multi-ethnic population. Diabetes Res. Clin. Pract. 104 (3), 427–434. doi:10.1016/j.diabres.2014.02.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Piccinini F., Bergman R. N. (2020). The measurement of insulin clearance. Diabetes Care 43 (9), 2296–2302. doi:10.2337/dc20-0750

PubMed Abstract | CrossRef Full Text | Google Scholar

Portet S. (2020). A primer on model selection using the Akaike Information Criterion. Infect. Dis. Model. 5, 111–128. doi:10.1016/j.idm.2019.12.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Röder P. V., Wu B., Liu Y., Han W. (2016). Pancreatic regulation of glucose homeostasis. Exp. Mol. Med. 48 (3), e219.

PubMed Abstract | CrossRef Full Text | Google Scholar

Røge R. M., Bagger J. I., Alskär O., Kristensen N. R., Klim S., Holst J. J., et al. (2017). Mathematical modelling of glucose-dependent insulinotropic polypeptide and glucagon-like peptide-1 following ingestion of glucose. Basic Clin. Pharmacol. Toxicol. 121 (4), 290–297. doi:10.1111/bcpt.12792

PubMed Abstract | CrossRef Full Text | Google Scholar

Saha B. (2006). Post prandial plasma glucose level less than the fasting level in otherwise healthy individuals during routine screening. Indian J. Clin. biochem. 21 (2), 67–71. doi:10.1007/BF02912915

PubMed Abstract | CrossRef Full Text | Google Scholar

Santoleri D., Titchenell P. M. (2019). Resolving the paradox of hepatic insulin resistance. Cell. Mol. Gastroenterol. Hepatol. 7 (2), 447–456. doi:10.1016/j.jcmgh.2018.10.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Sulston K. W., Ireland W. P., Praught J. C. (2006). Hormonal effects on glucose regulation. Atlantic 1 (1), 31–46.

Google Scholar

Suzuki K., Katsura D., Sagara M., Aoki C., Nishida M., Aso Y. (2016). Postprandial reactive hypoglycemia treated with a low-dose alpha-glucosidase inhibitor : Voglibose may suppress oxidative stress and prevent endothelial dysfunction. Int. Med. 55 (8), 949–953. doi:10.2169/internalmedicine.55.5737

CrossRef Full Text

Tian G., Sandler S., Gylfe E., Tengholm A (2011). Glucose- and hormone-induced cAMP oscillations in α- and β-cells within intact pancreatic islets. Diabetes 60 (5), 1535–1543. doi:10.2337/db10-1087

PubMed Abstract | CrossRef Full Text | Google Scholar

Titchenell P. M., Quinn W. J., Lu M., Chu Q., Lu W., Li C., et al. (2016). Direct hepatocyte insulin signaling is required for lipogenesis but is dispensable for the suppression of glucose production. Cell. Metab. 23 (6), 1154–1166. doi:10.1016/j.cmet.2016.04.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Topp B., Promislow K., Devries G., Miura R. M., Finegood D. T. (2000). A model of β-cell mass, insulin, and glucose kinetics: Pathways to diabetes. J. Theor. Biol. 206 (4), 605–619. doi:10.1006/jtbi.2000.2150

PubMed Abstract | CrossRef Full Text | Google Scholar

Topp B. G., Atkinson L. L., Finegood D. T. (2007). Dynamics of insulin sensitivity , Beta-cell function , and Beta-cell mass during the development of diabetes in fa/fa rats. Am. J. Physiol. Endocrinol. Metab. 293, E1730–E1735. doi:10.1152/ajpendo.00572.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Tura A., Bagger J. I., Ferrannini E., Holst J. J., Knop F. K., Vilsbøll T., et al. (2017). Impaired beta cell sensitivity to incretins in type 2 diabetes is insufficiently compensated by higher incretin response. Nutr. Metab. Cardiovasc. Dis. 27 (12), 1123–1129. doi:10.1016/j.numecd.2017.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Unger R. H., Aguilar-Parada E., Müller W. A., Eisentraut A. M. (1970). Studies of pancreatic alpha cell function in normal and diabetic subjects. J. Clin. Investig. 49 (4), 837–848. doi:10.1172/JCI106297

PubMed Abstract | CrossRef Full Text | Google Scholar

Unger R. H., Orci L. (1975). The essential role of glucagon in the pathogenesis of diabetes mellitus. Lancet 84, 14–16. doi:10.1016/s0140-6736(75)92375-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Utzschneider K. M., Younes N., Rasouli N., Barzilay J. I., Banerji M. A., Cohen R. M., et al. (2021). Shape of the OGTT glucose response curve: Relationship with β-cell function and differences by sex, race, and BMI in adults with early type 2 diabetes treated with metformin. BMJ Open Diabetes Res. Care 9 (1), e002264. doi:10.1136/bmjdrc-2021-002264

PubMed Abstract | CrossRef Full Text | Google Scholar

Villaverde A. F., Barreiro A., Papachristodoulou A. (2016). Structural identifiability of dynamic systems biology models. PLoS Comput. Biol. 12 (10), e1005153–22. doi:10.1371/journal.pcbi.1005153

PubMed Abstract | CrossRef Full Text | Google Scholar

Villaverde A. F., Evans N. D., Chappell M. J., Banga J. R. (2019). Input-dependent structural identifiability of nonlinear systems. IEEE Control Syst. Lett. 3 (2), 272–277. doi:10.1109/lcsys.2018.2868608

CrossRef Full Text | Google Scholar

Walker J. N., Ramracheya R., Zhang Q., Johnson P. R. V., Braun M., Rorsman P. (2011). Regulation of glucagon secretion by glucose: Paracrine. Diabetes Obes. Metab. 13, 95–105. doi:10.1111/j.1463-1326.2011.01450.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang G. (2014). Raison d’être of insulin resistance: The adjustable threshold hypothesis. J. R. Soc. Interface 11 (101), 20140892. doi:10.1098/rsif.2014.0892

PubMed Abstract | CrossRef Full Text | Google Scholar

Watts M., Ha J., Kimchi O., Sherman A. (2016). Paracrine regulation of glucagon secretion: The β/α/δ model. Am. J. Physiol. Endocrinol. Metab. 310 (8), E597-E611–E611. doi:10.1152/ajpendo.00415.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Watts M., Sherman A. (2014). Modeling the pancreatic α-cell: Dual mechanisms of glucose suppression of glucagon secretion. Biophys. J. 106 (3), 741–751. doi:10.1016/j.bpj.2013.11.4504

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolfram Research, Inc. (2019). Mathematica, Version 12.0. Champaign, IL.

Google Scholar

Yu Q., Shuai H., Ahooghalandari P., Gylfe E., Tengholm A. (2019). Glucose controls glucagon secretion by directly modulating cAMP in alpha cells, 1212–24.

PubMed Abstract | Google Scholar

Zmazek J., Grubelnik V., Markovič R., Marhl M. (2021). Role of cAMP in double switch of glucagon secretion. Cells 10 (4), 896. doi:10.3390/cells10040896

PubMed Abstract | CrossRef Full Text | Google Scholar