
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Physiol. , 10 March 2022
Sec. Exercise Physiology
Volume 13 - 2022 | https://doi.org/10.3389/fphys.2022.846284
This article is part of the Research Topic The Force-Velocity Relationship: Assessment and Adaptations provoked by Exercise, Disuse and Disease View all 5 articles
 Kathryn N. Seow1
Kathryn N. Seow1 Chun Y. Seow2,3*
Chun Y. Seow2,3*Muscles convert chemical energy to mechanical work. Mechanical performance of a muscle is often assessed by the muscle’s ability to shorten and generate power over a range of loads or forces, characterized by the force–velocity and force–power relationships. The hyperbolic force–velocity relationship of muscle, for a long time, has been regarded as a pure empirical description of the force–velocity data. Connections between mechanical manifestation in terms of force–velocity properties and the kinetics of the crossbridge cycle have only been established recently. In this review, we describe how the model of Huxley’s crossbridge kinetics can be transformed to the hyperbolic Hill equation, and link the changes in force–velocity properties to molecular events within the crossbridge cycle driven by ATP hydrolysis. This allows us to reinterpret some findings from previous studies on experimental interventions that altered the force–velocity relationship and gain further insight into the molecular mechanisms of muscle contraction under physiological and pathophysiological conditions.
An activated muscle is able to exert force or carry a load while shortening. The velocity of shortening decreases as the load or force on the muscle increases. The force–velocity relationship is not linear, rather, it can be described by a hyperbolic function, first proposed by Hill (1938):
where F and V are muscle force and velocity, respectively, and a, b, and c are Hill’s constants. Data from Hill’s (1938) study suggested that the mechanics of muscle contraction could be linked to the muscle’s energy metabolism, because the same hyperbolic force–velocity relationship could be derived from heat measurements and the constant a was derived from the thermal constant of shortening heat—α (Hill, 1938). A later study by Hill (1964) found that α was not a constant, but a function of shortening velocity and load, therefore α is not equivalent to a. The Hill equation has since been used as an empirical mathematical description of the force–velocity data (Abbott and Wilkie, 1953), until recently (Seow, 2013).
Our current understanding of the characteristic force–velocity behavior of muscle is based on Huxley’s (1957) kinetic model of cyclic interaction between myosin crossbridges and actin filaments. From a molecular basis, Huxley has demonstrated that the force–velocity relationship does not originate from the behavior of individual crossbridges, but from the collective action of all activated crossbridges in the muscle as they go through, asynchronously, the energy-dependent cyclic interaction with actin filaments. It is known that Huxley’s kinetic model predicts a force–velocity relationship that can be well-fitted by the Hill equation. It has been shown that this is not a coincidence, but rather that the two forms of description are mathematically identical when certain conditions are met (Seow, 2013). The recognition allowed us to link the molecular mechanisms of crossbridge cycle to the emergent relationship between muscle force and shortening velocity. Changes in the curvature of the force–velocity curve, for example, can now be interpreted in terms of changes in the rates of crossbridge attachment to, and detachment from, the actin filaments. Because the force–power relationship of a muscle can be derived from its force–velocity relationship, muscle performance in terms of power output can be understood at the crossbridge level through the changes in the force–velocity properties.
In isolated muscle preparations, force–velocity data are usually obtained using a method called isotonic quick release. Typically, during an isometric contraction, a step (or isotonic) release is applied so that the muscle shortens under a constant load, as illustrated in Figure 1A. It is known that the length change in response to the force step consists of four phases (Civan and Podolsky, 1966) and that each can be traced to certain cellular and subcellular origins (Ford et al., 1977). Phase 1 is primarily an elastic recoil immediately following the step release of tension. In striated muscle preparations with little stray compliance, phase 1 response stems mainly from the crossbridge and actin filament elasticity. Muscle stiffness assessed from the phase 1 response can therefore be used as an approximate index of the number of attached crossbridges. The phase 2 response originates mainly from the synchronous power strokes of some crossbridges after the step release (Dobbie et al., 1998; Suzuki et al., 1998). Phase 3 occurs when some of the crossbridges reach the end of their power stroke, and others start to detach from actin filaments. Phases 1 to 3 are transient responses, unlike phase 4, which occurs when the crossbridges enter steady-state asynchronous cycles. In force–velocity measurements, the initial slope of the phase 4 response is taken as the steady-state shortening velocity of the muscle under the externally applied isotonic load. The force–velocity properties of the muscle are therefore steady-state properties.
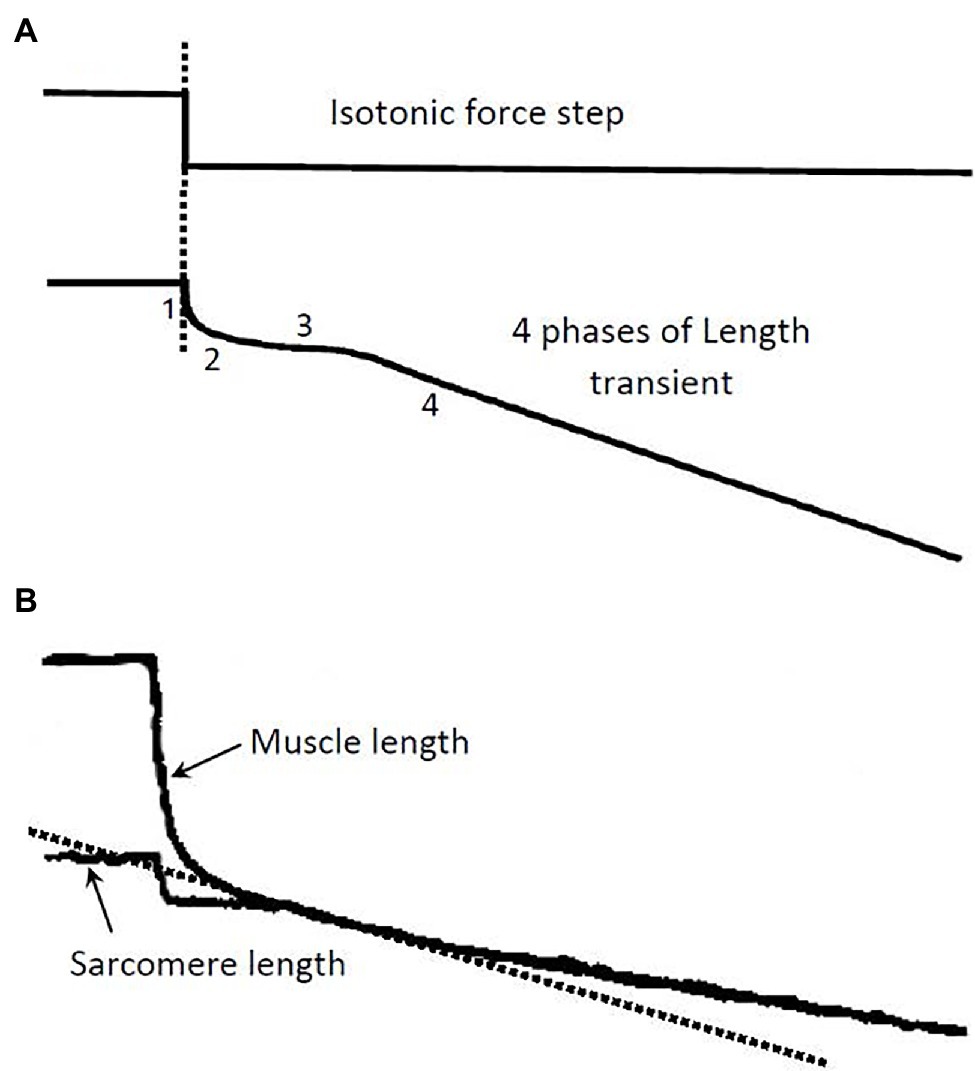
Figure 1. (A) Illustration of a step release in force and the ensuing length transient. The 4 phases of the length response and their underlying causes are described in the text. The isotonic load after the release is kept constant during the transient and the phase 4 contraction (Modified from Seow, 2013). (B) Records from an experiment showing length response to a force step. A skinned single fiber of rabbit psoas muscle was used in the experiment. Both the fiber length and the laser-diffracted sarcomere length signals were recorded. The initial slope (dotted line) of the phase 4 response in the sarcomere length record is taken as the shortening velocity corresponding to the isotonic load.
Many muscle preparations used in experiments contain a substantial amount of stray compliance, which usually stems from the crushed ends of the muscle preparation. The stray compliance is viscoelastic in nature (Seow and Ford, 1992), and its recoil during the step release can obscure the transient response of the muscle. Figure 1B shows a length response from a skinned (membrane-permeabilized) rabbit psoas fiber (cell), and a sarcomere length response from the same fiber. The muscle length response contains stray compliance which obscures the transients, whereas the sarcomere length response is free of the influence of the stray compliance and the transient phases are evident. It is clear from the sarcomere length record where to measure the steady-state shortening velocity (phase 4). It is crucial that this velocity is measured at the right time after the quick release; measurements made too early will overestimate the velocity, while measurements made too late will underestimate the velocity.
In fitting force–velocity data with the hyperbolic Hill equation, equation 1 is usually transformed to an explicit function, that is, shortening velocity as an explicit function of muscle load, as follows:
Alternatively, the Hill equation can be expressed as an explicit function of force:
A non-linear fit of force–velocity data is performed to obtain Hill’s constants a, b, and c. An example is shown in Figure 2. Curve fitting of force–velocity data by the Hill equation usually produces an excellent agreement between the data and the curve, especially in the force range of 5–80% of maximal isometric force (Fmax). Significant deviations of data from the curve can occur in the force ranges of 0–5% Fmax and 80–100% Fmax. Reasons for the deviation have been discussed in detail by Seow (2013).
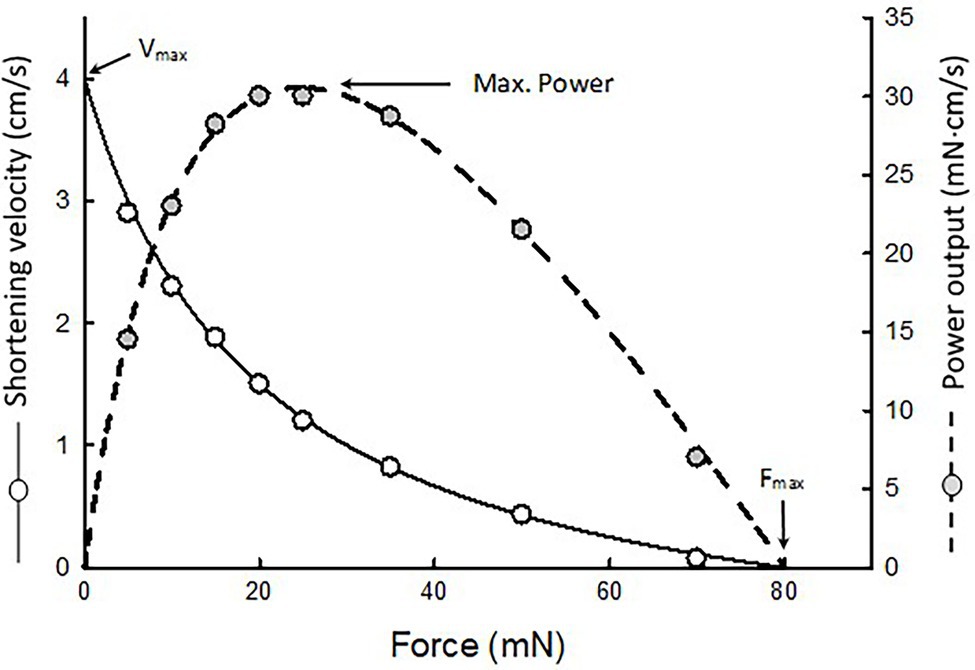
Figure 2. An example of force–velocity data fitted by the Hill equation. The maximal shortening velocity (Vmax) and maximal isometric force (Fmax) are extrapolated from the fitted curve. Because the muscle’s power output is the product of force and velocity, a force–power curve (dotted curve) can be derived from the force–velocity curve.
Because power equals force times velocity, the muscle’s force–power relationship can be derived from the force–velocity relationship, as shown in Figure 2 (dotted curve). Maximal power typically occurs in the force range of 10–50% Fmax. In this force range, curve fitting of the data is by interpolation. The maximal power output (Pmax) obtained from curve fitting is usually more reliable than the extrapolated values of maximal shortening velocity (Vmax) and Fmax.
The basic contractile unit in striated muscles is the half-sarcomere. In a muscle cell, all sarcomeres have the same structure and function. During contraction, each half-sarcomere contributes equally to the generation of force, shortening, and power by the muscle. Measured mechanical output of a muscle cell can vary depending on the cell size and how the sarcomeres are arranged within the cell. A muscle cell will generate more force if it has more sarcomeres packed in parallel. Because the cell’s cross-sectional area is proportional to the number of sarcomeres in parallel, muscle force is normalized by the cross-sectional area of the muscle preparation. Normalized force is called stress, which has the same unit as pressure, for example, kilopascal (kPa) which is also the same as mN/mm2.
The number of sarcomeres in series is proportional to the muscle length, therefore muscle length or shortening velocity is normalized by the resting length of the muscle preparation, if the sarcomere length is not known. The unit for the normalized shortening velocity is typically muscle length/s. If the sarcomere length is known, then the number of sarcomeres in series can be obtained by dividing the muscle length by the sarcomere length. Of course, the number of half-sarcomeres is twice that of sarcomeres. To normalize shortening velocity, the measured velocity is divided by the number of half-sarcomeres. The unit for normalized shortening velocity is therefore typically μm s−1 half-sarcomere−1.
The power output of a muscle is proportional to the total number of sarcomeres in the muscle, regardless of their arrangement (i.e., in series or in parallel). The total number of sarcomeres in a muscle is proportional to the volume of the muscle, that is, cross-sectional area of the muscle multiplied by the muscle length. Because muscle volume is more difficult to measure than muscle weight, the latter is typically used to normalize muscle power, since muscle weight is linearly proportional to muscle volume, with the muscle density (~1.06 g/cm3) being the constant of proportionality. The unit for normalized power is typically milliwatts per gram of muscle tissue, or mW/g.
The following section further illustrates the rationale for normalization of force–velocity properties.
We have found that in airway smooth muscle, partial activation (defined as a reduction in Fmax, Pmax, and the degree of phosphorylation of the regulatory myosin light chain, but without a change in Vmax) does not result in a change in the curvature of the force–velocity curve (Luo et al., 2019). Mathematically, the curvature of Hill’s hyperbola is determined by the ratio of maximal isometric force over the Hill constant a, or the ratio of maximal velocity over the Hill constant b, that is:
Figure 3 illustrates how curvature of a force–velocity curve could be altered by changes in the ratio of Fmax/a or Vmax/b.
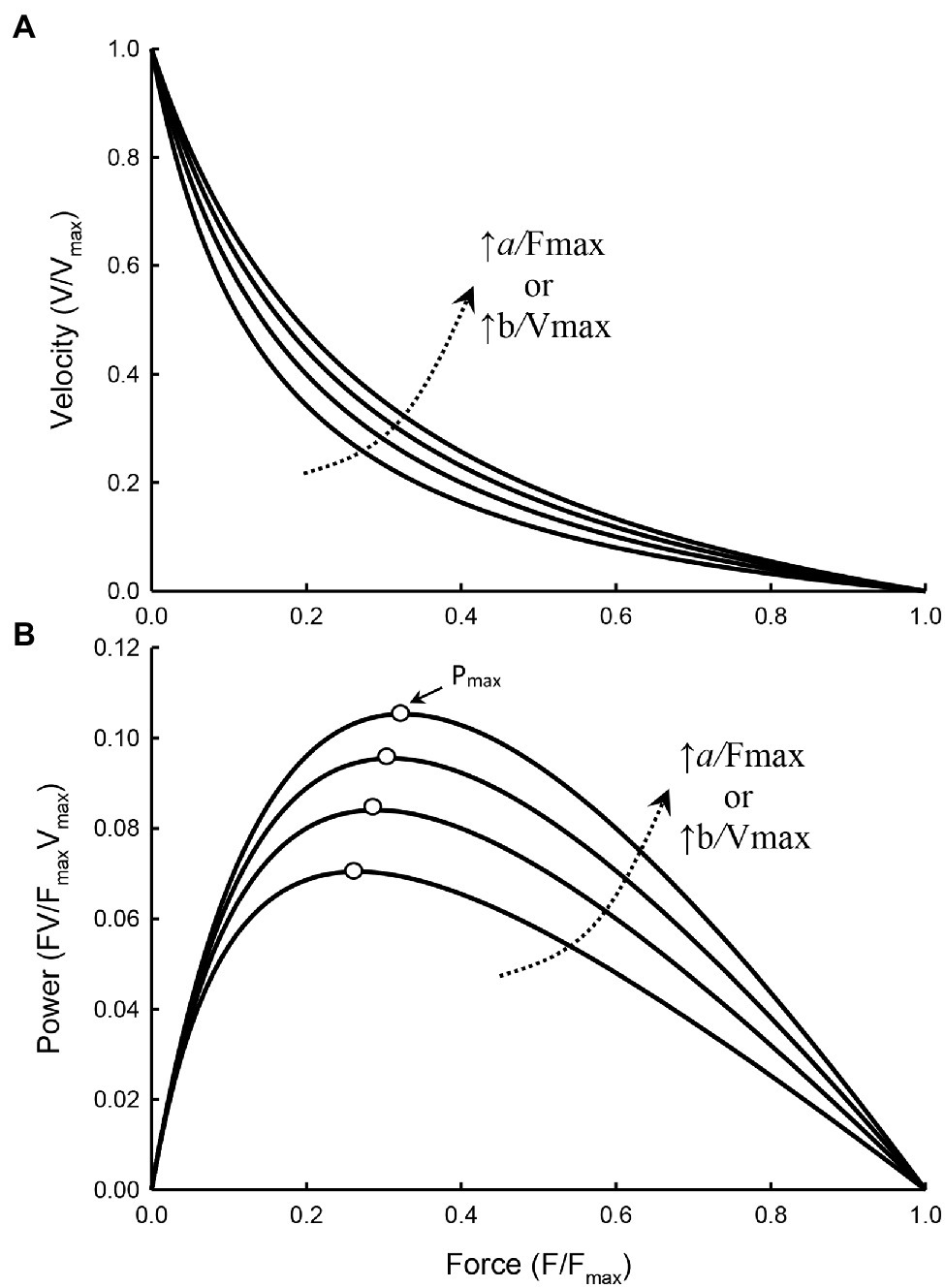
Figure 3. Force–velocity (A) and force–power (B) curves with the value of a/Fmax and b/Vmax increasing from 0.15, 0.2, 0.25, to 0.3, resulting in a decrease in the curvature of the force–velocity curves (i.e., less curved) and an increase in Pmax of the force–power curves. The force at which Pmax occurs (open symbols) also increases as the curvature decreases.
For interventions that do not alter the kinetics of actomyosin interaction, the force–velocity curvature will not be affected by such interventions. For example, in fully and partially activated muscles where the change in activation is strictly limited to a change in the number of activated crossbridges, with no change in the kinetics of actomyosin interaction, the curvature is not expected to change. The Hill equation for the fully and partially activated muscle can be written as follows:
In equations 5 and 6, Vf and Vp denote shortening velocity of fully and partially activated muscles, respectively, bp and ap are Hill’s constants for the partially activated muscle, and n is an index of activation with n = 1 for full activation and n < 1 for partial activation. We have shown that if partial activation only results in a reduction in the number of attached crossbridges, the Hill constant b remains unchanged (Luo et al., 2019). That is, bp = b. Because Vmax is the same in either full or partial activation, and Vmax occurs when F = 0, from equations 5 and 6:
From equation 7 one can derive: ap = na. The curvature of the force–velocity curve for the partially activated muscle is nFmax/ap or nFmax/na, or simply Fmax/a. The curvatures as defined by equation 4 (Fmax/a) for both fully and partially activated muscles are therefore the same.
Hypertrophy or atrophy of a striated muscle cell does not alter the structure or function of individual sarcomeres, but changes their number. Figure 4A shows a simplified illustration of a sarcomere, and Figure 4B shows three different arrangements of four such sarcomeres. Figure 4C shows force–velocity curves for each of the arrangements: a, bi, bii, and biii. Note that, graphically, curve bi is obtained by scaling the velocity values of curve a by a factor of 4; curve bii is obtained by scaling both force and velocity values of curve a by a factor of 2; and curve biii is obtained by scaling the force value of curve a by a factor of 4. Because the crossbridge kinetics is not altered by different geometric arrangements, the shape of the force–velocity curves after normalization by the number of sarcomeres in parallel and in series, bi, bii, and biii will all superimpose exactly on curve a. In other words, scaling of force and velocity in each of the cases, bi, bii, and biii, does not change the curvature of the force–velocity curves. The conservation of curvature can be illustrated mathematically. From equation 7 we learn that scaling the force by a factor n will lead to a change in the Hill constant a by the same factor. For example, in the case of partial activation, ap = na. It can be shown that n can be any positive number and it does not have to be less than 1 as in the case of partial activation. If we use an to denote the Hill constant a in a force–velocity relationship where force can be scaled up or down by a factor of n, then an = na. In a similar manner, it can be shown that bm = mb, where m is the scaling factor for velocity. An interesting property of the Hill equation is that the constants a and b are mutually exclusive in that changing the force scale only affects constant a, and changing the velocity scale only affects constant b. Therefore, for case bi (Figure 4C), bm = 4b. The curvature of curve bi, as defined by equation 4 is 4Vmax/bm or 4Vmax/4b or simply Vmax/b, is the same curvature as the unscaled curve a. For the case bii in Figure 4C, an = 2a and bm = 2b. The curvature does not change in this case either, because nFmax/an = 2Fmax/2a = Fmax/a and mVmax/bm = 2Vmax/2b = Vmax/b. Finally, for case biii in Figure 4C, nFmax/an = 4Fmax/4a = Fmax/a. Again, scaling force does not lead to a change in the curvature of the force–velocity curve. It should be pointed out that, in any case, the scaling factor has to be a constant, and not a function.
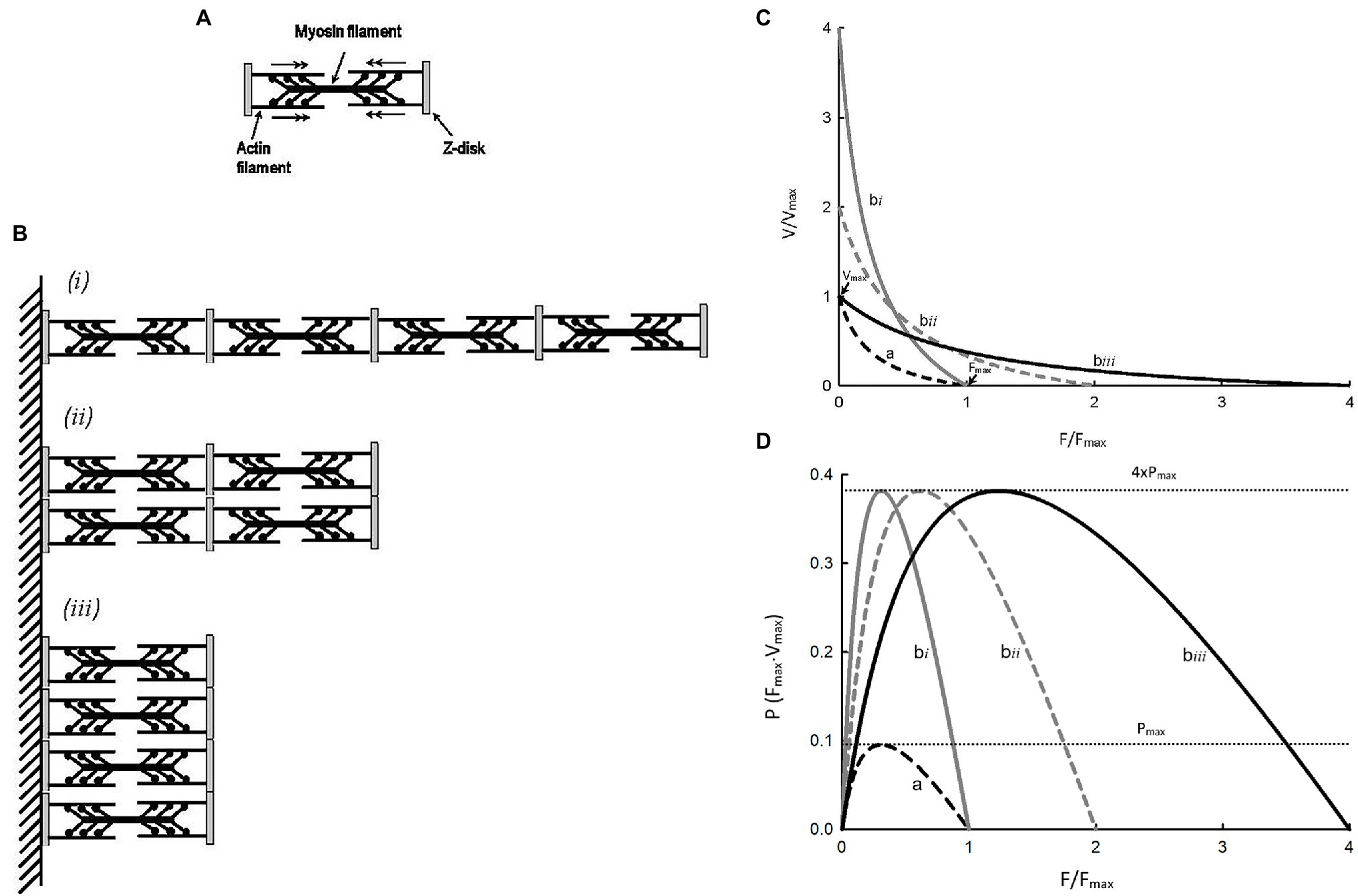
Figure 4. (A) Schematic representation of a sarcomere. (B) Three different arrangements of 4 identical sarcomeres in parallel and in series. (C)Force–velocity curves for a single sarcomere (a) and each of the sarcomere arrangements (bi, bii, biii). (D) Force–power curves for a single sarcomere (a) and each of the sarcomere arrangements (bi, bii, biii).
For the examples shown in Figure 4C, shortening velocity is proportional to the number of sarcomeres in series and force is proportional to the number of sarcomeres in parallel. From Figure 4D, it is clear that power output of a muscle is proportional to the number of sarcomeres, regardless of their arrangements. For curves bi, bii, and biii, the maximal power is the same, and it is 4 times the maximal power for curve a because they have 4 times more sarcomeres. The examples shown in Figure 4 support the rationale for how force, velocity, and power are normalized, as described earlier in the section Normalization of force, velocity, and power above.
Force in a force–velocity relationship usually refers to externally applied force or load against which the muscle shortens. The viscous and compressive loads within the muscle tissue are not part of the external load. In the absence of an internal load, the externally applied force is the total force “seen” by the muscle. In most studies, internal loads are neglected because they are relatively small compared to the maximal load (Fmax). However, even with an internal load less than 5% of Fmax, Vmax, and a/Fmax can be significantly altered. Internal loads are ubiquitous in muscle preparations. They stem from any loci within the muscle that offer impediments to shortening. They are present in smooth (Wang et al., 2002; Luo et al., 2019) and cardiac (Chiu et al., 1982; Walley et al., 1991) muscles. The internal load in skeletal muscle is relatively small and may be justifiably neglected, but under some experimental conditions, such as acidosis (Seow and Ford, 1993), the internal load can be significant.
Figure 5 graphically illustrates what an internal load is. Hill’s constants a and b are the asymptotes of the Hill hyperbola. In a typical force–velocity curve only the portion between Vmax and Fmax of the curve is plotted (Figure 5, solid curve). If an internal load is present, the force–velocity curve is truncated and only the portion of the curve between V’max and F’max is plotted. In order for a muscle to shorten, the contractile force developed by the muscle has to overcome both the internal and external loads. An internal load therefore functions to reduce the contractile force of the muscle, similar to partial activation. As in partial activation, an internal load affects the force–velocity relationship by changing the Hill constant a but not b (Seow and Stephens, 1986; Seow and Ford, 1993; Luo et al., 2019). The curvature of the force–velocity curve within the force range of F’max can be derived from:
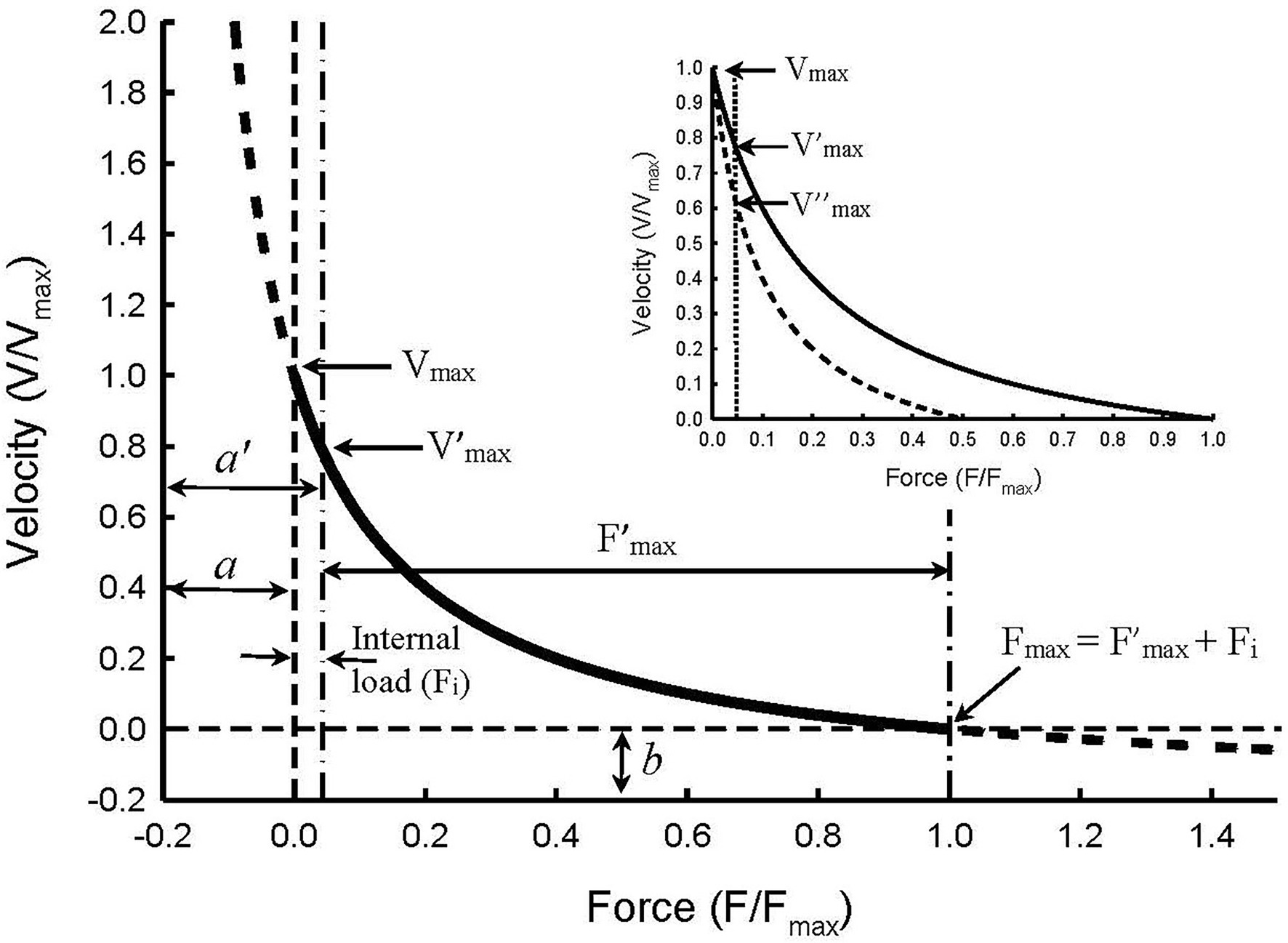
Figure 5. Illustration of force–velocity relationship in the presence of an internal load of 0.05 Fmax magnitude. The Hill constants a and b are asymptotes of the hyperbolic curve. An internal load effectively increases constant a so that the new asymptote a’ equals a + Fi. The internal load also reduces maximal isometric force so that F’max equals Fmax – Fi. The apparent force–velocity curvature (F’max/a’) decreases in the presence of an internal load, compared with the curvature in the absence of the internal load (Fmax/a), because F’max/a’ = (Fmax – Fi)/(a + Fi). The maximal velocity seen in the absence of both internal and external loads (Vmax) is not affected by the internal load. However, the internal load causes an apparent decrease in the maximal velocity (from Vmax to V’max). Inset: Illustration of how partial activation in the presence of an internal load causes an apparent decrease in the maximal velocity from V’max at full activation to V″max at half-activation. The changes in Vmax, Fmax, and Fmax/a due to an internal load are called “apparent” because the changes are artifacts caused by the internal load and not by changes in the kinetics of actomyosin interaction.
where a’ is the new asymptote for the curve with an internal load (Fi), and F’max is the maximal isometric force with an internal load. Because Fi is always positive, it follows that a’/F’max will always be greater than a/Fmax, and the greater the internal load, or ratio of Fi/Fmax, the greater the value of a’/F’max will be. Therefore, even though an internal load does not actually alter the shape of the force–velocity curve (Figure 5), the apparent curvature indicated by F’max/a’ is decreased.
The inset in Figure 5 illustrates a method with which internal loads can be determined. Without an internal load, Vmax will not be altered by partial activation of the muscle where only the number of activated crossbridges is reduced without changing the crossbridge kinetics (Luo et al., 2019). Therefore, by extending the force–velocity curve pass the vertical dot-dash line (Figure 5) to where the true zero load is (zero origin of the force axis), all curves with different amounts of internal load will converge to one point on the graph. That point is where both the internal and external loads are zero and where the true maximal shortening velocity (Vmax) occurs. The inset of Figure 5 shows two curves, one for full activation and the other for half-activation. Without taking internal loads into consideration, one would conclude that the maximal velocity obtained under full activation (V’max) is greater than that under half-activation (V″max). However, if the internal load is considered, we would conclude that the true maximal velocity (Vmax) is not changed, and the apparent difference among Vmax, V’max, and V″max is just an artifice created by the internal load and partial activation.
Hill’s hyperbola has been broadly used to describe the force–velocity relationship in muscle contraction despite significant deviations of the force–velocity data from the mathematical description at extreme high and low loads [See Seow (2013) for possible explanations for the deviation]. The extrapolated values of Fmax and Vmax are therefore approximations. Force–velocity data obtained in the force range between 5–80% Fmax are much better described by the Hill hyperbola, making the measurement of Pmax more accurate than the measurements of Vmax and Fmax. The curvature of the Hill hyperbola (mathematically represented by the term Fmax/a) is mainly determined by the force–velocity data obtained within the load range of 5–80% Fmax. Measurement of the curvature is therefore generally reliable. However, without a clear link between the Hill hyperbola and the kinetics of crossbridge cycle, interpretation of the curvature change in terms of physiological mechanisms has been vague.
When force and velocity in the Hill equation are normalized by their respective maximal values, that is, F = F/Fmax, V = V/Vmax, the Hill equation (equation 1) can be simplified to:
where K is a constant and equals a/Fmax [See Seow (2013) for details of derivation]. The Huxley (1957) model is the simplest example of two-state crossbridge kinetics, consisting of a detached and an attached state (Figure 6). In this model, the actomyosin crossbridges are either in the detached (D) or attached (A) state, and the fraction of bridges in the detached and attached states sum up to one. That is, A + D = 1. To link equation 9 to Huxley’s two-state model which assumes that force is proportional to the number of crossbridges in the attached state, F becomes pA, where p is force per bridge and A is the number of attached bridges. From the model shown in Figure 6, it can be derived that:
where fAPP and gAPP are the apparent attachment and detachment rates, respectively (Seow, 2013). Therefore,
Because p is inversely related to velocity and gAPP is linearly proportional to velocity (Piazzesi et al., 2007), that is, p = 1−V and gAPP = kV, (where k is a constant of proportionality) equation 11 becomes:
By defining that:
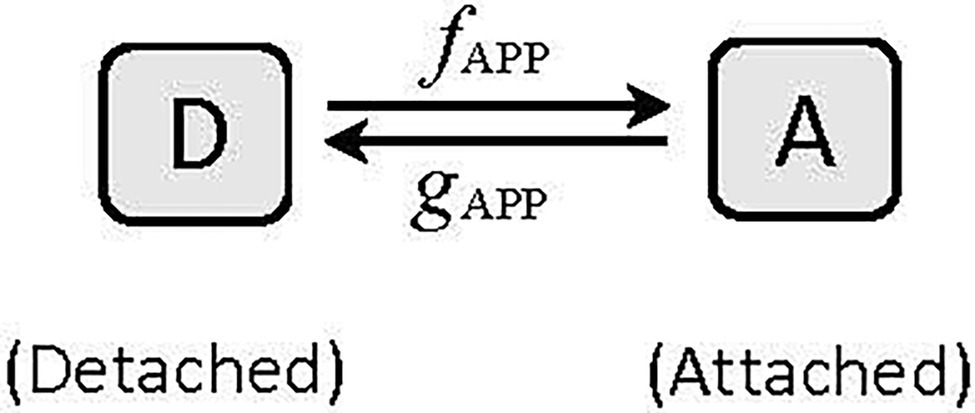
Figure 6. A two-state model of cyclic interaction of myosin crossbridges with actin filaments. A, attached state, D, detached state. fAPP and gAPP denote the apparent forward and reverse rate constants, respectively.
equation 12 becomes F = K(1−V)/(K + V), which is exactly the same as equation 9, the Hill equation.
In Hill’s equation, K = a/Fmax, and is inversely proportional to the curvature of the force–velocity curve. We can therefore define the curvature as follows:
Equation 14 provides a crucial link between the curvature of Hill’s hyperbola and the rate of attachment (fAPP) and the velocity-dependent rate of detachment of myosin crossbridges (k) in their cyclic interaction with actin filaments.
After a force–velocity curve has been properly normalized and internal loads taken into account, if its curvature is still different before and after an intervention, one can conclude that the crossbridge kinetics have been altered by the intervention. The intervention can come from Nature during evolution of species where the biochemical properties of isoforms of myosin and actin have been changed. The intervention can also come from changes in the chemical milieu in which actomyosin interaction occurs. The changes in chemical milieu in turn can be initiated by environmental factors, such as temperature and oxygen level, or pathological conditions, such as acidosis and alkalosis. A broader discussion on how interventions modify the force–velocity properties of muscle can be found in a review by Seow (2013). The following discussion focuses on interventions that specifically alter the force–velocity curvature.
It has been shown in earlier discussions that changes in the arrangement of sarcomeres, partial activation, and internal loads do not fundamentally alter the force–velocity relationship, because after normalization of force and velocity, the force–velocity curvature remains the same. Fast and slow muscle fibers contain different myosin isoforms. Observations from many studies comparing the force–velocity relationships in fast and slow muscles, revealed that fast muscles, besides having higher Vmax, also have less curvature (lower values for Fmax/a; Katz, 1939; Close, 1964; Woledge, 1968; Cecchi et al., 1978; Lännergren, 1978; Luff, 1981; Lännergren et al., 1982; Ranatunga, 1982; Brooks and Faulkner, 1988; Stienen et al., 1988; Barclay et al., 1993; Wahr and Metzger, 1998; Gilliver et al., 2009). This means that fast muscles possess a greater power output than slow muscles do, not only by having a faster shortening velocity, but also by having less curvature in their force–velocity curves. Cardiac myocytes containing the faster isoform α-MHC have a higher shortening velocity and power output than those containing the slower isoform β-MHC. The faster isoform α-MHC is also associated with a reduction in the curvature of the force–velocity curve, Fmax/a (Herron et al., 2001).
Because shortening velocity is proportional to the apparent rate of crossbridge detachment (gAPP), and from equation 13, K = fAPP/k, we can deduce that the molecular mechanisms conferring the phenotype of fast myosin isoforms are (1) a faster rate of crossbridge detachment (gAPP), likely due to an increased rate of dissociation of ADP from its myosin binding site (Siemankowski et al., 1985; Rayment et al., 1993; Elangovan et al., 2012), (2) an increase in the rate of crossbridge attachment (fAPP) and/or (3) a decrease in the velocity–dependent rate of detachment (k). The first mechanism gives rise to higher shortening velocities and the second and third mechanisms, individually or together, can explain the increase in K value observed in muscles with fast myosin.
It has been observed that the slow tortoise muscle is more energetically efficient than the faster frog muscle and that the former also possesses a greater curvature in its force–velocity curve than the latter (Woledge, 1968). It is possible that a greater value for k is associated with the slow tortoise muscle. This makes the dissociation rate of crossbridges from their actin binding sites faster as the shortening velocity increases, reaching its maximal value at Vmax. This could lead to less bridges being dragged into the negative-force region (Huxley, 1957). The improvement in energetic efficiency may come as a result of fewer negatively strained bridges.
It has been found that Vmax and a/Fmax both increase with temperature, with a strong correlation between Vmax and a/Fmax over a temperature range of 10°–35° (Ranatunga, 1984). Furthermore, Vmax and a/Fmax in fast muscles, compared with those in slow muscles, have higher temperature sensitivity. Fmax has also been found to be temperature-dependent, and the augmentation of Fmax by temperature appears to be due to enhancement of a step transition of crossbridges from the detached state to a force-generating state before the release of inorganic phosphate from the myosin head (Ranatunga, 2010). The temperature-dependent increase in Vmax, Fmax, and a/Fmax will tend to increase the power output of the muscle. Interestingly, analysis by Ranatunga (1998) showed that among the force–velocity parameters, Pmax has the highest temperature sensitivity. This perhaps can be understood as a consequence of a synergistic effect from the contribution of Vmax, Fmax, and a/Fmax to Pmax. For example, if velocity and force both increase by 10% due to temperature increase, this alone would lead to an increase in power output by 21% because power equals velocity times force, assuming no change in a/Fmax. An increase in a/Fmax with temperature will further contribute to the increase in Pmax.
From equation 13 we know that a/Fmax (or K) is determined by fAPP and k. A study on the effects of temperature on the crossbridge cycle has revealed that the fraction of detached bridges decreases as temperature increases (Zhao and Kawai, 1994), indicating that fAPP is enhanced and/or k is diminished by increasing temperature. In homeothermic species, the temperature sensitivity of a/Fmax is perhaps physiologically less relevant. For ectotherms, such as fish living in water with large, depth-dependent temperature gradient, a large change in a/Fmax (hence Pmax) could significantly impact their function. This is perhaps why, in some cold-water fish, a/Fmax is temperature insensitive (Johnston and Salamonski, 1984; Johnston and Sidell, 1984). In carp red muscle, the temperature-dependent change in a/Fmax is opposite to that in mammalian skeletal muscle (Rome and Sosnicki, 1990). This is perhaps a compensatory mechanism for ectotherms to reduce power loss in muscle at low temperature by increasing a/Fmax (decreasing the curvature).
In muscle contraction, the immediate energy source is ATP hydrolysis. When an ATP molecule is hydrolyzed, Pi (inorganic phosphate), ADP (adenosine diphosphate), and H+ (hydrogen ion) are produced. The hydrolysis products are known to alter the kinetics of the crossbridge cycle and hence the force–velocity relationship.
In experiments using membrane-permeabilized muscle fibers, it has been shown that when ADP release is partially blocked by high concentrations of ADP in the intracellular milieu, Fmax is increased and Vmax is decreased (Cooke and Pate, 1985; Seow and Ford, 1997). Furthermore, the curvature of the force–velocity curve is reduced by high concentrations of ADP (Seow and Ford, 1997). The increase in a/Fmax (reduced curvature) is likely due to a decrease in the sensitivity of gAPP on shortening velocity, that is, a reduction in the value of k in equation 13. The effect of slowing ADP release in the crossbridge cycle can also be demonstrated in experiments using a bipyridine compound (amrinone), which is known to increase ADP affinity to myosin. The presence of amrinone enhances Fmax, diminishes Vmax, and augments a/Fmax (Albet-Torres et al., 2009). Low [ATP] has a very similar effect as high [ADP] on the crossbridge cycle and hence the force–velocity relationship (Ferenczi et al., 1984; Cooke and Pate, 1985; Stienen et al., 1988; Seow and Ford, 1997). Furthermore, low [ATP] has been found to cause an increase in a/Fmax (Ferenczi et al., 1984; Stienen et al., 1988; Seow and Ford, 1997; Wakayama and Yamada, 2000; Cheng et al., 2020).
The effect of high [H+] on force–velocity curvature is more complicated, because it affects multiple points in the crossbridge cycle. Detention of crossbridges in the low-force states by high (H+; Seow and Ford, 1993) tends to decrease fAPP, which would increase the curvature (Overgaard et al., 2010). On the other hand, slowing of ADP release (Debold et al., 2008) would tend to decrease the value of k and hence curvature (Albet-Torres et al., 2009). This may explain the mixed reports on the effects of high [H+] on the force–velocity curvature. In addition, the high [H+] effect on the force–velocity curvature is dependent on temperature and muscle type. For example, at low temperature (15°C), Knuth et al. (2006) found that in type I muscle, a/Fmax increased at low pH and decreased at high pH, but at a higher temperature (30°C), a/Fmax decreased at low pH and increased at high pH. In type II muscle at 15°C, a/Fmax increased at low pH and decreased at high pH, just like that in type I muscle, but at 30°C, pH had no significant effect on a/Fmax in type II muscle. In rabbit psoas (fast) muscle at 10°C, Cooke et al. (1988) found no significant change in a/Fmax due to pH change. For the same muscle at 1.5°C, Seow and Ford (1993) found a significant increase in a/Fmax at low pH. From the scattered results one can conclude that to understand the effect of low pH on physiological function of muscle, the force–velocity parameters should be measured at or near body temperature.
At the muscle cell level, fatigue is often a consequence of energy demand exceeding supply. The immediate energy supply for muscle contraction is derived from the intracellular pool of ATP, normally at a concentration of about 5 mM. Metabolism of ATP produces metabolites that include ADP, Pi, and H+. The intracellular concentration of ATP is usually maintained at a constant level by buffering systems that involve phosphocreatine, glycolysis, and oxidative phosphorylation. When oxygen supply lags demand, lactic acid accumulates, leading to acidosis. To make things worse, both Pi and H+ reduce myofibrillar Ca2+ sensitivity (Debold et al., 2006; Nelson and Fitts, 2014). Effects of muscle fatigue on the force–velocity relationship are therefore multifaceted due to the many contributing factors.
The consequence of muscle fatigue involves a reduction in the ability of the muscle to generate force and reduced shortening velocity. However, there are mixed reports regarding changes in the curvature of the force–velocity curve (Barclay, 1996; Fitts, 2008; Jones, 2010; Devrome and MacIntosh, 2018; Kristensen et al., 2019, 2020). The ratio of ADP/ATP is usually well maintained and is thought to play little role in causing fatigue (Cooke, 2007). Reduction in myofibrillar Ca2+ sensitivity leads to a reduced number of activated crossbridges, similar to the situation in partial activation. If lower myofibrillar Ca2+ sensitivity is equivalent to partial activation (discussed above), it would decrease Fmax but have no effect on a/Fmax, as reported by Langeron et al. (1999). However, other studies showed that lowering intracellular [Ca2+] led to a slight increase in a/Fmax, and augmenting intracellular [Ca2+] led to a decrease in a/Fmax (Kristensen et al., 2018). The effect of intracellular [Ca2+] on the force–velocity curvature is therefore inconclusive. Note that the presence of an internal load tends to increase the ratio a/Fmax, as discussed above. Taking internal loads into account in the determination of force–velocity properties may help to resolve some of the discrepancies.
In a muscle cell, ADP produced from ATP hydrolysis is used in the phosphocreatine buffering system to replenish ATP, but Pi produced by ATP hydrolysis is not used in this buffering system and therefore can accumulate inside the muscle cell. As discussed above, high [Pi] depresses Fmax but has little effect on Vmax. In mild fatigue, a small decrease in Fmax occurs without a significant decrease in Vmax (Edman and Mattiazzi, 1981; Jones et al., 2006). It is likely that Pi accumulation is responsible for the initial phase of muscle fatigue (Wilson et al., 1988). In later phases of fatigue, accumulation of H+ and lactic acid, combined with high [Pi] likely lead to a large depression of Fmax and Vmax due to the direct effects of low pH and high [Pi], and indirect effect of low myofibrillar Ca2+ sensitivity. Low pH at near body temperature has been shown to increase the curvature (decrease in a/Fmax; Knuth et al., 2006). Low pH is therefore one of the contributors to the increase in force–velocity curvature observed in muscle fatigue. As discussed above, high [H+] detains crossbridges in the low-force states and reduces the apparent rate of attachment (fAPP). A similar conclusion is reached by Jones (2010) in that there must be a substantial decrease in the rate constant for attachment in the Huxley (1957) model to account for the observed decrease in power and increase in force–velocity curvature in fatigued muscle.
Mechanical manifestation of muscle activation captured in the force–velocity relationship is a window through which the molecular events of the crossbridge cycle can be observed. The presence of an internal load can lead to an apparent decrease in the curvature of a force–velocity curve, and the apparent decrease in the curvature can be exaggerated under conditions of partial activation or interventions that change the number of activated crossbridges. All these interventions do not alter the true curvature of the force–velocity curve, because, after proper normalization, the apparent changes in the curvature will disappear. When the kinetics of the crossbridge cycle is interrupted by experimental interventions, changes in the true curvature of the force–velocity curve can be linked to specific changes in the velocity-dependent rate functions governing the cyclic actomyosin interaction.
KS and CS contributed to the drafting and editing of the review. All authors contributed to the article and approved the submitted version.
This work was supported by a Discovery Grant from the Natural Science and Engineering Research Council (NSERC) of Canada.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbott, B. C., and Wilkie, D. R. (1953). The relation between velocity of shortening and the tension-length curve of skeletal muscle. J. Physiol. 120, 214–223. doi: 10.1113/jphysiol.1953.sp004886
Albet-Torres, N., Bloemink, M. J., Barman, T., Candau, R., Frölander, K., Geeves, M. A., et al. (2009). Drug effect unveils inter-head cooperativity and strain-dependent ADP release in fast skeletal actomyosin. J. Biol. Chem. 284, 22926–22937. doi: 10.1074/jbc.M109.019232
Barclay, C. J. (1996). Mechanical efficiency and fatigue of fast and slow muscles of the mouse. J. Physiol. 497, 781–794. doi: 10.1113/jphysiol.1996.sp021809
Barclay, C. J., Constable, J. K., and Gibbs, C. L. (1993). Energetics of fast- and slow-twitch muscles of the mouse. J. Physiol. 472, 61–80. doi: 10.1113/jphysiol.1993.sp019937
Brooks, S. V., and Faulkner, J. A. (1988). Contractile properties of skeletal muscles from young, adult and aged mice. J. Physiol. 404, 71–82. doi: 10.1113/jphysiol.1988.sp017279
Cecchi, G., Colomo, F., and Lombardi, V. (1978). Force-velocity relation in normal and nitrate-treated frog single muscle fibres during rise of tension in an isometric tetanus. J. Physiol. 285, 257–273. doi: 10.1113/jphysiol.1978.sp012570
Cheng, Y. S., de Souza Leite, F., and Rassier, D. E. (2020). The load dependence and the force-velocity relation in intact myosin filaments from skeletal and smooth muscles. Am. J. Physiol. Cell Physiol. 318, C103–C110. doi: 10.1152/ajpcell.00339.2019
Chiu, Y. L., Ballou, E. W., and Ford, L. E. (1982). Internal viscoelastic loading in cat papillary muscle. Biophys. J. 40, 109–120. doi: 10.1016/S0006-3495(82)84465-2
Civan, M. M., and Podolsky, R. J. (1966). Contraction kinetics of striated muscle fibres following quick changes in load. J. Physiol. 184, 511–534. doi: 10.1113/jphysiol.1966.sp007929
Close, R. (1964). Dynamic properties of fast and slow skeletal muscles of the rat during development. J. Physiol. 173, 74–95. doi: 10.1113/jphysiol.1964.sp007444
Cooke, R. (2007). Modulation of the actomyosin interaction during fatigue of skeletal muscle. Muscle Nerve 36, 756–777. doi: 10.1002/mus.20891
Cooke, R., Franks, K., Luciani, G. B., and Pate, E. (1988). The inhibition of rabbit skeletal muscle contraction by hydrogen ions and phosphate. J. Physiol. 395, 77–97. doi: 10.1113/jphysiol.1988.sp016909
Cooke, R., and Pate, E. (1985). The effects of ADP and phosphate on the contraction of muscle fibers. Biophys. J. 48, 789–798. doi: 10.1016/S0006-3495(85)83837-6
Debold, E. P., Beck, S. E., and Warshaw, D. M. (2008). Effect of low pH on single skeletal muscle myosin mechanics and kinetics. Am. J. Physiol. Cell Physiol. 295, C173–C179. doi: 10.1152/ajpcell.00172.2008
Debold, E. P., Romatowski, J., and Fitts, R. H. (2006). The depressive effect of pi on the force-pCa relationship in skinned single muscle fibers is temperature dependent. Am. J. Physiol. Cell Physiol. 290, C1041–C1050. doi: 10.1152/ajpcell.00342.2005
Devrome, A. N., and MacIntosh, B. R. (2018). Force-velocity relationship during isometric and isotonic fatiguing contractions. J. Appl. Physiol. 125, 706–714. doi: 10.1152/japplphysiol.01119.2017
Dobbie, I., Linari, M., Piazzesi, G., Reconditi, M., Koubassova, N., Ferenczi, M. A., et al. (1998). Elastic bending and active tilting of myosin heads during muscle contraction. Nature 396, 383–387. doi: 10.1038/24647
Edman, K. A., and Mattiazzi, A. R. (1981). Effects of fatigue and altered pH on isometric force and velocity of shortening at zero load in frog muscle fibres. J. Muscle Res. Cell Motil. 2, 321–334. doi: 10.1007/BF00713270
Elangovan, R., Capitanio, M., Melli, L., Pavone, F. S., Lombardi, V., and Piazzesi, G. (2012). An integrated in vitro and in situ study of kinetics of myosin II from frog skeletal muscle. J. Physiol. 590, 1227–1242. doi: 10.1113/jphysiol.2011.222984
Ferenczi, M. A., Goldman, Y. E., and Simmons, R. M. (1984). The dependence of force and shortening velocity on substrate concentration in skinned muscle fibres from Rana temporaria. J. Physiol. 350, 519–543. doi: 10.1113/jphysiol.1984.sp015216
Fitts, R. H. (2008). The cross-bridge cycle and skeletal muscle fatigue. J. Appl. Physiol. 104, 551–558. doi: 10.1152/japplphysiol.01200.2007
Ford, L. E., Huxley, A. F., and Simmons, R. M. (1977). Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J. Physiol. 269, 441–515. doi: 10.1113/jphysiol.1977.sp011911
Gilliver, S. F., Degens, H., Rittweger, J., Sargeant, A. J., and Jones, D. A. (2009). Variation in the determinants of power of chemically skinned human muscle fibres. Exp. Physiol. 94, 1070–1078. doi: 10.1113/expphysiol.2009.048314
Herron, T. J., Korte, F. S., and McDonald, K. S. (2001). Loaded shortening and power output in cardiac myocytes are dependent on myosin heavy chain isoform expression. Am. J. Physiol. Heart Circ. Physiol. 281:H1217. doi: 10.1152/ajpheart.2001.281.3.H1217
Hill, A. V. (1938). The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. B Biol. Sci. 126, 136–195. doi: 10.1098/rspb.1938.0050
Hill, A. V. (1964). The effect of load on the heat of shortening of muscle. Proc. R. Soc. Lond. B Biol. Sci. 159, 297–318. doi: 10.1098/rspb.1964.0004
Huxley, A. F. (1957). Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 7, 255–318. doi: 10.1016/S0096-4174(18)30128-8
Johnston, I. A., and Salamonski, J. (1984). Power output and force-velocity relationship of red and white muscle fibres from the Pacific blue marlin (Makaira nigricans). J. Exp. Biol. 111, 171–177. doi: 10.1242/jeb.111.1.171
Johnston, I. A., and Sidell, B. D. (1984). Differences in temperature dependence of muscle contractile properties and myofibrillar ATPase activity in a cold-temperature fish. J. Exp. Biol. 111, 179–189. doi: 10.1242/jeb.111.1.179
Jones, D. A. (2010). Changes in the force-velocity relationship of fatigued muscle: implications for power production and possiblecauses. J. Physiol. 588, 2977–2986. doi: 10.1113/jphysiol.2010.190934
Jones, D. A., de Ruiter, C. J., and de Haan, A. (2006). Change in contractile properties of human muscle in relationship to the loss of power and slowing of relaxation seen with fatigue. J. Physiol. 576, 913–922. doi: 10.1113/jphysiol.2006.116343
Katz, B. (1939). The relation between force and speed in muscular contraction. J. Physiol. 96, 45–64. doi: 10.1113/jphysiol.1939.sp003756
Knuth, S. T., Dave, H., Peters, J. R., and Fitts, R. H. (2006). Low cell pH depresses peak power in rat skeletal muscle fibres at both 30 degrees C and 15 degrees C: implications for muscle fatigue. J. Physiol. 575, 887–899. doi: 10.1113/jphysiol.2006.106732
Kristensen, A. M., MacDougall, K. B., MacIntosh, B. R., and Overgaard, K. (2020). Is curvature of the force-velocity relationship affected by oxygen availability? Evidence from studies in ex vivo and in situ rat muscles. Pflugers Arch. 472, 597–608. doi: 10.1007/s00424-020-02390-5
Kristensen, A. M., Nielsen, O. B., and Overgaard, K. (2018). Effects of manipulating tetanic calcium on the curvature of the force-velocity relationship in isolated rat soleus muscle. Acta Physiol. 222:e12977. doi: 10.1111/apha.12977
Kristensen, A. M., Nielsen, O. B., Pedersen, T. H., and Overgaard, K. (2019). Fatiguing stimulation increases curvature of the force-velocity relationship in isolated fast-twitch and slow-twitch rat muscles. J. Exp. Biol. 222:jeb204545. doi: 10.1242/jeb.204545
Langeron, O., Coirault, C., Fratea, S., Orliaguet, G., Coriat, P., and Riou, B. (1999). The effects of dantrolene on the contraction, relaxation, and energetics of the diaphragm muscle. Anesth. Analg. 89, 466–471. doi: 10.1213/00000539-199908000-00041
Lännergren, J. (1978). The force-velocity relation of isolated twitch and slow muscle fibres of Xenopus laevis. J. Physiol. 283, 501–521. doi: 10.1113/jphysiol.1978.sp012516
Lännergren, J., Lindblom, P., and Johansson, B. (1982). Contractile properties of two varieties of twitch muscle fibres in Xenopus laevis. Acta Physiol. Scand. 114, 523–535. doi: 10.1111/j.1748-1716.1982.tb07020.x
Luff, A. R. (1981). Dynamic properties of the inferior rectus, extensor digitorum longus, diaphragm and soleus muscles of the mouse. J. Physiol. 313, 161–171. doi: 10.1113/jphysiol.1981.sp013656
Luo, L., Wang, L., Paré, P. D., Seow, C. Y., and Chitano, P. (2019). The Huxley crossbridge model as the basic mechanism for airway smooth muscle contraction. Am. J. Physiol. Lung Cell. Mol. Physiol. 317, L235–L246. doi: 10.1152/ajplung.00051.2019
Nelson, C. R., and Fitts, R. H. (2014). Effects of low cell pH and elevated inorganic phosphate on the pCa-force relationship in single muscle fibers at near-physiological temperatures. Am. J. Physiol. Cell Physiol. 306, C670–C678. doi: 10.1152/ajpcell.00347.2013
Overgaard, K., Højfeldt, G. W., and Nielsen, O. B. (2010). Effects of acidification and increased extracellular potassium on dynamic muscle contractions in isolated rat muscles. J. Physiol. 588, 5065–5076. doi: 10.1113/jphysiol.2010.195727
Piazzesi, G., Reconditi, M., Linari, M., Lucii, L., Bianco, P., Brunello, E., et al. (2007). Skeletal muscle performance determined by modulation of number of myosin motors rather than motor force or stroke size. Cell 131, 784–795. doi: 10.1016/j.cell.2007.09.045
Ranatunga, K. W. (1982). Temperature-dependence of shortening velocity and rate of isometric tension development in rat skeletal muscle. J. Physiol. 329, 465–483. doi: 10.1113/jphysiol.1982.sp014314
Ranatunga, K. W. (1984). The force-velocity relation of rat fast- and slow-twitch muscles examined at different temperatures. J. Physiol. 351, 517–529. doi: 10.1113/jphysiol.1984.sp015260
Ranatunga, K. W. (1998). Temperature dependence of mechanical power output in mammalian (rat) skeletal muscle. Exp. Physiol. 83, 371–376. doi: 10.1113/expphysiol.1998.sp004120
Ranatunga, K. W. (2010). Force and power generating mechanism(s) in active muscle as revealed from temperature perturbation studies. J. Physiol. 588, 3657–3670. doi: 10.1113/jphysiol.2010.194001
Rayment, I., Holden, H. M., Whittaker, M., Yohn, C. B., Lorenz, M., Holmes, K. C., et al. (1993). Structure of the actin-myosin complex and its implications for muscle contraction. Science 261, 58–65. doi: 10.1126/science.8316858
Rome, L. C., and Sosnicki, A. A. (1990). The influence of temperature on mechanics of red muscle in carp. J. Physiol. 427, 151–169. doi: 10.1113/jphysiol.1990.sp018165
Seow, C. Y. (2013). Hill's equation of muscle performance and its hidden insight on molecular mechanisms. J. Gen. Physiol. 142, 561–573. doi: 10.1085/jgp.201311107
Seow, C. Y., and Ford, L. E. (1992). Contribution of damped passive recoil to the measured shortening velocity of skinned rabbit and sheep muscle fibres. J. Muscle Res. Cell Motil. 13, 295–307. doi: 10.1007/BF01766457
Seow, C. Y., and Ford, L. E. (1993). High ionic strength and low pH detain activated skinned rabbit skeletal muscle crossbridges in a low force state. J. Gen. Physiol. 101, 487–511. doi: 10.1085/jgp.101.4.487
Seow, C. Y., and Ford, L. E. (1997). Exchange of ATP for ADP on high-force cross-bridges of skinned rabbit muscle fibers. Biophys. J. 72, 2719–2735. doi: 10.1016/S0006-3495(97)78915-X
Seow, C. Y., and Stephens, N. L. (1986). Force-velocity curves for smooth muscle: analysis of internal factors reducing velocity. Am. J. Phys. 251:C362. doi: 10.1152/ajpcell.1986.251.3.C362
Siemankowski, R. F., Wiseman, M. O., and White, H. D. (1985). ADP dissociation from actomyosin subfragment 1 is sufficiently slow to limit the unloaded shortening velocity in vertebrate muscle. Proc. Natl. Acad. Sci. U. S. A. 82, 658–662. doi: 10.1073/pnas.82.3.658
Stienen, G. J. M., Van der Laarse, W. J., and Elzinga, G. (1988). Dependency of the force-velocity relationships on mg ATP in different types of muscle fibers from Xenopus laevis. Biophys. J. 53, 849–855. doi: 10.1016/S0006-3495(88)83165-5
Suzuki, Y., Yasunaga, T., Ohkura, R., Wakabayashi, T., and Sutoh, K. (1998). Swing of the lever arm of a myosin motor at the isomerization and phosphate-release steps. Nature 396, 380–383. doi: 10.1038/24640
Wahr, P. A., and Metzger, J. M. (1998). Peak power output is maintained in rabbit psoas and rat soleus single muscle fibers when CTP replaces ATP. J. Appl. Physiol. 85, 76–83. doi: 10.1152/jappl.1998.85.1.76
Wakayama, J., and Yamada, T. (2000). Contractility of single myofibrils of rabbit skeletal muscle studied at various MgATP concentrations. Jpn. J. Physiol. 50, 533–542. doi: 10.2170/jjphysiol.50.533
Walley, K. R., Ford, L. E., and Wood, L. D. (1991). Effects of hypoxia and hypercapnia on the force-velocity relation of rabbit myocardium. Circ. Res. 69, 1616–1625. doi: 10.1161/01.res.69.6.1616
Wang, L., Paré, P. D., and Seow, C. Y. (2002). Changes in force-velocity properties of trachealis due to oscillatory strains. J. Appl. Physiol. 92, 1865–1872. doi: 10.1152/japplphysiol.01155.2001
Wilson, J. R., McCully, K. K., Mancini, D. M., Boden, B., and Chance, B. (1988). Relationship of muscular fatigue to pH and deprotonated pi in humans: a 31P-NMR study. J. Appl. Physiol. 64, 2333–2339. doi: 10.1152/jappl.1988.64.6.2333
Woledge, R. C. (1968). The energetics of tortoise muscle. J. Physiol. 197, 685–707. doi: 10.1113/jphysiol.1968.sp008582
Keywords: muscle mechanics, isometric contraction, isotonic shortening, power output, internal load, crossbridge cycle
Citation: Seow KN and Seow CY (2022) Molecular Events of the Crossbridge Cycle Reflected in the Force–Velocity Relationship of Activated Muscle. Front. Physiol. 13:846284. doi: 10.3389/fphys.2022.846284
Received: 31 December 2021; Accepted: 15 February 2022;
Published: 10 March 2022.
Edited by:
Luis M. Alegre, University of Castilla-La Mancha, SpainReviewed by:
D. George Stephenson, La Trobe University, AustraliaCopyright © 2022 Seow and Seow. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chun Y. Seow, Y2h1bi5zZW93QGhsaS51YmMuY2E=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.