- 1Theory and Simulation of Complex Fluids, Department of Scale-Bridging Thermodynamic and Kinetic Simulation, Interdisciplinary Center for Advanced Materials Simulation (ICAMS), Ruhr-Universität Bochum, Bochum, Germany
- 2Department of Civil and Environmental Engineering, Chair of Continuum Mechanics, Ruhr-Universität Bochum, Bochum, Germany
- 3Department of Mechanical Engineering, Columbia University in the City of New York, New York, NY, United States
Tissue degradation plays a crucial role in the formation and rupture of aneurysms. Using numerical computer simulations, we study the combined effects of blood flow and tissue degradation on intra-aneurysm hemodynamics. Our computational analysis reveals that the degradation-induced changes of the time-averaged wall shear stress (TAWSS) and oscillatory shear index (OSI) within the aneurysm dome are inversely correlated. Importantly, their correlation is enhanced in the process of tissue degradation. Regions with a low TAWSS and a high OSI experience still lower TAWSS and higher OSI during degradation. Furthermore, we observed that degradation leads to an increase of the endothelial cell activation potential index, in particular, at places experiencing low wall shear stress. These findings are robust and occur for different geometries, degradation intensities, heart rates and pressures. We interpret these findings in the context of recent literature and argue that the degradation-induced hemodynamic changes may lead to a self-amplification of the flow-induced progressive damage of the aneurysmal wall.
1. Introduction
Both microscopic degradation in vascular tissues and hemodynamic (fluid-dynamic) forces play a crucial role in the initiation, growth and focal rupture of aneurysms (Sforza et al., 2009; Salman et al., 2019; Lipp et al., 2020; Wu et al., 2020). Aneurysms are vascular diseases characterized by excessive tissue degradation and chronic inflammation (Frösen, 2014). There are relations among aneurysmal geometry, intra-aneurysmal hemodynamics (flow), and aneurysm pathobiology (Meng et al., 2014): Geometry instantaneously alters flow conditions (short-term effect) (Wang et al., 2020, 2021a); abnormal-flow-induced hemodynamic-biomechanical triggers are transduced into biological signals and lead to the degradation, growth and/or remodeling of aneurysms via pathobiology (Meng et al., 2014); the interplay between the local flow environment and aneurysm pathobiology dominates the growth and geometric changes of the aneurysm (long-term effect) (Tarbell et al., 2014). Within an aneurysm wall, constructive (eutrophic) changes (cell proliferation and extracellular matrix production) and destructive (degradative) changes (cell death and extracellular matrix degradation) are ongoing concurrently (Frösen et al., 2012; Frösen, 2014; Meng et al., 2014). Wall shear stress (WSS), defined as the tangential stress component induced by the flowing blood and acting on endothelial cells, regulates the near-wall transport of chemicals and proteins (Kadirvel et al., 2007; Nixon et al., 2010; Meng et al., 2014). WSS, however, is usually calculated for a stationary/instantaneous blood flow and does not, per se, consider the pulsatility within a cardiac cycle. In order to better elucidate the mechanistic link between blood flow and vascular diseases (in particular, aneurysms), a number of WSS-related metrics have been proposed. Among these, the time-averaged wall shear stress (TAWSS) (He and Ku, 1996) and oscillatory shear index (OSI) (Ku et al., 1985) are the two most common candidates that are important for aneurysms' progression and rupture. TAWSS measures the average magnitude of WSS within a full cardiac cycle. OSI indicates the change in the direction along which WSS is acting on the vascular tissue. Abnormal WSS is a major cause of the imbalance between the constructive and destructive processes (Meng et al., 2014) and leads to vascular degradation and inflammation by activating inflammatory markers of endothelial cells (Franck et al., 2013; Meng et al., 2014), thereby causing the breakdown of the internal elastic lamina and loss of structural strength within the vessel wall (Kataoka et al., 1999). An aneurysm can grow and even rupture with continuous vascular injury, inflammation, and prolonged activation (Fisher and Demel, 2019).
On the one hand, although mechanisms underlying the effects of hemodynamic forces on aneurysm pathogenesis remain unclear, there is growing evidence that hemodynamic factors (in particular, TAWSS and OSI) act as crucial contributors to the progression and rupture of aneurysms. Low TAWSS and high OSI are commonly used risk factors for a rupture-prone phenotype (Xiang et al., 2011; Meng et al., 2014; Zhang et al., 2016; Liu et al., 2019a). Previous in vitro (Davies et al., 1984; Dai et al., 2004) and numerical (Sáez et al., 2015) studies have indicated that the remodeling of endothelial cells is dependent on the combined effects of TAWSS and OSI. Liu et al. (2019a) have recently suggested that low WSS and high OSI shall be considered as independent hemodynamic-morphological risk factors and proposed to use them as predictors for intra-operative aneurysm rupture. Low TAWSS and high OSI have also been shown to be significantly associated with thrombus formation in aneurysms (Les et al., 2010; Kelsey et al., 2017). In addition, Cebral et al. (2019) have argued that high WSS and low OSI, prevalent in the flow impingement region, may be also associated with the degradation and local thinning of aneurysmal walls. Both the TAWSS and OSI affect the endothelial mechanobiology locally. To localize regions exposed to both low TAWSS and high OSI, the so-called endothelial cell activation potential (ECAP) is used (Di Achille et al., 2014; Zambrano et al., 2016; Kelsey et al., 2017; Ong et al., 2019). It has been shown that low TAWSS, high OSI ang high ECAP correlate with regions of thrombus development in aneurysms (Zambrano et al., 2016; Kelsey et al., 2017; Ong et al., 2019). The effects of geometry on intra-aneurysmal hemodynamics have also been extensively studied (Hassan et al., 2005; Cebral et al., 2007; Baharoglu et al., 2010; Kawaguchi et al., 2012; Wang et al., 2020).
On the other hand, degradation-induced changes in mechanical properties of an aneurysmal wall may have an influence on hemodynamics inside the aneurysm, which is poorly studied though. Recently, we have developed a novel computational framework by combining a tissue degradation model and a finite element-based fluid-structure interaction (FSI) solver (Wang et al., 2021b). Using this model, we have shown that TAWSS increases near the flow-impingement region of idealized aneurysms and decreases away from it in the process of degradation (Wang et al., 2021b).
While several longitudinal studies (Arzani et al., 2014; Zambrano et al., 2016) have been conducted to understand the role of TAWSS and OSI in thrombus deposition in aneurysms, it remains unclear how degradation may affect the oscillatory shear index and its potential connection to TAWSS, and the endothelial cell activation potential. The present study aims at investigating this topic. To the best of our knowledge, this paper presents the first preliminary results uncovering qualitative trends and correlations of biomechanically important metrics upon degradation. Potential consequences of the central finding are discussed in the context of recent literature.
2. Materials and Methods
2.1. Numerical Model
As mentioned above, in this work, we use a recently developed FSI framework to account for the interaction between blood flow and aneurysmal walls, and at the same time to capture the degradation of vascular tissues (Wang et al., 2021b). In this computational framework, a tissue degradation model (Balzani et al., 2012; Anttila et al., 2019) is combined with the open-source software, SimVascular/svFSI (2021) which is finite-element-method-based and uses an arbitrary Lagrangian-Eulerian formulation of Navier-Stokes equations to model incompressible Newtonian fluid (blood) flows on moving domains (Vedula et al., 2017). The degradation model employed here has been validated in previous studies (Balzani et al., 2012; Anttila et al., 2019) and proved to reproduce the experimental cyclic responses of different types of arteries. The current model is able to account for stress softening (Balzani et al., 2012; Anttila et al., 2019; Wang et al., 2021b), a phenomenon commonly observed in biological tissues. The present study is qualitative research and a first step toward a more realistic model.
For flow boundary conditions, we prescribe a pulsatile flow (Figure 1A) at the inlet with a parabolic velocity profile, together with a three-element Windkessel-type boundary condition at each outlet. The Windkessel parameters are tuned to match the systolic, diastolic and mean blood pressures. At each cross-sectional end of the structural domain, homogeneous Dirichlet boundary conditions are applied to anchor its location. The fluid and wall domains share a contact surface. Through each contact surface point, the flow velocity is projected onto the wall. Indeed, we impose the non-slip condition on the surface regardless of the thickness of the wall.
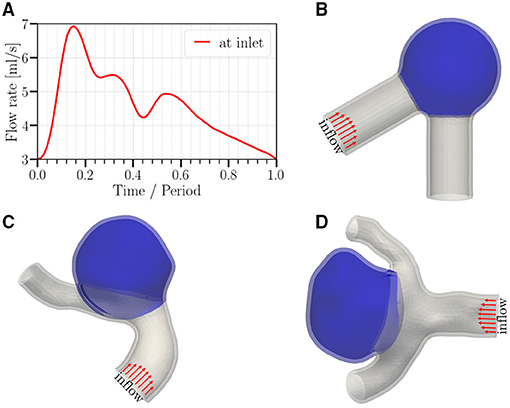
Figure 1. (A) Temporal variation of the imposed flow rate at the inlet (period T = 0.6 s or 0.8 s, depending on the studied case). (B–D) Geometries studied in this work; (B) a canonical aneurysm model based on data in (Usmani and Muralidhar, 2018; Chassagne et al., 2021); (C,D) patient-specific cerebral aneurysm models based on the cases C0034 and C0020 in the open-source Aneurisk dataset repository (Aneurisk-Team, 2012), respectively. In order to keep the computational cost in a reasonable range, we select a short representative section from each full image available in the Aneurisk repository. All meshes use quadratic tetrahedrons having a mean effective spatial resolution of 0.07 mm. Arrows serve to highlight the parabolic velocity profile imposed at the inlet. The tissue degradation model is applied only on the aneurysmal region (colored in blue); the remaining of the vessel (gray) is modeled as Neo-Hookean.
2.2. Study Cases
Three geometries are employed in this study (Figure 1). For the idealized aneurysm (Figure 1B), the inner diameter of the parent vessel is 0.41 cm (Chnafa et al., 2017) with an angle of 60° between the two vessel parts. The inner diameter of the spherical cap (aneurysm) is 1.0 cm. The mean diameter of the parent vessel in Figures 1C,D is approximately identical and equal to 0.4 cm. The average diameter of the aneurysm dome in Figures 1C,D is 1.2 and 0.8 cm, respectively. The aspect ratio (perpendicular height to neck diameter) of the aneurysm sac in Figures 1C,D is approximately 1.0 and 1.2, respectively.
Following the literature, the wall thickness has been chosen to be 0.04cm (Isaksen et al., 2008; Wang et al., 2021b). As shown in Figure 2, a variation of wall thickness by a factor of three (from 0.02 to 0.06 cm) leads to less than 15% change in degradation-induced effect on strain. Other quantities behave similarly (not shown). Therefore, for simplicity, we assume a spatially homogeneous wall thickness.
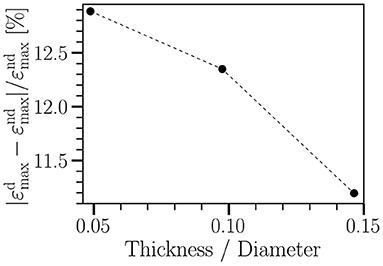
Figure 2. Relative change in radial strain of a straight tube between non-degraded (εnd) and degraded (εd) cases vs. wall thickness of the tube. The tube diameter is 0.41 cm. The wall thickness varies from 0.02 cm to 0.06 cm. The imposed cyclic load ranges from 8.7 kPa to 20 kPa, having the same waveform as shown in Figure 1A. Each simulation runs for five cycles. T = 0.8 s; γ∞ = 18 kPa. Other material parameters are given in Table 1.
Unless otherwise stated, material parameters given in Table 1 are used in this study. The fluid density and viscosity are 1.055 g cm−3 and 0.04 g cm−1 s−1, respectively (Isaksen et al., 2008).

Table 1. Material parameters for the aneurysm region (colored in blue in Figures 1B–D) used in this study [based on data shown in Balzani et al. (2012)].
The pressure levels are controlled by varying the three-element Windkessel parameters (i.e., distal resistance Rd, proximal resistance Rp, and capacitance C). For a bifurcation artery, the total resistance, Rtot, at each outlet is calculated assuming the power law relationship between the blood flow rate and the internal vessel diameter (Chnafa et al., 2017). The distal and proximal resistance at each outlet is given by Rd = kdRtot, and Rp = (1−kd)Rtot, where the factor kd defines the ratio of distal to total resistance and is fixed for all outlets to kd = 0.9 (Kim et al., 2010). Rd is often chosen to be higher than Rp as the most resistance occurs in the downstream vascular system. The capacitance C controls the amplitude of the pressure waveform; a low capacitance leads to a high pressure amplitude.
In order to gain a qualitative understanding of the effects arising from tissue degradation, we start with an idealized aneurysm model shown in Figure 1B with pressure ranging from 90 mmHg (diastole) to 160 mmHg (systole) and a heart rate of 100 bpm (T = 0.6 s). The total resistance and capacitance at each branch are Rtot = 7.3·104 g cm−4 s−1 and C = 10−6 cm4 s2 g−1, respectively. We then investigate the influence of different parameters as follows:
1. Morphology-related effects: Here we perform simulations using the same parameters as described above for two patient-specific aneurysm geometries (Figures 1C,D).
2. Effect of degradation intensity: In this case we change the value of the damage parameter γ∞ from 11 to 18 kPa ; note that γ∞ = 18kPa corresponds to a lower damage intensity than the case with γ∞ = 11kPa (see Supplementary Material and Wang et al., 2021b).
3. Influence of heart rate (flow frequency): Here the heart rate is changed from 100 bpm (T = 0.6 s) to 75 bpm (T = 1 s) for the two patient-specific geometries.
4. Pressure (tension)-dependence: Here we impose a different blood pressure ranging from 70 mmHg (diastole) to 140 mmHg (systole), again for the two patient-specific aneurysms.
In order to highlight effects arising from the degradation of blood vessel tissue, all the above simulations are performed twice: once with and once without material degradation.
All meshes use quadratic tetrahedrons (Balzani et al., 2016; Wang et al., 2021b). For each case investigated in the present study, the fluid and solid domains consist of approximately 93,000 nodes/67,000 tetrahedral elements. The discrete time step is set to 10−4 s; for a cycle with a duration of 0.8 s, the temporal resolution is 8,000 time-steps per cardiac cycle. As to the computation time, each simulation with a typical duration of five cardiac cycles takes roughly 10 days using 38 cores on a multi-core workstation (Intel(R) Xeon(R) Gold 6148, 2.40 GHz).
2.3. Metrics for Analysis
As motivated in the Introduction, time-averaged wall shear stress and oscillatory shear index play a pivotal role in mechanobiological development and focal rupture of aneurysms.
The TAWSS at an arbitrary position x is simply the average magnitude of the wall shear stress vector τw over one cardiac cycle of duration T at that point (He and Ku, 1996),
The oscillatory shear index quantifies the change in the orientation of the wall shear stress vector during a cardiac cycle and is calculated as (Ku et al., 1985),
The value of OSI ranges from 0 in a uni-directional flow to 0.5 in a reversing flow with a 180° change in the direction of the shear force acting on the tissue surface.
Another interesting metric is the so-called endothelial cell activation potential, ECAP, which combines TAWSS and OSI as
The ECAP is usually used to characterize the degree of ‘thrombotic susceptibility' of arterial walls (Di Achille et al., 2014). A large value of the ECAP signals low TAWSS together with high OSI and vise versa. All the above-mentioned hemodynamic quantities are used to quantify the flow environment and flow-induced shear stress experienced by endothelium.
To quantify the effects of tissue degradation on intra-aneurysm hemodynamics, we analyze the relative changes in these metrics upon degradation. For this purpose, given a time-averaged quantity f(x) at point x, the relative percentage change in f(x) between the degraded (fd) and non-degraded (fnd) cases is defined via
3. Results
In this section, we investigate the effect of tissue degradation on two commonly used intra-aneurysmal hemodynamic quantities, TAWSS and OSI, and ECAP. Since the fluid is at rest at the beginning of our simulations, we wait for two full cardiac cycles before gathering the data on WSS and OSI. This way, we focus on cyclic dynamics, which regularly repeats itself.
In order to quantify the effects of tissue degradation on TAWSS, OSI and ECAP, we use Equation (4) and determine the tissue-degradation-induced relative changes of these hemodynamic quantities (Figure 3). Using this approach, a decrease or increase of TAWSS, OSI, and ECAP upon degradation shows itself in a negative or positive value and will be made visible by blue or red color, respectively.
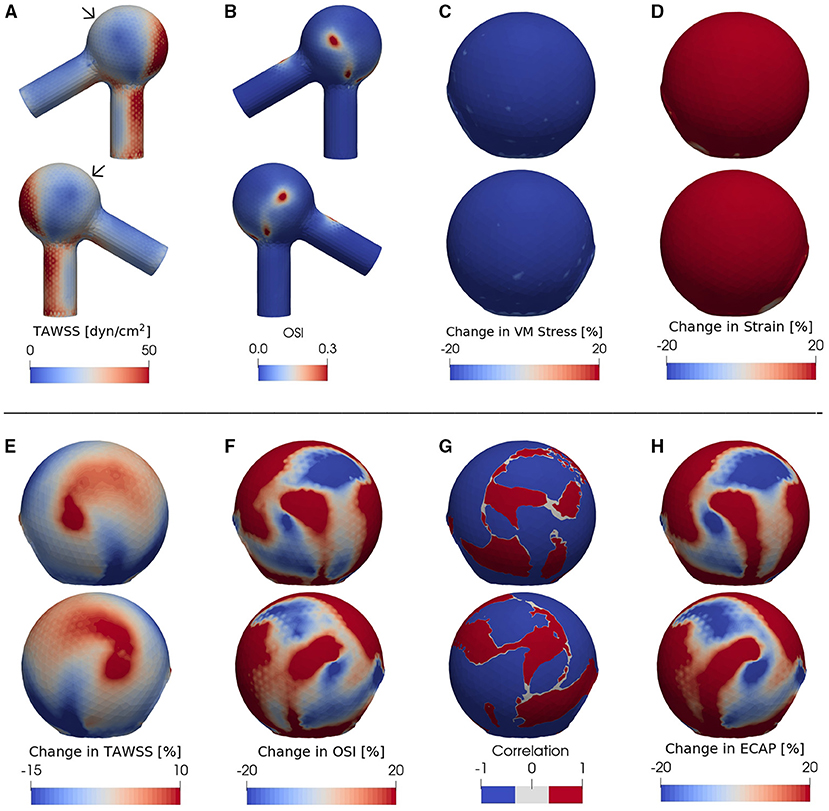
Figure 3. (A) TAWSS and (B) OSI fields in the presence of degradation using an idealized aneurysm model. Relative percentage change (Equation 4) of (C) Von Mises stress, (D) strain magnitude, (E) TAWSS and (F) OSI between non-degraded and degraded cases; the blue (red) color indicates a decrease (increase) of each metric upon tissue degradation. Panel (G) illustrates the correlation function between the data shown in the panels (E,F), calculated via Equation (5) and digitized to –1 or 1 for all data points with a magnitude >5%. The region with blue color corresponds to an inverse effect of degradation on TAWSS as opposed to OSI: In places where TAWSS decreases due to degradation, OSI increases and vice versa. A positive correlation, on the other hand, is represented by a red color in (G). (H) shows the relative change of ECAP upon degradation. In all cases, the pressure ranges from 90 (diastole) to 160 mmHg (systole) and T = 0.6 s. For each case investigated, the locations of low-WSS (indicated by arrows) remain nearly intact during a full cardiac cycle. In order to better visualize the data, the second (fourth) row shows the same simulated data as in the first (third) row but after rotating the aneurysm dome by an angle of π around the polar axis. In (C–H) we show only the aneurysm region since the degradation model is applied only on the aneurysm domain.
As revealed by our simulations, degradation effects seem to be nearly homogeneous on wall stress (Figure 3C) and strain magnitude (Figure 3D) [in line with our previous study (Wang et al., 2021b)] but spatially heterogeneous on TAWSS (Figure 3E), OSI (Figure 3F) and ECAP (Figure 3H). Importantly, the degradation process appears to bring locally opposite influences on the TAWSS and OSI; a region with a decrease in TAWSS shows an increase in OSI (and thus an increase in ECAP as visualized by red color in Figure 3H), and vice versa.
To further highlight the enhancement of the inverse correlation between TAWSS and OSI in the progress of degradation, we quantify their correlation via
The degradation-induced local enhancement of the inverse correlation between TAWSS and OSI is indicated by negative CΔTAWSS·ΔOSI and is visualized by blue color in Figure 3G. The main advantage of introducing this quantity is that its negative value indicates opposite changes of TAWSS and OSI during degradation. When combined with the information contained in ECAP, one can then uniquely distinguish which of the two quantities has increased and which one has decreased. However, if TAWSS and OSI change in a similar manner (both increase or both decrease, leading to a positive correlation), ECAP will raise if (i) the percentage increase in OSI is larger than that of TAWSS but also if (ii) percentage decrease of OSI is lower than that of TAWSS. Similarly, two possibilities exist for a decrease of ECAP in the case of a positive correlation value.
In view of possible clinical consequences of an inverse correlation between TAWSS and OSI, we have examined the robustness of the observed behavior and have performed two new sets of simulations using patient-specific aneurysm geometries shown in Figures 1C,D. The data for these geometries are obtained from the Aneurisk repository (Aneurisk-Team, 2012).
We find that, at certain areas of each aneurysm sac investigated in this study, TAWSS and OSI are oppositely affected by degradation. This feature is stronger at places with low WSS (compare Figures 3A,G,H, 4A,C–F, 5A,C–F). In this study, a threshold value of 25 dyn/cm2 is used to define the low and high TAWSS, also in agreement with reported values in the literature (Mendieta et al., 2020; Morbiducci et al., 2020; Tian et al., 2021). High OSI is considered to be larger than 0.15 (Xu et al., 2020).
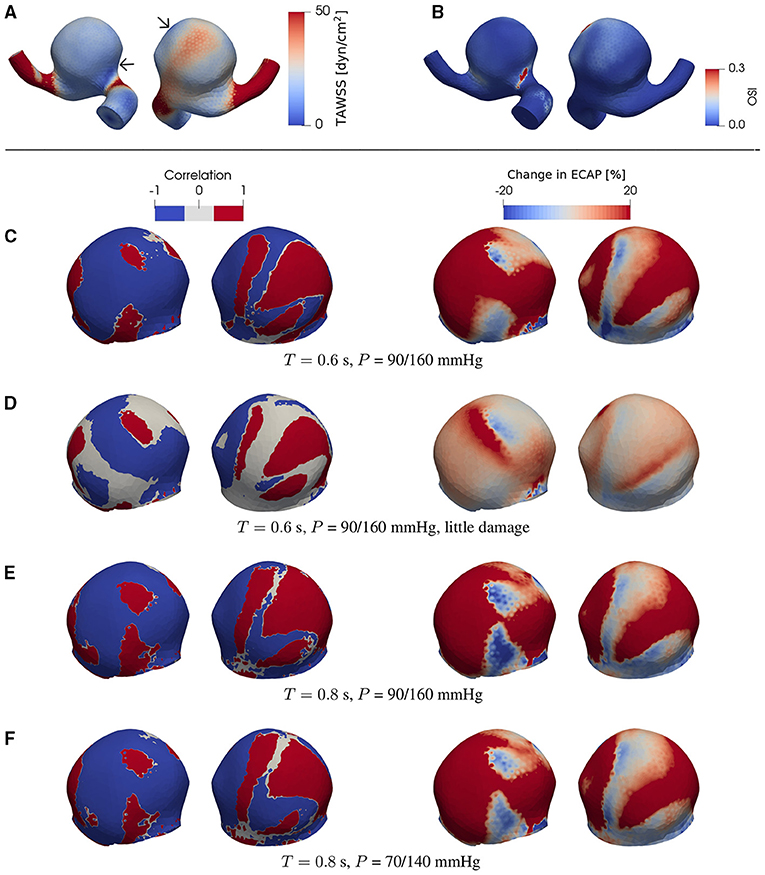
Figure 4. (A) TAWSS and (B) OSI field in the presence of degradation using a patient-specific aneurysm geometry [C0034 in Aneurisk dataset repository (Aneurisk-Team, 2012); Figure 1C]. (C–F) Product of degradation-induced relative changes in TAWSS and OSI (two left-hand columns; Equation 5) and the relative change in ECAP (two right-hand columns; Equation 4) under different damage intensities and flow conditions. The damage intensity in (C) is larger than that in (D). (C,E) differ in only the heart rate (or duration of cardiac cycle T). Compared to (E), the pressure P in (F) is lower. In (C–F), all negative and positive products (threshold = ∓5%) of the relative changes in TAWSS and OSI are set to –1 and 1, respectively. As indicated by comparisons between (A) and (C–F), the degradation-enhanced inverse correlation between TAWSS and OSI remains intact particularly at regions with low WSS. For each case investigated, the locations of low-WSS (indicated by arrows) remain intact during a full cardiac cycle. The second (fourth) column shows the same simulated data as in the first (third) column but after rotating the aneurysm dome by an angle of π around the polar axis. In (C–F) we show only the aneurysm region since the degradation model is applied only on the aneurysm domain.
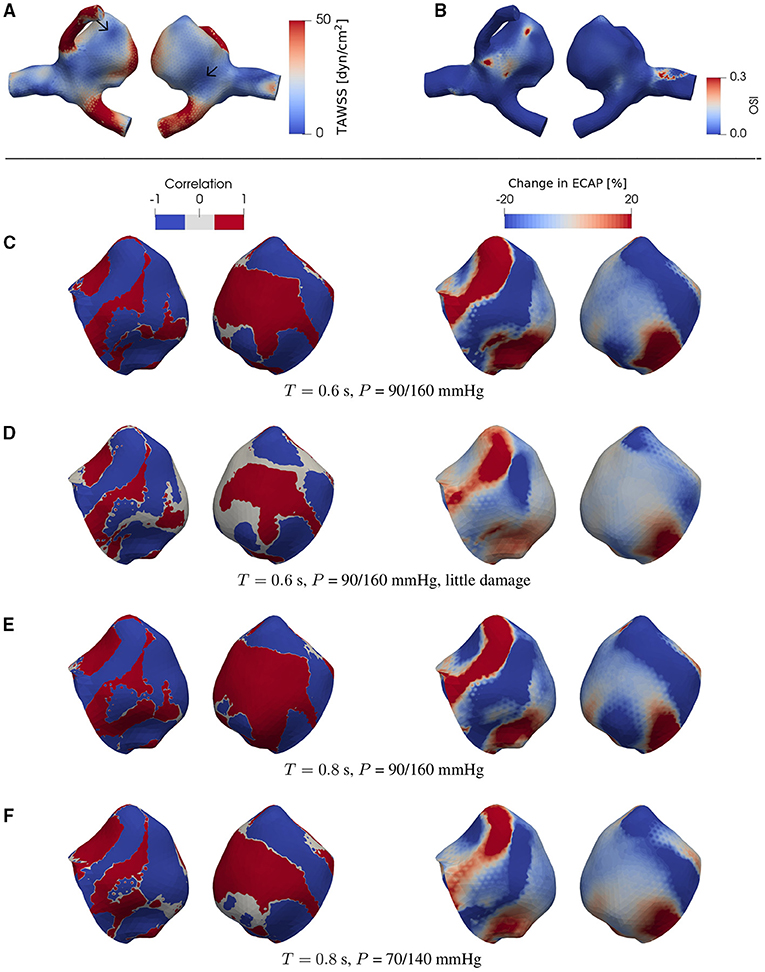
Figure 5. The same type of data as in Figure 4 but now for a different patient-specific aneurysm [C0020 in Aneurisk dataset repository (Aneurisk-Team, 2012); see as Figure 1D]. For each case investigated, the locations of low-WSS (indicated by arrows) remain intact during a full cardiac cycle.
As will be discussed in more detail below, this feature is robust and is confirmed in the case of both ideal and patient-specific geometries, and different degradation intensities, heart rates, and blood pressures.
4. Discussion
Although mechanisms in aneurysm pathogenesis have not yet been fully elucidated, there is growing evidence that hemodynamic factors and tissue degradation act as crucial contributors to the progression of aneurysms (Kadirvel et al., 2007; Sforza et al., 2009; Nixon et al., 2010; Meng et al., 2014; Cebral et al., 2019; Salman et al., 2019). Abnormal flow-induced WSS often causes disruption and dysfunction of endothelial cells (Sorokin et al., 2020), initiating an aneurysm (Meng et al., 2014). Subsequently, a vascular wall may degrade due to inflammation-triggered biochemical reactions such as apoptosis and migration of smooth muscle cells, infiltration of inflammatory cells, and secretion of various cytokines (Pentimalli et al., 2004; Kwak et al., 2014; Meng et al., 2014; Liu et al., 2019b). Chronic hemodynamic stress and inflammation induce the structure change or damage in the endothelial cells and lead to the progression and eventual rupture of aneurysms (Frösen et al., 2012; Signorelli et al., 2018). Time-averaged wall shear stress and oscillatory shear index are commonly used to quantify changes in magnitude and direction of WSS.
Using computer simulations, we studied the effects of tissue degradation on these two hemodynamic stimuli, TAWSS and OSI, for the case of aneurysm geometry. The results obtained within this work revealed a strong heterogeneity in the effects arising from degradation on TAWSS and OSI.
Importantly, the degradation-induced variations of these two hemodynamic factors turned out to be opposite to each other. In places with decreased TAWSS due to tissue degradation, we found an increase in OSI and vice versa. For both the ideal and patient-specific aneurysm geometries investigated in this work, we observed that the degradation-related enhancement of this inverse correlation between TAWSS and OSI occurs predominantly at low-WSS regions.
Although intra-aneurysm flow patterns and hemodynamic quantities depend on the specific geometry (Varble et al., 2016; Wang et al., 2020, 2021a; Khan et al., 2021), effects of tissue degradation turn out to be qualitatively similar in all the investigated cases, i.e., for different geometries, degradation intensities, heart rates and blood pressures: at low-WSS sites, degradation leads to a lower TAWSS and at the same time a higher OSI.
Low TAWSS accompanied by high OSI has been associated with the thrombus accumulation in aneurysms (Frösen et al., 2012; Zambrano et al., 2016; Kelsey et al., 2017; Ong et al., 2019) via promoting a prothrombogenic phenotype (Chiu and Chien, 2011; Wolberg et al., 2012), and with the aneurysm's progression and a rupture-prone phenotype (Les et al., 2010; Xiang et al., 2011; Meng et al., 2014; Zhang et al., 2016; Liu et al., 2019a). Such hemodynamic characteristics also promote the formation of atherosclerotic plaques on aneurysms (Galis et al., 1999; Tateshima et al., 2008; Chiu and Chien, 2011; Yang et al., 2011; Frösen et al., 2012) and thus make the aneurysmal walls vulnerable to rupture. A number of molecules are involved in the formation and rupture of aneurysms. The combination of low WSS and high OSI is known to elicit the inflammatory response in the endothelium (Meng et al., 2014). When endothelial cells are exposed to low and oscillatory shear stress, they respond by producing reactive oxygen species (Galis et al., 1999; Chiu and Chien, 2011), recruiting more inflammatory cells (van Varik et al., 2012), upregulating vascular cell adhesion molecules and cytokines in the vessel wall (Aoki et al., 2011; van Varik et al., 2012), and increasing endothelial permeability (Malek et al., 1999; Bian et al., 2009; Chiu and Chien, 2011). Conway et al. (2010) have reported that low average shear stress and high OSI (or flow reversal) act as significant mechanical stimuli on the regulation of endothelial cell gene expression and monocyte adhesion, respectively. A “sticky” and “leaky” proinflammatory endothelium tends to promote leukocyte transmigration into the vascular wall during the progression of aneurysms (Chiu and Chien, 2011; Meng et al., 2014). Low WSS together with high OSI also causes smooth muscle cells to undergo phenotypic modulation and apoptosis (Hsu et al., 2011; Liu et al., 2019b), and facilitates inflammatory cell infiltration (Malek et al., 1999; Nixon et al., 2010; Soldozy et al., 2019). These inflammatory responses in vessel walls can produce matrix metalloproteinases to destroy internal elastic lamina and degrade the extracellular matrix (Galis et al., 1994), thereby leading to an imbalance between the constructive and destructive processes (Meng et al., 2014).
Importantly, if we combine our findings with prior observations, we obtain a ‘degradation loop': Degradation of an aneurysm wall leads to lower TAWSS and higher OSI which correspond to a favorable environment for pathological changes such as atherosclerosis and thrombus formation in the aneurysm; such flow environment, in turn, may induce further degradation. Hence, the present study suggests that degradation enhances this pathological process via a self-amplification mechanism: sites with a low TAWSS and at the same time a high OSI experience still lower TAWSS and higher OSI during degradation.
A degradation process may thus self-amplify/accelerate itself via enhancing the contrast between TAWSS and OSI. That is, tissue degradation may promote the aneurysm's pathological progression to rupture by accelerating the usually slow processes, which leads to enhanced vulnerability of the wall.
Several improvements can be added to the numerical approach used in this study. First, it assumes the blood to be a Newtonian fluid with constant viscosity. This is a good approximation at low flow rates but may need correction in large arteries, where shear rate varies over a wider range from the center toward the vessel wall. Second, active response and fatigue of the aneurysmal wall are not accounted for in the material model. Third, idealized fiber orientations are employed. Fourth, a uniform wall thickness is assumed in this study. Fifth, we assume a parabolic velocity profile at the inlet. The main reason for these simplifying assumptions is that the patient-specific data of the mechanical response of aneurysmal walls, the fiber architecture, the distribution of wall thickness and the boundary conditions are not yet available. This is presumably related to the complexity of the degradation phenomenon and difficulties associated with the measurements of these properties of the arterial wall during the degradation process. Indeed, the model can be easily improved if the corresponding experimental and clinical data become available.
This study is a first step to investigate the effects of tissue degradation on the hemodynamic factors and the potential evolution of an aneurysm. In the future, if clinical/experimental data of fiber orientations in an individual aneurysm becomes available, the current model could be used to predict if the aneurysm is susceptible to develop further damage and, if so, to estimate the regions where rupture is more likely to occur.
5. Conclusion
Using computer simulations with an idealized aneurysm and two patient-specific ones, we investigated the effects of tissue degradation on the mechanical stimuli, time-averaged wall shear stress and oscillatory shear index, which are commonly associated with aneurysms.
We found that the degradation-induced variations of TAWSS and OSI are opposite to each other: If in the course of degradation the time-averaged wall shear stress is decreased at a given site, we observed an increase in OSI at the same site and vice versa. This process is most prominent at sites that are already subject to a low TAWSS and at the same time a high OSI. This finding turned out to be robust and was confirmed in the case of all the three investigated aneurysm geometries and different degradation intensities, heart rates, and blood pressures.
Our findings are discussed in the light of the present state of understanding in the literature regarding biomechanical mechanisms responsible for aneurysm development and rupture. We argue that degradation is likely to enhance the existing contrast between these two hemodynamic factors (in particular, at sites subject to a low time-averaged wall shear stress and a high oscillatory shear index), and thereby pave the way for the next degradation step. This study thus underlines the importance of the inverse correlation between TAWSS and OSI as an independent risk factor for aneurysm degradation and rupture. Further investigations are warranted to examine these findings in a clinical setting.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Author Contributions
HW and FV designed the details of the specific computational and analysis protocols including the study of patient-specific geometries. HW, VV, KU, and DB contributed to the algorithmic implementation. HW performed the simulations and analyses and wrote the first draft. HW and FV revised the manuscript. All authors contributed equally to the development of the original hypothesis of self-amplification and the design of suitable numerical analysis, read, and approved the final version of the manuscript.
Funding
This work was performed with support from the IMPRS-SurMat program and by the German Research Foundation (DFG) within SFB-TRR 287/1 (project A4).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We acknowledge support by the DFG Open Access Publication Funds of the Ruhr-Universität Bochum.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2021.785780/full#supplementary-material
References
Aneurisk-Team (2012). AneuriskWeb Project Website. Emory University, Department of Math & CS. Available online at: http://ecm2.mathcs.emory.edu/aneuriskweb
Anttila, E., Balzani, D., Desyatova, A., Deegan, P., MacTaggart, J., and Kamenskiy, A. (2019). Mechanical damage characterization in human femoropopliteal arteries of different ages. Acta Biomater. 90, 225–240. doi: 10.1016/j.actbio.2019.03.053
Aoki, T., Nishimura, M., Matsuoka, T., Yamamoto, K., Furuyashiki, T., Kataoka, H., et al. (2011). PGE2-EP2 signalling in endothelium is activated by haemodynamic stress and induces cerebral aneurysm through an amplifying loop via NF-κB. Br. J. Pharmacol. 163, 1237–1249. doi: 10.1111/j.1476-5381.2011.01358.x
Arzani, A., Suh, G., Dalman, R., and Shadden, S. (2014). A longitudinal comparison of hemodynamics and intraluminal thrombus deposition in abdominal aortic aneurysms. Am. J. Physiol. Heart Circ. Physiol. 307, H1786–H1795. doi: 10.1152/ajpheart.00461.2014
Baharoglu, M. I., Schirmer, C. M., Hoit, D. A., Gao, B. L., and Malek, A. M. (2010). Aneurysm inflow-angle as a discriminant for rupture in sidewall cerebral aneurysms: Morphometric and computational fluid dynamic analysis. Stroke 41, 1423–1430. doi: 10.1161/STROKEAHA.109.570770
Balzani, D., Brinkhues, S., and Holzapfel, G. (2012). Constitutive framework for the modeling of damage in collagenous soft tissues with application to arterial walls. Comput. Methods Appl. Mech. Engrg. 213–216:139–151. doi: 10.1016/j.cma.2011.11.015
Balzani, D., Deparis, S., Fausten, S., Forti, D., Heinlein, A., Klawonn, A., et al. (2016). Numerical modeling of fluid structure interaction in arteries with anisotropic polyconvex hyperelastic and anisotropic viscoelastic material models at finite strains. Int. J. Numer. Method Biomed. Eng. 32:e02756. doi: 10.1002/cnm.2756
Bian, C., Xu, G., Wang, J., Ma, J., Xiang, M., and Chen, P. (2009). Hypercholesterolaemic serum increases the permeability of endothelial cells through zonula occludens-1 with phosphatidylinositol 3-kinase signaling pathway. J. Biomed. Biotechnol. 2009:814979. doi: 10.1155/2009/814979
Cebral, J., Detmer, F., Chung, B., Choque-Velasquez, J., Rezai, B., Lehto, H., et al. (2019). Local hemodynamic conditions associated with focal changes in the intracranial aneurysm wall. AJNR Am. J. Neuroradiol. 40, 510–516.
Cebral, J. R., Radaelli, A., Frangi, A., and Putman, C. M. (2007). Hemodynamics before and after bleb formation in cerebral aneurysms. progress in biomedical optics and imaging. Proc. SPIE 6511:65112C–65112C-9. doi: 10.1117/12.709240
Chassagne, F., Barbour, M., Chivukula, V., Machicoane, N., Kim, L., Levitt, M., et al. (2021). The effect of Dean, Reynolds, and Womersley number on the flow in a spherical cavity on a curved round pipe. Part 1. Fluid mechanics in the cavity as a canonical flow representing intracranial aneurysms. J. Fluid. Mech. 915:A123. doi: 10.1017/jfm.2020.1114
Chiu, J.-J., and Chien, S. (2011). Effects of disturbed flow on vascular endothelium: pathophysiological basis and clinical perspectives. Physiol. Rev. 91, 327–387. doi: 10.1152/physrev.00047.2009
Chnafa, C., Bouillot, P., Brina, O., Delattre, B., Vargas, M., Lovblad, K., et al. (2017). Vessel calibre and flow splitting relationships at the internal carotid artery terminal bifurcation. Physiol. Meas. 38, 2044–2057. doi: 10.1088/1361-6579/aa92bf
Conway, D., Williams, M., Eskin, S., and McIntire, L. (2010). Endothelial cell responses to atheroprone flow are driven by two separate flow components: low time-average shear stress and fluid flow reversal. Am. J. Physiol. Heart Circ. Physiol. 298, H367–H374. doi: 10.1152/ajpheart.00565.2009
Dai, G., Kaazempur-Mofrad, M., Natarajan, S., Zhang, Y., Vaughn, S., Blackman, B., et al. (2004). Distinct endothelial phenotypes evoked by arterial waveforms derived from atherosclerosis-susceptible and -resistant regions of human vasculature. Proc. Natl. Acad. Sci. U.S.A. 101, 14871–14876. doi: 10.1073/pnas.0406073101
Davies, P., Dewey, C. J., Bussolari, S., Gordon, E., and Gimbrone, M. J. (1984). Influence of hemodynamic forces on vascular endothelial function. in vitro studies of shear stress and pinocytosis in bovine aortic cells. J. Clin. Invest. 73, 1121–1129. doi: 10.1172/JCI111298
Di Achille, P., Tellides, G., Figueroa, C. A., and Humphrey, J. D. (2014). A haemodynamic predictor of intraluminal thrombus formation in abdominal aortic aneurysms. Proc. R. Soc. A Math. Phys. Eng. Sci. 470, 20140163. doi: 10.1098/rspa.2014.0163
Fisher, C., and Demel, S. (2019). Nonsteroidal anti-inflammatory drugs: a potential pharmacological treatment for intracranial aneurysm. Cerebrovasc. Dis. Extra. 9, 31–45. doi: 10.1159/000499077
Franck, G., Dai, J., Fifre, A., Ngo, S., Justine, C., Michineau, S., et al. (2013). Reestablishment of the endothelial lining by endothelial cell therapy stabilizes experimental abdominal aortic aneurysms. Circulation 127, 1877–1887. doi: 10.1161/CIRCULATIONAHA.113.001677
Frösen, J.. (2014). Smooth muscle cells and the formation, degeneration, and rupture of saccular intracranial aneurysm wall–a review of current pathophysiological knowledge. Transl. Stroke Res. 5, 347–356. doi: 10.1007/s12975-014-0340-3
Frösen, J., Tulamo, R., Paetau, A., Laaksamo, E., Korja, M., Laakso, A., et al. (2012). Saccular intracranial aneurysm: pathology and mechanisms. Acta Neuropathol. 123, 773–786. doi: 10.1007/s00401-011-0939-3
Galis, Z., Sukhova, G., Lark, M., and Libby, P. (1994). Increased expression of matrix metalloproteinases and matrix degrading activity in vulnerable regions of human atherosclerotic plaques. J. Clin. Invest. 96, 2493–2503. doi: 10.1172/JCI117619
Galis, Z., Sukhova, G., Lark, M., and Libby, P. (1999). Atherosclerosis-an inflammatory disease. N. Engl. J. Med. 340, 115–126. doi: 10.1056/NEJM199901143400207
Hassan, T., Timofeev, E., Saito, T., Shimizu, H., Ezura, M., Matsumoto, Y., et al. (2005). A proposed parent vessel geometry-based categorization of saccular intracranial aneurysms: computational flow dynamics analysis of the risk factors for lesion rupture. J. Neurosurg. 103, 662–680. doi: 10.3171/jns.2005.103.4.0662
He, X., and Ku, D. (1996). Pulsatile flow in the human left coronary artery bifurcation: average conditions. J. Biomech. Eng. 118, 74–82. doi: 10.1115/1.2795948
Hsu, S., Chu, J., Chen, F., Wang, A., and Li, S. (2011). Effect of fluid shear stress on a distinct population of vascular smooth muscle cells. Cell. Mol. Bioeng. 4:627–636. doi: 10.1007/s12195-011-0205-8
Isaksen, J. G., Bazilevs, Y., Kvamsdal, T., Zhang, Y., Kaspersen, J. H., Waterloo, K., et al. (2008). Determination of wall tension in cerebral artery aneurysms by numerical simulation. Stroke 39, 3172–3179. doi: 10.1161/STROKEAHA.107.503698
Kadirvel, R., Ding, Y., Dai, D., Zakaria, H., Robertson, A., Danielson, M., et al. (2007). The influence of hemodynamic forces on biomarkers in the walls of elastase-induced aneurysms in rabbits. Neuroradiology 49, 1041–1053. doi: 10.1007/s00234-007-0295-0
Kataoka, K., Taneda, M., Asai, T., Kinoshita, A., Ito, M., and Kuroda, R. (1999). Structural fragility and inflammatory response of ruptured cerebral aneurysms. A comparative study between ruptured and unruptured cerebral aneurysms. Stroke 30, 1396–1401. doi: 10.1161/01.STR.30.7.1396
Kawaguchi, T., Nishimura, S., Kanamori, M., Takazawa, H., Omodaka, S., Sato, K., et al. (2012). Distinctive flow pattern of wall shear stress and oscillatory shear index: similarity and dissimilarity in ruptured and unruptured cerebral aneurysm blebs. J. Neurosurg. 117, 774–780. doi: 10.3171/2012.7.JNS111991
Kelsey, L. J., Powell, J. T., Norman, P. E., Miller, K., and Doyle, B. J. (2017). A comparison of hemodynamic metrics and intraluminal thrombus burden in a common iliac artery aneurysm. Int. J. Numer. Method Biomed. Eng. 33, e2821. doi: 10.1002/cnm.2821
Khamdaeng, T., Luo, J., Vappou, J., Terdtoon, P., and Konofagou, E. (2012). Arterial stiffness identification of the human carotid artery using the stress-strain relationship in vivo. Ultrasonics 52, 402–411. doi: 10.1016/j.ultras.2011.09.006
Khan, M., Toro Arana, V., Najafi, M., MacDonald, D., Natarajan, T., Valen-Sendstad, K., et al. (2021). On the prevalence of flow instabilities from high-fidelity computational fluid dynamics of intracranial bifurcation aneurysms. J. Biomech. 127:110683. doi: 10.1016/j.jbiomech.2021.110683
Kim, H., Vignon-Clementel, I., Figueroa, C., Jansen, K., and Taylor, C. (2010). Developing computational methods for three-dimensional finite element simulations of coronary blood flow. Finite Elem. Anal. Des. 46, 514–525. doi: 10.1016/j.finel.2010.01.007
Ku, D., Giddens, D., Zarins, C., and Glagov, S. (1985). Pulsatile flow and atherosclerosis in the human carotid bifurcation. positive correlation between plaque location and low oscillating shear stress. Arterioscler. Thromb. Vasc. Biol. 5:293–302. doi: 10.1161/01.ATV.5.3.293
Kwak, B., Bäck, M., Bochaton-Piallat, M., Caligiuri, G., Daemen, M., Davies, P., et al. (2014). Biomechanical factors in atherosclerosis: mechanisms and clinical implications. Eur. Heart J. 35, 3013–3020. doi: 10.1093/eurheartj/ehu353
Les, A., Shadden, S., Figueroa, C., Park, J., Tedesco, M., Herfkens, R., et al. (2010). Quantification of hemodynamics in abdominal aortic aneurysms during rest and exercise using magnetic resonance imaging and computational fluid dynamics. Ann. Biomed. Eng. 38, 1288–1313. doi: 10.1007/s10439-010-9949-x
Lipp, S. N., Niedert, E. E., Cebull, H. L., Diorio, T. C., Ma, J. L., Rothenberger, S. M., et al. (2020). Computational hemodynamic modeling of arterial aneurysms: a mini-review. Front. Physiol. 11:454. doi: 10.3389/fphys.2020.00454
Liu, Q., Jiang, P., Wu, J., Gao, B., and Wang, S. (2019a). The morphological and hemodynamic characteristics of the intraoperative ruptured aneurysm. Front. Neurosci. 13:233. doi: 10.3389/fnins.2019.00233
Liu, Z., Ajimu, K., Yalikun, N., Zheng, Y., and Xu, F. (2019b). Potential therapeutic strategies for intracranial aneurysms targeting aneurysm pathogenesis. Front. Neurosci. 13:1238. doi: 10.3389/fnins.2019.01238
Malek, A., Alper, S., and Izumo, S. (1999). Hemodynamic shear stress and its role in atherosclerosis. JAMA 282, 2035–2042. doi: 10.1001/jama.282.21.2035
Mendieta, J. B., Fontanarosa, D., Wang, J., Paritala, P. K., McGahan, T., Lloyd, T., et al. (2020). The importance of blood rheology in patient-specific computational fluid dynamics simulation of stenotic carotid arteries. Biomech. Model Mechanobiol. 19, 1477–1490. doi: 10.1007/s10237-019-01282-7
Meng, H., Tutino, V. M., Xiang, J., and Siddiqui, A. (2014). High WSS or Low WSS? Complex interactions of hemodynamics with intracranial aneurysm initiation, growth, and rupture: toward a unifying hypothesis. AJNR Am. J. Neuroradiol. 35, 1254–1262. doi: 10.3174/ajnr.A3558
Morbiducci, U., Mazzi, V., Domanin, M., De Nisco, G., Vergara, C., Steinman, D., et al. (2020). Wall shear stress topological skeleton independently predicts long-term restenosis after carotid bifurcation endarterectomy. Ann. Biomed. Eng. 48, 2936–2949. doi: 10.1007/s10439-020-02607-9
Nixon, A., Gunel, M., and Sumpio, B. (2010). The critical role of hemodynamics in the development of cerebral vascular disease. J. Neurosurg. 112:1240–1253. doi: 10.3171/2009.10.JNS09759
Ong, C., Xiong, F., Kabinejadian, F., Praveen Kumar, G., Cui, F., Chen, G., et al. (2019). Hemodynamic analysis of a novel stent graft design with slit perforations in thoracic aortic aneurysm. J. Biomech. 85:210–217. doi: 10.1016/j.jbiomech.2019.01.019
Pentimalli, L., Modesti, A., Vignati, A., Marchese, E., Albanese, A., Di, R., occo, F., et al. (2004). Role of apoptosis in intracranial aneurysm rupture. J. Neurosurg. 101:1018–1025. doi: 10.3171/jns.2004.101.6.1018
Sáez, P., Malvè, M., and Martínez, M. A. (2015). A theoretical model of the endothelial cell morphology due to different waveforms. J. Theor. Biol. 379:16–23. doi: 10.1016/j.jtbi.2015.04.038
Salman, H., Ramazanli, B., Yavuz, M., and Yalcin, H. (2019). Biomechanical investigation of disturbed hemodynamics-induced tissue degeneration in abdominal aortic aneurysms using computational and experimental techniques. Front. Bioeng. Biotechnol. 7:111. doi: 10.3389/fbioe.2019.00111
Sforza, D. M., Putman, C. M., and Cebral, J. R. (2009). Hemodynamics of cerebral aneurysms. Annu. Rev. Fluid Mech. 41, 91–107. doi: 10.1146/annurev.fluid.40.111406.102126
Signorelli, F., Sela, S., Gesualdo, L., Chevrel, S., Tollet, F., Pailler-Mattei, C., et al. (2018). Hemodynamic stress, inflammation, and intracranial aneurysm development and rupture: a systematic review. World Neurosurg. 115:234–244. doi: 10.1016/j.wneu.2018.04.143
SimVascular/sv,FS. I. (2021). https://github.com/SimVascular/svFSI
Soldozy, S., Norat, P., Elsarrag, M., Chatrath, A., Costello, J., Sokolowski, J., et al. (2019). The biophysical role of hemodynamics in the pathogenesis of cerebral aneurysm formation and rupture. Neurosurg. Focus. 47, E11. doi: 10.3171/2019.4.FOCUS19232
Sorokin, V., Vickneson, K., Kofidis, T., Woo, C. C., Lin, X. Y., Foo, R., et al. (2020). Role of vascular smooth muscle cell plasticity and interactions in vessel wall inflammation. Front. Immunol. 11:3053. doi: 10.3389/fimmu.2020.599415
Tarbell, J., Shi, Z., Dunn, J., and Jo, H. (2014). Fluid mechanics, arterial disease, and gene expression. Annu. Rev. Fluid Mech. 46, 591–614. doi: 10.1146/annurev-fluid-010313-141309
Tateshima, S., Tanishita, K., Omura, H., Sayre, J., Villablanca, J., Martin, N., et al. (2008). Intra-aneurysmal hemodynamics in a large middle cerebral artery aneurysm with wall atherosclerosis. Surg. Neurol. 70, 454–462. doi: 10.1016/j.surneu.2008.03.035
Tian, S., Pan, W., Peng, J., Wang, H., Deng, B., Liang, Y., et al. (2021). Hemodynamic responses in carotid bifurcation induced by enhanced external counterpulsation stimulation in healthy controls and patients with neurological disorders. Front. Physiol. 12:1281. doi: 10.3389/fphys.2021.717080
Usmani, A., and Muralidhar, K. (2018). Flow in an intracranial aneurysm model: effect of parent artery orientation. J. Vis. 21, 795–818. doi: 10.1007/s12650-018-0491-5
van Varik, B., Rennenberg, R., Reutelingsperger, C., Kroon, A., de Leeuw, P., and Schurgers, L. (2012). Mechanisms of arterial remodeling: lessons from genetic diseases. Front. Genet. 3:290. doi: 10.3389/fgene.2012.00290
Varble, N., Xiang, J., Lin, N., and Meng, H. (2016). Flow instability detected by high-resolution CFD in fifty-six middle cerebral artery aneurysms. J. Biomech. Eng. 138, 061009. doi: 10.1115/1.4033477
Vedula, V., Lee, J., Xu, H., Kuo, C., Hsiai, T., and Marsden, A. (2017). A method to quantify mechanobiologic forces during zebrafish cardiac development using 4-D light sheet imaging and computational modeling. PLoS Comput. Biol. 13:e1005828. doi: 10.1371/journal.pcbi.1005828
Wang, H., Krüger, T., and Varnik, F. (2020). Effects of size and elasticity on the relation between flow velocity and wall shear stress in side-wall aneurysms: a lattice Boltzmann-based computer simulation study. PLoS ONE 15:e0227770. doi: 10.1371/journal.pone.0227770
Wang, H., Krüger, T., and Varnik, F. (2021a). Geometry and flow properties affect the phase shift between pressure and shear stress waves in blood vessels. Fluids 6, 378. doi: 10.3390/fluids6110378
Wang, H., Uhlmann, K., Vedula, V., Balzani, D., and Varnik, F. (2021b). Fluid-structure interaction simulation of tissue degradation and its effects on intra-aneurysm hemodynamics. bioRxiv. doi: 10.1101/2021.09.01.458529
Wolberg, A., Aleman, M., Leiderman, K., and Machlus, K. (2012). Procoagulant activity in hemostasis and thrombosis: virchow's triad revisited. Anesth. Analg. 114, 275–285. doi: 10.1213/ANE.0b013e31823a088c
Wu, D., Wang, S., Xie, J., Mao, B., Li, B., Jin, C., et al. (2020). Hemodynamic mechanism of coronary artery aneurysm high occurrence on right coronary artery. Front. Physiol. 11:323. doi: 10.3389/fphys.2020.00323
Xiang, J., Natarajan, S., Tremmel, M., Ma, D., Mocco, J., Hopkins, L., et al. (2011). Hemodynamic-morphologic discriminants for intracranial aneurysm rupture. Stroke 42, 144–115. doi: 10.1161/STROKEAHA.110.592923
Xu, L., Chen, X., Cui, M., Ren, C., Yu, H., Gao, W., et al. (2020). The improvement of the shear stress and oscillatory shear index of coronary arteries during enhanced external counterpulsation in patients with coronary heart disease. PLoS ONE 15:e0230144. doi: 10.1371/journal.pone.0230144
Yang, J., Cui, C., and Wu, C. (2011). Cerebrovascular hemodynamics in patients with cerebral arteriosclerosis. Neural Regen. Res. 6, 2532–2536.
Zambrano, B., Gharahi, H., Lim, C., Jaberi, F., Choi, J., Lee, W., et al. (2016). Association of intraluminal thrombus, hemodynamic forces, and abdominal aortic aneurysm expansion using longitudinal CT images. Ann. Biomed. Eng. 44, 1502–1514. doi: 10.1007/s10439-015-1461-x
Keywords: aneurysms, tissue degradation, fluid-structure interaction (FSI), hemodynamics, wall shear stress (WSS), oscillatory shear index (OSI)
Citation: Wang H, Balzani D, Vedula V, Uhlmann K and Varnik F (2021) On the Potential Self-Amplification of Aneurysms Due to Tissue Degradation and Blood Flow Revealed From FSI Simulations. Front. Physiol. 12:785780. doi: 10.3389/fphys.2021.785780
Received: 29 September 2021; Accepted: 09 November 2021;
Published: 10 December 2021.
Edited by:
Liang Zhong, National Heart Centre Singapore, SingaporeReviewed by:
Fangsen Cui, Technology and Research (A*STAR), SingaporeHuseyin Enes Salman, TOBB University of Economics and Technology, Turkey
Copyright © 2021 Wang, Balzani, Vedula, Uhlmann and Varnik. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haifeng Wang, aGFpZmVuZy53YW5nQHJ1Yi5kZQ==; Fathollah Varnik, ZmF0aG9sbGFoLnZhcm5pa0BydWIuZGU=
 Haifeng Wang
Haifeng Wang Daniel Balzani2
Daniel Balzani2 Fathollah Varnik
Fathollah Varnik