Symbiosis of Electrical and Metabolic Oscillations in Pancreatic β-Cells

Insulin is secreted in a pulsatile pattern, with important physiological ramifications. In pancreatic β-cells, which are the cells that synthesize insulin, insulin exocytosis is elicited by pulses of elevated intracellular Ca²⁺ initiated by bursts of electrical activity. In parallel with these electrical and Ca²⁺ oscillations are oscillations in metabolism, and the periods of all of these oscillatory processes are similar. A key question that remains unresolved is whether the electrical oscillations are responsible for the metabolic oscillations via the effects of Ca²⁺, or whether the metabolic oscillations are responsible for the electrical oscillations due to the effects of ATP on ATP-sensitive ion channels? Mathematical modeling is a useful tool for addressing this and related questions as modeling can aid in the design of well-focused experiments that can test the predictions of particular models and subsequently be used to improve the models in an iterative fashion. In this article, we discuss a recent mathematical model, the Integrated Oscillator Model (IOM), that was the product of many years of development. We use the model to demonstrate that the relationship between calcium and metabolism in beta cells is symbiotic: in some contexts, the electrical oscillations drive the metabolic oscillations, while in other contexts it is the opposite. We provide new insights regarding these results and illustrate that what might at first appear to be contradictory data are actually compatible when viewed holistically with the IOM.

Introduction

Pancreatic β-cells contribute to maintaining glucose homeostasis in the body by producing and secreting insulin in a pulsatile fashion, with a period of 4–5 min (Laurenti et al., 2020, 2021; Shukla et al., 2021). Pulses of insulin are more efficient than constant secretion at lowering the level of plasma glucose by suppressing hepatic glucose production and stimulating uptake of glucose by muscle and adipose tissue (Komjati et al., 1986; Paolisso et al., 1991; Matveyenko et al., 2012), and plasma insulin oscillations are disrupted in patients with type I and II diabetes (reviewed in Satin et al., 2015). Insulin secretion is evoked by elevations in the intracellular Ca²⁺ concentration, so pulsatile insulin secretion is associated with oscillations in the intracellular Ca²⁺ concentration.

This has been studied most directly in mice, where it has been possible to measure both in vivo insulin oscillations and in vitro calcium oscillations from the same mouse and show that the frequencies are well correlated (Nunemaker et al., 2005). Although the oscillation patterns are more varied and complex in humans, slow oscillations of appropriate frequency in calcium (Martin and Soria, 1996; Bertram et al., 2018), membrane potential (Riz et al., 2014), and insulin secretion (Marchetti et al., 1994; Lin et al., 2002; Misun et al., 2020) have been observed in human islets in vitro. Thus, these oscillations all originate from bursting electrical activity. In addition, they are accompanied by oscillations in metabolism, as demonstrated by multiple observations in mouse islets of ATP concentration (Li et al., 2013; Merrins et al., 2016), NAD(P)H fluorescence (Luciani et al., 2006; Merrins et al., 2010), mitochondrial membrane potential (Krippeit-Drews et al., 2000; Merrins et al., 2016), and the glycolytic metabolite fructose-1,6-bisphosphate (FBP) (Merrins et al., 2013, 2016).

Bursting electrical activity consists of an episode of action potentials (the active phase) followed by a period of membrane repolarization (the silent phase), repeated periodically. Since the electrical impulses are produced by Ca²⁺ influx through voltage-dependent Ca²⁺ channels (Ca²⁺ channels), the intracellular Ca²⁺ concentration is higher during each burst active phase and lower during each silent phase. These periodic rises in Ca²⁺ evoke exocytosis of insulin-containing vesicles during each active phase (Rorsman and Ashcroft, 2018).

The mechanism responsible for bursting activity remains elusive. It has been proposed that Ca²⁺ oscillations are responsible for periodically switching the cell between the active and silent phases by acting on Ca²⁺-dependent K⁺ channels [K(Ca) channels], or (indirectly) on ATP-sensitive K⁺ channels [K(ATP) channels] (Chay and Keizer, 1983; Keizer and Smolen, 1991; Smolen and Keizer, 1992; Magnus and Keizer, 1998; Fridlyand et al., 2005; Diederichs, 2006; Cha et al., 2011). However, alongside these Ca²⁺ oscillations are metabolic oscillations that have a similar period. These oscillations are manifested as oscillations in the ATP/ADP ratio, which determines K(ATP) channel activity (Ashcroft et al., 1984; Cook and Hales, 1984; Henquin, 1988), thus linking oscillations in metabolism to oscillations in electrical activity and Ca²⁺. Whether these metabolic oscillations are intrinsic (Tornheim, 1997) or passively driven by the downstream effects of Ca²⁺ oscillations (Fridlyand et al., 2005; Cha et al., 2011) has been a matter of debate. One proposal is that metabolic oscillations are driven by oscillations in glycolysis (Tornheim, 1997), as has been demonstrated in extracts from skeletal muscle cytosol (Tornheim and Lowenstein, 1974). Another is that ATP/ADP varies dynamically due to the hydrolysis of ATP to power the Ca²⁺ pumps of the plasma and ER membranes. These pumps remove Ca²⁺ from the cytosol during each active phase (Detimary et al., 1998).

Although both the cytosolic Ca²⁺ concentration and ATP (and other metabolites) oscillate with similar periods, the question of “who is driving bursting?” has yet to be answered. Are Ca²⁺ oscillations driving metabolic oscillations, or vice versa? Mathematical modeling provides a valuable tool for addressing this question, as we demonstrate herein. Models can incorporate different oscillation mechanisms that yield differential predictions. One model, the Integrated Oscillator Model (IOM) (McKenna et al., 2016; Marinelli et al., 2018), incorporates both bursting mechanisms, with different parameter combinations determining which mechanism wins out. In this perspectives article, we use the IOM to demonstrate how the model has been and can be used to investigate the origin of pulsatile insulin secretion, electrical bursting oscillations, and Ca²⁺ and metabolic oscillations of pancreatic β-cells. We also use the IOM to demonstrate how modeling can resolve apparently contradictory data concerning the effects of Ca²⁺ on the polarization of the mitochondrial inner membrane.

Materials and Methods

Mathematical Model

We used the Integrated Oscillator Model (IOM) to simulate a representative β-cell in a well-coupled islet. Figure 1 shows key elements of the model. The current model is an extension of a prior IOM implementation (Marinelli et al., 2018). In particular, we added a third module to account for mitochondrial metabolism (adapted from Bertram et al., 2007a) to the previous two modules representing cellular electrical activity and glycolysis. The differential equations were integrated numerically using MATLAB (MathWorks Inc., Natick, MA); the computer code can be downloaded from https://www.math.fsu.edu/∼bertram/software/islet/.

FIGURE 1

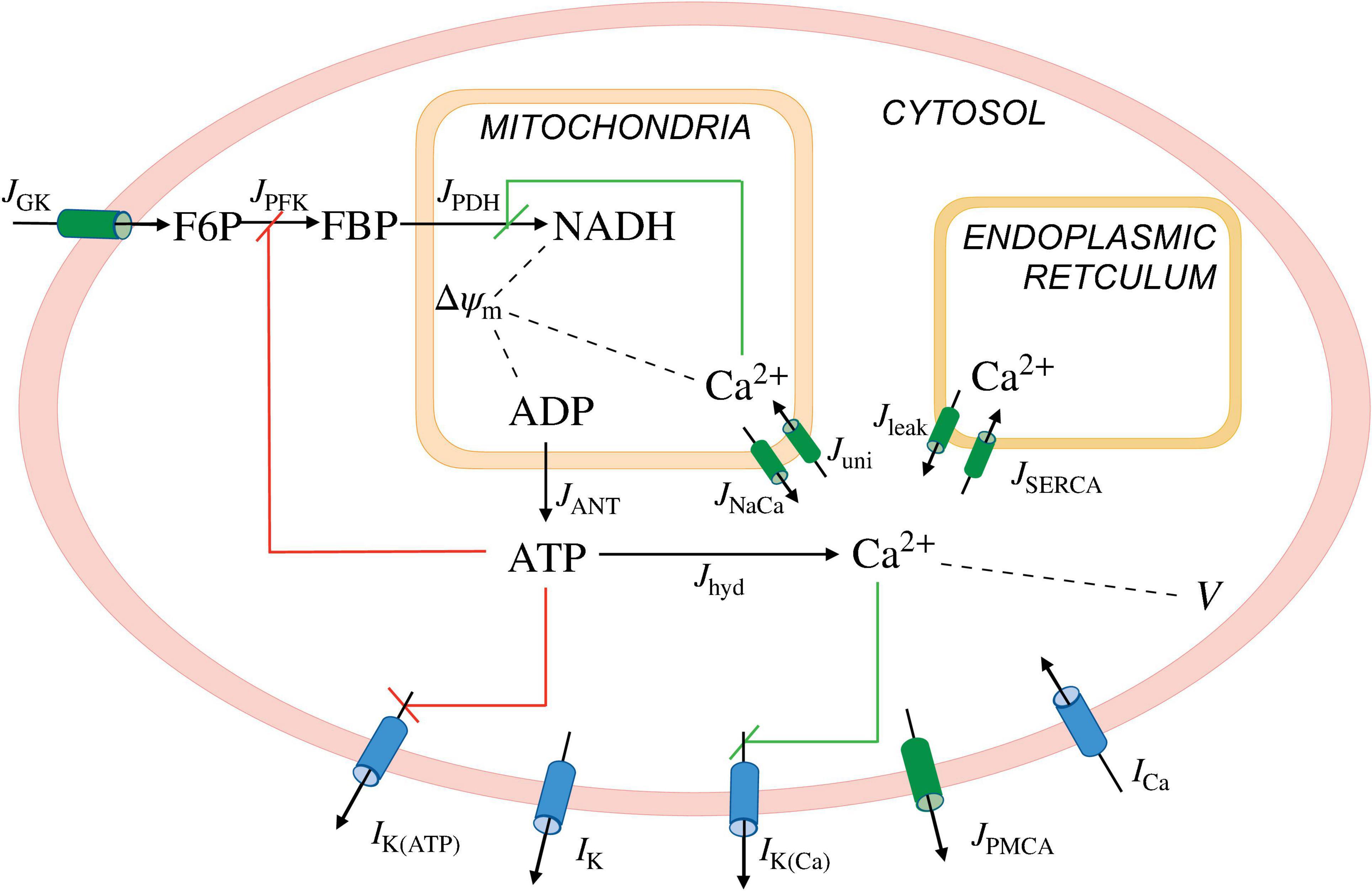
Figure 1. Illustration of the IntegratedOscillatorModel(IOM). The model consists of three modules. A first module describes the β-cell electrical activity and Ca²⁺ dynamics, the second describes key elements of glycolysis, and the third accounts for the mitochondrial metabolism. The second and third modules together make up the metabolic subsystem. I, ionic currents; J, fluxes; K(ATP), ATP-sensitive K⁺ channels; K, delayed rectifier K⁺ channels; K(Ca), Ca²⁺-activated K⁺ channels; PMCA, plasma membrane Ca²⁺ ATPase; Ca, V-dependent Ca²⁺ current; GK, glucokinase; PFK, phosphofructokinase; PDH, phosphate dehydrogenase; ANT, adenine nucleotide translocator; hyd, hydrolysis; NaCa, Na⁺-Ca²⁺ exchanger; uni, uniporter; leak, Ca²⁺ leak across the ER membrane; SERCA, sarcoplasmic endoplasmic reticulum Ca²⁺ pumps; V and △ψ_m, cellular and mitochondrial membrane potential, respectively. The red and green lines represent negative and positive feedback, respectively.

In this model, the flux through the pyruvate dehydrogenase (PDH) reaction (J_PDH) is given by

$$J_{\text{PDH}}=v_{\text{PDH}}\frac{1}{K_{{\text{NADH}}_{\text{m}},\mathrm{PDH}}+\frac{{\text{NADH}}_{\text{m}}}{{\text{NAD}}_{\text{m}}}}{J}_{\text{GPDH}},(1)$$

where v_PDH is the maximum PDH reaction rate, J_GPDH is the flux through the glycerol-3-phosphate dehydrogenase (GPDH) reaction, and NADH_m and NAD_m are dinucleotides of mitochondria. The GPDH reaction rate (J_GPDH) is given by

$$J_{\text{GPDH}}=\frac{{\text{Ca}}_{\text{m}}^{2+}}{{\text{K}}_{\text{GPDH}}+{\text{Ca}}_{\text{m}}^{2+}}\sqrt{\text{FBP}},(2)$$

with ${\text{Ca}}_{\text{m}}^{2+}$ representing the Ca²⁺ concentration of the mitochondria. In the IOM, the K(ATP) current (I_K(ATP)) is described by

$$I_{\text{K}\left(\text{ATP}\right)}=g_{\text{K}\left(\text{ATP}\right)}{o}_{\mathrm{\infty }}(\mathrm{ATP},\mathrm{ADP})\left(V-V_{\text{K}}\right),(3)$$

where g_K(ATP) is the maximum conductance, V is the plasma membrane potential, V_K is the K⁺ Nernst potential, and o_∞(ATP,ADP) is the fraction of activated K(ATP) channels,

$$o_{\mathrm{\infty }}(\mathrm{ADP},\mathrm{ATP})=\frac{0.08+0.89{\left(\frac{\text{MgADP}}{k_{dd}}\right)}^2+0.16\left(\frac{\text{MgADP}}{k_{dd}}\right)}{{\left(1+\frac{\text{MgADP}}{k_{dd}}\right)}^2\left(1+\frac{{\text{ATP}}^{4-}}{k_{tt}}+\frac{{\text{ADP}}^{3-}}{k_{td}}\right)}.(4)$$

Here, MgADP = 0.165 ADP, ADP^3– = 0.135 ADP, and ATP^4– = 0.05 ATP, while the parameters k_tt, k_td and k_dd represent the dissociation constants for ATP, ADP, and MgADP, respectively.

We simulated the addition of the K(ATP) channel activator diazoxide (Dz) by increasing the dissociation constants for ATP (k_tt) from 1 to 2μM. The application of KCl, which induces cell depolarization, was simulated by increasing the K⁺ Nernst potential (V_K) from –75 to −70mV.

The model used here should be thought of as simulating a representative β-cell in a well synchronized islet. There has been a great deal of interest recently in β-cell heterogeneity within the islets, which is beyond our scope, as it doesn’t generate the oscillations, though it does strongly influence the characteristics of the oscillations. The hypothesis that the mechanisms of oscillations are inherent in the β-cells rather than the network is supported by calcium imaging in isolated β-cells and in islets lacking gap junctions. Oscillations are observed but are irregular (likely due to noise) and occur out of the normal glucose range (likely due to heterogeneity) and, in islets, asynchronous (Ravier et al., 2005; Benninger et al., 2011; Dwulet et al., 2019; Scarl et al., 2019). See the following for recent work on the roles of heterogeneity (Cappon and Pedersen, 2016; Benninger and Hodson, 2018; Nasteska and Hodson, 2018; Stozer et al., 2019; Joglekar et al., 2021; Zmazek et al., 2021).

Results

Electrical, Ca²⁺, and Metabolic Subsystems Are Symbiotic

The transduction of glucose input to insulin output in β-cells is complex, and can be thought of in terms of feedforward and feedback pathways implemented through the metabolism of glucose (which, unlike most cells, plays a key role not only in providing energy but also in intracellular signaling), intracellular Ca²⁺ signaling, and membrane electrical activity. We describe these pathways in some detail below, but begin with an overview illustrated in Figure 2.

FIGURE 2

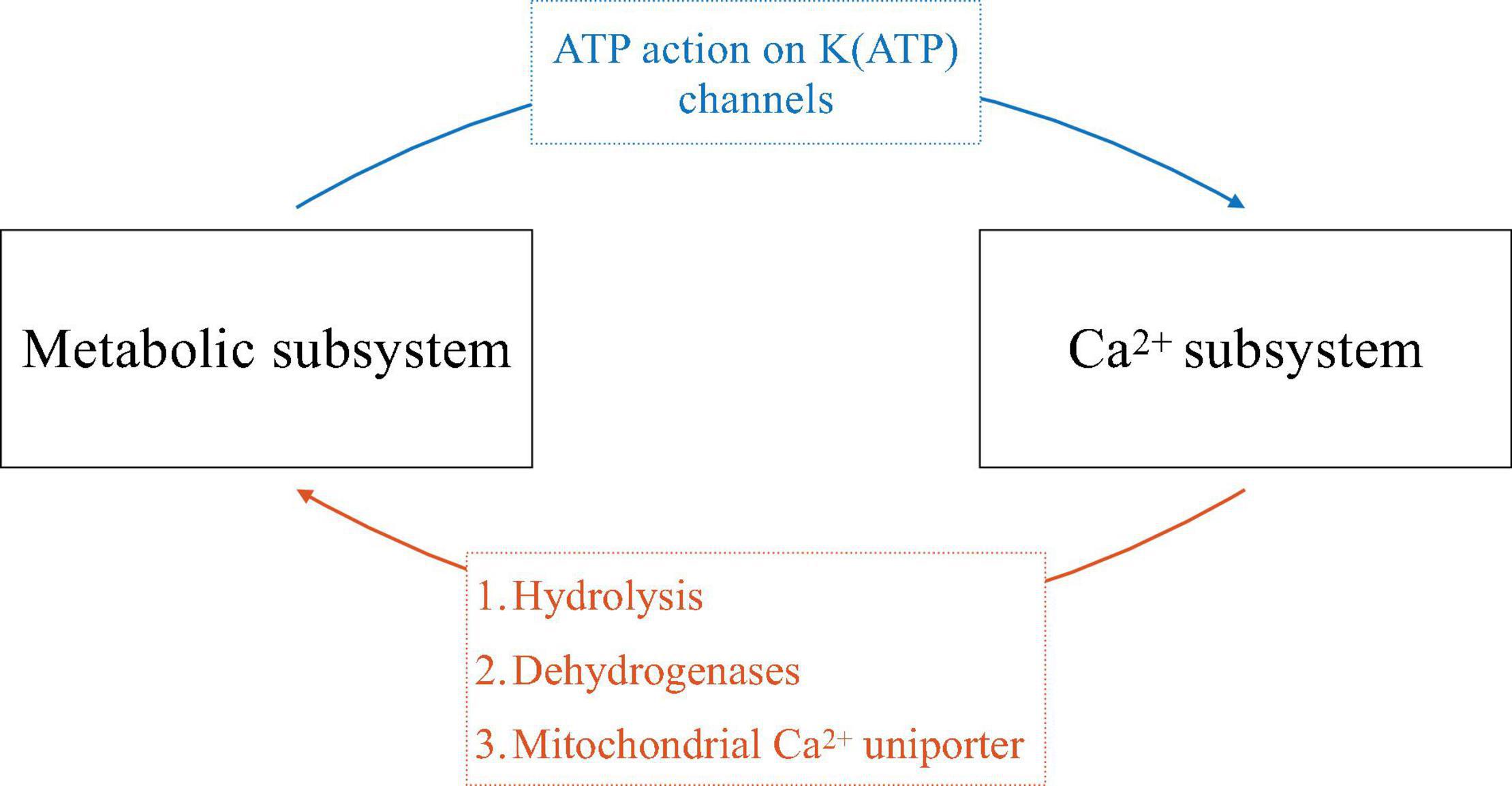
Figure 2. Schematic of the symbiosis of electrical and metabolic oscillators. The ways that one subsystem affects the other is indicated on the arrows.

Glucose triggers β-cell electrical activity through the metabolic production of ATP from ADP, resulting in an increase in cytosolic ATP/ADP. This increase inhibits K(ATP) channels and thereby reduces net outward K⁺ current, resulting in cell depolarization. This depolarization opens voltage-dependent Ca²⁺ channels and allows Ca²⁺ influx, producing electrical impulses and increasing the intracellular Ca²⁺ concentration (blue arrow, Figure 2). In this way, metabolism feeds forward onto the cell’s electrical activity and Ca²⁺ subsystem. If metabolism oscillates, this pathway can produce bursting electrical activity and Ca²⁺ oscillations.

Cytosolic Ca²⁺, as well as Ca²⁺ entering organelles such as the endoplasmic reticulum (ER) and mitochondria, in turn affects metabolism through several pathways (orange arrow, Figure 2). One is via ATP hydrolysis needed to power the Ca²⁺ pumps of the plasma membrane and ER membrane. These pumps, or Ca²⁺-ATPases, are particularly active during the active phases of bursting, when cytosolic Ca²⁺ is elevated. The hydrolysis of ATP that results in turn reduces cytosolic ATP/ADP. If the Ca²⁺ concentration oscillates, then ATP/ADP, and the levels of other metabolites, will concomitantly oscillate as ATP is hydrolyzed by Ca²⁺ pump activity (Detimary et al., 1998). A second way for Ca²⁺ to affect metabolism is by activating dehydrogenases of the glycolytic pathway and tricarboxylic acid cycle (TCA cycle), speeding up metabolism (Denton, 2009). If the Ca²⁺ concentration is oscillatory, then ATP production in this case will be facilitated during each active phase, leading to ATP/ADP oscillations. A third way for Ca²⁺ to influence metabolism is due to Ca²⁺ flux through the mitochondrial Ca²⁺ uniporter, the main path for Ca²⁺ transport across the mitochondrial inner membrane (De Stefani et al., 2015). This influx depolarizes the mitochondrial membrane potential, reducing ATP synthesis through oxidative phosphorylation (Magnus and Keizer, 1998). If the Ca²⁺ concentration oscillates, then there will be increased flux across the mitochondrial inner membrane during each active phase of the oscillation, resulting in oscillations in ATP synthesis and thus in cytosolic ATP/ADP.

Symbiosis of the Two Subsystems Provides Multiple Mechanisms for Rhythm Generation

The symbiotic relationship between the metabolic and Ca²⁺ subsystems described here, with mutual feedback from one subsystem to the other, provides for several potential mechanisms underlying electrical bursting and oscillations in Ca²⁺ and metabolism. In one mechanism, oscillations can be generated purely within the metabolic subsystem, and project out to the other subsystems (blue arrow, Figure 2). This intrinsic metabolic oscillator can be mediated by glycolysis, due to the allosteric enzyme phosphofructokinase (PFK), which is positively regulated by its product FBP. This positive autoregulation can lead to oscillations due to the negative feedback that occurs through substrate pool depletion (Smolen, 1995). Indeed, evidence for this comes from work done on skeletal muscle extracts, where the M-type (for muscle) isoform of PFK is dominant (Tornheim and Lowenstein, 1974). This isoform is also dominant in β-cells (Yaney et al., 1995), prompting the proposal that the same rhythmogenic mechanism applies (Tornheim, 1997). We refer to these intrinsic metabolic oscillations as Active Metabolic Oscillations (AMOs). [We previously referred to them as Active Glycolytic Oscillations (Bertram et al., 2018), but have generalized the nomenclature to make clear that the concept applies to oscillations of all metabolites, whether they are part of glycolysis or oxidative phosphorylation].

At the other extreme, metabolic oscillations can be generated purely due to the elevations in Ca²⁺ that occur during each active phase, and downstream effects resulting from that elevation (orange arrow, Figure 2), primarily due to ATP hydrolysis by the Ca²⁺ ATPases (Detimary et al., 1998). We refer to these Ca²⁺-dependent metabolic oscillations as Passive Metabolic Oscillations (PMOs), since the metabolic variables in this case are only responding to Ca²⁺.

In either case, the cell’s electrical activity is ultimately determined by ion channels. Several spiking patterns have been reported in the literature: fast spiking with a period of about 100 ms; fast bursting with superimposed spikes, with a period of tens of seconds (Meissner, 1976; Henquin and Meissner, 1984); and slow bursting with a period of 5 min or more (Henquin et al., 1982; Cook, 1983). Each electrical pattern is associated with a corresponding oscillation in Ca²⁺. For recent work on the interactions of spikes and bursts see Zmazek et al. (2021). In the case of slow bursting, the most likely channel type for turning burst active phases on and off is the K(ATP) channel (Keizer and Magnus, 1989; Detimary et al., 1998; Magnus and Keizer, 1998). If this is correct, then ATP/ADP oscillations drive bursting through the activation/deactivation of K(ATP) channels. A likely mechanism for fast bursting oscillations is cyclic activation of K(Ca) channels.

While it can be difficult to ascribe one of these mechanisms or the other to a particular pattern of bursting by period alone, this can be addressed using computer simulations with the IOM, as in Figure 3. The left panels show slow oscillations in which the metabolic oscillations are passive (PMOs), and the right panels show bursting with AMOs. These different scenarios were obtained using different values of the maximum catalytic rate for PDH, v_PDH (Eq. 1). Slow oscillations exist for intermediate range of values of v_PDH, as described in Bertram et al. (2018) and explored quantitatively in Marinelli et al. (2018). The Ca²⁺ traces (Figures 3A,B) share the same basic features (a rapid rise at the start of an active phase, a plateau throughout most of the active phase, and a sharp drop initially, followed by a slower drop during the silent phase). The ATP oscillations (Figures 3E,F) also have roughly the same shapes. The only clear difference between the two cases is the shape of the FBP time course. With PMOs it has a sawtooth pattern (Figure 3C) with peaks at the beginning of the active phase and nadirs at the end. With AMOs, FBP is pulsatile (Figure 3D), exhibiting peaks at the beginning of the active phase and then slowly decreasing to almost zero, where it remains during most of the silent phase. While a FRET sensor has been developed in our lab that reports FBP dynamics (PKAR, for Pyruvate Kinase Activity Reporter) (Merrins et al., 2013), our analysis (unpublished observations) of data from a population of islets indicates that it is difficult in practice to experimentally distinguish between the sawtooth and pulsatile FBP patterns.

FIGURE 3

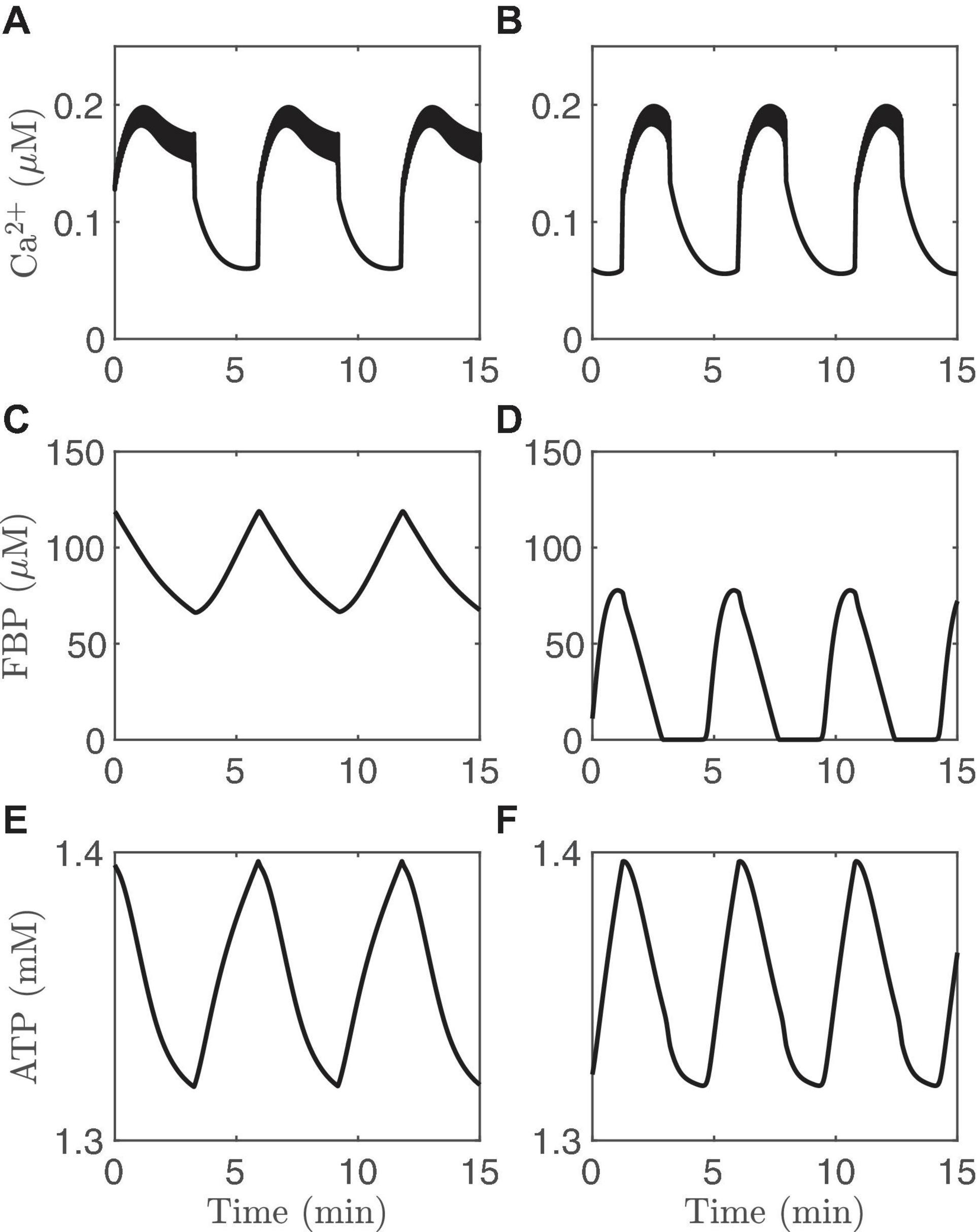
Figure 3. Time courses generated with the IOM. The columns on the left (A,C,E) show an example of PMOs, while those on the right (B,D,F) show an example of AMOs. For the left column, v_PDH = 0.4 μM/ms while for the right column and v_PDH = 2 μM/ms. In both cases, g_K(Ca) = 150pS and the glucose concentration in 11 mM.

Clamping the Ca²⁺ Concentration Can Distinguish Active Metabolic Oscillations and Passive Metabolic Oscillations

Another way to distinguish AMOs and PMOs theoretically is illustrated in Figure 4. As in the previous figure, the traces on the left are from an oscillating system exhibiting PMOs, while those on the right are from a system exhibiting AMOs. At time t=15 min, the Ca²⁺ concentration is clamped in both cases to a fixed level. This terminates the metabolic oscillations in the case of PMOs (left), while metabolic oscillations persist in the case of AMOs (right). This is a clear qualitative difference between the two oscillation mechanisms that does not require distinguishing between small changes in the shapes of variables. It is a perfect model prediction. But can it be tested experimentally?

FIGURE 4

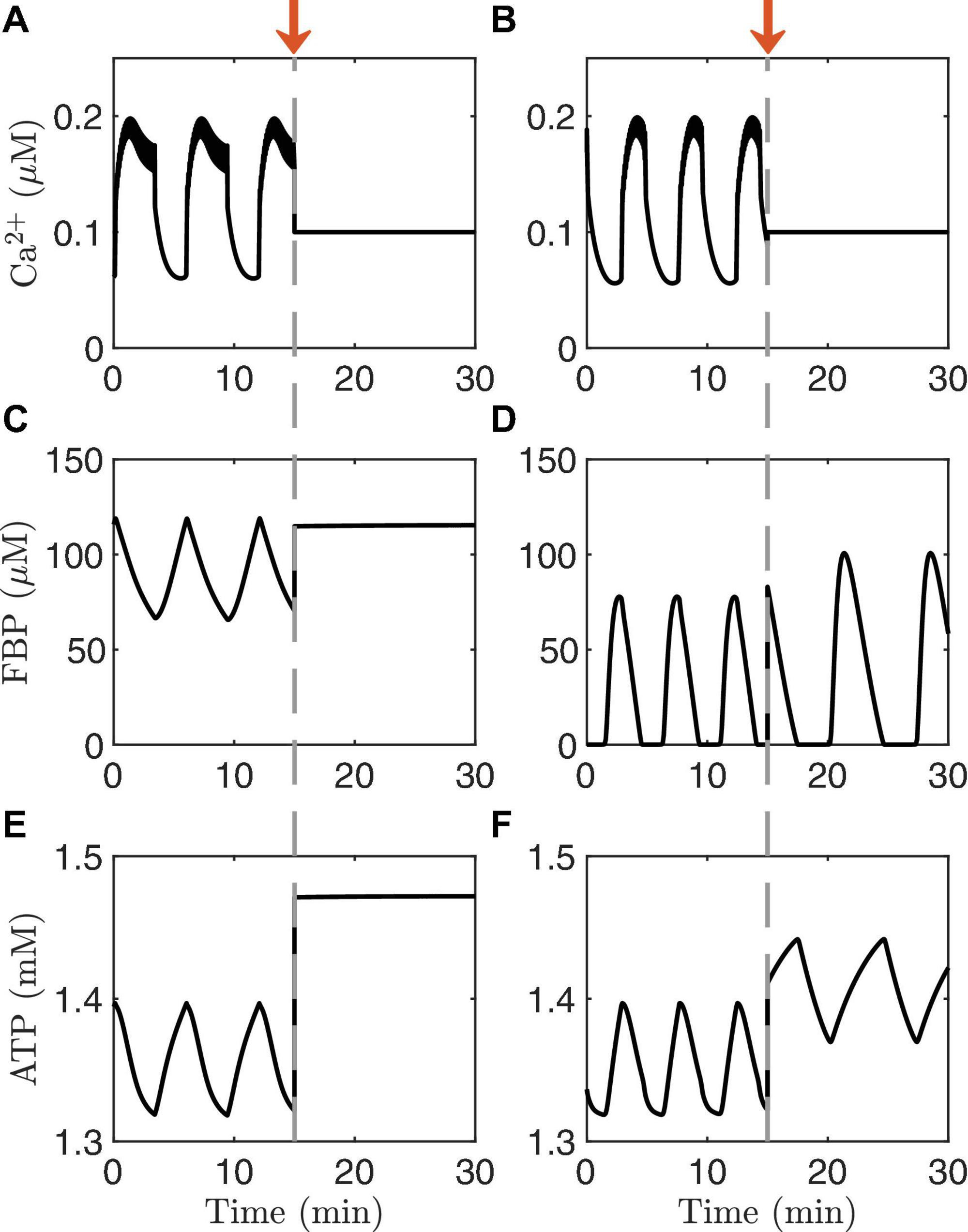
Figure 4. Time courses generated with the IOM. The columns on the left (A,C,E) show an example of PMOs, while those on the right (B,D,F) show an example of AMOs. At time t = 15 min (arrow), the Ca²⁺ concentration is clamped. In the model with the PMOs (left column) all oscillations stop, while in case of AMOs (right column) the metabolic oscillations persist. The values of v_PDH and g_K(Ca) and glucose are the same as in Figure 3.

It is possible to clamp the Ca²⁺ level of a single cell pharmacologically by bath applying diazoxide (Dz), an activator of K(ATP) channels. The level at which Ca²⁺ is clamped, moreover, can be raised by increasing the concentration of KCl in the bath solution, which depolarizes the cells and thereby opens more Ca²⁺ channels. This procedure for clamping islet Ca²⁺ has been used to better understand intracellular signaling in islet β-cells by short-circuiting the dynamics of the Ca²⁺ subsystem (Gembal et al., 1992; Merrins et al., 2010). Model simulations depicting this are shown in Figure 5. Each panel of the figure shows a simulation of what can happen when Ca²⁺ is first clamped with Dz, and then the Ca²⁺ level is increased by raising the KCl concentration in the continued presence of Dz. We illustrate the results in different cases, represented by different values set for the parameter v_PDH. The first three panels exhibit AMOs prior to clamping, while the last exhibits PMOs.

FIGURE 5

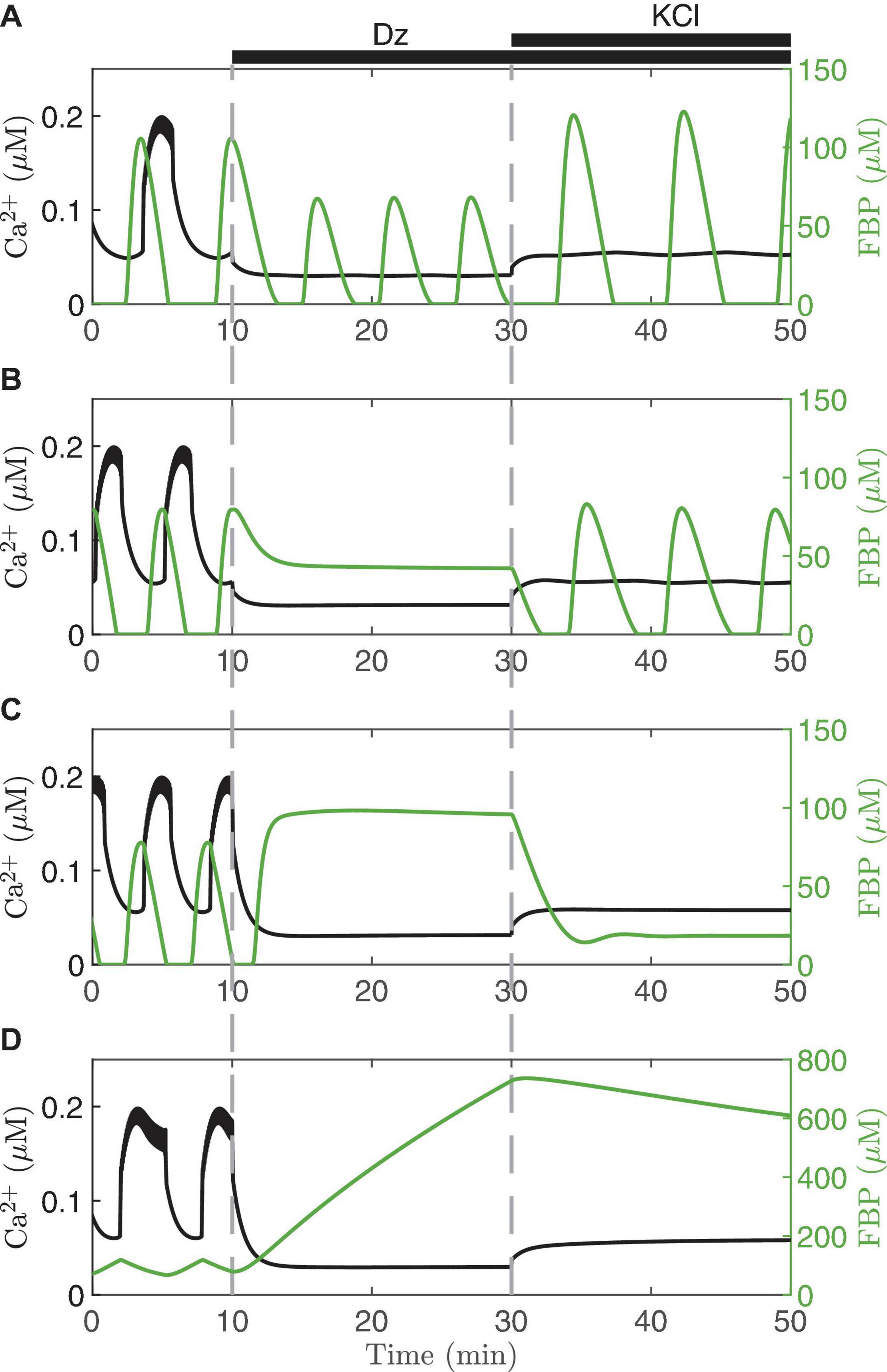
Figure 5. Model simulations in which the membrane potential is clamped with diazoxide (Dz) and elevated KCl. Each panel illustrates the model predictions for v_PDH = 7 μM/ms (A), 3 μM/ms (B), 2 μM/ms (C), 0.4 μM/ms (D). In all cases, g_K(Ca) = 150pS and the glucose concentration is 11 mM.

When Dz is first applied, the Ca²⁺ oscillations stop in all four cases (Ca²⁺ is clamped to a low value since the cell is hyperpolarized due to K(ATP) opening). However, in the top case (Figure 5A) the metabolic oscillations (shown here by the glycolytic metabolite FBP) persist in Dz. When KCl is applied with Dz, the Ca²⁺ level is increased, and at this higher Ca²⁺ level the metabolic oscillations become slower and larger in amplitude. This is a clear demonstration that, in this case, the metabolic oscillations are AMOs, as in the right panels of Figure 4. They thus do not require oscillatory Ca²⁺ for them to occur, although they do require Ca²⁺ to be at a sufficiently high, but not too high, level (achieved by adding KCl). We also note that the Ca²⁺ level in the presence of Dz does modulate AMO period and amplitude. What is perhaps more surprising is that in the middle two cases (Figures 4B,C), which both also show AMOs, clamping Ca²⁺ with Dz can be seen to terminate the metabolic oscillations. Indeed, a similar finding done experimentally [where NAD(P)H or oxygen consumption was measured as the metabolic variable] led to the conclusion that metabolic oscillations are not intrinsic (AMOs), but must be driven by the Ca²⁺ oscillations (PMOs) (Kennedy et al., 2002; Luciani et al., 2006). As our simulation in Figure 4B shows, however, when Ca²⁺ was subsequently elevated to a higher level, the metabolic oscillations re-emerged. Thus, in this case, metabolic oscillations clearly do not require Ca²⁺ oscillations, just a more elevated level of Ca²⁺. Measurements of NAD(P)H were made to test this prediction (Merrins et al., 2010), and it was found that while Dz often terminated the metabolic oscillations, in some of the cases the oscillations re-emerged following the addition of KCl. Thus, the experimental data showed examples that matched both panels A and B of the simulations in Figure 5. A later experimental study also found recovery of the metabolic oscillations with the application of KCl, but in this case measurements were made using PKAR (Merrins et al., 2016), a more direct readout of glycolytic oscillations.

The bottom two panels of Figure 5 show examples where the metabolic oscillations were terminated by simulated application of Dz, and did not recover even following islet depolarization by KCl. This behavior was also observed experimentally (Merrins et al., 2010, 2016). However, it is not known in this case whether the metabolic oscillations present before Ca²⁺ was clamped were AMOs (as in Figure 5C) or PMOs (as in Figure 5D). The latter type would be expected from Figure 4 (left column), as these passive metabolic oscillations must stop when Ca²⁺ does not oscillate. It is harder to understand the former case (Figure 4C) since the metabolic oscillations that existed before Ca²⁺ was clamped were AMOs that do not require Ca²⁺ oscillations. So why were the metabolic oscillations not rescued by elevating Ca²⁺ with KCl? Put simply, it is because the Ca²⁺ level induced by the KCl in this case was not sufficiently large; increasing the Ca²⁺ level further indeed rescues the metabolic oscillations. For more details (see Watts et al., 2014; Marinelli et al., 2018).

Islet Ca²⁺ can also be clamped by exposing islets to glucose concentrations below the threshold for electrical activity. This was done in Nunemaker et al. (2006) and small oscillations in the Ca²⁺ concentration could be detected even in the absence of electrical activity. Figure 6 illustrates the model prediction when the concentration of glucose was reduced from a stimulatory level (11 mM) to a substimulatory level near the threshold (5 mM, arrow). At 5 mM, the cell is not bursting, although small fluctuations in Ca²⁺ concentration occur. Where do these fluctuations come from? Examination of the superimposed FBP trace shows that even in subthreshold glucose, intrinsic metabolic oscillations are produced that act on the Ca²⁺ concentration by causing oscillations in ATP/ADP (blue arrow, Figure 2); these produce small voltage fluctuations that result in small Ca²⁺ fluctuations. Note that these subthreshold Ca²⁺ fluctuations are much smaller than the oscillations produced at a stimulatory glucose level, and are too small to drive any plausible Ca²⁺-dependent oscillation mechanism, but they are large enough to be detected experimentally, as shown in Nunemaker et al. (2006).

FIGURE 6

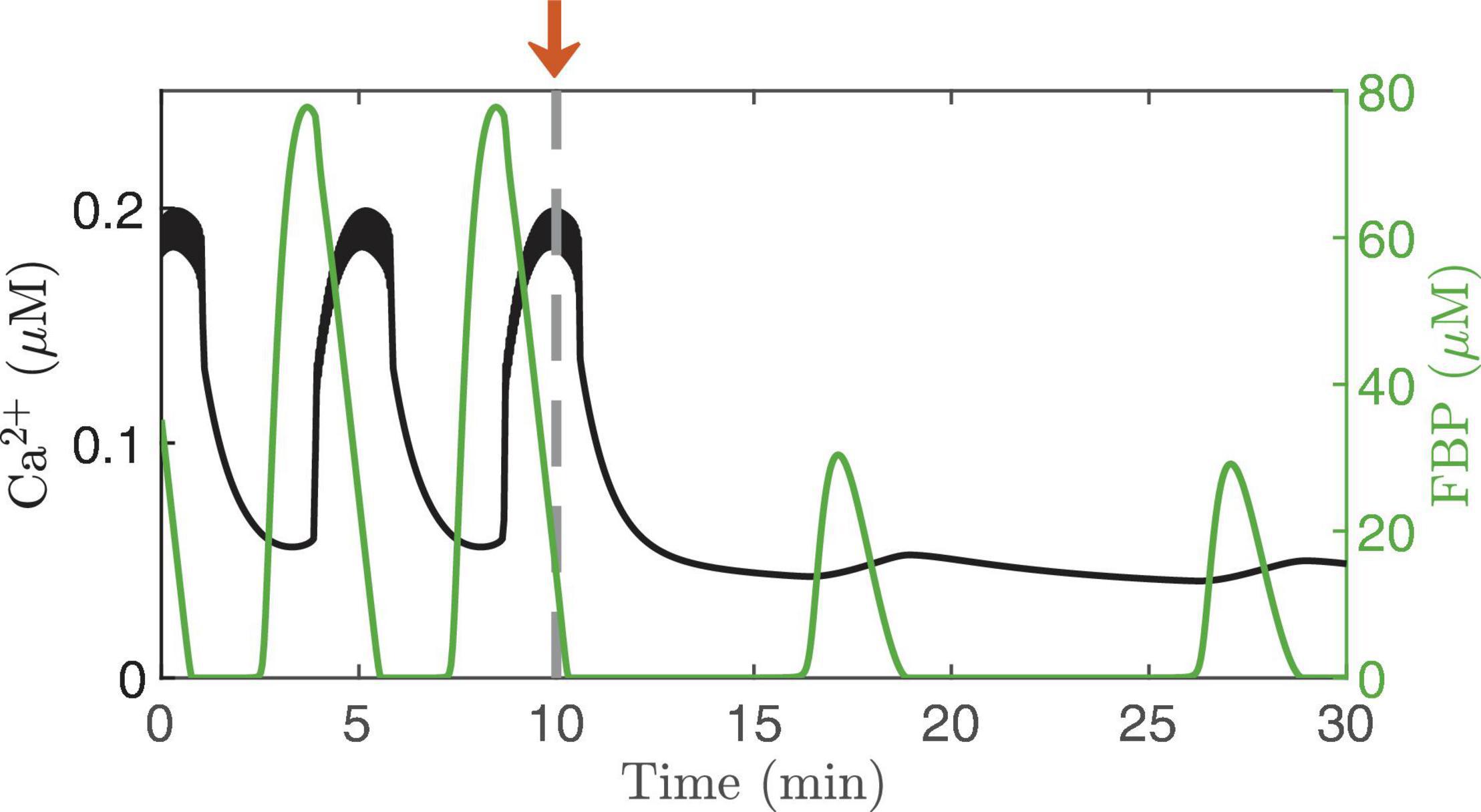
Figure 6. Ca²⁺ oscillations generated by the IOM, with FBP pulses superimposed. The glucose concentration is lowed from 11 to 5 mM at time t = 10 min. The electrical activity stops at the subthreshold glucose concentration, but intrinsic oscillations persist, resulting in small-amplitude Ca²⁺ fluctuation. For this simulation, v_PDH = 2 μM/ms and g_K(Ca) = 150pS.

The subthreshold Ca²⁺ oscillations are likely also too small to drive the oscillations that occur in basal insulin secretion (Satin et al., 2015). They are very slow, which suggests they are the product of intrinsic metabolic oscillations, and it is likely that the metabolic oscillations drive the oscillations in basal secretion. They would do this directly through increasing delivery of insulin granules to the plasma membrane and to the vicinity of the small number of Ca²⁺ channels that open spontaneously even when membrane potential is low. This is supported by observations in super-threshold glucose with Ca²⁺ clamped and glucose artificially pulsed (Ravier et al., 1999; Kjems et al., 2002). The oscillations of secretion under these conditions were only about one-tenth the size of those when Ca²⁺ was free to oscillate, but that would be sufficient to account for oscillations in basal secretion. When Ca²⁺ is free to oscillate, the metabolic oscillations synergize with Ca²⁺ to markedly amplify the secretory pulses, as modeled in Figure 6 of Satin et al. (2015).

Direct confirmation of metabolic oscillations in basal glucose through measurements of a metabolite such as NAD(P)H, FBP, or ATP/ADP remains to be done. This is a particularly tricky experiment since, from an analysis of the model, subthreshold AMOs do not always occur. That is, the result will likely vary from islet to islet, so that many trials might be needed to firmly establish that subthreshold AMOs occur. Indeed, this could be why subthreshold Ca²⁺ oscillations have so rarely been reported in the islet literature. Regardless, subthreshold glucose is an excellent condition in which to bypass the cell’s electrical activity and isolate oscillations in the metabolic subsystem.

Compound Oscillations Demonstrate the Coexistence of Intrinsic Metabolic Oscillations and Ca²⁺-Driven Oscillations

The observation that islets exhibit compound electrical or Ca²⁺ oscillations is the strongest evidence to date that β-cells have intrinsic metabolic oscillations. Compound oscillations consist of fast V bursts (or Ca²⁺ oscillations) that are grouped into slower episodes. This type of oscillatory pattern has been observed since the earliest reports of islet electrical activity (Henquin et al., 1982; Cook, 1983), and has been confirmed using Ca²⁺ imaging (Valdeolmillos et al., 1989; Bertram et al., 2004) or using simultaneous recordings of islet membrane potential and Ca²⁺ (Beauvois et al., 2006). The period of the burst episodes is about 5 min, corresponding closely to the period of insulin pulsatility. We have hypothesized that the fast oscillations within compound oscillations reflect the feedback of intracellular Ca²⁺ onto K(Ca) channels, while intrinsic slow metabolic oscillations group the fast oscillations into slower episodes (Bertram et al., 2004, 2007b). The mechanism of compound oscillations can be thought of as a combination of the first mathematical model of bursting in β-cells (Chay and Keizer, 1983) [for the fast bursts, and based on K(Ca)] with the first model in which bursting (for the slow burst episodes) relied upon intrinsic metabolic oscillations (Tornheim, 1997). Since both mechanisms are incorporated into the IOM, this model can produce compound oscillations, as shown in Figure 7. Here it can be seen that pulses of FBP (Figure 7D) lead to rises in ATP (Figure 7C) that are responsible for packaging bursts (Figure 7A) and fast Ca²⁺ oscillations (Figure 7B) into episodes via the activation and deactivation of K(ATP) channels. The FBP pulses in this simulation result from AMOs, and the effect of Ca²⁺ on the AMOs is seen only as the “teeth” in the ATP profile. The elevated Ca²⁺ concentration that accompanies each fast burst leads to increased ATP hydrolysis by Ca²⁺ ATPases (orange arrow in Figure 2), resulting in a downward deflection in the ATP trace shown. Such “teeth” have been observed for other metabolic variables and for glucose consumption during compound bursting (Jung et al., 1999; Dahlgren et al., 2005).

FIGURE 7

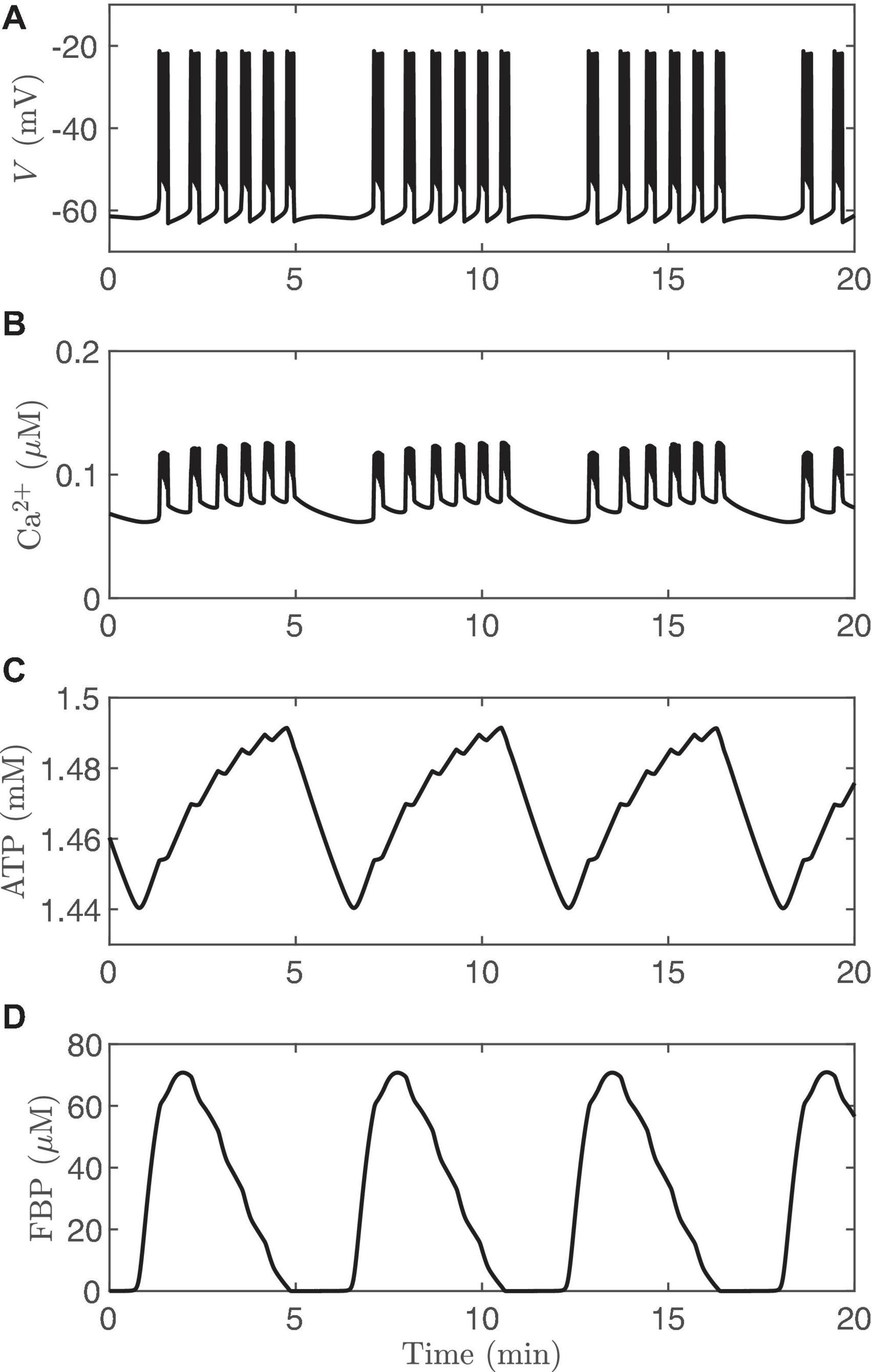
Figure 7. Compound bursting generated by the IOM, and the calcium time courses are similar (Figures 9A,B). (A) Membrane potential. (B) Cytosolic calcium. (C) ATP. (D) FBP. For this simulation, v_PDH = 2 μM/ms, g_K(Ca) = 600pS, and the glucose concentration in 11 mM.

FIGURE 8

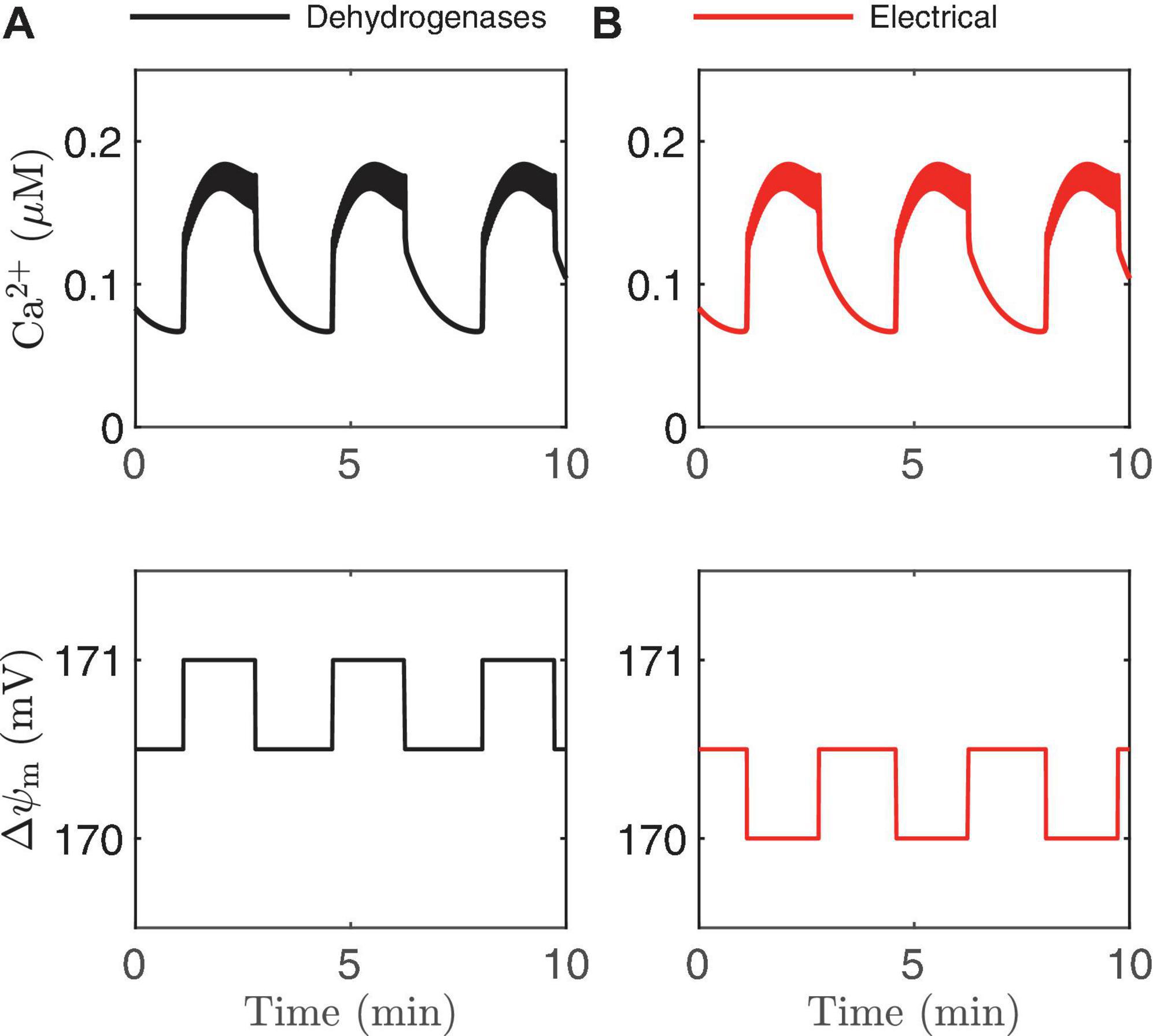
Figure 8. Schematic of experimental findings on the mitochondrial membrane potential △ψ_m If the dehydrogenase effects prevail, △ψ_m hyperpolarizes during the active phase (A), while △ψ_m depolarizes during the active phase if the electrical effect dominates (B).

FIGURE 9

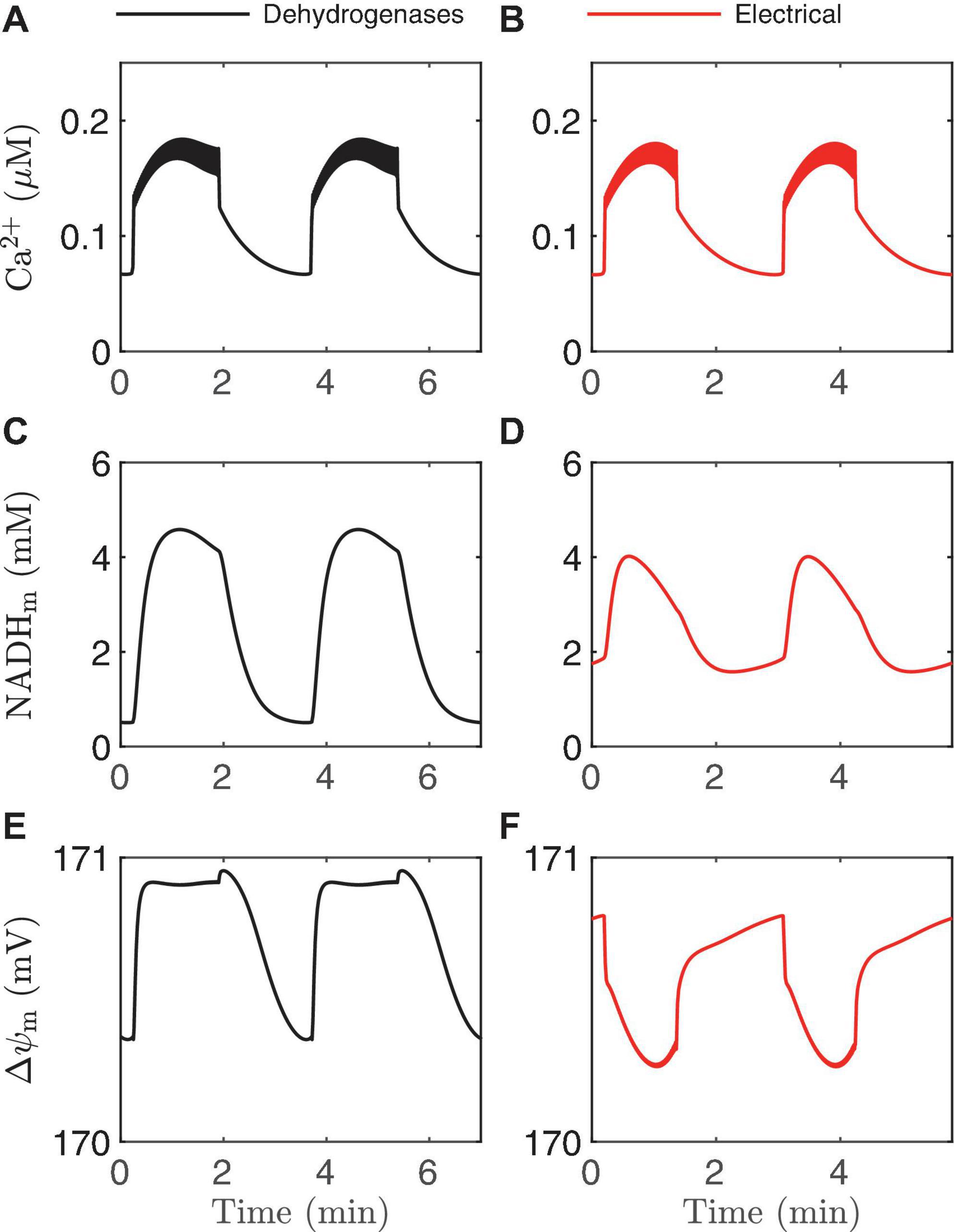
Figure 9. Time courses generated by the IOM with p₂₁ = 0.013μM/ms (A,C,E) and 0.03μM/ms (B,D,F). In both cases, v_PDH = 0.4 μM/ms, g_K(Ca) = 150pS, and the glucose concentration in 11 mM. In the left panel, the effect of Ca²⁺ on dehydrogenases dominates, while on the right the electrical effect of Ca²⁺ current across the inner membrane dominates.

Although we know of no other reasonable explanation for compound bursting, we cannot rule out other possibilities. Thus, although the existence of compound oscillations is suggestive of AMOs, as both metabolism and Ca²⁺ are oscillating during compound bursting, disentangling the effects of one on the other experimentally is difficult. This highlights why clamping Ca²⁺, either pharmacologically or by using subthreshold glucose remains the best approach for unequivocally distinguishing between AMOs from PMOs experimentally.

The Model Can Be Used to Resolve Contradictory Behaviors

Models can also be useful for interpreting data from experiments post hoc. This is particularly important when the data defy straightforward explanations, or when data from different labs appear to be contradictory. As an example of this, we consider the measurements that have been made of mitochondrial inner membrane potential (△ψ_m) during bursting. The inner membrane potential is very important as it provides the electrochemical driving force needed for mitochondrial ATP synthesis. In one study, the measurement of △ψ_m using the fluorescent dye rhodamine-1,2,3 showed that △ψ_m depolarized during each burst active phase (Krippeit-Drews et al., 2000), decreasing mitochondrial electrochemical driving force. In a later study, measurements made using the same technique found that △ψ_m hyperpolarized during each active phase, increasing the electrochemical driving force (Merrins et al., 2016). How can one interpret these apparently contradictory findings? How can they both be right?

In Figure 2 we illustrated two ways that Ca²⁺ can influence ATP production: through the activation of Ca²⁺-dependent dehydrogenases which hyperpolarize △ψ_m, and via the direct depolarization of △ψ_m by the Ca²⁺ current flowing across the mitochondrial inner membrane through the Ca²⁺ uniporter. During a burst active phase, cytosolic Ca²⁺ concentration is elevated, and when some of this Ca²⁺ enters the mitochondria it will thus likely have both hyperpolarizing and depolarizing effects on △ψ_m. Which effect dominates will determine the direction of △ψ_m during each burst active phase, as illustrated in Figure 8. If the activation of dehydrogenases by Ca²⁺ dominates, then △ψ_m will hyperpolarize during the active phase (left panels, increases in △ψ_m indicate hyperpolarization), while if the electrical effect of the Ca²⁺ flux dominates, then △ψ_m will depolarize during the active phase (right panels).

This result is intuitive, and modeling is not needed to make the point. What is not clear, however, is what system parameter controls this competition? A key parameter that can change the effect of mitochondrial Ca²⁺ influx during the active phase from △ψ_mhyperpolarization to depolarization (Bertram et al., 2006) is p₂₁, which appears in the term for Ca²⁺ uniporter flux,

$$J_{\text{uni}}=\left(p_{21}\mathrm{△}{\mathrm{\psi }}_m-p_{22}\right){\text{Ca}}^{2+},(5)$$

where Ca²⁺ is the cytosolic Ca²⁺ concentration. In the uniporter flux function the term in parentheses is the effect of △ψ_m on Ca²⁺ influx across the mitochondrial inner membrane. The relationship is approximately linear in the relevant range of △ψ_m, with slope p₂₁ and intercept p₂₂ (Bertram et al., 2007a). For small values of p₂₁, the electrical effect produced is small and the dehydrogenase effect will therefore dominate so that the inner membrane hyperpolarizes during the burst active phase (Figure 9E). Increasing p₂₁increases the electrical effect, to the point where it will dominate the dehydrogenase effect. As a result, the inner membrane potential now depolarizes during each burst active phase (Figure 9F). In both cases, NADH_m peaks near the beginning of the active phases (Figures 9C,D), as shown experimentally in Merrins et al. (2016). Thus, measurements of NAD(P)H fluorescence alone cannot predict the effects of Ca²⁺ on △ψ_m. In summary, islet-to-islet variation in this single parameter, p₂₁, can account for the different findings that have been reported concerning the relationship between burst active phase and △ψ_m (Krippeit-Drews et al., 2000; Merrins et al., 2016). Again, this reinforces the utility of modeling in understanding and interpreting published data in the literature.

Discussion

In this perspectives article, we illustrated that there is a symbiotic relationship between the metabolic and electrical/calcium subsystems of pancreatic β-cells. What couples these systems together in a way that is different from most other cells are the K(ATP) channels, which are found in cardiac myocytes (Noma, 1983), smooth muscle cells (Hibino et al., 2010), a small population of glucose-sensing neurons in the hypothalamus (Burdakov et al., 2005), glucagon-like-peptide-1-secreting L-cells of the small intestine (Reimann and Gribble, 2002), in addition to β-cells (Ashcroft and Rorsman, 2013). While it is widely appreciated that K(ATP) channels are a key player in the transduction of blood glucose level to insulin secretion by β-cells (Ashcroft and Rorsman, 2013), their role in the generation of insulin pulsatility remains a matter of debate. Our goal in this perspectives article was to illustrate the several interacting signaling pathways that exist in β-cells and their influence on electrical bursting oscillations, oscillations in cytosolic Ca²⁺ concentration, and metabolism, the sum of which produces pulsatile insulin secretion.

Figure 10 summarizes these feedback loops and their contributions to slow, fast, and compound bursting oscillations. The first of these loops (loop I) describes the action of Ca²⁺ on ATP production and consumption through hydrolysis, dehydrogenases, and the mitochondrial Ca²⁺ uniporter. Oscillations in the Ca²⁺ concentration produce oscillations in ATP that are carried forward to the K(ATP) conductance, which in turn, influences the cell membrane potential. The loop is closed by the influence of the membrane potential on voltage-dependent Ca²⁺ channels, which determine the cytosolic Ca²⁺ concentration through Ca²⁺ influx. This feedback loop is responsible for slow bursting oscillations associated with PMOs in the IOM, and is represented as a large loop for the slow oscillations. While the loop is still active during fast and compound oscillations and slow oscillations with AMOs, we propose that it plays a lesser role in either, so we depict it as being small in the diagram.

FIGURE 10

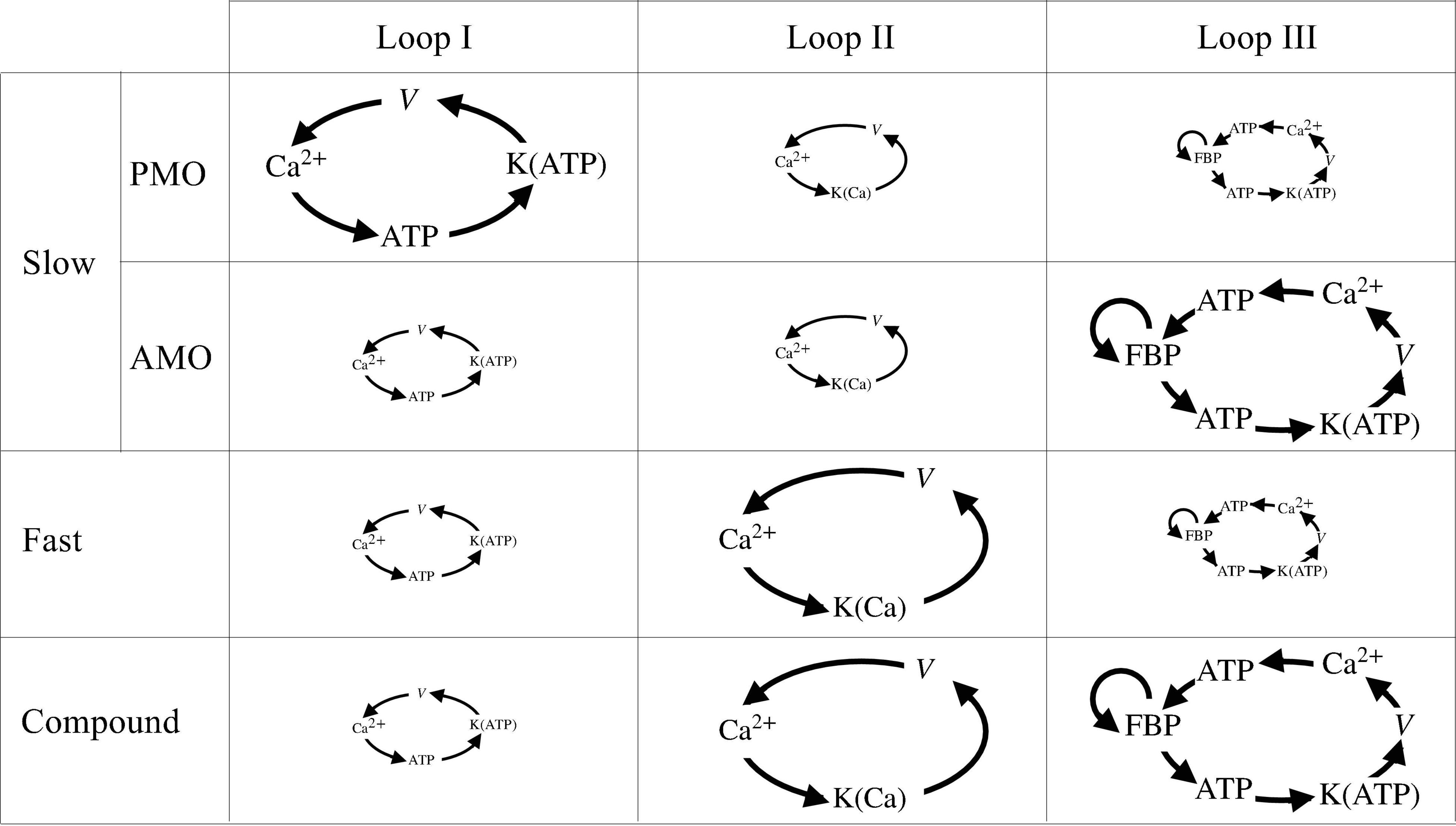
Figure 10. Schematic of the three main loops encapsulating the symbiosis between metabolism and Ca²⁺ activity. The size of each loop is proportional to the importance of its role played in slow, fast, and compound bursting. Note that slow bursting can be driven by two different mechanisms, loop I for PMOs or loop III for AMOs.

The second loop (loop II) describes the action of cytosolic Ca²⁺ on K(Ca) ion channels. Activation of these channels has a hyperpolarizing effect on the cell’s membrane potential, which in turn closes V-dependent Ca²⁺ channels, reducing the cytosolic Ca²⁺ concentration. We propose that while this loop has only a minor role to play in slow bursting, it is the main driver of fast bursting, including fast bursting that occurs during each episode of compound bursting.

The third feedback loop (loop III) describes the positive feedback effect of FBP on PFK, which produces intrinsic glycolytic oscillations (AMOs). These glycolytic oscillations result in oscillations in ATP, which affect the membrane potential again through K(ATP) channels. The electrical bursting results in Ca²⁺ oscillations, which affect the cell’s ATP level, which in turn affects PFK since ATP is an allosteric inhibitor of PFK (Passonneau and Lowry, 1962). Loop III has the potential to produce slow bursting with AMOs in our model, and we believe it is responsible for the slow wave underlying compound bursting as well as slow sub-threshold Ca²⁺ oscillations. It is unlikely to be active during fast bursting and slow bursting with PMOs, however.

It is our belief that the vast majority of observed phenomena regarding oscillations in β-cell activity in mouse islets, where most of the research on islet oscillations has been performed, can be understood from the standpoint of these three canonical feedback loops. Because all three are incorporated into the IOM, the model is a useful tool for determining the conditions that must hold to explain various phenomena. This article focused on a few specific behaviors that can be interpreted with the use of the model; some others have been the focus of prior reports (see Bertram et al., 2018 for a recent review). The success of the IOM stems from the fact that it incorporates feedback pathways that can account for the symbiotic relationships observed among the metabolic, electrical, and Ca²⁺ subsystems of β-cells.

Author Contributions

IM performed mathematical simulations and analysis. PF provided conceptual advice on the model. AS, LS, and RB provided resources and supervision. All authors contributed to writing the manuscript.

Funding

RB was partially supported by the NSF grant no. DMS 1853342. LS was partially supported by NIH grant no. RO1 DK46409. PF and AS were supported by the Intramural Research Program of the National Institutes of Health (NIDDK). Part of this research was performed when IM was with BCAM, the Basque Center for Applied Mathematics, Bilbao, Spain. IM acknowledges the support of the Basque Government through the BERC 2018–2021 program, and of the Spanish State Research Agency through the BCAM Severo Ochoa excellence accreditation SEV-2017-0718, and grant RTI2018-093416-B-I00 MULTIQUANT. IM acknowledges financial support from the University of Birmingham Dynamic Investment Fund.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ashcroft, F. M., Harrison, D. E., and Ashcroft, S. J. H. (1984). Glucose induces closure of single potassium channels in isolated rat pancreatic β-cells. Nature 312, 446–448. doi: 10.1038/312446a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashcroft, F. M., and Rorsman, P. (2013). K_ATP channels and islet hormone secretion: new insights and controversies. Nat. Rev. Endocrinol. 9, 660–669. doi: 10.1038/nrendo.2013.166

PubMed Abstract | CrossRef Full Text | Google Scholar

Beauvois, M. C., Merezak, C., Jonas, J.-C., Ravier, M. A., Henquin, J.-C., and Gilon, P. (2006). Glucose-induced mixed [Ca^{2 +} ]_c oscillations in mouse β-cells are controlled by the membrane potential and the SERCA3 Ca^{2 +} -ATPase of the endoplasmic reticulum. Am. J. Physiol. 290, C1503–C1511. doi: 10.1152/ajpcell.00400.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Benninger, R. K., Head, W. S., Zhang, M., Satin, L. S., and Piston, D. W. (2011). Gap junctions and other mechanisms of cell-cell communication regulate basal insulin secretion in the pancreatic islet. J. Physiol. 589, 5453–5466. doi: 10.1113/jphysiol.2011.218909

PubMed Abstract | CrossRef Full Text | Google Scholar

Benninger, R. K. P., and Hodson, D. J. (2018). New understanding of β-cell heterogeneity and in situ islet function. Diabetes 67, 537–547. doi: 10.2337/dbi17-0040

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertram, R., Pedersen, M. G., Luciani, D. S., and Sherman, A. (2006). A simplified model for mitochondrial ATP production. J. Theor. Biol. 243, 575–586. doi: 10.1016/j.jtbi.2006.07.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertram, R., Satin, L. S., Pedersen, M. G., Luciani, D. S., and Sherman, A. (2007a). Interaction of glycolysis and mitochondrial respiration in metabolic oscillations of pancreatic islets. Biophys. J. 92, 1544–1555. doi: 10.1529/biophysj.106.097154

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertram, R., Sherman, A., and Satin, L. S. (2007b). Metabolic and electrical oscillations: partners in controlling pulsatile insulin secretion. Am. J. Physiol. 293, E890–E900. doi: 10.1152/ajpendo.00359.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertram, R., Satin, L. S., and Sherman, A. S. (2018). Closing in on the mechanisms of pulsatile insulin secretion. Diabetes 67, 351–359. doi: 10.2337/dbi17-0004

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertram, R., Satin, L. S., Zhang, M., Smolen, P., and Sherman, A. (2004). Calcium and glycolysis mediate multiple bursting modes in pancreatic islets. Biophys. J. 87, 3074–3087. doi: 10.1529/biophysj.104.049262

PubMed Abstract | CrossRef Full Text | Google Scholar

Burdakov, D., Luckman, S. M., and Verkhratsky, A. (2005). Glucose-sensing neurons of the hypothalamus. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 2227–2235. doi: 10.1098/rstb.2005.1763

PubMed Abstract | CrossRef Full Text | Google Scholar

Cappon, G., and Pedersen, M. G. (2016). Heterogeneity and nearest-neighbor coupling can explain small-worldness and wave properties in pancreatic islets. Chaos 26:053103. doi: 10.1063/1.4949020

CrossRef Full Text | Google Scholar

Cha, C. Y., Nakamura, Y., Himeno, Y., Wang, J. W., Fujimoto, S., Inagaki, N., et al. (2011). Ionic mechanisms and Ca^{2 +} dynamics underlying the glucose response of pancreatic β cells: a simulation study. J. Gen. Physiol. 138, 21–37. doi: 10.1085/jgp.201110611

PubMed Abstract | CrossRef Full Text | Google Scholar

Chay, T. R., and Keizer, J. (1983). Minimal model for membrane oscillations in the pancreatic β-cell. Biophys. J. 42, 181–190.

Google Scholar

Cook, D. L. (1983). Isolated islets of Langerhans have slow oscillations of electrical-activity. Metab. Clin. Exp. 32, 681–685. doi: 10.1016/0026-0495(83)90124-5

CrossRef Full Text | Google Scholar

Cook, D. L., and Hales, N. (1984). Intracellular ATP directly blocks K⁺ channels in pancreatic B-cells. Nature 311, 271–273. doi: 10.1038/311271a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Dahlgren, G., Kauri, L., and Kennedy, R. T. (2005). Substrate effects on oscillations in metabolism, calcium and secretion in single mouse islets of Langerhans. Biochim. Biophys. Acta 1724, 23–36. doi: 10.1016/j.bbagen.2005.04.007

PubMed Abstract | CrossRef Full Text | Google Scholar

De Stefani, D., Patron, M., and Rizzuto, R. (2015). Structure and function of the mitochondrial calcium uniporter complex. Biochim. Biophys. Acta 1853, 2006–2011. doi: 10.1016/j.bbamcr.2015.04.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Denton, R. M. (2009). Regulation of mitochondrial dehydrogenases by calcium ions. Biochim. Biophys. Acta 1787, 1309–1316. doi: 10.1016/j.bbabio.2009.01.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Detimary, P., Gilon, P., and Henquin, J. C. (1998). Interplay between cytoplasmic Ca^{2 +} and the ATP/ADP ratio: a feedback control mechanism in mouse pancreatic islets. Biochem. J. 333, 269–274. doi: 10.1042/bj3330269

PubMed Abstract | CrossRef Full Text | Google Scholar

Diederichs, F. (2006). Mathematical simulation of membrane processes and metabolic fluxes of the pancreatic β-cell. Bull. Math. Biol. 68, 1779–1818. doi: 10.1007/s11538-005-9053-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Dwulet, J. M., Ludin, N. W. F., Piscopio, R. A., Schleicher, W. E., Moua, O., Westacott, M. J., et al. (2019). How heterogeneity in glucokinase and gap-junction coupling determines the islet [Ca^{2 +} ] response. Biophys. J. 117, 2188–2203. doi: 10.1016/j.bpj.2019.10.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Fridlyand, L. E., Ma, L., and Philipson, L. H. (2005). Adenine nucleotide regulation in pancreatic β-cells: modeling of ATP/ADP-Ca^{2 +} interactions. Am. J. Physiol. Endocrinol. Metab. 289, E839–E848. doi: 10.1152/ajpendo.00595.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Gembal, M., Gilon, P., and Henquin, J. C. (1992). Evidence that glucose can control insulin release independently from its action on ATP-sensitive K⁺ channels in mouse b cells. J. Clin. Invest. 89, 1288–1295. doi: 10.1172/JCI115714

PubMed Abstract | CrossRef Full Text | Google Scholar

Henquin, J. C. (1988). ATP-sensitive K⁺ channels may control glucose-induced electrical activity in pancreatic B-cells. Biochem. Biophys. Res. Commun. 156, 769–775. doi: 10.1016/s0006-291x(88)80910-0

CrossRef Full Text | Google Scholar

Henquin, J. C., and Meissner, H. P. (1984). Significance of ionic fluxes and changes in membrane potential for stimulus-secretion coupling in pancreatic B-cells. Experientia 40, 1043–1052. doi: 10.1007/BF01971450

PubMed Abstract | CrossRef Full Text | Google Scholar

Henquin, J. C., Meissner, H. P., and Schmeer, W. (1982). Cyclic variations of glucose-induced electrical-activity in pancreatic B-cells. Pflugers Arch. 393, 322–327.

Google Scholar

Hibino, H., Inanobe, A., Furutani, K., Murakami, S., Findlay, I., and Kurachi, Y. (2010). Inwardly rectifying potassium channels: their structure, function, and physiological roles. Physiol. Rev. 90, 291–366. doi: 10.1152/physrev.00021.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Joglekar, M. V., Dong, C. X., Wong, W. K. M., Dalgaard, L. T., and Hardikar, A. A. (2021). A bird’s eye view of the dynamics of pancreatic β-cell heterogeneity. Acta Physiol. (Oxf) 233, e13664. doi: 10.1111/apha.13664

PubMed Abstract | CrossRef Full Text | Google Scholar

Jung, S. K., Aspinwall, C. A., and Kennedy, R. T. (1999). Detection of multiple patterns of oscillatory oxygen consumption in single mouse islets of Langerhans. Biochem. Biophys. Res. Commun. 259, 331–335. doi: 10.1006/bbrc.1999.0784

PubMed Abstract | CrossRef Full Text | Google Scholar

Keizer, J., and Magnus, G. (1989). ATP-sensitive potassium channel and bursting in the pancreatic beta cell. A theoretical study. Biophys. J. 56, 229–242.

Google Scholar

Keizer, J., and Smolen, P. (1991). Bursting electrical-activity in pancreatic β-cells caused by Ca^{2 +} -inactivated and voltage-inactivated Ca^{2 +} channels. Proc. Natl. Acad. Sci. U. S. A. 88, 3897–3901. doi: 10.1073/pnas.88.9.3897

PubMed Abstract | CrossRef Full Text | Google Scholar

Kennedy, R. T., Kauri, L. M., Dahlgren, G. M., and Jung, S. K. (2002). Metabolic oscillations in β-cells. Diabetes 51, S152–S161.

Google Scholar

Kjems, L. L., Ravier, M. A., Jonas, J. C., and Henquin, J. C. (2002). Do oscillations of insulin secretion occur in the absence of cytoplasmic Ca^{2 +} oscillations in β-cells? Diabetes 51, S177–S182. doi: 10.2337/diabetes.51.2007.s177

PubMed Abstract | CrossRef Full Text | Google Scholar

Komjati, M., Bratusch-Marrain, P., and Waldhausl, W. (1986). Superior efficacy of pulsatile versus continuous hormone exposure on hepatic glucose production in vitro. Endocrinology 118, 312–319. doi: 10.1210/endo-118-1-312

PubMed Abstract | CrossRef Full Text | Google Scholar

Krippeit-Drews, P., Dufer, M., and Drews, G. (2000). Parallel oscillations of intracellular calcium activity and mitochondrial membrane potential in mouse pancreatic B-cells. Biochem. Biophys. Res. Commun. 267, 179–183. doi: 10.1006/bbrc.1999.1921

PubMed Abstract | CrossRef Full Text | Google Scholar

Laurenti, M. C., Dalla Man, C., Varghese, R. T., Andrews, J. C., Rizza, R. A., Matveyenko, A., et al. (2020). Diabetes-associated genetic variation in TCF7L2 alters pulsatile insulin secretion in humans. JCI Insight 5:e136136. doi: 10.1172/jci.insight.136136

PubMed Abstract | CrossRef Full Text | Google Scholar

Laurenti, M. C., Matveyenko, A., and Vella, A. (2021). Measurement of pulsatile insulin secretion: rationale and methodology. Metabolites 11:409. doi: 10.3390/metabo11070409

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Shuai, H. Y., Gylfe, E., and Tengholm, A. (2013). Oscillations of sub-membrane ATP in glucose-stimulated β cells depend on negative feedback from Ca^{2 +}. Diabetologia 56, 1577–1586. doi: 10.1007/s00125-013-2894-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, J. M., Fabregat, M. E., Gomis, R., and Bergsten, P. (2002). Pulsatile insulin release from islets isolated from three subjects with type 2 diabetes. Diabetes 51, 988–993. doi: 10.2337/diabetes.51.4.988

PubMed Abstract | CrossRef Full Text | Google Scholar

Luciani, D. S., Misler, S., and Polonsky, K. S. (2006). Ca^{2 +} controls slow NAD(P)H oscillations in glucose-stimulated mouse pancreatic islets. J. Physiol. 572, 379–392. doi: 10.1113/jphysiol.2005.101766

PubMed Abstract | CrossRef Full Text | Google Scholar

Magnus, G., and Keizer, J. (1998). Model of β-cell mitochondrial calcium handling and electrical activity. II. Mitochondrial variables. Am. J. Physiol. 274, C1174–C1184. doi: 10.1152/ajpcell.1998.274.4.C1174

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchetti, P., Scharp, D. W., McLear, M., Gingerich, R., Finke, E., Olack, B., et al. (1994). Pulsatile insulin secretion from isolated human pancreatic islets. Diabetes 43, 827–830.

Google Scholar

Marinelli, I., Vo, T., Gerardo-Giorda, L., and Bertram, R. (2018). Transitions between bursting modes in the integrated oscillator model for pancreatic β-cells. J. Theor. Biol. 454, 310–319. doi: 10.1016/j.jtbi.2018.06.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, F., and Soria, B. (1996). Glucose-induced [Ca^{2 +} ]_i oscillations in single human pancreatic islets. Cell Calcium 20, 409–414. doi: 10.1016/s0143-4160(96)90003-2

CrossRef Full Text | Google Scholar

Matveyenko, A. V., Liuwantara, D., Gurlo, T., Kirakossian, D., Dalla Man, C., Cobelli, C., et al. (2012). Pulsatile portal vein insulin delivery enhances hepatic insulin action and signaling. Diabetes 61, 2269–2279. doi: 10.2337/db11-1462

PubMed Abstract | CrossRef Full Text | Google Scholar

McKenna, J. P., Ha, J., Merrins, M. J., Satin, L. S., Sherman, A., and Bertram, R. (2016). Ca^{2 +} effects on ATP production and consumption have regulatory roles on oscillatory islet activity. Biophys. J. 110, 733–742. doi: 10.1016/j.bpj.2015.11.3526

PubMed Abstract | CrossRef Full Text | Google Scholar

Meissner, H. P. (1976). Electrophysiological evidence for coupling between β cells of pancreatic islets. Nature 262, 502–504. doi: 10.1038/262502a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Merrins, M. J., Fendler, B., Zhang, M., Sherman, A., Bertram, R., and Satin, L. S. (2010). Metabolic oscillations in pancreatic islets depend on the intracellular Ca^{2 +} level but not Ca^{2 +} oscillations. Biophys. J. 99, 76–84. doi: 10.1016/j.bpj.2010.04.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Merrins, M. J., Poudel, C., McKenna, J. P., Ha, J., Sherman, A., Bertram, R., et al. (2016). Phase analysis of metabolic oscillations and membrane potential in pancreatic islet β cells. Biophys. J. 110, 691–699. doi: 10.1016/j.bbrc.2013.03.084

PubMed Abstract | CrossRef Full Text | Google Scholar

Merrins, M. J., Van Dyke, A. R., Mapp, A. K., Rizzo, M. A., and Satin, L. S. (2013). Direct measurements of oscillatory glycolysis in pancreatic islet β-cells using novel FRET biosensors for pyruvate kinase M2 activity. J. Biol. Chem. 288, 33312–33322. doi: 10.1074/jbc.M113.508127

PubMed Abstract | CrossRef Full Text | Google Scholar

Misun, P. M., Yesildag, B., Forschler, F., Neelakandhan, A., Rousset, N., Biernath, A., et al. (2020). In vitro platform for studying human insulin release dynamics of single pancreatic islet microtissues at high resolution. Adv. Biosyst. 4:e1900291. doi: 10.1002/adbi.201900291

PubMed Abstract | CrossRef Full Text | Google Scholar

Nasteska, D., and Hodson, D. J. (2018). The role of β cell heterogeneity in islet function and insulin release. J. Mol. Endocrinol. 61, R43–R60.

Google Scholar

Noma, A. (1983). ATP-regulated. Nature 305, 147–148.

Google Scholar

Nunemaker, C. S., Bertram, R., Sherman, A., Tsaneva-Atanasova, K., Daniel, C. R., and Satin, L. S. (2006). Glucose modulates [Ca^{2 +} ]_i oscillations in pancreatic islets via ionic and glycolytic mechanisms. Biophys. J. 91, 2082–2096. doi: 10.1529/biophysj.106.087296

PubMed Abstract | CrossRef Full Text | Google Scholar

Nunemaker, C. S., Zhang, M., Wasserman, D. H., McGuinness, O. P., Powers, A. C., Bertram, R., et al. (2005). Individual mice can be distinguished by the period of their islet calcium oscillations: is there an intrinsic islet period that is imprinted in vivo? Diabetes 54, 3517–3522. doi: 10.2337/diabetes.54.12.3517

PubMed Abstract | CrossRef Full Text | Google Scholar

Paolisso, G., Scheen, A. J., Giugliano, D., Sgambato, S., Albert, A., Varricchio, M., et al. (1991). Pulsatile insulin delivery has greater metabolic effects than continuous hormone administration in man: importance of pulse frequency. J. Clin. Endocrinol. Metab. 72, 607–615. doi: 10.1210/jcem-72-3-607

PubMed Abstract | CrossRef Full Text | Google Scholar

Passonneau, J. V., and Lowry, O. H. (1962). Phosphofructokinase and the Pasteur effect. Biochem. Biophys. Res. Commun. 7, 10–15.

Google Scholar

Ravier, M. A., Gilon, P., and Henquin, J. C. (1999). Oscillations of insulin secretion can be triggered by imposed oscillations of cytoplasmic Ca2+ or metabolism in normal mouse islets. Diabetes 48, 2374–2382. doi: 10.2337/diabetes.48.12.2374

PubMed Abstract | CrossRef Full Text | Google Scholar

Ravier, M. A., Guldenagel, M., Charollais, A., Gjinovci, A., Caille, D., Sohl, G., et al. (2005). Loss of connexin36 channels alters β-cell coupling, islet synchronization of glucose-induced Ca^{2 +} and insulin oscillations, and basal insulin release. Diabetes 54, 1798–1807. doi: 10.2337/diabetes.54.6.1798

PubMed Abstract | CrossRef Full Text | Google Scholar

Reimann, F., and Gribble, F. M. (2002). Glucose-sensing in glucagon-like-peptide-1-secreting cells. Diabetes 51, 2757–2763. doi: 10.2337/diabetes.51.9.2757

PubMed Abstract | CrossRef Full Text | Google Scholar

Riz, M., Braun, M., and Pedersen, M. G. (2014). Mathematical modeling of heterogeneous electrophysiological responses in human β-cells. PLoS Comput. Biol. 10:e1003389. doi: 10.1371/journal.pcbi.1003389

PubMed Abstract | CrossRef Full Text | Google Scholar

Rorsman, P., and Ashcroft, F. M. (2018). Pancreatic β-cell electrical activity and insulin secretion: of mice and men. Physiol. Rev. 98, 117–214. doi: 10.1152/physrev.00008.2017

PubMed Abstract | CrossRef Full Text | Google Scholar

Satin, L. S., Butler, P. C., Ha, J., and Sherman, A. S. (2015). Pulsatile insulin secretion, impaired glucose tolerance and type 2 diabetes. Mol. Aspects Med. 42, 61–77. doi: 10.1016/j.mam.2015.01.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Scarl, R. T., Corbin, K. L., Vann, N. W., Smith, H. M., Satin, L. S., Sherman, A., et al. (2019). Intact pancreatic islets and dispersed beta-cells both generate intracellular calcium oscillations but differ in their responsiveness to glucose. Cell Calcium 83:102081. doi: 10.1016/j.ceca.2019.102081

PubMed Abstract | CrossRef Full Text | Google Scholar

Shukla, N., Kadam, S., Padinhateeri, R., and Kolthur-Seetharam, U. (2021). Continuous variable responses and signal gating form kinetic bases for pulsatile insulin signaling and emergence of resistance. Proc. Natl. Acad. Sci. U. S. A. 118:e2102560118. doi: 10.1073/pnas.2102560118

PubMed Abstract | CrossRef Full Text | Google Scholar

Smolen, P. (1995). A model for glycolytic oscillations based on skeletal muscle phosphofructokinase kinetics. J. Theor. Biol. 174, 137–148. doi: 10.1006/jtbi.1995.0087

PubMed Abstract | CrossRef Full Text | Google Scholar

Smolen, P., and Keizer, J. (1992). Slow voltage inactivation of Ca^{2 +} currents and bursting mechanisms for the mouse pancreatic beta-cell. J. Membrane Biol. 127, 9–19. doi: 10.1007/BF00232754

PubMed Abstract | CrossRef Full Text | Google Scholar

Stozer, A., Markovic, R., Dolensek, J., Perc, M., Marhl, M., Slak Rupnik, M., et al. (2019). Heterogeneity and delayed activation as hallmarks of self-organization and criticality in excitable tissue. Front. Physiol. 10:869. doi: 10.3389/fphys.2019.00869

PubMed Abstract | CrossRef Full Text | Google Scholar

Tornheim, K. (1997). Are metabolic oscillations responsible for normal oscillatory secretion? Diabetes 46, 1375–1380.

Google Scholar

Tornheim, K., and Lowenstein, J. M. (1974). The purine nucleotide cycle. IV. Interactions with oscillations of the glycolytic pathway in muscle extracts. J. Biol. Chem. 249, 3241–3247.

Google Scholar

Valdeolmillos, M., Santos, R. M., Contreras, D., Soria, B., and Rosario, L. M. (1989). Glucose-induced oscillations of intracellular Ca^{2 +} concentration resembling bursting electrical activity in single mouse islets of Langerhans. FEBS Lett. 259, 19–23. doi: 10.1016/0014-5793(89)81484-x

CrossRef Full Text | Google Scholar

Watts, M., Fendler, B., Merrins, M. J., Satin, L. S., Bertram, R., and Sherman, A. (2014). Calcium and metabolic oscillations in pancreatic islets: who’s driving the bus? SIAM J. App. Dyn. Syst. 13, 683–703. doi: 10.1137/130920198

PubMed Abstract | CrossRef Full Text | Google Scholar

Yaney, G. C., Schultz, V., Cunningham, B. A., Dunaway, G. A., Corkey, B. E., and Tornheim, K. (1995). Phosphofructokinase isozymes in pancreatic islets and clonal β-cells (INS-1). Diabetes 44, 1285–1289. doi: 10.2337/diab.44.11.1285

PubMed Abstract | CrossRef Full Text | Google Scholar

Zmazek, J., Klemen, M. S., Markovic, R., Dolensek, J., Marhl, M., Stozer, A., et al. (2021). Assessing different temporal scales of calcium dynamics in networks of beta cell populations. Front. Physiol. 12:612233.

Google Scholar