Building Valveless Impedance Pumps From Biological Components: Progress and Challenges

Valveless pumping based on Liebau mechanism entails asymmetrical positioning of the compression site relative to the attachment sites of the pump’s elastic segment to the rest of the circuit. Liebau pumping is believed to play a key role during heart development and be involved in several other physiological processes. Until now studies of Liebau pump have been limited to numerical analyses, in silico modeling, experiments using non-biological elements, and a few indirect in vivo measurements. This review aims to stimulate experimental efforts to build Liebau pumps using biologically compatible materials in order to encourage further exploration of the fundamental mechanisms behind valveless pumping and its role in organ physiology. The covered topics include the biological occurrence of Liebau pumps, the main differences between them and the peristaltic flow, and the potential uses and body sites that can benefit from implantable valveless pumps based on Liebau principle. We then provide an overview of currently available tools to build such pumps and touch upon limitations imposed by the use of biological components. We also talk about the many variables that can impact Liebau pump performance, including the concept of resonant frequencies, the shape of the flowrate-frequency relationship, the flow velocity profiles, and the Womersley numbers. Lastly, the choices of materials to build valveless impedance pumps and possible modifications to increase their flow output are briefly discussed.

Brief History

About 70 years ago, German physician Gerhard Liebau came up with a new concept of valveless pumping (Liebau, 1954, 1955). It involves a periodic compression of a compliant tube connected to a stiffer tubing on both ends (Figure 1). Asymmetric positioning of the pincher is required to generate the flow, and the relationship between the pinching frequency and the flow is highly non-linear. This mechanism acquired the name of a “Liebau-pump” or a “Liebau-based” principle. Due to a common assumption that it is a mismatch in impedance at the junctions between compliant and stiff segments that generates net flow, the Liebau pump has also been referred to as a “valveless impedance pump.”

FIGURE 1

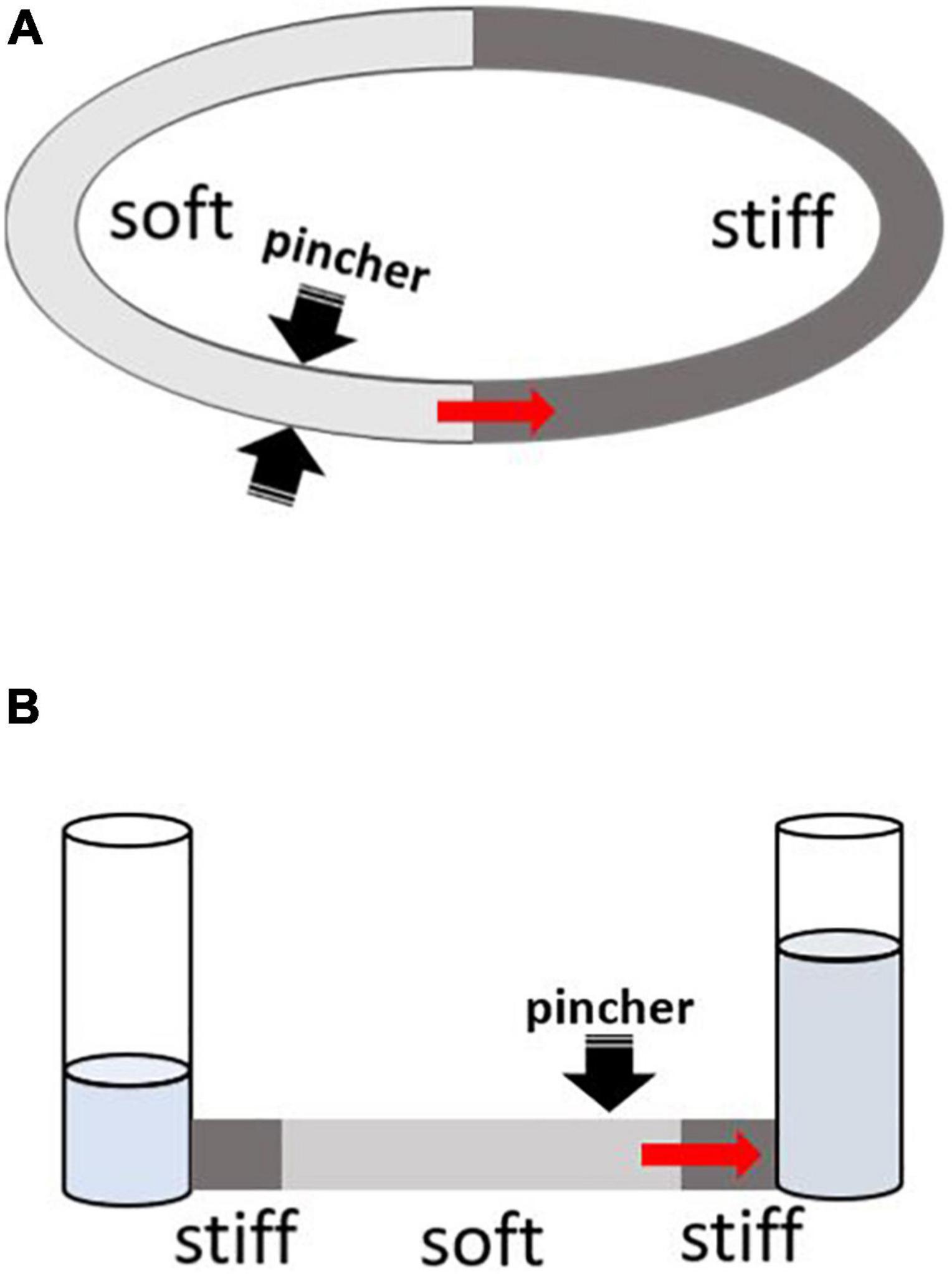
Figure 1. Two main configurations for testing Liebau-based pumping. The red arrow depicts the direction of mean flow as originally reported by G. Liebau from pincher toward the nearest junction with stiff tubing. Depending on the compression frequency, the flow can also occur in an opposite direction. (A) Two tubes with different compliances are connected to form a close loop conduit. Pincher is typically a rectangular piston being pushed into soft tubing (light gray) by some form of linear actuator. When the asymmetrically positioned pincher is periodically compressed, it creates pulsative flow. (B) The compliant segment is depicted in light gray. On both ends, it connects to stiff tubes that are attached to open tanks filled with fluid. Pincher is an asymmetrically positioned piston that compresses the soft segment with a defined frequency.

Initially, the physiological significance of the Liebau pump was largely hypothetical; therefore, for the next 50 years, this concept remained of interest mainly to physicists (Thomann, 1978; Jung and Peskin, 2002; Borzì and Propst, 2003; Ottesen, 2003; Auerbach et al., 2004; Jung, 2007). However, in 2006, a landmark paper by Gharib’s group provided the first direct experimental evidence that the Liebau-type mechanism might be involved in driving blood flow in vivo (Forouhar et al., 2006). The authors’ conclusions were based on tracking erythrocyte movement in the hearts of live zebrafish embryos. The data suggested that the observed flow pattern was more consistent with the Liebau pumping mechanism than that based on peristalsis. Modification of the Liebau pump that included an additional gelatinous layer was soon proposed to explain the physiological role of cardiac jelly in helping drive blood flow in embryonic hearts (Loumes et al., 2008). Additional modifications that mimic possible biological scenarios and further increase flow efficiency, have also been suggested. These included inclusion of bends (Hiermeier and Männer, 2017), insertion of cavities (Kozlovsky et al., 2015), use of tapered connectors (Lee et al., 2017), or asymmetric arrangement of resistances between the two sides of the compliant tube (Wen and Chang, 2009). Due to its complexity and dependence on many variables, the pumping mechanism proposed by Liebau remains the subject of interest across a wide range of disciplines, including physiology, engineering, physics, and biomedical research (Hickerson et al., 2005; Rinderknecht et al., 2005; Hickerson and Gharib, 2006; Manopoulos et al., 2006, 2020; Bringley et al., 2008; Timmermann and Ottesen, 2009; Rosenfeld and Avrahami, 2010; Meier, 2011; Lee et al., 2013; Kozlovsky et al., 2016; Zislin and Rosenfeld, 2018; Li et al., 2019; Davtyan and Sarvazyan, 2021).

Biological Occurrence of Liebau Pumps

Today, the possibility of the physiological existence of Liebau-like pumps is rarely disputed, with ongoing discussions as to what degree embryonic heart tubes function as peristaltic vs. impedance-based pump (Männer et al., 2010). A number of papers have suggested that it is the combination of the two mechanisms that is involved (Santhanakrishnan et al., 2009; Santhanakrishnan and Miller, 2011; Kozlovsky et al., 2016). Indeed, at the end of the first month, the heart of the human embryo is still valveless, yet its beating yields unidirectional blood flow with a non-linear flow-frequency pattern (Forouhar et al., 2006). Behavior of an embryonic heart can be seen as a stage of early evolutionary development since the valveless circulatory system has been described for several classes of invertebrates and some lower vertebrates (Anderson, 1981). It was also suggested that circulation of cerebrospinal fluid (Longatti, 2018) as well as blood flow caused by compressions during cardiopulmonary resuscitation (Ottesen, 2003) can be explained, at least in part, by Liebau-type pumping. There is also an indirect evidence that the latter contributes to blood flow in other body locations, such as an aorta (Pahlevan and Gharib, 2013).

Main Differences Between Peristaltic and Liebau Pumps

There are number of fundamental differences that distinguish the two types of valveless pumps found in Nature. Peristaltic pumps belong to the class of so-called positive displacement pumps. Contraction waves passing through the wall of the vessel lead to lumen compression, which squeezes the content of the vessel in the same direction as the contraction wave. As a result, continuous flow is generated with peak flow velocity equal to the speed of the propagating contraction wave. Peristaltic pumps exhibit a linear relationship between the compression frequency and the flowrate (Jaffrin and Shapiro, 1971).

The behavior of a Liebau pump exhibits a number of key differences. Only a small segment of the wall is actively compressed, with the rest of the pressure wave passively propagating through the vessel. Instant flow pattern is pulsatile with direction of flow changing back and forth within each compression event. The mean flowrate can be significant even in the absence of full lumen closure. When recorded over a wide range of compression frequencies, the relationship between the frequency and the mean flow rate is non-linear, including reversals in the direction of flow (Liebau, 1955).

Potential Uses of Liebau Pumps Made From Biological Components

As of today (with two exceptions detailed below), studies of Liebau pumps have been limited to numerical analyses, in silico modeling, experiments using non-biological elements, and a few indirect in vivo measurements. Therefore, there is a need for experimental studies that recreate Liebau pumps from biological materials using tissue engineering methods, biofabrication tools or biomimetric approaches. Such efforts can yield multiple benefits. First, they will lead to a better understanding of physiological mechanisms responsible for blood flow generation during heart development, including cases of collapsed flow caused by cardiac malformations or genetic defects. Second, the creation of biofabricated Liebau pumps (abbreviated as BLP thereafter) will be of interest from a purely biological perspective. There is ample evidence that Liebau-type pumping is involved in the circulation of fluids in a wide variety of biological forms, including both vertebrates and invertebrates (Johansen et al., 1980) and it will be quite interesting to look into the evolutionary adaptation of these valveless pumps. Third, miniature self-beating BLPs can be used to circulate fluids in organ-on-a-chip or human-on-chip platforms (Zhang et al., 2018; Ma et al., 2021). Lastly, in the long term, one can envision the clinical use of biomimetic devices, such as those based on the Liebau principle, that will help drive the flow of fluids at various locations within the human body (Dai et al., 2006; Sarvazyan, 2014a,b; Swift et al., 2014). The next paragraph will consider the later possibilities in slightly more detail.

Possible Body Sites That Can Benefit From Implantable Biofabricated Liebau Pumps

There are multiple types of fluids in the human body, including blood, lymph, saliva, gastric juice, semen, urine, tears, and many others. Some fluids are delivered by simple secretion into the target compartment or a duct, while others are delivered by active circulation. The most obvious instance of the latter is blood that circulates due to active pumping by the beating heart aided by contraction of skeletal muscle that surrounds valve-containing veins. Another example is a lymph flow, which is enabled by the presence of one-way valves and repetitive contractions of smooth muscle within walls of lymphatic vessels (Zawieja, 2009), again aided by compression by the surrounding skeletal muscle. An additional case is semen ejection, which is caused by contraction of smooth muscle within walls of vas deferens. One can also mention peristalsis of smooth muscle in the walls of the ureters that moves urine toward the urinary bladder. When, for a variety of reasons, these physiological pumping mechanisms become impaired, one can envision the use of BLP-based therapies to either aid or restore the flow. Importantly, the key components of BLPs can be added without disrupting the integrity of the vessel, and there are no requirements to create one-way valves. These key components can be positioned outside the vessel of interest and include a pair of low compliance cuffs and a band of periodically contracting muscles. The latter can be made from a patient’s induced pluripotent stem cell (iPS) derived cardiomyocytes, or a stimulable ring of skeletal muscle cells. The most attractive aspect of such a design is that the integrity of the inner endothelial layer does not have to be disrupted, avoiding possible fibrosis, blockage, or, in case of blood flow, thrombi formation.

Available Biofabrication Tools

The last two decades have led to an explosion of biofabrication tools and approaches. It is now possible to build cell-free or cell-seeded vessels with different degrees of elasticity and compliance (Schuurman et al., 2011; Nguyen et al., 2016). Tissue engineered cardiac and skeletal muscle strips have been developed (Juhas et al., 2014). Initially, force generation by these engineered muscle constructs was quite low (Zimmermann et al., 2002), yet the use of electrical and mechanical stimulation (Radisic et al., 2004; Tandon et al., 2009; Khodabukus et al., 2019), enhanced perfusion (Carrier et al., 1999), and seeding cells into stretchable scaffolds (Zhang et al., 2013) or around suture templates (Nunes et al., 2013) led to a significant increase in the force of contraction that such engineered muscles can create. Tissue engineered muscle strips can now be developed from patient-specific iPSCs (Karabekian et al., 2015a; Breckwoldt et al., 2017) alleviating concerns of immunorejection when such constructs are implanted back into the patient (Karabekian et al., 2015a,b). Another set of useful tools comes from the optogenetic field. One can now repetitively stimulate muscle constructs made from cells that express light-sensitive channels using pulses of light (Burton et al., 2015; Raman et al., 2016; Entcheva and Kay, 2020). Optogenetics also offers the possibility of a programmable spatiotemporal coordination of excitability along the tissue engineered muscular construct (Entcheva, 2013). Ability to 3D-bioprint multicellular multilayered constructs (Cvetkovic et al., 2014; Kang et al., 2016; Zhang et al., 2017; Koti et al., 2019) is yet another tool that can be used to create BLPs. A particularly promising approach for this task is additive-lathe 3D printing, an approach that uses rotating cylindrical mandrel to bioprint tubular constructs (Reeser and Doiron, 2019).

Published Attempts to Create Functional Biofabricated Liebau Pumps

The design shown in Figure 1A is deceivingly simple. In fact, creating any sizable pressure or flow using Liebau pump built from biological elements has been a real challenge. To the best of our knowledge, as of today there is just one published peer-reviewed attempt to create a BLP (Li et al., 2019). Yet even this study created only a partial BLP, with its compression element made from biological material while the vessel parts were not. Specifically, Li et al. (2019) examined the ability of a ring formed by differentiated cells from mouse myoblast cell line C2C12 to create flow in a polyacrylamide-based compliant tube inserted into a more rigid PDMS mold. Repetitive compression of the tube by the tissue engineered muscle led to a 0.3–1% decrease in tube radius, yielding mean flowrates of < 0.4 μL/s. Non-peer reviewed attempts to build BLPs can also be found in the PhD thesis of Hesham Azizgolshani from Gharib’s lab (Azizgolshani, 2013). These studies attempted to create BLPs using neonatal rat cardiac myocytes seeded onto vessels made from decellularized small intestinal submucosa. Cell contraction led to < 2% change in tube radius yielding < 20 nL/s mean flowrate.

The very low mean flow rates seen in these two studies (Azizgolshani, 2013; Li et al., 2019) are troublesome for two reasons. First, they offer little use for any real flow improvement in physiologically relevant settings. Second, they are in sharp contrast with much higher flow rate values obtained when using non-biological components of Liebau pumps. In the next section, we will consider factors that may limit the efficiency of BLPs, followed by the sections that consider ways to circumvent or minimize these limitations.

Limitations Imposed by the Use of Biological Components

There are several reasons behind the low flow rates reported by the above-mentioned attempts to build BLPs. The same reasons are likely to play a role in any future attempts to create Liebau pumps using biological components, particularly from mammalian cells and more specifically from their human counterparts.

The first reason is that, when compared to mechanical actuators, the pincher segment of a BLP can operate within a very limited range of compression frequencies. Cardiac myocytes isolated or derived from iPSC of animals with intrinsically high heart rates, such as mice, can be continually paced at frequencies up to 7–8 Hz (Bers, 2001). Their human counterparts are unlikely to go over 3 Hz. In most cases of skeletal muscle-based constructs, stimulation frequency can be increased to 10 Hz (Khodabukus et al., 2019), after which contractions become fused, leading to tetanus. Maximal frequency of smooth muscle contractions varies depending on muscle subtype and location, but in general, due to different molecular mechanisms underlying excitation-contraction coupling and relaxation cycles of smooth muscle, these cells are too slow to be viable candidates for repetitive fast contractions. To conclude, compression frequencies by a BLP pincher can hardly exceed 10 Hz, with 1–4 Hz being the most realistic range.

This leads us to the second reason: the limited degree of muscle shortening. By excluding smooth muscle as a main component of a BLP pincher, one is left with cross-striated muscle candidates, such as cardiac and skeletal muscle. Cross-striated muscle can shorten to only 15–20% of its resting length (Bers, 2001). Therefore, a pincher made from a muscular ring of cross-striated muscle has a limited ability to decrease the lumen. This limitation can be overcome by a non-conventional way of arranging muscle elements—some of which will be considered later. Notably, in previously mentioned studies by Azizgolshani (2013) and Li et al. (2019), decreases in lumen diameter were much smaller than the above-mentioned limit of 15–20%, leading us to the third reason.

The third reason involves the way in which the muscle layer is created. Both above-cited studies used a simple cell seeding approach to create a ring of tissue-engineered muscle (Zimmermann et al., 2002). It is now well recognized that such an approach yields a weakly contracting muscle due to underdeveloped connections between the cells and the lack of a well-organized sarcomere structure inside the cells. The use of preconditioned tissue-engineered muscle strips, strength of which has been increased by electrical and mechanical stimuli (Tandon et al., 2009; Nunes et al., 2013; Ronaldson-Bouchard et al., 2019) should significantly improve the outcome of BLPs. An additional consideration should be given to a spiral arrangement of multiple fibers within the pincher. The latter has been shown to greatly increase the efficiency of cardiac ejection (Torrent-Guasp et al., 2001) and is likely to do the same for the efficiency of the BLP pincher.

The fourth and the last reason why reported BLP yielded such low flow rates is that their design did not take into consideration insights from theoretical and experimental studies that used non-biological components. In the next sections, we will review available experimental reports and a few numerical studies with the goal of outlining strategies for more effective implementation of Liebau pumps using biofabrication tools. We will start by listing different parameters that can influence the performance of the Liebau pump.

Variables That Impact Liebau Pump Performance

Despite its apparent simplicity, the physics behind flow and pressure generation by a Liebau pump is quite complex and, as such, remains the subject of intense interest by several generations of physicists and mathematicians (Takagi and Takahashi, 1985; Borzì and Propst, 2003; Manopoulos et al., 2006; Jung, 2007; Loumes et al., 2008; Kozlovsky et al., 2015). Because of its complexity, all modeling studies had to omit many involved variables. The list of such variables, each of which can potentially affect the mean flow rate created by a Liebau pump, can be seen in Table 1. They can be divided into four categories. The first category describes the overall pump design, including the tubing being closed or open, number of pinchers, presence of kinks or gelatinous inner layer, or difference in resistances by the two stiff ends. The second category includes the physical properties of compliant tube segments (notably, the impact of the physical properties of stiff tube segments remains to be explored). The third category includes properties of the pincher, such as its length, degree of vessel occlusion, its relative position with respect to the two ends of the compliant segment, compression frequency, duty cycle, and its dynamic waveform (i.e., square form vs. sinusoid). The fourth category includes properties of the fluid, including density, viscosity, and fluid volume, the latter having a direct impact on transmural pressure and therefore compliance of the elastic segment. For readers wanted to learn more, Table 1 lists studies that considered, either numerically or experimentally, the impact of specific variables. Notably, the non-linear character of Liebau pumps precludes predicting, in a simple manner, the effect of many variables. Therefore, changing the frequency of pinching from, for example, 10–20 Hz for the Liebau pump with one set of dimensions will increase the flow, while it will decrease it for the pump with different geometry. Such non-linearity and involvement of multiple variables explains a vast range of measured flow rate values created by experimental variations of the Liebau pump (Table 2).

TABLE 1

Table 1. Major variables that affect performance of Liebau pump.

TABLE 2

Table 2. Flow rate values created by experimental variations of the Liebau pump.

Resonant Frequencies

Natural Frequency Concept

Based on the currently prevailing view, the main mechanism as to how the Liebau pump generates flow is depicted in Figure 2. Pressure waves generated by the periodic compression of the compliant segment reach the points of impedance mismatch. When the pincher is positioned asymmetrically, it leads to a dynamic pressure difference between the two ends of the compliant tube, which in turn generates the flow. It has been argued that for such a difference to be maximal, the system has to be near its resonant frequency (Hickerson et al., 2005; Hickerson and Gharib, 2006). Yet many experimental studies, including our own work (Davtyan and Sarvazyan, 2021), observed significant flow rates at frequencies that are far below the estimated natural frequency (F_n) of the compliant segment. Let us consider the concept of F_n in more detail.

FIGURE 2

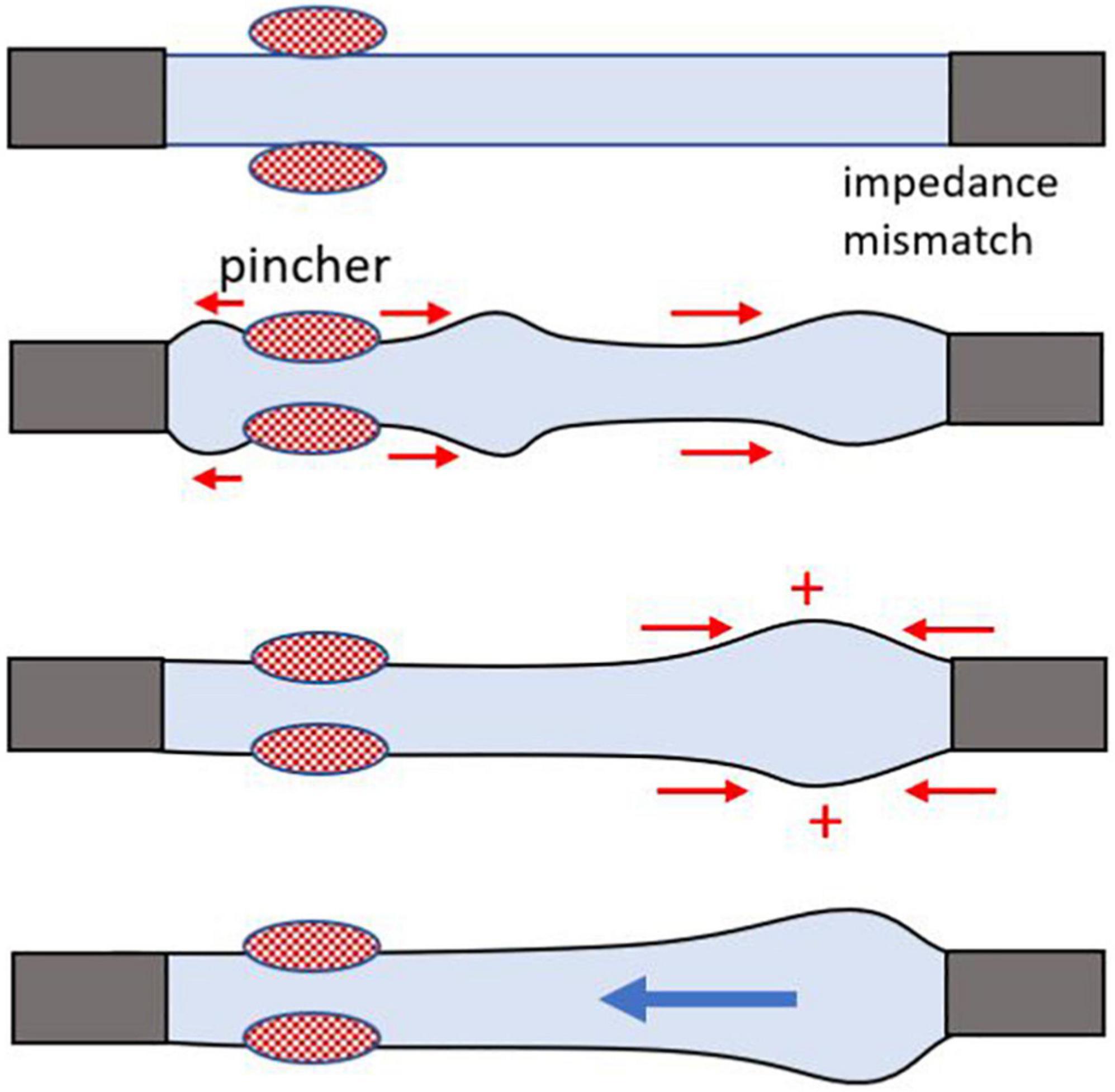
Figure 2. Cartoon illustrating mismatch of impedance that creates a wave reflection site, leading to a one-way flow. A general cartoon of Liebau’s principle for an open tube system. Rhythmic compressions of the flexible tube in the middle do not generate flow, while asymmetrically positioned pinch sites yield a one-way flow. The mismatch of impedance at the junction of the two tubes with different wall compliance creates a wave reflection site, a necessary condition to achieve pumping. Flow direction depends on the compression frequency, geometry, and physical properties of the tubes.

Frequencies at which the system resonates can be determined experimentally upon hitting the tube with a substantial force and applying a fast Fourier transform analysis to pressure signals (Manopoulos et al., 2020). There is also a simple formula to calculate the natural frequency of a tube:

$F_n=c/2\text{L}(1)$

where L is the length of a tube and c is the velocity of the pressure or pulse wave. The latter can be measured experimentally by tracking the speed of wall deformation or via distally positioned pressure transducers. For thin-walled tubes, pulse wave velocity can be estimated using the Moens-Korteweg equation, where E is the Young modulus of the wall, h is wall thickness, D is the internal diameter, and ρ is fluid density:

$c={(Eh/\rho D)}^{1/2}(2)$

For thick-walled vessels, the equation can be further modified using Poisson’s ratio υ:

$c^{\prime }={(Eh\text{/}\rho D(1-{\upsilon }^2))}^{1/2}(3)$

Most biological materials can be considered incompressible with Poisson’s ratio close to 0.5. Therefore, correcting for Poisson’s ratio basically increases the estimated pulse velocity values by ∼15%.

Equation 1 implies that F_n is inversely proportional to the length of the compliant segment. Therefore, the smaller Liebau pump is, the higher F_n it is expected to have. Moreover, F_n is likely to increase as a result of increased values of c. This is because wall thickness h cannot decrease at the same rate as vessel diameter since this will render vessel too fragile to handle and/or to repetitively compress. Therefore, for very small Liebau pumps, one should expect h/D ratio in Equation 2 to increase, leading to a further increase in c and consequently in F_n as per Equation 1.

Calculated F_n value is affected by the energy losses in the system and is referred to as “damped natural frequency.” These energy losses can be linked to the mass and viscosity of the moving fluid and expanding vessel walls (Babbs, 2010). They also include frictional losses from the interaction of flowing fluid with the walls of the vessel. More friction will occur in vessels with smaller diameters, with more F_n damping expected in narrow vessels. Additional changes to the calculated F_n of the complaint segment of the Liebau pump are imposed by the differences in compliance between the soft and stiff tube segments as well as the length of the latter. In the case of a closed flow loop, when the difference between the Young modules of compliant and stiff tubing decreases, the latter becomes part of the resonant system (Meier, 2011).

For the surveyed experimental studies of the Liebau pump listed in Table 2, we calculated pulse wave velocities c and undamped F_n values. This enabled us to compare F_n with the frequency at which the experimentally recorded flow rate was maximal (F_max). Notably, here F_max is simply a frequency for which maximal mean flow rate was observed in each specific study and not what would have been observed if the entire range of frequencies had been examined. For calculations of F_n we used vessel dimensions and Young modulus provided by the authors, while filling any gaps by using information available elsewhere (indicated by asterisks). As Table 2 shows, with few exceptions, most studies tested frequency ranges that lie below calculated undamped F_n. In a few studies that examined frequency ranges that included the predicted F_n, the F_max was actually very close to the calculated F_n.

The overall conclusion from this section is the following: while the maximal flowrates created by Liebau pumps are predicted to occur near F_n, published experimental studies suggest that sizable flowrates can be created using much lesser frequencies. What we mean by the word “sizable” is considered next.

Comparison With Peristaltic Pumps of Similar Dimensions

One way to evaluate the performance of Liebau pumps across different experimental studies is to compare them to peristaltic pumps of the same dimensions operating at the same frequency. To find a flow rate by a comparable peristaltic pump, F_max was multiplied by the volume of displaced fluid, the latter being a product of pincher width (w) and cross-sectional area of the tube (A):

$\mathbf{\text{Q}}{}_{\mathbf{p}}=\mathbf{\text{F}}{}_{\mathbf{max}}\mathbf{\text{wA}}(4)$

Note that to calculate the expected flow rate by peristaltic pumps, we assumed a complete closure of the lumen. The same cannot be expected for all Liebau pumps listed in Table 2, since the degree of lumen occlusion varied between the studies (the latter value is often omitted, with only ∼30% of surveyed studies mentioning it). Therefore, the reported maximal flow rates created by the Liebau pumps could have been higher if a complete lumen closure had been achieved. The outcome of the comparison is shown graphically in Figure 3 using values listed in Table 2. The Figure 3A shows data from all surveyed experimental studies, while Figure 3B zooms in on pumps with the smallest dimensions. These plots suggest two things. First, there is a high degree of correlation between the maximal flow rates achievable by peristaltic vs. Liebau-based pumps of the same dimensions (R² = 0.97). Second, for larger pumps, this relationship is approaching 1:1, with two studies (Hickerson et al., 2005; Bringley et al., 2008) reporting flow rates exceeding the estimated peristaltic-based flow. The latter is rather remarkable since in the case of the peristaltic pump it is the entire length of the tube that needs to be engaged in active contraction, while in the Liebau pump it is only a small segment of the tube. In fact, when averaged across surveyed experimental studies, the width of the pincher was only about 12 ± 6% of the total length of the tube.

FIGURE 3

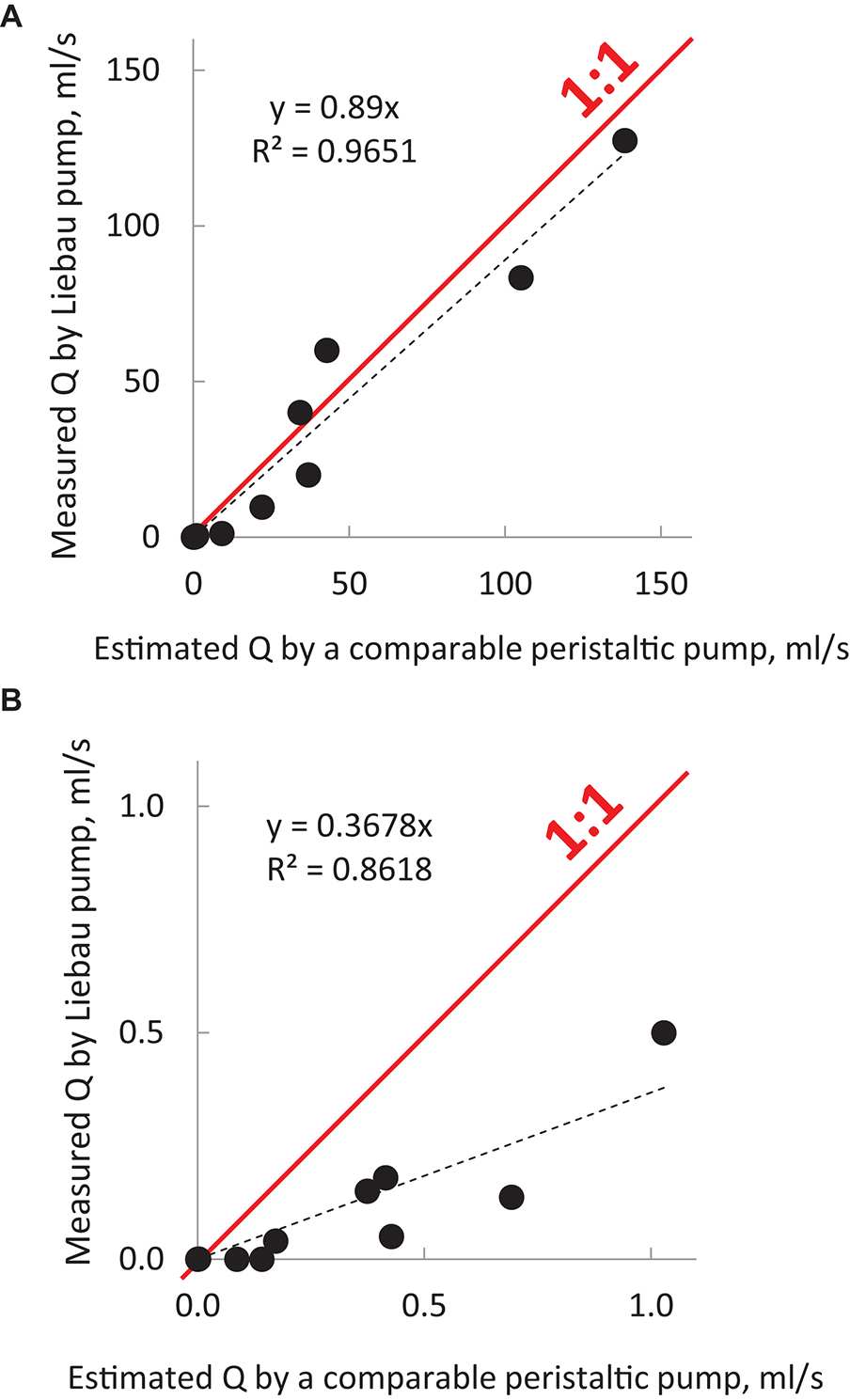
Figure 3. Output of Liebau pumps in comparison to peristaltic pumps of the same dimensions. The graphs were compiled using MS Excel from published studies listed in Table 2. They illustrate the relative efficiency of Liebau pumps compared to peristaltic pumps of the same dimensions and compression frequencies. Dots above the red line indicate flow rates that were higher than the ones created by the peristaltic pumps; below the red line are lower. For macroscopic pumps, flow created by Liebau pumps was ∼90% from that of peristaltic flow, while for smaller pumps it was ∼40%. Data also point to a significant correlation between the two ways to pump fluid. To calculate the output of a comparable peristaltic pump, the cross-sectional area of the tube was multiplied by the width of the pincher element and the compression frequency at which the maximal flow was observed in each cited study of the Liebau pump. Red rectangle in (A) encompasses datapoints for micropumps. The latter has been shown in (B) using different scales.

Flow Rate-Frequency Relationship

Nearly all studies of Liebau pumps report pulsatile flow, the presence of flow reversals, and a non-linear flow rate-frequency relationship. Yet the exact shape of the latter curve, as well as the number of flow-frequency peaks, varies dramatically across studies. In addition, while some report maximal flowrate near F_n (Hickerson et al., 2005; Kozlovsky et al., 2015; Manopoulos et al., 2020), others report it being close to zero (Takagi and Takahashi, 1985; Borzì and Propst, 2003; Meier, 2011). In the latter cases, the performance of the valveless pump is maximum on either side of the resonant frequency, passing through zero flow rate at the resonant frequency. An interesting suggestion as to why such different patterns have been observed was made by Wen and Chang (2009). They have shown that the flow-frequency relationship shifts when the resistances between the two sides of stiff tubing to which the compliant tube is connected are different. Whether unintended small variations in resistances between the two sides can explain differently shaped frequency-flow rate curves near F_n values awaits further exploration.

Flow Velocity Profiles and Womersley Number

To scale and characterize the dynamics of flow in differently sized vessels, dimensionless Reynolds and Womersley numbers are commonly used. For cylindrical vessels under a steady pressure gradient, the Reynolds number<2,000 predicts laminar flow with a parabolic velocity profile. The Womersley number is used to characterize the velocity profile during pulsatile pressure conditions. The Womersley number is calculated using the values of fluid density ρ, dynamic viscosity μ, angular frequency ω, and the vessel radius R:

$W_o{}_{=}R{(\rho \omega /\mu )}^{1/2}(5)$

When W_o < 1, the flow tracks the oscillating pressure gradient, and the velocity profiles exhibit a parabolic shape. When W_o > 10, the velocity profile is flat or plug-like, and the flow is phase-shifted relative to the oscillating pressure gradient. Values of 1 < W_o < 10 represents intermediate regimes (Manopoulos et al., 2020). For the surveyed non-biological studies of Liebau pumps listed under Table 2, typical W_o values exceed 10. In contrast, the two experimental attempts at creating BLPs (Azizgolshani, 2013; Li et al., 2019) described under see section “Published Attempts to Create Functional Biofabricated Liebau Pumps” had W_o < 10. This was due to a combination of low frequency and small vessel diameters. In cases when solutions that mimic blood viscosity were used, the W_o values further declined. This was the case in our own experiments that tested the performance of the Liebau pump with physiologically relevant vessel dimensions, viscosity, and compression frequencies (Davtyan and Sarvazyan, 2021).

The Womersley number plays a role in calculating the mean flow rate Q from particle tracking, the latter method being one of the easiest ways to estimate the flow experimentally:

$\mathbf{\text{Q}}=\mathbf{\pi }\mathbf{\text{R}}{}^2\mathbf{\text{K}}{}_{\mathbf{w}}\mathbf{\text{v}}(6)$

where R is the radius of the cylindrical vessel and v is the maximal linear velocity of the particles flowing midstream. Coefficient K_w enables one to account for different velocity profiles. It is equal to 0.5 when Wo < 1 and the velocity profile is parabolic. When Wo > 10, the K_w becomes close to 1, since when flow is plug-like, the velocity profile of flowing particles is nearly the same across the entire volume of the tube. For intermediate regimes when 1 < W_o < 10 an empirically derived formula can be used to derive coefficient K_w. This formula was developed by Ponzini et al. (2010) and is included in Supplementary Excel File.

Choice of Vessel Material to Build Biofabricated Liebau Pumps ex vivo

To get closer to F_n within the physiological range of frequencies, i.e., 1–4 Hz, it is best to select highly stretchable materials with low Young modulus while having high tensile strength to prevent breakage. There are two possible approaches. The first approach is to excise tubular structures from an organism of choice and use them in their native, processed, or decellularized form. The most obvious choice appears to be pieces of arteries or veins. However, in their natural form, the values of Young modulus for blood vessels are still rather high. When stretched transversally, reported values of Young modulus for blood vessels span from 0.5 to 5 MPa (Riley et al., 1992; Egorov et al., 2008). When non-destructive decellularization protocols are being used, the elastic modulus of vessels changes very little (Daniel et al., 2005; Crapo et al., 2011). This is because the mechanical properties of vessels are mainly determined by interwoven collagen and elastin fibers. Other tubular structures that can be excised and used to create a compliant segment for BLPs include intestine (Herbert et al., 1993), ureter (Narita et al., 2008), or their components such as small-intestine submucosa, for example (Roeder et al., 1999). One can also consider additional treatments that can lower E values of these vessels while retaining their integrity, mild enzymatic treatment being one example (Trabelsi et al., 2020).

The second approach to creating BLP-compliant segments is to use the ever-expanding arsenal of biofabrication tools (Pashneh-Tala et al., 2016). Suitable tubular scaffolds can be created using casting, 3D printing, electrospinning, weaving, or other techniques (Chang and Niklason, 2017; Elomaa and Yang, 2017; Song et al., 2018). The range of biocompatible materials that can be used is vast, and they can be mixed or modified to achieve the desired stiffness (Bello et al., 2020). The Young modulus of unenforced simple hydrogels, such as gelatin, acrylamide, or agarose, is on the order of a few kPA (Chen et al., 2018; Lee et al., 2019). It can be enhanced by several orders of magnitude by including different additives (Le Goff et al., 2015; Yan et al., 2017). Collagen, elastin, and other extracellular matrix components are other obvious choices. Although pure collagen fibers are very stiff, with E reaching 1.2 GPa, the strength of structures made from collagen fibers can be adjusted by changing protein concentration, type, crosslinking, and inclusion of other ECM components (Gosline et al., 2002).

Creation of Biofabricated Liebau Pumps in vivo

The above-described strategies to approach F_n (i.e., by decreasing elastic modulus and h/D ratio, while increasing vessel length L) can work to create and test ex vivo BLPs. But what about creating BLPs in vivo by wrapping tissue engineered muscle around a vessel of choice? For medium-sized blood vessels, the h/D ratio is about 0.3 for arteries and 0.1 for veins. The lowest reported values of Young modulus for collagen-rich arteries and veins are about 0.2–0.5 MPa (Daniel et al., 2005). Therefore, if a 10 cm piece of vein with a diameter of 1 cm and an E of 0.2 MPa is used as a compliant segment of the Liebau pump, the Moens-Korteweg equation yields c = ∼4 m/s and F_n = 22 Hz (see Supplementary Appendix for formulas). The later value is too high for a pincher made from muscle cells. For smaller vessels, the F_n will be even higher. And if one estimates F_n values for an embryonic heart tube of a zebrafish by eyeballing its dimensions [200, 60, 20 μm for L, D, and h, respectively (Forouhar et al., 2006)], while assuming the lowest possible E of 2 kPA, the F_n will be > 2000 Hz, which is an impossible range of frequencies for biological pumps.

The above estimates of F_n seems to question the feasibility of creating in vivo BLPs while using a muscle ring as a pincher element. However, this is far from the case. Data shown in Figure 3B illustrate that despite being less efficient than their macro versions (i.e., Figure 3A), micro Liebau pumps working far from their F_n values generate flows that are about 10–30% of their peristaltic equivalents. Also, several modifications of Liebau pumps have been suggested. These modifications resemble features of embryonic hearts and parts of circulation in lower invertebrates. They can help to increase flow rates at frequencies lower than F_n and are considered next.

Modifications to Increase Biofabricated Liebau Pump Output

Previous paragraphs considered the simplest configuration of Liebau pumps that consisted of a single-walled cylindrical compliant segment with a single compression element. As we argued above, in this basic configuration BLPs with the length ranging from millimeters to several centimeters will yield miniscule flowrates when compressed with physiological frequencies. By mimicking scenarios that can be encountered in vivo, one can try to modify the basic configuration of the Liebau pump to increase the flow. One study, for example, documented the beneficial effect of kinks by showing that by bending compliant tubes in several places, one can significantly increase its performance (Hiermeier and Männer, 2017). Another way to increase the mean flow rate was suggested by a theoretical study by Loumes et al. (2008). The authors tried to mimic the effects of cardiac jelly, which is present during the early stages of embryonic heart development. The proposed model predicted that the addition of a thick gelatinous layer to the inner wall of the complaint segment would greatly increase the amplitude of the pressure waves and increase the mean flow rates of the pump. Notably, in the presence of such a gelatinous layer, the vessel’s lumen can be constricted to a larger degree using the same degree of outer layer shortening. The letter is particularly important for a pincher element made of striated muscle, which can only shorten to a ∼15% of its initial length. Another interesting approach to better mimic putative Liebau pumps was to add cavities before and after the pincher element (Kozlovsky et al., 2015). This was again a purely computational study, conclusions from which await experimental proof. An additional way to increase the force by which muscular band compresses the compliant tube can be to mimic the spiral structure of the cardiac wall by creating a pincher using multiple bands with alternating directions of the fibers (Torrent-Guasp et al., 2001).

One can also suggest building a Liebau pump using biological elements but without mimicking in vivo scenarios. This can be done by changing the position of the compression element relative to the vessel. Different configurations that can help to increase the degree of lumen compression can be envisioned (Figure 4). Although such configurations are unlikely to be considered in lieu of clinical treatments, one can imagine using them for organ-on-a-chip or similar applications.

FIGURE 4

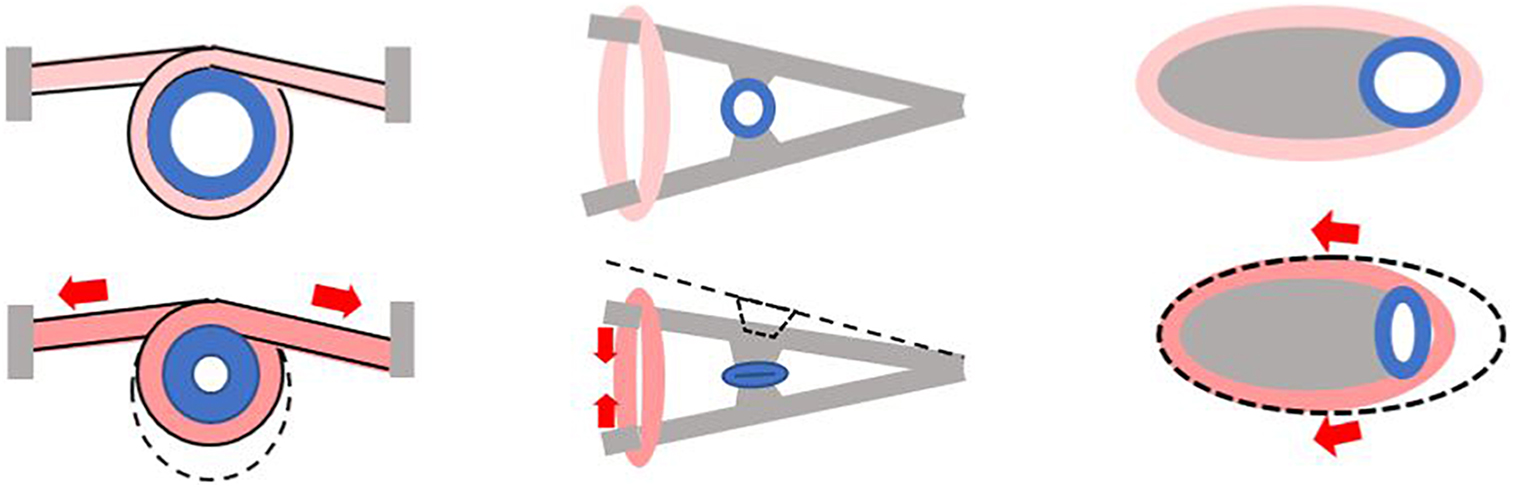
Figure 4. Alternative ways to create a pincher from tissue engineered muscle. Gray color depicts stationary elements that can be created from bone-like or similar material. Pink color indicates tissue engineered muscle. Cross section of the compliant segment of Liebau pump is shown in blue. Each panel shows a pincher before (top) and during (bottom) contraction with red arrows depicting direction of muscle shortening.

Relative Efficiency of Liebau Pumps

Flow and pressure outputs of Liebau pumps are highly non-linear and depend on multiple factors, including those listed in Tables 1, 2. Therefore, it is rather difficult to quantitively compare their energy efficiency to other types of pumping devices. As a rough estimate one can use a relationship between the maximal flowrate and the pump dimensions, an approach taken by Laser and Santiago to create a chart comparing a wide range of micropumps, including piezoelectric, thermopneumatic, electrostatic and electroosmotic devices (Laser and Santiago, 2004). The experimental data from Table 2 and as well as evaluation by Meier (2011), places Liebau pumps on the top of that chart. Data shown Figure 3 also suggest that at their optimal frequencies the output of Liebau pumps, particularly those on a centimeter scale, is comparable to their peristaltic counterparts. Interestingly, a significant increase in the flowrate can be achieved by the inclusion of the valves into the Liebau pump circuit (Moser et al., 1998). From the viewpoint of future clinical implementation though, addition of the valves makes little sense since their absence is probably the most beneficial feature of the Liebau pump design.

Insights From the First Biofabricated Liebau Pump Attempt

Although the first published BLP attempt (Li et al., 2019) using tissue engineered rings of skeletal muscle around hydrogel tubes yielded negligible flow rates, it enabled the authors to make several interesting observations. Notably, such insights were never brought up by studies that built Liebau pumps from non-biological components or relied on simulations. Indeed, contraction of a ring of muscle cells wrapped around a vessel does not work like a mechanical pincher that compresses vessels in one dimension. Instead, the authors observed that in many cases, any significant contraction of the muscular ring led to an inward deformation of the vessel wall. Such “buckling” then impacted the calculation of a new radius of the tube as well as the degree of lumen compression. Also, the authors revealed that buckling had an unexpected effect on the flow rate-frequency relationship. When the tube was buckled, there was less resistance to the act of compression, so the degree of muscle shortening was higher at the same degree of electrical stimulation. Moreover, when stimulation frequency increased with electrical pulses arriving during relaxation, contraction amplitude decreased, giving rise to frequency dependence of contraction amplitude, i.e., the higher was the frequency, the lower was the amplitude of contraction. The authors argued that for the unbuckled case, restoring force of the elastic tube was high compared with the buckled tube, and contraction amplitude was less sensitive to the contraction frequency.

New insights, such as above, are expected from future attempts to build Liebau pumps using biological materials. We hope that this publication will encourage others to explore this fascinating phenomenon and stimulate additional experimental efforts to build valveless impedance pumps using biological materials.

Conclusion

Cumulative evidence from different labs point to physiological feasibility of Liebau-based valveless pumping warranting efforts to create such pumps using tissue engineering and other biofabrication tools. Such efforts will provide additional insights into performance of these pumps in vivo as well as further our understanding of the fundamental mechanisms driving blood flow during early development. Liebau-based biomimetic pumps can also serve as energy-efficient flow generators in organ-on-a-chip devices or be implanted to assist flow during various disease states.

Author Contributions

NS conceived and wrote the manuscript.

Funding

This work was supported by the United States National Science Foundation EAGER award (#1927694).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Rubina Davtyan is gratefully acknowledged for her help in compiling published values for Table 2.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2021.770906/full#supplementary-material

References

Anderson, R. H. (1981). Hearts and Heart-like Organs. Volume 1. Comparative anatomy and development. J. Anat. 133(Pt 1), 104.

Google Scholar

Auerbach, D., Moehring, W., and Moser, M. (2004). An analytic approach to the Liebau problem of valveless pumping. Cardiovasc. Eng. 4, 201–207. doi: 10.1023/b:care.0000031549.13354.5e

CrossRef Full Text | Google Scholar

Azizgolshani, H. (2013). Tissue Engineering Active Biological Machines: Bio-Inspired Design, Directed Self-Assembly, and Characterization of Muscular Pumps Simulating the Embryonic Heart. Ph.D. Thesis. California, CA: California Institute of Technology.

Google Scholar

Babbs, C. F. (2010). Behavior of a viscoelastic valveless pump: a simple theory with experimental validation. Biomed. Eng. Online 9:42. doi: 10.1186/1475-925X-9-42

PubMed Abstract | CrossRef Full Text | Google Scholar

Bello, A. B., Kim, D., Kim, D., Park, H., and Lee, S. H. (2020). Engineering and functionalization of gelatin biomaterials: from cell culture to medical applications. Tissue Eng. Part B Rev. 26, 164–180. doi: 10.1089/ten.TEB.2019.0256

PubMed Abstract | CrossRef Full Text | Google Scholar

Bers, D. (2001). Excitation-Contraction Coupling and Cardiac Contractile Force, 2nd Edn. Berlin: Springer Science & Business Media.

Google Scholar

Borzì, A., and Propst, G. (2003). Numerical investigation of the Liebau phenomenon. Zeitschrift Angew Math. Phys. 54, 1050–1072.

Google Scholar

Breckwoldt, K., Letuffe-Brenière, D., Mannhardt, I., Schulze, T., Ulmer, B., Werner, T., et al. (2017). Differentiation of cardiomyocytes and generation of human engineered heart tissue. Nat. Protoc. 12, 1177–1197.

Google Scholar

Bringley, T. T., Chilress, S., Vandenberghe, N., and Zhang, J. (2008). An experimental investigation and a simple model of a valveless pump. Phys. Fluids 20:33602.

Google Scholar

Burton, R. A. B., Klimas, A., Ambrosi, C. M., Tomek, J., Corbett, A., Entcheva, E., et al. (2015). Optical control of excitation waves in cardiac tissue. Nat. Photonics 9, 813–816. doi: 10.1038/nphoton.2015.196

PubMed Abstract | CrossRef Full Text | Google Scholar

Carrier, R. L., Papadaki, M., Rupnick, M., Schoen, F. J., Bursac, N., Langer, R., et al. (1999). Cardiac tissue engineering: cell seeding, cultivation parameters, and tissue construct characterization. Biotechnol. Bioeng. 64, 580–589. doi: 10.1002/(sici)1097-0290(19990905)64:5<580::aid-bit8>3.0.co;2-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, W. G., and Niklason, L. E. (2017). A short discourse on vascular tissue engineering. NPJ Regen. Med. 2:7. doi: 10.1038/s41536-017-0011-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, R., Xu, X., Yu, D., Xiao, C., Liu, M., Huang, J., et al. (2018). Highly stretchable and fatigue resistant hydrogels with low Young’s modulus as transparent and flexible strain sensors. J. Mater. Chem. C. R. Soc. Chem. 6:11193. doi: 10.1039/c8tc02583e

CrossRef Full Text | Google Scholar

Crapo, P. M., Gilbert, T. W., and Badylak, S. F. (2011). An overview of tissue and whole organ decellularization processes. Biomaterials 32, 3233–3243. doi: 10.1016/j.biomaterials.2011.01.057

PubMed Abstract | CrossRef Full Text | Google Scholar

Cvetkovic, C., Raman, R., Chan, V., Williams, B. J., Tolish, M., Bajaj, P., et al. (2014). Three-dimensionally printed biological machines powered by skeletal muscle. Proc. Natl. Acad. Sci. U.S.A. 111, 10125–10130. doi: 10.1073/pnas.1401577111

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, W., Hale, S. L., and Kloner, R. A. (2006). Cardiac cells implanted within the outer aortic wall of rats generate measurable contractile force. Regen. Med. 1, 119–124. doi: 10.2217/17460751.1.1.119

PubMed Abstract | CrossRef Full Text | Google Scholar

Daniel, J., Abe, K., and McFetridge, P. S. (2005). Development of the human umbilical vein scaffold for cardiovascular tissue engineering applications. ASAIO J. 51, 252–261. doi: 10.1097/01.mat.0000160872.41871.7e

PubMed Abstract | CrossRef Full Text | Google Scholar

Davtyan, R., and Sarvazyan, N. A. (2021). Output of a valveless Liebau pump with biologically relevant vessel properties and compression frequencies. Sci. Rep. 11:11505. doi: 10.1038/s41598-021-90820-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Egorov, V., Tsyuryupa, S., Kanilo, S., Kogit, M., and Sarvazyan, A. (2008). Soft tissue elastometer. Med. Eng. Phys. 30, 206–212. doi: 10.1016/j.medengphy.2007.02.007

CrossRef Full Text | Google Scholar

Elomaa, L., and Yang, Y. P. (2017). Additive manufacturing of vascular grafts and vascularized tissue constructs. Tissue Eng. Part B Rev. 23, 436–450. doi: 10.1089/ten.TEB.2016.0348

PubMed Abstract | CrossRef Full Text | Google Scholar

Entcheva, E. (2013). Cardiac optogenetics. Am. J. Physiol. Heart Circ. Physiol. 304, H1179–H1191.

Google Scholar

Entcheva, E., and Kay, M. W. (2020). Cardiac optogenetics: a decade of enlightenment. Nat. Rev. Cardiol. 18, 349–367. doi: 10.1038/s41569-020-00478-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Forouhar, A. S., Liebling, M., Hickerson, A., Nasiraei-Moghaddam, A., Tsai, H. J., Hove, J. R., et al. (2006). The embryonic vertebrate heart tube is a dynamic suction pump. Science 312, 751–753. doi: 10.1126/science.1123775

PubMed Abstract | CrossRef Full Text | Google Scholar

Gosline, J., Lillie, M., Carrington, E., Guerette, P., Ortlepp, C., and Savage, K. (2002). Elastic proteins: biological roles and mechanical properties. Philos. Trans. R Soc. B Biol. Sci. 357, 121–132. doi: 10.1098/rstb.2001.1022

PubMed Abstract | CrossRef Full Text | Google Scholar

Herbert, S. T., Badylak, S. F., Geddes, L. A., Hillberry, B., Lantz, G. C., and Kokini, K. (1993). Elastic modulus of prepared canine jejunum, a new vascular graft material. Ann. Biomed. Eng. 21, 727–733. doi: 10.1007/BF02368651

PubMed Abstract | CrossRef Full Text | Google Scholar

Hickerson, A. I., and Gharib, M. (2006). On the resonance of a pliant tube as a mechanism for valveless pumping. J. Fluid. Mech. 555, 141–148. doi: 10.1017/s0022112006009220

CrossRef Full Text | Google Scholar

Hickerson, A. I., Rinderknecht, D., and Gharib, M. (2005). Experimental study of the behavior of a valveless impedance pump. Exp. Fluids 38, 534–540. doi: 10.1007/s00348-005-0946-z

CrossRef Full Text | Google Scholar

Hiermeier, F., and Männer, J. (2017). Kinking and torsion can significantly improve the efficiency of valveless pumping in periodically compressed tubular conduits. Implications for understanding of the form-function relationship of embryonic heart tubes. J. Cardiovasc. Dev. Dis. 4:19. doi: 10.3390/jcdd4040019

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaffrin, M. Y., and Shapiro, A. H. (1971). Peristaltic pumping. Annu. Rev. Fluid Mech. 3, 13–37.

Google Scholar

Johansen, K., Burggren, W., and Bourne, G. H. (1980). “Cardiovascular function in the lower vertebrates,” in Hear Hear Organs, ed. G. H. Bourne (London: Academic Press), 61–117. doi: 10.1016/b978-0-12-119401-7.50009-8

CrossRef Full Text | Google Scholar

Juhas, M., Engelmayr, G. C., Fontanella, A. N., Palmer, G. M., and Bursac, N. (2014). Biomimetic engineered muscle with capacity for vascular integration and functional maturation in vivo. Proc. Natl. Acad. Sci. U.S.A. 111, 5508–5513. doi: 10.1073/pnas.1402723111

PubMed Abstract | CrossRef Full Text | Google Scholar

Jung, E. (2007). A mathematical model of valveless pumping: a lumped model with time-dependent compliance, resistance, and inertia. Bull. Math. Biol. 69, 2181–2198. doi: 10.1007/s11538-007-9208-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Jung, E., and Peskin, C. S. (2002). Two-dimensional simulations of valveless pumping using the immersed boundary method. SIAM J. Sci. Comput. 23, 19–45. doi: 10.1007/s12013-011-9157-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Kang, H. W., Lee, S. J., Ko, I. K., Kengla, C., Yoo, J. J., and Atala, A. (2016). A 3D bioprinting system to produce human-scale tissue constructs with structural integrity. Nat. Biotechnol. 34, 312–319. doi: 10.1038/nbt.3413

PubMed Abstract | CrossRef Full Text | Google Scholar

Karabekian, Z., Ding, H., Stybayeva, G., Ivanova, I., Muselimyan, N., Haque, A., et al. (2015a). HLA Class I depleted hESC as a source of hypoimmunogenic cells for tissue engineering applications. Tissue Eng. Part A 21, 2559–2571. doi: 10.1089/ten.TEA.2015.0105

PubMed Abstract | CrossRef Full Text | Google Scholar

Karabekian, Z., Idress, S., Jamshidi, A., Posnack, N. G., Sarvazyan, N. A., Idrees, S., et al. (2015b). Downregulation of beta-microglobulin to diminish T-lymphocyte lysis of non-syngeneic cell sources of engineered heart tissue constructs. Biomed. Mater. 10:34101. doi: 10.1088/1748-6041/10/3/034101

PubMed Abstract | CrossRef Full Text | Google Scholar

Khodabukus, A., Madden, L., Prabhu, N. K., Koves, T. R., Jackman, C. P., Muoio, D. M., et al. (2019). Electrical stimulation increases hypertrophy and metabolic flux in tissue-engineered human skeletal muscle. Biomaterials 198, 259–269. doi: 10.1016/j.biomaterials.2018.08.058

PubMed Abstract | CrossRef Full Text | Google Scholar

Koti, P., Muselimyan, N., Mirdamadi, E., Asfour, H., and Sarvazyan, N. A. (2019). Use of GelMA for 3D printing of cardiac myocytes and fibroblasts. J. 3D Print Med. 3, 11–22. doi: 10.2217/3dp-2018-0017

PubMed Abstract | CrossRef Full Text | Google Scholar

Kozlovsky, P., Bryson-Richardson, R. J., Jaffa, A. J., Rosenfeld, M., and Elad, D. (2016). The driving mechanism for unidirectional blood flow in the tubular embryonic heart. Ann. Biomed. Eng. Springer N. Y. LLC 44:3069. doi: 10.1007/s10439-016-1620-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Kozlovsky, P., Rosenfeld, M., Jaffa, A. J., and Elad, D. (2015). Dimensionless analysis of valveless pumping in a thick-wall elastic tube: application to the tubular embryonic heart. J. Biomech. 48:1652. doi: 10.1016/j.jbiomech.2015.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Laser, D. J., and Santiago, J. G. (2004). A review of micropumps. J. Micromech. Microeng. 14:R35.

Google Scholar

Le Goff, K. J., Gaillard, C., Helbert, W., Garnier, C., and Aubry, T. (2015). Rheological study of reinforcement of agarose hydrogels by cellulose nanowhiskers. Carbohydr. Polym. 116, 117–123. doi: 10.1016/j.carbpol.2014.04.085

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, D., Zhang, H., and Ryu, S. (2019). “Elastic modulus measurement of hydrogels,” in Cellulose-Based Superabsorbent Hydrogels. Polymers and Polymeric Composites: A Reference Series, ed. M. Mondal (Cham: Springer), 865–884. doi: 10.1007/978-3-319-77830-3_60

CrossRef Full Text | Google Scholar

Lee, V. C. C., Abakr, Y. A., and Woo, K. C. (2013). Valveless pumping using a two-stage impedance pump. Front. Mech. Eng. 8:311. doi: 10.1007/s11465-013-0270-x

CrossRef Full Text | Google Scholar

Lee, V. C. C., Chai, C. H., Law, M. C., and Wee, S. K. (2017). On the analysis of impedance-driven reverse flow dynamics. J. Eng. Sci. Technol. 12, 451–459.

Google Scholar

Li, Z., Seo, Y., Aydin, O., Elhebeary, M., Kamm, R. D., Kong, H., et al. (2019). Biohybrid valveless pump-bot powered by engineered skeletal muscle. Proc. Natl. Acad. Sci. U.S.A. 116, 1543–1548. doi: 10.1073/pnas.1817682116

PubMed Abstract | CrossRef Full Text | Google Scholar

Liebau, G. (1954). Uber ein ventilloses Pumpprinzip. Naturwissenschaften 41:327. doi: 10.1007/bf00644490

PubMed Abstract | CrossRef Full Text | Google Scholar

Liebau, G. (1955). Die Strömungsprinzipien des Herzens. Z. Kreislaufforsch. 44:677.

Google Scholar

Longatti, P. (2018). The Liebau phenomenon: a translational approach to new paradigms of CSF circulation and related flow disturbances. Child’s Nerv. Syst. 34, 227–233. doi: 10.1007/s00381-017-3653-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Loumes, L., Avrahami, I., and Gharib, M. (2008). Resonant pumping in a multilayer impedance pump. Phys. Fluids 20:23013.

Google Scholar

Ma, C., Peng, Y., Li, H., and Chen, W. (2021). Organ-on-a-Chip: a new paradigm for drug development. Trends Pharmacol. Sci. 42, 119–133. doi: 10.1016/j.tips.2020.11.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Männer, J., Wessel, A., and Yelbuz, T. M. (2010). How does the tubular embryonic heart work? Looking for the physical mechanism generating unidirectional blood flow in the valveless embryonic heart tube. Dev. Dyn. 239, 1035–1046. doi: 10.1002/dvdy.22265

PubMed Abstract | CrossRef Full Text | Google Scholar

Manopoulos, C., Tsangaris, S., and Mathioulakis, D. (2020). Net flow generation in closed-loop valveless pumping. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 234:2126. doi: 10.1177/0954406220904110

CrossRef Full Text | Google Scholar

Manopoulos, C. G., Mathioulakis, D. S., and Tsangaris, S. G. (2006). One-dimensional model of valveless pumping in a closed loop and a numerical solution. Phys. Fluids 18:17106.

Google Scholar

Meier, J. (2011). A Novel Experimental Study of A Valveless Impedance Pump for Applications at Lab-On-Chip, Microfluidic, and Biomedical Device Size Scales. Ph.D. Thesis. California, CA: California Institute of Technology.

Google Scholar

Moser, M., Huang, J., Schwarz, G., Kenner, T., and Noordergraaf, A. (1998). Impedance defined flow. Generalisation of William Harvey’s concept of the circulation—370 years later. Int. J. Cardiovasc. Med. Sci. 1, 205–211.

Google Scholar

Narita, Y., Kagami, H., Matsunuma, H., Murase, Y., Ueda, M., and Ueda, Y. (2008). Decellularized ureter for tissue-engineered small-caliber vascular graft. J. Artif. Organs 11, 91–99. doi: 10.1007/s10047-008-0407-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, T.-U., Bashur, C. A., and Kishore, V. (2016). Impact of elastin incorporation into electrochemically aligned collagen fibers on mechanical properties and smooth muscle cell phenotype. Biomed. Mater. 11:25008. doi: 10.1088/1748-6041/11/2/025008

PubMed Abstract | CrossRef Full Text | Google Scholar

Nunes, S. S., Miklas, J. W., Liu, J., Aschar-Sobbi, R., Xiao, Y., Zhang, B., et al. (2013). Biowire: a platform for maturation of human pluripotent stem cell-derived cardiomyocytes. Nat. Methods 10, 781–787.

Google Scholar

Ottesen, J. T. (2003). Valveless pumping in a fluid-filled closed elastic tube-system: one-dimensional theory with experimental validation. J. Math. Biol. 46, 309–332. doi: 10.1007/s00285-002-0179-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Pahlevan, N. M., and Gharib, M. (2013). In-vitro investigation of a potential wave pumping effect in human aorta. J. Biomech. 46, 2122–2129. doi: 10.1016/j.jbiomech.2013.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Pashneh-Tala, S., MacNeil, S., and Claeyssens, F. (2016). The tissue-engineered vascular graft - Past, present, and future. Tissue Eng. Part B Rev. 22, 68–100. doi: 10.1089/ten.teb.2015.0100

PubMed Abstract | CrossRef Full Text | Google Scholar

Ponzini, R., Vergara, C., Rizzo, G., Veneziani, A., Roghi, A., Vanzulli, A., et al. (2010). Womersley number-based estimates of blood flow rate in doppler analysis: in vivo validation by means of phase-contrast MRI. IEEE Trans. Biomed. Eng. 57, 1807–1815. doi: 10.1109/TBME.2010.2046484

PubMed Abstract | CrossRef Full Text | Google Scholar

Radisic, M., Park, H., Shing, H., Consi, T., Schoen, F. J., Langer, R., et al. (2004). Functional assembly of engineered myocardium by electrical stimulation of cardiac myocytes cultured on scaffolds. Proc. Natl. Acad. Sci. U.S.A. 101, 18129–18134. doi: 10.1073/pnas.0407817101

PubMed Abstract | CrossRef Full Text | Google Scholar

Raman, R., Cvetkovic, C., Uzel, S. G. M., Platt, R. J., Sengupta, P., Kamm, R. D., et al. (2016). Optogenetic skeletal muscle-powered adaptive biological machines. Proc. Natl. Acad. Sci. U.S.A. 113, 3497–3502. doi: 10.1073/pnas.1516139113

PubMed Abstract | CrossRef Full Text | Google Scholar

Reeser, K., and Doiron, A. L. (2019). Three-dimensional printing on a rotating cylindrical mandrel: a review of additive-lathe 3D printing technology. 3D Print. Addit. Manuf. Mary Ann. Liebert Inc. 6, 293–307. doi: 10.1089/3dp.2019.0058

CrossRef Full Text | Google Scholar

Riley, W. A., Barnes, R. W., Evans, G. W., and Burke, G. L. (1992). Ultrasonic measurement of the elastic modulus of the common carotid artery: the atherosclerosis risk in communities (aric) study. Stroke 23, 952–956. doi: 10.1161/01.str.23.7.952

PubMed Abstract | CrossRef Full Text | Google Scholar

Rinderknecht, D., Hickerson, A. I., and Gharib, M. (2005). A valveless micro impedance pump driven by electromagnetic actuation. J. Micromech. Microeng. 15:861. doi: 10.1088/0960-1317/15/4/026

CrossRef Full Text | Google Scholar

Roeder, R., Wolfe, J., Lianakis, N., Hinson, T., Geddes, L. A., and Obermiller, J. (1999). Compliance, elastic modulus, and burst pressure of small-intestine submucosa (SIS), small-diameter vascular grafts. J. Biomed. Mater. Res. 47:65. doi: 10.1002/(sici)1097-4636(199910)47:1<65::aid-jbm9>3.0.co;2-f

PubMed Abstract | CrossRef Full Text | Google Scholar

Ronaldson-Bouchard, K., Yeager, K., Teles, D., Chen, T., Ma, S., Song, L. J., et al. (2019). Engineering of human cardiac muscle electromechanically matured to an adult-like phenotype. Nat. Protoc. 14, 2781–2817. doi: 10.1038/s41596-019-0189-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenfeld, M., and Avrahami, I. (2010). Net flow rate generation by a multi-pincher impedance pump. Comput. Fluids 39:1634. doi: 10.1016/j.compfluid.2010.05.016

CrossRef Full Text | Google Scholar

Santhanakrishnan, A., and Miller, L. A. (2011). Fluid dynamics of heart development. Cell Biochem. Biophys. 61, 1–22. doi: 10.1007/s12013-011-9158-8

CrossRef Full Text | Google Scholar

Santhanakrishnan, A., Nguyen, N., Cox, J. G., and Miller, L. A. (2009). Flow within models of the vertebrate embryonic heart. J. Theor. Biol. 259, 449–461. doi: 10.1016/j.jtbi.2009.04.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarvazyan, N. (2014a). Creating biological pumps using engineered heart tissue. Tissue Eng. Part A. 20:S46.

Google Scholar

Sarvazyan, N. (2014b). Thinking outside the heart: use of engineered cardiac tissue for treatment of chronic deep venous insufficiency. J. Cardiovasc. Pharmacol. Ther. 19, 394–401. doi: 10.1177/1074248413520343

PubMed Abstract | CrossRef Full Text | Google Scholar

Schuurman, W., Khristov, V., Pot, M. W., Van Weeren, P. R., Dhert, W. J. A., and Malda, J. (2011). Bioprinting of hybrid tissue constructs with tailorable mechanical properties. Biofabrication 3:21001. doi: 10.1088/1758-5082/3/2/021001

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, H. H. G., Rumma, R. T., Ozaki, C. K., Edelman, E. R., and Chen, C. S. (2018). Vascular tissue engineering: progress, challenges, and clinical promise. Cell Stem Cell 22, 340–354. doi: 10.1016/j.stem.2018.02.009

CrossRef Full Text | Google Scholar

Swift, L., Karimi, V., Velez, M., Simonyan, H., Patev, N., Posnack, N. G., et al. (2014). Engineered heart tissue to aid venous flow. Tissue Eng. Part A. 20, S119.

Google Scholar

Takagi, S., and Takahashi, K. (1985). Study of a piston pump without valves: pumping effect and resonance in a pipe-capacity-system with a t-junction. Bull. Japan Soc. Mech. Eng. 28, 831–836.

Google Scholar

Tandon, N., Cannizzaro, C., Chao, P.-H. G., Maidhof, R., Marsano, A., Au, H. T. H., et al. (2009). Electrical stimulation systems for cardiac tissue engineering. Nat. Protoc. 4, 155–173. doi: 10.1038/nprot.2008.183

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomann, H. (1978). A simple pumping mechanism in a valveless tube. Zeitschrift. Angew Math. Phys. ZAMP. 29:169.

Google Scholar

Timmermann, S., and Ottesen, J. T. (2009). Novel characteristics of valveless pumping. Phys. Fluids 21:53601.

Google Scholar

Torrent-Guasp, F., Buckberg, G. D., Clemente, C., Cox, J. L., Coghlan, H. C., and Gharib, M. (2001). The structure and function of the helical heart and its buttress wrapping. I. The normal macroscopic structure of the heart. Semin. Thorac. Cardiovasc. Surg. 13, 301–319.

Google Scholar

Trabelsi, O., Dumas, V., Breysse, E., Laroche, N., and Avril, S. (2020). In vitro histomechanical effects of enzymatic degradation in carotid arteries during inflation tests with pulsatile loading. J. Mech. Behav. Biomed. Mater. 103:103550. doi: 10.1016/j.jmbbm.2019.103550

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, C. Y., and Chang, H. T. (2009). Design and characterization of valveless impedance pumps. J. Mech. 25:345. doi: 10.1017/s1727719100002835

CrossRef Full Text | Google Scholar

Yan, X., Chen, Q., Zhu, L., Chen, H., Wei, D., Chen, F., et al. (2017). High strength and self-healable gelatin/polyacrylamide double network hydrogels. J. Mater. Chem. B 5:7683. doi: 10.1039/c7tb01780d

PubMed Abstract | CrossRef Full Text | Google Scholar

Zawieja, D. C. (2009). Contractile physiology of lymphatics. Lymphat Res. Biol. 7, 87–96. doi: 10.1089/lrb.2009.0007

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, B., Korolj, A., Lai, B. F. L., and Radisic, M. (2018). Advances in organ-on-a-chip engineering. Nat. Rev. Mater. 3, 257–278.

Google Scholar

Zhang, D., Shadrin, I. Y., Lam, J., Xian, H.-Q., Snodgrass, H. R., and Bursac, N. (2013). Tissue-engineered cardiac patch for advanced functional maturation of human ESC-derived cardiomyocytes. Biomaterials 34, 5813–5820. doi: 10.1016/j.biomaterials.2013.04.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y. S., Yue, K., Aleman, J., Mollazadeh-Moghaddam, K., Bakht, S. M., Yang, J., et al. (2017). 3D bioprinting for tissue and organ fabrication. Ann. Biomed. Eng. 45, 148–163. doi: 10.1007/s10439-016-1612-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Zimmermann, W. H., Schneiderbanger, K., Schubert, P., Didié, M., Münzel, F., Heubach, J. F., et al. (2002). Tissue engineering of a differentiated cardiac muscle construct. Circ. Res. 90, 223–230. doi: 10.1161/hh0202.103644

PubMed Abstract | CrossRef Full Text | Google Scholar

Zislin, V., and Rosenfeld, M. (2018). Impedance pumping and resonance in a multi-vessel system. Bioengineering 5:63. doi: 10.3390/bioengineering5030063

PubMed Abstract | CrossRef Full Text | Google Scholar