Mechanical Principles Governing the Shapes of Dendritic Spines

Dendritic spines are small, bulbous protrusions along the dendrites of neurons and are sites of excitatory postsynaptic activity. The morphology of spines has been implicated in their function in synaptic plasticity and their shapes have been well-characterized, but the potential mechanics underlying their shape development and maintenance have not yet been fully understood. In this work, we explore the mechanical principles that could underlie specific shapes using a minimal biophysical model of membrane-actin interactions. Using this model, we first identify the possible force regimes that give rise to the classic spine shapes—stubby, filopodia, thin, and mushroom-shaped spines. We also use this model to investigate how the spine neck might be stabilized using periodic rings of actin or associated proteins. Finally, we use this model to predict that the cooperation between force generation and ring structures can regulate the energy landscape of spine shapes across a wide range of tensions. Thus, our study provides insights into how mechanical aspects of actin-mediated force generation and tension can play critical roles in spine shape maintenance.

1. Introduction

Dendritic spines are small, bulbous protrusions along the dendrites of neurons that occur at postsynaptic glutamatergic synapses (Bosch and Hayashi, 2012; Nakahata and Yasuda, 2018; Nishiyama, 2019). They respond to a glutamate release by orchestrating a series of biochemical and biophysical events that span multiple spatial and temporal scales (Gray, 1959; Harris and Kater, 1994; Shepherd, 1996). Spine morphology is tightly coupled to synaptic function, with larger spines tending to represent stronger synapses (Arellano et al., 2007; Patterson and Yasuda, 2011) due to their greater surface expression of functional glutamate receptors. Synaptic activity regulates spine shape and volume. For example, several forms of physiological synaptic plasticity, such as long-term potentiation (LTP) and long-term depression (LTD) are associated with spine enlargement and spine shrinkage, respectively (Bear and Malenka, 1994; Engert and Bonhoeffer, 1999; Harris et al., 2003). Although average spine volume is approximately 0.1 femtoliter, the shape and volume of dendritic spines are highly variable, depending both on the developmental stage and a combination of genetic and environmental factors, including the prior history of activity (Fifkova, 1985; Harris, 1999; Ostroff et al., 2002; Petrak et al., 2005). Moreover, spine morphology is highly dynamic on the scale of seconds to minutes, due to a dynamic actin-based cytoskeleton (calabrese et al., 2006; Nakahata and Yasuda, 2018).

Despite their broad range of morphological features and highly dynamic nature, dendritic spines can be classified into four broad categories. Spines in the mature nervous system are typically classified as being stubby, thin, or mushroom-shaped (Peters and Kaiserman-Abramof, 1970; Harris et al., 1992) (Figure 1A). These categories of spines can be identified in electron micrographs as postsynaptic structures connected to presynaptic nerve terminals. Stubby spines are short and wide, and lack a discernible neck. Such spines appear early during synaptogenesis and may represent an emerging spine, but they also might result from spine shrinkage driven by physiological or pathological conditions (Figure 1A) (Gray, 1959; Fiala et al., 1998; Harris, 1999).

FIGURE 1

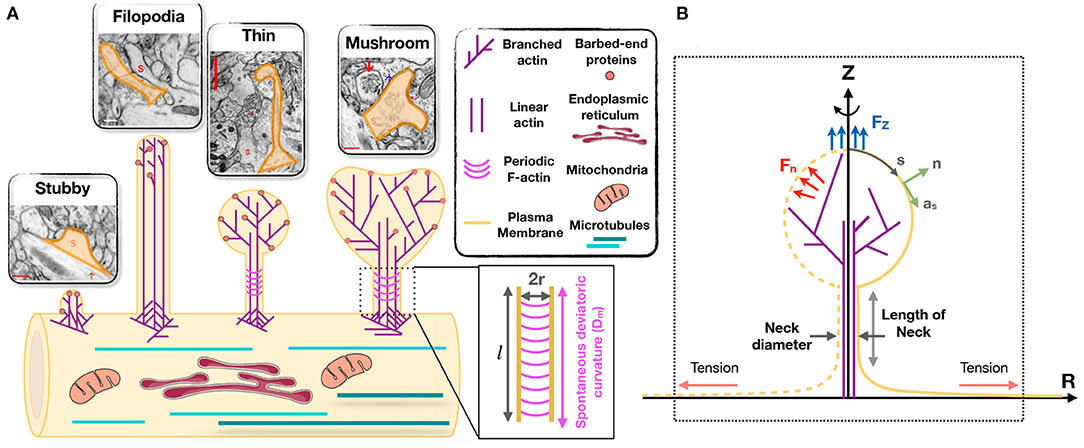
Figure 1. Modeling of forces relevant to spine shape. (A) Schematic depiction of different shape categories of dendritic spines (Reprinted with permission from SynapseWeb, Kristen M. Harris, PI, http://synapseweb.clm.utexas.edu/). The inset shows a schematic of a tubular neck with a radius r and a spontaneous deviatoric curvature D_m along the total neck length l. (B) The surface parametrization of the membrane geometry in axisymmetric coordinates. s is the arclength, n is the unit normal vector to the membrane surface, and a_s is the unit tangent vector in the direction of arclength. We assume that the actin filaments can apply axial (F_z) or normal (F_n) forces to the membrane surface. We assume that there is a large membrane reservoir with a fixed area, and we focused on the local region of the membrane under tension λ, as indicated by the dotted box.

The adult mammalian brain is dominated by either thin or mushroom-shaped spines. Thin spines have a long thin neck that is connected to a small bulbous head (Figure 1A) (Harris, 1999). Within the head is the postsynaptic density (PSD), an area just beneath the synaptic plasma membrane containing a high concentration of glutamate receptors, scaffolding molecules, and other proteins essential for postsynaptic function. Thin spines have flexible structures that allow them to adapt their morphology based on different levels of synaptic activity (Holtmaat et al., 2005; Zuo et al., 2005). It has been proposed that thin spines are “learning spines,” because they display a high capacity for expansion and strengthening via insertion of new AMPA-type glutamate receptors into the PSD, which is the key basis for synapse strengthening (Kasai et al., 2003; Holtmaat et al., 2005; Zuo et al., 2005; Bourne and Harris, 2007; Berry and Nedivi, 2017). Compared to thin spines, mushroom-shaped spines have a shorter neck and a greatly expanded head (Figure 1A) (Harris, 1999). Mature mushroom-shaped spines are more likely to be stable for months to years (Grutzendler et al., 2002; Trachtenberg et al., 2002; Holtmaat et al., 2005; Zuo et al., 2005; Berry and Nedivi, 2017), with slower turnover, and are associated with strong synapse functionality, as they contain on average higher concentrations of AMPA-type glutamate receptors. Such spines have therefore been called “memory spines,” in the sense that their potentiated strength reflects a history of high activity and thus “memory” storage, yet their capacity for further potentiation may be near saturation (Matsuzaki et al., 2001; Kasai et al., 2003; Ganeshina et al., 2004; Ashby et al., 2006; Bourne and Harris, 2007; Berry and Nedivi, 2017). Table 1 provides the reported dimensions for different shape categories of dendritic spines observed in hippocampal neurons (Harris et al., 1992; Spacek and Harris, 1997; Yuste and Bonhoeffer, 2004; Rodriguez et al., 2008; Kanjhan et al., 2016).

TABLE 1

Table 1. Dimensions of different spine shapes compiled from the literature.

In addition to synapse-bearing spines, the fourth category of spine-like protrusions is dendritic filopodia. These are commonly observed during early development, and are thought to facilitate the pairing of presynaptic and postsynaptic glutamatergic sites during synaptogenesis by spatially scanning the neuropil volume for a partner axon (Miller and Peters, 1981; Dailey and Smith, 1996; Ziv and Smith, 1996; Fiala et al., 1998). Thus, a fraction of these “protospines” become synapse-bearing spines if they come into contact with and are stabilized in partnership with presynaptic nerve terminals (Dailey and Smith, 1996; Koleske, 2013). Filopodia are long (>2 μm) and thin (<0.3 μm diameter) protrusions that lack a bulbous head (Figure 1A) (Kanjhan et al., 2016).

Because the size and shape of functional subcellular domains are closely tied to the mechanics of actin-membrane interactions (Harris et al., 1992; Yuste and Bonhoeffer, 2004; Kanjhan et al., 2016), a more complete understanding of dendritic spine dynamics, development, and function would benefit from biophysical models that address the underlying mechanical aspects. We have therefore begun to build a computational model of spines that incorporates both membrane forces and actin-based forces, and their interaction. This model is based on published experimental observations in dendritic spines, non-neuronal cells, and biochemical experiments. The goal of this model is to inform our understanding of the development of spines and the plasticity of their structure under different physiological scenarios.

Currently, there are hundreds of studies that address various aspects of the regulation of dendritic spine size and shape. In building our model, we have chosen to focus on several key observations, as follows.

1. Actin enrichment in spines: Dendritic spines are enriched in filamentous actin, which, along with scaffolding molecules, establish spine architecture (Landis and Reese, 1983; Hotulainen and Hoogenraad, 2010; Bertling and Hotulainen, 2017). Membrane-actin interactions associated with spine enlargement and shrinkage during plasticity can be modeled at the single filament level using the elastic Brownian ratchet and the net force acting on the membrane due to actin remodeling can be represented as work done by actin to deform the membrane (Peskin et al., 1993; Mogilner and Oster, 1996; Miermans et al., 2017).

2. Different subpopulations of actin: There appear to be distinct subpopulations of F-actin in dendritic spines, and spine actin can be thought of as an independent network with interconnected nodes (Frost et al., 2010). The spine head typically consists of short, cross-linked filaments; branched filaments have been observed in the spine head (Hotulainen and Hoogenraad, 2010; Korobova and Svitkina, 2010; Nanguneri et al., 2019). The spine neck was initially thought to contain long filaments (Halpain, 2000; Rao and Craig, 2000; Tada and Sheng, 2006; Hotulainen et al., 2009), but current evidence has suggested the presence of short, branched filaments (Korobova and Svitkina, 2010). Additionally, recent high resolution imaging techniques have shown that there are likely periodic F-actin structures along the neck region of dendritic spines (Bär et al., 2016; Bucher et al., 2020). These periodic F-actin structures are very stable and in contrast to long and branched filaments, resist depolymerization (Bär et al., 2016).

3. Membrane mechanics: All cells regulate their shape by coordinating the properties of the cytoskeleton with that of the plasma membrane. Proteins such as MARCKS that interact directly with both F-actin and the lipid bilayer can strongly influence spine shape (Calabrese and Halpain, 2005). Membrane curvature is especially important in spines and represents a specific mechanical force that is regulated by distribution of proteins and lipids. Additionally, membrane composition can regulate transport phenomena between two adjacent cells (Rahmaninejad and Vaughan, 2021). Bin/Amphiphysin/Rvs (BAR)-domain containing proteins assemble on the membrane to produce anisotropic curvature and promote tubulation. Studies have demonstrated critical roles for specific BAR-domain proteins in dendritic spines. Recently, the role of membrane mechanics has been elucidated in the initiation of dendritic spines (Hlushchenko et al., 2016). A series of studies showed that dendritic spines can be initiated by membrane bending due to protein patches containing BAR domains such as I-BAR and F-BAR proteins (Carlson et al., 2011; Wakita et al., 2011; Kessels and Qualmann, 2015; Saarikangas et al., 2015). These proteins are known to polymerize on the membrane (Peter et al., 2004; Shimada et al., 2007; Frost et al., 2008, 2009), induce anisotropic curvature (Kralj-Iglič et al., 2000; Iglič et al., 2005, 2007), and promote tubulation (Kralj-Iglič et al., 1996, 1999; Iglič et al., 1999; Frost et al., 2008; Kabaso et al., 2012).

The above findings suggest that membrane bending and actin-membrane interactions are major determinants of spine morphology. Recent studies have modeled the role of either membrane mechanics alone (Miermans et al., 2017) or actin dynamics alone in spines (Bonilla-Quintana et al., 2020), but the interaction between the two has not yet been addressed. Here, we present a general theoretical model that relates membrane bending and actin-mediated forces to spine morphology. Using this model, we investigate the mechanical landscape of the different shapes of spines and map the relationships among actin-mediated force generation, membrane elasticity, and curvature induced by periodic ring structures and proteins such as BAR domains.

2. Model Development

2.1. Assumptions

• We treat the lipid bilayer as a continuous thin elastic shell, assuming that the membrane thickness is negligible compared to the radii of membrane curvature (Helfrich, 1973; Deuling and Helfrich, 1976). This allows us to model the bending energy of the membrane using the modified version of the Helfrich-Canham energy, including the effect of spatially varying deviatoric curvature to represent the induced anisotropic curvatures by periodic F-actin rings and other ring-shaped structures (Canham, 1970; Helfrich, 1973; Kralj-Iglič et al., 1996, 1999; Iglič et al., 2006; Alimohamadi and Rangamani, 2018).

• We assume that the membrane is locally inextensible, since the stretching energy of the lipid bilayer is an order of magnitude larger than the membrane bending energy (Rawicz et al., 2000). We implemented this constraint using a Lagrange multiplier, which can be interpreted as the membrane tension (Steigmann, 1999; Alimohamadi et al., 2020a). We note that this membrane tension, in this study, is better interpreted as the cortical tension including the effective contribution of the membrane in-plane stresses, induced tension by actin polymerization, and myosin-driven contractility against membrane (Barfod et al., 2011; Diz-Muñoz et al., 2013; Orly et al., 2014; Alimohamadi et al., 2020b).

• We assume that the time scales of mechanical forces are much faster than other events (such as actin polymerization) in dendritic spines, allowing us to assume mechanical equilibrium and neglect inertia (Steigmann, 1999; Miermans et al., 2017). This assumption is justified by the fact that the timescale of the equilibration of the mechanical forces is much smaller than the timescale of actin polymerization in dendritic spines (Weichsel and Geissler, 2016).

• We assume that the force exerted by the actin cytoskeleton can be represented as work done on the membrane and do not include the molecular details of the actin network (Atilgan et al., 2006; Walani et al., 2015; Miermans et al., 2017; Alimohamadi et al., 2020b). Additionally, we assume that the periodic ring shaped structures of actin and related proteins such as βII spectrin and BAR-domain proteins can be represented using an anisotropic spontaneous curvature (Kralj-Iglič et al., 1996, 1999; Iglič et al., 2006, 2007).

• For ease of computation we assume that the geometry of a dendritic spine is rotationally symmetric (see Figure 1B) (Miermans et al., 2017). This assumption allows us to parametrize the whole surface by a single parameter, arclength.

2.2. Mechanical Force Balance

In this section, we present a concise derivation of the governing mathematical shape equations for the shape of dendritic spines at mechanical equilibrium. The complete derivation with details is given in Steigmann (1999), Agrawal and Steigmann (2009), and Walani et al. (2015). The total free energy of the system (E) includes the elastic storage energy of the membrane (E_elastic), and the work done by the applied forces due to actin filaments (W_force) (Lokar et al., 2012; Walani et al., 2014, 2015; Alimohamadi and Rangamani, 2018) is given by

$\begin{array}{ll}E=E_{\text{elastic}}-W_{\text{force}},& (1)\end{array}$

$\begin{array}{ll}{E}_{\text{elastic}}={\displaystyle {\int }_{\omega }}(\sigma (H,D;{\theta }^{\alpha })+\lambda ({\theta }^{\alpha }))da-pV,\text{ and}& (\mathrm{2a})\end{array}$

$\begin{array}{ll}{W}_{\text{force}}={\displaystyle {\int }_{\omega }}\text{f}({\theta }^{\alpha })·(\text{r}-{\text{r}}_0)da.& (\mathrm{2b})\end{array}$

Here, ω is the total membrane surface area, σ is the bending energy density per unit area, θ^α denotes the surface coordinate where α ∈ {1, 2}, H is the mean curvature of the surface, D is the curvature deviator, K is the Gaussian curvature of the surface, λ is the tension field and represents the Lagrange multiplier associated with the local area constraint, p is the transmembrane pressure and represents the Lagrange multiplier associated with the volume constraint, V is the enclosed volume, f is the applied force per unit area, r is the position vector in the current configuration, and r₀ is the position vector in the reference frame. To model the energy density σ in Equation (2a), we used the modified version of Helfrich energy including the effects of induced anisotropic curvature by periodic F-actin structures and BAR domain proteins (Canham, 1970; Helfrich, 1973; Iglič et al., 2005; Alimohamadi and Rangamani, 2018; Alimohamadi et al., 2018), given as

$\begin{array}{ll}\sigma (H,D;{\theta }^{\alpha })=(2k_1+k_2)H^2-k_2{(D-{\text{D}}_{\text{m}}({\theta }^{\alpha }))}^2,& (3)\end{array}$

where k₁ and k₂ are constants and D_m is the spontaneous (intrinsic) deviatoric curvature which can be spatially heterogeneous along the membrane surface (Kralj-Iglič et al., 1996, 1999; Iglič et al., 2005). For an isotropic case (D_m = 0), Equation (3) reduces to the classical Helfrich energy with quadratic dependence on mean curvature and linear dependence on Gaussian curvature (Iglič et al., 2005), where k₁ = κ (bending modulus) and k₂ = κ_G (Gaussian modulus). In this study, we assume κ_G ~ −κ (Hu et al., 2012) and simplify the bending energy density in Equation (3) as (Iglič et al., 2005; Walani et al., 2014)

$\begin{array}{ll}\sigma (H,D;{\theta }^{\alpha })=\kappa H^2+\kappa {(D-{\text{D}}_{\text{m}}({\theta }^{\alpha }))}^2.& (4)\end{array}$

It should be mentioned that in Equation (4), we assumed that periodic rings can only induce anisotropic curvature and we set the isotropic curvature (spontaneous curvature) to be zero throughout this study. Substituting Equations (2a), (2b), and (4) into Equation (1) gives

$\begin{array}{l}E=\underset{\begin{array}{l}\text{Bending energy }\\ \text{of the membrane}\end{array}}{\underbrace{{\displaystyle {\int }_{\omega }\kappa }{H}^{2}da}}+\underset{\begin{array}{l}\text{Bending energy due to }\\ \text{deviatoric curvature}\end{array}}{\underbrace{{\displaystyle {\int }_{\omega }\kappa }{(D-{\text{D}}_{\text{m}})}^{2}da}}+\underset{\begin{array}{l}\text{Work done}\\ \text{by tension}\end{array}}{\underbrace{{\displaystyle {\int }_{\omega }\lambda }da}}-\underset{\begin{array}{l}\text{Work done}\\ \text{by pressure}\end{array}}{\underbrace{\text{pV}}}\\ -\underset{\text{Work done by actin-mediated forces}}{\underbrace{{\displaystyle {\int }_{\omega }f}({\theta }^{\alpha })·(r-r_0)da}}& (5)\end{array}$

Minimization of the energy (Equation 5) using the variational approach results in the governing shape equation (Supplementary Equation 6) and the incompressibility condition (Supplementary Equation 7) for a heterogeneous membrane. The complete equations are presented in the Supplementary Material along with the complete notation in Supplementary Table 1.

2.3. Numerical Implementation

In axisymmetric coordinates, the membrane shape equation (Supplementary Equation 6) and the incompressibility condition (Supplementary Equation 7) simplify to a coupled system of first order differential equations (Supplementary Equation 20). In order to solve this system of equations along with the prescribed boundary conditions (Supplementary Equation 22), we used “bvp4c,” a boundary value problem solver in MATLAB. In all our simulations, we assume that the total area of the membrane is conserved and we also fixed the bending modulus to be κ = 0.18 pN·μm based on previous models for spines (Pontes et al., 2013; Bonilla-Quintana et al., 2020). We also set the transmembrane pressure to zero (p = 0) to focus only on the mechanism of membrane-actin interactions in governing the shapes of dendritic spines.

3. Results

Using the model described above, we conducted simulations for different mechanical parameters with the goal of identifying the range of forces, the associated heterogeneities, and the protein-induced and cytoskeleton-induced anisotropic curvatures that could result in shapes and sizes of spines corresponding to those observed experimentally (Table 1). Specifically, we sought to recreate the filopodial, stubby, thin, and mushroom-shaped spines as shown in Figure 1. We must emphasize that all the shapes are equilibrium shapes, and our model does not provide insight into dynamic transitions from one shape to another. Our simulation results are described below. In these data, we emphasize the relationships among different mechanical parameters to obtain the desired shapes, and give specific values for mechanical parameters that result in sizes as listed in Table 1. These provide some realistic magnitudes for forces present at various locations within the compact spine volume.

3.1. Localized Axial Forces Along the Membrane Are Sufficient for the Formation of Stubby and Filopodial Shaped Spines

We begin with an analysis of the force-shape relationship of stubby spines. We assumed that actin filaments exert axial forces in the nascent PSD area, which is a small fraction of the membrane surface area (Table 1). This heterogeneous force distribution along the membrane was implemented using a hyperbolic tangent function (Supplementary Equation 23). We observed that the relationship between the magnitude of the forces and the length of the stubby spines depends on the value of tension. To map this relationship, we performed the simulation for (i) a fixed height (L = 0.44 μm) and a wide range of tensions (Figure 2A) and (ii) a fixed tension (e.g., λ = 10 pN/μm) and different heights of the stubby spine (Figure 2B). As shown in previous studies (Derényi et al., 2002; Powers et al., 2002), for a small membrane deformation, such as a stubby spine, the axial force is linearly proportional to both tension and the height of the stubby spine (Figures 2A,B) (Derényi et al., 2002; Powers et al., 2002). Thus, from a mechanical standpoint, the stubby spine shape is accessible for a wide range of forces and tensions in the physiological range. For example, based on our simulation, when tension is λ = 10 pN/μm, an axial force of F_z = 7.5 pN is required to form a stubby spine of the length of L = 0.44 μm (Table 1 and Figure 2C).

FIGURE 2

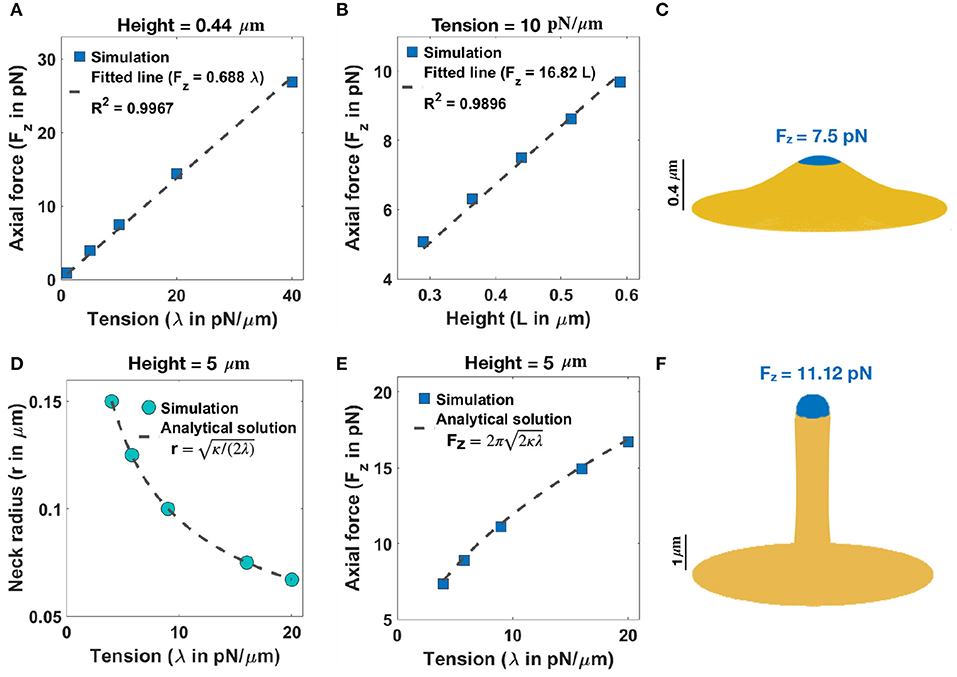
Figure 2. Formation of stubby and filopodia shaped spines with a localized axial force. (A) Linear relationship between the magnitude of axial force and tension in a small stubby-shaped membrane deformation (Derényi et al., 2002; Powers et al., 2002). The dashed line is the fitted curve (F_z = 0.688λ) with R² = 0.9967. (B) Linear relationship between the magnitude of axial force and the height of the stubby spine for a fixed tension (Derényi et al., 2002; Powers et al., 2002). The dashed line is the fitted curve (F_z = 16.82L) with R² = 0.9896. (C) A stubby-shaped spine with a total length L = 0.44 μm is formed with F_z = 7.5 pN applied along the blue area (λ = 10 pN/μm). (D) Neck radius of a filopodium as a function of tension (r $=\sqrt{\kappa /(2\lambda )}$) (Derényi et al., 2002). (E) The magnitude of axial force needed to form a filopodium as a function of tension (${\text{F}}_{\text{z}}=2\pi \sqrt{2\kappa \lambda }$) (Derényi et al., 2002). (F) A filopodium-shaped protrusion with a total length L = 5 μm and neck radius r = 0.2 μm is formed with F_z = 11.2 pN applied along the spherical cap of the filopodium, which is shown in blue (λ = 9 pN/μm).

Next, we investigated the role of forces in the formation of long spines that resembled filopodia. For the simplest case with no steric interaction between membrane and bundled actin, we found that the formation of a long filopodium follows well-established results for tube formation from a membrane reservoir (Derényi et al., 2002). Ignoring the spherical cap, a filopodium is a tubular membrane and its equilibrium radius (r) depends on the tension and bending rigidity of the membrane as r $=\sqrt{\kappa /(2\lambda )}$ (Figure 2D) (Derényi et al., 2002). The axial force F_z required to maintain the tubule with radius r is given as ${\text{F}}_{\text{z}}=2\pi \sqrt{2\kappa \lambda }$ (Figures 2E,F) (Derényi et al., 2002), which is independent of the length of the protrusion (Supplementary Figure 3A). In addition to the actin-mediated filopodium formation from a large membrane reservoir (fixed membrane area) that we focused on here, Miermans et al. showed that an increase in the surface area of a spine can drive a filopodium elongation from a stubby-shaped spine (Miermans et al., 2017). They suggested that exocytosis of endosomes at synapses provides this membrane addition to the system (Miermans et al., 2017).

3.2. Normal Forces Along the Membrane Support the Formation of Thin Shaped Spines

We next investigated the nature of forces that could be associated with the formation of thin-shaped spines. Because thin-shaped spines have a bulbous head, axial forces such as those used in Figure 2 are insufficient to generate the spherical shape of the head. Since spherical shapes can be obtained by a normal force acting locally on the head region, we repeated the simulation in Figure 2 but now included a localized uniform normal force density along the area of the spine head (A_force = A_{spine head}). It is possible that such normal forces result from the dense actin meshwork in the spine heads (Borisy and Svitkina, 2000; Miermans et al., 2017). We estimated the forces required to generate a spherical head by assuming that a thin spine is ideally a sphere with radius R which is connected to a cylinder with radius r and height l (Supplementary Figure 1B). If a uniform normal force density, f_n, is applied all along the sphere, then, ignoring the interface between the sphere and the cylinder, the total energy of the system can be written as

$\begin{array}{ll}E=E_{\text{sphere}}+E_{\text{cylinder}},& (6)\end{array}$

where E_sphere =$(\kappa /R^2+\lambda )4\pi R^2-(4\pi /3)R^3{\text{f}}_{\text{n}}$ and E_cylinder =$2\pi \sqrt{2\lambda \kappa }l$ (see section 1.5.2 in the Supplementary Material). Minimizing the total energy of the system with respect to R by taking ∂E/∂R = 0, we obtain the equilibrium normal force density as f_n = 2λ/R. This resembles the Young-Laplace equation where normally pressure (normal force density) is a global parameter; in this case, f_n is a local normal force density. In our simulation, we prescribe the area of the applied force and thus we can rewrite the force density as

$\begin{array}{ll}{\text{f}}_{\text{n}}=4\lambda \sqrt{\frac{\pi }{{\text{A}}_{\text{force}}}}.& (7)\end{array}$

In order to generate thin-shaped spines, we first fixed the neck diameter based on the magnitude of tension (r $=\sqrt{\kappa /(2\lambda )}$) as shown in Figure 2D. Similar to filopodia, in thin spines, the radius of the neck is related to the tension and the bending rigidity, given by r $=\sqrt{\kappa /(2\lambda )}$ (Derényi et al., 2002) (Figure 3A). This relationship suggests that in order to have a thin spine with a neck radius between 0.035 μm < r <0.065 μm (given range in Table 1), the tension can vary between 20 pN/μm < λ < 80 pN/μm. Based on Equation (7), the magnitude of the normal force density linearly depends on the tension, while it varies as the inverse of the square root of the area of applied force.

FIGURE 3

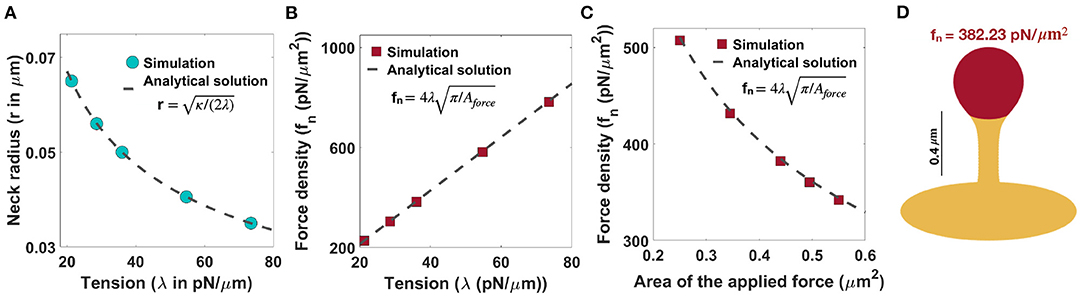
Figure 3. Formation of thin-shaped spines with localized normal force density along the spine head. (A) Neck radius of a thin-shaped spine as a function of tension (r $=\sqrt{\kappa /(2\lambda )}$) (Derényi et al., 2002). (B) Linear relationship between the magnitude of normal force density needed to form a thin-shaped spine and the tension. Here, the area of the applied force is set at A_force = 0.44 μm². The red squares represent the results obtained from simulation and the dashed line is the derived analytical solution (${\text{f}}_{\text{n}}=4\lambda \sqrt{\pi /A_{\text{force}}}$, Equation (7)). (C) The magnitude of a normal force density needed to form a thin-shaped spine as a function of the area of the spine head. The tension is set at λ = 36 pN/μm. The red squares represent the results obtained from our simulations and the dashed line is the derived analytical solution ($({\text{f}}_{\text{n}}=4\lambda \sqrt{\pi /A_{\text{force}}}$, Equation (7). (D) A thin-shaped spine with a total length L = 0.98 μm, neck radius r = 0.05 μm, and head volume V = 0.033 μm³ is formed with f_n = 382.23 pN/μm² applied along the head of spine which is shown in red (λ = 36 pN/μm and A_force = 0.44 μm²).

In Figure 3B, we plotted the magnitude of the normal force density as a function of tension obtained from numerical solutions (red squares) vs. the analytical expression given in Equation (7) (dotted line) for fixed A_force = 0.44 μm². We found a good agreement between the analytical solution and the results obtained from simulation such that by changing tension between 20pN/μm < λ < 80pN/μm, the magnitude of the normal force density required to form a thin-shaped spine varies in a large range between $200\text{pN}/\text{μ}{\text{m}}^2<{\text{f}}_{\text{n}}<900\text{pN}/\text{μ}{\text{m}}^2$ (Figure 3B). To further validate our numerical results, we plotted the magnitude of the normal force density as a function of the area of the applied force (A_force) obtained from numerical solution (red squares) vs. the analytical expression given in Equation (7) (dotted line) for a fixed tension, λ = 36 pN/μm (Figure 3C). We observed a good agreement between the analytical solution and the numerical results where by increasing the area of the applied force from $A_{\text{force}}=0.25\text{μ}{\text{m}}^2$ to $A_{\text{force}}=0.55\text{μ}{\text{m}}^2$, the magnitude of the normal applied force density needed to form a thin spine decreases from f_n ~ 500 pN/μm² to f_n ~ 300 pN/μm² (Figure 3C).

As an example, to form a thin spine with an average neck diameter of r = 0.05 μm (see Table 1), we set our tension to be λ = 36 pN/μm (r $=\sqrt{\kappa /(2\lambda )}$). Based on our calculation for λ = 36 pN/μm and A_force = 0.44 μm² (average area of the spine head in Table 1), a total normal force density of f_n = 382.23 pN/μm² (applied along the red area) is required to form a thin spine with a total length L = 0.98 μm, a neck radius r = 0.05 μm, and a head volume V = 0.033 μm³ (Figure 3D). Also, in Supplementary Figure 3B, we show that the magnitude of the normal force density needed to form a thin spine is independent of the height of the spine.

3.3. Non-uniform Normal Force Distributions Can Result in Mushroom-Shaped Spines

We next asked if changes to the force distributions could result in mushroom-shaped spines. We hypothesized that one possible way is to have a heterogeneous force distribution along the spine head and the PSD area. The heterogeneous force distribution assumption comes in part from the observation that the presence of the presynaptic terminal might cause the concave structure of the PSD on the dendritic spine, suggesting the possibility that the net force on the membrane would be altered at the PSD region (Kashiwagi et al., 2019). To understand how non-uniform distributions of normal forces can characterize the morphology of mushroom spines, we performed simulations assuming that the normal force applied along the PSD area is different from the normal force density applied along the rest of the spine head (Figure 4A).

FIGURE 4

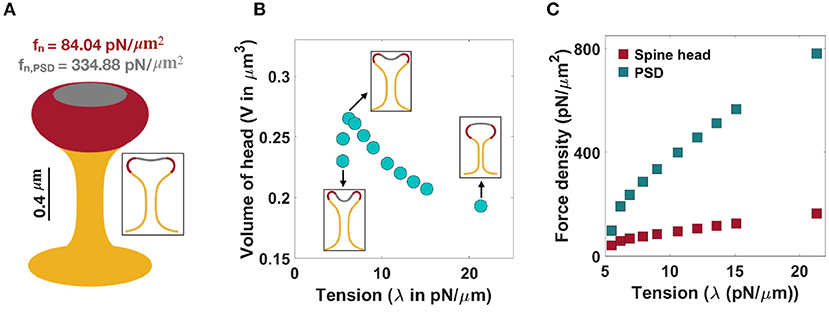
Figure 4. Formation of mushroom-shaped spines with localized normal forces along the spine head and PSD. (A) A mushroom-shaped spine with a total length L = 1.51 μm, neck radius r = 0.1 μm, head volume V = 0.25 μm³, and area of PSD/area of head = 0.2 is formed with f_n = 84.04 pN/μm² applied along the head of spine (red domain) and f_n,PSD = 334.88 pN/μm² applied along the PSD (gray domain) (λ = 9 pN/μm). (B) The non-monotonic behavior of the volume of a mushroom-shaped spine head when increasing tension. Three different shapes of mushroom-shaped spines are shown for low, intermediate, and high tensions. With increasing magnitude of tension, the mushroom-shaped spine head flattens. (C) The magnitude of normal force densities in the spine head (red squares) and in PSD (gray squares) increases with increasing tension.

In the case of mushroom-shaped spines, we have multiple geometric parameters to consider—(a) head volume, (b) area fraction of the PSD, and (c) neck diameter determined by tension. For example, to form a mushroom-shaped spine with a total length L = 1.51 μm, head volume V = 0.25 μm³, and area of PSD/ area of head ratio = 0.2 (see Table 1), normal force densities of f_n = 84.04 pN/μm² and f_n,PSD = 334.88 pN/μm² are required along the spine head (red region) and the PSD area (gray region), respectively (Figure 4A). The value of tension was set to λ = 9 pN/μm to obtain a neck radius of about r ≈ 0.1 μm (see Table 1 and Supplementary Figure 4). The magnitude of these force densities is independent of the height of the spine (Supplementary Figure 3C).

We observed that the morphology of the spine head changes with varying magnitude of tension; the spine head flattens for large tensions (Figure 4B). This is consistent with previous studies that have investigated membrane shape at high tensions, e.g., the membrane remains almost flat during vesicle budding (Saleem et al., 2015), or in the case of a red blood cell, the biconcave cell flattens to a pancake shape (Evans, 2018; Alimohamadi et al., 2020b). To further investigate how a change in the morphology of the spine head can affect the volume of the head, we plotted the volume of the head (V) as a function of tension (Figure 4B). We found that the head volume is a non-monotonic function of tension; as tension increases, the volume of the spine head increases and then decreases (Figure 4B).

This is because initially when increasing tension from low to intermediate values the head flattens and the volume of the head increases. However, for high tensions, the shrinkage of the head becomes dominant and as a result the volume decreases (Figure 4B). Consistent with these observations, a larger normal force is required to bend a stiffer membrane and form a mushroom-shaped spine (Figure 4C). For example, based on our calculation, when increasing tension from λ = 5 pN/μm to λ = 20 pN/μm, the normal force densities in the spine head and PSD area increase by almost 120 and 680 pN/μm², respectively (Figure 4C).

To study how the ratio of PSD area to the total area of the spine head affects the magnitude of normal force densities, we performed simulations for a range of area of PSD/area of head ratios (Supplementary Figure 5). Our results show that with increasing area of PSD/area of head ratio, a larger normal force density in the spine head and a smaller normal force in the PSD region are required (Supplementary Figure 5A). Additionally, increasing the ratio of the PSD area to the total area of the head results in the flattening of the spine head with a larger volume (Supplementary Figure 5B). Thus, mushroom-shaped spines can be formed from a multitude of mechanical pathways—heterogeneous forces in the spine head, balancing tension and force distributions, and using different area localizations of the forces.

3.4. Induced Spontaneous Deviatoric Curvature by Periodic F-Actins Structures and BAR Domain Proteins Can Generate Characteristic Dendritic Spine Necks

Recently, super-resolution microscopy methods have revealed the presence of ubiquitous actin ring structures along spine necks (Bär et al., 2016; Bucher et al., 2020). It has been suggested that these ring-like structures and BAR-domain proteins can together support the tubular shape of dendritic spines (Ebrahimi and Okabe, 2014; Bertling and Hotulainen, 2017). To understand how periodic F-actin structures and BAR domain proteins can regulate the tubular shape of spine necks, we implemented their net effect in our model by including spontaneous deviatoric curvature in the energy density of the system (Equation 4) (Kralj-Iglič et al., 1996, 1999; Iglič et al., 1999, 2005; Kabaso et al., 2012).

Consider a tubular membrane with radius r and a spontaneous deviatoric curvature D_m along the neck with total length l (Figure 1A), the equilibrium radius in the presence of spontaneous deviatoric curvature is given by $\text{r}=\sqrt{\kappa /(2(\lambda +\kappa {\text{D}}_{\text{m}}^2))}$ (Supplementary Equation 37). Since this radius depends on both the value of tension and the spontaneous deviatoric curvature (Figure 5A), we define an effective tension ($\lambda +\kappa {\text{D}}_{\text{m}}^2$). As a result, the relationship between neck radius, spontaneous deviatoric curvature, and tension in Figure 5A collapses onto a single curve (Supplementary Figure 6B) as a function of this effective tension. Simulations confirm that the radii of tubular necks obtained from numerical solutions collapse onto a single curve as a function of effective tension (Figure 5B).

FIGURE 5

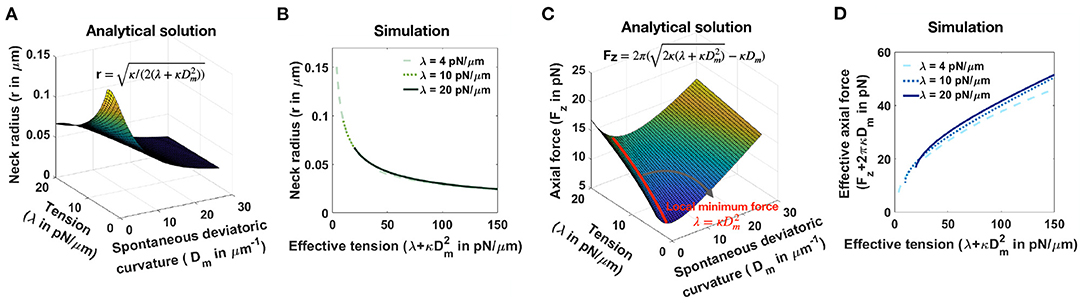
Figure 5. Effective tension including spontaneous deviatoric curvature regulates the neck radius and the magnitude of axial force in a tubular membrane. (A) Analytical solution for the neck radius of a tubular membrane as a function of spontaneous deviatoric curvature and tension ($\text{r}=\sqrt{\kappa /(2(\lambda +\kappa {\text{D}}_{\text{m}}^2))}$, Supplementary Equation 37). (B) The neck radius obtained from numerical solutions as a function of effective tension ($\lambda +\kappa {\text{D}}_{\text{m}}^2$). Here, for fixed three different tensions, we varied the effective tension by changing the spontaneous deviatoric curvature between $0<{\text{D}}_{\text{m}}<30\text{μ}{\text{m}}^{-1}$. The radii of the membrane necks collapse onto a single curve for different tensions. (C) Analytical solution for the magnitude of an axial force needed to maintain a tubular protrusion as a function of spontaneous deviatoric curvature and tension (${\text{F}}_{\text{z}}=2\pi (\sqrt{2\kappa (\lambda +\kappa {\text{D}}_{\text{m}}^2)}-\kappa {\text{D}}_{\text{m}})$, Supplementary Equation 37). The axial force needed to maintain a tubular protrusion has a local minimum along the red line where λ =$\kappa {\text{D}}_{\text{m}}^2$ (Supplementary Equation 39). (D) The effective axial force (F_z+2πκD_m) obtained from numerical solutions as a function of effective tension ($\lambda +\kappa {\text{D}}_{\text{m}}^2$). Here, for fixed three different tensions, we varied the effective tension by changing the spontaneous deviatoric curvature between $0<{\text{D}}_{\text{m}}<30\text{μ}{\text{m}}^{-1}$. Effective axial forces collapse onto a single curve for different tensions.

Similarly, the axial force required to maintain a tubular membrane with radius r and spontaneous deviatoric curvature D_m along the total length L, is given by ${\text{F}}_{\text{z}}=2\pi (\sqrt{2\kappa (\lambda +\kappa {\text{D}}_{\text{m}}^2)}-\kappa {\text{D}}_{\text{m}})$ (Supplementary Equation 37). In Figure 5C, we plotted the axial force as a function of tension and spontaneous deviatoric curvature. We found that for a fixed value of tension, the axial force has a local minimum along the red line (Figure 5C) where λ =$\kappa {\text{D}}_{\text{m}}^2$ (Supplementary Equation 38) and F_z,min = 2πκD_m (Supplementary Equation 38). The 3D surface in Figure 5C can be reduced to a single curve by defining the effective axial force as F_z+2πκD_m and plotting it as a function of effective tension (Supplementary Figure 6D). We also plotted the effective axial force obtained from numerical solutions as a function of effective tension (Figure 5D). We observed that consistent with the analytical prediction, for different tensions, the effective axial forces collapse onto a single curve as a function of effective tension (Figure 5D). These results suggest that effective tension ($\lambda +\kappa {\text{D}}_{\text{m}}^2$) regulates the radius of dendritic spine necks.

3.5. Cooperation of Forces and Induced Spontaneous Deviatoric Curvature Offers Multiple Pathways for Spine Shape Maintenance

Thus far, we have focused on the role of forces (axial and normal) on spine head shape and the role of spontaneous deviatoric curvature representing periodic rings on the spine neck radius. Next, we asked if the cooperation of these two different mechanisms could further influence the spine geometries and the energy landscape associated with these features. In other words, we asked if the combination of spontaneous deviatoric curvature and applied forces could result in lower energy states for the same spine geometry. To answer this question, we sought to identify the parameters that give rise to thin spines with the same geometric parameters. We explain this approach with a specific example below.

As noted before, when only normal forces are used, a normal force density of f_n = 382.23 pN/μm² under a tension of λ = 36 pN/μm is required to form a thin spine with a neck radius of r = 0.05 μm and head volume of V = 0.033 μm³ (Figure 6A, left). We can also obtain a thin spine with the same dimensions, by using a prescribed spontaneous deviatoric curvature D_m = 10 μm⁻¹ along the neck and an applied force density of f_n = 143.33 pN/μm² along the head for λ = 10 pN/μm (Figure 6A, right). Thus, for the same shape parameters, in the presence of spontaneous deviatoric curvature, the value of force density required is roughly one-third of the force density required in the absence of spontaneous deviatoric curvature (Figure 6A). Similarly, when a combination of axial force along the spine head and spontaneous deviatoric curvature along the neck is used, a thin spine with r ~ 0.05 μm and head volume V ~ 0.033 μm³ can be formed with F_z = 7.71 pN and spontaneous deviatoric curvature D_m = 10 μm⁻¹ when λ = 10 pN/μm (Figure 6B). Thus, in both these cases (axial and normal forces) for the formation of thin spines, we note that access to spontaneous deviatoric curvature significantly reduces the forces required to form and maintain thin spines.

FIGURE 6

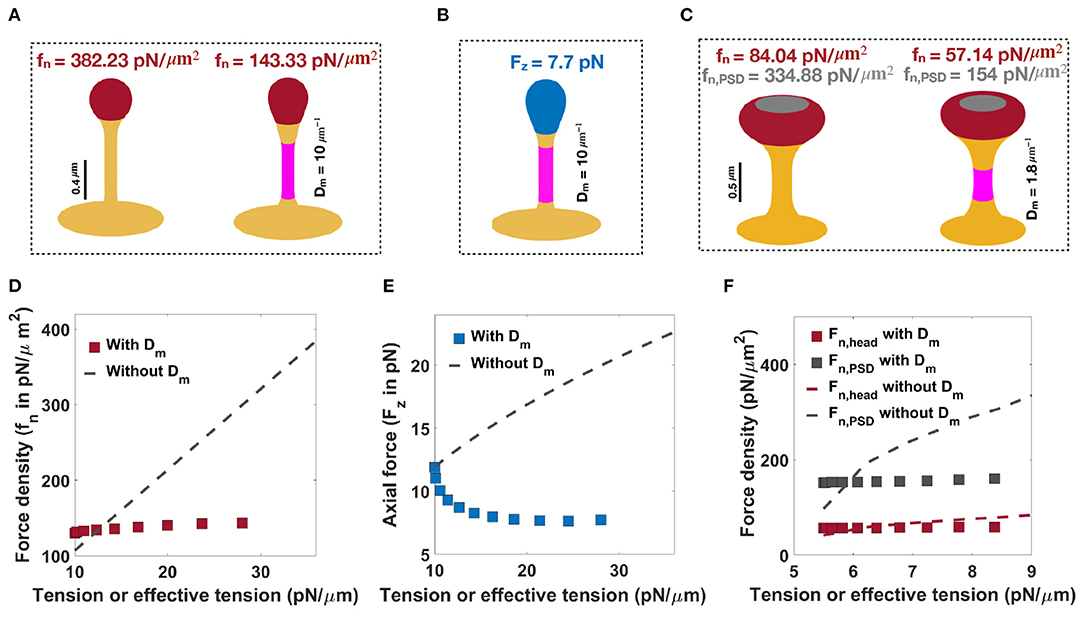
Figure 6. Formation of thin and mushroom shaped spines with a combination of forces and spontaneous deviatoric curvature. (A) Formation of a thin-shaped spine by applying a uniform normal force density along the spine head (left) vs. applying a uniform normal force density along the head and spontaneous deviatoric curvature (purple region) along the spine neck (right) (λ = 10 pN/μm). (B) Formation of a thin-shaped spine by applying an axial force along the spherical cap (blue region) and spontaneous deviatoric curvature along the spine neck (purple region), λ = 10 pN/μm. All thin spines in (A,B) have a neck radius r ~ 0.05 μm and head volume V ~ 0.033 μm³. (C) Formation of a mushroom-shaped spine by applying a non-uniform normal force density along the spine head (left) vs. applying a non-uniform normal force density along the head and spontaneous deviatoric curvature along the spine neck (purple region), (right), λ = 5.5 pN/μm. The formed mushroom spine with normal force densities f_n = 57.14 pN/μm² and f_n,PSD = 154 pN/μm² and deviatoric curvature D_m = 1.8 μm⁻¹ has a neck radius r ~ 0.1 μm and head volume V ~ 0.27 μm³. (D) The magnitude of a normal force density that is required to form a thin-shaped spine with and without spontaneous deviatoric curvature as a function of effective tension and tension, respectively. (E) The magnitude of an axial force that is required to form a thin-shaped spine with and without spontaneous deviatoric curvature as a function of effective tension and tension, respectively. (F) The magnitude of normal force densities in the spine head and in PSD that is required to form a mushroom spine with and without spontaneous deviatoric curvature as a function of effective tension and tension, respectively.

Not surprisingly, these same results hold for mushroom-shaped spines too. As we have shown before, to form a mushroom spine with a neck radius of r = 0.1 μm and head volume of V ~ 0.25 μm³, normal force densities of f_n = 84.04 pN/μm² along the spine head and f_n,PSD = 334.88 pN/μm² along the PSD are required under a tension of λ = 9 pN/μm (Figure 6C, left). We can also form a mushroom spine with the same dimensions and lower tension (λ = 5.5 pN/μm) by prescribing a spontaneous deviatoric curvature D_m = 1.8 μm⁻¹ along the spine neck and normal force densities of f_n = 57.14 pN/μm² and f_n,PSD = 154 pN/μm² along the spine head and PSD, respectively (Figure 6C, right).

In Figures 6D–F, we plotted the magnitude of forces that are required to form thin and mushroom-shaped spines with or without spontaneous deviatoric curvature as a function of tension alone (with no spontaneous deviatoric curvature) or effective tension (with spontaneous deviatoric curvature). We observed that with increasing effective tension, the magnitude of the normal force density that is required to form a thin spine with spontaneous deviatoric curvature (red squares) is almost constant (Figure 6D). However, the magnitude of the normal force density that is needed to form a thin spine without spontaneous deviatoric curvature (dashed line) increases linearly with increasing tension (Equation (7) and Figure 6D). In the case of the formation of a thin spine with an axial force, we found that in the presence of spontaneous deviatoric curvature, the magnitude of axial force (blue squares) decreases slightly and then becomes constant with increasing effective tension (Figure 6E). In contrast, without spontaneous deviatoric curvature, the magnitude of axial force (dashed line) increases with increasing tension (Figure 6E). Similar to the thin-shaped spine, with spontaneous deviatoric curvature along the spine neck, the magnitude of normal force densities in the head (red square) and PSD (gray square) region that are required to form a mushroom spine is almost constant with increasing effective tension (Figure 6F). However, without spontaneous deviatoric curvature, the magnitude of force densities in both regions increases with increasing tension (Figure 6F).

To further compare thin and mushroom spines shown in Figure 6, we computed the components of energy (Equation 1) and the total energy of the system for each shape (Supplementary Tables 2, 3 and Figures 7C,D). Based on our results, by prescribing spontaneous deviatoric curvature D_m along the spine neck, the bending energy due to deviatoric curvature decreases (Supplementary Tables 2, 3). This is because the deviatoric curvature D along the neck tends to D_m and minimizes the bending energy (Supplementary Tables 2, 3). Additionally, in the presence of spontaneous deviatoric curvature, in our simulation, we set the tension to lower values compared to the condition that D_m = 0. Therefore, the work that is done by tension and forces to bend the membrane reduces for the case that the spines obtained with a combination of force and spontaneous deviatoric curvature (Supplementary Tables 2, 3). For example, to form a thin spine shown in Figure 6, the work that is done by an axial force with a spontaneous deviatoric curvature (Figure 6B) is almost one third of the work that is done by a normal force without spontaneous deviatoric curvature (Figure 6A and Supplementary Tables 2, 3).

FIGURE 7

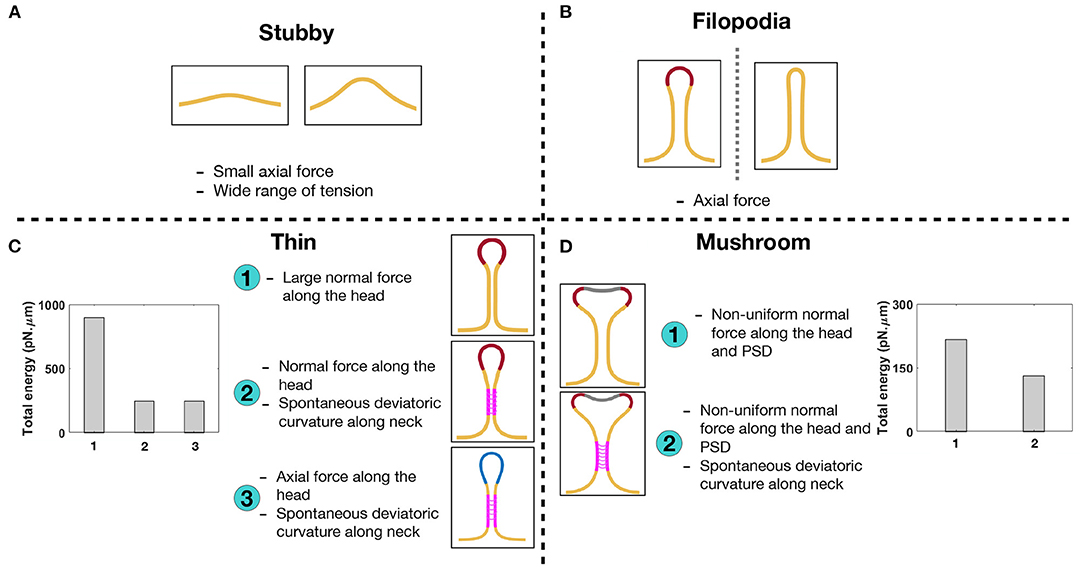
Figure 7. Characterizing different shapes of dendritic spines based on the mechanical model. (A) Stubby spines can be formed with an axial force and in a wide range of tensions. (B) An axial force is sufficient to form a long filopodial spine. (C) A thin-shaped spine can be formed with three different mechanisms; (1) a uniform normal force density along the spine head, (2) a uniform normal force density along the spine head and spontaneous deviatoric curvature along the neck, and (3) a uniform axial force density along the spine head and spontaneous deviatoric curvature along the neck. In the bar plot, the total energy of the system is shown for three different mechanisms. The total energy of the system for the second and third mechanisms with spontaneous deviatoric curvature is much less than the energy for the first mechanism with just a normal force. (D) A mushroom-shaped spine can be formed with two different mechanisms; (1) a non-uniform normal force density along the spine head and PSD region and (2) a non-uniform normal force density along the spine head and PSD region plus a spontaneous deviatoric curvature along the spine neck. The resulting mushroom spine with a combination of normal forces and spontaneous deviatoric curvature has lower energy compared to the spine that is formed with just normal forces (bar graph).

In the bar plots of Figures 7C,D, we compared the total energy of thin and mushroom spines formed with different mechanisms. We observed that in both thin and mushroom spines, the total energy of the system dramatically decreases when the spines form with a combination of forces and spontaneous deviatoric curvature (Figures 7C,D). This result suggests that spontaneous deviatoric curvature can alter the energy landscape of thin and mushroom dendritic spines to a lower energy state.

4. Discussion

Previous studies have showed that the coupled dynamics of signaling and actin remodeling can alter spine volume in a biophysical model (Rangamani et al., 2016) without considering the geometry of the spines or considering the role of spine shape in regulating different signaling pathways (Colgan and Yasuda, 2014; Yasuda, 2017; Bell et al., 2019; Rahmaninejad et al., 2020). In this work, we present a simplified mechanical model for studying the role of different force distributions and energy contributions that are associated with the different spine shapes noted in the literature. Our results show that different spine shapes can be associated with different forces and spontaneous deviatoric curvature distributions, giving us insight into the mechanical design principles of spine formation and maintenance (Figure 7).

We show that stubby spines can be formed for a wide range of tensions and low forces (Figure 2). From a spine formation viewpoint, this makes sense, since during development the stubby spines can be the initial protrusions that form out of the dendrites. Given the ubiquitous nature of stubby spines (Gray, 1959; Fiala et al., 1998; Harris, 1999), our results suggest that the prevalence of stubby spines could be due to the mechanical ease which they can be formed. They may also represent a temporarily stable state adopted by shrinking spines during synapse removal. Filopodia have the same force-length and force-radius relationships as membrane tubules that can be formed with micropipettes (Evans et al., 1996), optical tweezers (Raucher and Sheetz, 1999), or by kinesin motor proteins (Roux et al., 2002) (Figure 2).

Based on our results, dendritic filopodia can be formed with a relatively small axial force, which make them good candidates as initial protrusions for the formation of mature thin and mushroom spines. Thin and mushroom spines, which have defined head shapes, require more mechanical features—heterogeneous force distributions, normal or axial forces, and an induced spontaneous deviatoric curvature representing the periodic protein rings or other deviatoric curvature inducing mechanics along the neck. The heterogeneous distribution of actin-mediated forces and BAR domain proteins can be related to the nanoscale organization of actin filaments and protein phase separation on the membrane surface (Nowak et al., 2021; Yuan et al., 2021).

In the case of thin spines, we find that the mechanical design principles that support the formation of a spherical head are (1) large normal force along the head (Figure 3), (2) normal force along the head with a spontaneous deviatoric curvature along the neck (Figure 6A), and (3) an axial force along the head with a spontaneous deviatoric curvature along the neck (Figure 6B). Within these mechanisms, the presence of spontaneous deviatoric curvature significantly reduces the total energy of the spine (Figure 7C). Similarly, for mushroom spines, in addition to non-uniform forces along the head and the PSD (Figure 4), the spine can be formed with a combination of forces in the head and spontaneous deviatoric curvature along the neck (Figure 6C) while the spontaneous deviatoric curvature results in a lower energy state (Figure 7D).

These findings have implications for our understanding of how mechanical aspects of membrane dynamics such as bending, tension, membrane-protein interactions, and interactions of the membrane with the cytoskeleton play critical roles in spine geometry maintenance, particularly in structural plasticity. Many of the events associated with synaptic plasticity alter spine size and shape through changes in F-actin dynamics and the dynamics of the actin related proteins (Landis and Reese, 1983; Hotulainen and Hoogenraad, 2010; Bertling and Hotulainen, 2017). The net impact of changes in actin remodeling would likely result in changes in force distribution.

Another important and, as yet, under explored aspect of synaptic plasticity is the role of cortical membrane tension, including the effect of the membrane in-plane stresses and membrane-cytoskeleton interactions. We know that spines are sites of active vesicle trafficking events, such as endo- and exocytosis, and that these processes alter the membrane surface area and thereby alter the membrane tension (Blanpied et al., 2002; Collingridge et al., 2004). Here, we show that the effective membrane tension can play an important role in altering the energy required for the maintenance of different spine shapes. One of the main impacts of such effective tension is that because of the cooperative effects of spontaneous deviatoric curvature and the applied forces, the energy required to maintain certain spine shapes may be lower. Thus, we show that there are different mechanical pathways that are likely associated with the different spine shapes and that some mechanisms may be energetically more favorable than others.

Despite these insights, our model has certain limitations. We do not explicitly consider the remodeling of the actin network or the dynamics of the associated proteins, but use force as a lumped parameter. Additionally, the use of axisymmetric coordinates restricts our ability to obtain realistic spine shapes (Lee et al., 2020).

The impact of mechanical aspects of actin remodeling and membrane mechanics on structural plasticity is highly intriguing and we are only beginning to understand their effects on spine functionality. This complexity is immediately apparent in dendritic spines, which undergo dynamic changes, both mechanical and biochemical during structural plasticity spatiotemporal scales. For example, it is known that electromagnetic forces can alter membrane shape either through signaling or direct forces (Tasaki and Byrne, 1992; El Hady and Machta, 2015). The change in the geometry of the spine affects the membrane capacitance and ultimately neural activities (Ma et al., 2019). While in our model we do not consider the induced forces from time-dependent neural activities such as a change in membrane potential, the electrostatic contributions have been implicitly considered in the membrane elastic properties and induced spontaneous curvatures (Winterhalter and Helfrich, 1988; Andelman, 1995; Steigmann and Agrawal, 2016; Tarun et al., 2020). We believe that our minimal model provides insights into the possible mechanical aspects underlying the characteristic geometries associated with dendritic spines. This is an important step toward deciphering the intricate mechanochemistry of structural plasticity and dendritic spine development.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

HA and PR conceived the research. HA, MB, and PR conducted the research and analyzed the data. HA, MB, SH, and PR wrote the paper. All authors reviewed the manuscript and agreed on the contents of the paper.

Funding

This work was supported by Air Force Office of Scientific Research FA9550-18-1-0051 to PR and MB was supported by a National Defense Science and Engineering Graduate (NDSEG) Fellowship.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Dr. Christopher Lee, Can Uysalel, Arijit Mahapatra, and Andrew Nguyen for critical discussions and feedback on the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2021.657074/full#supplementary-material

References

Agrawal, A., and Steigmann, D. J. (2009). Modeling protein-mediated morphology in biomembranes. Biomech. Model. Mechanobiol. 8, 371–379. doi: 10.1007/s10237-008-0143-0

CrossRef Full Text | Google Scholar

Alimohamadi, H., Ovryn, B., and Rangamani, P. (2020a). Modeling membrane nanotube morphology: the role of heterogeneity in composition and material properties. Sci. Rep. 10, 1–15. doi: 10.1038/s41598-020-59221-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Alimohamadi, H., and Rangamani, P. (2018). Modeling membrane curvature generation due to membrane-protein interactions. Biomolecules 8:120. doi: 10.3390/biom8040120

CrossRef Full Text | Google Scholar

Alimohamadi, H., Smith, A. S., Nowak, R. B., Fowler, V. M., and Rangamani, P. (2020b). Non-uniform distribution of myosin-mediated forces governs red blood cell membrane curvature through tension modulation. PLoS Comput. Biol. 16:e1007890. doi: 10.1371/journal.pcbi.1007890

PubMed Abstract | CrossRef Full Text | Google Scholar

Alimohamadi, H., Vasan, R., Hassinger, J., Stachowiak, J. C., and Rangamani, P. (2018). The role of traction in membrane curvature generation. Mol. Biol. Cell 29, 2024–2035. doi: 10.1091/mbc.E18-02-0087

PubMed Abstract | CrossRef Full Text | Google Scholar

Andelman, D. (1995). “Electrostatic properties of membranes: the Poisson-Boltzmann theory,” in Handbook of Biological Physics 1, Vol. 1, eds R. Lipowsky and E. Sackmann (Amsterdam: Elsevier), 603–642. doi: 10.1016/S1383-8121(06)80005-9

CrossRef Full Text | Google Scholar

Arellano, J. I., Benavides-Piccione, R., DeFelipe, J., and Yuste, R. (2007). Ultrastructure of dendritic spines: correlation between synaptic and spine morphologies. Front. Neurosci. 1, 131–143. doi: 10.3389/neuro.01.1.1.010.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashby, M. C., Maier, S. R., Nishimune, A., and Henley, J. M. (2006). Lateral diffusion drives constitutive exchange of AMPA receptors at dendritic spines and is regulated by spine morphology. J. Neurosci. 26, 7046–7055. doi: 10.1523/JNEUROSCI.1235-06.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Atilgan, E., Wirtz, D., and Sun, S. X. (2006). Mechanics and dynamics of actin-driven thin membrane protrusions. Biophys. J. 90, 65–76. doi: 10.1529/biophysj.105.071480

PubMed Abstract | CrossRef Full Text | Google Scholar

Bär, J., Kobler, O., Van Bommel, B., and Mikhaylova, M. (2016). Periodic f-actin structures shape the neck of dendritic spines. Sci. Rep. 6:37136. doi: 10.1038/srep37136

PubMed Abstract | CrossRef Full Text | Google Scholar

Barfod, E. T., Moore, A. L., Van de Graaf, B. G., and Lidofsky, S. D. (2011). Myosin light chain kinase and src control membrane dynamics in volume recovery from cell swelling. Mol. Biol. Cell 22, 634–650. doi: 10.1091/mbc.e10-06-0514

PubMed Abstract | CrossRef Full Text | Google Scholar

Bear, M. F., and Malenka, R. C. (1994). Synaptic plasticity: LTP and LTD. Curr. Opin. Neurobiol. 4, 389–399. doi: 10.1016/0959-4388(94)90101-5

CrossRef Full Text | Google Scholar

Bell, M., Bartol, T., Sejnowski, T., and Rangamani, P. (2019). Dendritic spine geometry and spine apparatus organization govern the spatiotemporal dynamics of calcium. J. Gen. Physiol. 151, 1017–1034. doi: 10.1085/jgp.201812261

PubMed Abstract | CrossRef Full Text | Google Scholar

Berry, K. P., and Nedivi, E. (2017). Spine dynamics: are they all the same? Neuron 96, 43–55. doi: 10.1016/j.neuron.2017.08.008

CrossRef Full Text | Google Scholar

Bertling, E., and Hotulainen, P. (2017). New waves in dendritic spine actin cytoskeleton: From branches and bundles to rings, from actin binding proteins to post-translational modifications. Mol. Cell. Neurosci. 84, 77–84. doi: 10.1016/j.mcn.2017.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Blanpied, T. A., Scott, D. B., and Ehlers, M. D. (2002). Dynamics and regulation of clathrin coats at specialized endocytic zones of dendrites and spines. Neuron 36, 435–449. doi: 10.1016/S0896-6273(02)00979-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonilla-Quintana, M., Wörgötter, F., Tetzlaff, C., and Fauth, M. (2020). Modeling the shape of synaptic spines by their actin dynamics. Front. Synaptic Neurosci. 12:9. doi: 10.3389/fnsyn.2020.00009

PubMed Abstract | CrossRef Full Text | Google Scholar

Borisy, G. G., and Svitkina, T. M. (2000). Actin machinery: pushing the envelope. Curr. Opin. Cell Biol. 12, 104–112. doi: 10.1016/S0955-0674(99)00063-0

CrossRef Full Text | Google Scholar

Bosch, M., and Hayashi, Y. (2012). Structural plasticity of dendritic spines. Curr. Opin. Neurobiol. 22, 383–388. doi: 10.1016/j.conb.2011.09.002

CrossRef Full Text | Google Scholar

Bourne, J., and Harris, K. M. (2007). Do thin spines learn to be mushroom spines that remember? Curr. Opin. Neurobiol. 17, 381–386. doi: 10.1016/j.conb.2007.04.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Bucher, M., Fanutza, T., and Mikhaylova, M. (2020). Cytoskeletal makeup of the synapse: shaft versus spine. Cytoskeleton 77, 55–64. doi: 10.1002/cm.21583

PubMed Abstract | CrossRef Full Text | Google Scholar

Calabrese, B., and Halpain, S. (2005). Essential role for the pkc target marcks in maintaining dendritic spine morphology. Neuron 48, 77–90. doi: 10.1016/j.neuron.2005.08.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Calabrese, B., Wilson, M. S., and Halpain, S. (2006). Development and regulation of dendritic spine synapses. Physiology 21, 38–47. doi: 10.1152/physiol.00042.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Canham, P. B. (1970). The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theoret. Biol. 26, 61–81. doi: 10.1016/S0022-5193(70)80032-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Carlson, B. R., Lloyd, K. E., Kruszewski, A., Kim, I.-H., Rodriguiz, R. M., Heindel, C., et al. (2011). WRP/srGAP3 facilitates the initiation of spine development by an inverse F-BAR domain, and its loss impairs long-term memory. J. Neurosci. 31, 2447–2460. doi: 10.1523/JNEUROSCI.4433-10.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Colgan, L. A., and Yasuda, R. (2014). Plasticity of dendritic spines: subcompartmentalization of signaling. Annu. Rev. Physiol. 76, 365–385. doi: 10.1146/annurev-physiol-021113-170400

PubMed Abstract | CrossRef Full Text | Google Scholar

Collingridge, G. L., Isaac, J. T., and Wang, Y. T. (2004). Receptor trafficking and synaptic plasticity. Nat. Rev. Neurosci. 5, 952–962. doi: 10.1038/nrn1556

CrossRef Full Text | Google Scholar

Dailey, M. E., and Smith, S. J. (1996). The dynamics of dendritic structure in developing hippocampal slices. J. Neurosci. 16, 2983–2994. doi: 10.1523/JNEUROSCI.16-09-02983.1996

PubMed Abstract | CrossRef Full Text | Google Scholar

Derényi, I., Jülicher, F., and Prost, J. (2002). Formation and interaction of membrane tubes. Phys. Rev. Lett. 88:238101. doi: 10.1103/PhysRevLett.88.238101

CrossRef Full Text | Google Scholar

Deuling, H., and Helfrich, W. (1976). Red blood cell shapes as explained on the basis of curvature elasticity. Biophys. J. 16, 861–868. doi: 10.1016/S0006-3495(76)85736-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Diz-Muñoz, A., Fletcher, D. A., and Weiner, O. D. (2013). Use the force: membrane tension as an organizer of cell shape and motility. Trends Cell Biol. 23, 47–53. doi: 10.1016/j.tcb.2012.09.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebrahimi, S., and Okabe, S. (2014). Structural dynamics of dendritic spines: molecular composition, geometry and functional regulation. Biochim. Biophys. Acta Biomemb. 10, 2391–2398. doi: 10.1016/j.bbamem.2014.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

El Hady, A., and Machta, B. B. (2015). Mechanical surface waves accompany action potential propagation. Nat. Commun. 6, 1–7. doi: 10.1038/ncomms7697

PubMed Abstract | CrossRef Full Text | Google Scholar

Engert, F., and Bonhoeffer, T. (1999). Dendritic spine changes associated with hippocampal long-term synaptic plasticity. Nature 399:66. doi: 10.1038/19978

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, E., Bowman, H., Leung, A., Needham, D., and Tirrell, D. (1996). Biomembrane templates for nanoscale conduits and networks. Science 273, 933–935. doi: 10.1126/science.273.5277.933

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, E. A. (2018). Mechanics and Thermodynamics of Biomembranes. Boca Raton, FL: CRC Press. doi: 10.1201/9781351074339

CrossRef Full Text | Google Scholar

Fiala, J. C., Feinberg, M., Popov, V., and Harris, K. M. (1998). Synaptogenesis via dendritic filopodia in developing hippocampal area CA1. J. Neurosci. 18, 8900–8911. doi: 10.1523/JNEUROSCI.18-21-08900.1998

PubMed Abstract | CrossRef Full Text | Google Scholar

Fifkova, E. (1985). A possible mechanism of morphometric changes in dendritic spines induced by stimulation. Cell. Mol. Neurobiol. 5, 47–63. doi: 10.1007/BF00711085

PubMed Abstract | CrossRef Full Text | Google Scholar

Frost, A., Perera, R., Roux, A., Spasov, K., Destaing, O., Egelman, E. H., et al. (2008). Structural basis of membrane invagination by F-BAR domains. Cell 132, 807–817. doi: 10.1016/j.cell.2007.12.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Frost, A., Unger, V. M., and De Camilli, P. (2009). The bar domain superfamily: membrane-molding macromolecules. Cell 137, 191–196. doi: 10.1016/j.cell.2009.04.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Frost, N. A., Shroff, H., Kong, H., Betzig, E., and Blanpied, T. A. (2010). Single-molecule discrimination of discrete perisynaptic and distributed sites of actin filament assembly within dendritic spines. Neuron 67, 86–99. doi: 10.1016/j.neuron.2010.05.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganeshina, O., Berry, R., Petralia, R., Nicholson, D., and Geinisman, Y. (2004). Synapses with a segmented, completely partitioned postsynaptic density express more AMPA receptors than other axospinous synaptic junctions. Neuroscience 125, 615–623. doi: 10.1016/j.neuroscience.2004.02.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Gray, E. G. (1959). Electron microscopy of synaptic contacts on dendrite spines of the cerebral cortex. Nature 183, 1592–1593. doi: 10.1038/1831592a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Grutzendler, J., Kasthuri, N., and Gan, W.-B. (2002). Long-term dendritic spine stability in the adult cortex. Nature 420, 812–816. doi: 10.1038/nature01276

PubMed Abstract | CrossRef Full Text | Google Scholar

Halpain, S. (2000). Actin and the agile spine: how and why do dendritic spines dance? Trends Neurosci. 23, 141–146. doi: 10.1016/S0166-2236(00)01576-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, K. M. (1999). Structure, development, and plasticity of dendritic spines. Curr. Opin. Neurobiol. 9, 343–348. doi: 10.1016/S0959-4388(99)80050-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, K. M., Fiala, J. C., and Ostroff, L. (2003). Structural changes at dendritic spine synapses during long-term potentiation. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 358, 745–748. doi: 10.1098/rstb.2002.1254

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, K. M., Jensen, F. E., and Tsao, B. (1992). Three-dimensional structure of dendritic spines and synapses in rat hippocampus (CA1) at postnatal day 15 and adult ages: implications for the maturation of synaptic physiology and long-term potentiation. J. Neurosci. 12, 2685–2705. doi: 10.1523/JNEUROSCI.12-07-02685.1992

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, K. M., and Kater, S. (1994). Dendritic spines: cellular specializations imparting both stability and flexibility to synaptic function. Annu. Rev. Neurosci. 17, 341–371. doi: 10.1146/annurev.ne.17.030194.002013

PubMed Abstract | CrossRef Full Text | Google Scholar

Helfrich, W. (1973). Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforschung C 28-12, 693–703. doi: 10.1515/znc-1973-11-1209

PubMed Abstract | CrossRef Full Text | Google Scholar

Hlushchenko, I., Koskinen, M., and Hotulainen, P. (2016). Dendritic spine actin dynamics in neuronal maturation and synaptic plasticity. Cytoskeleton 73, 435–441. doi: 10.1002/cm.21280

PubMed Abstract | CrossRef Full Text | Google Scholar

Holtmaat, A. J., Trachtenberg, J. T., Wilbrecht, L., Shepherd, G. M., Zhang, X., Knott, G. W., et al. (2005). Transient and persistent dendritic spines in the neocortex in vivo. Neuron 45, 279–291. doi: 10.1016/j.neuron.2005.01.003

CrossRef Full Text | Google Scholar

Hotulainen, P., and Hoogenraad, C. C. (2010). Actin in dendritic spines: connecting dynamics to function. J. Cell Biol. 189, 619–629. doi: 10.1083/jcb.201003008

PubMed Abstract | CrossRef Full Text | Google Scholar

Hotulainen, P., Llano, O., Smirnov, S., Tanhuanpää, K., Faix, J., Rivera, C., et al. (2009). Defining mechanisms of actin polymerization and depolymerization during dendritic spine morphogenesis. J. Cell Biol. 185, 323–339. doi: 10.1083/jcb.200809046

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, M., Briguglio, J. J., and Deserno, M. (2012). Determining the gaussian curvature modulus of lipid membranes in simulations. Biophys. J. 102, 1403–1410. doi: 10.1016/j.bpj.2012.02.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Iglič, A., Babnik, B., Bohinc, K., Fošnarič, M., Hägerstrand, H., and Kralj-Iglič, V. (2007). On the role of anisotropy of membrane constituents in formation of a membrane neck during budding of a multicomponent membrane. J. Biomech. 40, 579–585. doi: 10.1016/j.jbiomech.2006.02.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Iglič, A., Babnik, B., Gimsa, U., and Kralj-Iglič, V. (2005). On the role of membrane anisotropy in the beading transition of undulated tubular membrane structures. J Phys. A Math. Gen. 38:8527. doi: 10.1088/0305-4470/38/40/004

CrossRef Full Text | Google Scholar

Iglič, A., Hägerstrand, H., Veranič, P., Plemenitaš, A., and Kralj-Iglič, V. (2006). Curvature-induced accumulation of anisotropic membrane components and raft formation in cylindrical membrane protrusions. J. Theoret. Biol. 240, 368–373. doi: 10.1016/j.jtbi.2005.09.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Iglič, A., Kralj-Iglič, V., and Majhenc, J. (1999). Cylindrical shapes of closed lipid bilayer structures correspond to an extreme area difference between the two monolayers of the bilayer. J. Biomech. 32, 1343–1347. doi: 10.1016/S0021-9290(99)00136-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kabaso, D., Bobrovska, N., Góźdź, W., Gov, N., Kralj-Iglič, V., Veranič, P., et al. (2012). On the role of membrane anisotropy and bar proteins in the stability of tubular membrane structures. J. Biomech. 45, 231–238. doi: 10.1016/j.jbiomech.2011.10.039

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanjhan, R., Noakes, P. G., and Bellingham, M. C. (2016). Emerging roles of filopodia and dendritic spines in motoneuron plasticity during development and disease. Neural Plastic. 2016, 1–31. doi: 10.1155/2016/3423267

PubMed Abstract | CrossRef Full Text | Google Scholar

Kasai, H., Matsuzaki, M., Noguchi, J., Yasumatsu, N., and Nakahara, H. (2003). Structure-stability-function relationships of dendritic spines. Trends Neurosci. 26, 360–368. doi: 10.1016/S0166-2236(03)00162-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kashiwagi, Y., Higashi, T., Obashi, K., Sato, Y., Komiyama, N. H., Grant, S. G., et al. (2019). Computational geometry analysis of dendritic spines by structured illumination microscopy. Nat. Commun. 10, 1–14. doi: 10.1038/s41467-019-09337-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kessels, M. M., and Qualmann, B. (2015). Different functional modes of bar domain proteins in formation and plasticity of mammalian postsynapses. J. Cell Sci. 128, 3177–3185. doi: 10.1242/jcs.174193

PubMed Abstract | CrossRef Full Text | Google Scholar

Koleske, A. J. (2013). Molecular mechanisms of dendrite stability. Nat. Rev. Neurosci. 14, 536–550. doi: 10.1038/nrn3486

CrossRef Full Text | Google Scholar

Korobova, F., and Svitkina, T. (2010). Molecular architecture of synaptic actin cytoskeleton in hippocampal neurons reveals a mechanism of dendritic spine morphogenesis. Mol. Biol. Cell 21, 165–176. doi: 10.1091/mbc.e09-07-0596

PubMed Abstract | CrossRef Full Text | Google Scholar

Kralj-Iglič, V., Heinrich, V., Svetina, S., and Žekš, B. (1999). Free energy of closed membrane with anisotropic inclusions. Eur. Phys. J. B Cond. Matter Complex Syst. 10, 5–8. doi: 10.1007/s100510050822

CrossRef Full Text | Google Scholar

Kralj-Iglič, V., Iglič, A., Hägerstrand, H., and Peterlin, P. (2000). Stable tubular microexovesicles of the erythrocyte membrane induced by dimeric amphiphiles. Phys. Rev. E 61:4230. doi: 10.1103/PhysRevE.61.4230

PubMed Abstract | CrossRef Full Text | Google Scholar

Kralj-Iglič, V., Svetina, S., and Žekš, B. (1996). Shapes of bilayer vesicles with membrane embedded molecules. Eur. Biophys. J. 24, 311–321. doi: 10.1007/BF00180372

PubMed Abstract | CrossRef Full Text | Google Scholar

Landis, D., and Reese, T. S. (1983). Cytoplasmic organization in cerebellar dendritic spines. J. Cell biol. 97, 1169–1178. doi: 10.1083/jcb.97.4.1169

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C. T., Laughlin, J. G., de La Beaumelle, N. A., Amaro, R. E., McCammon, J. A., Ramamoorthi, R., et al. (2020). 3D mesh processing using gamer 2 to enable reaction-diffusion simulations in realistic cellular geometries. PLoS Comput. Biol. 16:e1007756. doi: 10.1371/journal.pcbi.1007756

PubMed Abstract | CrossRef Full Text | Google Scholar

Lokar, M., Kabaso, D., Resnik, N., Sepčić, K., Kralj-Iglič, V., Veranič, P., et al. (2012). The role of cholesterol-sphingomyelin membrane nanodomains in the stability of intercellular membrane nanotubes. Int. J. Nanomed. 7:1891. doi: 10.2147/IJN.S28723

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, J., and Yang, Z.-Q, Yang, L.-J, Tang, J. (2019). A physical view of computational neurodynamics. J. Zhejiang Univ. Sci. A 20, 639–659. doi: 10.1631/jzus.A1900273

CrossRef Full Text | Google Scholar

Matsuzaki, M., Ellis-Davies, G. C., Nemoto, T., Miyashita, Y., Iino, M., and Kasai, H. (2001). Dendritic spine geometry is critical for AMPA receptor expression in hippocampal CA1 pyramidal neurons. Nat. Neurosci. 4:1086. doi: 10.1038/nn736

PubMed Abstract | CrossRef Full Text | Google Scholar

Miermans, C., Kusters, R., Hoogenraad, C., and Storm, C. (2017). Biophysical model of the role of actin remodeling on dendritic spine morphology. PLoS ONE 12:e0170113. doi: 10.1371/journal.pone.0170113

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, M., and Peters, A. (1981). Maturation of rat visual cortex. II. A combined golgi-electron microscope study of pyramidal neurons. J. Comp. Neurol. 203, 555–573. doi: 10.1002/cne.902030402

PubMed Abstract | CrossRef Full Text | Google Scholar

Mogilner, A., and Oster, G. (1996). Cell motility driven by actin polymerization. Biophys. J. 71, 3030–3045. doi: 10.1016/S0006-3495(96)79496-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakahata, Y., and Yasuda, R. (2018). Plasticity of spine structure: local signaling, translation and cytoskeletal reorganization. Front. Synaptic Neurosci. 10:29. doi: 10.3389/fnsyn.2018.00029

PubMed Abstract | CrossRef Full Text | Google Scholar

Nanguneri, S., Pramod, R., Efimova, N., Das, D., Jose, M., Svitkina, T., et al. (2019). Characterization of nanoscale organization of f-actin in morphologically distinct dendritic spines in vitro using supervised learning. eNeuro 6, 1–13. doi: 10.1523/ENEURO.0425-18.2019

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishiyama, J. (2019). Plasticity of dendritic spines: molecular function and dysfunction in neurodevelopmental disorders. Psychiatry Clin. Neurosci. 73, 541–550. doi: 10.1111/pcn.12899

PubMed Abstract | CrossRef Full Text | Google Scholar

Nowak, R. B., Alimohamadi, H., Pestonjamasp, K., Rangamani, P., and Fowler, V. M. (2021). Nanoscale organization of actin filaments in the red blood cell membrane skeleton. bioRxiv. 1, 1–52. doi: 10.1101/2021.03.07.434292

CrossRef Full Text | Google Scholar

Orly, G., Naoz, M., and Gov, N. (2014). Physical model for the geometry of actin-based cellular protrusions. Biophys. J. 107, 576–587. doi: 10.1016/j.bpj.2014.05.040

PubMed Abstract | CrossRef Full Text | Google Scholar

Ostroff, L. E., Fiala, J. C., Allwardt, B., and Harris, K. M. (2002). Polyribosomes redistribute from dendritic shafts into spines with enlarged synapses during LTP in developing rat hippocampal slices. Neuron 35, 535–545. doi: 10.1016/S0896-6273(02)00785-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Patterson, M., and Yasuda, R. (2011). Signalling pathways underlying structural plasticity of dendritic spines. Brit. J. Pharmacol. 163, 1626–1638. doi: 10.1111/j.1476-5381.2011.01328.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Peskin, C. S., Odell, G. M., and Oster, G. F. (1993). Cellular motions and thermal fluctuations: the brownian ratchet. Biophys. J. 65, 316–324. doi: 10.1016/S0006-3495(93)81035-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Peter, B. J., Kent, H. M., Mills, I. G., Vallis, Y., Butler, P. J. G., Evans, P. R., et al. (2004). Bar domains as sensors of membrane curvature: the amphiphysin bar structure. Science 303, 495–499. doi: 10.1126/science.1092586

PubMed Abstract | CrossRef Full Text | Google Scholar

Peters, A., and Kaiserman-Abramof, I. R. (1970). The small pyramidal neuron of the rat cerebral cortex. The perikaryon, dendrites and spines. Am. J. Anat. 127, 321–355. doi: 10.1002/aja.1001270402

PubMed Abstract | CrossRef Full Text | Google Scholar

Petrak, L. J., Harris, K. M., and Kirov, S. A. (2005). Synaptogenesis on mature hippocampal dendrites occurs via filopodia and immature spines during blocked synaptic transmission. J. Comp. Neurol. 484, 183–190. doi: 10.1002/cne.20468

PubMed Abstract | CrossRef Full Text | Google Scholar

Pontes, B., Ayala, Y., Fonseca, A. C. C., Romao, L. F., Amaral, R. F., Salgado, L. T., et al. (2013). Membrane elastic properties and cell function. PLoS ONE 8:e67708. doi: 10.1371/journal.pone.0067708

PubMed Abstract | CrossRef Full Text | Google Scholar

Powers, T. R., Huber, G., and Goldstein, R. E. (2002). Fluid-membrane tethers: minimal surfaces and elastic boundary layers. Phys. Rev. E 65:041901. doi: 10.1103/PhysRevE.65.041901

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahmaninejad, H., Pace, T., Bhatt, S., Sun, B., and Kekenes-Huskey, P. (2020). Co-localization and confinement of ecto-nucleotidases modulate extracellular adenosine nucleotide distributions. PLoS Comput. Biol. 16:e1007903. doi: 10.1371/journal.pcbi.1007903

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahmaninejad, H., and Vaughan, D. D. (2021). Effect of membrane cholesterol on dynamical properties of solvent molecules. bioRxiv. 1, 1–8. doi: 10.1101/2021.02.19.432063

CrossRef Full Text | Google Scholar

Rangamani, P., Levy, M. G., Khan, S., and Oster, G. (2016). Paradoxical signaling regulates structural plasticity in dendritic spines. Proc. Natl. Acad. Sci. U.S.A. 113, E5298–E5307. doi: 10.1073/pnas.1610391113

PubMed Abstract | CrossRef Full Text | Google Scholar

Rao, A., and Craig, A. M. (2000). Signaling between the actin cytoskeleton and the postsynaptic density of dendritic spines. Hippocampus 10, 527–541. doi: 10.1002/1098-1063(2000)10:5<527::AID-HIPO3>3.0.CO;2-B

PubMed Abstract | CrossRef Full Text | Google Scholar

Raucher, D., and Sheetz, M. P. (1999). Characteristics of a membrane reservoir buffering membrane tension. Biophys. J. 77, 1992–2002. doi: 10.1016/S0006-3495(99)77040-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Rawicz, W., Olbrich, K., McIntosh, T., Needham, D., and Evans, E. (2000). Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79, 328–339. doi: 10.1016/S0006-3495(00)76295-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodriguez, A., Ehlenberger, D. B., Dickstein, D. L., Hof, P. R., and Wearne, S. L. (2008). Automated three-dimensional detection and shape classification of dendritic spines from fluorescence microscopy images. PLoS ONE 3:e1997. doi: 10.1371/journal.pone.0001997

PubMed Abstract | CrossRef Full Text | Google Scholar

Roux, A., Cappello, G., Cartaud, J., Prost, J., Goud, B., and Bassereau, P. (2002). A minimal system allowing tubulation with molecular motors pulling on giant liposomes. Proc. Natl. Acad. Sci. U.S.A. 99, 5394–5399. doi: 10.1073/pnas.082107299

PubMed Abstract | CrossRef Full Text | Google Scholar

Saarikangas, J., Kourdougli, N., Senju, Y., Chazal, G., Segerstråle, M., Minkeviciene, R., et al. (2015). Mim-induced membrane bending promotes dendritic spine initiation. Dev. Cell 33, 644–659. doi: 10.1016/j.devcel.2015.04.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Saleem, M., Morlot, S., Hohendahl, A., Manzi, J., Lenz, M., and Roux, A. (2015). A balance between membrane elasticity and polymerization energy sets the shape of spherical clathrin coats. Nat. Commun. 6, 1–10. doi: 10.1038/ncomms7249

PubMed Abstract | CrossRef Full Text | Google Scholar

Shepherd, G. M. (1996). The dendritic spine: a multifunctional integrative unit. J. Neurophysiol. 75, 2197–2210. doi: 10.1152/jn.1996.75.6.2197

PubMed Abstract | CrossRef Full Text | Google Scholar

Shimada, A., Niwa, H., Tsujita, K., Suetsugu, S., Nitta, K., Hanawa-Suetsugu, K., et al. (2007). Curved EFC/F-BAR-domain dimers are joined end to end into a filament for membrane invagination in endocytosis. Cell 129, 761–772. doi: 10.1016/j.cell.2007.03.040

PubMed Abstract | CrossRef Full Text | Google Scholar

Spacek, J., and Harris, K. M. (1997). Three-dimensional organization of smooth endoplasmic reticulum in hippocampal CA1 dendrites and dendritic spines of the immature and mature rat. J. Neurosci. 17, 190–203. doi: 10.1523/JNEUROSCI.17-01-00190.1997

PubMed Abstract | CrossRef Full Text | Google Scholar

Steigmann, D. (1999). Fluid films with curvature elasticity. Arch. Rational Mech. Anal. 150, 127–152. doi: 10.1007/s002050050183

CrossRef Full Text | Google Scholar

Steigmann, D., and Agrawal, A. (2016). Electromechanics of polarized lipid bilayers. Math. Mech. Complex Syst. 4, 31–54. doi: 10.2140/memocs.2016.4.31

CrossRef Full Text | Google Scholar

Tada, T., and Sheng, M. (2006). Molecular mechanisms of dendritic spine morphogenesis. Curr. Opin. Neurobiol. 16, 95–101. doi: 10.1016/j.conb.2005.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Tarun, O., Okur, H. I., Rangamani, P., and Roke, S. (2020). Transient domains of ordered water induced by divalent ions lead to lipid membrane curvature fluctuations. Commun. Chem. 3, 1–8. doi: 10.1038/s42004-020-0263-8

CrossRef Full Text | Google Scholar

Tasaki, I., and Byrne, P. (1992). Rapid structural chances in nerve fibers evoked by electric current pulses. Biochem. Biophys. Res. Commun. 188, 559–564. doi: 10.1016/0006-291X(92)91092-5

CrossRef Full Text | Google Scholar

Trachtenberg, J. T., Chen, B. E., Knott, G. W., Feng, G., Sanes, J. R., Welker, E., et al. (2002). Long-term in vivo imaging of experience-dependent synaptic plasticity in adult cortex. Nature 420, 788–794. doi: 10.1038/nature01273

PubMed Abstract | CrossRef Full Text | Google Scholar

Wakita, Y., Kakimoto, T., Katoh, H., and Negishi, M. (2011). The F-BAR protein rapostlin regulates dendritic spine formation in hippocampal neurons. J. Biol. Chem. 286, 32672–32683. doi: 10.1074/jbc.M111.236265

PubMed Abstract | CrossRef Full Text | Google Scholar

Walani, N., Torres, J., and Agrawal, A. (2014). Anisotropic spontaneous curvatures in lipid membranes. Phys. Rev. E 89:062715. doi: 10.1103/PhysRevE.89.062715

PubMed Abstract | CrossRef Full Text | Google Scholar

Walani, N., Torres, J., and Agrawal, A. (2015). Endocytic proteins drive vesicle growth via instability in high membrane tension environment. Proc. Natl. Acad. Sci. U.S.A. 112, E1423–E1432. doi: 10.1073/pnas.1418491112

PubMed Abstract | CrossRef Full Text | Google Scholar

Weichsel, J., and Geissler, P. L. (2016). The more the tubular: dynamic bundling of actin filaments for membrane tube formation. PLoS Comput. Biol. 12:e1004982. doi: 10.1371/journal.pcbi.1004982

PubMed Abstract | CrossRef Full Text | Google Scholar

Winterhalter, M., and Helfrich, W. (1988). Effect of surface charge on the curvature elasticity of membranes. J. Phys. Chem. 92, 6865–6867. doi: 10.1021/j100335a004

CrossRef Full Text | Google Scholar

Yasuda, R. (2017). Biophysics of biochemical signaling in dendritic spines: implications in synaptic plasticity. Biophys. J. 113, 2152–2159. doi: 10.1016/j.bpj.2017.07.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, F., Alimohamadi, H., Bakka, B., Trementozzi, A. N., Day, K. J., Fawzi, N. L., et al. (2021). Membrane bending by protein phase separation. Proc. Natl. Acad. Sci. U.S.A. 118, 1–11. doi: 10.1073/pnas.2017435118

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuste, R., and Bonhoeffer, T. (2004). Genesis of dendritic spines: insights from ultrastructural and imaging studies. Nat. Rev. Neurosci. 5:24. doi: 10.1038/nrn1300

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziv, N. E., and Smith, S. J. (1996). Evidence for a role of dendritic filopodia in synaptogenesis and spine formation. Neuron 17, 91–102. doi: 10.1016/S0896-6273(00)80283-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuo, Y., Lin, A., Chang, P., and Gan, W.-B. (2005). Development of long-term dendritic spine stability in diverse regions of cerebral cortex. Neuron 46, 181–189. doi: 10.1016/j.neuron.2005.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar