
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Physiol. , 08 January 2021
Sec. Fractal Physiology
Volume 11 - 2020 | https://doi.org/10.3389/fphys.2020.583082
 Zengbing Lu1,2*†
Zengbing Lu1,2*† Yu Zhou3†
Yu Zhou3† Longlong Tu1
Longlong Tu1 Sze Wa Chan2
Sze Wa Chan2 Man P. Ngan1
Man P. Ngan1 Dexuan Cui1
Dexuan Cui1 Yuen Hang Julia Liu1
Yuen Hang Julia Liu1 Ianto Bosheng Huang1
Ianto Bosheng Huang1 Jeng S. C. Kung1
Jeng S. C. Kung1 Chung Man Jessica Hui1
Chung Man Jessica Hui1 John A. Rudd1,4*
John A. Rudd1,4*Nausea and emesis resulting from disease or drug treatment may be associated with disrupted gastric myoelectric activity (GMA). Conventional analytical techniques can determine the relative degrees of brady-, normo-, and tachygastric power, but lose information relative to the basic slow wave shape. The aim of the present study was to investigate the application of advanced analytical techniques in the analysis of disrupted GMA recorded after administration of sulprostone, a prostaglandin E3/1 agonist, in ferrets. Ferrets were implanted with radiotelemetry devices to record GMA, blood pressure, heart rate (HR) and core body temperature 1 week before the administration of sulprostone (30 μg/kg) or vehicle (saline, 0.5 mL/kg). GMA was initially analyzed using fast Fourier transformations (FFTs) and a conventional power partitioning. Detrended fluctuation analysis (DFA) was also applied to the GMA recordings to reveal information relative to the fluctuation of signals around local trends. Sample entropy (SampEn) analysis was used for examining the regularity of signals. Conventional signal processing techniques revealed that sulprostone increased the dominant frequency (DF) of slow waves, with an increase in the percentage power of the tachygastric range and a decrease in the percentage power of the normogastric range. DFA revealed that sulprostone decreased the fluctuation function, indicative of a loss of the variability of GMA fluctuations around local trends. Sulprostone increased SampEn values, indicating a loss of regularity in the GMA data. Behaviorally, sulprostone induced emesis and caused defecation. It also increased blood pressure and elevated HR, with an associated decrease in HR variability (HRV). Further analysis of HRV revealed a decrease in both low-frequency (LF) and high-frequency (HF) components, with an overall increase in the LF/HF ratio. Sulprostone did not affect core body temperature. In conclusion, DFA and SampEn permit a detailed analysis of GMA, which is necessary to understand the action of sulprostone to modulate gastric function. The action to decrease HRV and increase the LF/HF ratio may be consistent with a shift toward sympathetic nervous system dominance, commonly seen during nausea.
Gastric dysfunction caused by altered motility occurs in a number of diseases and in response to drug treatments that cause nausea (Sanger et al., 2013). In situations of unexplained nausea and emesis, electrogastrography may be used to examine the electrical pacing of the stomach (Koch, 1989; Parkman et al., 2003). This technique records gastric myoelectric activity (GMA), which comprises low-frequency slow waves and neuronal spike activity. Slow waves originate from the interstitial cells of Cajal (ICCs), which show a specific distribution, arrangement and cell shape depending on their location within various regions and tissue layers of the gastrointestinal tract (Komuro, 2006). In healthy individuals, the frequency at which the power spectrum of slow waves with the highest power occurs approximately three times per minute; this is termed the dominant frequency (DF). During nausea, the frequency and power of these waves may increase or decrease, and other disordered waves may occur, leading to dysrhythmia. To classify the electrical state of the stomach as dysrhythmic, clinicians may observe a loss of normal rhythm either quantitatively, changes in DF, or qualitatively, by looking at signal shapes or inspecting a running spectral analysis (RSA) of data (Verhagen et al., 1999).
Using state-of-the-art radiotelemetric technology, our previous studies successfully recorded the GMA from freely moving ferrets, shrews and mice (Percie du Sert et al., 2010; Lu et al., 2014; Tu et al., 2017; Wang et al., 2018). In the ferrets, analysis of the DF and power partition of GMA revealed that GMA could be disrupted by emetics such as apomorphine (Percie du Sert et al., 2009a), cisplatin (Percie du Sert et al., 2009a), and exendin-4 (Lu et al., 2017b). In shrews, disrupted GMA was observed in animals following motion (Percie du Sert et al., 2010; Rudd et al., 2018). MFDFA has been used to analyze stationary or non-stationary time series in electromyography (EMG), electroencephalography (EEG), electrocardiography (ECG), gait variability, glycemic variability and respiration (Ihlen, 2012), in which signal shapes change in complexity. However, the correct implementation of the MFDFA assumes the power law can be found in the scaling behavior of fluctuation function and the detected multifractality should be examined by surrogate tests (Racz et al., 2019). Here, we study the series by detrended fluctuation analysis (DFA), which is a special case of MFDFA by considering only the second moment of the fluctuation function. Theoretically, the scaling power estimated by DFA can be connected to the Hurst exponent for quantifying long-range correlation. Because of its effectiveness and efficiency, DFA is recommended as the most appropriate method among many different methods to estimate the Hurst exponent, especially when the functional form of the trend is not a priori known (Bashan et al., 2008). Although DFA studies mainly focus on the scaling behavior via estimating the scaling power, such power actually contains part of the information about the fluctuation function (Peng et al., 1994; Kantelhardt et al., 2001). As pointed out by Kantelhardt et al. (2001), the fluctuation function is the average over the fluctuations around the local trend in each segment, which plays a role similar to variance to measure the variability of the series around the local trend. It should be emphasized that even when the fluctuation function turns out to not follow the power-law scaling behavior, the information about the variability contained in the fluctuation function at each scale is still valid. In this study, we therefore focus on the values of fluctuation function but not the DFA exponent based on its scaling behavior.
The concept of entropy has been invoked to measure irregularity in complex systems, which can usually be characterized using time series. Physiological signals such as heart rate (HR), blood pressure (BP) and respiratory variability are regulated by multiple control mechanisms, so they may constitute a complex system from the perspective of information content (Castiglioni et al., 2013; Wu et al., 2013; Diab et al., 2014; Haeufle et al., 2014). Many different definitions of entropy have been proposed, but the term is commonly defined as the rate of information production, with larger values indicating more irregularity (Costa et al., 2002). Entropy analysis has been applied to electrogastrogram (EGG) recordings in man. Peupelmann et al. used an approximate entropy (ApEn) approach to analyze EGG data from patients diagnosed with schizophrenia and found that the ApEn level of GMA during tachygastria after a test meal was higher than in controls (Peupelmann et al., 2009). A similar study showed that patients diagnosed with major depression had higher ApEn levels than controls, as well as tachygastria (Quick et al., 2010). An elevated ApEn level indicates increased complexity and dysregulation of GMA. Despite the wide application of the ApEn in physiological studies, it is actually prone to noisy or the short length of the signal (Richman and Moorman, 2000). Because of this drawback, a slightly different analytical approach, i.e., the sample entropy (SampEn), was introduced by Richman and Moorman (2000) to determine system complexity. In this study, we employed the improved entropy analysis, i.e., the SampEn analysis.
The aim of the present study was to apply conventional and advanced signal processing techniques to GMA data generated from another emetic challenge, sulprostone, that disrupts gastric function and causes nausea and emesis via activation of prostanoid receptors. Prostaglandins and thromboxane A2 are lipid-mediators that play a major role in physiological and pathological processes. Five major types of prostanoid receptors have been identified: DP, EP, FP, IP, and TP (Coleman et al., 1994). Prostanoids acting on DP, EP, and TP receptors are associated with emesis in animals and man. Sulprostone is a relatively potent EP1/3 receptor agonist, with lower affinity FP receptors (Boie et al., 1997; Abramovitz et al., 2000). In our previous investigations, sulprostone dose-dependently induced emesis in ferrets, with the response being resistant to bilateral abdominal vagotomy and conventional anti-emetic drugs (Kan et al., 2002). Given that sulprostone also causes diarrhea, we reasoned that it would be an ideal exemplar to cause gastric changes so that we could compare different analytical approaches to the assessment of normal and disturbed gastric rhythm.
Eight castrated male fitch ferrets (1.68 ± 0.06 kg) were purchased from Southland Ferrets (Invercargill, New Zealand) and housed in a temperature-controlled room at 24°C ± 1°C under artificial lighting, with lights on between 06:00 and 18:00. The relative humidity was maintained at 50% ± 5%. Water and food (TriPro super premium chicken meal formula dog food, American Nutrition, United States) were given ad libitum unless otherwise stated. All experiments were conducted under license from the Government of Hong Kong Special Administrative Region and the Animal Experimentation Ethics Committee of The Chinese University of Hong Kong.
Eight ferrets were fasted overnight but allowed free access to water. The surgical procedures for implanting radiotelemetric devices (C50-PXT; Data Sciences International, United States) have been described in our previous studies (Tu et al., 2017). Briefly, in the anesthetized animals, following a midline abdominal incision, a 19G needle was used to pierce the aorta, and then the catheter of a C50-PXT transmitter (Data Sciences, Inc, United States) was inserted up to a length of approximately 2 cm. A 2 × 2 mm piece of sterile gauze was placed over the catheter’s entry point, and fixed with a drop of tissue glue. The body of the transmitter was then sutured to the left side of the ferret’s abdominal wall muscle with the biopotential wires and catheter facing caudally. The gastric antrum was exposed and the biopotential wires were inserted into the muscle and secured in place by suturing the serosa. The abdominal cavity was sutured in closed layers and covered with a permeable spray dressing (Opsite®, Smith and Nephew, United Kingdom). After the surgery, animals were allowed to recover for 7 days before drug treatment.
The animals were divided into two groups (n = 4 for each group) and were randomized to receive a single treatment of saline (1 mL/kg, i.p.) or sulprostone (30 μg/kg, i.p.). At 08.00, the ferrets were presented with 20 g of food and allowed to eat. At 08.30, any uneaten food was removed and the animals were fasted again. At 10.00 (t = 0), they were injected with either sterile saline (1 mL/kg, i.p.) or sulprostone (30 μg/kg, i.p.). Their behavior was then recorded for 4 h. Radiotelemetry of cardiovascular parameters, core body temperature and GMA were recorded throughout the experiment using Dataquest ART 4.1 (Data Sciences International, United States). At the end of the experiments, the ferrets were euthanized using an overdose of pentobarbitone (80 mg/kg, i.p.).
After sulprostone injection, behavior was recorded for 4 h via a video system (Panasonic WV-PC-240, China). Emesis was characterized as rhythmic abdominal contractions that were either associated with the oral expulsion of solid or liquid material from the gastrointestinal tract (i.e., vomiting), or not associated with passage of material (i.e., retching). An episode of retching and/or vomiting was considered separate when the animal changed its location in the observation cage, or when the interval between retches and/or vomits exceeded 5 s (Rudd et al., 1994). An episode of defecation was characterized as a series of lower abdominal contractions and expulsion of solid or liquid fecal matter from the anus. Episodes of tenesmus were characterized as non-productive lower abdominal contractions; only tenesmus involving spasm of the anal sphincter was recorded to differentiate tenesmus from non-productive attempts of the animals to micturate. Furthermore, the animals had raised tails during all episodes of defecation and tenesmus, and episodes were considered separate when the animal changed its location in the observation cage (Kan et al., 2017).
All telemetric data were processed using Spike2 (Version 7; Cambridge Electronic Design). The method of telemetric GMA data analysis has been described in previous studies; dominant power was defined as the highest power in the 0–15 cpm range, and DF was defined as the frequency bin with the highest power in the 0–15 cpm range; the definition of brady-, normo-, and tachy-gastria ranges were as follow: bradygastria: 0 to (DF - 1) cpm, normogastria: DF ± 1 cpm, tachygastria: (DF + 1) to 15 cpm (Percie du Sert et al., 2009b). Systolic BP was calculated from the peak of the BP recording trace, while diastolic BP was calculated from the trough of the BP recording trace. To measure HR (in bpm), the peak-to-peak interval was first calculated using the following formula: HR = 60/P-P interval. The standard deviation of the R-R intervals (SDNN) was measured based on the P-P wave interval of the BP in 5-min segments. It was then used as an index of HR variability (HRV) (Lu et al., 2017a). Frequency-domain analysis was performed using fast Fourier transform (FFT). The total power of all R-R intervals in 5-min segments was determined, along with its low-frequency component (LF: 0.04–0.15 Hz), high-frequency component (HF: 0.15–0.7 Hz) and LF/HF ratio (Lu et al., 2017c). Core body temperature data were calculated by averaging the data. All data were averaged in 1-h segments for statistical analysis.
To carry out DFA, the GMA data were subjected to the following formulas (Peng et al., 1994; Kantelhardt et al., 2001): By dividing the cumulative sum of the given series to Ns = N/s non-overlapping segments with length s, the variance for ν-th segment can be calculated to measure the fluctuations around the m-th order polynomial local trend pt(v) as The fluctuation function F(s) at the scale s can be obtained as . The scaling behavior of F(s) can be obtained with varying scale s. The code for DFA analysis in the MATLAB software was provided in the Supplementary Material. Typically, DFA focuses on the DFA exponent h, which assumes the power-law asymptotic behavior F(s)∼sh, because it can be connected to the auto-correlation of a time series. In principle, the segmented statistical equivalence is a crucial condition of DFA validation; this implies that the fluctuations around the local trend were statistically distinguishable in all segments (Höll et al., 2016). It is easy to see that the DFA exponent h only extracts part of such information: the power of the scaling behavior of the fluctuation function F(s). As seen from its calculation, the fluctuation function F(s) contains rich information about the fluctuations around the local trends at each s, which plays a role similar to that of variance in probability theory. In the general sense, direct consideration of F(s) has two advantages for characterizing the difference between two series. On one hand, only for the series with the fluctuation function F(s) following the power law, it is possible to estimate the DFA exponent. On the other hand, taking two series z1 and z2with the same DFA exponent h1 = h2, their fluctuation functions can be expressed as logF1(s) = a1 + h1logs and logF2(s) = a2 + h2logs. Although the DFA exponent cannot distinguish these two series because of the same value, the fluctuation functions F1(s) and F2(s) may do so if a1≠a2. Therefore, in this study we prefer the fluctuation function F(s) to the estimated DFA exponent h for characterizing the given signals. However, we by no means imply that the DFA exponent is not important. We only want to extract useful information from the DFA fluctuation function when its scaling behavior is not a power law, which makes it impossible to estimate the DFA exponent.
To capture information about irregularity at multiple scales, multiscale entropy (MSE) analysis, which is based on SampEn, has been proposed (Costa et al., 2002).
For a given time series , MSE analysis calculates SampEn(m,r,s) at the concerned scales, s. The computation procedure and the meaning of the parameters m, r, and Nτ are as follows (Costa et al., 2002): By coarsening the given series at a given scale s to construct as , where , the regularity of at the scale s can be obtained as . By respectively defining the embedded vectors with j = 1, 2,…,Ns−m + 1 and with j = 1, 2,…,Ns−m, A(m,r) and B(m,r) is the probability of observation of pairs of and with the distance less than r×SD, where SD is the standard deviation of the series. In formula, and . Where # denotes the set cardinality and d is the distance function defined as .
The code for SampEn analysis in the MATLAB software was provided in the Supplementary Material.
All data analyses were performed using GraphPad Prism version 6 (GraphPad Prism Software, La Jolla, CA, United States) and MATLAB (MathWorks, Natick, MA, United States). Differences in emesis and defecation between treatment groups were assessed using unpaired Student’s t-tests, as appropriate. Differences in BP, HR, HRV, core body temperature, GMA, DFA and entropy were assessed using repeated-measures two-way ANOVA and Bonferroni tests. All data are expressed as mean ± standard error of the mean. Differences were considered statistically significant at P-values < 0.05.
Sulprostone (Sigma-Aldrich, St. Louis, United States) was dissolved in saline (0.9% w/v) and administered in a volume of 1 mL/kg, i.p.
The i.p. administration of saline did not induce either retching or vomiting in any of the animals tested, but it was associated with 2.3 ± 0.8 episodes of defecation. Sulprostone at 30 μg/kg, i.p. induced emesis in all ferrets. The emetic response comprised 208.5 ± 22.3 retches and 27.8 ± 4.7 vomits, following a median latency of 9.8 min (Figure 1; P < 0.05). Sulprostone also induced 6.8 ± 0.9 episodes of defecation/tenesmus, with a median latency of 10.7 min (P < 0.05, compared to saline-treated animals).
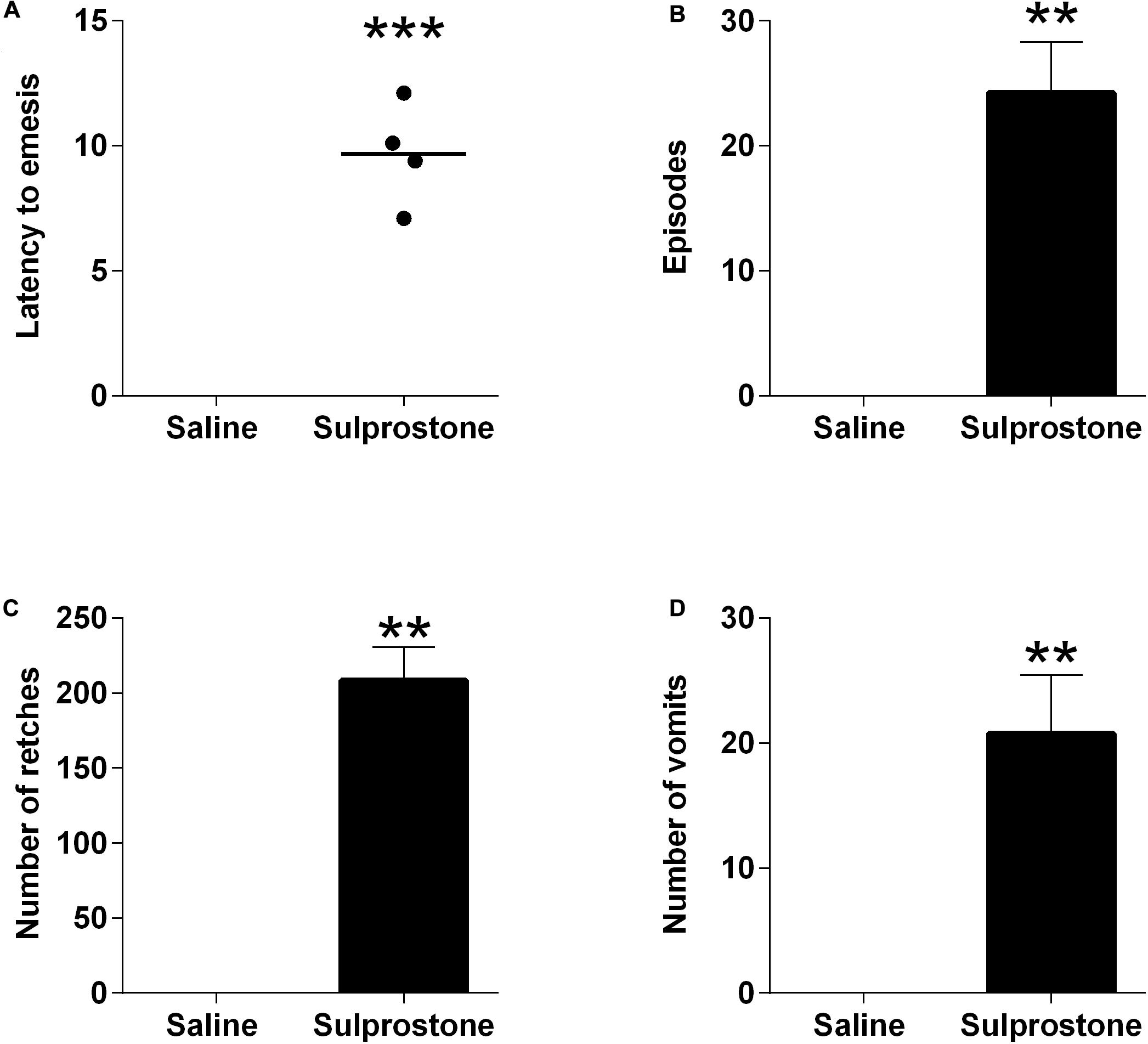
Figure 1. Effect of intraperitoneal administration of sulprostone (30 μg/kg) or saline (1 mL/kg) in the ferret. (A) Latency to the first emetic episode. (B) Number of episodes. (C) Number of retches. (D) Number of vomits. The episodes, retching and vomiting data are represented as mean ± SEM, using four animals. Latency data are shown as individual responses, with lines indicating the median response. Significant differences compared to the saline control group are indicated as **P < 0.01 and ***P < 0.001 (unpaired Student’s t-test).
Visual comparison of the GMA traces with traces obtained from saline-treated animals showed that sulprostone tended to reduce the power of the signal and disrupted the normal rhythm (Figure 2). RSA revealed that sulprostone diminished the dominant power, and that the DF increased toward the tachygastric range, whereas saline had little effect (Figure 3A). Thus, baseline GMA recordings (0–1 h) revealed a DF of 9.3 ± 0.2 cpm (expected normal DF: ∼9.0-9.4; Percie du Sert et al., 2009a; Lu et al., 2017a), whereby 19.7% ± 3.3% of power was in the bradygastric range, 56.5% ± 4.2% was in the normogastric range, and 13.2% ± 2.1% was in the tachygastric range (pooled data, n = 8; Figure 3). Saline did not affect any of the GMA parameters, but sulprostone increased the DF significantly by approximately 2.6 cpm (DF with saline = 9.6 ± 0.2 cpm vs. DF with sulprostone = 12.2 ± 0.3; Figure 3A). Furthermore, sulprostone conferred a 77.6% decrease in the percentage power of normogastria and a 115.8% increase in the percentage power of tachygastria when compared with saline control; these effects persisted for approximately 4 h (Figures 3D,E). The percentage power of the bradygastric range was unaffected (Figure 3C).
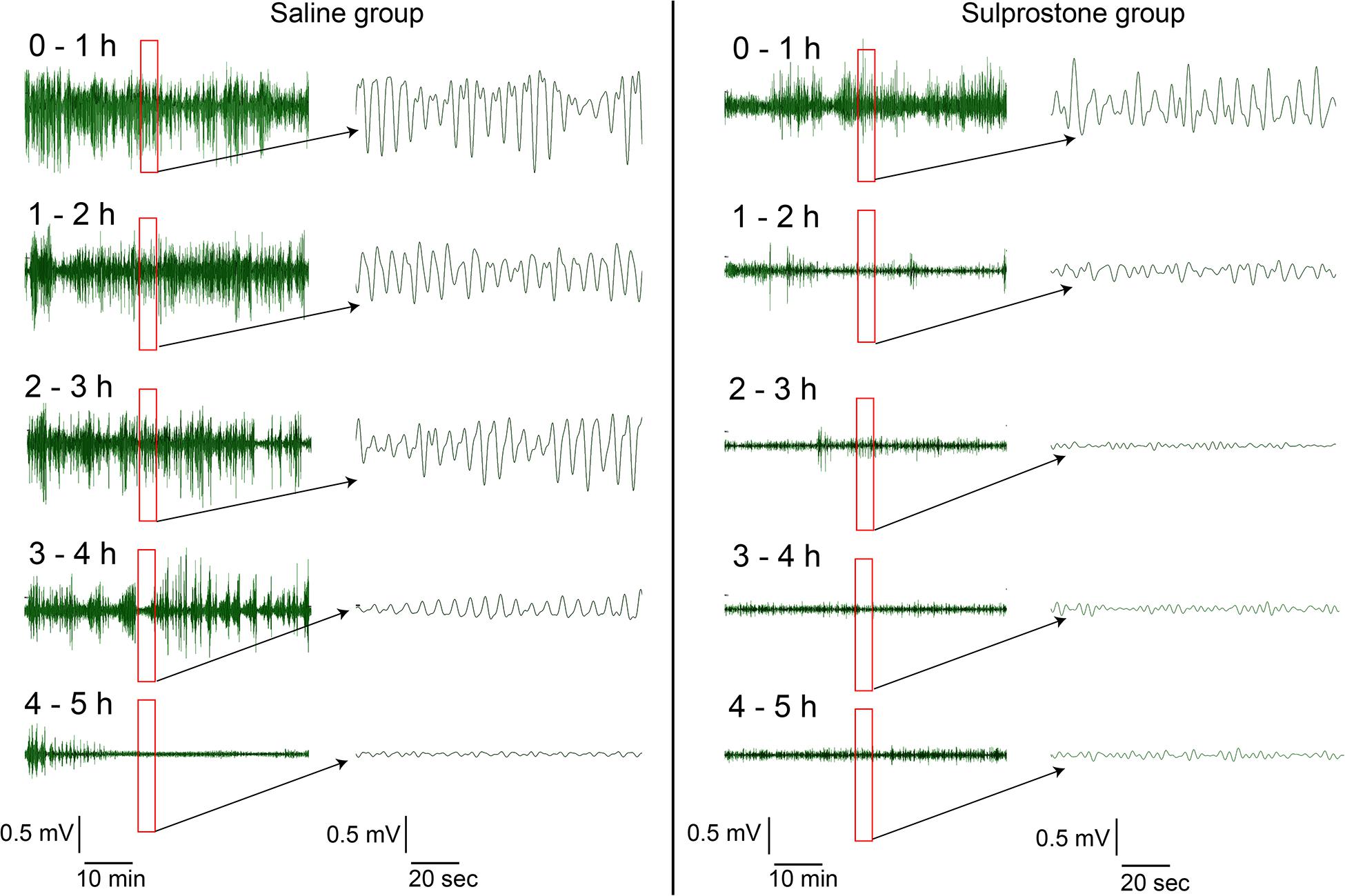
Figure 2. Representative traces of gastric myoelectric activity in a ferret that had received i.p. administration of sulprostone (30 μg/kg) or saline (1 mL/kg). Visual inspection of the GMA signal shows that sulprostone decreases the power of the signal, but increases the number of oscillations.
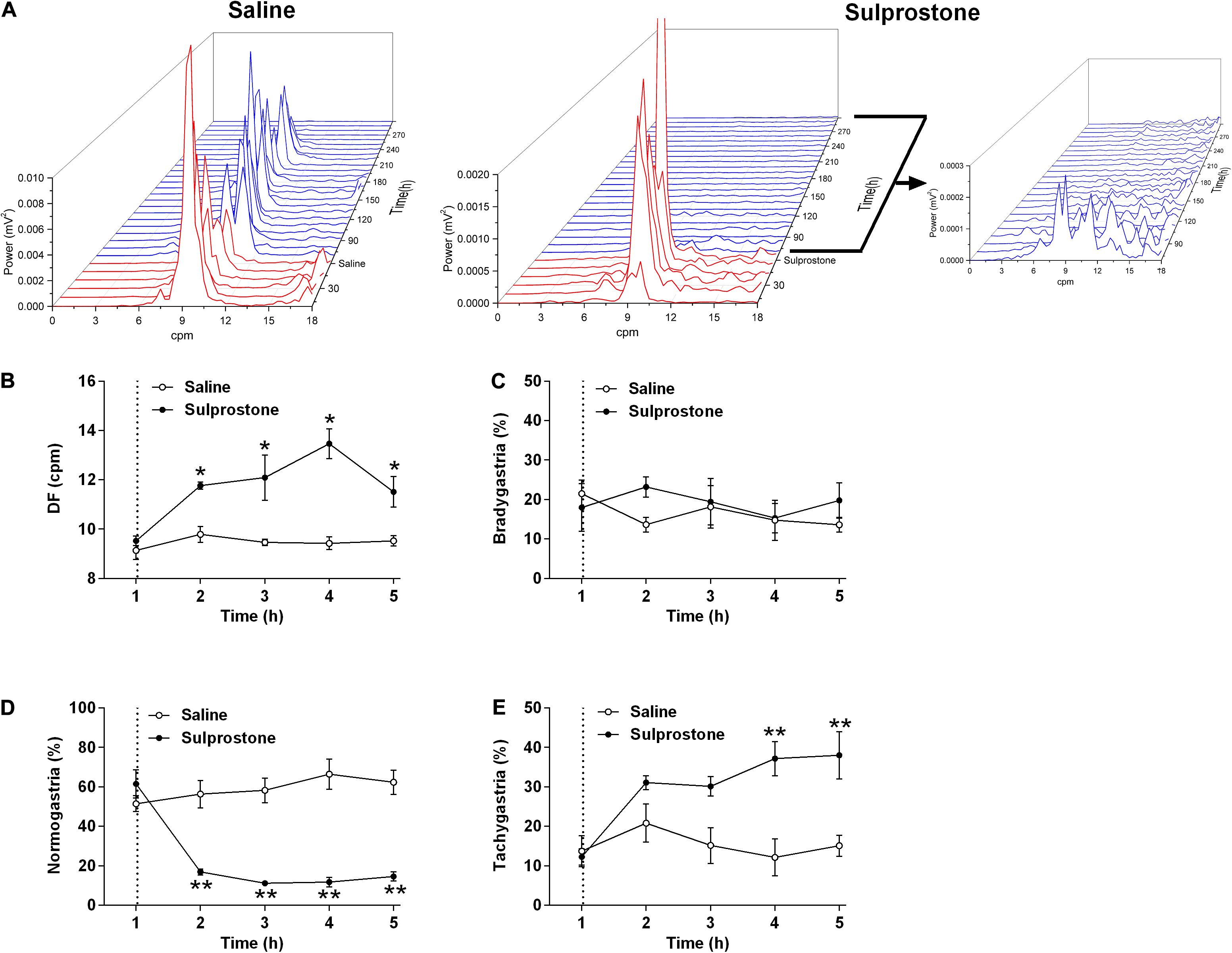
Figure 3. Effect of i.p. administration of sulprostone (30 μg/kg) or saline (1 mL/kg) on gastric myoelectric activity (GMA), as determined using running spectral analysis in the ferret. (A) RSA of GMA from the start of baseline recording 1 h prior to sulprostone or saline administration to 4 h after sulprostone or saline administration. (B) DF, (C) bradygastria (%), (D) normogastria (%), and (E) tachygastria (%) in animals that had received sulprostone or saline. Dashed line: injection of sulprostone or saline. Data represent the mean ± SEM of four animals. Significant differences compared to the saline control group are indicated as *P < 0.05 and **P < 0.01 (repeated-measures two-way ANOVA).
As pointed out by Hu et al. (2001), the observed periodic trend in GMA may invalidate the power-law scaling behavior. In this case, it is meaningless to estimate the DFA exponent. Therefore, we can only directly focus on the fluctuation function F(s). We set it at a common order 2, and find with this order, the effect of sulprostone can be well identified. Therefore, it should be sufficient to use the second detrending order. The DFA fluctuation function of GMA at multiple scales was significantly lower in the sulprostone-treated animals than in the saline-treated animals (P < 0.05; Figures 4A,B). For example, the DFA fluctuations of GMA at a scale of 28, i.e., F(s = 28), decreased in both the saline and sulprostone-treated animals (Figure 4C). However, the effect of sulprostone to decrease the DFA fluctuations was much stronger than that of saline, while the saline effect was more persistent and lasted for a longer period. Consequently, a significant difference in DFA fluctuation between the saline and sulprostone group only occurred during the 2- to 4-h post-administration period (P < 0.05) and was not present after 4 h. To characterize each signal by one single indictor, we further calculate the averaged fluctuation function as the mean of F(s) over all scales s. It can be seen in Figure 4D the results of similar to that for F(s = 28) shown in Figure 4C.
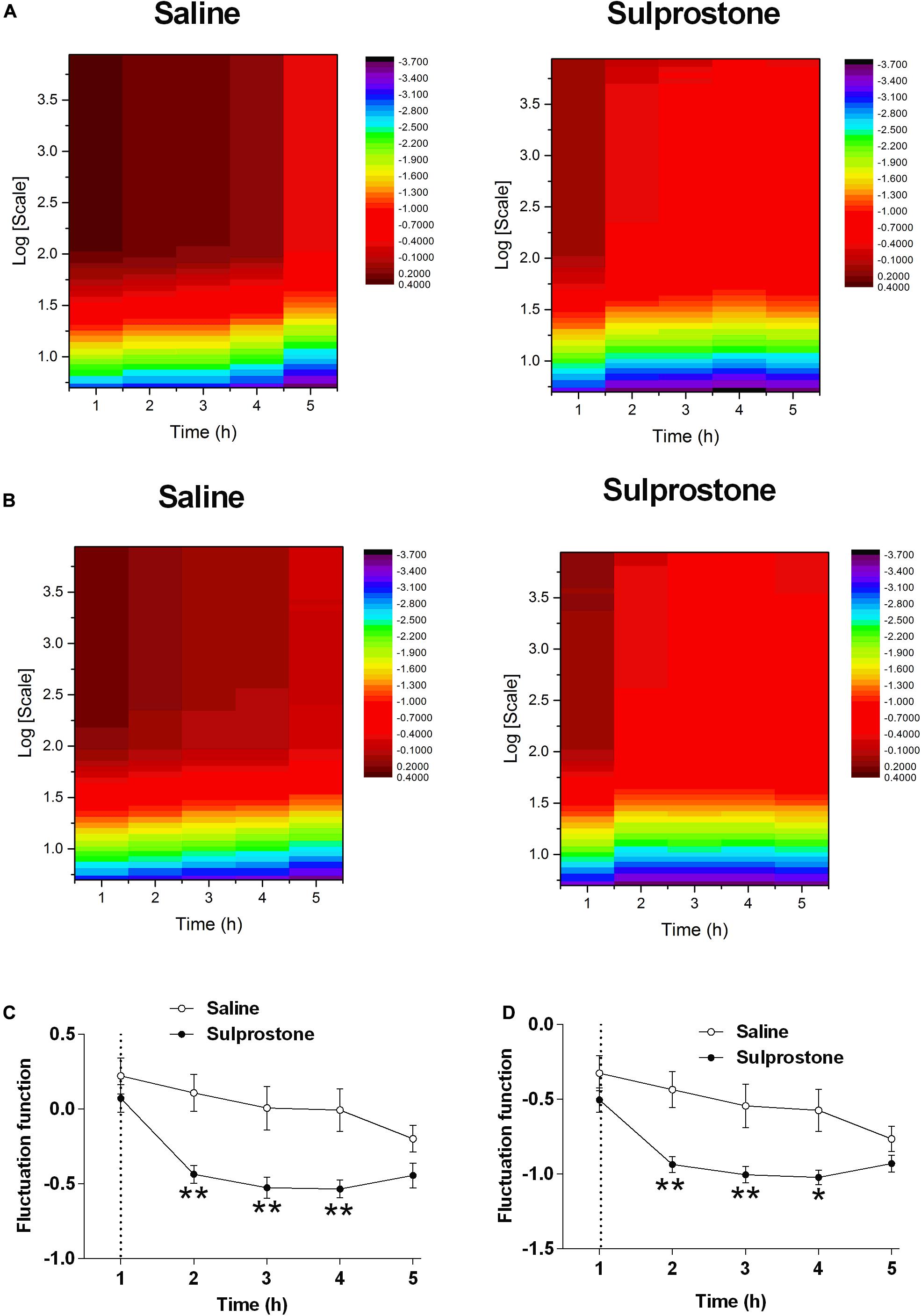
Figure 4. Effect of i.p. administration of sulprostone (30 μg/kg) or saline (1 mL/kg) on gastric myoelectric activity (GMA), as determined using detrended fluctuation analysis (DFA) in the ferret. (A) DFA fluctuation function of GMA in one sample ferret that had received i.p. administration of sulprostone (30 μg/kg) or saline (1 mL/kg). For each scale s and each time h, the fluctuation functions F(s) of the corresponding sample can be calculated. For example, the value of the heatmap corresponding to h = 1 and logs = 1 indicates F(s = 10) of the sample collected at h = 1. (B) Averaged DFA fluctuation function of GMA over all samples in the sulprostone and saline groups. For example, the value of the heatmap corresponding to h = 1 and logs = 1 indicates the averaged F(s = 10) over all samples in each group collected at h = 1. (C) Averaged DFA fluctuation function of GMA over all samples in each group at one scale of 28, i.e., F(s = 28). (D) DFA fluctuation function of GMA averaged over all scales, i.e., . Dashed line: injection of sulprostone or saline. Data represent the mean ± SEM of four animals. Significant differences compared to the saline control group are indicated as *P < 0.05 and **P < 0.01 (repeated-measures two-way ANOVA).
SampEn was used to evaluate the changes in signal regularity induced by sulprostone. The heatmaps shown in Figures 5A,B illustrate variations in the SampEn of GMA at multiple scales over time using one ferret and the average data from all ferrets, respectively. Generally, singular or averaged data exhibited a similar pattern: at each scale, saline decreased the SampEn over time (Figures 5C,D). In particular, at a scale of 5.0, sulprostone conferred a SampEn ∼60% than that of saline 1–4 h after administration (Figure 5C). Thus, although sulprostone increased SampEn, the increase over time appeared more gradual, and it may even have stopped or decreased 4 h after sulprostone administration.
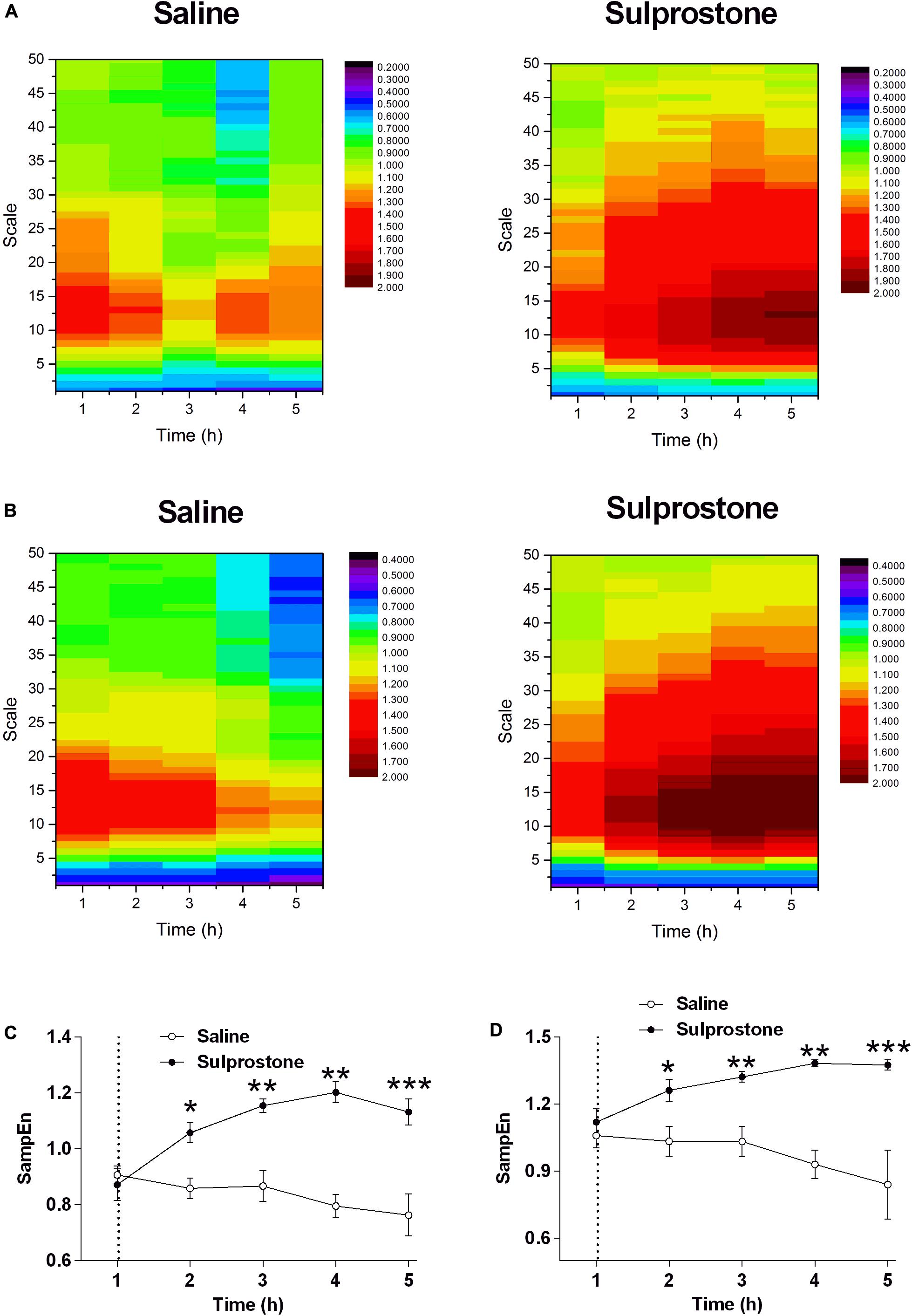
Figure 5. Effect of i.p. administration of sulprostone (30 μg/kg) or saline (1 mL/kg) on entropy of GMA in the ferret. (A) Entropy analysis of gastric myoelectric activity (GMA) in a ferret that had received an i.p. administration of sulprostone (30 μg/kg) or saline (1 mL/kg). (B) Averaged entropy of GMA in the sulprostone and saline groups. (C) Entropy analysis of GMA at a scale of 5.0. (D) Entropy analysis of GMA averaged over all scales. Data represent the mean ± SEM of four animals. Dashed line: injection of sulprostone or saline. Significant differences compared to the saline control group are indicated as *P < 0.05, **P < 0.01, and ***P < 0.001 (repeated-measures two-way ANOVA).
Examination of pooled data revealed a baseline systolic BP of 135.2 ± 3.7 mm Hg and a baseline diastolic BP of 94.3 ± 3.9 mm Hg (n = 8; Figures 6A,B). The basal HR was 219.8 ± 5.8 bpm, and the HRV (SD of R-R intervals) was 0.058 ± 0.002 arbitrary units (Figures 6C,D). The frequency domains of the HRV were as follows: LF, 647.3 ± 49.7 ms2; HF, 2106.0 ± 26.15 ms2; and LF/HF ratio, 0.347 ± 0.038 (Figures 6E–G). The mean basal core body temperature was 38.2°C ± 0.1°C (n = 8; Figure 6H).
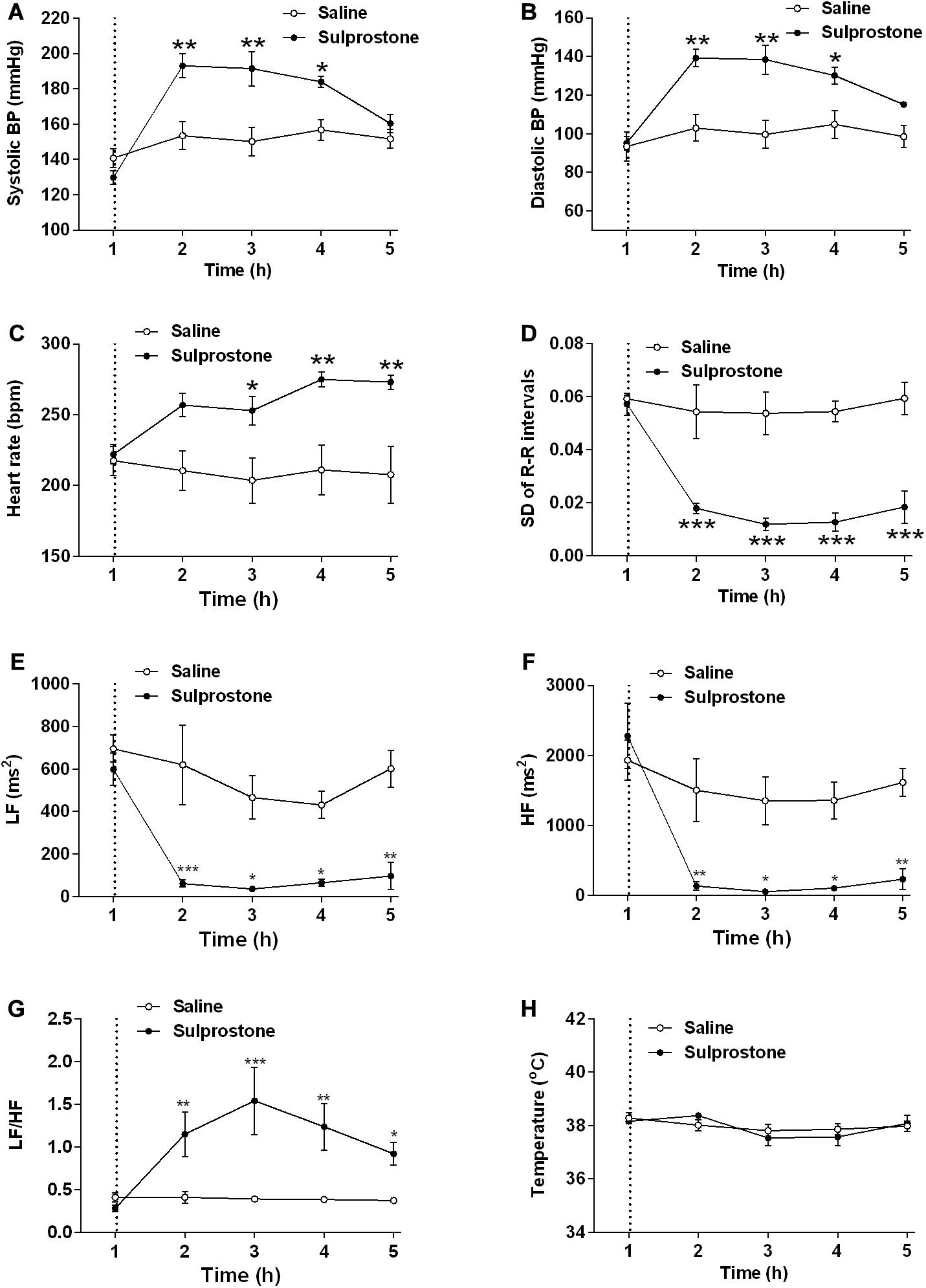
Figure 6. Effect of an i.p. administration of sulprostone (30 μg/kg) or saline (1 mL/kg) on cardiovascular functions and core body temperature in the ferret. (A) Systolic blood pressure (BP), (B) diastolic BP, (C) heart rate, (D) heart rate variability (HRV; SD of R-R intervals), (E) high frequency (HF) HRV, (F) low frequency (LF) HRV, (G) LF/HF ratio, and (H) core body temperature. Dashed line: injection of sulprostone or saline. Data represent the mean ± SEM of four animals. Significant differences compared to the saline control group are indicated as *P < 0.05, **P < 0.01, and ***P < 0.001 (repeated-measures two-way ANOVA).
Sulprostone significantly increased systolic and diastolic BP by 19.1 and 28.9%, respectively, with significant differences observed 1–3 h after administration (Figures 6A,B); there was also a 26.9% increase in HR 2–4 h after sulprostone administration (Figure 6C). Further analysis revealed that sulprostone decreased HRV by 72.4% within 1 h of administration and the effects lasted up to 4 h (Figure 6D); it also caused a marked decrease in both the LF and HF frequency domains (Figures 6E,F), leading to an overall increase in the LF/HF ratio (Figure 6G). However, sulprostone did not affect core body temperature (Figure 6H).
The present study was the first to use different analytical methods to investigate the effect of sulprostone on GMA in ferrets implanted with telemetric devices. The dose of sulprostone to induce a reliable emetic response was based on our previous publications (Kan et al., 2002). Sulprostone administered peripherally predictably induced emesis and increased the frequency of defecation. This is consistent with previous studies implicating EP1/3 and FP receptors in the responses (Kan et al., 2002, 2017).
We primarily embarked on the present study to compare three analytical techniques used to assess drug action on GMA. As sulprostone induces emesis and defecation, we expected a dramatic GMA profile. In a previous study, sulprostone increased the slow wave frequency, but reduced the slow wave amplitude recorded from isolated antral muscles in mice; moreover, it increased the frequency of spontaneous inward currents from the ICCs. These effects were not prevented by SC-19220, an EP1 receptor antagonist, suggesting that sulprostone may affect slow wave activity via EP3 receptors (Kim et al., 2002). Furthermore, other studies have demonstrated that sulprostone increased the frequency of peristaltic contractions in isolated mouse antral muscles via the EP3 receptor (Forrest et al., 2009). In ex vivo perfused canine stomachs, prostaglandin E2 infusion increases slow wave frequency whilst decreasing the force of antral contractions (Kowalewski and Kolodej, 1975). Comparatively, data from patients with tachygastria and impaired gastric emptying have indicated that these symptoms are associated with higher levels of prostaglandin E2 (Sanders, 1984).
Visual inspection of the GMA signal showed that sulprostone decreased the power of the signal, but increased the number of oscillations. The slow wave signal shape became more regular, with less variation. Although the power decreased, the clustering of frequencies in the tachygastric range showed an overall increase. Indeed, conventional GMA signal processing using FFT and power spectral analysis revealed that sulprostone caused an increase in slow wave DF and reduced the power of the signals. Upon partitioning, this manifested as an increase in the percentage power of the tachygastric range and a consequent reduction in the percentage power of the normogastric range.
The detrending order is a parameter of DFA used to control the order of the fitted local polynomial trend in each segment. Mathematically, to completely remove the polynomial trend with the order m, the detrending order has to be at least m+1. Therefore, in traditional analysis, the detrending order has to be sufficiently large to ensure that the impact of local trends on the DFA scaling behavior can be completely removed. However, here we do not focus on the DFA scaling behavior and aim at fully using all information in series. It is unnecessary to completely remove the local trend. Actually, the series can be decomposed into two components at each scale, namely local trends and the fluctuations around local trends. In this sense, the DFA detrending order is not important in the traditional sense, i.e., we do not need to set it at a sufficiently large value to completely eliminate all impact of trends. Instead, we only need to see if the fluctuation around the local trends can successfully characterize the effect of sulprostone. The DFA analysis of GMA revealed that both saline and sulprostone decreased the variability of fluctuations in the GMA signals at multiple scales, indicating the loss of the signal energy over time. However, the effect of sulprostone was much greater than that of saline, and this difference was easily detected after 2–4 h. In this sense, sulprostone decreased the variability of the fluctuations, compared to the effect of saline.
In our previous studies, the analysis of GMA focused on the DF and its associated GMA power distribution. We found that the fluctuation of GMA was suppressed after cisplatin treatment in the delayed phase of emesis, while the DF of GMA was unaffected. In the present study, we applied two analytical strategies: (1) DFA and (2) MSE. DFA is used to analyze auto-correlation in either stationary or non-stationary time series, and it has been applied to various types of physiological data. In ECG analysis using DFA, pharmacological intervention that changes the sympathetic and vagal cardiac outputs (atenolol or atropine treatment) also affected the DFA scaling properties of HRV (Silva et al., 2017). It follows that DFA analysis of ECG may uncover novel implications during pathophysiological conditions. Yeh et al. (2013) pointed out that the dynamic properties of HRV revealed by DFA constitute an important feature of autonomic nervous system activity during sleep. In EEG, brain state variation, normal development, or pathological states can be detected using DFA, as can phase modulation of cortical oscillations. Furthermore, Márton et al. (2014) recently published a methodology to analyze EEG signaling using DFA. A study by Adda and Benoudnine (2016) showed that DFA of EEG achieved high detection accuracy to distinguish epileptic seizures from normal healthy EEG. To date, only limited information is available regarding DFA of GMA, probably because the time series of EGG recordings in humans have a short-duration. With the advent of radiotelemetric technology, long-term GMA from the antrum has been recorded in different species (Percie du Sert et al., 2010; Rudd et al., 2018; Wang et al., 2018). Theoretically, the observed periodic trend in GMA may invalidate the power-law scaling behavior (Hu et al., 2001). In this case, it is meaningless to estimate the DFA exponent. Therefore, we can only directly focus on the fluctuation function F(s). In the present study, the reduced DFA fluctuation of GMA was observed in sulprostone-treated animals, which may indicate reduced fluctuation of the signals. Inspection of the raw traces indicated that sulprostone caused a reduction in the GMA amplitude, perhaps because it reduced the fluctuation of GMA.
In a further analysis, we applied SampEn analysis to the ferret GMA and found that sulprostone increased the SampEn of the ferret GMA. It was difficult to distinguish the GMA irregularity by inspecting the raw traces alone. In addition, the collected GMA contains some noises. Given the advantage of SampEn for the noisy data (Richman and Moorman, 2000), it should be more appropriate to SampEn analysis rather than other entropy analysis, like ApEn. Using SampEn analysis, we showed that the SampEn of GMA was significantly higher in the sulprostone-treated than the saline-treated ferrets, and that this increase in SampEn lasted up to 4 h after sulprostone administration. In previous studies, ApEn analysis of GMA from patients with acute schizophrenia or major depression has detected increased ApEn levels and tachygastria in these patients compared with controls (Peupelmann et al., 2009; Quick et al., 2010). Taken together with our own findings, this may indicate that an elevated SampEn value points to increased complexity and dysregulation of ferret GMA after sulprostone intervention. In the present study, sulprostone reduced both the LF and HF components of HRV, with an overall increase in the LF/HF ratio, indicating a shift toward sympathetic dominance. In patients with major depression or acute schizophrenia, the increased ApEn of GMA was accompanied by an increase in sympathetic modulation, as determined by autonomic nervous symptom scores (Peupelmann et al., 2009; Quick et al., 2010). These results imply that the sulprostone-induced increase in SampEn and tachygastria is associated with an increase in sympathetic dominance, although this needs to be confirmed in further pharmacological studies. Our data inclusive of entropy and autonomic changes provide a fingerprint of prostanoid-induced changes in GI function that may underlie emesis and diarrhea. However, further studies are required to fully understand the relationships involved and if the changes are specific to EP/FP receptor activation or not.
The present study had several limitations. First, the relatively small sample size made it difficult to correlate the measured parameters, including DF, DFA and SampEn, with the severity of the emetic response. Second, it is not yet clear whether the sulprostone-induced changes in DF, DFA, and SampEn could be pharmacologically reversed by appropriate antagonists. Third, measurement of GMA using few electrodes has been demonstrated to be unreliable at capturing all types of gastric dysrhythmias (O’Grady et al., 2012), and future studies may consider multiple electrodes to investigate the spatial patterns of GMA. It would also be interesting to apply the analytical techniques identified in the present study to datasets generated using multielectrode arrays.
In conclusion, the present study revealed that sulprostone induced emesis, disrupted GMA and modulated cardiovascular function in ferrets. A further comprehensive analysis in GMA using RSA, DFA, and SampEn measures showed that sulprostone induced tachygastria, decreased GMA fluctuation and increased the SampEn level of GMA, suggesting loss of variability around local trends, increased multifractality and GMA irregularity. Further studies involving other emetic stimuli such as cisplatin are needed to clarify the biological significance of DFA and SampEn in GMA analysis.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
The animal study was reviewed and approved by All experiments were conducted under license from the Government of Hong Kong Special Administrative Region and the Animal Experimentation Ethics Committee of The Chinese University of Hong Kong.
JR conceived the study and was in charge of overall direction and planning. ZL performed the animal surgery, experiments, and data collection. YZ performed the DFA and entropy analysis of GMA and interpreted the results. MN recorded the animal behaviors. ZL, LT, SC, YL, IH, JK, CH, and JR finalized the manuscript. All authors reviewed the final version of the manuscript and approved submission.
This work was supported by the Emesis Research Group, The Chinese University of Hong Kong.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2020.583082/full#supplementary-material
Abramovitz, M., Adam, M., Boie, Y., Carrière, M., Denis, D., Godbout, C., et al. (2000). The utilization of recombinant prostanoid receptors to determine the affinities and selectivities of prostaglandins and related analogs. Biochim. Biophys. Acta. 1483, 285–293. doi: 10.1016/s1388-1981(99)00164-x
Adda, A., and Benoudnine, H. (2016). Detrended fluctuation analysis of EEG recordings for epileptic seizure detection”, in: International Conference on Bio-engineering for Smart Technologies (BioSMART). Dubai: IEEE, 1–4.
Bashan, A., Bartsch, R., Kantelhardt, J. W., and Havlin, S. (2008). Comparison of detrending methods for fluctuation analysis. Physica. A: Stat. Mech. Appl. 387, 5080–5090. doi: 10.1016/j.physa.2008.04.023
Boie, Y., Stocco, R., Sawyer, N., Slipetz, D. M., Ungrin, M. D., Neuschäfer-Rube, F., et al. (1997). Molecular cloning and characterization of the four rat prostaglandin E2 prostanoid receptor subtypes. Eur. J. Pharmacol. 340, 227–241. doi: 10.1016/s0014-2999(97)01383-6
Castiglioni, P., Zurek, S., Piskorski, J., Kosmider, M., Guzik, P., Ce, E., et al. (2013). Assessing sample entropy of physiological signals by the norm component matrix algorithm: application on muscular signals during isometric contraction. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2013, 5053–5056.
Coleman, R. A., Smith, W. L., and Narumiya, S. (1994). International union of pharmacology classification of prostanoid receptors: properties, distribution, and structure of the receptors and their subtypes. Pharmacol. Rev. 46, 205–229.
Costa, M., Goldberger, A. L., and Peng, C. K. (2002). Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 89:068102.
Diab, A., Hassan, M., Marque, C., and Karlsson, B. (2014). Performance analysis of four nonlinearity analysis methods using a model with variable complexity and application to uterine EMG signals. Med. Eng. Phys. 36, 761–767. doi: 10.1016/j.medengphy.2014.01.009
Forrest, A. S., Hennig, G. W., Jokela-Willis, S., Park, C. D., and Sanders, K. M. (2009). Prostaglandin regulation of gastric slow waves and peristalsis. Am. J. Physiol. Gastrointest Liver Physiol. 296, G1180–G1190.
Haeufle, D. F., Gunther, M., Wunner, G., and Schmitt, S. (2014). Quantifying control effort of biological and technical movements: an information-entropy-based approach. Phys. Rev. E Stat. Nonlin Soft Matter. Phys. 89:012716.
Höll, M., Kantz, H., and Zhou, Y. (2016). Detrended fluctuation analysis and the difference between external drifts and intrinsic diffusionlike nonstationarity. Phys. Rev. E. 94:042201.
Hu, K., Ivanov, P. C., Chen, Z., Carpena, P., and Stanley, H. E. (2001). Effect of trends on detrended fluctuation analysis. Phys. Rev. E Stat. Nonlin Soft. Matter. Phys. 64:011114.
Ihlen, E. (2012). Introduction to multifractal detrended fluctuation analysis in matlab. Front. Physiol. 3:141. doi: 10.3389/fphys.2012.00141
Kan, K. K. W., Wai, M. K., Jones, R. L., and Rudd, J. A. (2017). Role of prostanoid EP(3/1) receptors in mechanisms of emesis and defaecation in ferrets. Eur. J. Pharmacol. 803, 112–117. doi: 10.1016/j.ejphar.2017.03.035
Kan, K. K., Jones, R. L., Ngan, M. P., and Rudd, J. A. (2002). Actions of prostanoids to induce emesis and defecation in the ferret. Eur J Pharmacol 453, 299–308. doi: 10.1016/s0014-2999(02)02424-x
Kantelhardt, J. W., Koscielny-Bunde, E., Rego, H. H. A., Havlin, S., and Bunde, A. (2001). Detecting long-range correlations with detrended fluctuation analysis. Physica. A: Stat. Mech. Appl. 295, 441–454. doi: 10.1016/s0378-4371(01)00144-3
Kim, T. W., Beckett, E. A., Hanna, R., Koh, S. D., Ordog, T., Ward, S. M., et al. (2002). Regulation of pacemaker frequency in the murine gastric antrum. J. Physiol. 538, 145–157. doi: 10.1113/jphysiol.2001.012765
Koch, K. L. (1989). Gastric dysrhythmias and the current status of electrogastrography. Pract. Gastroenterol. 13, 41–44.
Komuro, T. (2006). Structure and organization of interstitial cells of cajal in the gastrointestinal tract. J. Physiol. 576, 653–658. doi: 10.1113/jphysiol.2006.116624
Kowalewski, K., and Kolodej, A. (1975). Effect of prostaglandin-E2 on myoelectrical and mechanical activity of totally isolated, ex-vivo-perfused, canine stomach. Pharmacology 13, 325–339. doi: 10.1159/000136922
Lu, Z., Du Sert, N., Chan, S. W., Yeung, C. K., Lin, G., Yew, D. T., et al. (2014). Differential hypoglycaemic, anorectic, autonomic and emetic effects of the glucagon-like peptide receptor agonist, exendin-4, in the conscious telemetered ferret. J. Transl. Med. 12:327.
Lu, Z., Ngan, M. P., Lin, G., Yew, D. T. W., Fan, X., Andrews, P. L. R., et al. (2017a). Gastric myoelectric activity during cisplatin-induced acute and delayed emesis reveals a temporal impairment of slow waves in ferrets: effects not reversed by the GLP-1 receptor antagonist, exendin (9-39). Oncotarget 8, 98691–98707. doi: 10.18632/oncotarget.21859
Lu, Z., Yeung, C. K., Lin, G., Yew, D. T. W., Andrews, P. L. R., and Rudd, J. A. (2017c). Centrally located GLP-1 receptors modulate gastric slow waves and cardiovascular function in ferrets consistent with the induction of nausea. Neuropeptides 65, 28–36. doi: 10.1016/j.npep.2017.04.006
Lu, Z., Yeung, C.-K., Lin, G., Yew, D. T. W., Andrews, P. L. R., and Rudd, J. A. (2017b). Centrally located GLP-1 receptors modulate gastric slow waves and cardiovascular function in ferrets consistent with the induction of nausea. Neuropeptides 65, 28–36.
Márton, L. F., Brassai, S. T., Bakó, L., and Losonczi, L. (2014). Detrended fluctuation analysis of EEG signals. Procedia Technol. 12, 125–132. doi: 10.1016/j.protcy.2013.12.465
O’Grady, G., Angeli, T. R., Du, P., Lahr, C., Lammers, W., Windsor, J. A., et al. (2012). Abnormal initiation and conduction of slow-wave activity in gastroparesis, defined by high-resolution electrical mapping. Gastroenterology 143:e583.
Parkman, H. P., Hasler, W. L., Barnett, J. L., and Eaker, E. Y. (2003). Electrogastrography: a document prepared by the gastric section of the american motility society clinical GI motility testing task force. Neurogastroenterol. Motil. 15, 89–102. doi: 10.1046/j.1365-2982.2003.00396.x
Peng, C. K., Buldyrev, S. V., Havlin, S., Simons, M., Stanley, H. E., and Goldberger, A. L. (1994). Mosaic organization of DNA nucleotides. Physical. Rev. E. 49, 1685–1689. doi: 10.1103/physreve.49.1685
Percie du Sert, N., Chu, K. M., Wai, M. K., Rudd, J. A., and Andrews, P. L. (2009a). Reduced normogastric electrical activity associated with emesis: a telemetric study in ferrets. World J. Gastroenterol. 15, 6034–6043. doi: 10.3748/wjg.15.6034
Percie du Sert, N., Chu, K. M., Wai, M. K., Rudd, J. A., and Andrews, P. L. (2010). Telemetry in a motion-sickness model implicates the abdominal vagus in motion-induced gastric dysrhythmia. Exp. Physiol. 95, 768–773. doi: 10.1113/expphysiol.2009.052001
Percie du Sert, N., Rudd, J. A., Moss, R., and Andrews, P. L. (2009b). The delayed phase of cisplatin-induced emesis is mediated by the area postrema and not the abdominal visceral innervation in the ferret. Neurosci. Lett. 465, 16–20. doi: 10.1016/j.neulet.2009.08.075
Peupelmann, J., Quick, C., Berger, S., Hocke, M., Tancer, M. E., Yeragani, V. K., et al. (2009). Linear and non-linear measures indicate gastric dysmotility in patients suffering from acute schizophrenia. Prog. Neuropsychopharmacol. Biol. Psychiatry. 33, 1236–1240. doi: 10.1016/j.pnpbp.2009.07.007
Quick, C., Kliem, A., Berger, S., Hocke, M., Tancer, M., Juckel, G., et al. (2010). Gastric dysmotility in major depression. Prog. Neuropsychopharmacol. Biol. Psychiatry 34, 92–97. doi: 10.1016/j.pnpbp.2009.10.003
Racz, F. S., Stylianou, O., Mukli, P., and Eke, A. (2019). Multifractal and entropy analysis of resting-state electroencephalography reveals spatial organization in local dynamic functional connectivity. Sci. Rep. 9:13474.
Richman, J. S., and Moorman, J. R. (2000). Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 278, H2039–H2049.
Rudd, J. A., Chan, S. W., Ngan, M. P., Tu, L., Lu, Z., Giuliano, C., et al. (2018). Anti-emetic Action of the brain-penetrating new ghrelin agonist, HM01, alone and in combination with the 5-HT3 antagonist, palonosetron and with the NK1 antagonist, netupitant, against cisplatin- and motion-induced emesis in suncus murinus (house musk shrew). Front. Pharmacol. 9:869. doi: 10.3389/fphar.2018.00869
Rudd, J. A., Jordan, C. C., and Naylor, R. J. (1994). Profiles of emetic action of cisplatin in the ferret: a potential model of acute and delayed emesis. Eur. J. Pharmacol. 262, R1–R2.
Sanders, K. M. (1984). Role of prostaglandins in regulating gastric motility. Am. J. Physiol. 247, G117–G126.
Sanger, G. J., Broad, J., and Andrews, P. L. (2013). The relationship between gastric motility and nausea: gastric prokinetic agents as treatments. Eur. J. Pharmacol. 715, 10–14. doi: 10.1016/j.ejphar.2013.06.031
Silva, L. E., Silva, C. A., Salgado, H. C., and Fazan, R. Jr. (2017). The role of sympathetic and vagal cardiac control on complexity of heart rate dynamics. Am. J. Physiol. Heart. Circ. Physiol. 312, H469–H477.
Tu, L., Lu, Z., Dieser, K., Schmitt, C., Chan, S. W., Ngan, M. P., et al. (2017). Brain activation by H1 antihistamines challenges conventional view of their mechanism of action in motion sickness: a behavioral, c-Fos and physiological study in suncus murinus (house musk shrew). Front. Physiol. 8:412. doi: 10.3389/fphys.2017.00412
Verhagen, M. A., Van Schelven, L. J., Samsom, M., and Smout, A. J. (1999). Pitfalls in the analysis of electrogastrographic recordings. Gastroenterology 117, 453–460. doi: 10.1053/gast.1999.0029900453
Wang, H., Lu, Z., Liu, Y. H., Sun, Y., Tu, L., Ngan, M. P., et al. (2018). Establishment of a radiotelemetric recording technique in mice to investigate gastric slow waves: modulatory role of putative neurotransmitter systems. Exp. Physiol. 103, 827–837. doi: 10.1113/ep086815
Wu, H. T., Liu, C. C., Lo, M. T., Hsu, P. C., Liu, A. B., Chang, K. Y., et al. (2013). Multiscale cross-approximate entropy analysis as a measure of complexity among the aged and diabetic. Comput. Math. Methods Med. 2013:32 4325.
Keywords: sulprostone, ferret, gastric myoelectric activity, running spectrum analysis, detrended fluctuation analysis, entropy
Citation: Lu Z, Zhou Y, Tu L, Chan SW, Ngan MP, Cui D, Liu YHJ, Huang IB, Kung JSC, Hui CMJ and Rudd JA (2021) Sulprostone-Induced Gastric Dysrhythmia in the Ferret: Conventional and Advanced Analytical Approaches. Front. Physiol. 11:583082. doi: 10.3389/fphys.2020.583082
Received: 14 July 2020; Accepted: 07 December 2020;
Published: 08 January 2021.
Edited by:
F. Argoul, Centre National de la Recherche Scientifique (CNRS), FranceReviewed by:
Armen Gharibans, The University of Auckland, New ZealandCopyright © 2021 Lu, Zhou, Tu, Chan, Ngan, Cui, Liu, Huang, Kung, Hui and Rudd. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zengbing Lu, emVuZ2JpbmdsdS5qYWNrQGdtYWlsLmNvbQ==; John A. Rudd, amFyQGN1aGsuZWR1Lmhr
†These authors have contributed equally to this work
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.