Gauging Functional Brain Activity: From Distinguishability to Accessibility

Papo, David

doi:10.3389/fphys.2019.00509

PERSPECTIVE article

Front. Physiol., 08 May 2019

Sec. Fractal Physiology

Volume 10 - 2019 | https://doi.org/10.3389/fphys.2019.00509

Gauging Functional Brain Activity: From Distinguishability to Accessibility

$\r\nDavid Papo*$ David Papo^*

SCALab, UMR CNRS 9193, Université de Lille, Villeneuve d’Ascq, France

Standard neuroimaging techniques provide non-invasive access not only to human brain anatomy but also to its physiology. The activity recorded with these techniques is generally called functional imaging, but what is observed per se is an instance of dynamics, from which functional brain activity should be extracted. Distinguishing between bare dynamics and genuine function is a highly non-trivial task, but a crucially important one when comparing experimental observations and interpreting their significance. Here we illustrate how neuroimaging’s ability to extract genuine functional brain activity is bounded by functional representations’ structure. To do so, we first provide a simple definition of functional brain activity from a system-level brain imaging perspective. We then review how the properties of the space on which brain activity is represented induce relations on observed imaging data which allow determining the extent to which two observations are functionally distinguishable and quantifying how far apart they are. It is also proposed that genuine functional distances would require defining accessibility, i.e., how a given observed condition can be accessed from another given one, under the dynamics of some neurophysiological process. We show how these properties result from the structure defined on dynamical data and dynamics-to-function projections, and consider some implications that the way and extent to which these are defined have for the interpretation of experimental data from standard system-level brain recording techniques.

Introduction

System-level neuroimaging techniques such as PET and MRI make it possible to non-invasively access not only the anatomy of the human brain but also its physiology (Raichle, 2000). Brain activity recorded with these techniques, and others such as EEG or MEG is generally called functional imaging. However, observed activity is not genuinely functional per se, and neuroimaging data should a priori be treated as brain dynamics. Extracting functional brain activity from bare dynamics represents a non-trivial though often implicit process (Atmanspacher and Beim Graben, 2007; Allefeld et al., 2009).

Defining functional brain activity and how the brain implements given functions are arduous tasks. Here we address neither these ontological issues, nor the comparably complex one of state-space reconstruction from data, but a more circumscribed methodological question: how does neuroimaging data structure determine our ability to define functional activity?

Experimentalists typically compare representations associated with different recording sessions from the same individual, different individuals, or experimental conditions, addressing questions such as: when are two representations distinguishable? How far apart are they? What do neighboring representations look like? Is a transition possible from a given representation to another?

We illustrate how neuroimaging’s ability to address these questions is bounded by functional representations’ structure. We first provide a simple but convenient definition of functional brain activity from a system-level brain imaging perspective, a more comprehensive one being beyond the present work’s scope. We then review how the structure of the space on which brain activity is represented allows defining relations among observed instances of the dynamics, and show how these result from dynamics-to-function projections.

Defining Functional Brain Activity

Function can be defined as the ability to perform a given cognitive or physiological task. Insofar as individuals’ behavioral performance results from brain properties, functional activity refers to both behavior and neural structures reflecting two complementary goals: understanding how brain anatomical structure and dynamics control function, and how task performance’s action produces functional brain subdivisions. In the former, a space Ψ of (typically non-observable) cognitive or physiological functions {ψ₁, ψ₂, ..., ψ_J} is described using a finite set {φ₁, φ₂, ..., φ_K} ∈ Φ_Obs of carefully selected coarse-grained aspects of brain anatomy or physiology (reflecting at a macroscopic level neurophysiological phenomena Φ_NObs not observable when using a given system-level neuroimaging technique) associated with observable performance measures {γ₁, γ₂, ..., γ_L} ∈ Γ from subjects at rest or carrying out given tasks. In the latter, the ability to carry out given tasks is used as a probe exposing information on brain properties Φ.

Defining functional brain activity using system-level neuroimaging techniques involves partitioning two complex spaces, respectively made observable by behavior and brain recording techniques, putting some structure, i.e., a relationship among the set’s elements, on the set of equivalence classes, and mapping the corresponding structures.

Brain Parcellation

Characterizing functional activity is in essence a parcellation problem. When using Φ to make sense of Ψ one ultimately aims at partitioning the space of cognitive functions f : Ψ → Ψ/ℜ where Ψ = Ψ(Γ, Φ) and Ψ/ℜ is the space of equivalence classes under the relation ℜ. In the opposite case, Φ is partitioned into functionally meaningful units g : Φ → Φ/ℜ′ using cognitive tasks as probes. This implies evaluating the sets U = π⁻¹(V) where U ⊂ Ψ, V ⊂ Φ/ℜ′, π : Ψ → Φ/ℜ′ and ℜ′ is a relation defined on Φ or the equivalent in the opposite case. Since typically L ≪ K the structure on Φ is finer than that on Γ and physiology is more often used to define the cognitive space than the opposite case. Meaningful functional units correspond to the family of sets 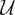www.frontiersin.org _π = {U = π⁻¹(V)} (or, equivalently, 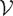_π′ = {V = π′⁻¹(U)}). How to construct 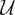_π (or 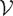_π′) what form the corresponding space may take, and therefore what may be regarded as functional, depends on the way (Ψ, 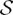_Ψ) and (Φ, 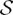_Φ) are defined and mapped onto each other through π (orπ′), 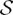www.frontiersin.org denoting a generic structure.

Classical neuropsychological descriptions map Γ onto the anatomical orthonormal Euclidean space (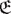 www.frontiersin.org ; d) where d is the usual metric, so that Φ 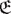⊂ ℝ³. Brain lesions induce a coarse partition Φ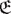_/L.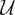_π is extrapolated from the overlap between lesions and cortical areas, i.e., anatomical space partitions defined on the basis of cytoarchitecture, histological structure or organization homogeneity (Brodmann, 1909), associated with a map Ψ → Φ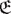, using double dissociations together with the assumption of modularity of both Φ 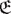and Ψ (Dunn and Kirsner, 2003).

System-level neuroimaging maps Ψ onto some function of macroscopic observables φ_i ∈ Φ of brain physiology. Neuroimaging data are typically treated as (scalar, vector, or tensor) fields 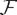www.frontiersin.org = {f_X (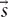, t)} where 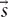lives in a subspace isomorphic to ℝ³ and t ∈ ℝ is the physical time, and described in terms of some convenient function of this field, in the spatial (anatomical), temporal, frequency domains or in phase space, at experimental, developmental or evolutionary time-scales. On the other hand, while Γ is typically a scalar or vector field, it can sometimes take the form a complex function space.

Functional parcellations are defined in a recording technique- and scale-dependent manner. For fast sensory processes, functional equivalence classes can be defined by characterizing the dynamical range, i.e., the range of stimulus intensities resulting in distinguishable neural responses, while the dynamical repertoire, i.e., the number of distinguishable responses, quantifies the functional phase space extension. How to define distinguishability represents the most crucial question. For processes with non-trivial temporal scales such as thinking or reasoning (Papo, 2015) extracting function from dynamics is conceptually and technically arduous and involves understanding the structure of brain dynamics and how this can be used to ultimately define function.

Superstructure of Brain Imaging Representations

The space on which parcellations are defined is in general endowed with some superstructure. First, brain anatomy and dynamics can be endowed with a network structure (Bullmore and Sporns, 2009), and, as a consequence, with topological properties (Boccaletti et al., 2006) and symmetries (Pecora et al., 2014). Network structures indicate that parcellations may not necessarily be local in the anatomical space.

Φ is typically embedded into (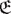 www.frontiersin.org ; d), and treated as a field (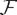; d) equipped with d. This translates the fact that, at least at the temporal scales at which anatomy represents a genuine boundary condition for brain anatomy and dynamics (Papo, 2017), the brain can be thought of as a spatial network (Barthélemy, 2011), submitted to geometric alongside topological constraints (Robinson P. A., 2013; Stiso and Bassett, 2018).

While Φ should not be regarded as homeomorphic to ℝⁿ, it may be treated as almost everywhere locally isomorphic to it, and represented as a topological manifold (X,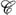 www.frontiersin.org ) i.e., a paracompact topological space X equipped with an atlas, a cover 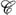of open sets where each C ∈ 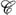is homeomorphic to an open subset D ⊆ ℝⁿ through a map φ_C: C → D called a chart of 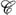(Robinson M., 2013). Whenever data can effectively be treated as the output of a dynamical system, Φ may be modeled as a topological dynamical system, i.e., a triple (Φ, 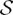www.frontiersin.org , T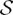) where Φ is a Hausdorff (separable) topological space, 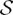a topological semigroup prescribing the matching conditions between overlapping local trivialization charts, and T 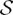a continuous function T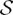: 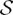× Φ → Φ. For instance, long time scales fluctuations are characterized by non-trivial scaling properties such as scale-invariance (Novikov et al., 1997; Linkenkaer-Hansen et al., 2001; Allegrini et al., 2010; Expert et al., 2010; Papo, 2013), and the set of associated renormalization operators has a multiplicative semigroup structure on the time-scale space (Papo, 2014).

Φ can nonetheless be equipped with a geometry in various ways. First, geometry may be derived from topology. A network can always be embedded in a surface, provided it has sufficiently high genus (Aste et al., 2005); continuous space geometry may also emerge from the discrete network structure at microscopic scales, as in pregeometric models of quantum gravity (Bianconi and Rahmede, 2017). Furthermore, time series may be mapped into geometry, e.g., by representing observed brain activity in terms of probability distribution functions (Amari and Nagaoka, 2007; Lesne, 2014; Ali et al., 2018). This induces a smooth manifold www.frontiersin.org whose points are probability distributions defined on a common probability space (Amari and Nagaoka, 2007). Fluctuations’ scaling properties may help equipping the space with a specific geometry. For instance, scale-free distributions suggest a fractal geometry, for the temporal structure of spatially local fluctuations (Novikov et al., 1997; Linkenkaer-Hansen et al., 2001; Allegrini et al., 2010; Expert et al., 2010; Papo, 2013), but also for network representations of brain activity (Pasemann, 2002) whereas accounting for the history-dependence of brain fluctuations may require a non-commutative one or a quasi-metric space.

Gauging Neuroimaging Data

Interpreting neuroimaging data requires introducing relations among experimental conditions and this, in turn, understanding the implications that given structures have on the definition of the families www.frontiersin.org _π or, equivalently,_π′. Endowing data with given structural properties induces specific equivalence classes, e.g., two dynamical systems are dynamically equivalent if they are topologically conjugate (Xue and Bogdan, 2017). More generally, observed data may be classified up to a given property (e.g., homotopy, symmetry, etc) or by obstructions to one of them. Conversely, comparing experimental conditions involves comparing their associated (e.g., network) structure, each structure involving its own set of operations and restrictions, and sometimes adding further structure (Simas et al., 2015; Gadiyaram et al., 2016; Schieber et al., 2017).

At the most basic level, comparing experimental conditions requires evaluating the topological distinguishability of two sets V₁ and V₂ in φ/ℜ′ and the corresponding U₁ and U₂ in Ψ/ℜ. For the bare field representation, this requires comparing two fields f_X and f_Y a seemingly tractable task. However, noise, inter-individual differences and the possible organization of functional brain activity into patterns with similar meaning but considerably different anatomical structure (Ganmor et al., 2015) render distinguishability in terms of pattern similarity in ( www.frontiersin.org ; d) misleading.

The extent to which two parcellations can be distinguished depends on the space’s separation properties (Dodson and Parker, 1997). The functional space is not necessarily separable, even when Φ is embedded in (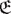 www.frontiersin.org ; d). This is the case for fuzzy relations (Grzegorzewski, 2017) or overlapping communities (Palla et al., 2005) for which the manifold’s atlas charts overlap, and transition functions are needed to resolve these areas.

Observed data can be regarded as instances of an ensemble of objects with given properties, and equivalence class membership assessed using maximum entropy methods (Bianconi, 2007; Cimini et al., 2019). These properties’ meaningfulness can be gauged by their ability to perform a given task, e.g., classification or prediction (Zanin et al., 2016).

Often, it is also necessary to quantify how far V₁ and V₂ and the corresponding U₁ and U₂ are from each other. This implies defining some property intuitively translating the concept of distance. While the anatomically-embedded functional space can only locally be considered a Euclidean metric space, distances may be defined for other structures in a way that is dictated by the structure itself (Rossi et al., 2015; De Domenico and Biamonte, 2016). When operating in a probability distribution space, Φ can be equipped with the Fisher information metric e.g., by using the covariance matrix as a metric tensor (Crooks, 2007). This endows the space 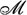www.frontiersin.org with a Riemannian differential manifold structure (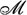, g, θ), g being the Fisher-Rao information metric and the parameters θ probability measures representing the manifold’s coordinates. The Fisher metric can be used to quantify the informational difference between measurements, and model predictions’ sensitivity to changes in parameters (Machta et al., 2013). Whenever neuroimaging data can be treated as a dynamical system, a dynamical distance can be derived from the dynamics itself. This distance allows a coarse-graining which in some sense is optimal with respect to the dynamics (Gaveau and Schulman, 2005). Finally, whether considering static or dynamic structures, perturbation methods can induce both a metric and proximity relations in Φ (Peters, 2016).

From Dynamics to Function

To move from dynamical equivalence classes, comprising identical dynamical properties and symmetries, to functional equivalence classes, comprising patterns of neural activity that can achieve given functional properties (Ma et al., 2009) requires considering the structure induced by T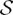_{_Ψ}: Φ/Γ → Φ/Γ. While dynamical properties may sometimes be interpreted in functional terms, e.g., the co-existence of different attractors points to a given system’s multi-functionality (Xue and Bogdan, 2017), the dynamical system T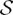_{_Ψ}: Φ/Γ → Φ/Γ may give rise to non-trivial properties that cannot be anticipated based on dynamics alone.

While each recording technique’s precision induces specific a priori parcellations of Φ, these are in general not functionally relevant. To be functionally meaningful, metrics in Φ need to be appraised in the space Ψ made observable through Γ. How properties in one structure are transferred onto those of the other depends on the map π. Ideally, one seeks the finest topology in Φ/ℜ′ that renders the π: Γ → Φ surjection continuous. This means endowing Φ with the quotient topology with respect to π i.e., the family V_π = {V |π⁻¹(V) is open in Γ}. Thus, from a neuroimaging view-point, functional brain activity can be thought of as a fiber bundle, i.e., a quadruple (Ψ, Φ, π, 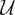www.frontiersin.org _π), where Ψ is the total space, Φ the base π: Ψ → Φ a continuous surjective function called projection, and 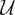_π the fibers. Φ can be identified with a subspace of Ψ through a fiber bundle section, i.e., a continuous right inverse of the projection function π defined on open sets of Φ. Ψ is locally but not necessarily globally isomorphic to a Cartesian product Φ × 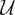www.frontiersin.org _π (see Figure 1).

FIGURE 1

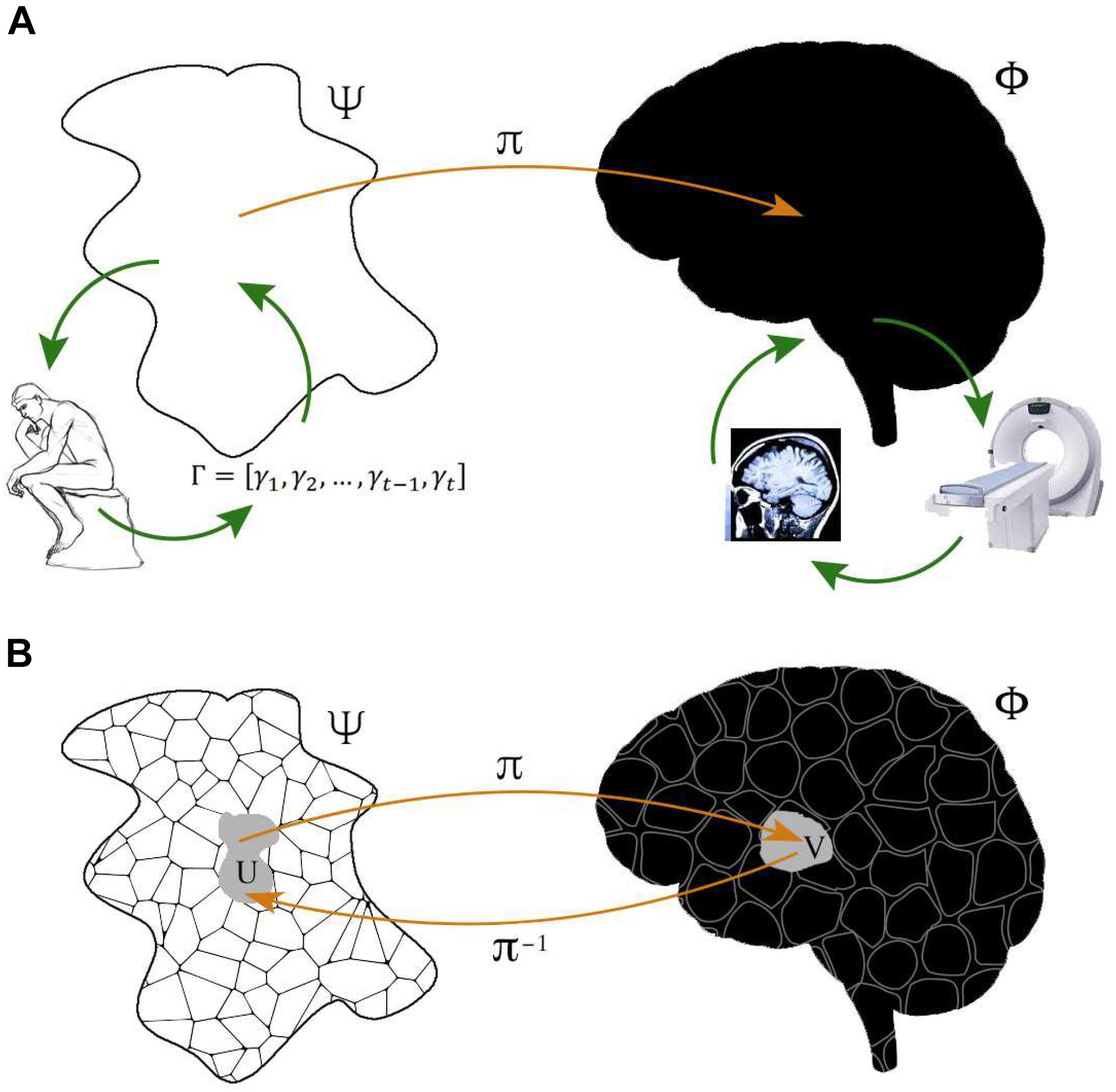
Figure 1. Representation of system-level functional brain mapping. (A) Typical neuroimaging experiments are designed to reconstruct a space Ψ of cognitive or physiological functions, made behaviorally observable by performance measures Γ from subjects at rest or carrying out given tasks, which can be associated, via some mapping π, with a space Φ defined by some brain property, observed through some neuroimaging technique. Experiments may also address the somehow dual aim of reconstructing Φ by using carefully selected cognitive of physiological probes, indirectly reflecting the space Ψ. Each neuroimaging technique documents specific neurophysiological phenomena Φ_Obs which result from brain activity Φ_NObs inaccessible to this particular technique. Note that functional brain activity Φ is typically identified with the anatomical space with Cartesian coordinates, but may in principle represent any other brain feature. (B) Φ and Ψ both have their own, usually non-trivial, structure i.e., a collection of elements together with a relation among them. The crucial point is that what is observed with a neuroimaging technique is not functional per se. Observed brain activity is genuinely functional if structure of the neurophysiological space Φ is reflected by structure in Ψ. Accordingly, neuroimaging’s goal is to use the structure of one space to refine the structure of the other, for all the elements of these spaces. The problem addressed by functional brain imaging can be thought of as a fiber bundle, in essence a family of spaces (fibers) parameterized by another space (base). Such a structure can be used to define properties that are useful when gauging the significance of observed brain activity.

Before examining the properties of the π: Ψ → Φ map, it is worth recalling that there exists a non-observable map 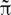www.frontiersin.org : Φ_NObs → Φ_Obs which can show permutation symmetry but also combinatorial complexity with respect to more fine-grained Φ_NObs configurations (Brezina, 2010). A faithful representation of the hidden microscopic structure preserving given properties, e.g., symmetry (Cross and Gilmore, 2010), and the possibility to obtain a dynamical rule for the system (Allefeld et al., 2009) requires finding a generating partition, an arduous task in practice (Kantz and Schreiber, 2004). While macroscopic scale descriptions are stricto sensu dynamically emergent states only if they correspond to a Markov coarse-graining of lower-level dynamics (Adler, 1998; Shalizi and Moore, 2003; Bollt and Skufca, 2005; Gaveau and Schulman, 2005; Allefeld et al., 2009), both Φ_Obs and Γ can loosely be thought to emerge from the renormalization of microscopic neural fluctuations. How microscopic scales renormalize into macroscopic ones determines the scale at which the space is locally isomorphic to ℝⁿ and can effectively be treated as a topological manifold. This scale may be induced by permutation symmetry with respect to a given property at microscopic scales. On the other hand, topologically equivalent structures may not have the same functional meaning in Φ_Obs and Φ_NObs For example, the robust computational properties associated with motifs in microcircuits (Klemm and Bornholdt, 2005; Gollo and Breakspear, 2014) do not necessarily characterize structurally isomorphic macroscopic circuits. Observability may also be increased by taking into account processes that are not directly observed when reconstructing the underlying dynamical system (Gupta et al., 2018).

The Φ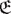 → Ψ map the lesion-based framework is in general ill-defined, due to fuzzy lesion contour geometry, and global non-Euclideanity but also to Φ′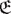s lack of temporal dimension and brain degeneracy (Price and Friston, 2002). However, Φ → Ψ maps can sometimes be well-behaved. A notable example is represented by Kelso’s bimanual finger coordination paradigm (Kelso, 1995). Once the relative phase ϕ between the fingers is chosen as the order parameter describing the dynamics, Φ and Ψ are both differentiable and Ψ turns out to be diffeomorphic to the macroscopic velocity field ∇ Φ, which in turn can be thought of as collective modes of underlying neurophysiological activity (Kelso et al., 1998). Since total space, base and fiber are all smooth differentiable manifolds and π is surjective, the functional space can be considered as a differentiable fiber bundle. While in most contexts Ψ cannot be described in terms of differential equations or even dynamical rules, relatively well-behaved mappings may occur in other contexts as well. For instance, both brain networks (Meunier et al., 2010), and brain temporal fluctuations (Papo, 2014) display generic hierarchical structure which may be mirrored by one in Ψ, e.g., linguistic functions may be defined in terms of hierarchical relations, rules, and operations.

From Measure to Accessibility

Proximity relations are usually quantified in terms of static representations, both for truly quasi-static data (e.g., fMRI images) and for dynamic ones (e.g., EEG recordings). However, these properties depend on the way one state in Φ/Γ may be transformed into another under some neurophysiological process.

To understand how the functional space inherits Φ′s properties, one may think of neurophysiological processes being only partially observable at the system level of non-invasive neuroimaging techniques, as genotype, and of observed behavior or macroscopic brain activity as the corresponding phenotype, resulting from coarse-graining of physiological processes. The crucial question is: what space does the genotype-to-phenotype map induce?

A smooth genotype-to-phenotype map can sometimes be ensured. For instance, in Kelso’s paradigm (Kelso et al., 1998), functional discontinuities in Ψ can be explained in terms of genuine brain dynamics. This results from the simultaneous fulfillment of various conditions: Φ′s differentiable manifold structure allows for differential calculus on the manifold; function is defined in terms of dynamical variables, i.e., synchronization and syncopation; components and collective variables in Ψ can both be endowed with explicit differentiable analytical expressions, and cognitive demands can be construed as their boundary conditions (Kelso, 1995).

However, Ψ → Φ can induce non-trivial structure, and the phenotype space induced by T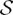_{_Ψ} may be non-metric, and even the less stringent notion of topology may not hold (Stadler et al., 2001; Stadler and Stadler, 2006). Nearness and neighborhood in the phenotype space should reflect the structure induced by genotype space’s accessibility, i.e., the ability to reach a given state x from another given state y, under the action of some underlying neurophysiological process: the variation operators establishing which configurations are accessible from given ones should reflect the dynamics of physiological processes (see Figure 2).

FIGURE 2

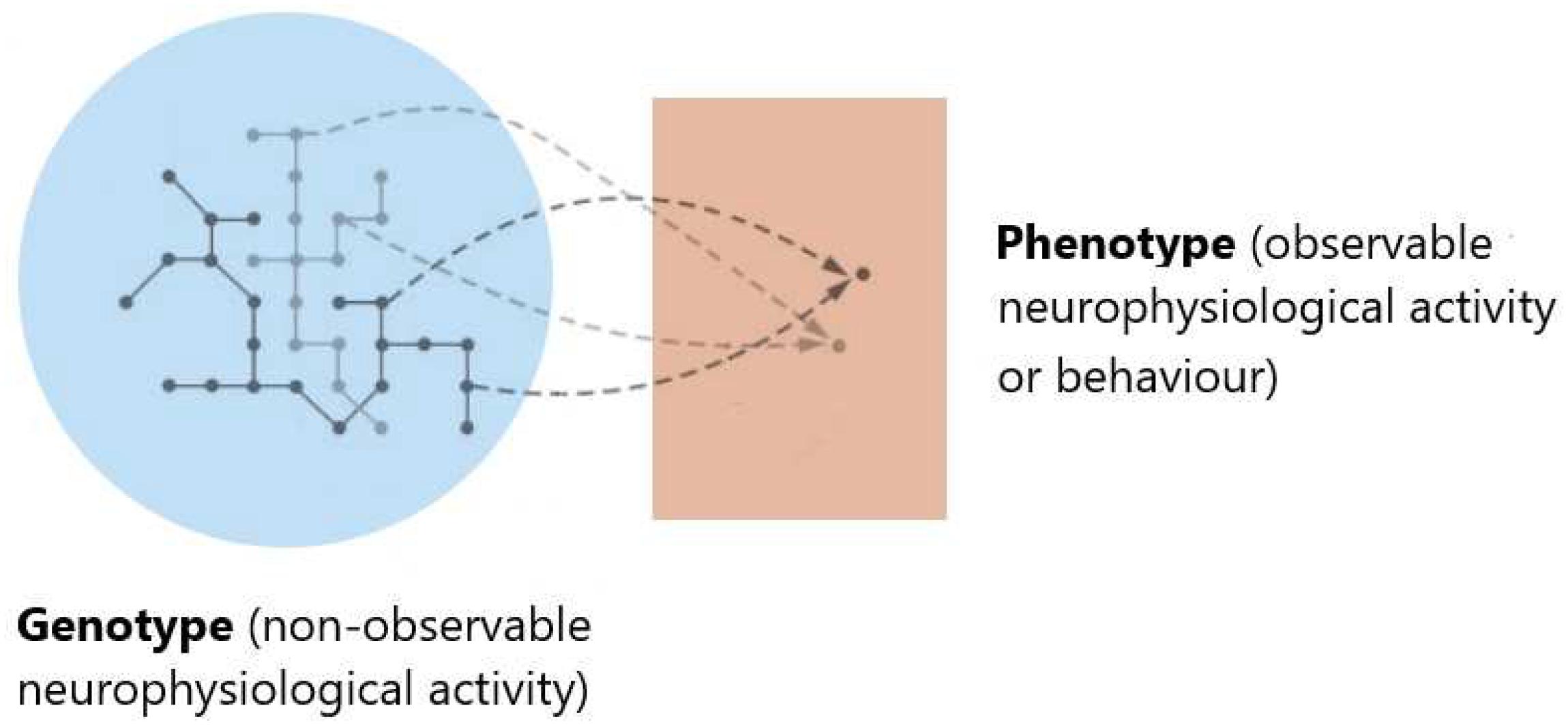
Figure 2. Gauging the functional space. Evaluating the significance of brain activity may require comparing data from different experimental conditions or subjects. This may involve not only asking whether given data sets are distinguishable, and quantifying how far apart they are but also establishing which configurations can be attained from given ones. Rather than the similarity of neuroimaging data representations, a dynamical definition of nearness and neighborhood should reflect the structure induced by the accessibility of given states induced by physiological process dynamics. This notion can be understood by thinking of Φ_NObs as genotype, and Φ_Obs (or observed behavior) as the corresponding phenotype. Characterizing accessibility in the phenotype space means understanding which phenotypic variations (corresponding to genuine functional differences) are realizable and which dynamical changes or image representation differences (depicted by networks of different gray shades in the genotype space) are functionally neutral, i.e., have equivalent function, with respect to underlying neurophysiological processes.

Ultimately, the phenotype’s properties depend on which variations are neurophysiologically neutral and which ones are realizable in the neighborhood of underlying neuronal variations. Since accessibility lacks symmetry in general, nearness in the induced space should be non-symmetric. Furthermore, dynamical patterns including intermittencies, degeneracy, and redundancy can result from the phenotype’s topological properties induced by the genotype-to-phenotype map.

Concluding Remarks

Though not necessarily the case, some structures used in data analysis, viz. in topological data analysis, may reflect the way function impacts on brain dynamics. The brain can be thought of as a “geometric engine,” implementing structures (e.g., fiber bundles) through task-specific functional architectures, i.e., a hard-wired anatomical apparatus together with some dynamics (Koenderink and van Doorn, 1987), with non-random topological properties (Giusti et al., 2015; Curto et al., 2017), and (possibly non-Euclidean) geometry (Petitot, 2013, 2017). Moreover, representing brain data as probability distributions allows characterizing function as a perturbation of brain dynamics’ functional form, amplitude, or frequency modulations representing a short temporal scales special case (Papo, 2014). This representation induces a space of functions on Φ straightforwardly mirroring the non-observable space Ψ.

Topological signal processing tools are consistent with information locality (in space, time, and frequency, etc) (Robinson M., 2013). Likewise, despite novel techniques and high-performance computing, cortical areas are typically defined based on anatomically local structure-function associations (Amunts and Zilles, 2015), under the assumption that information is (locally) compact in www.frontiersin.org . However, the brain also shows genuine non-locality, i.e., interaction-induced emergence, and the role of non-local information cannot be neglected (Santos et al., 2018).

Representing Φ as a space that does not derive its topology from a metric (Baruchi and Ben-Jacob, 2004; Petri et al., 2014) allows treating multiple observables, observation scales and geometries, and defining relationships between geometric objects constructed using different parameter values and continuous maps relating these objects (Carlsson, 2009).

Endowing Φ with a structure involves discretionary choices somehow associated with assumptions on what should be regarded as functional in brain activity, introducing circularity between definition and quantification of functional brain activity (Papo et al., 2014b). For instance, there are no criteria to elect the space to equip with a network structure, or to define its boundaries, constituent nodes and edges (Papo et al., 2014a). Brain function “stylized facts,” topological and geometrical constructs, and thorough behavioral studies (Krakauer et al., 2017) may all help defining and quantifying brain function. Finally, whether at the computational, algorithmic or implementation level (Marr, 1982), genuine mechanistic descriptions (Illari and Williamson, 2012) will help determining when the functional space can be endowed with a given representation and how reproducible it is.

Data Availability

All datasets analyzed for this study are cited in the manuscript and the supplementary files.

Author Contributions

DP thought and wrote the manuscript.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author acknowledges financial support from the Program “Accueil de Talents” of the Métropole Européenne de Lille and from the Labex (laboratory of excellence) DISTALZ (development of innovative strategies for a transdisciplinary approach to Alzheimer’s disease).

References

Adler, R. (1998). Symbolic dynamics and Markov partitions. Bull. New Ser. Am. Math. Soc. 35, 1–56.