
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
METHODS article
Front. Physiol., 24 August 2018
Sec. Computational Physiology and Medicine
Volume 9 - 2018 | https://doi.org/10.3389/fphys.2018.01003
This article is part of the Research TopicMathematical Modeling of Cardiovascular Systems: From Physiology to the ClinicView all 24 articles
The pathophysiological mechanisms underlying preserved left ventricular (LV) ejection fraction (EF) in patients with heart failure and preserved ejection fraction (HFpEF) remain incompletely understood. We hypothesized that transmural variations in myofiber contractility with existence of subendocardial dysfunction and compensatory increased subepicardial contractility may underlie preservation of LVEF in patients with HFpEF. We quantified alterations in myocardial function in a mathematical model of the human LV that is based on the finite element method. The fiber-reinforced material formulation of the myocardium included passive and active properties. The passive material properties were determined such that the diastolic pressure-volume behavior of the LV was similar to that shown in published clinical studies of pressure-volume curves. To examine changes in active properties, we considered six scenarios: (1) normal properties throughout the LV wall; (2) decreased myocardial contractility in the subendocardium; (3) increased myocardial contractility in the subepicardium; (4) myocardial contractility decreased equally in all layers, (5) myocardial contractility decreased in the midmyocardium and subepicardium, (6) myocardial contractility decreased in the subepicardium. Our results indicate that decreased subendocardial contractility reduced LVEF from 53.2 to 40.5%. Increased contractility in the subepicardium recovered LVEF from 40.5 to 53.2%. Decreased contractility transmurally reduced LVEF and could not be recovered if subepicardial and midmyocardial contractility remained depressed. The computational results simulating the effects of transmural alterations in the ventricular tissue replicate the phenotypic patterns of LV dysfunction observed in clinical practice. In particular, data for LVEF, strain and displacement are consistent with previous clinical observations in patients with HFpEF, and substantiate the hypothesis that increased subepicardial contractility may compensate for subendocardial dysfunction and play a vital role in maintaining LVEF.
Heart Failure (HF) is the only cardiovascular disease for which incidence, prevalence, morbidity, mortality, and costs are not decreasing. According to the 2017 Update (Benjamin et al., 2017), the prevalence of HF has increased from 5.7 million (2009 to 2012) to 6.5 million (2011 to 2014) in Americans >20 years of age and projections show prevalence will increase 46% by 2030, resulting in over 8 million adults with HF (Heidenreich et al., 2013). In 2012, the total cost for HF was estimated to be $31 billion and projections show that by 2030, the total cost will increase to $70 billion or roughly ~$244 for every US adult (Heidenreich et al., 2013). Among patients hospitalized for an HF incident, 47% had HF with preserved ejection fraction (HFpEF) or systolic function, which is the focus of this paper.
The mechanism of the development of HFpEF is not well-understood (Aurigemma and Gaasch, 2004; Shah and Solomon, 2012; Steinberg et al., 2012; Sengupta and Marwick, 2018), and optimal treatment options remain unclear (Vasan et al., 1995; Bhuiyan and Maurer, 2011). Recent studies have suggested that HFpEF is associated with transmural changes in myocardial deformation (Shah and Solomon, 2012; Omar et al., 2016, 2017). Understanding the transmural variations in left ventricular (LV) mechanics associated with HFpEF may offer pathophysiological insights for developing potential therapeutic targets. We therefore explored a physics-based mathematical [finite element (FE)] model of the normal human LV to test the hypothesis that reduced subendocardial contractility combined with compensatory high subepicardial contractility may help in preserving LVEF independent of changes in myocardial geometry and material properties. We used our established computational framework in this paper. To the best of our knowledge, this is the first study that quantifies the development of HFpEF based on transmural variation in contractility, using patient-specific parameters.
In vivo echocardiographic recordings were obtained under a protocol approved by our institutional review board. Individual patients provided informed consent and anonymized data were sent to a core laboratory for analysis.
The ventricle model pertains to a normal human subject. The LV was modeled as a truncated thick-walled ellipsoid (Mercier et al., 1982; LeGrice et al., 2001). Based on echocardiography recordings for end diastolic volume (EDV), LV diameter and wall thicknesses for the posterior and septal wall, we back-calculated ellipsoidal surfaces for the endocardium and epicardium at end diastole (ED).
Using a linearly regressed estimation of the unloaded LV cavity volume V0 (Klotz et al., 2006) we scaled the dimensions of the endocardium surface to match the calculated volume V0. The epicardium dimensions were then scaled to maintain the same myocardial wall volume ascertained at the ED configuration (preservation of mass).
TruGrid (XYZ Scientific Applications Inc, Pleasant Hill, California, USA) was used to mesh LV surfaces. The ventricle was meshed to produce eight layers through the radial direction (Figure 1). Finite element calculations were performed in ABAQUS (SIMULIA, Providence, RI, USA). The FE meshes are shown in Figure 1.
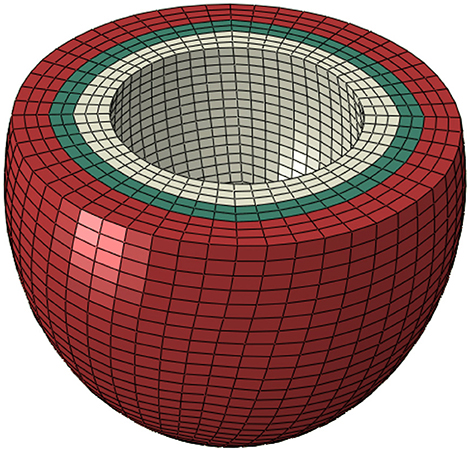
Figure 1. In normal conditions, contractility (Tmax) was uniform in all layers (scenario 1). To simulate no contraction in the subendocardial region, contractility in three layers in white was set to zero (scenario 2). The three layers in red were used to simulate alterations in subepicardial contractility (scenario 3). The three white layers, the two green layers, and the three red layers comprise subendocardial, midmyocardial, and subepicardial regions, respectively.
We used a rule-based approach coded in MATLAB 2012b (The MathWorks, Inc., Natick, Massachusetts, United States) to assign myofiber orientations to the centroid of each element in the meshed LV geometry. The aggregated myofiber orientation was assumed to present with an angle of −60° from the local circumferential direction on the epicardium surface that varies linearly through the LV wall thickness to an angle of +60° on the endocardial surface. This assumption is well-established in LV modeling studies (Carrick et al., 2012; Lee et al., 2013, 2015; Genet et al., 2014), and based on histological studies (Streeter et al., 1969), and diffusion tensor MRI studies (Lombaert et al., 2011).
The material formulation of the LV tissue includes passive and active properties. The passive behavior of the tissue was described using the model introduced by Holzapfel and Ogden (Holzapfel and Ogden, 2009; Göktepe et al., 2011). Briefly, the strain energy function used to compute passive stresses is composed of deviatoric (Ψdev) and volumetric (Ψvol) parts as follows:
where a and b represent isotropic stiffness of the tissue, af and bf represent tissue stiffness in the fiber direction, and afs and bfs represent the stiffness resultant from connection between fiber and sheet directions; l1, l4i, and l8fs are invariants, defined as follows:
where C is the right Cauchy-Green tensor, and f0 and s0 are vectors specifying the fiber and sheet directions, respectively. J is the deformation gradient invariant, and D is a multiple of the Bulk Modulus K (i.e., D = 2/K).
The material constants a, ai, and afs scale the strain-stress curve, whereas material constants b, bi, and bfs determine the shape of the strain-stress curve. To determine these parameters we used the End Diastolic Pressure Volume (ED PV) curve as described by Klotz et al. who reported an analytical expression for the ED PV curve based on a single PV point that is applicable for multiple species, including humans (Klotz et al., 2006). The LV EDV of 53 ml was recorded using echocardiography and the LV EDP of 14.3 mmHg was approximated from echocardiography data using Nagueh's formula (Nagueh et al., 1997).
The optimized material properties were found using an in-house Python script that minimized the error between the ED PV curve from the FE model and the analytical expression (Klotz et al., 2006). The sequential least squares (SLSQP) algorithm (Jones et al., 2001) was used in the Python script, and ABAQUS was used for the FE modeling, as the forward solver (Table 1 and Figure 2).

Table 1. Passive material properties that produced a pressure-volume curve close to the experimental pressure-volume curve (Figure 2).
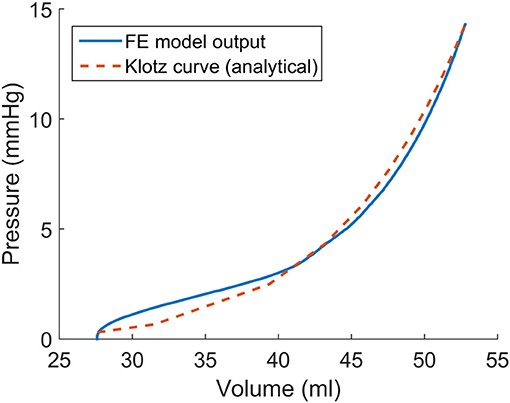
Figure 2. The passive material properties were determined such that the end diastolic pressure volume (ED PV) curve from finite element model was close to the experimental ED PV curve determined by Klotz et al. (2006).
The formulation for the active stress has been described extensively in the literature (Guccione and McCulloch, 1993; Walker et al., 2005; Genet et al., 2014; Sack et al., 2016). In short, the active stress in the myofiber direction was calculated as:
where Tmax is the isometric tension at the largest sarcomere length and highest calcium concentration, Ca0 is the peak intracellular calcium concentration, and
m, b = constants that govern the shape of the linear relaxation duration and sarcomere length relaxation.
Also,
where Eff is the Lagrangian strain in the fiber direction, B is a constant that governs the shape of the peak isometric tension-sarcomere length relation, l0 is the sarcomere length that does not produce active stress, lR is the sarcomere length with the stress-free condition, and (Ca0)max is the maximum peak intracellular calcium concentration.
The active stress was added to the passive stress to compute total stress:
where S is the total stress.
The boundary and load conditions generally follow the ABAQUS Living Heart Model (Baillargeon et al., 2014, 2015; Sack et al., 2016). In particular, the center of the LV proximal cross-section (base) was fixed. The average rotation and translation of nodes of the endocardial annulus were coupled to the center of the LV base. This boundary condition prevents rigid body rotation, but allows inflations and contractions of the annulus. The nodes of the base were fixed in the longitudinal direction. A pressure load was applied to the LV surface to simulate diastole, whereas the contraction of the LV muscles caused systole. Surface-based fluid cavities and fluid exchanges were used to model blood flow (ABAQUS Analysis User's Guide).
When Tmax is changed in Equation (2), the total contractile force of the tissue is altered, and other parameters related to the passive and active material formulations (Equations 1, 2) either do not change or change in a consistent way. We can prescribe different values of Tmax in transmural layers to introduce regionally varying contractility throughout the LV. We considered six scenarios with different contractile properties, as explained in Table 2. Homogenous contractile properties were considered in scenario 1, which also served to establish a baseline value for normal Tmax. Tmax was calibrated to produce the echocardiogram-recorded value for end- systolic volume (ESV) for this patient (24.8 ml). To simulate the diseased condition, subendocardial contractility was set to zero by setting Tmax = 0 (scenario 2). To recover ESV, a scenario was considered in which Tmax was increased in the subepicardial layers (scenario 3). To further assess the effects of transmural contractility, three more scenarios with different contractility in the transmural layers were created. In scenario 4, Tmax in all regions was reduced by 50%. In scenario 5, Tmax was set to zero in subepicardial and midmyocardial regions. In scenario 6, Tmax was set to zero in the subepicardial region.
To calculate LV torsion, we use the following formula (Aelen et al., 1997; Rüssel et al., 2009).
Where τ is normalized LV torsion; Øapex and Øbase are rotations in the apex and base, respectively; ρapex and ρbase are the radius of the apex and base, respectively; and D is the distance between the apex and base (Figure 3).
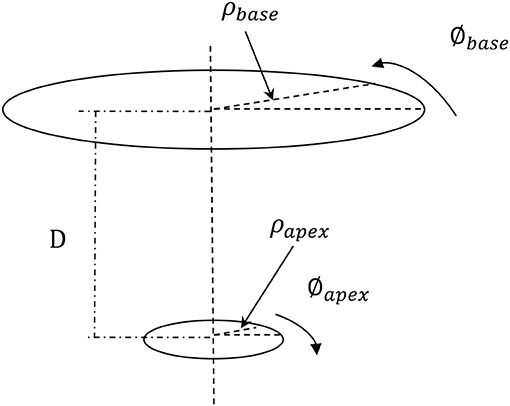
Figure 3. The torsion of the LV was computed based on the apical and basal rotations, the apical and basal radius, and the distance between the apex and base. The formula used to compute the LV torsion (Equation 4) makes the LV torsion comparable for hearts of different sizes (Aelen et al., 1997; Rüssel et al., 2009). The positive rotation is counterclockwise when seen from apex.
The EF decreased from 53.2 to 40.5% when Tmax was set to zero in the subendocardial layers (Table 2 and Figure 4: scenario 2 vs. 1: 23.9% reduction in EF). The depressed contractility in the subendocardial region was enough to drop EF below 50%, producing HF with reduced EF (HFrEF). The EF normalized when Tmax was increased in the subepicardial layers (Table 2 and Figure 4: scenario 3 vs. 1). This increased subepicardial contractility was enough to recover EF from the failing value of 40.5% and reach 53.2% (vs. 53.2% in the normal scenario). End-systolic pressure (ESP) and ESV increased when subendocardial contractility was zero. After subepicardial contractility increased, ESV and ESP decreased (Table 2, scenario 3 vs. 1 and 2).
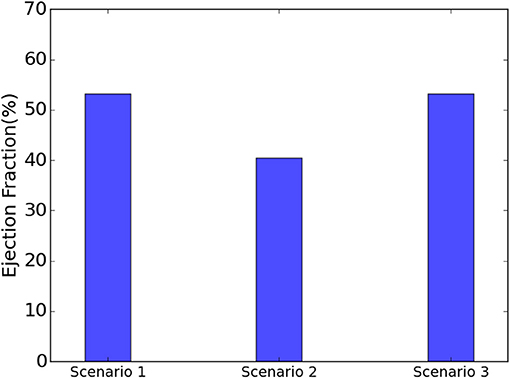
Figure 4. When the subendocardial contractility was zero, EF reduced by 23.9% relative to scenario 1 (scenarios 1 and 2). Increased subepicardial contractility recovered EF to scenario 1 (scenarios 1 and 3).
The EF decreased by 75% when contractility decreased by 50% in all layers (Table 2: scenario 4 vs. 1). When subepicardial and midmyocardial contractility was zero, EF became almost zero (0.3% in scenario 5, Table 2). Similarly, when subepicardial contractility was zero, EF decreased dramatically compared to the normal scenario (12.7% in scenario 6 vs. 53.2% in scenario 1, Table 2). ESV noticeably increased and ESP decreased in scenarios 4, 5, and 6 vs. scenario 1.
When subendocardial contractility was zero, LV torsion increased (scenario 2 vs. 1). The torsion further increased after contractility in a remaining region was increased to compensate (scenario 3 vs. 1 and 2). The torsion decreased when contractility in all transmural regions decreased by 50% (scenario 4 vs. 1). The torsion reversed when midmyocardial and subepicardial contractility were decreased to zero (scenario 5 vs. 1). The reversed torsion increased when only subepicardial contractility was zero (scenario 6 vs. 5).
Strains (which are independent of displacement boundary conditions) were altered in diseased conditions. The global longitudinal, circumferential, and radial strains decreased in HFpEF, but recovered after subepicardial contractility increased (Table 2, scenarios 2 and 3 vs. scenario 1). In addition, the global strains decreased when contractility decreased by half in all layers, and when subepicardial and midmyocardial contractility were zero, and also when subepicardial contractility was zero (Table 2, scenarios 4, 5, and 6 vs. scenario 1). The direction of circumferential strain changed when midmyocardial and subepicardial contractility were both zero (Scenario 5 vs. 1, Table 2). With normal homogenous contractility (scenario 1), all layers experienced contractile strains (Figures 5–7). Regional changes in contractility to simulate HFrEF (scenario 2) and HFpEF (scenario 3) both presented with tensile strains in the subendocardial regions where contractility was set to zero (Figures 5–7). However, the increased subepicardial contractility in HFpEF had a global effect on strains throughout all layers, reducing the strains in all regions. Qualitatively, the transmural strain curve of the HFpEF case (scenario 3) replicated the pathological HFrEF curve (scenario 2), albeit with strains that were 23.8% lower on average.
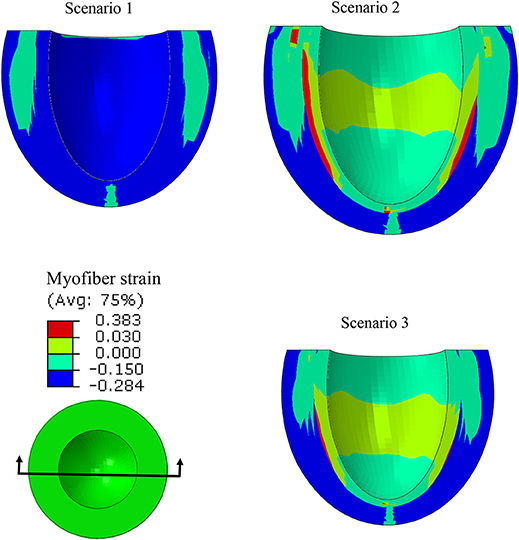
Figure 5. A long-axis view showing that at end systole, with uniform Tmax (scenario 1), all layers experienced compressive strain in myofiber directions. When subendocardial contractility was zero, the strain pattern was altered (scenarios 1 and 2), but it partially recovered when subepicardial contractility increased (scenarios 1 and 3).
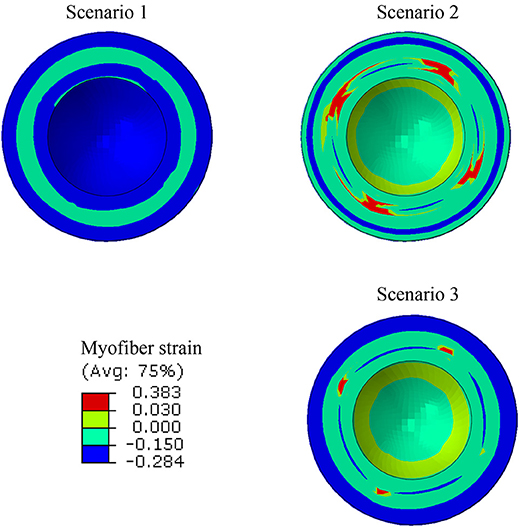
Figure 6. A short-axis view showing that the ES myofiber strain pattern altered when subendocardial contractility was zero (scenarios 1 and 2), but a partial recovery in strain pattern was observed when subepicardial contractility increased (scenarios 1 and 3).
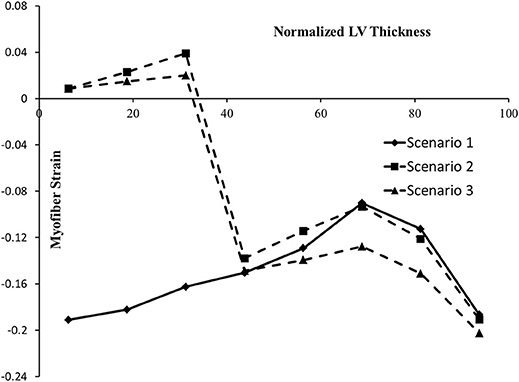
Figure 7. The ES myofiber strain at various points along LV thickness. In the horizontal axis, 0% represents the endocardium and100% represents the epicardium. The alterations in strains in scenario 2 are noticeable, compared to scenario 1. In scenario 3, the tensile strains decreased compared to scenario 2.
ES stress in the myofiber direction was noticeably reduced when subendocardial contractility decreased (scenarios 1 and 2, Figure 8). A trend to recovery in the stress distribution was observed when subepicardial contractility increased (scenarios 1 and 3, Figure 8).
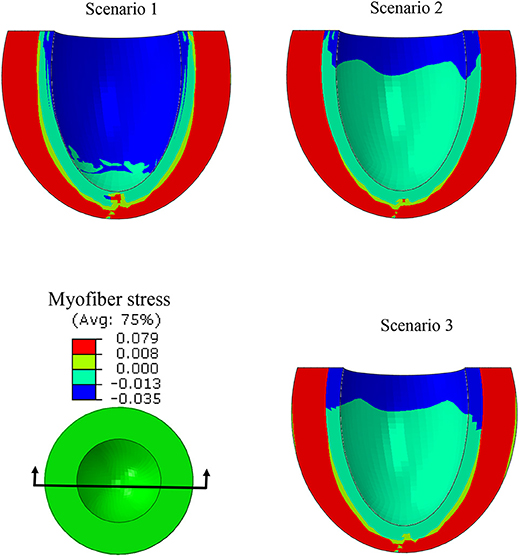
Figure 8. A long-axis view showing the ES myofiber compressive stress decreased when the subendocardial contractility was zero (scenarios 1 and 2). The stress pattern became partially similar to the normal case when subepicardial contractility increased (scenarios 1 and 3).
The ES-shortening longitudinal displacement of the LV was profoundly decreased when subendocardial contractility was zero (scenarios 1 and 2, Figure 9). The longitudinal displacement was partially recovered when subepicardial contractility increased (scenarios 1 and 3, Figure 9).
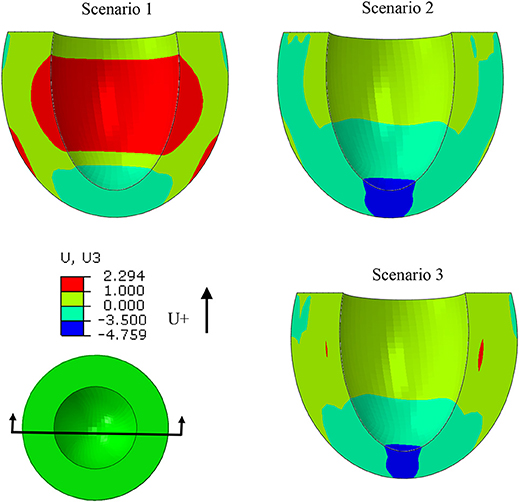
Figure 9. The ES longitudinal deformation was altered when subendocardial contractility was zero (scenarios 1 and 2). Deformation partially recovered when subepicardial contractility increased (scenarios 1 and 3).
The ES sphericity index (defined as the ratio between the lengths of the LV long axis and the short axis) was approximated as 1.1, 1.0, and 1.1 for scenarios 1, 2, and 3, respectively. In the HFrEF case (scenario 2), the ES sphericity index decreased compared to scenario 1. However, the ES sphericity index in the HFpEF scenario normalized toward the normal scenario. In other words, when the subendocardial contractility was zero, the LV shape became more spherical, compared to scenario 1. The shape of the LV recovered toward the normal scenario when subepicardial contractility increased.
In this study, we used a realistic FE model of the human LV to examine the role of altered LV systolic mechanics as a mechanism of HFpEF. Our findings support the hypothesis that HFpEF could be a result of lower subendocardial contractility linked with increased subepicardial contractility (Sengupta and Narula, 2008; Shah and Solomon, 2012; Omar et al., 2016, 2017). When subendocardial contractility was zero, LVEF decreased by 23.9% (Table 2: 53.2% in scenario 1 vs. 40.5% in scenario 2). The EF normalized when subepicardial contractility increased (Table 2: 53.2% in scenario 3 vs. 53.2% in scenario 1). The change in subepicardial contractility (less than a 40% increase from normal values) resulted in a 31.4% improvement in EF. Unlike scenario 1, scenarios 2 and 3 experienced abnormal strains within the subendocardial region (Figures 5–7), even though scenario 3 experienced normal EF. The ES sphericity index decreased in scenario 2 (1.0) compared to scenario 1 (1.1), but it recovered in scenario 3 (1.1). The LV torsion increased in scenario 2 (26.7°) compared to scenario 1 (24.7°), and it further increased in scenario 3 (30.2°).
The subendocardial region played an important role in the LV systolic mechanics, as our results showed. In particular, when subendocardial contractility was zero, the EF was reduced below 50%. A scenario with EF below 50% and zero subendocardial contractility corresponds to HFrEF (Vasan et al., 1999; Owan and Redfield, 2005; Yancy et al., 2013). Also, reducing EF below 50% by zeroing subendocardial contractility is in line with previous studies that reported the important role of the subendocardial region in the mechanics of the LV (Sabbah et al., 1981; Algranati et al., 2011). Based on our adopted definition of end-systolic elastance (EES) (Chen et al., 2001), our results imply that EES decreased after subendocardial contractility was zero, but EES recovered when subepicardial contractility increased (Table 2, scenarios 2 and 3 vs. scenario 1). Increased ESP in HFpEF could be due to alterations in the ejection period of the LV (scenario 2). After subendocardial contractility was lost, the ejection period shortened and ended with a higher pressure.
The EF decreased by 75% when contractility decreased by 50% in all layers (scenario 4 vs. scenario 1, Table 2). On the other hand, setting subepicardial and midmyocardial contractility to zero affected EF more than subendocardial contractility (0.3% in scenario 5 and 12.7% in scenario 6 vs. 40.5% in scenario 2, Table 2). This result illustrates the important role of subepicardial and midmyocardial regions and confirms previous experimental (Haynes et al., 2014) and computational (Wang et al., 2016) studies that indicated the important roles of the epicardium and midmyocardium in systolic mechanics of the LV. Also, based on our adopted definition of EES, this parameter decreased when contractility decreased in all layers by 50%, and when subepicardial and midmyocardial contractility were zero, and also when subepicardial contractility was set to zero (Table 2, scenarios 4, 5, and 6 vs. scenario 1).
Quantifying changes in torsional deformation related to changes in transmural contractility revealed an interesting relationship between the two. Abnormally high torsion could be a useful index of pathology, as we showed when subendocardial contractility was lost (Table 2, scenarios 2 and 3 vs. 1). This result confirms previous reports according to which the LV torsion increases in subendocardial ischemia (Prinzen et al., 1984), which has been related to the counter torque applied by the subendocardial region against the subepicardial region (Aelen et al., 1997). Also, this counter torque effect between subendocardium and subepicarium can be seen in scenarios 5 and 6 (Table 2). In these scenarios a negative torsion was seen after midmyocardium and subepicardium contractility was set to zero. The torsion of the LV is strongly coupled to the LV contractility and the inability to complete ejection properly (Table 2).
The longitudinal strain has been reported as a criterion to diagnose normal and diseased hearts (Henein and Gibson, 1999; Takeda et al., 2001; Yu et al., 2002; Vinereanu et al., 2005). The decreased longitudinal strain in our results (Table 2) corresponds to clinical studies that reported longitudinal strains decrease in HFpEF (Mizuguchi et al., 2010). Also, the contour of ES longitudinal displacement, which is directly related to longitudinal strain, was noticeably altered in the diseased scenario compared to the normal scenario (Figure 9, scenarios 1 and 2). However, when subepicardial contractility increased, the pattern of longitudinal displacement became more similar to the normal scenario (Figure 9, scenarios 1 and 3). The ES strain pattern across the regional layers of the LV wall (Figure 7) also supported the hypothesis that increased subepicardial contractility in HFpEF improves function globally (Sengupta and Narula, 2008). Moreover, the alterations in circumferential and radial strains are in line with clinical studies that reported these strains decrease in HFpEF (Wang et al., 2008; Mizuguchi et al., 2010). Yet, our results should be interpreted with caution. The circumferential and radial strains for normal conditions (scenario 1) were in line with clinical data reported in the literature, whereas the longitudinal strain was smaller than reported clinical data (Moore et al., 2000; Yingchoncharoen et al., 2013). The methodology of our study is similar to previous computational models of LV in our group. The longitudinal strain results of these previous models have been validated against experimental strain data (for example, Genet et al., 2014).
It has been well-documented that the shape of the LV changes in HF (Grossman et al., 1975; Carabello, 1995; Gaasch and Zile, 2011). In particular, LV concentric hypertrophy is seen in patients with HFpEF (Melenovsky et al., 2007), and exercise capacity is correlated with the sphericity index of the LV (Tischler et al., 1993). In line with previous studies, in our simulations, the shape of the LV was altered when the subendocardial contractility was zero. The ES sphericity index decreased in scenario 2 (1.0) compared to scenario 1 (1.1). When subepicardial contractility increased, the shape of the LV recovered toward the normal case, as seen in the ES sphericity index in scenario 3 (1.1) compared to scenario 2 (1.0). Thus, the increased subepicardial contractility may prevent LV dilatation in HFpEF, and help preserve the LV shape. This phenomenon will further support the normalization of LVEF due to the direct interplay between the LV shape and function (Grossman et al., 1975; Stokke et al., 2017).
In this study we used tissue-level load-independent properties (Tmax) to alter myocardium contractility. This approach is more appropriate than using the LV strains. In fact, the popular notion of equating myocardial contractility with strain measurements (that are load dependent) is “off the mark [and] if contractility means anything, it is as an expression of the ability of a given piece of myocardium to generate tension and shortening under any loading conditions” (Reichek, 2013). Therefore, our approach to alter transmural contractility, which might not be feasible using current experimental methods, could lead to a better understanding of the development of HFpEF.
Novel physics-based mathematical modeling was used in this study to examine a possible mechanism underlying preservation of LVEF in HFpEF. The results from the simulations provide evidence of the potential role of myocardial contractility in the genesis of preserved EF in the HFpEF phenotype. Previous studies on HFpEF were mostly based on experimental data (for example, Phan et al., 2009), where the contribution of a single feature like myocardial contractility could not be varied in isolation of other parameters. However, we used FE modeling to simulate and isolate transmural contractility as a feature and study its effect on LV systolic mechanics. Our results provide important first steps toward eventual development of a computational model of HFpEF.
The simulation addressed only the relationship between transmural myocardial contractility and LV systolic mechanics. Modeling all aspects of HFpEF was beyond the scope of this paper. In clinical conditions, several factors contribute to the development of HFpEF (Bench et al., 2009; Shah and Solomon, 2012; Sengupta and Marwick, 2018). These factors include abnormalities in both the systolic and the diastolic mechanics of the LV (MacIver and Townsend, 2008; MacIver, 2009; Shah and Solomon, 2012), the LV hypertrophy and geometric changes (Aurigemma et al., 1995; Vasan et al., 1999; Adeniran et al., 2015) and material properties of the LV (stiffness). A recent study employed computational models with heterogeneous transmural distributions of Tmax (Wang et al., 2016). In our investigation, only in one scenario (scenario 1) did we assume Tmax to be uniform in the transmural direction. Also, since this study focused on the LV, we assumed timing and activation of contractility are homogenous. A more realistic assumption would be to consider the sequence of electrical stimulations in the tissue (Chabiniok et al., 2012; Villongco et al., 2014; Crozier et al., 2016; Giffard-Roisin et al., 2017), particularly in the septum. However, a heterogeneous distribution of Tmax would be more important if atria were also included in the model. Moreover, we only modeled LV data from one human subject in our study. Modeling data from multiple subjects is the goal of a subsequent study. Here, our intent was to document our modeling methodology and demonstrate its utility.
Alterations in strain distributions might lead to remodeling in the LV tissue (Figures 5–7). The response of myocardial tissue to an altered mechanical environment will likely lead to changes in tissue properties that will in turn affect the LV inflation, contraction, and relaxation. It is well-documented that diastolic LV tissue stiffness becomes abnormally high in HFpEF (Zile et al., 2004). Our study focused on the systolic mechanics of the LV. As a future direction, integration of tissue response in diastole and systole will provide a more realistic and informative model to understand the mechanisms involved during the onset and development of HFpEF. Integration of cell-based cross-bridge cycling and contractility could provide more realistic information about the tissue alterations over the course of HFpEF development (Adeniran et al., 2015; Shavik et al., 2017).
Although our study explored a simplified representation of HFpEF (appropriately so, to isolate mechanical effects), the clinical definition and diagnosis of HFpEF and HFrEF are more complex than just calculations of EF (Borlaug and Paulus, 2011). In fact, HFpEF lacks a clear validated diagnostic guideline (Lam, 2010; Oghlakian et al., 2011). In this hypothesis-generating study, we simply assumed EF < 50% represents HFrEF. This assumption is in line with some definitions used for HFrEF in the literature (Vasan et al., 1999; Paulus et al., 2007). However, an EF = 40.5% (scenario 2) might also be defined as borderline HFpEF (for example, Yancy et al., 2013). These points may be considered semantic because they do not affect the conclusions of our study, which quantified alterations in contractility with changes in EF, torsion and strain. It would be interesting to apply these methods to personalized models derived from patients diagnosed clinically with HFpEF and HFrEF.
Several other scenarios need to be investigated, including more graded loss of subendocardial contractility, and graded decrease of subendocardial contractility, with both coupled to a graded increase in subepicardial contractility. Moreover, the definitions of subendocardium, midmyocardium, and subepicardium regions were arbitrary in this study because exact definitions are not available. A more realistic imaging approach might better delineate transmural layers and their related contractility. Furthermore, exercise intolerance has been reported as a key factor in HFpEF (Roh et al., 2017), and could be implemented in our modeling methodology to better understand the mechanisms of HFpEF development. Despite these limitations, this paper reports instructive quantitative information about development of HFpEF, as we could change one aspect of the model (contractility at a particular location) and determine its effects alone.
The results of this study support the hypothesis that preservation of LVEF in patients with HFpEF could be explained on the basis of reduced subendocardial contractility with a compensatory increase in subepicardial contractility. These findings underscore the roles of regional LV myocardial contractility in HF syndromes and emphasize the importance of computational models in understanding pathophysiological mechanisms underlying complex phenotypic presentations like HFpEF.
PS and JG designed the study. KS developed the constitutive model. YD and KS created the computational models. YD ran simulations, compiled results, and wrote the initial draft of the paper. SS helped with the modeling process. YD, KS, JG, and PS contributed to analysis of the results, and manuscript writing.
This work was supported by NIH grants R01-HL-077921, R01-HL-118627, and U01-HL-119578. Further financial support was provided by the Oppenheimer Memorial Trust (OMT) and the National Research Foundation (NRF) of South Africa. Opinions expressed and conclusions arrived at are those of the authors and are not necessarily to be attributed to the NRF or OMT.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We thank Pamela Derish in the Department of Surgery, University of California San Francisco, for assistance with proofreading the manuscript.
Adeniran, I., MacIver, D. H., Hancox, J. C., and Zhang, H. (2015). Abnormal calcium homeostasis in heart failure with preserved ejection fraction is related to both reduced contractile function and incomplete relaxation: an electromechanically detailed biophysical modeling study. Front. Physiol. 6:78. doi: 10.3389/fphys.2015.00078
Aelen, F. W., Arts, T., Sanders, D. G., Thelissen, G. R., Muijtjens, A. M., Prinzen, F. W., et al. (1997). Relation between torsion and cross-sectional area change in the human left ventricle. J. Biomech. 30, 207–212. doi: 10.1016/S0021-9290(96)00147-9
Algranati, D., Kassab, G. S., and Lanir, Y. (2011). Why is the subendocardium more vulnerable to ischemia? A new paradigm. Am. J. Physiol. Heart Circ. Physiol. 300, H1090–H1100. doi: 10.1152/ajpheart.00473.2010
Aurigemma, G. P., and Gaasch, W. H. (2004). Clinical practice. Diastolic heart failure. N. Engl. J. Med. 351, 1097–1105. doi: 10.1056/NEJMcp022709
Aurigemma, G. P., Silver, K. H., Priest, M. A., and Gaasch, W. H. (1995). Geometric changes allow normal ejection fraction despite depressed myocardial shortening in hypertensive left ventricular hypertrophy. J. Am. Coll. Cardiol. 26, 195–202. doi: 10.1016/0735-1097(95)00153-Q
Baillargeon, B., Costa, I., Leach, J. R., Lee, L. C., Genet, M., Toutain, A., et al. (2015). Human cardiac function simulator for the optimal design of a novel annuloplasty ring with a sub-valvular element for correction of ischemic mitral regurgitation. Cardiovasc. Eng. Technol. 6, 105–116. doi: 10.1007/s13239-015-0216-z
Baillargeon, B., Rebelo, N., Fox, D. D., Taylor, R. L., and Kuhl, E. (2014). The living heart project: a robust and integrative simulator for human heart function. Eur. J. Mech. A Solids 48, 38–47. doi: 10.1016/j.euromechsol.2014.04.001
Bench, T., Burkhoff, D., O'Connell, J. B., Costanzo, M. R., Abraham, W. T., St John Sutton, M., et al. (2009). Heart failure with normal ejection fraction: consideration of mechanisms other than diastolic dysfunction. Curr. Heart Fail. Rep. 6, 57–64. doi: 10.1007/s11897-009-0010-z
Benjamin, E. J., Blaha, M. J., Chiuve, S. E., Cushman, M., Das, S. R., Deo, R., et al. (2017). American heart association statistics committee and stroke statistics Subcommittee. heart disease and stroke statistics-2017 update: a report from the American Heart Association. Circulation 135, e146–e603. doi: 10.1161/CIR.0000000000000485
Bhuiyan, T., and Maurer, M. S. (2011). Heart failure with preserved ejection fraction: persistent diagnosis, therapeutic enigma. Curr. Cardiovasc. Risk Rep. 5, 440–449. doi: 10.1007/s12170-011-0184-2
Borlaug, B. A., and Paulus, W. J. (2011). Heart failure with preserved ejection fraction: pathophysiology, diagnosis, and treatment. Eur. Heart J. 32, 670–679. doi: 10.1093/eurheartj/ehq426
Carabello, B. A. (1995). The relationship of left ventricular geometry and hypertrophy to left ventricular function in valvular heart disease. J. Heart Valve Dis. 4(Suppl. 2), S132–S138.
Carrick, R., Ge, L., Lee, L. C., Zhang, Z., Mishra, R., Axel, L., et al. (2012). Patient-specific finite element-based analysis of ventricular myofiber stress after Coapsys: importance of residual stress. Ann. Thorac. Surg. 93, 1964–1971. doi: 10.1016/j.athoracsur.2012.03.001
Chabiniok, R., Moireau, P., Lesault, P. F., Rahmouni, A., Deux, J. F., and Chapelle, D. (2012). Estimation of tissue contractility from cardiac cine-MRI using a biomechanical heart model. Biomech. Model. Mechanobiol. 11, 609–630. doi: 10.1007/s10237-011-0337-8
Chen, C. H., Fetics, B., Nevo, E., Rochitte, C. E., Chiou, K. R., Ding, P. A., et al. (2001). Noninvasive single-beat determination of left ventricular end-systolic elastance in humans. J. Am. Coll. Cardiol. 38, 2028–2034. doi: 10.1016/S0735-1097(01)01651-5
Crozier, A., Blazevic, B., Lamata, P., Plank, G., Ginks, M., Duckett, S, et al. (2016). The relative role of patient physiology and device optimisation in cardiac resynchronisation therapy: a computational modelling study. J. Mol. Cell. Cardiol. 96, 93–100. doi: 10.1016/j.yjmcc.2015.10.026
Gaasch, W. H., and Zile, M. R. (2011). Left ventricular structural remodeling in health and disease: with special emphasis on volume, mass, and geometry. J. Am. Coll. Cardiol. 58, 1733–1740. doi: 10.1016/j.jacc.2011.07.022
Genet, M., Lee, L. C., Nguyen, R., Haraldsson, H., Acevedo-Bolton, G., Zhang, Z., et al. (2014). Distribution of normal human LV myofiber stress at end diastole and end systole: a target for in silico design of heart failure treatments. J. Appl. Physiol. 117, 142–152. doi: 10.1152/japplphysiol.00255.2014
Giffard-Roisin, S., Jackson, Th, Fovargue, L., Lee, J., Delingette, H., Razavi, R., et al. (2017). Noninvasive personalization of a cardiac electrophysiology model from body surface potential mapping. IEEE Trans. Biomed. Eng. 64, 2206–2218. doi: 10.1109/TBME.2016.2629849
Göktepe, S., Acharya, S. N. S., Wong, J., and Kuhl, E. (2011). Computational modeling of passive myocardium. Int. J. Numer. Methods Biomed. Eng. 27, 1–12. doi: 10.1002/cnm.1402
Grossman, W., Jones, D., and McLaurin, L. P. (1975). Wall stress and patterns of hypertrophy in the human left ventricle. J. Clin. Invest. 56, 56–64. doi: 10.1172/JCI108079
Guccione, J. M., and McCulloch, A. D. (1993). Mechanics of active contraction in cardiac muscle. I. Constitutive relations for fiber stress that describe deactivation. J. Biomech. Eng. 115, 72–81. doi: 10.1115/1.2895473
Haynes, P., Nava, K. E., Lawson, B. A., Chung, C. S., Mitov, M. I., Campbell, S. G., et al. (2014). Transmural heterogeneity of cellular level power output is reduced in human heart failure. J. Mol. Cell Cardiol. 72, 1–8. doi: 10.1016/j.yjmcc.2014.02.008
Heidenreich, P. A., Albert, N. M., Allen, L. A., Bluemke, D. A., Butler, J., Fonarow, G. C., et al. (2013). Forecasting the impact of heart failure in the United States: a policy statement from the American Heart Association. Circ. Heart Fail. 6, 606–619. doi: 10.1161/HHF.0b013e318291329a
Henein, M. Y., and Gibson, D. G. (1999). Long axis function in disease. Heart 81, 229–231. doi: 10.1136/hrt.81.3.229
Holzapfel, G. A., and Ogden, R. W. (2009). Constitutive modelling of passive myocardium: a structurally based framework for material characterization. Philos. Trans. A Math. Phys. Eng. Sci. 367, 3445–3475. doi: 10.1098/rsta.2009.0091
Jones, E., Oliphant, T., and Peterson, P. (2001). SciPy: Open Source Scientific Tools for Python. Available online at: http://www.scipy.org
Klotz, S., Hay, I., Dickstein, M. L., Yi, G. H., Wang, J., Maurer, M. S., et al. (2006). Single-beat estimation of end-diastolic pressure-volume relationship: a novel method with potential for noninvasive application. Am. J. Physiol. Heart Circ. Physiol. 291, H403–H412. doi: 10.1152/ajpheart.01240.2005
Lam, C. S. (2010). Heart failure with preserved ejection fraction: invasive solution to diagnostic confusion? J. Am. Coll. Cardiol. 55, 1711–1712. doi: 10.1016/j.jacc.2009.12.034
Lee, L. C., Genet, M., Acevedo-Bolton, G., Ordovas, K., Guccione, J. M., and Kuhl, E. (2015). A computational model that predicts reverse growth in response to mechanical unloading. Biomech. Model. Mechanobiol. 14, 217–229. doi: 10.1007/s10237-014-0598-0
Lee, L. C., Zhihong, Z., Hinson, A., and Guccione, J. M. (2013). Reduction in left ventricular wall stress and improvement in function in failing hearts using Algisyl-LVR. J. Vis. Exp. 74:50096. doi: 10.3791/50096
LeGrice, I., Hunter, P., Young, A., and Small, B. (2001). The architecture of the heart: a data-based model. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 359, 1217–1232. doi: 10.1098/rsta.2001.0827
Lombaert, H., Peyrat, J.-M., Croisille, P., Rapacchi, S., Fanton, L., Clarysse, P., et al. (2011). “Statistical analysis of the human cardiac fiber architecture from DT-MRI,” in Functional Imaging and Modeling of the Heart (Berlin; Heidelberg: Springer), 171–179.
MacIver, D. H. (2009). Heart failure with preserved ejection fraction: is it due to contractile dysfunction? Circ. J. 73:1169. doi: 10.1253/circj.CJ-09-0190
MacIver, D. H., and Townsend, M. (2008). A novel mechanism of heart failure with normal ejection fraction. Heart 94, 446–449. doi: 10.1136/hrt.2006.114082
Melenovsky, V., Borlaug, B. A., Rosen, B., Hay, I., Ferruci, L., Morell, C. H., et al. (2007). Cardiovascular features of heart failure with preserved ejection fraction versus nonfailing hypertensive left ventricular hypertrophy in the urban Baltimore community: the role of atrial remodeling/dysfunction. J. Am. Coll. Cardiol. 49, 198–207. doi: 10.1016/j.jacc.2006.08.050
Mercier, J. C., DiSessa, T. G., Jarmakani, J. M., Nakanishi, T., Hiraishi, S., Isabel-Jones, J., et al. (1982). Two-dimensional echocardiographic assessment of left ventricular volumes and ejection fraction in children. Circulation 65, 962–969. doi: 10.1161/01.CIR.65.5.962
Mizuguchi, Y., Oishi, Y., Miyoshi, H., Iuchi, A., Nagase, N., and Oki, T. (2010). Concentric left ventricular hypertrophy brings deterioration of systolic longitudinal, circumferential, and radial myocardial deformation in hypertensive patients with preserved left ventricular pump function. J. Cardiol. 55, 23–33. doi: 10.1016/j.jjcc.2009.07.006
Moore, C. C., Lugo-Olivieri, C. H., McVeigh, E. R., and Zerhouni, E. A. (2000). Three-dimensional systolic strain patterns in the normal human left ventricle: characterization with tagged MR imaging. Radiology 214, 453–466. doi: 10.1148/radiology.214.2.r00fe17453
Nagueh, S. F., Middleton, K. J., Kopelen, H. A., Zoghbi, W. A., and Quiñones, M. A. (1997). Doppler tissue imaging: a noninvasive technique for evaluation of left ventricular relaxation and estimation of filling pressures. J. Am. Coll. Cardiol. 30, 1527–1533. doi: 10.1016/S0735-1097(97)00344-6
Oghlakian, G. O., Sipahi, I., and Fang, J. C. (2011). Treatment of heart failure with preserved ejection fraction: have we been pursuing the wrong paradigm? Mayo Clin. Proc. 86, 531–539.
Omar, A. M., Bansal, M., and Sengupta, P. P. (2016). Advances in echocardiographic imaging in heart failure with reduced and preserved ejection fraction. Circ. Res. 119, 357–374. doi: 10.1161/CIRCRESAHA.116.309128
Omar, A. M. S., Narula, S., Abdel Rahman, M. A., Pedrizzetti, G., Raslan, H., Rifaie, O., et al. (2017). Precision phenotyping in heart failure and pattern clustering of ultrasound data for the assessment of diastolic dysfunction. JACC Cardiovasc. Imaging 10, 1291–1303. doi: 10.1016/j.jcmg.2016.10.012
Owan, T. E., and Redfield, M. M. (2005). Epidemiology of diastolic heart failure. Prog. Cardiovasc. Dis. 47, 320–332.
Paulus, W. J., Tschöpe, C., Sanderson, J. E., Rusconi, C., and Flachskampf, F. A. (2007). How to diagnose diastolic heart failure: a consensus statement on the diagnosis of heart failure with normal left ventricular ejection fraction by the Heart Failure and Echocardiography Associations of the European Society of Cardiology. Eur. Heart J. 28, 2539–2550. doi: 10.1093/eurheartj/ehm037
Phan, T. T., Abozguia, K., Nallur Shivu, G., Mahadevan, G., Ahmed, I., Williams, L., et al. (2009). Heart failure with preserved ejection fraction is characterized by dynamic impairment of active relaxation and contraction of the left ventricle on exercise and associated with myocardial energy deficiency. J. Am. Coll. Cardiol. 54, 402–409. doi: 10.1016/j.jacc.2009.05.012
Prinzen, F. W., Arts, T., van der Vusse, G. J., and Reneman, R. S. (1984). Fiber shortening in the inner layers of the left ventricular wall as assessed from epicardial deformation during normoxia and ischemia. J. Biomech. 17, 801–811.
Rüssel, I. K., Götte, M. J., Bronzwaer, J. G., Knaapen, P., Paulus, W. J., and van Rossum, A. C. (2009). Left ventricular torsion: an expanding role in the analysis of myocardial dysfunction. JACC Cardiovasc. Imaging 2, 648–655. doi: 10.1016/j.jcmg.2009.03.001
Reichek, N. (2013). Right ventricular strain in pulmonary hypertension: flavor du jour or enduring prognostic index? Circul. Cardiovasc. Imaging 6, 609–611. doi: 10.1161/CIRCIMAGING.113.000936
Roh, J., Houstis, N., and Rosenzweig, A. (2017). Why Don't we have proven treatments for HFpEF? Circ. Res. 120, 1243–1245. doi: 10.1161/CIRCRESAHA.116.310119
Sabbah, H. N., Marzilli, M., and Stein, P. D. (1981). The relative role of subendocardium and subepicardium in left ventricular mechanics. Am. J. Physiol. 240, H920–H926.
Sack, K. L., Baillargeon, B., Acevedo-Bolton, G., Genet, M., Rebelo, N., Kuhl, E., et al. (2016). Partial LVAD restores ventricular outputs and normalizes LV but not RV stress distributions in the acutely failing heart in silico. Int. J. Artif. Organs. 39, 421–430. doi: 10.5301/ijao.5000520
Sengupta, P. P., and Marwick, T. H. (2018). The many dimensions of diastolic function: a curse or a blessing? JACC Cardiovasc. Imaging. 11, 409–410. doi: 10.1016/j.jcmg.2017.05.015
Sengupta, P. P., and Narula, J. (2008). Reclassifying heart failure: predominantly subendocardial, subepicardial, and transmural. Heart Fail. Clin. 4, 379–382. doi: 10.1016/j.hfc.2008.03.013
Shah, A. M., and Solomon, S. D. (2012). Phenotypic and pathophysiological heterogeneity in heart failure with preserved ejection fraction. Eur. Heart J. 33, 1716–1717. doi: 10.1093/eurheartj/ehs124
Shavik, S. M., Wall, S. T., Sundnes, J., Burkhoff, D., and Lee, L. C. (2017). Organ-level validation of a cross-bridge cycling descriptor in a left ventricular finite element model: effects of ventricular loading on myocardial strains. Physiol. Rep. 5:e13392. doi: 10.14814/phy2.13392
Steinberg, B. A., Zhao, X., Heidenreich, P. A., Peterson, E. D., Bhatt, D. L., Cannon, C. P., et al. (2012). Trends in patients hospitalized with heart failure and preserved left ventricular ejection fraction: prevalence, therapies, and outcomes. Circulation 126, 65–75. doi: 10.1161/CIRCULATIONAHA.111.080770
Stokke, T. M., Hasselberg, N. E., Smedsrud, M. K., Sarvari, S. I., Haugaa, K. H., Smiseth, O. A., et al. (2017). Geometry as a confounder when assessing ventricular systolic function: comparison between ejection fraction and strain. J. Am. Coll. Cardiol. 70, 942–954. doi: 10.1016/j.jacc.2017.06.046
Streeter, D. D., Spotnitz, H. M., Patel, D. P., Ross, J., and Sonnenblick, E. H. (1969). Fiber orientation in the canine left ventricle during diastole and systole. Circ. Res. 24, 339–347.
Takeda, S., Rimington, H., Smeeton, N., and Chambers, J. (2001). Long axis excursion in aortic stenosis. Heart 86, 52–56. doi: 10.1136/heart.86.1.52
Tischler, M. D., Niggel, J., Borowski, D. T., and LeWinter, M. M. (1993). Relation between left ventricular shape and exercise capacity in patients with left ventricular dysfunction. J. Am. Coll. Cardiol. 22, 751–757.
Vasan, R. S., Benjamin, E. J., and Levy, D. (1995). Prevalence, clinical features and prognosis of diastolic heart failure: an epidemiologic perspective. J. Am. Coll. Cardiol. 26, 1565–1574.
Vasan, R. S., Larson, M. G., Benjamin, E. J., Evans, J. C., Reiss, C. K., and Levy, D. (1999). Congestive heart failure in subjects with normal versus reduced left ventricular ejection fraction: prevalence and mortality in a population-based cohort. J. Am. Coll. Cardiol. 33, 1948–1955.
Villongco, C. T., Krummen, D. E., Stark, P., Omens, J. H., and McCulloch, A. D. (2014). Patient-specific modeling of ventricular activation pattern using surface ECG-derived vectorcardiogram in bundle branch block. Prog. Biophys. Mol. Biol. 115, 305–313. doi: 10.1016/j.pbiomolbio.2014.06.011
Vinereanu, D., Nicolaides, E., Tweddel, A. C., and Fraser, A. G. (2005). “Pure” diastolic dysfunction is associated with long-axis systolic dysfunction. Implications for the diagnosis and classification of heart failure. Eur. J. Heart Fail. 7, 820–828. doi: 10.1016/j.ejheart.2005.02.003
Walker, J. C., Ratcliffe, M. B., Zhang, P., Wallace, A. W., Fata, B., Hsu, E. W., et al. (2005). MRI-based finite-element analysis of left ventricular aneurysm. Am. J. Physiol. Heart Circ. Physiol. 289, H692–H700. doi: 10.1152/ajpheart.01226.2004
Wang, H., Zhang, X., Dorsey, S. M., McGarvey, J. R., Campbell, K. S., Burdick, J. A., et al. (2016). Computational investigation of transmural differences in left ventricular contractility. ASME J. Biomech. Eng. 138:114501. doi: 10.1115/1.4034558
Wang, J., Khoury, D. S., Yue, Y., Torre-Amione, G., and Nagueh, S. F. (2008). Preserved left ventricular twist and circumferential deformation, but depressed longitudinal and radial deformation in patients with diastolic heart failure. Eur. Heart J. 29, 1283–1289. doi: 10.1093/eurheartj/ehn141
Yancy, C. W., Jessup, M., Bozkurt, B., Butler, J., Casey, D. E. Jr, Drazner, M. H., et al. (2013). ACCF/AHA guideline for the management of heart failure: a report of the American College of Cardiology Foundation/American Heart Association task force on practice guidelines. J. Am. Coll. Cardiol. 62, e147–e239. doi: 10.1016/j.jacc.2013.05.019
Yingchoncharoen, T., Agarwal, S., Popović, Z. B., and Marwick, T. H. (2013). Normal ranges of left ventricular strain: a meta-analysis. J. Am. Soc. Echocardiogr. 26, 185–191. doi: 10.1016/j.echo.2012.10.008
Yu, C. M., Lin, H., Yang, H., Kong, S. L., Zhang, Q., and Lee, S. W. (2002). Progression of systolic abnormalities in patients with “isolated” diastolic heart failure and diastolic dysfunction. Circulation. 105, 1195–1201. doi: 10.1161/hc1002.105185
Keywords: heart failure and preserved ejection fraction, left ventricle, myocardial contractility, finite element method, simulation
Citation: Dabiri Y, Sack KL, Shaul S, Sengupta PP and Guccione JM (2018) Relationship of Transmural Variations in Myofiber Contractility to Left Ventricular Ejection Fraction: Implications for Modeling Heart Failure Phenotype With Preserved Ejection Fraction. Front. Physiol. 9:1003. doi: 10.3389/fphys.2018.01003
Received: 13 January 2018; Accepted: 09 July 2018;
Published: 24 August 2018.
Edited by:
Massimo Pagani, Università degli Studi di Milano, ItalyReviewed by:
Peter L. Kerkhof, VU University Medical Center, NetherlandsCopyright © 2018 Dabiri, Sack, Shaul, Sengupta and Guccione. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Julius M. Guccione, anVsaXVzLmd1Y2Npb25lQHVjc2YuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.