
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Physiol., 20 July 2018
Sec. Computational Physiology and Medicine
Volume 9 - 2018 | https://doi.org/10.3389/fphys.2018.00958
This article is part of the Research TopicRecent Advances in Understanding the Basic Mechanisms of Atrial Fibrillation Using Novel Computational ApproachesView all 28 articles
In cardiac electrophysiology, there exist many sources of inter- and intra-personal variability. These include variability in conditions and environment, and genotypic and molecular diversity, including differences in expression and behavior of ion channels and transporters, which lead to phenotypic diversity (e.g., variable integrated responses at the cell, tissue, and organ levels). These variabilities play an important role in progression of heart disease and arrhythmia syndromes and outcomes of therapeutic interventions. Yet, the traditional in silico framework for investigating cardiac arrhythmias is built upon a parameter/property-averaging approach that typically overlooks the physiological diversity. Inspired by work done in genetics and neuroscience, new modeling frameworks of cardiac electrophysiology have been recently developed that take advantage of modern computational capabilities and approaches, and account for the variance in the biological data they are intended to illuminate. In this review, we outline the recent advances in statistical and computational techniques that take into account physiological variability, and move beyond the traditional cardiac model-building scheme that involves averaging over samples from many individuals in the construction of a highly tuned composite model. We discuss how these advanced methods have harnessed the power of big (simulated) data to study the mechanisms of cardiac arrhythmias, with a special emphasis on atrial fibrillation, and improve the assessment of proarrhythmic risk and drug response. The challenges of using in silico approaches with variability are also addressed and future directions are proposed.
Beginning with the seminal paper by Hodgkin and Huxley, 1952, mathematical models of electrophysiology have proven to be valuable tools for better understanding many physiological processes, especially in cardiac arrhythmia research (Noble et al., 2012; Dibb et al., 2015). Fifty-six years after publication of the first cardiac model (Noble, 1962), there is currently a computational model for almost every cell type of the heart, including nodal, atrial, ventricular, and Purkinje cells (Beeler and Reuter, 1977; Difrancesco and Noble, 1985; Luo and Rudy, 1991; Inada et al., 2009; Maltsev and Lakatta, 2009; Sampson et al., 2010; Grandi et al., 2011; O'Hara et al., 2011), for numerous species, and for various levels of complexity across multiple spatial scales (e.g., inclusion of disease-associated remodeling, drug action, contractile, energetics, and signaling modules) (Fink et al., 2011). Most of these models use average data from voltage-clamp experiments of individual ionic membrane currents, and while they have led to many important advances in studies of cardiac electrophysiology and pathology, especially cardiac arrhythmias (Sepulveda et al., 1989; Courtemanche and Winfree, 1991; Panfilov and Holden, 1991; Gray et al., 1995; Krogh-Madsen and Christini, 2012; Roberts et al., 2012; Bueno-Orovio et al., 2014), they typically represent the average behavior of a particular cell type. Because these models ignore evident inter- and intra-personal variability, they can fail to capture the properties of any given individual cell or cells in a given patient (Golowasch et al., 2002; Dokos and Lovell, 2004; Sarkar and Sobie, 2010; Marder, 2011; Zaniboni, 2011; Groenendaal et al., 2015; Pathmanathan et al., 2015). This is in part because incorporating variance that reflects biological data into cardiac models requires significant computational capacity, particularly as compared to what was available when mathematical modeling of electrophysiology first emerged. Given ever-increasing computational capabilities, new modeling approaches have been developed to reproduce and analyze the immense physiological diversity observed in electrophysiology.
In this review, we discuss the importance of accounting for variability when building models of cardiac electrophysiology in both physiological and diseased conditions, and describe new tools being developed to address the limitations of traditional modeling approaches. In particular, we focus on two computational approaches that have emerged as leading methodologies for studying variability in cardiac electrophysiology, which we will refer to as (1) population-based modeling and (2) sample-specific modeling. Both methodologies have provided valuable insights in the fields of neuroscience, cardiology, and pharmacology. Here we review how they have advanced our understanding of the basic mechanisms of cardiac arrhythmias, and particularly atrial fibrillation (AF). As these in silico approaches have led to important insights into arrhythmia risks, mechanisms of arrhythmogenesis, and variable response to drugs, they should be considered when determining the regulatory requirements for the proarrhythmia assessment and drug efficacy and safety evaluation of candidate compounds.
Sources of variability in cardiac electrophysiology encompass multiple spatial and temporal scales, and include inter-species (Sham et al., 1995; Su et al., 2003), inter-ethnic (Lau et al., 2012; Fender et al., 2014), inter-subject (Taneja et al., 2001; Batchvarov et al., 2002), regional (Feng et al., 1998; Yan et al., 1998), and temporal (Jeyaraj et al., 2012) differences. Variability in experimental electrophysiological data does not only represent natural physiological diversity, but also reflects, in part, differences in the experimental conditions in which electrophysiological measurements are performed (Groenendaal et al., 2015). These conditions can vary from laboratory to laboratory (Niederer et al., 2009; Fink et al., 2011), experiment to experiment, or during the same experiment, e.g., due to deterioration of the experimental preparations over time (Fink et al., 2011). There is also instrument noise (Mirams et al., 2016), artifacts, and use of non-physiological temperatures and solutions (Groenendaal et al., 2015), all of which impact the structure and function of the cellular or tissue components being studied. These sources of variation are difficult to control even for experienced electrophysiologists and are equally as challenging to account for by modelers.
Mathematical cardiomyocyte models have remained useful tools for unraveling physiological and pathophysiological mechanisms, including mechanisms of arrhythmia, and identifying antiarrhythmic strategies without accounting for variability (Sepulveda et al., 1989; Courtemanche and Winfree, 1991; Clancy and Rudy, 1999, 2002; Clancy et al., 2002; Rivolta et al., 2002; Gong et al., 2007; Noble et al., 2007; Tsujimae et al., 2007; Zhang et al., 2007; Zhu and Clancy, 2007; Campbell et al., 2008; Comtois et al., 2008; Kharche et al., 2008; Sale et al., 2008; Ahrens-Nicklas et al., 2009; Butters et al., 2010; Adeniran et al., 2012; Edwards et al., 2014; Grandi and Maleckar, 2016; Morotti et al., 2016; Ni et al., 2017). Although average models have also been successfully applied to the study of sources of variability, such as sexual and hormonal factors (Yang et al., 2010, 2017; Yang and Clancy, 2012), age (Behar and Yaniv, 2017), and circadian regulation (Fotiadis and Forger, 2013), the rationale for developing novel computational approaches that specifically account for electrophysiological variability can be summarized by two main reasons.
The traditional cardiac model-building scheme involves averaging over samples from multiple experiments from many individuals, both to parameterize the model and validate it, which may not represent any specific measured physiological behavior very well. This “failure of averaging” has been demonstrated in many fields, most recently in neuroscience (Golowasch et al., 2002; Marder, 2011), and was particularly well-documented in 1952, the same year that the seminal Hodgkin and Huxley paper was published, when Lt. Gilbert S. Daniels of the U.S. Air Force published a Technical Note that highlighted the fundamental problem with fitting data to the mean (Daniels, 1952; Rose, 2017). Using data from 4,063 pilots, Lt. Daniels calculated the average of 10 physical dimensions believed to be most relevant for design of the cockpit on a plane, including a pilot's height, chest circumference, and sleeve length. Surprisingly, he found that a total of zero individuals fit within the middle 30% of the range of values for each dimension, and less than 3.5% of pilots would be average sized on any three dimensions. After this finding, the U.S. Air Force completely moved from standardizing all dimensions to an “average pilot,” to making all the dimensions adjustable to each individual pilot, which immediately and drastically improved performance and was soon adopted by all branches of the American military. Modeling of electrophysiology is undergoing a similar evolution, which will likely improve the translational significance of the models.
Variability plays an important role in arrhythmia generation and treatment, as exemplified by AF. The atria are characterized by a high degree of phenotypic variability in physiological properties, with broad and diverging distributions of biomarkers in patients in normal sinus rhythm (nSR) or chronic AF (cAF, Figure 1A) (Ravens et al., 2015), likely due to innate variability of the ionic currents (perhaps due to stochastic gating) that can affect whole cell and/or tissue proarrhythmic behavior (Pueyo et al., 2011; Heijman et al., 2013). This phenotypic variability can be captured by adding variability in the conductance parameters of a mathematical model of the action potential (AP, Figures 1B,C). In some circumstances, physiological variability itself can be the substrate for arrhythmia. For example, increased heterogeneity of refractoriness is important for the maintenance of AF (Moe et al., 1964; Boutjdir et al., 1986; Misier et al., 1992; Sato et al., 1992; Wang et al., 1995, 1996; Gaspo et al., 1997; Liu and Nattel, 1997; Ramirez et al., 2000), and regional differences in atrial ionic currents play a significant role in atrial arrhythmia initiation (Feng et al., 1998; Gaborit et al., 2007; Colman et al., 2013). Consequently, pharmacotherapy that increases dispersion of refractoriness is an adverse side effect of drugs for the treatment of AF (Ramanna et al., 2001; Soylu et al., 2003).
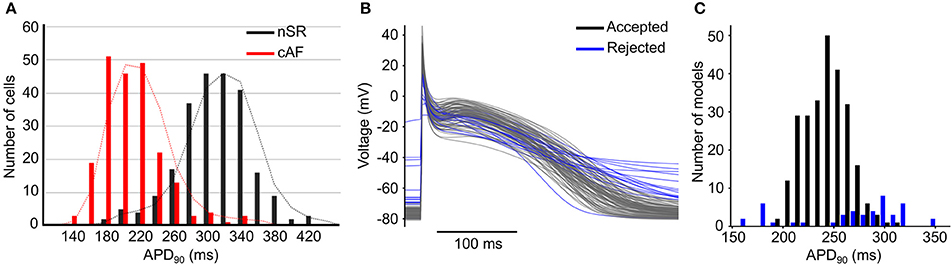
Figure 1. Variability in cardiac electrophysiology.(A) Histograms of AP duration at 90% repolarization (APD90) for patients in nSR (black) and cAF (red) show substantial variability. Reproduced from Ravens et al. (2015) with permission. (B) Example of APs and (C) histogram of APD90 produced using models incorporating variability in conductances of ionic currents; some models (in blue) are rejected due to non-physiological behaviors.
It is well-known that individuals may present largely different responses to same pharmacological interventions. As an example, it has been shown that drugs that block the hERG (human ether-à-go-go-related gene) channel are generally responsible for drug-induced long QT syndrome (diLQTS), but in a population this adverse response is highly variable, from minimum changes in the electrocardiogram (ECG) to induction of lethal ventricular arrhythmias (Singh et al., 2000; Kannankeril et al., 2011). Accounting for physiological variability may help better understand why some individuals display adverse side effects, while others do not. Given the different etiologies of many cardiac arrhythmias, such as AF, computational approaches that take into account variability may help us identify subpopulations in which a particular antiarrhythmic therapy will be effective and safe, or toxic. Furthermore, when assessing the efficacy and safety of a drug administration for heart conditions, it is important to take into account physiological and pathological variabilities to make sure that results are quantified and valid at the population level. Such approaches will potentially be more clinically useful in simulating the effects of drugs and aiding the design of safer and more effective therapies (Britton et al., 2013, 2017a; Passini et al., 2016; Yang et al., 2016).
Although many methods have been developed, two families of approaches have emerged as leading methodologies to account for variability in cardiac electrophysiology: (1) population-based and (2) sample-specific modeling (Figure 2). Both methods generally start with the building or use of a baseline cardiac cell model, which has been parameterized and validated to average data. Population-based approaches generate model variants of the baseline model that fit given experimental distributions of electrophysiological outcomes or biomarkers, while sample-specific modeling approaches re-parameterize the baseline model based on cell- or patient-specific datasets (Figure 2). Because their implementation requires computational power, the advancements in computing capabilities and techniques (Pitt-Francis et al., 2006; Abramson et al., 2010), especially in parallel computing (Wang et al., 2011), have helped these methods gain traction in the last decade.
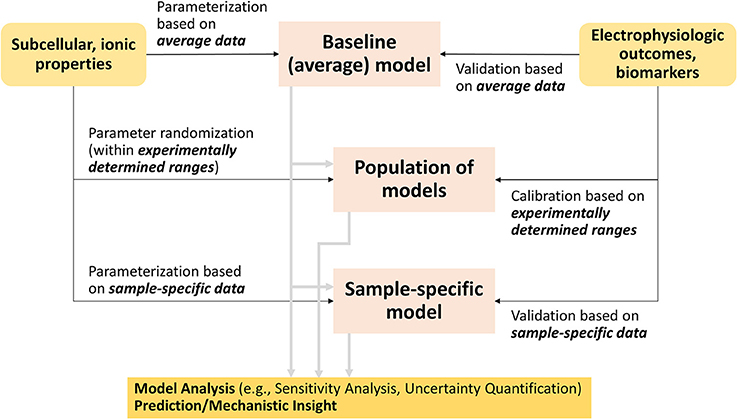
Figure 2. Flowchart connecting traditional cardiac modeling approach to the new methodologies that account for variability.
Population-based modeling approaches have been developed and employed to obtain results at the population level, which led to many novel insights into physiological and pathophysiological variabilities, and variable responses to drug administration. We refer the readers to a recent review from the Rodriguez group (Muszkiewicz et al., 2016), where this methodology is described in detail. Here, we briefly describe the general approach of population-based modeling, and summarize how it has contributed to advancing the field as exemplified by some important studies.
Populations of models are generally created by modifying sets of parameters in a baseline model (Figure 2). This process involves determination of the parameters to be varied, over what range, and a sampling method to select the parameter values. Frequently, maximal conductances or maximum transport rates of ion channels, pumps and transporters in AP models are selected to vary. The parameter space over which these model parameters vary can be chosen either to reflect the experimental range, when available, or theoretical upper and lower bounds. Then, populations of parameter sets are created by sampling the parameters within the predefined parameter spaces. Typically, four types of sampling methods have been applied to obtain the populations of parameter sets: uniform-interval sampling (Romero et al., 2009, 2011; Corrias et al., 2011), log-normal sampling (Sobie, 2009; Sadrieh et al., 2013; Ellinwood et al., 2017a; Morotti and Grandi, 2017), Latin hypercube sampling (LHS) (Britton et al., 2013) and its variants such as orthogonal sampling (Burrage et al., 2015; Donovan et al., 2018), and sequential Monte Carlo sampling (Muszkiewicz et al., 2017).
After generating hundreds or thousands of model variants, calibration can be performed to exclude models that display non-physiological behaviors (Figure 2). This can be done, for example, by removing models showing repolarization failure (Sobie, 2009), or exhibiting AP duration (APD) more than three standard deviations from the population mean (Devenyi and Sobie, 2016). Population of models are also calibrated to measured data from patient samples, whereby model variants are selected based on simulated electrophysiological properties, such as APD, upstroke velocity, resting membrane potential and/or Ca2+ transient (CaT) (Britton et al., 2013, 2017a; Sanchez et al., 2014; Passini et al., 2016; Rees et al., 2018). Other studies use additional information such as ionic current data (Muszkiewicz et al., 2017), or ECG data (Mann et al., 2016). This calibration step is meant to ensure that (1) variants displaying non-physiological properties are discarded before analysis, and (2) the simulated electrophysiological properties of models in a given population are in the same range as experimental data, or, more recently, correspond to the same distribution of observed experimental biomarkers (Lawson et al., 2018), thus possibly making inferences from in silico experiments more physiologically relevant.
Once a population of cardiac AP models is generated, and electrophysiological simulations have been performed corresponding to the scientific question at hand, mechanistic insights can be obtained using various analysis techniques. These analyses have contributed to our understanding of the relative role of the underlying parameters in modulating the physiological properties of interest (i.e., sensitivity analysis), or revealing association of certain parameter ranges or properties with specific physiological behaviors (e.g., repolarization abnormalities, ectopic activity, drug response). Many relevant examples have recently been reviewed (Muszkiewicz et al., 2016). Here we highlight new recent developments and discuss details of parameter sensitivity analysis.
A common systematic analysis of populations of models is sensitivity analysis. It assesses how model outputs, which typically represent whole cell behavior (e.g., APD), are sensitive to changes in model parameters, (e.g., conductances and maximum transport rates). Because many parameters are often varied to generate the populations of models, multivariable linear regression (Hair et al., 2010; Draper and Smith, 2014) has emerged as a frequently utilized tool to perform sensitivity analysis in cardiac electrophysiology. Moreover, as the number of independent parameters varied is used to predict a smaller set of dependent variables, sensitivity analysis is typically performed using partial least squares regression (Geladi and Kowalski, 1986; Sobie, 2009), as compared to standard multivariable regression. The result of linear regression is a set of coefficients (forming a “regression model”) describing how perturbing a particular parameter influences an output of interest. This method has been successfully utilized in other fields such as molecular biology (Janes et al., 2005) and neuroscience (Weaver and Wearne, 2008), and was first used in cardiac electrophysiology by Sobie (2009), who applied it to study sensitivities of properties such as APD and pacing rate threshold for inducing AP alternans. Since the regression model represents a linear approximation of a highly non-linear system, it is important to always check the goodness of fit. Several papers by the Sobie's group have indeed shown that the linear approximation actually provides a very good fit of the AP biomarkers, which was not trivially predictable (Sarkar et al., 2012).
The approach of varying multiple ionic conductances at once in a systematic fashion (as opposed to one at a time) and employing sensitivity analysis using multivariable regression has led to many important insights in cardiac electrophysiology (Sarkar and Sobie, 2011; Mann et al., 2012; Heijman et al., 2013; Walmsley et al., 2013), some of which have been confirmed experimentally (Lee et al., 2013; Devenyi and Sobie, 2016; Devenyi et al., 2017). For example, it has been used to study how different diseased conditions affect the sensitivities of given electrophysiological properties (Sadrieh et al., 2013; Ellinwood et al., 2017a; Vagos et al., 2017; Koivumaki et al., 2018), mechanisms of physiological phenomena (Lee et al., 2013), and for constraining free parameters (Sarkar and Sobie, 2010). Through sensitivity analysis, Cummins et al. identified multiple potential ionic targets mediating forward rate dependence (FRD) of AP, and demonstrated that modulation of the inward rectifier K+ current (IK1) or the Na+/K+ pump current was more likely to produce FRD (Cummins et al., 2014). Devenyi and Sobie performed sensitivity analysis of rat ventricular myocyte models, and quantitatively compared the modulatory role of transient outward K+ current (Ito) and sarco/endoplasmic reticulum Ca2+-ATPase (SERCA) in CaT amplitude. They found that in rat epicardial cells Ito plays a more important role than SERCA in regulating CaT amplitude, and this was analogous to human atrial cells, where both Ito and ultra-rapid delayed-rectifier K+ current (IKur) had greater impacts on CaT amplitude than did SERCA (Devenyi and Sobie, 2016). These studies highlight how sensitivity analysis can be applied to compare and contrast roles of different ionic processes and Ca2+ handling in regulating physiological properties and behaviors between cell types and species. Sensitivity analysis has also been used to compare the dependence of AP biomarkers on ionic processes in healthy and diseased conditions. For example, Lee et al. compared the impact of ionic processes on APD in control and AF-remodeled cells and found that the Na+/Ca2+ exchanger (NCX) current has little influence on APD in control cells but more markedly impacts AF cells; the analysis also revealed that IK1 upregulation plays a dominant role in APD shortening in AF, and that the L-type Ca2+ current (ICaL) significantly contributes to rate-dependent APD changes in both control and AF myocytes (Lee Y. S. et al., 2016). Most recently, Gong and Sobie described a novel use of regression models, cross-cell regression, to predict adult myocyte drug responses from induced pluripotent stem-cell-derived cardiomyocytes (iPSC-CMs) behaviors (Gong and Sobie, 2018).
Multivariable linear regression is used if the physiological output of interest is continuous, but, for the study of arrhythmia mechanisms, another particularly useful and efficient regression technique is logistic regression, which is used when the outcome of interest is Boolean (i.e., yes/no, true/false). Applying logistic regression in studies of physiology is well-described by Lee et al. who examined Ca2+ spark triggering (an all-or-none event), and demonstrated the accuracy of logistic regression using receiver operator characteristic curves (Lee et al., 2013). This method has since been used to study the probability that a certain arrhythmic event such as early afterdepolarizations (EADs) will occur and suggest underlying factors (Morotti and Grandi, 2017).
The main limitation of regression (both linear and logistic) analysis is that it only highlights how inputs are correlated to outputs, so the conclusions drawn from the analysis can be misleading if only a few outputs are considered. For example, it has been shown that completely different parameter combinations could produce essentially identical AP shapes but substantially different CaT amplitudes (Figure 3) (Sarkar and Sobie, 2010). However, sensitivity analysis can still help determine whether the relationships between inputs and outputs in computational models match experimental findings and assumptions, and whether there are particularly influential parameters that can be exploited therapeutically or targeted to better understand a given physiological phenomena (e.g., arrhythmia mechanism).
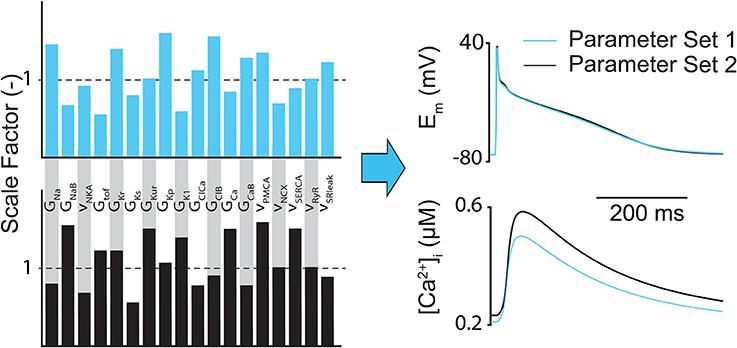
Figure 3. Different subcellular parameter combinations can lead to same AP shape. Example of how different model parameter combinations (e.g., ion channel conductances and maximum transport rates) can produce nearly identical atrial AP morphologies, but notably different CaTs.
Comparing subgroups in a population of models (often using statistical difference tests of parameters of interest) can help identify underlying determinants of different phenotypes, behaviors, and pathological conditions (Sanchez et al., 2014; Zhou et al., 2016; Britton et al., 2017b; Muszkiewicz et al., 2017; Vagos et al., 2017; Lawson et al., 2018). For example, through characterizing ionic parameters of models that are prone to repolarization abnormalities, Britton et al. found that the electrogenic Na+/K+ pump is a key determinant of susceptibility to repolarization abnormalities in human ventricular cardiomyocytes by applying arrhythmia-provoking conditions to a population of experimentally-calibrated cardiac cells (Britton et al., 2017b). A population-based approach has also been used to tease out the ionic mechanisms underlying variability in iPSC-CMs (Paci et al., 2017). By calibrating generated subpopulations of human atrial myocyte models to ranges of experimental data from a large number of patients with nSR or cAF, Sanchez et al. characterized potential ionic determinants of inter-subject variability in AP biomarkers, and identified similar changes in IK1, IKur, and Ito in cAF vs. nSR subpopulations that were consistent with experimentally reported AF-induced remodeling effects (Sanchez et al., 2014). In a more recent study, instead of calibrating population of models to the range of experimental dataset, Lawson et al. proposed a novel method to calibrate these models to the distributions of multiple experimentally measured biomarkers (Lawson et al., 2018), which led to an improved characterization of ionic differences between nSR and cAF. These studies focused on AP biomarkers at a fixed pacing rate. In a different study, Vagos et al. expanded the use of population of models to compare the steady state and dynamic restitution behaviors of AP in nSR and cAF populations (Vagos et al., 2017). By combining population-based modeling and experiments, Muszkiewicz et al. characterized variability in AP and ionic densities and their impact on CaT in atrial cells from right atrial appendage of patients exhibiting nSR (Muszkiewicz et al., 2017). In addition to calibrating model outputs to measured AP biomarkers, they also extended the experimental calibration of population of human atrial models to model parameter (inputs) by using experimental data of major ionic currents.
By using a population of models that incorporate variabilities, drug modulatory effects on electrophysiological properties can be interpreted at a whole population level, which also contributes to limiting potential model-dependent results. For example, Yang et al. used a population-based approach to simulate effects of late Na+ current (INaL) and hERG block and found that the selective INaL blocker GS-458967 could suppress proarrhythmic markers after hERG block in ventricular myocytes (Yang et al., 2016). Population-based modeling has also allowed for more rigorous quantitative comparison of modulatory effects between multiple drugs. A recent study by Britton et al. calibrated populations of ventricular models to specific individuals using data from human trabeculae (Britton et al., 2017a). They then assessed the effects of four different (selective and non-selective) blockers of the rapid delayed-rectifier K+ current (IKr), dofetilide, sotalol, quinidine, and verapamil, to quantitatively compare changes in AP biomarkers, and demonstrated good agreement with experiments for the selective IKr blockers (dofetilide and sotalol) but not for the non-selective IKr inhibitors (quinidine and verapamil). Paci et al. utilized populations of in silico iPSC-CMs to evaluate antiarrhythmic effects of mexiletine and ranolazine to treat iPSC-CM long QT syndrome type 3 (LQT3) mutants and demonstrated that mexilitine stops spontaneous APs in more LQT3 models than ranolazine due to its stronger effects on the fast Na+ current (INa) (Paci et al., 2017). In contrast to the traditional modeling approach using a single model, the population-based modeling can gain insights into the physiologically relevant variability of predictions made in silico, as demonstrated in these studies.
By taking a step further, simulations using populations of models incorporating variabilities can also help recognize the contributing factors underlying the variability observed in response to drugs. One relevant example is the variable outcomes of hERG inhibition, which is frequently linked with diLQTS. Population-based modeling has offered insights into the mechanisms underlying the fact that individuals will not exhibit the same degree of QT interval prolongation after hERG block (Singh et al., 2000; Kannankeril et al., 2011; Weeke et al., 2014). Employing a population of models of ventricular myocytes, Sobie and Sarkar attributed the variable outcomes to the different ionic properties of the cells (Sarkar and Sobie, 2011). In another interesting application, Passini et al. implemented an in silico drug trial using experimentally-calibrated populations of AP models to investigate the risk of drug-induced arrhythmias, and to identify specific subpopulations at higher risk for proarrhythmic cardiotoxicity (Passini et al., 2017). Their methodology not only demonstrated higher accuracy than animal models in predicting arrhythmia risk, but also provided mechanistic insight into the underlying ionic contributors to repolarization/depolarization abnormalities.
Understanding the bases of variability in electrophysiological behavior and arrhythmia proclivity may also allow developing specific antiarrhythmic therapies for different disease phenotypes. For example, Liberos et al. compared AF models that had self-sustained vs. self-terminating reentries (Liberos et al., 2016). They found that AF maintenance was correlated with high ICaL and INa, and that ICaL block could be an effective treatment depending on the basal availability of Na+ and Ca2+ ion channel conductivities (INa depression increased efficacy). Mayourian et al. employed a comprehensive integrated approach to study the mechanisms of cardiac contractility and arrhythmogenicity using experimentally-calibrated human mesenchymal stem cells (hMSCs) (Mayourian et al., 2017). In simulations testing proarrhythmic effects, they found that hMSCs paracrine signaling protected such adverse effects of heterocellular coupling at various levels of engraftment. This work highlights that antiarrhythmic strategies can move beyond simply considering repolarization abnormalities.
Instead of taking a baseline cardiac model and introducing variability by randomly varying the ionic conductances, optimization and statistical techniques can also be used to tailor the baseline model to describe a specific experimental sample. Depending on the characteristics of the dataset at hand, sample-specific models can be representative of either individual myocytes or a particular group of cells. The former approach, cell-specific modeling, can be helpful when integrating mathematical modeling into an experimental setup. For example, Ravagli et al. characterized the role of the “funny” current If in sinoatrial myocytes using the dynamic clamp technique by adapting the extent of injected If in a cell-specific fashion, i.e., based on the basal firing rate measured in each individual cell (Ravagli et al., 2016). Despite the use of average data, sample-specific models built from a group of cells (e.g., a cell line developed in a certain laboratory, myocytes isolated from disease models, iPSC-CMs derived from a single patient) can allow for specific characterization of conditions that are far from the average, or even of personalized physiology (Barichello et al., 2018). For example, monophasic AP data recorded in AF patients undergoing ablation procedures have been used to construct atrial cell models that capture patient-specific electrophysiological properties (Lombardo et al., 2016). This approach has the promise of making patient-specific predictions given interventions such as arrhythmia-provoking protocols or drug application. Here we summarize methodologies for building and improving sample-specific cell models. For more detail, we refer the readers to a previous review on the topic (Krogh-Madsen et al., 2016).
Sample-specific models can be constructed by fitting the parameters of a baseline model so that the model outputs match the corresponding physiological behaviors seen in a single patient or myocyte (Figure 2). Cardiac electrophysiology models can be optimized using many different fitness functions (Druckmann et al., 2007; Tomaiuolo et al., 2012), such as global search heuristics (Vanier and Bower, 1999; Dokos and Lovell, 2004; Bueno-Orovio et al., 2008; Guo et al., 2010). Recently, many sample-specific models are generated using the genetic algorithm (GA), which traces its beginnings to evolutionary biology (Fraser and Burnell, 1970; Crosby, 1982), but is still being applied in new ways today (Chen and Guan, 2004; Hussein and El-Ghazaly, 2004; Leung et al., 2004; Vieira et al., 2004). Its use for optimization of ionic models is relatively new in both neuroscience (Achard and De Schutter, 2006; Gurkiewicz and Korngreen, 2007; Hobbs and Hooper, 2008; Ben-Shalom et al., 2012) and cardiac electrophysiology (Syed et al., 2005; Bot et al., 2012; Kaur et al., 2014; Groenendaal et al., 2015). Syed et al. demonstrated its feasibility for atrial cell models when they proved they could fit two different cell models (Courtemanche et al., 1998; Nygren et al., 1998) to any given atrial AP (Syed et al., 2005). Essentially, the GA optimization procedure is initialized in the same way as for the population-based approach (varying maximal conductance and/or transport rates), and then it iteratively evolves toward better solutions in generations, while the underlying parameters can be varied, swapped, or discarded. Sensitivity analysis can be used in conjunction with generating sample-specific models as it can inform the design of the error function (i.e., weights) by revealing the conductances that more significantly impact the electrophysiological outputs used for fitting. For example, Krogh-Madsen et al. recently combined sensitivity analysis and global optimization (using a GA) of a ventricular myocyte model to clinical long QT data and intracellular Ca2+ and Na+ concentrations, to better constrain the model parameters (Krogh-Madsen et al., 2017). They found that this improved prediction of drug-induced torsades de pointes (TdP), especially in eliminating false-positive outcomes generated by the baseline model parameters.
The final solution of an optimization procedure using some fitness function may not match experimental data well if only fitting to a single electrophysiological output such as a single AP, because multiple parameter combinations can potentially produce the same AP (Figure 3) (Syed et al., 2005; Druckmann et al., 2007; Sarkar and Sobie, 2010; Guo et al., 2013; Kaur et al., 2014; Groenendaal et al., 2015). In this case, although fitness function itself can be improved, for example, by increasing the population size or diversity for GAs can improve the fit of a sample-specific model, it may not necessarily guarantee that the final solution relates to the global minimum. To address this issue, many methods have been developed using (1) additional electrophysiological properties for fitting and/or (2) more complex electrophysiological protocols to improve model fidelity. It has been shown that model faithfulness can be improved by adding membrane resistance as an objective (Kaur et al., 2014), by optimizing to Ca2+ handling (Dokos and Lovell, 2004; Sarkar and Sobie, 2010; Rees et al., 2018), or by accounting for experimental data generated from multiple pacing frequencies (Syed et al., 2005; Lombardo et al., 2016) or irregular pacing protocols (Guo et al., 2013; Groenendaal et al., 2015).
In addition to using multiple electrophysiological properties to improve the fit of sample-specific models, more intricate voltage-clamp protocols that capture complex and rich electrophysiological dynamics have been employed, as first demonstrated to improve the fit of Markov models of ionic currents with many parameters (Dokos and Lovell, 2004; Zhou et al., 2009; Beattie et al., 2018). These can be implemented over a short time frame and may be used to emphasize certain currents over others. In the absence of pharmacological isolation, Groenendaal et al. used only a 6-s protocol that effectively isolated IK1, ICaL, and slow delayed-rectifier K+ current (IKs) given their disproportionately large contribution at voltage steps of −120, +20, +40, and −30 mV, respectively (Groenendaal et al., 2015). They found that using this protocol alone cannot isolate all ionic currents, and when used in combination with a stochastic pacing protocol there was a considerable improvement in parameter estimation. Developing short but information-rich protocols is useful especially when trying to improve the results of an optimization procedure for cell-specific modeling, because longer protocols take longer to implement experimentally and thus are difficult to perform in a single cell. In a recent study, Beattie et al. proposed an innovative experimental and mathematical modeling method that allows to concisely measure the dominant processes involved in hERG channel gating by applying a short (8-s long) “sum of sinusoids” voltage-clamp protocol (Beattie et al., 2018). The sinusoidal waves were able to provoke a wider range of non-equilibrium behavior than traditional square voltage steps, thus allowing rich and complete characterization of hERG channel kinetics in the same cell and efficient model fitting (Figure 4A).
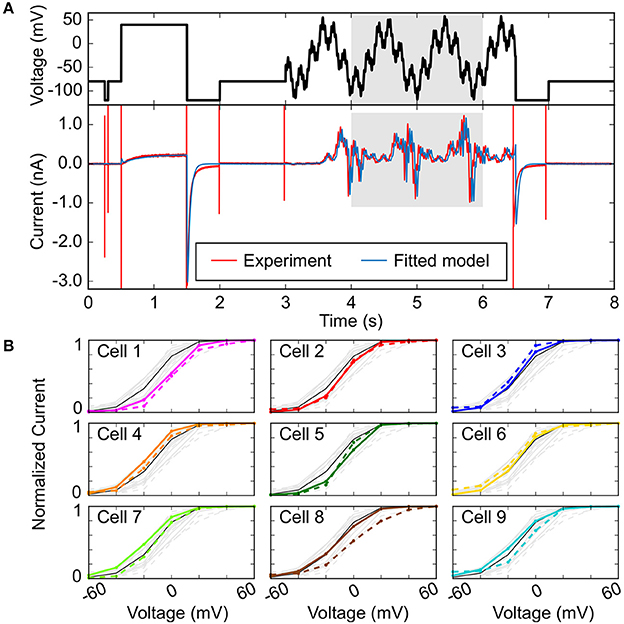
Figure 4. Improving fit of sample-specific models. (A) Experimental and simulated IKr time courses (bottom) evoked in response to an efficient, information-rich sum-of-sinusoid voltage protocol (top) that allows rapid characterization of IKr behavior. (B) Steady-state peak IKr-voltage curves comparing cell-specific model predictions (bold, colored) to cell-specific experimental recordings (dashed, colored). The black lines in each plot are from the model calibrated to averaged sinusoidal data from all the cells (light gray). Reproduced from Beattie et al. (2018) with permission.
The final step in improving fidelity of sample-specific models is to directly experimentally test the predictions of the model given new protocols (Groenendaal et al., 2015; Devenyi et al., 2017; Beattie et al., 2018). Figure 4B reports an example of such validation experiments, where predictions obtained with cell-specific IKr models (identified applying the sinusoidal protocol in Figure 4A in 9 cells) are compared to the IKr-voltage relationships experimentally determined in each cell (Beattie et al., 2018). The order of the panels in Figure 4B is based on an index of recording stability (lowest to highest difference in leak resistance between the vehicle and dofetilide recordings) that is associated to “data quality”. Cell-specific predictions are excellent for cells 1–5 (higher data quality), but less accurate for cells 6–9 (lower data quality). The analysis also shows that cell-specific models provide better predictions than the average model for the cells with the highest data quality (cells 1–5). Experimental validation is an important last step in improving cell-specific models, as generating cell-specific models is potentially more susceptible to observational error. Devenyi et al. used a GA to re-parameterize the Livshitz-Rudy model of the guinea pig ventricular cardiomyocyte (Livshitz and Rudy, 2009), and predicted an increase in IKr and a drastic decrease in IKs given a dynamic clamp protocol as compared to the original model, and this was validated experimentally (Devenyi et al., 2017). Their adjusted model predicted that IKs can stabilize the AP and EADs better as compared to IKr—which improved the ability to assess arrhythmia risk, given the baseline model did not produce physiological behaviors that were quantitatively similar to their experiments.
While a detailed discussion of patient-specific anatomical models is beyond the scope of our review, recent studies have begun investigating how inter-patient differences in myocardial structure affects atrial arrhythmia, as reviewed by Barichello et al. (2018). For example, Zhao et al. developed a 3D human heart-specific atrial computer model integrating 3D high resolution structural and functional mapping data to test the impact of wall thickness, fibrosis, and myofiber orientation on AF induction, maintenance, and ablation strategies (Zhao et al., 2017). Deng et al. demonstrated that reentrant driver localization dynamics are influenced by inter-patient variability in the spatial distribution of atrial fibrosis, APD, and conduction velocity (Deng et al., 2017). This suggests that incorporating patient-specific electrophysiological models in patient-specific geometries might enhance their predictive value. We discuss the computational challenges associated to this task in the section entitled “Arrhythmia Research Requires Understanding Variability at Larger Spatial Scales”. Furthermore, obtaining patient-specific electrophysiological data might constitute another logistical roadblock.
Overall, methods that incorporate variability are particularly useful for (1) analyzing variability in cardiac electrophysiology, (2) assessing proarrhythmic risk, (3) determining the underlying factors contributing to variable drug response, and (4) identifying phenotype-specific (and in the future patient-specific) antiarrhythmic targets. Table 1 summarizes applications of these approaches and new insights provided by the studies (shaded areas indicate atrial studies).
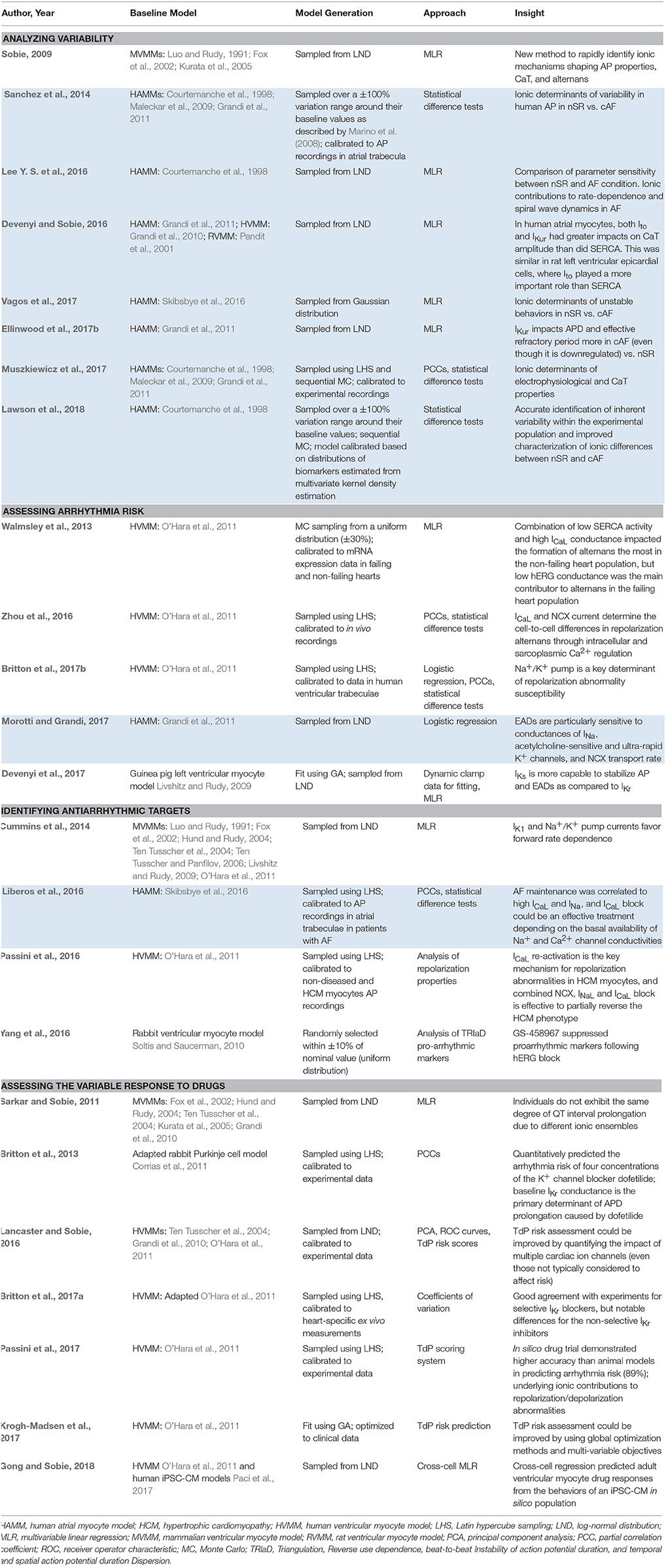
Table 1. Applications and main findings of computational methods incorporating cardiac electrophysiological variability (**shaded areas indicate atrial studies).
We reviewed the most common methods used to account for variability in cardiac electrophysiology, which largely fall into the two categories of (1) population-based modeling and (2) sample-specific modeling. These methods complement each other well, as population-based methods can help characterize behavior in a particular patient group (healthy, diseased, stressed, etc.), and sample-specific modeling shows significant promise to develop personalized medical approaches for individual patients. Both methods have led to many important insights into the mechanisms of arrhythmogenesis and antiarrhythmic strategies. However, there are several important limitations to consider, which suggest potential future developments in modeling of cardiac electrophysiology.
As opposed to the traditional approach of producing a single value from a single baseline model, models that incorporate variability have allowed statistical methods to be applied that can either ask new scientific questions or quantify the impact of variability on electrophysiological outputs, as performed in experimental studies. While the statistical analysis methods used in experimental studies can be directly applied in the in silico population-based studies, differences in the nature of experimental and simulation studies may need to be considered. For example, some population-based techniques generate model population sizes (often sample sizes in the 1000s) that are much greater than could be achieved by experiments (often sample sizes of 3–12) or the traditional cardiac modeling approach alone. Therefore, given similar effects, results produced in the population-based simulations have greater statistical power to detect differences. Furthermore, because even very small effects can reach statistical significance with large samples, physiological significance should be assessed (White et al., 2014). Additionally, when evaluating drug effects on electrophysiology, in simulations of the same virtual cell (a single model out of the population-models) can be used to perform both control and with-drug studies, allowing for paired comparisons, which is often not practical in experimental studies. The methodologies for analyzing and interpreting the “big data” produced by the population of models should be carefully considered and standards should be established going forward.
Physiologic variability should be thought of in the context of the broader umbrella of uncertainty, which is the confidence (or precision) with which a quantity, such as an electrophysiological output, can be given a value (Mirams et al., 2016). While here we reviewed how cardiac electrophysiology models have begun to account for physiological and experimental variability, uncertainty analysis should determine whether the baseline model itself is a valid representation of its physical system. The extent and rigor of validation during model development affects uncertainty, whereby the broader the set of constraints, e.g., the model recapitulates both voltage and Ca2+ responses, their pacing rate-dependence, short- and long-term behavior, the lesser the uncertainty in the obtained parameters. Uncertainty analysis should also verify that the experiments used to construct the model are appropriate. For example, in experiments, voltage-clamp protocols used to characterize ionic currents are often done using non-selective pharmacological block which may have unidentified effects, over a range narrower than the entire physiological range, or on larger cells that are easier to patch-clamp with intrinsically greater than normal maximal conductances (Courtemanche et al., 1998). All of these would lead to uncertainties in the initial parameters and conditions due to experimental error and lack of knowledge. Likewise, the choice of the computational methods or resources used to perform the model parameterization and simulations can produce uncertainty in model results. This is because cardiac models may use different mathematical equations to describe the same physiological process, perhaps based on different analyses or assumptions on the physical-world process. Using more than one (e.g., cell) model to confirm predictions or validate the mechanistic understanding of a process is therefore a useful strategy (see for example Sarkar and Sobie, 2011; Sanchez et al., 2014; Lancaster and Sobie, 2016; Muszkiewicz et al., 2017). Additionally, even the choice of the numerical solver used by the software can lead to variability in model outputs, i.e., simulator uncertainty (Pathmanathan et al., 2012). Moreover, uncertainty in model outputs may arise if the code has not been verified to truly represent the mathematical equations in the computational model (Niederer et al., 2011a). Finally, optimization procedures can also introduce uncertainty, whereby the choice of whether to optimize simplified models with few parameters (Bueno-Orovio et al., 2008; Al Abed et al., 2013; Guo et al., 2013) or detailed models but only a few properties (e.g., focusing on specific currents) (Zhou et al., 2009; Fink et al., 2011) can lead to multiple distinct models given the same experimental data.
Used in conjunction with the approaches discussed in this review that take into account electrophysiological variability, new methods have been developed that try to quantify uncertainty more generally (Marino et al., 2008). Uncertainty quantification methods aim to quantify uncertainties in model inputs and propagation through the model to see how they affect model predictions (Pathmanathan et al., 2015; Mirams et al., 2016). This is typically done by assigning probability distribution functions, rather than fixed values to model parameters, as done for example by Pathmanathan et al. and applied to the study of INa steady-state inactivation (Pathmanathan et al., 2015). However, this process can be slow and tedious (requiring lots of simulations), especially if using a Monte Carlo sampling method that chooses input values from a statistical distribution. Also, in some cases, this statistical distribution of input parameters can be difficult to obtain or justify experimentally. To solve this issue, uncertainty quantification analysis has developed surrogate models or emulators (e.g., polynomial chaos expansions, and Gaussian process emulators; Chang et al., 2015), which are fast-running statistical approximations of the computational models and are quite powerful when fit to carefully constructed training data. Formal studies using uncertainty quantification in cardiac models are still limited, given the huge number of parameters in cardiac models, and may require the development of new methods or computational techniques (Johnstone et al., 2016).
Currently, populations of cardiac models and sample-specific models typically calibrate or fit to maximal conductance values or transport rates of channels or receptors, based on the observation that changes in expression levels of ion channels and transport proteins are the primary contributors to (inter-species) variability (Rosati et al., 2008). However, this approach does not take into account that the expression of ion channels will vary over relatively short time scales given changes in transcription, translation, degradation, or even circadian rhythm. Moreover, with a few exceptions (Sarkar and Sobie, 2011; Cummins et al., 2014) these methods do not typically account for variability in ion channel kinetics, which is known to change especially in response to drugs (Clancy et al., 2007). The methods discussed in this review can attempt to account for these properties using additional parameters.
Although the correlation between parameters (i.e., maximal conductances) is assessed sometimes (Britton et al., 2013), neither population-based nor the sample-specific approaches account for possible covariance in ion channel conductances, despite the fact it has been observed in neurons (Schulz et al., 2006, 2007; Tobin et al., 2009) and cardiac tissue (Schram et al., 2002; Rosati and Mckinnon, 2004; Deschenes et al., 2008; Xiao et al., 2008; Banyasz et al., 2011; Milstein et al., 2012). The exact mechanisms responsible for these covariances are still being explored. Xiao et al. found that sustained reductions in IKr may lead to compensatory upregulation of IKs through post-transcriptional upregulation of underlying subunits (Xiao et al., 2008), which potentially underlie the observed phenomenon of repolarization reserve (Roden, 2008). Macromolecular complexes or post-transcriptional modifications could also facilitate coregulation of ionic conductances, as demonstrated by the observed structural or functional complex between Ito and INa (Deschenes et al., 2008). Rees et al. recently argued that sensing of aggregate CaT may be sufficient in itself to regulate ionic conductances (of K+ and inward Ca2+) to maintain normal Ca2+ handling (Rees et al., 2018). Moreover, knockout and knockdown studies are consistent with the idea that cardiac cells have compensatory mechanisms to maintain AP or CaTs (perhaps to prevent arrhythmias) (Guo et al., 1999; Zhou et al., 2003). The covariance of ionic conductance can have significant implications for both calibrating populations of models or fitting sample-specific models, because it could propose additional constraints for how the underlying parameters of the computational model can be varied. Thus, new methods have begun to be developed that measure all ionic conductances at once, and can not only tease out how ionic conductances are correlated, but the extent to which they vary between cells (Banyasz et al., 2011; Groenendaal et al., 2015).
Accounting for variability at tissue and organ-level scales is a logical, but not trivial (Elshrif and Cherry, 2014), next step. A thorough investigation of variability would first require including differences among the cells in the same tissue, and evaluating the impact of diverse geometrical distributions. One should also account for patient-specific structural differences, based on measures of tissue conductivity and anatomic properties, including heterogeneity in signaling due to non-uniform innervation. This last step can be particularly problematic when investigating diseased conditions affected by pronounced structural remodeling, such as fibrosis, organ dilation, and alterations in gap junction coupling. Where there has been meaningful progress in accounting for variability is in developing personalized atrial model structures based on medical images (Dossel et al., 2012; Trayanova, 2014). These methods have shown some promise in developing personalized ablation strategies (Mcdowell et al., 2015). For example, recently, Soor et al. implemented a modeling approach to optimize ablation times based on patient-specific atrial geometries to create lesions for a given atrial wall thickness (Soor et al., 2016). Combining these methods that utilize medical images with the methods described here, could significantly improve the clinical value of both methods alone (Hansen et al., 2017; Zhao et al., 2017). For example, Arevalo et al. developed personalized heart models based on cardiac imaging and published patch-clamp data to better predict arrhythmic events and possibly avoid unnecessary implantable cardioverter defibrillators (Arevalo et al., 2016). Developing multi-scale frameworks that account for variability is the next frontier in cardiac modeling that will greatly benefit from further advancements in computing capabilities. Beyond the availability of large experimental and clinical datasets, the development of novel techniques to speed model derivations and to integrate automation will be crucial to capture variability for different cell types and conditions at various scales.
The in silico approaches described here are being combined with other state-of-the-art tools to improve the evaluation of drug safety. Of significance, these approaches can help further the mission of the CiPA (Comprehensive in vitro Proarrhythmia Assay) initiative, which aspires to develop better methods to predict TdP. Beyond exclusively using steady-state hERG block as the main predictor of arrhythmia and not at all using QT interval prolongation, the CiPA initiative attempts to gain a more comprehensive understanding of proarrhythmic risk by combining (1) mechanistically-based in vitro assays, (2) in silico reconstructions of cardiac electrophysiology, and (3) confirmation using human iPSC-CMs (Colatsky et al., 2016). The methods described in this review are being utilized to help meet the mission of the CiPA initiative (Cummins et al., 2014; Lancaster and Sobie, 2016; Britton et al., 2017a; Passini et al., 2017). Most of the methods described here that assess the effects of drugs on populations of cardiac myocytes use simple pore block schemes. However, it is also clear that the sole use of steady-state hERG block assays is insufficient to predict arrhythmia risk, and thus studies are beginning to simulate the effects drug-binding kinetics and state-specific binding, which have been shown to affect electrophysiological outcomes (Lee W. et al., 2016; Dutta et al., 2017; Ellinwood et al., 2017b; Li et al., 2017). Incorporating more detailed drug-binding effects may allow studying the effects of populations of drugs characteristics (e.g., state-dependent block and kinetics) on populations of cardiomyocytes.
Computational approaches that have been developed over the past decade to account for variability in cardiac electrophysiology have led to important insights into mechanisms of arrhythmogenesis, etiology of disease, and variable response to drugs. The approaches outlined in this review are used in basic research studies, i.e., quite separately from actual clinical workflows, where decisions are made sometimes for a particular patient within minutes. Advanced computing facilities now allow near real-time simulations of anatomically realistic, biophysically detailed models of human cardiac electrophysiology (Niederer et al., 2011b; Okada et al., 2015, 2017). Such massively parallel processes could be optimized to run personalized cardiac simulations pre-determined to have clinical value. However, implementing these approaches more comprehensively into clinical workflows still presents challenges and simulation of variability may not find immediate application.
HN, SM, and EG reviewed the literature and wrote the manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was supported by the American Heart Association grant 15SDG24910015 (EG); the National Institutes of Health (NIH) Stimulating Peripheral Activity to Relieve Conditions grant 1OT2OD023848-01 (EG), the National Heart, Lung, and Blood Institute R01HL131517 and R01HL141214 grants (EG) and K99HL138160 award (SM); and the Heart Rhythm Society post-doctoral fellowship 16OA9HRS (SM). An early version of this article was drafted by Dr. Nicholas Ellinwood.
AF, atrial fibrillation; AP, action potential; APD, AP duration; cAF, chronic AF; CaT, Ca2+ transient; CiPA, Comprehensive in vitro Proarrhythmia Assay; DAD, delayed afterdepolarization; diLQTS, drug-induced long QT syndrome; EAD, early afterdepolarization; ECG, electrocardiogram; FRD, forward rate dependence; GA, genetic algorithm; hERG, human ether-à-go-go-related gene; hMSCs, human mesenchymal stem cells; ICaL, L-type Ca2+ current; Ito, transient outward K+ current; IKur, ultra-rapid delayed-rectifier K+ current; IKr, rapid delayed-rectifier K+ current; IKs, slow delayed-rectifier K+ current; IK1, inward rectifier K+ current; INa, fast Na+ current; INaL, late Na+ current; iPSC-CM, induced pluripotent stem-cell-derived cardiomyocyte; LHS, latin hypercube sampling; LQT3, long QT syndrome type 3; NCX, Na+/Ca2+ exchanger; nSR, normal sinus rhythm; SERCA, sarco/endoplasmic reticulum Ca2+-ATPase; TdP, torsades de pointes.
Abramson, D., Bernabeu, M. O., Bethwaite, B., Burrage, K., Corrias, A., Enticott, C., et al. (2010). High-throughput cardiac science on the Grid. Philos. Trans. A Math. Phys. Eng. Sci. 368, 3907–3923. doi: 10.1098/rsta.2010.0170
Achard, P., and De Schutter, E. (2006). Complex parameter landscape for a complex neuron model. PLoS. Comput. Biol. 2:e94. doi: 10.1371/journal.pcbi.0020094
Adeniran, I., El Harchi, A., Hancox, J. C., and Zhang, H. (2012). Proarrhythmia in KCNJ2-linked short QT syndrome: insights from modelling. Cardiovasc. Res. 94, 66–76. doi: 10.1093/cvr/cvs082
Ahrens-Nicklas, R. C., Clancy, C. E., and Christini, D. J. (2009). Re-evaluating the efficacy of beta-adrenergic agonists and antagonists in long QT-3 syndrome through computational modelling. Cardiovasc. Res. 82, 439–447. doi: 10.1093/cvr/cvp083
Al Abed, A., Guo, T., Lovell, N. H., and Dokos, S. (2013). Optimisation of ionic models to fit tissue action potentials: application to 3D atrial modelling. Comput. Math. Methods Med. 2013:951234. doi: 10.1155/2013/951234
Arevalo, H. J., Vadakkumpadan, F., Guallar, E., Jebb, A., Malamas, P., Wu, K. C., et al. (2016). Arrhythmia risk stratification of patients after myocardial infarction using personalized heart models. Nat. Commun. 7:11437. doi: 10.1038/ncomms11437
Banyasz, T., Horvath, B., Jian, Z., Izu, L. T., and Chen-Izu, Y. (2011). Sequential dissection of multiple ionic currents in single cardiac myocytes under action potential-clamp. J. Mol. Cell. Cardiol. 50, 578–581. doi: 10.1016/j.yjmcc.2010.12.020
Barichello, S., Roberts, J. D., Backx, P., Boyle, P. M., and Laksman, Z. (2018). Personalizing therapy for atrial fibrillation: the role of stem cell and in silico disease models. Cardiovasc. Res. 114, 931–943. doi: 10.1093/cvr/cvy090
Batchvarov, V. N., Ghuran, A., Smetana, P., Hnatkova, K., Harries, M., Dilaveris, P., et al. (2002). QT-RR relationship in healthy subjects exhibits substantial intersubject variability and high intrasubject stability. Am. J. Physiol. Heart Circ. Physiol. 282, H2356–H2363. doi: 10.1152/ajpheart.00860.2001
Beattie, K. A., Hill, A. P., Bardenet, R., Cui, Y., Vandenberg, J. I., Gavaghan, D. J., et al. (2018). Sinusoidal voltage protocols for rapid characterisation of ion channel kinetics. J. Physiol. 596, 1813–1828. doi: 10.1113/JP275733
Beeler, G. W., and Reuter, H. (1977). Reconstruction of the action potential of ventricular myocardial fibres. J. Physiol. 268, 177–210. doi: 10.1113/jphysiol.1977.sp011853
Behar, J., and Yaniv, Y. (2017). Age-related pacemaker deterioration is due to impaired intracellular and membrane mechanisms: insights from numerical modeling. J. Gen. Physiol. 149, 935–949. doi: 10.1085/jgp.201711792
Ben-Shalom, R., Aviv, A., Razon, B., and Korngreen, A. (2012). Optimizing ion channel models using a parallel genetic algorithm on graphical processors. J. Neurosci. Methods 206, 183–194. doi: 10.1016/j.jneumeth.2012.02.024
Bot, C. T., Kherlopian, A. R., Ortega, F. A., Christini, D. J., and Krogh-Madsen, T. (2012). Rapid genetic algorithm optimization of a mouse computational model: benefits for anthropomorphization of neonatal mouse cardiomyocytes. Front. Physiol. 3:421. doi: 10.3389/fphys.2012.00421
Boutjdir, M., Le Heuzey, J. Y., Lavergne, T., Chauvaud, S., Guize, L., Carpentier, A., et al. (1986). Inhomogeneity of cellular refractoriness in human atrium: factor of arrhythmia? Pacing Clin. Electrophysiol. 9, 1095–1100. doi: 10.1111/j.1540-8159.1986.tb06676.x
Britton, O. J., Abi-Gerges, N., Page, G., Ghetti, A., Miller, P. E., and Rodriguez, B. (2017a). Quantitative comparison of effects of dofetilide, sotalol, quinidine, and verapamil between human ex vivo trabeculae and in silico ventricular models incorporating inter-individual action potential variability. Front. Physiol. 8:597. doi: 10.3389/fphys.2017.00597
Britton, O. J., Bueno-Orovio, A., Van Ammel, K., Lu, H. R., Towart, R., Gallacher, D. J., et al. (2013). Experimentally calibrated population of models predicts and explains intersubject variability in cardiac cellular electrophysiology. Proc. Natl. Acad. Sci. U.S.A. 110, E2098–E2105. doi: 10.1073/pnas.1304382110
Britton, O. J., Bueno-Orovio, A., Virag, L., Varro, A., and Rodriguez, B. (2017b). The Electrogenic Na(+)/K(+) Pump is a key determinant of repolarization abnormality susceptibility in human ventricular cardiomyocytes: a population-based simulation study. Front. Physiol. 8:278. doi: 10.3389/fphys.2017.00278
Bueno-Orovio, A., Cherry, E. M., and Fenton, F. H. (2008). Minimal model for human ventricular action potentials in tissue. J. Theor. Biol. 253, 544–560. doi: 10.1016/j.jtbi.2008.03.029
Bueno-Orovio, A., Sánchez, C., Pueyo, E., and Rodriguez, B. (2014). Na/K pump regulation of cardiac repolarization: insights from a systems biology approach. Pflugers Arch. 466, 183–193. doi: 10.1007/s00424-013-1293-1
Burrage, K., Burrage, P., Donovan, D., and Thompson, B. (2015). Populations of models, experimental designs and coverage of parameter space by latin hypercube and orthogonal sampling. Procedia Comp. Sci. 51, 1762–1771. doi: 10.1016/j.procs.2015.05.383
Butters, T. D., Aslanidi, O. V., Inada, S., Boyett, M. R., Hancox, J. C., Lei, M., et al. (2010). Mechanistic links between Na+ channel (SCN5A) mutations and impaired cardiac pacemaking in sick sinus syndrome. Circ. Res. 107, 126–137. doi: 10.1161/CIRCRESAHA.110.219949
Campbell, S. G., Flaim, S. N., Leem, C. H., and Mcculloch, A. D. (2008). Mechanisms of transmurally varying myocyte electromechanics in an integrated computational model. Philos. Trans. A Math. Phys. Eng. Sci. 366, 3361–3380. doi: 10.1098/rsta.2008.0088
Chang, E. T., Strong, M., and Clayton, R. H. (2015). Bayesian sensitivity analysis of a cardiac cell model using a gaussian process emulator. PLoS ONE 10:e0130252. doi: 10.1371/journal.pone.0130252
Chen, Q., and Guan, S. U. (2004). Incremental multiple objective genetic algorithms. IEEE. Trans. Syst. Man. Cybern. B Cybern. 34, 1325–1334. doi: 10.1109/TSMCB.2003.822958
Clancy, C. E., and Rudy, Y. (1999). Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature 400, 566–569. doi: 10.1038/23034
Clancy, C. E., and Rudy, Y. (2002). Na(+) channel mutation that causes both Brugada and long-QT syndrome phenotypes: a simulation study of mechanism. Circulation 105, 1208–1213. doi: 10.1161/hc1002.105183
Clancy, C. E., Tateyama, M., and Kass, R. S. (2002). Insights into the molecular mechanisms of bradycardia-triggered arrhythmias in long QT-3 syndrome. J. Clin. Invest. 110, 1251–1262. doi: 10.1172/JCI0215928
Clancy, C. E., Zhu, Z. I., and Rudy, Y. (2007). Pharmacogenetics and anti-arrhythmic drug therapy: a theoretical investigation. Am. J. Physiol. Heart Circ. Physiol. 292, H66–H75. doi: 10.1152/ajpheart.00312.2006
Colatsky, T., Fermini, B., Gintant, G., Pierson, J. B., Sager, P., Sekino, Y., et al. (2016). The Comprehensive in Vitro Proarrhythmia Assay (CiPA) initiative - Update on progress. J. Pharmacol. Toxicol. Methods 81, 15–20. doi: 10.1016/j.vascn.2016.06.002
Colman, M. A., Aslanidi, O. V., Kharche, S., Boyett, M. R., Garratt, C., Hancox, J. C., et al. (2013). Pro-arrhythmogenic effects of atrial fibrillation-induced electrical remodelling: insights from the three-dimensional virtual human atria. J. Physiol. 591, 4249–4272. doi: 10.1113/jphysiol.2013.254987
Comtois, P., Sakabe, M., Vigmond, E. J., Munoz, M., Texier, A., Shiroshita-Takeshita, A., et al. (2008). Mechanisms of atrial fibrillation termination by rapidly unbinding Na+ channel blockers: insights from mathematical models and experimental correlates. Am. J. Physiol. Heart. Circ. Physiol. 295, H1489–H1504. doi: 10.1152/ajpheart.01054.2007
Corrias, A., Giles, W., and Rodriguez, B. (2011). Ionic mechanisms of electrophysiological properties and repolarization abnormalities in rabbit Purkinje fibers. Am. J. Physiol. Heart Circ. Physiol. 300, H1806–H1813. doi: 10.1152/ajpheart.01170.2010
Courtemanche, M., Ramirez, R. J., and Nattel, S. (1998). Ionic mechanisms underlying human atrial action potential properties: insights from a mathematical model. Am. J. Physiol. 275, H301–H321. doi: 10.1152/ajpheart.1998.275.1.H301
Courtemanche, M., and Winfree, A. T. (1991). Re-entrant rotating waves in a beeler-reuter based model of two-dimensional cardiac electrical activity. Int. J. Bifurcation Chaos 1, 431–444. doi: 10.1142/S0218127491000336
Cummins, M. A., Dalal, P. J., Bugana, M., Severi, S., and Sobie, E. A. (2014). Comprehensive analyses of ventricular myocyte models identify targets exhibiting favorable rate dependence. PLoS. Comput. Biol. 10:e1003543. doi: 10.1371/journal.pcbi.1003543
Daniels, G. S. (1952). The Average Man? Technical Note WCRD53-7, Wright Air Development Center, Ohio AD-10203.
Deng, D., Murphy, M. J., Hakim, J. B., Franceschi, W. H., Zahid, S., Pashakhanloo, F., et al. (2017). Sensitivity of reentrant driver localization to electrophysiological parameter variability in image-based computational models of persistent atrial fibrillation sustained by a fibrotic substrate. Chaos 27, 093932. doi: 10.1063/1.5003340
Deschênes, I., Armoundas, A. A., Jones, S. P., and Tomaselli, G. F. (2008). Post-transcriptional gene silencing of KChIP2 and Navbeta1 in neonatal rat cardiac myocytes reveals a functional association between Na and Ito currents. J. Mol. Cell. Cardiol. 45, 336–346. doi: 10.1016/j.yjmcc.2008.05.001
Devenyi, R. A., Ortega, F. A., Groenendaal, W., Krogh-Madsen, T., Christini, D. J., and Sobie, E. A. (2017). Differential roles of two delayed rectifier potassium currents in regulation of ventricular action potential duration and arrhythmia susceptibility. J. Physiol. 595, 2301–2317. doi: 10.1113/JP273191
Devenyi, R. A., and Sobie, E. A. (2016). There and back again: iterating between population-based modeling and experiments reveals surprising regulation of calcium transients in rat cardiac myocytes. J. Mol. Cell. Cardiol. 96, 38–48. doi: 10.1016/j.yjmcc.2015.07.016
Dibb, K., Trafford, A., Zhang, H., and Eisner, D. (2015). A model model: a commentary on DiFrancesco and Noble (1985) 'A model of cardiac electrical activity incorporating ionic pumps and concentration changes'. Philos. Trans. R Soc. Lond. B Biol. Sci. 370:20140316. doi: 10.1098/rstb.2014.0316
Difrancesco, D., and Noble, D. (1985). A model of cardiac electrical activity incorporating ionic pumps and concentration changes. Philos. Trans. R Soc. Lond. B Biol. Sci. 307, 353–398. doi: 10.1098/rstb.1985.0001
Dokos, S., and Lovell, N. H. (2004). Parameter estimation in cardiac ionic models. Prog. Biophys. Mol. Biol. 85, 407–431. doi: 10.1016/j.pbiomolbio.2004.02.002
Donovan, D., Burrage, K., Burrage, P., Mccourt, T. A., Thompson, B., and Yazici, E. S. (2018). Estimates of the coverage of parameter space by latin hypercube and orthogonal array-based sampling. Appl. Math. Model. 57, 553–564. doi: 10.1016/j.apm.2017.11.036
Dössel, O., Krueger, M. W., Weber, F. M., Wilhelms, M., and Seemann, G. (2012). Computational modeling of the human atrial anatomy and electrophysiology. Med. Biol. Eng. Comput. 50, 773–799. doi: 10.1007/s11517-012-0924-6
Draper, N. R., and Smith, H. (2014). Applied Regression Analysis. Hoboken; Somerset, NJ: John Wiley and Sons.
Druckmann, S., Banitt, Y., Gidon, A., Schürmann, F., Markram, H., and Segev, I. (2007). A novel multiple objective optimization framework for constraining conductance-based neuron models by experimental data. Front. Neurosci. 1, 7–18. doi: 10.3389/neuro.01.1.1.001.2007
Dutta, S., Chang, K. C., Beattie, K. A., Sheng, J., Tran, P. N., Wu, W. W., et al. (2017). Optimization of an in silico cardiac cell model for proarrhythmia risk assessment. Front. Physiol. 8:616. doi: 10.3389/fphys.2017.00616
Edwards, A. G., Grandi, E., Hake, J. E., Patel, S., Li, P., Miyamoto, S., et al. (2014). Nonequilibrium reactivation of Na+ current drives early afterdepolarizations in mouse ventricle. Circ. Arrhythm Electrophysiol. 7, 1205–1213. doi: 10.1161/CIRCEP.113.001666
Ellinwood, N., Dobrev, D., Morotti, S., and Grandi, E. (2017a). In silico assessment of efficacy and safety of IKur inhibitors in chronic atrial fibrillation: role of kinetics and state-dependence of drug binding. Front. Pharmacol. 8, 799. doi: 10.3389/fphar.2017.00799
Ellinwood, N., Dobrev, D., Morotti, S., and Grandi, E. (2017b). Revealing kinetics and state-dependent binding properties of IKur-targeting drugs that maximize atrial fibrillation selectivity. Chaos 27, 093918. doi: 10.1063/1.5000226
Elshrif, M. M., and Cherry, E. M. (2014). A quantitative comparison of the behavior of human ventricular cardiac electrophysiology models in tissue. PLoS ONE 9:e84401. doi: 10.1371/journal.pone.0084401
Fender, E. A., Henrikson, C. A., and Tereshchenko, L. (2014). Racial differences in sudden cardiac death. J. Electrocardiol. 47, 815–818. doi: 10.1016/j.jelectrocard.2014.07.023
Feng, J., Yue, L., Wang, Z., and Nattel, S. (1998). Ionic mechanisms of regional action potential heterogeneity in the canine right atrium. Circ. Res. 83, 541–551. doi: 10.1161/01.RES.83.5.541
Fink, M., Niederer, S. A., Cherry, E. M., Fenton, F. H., Koivumäki, J. T., Seemann, G., et al. (2011). Cardiac cell modelling: observations from the heart of the cardiac physiome project. Prog. Biophys. Mol. Biol. 104, 2–21. doi: 10.1016/j.pbiomolbio.2010.03.002
Fotiadis, P., and Forger, D. B. (2013). Modeling the effects of the circadian clock on cardiac electrophysiology. J. Biol. Rhythms 28, 69–78. doi: 10.1177/0748730412469499
Fox, J. J., Mcharg, J. L., and Gilmour, R. F. (2002). Ionic mechanism of electrical alternans. Am. J. Physiol. Heart Circ. Physiol. 282, H516–H530. doi: 10.1152/ajpheart.00612.2001
Gaborit, N., Le Bouter, S., Szuts, V., Varro, A., Escande, D., Nattel, S., et al. (2007). Regional and tissue specific transcript signatures of ion channel genes in the non-diseased human heart. J. Physiol. 582, 675–693. doi: 10.1113/jphysiol.2006.126714
Gaspo, R., Bosch, R. F., Talajic, M., and Nattel, S. (1997). Functional mechanisms underlying tachycardia-induced sustained atrial fibrillation in a chronic dog model. Circulation 96, 4027–4035. doi: 10.1161/01.CIR.96.11.4027
Geladi, P., and Kowalski, B. R. (1986). Partial least-squares regression - a tutorial. Anal. Chim. Acta 185, 1–17. doi: 10.1016/0003-2670(86)80028-9
Golowasch, J., Goldman, M. S., Abbott, L. F., and Marder, E. (2002). Failure of averaging in the construction of a conductance-based neuron model. J. Neurophys. 87, 1129–1131. doi: 10.1152/jn.00412.2001
Gong, J. Q. X., and Sobie, E. A. (2018). Population-based mechanistic modeling allows for quantitative predictions of drug responses across cell types. NPJ. Syst. Biol. Appl. 4, 11. doi: 10.1038/s41540-018-0047-2
Gong, Y., Xie, F., Stein, K. M., Garfinkel, A., Culianu, C. A., Lerman, B. B., et al. (2007). Mechanism underlying initiation of paroxysmal atrial flutter/atrial fibrillation by ectopic foci: a simulation study. Circulation 115, 2094–2102. doi: 10.1161/CIRCULATIONAHA.106.656504
Grandi, E., and Maleckar, M. M. (2016). Anti-arrhythmic strategies for atrial fibrillation: the role of computational modeling in discovery, development, and optimization. Pharmacol. Ther. 168, 126–142. doi: 10.1016/j.pharmthera.2016.09.012
Grandi, E., Pandit, S. V., Voigt, N., Workman, A. J., Dobrev, D., Jalife, J., et al. (2011). Human atrial action potential and Ca2+ model: sinus rhythm and chronic atrial fibrillation. Circ. Res. 109, 1055–1066. doi: 10.1161/CIRCRESAHA.111.253955
Grandi, E., Pasqualini, F. S., and Bers, D. M. (2010). A novel computational model of the human ventricular action potential and Ca transient. J. Mol. Cell. Cardiol. 48, 112–121. doi: 10.1016/j.yjmcc.2009.09.019
Gray, R. A., Jalife, J., Panfilov, A., Baxter, W. T., Cabo, C., Davidenko, J. M., et al. (1995). Nonstationary vortexlike reentrant activity as a mechanism of polymorphic ventricular tachycardia in the isolated rabbit heart. Circulation 91, 2454–2469. doi: 10.1161/01.CIR.91.9.2454
Groenendaal, W., Ortega, F. A., Kherlopian, A. R., Zygmunt, A. C., Krogh-Madsen, T., and Christini, D. J. (2015). Cell-specific cardiac electrophysiology models. PLoS Comput. Biol. 11:e1004242. doi: 10.1371/journal.pcbi.1004242
Guo, T., Abed, A. A., Lovell, N. H., and Dokos, S. (2010). A generic ionic model of cardiac action potentials. Conf. Proc. IEEE. Eng. Med. Biol. Soc. 2010, 1465–1468. doi: 10.1109/IEMBS.2010.5626853
Guo, T., Al Abed, A., Lovell, N. H., and Dokos, S. (2013). Optimisation of a generic ionic model of cardiac myocyte electrical activity. Comput. Math. Methods Med. 2013:706195. doi: 10.1155/2013/706195
Guo, W., Xu, H., London, B., and Nerbonne, J. M. (1999). Molecular basis of transient outward K+ current diversity in mouse ventricular myocytes. J. Physiol. 521(Pt 3), 587–599. doi: 10.1111/j.1469-7793.1999.00587.x
Gurkiewicz, M., and Korngreen, A. (2007). A numerical approach to ion channel modelling using whole-cell voltage-clamp recordings and a genetic algorithm. PLoS Comput. Biol. 3:e169. doi: 10.1371/journal.pcbi.0030169
Hair, J. F., Black, W. C., Babin, B. J., and Anderson, R. E. (2010). Multivariate Data Analysis. Upper Saddle River, NJ: Pearson Prentice Hall.
Hansen, B. J., Zhao, J., and Fedorov, V. V. (2017). Fibrosis and atrial fibrillation: computerized and optical mapping; a view into the human atria at submillimeter resolution. JACC Clin. Electrophysiol. 3, 531–546. doi: 10.1016/j.jacep.2017.05.002
Heijman, J., Zaza, A., Johnson, D. M., Rudy, Y., Peeters, R. L., Volders, P. G., et al. (2013). Determinants of beat-to-beat variability of repolarization duration in the canine ventricular myocyte: a computational analysis. PLoS Comput. Biol. 9:e1003202. doi: 10.1371/journal.pcbi.1003202
Hobbs, K. H., and Hooper, S. L. (2008). Using complicated, wide dynamic range driving to develop models of single neurons in single recording sessions. J. Neurophysiol. 99, 1871–1883. doi: 10.1152/jn.00032.2008
Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544. doi: 10.1113/jphysiol.1952.sp004764
Hund, T. J., and Rudy, Y. (2004). Rate dependence and regulation of action potential and calcium transient in a canine cardiac ventricular cell model. Circulation 110, 3168–3174. doi: 10.1161/01.CIR.0000147231.69595.D3
Hussein, Y. A., and El-Ghazaly, S. M. (2004). Modeling and optimization of microwave devices and circuits using genetic algorithms. IEEE Trans. Microwave Theory Tech. 52, 329–336. doi: 10.1109/TMTT.2003.820899
Inada, S., Hancox, J. C., Zhang, H., and Boyett, M. R. (2009). One-dimensional mathematical model of the atrioventricular node including atrio-nodal, nodal, and nodal-his cells. Biophys. J. 97, 2117–2127. doi: 10.1016/j.bpj.2009.06.056
Janes, K. A., Albeck, J. G., Gaudet, S., Sorger, P. K., Lauffenburger, D. A., and Yaffe, M. B. (2005). A systems model of signaling identifies a molecular basis set for cytokine-induced apoptosis. Science 310, 1646–1653. doi: 10.1126/science.1116598
Jeyaraj, D., Haldar, S. M., Wan, X., Mccauley, M. D., Ripperger, J. A., Hu, K., et al. (2012). Circadian rhythms govern cardiac repolarization and arrhythmogenesis. Nature 483, 96–99. doi: 10.1038/nature10852
Johnstone, R. H., Chang, E. T. Y., Bardenet, R., de Boer, T. P., Gavaghan, D. J., Pathmanathan, P., et al. (2016). Uncertainty and variability in models of the cardiac action potential: can we build trustworthy models? J. Mol. Cell. Cardiol. 96, 49–62. doi: 10.1016/j.yjmcc.2015.11.018
Kannankeril, P. J., Norris, K. J., Carter, S., and Roden, D. M. (2011). Factors affecting the degree of QT prolongation with drug challenge in a large cohort of normal volunteers. Heart Rhythm 8, 1530–1534. doi: 10.1016/j.hrthm.2011.03.042
Kaur, J., Nygren, A., and Vigmond, E. J. (2014). Fitting membrane resistance along with action potential shape in cardiac myocytes improves convergence: application of a multi-objective parallel genetic algorithm. PLoS ONE 9:e107984. doi: 10.1371/journal.pone.0107984
Kharche, S., Garratt, C. J., Boyett, M. R., Inada, S., Holden, A. V., Hancox, J. C., et al. (2008). Atrial proarrhythmia due to increased inward rectifier current (I(K1)) arising from KCNJ2 mutation–a simulation study. Prog. Biophys. Mol. Biol. 98, 186–197. doi: 10.1016/j.pbiomolbio.2008.10.010
Koivumäki, J. T., Naumenko, N., Tuomainen, T., Takalo, J., Oksanen, M., Puttonen, K. A., et al. (2018). Structural immaturity of human iPSC-Derived cardiomyocytes: in silico investigation of effects on function and disease modeling. Front. Physiol. 9:80. doi: 10.3389/fphys.2018.00080
Krogh-Madsen, T., and Christini, D. J. (2012). Nonlinear dynamics in cardiology. Annu. Rev. Biomed. Eng. 14, 179–203. doi: 10.1146/annurev-bioeng-071811-150106
Krogh-Madsen, T., Jacobson, A. F., Ortega, F. A., and Christini, D. J. (2017). Global optimization of ventricular myocyte model to multi-variable objective improves predictions of drug-induced torsades de pointes. Front. Physiol. 8:1059. doi: 10.3389/fphys.2017.01059
Krogh-Madsen, T., Sobie, E. A., and Christini, D. J. (2016). Improving cardiomyocyte model fidelity and utility via dynamic electrophysiology protocols and optimization algorithms. J. Physiol. 594, 2525–2536. doi: 10.1113/JP270618
Kurata, Y., Hisatome, I., Matsuda, H., and Shibamoto, T. (2005). Dynamical mechanisms of pacemaker generation in IK1-downregulated human ventricular myocytes: insights from bifurcation analyses of a mathematical model. Biophys. J. 89, 2865–2887. doi: 10.1529/biophysj.105.060830
Lancaster, M. C., and Sobie, E. A. (2016). Improved prediction of drug-induced torsades de pointes through simulations of dynamics and machine learning algorithms. Clin. Pharmacol. Ther. 100, 371–379. doi: 10.1002/cpt.367
Lau, C. P., Tse, H. F., Siu, C. W., and Gbadebo, D. (2012). Atrial electrical and structural remodeling: implications for racial differences in atrial fibrillation. J. Cardiovasc. Electrophysiol. 23(Suppl. 1), S36–S40. doi: 10.1111/jce.12022
Lawson, B. A. J., Drovandi, C. C., Cusimano, N., Burrage, P., Rodriguez, B., and Burrage, K. (2018). Unlocking data sets by calibrating populations of models to data density: a study in atrial electrophysiology. Sci. Adv. 4:e1701676. doi: 10.1126/sciadv.1701676
Lee, W., Mann, S. A., Windley, M. J., Imtiaz, M. S., Vandenberg, J. I., and Hill, A. P. (2016). In silico assessment of kinetics and state dependent binding properties of drugs causing acquired LQTS. Prog. Biophys. Mol. Biol. 120, 89–99. doi: 10.1016/j.pbiomolbio.2015.12.005
Lee, Y. S., Hwang, M., Song, J. S., Li, C., Joung, B., Sobie, E. A., et al. (2016). The contribution of ionic currents to rate-dependent action potential duration and pattern of reentry in a mathematical model of human atrial fibrillation. PLoS ONE 11:e0150779. doi: 10.1371/journal.pone.0150779
Lee, Y. S., Liu, O. Z., Hwang, H. S., Knollmann, B. C., and Sobie, E. A. (2013). Parameter sensitivity analysis of stochastic models provides insights into cardiac calcium sparks. Biophys. J. 104, 1142–1150. doi: 10.1016/j.bpj.2012.12.055
Leung, F. H. F., Lam, H. K., Ling, S. H., and Tam, P. K. S. (2004). Optimal and stable fuzzy controllers for nonlinear systems based on an improved genetic algorithm. IEEE Trans. Indus. Electron. 51, 172–182. doi: 10.1109/TIE.2003.821898
Li, Z., Dutta, S., Sheng, J., Tran, P. N., Wu, W., Chang, K., et al. (2017). Improving the in silico assessment of proarrhythmia risk by combining herg (human ether-a-go-go-related gene) channel-drug binding kinetics and multichannel pharmacology. Circ. Arrhythm. Electrophysiol. 10:e004628. doi: 10.1161/CIRCEP.116.004628
Liberos, A., Bueno-Orovio, A., Rodrigo, M., Ravens, U., Hernandez-Romero, I., Fernandez-Aviles, F., et al. (2016). Balance between sodium and calcium currents underlying chronic atrial fibrillation termination: an in silico intersubject variability study. Heart Rhythm 13, 2358–2365. doi: 10.1016/j.hrthm.2016.08.028
Liu, L., and Nattel, S. (1997). Differing sympathetic and vagal effects on atrial fibrillation in dogs: role of refractoriness heterogeneity. Am. J. Physiol. 273, H805–H816. doi: 10.1152/ajpheart.1997.273.2.H805
Livshitz, L., and Rudy, Y. (2009). Uniqueness and stability of action potential models during rest, pacing, and conduction using problem-solving environment. Biophys. J. 97, 1265–1276. doi: 10.1016/j.bpj.2009.05.062
Lombardo, D. M., Fenton, F. H., Narayan, S. M., and Rappel, W. J. (2016). Comparison of detailed and simplified models of human atrial myocytes to recapitulate patient specific properties. PLoS Comput. Biol. 12:e1005060. doi: 10.1371/journal.pcbi.1005060
Luo, C. H., and Rudy, Y. (1991). A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction. Circ. Res. 68, 1501–1526. doi: 10.1161/01.RES.68.6.1501
Maleckar, M. M., Greenstein, J. L., Giles, W. R., and Trayanova, N. A. (2009). K+ current changes account for the rate dependence of the action potential in the human atrial myocyte. Am. J. Physiol. Heart Circ. Physiol. 297, H1398–H1410. doi: 10.1152/ajpheart.00411.2009
Maltsev, V. A., and Lakatta, E. G. (2009). Synergism of coupled subsarcolemmal Ca2+ clocks and sarcolemmal voltage clocks confers robust and flexible pacemaker function in a novel pacemaker cell model. Am. J. Physiol. Heart Circ. Physiol. 296, H594–H615. doi: 10.1152/ajpheart.01118.2008
Mann, S. A., Imtiaz, M., Winbo, A., Rydberg, A., Perry, M. D., Couderc, J. P., et al. (2016). Convergence of models of human ventricular myocyte electrophysiology after global optimization to recapitulate clinical long QT phenotypes. J. Mol. Cell. Cardiol. 100, 25–34. doi: 10.1016/j.yjmcc.2016.09.011
Mann, S. A., Otway, R., Guo, G., Soka, M., Karlsdotter, L., Trivedi, G., et al. (2012). Epistatic effects of potassium channel variation on cardiac repolarization and atrial fibrillation risk. J. Am. Coll. Cardiol. 59, 1017–1025. doi: 10.1016/j.jacc.2011.11.039
Marder, E. (2011). Variability, compensation, and modulation in neurons and circuits. Proc. Natl. Acad. Sci. U.S.A. 108(Suppl. 3), 15542–15548. doi: 10.1073/pnas.1010674108
Marino, S., Hogue, I. B., Ray, C. J., and Kirschner, D. E. (2008). A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 254, 178–196. doi: 10.1016/j.jtbi.2008.04.011
Mayourian, J., Cashman, T. J., Ceholski, D. K., Johnson, B. V., Sachs, D., Kaji, D. A., et al. (2017). Experimental and computational insight into human mesenchymal stem cell paracrine signaling and heterocellular coupling effects on cardiac contractility and arrhythmogenicity. Circ. Res. 121, 411–423. doi: 10.1161/CIRCRESAHA.117.310796
McDowell, K. S., Zahid, S., Vadakkumpadan, F., Blauer, J., Macleod, R. S., and Trayanova, N. A. (2015). Virtual electrophysiological study of atrial fibrillation in fibrotic remodeling. PLoS ONE 10:e0117110. doi: 10.1371/journal.pone.0117110
Milstein, M. L., Musa, H., Balbuena, D. P., Anumonwo, J. M., Auerbach, D. S., Furspan, P. B., et al. (2012). Dynamic reciprocity of sodium and potassium channel expression in a macromolecular complex controls cardiac excitability and arrhythmia. Proc. Natl. Acad. Sci. U.S.A. 109, E2134–E2143. doi: 10.1073/pnas.1109370109
Mirams, G. R., Pathmanathan, P., Gray, R. A., Challenor, P., and Clayton, R. H. (2016). Uncertainty and variability in computational and mathematical models of cardiac physiology. J. Physiol. 594, 6833–6847. doi: 10.1113/JP271671
Misier, A. R., Opthof, T., Van Hemel, N. M., Defauw, J. J., de Bakker, J. M., Janse, M. J., et al. (1992). Increased dispersion of “refractoriness” in patients with idiopathic paroxysmal atrial fibrillation. J. Am. Coll. Cardiol. 19, 1531–1535. doi: 10.1016/0735-1097(92)90614-S
Moe, G. K., Rheinboldt, W. C., and Abildskov, J. A. (1964). A computer model of atrial fibrillation. Am. Heart J. 67, 200–220. doi: 10.1016/0002-8703(64)90371-0
Morotti, S., and Grandi, E. (2017). Logistic regression analysis of populations of electrophysiological models to assess proarrythmic risk. MethodsX 4, 25–34. doi: 10.1016/j.mex.2016.12.002
Morotti, S., Mcculloch, A. D., Bers, D. M., Edwards, A. G., and Grandi, E. (2016). Atrial-selective targeting of arrhythmogenic phase-3 early afterdepolarizations in human myocytes. J. Mol. Cell. Cardiol. 96, 63–71. doi: 10.1016/j.yjmcc.2015.07.030
Muszkiewicz, A., Britton, O. J., Gemmell, P., Passini, E., Sánchez, C., Zhou, X., et al. (2016). Variability in cardiac electrophysiology: using experimentally-calibrated populations of models to move beyond the single virtual physiological human paradigm. Prog. Biophys. Mol. Biol. 120, 115–127. doi: 10.1016/j.pbiomolbio.2015.12.002
Muszkiewicz, A., Liu, X., Bueno-Orovio, A., Lawson, B. A. J., Burrage, K., Casadei, B., et al. (2017). From ionic to cellular variability in human atrial myocytes: an integrative computational and experimental study. Am. J. Physiol. Heart Circ. Physiol. 314, H895–H916. doi: 10.1152/ajpheart.00477.2017
Ni, H., Whittaker, D. G., Wang, W., Giles, W. R., Narayan, S. M., and Zhang, H. (2017). Synergistic anti-arrhythmic effects in human atria with combined use of sodium blockers and acacetin. Front. Physiol. 8:946. doi: 10.3389/fphys.2017.00946
Niederer, S. A., Fink, M., Noble, D., and Smith, N. P. (2009). A meta-analysis of cardiac electrophysiology computational models. Exp. Physiol. 94, 486–495. doi: 10.1113/expphysiol.2008.044610
Niederer, S. A., Kerfoot, E., Benson, A. P., Bernabeu, M. O., Bernus, O., Bradley, C., et al. (2011a). Verification of cardiac tissue electrophysiology simulators using an N-version benchmark. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 369, 4331–4351. doi: 10.1098/rsta.2011.0139
Niederer, S., Mitchell, L., Smith, N., and Plank, G. (2011b). Simulating human cardiac electrophysiology on clinical time-scales. Front. Physiol. 2:14. doi: 10.3389/fphys.2011.00014
Noble, D. (1962). A modification of the Hodgkin–Huxley equations applicable to Purkinje fibre action and pace-maker potentials. J. Physiol. 160, 317–352. doi: 10.1113/jphysiol.1962.sp006849
Noble, D., Garny, A., and Noble, P. J. (2012). How the Hodgkin-Huxley equations inspired the Cardiac Physiome Project. J. Physiol. Lond. 590, 2613–2628. doi: 10.1113/jphysiol.2011.224238
Noble, D., Sarai, N., Noble, P. J., Kobayashi, T., Matsuoka, S., and Noma, A. (2007). Resistance of cardiac cells to NCX knockout: a model study. Ann. N. Y. Acad. Sci. 1099, 306–309. doi: 10.1196/annals.1387.018
Nygren, A., Fiset, C., Firek, L., Clark, J. W., Lindblad, D. S., Clark, R. B., et al. (1998). Mathematical model of an adult human atrial cell: the role of K+ currents in repolarization. Circ. Res. 82, 63–81. doi: 10.1161/01.RES.82.1.63
O'Hara, T., Virág, L., Varró, A., and Rudy, Y. (2011). Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Comput. Biol. 7:e1002061. doi: 10.1371/journal.pcbi.1002061
Okada, J. I., Washio, T., Nakagawa, M., Watanabe, M., Kadooka, Y., Kariya, T., et al. (2017). Multi-scale, tailor-made heart simulation can predict the effect of cardiac resynchronization therapy. J. Mol. Cell. Cardiol. 108, 17–23. doi: 10.1016/j.yjmcc.2017.05.006
Okada, J., Yoshinaga, T., Kurokawa, J., Washio, T., Furukawa, T., Sawada, K., et al. (2015). Screening system for drug-induced arrhythmogenic risk combining a patch clamp and heart simulator. Sci. Adv. 1:e1400142. doi: 10.1126/sciadv.1400142
Paci, M., Passini, E., Severi, S., Hyttinen, J., and Rodriguez, B. (2017). Phenotypic variability in LQT3 human induced pluripotent stem cell-derived cardiomyocytes and their response to antiarrhythmic pharmacologic therapy: an in silico approach. Heart Rhythm 14, 1704–1712. doi: 10.1016/j.hrthm.2017.07.026
Pandit, S. V., Clark, R. B., Giles, W. R., and Demir, S. S. (2001). A mathematical model of action potential heterogeneity in adult rat left ventricular myocytes. Biophys. J. 81, 3029–3051. doi: 10.1016/S0006-3495(01)75943-7
Panfilov, A. V., and Holden, A. V. (1991). Spatiotemporal irregularity in a two-dimensional model of cardiac tissue. Int. J. Bifurcation Chaos 1, 219–225. doi: 10.1142/S0218127491000142
Passini, E., Britton, O. J., Lu, H. R., Rohrbacher, J., Hermans, A. N., Gallacher, D. J., et al. (2017). Human in silico drug trials demonstrate higher accuracy than animal models in predicting clinical pro-arrhythmic cardiotoxicity. Front. Physiol. 8:668. doi: 10.3389/fphys.2017.00668
Passini, E., Mincholé, A., Coppini, R., Cerbai, E., Rodriguez, B., Severi, S., et al. (2016). Mechanisms of pro-arrhythmic abnormalities in ventricular repolarisation and anti-arrhythmic therapies in human hypertrophic cardiomyopathy. J. Mol. Cell. Cardiol. 96, 72–81. doi: 10.1016/j.yjmcc.2015.09.003
Pathmanathan, P., Bernabeu, M. O., Niederer, S. A., Gavaghan, D. J., and Kay, D. (2012). Computational modelling of cardiac electrophysiology: explanation of the variability of results from different numerical solvers. Int. J. Numer. Methods Biomed. Eng. 28, 890–903. doi: 10.1002/cnm.2467
Pathmanathan, P., Shotwell, M. S., Gavaghan, D. J., Cordeiro, J. M., and Gray, R. A. (2015). Uncertainty quantification of fast sodium current steady-state inactivation for multi-scale models of cardiac electrophysiology. Prog. Biophys. Mol. Biol. 117, 4–18. doi: 10.1016/j.pbiomolbio.2015.01.008
Pitt-Francis, J., Garny, A., and Gavaghan, D. (2006). Enabling computer models of the heart for high-performance computers and the grid. Philos. Trans. A Math. Phys. Eng. Sci. 364, 1501–1516. doi: 10.1098/rsta.2006.1783
Pueyo, E., Corrias, A., Virág, L., Jost, N., Szél, T., Varró, A., et al. (2011). A multiscale investigation of repolarization variability and its role in cardiac arrhythmogenesis. Biophys. J. 101, 2892–2902. doi: 10.1016/j.bpj.2011.09.060
Ramanna, H., Elvan, A., Wittkampf, F. H., de Bakker, J. M., Hauer, R. N., and Robles de Medina, E. O. (2001). Increased dispersion and shortened refractoriness caused by verapamil in chronic atrial fibrillation. J. Am. Coll. Cardiol. 37, 1403–1407. doi: 10.1016/S0735-1097(01)01132-9
Ramirez, R. J., Nattel, S., and Courtemanche, M. (2000). Mathematical analysis of canine atrial action potentials: rate, regional factors, and electrical remodeling. Am. J. Physiol. Heart Circ. Physiol. 279, H1767–H1785. doi: 10.1152/ajpheart.2000.279.4.H1767
Ravagli, E., Bucchi, A., Bartolucci, C., Paina, M., Baruscotti, M., DiFrancesco, D., et al. (2016). Cell-specific Dynamic Clamp analysis of the role of funny If current in cardiac pacemaking. Prog. Biophys. Mol. Biol. 120, 50–66. doi: 10.1016/j.pbiomolbio.2015.12.004
Ravens, U., Katircioglu-Öztürk, D., Wettwer, E., Christ, T., Dobrev, D., Voigt, N., et al. (2015). Application of the RIMARC algorithm to a large data set of action potentials and clinical parameters for risk prediction of atrial fibrillation. Med. Biol. Eng. Comput. 53, 263–273. doi: 10.1007/s11517-014-1232-0
Rees, C., Yang, J.-H., Santolini, M., Lusis, A. J., Weiss, J. N., and Karma, A. (2018). Variability and compensation of cardiomycoyte ionic conductances at the population level. bioRxiv [Preprint]. doi: 10.1101/283275
Rivolta, I., Clancy, C. E., Tateyama, M., Liu, H., Priori, S. G., and Kass, R. S. (2002). A novel SCN5A mutation associated with long QT-3: altered inactivation kinetics and channel dysfunction. Physiol. Genomics 10, 191–197. doi: 10.1152/physiolgenomics.00039.2002
Roberts, B. N., Yang, P. C., Behrens, S. B., Moreno, J. D., and Clancy, C. E. (2012). Computational approaches to understand cardiac electrophysiology and arrhythmias. Am. J. Physiol. Heart Circ. Physiol. 303, H766–H783. doi: 10.1152/ajpheart.01081.2011
Roden, D. M. (2008). Repolarization reserve: a moving target. Circulation 118, 981–982. doi: 10.1161/CIRCULATIONAHA.108.798918
Romero, L., Carbonell, B., Trenor, B., Rodríguez, B., Saiz, J., and Ferrero, J. M. (2011). Systematic characterization of the ionic basis of rabbit cellular electrophysiology using two ventricular models. Prog. Biophys. Mol. Biol. 107, 60–73. doi: 10.1016/j.pbiomolbio.2011.06.012
Romero, L., Pueyo, E., Fink, M., and Rodríguez, B. (2009). Impact of ionic current variability on human ventricular cellular electrophysiology. Am. J. Physiol. Heart Circ. Physiol. 297, H1436–H1445. doi: 10.1152/ajpheart.00263.2009
Rosati, B., Dong, M., Cheng, L., Liou, S. R., Yan, Q., Park, J. Y., et al. (2008). Evolution of ventricular myocyte electrophysiology. Physiol. Genomics 35, 262–272. doi: 10.1152/physiolgenomics.00159.2007
Rosati, B., and Mckinnon, D. (2004). Regulation of ion channel expression. Circ. Res. 94, 874–883. doi: 10.1161/01.RES.0000124921.81025.1F
Sadrieh, A., Mann, S. A., Subbiah, R. N., Domanski, L., Taylor, J. A., Vandenberg, J. I., et al. (2013). Quantifying the origins of population variability in cardiac electrical activity through sensitivity analysis of the electrocardiogram. J. Physiol. 591, 4207–4222. doi: 10.1113/jphysiol.2013.251710
Sale, H., Wang, J., O'Hara, T. J., Tester, D. J., Phartiyal, P., He, J. Q., et al. (2008). Physiological properties of hERG 1a/1b heteromeric currents and a hERG 1b-specific mutation associated with Long-QT syndrome. Circ. Res. 103, e81–95. doi: 10.1161/CIRCRESAHA.108.185249
Sampson, K. J., Iyer, V., Marks, A. R., and Kass, R. S. (2010). A computational model of Purkinje fibre single cell electrophysiology: implications for the long QT syndrome. J. Physiol. 588, 2643–2655. doi: 10.1113/jphysiol.2010.187328
Sánchez, C., Bueno-Orovio, A., Wettwer, E., Loose, S., Simon, J., Ravens, U., et al. (2014). Inter-subject variability in human atrial action potential in sinus rhythm versus chronic atrial fibrillation. PLoS ONE 9:e105897. doi: 10.1371/journal.pone.0105897
Sarkar, A. X., Christini, D. J., and Sobie, E. A. (2012). Exploiting mathematical models to illuminate electrophysiological variability between individuals. J. Physiol. 590, 2555–2567. doi: 10.1113/jphysiol.2011.223313
Sarkar, A. X., and Sobie, E. A. (2010). Regression analysis for constraining free parameters in electrophysiological models of cardiac cells. PLoS Comput. Biol. 6:e1000914. doi: 10.1371/journal.pcbi.1000914
Sarkar, A. X., and Sobie, E. A. (2011). Quantification of repolarization reserve to understand interpatient variability in the response to proarrhythmic drugs: a computational analysis. Heart Rhythm 8, 1749–1755. doi: 10.1016/j.hrthm.2011.05.023
Sato, S., Yamauchi, S., Schuessler, R. B., Boineau, J. P., Matsunaga, Y., and Cox, J. L. (1992). The effect of augmented atrial hypothermia on atrial refractory period, conduction, and atrial flutter/fibrillation in the canine heart. J. Thorac. Cardiovasc. Surg. 104, 297–306.
Schram, G., Pourrier, M., Melnyk, P., and Nattel, S. (2002). Differential distribution of cardiac ion channel expression as a basis for regional specialization in electrical function. Circ. Res. 90, 939–950. doi: 10.1161/01.RES.0000018627.89528.6F
Schulz, D. J., Goaillard, J. M., and Marder, E. (2006). Variable channel expression in identified single and electrically coupled neurons in different animals. Nat. Neurosci. 9, 356–362. doi: 10.1038/nn1639
Schulz, D. J., Goaillard, J. M., and Marder, E. E. (2007). Quantitative expression profiling of identified neurons reveals cell-specific constraints on highly variable levels of gene expression. Proc. Natl. Acad. Sci. U.S.A. 104, 13187–13191. doi: 10.1073/pnas.0705827104
Sepulveda, N. G., Roth, B. J., and Wikswo, J. P. (1989). Current injection into a two-dimensional anisotropic bidomain. Biophys. J. 55, 987–999. doi: 10.1016/S0006-3495(89)82897-8
Sham, J. S., Hatem, S. N., and Morad, M. (1995). Species differences in the activity of the Na(+)-Ca2+ exchanger in mammalian cardiac myocytes. J. Physiol. 488 (Pt 3), 623–631. doi: 10.1113/jphysiol.1995.sp020995
Singh, S., Zoble, R. G., Yellen, L., Brodsky, M. A., Feld, G. K., Berk, M., et al. (2000). Efficacy and safety of oral dofetilide in converting to and maintaining sinus rhythm in patients with chronic atrial fibrillation or atrial flutter: the symptomatic atrial fibrillation investigative research on dofetilide (SAFIRE-D) study. Circulation 102, 2385–2390. doi: 10.1161/01.CIR.102.19.2385
Skibsbye, L., Jespersen, T., Christ, T., Maleckar, M. M., Van den Brink, J., Tavi, P., et al. (2016). Refractoriness in human atria: time and voltage dependence of sodium channel availability. J. Mol. Cell. Cardiol. 101, 26–34. doi: 10.1016/j.yjmcc.2016.10.009
Sobie, E. A. (2009). Parameter sensitivity analysis in electrophysiological models using multivariable regression. Biophys. J. 96, 1264–1274. doi: 10.1016/j.bpj.2008.10.056
Soltis, A. R., and Saucerman, J. J. (2010). Synergy between CaMKII Substrates and beta-Adrenergic Signaling in Regulation of Cardiac Myocyte Ca2+ Handling. Biophys. J. 99, 2038–2047. doi: 10.1016/j.bpj.2010.08.016
Soor, N., Morgan, R., Varela, M., and Aslanidi, O. V. (2016). Towards patient-specific modelling of lesion formation during radiofrequency catheter ablation for atrial fibrillation. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2016, 489–492. doi: 10.1109/EMBC.2016.7590746
Soylu, M., Demir, A. D., Ozdemir, O., Soylu, O., Topaloglu, S., Kunt, A., et al. (2003). Increased dispersion of refractoriness in patients with atrial fibrillation in the early postoperative period after coronary artery bypass grafting. J. Cardiovasc. Electrophysiol. 14, 28–31. doi: 10.1046/j.1540-8167.2003.02218.x
Su, Z., Li, F., Spitzer, K. W., Yao, A., Ritter, M., and Barry, W. H. (2003). Comparison of sarcoplasmic reticulum Ca2+-ATPase function in human, dog, rabbit, and mouse ventricular myocytes. J. Mol. Cell. Cardiol. 35, 761–767. doi: 10.1016/S0022-2828(03)00119-6
Syed, Z., Vigmond, E., Nattel, S., and Leon, L. J. (2005). Atrial cell action potential parameter fitting using genetic algorithms. Med. Biol. Eng. Comput. 43, 561–571. doi: 10.1007/BF02351029
Taneja, T., Mahnert, B. W., Passman, R., Goldberger, J., and Kadish, A. (2001). Effects of sex and age on electrocardiographic and cardiac electrophysiological properties in adults. Pacing Clin. Electrophysiol. 24, 16–21. doi: 10.1046/j.1460-9592.2001.00016.x
ten Tusscher, K. H., Noble, D., Noble, P. J., and Panfilov, A. V. (2004). A model for human ventricular tissue. Am. J. Physiol. Heart Circ. Physiol. 286, H1573–H1589. doi: 10.1152/ajpheart.00794.2003
ten Tusscher, K. H., and Panfilov, A. V. (2006). Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Heart Circ. Physiol. 291, H1088–H1100. doi: 10.1152/ajpheart.00109.2006
Tobin, A. E., Cruz-Bermúdez, N. D., Marder, E., and Schulz, D. J. (2009). Correlations in ion channel mRNA in rhythmically active neurons. PLoS ONE 4:e6742. doi: 10.1371/journal.pone.0006742
Tomaiuolo, M., Bertram, R., Leng, G., and Tabak, J. (2012). Models of electrical activity: calibration and prediction testing on the same cell. Biophys. J. 103, 2021–2032. doi: 10.1016/j.bpj.2012.09.034
Trayanova, N. A. (2014). Mathematical approaches to understanding and imaging atrial fibrillation significance for mechanisms and management. Circ. Res. 114, 1516–1531. doi: 10.1161/CIRCRESAHA.114.302240
Tsujimae, K., Suzuki, S., Murakami, S., and Kurachi, Y. (2007). Frequency-dependent effects of various IKr blockers on cardiac action potential duration in a human atrial model. Am. J. Physiol. Heart Circ. Physiol. 293, H660–H669. doi: 10.1152/ajpheart.01083.2006
Vagos, M. R., Arevalo, H., de Oliveira, B. L., Sundnes, J., and Maleckar, M. M. (2017). A computational framework for testing arrhythmia marker sensitivities to model parameters in functionally calibrated populations of atrial cells. Chaos 27, 093941. doi: 10.1063/1.4999476
Vanier, M. C., and Bower, J. M. (1999). A comparative survey of automated parameter-search methods for compartmental neural models. J. Comput. Neurosci. 7, 149–171. doi: 10.1023/A:1008972005316
Vieira, D., Adriano, R. L. S., Vasconcelos, J. A., and Krahenbuhl, L. (2004). Treating constraints as objectives in multiobjective optimization problems using niched pareto genetic algorithm. IEEE Trans. Magn. 40, 1188–1191. doi: 10.1109/TMAG.2004.825006
Walmsley, J., Rodriguez, J. F., Mirams, G. R., Burrage, K., Efimov, I. R., and Rodriguez, B. (2013). mRNA expression levels in failing human hearts predict cellular electrophysiological remodeling: a population-based simulation study. PLoS ONE 8:e56359. doi: 10.1371/journal.pone.0056359
Wang, J., Liu, L., Feng, J., and Nattel, S. (1996). Regional and functional factors determining induction and maintenance of atrial fibrillation in dogs. Am. J. Physiol. 271, H148–H158. doi: 10.1152/ajpheart.1996.271.1.H148
Wang, W., Huang, H. H., Kay, M., and Cavazos, J. (2011). GPGPU accelerated cardiac arrhythmia simulations. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2011, 724–727. doi: 10.1109/IEMBS.2011.6090164
Wang, Z., Feng, J., and Nattel, S. (1995). Idiopathic atrial fibrillation in dogs: electrophysiologic determinants and mechanisms of antiarrhythmic action of flecainide. J. Am. Coll. Cardiol. 26, 277–286. doi: 10.1016/0735-1097(95)90845-F
Weaver, C. M., and Wearne, S. L. (2008). Neuronal firing sensitivity to morphologic and active membrane parameters. PLoS Comput. Biol. 4:e11. doi: 10.1371/journal.pcbi.0040011
Weeke, P., Mosley, J. D., Hanna, D., Delaney, J. T., Shaffer, C., Wells, Q. S., et al. (2014). Exome sequencing implicates an increased burden of rare potassium channel variants in the risk of drug-induced long QT interval syndrome. J. Am. Coll. Cardiol. 63, 1430–1437. doi: 10.1016/j.jacc.2014.01.031
White, J. W., Rassweiler, A., Samhouri, J. F., Stier, A. C., and White, C. (2014). Ecologists should not use statistical significance tests to interpret simulation model results. Oikos 123, 385–388. doi: 10.1111/j.1600-0706.2013.01073.x
Xiao, L., Xiao, J., Luo, X., Lin, H., Wang, Z., and Nattel, S. (2008). Feedback remodeling of cardiac potassium current expression: a novel potential mechanism for control of repolarization reserve. Circulation 118, 983–992. doi: 10.1161/CIRCULATIONAHA.107.758672
Yan, G. X., Shimizu, W., and Antzelevitch, C. (1998). Characteristics and distribution of M cells in arterially perfused canine left ventricular wedge preparations. Circulation 98, 1921–1927. doi: 10.1161/01.CIR.98.18.1921
Yang, P. C., and Clancy, C. E. (2012). In silico prediction of sex-based differences in human susceptibility to cardiac ventricular tachyarrhythmias. Front. Physiol. 3:360. doi: 10.3389/fphys.2012.00360
Yang, P. C., El-Bizri, N., Romero, L., Giles, W. R., Rajamani, S., Belardinelli, L., et al. (2016). A computational model predicts adjunctive pharmacotherapy for cardiac safety via selective inhibition of the late cardiac Na current. J. Mol. Cell. Cardiol. 99, 151–161. doi: 10.1016/j.yjmcc.2016.08.011
Yang, P. C., Kurokawa, J., Furukawa, T., and Clancy, C. E. (2010). Acute effects of sex steroid hormones on susceptibility to cardiac arrhythmias: a simulation study. PLoS Comput. Biol. 6:e1000658. doi: 10.1371/journal.pcbi.1000658
Yang, P. C., Perissinotti, L. L., López-Redondo, F., Wang, Y., Demarco, K. R., Jeng, M. T., et al. (2017). A multiscale computational modelling approach predicts mechanisms of female sex risk in the setting of arousal-induced arrhythmias. J. Physiol. 595, 4695–4723. doi: 10.1113/JP273142
Zaniboni, M. (2011). 3D current-voltage-time surfaces unveil critical repolarization differences underlying similar cardiac action potentials: a model study. Math. Biosci. 233, 98–110. doi: 10.1016/j.mbs.2011.06.008
Zhang, Z. S., Tranquillo, J., Neplioueva, V., Bursac, N., and Grant, A. O. (2007). Sodium channel kinetic changes that produce Brugada syndrome or progressive cardiac conduction system disease. Am. J. Physiol. Heart Circ. Physiol. 292, H399–H407. doi: 10.1152/ajpheart.01025.2005
Zhao, J., Hansen, B. J., Wang, Y., Csepe, T. A., Sul, L. V., Tang, A., et al. (2017). Three-dimensional integrated functional, structural, and computational mapping to define the structural “fingerprints” of heart-specific atrial fibrillation drivers in human heart ex vivo. J. Am. Heart. Assoc. 6:e005922. doi: 10.1161/JAHA.117.005922
Zhou, J., Kodirov, S., Murata, M., Buckett, P. D., Nerbonne, J. M., and Koren, G. (2003). Regional upregulation of Kv2.1-encoded current, IK,slow2, in Kv1DN mice is abolished by crossbreeding with Kv2DN mice. Am. J. Physiol. Heart Circ. Physiol. 284, H491–H500. doi: 10.1152/ajpheart.00576.2002
Zhou, Q., Zygmunt, A. C., Cordeiro, J. M., Siso-Nadal, F., Miller, R. E., Buzzard, G. T., et al. (2009). Identification of Ikr kinetics and drug binding in native myocytes. Ann. Biomed. Eng. 37, 1294–1309. doi: 10.1007/s10439-009-9690-5
Zhou, X., Bueno-Orovio, A., Orini, M., Hanson, B., Hayward, M., Taggart, P., et al. (2016). In vivo and in silico investigation into mechanisms of frequency dependence of repolarization alternans in human ventricular cardiomyocytes. Circ. Res. 118, 266–278. doi: 10.1161/CIRCRESAHA.115.307836
Keywords: cardiac electrophysiology, physiological variability, computational modeling, arrhythmia mechanisms, big data
Citation: Ni H, Morotti S and Grandi E (2018) A Heart for Diversity: Simulating Variability in Cardiac Arrhythmia Research. Front. Physiol. 9:958. doi: 10.3389/fphys.2018.00958
Received: 30 April 2018; Accepted: 29 June 2018;
Published: 20 July 2018.
Edited by:
Oleg Aslanidi, King's College London, United KingdomReviewed by:
Stefano Severi, Università degli Studi di Bologna, ItalyCopyright © 2018 Ni, Morotti and Grandi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eleonora Grandi, ZWxlLmdyYW5kaUBnbWFpbC5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.