- 1Julius Wolff Institute, Charité—Universitätsmedizin Berlin, Berlin, Germany
- 2Berlin-Brandenburg School for Regenerative Therapies, Charité—Universitätsmedizin Berlin, Berlin, Germany
Bone is a living part of the body that can, in most situations, heal itself after fracture. However, in some situations, healing may fail. Compromised conditions, such as large bone defects, aging, immuno-deficiency, or genetic disorders, might lead to delayed or non-unions. Treatment strategies for those conditions remain a clinical challenge, emphasizing the need to better understand the mechanisms behind endogenous bone regeneration. Bone healing is a complex process that involves the coordination of multiple events at different length and time scales. Computer models have been able to provide great insights into the interactions occurring within and across the different scales (organ, tissue, cellular, intracellular) using different modeling approaches [partial differential equations (PDEs), agent-based models, and finite element techniques]. In this review, we summarize the latest advances in computer models of bone healing with a focus on multiscale approaches and how they have contributed to understand the emergence of tissue formation patterns as a result of processes taking place at the lower length scales.
Introduction
Bones have a number of different functions, but two of the most important ones are that bones provide structural support and physical protection of vital organs. Especially in elderly patients, bones can be fragile and frequently experience fractures. Although, bones have the fascinating and unique capacity to completely self-regenerate without leaving a scar; in some cases, such as in pathological fractures or those situations leading to large bone defects, bones fail to reach a complete healing. Delayed or incomplete bone regeneration represents a major clinical challenge. Nowadays, there is a need to understand the mechanisms involved in the bone healing process in order to develop treatment strategies which ensure the successful repair of the bone.
The unique process of bone healing is highly complex and dynamic and spans many different time and length scales. The process of healing can be divided into five overlapping phases: hematoma formation (pro-inflammation) phase, anti-inflammatory phase, soft callus formation (proliferative) phase, hard callus formation (maturing or modeling) phase, and remodeling phase (Schmidt-Bleek et al., 2014). During all these phases, many processes at the intracellular, cellular and tissue level scales are coordinated and interact to achieve bone restoration at the organ scale. At the intracellular level, a complex array of signaling molecules interacts and gives rise to the activation of specific genes that, ultimately, determine cell function. At the cellular level, cells proliferate, migrate, differentiate, and synthesize extracellular matrix. At the tissue level, bone, cartilage, and fibrous tissue are organized to provide the extracellular environment for the cells.
Over the last decades, experimental human and animal studies have provided detailed insights into the processes that occur during the bone healing response at individual length and time scales. For example, at the tissue level, it has been shown that bone healing is influenced by fixation stability (Schell et al., 2005), aging (Strube et al., 2008), fracture size (Claes et al., 1997), etc. At the cellular level, experimental studies have determined the contribution of the different cell phenotypes (immune cells, progenitor cells, etc.) to the healing response (Konnecke et al., 2014). At the intracellular level, the role of intracellular signaling pathways and their potential as therapeutic targets for bone regeneration have been investigated (Secreto et al., 2009). Despite great advances in the field at the individual length and time scales, the behavior of the process as a whole remains unclear.
The complexity involved in bone regeneration has brought computational modeling as a core discipline into regenerative research. In bone healing, such computer models aim to identify underlying rules driving bone regeneration cascades. First computer models of bone healing were focused on understanding how mechanical stability and/or loading influence the bone healing outcome. Using finite element techniques, those models aimed to determine the local mechanical signals (strains, pressure, fluid velocity, etc.) within the regenerating region and how they relate to the formation of different tissue phenotypes over the course of healing (Carter et al., 1988; Claes and Heigele, 1999). Although, they were a breakthrough in the field, they were mainly focused on the mechanical aspects of bone healing, ignoring or highly simplifying the biology of the process. As a result, they could not explain many of the experimental observations, such as non-healing in large bone defects or the effect of growth factor stimulation (Carlier et al., 2014; Ribeiro et al., 2015).
Over the years, computer models have progressively increased their complexity, by adding more and more biological details and giving rise to a new generation of computer models that try to understand mechanical and biological interactions occurring at the different time and length scales. One of the advantages of these more recent models lies in their ability not only to predict the bone healing outcome and how it might be influenced by, for example, fixation stability; but also to explain the mechanisms behind. Although mechanics can be used to predict the progression of bone healing in many situations, the mechanical conditions do not explain the bone healing process. Computer models that aim not only to predict but also to explain bone regeneration are based, at least to some extent, on the biological processes behind. Although some of these models have recently shown their potential to support the development of new treatment strategies for the promotion of bone repair (Carlier et al., 2014), most models have so far focused on understanding the mechanisms behind the bone healing response.
In what follows, we review how multiscale computer models have contributed to better understand the systems biology of the bone healing process. In the next section, we briefly describe the different modeling approaches that have been used to simulate bone regeneration. Thereafter, we group the models in three main categories based on the main biological processes under investigation: cellular activity (including migration, proliferation, differentiation, extracellular matrix production), growth factor production and effect, and angiogenesis.
Modeling Approaches
Modeling approaches in the field of bone regeneration have mostly focused on finite element, partial differential equations (PDEs) and agent-based techniques (Table 1). Finite element analyses have been used to solve the mechanical equations, i.e., to determine the mechanical signals within the regeneration region. Many models have then coupled these mechanical signals to changes in biological parameters; for example the differentiation or migration of the cells (Lacroix et al., 2002; Gomez-Benito et al., 2005; Isaksson et al., 2008; Nagel and Kelly, 2010; Checa et al., 2011). Following an iterative approach, these models simulate how changes in tissue patterning influence mechanical signals within the healing region and how these signals further influence tissue formation (Lacroix et al., 2002; Isaksson et al., 2006; Checa et al., 2011). Systems of PDEs have been used to simulate temporal and spatial changes in cell and tissue density or protein concentrations over the course of healing (Bailon-Plaza and van der Meulen, 2003; Gomez-Benito et al., 2005; Geris et al., 2010b). This modeling approach focuses on the processes occurring at the tissue and cell population (i.e., cell density) level. Models that take into account the processes at the cellular level are based on agent-based approaches. These models employ experimentally derived computational-coded rules to define the behavior of individual cells (Byrne et al., 2011; Checa et al., 2011). These models simulate the bone regeneration process at the cellular scale and aim to understand how cellular behavior gives rise to tissue formation pattern and bone regeneration.
The Role of Cellular Activity on Tissue Formation Patterns
Tissue patterning over the course of bone healing is an emergent event that results from multiple processes taking place at the lower length and time scales. For example, tissue patterning is determined by the number of cells present in the healing region, their location, migration, and proliferation capacity, as well as by the amount of extracellular matrix produced by the different cell phenotypes. Bailon-Plaza et al. were the first to explicitly introduce biological factors into a computer model of the bone healing process, including simulation of cell migration, proliferation and differentiation, as well as production and resorption of corresponding tissues (Bailon-Plaza and van der Meulen, 2001). Using PDEs, they determined spatial and temporal changes in the density of mesenchymal stem cells, osteoblasts and chondrocytes, as well as changes in bone and cartilage tissue densities inside the callus. Although, the model presented some major limitations, such as a highly simplified callus geometry, they were able to predict early periosteal bone formation and endochondral ossification in the external callus according to experimental observations. Thereafter, Bailon-Plaza et al. (Bailon-Plaza and van der Meulen, 2003) and others (Gomez-Benito et al., 2005; Isaksson et al., 2006, 2008; Garcia-Aznar et al., 2007; Geris et al., 2008, 2010a,b; Burke and Kelly, 2012) adapted and extended this model to investigate different aspects of the bone healing process, such as the effect of mechanical loading on the bone healing process. Bailon-Plaza et al. (Bailon-Plaza and van der Meulen, 2003) simulated the stimulatory or inhibitory effect of mechanical signals on the ossification process according to Claes et al. (Claes and Heigele, 1999). With this model, they were able to explain the beneficial and adverse effects of moderate and excessive loading, respectively, as well as the negative effects of delaying mechanical stimulation of rigidly fixed calluses; as observed experimentally. Geris et al. investigated the occurrence of non-unions due to mechanical over-loading (Geris et al., 2010b). In their model, they showed that the mechanical regulation of both angiogenesis and osteogenesis was able to predict overload-induced non-union, confirming the hypotheses of experimental studies investigating the interconnection between angiogenesis and osteogenesis. All these models based on PDEs make use of diffusion equations to simulate cellular invasion within the callus. Several models have used this approach to investigate the effect of the origin of the cells on the healing pattern (Lacroix et al., 2002; Vetter et al., 2012). Comparing model predictions with histological data, Vettel et al. showed that the source of progenitor cells needs to be stronger at the periosteum than at the marrow space in order to achieve early periosteal and delayed endosteal bone formation, as seen in bone healing experiments in sheep (Vetter et al., 2012).
Several computer models have used agent-based approaches to simulate the behavior of individual cells and to investigate their contribution to tissue patterning over the course of healing (Byrne et al., 2011; Checa et al., 2011; Carlier et al., 2012; Borgiani et al., 2015; O'Reilly et al., 2016). Using this approach, Checa et al. (2011) and Borgiani et al. (2015) showed that differences in the healing pattern (e.g., endosteal, periosteal, time to bringing) of different species (sheep, rat, and mice) can be explained by differences in the regulation of cellular activity by mechanical signals during the course of healing.
Statistical methods have been used to investigate the robustness of the models and to identify the influence of model parameters on model outcome. Using a design of experiments approach, Isaksson et al. determined the rate of bone tissue formation and cartilage degradation as key players for the prediction of uneventful bone fracture healing (Isaksson et al., 2008). Using the same approach, Carlier et al. identified the impaired endochondral ossification process and increased infiltration of fibroblastic cells as key contributors to the degree of severity of congenital pseudarthrosis of the tibia (Carlier et al., 2016).
The Role of Intrinsic and Extrinsic Growth Factors on Cellular Activity
Growth factors play a key role in the bone healing process by modulating cellular activity and serving as communication between the cells. A single growth factor may have effects on multiple cell types and induce different functions, resulting in a cascade of highly complex interactions. Several computer models have aimed to understand the role of growth factors on cellular activity, and thereof on tissue formation over the course of healing (Bailon-Plaza and van der Meulen, 2001; Moore et al., 2014; Ribeiro et al., 2015). Bailon-Plaza et al. assumed two initial sources of an osteogenic and a chondrogenic growth factor located at the periosteum and the hematoma, respectively; while keeping the duration of the release and the magnitude as parameters. They predicted that the duration of the release in the hematoma needs to be sufficiently long to initiate the healing response. They found an agreement with experimental data in the time point of peak osteogenic growth factor concentration (Bailon-Plaza and van der Meulen, 2001).
The chemotactic potential of vascular endothelial growth factors on the angiogenic process during bone healing has also been investigated using a computer model (Geris et al., 2008). This model suggested that endothelial cells are attracted toward gradients of vascular endothelial growth factor secreted by chondrocytes and osteoblast and that these gradients are ensured by the consumption of the growth factor by the endothelial cells. Based on these assumptions, the model was able to simulate compromised healing conditions due to impaired angiogenesis. However, the model did not take into account the influence of the mechanical environment on growth factor production or its effect on vascular growth.
Moore et al. explicitly included the effect of mechanics on the production of bone morphogenetic protein 2 (BMP-2) by progenitor cells located in the periosteum of a critical sized femoral defect in sheep stabilized with an intramedullary nail (Moore et al., 2014). Assuming that BMP-2 in turn regulates cell proliferation and differentiation, they were able to predict experimentally observed tissue formation over the course of healing.
The potential of growth factor BMP-2 incorporation to promote cellular activity and enhance tissue regeneration in the context of large bone defects has been shown not only in a clinic setting (Schmidt-Bleek et al., 2016), but also using computer modeling techniques (Ribeiro et al., 2015). Ribeiro et al. collected quantitative experimental data from the literature on the effect of BMP-2 on cellular activity (proliferation, migration, differentiation, extracellular matrix production, etc.) and implemented them into a model to simulate bone healing in a large defect stimulated with BMP-2 (Ribeiro et al., 2015). The authors showed a good agreement with experimental data on the amount of bone tissue formed over the course of healing; however they were not able to predict endosteal bone formation.
Angiogenesis and the Role of Oxygen Supply for Successful Healing
Angiogenesis, defined by the formation of new capillaries, plays a key role in bone repair. Several computational studies have been developed to investigate the relative role of revascularization on bone healing progression (Geris et al., 2008; Chen et al., 2009; Peiffer et al., 2011; Simon et al., 2011; Burke and Kelly, 2012; O'Reilly et al., 2016). These models have seen a clear evolution toward a multiscale approach with the aim to better reflect and understand the biology of the process. While early models simulated vascular growth as a simple diffusion process (Geris et al., 2008; Chen et al., 2009; Burke and Kelly, 2012), more recent models use a discrete approach in order to simulate the complex structure of the newly formed capillary network (Carlier et al., 2015; O'Reilly et al., 2016).
Diffusion based models have investigated the influence of angiogenic growth factor production or callus size on the establishment of the vascular network and in turn on successful bone healing (Geris et al., 2008; Chen et al., 2009). Computer models at the cellular level have focused on understanding how progenitor cell fate might be affected by the altered conditions present in fractures with disrupted vasculature (O'Reilly et al., 2016) or in genetically modified mouse animal models (Burke et al., 2013). The MOSAIC model, developed by Carlier and her group, is the only multiscale computer model of bone healing that incorporates processes at the intracellular scale (Carlier et al., 2012). It implements an intracellular module that includes Dll4/Notch1 signaling to determine tip cell selection. The model was able to simulate the salt and pepper pattern seen for cell fates, an increased tip cell density due to the loss of Dll4 and an excessive number of tip cells in high VEGF environments (Carlier et al., 2012).
Discussion and Future Perspectives
Computer models can provide great insights into the complexity of the bone regeneration process, especially on the interactions between the different length and time scales. Despite significant advances in the field of computer modeling of bone healing and its clear trend toward a multiscale approach to provide a systems biology overview of the process, many limitations remain. In what follows, we describe some of the remaining challenges and give insights into possibilities for future work.
Cells as “Sensors” of the Mechanical Environment
So far, models have considered that the mechanical signals at the tissue level regulate the bone healing progression (e.g., Lacroix et al., 2002). However, it is well-known that, in reality, it is the cells that feel mechanical signals and respond with changes in cellular function (review in Su et al., 2011). We and others have shown that mechanical strains at the tissue level differ from those at the cellular scale (Bell et al., 2012; Shoham and Gefen, 2012; Checa et al., 2015). It is known that cells can sense mechanical stimuli provided by the surrounding matrix and that these stimuli influence cellular function, such as proliferation (Hadjipanayi et al., 2009), migration (Lo et al., 2000), and differentiation (Engler et al., 2006). However, the role of the mechanical regulation of cellular activity on processes at a larger scale, such as the formation/regeneration of bone, remains poorly understood.
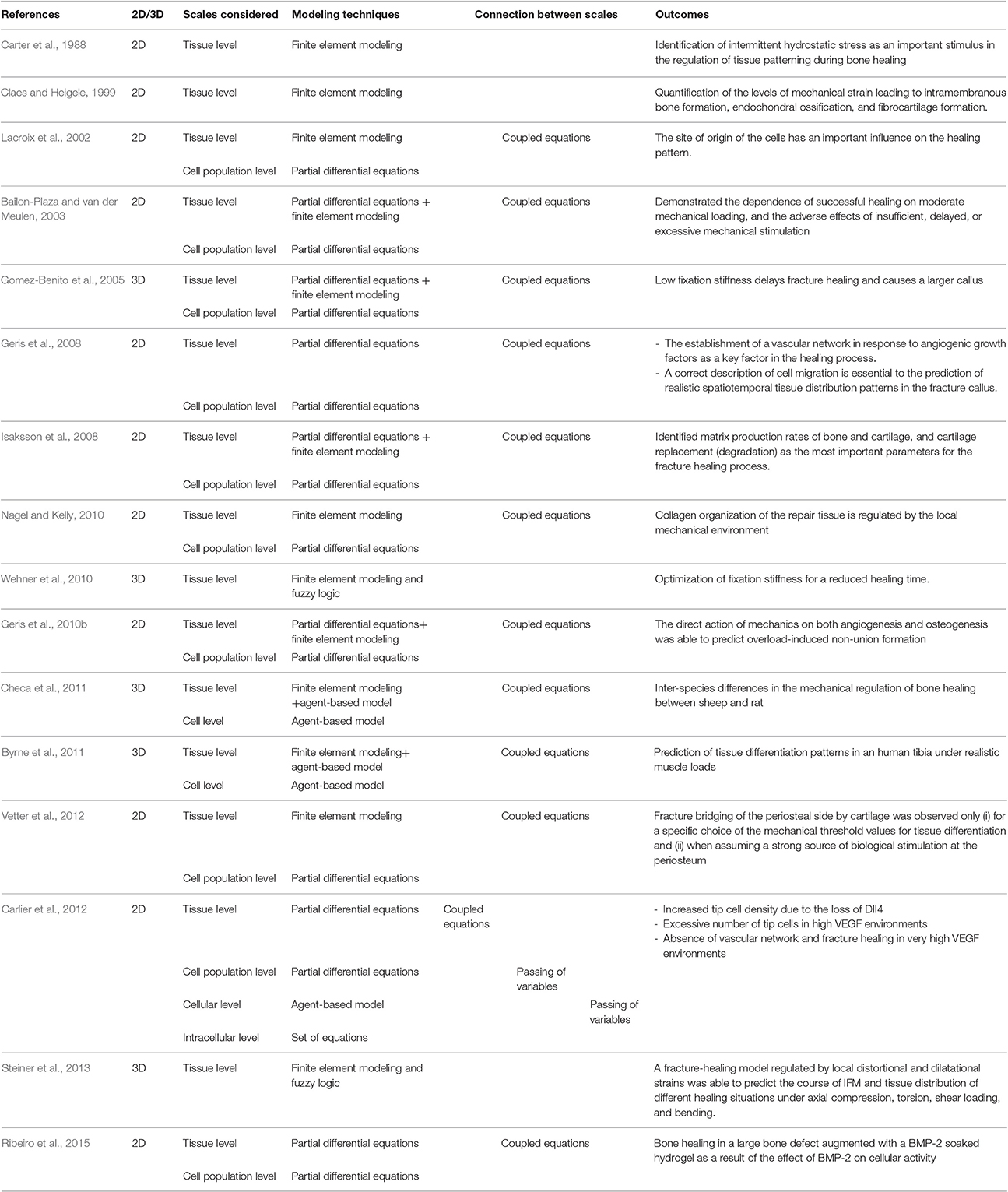
Cells produce highly organized fibrous and mineralized structures with preferential orientations (Liu et al., 2010; Preininger et al., 2011), resulting in highly heterogeneous and anisotropic material behavior. One of the current limitations of computer models of bone healing is that they assume homogeneous distributions of tissues while, in reality, tissues within the healing region form very organized structures (Figure 1). A first step toward understanding the role of cellular mechanosensation on bone healing is to be able to determine how mechanical signals are transferred from the tissue to the cellular level. To achieve this, there is a need to develop realistic computer models of extracellular matrix production and organization.
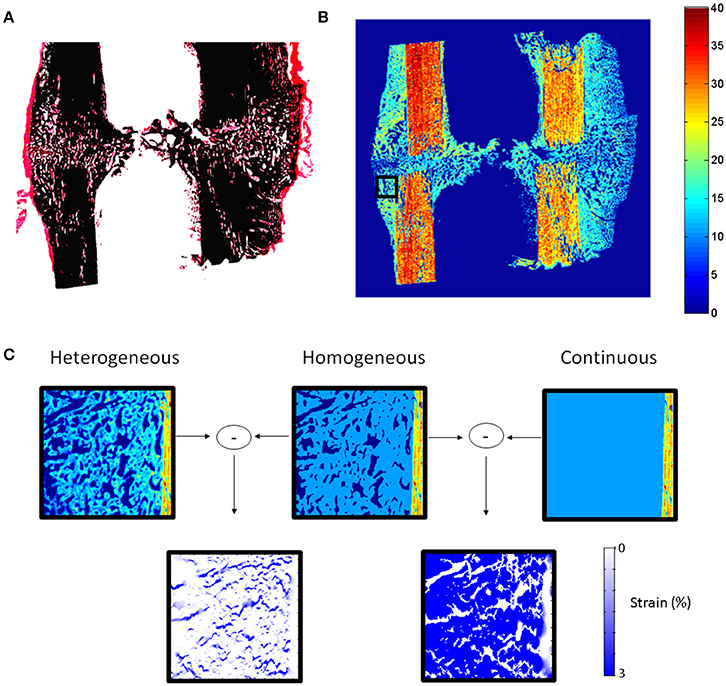
Figure 1. (A) Histological section (Safranin-O von Kossa staining) of sheep callus stabilized with an external fixator (9 weeks). (B) Map of elastic coefficient (GPa) of the same sample measured by quantitative acoustic scanning microscopy. (C) FEMs of callus region (black square B) under 10% compression showing the influence of callus tissue structure and heterogeneity on the mechanical strains within the healing region. High mechanical strains are induced in regions between the highly organized bone tissue, which cannot be predicted when describing the tissues as continuous and homogeneous materials.
Early Phases of Healing: Inflammation and the Immune Response
During the first phase of bone fracture healing, a hematoma is formed where platelets and macrophages are known to release different signaling molecules such as cytokines and growth factors. These molecules play a key role in the regulation of the subsequent cellular events during the healing process. More and more, it is becoming obvious that the initial healing and inflammation phases play a main role in the bone healing outcome and that understanding the mechano-biology of the initial stages of healing is important to improve bone fracture healing (Klein et al., 2003; Schlundt et al., 2015). Up to now, there are no computer models investigating the interactions occurring during this healing phase or considering the role of immune cells on bone regeneration. Future computer models of bone healing should aim at investigating the interactions that occur during the initial healing phases and how they influence healing progression.
Reaching the Intracellular Level
Ultimately, cell decisions about differentiation, proliferation, and other cellular activities, are made on the basis of external signals. These signals are transmitted to the interior of the cells activating diverse signaling pathways which, in turn, activate genes involved in the specified cellular function. Several signaling pathways (Wnt, BMP, and ER receptor) have been shown to play a key role in the bone formation response (Hayrapetyan et al., 2015) and clinical strategies are being developed based on the modulation of these pathways to promote bone repair. However, experimentally, it is difficult to investigate the detailed mechanism of these pathways, their interactions and their implications at the cellular and tissue levels. Several studies have shown a great potential of computational approaches to elucidate non-obvious interactions between signaling pathways and their implications for cellular function (Gilbert et al., 2006). To date, the intracellular level has been mainly ignored in computer models of bone healing (Figure 2). Future in silico studies should aim at integrating information within and across all the different scales in order to get a mechanistic insight of the process as a whole.
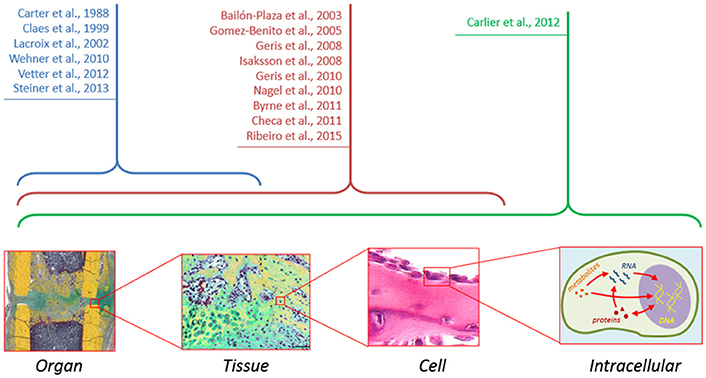
Figure 2. Although computer models of bone healing tend toward a multiscale approach to understand interactions between and within the different length and time scales, computer models at the intracellular level are still lacking.
Modeling Reusability and Reproducibility
While computer modeling in systems biology has seen a strong advancement toward the development of model standards, reusability and reproducibility (Waltemath and Wolkenhauer, 2016), the field of computer modeling of bone regeneration lags clearly behind in this respect. To the author's knowledge, none of the computer models of bone regeneration developed so far has been made publically available in an open database. This, despite the fact that several journals, such as BMC, FEBS, or PLOS, request the authors to provide the model code through open repositories. Future developments in the field would definitely benefit from sharing, not only of model equations and parameters, as done so far, but also of model code and software. This would clearly facilitate the reproducibility of study results and the further development of the models.
Conclusions
Despite advances in modeling being rather rapid, the present computer models are still unable to capture many of the mechanical and biological interactions that occur across and within the different time and length scales. More importantly, in most cases, they lack prediction power in compromised repair conditions. Old age (Bak and Andreassen, 1989), immune compromise (Claes et al., 2012) or genetic disorders (El Khassawna et al., 2012) have been shown to negatively affect the bone healing response; however little is known about the mechanisms behind these phenomena. From a computational point of view, very little has been done to understand how these factors influence the bone healing cascade. In silico studies show a great potential to contribute to the understanding of bone healing in compromised conditions and the consequences of alterations in cellular function on the bone healing outcome.
Author Contributions
EB and SC drafted the manuscript; all authors read and revised the manuscript and approved its content.
Funding
This study was supported by the German Research Foundation (Deutsche Forschungsgemeinschaft: DU298/14-1; CH 1123/4-1).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Bailon-Plaza, A., and van der Meulen, M. C. (2001). A mathematical framework to study the effects of growth factor influences on fracture healing. J. Theor. Biol. 212, 191–209. doi: 10.1006/jtbi.2001.2372
Bailon-Plaza, A., and van der Meulen, M. C. (2003). Beneficial effects of moderate, early loading and adverse effects of delayed or excessive loading on bone healing. J. Biomech. 36, 1069–1077. doi: 10.1016/S0021-9290(03)00117-9
Bak, B., and Andreassen, T. T. (1989). The effect of aging on fracture-healing in the rat. Calcif. Tissue Int. 45, 292–297. doi: 10.1007/BF02556022
Bell, B. J., Nauman, E., and Voytik-Harbin, S. L. (2012). Multiscale strain analysis of tissue equivalents using a custom-designed biaxial testing device. Biophys. J. 102, 1303–1312. doi: 10.1016/j.bpj.2012.02.007
Borgiani, E. D. G., Willie, B., and Checa, S. (2015). Bone Healing in Mice: Does It Follow Generic Mechano-Regulation Rules? Series: Mechanical Engineering, Facta Universitatis. 13, 217–227.
Burke, D., Dishowitz, M., Sweetwyne, M., Miedel, E., Hankenson, K. D., and Kelly, D. J. (2013). The role of oxygen as a regulator of stem cell fate during fracture repair in TSP2-null mice. J. Orthop. Res. 31, 1585–1596. doi: 10.1002/jor.22396
Burke, D. P., and Kelly, D. J. (2012). Substrate stiffness and oxygen as regulators of stem cell differentiation during skeletal tissue regeneration: a mechanobiological model. PLoS ONE 7:e40737. doi: 10.1371/journal.pone.0040737
Byrne, D. P., Lacroix, D., and Prendergast, P. J. (2011). Simulation of fracture healing in the tibia: mechanoregulation of cell activity using a lattice modeling approach. J. Orthop. Res. 29, 1496–1503. doi: 10.1002/jor.21362
Carlier, A., Brems, H., Ashbourn, J. M., Nica, I., Legius, E., and Geris, L. (2016). Capturing the wide variety of impaired fracture healing phenotypes in Neurofibromatosis Type 1 with eight key factors: a computational study. Sci. Rep. 7:20010. doi: 10.1038/srep20010
Carlier, A., Geris, L., Bentley, K., Carmeliet, G., Carmeliet, P., and Van Oosterwyck, H. (2012). MOSAIC: a multiscale model of osteogenesis and sprouting angiogenesis with lateral inhibition of endothelial cells. PLoS Comput. Biol. 8:e1002724. doi: 10.1371/journal.pcbi.1002724
Carlier, A., Geris, L., van Gastel, N., Carmeliet, G., and Van Oosterwyck, H. (2015). Oxygen as a critical determinant of bone fracture healing-A multiscale model. J. Theor. Biol. 365, 247–264. doi: 10.1016/j.jtbi.2014.10.012
Carlier, A., van Gastel, N., Geris, L., Carmeliet, G., and Van Oosterwyck, H. (2014). Size does matter: an integrative in vivo-in silico approach for the treatment of critical size bone defects. PLoS Comput. Biol. 10:e1003888. doi: 10.1371/journal.pcbi.1003888
Carter, D. R., Blenman, P. R., and Beaupre, G. S. (1988). Correlations between mechanical-stress history and tissue differentiation in initial fracture-healing. J. Orthop. Res. 6, 736–748. doi: 10.1002/jor.1100060517
Checa, S., Prendergast, P. J., and Duda, G. N. (2011). Inter-species investigation of the mechano-regulation of bone healing: comparison of secondary bone healing in sheep and rat. J. Biomech. 44, 1237–1245. doi: 10.1016/j.jbiomech.2011.02.074
Checa, S., Rausch, M. K., Petersen, A., Kuhl, E., and Duda, G. N. (2015). The emergence of extracellular matrix mechanics and cell traction forces as important regulators of cellular self-organization. Biomech. Model. Mechanobiol. 14, 1–13. doi: 10.1007/s10237-014-0581-9
Chen, G., Niemeyer, F., Wehner, T., Simon, U., Schuetz, M. A., Pearcy, M. J., et al. (2009). Simulation of the nutrient supply in fracture healing. J. Biomech. 42, 2575–2583. doi: 10.1016/j.jbiomech.2009.07.010
Claes, L., Augat, P., Suger, G., and Wilke, H. J. (1997). Influence of size and stability of the osteotomy gap on the success of fracture healing. J. Orthop. Res. 15, 577–584. doi: 10.1002/jor.1100150414
Claes, L. E., and Heigele, C. A. (1999). Magnitudes of local stress and strain along bony surfaces predict the course and type of fracture healing. J. Biomech. 32, 255–266. doi: 10.1016/S0021-9290(98)00153-5
Claes, L., Recknagel, S., and Ignatius, A. (2012). Fracture healing under healthy and inflammatory conditions. Nat. Rev. Rheumatol. 8, 133–143. doi: 10.1038/nrrheum.2012.1
El Khassawna, T., Toben, D., Kolanczyk, M., Schmidt-Bleek, K., Koennecke, I., Schell, H., et al. (2012). Deterioration of fracture healing in the mouse model of NF1 long bone dysplasia. Bone 51, 651–660. doi: 10.1016/j.bone.2012.07.011
Engler, A. J., Sen, S., Sweeney, H. L., and Discher, D. E. (2006). Matrix elasticity directs stem cell lineage specification. Cell 126, 677–689. doi: 10.1016/j.cell.2006.06.044
Garcia-Aznar, J. M., Kuiper, J. H., Gomez-Benito, M. J., Doblare, M., and Richardson, J. B. (2007). Computational simulation of fracture healing: influence of interfragmentary movement on the callus growth. J. Biomech. 40, 1467–1476. doi: 10.1016/j.jbiomech.2006.06.013
Geris, L., Gerisch, A., Sloten, J. V., Weiner, R., and Oosterwyck, H. V. (2008). Angiogenesis in bone fracture healing: a bioregulatory model. J. Theor. Biol. 251, 137–158. doi: 10.1016/j.jtbi.2007.11.008
Geris, L., Reed, A. A., Vander Sloten, J., Simpson, A. H., and Van Oosterwyck, H. (2010a). Occurrence and treatment of bone atrophic non-unions investigated by an integrative approach. PLoS Comput. Biol. 6:e1000915. doi: 10.1371/journal.pcbi.1000915
Geris, L., Vander Sloten, J., and Van Oosterwyck, H. (2010b). Connecting biology and mechanics in fracture healing: an integrated mathematical modeling framework for the study of nonunions. Biomech. Model. Mechanobiol. 9, 713–724. doi: 10.1007/s10237-010-0208-8
Gilbert, D., Fuss, H., Gu, X., Orton, R., Robinson, S., Vyshemirsky, V., et al. (2006). Computational methodologies for modelling, analysis and simulation of signalling networks. Brief. Bioinformatics 7, 339–353. doi: 10.1093/bib/bbl043
Gomez-Benito, M. J., Garcia-Aznar, J. M., Kuiper, J. H., and Doblare, M. (2005). Influence of fracture gap size on the pattern of long bone healing: a computational study. J. Theor. Biol. 235, 105–119. doi: 10.1016/j.jtbi.2004.12.023
Hadjipanayi, E., Mudera, V., and Brown, R. A. (2009). Close dependence of fibroblast proliferation on collagen scaffold matrix stiffness. J. Tissue Eng. Regen. Med. 3, 77–84. doi: 10.1002/term.136
Hayrapetyan, A., Jansen, J. A., and van den Beucken, J. J. (2015). Signaling pathways involved in osteogenesis and their application for bone regenerative medicine. Tissue Eng. Part B Rev. 21, 75–87. doi: 10.1089/ten.teb.2014.0119
Isaksson, H., van Donkelaar, C. C., Huiskes, R., and Ito, K. (2006). Corroboration of mechanoregulatory algorithms for tissue differentiation during fracture healing: comparison with in vivo results. J. Orthop. Res. 24, 898–907. doi: 10.1002/jor.20118
Isaksson, H., van Donkelaar, C. C., Huiskes, R., Yao, J., and Ito, K. (2008). Determining the most important cellular characteristics for fracture healing using design of experiments methods. J. Theor. Biol. 255, 26–39. doi: 10.1016/j.jtbi.2008.07.037
Klein, P., Schell, H., Streitparth, F., Heller, M., Kassi, J. P., Kandziora, F., et al. (2003). The initial phase of fracture healing is specifically sensitive to mechanical conditions. J. Orthop. Res. 21, 662–669. doi: 10.1016/S0736-0266(02)00259-0
Konnecke, I., Serra, A., El Khassawna, T., Schlundt, C., Schell, H., Hauser, A., et al. (2014). T and B cells participate in bone repair by infiltrating the fracture callus in a two-wave fashion. Bone 64, 155–165. doi: 10.1016/j.bone.2014.03.052
Lacroix, D., Prendergast, P. J., Li, G., and Marsh, D. (2002). Biomechanical model to simulate tissue differentiation and bone regeneration: application to fracture healing. Med. Biol. Eng. Comput. 40, 14–21. doi: 10.1007/BF02347690
Liu, Y. F., Manjubala, I., Schell, H., Epari, D. R., Roschger, P., Duda, G. N., et al. (2010). Size and habit of mineral particles in bone and mineralized callus during bone healing in sheep. J. Bone Miner. Res. 25, 2029–2038. doi: 10.1002/jbmr.84
Lo, C. M., Wang, H. B., Dembo, M., and Wang, Y. L. (2000). Cell movement is guided by the rigidity of the substrate. Biophys. J. 79, 144–152. doi: 10.1016/S0006-3495(00)76279-5
Moore, S. R., Saidel, G. M., Knothe, U., and Knothe Tate, M. L. (2014). Mechanistic, mathematical model to predict the dynamics of tissue genesis in bone defects via mechanical feedback and mediation of biochemical factors. PLoS Comput. Biol. 10:e1003604. doi: 10.1371/journal.pcbi.1003604
Nagel, T., and Kelly, D. J. (2010). Mechano-regulation of mesenchymal stem cell differentiation and collagen organisation during skeletal tissue repair. Biomech. Model. Mechanobiol. 9, 359–372. doi: 10.1007/s10237-009-0182-1
O'Reilly, A., Hankenson, K. D., Kelly, D. J. (2016). A computational model to explore the role of angiogenic impairment on endochondral ossification during fracture healing. Biomech. Model. Mechanobiol. 15, 1279–1294. doi: 10.1007/s10237-016-0759-4
Peiffer, V., Gerisch, A., Vandepitte, D., Van Oosterwyck, H., and Geris, L. (2011). A hybrid bioregulatory model of angiogenesis during bone fracture healing. Biomech. Model. Mechanobiol. 10, 383–395. doi: 10.1007/s10237-010-0241-7
Preininger, B., Checa, S., Molnar, F. L., Fratzl, P., Duda, G. N., and Raum, K. (2011). Spatial-temporal mapping of bone structural and elastic properties in a sheep model following osteotomy. Ultrasound Med. Biol. 37, 474–483. doi: 10.1016/j.ultrasmedbio.2010.12.007
Ribeiro, F. O., Gomez-Benito, M. J., Folgado, J., Fernandes, P. R., and Garcia-Aznar, J. (2015). In silico mechano-chemical model of bone healing for the regeneration of critical defects: the effect of BMP-2. PLoS ONE 10:e0127722. doi: 10.1371/journal.pone.0127722
Schell, H., Epari, D. R., Kassi, J. P., Bragulla, H., Bail, H. J., and Duda, G. N. (2005). The course of bone healing is influenced by the initial shear fixation stability. J. Orthop. Res. 23, 1022–1028. doi: 10.1016/j.orthres.2005.03.005
Schlundt, C., Schell, H., Goodman, S. B., Vunjak-Novakovic, G., Duda, G. N., and Schmidt-Bleek, K. (2015). Immune modulation as a therapeutic strategy in bone regeneration. J. Exp. Orthop. 2:1. doi: 10.1186/s40634-014-0017-6
Schmidt-Bleek, K., Petersen, A., Dienelt, A., Schwarz, C., and Duda, G. N. (2014). Initiation and early control of tissue regeneration - bone healing as a model system for tissue regeneration. Expert Opin. Biol. Ther. 14, 247–259. doi: 10.1517/14712598.2014.857653
Schmidt-Bleek, K., Willie, B. M., Schwabe, P., Seemann, P., and Duda, G. N. (2016). BMPs in bone regeneration: less is more effective, a paradigm-shift. Cytokine Growth Factor Rev. 27, 141–148. doi: 10.1016/j.cytogfr.2015.11.006
Secreto, F. J., Hoeppner, L. H., and Westendorf, J. J. (2009). Wnt signaling during fracture repair. Curr. Osteoporos. Rep. 7, 64–69. doi: 10.1007/s11914-009-0012-5
Shoham, N., and Gefen, A. (2012). Deformations, mechanical strains and stresses across the different hierarchical scales in weight-bearing soft tissues. J. Tissue Viabil. 21, 39–46. doi: 10.1016/j.jtv.2012.03.001
Simon, U., Augat, P., Utz, M., and Claes, L. (2011). A numerical model of the fracture healing process that describes tissue development and revascularisation. Comput. Methods Biomech. Biomed. Eng. 14, 79–93. doi: 10.1080/10255842.2010.499865
Steiner, M., Claes, L., Ignatius, A., Niemeyer, F., Simon, U., and Wehner, T. (2013). Prediction of fracture healing under axial loading, shear loading and bending is possible using distortional and dilatational strains as determining mechanical stimuli. J. R. Soc. Interface 10:20130389. doi: 10.1098/rsif.2013.0389
Strube, P., Sentuerk, U., Riha, T., Kaspar, K., Mueller, M., Kasper, G., et al. (2008). Influence of age and mechanical stability on bone defect healing: age reverses mechanical effects. Bone 42, 758–764. doi: 10.1016/j.bone.2007.12.223
Su, F. C., Wu, C. C., and Chien, S. (2011). Review: roles of microenvironment and mechanical forces in cell and tissue remodeling. J. Med. Biol. Eng. 31, 233–244. doi: 10.5405/jmbe.944
Vetter, A., Witt, F., Sander, O., Duda, G. N., and Weinkamer, R. (2012). The spatio-temporal arrangement of different tissues during bone healing as a result of simple mechanobiological rules. Biomech. Model. Mechanobiol. 11, 147–160. doi: 10.1007/s10237-011-0299-x
Waltemath, D., and Wolkenhauer, O. (2016). How modeling standards, software, and initiatives support reproducibility in systems biology and systems medicine. IEEE Trans. Biomed. Eng. 63, 1999–2006. doi: 10.1109/TBME.2016.2555481
Keywords: bone healing, computer modeling, multiscale modeling, systems biology, tissue regeneration
Citation: Borgiani E, Duda GN and Checa S (2017) Multiscale Modeling of Bone Healing: Toward a Systems Biology Approach. Front. Physiol. 8:287. doi: 10.3389/fphys.2017.00287
Received: 20 December 2016; Accepted: 19 April 2017;
Published: 08 May 2017.
Edited by:
Ioannis P. Androulakis, Rutgers University, USAReviewed by:
Monika Heiner, Brandenburg University of Technology, GermanyHisham Bahmad, American University of Beirut, Lebanon
Copyright © 2017 Borgiani, Duda and Checa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sara Checa, c2FyYS5jaGVjYUBjaGFyaXRlLmRl
 Edoardo Borgiani
Edoardo Borgiani Georg N. Duda1,2
Georg N. Duda1,2 Sara Checa
Sara Checa