Arrhythmogenic right ventricular cardiomyopathy: considerations from in silico experiments

Objective: Arrhythmogenic right ventricular cardiomyopathy (ARVC) is associated with remodeling of gap junctions and also, although less well-defined, down-regulation of the fast sodium current. The gap junction remodeling and down-regulation of sodium current have been proposed as contributors to arrhythmogenesis in ARVC by slowing conduction. The objective of the present study was to assess the amount of conduction slowing due to the observed gap junction remodeling and down-regulation of sodium current. Methods: The effects of (changes in) gap junctional conductance, cell dimensions, and sodium current on both longitudinal and transversal conduction velocity were tested by simulating action potential propagation in linear strands of human ventricular cells that were either arranged end-to-end or side-by-side. Results: A 50% reduction in gap junction content, as commonly observed in ARVC, gives rise to an 11% decrease in longitudinal conduction velocity and a 29% decrease in transverse conduction velocity. A down-regulation of the sodium current through a 50% decrease in peak current density as well as a −15 mV shift in steady-state inactivation, as observed in an experimental model of ARVC, decreases conduction velocity in either direction by 32%. In combination, the gap junction remodeling and down-regulation of sodium current result in a 40% decrease in longitudinal conduction velocity and a 52% decrease in transverse conduction velocity. Conclusion: The gap junction remodeling and down-regulation of sodium current do result in conduction slowing, but heterogeneity of gap junction remodeling, in combination with down-regulation of sodium current, rather than gap junction remodeling per se may be a critical factor in arrhythmogenesis in ARVC.

Introduction

Arrhythmogenic right ventricular cardiomyopathy (ARVC), also known as arrhythmogenic right ventricular dysplasia (ARVD) or arrhythmogenic right ventricular dysplasia/cardiomyopathy (ARVD/C), is an inheritable arrhythmogenic disease characterized by ventricular tachyarrhythmias and sudden cardiac death. These occur mostly in the early “concealed” phase of the disease, in the absence of the extensive structural damage, including the fibro-fatty replacement of the myocardium, that characterizes the later phases. These and other characteristics of ARVC have been reviewed in detail elsewhere (Thiene et al., 2007; Basso et al., 2009, 2012; Sen-Chowdhry et al., 2010; Sen-Chowdhry and McKenna, 2012). The disease does not only occur in humans, but has also been described for cats (Fox et al., 2000; Harvey et al., 2005), dogs (Basso et al., 2004; Oxford et al., 2011), and horses (Freel et al., 2010).

Initially, ARVC was considered to be a developmental defect of the right ventricular myocardium, explaining the original term dysplasia, which was replaced once it was recognized that ARVC was not a structural defect present at birth. Furthermore, it became clear that the disease is not restricted to the right ventricle, but may also be biventricular or even left-dominant, leading to the introduction of the broader term arrhythmogenic cardiomyopathy (Basso et al., 2009, 2012; Sen-Chowdhry et al., 2010), abbreviated to AC by Basso et al. (2012), but, referring to a recent “Expert Consensus Statement,” to ACM by Jacoby and McKenna (2012). The latter authors, however, also use the term arrhythmogenic ventricular cardiomyopathy (AVC). Here, we will use the term ARVC, although we are aware that the disease may also affect the left ventricle.

A common observation in ARVC is remodeling of cardiac gap junctions early in the disease, with a diminished expression of the major gap junction protein connexin43 (Cx43) at the intercalated disks (IDs), which establish the mechanical and electrical coupling between adjacent cells (Saffitz, 2009). In samples from a single early-stage patient with Naxos disease, a rare variant of ARVC caused by a recessive mutation in the JUP gene encoding plakoglobin, electron microscopy revealed 2–5 times smaller and 1.5–4 times fewer gap junctions between both left and right ventricular myocytes as compared to left ventricular control samples (Kaplan et al., 2004). Of note, we have previously demonstrated that the number of gap junctions is more important for net intercellular coupling than gap junction size (Jongsma and Wilders, 2000). In another electron microscopic study, Basso et al. (2006) found a 2.5-fold reduction in number, but not length, of gap junctions at the IDs in right ventricular biopsies from 21 ARVC patients as compared to controls. In Boxer dogs with ARVC, a significant reduction in number, but again not length, of gap junctions between both left and right ventricular myocytes was observed (Oxford et al., 2011). The median number of gap junctions per 10 μm of ID, as revealed by electron microscopy, was reduced by a factor of 2 in the left ventricle and by a factor of 3 in the right, as compared to non-ARVC dogs, with a large variation in this median number between ARVC dogs.

In the young, i.e., in people aged ≤35 years, ARVC is a leading cause of sudden cardiac death, which is often the first clinical manifestation of the disease (see Sen-Chowdhry et al., 2010; and primary references cited therein). The prevalence of ARVC is commonly estimated to vary from 1:2,000 to 1:5,000 (Basso et al., 2012), but a higher prevalence has also been suggested (Peters et al., 2004; Lahtinen et al., 2011). In 50–60% of clinically diagnosed ARVC patients one or more mutations in desmosomal protein genes, like the aforementioned JUP gene, are found (Bhuiyan et al., 2009; den Haan et al., 2009; Kapplinger et al., 2011). These mutations particularly occur in PKP2, encoding plakophilin-2 (PKP2), which is known to interact with other molecules of the IDs. Using RNA silencing techniques to decrease the expression of PKP2 in cardiac cells, Oxford et al. (2007) demonstrated that Cx43 and PKP2 are part of a common macromolecular complex and that a loss of PKP2 expression leads to loss of gap junction plaques and a decrease in intercellular coupling as assessed by dye transfer. In a subsequent study on cultured cardiomyocytes (Sato et al., 2009), it was shown that PKP2 associates with the SCN5A encoded sodium channel protein Na_V1.5 and that knockdown of PKP2 expression alters the properties of the sodium current. Patch clamp studies revealed a decrease in peak current density by ≈50%, a −15 to −20 mV shift in the steady-state inactivation curve, and a slowed recovery from inactivation, all reducing membrane excitability. Given the strong association in expression levels of Cx43 and Na_V1.5 observed in recent studies (Desplantez et al., 2012; Jansen et al., 2012), the decrease in peak current density may be directly related to the decrease in intercellular coupling. Further evidence for the involvement of sodium current in ARVC comes from a recent study by Gomes et al. (2012), who studied right ventricular biopsies from three ARVC patients and observed Na_V1.5 mislocalization in biopsies from two early-stage patients. On the other hand, in the same study no difference was observed in sodium current properties in a desmoplakin^+/− murine model of ARVC, despite a reduced Cx43 expression at the IDs.

Although ARVC is associated with a clear reduction in intercellular coupling and probably also in membrane excitability, which is largely determined by the fast sodium current, it remains questionable whether the observed changes, either alone or in combination, can explain the arrhythmogenic nature of early-stage ARVC. The aim of the present study is to assess the functional implications of the ARVC related gap junction remodeling and down-regulation of sodium current in human ventricle. To this end, we carried out computer simulations using linear strands of cardiac cells, which were either arranged end-to-end or side-by-side. Individual cells of the strand were described by a mathematical model of a human (left) ventricular cell. After defining “normal” gap junctional conductance, based on data from literature, we tested the effects of (changes in) gap junctional conductance, myoplasmic resistivity, cell dimensions, and sodium current on conduction velocity in these strands.

Our simulation results show that conduction velocity is only moderately sensitive to changes in gap junctional conductance, cell length, cell width, or sodium current per se. The combined effects of gap junction remodeling and down-regulation of sodium current are larger, but still not definitely arrhythmogenic, suggesting that heterogeneity of gap junction remodeling rather than gap junction remodeling itself may be a critical factor in arrhythmogenesis, in particular if it occurs in combination with down-regulation of sodium current.

Materials and Methods

Linear Strand Model

Action potential conduction is studied in a linear strand of 90 cells that are either arranged end-to-end (Figure 1A) or side-by-side (Figure 1B) and coupled by an ohmic gap junctional conductance g_j. For each cell in the strand, ionic currents, and concentration changes are computed using the human ventricular cell model by Priebe and Beuckelmann (1998). This model is based on the Luo-Rudy dynamic model of the guinea pig-type ventricular action potential (Luo and Rudy, 1994), but equations for ionic currents and calcium handling have been modified to account for data from isolated human ventricular cells (Priebe and Beuckelmann, 1998). A propagating action potential is elicited by applying a 2-ms, 20–25% suprathreshold stimulus to the leftmost cell of the strand at 1 Hz. Conduction velocity is computed across the middle third of the strand.

FIGURE 1

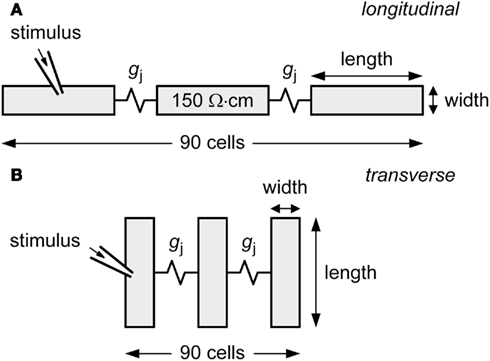
Figure 1. Diagram of linear strand model. The strand is composed of 90 human ventricular cells, coupled by an ohmic gap junctional conductance g_j. Myoplasmic resistivity is set to 150 Ω cm. Action potential propagation is initiated by applying an external stimulus to the leftmost cell of the strand. (A) Cells arranged longitudinally. (B) Cells arranged transversally.

Myoplasmic specific resistance (myoplasmic resistivity; ρ_myo) is set to 150 Ω cm. To allow comparison between g_j and ρ_myo, we compute the gap junctional resistivity ρ_j by “spreading out” g_j across the length – or width, in case of transverse conduction – of the cell. Thus, for longitudinal conduction, we have ρ_j = A/(g_j·l), where A denotes the 19.5-μm² × 19.5-μm² cross-sectional area and l denotes the 100-μm cell length. Total resistivity in the direction of conduction is computed as the sum of ρ_myo and ρ_j. In simulations with an increase in cell length or cell width, the membrane current densities were kept constant.

Numerical Methods

Since earlier simulations have shown that subcellular discretization is not required for accurate computation of conduction velocity (Shaw and Rudy, 1997), we use entire cells as computational elements with ρ_myo and ρ_j lumped together at each discretization point. No-flux boundary conditions are used at both ends of the strand. Stimulation and termination artifacts are restricted to ≈5 cells from both ends. For numerical integration of differential equations we applied a simple and efficient Euler-type integration scheme (Rush and Larsen, 1978) with a 1-μs time step. All software was compiled as a 32-bit Windows application using Compaq Visual Fortran 6.6C and run on an Intel Xeon processor based workstation.

Results

“Normal” Gap Junctional Conductance

Before assessing the effects of a reduction in g_j, we need to define a control value of g_j, both for side-by-side and end-to-end coupled cells. Studies on isolated cell pairs report widely different values for the gap junctional conductance between adult mammalian ventricular cells, ranging from 5 nS to 4 μS, as summarized by Wilders and Jongsma (1992). Most likely, each of these values is an underestimate of true gap junctional conductance, because these pairs consist of cells that have not become completely separated during the enzymatic isolation procedure to which they were subjected. Therefore, we chose another approach to estimate “normal” g_j, using data from confocal microscopy studies. In normal human left ventricular myocardium, mean gap junction plaque area is 0.21 μm² (Kaprielian et al., 1998). For such gap junctions, effective gap junctional conductance is ≈0.6 μS/μm² (Jongsma and Wilders, 2000). Gap junction labeling is confined to IDs in normal human left ventricle, and gap junction surface density is 0.0051–0.0055 μm²/μm³ (Peters et al., 1993; Kostin et al., 2003). Combining these numbers with the human left ventricular myocyte volume of 27,947 μm³ (Zafeiridis et al., 1998) and the total of 11.55 IDs per myocyte (Peters et al., 1993), which implies – given that left ventricular myocytes are connected to 11.3 ± 2.2 neighbors (Kanno and Saffitz, 2001) – that neighboring myocytes are typically connected by a single ID, which provides an intercellular pathway with an effective conductance of ≈7.7 μS.

From the above, our round estimate for normal g_j in case of longitudinal conduction would be 8 μS. Since gap junctions are largely confined to IDs in normal ventricular myocardium, a similar estimate would hold for transverse conduction. Figure 2 shows longitudinal and transverse conduction velocity (θ_L and θ_T, respectively) in the strands of Figure 1 as a function of g_j, which is varied between 10 nS and 20 μS. The value of 10 nS is about twice the minimum value of 5.4 nS required for successful action potential conduction (with θ_L and θ_T values as low as 0.5 and 0.1 cm/s, respectively). The g_j value of 8 μS results in θ_L and θ_T values of 67 and 26 cm/s, respectively. The longitudinal conduction velocity of 67 cm/s agrees well with the control value of 65 ± 4 cm/s (mean ± SEM, n = 7) for planar wave propagation in longitudinal direction in human left ventricular myocardium reported by Taggart et al. (2000).

FIGURE 2

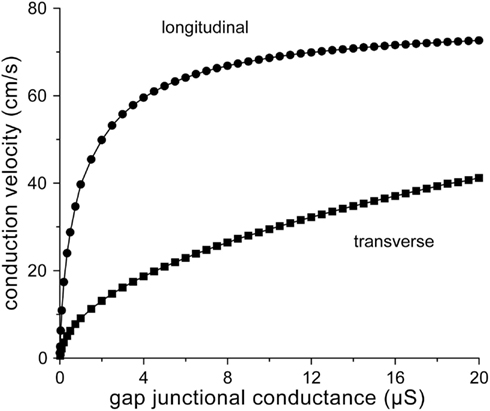
Figure 2. Relation between conduction velocity and gap junctional conductance for the strands of Figure 1.

Now that we have defined “normal” g_j, we can determine the decrease in conduction velocity upon a 50% or even larger decrease in g_j as observed in ARVC (see Introduction) or the 25–50% decrease as observed in various other cardiomyopathies (Smith et al., 1991; Peters et al., 1993; Kaprielian et al., 1998; Dupont et al., 2001; Kostin et al., 2003). A 25–50% decrease in g_j from 8 to 4–6 μS results in a 4–11% decrease in θ_L from 67 to 60–64 cm/s and a 13–29% decrease in θ_T from 26 to 19–23 cm/s (Figure 2). These effects may be considered moderate. However, larger effects are observed upon a 75% decrease in g_j to 2 μS, which may reflect the remodeling that occurs in ARVC. Then, θ_L and θ_T decrease to 50 and 13 cm/s, respectively, i.e., a 25% decrease in θ_L and a 50% decrease in θ_T (Figure 2).

From Figure 2, it can also be appreciated that θ_L tends to “saturate” near 70 cm/s with increasing g_j, whereas θ_T is more steeply dependent on g_j. The relative insensitivity of θ_L to g_j can be explained in terms of the gap junctional resistivity ρ_j (see Materials and Methods). To this end, we have plotted ρ_j as a function of g_j in Figure 3A. For longitudinal conduction, ρ_j falls below the myoplasmic resistivity of 150 Ω cm (horizontal dashed line) at a gap junctional conductance as low as 2.5 μS, whereas for transverse conduction ρ_j is considerably larger than ρ_myo at all values of g_j. At the normal g_j of 8 μS, gap junctions are responsible for only 24% of total resistivity in the longitudinal direction, whereas this number is 89% in the transverse direction (Figure 3B).

FIGURE 3

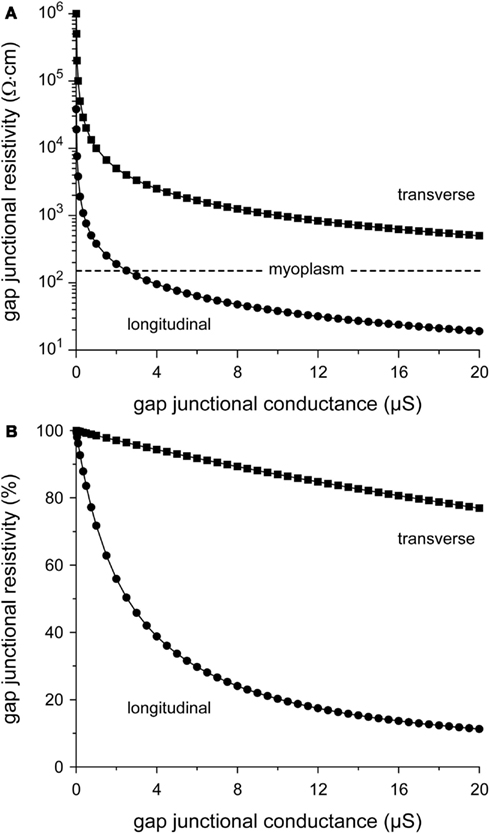
Figure 3. Relation between gap junctional resistivity and gap junctional conductance for longitudinal (circles) or transverse arrangement of cells (squares). (A) Gap junctional resistivity in Ω·cm. Dashed horizontal line indicates the myoplasmic resistivity of 150 Ω cm. Note logarithmic ordinate scale. (B) Gap junctional resistivity expressed as percent of total resistivity.

Conduction Velocity and Cell Dimensions

“Myocyte atrophy” is a common observation in ARVC (Gomes et al., 2012), but quantitative data are scarce. In a study with transgenic mice overexpressing a desmoplakin mutant gene, Yang et al. (2006) observed that ventricular cardiomyocyte cross-sectional areas were 40% higher in mutant mice as compared to control mice. Changes in cell dimensions are not limited to ARVC. Both hypertrophy and heart failure are associated with changes in myocyte dimensions. Length and width of failing human left ventricular myocytes are increased by 48 and 20%, respectively (Zafeiridis et al., 1998). Similarly, failing rabbit left ventricular myocytes show an increase by 39 and 50%, respectively (de Groot et al., 2003). Left ventricular myocytes from patients with ischemic heart disease show a 49% increase in length-to-width ratio without a significant change in cell width (Gerdes et al., 1992). To test to which extent an increase in myocyte length or width adds to changes in conduction velocity, simulations were run with myocyte length or width increased by 50%. Results are shown in Figure 4. Note that, for reasons of clarity, a descending abscissa scale is used in this and subsequent figures.

FIGURE 4

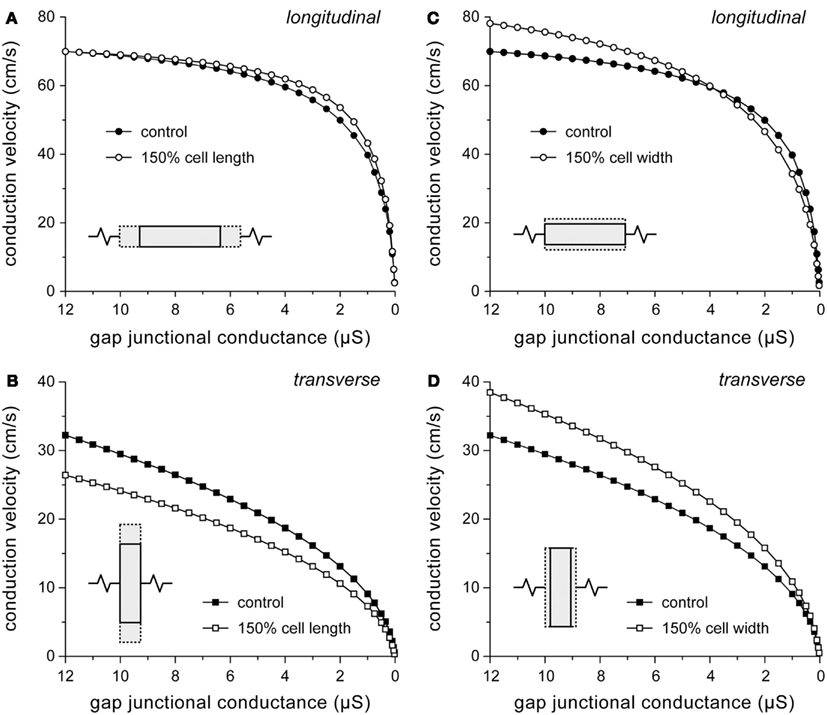
Figure 4. Effect of changes in cell dimensions on conduction velocity. (A,B) Effect of 50% increase in cell length on (A) longitudinal and (B) transverse conduction velocity. (C,D) Effect of 50% increase in cell width on (C) longitudinal and (D) transverse conduction velocity.

An increase in cell length has a beneficial effect on θ_L, because the number of gap junctions per unit distance decreases. However, the effect is small at high g_j (Figure 4A) because the strand is then essentially a uniform cable with a total resistivity that is largely determined by the resistivity of the myoplasm (Figure 3B). At very low values of g_j (<30 nS), at which propagation is slow and discontinuous, θ_L is considerably depressed by the increase in cell length. The time required to supply enough current, by the combination of sodium and L-type calcium current, to the downstream cell to reach threshold is then increased by >50%. Loading effects also play a role in case of transverse conduction (Figure 4B). If cell length is increased without a concomitant increase in g_j, the increased load of the downstream cells hampers conduction, resulting in reduced θ_T.

Opposing effects on θ_L are observed upon an increase in cell width (Figure 4C). The increased cross-sectional area of the cells reduces the intracellular resistance per unit of distance, thus facilitating intracellular current flow, but on the other hand more excitatory current is required due to the increased membrane surface area. At 4 μS, the two effects cancel out, but at the normal g_j of 8 μS, θ_L is increased by 8%. For transverse conduction, the decrease in the number of gap junctions per unit distance upon an increase in cell width results in increased θ_T (Figure 4D) despite the increased downstream load. Only if g_j is very low (<30 nS), θ_T is considerably depressed by a >50% increase in conduction time.

According to our simulation results, a 20% increase in cell width (or cell radius), as suggested by the aforementioned 40% increase in ventricular cardiomyocyte cross-sectional area in a transgenic mouse model of ARVC (Yang et al., 2006), would not contribute to the ARVC related conduction slowing, but rather increase conduction velocity. Additional simulations show that a 20% increase in cell width increases θ_L by 5% to 70 cm/s and increases θ_T by 9% to 28 cm/s.

Conduction Velocity and Myoplasmic Resistivity

Our simulation results so far suggest that myoplasmic resistivity is an important determinant of (longitudinal) conduction velocity. To test to which extent this model parameter affects simulation results, we computed conduction velocity at ρ_myo values that are higher or lower than our model value of 150 Ω cm. If ρ_myo is raised to 250 Ω cm, θ_L is reduced at all values of g_j (by 20% at 8 μS) and it eventually “saturates” at ≈59 cm/s. If ρ_myo is lowered to 100 Ω cm, θ_L increases at all values of g_j (by 17% at 8 μS; Figure 5A) and eventually “saturates” at ≈96 cm/s (not shown). Effects on θ_T are minimal, as expected from the large contribution of gap junctional resistivity (Figure 3), with a <4% change at 8 μS (Figure 5B).

FIGURE 5

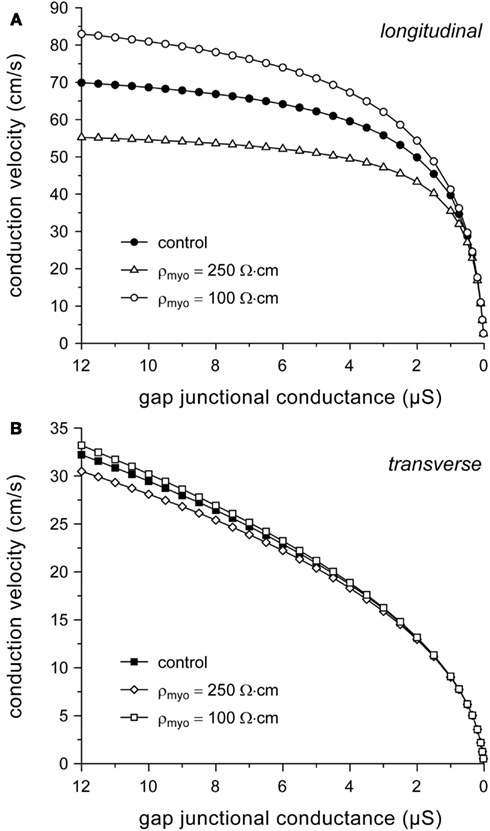
Figure 5. Dependence on myoplasmic resistivity (ρ_myo) of relationship between (A) longitudinal or (B) transverse conduction velocity and gap junctional conductance.

Given the dependence of (longitudinal) conduction velocity on myoplasmic resistivity, it is important to document the selection of the model value for this parameter. With typical values of 150 (Shaw and Rudy, 1997; Kucera et al., 2002), 200 (Rudy and Quan, 1987), and 250 Ω cm (Spach et al., 2000), our value of 150 Ω cm is at the lower end of the range of values used in these and subsequent theoretical studies, but near the experimentally observed value of 166 ± 19 Ω cm (mean ± SEM, n = 11) at 35°C (Kléber and Riegger, 1987). Impedance measurements on guinea pig left ventricular myocardium yield a value of 100 ± 9 Ω cm (mean ± SEM, n = 31) at 37°C (Cooklin et al., 1997), which is only two times the value of 49 ± 1 Ω cm for the resistivity of Tyrode solution (Sui et al., 2003).

Conduction Velocity and Membrane Excitability

Conduction velocity is not only determined by the passive characteristics of the cardiac cell network that constitutes the substrate for impulse propagation, but also by the active properties of the cardiac cell membrane, in particular of the fast sodium current (I_Na). It is likely that the expression of sodium channels is reduced in ARVC (see Introduction), with a decrease in current density of I_Na of ≈50% (Sato et al., 2009). A down-regulation of I_Na has not only been implicated in ARVC. For example, a 32% reduction in I_Na conductance was observed in isolated ventricular myocytes from dogs with chronic heart failure (Maltsev et al., 2002).

To gain insight into the role of I_Na in determining conduction velocity, we ran simulations with the number of sodium channels increased or decreased by 50%, which was accomplished by a 50% increase or decrease in the fully activated I_Na conductance (g_Na), respectively. The increased excitability results in an increase in both θ_L and θ_T. At the normal g_j of 8 μS, θ_L and θ_T are both increased by 24%. Similarly, halving g_Na results in a 22–23% decrease in both θ_L and θ_T (Figure 6).

FIGURE 6

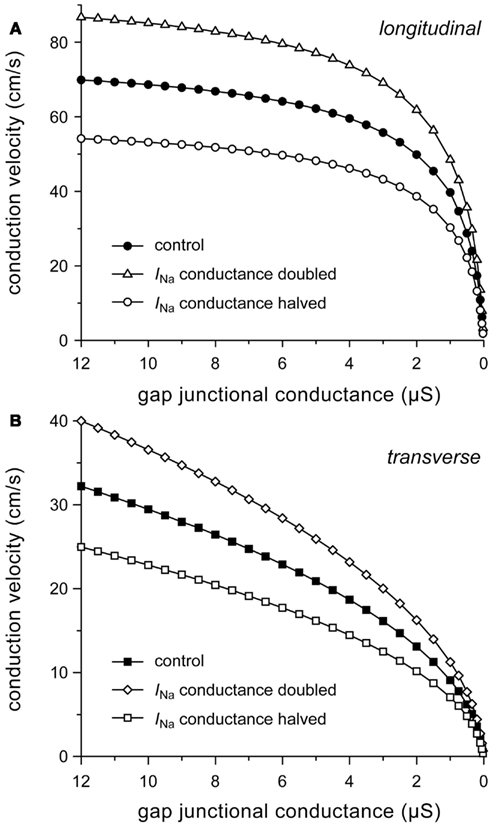
Figure 6. Effect of halving or doubling sodium current (I_Na) conductance on (A) longitudinal and (B) transverse conduction velocity.

Major Determinants of Conduction Velocity

In the above, we have investigated how conduction velocity is related to structural determinants of conduction (gap junctional conductance, myocyte dimensions, myoplasmic resistivity) and active membrane properties (conductance of I_Na). In Figure 7, we compare their relative importance at different levels of intercellular coupling. We have determined the relative change in θ_L and θ_T in response to a plus or minus 50% change in gap junctional conductance, cell length, cell width, myoplasmic resistivity, and I_Na conductance at g_j values of 2, 4, 8, and 12 μS.

FIGURE 7

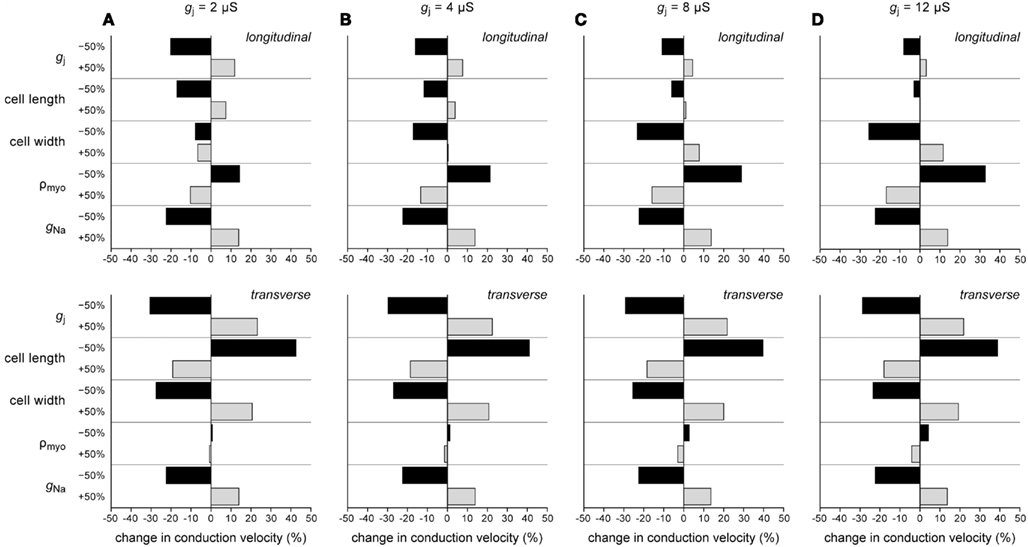
Figure 7. Percent change in longitudinal (top) and transverse conduction velocity (bottom) upon −50% or +50% change in gap junctional conductance (g_j), cell length, cell width, myoplasmic resistivity (ρ_myo), or sodium current conductance (g_Na). (A) g_j = 2 μS. (B) g_j = 4 μS. (C) g_j = 8 μS. (D) g_j = 12 μS.

Several conclusions can be drawn from Figure 7. (1) None of the changes exerts a 1:1 effect on conduction velocity: the change in conduction velocity upon a 50% change in any of the parameters is always <50%. (2) For transverse conduction (bottom panels), the effects at 2, 4, 8, and 12 μS are largely similar. (3) The effects of changes in active membrane properties (conductance of I_Na) are almost identical for longitudinal and transverse conduction and relatively constant over the range of g_j values examined. (4) Gap junctional conductance is not the single major determinant of conduction velocity. At normal g_j, myocyte dimensions and I_Na conductance are equally important.

Figure 7A shows an interesting phenomenon occurring at g_j = 2 μS. The longitudinal strand then operates at an optimum cell width: both an increase and a decrease in cell width result in a decrease in θ_L. This phenomenon is related to the opposing effects on θ_L of changes in cell width, which also underlie the “cross-over” at 4 μS in Figure 4C.

Conduction Velocity in ARVC

In ARVC, the number of gap junctions may be decreased by 50% while at the same time sodium current is down-regulated. The study by Sato et al. (2009) shows that the sodium current density may be decreased by ≈50%, whereas the steady-state inactivation curve may be shifted in the negative direction by 15–20 mV. Therefore, we also assessed the combined effects of changes in intercellular coupling and sodium current, using 8 μS as the control value for gap junctional conductance. Figure 8 displays the separate effects of a 50% reduction in gap junctional conductance, a 50% reduction in I_Na conductance, and a −15 mV shift in the steady-state inactivation curve of I_Na on both θ_L (Figure 8A) and θ_T (Figure 8B). The combined effects of the reduction in I_Na conductance and shift in inactivation curve are also shown. The rightmost bars show θ_L (Figure 8A) and θ_T (Figure 8B) under ARVC like conditions, i.e., if the intercellular coupling is reduced by 50% and the sodium current is down-regulated through a 50% decrease in current density as well as a −15 mV shift in steady-state inactivation.

FIGURE 8

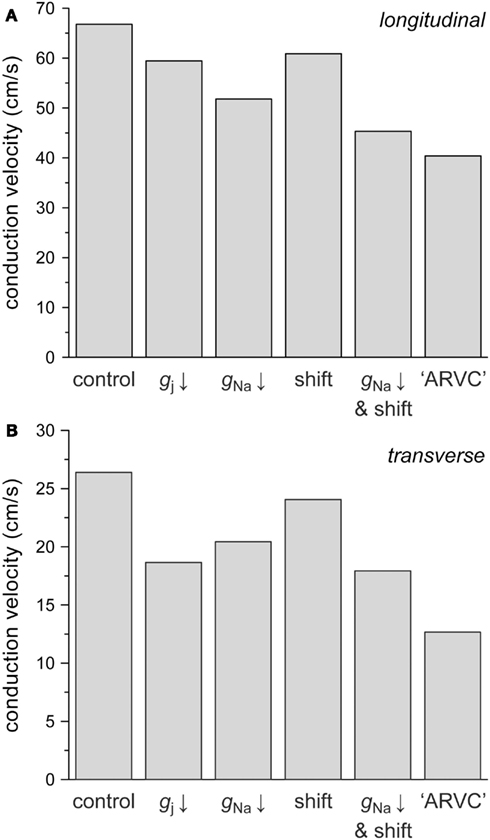
Figure 8. Effect of a 50% decrease in gap junctional conductance (labeled “g_j ↓”), a 50% decrease in sodium current conductance (“g_Na ↓”) or a −15 mV shift in the I_Na steady-state inactivation curve (“shift”), as implicated in ARVC, on (A) longitudinal and (B) transverse conduction velocity. Also shown are the combined effects of a 50% decrease in g_Na and a −15 mV shift (“g_Na ↓ and shift”) and the combined effects of a 50% decrease in g_j, a 50% decrease in g_Na and a −15 mV shift (“ARVC”).

The 50% decrease in gap junctional conductance reduces θ_L by 11% and θ_T by 29%, again demonstrating that transverse conduction is more sensitive to gap junctional conductance than longitudinal conduction. The 50% decrease in I_Na conductance reduces θ_L by 22% and θ_T by 23%, whereas the −15 mV shift in steady-state inactivation reduces both θ_L and θ_T by 9%. In combination, the decrease in I_Na conductance and shift in inactivation result in a 32% decrease in both θ_L and θ_T. Under ARVC like conditions, not taking into account a potential change in cell dimensions, θ_L and θ_T are decreased by 40 and 52%, respectively.

We have also run simulations in which the ARVC like conditions were extended with a tentative 20% increase in cell width (or cell radius), as suggested by the 40% increase in ventricular cardiomyocyte cross-sectional area in a transgenic mouse model of ARVC (Yang et al., 2006). With a 39% decrease in θ_L instead of the above 40%, the effect on θ_L is small, as might be expected from the “cross-over” at 4 μS in Figure 4C. The effect on θ_T is larger, with a decrease in θ_T of 48% instead of the above 52%.

Discussion

We used computer simulations to assess the functional implications of gap junction remodeling and down-regulation of I_Na, as implicated in ARVC. We investigated how conduction velocity is related to both structural determinants of conduction (gap junctional conductance, cell length and width, myoplasmic resistivity) and active membrane properties (conductance and kinetics of sodium current). Our simulation results show that the slowing effects of gap junction remodeling per se are only moderate and that conduction may be more sensitive to changes in membrane excitability, i.e., in I_Na, which is line with experimental data obtained from mouse models of reduced excitability or intercellular coupling (Stein et al., 2011). Our data also show that θ_T is more sensitive to changes in g_j than θ_L, which agrees with experimental studies in which uncoupling agents were used to induce a uniform reduction in g_j (see Dhein et al., 1999; and primary references cited therein).

Model Parameters

We have used a control value of 8 μS for the gap junctional conductance between ventricular cells. This value is higher than values that have been used in previous simulation studies, e.g., 0.77 μS (Spach et al., 2000) and 2.5 μS (Shaw and Rudy, 1997; Kucera et al., 2002). Our value is, however, based on data from literature and yields a value for longitudinal conduction velocity that is in accordance with data from human ventricle as obtained by Taggart et al. (2000). The θ_L value of 67 cm/s may seem somewhat large compared to the mean value of ≈56 cm/s obtained from “classic” animal studies as summarized by Kléber et al. (2001). However, more recent studies typically show θ_L values near 65 cm/s in mouse (Gutstein et al., 2001a), guinea pig (Girouard et al., 1996), and dog (Watanabe et al., 2000).

Our myocyte dimensions follow from the single human ventricular cell model we employed (Priebe and Beuckelmann, 1998), which in turn uses the same dimensions as the Luo-Rudy model of a guinea pig-type ventricular myocyte (Luo and Rudy, 1994). The model values for myocyte length (100 μm) and width (≈20 μm) are small compared to the values of 136 ± 4 and 26.2 ± 1.3 μm (mean ± SEM, n = 210), respectively, reported for human ventricular myocytes (Zafeiridis et al., 1998), which are similar to the dimensions reported for guinea pig and rabbit myocytes (Cooklin et al., 1997; de Groot et al., 2003; Wiegerinck et al., 2006). The apparent underestimation of cell length and width does not affect the simulation results to a large extent. A 30% increase in the control values for both cell length and width, to match these experimental data, increases θ_L by 9% and decreases θ_T by 1% (data not shown).

Our simulation results identify myoplasmic resistivity as an important determinant of θ_L, but not θ_T. Unfortunately, this parameter is difficult to determine experimentally (see, Kléber and Riegger, 1987). As mentioned above, the model value of 150 Ω cm is at the lower end of values used in simulation studies. However, if we had for example set ρ_myo to 250 Ω cm, θ_L would have been limited to values below 60 cm/s, irrespective of the value of g_j (Figure 5A). On the other hand, our value of 150 Ω cm is in line with a simulation study of propagation in synthetic strands of cultured neonatal ventricular myocytes, in which the fit to experimental data required a myoplasmic resistivity of 124 Ω cm (Thomas et al., 2003).

Limitations

In this study, we have assessed action potential propagation in linear strands with a simple and uniform arrangement of cells within the strands. Such reconstruction represents the propagation of broad planar wavefronts, either on the myocardial surface or transmurally, from endocardium to epicardium, during normal ventricular excitation. Thus, the complex architecture of the cardiac syncytium is much simplified and some important determinants of cardiac activation, including current-to-load mismatch (Derksen et al., 2003) and wavefront curvature (Fast and Kléber, 1997; Chow et al., 2002), have been excluded from our analysis. In particular, enhanced anisotropy may have an attenuating effect on the reduction in longitudinal conduction velocity in case of impaired membrane excitability and intercellular coupling by forcing intercellular current flow in the axial direction (Wilders et al., 2000; Stein et al., 2009).

We have used the human ventricular cell model by Priebe and Beuckelmann (1998). This model dates from the late 1990s, but seems suited for the present study that focuses on generic properties of cardiac tissue. Notably, the cell dimensions and the sodium current equations are identical to those of the original and updated versions of the Luo-Rudy dynamic model of mammalian subepicardial ventricular myocytes that we and others employed in more recent studies (Wiegerinck et al., 2006; Petitprez et al., 2008; Gaur et al., 2009). Although our simulations are of a generic nature, we cannot exclude that our results and conclusions are to some extent dependent on the chosen ventricular cell model.

We have subjected our simulated strands to relatively “mild” ARVC related conditions. First, gap junctional conductance and sodium current conductance have been reduced by 50%, whereas the actual reduction may be larger. Second, we have limited the shift in the steady-state I_Na inactivation curve to −15 mV, whereas the actual shift may be as large as −20 mV (Sato et al., 2009). Third, we have not investigated the effects of high frequency stimulation or the experimentally observed prolongation in the recovery from I_Na inactivation (Sato et al., 2009), which may both impair conduction. Indeed, preliminary simulations with 2-Hz stimulation and a −20 mV shift in inactivation result in 2:1 conduction block, both longitudinally and transversally (data not shown). The latter results underscore the potentially important role of sodium current kinetics in ARVC rather than gap junctional conductance or I_Na density, as do the simulation results of Deo et al. (2011). It should, however, be noted that a direct comparison with the study by Deo et al. (2011) is not possible, because this study aimed at simulating conduction in a two-dimensional isotropic monolayer of rat ventricular myocytes with a conduction velocity of ≈25 cm/s.

Implications for Arrhythmogenesis

Although a causative role in vivo remains speculative, gap junction remodeling has been postulated to contribute to the increased propensity for arrhythmogenesis in the diseased myocardium of ARVC patients. Gap junction remodeling could potentially induce significant slowing of conduction, thereby facilitating micro-reentrant arrhythmias. However, our simulation results demonstrate that a 50% reduction in gap junctional conductance, as expected from the ≈50% reduction in Cx43 expression in diseased hearts, gives rise to relatively small changes in conduction velocity. In line with these simulation results, Cx43^+/− mice, which show a ≈50% decrease in Cx43 expression, are not prone to arrhythmias, as tested by subjecting them to aggressive extra-stimulation protocols (Thomas et al., 1998; Vaidya et al., 2001).

Given the relatively small effects of gap junctional remodeling on conduction velocity, other factors, like (changes in) membrane excitability and cell dimensions, come into play as contributors to arrhythmogenesis. However, our simulations demonstrate that neither the observed decrease in sodium current density, as a main determinant of membrane excitability, nor the observed increase in myocyte cross-sectional area would give rise to highly significant changes in conduction velocity. As discussed above, changes in sodium current kinetics, rather than gap junctional conductance or sodium current density, may play an important role in the arrhythmogenesis of ARVC. In particular, incomplete recovery from inactivation during extra-stimuli and premature beats may play an important role in triggering ARVC related arrhythmias.

The prediction from our model that a 50% decrease in Cx43 levels would not have a major effect on conduction velocity may seem to question the idea that a reduced Cx43 expression contributes to the arrhythmogenesis of ARVC. However, it should be kept in mind – as a common observation that seems also applicable to ARVC – that the extent of Cx43 reduction may vary considerably between patients, sometimes reaching a reduction of >90% of control values, where conduction velocity becomes steeply dependent on gap junctional conductance (Figure 2), and that such reduction is often superimposed on heterogeneity of Cx43 distribution (Dupont et al., 2001; Severs, 2001). A high degree of cellular uncoupling may occur locally without affecting global conduction characteristics, and may predispose to the formation of unidirectional block and reentry. This is in line with the observation that Cx43^−/− conditional knockout mice, which show a large and heterogeneous decrease in Cx43 expression but only a moderate decrease in conduction velocity, are extremely prone to arrhythmias (Gutstein et al., 2001a; van Rijen et al., 2004), and with the observation of conduction defects in a murine model of heterogeneous gap junction channel expression (Gutstein et al., 2001b). If heterogeneity of gap junction remodeling occurs in combination with down-regulation of sodium current, it may create the substrate for the ventricular tachyarrhythmias observed in ARVC.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Basso, C., Bauce, B., Corrado, D., and Thiene, G. (2012). Pathophysiology of arrhythmogenic cardiomyopathy. Nat. Rev. Cardiol. 9, 223–233.

CrossRef Full Text

Basso, C., Corrado, D., Marcus, F. I., Nava, A., and Thiene, G. (2009). Arrhythmogenic right ventricular cardiomyopathy. Lancet 373, 1289–1300.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Basso, C., Czarnowska, E., Della Barbera, M., Bauce, B., Beffagna, G., Wlodarska, E. K., Pilichou, K., Ramondo, A., Lorenzon, A., Wozniek, O., Corrado, D., Daliento, L., Danieli, G. A., Valente, M., Nava, A., Thiene, G., and Rampazzo, A. (2006). Ultrastructural evidence of intercalated disc remodelling in arrhythmogenic right ventricular cardiomyopathy: an electron microscopy investigation on endomyocardial biopsies. Eur. Heart J. 27, 1847–1854.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Basso, C., Fox, P. R., Meurs, K. M., Towbin, J. A., Spier, A. W., Calabrese, F., Maron, B. J., and Thiene, G. (2004). Arrhythmogenic right ventricular cardiomyopathy causing sudden cardiac death in Boxer dogs: a new animal model of human disease. Circulation 109, 1180–1185.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bhuiyan, Z. A., Jongbloed, J. D. H., van der Smagt, J., Lombardi, P. M., Wiesfeld, A. C. P., Nelen, M., Schouten, M., Jongbloed, R., Cox, M. G. P. J., van Wolferen, M., Rodriguez, L. M., van Gelder, I. C., Bikker, H., Suurmeijer, A. J. H., van den Berg, M. P., Mannens, M. M. A. M., Hauer, R. N. W., Wilde, A. A. M., and van Tintelen, J. P. (2009). Desmoglein-2 and desmocollin-2 mutations in Dutch arrhythmogenic right ventricular dysplasia/cardiomypathy patients: results from a multicenter study. Circ. Cardiovasc. Genet. 2, 418–427.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chow, A. W. C., Schilling, R. J., Davies, D. W., and Peters, N. S. (2002). Characteristics of wavefront propagation in reentrant circuits causing human ventricular tachycardia. Circulation 105, 2172–2178.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cooklin, M., Wallis, W. R. J., Sheridan, D. J., and Fry, C. H. (1997). Changes in cell-to-cell electrical coupling associated with left ventricular hypertrophy. Circ. Res. 80, 765–771.

Pubmed Abstract | Pubmed Full Text

de Groot, J. R., Schumacher, C. A., Verkerk, A. O., Baartscheer, A., Fiolet, J. W. T., and Coronel, R. (2003). Intrinsic heterogeneity in repolarization is increased in isolated failing rabbit cardiomyocytes during simulated ischemia. Cardiovasc. Res. 59, 705–714.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

den Haan, A. D., Tan, B. Y., Zikusoka, M. N., Lladó, L. I., Jain, R., Daly, A., Tichnell, C., James, C., Amat-Alarcon, N., Abraham, T., Russell, S. D., Bluemke, D. A., Calkins, H., Dalal, D., and Judge, D. P. (2009). Comprehensive desmosome mutation analysis in North Americans with arrhythmogenic right ventricular dysplasia/cardiomyopathy. Circ. Cardiovasc. Genet. 2, 428–435.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Deo, M., Sato, P. Y., Musa, H., Lin, X., Pandit, S. V., Delmar, M., and Berenfeld, O. (2011). Relative contribution of changes in sodium current versus intercellular coupling on reentry initiation in 2-dimensional preparations of plakophilin-2-deficient cardiac cells. Heart Rhythm 8, 1740–1748.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Derksen, R., van Rijen, H. V. M., Wilders, R., Tasseron, S., Hauer, R. N. W., Rutten, W. L. C., and de Bakker, J. M. T. (2003). Tissue discontinuities affect conduction velocity restitution: a mechanism by which structural barriers may promote wave break. Circulation 108, 882–888.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Desplantez, T., McCain, M. L., Beauchamp, P., Rigoli, G., Rothen-Rutishauser, B., Parker, K. K., and Kleber, A. G. (2012). Connexin43 ablation in foetal atrial myocytes decreases electrical coupling, partner connexins, and sodium current. Cardiovasc. Res. 94, 58–65.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dhein, S., Krusemann, K., and Schaefer, T. (1999). Effects of the gap junction uncoupler palmitoleic acid on the activation and repolarization wavefronts in isolated rabbit hearts. Br. J. Pharmacol. 128, 1375–1384.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dupont, E., Matsushita, T., Kaba, R., Vozzi, C., Coppen, S. R., Khan, N., Kaprielian, R., Yacoub, M. H., and Severs, N. J. (2001). Altered connexin expression in human congestive heart failure. J. Mol. Cell. Cardiol. 33, 359–371.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fast, V. G., and Kléber, A. G. (1997). Role of wavefront curvature in propagation of cardiac impulse. Cardiovasc. Res. 33, 258–271.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fox, P. R., Maron, B. J., Basso, C., Liu, S. K., and Thiene, G. (2000). Spontaneously occurring arrhythmogenic right ventricular cardiomyopathy in the domestic cat: a new animal model similar to the human disease. Circulation 102, 1863–1870.

Pubmed Abstract | Pubmed Full Text

Freel, K. M., Morrison, L. R., Thompson, H., and Else, R. W. (2010). Arrhythmogenic right ventricular cardiomyopathy as a cause of unexpected cardiac death in two horses. Vet. Rec. 166, 718–721.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gaur, N., Rudy, Y., and Hool, L. (2009). Contributions of ion channel currents to ventricular action potential changes and induction of early afterdepolarizations during acute hypoxia. Circ. Res. 105, 1196–1203.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerdes, A. M., Kellerman, S. E., Moore, J. A., Muffly, K. E., Clark, L. C., Reaves, P. Y., Malec, K. B., McKeown, P. P., and Schocken, D. D. (1992). Structural remodeling of cardiac myocytes in patients with ischemic cardiomyopathy. Circulation 86, 426–430.

Pubmed Abstract | Pubmed Full Text

Girouard, S. D., Pastore, J. M., Laurita, K. R., Gregory, K. W., and Rosenbaum, D. S. (1996). Optical mapping in a new guinea pig model of ventricular tachycardia reveals mechanisms for multiple wavelengths in a single reentrant circuit. Circulation 93, 603–613.

Pubmed Abstract | Pubmed Full Text

Gomes, J., Finlay, M., Ahmed, A. K., Ciaccio, E. J., Asimaki, A., Saffitz, J. E., Quarta, G., Nobles, M., Syrris, P., Chaubey, S., McKenna, W. J., Tinker, A., and Lambiase, P. D. (2012). Electrophysiological abnormalities precede overt structural changes in arrhythmogenic right ventricular cardiomyopathy due to mutations in desmoplakin: a combined murine and human study. Eur. Heart J. doi:10.1093/eurheartj/ehr472

CrossRef Full Text

Gutstein, D. E., Morley, G. E., Tamaddon, H., Vaidya, D., Schneider, M. D., Chen, J., Chien, K. R., Stuhlmann, H., and Fishman, G. I. (2001a). Conduction slowing and sudden arrhythmic death in mice with cardiac-restricted inactivation of connexin43. Circ. Res. 88, 333–339.

Gutstein, D. E., Morley, G. E., Vaidya, D., Liu, F., Chen, J., Stuhlmann, H., and Fishman, G. I. (2001b). Heterogeneous expression of gap junction channels in the heart leads to conduction defects and ventricular dysfunction. Circulation 104, 1194–1199.

CrossRef Full Text

Harvey, A. M., Battersby, I. A., Faena, M., Fews, D., Darke, P. G., and Ferasin, L. (2005). Arrhythmogenic right ventricular cardiomyopathy in two cats. J. Small Anim. Pract. 46, 151–156.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jacoby, D., and McKenna, W. J. (2012). Genetics of inherited cardiomyopathy. Eur. Heart J. 33, 296–304.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jansen, J. A., Noorman, M., Musa, H., Stein, M., de Jong, S., van der Nagel, R., Hund, T. J., Mohler, P. J., Vos, M. A., van Veen, T. A., de Bakker, J. M., Delmar, M., and van Rijen, H. V. (2012). Reduced heterogeneous expression of Cx43 results in decreased Nav1.5 expression and reduced sodium current that accounts for arrhythmia vulnerability in conditional Cx43 knockout mice. Heart Rhythm 9, 600–607.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jongsma, H. J., and Wilders, R. (2000). Gap junctions in cardiovascular disease. Circ. Res. 86, 1193–1197.

Pubmed Abstract | Pubmed Full Text

Kanno, S., and Saffitz, J. E. (2001). The role of myocardial gap junctions in electrical conduction and arrhythmogenesis. Cardiovasc. Pathol. 10, 169–177.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kaplan, S. R., Gard, J. J., Protonotarios, N., Tsatsopoulou, A., Spiliopoulou, C., Anastasakis, A., Squarcioni, C. P., McKenna, W. J., Thiene, G., Basso, C., Brousse, N., Fontaine, G., and Saffitz, J. E. (2004). Remodeling of myocyte gap junctions in arrhythmogenic right ventricular cardiomyopathy due to a deletion in plakoglobin (Naxos disease). Heart Rhythm 1, 3–11.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kapplinger, J. D., Landstrom, A. P., Salisbury, B. A., Callis, T. E., Pollevick, G. D., Tester, D. J., Cox, M. G. P. J., Bhuiyan, Z., Bikker, H., Wiesfeld, A. C. P., Hauer, R. N. W., van Tintelen, J. P., Jongbloed, J. D. H., Calkins, H., Judge, D. P., Wilde, A. A. M., and Ackerman, M. J. (2011). Distinguishing arrhythmogenic right ventricular cardiomyopathy/dysplasia-associated mutations from background genetic noise. J. Am. Coll. Cardiol. 57, 2317–2327.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kaprielian, R., Gunning, M., Dupont, E., Sheppard, M. N., Rothery, S. M., Underwood, R., Pennell, D. J., Fox, K., Pepper, J., Poole-Wilson, P. A., and Severs, N. J. (1998). Downregulation of immunodetectable connexin43 and decreased gap junction size in the pathogenesis of chronic hibernation in the human left ventricle. Circulation 97, 651–660.

Pubmed Abstract | Pubmed Full Text

Kléber, A. G., Janse, M. J., and Fast, V. G. (2001). “Normal and abnormal conduction in the heart,” in Handbook of Physiology, Section 2: The Cardiovascular System, Volume I: The Heart, eds. E. Page, H. A. Fozzard, and R. J. Solaro (New York, NY: Oxford University Press), 455–530.

Kléber, A. G., and Riegger, C. B. (1987). Electrical constants of arterially perfused rabbit papillary muscle. J. Physiol. 385, 307–324.

Pubmed Abstract | Pubmed Full Text

Kostin, S., Rieger, M., Dammer, S., Hein, S., Richter, M., Klövekorn, W. P., Bauer, E. P., and Schaper, J. (2003). Gap junction remodeling and altered connexin43 expression in the failing human heart. Mol. Cell. Biochem. 242, 135–144.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kucera, J. P., Rohr, S., and Rudy, Y. (2002). Localization of sodium channels in intercalated disks modulates cardiac conduction. Circ. Res. 91, 1176–1182.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lahtinen, A. M., Lehtonen, E., Marjamaa, A., Kaartinen, M., Heliö, T., Porthan, K., Oikarinen, L., Toivonen, L., Swan, H., Jula, A., Peltonen, L., Palotie, A., Salomaa, V., and Kontula, K. (2011). Population-prevalent desmosomal mutations predisposing to arrhythmogenic right ventricular cardiomyopathy. Heart Rhythm 8, 1214–1221.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Luo, C. H., and Rudy, Y. (1994). A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ. Res. 74, 1071–1096.

Pubmed Abstract | Pubmed Full Text

Maltsev, V. A., Sabbab, H. N., and Undrovinas, A. I. (2002). Down-regulation of sodium current in chronic heart failure: effect of long-term therapy with carvedilol. Cell. Mol. Life Sci. 59, 1561–1568.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Oxford, E. M., Danko, C. G., Kornreich, B. G., Maass, K., Hemsley, S. A., Raskolnikov, D., Fox, P. R., Delmar, M., and Moïse, N. S. (2011). Ultrastructural changes in cardiac myocytes from Boxer dogs with arrhythmogenic right ventricular cardiomyopathy. J. Vet. Cardiol. 13, 101–113.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Oxford, E. M., Musa, H., Maass, K., Coombs, W., Taffet, S. M., and Delmar, M. (2007). Connexin43 remodeling caused by inhibition of plakophilin-2 expression in cardiac cells. Circ. Res. 101, 703–711.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Peters, N. S., Green, C. R., Poole-Wilson, P. A., and Severs, N. J. (1993). Reduced content of connexin43 gap junctions in ventricular myocardium from hypertrophied and ischemic human hearts. Circulation 88, 864–875.

Pubmed Abstract | Pubmed Full Text

Peters, S., Trümmel, M., and Meyners, W. (2004). Prevalence of right ventricular dysplasia-cardiomyopathy in a non-referral hospital. Int. J. Cardiol. 97, 499–501.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Petitprez, S., Jespersen, T., Pruvot, E., Keller, D. I., Corbaz, C., Schläpfer, J., Abriel, H., and Kucera, J. P. (2008). Analyses of a novel SCN5A mutation (C1850S): conduction vs. repolarization disorder hypotheses in the Brugada syndrome. Cardiovasc. Res. 78, 494–504.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Priebe, L., and Beuckelmann, D. J. (1998). Simulation study of cellular electric properties in heart failure. Circ. Res. 82, 1206–1223.

Pubmed Abstract | Pubmed Full Text

Rudy, Y., and Quan, W. L. (1987). A model study of the effects of the discrete cellular structure on electrical propagation in cardiac tissue. Circ. Res. 61, 815–823.

Pubmed Abstract | Pubmed Full Text

Rush, S., and Larsen, H. (1978). A practical algorithm for solving dynamic membrane equations. IEEE Trans. Biomed. Eng. 25, 389–392.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Saffitz, J. E. (2009). Arrhythmogenic cardiomyopathy and abnormalities of cell-to-cell coupling. Heart Rhythm 6, S62–S65.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sato, P. Y., Musa, H., Coombs, W., Guerrero-Serna, G., Patiño, G. A., Taffet, S. M., Isom, L. L., and Delmar, M. (2009). Loss of plakophilin-2 expression leads to decreased sodium current and slower conduction velocity in cultured cardiac myocytes. Circ. Res. 105, 523–526.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sen-Chowdhry, S., and McKenna, W. J. (2012). Sudden death from genetic and acquired cardiomyopathies. Circulation 125, 1563–1576.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sen-Chowdhry, S., Morgan, R. D., Chambers, J. C., and McKenna, W. J. (2010). Arrhythmogenic cardiomyopathy: etiology, diagnosis, and treatment. Annu. Rev. Med. 61, 233–253.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Severs, N. J. (2001). Gap junction remodeling and cardiac arrhythmogenesis: cause or coincidence? J. Cell. Mol. Med. 5, 355–366.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shaw, R. M., and Rudy, Y. (1997). Ionic mechanisms of propagation in cardiac tissue: roles of the sodium and L-type calcium currents during reduced excitability and decreased gap junction coupling. Circ. Res. 81, 727–741.

Pubmed Abstract | Pubmed Full Text

Smith, J. H., Green, C. R., Peters, N. S., Rothery, S., and Severs, N. J. (1991). Altered patterns of gap junction distribution in ischemic heart disease: an immunohistochemical study of human myocardium using laser scanning confocal microscopy. Am. J. Pathol. 139, 801–821.

Pubmed Abstract | Pubmed Full Text

Spach, M. S., Heidlage, F. J., Dolber, P. C., and Barr, R. C. (2000). Electrophysiological effects of remodeling cardiac gap junctions and cell size: experimental and model studies of normal cardiac growth. Circ. Res. 86, 302–311.

Pubmed Abstract | Pubmed Full Text

Stein, M., van Veen, T. A. B., Hauer, R. N. W., de Bakker, J. M. T., and van Rijen, H. V. M. (2011). A 50% reduction of excitability but not of intercellular coupling affects conduction velocity restitution and activation delay in the mouse heart. PLoS ONE 6, e20310. doi:10.1371/journal.pone.0020310

CrossRef Full Text

Stein, M., van Veen, T. A. B., Remme, C. A., Boulaksil, M., Noorman, M., van Stuijvenberg, L., van der Nagel, R., Bezzina, C. R., Hauer, R. N. W., de Bakker, J. M. T., and van Rijen, H. V. M. (2009). Combined reduction of intercellular coupling and membrane excitability differentially affects transverse and longitudinal cardiac conduction. Cardiovasc. Res. 83, 52–60.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sui, G. P., Coppen, S. R., Dupont, E., Rothery, S., Gillespie, J., Newgreen, D., Severs, N. J., and Fry, C. H. (2003). Impedance measurements and connexin expression in human detrusor muscle from stable and unstable bladders. BJU Int. 92, 297–305.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Taggart, P., Sutton, P. M. I., Opthof, T., Coronel, R., Trimlett, R., Pugsley, W., and Kallis, P. (2000). Inhomogeneous transmural conduction during early ischaemia in patients with coronary artery disease. J. Mol. Cell. Cardiol. 32, 621–630.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thiene, G., Corrado, D., and Basso, C. (2007). Arrhythmogenic right ventricular cardiomyopathy/dysplasia. Orphanet J. Rare Dis. 2, 45. doi:10.1186/1750-1172-2-45

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thomas, S. A., Schuessler, R. B., Berul, C. I., Beardslee, M. A., Beyer, E. C., Mendelsohn, M. E., and Saffitz, J. E. (1998). Disparate effects of deficient expression of connexin43 on atrial and ventricular conduction: evidence for chamber specific molecular determinants of conduction. Circulation 97, 686–691.

Pubmed Abstract | Pubmed Full Text

Thomas, S. P., Kucera, J. P., Bircher-Lehmann, L., Rudy, Y., Saffitz, J. E., and Kléber, A. G. (2003). Impulse propagation in synthetic strands of neonatal cardiac myocytes with genetically reduced levels of connexin43. Circ. Res. 92, 1209–1216.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vaidya, D., Tamaddon, H. S., Lo, C. W., Taffet, S. M., Delmar, M., Morley, G. E., and Jalife, J. (2001). Null mutation of connexin43 causes slow propagation of ventricular activation in the late stages of mouse embryonic development. Circ. Res. 88, 1196–1202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Rijen, H. V. M., Eckardt, D., Degen, J., Theis, M., Ott, T., Willecke, K., Jongsma, H. J., Opthof, T., and de Bakker, J. M. T. (2004). Slow conduction and enhanced anisotropy increase the propensity for ventricular tachyarrhythmias in adult mice with induced deletion of connexin43. Circulation 109, 1048–1055.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Watanabe, T., Yamaki, M., Tachibana, H., Yamauchi, S., Kubota, I., and Tomoike, H. (2000). Anisotropic effects of sodium channel blockers on the wavelength for ventricular excitation in dogs. Jpn. Circ. J. 64, 689–694.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wiegerinck, R. F., Verkerk, A. O., Belterman, C. N., van Veen, T. A. B., Baartscheer, A., Opthof, T., Wilders, R., de Bakker, J. M. T., and Coronel, R. (2006). Larger cell size in rabbits with heart failure increases myocardial conduction velocity and QRS duration. Circulation 113, 806–813.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilders, R., and Jongsma, H. J. (1992). Limitations of the dual voltage clamp method in assaying conductance and kinetics of gap junction channels. Biophys. J. 63, 942–953.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilders, R., Wagner, M. B., Golod, D. A., Kumar, R., Wang, Y. G., Goolsby, W. N., Joyner, R. W., and Jongsma, H. J. (2000). Effects of anisotropy on the development of cardiac arrhythmias associated with focal activity. Pflügers Arch. 441, 301–312.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yang, Z., Bowles, N. E., Scherer, S. E., Taylor, M. D., Kearney, D. L., Ge, S., Nadvoretskiy, V. V., DeFreitas, G., Carabello, B., Brandon, L. I., Godsel, L. M., Green, K. J., Saffitz, J. E., Li, H., Danieli, G. A., Calkins, H., Marcus, F., and Towbin, J. A. (2006). Desmosomal dysfunction due to mutations in desmoplakin causes arrhythmogenic right ventricular dysplasia/cardiomyopathy. Circ. Res. 99, 646–655.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zafeiridis, A., Jeevanandam, V., Houser, S. R., and Margulies, K. B. (1998). Regression of cellular hypertrophy after left ventricular assist device support. Circulation 98, 656–662.

Pubmed Abstract | Pubmed Full Text