- 1 Department of Biomedical Engineering, University of Virginia, Charlottesville, VA, USA
- 2 Department of Biomedical Engineering, Texas A&M University, College Station, TX, USA
- 3 Department of Biomedical Engineering, Yale University, New Haven, CT, USA
Agent-based models (ABMs) represent a novel approach to study and simulate complex mechano chemo-biological responses at the cellular level. Such models have been used to simulate a variety of emergent responses in the vasculature, including angiogenesis and vasculogenesis. Although not used previously to study large vessel adaptations, we submit that ABMs will prove equally useful in such studies when combined with well-established continuum models to form multi-scale models of tissue-level phenomena. In order to couple agent-based and continuum models, however, there is a need to ensure that each model faithfully represents the best data available at the relevant scale and that there is consistency between models under baseline conditions. Toward this end, we describe the development and verification of an ABM of endothelial and smooth muscle cell responses to mechanical stimuli in a large artery. A refined rule-set is proposed based on a broad literature search, a new scoring system for assigning confidence in the rules, and a parameter sensitivity study. To illustrate the utility of these new methods for rule selection, as well as the consistency achieved with continuum-level models, we simulate the behavior of a mouse aorta during homeostasis and in response to both transient and sustained increases in pressure. The simulated responses depend on the altered cellular production of seven key mitogenic, synthetic, and proteolytic biomolecules, which in turn control the turnover of intramural cells and extracellular matrix. These events are responsible for gross changes in vessel wall morphology. This new ABM is shown to be appropriately stable under homeostatic conditions, insensitive to transient elevations in blood pressure, and responsive to increased intramural wall stress in hypertension.
Introduction
Vascular development, homeostasis, adaptation, disease progression, and responses to injury or surgical intervention are governed, in large part, by underlying mechanobiological processes. All three primary cell types within the normal vascular wall (endothelial cells, smooth muscle cells [SMCs], and fibroblasts) and often invading monocytes/macrophages are extremely sensitive to changes in mechanical stimuli, including changes in blood flow, pressure, and axial extension (Humphrey, 2008). As more and more is learned about the complex mechanisms at molecular and cellular levels and their manifestations at the tissue level, it is becoming increasingly evident that computational modeling will need to play a greater role in integrating these vast knowledge bases, thereby deepening our understanding of both the vascular biology and the pathophysiology. Toward this end, multi-scale models hold great promise, as they allow details at different spatial and temporal scales to be modeled in the most natural way and then to be linked together in computationally efficient ways. For example, consider a natural progression of mathematical modeling of arterial adaptations from the tissue level (e.g., clinical presentation and possible surgical treatment) to the molecular level (e.g., underlying mechanism and possible pharmacologic treatment). In such cases, continuum mechanical analyses are essential for relating global loads (blood pressure and flow) to local metrics such as stress and strain; constrained mixture models (CMMs) of growth and remodeling allow one to prescribe lumped-parameter models of local cell-mediated production and turnover based on altered stresses and strains; agent-based models (ABMs) address discrete cell level activity and production of diverse molecules; molecular level models of both the mechanics (e.g., molecular dynamic models) and the reaction kinetics (e.g., intracellular signaling models) permit mechanistic considerations. Although models at each scale should be developed in ways that are most natural, we must also begin to anticipate how such models will need to be linked in multi-scale computations to ensure consistency and communication across scales.
In this paper, we present the development, refinement, and verification of a novel ABM at the cell level to facilitate linking with a CMM of vascular adaptation at the tissue level. This work is motivated by observations that the vascular wall often maintains a mechanical homeostasis through short-term changes in vascular tone and long-term changes in extracellular matrix microstructure and cell phenotype. For example, many arterial adaptations occur largely via changes in vasoactivity, proliferation, and apoptosis of SMCs, as well as production or degradation of collagens and other extracellular matrix components (Zeller and Skalak, 1998; Humphrey and Rajagopal, 2002; Dajnowiec and Langille, 2007). Since the mid-1990s, there has been considerable attention directed toward developing continuum-based (tissue level) models of large vessel adaptation. Whereas some models have focused on consequences of cell activity (Taber, 1998; Rachev et al., 2000; Tsamis et al., 2009), others have focused on the means by which these consequences are realized (Humphrey and Rajagopal, 2002). For example, by employing lumped-parameter constitutive relations for mass production and removal in evolving mechanical states, CMMs of tissue-level growth and remodeling have captured salient aspects of cerebral aneurysm enlargement (Baek et al., 2006), cerebral vasospasm (Baek et al., 2007), and adaptations to altered blood pressure and flow (Valentin et al., 2009). Such models have also been refined and verified using methods of numerical hypothesis testing and parameter sensitivity studies (Valentin and Humphrey, 2009). Our long-term goal is to couple ABMs with CMMs to enable cell-specific processes involved in cell and matrix turnover to be modeled directly, not simply via lumped-parameter constitutive relations. Toward this end, the present goal is to develop an ABM suitable for coupling with a prior CMM by ensuring appropriate inputs and outputs derived from the most reliable data and a comparable level of model verification.
Materials and Methods
ABM Design
Agent-based models, in which autonomous cells act according to a set of literature-derived rules, are capable of simulating autocrine and paracrine functions with a high level of spatial and temporal resolution. In this work, we build on our general approach to ABM design (Bailey et al., 2007; Thorne et al., 2007) to construct a new model of the mouse aorta (Figure 1). This vessel consists of an intimal monolayer of endothelial cells, a 4–6 SMC thick medial layer rich in elastin and collagens I and III, and a thin adventitial layer consisting primarily of fibroblasts and collagen I. We have neglected the adventitia in our initial model, however, because of its thinness and the lack of information on arterial fibroblast mechanobiology. Each endothelial cell or SMC is represented discretely by an agent that interacts with its environment and other agents, performing behaviors such as proliferation, apoptosis, matrix production or degradation, and growth factor production according to a literature-derived rule-set. Recalling the goal of eventually coupling this ABM with a prior CMM (Valentin et al., 2009), we matched model inputs and outputs with those of the CMM, including vessel geometry, shear stress, and circumferential stress as inputs and collagen mass and SMC number as outputs. Because the ABM assumes an essentially 2-D arterial cross-section 10 μm in thickness, SMC number was normalized and collagen mass converted for comparison with a CMM of an aortic segment of 1 cm in length. A computational time step of 6 h was also selected to match the time step of the CMM (Valentin et al., 2009). The ABM was built-in NetLogo 4.1 (Wilensky, 1999) and controlled using a MatLab (2010) script for ease of analysis of model outputs.
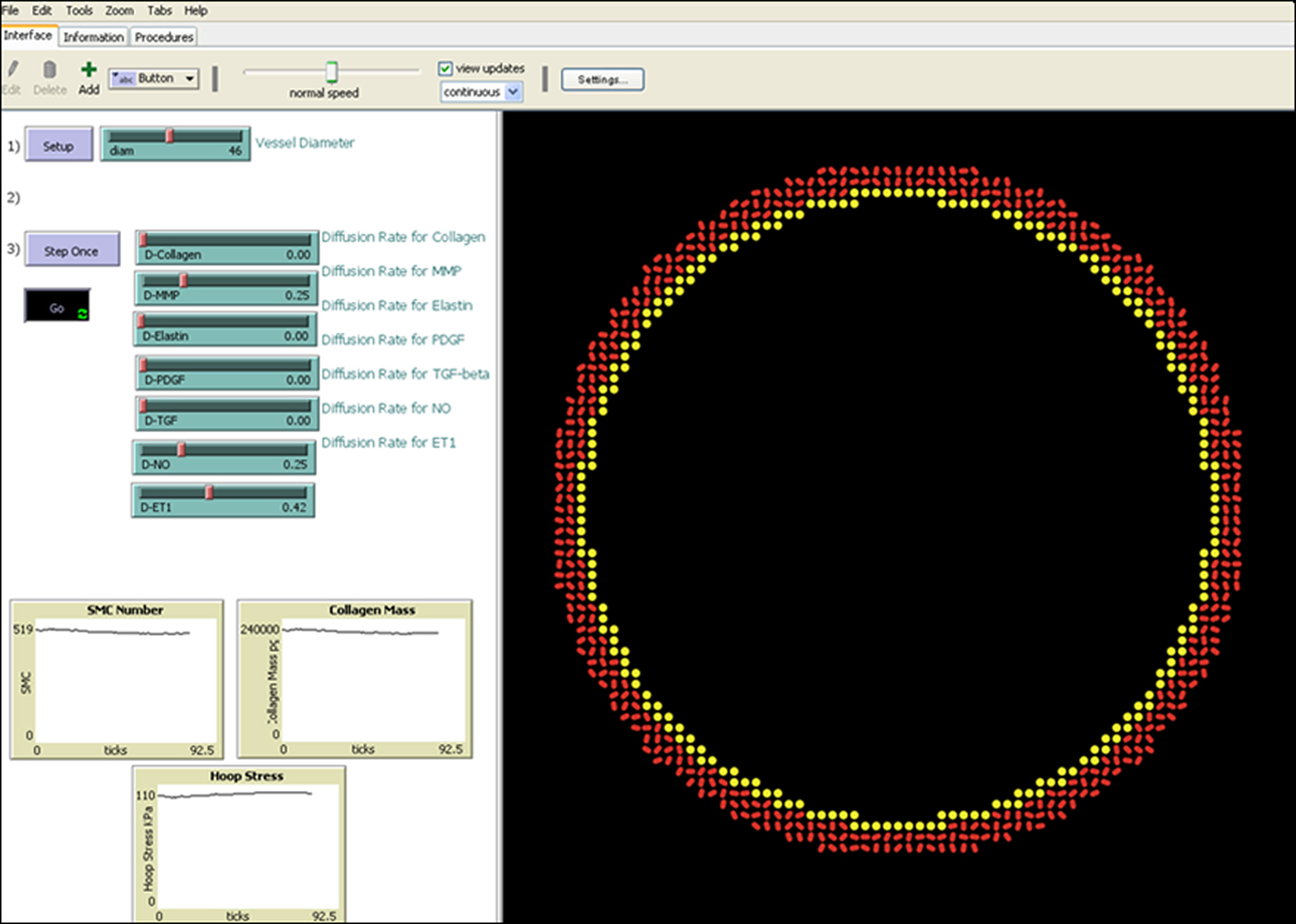
Figure 1. Screen shot of the ABM during a homeostatic run, displaying a 2-D representation of a transverse section of the model mouse abdominal aorta on the right and user controls as well as a display of progress on the left. Inner diameter of the vessel is 460 μm.
Rule Development
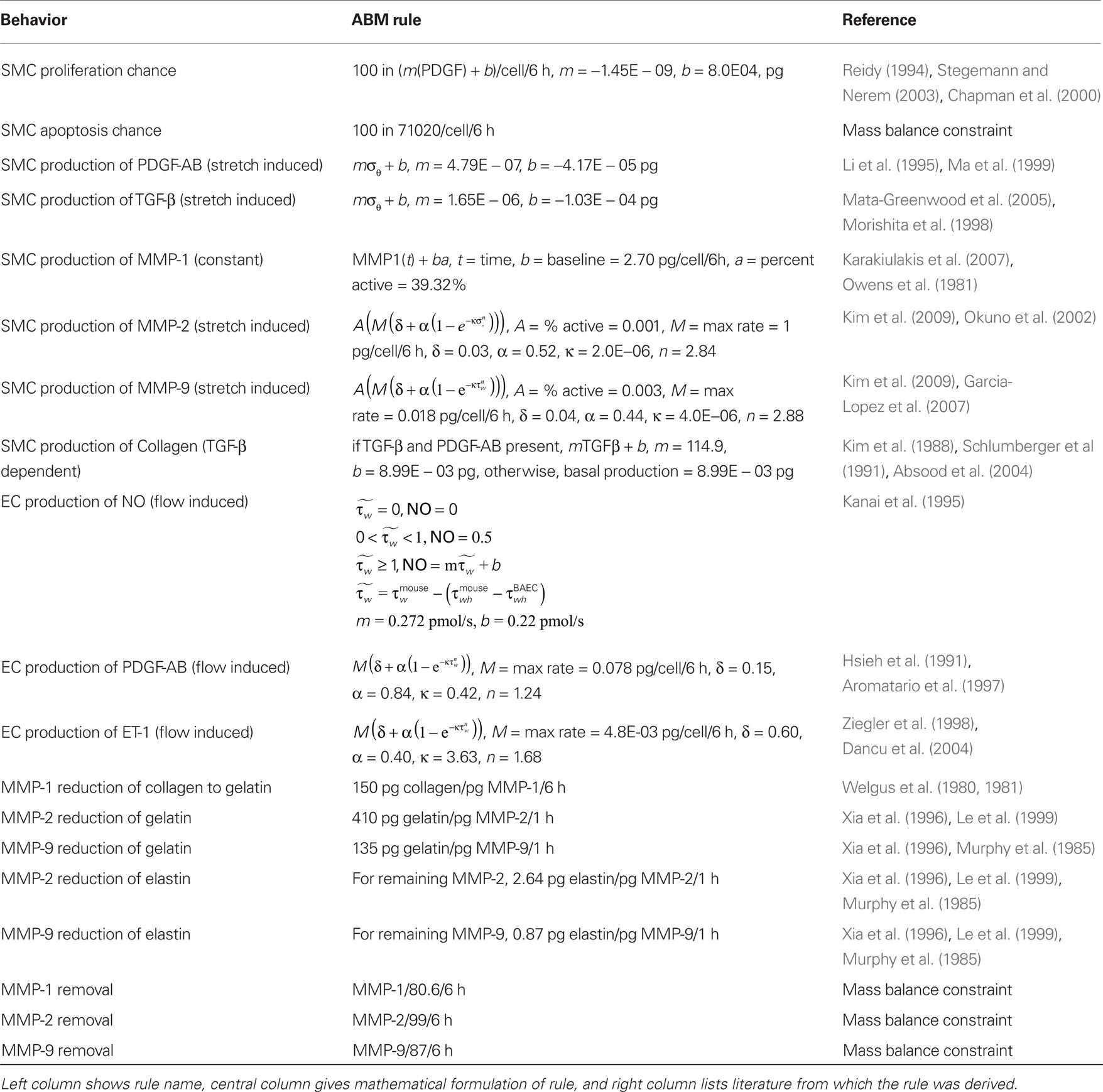
We focused our model on the cellular production of key vasoactive molecules, growth factors, and proteases involved in the mechanobiological control of arterial adaptations to altered blood pressure and flow. These molecules include nitric oxide (NO), endothelin-1 (ET-1), platelet-derived growth factor AB (PDGF-AB), transforming growth factor – beta (TGF-β), and the matrix metalloproteases 1, 2, and 9 (MMP-1, MMP-2, MMP-9). The primary structurally significant matrix proteins were assumed to be elastin and fibrillar collagen, the former of which does not turn over significantly in normal adaptations. Initial rules for the production and/or removal of these molecules, as well as their effects on the SMCs, were developed from the literature (Table 1).
Rule Scoring
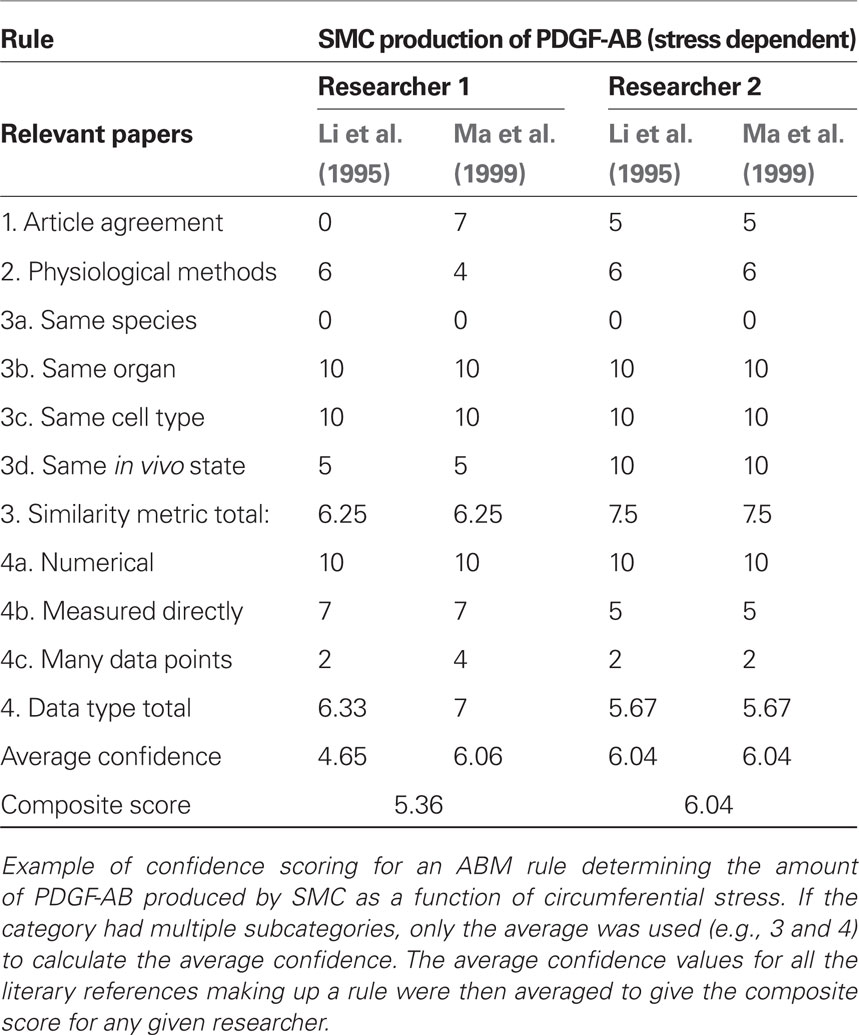
We scored the quality of each rule in the ABM using a weighted average of four different metrics. In particular, we expect rules to be more reliable when supported by multiple peer-reviewed articles, when the parameters of interest have been measured directly rather than simply extrapolated or inferred, and when the research was performed on the same cell type of interest under culture conditions most representative of the in vivo environment. Thus, points were awarded to each rule on a scale from 1 to 10 for: (1) a “literature consensus” metric representing the number of published articles that were in agreement, (2) a “physiological methods” metric that considered whether the experimental conditions were similar to the in vivo environment, (3) a “similarity metric” in which points were awarded for research using the same cell type, same organ system, same species, and same physical environmental conditions as the in silico model, and (4) a “data type” metric that accounted for whether the data underpinning the rule were numerical rather than from a textual description and whether parameters were measured directly or simply extrapolated. Table 2 shows how points were awarded for each metric. These four metrics were then averaged to produce a score between 0 and 10 for each rule. An article was determined to be “in agreement” with other articles underpinning a rule if the response to a stimulus of the same order of magnitude occurred in the same direction and was of the same order of magnitude as the response in the original paper. Because such scoring is subjective, rules were scored by two researchers and the results averaged (see example in Table 3). Rules receiving composite scores below the overall average were reexamined, re-derived if possible to improve quality, and re-scored. Rules with final scores below the new average for the rule set were deemed less reliable and thus subjected to a parametric study (see below).
Parameterization to Ensure Homeostatic Stability
Although the primary goal of numerical simulations is to predict emergent behaviors for cases where data do not exist, the models must also recover simpler cases that are well known. For example, cells and matrix turn over continually within healthy arteries, but there is no net change in geometry or properties when the turnover is balanced precisely and occurs under stable mechanical conditions. A computational model must similarly yield such “tissue maintenance” by ensuring that parameter values within relevant rule-sets balance precisely, something that should not be expected a priori when rule-sets and parameter values come from different papers. A parameter refinement study was thus performed using the genetic algorithm functions from MATLAB’s (2010) Global Optimization Toolbox to ensure long-term self-equilibrating cell proliferation versus apoptosis and collagen production versus removal under homeostatic conditions. The genetic algorithm used a population of 50 individuals for a maximum of 100 generations. The model was run for 100 simulated days (400 time steps) at healthy baseline levels of wall shear and circumferential stress for the mouse aorta (τ = 8.8 Pa and σ = 100 kPa, respectively; Humphrey, 2002; Greve et al., 2006). Because of stochasticity in the cell proliferation rules, each parameter set was simulated 100 times while respecting upper and lower bounds that were determined from the margin of error in the experimental literature. The genetic algorithm refined the literature-based parameter values for the different rules to minimize the error function:
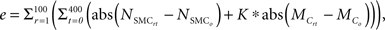
where r is the replication number, t the computational time step, NSMC the number of SMCs, Mc the accumulated mass of collagen, and K is a weight parameter that scales the collagen error to be of the same order of magnitude as SMC error. The subscript 0 denotes the original homeostatic target value.
Sensitivity Analysis
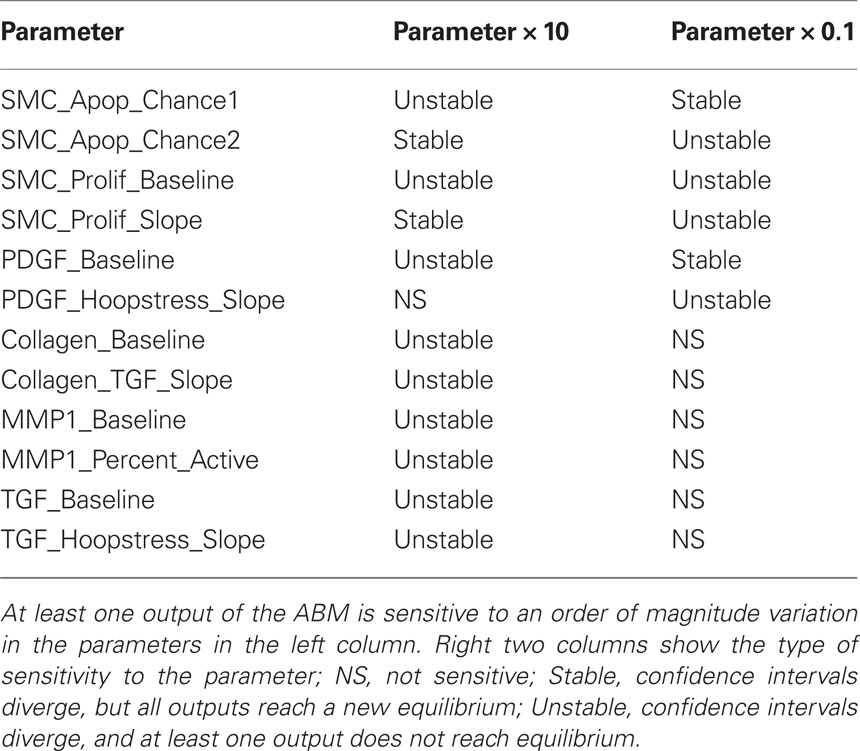
Notwithstanding refinements achieved by imposing both our new rule scoring method and the parametric homeostasis check, there is still uncertainty in rule development because of the inherent limitations in the experiments from which the rules are originally gleaned. To determine whether such uncertainties could influence the overall predictions, we also performed a one-dimensional sensitivity analysis for both homeostatic and hypertensive conditions. Each parameter was increased and decreased by an order of magnitude (i.e., 10-fold) and 100 replications were performed for each parameter variation. The 95% confidence intervals were constructed for each parameter variation and output metric (i.e., SMC number, collagen mass, hoop stress, PDGF and TGF masses). The ABM was designated as sensitive to a parameter if there was a time step beyond which the confidence interval of an output for the varied parameter diverged from the confidence interval of that output for the baseline value of that parameter. Moreover, an increasingly detailed sensitivity analysis was performed for the parameters for which the ABM was sensitive at the 10-fold level. Each of these parameters was increased and decreased by 1.5-, 2-, and 5-fold, again for 100 simulations under homeostatic and hypertensive conditions.
Transient Insensitivity
Whereas large arteries are subjected to frequent transient changes in hemodynamic loading (e.g., during standing, momentary exertion, and so forth), we do not expect such transients to result in an adaptation per se. Rather, we expect adaptations to result from consistent strenuous activities (e.g., exercise) or sustained changes in loading (e.g., hypertension or arterio-venous fistula). Stability of the ABM against transient changes in loading was tested by running the model for 100 simulated days under “healthy” homeostatic conditions (τ = 8.8 Pa and σ = 100 kPa; Greve et al., 2006) with two transient (one time step duration each) 10% increases in pressure imposed at simulated days 2 and 60. For contrast with the response to transient loading, we also simulated the response to hypertensive conditions by prescribing a 30% step increase in pressure at day 2 that persisted for the remainder of the 1000 simulation days.
Comparison to CMM Predictions
Finally, we used a CMM (Valentin et al., 2009) that has previously passed numerical hypothesis testing, homeostasis checks, and parameter sensitivity studies, as well as predicted salient features of large artery remodeling (Valentin and Humphrey, 2009; Valentin et al., 2009). The CMM was run using the same homeostatic conditions and transient and sustained increases in pressure as the ABM to provide yet another check of the validity of the ABM. Predicted changes in SMC mass by the CMM were normalized as fold changes in mass for comparison to those results from the ABM.
Results
Rule-Set Confidence Scoring
After designing the initial ABM consisting of 19 rules and 37 parameters (Table 1), each rule was then scored individually for confidence. The initial rule-set had an average score of 5.14, with scores ranging from 2.63 to 7.75. The 10 rules with confidence scores below the rule-set average of 5.14 were re-derived in an attempt to achieve higher overall confidence. After refinement, the average score increased to 5.49, with scores ranging from 3.10 to 7.75. The difference between the two investigators in average score over the entire rule-set was 0.04, while the difference on average between investigators on an individual rule was 1.52. The scoring breakdown of a representative rule governing PDGF-AB production by SMCs in response to circumferential stress is shown in Table 3. Final scores for each rule used in the model are in the Supplemental Material and Table S1. Recall that a screenshot of the model at computational time t = 20 days is in Figure 1.
Model Sensitivity
Agent-based model parameters were then individually increased and decreased by an order of magnitude to examine the sensitivity of the model’s outputs to each input, and 95% confidence intervals were plotted and used to determine sensitivity. For example, the confidence intervals for all outputs overlapped when the δ parameter in the rule for endothelin-1 production by ECs was varied systematically (Figure 2). This finding suggests that the model is insensitive to 10-fold and greater variations in this parameter. The model was considered sensitive to a parameter value when the output confidence intervals did not overlap. This analysis uncovered 12 parameters to which the model was sensitive (Table 4). A more detailed sensitivity analysis of these 12 parameters (varying parameters by as little as 1.5-fold) was then performed to examine the behavior of the model for the associated rule-sets. Note that the “sensitive parameters” were restricted to a few major categories: growth factor production in response to circumferential stress, proliferation and apoptosis of SMCs in response to growth factors, and production and degradation of collagen in response to growth factors. We found two primary types of responses to variations of these parameters, those for which the model was able to reach a new steady state (stable response) and those for which the model was unable to reach a steady state (unstable response). For example, recall from Table 1 that the rule governing likelihood of SMC proliferation in response to PDGF-AB is:
SMC_Prolif_Chance = 100 in (m(PDGF) + b)/cell/6 h,
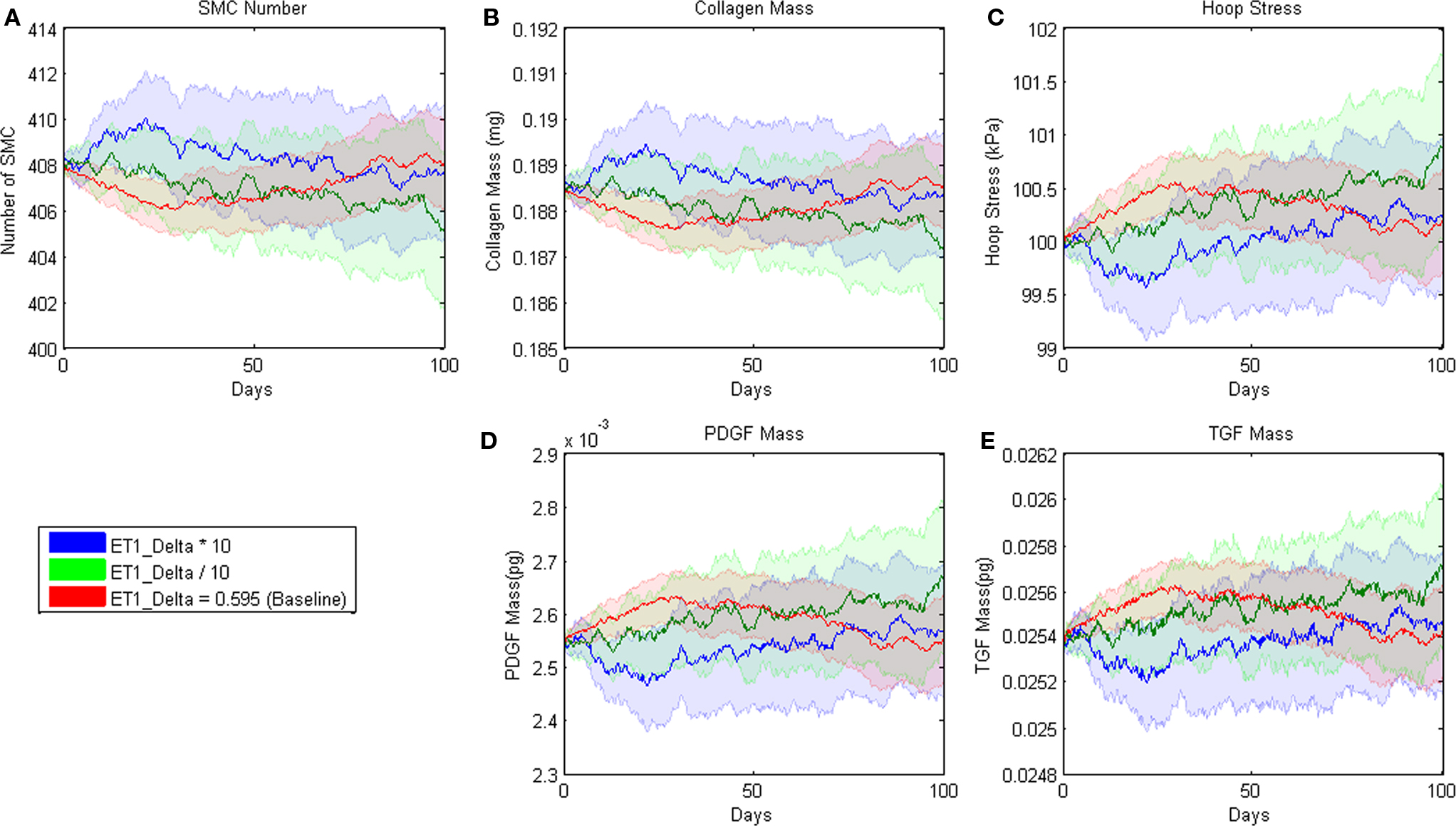
Figure 2. Parameter sensitivity analysis for the parameter δ in the rule for ET-1 production (cf. Table 3.1). This rule states that the production of ET-1 by ECs depends on wall shear stress in a sigmoid fashion. Each solid line represents the mean value based on 100 replications of the ABM. Blue indicates the response when the parameter was increased an order of magnitude, green when the parameter was decreased an order of magnitude, and red when the parameter remained at its original value. The pastel colors represent the 95% confidence intervals surrounding each result.
where m = −1.45E − 09 and b = 8.0E04 pg. Small changes in the slope parameter m led the model to a different steady state value whereas large changes led to a steady decline in SMC mass (Figure 3). Sensitivity plots for each parameter can be found in the Supplemental Material.
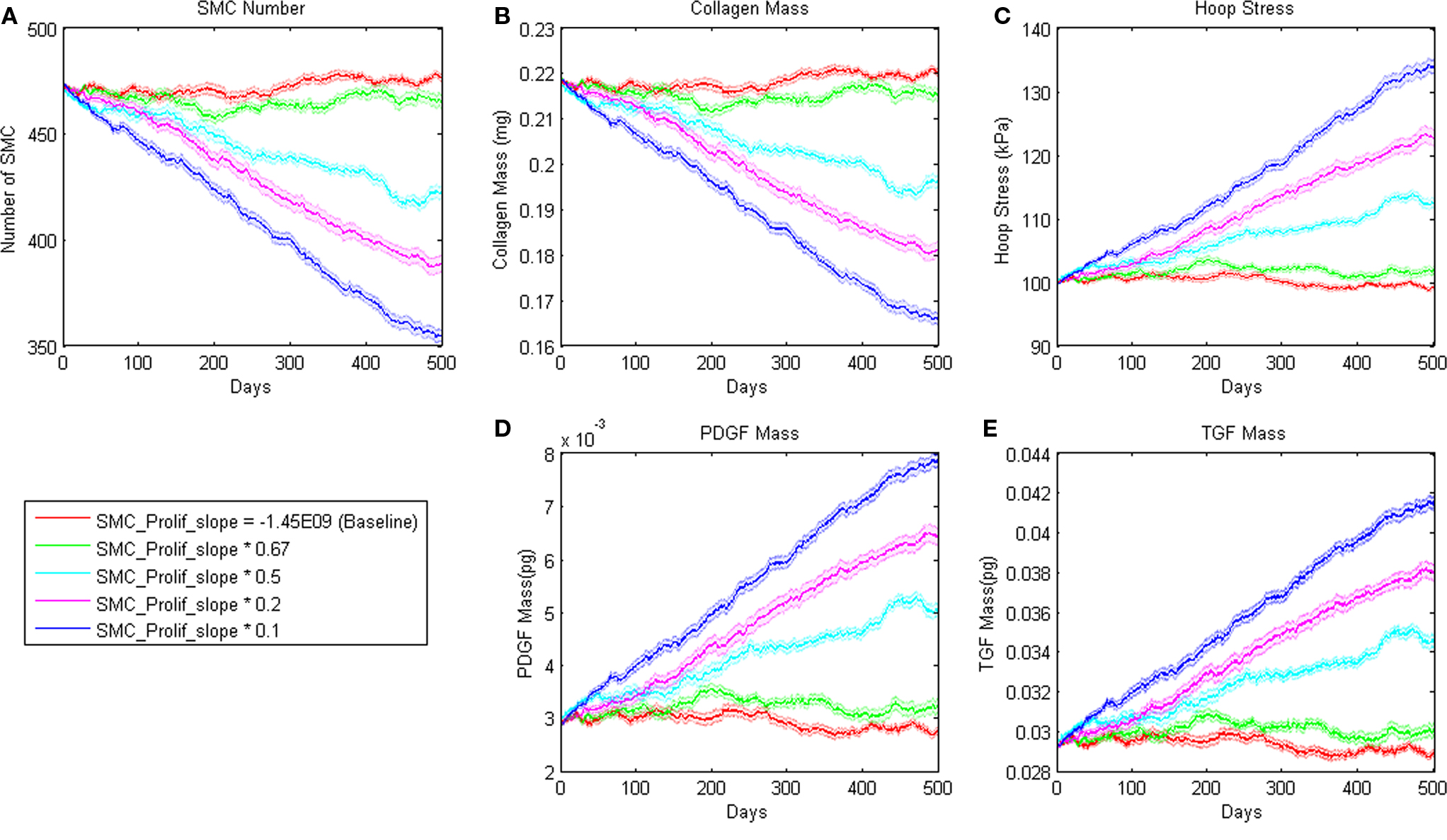
Figure 3. Sensitivity of ABM outputs to changes in proliferation rate of SMC in response to PDGF-AB. Note that for smaller changes in this parameter, SMC number and collagen mass reach a new equilibrium as hoop stress increases enough to support PDGF-AB and TGF-β production and therefore cell proliferation and collagen production.
ABM Stability
To assess homeostatic stability, the ABM was run under baseline conditions for 100 simulated days. Figure 4 shows resulting change in SMC number, collagen mass, and the masses of the growth factors TGF-β and PDGF-AB. The CMM was run under the same conditions and results for collagen mass, change in SMC mass, and circumferential stress were plotted in the same figure for comparison. Under these baseline conditions, the ABM yielded an average variation of less than 1%, which appeared to result from the stochasticity in the rules for cell proliferation and apoptosis. These changes led to small changes in circumferential stress, which in turn caused changes in growth factor production that returned the simulated vessel to its initial equilibrium state. In response to a transient (one time step) 10% increase in pressure on days 2 and 60 (Figure 5A), production of growth factors increased in response to the associated transient increase in circumferential stress (Figures 5D,E), but the elevation in these factors was not sustained long enough to initiate SMC proliferation and matrix production. Indeed, the slight changes in these two outputs were indistinguishable from those due to random cell proliferation and apoptosis (Figures 5B,C). Outputs of SMC number and collagen mass under both stability checks (homeostatic and transient) thus compared favorably to results from the established CMM (Figures 4 and 5).
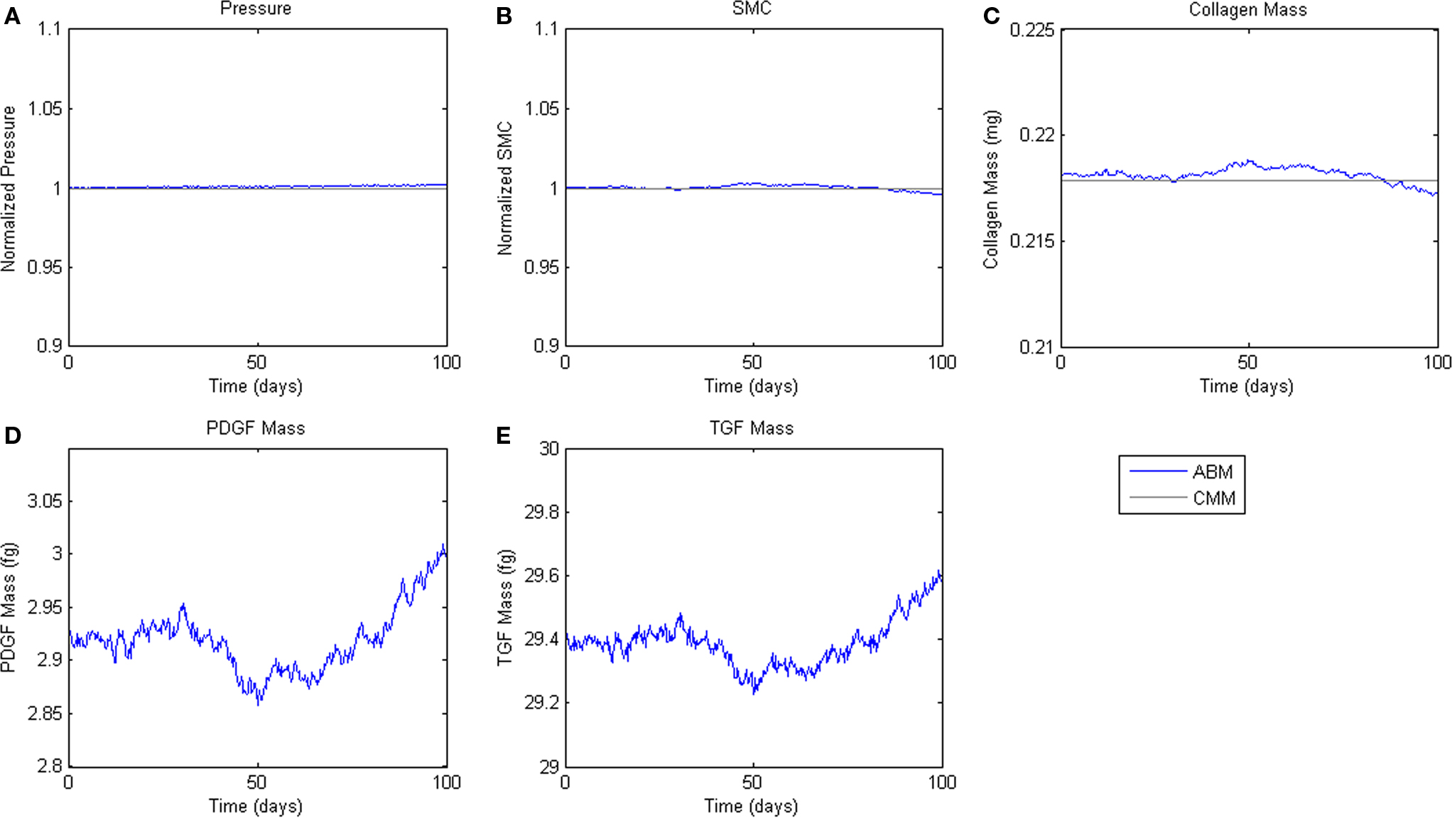
Figure 4. Homeostatic Conditions. ABM results are shown in blue, CMM results in black. ABM results are an average of 100 simulations. Stochastic fluctuations in cell number lead to some changes in stress and growth factor production. Overall change in cell number is <1%. (A) Pressure, (B) SMC, (C) Collagen, (D) PDGF-AB, (E) TGF-β.
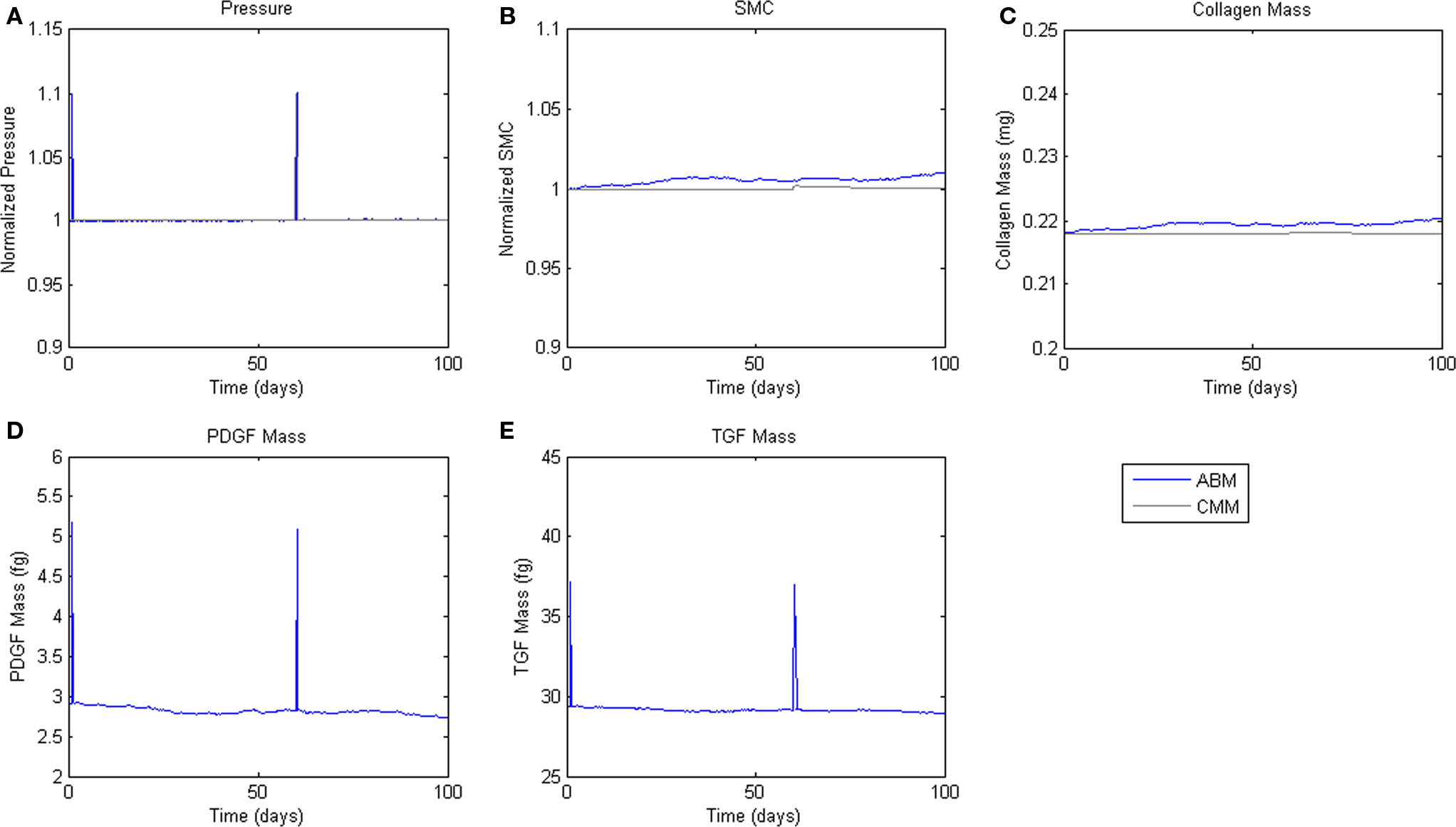
Figure 5. Transient Pressure Increases. ABM results are shown in blue, CMM results in black. ABM results are an average of 100 simulations. Transient increases in pressure of 10% for 6 h drive short-term changes in growth factor expression, but not SMC mass or collagen production. (A) Pressure, (B) SMC, (C) Collagen, (D) PDGF-AB, (E) TGF-β.
Hypertension
Finally, we simulated the response of the ABM to a sustained 30% increase in pressure (Figure 6A), which is consistent with pressure increases seen in a number of experimental surgical models of hypertension (Xu et al., 2001; Hu et al., 2007, 2008). This increase in pressure and associated increase in circumferential stress resulted in sharp increases in PDGF-AB and TGF-β (Figures 6B,C). Increases in these growth factors drove increased SMC proliferation and collagen production, which together thickened the vessel wall and relieved the increased circumferential stress (Figure 6).
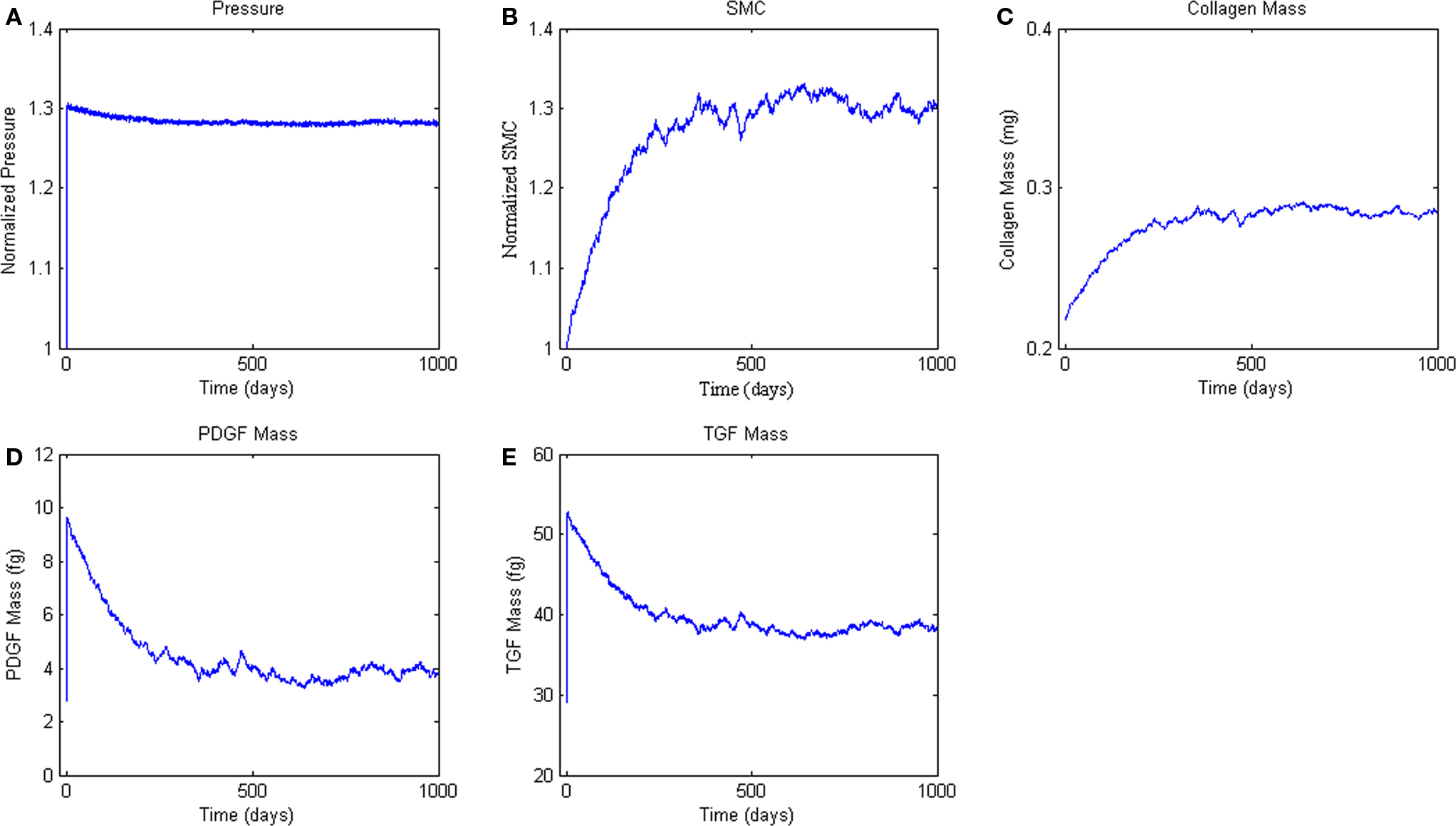
Figure 6. Agent-based model Hypertension Response. ABM results are an average of five simulations. Panel (A) ABM is subjected to a step increase in mean arterial pressure of 30%. (B, C) Response of SMC proliferation and collagen production to increased growth factor levels. (D, E) Production of the growth factors PDGF-AB and TGF-β in response to the elevated pressure and circumferential stress.
Discussion
Prior ABMs in vascular research have been restricted to examining mechanically driven processes involved in microvascular remodeling. Some of these models have accounted for mechanical stimuli of cellular protein expression (Peirce et al., 2004; Bailey et al., 2007, 2009) and/or the effects of growth factors on angiogenesis (Peirce et al., 2004), but no ABM had yet coupled mechanosensation with growth factor and protease production to describe structural remodeling of the vascular wall, and no ABM has been combined with mechanical models at higher levels of scale (Peirce et al., 2006; Robertson et al., 2007). The present work thus represents the first attempt to develop an ABM suitable for linking to a continuum-level model to describe cell-mediated changes in the geometry, composition, and properties of an adapting vascular wall. In order to achieve this goal, however, we needed to introduce a number of model verification steps that have heretofore been absent in agent-based modeling. Whereas a commonly asked question when presenting ABMs is, “How confident are you in the ability of your rules to accurately reflect the biology?,” we now must ask further how well the associated biology yields results that are appropriate at the tissue-level in vivo. In particular, whereas many rules for ABMs are of necessity based on cell culture experiments, the cell behavior in culture need not reflect in vivo responses in native tissues. There was a need, therefore, to critically assess the initial rules that one typically builds from the literature.
Toward this end, we first developed a new system for scoring confidence in ABM rules and tested it while building the model above. This system provides a formal means for determining rule quality by gaging overall utility of the input data to the intended ABM. Moreover, this method naturally suggests which rules should be improved before implementation and even suggests starting points for rule refinement when model outputs do not match a validation data set. We found this formalized evaluation process to be extremely useful in building the present ABM for it encouraged us to rethink assumptions and search more deeply in the literature for potentially relevant work. Others have also proposed formalized methods for ensuring the quality of an ABM’s rule-set. An proposed using ABMs to represent the state of knowledge in a given field by basing ABM rules on the consensus view of a committee of experts (An, 2006). This method requires a large amount of buy-in from the scientific community. Our scoring system differs in that it provides a systematic method for evaluating rules even when a consensus does not exist in the literature; we included a measure of literature support, but also evaluated the specific experiments and types of data reported in the archival papers that provide the foundation for a given rule. Hunt proposed the “functional unit representation method,” (FURM) which involves building a set of modules, each with slightly different rules, selecting those whose output possesses a progressively more stringent set of functional attributes (Grant et al., 2006; Hunt, 2010). FURM excels in evaluating mechanistic explanations for observed biological phenomena, but computational constraints in more complex models may prevent testing as many modules as one would prefer. The method presented here focuses on improving rules prior to instantiation of the conceptual model, potentially reducing the number of alternative modules that would need to be tested.
Because an ABM at the cellular scale treats most intracellular protein interactions as a “black box,” where the cellular response to an extracellular stimulus is captured by a single mathematical relationship, or rule, these rules and associated parameters often represent multiple in vivo intracellular protein interactions. This one-dimensional sensitivity analysis examines the types of changes in pathways or behaviors that the system can compensate for without compensatory changes in other parameters. For example, SMC_Prolif_Baseline represents the baseline proliferation rate of SMC in the absence of growth factors such as PDGF. Our model had an unstable response to a 10-fold change in this parameter (Table 4); this finding is important mathematically because it helps bound the parameter space based on comparisons of simulated results to well accepted vascular responses. Biologically, this finding could also suggest that if a mutation or combination of mutations occurred in the cell cycle control pathway that increased the proliferation rate of SMC by 10-fold without changing the apoptosis rate or the cells’ sensitivity to PDGF, the cells would proliferate unchecked, leading to essentially a cancerous phenotype. In contrast, a mutation leading to a lesser increase in the growth rate, for example dividing SMC_Prolif_Baseline by 1.5 (see detailed sensitivity analysis in Supplemental Material), could potentially be compensated for by other aspects of the ABM. Increased numbers of SMC and associated increases in wall thickness would decrease the circumferential stress sensed by the SMC, which would decrease stress-mediated PDGF production. This decrease in PDGF in the tissue would, in turn, lead to a decrease in PDGF-driven proliferation of SMC. Assuming that the baseline SMC proliferation rate is increased by an amount less than that driven by PDGF at baseline, the vessel could stabilize at a slightly increased wall thickness. Similarly, a decrease in the baseline proliferation of SMC could be compensated up to a point by increased production of PDGF stimulated by increased circumferential stress and the vessel could stabilize with a thinner wall. Beyond a certain level of variation in SMC_Prolif_Baseline, however, stability could only be maintained by compensatory changes/mutations in the baseline apoptosis rate of SMC (SMC_Apoptosis_Chance1, SMC_Apoptosis_Chance2), the sensitivity of SMC to PDGF (SMC_Prolif_Slope), the production of PDGF (PDGF_Baseline, PDGF_Hoopstress_Slope), or a combination of all three. Other parameters involved in cellular proliferation (highlighted in gray in Table 4) have similar effects on the overall stability of the vessel.
These sensitivity results suggest something often observed in vivo: small mutations can often be compensated by built-in feedback loops. Valentin and Humphrey thus suggested that vessels are “fault tolerant” structures (Valentin et al., 2009). Yet, an accumulation of small mutations (or a single large mutation in a key pathway regulating cell proliferation), if not balanced by changes in other pathways, can lead to pathologic proliferation or apoptosis, resulting in a pre-disposition to embryonic lethality, subsequent vascular disease, or perhaps even cancer. Analogous to the unstable sensitivity response described above, expression of VEGF is so tightly regulated that manipulations reducing its expression by 50% or increasing it by 2- to 3-fold are both embryonic lethal (Carmeliet et al., 1996; Ferrara et al., 1996; Miquerol et al., 2000). Conversely, a response similar to “stable sensitivity” is described by Wagenseil et al. (2005) in the elastin mutant mouse ELN+/−. While the ELN−/− mouse is perinatally lethal (Li et al., 1998a), the haploinsufficient ELN+/− mouse demonstrates a distinct vascular phenotype (hypertension, decreased compliance, and inward remodeling), yet is able to adapt to the deficiency and has a normal lifespan (Li et al., 1998b; Faury et al., 2003; Wagenseil et al., 2005). While our present goal was to develop an ABM capable of recapitulating “normal adaptations,” the types of sensitivity demonstrated above suggest that the model could also be useful in the future for simulating diseases based on known mutations by perturbing the rules/parameters associated with those key pathways.
Because our intention is for this ABM to be combined with a CMM to enable tissue-level adaptations to be modeled based on molecular and cellular level mechanisms, it is important that the ABM be held to the same standards for computational and biological stability as the CMM. Comparison of results for the two models revealed that, following necessary refinement of the initial ABM rule-set, both models exhibited similar long-term stability under homeostatic conditions and both models were similarly insensitive to pressure transients as desired. Passing such tests provided confidence in using the model to predict adaptations in response to perturbations in loading from homeostatic conditions.
In response to an abrupt and sustained 30% step increase in pressure, the ABM predicted a 26% increase in SMC number at 365 days (i.e., 1 year) and an overall 28% increase at 500 days; collagen mass increased by a comparable percent. Measurements reported in the literature on arterial remodeling in response to hypertension are inconsistent in both the amount and time-course of remodeling, due in part to the use of different species, different experimental manipulations, and a focus on different arteries. For example, Xu et al. (2001) reports a 38% increase in wall thickness at 1 week in the rat aorta in response to a 25% increase in mean arterial pressure. This thickness increase was maintained over at least 4 weeks. Elevated cellular proliferation occurred through 2 weeks, and elevated levels of TGF-β persisted through 1 week. In the rabbit, however, Xu et al. reported no significant change in wall thickness over 8 weeks in response to coarctation induced hypertension, with a final pressure increase of 39% at 8 weeks (Xu et al., 2000). Hu et al. (2008) showed increased procollagen through 8 weeks and increased SMC proliferation through 4 weeks in a porcine aortic model of hypertension wherein mean arterial pressure increased 29% above normal. Other studies have shown similar results (Owens and Reidy, 1985).
Although the absolute changes in SMC number and collagen mass predicted by the ABM are within the range that would be expected based on actual measurements of altered wall thickness due to hypertension, the time-course of the changes predicted by the ABM is longer than that reported in the papers cited above. This difference may be a function of differences between SMC proliferation rates in vivo versus in silico. SMC proliferation in the ABM was governed by the baseline proliferation rate of SMC plus additional proliferation in response to PDGF-AB, with the production of PDGF-AB changing in response to changes in circumferential stress. When scoring these rules for confidence, it was noted that the baseline in vivo proliferation rate of SMC had lower confidence, while changes in the proliferation of SMC in response to PDGF-AB in vitro had been studied more thoroughly. Production of PDGF-AB by SMC in response to stretch achieved a score of 5.5, near the average for the rule-set. The model is sensitive to parameters in all three rules above. Because of the design of the model, changes in these parameters would be expected to synergize with each other, and small changes to these parameters (within the standard deviations reported in the literature) could radically alter the time-course of the predicted remodeling response to circumferential stress.
In contrast, the CMM has predicted a time-course for hypertensive remodeling much closer to that expected from in vivo animal studies reported in the literature (Valentin and Humphrey, 2009). This result should not be surprising, however; the lumped-parameter constitutive relations used in the CMM were derived from in vivo tissue-level data in the literature. We expect that minimization of differences between outputs common to the two models will result in more realistic parameters in the ABM for PDGF-AB production and the associated SMC proliferative response, thus resulting in an overall model that more closely reflects the rate of structural remodeling reported in the literature.
In conclusion, we developed and verified a novel ABM of structural remodeling of the arterial wall in response to biomechanical forces. The ABM was designed from the outset with inputs and outputs that compare favorably with a previously published CMM to facilitate the future coupling of these two models and thereby to exploit their individual advantages. We showed that the ABM running independently is stable under homeostatic conditions and robust to transient changes in mean arterial pressure. When subjected to an abrupt but sustained 30% increase of pressure, the ABM responded as expected via increased smooth muscle proliferation and collagen production that approximates values reported in the literature. Because of the axisymmetry of the problem, these changes in cell number and collagen mass could then be correlated a priori with changes in wall thickness. Such cell-mediated changes were seen to return the circumferential stress toward its baseline value as would be expected from the literature (Zeller and Skalak, 1998; Humphrey and Rajagopal, 2002; Dajnowiec and Langille, 2007). We note, however, that this illustrative problem was chosen carefully to allow the ABM to be evaluated independently. That is, we isolated the effects of pressure on circumferential stress alone (Laplace’s equation), hence ignoring the axial direction. Moreover, we did not allow the step increase in pressure to change the inner radius of the model vessel for we expect a rapid (i.e., less than one time step of 6 h) vasoregulatory response to restore the radius to normal and thereby restore wall shear stress. This ABM was not designed to simulate deformations under the influence of changing hemodynamic loads according to fundamental postulates of mechanics such as linear momentum balance. Having demonstrated the utility of the ABM in this simple illustrative problem, however, reveals that it is ready to be linked to a CMM which is based on the fundamental postulates of mechanics. In this way, there is promise for developing multi-scale models that enable one to satisfy simultaneously the tissue-level mechanics and the cell level biology that are fundamental to arterial adaptations.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported, in part, via NIH grants HL-082838 (to Shayn M. Peirce) and HL-86418 (to Jay D. Humphrey).
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/computational_physiology_and_medicine/10.3389/fphys.2011.00020/abstract
References
Absood, A., Furutani, A., Kawamura, T., and Graham, L. M. (2004). A comparison of oxidized LDL-induced collagen secretion by graft and aortic SMCs: role of PDGF. Am. J. Physiol. Heart Circ. Physiol. 287, H1200–H1206.
An, G. (2006). Concepts for developing a collaborative in silico model of the acute inflammatory response using agent-based modeling. J. Crit. Care 21, 105–110; discussion 110–101.
Aromatario, C., Sterpetti, A. V., Palumbo, R., Patrizi, A. L., Di Carlo, A., Proietti, P., Guglielmi, M. B., Cavallaro, A., Santoro-D’angelo, L., and Cucina, A. (1997). Fluid shear stress increases the release of platelet derived growth factor BB (PDGF BB) by aortic endothelial cells. Minerva Cardioangiol. 45, 1–7.
Baek, S., Rajagopal, K. R., and Humphrey, J. D. (2006). A theoretical model of enlarging intracranial fusiform aneurysms. J. Biomech. Eng. 128, 142–149.
Baek, S., Valentin, A., and Humphrey, J. D. (2007). Biochemomechanics of cerebral vasospasm and its resolution: II. Constitutive relations and model simulations. Ann. Biomed. Eng. 35, 1498–1509.
Bailey, A. M., Lawrence, M. B., Shang, H., Katz, A. J., and Peirce, S. M. (2009). Agent-based model of therapeutic adipose-derived stromal cell trafficking during ischemia predicts ability to roll on P-selectin. PLoS Comput. Biol. 5, e1000294. doi: 10.1371/journal.pcbi.1000294
Bailey, A. M., Thorne, B. C., and Peirce, S. M. (2007). Multi-cell agent-based simulation of the microvasculature to study the dynamics of circulating inflammatory cell trafficking. Ann. Biomed. Eng. 35, 916–936.
Carmeliet, P., Ferreira, V., Breier, G., Pollefeyt, S., Kieckens, L., Gertsenstein, M., Fahrig, M., Vandenhoeck, A., Harpal, K., Eberhardt, C., Declercq, C., Pawling, J., Moons, L., Collen, D., Risau, W., and Nagy, A. (1996). Abnormal blood vessel development and lethality in embryos lacking a single VEGF allele. Nature 380, 435–439.
Chapman, G. B., Durante, W., Hellums, J. D., and Schafer, A. I. (2000). Physiological cyclic stretch causes cell cycle arrest in cultured vascular smooth muscle cells. Am. J. Physiol. Heart Circ. Physiol. 278, H748–H754.
Dajnowiec, D., and Langille, B. L. (2007). Arterial adaptations to chronic changes in haemodynamic function: coupling vasomotor tone to structural remodelling. Clin. Sci. (Lond) 113, 15–23.
Dancu, M. B., Berardi, D. E., Vanden Heuvel, J. P., and Tarbell, J. M. (2004). Asynchronous shear stress and circumferential strain reduces endothelial NO synthase and cyclooxygenase-2 but induces endothelin-1 gene expression in endothelial cells. Arterioscler. Thromb. Vasc. Biol. 24, 2088–2094.
Faury, G., Pezet, M., Knutsen, R. H., Boyle, W. A., Heximer, S. P., Mclean, S. E., Minkes, R. K., Blumer, K. J., Kovacs, A., Kelly, D. P., Li, D. Y., Starcher, B., and Mecham, R. P. (2003). Developmental adaptation of the mouse cardiovascular system to elastin haploinsufficiency. J. Clin. Invest. 112, 1419–1428.
Ferrara, N., Carver-Moore, K., Chen, H., Dowd, M., Lu, L., O’shea, K. S., Powell-Braxton, L., Hillan, K. J., and Moore, M. W. (1996). Heterozygous embryonic lethality induced by targeted inactivation of the VEGF gene. Nature 380, 439–442.
Garcia-Lopez, G., Vadillo-Ortega, F., Merchant-Larios, H., Maida-Claros, R., Osorio, M., Soriano-Becerril, D., Flores-Herrera, H., Beltran-Montoya, J., Garfias-Becerra, Y., and Zaga-Clavellina, V. (2007). Evidence of in vitro differential secretion of 72 and 92 kDa type IV collagenases after selective exposure to lipopolysaccharide in human fetal membranes. Mol. Hum. Reprod. 13, 409–418.
Grant, M. R., Mostov, K. E., Tlsty, T. D., and Hunt, C. A. (2006). Simulating properties of in vitro epithelial cell morphogenesis. PLoS Comput. Biol. 2, e129. doi: 10.1371/journal.pcbi.0020129
Greve, J. M., Les, A. S., Tang, B. T., Draney Blomme, M. T., Wilson, N. M., Dalman, R. L., Pelc, N. J., and Taylor, C. A. (2006). Allometric scaling of wall shear stress from mice to humans: quantification using cine phase-contrast MRI and computational fluid dynamics. Am. J. Physiol. Heart Circ. Physiol. 291, H1700–H1708.
Hsieh, H. J., Li, N. Q., and Frangos, J. A. (1991). Shear stress increases endothelial platelet-derived growth factor mRNA levels. Am. J. Physiol. 260, H642–H646.
Hu, J. J., Ambrus, A., Fossum, T. W., Miller, M. W., Humphrey, J. D., and Wilson, E. (2008). Time courses of growth and remodeling of porcine aortic media during hypertension: a quantitative immunohistochemical examination. J. Histochem. Cytochem. 56, 359–370.
Hu, J. J., Fossum, T. W., Miller, M. W., Xu, H., Liu, J. C., and Humphrey, J. D. (2007). Biomechanics of the porcine basilar artery in hypertension. Ann. Biomed. Eng. 35, 19–29.
Humphrey, J. D. (2002). Cardiovascular solid mechanics: cells, tissues, and organs. New York: Springer.
Humphrey, J. D. (2008). Vascular adaptation and mechanical homeostasis at tissue, cellular, and sub-cellular levels. Cell Biochem. Biophys. 50, 53–78.
Humphrey, J. D., and Rajagopal, K. R. (2002). A constrained mixture model for growth and remodeling of soft tissues. Math. Model. Meth. Appl. Sci. 12, 407–430.
Hunt, C. A. (2010). FURM: A Functional Unit Representation Method [Online]. Available at: http://furm.org [accessed December 21, :2010].
Kanai, A. J., Strauss, H. C., Truskey, G. A., Crews, A. L., Grunfeld, S., and Malinski, T. (1995). Shear stress induces ATP-independent transient nitric oxide release from vascular endothelial cells, measured directly with a porphyrinic microsensor. Circ. Res. 77, 284–293.
Karakiulakis, G., Papakonstantinou, E., Aletras, A. J., Tamm, M., and Roth, M. (2007). Cell type-specific effect of hypoxia and platelet-derived growth factor-BB on extracellular matrix turnover and its consequences for lung remodeling. J. Biol. Chem. 282, 908–915.
Kim, Y. J., Sah, R. L., Doong, J. Y., and Grodzinsky, A. J. (1988). Fluorometric assay of DNA in cartilage explants using Hoechst 33258. Anal. Biochem. 174, 168–176.
Kim, Y. S., Galis, Z. S., Rachev, A., Han, H. C., and Vito, R. P. (2009). Matrix metalloproteinase-2 and -9 are associated with high stresses predicted using a nonlinear heterogeneous model of arteries. J. Biomech. Eng. 131, 011009.
Le, J., Dauchot, P., Perrot, J. L., Cambazard, F., Frey, J., and Chamson, A. (1999). Quantitative zymography of matrix metalloproteinases by measuring hydroxyproline: application to gelatinases A and B. Electrophoresis 20, 2824–2829.
Li, D. Y., Brooke, B., Davis, E. C., Mecham, R. P., Sorensen, L. K., Boak, B. B., Eichwald, E., and Keating, M. T. (1998a). Elastin is an essential determinant of arterial morphogenesis. Nature 393, 276–280.
Li, D. Y., Faury, G., Taylor, D. G., Davis, E. C., Boyle, W. A., Mecham, R. P., Stenzel, P., Boak, B., and Keating, M. T. (1998b). Novel arterial pathology in mice and humans hemizygous for elastin. J. Clin. Invest. 102, 1783–1787.
Li, Z., Moore, S., and Alavi, M. Z. (1995). Mitogenic factors released from smooth muscle cells are responsible for neointimal cell proliferation after balloon catheter deendothelialization. Exp. Mol. Pathol. 63, 77–86.
Ma, Y. H., Ling, S., and Ives, H. E. (1999). Mechanical strain increases PDGF-B and PDGF beta receptor expression in vascular smooth muscle cells. Biochem. Biophys. Res. Commun. 265, 606–610.
Mata-Greenwood, E., Grobe, A., Kumar, S., Noskina, Y., and Black, S. M. (2005). Cyclic stretch increases VEGF expression in pulmonary arterial smooth muscle cells via TGF-beta1 and reactive oxygen species: a requirement for NAD(P)H oxidase. Am. J. Physiol. Lung Cell. Mol. Physiol. 289, L288–L289.
Miquerol, L., Langille, B. L., and Nagy, A. (2000). Embryonic development is disrupted by modest increases in vascular endothelial growth factor gene expression. Development 127, 3941–3946.
Morishita, R., Gibbons, G. H., Horiuchi, M., Kaneda, Y., Ogihara, T., and Dzau, V. J. (1998). Role of AP-1 complex in angiotensin II-mediated transforming growth factor-beta expression and growth of smooth muscle cells: using decoy approach against AP-1 binding site. Biochem. Biophys. Res. Commun. 243, 361–367.
Murphy, G., Mcalpine, C. G., Poll, C. T., and Reynolds, J. J. (1985). Purification and characterization of a bone metalloproteinase that degrades gelatin and types IV and V collagen. Biochim. Biophys. Acta 831, 49–58.
Okuno, T., Andoh, A., Bamba, S., Araki, Y., Fujiyama, Y., Fujiyama, M., and Bamba, T. (2002). Interleukin-1beta and tumor necrosis factor-alpha induce chemokine and matrix metalloproteinase gene expression in human colonic subepithelial myofibroblasts. Scand. J. Gastroenterol. 37, 317–324.
Owens, G. K., Rabinovitch, P. S., and Schwartz, S. M. (1981). Smooth muscle cell hypertrophy versus hyperplasia in hypertension. Proc. Natl. Acad. Sci. U.S.A. 78, 7759–7763.
Owens, G. K., and Reidy, M. A. (1985). Hyperplastic growth response of vascular smooth muscle cells following induction of acute hypertension in rats by aortic coarctation. Circ. Res. 57, 695–705.
Peirce, S. M., Skalak, T. C., and Papin, J. A. (2006). Multiscale biosystems integration: coupling intracellular network analysis with tissue-patterning simulations. IBM J. Res. Dev. 50, 601–615.
Peirce, S. M., Van Gieson, E. J., and Skalak, T. C. (2004). Multicellular simulation predicts microvascular patterning and in silico tissue assembly. FASEB J. 18, 731–733.
Rachev, A., Manoach, E., Berry, J., and Moore, J. E. Jr. (2000). A model of stress-induced geometrical remodeling of vessel segments adjacent to stents and artery/graft anastomoses. J. Theor. Biol. 206, 429–443.
Reidy, M. A. (1994). Growth factors and arterial smooth muscle cell proliferation. Ann. N. Y. Acad. Sci. 714, 225–230.
Robertson, S. H., Smith, C. K., Langhans, A. L., Mclinden, S. E., Oberhardt, M. A., Jakab, K. R., Dzamba, B., Desimone, D. W., Papin, J. A., and Peirce, S. M. (2007). Multiscale computational analysis of Xenopus laevis morphogenesis reveals key insights of systems-level behavior. BMC Syst. Biol. 1, 46.
Schlumberger, W., Thie, M., Rauterberg, J., and Robenek, H. (1991). Collagen synthesis in cultured aortic smooth muscle cells. Modulation by collagen lattice culture, transforming growth factor-beta 1, and epidermal growth factor. Arterioscler. Thromb. 11, 1660–1666.
Stegemann, J. P., and Nerem, R. M. (2003). Altered response of vascular smooth muscle cells to exogenous biochemical stimulation in two- and three-dimensional culture. Exp. Cell Res. 283, 146–155.
Taber, L. A. (1998). A model for aortic growth based on fluid shear and fiber stresses. J. Biomech. Eng. 120, 348–354.
Thorne, B. C., Bailey, A. M., and Peirce, S. M. (2007). Combining experiments with multi-cell agent-based modeling to study biological tissue patterning. Brief. Bioinform. 8, 245–257.
Tsamis, A., Stergiopulos, N., and Rachev, A. (2009). A structure-based model of arterial remodeling in response to sustained hypertension. J. Biomech. Eng. 131, 101004.
Valentin, A., Cardamone, L., Baek, S., and Humphrey, J. D. (2009). Complementary vasoactivity and matrix remodelling in arterial adaptations to altered flow and pressure. J. R. Soc. Interface 6, 293–306.
Valentin, A., and Humphrey, J. D. (2009). Parameter sensitivity study of a constrained mixture model of arterial growth and remodeling. J. Biomech. Eng. 131, 101006.
Wagenseil, J. E., Nerurkar, N. L., Knutsen, R. H., Okamoto, R. J., Li, D. Y., and Mecham, R. P. (2005). Effects of elastin haploinsufficiency on the mechanical behavior of mouse arteries. Am. J. Physiol. Heart Circ. Physiol. 289, H1209–H1217.
Welgus, H. G., Jeffrey, J. J., and Eisen, A. Z. (1981). The collagen substrate specificity of human skin fibroblast collagenase. J. Biol. Chem. 256, 9511–9515.
Welgus, H. G., Jeffrey, J. J., Stricklin, G. P., Roswit, W. T., and Eisen, A. Z. (1980). Characteristics of the action of human skin fibroblast collagenase on fibrillar collagen. J. Biol. Chem. 255, 6806–6813.
Wilensky, U. (1999). “NetLogo”. Evanston, IL: Center for Connected Learning and Computer-Based Modeling, Northwestern University.
Xia, T., Akers, K., Eisen, A. Z., and Seltzer, J. L. (1996). Comparison of cleavage site specificity of gelatinases A and B using collagenous peptides. Biochim. Biophys. Acta 1293, 259–266.
Xu, C., Lee, S., Singh, T. M., Sho, E., Li, X., Sho, M., Masuda, H., and Zarins, C. K. (2001). Molecular mechanisms of aortic wall remodeling in response to hypertension. J. Vasc. Surg. 33, 570–578.
Xu, C., Zarins, C. K., Bassiouny, H. S., Briggs, W. H., Reardon, C., and Glagov, S. (2000). Differential transmural distribution of gene expression for collagen types I and III proximal to aortic coarctation in the rabbit. J. Vasc. Res. 37, 170–182.
Zeller, P. J., and Skalak, T. C. (1998). Contribution of individual structural components in determining the zero-stress state in small arteries. J. Vasc. Res. 35, 8–17.
Keywords: agent-based modeling, constrained mixture modeling, hypertension, vascular remodeling, multi-scale modeling
Citation: Thorne BC, Hayenga HN, Humphrey JD and Peirce SM (2011) Toward a multi-scale computational model of arterial adaptation in hypertension: verification of a multi-cell agent based model. Front. Physio. 2:20. doi: 10.3389/fphys.2011.00020
Received: 08 February 2011; Accepted: 25 April 2011;
Published online: 09 May 2011.
Edited by:
Robert Hester, University of Mississippi, USAReviewed by:
William Andrew Pruett, University of Mississippi Medical Center, USASarah S. Knox, West Virginia University School of Medicine, USA
Aleksander S. Popel, Johns Hopkins University, USA
Copyright: © 2011 Thorne, Hayenga, Humphrey and Peirce. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Shayn M. Peirce, Department of Biomedical Engineering, University of Virginia, P.O. Box 800759, Charlottesville, VA 22908, USA. e-mail: shayn@virginia.edu