Multifractal analysis and modification of coal pore structures with impact of clean compound biomass surfactants

This study investigates the modification of coal pore structures using composite biomass surfactants and explores its implications for methane adsorption and desorption characteristics. Coal samples from the 13–1 coal seam in Liuzhuang Mine, Huainan, China, are analyzed using low-temperature nitrogen adsorption experiments. The box-counting-based multifractal theory is used to assess coal pore heterogeneity and connectivity before and after surfactant treatment. The results reveal significant improvements in pore structure uniformity and connectivity, providing insights into the relationship between pore characteristics and methane adsorption behavior. This research offers a foundational understanding for optimizing coalbed methane extraction and enhancing environmental sustainability in coal mining operations.

1 Introduction

The extraction of coalbed methane (CBM) plays a critical role in addressing global energy demands while concurrently reducing greenhouse gas emissions. Nevertheless, the efficiency of CBM recovery is significantly constrained by the complex pore systems in coal, which are characterized by heterogeneous pore size distributions, low connectivity, and limited permeability [1]. These structural attributes directly impact key processes such as methane adsorption and desorption, as well as diffusion and migration, thereby posing substantial challenges for effective gas extraction [2–4]. While traditional fractal models have been employed to describe the self-similarity inherent in porous materials, they often fail to fully capture the complex and multifactorial heterogeneity native to coal pores, particularly under chemical modification. This gap underscores the necessity for advanced analytical frameworks capable of quantifying structural intricacies and informing targeted enhancements.

Multifractal theory has arisen as a robust analytical approach for examining the hierarchical and non-uniform characteristics of coal pore networks. Unlike conventional monofractal models, multifractal analysis decomposes complex systems into a spectrum of singular metrics, enabling precise quantification of spatial heterogeneity and connectivity [5–7]. By analyzing scaling behaviors across diverse probability distributions, multifractal methods offer critical insights into the evolution of pore structures under external modifications, such as those resulting from the application of surfactants [8–11]. Recent investigations highlight the efficacy of multifractal theory in correlating pore geometry with gas storage and transport capacities [12–14]. However, its application to assess structural changes induced by biomass-based surfactants remains limited, leaving critical knowledge gaps in the development of environmentally sustainable CBM extraction techniques.

Chemical surfactants, predominantly synthetic variants, have been extensively studied for their ability to improve coal wettability and enhance pore connectivity [15, 16]. Nonetheless, their persistence in the environment and associated toxicity raise concerns that conflict with global sustainability objectives. Biomass-derived surfactants, made from renewable sources such as soybean protein isolates, offer a promising alternative due to their amphiphilic properties and high biodegradability [17–20]. For example, soybean protein isolates (SPIs) modified with glucose have demonstrated improved adsorption capabilities on coal surfaces, leading to altered surface hydrophobicity and more uniform pore networks [21, 22]. Despite these advancements, the multifractal response of coal pores to such biomass-based surfactants remains underexplored, impeding the systematic design of green chemical modification strategies. Expanding our understanding of this area is vital for achieving sustainable CBM recovery solutions.

This study addresses these gaps by integrating multifractal theory with low-temperature nitrogen adsorption experiments to evaluate pore structure modifications in anthracite coal treated with composite biomass surfactants. Coal samples from the Liuzhuang Mine were analyzed before and after surfactant treatment, focusing on multifractal spectra (e.g., f(α)∼α, Dq∼q) and connectivity parameters such as the Hurst index. The objectives are threefold: 1) to establish quantitative links between surfactant-induced pore modifications and methane adsorption-desorption behavior, 2) to assess the efficacy of biomass surfactants in reducing structural heterogeneity, and 3) to provide a theoretical foundation for optimizing CBM recovery through sustainable chemical interventions. By bridging multifractal analysis with green chemistry, this work advances both fundamental understanding and practical applications in energy resource management.

The subsequent sections are organized as follows: Section 2 details coal sample preparation and surfactant modification protocols and introduces experimental methods for pore structure characterization. Section 3 presents multifractal analyses and connectivity assessments, while Section 4 discusses implications for CBM extraction and environmental sustainability.

2 Coal sample collection and experimental methods

2.1 Coal sample collection

Coal samples were extracted from the 13-1 coal seam situated in Liuzhuang Mine, Huainan, China. This seam exhibits structural variability, ranging from simple to complex formations. Positioned within the central portion of the fourth coal-bearing stratum, the seam’s thickness spans from 0.98 m to 11.07 m, averaging 4.34 m. The primary coal seams exhibit gas content values between 0.21 and 1.47 m³/t, with a mean of 0.65 m³/t. The gas saturation is very low, and the maximum value is only 18%, which belongs to reservoirs with poor permeability.

According to the industrial analysis method of coal (GB/T 212-2008), the collected coal samples are tested for industrial analysis. The coal quality characteristics are shown in Table 1.

Table 1

Table 1. Coal quality characteristics.

In Table 1, Mad (Moisture Content as Determined by Air-Drying, %), refers to the percentage of moisture present in a coal sample after it has been subjected to air drying at ambient conditions. This parameter is crucial for understanding the water content that affects the coal’s heating value and combustion efficiency; Aad (Ash Content as Determined in Air-Dried Condition, %), denotes the percentage of inorganic residue or ash remaining after the combustion of a coal sample that has been air-dried. The ash content is significant as it impacts the coal’s combustibility, ash disposal, and overall energy yield; Vdaf (Volatile Matter Content as Determined in Dry and Ash-Free Condition, %), represents the percentage of volatile matter in the coal, expressed on a dry and ash-free basis. This parameter is essential for assessing the coal’s behavior during combustion and gasification, as volatile matter influences ignition, flame characteristics, and overall energy release; Fcd (Fixed Carbon Density, %), indicates the density of fixed carbon within a coal sample, which is a key indicator of the coal’s carbon content remaining after the volatile matter has been released. The fixed carbon density is vital for determining the coal’s heating capacity and its suitability for various industrial applications.

2.2 Preparation of modified solution

In this paper, soybean protein isolate was used as the main raw material, and based on alkaline protease hydrolysis reaction, soybean protein isolate hydrolysate was grafted with glucose to obtain modified soybean protein isolate based surfactant (modified SPI). The structure is shown in Figure 1. Using the modified SPI as the main body, the modified solution was prepared with 1wt%KCl base solution and rhamnolipidemic biomass surfactant.

Figure 1

Figure 1. Basic unit structure diagram of modified soybean protein isolate (modified SPI).

Figure 1 illustrates the basic unit structure of the modified soybean protein isolate (SPI), which serves as the primary component of the biomass surfactant used in this study. This structural representation is crucial for understanding the chemical modifications made to the SPI, such as the grafting of glucose through alkaline protease hydrolysis. These modifications enhance the surfactant’s functionality, enabling it to improve the pore structure of coal by optimizing uniformity and connectivity.

2.3 Coal sample modification treatment

Following the crushing of the original coal sample, coal powder with a particle size range of 60–80 mesh was carefully screened and subsequently immersed in six different composite modification solutions with varying ratios (1:9 to 3:2). The samples were thoroughly soaked, rinsed, and filtered, then dried to achieve a constant weight. Finally, the treated samples were bagged, sealed, and stored for further use.

2.4 Experimental instruments and conditions

In compliance with the Chinese national standard for determining the specific surface area of solid materials via the gas adsorption BET method (GB/T 19587-2017), a specific surface area and micropore adsorption analyzer was employed for the low-temperature nitrogen adsorption experiments (refer to Figure 2). The experimental process was conducted at a temperature of 77 K, utilizing approximately 5 g of the sample, with an equilibrium time interval of 10 s.

Figure 2

Figure 2. ASAP 2460 automatic rapid surface area and porosity analyzer (mack corporation).

2.5 Analysis method

The Barrett–Joyner–Halenda (BJH) method, which is based on Kelvin capillary condensation theory and assumes cylindrical pore geometry, is a widely used approach for pore size analysis (see [23, 24]). Nonetheless, traditional methods remain inadequate for accurately characterizing micropores or narrow mesopores, particularly when analyzing pore size distributions below 10 nm. These techniques often underestimate pore diameters by approximately 20%–30%. In comparison, Nonlocal Density Functional Theory (NLDFT) has emerged as a more advanced and dependable framework for investigating the pore structures and adsorption properties of porous materials. Unlike conventional approaches, NLDFT integrates both statistical and spatial correlations between adsorbate molecules as well as their interactions with pore walls, achieving molecular-level precision in representing adsorption phenomena. This methodology has been widely employed in the analysis of microporous and mesoporous materials, such as activated carbons, zeolites, and coal matrices, due to its ability to accurately model intricate adsorption isotherms and pore size distributions. By addressing the shortcomings of classical models like Brunauer–Emmett–Teller (BET) and Barrett–Joyner–Halenda (BJH)—which often rely on simplified geometric assumptions—NLDFT offers a more nuanced depiction of pore connectivity, heterogeneity, and molecular-scale interactions. Specifically, NLDFT enables the prediction of adsorption energies and the spatial distribution of adsorbed molecules within porous networks, rendering it an effective tool for evaluating both microporous and mesoporous structures. In this study, the NLDFT methodology is leveraged for the quantitative characterization of mesopore size distributions, establishing a robust framework for elucidating the pore structures of coal and other porous systems.

3 Multifractal characteristics of coal pore structure

3.1 Multifractal theory

The multifractal characteristics of pores are studied by the box-counting method. Considering that N₂ (77K) adsorption is suitable for mesoporous, that is, the pore size range is 2nm–50 nm. In this section, the aperture range of 2–50 nm is taken as an example. According to the Kelvin equation (see [23–26]),

$r_i=-\frac{0.414}{\lg \left(\frac{P}{P_0}\right)},$

$r_i$ is the curvature radius of the gas adsorbed in the pore, and the relative pressure range corresponding to the aperture range of 2–50 nm can be calculated. The interval I measured by the relative pressure (P/P₀) distribution is tested experimentally, and the interval is divided into N small partitions, and the sampling interval is carried out in the form of logarithmic arithmetic increase. In the context of gas adsorption, the relative pressure is partitioned into multiple equally sized intervals, denoted by ε. To quantitatively evaluate the distribution characteristics of gas adsorption within each interval, the mass probability function corresponding to the i-th interval is defined, focusing on the relative pressure associated with gas adsorption.

${\mu }_i\left(\epsilon \right)=\frac{N_i\left(\epsilon \right)}{N_t}(1)$

where $N_i\left(\epsilon \right)$ is the gas adsorption capacity of box i, which is the sum of all pore size distribution results in subinterval I_i. $N_t$ is the total amount of gas adsorption. Calculating

${\mu }_i\left(q,\epsilon \right)=\frac{{\mu }_i^q\left(\epsilon \right)}{{\sum }_{i=1}^{N\left(\epsilon \right)}{\mu }_i^q\left(\epsilon \right)}(2)$

${\mu }_i\left(q,\epsilon \right)$ is the probability of order q in the i-th subinterval. Define the denominator in the above formula as follows:

$U\left(q,\epsilon \right)={\sum }_{i=1}^{N\left(\epsilon \right)}{\mu }_i^q\left(\epsilon \right),(3)$

which is called partition function or statistical moment function. Define

$\alpha \left(q\right)={\lim }_{\epsilon \to 0}\frac{{\sum }_{i=1}^{N\left(\epsilon \right)}{\mu }_i\left(q,\epsilon \right)\lg {\mu }_i\left(\epsilon \right)}{\lg \epsilon }(4)$

characterizes the local singular intensity of the object, and the larger the value of α(q), the higher the regularity of the aperture distribution. The multifractal spectral function of the aperture distribution with respect to α(q) can be expressed as:

$f\left(\alpha \left(q\right)\right)={\lim }_{\epsilon \to 0}\frac{{\sum }_{i=1}^{N\left(\epsilon \right)}{\mu }_i\left(q,\epsilon \right)\lg {\mu }_i\left(q,\epsilon \right)}{\lg \epsilon }.(5)$

The multifractal spectrum, denoted as f (α(q)), characterizes the fractal dimension of subsets sharing an equivalent singularity index. If the aperture distribution exhibits multifractal properties, f (α(q)) will display a unimodal convex function profile. Within this analysis, the q value spans from −10 to 10 with an increment of 1 for each step.

Define the generalized fractal dimension as

$D\left(q\right)={\lim }_{\epsilon \to 0}\frac{1}{q-1}\frac{\lg \left[{\sum }_{i=1}^{N\left(\epsilon \right)}{\mu }_i{\left(\epsilon \right)}^q\right]}{\lg \epsilon },\left(q\ne 1\right).(6)$

Specifically,

$D\left(1\right)={\lim }_{\epsilon \to 0}\frac{{\sum }_{i=1}^{N\left(\epsilon \right)}{\mu }_i\left(\epsilon \right)\lg {\mu }_i\left(\epsilon \right)}{\lg \epsilon }.(7)$

Multifractal theory is a theoretical framework for describing systems with complex distributions or structures. It describes the inhomogeneity and complexity of systems through a series of fractal dimensions (see Equations 1-7). In multifractal theory, the generalized fractal dimension D(q) is a key parameter used to characterize the distribution characteristics of the system at different scales, where q is a real number and can take any value. Different values of generalized fractal dimensions correspond to different types of dimensions, of which D₀, D₁, and D₂ are the three most commonly used dimensions, each of which has a specific meaning.

Capacity dimension D₀: Also known as the box dimension, it is the most basic fractal dimension used to describe the rough structure of a set. D₀ reflects the global distribution characteristics of the entire coal sample pore diameter, regardless of the internal details of the coal sample pore diameter or the uneven distribution. The larger the result, the wider the distribution range of the pore diameter. Information dimension D₁: Also known as information dimension or Shannon dimension, is defined by the concept of Shannon entropy. D₁ reveals the detail structure and non-uniformity of coal sample pore size distribution, which is a measure of the complexity of coal sample pore size. The larger the result, the more concentrated the pore size distribution. Correlation dimension D₂: Also known as correlation dimension or correlation dimension, it is defined by considering the correlation between the points within the pore diameter of the coal sample. D₂ can be regarded as a measure to describe the correlation between the internal structure of coal sample pore size, reflecting the density of some areas in coal sample pore size and the uniformity of distribution. The larger the result, the more uniform the spacing of pore size distribution. D₀, D₁ and D₂ describe the fractal characteristics of coal sample pore size from different perspectives, including its global structure, information complexity and internal correlation, which together form the basis of multifractal analysis, and can be used to comprehensively reveal the distribution characteristics and internal laws of complex systems. D (-q)-D(q) describes the difference in fractal dimensions between sparse and dense regions of the system. This difference reflects the heterogeneity and complexity of the internal structure of the system. When D (-q)-D(q) > 0, it indicates that the fractal dimension of the sparse region in the system is higher than that of the dense region, which means that the non-uniformity of the system is strong, and the sparse region contributes more to the fractal characteristics of the system.

3.2 Characteristics of pore multifractal parameters

Taking mixed 3:7 as an example, let the total interval I = [0.38, 0.94]. Using the same dichotomy as [12, 27], the interval I of length L is divided into $N\left(\epsilon \right)=2^k$ boxes of scale ε, and the length of the boxes $\epsilon =2^{-k}L$. In order to make the minimum subinterval contain the measured value, k = 0,1,2,3,4 is selected in this paper.

3.2.1 Generalized dimension spectrum

In the multifractal analysis of aperture distribution, the first step is to verify whether the object of study exhibits multifractal properties at the spatial scale under investigation. The existence of a linear relationship between U (q,ε) and lgε is a key prerequisite to confirm that an object has multifractal characteristics. The relationship between the generalized fractal dimension U (q,ε) and log-aperture lgε (see Figure 3) of the coal sample modified with the mixed biomass surfactant shows a significant linear correlation. The results confirm the multifractal properties revealed by the pore size distribution data of N₂ (77K) adsorption experiments at low temperature.

Figure 3

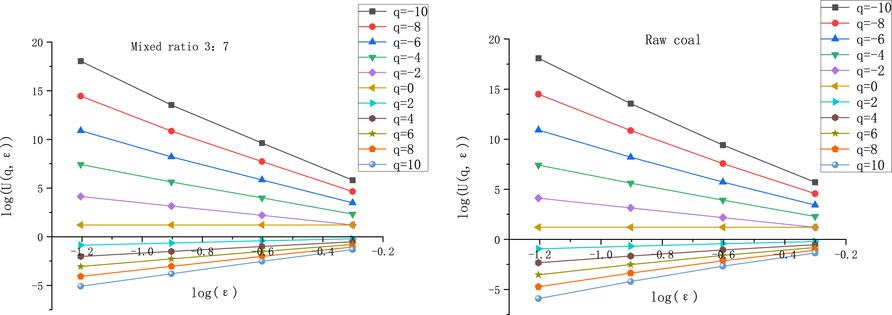
Figure 3. Linear fitting relationship between partition function and scale (taking LZ coal sample 3:7 as example).

The generalized dimension spectrum D(q)∼q curves of coal samples treated with biomass surfactants are shown in Figure 4. Combined with the inverse “S” shape of the curve, the pore size distribution of coal samples is characterized by non-uniform distribution. The larger the range of D(q), the greater the heterogeneity of the fractal structure. It can also be seen from the figure that after the coal sample is modified, the generalized dimension spectrum curve becomes more and more gentle, that is, the volatility of the curve is weakened, and the range of the curve (that is, the numerical range covered by the curve) is also gradually shrinking, which indicates that the non-uniformity of high-rank coal is smaller. In other words, the internal structural complexity of the modified coal is reduced, and it has weaker inhomogeneity.

Figure 4

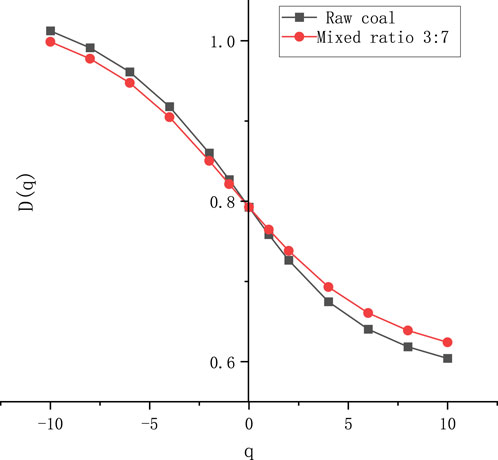
Figure 4. Generalized dimensional spectral D (q)∼q curve of pore size distribution of coal samples (taking LZ coal sample 3:7 as example).

The results of D₀, D₁, D₂ and D_-10-D₁₀ in the generalized fractal dimensions of coal samples are shown in Table 2. For raw coal and composite (3:7) coal samples, their D₀ values are the same (0.7925), which indicates that the degree of pore space filling of the two is consistent in fractal dimension. However, on D₁ and D₂ values, the coal treated with the mixed biomass surfactant is 0.7645 and 0.7382, respectively, which are higher than that of raw coal (0.7584 and 0.7264). This means that compared with raw coal, the uniformity of pore distribution and the degree of correlation between pores are improved. The values of D_-10-D₁₀ reflect the diversity and complexity of pore structure. The D_-10-D₁₀ value of raw coal is 0.4084, while that of coal treated with mixed biomass surfactant is 0.3746, indicating that the pore structure of raw coal has higher diversity and complexity than that of coal treated with mixed biomass surfactant. Although there is no difference in the degree of pore space filling between raw coal and the coal treated with mixed biomass surfactant, the coal treated with mixed biomass surfactant performs better in the uniformity of pore distribution and the degree of pore correlation. These differences may have an impact on the physical and chemical properties of coal samples, which in turn affect their performance in practical applications.

Table 2

Table 2. Spectral parameters of generalized fractal dimension of coal samples.

3.2.2 Multifractal singular spectrum

In multifractal analysis, △α and △f are two important parameters, which are used to describe the heterogeneity and complexity of coal sample pores (see [12]). These two parameters are derived from the analysis of multifractal spectrum, which is extracted from coal sample pores through a series of operations to represent the fractal dimension of coal sample pores at different scales. The following are the meanings of these two parameters.

In the multifractal spectrum, the minimum and maximum values of α(q) represent the local shape characteristics of the sparsest and densest parts of the coal sample pores, respectively. Thus, △α = α_max-α_min describes the difference in fractal properties between the densest and the sparsest parts of the coal sample pores. The larger △α value indicates that the pore space distribution of coal sample is non-uniform.

In the multifractal spectrum, f(α) describes the fractal dimension of coal sample pores with a specific local Holder index. It can be understood as the richness or complexity of coal sample pores under this fractal property. Something like △f = f (α_max) - f (α_min) describes the difference in fractal dimension between the densest and the sparsest parts. However, because of the way f(α) is defined and calculated, △f is often used to represent the width of the multifractal spectrum, that is, the shape and range of the spectrum, and is not directly used to compare the fractal dimension of the densest and sparsest parts.

The multifractal spectrum curve illustrating the pore distribution of the coal sample treated with the mixed biomass surfactant, compared to that of raw coal, is presented in Figure 5. This confirms the presence of multifractal characteristics in the pore size distribution. Correspondingly, the multifractal singular spectrum parameters of the coal samples were computed, with the results summarized in Table 3.

Figure 5

Figure 5. Multifractal spectral curve of pore size distribution of coal samples (taking LZ coal sample 3:7 as example).

Table 3

Table 3. Parameters of multifractal singular spectra.

As depicted in Figure 5, the spectrum curve of pore distribution, comparing treated coal samples to raw coal following surfactant modification, exhibits a unimodal convex profile. This finding demonstrates that the pore size distribution, determined via the low-temperature N₂ adsorption method at 77 K, possesses multifractal features. Table 3 provides the detailed results of the calculated multifractal singular spectrum parameters for the coal samples.

From the data in Table 3, it is evident that the treated coal exhibits a smaller △α value and a larger △f value compared to raw coal. These observations suggest that biomass surfactant modification enhances the local density of the pore size distribution, leading to a more uniform fractal behavior across different scales relative to untreated coal. Such changes in pore structure likely exert a favorable influence on the physical and chemical properties of the coal samples, with potential implications for energy applications and environmental sustainability.

3.3 Multifractal characteristic and connectivity complexity

In the field of coal science, the Hurst index plays a significant role in characterizing the pore structure of materials such as coal seams, with a particular emphasis on their connectivity (see [28–30]). Ranging from 0 to 1, the Hurst index reflects the degree of long-range dependence and structural self-similarity, with values closer to 1 indicating stronger self-similarity and persistence in the material’s structural patterns. As a fundamental tool in fractal and multifractal analysis, the Hurst index not only aids in assessing pore connectivity but also provides insights into the anisotropic and heterogeneous properties of coal seams. Building on the multifractal framework, the generalized Hurst index extends this concept to better capture the complex, scale-dependent nature of pore connectivity in coal. Represented as H(q), the generalized Hurst index is determined using the scale index τ(q) and the multifractal spectrum f(α). It is expressed as follows:

$H\left(q\right)=\frac{\tau \left(q\right)+1}{q}(8)$

In Equation 8, H(q) signifies the generalized Hurst index, which describes the connectivity of apertures, while τ(q) denotes the scale index. Notably, when q = 2, H(q) reduces to the classical Hurst index, typically ranging from 0.5 to 1. A higher Hurst index indicates stronger aperture connectivity, whereas a lower value reflects weaker connectivity. Refer to Table 4 below for further details.

Table 4

Table 4. Hurst index of coal samples (taking LZ coal sample as an example).

It can be found from the table that the Hurst index of the coal treated with the mixed biomass surfactant is higher than that of the raw coal, indicating that the pore connectivity is improved after the mixed modification.

4 Conclusion

The study systematically investigates the multifractal characteristics of coal pore structures under the influence of mixed biomass surfactants, providing significant insights into the optimization of coal pore connectivity and uniformity. The findings reveal that the pore size distribution of coal samples, as determined by low-temperature N2 adsorption experiments, exhibits distinct multifractal properties. The application of mixed biomass surfactants leads to a notable enhancement in the uniformity of the pore structure, reducing internal heterogeneity and improving the overall connectivity of the pore network. This is evidenced by the increase in the Hurst index of treated coal samples compared to raw coal, indicating improved self-similarity and a more consistent distribution pattern across larger spatial scales.

The generalized dimension spectrum (Dq∼q) and multifractal singular spectrum (f(α)∼α) analyses further demonstrate the reduction in structural complexity and heterogeneity of coal pores after surfactant treatment. A reduced slope and a narrower range in the generalized dimension spectrum suggest that the treated coal exhibits a more homogeneous pore distribution. Similarly, the decrease in Δα and Δf values in the multifractal singular spectrum analysis confirms the reduction in pore heterogeneity and complexity. These structural improvements are critical for enhancing methane desorption, diffusion, and migration, thereby addressing challenges in coalbed methane (CBM) recovery.

However, the study has certain limitations. The scalability of biomass surfactant applications in industrial settings remains uncertain, as the study was conducted under controlled laboratory conditions. Future research should evaluate the economic feasibility and operational challenges of large-scale implementation. Additionally, the study focuses on a specific biomass surfactant formulation (such as subdivide the mixing ratios) and coal seam. Exploring alternative biomass surfactant formulations and testing their effects under varying coal seam conditions could provide broader insights into their applicability and effectiveness. These directions will further enhance the understanding of biomass surfactants as sustainable solutions for optimizing coalbed methane recovery and improving energy resource management.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

LY: Conceptualization, Methodology, Resources, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. YY: Writing–original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This paper was supported by the Key Project of the Natural Science Foundation of Universities in Anhui Province (KJ2021A1389), Anhui Province Outstanding Young Talents Support Program (No. gxyg2021270), Anhui University Collaborative Innovation Project GXXT-2020-057, and Key Project of University Humanities and Social Science in Anhui Province (No. SK2019A0102).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Xu C, Nie W, Liu Z, Peng H, Yang S, Liu Q. Multi-factor numerical simulation study on spray dust suppression device in coal mining process. Energy (2019) 182:544–58. doi:10.1016/j.energy.2019.05.201

CrossRef Full Text | Google Scholar

2. Bardestani R, Patience GS, Kaliaguine S. Experimental methods in chemical engineering: specific surface area and pore size distribution measurements—BET, BJH, and DFT. Can J Chem Eng (2019) 97(11):2781–91. doi:10.1002/cjce.23632

CrossRef Full Text | Google Scholar

3. Ji B, Jiang B, Yuan L, Yu C, Zhou G, Zhao Y, et al. Experimental and molecular dynamics simulation study on the influence of SDS and JFC composite ratios on bituminous coal wettability. Process Saf Environ Prot (2023) 174:473–84. doi:10.1016/j.psep.2023.03.081

CrossRef Full Text | Google Scholar

4. Nikolova C, Gutierrez T. Biosurfactants and their applications in the oil and gas industry: current state of knowledge and future perspectives. Front Bioeng Biotechnol (2021) 9:626639. doi:10.3389/fbioe.2021.626639

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Cai F, Zhang Q, Yang L. Fractal characteristics and microstructure of coal with impact of starch-polymerized aluminum sulfate fracturing fluids. Fractal and Fractional (2024) 8(4):228. doi:10.3390/fractalfract8040228

CrossRef Full Text | Google Scholar

6. Yang L, Cai F, Yuan Y. Fractal dimension and nuclear magnetic resonance characteristics of surfactants for coal gas desorption. Fractal and Fractional (2023) 7(3):217. doi:10.3390/fractalfract7030217

CrossRef Full Text | Google Scholar

7. Zhao Y, Lin B, Liu T, Zheng Y, Sun Y, Zhang G, et al. Multifractal analysis of coal pore structure based on NMR experiment: a new method for predicting T2 cutoff value. Fuel (2021) 283:119338. doi:10.1016/j.fuel.2020.119338

CrossRef Full Text | Google Scholar

8. Miao Z, Qiu Z, Guofu L, Xuehai F, Chaochao D, Huihu L, et al. Fluid distribution and pore structure multifractal characteristics analysis of coal measure mudstone. J Nat Gas Sci Eng (2021) 88:103810. doi:10.1016/j.jngse.2021.103810

CrossRef Full Text | Google Scholar

9. Sun Y, Zhai C, Zhao Y, Xu J, Cong Y, Zheng Y, et al. Multifractal analysis and neural network prediction of pore structures in coal reservoirs based on NMR T2 spectra. Energy and Fuels (2021) 35(14):11306–18. doi:10.1021/acs.energyfuels.1c01409

CrossRef Full Text | Google Scholar

10. Li T, Li HL, Zhang L, Zheng S. Complete synchronization of discrete-time variable-order fractional neural networks with time delays. Chin J Phys (2024) 91:883–94. doi:10.1016/j.cjph.2024.08.022

CrossRef Full Text | Google Scholar

11. Johansyah MD, Sambas A, Farman M, Vaidyanathan S, Zheng S, Foster B, et al. Global mittag-leffler attractive sets, boundedness, and finite-time stabilization in novel chaotic 4d supply chain models with fractional order form. Fractal and Fractional (2024) 8(8):462. doi:10.3390/fractalfract8080462

CrossRef Full Text | Google Scholar

12. Zheng S, Yao Y, Liu D, Cai Y, Liu Y, Li X. Nuclear magnetic resonance T2 cutoffs of coals: a novel method by multifractal analysis theory. Fuel (2019) 241:715–24. doi:10.1016/j.fuel.2018.12.044

CrossRef Full Text | Google Scholar

13. Wang D, Hu H, Wang T, Tang T, Li W, Zhu G, et al. Difference between of coal and shale pore structural characters based on gas adsorption experiment and multifractal analysis. Fuel (2024) 371:132044. doi:10.1016/j.fuel.2024.132044

CrossRef Full Text | Google Scholar

14. Zhang S, Liu H, Wu C, Jin Z. Influence of particle size on pore structure and multifractal characteristics in coal using low-pressure gas adsorption. J Pet Sci Eng (2022) 212:110273. doi:10.1016/j.petrol.2022.110273

CrossRef Full Text | Google Scholar

15. Gan J, Wang D, Xiao Z, Wang YN, Zhang K, Zhu X, et al. Experimental and molecular dynamics investigations of the effects of ionic surfactants on the wettability of low-rank coal. Energy (2023) 271:127012. doi:10.1016/j.energy.2023.127012

CrossRef Full Text | Google Scholar

16. Niu W, Nie W, Yuan M, Bao Q, Zhou W, Yan J, et al. Study of the microscopic mechanism of lauryl glucoside wetting coal dust: environmental pollution prevention and control. J Hazard Mater (2021) 412:125223. doi:10.1016/j.jhazmat.2021.125223

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Chen Y, Xu G, Albijanic B. Evaluation of SDBS surfactant on coal wetting performance with static methods: preliminary laboratory tests. Energy Sourc A: Recovery, Utilization Environ Effects (2017) 39(23):2140–50. doi:10.1080/15567036.2017.1403503

CrossRef Full Text | Google Scholar

18. Dou J, Liu J, Wang Y, Zhi L, Shen J, Wang G. Surface activity, wetting, and aggregation of a perfluoropolyether quaternary ammonium salt surfactant with a hydroxyethyl group. Molecules (2023) 28(20):7151. doi:10.3390/molecules28207151

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ni G, Sun Q, Xun M, Wang H, Xu Y, Cheng W, et al. Effect of NaCl-sds compound solution on the wettability and functional groups of coal. Fuel (2019) 257:116077. doi:10.1016/j.fuel.2019.116077

CrossRef Full Text | Google Scholar

20. Tian Q, Nie W, Bao Q, Niu W, Li R, Zhang X, et al. Research on coal dust pollution prevention and control based on co-solvent association: macro-micro experiments and molecular dynamics simulations. Appl Surf Sci (2024) 651:159289. doi:10.1016/j.apsusc.2024.159289

CrossRef Full Text | Google Scholar

21. Niu W, Nie W, Bao Q, Tian Q, Liu F, Li R, et al. Interactions between fluorocarbon surfactant and coal dust at macro, meso and molecular scales and their applications in coal dust control. Chem Eng J (2023) 475:146059. doi:10.1016/j.cej.2023.146059

CrossRef Full Text | Google Scholar

22. Xu F, Wang S, Kong R, Wang C. Synergistic effects of dodecane-castor oil acid mixture on the flotation responses of low-rank coal: a combined simulation and experimental study. Int J Mining Sci Technology (2023) 33(5):649–58. doi:10.1016/j.ijmst.2022.11.010

CrossRef Full Text | Google Scholar

23. Wang Y, Shardt N, Lu C, Li H, Elliott JA, Jin Z. Validity of the Kelvin equation and the equation-of-state-with-capillary-pressure model for the phase behavior of a pure component under nanoconfinement. Chem Eng Sci (2020) 226:115839. doi:10.1016/j.ces.2020.115839

CrossRef Full Text | Google Scholar

24. Stahlfeld KW, Belmont EL. BET and Kelvin analyses by thermogravimetric desorption. Langmuir (2023) 39(25):8814–23. doi:10.1021/acs.langmuir.3c00854

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Shi K, Santiso EE, Gubbins KE. Current advances in characterization of nano-porous materials: pore size distribution and surface area. In: JC Moreno-Piraján, L Giraldo-Gutierrez, and F Gómez-Granados, editors. Porous materials. Engineering materials. Cham: Springer (2021).

Google Scholar

26. Ullah R, Siraj M, Zarshan F, Ahsan Abbasi B, Yaseen T, Abdul W, et al. A comprehensive overview of fabrication of biogenic multifunctional metal/metal oxide nanoparticles and applications. Rev Inorg Chem (2024). doi:10.1515/revic-2024-0031

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhang M, Liu Q, Wang X, Dong Z. Multiple fractal characterization of medium-high rank coal integrating mercury intrusion porosimetry, N2 and CO2 adsorption experiments. J China coal Soc (2024) 49(5):2394–404. doi:10.13225/j.cnki.jccs.2023.0433

CrossRef Full Text | Google Scholar

28. Prajapati R, Kumar R, Singh UK. Assessment of reservoir heterogeneities and hydrocarbon potential zones using wavelet-based fractal and multifractal analysis of geophysical logs of Cambay basin, India. Mar Pet Geology (2024) 160:106633. doi:10.1016/j.marpetgeo.2023.106633

CrossRef Full Text | Google Scholar

29. Chen S, Liu D, Wang Z, Xu L, Li Q, Ren L, et al. Predicting T2 cutoffs from nmr logging based on multifractal theory: a case study of a shale reservoir in the songliao basin, China. Energy and Fuels (2025) 39:4292–303. doi:10.1021/acs.energyfuels.5c00022

CrossRef Full Text | Google Scholar

30. Kumar C, Shrivastav M, Escrig J, Ţălu Ş, Yadav RP, Guzman F. Unravelling the impact of surface roughness and cationic Ni2+ vacancies to Ni3+ ions ratio on optical properties of NiOx thin film: insights fractal and multifractal dimension. Ceramics Int Online (2025). doi:10.1016/j.ceramint.2025.01.362

CrossRef Full Text | Google Scholar