Permittivity-asymmetric chiral metasurfaces empowered by bound states in the continuum

The intrinsic chirality of natural materials is usually weak or absent. To enlarge circular dichroism, chiral metasurfaces supporting bound states in the continuum have been widely investigated. These chiral metasurfaces have demonstrated considerable potential to achieve high quality (Q) factors but require ultra-small structure asymmetry and complicated fabrication processes. Here we propose a novel approach to break the in-plane symmetry of the structure by introducing refractive index perturbations. Furthermore, we demonstrate the efficient intrinsic chiral emission from resonant metasurfaces which are composed of two slant titanium dioxide (TiO₂) bars arranged on a square lattice. Numerical calculations indicate that the intrinsic chirality of our metasurfaces at normal incidence achieves near-unity circular dichroism of 0.99 and an ultra-high Q factor exceeding ${10}^6$. The relationship between the two perturbations and CD and Q factor has also been studied, offering the flexibility to enhance and tailor chirality and Q factor simultaneously. Our chiral metasurfaces may lead to applications in chiral lasers, chiral light detectors, chiral biosensing, and chiral nonlinear filters.

1 Introduction

Chirality exists widely in nature and means that an object cannot be coincident with its mirror image. Chiral materials usually exhibit different optical responses under different circularly polarized light, which can be measured by circular dichroism (CD) [1]. CD represents differential absorption or reflection between left-handed circularly polarized (LCP) light and right-handed circularly polarized (RCP) light. Chiral optics have shown great importance in the fields of bioscience, chemistry and medicine [2–5]. For example, Chanda and his colleagues report that they used an achiral plasma cavity structure to enhance the brational circular dichroism (VCD) signal, allowing them to distinguish the chirality of thalidomide [6, 7]. Compared to traditional VCD technology, their system improves detection sensitivity by 13 orders of magnitude. Most naturally occurring chiral materials have very small CD values, limiting their further application. In recent years, optical metamaterials with strong optical chirality have been proposed and widely investigated [8–12]. In 2009, Gansel et al. [8] fabricated a single-axis photonic metamaterial composed of three-dimensional gold helices. Due to the internal and Bragg resonances, the structure blocks circular polarization with the same handedness as the helix, while transmitting the other. The transmittance difference between LCP and RCP reaches up to 0.76. Moreover, other three-dimensional (3D) nanostructures, such as L-shaped and cross-shaped ones have also demonstrated optical chirality by breaking multiple mirror symmetries [9–12].

Although 3D metamaterials have demonstrated excellent optical chiral properties, their manufacturing processes are complex and challenging [13]. Recently, some planar metasurfaces have experimentally shown strong CD signals through structural anisotropy under oblique incidence [14–16], which are called ‘extrinsic chirality’. On the other hand, there is another type of metasurfaces demonstrating chirality at normal incidence, known as intrinsic chirality. In 2014, Wu et al. [13] suggested the Fano-resonant all-dielectric metasurfaces that exhibit extreme intrinsic planar chirality. Each unit cell of the metasurface consists of one straight and one bent silicon nanorod, where the bend is responsible for breaking the two mirror inversion symmetries of the cell and coupling the electric dipole and the electric quadrupole/magnetic dipole resonances.

To further enhance the chiral light-matter interactions, chiroptical metasurfaces mediated by bound states in the continuum (BICs) have been proposed [17–19]. BICs represent specific states situated within the light cone, allowing for the localization of light for an infinitely long time [20–22]. Since BICs cannot be accessed externally, quasi-BICs are introduced by breaking the in-plane symmetry of the structure. Quasi-BICs exhibit finite but still very high Q factors by coupling out the resonant mode to free-space radiation [23–25]. In 2023, by employing the tilted trapezoidal hollow photonic crystal plate that supports a quasi-BIC, Chen et al. [26] broke the in-plane geometric symmetry and out-of-plane symmetry of the metasurfaces and eventually achieved an intrinsic chiral response with a CD value of 0.93 and a high quality factor exceeding 2,663 for visible frequencies. Although the fabrication challenges of metasurfaces have been greatly improved by superior technologies [27, 28], the realization of small geometric perturbations in nanostructures remains a great challenge [29].

Here we propose and demonstrate a new paradigm for designing chiral dielectric metasurfaces. Unlike previous studies that predominantly break in-plane symmetry by disrupting geometric symmetry, our metasurface introduces refractive index perturbations within the plane, enabling it to support quasi-BIC modes. Subsequently, by incorporating tilted perturbations, the metasurface is further capable of supporting far-field chiral light emission. By studying the relationship between the two perturbations, the CD value, and the Q factor, we reveal a new method for designing metasurfaces with strong chirality and high Q factors. We believe that our metasurface may boost applications such as surface-emitting lasing [30], biomedical sensing [31–33], polarization converters [34–36] and nonlinear frequency converters [18, 37].

2 Materials and methods

As shown in Figure 1a, our metasurface consists of a three-layer structure: the top layer is polymethyl methacrylate (PMMA), the bottom layer is a glass substrate, and the middle layer of the metasurface is composed of titanium dioxide (TiO₂) bars surrounded by a polycarbonate (PC) filling medium. The thickness of both the glass substrate and PMMA is h = 400 nm, with a refractive index of 1.45 for both materials. Figure 1b shows the cross-section of the unit cell of our proposed planar metasurface. The two bars have the same width, height, and length. The bars are embedded in polycarbonate (PC) with a refractive index of 1.63. The lattice constant and the distance between the centers of the two bars are fixed at a = 360 nm and d = 150 nm, respectively. As pointed out by previous research, the key to enabling the chiral BIC is to break all the mirror symmetries of the structure [38–40]. Unlike other studies that break the in-plane geometry asymmetry, we introduce refractive index perturbation α to break the in-plane mirror symmetry. The two bars have different refractive indices. One has a refractive index of n₁ = 2.13 and the other has a refractive index of n₂ = n₁ - α. Minute refractive index perturbation α can be finely tuned through carrier injection, chemical doping or annealing temperature adjustment [29, 41–43]. Then we introduce slant angle perturbation θ to break the out-of-plane mirror symmetry. Thus, all the mirror symmetries are broken.

Figure 1

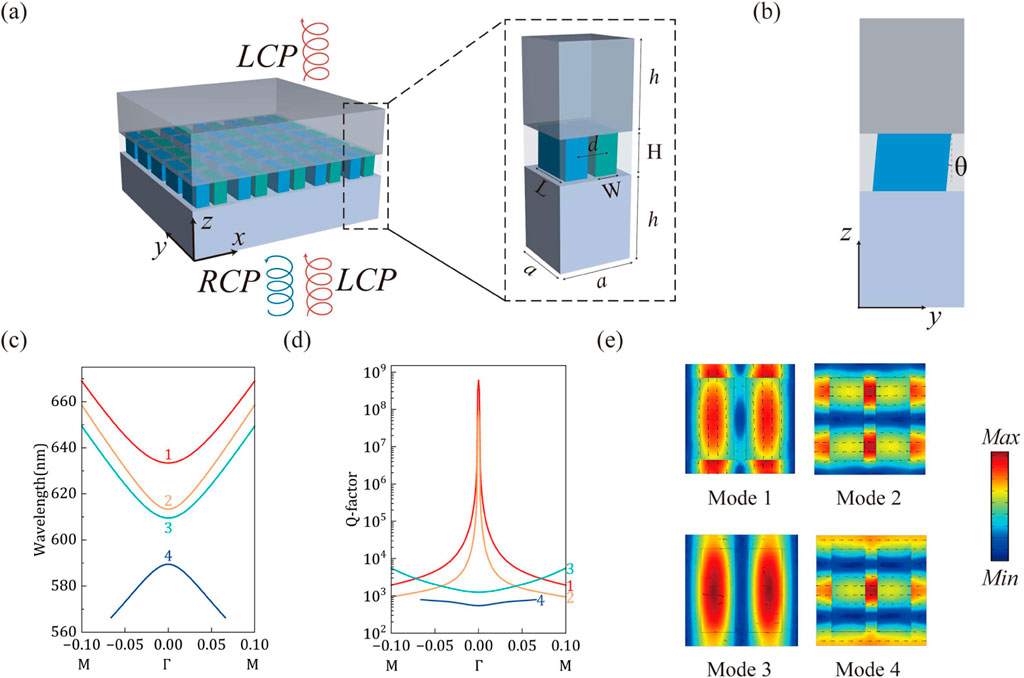
Figure 1. (a) Schematic of the proposed intrinsic chiral metasurface empowered by BICs. The geometric parameters are as follows: L = 270 nm, W = 110 nm, and H = 200 nm. (b) Side view of the unit cell. (c) Simulated band structure of the proposed metasurface near the Г point. The insets show the first Brillouin zone with high symmetries. (d) Simulated Q-factors of the typical eigenmodes in the k space in the vicinity of the Г point. (e) The corresponding electric field patterns of the four eigenmodes at the Γ point. The black arrows represent the electric field vectors.

We conducted numerical simulations using the Wave Optics Module in COMSOL Multiphysics. Additionally, we utilized the eigenfrequency solver to calculate the eigenmodes and Stokes parameters of the planar metasurface, thereby simulating the splitting and displacement processes of the topological charge. When no perturbations are introduced, the structure exhibits a symmetry-protected BIC at the Γ point of the Brillouin zone and supports a series of Bloch modes. The dispersion curve, calculated using the finite element method (FEM), is depicted in Figure 1c. Both the first and second eigenmodes support an infinitely high Q factor at the Γ point, as shown in Figure 1d. Figure 1e shows the electric field distribution and electric field vectors of different eigenmodes at the Γ point. Due to time-reversal symmetry, the electromagnetic near fields of BICs are always linearly polarized, and their distributions cancel each other out, blocking far-field radiation.

Once the in-plane C₂ symmetry is broken, such as by refractive index perturbations introduced through carrier injection or chemical doping [41, 42], the BIC transforms into a quasi-BIC that generates circular polarization in the near field. We measure the chirality of a quasi-BIC with the optical chirality density (OCD) Equation 1 [44]:

$OCD=-\frac{1}{2}\omega \text{Re}\left[\mathit{D}·{\mathit{B}}^{*}\right](1)$

where ω is the angular frequency of light, D is the electric displacement field and B^∗ is the complex conjugate of magnetic flux density. For the case of α ≠ 0, θ = 0, since OCD is a parity-odd scalar [45], the presence of mirror symmetry causes OCD to have opposite values on both sides of the mirror, as shown in Figure 2a. Optical chirality follows the conservation law, and the relationship between the optical chirality flux F and the near-field OCD of the relevant resonance is given by Equation 2:

$-2\omega {\int }_{V}OCD\mathrm{d}\mathrm{v}+{\int }_V\text{Re}\left(\nabla ·\mathit{F}\right)\mathrm{d}\mathrm{v}=0(2)$

where V is a finite volume that includes the dielectric bars and the surrounding background medium. F is directly proportional to the degree of circular polarization and is defined by Equation 3:

$\mathit{F}=\frac{1}{4}\left[\mathit{E}\times \left(\nabla \times {\mathit{H}}^{*}\right)-{\mathit{H}}^{*}\times \left(\nabla \times \mathit{E}\right)\right](3)$

Figure 2

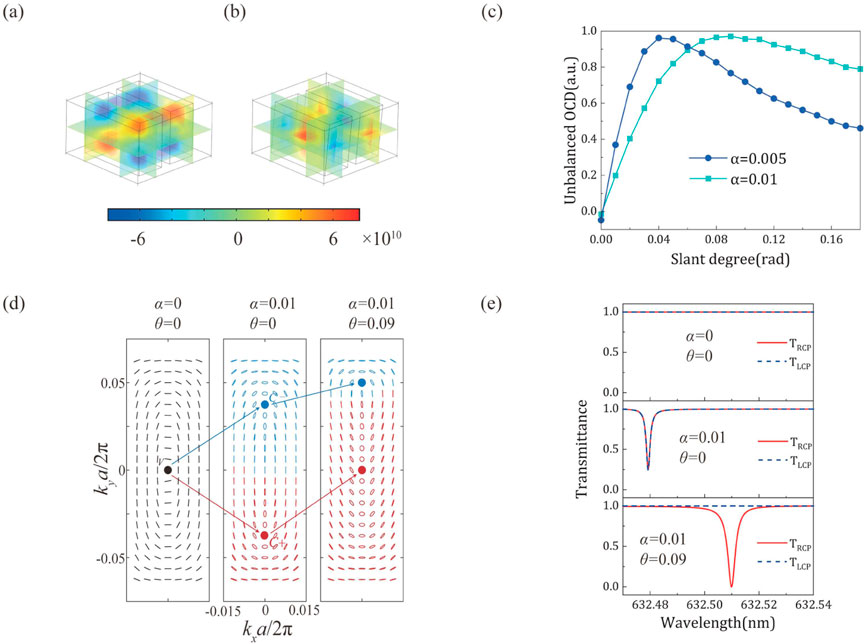
Figure 2. (a) OCD distribution in cross section when α ≠ 0 and θ = 0. (b) OCD distribution in cross section when α ≠ 0 and θ ≠ 0. (c) Unbalanced OCD as a function of slant angle for two different α values. (d) Evolution of C points in momentum space for different α and θ. The black lines represent linear polarization states. The red and blue ellipses indicate right-handed and left-handed elliptical polarization, respectively. (e) The transmission spectra of right-circularly polarized light and left-circularly polarized light for different asymmetric parameters.

The antisymmetric OCD distributions cancel each other in the near field of the metasurface, so no chiral flux is generated in the far field. Due to the out-of-plane mirror symmetry, the far field chiral flux is absent and unaffected by the in-plane geometry. To break the out-of-plane mirror symmetry, we tilt the dielectric bars along the y-axis. This results in an imbalance in the near-field OCD distribution on the metasurface, which in turn causes a non-zero optical chiral flux in the far field, i.e., circularly polarized radiation, as depicted in Figure 2b.

3 Results and discussion

The relationship between the unbalanced OCD (equal to ${\int }_{V}OCDdv$) and the slant angle θ of mode1 for two different α values is calculated using the Wave Optics Module in COMSOL Multiphysics, as shown in Figure 2c. As the slant angle increases, the unbalanced OCD reaches the maximum value and then decreases. This maximum value corresponds to the highest degree of circular polarization at the Γ point. The metasurface with the largest unbalanced OCD is suitable for realizing an intrinsic chiral metasurface with the maximum CD value. We can infer that for any refractive index perturbation α, there exists a specific slant angle that makes far field of the metasurface highly circularly polarized.

Furthermore, the evolution of polarization states in momentum space for the mode1 with perturbations is depicted in Figure 2d. When no perturbation is applied, the polarization states exhibit linear characteristics, and a V point corresponding to a BIC is present at the Γ point. When in-plane refractive index perturbation α is introduced, the in-plane symmetry is broken. The V point with an integer topological charge is decomposed into a pair of C points with half-integer topological charges [22], which are symmetrically distributed along the $k_y$ direction on both sides of the Γ point. The C+ and C- points represent right-handed circular polarization (RCP) and left-handed circular polarization (LCP), respectively. To achieve intrinsic chirality, the C points should be manipulated and moved back to the Γ point. By introducing a slant angle perturbation θ to break the out-of-plane symmetry, the C+ point is moved to the Γ point. When the dielectric bars are tilted along the $k_y$ direction, the C points also move along the $k_y$ direction. It is noteworthy that for a perturbation α, the perturbation θ that moves the C+ point to the Γ point is the same as the perturbation θ that maximizes the unbalanced OCD. For example, when α = 0.01 and θ = 0.09, the C+ point is located at the Γ point in the momentum space, and the unbalanced OCD reaches the maximum, leading to the realization of an intrinsic chiral BIC. Figure 2e shows the transmission peak curves of RCP and LCP for different perturbation parameters. This is consistent with the predicted evolution of the intrinsic polarization states. When α = 0 and θ = 0, a BIC appears at the Γ point and the eigenstate is completely decoupled from all normally incident plane waves, resulting in no radiation loss. When a perturbation α = 0.01 is introduced, the V point splits into two C points symmetrically distributed on both sides of the Γ point. Due to the mirror symmetry in the z-direction of the metasurface, there is no chiral response. When a perturbation θ = 0.09 is introduced, the C+ point is moved to the Γ point, exhibiting intrinsic RCP states in the far field. Thus, for inclined metasurfaces, asymmetric transmission of RCP and LCP light can be observed.

To verify the chirality of the metasurface, we employed the wavelength domain solver in COMSOL Multiphysics to calculate the transmission spectrum of the metasurface at α = 0.01. Figure 3a shows the calculated transmission and CD spectra of the metasurface at normal incidence. Here, T_ij represents the transmittance of the output polarization i for the input polarization j. r represents RCP, and l represents LCP. Circular dichroism (CD) describes the difference in absorption between left-handed and right-handed circularly polarized light by chiral molecules. It is defined by Equation 4:

$CD=\frac{\left(T_{rl}+T_{ll}\right)-\left(T_{rr}+T_{lr}\right)}{\left(T_{rl}+T_{ll}\right)+\left(T_{rr}+T_{lr}\right)}(4)$

T_rr exhibits a sharp drop at the q-BIC resonant wavelength (632.51 nm), while the other three transmittance values remain basically stable, resulting in a super-sharp spike in the CD spectrum at this wavelength, with a maximum value exceeding 0.99 (green curve in Figure 3a).

Figure 3

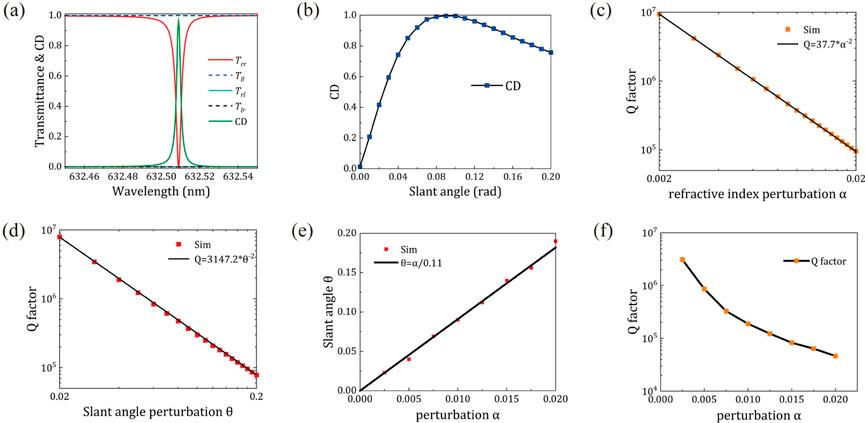
Figure 3. (a) Calculated transmission and CD spectra of the metasurface at normal incidence. (b) CD amplitude as a function of θ when α is fixed at 0.01. (c, d) Dependence of the Q-factors of the mode1 on the relative asymmetry perturbation (c) α = n₁−n₂, (d) θ around the chiral q-BIC state. The solid line represents an inverse quadratic fitting. (e) Relation between ϕ and θ for maximizing CD. (f) Simulated Q-factor (in log scale) of the mode1 chiral BIC as a function of the cooperative change in perturbations α and θ, where θ = α/0.11.

In addition, we investigated the relationship between the CD amplitude and the slant angle θ when α was fixed at 0.01, as shown in Figure 3b. As the slant angle θ increases, the CD value first reaches its maximum at θ = 0.09, and then gradually decreases. The variation trend of CD is the same as that of the unbalanced OCD (Figure 2c), which reaches its maximum at θ = 0.09, suggesting that the maximum unbalanced OCD corresponds to the highest circular polarization at the Γ point. As shown in Figures 3c and 3d, the Q-factor of symmetry-protected BICs approximately follows the inverse quadratic law of asymmetric perturbations: Q∼1/(α²+Aθ²), where A represents the different sensitivities of the Q factor to α and θ. By fitting, the scale factors for the Q-factor are determined to be 37.7 and 3147.2 for α and θ, respectively. As a result, the parameter A in the equation is calculated to be A = 37.7/3147.2 = 0.012.

When the two perturbations α and θ are small, the intrinsic chirality of quasi-BICs, characterized by CD, can be estimated as [26]:

$CD\sim \frac{\sin \left(\theta \right)}{{\alpha }^2+A{\theta }^2}\approx \frac{\theta }{{\alpha }^2+A{\theta }^2}(5)$

As can be seen from Equation 5, when α is fixed, CD first rapidly increases to the maximum value with increasing θ, and then gradually decrease. The simulation results reproduce this behavior well (Figure 3b). By calculating the reciprocal of CD with respect to θ, we find that CD reaches its maximum at θ = α/ $\sqrt{A}$. This provides a new approach to modulating the perturbations to achieve the strongest intrinsic chirality. The value of A depends on the different structures and field patterns of the chiral metasurface. In our designed metasurface, the maximum chirality is achieved when θ and α satisfy θ = α/0.11. As shown in Figure 3e, for each fixed α, we simulate the θ that maximizes the CD value, which is in good agreement with the theoretical value. As mentioned earlier, the Q factor decreases as the perturbation increases. Therefore, one way to increase the Q factor is to decrease α and θ proportionally while maintaining the maximum CD amplitude. As shown in Figure 3f, we calculate the Q factor of the chiral BIC as a function of the cooperative changes in perturbations α and θ, where α and θ always satisfy the relationship θ = α/0.11. The infinitely high Q-factor can be precisely tailored by simultaneously adjusting α and θ, and the maximum Q factor can exceed 10⁶.

4 Conclusion

In summary, using the concept of BICs, we propose a new intrinsic chiral metasurface with Q factor values over 10⁶ and CD amplitudes up to 0.99. By introducing refractive index perturbations, we break the in-plane symmetry and avoid the complex manufacturing process associated with geometric perturbations. We then break the out-of-plane symmetry by introducing the slant angle θ and move the C+ point in the momentum space to the Γ point, achieving the intrinsic chirality. The relationship between Q factor, CD value, and two kinds of perturbations has been thoroughly investigated, resulting in a tunable metasurface. Due to the high Q-factor and CD values of chiral q-BICs in the metasurface, along with their accessibility and controllability, our results may have applications in various fields, including chiral biosensing, chiral lasing, and quantum optics.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YL: Writing–original draft, Writing–review and editing. YM: Writing–review and editing. SY: Writing–review and editing. YZ: Writing–review and editing. ZS: Writing–review and editing. ZT: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Supported by Hunan Provincial lnnovation Foundation for Postgraduate (CX20240410).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Fasman GD. Circular dichroism and the conformational analysis of biomolecules. Springer Science and Business Media (2013).

Google Scholar

2. Haesler J, Schindelholz I, Riguet E, Bochet CG, Hug W. Absolute configuration of chirally deuterated neopentane. Nature (2007) 446:526–9. doi:10.1038/nature05653

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Schreiber R, Luong N, Fan Z, Kuzyk A, Nickels PC, Zhang T, et al. Chiral plasmonic DNA nanostructures with switchable circular dichroism. Nat Commun (2013) 4:2948. doi:10.1038/ncomms3948

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Selinger RLB, Selinger JV, Malanoski AP, Schnur JM. Shape selection in chiral self-assembly. Phys Rev Lett (2004) 93:158103. doi:10.1103/PhysRevLett.93.158103

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Brunetti G, Saha N, Colapietro P, Ciminelli C. Optical slot-assisted metasurface for IgG protein detection. J Phys Conf Ser (2024) 2725:012001. doi:10.1088/1742-6596/2725/1/012001

CrossRef Full Text | Google Scholar

6. Biswas A, Cencillo-Abad P, Shabbir MW, Karmakar M, Chanda D. Tunable plasmonic superchiral light for ultrasensitive detection of chiral molecules. Sci Adv (2024) 10:eadk2560. doi:10.1126/sciadv.adk2560

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Im S, Mousavi S, Chen Y-S, Zhao Y. Perspectives of chiral nanophotonics: from mechanisms to biomedical applications. npj Nanophoton (2024) 1:46–20. doi:10.1038/s44310-024-00045-2

CrossRef Full Text | Google Scholar

8. Gansel JK, Thiel M, Rill MS, Decker M, Bade K, Saile V, et al. Gold helix photonic metamaterial as broadband circular polarizer. Science (2009) 325:1513–5. doi:10.1126/science.1177031

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Decker M, Ruther M, Kriegler CE, Zhou J, Soukoulis CM, Linden S, et al. Strong optical activity from twisted-cross photonic metamaterials. Opt Lett OL (2009) 34:2501–3. doi:10.1364/OL.34.002501

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Kuzyk A, Schreiber R, Fan Z, Pardatscher G, Roller E-M, Högele A, et al. DNA-based self-assembly of chiral plasmonic nanostructures with tailored optical response. Nature (2012) 483:311–4. doi:10.1038/nature10889

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zhang M, Pacheco-Peña V, Yu Y, Chen W, Greybush NJ, Stein A, et al. Nanoimprinted chiral plasmonic substrates with three-dimensional nanostructures. Nano Lett (2018) 18:7389–94. doi:10.1021/acs.nanolett.8b03785

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Kakkar T, Keijzer C, Rodier M, Bukharova T, Taliansky M, Love AJ, et al. Superchiral near fields detect virus structure. Light Sci Appl (2020) 9:195–10. doi:10.1038/s41377-020-00433-1

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wu C, Arju N, Kelp G, Fan JA, Dominguez J, Gonzales E, et al. Spectrally selective chiral silicon metasurfaces based on infrared Fano resonances. Nat Commun (2014) 5:3892. doi:10.1038/ncomms4892

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Plum E, Fedotov VA, Zheludev NI. Optical activity in extrinsically chiral metamaterial. Appl Phys Lett (2008) 93:191911. doi:10.1063/1.3021082

CrossRef Full Text | Google Scholar

15. Plum E, Liu X-X, Fedotov VA, Chen Y, Tsai DP, Zheludev NI. Metamaterials: optical activity without chirality. Phys Rev Lett (2009) 102:113902. doi:10.1103/PhysRevLett.102.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Cao T, Wei C, Mao L, Li Y. Extrinsic 2D chirality: giant circular conversion dichroism from a metal-dielectric-metal square array. Sci Rep (2014) 4:7442. doi:10.1038/srep07442

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Shi T, Deng Z-L, Geng G, Zeng X, Zeng Y, Hu G, et al. Planar chiral metasurfaces with maximal and tunable chiroptical response driven by bound states in the continuum. Nat Commun (2022) 13:4111. doi:10.1038/s41467-022-31877-1

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Cai S, Chen J, Liu X, Fu G, Liu G, Chen J, et al. Perfect intrinsic and nonlinear chirality simultaneously driven by half-integer topological charge. Phys Rev B (2024) 109:165420. doi:10.1103/PhysRevB.109.165420

CrossRef Full Text | Google Scholar

19. Zhang X, Liu Y, Han J, Kivshar Y, Song Q. Chiral emission from resonant metasurfaces. Science (2022) 377:1215–8. doi:10.1126/science.abq7870

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kodigala A, Lepetit T, Gu Q, Bahari B, Fainman Y, Kanté B. Lasing action from photonic bound states in continuum. Nature (2017) 541:196–9. doi:10.1038/nature20799

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Huang C, Zhang C, Xiao S, Wang Y, Fan Y, Liu Y, et al. Ultrafast control of vortex microlasers. Science (2020) 367:1018–21. doi:10.1126/science.aba4597

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhen B, Hsu CW, Lu L, Stone AD, Soljačić M. Topological nature of optical bound states in the continuum. Phys Rev Lett (2014) 113:257401. doi:10.1103/PhysRevLett.113.257401

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Koshelev K, Lepeshov S, Liu M, Bogdanov A, Kivshar Y. Asymmetric metasurfaces with high- Q resonances governed by bound states in the continuum. Phys Rev Lett (2018) 121:193903. doi:10.1103/PhysRevLett.121.193903

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Liu M, Choi D-Y. Extreme huygens’ metasurfaces based on quasi-bound states in the continuum. Nano Lett (2018) 18:8062–9. doi:10.1021/acs.nanolett.8b04774

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Overvig AC, Malek SC, Carter MJ, Shrestha S, Yu N. Selection rules for quasibound states in the continuum. Phys Rev B (2020) 102:035434. doi:10.1103/PhysRevB.102.035434

CrossRef Full Text | Google Scholar

26. Chen Y, Deng H, Sha X, Chen W, Wang R, Chen Y-H, et al. Observation of intrinsic chiral bound states in the continuum. Nature (2023) 613:474–8. doi:10.1038/s41586-022-05467-6

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Yang S, He M, Hong C, Caldwell JD, Ndukaife JC. Engineering electromagnetic field distribution and resonance quality factor using slotted quasi-BIC metasurfaces. Nano Lett (2022) 22:8060–7. doi:10.1021/acs.nanolett.2c01919

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yang G, Dev SU, Allen MS, Allen JW, Harutyunyan H. Optical bound states in the continuum enabled by magnetic resonances coupled to a mirror. Nano Lett (2022) 22:2001–8. doi:10.1021/acs.nanolett.1c04764

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Sun G, Wang Y, Cui Z, Xie R, Zhao X. Enhanced terahertz high-harmonic generation from high-Q quasi-bound states in the continuum empowered by permittivity-broken metasurface. Appl Phys Lett (2024) 124:111704. doi:10.1063/5.0196849

CrossRef Full Text | Google Scholar

30. Ha ST, Fu YH, Emani NK, Pan Z, Bakker RM, Paniagua-Domínguez R, et al. Directional lasing in resonant semiconductor nanoantenna arrays. Nat Nanotech (2018) 13:1042–7. doi:10.1038/s41565-018-0245-5

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Leung D, Ok Kang S, Anslyn E V. Rapid determination of enantiomeric excess: a focus on optical approaches. Chem Soc Rev (2012) 41:448–79. doi:10.1039/C1CS15135E

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Kumar J, Eraña H, López-Martínez E, Claes N, Martín VF, Solís DM, et al. Detection of amyloid fibrils in Parkinson’s disease using plasmonic chirality. Proc Natl Acad Sci (2018) 115:3225–30. doi:10.1073/pnas.1721690115

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Yesilkoy F, Arvelo ER, Jahani Y, Liu M, Tittl A, Cevher V, et al. Ultrasensitive hyperspectral imaging and biodetection enabled by dielectric metasurfaces. Nat Photon (2019) 13:390–6. doi:10.1038/s41566-019-0394-6

CrossRef Full Text | Google Scholar

34. Shao L, Li Z, Feng J, Zhang J, Shi H, Bai X, et al. Transmissive metasurface for multi-channel and full-polarization modulation of electromagnetic wavefronts. Photon Res, (2023) 11:245–51. doi:10.1364/PRJ.475364

CrossRef Full Text | Google Scholar

35. Zanotto S, Colombano M, Navarro-Urrios D, Biasiol G, Sotomayor-Torres CM, Tredicucci A, et al. Broadband dynamic polarization conversion in optomechanical metasurfaces. Front Phys (2020) 7:7. doi:10.3389/fphy.2019.00231

CrossRef Full Text | Google Scholar

36. Wang M, Zhai Z. Wide-angle circular polarization converter based on a metasurface of Z-shaped unit cells. Front Phys (2020) 8:8. doi:10.3389/fphy.2020.527394

CrossRef Full Text | Google Scholar

37. Koshelev K, Kruk S, Melik-Gaykazyan E, Choi J-H, Bogdanov A, Park H-G, et al. Subwavelength dielectric resonators for nonlinear nanophotonics. Science (2020) 367:288–92. doi:10.1126/science.aaz3985

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Gorkunov MV, Antonov AA, Kivshar YS. Metasurfaces with maximum chirality empowered by bound states in the continuum. Phys Rev Lett (2020) 125:093903. doi:10.1103/PhysRevLett.125.093903

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Overvig A, Yu N, Alù A. Chiral quasi-bound states in the continuum. Phys Rev Lett (2021) 126:073001. doi:10.1103/PhysRevLett.126.073001

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Dixon J, Lawrence M, Barton DR, Dionne J. Self-isolated Raman lasing with a chiral dielectric metasurface. Phys Rev Lett (2021) 126:123201. doi:10.1103/PhysRevLett.126.123201

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Berté R, Weber T, de Souza Menezes L, Kühner L, Aigner A, Barkey M, et al. Permittivity-asymmetric quasi-bound states in the continuum. Nano Lett (2023) 23:2651–8. doi:10.1021/acs.nanolett.2c05021

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Soref R, Bennett B. Electrooptical effects in silicon. IEEE J Quan Electronics (1987) 23:123–9. doi:10.1109/JQE.1987.1073206

CrossRef Full Text | Google Scholar

43. Mathews NR, Morales ER, Cortés-Jacome MA, Toledo Antonio JA. TiO2 thin films – influence of annealing temperature on structural, optical and photocatalytic properties. Solar Energy (2009) 83:1499–508. doi:10.1016/j.solener.2009.04.008

CrossRef Full Text | Google Scholar

44. Poulikakos LV, Gutsche P, McPeak KM, Burger S, Niegemann J, Hafner C, et al. Optical chirality flux as a useful far-field probe of chiral near fields. ACS Photon (2016) 3:1619–25. doi:10.1021/acsphotonics.6b00201

CrossRef Full Text | Google Scholar

45. Tang Y, Cohen AE. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science (2011) 332:333–6. doi:10.1126/science.1202817

PubMed Abstract | CrossRef Full Text | Google Scholar