Mutual authentication quantum key agreement protocol with single-particle measurement

In this paper, a mutual authentication quantum key agreement protocol with single-particle measurement is proposed. The participants can authenticate each other’s identity through their secret identity information and the entanglement property of Bell states. After the authentication phase, the participants can negotiate a private key with equal contribution. We prove that the proposed scheme is unconditional security. In comparison to the previous mutual authentication quantum key agreement protocols, the proposed method utilizes Bell states as the quantum resource states in both the identity authentication and key agreement stages. It requires single-particle measurement without the need for Bell measurements or the involvement of trusted or semi-trusted other participants. Additionally, our proposed scheme demonstrates significant advantages in terms of qubit efficiency.

1 Introduction

As one of the important branches of cryptography, key agreement allows all the participants to contribute equally to generating a negotiated key, where any nontrivial subset cannot privately determine the negotiated key. Since the first key agreement protocol was proposed by Diffie and Hellman in 1976 [1], many key agreement protocols have been proposed [2–5]. However, with the rapid development of quantum computing and quantum computers, the classical cryptography schemes based on the complexity of mathematical algorithms will be seriously endangered. Different from classical cryptography, quantum cryptography is theoretically unconditionally secure. For this reason, quantum cryptography has garnered widespread attention from numerous cryptography researchers and has gradually evolved into a popular research direction in the field of cryptography.

Quantum cryptography encompasses various branches, such as quantum key distribution (QKD) [6–8], quantum key agreement (QKA) [9, 10], quantum secure direct communication (QSDC) [11–13], quantum secret sharing (QSS) [14, 15], quantum signature (QS) [16–18], quantum private query (QPQ) [19–21], quantum private comparison (QPC), [22–24]. Currently, quantum key agreement is a novel and highly significant research topic that has attracted considerable attention within the academic sphere.

In 2004, Zhou et al. [9], achieved the first QKA protocol by utilizing quantum teleportation, thereby pioneering the application of quantum technology in key negotiation. However, Tsai et al. [25] identified a critical flaw in Zhou et al.’s protocol, wherein a participant could unilaterally determine the shared key. Subsequently, in the same year, Hsueh et al. [26] proposed a QKA scheme using unitary operations and single photons. Nevertheless, Tsai et al. [27] pointed out that this scheme lacked sufficient security, as an attacker could acquire the shared key through controlled attacks without detection. In 2010, Chong et al. [10] successfully proposed an efficient two-party QKA protocol, building upon the foundation of the BB84 protocol. This QKA protocol primarily leverages unitary operations and delayed measurement techniques. Subsequently, numerous research efforts have been proposed to enhance the QKA protocol from various perspectives, such as multi-party QKA [28–32], improved communication efficiency [33–37], enhanced security [38, 39], and against noise environments [34, 40–44], semi-quantum capabilities [45–50].

However, the aforementioned QKA protocols lack the capability to authenticate the identities of the involved parties. In practical settings, attackers often attempt to impersonate participants to gain access to the shared key and carry out man-in-the-middle attacks on the QKA protocol. To counteract this attack, it is crucial to authenticate the identity of the key negotiators before the key establishment process, which holds significant importance for ensuring the security of the QKA protocol. In 2021, Zhu et al. [51] proposed a semi-honest three-party mutual authentication quantum key agreement (MAQKA) scheme based on three-particle entangled states, which requires a semi-honest third party to assist two key negotiators in achieving mutual authentication and key agreement. In the same year, Ma et al. [52] presented a MAQKA protocol based on five-particle entangled states, involving four participants and relying on two users to assist the other two users in achieving identity authentication and key agreement. However, this scheme exhibits relatively low qubit efficiency. In 2022, He et al. [53] presented a novel MAQKA protocol based on Bell states, which improves qubit efficiency and achieves the identity authentication and key agreement without relying on a trusted or semi-trusted third party.

In this paper, we propose a mutual authentication quantum key agreement protocol with single-particle measurement. The protocol utilizes Bell entangled states as the quantum source, enabling identity verification of participants before key agreement and against potential attacks. Compared to the previous MAQKA schemes, our proposed protocol has significant improvements in terms of quantum sources, auxiliary requirements from other participants, measurement bases, and qubit efficiency.

The rest of the paper is organized as follows. In Section 2, the proposed two-party mutual authentication quantum key agreement protocol is described in detail. In Section 3, we provide concrete examples. In Section 4, we analyze its security. In Section 5, we discuss the performance of our scheme and provide a conclusion.

2 The proposed mutual authentication quantum key agreement protocol

Two participants Alice and Bob want to authenticate their identity and negotiate a key. We assume that Alice and Bob need a secret identity information $K_{AB}$ through a secure channel in advance [53–55]. Two hash functions $H_1(x)$ outputting m-bit value and $H_2(x)$ outputting n-bit value are used. The process is described as follows.

Step 1: Bell sates preparation and transmission. Alice prepares m + n Bell states all in $\left|{\phi }^{+},\rangle \right.=\frac{1}{\sqrt{2}}\left(\left|00,\rangle \right.+\left|11\rangle \right.,\right)$, where m denotes the number of the authentication particles, n denotes the number of the information particles. Alice records the first particles as qubit sequence $S_A=\left\{S_A^1,S_A^2,\dots ,S_A^{m+n}\right\}$, the second particles as qubit sequence $S_B=\left\{S_B^1,S_B^2,\dots ,S_B^{m+n}\right\}$. Alice randomly inserts some decoy states into the qubit sequence $S_B$. These particles form a new sequence $S_{DB}$, where the decoy states are random in the set $\{|0\rangle ,|1\rangle ,|+\rangle ,|-\rangle \}$. Alice sends the qubit sequence $S_{DB}$ to Bob, and keeps the qubit sequence $S_A$.

Step 2: Eavesdropping detection. After Bob received $S_{DB}$, Alice publishes the positions and the measurement bases of the decoy states. Bob measures the decoy states and publishes the results. Alice calculates the error rate and determines whether the quantum channel is safe or not. If the quantum channel is safe, the protocol continues. Otherwise, the protocol aborts.

Step 3: Mutual authentication. After the eavesdropping detection, the qubit sequence $S_{DB}$ has been restored as the sequence $S_B$. For the qubit sequence $S_A$ $(S_B)$, we use the first m particles as the authentication sequence $L_A$ $(L_B)$ and the last n particles as the information particles $R_A$ $(R_B)$, where $L_A=\left\{L_A^1,L_A^2,\dots ,L_A^m\right\}$, $L_B=\left\{L_B^1,L_B^2,\dots ,L_B^m\right\}$, $R_A=\left\{R_A^1,R_A^2,\dots ,R_A^n\right\}$, $R_B=\left\{R_B^1,R_B^2,\dots ,R_B^n\right\}$. Bob generates two random numbers $r_1$, $r_2$ and publishes them. Alice and Bob calculate the value $K_{\mathit{auth}}=H_1\left(K_{AB}\Vert r_1\right)$, where $K_{\mathit{auth}}=\left\{K_{\mathit{auth}}^1,K_{\mathit{auth}}^2,\dots ,K_{\mathit{auth}}^m\right\}$, $K_{\mathit{auth}}^i\in \left\{\mathrm{0,1}\right\}$, $i\in \left\{\mathrm{1,2},\dots ,m\right\}$. Then, according to the value of $K_{\mathit{auth}}$, Alice and Bob choose the measurement bases to measure the particles $L_A$ and $L_B$. For the i-th particle $L_A^i$ $(L_B^i)$, if the value of $K_{\mathit{auth}}^i=0$, Alice (Bob) chooses $Z=\left\{\left|0,\rangle \right.,\left|1,\rangle \right.,\right\}$ to measure the particle $L_A^i$ $(L_B^i)$. If the value of $K_{\mathit{auth}}^i=1$, Alice (Bob) chooses $X=\left\{\left|+,\rangle \right.,\left|-,\rangle \right.,\right\}$ to measure the particle $L_A^i$ $(L_B^i)$. After measuring the particles $L_A^i$ $(L_B^i)$, Alice (Bob) obtains the measurement results $L_{MA}^i$ $(L_{MB}^i)$ and encodes the measurement results as $L_{EA}^i$ $(L_{EB}^i)$. If the measurement result of $L_{MA}^i$ $(L_{MB}^i)$ is $\left|0\right.⟩$ or $|+\rangle$, take the value of $L_{EA}^i$ $(L_{EB}^i)$ as 0. If the measurement result of $L_{MA}^i$ $(L_{MB}^i)$ is $|1\rangle$ or $|-\rangle$, take the value of $L_{EA}^i$ $(L_{EB}^i)$ as 1. Next, Alice announces the value of $L_{EA}^i$ at the position corresponding to an odd number $i$, where $i\in \left\{\mathrm{1,2},\dots ,m\right\}$. Bob can judge whether Alice’s identity is legal. Obviously, Alice’s identity is correct when $L_{EA}^i=L_{EB}^i$. Otherwise, Alice’ identity is illegal. Similarly, Bob announces the value of $L_{EB}^j$ at the position corresponding to an even number $j$, where $j\in \left\{\mathrm{1,2},\dots ,m\right\}$. Alice can judge whether Bob’s identity is legal. Obviously, Bob’s identity is correct when $L_{EA}^j=L_{EB}^j$. Table 1 shows the process of the mutual authentication phase when the identities of Alice and Bob are legal.

Step 4: Key negotiation. After the mutual authentication phase, Alice and Bob negotiate a session key together. They calculate the value $K_{\mathit{info}}=H_2\left(K_{AB}\Vert r_2\right)$, where $K_{\mathit{info}}=\left\{K_{\mathit{info}}^1,K_{\mathit{info}}^2,\dots ,K_{\mathit{info}}^n\right\}$, $K_{\mathit{info}}^i\in \left\{\mathrm{0,1}\right\}$, $i\in \left\{\mathrm{1,2},\dots ,n\right\}$. Then, according to the value of $K_{\mathit{info}}$, Alice and Bob choose the measurement bases to measure owned particles $R_A$ and $R_B$. For the i-th particle $R_A^i$ $(R_B^i)$, if the value of $K_{\mathit{info}}^i=0$, Alice (Bob) chooses $Z=\left\{\left|0,\rangle \right.,\left|1,\rangle \right.,\right\}$ to measure the particle $R_A^i$ $(R_B^i)$. If the value of $K_{\mathit{info}}^i=1$, Alice (Bob) chooses $X=\left\{\left|+,\rangle \right.,\left|-,\rangle \right.\right\}$ to measure the particle $R_A^i$ $(R_B^i)$. Obviously, there are four kinds of different measurement results $\left\{\left|0,\rangle \right.,\left|1,\rangle \right.,\left|+,\rangle \right.,\left|-,\rangle \right.\right\}$ of $R_A^i$ $(R_B^i)$. For the measurement results $R_{MA}^i$ $(R_{MB}^i)$, Alice and Bob negotiate an encoding rule, that is, $\left|0\right.⟩$ and $|+\rangle$ correspond to 0, $|1\rangle$ and $|-\rangle$ correspond to 1. According to the encoding rule and the measurement results $R_{MA}^i$, $R_{MB}^i$, Alice and Bob can obtain the negotiated key $K=\left\{K^1,K^2,\dots ,K^n\right\}$. The key $K$ is negotiated by both parties. Table 2 shows the process of the key negotiation phase.

Table 1

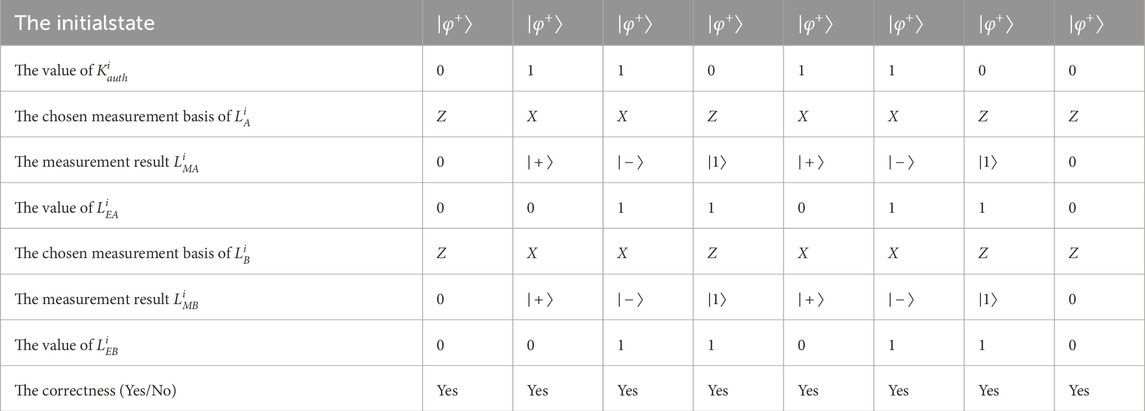
Table 1. The process of the mutual authentication phase when the identifies of Alice and Bob are legal.

Table 2

Table 2. The process of the key negotiation phase.

As shown in Figure 1, the flowchart depicts the mechanism of the proposed protocol.

Figure 1

Figure 1. The flowchart depicts the mechanism of the proposed protocol.

3 Examples

In this section, we provide concrete examples of our scheme to help readers better understand it. For simplicity, we have omitted the steps involved in eavesdropping detection.

Step 1: Bell states preparation and transmission. Alice prepares 16 Bell states all in $\left|{\phi }^{+}\rangle \right.=\frac{1}{\sqrt{2}}\left(\left|00,\rangle \right.+\left|11\right.⟩\right)$. Alice records the first particles as qubit sequence $S_A=\{S_A^1,S_A^2,\dots ,S_A^{16}\}$, the second particles as qubit sequence $S_B=\{S_B^1,S_B^2,\dots ,S_B^{16}\}$. Alice sends the qubit sequence $S_B$ to Bob, and keeps the qubit sequence $S_A$.

Step 2: Mutual authentication. For the qubit sequence $S_A$ $(S_B)$, we use the particles $\{S_A^1,S_A^2,\dots ,S_A^8\}$ $(\{S_B^1,S_B^2,\dots ,S_B^8\})$ as the authentication sequence $L_A$ $(L_B)$ and the particles $\{S_A^9,S_A^{10},\dots ,S_A^{16}\}$ $(\{S_B^9,S_B^{10},\dots ,S_B^{16}\})$ as the information particles $R_A$ $(R_B)$, where $L_A=\{L_A^1,L_A^2,\dots ,L_A^8\}$, $L_B=\{L_B^1,L_B^2,\dots ,L_B^8\}$, $R_A=\{R_A^1,R_A^2,\dots ,R_A^8\}$, $R_B=\{R_B^1,R_B^2,\dots ,R_B^8\}$. Bob generates two random numbers $r_1$, $r_2$ and publishes them. Alice and Bob calculate the value $K_{\text{auth}}=H_1(K_{\text{AB}}\Vert r_1)=01101100$. Then, according to the value of $K_{\mathit{auth}}$, Alice and Bob choose the measurement bases $ZXXZXXZZ$ to measure the particles $L_A$ and $L_B$. After measuring the particles $L_A$ $(L_B)$, Alice (Bob) obtains the measurement results $L_{MA}=\{\left|0,\rangle \right.,\left|+\right.\rangle ,\left|-,\rangle \right.,\left|1,\rangle \right.,\left|+,\rangle \right.,\left|-,\rangle \right.,\left|1,\rangle \right.,\left|0,\rangle \right.\}$ $(L_{MB}=\{\left|0,\rangle \right|,\left|+,\rangle \right.,\left|-,\rangle \right.,\left|1,\rangle \right.,\left|+,\rangle \right.,\left|-,\rangle \right.,\left|1,\rangle \right.,\left|0,\rangle \right.\})$ and encodes the measurement results as $L_{EA}=00110110$ $(L_{EB}=00110110)$. Next, Alice announces the value of $L_{EA}^1{L}_{EA}^3{L}_{EA}^5{L}_{EA}^7=0101$. Obviously, since $L_{EB}^1{L}_{EB}^3{L}_{EB}^5{L}_{EB}^7=L_{EA}^1{L}_{EA}^3{L}_{EA}^5{L}_{EA}^7=0101$, Bob can judge that Alice is legal. Similarly, Bob announces the value of $L_{EB}^2{L}_{EB}^4{L}_{EB}^6{L}_{EB}^8=0110$. Since $L_{EA}^2{L}_{EA}^4{L}_{EA}^6{L}_{EA}^8=L_{EB}^2{L}_{EB}^4{L}_{EB}^6{L}_{EB}^8=0110$, Alice can judge that Bob is legal.

Step 3: Key negotiation. After the mutual authentication phase, Alice and Bob negotiate a session key together. They calculate the value $K_{\mathit{info}}=H_2(K_{AB}\Vert r_2)=10100110$. Then, according to the value of $K_{\mathit{info}}$, Alice and Bob choose the measurement bases $XZXZZXXZ$ to measure owned particles $R_A$ and $R_B$. For the measurement results $R_{MA}=\{\left|-,\rangle \right.,\left|1,\rangle \right.,\left|+,\rangle \right.,\left|1,\rangle \right.,\left|0,\rangle \right.,\left|+,\rangle \right.,\left|-,\rangle \right.,\left|0,\rangle \right.\}$, Alice can obtain the negotiated key $K=11010010$. Similarly, For the measurement results $R_{MB}=\{\left|-,\rangle \right.,\left|1,\rangle \right.,\left|+,\rangle \right.,\left|1,\rangle \right.,\left|0,\rangle \right.,\left|+,\rangle \right.,\left|-,\rangle \right.,\left|0,\rangle \right.\}$, Bob can obtain the negotiated key $K=11010010$.

4 Security analysis

4.1 Security analysis of mutual authentication phase

We analyze the security of mutual authentication phase from the following aspects.

Correctness: According to the process of the mutual authentication, Alice (Bob) can judge that the identity of Bob (Alice) is legal. If the identities of Alice and Bob are correct, they must have $K_{AB}$ and calculate the correct value of $K_{\mathit{auth}}=H_1\left(K_{AB}\Vert r_1\right)$. Then, they measure owned authentication parties $L_A$, $L_B$, and obtain the measurement results $L_{MA}$, $L_{MB}$. Alice and Bob encodes their measurement results and get $L_{EA}$, $L_{EB}$. According to the property of Bell state, the value must satisfy $L_{EA}=L_{EB}$ when the identities of Alice and Bob are correct. For examples, suppose that the initial prepared states are $S=\left\{\left|{\phi }^{+}\right.\rangle ,\left|{\phi }^{+}\right.\rangle ,\left|{\phi }^{+}\right.\rangle ,\left|{\phi }^{+}\right.\rangle ,\left|{\phi }^{+}\rangle \right.,\left|{\phi }^{+}\right.\rangle ,\left|{\phi }^{+}\right.\rangle ,\left|{\phi }^{+}\rangle \right.,\right\}$. Alice holds the first qubit sequence $L_A=\left\{L_A^1,L_A^2,\dots ,L_A^8\right\}$, Bob holds the second qubit sequence $L_B=\left\{L_B^1,L_B^2,\dots ,L_B^8\right\}$. The hash value $K_{\mathit{auth}}=01101100$, corresponding to the measurement bases $ZXXZXXZZ$. When the measurement results $L_A^1{L}_A^3{L}_A^5{L}_A^7=|0\rangle |-\rangle |+\rangle |1\rangle$, the corresponding encoding value $L_{EA}^1{L}_{EA}^3{L}_{EA}^5{L}_{EA}^7=0101$. Alice publishes the value $L_{EA}^1{L}_{EA}^3{L}_{EA}^5{L}_{EA}^7$. As the measurement bases Bob selected are the same Alice, Bob’s measurement results must satisfy $L_B^1{L}_B^3{L}_B^5{L}_B^7=|0\rangle |-\rangle |+\rangle |1\rangle$. Then, Bob gets the value $L_{EB}^1{L}_{EB}^3{L}_{EB}^5{L}_{EB}^7=0101$, and judges Alice’s identity is correct by $L_{EA}^1{L}_{EA}^3{L}_{EA}^5{L}_{EA}^7=L_{EB}^1{L}_{EB}^3{L}_{EB}^5{L}_{EB}^7$. Similarly, when the measurement results $L_B^2{L}_B^4{L}_B^6{L}_B^8=|+\rangle |1\rangle |-\rangle |0\rangle$, the corresponding encoding value $L_{EB}^2{L}_{EB}^4{L}_{EB}^6{L}_{EB}^8=0110$. Bob publishes the value $L_{EB}^2{L}_{EB}^4{L}_{EB}^6{L}_{EB}^8$. According to the property of Bell state, Alice’s measurement results must satisfy $L_A^2{L}_A^4{L}_A^6{L}_A^8=|+\rangle |1\rangle |-\rangle |0\rangle$. Then, Alice gets the value $L_{EA}^2{L}_{EA}^4{L}_{EA}^6{L}_{EA}^8=0110$, and judges Bob’s identity is correct by $L_{EB}^2{L}_{EB}^4{L}_{EB}^6{L}_{EB}^8=L_{EA}^2{L}_{EA}^4{L}_{EA}^6{L}_{EA}^8$.

Forgery attack: If charlie wants to disguise herself as Alice, she must get the correct value of $L_{EA}$. In order to get $L_{EA}$, she should obtain the measurement results $L_{MA}$ of the particles $L_A$. However, she cannot get the right $K_{\mathit{auth}}$ and choose the right measurement bases. For each particle of $L_A$, she can only randomly selects measurement basis $Z=\left\{\left|0,\rangle \right.,\left|1,\rangle \right.,\right\}$ or $X=\left\{\left|+,\rangle \right.,\left|-,\rangle \right.,\right\}$, where the probability of each measurement basis is $\frac{1}{2}$. Continue to use the previous example, for the first particle $L_A^1$, $L_B^1$, the initial system state is $\left|{\phi }^{+}\rangle \right.=\frac{1}{\sqrt{2}}\left(\left|00,\rangle \right.+\left|11\right.⟩,\rangle \right)$, $K_{\mathit{auth}}^1=0$, the correct choosed basis is $Z=\left\{\left|0\right.\rangle ,\left|1\right.\rangle \right\}$, the correct measurement results $L_{MA}^1=\left|0\right.⟩$, $L_{MB}^1=\left|0\right.⟩$ and the correct encoding value $L_{EA}^1=0$, $L_{EB}^1=0$. Form the aspect of Charlie, Charlie may choose the measurement basis $Z=\left\{\left|0\right.⟩,\left|1\right.⟩\right\}$ to measurement the particle $L_A^1$ with a probability of $\frac{1}{2}$, and obtain the correct measurement result $\left|0\right.⟩$ and the correct encoding value 0. Meanwhile, Charlie may choose the measurement basis $X=\left\{\left|+\right.\rangle ,\left|-\right.\rangle \right\}$ to measurement the particle $L_A^1$ with a probability of $\frac{1}{2}$. Since $|0\rangle =\frac{1}{\sqrt{2}}\left(|+\rangle +|-\rangle \right)$, the probability of each result is $\frac{1}{2}$. When Charlie’s measurement result is $|+\rangle$, she can obtain the correct encoding value 0. When Charlie’s measurement result is $|-\rangle$, she can obtain the false encoding value 1. Thereby, for each particle, Charlie gets the correct encoding value is $\frac{1}{2}+\frac{1}{2}\times \frac{1}{2}=\frac{3}{4}$. Evidently, with the number of the authentication particles increases, the probability will converge to 0.

Unconditional security: In our scheme, the value of the hash function $H_1(x)$ is used to determine the measurement bases of Alice and Bob. In Step 3, Alice publishes the corresponding encoding value of $L_{EA}$ after measuring the particles $L_A$. However, an attacker cannot obtain any useful information from $L_{EA}$. For example, when $L_{EA}=0110$, there are 16 kinds of possible hash value $K_{\mathit{auth}}$, which corresponds to 16 kinds of different measurement bases and measurement results $L_{MB}$, as shown in Table 3. Therefore, the attacker cannot know the hash value $K_{\mathit{auth}}$ $(K_{\mathit{auth}}=H_1\left(K_{AB}\Vert r_1\right))$ and infer the private identity information $K_{AB}$. Actually, we merely use the information compression ability of the hash function $H_1(x)$, instead of the one-way property and anti-collision property of the hash function. Thereby, for each different random number $r_1$, the hash value $K_{\mathit{auth}}$ is different. Thus, our mutual authentication scheme is still unconditional security.

Table 3

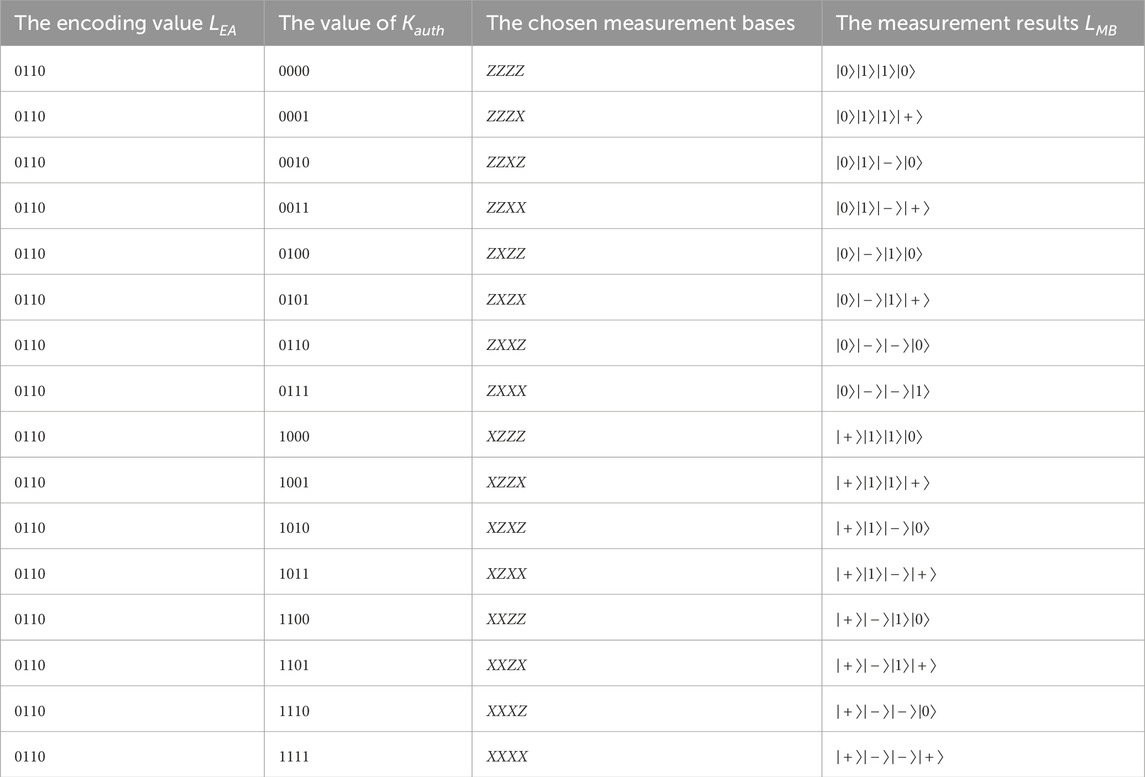
Table 3. The correlation among the encoding value $L_{EA}$, the hash value $K_{\mathit{auth}}$, the chosen measurement bases, the measurement results $L_{MB}$.

4.2 Security analysis of key negotiation phase

In this part, we analyze the participant attacks and the external attacks.

The participant attacks: The private key negotiation of our scheme is realized by the property of Bell states. The entanglement characteristic of Bell states ensures that the key negotiated by both parties is equal and random. Neither Alice nor Bob can change this randomness, so neither of them can independently control the private key. That is, they cannot successfully launch this attack.

The external attacks: Here, we consider four kinds of external attacks, including Trojan horse attacks, intercept-resend attack, measure-resend attack, and entangle-measure attack. As all the quantum states are transmitted only once, our scheme is naturally immune to the invisible photon eavesdropping Trojan horse attack [56] and the delay-photon Trojan horse attack [57]. Furthermore, in our scheme, we employ decoy states to detect the channel security, thereby ensuring the security of the transmitted qubit sequence $S_{DB}$. By randomly selecting decoy states from two different orthogonal bases, our scheme enables the detection of all types of attacks, such as intercept-resend attack, measure-resend attack, and entangled-measure attack, during the eavesdropping detection in Step 2. The probability of security verification can be referenced from the reference [40]. Besides, as our scheme only publishes the encoding value, the entanglement property of Bell state ensures no information leakage in the key negotiation [58].

It should be noted that we use the information compression ability of the hash function $H_2(x)$ to determine the measurement bases of the information particles $R_A$, $R_B$. For each different random number $r_2$, the hash value $K_{\mathit{info}}$ is different.

Thereby, the key negotiation of our scheme is unconditional security.

5 Discussions and conclusion

In this section, we discuss the performance of our scheme, and provide a conclusion.

As pointed in the reference [59], the qubit efficiency is defined as $\eta =\frac{f}{q+c}$, where $f$, $q$, $c$ are the number of bits of the negotiated key, the consumed qubits, the classical bits needed for the classical communication, respectively. Suppose that the number of the decoy states is equal to the number of the transmitted qubits, and the length of pre-shared identity information $K_{AB}$ is $n$. Here, we consider the qubit efficiency in two cases, one of which includes the authentication part, and the other does not. First, we consider the qubit efficiency without authentication phase. The length of the negotiated key is $n$, the number of the consumed decoy states is $n$, the number of the consumed Bell states is also $n$, and the number of the classical bits is $n$. We can obtain $f=n$, $q=2n+n$, $c=n$. Therefore, the qubit efficiency of the key negotiation phase is $\eta =\frac{n}{2n+n+n}=\frac{1}{4}\approx 25\%$. Second, we consider the qubit efficiency including the authentication phase. The authentication phase consumes the number of $m$ Bell states, and the number of $m$ decoy states. Thereby, the qubit efficiency including the authentication phase is $\bar{\eta }=\frac{n}{2(m+n)+m+n+n}$. When $n$ is the same as $m$, the qubit efficiency $\bar{\eta }\approx 14.29\mathrm{\%}$. In comparison to the existing MAQKA protocol, as illustrated in Table 4, our MAQKA protocol demonstrates great advantages.

Table 4

Table 4. Comparison between our protocol and the previous MAQKA protocols.

In our protocol, from the perspective of the quantum source, our scheme utilizes Bell states, which are easier to implement with existing technology compared to three-particle entangled states [51] and five-particle entangled states [52]. Unlike scheme [52] that necessitates the involvement of a trusted or semi-trusted third party, and scheme [52] that relies on the assistance of two additional participants, our approach does not require auxiliary support from other participants. Furthermore, our scheme only requires single-particle measurement ($Z$ basis, $X$ basis), without the need for Bell measurements as in schemes [52] and [53]. In terms of qubit efficiency, our scheme exhibits significant improvements compared to [51] and [52]. It is evident that our scheme is more feasible to implement in realistic scenarios.

In this paper, we propose a mutual authentication quantum key agreement protocol with single-particle measurement. By utilizing the secret identity information and the entanglement property of Bell states, our protocol enables mutual identity authentication to be realized. After the authentication phase, the participants can negotiate a private key with equal contribution. We prove that our scheme is unconditionally secure and can resist potential attacks. In contrast to the previous MAQKA schemes, our proposed protocol has significant improvements in terms of quantum sources, assistance requirements from other participants, measurement bases, and qubit efficiency.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HY: Writing–original draft, Writing–review and editing. ZY: Writing–original draft, Writing–review and editing. SL: Writing–review and editing. MW: Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Major Research Plan of Hubei Province under Grant/Award NO. 2023BAA027; the Key Research & Development Plan of Hubei Province of China under Grant No. 2024BAB049 and the project of Science, Technology and Innovation Commission of Shenzhen Municipality of China under Grant No. GJHZ20240218114659027.

Acknowledgments

We are deeply grateful to all the authors for their steadfast guidance and support throughout the entire research process. Their valuable insights and encouragement are crucial in shaping the direction and quality of this research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Diffie W, Hellman M. New directions in cryptography. IEEE Trans Inf Theor (1976) 22:644–54. doi:10.1109/tit.1976.1055638

CrossRef Full Text | Google Scholar

2. Steiner M, Tsudik G, Waidner M. CLIQUES: a new approach to group key agreement. In: Proceedings of the 18th international conference on distributed computing systems. Amsterdam, Netherlands (1998). p. 380–7. doi:10.1109/ICDCS.1998.679745

CrossRef Full Text | Google Scholar

3. Steiner M, Tsudik G, Waidner M. Key agreement in dynamic peer groups. IEEE Trans Parallel Distrib Syst (2000) 11:769–80. doi:10.1109/71.877936

CrossRef Full Text | Google Scholar

4. Pieprzyk J, Li CH. Multiparty key agreement protocols. IEEE Proc Comput Digital Tech (2000) 147:229–36. doi:10.1049/ip-cdt:20000531

CrossRef Full Text | Google Scholar

5. Ateniese G, Steiner M, Tsudik G. New multiparty authentication services and key agreement protocols. IEEE J Sel Areas Commun (2000) 18(4):628–39. doi:10.1109/49.839937

CrossRef Full Text | Google Scholar

6. Bennett CH, Brassard G. Quantum cryptography: public-key distribution and coin tossing. In: Proceedings of IEEE international conference on computers. Systems and signal processing. Bangalore, India (1984). p. 175–9.

Google Scholar

7. Bennett CH. Quantum cryptography using any two nonorthogonal states. Phys Rev Lett (1992) 68:3121–4. doi:10.1103/physrevlett.68.3121

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Boyer M, Kenigsberg D, Mor T. Quantum key distribution with classical Bob. Phys Rev Lett (2007) 99(14):140501. doi:10.1103/physrevlett.99.140501

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhou N, Zeng G, Xiong J. Quantum key agreement protocol. Electron Lett (2004) 40(18):1149–50. doi:10.1049/el:20045183

CrossRef Full Text | Google Scholar

10. Chong SK, Hwang T. Quantum key agreement protocol based on BB84. Opt Commun (2010) 283:1192–5. doi:10.1016/j.optcom.2009.11.007

CrossRef Full Text | Google Scholar

11. Zhang W, Ding D-S, Sheng Y-B, Zhou L, Shi B-S, Guo G-C. Quantum secure direct communication with quantum memory. Phys Rev Lett (2017) 118(22):220501. doi:10.1103/physrevlett.118.220501

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Panda SS, Yasir PA, Chandrashekar C. Quantum direct communication protocol using recurrence in k-cycle quantum walks. Phys Rev A (2023) 107(2):022611. doi:10.1103/physreva.107.022611

CrossRef Full Text | Google Scholar

13. Hong YP, Zhou L, Zhong W, Sheng YB. Measurement-device-independent three-party quantum secure direct communication. Quant Inform Process (2023) 22:111. doi:10.1007/s11128-023-03853-1

CrossRef Full Text | Google Scholar

14. Hillery M, Buek V, Berthiaume A. Quantum secret sharing. Phys Rev A (1999) 59:1829–34. doi:10.1103/physreva.59.1829

CrossRef Full Text | Google Scholar

15. Senthoor K, Sarvepalli PK. Theory of communication efficient quantum secret sharing. IEEE Trans Inf Theor (2022) 68(5):3164–86. doi:10.1109/tit.2021.3139839

CrossRef Full Text | Google Scholar

16. Gottesman D, Chuang I. Quantum digital signatures. arXiv:quant-ph/0105032 (2001). doi:10.48550/arXiv.quant-ph/0105032

CrossRef Full Text | Google Scholar

17. Collins RJ, Donaldson RJ, Dunjko V, Wallden P, Clarke PJ, Andersson E, et al. Realization of quantum digital signatures without the requirement of quantum memory. Phys Rev Lett (2014) 113:040502. doi:10.1103/physrevlett.113.040502

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Yin HL, Fu Y, Chen ZB. Practical quantum digital signature. Phys Rev A (2016) 93:032316. doi:10.1103/physreva.93.032316

CrossRef Full Text | Google Scholar

19. Giovannetti V, Lloyd S, Maccone L. Quantum private queries. Phys Rev Lett (2008) 100(23):230502. doi:10.1103/physrevlett.100.230502

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Gao F, Qin SJ, Huang W, Wen QY. Quantum private query: a new kind of practical quantum cryptographic protocol. Sci China Phys Mech Astron (2019) 62(7):70301. doi:10.1007/s11433-018-9324-6

CrossRef Full Text | Google Scholar

21. Yang H, Xiao M. Multi-user quantum private query. Quan Inf. Process. (2020) 19:253. doi:10.1007/s11128-020-02732-3

CrossRef Full Text | Google Scholar

22. Yang YG, Cao WF, Wen QY. Secure quantum private comparison. Phys Scr (2009) 80(6):065002. doi:10.1088/0031-8949/80/06/065002

CrossRef Full Text | Google Scholar

23. Yang YG, Wen QY. An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement. J Phys A: Math Theor (2009) 42(5):055305. doi:10.1088/1751-8113/42/5/055305

CrossRef Full Text | Google Scholar

24. Geng MJ, Chen Y, Xu TJ, Ye TY. Single-state semiquantum private comparison based on bell states. EPJ Quan Technol. (2022) 9(36):36. doi:10.1140/epjqt/s40507-022-00156-9

CrossRef Full Text | Google Scholar

25. Tsai C, Hwang T. On quantum key agreement protocol. Technical Report, C-S-I-E, NCKU, Taiwan ROC (2009)

Google Scholar

26. Hsueh CC, Chen CY. Quantum key agreement protocol with maximally entangled states. In: Proceedings of the 14th information security conference (ISC 2004). Taipei, Taiwan: National Taiwan University of Science and Technology (2004). p. 236‖242.

Google Scholar

27. Tsai CW, Chong SK, Hwang T. Comment on quantum key agreement protocol with maximally entangled states. In: Proceedings of the 20th cryptology and information security conference (CISC 2010). Hsinchu, Taiwan: National Chiao Tung University (2010). p. 210–3.

Google Scholar

28. Shi RH, Zhong H. Multi-party quantum key agreement with bell states and bell measurements. Quan Inf Process (2013) 12:921–32. doi:10.1007/s11128-012-0443-2

CrossRef Full Text | Google Scholar

29. Xu GB, Wen QY, Gao F, Qin SJ. Novel multiparty quantum key agreement protocol with GHZ states. Quan Inf Process (2014) 13:2587–94. doi:10.1007/s11128-014-0816-9

CrossRef Full Text | Google Scholar

30. Yang H, Lu S, Zhu J, Wu J, Zhou Q, Li T. A tree-type multiparty quantum key agreement protocol against collusive attacks. Int J Theor Phys (2023) 62:7. doi:10.1007/s10773-022-05265-w

CrossRef Full Text | Google Scholar

31. Liu B, Gao F, Huang W, Wen Q. Multiparty quantum key agreement with single particles. Quan Inf. Process. (2013) 12(4):1797–805. doi:10.1007/s11128-012-0492-6

CrossRef Full Text | Google Scholar

32. Sun Z, Yu J, Wang P. Efficient multi-party quantum key agreement by cluster states. Quan Inf Process (2016) 15:373–84. doi:10.1007/s11128-015-1155-1

CrossRef Full Text | Google Scholar

33. He YF, Ma WP. Quantum key agreement protocols with four-qubit cluster states. Quan Inf Process (2015) 14:3483–98. doi:10.1007/s11128-015-1060-7

CrossRef Full Text | Google Scholar

34. Yang YG, Li BR, Li D, Zhou YH, Shi WM. New quantum key agreement protocols based on Bell states. Quan Inf Process (2019) 18:322. doi:10.1007/s11128-019-2434-z

CrossRef Full Text | Google Scholar

35. Yang YG, Gao S, Li D, Zhou YH, Shi WM. Two-party quantum key agreement over a collective noisy channel. Quan Inf Process (2019) 18:74. doi:10.1007/s11128-019-2187-8

CrossRef Full Text | Google Scholar

36. Huang X, Zhang SB, Chang Y, Qiu C, Liu DM, Hou M. Quantum key agreement protocol based on quantum search algorithm. Int J Theor Phys (2021) 60:838–47. doi:10.1007/s10773-020-04703-x

CrossRef Full Text | Google Scholar

37. Zhao XQ, Wan H, Li LZ. High-efficient quantum key agreement protocol with entanglement measure. Int J Theor Phys (2022) 61:183. doi:10.1007/s10773-022-05166-y

CrossRef Full Text | Google Scholar

38. Zhu ZC, Hu AQ, Fu AM. Improving the security of protocols of quantum key agreement solely using Bell states and Bell measurement. Quan Inf. Process. (2015) 14:4245–54. doi:10.1007/s11128-015-1110-1

CrossRef Full Text | Google Scholar

39. Yang YG, Huang RC, Xu GB, Zhou YH, Shi WM, Li D. Measurement-device-independent quantum key agreement based on entanglement swapping. Quan Inf Process (2023) 22:438. doi:10.1007/s11128-023-04189-6

CrossRef Full Text | Google Scholar

40. He YF, Ma WP. Two-party quantum key agreement against collective noise. Quan Inf Process (2016) 15:5023–35. doi:10.1007/s11128-016-1436-3

CrossRef Full Text | Google Scholar

41. Gao H, Chen XG, Qian SR. Two-party quantum key agreement protocols under collective noise channel. Quan Inf Process (2018) 17:140. doi:10.1007/s11128-018-1910-1

CrossRef Full Text | Google Scholar

42. Zhou YH, Wang MF, Shi WM, Yang YG, Zhang J. Two-party quantum key agreement against collective noisy channel. Quan Inf Process (2020) 19:100. doi:10.1007/s11128-020-2593-y

CrossRef Full Text | Google Scholar

43. Li L, Zhou RG, Zhang XX. Three-party quantum key agreement protocol based on logical four-particle Cluster state to resist collective noise. Quan Inf Process (2023) 22:453. doi:10.1007/s11128-023-04206-8

CrossRef Full Text | Google Scholar

44. Mu Q, Liu J, Wang Q, Li G, Sun W. Two-layer multiparty quantum key agreement protocol with collective detection. Int J Theor Phys (2024) 63:56. doi:10.1007/s10773-024-05564-4

CrossRef Full Text | Google Scholar

45. Shukla C, Thapliyal K, Pathak A. Semi-quantum communication: protocols for key agreement, controlled secure direct communication and dialogue. Quan Inf. Process. (2017) 16:295. doi:10.1007/s11128-017-1736-2

CrossRef Full Text | Google Scholar

46. Liu WJ, Chen ZY, Ji S, Wang HB, Zhang J. Multi-party semi-quantum key agreement with delegating quantum computation. Int J Theor Phys (2017) 56:3164–74. doi:10.1007/s10773-017-3484-6

CrossRef Full Text | Google Scholar

47. Li HH, Gong LH, Zhou NR. New semi-quantum key agreement protocol based on high-dimensional single-particle states. Chin Phys B (2020) 29(11):110304. doi:10.1088/1674-1056/abaedd

CrossRef Full Text | Google Scholar

48. Xu TJ, Gan ZG, Ye TY. Multiparty semiquantum key agreement with d-level single-particle states. Physica A: Stat Mech its Appl (2023) 625:128991. doi:10.1016/j.physa.2023.128991

CrossRef Full Text | Google Scholar

49. Yi HM, Zhou RG, Xu RQ. Semi-quantum key agreement protocol using W states. Int J Theor Phys (2023) 62:212. doi:10.1007/s10773-023-05467-w

CrossRef Full Text | Google Scholar

50. Hong WL, Bai CM, Zhang SJ, Liu L. Multiparty semi-quantum key agreement protocol based on multiparticle entangled states. Laser Phys Lett (2024) 21:125212. doi:10.1088/1612-202x/ad8cc5

CrossRef Full Text | Google Scholar

51. Zhu H, Wang C, Li Z. Semi-honest three-party mutual authentication quantum key agreement protocol based on GHZ-like state. Int J Theor Phys (2021) 60:293–303. doi:10.1007/s10773-020-04692-x

CrossRef Full Text | Google Scholar

52. Ma X, Hur J, Li Z, Zhu H. Quantum mutual authentication key agreement scheme using five-qubit entanglement towards different realm architecture. Int J Theor Phys (2021) 60:1933–48. doi:10.1007/s10773-021-04812-1

CrossRef Full Text | Google Scholar

53. He YF, Pang Y, Di M. Mutual authentication quantum key agreement protocol based on Bell states. Quan Inf Process (2022) 21:290. doi:10.1007/s11128-022-03640-4

CrossRef Full Text | Google Scholar

54. Zhang L, Han ZW, Ma QM, Li LL. Authenticated quantum key agreement based on cluster states against collective noise. Phys Scr (2024) 99:075104. doi:10.1088/1402-4896/ad514c

CrossRef Full Text | Google Scholar

55. Zhang L, Han ZW, Li TH, Ma QY, Li LL. Authenticated multi-party quantum key agreement protocol based on cluster states. Laser Phys (2024) 34:095205. doi:10.1088/1555-6611/ad6d52

CrossRef Full Text | Google Scholar

56. Cai QY. Eavesdropping on the two-way quantum communication protocols with invisible photons. Phys Lett A (2006) 351(12):23–5. doi:10.1016/j.physleta.2005.10.050

CrossRef Full Text | Google Scholar

57. Li XH, Deng FG, Zhou HY. Improving the security of secure direct communication based on the secret transmitting order of particles. Phys Rev A (2006) 74:054302. doi:10.1103/physreva.74.054302

CrossRef Full Text | Google Scholar

58. Gao F, Qin SJ, Wen QY, Zhu FC. Comment on: three-party quantum secure direct communication based on GHZ states. Phys Lett A (2008) 372:3333–6. doi:10.1016/j.physleta.2008.01.043

CrossRef Full Text | Google Scholar

59. Cabello A. Quantum key distribution in the Holevo limit. Phys Rev Lett (2000) 85:5635–8. doi:10.1103/physrevlett.85.5635

PubMed Abstract | CrossRef Full Text | Google Scholar