A first-principles density functional theory study on the piezocatalytic activity of tetragonal perovskite PbTiO3

Piezoelectric materials have been found to possess high catalytic activity under external mechanical excitations, such as ultrasonic waves or collisions. Energy band theory (EBT) based on electronic excitation in semiconductors has been widely used to investigate piezocatalytic activity from a macroscopic perspective, while the microscopic correlation between the piezoelectric feature and surface chemical reactivity was not fully understood at the current stage. In this work, to overcome the limitation of conventional finite element modeling of piezoelectric materials, we employ the first-principles density functional theory (DFT) to study the electronic properties, macroscopic electrostatic potential, surface polarization, and chemical adsorption energy of tetragonal PbTiO₃ under external mechanical strains. The correlations between the band structure, piezopotential, space charge distribution, and surface adsorption energy of the *OH/H groups are discussed in our work. Our simulation shows that the bulk PTO and layered PTO exhibit opposite trends in the band gap change under external strain. In addition, a nonmonotonic correlation between the change of dipole moment piezopotential versus the applied strain was found in few-layer PTO, which could directly quantify the driving force of piezocatalysis. Finally, the enhanced surface adsorption of *OH and *H on PTO was observed under both tensile and compressive strain, which reveals how piezoelectric features affect the surface chemical process in thermodynamics. Our work provides a significant mechanistic insight into the piezocatalytic behavior of general polar perovskite, which could facilitate the development of piezoelectric materials in energy conversion and environmental applications.

GRAPHICAL ABSTRACT

Introduction

Energy harvesting and conversion technologies have received tremendous attention in recent decades due to the increasing energy consumption as well as serious environmental problems [1–5]. Direct utilization of energy from the natural environment is an effective way to deal with energy and environmental problems. In addition to the most well-known photovoltaic technology that can directly convert solar energy from nature into electricity, energy conversion via the piezoelectric effect is another way to exploit natural energy that can convert mechanical energy into electricity or chemical energy [6–8]. According to the fundamental concept of electrostatics and electrochemistry, a large electrical potential drop on a material surface can govern the electrochemical reaction and electron transfer. The concept of “piezocatalysis” was proposed based on the electrocatalytic process induced by a large potential drop on the piezo-electrified surface [9]. This phenomenon has been validated in many experimental studies. For instance, Hong et al. discovered piezocatalytic water splitting on the ZnO fiber and BaTiO₃ dendrite, which could generate oxygen and hydrogen gas from pure water in a stoichiometric ratio under the excitation of ultrasonic vibration [10]. Starr et al. made a similar observation in Pb(Mg_1/3Nb_2/3)O₃-32PbTiO₃ (PMN-PT) material and reported the direct hydrogen generation induced by piezoelectric effects [11]. In addition to the water-splitting reaction, piezocatalysis has also been employed in pollutant degradation, medical cleaning, and organic synthesis [12–18].

To understand the mechanism of piezocatalysis, the energy band theory (EBT) was developed to interpret the driving force of the piezocatalytic process [19]. Due to the spontaneous polarization in piezoelectric materials and the effects of mechanical strain, the band edge usually exhibits a linear shift along the direction of polarization under the external strain [11, 20]. This effect causes the possible redox reaction that occurs when the modified band edge reaches the redox potential of chemical species on the surface. Under the frame of EBT, the driving force of piezocatalysis was attributed to electronic excitation by thermal effect during the vibrational excitation, which is highly similar to photocatalysis. This indicates that the piezopotential is determined by the band structure of the material under mechanical strain [21, 22]. Different from EBT, the screening charge effect (SCE) model was proposed based on the electrostatics of the piezo-electrified medium [19]. According to the SCE model, piezocatalysis is dominated by the presence of a screening charge on the electrified surface. With the help of finite-element simulation, numerical solutions of the global electrostatic potential can be obtained at any mechanical strain, which clearly visualizes the polarity of the piezoelectric material [14, 23, 24]. The piezopotential is defined as the electrostatic potential difference between two sides and determines the size of the driving force of piezocatalysis [11, 22, 25]. Although EBT and SCE models have been extensively used to provide a mechanistic understanding of piezocatalysis from different physical scales and perspectives, the microscopic reaction process and mechanism on the surface of piezoelectric materials are not well understood. In addition, the intrinsic connection between EBT and SCE models is still blurry at the current stage, which limits further mechanistic investigation of piezocatalysis. To fully understand the mechanism of piezocatalysis, in this work, we take the typical piezoelectric perovskite PbTiO₃ (PTO) as an example and carry out the first-principles density functional theory (DFT) calculation to investigate the electronic structure, polarization, space charge distribution, and surface reactivity under mechanical strain. Our work could provide fundamental insights into the physical picture of piezocatalysis and further benefit the development of piezoelectric materials in renewable energy applications.

Simulation method

Density functional theory calculations were carried out by using the Vienna ab initio Simulation Package (VASP) software [26, 27]. The ion–electron interaction was treated by the projector augmented-wave (PAW) pseudopotential [28]. The generalized gradient approximation with the Perdew–Burke–Enzerhof (GGA-PBE) formalism was used to describe the exchange-correlation effect [29, 30]. The plane-wave basis set with a cutoff energy of 550 eV was adopted to expand the wave function under periodic boundary conditions. The van der Waals (vdW) interaction was captured through Grimme’s DFT-D3 correction method [31]. The convergence criteria of geometric optimization and electronic iteration were set as 0.02 eV/Å and 10^–5 eV, respectively. The k-point sampling of the Brillouin zone was carried out using the Monkhorst–Pack scheme with the k-mesh resolution of 0.04 (in the unit of 2π/Å) [32]. To reasonably deal with the strong correlation effect of 3d electrons, the GGA + U method was employed for Ti with the U value of 3.0 eV from early literature [33]. In addition, the hybrid functional calculation was also performed using the HSE06 formalism to obtain an accurate band structure and band gap [34, 35]. The surface slab model of the 2/3/4 layers PbTiO₃ in the [001] direction was created in contact with a vacuum slab with a thickness of 40 Å to avoid the layer–layer interaction and reliably capture the dipole moment along the z direction. To investigate the effect of mechanical strain on the polarization and electronic properties in PTO, a biaxial strain was introduced on the equilibrated lattice, which has been validated as an effective strategy for understanding piezoelectric materials [22, 36, 37]. The mechanical strain (δ) was defined as δ = (a − a₀)/a, where a₀ and a refer to the equilibrated and compressed/stretched lattice constant, respectively. In addition, dipole correction was employed to treat the highly polarized surface in the electrostatic potential calculation because our test calculation has shown that the electrostatic potential is not able to converge in the center of the vacuum slab if dipole correction is not included, as shown in Supplementary Figure S1; [38].

The electronic polarization of PTO was calculated using the Berry phase method developed by King-Smith and Vanderbilt, which directly provides the electronic dipole moment in each direction [39]. The ionic part of polarization is directly defined by the ion valance and location, giving the expression of total polarization along the z direction as Equation 1:

$P=P_{\text{ion}}+P_{\text{elec}}={\displaystyle \sum _{\mathrm{i}}}\left(r-r_0\right)Z_{\mathrm{i}}\left(r\right)+P_{\text{elec},}(1)$

where the first and second terms refer to the contribution of ionic and electronic dipole moment in the z direction. The r₀, Z_i refers to the reference location and valence charge of ion along the z direction, respectively. P_elec is given by the Berry phase calculation.

Results and discussion

Effects of Hubbard U and exchange-correlation functional on the geometry, polarization, electronic, and mechanical properties of bulk PTO

Because the accuracy of lattice parameters significantly affects the calculated polarization of ionic contribution, different functionals were tested as a comparison, including PBE [30], PBEsol [40], and HSE06 [34], with and without Hubbard correction, as listed in Table 1. The calculated structure parameters, polarization, and mechanical properties were compared with previous experimental results. As listed in Table 1, our simulation indicates that PBE + U shows good consistency with experimental data in structural parameters and polarization charge density P_s, whereas PBE, PBEsol, and HSE06 overestimate P_s. Conversely, PBEsol + U underestimates the P_s value, which suggests that the introduction of Hubbard U could lower the calculated P_s. However, the introduction of Hubbard U makes the mechanical property calculation worse than the experimental results. Additionally, PBEsol predicts the band gap as 1.61 eV, which significantly underestimates the band gap compared with the HSE06 (E_g = 3.05 eV) and experimental data (E_g = 3.10 eV). Early DFT study has indicated that applying the Hubbard U correction could push the Ti (3d) states to be more localized on Ti ions, which significantly affects the length of the Ti–O bond along [001] direction and the ionic polarization [41]. Our results similarly find that the Hubbard U suppresses Ti (3d)-O (2p) hybridization (Supplementary Figure S2) and leads to a smaller c parameter than PBE and PBEsol. Because the piezocatalytic activity in PTO is dominated by mechanical excitation in the planar direction (x and y direction) and polarization response in the vertical direction (z direction), it is important to accurately capture the effects of in-plane strain (x/y direction, which is related to C₁₁, C₁₂, and C₁₃) on the electronic structure and polarization. Thus, to obtain a reliable result on the polarization property under in-plane strain, we will employ the PBE + U calculation for geometry optimization and polarization calculation, which has exhibited reasonable accuracy compared with early experimental results [42–44]. The electronic structure and band gap will be calculated via HSE06 based on a single-point calculation after structure optimization by PBE + U.

Table 1

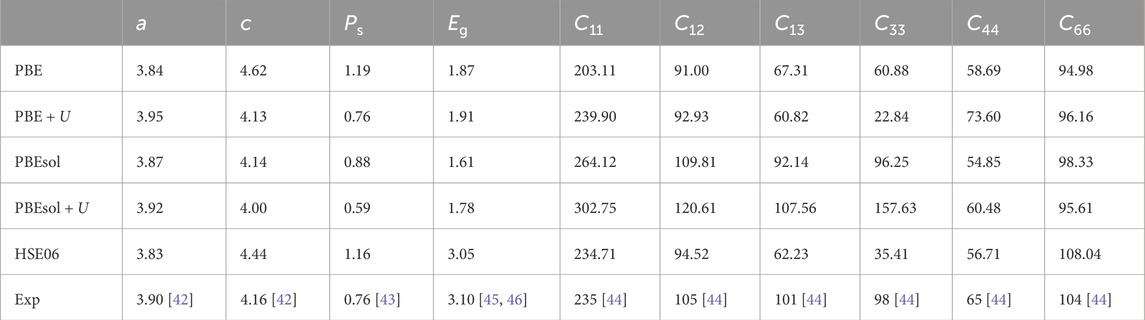
Table 1. Calculated lattice parameters (in Å), spontaneous polarization (P_s in C/m²), band gap (E_g in eV), and elastic constants (in GPa). Experimental results were taken from early literature [42–46].

Effects of mechanical strain on the band structure

To understand the change of electronic structure under piezoelectric polarization, we first studied the band structure of bulk PTO under biaxial strain on the lattice, as shown in Supplementary Figures S3, S4. We compared the band structure calculation results from PBE, PBE + U, and HSE06 functionals in Supplementary Figure S3. It shows that all the methods predicted the bulk PTO as an indirect semiconductor with the valence band maximum (VBM) located at X and the conduction band minimum (CBM) located at the Γ and Z points. The flat region of the conduction band in the K-path (Γ to Z) is also consistent with an early study by Bendaoudi et al. [37]. The HSE06 predicts the E_g of bulk PTO as 3.05 eV, which is very close to the experimentally measured E_g = 3.10 eV, while PBE and PBE + U predict the E_g = 1.81 eV and E_g = 1.97 eV, respectively. (Figure 1B). The band structure of PTO from PBE + U and HSE06 is like the BaTiO₃ in our previous work [22].

Figure 1

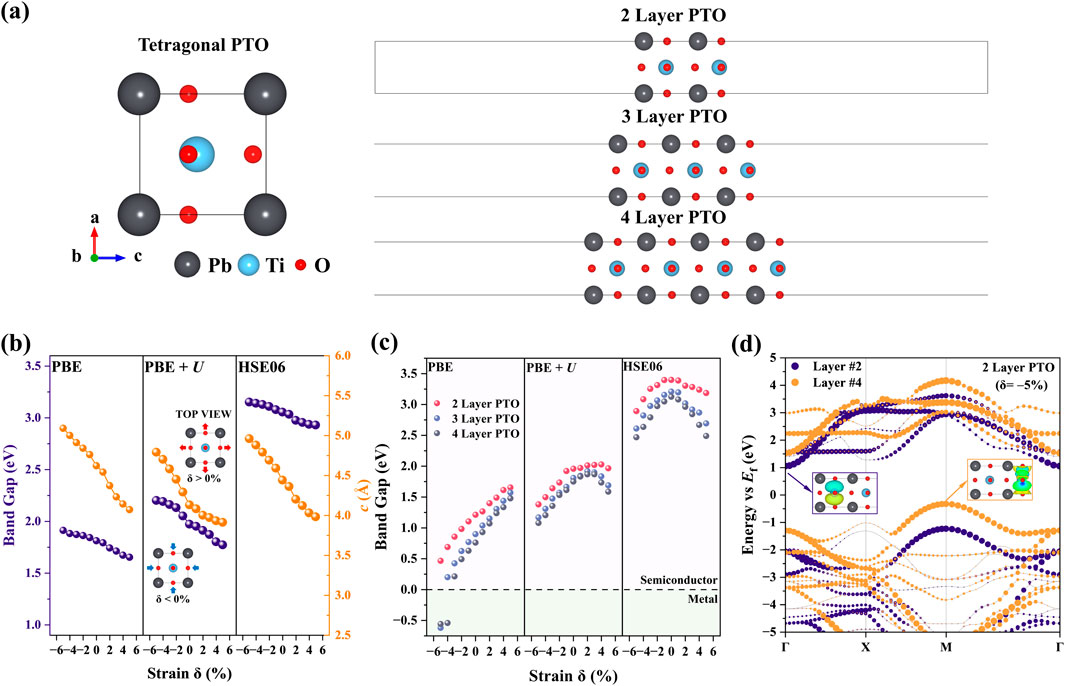
Figure 1. Strain-induced band structure change of PTO. (A) Bulk PTO model and 2L/3L/4L PTO surface model. (B) Band gap and lattice constant of c of the bulk PTO under different strains calculated by PBE, PBE + U, and HSE06. (C) Band gap of 2L/3L/4L PTO surfaces at different applied strains calculated by PBE, PBE + U, and HSE06 methods. (D) Band structure and visualized |Ψ|² near the Fermi level for 2L PTO under a −5% applied strain.

As shown in Figure 1B and Supplementary Figure S4, with the introduction of biaxial strain (δ = −5% to +5%), we observed a monotonic variation of E_g with the strain with the PBE, PBE + U, and HSE06. Under a compressive strain of δ = −5%, E_g increases to 2.20 eV, while E_g decreases to 1.77 eV when a tensile strain of δ = +5% is introduced along the lattice vector a in the xy plane. The projected density of states (PDOS) (Supplementary Figure S5) indicates that the CBM is primarily contributed by Ti, while the VBM is mainly contributed by O. Compressive strain causes a displacement of the Ti ion from its centrosymmetric position, leading to polarity change. This structural distortion enhances the hybridization between the Ti-3d and O-2p orbitals, thus increasing the VBM-CBM energy difference and leading to a wider band gap. Berger et al. also reported the effect of polarity change on the band gap [47]. The location of VBM and CBM remain unchanged under the compressive and tensile strain on bulk PTO.

To explore the piezoelectric effects on the band structure of PTO under realistic experimental conditions, we established the few-layer PTO model shown in Figure 1A. The PTO surface model was built along the (001) direction of the bulk PTO, and we created three PTO surface models: 2L-, 3L-, and 4L-PTO, which are shown in Figure 1A. The effect of biaxial strain on the E_g of 2L/3L/4L PTO is systematically studied in Figure 1C. Compared with the results of bulk PTO (Figure 1B), the few-layer PTO shows an opposite trend in the E_g-δ relation, as shown in Figure 1C. The E_g of few-layer PTO shows a nonmonotonic trend with the mechanical strain that varies from compressive (−5%) to tensile (+5%). In Figure 1C, the HSE06 results show that compressive or tensile strain both decrease the E_g, leading to a “bell” shape in the E_g-δ relation. Interestingly, PBE + U predicts a slightly decreased E_g in the tensile strain region, while PBE results show a monotonically increasing E_g with δ. The opposite trend given by PBE in the tensile strain region suggests that the strong correlation effect of 3d electron in Ti plays a crucial role in determining the band gap of the tensile PTO surface. We visualized the wavefunction of 2L PTO at VBM (M point) and CBM (Γ) in Figure 1D, which shows that the VBM and CBM were both contributed by the TiO₂ layer.

According to the projected density of states (PDOS) analysis in Supplementary Figure S6, it can be seen that the CBM of the PTO surface is mainly dominated by the O, while the CBM is mainly contributed by Ti. To validate the contribution of each layer in the band structure, we further decomposed the band in the real space in Supplementary Figure S7 (layer index definition) and Supplementary Figure S8 (layer-resolved band structure). It can be clearly found that the CBM and VBM are contributed by layer 2 (inner TiO₂ layer) and layer 4 (surface TiO₂ layer), respectively, while layer 1 (surface PbO layer) and layer 3 (inner PbO layer) make little contribution. This situation is not affected by the introduction of mechanical strain, as shown in Supplementary Figure S9. Compared with our previous study on BTO [22], our simulation of PTO exhibits a decreasing E_g under the tensile strain, which might weaken the driving force of piezocatalysis according to the EBT.

Space charge redistribution and strain-induced polarization response

Because the polarization is determined by the charge distribution inside the material, to understand the polarization of PTO, we investigated the distribution of atomic charge in bulk and few-layer PTO. The Bader charge [48] was used to describe the atomic charge and further calculate the layer-resolved charge transfer. As shown in Figure 2A, in bulk PTO, according to the sum of Bader charge, the TiO₂ layer gains 0.2 e⁻ from the PbO layer, leading to the TiO₂ node holding a −0.2 |e| charge and PbO node holding a +0.2 |e| charge. Under the compressive strain, the PbO layer sucks back 0.04 e⁻ from the TiO₂ layer, leading to the partial charge decreasing to −0.16 |e| on the TiO₂ layer. However, under tensile strain, we observed the 0.01 e⁻ electron transfer from the PbO to the TiO₂ layer, leading to the −0.21 |e| partial charge on the TiO₂ node.

Figure 2

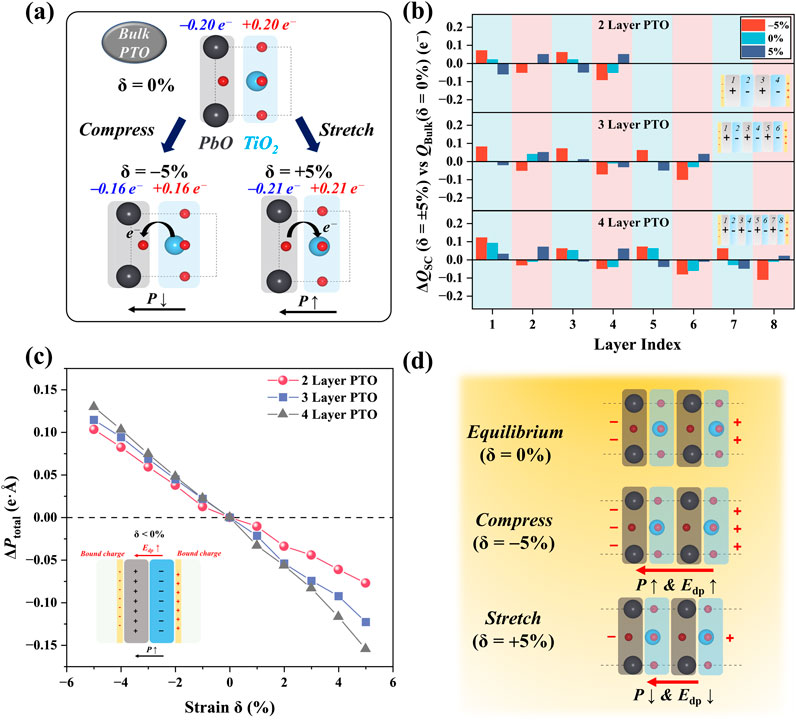
Figure 2. Space charge distribution and dipole moment under strain. (A) Electron transfer and strain-induced space charge redistribution for bulk (referenced to the = 0% state). (B) Strain-induced space charge redistribution for the 2L, 3L, and 4L PTO surfaces (referenced to the δ = 0% state). (C) Change of total dipole moment vs. strain. (C) Change of total dipole moment vs. strain. (D) Schematic description of the bound charge accumulation and depolarization field under compress and stretch conditions.

We chose the bulk PTO as a reference and evaluated the partial charge distribution of few-layer PTO in Figure 2B. Comparing the few-layer PTO and bulk PTO under zero strain, a partial electron suck back to PbO layers was observed (cyan bar in Figure 2B) in 2L- and 4L-PTO. Electron accumulation was observed in layers 1/3 in 2L PTO and layers 1/3/5 in 4L PTO, while electron loss was observed in layer 4 in 2L-PTO, layer 6 in 3L-PTO, and layers 4/6/7 in 4L-PTO. This reverse electron transfer can be explained by the effect of depolarization. When extracting few-layer PTO from the bulk, electron transfer occurs due to the suddenly disappearing constraint from the macroscopic polarization of the whole system. This electron transfer usually tends to weaken the polarization, leading to the electron transfer from the negatively charged node (TiO₂) to the positively charged node (PbO). With the introduction of strain, a relatively larger variation of space charge was observed in the compressive strain rather than tensile strain, as shown in Figure 2B. This can be explained by the change of Ti-O bond length under strain in Figure 2D: compressive strain pushes the O of the PbO layer and the Ti of the TiO₂ layer to be closer, while tensile strain enlarges the Ti-O distance. The closer contact of Ti and O causes more electron transfer, leading to a stronger degree of space charge redistribution.

The change of total dipole moment versus mechanical strain was also studied, as shown in Figure 2C. Interestingly, all the few-layer PTO models show enhanced polarization under compressive strain and weakened polarization under tensile strain. Although the space charge distribution shows that the electron transfer under compressive strain should decrease the polarization, an increase in dipole moment was still observed. This suggests that the contribution of the ionic dipole moment is more dominant than the electronic dipole moment in total dipole moment change. In addition, under the same degree of strain, a thicker layer exhibits larger dipole moment variation than a thin layer PTO. This finding indicates that the increase of overall polarization from the additional PTO layer cannot be perfectly counterbalanced by the depolarization field. The stronger polarization enhancement under strain in thicker layer PTO also suggests a stronger driving force of piezocatalysis, which will be discussed in the next section.

We also investigated the correlation between the band gap and dipole moment of 4L PTO, as shown in Supplementary Figure S10. It shows that there is a linear correlation between polarization and the variation of E_g under lattice strain. Specifically, Supplementary Figure S10 highlights that under compressive strain, a negative correlation is observed, while under tensile strain, a positive correlation emerges, with R² values close to 1. This relationship aligns well with trends reported in previous literature [49, 50].

Work function and piezopotential

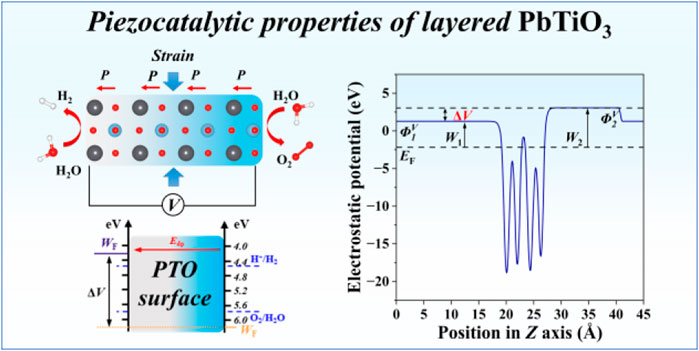
Because the redox ability of a material under an external electric field or polarization is determined by the surface work function, we also investigated the work function of each side of PTO under various mechanical strains. Two vacuum references coexist due to the presence of dipole moment across the PTO along the z direction, which leads to different surface work functions on each side. As shown in Figure 3A, due to the negative charge accumulation on the TiO₂ node, the upper side (TiO₂ side on the right) possesses a larger work function than the lower side (PbO side on the left). We individually calculated the W₁ and W₂ at various strains, as shown in Figure 3B. It shows that both PBE + U and HSE06 predict a monotonically increasing W₁ with strain δ, while the W₂ exhibits a fluctuating trend with the strain δ changes from compressive to tensile, as shown in Figure 3B. In addition, HSE06 always predicts higher work function than PBE + U. Comparing the calculated work function with the energy level of redox potential of O₂ and H₂, the HSE06 calculation shows that the work function of the TiO₂ side is always beyond the oxidation potential of H₂O when δ changes from −5% to +5%, while work function of the PbO side is below H⁺/H₂ redox potential only when the δ decrease below −3% in 2L-PTO. With the layer thickness increase to 3L and 4L, the work function W₁ of the lower side tends to decrease, indicating a stronger driving force of hydrogen evolution reaction (HER) on the low potential side. In the 4L PTO, only a slight compressive strain of δ = −1% can push the W₁ to below 4.5 eV (standard hydrogen electrode reference), while the W₂ is still located beyond 5.73 eV (H₂O oxidation potential). This observation suggests that increasing the PTO thickness could effectively benefit HER activity but have little influence on the driving force of OER.

Figure 3

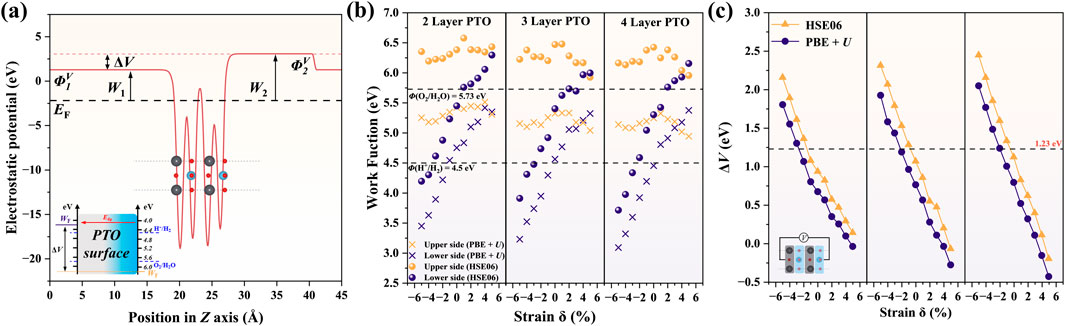
Figure 3. Surface work function under piezoelectric polarization. (A) Schematic description of the work function and piezopotential ΔV in PTO surface. Under the introduction of dipole correction along the z-axis, the surface electrostatic potential converges to different vacuum levels on each side, reflecting different electrochemical activities of the surface electrons. W = Φ_V − E_F directly computed the work function for each side. Φ_V refers to the electrostatic potential near the surface’s vacuum region, and E_F is the Fermi level. The ΔV driven piezocatalytic mechanism is shown in the inset. (B) The work function of 2L, 3L, and 4L PTO surfaces. The upper side refers to the TiO₂ side (right), and the lower side refers to the PbO side (left). (C) Piezopotential ΔV under different strains for 2L, 3L, and 4L PTO.

We further calculated the potential difference between the PbO and TiO₂ sides, which is defined as the piezopotential ΔV. As shown in Figure 3C, we find that compressive strain increases ΔV while tensile strain decreases ΔV. This is consistent with the dipole moment change in Figure 2C, which indicates enhanced polarization by compressive strain and weakened polarization by tensile strain. In addition, the HSE06 method tends to predict a higher ΔV than PBE + U, indicating the significance of a strong correlation effect in the simulation of the piezoelectric property. More importantly, with the layer number increase, we found a larger ΔV variation under the same degree of mechanical strain, suggesting better activity in thicker PTO film. This observation is closely related to the depolarization field, which becomes more pronounced in thinner films and can partially suppress the net polarization and its associated potential. In thicker films, the depolarization field is effectively reduced, leading to a larger polarity and piezopotential. This phenomenon has been discussed from a theoretical approach [22, 51]. From the experimental perspective, promising piezocatalytic performance was usually observed in the thick PTO, which indirectly validates that thick PTO is better than thin PTO in piezocatalysis [52–54].

Finally, it is found that the correlation between ΔV and strain δ is nearly linear in Figure 3C. This linear relation between piezopotential and lattice strain was previously reported by Liu et al. in general piezoelectric materials, but it is derived based on a simple capacitor model with polarization along the z direction [21]. Our simulation indicates that this linear ΔV-δ correlation also exists with the vibrational excitation in the xy plane, which enriches the mechanistic understanding of piezocatalysis.

Piezoelectric effects on the surface adsorption of*H/*OH group

To understand the chemical activity of piezo-electrified PTO surface, we investigate the adsorption energy of *H and *OH groups as examples, which are important adsorbates of the water splitting reaction. The adsorption enthalpy of an adsorbate from DFT calculation is defined by Equation 2:

$∆E_{\mathrm{A}}=E_{*\mathrm{A}}-E_{*}-E_{\mathrm{A},}(2)$

where the index A refers to the adsorbates (H and OH groups in this work), and ‘‘*’’ refers to the clean surface or active site. The total energy E can be directly obtained from DFT calculation. Considering the energy variation with the applied strain δ, the adsorption can be written as Equation 3:

$\begin{array}{ll}\hfill ∆E_{\mathrm{A}}\left(\mathrm{\delta }\right)& =E_{*\mathrm{A}}\left(\mathrm{\delta }\right)-E_{*}\left(\mathrm{\delta }\right)-E_{\mathrm{A}}\\ \hfill & =\left(∆E_{*\mathrm{A}}\left(\mathrm{\delta }\right){+E}_{*\mathrm{A}}\left(\mathrm{\delta }=0\right)\right)-\left(∆E_{*}\left(\mathrm{\delta }\right){+E}_{*}\left(\mathrm{\delta }=0\right)\right)-E_{\mathrm{A}}\hfill \\ \hfill & =∆E_{*\mathrm{A}}\left(\mathrm{\delta }\right)-∆E_{*}\left(\mathrm{\delta }\right){+E}_{*\mathrm{A}}\left(\mathrm{\delta }=0\right){-E}_{*}\left(\mathrm{\delta }=0\right)-E_{\mathrm{A}}\hfill \\ \hfill & =∆E_{*\mathrm{A}}\left(\mathrm{\delta }\right)-∆E_{*}\left(\mathrm{\delta }\right)+Constant\hfill \end{array}(3)$

The ΔE_A(δ) refers to the strain-induced energy variation of the surface with reference to the equilibrium state. Thus, the effect of applied strain on the adsorption enthalpy can be evaluated via the ΔE*A(δ) – ΔE*(δ). We calculated the strain-induced energy variation ΔE_*A(δ) for clean, H-, and OH-absorbed PTO surfaces in Figure 4A. The clean surface exhibits larger ΔE_*A(δ) values than the H- and OH-absorbed surfaces. In addition, on the compressive strain side, the H-absorbed surface shows larger energy variation than the OH-absorbed surface, while their energy variation on the tensile strain region is very close. We further calculated the ΔE*A(δ)–ΔE*(δ) to evaluate the effect of strain δ on the adsorption enthalpy, as shown in Figure 4B. One can see that either compressive or tensile strain can enhance the adsorption for both *H and *OH groups on PTO. This enhancement of adsorption enthalpy is nonsymmetric. Compressive strain enhances the OH adsorption more than H adsorption, while tensile strain enhances the H adsorption more than OH adsorption.

Figure 4

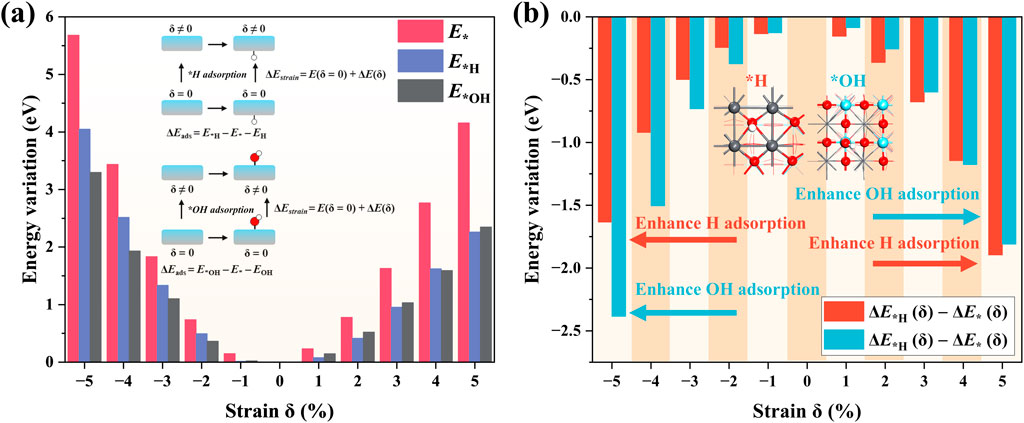
Figure 4. (A) Total energy variation versus applied strain δ; and (B) adsorption energy of *H/*OH versus δ.

These results suggest that the chemical activity of the PTO surface can be significantly tuned via mechanical strain due to the piezoelectric effect. Here, one should note that neither excessively strong nor weak adsorption is favorable for the catalytic process. In this work, we only performed a simple analysis of the adsorption energies, but we did not conduct any detailed study on the optimal adsorption strength and its impact on the HER/OER mechanisms, which will be planned in our further work. To conclude, this strain-induced activity change should be an important part of piezocatalysis from the perspective of reaction on a molecular scale.

Summary and conclusion

In this work, we employed the first-principles DFT calculation to study the piezocatalytic activity and mechanism of tetragonal perovskite PTO. The band structure calculation of bulk PTO shows that PTO is an indirect semiconductor with the VBM and CBM located at the X and Γ points in the reciprocal space. The PDOS and band decomposition of few-layer PTO indicate that the VBM and CBM were mainly contributed by the surface TiO₂ layer and inner TiO₂ layer, respectively.

Under mechanical strain, HSE06 calculation predicts an increasing E_g under compressive strain and a decreasing E_g under tensile strain, giving a monotonical trend of E_g vs. δ. The E_g variation under strain in few-layer PTO is different from that in bulk PTO, which shows a “bell” shape across the whole region, indicating that both compressive and tensile strain leads to E_g decrease. The space charge analysis indicates that few-layer PTO is less polarized than bulk PTO due to the depolarization effect. This effect leads to a reverse electron transfer from the TiO₂ node to the PbO node that should effectively weaken the electronic polarization. However, an enhanced total dipole moment was observed under the compressive strain side, while the tensile strain was found to decrease the total dipole moment. This can be explained by the dominant role of the ionic dipole moment in determining the total polarization.

By looking at the surface work function and piezopotential, we found that the work function of the TiO₂ side (upper side) is always located beyond the H₂O oxidation potential, while the work function of the PbO side is below the HER potential only when the compressive strain was introduced. The reduction potential of the PbO side can be further reduced if the thicker PTO film is used under similar strain conditions. In addition, a linear correlation exists between piezopotential ΔV and biaxial strain δ in the xy plane, which extends linear response ansatz to the mechanical excitation on the basal plane (xy direction) of piezoelectric perovskite.

Finally, by looking at the adsorption enthalpy change under strain, we found that both compressive and tensile strain could promote the H and OH adsorption, which should be an important part when capturing the reaction mechanism under molecular scale during piezocatalysis. Our work could provide in-depth mechanistic insight into the piezocatalytic water splitting in the piezoelectric perovskite family.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

XS: writing–original draft and writing–review and editing. XZ: conceptualization, software, validation, and writing–review and editing. EK: conceptualization, investigation, methodology, supervision, and writing–review and editing. CZ: conceptualization, funding acquisition, project administration, resources, supervision, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by the Funding of NJUST (No. TSXK2022D002), the Natural Science Foundation of Jiangsu Province (No. BK20220929), the Natural Science Foundation of China (No. 22303039), the Fundamental Research Funds for the Central Universities (No. 30922010102), and a Startup Grant of NJUST.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1562239/full#supplementary-material

References

1. Fujishima A, Honda K. Electrochemical photolysis of water at a semiconductor electrode. Nature (1972) 238:37–8. doi:10.1038/238037a0

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Haryanto A, Fernando S, Murali N, Adhikari S. Current status of hydrogen production techniques by steam reforming of ethanol: a review. Energy Fuels (2005) 19:2098–106. doi:10.1021/ef0500538

CrossRef Full Text | Google Scholar

3. Seh ZW, Kibsgaard J, Dickens CF, Chorkendorff I, Nørskov JK, Jaramillo TF. Combining theory and experiment in electrocatalysis: insights into materials design. Science (2017) 355:eaad4998. doi:10.1126/science.aad4998

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Luo J, Zhang S, Sun M, Yang L, Luo S, Crittenden JC. A critical review on energy conversion and environmental remediation of photocatalysts with remodeling crystal lattice, surface, and interface. ACS Nano (2019) 13:9811–40. doi:10.1021/acsnano.9b03649

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Liu C, Chen F, Zhao B-H, Wu Y, Zhang B. Electrochemical hydrogenation and oxidation of organic species involving water. Nat Rev Chem (2024) 8:277–93. doi:10.1038/s41570-024-00589-z

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Wang ZL, Song J. Piezoelectric nanogenerators based on zinc oxide nanowire arrays. Science (2006) 312:242–6. doi:10.1126/science.1124005

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Dai B, Biesold GM, Zhang M, Zou H, Ding Y, Wang ZL, et al. Piezo-phototronic effect on photocatalysis, solar cells, photodetectors and light-emitting diodes. Chem Soc Rev (2021) 50:13646–91. doi:10.1039/D1CS00506E

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Deng W, Zhou Y, Libanori A, Chen G, Yang W, Chen J. Piezoelectric nanogenerators for personalized healthcare. Chem Soc Rev (2022) 51:3380–435. doi:10.1039/D1CS00858G

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Tu S, Guo Y, Zhang Y, Hu C, Zhang T, Ma T, et al. Piezocatalysis and piezo-photocatalysis: catalysts classification and modification strategy, reaction mechanism, and practical application. Adv Funct Mater (2020) 30:2005158. doi:10.1002/adfm.202005158

CrossRef Full Text | Google Scholar

10. Hong K-S, Xu H, Konishi H, Li X. Direct water splitting through vibrating piezoelectric microfibers in water. J Phys Chem Lett (2010) 1:997–1002. doi:10.1021/jz100027t

CrossRef Full Text | Google Scholar

11. Starr MB, Shi J, Wang X. Piezopotential-driven redox reactions at the surface of piezoelectric materials. Angew Chem Int (2012) Ed(51):5962–6. doi:10.1002/anie.201201424

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wang M, Zuo Y, Wang J, Wang Y, Shen X, Qiu B, et al. Remarkably enhanced hydrogen generation of organolead halide perovskites via piezocatalysis and photocatalysis. Adv Energ Mater (2019) 9:1901801. doi:10.1002/aenm.201901801

CrossRef Full Text | Google Scholar

13. Wang Y, Wen X, Jia Y, Huang M, Wang F, Zhang X, et al. Piezo-catalysis for nondestructive tooth whitening. Nat Commun (2020) 11:1328. doi:10.1038/s41467-020-15015-3

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Su R, Hsain HA, Wu M, Zhang D, Hu X, Wang Z, et al. Nano-ferroelectric for high efficiency overall water splitting under ultrasonic vibration. Angew Chem Int (2019) Ed(58):15076–81. doi:10.1002/anie.201907695

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zhang A, Liu Z, Xie B, Lu J, Guo K, Ke S, et al. Vibration catalysis of eco-friendly Na_0.5K_0.5NbO₃-based piezoelectric: an efficient phase boundary catalyst. Appl Catal B (2020) 279:119353. doi:10.1016/j.apcatb.2020.119353

CrossRef Full Text | Google Scholar

16. Wang Y-C, Wu JM. Effect of controlled oxygen vacancy on H₂-production through the piezocatalysis and piezophototronics of ferroelectric R3c ZnSnO₃ nanowires. Adv Funct Mater (2020) 30:1907619. doi:10.1002/adfm.201907619

CrossRef Full Text | Google Scholar

17. Kubota K, Pang Y, Miura A, Ito H. Redox reactions of small organic molecules using ball milling and piezoelectric materials. Science (2019) 366:1500–4. doi:10.1126/science.aay8224

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wu M-H, Lee J-T, Chung YJ, Srinivaas M, Wu J-M. Ultrahigh efficient degradation activity of single- and few-layered MoSe₂ nanoflowers in dark by piezo-catalyst effect. Nano Energy (2017) 40:369–75. doi:10.1016/j.nanoen.2017.08.042

CrossRef Full Text | Google Scholar

19. Wang K, Han C, Li J, Qiu J, Sunarso J, Liu S. The mechanism of piezocatalysis: energy band theory or screening charge effect? Angew Chem Int (2022). doi:10.1002/anie.202110429

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Starr MB, Wang X. Fundamental analysis of piezocatalysis process on the surfaces of strained piezoelectric materials. Sci Rep (2013) 3:2160. doi:10.1038/srep02160

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Liu Z, Wang B, Chu D, Cazorla C. First-principles high-throughput screening of bulk piezo-photocatalytic materials for sunlight-driven hydrogen production. J Mater Chem A (2022) 10:18132–46. doi:10.1039/D2TA05941J

CrossRef Full Text | Google Scholar

22. Zhou Z, Zhan C, Kan E. Understanding the piezocatalytic properties of the BaTiO₃(001) surface via density functional theory. Phys Chem Chem Phys (2023) 25:8631–40. doi:10.1039/D2CP05631C

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Su R, Wang Z, Zhu L, Pan Y, Zhang D, Wen H, et al. Strain-engineered nano-ferroelectrics for high-efficiency piezocatalytic overall water splitting. Angew Chem Int (2021) Ed(60):16019–26. doi:10.1002/anie.202103112

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Zhu P, Chen Y, Shi J. Piezocatalytic tumor therapy by ultrasound-triggered and BaTiO₃-mediated piezoelectricity. Adv Mater (2020) 32:2001976. doi:10.1002/adma.202001976

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Starr MB, Wang X. Coupling of piezoelectric effect with electrochemical processes. Nano Energy (2015) 14:296–311. doi:10.1016/j.nanoen.2015.01.035

CrossRef Full Text | Google Scholar

26. Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci (1996) 6:15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

27. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B (1996) 54:11169–86. doi:10.1103/PhysRevB.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Blöchl PE. Projector augmented-wave method. Phys Rev B (1994) 50:17953–79. doi:10.1103/PhysRevB.50.17953

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Hammer B, Hansen LB, Nørskov JK. Improved adsorption energetics within density-functional theory using revised perdew-burke-ernzerhof functionals. Phys Rev B (1999) 59:7413–21. doi:10.1103/PhysRevB.59.7413

CrossRef Full Text | Google Scholar

30. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Grimme S, Antony J, Ehrlich S, Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys (2010) 132:154104. doi:10.1063/1.3382344

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Chadi DJ, Cohen ML. Special points in the Brillouin zone. Phys Rev B (1973) 8:5747–53. doi:10.1103/PhysRevB.8.5747

CrossRef Full Text | Google Scholar

33. Majumder S, Basera P, Tripathi M, Choudhary RJ, Bhattacharya S, Bapna K, et al. Elucidating the origin of magnetic ordering in ferroelectric BaTiO_3-D thin film via electronic structure modification. J Phys Condens Matter (2019) 31:205001. doi:10.1088/1361-648X/ab06d5

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Heyd J, Scuseria GE, Ernzerhof M. Hybrid functionals based on a screened coulomb potential. J Chem Phys (2003) 118:8207–15. doi:10.1063/1.1564060

CrossRef Full Text | Google Scholar

35. Becke AD. Density-functional thermochemistry. Iii. The role of exact exchange. J Chem Phys (1993) 98:5648–52. doi:10.1063/1.464913

CrossRef Full Text | Google Scholar

36. Sághi-Szabó G, Cohen RE, Krakauer H. First-principles study of piezoelectricity in PbTiO₃. Phys Rev Lett (1998) 80:4321–4. doi:10.1103/PhysRevLett.80.4321

CrossRef Full Text | Google Scholar

37. Bendaoudi L, Ouahrani T, Daouli A, Rerbal B, Boufatah RM, Morales-García Á, et al. Electronic and electrocatalytic properties of PbTiO₃: unveiling the effect of strain and oxygen vacancy. Dalton Trans (2023) 52:11965–80. doi:10.1039/D3DT01478A

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Neugebauer J, Scheffler M. Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al(111). Phys Rev B (1992) 46:16067–80. doi:10.1103/PhysRevB.46.16067

PubMed Abstract | CrossRef Full Text | Google Scholar

39. King-Smith RD, Vanderbilt D. Theory of polarization of crystalline solids. Phys Rev B (1993) 47:1651–4. doi:10.1103/PhysRevB.47.1651

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Perdew JP, Ruzsinszky A, Csonka GI, Vydrov OA, Scuseria GE, Constantin LA, et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys Rev Lett (2008) 100:136406. doi:10.1103/PhysRevLett.100.136406

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Gebreyesus G, Bastonero L, Kotiuga M, Marzari N, Timrov I. Understanding the role of hubbard corrections in the rhombohedral phase of BaTiO₃. Phys Rev B (2023) 108:235171. doi:10.1103/PhysRevB.108.235171

CrossRef Full Text | Google Scholar

42. Mabud SA, Glazer AM. Lattice parameters and birefringence in PbTiO₃ single crystals. J Appl Crystallogr (1979) 12:49–53. doi:10.1107/S0021889879011754

CrossRef Full Text | Google Scholar

43. Wójcik K. Electrical properties of PbTiO₃ single crystals doped with lanthanum. Ferroelectrics (1989) 99:5–12. doi:10.1080/00150198908221435

CrossRef Full Text | Google Scholar

44. Li Z, Grimsditch M, Xu X, Chan SK. The elastic, piezoelectric and dielectric constants of tetragonal PbTiO₃ single crystals. Ferroelectrics (1993) 141:313–25. doi:10.1080/00150199308223459

CrossRef Full Text | Google Scholar

45. Lemziouka H, Omari LEH, Moubah R, Boutahar A, Bahhar S, Abid M, et al. Structural, dielectric and optical properties of Cu-doped PbTiO₃ ceramics prepared by sol–gel. Mater Today Proc (2021) 37:3940–5. doi:10.1016/j.matpr.2020.09.094

CrossRef Full Text | Google Scholar

46. Prajapati P, Singh AK. Band gap tuning of ferroelectric PbTiO₃ by Mo doping. J Mater Sci:mater Electron (2022) 33:2550–65. doi:10.1007/s10854-021-07461-6

CrossRef Full Text | Google Scholar

47. Berger RF, Fennie CJ, Neaton JB. Band gap and edge engineering via ferroic distortion and anisotropic strain: the case of SrTiO₃. Phys Rev Lett (2011) 107:146804. doi:10.1103/PhysRevLett.107.146804

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Tang W, Sanville E, Henkelman G. A grid-based bader analysis algorithm without lattice bias. J Phys Condens Matter (2009) 21:084204. Epub 20090130. doi:10.1088/0953-8984/21/8/084204

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Vonrüti N, Aschauer U. Epitaxial strain dependence of band gaps in perovskite oxynitrides compared to perovskite oxides. Phys Rev Mater (2018) 2:105401. doi:10.1103/PhysRevMaterials.2.105401

CrossRef Full Text | Google Scholar

50. Parker WD, Rondinelli JM, Nakhmanson SM. First-principles study of misfit strain-stabilized ferroelectric SnTiO₃. Phys Rev B (2011) 84:245126. doi:10.1103/PhysRevB.84.245126

CrossRef Full Text | Google Scholar

51. Jung S, Pizzolitto C, Biasi P, Dauenhauer PJ, Birol T. Programmable catalysis by support polarization: elucidating and breaking scaling relations. Nat Commun (2023) 14:7795. doi:10.1038/s41467-023-43641-0

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Amiri O, Salar K, Othman P, Rasul T, Faiq D, Saadat M. Purification of wastewater by the piezo-catalyst effect of PbTiO₃ nanostructures under ultrasonic vibration. J Hazard Mater (2020) 394:122514. doi:10.1016/j.jhazmat.2020.122514

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Wan G, Yin L, Chen X, Xu X, Huang J, Zhen C, et al. Photocatalytic overall water splitting over PbTiO₃ modulated by oxygen vacancy and ferroelectric polarization. J Am Chem Soc (2022) 144:20342–50. doi:10.1021/jacs.2c08177

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Huang X, Lei R, Yuan J, Gao F, Jiang C, Feng W, et al. Insight into the piezo-photo coupling effect of PbTiO₃/CdS composites for piezo-photocatalytic hydrogen production. Appl Catal B (2021) 282:119586. doi:10.1016/j.apcatb.2020.119586

CrossRef Full Text | Google Scholar