Modeling social conformity and peer pressure in opinion dynamics: the role of dynamic interaction structures

With the advent of modern media platforms, the dissemination of information has become faster and more far-reaching than ever before. These platforms amplify susceptibility to societal influences, as individuals respond to widely circulating information while being shaped by the perspectives of those around them. By aligning with others’ opinions, individuals contribute to establishing shared norms through both macroscopic and microscopic influences. This paper explores the roles of these influences—social conformity at the population-wide level and peer pressure at the localized level—in shaping opinion dynamics within today’s information-rich environment. Building on the Hegselmann-Krause opinion dynamics model, we introduce modifications to incorporate peer pressure through three modes of dynamic social circles. While conformity and peer pressure have been studied previously, we focus specifically on how properties and behaviors evolve in an opinion-dependent manner from both individual and social circle perspectives. Furthermore, we incorporate radical agents, characterized by resistance to influence. However, unlike radicals as referred to the stubborn agents commonly discussed in previous literature, our radical agents adjust their behavior based on their position in the opinion spectrum rather than remaining entirely fixed in their views. Simulations reveal that removing agents with distant opinions from social circles facilitates population convergence more than adding agents with similar opinions. Our model suggests that increasing the number of agents within social circles accelerates opinion shifts. Similarly, broadening confidence bounds fosters cluster formation. In addition, a higher initial number of radical agents makes it more likely for non-radical agents to adopt radical views. Likewise, when agents are influenced more by macroscopic rather than microscopic forces, radicalization becomes more likely. Together, one or more of these dynamics drive convergence between radical and non-radical agents.

1 Introduction

Contemporary media has redefined societal interactions, driving unprecedented changes in the speed and breadth of information dissemination. Today’s social media platforms connect to distant trends and diverse content, creating broader and more dynamic spheres of influence [1]. This rapid flow of information has also been linked to the formation of echo chambers, where selective exposure to similar viewpoints reinforces beliefs and amplifies polarization [2, 3].

This shift suggests a heightened susceptibility to conform to broader societal opinions, as people respond to information that circulates widely across media platforms. As individuals consume diverse and, at times, contradictory content, their opinions may increasingly align with dominant narratives, fostering a sense of shared outlook even among people who are geographically or culturally distant. Research on homophily demonstrates that individuals tend to cluster with those who share similar beliefs, further amplifying dominant viewpoints [4–6]. Conversely, this global information network provides those seeking to advance specific viewpoints, such as political ideologies, with more extensive means to engage with and sway public opinion [7, 8]. As a result, voices that may have once remained marginal, including radical perspectives, can now gain visibility and exert influence through various media channels, amplifying their impact on society [9].

Amid the constant flow of information in modern society, individuals rarely form opinions in isolation. Instead, opinions are shaped by interactions with others, as individuals naturally adjust their views in response to social cues [10, 11]. This process aligns with Festinger’s social comparison theory, which suggests that people evaluate their own opinions by comparing them with others [12]. Beyond mere information absorption, individuals also seek social approval and aim to align with the views of their peers, contributing to establishing shared norms and influencing public opinion on a broader scale [13]. This behavior is reinforced through both normative social influence, where individuals conform to meet social expectations, and informational social influence, which occurs when people rely on others as a source of guidance [14]. This paper explores social conformity and peer pressure—the tendency for individuals to adjust their opinions to match those of others—and their role in shaping opinion formation within today’s information-rich environment.

In social psychology, social conformity is defined as the tendency for individuals to adjust their behaviors to align with group norms, driven by a desire for social acceptance or to avoid rejection, even when those judgements contradict personal beliefs [15, 16]. Peer pressure refers to the influence exerted by peers to encourage conformity within a social circle. Research has identified mechanisms such as normative social influence, where individuals conform to meet others’ expectations, and informational social influence, where individuals rely on the group for guidance in ambiguous situations [14].

In our model, we distinguish these influences by defining social conformity as a macroscopic force that aligns individuals with prevalent societal views, reflecting broad-scale normative pressures. Peer pressure, by contrast, serves as a microscopic influence, shaped by the dynamics of individual relationships and immediate social circles. This distinction allows us to investigate how these two levels of influence interact and contribute to opinion dynamics within diverse social contexts [17].

Opinion dynamics explores how individual opinions change and spread within a group on the basis of social interactions [18–20]. This field models complex social interactions where opinions change through influence, selective exposure, and reinforcement mechanisms and reveals how collective beliefs emerge from individual perspectives [21–24]. Classical approaches, such as the DeGroot model, illustrate how iterative averaging can lead to consensus under certain conditions [25], while confidence bound models capture how agents form opinion clusters when limited to interacting within specific belief ranges [23, 26, 27]. Networked frameworks in opinion dynamics simulate how social structures and individual characteristics shape the stability or fragmentation of group beliefs [25, 28, 29].

By integrating psychological literature with opinion dynamics modeling, we incorporate social conformity and peer pressure into an opinion dynamics model. We base our model on the Hegselmann-Krause (HK) model of opinion dynamics, which considers macroscopic influence. The HK model explores how individuals form clusters of shared beliefs on the basis of confidence bounds. It assumes that individuals only interact with others whose opinions fall within this confidence range. Each agent averages its opinion with those of neighbors within this confidence interval, gradually moving toward a common position with agents holding similar views while ignoring those with divergent opinions [26, 27, 30].

The confidence bound mechanisms in the HK model lead to emergent patterns of opinion clustering, often resulting in either a consensus, polarization or fragmentation, depending on the confidence bound and initial distribution of opinions [26]. When confidence bounds are broad, agents are more likely to achieve consensus. Conversely, with narrower bounds, the population is more likely to polarize [23].

However, the HK model does not consider microscopic influence, which we also aim to incorporate. A similar approach has been studied, but it is based on a network-based opinion dynamics model [31]. This model examines the interplay between network connections formed through personal acquaintances and those formed between individuals with similar beliefs. While it considers the interdependence of these two factors, our focus is on the opinion-dependent evolution of social circles and individuals, incorporating confidence bounds. Despite previous studies on conformity at both macroscopic and microscopic levels in opinion dynamics [32–35], this specific aspect has received little attention. Therefore, our approach emphasizes how these evolving dynamics shape opinion dynamics. Consequently, we modify the HK model to include microscopic influence by assuming that agents are influenced by both macroscopic and microscopic influences.

In particular, when dynamizing social circles, agents are added or removed based on the closeness of opinions within the circle at each timestep. From an individual perspective, an agent’s behavior—both independently and within social circles—varies depending on its opinion value.

To model these dynamics, we first modify the model to construct social circles (referred to as “friend sets” in this paper) consisting of a fixed number of friends. Within these friend sets, agents interact with others in their circle and update their opinions on the basis of their friends’ views. To allow agents to enter and leave friend sets, we set up three modes of updating friend sets: Fermi-Birth, Fermi-Death, and Random-out-random-in. In the Fermi-Birth mode, an agent with a close opinion to the friend set is added while another agent is removed at random. In Fermi-Death, a random agent is added, and an agent with a distant opinion is removed. In Random-out-random-in, a random agent is added, and another random agent is removed.

Second, we modify the opinion-updating rules of the HK model. In the original HK model, agents update their opinions if their opinions are within a given confidence bound. While we remain in this setup, we incorporate both macroscopic and microscopic influences. In contrast to the HK model, which assumes agents update solely on the basis of the opinions of the entire population within the confidence bound, we assume that agents update on the basis of both the population and their friend sets. We therefore establish a ratio for how much agents are influenced by macroscopic (population) and microscopic (friend set) influences.

Furthermore, we extend our model to include radical opinions—extreme viewpoints resistant to influence. Studies by [36, 37] show that radical agents often act as sources of stability for fringe views and contribute to polarization within communities. Their presence can lead to the formation of “opinion islands,” where like-minded individuals cluster around extreme beliefs, increasing fragmentation and preventing broader societal consensus [29, 38, 39]. Experiments indicate that the stubbornness effect of radical agents varies depending on the network topology of communication and affinity [40]. To account for these effects, we differentiate between radical and non-radical agents based on the range of opinions they hold. While prior literature typically defines “radical agents” as stubborn individuals whose opinions remain fixed, our approach instead characterizes radicals by their position in the opinion spectrum rather than their resistance to change. Contrary to non-radical agents, radicals are less influenced by macroscopic forces and instead respond more strongly to microscopic interactions within their friend sets.

Our simulations demonstrate that the dynamics of friend sets significantly influence opinion dynamics. Specifically, determining whom to remove from friend sets, rather than whom to add, plays a critical role in achieving consensus. Populations in the Fermi-Death mode consistently exhibit convergence, while those in the Fermi-Birth and Random-out-random-in modes exhibit a range of opinion distributions—such as convergence, polarization and fragmentation—depending on parameter settings.

Simulation results across parameter variations show that increasing all parameter values accelerates cluster formation and the speed of opinion dynamics. In other words, when agents have more friends to interact with, the population is likely to change more rapidly and form clusters. Similarly, higher confidence bound values lead to early cluster formation and faster consensus. Moreover, with a higher initial number of radical agents or agents influenced predominantly by macroscopic rather than microscopic forces, non-radical agents are more likely to adopt radical views, and vice versa. This dynamic fosters convergence between radical and non-radical agents.

2 Models

We present our opinion dynamics model of social conformity and peer pressure. Since our model is an extension of the HK bounded confidence model, we will first introduce their model. Then, we will explain the primary four parameters for agent properties and three modes for dynamic interaction structures.

2.1 The original Hegselmann-Krause model

We will begin by giving an overview of the HK model.

In the HK model, there are $N$ agents, indexed by $i=1\dots N$, who interact with each other in discrete time intervals. Each agent $i$ has an opinion, represented by $s_i(t)$ on a topic at time $t$. Opinions are expressed as real numbers within the interval [0,1]. The initial opinions of all agents are assigned random values uniformly within the interval [26].

Agents interact and adjust their opinions on the basis of those of other agents within a certain confidence bound value, denoted by $ϵ\in (\mathrm{0,1})$. This value represents the degree of tolerance that agents have towards differing opinions. Agents are assumed to interact with others whose opinions are close to their own, specifically where the absolute difference between an agent’s current opinion and the opinions of their friends is less than a given confidence bound, $ϵ$. In other words, if the distance between an agent’s opinion and others’ opinions exceeds the confidence bound $ϵ$, no interaction between them occurs. Every agent interacts with everyone else only if their opinion difference is within the confidence bound. The opinion of an agent $i$ at time $t+1$, is updated on the basis of the average opinions of all agents whose opinions are within the confidence bound interval $ϵ$ of $s_i(t)$. This is defined as:

$s_i\left(t+1\right)=s_i\left(t\right)+\frac{1}{\left|N_i^{\prime }\right|}{\displaystyle \sum _{j\in N_i^{\prime }}}\left(s_j\left(t\right)-s_i\left(t\right)\right)$

where $N_i^{\prime }=\{j\Vert s_j(t)-s_i(t)|<ϵ\}$.

Note that in the original HK model, agents are represented as nodes and are connected through interactions as links in a complete graph. This implies that every agent is connected to all others in the population, regardless of their opinion values. However, interactions occur only when the opinions of agents fall within the confidence bound; otherwise, their opinions remain unchanged [26].

2.2 Extension of the Hegselmann-Krause model

We extend the HK model to model social conformity and peer pressure within the interaction structure. We introduce dynamic interaction graphs and modify agents’ properties. The key differences between the HK model and our model are shown in Table 1.

Table 1

Table 1. Comparison of key elements between the original Hegselmann-Krause model and our model.

2.2.1 Friend set updating modes

The network structures of the HK model and our model are illustrated in Figure 1. The HK model assumes that interactions occur between agents on the basis of the similarity of their opinions with all other agents [26]. In contrast, while our model also assumes that agents are influenced by the opinions of all others, it also introduces friend sets, where agents interact exclusively within their own friend groups. Note that these friend relationships are not necessarily symmetrical; for instance, while Agent A may consider Agent B a friend, Agent B may not necessarily reciprocate this view.

Figure 1

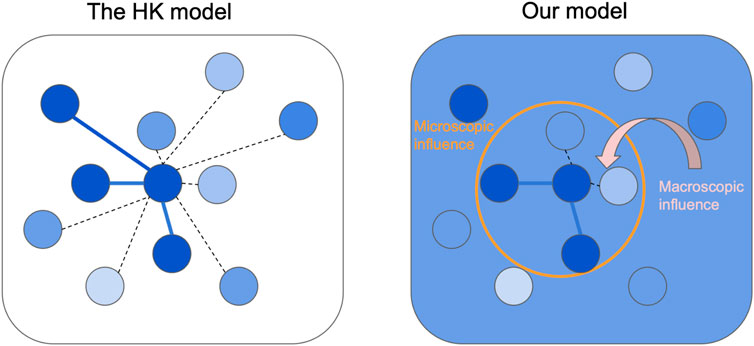
Figure 1. Comparison of the network structures between the original Hegselmann-Krause model and our model Left: The original HK model is based on a complete graph structure, where every agent is connected to every other agent, allowing influence from the entire population. Right: Our model incorporates two types of influences on agents: macroscopic and microscopic. Macroscopic influence captures the effect of the entire population, where each agent’s opinion is influenced by the average opinion of all agents, representing social conformity. Microscopic influence, on the other hand, represents peer pressure, where agents are influenced through connections within a defined “friend set”. Each agent maintains connections with $f\times N$ friends, where $f$ is the proportion of connected friends (other agents in the same group) per agent. This proportion ranges from 0 to 1.

To reflect the tendency for stronger ties with friends, our model introduces dynamic adjustments of agents within these friend sets. Let $N_i(t)$ be Agent $i$’s friend set at simulation time $t$ and $N_i(t)$ be a constant where $|N_i(t)|=f\times N$ and $f$ represents network density. The dynamization of $N_i(t)$ follows a one-out-one-in rule. In other words, one friend exits the friend set while one newcomer joins the friend set during each time step. Note that each agent includes itself in its set of neighbors. We first consider the Random-out-random-in mode, where both the leaving and entering agents are randomly selected from the friend set. In addition, we introduce two other agent updating modes: Fermi-Birth and Fermi-Death (Figure 2).

Figure 2

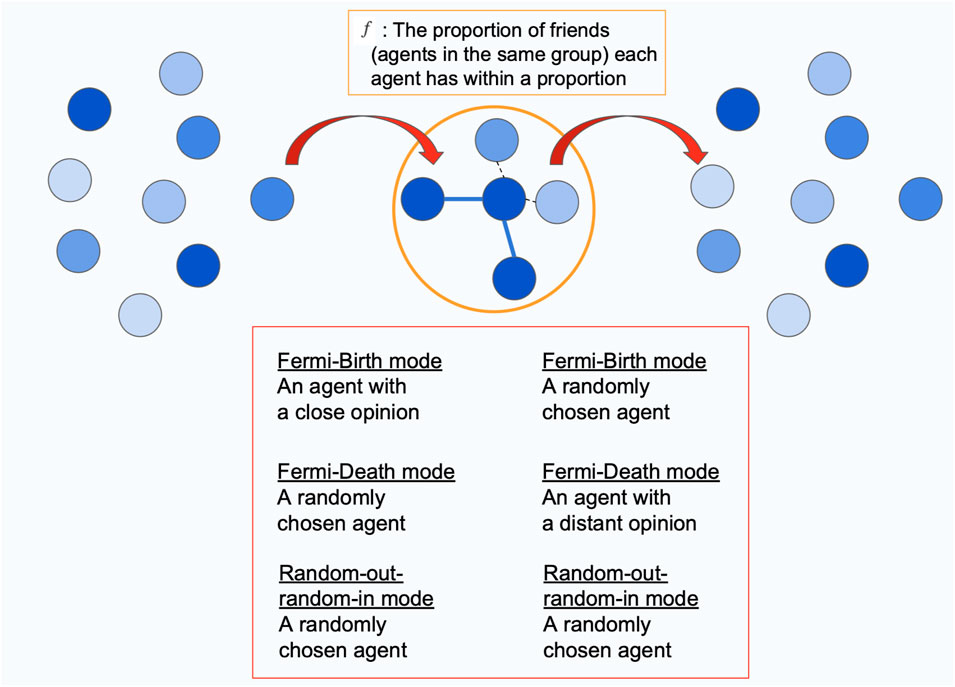
Figure 2. Friend set updating rules - Fermi-Birth mode, Fermi-Death mode, and Random-out-random-in mode This figure illustrates how agents enter and exit a friend set in each mode. Agents are represented as small, cool-colored circles, with links indicating their connections. The orange circle denotes immediate neighbors, referred to as the friend set in this paper. Each agent is assumed to have a fixed number of friends. (four in this example). Interactions occur by adding one agent and removing another during each update. In the Fermi-Birth mode, an agent with an opinion similar to the friend set joins, while a randomly chosen agent leaves. In the Fermi-Death mode, a randomly chosen agent joins, and an agent with an opinion distant from the friend set leaves. In the Random-out-random-in mode, a randomly chosen agent joins, and another randomly chosen agent exits the friend set.

In the Fermi-Death mode, an agent with a distant opinion is removed from the friend set. In other words, the probability of a friend $j$ in $N_i(t)$ exiting is determined by the formula $p_{\text{out}}(j|i)=|s_j(t)-s_i(t)|/{\sum }_j|s_j(t)-s_i(t)|$. Subsequently, a new random agent is added to the friend set. In contrast, in the Fermi-Birth mode, one friend is randomly chosen to leave the friend set, and an agent whose opinion closely matches that of the friend set is added. The probability of an agent $j$ joining, denoted as $p_{\text{in}}(j|i)$ among all where $p_{\text{in}}(j|i)=[s_{\max }-|s_j(t)-s_i(t)]/{\sum }_j[s_{\max }-|s_i(t)-s_i(t)|]$, where $s_{\max }$ represents the theoretical maximum opinion distance.

2.2.2 Introduction of four parameters

The properties of agents in our model are defined in Table 1. Agents are assumed to update their opinions on the basis of two types of influences: social conformity and peer pressure. Social conformity reflects a macroscopic perspective, representing the overall opinion of the entire society. It is calculated as the average opinion across all agents, denoted as $M={\sum }_i{s}_i(t)/N$, where $M(t)$ is the average opinion of the population at time $t$ that we assume social conformity covers the overall atmosphere. Peer pressure, on the other hand, influences agents at a microscopic level, representing the pressure from surrounding peers with similar opinions. We specifically introduce peer pressure by defining a friend set into the original HK model. Peer pressure is calculated as the average opinion of the agents within the friend set who share similar opinions.

To weigh these two types of influences, we introduce a parameter $c$, which lies in the interval [0,1]. This parameter represents the ratio of social conformity to peer pressure influences acting on agents. The opinion of agent $i$ is updated by combining the influence of social conformity, weighted by $c_i$, and peer pressure, weighted by $1-c_i$. Therefore, the opinion update rule is given by:

$s_i\left(t+1\right)=c_{i}M+\left(1-c_i\right){\displaystyle \sum _{j\in N_i^{\prime }\left(t\right)}}\frac{s_j\left(t\right)}{|N_i^{\prime }\left(t\right)|}$

where $N_i^{\prime }(t)=\{j|j\in N_i(t)\cap |s_j(t)-s_i(t)|<{ϵ}_i\}$. Here, ${ϵ}_i$ is a confidence bound randomly assigned from a uniform distribution between 0 and $ϵ$, which remains constant throughout the simulation. The value of $c_i$ is also randomly assigned from a uniform distribution between 0 and $c\times k_i$ and remains constant throughout the simulation, where $k_i$ will be defined later.

This model introduces radical agents by extending the opinion range from [0,1] to $[-\mathrm{1,1}]$ (Table 2). Radical agents are defined as those with opinions between $-1$ and 0, while non-radical agents have opinions between 0 and 1. Agents with an opinion value of 0 are included among non-radicals. The initial proportion of agents with radical opinions is denoted by $\beta$, thus the initial proportion of non-radical agents is denoted as $1-\beta$. To model the tendency for radicalized agents to maintain their opinions [41], we assume $k_i=1-\beta$ for non-radicalized agents and $k_i=\beta$ for radicalized ones.

Table 2

Table 2. Distributions of each parameter In this model, agents with opinion ranging from −1 to 0 are categorized as radical, while those with opinions from 0 to 1 are categorized as non-radical.

3 Simulation results and findings

We conduct simulations of our model using an agent-based approach to compare two main aspects: three different friend set updating modes and four parameters that may represent how social conformity and peer pressure influence opinion dynamics. The population size is set to $N=100$ in Figures 3, 4 and $N=1000$ in Figures 5–8, with each simulation running for $T=1000$ time steps. Initial opinions are assigned randomly and uniformly. To observe the overall outcomes, we generate heatmaps and box plots showing the average, variance, and Gini coefficient of the opinion distribution under different parameter settings at the end time of each simulation run. We then examine the opinion dynamics to analyze how the population’s opinions evolve over time. Note that all agents’ opinion values are increased by two to avoid negative values when calculating the Gini coefficient.

Figure 3

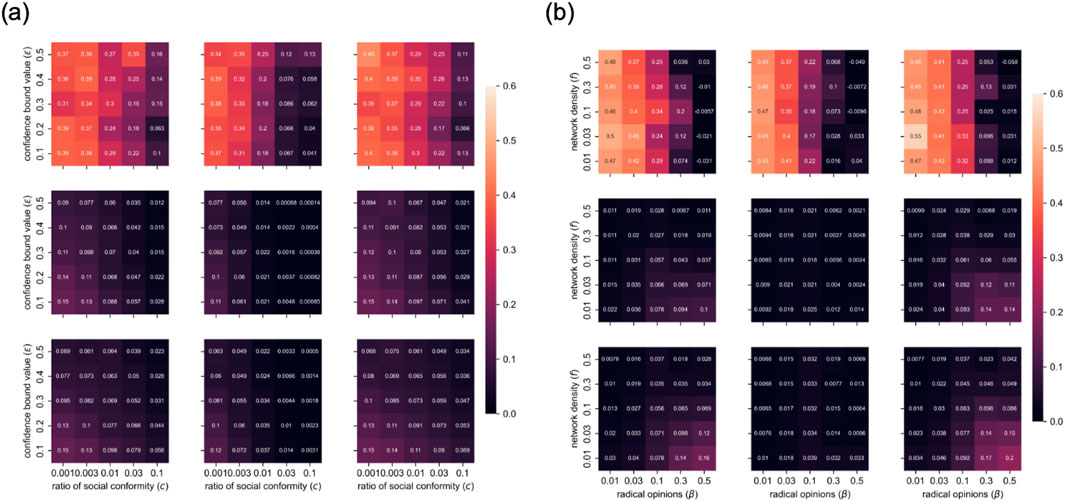
Figure 3. Heat maps of the average, variance, and Gini coefficient of the population’s opinions in three modes Heatmaps and box plots were generated to illustrate the average, variance and Gini coefficient of the population’s opinions across different parameter values. Each box depicts the value of the respective statistic, with lighter colors corresponding to higher values. Each simulation consisted of 30 iterations with varying random seeds, with N = 100 agents and T = 1000 time steps per iteration. The results are displayed as follows: Left: Fermi-Birth mode, Center: Fermi-Death mode, and Right: Random-out-random-in mode. Top: Average of the population’s opinions, Middle: Variance of the population’s opinions, Bottom: Gini coefficient of the population’s opinions. (a) shows the average, variance, and Gini coefficient of the population’s opinions based on varying confidence bound $ϵ$ and the ratio of social conformity to peer pressure influences acting on agents $c$. The ratio of social conformity is shown on the horizontal axis, while the confidence bound is shown on the vertical axis. Other parameters are set to $f=0.03$ and $\beta =0.1$ for this heat map. As the confidence bound increases, both the variance and Gini coefficient decrease. Similarly, a higher influence from social conformity results in lower variance and Gini coefficients. These trends are more pronounced in the Fermi-Birth and Random-out-random-in modes than in the Fermi-Death mode. (b) explores the relationship between the proportion of radical agents and the proportion of friends each agent has. The proportion of radical agents $\beta$ is displayed on the horizontal axis, while the proportion of friends $f$ is shown on the vertical axis. For this heatmap, other parameters are set to $c=0.01$ and $ϵ=0.3$. As the number of friends increases, the variance and Gini coefficient decrease. Conversely, a higher proportion of radical agents correlates with increased variance and Gini coefficient. These trends are again more apparent in the Fermi-Birth and Random-out-random-in modes than in the Fermi-Death mode.

Figure 4

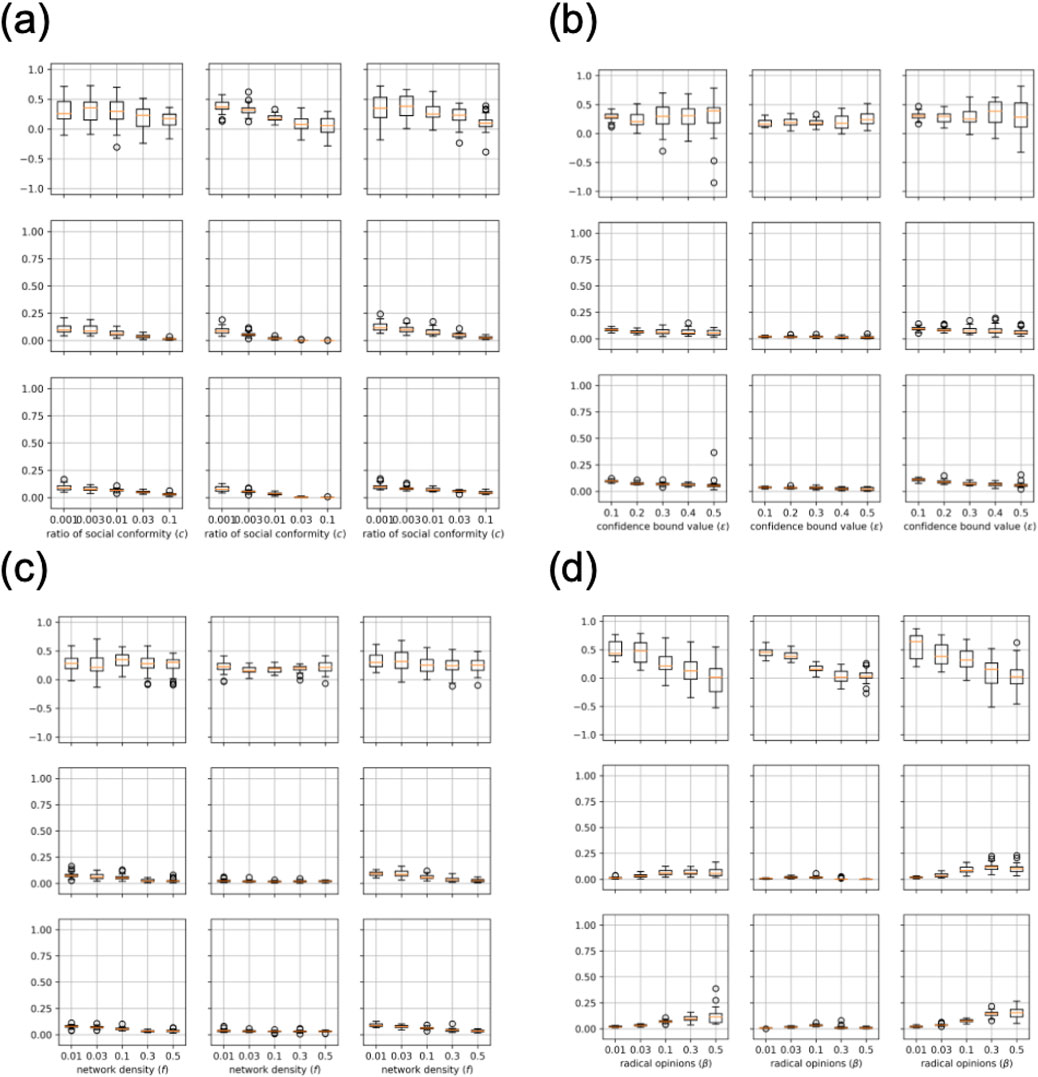
Figure 4. Box plots of the average, variance, and Gini coefficient of the population’s opinions in three modes Each box plot represents the distribution of 30 iterations with different random seeds for the average, variance, and Gini coefficient of the population’s opinions. Each plot is organized as follows: Left: Fermi-Birth mode, Center: Fermi-Death mode, and Right: Random-out-random-in mode. Top: Average of the population’s opinions, Middle: Variance, and Bottom: Gini coefficient. The horizontal axis in each plot shows the parameter being varied, while the vertical axis shows the respective metric. Overview The heat maps in Figure 3 indicate consistent overall trends in the average, variance, and Gini coefficient across the three modes and four parameters. However, the box plots provide deeper insights into their distributions within each mode. The average typically ranges from -0.5 to 1, while variance and Gini coefficient fall between 0 and 0.25. Compared to the Fermi-Death mode, the Fermi-Birth and Random-out-random-in modes exhibit broader distributions for all metrics. Variance and Gini coefficient show more significant changes with the ratio of social conformity and the proportion of radical agents than with confidence bounds or network density. Observations (a) Boxplot across different values of the ratio of social conformity to peer pressure. The other parameters are set to $ϵ=0.3$, $f=0.03$, and $\beta =0.1$. As social conformity increases, the average, variance and Gini coefficient decrease. This indicates that as stronger conformity to macroscopic influences leads to opinion convergence and reduced opinion diversity. (b) Boxplot across different values of confidence bounds. The other parameters are set to $c=0.01$, $f=0.03$, and $\beta =0.1$. While no clear pattern is observed for the average, higher confidence bounds reduce both variance and Gini coefficient. This indicates that tolerant populations are more likely to converge on similar opinions. (c) Boxplot across different values of network density, defined as the proportion of friends that each agent has. The other parameters are set to $c=0.01$, $ϵ=0.3$, and $\beta =0.1$. No consistent pattern emerges for the average, but a higher network density (more connections per agent) corresponds to lower variance and Gini coefficient. This indicates that well-connected populations share more similar opinions. (d) Boxplot across different values of the proportion of agents with radical opinions. The other parameters are set to $c=0.01$, $ϵ=0.3$, and $f=0.03$. As the proportion of radical agents increases, the average opinion decreases, while both variance and Gini coefficient diminish, especially in the Fermi-Birth and Random-out-random-in modes.

Figure 5

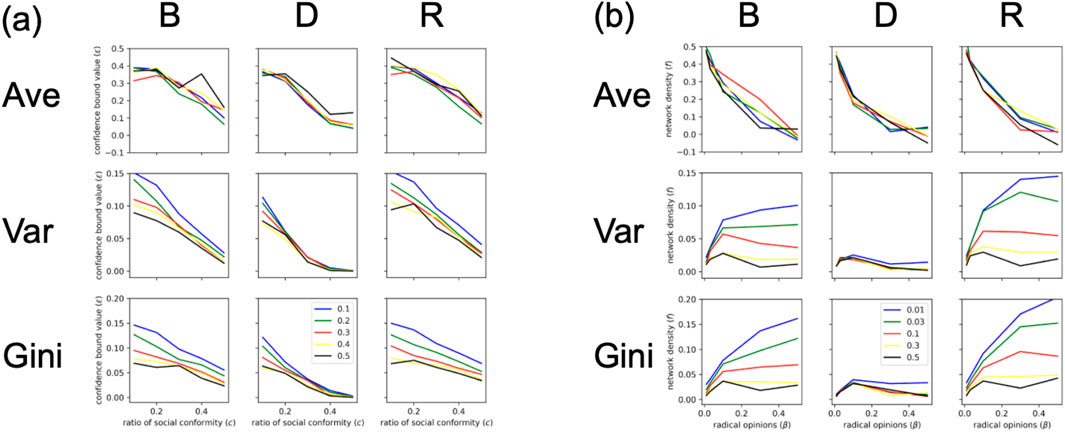
Figure 5. Line Graphs of Changes in Population’s Opinions The line graphs illustrate the changes in the average, variance and Gini coefficient of the population’s opinions. Left: Fermi-Birth mode, Middle: Fermi-Death mode, Right: Random-out-random-in mode. The vertical axis in both figures represents the average opinion (Top), opinion variance (Middle), and Gini coefficient (Bottom). (a) The horizontal axis represents the ratio of social conformity to peer pressure $(c)$ influences acting on agents, while the color indicates different values of the confidence bound $(ϵ)$. (b) The horizontal axis represents the proportion of agents with radical opinions $(\beta )$, with color representing network density defined as the proportion of friends that each agent has. These simulation results offer an analysis from four perspectives 1. Overall tendencies across modes: Across all modes, the overall trends in the average, variance, and Gini coefficient (whether they increase, decrease, or remain stable) are consistent when adjusting each parameter. 2. Differences across modes: The Fermi-Birth and Random-out-random-in modes show more significant variations than the Fermi-Death mode. 3. Influence of Parameters: Changes in the ratio of social conformity, the proportion of friends (network density), and the proportion of radical agents impact the population’s opinions more than the confidence bound. 4. Sensitivity of Measures: The variance and Gini coefficient are more sensitive to changes in parameter values than the average opinion. In other words, while the average opinion can remain stable, both the variance and Gini coefficient can fluctuate considerably.

Figure 6

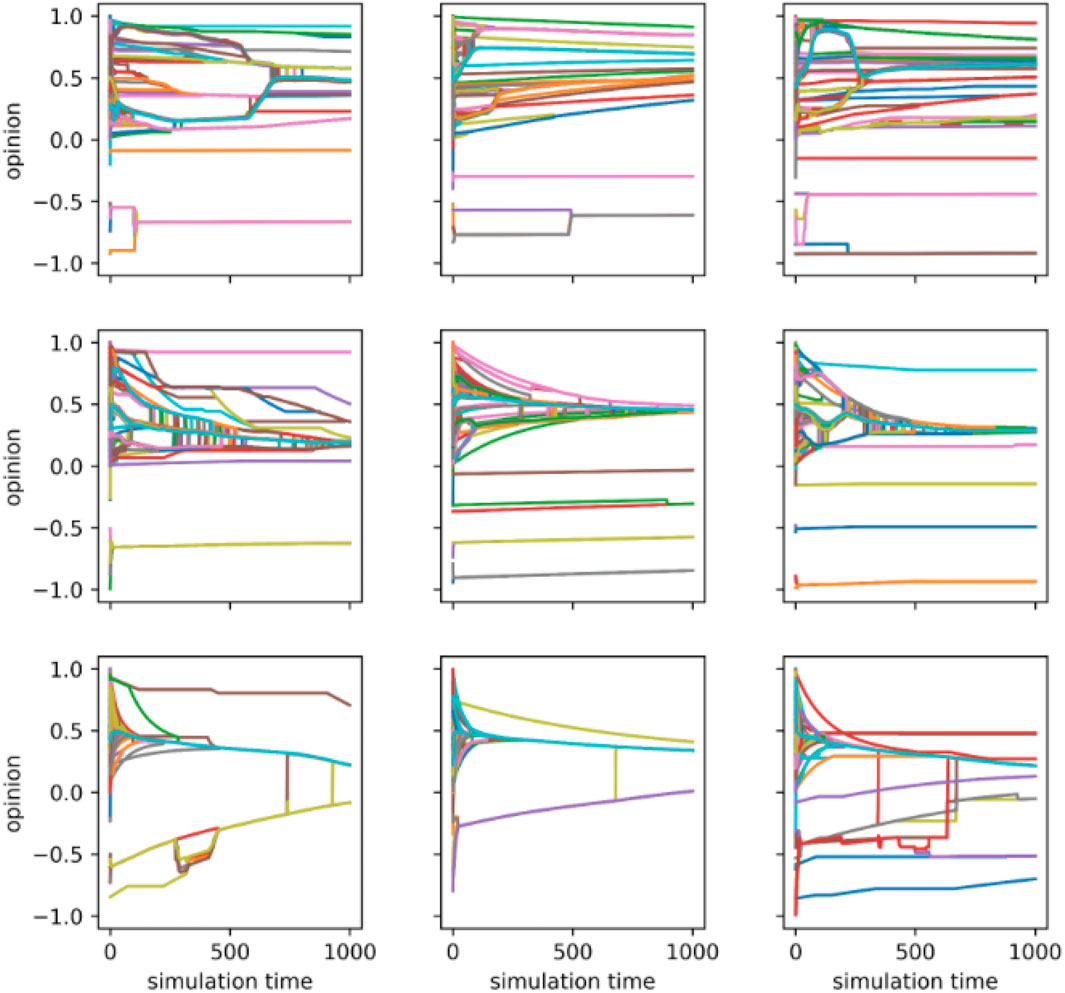
Figure 6. Opinion Dynamics with Varying Ratios of Social Conformity to Peer Pressure influences Each panel represents the time series of the opinions for all agents over a simulation with a population size of $N=1000$ and $T=1000$ time steps. Left: Fermi-Birth mode, Middle: Fermi-Death mode, Right: Random-out-random-in mode. The ratios of social conformity to peer pressure, $c$, are set as follows: 0.001 (Top), 0.01 (Middle), and 0.1 (Bottom). Other parameters are set to $(ϵ,f,\beta )=(0.5,0.3,0.01)$. An increase in the ratio of social conformity $c$ accelerates the shift of radical agents towards less radical opinions while simultaneously pushing non-radical agents toward more radical opinions. This dynamic results in a faster convergence of opinions within the population as $c$ increases. In other words, a higher $c$ leads non-radical agents to become more influenced by radical agents, facilitating overall convergence.

Figure 7

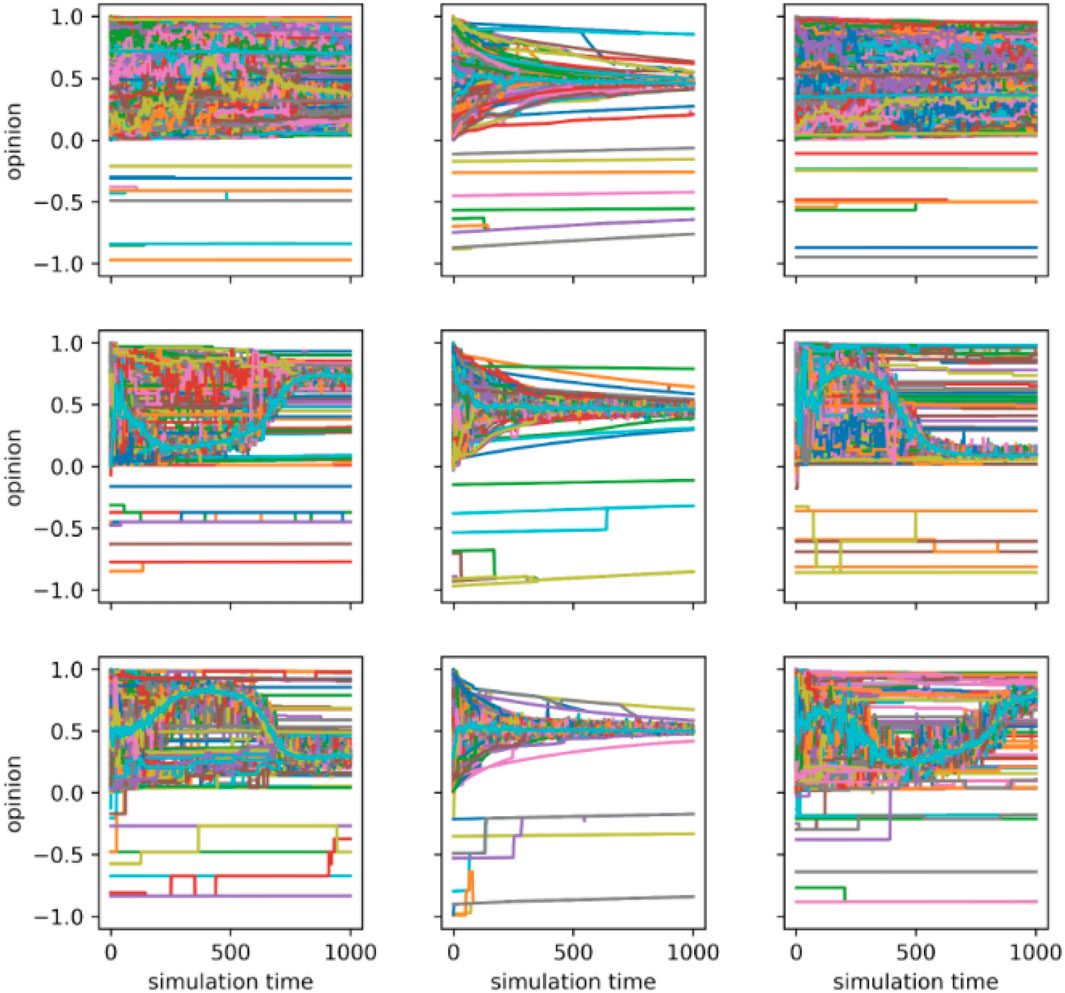
Figure 7. Opinion Dynamics with Different Confidence Bound Values Each panel illustrates the time series of opinions for all agents over a simulation with a population size of $N=1000$ and $T=1000$ time steps. Left: Fermi-birth mode, Middle: Fermi-death mode, Right: Random-out-random-in mode. The confidence bound value, $ϵ$, is set to 0.1 (Top), 0.3 (Middle), 0.5 (Bottom). Other parameters are set to $(c,f,\beta )$ = (0.01,0.003,0.01). As the confidence bound value increases, agents with similar opinions tend to form clusters more rapidly. These clusters can merge into large ones, leading to more agents aligning their opinions within the same cluster than in scenarios with lower $ϵ$. However, not all agents join these clusters; some may choose to maintain their individual opinions. This divergence can hinder overall convergence and result in fragmentation within the population. Moreover, a higher confidence bound value accelerates the rate at which agents adjust their opinions. Thus, increasing the confidence bound impacts both the dynamics of cluster formation and the speed of changing opinion dynamics.

Figure 8

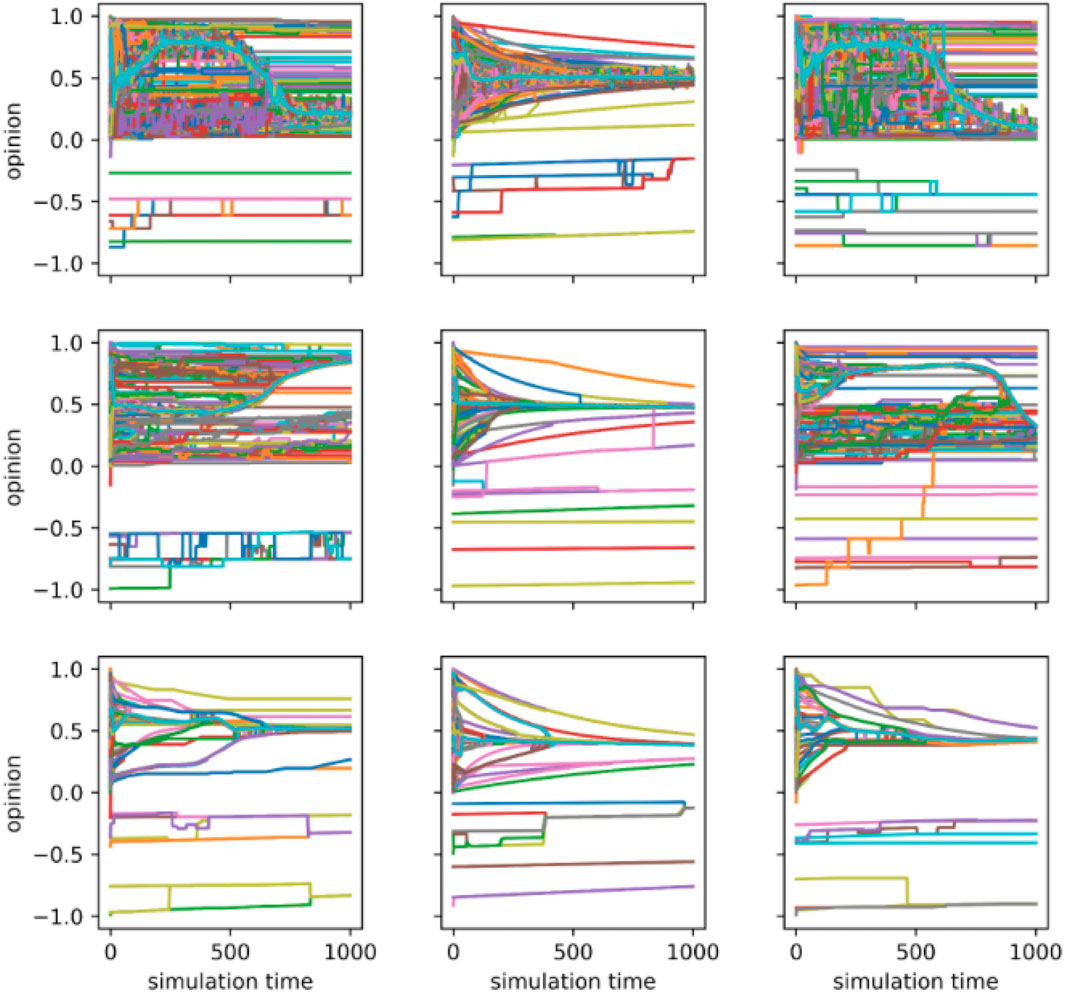
Figure 8. Opinion dynamics with different proportions of friends within a population that each agent has in three modes Opinion dynamics with different proportions of friends within a population that each agent has across three modes. Each panel displays the time series of opinions for all agents over a simulation with a population size of $N=1000$ and $T=1000$ time steps. Left: Fermi-Birth mode, Middle: Fermi-Death mode, and Right: Random-out-random-in mode. The proportion of friends that each agents has, $f$, is set to 0.003 (Top), 0.03 (Middle), and 0.3 (Bottom). Other parameters are held constant at $(c,ϵ,\beta )$ = (0.01,0.3,0.01). Increasing the proportion of friends significantly influences consensus formation. Although higher friend proportions do not create notable patterns in the average opinion of the population, they do affect the distribution of opinions. When the proportion of friends each agent has increases, agents are more inclined to cluster together. Even agents with radical opinions tend to converge, whether by shifting toward more neutral opinions or aligning with others holding similar radical opinions. In contrast, when friend proportions are lower, opinion fragmentation is more likely to occur, with agents maintaining a range of divergent opinions. However, as friend proportions rise, convergence becomes more feasible, leading agents to increasingly share similar opinions. In addition, increased friend proportions accelerate the pace at which agents adjust their opinions, producing more rapid shifts in opinion dynamics.

3.1 The overview of simulation results

First, we briefly present an overview of the simulation results. The parameter spaces are defined as follows: $c\in [0.001,0.003,0.01,0.03,0.1]$, $ϵ\in [0.1,0.2,0.3,0.4,0.5]$, $f\in [0.003,0.01,0.03,0.1,0.3]$, and $\beta \in [0.01,0.03,0.1,0.3,0.5]$. Overall, according to both the heat maps (Figure 3) and box plots (Figure 4), the Fermi-Birth and Random-out-random-in modes produce relatively similar simulation results, while the Fermi-Death mode leads to different outcomes. In the Fermi-Death mode, the population tends to converge. In contrast, the Fermi-Birth and Random-out-random-in modes result in varying opinion distributions, depending on the parameter settings. These trends remain consistent across all three modes. However, changes in the four parameters more significantly affect the population’s opinions in the Fermi-Birth and Random-out-random-in modes than in the Fermi-Death mode. Specifically, the range of changes in the average opinion, opinion variance, and Gini coefficient is smaller in the Fermi-Death mode, which also shows a narrower spread of opinions than the other two modes.

Regardless of the friend set updating mode, simulating the four parameters reveals some consistent patterns. Increasing $c$ reduces the average, variance, and Gini coefficient of the population’s opinions. Although $ϵ$ shows no clear effect on the average, it decreases both the variance and the Gini coefficient. An increase in the parameter $f$ causes either a slight decrease or stabilization in the average and reduces variance, but it increases the Gini coefficient. Lastly, $\beta$ significantly lowers both the average and Gini coefficient, while slightly increasing variance (Table 3; Figure 3).

Table 3

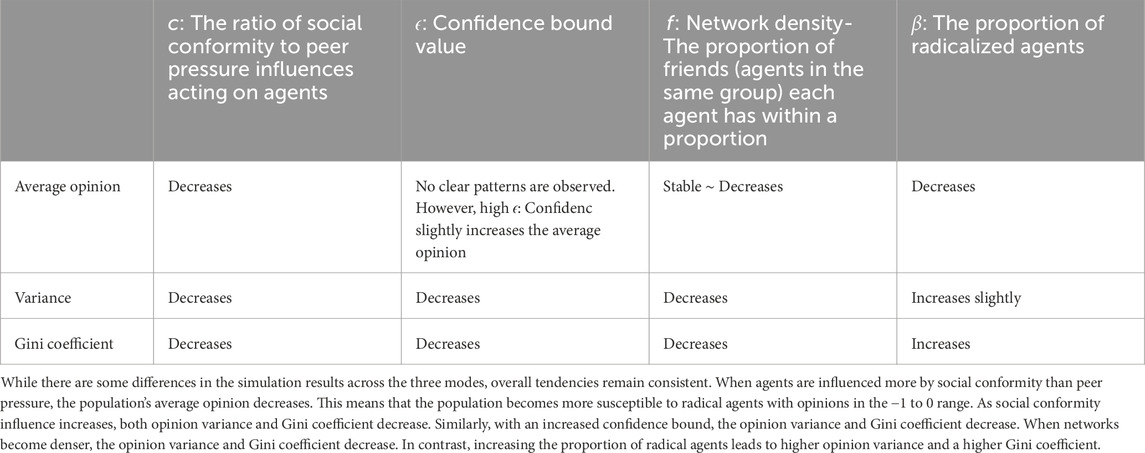
Table 3. Summary of the simulation results in the average, variance, and Gini coefficient of the population’s opinions across different parameters This table summarizes the effects of increasing each parameter on the population’s average opinion, the opinion variance, and Gini coefficient.

3.2 Comparison of opinion dynamics among three network modes

From the heat maps and box plots, all three modes show similar overall trends in the average, variance, and Gini coefficient of the population’s opinions as the values of the four parameters change (Table 3; Figure 3). Despite these overall similarities, the opinion distributions in the Fermi-Birth and Random-out-random-in modes are more sensitive to changes in the four parameters. The values for average, variance, and Gini coefficient of opinions in these two modes tend to increase or decrease more significantly with changes in the four parameters. In contrast, the average, variance, and Gini coefficient in the Fermi-Death mode exhibit smaller fluctuations when each parameter changes. Similarly, the range of the average, variance, and Gini coefficient is larger in the Fermi-Birth and Random-out-random-in modes while the Fermi-Death exhibits a smaller range of these metrics, which indicates that the population’s opinions are distributed more narrowly. The time series of opinion distributions reveals different features across different parameters and different modes (Figures 4–7). One notable observation is that the Fermi-Death mode tends to lead to opinion convergence. In contrast, the Fermi-Birth and Random-out-random-in modes display relatively similar dynamics, with wider opinion distributions that can result in outcomes such as consensus, polarization, or fragmentation. In addition, agents in the Fermi-Death mode change their opinions more rapidly than those in the Fermi-Birth and Random-out-random-in modes. A second observation concerns the behavior of agents with radical opinions, which differs between the Fermi-Birth and Random-out-random-in modes and the Fermi-Death mode. In the Fermi-Death mode, agents holding radical opinions are more likely to shift toward the majority opinion. In contrast, in the Fermi-Birth and Random-out-random-in modes, these agents tend to retain their initial opinions. When they do shift, they move more gradually toward neutral opinions than agents in the Fermi-Death mode. Third, in some cases, particularly in the Fermi-Birth and Random-out-random-in modes, radical opinion shifts are observed. In these instances, clusters of agents holding similar opinions form a majority, leading to a drastic opinion shift under certain parameter conditions (Figures 7–9). The fluctuation range of opinions hovers around 0.5. Note that this phenomenon occurs only in the Fermi-Birth and Random-out-random-in modes and not in the Fermi-Death mode.

Figure 9

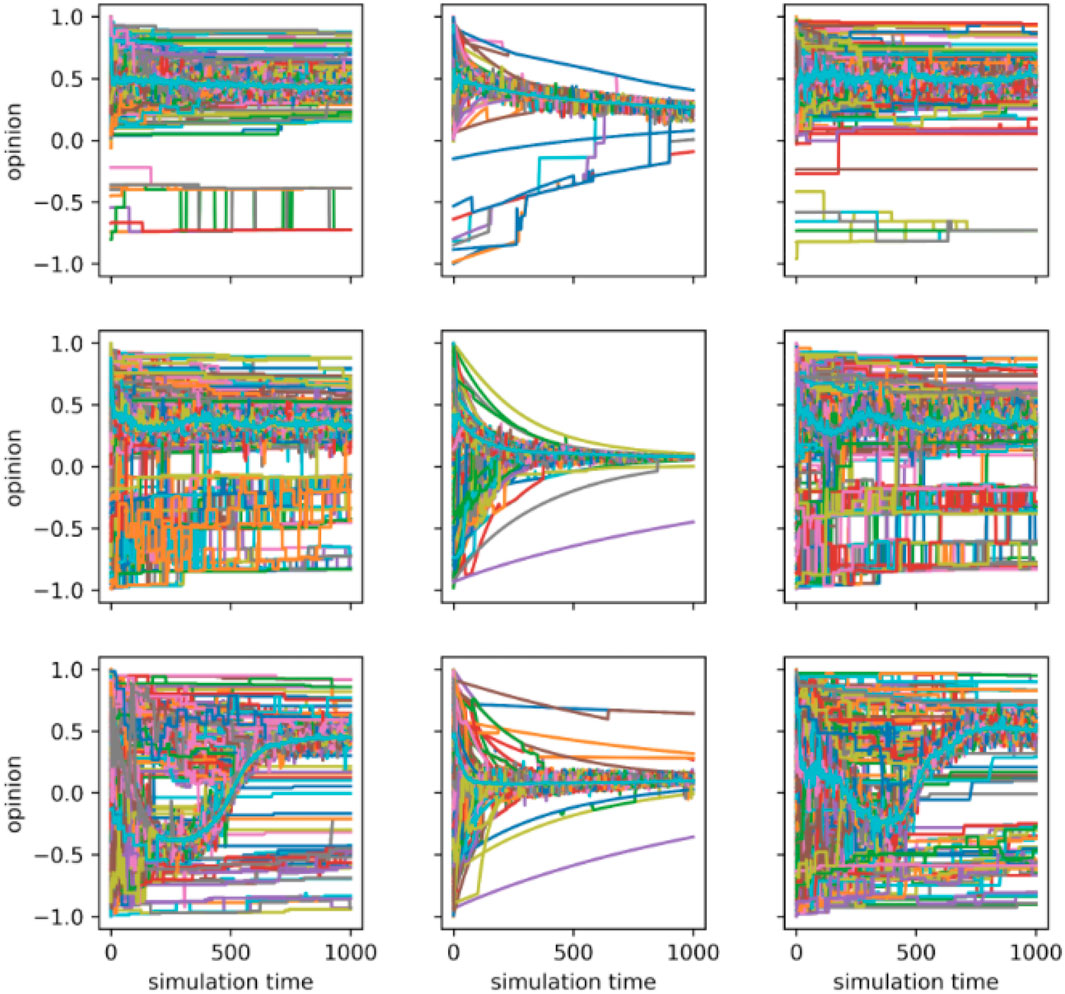
Figure 9. Opinion dynamics with different proportions of agents with radical opinions in three modes Opinion dynamics with different proportions of agents with radical opinions across three modes. Each panel presents the time series of opinions for all agents over a simulation with a population size $N=1000$ and $T=1000$ time steps. Left: Fermi-birth mode, Middle: Fermi-death mode, and Right: Random-out-random-in mode. The proportion of agents with radical opinions is set to 0.01 (Top), 0.1 (Middle), and 0.3 (Bottom). Other parameters are fixed at $(c,ϵ,f)$ = (0.1,0.5,0.003). As the proportion of radical agents increases, some non-radical agents tend to adopt more radical positions, while certain radical agents shift toward less radical views. This bidirectional adjustment increases the likelihood of convergence within the population. In addition, when the initial proportion of radical agents is higher, these shifts occur more rapidly. Despite this increased likelihood of convergence, higher proportions of radical agents can also lead to polarization or fragmentation. The opinion distribution becomes sparser as not all agents merge into a single cluster. This polarization creates distinct clusters of radical and non-radical agents. This polarization may hinder population convergence. In contrast, when the proportion of radical agents is low, they tend to remain isolated from the larger group of non-radical agents, resulting in fewer interactions and less influence between these groups.

In summary, the Fermi-Birth and Random-out-random-in modes generate diverse opinion distribution patterns, including consensus, polarization, and fragmentation, depending on parameter conditions. In contrast, the Fermi-Death mode generally leads to convergence. Another key difference lies in the behavior of radical agents: in the Fermi-Birth and Random-out-random-in modes, radical agents generally retain their opinions, whereas, in the Fermi-Death mode, they are more likely to shift toward the majority. Furthermore, radical opinion shifts are observed in the Fermi-Birth and Random-out-random-in modes, a phenomenon not seen in the Fermi-Death mode. These differences in simulation outcomes may be attributed to mechanisms by which agents are removed from their immediate friend sets. Counterintuitively, it is the removal of agents, rather than the addition of new ones, that plays a more significant role in shaping opinion dynamics.

3.3 Comparison of four key parameters

Next, we will examine the effects of the four parameters on opinion dynamics each by each.

First, we focus on $c$, which represents the ratio of social conformity to peer pressure influences acting on agents. As shown in Figure 5, an increase in $c$ accelerates the shift of radical agents towards less radical opinions and the shift of non-radical agents towards more radical opinions, leading to quicker convergence within the population than at lower values of $c$. In other words, a higher $c$ not only facilitates convergence but also achieves it in a shorter time.

Second, we consider $ϵ$, which represents the tolerance of agents towards different opinions. Figure 6 shows that when $ϵ$ is high, agents with similar opinions tend to form clusters that merge into larger ones. This results in more agents belonging to the same cluster than when $ϵ$ is low. However, in certain cases, not all agents join these clusters but rather keep their opinions, which impedes overall convergence and results in fragmentation. Beyond its effect on opinion distributions, a higher $ϵ$ causes agents to change their opinions more rapidly, allowing to reach a stable configuration in less time.

Third, we examine $f$, which represents the proportion of friends each agent has within the population, reflecting interaction density among agents. As illustrated in Figure 7, a higher $f$ value significantly accelerates changes in opinion dynamics and facilitates cluster formation. When $f$ is low, the population’s opinions are likely to fragment. However, increasing $f$ can foster greater convergence. Furthermore, at higher values of $f$, radical agents tend to shift towards less extreme opinions, potentially leading to convergence around extreme or less extreme opinions.

Finally, we consider $\beta$, which represents the proportion of agents with radical opinions. As $\beta$ increases, some non-radical agents become more radical while some radical agents become less radical. However, as not all agents agglomerate to one cluster, leading to a more sparse opinion distribution, which causes polarization or fragmentation between radical and non-radical agents (Figure 8). In contrast, a smaller $\beta$ tends to isolate radical agents from the majority of non-radical agents.

3.4 Characteristics of specific parameters

An intriguing pattern emerges beyond the findings discussed above: under certain parameter conditions, a subset of agents undergoes radical opinion shifts, as shown in Figures 6–8. These shifts are unique to the Fermi-Birth and Random-out-random-in modes and do not occur in Fermi-Death mode. This phenomenon is particularly pronounced when the value of $f$ is low and $ϵ$ is high. In addition, a small value of $c$ or a high value of $\beta$ appears to further increase the likelihood of these shifts. Conversely, when $f$ is sufficiently large or $ϵ$ is sufficiently low, these radical opinion changes do not occur.

While we have observed these opinion shifts to be more frequent under parameter settings in the Fermi-Birth and Random-out-random-in modes, no clear pattern has been identified regarding the movement or direction of these shifts. As agents begin to cluster, they experience rapid and radical opinion changes, incorporating other agents in the process. However, the trajectory of these radical opinion shifts remains unpredictable.

4 Discussion and conclusion

Driven by an interest in how social conformity and peer pressure shape society, we developed an opinion dynamics model to capture individuals’ susceptibility to both influences. In our model, we assume that social conformity represents a macroscopic influence, where individuals are swayed by the population at large, while peer pressure represents a microscopic influence, where individuals are affected by their immediate contacts such as friends. Thus, each agent is influenced by both social conformity and peer pressure in this model.

Our model builds upon the HK model, which assumes agents update their opinions on the basis of confidence bounds. We introduce three additional parameters to modify opinion-updating rules: (i) the ratio of social conformity to peer pressure influences acting on individuals, (ii) the proportion of friends each agent has within a population, and (iii) the proportion of agents with radical opinions. In our model, individual opinions are represented on a continuous scale from $-1$ to 1, with agents holding opinions in the range from $-1$ to 0 classified as radical and those holding opinions from 0 to 1 classified as non-radical.

Beyond exploring how agents update their opinions on the basis of these parameters, we set up “friend sets” to simulate the peer pressure influence from immediate social circles. Friend sets represent a social circle where a fixed number of agents is connected through links, which update at each time step. This allows agents to enter and leave friend sets dynamically. To observe how different types of agents influence opinion dynamics, we implemented three modes of friend set updates: Fermi-Birth, Fermi-Death, and Random-out-random-in modes. An overview of each mode, along with its simulation results, key insights, and real-world examples, is presented in Table 4.

Table 4

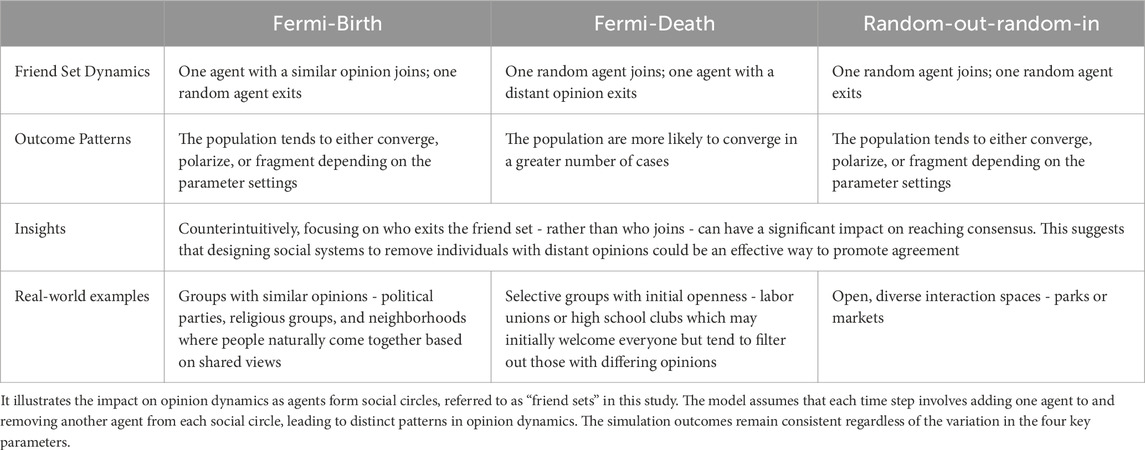
Table 4. Overview and insights of simulation results of three modes This table provides an overview of the simulation results across three modes.

In the Fermi-Birth mode, one agent with a similar opinion joins the friend set, while a random agent leaves. This may foster environments where like-minded individuals form groups with similar opinions. Examples of such real-world scenarios might include political parties, religious congregations, and urban communities, where people naturally gather around shared views. The Fermi-Death mode, in contrast, accepts any agent into a friend set but removes those with the most divergent opinions. This scenario may resemble labor unions or school clubs, which may initially welcome all individuals but gradually filter out those with contrasting viewpoints over time. Lastly, the Random-out-random-in mode simulates an environment where agents are randomly added or removed, regardless of opinion. This may reflect situations where social interactions occur more spontaneously and are not strongly influenced by shared opinions, such as parks, markets, or other public spaces where people of diverse perspectives interact without selection criteria based on viewpoints.

Simulation results show that populations in Fermi-Death modes tend to converge, while those in Fermi-Birth and Random-out-random-in modes either converge, polarize, or fragment depending on the parameter settings. This outcome may be attributed to radical agents being more likely to maintain their opinions in Fermi-Birth and Random-out-random-in modes but more likely to conform to the majority in Fermi-Death mode. These phenomena can be explained by the underlying process of deciding who to include or exclude within a group of friends. Intuitively, as in Fermi-Birth mode, individuals with similar opinions are welcomed, reinforcing shared views, which may create close-knit groups of like-minded individuals. In the Fermi-Death mode, as agents with differing opinions of the groups are excluded, agents may form groups of relatively similar opinions. In the Random-out-random-in mode, as agents with any opinions come and exit, agents may foster more diverse groups.

Furthermore, the simulation of opinion dynamics in Fermi-Birth and Random-out-random-in modes are more sensitive to parameter variations, whereas the Fermi-Death mode tends to converge in a greater number of cases. This suggests that the decision of whom to remove from a friend set may be critical in attaining population convergence. In other words, counterintuitively, it may be more effective to focus on excluding individuals from the friend set rather than determining whom to include. When designing social systems to achieve consensus, it could be beneficial to create mechanisms that facilitate the removal of individuals with distant opinions.

In exploring the parameters, Table 5 summarizes the characteristics of each, along with their simulation results, key insights, and real-world examples.

Table 5

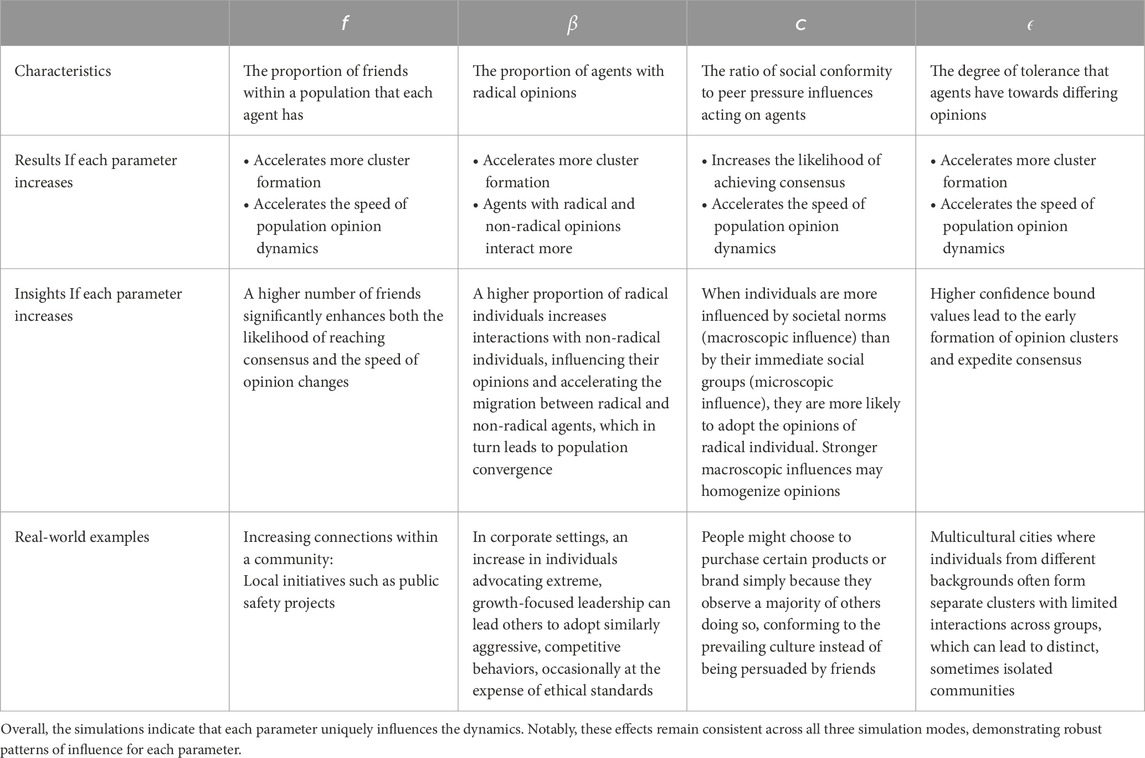
Table 5. Overview and insights of simulation results of four parameters The table provides an overview of the simulation results, highlighting the effects of increasing each parameter on opinion dynamics.

This study demonstrates that opinion dynamics are profoundly influenced by the number of friends and the presence of radical individuals. Our model introduced a variable representing the number of friends that each individual interacts with. The simulation results show that a higher number of friends significantly enhances both the likelihood of convergence and the speed of opinion changes. In real-world contexts, increasing connections within a community, such as local projects like public safety, may help members find common ground. Personal bonds may encourage people to align on priorities and cooperate on initiatives, reducing disagreements and driving the group toward consensus [42, 43].

Regarding radical individuals, our simulation reveals that the presence of individuals with radical opinions plays a crucial role in opinion dynamics. In cases where there is a small proportion of radical individuals, as described by the opinion update process in the HK model, they tend not to interact with non-radical individuals and maintain their radical opinions. However, a higher proportion of radical individuals increases interactions with non-radical individuals, influencing their opinions and accelerating the migration between radical and non-radical agents, which in turn leads to population convergence. For instance, in corporate settings, an increase in radical individuals who emphasize extreme growth-oriented leadership may influence others to adopt similar competitive behaviors, sometimes at the expense of ethical considerations. Conversely, a cult group with a small number of extreme adherents may not significantly impact the broader population.

The ratio of social conformity to peer pressure also affects the overall convergence of opinions. Our model shows that when individuals are more influenced by societal norms (macroscopic influence) than by their immediate social groups (microscopic influence), they are more likely to adopt the opinions of radical individuals. Macroscopic influence refers to societal forces (social conformity), while microscopic influence comes from an individual’s close social circle (peer pressure), such as friend groups, family, or coworkers. As the ratio of social conformity increases, opinion differences across the population decrease, reducing both variance and the Gini coefficient of the opinions. This suggests that stronger macroscopic influences tend to homogenize opinions. In real-world scenarios, such as the filter bubble effect on social media, individuals may perceive their environments as the norm, which can reinforce specific ideologies and make them susceptible to extreme views or misinformation.

Confidence bound values, representing an individual’s tolerance toward differing opinions, also play a role in opinion dynamics [23, 26, 27]. Our simulation results show that higher confidence bound values lead to the early formation of opinion clusters and expedite consensus. This may be observed in multicultural cities where people with differing viewpoints form distinct clusters, with limited interaction between different groups.

For unique opinion dynamics, our simulations identify cases where some agents shift toward less popular opinions in Fermi-Birth and Random-out-random-in modes. This radical opinion shift may be linked to the variance and Gini coefficient, especially when comparing these modes with Fermi-Death. Such phenomena are particularly evident when confidence bounds are high, the number of friends is small, the ratio of social conformity is low, or radical agents are fewer. The timing and dynamics of this shift are unpredictable, but similar events occur in real life. For example, controversial science-related issues can lead to the spread of misinformation, causing the majority to adopt false beliefs [8, 44, 45]. This indicates that the number of social connections an individual has may be a crucial factor in shaping opinion dynamics. Insights from related research illuminate how network density and structure influences these dynamics, shedding light on the mechanisms of collective behavior [46, 47].

While this study on opinion dynamics has developed a theoretical model to explore how individual interactions and factors such as friend set updating modes and exclusive interactions among agents drive the societal consensus via social conformity and peer pressure. The next challenge in applying it to real-world scenarios lies in identifying the appropriate data to represent each parameter [48]. We believe this can be achieved by incorporating insights from related fields such as social sciences and data science to better represent reality through modeling and simulations.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

KS: Conceptualization, Formal Analysis, Investigation, Methodology, Project administration, Validation, Visualization, Writing–original draft, Writing–review and editing. IO: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by JSPS KAKENHI Grant Numbers JP21KK0027, JP23K21017, and JP23K25160.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. The authors used generative AI to assist in drafting the document; however, the final text was written by the authors themselves.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Castells M. Communication power. Oxford University Press (2009). p. 624.

Google Scholar

2. Pariser E. The filter bubble: how the new personalized web is changing what we read and how we think. Penguin Press (2011). p. 304.

Google Scholar

3. Sunstein CR. Republic: divided democracy in the age of social media. Princeton University Press (2017). p. 328. doi:10.1515/9781400884711

CrossRef Full Text | Google Scholar

4. McPherson M, Smith-Lovin L, Cook JM. Birds of a feather: homophily in social networks. Annu Rev Sociol (2001) 27:415–44. doi:10.1146/annurev.soc.27.1.415

CrossRef Full Text | Google Scholar

5. Gilbert E, Bergstrom T, Karahalios K. Blogs are echo chambers: blogs are echochambers. In: 2009 42nd Hawaii International Conference on System Sciences; 2009 05–08 Jan; Waikoloa, HI. IEEE (2009). p. 1–10. doi:10.1109/HICSS.2009.91

CrossRef Full Text | Google Scholar

6. Baront RS, Hoppet SI, Kaot CF, Brunsmant B, Linneweht B, Rogerst D. Social corroboration and opinion extremity. J Exp Soc Psychol (1996) 32:537–60. doi:10.1006/jesp.1996.0024

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Benkler Y, Robert F, Roberts H. Network propaganda: manipulation, disinformation, and radicalization in American politics. Oxford University Press (2018).

Google Scholar

8. Vosough S, Roy D, Aral S. The spread of true and false news online. Science (2018) 359:1146–51. doi:10.1126/science.aap9559

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Bakshy E, Messing S, Adamic LA. Exposure to ideologically diverse news and opinion on Facebook. Science (2015) 348:1130–2. doi:10.1126/science.aaa1160

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Asch SE. Effects of group pressure upon the modification and distortion of judgments. Carnegie Press (1951). p. 177–90.

Google Scholar

11. Bikhchandani S, Hirshleifer D, Welch I. A theory of fads, fashion, custom, and cultural change as informational cascades. J Polit Economy (1992) 100:992–1026. doi:10.1086/261849

CrossRef Full Text | Google Scholar

12. Festinger L. A theory of social comparison processes. Hum Relations (1954) 7:117–40. doi:10.1177/001872675400700202

CrossRef Full Text | Google Scholar

13. Cialdini RB, Goldstein NJ. Social influence: compliance and conformity. Annu Rev Psychol (2004) 55:591–621. doi:10.1146/annurev.psych.55.090902.142015

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Deutsch M, Gerard HB. A study of normative and informational social influences upon individual judgment. J Abnormal Soc Psychol (1955) 51:629–36. doi:10.1037/h0046408

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Asch SE. Opinions and social pressure. Scientific Am (1955) 193:31–5. doi:10.1038/scientificamerican1155-31

CrossRef Full Text | Google Scholar

16. Sherif M. The psychology of social norms. Harper (1936).

Google Scholar

17. Nowak A, Szamrej J, Latané B. From private attitude to public opinion: a dynamic theory of social impact. Psychol Rev (1990) 97:362–76. doi:10.1037/0033-295X.97.3.362

CrossRef Full Text | Google Scholar

18. Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev Mod Phys (2009) 81:591–646. doi:10.1103/revmodphys.81.591

CrossRef Full Text | Google Scholar

19. Moussaïd M, Kämmer JE, Analytis PP, Neth H. Social influence and the collective dynamics of opinion formation. PLoS One (2013) 8:e78433. doi:10.1371/journal.pone.0078433

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Acemoğlu D, Como G, Fagnani F, Ozdaglar A. Opinion fluctuations and disagreement in social networks. Mathematics Operations Res (2012) 38:1–27. doi:10.1287/moor.1120.0570

CrossRef Full Text | Google Scholar

21. Axelrod R. The dissemination of culture: a model with local convergence and global polarization. J Conflict Resolution (1997) 41:203–26. doi:10.1177/0022002797041002001

CrossRef Full Text | Google Scholar

22. Epstein JM. Generative social science: studies in agent-based computational modeling. Princeton University Press (2006). p. 352.

Google Scholar

23. Deffuant G, Neau D, Amblard F, Weisbuch G. Mixing beliefs among interacting agents. Adv Complex Syst (2000) 3:87–98. doi:10.1142/S0219525900000078

CrossRef Full Text | Google Scholar

24. Franco B, Timoteo C, Duccio F, Alessio G, Andrea G. Dynamical affinity in opinion dynamics modeling. Phys Rev E (2007) 76:066105. doi:10.1103/PhysRevE.76.066105

CrossRef Full Text | Google Scholar

25. DeGroot MH. Reaching a consensus. J Am Stat Assoc (1974) 69:118–21. doi:10.2307/2285509

CrossRef Full Text | Google Scholar

26. Rainer H, Krause U. Opinion dynamics and bounded confidence models, analysis and simulation. J Artif Societies Soc Simulation (2002) 5.

Google Scholar

27. Lorenz J. Continuous opinion dynamics under bounded confidence: a survey. Int J Mod Phys C (2007) 18:1819–38. doi:10.1142/s0129183107011789

CrossRef Full Text | Google Scholar

28. Centola D. The spread of behavior in an online social network experiment. Science (2010) 329:1194–7. doi:10.1126/science.1185231

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Flache A, Macy MW. Small worlds and cultural polarization. J Math Sociol (2011) 35:146–76. doi:10.1080/0022250X.2010.532261

CrossRef Full Text | Google Scholar

30. Bernardo C, Altafini C, Proskurnikov A, Vasca F. Bounded confidence opinion dynamics: a survey. Automatica (2024) 159:111302. doi:10.1016/j.automatica.2023.111302

CrossRef Full Text | Google Scholar

31. Holme P, Newman MEJ. Nonequilibrium phase transition in the coevolution of networks and opinions. Phys Rev E (2006) 74:056108. doi:10.1103/PhysRevE.74.056108

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Javarone MA. Social influences in opinion dynamics: the role of conformity. Physica A: Stat Mech its Appl (2014) 414:19–30. doi:10.1016/j.physa.2014.07.018

CrossRef Full Text | Google Scholar

33. Das A, Gollapudi S, Khan S, Paes Leme R. Role of conformity in opinion dynamics in social networks. In: Proceedings of the Second ACM Conference on Online Social Networks (ACM) (2014). p. 25–36. doi:10.1145/2660460.2660479

CrossRef Full Text | Google Scholar

34. Stepień S, Jankowski J, Bródka P, Michalski R. The role of conformity in opinion dynamics modelling with multiple social circles. Comput Sci – ICCS 2023 (2023) 14075:30–42. doi:10.48550/arXiv.2403.04480

CrossRef Full Text | Google Scholar

35. Liu L, Wang X, Tang S, Zhen Z, Zheng Z. Modeling confirmation bias and peer pressure in opinion dynamics. Front Phys (2021) 9. doi:10.3389/fphy.2021.649852

CrossRef Full Text | Google Scholar

36. Deffuant G, Huet S, Amblard F. An individual-based model of innovation diffusion mixing social value and individual benefit. Am J Sociol (2005) 110:1041–69. doi:10.1086/430220

CrossRef Full Text | Google Scholar

37. Borum R. Radicalization into violent extremism i: a review of social science theories. J Strateg Security (2011) 4:7–36. doi:10.5038/1944-0472.4.4.1

CrossRef Full Text | Google Scholar

38. Deffuant G, Amblard F, Weisbuch G. Modelling group opinion shift to extreme: the smooth bounded confidence model. arXiv: Other Condensed Matter (2004).

Google Scholar

39. Deffuant G, Amblard F, Weisbuch G, Faure T. How can extremism prevail? a study based on the relative agreement interaction model. J Artif Societies Soc Simulation (2002) 5.

Google Scholar

40. Guazzini A, Cini A, Bagnoli F, Ramasco JJ. Opinion dynamics within a virtual small group: the stubbornness effect. Front Phys (2015) 3. doi:10.3389/fphy.2015.00065

CrossRef Full Text | Google Scholar

41. Festinger L. A theory of cognitive dissonance. Stanford University Press (1957).

Google Scholar

42. Granovetter MS. The strength of weak ties. Am J Sociol (1973) 78:1360–80. doi:10.1086/225469

CrossRef Full Text | Google Scholar

43. Putnam RD. Bowling alone: the collapse and revival of American community. Simon and Schuster (2000). doi:10.1145/358916.361990

CrossRef Full Text | Google Scholar

44. Scheufele DA, Krause NM. Science audiences, misinformation, and fake news. Proc Natl Acad Sci USA (2019) 116:7662–9. doi:10.1073/pnas.1805871115

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Bode L, Vraga EK. See something, say something: correction of global health misinformation on social media. Health Commun (2018) 33:1131–40. doi:10.1080/10410236.2017.1331312

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Centola D, González-Avella JC, Eguíluz VM, Miguel MS. Homophily, cultural drift, and the co-evolution of cultural groups. J Conflict Resolution (2007) 51:905–29. doi:10.1177/0022002707307632

CrossRef Full Text | Google Scholar

47. Lee E, Karimi F, Wagner C, Hang-Hyun J, Strohmaier M, Galesic M. Homophily and minority-group size explain perception biases in social networks. Nat Hum Behav (2019) 3:1078–87. doi:10.1038/s41562-019-0677-4

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Sobkowicz P. Modelling opinion formation with physics tools: call for closer link with reality. J Artif Societies Soc Simulation (2009) 12.

Google Scholar