The influence of bank-firm loan network structure on systemic risk: from the perspective of complex networks

The structure of the bank-firm loan network is crucial for understanding the transmission of systemic risk within the banking system. Drawing on complex network theory, this study analyzes loan data from 370 Chinese commercial banks spanning January 2013 to December 2023 to construct a syndicated loan network, wherein different banks lend to the same enterprise. This analysis reveals how the structure of this network influences systemic risk in the banking sector across various periods. Our findings indicate that, in the long term, network density and centralization significantly mitigate systemic risk, whereas transitivity and average clustering coefficients have a positive effect on systemic risk. In the short term, the network demonstrates strong mean-reverting properties. Additionally, we observe a noteworthy phenomenon: the bank-firm loan relationships exhibit a ‘core-periphery’ hierarchical structure, characterized by a network that is both robust and fragile. These insights offer a novel perspective on the relationship between bank network structures and systemic risk, contributing to the interdisciplinary application of physics in economic and financial studies.

1 Introduction

Banks play a crucial role in the financial systems and economic growth of countries [1]. As the primary intermediaries of capital flows, banks not only provide essential financing support to the real economy but also significantly promote the growth of social financing. From March 2015 to March 2024, the renminbi loans extended by Chinese financial institutions to the real economy increased from 85.09 trillion yuan to 244.59 trillion yuan, representing an average of 61.5% of the total social financing scale. This trend indicates that the real economy is highly reliant on bank loans for financing [2, 3], particularly large enterprises that utilize bank financing to sustain their operations and expand, thereby underscoring the indispensable role of banks in economic development.

Bank loans are an essential corporate financing tool in contemporary financial markets. They not only address the substantial financing needs of enterprises but also facilitate the efficient allocation of financial resources, thereby serving as a crucial pillar for economic growth. However, with the rapid advancement of financial markets and the deepening of financial innovation, bank loans have transformed from simple credit transactions into a complex network of bank-firm loans [4]. This networked characteristic has not only improved financing efficiency but also introduced new challenges: the high interconnectedness among banks, as well as between banks and enterprises, may result in the swift transmission and accumulation of risks within the network, potentially jeopardizing the stability of the financial system [5].

Despite this, traditional financial regulation often prioritizes the risk status of individual commercial banks, neglecting the influence of interbank interconnectedness on systemic risk. This oversight was starkly illustrated during the 2008 global financial crisis, which revealed that the intricate network relationships among banks could intensify risk transmission and increase the likelihood of systemic collapse [6]. In recent years, chain reactions initiated by problems within individual banks—such as the successive failures of Silicon Valley Bank, Signature Bank, and First Republic Bank—have further underscored the necessity of addressing systemic risk within the banking system [7]. When a single bank within the system encounters difficulties, these complex interconnections can trigger a chain reaction throughout the entire network, generating systemic risk and posing a significant threat to the sustainable development of the national economy.

Given the complex and interconnected nature of the banking system [8], when individual banks within this system face difficulties, it may trigger a chain reaction throughout the entire banking network, resulting in systemic risk [9]. Systemic risk refers to the potential for a chain reaction initiated by the failure of a single node or a localized event within a system, which can ultimately result in the loss of functionality or the collapse of the entire system [6, 10]. characteristics of loss-sharing and risk transmission between the banking system and the real economy highlight the interconnectedness and cohesiveness of the banking system, as well as its links to the real economy, which are primary sources and accelerators of systemic risk formation and propagation (as illustrated in Figure 1). Consequently, the implementation of macroprudential regulatory tools to address issues of interbank interconnectedness has become essential for preventing systemic risk.

Figure 1

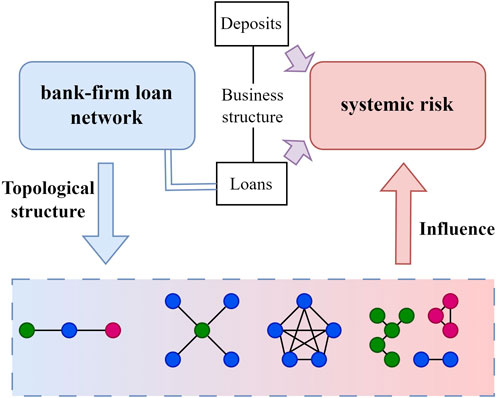
Figure 1. The impact of the network structure of bank-firm loans on systemic risk in the banking system.

This study makes three significant contributions to the existing literature. First, it offers broader sample coverage. Unlike previous studies that typically focus on a limited sample of listed banks or systemically important banks [11], this research utilizes a comprehensive loan dataset encompassing 370 Chinese commercial banks. This dataset includes banks of various sizes and types, thereby significantly enhancing the breadth of the research and the generalizability of the findings. It provides a more robust empirical foundation for understanding the overall network characteristics and risk relationships within the Chinese banking system. Second, the study employs a complex network model to illustrate the bank-firm loan network, quantifying the dynamic evolution of loan relationship structures over different periods by extracting network features such as density, centralization, transitivity, and clustering coefficient. Third, to thoroughly explore the dynamic relationship between loan relationship structures and systemic risk, the study employs the ECM to differentiate and validate short-term and long-term impacts. Through this approach, the study not only elucidates how the structural characteristics of the loan network influence systemic risk across various time scales but also offers policymakers more targeted, time-sensitive risk management recommendations.

The remainder of this paper is organized as follows: Section 2 reviews and summarizes the main points and findings of existing literature. Section 3 details the research methodology employed, including the construction of the stress index, network construction, and the error correction model. Section 4 presents the empirical analysis results. Section 5 discusses the conclusions and policy recommendations of this study and proposes directions for future research.

2 Literature review

2.1 Bank-firm loan

China’s financial system is predominantly bank-driven [12, 13]. Existing literature on financial systemic risk has primarily concentrated on modeling interbank lending markets [14–16]. However, the increasing scale of renminbi loans extended by Chinese financial institutions to the real economy suggests that financing for the real economy remains largely reliant on bank loans. In particular, some large enterprises, which possess thousands of subsidiary companies, have substantial credit lines and loan amounts [17]. These enterprises typically serve as the core of supply chains [18], linking numerous upstream and downstream firms of various types. The business activities of these enterprises not only influence the sound operation of the financial institutions that provide financing but also significantly impact the overall structure and stability of the financial network.

Currently, there are limited studies that construct bank-firm loan networks based on bank-firm lending data [19–21]. Syndicated loans serve as a financial tool whereby banks collaborate to address the substantial financing needs of enterprises [22, 23]. In contrast to traditional single-bank loans, syndicated loans allow multiple banks to share both risk and return, thereby providing enterprises—especially those engaged in capital-intensive and green projects—with more reliable financing options [24, 25]. In recent years, syndicated loans have gained widespread adoption globally and have become a crucial area for examining the relationship between systemic risk in banking [19]. The credit lending activities between banks and enterprises establish complex relationships, forming an interdependent financial network within the system through credit-based lending [6].

2.2 Structure of the bank-firm loan network and systemic risk

The credit lending activities between banks and enterprises create complex relationships, forming an interdependent financial network within the banking system. Graph theory provides a natural conceptual framework for analyzing this network. In this framework, participants within the banking system are represented as nodes, while the connections between them indicate relationships, thereby depicting the entire banking system as a network [26]. When a bank node encounters issues, other bank nodes in the network may also be affected through these connections. Network models, which are capable of illustrating risk transmission within the banking system on a micro-level while simultaneously reflecting and predicting the impact of contagion on the broader economic system at a macro-level, have garnered increasing research attention for modeling banking and economic systems [19, 26, 27]. Consequently, complex network theory has emerged as a valuable tool for analyzing and predicting banking risk contagion.

By selecting appropriate metrics to describe the characteristics of the bank-firm loan network, the structure of these relationships can be quantified. Multiple methods are currently available for feature extraction or identification within networks, including neural networks [28], CART decision trees [29], Bayesian networks [30], and complex network models [31, 32]. Among these methods, indicators such as network density, network centralization, transitivity coefficient, and average clustering coefficient in complex network models effectively reflect the concentration of risk, potential contagion strength, and degree of risk clustering within the bank-firm loan network. Therefore, this study employs a complex network model to extract the features of the bank-firm loan network between banks and enterprises, with the aim of quantifying the evolution of interbank risk correlation structures over different periods.

Existing research has examined the characteristics of bank-firm loan networks between banks and enterprises, as well as their impact on the banking system and the economy from various perspectives. Some scholars have concentrated on the topological structure of these networks and their role in risk contagion. For example, network density and centralization are regarded as effective measures of the concentration and dispersion of risk within loan networks [33]. A higher network density signifies closer interbank collaboration, which aids in distributing loan risk; however, excessive centralization may result in the accumulation of systemic risk at certain critical nodes, thereby posing a threat to the overall stability of the network [34].

On the other hand, the contagion properties within bank-firm loan networks have also drawn significant attention from the academic community. Research indicates that when a default event occurs at an enterprise or bank node, its effects can propagate through the network structure, thereby accelerating the formation and dissemination of systemic risk [6, 35]. In light of this, optimizing the structure of bank-firm loan networks to achieve a balance between risk and return has emerged as a primary concern for scholars and policymakers.

3 Methodology

The Financial Market Stress Index has proven effective in assessing systemic risk conditions within financial systems and in identifying risk events, thereby offering practical implications [32, 36, 37]. The emphasis is placed on comparing financial risks rather than on absolute values to monitor the operations of financial markets.

This study utilizes the Chinese Banks Stress Index (CBSI) synthesis method of cumulative distribution function [32, 38], which involves ranking the original observed indicators $\left({\mathrm{X}}_1,{\mathrm{X}}_2,\dots ,{\mathrm{X}}_n\right)$ according to their economic significance. The ranking is performed in ascending order if a higher observation indicates greater risk or in descending order if a lower observation indicates greater risk. The newly ranked indicator $X_{[1]}<X_{[2]}<\dots <X_{[n]}$ is then mapped under the empirical cumulative distribution function to a new indicator $Z_t$ based on the original indicator $X_t$:

$Z_t=\left\{\begin{array}{c}\frac{r}{n},x_{i,\left[r\right]}\le x_{i,t}<x_{i,\left[r+1\right]},r=\mathrm{1,2},\dots ,n-1\hfill \\ 1,x_i\ge x_{\left[n\right]}\hfill \end{array}\right.(1)$

where the subscript $[r]$ represents the ranking position of $X_t$.

Using the empirical cumulative distribution function, we map the observed values representing risk conditions to the interval (0,1]. To give the stress index a more intuitive economic meaning, each mapped indicator is equally weighted to synthesize the CBSI. The CBSI is constructed as follows:

$\text{CBSI}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{Z}_t(2)$

where $N$ represents the number of original indicators.

3.1 Construction of the bank-firm loan network

Following the approach outlined by Hao et al. and Jia et al. [19, 39], this study begins by analyzing loan data from publicly listed companies. A connection is established between a bank and a listed company if a loan is extended during a specific period; otherwise, the connection is considered absent. Figure 2a depicts a simplified bipartite network consisting of four banks and five listed companies. To focus on the interbank network structure, the bipartite network is transformed into a network comprising only commercial banks, where each bank serves as a node. To measure the strength of connections between banks and listed companies, the study opts not to use the number of loans as the weight of the link [19]. Instead, the loan amount shared by two banks with a bank-firm loan relationship is utilized as the link weight between them. For instance, Bank one and Bank three have a shared loan relationship with three companies (Company 2, Company 3, and Company 4), resulting in a link weight of $2130\{(10+1000)+(10+100)+(10+1000)\}$. Conversely, Bank two and Bank 3, sharing loans with two companies (Company two and Company 4), have a link weight of $2200\{(100+1000)+(100+1000)\}$. On the other hand, Bank one and Bank 2, which also share loans with two companies (Company two and Company 4), have a link weight of $220\{(10+100)+(10+100)\}$. This method of using loan amounts as link weights provides a more comprehensive understanding of potential risk relationships among commercial banks. Figure 2b illustrates the resulting commercial bank network derived from the bipartite network, with each link weight indicating the shared loan amount.

Figure 2

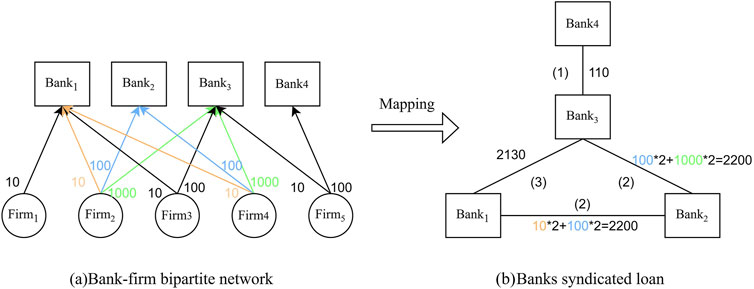
Figure 2. Network mapping of bank-firm loan relationships. (a) Bank-firm bipartite network, (b) Banks syndicated loan.

3.2 Structural characteristics of the bank-firm loan network

The mapped one-mode commercial bank network is denoted by set $G=(V,W)$, where $G$ is a network consisting of interconnected commercial banks represented by $V$. The set $V=\left\{v_1,v_2,\dots ,v_n\right\}$ represents nodes, with elements $v_i$ representing individual commercial banks, and set $W=\left\{w_{ij}\right\}$ represents the weighted edges in the network, indicating the bank-firm loan amounts between commercial bank $i$ and commercial bank $j$.

In this study, we analyze a weighted undirected network, where $w_{ij}$ is considered equal to $w_{ji}$. The topological network can be represented by an adjacency matrix $A=\left(a_{ij}\right)$, as shown in Equation 3.

$a_{ij}=\left\{\begin{array}{c}1,w_{ij}>0\hfill \\ 0,w_{ij}=0\hfill \end{array}\right.(3)$

The unique characteristics of the topological structure of the bank-firm loan network may exhibit specific properties that cannot be fully captured through network diagrams alone. Hence, choosing suitable measurement criteria becomes crucial in examining the topological characteristics and evolutionary trends of bank-firm loan networks. This research delves into four complex network topological metrics to investigate the alterations in the general properties of commercial banking bank-firm loan network, including network density, network centralization, transitivity coefficient, and average clustering coefficient.

3.2.1 Network density

The density of a network is a metric that quantifies the level of connection between nodes in the network and is computed by dividing the existing edges by the total potential edges. It is denoted by a numerical value ranging from 0 to 1, wherein higher values signify increased interconnectedness. The calculation for network density can be expressed by the following Equation 4:

$\text{\hspace{0.17em}Density\hspace{0.17em}}=\frac{2m}{n\left(n-1\right)}(4)$

where $m$ represents the total number of edges in the network and $n$ signifies the number of nodes.

Within the framework of the bank-firm loan network in commercial banking, a higher level of network density suggests an increased amount of bank-firm loan relationships between banks, leading to a more varied network configuration. With a constant total loan demand from enterprises, this diversification allows the risk of bank-firm loans from a single bank to be spread across multiple banks, avoiding the concentration of risk in any one bank. As a result, in the event of a risk occurrence in one bank, other banks can help absorb and distribute this risk through diverse connections, ultimately reducing systemic risk.

3.2.2 Network centralization

Network centralization measures the importance of specific nodes within a network. Centralization is highest in star-shaped networks and lowest in fully connected networks. The calculation for centralization can be expressed by the following Equation 5:

$\text{\hspace{0.17em}Centralization\hspace{0.17em}}=\frac{{\sum }_{i=1}^n\left(C_{\max }-k_i\right)}{n^2-3n+2}(5)$

where $C_{\max }$ represents the maximum centrality in the network, $k_i$ is the degree of node $v_i$, and $n$ is as previously defined. This metric assesses the control capacity of core nodes in a network [40].

In the specific case of the bank-firm loan network, centralization refers to the extent to which a small number of banks have control over loan relationships. A high level of centralization suggests that these banks wield significant influence and control within the system, and their risk status can greatly affect systemic risk.

3.2.3 Transitivity coefficient

According to Barrat et al. [41], the transitivity coefficient is a measure that indicates the probability of neighboring nodes being linked to a particular node, reflecting the degree of clustering within the network. Increased transitivity coefficient values indicate more pronounced clustering among nodes in the network, particularly in the realm of weighted networks. The calculation for transitivity can be expressed by the following Equations 6, 7:

$T_i=\frac{1}{s_i\left(k_i-1\right)}{\displaystyle \sum _{j,h}}\frac{w_{ij}+w_{ih}}{2}{a}_{ij}{a}_{ih}{a}_{jh}(6)$

$\text{\hspace{0.17em}Transitivity\hspace{0.17em}}=\frac{{\sum }_i^n{T}_i}{n}(7)$

where $T_i$ denotes the transitivity of node $v_i$, $s_i={\sum }_{j=1}^N{a}_{ij}{w}_{ij}$ represents the strength of node $v_i$, and $k_i$ is as previously defined.

In the bank-firm loan network of commercial banks, a high transitivity coefficient suggests the existence of triangular connections among banks. For instance, if Bank A is in a loan agreement with Bank B, and Bank B has a loan deal with Bank C, it implies that Bank A is also connected with Bank C through a loan arrangement. These triangular connections generate additional routes for risk transmission, potentially increasing systemic risk.

3.2.4 Average clustering coefficient

The average clustering coefficient is calculated as the mean value of the clustering coefficients in the network. This coefficient represents the degree to which nodes are interconnected within their immediate surroundings. The calculation for average clustering coefficient can be expressed by the following Equations 8, 9:

${\text{\hspace{0.17em}Clustering\hspace{0.17em}}}_i=\frac{2e_i}{k_i\left(k_i-1\right)}(8)$

${\text{\hspace{0.17em}Clustering\hspace{0.17em}}}^{\text{avg}}=\frac{{\sum }_i^n{\text{\hspace{0.17em}Clustering\hspace{0.17em}}}_i}{n}(9)$

where $e_i$ represents the number of edges between the neighbors of node $v_i$, and $k_i$ is as previously defined.

Within the bank-firm loan network, the clustering coefficient reflects the tightness of the network, showing the level of interconnected bank-firm loan relationships among banks. A high average clustering coefficient indicates the presence of numerous small cliques or subnetworks among the banks. These closely linked groups can accelerate the spread of risk within cliques, potentially affecting the overall stability of the banking system.

3.3 Error correction model (ECM)

Constructing a monthly trade network of bank-firm loans among various commercial banks reveals evolving syndication relationship structures over time. This study seeks to investigate how these relationship characteristics impact banks’ systemic risk. While the ordinary least squares (OLS) method is commonly used, it assumes that economic variables are stationary. However, many macroeconomic variables are time series data and nonstationary in practice. Utilizing the OLS method in such cases can lead to ‘spurious regression.’ Engle and Granger [42] introduced the cointegration method and ECM to address this issue by examining the significance of variable coefficients to determine short-term and long-term relationships among variables. Therefore, this research aims to empirically analyze the network structure characteristics of the commercial banking system and banks’ systemic risk using cointegration and ECM methods. The model is outlined as follows:

${\text{CBSI}}_t={\alpha }_0+{\alpha }_1{\text{Network}}_{i,t}+{\alpha }_2{\text{Control}}_{i,t}+{\epsilon }_t(10)$

$\mathrm{\Delta }{\text{\hspace{0.17em}CBSI\hspace{0.17em}}}_t={\beta }_0+\lambda {\text{ECM}}_{t-1}+{\beta }_1{\text{\hspace{0.17em}Network\hspace{0.17em}}}_{i,t}+{\beta }_2{\text{\hspace{0.17em}Control\hspace{0.17em}}}_{i,t}+{\omega }_t(11)$

Equation 10 represents the cointegration regression equation, while Equation 11 represents the ECM. In these equations, $\text{CBSI}$ denotes the Chinese Commercial Bank Stress Index (CBSI), while $\mathrm{\Delta }\text{CBSI}$ represents the first-order difference of the CBSI; ${\alpha }_0$ and ${\beta }_0$ are constants; ${\alpha }_1$ and ${\alpha }_2$ denote the long-term correlation coefficients of the variables; $Networ{k}_{i,t}$ is the characteristic value of the ith topological feature indicator at period $t$; $Contro{l}_i,t$ represents the characteristic value of the ith control variable at period $t$; ${\epsilon }_t$ and ${\omega }_t$ are random error terms; $\lambda$ is the adjustment speed coefficient, indicating short-term correction to equilibrium; $EC{M}_{t-1}$ denotes the lagged error correction term; ${\beta }_1$ and ${\beta }_2$ are the short-term correlation coefficients of the variables.

4 Results

4.1 Construction of the stress index for Chinese Commercial Banks

China has not faced systemic banking risk; therefore, the banking stress index is utilized to assess systemic risk. Monthly data on various factors, such as the nonperforming loan ratio (NPL), the TED spread, the weighted interest rate of the 7-day interbank pledged repo (RR), the liquidity ratio (LR), the capital adequacy ratio (CR), and the excess reserve ratio (PR) from January 2013 to December 2023 were collected. By applying Formulas 1, 2, a monthly CBSI was calculated for the mentioned period. All the data used in this analysis were obtained from the WIND database. To address the fact that NPL, LR, CR, and PR are reported quarterly, cubic spline interpolation was employed to convert quarterly data into monthly data. The systemic stress index for commercial banks, synthesized using the cumulative distribution function method in this study, is calculated as shown in Equation 12:

$\text{CBSI}=\frac{\text{NPL\_ecdf}+\text{TED\_ecdf}+\text{RR\_ecdf}+\text{LR\_ecdf}+\text{C\_ecdf}+\text{PR\_ecdf}}{6}(12)$

Where, $\text{\_}ecdf$ denotes the empirical cumulative distribution function values of the respective indicators.

Figure 3 illustrates the monthly trend of the CBSI from January 2013 to December 2023. This index is constructed from multiple indicators, including the nonperforming loan ratio (NPL), the TED spread, the 7-day interbank pledged repo weighted interest rate (RR), the liquidity ratio (LR), the capital adequacy ratio (CR), and the excess reserve ratio (PR). Data obtained from the WIND database reflects systemic risk within the Chinese banking sector over time. Key observations include the ‘money shortage’ events in June and December 2013, which resulted in a significant increase in liquidity risk for commercial banks; the prolonged Sino-US trade war during 2018–2019, which hampered trade financing and credit activities, leading to a deterioration in asset quality within affected industries and an escalation of the CBSI; and the financial strain on enterprises during the COVID-19 pandemic (2020-2021). This strain was coupled with diminished demand for corporate loans and challenges in loan repayments, which exerted additional pressure on the banking sector, culminating in a peak of the CBSI in December 2021.

Figure 3

Figure 3. Trend of the Chinese banking system stress index (CBSI).

This index effectively captures the varying levels of systemic risk confronting Chinese commercial banks, closely aligning with real-world events and reflecting the broader economic challenges faced by the banking industry during these periods.

4.2 Evolution of bank-firm loan structures in Commercial Banks

This study establishes a bank-firm loan network among Chinese banks by analyzing loan data from listed companies in the CSMAR database. The dataset covers the period from January 2013 to December 2023 and includes five state-owned commercial banks, 13 joint-stock commercial banks, 125 urban commercial banks, and 227 rural commercial banks, for a total of 370 commercial banks. The data processing steps involved excluding information from the People’s Bank of China, three policy banks, foreign banks, and some nonbanking financial institutions to ensure sample homogeneity. Additionally, invalid data such as undisclosed loan details, non-RMB settlements, vague bank names, and loans from nontraditional banks were eliminated. The monthly aggregation of daily loan data and consolidation of loans from different branches at the head office level resulted in 132 months of data and 84,210 bank loan records. Considering that bank-firm loan involve long-term loan risks, this study focuses on the stock amount of bank-firm loans between banks.

Figure 4 illustrates the evolution of the bank-firm loan network in China, highlighting the relationships between banks and firms in December of each year from 2013 to 2023. The network comprises various types of banks, with state-owned commercial banks (red triangles) and joint-stock commercial banks (blue quadrilaterals) forming the core tier, while urban commercial banks (green pentagons) and rural commercial banks (yellow circles) occupy the periphery. Key observations include: (1) December 2013: The bank-firm loan relationships were predominantly organized into dense clusters led by large banks, with limited inter-cluster connections. This suggests that financial activities were concentrated in the core institutions, while peripheral banks had fewer direct connections to firms. (2) December 2023: Over the years, the network has evolved to become more interconnected, forming a ‘core-periphery’ tiered structure [43–45]. This indicates that smaller banks are gradually becoming more integrated into the financial system, contributing to better resource allocation and risk diversification. (3) The transformation of the network into a ‘group loan model’ signifies that multiple city commercial banks are now revolving around key listed companies. This shift underscores the growing role of small- and medium-sized banks in crucial financial activities, enhancing the inclusivity and sustainability of the financial system. (4) The increasing involvement of city and rural commercial banks at the network’s center suggests that these banks are emerging as new “systemically important institutions” [46, 47], reflecting a trend toward a more balanced and equitable distribution of financial resources, particularly between urban and rural areas.

Figure 4

Figure 4. Bank-firm loan networks (December of each year).

This evolution enhances the overall resilience and stability of the financial system, contributing to improved financial inclusion and a more sustainable allocation of resources.

Figure 5 illustrates the evolution of four key topological indicators—network density, network centralization, transitivity coefficient, and average clustering coefficient—from January 2013 to December 2023. These indicators provide critical insights into the structure and dynamics of the bank-firm loan network, highlighting the changing patterns of collaboration among commercial banks in China over the past decade. Key observations include: (1) Network Density: Fluctuating between 0.22 and 0.25, network density exhibits a cyclical pattern. During periods of robust economic activity, density increases as bank-firm loan relationships expand, indicating more frequent collaborations. Conversely, during economic downturns, the frequency of interbank cooperation diminishes, resulting in reduced density. This trend suggests that the network is highly responsive to economic conditions, with banks adjusting their loan relationships in response to fluctuations in demand. (2) Network Centralization: Ranging from 0.50 to 0.55, network centralization remains relatively stable, albeit with some volatility. A higher centralization score indicates that certain banks consistently occupy central roles within the network, underscoring their significance in lending activities and their influence on systemic risk. (3) Transitivity Coefficient: With an average value of approximately 0.50, the transitivity coefficient remains stable over time. This stability suggests that banks in the network tend to maintain consistent relationships with their partners, thereby reinforcing a dense and stable cooperation structure. (4) Average Clustering Coefficient: Varying between 0.18 and 0.20, the clustering coefficient shows a gradual increase over the period. This trend indicates that interbank cooperative relationships are becoming more tightly-knit, reflecting a clustering effect. A higher clustering coefficient may signify stronger, more resilient cooperative ties among banks, which could contribute to enhancing the stability of the financial system.

Figure 5

Figure 5. Evolution of key network indicators of bank-firm loan relationships (2013–2023).

The dynamic analysis of these indicators offers a deeper understanding of how changes in bank-firm loan networks can influence systemic risk, highlighting the evolving nature of interbank collaborations. This comprehensive view is crucial for assessing financial stability and formulating policies to mitigate potential risks in the banking sector.

4.3 Impact of bank-firm loan structures on the systemic risk of Commercial Banks

4.3.1 Descriptive statistics of variables

This study draws on the relevant literature on financial crises and includes traditional macrolevel control variables. These variables consist of the year-on-year growth rate of the money supply (M1), which reflects the central bank’s monetary policy position; the banking prosperity index (Bank); and the corporate prosperity index (Cop). Detailed descriptive statistics can be found in Table 1.

Table 1

Table 1. Descriptive statistics of the variables.

4.3.2 Model testing

4.3.2.1 Unit root test

The ADF unit root test method was used to assess the stationarity of the variables, with the lag length determined based on the Akaike information criterion (AIC). The test results in Table 2 reveal that the original variables all fail to reject the null hypothesis, indicating that they are nonstationary series. However, after first-order differencing, the ADF values of the variables are all below the critical value at the $1\%$ significance level, leading to the rejection of the null hypothesis. Therefore, all first-order differenced variables are stationary series, denoted as I (1). These results suggest that although the original multivariate time series variables are nonstationary, their first-order differences are stationary, implying the presence of a long-term equilibrium relationship among them.

Table 2

Table 2. ADF test results for the variables.

4.3.2.2 Cointegration test

This study utilizes the Engle-Granger two-step method to investigate the cointegration between variables [42]. The first step involves using the ordinary least squares method to regress the equation formulated in Equation 10, which depicts the correlation between the bank-firm loan network structure and the systemic risk of commercial banks. The findings of the model calculations are outlined in Equation 13.

$\begin{array}{cc}\hfill {\text{CBSI}}_t& =-1.3267{\text{Density}}_t-0.0582{\text{Centralization}}_t\hfill \\ \hfill & +1.5296{\text{Transitivity}}_t+0.9977{\text{AverageClustering}}_t\hfill \\ \hfill & -0.2774M{1}_t-0.1903{\text{Bank}}_t+0.2138{\text{Enterprise}}_t+0.0981\hfill \end{array}(13)$

Subsequently, the residual series ${\epsilon }_t$ from the model is derived and subjected to a stationarity test. As shown in Table 3, the Augmented Dickey-Fuller (ADF) value for the unit root test of the residual series ${\epsilon }_t$ is compared to the critical value at the $1\%$ significance level, revealing that the residual series ${\epsilon }_t$ is stationary (I (0)). This indicates the presence of a cointegration relationship among the variables, making Equation 13 a cointegration regression equation. This implies a long-term equilibrium relationship between the bank-firm loan network structure and the systemic risk of commercial banks.

Table 3

Table 3. ADF test results for the residual sequence.

The regression results in Table 4 indicate that the long-term impact coefficients of the bank-firm loan network structure on the systemic risk of banks are statistically significant. The regression coefficient for network density is −1.3267 and is almost significant at the $10\%$ level (p value of 0.0921), showing a negative influence of network density on the systemic risk of commercial banks. On one hand, high network density facilitates enhanced information sharing and cooperation. A high network density indicates closer interbank relationships and increased opportunities for collaboration. These closer relationships can mitigate information asymmetry through coordinated information sharing and risk management measures. On the other hand, high-density networks help disperse the impact of shocks. In such networks, the risks associated with individual banks are more readily distributed across multiple connected parties, thereby reducing the concentration of shocks. This risk dispersion contributes to alleviating systemic chain reactions that may arise from the failure of a single bank. This finding is consistent with the previous theoretical explanation that interbank cooperation and information sharing are key factors in reducing systemic risk over time.

Table 4

Table 4. OLS Regression results.

Similarly, the regression coefficient for network centralization is −0.5882, which is also nearly significant at the $10\%$ level (p value of 0.0959), indicating that network centralization has a negative impact on systemic risk. On one hand, a higher level of network centralization indicates the presence of a limited number of core nodes within the network. These core nodes, by maintaining a substantial number of connections and demonstrating high levels of resilience and shock-absorbing capacity, can act as stabilizing anchors for the entire network. In the context of interbank co-loan networks, central banks or key financial institutions often have superior access to information resources, ample liquidity reserves, and robust capital buffers, all of which contribute positively to the overall stability of the network. On the other hand, a centralized network structure can facilitate the swift transmission of rescue resources or stabilizing conditions from core nodes to peripheral nodes. For instance, when the risk level of peripheral nodes increases, core nodes can alleviate local shocks by enhancing liquidity supply, thereby limiting the spread of risk across a broader scope.

The regression coefficient for the transitivity coefficient is 1.5296, which is statistically significant at the $1\%$ level (p value of 0.0082), indicating a positive impact of transitivity on systemic risk. On one hand, high transitivity increases the number of pathways for risk propagation. The triangular relational networks among banks create additional channels for risk transmission, enabling local shocks to spread rapidly through multiple paths across the entire network. On the other hand, high transitivity signifies more complex and tightly knit relationships between banks, which can lead to the compounding and accumulation of local risks among multiple parties. Under certain contingent conditions, this may result in the rapid amplification of these risks.

Similarly, the regression coefficient for the average clustering coefficient is 0.9977, which is also significant at the $1\%$ level (p value of 0.0001), indicating a positive correlation between the average clustering coefficient and systemic risk. On one hand, a high clustering coefficient indicates that the relationships among banks are closely knit and tightly interconnected. This characteristic facilitates the rapid transmission of localized shocks within the system. For instance, if a financial institution experiences a liquidity shortage due to a default, its highly interconnected network may swiftly propagate the liquidity crisis to its directly linked counterparties, thereby amplifying the spread of the crisis. On the other hand, a high clustering coefficient reinforces positive feedback mechanisms. In networks characterized by high clustering coefficients, behaviors within localized sub-networks are more likely to generate feedback effects. For example, an increase in a particular bank’s risk level might prompt all banks within its cooperative network to simultaneously adopt more conservative lending strategies, further tightening liquidity conditions and exacerbating systemic risk.

To summarize, the results of the regression analysis indicate that the structural features of the network formed by bank-firm loans play a significant role in the overall risk faced by commercial banks. More precisely, network density and centralization are found to reduce systemic risk, whereas the transitivity coefficient and average clustering coefficient are associated with an increase in systemic risk. Additionally, the degree of monetary policy tightness is shown to have a moderate effect on systemic risk. These results provide concrete data that elucidate the relationship between interbank network structures and systemic risk, offering valuable insights for both bank risk mitigation strategies and policy-making.

4.3.3 ECM

The research reveals a notable long-term equilibrium relationship between the structure of the bank-firm loan network and systemic risk within banking institutions. However, there can be short-term deviations from this equilibrium. To remedy these deviations, the lagged term of the residuals from Equation 13 functions as the lagged error correction term. This effectively integrates both the short-term and long-term impacts of the bank-firm loan network structure on systemic risk in banks. Equation 11 defines the error correction model, with Equation 14 illustrating the derived effects of the bank-firm loan network structure on systemic bank risk.

$\begin{array}{cc}\hfill \mathrm{\Delta }{\text{CBSI}}_t& =-1.9557\mathrm{\Delta }{\text{Density}}_t+0.1905\mathrm{\Delta }{\text{Centralization}}_t\hfill \\ \hfill & +0.72\mathrm{\Delta }{\text{Transitivity}}_t+0.2182\mathrm{\Delta }{\text{AverageClustering}}_t\hfill \\ \hfill & -0.021\mathrm{\Delta }M{1}_t-0.6228\mathrm{\Delta }{\text{Bank}}_t+1.1187\mathrm{\Delta }{\text{Enterprise}}_t\hfill \\ \hfill & -0.4962EC{M}_{t-1}+0.0022\hfill \end{array}(14)$

Equation 14 depicts the short-term dynamic adjustment relationship between variables. The error correction model results are detailed in Table 5, showing a significant adjustment speed coefficient of −0.4962 at the $1\%$ level, indicating a strong capacity for the system to return to equilibrium. In the short term, the bank-firm loan network structure minimally impacts the systemic risk of commercial banks, with only network density significantly affecting systemic risk at the $5\%$ level. This suggests that the long-term influence of the bank-firm loan network structure on systemic risk in commercial banks outweighs its short-term impact. Several reasons support this observation:

$•$ Enterprises typically engage in medium to long-term borrowing from commercial banks to sustain production and operational activities, leading to persistent risk exposure for banks;

$•$ Short-term market fluctuations and economic events are often random and unpredictable, potentially making short-term relationships between variables insignificant. In contrast, long-term information dissemination and risk adjustment enhance the long-term impact of the bank-firm loan network structure on systemic risk;

$•$ The risk-sharing and buffering mechanisms within the bank-firm loan network may not fully materialize in the short term. Banks may turn to short-term financing for liquidity issues, while the risk-buffering effects of bank-firm loan relationships necessitate stable cash flows and credit cooperation over the long term.

Table 5

Table 5. Regression results for the ECM.

5 Discussion

This study explores the network of bank-firm loans between Chinese commercial banks through the analysis of loan announcements made by publicly traded companies. The evolution of its topological structure is examined using a complex network model. Additionally, an error correction model is employed to study how the bank-firm loan network structure impacts the systemic risk of commercial banks. The findings reveal that the connections among commercial banks in the modern banking system exhibit both resilience and vulnerability. The research results suggest the following:

$•$ The structure of the bank-firm loan network has a considerably greater impact on systemic risk in the long term compared to the short term. The inherent long-term stabilization mechanisms within the banking system are crucial for sustainable development, as they facilitate a gradual return to equilibrium when confronted with external shocks, thereby promoting continued economic growth. This finding emphasizes the significance of long-term collaboration and risk management, which closely aligns with the role of banks in pursuing sound operations and supporting enduring socio-economic objectives;

$•$ Furthermore, network density and centralization can mitigate systemic risk for commercial banks over the long term. This risk-sharing mechanism is well-suited to the stability objectives of sustainable development within the banking sector;

$•$ In the long run, such a network structure effectively addresses systemic risk and enhances the risk absorption capacity of the banking industry.In contrast, the transitivity coefficient and average clustering coefficient significantly elevate systemic risk for commercial banks in the long term. This phenomenon underscores the potential pitfalls of excessive network centralization: while transitivity and average clustering can improve internal collaboration and information flow within the network, they can also engender highly interlinked risk chains, thereby amplifying the impact of shocks from individual nodes across the entire network.

The outcomes of the error correction model and the risk characteristics of the bank-firm loan network highlight the necessity of balancing “short-term stability” with “long-term sustainability” within the banking system for sustainable development. By optimizing loan network structures, fostering medium-to long-term cooperation, and strengthening risk-buffering mechanisms, banks can not only diminish their systemic risk but also more effectively support the sustainable development goals of society and the environment.

Based on the above conclusions, the following policy recommendations are proposed to effectively reduce systemic risk in commercial banks and achieve sustainable development in the banking sector.

$•$ Promotion of interbank cooperation and information exchange. Regulatory bodies should encourage banks to work closely together, thereby increasing the network’s density. The Development of platforms and mechanisms for information sharing can enhance transparency and trust, which in turn disperses risks and mitigates systemic threats;

$•$ Foster the Growth of Core Banks. Considering the adverse effects of network centralization on systemic risk, policymakers should prioritize the support and oversight of key banks within the bank-firm loan network to ensure their stability. This involves monitoring their capital adequacy and liquidity requirements to boost resilience;

$•$ Mitigate risk transmission effects. To address the issues related to the transitivity coefficient, regulatory bodies should institute and improve mechanisms that isolate risks between banks, thereby preventing rapid risk spread. Setting limits on risk transmission and bolstering interbank risk monitoring are critical steps in this direction;

$•$ The structure of the interbank network is refined. To address systemic risks associated with a high average clustering coefficient, it is recommended to refine the interbank network structure by avoiding excessively tight-knit subgroups. Diversifying interbank loan relations and reducing highly concentrated cooperative clusters can help limit the extent and pace of risk spread across the network

$•$ Craft Tailored Regulatory Policies. Regulatory bodies should devise specific regulatory policies reflecting the varying roles and positions of banks within the bank-firm loan network. Core banks should adhere to stricter risk management protocols and capital requirements, whereas peripheral banks should receive additional support and guidance to enhance their risk resiliency.

While this study provides a comprehensive examination of the impact of bank-firm loan network structure on the systemic risk of commercial banks, several limitations must be acknowledged. Firstly, the analysis relies exclusively on loan data from publicly listed companies, whereas small and medium-sized enterprises (SMEs) are generally more susceptible to default risks. Secondly, we did not differentiate loan data across various industries, despite the fact that default risk associated with loans can vary significantly between sectors. Lastly, the ECM method does not comprehensively address all endogeneity issues, particularly the potential risks introduced by lagged variables. Due to constraints in the existing dataset and research design, more robust causal inference tools, such as the instrumental variable (IV) approach or a natural experiment framework, were not utilized in this study. Future research could benefit from incorporating loan data from SMEs and developing multi-layer network models to more effectively capture the network structures at the industry level. Additionally, further investigation into the influence of network structure on systemic risk is warranted. Furthermore, employing instrumental variables derived from exogenous shocks or utilizing a natural experiment framework should also be considered to enhance the robustness of conclusions through improved causal inference mechanisms. These significant issues will be explored in greater depth in our forthcoming studies.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, upon reasonable request. Requests to access these datasets should be directed to Zhengyong Li, bHp5MzMwM0BvdXRsb29rLmNvbQ==.

Author contributions

ZL: Conceptualization, Funding acquisition, Methodology, Project administration, Software, Validation, Writing–original draft. DF: Conceptualization, Supervision, Writing–review and editing. HL: Data curation, Formal Analysis, Resources, Visualization, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by Gansu Provincial Department of Education University Faculty Innovation Fund Project (2024A-076), Gansu Provincial Department of Education Soft Science Special Youth Project (23JRZA438) and the doctoral research innovation project of Lanzhou University of Finance and Economics (2022D03).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Allen F, Qian J, Qian M. Law, finance, and economic growth in China. J financial Econ (2005) 77(1):57–116. doi:10.1016/j.jfineco.2004.06.010

CrossRef Full Text | Google Scholar

2. He Z, Wei W. China’s financial system and economy: a review. Annu Rev Econ (2023) 15(1):451–83. doi:10.1146/annurev-economics-072622-095926

CrossRef Full Text | Google Scholar

3. Jiménez G, Mian A, Peydró J-L, Saurina J. The real effects of the bank lending channel. J Monetary Econ (2020) 115:162–79. doi:10.1016/j.jmoneco.2019.06.002

CrossRef Full Text | Google Scholar

4. Lu Y, Springer C, Steffen B. Cofinancing and infrastructure project outcomes in Chinese lending and overseas development finance. World Development (2024) 175:106473. doi:10.1016/j.worlddev.2023.106473

CrossRef Full Text | Google Scholar

5. Jackson MO, Pernoud A. Systemic risk in financial networks: a survey. Annu Rev Econ (2021) 13(1):171–202. doi:10.1146/annurev-economics-083120-111540

CrossRef Full Text | Google Scholar

6. Acemoglu D, Ozdaglar A, Tahbaz-Salehi A. Systemic risk and stability in financial networks. Am Econ Rev (2015) 105(2):564–608. doi:10.1257/aer.20130456

CrossRef Full Text | Google Scholar

7. Erer E, Erer D. The domino effect of silicon valley bank’s bankruptcy and the role of fed’s monetary policy. Borsa Istanbul Rev (2024) 24(3):573–91. doi:10.1016/j.bir.2024.03.002

CrossRef Full Text | Google Scholar

8. Chabot M, Bertrand J-L. Complexity, interconnectedness and stability: new perspectives applied to the european banking system. J Business Res (2021) 129:784–800. doi:10.1016/j.jbusres.2019.09.046

CrossRef Full Text | Google Scholar

9. Gao Q, Fan H. Systemic risk caused by the overlapping portfolios of banks under a bilateral network. Front Phys (2021) 9:638991. doi:10.3389/fphy.2021.638991

CrossRef Full Text | Google Scholar

10. Battiston S, Farmer JD, Flache A, Garlaschelli D, Haldane AG, Heesterbeek H, et al. Complexity theory and financial regulation. Science (2016) 351(6275):818–9. doi:10.1126/science.aad0299

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yan C, Ding Y, Liu W, Liu X, Liu J. Multilayer interbank networks and systemic risk propagation: evidence from China. Physica A: Stat Mech its Appl (2023) 628:129144. doi:10.1016/j.physa.2023.129144

CrossRef Full Text | Google Scholar

12. Dong J, Yin L, Liu X, Hu M, Li X, Liu L. Impact of internet finance on the performance of commercial banks in China. Int Rev Financial Anal (2020) 72:101579. doi:10.1016/j.irfa.2020.101579

CrossRef Full Text | Google Scholar

13. Allen F, Zhang C, Zhao M. China’s financial system: opportunities and challenges. (2012). doi:10.3386/w17828

CrossRef Full Text | Google Scholar

14. Wang C, He J, Ma J. Indirect correlation network between banks based on common assets. China Manag Sci (2019) 27(11):23–30. doi:10.16381/j.cnki.issn1003-207x.2019.11.003

CrossRef Full Text | Google Scholar

15. Wang Z, Zhao Q, Qiu L. Multi-dimensional factor correlation, multiple interbank network contagion, and conditional var of banks. Front Phys (2022) 10:895603. doi:10.3389/fphy.2022.895603

CrossRef Full Text | Google Scholar

16. Anand K, Craig B, Von Peter G. Filling in the blanks: network structure and interbank contagion. Quantitative Finance (2015) 15(4):625–36. doi:10.1080/14697688.2014.968195

CrossRef Full Text | Google Scholar

17. Chai S, Zhang K, Wei W, Ma W, Abedin MZ. The impact of green credit policy on enterprises’ financing behavior: evidence from Chinese heavily-polluting listed companies. J Clean Prod (2022) 363:132458. doi:10.1016/j.jclepro.2022.132458

CrossRef Full Text | Google Scholar

18. Jie Z. Coupling open innovation: network position, knowledge integration ability, and innovation performance. J Knowledge Economy (2023) 14(2):1538–58. doi:10.1007/s13132-022-00932-z

CrossRef Full Text | Google Scholar

19. Qingmin H, Shen JH, Lee C-C. Risk contagion of bank-firm loan network: evidence from China. Eurasian Business Rev (2023) 13(2):341–61. doi:10.1007/s40821-022-00237-w

CrossRef Full Text | Google Scholar

20. Drago D, Gallo R. The impact of financial crises on the syndicated loan spreads applied to public and private firms. J Financial Stab (2020) 46:100718. doi:10.1016/j.jfs.2019.100718

CrossRef Full Text | Google Scholar

21. Hasan I, Kim S-J, Politsidis PN, Wu E. Loan syndication under basel ii: how do firm credit ratings affect the cost of credit? J Int Financial Markets, Institutions Money (2021) 72:101331. doi:10.1016/j.intfin.2021.101331

CrossRef Full Text | Google Scholar

22. Dennis SA, Mullineaux DJ. Syndicated loans. J financial intermediation (2000) 9(4):404–26. doi:10.1006/jfin.2000.0298

CrossRef Full Text | Google Scholar

23. Gustafson MT, Ivanov IT, Meisenzahl RR. Bank monitoring: evidence from syndicated loans. J Financial Econ (2021) 139(2):452–77. doi:10.1016/j.jfineco.2020.08.017

CrossRef Full Text | Google Scholar

24. Del Gaudio BL, Previtali D, Sampagnaro G, Verdoliva V, Vigne S. Syndicated green lending and lead bank performance. J Int Financial Management and Account (2022) 33(3):412–27. doi:10.1111/jifm.12151

CrossRef Full Text | Google Scholar

25. Hale G, Meisenbacher B, Nechio F. Industrial composition of syndicated loans and banks’ climate commitments. Tech Rep Natl Bur Econ Res (2024) 2024:01–37. doi:10.24148/wp2024-23

CrossRef Full Text | Google Scholar

26. Galletta S, Mazzù S, Naciti V. A bibliometric analysis of esg performance in the banking industry: from the current status to future directions. Res Int Business Finance (2022) 62:101684. doi:10.1016/j.ribaf.2022.101684

CrossRef Full Text | Google Scholar

27. Liu J, Ding H, Shahroudy A, Duan L-Y, Jiang X, Wang G, et al. Feature boosting network for 3d pose estimation. IEEE Trans pattern Anal machine intelligence (2019) 42(2):494–501. doi:10.1109/tpami.2019.2894422

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Xin R, Zhang J, Shao Y. Complex network classification with convolutional neural network. Tsinghua Sci Technol (2020) 25(4):447–57. doi:10.26599/tst.2019.9010055

CrossRef Full Text | Google Scholar

29. Li H, Long F, Lin C. The impact of the overall network structure and cooperation intensity on innovation performance. Stud Sci Sci (2022) 1–18. doi:10.16192/j.cnki.1003-2053.20220602.001

CrossRef Full Text | Google Scholar

30. Gandy A, Veraart LAM. A bayesian methodology for systemic risk assessment in financial networks. Management Sci (2017) 63(12):4428–46. doi:10.1287/mnsc.2016.2546

CrossRef Full Text | Google Scholar

31. Xu J, Li J, Vincent C, Xin Z. Evolution of the rare earth trade network: a perspective of dependency and competition. Geosci Front (2024) 15(3):101653. doi:10.1016/j.gsf.2023.101653

CrossRef Full Text | Google Scholar

32. Li M, Liang S. Monitoring systemic financial risks: construction and state identification of China’s financial market stress index. J financial Res (2021) 6:21–38.

Google Scholar

33. Gai P, Kapadia S. Contagion in financial networks. Proc R Soc A: Math Phys Eng Sci (2010) 466(2120):2401–23. doi:10.1098/rspa.2009.0410

CrossRef Full Text | Google Scholar

34. Bhattacharya M, Inekwe JN, Valenzuela MR. Credit risk and financial integration: an application of network analysis. Int Rev Financial Anal (2020) 72:101588. doi:10.1016/j.irfa.2020.101588

CrossRef Full Text | Google Scholar

35. Pan H, Fan H. Systemic risk arising from shadow banking and sustainable development: a study of wealth management products in China. Sustainability (2024) 16(10):4280. doi:10.3390/su16104280

CrossRef Full Text | Google Scholar

36. Gil-Alana LA, Abakah EJA, Abakah MK. Financial stress spillover across asian countries. Rev Financial Econ (2021) 39(2):146–62. doi:10.1002/rfe.1113

CrossRef Full Text | Google Scholar

37. Sheng X, Kim WJ, Gupta R, Ji Q. The impacts of oil price volatility on financial stress: is the covid-19 period different? Int Rev Econ and Finance (2023) 85:520–32. doi:10.1016/j.iref.2023.02.006

CrossRef Full Text | Google Scholar

38. Tan S-R, Li C, Yeap XW. A time-varying copula approach for constructing a daily financial systemic stress index. The North Am J Econ Finance (2022) 63:101821. doi:10.1016/j.najef.2022.101821

CrossRef Full Text | Google Scholar

39. Jia K, He Y, Mohsin M. Digital financial and banking competition network: evidence from China. Front Psychol (2023) 13:1104120. doi:10.3389/fpsyg.2022.1104120

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Freeman LC. Centrality in social networks: conceptual clarification. Social Netw Crit concepts Sociol (2002) 1:215–39. doi:10.1016/0378-8733(78)90021-7

CrossRef Full Text | Google Scholar

41. Barrat A, Barthelemy M, Pastor-Satorras R, Vespignani A. The architecture of complex weighted networks. Proc Natl Acad Sci (2004) 101(11):3747–52. doi:10.1073/pnas.0400087101

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Engle RF, Granger CWJ. Co-integration and error correction: representation, estimation, and testing. Econometrica: J Econometric Soc (1987) 55:251–76. doi:10.2307/1913236

CrossRef Full Text | Google Scholar

43. Van der Leij M, Hommes C, Hommes C. The formation of a core-periphery structure in heterogeneous financial networks. J Econ Dyn Control (2020) 119:103972. doi:10.1016/j.jedc.2020.103972

CrossRef Full Text | Google Scholar

44. Peng S, Tanna S, Zhou D. Financial contagion in a core-periphery interbank network. The Eur J Finance (2020) 26(7-8):691–710. doi:10.1080/1351847x.2019.1630460

CrossRef Full Text | Google Scholar

45. Yanchenko E, Sengupta S. Core-periphery structure in networks: a statistical exposition. Statistic Surv (2023) 17:42–74. doi:10.1214/23-ss141

CrossRef Full Text | Google Scholar

46. Jiang C, Sun Q, Ye T, Wang Q. Identification of systemically important financial institutions in a multiplex financial network: a multi-attribute decision-based approach. Physica A: Stat Mech Its Appl (2023) 611:128446. doi:10.1016/j.physa.2023.128446

CrossRef Full Text | Google Scholar

47. Ouyang Z, Zhou X. Multilayer networks in the frequency domain: measuring extreme risk connectedness of Chinese financial institutions. Res Int Business Finance (2023) 65:101944. doi:10.1016/j.ribaf.2023.101944

CrossRef Full Text | Google Scholar