
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Phys. , 20 February 2025
Sec. Optics and Photonics
Volume 13 - 2025 | https://doi.org/10.3389/fphy.2025.1544914
This article is part of the Research Topic Advances in High-Power Lasers for Interdisciplinary Applications, Volume II View all 6 articles
Three-dimensional active imaging systems operating in photon-starved regimes have broad applications, including remote sensing, autonomous navigation, and military surveillance. In this study, we present a noncoaxial scanning imaging system capable of generating high-quality depth and reflectivity images with an average of only ∼1 detected photon per pixel, leveraging a single-photon avalanche diode (SPAD) detector. The accompanying depth retrieval algorithm integrates an l1-norm regularizer and operates without requiring prior knowledge of the number of targets in the scene. This design significantly enhances the algorithm’s robustness and reliability for practical applications. Experimental results validate the proposed algorithm’s effectiveness, underscoring its potential for advancing three-dimensional active imaging under photon-starved conditions.
Light detection and ranging (LiDAR) is an advanced optical remote sensing technology that utilizes pulsed lasers to measure target reflectivity and distance [1–3]. Depth estimation is achieved by calculating the time of flight (ToF) of photons, defined as the time interval between the emission of a laser pulse and the receipt of the reflected signal. To differentiate laser photons from ambient photons in ToF measurements, the time-correlated single-photon counting (TCSPC) technique is widely employed [4]. This technique detects individual photons and records their arrival times relative to a synchronized laser signal. By constructing a time-correlated histogram of photon arrival times and analyzing it, both depth and reflectivity information of the scene can be extracted.
Traditional LiDAR systems typically require the detection of hundreds of photons per pixel to compensate for the intrinsic Poisson noise associated with optical detection, even when single-photon detectors are utilized. However, in scenarios where the detector is positioned far from the target or rapid data acquisition is essential, the number of detected photons is significantly reduced. This limitation challenges the effectiveness of TCSPC-based techniques. Recent advancements in image processing have enabled imaging under low-light conditions, mitigating the constraints faced by conventional LiDAR systems in photon-limited scenarios.
A prominent technique for low-light imaging is first-photon imaging (FPI). In FPI, depth and reflectivity information are retrieved in low-photon flux environments by utilizing only the first detected photon at each pixel [5]. However, in FPI configurations, the detection time of the first photon is a random variable. This introduces inefficiencies in data acquisition, particularly when using single-photon avalanche diode (SPAD) array cameras with uniform dwell times for all pixels [6]. To address this challenge, the concept of photon-efficient imaging was proposed, which, unlike FPI, employs a fixed dwell time per pixel, thereby enabling faster data acquisition [7, 8]. The effectiveness of this approach was experimentally demonstrated using a SPAD array camera in a study reported in [9].
In this paper, we propose a SPAD-based LiDAR system designed to retrieve depth and reflectivity information within a photon-efficient imaging framework. Our approach builds upon prior work [9] by eliminating the need for prior knowledge of the number of targets in the scene. This advancement significantly enhances the system’s robustness, especially in real-world scenarios where the number of targets is often unknown. Experimental results demonstrate the effectiveness of our method, achieving accurate depth and reflectivity reconstruction with raw data containing an average of approximately one detected photon per pixel.
In this part, the reflectivity and depth of the scene are calculated by solving an unconstrained optimization problem with Total Variation (TV) and sparsity regularization, respectively. We define the scene’s reflectivity as
where c is the speed of light. Since we used the SPAD detector, the dark count rate of each pixel caused by the internal structure of the SPAD is similar, so we ignored this part of noise in data processing process.
We define the total number of time bins as
where
The reflectivity estimation model can be obtained from the Poisson-process rate function (Equation 3):
where
Due to the generally small spatial variance in images of natural scenes, we incorporate a transverse-smoothness constraint into the reflectivity image using the TV norm. The resulting reflectivity image,
where
where N defines the set of pixel neighborhoods and
The optical signal of the target, in the absence of background noise, was recorded only in a limited number of time bins. However, there were multiple non-zero entries in the collected dataset
It is observed that
where
The estimation of the target’s depth is performed within the valid depth interval determined in Section 2.2, using a processing method similar to that described in Section 2.1. The same TV norm is utilized to restrict the longitudinal sparsity of the target depth. As a result, the depth estimate
where
The experimental setup is depicted in Figure 1A, with the corresponding functional block diagram shown in Figure 1B. The primary parameters of the illumination source include wavelength, pulse width, power, and repetition rate. The light source was a pulsed broadband supercontinuum laser with a wavelength range of 470 nm–2,400 nm. The laser pulse width was approximately 100 ps (Tr ≈ 100 ps), which is a critical factor influencing the imaging resolution. The light source operated at a repetition rate of 2 MHz, determining the system’s sampling speed. Its power output was 500 mW, significantly impacting the imaging distance. The scanning system employed a dual-axis galvo scan head from Thorlabs (QS15−XY−AG−ϕ15 mm, protected silver mirrors). This system comprised a scan head with mirrors, a servo driver board, and power cables. The scanning range spanned from −22.5° to 22.5°, with an input voltage range of −5 V to 5 V.
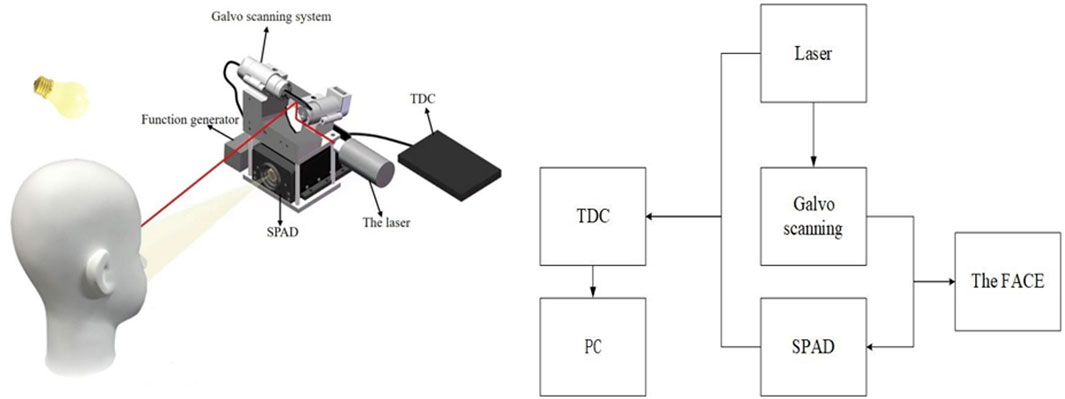
Figure 1. Single-photon imaging set-up and the functional block diagram for the experiments. (A) Experimental setup; (B) Functional block diagram.
The scan head turned 1° per input 0.22 V. The laser was incident on the center of the lower mirror (scanning X-Axis) and was emitted by the upper mirror (scanning Y-Axis) to illuminate the mannequin. The function generator controlled the scanning frequency and amplitude of the galvanometers. We chose a two-channel arbitrary waveform function generator (33612A) manufactured by Keysight Technologies. It can generate pulses up to 80 MHz and a jitter time ≤ 1 ps for precise timing.
The scan head is being controlled by a voltage signal, and for every 0.22 V of change in the voltage, the scan head turns by 1°. In the experiment, the laser beam was directed to the center of the lower mirror, which is responsible for scanning along the X-axis. The upper mirror was responsible for emitting the laser beam to illuminate the mannequin and for scanning along the Y-axis. The galvanometers are regulated by a two-channel arbitrary waveform function generator (33612A) manufactured by Keysight Technologies. This function generator has the capability of producing pulses with a frequency up to 80 MHz and precise timing with a jitter time of ≤ 1 ps, ensuring accurate and efficient 3D imaging results. In the experiment, the X-axis scan range was from −0.52° to 0.56°, which corresponds to an input voltage range of −1150 mV to 1230 mV. The Y-axis scan range was from −0.17° to 0.54°, which corresponds to an input voltage range of −370 mV to 1810 mV.
The detector utilized in the experiment was the SPAD (IDQ 100) manufactured by ID Quantique (IDQ) of Switzerland. With a time resolution of Δ = 40 ps and a photosensitive area 50 µm, the SPAD demonstrated a single-photon detection probability of 35% at λ = 500 nm. This improvement in detection efficiency led to a higher generated key rate and faster image acquisition. The high timing resolution also resulted in smaller coincidence detection windows, reducing the number of false pair detections and thus improving the signal-to-noise ratio in imaging. The signals received by the SPAD were statistically processed using a Time-to-Digital Converter (TDC) manufactured by IDQ. Each frame had a capture window of 200 ns, with a total capture duration of 1 µs. Prior to scanning, the galvanometer scanning area was adjusted, and continuous laser pulses were emitted. This setup ensured that the SPAD effectively captured the scene information for each pixel during the TDC acquisition period.
We employed a low-power laser to illuminate the face of mannequin to simulate the low luminous flux detection. The resulting reconstructed reflectivity and depth images are presented in Figure 2. The size of the reconstructed image is 110 × 120 pixels, with an average of approximately one detected photon per pixel. In order to compare the performance of the proposed algorithm, we compared its results to those obtained using the conventional algorithm, as reported in [16]. Figure 2A displays the reflectivity results obtained using the conventional algorithm. This approach fails to account for the impact of noise on the image and as a result, the reconstructed reflectivity image exhibits significant noise artifacts. In contrast, Figure 2B presents the reflectivity image obtained using the proposed algorithm, which is significantly superior to that produced by the conventional algorithm. This improvement highlights the effectiveness of the proposed algorithm in mitigating the effects of noise in low luminous flux detection.
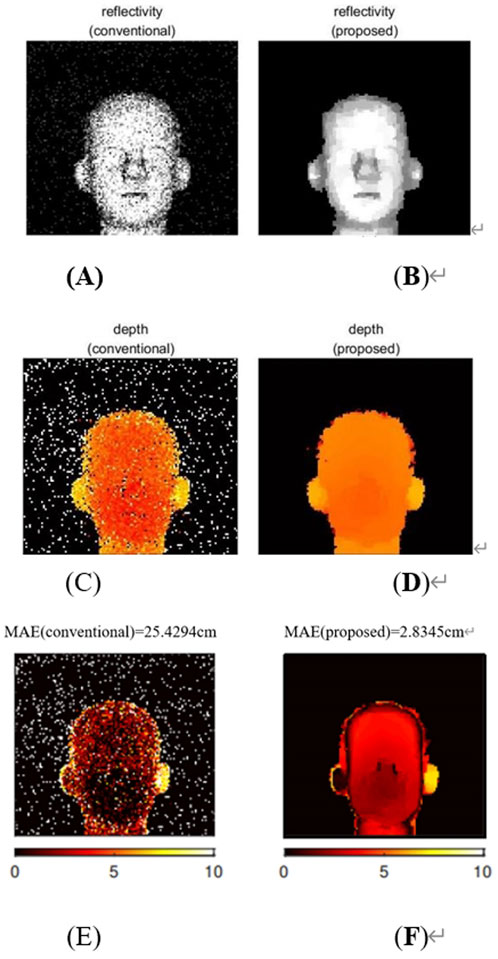
Figure 2. Reflectivity and depth reconstructions of mannequin’s face. (A, C) The reflectivity and depth estimation using pixelwise reconstruction method from Ref. [14]. (B, D) Reflectivity and depth reconstruction using the proposed method. (E, F) The mean absolute error using the proposed method.
Figures 2C, D displays the depth reconstruction results obtained through the conventional and proposed methods. As depicted in Figure 2C, the conventional algorithms utilize the time-bin with the highest photon count for each pixel as the depth interval. However, this approach entails processing data from all time-bins for each pixel, which results in poor noise filtering and longer imaging times. In contrast, the proposed FISTA algorithm selects the effective time-bins without prior knowledge of the number of scene features. By excluding irrelevant signal interference, depth estimation is performed only using these effective time-bins, a process that resembles reflectivity estimation. The resulting image is smoothed using the TV norm, effectively removing noise while preserving character features. The final depth result is presented in Figure 2D.
In the low-flux depth imaging experiments, the mean absolute error (MAE) was used to quantify the computational results of the two algorithms (Figures 2E, F). Because it does not preprocess the noise, the conventional method resulted in a high depth error, where the ground truth is obtained by detecting approximately 1,100 signal photons per pixel. Compared with conventional methods, our framework reduces the error evidently. In conclusion, our proposed algorithm successfully achieves few-photon imaging without the requirement of prior knowledge of the number of scene features, making it both effective and widely applicable.
The LiDAR system presented in this paper is specifically designed to operate in low-light conditions, where only a limited number of photons are available for detection. The primary objective of the system is to accurately retrieve reflectivity and depth information of target objects. The associated reconstruction algorithm is both robust and flexible, requiring no prior knowledge of the number of objects in the scene. This adaptability makes it particularly well-suited for real-world applications, where the number and characteristics of objects can vary significantly. The algorithm employs a mathematical framework to reconstruct target information from the sparse and noisy signals detected by the LiDAR system. Additionally, the proposed approach is versatile and can be extended to non-scanning LiDAR systems. The paper further suggests potential improvements to the reconstruction algorithm by incorporating more advanced regularization terms. Techniques such as joint basis pursuit [17] or data-driven neural networks [18] could enhance the quality and resolution of the reconstructed images. This technology holds significant potential for a wide range of applications, including scenarios with low photon reflectivity in underwater environments, long-distance imaging, and conditions affected by atmospheric turbulence.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
YC: Methodology, Writing–original draft. YS: Formal Analysis, Project administration, Supervision, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The National Key Research and Development Program of China (Nos. 2023YFF0720402, and 2023YFF0616203); and the National Natural Science Foundation of China (No. T2293751).
Author YC was employed by Hengdian Group Tospo Lighting Company Limited.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declare that no Generative AI was used in the creation of this manuscript.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Barbosa PR. Remapping the world in 3D. IEEE Potentials (2010) 29(2):21–5. doi:10.1109/MPOT.2009.935239
2. Chen H, Bai Z, Chen J, Li X, Zhu ZH, Wang Y, et al. Diamond Raman vortex lasers. ACS Photon (2025) 12(1):55–60. doi:10.1021/acsphotonics.4c01852
3. Xu G, Pang Y, Bai Z, Wang Y, Lu Z. A fast point clouds registration algorithm for laser scanners. Appl Sci (2021) 11(8):3426. doi:10.3390/app11083426
4. Castleman AW, Toennies JP, Zinth W. Advanced time-correlated single photon counting techniques. Springer Berlin Heidelberg (2005).
5. Kirmani A, Venkatraman , Shin D, Colaço A, Wong FNC, Shapiro JH, et al. First-photon imaging. Science (2014) 343(6166):58–61. doi:10.1126/science.1246775
6. Morimoto K, Ardelean A, Wu ML, Ulku AC, Antolovic IM, Bruschini C, et al. Megapixel time-gated SPAD image sensor for 2D and 3D imaging applications. Optica (2020) 7(4):346. doi:10.1364/OPTICA.386574
7. Shin D, Kirmani A, Goyal VK, Shapiro JH. Computational 3D and reflectivity imaging with high photon efficiency. IEEE (2015) 46–50. doi:10.1109/ICIP.2014.7025008
8. Shin D, Kirmani A, Goyal VK, Shapiro JH. Photon-efficient computational 3-D and reflectivity imaging with single-photon detectors. IEEE Trans Comput Imaging (2014) 1(2):112–25. doi:10.1109/TCI.2015.2453093
9. Shin D, Xu F, Venkatraman D, Lussana R, Villa F, Zappa F, et al. Photon-efficient imaging with a single-photon camera. Nat Commun (2016) 7:12046. doi:10.1038/ncomms12046
10. Fox M, Javanainen J. Quantum optics: an introduction. Phys Today (2007) 60(9):74–5. doi:10.1063/1.2784691
11. Coates PB. The correction for photon `pile-up' in the measurement of radiative lifetimes. J Phys E Scientific Instr (2002) 1(8):878–9. doi:10.1088/0022-3735/1/8/437
12. Measurements FL, Tomogrphy O, Imaging FL, et al. Time correlated single photon counting. (2011).
13. Dou Z, Zhang B, Yu X. A new alternating minimization algorithm for total Variation image reconstruction. In: International conference on wireless. IET (2016). doi:10.1049/cp.2015.0936
14. Afonso MV, Bioucas-Dias , José M, Figueiredo MAT. Fast image recovery using variable splitting and constrained optimization. IEEE Trans Image Process (2010) 19(9):2345–56. doi:10.1109/TIP.2010.2047910
15. Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. Siam J Imaging Sci (2009) 2(1):183–202. doi:10.1137/080716542
16. Buller G, Wallace A. Ranging and three-dimensional imaging using time-correlated single-photon counting and point-by-point acquisition. IEEE J Selected Top Quan Electronics (2007) 13(4):1006–15. doi:10.1109/JSTQE.2007.902850
17. Tosic I, Drewes S. Learning joint intensity-depth sparse representations. Image Process IEEE Trans (2014) 23(5):2122–32. doi:10.1109/TIP.2014.2312645
Keywords: lidar, 3D imaging, SPAD detector, TCSPC, TOF
Citation: Chen Y, Zhang Z, Wang L, Liu P and Shi Y (2025) Single-photon imaging for 3D reflectivity and depth estimation in low-light conditions. Front. Phys. 13:1544914. doi: 10.3389/fphy.2025.1544914
Received: 13 December 2024; Accepted: 13 January 2025;
Published: 20 February 2025.
Edited by:
Zhenxu Bai, Hebei University of Technology, ChinaReviewed by:
Yajun Pang, Hebei University of Technology, ChinaCopyright © 2025 Chen, Zhang, Wang, Liu and Shi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yi Chen, Y2hlbnlpQGNqbHUuZWR1LmNu; Yan Shi, c2hpeWFuQGNqbHUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.