A tripartite evolutionary game analysis of stakeholder decision-making behavior in the internet of vehicles data supply chain

The Internet of Vehicles, as a new generation of information infrastructure that integrates multiple industries such as automotive, information communication, and transportation, is currently in a rapid development stage. However, its data supply chain involves numerous stakeholders and faces severe challenges in terms of data sharing, security, and regulation. To address this issue, this paper utilizes evolutionary game theory, setting key variables such as the strategy set, probability combination, and game behavior of each stakeholder to construct a tripartite evolutionary game model and its replicator dynamic equations, involving the Internet of Vehicles data sharing platform, vehicle manufacturers, and sellers. We studied the equilibrium solutions of this model and conducted an in-depth analysis of the local stability of the equilibrium state. Through simulation analysis, we explored the interference factors and their mechanisms of action in the interaction and dynamic changes during the evolutionary process and analyzed the impact of different parameters on the system’s evolution. The experimental results show that compensation mechanisms and the risk of information leakage have a significant impact on decision-making behavior; enhancing the security technology of the data-sharing platform and the construction of the data governance system, as well as implementing corresponding incentive and punitive measures, can promote the system to reach a stable state. The results of this study provide a scientific and reasonable decision-making basis for core enterprises in the Internet of Vehicles data supply chain, helping them to more effectively supervise and coordinate the data sharing behavior of downstream enterprises, thereby enhancing the collaborative effect of the entire supply chain system and improving the overall competitiveness and stability of the supply chain.

1 Introduction

As a new generation of information infrastructure that links multiple industries such as the automotive industry, information and communication, transportation, and electric power, the Internet of Vehicles has become an important driving force for promoting the transformation and upgrading of the automotive industry. Not only has it promoted the vigorous development of the digital economy, but it has also improved the efficiency of data resource utilization. With the integration of cutting-edge technologies such as smart cars and the Internet of Things, vehicles are no longer merely simple means of transportation but have become huge data generation terminals. This development trend has not only posed new demands on transportation systems and urban planning but has also made the scientific management and efficient utilization of Internet of Vehicles data urgent. Currently, the Internet of Vehicles not only involves the massive data generated by built-in and external vehicle devices but also includes numerous data processing entities such as intelligent connected vehicle manufacturers, Internet of Vehicles service platforms, and operating enterprises. Moreover, data collaboration among various institutions in the industry chain has gradually exposed difficulties such as data sharing, data security, and data regulation [1–3].

To address these issues, scholars have conducted extensive work in areas such as privacy protection in vehicular networks, data classification and grading, and trust mechanisms. In terms of privacy protection, He et al. [4] proposed a method based on blockchain technology and local differential privacy, aiming to protect the location data privacy in vehicular networks. Han et al. [5] utilized an NDN-based IoV architecture combined with mobile edge computing technology to address issues related to data transmission, security, and privacy protection in IoV. Xu et al. [6] proposed a secure privacy protection communication protocol based on elliptic curve cryptography to tackle various security threats and attacks that may arise in vehicular network systems. Wang et al. [7] proposed a blockchain-based privacy-preserving federated learning scheme, on which they developed a reputation-based incentive mechanism to encourage vehicular network users to actively participate in federated learning and remain honest. In terms of data classification and grading, Chen et al. [8] proposed a blockchain model based on master-slave multi-chains, aiming to address the challenges of data classification, grading, storage, and access control. This model, based on data stakeholders, master-slave chain networks, and IPFS, enables data owners to classify and manage sensitive data. Bai et al. [9] proposed a hierarchical model for transportation administrative data, which is based on factors such as scale, precision, and depth. This model establishes data levels through security risk analysis, addressing the classification and grading issues in transportation administrative data management, and helps prevent data leakage and illegal use. Feng et al. [10] introduced the development of data security classification and grading, analyzed the principles of data security classification and grading in some fields and shared practices, and finally put forward ideas and development suggestions for data security classification and grading. In terms of trust mechanisms, Chen et al. [11] adopted a deep reinforcement learning approach and proposed an algorithm called deep policy gradient action quantization (DPGAQ) to address trust and security issues in intelligent vehicular networks. Rathee et al. [12] proposed a vehicular network trust framework based on the tidal trust mechanism (TTM) and contract theory (CT). TTM evaluates the trustworthiness between devices, and CT verifies the reliability of context predictions, improving the trust and accuracy of data sharing. Haseeb et al. [13] proposed an autonomous vehicle routing protocol for vehicular networks based on 6G technology, employing simulated annealing optimization technology to establish the routing process, and improving the energy optimization of IoT vehicles. Wang et al. [14] proposed a federated learning-based trust evaluation scheme for vehicular cloud collaborative systems, constructing a hierarchical trust model. Through federated learning, they achieved personalization at the device, data, and model levels, addressing the issue of node trust changes caused by network topology changes.

Most of the aforementioned literature has partially achieved the security and governance of vehicular network data sharing from a technical perspective. However, these solutions have some limitations and ignore the impact and constraints of different stakeholders’ behavioral strategies on other participants. They fail to use dynamic system theory to analyze the decision-making behaviors of each participant [15]. From an economic perspective, vehicular networks involve data processing entities composed of multiple stakeholders, and data sharing in vehicular networks is a continuous and bounded rationality process in which all parties seek to maximize their own interests [16]. For example, vehicle manufacturers may choose not to share or provide false information services to evade legal responsibilities for data security governance. Vehicle sales companies may choose not to share or upload distorted data to avoid the leakage of trade secrets, which will hinder the development of the vehicular network industry.

Evolutionary game theory [17, 18] can analyze the costs, benefits, and losses of each stakeholder’s decision-making behavior in the system and dynamically reflect the evolutionary trends of each party’s strategic choices [19]. Therefore, this paper constructs a game model based on evolutionary game theory to model the behavioral interactions of the three stakeholders in the vehicular network data sharing platform (core enterprises), manufacturing enterprises, and sales enterprises (downstream enterprises). Through numerical simulations, the possibility of the existence of game equilibrium and its evolutionary trends are verified, focusing on the impact of factors such as data leakage risk, compensation mechanisms, and synergistic effects on each party’s strategic choices. This paper provides reasonable suggestions for the core enterprises in the vehicular network data supply chain to better regulate and coordinate the data sharing behaviors of downstream enterprises, in order to achieve synergistic effects among downstream enterprises, improve the connectivity of the supply chain system, and enhance the overall benefits of the supply chain.

2 Basic assumptions

2.1 Basic assumptions

Assumption 1. The game participants consist of three behavioral entities, namely, the Internet of Vehicles Data Sharing Platform (core enterprise), manufacturing enterprises (equipment manufacturers, car manufacturers, etc.), and sales enterprises (4S stores, insurance companies, etc.). The three parties play different roles in the supply chain game, with the Internet of Vehicles Data Sharing Platform serving as the core, holding a leadership position, and being responsible for the distribution of benefits and the supervision of downstream enterprises.

Assumption 2. The strategy sets of manufacturing enterprises and sales enterprises are both either to share data or not to share data. Not sharing data will lead to information lag. The core enterprise needs to share information with other members of the supply chain and monitor their data-sharing behavior. Its strategy set is either to supervise or not to supervise.

Assumption 3. The core enterprise encourages downstream enterprises to share data through management mechanisms to improve supply chain efficiency. If downstream enterprises fail to share key information in a timely manner and cause damage to the overall interests of the supply chain, the platform will impose penalties, reducing their benefits and compensating other enterprises that share data. This mechanism is only activated when the platform implements a supervision strategy.

Assumption 4. When both manufacturing enterprises and sales enterprises share data, a synergistic effect is triggered, meaning the total revenue of the entire supply chain will exceed the sum of the revenues of each enterprise. Conversely, if either party or both parties do not share data, the synergistic effect cannot be achieved.

Assumption 5. The probability of the core enterprise choosing the “supervision” strategy is $x$, and the probability of “no supervision” is 1-$x$; The probability that the manufacturing enterprise chooses the strategy of “data sharing” is $y$, and the probability of “not data sharing” is 1-$y$; The probability of sales enterprises choosing the “share data” strategy is $z$, and the probability of “not sharing” is 1-$z$. Where $x$, $y$, and $z$ are variables whose values range from [0,1].

Based on the aforementioned assumptions, the profit and loss analysis for the core enterprise encompasses its fundamental revenue, synergistic gains from supply chain collaboration, data sharing incentives, supervision costs, sharing costs, and the potential risks associated with data leakage. Similarly, the profit and loss analysis for downstream enterprises includes their basic revenue, synergistic benefits, data sharing rewards, sharing costs, and information leakage risks. Evidently, synergistic gains exhibit a positive correlation with the synergy coefficient, the enterprises’ data utilization efficiency, and the sufficiency of data sharing. Specifically, the synergistic gains for the IoV platform, manufacturing enterprises, and sales enterprises are denoted as $\beta \left(A_2+A_3\right)B_1$, $\beta \left(A_1+A_3\right)B_2$, and $\beta \left(A_1+A_2\right)B_3$, respectively. When the IoV data-sharing platform implements a monitoring strategy, a compensation mechanism is activated. Entities that do not share data are required to provide compensation to those who do, and the compensation amount is positively correlated with the compensation coefficient and the sufficiency of data provided by other entities. For instance, if the IoV platform shares data while the manufacturing enterprise does not, the manufacturer is obligated to pay a compensation fee, denoted as $\gamma A_1$, to the platform. Should the sales enterprise also abstain from data sharing, it is likewise required to remit compensation to the platform. In this scenario, the IoV platform will receive a total compensation of $2\gamma A_1$ from its downstream enterprises. All three parties involved in data sharing face the risk of data leakage, with the magnitude of this risk being contingent upon the sufficiency of data provided by each entity. The data leakage risks for the IoV platform, manufacturing enterprises, and sales enterprises are represented by $\alpha A_1$, $\alpha A_2$ and $\alpha A_3$., respectively. Table 1 provides a comprehensive list of the parameters employed in the model, along with their corresponding descriptions.

Table 1

Table 1. Description of model parameters.

2.2 Payoff matrix

In this paper, the strategy combination of the three parties will be represented in the form of a set, denoted as $S_i=\left\{m,n,k\right\}$, where $i=\left(1,2,3,4,5,6,7,8\right)$. The values of $m,n,k$ are either 0 or 1. The strategy of the Internet of Vehicles (IoV) platform is represented by $m$, where $m=0$ indicates that the IoV platform adopts a non-supervision strategy, and $m=1$ indicates that a supervision strategy is implemented; $n$ represents the strategy adopted by the manufacturing enterprise, where $n=0$ indicates a non-sharing strategy, and $n=1$ indicates a sharing strategy; $k$ represents the strategy adopted by the sales enterprise, where $k=0$ indicates a non-sharing strategy, and $k=1$ indicates a sharing strategy. The specific payoff matrix is shown in Table 2.

Table 2

Table 2. The profit matrix of the three participants.

3 Model establishment

3.1 Replicator dynamics equation and phase diagram of the internet of vehicles platform

When the Internet of Vehicles (IoV) platform selects “no supervision”, the expected return is $P_{11}$, the expected return when it selects “supervision” is $P_{12}$, the average expected return is $P_1$.

$\left\{\begin{array}{l}\begin{array}{l}\begin{array}{l}{P}_{11}=\left(1-y\right)\left(1-z\right)\left(E_1-K_1-\alpha A_1\right)+y\left(1-z\right)\\ \left(E_1-K_1-\alpha A_1+A_2{B}_1\right)+\left(1-y\right)z\left(E_1-K_1-\alpha A_1+A_3{B}_1\right)\\ +yz\left(E_1-K_1-\alpha A_1+\beta \left(A_2+A_3\right)B_1\right);\end{array}\\ \begin{array}{l}{P}_{12}=\left(1-y\right)\left(1-z\right)\left(E_1-K_1-\alpha A_1-K_2+2\gamma A_1\right)+y\left(1-z\right)\\ \left(E_1-K_1-\alpha A_1-K_2+A_2{B}_1+\gamma A_1\right)\\ +\left(1-y\right)z\left(E_1-K_1-\alpha A_1-K_2+A_3{B}_1+\gamma A_1\right)\\ +yz\left(E_1-K_1-\alpha A_1-K_2+\beta \left(A_2+A_3\right)B_1\right);\end{array}\end{array}\\ P_1=\left(1-x\right)P_{11}+x{P}_{12}\end{array}\right)(1)$

The replication dynamic equation of the IoV platform is

$F\left(x\right)=\frac{dx}{dt}=x\left(P_{12}-P_1\right)=x\left(1-x\right)\left(2\gamma A_1-y{A}_1\gamma -A_1\gamma z-K_2\right)(2)$

Take the first derivative of $x$:

$\frac{dF\left(x\right)}{dx}=\left(2x-1\right)G\left(y,z\right)=\left(2x-1\right)\left(K_2-2\gamma A_1+\gamma A_{1}y+\gamma A_{1}z\right)(3)$

$G\left(y,z\right)=\left(K_2-2\gamma A_1+\gamma A_{1}y+\gamma A_{1}z\right)(4)$

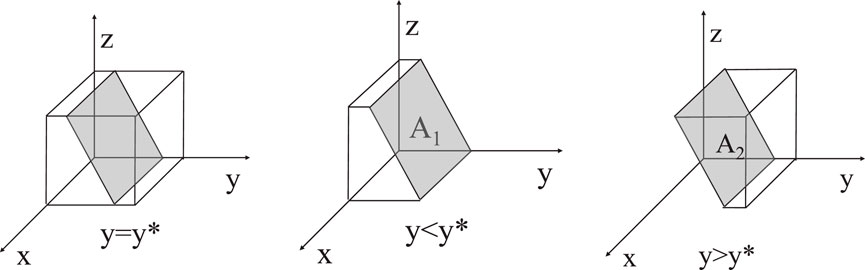
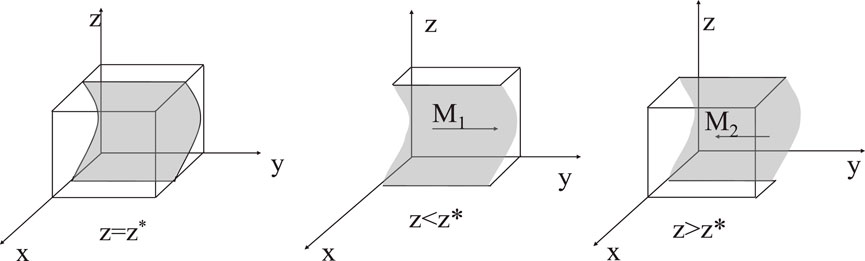
The probability that the IoV platform chooses supervision is in a stable state, it needs to satisfy condition $F\left(x\right)=0$ and $\frac{dF\left(x\right)}{x}<0$. The derivative of $G\left(y,z\right)$ with respect to y is less than 0. Therefore, $G\left(y,z\right)$ is a decreasing function of $y$. Let $y=y^{*}=\frac{2\gamma A_1-K_2-\gamma A_{1}z}{\gamma A_1}$, at this time $G\left(y,z\right)=0$, $\frac{dF\left(x\right)}{x}=0$ the IoV platform can not determine the stability strategy; when $y<y^{*}$, then $G\left(y\right)<0$, and at this point $\frac{dF\left(x\right)}{x}<0$, $x=1$ is the stable point for the IoV platform. In the same way, if $y>y^{*}$, then $G\left(y\right)>0$, and at this point $\frac{dF\left(x\right)}{x}<0$, $x=0$ is the stable point of the IoV platform. Figure 1 shows the strategy evolution phase diagram of the platform.

Figure 1

Figure 1. Phase diagram of IoV data sharing platform.

3.2 Replicator dynamics equation and phase diagram of manufacturing enterprise

The expected return of the manufacturing enterprise when it selects “not sharing” is $P_{21}$, the expected return when it selects “sharing” is $P_{22}$, and the average expected return is $P_2$.

$\begin{array}{l}\begin{array}{l}\begin{array}{l}{P}_{21}=\left(1-x\right)\left(1-z\right)\left(E_2+A_1{B}_2\right)+\left(1-x\right)z\left(E_2+\left(A_1+A_3\right)B_2\right)\\ +x\left(1-z\right)\left(E_2+A_1{B}_2-\gamma A_1\right)\\ +xz\left(E_2+\left(A_1+A_3\right)B_2-\gamma \left(A_1+A_3\right)\right);\end{array}\\ \begin{array}{l}{P}_{22}=\left(1-x\right)\left(1-z\right)\left(E_2+A_1{B}_2-K_3-\alpha A_2\right)\\ +\left(1-x\right)z\left(E_2+\beta \left(A_1+A_3\right)B_2-K_3-\alpha A_2\right)\\ +x\left(1-z\right)\left(E_2+A_1{B}_2+\gamma A_2-K_3-\alpha A_2\right)\\ +xz\left(E_2-K_3-\alpha A_2+\beta \left(A_1+A_3\right)B_2\right);\end{array}\end{array}\\ P_2=\left(1-y\right)P_{21}+y{P}_{22};\end{array}(5)$

The replication dynamic equation of a manufacturing firm is:

$\begin{array}{l}F\left(y\right)=\frac{dy}{dt}=\mathrm{y}\left(P_{22}-P_2\right)=y\left(y-1\right)(K_3+\alpha A_2+z{A}_1{B}_2+z{A}_3{B}_2\\ -\gamma A_{1}x-\gamma A_{2}x-z{A}_1{B}_2\beta -z{A}_3{B}_2\beta +A_2\beta xz-A_3\beta xz);\end{array}(6)$

By taking the derivative of y, can obtain

$\begin{array}{l}\frac{dF\left(y\right)}{dy}=\left(2y-1\right)(k_3+\alpha A_2+A_1{B}_{2}z+A_3{B}_{2}z-\gamma A_{1}x-\gamma A_{2}x\\ -\beta A_1{B}_{2}z-\beta A_3{B}_{2}z+\gamma A_{2}xz-\gamma A_{3}xz)\end{array}(7)$

Based on the stability theorem of differential equation, the probability that the manufacturing enterprise chooses to share is in a stable state must meet the following conditions: $F\left(y\right)=0$ and $\frac{dF\left(y\right)}{y}<0$, because $G\left(z\right)$ is an increasing function, so when

$z=z^{*}=\frac{x\left(\gamma A_1+\gamma A_2\right)-k_3-\alpha A_2}{\left(A_1{B}_2+A_3{B}_2-\beta A_1{B}_2-\beta A_3{B}_2+\gamma A_{2}x-\gamma A_{3}x\right)}(8)$

$G\left(z\right)=0$, $\frac{dF\left(z\right)}{dz}=0$, can not determine the stability strategy; When $z<z^{*}$, $G\left(z\right)<0$, $\frac{dF\left(z\right)}{dz}<0y=1$ reaches the stable state, the strategy evolution phase diagram of the manufacturing enterprise is shown in Figure 2.

Figure 2

Figure 2. Phase diagram of manufacturing enterprise.

3.3 Replicator dynamics equation and phase diagram of sales enterprise

The expected return of a selling firm when it selects “Not share” is $P_{31}$, the expected return when it selects “share” is $P_{32}$, and the average expected return is $P_3$.

$\begin{array}{l}\begin{array}{l}{P}_{31}=\left(1-x\right)\left(1-y\right)\left(E_3+A_1{B}_3\right)+\left(1-x\right)y\left(E_3+\left(A_1+A_2\right)B_3\right)\\ +x\left(1-y\right)\left(E_3+A_1{B}_3-\gamma A_1\right)\\ +xy\left(E_3+\left(A_1+A_2\right)B_3-\gamma \left(A_1-A_2\right)\right);\end{array}\\ \begin{array}{l}{P}_{32}=\left(1-x\right)\left(1-y\right)\left(E_3+A_1{B}_3-K_4-\alpha A_3\right)\\ +\left(1-x\right)y\left(E_3+\beta \left(A_1+A_2\right)B_3-K_4-\alpha A_3\right)\\ +x\left(1-y\right)\left(E_3+A_1{B}_3+\gamma A_3-K_4-\alpha A_3\right)\\ +xy\left(E_3-K_4-\alpha A_3+\beta \left(A_1+A_2\right)B_3\right);\end{array}\\ P_3=\left(1-z\right)P_{31}+z{P}_{32};\end{array}(9)$

The replication dynamic equation for a sales enterprise is:

$\begin{array}{l}F\left(z\right)=\frac{dz}{dt}=x\left(P_{32}-P_3\right)=z\left(z-1\right)(K_4+\alpha A_3+y{A}_1{B}_3+y{A}_2{B}_3\\ -\gamma x{A}_1-\gamma x{A}_3-y\beta A_1{B}_3-y\beta A_2{B}_3-\gamma xy{A}_2+\gamma xy{A}_3);\end{array}(10)$

For derivation $F\left(z\right)$:

$\begin{array}{l}\frac{dF\left(z\right)}{z}=\left(2z-1\right)(k_4+\alpha A_3+y(A_1{B}_3+A_2{B}_3-\beta A_1{B}_3-\beta A_2{B}_3\\ +x\left(-\gamma A_2+\gamma A_3\right))+x\left(-\gamma A_1-\gamma A_3\right));\end{array}(11)$

Based on the stability theorem of differential equation, the probability that the sales enterprise chooses to share is in a stable state must meet the following conditions: $F\left(z\right)=0,\frac{dF\left(z\right)}{dz}<0$. Because $\frac{dH\left(y\right)}{dy}>0$, so $H\left(y\right)$ is an increasing function of $y$. When $y=y^{*}=\frac{x\left(\gamma A_1+\gamma A_3\right)-k_4-\alpha A_3}{\left(A_1{B}_3+A_2{B}_3-\beta A_1{B}_3-\beta A_2{B}_3+x\left(-\gamma A_2+\gamma A_3\right)\right)}$, $H\left(y\right)=0,\frac{dF\left(z\right)}{dz}=0$, the stability strategy could not be determined; When $y<y^{*},H\left(y\right)<0,\frac{dF\left(z\right)}{dz}<0$, $z=1$ a steady state is attained, and vice versa $z=0$, a steady state is attained. The strategy evolution phase diagram of the sales enterprise is shown in Figure 3.

Figure 3

Figure 3. Sales enterprise phase diagram1.

4 Stability analysis of the model’s equilibrium points

4.1 Jacobian matrix

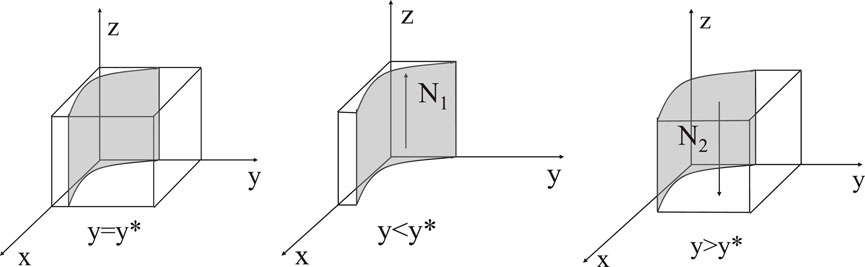
The asymptotically stable solution of the replicator dynamics equation is a strict Nash equilibrium. In the evolutionary game system, eight pure strategy equilibrium solutions can be obtained. According to Lyapunov’s stability theory [20], when all eigenvalues of the Jacobian matrix are negative, the corresponding equilibrium point is the asymptotically stable point of the system. The Jacobian matrix is shown as (12).

$J=\left[\begin{array}{ccc}\frac{\mathrm{\partial }F\left(x\right)}{\mathrm{\partial }x}& \frac{\mathrm{\partial }F\left(x\right)}{\mathrm{\partial }y}& \frac{\mathrm{\partial }F\left(x\right)}{\mathrm{\partial }z}\\ \frac{\mathrm{\partial }F\left(y\right)}{\mathrm{\partial }x}& \frac{\mathrm{\partial }F\left(y\right)}{\mathrm{\partial }y}& \frac{\mathrm{\partial }F\left(y\right)}{\mathrm{\partial }z}\\ \frac{\mathrm{\partial }F\left(z\right)}{\mathrm{\partial }x}& \frac{\mathrm{\partial }F\left(z\right)}{\mathrm{\partial }y}& \frac{\mathrm{\partial }F\left(z\right)}{\mathrm{\partial }z}\end{array}\right]=\left[\begin{array}{ccc}{F}_{11}& F_{12}& F_{13}\\ F_{21}& F_{22}& F_{23}\\ F_{31}& F_{32}& F_{33}\end{array}\right](12)$

Among them,

$\left\{\begin{array}{l}{F}_{11}=\left(2x-1\right)\left(K_2-2\gamma A_1+\gamma A_{1}y+\gamma A_{1}z\right)\\ F_{12}=x\left(x-1\right)\gamma A_1\\ F_{13}=x\left(x-1\right)\gamma A_1\\ F_{21}=-y\left(y-1\right)\left(\gamma A_1+\gamma A_2-\gamma A_{2}z+\gamma A_{3}z\right)\\ \begin{array}{l}{F}_{22}=\left(2y-1\right)(k_3+\alpha A_2+A_1{B}_{2}z+A_3{B}_{2}z-\gamma A_{1}x\\ -\gamma A_{2}x-\beta A_1{B}_{2}z-\beta A_3{B}_{2}z+\gamma A_{2}xz-\gamma A_{3}xz)\end{array}\\ F_{23}=y\left(y-1\right)\left(A_1{B}_2+A_3{B}_2-\beta A_1{B}_2-\beta A_3{B}_2+\gamma A_{2}x-\gamma A_{3}x\right)\\ F_{31}=-z\left(z-1\right)\left(\gamma A_1+\gamma A_3-\gamma A_{2}y-\gamma A_{3}y\right)\\ F_{32}=z\left(z-1\right)\left(A_1{B}_3+A_2{B}_3-\beta A_1{B}_3-\beta A_2{B}_3+\gamma A_{2}x+\gamma A_{3}x\right)\\ \begin{array}{l}{F}_{33}=\left(2z-1\right)(k_4+\alpha A_3+A_1{B}_{3}y+A_2{B}_{3}y-\gamma A_{1}x\\ -\gamma A_{3}x-\beta A_1{B}_{3}y-\beta A_2{B}_{3}y-\gamma A_{2}xy+\gamma A_{3}xy)\end{array}\end{array}\right.(13)$

4.2 Stability analysis

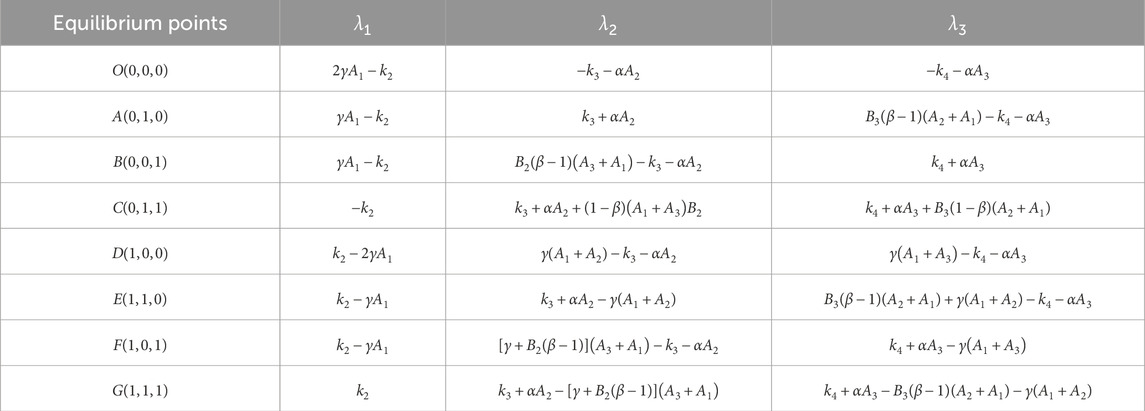
By substituting the eight equilibrium points into the Jacobian matrix, the eigenvalues of each equilibrium point can be obtained, as shown in Table 3. From the above analysis, it can be seen that when the parameters change, the evolutionary stability strategy of the system will also change. The stability of the equilibrium points is shown in Table 4. Among them, there are three unstable points, and the remaining uncertain points will be discussed next.

Table 3

Table 3. System equilibrium points and eigenvalues.

Table 4

Table 4. Stability analysis of equilibrium points.

Case1: When $2\gamma A_1-k_2<0$, Figure 4 shows the evolutionary process of the three-way evolutionary game at this time. There was an evolutionary stability point in the system, and the corresponding strategy was (no supervision, no sha no sharing). Because the low compensation cost failed to cover the supervision cost, the platform tended to give up supervision, resulting in the inability to effectively restrict the behavior of subordinate enterprises. At this time, the compensation coefficient can be increased to encourage the IoV platform to take regulatory measures. When the compensation amount reaches the corresponding level, $2\gamma A_1-k_2<0$ it is no longer met. At this time, the probability of the IoV platform choosing supervision increases, and its strategy will also affect the strategic choice of the other two subjects. Similarly, reducing regulatory costs or increasing $A_1$ will also have an impact on their strategies. Figure 4 shows that the adjustment of initial probability has no significant effect on the evolution of the system, which means that other factors may play a more critical role in the outcome of the game.

Figure 4

Figure 4. Diagram of the evolution path under case1.

Case 2: when $k_3+\alpha A_2+\left(1-\beta \right)\left(A_1+A_3\right)B_2<0$, $k_4+\alpha A_3+B_3\left(1-\beta \right)\left(A_2+A_1\right)<0$, Figure 5 shows the evolutionary process of the three-way evolutionary game at this time. For the manufacturing enterprise,the cost of data sharing and the loss caused by data leakage are smaller than the benefits obtained by using the sharing platform of the IoV and data of sales companies. Similarly, for sales enterprises, the cost of data sharing and the loss caused by data leakage are smaller than the benefit obtained by using the data of IoV sharing platform and manufacturing enterprises. At this time, the system has an evolutionary stability point, and the evolutionary strategy is (no supervision, sharing, sharing), which is a relatively ideal equilibrium state, that is, the downstream enterprises adopt an active sharing strategy, while the sharing platform does not need to spend regulatory costs for supervision. In this case, the sum of the marginal cost of data sharing by the manufacturer plus the potential loss caused by data leakage is lower than the marginal benefit of data sharing with the seller through the sharing platform. Similarly, the cost of data sharing and the risk of data breach for vendors are lower than the economic benefit of the data obtained from the shared platform. Under this condition, the system achieves an evolutionarily stable strategy, that is, downstream enterprises tend to implement active data sharing strategies, while the sharing platform does not have to bear additional regulatory costs to ensure the overall stability of the data supply chain of the Internet of vehicles.

Figure 5

Figure 5. Diagram of the evolution path under case 2.

Case 3: When $k_2-2\gamma A_1<0$, $\gamma \left(A_1+A_2\right)-k_3-\alpha A_2<0$, $\gamma \left(A_1+A_3\right)-k_4-\alpha A_3<0$, Figure 6 shows the evolutionary process of the three-way evolutionary game at this time. The system reaches a stable point, the corresponding strategy is (supervision, no sharing, no sharing). At this time, the compensation obtained by the supervision of the sharing platform is greater than the cost of supervision, which makes the sharing platform more inclined to supervision for benefits, while the compensation obtained by vehicle manufacturers and sales companies is not enough to make up for the loss caused by the sharing cost and information disclosure. And they are more inclined to not share strategy. When the compensation coefficient increases, it will make the IoV data sharing platform more inclined to the regulatory strategy. When the compensation coefficient reaches a certain threshold, the latter two inequalities are no longer valid. At this time, all parties in the data supply chain will change their strategies, which will affect the strategy of the IoV data sharing platform, that is, tend to be non-regulated. In addition, increasing the adequacy of shared information and reducing the sharing cost and information leakage risk will cause the sharing platform to modify its strategy and tend to not supervise, and finally all parties in the data supply chain will tend to share the strategy.

Figure 6

Figure 6. Diagram of the evolution path under case 3.

Case 4: when $k_2-\gamma A_1<0$, $k_4+\alpha A_3-\gamma \left(A_1+A_3\right)<0$, $\left[\gamma +B_2\left(\beta -1\right)\right]\left(A_3+A_1\right)-k_3-\alpha A_2<0$, Figure 7 shows the evolutionary process of the three-way evolutionary game at this time. The system’s stable strategy is (supervision, non-sharing, sharing), then the sharing platform accepts the compensation of a single entity greater than the supervision cost, which makes it tend to choose the supervision strategy. For manufacturing enterprises, the benefits and compensation from processing information are less than the costs and losses from data leakage, so they choose not to share. On the other hand, the compensation accepted by the sales enterprises can make up for the cost and loss of information leakage, so they choose to share. When the compensation factor is increased, the sharing platform will choose the regulatory strategy. When the compensation coefficient reaches a certain threshold, manufacturing companies will rely on compensation to cover the sharing costs and losses caused by data breaches, and choose the sharing strategy. Therefore, the strategies of the downstream enterprises will affect the strategic choice of the sharing platform. Since the compensation coefficient has sufficient binding force on the downstream enterprises, the sharing platform does not need to choose a regulatory strategy.

Figure 7

Figure 7. Diagram of the evolution path under case 4.

Case 5: when $k_3+\alpha A_2-\gamma \left(A_1+A_2\right)<0,k_2-\gamma A_1<0$, $B_3\left(\beta -1\right)\left(A_2+A_1\right)+\gamma \left(A_1+A_2\right)-k_4-\alpha A_3<0$, there is a stability point in the system, and the corresponding stability strategies are (supervision, sharing, not sharing); Similar to case 4, the compensation of a single entity accepted by the IoV data sharing platform is still greater than the regulatory cost. At this time, the revenue and compensation obtained by the sales enterprise are less than the sharing cost and loss of data leakage, so they choose not to share, while the compensation accepted by the manufacturing enterprise can make up for the cost and loss of data leakage, so they choose to share.

5 Simulation analysis

5.1 The impact of various initial strategies on evolution

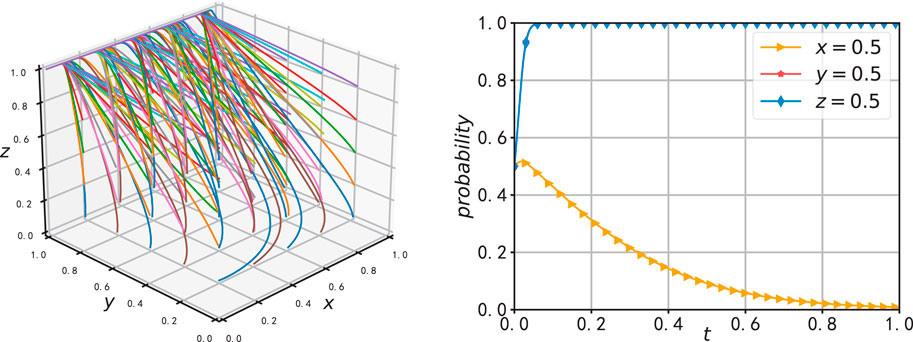
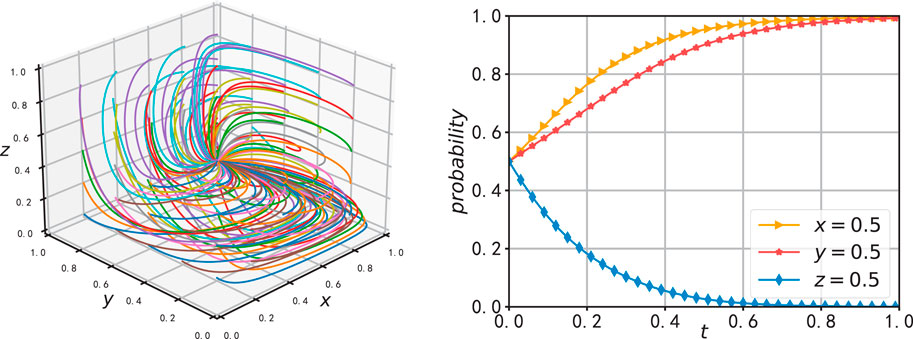
Due to the interconnected nature of the data-sharing platform for vehicle networks, manufacturing enterprises, and sales enterprises within the same dynamic system, the stability of strategies from one side will affect the other two. In the simulation experiment, the same initial parameters as in Case 2 were used. The initial selection probabilities of the three stakeholders were incrementally increased to analyze the impact of these changes on the evolutionary path.

In Figure 8, the initial selection probabilities of $y$ and $z$ are set to 0.5. By changing the initial probability value of the Internet of Vehicles data sharing platform (core enterprise), the evolution trend of the system is observed. As shown in Figures 9A, B, when $x$ is gradually increased from 0.2 to 0.8, the evolution speed of the data sharing strategy adopted by manufacturing and sales enterprises is increased and converges at a relatively stable speed. This indicates that the gradual increase in the regulatory intensity of the sharing platform will further accelerate the decision-making of downstream enterprises regarding data sharing.

Figure 8

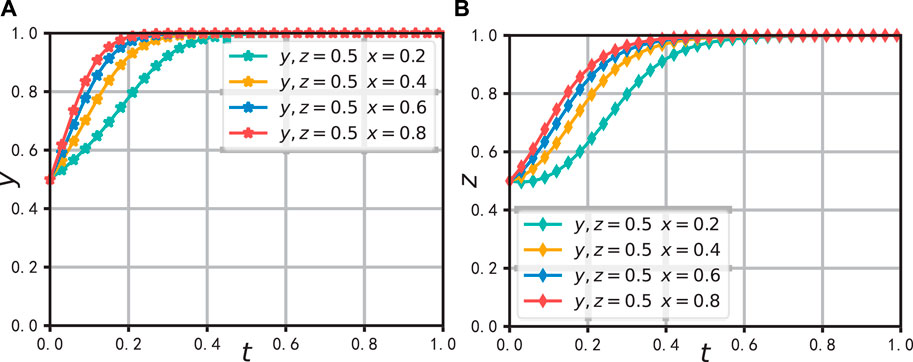
Figure 8. The effect of a change in x on the evolution of system. (A) Effect on the evolution of y (B) Effect on the evolution of z.

Figure 9

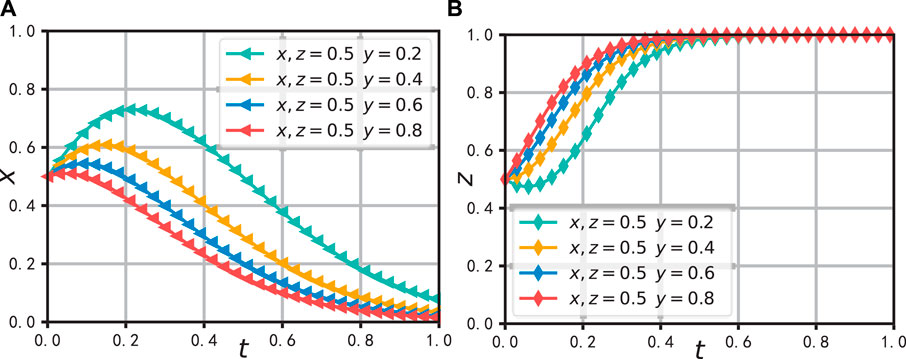
Figure 9. The effect of a change in y on the evolution of system. (A) Effect on the evolution of x (B) Effect on the evolution of z.

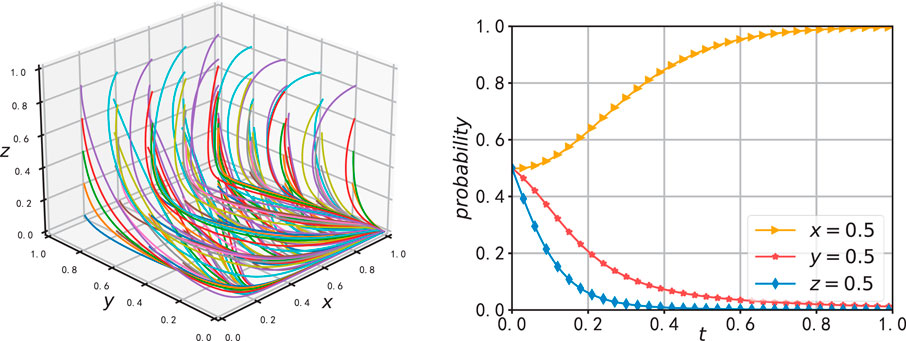
In Figure 9, the probability of strategy selection by manufacturing enterprises was increased from 0.2 to 0.8 to observe the evolution trend of the entire system. As shown in Figure 10A, the data-sharing platform of the Internet of Vehicles would quickly converge to an unsupervised strategy and remain relatively stable, while sales enterprises would adopt an active data sharing strategy, as illustrated in Figure 9B. This indicates that the active data sharing behavior of manufacturing enterprises would prompt sales enterprises to select data sharing strategies, thereby achieving synergistic benefits. Similarly, it would also encourage the sharing platform to reduce the intensity of supervision, thereby achieving the goal of saving supervision costs.

In Figure 10, the probability of strategy selection by sales enterprises is increased from 0.2 to 0.8 to observe the evolution trend of the entire system. Similar to Figure 9, the proactive data sharing behavior of sales enterprises will induce manufacturing enterprises to choose a data sharing strategy, thereby achieving collaborative benefits, and will likewise prompt the data sharing platform to reduce the supervision intensity, thus achieving the goal of saving supervision costs.

Figure 10

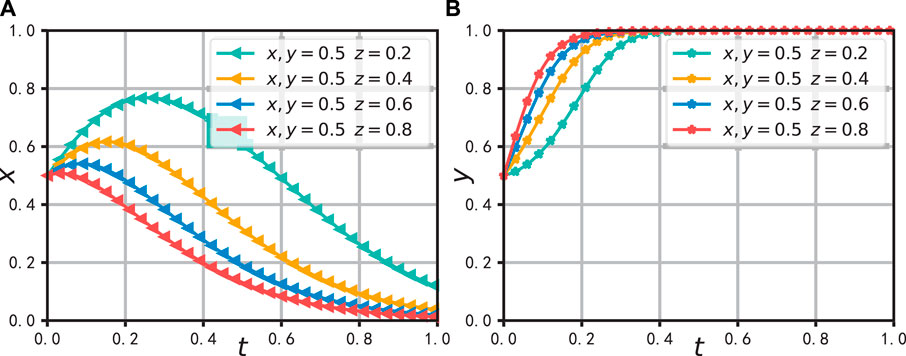
Figure 10. The effect of a change in z on the evolution of system. (A) Effect on the evolution of x (B) Effect on the evolution of y.

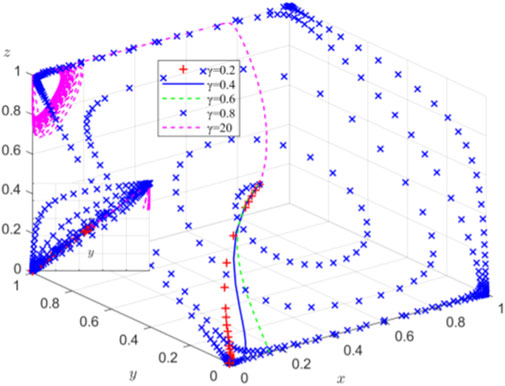
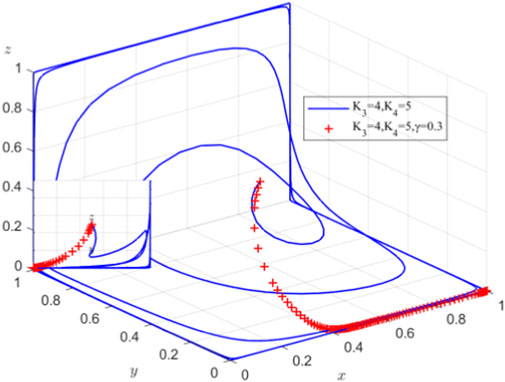
5.2 Influence of compensation coefficient $\gamma$ on system evolution at equilibrium point (0, 0, 0)

When $2\gamma A_1-k_2<0$, and setting the initial values as $A_1=40$, $A_2=20$, $A_3=20$, $B_2=0.6$, $B_3=0.4$, $K_2=40$, $K_3=22$, $K_4=19$, $\alpha =0.5$, $\beta =2$. As shown in Figure 11, when $\gamma$ is 0.2 or 0.4, the system evolution direction tends to (0,0,0). At this time, the sharing platform adopts an unsupervised strategy, while the manufacturing and sales companies choose a non-sharing strategy. When the compensation coefficient value increases to 0.6, the equation is no longer satisfied, causing the strategy of the sharing platform to gradually adjust in the direction of supervision. However, the change of $\gamma$ is small, so the degree of deviation is limited, and it will not significantly affect the strategy selection of the parties in the data supply chain. However, when $\gamma$ is 20, the compensation coefficient increases significantly, prompting the parties in the data supply chain to choose to share data in order to obtain benefits. Due to the high compensation coefficient, the market activity increases significantly, and the sharing platform does not need to adopt a supervision strategy, then the system evolution reaches a new equilibrium point (0,1,1).

Figure 11

Figure 11. Simulation analysis of γ-value in case 1.

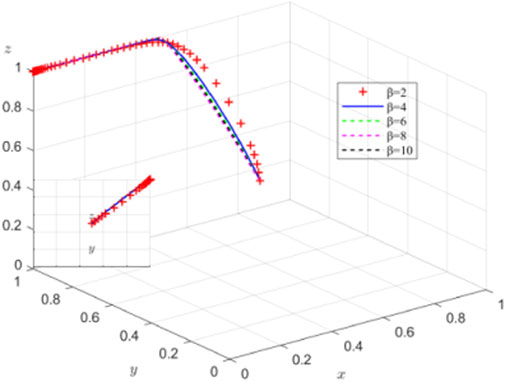
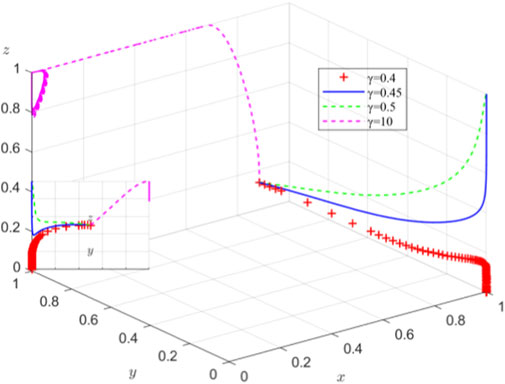
5.3 Influence of cooperation coefficient $\beta$ on system evolution at equilibrium point (0,1,1)

When $k_3+\alpha A_2+\left(1-\beta \right)\left(A_1+A_3\right)B_2<0$, $k_4+\alpha A_3+B_3\left(1-\beta \right)\left(A_2+A_1\right)<0$, and setting the initial values as $A_1=25$, $A_2=30$, $A_3=35$, $B_2=0.4$, $B_3=0.5$, $K_2=5$, $K_3=3$, $K_4=4$, $\alpha =0.5$, $\beta =2$, $\gamma =0.6$. As shown in Figure 12, the system evolves towards a stable point (0,1,1). When the cooperation coefficient $\beta$ increases from 2 to 10, the corresponding system evolution results are shown in Figure 9. As can be seen in the figure, the rate at which the system reaches the equilibrium point (0,1,1) increases significantly. In addition, when the information processing efficiency of each participant is enhanced, the adequacy of data sharing is improved, or the cost of data sharing is reduced and the risk loss caused by data leakage is reduced, the synergy coefficient can be improved. For instance, increasing the information processing capacity of participants $B_{i(i=2,3)}$ from (0.4,0.5) to (0.7,0.8) has a similar effect to that observed by increasing the parameters of the cooperation coefficient. Similarly, increasing the adequacy of data sharing by increasing it from (25, 30, 30) to (35, 40, 40), reducing the cost of data sharing from the original value to (3,1,2), and reducing the loss of data breach risk to 0.2 can replicate the experimental effect of increasing the synergy coefficient.

Figure 12

Figure 12. Simulation analysis diagram of βvalues in case 2.

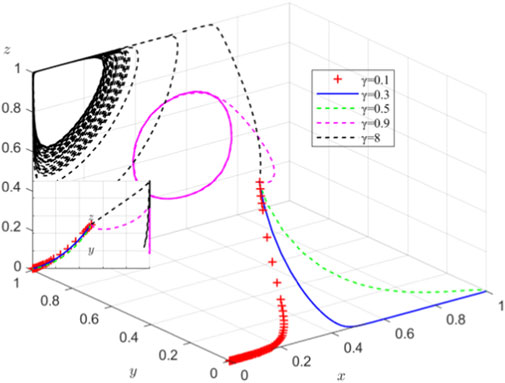
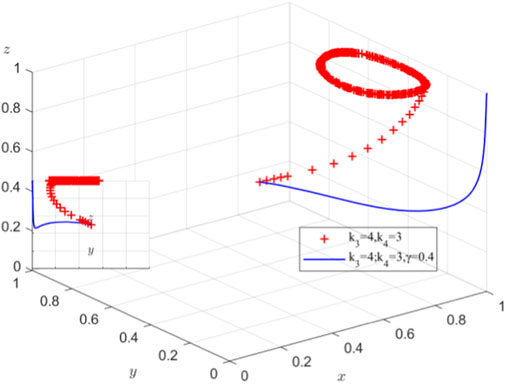
5.4 Effects of compensation coefficient and cost on system evolution at equilibrium point (1,0,0)

When $\gamma \left(A_1+A_3\right)-k_4-\alpha A_3<0$, $k_2-2\gamma A_1<0,\gamma \left(A_1+A_2\right)-k_3-\alpha A_2<0$, and setting the initial values as $A_1=15$, $A_2=15$, $A_3=20$, $B_2=0.6$, $B_3=0.4$, $K_2=8$, $K_3=10$, $K_4=12$, $\alpha =0.5$, $\beta =2$, $\gamma =0.3$. When the compensation coefficient $\gamma$ is 0.2, the above inequality is not satisfied, indicating that the compensation mechanism cannot effectively offset the cost burden and the loss caused by data leakage. The system evolves to (0,0,0), as shown in Figure 13. When $\gamma$ is adjusted to 0.3 and 0.4, all inequalities are satisfied, and the system evolves to the stable equilibrium point (1,0,0), indicating that the sharing platform has implemented regulatory strategies, while downstream enterprises adopt a non-sharing strategy. As the value of $\gamma$ continues to increase to 0.9, the stability of the system is disrupted. Although it does not completely reach a stable state, the evolution path shows a clear tendency in strategy selection. When $\gamma$ increases to 8, high compensation leads downstream enterprises in the data supply chain to adopt a sharing strategy. At this time, the Internet of Vehicles data sharing platform can adopt a non-regulatory strategy, and the system eventually tends towards the stable point (0,1,1). Additionally, we analyzed the impact of adjusting the data sharing costs of manufacturing and sales enterprises on the system evolution, i.e., when $K_3$ and $K_4$ are reduced from 8 to 10 to 4 and 5 respectively, the experimental results are shown in Figures 14, 15. Although the costs for manufacturing and sales enterprises decrease, the stability of the system is undermined, and its evolutionary trend becomes unclear. If the compensation coefficient is comprehensively adjusted at this time, the system will return to the stable equilibrium point (0,1,1).

Figure 13

Figure 13. Simulation analysis diagram of values $\gamma$ in Case 3.

Figure 14

Figure 14. Simulation analysis diagram of $K_3,K_4,\gamma$ in case 3.

Figure 15

Figure 15. Simulation analysis diagram of $\gamma$ in Case 4.

5.5 Effects of compensation coefficient and cost on system evolution at equilibrium point (1,0,1)

When $k_2-\gamma A_1<0$, $k_4+\alpha A_3-\gamma \left(A_1+A_3\right)<0$, $\left[\gamma +B_2\left(\beta -1\right)\right]$, $\left(A_3+A_1\right)-k_3-\alpha A_2<0$ . And setting the initial values as $A_1=15$, $A_2=35$, $A_3=15$, $B_2=0.6$, $B_3=0.4$, $K_2=5$, $K_3=8$, $K_4=5$, $\alpha =0.5$, $\beta =1.5$, $\gamma =0.45$. As shown in Figure 14, when $\gamma$ is 0.4, the above inequality conditions are not satisfied, meaning that compensation cannot make up for the losses caused by cost and information leakage. The evolution trend of the system tends towards the unstable point (0,0,1). When $\gamma$ is 0.45 and 0.5, all three inequality conditions are met, and the system evolves to (1,0,1), indicating that the vehicle network data sharing platform adopts a regulatory strategy, sales enterprises choose a sharing strategy, while manufacturing enterprises choose a non-sharing strategy. Subsequently, when $\gamma$ gradually increases to 10, the situation is similar to Case 1. This is because the compensation mechanism triggers both manufacturing and sales enterprises to choose a sharing strategy, while the vehicle network data sharing platform adopts a non-regulatory strategy, and the system ultimately stabilizes at (0,1,1). As shown in Figure 16, when the data sharing costs of manufacturing and sales enterprises are reduced, the stable state of the system is disturbed, and the evolution trend becomes unclear. However, by simultaneously adjusting the compensation coefficient $\gamma$, it can be observed that the system will reach a stable point (1,0,1) again.

Figure 16

Figure 16. Simulation analysis diagrams of $K_3,K_4,\gamma$ in case 4.

6 Conclusion

In this paper, we investigate the dynamic game process of data sharing behaviors among shared platforms, manufacturing enterprises, and sales enterprises in the Internet of Vehicles data supply chain. We establish an evolutionary game model for the data sharing behavior decisions of the three game participants and conduct an in-depth analysis of the model to determine the key factors affecting stable cooperation among supply chain decision-makers. By summarizing the previous content, the following conclusions are drawn.

(1) Clarifying the positive and negative impacts of key factors is crucial for the effective management of the Internet of Vehicles (IoV) data supply chain. Studies have shown that improving the adequacy of data sharing, enhancing the understanding and utilization capabilities of data by various entities in the supply chain, increasing reasonable compensation coefficients, and enhancing collaborative coefficients can all positively promote the optimization of the IoV data supply chain game system. Conversely, an increase in the supervision costs of the sharing platform, an increase in the data sharing costs of manufacturing and sales enterprises, and an increase in the risk coefficient of data leakage will negatively affect system optimization. Therefore, in practical applications, the positive effects of favorable factors should be actively amplified, and the negative effects of unfavorable factors should be effectively controlled within a reasonable range. This will stimulate the cooperation willingness of all entities in the industry chain and promote the coordinated and sustainable development of the IoV data supply chain.

(2) In the IoV data supply chain, the decision-making behaviors of various participating entities are intertwined and influence each other. To comprehensively and deeply analyze the evolutionary game process, it is necessary to organically combine theoretical analysis with numerical simulation experiments. In terms of theoretical analysis, we used Lyapunov stability theory to derive the inequality conditions that ensure the asymptotic stability of each equilibrium point. These inequality conditions preliminarily reveal the intrinsic rules of strategy evolution for participants in the IoV data supply chain. However, due to the interdependence of participants’ decisions, relying solely on theoretical analysis makes it difficult to accurately judge the overall evolutionary trend of the system. Therefore, combining numerical simulation experiments can not only verify the correctness of theoretical analysis but, more importantly, vividly show the specific paths and trends of system evolution, thereby obtaining more comprehensive and in-depth research conclusions.

(3) The strategy combination {No supervision, Share data, Share data} (i.e., strategy set {0,1,1}) has been proven to be the optimal strategy choice for the tripartite game entities in the IoV data supply chain. The optimization analysis results of the equilibrium point indicate that the system’s final evolutionary trend stabilizes at the equilibrium point (0,1,1). This suggests that, ideally, the IoV data sharing platform does not need to invest excessive supervision costs, while manufacturing and sales enterprises can still actively and proactively share data and maintain high enthusiasm for cooperation without external supervisory constraints. Under this positive interaction, the entire IoV data supply chain system is expected to generate robust synergistic effects with the active collaboration of all participants, ultimately achieving long-term stability and high-quality development of the supply chain. This research conclusion provides valuable theoretical insights and practical guidance for constructing an efficient and stable IoV data supply chain system.

In summary, this paper delves into the dynamic game mechanism of data sharing behavior in the IoV data supply chain and, through the construction and analysis of an evolutionary game model, reveals the key factors affecting stable cooperation in the supply chain and the realization path of the optimal strategy combination. The research results not only provide new perspectives for the academic community to deeply understand the data sharing behavior in the IoV data supply chain but also offer valuable decision-making references for the industry to enhance data supply chain management levels.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RW: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. JY: Formal Analysis, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hemmati A, Zarei M, Rahmani AM. A systematic review of congestion control in internet of vehicles and vehicular ad hoc networks: techniques, challenges, and open issues. Int J Commun Syst (2024) 37(1):e5625. doi:10.1002/dac.5625

CrossRef Full Text | Google Scholar

2. Guo J, Bilal M, Qiu Y, Qian C, Xu X, Raymond Choo KK. Survey on digital twins for Internet of Vehicles: fundamentals, challenges, and opportunities. Digital Commun Networks (2024) 10(2):237–47. doi:10.1016/j.dcan.2022.05.023

CrossRef Full Text | Google Scholar

3. Sahu BL, Chandrakar P. Blockchain-oriented secure communication and smart parking model for internet of electric vehicles in smart cities. Peer-to-Peer Networking Appl (2025) 18(1):51–17. doi:10.1007/s12083-024-01872-y

CrossRef Full Text | Google Scholar

4. Han X, Tian D, Duan X, Sheng Z, Zhou J, Leung VC. A dual mode privacy-preserving scheme enabled secure and anonymous for edge computing assisted internet of vehicle networks. Proc 11th ACM Symp Des Anal Intell Vehicular Networks Appl (2021) 65–70. doi:10.1145/3479243.3487310

CrossRef Full Text | Google Scholar

5. He M, Bai F, Zhang C, Shen T, Gong B. A blockchain-enabled location privacy-preserving under local differential privacy for internet of vehicles. Proc 2022 4th Blockchain Internet Things Conf (2022) 84–91. doi:10.1145/3559795.3559807

CrossRef Full Text | Google Scholar

6. Xu J, Li M, He Z, Anwlnkom T. Security and privacy protection communication protocol for Internet of vehicles in smart cities. Comput Electr Eng (2023) 109:108778. doi:10.1016/j.compeleceng.2023.108778

CrossRef Full Text | Google Scholar

7. Wang N, Yang W, Wang X, Wu L, Guan Z, Du X, et al. A blockchain based privacy-preserving federated learning scheme for Internet of Vehicles. Digital Commun Networks (2024) 10(1):126–34. doi:10.1016/j.dcan.2022.05.020

CrossRef Full Text | Google Scholar

8. Chen M, Yuan L, Xia T. Data classified and graded access control model based on master-slave multi-chain. J Comput Appl (2024) 44:1148–57. doi:10.11772/j.issn.1001-9081.2023040529

CrossRef Full Text | Google Scholar

9. Bai Z, Wang T, Guo M. Classification and grading method of transportation government data. J Inf Security Res (2023) 9(8):808. doi:10.12379/j.issn.2096-1057.2023.08.13

CrossRef Full Text | Google Scholar

10. Feng Z, Yu L, Ma Y, Zhong H, Jiang W. Research and practice of data security classification and grading. Inf Commun Technol Pol (2021) 47(8):45. doi:10.12267/j.issn.2096-5931.2021.08.007

CrossRef Full Text | Google Scholar

11. Chen M, Yi M, Huang M, Huang G, Ren Y, Liu A. A novel deep policy gradient action quantization for trusted collaborative computation in intelligent vehicle networks. Expert Syst Appl (2023) 221:119743. doi:10.1016/j.eswa.2023.119743

CrossRef Full Text | Google Scholar

12. Rathee G, Garg S, Kaddoum G, Choi BJ, Benslimane A, Hassan MM. A secure and trusted context prediction for next generation autonomous vehicles. Alexandria Eng J (2023) 78:131–40. doi:10.1016/j.aej.2023.07.020

CrossRef Full Text | Google Scholar

13. Haseeb K, Rehman A, Saba T, Bahaj SA, Wang H, Song H. Efficient and trusted autonomous vehicle routing protocol for 6G networks with computational intelligence. ISA Trans (2023) 132:61–8. doi:10.1016/j.isatra.2022.09.035

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang D, Yi Y, Yan S, Wan N, Zhao J. A node trust evaluation method of vehicle-road-cloud collaborative system based on federated learning. Ad Hoc Networks (2023) 138:103013. doi:10.1016/j.adhoc.2022.103013

CrossRef Full Text | Google Scholar

15. Gao Y, Zhu Z, Yang J. An evolutionary game analysis of stakeholders’ decision-making behavior in medical data sharing. Mathematics (2023) 11(13):2921. doi:10.3390/math11132921

CrossRef Full Text | Google Scholar

16. Hu C, Yang J, Gao P, Zhang Y. Evolutionary game analysis of three stakeholders in big data trading market. J Ind Manage Optimization (2024) 20(6):2135–52. doi:10.3934/jimo.2023159

CrossRef Full Text | Google Scholar

17. Feng L, Zhang L, Wang J, Feng J. How to promote the participation of enterprises using open government data? Evolutionary game analysis by applying dynamic measures. Expert Syst Appl (2024) 238:122348. doi:10.1016/j.eswa.2023.122348

CrossRef Full Text | Google Scholar

18. Lv Y, Yang J, Sun X, Wu H. Evolutionary game analysis of stakeholder privacy management in the AIGC model. Operations Res Perspect (2025) 14:100327. doi:10.1016/j.orp.2025.100327

CrossRef Full Text | Google Scholar

19. Tang J, Wu W, Zhao D, Chen X. Evolutionary game and simulation analysis of intelligent connected vehicle industry with cross-border collaborative innovation. IEEE Access (2023) 11:17721–30. doi:10.1109/access.2023.3245078

CrossRef Full Text | Google Scholar

20. Srivastava V, Srivastava S, Chaudhary G, Blanco Valencia XP. Performance improvement and Lyapunov stability analysis of nonlinear systems using hybrid optimization techniques. Expert Syst (2024) 41(6):e13140. doi:10.1111/exsy.13140

CrossRef Full Text | Google Scholar