Systematic trends in the spin-orbit splitting toward weak-binding

Spin–orbital (SO) splitting in atomic nuclei results from the coupling between a nucleon’s spin and its orbital angular momentum, fundamentally influencing nuclear structure, especially near the magic numbers. This paper reviews the impact of various effects on SO-splitting, including tensor and weak-binding effects in neutron-rich and weakly bound nuclei, focusing on both theoretical interpretations and recent experimental results. The study summarizes new experimental results on SO-splitting in isotopes such as ³⁴Si, ³²Si, and ¹³²Sn, showing a consistent smooth reduction in SO energy for weakly bound orbits, attributed to extended radial wave functions rather than a reduced SO potential strength. These findings reinforce the need for further experimental research with advanced radioactive ion beam facilities to understand the intricate behaviors of SO interactions in exotic nuclei.

1 Introduction

The study of atomic nuclei remains an important topic for understanding it as a complex system governed by the strong nuclear force. One of the key concepts in nuclear structure is the nuclear shell model [1, 2], which granted enormous success in understanding the nuclear structure near stability. In the nuclear shell model, the nucleons group in quantized energy levels or “shells” within the nucleus, which is analogous to electrons in an atom where electrons fill up discrete energy levels. The concept of “magic numbers” was introduced to denote specific numbers of nucleons that result in particularly stable atomic nuclei. Unstable nuclei generally possess lower binding energies, rendering them more susceptible to various quantum effects not observed in stable nuclei. With advancements in radioactive beam facilities worldwide, numerous new phenomena have been discovered, including halo nuclei [3], cluster structures [4], and the migration of magic numbers [5].

Spin–orbital (SO) splitting refers to the energy difference between nuclear states that arises due to the coupling of a nucleon’s spin with its orbital angular momentum. It was first proposed to interpret the fine structure in atomic spectra, and the concept was later adapted to nuclear physics by Goeppert-Mayer and Haxel et al. [1, 2] to explain similar splittings observed in nuclear energy levels. This phenomenon is a direct consequence of the SO interaction, which was manually added to the shell model to explain the “magic numbers.” Magic numbers 2, 8, and 20 are formed by the harmonic oscillator levels, while all the magic numbers above 20 are dominantly driven by the SO splittings. For example, the lowering of the $j=\ell +1/2$ orbitals with large $\ell$ ($f_{7/2}$, $g_{9/2}$, and $h_{11/2}$) caused by strong SO splittings results in the shell closure at 28, 50, 82, etc. Any changes in SO potential may impact the shell gaps, binding energies, and lifetime of the nuclei, which possibly influence the neutron capture rate determining the heavy element synthesis [6]. In heavy elements, different theoretical descriptions of the SO potential can also affect predictions of the dripline and the location of the island of stability. Some theoretical predictions suggest that the SO interaction contributes to the stability of superheavy elements by creating energy gaps at higher nucleon numbers, leading to islands of stability in the superheavy region.

Although there is not yet a quantitative understanding of the microscopic origins of the SO term in the nuclear Hamiltonian, it appears to be influenced by the meson-theoretical three-body force [7], the tensor force [8], and the two-body SO term from the meson exchange. Fujita and Miyazawa first proposed that the three-body nucleon force with an intermediate $\mathrm{\Delta }$ excitation results in an SO-splitting [7]. Second, Terasawa showed that the tensor-force also contributes to the SO-splitting [9]. Later, in the proposed relativistic mean field (RMF) theory [10], nucleons are treated as relativistic particles that interact through the exchange of mesons, and the SO interaction term arises due to the coupling between the nucleon’s spin and its motion in the central potential field created by the mesons. When the non-relativistic expansion is performed, the SO coupling term appears as

$V_{\text{so\hspace{0.17em}}}=\frac{1}{2M^{2}R}\frac{d{V}_{\text{eff\hspace{0.17em}}}}{dR}\left(\mathit{\ell }\cdot \mathit{s}\right),(1)$

where M is the mass of the nucleon (proton or neutron), $V_{\text{eff\hspace{0.17em}}}$ is an effective potential that includes contributions from the scalar and vector meson fields, $\mathit{\ell }$ is the orbital angular momentum, $\mathit{s}$ is the intrinsic spin of the nucleon, and $R$ is the radial distance from the center of the nucleus. The derivative of the effective potential indicates how steeply this potential changes with distance. The resulting SO-splitting scales approximately with node number and angular momentum of the orbitals as $24.5/n(\ell +1/2)A^{-0.597}$ [11], where $A$ refers to the mass number and $n$ refers to the quantum number of the harmonic oscillator. However, it has been observed in many cases that the SO-splitting may deviate from this trend due to different effects, which will be discussed below.

From Equation 1, we can see that the SO interaction can be influenced by the mass of the nuclei and depends on the orbital angular momentum of the nucleon. Higher orbital angular momentum states experience a more substantial SO-splitting. Therefore, the SO splittings generate all the magic numbers above 20 for orbitals with higher $\ell$ values, as stated above. The orientation of the orbital angular momentum and the intrinsic spin lead to splittings of different states with $j=\ell \pm s$. The dependence on the $1/R$ term in the formula indicates that this interaction has a significant impact at smaller radii. Given its proportionality to the derivative of the potential with respect to distance, it is natural to expect the SO interaction to be a surface term. This is because the density in the central region of nuclei is remarkably consistent across most stable nuclei, despite the wide variety in nuclear sizes. However, there are some theoretical predictions that suggest depletion in central density in some exotic nuclei, which leads to a sudden change in the SO potential of these nuclei.

This article aims to provide a succinct summary of the recent research on SO-splitting in nuclei, with a focus on the weak-binding effect on it. We will examine the current experimental status of SO-splitting with a focus on the Si isotopes and discuss possible underlying mechanisms. By delving into these specific studies, we will analyze the evolution of SO-splitting in these nuclei and its implications.

2 SO interaction evolution as a function of proton and neutron numbers

There are many factors that contribute to the SO interactions, including, but not limited to the tensor force, the three-body force. Moreover, as experimental studies extend to nuclei away from stability, the finite binding energy may also impact the SO splittings. Reference [12] provides a comprehensive historical overview on the impact of the three-body force on the SO-splitting, so we will focus on the other two aspects.

2.1 Effect of tensor force on SO splittings

The tensor force is a crucial component of the nuclear interaction that plays a significant role in determining the energy levels of nuclei, especially for nucleons in high-angular-momentum states and in nuclei far from the stability (23). In the nuclei far from stability or with high isospin asymmetry, the neutrons and protons can occupy different orbitals. Since the tensor component of the nuclear force arises primarily from the exchange of pions ($\pi$-mesons) between nucleons, the exchange process contributes dominantly to the monopole part of the tensor force, which is much stronger for the proton–neutron $(T=0)$ interaction, and is approximately twice as strong as the $(T=1)$ interaction. The tensor force causes the effective interactions between the proton orbital with $j_{>}=\ell +1/2$ (or $j_{<}=\ell -1/2$) and neutron orbitals $j_{<}^{\prime }$ (or $j_{>}^{\prime }$) to be more attractive, whereas $j_{>}$ and $j_{>}^{\prime }$ (or $j_{<}^{\prime }$ and $j_{<}^{\prime }$) repel each other. This effect accumulates as the proton–neutron asymmetry increases, and the shell evolution occurs consequently.

It is, therefore, natural to expect that the neutron SO splittings evolve with the change in the proton number. As the proton fills the $j_{>}$ orbitals, the SO-splitting decreases, and vice versa, which is supported by experimental data. For example, in the Ca isotopes, it was shown that the proton $0d_{3/2}$ is attracted (lowered in energy), while $0d_{5/2}$ is repelled (raised in energy) due to the neutron filling of the $0f_{7/2}$ orbit [13]. Similarly, in the Sb isotopes, as more neutrons occupy $0h_{11/2}$, the protons $0h_{11/2}$ and $0g_{7/2}$ move apart [14]. This trend is also consistent with a decrease in the nuclear SO interaction.

2.2 SO splittings in weakly bound nuclei

Since the SO interaction is majorly a surface term, it could be modified in neutron-rich nuclei away from stability, where neutrons may have a diffuse surface density distribution due to weak binding. Hamamoto et al. [15] predicted the SO splittings of weakly bound orbits in light, neutron-rich nuclei to decrease due to the extended radial wavefunctions of neutron orbits, with no reduction in the SO potential strength.

By approximating SO potential to a $\delta$ function at the nuclear surface, a simple evaluation of the SO-splitting was established in Reference [16],

${\mathrm{\Delta }}_{\text{S}\text{O}}\propto {\text{V}}_{\text{s}\text{o}}\left(\mathit{\ell }\cdot \mathit{s}\right){\text{r}}_0^2\text{R}{\mathrm{\Psi }}^2\left(\text{R}\right),(2)$

where $V_{so}$ is the SO potential strength, $\mathrm{\Psi }(R)$ is the radial wavefunction, $r_0$ is the scaling parameter for the radius of nuclei (usually taken as 1.2 fm), and R is the radial distance from the center of nuclei. Figure 1A plots the radial $1p_{3/2}$ wavefunctions multiplied by the radius under different binding energies, showing that the SO-splitting decreases as the corresponding orbitals become less bound.

Figure 1

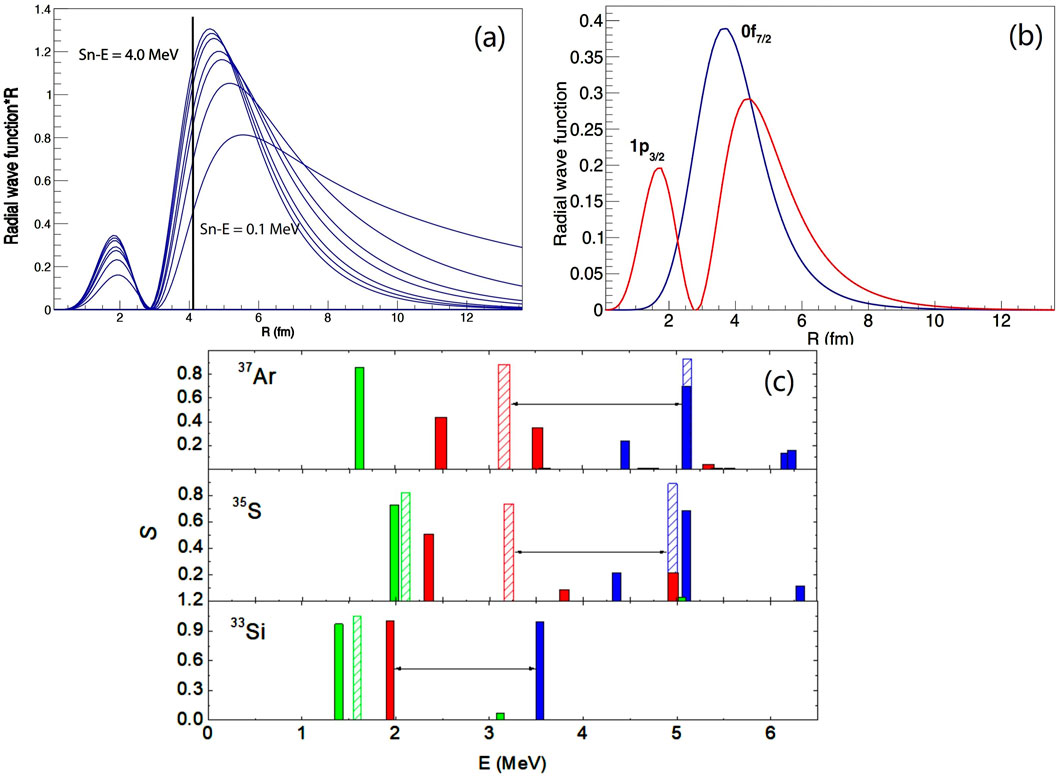
Figure 1. (A) Term $R\mathrm{\Psi }(R)$ plotted as a function of the radius $R$ under different binding energies $S_n-E$. (B) Radial neutron wave functions of the $1p_{3/2}$ (red solid line) and $0f_{7/2}$ orbital (blue solid line). The vertical solid black line shows the estimated matter radius of the nucleus ³⁴Si $R_0=4.05$ fm. (C) Excitation energies and corresponding spectroscopic factors of the low-lying states in ³⁷Ar, ³⁵S, and ³³Si measured in the $(d,p)$ reaction, with transitions to the $0f_{7/2}$ (green), $1p_{3/2}$ (red), and $1p_{1/2}$ (blue) orbitals. The weighted average of the corresponding orbitals is labeled with the slashed bars, if different from the dominant states.

3 SO interaction evolution near the proposed “bubble” nucleus

3.1 SO splittings in N = 21 isotones

Due to the saturation and short-range nature of the nuclear force, it is natural to expect that the density in the center of nuclei is constant. However, there have been many theoretical studies supporting the existence of central depletion in ³⁴Si [17, 18]. ³⁴Si is a candidate for a so-called “bubble” nuclei, providing a valuable test case for the SO potential in the center of nuclei. The prediction of central depletion in ³⁴Si arises from its doubly magic characteristic ($N=20$ and $Z=14$), which results in an extremely low proton occupancy number in the $1s_{1/2}$ orbital. This occupancy was determined to be between 0.17 and 0.24 in the proton knockout reaction [19]. As a large fraction of the radial part of the $1s_{1/2}$ orbital peaks in the center of the nucleus, the lack of $1s_{1/2}$ naturally induces a central density depletion. Despite no direct proof of such central depletion, experimental developments in electron scattering measurements, ideally suited for such studies, of radioactive isotopes are being made [20].

Since the SO-splitting is proportional to the derivative of the density distribution (see Equation 1), it is expected to change due to the presence of density depletion. The one-neutron adding reaction is useful for determining the angular momentum transfer $\ell$ and spectroscopic factors through comparison to the reaction models, and the population strength indicates the single-particle strength in each state. Therefore, the SO splittings can be mapped out with the addition and removal of single-particle strengths and the corresponding binding energies [21],

$E_j=\sum G_j^{+}{E}_j^{+}+\sum G_j^{-}{E}_j^{-},(3)$

with $G_j^{+}+G_j^{-}=1.0$. For the case in which the single-particle removal strengths were not measured, the energy centroid can be used to determine the single-particle energies

$E_j=\sum G_j^{+}{E}_j^{+},(4)$

with $G_j^{+}=1$.

A significant reduction in SO-splitting is predicted for ³⁴Si compared to other $N=20$ isotones due to central density depletion. This prediction seems to be supported by the nearly 50$\%$ reduction in the SO-splitting in ³⁴Si compared to ³⁶S, as determined using the dominant single-particle component [19, 22] (see Figure 2A). However, this assertion was questioned because only dominant single-particle strength was considered, instead of including the fragmented components of the $\ell =1$ single-particle strength as in Equation 3, which may result in overestimation of SO splittings. After taking them into account, a smooth reduction from ⁴¹Ca via ³⁹Ar and ³⁷S to ³⁵Si was shown (see Figure 2A), which was explained by the finite binding energies of the neutron states [23]. So far, the interpretation remains highly debated. There is an ongoing investigation into whether the observed changes in the $1p$ SO-splitting are driven by the weak-binding effect or by the weakening of the two-body SO potential in this region [6, 24]. This motivated the recent measurement of the $N=19$ isotones.

Figure 2

Figure 2. (A) Evolution of the $1p_{3/2}-1p_{1/2}$ or $3/2^{-}$-$1/2^{-}$ SO-splitting, for the $N=21$ isotones. Black open circles (with estimated error bars) correspond to the centroid of the single-particle strength derived in [23], in which Woods–Saxon calculations were made (orange band). Red filled triangles are obtained using the energy difference between the $3/2^{-}$ and $1/2^{-}$ states having the dominating spectroscopic factor value, when populated by the $(d,p)$ reaction. Blue squares correspond to covariant energy density functional calculations with the DDME2 parametrization of the $3/2^{-}$ and $1/2^{-}$ states shifted upward by 340 keV. Some symbols have been slightly shifted to the left or right to be better distinguished. This figure is adopted from Reference [24]. (B) Evolution of the $1p_{3/2}-1p_{1/2}$ or $3/2^{-}1/2^{-}$ SO-splitting, for the $N=19$ isotones. Red squares (with estimated error bars) correspond to the centroid of the single-particle strength derived in [30]. Black squares correspond to covariant energy density functional calculations, shifted downward by 450 keV. This figure is adopted from Reference [30]. Proton density of ³⁴Si and ³⁶S calculated with the DD–ME2 interaction using the covariant energy density functional method. (D) Same as (C), but for ³²Si and ³⁴S. This figure is adopted from Reference.

3.2 SO splittings in N = 19 isotones

In order to enhance our understanding of the microscopic origins of the SO interaction, studying the SO interaction near the S and Si isotopes is crucial. The evolution from Si to S is particularly important since only the $1s_{1/2}$ proton orbital is filled between these two nuclei. Consequently, the resulting proton–neutron interaction involves no tensor component because it vanishes for $\ell =0$; only the SO part of the nuclear force plays a role.

For ³²S to ³⁰Si $(N=16)$, the proton $1s_{1/2}$ occupancy changes from 1.35 to 0.65 (not 2.0 to 0.0) based on the proton knockout reaction data [25], making ³⁰Si not an ideal candidate to study the proton central depletion. However, for ³²Si, the neighboring even–even isotope of ³⁴Si, both density functional theory and shell model calculation predict a very small proton $1s_{1/2}$ occupancy ($\sim$0.3) compared to ³⁴S, where $1s_{1/2}$ is almost fully occupied. Furthermore, density functional theory calculations of ³²Si predict a depletion similar to that of ³⁴Si in the proton density distribution, as well as a sudden reduction in SO-splitting in ³²Si compared to ³⁴S (see Figures 2C, D). It provides another testing ground for investigating if there is a sudden reduction in SO-splitting due to proton depletion. It should also be noted that one major difference in ³²Si is that its neutrons are more deeply bound than ³⁴Si, so it should be less influenced by the weak binding effect.

The single-particle energies of shell-model orbitals in $N=19$ isotones (³³Si, ³⁵S, and ³⁷Ar) can be mapped out with the addition and removal of single-particle strengths using Equations 3, 4. The neutron addition data of the $N=19$ isotone ³⁷Ar and ³⁵S can be found in Refs. [26–29]. With these data, the weighted average values of the $0f_{7/2}$ and $1p_{1/\mathrm{2,3}/2}$ orbitals were obtained and are plotted in Figure 1C. It was found that the location of the weighted average is clearly different from the dominant strength, showing that considering the fragmented strength is important. The single-particle removal strength of these orbitals was also considered where one-neutron removal data exist for ³⁷Ar and ³⁵S. Only the $1p_{3/2}$ and $0f_{7/2}$ single-particle energies of ³⁷Ar have been shifted downward by approximately 100 and 250 keV, respectively. The $pf$-shell orbitals of ³⁵S have been shifted less than 50 keV. However, no such previous addition or removal data exist for ³³Si.

In order to quantitatively determine the SO-splitting, a measurement of ³²Si${(d,p)}^{33}$Si cross-sections was carried out at the ReA6 beamline in FRIB using the newly constructed solenoid spectrometer SOLARIS in the silicon array mode [30]. The solenoid spectrometer is capable of measuring the transfer reactions, in particular the one-neutron adding $(d,p)$ reactions with high resolution. The experimental spectroscopic factors and the single-particle energies of the $1p_{3/\mathrm{2,1}/2}$ and $0f_{7/2}$ orbitals are plotted in Figure 1C and compared with its S and Ar $N=19$ isotones.

In the relativistic mean field (RMF) calculation with the DD-ME2 interaction [31], ³²Si was predicted to exhibit a depletion in central density, similar to ³⁴Si, due to low $1s_{1/2}$ proton occupancy. This calculation predicts a sudden reduction of the neutron $1p$-shell SO-splitting ${\text{in}}^{33}$Si compared to ³⁵S, similar to the $N=21$ isotones. However, as observed from the present measurement, the SO-splitting in ³³Si is similar to that of ³⁵S, in contradiction to the RMF calculation (see Figure 2B). The mismatch of this calculation might be attributed to the fact that the proton–neutron quadrupole correlations are not taken into account in the RMF calculation. Therefore, this study does not support the existence of a sudden reduction in SO-splitting associated with a proton bubble.

3.3 Systematic description of the SO splittings with the weak binding effect

To explore this weak binding effect on SO splittings, the calculation was carried out with a Woods–Saxon (WS) potential. Figure 4 of Reference [30] shows the binding energy of $1p_{1/2}$ and $1p_{3/2}$ orbitals from existing experimental data, together with the WS calculation, using the radius and diffuseness parameters $r_0=1.2$ fm, $a_0=0.7$ fm, $r_{so}=1.3$ fm, $a_{so}=0.65$ fm, and SO strength $V_{so}=6$ MeV. The depth of the potential was chosen to reproduce the binding energies of these two orbitals with a ${\chi }^2$ minimization method. The SO strength is not varied in the calculation.

It can be seen immediately that the SO-splitting and single-particle energies of the $1p$ orbitals have been reproduced by the calculation without changing the SO potential strength. The good agreement with the calculation with WS formalism indicates that the evolution of the $p$-shell single-particle energies was described by the behavior of the wavefunctions resulted from the geometric effect (a large radius or diffuseness) of the low-$\ell$ orbitals as they become less bound. This was achieved without inducing a weakening of the SO potential strength or other additional effects.

From Equation 2, it is seen that the SO-splitting depends on the term $R\mathrm{\Psi }(R)$ if the strength of the SO potential $V_{so}$ remains unchanged. In Figure 1A, this term is plotted as a function of R. The radius of the nucleus $R_0$ was taken as 1.25 fm$\times A^{1/3}=4.05$ fm. It is clearly seen that the term $R\mathrm{\Psi }(R)$ reduces as the binding energies approach to 0, diminishing to more than 60$\%$ of its original value. This indicates that the reduction observed in the $1p$-orbital SO-splitting can be fully accounted for by the evolution of the wavefunctions toward weak binding.

³²Si should have a similar $1s_{1/2}$ occupancy as ³⁴Si, according to the latest safe Coulomb excitation measurement [32], as also supported by the theories. It is noted that there is yet no experimental measurement informing on the proton occupancy. Related measurements to determine its proton occupancy in the $1s_{1/2}$ orbital are being planned with the Active-Target Time Projection Chamber (AT-TPC) [33] coupled with the HELIOS solenoid. Using the proton addition or removal reaction, the proton occupancy of ³²Si in the $s_{1/2}$ orbital will be determined.

3.4 SO splittings of orbitals with $\ell =1$ and $\ell =3$

The discussion above mostly focuses on the SO-splitting of the $1p$-shell orbitals. One may wonder if the weak binding or central depletion effect may be revealed in the SO-splitting of the $0f$ orbitals. The radial wavefunction of the $0f$ orbital is compared with that of the $1p$ orbital in Figure 1B. In addition, Equation 1 shows that the changes in the wavefunction at the smaller radius would have a larger impact on the SO potential. Therefore, some may expect that there would be a sudden reduction in the SO-splitting in case of a central depletion. However, the $0f$ orbital wavefunction seems to have very little sensitivity to the change in the potentials in the very center of nuclei ($R<2$ fm), where the depletion was presented. Consequently, the central depletion should have very little impact on the SO-splitting of the $0f$ orbitals.

On the other hand, the weak binding effect may still impact the SO-splitting of the $0f$ orbitals, although much less than the $1p$ orbital. According to a calculation with the WS potential, the change in the SO-splitting from binding energy is approximately $50\%$ less compared to that of $1p$ orbitals. However, this effect will still be clearly seen based on the usual uncertainties of approximately 100–200 keV for determining the single-particle energies from the transfer reactions. Future experiments to measure the $0f$ orbital SO splittings in Si and S under weak binding would be important to further study whether the weak binding effect or the central density depletion plays a major role.

4 SO interactions in heavy nuclei

In heavy nuclei, the SO interaction is even stronger due to the higher angular momentum and larger node number. For examples, in the nucleus of ¹³²Sn, the SO splittings of the $1f$, $2p$, and $1d$ orbits were investigated, which shows a reduction in the SO-splitting of weakly bound $1p$ orbits compared to well-bound $1d$ orbits [34]. Similarly to the $N=19$ and $N=21$ cases discussed before, the reduction can be explained by the extended radial wavefunctions of the weakly bound orbits rather than a weakened SO interaction strength. The work also highlights the importance of understanding the SO interaction for calculations related to neutron-capture cross-sections in the r-process. Although the weak binding effect was shown to be dominant in this case, the effect of tensor force on the single-particle energies of the odd-mass Sb isotopes can also convincingly describe the data [8, 14]. More experimental studies are still needed in the future for a systematic study to understand the microscopic origins of the SO-splitting in heavy nuclei, which will be important for the predictions for the stability of superheavy elements. For example, the SO splittings near the $2s_{1/2}$ orbital would be interesting since there is no tensor component evolved.

5 Summary

SO-splitting plays a critical role in the nuclear shell model and the stability of nuclei, particularly those with magic numbers. An overview of the recent research on SO-splittings in atomic nuclei was presented. The microscopic origins of the SO term in the nuclear Hamiltonian and the possible contribution of the tensor forces and the weak-binding effect were examined. The concept of central density depletion in “bubble” nuclei like ³⁴Si and its impact on SO-splitting is investigated, using experimental data and theoretical calculations, which shows a smooth reduction in SO-splitting and the need for considering the fragmented single-particle strengths. Overall, the importance of the weak binding effect is highlighted in explaining the existing experimental data. The present review also emphasizes the need for advanced experimental studies to further unravel the driven mechanism of the SO interactions for the understanding of nuclear structure, the synthesis of heavy elements, and the prediction of stability in superheavy regions.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

JC: writing–original draft and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (Grant Numbers 12475120 and 12435010).

Acknowledgments

The author would like to express deepest gratitude to all those who provided the assistance to complete this project. The author is particularly grateful for the assistance given by the author’s colleagues Calem R. Hoffman and Ben P. Kay at Argonne National Laboratory, who offered invaluable suggestions for the research.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor SF declared a past co-authorship with the author.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mayer MG. On closed shells in nuclei. II. Phys Rev (1949) 75:1969–70. doi:10.1103/PhysRev.75.1969

CrossRef Full Text | Google Scholar

2. Haxel O, Jensen JHD, Suess HE. On the “magic numbers” in nuclear structure. Phys Rev (1949) 75:1766. doi:10.1103/PhysRev.75.1766.2

CrossRef Full Text | Google Scholar

3. Tanihata I, Savajols H, Kanungo R. Recent experimental progress in nuclear halo structure studies. Prog Part Nucl Phys (2013) 68:215–313. doi:10.1016/j.ppnp.2012.07.001

CrossRef Full Text | Google Scholar

4. Freer M, Horiuchi H, Kanada-En’yo Y, Lee D, Meißner UG. Microscopic clustering in light nuclei. Rev Mod Phys (2018) 90:035004. doi:10.1103/RevModPhys.90.035004

CrossRef Full Text | Google Scholar

5. Sorlin O, Porquet MG. Nuclear magic numbers: new features far from stability. Prog Part Nucl Phys (2008) 61:602–73. doi:10.1016/j.ppnp.2008.05.001

CrossRef Full Text | Google Scholar

6. Otsuka T, Gade A, Sorlin O, Suzuki T, Utsuno Y. Evolution of shell structure in exotic nuclei. Rev Mod Phys (2020) 92:015002. doi:10.1103/RevModPhys.92.015002

CrossRef Full Text | Google Scholar

7. Ji F, Miyazawa H. Spin-orbit coupling in heavy nuclei. Prog Theor Phys (1957) 17:366–72. doi:10.1143/PTP.17.366

CrossRef Full Text | Google Scholar

8. Otsuka T, Suzuki T, Fujimoto R, Grawe H, Akaishi Y. Evolution of nuclear shells due to the tensor force. Phys Rev Lett (2005) 95:232502. doi:10.1103/PhysRevLett.95.232502

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Terasawa T. Spin-orbit splitting and tensor force. i. Prog Theor Phys (1960) 23:87–105. doi:10.1143/ptp.23.8723.87

CrossRef Full Text | Google Scholar

10. Meng J, Ring P, Zhao P. Relativistic mean-field theory. In Relativistic Density Functional for Nuclear Structure. World Scientific Publishing Co. Pvt. Ltd. (2016). 21–81.

CrossRef Full Text | Google Scholar

11. Mairle G. Scaling of measured nuclear spin-orbit splittings. Phys Lett B (1993) 304:39–44. doi:10.1016/0370-2693(93)91396-5

CrossRef Full Text | Google Scholar

12. Uesaka T. Spins in exotic nuclei: ri beam experiments with polarized targets. Eur Phys J Plus (2016) 131:403. doi:10.1140/epjp/i2016-16403-1

CrossRef Full Text | Google Scholar

13. Cottle PD, Kemper KW. Persistence of the N = 28 shell closure in neutron-rich nuclei. Phys Rev C (1998) 58:3761–2. doi:10.1103/PhysRevC.58.3761

CrossRef Full Text | Google Scholar

14. Schiffer JP, Freeman SJ, Caggiano JA, Deibel C, Heinz A, Jiang CL, et al. Is the nuclear spin-orbit interaction changing with neutron excess? Phys Rev Lett (2004) 92:162501. doi:10.1103/PhysRevLett.92.162501

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Hamamoto I, Lukyanov S, Zhang X. Kinetic energy and spin-orbit splitting in nuclei near neutron drip line. Nucl Phys A (2001) 683:255–65. doi:10.1016/S0375-9474(00)00443-7

CrossRef Full Text | Google Scholar

16. Bohr A, Mottelson BR. Nulear struture. Singapore: World Sientific (1998). 218.

Google Scholar

17. Karakatsanis K, Lalazissis GA, Ring P, Litvinova E. Spin-orbit splittings of neutron states in n = 20 isotones from covariant density functionals and their extensions. Phys Rev C (2017) 95:034318. doi:10.1103/PhysRevC.95.034318

CrossRef Full Text | Google Scholar

18. Grasso M, Anguiano M. Neutron 2p and 1f spin-orbit splittings in 40Ca, 36S, and 34Si n = 20 isotones: tensor-induced and pure spin-orbit effects. Phys Rev C (2015) 92:054316. doi:10.1103/PhysRevC.92.054316

CrossRef Full Text | Google Scholar

19. Mutschler A, Lemasson A, Sorlin O, Bazin D, Borcea C, Borcea R, et al. A proton density bubble in the doubly magic ³⁴Si nucleus. Nat Phys (2017) 13:152–6. doi:10.1038/nphys3916

CrossRef Full Text | Google Scholar

20. Tsukada K, Abe Y, Enokizono A, Goke T, Hara M, Honda Y, et al. First observation of electron scattering from online-produced radioactive target. Phys Rev Lett (2023) 131:092502. doi:10.1103/PhysRevLett.131.092502

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Baranger M. A definition of the single-nucleon potential. Nucl Phys A (1970) 149:225–40. doi:10.1016/0375-9474(70)90692-5

CrossRef Full Text | Google Scholar

22. Burgunder G, Sorlin O, Nowacki F, Giron S, Hammache F, Moukaddam M, et al. Experimental study of the two-body spin-orbit force in nuclei. Phys Rev Lett (2014) 112:042502. doi:10.1103/PhysRevLett.112.042502

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Kay BP, Hoffman CR, Macchiavelli AO. Effect of weak binding on the apparent spin-orbit splitting in nuclei. Phys Rev Lett (2017) 119:182502. doi:10.1103/PhysRevLett.119.182502

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Sorlin O, de Oliveira Santos F, Ebran J. Reduced spin-orbit splitting in ³⁵Si: weak binding or density-depletion effect? Phys Lett B (2020) 809:135740. doi:10.1016/j.physletb.2020.135740

CrossRef Full Text | Google Scholar

25. Mackh H, Mairle G, Wagner GJ. Proton shell structure of mass 28–32 nuclei Z Physik (1974) 269:353–364. doi:10.1007/BF01668607

CrossRef Full Text | Google Scholar

26. Piskoř S, Franc P, Křemének J, Schäferlingová W. Spectroscopic information on ³⁵S and ³⁷S from the (d, p) reaction. Nucl Phys A (1984) 414:219–39. doi:10.1016/0375-9474(84)90641-9

CrossRef Full Text | Google Scholar

27. Mermaz MC, Whitten CA, Champlin JW, Howard AJ, Bromley DA. Study of the (d, p) reaction on ²⁸Si, ³²S, and ³⁶Ar at E_d = 18.00 mev. Phys Rev C (1971) 4:1778–800. doi:10.1103/PhysRevC.4.1778

CrossRef Full Text | Google Scholar

28. Van Der Baan J, Leighton H. Investigation of the ³⁴S(d, p)³⁵S reaction at ed = 10 mev. Nucl Phys A (1971) 170:607–15. doi:10.1016/0375-9474(71)90240-5

CrossRef Full Text | Google Scholar

29. Sen S, Hollas CL, Riley PJ. Reaction ³⁶Ar(d, p)³⁷Ar. Phys Rev C (1971) 3:2314–22. doi:10.1103/PhysRevC.3.2314

CrossRef Full Text | Google Scholar

30. Chen J, Kay B, Hoffman C, Tang T, Tolstukhin I, Bazin D, et al. Evolution of the nuclear spin-orbit splitting explored via the ³²Si(d, p)³³Si reaction using solaris. Phys Lett B 853 (2024) 138678. doi:10.1016/j.physletb.2024.138678

CrossRef Full Text | Google Scholar

31. Lalazissis GA, Nikšić T, Vretenar D, Ring P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys Rev C (2005) 71:024312. doi:10.1103/PhysRevC.71.024312

CrossRef Full Text | Google Scholar

32. Heery J, Henderson J, Hoffman CR, Hill AM, Beck T, Cousins C, et al. Suppressed electric quadrupole collectivity in ³²Si. Phys Rev C (2024) 109:014327. doi:10.1103/PhysRevC.109.014327

CrossRef Full Text | Google Scholar

33. Bradt J, Bazin D, Abu-Nimeh F, Ahn T, Ayyad Y, Beceiro-Novo S, et al. Commissioning of the active-target time projection chamber. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2017) 875:65–79. doi:10.1016/j.nima.2017.09.013

CrossRef Full Text | Google Scholar

34. Orlandi R, Pain S, Ahn S, Jungclaus A, Schmitt K, Bardayan D, et al. Neutron-hole states in ¹³¹Sn and spin-orbit splitting in neutron-rich nuclei. Phys Lett B (2018) 785:615–20. doi:10.1016/j.physletb.2018.08.005

CrossRef Full Text | Google Scholar