Relativistic nonlinear Thomson scattering of excited electron in ultra-tightly focused circularly polarized laser pulses with different beam waist radius

Based on Thomson scattering classical theory and single-electron model, we explore the influence of variations in the laser beam waist radius on the interaction between an ultra-tightly focused (UTF) laser and off-axis electron. In practical experiments, off-axis collisions predominate, and our study specifically addresses this scenario. Under UTF conditions ($b_0=2{\lambda }_0$), electron experience significant asymmetric forces, leading to deviations in axial trajectories, acceleration, and oscillations in energy. Simultaneously, observable asymmetries emerge in the electron’s radiated power and spectrum, gradually diminishing as the beam waist radius increases. These findings are pivotal for generating ultrashort pulses, particularly in ultrashort optics, and hold significance for applications leveraging nonlinear inverse Thomson scattering radiation.

1 Introduction

Over the past few decades, laser technology has advanced rapidly, catalyzing the continuous expansion and deepening of the field of laser-matter interaction [1–3]. Nonlinear inverse Thomson scattering (NITS), as an essential high-quality X-ray source [4, 5], has garnered significant attention from researchers due to its diverse applications ranging from biomedicine to atomic physics [6–8].

NITS devices utilize high-power lasers and relativistic electron beams within a controlled interaction region. Extensive research has been conducted to explore the characteristics of NITS under various parameters, aiming to enhance the modulation of X-rays, as illustrated in Figure 1. Extensive research has explored the characteristics of NITS under various parameters, aiming to enhance the modulation of X-rays [9–11]. Chris Harvey et al. investigated temporal envelope and focusing effects in laser-electron Thomson scattering [12], while S. G. Rykovanov’s team utilized laser chirping to control spectrum broadening for high laser pulse intensities [13].

Figure 1

Figure 1. Schematic diagram of relativistic nonlinear Thomson inverse scattering.

Previous studies have primarily focused on direct electron collisions with tightly focused laser pulses. However, achieving complete confinement of electron along the laser pulse axis under practical conditions presents significant challenges. Therefore, there is an urgent need to investigate and understand electron-laser interactions under off-axis conditions. Furthermore, there is a lack of research examining the impact of the laser beam waist radius on electron radiation properties, necessitating further investigation.

This paper provides an exploration into how the beam waist radius of a laser pulse influences electron dynamic properties, spatial radiated power characteristics, and spectral attributes during off-axis collisions within a circularly polarized tightly focused laser environment.

The findings demonstrate that the aforementioned characteristics are influenced by the laser beam waist radius, notably revealing distinct properties under ultra-tightly focused (UTF) conditions ($b_0=2{\lambda }_0$), which diminish or disappear as the beam waist radius increases. Under UTF ($b_0=2{\lambda }_0$), the electron experience pronounced asymmetrical forces at the beam waist, leading to considerable axial trajectory deviations, accelerated motion, and energy oscillations.

Observable asymmetries also manifest in the radiation’s spatial distribution, temporal spectrum, and angular distribution. A temporal spectral bias towards the x+axis and spatial spectral disparities around 130° and 230° are observed. Increasing the beam waist radius attenuates these asymmetries and reduces axial trajectory shift, electron acceleration, and energy oscillations along the z-direction. This is attributed to reduced laser intensity attenuation and reduced force disparities at electron positions with increased beam waist radius.

The remaining part of this paper is organized as follows: Section 2 derives analytical expressions encompassing the laser pulse vector potential, electron kinematics, radiation spectrum, and power factors, grounded in classical electrodynamics principles. Section 3 examines the influence of the laser beam waist radius on electron motion dynamics, spatial radiated power distribution, and radiation spectrum characteristics. In Section 4, we consolidate the impact of the laser beam waist radius on electron kinematics, spatial radiated power, and radiation spectrum. Furthermore, we explore methods to generate isolated narrow-second pulses with high signal-to-noise ratios by modulating the laser beam waist radius.

2 Theory and formula

In this paper we introduce a Laguerre–Gaussian (LG) laser pulse propagating along the z-axis at a fluctuation angle ${\sigma }_{in}=0$ based on the RNTS (relativistic nonlinear Thomson scattering) model. And the medium is isotropic, homogeneous, nonmagnetic and nonconducting.

Here the wavelength of the laser ${\lambda }_0=1\mathrm{\mu }\mathrm{m}$, $c$ is the speed of light, $ϵ$ is the dielectric constant, and $m$ and $e$ denote the mass and charge of the electron. The first thing to state is that for all the following formula definitions, the spatial and temporal coordinates are normalized by the wave number of the laser $k_0^{-1}={\lambda }_0/2\pi$ and the frequency of the laser ${\omega }_0^{-1}={\lambda }_0/2\pi c$. In a tightly focused Gaussian laser field, the electric field $\mathit{E}$ and magnetic field $\mathit{B}$ can be stated by the following [14]:

$\mathit{E}=\nabla \times \mathit{\Lambda }(1)$

$\mathit{B}=\sqrt{ϵ}\left[\left(\frac{i}{k}\right)\nabla \left(\nabla ·\mathit{\Lambda }\right)+ik\mathit{\Lambda }\right](2)$

the above electric field $\mathit{E}$ and magnetic field $\mathit{B}$ satisfy Maxwell’s system of equations. And it is worth noting that $\mathit{\Lambda }$ is the solution to the Helmholtz equation:

${\nabla }^{\mathbf{2}}\mathit{\Lambda }+{\mathit{k}}_{\mathbf{0}}^{\mathbf{2}}\mathit{\Lambda }=\mathbf{0}(3)$

Circularly polarized lasers and their electromagnetic fields can be decomposed into x-axis and y-axis linearly polarized lasers whose phase difference is $\frac{\pi }{2}$, viz. $\mathit{E}={\mathit{E}}_{\mathit{x}\mathit{p}}+{\mathit{E}}_{\mathit{y}\mathit{p}}$, $\mathit{B}={\mathit{B}}_{\mathit{x}\mathit{p}}+{\mathit{B}}_{\mathit{y}\mathit{p}}$. Salamin et al. [15] and Zhang [16] derived $\mathit{\Lambda }$, $\mathit{B}$ and $\mathit{E}$ in the x-axis and y-axis linearly polarized laser field from Equations 1–3 respectively. By combining the aforementioned equations, the magnetic field components $\mathit{B}=\left\{B_x,B_y,B_z\right\}$ are described as Equations 4–6 [17]:

$\begin{array}{ll}\hfill {\mathit{B}}_{\mathit{x}}& ={\mathit{A}}_{\mathit{L}}[{\mathit{\varpi }}_{\mathbf{0}}^{\mathbf{0}}+{\mathit{\epsilon }}^{\mathbf{2}}\left[\frac{{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{0}}}{\mathbf{2}}-\frac{{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{0}}}{\mathbf{4}}\right]\hfill \\ \hfill & +{\mathit{\epsilon }}^{\mathbf{4}}\left[-\frac{{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{0}}}{\mathbf{8}}+\frac{{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{0}}}{\mathbf{4}}+\frac{\mathbf{5}{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{0}}}{\mathbf{16}}-\frac{{\mathit{r}}^{\mathbf{6}}{\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{0}}}{\mathbf{4}}+\frac{{\mathit{r}}^{\mathbf{8}}{\mathit{\varpi }}_{\mathbf{6}}^{\mathbf{0}}}{\mathbf{32}}\right]\hfill \end{array}(4)$

${\mathit{B}}_{\mathit{y}}={\mathit{A}}_{\mathit{L}}\left\{{\mathit{\varpi }}_{\mathbf{0}}^{\mathbf{1}}+{\mathit{\epsilon }}^{\mathbf{2}}\left[\frac{{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{1}}}{\mathbf{2}}-\frac{{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{1}}}{\mathbf{4}}\right]+{\mathit{\epsilon }}^{\mathbf{4}}\left[-\frac{{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{1}}}{\mathbf{8}}+\frac{{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{1}}}{\mathbf{4}}+\frac{\mathbf{5}{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{1}}}{\mathbf{16}}-\frac{{\mathit{r}}^{\mathbf{6}}{\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{1}}}{\mathbf{4}}+\frac{{\mathit{r}}^{\mathbf{8}}{\mathit{\varpi }}_{\mathbf{6}}^{\mathbf{1}}}{\mathbf{32}}\right]\right\}(5)$

$\begin{array}{c}{\mathit{B}}_{\mathit{z}}={\mathit{A}}_{\mathit{L}}\mathit{\beta }\left\{\mathit{\epsilon }{\mathit{\varpi }}_{\mathbf{1}}^{\mathbf{0}}+{\mathit{\epsilon }}^{\mathbf{3}}\left[\frac{{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{0}}}{\mathbf{2}}+\frac{{\mathit{r}}_{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{0}}}{\mathbf{2}}-\frac{{\mathit{r}}_{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{0}}}{\mathbf{4}}\right]+{\mathit{\epsilon }}_{\mathbf{5}}\left[\frac{\mathbf{3}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{0}}}{\mathbf{8}}+\frac{\mathbf{3}{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{0}}}{\mathbf{8}}+\frac{\mathbf{3}{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{0}}}{\mathbf{16}}-\frac{{\mathit{r}}^{\mathbf{6}}{\mathit{\varpi }}_{\mathbf{6}}^{\mathbf{0}}}{\mathbf{4}}+\frac{{\mathit{r}}^{\mathbf{8}}{\mathit{\varpi }}_{\mathbf{7}}^{\mathbf{0}}}{\mathbf{32}}\right]\right\}\\ -{\mathit{A}}_{\mathit{L}}\mathit{\sigma }\left\{\mathit{\epsilon }{\mathit{\varpi }}_{\mathbf{1}}^{\mathbf{1}}+{\mathit{\epsilon }}^{\mathbf{3}}\left[\frac{{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{1}}}{\mathbf{2}}+\frac{{\mathit{r}}_{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{1}}}{\mathbf{2}}-\frac{{\mathit{r}}_{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{1}}}{\mathbf{4}}\right]+{\mathit{\epsilon }}_{\mathbf{5}}\left[\frac{\mathbf{3}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{1}}}{\mathbf{8}}+\frac{\mathbf{3}{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{1}}}{\mathbf{8}}+\frac{\mathbf{3}{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{1}}}{\mathbf{16}}-\frac{{\mathit{r}}^{\mathbf{6}}{\mathit{\varpi }}_{\mathbf{6}}^{\mathbf{1}}}{\mathbf{4}}+\frac{{\mathit{r}}^{\mathbf{8}}{\mathit{\varpi }}_{\mathbf{7}}^{\mathbf{1}}}{\mathbf{32}}\right]\right\}\end{array}(6)$

and the electric field component $\mathit{E}=\left\{E_x,E_y,E_z\right\}$ can be derived as Equations 7–9:

$\begin{array}{l}{\mathit{E}}_{\mathit{x}}={\mathit{A}}_{\mathit{L}}\{{\mathit{\varpi }}_{\mathbf{0}}^{\mathbf{1}}+{\mathit{\epsilon }}^{\mathbf{2}}\left[{\mathit{\varsigma }}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{1}}-\frac{{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{1}}}{\mathbf{4}}\right]\\ +{\mathit{\epsilon }}^{\mathbf{4}}\left[\frac{{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{1}}}{\mathbf{8}}-\frac{{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{1}}}{\mathbf{4}}-\frac{{\mathit{r}}^{\mathbf{2}}\left({\mathit{r}}^{\mathbf{2}}-\mathbf{16}{\mathit{\alpha }}^{\mathbf{2}}\right){\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{1}}}{\mathbf{16}}-\frac{{\mathit{r}}^{\mathbf{4}}\left({\mathit{r}}^{\mathbf{2}}+\mathbf{2}{\mathit{\alpha }}^{\mathbf{2}}\right){\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{1}}}{\mathbf{8}}+\frac{{\mathit{r}}^{\mathbf{8}}{\mathit{\varpi }}_{\mathbf{6}}^{\mathbf{1}}}{\mathbf{32}}\right]\\ +{\mathit{\epsilon }}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{0}}+{\mathit{\epsilon }}^{\mathbf{4}}\left[{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{0}}-\frac{{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{0}}}{\mathbf{4}}\right]\}\end{array}(7)$

$\begin{array}{l}{\mathit{E}}_{\mathit{y}}={\mathit{A}}_{\mathit{L}}\{{\mathit{\varpi }}_{\mathbf{0}}^{\mathbf{0}}+{\mathit{\epsilon }}^{\mathbf{2}}\left[{\mathit{\beta }}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{0}}-\frac{{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{0}}}{\mathbf{4}}\right]\\ +{\mathit{\epsilon }}^{\mathbf{4}}\left[\frac{{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{0}}}{\mathbf{8}}-\frac{{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{0}}}{\mathbf{4}}-\frac{{\mathit{r}}^{\mathbf{2}}\left({\mathit{r}}^{\mathbf{2}}-\mathbf{16}{\mathit{\beta }}^{\mathbf{2}}\right){\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{0}}}{\mathbf{16}}-\frac{{\mathit{r}}^{\mathbf{4}}\left({\mathit{r}}^{\mathbf{2}}+\mathbf{2}{\mathit{\beta }}^{\mathbf{2}}\right){\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{0}}}{\mathbf{8}}+\frac{{\mathit{r}}^{\mathbf{8}}{\mathit{\varpi }}_{\mathbf{6}}^{\mathbf{0}}}{\mathbf{32}}\right]\\ +{\mathit{\epsilon }}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{1}}+{\mathit{\epsilon }}^{\mathbf{4}}\left[{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{1}}-\frac{{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{1}}}{\mathbf{4}}\right]\}\end{array}(8)$

$\begin{array}{l}\begin{array}{l}\begin{array}{l}{\mathit{E}}_{\mathit{z}}={\mathit{A}}_{\mathit{L}}\mathit{\sigma }\{\mathit{\epsilon }{\mathit{\varpi }}_{\mathbf{1}}^{\mathbf{0}}+{\mathit{\epsilon }}^{\mathbf{3}}\left[-\frac{{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{0}}}{\mathbf{2}}+{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{0}}-\frac{{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{0}}}{\mathbf{4}}\right]\\ +{\mathit{\epsilon }}^{\mathbf{5}}\left[-\frac{\mathbf{3}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{0}}}{\mathbf{8}}-\frac{\mathbf{3}{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{0}}}{\mathbf{8}}+\frac{\mathbf{17}{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{0}}}{\mathbf{16}}-\frac{\mathbf{3}{\mathit{r}}^{\mathbf{6}}{\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{0}}}{\mathbf{16}}-\frac{\mathbf{3}{\mathit{r}}^{\mathbf{6}}{\mathit{\varpi }}_{\mathbf{6}}^{\mathbf{0}}}{\mathbf{8}}+\frac{{\mathit{r}}^{\mathbf{8}}{\mathit{\varpi }}_{\mathbf{7}}^{\mathbf{0}}}{\mathbf{32}}\right]\}\end{array}\\ -{\mathit{K}}_{\mathit{L}}\mathit{\beta }\{\mathit{\epsilon }{\mathit{\varpi }}_{\mathbf{1}}^{\mathbf{1}}+{\mathit{\epsilon }}^{\mathbf{3}}\left[-\frac{{\mathit{\varpi }}_{\mathbf{2}}^{\mathbf{1}}}{\mathbf{2}}+{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{1}}-\frac{{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{1}}}{\mathbf{4}}\right]\end{array}\\ +{\mathit{\epsilon }}^{\mathbf{5}}\left[-\frac{\mathbf{3}{\mathit{\varpi }}_{\mathbf{3}}^{\mathbf{1}}}{\mathbf{8}}-\frac{\mathbf{3}{\mathit{r}}^{\mathbf{2}}{\mathit{\varpi }}_{\mathbf{4}}^{\mathbf{1}}}{\mathbf{8}}+\frac{\mathbf{17}{\mathit{r}}^{\mathbf{4}}{\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{1}}}{\mathbf{16}}-\frac{\mathbf{3}{\mathit{r}}^{\mathbf{6}}{\mathit{\varpi }}_{\mathbf{5}}^{\mathbf{1}}}{\mathbf{16}}-\frac{\mathbf{3}{\mathit{r}}^{\mathbf{6}}{\mathit{\varpi }}_{\mathbf{6}}^{\mathbf{1}}}{\mathbf{8}}+\frac{{\mathit{r}}^{\mathbf{8}}{\mathit{\varpi }}_{\mathbf{7}}^{\mathbf{1}}}{\mathbf{32}}\right]\}\end{array}(9)$

where fifth-order expansion of the electromagnetic field accurate to the diffraction angle $\epsilon =w_0/z_r$, and $\sigma =x/w_0$, $\beta =y/w_0$, $r=\rho /w_0$, $w_0$ represents the minimum waist radius. $A_L$ can be described as follows:

${\mathit{A}}_{\mathit{L}}={\mathit{a}}_{\mathbf{0}}\frac{{\mathit{w}}_{\mathbf{0}}}{\mathit{w}}\mathit{exp}\left(-\frac{{\mathit{\eta }}^{\mathbf{2}}}{{\mathit{L}}^{\mathbf{2}}}\right)\mathit{exp}\left(-\frac{{\mathit{\rho }}^{\mathbf{2}}}{{\mathit{w}}^{\mathbf{2}}}\right)(10)$

when the laser at $z$, the waist radius $w=w_0\sqrt{1+\frac{z_f^2}{z^2}}$, $z_r=w_0^2/2$ indicates the Rayleigh distance, $\eta =z-t$, $\rho =\sqrt{x^2+y^2}$ denotes the perpendicular distance, and $a_0$ indicates the peak amplitude, whose relationship between laser intensity is $a_0=\sqrt{I{\lambda }_0^2/1.37}\times {10}^9$.

The electromagnetic field is fifth-order expanded accurate to the diffraction angle $\epsilon =w_0/z_r$, among them, ${\varpi }_n^0$ and ${\varpi }_n^1$ are shown as Equation 11:

${\mathit{\varpi }}_{\mathit{n}}^{\mathit{i}}={\left(\frac{{\mathit{w}}_{\mathbf{0}}}{\mathit{w}}\right)}^{\mathit{n}}\mathit{cos}\left(\mathit{\phi }+\mathit{n}{\mathit{\phi }}_{\mathit{G}}+\frac{\mathit{i}\mathit{\pi }}{\mathbf{2}}\right)\mathit{n}=\mathbf{0},\mathbf{1},\mathbf{2},\dots (11)$

$\phi =\eta +{\phi }_R-{\phi }_G+{\phi }_0$, where ${\phi }_R=\frac{\left(x^2+y^2\right)}{2R\left(z\right)}$, $R\left(z\right)=z\left(1+\frac{z_f^2}{z^2}\right)$ and ${\phi }_G={\mathit{tan}}^{-1}\left(\frac{z}{z_f}\right)$. ${\phi }_R$ is the phase associated with the curvature of the wave fronts, and that $R\left(z\right)$ is the radius of a curvature of a wave front intersecting the beam axis at the coordinate $z$. ${\phi }_G$ is the Guoy phase associated with the fact that a Gaussian beam undergoes a total phase change of $\pi$ as $z$ changes from $-\infty$ to $+\infty$, ${\phi }_0$ is the initial phase of the laser pulse, which is determined by the pulse. ${\phi }_0$ is different from the initial phase that electron experiences when it enters the field.

In the course of the calculation, the focal point of the laser pulse was established as the origin, and the electron move from {$d_0,0,z_0$} toward the laser, where $z_0$ represents the enough far away position, and $d_0$ denotes the initial off-axis position of the electron.

The following Lorentz and energy (Equations 12, 13) can be used to compute the momentum of the electron in an intense laser pulse:

$\frac{\mathit{d}\mathit{p}}{\mathit{d}\mathit{t}}=-\mathit{e}\left(\mathit{E}+\frac{\mathit{u}}{\mathit{c}}\times \mathit{B}\right)(12)$

$\frac{\mathit{d}\mathit{\Gamma }}{\mathit{d}\mathit{t}}=-\mathit{e}\left(\mathit{v}·\mathit{E}\right)(13)$

In this context, $\mathrm{\Gamma }=\mathrm{\gamma }m{c}^2$ represents the electron energy, which is defined in terms of the Lorentz factor $\mathrm{\gamma }={\left[1-{\left(\mathit{v}/c\right)}^2\right]}^{-1/2}$. The momentum $\mathit{p}$ is given by the relation $\mathit{p}=\mathrm{\Gamma }\mathit{u}/c^2$, $\mathit{v}$ is the electron velocity, and $\mathit{u}=\mathit{v}/c$.

When an electron is in relativistic motion, it emits radiation. The radiated power or energy per unit solid angle is given below [18, 19]:

${\mathit{P}}_{\mathit{\Omega }}=\frac{\mathit{d}\mathit{P}\left(\mathit{t}\right)}{\mathit{d}\mathit{\Omega }}={\left[\frac{{\left|\mathit{n}\times \left[\left(\mathit{n}-\mathit{u}\right)\times \mathit{u}\right]\right|}^{\mathbf{2}}}{{\left(\mathbf{1}-\mathit{n}\cdot \mathit{u}\right)}^{\mathbf{6}}}\right]}_{{\mathit{t}}^{\prime }}(14)$

Here, the power radiated per unit solid angle $P_{\mathrm{\Omega }}$ is normalized. The direction of radiation represented by $\mathit{n}=\left\{\sin \theta \cos \varphi ,\sin \theta \sin \varphi ,\cos \theta \right\}$, is specified in terms of the polar angle θ relative to the laser movement direction. And $\varphi$ denotes the azimuth in the plane perpendicular to the origin. The time at which the electron interacts with the laser pulse $t^{\prime }$, can be expressed as $t=t^{\prime }+R,\text{where\hspace{0.17em}}R\sim R_0-\mathit{n}·\mathit{r}$. $R_0$ denotes the distance from the origin to the observer, $\mathit{r}$ is the position vector of the electron.

Lee et al. proposed power factor (Equation 15) as a means of characterizing the peak power radiated by the electron in RNTS [20]:

$\mathit{F}\mathit{a}\mathit{c}\mathit{t}\mathit{o}\mathit{r}=\frac{{\left(\frac{\mathit{d}{\mathit{u}}_{\mathit{x}}}{\mathit{d}\mathit{t}}\right)}^{\mathbf{2}}+{\left(\frac{\mathit{d}{\mathit{u}}_{\mathit{y}}}{\mathit{d}\mathit{t}}\right)}^{\mathbf{2}}}{{\left(\mathbf{1}-{\left|\mathit{u}\right|}^{\mathbf{2}}\right)}^{\mathbf{4}}}(15)$

The equation for the radiant energy per unit steradian angle per unit frequency interval during the interaction of electron with a laser pulse can be expressed as follows [21]:

$\frac{{\mathit{d}}^{\mathbf{2}}\mathit{I}}{\mathit{d}\mathit{\omega }\mathit{d}\mathit{\Omega }}={\left|{\displaystyle \underset{-\mathit{\infty }}{\overset{\mathit{\infty }}{\int }}}\frac{\mathit{n}\times \left[\left(\mathit{n}-\mathit{u}\right)\times \mathit{u}\right]}{{\left(\mathbf{1}-\mathit{n}\cdot \mathit{u}\right)}^{\mathbf{2}}}{\mathit{e}}^{\mathit{i}\mathit{s}\left(\mathit{t}-\mathit{n}\cdot \mathit{r}\right)}\mathit{d}\mathit{t}\right|}^{\mathbf{2}}(16)$

The normalized expression $\frac{d^{2}I}{d\omega d\mathrm{\Omega }}$ is derived by employing the constant $\frac{e^2}{4{\pi }^{2}c}$, as well as the harmonic frequency ratio $s=\frac{{\omega }_s}{{\omega }_0}$, ${\omega }_s$ is the frequency of the harmonic radiation. Solving Equations 14, 16 gives the full time, space, and spectral characteristics of electron harmonic radiation.

3 Numerical results

In our observations, we directed our focus towards the radiation emanating from a precisely defined sphere with a radius of 1 m, positioned at the origin of the coordinate system. The peak amplitude of the laser pulse $a_0=5$, while the pulse duration L is tuned to 6.6 fs. The initialization of the phase ${\phi }_0=0$. Initially, the electron is endowed with an energy of 5 (equivalent to 2.56 MeV), which is denoted as ${\gamma }_0$, and its initial off-axis distance $d_0=0.4$, moving in the opposite direction of the z-axis. The electron can be accelerated to this energy level by a linear accelerator. In view of the characteristics of circularly polarized laser pulses, at the radial off-axis angle ${\alpha }_0$, the effect of the pulse with initial phase ${\phi }_0$ on the electron is equivalent to the effect of the pulse with initial phase ${\phi }_0+{\beta }_0-{\alpha }_0$ at the radial off-axis angle ${\beta }_0$, which means that the effect of the off-axis position of the electron on their collision with the off-axis of the laser pulse can be adjusted by the initial phase ${\phi }_0$ of the laser pulse. Thus, the point of collision of the electron with the laser pulse, namely, the maximum value of the amplitude of the electron motion, is located on the x-axis of the Cartesian coordinate system. In our discussion, the peak radiated power per unit solid angle will be formally designated as $dP/d\mathrm{\Omega }$. It should be emphasized that every numerical datum described here has its genesis in the unchanging foundation of physical principles and equations outlined in Section 2.

3.1 Electronic motion properties

As indicated in Figures 2A–F, the motion trajectories of off-axis electron are finally shifted in the x+axis direction after interacting with the laser at UTF ($b_0=2{\lambda }_0$). As the radius of the laser beam waist increases, the resultant axial displacement of the off-axis electron trajectory decreases. This phenomenon stems from the significant imbalance of forces exerted on the electron along the x+axis and x-axis directions at positions of asymmetry inherent in UTF ($b_0=2{\lambda }_0$), consequently yielding a more substantial final axial shift in the electron’s motion trajectory. When the radius of the laser beam waist increases, the laser intensity attenuation decreases, and the discrepancy between forces acting along the x+axis and x-axis directions on the electron is reduced which leads to the weakening of the final offset phenomenon.

Figure 2

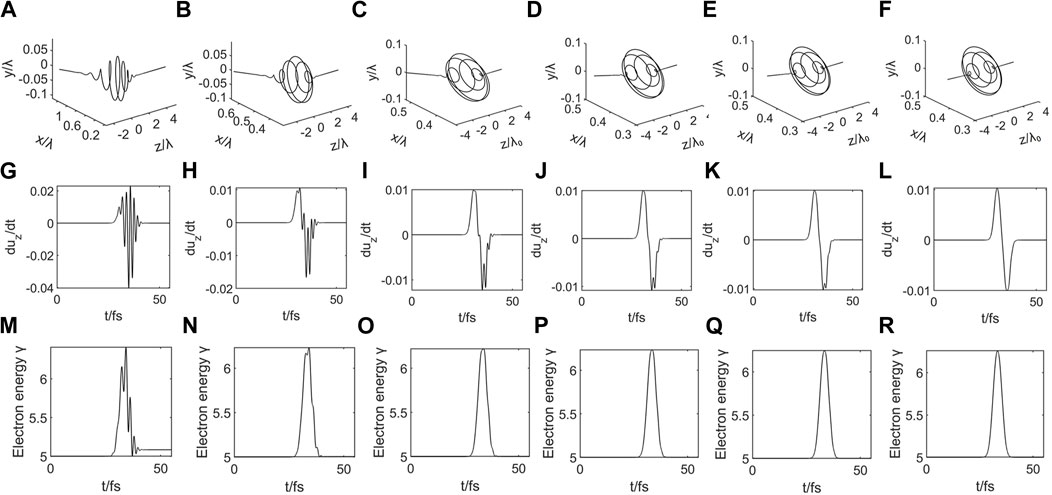
Figure 2. The effect of laser pulses with different laser beam waist radius on the motion of electron, where (A–F) are the trajectory plots of the electron which show the variations in the degree of final axial deflection of the electron, (G–L) are the changes in acceleration of the electron in the z-axis direction at different moments, and (M–R) reflect the variations in the electron energy. (A) b₀ = 2λ₀. (B) b₀ = 4. (C) b₀ = 6. (D) b₀ = 8. (E) b₀ = 10. (F) b₀ = 20. (G) b₀ = 2. (H) b₀ = 4. (I) b₀ = 6. (J) b₀ = 8. (K) b₀ = 10. (L) b₀ = 20. (M) b₀ = 2. (N) b₀ = 4. (O) b₀ = 6. (P) b₀ = 8. (Q) b₀ = 10. (R) b₀ = 20.

It can be observed in Figures 2G–L that both the acceleration and deceleration oscillation phenomena along the z-axis are more pronounced at UTF ($b_0=2{\lambda }_0$). Furthermore, with an increase in the radius of the laser beam waist, the intensity of these oscillatory phenomena gradually weakens. Specifically, the acceleration oscillation basically disappeared at $b_0=6{\lambda }_0$, while the deceleration oscillation lasted until the $b_0=20{\lambda }_0$ place before it disappeared.

Moreover, the electron energy oscillation phenomenon is very significant in the UTF ($b_0=2{\lambda }_0$), yet with the increase of the laser beam waist radius, the energy oscillation phenomenon is gradually weakened until it vanishes, exhibiting a stable trend characterized by an initial increase followed by a subsequent decrease, and this change can be reflected in Figures 2M–R.

The oscillation of electron acceleration and energy is induced by the degree of nonlinearity of the laser. In the realm of UTF ($b_0=2{\lambda }_0$), the laser’s nonlinearity manifests prominently, and the electron are subjected to the qualitative force at the laser beam waist which exhibits significant asymmetry in the x+axis and x-axis directions. Consequently, the electron are object to the combined qualitative force oscillations, resulting in oscillations in its z-direction acceleration; and with an increase in $b_0$, the nonlinear nature of the laser is lessened, and so does the asymmetry of the qualitative force in the x+axis and x-axis directions which the electron subjected to at the laser beam waist, leading to a smoother trajectory of z-direction acceleration for the electron.

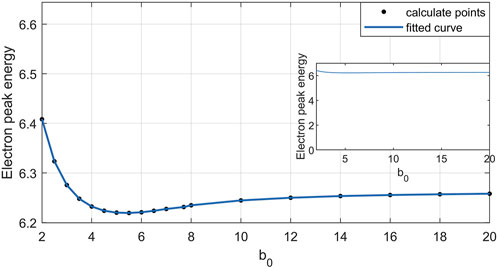
The graphical representation in Figure 3 illustrates the dynamic relationship between the peak electron energy and the expansion of the laser beam waist radius. Evidently, as the laser beam waist radius transitions from $b_0=2{\lambda }_0$ to $b_0=20{\lambda }_0$, there is a descent followed by a subsequent ascent in the peak electron energy, achieving the nadir at about $b_0=5.5{\lambda }_0$.

Figure 3

Figure 3. Variation of peak electron energy with increasing laser beam waist radius.

3.2 Electron space radiation properties of relativistic nonlinear Thomson inverse scattering

3.2.1 Power properties of electron space radiation

Figures 4A–F delineate that the spatial distribution of electron radiated power has an evident asymmetry at UTF ($b_0=2{\lambda }_0$), and the asymmetry of electron spatial radiation becomes weaker and weaker with the expanding radius of the laser beam waist. This phenomenon can be attributed to the qualitative force in the x+axis and x-axis directions acting upon the electron at the laser beam waist. There is a significant asymmetry at UTF ($b_0=2{\lambda }_0$), while this asymmetry undergoes a gradual attenuation with the increase of $b_0$. Remarkably, during this process, there is always a distinct vortex state, consistent with the findings of Wang et al. [17].

Figure 4

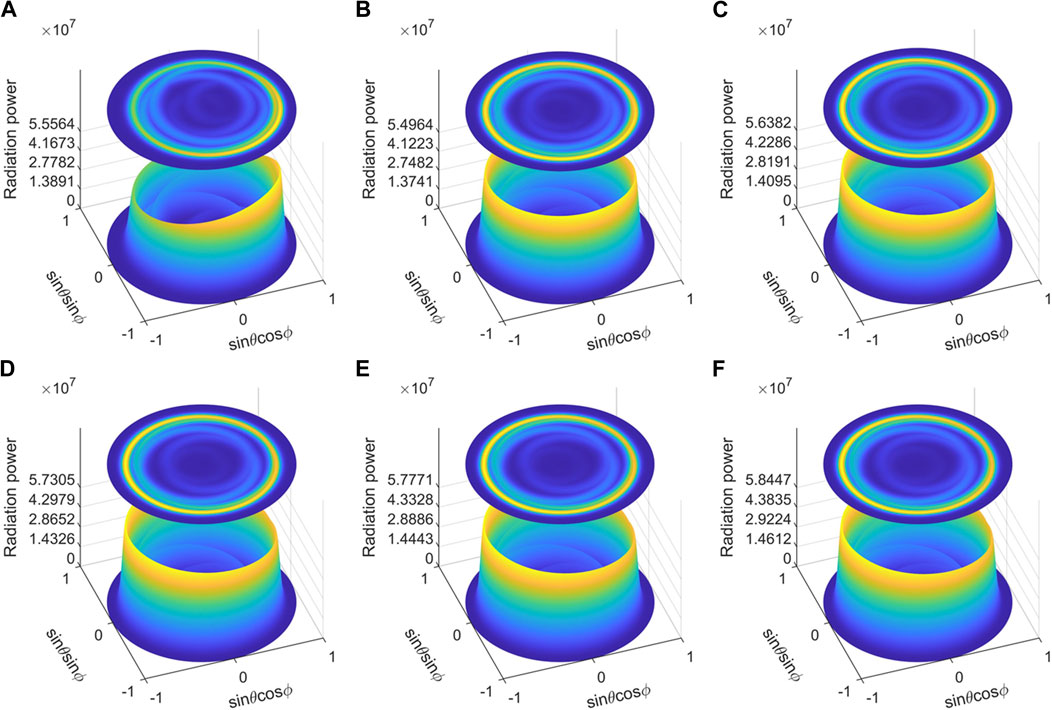
Figure 4. Spatial distribution of electron radiated power in the presence of laser pulses with different beam waist radius $b_0$. (A) b₀ = 2λ₀. (B) b₀ = 4λ₀. (C) b₀ = 6λ₀. (D) b₀ = 8λ₀. (E) b₀ = 10λ₀. (F) b₀ = 20λ₀.

Curve fitting analysis was conducted on the peak power of electron radiation under the influence of laser pulses with varying beam waist radius, and it was found that the peak power of electron radiation shows a changing trend as depicted in Figure 5: Within the range of $b_0=2{\lambda }_0$ to $b_0=20{\lambda }_0$, the electron peak energy initially declines with the waist radius, and subsequently escalates. Notably, at approximately $b_0=3{\lambda }_0$, the peak radiation power reaches its nadir. As can be seen in Figure 6, the trends of the fitted curves of the electron power factor under the influence of laser pulses with different beam waist radii are roughly the same as that of the peak electron power, and both of them display excellent consistency.

Figure 5

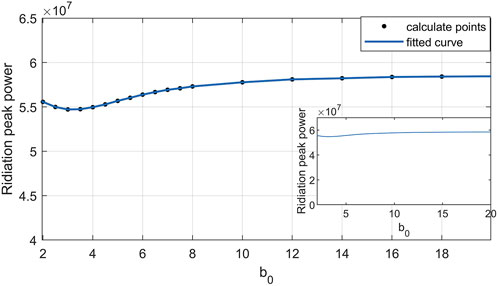
Figure 5. Fitting curves of peak power of electron radiation under the action of laser pulses with different beam waist radius $b_0$.

Figure 6

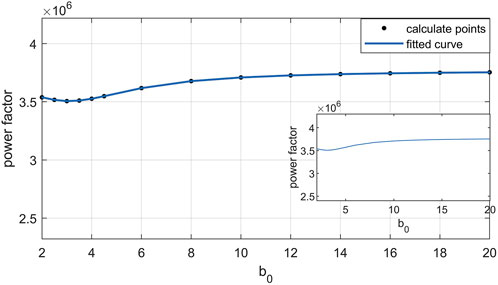
Figure 6. Fitting curves of power factor of electron radiation under the action of laser pulses with different beam waist radius $b_0$.

At $b_0=2{\lambda }_0$ to $b_0=3{\lambda }_0$, although there is an asymmetry in the x+axis and x-axis directions in the qualitative force on the electron at the waist of the laser beam, the difference between the two decreases with the increase of $b_0$, and the electron are subjected to a decrease in the combined qualitative force, and thus the radiated power of the electron decreases; at $b_0=3{\lambda }_0$ to $b_0=20{\lambda }_0$, since the variable studied in this paper is only $b_0$, the vector potential term $a_0=\exp \left(-\frac{{\eta }^2}{L^2}-\frac{{\rho }^2}{b^2}\right)$ in Equation 10 can be regarded as a term positively correlated only with $\exp \left(-\frac{{\rho }^2}{b^2}\right)$. $-\frac{{\rho }^2}{b^2}$ increases when $b_0$ increases, so the electron are subjected to an increased mass-power interaction, and hence the radiated power of the electron increases.

3.2.2 Electron temporal relativistic nonlinear Thomson inverse scattering properties

Figures 7A–F show that at UTF ($b_0=2{\lambda }_0$), it exhibits a small disparity between the principal and secondary peaks within the same theta direction, and the gap between the two gradually widens with increasing $b_0$.

Figure 7

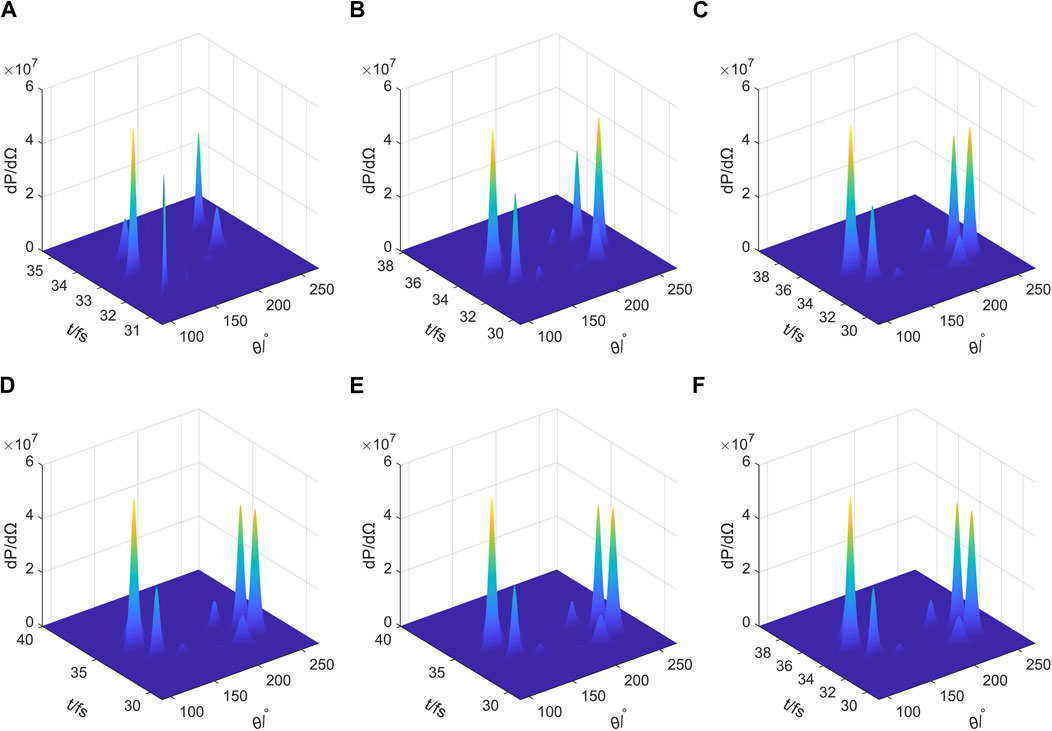
Figure 7. Angular distribution of electron radiation pulse time spectra θ under the action of laser pulses with different beam waist radius $b_0$. (A) b₀ = 2λ₀. (B) b₀ = 4λ₀. (C) b₀ = 6λ₀. (D) b₀ = 8λ₀. (E) b₀ = 10λ₀. (F) b₀ = 20λ₀.

It can be seen from Figures 8A–F that the radiation pulse time spectrum about the phi = 180 asymmetry is conspicuous at UTF ($b_0=2{\lambda }_0$), and the asymmetry diminishes with increasing $b_0$. Notably, under UTF conditions ($b_0=2{\lambda }_0$), the time spectrum’s radiation pulse power tilts towards the x + axis direction, a pattern that reverses with increasing $b_0$, favoring the x-axis direction.

Figure 8

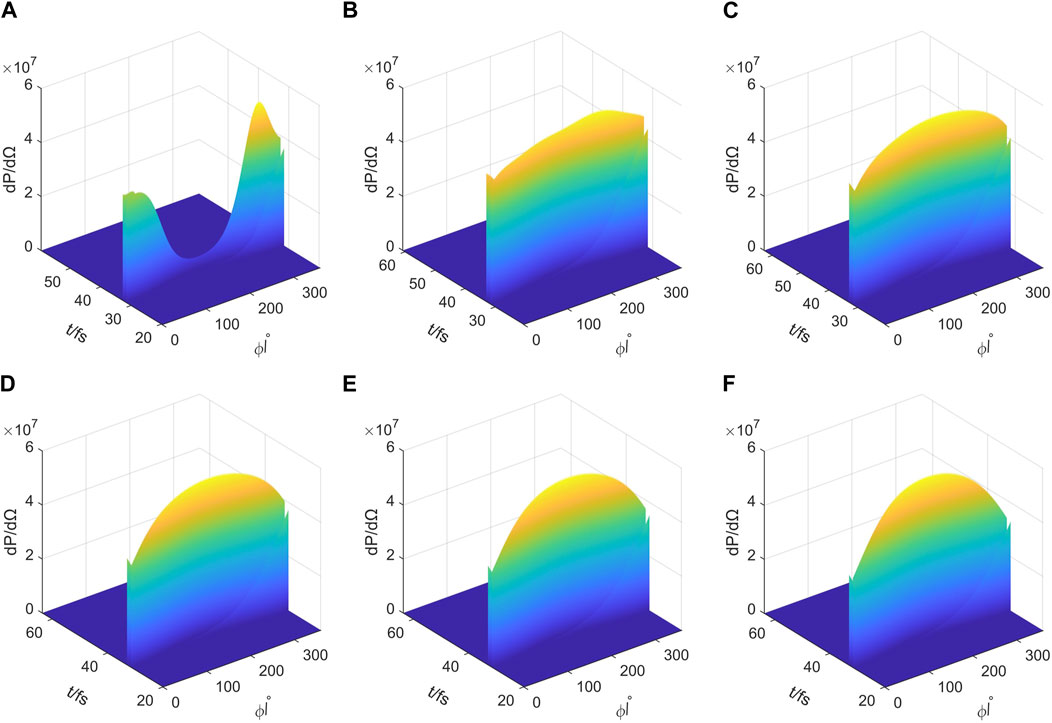
Figure 8. Angular distribution of the electron radiation pulse time spectrum Φ under the action of laser pulses with different beam waist radius $b_0$. (A) b₀ = 2λ₀. (B) b₀ = 4λ₀. (C) b₀ = 6λ₀. (D) b₀ = 8λ₀. (E) b₀ = 10λ₀. (F) b₀ = 20λ₀.

This segment delves into the effect of electron on the time distribution in the direction of peak radiated power generation, modulated by the laser beam waist radius. The comparative analysis employs varied laser beam waist radius $b_0=2{\lambda }_0$, 4 ${\lambda }_0$, 6 ${\lambda }_0$, 8 ${\lambda }_0$, 10 ${\lambda }_0$, and 20 ${\lambda }_0$, as shown in Figure 9. At UTF ($b_0=2{\lambda }_0$), the gap between the primary and secondary peak powers in the same radiation direction is small, and as $b_0$ escalates, the secondary peak value significantly decreases, concurrently expanding the gap, a phenomenon consistently observed across Figures 9A–F. In addition, the half-peak full-width changes less and is hovering around $5\times {10}^{-4}$ fs. This suggests that the beam waist radius of the laser pulse is less correlated with the half-peak full width. Anticipatedly, when $b_0$ attains or exceeds 10 ${\lambda }_0$, we can acquire isolated narrow-second pulses with high signal-to-noise ratios, which is of greater practical value for experiments in ultrashort and ultrafast optics.

Figure 9

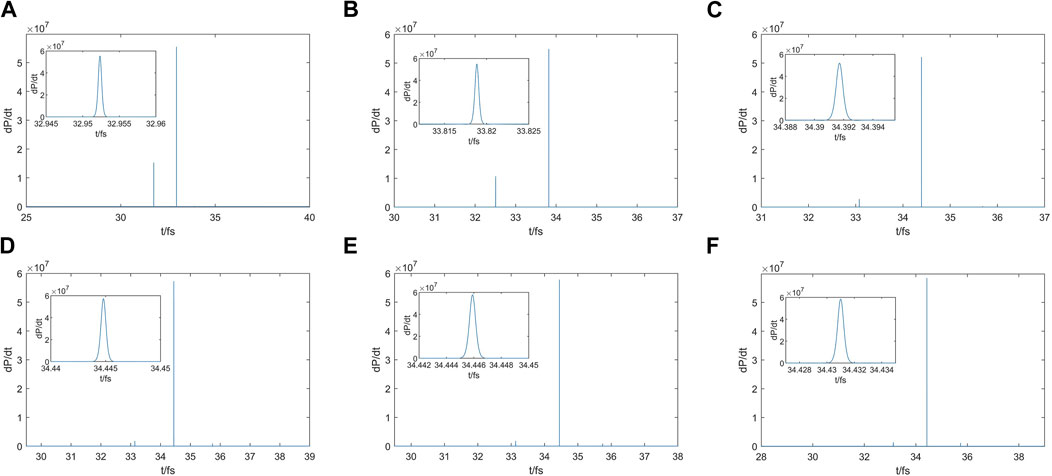
Figure 9. Radiation time distribution in the direction of the maximum power of electron radiation and amplification of the main radiation pulse in the direction of the maximum power of electron radiation in the presence of laser pulses with different beam-waist radius $b_0=2{\lambda }_0$, 4 ${\lambda }_0$, 6 ${\lambda }_0$, 8 ${\lambda }_0$, 10 ${\lambda }_0$ and 20 ${\lambda }_0$. (A) b₀ = 2λ₀. (B) b₀ = 4λ₀. (C) b₀ = 6λ₀. (D) b₀ = 8λ₀. (E) b₀ = 10λ₀. (F) b₀ = 20λ₀.

3.2.3 Spectral properties of electron radiation

Figures 10A–F demonstrate that as the parameter Φ attains its peak radiant power Φ, the spectral radiation reaches its pinnacle intensity, accompanied by the highest peak frequency of the spectral harmonic, occurring at theta of about $130°$ in the UTF state. But at approximately $230°$, the brightness decreases a bit, along with a drop in harmonic frequency, and the radiation harmonics are red-shifted as $b_0$ increases. In addition, the angular distribution of harmonics about $180°$ shows asymmetry, which is specifically manifested by the difference between the frequencies at which the harmonic peaks are located and the harmonic peak light intensity when theta is $130°$ and $230°$. However, with the increase of $b_0$, the above gap becomes less obvious, and the asymmetry is weakened and finally disappears.

Figure 10

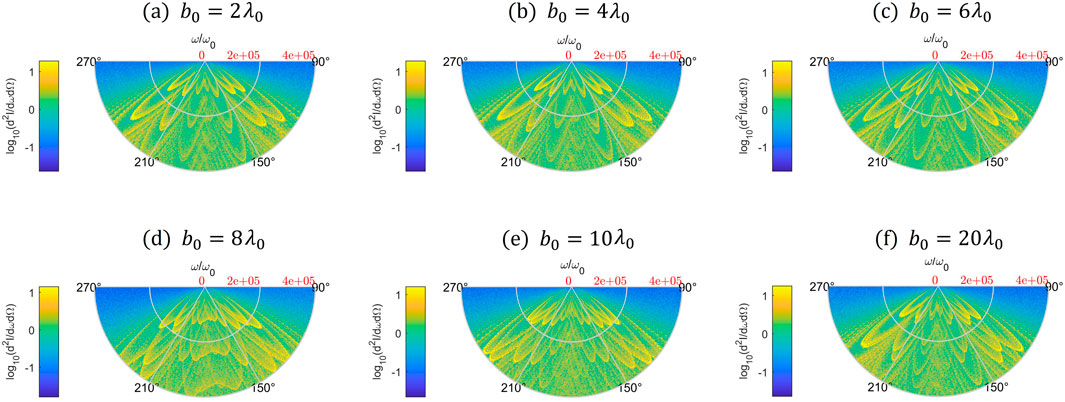
Figure 10. Changes in $\theta$ angular distribution of the spatial radiation spectra of electron in the presence of laser pulses with different beam waist radius $b_0$. (A) b₀ = 2λ₀. (B) b₀ = 4λ₀. (C) b₀ = 6λ₀. (D) b₀ = 8λ₀. (E) b₀ = 10λ₀. (F) b₀ = 20λ₀.

As can be seen from Figure 11A, when θ coincides with the peak radiated power θ, the radial distribution of the spectrum is concentrated in the x+axis direction and its vicinity during UTF, with a conspicuous phenomenon of harmonic overlap. Also, the spectral distribution with the x-axis as the symmetry axis exhibits obvious asymmetry. Nonetheless, as $b_0$ escalates, both the harmonic overlap and asymmetry gradually diminish until they are absent, as illustrated in Figures 11A–F. The above phenomenon is fully consistent with the trend of the electron spatial radiated power performance shown in Figure 4, and its causes are also the same.

Figure 11

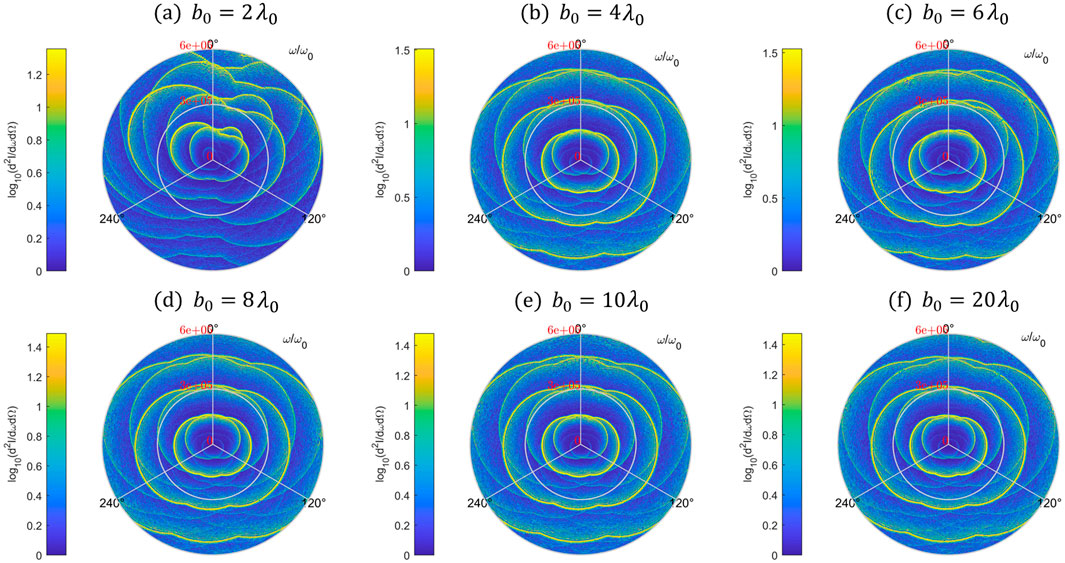
Figure 11. Changes in the Φ angular distribution of the spatial radiation spectra of electron in the presence of laser pulses with different beam waist radius $b_0$. (A) b₀ = 2λ₀. (B) b₀ = 4λ₀. (C) b₀ = 6λ₀. (D) b₀ = 8λ₀. (E) b₀ = 10λ₀. (F) b₀ = 20λ₀.

4 Conclusion

In this investigation, we carefully explore the effect of laser beam waist radius variations on the radiation properties in nonlinear Thomson scattering, particularly as it pertains to the interaction with off-axis electron. In practical experimental setups, the prevalent scenario involves electron engaging in off-axis collisions, underscoring the profound practical relevance of our study. Under conditions of UTF, denoted by $b_0=2{\lambda }_0$, electron are exposed to a pronounced asymmetry in the qualitative force along the x+axis and x-axis directions at the laser beam waist. This imbalance leads to a substantial axial deviation in electron trajectory, accompanied by notable instances of electron acceleration and energy oscillations.

Simultaneously, significant asymmetry emerges in the spatial distribution of the electron-radiated power, the temporal spectrum of the electron-radiated pulse, and the angular distribution of the spatial radiation spectrum. Specifically, the radiated pulse power within the temporal spectrum exhibits a marked bias towards the x+axis direction. Moreover, the spatial spectrum’s asymmetry manifests in the disparities observed in spectral peak radiation intensity and harmonic peak frequency at angles around 130°and 230° when Φ coincides with the peak radiated power Φ,and when θ serves as the peak radiant power reference, the spectral distribution showcases evident asymmetry.

With an increase in the beam waist radius $b_0$, the aforementioned asymmetries in spatial distribution, temporal spectrum, and angular distributions of spatial radiation spectra, are gradually weakened. At the same time, the magnitude of axial offset in off-axis electron trajectory diminishes, as well as the acceleration of the electron and the energy oscillations along the Z-direction. These phenomena are attributable to the decrease in the laser intensity attenuation after the beam waist radius is increased, coupled with a reduction in the disparity between forces acting along the x+axis and x-axis directions at the specified electron position.

In summary, the manipulation of the laser beam waist radius, particularly when $b_0$ equals or exceeds 10 ${\lambda }_0$, is of great significance for the generation of isolated narrow-second pulses boasting remarkable signal-to-noise ratios. This optimization bears greater practical value for investigations within the realms of ultrashort and ultrafast optics. Discerning the laser beam waist radius’s impact on radiation properties in nonlinear Thomson scattering of off-axis electron constitutes a pivotal stride towards utilizing nonlinear inverse Thomson scattering radiation (NITS) as an important source of radiation for both scientific research and practical applications, such as those in cancer therapy. By judiciously fine-tuning the laser beam waist radius, researchers can achieve an optimal balance between electron energy and radiation power for their specific experimental needs.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

QZ: Conceptualization, Data curation, Methodology, Writing–original draft, Writing–review and editing. JL: Formal Analysis, Supervision, Writing–review and editing. ZW: Data curation, Writing–original draft. YT: Conceptualization, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wiste T, Maliuk O, Tikhonchuk V, Lastovicka T, Homola J, Chadt K, et al. Additive manufactured foam targets for experiments on high-power laser–matter interaction. J Appl Phys (2023) 133:043101. doi:10.1063/5.0121650

CrossRef Full Text | Google Scholar

2. Sun J, Wang S, Zhu W, Li X, Jiang L. Simulation of femtosecond laser-induced periodic surface structures on fused silica by considering intrapulse and interpulse feedback. J Appl Phys (2024) 136:013103. doi:10.1063/5.0205299

CrossRef Full Text | Google Scholar

3. Bergner K, Flamm D, Jenne M, Kumkar M, Tünnermann A, Nolte S. Time-resolved tomography of ultrafast laser-matter interaction. Opt Express (2018) 26:2873–83. doi:10.1364/oe.26.002873

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Frydrych S, Vorberger J, Hartley NJ, Schuster AK, Ramakrishna K, Saunders AM, et al. Demonstration of X-ray Thomson scattering as diagnostics for miscibility in warm dense matter. Nat Commun (2020) 11:2620. doi:10.1038/s41467-020-16426-y

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Chi Z, Du Y, Huang W, Tang C. Linearly polarized X-ray fluorescence computed tomography based on a Thomson scattering light source: a Monte Carlo study. J Synchrotron Radiat (2020) 27:737–45. doi:10.1107/s1600577520003574

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Panetta D, Labate L, Billeci L, Di Lascio N, Esposito G, Faita F, et al. Numerical simulation of novel concept 4D cardiac microtomography for small rodents based on all-optical Thomson scattering X-ray sources. Sci Rep (2019) 9:8439. doi:10.1038/s41598-019-44779-y

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yamaguchi R, Tanaka G, Shafii NS, Osman K, Shimizu Y, Saqr KM, et al. Characteristic effect of wall elasticity on flow instability and wall shear stress of a full-scale, patient-specific aneurysm model in the middle cerebral artery: an experimental approach. J Appl Phys (2022) 131:184701. doi:10.1063/5.0085417

CrossRef Full Text | Google Scholar

8. Vais OE, Bychenkov VY. Nonlinear Thomson scattering of a tightly focused relativistically intense laser pulse by an ensemble of particles. Quan Electron. (2020) 50:922–8. doi:10.1070/qel17344

CrossRef Full Text | Google Scholar

9. Chi Z, Du Y, Huang W, Tang C. Focal spot characteristics of Thomson scattering x-ray sources. J Appl Phys (2018) 124:124901. doi:10.1063/1.5048457

CrossRef Full Text | Google Scholar

10. Chang Y, Zeng Z, Wang C, Long Z, Tian Y. Modulation of high-energy γ-rays by collision of an ultra-high-energy electron with a tightly focused circularly polarized laser pulse. Appl Opt (2022) 61:6038–45. doi:10.1364/ao.459665

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wang Y, Zhou Q, Zhuang J, Yu P, Tian Y. Vortex and symmetric radiation character of nonlinear Thomson scattering in Laguerre-Gaussian circularly polarized laser pulses. Opt Express (2021) 29:22636–47. doi:10.1364/oe.426529

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Harvey C, Marklund M, Holkundkar AR. Focusing effects in laser-electron Thomson scattering. Phys Rev Accel Beams (2016) 19:094701. doi:10.1103/physrevaccelbeams.19.094701

CrossRef Full Text | Google Scholar

13. Rykovanov SG, Geddes C, Schroeder C, Esarey E, Leemans W. Controlling the spectral shape of nonlinear Thomson scattering with proper laser chirping. Phys Rev Accel Beams (2016) 19:030701. doi:10.1103/physrevaccelbeams.19.030701

CrossRef Full Text | Google Scholar

14. Barton JP, Alexander DR. Fifth-order corrected electromagnetic field components for a fundamental Gaussian beam. J Appl Phys (1989) 66:2800–2. doi:10.1063/1.344207

CrossRef Full Text | Google Scholar

15. Salamin YI, Keitel CH. Electron acceleration by a tightly focused laser beam. Phys Rev Lett (2002) 88:095005. doi:10.1103/physrevlett.88.095005

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Zhang SY. Accurate correction field of circularly polarized laser and its acceleration effect. J Mol Sci (2010) 1:308–17. doi:10.4208/jams.042110.051010a

CrossRef Full Text | Google Scholar

17. Wang Y, Yang Q, Chang Y, Lin Z, Tian Y. Collision off-axis position dependence of relativistic nonlinear Thomson inverse scattering of an excited electron in a tightly focused circular polarized laser pulse. Chin Phys B (2023) 33:013301. doi:10.1088/1674-1056/acd921

CrossRef Full Text | Google Scholar

18. He F, Lau Y, Umstadter DP, Kowalczyk R. Backscattering of an intense laser beam by an electron. Phys Rev Lett (2003) 90:055002. doi:10.1103/physrevlett.90.055002

PubMed Abstract | CrossRef Full Text | Google Scholar

19. He F, Yu W, Lu P, Xu H, Qian L, Shen B, et al. Ponderomotive acceleration of electrons by a tightly focused intense laser beam. Phys Rev E (2003) 68:046407. doi:10.1103/physreve.68.046407

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Lee H, Kim D, Chung S, Lee K. Attosecond keV x-ray pulses driven by Thomson scattering in a tight focus regime. New J Phys (2009) 11:063050. doi:10.1088/1367-2630/11/6/063050

CrossRef Full Text | Google Scholar

21. Gao J. Thomson scattering from ultrashort and ultraintense laser pulses. Phys Rev Lett (2004) 93:243001. doi:10.1103/physrevlett.93.243001

PubMed Abstract | CrossRef Full Text | Google Scholar