Novel features of asymmetric nuclear matter from terrestrial experiments and astrophysical observations of neutron stars

The accurate measurement of neutron skin thickness of ²⁰⁸Pb by the PREX Collaboration suggests a large value of the nuclear symmetry energy slope parameter, $L$, whereas the smaller $L$ is preferred to account for the small neutron-star radii from NICER observations. To resolve this discrepancy between nuclear experiments and astrophysical observations, new effective interactions have been developed using relativistic mean-field models with the isoscalar- and isovector-meson mixing. We investigate the effects of $\delta$-nucleon coupling and $\sigma$–$\delta$ mixing on the ground-state properties of finite nuclei, as well as the characteristics of isospin-asymmetric nuclear matter and neutron stars. Additionally, we explore the role of the quartic $\rho$-meson self-interaction in dense nuclear matter to mitigate the stiff equation of state for neutron stars resulting from the large $\delta$-nucleon coupling. It is found that the nuclear symmetry energy undergoes a sudden softening at approximately twice the saturation density of nuclear matter, taking into account the PREX-2 result, the recent NICER observation of PSR J0437$-$4715, and the binary neutron star merger, GW170817.

1 Introduction

The astrophysical phenomena concerning compact stars as well as the characteristics of finite nuclei and nuclear matter are determined by the nuclear equation of state (EoS), characterized by the relation between the energy density and pressure of the system [1, 2]. Many nuclear EoSs have been contemplated so far through realistic nuclear models in a non-relativistic or relativistic framework [3, 4]. Relativistic mean-field (RMF) calculations, based on the one-boson exchange potential for nuclear interactions [5, 6], have achieved great success in understanding of the properties of nuclear matter and finite nuclei [7]. To reproduce a reasonable nuclear incompressibility and properties of unstable nuclei, the RMF models have been developed by introducing the non-linear self-couplings of isoscalar, Lorentz-scalar $(\sigma )$ and Lorentz-vector $({\omega }^{\mu })$ mesons [8, 9]. In addition, the isovector, Lorentz-vector $({\mathit{\rho }}^{\mu })$ meson and its non-linear couplings have been considered to describe a neutron skin thickness of heavy nuclei and characteristics of isospin-asymmetric nuclear matter [10, 11]. The RMF approach is, at present, one of the most powerful tools to study neutron star physics [12–14], as in the case of the Skyrme energy density functional [15–18].

The nuclear symmetry energy, $E_{\text{sym}}$, which is defined as the difference between the energies of pure neutron and symmetric nuclear matter, is recognized to be an important physical quantity to study the properties of isospin-asymmetric nuclear EoS [19, 20]. In addition, the slope parameter of nuclear symmetry energy, $L$, gives a significant constraint on the density dependence of $E_{\text{sym}}$ and is related to the neutron skin thickness of heavy nuclei [21]. Laboratory experiments have been also performed to investigate the properties of low-density nuclear matter and to impose constraints on $E_{\text{sym}}$ and $L$ through the heavy-ion collisions (HICs) [22, 23]. Recently, the impacts of the higher-order coefficients—the curvature and skewness of nuclear symmetry energy, $K_{\text{sym}}$ and $J_{\text{sym}}$—have been studied in light of some astrophysical observations, for instance the mass-radius relations of neutron stars and the cooling process of proto-neutron stars [24–26].

Owing to the precise observations of neutron stars, such as the Shapiro delay measurement of a binary millisecond pulsar J1614$-$2230 [27, 28] and the radius measurement of PSR J0740$+$6620 from Neutron Star Interior Composition Explorer (NICER) and from X-ray Multi-Mirror (XMM-Newton) Data [29–32], theoretical studies have been currently performed more than ever to elucidate neutron star physics through the nuclear EoS for dense matter. It has been found that the nuclear EoS should satisfy at least $2M_{\odot }$ to support the high-mass PSR J0740$+$6620 event, and that the precise measurements of neutron-star radii provide the valuable information in determining the features of isospin-asymmetric nuclear matter. In addition, the direct detection of gravitational-wave (GW) signals from a binary neutron star merger, GW170817, observed by Advanced LIGO and Advanced Virgo detectors has placed stringent restrictions on the mass–radius relation of neutron stars [33–35]. In particular, the tidal deformability of a neutron star [36, 37] plays a critical role in constructing the EoS for neutron star matter [38–41]. It has been reported that there are the strong correlations of neutron-star radii with $E_{\text{sym}}$ and $L$, and the radius of a typical neutron star is determined by $L$ [42–45]. Using a Bayesian analysis based on constraints from NICER and GW170817 within chiral effective field theory calculations, $L$ is currently estimated as $L$ = (43.7–70.0) MeV [46].

The accurate measurement of neutron skin thickness of ²⁰⁸Pb, $R_{\text{skin}}^{208}$, by the PREX Collaboration, using the parity-violating electron scattering, has revealed a serious discrepancy between the measured $R_{\text{skin}}^{208}$ and theoretical predictions [47]. The neutron skin thickness, $R_{\text{skin}}$, is defined here as the difference between the root-mean-square radii of point neutrons and protons, $R_n$ and $R_p$, in a nucleus:

$R_{\text{skin}}=R_n-R_p.(1)$

To explain the PREX-2 result, Reed et al. [48] have proposed the large $L$ value as $L=106\pm 37$ MeV, by exploiting the strong correlation between $R_{\text{skin}}^{208}$ and $L$. In contrast, Reinhard et al. [49], using modern relativistic and non-relativistic energy density functionals, have predicted the smaller value, $L=54\pm 8$ MeV, by carefully assessing theoretical uncertainty on the parity-violating asymmetry, $A_{\text{PV}}$, in ²⁰⁸Pb. Additionally, the CREX experiment, which provides a precise measurement of the neutron skin thickness of ⁴⁸Ca, $R_{\text{skin}}^{48}$, through the parity-violating electron scattering [50], complicates the understanding of isospin-asymmetric nuclear matter. This complexity arises from the difficulty of reconciling the PREX-2 and CREX results simultaneously. In addition, the measurements from polarized proton scattering off ²⁰⁸Pb indicate smaller $R_{\text{skin}}^{208}$, and consequently smaller $L$, compared to those obtained from the PREX-2 experiment [51, 52]. As a result, $R_{\text{skin}}^{208}$ and $L$ remain uncertain in theoretical calculations [53, 54]. At present, many species of neutron skin thickness have been reported from a combination of experimental and theoretical results [55].

In this article, we review the recently updated RMF models with non-linear couplings by introducing the isoscalar- and isovector-meson mixing, ${\sigma }^2{\mathit{\delta }}^2$ and ${\omega }_{\mu }{\omega }^{\mu }{\mathit{\rho }}_{\nu }{\mathit{\rho }}^{\nu }$, which can cover both data from stable nuclear ground states and astrophysical observations of neutron stars. Although the isovector, Lorentz-scalar $(\mathit{\delta })$ meson has been claimed to be less important than the isovector, Lorentz-vector $({\mathit{\rho }}^{\mu })$ meson so far, it has been recently realized that the $\delta$ meson considerably affects the properties of isospin-asymmetric nuclear EoS, such as neutron skin thickness of heavy nuclei and neutron-star radii [56–59] The new effective interactions discussed in this review are constructed under the constraints from the terrestrial experiments and astrophysical observations of neutron stars, especially focusing on the PREX-2 and CREX experiments. The resulting nuclear EoS have to support the following conditions:

(1) The EoSs for symmetric nuclear matter and pure neutron matter satisfy the particle flow data in heavy-ion collisions (HICs) [60–63],

(2) The EoS for neutron stars attains to the observed mass of PSR J0740$+$6620 $M=2.072_{-0.066}^{+0.067}$ $M_{\odot }$ [32, 64, 65],

(3) The EoS for neutron stars explains the dimensionless tidal deformability from the binary merger event, GW170817 $({\mathrm{\Lambda }}_{1.4}=190_{-120}^{+390})$ [34, 35].

Under these constraints, we examine the effects of the $\delta$-nucleon coupling and $\sigma$–$\delta$ mixing on the ground-state properties of finite nuclei, and consider the PREX-2 and CREX results. Additionally, we investigate the impact of the quartic self-interactions of $\delta$ and $\rho$ mesons on the nuclear EoS to study the properties of neutron star matter.

This paper is organized as follows. A summary and analytical calculations concerning the RMF model with non-linear couplings are described in Section 2. Numerical results and detailed discussions are presented in Section 3. Finally, we give a summary in Section 4.

2 Theoretical framework

2.1 Lagrangian density

In quantum hydrodynamics [7], we employ the recently updated effective Lagrangian density including the isoscalar ($\sigma$ and ${\omega }^{\mu }$) and isovector ($\mathit{\delta }$ and ${\mathit{\rho }}^{\mu }$) mesons as well as nucleons $(N=p,n)$ [57, 58]. The total Lagrangian density is then given by

$\begin{array}{ll}\hfill \mathcal{L}& ={\bar{\psi }}_N\left[i{\gamma }_{\mu }{\partial }^{\mu }-\left(M_N-g_{\sigma }\sigma -g_{\delta }\mathit{\delta }\cdot {\mathit{\tau }}_N\right)-g_{\omega }{\gamma }_{\mu }{\omega }^{\mu }-g_{\rho }{\gamma }_{\mu }{\mathit{\rho }}^{\mu }\cdot {\mathit{\tau }}_N\right]{\psi }_N\hfill \\ \hfill & +\frac{1}{2}\left({\partial }_{\mu }\sigma {\partial }^{\mu }\sigma -m_{\sigma }^2{\sigma }^2\right)+\frac{1}{2}{m}_{\omega }^2{\omega }_{\mu }{\omega }^{\mu }-\frac{1}{4}{W}_{\mu \nu }{W}^{\mu \nu }+\frac{1}{2}\left({\partial }_{\mu }\mathit{\delta }\cdot {\partial }^{\mu }\mathit{\delta }-m_{\delta }^2\mathit{\delta }\cdot \mathit{\delta }\right)\hfill \\ \hfill & +\frac{1}{2}{m}_{\rho }^2{\mathit{\rho }}_{\mu }\cdot {\mathit{\rho }}^{\mu }-\frac{1}{4}{\mathit{R}}_{\mu \nu }\cdot {\mathit{R}}^{\mu \nu }+{\mathcal{L}}_{\text{EM}}-U_{\text{NL}}\left(\sigma ,\omega ,\mathit{\delta },\mathit{\rho }\right),\hfill \end{array}(2)$

where ${\psi }_N=\left({}_{{\psi }_n}^{{\psi }_p}\right)$ is the iso-doublet, nucleon field, ${\mathit{\tau }}_N$ is its isospin matrix, $W_{\mu \nu }={\partial }_{\mu }{\omega }_{\nu }-{\partial }_{\nu }{\omega }_{\mu }$, and ${\mathit{R}}_{\mu \nu }={\partial }_{\mu }{\mathit{\rho }}_{\nu }-{\partial }_{\nu }{\mathit{\rho }}_{\mu }$. The meson-nucleon coupling constants are respectively denoted by $g_{\sigma }$, $g_{\omega }$, $g_{\delta }$, and $g_{\rho }$. The photon-$N$ interaction, ${\mathcal{L}}_{\text{EM}}=-e{\bar{\psi }}_p{\gamma }_{\mu }{A}^{\mu }{\psi }_p-\frac{1}{4}{F}_{\mu \nu }{F}^{\mu \nu }$ with $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$, is also taken into account to describe the characteristics of finite nuclei [7, 66]. Additionally, a non-linear potential in Equation 1 is supplemented as follows:

$\begin{array}{ll}\hfill U_{\text{NL}}\left(\sigma ,\omega ,\mathit{\delta },\mathit{\rho }\right)& =\frac{1}{3}{g}_2{\sigma }^3+\frac{1}{4}{g}_3{\sigma }^4-\frac{1}{4}{c}_3{\left({\omega }_{\mu }{\omega }^{\mu }\right)}^2+\frac{1}{4}{d}_3{\left(\mathit{\delta }\cdot \mathit{\delta }\right)}^2-\frac{1}{4}{e}_3{\left({\mathit{\rho }}_{\mu }\cdot {\mathit{\rho }}^{\mu }\right)}^2\hfill \\ \hfill & -{\mathrm{\Gamma }}_{\sigma \delta }\sigma \left(\mathit{\delta }\cdot \mathit{\delta }\right)-{\mathrm{\Lambda }}_{\sigma \delta }{\sigma }^2\left(\mathit{\delta }\cdot \mathit{\delta }\right)-{\mathrm{\Lambda }}_{\omega \rho }\left({\omega }_{\mu }{\omega }^{\mu }\right)\left({\mathit{\rho }}_{\nu }\cdot {\mathit{\rho }}^{\nu }\right).\hfill \end{array}(3)$

The first and second terms in Equation 2 are introduced to obtain a quantitative description of ground-state properties for symmetric nuclear matter [8, 67]. The quartic self-interactions of $\omega$, $\delta$, and $\rho$ mesons are also introduced in Equation 2 [9, 10, 68, 69]. We also consider the isoscalar- and isovector-meson mixing, which only affects the characteristics of $N\ne Z$ finite nuclei and isospin-asymmetric nuclear matter [56, 70, 71], while the scalar-vector mixing is not included in the present study [11, 72–75].

2.2 Field equations for finite nuclei in mean-field approximation

In mean-field approximation, the meson and photon fields are replaced by the mean-field values: $\bar{\sigma }$, $\bar{\omega }$, $\bar{\delta }$, $\bar{\rho }$, and $\bar{A}$. Then, the effective nucleon mass in matter is simply expressed as

$M_{N=\left({}_n^p\right)}^{*}\left(\bar{\sigma },\bar{\delta }\right)=M_N-g_{\sigma }\bar{\sigma }\mp g_{\delta }\bar{\delta },(4)$

where $M_N$ ($=939$ MeV) is the nucleon mass in free space. If we restrict consideration to spherical finite nuclei, the equation of motion for $N$ is given by

$\left[-i\mathit{\alpha }\cdot \mathbf{\nabla }+\beta M_{\left({}_n^p\right)}^{*}\left(\bar{\sigma },\bar{\delta }\right)+g_{\omega }\bar{\omega }\pm g_{\rho }\bar{\rho }+e\frac{1\pm 1}{2}\bar{A}\right]{\psi }_{\left({}_n^p\right)}=E_{\alpha \left({}_n^p\right)}{\psi }_{\left({}_n^p\right)},(5)$

with $E_{\alpha N}$ being the nucleon single-particle energy. The meson and photon fields are then given by

$\left[-{\mathbf{\nabla }}^2+m_{\sigma }^{*2}\left(\bar{\sigma },\bar{\delta }\right)\right]\bar{\sigma }=g_{\sigma }\left({\rho }_p^s+{\rho }_n^s\right),(6)$

$\left[-{\mathbf{\nabla }}^2+m_{\omega }^{*2}\left(\bar{\omega },\bar{\rho }\right)\right]\bar{\omega }=g_{\omega }\left({\rho }_p+{\rho }_n\right),(7)$

$\left[-{\mathbf{\nabla }}^2+m_{\delta }^{*2}\left(\bar{\sigma },\bar{\delta }\right)\right]\bar{\delta }=g_{\delta }\left({\rho }_p^s-{\rho }_n^s\right),(8)$

$\left[-{\mathbf{\nabla }}^2+m_{\rho }^{*2}\left(\bar{\omega },\bar{\rho }\right)\right]\bar{\rho }=g_{\rho }\left({\rho }_p-{\rho }_n\right),(9)$

and

$-{\mathbf{\nabla }}^2\bar{A}=e{\rho }_p,(10)$

where ${\rho }_N^s$ $({\rho }_N)$ is the scalar (baryon) density for $N$, which is computed self-consistently using nucleon wave functions in Equation 4 that are solutions to the Dirac equation in the spatially dependent meson and photon fields. The effective meson masses are defined by

$m_{\sigma }^{*2}\left(\bar{\sigma },\bar{\delta }\right)=m_{\sigma }^2+g_2\bar{\sigma }+g_3{\bar{\sigma }}^2-{\mathrm{\Gamma }}_{\sigma \delta }{\bar{\delta }}^2/\bar{\sigma }-2{\mathrm{\Lambda }}_{\sigma \delta }{\bar{\delta }}^2,(11)$

$m_{\omega }^{*2}\left(\bar{\omega },\bar{\rho }\right)=m_{\omega }^2+c_3{\bar{\omega }}^2+2{\mathrm{\Lambda }}_{\omega \rho }{\bar{\rho }}^2,(12)$

$m_{\delta }^{*2}\left(\bar{\sigma },\bar{\delta }\right)=m_{\delta }^2+d_3{\bar{\delta }}^2-2{\mathrm{\Gamma }}_{\sigma \delta }\bar{\sigma }-2{\mathrm{\Lambda }}_{\sigma \delta }{\bar{\sigma }}^2,(13)$

$m_{\rho }^{*2}\left(\bar{\omega },\bar{\rho }\right)=m_{\rho }^2+e_3{\bar{\rho }}^2+2{\mathrm{\Lambda }}_{\omega \rho }{\bar{\omega }}^2.(14)$

The total energy of the system is thus written as

$\begin{array}{ll}\hfill E_{\text{tot}}& ={\displaystyle \sum _{N=p,n}}{\displaystyle \sum _{\alpha }^{\text{occ}}}\left(2j_{\alpha }+1\right)E_{\alpha N}+\frac{1}{2}\int d\mathit{r}\left[g_{\sigma }\left({\rho }_p^s+{\rho }_n^s\right)\bar{\sigma }\right.\hfill \\ \hfill & -g_{\omega }\left({\rho }_p+{\rho }_n\right)\bar{\omega }+g_{\delta }\left({\rho }_p^s-{\rho }_n^s\right)\bar{\delta }-g_{\rho }\left({\rho }_p-{\rho }_n\right)\bar{\rho }-e{\rho }_p\bar{A}\hfill \\ \hfill & +\frac{1}{2}\int d\mathit{r}\left(-\frac{1}{3}{g}_2{\bar{\sigma }}^3-\frac{1}{2}{g}_3{\bar{\sigma }}^4+\frac{1}{2}{c}_3{\bar{\omega }}^4-\frac{1}{2}{d}_3{\bar{\delta }}^4\right.\hfill \\ \hfill & \left.\left.+\frac{1}{2}{e}_3{\bar{\rho }}^4+{\mathrm{\Gamma }}_{\sigma \delta }\bar{\sigma }{\bar{\delta }}^2+2{\mathrm{\Lambda }}_{\sigma \delta }{\bar{\sigma }}^2{\bar{\delta }}^2+2{\mathrm{\Lambda }}_{\omega \rho }{\bar{\omega }}^2{\bar{\rho }}^2\right)\right],\hfill \end{array}(15)$

where the sum $\alpha$ runs over the occupied states of $E_{\alpha N}$ with the degeneracy $\left(2j_{\alpha }+1\right)$ [7].

2.3 Infinite nuclear matter

To study the bulk properties of nuclear and neutron star matter, it is necessary to compute the nuclear equation of state (EoS)—a relation between the energy density, ${\epsilon }_B$, and pressure, $P_B$. In infinite nuclear matter, the surface terms in Equations 5–9 have no influence on its characteristics as the gradient reads zero. The scalar and baryon density for $N\left(=p,n\right)$ are then obtained as

$\begin{array}{ll}\hfill {\rho }_N^s& =⟨{\bar{\psi }}_N{\psi }_N⟩\hfill \\ \hfill & =\frac{1}{{\pi }^2}{\int }_0^{k_{F_N}}dk{k}^2\frac{M_N^{*}}{\sqrt{k^2+M_N^{*2}}}=\frac{M_N^{*3}}{2{\pi }^2}\left[\frac{k_{F_N}{E}_N^{*}}{M_N^{*2}}-\ln \left(\frac{k_{F_N}+E_N^{*}}{M_N^{*}}\right)\right],\hfill \end{array}(16)$

$\begin{array}{ll}\hfill {\rho }_N& =⟨{\psi }_N^{†}{\psi }_N⟩\hfill \\ \hfill & =\frac{1}{{\pi }^2}{\int }_0^{k_{F_N}}dk{k}^2=\frac{k_{F_N}^3}{3{\pi }^2},\hfill \end{array}(17)$

where $k_{F_N}$ and $E_N^{*}\left(=\sqrt{k_{F_N}^2+M_N^{*2}}\right)$ are the Fermi momentum and energy for $N$. With the self-consistent calculations of the meson fields, ${\epsilon }_B$ and $P_B$ are respectively given by ${\epsilon }_B={\sum }_N{\epsilon }_N+{\epsilon }_M$ and $P_B={\sum }_N{P}_N+P_M$ where the nucleon and meson parts are expressed as

${\epsilon }_N=\frac{1}{{\pi }^2}{\int }_0^{k_{F_N}}dk{k}^2\sqrt{k^2+M_N^{*2}}=\frac{1}{4}\left(3E_N^{*}{\rho }_N+M_N^{*}{\rho }_N^s\right),(18)$

$P_N=\frac{1}{3{\pi }^2}{\int }_0^{k_{F_N}}dk\frac{k^4}{\sqrt{k^2+M_N^{*2}}}=\frac{1}{4}\left(E_N^{*}{\rho }_N-M_N^{*}{\rho }_N^s\right),(19)$

and

$\begin{array}{ll}\hfill {\epsilon }_M& =\frac{1}{2}\left(m_{\sigma }^2{\bar{\sigma }}^2+m_{\omega }^2{\bar{\omega }}^2+m_{\delta }^2{\bar{\delta }}^2+m_{\rho }^2{\bar{\rho }}^2\right)+\frac{1}{3}{g}_2{\bar{\sigma }}^3+\frac{1}{4}{g}_3{\bar{\sigma }}^4\hfill \\ \hfill & +\frac{3}{4}{c}_3{\bar{\omega }}^4+\frac{1}{4}{\bar{\delta }}^4+\frac{3}{4}{e}_3{\bar{\rho }}^4-{\mathrm{\Gamma }}_{\sigma \delta }\bar{\sigma }{\bar{\delta }}^2-{\mathrm{\Lambda }}_{\sigma \delta }{\bar{\sigma }}^2{\bar{\delta }}^2+3{\mathrm{\Lambda }}_{\omega \rho }{\bar{\omega }}^2{\bar{\rho }}^2,\hfill \end{array}(20)$

$\begin{array}{ll}\hfill P_M& =-\frac{1}{2}\left(m_{\sigma }^2{\bar{\sigma }}^2-m_{\omega }^2{\bar{\omega }}^2+m_{\delta }^2{\bar{\delta }}^2-m_{\rho }^2{\bar{\rho }}^2\right)-\frac{1}{3}{g}_2{\bar{\sigma }}^3-\frac{1}{4}{g}_3{\bar{\sigma }}^4\hfill \\ \hfill & +\frac{1}{4}{c}_3{\bar{\omega }}^4-\frac{1}{4}{\bar{\delta }}^4+\frac{1}{4}{e}_3{\bar{\rho }}^4+{\mathrm{\Gamma }}_{\sigma \delta }\bar{\sigma }{\bar{\delta }}^2+{\mathrm{\Lambda }}_{\sigma \delta }{\bar{\sigma }}^2{\bar{\delta }}^2+{\mathrm{\Lambda }}_{\omega \rho }{\bar{\omega }}^2{\bar{\rho }}^2.\hfill \end{array}(21)$

2.4 Nuclear bulk properties

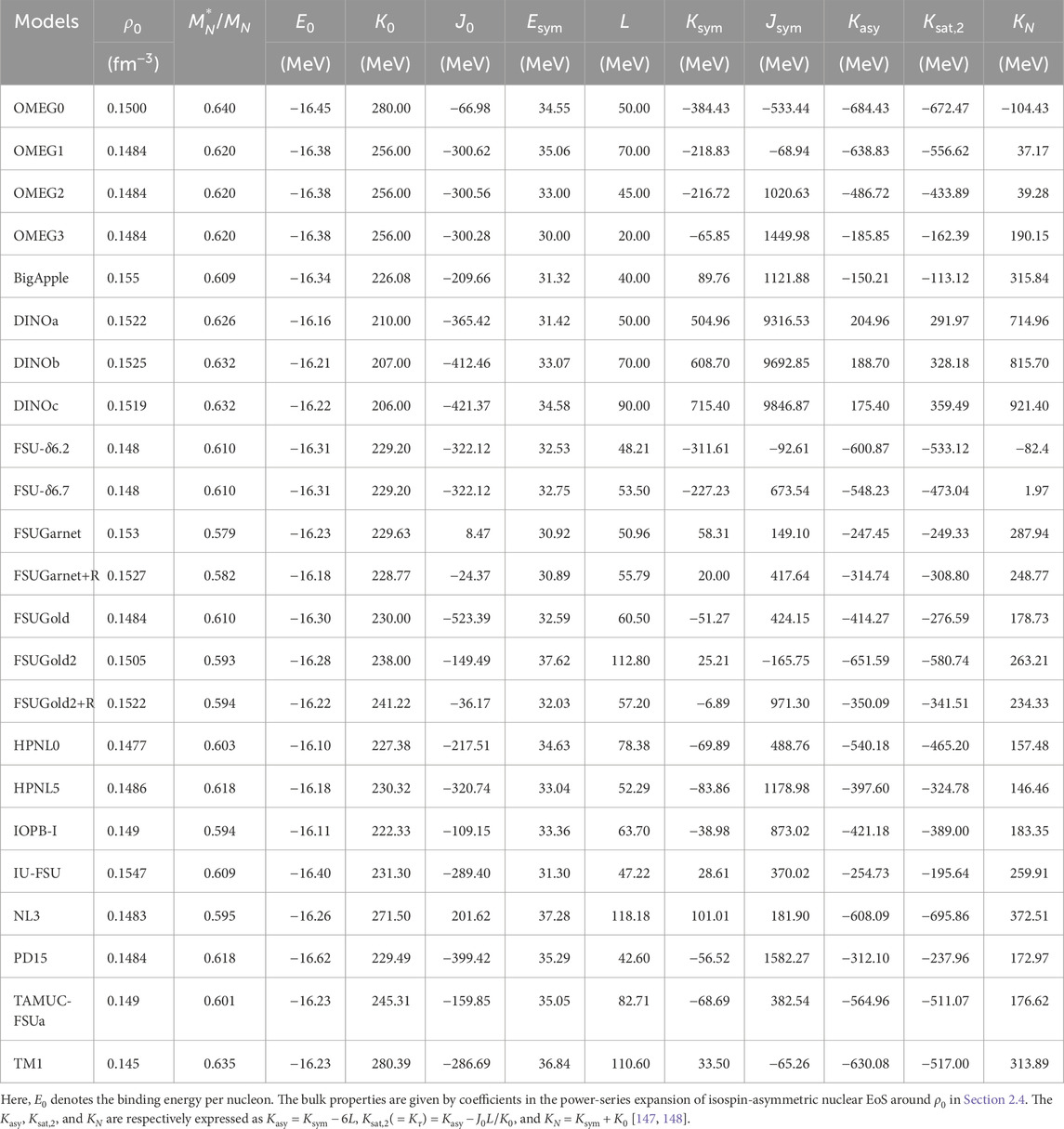
In general, the bulk properties of infinite nuclear matter are identified by the expansion of isospin-asymmetric nuclear EoS with a power series in the isospin asymmetry, $\alpha =({\rho }_n-{\rho }_p)/{\rho }_B$, and the total baryon density, ${\rho }_B\left(={\rho }_n+{\rho }_p\right)$ [76, 77]. The binding energy per nucleon is then written as

$\begin{array}{ll}\hfill E_B\left({\rho }_B,\alpha \right)& =\frac{{\epsilon }_B\left({\rho }_B,\alpha \right)}{{\rho }_B}-M_N\hfill \\ \hfill & =E_0\left({\rho }_B\right)+E_{\text{sym}}\left({\rho }_B\right){\alpha }^2+\mathcal{O}\left({\alpha }^4\right),\hfill \end{array}(22)$

where $E_0({\rho }_B)$ is the binding energy per nucleon of symmetric nuclear matter (SNM) and $E_{\text{sym}}({\rho }_B)$ is the nuclear symmetry energy (NSE),

$E_{\text{sym}}\left({\rho }_B\right)=\frac{1}{2}{\left.\frac{{\partial }^2{E}_B\left({\rho }_B,\alpha \right)}{\partial {\alpha }^2}\right|}_{\alpha =0}.(23)$

Besides, $E_0({\rho }_B)$ and $E_{\text{sym}}({\rho }_B)$ can be expanded around the nuclear saturation density, ${\rho }_0$, as

$E_0\left({\rho }_B\right)=E_0\left({\rho }_0\right)+\frac{K_0}{2}{\chi }^2+\frac{J_0}{6}{\chi }^3+\mathcal{O}\left({\chi }^4\right),(24)$

$E_{\text{sym}}\left({\rho }_B\right)=E_{\text{sym}}\left({\rho }_0\right)+L\chi +\frac{K_{\text{sym}}}{2}{\chi }^2+\frac{J_{\text{sym}}}{6}{\chi }^3+\mathcal{O}\left({\chi }^4\right),(25)$

with $\chi =({\rho }_B-{\rho }_0)/3{\rho }_0$ being the dimensionless variable characterizing the deviations of ${\rho }_B$ from ${\rho }_0$. The incompressibility coefficient of SNM, $K_0$, the slope and curvature parameters of NSE, $L$ and $K_{\text{sym}}$, and the third-order incompressibility coefficients of SNM and NSE, $J_0$ and $J_{\text{sym}}$, are respectively defined as

$K_0=9{\rho }_B^2{\left.\frac{d^2{E}_0\left({\rho }_B\right)}{d{\rho }_B^2}\right|}_{{\rho }_B={\rho }_0},(26)$

$L=3{\rho }_B{\left.\frac{d{E}_{\text{sym}}\left({\rho }_B\right)}{d{\rho }_B}\right|}_{{\rho }_B={\rho }_0},K_{\text{sym}}=9{\rho }_B^2{\left.\frac{d^2{E}_{\text{sym}}\left({\rho }_B\right)}{d{\rho }_B^2}\right|}_{{\rho }_B={\rho }_0},(27)$

$J_0=27{\rho }_B^3{\left.\frac{d^3{E}_0\left({\rho }_B\right)}{d{\rho }_B^3}\right|}_{{\rho }_B={\rho }_0},J_{\text{sym}}=27{\rho }_B^3{\left.\frac{d^3{E}_{\text{sym}}\left({\rho }_B\right)}{d{\rho }_B^3}\right|}_{{\rho }_B={\rho }_0}.(28)$

Taking into account the thermodynamic condition, the pressure of infinite nuclear matter, $P_B({\rho }_B,\alpha )$, is given by

$\begin{array}{ll}\hfill P_B\left({\rho }_B,\alpha \right)& ={\rho }_B^2\frac{\partial E_B\left({\rho }_B,\alpha \right)}{\partial {\rho }_B}\hfill \\ \hfill & ={\rho }_B^2\frac{\partial }{\partial {\rho }_B}\left[\frac{{\epsilon }_B\left({\rho }_B,\alpha \right)}{{\rho }_B}-M_N\right]\hfill \\ \hfill & ={\rho }_B\frac{\partial {\epsilon }_B\left({\rho }_B,\alpha \right)}{\partial {\rho }_B}-{\epsilon }_B\left({\rho }_B,\alpha \right),\hfill \end{array}(29)$

with the binding energy per nucleon in Equation 14. The nuclear incompressibility, $K_B({\rho }_B,\alpha )$, is then expressed as

$\begin{array}{ll}\hfill K_B\left({\rho }_B,\alpha \right)& =9{\rho }_B^2\frac{{\partial }^2{E}_B\left({\rho }_B,\alpha \right)}{\partial {\rho }_B^2}\hfill \\ \hfill & =9{\rho }_B^2\frac{\partial }{\partial {\rho }_B}\left[\frac{P_B\left({\rho }_B,\alpha \right)}{{\rho }_B^2}\right]\hfill \\ \hfill & =9\left[\frac{\partial P_B\left({\rho }_B,\alpha \right)}{\partial {\rho }_B}-2\frac{P_B\left({\rho }_B,\alpha \right)}{{\rho }_B}\right].\hfill \end{array}(30)$

Hence, the incompressibility coefficient of SNM, $K_0$, in Equation 16 is related with $K_B$ through $K_0=K_B({\rho }_0,0)$. In the RMF calculation, we can obtain the analytical expression of $K_B({\rho }_B,\alpha )$ using the following equation:

$\begin{array}{ll}\hfill \frac{\partial P_B}{\partial {\rho }_B}& =\frac{1}{3{\rho }_B}{\displaystyle \sum _{N=p,n}}{\rho }_N\frac{k_{F_N}^2}{E_N^{*}}-{\displaystyle \sum _{N=p,n}}{\rho }_N\frac{M_N^{*}}{E_N^{*}}\left[g_{\sigma }\frac{\partial \bar{\sigma }}{\partial {\rho }_B}+g_{\delta }{\left({\mathit{\tau }}_N\right)}_3\frac{\partial \bar{\delta }}{\partial {\rho }_B}\right]\hfill \\ \hfill & +m_{\omega }^{*2}\bar{\omega }\frac{\partial \bar{\omega }}{\partial {\rho }_B}+m_{\rho }^{*2}\bar{\rho }\frac{\partial \bar{\rho }}{\partial {\rho }_B},\hfill \end{array}(31)$

where the density derivatives of meson fields are calculated through the relation

$\frac{\partial \mathcal{M}}{\partial {\rho }_B}={\displaystyle \sum _{N=p,n}}\frac{{\rho }_N}{{\rho }_B}\frac{\partial \mathcal{M}}{\partial {\rho }_N}\left(\mathcal{M}=\bar{\sigma },\bar{\omega },\bar{\delta },\bar{\rho }\right),(32)$

with

$\frac{\partial \bar{\sigma }}{\partial {\rho }_N}=\frac{M_N^{*}}{E_N^{*}}\frac{G_{\sigma }+G_{\delta }{\left({\mathit{\tau }}_N\right)}_3{H}_{\sigma \delta }}{1-H_{\sigma \delta }{H}_{\delta \sigma }},\frac{\partial \bar{\omega }}{\partial {\rho }_N}=\frac{G_{\omega }-G_{\rho }{\left({\mathit{\tau }}_N\right)}_3{H}_{\omega \rho }}{1-H_{\omega \rho }{H}_{\rho \omega }},(33)$

$\frac{\partial \bar{\delta }}{\partial {\rho }_N}=\frac{M_N^{*}}{E_N^{*}}\frac{G_{\sigma }{H}_{\delta \sigma }+G_{\delta }{\left({\mathit{\tau }}_N\right)}_3}{1-H_{\sigma \delta }{H}_{\delta \sigma }},\frac{\partial \bar{\rho }}{\partial {\rho }_N}=\frac{-G_{\omega }{H}_{\rho \omega }+G_{\rho }{\left({\mathit{\tau }}_N\right)}_3}{1-H_{\omega \rho }{H}_{\rho \omega }},(34)$

and

${\left({\mathit{\tau }}_N\right)}_3=\left\{\begin{array}{c}+1\hfill \\ -1\hfill \end{array}\right.\text{for}N=\left({}_n^p\right).(35)$

We here use the following quantities:

$G_{\sigma }=\frac{g_{\sigma }}{M_{\sigma }^2},G_{\omega }=\frac{g_{\omega }}{M_{\omega }^2},G_{\delta }=\frac{g_{\delta }}{M_{\delta }^2},G_{\rho }=\frac{g_{\rho }}{M_{\rho }^2},(36)$

and

$H_{\sigma \delta }=\frac{L_{\sigma \delta }^2}{M_{\sigma }^2},H_{\delta \sigma }=\frac{L_{\sigma \delta }^2}{M_{\delta }^2},H_{\omega \rho }=\frac{4{\mathrm{\Lambda }}_{\omega \rho }\bar{\omega }\bar{\rho }}{M_{\omega }^2},H_{\rho \omega }=\frac{4{\mathrm{\Lambda }}_{\omega \rho }\bar{\omega }\bar{\rho }}{M_{\rho }^2},(37)$

with

$M_{\sigma }^2\left(\bar{\sigma },\bar{\delta }\right)=m_{\sigma }^{*2}\left(\bar{\sigma },\bar{\delta }\right)+g_2\bar{\sigma }+2g_3{\bar{\sigma }}^2+{\mathrm{\Gamma }}_{\sigma \delta }{\bar{\delta }}^2/\bar{\sigma }+g_{\sigma }^2\left(J_p+J_n\right),(38)$

$M_{\omega }^2\left(\bar{\omega },\bar{\rho }\right)=m_{\omega }^{*2}\left(\bar{\omega },\bar{\rho }\right)+2c_3{\bar{\omega }}^2,(39)$

$M_{\delta }^2\left(\bar{\sigma },\bar{\delta }\right)=m_{\delta }^{*2}\left(\bar{\sigma },\bar{\delta }\right)+2d_3{\bar{\delta }}^2+g_{\delta }^2\left(J_p+J_n\right),(40)$

$M_{\rho }^2\left(\bar{\omega },\bar{\rho }\right)=m_{\rho }^{*2}\left(\bar{\omega },\bar{\rho }\right)+2e_3{\bar{\rho }}^2,(41)$

$L_{\sigma \delta }^2\left(\bar{\sigma },\bar{\delta }\right)=2{\mathrm{\Gamma }}_{\sigma \delta }\bar{\delta }+4{\mathrm{\Lambda }}_{\sigma \delta }\bar{\sigma }\bar{\delta }-g_{\sigma }{g}_{\delta }\left(J_p-J_n\right),(42)$

where the effective meson masses, $m_{\sigma }^{*2}$, $m_{\omega }^{*2}$, $m_{\delta }^{*2}$ and $m_{\rho }^{*2}$, are given in Equations 10–13, and $J_N$ for $N\left(=p,n\right)$ reads

$J_N=3\left(\frac{{\rho }_N^s}{M_N^{*}}-\frac{{\rho }_N}{E_N^{*}}\right).(43)$

According to the Hugenholtz-Van Hove theorem in nuclear matter, $E_{\text{sym}}$ defined in Equation 15 can be generally written as

$\begin{array}{ll}\hfill E_{\text{sym}}\left({\rho }_B\right)& =\frac{1}{2}\frac{\partial }{\partial \alpha }{\left[\frac{\partial E_B\left({\rho }_B,\alpha \right)}{\partial \alpha }\right]}_{\alpha =0}\hfill \\ \hfill & =\frac{1}{8}{\rho }_B{\left.\left(\frac{\partial }{\partial {\rho }_p}-\frac{\partial }{\partial {\rho }_n}\right)\left[E_p\left(k_{F_p}\right)-E_n\left(k_{F_n}\right)\right]\right|}_{{\rho }_p={\rho }_n},\hfill \end{array}(44)$

where $E_N$ is the single-particle energy for $N$, which is determined self-consistently by solving the following transcendental equation [78, 79]:

$E_N\left(k\right)={\left[E_N^{*}\left(k\right)-{\displaystyle \sum _N^0}\left(k\right)\right]}_{k^0=E_N\left(k\right)}.(45)$

The effective mass, (four) momentum, and energy for $N$ are here defined as [80, 81]

$M_N^{*}\left(k\right)=M_N+\underset{N}{\overset{s}{\mathrm{\Sigma }}}\left(k\right),(46)$

$\begin{array}{ll}\hfill k_N^{\mu *}& =\left(k_N^{*0},{\mathit{k}}_N^{*}\right)\hfill \\ \hfill & =\left(k^0+{\displaystyle \sum _N^0}\left(k\right),\mathit{k}+\widehat{k}{\displaystyle \sum _N^v}\left(k\right)\right),\hfill \end{array}(47)$

$E_N^{*}\left(k\right)=\sqrt{{\mathit{k}}_N^{*2}+M_N^{*2}\left(k\right)},(48)$

with ${\mathrm{\Sigma }}_N^{s(0)[v]}$ being the scalar (time) [space] component of nucleon self-energy. In addition, $E_{\text{sym}}$ is divided into the kinetic and potential terms as

$E_{\text{sym}}\left({\rho }_B\right)=E_{\text{sym}}^{\text{kin}}\left({\rho }_B\right)+E_{\text{sym}}^{\text{pot}}\left({\rho }_B\right).(49)$

Based on the Lorentz-covariant decomposition of NSE [82], $E_{\text{sym}}^{\text{pot}}$ is expressed as

$E_{\text{sym}}^{\text{pot}}\left({\rho }_B\right)=E_{\text{sym}}^s\left({\rho }_B\right)+E_{\text{sym}}^0\left({\rho }_B\right)+E_{\text{sym}}^v\left({\rho }_B\right),(50)$

with the scalar $(s)$, time (0), and space $(v)$ components. The $E_{\text{sym}}$ is thus computed as follows:

$E_{\text{sym}}^{\text{kin}}\left({\rho }_B\right)=\frac{1}{6}\frac{k_F^{*}}{E_F^{*}}{k}_F,(51)$

$E_{\text{sym}}^s\left({\rho }_B\right)=\frac{1}{8}{\rho }_B\frac{M_F^{*}}{E_F^{*}}{\left.\left(\frac{\partial }{\partial {\rho }_p}-\frac{\partial }{\partial {\rho }_n}\right)\left({\displaystyle \sum _p^s}-{\displaystyle \sum _n^s}\right)\right|}_{{\rho }_p={\rho }_n},(52)$

$E_{\text{sym}}^0\left({\rho }_B\right)=-\frac{1}{8}{\rho }_B{\left.\left(\frac{\partial }{\partial {\rho }_p}-\frac{\partial }{\partial {\rho }_n}\right)\left({\displaystyle \sum _p^0}-{\displaystyle \sum _n^0}\right)\right|}_{{\rho }_p={\rho }_n},(53)$

$E_{\text{sym}}^v\left({\rho }_B\right)=\frac{1}{8}{\rho }_B\frac{k_F^{*}}{E_F^{*}}{\left.\left(\frac{\partial }{\partial {\rho }_p}-\frac{\partial }{\partial {\rho }_n}\right)\left({\displaystyle \sum _p^v}-{\displaystyle \sum _n^v}\right)\right|}_{{\rho }_p={\rho }_n},(54)$

where the effective quantities at the Fermi surface in Equations 22–25 are then given by $M_F^{*}=M_p^{*}(k_F)=M_n^{*}(k_F)$, $k_F^{*}=|{\mathit{k}}_p^{*}(k_F)|=|{\mathit{k}}_n^{*}(k_F)|$, and $E_F^{*}=E_p^{*}(k_F)=E_n^{*}(k_F)$ at ${\rho }_p={\rho }_n$, namely, $k_{F_p}=k_{F_n}=k_F$. In RMF approximation, ${\mathrm{\Sigma }}_N^{s,0,v}$ are respectively given by

${\displaystyle \sum _N^s}=-g_{\sigma }\bar{\sigma }-g_{\delta }{\left({\mathit{\tau }}_N\right)}_3\bar{\delta },(55)$

${\displaystyle \sum _N^0}=-g_{\omega }\bar{\omega }-g_{\rho }{\left({\mathit{\tau }}_N\right)}_3\bar{\rho },(56)$

${\displaystyle \sum _N^v}=0.(57)$

Using Equations 20, 21, $E_{\text{sym}}$ can be finally expressed as

$\begin{array}{ll}\hfill E_{\text{sym}}\left({\rho }_B\right)& =E_{\text{sym}}^{\text{kin}}\left({\rho }_B\right)+E_{\text{sym}}^s\left({\rho }_B\right)+E_{\text{sym}}^0\left({\rho }_B\right)\hfill \\ \hfill & =\frac{1}{6}\frac{k_F^2}{E_F^{*}}-\frac{1}{2}\frac{g_{\delta }^2}{M_{\delta }^2\left(\bar{\sigma },0\right)}{\left(\frac{M_F^{*}}{E_F^{*}}\right)}^2{\rho }_B+\frac{1}{2}\frac{g_{\rho }^2}{M_{\rho }^2\left(\bar{\omega },0\right)}{\rho }_B.\hfill \end{array}(58)$

Note that $k_F^{*}=k_F$ and $E_{\text{sym}}^v({\rho }_B)=0$ in RMF approximation.

The $L$ and $K_{\text{sym}}$ given in Equation 17 are also expressed as

$\begin{array}{ll}\hfill L& =L^{\text{kin}}+L^{\text{pot}}\hfill \\ \hfill & =L^{\text{kin}}+L^s+L^0,\hfill \end{array}(59)$

$\begin{array}{ll}\hfill K_{\text{sym}}& =K_{\text{sym}}^{\text{kin}}+K_{\text{sym}}^{\text{pot}}\hfill \\ \hfill & =K_{\text{sym}}^{\text{kin}}+K_{\text{sym}}^s+K_{\text{sym}}^0,\hfill \end{array}(60)$

where the kinetic, scalar, and time components are respectively given by

$L^{\text{kin}}=E_{\text{sym}}^{\text{kin}}\left({\rho }_0\right)\left[1+{\left(\frac{M_F^{*}}{E_F^{*}}\right)}^2{\mathcal{K}}_B\left({\rho }_0\right)\right],(61)$

$L^{s(0)}=3E_{\text{sym}}^{s(0)}\left({\rho }_0\right)\left[1-{\rho }_0{\mathcal{T}}_B^{s(0)}\left({\rho }_0\right)\right],(62)$

$K_{\text{sym}}^{\text{kin}}=-2L^{\text{kin}}+{\left(\frac{M_F^{*}}{E_F^{*}}\right)}^2\left[E_{\text{sym}}^{\text{kin}}\left({\rho }_0\right){\mathcal{N}}_B\left({\rho }_0\right)+L^{\text{kin}}{\mathcal{K}}_B\left({\rho }_0\right)\right],(63)$

$K_{\text{sym}}^{\text{s}\left(\text{0}\right)}=3L^{s(0)}\left[1-{\rho }_0{\mathcal{T}}_B^{s(0)}\left({\rho }_0\right)\right]-9E_{\text{sym}}^{s(0)}\left[1+{\rho }_0^2{\left.\frac{d{\mathcal{T}}_B^{s(0)}\left({\rho }_B\right)}{d{\rho }_B}\right|}_{{\rho }_B={\rho }_0}\right],(64)$

with

${\mathcal{K}}_B\left({\rho }_B\right)=1+3\frac{g_{\sigma }^2}{M_{\sigma }^2\left(\bar{\sigma },0\right)}\frac{{\rho }_B}{E_F^{*}},(65)$

$\begin{array}{ll}\hfill {\mathcal{T}}_B^s\left({\rho }_B\right)& =\frac{2}{3{\rho }_B}{\left(\frac{k_F}{E_F^{*}}\right)}^2{\mathcal{K}}_B\left({\rho }_B\right)-\frac{g_{\sigma }\left(2{\mathrm{\Gamma }}_{\sigma \delta }+4{\mathrm{\Lambda }}_{\sigma \delta }\bar{\sigma }\right)}{M_{\sigma }^2\left(\bar{\sigma },0\right)M_{\delta }^2\left(\bar{\sigma },0\right)}\frac{M_F^{*}}{E_F^{*}}\hfill \\ \hfill & +\frac{g_{\delta }^2}{M_{\delta }^2\left(\bar{\sigma },0\right)}\left[{\left(\frac{k_F}{E_F^{*}}\right)}^2\frac{{\mathcal{K}}_B\left({\rho }_B\right)}{E_F^{*}}-2\frac{g_{\sigma }^2}{M_{\sigma }^2\left(\bar{\sigma },0\right)}\frac{J_p+J_n}{E_F^{*}}\right],\hfill \end{array}(66)$

${\mathcal{T}}_B^0\left({\rho }_B\right)=\frac{4g_{\omega }{\mathrm{\Lambda }}_{\omega \rho }\bar{\omega }}{M_{\omega }^2\left(\bar{\omega },0\right)M_{\rho }^2\left(\bar{\omega },0\right)},(67)$

${\mathcal{N}}_B\left({\rho }_B\right)=3{\rho }_B\frac{d{\mathcal{K}}_B\left({\rho }_B\right)}{d{\rho }_B}-2{\left(\frac{k_F}{E_F^{*}}\right)}^2{\mathcal{K}}_B^2\left({\rho }_B\right).(68)$

2.5 Stability of nuclear and neutron star matter

In order to move on the calculations of neutron stars in which the charge neutrality and $\beta$ equilibrium conditions are imposed, we introduce the degrees of freedom of leptons (electrons and muons) as well as nucleons and mesons in Equation 2.

${\mathcal{L}}_L={\bar{\psi }}_{\ell }\left(i{\gamma }_{\mu }{\partial }^{\mu }-{\widehat{m}}_{\ell }\right){\psi }_{\ell },(69)$

where ${\psi }_{\ell }=\left({}_{{\psi }_{\mu }}^{{\psi }_e}\right)$ is the lepton field and its mass is given by ${\widehat{m}}_{\ell }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(m_e,m_{\mu })$.

When we consider the stability of matter in cold neutron stars, the first principle of thermodynamics should be considered:

$du=-Pdv-\mu dq,(70)$

with $u$, $P$, $v\left(=1/{\rho }_B\right)$, $\mu$, and $q$ being the total internal energy per nucleon, pressure, volume per nucleon, chemical potential, and charge fraction, respectively [83–86]. In neutron star matter, the charge neutrality and $\beta$ equilibrium conditions read

$\mu ={\mu }_n-{\mu }_p={\mu }_e={\mu }_{\mu },(71)$

$q=Y_p-Y_L={\rho }_p/{\rho }_B-{\displaystyle \sum _{\ell =e,\mu }}{\rho }_{\ell }/{\rho }_B=0,(72)$

with ${\rho }_{\ell }$ the lepton density. The stability of neutron star matter are then expressed as the following two constraints on chemical potential and pressure:

$-{\left(\frac{\partial \mu }{\partial q}\right)}_v>0,(73)$

$-{\left(\frac{\partial P}{\partial v}\right)}_{\mu }>0.(74)$

The total internal energy per baryon, $u(v,q)$, can be decomposed into the baryon $(B)$ and lepton $(L)$ contributions as

$u\left(v,q\right)=u\left({\rho }_B,\alpha \right)=E_B\left({\rho }_B,\alpha \right)+E_L\left({\rho }_B,\alpha \right),(75)$

with $\alpha =1-2Y_p$. At zero temperature, the $\beta$ equilibrium condition leads to the relation [87].

$\begin{array}{ll}\hfill \mu & =-{\left(\frac{\partial E_B}{\partial Y_p}\right)}_{{\rho }_B}\hfill \\ \hfill & =2{\left(\frac{\partial E_B}{\partial \alpha }\right)}_{{\rho }_B}=2E_{\text{ISB}}\left({\rho }_B,\alpha \right).\hfill \end{array}(76)$

where the isospin symmetry breaking (ISB) energy of infinite nuclear matter is given by

$\begin{array}{ll}\hfill E_{\text{ISB}}\left({\rho }_B,\alpha \right)& ={\left[\frac{\partial E_B\left({\rho }_B,\alpha \right)}{\partial \alpha }\right]}_{{\rho }_B}\hfill \\ \hfill & =\frac{1}{2}\left[E_n\left(k_{F_n}\right)-E_p\left(k_{F_p}\right)\right].\hfill \end{array}(77)$

Considering the differentiation of $\mu (v,q)\left(=\mu ({\rho }_B,\alpha )\right)$, we find

$\begin{array}{ll}\hfill -{\left(\frac{\partial q}{\partial \mu }\right)}_v& =\frac{1}{2}{\left(\frac{\partial \alpha }{\partial \mu }\right)}_{{\rho }_B}+\frac{1}{{\rho }_B}{\displaystyle \sum _{\ell =e,\mu }}{\left(\frac{\partial {\rho }_{\ell }}{\partial \mu }\right)}_{{\rho }_B}\hfill \\ \hfill & =\frac{1}{8E_{\text{sym}}\left({\rho }_B,\alpha \right)}+\frac{\mu }{{\pi }^2{\rho }_B}\left(k_{F_e}+k_{F_{\mu }}\right)≕V_{\mu }\left({\rho }_B,\alpha \right),\hfill \end{array}(78)$

where $k_{F_e}$ and $k_{F_{\mu }}$ are respectively the Fermi momenta for electrons $(e)$ and muons $(\mu )$. For simplicity, we here define the nuclear symmetry energy involving the isospin asymmetry, $\alpha$, as

$\begin{array}{ll}\hfill E_{\text{sym}}\left({\rho }_B,\alpha \right)& =\frac{1}{2}\frac{{\partial }^2{E}_B\left({\rho }_B,\alpha \right)}{\partial {\alpha }^2}\hfill \\ \hfill & =\frac{1}{2}\frac{\partial E_{\text{ISB}}\left({\rho }_B,\alpha \right)}{\partial \alpha }.\hfill \end{array}(79)$

Note that we explicitly keep $\alpha$ to consider the stability of nuclear and neutron star matter, though the nuclear symmetry energy is in general calculated at ${\rho }_p={\rho }_n$, namely, $\alpha =0$, as shown in Equation 15. Hence the stability constraint on chemical potential, $V_{\mu }({\rho }_B,\alpha )>0$, can be satisfied by assuming that $E_{\text{sym}}({\rho }_B,\alpha )$ is positive at any ${\rho }_B$.

As for the pressure stability, the differentiation of $P(v,q)\left(=P({\rho }_B,\alpha )\right)$ reads

$-{\left(\frac{\partial P}{\partial v}\right)}_{\mu }={\rho }_B^2\left[{\left(\frac{\partial P_B}{\partial {\rho }_B}\right)}_{\mu }+{\left(\frac{\partial P_L}{\partial {\rho }_B}\right)}_{\mu }\right],(80)$

with the baryon and lepton contributions. Similar to Equation 27, the baryon contribution is given by

$\begin{array}{ll}\hfill {\left(\frac{\partial P_B}{\partial {\rho }_B}\right)}_{\mu }& =2{\rho }_B\frac{\partial E_B\left({\rho }_B,\alpha \right)}{\partial {\rho }_B}+{\rho }_B^2\frac{{\partial }^2{E}_B\left({\rho }_B,\alpha \right)}{{\partial }^2{\rho }_B}\hfill \\ \hfill & -{\rho }_B^2{\left[\frac{{\partial }^2{E}_B\left({\rho }_B,\alpha \right)}{\partial {\rho }_B\partial \alpha }\right]}^2/\frac{{\partial }^2{E}_B\left({\rho }_B,\alpha \right)}{{\partial }^2\alpha }.\hfill \end{array}(81)$

Using the thermodynamic definitions of pressure and incompressibility of infinite nuclear matter in Equations 18, 19, this equation can be simplified as

${\left(\frac{\partial P_B}{\partial {\rho }_B}\right)}_{\mu }=2\frac{P_B\left({\rho }_B,\alpha \right)}{{\rho }_B}+\frac{1}{9}{K}_B\left({\rho }_B,\alpha \right)-\frac{1}{18}\frac{L_{\text{ISB}}^2\left({\rho }_B,\alpha \right)}{E_{\text{sym}}\left({\rho }_B,\alpha \right)},(82)$

where the slope of ISB energy, $L_{\text{ISB}}({\rho }_B,\alpha )$, is defined as

$L_{\text{ISB}}\left({\rho }_B,\alpha \right)=3{\rho }_B\frac{\partial E_{\text{ISB}}\left({\rho }_B,\alpha \right)}{\partial {\rho }_B}.(83)$

The lepton contribution is also given by the simple form under the $\beta$ equilibrium condition:

${\left(\frac{\partial P_L}{\partial {\rho }_B}\right)}_{\mu }=\frac{{\rho }_e{k}_{F_e}^2+{\rho }_{\mu }{k}_{F_{\mu }}^2}{3\mu {\rho }_B}.(84)$

Therefore, the stability of neutron star matter under the charge neutrality and $\beta$ equilibrium conditions can be clarified by the thermodynamic constraints on chemical potential and pressure, namely, $V_{\mu }({\rho }_B,\alpha )>0$ and

$V_P\left({\rho }_B,\alpha \right)≔{\left(\frac{\partial P_B}{\partial {\rho }_B}\right)}_{\mu }+{\left(\frac{\partial P_L}{\partial {\rho }_B}\right)}_{\mu }>0.(85)$

The thermodynamic stability is used in several calculations of nuclear and neutron star matter, for instance, the compressibility of $\beta$-equilibrated matter [56, 88] and the phase transition between the crust and core regions in neutron stars [89–91].

3 Results and discussions

3.1 Nuclear models

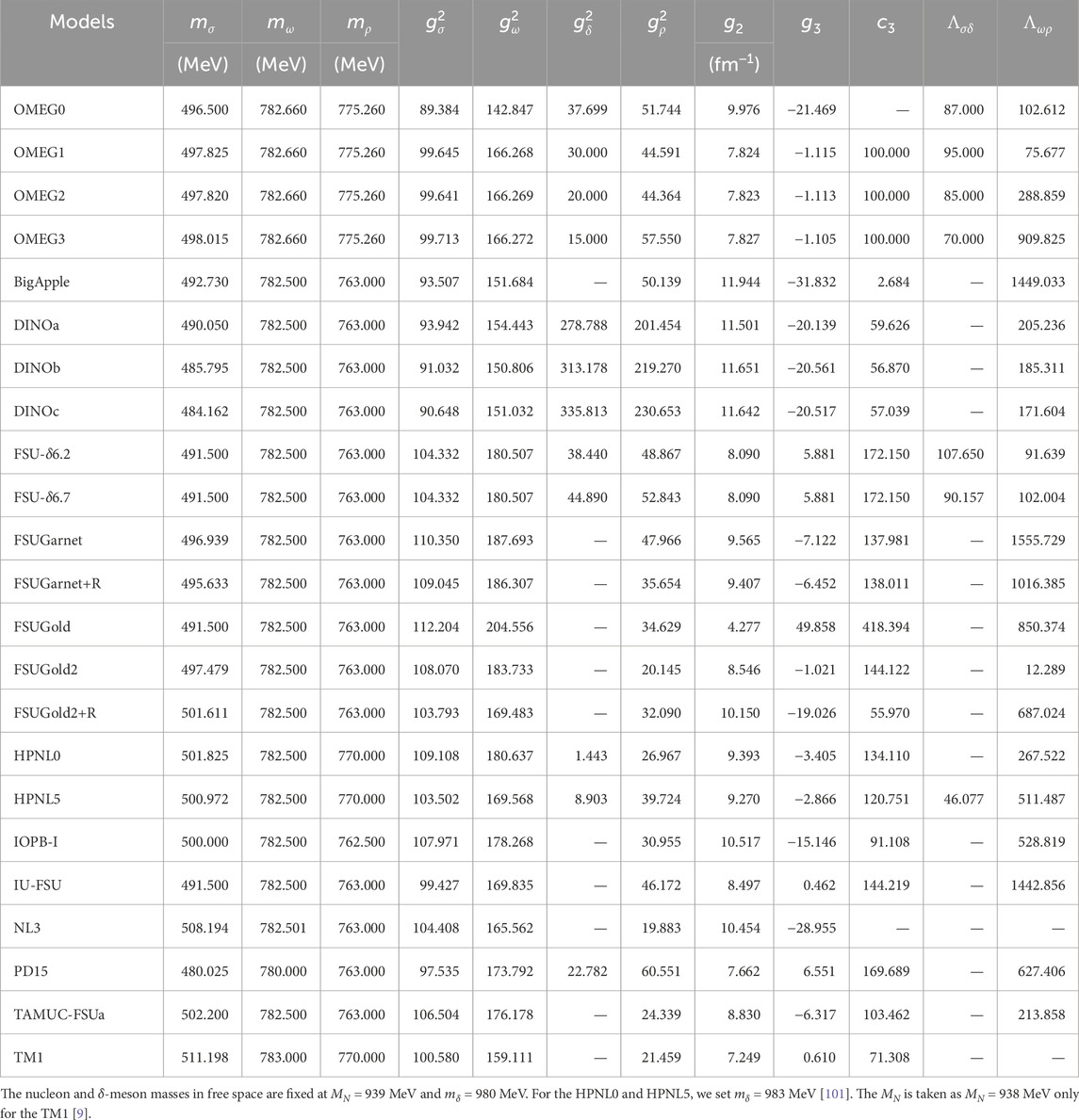
We adopt the recently developed effective interactions labeled as the OMEG family, which are constructed to reproduce the characteristics of finite nuclei, nuclear matter, and neutron stars [58, 92]. In particular, the $\delta$–$N$ coupling and $\sigma$–$\delta$ mixing in the OMEG family are determined so as to support the astrophysical constraints on the neutron-star radii from the NICER mission [29–32] and the tidal deformabilities from the binary merger events due to GW signals [34, 93]. Various theoretical calculations using the well-calibrated parameter sets based on the RMF models are also presented: BigApple [94], DINO [95], FSU-$\delta$ [59], FSUGarnet [96], FSUGold [97], FSUGold2 [98], Bayesian refinement of FSUGarnet and FSUGold2, FSUGarnet+R and FSUGold2+R [99, 100], HPNL0 and HPNL5 [101], IOPB-I [102], IU-FSU [103], NL3 [67], PD15 [104], TAMUC-FSUa [105, 106], and TM1 [9]. In Tables 1, 2, we summarize the model parameters and the properties of symmetric nuclear matter at ${\rho }_0$ for the effective interactions used in the present study.

Table 1

Table 1. Model parameters for various effective interactions.

Table 2

Table 2. Properties of symmetric nuclear matter at ${\rho }_0$ for various effective interactions.

In addition, we present the extended interactions based on the FSUGarnet, TAMUC-FSUa, and FSUGold2 models, in which the $\delta$–$N$ coupling are introduced to investigate the effect of $\delta$ meson. Since the $\delta$–$N$ coupling only influences the properties of $N\ne Z$ finite nuclei and isospin-asymmetric nuclear matter, we adjust $g_{\rho }^2$ and ${\mathrm{\Lambda }}_{\omega \rho }$ to preserve the original model’s predictions for $L$ when the $\delta$–$N$ coupling is included. Simultaneously, the other coupling constants related to the properties of $N=Z$ finite nuclei and isospin-symmetric nuclear matter—$g_{\sigma }^2$, $g_{\omega }^2$, $g_2$, and $g_3$—are readjusted to closely match the experimental data for the binding energy per nucleon and charge radius of several closed-shell nuclei, as well as to maintain the original $K_0$ value. The resultant coupling constants and nuclear properties for the FSUGarnet, TAMUC-FSUa, and FSUGold2 series are listed in Table 3. Furthermore, the parameter sets for the FSUGold2 with the $\delta$–$N$ coupling and the quartic self-interaction of $\rho$ meson are also given in Table 4, where the quartic coupling constant, $e_3$, is varied in the range of $0\le e_3\le 800$ with the fixed parameters, $c_3=144.12$ and $g_{\delta }^2=300$.

Table 3

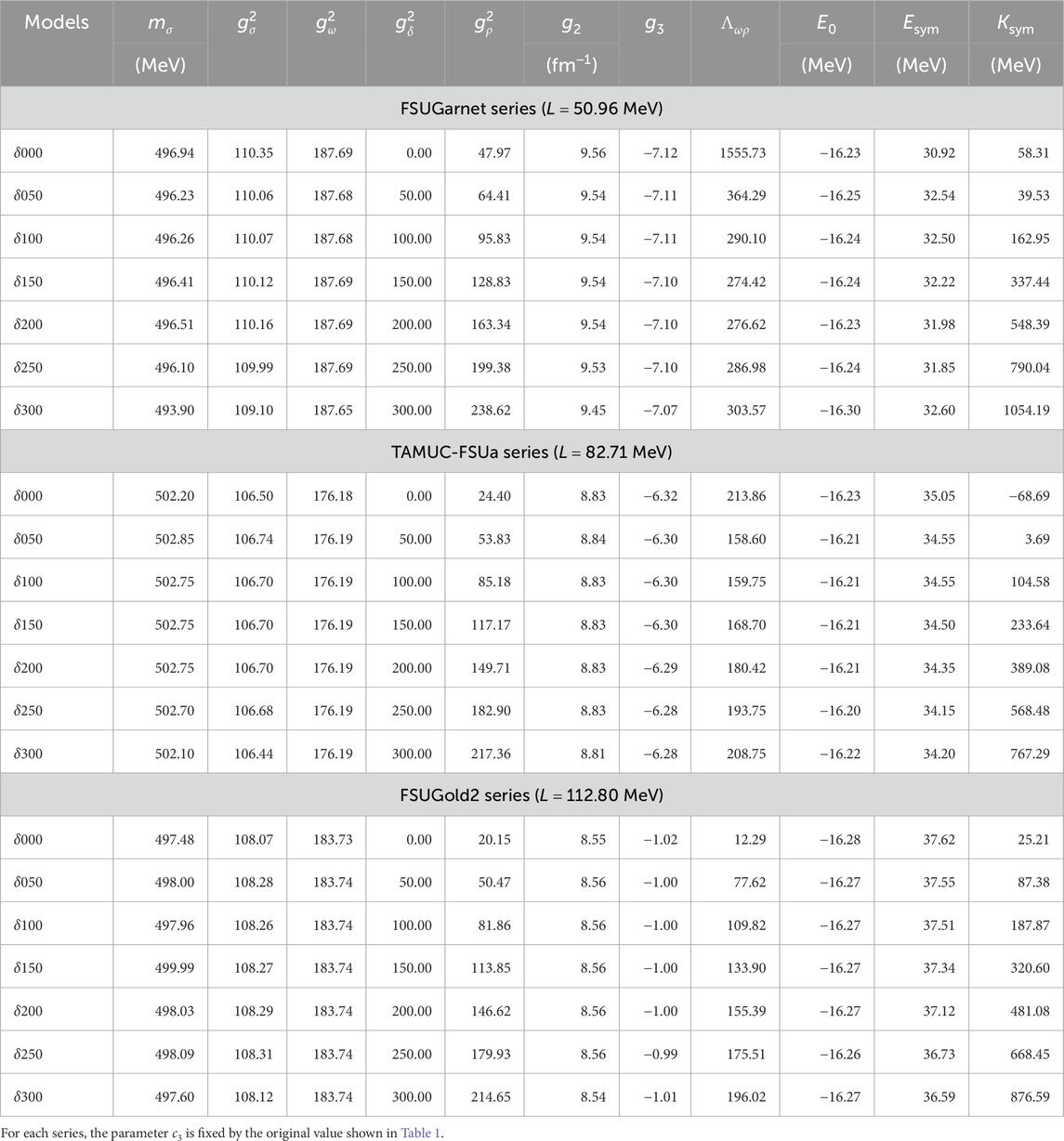
Table 3. Model parameters and nuclear properties for the extended version of the FSUGarnet, TAMUC-FSUa, and FSUGold2 models.

Table 4

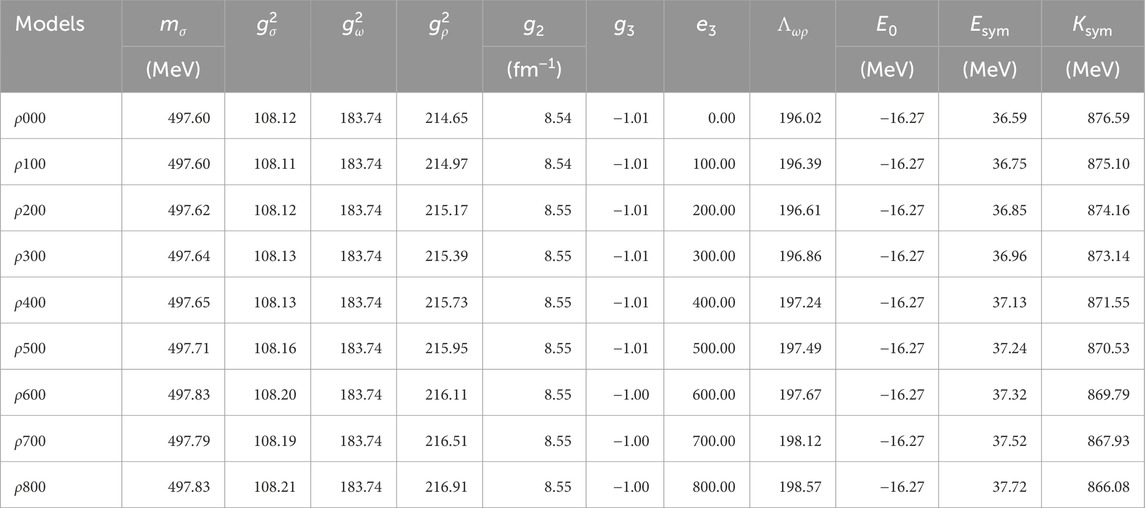
Table 4. Model parameters and several properties for the FSUGold2 with the $\delta$-$N$ coupling and the quartic self-interaction of $\rho$ meson. We set $c_3=144.12$ and $g_{\delta }^2=300.00$.

3.2 Finite nuclei

The theoretical predictions for the neutron skin thickness of ⁴⁰Ca and ²⁰⁸Pb, $R_{\text{skin}}^{48}$ and $R_{\text{skin}}^{208}$, in the RMF models are presented in Figure 1, compared with the experimental data: the electric dipole polarizability of ⁴⁸Ca (RCNP; $R_{\text{skin}}^{48}=0.14$–0.20 fm) [107], the complete electric dipole response on ²⁰⁸Pb (RCNP; $R_{\text{skin}}^{208}=0.156_{-0.021}^{+0.025}$ fm) [52], the coherent pion photoproduction cross sections measurement of ²⁰⁸Pb (MAMI; $R_{\text{skin}}^{208}=0.15\pm 0.03{(\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}.)}_{-0.03}^{+0.01}(\mathrm{s}\mathrm{y}\mathrm{s}.)$ fm) [108], and the parity-violating electron scattering off ⁴⁸Ca (CREX; $R_{\text{skin}}^{48}=0.121\pm 0.026(\mathrm{e}\mathrm{x}\mathrm{p}.)\pm 0.024(\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l})$ fm) [50] and off ²⁰⁸Pb (PREX-2; $R_{\text{skin}}^{208}=0.283\pm 0.071$ fm) [47].

Figure 1

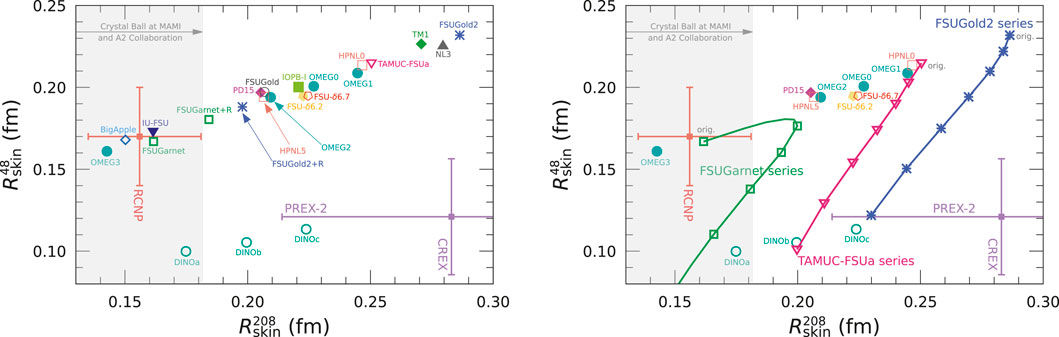
Figure 1. Neutron skin thickness of ⁴⁰Ca and ²⁰⁸Pb, $R_{\text{skin}}^{48}$ and $R_{\text{skin}}^{208}$. The left panel shows the results from the effective interactions presented in Tables 1, 2. The right panel is for the FSUGarnet, TAMUC-FSUa, and FSUGold2 series in Table 3.

As for the OMEG family, the OMEG0 and OMEG1 give the large values, $R_{\text{skin}}^{208}=0.227$ fm and $R_{\text{skin}}^{208}=0.245$ fm, respectively, which meet the PREX-2 result. The OMEG2 is selected so as to match the predicted result, $R_{\text{skin}}^{208}=0.19\pm 0.02$ fm, by the assessment of the theoretical uncertainty on parity-violating asymmetry in ²⁰⁸Pb [49]. Meanwhile, the OMEG3 exhibits the small value, $R_{\text{skin}}^{48}=0.161$ fm, which satisfies the experimental result in RCNP and is near the range of CREX experiment, $R_{\text{skin}}^{48}=0.121\pm 0.035$ fm. We summarize the predictions for the charge radius, $R_{\text{ch}}$, neutron skin thickness, $R_{\text{skin}}$, and weak radius, $R_{\text{wk}}$, of ⁴⁸Ca and ²⁰⁸Pb in Table 5. We here consider the zero-point energy correction taken from the conventional Skyrme Hartree–Fock calculations [9, 109]. The $R_{\text{ch}}$ is defined as

$R_{\text{ch}}=\sqrt{R_p^2+{\left(0.8783\right)}^2},(86)$

with $R_p$ being the point proton radius [98].

Table 5

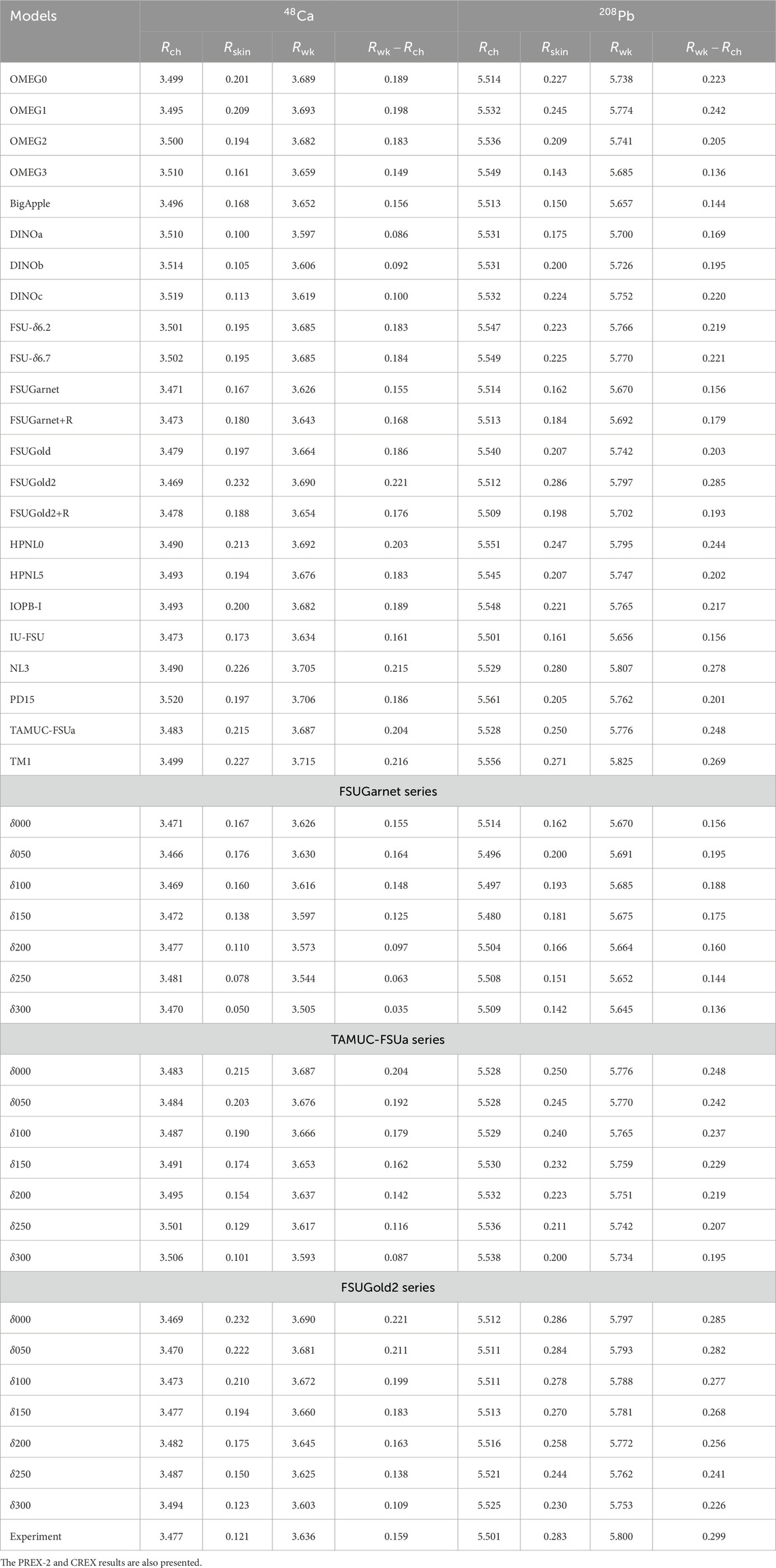
Table 5. Predictions for the charge radius, $R_{\text{ch}}$, neutron skin thickness, $R_{\text{skin}}$, weak radius, $R_{\text{wk}}$, and weak skin thickness, $R_{\text{wk}}-R_{\text{ch}}$, of ⁴⁸Ca and ²⁰⁸Pb in fm.

We see the linear correlation between $R_{\text{skin}}^{48}$ and $R_{\text{skin}}^{208}$ in the left panel of Figure 1. In general, the larger $R_{\text{skin}}^{48}$ and $R_{\text{skin}}^{208}$ are obtained by the models with the larger $L$ (see Table 2). To explain the results from RCNP, $L$ should be small such as the OMEG3, BigApple, FSUGarnet, and IU-FSU. In contrast, the DINO family is located far from the points calculated by the other RMF models. As explained in Reed et al. [95], the DINO family expresses the large $K_{\text{sym}}$ by means of the huge $\delta$–$N$ and $\rho$–$N$ couplings. Although it is difficult to support the PREX-2 and CREX results simultaneously, only the DINOc successfully aligns with both data sets. We note that the $\delta$-$N$ coupling and $\sigma$-$\delta$ mixing affect the charge radii of finite nuclei and hence $R_{\text{skin}}$ while they have less influence on the binding energy because we focus on the finite, closed-shell nuclei, ¹⁶O, ^40,48Ca, ⁶⁸Ni, ⁹⁰Zr, ^100,116,132Sn, and ²⁰⁸Pb, in the present study [110].

To clarify the effect of $\delta$ meson on the characteristics of finite nuclei, we describe the correlation between $R_{\text{skin}}^{48}$ and $R_{\text{skin}}^{208}$ for the FSUGarnet, TAMUC-FSUa, and FSUGold2 series in the right panel of Figure 1. We also display the calculations based on the other RMF models including the $\delta$ meson as well as the $\sigma$, $\omega$, and $\rho$ mesons. As shown in Table 3, $K_{\text{sym}}$ becomes large as $g_{\delta }^2$ increases. Consequently, the TAMUC-FSUa, and FSUGold2 series draw the lines from the upper right to the bottom left. In particular, the FSUGold2 with the large $\delta$–$N$ coupling $(g_{\delta }^2\ge 250)$ supports both experimental data from the parity-violating electron scattering. On the other hand, the FSUGarnet series moves away from the PREX-2 and CREX results when the large $g_{\delta }^2$ is introduced.

The density profiles in ²⁰⁸Pb are displayed in Figure 2. We here present the baryon, charge, and weak charge densities, ${\rho }_B$ $(={\rho }_p+{\rho }_n)$, ${\rho }_{\text{ch}}$, and ${\rho }_W$, with the experimental results [47, 111]. The ${\rho }_W$ is approximately expressed as

${\rho }_W\left(\mathit{r}\right)\simeq Q_p{\rho }_{\text{ch}}\left(\mathit{r}\right)+Q_n\int d{\mathit{r}}^{\prime }{G}_p^E\left(\left|\mathit{r}-{\mathit{r}}^{\prime }\right|\right){\rho }_n\left(\mathit{r}\right),(87)$

with $Q_{p(n)}$ being the proton (neutron) weak charge and $G_p^E$ being the proton electric form factor [112–114]. The OMEG family is calibrated so as to reproduce $-{\rho }_W$ and ${\rho }_B$ in ²⁰⁸Pb by the PREX-2 experiment.

Figure 2

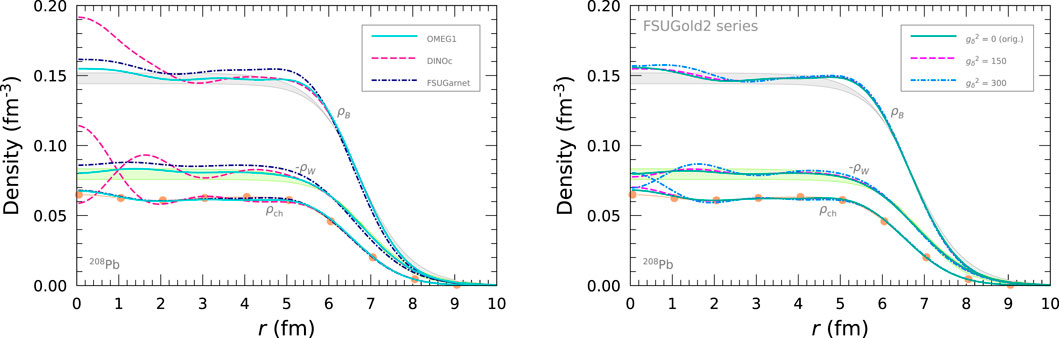
Figure 2. Baryon, charge, and weak change densities, ${\rho }_B$, ${\rho }_{\text{ch}}$, and ${\rho }_W$, for ²⁰⁸Pb. The density profiles for the OMEG1, DINOc, and FSUGarnet are given in the left panel. The right panel is for the FSUGold2 series.

In the left panel of Figure 2, we present the density profiles for the OMEG1, DINOc, FSUGarnet. The OMEG1 and FSUGarnet adequately satisfy the density distributions of ${\rho }_{\text{ch}}$ from the elastic electron scattering [111]. On the other hand, the DINOc possesses the instability around the core of nuclei because of the strong $\delta$–$N$ coupling constant [95]. As a result, the density profiles, ${\rho }_B$, ${\rho }_{\text{ch}}$, and ${\rho }_W$, show the large density fluctuations around the core.

The effect of $\delta$–$N$ coupling on the density profiles for the FSUGold2 series is illustrated in the right panel of Figure 2. There is almost no difference up to $g_{\delta }^2=150$. In the case of $g_{\delta }^2=300$, ${\rho }_{\text{ch}}$ and ${\rho }_W$ begin to show the instability around the core, but ${\rho }_B$ still matches the experimental data from PREX-2 [47]. When the larger value, $g_{\delta }^2>300$, is taken, the unexpectedly large fluctuations of ${\rho }_{\text{ch}}$ and ${\rho }_W$ emerge around the core, and the wave functions do not converge numerically. In the present study, we thus impose the limit on the $\delta$–$N$ coupling as $g_{\delta }^2\le 300$ for the FSUGold2 series. We here comment that this defect can not be solved even if one considers the quartic self-interactions of $\delta$ and/or $\rho$ mesons in Equation 3, which less affect $R_{\text{skin}}^{48}$ and $R_{\text{skin}}^{208}$.

3.3 Infinite nuclear matter

The $\delta$-meson effect can be clearly seen in the effective nucleon mass, $M_N^{*}$, in Equation 3. Displayed in Figure 3 is the density dependence of $M_N^{*}$ in pure neutron matter for the OMEG family and the FSUGold2 series. When the $\rho$ meson only is included, the RMF model gives the equal effective mass of proton and neutron. However, the iso-scalar $\delta$ meson is responsible for the mass splitting between protons and neutrons, where $M_p^{*}$ is much heavier than $M_n^{*}$ at high densities. Compared with the OMEG family, the FSUGold2 series shows the strong mass splitting, as $g_{\delta }^2$ increases, even at low densities. It is implied that the neutron distribution is more spread out than the proton one, because $M_n^{*}$ is lighter, and then, the large fluctuations of ${\rho }_{\text{ch}}$ and ${\rho }_W$ appear around the core of ²⁰⁸Pb as shown in Figure 2. Due to the $\delta$–$N$ coupling and the $\sigma$–$\delta$ mixing, $M_p^{*}$ and $M_n^{*}$ respectively reach the almost constant values at high densities in all the cases.

Figure 3

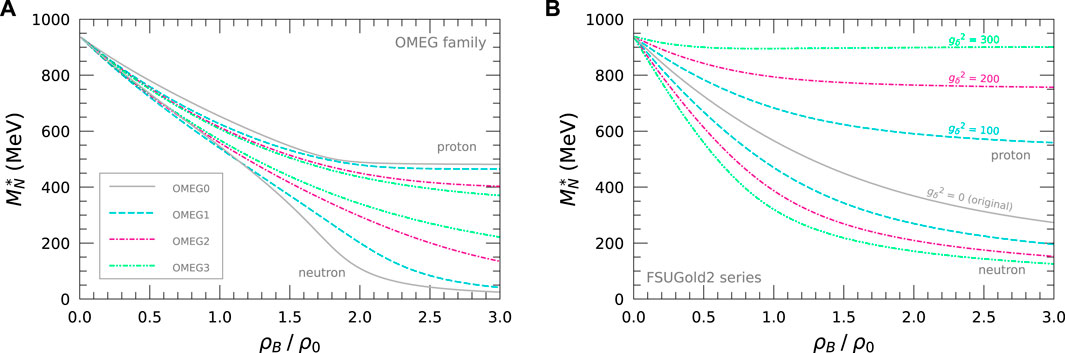
Figure 3. Effective nucleon mass, $M_N^{*}$, as a function of ${\rho }_B/{\rho }_0$ for the OMEG family (A) and the FSUGold2 series (B).

The density dependence of nuclear symmetry energy, $E_{\text{sym}}$, in Equation 26 is depicted in Figure 4. We here present the calculations using the OMEG, FSU-$\delta$, and DINO families. Furthermore, we use the conventional ones (the NL3, FSUGold2, TAMUC-FSUa, IOPB-I, and FSUGarnet models). In addition, several experimental or theoretical constraints are presented. Figure 4 highlights significant differences in $E_{\text{sym}}$ at high densities, that is, whereas the conventional calculations show a monotonic increase in $E_{\text{sym}}$, the models with the $\delta$ meson exhibit more complex behavior. In particular, the DINO family predicts a large $E_{\text{sym}}$ above $1.5{\rho }_0$ as the $\delta$ meson amplifies $E_{\text{sym}}$ in dense nuclear matter [57]. The OMEG and FSU-$\delta$ families, on the other hand, display unusual $E_{\text{sym}}$ trends depending on the strength of $\delta$–$N$ coupling and $\sigma$–$\delta$ mixing. The $\sigma$–$\delta$ mixing has a weak influence on $E_{\text{sym}}$ below ${\rho }_0$, but, as discussed by Zabari et al. [56], it becomes substantial above ${\rho }_0$. Specifically, the $\sigma$–$\delta$ mixing reduces $E_{\text{sym}}$ at high densities, partially offsetting the increase from the $\delta$–$N$ interaction. Furthermore, in the OMEG0 and FSU-$\delta 6.2$, the inflection points appear above ${\rho }_0$ and the dip emerges around $2.5{\rho }_0$–$3.5{\rho }_0$. This behavior is similar to the cusp in $E_{\text{sym}}$ in the skyrmion crystal approach [115, 116] and to the results from the Skyrme Hartree-Fock calculations [117]. We note that, as explained in Section 2.5, the thermodynamic constraint on chemical potential in isospin-asymmetric nuclear matter, $V_{\mu }({\rho }_B,\alpha )>0$, is satisfied over all densities, namely, $E_{\text{sym}}({\rho }_B,\alpha )>E_{\text{sym}}({\rho }_B)>0$.

Figure 4

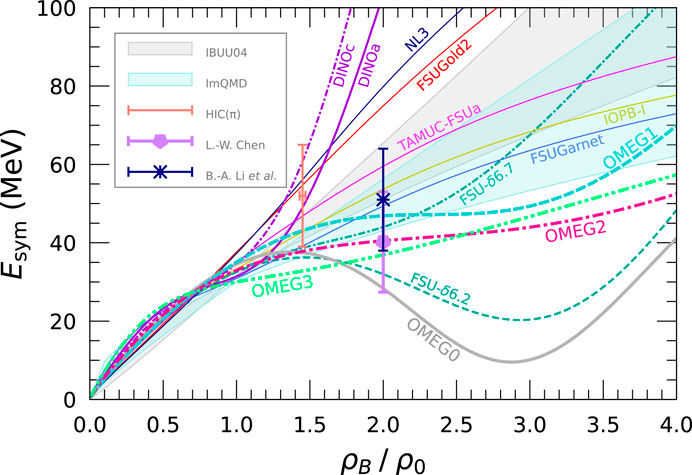
Figure 4. Density dependence of nuclear symmetry energy, $E_{\text{sym}}$. The shaded regions are the results from analyses of HIC data using the isospin-dependent Boltzmann-Uehling-Uhlenbec (IBUU04) and improved quantum molecular dynamics (ImQMD) transport models [22, 139, 140]. The recent experimental constraint from the pion emission in heavy-ion reactions is expressed as HIC$(\pi )$ with $E_{\text{sym}}({\rho }_B)=52\pm 13$ MeV at ${\rho }_B/{\rho }_0=1.45\pm 0.2$ [141–143]. We also present two theoretical constraints on the magnitude of $E_{\text{sym}}$ at $2{\rho }_0$ with $E_{\text{sym}}(2{\rho }_0)\simeq 40.2\pm 12.8$ MeV by Chen [144] and $E_{\text{sym}}(2{\rho }_0)\simeq 51\pm 13$ MeV by Li et al. [145].

Based on the Lorentz decomposition of nucleon self-energy in Section 2.4, $E_{\text{sym}}$ is generally divided into the kinetic and potential terms, $E_{\text{sym}}^{\text{kin}}$ and $E_{\text{sym}}^{\text{pot}}$, as $E_{\text{sym}}=E_{\text{sym}}^{\text{kin}}+E_{\text{sym}}^{\text{pot}}$. In RMF approximation, only the isovector mesons contribute to $E_{\text{sym}}^{\text{pot}}$ as $E_{\text{sym}}^{\text{pot}}=E_{\text{sym}}^s+E_{\text{sym}}^0$, where the scalar $(s)$ and time (0) components, $E_{\text{sym}}^s$ and $E_{\text{sym}}^0$, are respectively given by the $\delta$ and $\rho$ mesons. We show the Lorentz decomposition of $E_{\text{sym}}$ for the OMEG family and the FSUGold2 series as a function of ${\rho }_B/{\rho }_0$ in Figure 5. The top panels are the density dependence of $E_{\text{sym}}$ and $E_{\text{sym}}^{\text{kin}}$. We see that the unique behavior of $E_{\text{sym}}$ in the OMEG family is caused by $E_{\text{sym}}^{\text{pot}}$ because $E_{\text{sym}}^{\text{kin}}$ is almost the same as in both cases. The contents of $E_{\text{sym}}^{\text{pot}}$ are given in the middle and bottom panels of Figure 5. It is found that $E_{\text{sym}}^s$ is negative while $E_{\text{sym}}^0$ is positive, which is similar to the general understanding of $N$–$N$ interaction described by the nuclear attractive and repulsive forces. Note that a similar description of $E_{\text{sym}}^{\text{pot}}$ has been reported using the RMF model with a contact interaction of isovector mesons, where the scalar contribution, ${({\bar{\psi }}_N{\mathit{\tau }}_N{\psi }_N)}^2$, is positive while the vector one, ${({\bar{\psi }}_N{\gamma }_{\mu }{\mathit{\tau }}_N{\psi }_N)}^2$, is negative [118, 119]. It is noticeable that, for the FSUGold2 series, $E_{\text{sym}}^s$ is strongly influenced by the $\delta$–$N$ coupling above ${\rho }_0$, and the contribution of $E_{\text{sym}}^s$ is small at high densities. Conversely, for the OMEG family, the $\sigma$–$\delta$ mixing shows less impact on $E_{\text{sym}}^s$ below ${\rho }_0$, but it strongly affects $E_{\text{sym}}^s$ at high densities. When the absolute value of $E_{\text{sym}}^s$ is larger than that of $E_{\text{sym}}^0$, $E_{\text{sym}}^{\text{pot}}$ has the rapid reduction, and then $E_{\text{sym}}$ shows a dip around $3{\rho }_0$ as in the cases for the OMEG0 and FSU-$\delta 6.2$ in Figure 4.

Figure 5

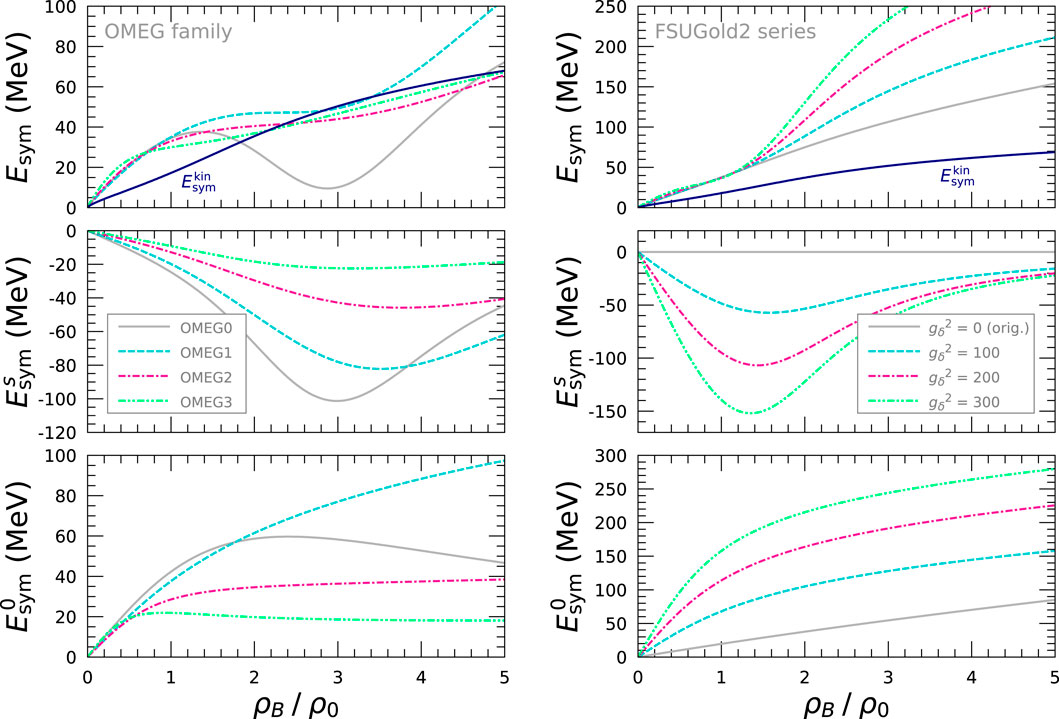
Figure 5. Lorentz decomposition of nuclear symmetry energy, $E_{\text{sym}}$, for the OMEG family (left panels) and the FSUGold2 series (right panels). The total $E_{\text{sym}}$ and the kinetic term, $E_{\text{sym}}^{\text{kin}}$, are presented in the top panels. The scalar (time) component of potential term, $E_{\text{sym}}^s(E_{\text{sym}}^0)$, is given in the middle (bottom) panels.

The EoSs for symmetric nuclear matter and pure neutron matter are displayed in Figure 6 with the constraints on the nuclear EoS extracted from the analyses of particle flow data in HICs [60–62]. In both panels, we show the various EoSs calculated by the OMEG, DINO, and FSU-$\delta$ families, and the FSUGarnet and FSUGold2 models. The $\delta$ meson does not affect $P$ in symmetric nuclear matter. All the cases except for the OMEG0 are well constructed to match the HIC data in symmetric nuclear matter because of the small $K_0$. However, the stiffer EoS with $K_0\simeq 285$ MeV is still acceptable, taking into account the recent simulation of Au$+$Au collisions [63]. In contrast, the $\delta$ meson has a large impact on $P$ in pure neutron matter. The DINOa and DINOc show the hard EoSs, which are far from the constraints from HICs, due to the large $\delta$–$N$ coupling. Meanwhile, the strong $\sigma$–$\delta$ mixing softens the EoSs extremely for the OMEG and FSU-$\delta$ families in the density region from ${\rho }_0$ to $2{\rho }_0$, around which the characteristics of a canonical $1.4M_{\odot }$ neutron star are generally determined.

Figure 6

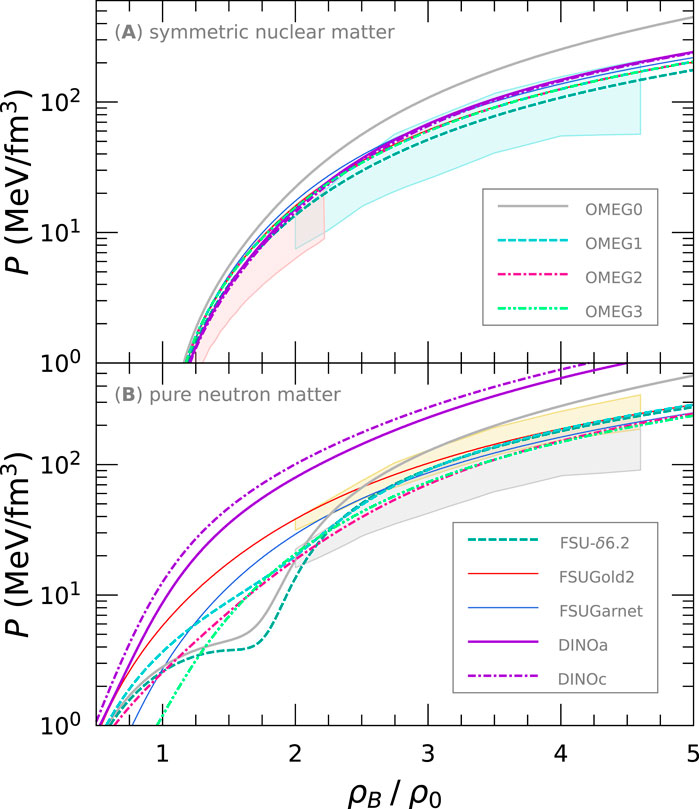
Figure 6. EoS—pressure, $P$, as a function of ${\rho }_B/{\rho }_0$—for (A) symmetric nuclear matter and for (B) pure neutron matter. The shaded areas represent the constraints from elliptical flow data [60] and kaon production data [61, 62].

We present the EoS for pure neutron matter for the FSUGold2 series in Figure 7. In the left panel, the EoS becomes hard with increasing the $\delta$–$N$ coupling, and the EoS with $g_{\delta }^2=300$ exceeds the HIC results as in the cases for the DINO family in Figure 6. Hence, we find that, even if the large $\delta$–$N$ coupling is introduced simply, it is not easy to explain simultaneously both properties of dense nuclear matter and characteristics of finite nuclei for $R_{\text{skin}}^{48}$ and $R_{\text{skin}}^{208}$ in Figure 1. In order to suppress such excessive stiffness of EoSs for pure neutron matter due to the $\delta$–$N$ coupling, we additionally include the quartic self-interaction of $\rho$ meson in the FSUGold2 model with the upper limit of $g_{\delta }^2=300$ (see Table 4), given in the right panel of Figure 7. The EoS is soft and again reaches the upper edge of the constraint from HICs with increasing the quartic coupling, $e_3$, whose effect is almost imperceptible below ${\rho }_0$.

Figure 7

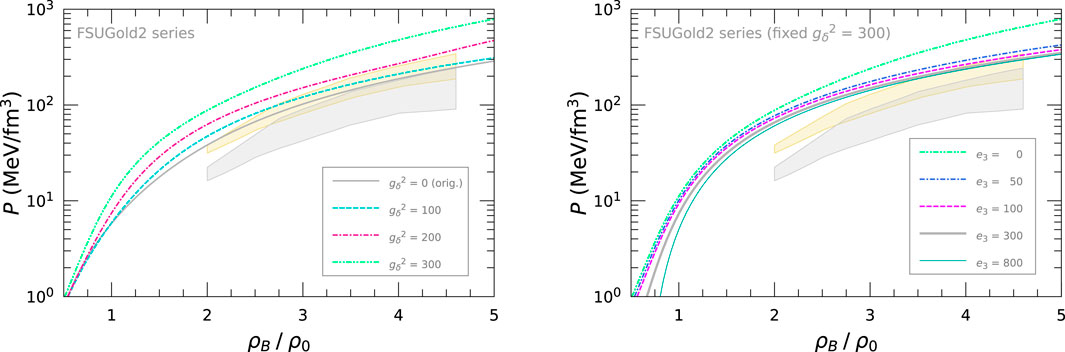
Figure 7. EoS for pure neutron matter for the FSUGold2 series. The left panel shows the dependence of $\delta$–$N$ coupling square, $g_{\delta }^2$. In the right panel, the influence of quartic $\rho$-meson self-interaction, $e_3$, is presented with the fixed parameter of $g_{\delta }^2=300$ (see Table 4).

3.4 Neutron star physics

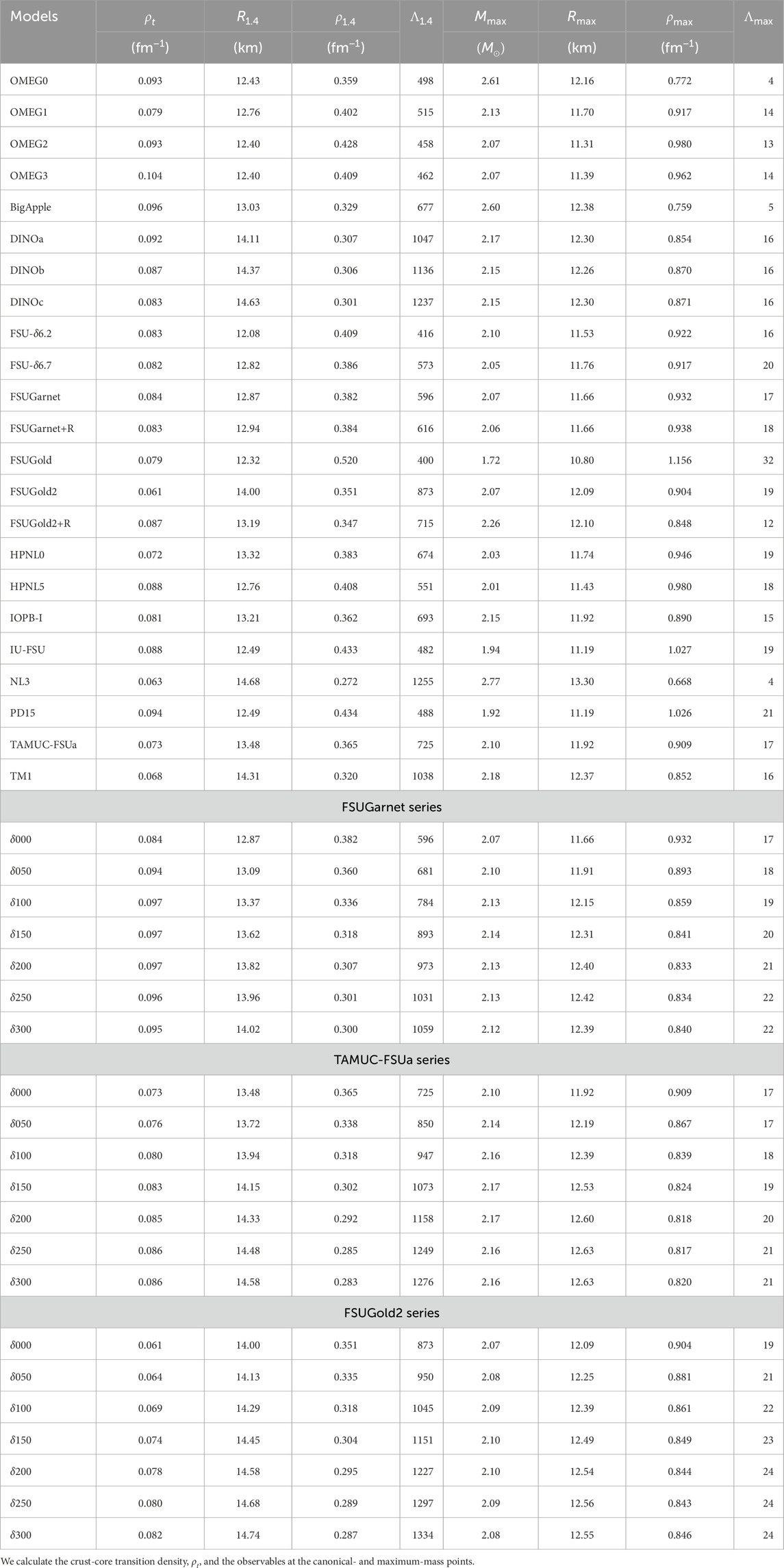
In studying neutron star physics, the EoS for non-uniform matter is additionally required as well as that for uniform nuclear matter since the radius of a neutron star is remarkably sensitive to the nuclear EoS at very low densities [120]. In the present study, to cover the crust region, we adopt the MYN13 EoS, in which nuclei are taken into consideration using the Thomas-Fermi calculation in non-uniform matter and the EoS for infinite nuclear matter is constructed with the relativistic Hartree-Fock calculation [80, 81, 121, 122]. We list in Table 6 the predicted stellar properties, which are calculated by solving the Tolman–Oppenheimer–Volkoff (TOV) equation [123, 124].

Table 6

Table 6. Properties of neutron stars.

There are three methods used widely to determine the crust-core transition density, ${\rho }_t$ [125]: the thermo-dynamical method, the dynamical method, and the random-phase-approximation method. We employ the first method in the present study. As explained in Section 2.5, the stability of nuclear and neutron star matter is determined by the constraints on chemical potential and pressure, $V_{\mu }({\rho }_B,\alpha )>0$ and $V_P({\rho }_B,\alpha )>0$, in the first law of thermodynamics. Since the proton fraction, $Y_p$, is supposed to be small in the crust region, the second-order Taylor series approximation of the nuclear EoS is generally adopted in the density derivative of baryon pressure, ${\left(\partial P_B/\partial {\rho }_B\right)}_{\mu }$, in Equation 28 [83]. However, it has been reported that the parabolic approximation of isospin-asymmetric nuclear EoS may be misleading as regards the predictions for ${\rho }_t$ [89]. We thus employ the exact nuclear EoS to calculate $V_P$ defined in Equation 29.

We summarize the results of ${\rho }_t$ in the second column of Table 6. Compared with the results from the Taylor series expansion, the our results settle between the second-order and fourth-order calculations. For example, for the FSUGold, the exact value is ${\rho }_t=0.079$ ${\text{fm}}^{-3}$ while the second-order (fourth-order) result is ${\rho }_t^{2\mathrm{n}\mathrm{d}}=0.089$ $({\rho }_t^{4\mathrm{t}\mathrm{h}}=0.051)$ ${\text{fm}}^{-3}$ (see Table 2 in Routray et al. [89]). In addition, the current results are almost the same as the transition density from the pasta phase to the homogeneous nuclear matter in the model calculation with Thomas-Fermi approximation [126]. The EoS for neutron star matter in the OMEG family is presented in Figure 8. The crust-core phase transition occurs at $V_P=0$, which is also described in the left panel of Figure 9. As it is well known, the EoS with larger $L$ gives the smaller ${\rho }_t$ [127].

Figure 8

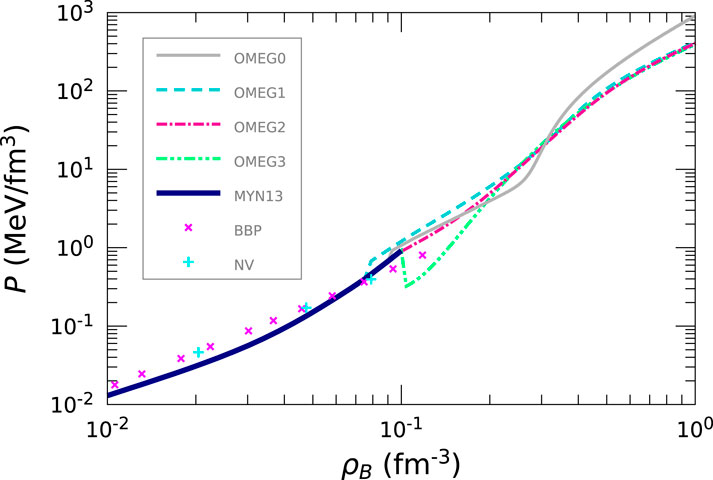
Figure 8. EoS for neutron star matter for the OMEG family. The inner-crust region is described by the EoSs of MYN13 [121], BBP [1], and NV [146].

Figure 9

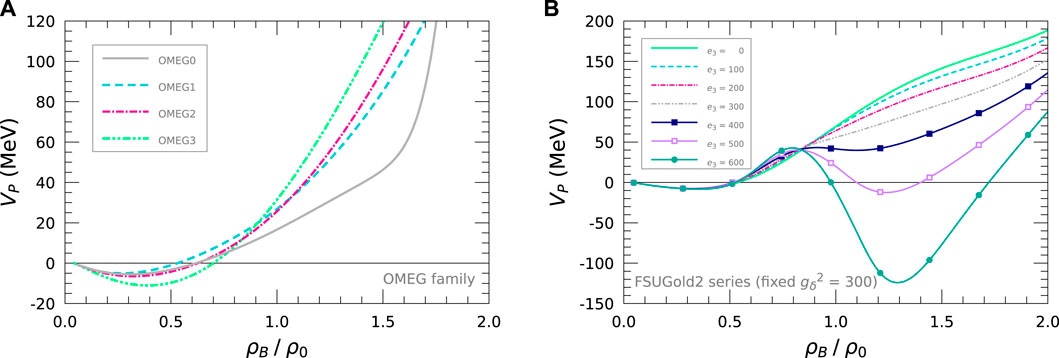
Figure 9. Thermodynamic stability of pressure, $V_p$, in neutron star matter for the OMEG family (A) and for the FSUGold2 series with the fixed parameter of $g_{\delta }^2=300$ (B).

Since the large $\sigma$–$\delta$ mixing enhances the rapid reduction of $E_{\text{sym}}$ around $3{\rho }_0$ as shown in Figure 4, we have to investigate the stability of neutron star matter. Similar to the crust-core phase transition, we adopt the thermo-dynamical method. It is especially important to apply the exact nuclear EoS to $V_P$ because $Y_p$ is by no means small and the Taylor series expansion is prohibited at high densities. It is found that the constraint on chemical potential, $V_{\mu }>0$, is always satisfied as $E_{\text{sym}}$ is positive at any densities. Hence, all we have to do is check the thermodynamic stability of pressure, $V_P$. In Figure 9, we show $V_P$ in neutron star matter. In general, $V_P$ changes from negative to positive at ${\rho }_t$, and the stable EoS possesses $V_P>0$ even at high densities. Despite the OMEG0 give a strong concavity in $E_{\text{sym}}$ by the $\sigma$–$\delta$ mixing, it satisfies the thermodynamic stability. In the right panel of Figure 9, we show $V_P$ for the FSUGold2 series. The neutron star matter keeps $V_P>0$ when the $\delta$–$N$ coupling only is included, whereas the large quartic self-interaction of $\rho$ meson, $e_3$, makes the matter unstable. Though the quartic $\rho$-meson self-interaction is useful to figure out the HIC data as mentioned in the right panel of Figure 7, the large value of $e_3$ is unfavorable to the neutron star physics.

We illustrate in Figure 10 the proton fraction, $Y_p$, in neutron star matter with the threshold for the direct URCA process. The direct URCA process is visible only when $Y_p$ is large enough to conserve momentum in $\beta$-equilibrated matter, in which the Fermi momenta of neutrons, protons, and electron must satisfy the relation: $k_{F_n}\le k_{F_p}+k_{F_e}$. Hence, $Y_p$ can be estimated as $0.111\le Y_p\le 0.148$, above which the direct URCA cooling occurs [118, 128, 129]. We find that as ${\rho }_B$ increases, the threshold of $Y_p$ for the direct URCA process shifts toward the upper boundary where muons are present. The $Y_p$ for the DINOa grows quickly with increasing ${\rho }_B$ due to the large $\delta$–$N$ coupling, and then the direct URCA process is allowed sufficiently at $2{\rho }_0$, which corresponds to the core density of a canonical $1.4M_{\odot }$ neutron star. Conversely, in the OMEG and FSU-$\delta$ families, the $\sigma$–$\delta$ mixing suppresses $Y_p$, and then delays the direct URCA process. Particularly, the direct URCA process never occurs for the OMEG0, OMEG2, and OMEG3 in the current density region, and thus the so-called modified URCA process, which is the standard model of neutron-star coolings, mainly takes place for the neutrino emission [130]. Alternatively, the possibility of exotic degrees of freedom in the core of a neutron star, such as hyperons, quarks, gluons and/or some unusual condensations of boson-like matter, should be taken into account to understand the rapid neutron star cooling.

Figure 10

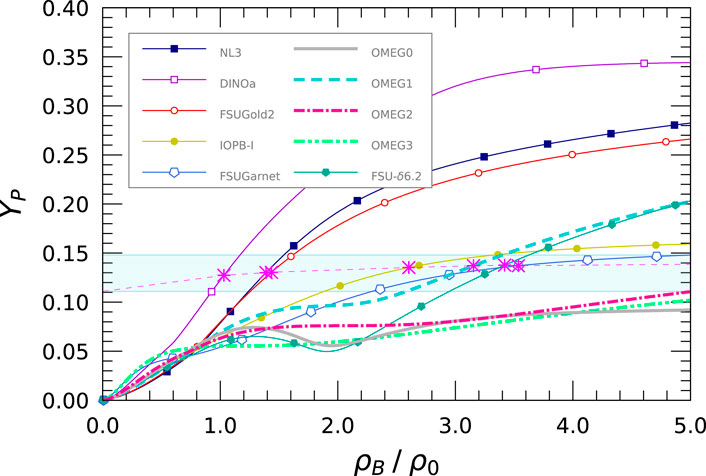
Figure 10. Proton fraction, $Y_p(={\rho }_p/{\rho }_B)$, in neutron star matter. The shaded band is the threshold for the direct URCA process [118, 128]. The asterisks indicate the densities at which the direct URCA process actually begins.

The mass$(M)$–radius$(R)$ relations of neutron stars are displayed in Figure 11. We here show the astrophysical constraints from the NICER observations: PSR J0030$+$0451 [29, 31], PSR J0740$+$6620 [32, 64, 65], and PSR J0437$-$4715 [131, 132]. According to the observation from PSR J0740$+$6620, the maximum mass of a neutron star, $M_{\text{max}}$, should be larger than $2M_{\odot }$. Thus the EoS involving the large $R$, such as the NL3, is ruled out. It is found that the large $\delta$–$N$ coupling affects the large $R$ in the DINO family, whereas the $\sigma$–$\delta$ mixing makes $R$ small in the OMEG family. In particular, though the DINOa and OMEG0 have the same $L$ as $L=50$ MeV, their $M$–$R$ relations are completely different and the difference of $R$ at canonical-mass point reads approximately 1.7 km (see also Table 6). The OMEG family can support not only the NICER constraint on $R_{1.4}$ from PSR J0030$+$0451 but also that from PSR J0437$-$4715, which is the latest result based on new chiral effective field theory inputs [131].

Figure 11

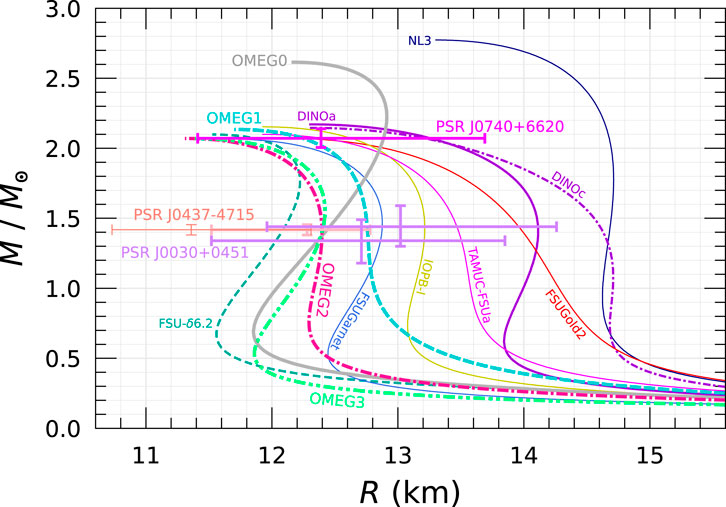
Figure 11. Mass–radius relations of neutron stars. The NICER observation data are supplemented by the constraints from PSR J0030$+$0451 ($1.44_{-0.14}^{+0.15}$ $M_{\odot }$ and $13.02_{-1.06}^{+1.24}$ km, and $1.34_{-0.16}^{+0.15}$ $M_{\odot }$ and $12.71_{-1.19}^{+1.14}$ km) [29, 31], PSR J0740$+$6620 ($2.072_{-0.066}^{+0.067}$ $M_{\odot }$ and $12.39_{-0.98}^{+1.30}$ km) [32, 64, 65], and PSR J0437$-$4715 ($12.28_{-0.76}^{+0.50}$ km at 1.4 $M_{\odot }$, and $1.418\pm 0.037$ $M_{\odot }$ and $11.36_{-0.63}^{+0.95}$ km) [131, 132].

The dimensionless tidal deformability, $\mathrm{\Lambda }$, of neutron stars is displayed in Figure 12 as a function of $M/M_{\odot }$. The $\mathrm{\Lambda }$ is defined as $\mathrm{\Lambda }=\frac{2}{3}{k}_2{\left(R/M\right)}^5$ with $k_2$ being the second Love number [36, 37]. The astrophysical constraints on $\mathrm{\Lambda }$ at the canonical-mass point, ${\mathrm{\Lambda }}_{1.4}$, from the binary merger events detected by the Advanced LIGO and Advanced Virgo observatories are also presented as follows: ${\mathrm{\Lambda }}_{1.4}=190_{-120}^{+390}$ for GW170817 [34] and ${\mathrm{\Lambda }}_{1.4}=616_{-158}^{+273}$ for GW190814 [93]. As explained in Miyatsu et al. [57], the $\delta$–$N$ coupling enlarges $\mathrm{\Lambda }$ for the DINOa, and then ${\mathrm{\Lambda }}_{1.4}$ lies far from the constraints on ${\mathrm{\Lambda }}_{1.4}$ from GW190814. On the other hand, the $\sigma$–$\delta$ mixing has a promising effect on $\mathrm{\Lambda }$, and thus the OMEG family sufficiently matches the severe constraints from both GW170817 and GW190814.

Figure 12

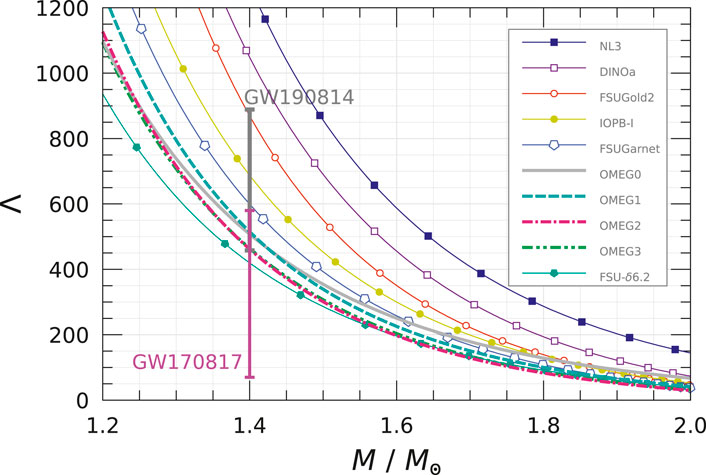
Figure 12. Dimensionless tidal deformability, $\mathrm{\Lambda }$, of neutron stars. We present the constraints on ${\mathrm{\Lambda }}_{1.4}$ from the binary merger events, GW170817 $({\mathrm{\Lambda }}_{1.4}=190_{-120}^{+390})$ [34] and GW190814 $({\mathrm{\Lambda }}_{1.4}=616_{-158}^{+273})$ [93].

4 Summary and conclusion

We have developed a new family of nuclear EoSs, referred to as the OMEG family, using the RMF model with non-linear couplings between the isoscalar and isovector mesons. In addition to the $\sigma$, $\omega$, and $\rho$ mesons, we have also included the $\delta$ meson to examine the ground-state properties of finite, closed-shell nuclei as well as the characteristics of nuclear and neutron star matter. Specifically, we have investigated the effects of $\delta$–$N$ coupling and $\sigma$–$\delta$ mixing on the EoS for both nuclear and neutron star matter. The model parameters for the OMEG family have been calibrated so as to satisfy the constraints from the particle flow data in HICs [60–62], the observed neutron-star mass of PSR J0740$+$6620 [32, 64, 65], and the dimensionless tidal deformability, ${\mathrm{\Lambda }}_{1.4}$, from the neutron star merger, GW170817 [34], as well as the results from the PREX-2 and CREX experiments [47, 50].

It has been found that the $\delta$–$N$ coupling and the $\sigma$–$\delta$ mixing significantly influence the properties of isospin-asymmetric nuclear matter and finite nuclei, playing a crucial role in reconciling terrestrial experiments with astrophysical observations of neutron stars. The strong $\delta$–$N$ coupling for the FSUGold2 series can simultaneously explain the large $R_{\text{skin}}^{208}$ and the small $R_{\text{skin}}^{48}$ measured by the PREX-2 and CREX experiments. However, it seems difficult that the FSUGold2 series satisfy the combined constraints from the particle flow data in HICs and astrophysical observations, such as the EoS for pure neutron matter and the $\mathrm{\Lambda }$ of neutron stars. Even with the inclusion of quartic $\rho$-meson self-interaction in the FSUGold2 series, both experimental and observational results can not be understood, because the large $e_3$ destabilizes neutron star matter. In contrast, the OMEG family can satisfy the recent measurement of $R_{1.4}=12.28_{-0.76}^{+0.50}$ km for PSR J0437$-$4715 from NICER [131] and the stringent constraint on ${\mathrm{\Lambda }}_{1.4}=190_{-120}^{+390}$ from GW170817 [34]. This is attributed to the $\sigma$–$\delta$ mixing, which suppresses $E_{\text{sym}}$ above $2{\rho }_0$, resulting in a softer nuclear EoS in the density region corresponding to the core density of the canonical neutron stars.

In a future work, we plan to extend the present study to global calculations of finite nuclei properties covered the periodic table, aiming to achieve well-calibrated parameter sets for the RMF models. Finally, we comment that the further theoretical studies are necessary to reconcile the $R_{\text{skin}}$ measured by proton (in)elastic scattering with that obtained from parity-violating electron scattering. In particular, it is very significant to investigate the discrepancy between the PREX-2 data [47] and the results from RCNP [51, 52] and MAMI [108]. It is also essential to consider the effect of isospin symmetry breaking on asymmetric nuclear matter from the quark level [133–138].

Author contributions

TM: Writing–original draft, Writing–review and editing. M-KC: Writing–review and editing. KK: Writing–review and editing. KS: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Research Foundation of Korea (Grant Nos. RS-2023-00242196, NRF-2021R1A6A1A03043957, NRF-2020R1A2C3006177, and NRF-2018R1A5A1025563).

Acknowledgments

TM would like to thank H. Sagawa and G. Colò for informative discussions of the neutron skin thickness of heavy nuclei.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Baym G, Bethe HA, Pethick C. Neutron star matter. Nucl Phys A (1971) 175:225–71. doi:10.1016/0375-9474(71)90281-8

CrossRef Full Text | Google Scholar

2. Bethe HA, Brown GE, Applegate J, Lattimer JM. Equation of state in the gravitational collapse of stars. Nucl Phys A (1979) 324:487–533. doi:10.1016/0375-9474(79)90596-7

CrossRef Full Text | Google Scholar

3. Lattimer JM, Swesty FD. A Generalized equation of state for hot, dense matter. Nucl Phys A (1991) 535:331–76. doi:10.1016/0375-9474(91)90452-C

CrossRef Full Text | Google Scholar

4. Glendenning NK, Moszkowski SA. Reconciliation of neutron star masses and binding of the lambda in hypernuclei. Phys Rev Lett (1991) 67:2414–7. doi:10.1103/PhysRevLett.67.2414

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Machleidt R, Holinde K, Elster C. The bonn meson exchange model for the nucleon nucleon interaction. Phys Rept (1987) 149:1–89. doi:10.1016/S0370-1573(87)80002-9

CrossRef Full Text | Google Scholar

6. Machleidt R. The Meson theory of nuclear forces and nuclear structure. Adv Nucl Phys (1989) 19:189–376. doi:10.1007/978-1-4613-9907-0_2

CrossRef Full Text | Google Scholar

7. Serot BD, Walecka JD. The relativistic nuclear many body problem. Adv Nucl Phys (1986) 16:1–327.

Google Scholar

8. Boguta J, Bodmer AR. Relativistic calculation of nuclear matter and the nuclear surface. Nucl Phys A (1977) 292:413–28. doi:10.1016/0375-9474(77)90626-1

CrossRef Full Text | Google Scholar

9. Sugahara Y, Toki H. Relativistic mean field theory for unstable nuclei with nonlinear sigma and omega terms. Nucl Phys A (1994) 579:557–72. doi:10.1016/0375-9474(94)90923-7

CrossRef Full Text | Google Scholar

10. Mueller H, Serot BD. Relativistic mean field theory and the high density nuclear equation of state. Nucl Phys A (1996) 606:508–37. doi:10.1016/0375-9474(96)00187-X

CrossRef Full Text | Google Scholar

11. Horowitz CJ, Piekarewicz J. The Neutron radii of Pb-208 and neutron stars. Phys Rev C (2001) 64:062802. doi:10.1103/PhysRevC.64.062802

CrossRef Full Text | Google Scholar

12. Oertel M, Hempel M, Klähn T, Typel S. Equations of state for supernovae and compact stars. Rev Mod Phys (2017) 89:015007. doi:10.1103/RevModPhys.89.015007

CrossRef Full Text | Google Scholar

13. Alford MG, Brodie L, Haber A, Tews I. Relativistic mean-field theories for neutron-star physics based on chiral effective field theory. Phys Rev C (2022) 106:055804. doi:10.1103/PhysRevC.106.055804

CrossRef Full Text | Google Scholar

14. Patra NK, Venneti A, Imam SMA, Mukherjee A, Agrawal BK. Systematic analysis of the impacts of symmetry energy parameters on neutron star properties. Phys Rev C (2023) 107:055804. doi:10.1103/PhysRevC.107.055804

CrossRef Full Text | Google Scholar

15. Stone JR. Nuclear physics and astrophysics constraints on the high density matter equation of state. Universe (2021) 7:257. doi:10.3390/universe7080257

CrossRef Full Text | Google Scholar

16. Stone JR. Nuclear symmetry energy in strongly interacting matter: past, present and future. Symmetry (2024) 16:1038. doi:10.3390/sym16081038

CrossRef Full Text | Google Scholar

17. Zhou J, Xu J, Papakonstantinou P. Bayesian inference of neutron-star observables based on effective nuclear interactions. Phys Rev C (2023) 107:055803. doi:10.1103/PhysRevC.107.055803

CrossRef Full Text | Google Scholar

18. Sun B, Bhattiprolu S, Lattimer JM. Compiled properties of nucleonic matter and nuclear and neutron star models from nonrelativistic and relativistic interactions. Phys Rev C (2024) 109:055801. doi:10.1103/PhysRevC.109.055801

CrossRef Full Text | Google Scholar

19. Li B-A, Chen L-W, Ko CM. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys Rept (2008) 464:113–281. doi:10.1016/j.physrep.2008.04.005

CrossRef Full Text | Google Scholar

20. Lattimer JM. Symmetry energy in nuclei and neutron stars. Nucl Phys A (2014) 928:276–95. doi:10.1016/j.nuclphysa.2014.04.008

CrossRef Full Text | Google Scholar

21. Typel S, Brown BA. Neutron radii and the neutron equation of state in relativistic models. Phys Rev C (2001) 64:027302. doi:10.1103/PhysRevC.64.027302

CrossRef Full Text | Google Scholar

22. Tsang MB, Zhang Y, Danielewicz P, Famiano M, Li Z, Lynch WG, et al. Constraints on the density dependence of the symmetry energy. Phys Rev Lett (2009) 102:122701. doi:10.1103/PhysRevLett.102.122701

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Tsang MB, Stone JR, Camera F, Danielewicz P, Gandolfi S, Hebeler K, et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys Rev C (2012) 86:015803. doi:10.1103/PhysRevC.86.015803

CrossRef Full Text | Google Scholar

24. Zhang N-B, Li B-A. Impact of NICER’s radius measurement of PSR J0740+6620 on nuclear symmetry energy at suprasaturation densities. Astrophys J (2021) 921:111. doi:10.3847/1538-4357/ac1e8c

CrossRef Full Text | Google Scholar

25. Richter J, Li B-A. Empirical radius formulas for canonical neutron stars from bidirectionally selecting features of equations of state in extended Bayesian analyses of observational data. Phys Rev C (2023) 108:055803. doi:10.1103/PhysRevC.108.055803

CrossRef Full Text | Google Scholar

26. Xie W-J, Li B-A, Zhang N-B. Impact of the newly revised gravitational redshift of x-ray burster GS 1826-24 on the equation of state of supradense neutron-rich matter. Phys Rev D (2024) 110:043025. doi:10.1103/PhysRevD.110.043025

CrossRef Full Text | Google Scholar

27. Demorest P, Pennucci T, Ransom S, Roberts M, Hessels J. Shapiro delay measurement of A two solar mass neutron star. Nature (2010) 467:1081–3. doi:10.1038/nature09466

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Arzoumanian Z, Brazier A, Burke-Spolaor S, Chamberlin S, Chatterjee S, Christy B, et al. The NANOGrav 11-year data set: high-precision timing of 45 millisecond pulsars. Astrophys J Suppl (2018) 235:37. doi:10.3847/1538-4365/aab5b0

CrossRef Full Text | Google Scholar

29. Miller MC, Lamb FK, Dittmann AJ, Bogdanov S, Arzoumanian Z, Gendreau KC, et al. PSR J0030+0451 mass and radius from NICER data and implications for the properties of neutron star matter. Astrophys J Lett (2019) 887:L24. doi:10.3847/2041-8213/ab50c5

CrossRef Full Text | Google Scholar

30. Miller MC, Lamb FK, Dittmann AJ, Bogdanov S, Arzoumanian Z, Gendreau KC, et al. The radius of PSR J0740+6620 from NICER and XMM-Newton data. Astrophys J Lett (2021) 918:L28. doi:10.3847/2041-8213/ac089b

CrossRef Full Text | Google Scholar

31. Riley TE, Watts AL, Bogdanov S, Ray PS, Ludlam RM, Guillot S, et al. A NICER view of PSR J0030+0451: millisecond pulsar parameter estimation. Astrophys J Lett (2019) 887:L21. doi:10.3847/2041-8213/ab481c

CrossRef Full Text | Google Scholar

32. Riley TE, Watts AL, Ray PS, Bogdanov S, Guillot S, Morsink SM, et al. A NICER view of the massive pulsar PSR J0740+6620 informed by radio timing and XMM-Newton spectroscopy. Astrophys J Lett (2021) 918:L27. doi:10.3847/2041-8213/ac0a81

CrossRef Full Text | Google Scholar

33. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett (2017) 119:161101. doi:10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. GW170817: measurements of neutron star radii and equation of state. Phys Rev Lett (2018) 121:161101. doi:10.1103/PhysRevLett.121.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. Properties of the binary neutron star merger GW170817. Phys Rev X (2019) 9:011001. doi:10.1103/PhysRevX.9.011001

CrossRef Full Text | Google Scholar

36. Hinderer T. Tidal Love numbers of neutron stars. Astrophys J (2008) 677:1216–20. Erratum: Astrophys.J. 697, 964 (2009) doi:10.1086/533487

CrossRef Full Text | Google Scholar

37. Hinderer T, Lackey BD, Lang RN, Read JS. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys Rev D (2010) 81:123016. doi:10.1103/PhysRevD.81.123016

CrossRef Full Text | Google Scholar

38. Annala E, Gorda T, Kurkela A, Vuorinen A. Gravitational-wave constraints on the neutron-star-matter equation of state. Phys Rev Lett (2018) 120:172703. doi:10.1103/PhysRevLett.120.172703

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Lim Y, Holt JW. Neutron star tidal deformabilities constrained by nuclear theory and experiment. Phys Rev Lett (2018) 121:062701. doi:10.1103/PhysRevLett.121.062701

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Most ER, Weih LR, Rezzolla L, Schaffner-Bielich J. New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys Rev Lett (2018) 120:261103. doi:10.1103/PhysRevLett.120.261103

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Raithel C, Özel F, Psaltis D. Tidal deformability from GW170817 as a direct probe of the neutron star radius. Astrophys J Lett (2018) 857:L23. doi:10.3847/2041-8213/aabcbf

CrossRef Full Text | Google Scholar

42. Alam N, Agrawal BK, Fortin M, Pais H, Providência C, Raduta AR, et al. Strong correlations of neutron star radii with the slopes of nuclear matter incompressibility and symmetry energy at saturation. Phys Rev C (2016) 94:052801. doi:10.1103/PhysRevC.94.052801

CrossRef Full Text | Google Scholar

43. Hu J, Bao S, Zhang Y, Nakazato K, Sumiyoshi K, Shen H. Effects of symmetry energy on the radius and tidal deformability of neutron stars in the relativistic mean-field model. PTEP (2020) 2020:043D01. doi:10.1093/ptep/ptaa016

CrossRef Full Text | Google Scholar

44. Li B-A, Magno M. Curvature-slope correlation of nuclear symmetry energy and its imprints on the crust-core transition, radius and tidal deformability of canonical neutron stars. Phys Rev C (2020) 102:045807. doi:10.1103/PhysRevC.102.045807

CrossRef Full Text | Google Scholar

45. Lopes LL. Role of the symmetry energy slope in neutron stars: exploring the model dependency. Phys Rev C (2024) 110:015805. doi:10.1103/PhysRevC.110.015805

CrossRef Full Text | Google Scholar

46. Lim Y, Schwenk A. Symmetry energy and neutron star properties constrained by chiral effective field theory calculations. Phys Rev C (2024) 109:035801. doi:10.1103/PhysRevC.109.035801

CrossRef Full Text | Google Scholar

47. Adhikari D, Albataineh H, Androic D, Aniol K, Armstrong D, Averett T, et al. Accurate determination of the neutron skin thickness of ²⁰⁸Pb through parity-violation in electron scattering. Phys Rev Lett (2021) 126:172502. doi:10.1103/PhysRevLett.126.172502

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Reed BT, Fattoyev FJ, Horowitz CJ, Piekarewicz J. Implications of PREX-2 on the equation of state of neutron-rich matter. Phys Rev Lett (2021) 126:172503. doi:10.1103/PhysRevLett.126.172503

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Reinhard P-G, Roca-Maza X, Nazarewicz W. Information content of the parity-violating asymmetry in Pb208. Phys Rev Lett (2021) 127:232501. doi:10.1103/PhysRevLett.127.232501

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Adhikari D, Albataineh H, Androic D, Aniol K, Armstrong D, Averett T, et al. Precision determination of the neutral weak form factor of ⁴⁸Ca. Phys Rev Lett (2022) 129:042501. doi:10.1103/PhysRevLett.129.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Zenihiro J, Sakaguchi H, Murakami T, Yosoi M, Yasuda Y, Terashima S, et al. Neutron density distributions of Pb-204, Pb-206, Pb-208 deduced via proton elastic scattering at Ep=295 MeV. Phys Rev C (2010) 82:044611. doi:10.1103/PhysRevC.82.044611

CrossRef Full Text | Google Scholar

52. Tamii A, Poltoratska I, von Neumann-Cosel P, Fujita Y, Adachi T, Bertulani CA, et al. Complete electric dipole response and the neutron skin in 208Pb. Phys Rev Lett (2011) 107:062502. doi:10.1103/PhysRevLett.107.062502

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Centelles M, Roca-Maza X, Vinas X, Warda M. Nuclear symmetry energy probed by neutron skin thickness of nuclei. Phys Rev Lett (2009) 102:122502. doi:10.1103/PhysRevLett.102.122502

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Dutra M, Lourenço O, Avancini SS, Carlson BV, Delfino A, Menezes DP, et al. Relativistic mean-field hadronic models under nuclear matter constraints. Phys Rev C (2014) 90:055203. doi:10.1103/PhysRevC.90.055203

CrossRef Full Text | Google Scholar

55. Trzcinska A, Jastrzebski J, Lubinski P, Hartmann FJ, Schmidt R, von Egidy T, et al. Neutron density distributions deduced from anti-protonic atoms. Phys Rev Lett (2001) 87:082501. doi:10.1103/PhysRevLett.87.082501

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Zabari N, Kubis S, Wójcik W. Influence of the interactions of scalar mesons on the behavior of the symmetry energy. Phys Rev C (2019) 99:035209. doi:10.1103/PhysRevC.99.035209

CrossRef Full Text | Google Scholar

57. Miyatsu T, Cheoun M-K, Saito K. Asymmetric nuclear matter in relativistic mean-field models with isoscalar- and isovector-meson mixing. Astrophys J (2022) 929:82. doi:10.3847/1538-4357/ac5f40

CrossRef Full Text | Google Scholar

58. Miyatsu T, Cheoun M-K, Kim K, Saito K. Can the PREX-2 and CREX results be understood by relativistic mean-field models with the astrophysical constraints? Phys Lett B (2023) 843:138013. doi:10.1016/j.physletb.2023.138013

CrossRef Full Text | Google Scholar

59. Li F, Cai B-J, Zhou Y, Jiang W-Z, Chen L-W. Effects of isoscalar- and isovector-scalar meson mixing on neutron star structure. Astrophys J (2022) 929:183. doi:10.3847/1538-4357/ac5e2a

CrossRef Full Text | Google Scholar

60. Danielewicz P, Lacey R, Lynch WG. Determination of the equation of state of dense matter. Science (2002) 298:1592–6. doi:10.1126/science.1078070

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Fuchs C. Kaon production in heavy ion reactions at intermediate energies. Prog Part Nucl Phys (2006) 56:1–103. doi:10.1016/j.ppnp.2005.07.004

CrossRef Full Text | Google Scholar

62. Lynch WG, Tsang MB, Zhang Y, Danielewicz P, Famiano M, Li Z, et al. Probing the symmetry energy with heavy ions. Prog Part Nucl Phys (2009) 62:427–32. doi:10.1016/j.ppnp.2009.01.001

CrossRef Full Text | Google Scholar

63. Oliinychenko D, Sorensen A, Koch V, McLerran L. Sensitivity of Au+Au collisions to the symmetric nuclear matter equation of state at 2–5 nuclear saturation densities. Phys Rev C (2023) 108:034908. doi:10.1103/PhysRevC.108.034908

CrossRef Full Text | Google Scholar

64. Cromartie HT, Fonseca E, Ransom SM, Demorest PB, Arzoumanian Z, Blumer H, et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat Astron (2019) 4:72–6. doi:10.1038/s41550-019-0880-2

CrossRef Full Text | Google Scholar

65. Fonseca E, Cromartie HT, Pennucci TT, Ray PS, Kirichenko AY, Ransom SM, et al. Refined mass and geometric measurements of the high-mass PSR J0740+6620. Astrophys J Lett (2021) 915:L12. doi:10.3847/2041-8213/ac03b8

CrossRef Full Text | Google Scholar

66. Ring P. Relativistic mean field theory in finite nuclei. Prog Part Nucl Phys (1996) 37:193–263. doi:10.1016/0146-6410(96)00054-3

CrossRef Full Text | Google Scholar

67. Lalazissis GA, Konig J, Ring P. A New parametrization for the Lagrangian density of relativistic mean field theory. Phys Rev C (1997) 55:540–3. doi:10.1103/PhysRevC.55.540

CrossRef Full Text | Google Scholar

68. Pradhan BK, Chatterjee D, Gandhi R, Schaffner-Bielich J. Role of vector self-interaction in neutron star properties. Nucl Phys A (2023) 1030:122578. doi:10.1016/j.nuclphysa.2022.122578

CrossRef Full Text | Google Scholar

69. Malik T, Dexheimer V, Providência C. Astrophysics and nuclear physics informed interactions in dense matter: inclusion of PSR J0437-4715. Phys Rev D (2024) 110:043042. doi:10.1103/PhysRevD.110.043042

CrossRef Full Text | Google Scholar

70. Todd-Rutel BG, Piekarewicz J. Neutron-Rich nuclei and neutron stars: a new accurately calibrated interaction for the study of neutron-rich matter. Phys Rev Lett (2005) 95:122501. doi:10.1103/PhysRevLett.95.122501

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Miyatsu T, Cheoun M-K, Saito K. Equation of state for neutron stars in SU(3) flavor symmetry. Phys Rev C (2013) 88:015802. doi:10.1103/PhysRevC.88.015802

CrossRef Full Text | Google Scholar

72. Horowitz CJ, Piekarewicz J. Neutron star structure and the neutron radius of Pb-208. Phys Rev Lett (2001) 86:5647–50. doi:10.1103/PhysRevLett.86.5647

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Haidari MM, Sharma MM. Sigma-omega meson coupling and properties of nuclei and nuclear matter. Nucl Phys A (2008) 803:159–72. doi:10.1016/j.nuclphysa.2008.02.296

CrossRef Full Text | Google Scholar

74. Sharma MM. Scalar-vector Lagrangian without nonlinear self-interactions of bosonic fields in the relativistic mean-field theory. Phys Lett B (2008) 666:140–4. doi:10.1016/j.physletb.2008.07.005

CrossRef Full Text | Google Scholar

75. Kubis S, Wójcik W, Castillo DA, Zabari N. Relativistic mean-field model for the ultracompact low-mass neutron star HESS J1731-347. Phys Rev C (2023) 108:045803. doi:10.1103/PhysRevC.108.045803

CrossRef Full Text | Google Scholar

76. Chen L-W, Ko CM, Li B-A. Isospin-dependent properties of asymmetric nuclear matter in relativistic mean-field models. Phys Rev C (2007) 76:054316. doi:10.1103/PhysRevC.76.054316

CrossRef Full Text | Google Scholar

77. Chen L-W, Cai B-J, Ko CM, Li B-A, Shen C, Xu J. Higher-order effects on the incompressibility of isospin asymmetric nuclear matter. Phys Rev C (2009) 80:014322. doi:10.1103/PhysRevC.80.014322

CrossRef Full Text | Google Scholar

78. Czerski P, De Pace A, Molinari A. Revisiting the Hugenholtz-Van Hove theorem in nuclear matter. Phys Rev C (2002) 65:044317. doi:10.1103/PhysRevC.65.044317

CrossRef Full Text | Google Scholar

79. Cai B-J, Chen L-W. Lorentz covariant nucleon self-energy decomposition of the nuclear symmetry energy. Phys Lett B (2012) 711:104–8. doi:10.1016/j.physletb.2012.03.058

CrossRef Full Text | Google Scholar

80. Miyatsu T, Katayama T, Saito K. Effects of Fock term, tensor coupling and baryon structure variation on a neutron star. Phys Lett B (2012) 709:242–6. doi:10.1016/j.physletb.2012.02.009

CrossRef Full Text | Google Scholar

81. Katayama T, Miyatsu T, Saito K. EoS for massive neutron stars. Astrophys J Suppl (2012) 203:22. doi:10.1088/0067-0049/203/2/22

CrossRef Full Text | Google Scholar

82. Miyatsu T, Cheoun M-K, Ishizuka C, Kim KS, Maruyama T, Saito K. Decomposition of nuclear symmetry energy based on Lorentz-covariant nucleon self-energies in relativistic Hartree-Fock approximation. Phys Lett B (2020) 803:135282. doi:10.1016/j.physletb.2020.135282

CrossRef Full Text | Google Scholar

83. Kubis S. Nuclear symmetry energy and stability of matter in neutron stars. Phys Rev C (2007) 76:025801. doi:10.1103/PhysRevC.76.025801

CrossRef Full Text | Google Scholar

84. Lattimer JM, Prakash M. Neutron star observations: prognosis for equation of state constraints. Phys Rept (2007) 442:109–65. doi:10.1016/j.physrep.2007.02.003

CrossRef Full Text | Google Scholar

85. Xu J, Chen L-W, Li B-A, Ma H-R. Nuclear constraints on properties of neutron star crusts. Astrophys J (2009) 697:1549–68. doi:10.1088/0004-637X/697/2/1549

CrossRef Full Text | Google Scholar

86. Moustakidis CC, Niksic T, Lalazissis GA, Vretenar D, Ring P. Constraints on the inner edge of neutron star crusts from relativistic nuclear energy density functionals. Phys Rev C (2010) 81:065803. doi:10.1103/PhysRevC.81.065803

CrossRef Full Text | Google Scholar

87. Psonis VP, Moustakidis CC, Massen SE. Nuclear symmetry energy effects on neutron stars properties. Mod Phys Lett A (2007) 22:1233–53. doi:10.1142/S0217732307023572

CrossRef Full Text | Google Scholar

88. Kubis S, Wójcik W, Zabari N. Multilayer neutron stars with scalar mesons crossing term. Phys Rev C (2020) 102:065803. doi:10.1103/PhysRevC.102.065803

CrossRef Full Text | Google Scholar

89. Routray TR, Viñas X, Basu DN, Pattnaik SP, Centelles M, Robledo L, et al. Exact versus Taylor-expanded energy density in the study of the neutron star crust–core transition. J Phys G (2016) 43:105101. doi:10.1088/0954-3899/43/10/105101

CrossRef Full Text | Google Scholar

90. Zhang N-B, Li B-A, Xu J. Combined constraints on the equation of state of dense neutron-rich matter from terrestrial nuclear experiments and observations of neutron stars. Astrophys J (2018) 859:90. doi:10.3847/1538-4357/aac027

CrossRef Full Text | Google Scholar

91. Xie W-J, Li B-A. Bayesian inference of high-density nuclear symmetry energy from radii of canonical neutron stars. Astrophys J (2019) 883:174. doi:10.3847/1538-4357/ab3f37

CrossRef Full Text | Google Scholar

92. Miyatsu T, Cheoun M-K, Kim K, Saito K. Massive neutron stars with small radii in relativistic mean-field models optimized to nuclear ground states. Preprint arXiv:2209.02861 (2022) [nucl–th]. doi:10.48550/arXiv.2209.02861

CrossRef Full Text | Google Scholar

93. Abbott R, Abbott TD, Abraham S, Acernese F, Ackley K, Adams C, et al. GW190814: gravitational waves from the coalescence of a 23 solar mass black hole with a 2.6 solar mass compact object. Astrophys J Lett (2020) 896:L44. doi:10.3847/2041-8213/ab960f

CrossRef Full Text | Google Scholar

94. Fattoyev FJ, Horowitz CJ, Piekarewicz J, Reed B. GW190814: impact of a 2.6 solar mass neutron star on the nucleonic equations of state. Phys Rev C (2020) 102:065805. doi:10.1103/PhysRevC.102.065805

CrossRef Full Text | Google Scholar

95. Reed BT, Fattoyev FJ, Horowitz CJ, Piekarewicz J. Density dependence of the symmetry energy in the post–PREX-CREX era. Phys Rev C (2024) 109:035803. doi:10.1103/PhysRevC.109.035803

CrossRef Full Text | Google Scholar

96. Chen W-C, Piekarewicz J. Searching for isovector signatures in the neutron-rich oxygen and calcium isotopes. Phys Lett B (2015) 748:284–8. doi:10.1016/j.physletb.2015.07.020

CrossRef Full Text | Google Scholar

97. Fattoyev FJ, Piekarewicz J. Sensitivity of the moment of inertia of neutron stars to the equation of state of neutron-rich matter. Phys Rev C (2010) 82:025810. doi:10.1103/PhysRevC.82.025810

CrossRef Full Text | Google Scholar

98. Chen W-C, Piekarewicz J. Building relativistic mean field models for finite nuclei and neutron stars. Phys Rev C (2014) 90:044305. doi:10.1103/PhysRevC.90.044305

CrossRef Full Text | Google Scholar

99. Salinas M, Piekarewicz J. Bayesian refinement of covariant energy density functionals. Phys Rev C (2023) 107:045802. doi:10.1103/PhysRevC.107.045802

CrossRef Full Text | Google Scholar

100. Salinas M, Piekarewicz J. Building an equation of state density ladder. Symmetry (2023) 15:994. doi:10.3390/sym15050994

CrossRef Full Text | Google Scholar

101. Kumar S, Kumar M, Kumar R, Dhiman SK. Implications of isoscalar and isovector scalar meson mixed interaction on nuclear and neutron star properties. Phys Rev C (2023) 108:055802. doi:10.1103/PhysRevC.108.055802

CrossRef Full Text | Google Scholar

102. Kumar B, Agrawal BK, Patra SK. New relativistic effective interaction for finite nuclei, infinite nuclear matter and neutron stars. Phys Rev C (2018) 97:045806. doi:10.1103/PhysRevC.97.045806

CrossRef Full Text | Google Scholar

103. Fattoyev FJ, Horowitz CJ, Piekarewicz J, Shen G. Relativistic effective interaction for nuclei, giant resonances, and neutron stars. Phys Rev C (2010) 82:055803. doi:10.1103/PhysRevC.82.055803

CrossRef Full Text | Google Scholar

104. Liliani N, Diningrum JP, Sulaksono A. Tensor and Coulomb-exchange terms in the relativistic mean-field model with δ-meson and isoscalar-isovector coupling. Phys Rev C (2021) 104:015804. doi:10.1103/PhysRevC.104.015804

CrossRef Full Text | Google Scholar

105. Fattoyev FJ, Piekarewicz J. Has a thick neutron skin in ²⁰⁸Pb been ruled out? Phys Rev Lett (2013) 111:162501. doi:10.1103/PhysRevLett.111.162501

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Piekarewicz J. Symmetry energy constraints from giant resonances: a theoretical overview. Eur Phys J (2014) A 50:25. doi:10.1140/epja/i2014-14025-x

CrossRef Full Text | Google Scholar

107. Birkhan J, Miorelli M, Bacca S, Bassauer S, Bertulani C, Hagen G, et al. Electric dipole polarizability of ⁴⁸Ca and implications for the neutron skin. Phys Rev Lett (2017) 118:252501. doi:10.1103/PhysRevLett.118.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Tarbert CM, Watts D, Glazier D, Aguar P, Ahrens J, Annand J, et al. Neutron skin of ²⁰⁸Pb from coherent pion photoproduction. Phys Rev Lett (2014) 112:242502. doi:10.1103/PhysRevLett.112.242502

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Reinhard PG, Rufa M, Maruhn J, Greiner W, Friedrich J. Nuclear ground state properties in a relativistic meson field theory. Z Phys A (1986) 323:13–25. doi:10.1007/bf01294551

CrossRef Full Text | Google Scholar

110. Liliani N, Nugraha AM, Diningrum JP, Sulaksono A. Tensor and isovector–isoscalar terms of relativistic mean field model: impacts on neutron-skin thickness, charge radius, and nuclear matter. Nucl Phys A (2024) 1042:122812. doi:10.1016/j.nuclphysa.2023.122812

CrossRef Full Text | Google Scholar

111. De Vries H, De Jager CW, De Vries C. Nuclear charge-density-distribution parameters from elastic electron scattering. Atom Data Nucl Data Tabl (1987) 36:495–536. doi:10.1016/0092-640X(87)90013-1

CrossRef Full Text | Google Scholar

112. Horowitz CJ, Pollock SJ, Souder PA, Michaels R. Parity violating measurements of neutron densities. Phys Rev C (2001) 63:025501. doi:10.1103/PhysRevC.63.025501

CrossRef Full Text | Google Scholar

113. Horowitz CJ, Ahmed Z, Jen CM, Rakhman A, Souder PA, Dalton MM, et al. Weak charge form factor and radius of 208Pb through parity violation in electron scattering. Phys Rev C (2012) 85:032501. doi:10.1103/PhysRevC.85.032501

CrossRef Full Text | Google Scholar

114. Niksic T, Vretenar D, Finelli P, Ring P. Relativistic Hartree-Bogoliubov model with density-dependent meson-nucleon couplings. Phys Rev C (2002) 66:024306. doi:10.1103/PhysRevC.66.024306

CrossRef Full Text | Google Scholar

115. Ma Y-L, Rho M. Topology change, emergent symmetries and compact star matter. AAPPS Bull (2021) 31:16. doi:10.1007/s43673-021-00016-1

CrossRef Full Text | Google Scholar

116. Lee HK, Ma Y-L, Paeng W-G, Rho M. Cusp in the symmetry energy, speed of sound in neutron stars and emergent pseudo-conformal symmetry. Mod Phys Lett A (2022) 37:2230003. doi:10.1142/S0217732322300038

CrossRef Full Text | Google Scholar

117. Chen L-W, Ko CM, Li B-A. Nuclear matter symmetry energy and the neutron skin thickness of heavy nuclei. Phys Rev C (2005) 72:064309. doi:10.1103/PhysRevC.72.064309

CrossRef Full Text | Google Scholar

118. Maruyama T, Chiba S. Equation of state of neutron star matter and the isovector nucleon optical model potential. J Phys G (1999) 25:2361–9. doi:10.1088/0954-3899/25/12/306

CrossRef Full Text | Google Scholar

119. Maruyama T, Balantekin AB, Cheoun M-K, Kajino T, Kusakabe M, Mathews GJ. A relativistic quantum approach to neutrino and antineutrino emission via the direct Urca process in strongly magnetized neutron-star matter. Phys Lett B (2022) 824:136813. doi:10.1016/j.physletb.2021.136813

CrossRef Full Text | Google Scholar

120. Glendenning NK (1997) Compact stars: nuclear physics, particle physics, and general relativity

Google Scholar

121. Miyatsu T, Yamamuro S, Nakazato K. A new equation of state for neutron star matter with nuclei in the crust and hyperons in the core. Astrophys J (2013) 777:4. doi:10.1088/0004-637X/777/1/4

CrossRef Full Text | Google Scholar

122. Miyatsu T, Cheoun M-K, Saito K. Equation of state for neutron stars with hyperons and quarks in the relativistic Hartree–Fock approximation. Astrophys J (2015) 813:135. doi:10.1088/0004-637X/813/2/135

CrossRef Full Text | Google Scholar

123. Tolman RC. Static solutions of Einstein’s field equations for spheres of fluid. Phys Rev (1939) 55:364–73. doi:10.1103/PhysRev.55.364

CrossRef Full Text | Google Scholar

124. Oppenheimer JR, Volkoff GM. On massive neutron cores. Phys Rev (1939) 55:374–81. doi:10.1103/PhysRev.55.374

CrossRef Full Text | Google Scholar

125. Sulaksono A, Alam N, Agrawal BK. Core–crust transition properties of neutron stars within systematically varied extended relativistic mean-field model. Int J Mod Phys E (2014) 23:1450072. doi:10.1142/S0218301314500724

CrossRef Full Text | Google Scholar

126. Providência C, Avancini SS, Cavagnoli R, Chiacchiera S, Ducoin C, Grill F, et al. Imprint of the symmetry energy on the inner crust and strangeness content of neutron stars. Eur Phys J (2014) A 50:44. doi:10.1140/epja/i2014-14044-7

CrossRef Full Text | Google Scholar

127. Li B-A, Krastev PG, Wen D-H, Zhang N-B. Towards understanding astrophysical effects of nuclear symmetry energy. Eur Phys J (2019) A 55:117. doi:10.1140/epja/i2019-12780-8

CrossRef Full Text | Google Scholar

128. Horowitz CJ, Piekarewicz J. Constraining URCA cooling of neutron stars from the neutron radius of Pb-208. Phys Rev C (2002) 66:055803. doi:10.1103/PhysRevC.66.055803

CrossRef Full Text | Google Scholar

129. Page D, Geppert U, Weber F. The Cooling of compact stars. Nucl Phys A (2006) 777:497–530. doi:10.1016/j.nuclphysa.2005.09.019

CrossRef Full Text | Google Scholar

130. Lattimer JM, Prakash M, Pethick CJ, Haensel P. Direct URCA process in neutron stars. Phys Rev Lett (1991) 66:2701–4. doi:10.1103/PhysRevLett.66.2701

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Rutherford N, Mendes M, Svensson I, Schwenk A, Watts AL, Hebeler K, et al. Constraining the dense matter equation of state with new NICER mass–radius measurements and new chiral effective field theory inputs. Astrophys J Lett (2024) 971:L19. doi:10.3847/2041-8213/ad5f02

CrossRef Full Text | Google Scholar

132. Choudhury D, Salmi T, Vinciguerra S, Riley TE, Kini Y, Watts AL, et al. A NICER view of the nearest and brightest millisecond pulsar: PSR J0437–4715. Astrophys J Lett (2024) 971:L20. doi:10.3847/2041-8213/ad5a6f

CrossRef Full Text | Google Scholar

133. Guichon PAM. A possible quark mechanism for the saturation of nuclear matter. Phys Lett B (1988) 200:235–40. doi:10.1016/0370-2693(88)90762-9

CrossRef Full Text | Google Scholar

134. Saito K, Thomas AW. A Quark - meson coupling model for nuclear and neutron matter. Phys Lett B (1994) 327:9–16. doi:10.1016/0370-2693(94)91520-2

CrossRef Full Text | Google Scholar

135. Saito K, Thomas AW. The Nolen-Schiffer anomaly and isospin symmetry breaking in nuclear matter. Phys Lett B (1994) 335:17–23. doi:10.1016/0370-2693(94)91551-2

CrossRef Full Text | Google Scholar

136. Saito K, Tsushima K, Thomas AW. Nucleon and hadron structure changes in the nuclear medium and the impact on observables. Prog Part Nucl Phys (2007) 58:1–167. doi:10.1016/j.ppnp.2005.07.003

CrossRef Full Text | Google Scholar

137. Saito K, Miyatsu T, Cheoun M-K. Effect of isoscalar and isovector scalar fields on baryon semileptonic decays in nuclear matter. Phys Rev D (2024) 110:113001. doi:10.1103/PhysRevD.110.113001

CrossRef Full Text | Google Scholar

138. Nagai S, Miyatsu T, Saito K, Tsushima K. Quark-meson coupling model with the cloudy bag. Phys Lett B (2008) 666:239–44. doi:10.1016/j.physletb.2008.07.065

CrossRef Full Text | Google Scholar

139. Chen L-W, Ko CM, Li B-A. Determination of the stiffness of the nuclear symmetry energy from isospin diffusion. Phys Rev Lett (2005) 94:032701. doi:10.1103/PhysRevLett.94.032701

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Li B-A, Chen L-W. Nucleon-nucleon cross sections in neutron-rich matter and isospin transport in heavy-ion reactions at intermediate energies. Phys Rev C (2005) 72:064611. doi:10.1103/PhysRevC.72.064611

CrossRef Full Text | Google Scholar

141. Estee J, Lynch W, Tsang C, Barney J, Jhang G, Tsang M, et al. Probing the symmetry energy with the spectral pion ratio. Phys Rev Lett (2021) 126:162701. doi:10.1103/PhysRevLett.126.162701

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Lynch WG, Tsang MB. Decoding the density dependence of the nuclear symmetry energy. Phys Lett B (2022) 830:137098. doi:10.1016/j.physletb.2022.137098

CrossRef Full Text | Google Scholar

143. Tsang CY, Tsang MB, Lynch WG, Kumar R, Horowitz CJ. Determination of the equation of state from nuclear experiments and neutron star observations. Nat Astron (2024) 8:328–36. doi:10.1038/s41550-023-02161-z

CrossRef Full Text | Google Scholar

144. Chen L-W. Symmetry energy systematics and its high density behavior. EPJ Web Conf (2015) 88:00017. doi:10.1051/epjconf/20158800017

CrossRef Full Text | Google Scholar

145. Li B-A, Cai B-J, Xie W-J, Zhang N-B. Progress in constraining nuclear symmetry energy using neutron star observables since GW170817. Universe (2021) 7:182. doi:10.3390/universe7060182

CrossRef Full Text | Google Scholar

146. Negele JW, Vautherin D. Neutron star matter at subnuclear densities. Nucl Phys A (1973) 207:298–320. doi:10.1016/0375-9474(73)90349-7

CrossRef Full Text | Google Scholar

147. Sotani H, Ota S. Neutron star mass formula with nuclear saturation parameters for asymmetric nuclear matter. Phys Rev D (2022) 106:103005. doi:10.1103/PhysRevD.106.103005

CrossRef Full Text | Google Scholar

148. Lattimer JM. Constraints on nuclear symmetry energy parameters. Particles (2023) 6:30–56. doi:10.3390/particles6010003

CrossRef Full Text | Google Scholar