Low-carbon optimal scheduling for distribution networks under supply and demand uncertainty

This paper presents a low-carbon optimal scheduling model for distribution networks with wind and photovoltaic (PV), accounting for supply and demand uncertainties. The model optimizes thermal generation costs, wind and PV maintenance costs, and carbon emissions using a chance-constrained approach with fuzzy variables. The clear equivalent class method simplifies these constraints for easier problem-solving. Validation on the IEEE-30 node system shows the model reduces costs by 32.9% and carbon emissions by 19.2% compared to traditional scheduling, effectively lowering both costs and the carbon footprint. This real-world optimization approach tackles uncertainty in renewable energy supply and improves system efficiency and sustainability.

1 Introduction

With the introduction of the ‘dual carbon’ targets and the growing energy demand, low-carbon scheduling has become a key focus in power systems research [1]. The increasing integration of renewable energy, especially wind and solar, presents both opportunities and challenges for low-carbon dispatch in distribution networks [2]. Exploring strategies that incorporate wind and solar power can improve renewable energy utilization [3], reduce carbon emissions, and enhance the safety, efficiency, and sustainability of power systems, supporting the achievement of the “dual carbon” goals [4].

Current research on low-carbon optimization scheduling for distribution networks includes efforts both domestically and internationally [5]. Early work introduced the carbon flow theory, which links power generation emissions to load-side consumption, highlighting the impact of load patterns on low-carbon scheduling [6]. Studies have developed methods for calculating carbon flow and node carbon potential, incorporating these constraints to reduce emissions from renewable energy stations [7, 8]. Other research has quantified the carbon intensity of high-penetration wind systems and proposed models for low-carbon grid transformation using carbon flow theory [9, 10]. Further developments have integrated low-carbon demand response and carbon flow to enhance carbon mitigation potential [11], and some models consider carbon tax costs on both supply and demand sides to increase renewable energy penetration [12, 13]. In addition, big data analytics has been applied to analyze energy consumption and carbon emissions, aiding in the optimization of low-carbon scheduling [14].

As the share of wind and solar power increases, the uncertainties in both supply and demand present new challenges for low-carbon optimization in distribution networks. To address these issues, this article focuses on integrated optimization of renewable energy output, demand response, and the carbon trading mechanism. It proposes a low-carbon scheduling model for distribution networks that considers uncertainties on both the supply and demand sides. The model optimizes thermal generation costs, wind and solar operation and maintenance costs, and carbon emission costs, using fuzzy chance constraint methods to handle uncertainties in wind power, PV output, and load demand. The effectiveness of the approach is validated through simulations based on the IEEE-30 node system.

2 Implementation technology for low-carbon optimal dispatching strategy in distribution networks accounting

2.1 Determination of objective function

We take into consideration the power generation costs associated with thermal power units, the operational and maintenance expenses of wind and solar power generation, as well as the carbon emission costs. Consequently, the objective function is defined as follows:

$minC=C_1+C_2+C_3(1)$

where $C_1$ represents the generation cost of thermal power units; $C_2$ represents the operation and maintenance costs of wind and solar power generation; $C_3$ represents the cost of carbon emissions.

The calculation formula for the generation cost $C_1$ of thermal power units is as follows:

$C_1={\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{j=1}^{N_{\text{G}}}}{a}_j{\left(P_{\text{G},j}^t\right)}^2+b_j{P}_{\text{G,}j}^t+c_j+{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{j=1}^{N_{\text{G}}}}{S}_j^t{u}_j^t\left(1-u_j^{t-1}\right)(2)$

where $a_j$, $b_j$, and $c_j$ respectively represent the coal consumption coefficient of the corresponding thermal power unit; $S_j^t$ represents the start stop cost of the thermal power unit at that time.

The calculation formula for the operation and maintenance cost $C_2$ of wind and solar power generation is as follows:

$C_2={\displaystyle \sum _{t=1}^T}\left[500\left({\tilde{P}}_{\text{W}}^t-P_{\text{W}}^t\right)+500\left({\tilde{P}}_{\text{V}}^t-P_{\text{V}}^t\right)\right](3)$

To effectively manage and control the carbon emissions of the system, the carbon emission cost is stratified into three distinct levels based on the volume of emissions. The formula for calculating the carbon emission cost $C_3$ is outlined as follows:

$C_3=\left\{\begin{array}{cc}\hfill & \omega \left(M_{\text{P}}^t-M_{\text{L}}^t\right),M_{\text{P}}^t\le M_{\text{L}}^t+d\hfill \\ \hfill & \left(1+\tau \right)\omega \left(M_{\text{P}}^t-M_{\text{L}}^t\right)-\tau \omega d,M_{\text{L}}^t+d\le M_{\text{P}}^t\le M_{\text{L}}^t+2d\hfill \\ \hfill & \left(1+2\tau \right)\omega \left(M_{\text{P}}^t-M_{\text{L}}^t\right)-3\tau \omega d,M_{\text{P}}^t\ge M_{\text{L}}^t+2d\hfill \end{array}\right.(4)$

where $\omega$ represents the carbon trading price; $d$represents the length of the carbon emission interval; $\tau$represents the growth rate. $M_{\text{L}}^t={\displaystyle {\sum }_{j=1}^{N_{\text{G}}}}{\epsilon }_j{P}_{\text{G},j}^t\mathrm{\Delta }T$ represents the total carbon emission quota of the system (${\epsilon }_j$ is the allocation coefficient $t/(\text{MW}\cdot \text{h})$ for unit electricity emissions; $\mathrm{\Delta }T$ represents the emission cycle). $M_{\text{P}}^t={\displaystyle {\sum }_{j=1}^{N_{\text{G}}}}{\lambda }_j{P}_{\text{G,}j}^t\mathrm{\Delta }T$ represents the total carbon emissions of the system within one cycle (${\lambda }_j$ represents the carbon emission intensity of thermal power unit $j$). When $C_3<0$,it indicates that the system has a surplus of carbon emission allowances greater than zero. These carbon emission allowances can be traded in the market at the base carbon price, and the system can obtain corresponding resource revenue from these transactions.

2.2 Determination of constraints

When integrating a wind-solar complementary power system into the grid, the system’s power balance is governed by an equation, and the rotating reserve balance is constrained by an inequality, as follows:

$P_{\text{L}}^t-P_{\text{W}}^t-P_{\text{V}}^t+P_{\text{Sc}}^t-P_{\text{Sd}}^t-{\displaystyle \underset{j=1}{{\displaystyle \sum ^N}}}{P}_{\text{G},j}^t=0(5)$

$P_{\text{L}}^t-P_{\text{W}}^t-P_{\text{V}}^t+P_{\text{Sc}}^t-P_{\text{Sd}}^t-{\displaystyle \underset{j=1}{{\displaystyle \sum ^N}}}{P}_{\text{G},j}^t\le 0(6)$

where $P_{\text{L}}^t$ represents the load value at time $t$; $P_{\text{W}}^t$ represents the wind power output value integrated into the grid at time $t$; $P_{\text{V}}^t$ represents the photovoltaic output value integrated into the power grid at time $t$; $P_{\text{G},j}^t$ represents the output value of the thermal power unit at time $t$; $P_{\text{Sc}}^t$ represents the charging capacity of the energy storage device at time $t$; $P_{\text{Sd}}^t$ represents the discharge capacity of the energy storage device at time $t$.

Due to the presence of uncertain variables, the system’s power balance equation and the rotating reserve inequality cannot be expressed deterministically. Therefore, it is necessary to account for system uncertainties in the day-ahead scheduling. In this article, we address these uncertainties by introducing wind power uncertainty parameter $P_{\text{W}}^t$, photovoltaic uncertainty parameter $P_{\text{V}}^t$, and load uncertainty parameter $P_{\text{L}}^t$. Equation 5 and Equation 6 are reformulated as power balance constraints with a specified reliability level, ensuring the probability of meeting these constraints is above a certain threshold. The set of uncertainty factors is established as follows:

$min{P}_{\text{r}}\left\{{\tilde{P}}_{\text{L}}^t-{\tilde{P}}_{\text{W}}^t-{\tilde{P}}_{\text{V}}^t-{\displaystyle \underset{j=1}{{\displaystyle \sum ^M}}}{P}_j^t-P_{\text{Sd}}^t=0\right\}\ge \alpha (7)$

$min{P}_{\text{r}}\left\{{\tilde{P}}_{\text{L}}^t-{\tilde{P}}_{\text{W}}^t-{\tilde{P}}_{\text{V}}^t-{\displaystyle \underset{j=1}{{\displaystyle \sum ^M}}}{P}_j^{\max }-P_{\text{Sd}}^t\le 0\right\}\ge \alpha (8)$

where $P_{\text{r}}\left\{\cdot \right\}$ represents the credibility of the event. From Equation 7 and Equation 8, it is evident that during the optimization process, the output of thermal power generation serves as a backup to address the uncertainties associated with wind and solar power generation outputs, as well as load power. This ensures that the probability of maintaining supply-demand balance in the system remains at a normal level. In comparison to deterministic constraints, system uncertainty chance constraint account for uncertain factors. Furthermore, by incorporating backup power into the output of thermal power units, the need for separately setting backup power is eliminated.

The low-carbon optimization scheduling model for distribution networks encompasses various complex constraints, including power balance, limitations on wind and solar power generation outputs, operational characteristics of thermal power units, energy storage system capacity, and rotational reserve requirements. The detailed expression of these constraints is as follows:

1) Power balance constraint

$\left(2-2\alpha \right)\left[P_{\text{L}2}^t-P_{\text{W}2}^t-P_{\text{V}2}^t\right]+\left(2\alpha -1\right)\left[P_{\text{L}3}^t-P_{\text{W}1}^t-P_{\text{V}1}^t\right]+P_{\text{Sc}}^t-P_{\text{Sd}}^t-{\displaystyle \sum _{j=1}^{N_{\text{G}}}}{u}_j^t{P}_{\text{G,}j}^t=0(9)$

2) Constraints on the output of wind and solar power generation

$\left\{\begin{array}{cc}\hfill & 0\le P_{\text{W}}^t\le P_{\text{W}}^{\max }\hfill \\ \hfill & 0\le P_{\text{V}}^t\le P_{\text{V}}^{\max }\hfill \\ \hfill & 0\le P_{\text{W}}^t+P_{\text{V}}^t\le P_{\text{L}}^t-P_{\text{G}}^{\min }\hfill \end{array}\right.(10)$

where $P_{\text{W}}^{\max }$ is the upper limit of wind power output; $P_{\text{V}}^{\max }$ is the upper limit of photovoltaic output, and $P_{\text{G}}^{\min }$ is the lower limit of total output of thermal power units.

3) Constraints pertaining to traditional thermal power units

(i) The output constraints of the unit are as follows:

(ii) The climbing constraints for the crew are as follows:

(iii) The constraint regarding the minimum start-stop time for the unit is as follows:

$P_{G,j}^{\min }\le P_{G,j}^t\le P_{G,j}^{\max }(11)$

In the formula, $P_{\text{G,}j}^{\max }$ and $P_{\text{G,}j}^{\min }$ respectively represent the maximum and minimum output values of the thermal power unit.

$-r_j^{\text{d}}\mathrm{\Delta }t\le P_{\text{G,}j}^t-P_{\text{G,}j}^{t-1}\le r_j^{\text{u}}\mathrm{\Delta }t(12)$

where $r_j^{\text{u}}$ and $r_j^{\text{d}}$ respectively denote the upper and lower bounds of the rate of change when the output of the thermal power unit is increased or decreased.

$\left\{\begin{array}{cc}\hfill & \left(u_j^{t-1}-u_j^t\right)\left(T_j^{t-1}-T_j^{\text{on}}\right)\ge 0\hfill \\ \hfill & \left(u_j^{t-1}-u_j^t\right)\left(T_j^{t-1}+T_j^{\text{off}}\right)\ge 0\hfill \end{array}\right.(13)$

where $u_j^t$ represent the binary variable indicating the start-stop state of the $j$th unit at time $t$. If $u_j^t=1$, it indicates that the unit is operational; if $u_j^t=0$, it signifies that the unit is shut down. The variable $T_j^{t-1}$ denotes the continuous operation or shutdown time of the $j$th unit up to time $t-1$. $T_j^{\text{on}}$ represents the minimum continuous startup time required for the $j$th unit, while $T_j^{\text{off}}$ signifies the minimum continuous shutdown time for the same unit.

4) Energy storage constraint

The calculation formula for the capacity $E_t$ of the energy storage system is as follows:

$E_t=E_{t-1}\left(1-{\theta }_i\right)+\left(u_{\text{Sc}}^t{\phi }_{\text{Sc}}^t{P}_{\text{Sc}}^t-u_{\text{Sd}}^t\frac{P_{\text{Sd}}^t}{{\phi }_{\text{Sd}}^t}\right)\mathrm{\Delta }t(14)$

where ${\theta }_i$ represents the self loss rate; ${\phi }_{\text{Sc}}^t$. and ${\phi }_{\text{Sd}}^t$ respectively represent the charging and discharging efficiency of the energy storage system at a given time; $u_{\text{Sc}}^t$ and $u_{\text{Sd}}^t$ respectively represent the charging and discharging states at time; $P_{\text{Sc}}^t$ and $P_{\text{Sd}}^t$ represent the charging and discharging power of the energy storage system at each moment.

The energy storage constraints are as follows:

$\left\{\begin{array}{cc}\hfill & u_{\text{Sc}}^t+u_{\text{Sd}}^t\le 1\hfill \\ \hfill & E_t^{\min }\le E_t\le E_t^{\max }\hfill \\ \hfill & E_t^{\text{T}}=E_t^1\hfill \end{array}\right.(15)$

where $E_t^{\min }$ and $E_t^{\max }$represent the upper and lower limits of capacity, respectively.

Furthermore, its charging and discharging power must also adhere to the following constraints:

$\left\{\begin{array}{cc}\hfill & 0\le P_{\text{Sc}}^t\le u_{\text{Sc}}^t{P}_{\text{Sc},\max }\hfill \\ \hfill & 0\le P_{\text{Sd}}^t\le u_{\text{Sd}}^t{P}_{\text{Sd},\max }\hfill \end{array}\right.(16)$

where $P_{\text{Sc},\max }$ and $P_{\text{Sd},\max }$ respectively represent the maximum charging and discharging power of the energy storage system.

5) Rotation backup constraint

$\left(2-2\alpha \right)\left[P_{\text{L}2}^t-P_{\text{W}2}^t-P_{\text{V}2}^t\right]+\left(2\alpha -1\right)\left[P_{\text{L}3}^t-P_{\text{W}1}^t-P_{\text{V}1}^t\right]+P_{\text{Sc}}^t-P_{\text{Sd}}^t-{\displaystyle \sum _{j=1}^{N_{\text{G}}}}{u}_j^t{P}_{\text{G,}j}^{\max }\le 0(17)$

2.3 Model solving

Managing chance constraints is a crucial aspect of solving fuzzy chance-constrained programming. We utilizes fuzzy chance-constrained programming and equivalent class processing techniques to address these constraints. Fuzzy chance-constrained programming is commonly used to tackle uncertain optimization problems. It sets a confidence level that determines how constraints are satisfied. This method not only handles randomness but also manages uncertainties from fuzziness, considering both the feasibility and optimality of solutions, particularly in complex systems with multiple interacting fuzzy parameters. The clear equivalence class method transforms fuzzy constraints into deterministic conditions, simplifying the solution process. This approach converts the original problem into an equivalent one with high confidence by analyzing the membership functions of fuzzy variables. It reduces the impact of fuzziness on model accuracy, enhances computational efficiency, and ensures solution stability. Since security is essential for system operation, establishing a reasonable reliability level is imperative. When the reliability level $\alpha$ is greater than or equal to 0.5, the clear equivalence class of the chance constraint $P_{\text{r}}\{g(x,\xi )\le 0\}\ge \alpha$ is expressed as follows:

$\left(2-2\alpha \right){\displaystyle \underset{k=1}{{\displaystyle \sum ^t}}}\left(z_{k3}{h}_k^{+}\left(x\right)-z_{k2}{h}_k^{-}\left(x\right)\right)+\left(2\alpha -1\right){\displaystyle \underset{k=1}{{\displaystyle \sum ^t}}}\left(z_{k4}{h}_k^{+}\left(x\right)-z_{k1}{h}_k^{-}\left(x\right)\right)+h_0\left(x\right)\le 0(18)$

In the formula, $h_k^{+}(x)$ and $h_k^{-}(x)$ represent the two assumed functions; $h_0(x)$ is a component of function $g(x,\xi )$; $z_{k1}\sim z_{k4}(k=\mathrm{1,2},\dots ,n,n\in R)$ represents the attribution parameter.

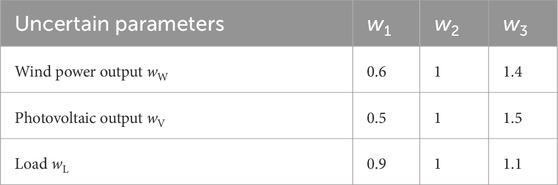
The expression for the trapezoidal uncertainty parameter $\tilde{P}$ is as follows:

$\tilde{P}=\left(z_1,z_2,z_3,z_4\right)=P_{\text{pre}}\left(w_1,w_2,w_3,w_4\right)(19)$

where $P_{\text{pre}}$ represents the predicted value; $z_1\sim z_4$ represents the attribution parameters of wind and solar power generation and load in each cycle; $w_1\sim w_4$ represents the proportionality coefficient, determined based on the historical values of uncertainty parameters.

Based on the aforementioned analysis, the system model is formulated as follows:

$\left\{\begin{array}{cc}\hfill & {\tilde{P}}_{\text{W}}^t=\left(P_{\text{W}1}^t,P_{\text{W}2}^t,P_{\text{W}3}^t\right)=P_{\text{Wpre}}^t\left(w_{\text{W}1},w_{\text{W}2},w_{\text{W}3}\right)\to F\left({\tilde{P}}_{\text{W}}^t\right)=\frac{1-\alpha }{2}{P}_{\text{W}1}^t+\frac{1}{2}{P}_{\text{W}2}^t+\frac{\alpha }{2}{P}_{\text{W}3}^t\hfill \\ \hfill & {\tilde{P}}_{\text{V}}^t=\left(P_{\text{V}1}^t,P_{\text{V}2}^t,P_{\text{V}3}^t\right)=P_{\text{Vpre}}^t\left(w_{\text{V}1},w_{\text{V}2},w_{\text{V}3}\right)\to F\left({\tilde{P}}_{\text{V}}^t\right)=\frac{1-\alpha }{2}{P}_{\text{V}1}^t+\frac{1}{2}{P}_{\text{V}2}^t+\frac{\alpha }{2}{P}_{\text{V}3}^t\hfill \\ \hfill & {\tilde{P}}_{\text{L}}^t=\left(P_{\text{L}1}^t,P_{\text{L}2}^t,P_{\text{L}3}^t\right)=P_{\text{Lpre}}^t\left(w_{\text{L}1},w_{\text{L}2},w_{\text{L}3}\right)\to F\left({\tilde{P}}_{\text{L}}^t\right)=\frac{1-\alpha }{2}{P}_{\text{L}1}^t+\frac{1}{2}{P}_{\text{L}2}^t+\frac{\alpha }{2}{P}_{\text{L}3}^t\hfill \end{array}\right)$

where $P_{\text{Wpre}}^t$ represents the predicted value of wind power output; $P_{\text{Vpre}}^t$ represents the predicted value of photovoltaic output; $P_{\text{Lpre}}^t$ represents the load forecast value.

The explicit equivalent class representation of power balance is as follows:

$\left(2-2\alpha \right)\left[P_{\text{L}2}^t-P_{\text{W}2}^t-P_{\text{V}2}^t\right]+\left(2\alpha -1\right)\left[P_{\text{L}3}^t-P_{\text{W}1}^t-P_{\text{V}1}^t\right]+P_{\text{Sc}}^t-P_{\text{Sd}}^t-{\displaystyle \sum _{j=1}^{N_{\text{G}}}}{u}_j^t{P}_{\text{G,}j}^t=0(20)$

The clear equivalence class representation for rotation backup is as follows:

$\left(2-2\alpha \right)\left[P_{\text{L}2}^t-P_{\text{W}2}^t-P_{\text{V}2}^t\right]+\left(2\alpha -1\right)\left[P_{\text{L}3}^t-P_{\text{W}1}^t-P_{\text{V}1}^t\right]+P_{\text{Sc}}^t-P_{\text{Sd}}^t-{\displaystyle \sum _{j=1}^{N_{\text{G}}}}{u}_j^t{P}_{\text{G,}j}^{\max }\le 0(21)$

3 Results

3.1 Parameter settings

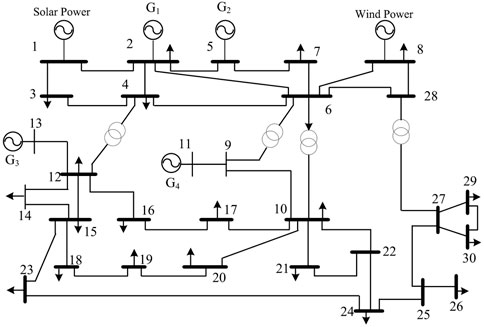
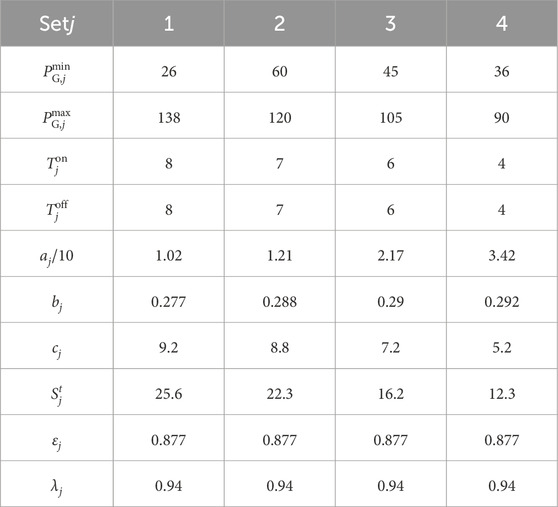
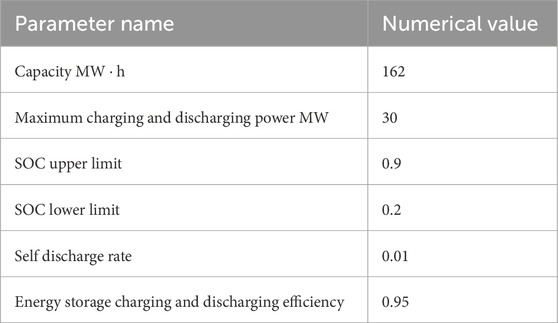
To assess the feasibility and efficacy of the proposed model, a case study was carried out utilizing the IEEE-30 node system, whose diagram is depicted in Figure 1. Initially, the IEEE-30 node system comprised six thermal power generators; however, two of these have been substituted with wind and photovoltaic power generation facilities. Consequently, the system now encompasses four thermal power generators and a hybrid wind-solar power generation system. The node system illustrated in Figure 1 features four thermal power generation units that simulate grid power. The detailed parameters for these units are presented in Table 1. Optimized scheduling calculations are performed in conjunction with wind and photovoltaic power. Furthermore, the system is equipped with wind turbines with a cumulative capacity of 75 MW and photovoltaic turbines with a total capacity of 150.3 MW. The energy storage system boasts a total capacity of 162 MW$•$ h and a maximum charging power of 30 MW. The specific parameters for the energy storage system are outlined in Table 2. To enhance the representativeness of the scheduling prediction, data from 1 day in each of the four seasons was chosen for optimization. The load, wind power, and photovoltaic power were forecasted utilizing the methodologies outlined in references [15, 16] The outcomes are depicted in Figure 2, which showcases the predictions for 1 day in spring, summer, autumn, and winter, respectively. Prior to executing the solving program, the initial carbon emission trading price is established at $\omega =50$ yuan/ton, and the carbon emission range is set to $d=100$ tons. With each increment in the first tier, the carbon emission trading price rises by 25% of the base price. Furthermore, the baseline emission coefficient of the system is designated as 0.75.

Figure 1

Figure 1. IEEE-30 node system.

Table 1

Table 1. Thermal generator data.

Table 2

Table 2. Energy storage unit parameter.

Figure 2

Figure 2. Load, wind, and PV forecast curves.

3.2 Analysis of case results

In order to quantitatively assess the capacity of a specific region’s power system to integrate wind and solar power generation during time period $t$, we define the wind power penetration rate $p_{\text{W}}^t=\frac{P_{\text{W}}^t}{P_{\text{L}}^t}\times 100$ and photovoltaic penetration rate $p_{\text{V}}^t=\frac{P_{\text{V}}^t}{P_{\text{L}}^t}\times 100$. The uncertainty parameters pertaining to wind power output, photovoltaic output, and load are established as presented in Table 3.

Table 3

Table 3. Uncertain parameter.

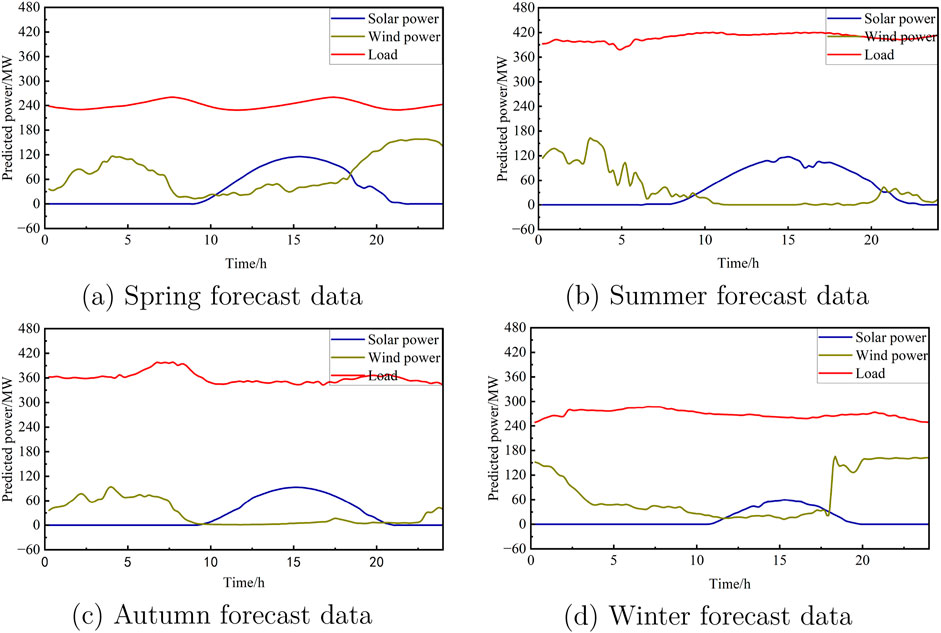
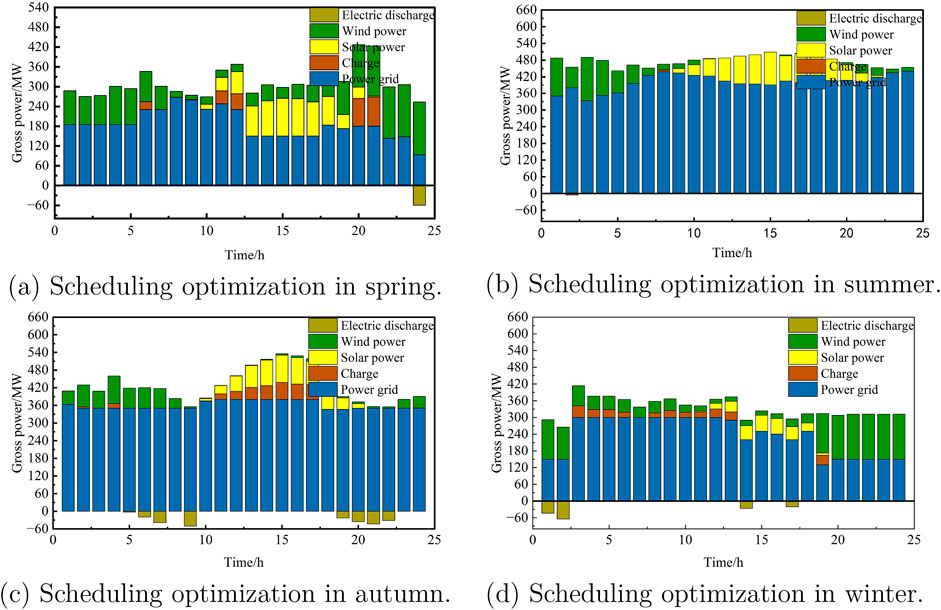
The system scheduling optimization results for different seasons are shown in Figure 3. In spring (Figure 2A), wind power remains stable throughout the day, compensating for the lack of photovoltaic (PV) generation at night. At night, the system primarily relies on wind and thermal power, with energy storage absorbing excess wind power. During the day, wind, PV, and thermal power are used together, reducing thermal output to maximize renewable energy penetration (59.38%). Energy storage absorbs surplus electricity when generation exceeds demand, while thermal power compensates for forecast inaccuracies. In summer (Figure 3B), the system fully absorbs wind and solar power. Due to increased load, thermal power output rises to meet demand, achieving a 32.01% penetration rate. When wind and solar, along with storage, cannot meet the load, all four thermal units may be activated. Excess power is stored and released as needed. In autumn (Figure 3C), wind power is sometimes unavailable, and the load is met by PV and thermal power, with a maximum renewable penetration of 30.16%. Even without wind, PV and thermal can meet grid demand, with energy storage helping to reduce emissions and costs. In winter (Figure 3D), shorter sunshine hours reduce PV output, and wind power compensates, achieving a peak penetration rate of 51.14%. In summary, wind power is higher in spring and winter, while summer has more PV generation due to longer daylight hours. Load demand varies seasonally, with summer requiring more thermal power to meet air conditioning loads during peak hours.

Figure 3

Figure 3. Scheduling optimization results for different seasons.

Seasonal differences in wind and photovoltaic (PV) power output affect the operating hours and frequency of traditional thermal power units. This impacts carbon emissions and, consequently, carbon trading costs. For instance, during seasons with high wind output, thermal units operate less, reducing carbon costs. In contrast, when wind output is low, thermal units run more, leading to higher emissions and carbon trading costs. Seasonal carbon cost variation is critical to the economic viability of system optimization. Additionally, during seasons with abundant wind and solar power, limited system flexibility or energy storage capacity may lead to curtailment, affecting system economics. The simulation confirms the model’s feasibility. Building on this, uncertainty chance constraints and carbon trading mechanisms are integrated into three scheduling models for comparison.

Model 1: A deterministic power balance model is used to handle wind, solar, and load uncertainties, with reserve capacities of 20% for wind and solar and 10% for load forecasting. A stepped carbon trading fee is included. Model 2: An uncertainty chance constraint model focuses on minimizing operating costs without considering carbon trading costs. Model 3: Similar to Model 2 but includes a stepped carbon trading fee and sets the reliability level at 0.9.

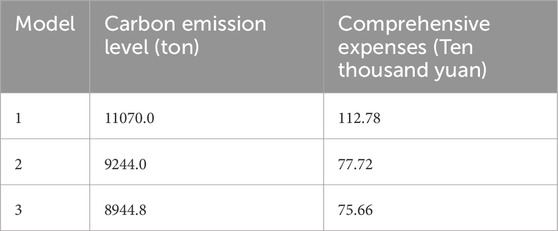
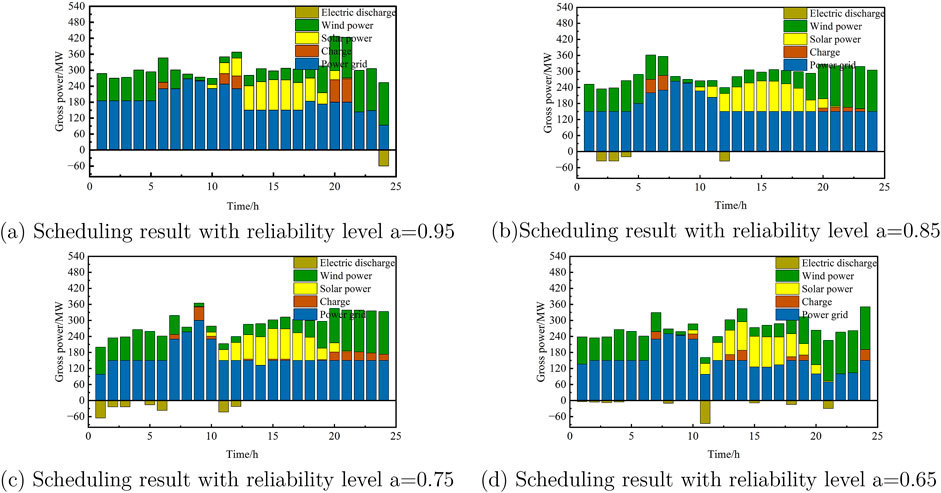
Table 4 shows Model 3 as the most effective, reducing total costs by 32.9% and carbon emissions by 19.2% compared to Model 1, and further lowering costs and emissions by 2.65% and 3.2% compared to Model 2. The wind-solar complementary scheduling model with uncertainty constraints minimizes system costs and emissions, aligning with China’s environmental policies. Figure 4 illustrates the system’s scheduling results under different reliability levels, using spring data.

Table 4

Table 4. Scheduling data for different models.

Figure 4

Figure 4. System scheduling results of different reliability levels.

As illustrated in Figure 4, the system’s backup capacity is intimately linked to its reliability level. A decrease in the reliability level reveals frequent charging and discharging of the energy storage device, accompanied by a reduction in the system’s rotational backup. The backup capacity of the system serves as an extra capacity to ensure its safety, safeguarding against any adverse effects caused by decreases in wind and solar power generation output or load growth. Configuring the backup capacity necessitates a thorough consideration of the system’s reliability requirements and operating costs, making it imperative to establish a reasonable reliability level. Enhancing the system’s backup capacity can elevate its reliability level and bolster its security. However, from an economic standpoint, augmenting the system’s backup capacity leads to an increase in the system’s construction cost. Therefore, to strike a balance between the system’s security and economy during scheduling, it is essential to choose the appropriate reliability level based on the actual needs of the system.

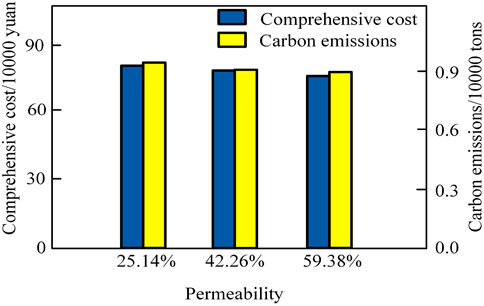
Using spring data as a case study, we investigated the influence of varying penetration rates of wind and solar power generation on scheduling optimization. The findings of this analysis are presented in Figure 5. As the penetration rate of wind and solar power generation diminishes, the reliance on thermal power units escalates. Furthermore, a decrease in the penetration rate results in an increase in overall costs. Specifically, when the penetration rate drops from 42.26% to 25.14%, the overall cost rises by 5%, while carbon emissions decrease by 5.5%. These findings suggest that the penetration rate of wind and solar power generation significantly influences the overall cost and carbon emissions associated with power generation. Hence, during the scheduling optimization process, it is imperative to prioritize the utilization of renewable energy to minimize carbon emissions and align with environmental standards. The simulation indicate that in comparison to Model 1 referenced in the article, the model proposed in this study has achieved a 32.9% reduction in comprehensive cost and a 19.2% decrease in carbon emission levels. Additionally, when compared to Model 2, Model 3 has further reduced the overall cost by 2.65% and carbon emissions by 3.2%. In conclusion, the grid-connected scheduling method for wind-solar complementary power generation systems, as proposed in this chapter, demonstrates the ability to effectively decrease both the overall cost and carbon emission levels of the system.

Figure 5

Figure 5. Combined costs and carbon emissions under different permeability.

4 Conclusion

This paper addresses the challenge of low-carbon scheduling in grid-connected wind and solar power systems, where supply and demand uncertainty is a key factor. It employs the fuzzy chance constraint method to handle this uncertainty and proposes an optimization scheduling model, leading to the following conclusions: (1) By using the fuzzy chance constraint method to represent supply and demand uncertainty, the proposed model reduces both carbon emissions and overall costs compared to traditional deterministic scheduling models. (2) The integration of a tiered carbon trading mechanism, while accounting for supply and demand uncertainty, further decreases carbon emissions and overall costs. (3) Although this study does not examine the renewable energy consumption rate, it acknowledges the potential negative impact of a low consumption rate on the power system’s overall economy. Future research could investigate the relationship between renewable energy consumption and its economic impact to achieve more comprehensive optimization.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YN: Conceptualization, Methodology, Writing–review and editing. ZL: Conceptualization, Methodology, Writing–review and editing. XG: Formal Analysis, Writing–original draft. XK: Conceptualization, Methodology, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by grants from State Grid Henan Electric Power Company Science and Technology Project (521790240007). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors YN, ZL, XG, and XK were employed by Henan Kaifeng Power Supply Company.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Qiuye S, Xiaohan Y, Jingao W. Discussion on challenges and countermeasures of “double-high” power distribution system. Proc CSEE (2024) 1-21(44):7115–36. doi:10.13334/j.0258-8013.pcsee.240077

CrossRef Full Text | Google Scholar

2. Jordehi AR. How to deal with uncertainties in electric power systems? a review. Renew Sustain Energ Rev (2018) 96:145–55. doi:10.1016/j.rser.2018.07.056

CrossRef Full Text | Google Scholar

3. Cui Mingyong HLEA, He J. Robust low-carbon economic scheduling of power system based on wind power consumption evaluation. J Solar Energ (2020) 41:270–80. doi:10.19912/j.0254-0096.2020.08.037

CrossRef Full Text | Google Scholar

4. Morales-España G, Martínez-Gordón R, Sijm J. Classifying and modelling demand response in power systems. Energy (2022) 242:122544. doi:10.1016/j.energy.2021.122544

CrossRef Full Text | Google Scholar

5. Li Q, Jiang Y, Du C, Zhou H, Chen T. Low-carbon optimization of distribution networks under the consideration of new energy integration. J Phys Conf Ser (2023) 2659:012017. doi:10.1088/1742-6596/2659/1/012017

CrossRef Full Text | Google Scholar

6. Tianrui Z, Chongqing K, Qianyao X. Study on carbon emission flow analysis theory of electric power system. Automation Electric Power Syst (2012) 36:38–43.

Google Scholar

7. Zhou Tianrui XQEA, Kang C. Characteristics and mechanism analysis of carbon emission flow distribution in electric power networks, 36 (2012). p. 39–44.

Google Scholar

8. Kang C, Zhou T, Chen Q, Wang J, Sun Y, Xia Q, et al. Carbon emission flow from generation to demand: a network-based model. IEEE Trans smart grid (2015) 6:2386–94. doi:10.1109/tsg.2015.2388695

CrossRef Full Text | Google Scholar

9. Cao Yitao JHEA, Wang D. Two-layer game expansion planning for regional integrated energy systems considering multi-energy carbon flow constraints. Automation Electric Power Syst (2023) 47:12–22. doi:10.7500/AEPS20220704007

CrossRef Full Text | Google Scholar

10. Shen W, Qiu J, Meng K, Chen X, Dong ZY. Low-carbon electricity network transition considering retirement of aging coal generators. IEEE Trans Power Syst (2020) 35:4193–205. doi:10.1109/tpwrs.2020.2995753

CrossRef Full Text | Google Scholar

11. Yaowang L, Ning Z, Ershun D, Yuliang L, Xiao C. Research and benefit analysis of low-carbon demand response mechanism in power system based on carbon emission flow. Chin J Electr Eng (2022) 42:2830–42. doi:10.13334/J.0258-8013.pcSE.220308

CrossRef Full Text | Google Scholar

12. Cui Yang ZPEA, Deng G. Source-charge multi-time scale scheduling method for power systems with wind power considering low-carbon characteristics of carbon capture power plants. Proc CSEE (2022) 42:5869–86+6163. doi:10.13334/j.0258-8013.pcsee.210697

CrossRef Full Text | Google Scholar

13. Cui Yang ZYEA, Deng G. Economic scheduling of power systems with wind power considering complementary source-charge low-carbon characteristics. Proc CSEE (2021) 41:4799–815. doi:10.13334/j.0258-8013.pcsee.202533

CrossRef Full Text | Google Scholar

14. Leijun X, Houyou X, Lihua N. Grain powder classification based on random forest algorithm and hardware acceleration. Comput Appl Res (2022) 39:1143–7. doi:10.19734/j.issn.1001-3695.2021.09.0418

CrossRef Full Text | Google Scholar

15. Hanyi O, Limei Z, Muke B. Combined prediction method for wind-photovoltaic-load in edge service center based on arima-gru. Mod Electric Power (2024) 41:65–71. doi:10.19725/j.cnki.1007-2322.2022.0180

CrossRef Full Text | Google Scholar

16. Wu Xiaogang GCEA, Yan J. Ultra-short term power prediction method of wind-water integration based on improved gru-cnn. China Electric Power (2023) 56:178–86+205. doi:10.11930/j.issn.1004-9649.202209120

CrossRef Full Text | Google Scholar