Using intermediate energy knockout, pickup, and charge exchange reactions with invariant mass spectroscopy for investigating nuclear structure beyond the proton drip line

The continuum structure of light p-rich elements has been extensively studied in recent years by invariant-mass spectroscopy. The feeble Coulomb barrier for light proton-rich nuclei makes proton decay an essential tool in this region not unlike alpha decay is in the trans-Pb region and neutron-deficient rare earths. Unlike binary alpha decay, the part of the Chart of the Nuclides this mini review will focus on can undergo decay into many-particle final states and invariant-mass spectroscopy is the frame-invariant and multi-particle replacement for simple binary alpha-particle spectroscopy. Here we highlight how pairing is reflected in the zig-zaggy pattern of the drip line, the decay of nuclides beyond the drip lines, and what the masses of nuclides exterior to the p-drip line have taught us about shell structure. In this context, the subtlety of removing the Wigner, or n-p congruence, energy when interpreting nucleon separation-energy systematics is discussed. We also present examples of where isospin symmetry is maintained in the continuum and where it is not.

1 Introduction

For medium and heavy nuclei, the large Coulomb barriers for fission, alpha, and proton decay retard these decays and allow weak decay modes to dominate over large regions of the nuclear chart. As the Coulomb barrier reduces with decreasing atomic number (Z), the proton decay rate increases becoming the dominate decay mode in the South-West part of the chart. Until one reaches decay rates commensurate with nucleon transit times across a nucleus, the nuclei that p-decay are no less real than those with positive Q-values for alpha decay, or for that matter, positive fission Q-values. These metastable nuclei exhibit structure and are amenable to study by a technique that is at its essence no different than what is done with alpha-particle spectroscopy. This technique is called invariant-mass spectroscopy (IMS) and is the tool employed for extracting the results reported here.

This mini-review presents some selected results which have employed IMS operating on knockout, charge exchange, and pickup reaction products. As soon will become clear, the primary utility of using the different reaction types is that the continuum structure of several nuclei in the region of a single secondary beam can be studied in one experiment. Some confirmation of the reaction mechanism can often be found in the velocity of the reconstructed decaying parent nucleus, e.g., a product of a simple knockout reaction will have a velocity close to that of the beam while pickup and charge-exchange products are notably slower [1]. The angular momentum mismatch in intermediate energy pick-up reactions favors population of high-spin states. This feature may, or may not, be advantageous, but cognizance of this bias is certainly required [1, 2].

We will start by showing how pairing is reflected in the zig-zaggy pattern of the drip line and in the total number and type (1p or prompt 2p) proton-decay steps. The second selected topic is a presentation of how the masses of some of the newly discovered light p-rich nuclei have informed us about the evolution of nuclear structure far from stability. In this exercise the subtlety of removing the Wigner, or n-p congruence, energy must be considered as the cases transit through $N\sim Z$. We then present examples where isospin symmetry is maintained, with textbook clarity, in the continuum. The first of these is two mated pairs of 2-proton decay from analog T = 2 to T = 1 states. One of each pair is from the ground-state of the $T_z=T$ nuclide and the decay of the mate from the excited analog in the $T_z=T-1$ nuclide. In both mated pairs, i.e., all 4 decays, 2p decay occurs as there is no 1p decay that is both energy and isospin allowed. The second isospin symmetry demonstration is paired rotational bands embedded in the continuum. We finish our selected topics with some counter balance to the above examples with selected cases of isospin symmetry breaking induced by asymmetric decay thresholds between the isospin partners. Not presented in this work are the many subtleties of employing IMS for complex nuclear decays, e.g., constructing backgrounds. For this technical detail the interested reader is directed elsewhere, e.g., [3].

2 Experimental methods

The invariant-mass technique requires an accurate determination of the energy-momentum 4-vectors of all the products in the final state. From this information, the decay energy $(E_T)$ of the parent relative to the multifragmented final state can be determined. The technique is not different in its base form from what is used in high-energy physics to, for example, determine the mass of the Higgs boson from detecting the final-state photon and the pairs of either electrons or muons that the Z boson decays into [4]. In fact, this example is similar to many nuclear IMS studies where the decay is concatenated and the intermediate is identified by correlations within a sub-event. In cases relevant to this mini-review, a decay that ultimately produces two protons and a residue can emit two protons at the same time, likely because there is no intermediate state, or sequentially emit two protons. In the latter case the intermediate can be identified because the invariant mass of one of the protons and the residue, one of two sub-events in this case, reconstruct the mass of a known resonance in the intermediate nucleus [5]. However, in another sense IMS is just an inversion of what is done in $\alpha$-particle spectroscopy where measuring the energy of the $\alpha$ particle provides an excitation spectrum of the daughter. As indicated in the introduction, there is another connection between $\alpha$-particle spectroscopy and the IMS employed to study p-rich nuclei. In both cases, the parents are energetically metastable and kinetically trapped by a Coulomb barrier.

A typical experiment is diagrammed in Figure 1A. The emitted light particles, residue, and any $\gamma$ ray from the deexcitation of the residue must be detected. If there are neutrons emitted they must be detected, but this review will not deal with such cases as the focus is on studies of p-rich nuclei. Some non-obvious subtleties are worth pointing out. The ultimate resolution is often limited by the undetermined energy losses in a finite-thickness target. The choice of target thickness is fixed by the width of the parent state one is seeking to study. (The wider this state, the thicker the target one can tolerate.) There is one - fortunate - case where the target thickness is usually not a significant contributor to the resolution. If there is no heavy residue and all the decay fragments have the same energy loss per unit mass, e.g., the decay of ¹⁰C into 2$\alpha$’s and 2p′s or the decay of ⁸C into one $\alpha$ and 4p′s, there is no differential velocity loss in the target. The transverse position of the reaction vertex in the target is a higher-order correction in that the IMS logic only requires a common vertex.

Figure 1

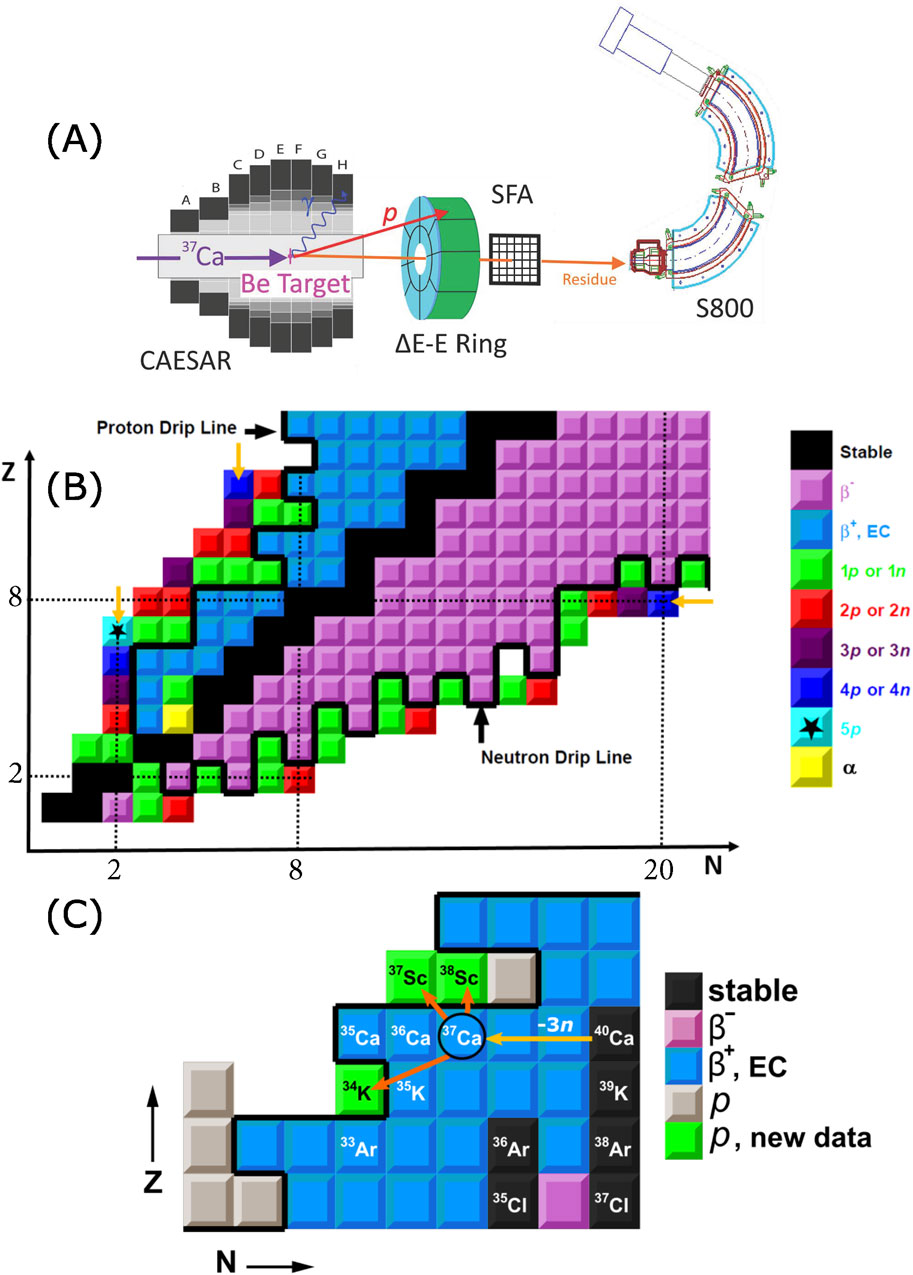
Figure 1. (A) Schematic of an invariant-mass experiment utilizing a position-sensitive $\mathrm{\Delta }$E-E [Si-CsI(Tl)] telescope for light charged-particle detection [6, 15], a spectrometer for identification and energy determination of the heavy residue (S800) [7], a scintillating fiber array (SFA) for an accurate determination of the position of the residue [15], and an array for detecting $\gamma$ rays from excited residues (CAESAR) [8]. (B) Lower portion of the Chart of the Nuclides where the drip lines, multi-nucleon decays, and the standard magic numbers (2, 8 and, for neutrons only, 20) are indicated, the latter by dotted lines. The orange arrows are decay sequences mentioned in the text (C). Starting from a primary beam of ⁴⁰Ca, the selected secondary, ³⁷Ca, produces the indicated products upon collisions with ⁹Be nuclei in the secondary target. Among the produced nuclei are three (³⁴K, ³⁷Sc, and ³⁸Sc, shown in lime) previously unobserved and for which ground-state masses were determined [9].

At intermediate energy, stopping of light charged particles requires rather thick scintillators. These scintillators have far inferior energy resolution as compared to double-sided Si detectors that are typically employed for the $\mathrm{\Delta }$E measurement and to fix the position of the light-charged particles. This difference in resolution translates into the general result that decays transverse to the beam, where the IMS resolution is largely fixed by the position, have superior resolution compared to longitudinal decays for which the IMS resolution is largely determined by the resolution of the scintillator and relative energy-loss considerations [10].

Related to the common vertex assumption, and the determination of the relative momentum vectors, an accurate position of the residue, should it exist, is important. All our recent work has employed some version of a 2-dimensional scintillating-fiber array positioned close the plane of the position determining Si detector, to fix the residue trajectory. This position fix of the residue that is ultimately detected in either a spectrometer [7] or in the Si array itself [6] comes at the cost of some modest efficiency loss ($\sim 15$ %) as the fibers have inactive cladding [11–14].

Finally, if the heavy daughter is produced in a bound excited state, the value of the decay energy $E_T$ determined by the particles alone will be that in reference to the excited daughter. To reconstruct the actual mass-difference relative to the ultimate (perhaps multi-particle) final ground state, the emitted gamma’s must be detected. This can be done in high efficiency, but not high resolution, with scintillation-based $\gamma$-ray detectors that surround the target [8]. These considerations have lead to several systems of which the schematic setup shown in Figure 1A is one.

3 Selected results

3.1 Decays beyond the drip lines

We start by showing a decays-eye view of the lower portion of the nuclear chart in Figure 1B. The zig-zaggy drip lines are defined in this part of the chart and these lines display easily understood pairing features. Namely, even atomic number (Z) elements have proton drip lines more removed from stability and the neutron-drip line is scalloped with even neutron number (N) isotopes inside and odd N isotopes outside the drip line. As required by the energetics, the number of nucleons emitted is that required to land inside the drip line. The N = 6 isotones, note upper orange arrow, extend from 1 to 4 protons emitted from ¹⁵F to ¹⁸Mg [14] (with the residue in each being ¹⁴O). The N = 2 isotones extend from ⁵Li up to ⁹N with the latter (see star) exhibiting the record length decay chain of 5 protons [15]. By examination of the subevents, it is often possible to reconstruct the kinetic decay chain, see, for example, [5]. If Z = odd, the first decay step is always emission of a single proton and long decay sequences are concatenations of 1p and prompt 2p decay steps. The latter principally, but not exclusively, occurs when there is no energy and isospin allowed 1p decay path.

3.2 Wigner-removed separation energies

Using a secondary beam of ³⁷Ca impinging on a ⁹Be target, resonances corresponding to the ground states of ³⁴K and ^37,38Sc were found, see Figure 1C. Using the IMS determined decay energies and the known mass excesses of the daughters, three new masses were determined [9]. These mass measurements allow for an extended look at neutron and proton separation-energy trends, which are shown in the upper panels of Figure 2 (The new masses allowed for calculation of the data represented by stars.) The lower panels in this figure show the separation energy differences defined by $\mathrm{\Delta }{S}_n(N,Z)=S_n(N,Z)-S_n(N+1,Z)$ = $[\mathrm{\Delta }M(N+1,Z)+\mathrm{\Delta }M(N-1,Z)]-2\mathrm{\Delta }M(N,Z)$ and an equivalent expression for protons.

Figure 2

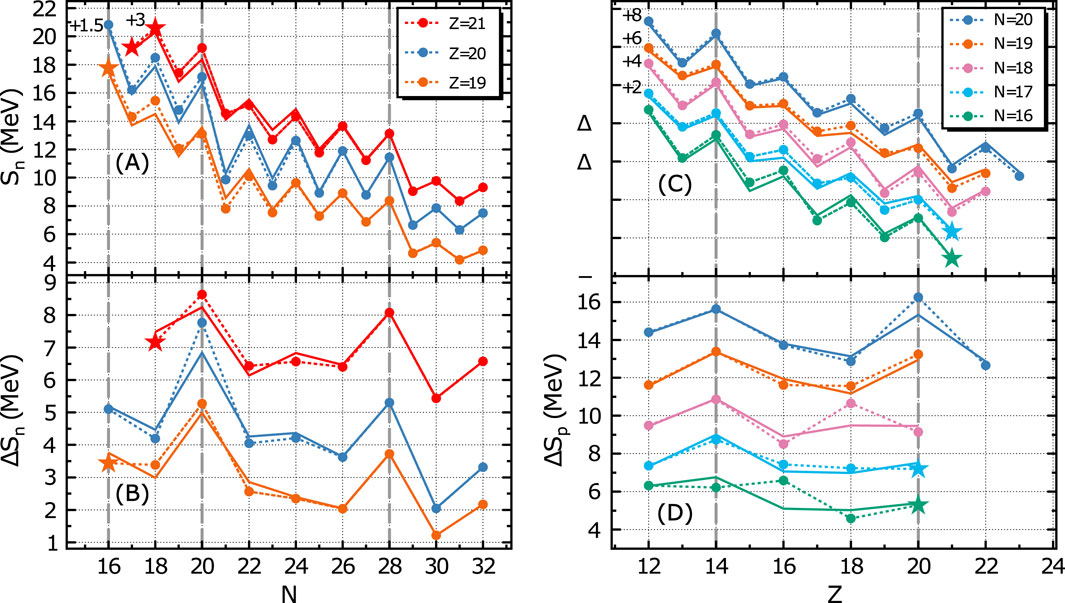
Figure 2. Experimental neutron (A) and proton (C) separation energies and changes in neutron (B) and proton (D) separation energies for even-$N$ isotopes and even $Z$ isotones. Data are represented by points (or stars for new values) connected by dashed lines and are shifted, as indicated, for visual clarity. Removing the Wigner energy results in the solid lines.

First, take note of the expected behavior. The jumps in $\mathrm{\Delta }{S}_n$ at $N=20$ and $N=28$ illustrate the classic neutron shell closures. The reduced increase in $\mathrm{\Delta }{S}_n$ ${\text{for}}_{21}^{41}{\text{Sc}}_{20}$ (red, top data sequence) should be noted and we shall return to this observation. Next, note that at $N=16$, the raw data (points connected with dotted lines) suggest a neutron shell closure for ³⁶Ca (blue). (The word “suggest” is used as one expects a general increase in neutron separation energy with decreasing neutron number.) This had previously been noted [16]. However, the new data point, for $Z$ = 19 (orange star), indicates that the enhanced binding for $N=16$ has largely diminished. Again, we shall return to this observation. Finishing on what is, more-or-less, expected; note that the change in proton separation energies exhibit a clear peak for ⁴⁰Ca (Figure 2D, blue points and dotted line). One observes a diminution of $\mathrm{\Delta }{S}_p$ and the apparent loss of the enhancement of the proton removal energy when $N$ recedes below 20.

Before proceeding to the explore the not-so-obvious trends, for which some inklings were provided above, we have to appreciate that there are three structure issues at play in these mass derived quantities. Two of these are the standard issues of nuclear shells and pairing of like nucleons. The remaining issue, unimportant for heavier nuclei or neutron-rich nuclei, is the so-called Wigner or n-p congruence energy [17, 18]. The latter, included early on in macroscopic mass models, results in extra stabilization near $N=Z$ and arises from $T=0$ (but not necessarily $J=1$) neutron-proton pairing correlations [19]. The real separation energies are enhanced if the parent $N/Z$ asymmetry is smaller, suppressing its mass, than that of the daughter. If one desires to focus only the impact of nuclear shells, pseudo separation energies should be constructed which remove congruence-energy effects. Such Wigner-“corrected” separation energies, are not observables as they remove, in a model-dependent way, one structure effect. As the Wigner energy rapidly reduces away from $N=Z$, Wigner-removed pseudo values of $\mathrm{\Delta }{S}_n(N,Z)$ are strongly reduced if the central nucleus has $N=Z$ (as the actual separation energies are inflated by n/p congruence) and will increase this quantity if either of the nuclei corresponding to one nucleon added or removed has $N=Z$. To generate the Wigner-removed pseudo-separation energies we employ the procedure suggested by Goriely $etal$ [20]. The results are shown as solid lines, without points, in Figure 2. The shading between the solid and dashed lines highlights the Wigner-energy contribution.

We are now ready to return to the not-so-obvious trends. The Wigner-energy-removed pseudo-separation energies confirm the suggestion of a $N=16$ subshell closure as one observes that $\mathrm{\Delta }{S}_n(N,Z)$ increases from $N=18$ to $N=16$ for potassium $(Z=19)$ isotopes similar to the trend observed for calcium isotopes, compare orange and blue solid lines without dots in Figure 2B. (Removing the Wigner energy suppresses the pseudo-separation energy ${\text{for}}_{19}^{37}{\text{K}}_{18}$ more than ${\text{for}}_{19}^{35}{\text{K}}_{16}$, as the former is closer to $N=Z$.)

A $Z=14$ subshell closure is most clearly seen as a peak in $\mathrm{\Delta }{S}_p$ between $N=20$ and $N=17$, see Figure 2D. At $N=16$, there is no evidence for this feature. With 16 neutrons, the $\nu 0d_{5/2}$ and $\nu 1s_{1/2}$ orbitals are nominally filled, so adding another neutron starts filling the $\nu 0d_{3/2}$ orbital. Through the tensor interaction [21], neutrons occupying the $\nu 0d_{3/2}$ will stabilize the $\pi 0d_{5/2}$, increasing the energy gap between it and the higher lying $\pi 1s_{1/2}$. This effect explains the observed low proton occupation of the $\pi 1s_{1/2}$ orbit ${\text{in}}_{14}^{34}{\text{Si}}_{20}$, which lead to the suggestion that this nucleus is doubly magic [22]. More insight into this topic can be found in the paper by J. Chen found in the present issue [23]. Finding the mirror of this effect ${\text{in}}_{20}^{34}{\text{Ca}}_{14}$ is a future research opportunity.

Neither the real nor the Wigner-removed pseudo-proton-separation energy differences show an increase at $Z=20$ for $N<19$ (The recent invariant-mass work added data allowing for the calculation of the values for $N=17$ and $N=16$, stars in Figure 2D.) In these cases, the Wigner modification is of little consequence. This analysis confirms that $Z=20$ has lost its “magicity” for $N<19$. This conclusion had previously been reached through the two-nucleon removal cross section for ³⁸Ca [24] and measurement of the B (E2) for ³⁶Ca [25]. This enfeebling of the $Z=20$ shell for neutron deficient isotopes has also been mentioned in a recent global examination of shell gaps over the whole chart of nuclides [26]. However, with some introspection, data from ⁴⁰Ca (e,e’p) [27] told us three decades ago that even ⁴⁰Ca had a somewhat open proton sd shell and an appreciable cross-shell $f_{7/2}$ spectroscopic factor of about 1/3, (results confirmed by (d,³He) proton knockout studies [28].) Another point of heuristic value deduced from panels (B) and (D) of Figure 2, is that congruence is a non-negligible contributor to the stability of ⁴⁰Ca.

Finally, we return to an observation made above from Figure 2B - the reduced increase in $\mathrm{\Delta }{S}_n$ ${\text{for}}_{21}^{41}{\text{Sc}}_{20}$ (red) compared to the two other isotones plotted (${\text{either}}_{20}^{40}{\text{Ca}}_{20}$ ${\text{or}}_{19}^{39}{\text{K}}_{20}$). The Wigner-energy-removal modification only amplifies this observation and therefore we must also conclude that the $N=20$ shell is significantly weakened for $Z>N$.

3.3 Isospin symmetry

One example of isospin symmetry found in the continuum is mated pairs of 2p emitters. Figure 3 shows two such cases [29, 30]. The schemes on the top show the ground-state 2p decay of Z = even, T = 2 nuclei. These decays are characterized by each proton removing 1/2 of the total available decay energy, a characteristic of decays unperturbed by intermediates and thus indicating “direct” 2p decay. (Experience has taught that if a potential intermediate is broad, it leaves no “finger print” on the decay.) The lower decay schemes show the same T = 2 to T = 1 decays rotated in isospace into the $T_z=T-1$ nuclei, i.e., the decays of the analogs. In these cases, while there are single-proton energetically-allowed narrow intermediates, there are no energetically and isospin allowed intermediates. (These potential intermediate states are T = 1/2.) As in the $T_z=2$ cases (top), the two protons share the decay energy equally. In the A = 8 analog decay, the charged-particle IMS was coupled with the gamma detection to confirm that the 2p decay populated the isobaric analog state in ⁶Li [31] (In the other case, the addition of excitation energy of the 2p daughter’s T = 1 gamma-decaying analog state to the measured 2p decay energy yielded the energy of the previously unobserved T = 2 state in ¹²N [30].) One would also expect another mated pair for A = 16, ${\text{i.e.}}^{16}{\text{Ne}}_{gs}$ and its T = 2 analog in ¹⁶F. Despite considerable effort, no clear evidence for the second of this pair has been found. We suspect that the resolution of the riddle lies in the failure of isospin allowed 2p decay to effectively compete (at Z = 9) with isospin violating 1p decay.

Figure 3

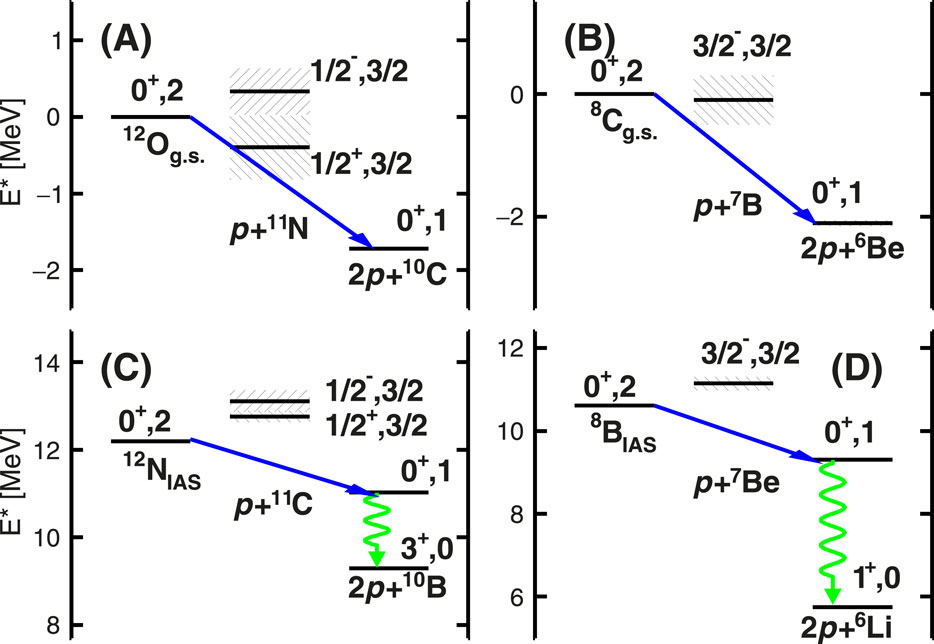
Figure 3. Decay schemes for two mated pairs, A = 12 Left and A = 8 Right, of T = 2 to T = 1 2p decays. (A,B) shows the $T_z=T$ cases and (C,D) shows the $T_z=T-1$ cases. Note that the former are ground-state 2p emitters and the latter are the highly excited analogs which decay to T = 1 analog states in the $T_z=0$ daughters that gamma decay to the respective ground states.

Another beautiful example of isospin symmetry in the continuum is the mated rotational bands in the A = 10 nuclei ¹⁰Be and ¹⁰C. These nuclei become unbound (to n and 2p emission) at 6.812 and 3.821 MeV, respectively. The ground and $2_1^{+}$ states are particle bound in both cases and have been known for decades. Other than the $0_2^{+}$ state in ¹⁰Be, all other states in either the ground rotational band or those built on the second $0^{+}$ state are in the continuum. Tentative, but highly plausible, reconstructions of the ground and excited rotational bands in these two nuclei, as well as the analog of the excited (T = 1) band in the intermediate odd-odd ¹⁰B nucleus, are shown in Figure 4. All of the states for ¹⁰Be shown in this standard rotational (excitation energy vs. spin) plot have been known for years. Only the spin of what is now assigned as $4_1^{+}$ was uncertain, although it was known to be T = 1 [32]. (Note that in the assignments made in Figure 4, $4_1^{+}$ belongs to the excited, but much lower moment-of-inertia, excited band while $4_2^{+}$ belongs to the ground-state band.). The spin assignments made for ¹⁰C only became possible when a highly plausible assignment could be made for $0_2^{+}$, the search for which was rather tortuous but for which the final chapters were IMS studies, one with an incorrect assignment [33] which prompted another study which lead to the assignment used in Figure 4 [34]. The correct assignment was made based on the similarity of the 3-body correlations for this state with those for other $0^{+}$ 2p decays. Using similar logic, the higher spin states could be given tentative assignments [34]. While this spin assignment method is novel and should be viewed with some measure of skepticism, confidence in the assignments is generated by the fact that the apparent moments-of-inertia are constant and the same in the two bands independent of isospin projection. (In three cases for the excited band.) While these assignments must be considered tentative, the results, taken at face value, show that the rotational structures in these clustered nuclei show remarkable insensitivity to decay thresholds.

Figure 4

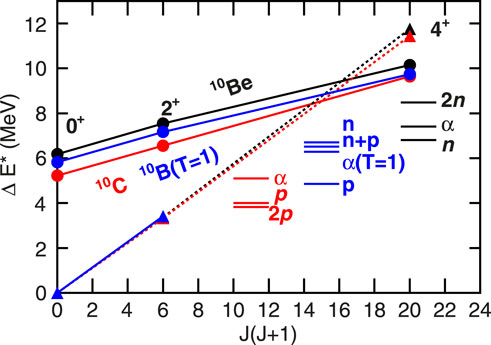
Figure 4. Comparison of analog rotational bands in ¹⁰C, ¹⁰B, and ¹⁰Be. The quantity $\mathrm{\Delta }{E}^{*}$ is the excitation energy relative to the first $T$ = 1, $J^{\pi }$ = $0^{+}$ state. The rotation bands built on the excited $0^{+}$ states have smaller moments of inertia compared to those built on the first $0^{+}$ states. The decay thresholds are indicated. The indicated $\alpha$ threshold for ¹⁰B (blue) is for decay to the T = 1 IAS in ⁶Li.

3.4 Breaking isospin symmetry

Isospin symmetry can be broken by asymmetric coupling to the continuum. The classic case, considered by both Ehrman [35] and Thomas [36] is for the A = 13 pair ¹³C and ¹³N, see Figure 5C, where the ground and first three excited states of the former are bound to neutron decay while for the latter all but the ground state are unbound to proton decay. The excitation energies of the $3/2^{-}$ and $5/2^{+}$ states are similar in the two nuclei while the excitation energy of the unbound $1/2^{+}$ state in ¹³N is downshifted by 0.73 MeV relative to its mirror state. The base explanation is simply that, for states unconfined by an angular momentum barrier, the Coulomb energy for the proton-rich case is less, i.e., the wave functions are slightly expanded, for states coupled to the continuum.

Figure 5

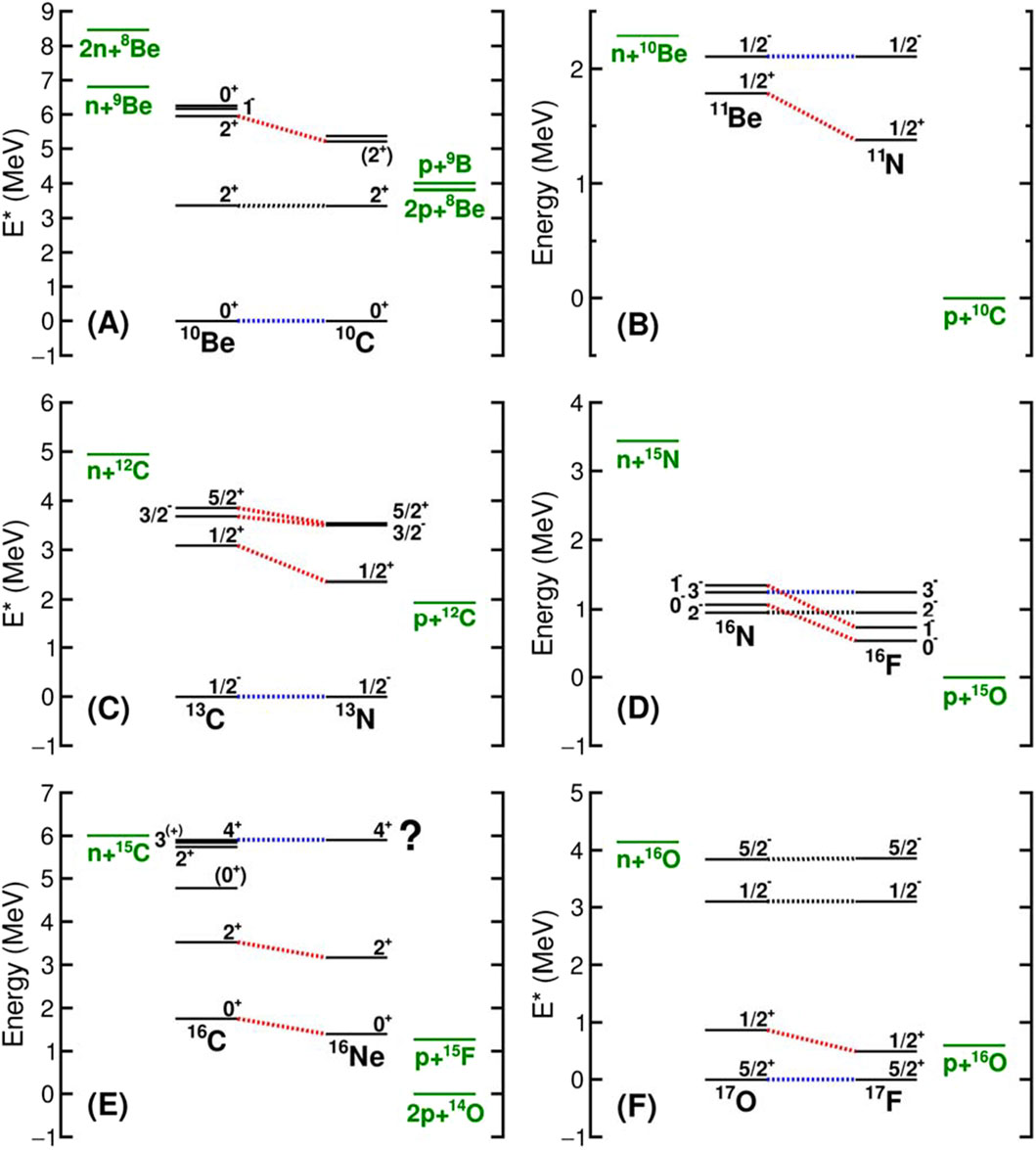
Figure 5. Selection of mirror nuclei which exhibit (or in one case - expected to exhibit) Thomas-Ehrman shifts. In each of the panels analog levels are connected by dotted lines and the relevant decay thresholds are indicated (in green) exterior to the level schemes. The analog levels connected by blue dotted lines are the reference level and those connected by red dotted lines are those with a downward shift for the p-rich nuclide suggesting a substantial s-wave component. When the ground state is the reference state, the ordinate is the actual excitation energy otherwise the ordinate zero is taken as the relevant p-decay threshold. The data for (A–D,F) are taken from ref. 32. The same is true for ¹⁶C in (E). However, as the reference (4⁺) level in ¹⁶Ne has not be observed, the positions of the lower levels and thresholds with respect to this level are not fixed.

While several examples of what has been come to be known as “Thomas-Ehrman” (TE) shifts have been known for decades, the study of proton-rich nuclei by IMS has extended the list of known examples several of which are shown in the other panels of Figure 5. The A = 11 and A = 17 cases, 5 (B) and (F) are similar to the A = 13 case (C) in that the $1/2^{+}$ state is down shifted relative to the $1/2^{-}$, and the $5/2^{-}$ state in (F). In the A = 17 case (F), the ground states are used as references and the ordinate is again (as in (C)) the excitation energy. However, to display the shift in the A = 11 case (B), we have chosen to fix the energy ordinate zero to the p + ¹⁰C decay threshold, the decay products of ¹¹N, and reference the mirror schemes to one another using levels with finite $\ell$ composition, blue dotted lines. For A = 16 (D), all the levels in the p-rich ¹⁶F are unbound while none of those in the mirror are. Using the graphical tool employed in (B), one notes that, if the two high-spin levels are used to align the level schemes, the two levels that can decay by s-wave emission are down shifted.

The ground and first excited states for both ¹⁰Be and ¹⁰C (A) are bound, however there are two levels in ¹⁰C well below the third excited state in ¹⁰Be but above both the 1p and 2p decay thresholds (The mirror 1n and 2n thresholds for ¹⁰Be are above all levels in question.) One of these levels is $0_2^{+}$, the band head of the second rotational band, see Figure 4, and the other, which decays to p + ⁹B, has been assigned $J^{\pi }=2^{+}$, see [37] and references cited therein, an assignment consistent with direct reaction data. (This state is not part of either of the rotational bands shown in Figure 4).

The remaining panel of Figure 5E represents a research opportunity. All the levels shown are known [32] except the $4^{+}$ in ¹⁶Ne. While states with $J^{\pi }\le 3$ can be reached with contributions from the second proton s orbit, $J^{\pi }=4^{+}$ states cannot. Finding this state, allows for an assessment of the actual downshifts of the lower levels, including the ground state, and thus estimates of the contribution from the second s orbit.

4 Conclusion

The lower portion of the Chart of the Nuclides is now mapped out to where nuclei convert from metastable to unstable and thus cease to exist. The pattern of nucleon decays, like the drip-lines themselves, reflect the strong influence of like-nucleon pairing. Sequences of single- and double-proton decay have been mapped out on the p-rich side with the longest chain starting with ⁹N emitting a single proton to the even Z and well ${\text{studied}}^{8}C$, which decays by two steps of 2p emission ending with an alpha-core residue.

As with any Fermion system, the punctuation of structure is the irregularity of single-particle levels. However, in the nuclear two-Fermion system, shell structure is conflated with n-p congruence effects. While generally not important, this latter structure effect is important in p-rich light nuclei [26]. Employing a reasonable prescription for removing n-p congruence effects, it was found that a $N=16$ subshell is a meaningful concept for both ³⁶Ca and ³⁵K. Another finding of note is a weakening of the $Z=20$ shell closure when $N<19$.

Two examples of isospin symmetry were presented. One of these, presented in duplicate, is mated pairs of two-proton decay, both T = 2 to T = 1, one from the ground state of the ${\text{T}}_Z$ = 2 nucleus and the other from its analog. Another example is the mated rotational bands, both ground and excited, in A = 10 systems. Finally, a selection of cases of isospin symmetry breaking, induced by differing decay thresholds, was presented. Generating a catalog of such cases, and explaining the systematics therein, presents a research opportunity.

In our view, the most interesting unresolved questions concerning the structure-reactions (they are intimately spliced) of nuclei near the proton-drip line are related to cases for which multiple open channels exist. Such cases are often found near the drip line but are exceedingly important at high excitation energy near stability, e.g., the ¹³C ($\alpha$,n)¹⁶O reaction which provides neutrons to the s-process. Advances in theory which allow for treatment of multiple open channels, especially when one of the channels is a cluster, should be a high priority for the field.

Author contributions

LS: Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Writing–original draft, Writing–review and editing, Conceptualization, Data curation, Validation. RC: Conceptualization, Formal Analysis, Investigation, Software, Supervision, Visualization, Writing–review and editing, Data curation, Methodology, Validation.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The work presented in this report is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics under Awards No. DE-FG02-87ER-40316.

Acknowledgments

The results presented here on the separation energies beyond the proton drip line are part of the thesis work of Nicolas Dronchi who, of course, did the hard analysis work on that project [38].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Charity RJ, Brown K, Webb T, Sobotka LG. Invariant-mass spectroscopy of ¹⁰B,¹¹C, ¹⁴F, ¹⁶F, and ¹⁸Na. Phys Rev C (2023) 107:054301. doi:10.1103/PhysRevC.107.054301

CrossRef Full Text | Google Scholar

2. Brink D. Kinematical effects in heavy-ion reactions. Phys Lett B (1972) 40:37–40. doi:10.1016/0370-2693(72)90274-2

CrossRef Full Text | Google Scholar

3. Charity RJ, Sobotka LG. Invariant-mass spectroscopy in projectile fragmentation reactions. Phys Rev C (2023) 108:044318. doi:10.1103/PhysRevC.108.044318

CrossRef Full Text | Google Scholar

4. Aad Gthe ATLAS collaboration. A detailed map of Higgs boson interactions by the ATLAS experiment ten years after the discovery. Nature (2022) 607:52–9. doi:10.1016/S0168-9002(98)00960-7

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Mercurio K, Charity RJ, Shane R, Sobotka LG, Elson JM, Famiano M, et al. Correlated two-proton decay from ¹⁰C. Phys Rev C (2008) 78:031602. doi:10.1103/PhysRevC.78.031602

CrossRef Full Text | Google Scholar

6. Wallace M, Famiano M, van Goethem MJ, Rogers A, Lynch W, Clifford J, et al. The high resolution array (HiRA) for rare isotope beam experiments. Nucl Instrum Methods A (2007) 583:302–12. doi:10.1016/j.nima.2007.08.248

CrossRef Full Text | Google Scholar

7. Yurkon J, Bazin D, Benenson W, Morrissey D, Sherrill B, Swan D, et al. Focal plane detector for the S800 high-resolution spectrometer. Nucl Instrum Methods A (1999) 422:291–5. doi:10.1016/S0168-9002(98)00960-7

CrossRef Full Text | Google Scholar

8. Weisshaar D, Gade A, Glasmacher T, Grinyer GF, Bazin D, Adrich P, et al. CAESAR-A high-efficiency CsI(Na) scintillator array for in-beam γ ray spectroscopy with fast rare-isotope beams. Nucl Instrum Methods A (2010) 624:615–23. doi:10.1016/j.nima.2010.09.148

CrossRef Full Text | Google Scholar

9. Dronchi N, Charity RJ, Sobotka LG, Brown BA, Weisshaar D, Gade A, et al. Evolution of shell gaps in the neutron-poor calcium region from invariant-mass spectroscopy of ^37,38Sc, ³⁵Ca, and ³⁴K. Phys Rev C (2024) 110:L031302. doi:10.1103/PhysRevC.110.L031302

CrossRef Full Text | Google Scholar

10. Charity RJ, Brown KW, Elson J, Reviol W, Sobotka LG, Buhro WW, et al. Invariant-mass spectroscopy of ¹⁸Ne, ¹⁶O, and ¹⁰C excited states formed in neutron-transfer reactions. Phys Rev C (2019) 99:044304. doi:10.1103/PhysRevC.99.044304

CrossRef Full Text | Google Scholar

11. Binns W, Connell J, Dowkontt P, Epstein J, Israel M, Klarmann J. A scintillating optical fiber track imaging detector. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (1986) 251:402–6. doi:10.1016/0168-9002(86)90808-9

CrossRef Full Text | Google Scholar

12. Ruchti R. Tracking with scintillating fibers. Nucl Phys B - Proc Supplements (1995) 44:308–19. doi:10.1016/S0920-5632(95)80049-2

CrossRef Full Text | Google Scholar

13. Back B, Betts R, Gillitzer A, Henning W, Hofman D, Nanal V A beam vertex detector using scintillating fibers. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (1998) 412:191–9. doi:10.1016/S0168-9002(98)00096-5

CrossRef Full Text | Google Scholar

14. Jin Y, Niu CY, Brown KW, Li ZH, Hua H, Anthony AK, et al. First observation of the four-proton unbound nucleus ¹⁸Mg. Phys Rev Lett (2021) 127:262502. doi:10.1103/PhysRevLett.127.262502

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Charity RJ, Wylie J, Wang SM, Webb TB, Brown KW, Cerizza G, et al. Strong evidence for ⁹N and the limits of existence of atomic nuclei. Phys Rev Lett (2023) 131:172501. doi:10.1103/PhysRevLett.131.172501

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Lalanne L, Sorlin O, Poves A, Assié M, Hammache F, Koyama S, et al. N=16 magicity revealed at the proton drip line through the study of ³⁵Ca. Phys Rev Lett (2023) 131:092501. doi:10.1103/PhysRevLett.131.092501

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Garvey GT, Gerace WJ, Jaffe RL, Talmi I, Kelson I. Set of nuclear-mass relations and a resultant mass table. Rev Mod Phys (1969) 41:S1–S80. doi:10.1103/RevModPhys.41.S1

CrossRef Full Text | Google Scholar

18. Myers WD. Droplet model of atomic nuclei. New York: Plenum (1977).

Google Scholar

19. Satuła W, Dean D, Gary J, Mizutori S, Nazarewicz W. On the origin of the Wigner energy. Phys Lett B (1997) 407:103–9. doi:10.1016/S0370-2693(97)00711-9

CrossRef Full Text | Google Scholar

20. Goriely S, Chamel N, Pearson JM. Further explorations of skyrme-Hartree-Fock-Bogoliubov mass formulas. xiii. the 2012 atomic mass evaluation and the symmetry coefficient. Phys Rev C (2013) 88:024308. doi:10.1103/PhysRevC.88.024308

CrossRef Full Text | Google Scholar

21. Otsuka T, Fujimoto R, Utsuno Y, Brown BA, Honma M, Mizusaki T. Magic numbers in exotic nuclei and spin-isospin properties of the NN interaction. Phys Rev Lett (2001) 87:082502. doi:10.1103/PhysRevLett.87.082502

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Mutschler A, Lemasson A, Sorlin O, Bazin D, Borcea C, Borcea R A proton density bubble in the doubly magic ³⁴Si nucleus. Nat Phys (2017) 13:152–6. doi:10.1038/nphys3916

CrossRef Full Text | Google Scholar

23. Chen J. Systematic trends in the spin-orbit splitting towards weak-binding. Front Phys. (2024).

PubMed Abstract | Google Scholar

24. Beck T, Gade A, Brown BA, Tostevin JA, Weisshaar D, Bazin D, et al. Probing proton cross-shell excitations through the two-neutron removal from ³⁸Ca. Phys Rev C (2023) 108:L061301. doi:10.1103/PhysRevC.108.L061301

CrossRef Full Text | Google Scholar

25. Dronchi N, Weisshaar D, Brown BA, Gade A, Charity RJ, Sobotka LG, et al. Measurement of the B(E2↑) strengths of ³⁶Ca and ³⁸Ca. Phys Rev C (2023) 107:034306. doi:10.1103/PhysRevC.107.034306

CrossRef Full Text | Google Scholar

26. Buskirk L, Godbey K, Nazarewicz W, Satuła W. Nucleonic shells and nuclear masses. Phys Rev C (2024) 109:044311. doi:10.1103/PhysRevC.109.044311

CrossRef Full Text | Google Scholar

27. Kramer G, Blok H, Van Den Brand J, Bulten H, Ent R, Jans E, et al. Proton ground-state correlations in ⁴⁰Ca studied with the reaction ⁴⁰Ca(e,e’p)³⁹K. Phys Lett B (1989) 227:199–203. doi:10.1016/S0370-2693(89)80022-X

CrossRef Full Text | Google Scholar

28. Chen J. Nuclear data sheets for A = 39. Nucl Data Sheets (2018) 149:1–251. doi:10.1016/j.nds.2018.03.001

CrossRef Full Text | Google Scholar

29. Charity RJ, Elson JM, Manfredi J, Shane R, Sobotka LG, Chajecki Z, et al. 2p-2p decay of ⁸C and isospin-allowed 2p decay of the isobaric-analog state in ⁸B. Phys Rev C (2010) 82:041304. doi:10.1103/PhysRevC.82.041304

CrossRef Full Text | Google Scholar

30. Jager MF, Charity RJ, Elson JM, Manfredi J, Mahzoon MH, Sobotka LG, et al. Two-proton decay of ¹²O and its isobaric analog state in ¹²N. Phys Rev C (2012) 86:011304. doi:10.1103/PhysRevC.86.011304

CrossRef Full Text | Google Scholar

31. Brown KW, Buhro WW, Charity RJ, Elson JM, Reviol W, Sobotka LG, et al. Two-proton decay from the isobaric analog state in ⁸B. Phys Rev C (2014) 90:027304. doi:10.1103/PhysRevC.90.027304

CrossRef Full Text | Google Scholar

32. NNDC. Evaluated nuclear structure data file (ENSDF) (2024). Available from: https://www.nndc.bnl.gov/ensdf/ (Accessed September, 2024).

Google Scholar

33. Curtis N, Achouri NL, Ashwood NI, Bohlen HG, Catford WN, Clarke NM, et al. Breakup reaction study of the brunnian nucleus ¹⁰C. Phys Rev C (2008) 77:021301. doi:10.1103/PhysRevC.77.021301

CrossRef Full Text | Google Scholar

34. Charity RJ, Sobotka LG, Webb TB, Brown KW. Two-proton decay from α-cluster states in ¹⁰C and ¹¹N. Phys Rev C (2022) 105:014314. doi:10.1103/PhysRevC.105.014314

CrossRef Full Text | Google Scholar

35. Ehrman JB. On the displacement of corresponding energy levels of ¹³C and ¹³N. Phys Rev (1951) 81:412–6. doi:10.1103/PhysRev.81.412

CrossRef Full Text | Google Scholar

36. Thomas RG. An analysis of the energy levels of the mirror nuclei, ¹³C and ¹³N. Phys Rev (1952) 88:1109–25. doi:10.1103/PhysRev.88.1109

CrossRef Full Text | Google Scholar

37. Charity RJ, Wiser TD, Mercurio K, Shane R, Sobotka LG, Wuosmaa AH, et al. Continuum spectroscopy with a ¹⁰C beam: cluster structure and three-body decay. Phys Rev C (2009) 80:024306. doi:10.1103/PhysRevC.80.024306

CrossRef Full Text | Google Scholar

38. Dronchi ND. Proton-decay branches and structures in ⁷Li and neutron-poor nuclides around calcium. Phd thesis. Saint Louis, MO: Washington University (2024). Available from: https://openscholarship.wustl.edu/art_sci_etds/3277/.

Google Scholar