Learning from knockout reactions using a dispersive optical model

We present the empirical dispersive optical model (DOM) as applied to direct nuclear reactions. The DOM links both scattering and bound-state experimental data through a dispersion relation, which allows for fully consistent, data-informed predictions for nuclei where such data exist. In particular, we review investigations of the electron-induced proton knockout reaction from both ⁴⁰Ca and ⁴⁸Ca in a distorted-wave impulse approximation (DWIA) utilizing the DOM for a fully consistent description. Viewing these reactions through the lens of the DOM allows us to connect the documented quenching of spectroscopic factors with the increased high-momentum proton content in neutron-rich nuclei. A similar DOM-DWIA description of the proton-induced knockout from ⁴⁰Ca, however, does not currently fit in the consistent story of its electron-induced counterpart. With the main difference in the proton-induced case being the use of an effective proton–proton interaction, we suggest that a more sophisticated in-medium interaction would produce consistent results.

1 Introduction

Independent particle models (IPMs) provide a simplified view of the nucleus in which correlations are neglected and all orbitals are completely filled up to the Fermi level according to the Pauli principle. However, due to residual interactions, orbitals below the Fermi energy are depleted, while those above it are filled. Knockout reactions, in which a nucleon is removed from a nuclear target after collision with a projectile, are suitable for studying this distortion of the Fermi sea. The importance of the $(e,e^{\prime }p)$ reaction in clarifying the details of this rearrangement near the Fermi energy is well-established and initially reviewed in [1]. Subsequent high-resolution work at the Nikhef facility in Amsterdam then provided a detailed view of the limitations of the IPMs in describing closed-shell nuclei [2–10]. The primary interaction in this reaction is electromagnetic and well-understood so that at sufficient high-electron beam energy, a distorted-wave impulse approximation (DWIA) provides an excellent reaction model [11–14].

In the traditional application of the DWIA to $(e,e^{\prime }p)$ cross sections, the Nikhef group typically utilized a global optical potential at the energy of the outgoing proton to describe the distorted wave. The overlap function from the ground state to the relevant state in the nucleus with one proton removed was obtained from a standard Woods–Saxon potential, with the depth adjusted to the separation energy and the radius constrained by the momentum dependence of the observed cross section. The cross sections obtained for targets consisting of closed shell nuclei then typically require a scaling factor of 0.6–0.7 to generate an accurate description of the data [9]. This scaling factor, usually referred to as the (reduced) spectroscopic factor, corresponds to the normalization of the overlap function between the target ground state and the excited state of the recoiling $A-1$ nucleus. A spectroscopic factor less than 1 indicates a divergence from the IPM. Furthermore, the data show that additional removal strength with essentially the same overlap function is located at nearby energies, providing clear evidence of the fragmentation of the single-particle strength [5, 15].

It has been argued in the literature that spectroscopic factors, while representing a useful concept, are not observables [16]. No doubt the $(e,e^{\prime }p)$ reaction provides the cleanest probe of removal probabilities. A similar approach in atoms for the $(e,2e)$ reaction supports this claim (see [17]). Apart from assessing the accuracy of the DWIA method for the $(e,e^{\prime }p)$ reaction, it is also necessary to clarify the validity of the chosen nuclear wave functions of the Nikhef analysis. We note that separate structure wave functions (phenomenological overlap function) and unrelated distorted scattering waves obtained from local optical potentials were employed. The dispersive optical model (DOM), which was first proposed by Mahaux and reviewed in [18], provides an approach to clarify these issues. In this article, we review the application of the DOM to DWIA calculations of knockout reactions [19–21]. Recent implementations of the DOM have introduced fully nonlocal dispersive potentials [22, 23], allowing additional data to be included in the description, like the particle number and the nuclear charge density, which were not considered in [18]. It is thus possible to extract all nuclear ingredients needed for a DWIA calculation of $(e,e^{\prime }p)$ from a DOM that is constrained by all available elastic nucleon scattering data, as well as separation energies, particle number, ground-state binding energy, charge radius, and the nuclear charge density for ⁴⁰Ca and ⁴⁸Ca in our case. Indeed, the distorted outgoing proton wave and the overlap function with its implied normalization are all provided by the DOM to allow for a consistent description of both ⁴⁰Ca$(e,e^{\prime }p)$ ³⁹K and ⁴⁸Ca$(e,e^{\prime }p)$ ⁴⁷K cross sections. The states analyzed for this reaction are the ground and first excited states of ³⁹K and ⁴⁷K, which correspond to the $0\mathrm{d}3/2$ and $1\mathrm{s}1/2$ valence hole states in the IPSM.

Although stable targets corresponding to closed-shell nuclei have been investigated using the $(e,e^{\prime }p)$ reaction, corresponding results for exotic nuclei are not available and may never be. Alternative reactions have been explored in inverse kinematics at rare isotope facilities. For example, the heavy-ion nucleon knockout reaction was employed by the researchers of the National Superconducting Cyclotron Laboratory at Michigan State University [24, 25]. The results suggested a strong dependence of the removal probability on the difference in separation energies between minority and majority species. The analysis of these data for open-shell nuclei relies on small model space shell model calculations, which already allow for partial orbital occupancy. The resulting reduction factors for overlap functions similarly generated as for the $(e,e^{\prime }p)$ reaction yield values close to 1 for the removal of valence majority nucleons and a strong suppression for the corresponding minority nucleons. The obtained results for closed-shell nuclei, with respect to the IPM description, are consistent with the $(e,e^{\prime }p)$ results mentioned above. This dependence on nucleon asymmetry is not consistent with the corresponding results of transfer reactions reviewed in [26] or the single-nucleon removal experiments recently reported in [27, 28]. At this time, no clear consensus has been reached on this intriguing difference. A comprehensive status report of these different approaches containing a theoretical background was reported in [29]. We provide an additional perspective on this situation based on our DOM analyses of ⁴⁰Ca$(e,e^{\prime }p)$ ³⁹K and ⁴⁸Ca$(e,e^{\prime }p)$ ⁴⁷K.

The electron-induced proton knockout reaction, $(e,e^{\prime }p)$, has been considered the cleanest spectroscopic method for decades. An alternative approach is proton-induced knockout or $(p,2p)$, which, despite some concerns about uncertainties [29–36], has been established as a complementary spectroscopic tool to $(e,e^{\prime }p)$ with approximately 15% uncertainty for incident energy above 200 MeV [36]. Although the $(e,e^{\prime }p)$ reaction involves one proton distorted wave, there are three such components in the $(p,2p)$ reaction. In addition, the interaction responsible for the transition to the final state, apart from being fundamentally two-body in nature, involves an in-medium proton–proton $(pp)$ interaction. The $pp$ interaction is not nearly as well-understood as the electromagnetic transition operator $(ep)$ in the $(e,e^{\prime }p)$ reaction, which is a predominantly one-body operator.

Using the same DOM bound-state and scattering wave functions that were employed in the DWIA analysis of ⁴⁰Ca${(e,e^{\prime }p)}^{39}$K, we performed a DWIA calculation of ⁴⁰Ca${(p,2p)}^{39}$K in [21]. This was not only the first DWIA calculation of ⁴⁰Ca${(p,2p)}^{39}$K to utilize consistent nuclear ingredients but also the first time that the distorted waves of the incoming and outgoing protons were generated by a nonlocal optical potential. The resulting analysis pointed to an inconsistency between the electron-induced and proton-induced knockout reactions; although the DOM-provided spectroscopic factor of 0.71 reproduces the $(e,e^{\prime }p)$ data, this factor had to be further reduced to 0.56 to reproduce the $(p,2p)$ data. Since the only difference between the descriptions of these two reactions is the $ep$ interaction vs the $pp$ interaction, the inevitable conclusion is that a further study of the in-medium $pp$ interaction is required. We note that transfer reactions have also been studied with DOM ingredients [37–39], but such studies require additional analysis of the reaction model, although applying current nonlocal DOM potentials may provide useful insights.

The underlying Green’s function formalism of the single-particle propagator is presented in Section 2.1, while the DOM framework is introduced in Section 2.2. The application of the DOM to the $(e,e^{\prime }p)$ reactions is described in Section 3. Results for the ⁴⁰Ca$(e,e^{\prime }p)$ and ⁴⁸Ca$(e,e^{\prime }p)$ reactions are presented in Sections 3.1, 3.2, respectively. A discussion of the $(p,2p)$ results employing DOM ingredients is provided in Section 4. Conclusions and some outlook are presented in Section 5.

2 Theory

This section is organized to provide brief introductions into the underlying theory of the DOM.

2.1 Single-particle propagator

The single-particle propagator describes the probability amplitude for adding (removing) a particle in state $\alpha$ at one time to (from) the non-degenerate ground state and propagating on top of that state until a later time when it is removed (added) in state $\beta$ [17]. In addition to the conserved orbital and total angular momentum ($\ell$ and $j$, respectively), the labels $\alpha$ and $\beta$ in Equation 1 refer to a suitably chosen single-particle basis. We employed a coordinate-space basis in our original ⁴⁸Ca calculation in [40], but we have switched to a Lagrange basis [41] in all subsequent calculations (including that of ²⁰⁸Pb from [42]). It is convenient to work with the Fourier-transformed propagator in the energy domain:

$\begin{array}{ll}{G}_{\ell j}\left(\alpha ,\beta ;E\right)\hfill & =\langle {\mathrm{\Psi }}_0^A|a_{\alpha \ell j}\frac{1}{E-\left(\widehat{H}-E_0^A\right)+i\eta }{a}_{\beta \ell j}^{†}|{\mathrm{\Psi }}_0^A\rangle \\ \hfill & +\langle {\mathrm{\Psi }}_0^A|a_{\beta \ell j}^{†}\frac{1}{E-\left(E_0^A-\widehat{H}\right)-i\eta }{a}_{\alpha \ell j}|{\mathrm{\Psi }}_0^A\rangle ,\hfill \end{array}(1)$

with $E_0^A$ representing the energy of the non-degenerate ground state $|{\mathrm{\Psi }}_0^A\rangle$. Many interactions can occur between the addition and removal of the particle (or vice versa), all of which need to be considered to calculate the propagator. No assumptions about the detailed form of the Hamiltonian $\widehat{H}$ need be made for the present discussion, but it is assumed that a meaningful Hamiltonian exists that contains two-body and three-body contributions. The application of perturbation theory then leads to the Dyson equation [17], which is given by

$G_{\ell j}\left(\alpha ,\beta ;E\right)=G_{\ell }^{\left(0\right)}\left(\alpha ,\beta ;E\right)+{\displaystyle \sum _{\gamma ,\delta }}{G}_{\ell }^{\left(0\right)}\left(\alpha ,\gamma ;E\right){\mathrm{\Sigma }}_{\ell j}^{*}\left(\gamma ,\delta ;E\right)G_{\ell j}\left(\delta ,\beta ;E\right),(2)$

where $G_{\ell }^{(0)}(\alpha ,\beta ;E)$ corresponds to the unperturbed propagator (the propagator derived from the unperturbed Hamiltonian, $H_0$, which in the DOM corresponds to the kinetic energy) and ${\mathrm{\Sigma }}_{\ell j}^{*}(\gamma ,\delta ;E)$ is the irreducible self-energy [17]. The hole spectral density for energies below ${\epsilon }_F$ is obtained from:

$S_{\ell j}^h\left(\alpha ,\beta ;E\right)=\frac{1}{\pi }\mathrm{I}\mathrm{m}{G}_{\ell j}\left(\alpha ,\beta ;E\right),(3)$

where the $h$ superscript signifies it as the hole spectral amplitude. For brevity, we drop this superscript for the rest of this review. The diagonal element of Equation 3 is known as the (hole) spectral function identifying the probability density for the removal of a single-particle state with the quantum number $\alpha \ell j$ at energy $E$. The single-particle density distribution can be calculated from the hole spectral function as

${\rho }_{\ell j}^{\left(p,n\right)}\left(r\right)={\displaystyle \sum _{\ell j}}\left(2j+1\right){\int }_{-\infty }^{{\epsilon }_F}dE{S}_{\ell j}^{\left(p,n\right)}\left(r,r;E\right),(4)$

where the $(p,n)$ superscript refers to protons or neutrons and ${\epsilon }_F=\frac{1}{2}(E_0^{A+1}-E_0^{A-1})$ is the average Fermi energy, which separates the particle and hole domains [17]. The number of protons and neutrons $(Z,N)$ is calculated by integrating ${\rho }_{\ell j}^{(p,n)}(r)$ over all spaces. In addition to the particle number, the total binding energy can be calculated from the hole spectral function using the Migdal–Galitski sum rule [17]:

$E_0^{N,Z}=\frac{1}{2}{\displaystyle \sum _{\alpha \beta }}{\int }_0^{{\epsilon }_F}dE\left[⟨\alpha |\widehat{T}|\beta ⟩S^h\left(\alpha ,\beta ;E\right)+{\delta }_{\alpha \beta }E{S}^h\left(\alpha ,\alpha ;E\right)\right].(5)$

The expression in Equation 5 assumes that the dominant contribution involves the two-nucleon interaction [43, 44].

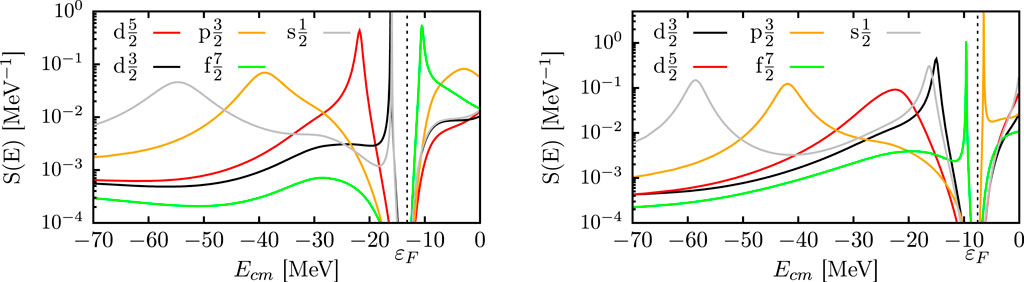
To visualize the spectral function of Equation 3, it is useful to sum (or integrate) over the basis variables, $\alpha$ so that only energy dependence, $S_{\ell j}(E)$, remains. The spectral strength $S_{\ell j}(E)$ is the contribution at energy $E$ to the occupation from all orbitals with the angular momentum $\ell j$. It reveals that the strength for a shell can be fragmented rather than isolated at the independent-particle model (IPM) energy levels. Figure 1 shows the spectral strength of a representative set of proton (panel (a)) and neutron (panel (b)) orbits in ⁴⁸Ca that would be considered bound in the IPM. The locations of the peaks shown in Figure 1 correspond to the energies of discrete bound states with one nucleon removed. For example, the s$1/2$ spectral function shown in Figure 1 has two peaks below ${\epsilon }_F$ that correspond to the 0s$1/2$ and 1s$1/2$ quasihole states, while the f$7/2$ spectral function has a peak below (neutrons) and above (protons) ${\epsilon }_F$ that corresponds to the 0f$7/2$ quasihole/particle state. The wave functions of these quasihole/particle states can be obtained by transforming the Dyson equation into a nonlocal Schrödinger-like equation by disregarding the imaginary part of ${\mathrm{\Sigma }}^{*}(\alpha ,\beta ;E)$:

${\displaystyle \sum _{\gamma }}\langle \alpha |T_{\ell }+\mathrm{R}\mathrm{e}{\mathrm{\Sigma }}_{\ell j}^{*}\left({\epsilon }_{\ell j}^n\right)|\gamma \rangle {\psi }_{\ell j}^n\left(\gamma \right)={\epsilon }_{\ell j}^n{\psi }_{\ell j}^n\left(\alpha \right),(6)$

where $\langle \alpha |T_{\ell }|\gamma \rangle$ is the kinetic-energy matrix element, including the centrifugal term. The wave function, ${\psi }_{\ell j}^n(\alpha )$, is the overlap between the $A$ and $A-1$ systems and the corresponding energy, ${\epsilon }_{\ell j}^n$, is the energy required to remove a nucleon with the particular quantum numbers $n\ell j$:

${\psi }_{\ell j}^n\left(\alpha \right)=\langle {\mathrm{\Psi }}_n^{A-1}|a_{\alpha \ell j}|{\mathrm{\Psi }}_0^A\rangle ,{\epsilon }_{\ell j}^n=E_0^A-E_n^{A-1}.(7)$

Figure 1

Figure 1. Proton (left) and neutron (right) spectral functions of a representative set of $\ell j$ shells in ⁴⁸Ca. The particle states are differentiated from the hole states by the dotted line representing ${\epsilon }_F$. Figure adapted from [20].

When solutions to Equations 6, 7 are found near the Fermi energy, where there is naturally no imaginary part of the self-energy, the normalization of the quasihole is well-defined as the spectroscopic factor:

${\mathcal{Z}}_{\ell j}^n={\left(1-\frac{\partial {\mathrm{\Sigma }}_{\ell j}^{*}\left({\alpha }_{qh},{\alpha }_{qh};E\right)}{\partial E}{|}_{{\epsilon }_{\ell j}^n}\right)}^{-1},(8)$

where ${\alpha }_{qh}$ corresponds to the quasihole state that solves Equation 6. The quasihole peaks in shown Figure 1 become narrower as the levels approach ${\epsilon }_F$, which is a consequence of the imaginary part of the irreducible self-energy decreasing when approaching ${\epsilon }_F$. The last mostly occupied neutron level in panel (b) of Figure 1 (0f$7/2$) has a spectral function that is essentially a delta function peaked at its energy level, where the imaginary part of the self-energy vanishes. Valence proton hole orbits (1s$1/2$ and 0 days $3/2$) exhibit the same behavior. For these orbitals, the strength of the spectral function at the peak corresponds to the spectroscopic factor shown in Equation 8. This spectroscopic factor is the very same we employ in the $(e,e^{\prime }p)$ calculations, which is discussed in Section 3.1 (see also [19, 20].

2.2 Dispersive optical model

The Dyson equation, Equation 2, simplifies the complicated task of calculating $G_{\ell j}(\alpha ,\beta ;E)$ from Equation 1 to find a suitable ${\mathrm{\Sigma }}^{*}(\alpha ,\beta ;E)$ to invert. It was recognized long ago that ${\mathrm{\Sigma }}^{*}(\alpha ,\beta ;E)$ represents the potential that describes elastic-scattering observables [45]. The link with the potential at negative energy is then provided by the Green’s function framework, as realized by Mahaux and Sartor, who introduced the DOM, as reviewed in [18]. The analytic structure of the nucleon self-energy allows one to apply the dispersion relation, which relates the real part of the self-energy at a given energy to a dispersion integral of its imaginary part over all energies. The energy-independent correlated Hartree–Fock (HF) contribution [17] is removed by employing a subtracted dispersion relation with the Fermi energy used as the subtraction point [18]. The subtracted form has the additional advantage of focusing on energies closer to the Fermi energy, for which more experimental data are available. We still refer to the energy-independent part of our potential as the HF term, and is sufficiently attractive to bind the relevant levels at exactly the correct energies. In practice, the imaginary part is assumed to reach the Fermi energy on both sides while being extremely small in its vicinity. The subtracted form of the dispersion relation employed in this work is given by

$\begin{array}{ll}\hfill \mathrm{R}\mathrm{e}{\mathrm{\Sigma }}^{*}\left(\alpha ,\beta ;E\right)& =\mathrm{R}\mathrm{e}{\mathrm{\Sigma }}^{*}\left(\alpha ,\beta ;{\epsilon }_F\right)\hfill \\ \hfill & -\mathcal{P}{\int }_{{\epsilon }_F}^{\infty }\frac{d{E}^{\prime }}{\pi }\mathrm{I}\mathrm{m}{\mathrm{\Sigma }}^{*}\left(\alpha ,\beta ;E^{\prime }\right)\left[\frac{1}{E-E^{\prime }}-\frac{1}{{\epsilon }_F-E^{\prime }}\right]\hfill \\ \hfill & +\mathcal{P}{\int }_{-\infty }^{{\epsilon }_F}\frac{d{E}^{\prime }}{\pi }\mathrm{I}\mathrm{m}{\mathrm{\Sigma }}^{*}\left(\alpha ,\beta ;E^{\prime }\right)\left[\frac{1}{E-E^{\prime }}-\frac{1}{{\epsilon }_F-E^{\prime }}\right],\hfill \end{array}(9)$

where $\mathcal{P}$ is the principal value. The static term, $\mathrm{R}\mathrm{e}{\mathrm{\Sigma }}^{*}(\alpha ,\beta ;{\epsilon }_F)$, is denoted by ${\mathrm{\Sigma }}_{\text{HF}}$ from here on. Equation 9 constrains the real part of ${\mathrm{\Sigma }}^{*}(\alpha ,\beta ;E)$ by empirical information on the HF and imaginary parts, which are closely tied to experimental data. Initially, standard functional forms for these terms were introduced by Mahaux and Sartor, who also cast the DOM potential in a local form by a standard transformation, which turns a nonlocal static HF potential into an energy-dependent local potential [46]. Such an analysis was extended in [47, 48] to a sequence of Ca isotopes and in [49] to semi-closed-shell nuclei heavier than Ca. The transformation to the exclusive use of local potentials precludes a proper calculation of the nucleon particle number and expectation values of the one-body operators, like the charge density in the ground state (see Equation 4). This obstacle was eliminated in [50], but it was shown that the introduction of nonlocality in the imaginary part was still necessary in order to accurately account for the particle number and the charge density [22]. Theoretical work provided further support for this introduction of a nonlocal representation of the imaginary part of the self-energy [51, 52]. A review detailing these developments was published in [23].

2.2.1 Functional form of the DOM self-energy

We employ a nonlocal representation of the self-energy, following [22], where ${\mathrm{\Sigma }}_{\text{HF}}(\mathit{r},{\mathit{r}}^{\prime })$ and $\mathrm{I}\mathrm{m}\mathrm{\Sigma }(\mathit{r},{\mathit{r}}^{\prime };E)$ are parametrized, and the energy dependence of the real part, $\mathrm{R}\mathrm{e}\mathrm{\Sigma }(\mathit{r},{\mathit{r}}^{\prime };E)$, is generated from the dispersion relation shown in Equation 9. The HF term consists of a volume term, spin-orbit term, and a wine-bottle-shape generating term [53]:

${\mathrm{\Sigma }}_{HF}\left(\mathit{r},{\mathit{r}}^{\prime }\right)=V_{\text{vol}}\left(\mathit{r},{\mathit{r}}^{\prime }\right)+V_{\text{so}}\left(\mathit{r},{\mathit{r}}^{\prime }\right)+V_{\text{wb}}\left(\mathit{r},{\mathit{r}}^{\prime }\right)+\delta \left(\mathit{r}-{\mathit{r}}^{\prime }\right)V_C\left(r\right),(10)$

where the Coulomb potential, $V_C(r)$, is also included. The radial part of the potentials in Equation 10 takes the following form:

$V_{\text{vol}}\left(\mathit{r},{\mathit{r}}^{\prime }\right)=V^{\text{vol}}f\left(\tilde{r},r_{\left(p,n\right)}^{\text{HF}},a^{\text{HF}}\right)H\left(\mathit{s};{\beta }^{\text{HF}}\right),(11)$

where $V^{\text{vol}}$ is a parameter that determines the depth of the potential and $r_{(p,n)}^{\text{HF}}$, $a^{\text{HF}}$, and ${\beta }^{\text{HF}}$ are parameters that control the shape of the Woods–Saxon form factor $f$ and Perey–Buck-shaped [46] nonlocality $H$:

$\begin{array}{c}f\left(r,r_i,a_i\right)={\left[1+\exp \left(\frac{r-r_i{A}^{1/3}}{a_i}\right)\right]}^{-1}\hfill \\ H\left(\mathit{s};\beta \right)=\exp \left(-{\mathit{s}}^2/{\beta }^2\right)/\left({\pi }^{3/2}{\beta }^3\right)\hfill \end{array}(12)$

and

$\tilde{r}=\frac{r+r^{\prime }}{2}\mathit{s}=\mathit{r}-{\mathit{r}}^{\prime }.(13)$

The radial form of $V_{\text{wb}}$ and $V_{\text{so}}$ are similar to those expressed in Equations 11–13; their explicit forms can be found in [54]. The imaginary self-energy consists of the volume, surface, and spin-orbit terms:

$\begin{array}{ll}\hfill \mathrm{I}\mathrm{m}\mathrm{\Sigma }\left(\mathit{r},{\mathit{r}}^{\prime };E\right)& =-W_{0\pm }^{\mathit{vol}}\left(E\right)f\left(\tilde{r};r_{\pm }^{\mathit{vol}};a_{\pm }^{\mathit{vol}}\right)H\left(\mathit{s};{\beta }^{\mathit{vol}}\right)\hfill \\ \hfill & +4a_{\pm }^{\mathit{sur}}{W}_{\pm }^{\mathit{sur}}\left(E\right)H\left(\mathit{s};{\beta }^{\mathit{sur}}\right)\frac{d}{d\tilde{r}}f\left(\tilde{r},r_{\pm }^{\mathit{sur}},a_{\pm }^{\mathit{sur}}\right)+\mathrm{I}\mathrm{m}{\mathrm{\Sigma }}_{so}\left(\mathit{r},{\mathit{r}}^{\prime };E\right),\hfill \end{array}(14)$

where $W_{0\pm }^{\mathit{vol}}(E)$ and $W_{\pm }^{\mathit{sur}}\left(E\right)$ are energy-dependent depths of the volume and surface potentials, respectively, and the $\pm$ subscript indicates that there are different forms used above and below the Fermi energy (see [54] for the exact forms of the potentials in Equation 14). When considering asymmetric nuclei, such as ⁴⁸Ca, additional terms proportional to the asymmetry, ${\alpha }_{\text{asy}}=\frac{N-Z}{A}$, are added to ${\mathrm{\Sigma }}_{\text{HF}}(\mathit{r},{\mathit{r}}^{\prime })$ and $\mathrm{I}\mathrm{m}\mathrm{\Sigma }(\mathit{r},{\mathit{r}}^{\prime };E)$ for a Lane-like representation [55]. These asymmetric terms introduce additional parameters describing both their radial shape and energy-dependent depths [54]. For the full list of parameters used in ⁴⁸Ca, see [20, 54].

As mentioned previously, it was typical in the past to replace nonlocal potentials by local, energy-dependent potentials [17, 18, 46, 56]. The introduction of an energy dependence alters the dispersive correction from Equation 9 and distorts normalization, leading to incorrect spectral functions and related quantities [50]. Thus, a nonlocal implementation permits the self-energy to accurately reproduce important observables such as charge density, particle number, and ground-state binding energy.

To use the DOM self-energy for predictions, the parameters of the self-energy are constrained through weighted ${\chi }^2$ minimization (using Powell’s method [57]) by measurements of elastic differential cross sections $(\frac{d\sigma }{d\mathrm{\Omega }})$, analyzing powers $(A_{\theta })$, reaction cross sections $({\sigma }_{\text{react}})$, total cross sections $({\sigma }_{\text{tot}})$, charge density $({\rho }_{\text{ch}})$, energy levels $({\epsilon }_{n\ell j})$, particle number, and the root mean square charge radius $(R_{\text{ch}})$. The angular dependence of $\mathrm{\Sigma }(\mathit{r},{\mathit{r}}^{\prime };E)$ is represented in a partial-wave basis, and the radial component is represented in a Lagrange basis using Legendre and Laguerre polynomials for scattering and bound states, respectively. The bound states are found by diagonalizing the Hamiltonian in Equation 6, the propagator is found by inverting the Dyson equation, Equation 2, while all scattering calculations are done in the framework of $R$-matrix theory [41].

The reproduction of all available experimental data (see [19, 20, 22, 40] for comparisons to training data) indicates that we have realistic self-energies of ⁴⁰Ca and ⁴⁸Ca capable of describing both bound-state and scattering processes. A parallel DOM analysis of these and other nuclei was conducted using Markov chain Monte Carlo (MCMC) methods to optimize the potential parameters employing the same experimental data and a very similar functional form but with a reduced number of parameters. All observables from this MCMC fit fell within one standard deviation of those presented above [58, 59].

3 DWIA description of the $(e,e^{\prime }p)$ cross section

In the past, $(e,e^{\prime }p)$ cross sections obtained at Nikhef in Amsterdam have been successfully described by utilizing the DWIA. This description is expected to be particularly good when kinematics that emphasize the longitudinal coupling of the excitation operator, which is dominated by a one-body operator, are used. The Nikhef group was able to fulfill this condition by choosing kinematic conditions, in which the removed proton carried momentum parallel or antiparallel to the momentum of the virtual photon. Under these conditions, the transverse contribution involving the spin and possible two-body currents is suppressed. Therefore, the process can be interpreted as requiring an accurate description of the transition amplitude from the resulting excited state to the ground state by a known one-body operator. This transition amplitude is contained in the polarization propagator, which can be analyzed with a many-body description involving a linear response [17]. Such an analysis demonstrates that the polarization propagator contains two contributions. The first term describes the propagation of a particle and a hole as they interact with the medium but not with each other. The other term involves their interaction. The latter term dominates at low energy when the proton that absorbs the photon participates in collective excitations like surface modes and giant resonances.

When the proton receives energy on the order of 100 MeV, it is expected that the resulting excited state can be well-approximated by the dressed particle and dressed hole excitation [60]. When strong transitions are considered, like in the present work, two-step processes have only minor influence [2, 5]. This interpretation forms the basis of the DWIA applied to exclusive $(e,e^{\prime }p)$ cross sections obtained by the Nikhef group. The ingredients of the DWIA, therefore, require a proton distorted wave describing the outgoing proton at the appropriate energy and an overlap function with its normalization for the removed proton. The distorted wave was typically obtained from a standard (local) global optical potential shown in [61] for ⁴⁰Ca. The overlap function was obtained by adjusting the radius of a local Woods–Saxon potential to the shape of the $(e,e^{\prime }p)$ cross section while adjusting its depth to the separation energy of the hole. Its normalization was obtained by adjusting the calculated DWIA cross section to the actual data [9]. Standard nonlocality corrections were applied to both the outgoing and removed proton wave functions [62], effectively making the bound-state wave function the solution of a nonlocal potential. We observe that such corrections are $\ell$-independent and, therefore, different from the nonlocal DOM implementation.

In order to describe the $(e,e^{\prime }p)$ reaction, the incoming electron, the electron–proton interaction, the outgoing electron, and the outgoing proton must be addressed. The cross section is calculated from the hadron tensor, $W^{\mu \nu }$, which contains matrix elements of the nuclear charge-current density, $J^{\mu }$ [14]. Using DWIA, which assumes that the virtual photon exchanged by the electron couples to the same proton that is detected [11, 13], the nuclear current can be written as

$J^{\mu }\left(\mathit{q}\right)=\int d\mathit{r}{e}^{i\mathit{q}\cdot \mathit{r}}{\chi }_{E\ell j}^{\left(-\right)*}\left(\mathit{r}\right){\left({\widehat{J}}_{\text{eff}}^{\mu }\right)}_{E\ell j}\left(\mathit{r}\right){\psi }_{\ell j}^n\left(\mathit{r}\right)\sqrt{{\mathcal{Z}}_{\ell j}^n},(15)$

where ${\chi }_E^{(-)*}(\mathit{r})$ is the outgoing proton distorted wave [14], ${\psi }_{\ell j}^n$ is the overlap function, ${\mathcal{Z}}_{\ell j}^n$ is its normalization, $\mathit{q}={\mathit{k}}_{\mathit{f}}-{\mathit{k}}_{\mathit{i}}$ is the electron three-momentum transfer, and ${\widehat{J}}_{\text{eff}}^{\mu }$ is the effective current operator [14]. The incoming and outgoing electron waves are treated within the effective momentum approximation, where the waves are represented by plane waves with effective momenta to account for distortion from the interaction with the target nucleus [12].

$k_{i\left(f\right)}^{\text{eff}}=k_{i\left(f\right)}+\int d\mathit{r}{V}_c\left(\mathit{r}\right){\varphi }_{\ell j}^2\left(\mathit{r}\right),(16)$

where $V_c(\mathit{r})$ is the Coulomb potential of the target nucleus. This alters Equation 15 by replacing $\mathit{q}$ with the ${\mathit{q}}_{\text{eff}}$ in Equation 16.

In the plane-wave impulse approximation (PWIA), in which the outgoing proton wave is approximated by a free scattering (plane) wave, the $(e,e^{\prime }p)$ cross section can be factorized into an off-shell electron–proton cross section and the spectral function [14]:

$S\left(E_m,{\mathit{p}}_m\right)=\frac{1}{k{\sigma }_{ep}}\frac{d^6\sigma }{d{E}_{e^{\prime }}d{\mathrm{\Omega }}_{e^{\prime }}d{E}_{p}d{\mathrm{\Omega }}_p}.(17)$

The off-shell electron–proton cross section, ${\sigma }_{ep}$, is approximated from the on-shell electron–proton cross section using the ${\sigma }_{\text{cc}1}$ model, as proposed in [63]. The factorization shown in Equation 17 does not hold true for the DWIA, but $(e,e^{\prime }p)$ cross sections, both experimental and theoretical, are typically divided by ${\sigma }_{\text{cc}1}$ when displayed. In principle, corrections due to two-step processes could be considered, but they are estimated to make negligible contributions for the transitions considered in this study [5].

The calculations of the $(e,e^{\prime }p)$ cross sections in [19] were performed by employing DOM ingredients that were constrained by the experimental data discussed in Section 2.2. Appropriate distorted waves and overlap functions with their normalization were thus generated that allow for a DWIA description of the exclusive $(e,e^{\prime }p)$ cross section for valence holes in ⁴⁰Ca. An agreement with cross sections, therefore, not only supports the description of the reaction in a DWIA framework but also confirms the overall consistency of the DOM approach including its interpretation of the normalization of the overlap functions as spectroscopic factors that can be confronted with data.

3.1 ⁴⁰Ca${(e,e^{\prime }p)}^{39}$K

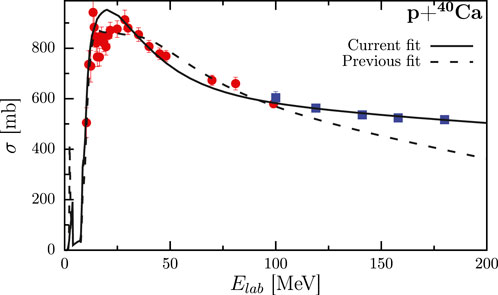
The first nonlocal DOM description of ⁴⁰Ca data is presented in [22]. Meanwhile, additional experimental higher-energy proton reaction cross sections [64] had been incorporated, which caused some adjustments of the DOM parameters compared to [22]. The updated parameters are collected in App. A of [19]. Adjusting the parameters from the previous values [22] to describe these additional experimental results leads to an equivalent description for all data except these reaction cross sections. These higher-energy data dictate that the proton reaction cross section remain flat for energies in the region of approximately 150 MeV, as shown in Figure 2. This means there is more absorption at higher energies than in the previous fit, leading to increased strength in the imaginary part of the self-energy. Due to the dispersion relation, Equation 9, this increases the spectral strength at positive energies when the Dyson equation is solved. The sum rule discussed in detail in [65], which relates to the integral over all energies of the strength of the valence holes, implies that strength is transferred from below the Fermi energy to the energies with an increased imaginary part. This resulting loss of strength below the Fermi energy reduces the spectroscopic factors by approximately 0.05 compared to the results reported in [22].

Figure 2

Figure 2. Proton reaction cross section for ⁴⁰Ca. The solid line represents the newest fit [19], while the dashed line depicts the original fit [22]. The circular data points were included in the original fit, while the square data points [64] were added in the newest fit. Figure adapted from [19].

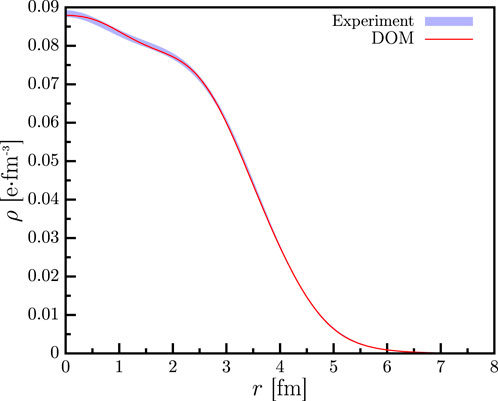
To accurately calculate the $(e,e^{\prime }p)$ cross section in the DWIA, it is imperative that the DOM self-energy not only precisely generates available elastic scattering data but also bound-state information. This is due to the fact that the shape of the cross section is primarily determined by the bound-state overlap function [5]. Thus, not only should the experimental charge radius be reproduced but also the charge density should match the experimental data, as shown in Figure 3, where the DOM charge density is shown as the solid line and compared with the deduced charge density (Fourier–Bessel parametrization) obtained from [66] with the band representing the 1% error.

Figure 3

Figure 3. Experimental and fitted ⁴⁰Ca charge density. The solid line is calculated using the DOM propagator, while the experimental band represents the 1% error associated with the extracted charge density from elastic electron scattering experiments [66, 67]. Figure adapted from Ref. [19].

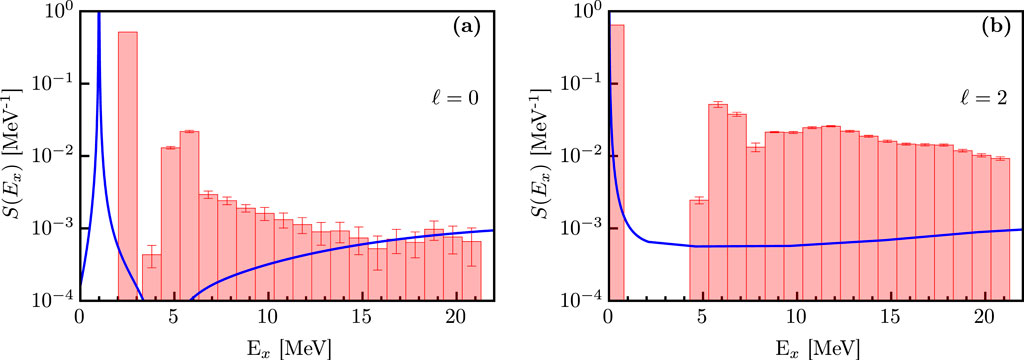
The ⁴⁰Ca DOM self-energy leads to the spectral strength distributions shown in Figure 4. The experimental bars are the results of an angular-momentum decomposition of the experimental spectral function at $T_p$ = 100 MeV, as described in [15]. The experimental distributions for $\ell =\mathrm{0,2}$ clearly show that the strength is already strongly fragmented at low energies. The main peak in each case represents the valence hole transition of interest. This fragmentation is smeared in the DOM via the non-zero imaginary component of the self-energy, which is why the DOM curves shown in Figure 4 are continuous rather than discrete. The imaginary part of the self-energy approaches 0 near ${\epsilon }_F$, which results in the sharp peaks of the DOM curve shown in Figure 4 (analogous to what is observed in Figure 1). The DOM, therefore, does not yet include the details of the low-energy fragmentation of the valence hole states, which requires the introduction of pole structure in the self-energy [68]. The spectroscopic factor of Equation 8 corresponds to the main peak of each distribution shown in Figure 4. It is calculated directly from the ⁴⁰Ca DOM self-energy, which results in values of 0.71 and 0.74 for the $0\mathrm{d}3/2$ and $1\mathrm{s}1/2$ peaks, respectively. The results are probed in more detail by analyzing the momentum distributions of the ⁴⁰Ca$(e,e^{\prime }p)$ ³⁹K reaction.

Figure 4

Figure 4. Spectral strength as a function of excitation energy for (A) the $1\mathrm{s}1/2$and (B) the $0\mathrm{d}3/2$proton orbitals, calculated from the DOM using Equation (3)) (solid line) and extracted from the ⁴⁰Ca$(e,e^{\prime }p)$ ³⁹K experiment [5, 15] (bars). The peaks in the DOM curves and experimental data correspond to the energies of the quasihole protons in ⁴⁰Ca. Notably, the experimental fragments in (B) above 4 MeV mostly correspond to $0\mathrm{d}5/2$strength. Figure adapted from [19].

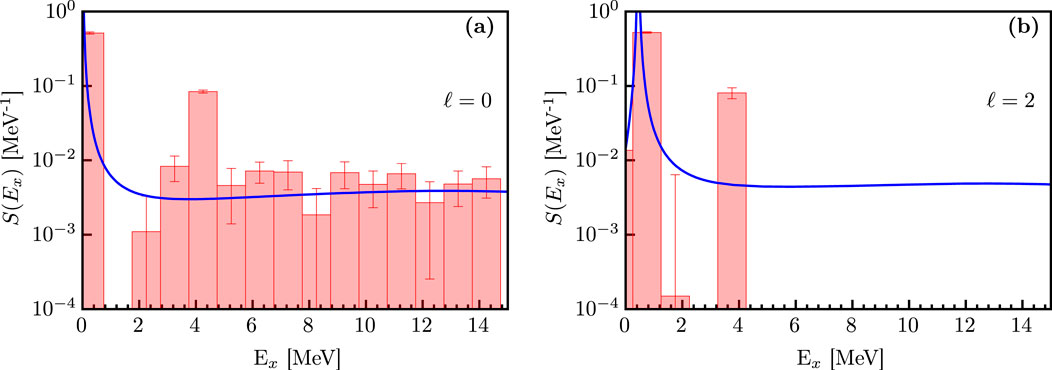
In the past, the DWIA calculations by the Nikhef group have been performed using the DWEEPY code [13]. The momentum distributions in [19] are calculated by adapting a recent version of the DWEEPY code [69] to use the DOM-bound states, distorted waves, and spectroscopic factors as inputs. Before confronting the DOM calculations with the experimental cross sections, it is necessary to consider the consequences of the low-energy fragmentation shown in Figure 4. For the $0\mathrm{d}3/2$ ground-state transition (panel (b) of Figure 4), there is a clear separation with higher-lying fragments, the majority of which cannot be distinguished from $0\mathrm{d}5/2$ contributions as the experiments did not provide the necessary polarization information. In addition, these higher-lying fragments appear to carry little $0\mathrm{d}3/2$ strength [70], so the DOM spectroscopic factor can, therefore, be directly used to calculate the cross section of the ground-state peak.

The situation is different for the $1\mathrm{s}1/2$ distribution, which, while dominated by the large fragment at 2.522 MeV, exhibits substantial surrounding strength, as shown in Figure 4a. These contributions come from other discrete poles in the propagator, reflecting the mixing of the $1\mathrm{s}1/2$ orbit to more complicated excitations nearby in energy. The origin of these additional discrete poles is not explicitly included in the DOM, although there is a smooth energy-dependent imaginary term in the self-energy to approximate their effect on the spectral strength [17]. This approximation is sufficient for discussing integrated values such as the charge density and particle number, but it falls short when considering the details of the low-energy fragmentation into discrete energies, as in the present situation. The calculated DOM spectroscopic factor, therefore, includes strength in the neighborhood of the quasihole energy, resulting in an inflated value. This effect is only noticeable in the $\ell =0$ case because there is a non-negligible amount of strength in the region near the peak. We turn to experimental data to account for this effect by enforcing that the ratio between the strength of the peak to the total spectral strength shown in the energy domain of Figure 4 is the same between the data as for the DOM:

$\frac{{\mathcal{Z}}_F^{\text{DOM}}}{\int dE{S}^{\text{DOM}}\left(E\right)}=\frac{{\mathcal{Z}}_F^{\text{exp}}}{\int dE{S}^{\text{exp}}\left(E\right)}.(18)$

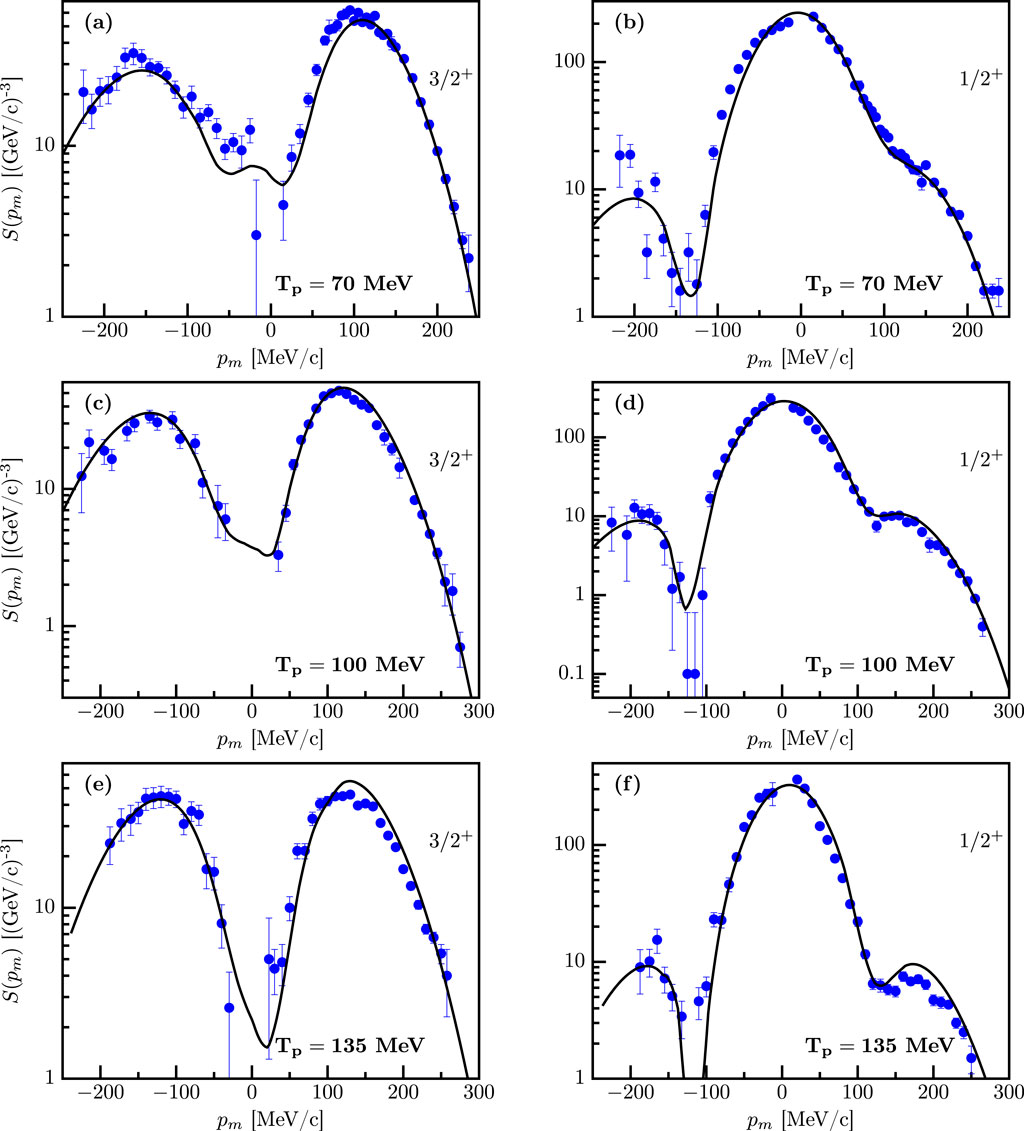
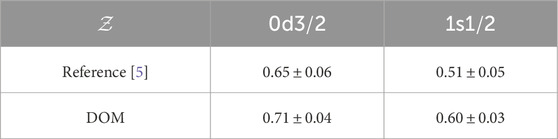
Accounting for the contributions to the momentum distribution from different energies by scaling the DOM spectroscopic factor is justified by observing that the shape of the momentum distribution calculated at similar energies is identical, with the strength being the only difference [5]. The scaling of the spectroscopic factor leads to a reduction from 0.74 to 0.60. As mentioned, no correction is needed for the $0\mathrm{d}3/2$ spectroscopic factor. The resulting momentum distributions are shown in Figure 5. The previous analysis of the Nikhef group at $T_p=100$ MeV [5] produced a comparable reproduction of the data with somewhat smaller spectroscopic factors, as shown in Table 1.

Figure 5

Figure 5. ⁴⁰Ca$(e,e^{\prime }p)$ ³⁹K spectral functions in parallel kinematics at an outgoing proton kinetic energies of 70, 100, and 135 MeV. The solid line is the calculation employing the DOM, while the points from the experiment are detailed in [5]. (A) Distribution for the removal of the $0\mathrm{d}3/2$. The curve contains the DWIA for the $3/2^{+}$ ground state including a spectroscopic factor of 0.71. (B) Distribution for the removal of the $1\mathrm{s}1/2$ proton with a spectroscopic factor of 0.60 for the $1/2^{+}$ excited state at 2.522 MeV. Panels (C) and (E) are the same as (A) except the outgoing proton energy is 100 MeV and 135 MeV, respectively. Panels (D) and (F) are the same as (A) except that the outgoing proton energy is 100 MeV and 135 MeV, respectively. Figure adapted from [19].

Table 1

Table 1. Comparison of spectroscopic factors deduced from the previous analysis [5] using the Schwandt optical potential [61] to the normalization of the corresponding overlap functions obtained in the present analysis from the DOM including an error estimate, as described in the text.

In order to estimate the uncertainty for the DOM spectroscopic factors, we followed the bootstrap method from [71], which was also employed in [40] to assess the uncertainty for the neutron skin in ⁴⁸Ca. New modified datasets were created from the original data by randomly renormalizing each angular distribution or excitation function within the experimental error to incorporate fluctuations from the systematic errors. The resulting uncertainties are listed in Table 1.

The DOM results yield at least as good agreement with the data as the standard analysis of [5] for the 100-MeV outgoing protons. The main difference in the description can be pinpointed to the use of nonlocal potentials to describe the distorted waves. Nonlocal potentials tend to somewhat suppress interior wave functions of scattering states and introduce an additional $\ell$ dependence, as compared to local potentials. We, therefore, concluded that this consistent treatment clarifies that spectroscopic factors will be larger by approximately 0.05 when the proper nonlocal dispersive potentials are employed.

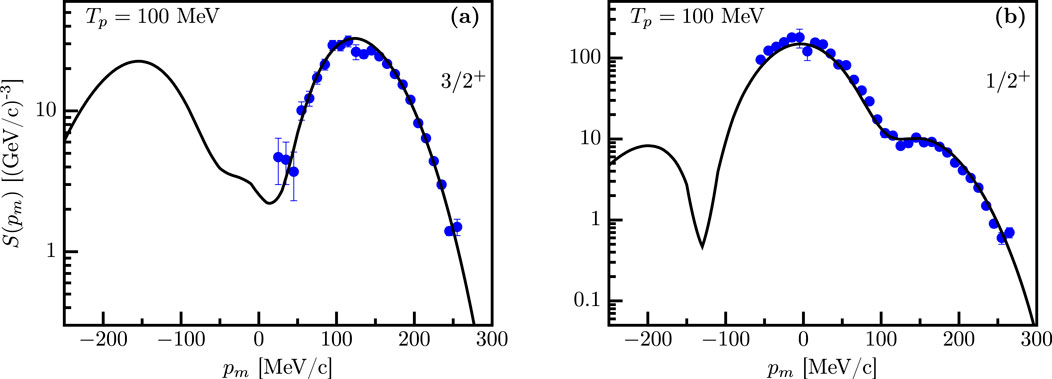
The DOM treatment of experimental data associated with both the particle and hole aspects of the single-particle propagator further allows for an assessment of the quality of the DWIA to describe exclusive $(e,e^{\prime }p)$ cross sections with outgoing proton energies of approximately 100 MeV. It is, therefore, fortunate that additional data were obtained at 70 and 135 MeV to further delineate the domain of validity for the DWIA description of the reaction. Figures 5A, B show the results when the DOM is employed at this lower energy for the two valence hole states in ³⁹K. The only difference in the DOM calculations for these cases is the energy of the outgoing proton wave function; the overlap functions and spectroscopic factors remain the same.

The agreement with the data at 135 MeV shown in Figures 5E, F is slightly worse but still acceptable. At this energy (and the corresponding value of the electron three-momentum transfer), the contribution of the transverse component of the excitation operator, where other mechanisms contribute in addition to those included in the present operator, will be larger. Given these results, it seems that parallel kinematics, with the longitudinal part of the operator dominating and proton energy of approximately 100 MeV, as chosen by the Nikhef group, is optimal for probing the removal probability of valence protons. We note that this can only be achieved if an analysis is conducted in which all nuclear constituents are provided by a nucleon self-energy constrained by all relevant available data, as in the DOM. The excellent agreement found here, therefore, supports the validity of the DOM approach, which can automatically account for the DWIA cross section in the domain where this approximation is expected to be valid.

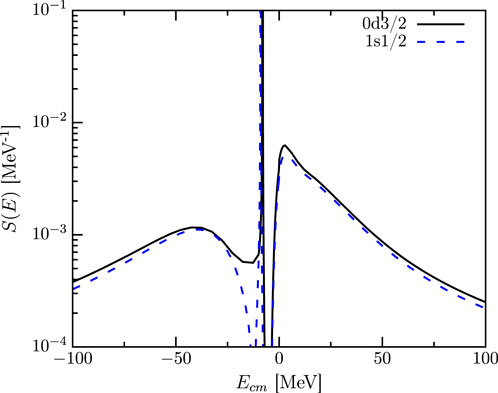
The DOM results also generate the complete spectral distribution for the $0\mathrm{d}3/2$ and $1\mathrm{s}1/2$ orbits according to

$S_{\ell j}^{n-}\left(E\right)={\displaystyle \sum _{\alpha ,\beta }}{\psi }_{\ell j}^n\left(\alpha \right)S_{\ell j}^h\left(\alpha ,\beta ;E\right){\psi }_{\ell j}^n\left(\beta \right)(19)$

and similarly for the strength above the Fermi surface [65]

$S_{\ell j}^{n+}\left(E\right)=\int dr{r}^2\int d{r}^{\prime }{r}^{\prime 2}{\psi }_{\ell j}^n\left(r\right)S_{\ell j}^p\left(r,r^{\prime };E\right){\psi }_{\ell j}^n\left(r^{\prime }\right),(20)$

where the actual procedure involves a double integral in coordinate space over the particle spectral amplitude. Distributions calculated using Equations 19, 20 are displayed in Figure 6 from −100 to 100 MeV. The energy axis refers to the $A-1$ system below the Fermi energy and the $A+1$ system above it. For clarity, a small imaginary strength in the self-energy near the Fermi energy was employed, providing the peaks a small width. The occupation probabilities are obtained from

$n_{\ell j}^n={\int }_{-\infty }^{{ϵ}_F}dE{S}_{\ell j}^{n-}\left(E\right).(21)$

For the 0d3/2 and 1s1/2 orbits, Equation 21 results in 0.80 and 0.82, respectively. The strength at negative energy not residing in the DOM peak, therefore, corresponds to 9% and 7%, respectively. This information is constrained by the proton particle number and the charge density. The strength above the Fermi energy is constrained by the elastic-scattering data and generates 0.17 and 0.15 for the $0\mathrm{d}3/2$ and $1\mathrm{s}1/2$ orbits, respectively, when Equation 22,

$d_{\ell j}^n={\int }_{{\epsilon }_F}^{\infty }dE{S}_{\ell j}^{n+}\left(E\right),(22)$

is employed up to 200 MeV. The sum rule given by Equation 23

$1=n_{\ell j}^n+d_{\ell j}^n=\langle {\mathrm{\Psi }}_0^A|a_{n\ell j}^{†}{a}_{n\ell j}+a_{n\ell j}{a}_{n\ell j}^{†}|{\mathrm{\Psi }}_0^A\rangle ,(23)$

associated with the anticommutation relation of the fermion operators, therefore, suggests that an additional 3% of the strength resides above 200 MeV, which is similar to what was found in [65]. Strength above the energy, where surface physics dominates, can be ascribed to the effects of short-range and tensor correlations. The main characterization of the strength distribution shown in Fig. 55 of [68] is therefore confirmed for ⁴⁰Ca. The present results, thus, suggest that it is possible to generate a consistent view of the strength distributions of these orbits while employing all the available experimental constraints. We, therefore, conclude that it is indeed quite meaningful to employ concepts like spectroscopic factors and occupation probabilities when discussing correlations in nuclei.

Figure 6

Figure 6. Spectral distribution of the $0\mathrm{d}3/2$ and $1\mathrm{s}1/2$ orbits as a function of energy. Additional strength outside this domain is not shown. Figure adapted from [19].

3.2 ⁴⁸Ca${(e,e^{\prime }p)}^{47}$K

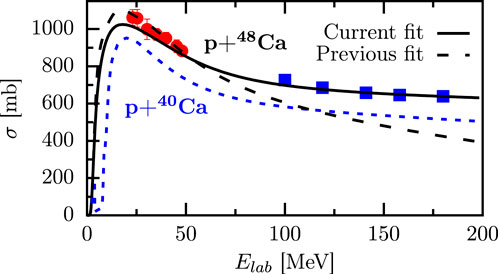
The first DOM fit of ⁴⁸Ca was published in [40]. However, just as in the case of ⁴⁰Ca in [19, 22], the proton reaction cross section is underestimated by approximately 200 MeV. Although there are no experimental data for ⁴⁸Ca at these energies, there is a data point at 700 MeV of the proton reaction cross section for ⁴⁰Ca and ⁴⁸Ca [72]. Comparing the available data for ${\sigma }_{\text{react}}^{40}(E)$ at 200 MeV and 700 MeV reveals that the reaction cross section essentially remains flat between these energies. It is reasonable to expect that ${\sigma }_{\text{react}}^{48}(E)$ assumes the same shape as ${\sigma }_{\text{react}}^{40}(E)$ at high energies. Thus, data points are extrapolated from the ⁴⁰Ca experimental data at energies above 100 MeV by applying the ratio that is seen in the 700 MeV data for ${\sigma }_{\text{react}}^{48}(E)/{\sigma }_{\text{react}}^{40}(E)$ [20]. The extrapolated points are shown as blue squares in Figure 7, while the updated fit is represented with the solid curve. The remainder of the fit did not change significantly from [40].

Figure 7

Figure 7. Proton reaction cross sections for ⁴⁸Ca and ⁴⁰Ca. The solid line represents the current ⁴⁸Ca fit [20], while the dashed line depicts the previous ⁴⁸Ca fit [40]. The dotted line represents the ⁴⁰Ca fit from [19]. The circular points are the same ⁴⁸Ca experimental data used in [49] and were included in the previous fit. The square points are extrapolated from the ${\sigma }_{\text{react}}^{40}(E)$ experimental data points at the corresponding energies and included in the current ⁴⁸Ca fit. Figure adapted from [20].

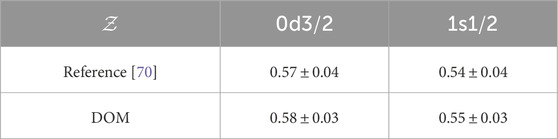
To analyze the proton spectroscopic factors, the ⁴⁸Ca${(e,e^{\prime }p)}^{47}$K cross section is calculated using the DWIA, following the same procedure detailed in Section 3.1 for ⁴⁰Ca. The experimental data on the ⁴⁸Ca${(e,e^{\prime }p)}^{47}$K reaction were obtained in parallel kinematics for outgoing proton kinetic energies of $T_p=100$ MeV at Nikhef and previously published in [70]. As shown in [19], the DOM spectroscopic factors need to be renormalized by incorporating the observed experimental fragmentation of the strength near the Fermi energy that is not yet included in the DOM self-energy. The experimental strength distributions for $\ell =0$ and the $\ell =2$ excitations of ⁴⁷K are shown in Figure 8, which are overlaid with the corresponding DOM spectral functions calculated from Equation 3. Similar to the ⁴⁰Ca calculation, the distributions shown in Figure 8 are used to renormalize the DOM spectroscopic factors using Equation 18. This scaling results in a reduction from 0.64 to 0.55 for the 1s$1/2$ orbital and 0.60 to 0.58 for the 0d$3/2$ orbital. These values are in good agreement with the originally published spectroscopic factors [70], as shown in Table 2. The uncertainties in the values of the spectroscopic factors were determined using the same bootstrap method discussed in Section 3.1.

Figure 8

Figure 8. Spectral strength as a function of excitation energy in ⁴⁸Ca. The solid lines are DOM spectral functions for (A) the $1\mathrm{s}1/2$ and (B) the $0\mathrm{d}3/2$ proton orbitals. The histograms are the excitation energy spectra in ⁴⁷K extracted from the ⁴⁸Ca$(e,e^{\prime }p)$ ⁴⁷K experiment [15, 70]. The peaks in the DOM curves and experimental data correspond to the quasihole energies of the protons in ⁴⁸Ca. The experimental spectrum in (B) is the isolated 0d$3/2$ orbital. Figure adapted from [20].

Table 2

Table 2. Comparison of spectroscopic factors in ⁴⁸Ca deduced from the previous analysis [70] using the Schwandt optical potential [61] to the normalization of the corresponding overlap functions obtained in the present analysis from the DOM including an error estimate, as described in the text.

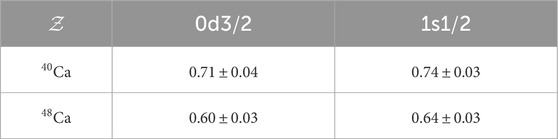
Employing the resulting renormalized spectroscopic factors leads to quantitative agreement with the experimental momentum distributions shown in Figure 9. The comparison of the spectroscopic factors in ⁴⁸Ca and ⁴⁰Ca, ${\mathcal{Z}}_{48}$ and ${\mathcal{Z}}_{40}$, shown in Table 3 reveals that both orbitals experience a reduction with the addition of eight neutrons. This indicates that strength from the spectroscopic factors is pulled to the continuum in $S(E)$ when eight neutrons are added to ⁴⁰Ca. Thus, the stronger coupling to surface excitations in ⁴⁸Ca, demonstrated by the larger proton reaction cross section when compared to ⁴⁰Ca (see Figure 7), strongly contributes to the quenching of the proton spectroscopic factor. It is important to note how crucial the extrapolated high-energy proton reaction cross-section data are in drawing these conclusions. Without them, there is no constraint for the strength of the spectral function at large positive energies, which could result in no quenching of the spectroscopic factors of ⁴⁸Ca due to the sum rule, Equation 23, that requires the strength to integrate to one when all energies are considered [17, 65].

Figure 9

Figure 9. ⁴⁸Ca$(e,e^{\prime }p)$ ⁴⁷K spectral functions in parallel kinematics at an outgoing proton kinetic energy of 100 MeV. The solid line is the calculation employing the DOM, while the points are from the experiment detailed in [70]. (A) Distribution for the removal of the $1\mathrm{s}1/2$ proton. The curve contains the DWIA for the $1/2^{+}$ ground state using the DOM-generated spectroscopic factor of 0.55 (renormalized using Equation (18)). (B) Distribution for the removal of the $0\mathrm{d}3/2$ with a DOM-generated spectroscopic factor of 0.58 (renormalized using Equation (18)) for the $3/2^{+}$ excited state at 0.36 MeV. Figure adapted from [20].

Table 3

Table 3. Comparison of DOM spectroscopic factors in ⁴⁸Ca and ⁴⁰Ca. These factors have not been renormalized and represent the aggregate strength near the Fermi energy.

In addition to the depletion of the spectroscopic factor due to long-range correlations, strength is also pulled to continuum energies due to SRC. A large portion of high-momentum content is caused by the tensor force in the nucleon–nucleon $(NN)$ interaction. In particular, the tensor force preferentially acts on pairs of neutrons and protons ($np$ pairs) with the total spin $S=1$. This phenomenon is known as $np$ dominance [73] and is demonstrated by a factor of 20 difference between the number of observed $np$ SRC pairs and the number of observed $pp$ and $nn$ SRC pairs in exclusive $(e,e^{\prime }pp)$ and $(e,e^{\prime }p)$ cross-section measurements of ¹²C, ²⁷Al, ⁵⁶Fe, and ²⁰⁸ Pb [73]. The dominance of $np$ SRC pairs would imply that the number of high-momentum protons observed in a nucleus is dependent on how many neutrons it contains. More specifically, one would expect that the high-momentum content of protons would increase with neutron excess since there are more neutrons available to make $np$ SRC pairs. The CLAS collaboration confirmed this asymmetry dependence by measuring the high-momentum content of protons and neutrons from $(e,e^{\prime }p)$ and $(e,e^{\prime }n)$ cross-section measurements in ¹²C, ²⁷Al, ⁵⁶Fe, and ²⁰⁸Pb [74].

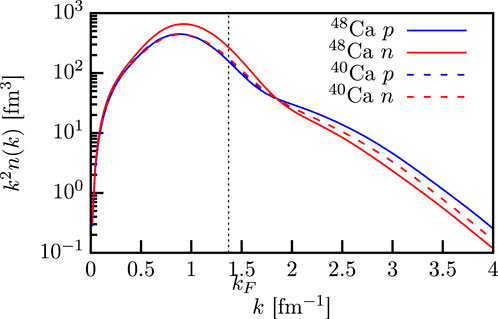
This effect can be studied by comparing the DOM-generated momentum distributions for ⁴⁰Ca and ⁴⁸Ca since the only difference between them is the eight additional neutrons in ⁴⁸Ca that mainly fill the 0f$7/2$ shell. It is clearly shown in Figure 10 that the ⁴⁸Ca proton momentum distribution (solid blue line) has more high-momentum content than the ⁴⁰Ca proton momentum distribution (dashed blue line). Since the number of protons does not change between ⁴⁰Ca and ⁴⁸Ca, the added high-momentum content in the tail of ⁴⁸Ca is accounted for by a reduction in the distribution of the $k<k_F$ region. Focusing on the neutrons shown in Figure 10 (red lines), the ⁴⁸Ca momentum distribution is significantly greater than the ⁴⁰Ca distribution for $k<k_F$. This is not surprising since there are now eight more neutrons that are dominated by a low-momentum content. The high-momentum content of the neutrons in ⁴⁰Ca decreases from $14.7\%$ to $12.6\%$ when eight neutrons are added to form ⁴⁸Ca, while the high-momentum content of the protons increases from 14.0% to 14.6%. The effects of the asymmetry of ⁴⁸Ca on the high-momentum content are evident in the fact that there are more high-momentum protons than neutrons. Both the increase in the proton high-momentum content and the decrease in the neutron high-momentum content are qualitatively consistent with the CLAS measurements of neutron-rich nuclei [74] and support the $np$-dominance picture, as predicted in [75, 76]. Notably, at this stage of the DOM development, no attempt has been made to quantitatively account (i.e., introduce additional constraints) for the CLAS observations.

Figure 10

Figure 10. Comparison of DOM-calculated momentum distributions of protons (blue) and neutrons (red) in ⁴⁸Ca (solid) and ⁴⁰Ca (dashed). The dotted line marks the value used for $k_F$. Figure adapted from [20].

Another manifestation of the more correlated protons can be seen in the spectral functions of Figure 1. The broader peaks of the proton spectral functions shown in Figure 1A, compared to those of the neutrons in Figure 1B, indicate that the protons are more correlated. Furthermore, the increased proton high-momentum content in ⁴⁸Ca is a result from the added strength in the continuum of the hole spectral function when compared to that of ⁴⁰Ca. To conserve the proton number (and preserve the sum rule of Equation 23), an increase in strength at continuum energies in $S_{\ell j}(E)$ of ⁴⁸Ca must be compensated by a decrease in strength from energies close to the proton Fermi energy in ⁴⁸Ca. In particular, this contributes to the quenching of the spectroscopic factors of the 0d$3/2$ and 1s$1/2$ orbitals, before renormalization (see Equation 18), in ⁴⁸Ca from the values for ⁴⁰Ca, as shown in Table 3. In this way, the spectroscopic factor provides a link between the low-momentum-knockout experiments done at Nikhef and the high-momentum-knockout experiments done at JLAB by the CLAS collaboration.

The success of the DOM in describing both ⁴⁰Ca${(e,e^{\prime }p)}^{39}$K and ⁴⁸Ca${(e,e^{\prime }p)}^{47}$K results has provided a foothold for understanding the quenching of spectroscopic factors. A DOM investigation across the nuclear chart would deepen our understanding as a data-informed spectroscopic factor could be generated for each nucleus using Equation 8. This would require a global parametrization of the DOM, which is currently in development. Meanwhile, we note that for ²⁰⁸Pb (see [54] for fit), the DOM values of the valence spectroscopic factors are consistent with the observations of [77] and the interpretation of [78]. The past extraction of spectroscopic factors using the ²⁰⁸Pb${(e,e^{\prime }p)}^{207}$Tl reaction yielded a value of approximately 0.65 for the valence $\mathrm{2}{\mathrm{s}}_{\mathrm{1}/\mathrm{2}}$ orbit [8] based on the results of [79, 80]. Although the use of nonlocal optical potentials may slightly increase this value, as shown in [19], it may be concluded that the value of 0.69 obtained from the DOM analysis is consistent with the past result. Nikhef data obtained in a large missing energy and momentum domain [81] can now be consistently analyzed, employing the complete DOM spectral functions.

4 Proton-induced knockouts

As discussed in Section 1, knockout reactions can be induced by nuclear projectiles such as protons. Although these reactions are not as clean due to the probe interacting through the nuclear $pp$ force rather than the electromagnetic $ep$ force, the DWIA description does a fairly good job of reproducing experimental data. Furthermore, these reactions are not limited to forward kinematics like their electron-induced counterparts; the proton can act as both the beam and the target. This is useful because it allows for the study of nuclei far from stability by utilizing rare isotope beams in laboratories such as the DOE flagship facility for rare isotope beams (FRIBs).

Since we have an accurate description of ⁴⁰Ca${(e,e^{\prime }p)}^{39}$K using the DOM, we are in a good position to investigate the reaction description of the analogous ⁴⁰Ca${(p,2p)}^{39}$K reaction. The kinematics of the $(p,2p)$ experiment are setup in a similar manner to those of the $(e,e^{\prime }p)$ experiment, and the outgoing proton energy is 100 MeV, which we showed is an optimal energy for a good DWIA description of knockout [19]. While the experiment we compare to was performed using a proton beam on a stable ⁴⁰Ca target [82], it serves as a benchmark for the DWIA description of proton-induced knockout, allowing it to be applied in more exotic cases where protons are used as targets for rare isotope beams.

4.1 DWIA in $(p,2p)$

In [21], the factorized form of the nonrelativistic DWIA with the spin degrees of freedom is employed. The transition matrix $T$ within the distorted wave impulse approximation framework is given by

$\begin{array}{ll}{T}_{{\mu }_1{\mu }_2{\mu }_0{\mu }_j}={\displaystyle \sum _{{\mu }_1^{\prime }{\mu }_2^{\prime }{\mu }_0^{\prime }{\mu }_p}}{\tilde{t}}_{{\mu }_1^{\prime }{\mu }_2^{\prime }{\mu }_0^{\prime }{\mu }_p}\int d\mathit{R}{\chi }_{1,{\mu }_1^{\prime }{\mu }_1}^{\left(-\right)*}\left(\mathit{R}\right){\chi }_{2,{\mu }_2^{\prime }{\mu }_2}^{\left(-\right)*}\left(\mathit{R}\right)\hfill & {\chi }_{0,{\mu }_0^{\prime }{\mu }_0}^{\left(+\right)}\left(\mathit{R}\right)e^{-i{\alpha }_R{\mathit{K}}_0\cdot \mathit{R}}\hfill \\ \times {\displaystyle \sum _m}\left(\ell m{s}_p{\mu }_p|j{\mu }_j\right){\psi }_{\ell jm}^n\left(\mathit{R}\right).\hfill & \hfill \end{array}(24)$

In Equation 24, the incident and two emitted protons are labeled as particle 0–2, while the bound proton in the initial state is labeled as $p$. ${\chi }_{i,{\mu }_i^{\prime }{\mu }_i}$ is a distorted wave of particle $i=\mathrm{0,1,2}$ having the asymptotic (local) third component ${\mu }_i$ $({\mu }_i^{\prime })$ of its spin $s_i=1/2$. The outgoing and incoming boundary conditions of the distorted waves are denoted by superscripts $(+)$ and $(-)$, respectively. ${\mathit{K}}_0$ is the momentum (wave number) of the incident proton, and ${\alpha }_R$ is the mass ratio of the struck particle and the target. $n$ is the radial quantum number, and $\ell ,j,m$ are the single-particle orbital angular momentum, total angular momentum, and third component of $\ell$, respectively. ${\psi }_{\ell jm}^n$ is the single-particle wave function (SPWF) normalized to unity. ${\tilde{t}}_{{\mu }_1^{\prime }{\mu }_2^{\prime }{\mu }_0^{\prime }{\mu }_p}$ is the matrix element of the $pp$ effective interaction $t_{pp}$:

${\tilde{t}}_{{\mu }_1^{\prime }{\mu }_2^{\prime }{\mu }_0^{\prime }{\mu }_p}=⟨{\mathit{\kappa }}^{\prime },{\mu }_1^{\prime }{\mu }_2^{\prime }|t_{pp}|\mathit{\kappa },{\mu }_0^{\prime }{\mu }_p⟩,(25)$

where $\mathit{\kappa }$ and ${\mathit{\kappa }}^{\prime }$ are relative momenta of two protons in the initial and the final states, respectively. The factorization procedure of $t_{pp}$ is explained using the local semi-classical approximation (LSCA) and the asymptotic momentum approximation (AMA) in the appendix of [21]. It should be noted that the factorized DWIA is often regarded as a result of the zero-range approximation, but $t_{pp}$ is a finite-range interaction.

The triple differential cross section (TDX) with respect to the emitted proton energy $T_1^{\mathrm{l}\mathrm{a}\mathrm{b}}$ and emission angles ${\mathrm{\Omega }}_1^{\mathrm{l}\mathrm{a}\mathrm{b}}$ and ${\mathrm{\Omega }}_2^{\mathrm{l}\mathrm{a}\mathrm{b}}$ is given as

$\frac{d^3{\sigma }^{\mathrm{l}\mathrm{a}\mathrm{b}}}{d{T}_1^{\mathrm{l}\mathrm{a}\mathrm{b}}d{\mathrm{\Omega }}_1^{\mathrm{l}\mathrm{a}\mathrm{b}}d{\mathrm{\Omega }}_2^{\mathrm{l}\mathrm{a}\mathrm{b}}}={\mathcal{Z}}_{lj}^n{\mathcal{J}}_{\mathrm{l}\mathrm{a}\mathrm{b}G}{F}_{\text{kin}}\frac{{\left(2\pi \right)}^4}{\hslash v_{\alpha }}\frac{1}{\left(2s_0+1\right)\left(2j+1\right)}{\displaystyle \sum _{{\mu }_1{\mu }_2{\mu }_0{\mu }_j}}{\left|T_{{\mu }_1{\mu }_2{\mu }_0{\mu }_j}\right|}^2,(26)$

with ${\mathcal{Z}}_{lj}^n$, ${\mathcal{J}}_{\mathrm{l}\mathrm{a}\mathrm{b}G}$, $F_{\text{kin}}$, and $v_{\alpha }$ being the spectroscopic factor, the Jacobian from the center-of-mass frame to the laboratory frame, kinetic factor, and the relative velocity of the incident proton and the target, respectively. Quantities in Equation 26 with the superscript $\mathrm{l}\mathrm{a}\mathrm{b}$ are evaluated in the laboratory frame, while the others are in the center-of-mass frame. For details, see Section 3.1 of [36].

Equations 15, 25, 26 for electron- and proton-induced knockout, respectively, have many similarities. They both employ the same spectroscopic factor, bound-state wave function, and 100-MeV outgoing proton distorted wave. The proton-induced expression includes two additional proton distorted waves to account for the incoming and outgoing projectile proton, but the main difference between these two equations is the appearance of the $pp$ interaction in the form of ${\tilde{t}}_{{\mu }_1^{\prime }{\mu }_2^{\prime }{\mu }_0^{\prime }{\mu }_p}$ in Equation 25. In the electron case, this is factorized outside of the hadronic part of the cross section, which is not possible in the proton-induced case. We probe this difference by employing the same DOM wave functions between $(e,e^{\prime }p)$ and $(p,2p)$ cases.

4.2 Results and discussion

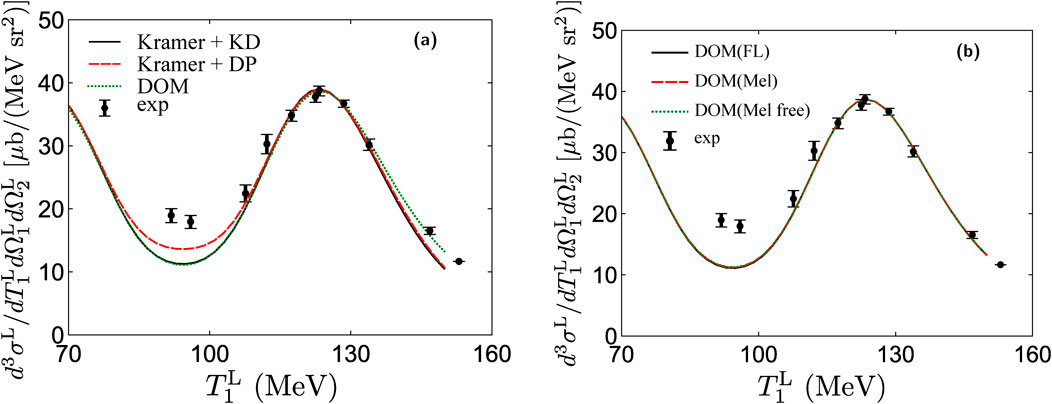
Theoretical knockout cross sections are calculated using the DWIA framework with the DOM SPWF and distorted waves. The reaction kinematics is in a coplanar kinematics, and the opening angles of the emitted protons are fixed at the same angle: ${\varphi }_1^{\text{L}}=0°$, ${\varphi }_2^{\text{L}}=180°$, and ${\theta }_1^{\text{L}}={\theta }_2^{\text{L}}=42.0°$ in the Madison convention [83]. The kinematics of the three particles is then uniquely determined by $T_1^{\text{L}}$. The DOM-DWIA result is compared with those of the phenomenological SPWF and the optical potential in panel (a) of Figure 11. For this comparison, the DOM-DWIA cross section is adjusted to the data rather than employing the DOM-generated spectroscopic factor from Equation 8. The phenomenological SPWF suggested by [70], the Koning–Delaroche optical potential parameter set (KD) [84], and the Dirac phenomenology (DP) [85–87] are also considered. Spectroscopic factors are, therefore, extracted from the ratio of the present calculations and the experimental data taken by the E258 experiment at the RCNP [82] by minimizing

${\chi }^2\left({\mathcal{Z}}_{0d_{3/2}}\right)={\displaystyle \sum _i}\frac{{\left({\mathcal{Z}}_{0d_{3/2}}{\sigma }_i^{\text{DWIA}}-{\sigma }_i\right)}^2}{{\delta }_i^2},(27)$

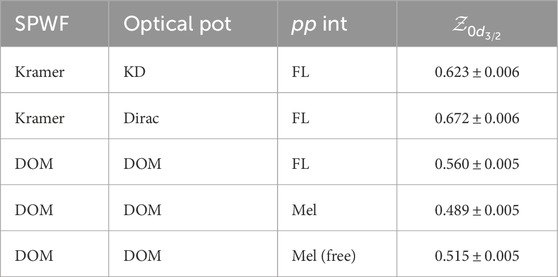
where ${\sigma }_i^{\text{DWIA}}$ and ${\sigma }_i$ are theoretical and experimental cross sections at data points $i$, respectively, and ${\delta }_i$ is the associated error of the experimental data. Obtained spectroscopic factors are summarized in Table 1. Following [36], only the data points around the peak, larger than $25\mu$b/(MeV ${\text{sr}}^2$), are fit to reduce the uncertainty.

Figure 11

Figure 11. (A) TDX with different optical potentials. The solid and dashed lines are TDXs with the Koning–Delaroche optical potential (KD) and Dirac phenomenology (DP), respectively. The result with the DOM is also shown as the dotted line. All results reflect cross sections that are normalized with the spectroscopic factors shown in Table 1. (B) TDX calculated using the DOM with different $pp$ effective interactions. The solid, dashed, and dotted lines are TDXs with the Franey–Love effective interaction [88] (FL), Melbourne $g$–matrix interaction at mean density [89] (Mel), and that at zero density (Mel free), respectively. See Table 1 for corresponding normalization (spectroscopic) factors. The experimental data taken by the E258 experiment at RCNP [82] are also shown. Figure adapted from [21].

The spectroscopic factors obtained from the phenomenological $(p,2p)$ analysis (the first two rows of Table 4) are consistent with the phenomenological $(e,e^{\prime }p)$ analysis, which resulted in $0.65\pm 0.06$ [5]. On the other hand, the spectroscopic factor obtained using the DOM wave functions to reproduce the $(p,2p)$ cross section is in disagreement with the DOM value (using Equation 8) of $0.71\pm 0.04$. Since the spectroscopic factor is a property of the quasihole bound state, it should not depend on the reaction mechanism or beam energy [90]. As shown in [36], the spectroscopic factors for the valence levels near the Fermi energies of stable nuclei extracted from $(p,2p)$ reactions above 200 MeV, using the DWIA with local potentials, are consistent with those from $(e,e^{\prime }p)$ with uncertainties ranging from 10% to 15%. The nonlocality correction to the SPWF and distorted waves is considered to be a primary source of uncertainty in determining these spectroscopic factors [36].

Table 4

Table 4. Normalization (spectroscopic) factors extracted in ⁴⁰Ca${(p,2p)}^{39}$K using Equation (27).

Employing different potentials to generate the proton scattering and bound-state wave functions complicates the interpretation of these results. However, the DOM bound-state and scattering wave functions are both fully consistent within the DWIA framework and equivalent between the $(e,e^{\prime }p)$ and $(p,2p)$ reactions. Nevertheless, ${\mathcal{Z}}_{0\mathrm{d}3/2}$ obtained with the DOM-DWIA analysis of the ⁴⁰Ca$(p,2p)$ data at 200 MeV, in which the nonlocality is treated in a sophisticated manner, differs by at least 21% from the value used to reproduce $(e,e^{\prime }p)$ data utilizing the same DOM. With the nucleus-dependent ingredients of the DWIA description eliminated as causes for this discrepancy (because the same DOM ingredients are used in both the $(e,e^{\prime }p)$ and $(p,2p)$ cases), we explore differences in the reaction descriptions to uncover the source of discrepancy.

We first consider the consequences of using three distorted proton waves in the $(p,2p)$ reaction, as compared to just one in $(e,e^{\prime }p)$. There is an uncertainty associated with the DOM distorted waves due to the experimental data points used in the DOM fit. Recalling the strong correlation between the proton reaction cross sections and the $(e,e^{\prime }p)$ cross sections demonstrated in Section 3, we look to uncertainties in the experimental proton reaction cross-section data points in energy regions corresponding to those of the distorted proton waves to get a rough estimate of the uncertainty associated with the DOM distorted waves. The proton reaction cross-section data points from [91, 92] suggest an uncertainty in the corresponding DOM distorted waves of approximately 3%. Furthermore, due to the kinematics of the reaction, one of the proton energies is as low as 36 MeV. In the DOM analysis of ⁴⁰Ca${(e,e^{\prime }p)}^{39}$K, the description of the experimental cross section for outgoing proton energies of 70 MeV, the lowest of the considered proton energies, is somewhat less satisfactory [19]. This indicates that the impulse approximation may not be applicable at proton energies of 70 MeV and below. Since one of the outgoing proton energies in this ⁴⁰Ca${(p,2p)}^{39}$K reaction is even less than 70 MeV, it is reasonable to expect some discrepancy in the ⁴⁰Ca${(p,2p)}^{39}$K TDX. This discrepancy may be reduced when higher proton beam energies are considered, but this implies that the DOM analysis has to be extended to higher energies. Noting that previous analyses of $(p,2p)$ and $(e,e^{\prime }p)$ resulted in consistent spectroscopic factors, we conclude that any inaccuracies caused by low-energy protons do not explain the high 21% discrepancy we are observing between DOM descriptions of $(e,e^{\prime }p)$ and $(p,2p)$. We also investigated the uncertainty arising from a different choice of the $pp$ effective interactions when employing the DOM in the DWIA. Three different types of $pp$ effective interaction were utilized: the Franey–Love effective interaction (FL) [88], the Melbourne $g$–matrix interaction at mean density (Mel) [89], and that at zero density (Mel free) were utilized. The Franey–Love interaction is a free-space $t$-matrix aimed at reproducing high-energy $pp$ scattering cross sections. The Melbourne interactions utilize the so-called $g$-matrix, which is an approximation to account for the fact that the $pp$ interaction in $(p,2p)$ takes place in a nucleus rather than a vacuum. The $g$-matrix is typically calculated from the $pp$ interaction via ladder diagrams in infinite nuclear matter and mapped to finite nuclei using the density [89]. The mean density of the $(p,2p)$ reaction is defined in Section 6.1. of [36]. The choice of the $pp$ effective interaction does not change the form of the TDX(see panel (b) of Figure 11), but it does change the magnitude of the TDX, causing the normalization factor to reproduce experimental data to vary (see Table 4).

The uncertainty due to the choice of the $pp$ effective interaction results in ${\mathcal{Z}}_{0d_{3/2}}=0.489$–0.560, which is still inconsistent with the DOM $(e,e^{\prime }p)$ results [19]. However, the variation in the spectroscopic factors using the different interactions (see Table 1) indicates that the $(p,2p)$ reaction is sensitive to the chosen effective $pp$ interaction. We note that the main difference between $(e,e^{\prime }p)$ and $(p,2p)$ is the need to employ an in-medium $pp$ interaction, which is not well-constrained. We, therefore, hypothesize that the $(p,2p)$ reaction must be investigated with a more sophisticated treatment of the $pp$ interaction beyond the standard $t$- or $g$-matrix approach. One immediate concern is that present treatments of this effective interaction do not allow for energy transfer in the elementary process. Since a substantial excitation energy is involved in the $(p,2p)$ reaction, it implies that the mediators of the strong interaction, in particular the pion, must be allowed to propagate [93]. The in-medium effective $pp$ interaction should be calculated in finite nuclei, which can be achieved by utilizing DOM propagators. The formalism for this nucleus-dressed interaction is analogous to that of the $g$-matrix, but instead of mapping the infinite nuclear matter propagator to ⁴⁰Ca via the density, we can explicitly employ the DOM propagator (Equation 2) of ⁴⁰Ca. The incorporation of the ⁴⁰Ca DOM propagator in the effective $pp$ interaction should contribute to improving the reaction description such that the DOM spectroscopic factor of ${\mathcal{Z}}_{0d_{3/2}}=0.71$ will ultimately describe both ⁴⁰Ca${(e,e^{\prime }p)}^{39}$K and ⁴⁰Ca${(p,2p)}^{39}$K cross sections.

5 Conclusion and outlook

We have reviewed a nonlocal dispersive optical-model analysis of ⁴⁰Ca and ⁴⁸Ca, in which we fit elastic-scattering angular distributions, absorption and total cross sections, single-particle energies, charge densities, ground-state binding energies, and particle numbers. When sufficient data are available to constrain the self-energy, the DOM can provide accurate predictions. In particular, the unique capability of the DOM to simultaneously describe bound-state and scattering wave functions leads to fully consistent DWIA descriptions of knockout reactions. After updating the high-energy reaction cross sections used to constrain the DOM self-energies in ⁴⁰Ca and ⁴⁸Ca, the predictions ⁴⁰Ca${(e,e^{\prime }p)}^{39}$K and ⁴⁸Ca${(e,e^{\prime }p)}^{47}$K reproduced the Nikhef experimental data, resulting in the updated spectroscopic factors for both ⁴⁰Ca and ⁴⁸Ca (see Table 3) [19, 20]. Furthermore, we observe a reduction in the spectroscopic factors from ⁴⁰Ca to ⁴⁸Ca, which is consistent with the quenching observed in the systematic analysis of [29]. Through the spectral function picture of the nucleus provided by the DOM, we connect the quenching of spectroscopic factors to the increase in the high-momentum content of protons when eight neutrons are added to ⁴⁰Ca to form ⁴⁸Ca.

The DOM-DWIA description of the proton-induced knockout from ⁴⁰Ca, however, does not currently fit in the consistent story of its electron-induced counterpart. Indeed, the DOM-DWIA overestimates the ⁴⁰Ca${(p,2p)}^{39}$K by 21% even though the same DOM wave functions (bound and scattering) are employed, which were so successful in describing the ⁴⁰Ca${(e,e^{\prime }p)}^{39}$K reaction. We hypothesize that the main cause of this discrepancy is the fact that the probe in $(p,2p)$ interacts with the nucleus through the nuclear $pp$ interaction rather than the electromagnetic $ep$ interaction in $(e,e^{\prime }p)$. We are, therefore, working on improving the $(p,2p)$ description by utilizing DOM propagators to explicitly treat the $pp$ interaction as scattering inside ⁴⁰Ca rather than in free-space ($t$-matrix) or infinite nuclear matter ($g$-matrix). The ability of the DOM to provide both bound and scattering nucleon wave functions is opening the door to a new research opportunity for the nucleon–nucleon scattering process in many-body systems. This is of particular importance as nucleus-induced reactions, which utilize the $NN$ interaction in their theoretical description (including $(p,2p)$), can be employed in inverse kinematics to study nuclei off stability at RIB facilities [27, 28]. There is, therefore, a definite need to improve the description of the effective interaction in the medium, which will also be influenced by the nucleon asymmetry studied in exotic systems.

Author contributions

MA: conceptualization, formal analysis, resources, visualization, writing–original draft, and writing–review and editing. WD: conceptualization, formal analysis, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under contract DE-AC52-07NA27344 and was supported by the LLNL-LDRD Program under Project No. 24-LW-062. This work was also supported by the U.S. National Science Foundation under grants PHY-1912643 and PHY-2207756.

Acknowledgments

The authors acknowledge the important contributions to some of this research from Henk Blok, Bob Charity, Louk Lapikás, Kazuyuki Ogata, and Kazuki Yoshida.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Frullani S, Mougey J. Advances in nuclear physics, volume 14. New York: Plenum Press (1984).

Google Scholar

2. van der Steenhoven G, Blok HP, den Herder JWA, Jans E, Keizer PHM, Lapikás L, et al. Two-step processes in the quasi-free (e,e’p) reaction. Phys Rev C (1985) 32:1787–8. doi:10.1103/physrevc.32.1787

CrossRef Full Text | Google Scholar

3. den Herder JWA, Blok HP, Jans E, Keizer PHM, Lapikás L, Quint ENM, et al. Single-particle properties of ⁵¹V and ⁹⁰Zr studied with the reaction. Nucl Phys A (1988) 490:507–55. doi:10.1016/0375-9474(88)90012-7

CrossRef Full Text | Google Scholar

4. Steenhoven GVD, Blok H, Jans E, Jong MD, Lapikás L, Quint E, et al. Knockout of protons from 12C induced by the reaction. Nucl Phys A (1988) 480:547–72. doi:10.1016/0375-9474(88)90463-0

CrossRef Full Text | Google Scholar

5. Kramer GJ, Blok HP, van den Brand JFJ, Bulten HJ, Ent R, Jans E, et al. Proton ground-state correlations in ⁴⁰ca studied with the reaction ⁴⁰CaK. Phys Lett B (1989) 227:199–203. doi:10.1016/S0370-2693(89)80022-X

CrossRef Full Text | Google Scholar

6. de Witt Huberts PKA. Proton spectral functions and momentum distributions in nuclei from high-resolution experiments. J Phys G: Nucl Part Phys (1990) 16:507–44. doi:10.1088/0954-3899/16/4/004

CrossRef Full Text | Google Scholar

7. Dieperink AEL, Huberts PKA. Ann Rev Nuc Part S (1990) 40:239–84. doi:10.1146/annurev.ns.40.120190.001323

CrossRef Full Text | Google Scholar

8. Sick I, de Witt Huberts PKA. Comm Nucl Part Phys (1991) 20:177.

Google Scholar

9. Lapikás L. Quasi-elastic electron scattering off nuclei. Nucl Phys A (1993) 553:297–308. doi:10.1016/0375-9474(93)90630-G

CrossRef Full Text | Google Scholar

10. Pandharipande VR, Sick I, Pkad H. Independent particle motion and correlations in fermion systems. Rev Mod Phys (1997) 69:981–91. doi:10.1103/RevModPhys.69.981

CrossRef Full Text | Google Scholar

11. Boffi S, Giusti C, Pacati FD. Electron-nucleon interaction in quasi-free scattering. Nucl Phys A (1980) 336:416–26. doi:10.1016/0375-9474(80)90218-3

CrossRef Full Text | Google Scholar

12. Giusti C, Pacati FD. Electron distortion in quasifree (e,e’p) reactions. Nucl Phys A (1987) 473:717–35. doi:10.1016/0375-9474(87)90276-4

CrossRef Full Text | Google Scholar

13. Giusti C, Pacati FD. Separation of structure functions and electron distortion in quasifree (e, ep) reactions. Nucl Phys A (1988) 485:461–80. doi:10.1016/0375-9474(88)90548-9

CrossRef Full Text | Google Scholar

14. Boffi S, Giusti C, Pacati FD, Radici M. Electromagnetic response of atomic nuclei. New York: Oxford (1996).

Google Scholar

15. Kramer GJ. Ph.D. thesis. Amsterdam: Universiteit van Amsterdam (1990).

Google Scholar

16. Furnstahl RJ, Hammer H. Phys Lett B (2002) 531:203–8. doi:10.1016/s0370-2693(01)01504-0

CrossRef Full Text | Google Scholar

17. Dickhoff WH, Van Neck D. Many-body theory exposed!, 2nd edition. New Jersey: World Scientific (2008).

Google Scholar

18. Mahaux C, Sartor R. Single-particle motion in nuclei. Boston, MA: Springer (1991) p. 1–223. doi:10.1007/978-1-4613-9910-0_1

CrossRef Full Text | Google Scholar

19. Atkinson MC, Blok HP, Lapikás L, Charity RJ, Dickhoff WH. Validity of the distorted-wave impulse-approximation description of Ca40(e,e′p)K39 data using only ingredients from a nonlocal dispersive optical model. Phys Rev C (2018) 98:044627. doi:10.1103/PhysRevC.98.044627

CrossRef Full Text | Google Scholar

20. Atkinson MC, Dickhoff WH. Investigating the link between proton reaction cross sections and the quenching of proton spectroscopic factors in 48ca. Phys Lett B (2019) 798:135027. doi:10.1016/j.physletb.2019.135027

CrossRef Full Text | Google Scholar

21. Yoshida K, Atkinson MC, Ogata K, Dickhoff WH. First application of the dispersive optical model to reaction analysis within the distorted-wave impulse approximation framework. Phys Rev C (2022) 105:014622. doi:10.1103/PhysRevC.105.014622

CrossRef Full Text | Google Scholar

22. Mahzoon MH, Charity RJ, Dickhoff WH, Dussan H, Waldecker SJ. Forging the link between nuclear reactions and nuclear structure. Phys Rev Lett (2014) 112:162503. doi:10.1103/PhysRevLett.112.162503

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Dickhoff WH, Charity RJ, Mahzoon MH. Novel applications of the dispersive optical model. J Phys G: Nucl Part Phys (2017) 44:033001. doi:10.1088/1361-6471/44/3/033001

CrossRef Full Text | Google Scholar

24. Gade A, Adrich P, Bazin D, Bowen MD, Brown BA, Campbell CM, et al. Reduction of spectroscopic strength: weakly-bound and strongly-bound single-particle states studied using one-nucleon knockout reactions. Phys Rev C (2008) 77:044306. doi:10.1103/PhysRevC.77.044306

CrossRef Full Text | Google Scholar

25. Tostevin JA, Gade A. Systematics of intermediate-energy single-nucleon removal cross sections. Phys Rev C (2014) 90:057602. doi:10.1103/PhysRevC.90.057602

CrossRef Full Text | Google Scholar

26. Dickhoff WH, Charity RJ. Recent developments for the optical model of nuclei. Prog Part Nucl Phys (2019) 105:252–99. doi:10.1016/j.ppnp.2018.11.002

CrossRef Full Text | Google Scholar

27. Atar L, Paschalis S, Barbieri C, Bertulani C, Díaz Fernández P, Holl M, et al. Quasifree reactions on oxygen isotopes: observation of isospin independence of the reduced single-particle strength. Phys Rev Lett (2018) 120:052501. doi:10.1103/PhysRevLett.120.052501

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Kawase S, Uesaka T, Tang TL, Beaumel D, Dozono M, Fukunaga T, et al. Exclusive quasi-free proton knockout from oxygen isotopes at intermediate energies. Prog Theor Exp Phys (2018) 2018. doi:10.1093/ptep/pty011.021D01

CrossRef Full Text | Google Scholar

29. Aumann T, Barbieri C, Bazin D, Bertulani CA, Bonaccorso A, Dickhoff WH, et al. Quenching of single-particle strength from direct reactions with stable and rare-isotope beams. Prog Part Nucl Phys (2021) 118:103847. doi:10.1016/j.ppnp.2021.103847

CrossRef Full Text | Google Scholar

30. Jacob G, Maris TAJ. Quasi-free scattering and nuclear structure. Rev Mod Phys (1966) 38:121–42. doi:10.1103/RevModPhys.38.121

CrossRef Full Text | Google Scholar

31. Jacob G, Maris TAJ. Quasi-free scattering and nuclear structure. ii. Rev Mod Phys (1973) 45:6–21. doi:10.1103/RevModPhys.45.6

CrossRef Full Text | Google Scholar

32. Chant NS, Roos PG. Distorted-wave impulse-approximation calculations for quasifree cluster knockout reactions. Phys Rev C (1977) 15:57–68. doi:10.1103/PhysRevC.15.57

CrossRef Full Text | Google Scholar

33. Chant NS, Roos PG. Spin orbit effects in quasifree knockout reactions. Phys Rev C (1983) 27:1060–72. doi:10.1103/PhysRevC.27.1060

CrossRef Full Text | Google Scholar

34. Samanta C, Chant NS, Roos PG, Nadasen A, Wesick J, Cowley AA. Tests of the factorized distorted wave impulse approximation for reactions. Phys Rev C (1986) 34:1610–9. doi:10.1103/PhysRevC.34.1610

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Cowley AA, Lawrie JJ, Hillhouse GC, Whittal DM, Förtsch SV, Pilcher JV, et al. Quasifree knockout in 16O15N at an incident energy of 151 MeV. Phys Rev C (1991) 44:329–35. doi:10.1103/PhysRevC.44.329

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wakasa T, Ogata K, Noro T. Proton-induced knockout reactions with polarized and unpolarized beams. Prog Part Nucl Phys (2017) 96:32–87. doi:10.1016/j.ppnp.2017.06.002

CrossRef Full Text | Google Scholar

37. Nguyen NB, Waldecker SJ, Nunes FM, Charity RJ, Dickhoff WH. Transfer reactions and the dispersive optical model. Phys Rev C (2011) 84:044611. doi:10.1103/PhysRevC.84.044611

CrossRef Full Text | Google Scholar

38. Ross A, Titus LJ, Nunes FM, Mahzoon MH, Dickhoff WH, Charity RJ. Effects of nonlocal potentials on transfer reactions. Phys Rev C (2015) 92:044607. doi:10.1103/PhysRevC.92.044607

CrossRef Full Text | Google Scholar

39. Potel G, Perdikakis G, Carlson BV, Atkinson M, Capel P, Dickhoff WH, et al. Toward a complete theory for predicting inclusive deuteron breakup away from stability. Eur Phys J A (2017) 53:178. doi:10.1140/epja/i2017-12371-9

CrossRef Full Text | Google Scholar

40. Mahzoon MH, Atkinson MC, Charity RJ, Dickhoff WH. Neutron skin thickness of Ca48 from a nonlocal dispersive optical-model analysis. Phys Rev Lett (2017) 119:222503. doi:10.1103/PhysRevLett.119.222503

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Descouvemont P, Baye D. The r -matrix theory. Rep Prog Phys (2010) 73:036301. doi:10.1088/0034-4885/73/3/036301

CrossRef Full Text | Google Scholar

42. Atkinson MC. Developing nucleon self-energies to generate the ingredients for the description of nuclear reactions. Springer (2020).

Google Scholar

43. Atkinson MC, Dickhoff WH, Piarulli M, Rios A, Wiringa RB. Reexamining the relation between the binding energy of finite nuclei and the equation of state of infinite nuclear matter. Phys Rev C (2020) 102:044333. doi:10.1103/PhysRevC.102.044333

CrossRef Full Text | Google Scholar

44. Atkinson MC, Dickhoff WH, Piarulli M, Rios A, Wiringa RB. Reply to “comment on ‘reexamining the relation between the binding energy of finite nuclei and the equation of state of infinite nuclear matter’ ”. Phys Rev C (2021) 104:059802. doi:10.1103/PhysRevC.104.059802

CrossRef Full Text | Google Scholar

45. Bell JS, Squires EJ. A formal optical model. Phys Rev Lett (1959) 3:96–7. doi:10.1103/PhysRevLett.3.96

CrossRef Full Text | Google Scholar

46. Perey F, Buck B. A non-local potential model for the scattering of neutrons by nuclei. Nucl Phys (1962) 32:353–80. doi:10.1016/0029-5582(62)90345-0

CrossRef Full Text | Google Scholar

47. Charity RJ, Sobotka LG, Dickhoff WH. Asymmetry dependence of proton correlations. Phys Rev Lett (2006) 97:162503. doi:10.1103/PhysRevLett.97.162503

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Charity RJ, Mueller JM, Sobotka LG, Dickhoff WH. Dispersive-optical-model analysis of the asymmetry dependence of correlations in ca isotopes. Phys Rev C (2007) 76:044314. doi:10.1103/PhysRevC.76.044314

CrossRef Full Text | Google Scholar

49. Mueller JM, Charity RJ, Shane R, Sobotka LG, Waldecker SJ, Dickhoff WH, et al. Asymmetry dependence of nucleon correlations in spherical nuclei extracted from a dispersive-optical-model analysis. Phys Rev C (2011) 83:064605. doi:10.1103/PhysRevC.83.064605

CrossRef Full Text | Google Scholar

50. Dickhoff WH, Van Neck D, Waldecker SJ, Charity RJ, Sobotka LG. Nonlocal extension of the dispersive optical model to describe data below the fermi energy. Phys Rev C (2010) 82:054306. doi:10.1103/PhysRevC.82.054306

CrossRef Full Text | Google Scholar

51. Waldecker SJ, Barbieri C, Dickhoff WH. Microscopic self-energy calculations and dispersive optical-model potentials. Phys Rev C (2011) 84:034616. doi:10.1103/PhysRevC.84.034616

CrossRef Full Text | Google Scholar

52. Dussan H, Waldecker SJ, Dickhoff WH, Müther H, Polls A. Microscopic self-energy of ⁴⁰ca from the charge-dependent bonn potential. Phys Rev C (2011) 84:044319. doi:10.1103/PhysRevC.84.044319

CrossRef Full Text | Google Scholar

53. Brida I, Pieper SC, Wiringa RB. Quantum Monte Carlo calculations of spectroscopic overlaps inA⩽7nuclei. Phys Rev C (2011) 84:024319. doi:10.1103/physrevc.84.024319

CrossRef Full Text | Google Scholar

54. Atkinson MC, Mahzoon MH, Keim MA, Bordelon BA, Pruitt CD, Charity RJ, et al. Dispersive optical model analysis of ²⁰⁸ generating a neutron-skin prediction beyond the mean field. Phys Rev C 101 (2020) 044303. doi:10.1103/PhysRevC.101.044303

CrossRef Full Text | Google Scholar

55. Lane AM. Isobaric spin dependence of the optical potential and quasi-elastic (p, n) reactions. OSTI.GOV (1962) 35:676–85. doi:10.1016/0029-5582(62)90153-0

CrossRef Full Text | Google Scholar

56. Fiedeldey H. The equivalent local potential and the perey effect. Nucl Phys (1966) 77:149–56. doi:10.1016/0029-5582(66)90682-1

CrossRef Full Text | Google Scholar

57. Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes in fortran 90. Cambridge University Press (1996).

Google Scholar

58. Pruitt CD, Charity RJ, Sobotka LG, Atkinson MC, Dickhoff WH. Systematic matter and binding-energy distributions from a dispersive optical model analysis. Phys Rev Lett (2020) 125:102501. doi:10.1103/PhysRevLett.125.102501

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Pruitt CD, Charity RJ, Sobotka LG, Elson JM, Hoff DEM, Brown KW, et al. Isotopically resolved neutron total cross sections at intermediate energies. Phys Rev C (2020) 102:034601. doi:10.1103/PhysRevC.102.034601

CrossRef Full Text | Google Scholar

60. Brand M, Allaart K, Dickhoff WH. Nucl Phys (1990) A509:1.

Google Scholar

61. Schwandt P, Meyer HO, Jacobs WW, Bacher AD, Vigdor SE, Kaitchuck MD, et al. Analyzing power of proton-nucleus elastic scattering between 80 and 180 mev. Phys Rev C (1982) 26:55–64. doi:10.1103/PhysRevC.26.55

CrossRef Full Text | Google Scholar

62. Direct Interactions FG, Reaction N. New York: Gordon & Breach (1963).

Google Scholar

63. Forest D. Off-shell electron-nucleon cross sections: the impulse approximation. Nucl Phys A (1983) 392:232–48. doi:10.1016/0375-9474(83)90124-0

CrossRef Full Text | Google Scholar

64. Auce A, Ingemarsson A, Johansson R, Lantz M, Tibell G, Carlson RF, et al. Reaction cross sections for protons on 12, and 208 at energies between 80 and 180 mev. Phys Rev C (2005) 71:064606. doi:10.1103/PhysRevC.71.064606

CrossRef Full Text | Google Scholar

65. Dussan H, Mahzoon MH, Charity RJ, Dickhoff WH, Polls A. Elastic nucleon-nucleus scattering as a direct probe of correlations beyond the independent-particle model. Phys Rev C (2014) 90:061603. doi:10.1103/PhysRevC.90.061603

CrossRef Full Text | Google Scholar

66. de Vries H, de Jager CW, de Vries C. Nuclear charge-density-distribution parameters from elastic electron scattering. Nucl Data Tables (1987) 36:495–536. doi:10.1016/0092-640x(87)90013-1

CrossRef Full Text | Google Scholar

67. Sick I, Bellicard JB, Cavedon JM, Frois B, Huet M, Leconte P, et al. Charge density of 40Ca. Phys Lett B (1979) 88:245–8. doi:10.1016/0370-2693(79)90458-1

CrossRef Full Text | Google Scholar

68. Dickhoff WH, Barbieri C. Self-consistent green’s function method for nuclei and nuclear matter. Prog Part Nucl Phys (2004) 52:377–496. doi:10.1016/j.ppnp.2004.02.038

CrossRef Full Text | Google Scholar

69. Giusti C, Meucci A, Pacati FD, Co’ G, De Donno V. Quasifree reactions on nuclei with neutron excess. Phys Rev C (2011) 84:024615. doi:10.1103/PhysRevC.84.024615

CrossRef Full Text | Google Scholar

70. Kramer G, Blok H, Lapikás L. Nucl Phys A (2001) 679:267–86. doi:10.1016/S0375-9474(00)00379-1

CrossRef Full Text | Google Scholar

71. Varner R, Thompson W, McAbee T, Ludwig E, Clegg T. A global nucleon optical model potential. Phys Rep (1991) 201:57–119. doi:10.1016/0370-1573(91)90039-O

CrossRef Full Text | Google Scholar

72. Anderson BD, Bevington PR, Cverna FH, McNaughton MW, Willard HB, Barrett RJ, et al. Proton total reaction cross section measurements for 40,44,48 at 700 mev. Phys Rev C (1979) 19:905–12. doi:10.1103/PhysRevC.19.905

CrossRef Full Text | Google Scholar

73. Hen O, Miller GA, Piasetzky E, Weinstein LB. Nucleon-nucleon correlations, short-lived excitations, and the quarks within. Rev Mod Phys (2017) 89:045002. doi:10.1103/RevModPhys.89.045002

CrossRef Full Text | Google Scholar

74. Duer M, Hen O, Piasetzky E, Hakobyan H, Weinstein LB, Braverman M, et al. Probing high-momentum protons and neutrons in neutron-rich nuclei. Nature (2018) 560:617–21. doi:10.1038/s41586-018-0400-z

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Rios A, Polls A, Dickhoff WH. Depletion of the nuclear fermi sea. Phys Rev C (2009) 79:064308. doi:10.1103/PhysRevC.79.064308

CrossRef Full Text | Google Scholar

76. Rios A, Polls A, Dickhoff WH. Density and isospin-asymmetry dependence of high-momentum components. Phys Rev C (2014) 89:044303. doi:10.1103/PhysRevC.89.044303

CrossRef Full Text | Google Scholar

77. Lichtenstadt J, Heisenberg J, Papanicolas CN, Sargent CP, Courtemanche AN, McCarthy JS. High-spin states of in 208 studied by. Phys Rev C (1979) 20:497–503. doi:10.1103/PhysRevC.20.497

CrossRef Full Text | Google Scholar

78. Pandharipande VR, Papanicolas CN, Wambach J. Occupation probabilities of shell-model orbits in the lead region. Phys Rev Lett (1984) 53:1133–6. doi:10.1103/PhysRevLett.53.1133

CrossRef Full Text | Google Scholar

79. Quint ENM, van den Brand JFJ, den Herder JWA, Jans E, Keizer PHM, Lapikás L, et al. Relative spectroscopic strength in 206 and 208 studied with the knockout reaction. Phys Rev Lett (1986) 57:186–9. doi:10.1103/PhysRevLett.57.186

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Quint ENM, Barnett BM, van den Berg AM, van den Brand JFJ, Clement H, Ent R, et al. Evidence for partial occupancy of the 3 proton orbit in ²⁰⁸. Phys Rev Lett (1987) 58:1088–91. doi:10.1103/PhysRevLett.58.1088

PubMed Abstract | CrossRef Full Text | Google Scholar

81. van Batenburg MF. Thesis (university of utrecht) (2001).

Google Scholar

82. Noro T, Sakaguchi S, Wakasa T, Dozono M, Fujioka H, Fujita K, et al. Experimental study of (p, 2p) reactions at 197 MeV on 12C, 16O, 40,48Ca, and 90Zr nuclei leading to low-lying states of residual nuclei. Prog Theor Exp Phys (2023) 2023. doi:10.1093/ptep/ptad116

CrossRef Full Text | Google Scholar

83. Darden SE. 39. University of Wisconsin Press, Madison (1971).

Google Scholar

84. Koning A, Delaroche J. Local and global nucleon optical models from 1 kev to 200 mev. Nucl Phys A (2003) 713:231–310. doi:10.1016/S0375-9474(02)01321-0

CrossRef Full Text | Google Scholar

85. Hama S, Clark BC, Cooper ED, Sherif HS, Mercer RL. Global Dirac optical potentials for elastic proton scattering from heavy nuclei. Phys Rev C (1990) 41:2737–55. doi:10.1103/PhysRevC.41.2737

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Cooper ED, Hama S, Clark BC, Mercer RL. Global Dirac phenomenology for proton-nucleus elastic scattering. Phys Rev C (1993) 47:297–311. doi:10.1103/PhysRevC.47.297

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Cooper ED, Hama S, Clark BC. Global Dirac optical potential from helium to lead. Phys Rev C (2009) 80:034605. doi:10.1103/PhysRevC.80.034605

CrossRef Full Text | Google Scholar

88. Franey MA, Love WG. Nucleon-nucleon matrix interaction for scattering at intermediate energies. Phys Rev C (1985) 31:488–98. doi:10.1103/PhysRevC.31.488

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Amos K, Dortmans PJ, von Geramb HV, Karataglidis S, Raynal J. Nucleon-nucleus scattering: a microscopic nonrelativistic approach. Adv Nucl Phys (2000) 25:276–536. doi:10.1007/0-306-47101-9_3

CrossRef Full Text | Google Scholar

90. Radici M, Dickhoff W, Roth Stoddard E. Consistency of spectroscopic factors from reactions at different momentum transfers. Phys Rev C (2002) 66:014613. doi:10.1103/PhysRevC.66.014613

CrossRef Full Text | Google Scholar

91. Carlson RF, Cox AJ, Nimmo JR, Davison NE, Elbakr SA, Horton JL, et al. Proton total reaction cross sections for the doubly magic nuclei 16, 40, and 208 in the energy range 20-50 mev. Phys Rev C (1975) 12:1167–75. doi:10.1103/PhysRevC.12.1167

CrossRef Full Text | Google Scholar

92. Turner J, Ridley B, Cavanagh P, Gard G, Hardacre A. Optical model studies of proton scattering at 30 mev: (ii). proton total reaction cross sections at 28.5 1.5 mev. Nucl Phys (1964) 58:509–14. doi:10.1016/0029-5582(64)90562-0

CrossRef Full Text | Google Scholar

93. Morris JM. Thesis Washington university in St. Louis (2011). doi:10.7936/K7959FN2

CrossRef Full Text | Google Scholar