Torsional vibration of a static drill-rooted nodular pile embedded in elastic media

This study examines the vibration characteristics of static drill-rooted nodular (SDRN) piles in elastic soils under time-harmonic torsional loads via an analytical approach. SDRN piles, which are characterized by uniformly distributed nodes and enhanced surrounding cemented soil, are able to increase the vertical bearing capacity of piles in soft soils. Piles are modelled using elastic rod theory, while surrounding soils are separated into two sublayers along radial direction: a core zone made up of cemented soil and an outer semi-infinite natural soil layer. An analytical method is proposed to solve the problem after formulating the wave equations for pile and radial soil layer. This methodology rigorously considers the continuity of twist angle and shear stress across the interface of the pile and radial soil layers. The simulation of nodes in the SDRN pile involves discretizing the pile-soil system and applying the principle of impedance function recursion to accurately compute the torsional stiffness at the top of the pile. Developed results are validated against the existing benchmarks for a cylindrical pile in elastic soil. Detailed numerical examples are carried out to assess the effect of major factors on the torsional impedance of the pile. For improved comprehension in engineering applications, the impedance function is applied to derive the twist angle of the rigid foundation, with the amplitude-frequency response expressed in a closed form. Results indicate that the vibration behavior of the piles is significantly influenced by the inner radius, outer radius, the dimension of the node, the radial width of the cemented soil and the damping ratio of the radial soil layer. The developed solution offers valuable insights for the optimization design of SDRN piles under dynamic torsional loads.

1 Introduction

Pile foundations are crucial for supporting large-scale structures like high-rise buildings [1], offshore bridges [2], and ocean platforms [3]. Therefore, understanding their response to complex dynamic loads is essential. While pile foundations are generally subjected to static and dynamic vertical and horizontal loads, wind and machine-induced vibrations can cause torsional loads that significantly affect their dynamic performance [4–6]. Accordingly, assessing the impact of dynamic torsional loads is vital to ensure the stability and safety of pile foundations. To address this, researchers have proposed various methods to investigate torsional vibration characteristics of piles.

Cai et al. [7] performed a comprehensive study on the torsional vibration of elastic piles in a uniform poroelastic medium. Based on this fundamental research, Chen et al. [8] introduced the concept of transverse isotropy to examine the vibration characteristics of piles embedded in saturated soils under transient loading. Their study emphasized the impact of soil transverse isotropy and the pile slenderness ratio on the vibration characteristics of the piles. Subsequent research further illustrated the effects of soil properties on end-bearing piles [9, 10] and pipe piles [11, 12]. Given the inherently layered and vertically non-uniform nature of soil profiles, Zou et al. [13] explored the mechanical behavior of single piles in a two-layer vertically non-uniform subgrade and subjected to axial-torsional combined loads. Liu and Zhang [14] expanded upon these findings by investigating the transient torsional vibration behavior of heterogeneous piles in multi-layered poroelastic media, with a focus on the influence of typical pile defects. To advance this field of study, Li et al. [15], Zhang and Pan [16] assessed the influences of construction disturbances on the surrounding soil, analyzing the impact of radial inhomogeneity induced by such disturbances on the vibration behavior of piles in layered media. Further research has addressed open-ended pipe piles [17–19], examining the effects of construction-induced inhomogeneity in radial direction on the torsional impedance of piles. Additionally, studies have investigated the impact of pile end soil [20] and variation in cross-sectional dimensions [21] on the torsional response of piles. Typically, these investigations model soil as a composite material composed of pore water and soil particles. However, this assumption does not always hold true in practical applications, particularly in surface or shallow soils where unsaturated conditions are prevalent. Unsaturated soils, characterized by incomplete pore saturation, exhibit markedly different mechanical behaviors compared to their saturated counterparts. Research concerning unsaturated soils primarily focused on the effects of transverse isotropy [22, 23], radial inhomogeneity [24, 25], vertical inhomogeneity of soil [25, 26], and pile end soil [27]. Despite the significant influence of torsional loads on pile performance, this factor has not been received adequate consideration in studies of nodular piles.

In soft soil regions, traditional piles, such as cast-in-situ and precast piles often face challenges such as low skin friction and construction-related defects in the pile body. To address these problems, static drill-rooted nodular (SDRN) piles, an innovative foundation type initially developed in Japan, have been increasingly used in engineering practice [28, 29]. As for SDRN pile, the prefabricated nodular pile is embedded into cemented soil via static drilling, effectively overcoming the limitations of conventional pile installation techniques and providing a more efficient, cost-effective scheme. Due to the construction similarities, SDRN piles are often evaluated in comparison to cast-in-situ piles. Research by Zhou et al. [30–33] has demonstrated, through extensive field studies and finite element simulations, that SDRN piles exhibit significantly superior skin friction and compressive bearing capacity compared to cast-in-situ piles, making them particularly advantageous for use in soft soil conditions. Li et al. [34] estimated the vibration characteristics of SDRN piles in layered soil profiles and under vertical loads, affirming the substantial benefits of SDRN piles in mitigating vertical deformation and vibration relative to cast-in-situ piles. Additionally, Wu et al. [35] investigated the impact of various cross-sectional geometries on vertical vibration. Despite considerable research on the performance of SDRN piles under vertical loads [36–38], the effects of torsional loads on SDRN piles remain underexplored.

The literature review above reveals that studies on the dynamic performance of SDRN piles under torsional loading are limited. Therefore, this article aims to examine the torsional vibration characteristics of SDRN piles in elastic soils using an analytical method. It should be pointed out that the analytical solutions presented here provides engineers with a precise, convenient, and efficient tool for quickly assessing the performance of SDRN piles. Specifically, it allows for the evaluation of factors such as pile inner and outer radii, node width, vertical node spacing, and variations in properties of the surrounding cemented soil on the overall performance of SDRN piles. The layout is as follows: Section 2 establishes the mathematical model. Section 3 derives the analytical solutions for the dynamic response problem. Numerical examples and the corresponding analysis and discussion are presented in Section 4. Section 5 applies the present solution into the vibration characteristic of pile-supported foundation. The main conclusions are summarized in Section 6.

2 Mathematical model

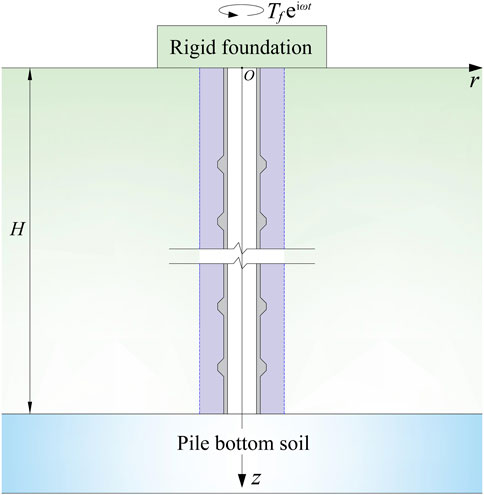
As depicted in Figure 1A, a SDRN pile in elastic soil, undergoing a time-harmonic torque is considered. This study considers the hardening surrounding cemented soil, a radially semi-infinite natural soil deposit and the nodular pile itself, but neglects the effect of the soil within the SDRN pile. Given the large slenderness ratio of the pile, it is approximated as an elastic rod with a fixed inner radius r_in and a series of equally spaced, enlarged nodes (see Figure 1B). The external (outer) radius of pile is r₀ at non-noded sections, while the maximum external radius at nodes is r_oumax. The vertical spacing between two adjacent nodes is l_b, and the radial protrusion thickness and length at each node are w_b. Based on the node distribution, the pile-soil interaction model is divided into N segments (elements), numbered sequentially from the bottom upward. Each segment has equal thickness in both the pile section and the surrounding soil section. The thickness and the radius of segment i are denoted by h_i and r_i, respectively. For node sections, sufficient segmentation is required to simulate the continuous variation in the pile’s outer radius. The soil around the pile is split into two distinct zones: (1) the inner zone, composed of cemented soil, extends to a distance r_c from the pile’s centroid, and (2) the outer zone, consisting of radially semi-infinite natural soil, lies beyond the cemented soil layer.

Figure 1

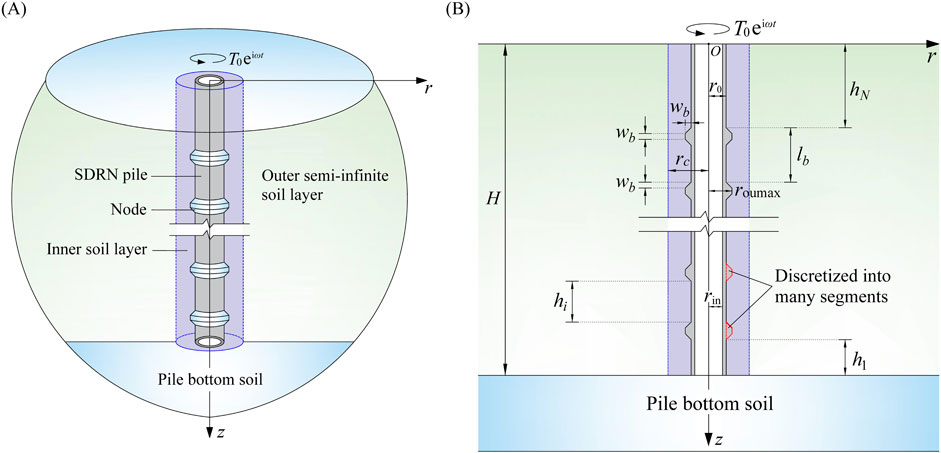
Figure 1. Diagram of a SDRN pile in elastic soil undergoing a time-harmonic torsional load: (A) 3D model; (B) section plan.

Previous studies [16, 39] have shown that neglecting the gradient of shear stress σ_θz along the z-axis (i.e., assuming a plane strain model) has a minimal effect on the dynamic impedance of the pile. Therefore, following the plane strain assumption, the wave equation for any soil layer under torsional load is given by [39].

$u_{\theta ,rr}\left(r,t\right)+r^{-1}{u}_{\theta ,r}\left(r,t\right)-r^{-2}{u}_{\theta }\left(r,t\right)=\frac{{\rho }_s}{G_s}{u}_{\theta ,tt}\left(r,t\right)(1)$

where the subscript, “j” denotes the partial derivative to the variable j (j = r, t); u_θ(r, t), G_s and ρ_s represents the tangential displacement, shear modulus and density of the soil, respectively.

The dynamic equilibrium equation for an elastic pile under torsional load is given by

$G_p{I}_p{\varphi }_{,zz}\left(z,t\right)+2\mathrm{\pi }{r}^2\tau \left(z,t\right)={\rho }_p{I}_p{\varphi }_{,tt}\left(z,t\right)(2)$

where ϕ(z, t), G_p, ρ_p and I_p represent the twist angle, shear modulus, density and polar moment of inertia of the pile, respectively; τ(z, t) denotes the tangential shear stress applied by the soil around the pile.

The boundary condition for the outer natural soil deposit can be specified as

$u_{\theta ij}\left(r\to \infty ,t\right)=0,\left(j=2\right)(3)$

where the subscript ij represents the component in the j-th (where j = 1, 2) radial region corresponding to the i-th (where i = 1-N) pile segment; Specifically, j = 1 and j = 2 refer to the inner and outer radial zones, respectively; In the subsequent sections, the subscript ij will maintain this definition, unless specified otherwise.

The boundary conditions at top and bottom of the i-th (i = 1-N) pile element are

${\varphi }_{i,z}\left(z=0,t\right)=-\frac{T_i\left(t\right)}{G_{pi}{I}_{pi}}(4)$

${\varphi }_{i,z}\left(z=h_i,t\right)+\frac{{\varphi }_i\left(z=h_i,t\right){\mathrm{\Theta }}_i}{G_{pi}{I}_{pi}}=0(5)$

where $I_{pi}=0.5\mathrm{\pi }\left(r_i^4-r_{\text{in}}^4\right)$; ϕ_i (z, t) denotes the twist angle in the i-th pile element; Θ_i represents the complex impedance at the lower end of the i-th pile element; T_i(t) represents the torque exerted on the top of the i-th pile element; For the N-th pile element (i.e., the top element), T_N(t) = T₀(t) holds; When i = 1, the impedance from the pile bottom soil is ${\mathrm{\Theta }}_1=16G_{su}\left(r_0^3-r_{\text{in}}^3\right)/3$ as described by Li et al. [17].

The continuity conditions at r = r_c can be given by

$u_{\theta i2}\left(r=r_c,t\right)=u_{\theta i1}\left(r=r_c,t\right)(6)$

${\tau }_{r\theta i2}\left(r=r_c,t\right)={\tau }_{r\theta i1}\left(r=r_c,t\right)(7)$

The continuity conditions at r = r_i can be formulated as

$u_{\theta ij}\left(r=r_i,t\right)={\varphi }_i\left(z,t\right)r_i(8)$

${\tau }_i\left(z,t\right)={\tau }_{r\theta i}\left(r=r_i,t\right)=G_{si}\left[u_{\theta i1,r}\left(r_i,t\right)-r^{-1}{u}_{\theta i1}\left(r_i,t\right)\right](9)$

3 Solutions

The time-harmonic solution of Equation 1 can be given by

$u_{\theta }\left(r\right)=A{K}_1\left(qr\right)+B{I}_1\left(qr\right)(10)$

where q = iω(ρ_s/G_s)^0.5; i=(−1)^0.5; ω is the angular frequency.

Substituting the boundary condition from Equation 3 into Equation 10, it follows that B = 0. Consequently, the field quantities in the natural soil deposit corresponding to the i-th element can be given by

$u_{\theta i2}\left(r\right)=A_{i2}{K}_1\left(q_{i2}r\right)(\mathrm{11a})$

${\tau }_{r\theta i2}\left(r\right)=-A_{i2}{G}_{si2}{q}_{i2}{K}_2\left(q_{i2}r\right)(\mathrm{11b})$

where q_i2 = iω(ρ_si2/G_si2)^0.5.

The field quantities in the cemented soil layer can be formulated as

$u_{\theta i1}\left(r\right)=A_{i1}{K}_1\left(q_{i1}r\right)+B_{i1}{I}_1\left(q_{i1}r\right)(\mathrm{12a})$

${\tau }_{r\theta i1}\left(r\right)=-A_{i1}{G}_{si1}{q}_{i1}{K}_2\left(q_{i1}r\right)+B_{i1}{G}_{si1}{q}_{i1}{I}_2\left(q_{i1}r\right)(\mathrm{12b})$

where q_i1 = iω(ρ_si1/G_si1)^0.5.

Substituting Equations 11, 12 into continuity conditions given by Equations 6, 7 results in

$B_{i1}={\kappa }_{i1}{A}_{i1}(13)$

where

${\kappa }_{i1}=\frac{G_{si1}{q}_{i1}{K}_2\left(q_{i1}{r}_c\right)K_1\left(q_{i2}{r}_c\right)-G_{si2}{q}_{i2}{K}_2\left(q_{i2}{r}_c\right)K_1\left(q_{i1}{r}_c\right)}{G_{si1}{q}_{i1}{I}_2\left(q_{i1}{r}_c\right)K_1\left(q_{i2}{r}_c\right)+G_{si2}{q}_{i2}{K}_2\left(q_{i2}{r}_c\right)I_1\left(q_{i1}{r}_c\right)}(14)$

Making use of Equation 13, Equation 12 can be rewritten as

$u_{\theta i1}\left(r\right)=A_{i1}{K}_1\left(q_{i1}r\right)+{\kappa }_{i1}{A}_{i1}{I}_1\left(q_{i1}r\right)(\mathrm{15a})$

${\tau }_{r\theta i1}\left(r\right)=-A_{i1}{G}_{si1}{q}_{i1}{K}_2\left(q_{i1}r\right)+{\kappa }_{i1}{A}_{i1}{G}_{si1}{q}_{i1}{I}_2\left(q_{i1}r\right)(\mathrm{15b})$

In the case of a time-harmonic load, Equation 2 can be reformulated as (for i-th element)

$G_{pi}{I}_{pi}\frac{{\mathrm{d}}^2{\varphi }_i\left(z\right)}{\mathrm{d}{z}^2}+2\mathrm{\pi }{r}_i^2{\tau }_i\left(z\right)=-{\rho }_{pi}{I}_{pi}{\omega }^2{\varphi }_i\left(z\right)(16)$

Combining Equations 8, 9, 15, 16 yields

$\frac{{\mathrm{d}}^2{\varphi }_i\left(z\right)}{\mathrm{d}{z}^2}+{\gamma }_i^2{\varphi }_i\left(z\right)=0(17)$

where

${\gamma }_i^2=\left({\delta }_{i1}+{\rho }_{pi}{I}_{pi}{\omega }^2\right)/\left(G_{pi}{I}_{pi}\right)(18)$

${\delta }_{i1}=\frac{2\mathrm{\pi }{r}_i^3{G}_{si1}{q}_{i1}\left[-K_2\left(q_{i1}{r}_i\right)+{\kappa }_{i1}{I}_2\left(q_{i1}{r}_i\right)\right]}{K_1\left(q_{i1}{r}_i\right)+{\kappa }_{i1}{I}_1\left(q_{i1}{r}_i\right)}(19)$

The solution of Equation 17 can be expressed as

${\varphi }_i\left(z\right)=C_i\cos \left({\gamma }_{i}z\right)+D_i\sin \left({\gamma }_{i}z\right)(20)$

Combining Equation 5 and Equation 20 results in

$D_i={\eta }_i{C}_i(21)$

where

${\eta }_i=\frac{{\overline{\gamma }}_i\sin \left({\overline{\gamma }}_i\right)-{\overline{\mathrm{\Theta }}}_i\cos \left({\overline{\gamma }}_i\right)}{{\overline{\gamma }}_i\cos \left({\overline{\gamma }}_i\right)+{\overline{\mathrm{\Theta }}}_i\sin \left({\overline{\gamma }}_i\right)};{\overline{\mathrm{\Theta }}}_i=\frac{{\mathrm{\Theta }}_i{h}_i}{G_{pi}{I}_{pi}};{\overline{\gamma }}_i={\gamma }_i{h}_i(22)$

Substituting Equation 20, 21 into Equation 4 yields

$k_{Ti}=\frac{T_i}{{\varphi }_i\left(z=0\right)}=-G_{pi}{I}_{pi}{\gamma }_i{\eta }_i(23)$

where k_Ti denotes the top-end torsional impedance of the i-th pile element.

The principle of impedance function recursion has been effectively used in past studies to address the vibration behavior of piles in layered soils [40]. According to this principle, the torque and twist angle at the interface between adjacent pile elements are continuous, meaning that the torsional impedance at the interface (i.e., torque/twist angle) is also continuous. That is to say, the impedance at the top of the i-th element is equal to the impedance at the bottom of (i+1)-th element (i.e., k_Ti = Θ_i+1). Hence based on Equation 23, the torsional impedance function at the top end of the pile can be determined via a step-by-step recursion from the first element to the N-th element, which can be written as follows

$k_{TN}=-G_{pN}{I}_{pN}{\gamma }_N{\eta }_N(24)$

Following Militano and Rajapakse [39], the normalized torsional impedance can be defined as

$k_T^{\prime }=-\frac{3G_{pN}{I}_{pN}{\gamma }_N{\eta }_N}{16G_0{r}_{0r}^3}(25)$

where $k_T^{\prime }$ denotes the normalized torsional impedance at the pile top; G₀ and r_0r denote the reference shear modulus and radius, respectively.

4 Numerical results and discussion

First, to confirm the correctness of the developed model, a comparison is made with the analytical results from Militano and Rajapakse [39]. For this comparison, the SDRN pile is reduced a solid cylindrical rod and the surrounding soil is assumed to be a uniform elastic material. The used parameters are ρ_p = 2,500 kg/m³, G_p = 12.1 or 16.5 GPa, r₀ = 0.3 m, r_in = 0 m, r_oumax = 0.3 m, r_c = 0.5 m, H = 10 m, w_b = 0 m, ρ_s1 = ρ_s2 = 1800 kg/m³, G_s1 = G_s2 = G_su = G_s0 = 20 MPa, β_s1 = β_s2 = 0. For analysis purposes, the normalized frequence is defined as a₀ = ωr_0r (ρ₀/G₀)^0.5, in which reference density ρ₀ = 1800 kg/m³ and G₀ = 20 MPa. In Figure 2, Re ( ) and Im ( ) denote respectively the real and imaginary components of the torsional impedance. Figure 2 demonstrates that an increase in excitation frequency leads to a decrease in real stiffness (real part) and an increase in damping (imaginary part). Additionally, the torsional impedance in the current solution corresponds well with those in the existing solution.

Figure 2

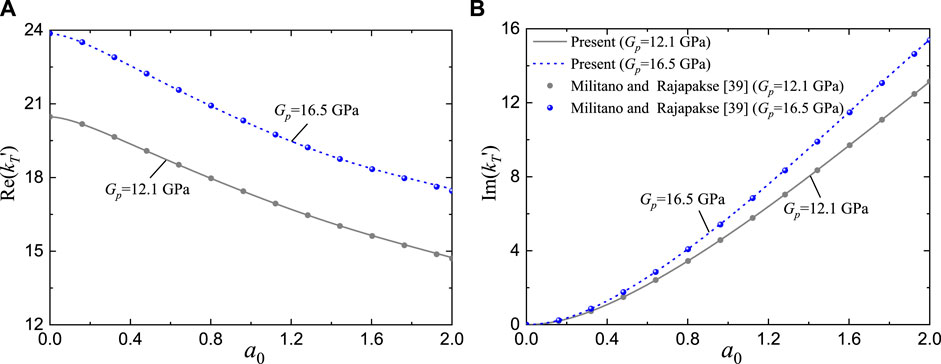
Figure 2. Comparison of torsional impedance results for an elastic cylindrical pile in homogeneous soil with those from existing solutions: (A) Real part; (B) Imaginary part.

After verifying the present solution, the effect of key parameters on the torsional impedance at the pile top is examined here. To account for soil damping, G_sj is replaced by G_sj (1+2iβ_sj), where β_sj denotes the damping ratio. Unless specified differently, the properties for SDRN pile and composite soil layers are outlined in Table 1. Additionally, each node is divided into 10 elements to simulate the continuous variation of cross-sectional dimension (see Figure 1B), where the length of the first pile segment h₁ fixed at 0.425 m.

Table 1

Table 1. Properties in SDRN pile and composite soil layers.

Figure 3 depicts the impact of inner radius (r_in) of the SDRN pile on the torsional impedance across different frequencies. The real stiffness initially decreases with an increase in frequency, then begins to increase at higher frequencies. In contrast, the imaginary part consistently increases as frequency rises. Moreover, both the real and imaginary parts decrease as r_in increases, indicating that the thinner wall (t_w = r₀−r_in) reduces the stiffness and damping of the pile, thereby decreasing its torsional resistance. This behavior is mainly attributed to the fact that a larger r_in decreases the polar moment of inertia of the pile, thereby reducing its dynamic resistance.

Figure 3

Figure 3. Torsional impedance for an elastic pile in elastic soil vs. excitation frequency for various inner radii: (A) Real part; (B) Imaginary part.

Figure 4 demonstrates the impact of outer radius (r₀) of the SDRN pile on the torsional impedance at various frequencies. For consistency, the radial width of cemented soil (r_c−r₀) is fixed at 0.2 m. As shown in Figure 4, r₀ has a greater impact on the torsional impedance than the inner radius. Both the real and imaginary components increase significantly as r₀ increases.

Figure 4

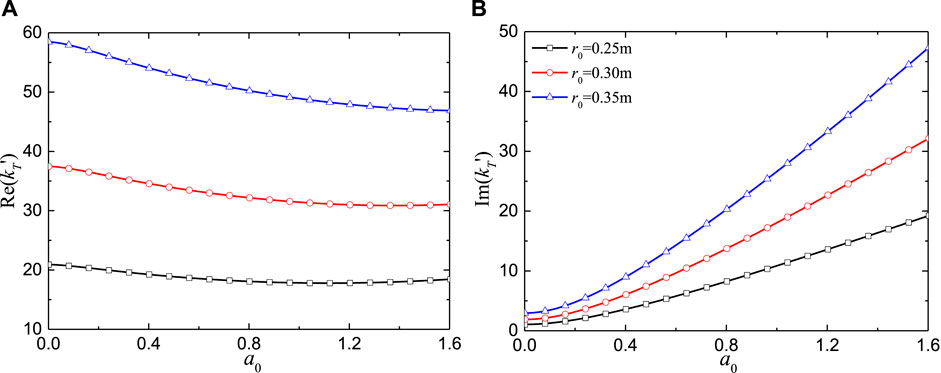
Figure 4. Torsional impedance for an elastic pile in elastic soil vs. excitation frequency for various outer radii: (A) Real part; (B) Imaginary part.

The effects of the node width (w_b) and vertical spacing (l_b) on the torsional impedance at different frequencies are presented in Figures 5, 6. It should be noted that for a fixed pile length, a smaller l_b corresponds to a greater number of nodes along the pile body. Figure 5 shows that increasing w_b leads to a rise in both the real and imaginary parts, revealing that a larger node width enhances the torsional resistance of the pile. This improvement is due to the increases in the polar moment of inertia at the node location, which enhances the dynamic resistance. It is evident from Figure 6 that the real part decreases as l_b increases, while the imaginary part is insensitive to l_b.

Figure 5

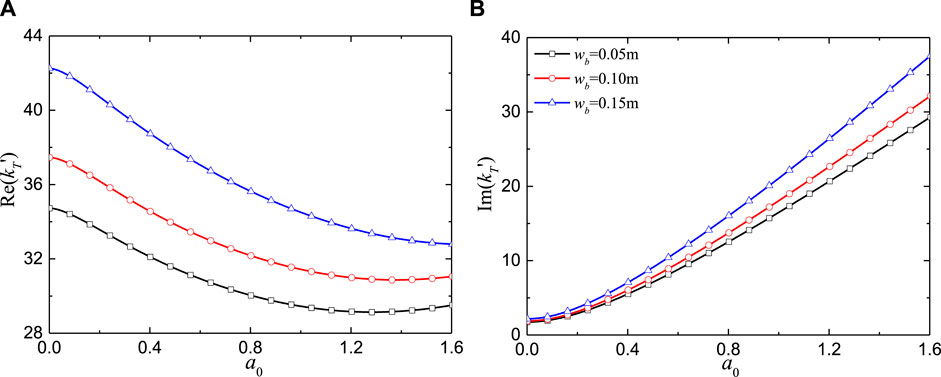
Figure 5. Torsional impedance for an elastic pile in elastic soil vs. excitation frequency for different node widths: (A) Real part; (B) Imaginary part.

Figure 6

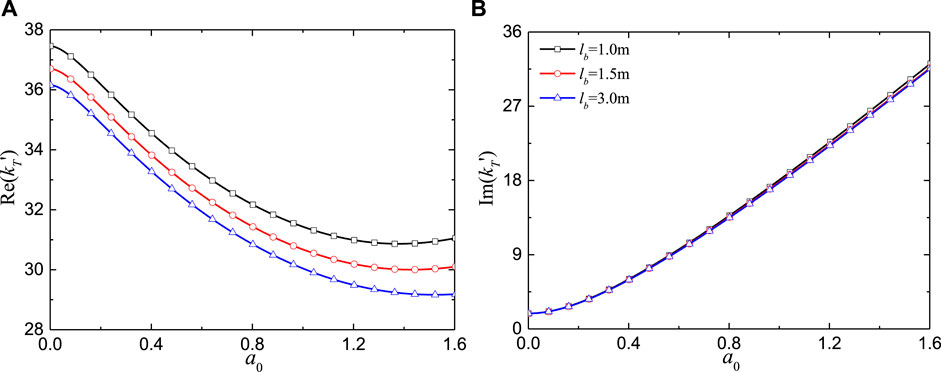
Figure 6. Torsional impedance for an elastic pile in elastic soil vs. excitation frequency for different vertical spacings of nodes: (A) Real part; (B) Imaginary part.

Figures 7, 8 describe the effects of the radial width and shear modulus of cemented soil on the torsional impedance at different frequencies. The radial width is represented by the outer radius of the cemented soil, with a larger r_c corresponding to a broader enhanced range. According to Figure 7, increasing the radial width leads to an increase in both the real and imaginary parts. In comparison, the effect of the shear modulus G_s1 is relatively smaller. As depicted in Figure 8, the components of torsional impedance increase as G_s1 increases, although the rate of increase slows down as G_s1 continues to rise. This suggests that enhancing the radial width of the cemented soil is more effective than increasing the shear modulus in improving the torsional impedance of the pile.

Figure 7

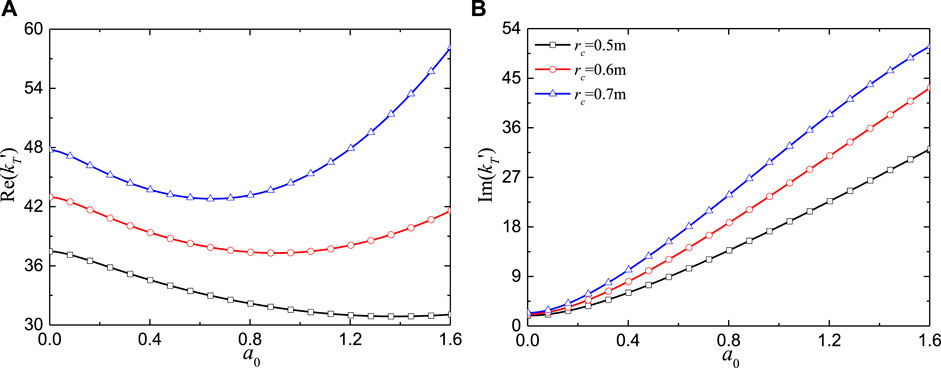
Figure 7. Torsional impedance for an elastic pile in elastic soil vs. excitation frequency for different radial widths of cemented soil: (A) Real part; (B) Imaginary part.

Figure 8

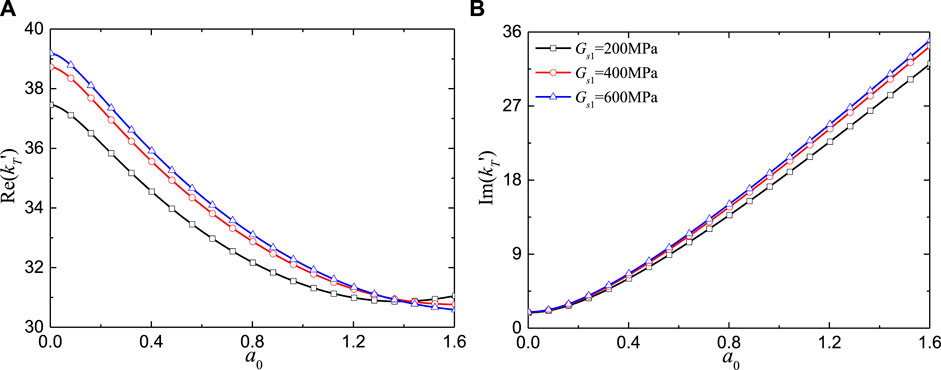
Figure 8. Torsional impedance for an elastic pile in elastic soil vs. excitation frequency for different shear modulus of cemented soil: (A) Real part; (B) Imaginary part.

Figure 9 describes the effect of the damping ratio of the outer soil layer on the torsional impedance for different frequencies. The focus here is to present the impact of the damping ratio of the outer natural soil layer due to minor effect of damping ratio of the inner soil. As shown in Figure 9, at lower frequencies, the damping ratio has little effect on the real part. However, at higher frequencies, the torsional impedance increases with increasing damping ratio.

Figure 9

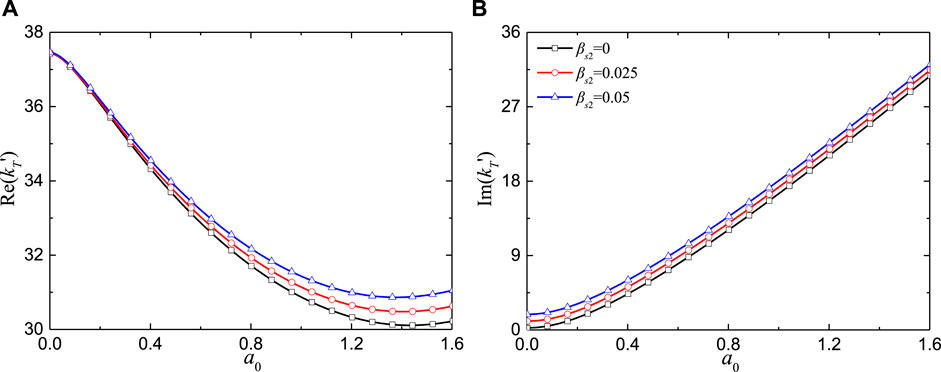
Figure 9. Torsional impedance for an elastic cylindrical pile in elastic soil vs. excitation frequency for different damping ratios of outer soil layer: (A) Real part; (B) Imaginary part.

5 Application to pile-supported rigid foundation

When a pile-supported rigid foundation is subjected to dynamic torsional loads (see Figure 10), the dynamic equilibrium of the foundation is defined by the equation given below

$I_f\frac{{\mathrm{d}}^2\phi \left(t\right)}{{\mathrm{d}t}^2}+\frac{\mathrm{d}\phi \left(t\right)}{\mathrm{d}t}+k_f\phi \left(t\right)=T_f\left(t\right)(26)$

where I_f and φ(t) represent the mass moment of inertia and angle of rotation of the foundation, respectively; k_f and c_f denote the stiffness and equivalent damping coefficient of the supported pile; T_f(t) denotes the external time-dependent torsional load.

Figure 10

Figure 10. Dynamic interaction between a rigid foundation and supported SDRN pile.

To obtain the solution for the foundation, Equation 24 can be reformulated as

$k_{TN}=k_f+\mathrm{i}\omega c_f(27)$

Assuming a time-harmonic external load on the foundation and making use of Equation 27, the solution to Equation 26 can be given by

$\phi =T_f/\left(k_f-I_f{\omega }^2+\mathrm{i}\omega c_f\right)(28)$

Making use of Equation 28, the normalized twist angle amplitude can be formulated as

$\left|A_{\phi }\right|=\left|\frac{16G_0{r}_0^3\phi }{3T_f}\right|=\frac{16G_0{r}_0^3}{3\sqrt{{\left(k_f-I_f{\omega }^2\right)}^2+{\left(\omega c_f\right)}^2}}(29)$

The following parts discuss the impact of key parameters on the twist angle amplitude, with the parameters listed in Table 1. To clearly observe the changing trends in resonant frequency and amplitude, we use the module of the twist angle amplitude instead of the real and imaginary part. In the analysis, I_f is fixed at 4,144 kg m². Figure 11 illustrates the effect of inner radius (r_in) and outer radius (r₀) of the SDRN pile on the twist angle amplitude at varying frequencies. The data in Figure 11A indicate that the twist angle amplitude initially ascends with frequency, reaches a peak, and then gradually approaches zero. The resonant peak shows obvious increase with an increase in r_in, while the resonant frequency slightly decreases as r_in increases. As shown in the Figure 11B, r₀ has a greater effect on the twist angle amplitude than the inner radius. The twist angle amplitude increases significantly as r₀ decreases. Furthermore, the resonant frequency increases markedly with an increase in r₀. This indicates that increasing the outer radius can substantially alter the natural frequency and reduce the twist angle of the whole system.

Figure 11

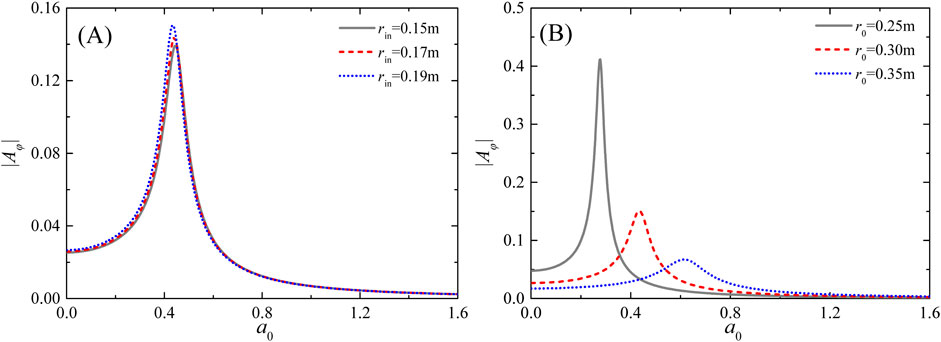
Figure 11. Variation of the normalized twist angle amplitude with excitation frequencies for different inner radii in (A) and outer radii in (B).

Figure 12 describes the effect of the node width (w_b) and vertical spacing (l_b) of the nodes on the twist angle amplitude for different frequencies. As observed in Figure 12A, the twist angle amplitude decreases significantly with an increase in w_b, revealing that a larger node width enhances the dynamic torsional resistance of the system. Besides, the resonant frequency rises with increasing w_b. Therefore, it can be concluded that increasing the node dimension is an effective strategy for improving the vibration behavior of the system in engineering practice. It can be observed in Figure 12B that contrary to expectations, the vertical spacing of the nodes has a relatively small impact on the twist angle amplitude. Additionally, the resonant peak shows a slight increase with increasing l_b.

Figure 12

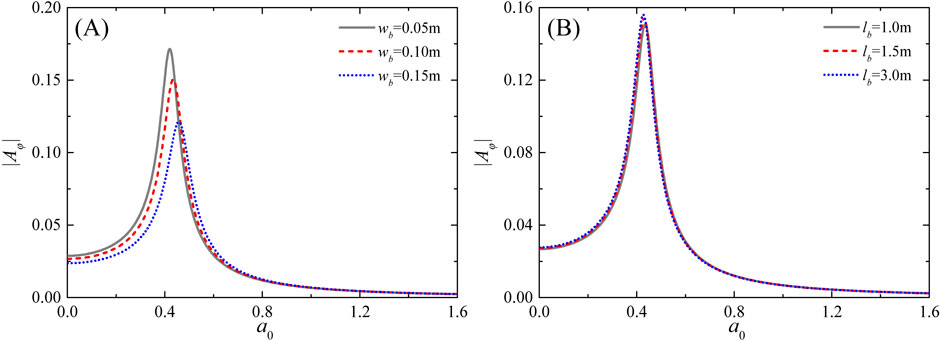
Figure 12. Variation of the normalized twist angle amplitude with excitation frequencies for different node widths in (A) and vertical spacings of nodes in (B).

Figure 13 describes the impact of the shear modulus and radial width of cemented soil on the twist angle amplitude at different frequencies. As observed in Figure 13A, the resonant peak decreases as G_s1 increases, while the resonant frequency increases with higher G_s1. At high frequencies, the influence of G_s1 becomes negligible. The impact of r_c is more pronounced than of the shear modulus of the cemented soil. The resonant peak significantly decreases as r_c increases, while the resonant frequency shows the opposite trend (see Figure 13B).

Figure 13

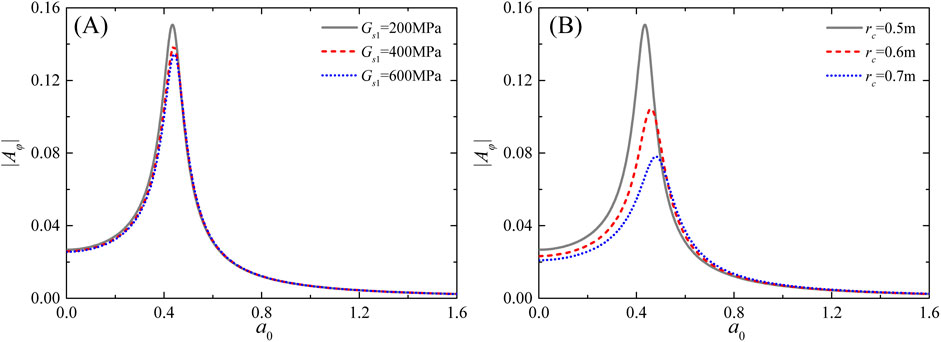
Figure 13. Variation of the normalized twist angle amplitude with excitation frequencies for different shear moduli in (A) and radial widths in (B) of cemented soil.

Figure 14 shows the effect of the damping ratio in the outer soil layer on the twist angle amplitude for different frequencies. The twist angle amplitude is notably affected by the damping ratio. The twist angle amplitude decreases substantially with increasing damping ratio, indicating that materials with a higher damping ratio are more effective in reducing vibrations.

Figure 14

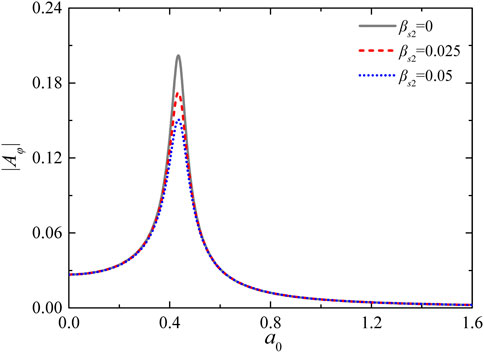
Figure 14. Variation of the normalized twist angle amplitude with excitation frequencies for different damping ratios of outer soil layer.

6 Conclusion

A closed-form solution is developed to address the time-harmonic torsional vibration of a SDRN pile embedded in elastic soils. The wave equations corresponding to the pile and surrounding soils are initially established. In the case of a time-harmonic load, the general solutions for the composite soil layers are derived. The pile and soil are partitioned into multiple elements, and interface continuity conditions of the pile and soil for each element are applied to derive the torsional impedance at the top end of each pile element. Using the principle of impedance function recursion, the torsional impedance of the pile and the twist angle amplitude are ultimately determined. The correctness of the proposed solution is meticulously checked, and detailed numerical analysis is conducted. The key findings are outlined as follows:

(1) Increasing the inner radius of the pile significantly reduces the torsional impedance of the pile and enhances the resonant peak of the system. In contrast, enlarging the outer radius markedly improves the torsional impedance of the pile, reduces the twist angle amplitude and raises the resonant frequency.

(2) Expanding the node width substantially increases the torsional impedance of the pile, reduces the twist angle amplitude and raises the resonant frequency, thereby improving the dynamic torsional resistance of the system. In contrast, variations in the vertical spacing of nodes have a relatively minor impact on the dynamic performance of the pile foundation.

(3) The radial width and shear modulus of the cemented soil are crucial in determining the dynamic characteristics of the system. Increasing the radial width of the cemented soil effectively increases the torsional impedance of the pile, attenuates both the resonant peak and frequency, thereby significantly enhancing the deformation resistance of the system. Moreover, enhancing the radial width of the cemented soil is more effective than increasing the shear modulus in improving the deformation resistance of the system.

(4) The damping ratio of the outer natural soil deposit is crucial for the dynamic response of the system. Increasing the damping ratio in the natural soil substantially improves the torsional impedance of the pile and reduces the twist angle amplitude, thereby effectively mitigating vibrations. These findings provide a solid theoretical foundation for optimizing SDRN pile designs.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HZ: Formal Analysis, Software, Validation, Writing–original draft. XL: Conceptualization, Funding acquisition, Project administration, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is funded by the National Natural Science Foundation of China (Grant No. 52478371).

Conflict of interest

Author HZ was employed by Hangzhou Transportation Investment and Construction Management Group Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tipsunavee T, Arangjelovski G, Jongpradist P. Numerical analysis on effects of soil improvement on pile forces on existing high-rise building. Buildings (2023) 13(6):1523. doi:10.3390/buildings13061523

CrossRef Full Text | Google Scholar

2. An-Jie W, Wan-Li Y. Numerical study of pile group effect on the hydrodynamic force on a pile of sea-crossing bridges during earthquakes. Ocean Eng (2020) 199:106999. doi:10.1016/j.oceaneng.2020.106999

CrossRef Full Text | Google Scholar

3. Fabo C, Ben H, Peng G, Xiangming G, Yong Z, Weijiang C. Effect of installation platform on bearing capacity of an offshore monopile foundation. Front Phys (2022) 9:809581. doi:10.3389/fphy.2021.809581

CrossRef Full Text | Google Scholar

4. Gupta BK. A hybrid formulation for torsional dynamic response of pile foundations in a layered soil deposits. Comput Geotech (2024) 168:106115. doi:10.1016/j.compgeo.2024.106115

CrossRef Full Text | Google Scholar

5. Luan L, Zheng C, Kouretzis G, Ding X. Dynamic analysis of pile groups subjected to horizontal loads considering coupled pile-to-pile interaction. Comput Geotech (2020) 117:103276. doi:10.1016/j.compgeo.2019.103276

CrossRef Full Text | Google Scholar

6. Liu X, El Naggar MH, Wang K, Wu W. Dynamic soil resistance to vertical vibration of pipe pile. Ocean Eng (2021) 220:108381. doi:10.1016/j.oceaneng.2020.108381

CrossRef Full Text | Google Scholar

7. Cai Y, Chen G, Xu C, Wu D. Torsional response of pile embedded in a poroelastic medium. Soil Dyn Earthq Eng (2006) 26(12):1143–8. doi:10.1016/j.soildyn.2005.10.009

CrossRef Full Text | Google Scholar

8. Chen G, Cai Y, Liu F, Sun H. Dynamic response of a pile in a transversely isotropic saturated soil to transient torsional loading. Comput Geotech (2008) 35(2):165–72. doi:10.1016/j.compgeo.2007.05.009

CrossRef Full Text | Google Scholar

9. Wang K, Zhang Z, Leo CJ, Xie K. Dynamic torsional response of an end bearing pile in saturated poroelastic medium. Comput Geotech (2008) 35(3):450–8. doi:10.1016/j.compgeo.2007.06.013

CrossRef Full Text | Google Scholar

10. Wang K, Zhang Z, Leo CJ, Xie K. Dynamic torsional response of an end bearing pile in transversely isotropic saturated soil. J Sound Vib (2009) 327(3-5):440–53. doi:10.1016/j.jsv.2009.06.017

CrossRef Full Text | Google Scholar

11. Zheng C, Liu H, Ding X, Lv Y. Torsional dynamic response of a large-diameter pipe pile in viscoelastic saturated soil. Int J Numer Anal Methods Geomech (2014) 38(16):1724–43. doi:10.1002/nag.2279

CrossRef Full Text | Google Scholar

12. Zheng C, Hua J, Ding X. Torsional vibration of a pipe pile in transversely isotropic saturated soil. Earthq Eng Eng Vib (2016) 15(3):509–17. doi:10.1007/s11803-016-0340-2

CrossRef Full Text | Google Scholar

13. Zou X, Du H, Zhou M, Zhou X. Analysis of a single pile under vertical and torsional combined loads in two-layered nonhomogeneous soil. Int J Geomech (2019) 19(6):04019054. doi:10.1061/(ASCE)GM.1943-5622.0001429

CrossRef Full Text | Google Scholar

14. Liu K, Zhang Z. Dynamic response of an inhomogeneous elastic pile in a multilayered saturated soil to transient torsional load. Math Probl Eng (2021) 2021(1):1–13. doi:10.1155/2021/5528237

CrossRef Full Text | Google Scholar

15. Li X, Zhang Z, Sheng J. Exact solution for the torsional vibration of an elastic pile in a radially inhomogeneous saturated soil. J Math (2021) 2021(1):1–12. doi:10.1155/2021/6644057

CrossRef Full Text | Google Scholar

16. Zhang Z, Pan E. Dynamic torsional response of an elastic pile in a radially inhomogeneous soil. Soil Dyn Earthq Eng (2017) 99:35–43. doi:10.1016/j.soildyn.2017.04.020

CrossRef Full Text | Google Scholar

17. Li Z, Gao Y. Influence of the inner soil on the torsional vibration of a pipe pile considering the construction disturbance. Acta Geotech (2021) 16(11):3647–65. doi:10.1007/s11440-021-01298-3

CrossRef Full Text | Google Scholar

18. Li Z, Pan Y, Gao Y, El Naggar MH, Wang K. Torsional vibration of open-ended pipe piles in saturated soil considering the construction disturbance. Ocean Eng (2023) 267:113253. doi:10.1016/j.oceaneng.2022.113253

CrossRef Full Text | Google Scholar

19. Sun M, Peng MQ, Chen Z, Zhao S, Li W, Chen F, et al. Dynamic torsional vibration of a pipe pile in radial heterogeneous transversely isotropic saturated soil. J Eng Mech (2024) 150(10):04024068. doi:10.1061/JENMDT.EMENG-7668

CrossRef Full Text | Google Scholar

20. Wu W, Liu H, El Naggar MH, Mei G, Jiang G. Torsional dynamic response of a pile embedded in layered soil based on the fictitious soil pile model. Comput Geotech (2016) 80:190–8. doi:10.1016/j.compgeo.2016.06.013

CrossRef Full Text | Google Scholar

21. Vega-Posada CA, Areiza-Hurtado M. Analysis of torsionally loaded non-uniform circular piles in multi-layered non-homogeneous elastic soils. Eng Struct (2022) 260:114205. doi:10.1016/j.engstruct.2022.114205

CrossRef Full Text | Google Scholar

22. Ma W, Wang B, Zhou S, Leong EC, Wang C. Torsional dynamic response of an end-bearing pile in homogeneous unsaturated transversely isotropic soil. Ocean Eng (2024) 299:117241. doi:10.1016/j.oceaneng.2024.117241

CrossRef Full Text | Google Scholar

23. Ma W, Shan Y, Xiang K, Wang B, Zhou S. Torsional dynamic response of a pipe pile in homogeneous unsaturated soils. Comput Geotech (2022) 143:104607. doi:10.1016/j.compgeo.2021.104607

CrossRef Full Text | Google Scholar

24. Ma W, Shan Y, Wang B, Zhou S, Wang C, Wang B, et al. Torsional dynamic response of a pipe pile embedded in unsaturated poroelastic transversely isotropic soil. Ocean Eng (2024) 310:118574. doi:10.1016/j.oceaneng.2024.118574

CrossRef Full Text | Google Scholar

25. Li Z, Zhao C, Xi Y, Jin N, Gao Y. Torsional vibration of a pile in unsaturated soil considering the construction disturbance. Comput Geotech (2024) 172:106409. doi:10.1016/j.compgeo.2024.106409

CrossRef Full Text | Google Scholar

26. Ma W, Shan Y, Wang B, Zhou S, Wang C. Analytical solution for torsional vibration of an end-bearing pile in nonhomogeneous unsaturated soil. J Build Eng (2022) 57:104863. doi:10.1016/j.jobe.2022.104863

CrossRef Full Text | Google Scholar

27. Li Z, Zhao C, Gao Y, Wu W, Wang K, Zhang Z. Torsional vibration of a floating pile in radially inhomogeneous unsaturated soil based on the fictitious unsaturated soil pile model. Soil Dyn Earthq Eng (2024) 183:108812. doi:10.1016/j.soildyn.2024.108812

CrossRef Full Text | Google Scholar

28. Honda T, Hirai Y, Sato E. Uplift capacity of belled and multi-belled piles in dense sand. Soils Found (2011) 51(3):483–96. doi:10.3208/sandf.51.483

CrossRef Full Text | Google Scholar

29. Horiguchi T, Karkee MB. Load tests on bored PHC nodular piles in different ground conditions and the bearing capacity based on simple soil parameters. AIJ J Technol Des (1995) 1(1):89–94. doi:10.3130/aijt.1.89

CrossRef Full Text | Google Scholar

30. Zhou JJ, Wang KH, Gong XN, Zhang RH. Bearing capacity and load transfer mechanism of a static drill rooted nodular pile in soft soil areas. J Zhejiang Univ Sci (2013) A(14):705–19. doi:10.1631/jzus.a1300139

CrossRef Full Text | Google Scholar

31. Zhou JJ, Gong XN, Wang KH, Zhang RH. A field study on the behavior of static drill rooted nodular piles with caps under compression. J Zhejiang Univ Sci (2015) A(16):951–63. doi:10.1631/jzus.a1500168

CrossRef Full Text | Google Scholar

32. Zhou JJ, Gong XN, Wang KH, Zhang RH, Yan TL. A model test on the behavior of a static drill rooted nodular pile under compression. Mar Georesour Geotech (2016) 34(3):293–301. doi:10.1080/1064119X.2015.1012313

CrossRef Full Text | Google Scholar

33. Zhou JJ, Gong XN, Wang KH, Zhang RH, Yan JJ. Testing and modeling the behavior of pre-bored grouting planted piles under compression and tension. Acta Geotech (2017) 12:1061–75. doi:10.1007/s11440-017-0540-6

CrossRef Full Text | Google Scholar

34. Li ZY, Wang KH, Wu WB, Leo CJ. Longitudinal dynamic impedance of a static drill rooted nodular pile embedded in layered soil. Mar. Georesour Geotech (2018) 36(3):253–63. doi:10.1080/1064119X.2016.1214194

CrossRef Full Text | Google Scholar

35. Wu JT, Wang KH, Liu X. Effect of a nodular segment on the dynamic response of a tubular pile subjected to longitudinal vibration. Acta Geotech (2020) 15:2925–40. doi:10.1007/s11440-020-00930-y

CrossRef Full Text | Google Scholar

36. Guo J, Dai GL. Study on vertical bearing capacity calculation method of the static drill rooted nodular piles. Spec Struct (2019) 36(05):44–50. (In Chinese). doi:10.19786/j.tzjg.2019.05.007

CrossRef Full Text | Google Scholar

37. Wang KH, Xiao S, Gao L, Wu JT. Vertical dynamic response of a static drill rooted nodular pile. J Vib Shock (2019) 38(15):49–56+86. (In Chinese). doi:10.13465/j.cnki.jvs.2019.15.007

CrossRef Full Text | Google Scholar

38. Liu QY, Zhou JJ, Gong XN, Zhang RH, Huang S. Numerical simulation of bearing performance of prestressed nodular pile in soft soil area. J Hunan Univ Nat Sci (2023) 50(03):235. (In Chinese). doi:10.16339/j.cnki.hdxbzkb.2023048

CrossRef Full Text | Google Scholar

39. Militano G, Rajapakse R. Dynamic response of a pile in a multi-layered soil to transient torsional and axial loading. Geotechnique (1999) 49(1):91–109. doi:10.1680/geot.1999.49.1.91

CrossRef Full Text | Google Scholar

40. Zhang Z, Zhou J, Wang K, Li Q, Liu K. Dynamic response of an inhomogeneous viscoelastic pile in a multilayered soil to transient axial loading. Math Probl Eng (2015) 2015(1):1–13. doi:10.1155/2015/495253

CrossRef Full Text | Google Scholar