A counter mode and multi-channel based chaotic image encryption algorithm for the internet of things

To deal with the threat of image privacy leakage in the Internet of things, this paper presents a novel batch images encryption algorithm using the counter mode and a multi-channel processing scheme. We employ multi-thread technique combined with an adapter to construct a novel multi-channel processing scheme, which can encrypt four different sized images in one round. Moreover, the counter encryption mode, which can compute round keys from a plaintext related session key, is introduced to decrease the difficulty of session key management when dealing with batch images. The security tests demonstrate the exceptional performance of the proposed algorithm in terms of security, as evidenced by P-values of statistical tests far larger than 0.01, correlation coefficients and entropies of cipher images close to 0 and greater than 7.99. Additionally, the results of NPCR and UACI tests closely approximate the theoretical values 99.6094% and 33.4635%, the proposed algorithm can better resist statistical, exhaustive, differential, or even chosen plaintext attacks. Moreover, due to the novel parallel scheme with a linear time complexity of O(2W+2H), which demonstrates an acceleration of over 300% compared to existing algorithms, it only takes 2.1sto encrypt one hundred images with varying sizes. Therefore, the proposed algorithm succeeds in exceeding existing algorithms in meeting the efficiency and security requirements for encrypting batch images.

1 Introduction

With the rapid proliferation of Internet of things (IoT) and wireless communication techniques, multimedia data has become an indispensable facet of daily life. Among various modes of multimedia representation, digital images have gained immense popularity owing to their affordability and easy accessibility. However, a looming threat of privacy breaches casts a shadow over image communication, resulting in financial losses or even endangering lives [1–3]. Scholars have endeavored to address this issue through encryption techniques [4, 5], watermarking [6, 7], steganography [8, 9], among others. Watermarking, whether blind or non-blind, offers creators an effective means to safeguard their copyright for image products. Steganography involves concealing secrets within host images and establishes a channel between sender and receiver for sharing less sensitive private information. Nevertheless, both techniques face challenges when it comes to securely transmitting high-capacity confidential images. Hence, encryption techniques remain crucial in transforming vivid images into disorderly forms as a defense against theft of classified information.

The limitations of well-known commercial ciphers, such as AES and ECC, in encrypting images have led to an increasing focus on the development of a dedicated cryptosystem for image encryption [10, 11]. The readability of a digital image can be compromised through various scrambling methods, such as Zigzag transformation [12, 13], Arnold transformation [14, 15] or magic cube [16, 17]. Therefore, despite the visual appearance of encryption, these methods are still susceptible to attacks based on frequency analysis and other techniques. Therefore, to completely conceal the relationship between the original and cipher images, various diffusion methods have been proposed to convert organized pixels into a state of statistical disorder. In general, a two-round cipher-block-chain (CBC) based diffusion process can provide protection against most cryptographic attacks by incorporating the previous ciphertext to encrypt the current plaintext and achieve an avalanche effect [5, 18, 19]. Additionally, pseudo random numbers play a crucial role in achieving satisfactory diffusion effects. Due to their high initial sensitivity and unpredictable randomness, chaotic systems naturally meet the requirements of an ideal cryptography pseudo random number generator [20–22]. Consequently, chaos-based image encryption algorithms have yielded significant advancements in preserving image privacy. For instance, Hua et al. [23] developed a novel 2D-LSM system to enhance the security of their color image encryption algorithm. Gao et al. [24] utilized DNA mutation operations and hyperchaotic systems to design a secure image encryption algorithm. Huang et al. [25] introduced compressive sensing and DWT techniques for enhanced security against attacks while Teng et al. [26] proposed a novel simultaneous permutation and diffusion structure that offers both high security and fast encryption speed.

However, in an actual communication between IoT devices, it usually involves hundreds of images to transfer. Since most existing algorithms aimed at single image encryption (hereinafter referred to as SIEA, single image encryption algorithm), it might emerge some imperfections when directly applied them to encrypt multiple images. First, in many SIEAs [27–29], the hash function is employed to provide a plaintext related session key which may cause extra communication overhead of session key exchange in multi-image encryption. Second, as the number of images grows, if a SIEA simply encrypts images in serial, the heavy time consumption of encryption will lead to low efficiency of image secure communications [23–29]. Third, some scholars attempted to reuse their SIEAs by composing multiple images into a single image with big size [30–32], but ignored the rapid growth of space complexity along with the increase of image numbers. Hence, researchers have gradually paid more attention to design specific algorithms for multi-image encryption (hereinafter referred to as MIEA, multi-image encryption algorithm).

Inspired by the 3D structure of the color image, some MIEAs operate on a three-dimensional image cube comprising all original images. In conjunction with conventional scrambling and rotation techniques, Sahasrabuddhe et al. [33] successfully achieved three-dimensional image cube scrambling prior to the diffusion process. Zhang et al. [34] applied Sarrus and 3D Fibonacci rules on the image cube to achieve scrambling and diffusion respectively. Zhou et al. [35] proposed a simultaneous scrambling-diffusion method on the image cube. Obviously, suchlike algorithms have an obvious limitation that they can only deal with multiple images with the same size. To address this issue, zero padding is commonly employed as a universal solution for smaller images [33–35]. Furthermore, considering the potential security issues of simple zero padding, Wang et al. [36] depended on blurred pixels method to fill smaller images to make their algorithm more robust against various attacks. In addition, the implementation of these algorithms necessitates additional computing resources, rendering they impractical for IoT devices with limited resources.

Another universal approach is that existing SIEA can work smoothly on a single image compounded from multiple images. Based on a so called NTMDP method, Tao et al. [37] realized multiple images encryption via a base-plane image, but the only shortcoming is that the high complexity of compound process makes their MIEA unsuitable for real-time communications. By using a P-tensor product compressive sensing technique, Xiao et al. [38] also presented a secure MIEA based on a compound single image, which not only had fast encryption speed but also had low storage consumption. However, reconstruction-induced data loss imposes limitations on the application of this method in secure transmissions of high-resolution images. Gao et al. [39] proposed an innovative scheme by integrating multiple images into a single image within the HSV channel. Subsequently, they employed a single-channel based scrambling and diffusion process to obtain the final cipher image. However, the overall efficiency of the MIEA is deemed unsatisfactory due to significant time consumption associated with color channel transformation.

1.1 Motivation and contribution

To design an applicable chaos-based image encryption algorithm for IoT devices, the complexity of the employed chaotic systems is also an important issue that cannot be ignored. The simple structures of low-dimensional chaotic systems make them suitable for implementation in resource-constrained IoT devices [40]. However, they may experience degradation, leading to the transformation of the chaotic system into a periodic system. The high-dimensional, especially hyperchaotic systems exhibit strong robustness against degradation, making them more complex to generate superior random sequences for enhanced security. However, this also poses implementation challenges, particularly in resource-constrained IoT devices [41].

In conclusion, given the escalating demand for secure image communications between IoT devices, the existing MIEAs still have notable deficiencies in terms of both efficiency and security. Therefore, this paper proposes an innovative encryption algorithm for batch images based on counter mode and a multi-channel processing scheme. Utilizing the multi-channel processing scheme, the proposed algorithm enables parallel encryption of four different sized images using any well-established SIEA. By introducing counter mode encryption, the novel scheme can easily be extended to handle batch images without heavy session key management.

The novelties and contributions of the proposed MIEA are summarized below:

1) To protect privacy of image data in IoT device, a fast and secure batch images encryption algorithm based on counter mode and multi-channel processing scheme is proposed.

2) A lightweight multi-channel pseudo random number generator is constructed from two 2D hyperchaotic systems, which can offer exceptional performance even in resource-constrained IoT devices.

3) By designing an adapter for key streams, four different sized images can be parallel encrypted using multi-thread technique, thereby eliminating additional operations on the original images.

4) The counter mode is introduced to obtain round keys from a session key on local device when dealing with batch images, which significantly simplifies session key management between IoT devices.

5) Various kinds of tests are performed on the proposed algorithm to verify its outstanding performances of feasibility, security, and efficiency, which can primely meet the requirements of batch images encryption.

The remainder of this paper is organized as follows. Section 2 presents the preliminaries for this work. In Section 3, we introduce the proposed image encryption algorithm. In Section 4, we present and analyze the experimental results of the proposed algorithm. Finally, we draw conclusions in Section 5.

2 Preliminaries

2.1 The employed 2D hyperchaotic systems

Pseudo random numbers are always critical to achieve high-strength image encryption to resist attacks. The hyperchaotic system, which contains two or more positive Lyapunov exponents, has extremely complex phase space trajectories, strong resistance against degradation in digital systems, and long-term unpredictable randomness. However, considering the heavy time consumption to solve equations, high dimensional continuous hyperchaotic systems are not so proper for time-sensitive encryption occasions. Recently, due to the progress of chaos control theory, 2D hyperchaotic systems have proven to be more suitable for image encryption, since they have simpler structure and faster iteration speed, while they still maintain good properties of other hyperchaotic systems. In this paper, to provide multi-channel pseudo random numbers with good properties, two novel 2D hyperchaotic systems are employed.

The first 2D hyperchaotic system 2D-SCCM [42] is defined as Equation 1 below:

$\left\{\begin{array}{l}{x}_1\left(n+1\right)=\sin \left({10}^{17}r{x}_1\left(n\right)+y_1\left(n\right)\right)\\ y_1\left(n+1\right)=\cos \left({10}^{19}r\pi y_1\left(n\right)\right)\end{array}\right.(1)$

where r is the control parameter, and x₁, y₁∈[-1,0)⋃(0,1]. When r locates in 100 and 200, as Figure 1 shows, two positive Lyapunov exponents occur, indicating the 2D-SCCM evolves into hyperchaotic state. In this paper, for better encryption effect, r is set as 200.

Figure 1

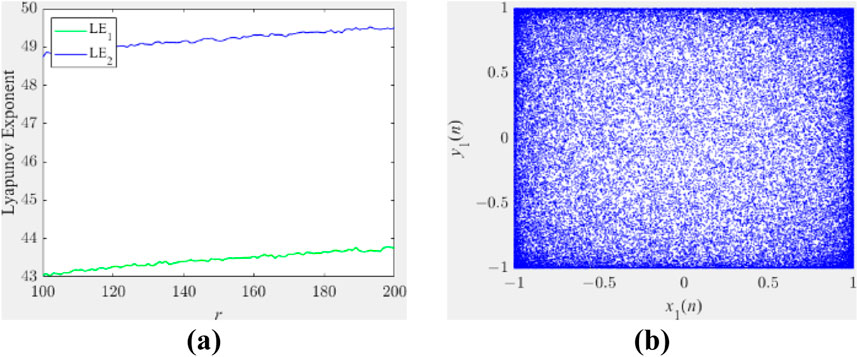
Figure 1. The chaotic behavior of 2D-SCCM. (A) LE distribution diagram. (B) Phase space trajectory diagram.

The another 2D hyperchaotic system 2D-SIDCM [43] is described as Equation 2:

$\left\{\begin{array}{l}{x}_2\left(n+1\right)=\sin \left(\frac{b}{\sin \left(a{y}_2\left(n\right)\right)}\right)\\ y_2\left(n+1\right)=\sin \left(a\sin \left(\frac{b}{x_2\left(n\right)y_2\left(n\right)}\right)\right)\end{array}\right.(2)$

which has two control parameters a, b and x₂, y₂∈[-1,0)⋃(0,1]. When a, b∈(0, 100], it contains two positive Lyapunov exponents and represents hyperchaotic behaviors as demonstrated in Figure 2. In this paper, for high-strength encryption, a and b are both set as 100.

Figure 2

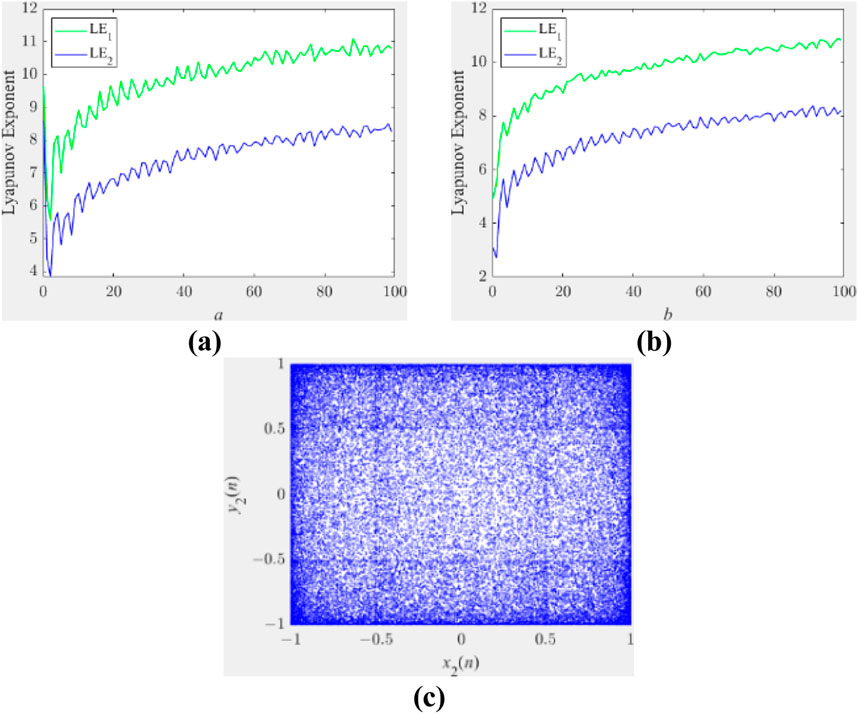
Figure 2. The chaotic behavior of 2D-SIDCM. (A) LE distribution diagram when b being set as 100. (B) LE distribution diagram when a being set as 100. (C) Phase space trajectory diagram.

2.2 The employed 1D chaotic maps

The 1D chaotic system is a proper tool for fast scrambling pixel positions. However, traditional 1D chaotic systems, such as Logistic map and Sine map, suffer from degeneration. Recently, by introducing cascade technique, many more robust 1D chaotic systems are proposed [44].

On the one hand, for scrambling, a cascade chaotic map 1D-CLLCM is employed, which is given by Equation 3, and x₃∈[-1,0)⋃(0,1].

$x_3\left(n+1\right)=1-2{\left({1-2x_3\left(n\right)}^2\right)}^2(3)$

On the other hand, for providing initial vectors of the encryption process, another cascade chaotic map 1D-CLSCM, as shown in Equation 4 with x₄∈(0,1], is utilized.

$x_4\left(n+1\right)=4\sin \left(\pi x_4\left(n\right)\right)\left(1-\sin \left(\pi x_4\left(n\right)\right)\right)(4)$

By comparing between Figures 3A, B and Figures 3C, D, two cascade chaotic maps have much larger Lyapunov exponents than traditional maps, meaning better chaotic properties against degeneration. Thus, they can ensure better scrambling effect and provide initial vectors with enough randomness.

Figure 3

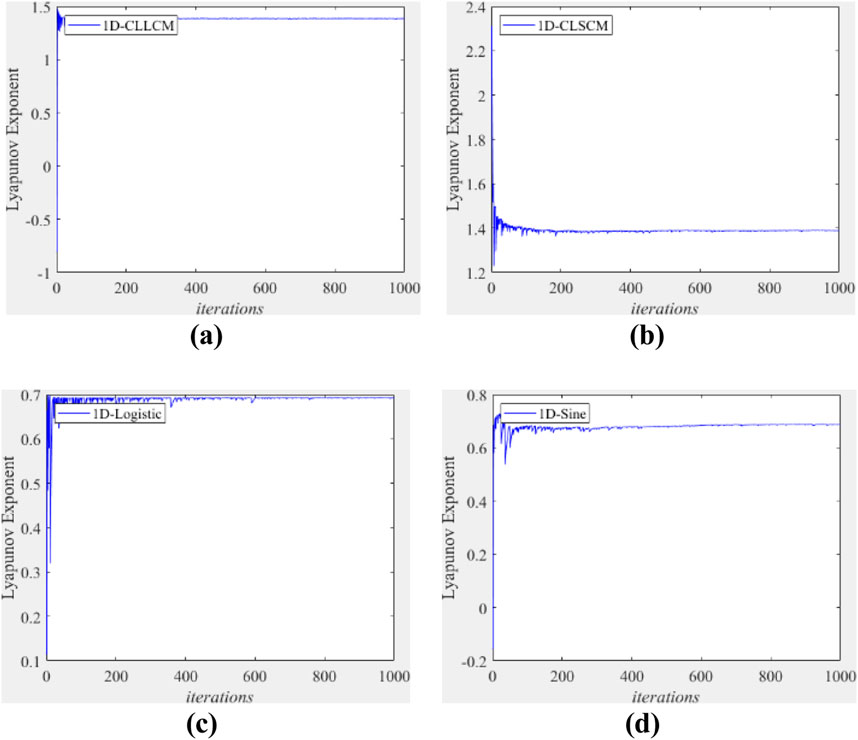
Figure 3. Largest Lyapunov exponents of (A) 1D-CLLCM, (B) 1D-CLSCM, (C) 1D-Logistic, and (D) 1D-Sine.

2.3 The counter encryption mode

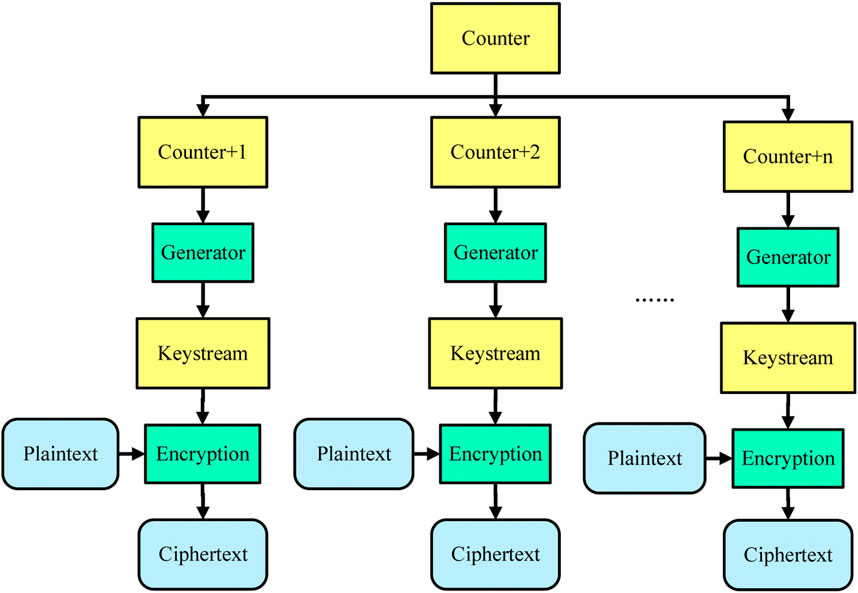
The counter mode was first introduced to turn a block cipher into a stream cipher [45, 46]. As demonstrated in Figure 4, the counter mode generates next keystream by encrypting successive counter values.

Figure 4

Figure 4. The schematic diagram of counter encryption mode.

In this paper, the counter mode is employed to generate round key of encrypting each four original images, which can reduce the difficulty of session key management. And as we can see in Figure 4, if all counter values are obtained before encryption, each round encryption can be parallel processed, which can further accelerate batch images encryption.

3 The proposed batch images encryption algorithm

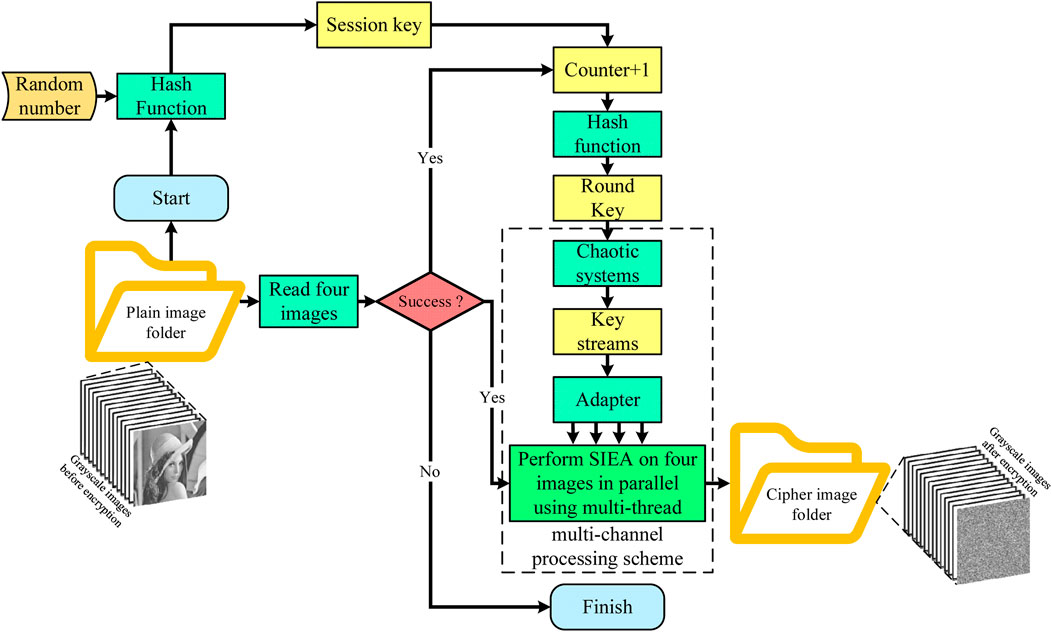
The flowchart of the proposed algorithm is demonstrated in Figure 5. Then, the details will be discussed from 1) how to obtain session key and round key, 2) how to generate the required key streams, 3) the employed SIEA, and 4) how the proposed algorithm works.

Figure 5

Figure 5. The flowchart of the proposed multi-image encryption algorithm.

3.1 The management of session key and round keys

To simplify session key management for batch images encryption task, this paper employs both hash function and random number. First, to resist differential attacks, the hash function is employed to quickly extract a global session key being sensitive to all under encrypted images. Second, to avoid invalid encryption when facing session key leakage, an external true random number is introduced to achieve one-time pad. At last, to accomplish encryption task, round keys for each four images will be calculated from the global session key.

The detail steps of generating session key and round keys are described below:

Step A1: Input an external 256-bit random number K_e and all original images into a secure hash function SHA-256, then a 256-bit session key SK can be created.

Step A2: For encrypting each four images, the SK will be further calculated by SHA-256 to obtain round keys, and since the number of images N is certain for every encryption task, round keys RK₁, RK₂, … , RK_N/4 can be obtained far before encryption.

Step A3: To launch chaotic systems, the round key will be post processed into floating point numbers. Take the round key RK₁ as an example, it can be converted into initial values for 2D-SCCM, 2D-SIDCM, 1D-CLLCM, and 1D-CLSCM by Equation 5, where operator ⊕ means a bitwise exclusive or operation:

$\left\{\begin{array}{l}{x}_1\left(1\right)=\left(\mathit{R}{\mathit{K}}_1\left(1:40\right)\oplus \mathit{R}{\mathit{K}}_1\left(217:256\right)\right)/2^{40}\\ y_1\left(1\right)=\left(\mathit{R}{\mathit{K}}_1\left(41:80\right)\oplus \mathit{R}{\mathit{K}}_1\left(177:216\right)\right)/2^{40}\\ x_2\left(1\right)=\left(\mathit{R}{\mathit{K}}_1\left(81:120\right)\oplus \mathit{R}{\mathit{K}}_1\left(137:176\right)\right)/2^{40}\\ y_2\left(1\right)=\left(\mathit{R}{\mathit{K}}_1\left(121:160\right)\oplus \mathit{R}{\mathit{K}}_1\left(97:136\right)\right)/2^{40}\\ x_3\left(1\right)=\left(\mathit{R}{\mathit{K}}_1\left(161:200\right)\oplus \mathit{R}{\mathit{K}}_1\left(57:96\right)\right)/2^{40}\\ x_4\left(1\right)=\left(\mathit{R}{\mathit{K}}_1\left(201:240\right)\oplus \mathit{R}{\mathit{K}}_1\left(17:56\right)\right)/2^{40}\end{array}\right.(5)$

3.2 The generation of key streams for diffusion

To perform multi-thread encryption on each four images, we combine 2D-SCCM and 2D-SIDCM to construct a multi-channel pseudo random numbers generator for diffusion, which not only has long-term unpredictable randomness, but also has ultra-fast generation speed. It consists of the following steps:

Step B1: Input x₁(1), y₁(1) and x₂(1), y₂(1) into 2D-SCCM and 2D-SIDCM respectively.

Step B2: Pre-iterate 2D-SCCM and 2D-SIDCM 100 times to overcome transient effect for better security, and let new x₁(1), y₁(1) and x₂(1), y₂(1) be the last state values.

Step B3: Create four empty sequences S₁, S₂, S₃, S₄.

Step B4: Read four images and obtain their width W₁, W₂, W₃, W₄, and height H₁, H₂, H₃, H₄.

Step B5: Let W_max = max{W₁, W₂, W₃, W₄} and H_max = max{H₁, H₂, H₃, H₄}.

Step B6: Continue to iterate 2D-SCCM and 2D-SIDCM W_max×H_max times and fill S₁, S₂, S₃, S₄ by Equation 6.

$\left\{\begin{array}{l}{\mathit{S}}_1=\left\{{\mathit{S}}_1,x_1\left(i\right)\right\},{\mathit{S}}_2=\left\{{\mathit{S}}_2,y_1\left(i\right)\right\}\\ {\mathit{S}}_3=\left\{{\mathit{S}}_3,x_2\left(i\right)\right\},{\mathit{S}}_4=\left\{{\mathit{S}}_4,y_2\left(i\right)\right\}\\ i=1,2,\cdots ,W_{\max }\times H_{\max }-1,W_{\max }\times H_{\max }\end{array}\right.(6)$

Step B7: Convert each element of the above generated sequences into integer number which locates in 0–255 as Equation 7 presents.

$\left\{\begin{array}{l}{\mathit{S}}_1=\lfloor \left(\left|{\mathit{S}}_1\right|-\lfloor \left|{\mathit{S}}_1\right|\rfloor \right)\times {10}^{15}\rfloor \%256\\ {\mathit{S}}_2=\lfloor \left(\left|{\mathit{S}}_2\right|-\lfloor \left|{\mathit{S}}_2\right|\rfloor \right)\times {10}^{15}\rfloor \%256\\ {\mathit{S}}_3=\lfloor \left(\left|{\mathit{S}}_3\right|-\lfloor \left|{\mathit{S}}_3\right|\rfloor \right)\times {10}^{15}\rfloor \%256\\ {\mathit{S}}_4=\lfloor \left(\left|{\mathit{S}}_4\right|-\lfloor \left|{\mathit{S}}_4\right|\rfloor \right)\times {10}^{15}\rfloor \%256\end{array}\right.(7)$

Step B8: Create four empty sequences DK₁, DK₂, DK₃, DK₄, then fill them by Equation 8.

$\left\{\begin{array}{l}\mathit{D}{\mathit{K}}_1={\mathit{S}}_1\oplus {\mathit{S}}_3\\ \mathit{D}{\mathit{K}}_2={\mathit{S}}_2\oplus {\mathit{S}}_4\\ \mathit{D}{\mathit{K}}_3={\mathit{S}}_1\oplus {\mathit{S}}_4\\ \mathit{D}{\mathit{K}}_4={\mathit{S}}_2\oplus {\mathit{S}}_3\end{array}\right.(8)$

Step B9: Delete S₁, S₂, S₃, S₄, then reshape DK₁, DK₂, DK₃, DK₄ to four matrices with size of W_max×H_max.

Step B10: At last, adapt the sizes of DK₁, DK₂, DK₃, DK₄ to sizes of W₁×H₁, W₂×H₂, W₃×H₃, W₄×H₄, then obtain four diffusion key matrices for four different size images.

3.3 The generation of key streams for initial vectors

A random initial vector is prerequisite to perform a favorable CBC-based diffusion process. Thus, we utilize the 1D-CLLCM to provide enough pseudo random numbers with good randomness and unpredictability as an initial vector.

Step C1: Input x₃(1) into 1D-CLLCM.

Step C2: Pre-iterate 1D-CLLCM 100 times to overcome transient effect for better security, and let new x₃(1) be the last state value.

Step C3: Create an empty sequences S.

Step C4: Continue to iterate 1D-CLLCM W_max times and let S = {x₃(i), i = 1, 2, … , W_max-1, W_max}.

Step C5: Convert all elements of S into integer numbers locating in 0–255 by Equation 9.

$\mathit{S}=\lfloor \left|\mathit{S}\right|\times {10}^{15}\rfloor \%256(9)$

Step C6: Delete S, then obtain the four initial vectors IV₁, IV₂, IV₃, IV₄, by Equation 10.

$\left\{\begin{array}{l}\mathit{I}{\mathit{V}}_1=\mathit{S}\left(W_{\max }-W_1+1:W_{\max }\right)\\ \mathit{I}{\mathit{V}}_2=\mathit{S}\left(W_{\max }-W_2+1:W_{\max }\right)\\ \mathit{I}{\mathit{V}}_3=\mathit{S}\left(W_{\max }-W_3+1:W_{\max }\right)\\ \mathit{I}{\mathit{V}}_4=\mathit{S}\left(W_{\max }-W_4+1:W_{\max }\right)\end{array}\right.(10)$

3.4 The generation of key streams for scrambling

To further complex the encryption process, we utilize 1D-CLSCM to generate key stream for scrambling by the following steps:

Step D1: Input x₄(1) into 1D-CLSCM.

Step D2: Pre-iterate 1D-CLSCM 100 times to overcome transient effect for better security, and let new x₄(1) be the last state value.

Step D3: Create an empty sequences S.

Step D4: Continue to iterate 1D-CLLCM W_max times and fill S = {x₄(i), i = 1, 2, … , W_max-1, W_max}

Step D5: Create four empty sequences S₁, S₂, S₃, S₄, then fill them by Equation 11.

$\left\{\begin{array}{l}{\mathit{S}}_1=\mathit{S}\left(W_{\max }-W_1+1:W_{\max }\right)\\ {\mathit{S}}_2=\mathit{S}\left(W_{\max }-W_2+1:W_{\max }\right)\\ {\mathit{S}}_3=\mathit{S}\left(W_{\max }-W_3+1:W_{\max }\right)\\ {\mathit{S}}_4=\mathit{S}\left(W_{\max }-W_4+1:W_{\max }\right)\end{array}\right.(11)$

Step D6: Obtain CSK₁, CSK₂, CSK₃, CSK₄ for scrambling columns of four images by Equation 12.

$\left\{\begin{array}{l}\mathit{C}\mathit{S}{\mathit{K}}_1=\lfloor \left({\mathit{S}}_1-\lfloor {\mathit{S}}_1\rfloor \right)\times {10}^{15}\rfloor \%H_1\\ \mathit{C}\mathit{S}{\mathit{K}}_2=\lfloor \left({\mathit{S}}_2-\lfloor {\mathit{S}}_2\rfloor \right)\times {10}^{15}\rfloor \%H_2\\ \mathit{C}\mathit{S}{\mathit{K}}_3=\lfloor \left({\mathit{S}}_3-\lfloor {\mathit{S}}_3\rfloor \right)\times {10}^{15}\rfloor \%H_3\\ \mathit{C}\mathit{S}{\mathit{K}}_4=\lfloor \left({\mathit{S}}_4-\lfloor {\mathit{S}}_4\rfloor \right)\times {10}^{15}\rfloor \%H_4\end{array}\right.(12)$

Step D7: Empty S, S₁, S₂, S₃, S₄, then continue to iterate1D-CLSCM 100 times, and let new x₄(1) be the last state value.

Step D8: Continue to iterate 1D-CLLCM H_max times and fill S = {x₄(i), i = 1, 2, … , H_max-1, H_max}

Step D9: Fill S₁, S₂, S₃, S₄ by Equation 13.

$\left\{\begin{array}{l}{\mathit{S}}_1=\mathit{S}\left(H_{\max }-H_1+1:H_{\max }\right)\\ {\mathit{S}}_2=\mathit{S}\left(H_{\max }-H_2+1:H_{\max }\right)\\ {\mathit{S}}_3=\mathit{S}\left(H_{\max }-H_3+1:H_{\max }\right)\\ {\mathit{S}}_4=\mathit{S}\left(H_{\max }-H_4+1:H_{\max }\right)\end{array}\right.(13)$

Step D10: Obtain RSK₁, RSK₂, RSK₃, RSK₄ for scrambling rows of four images by Equation 14.

$\left\{\begin{array}{l}\mathit{R}\mathit{S}{\mathit{K}}_1=\lfloor \left({\mathit{S}}_1-\lfloor {\mathit{S}}_1\rfloor \right)\times {10}^{15}\rfloor \%W_1\\ \mathit{R}\mathit{S}{\mathit{K}}_2=\lfloor \left({\mathit{S}}_2-\lfloor {\mathit{S}}_2\rfloor \right)\times {10}^{15}\rfloor \%W_2\\ \mathit{R}\mathit{S}{\mathit{K}}_3=\lfloor \left({\mathit{S}}_3-\lfloor {\mathit{S}}_3\rfloor \right)\times {10}^{15}\rfloor \%W_3\\ \mathit{R}\mathit{S}{\mathit{K}}_4=\lfloor \left({\mathit{S}}_4-\lfloor {\mathit{S}}_4\rfloor \right)\times {10}^{15}\rfloor \%W_4\end{array}\right.(14)$

Step D11: At last, delete S, S₁, S₂, S₃, S₄.

3.5 The encryption process

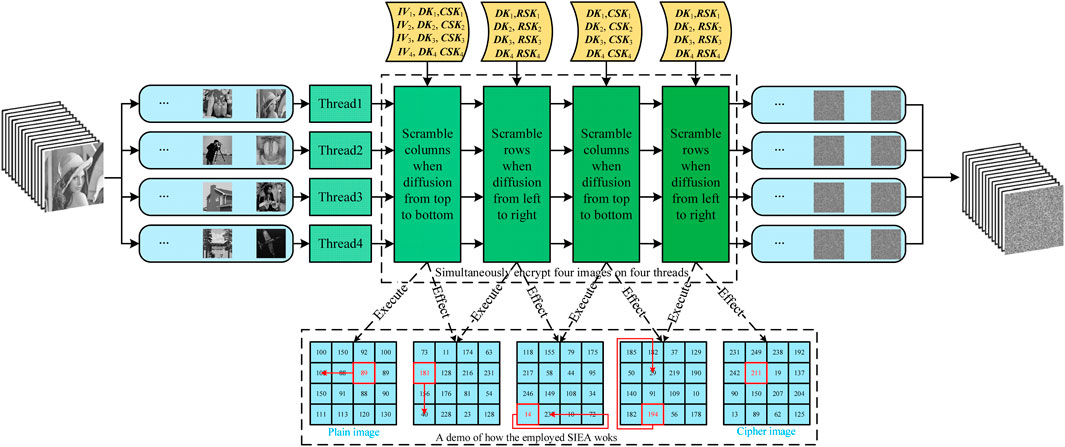
In this paper, we depend on the multi-thread technique to parallel encrypt four images in one round as shown in Figure 6.

Figure 6

Figure 6. The encryption details of the multi-channel processing scheme.

On each thread, a simultaneous scrambling and diffusion image encryption algorithm (as shown in Table 1: Algorithm SSDIEA) deal with original images one by one.

Table 1

Table 1. The employed single image encryption algorithm.

Then, the encryption process of the proposed algorithm is detailed below:

Step E1: Open four threads.

Step E2: Input four images into four threads respectively.

Step E3: Use round key RK_i, and perform Step B1-B10, Step C1-C6, Step D1-D10 to obtain key streams for encryption.

Step E4: Input key streams into each thread respectively as shown in Figure 6, then perform Algorithm SSDIEA to encrypt four images in parallel.

Step E5: Repeat Step E2-E4 until all images being encrypted.

Step E6: Close all threads.

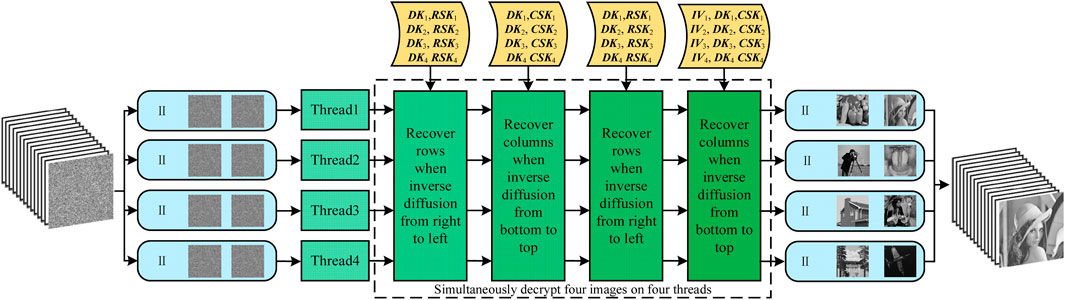
3.6 The decryption process

Since an 8-bit pixel value locates in [0,255], all operations of Algorithm SSDIEA have their inverse operations to recover the original image from a cipher image. Then the decryption process of the proposed batch images encryption algorithm is illustrated in Figure 7.

Figure 7

Figure 7. The decryption details of the multi-channel processing scheme.

4 Experimental results and analyses

In this section, the proposed algorithm is assessed from both security and efficiency aspects. All the employed tools and the proposed algorithm are implemented on MATLAB R2021b platform using a workstation equipped with 12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz, 32 GB 4800 MHz DDR5, 1 TB M.2 SSD, and running 64-bit Window 11 operating system (professional edition).

The true random numbers used in session key generation are obtained from Random.org [48] (which is an open organization to produce the highest quality true random numbers).

All test images with different sizes come from open image database. Part of the encryption and decryption results are demonstrated in the second and third column of Figure 8 respectively. As we can see, the proposed algorithm can successfully deal with images with different sizes.

Figure 8

Figure 8. Simulation results. The original images, the cipher images, and the decrypted images in second to fourth columns respectively, and their sizes are listed in the first column.

4.1 Histogram analysis

The uniform distribution is a typical characteristic of an ideal cipher image. Thus, we utilize histogram, as defined in Equation 15, to observe the changes of distributions between original and cipher images, then the results of histogram tests are presented in Figure 9. The comparison between the second and fourth columns of Figure 9 reveals that, regardless of the fluctuation in the histogram of an original image, it becomes uniformly distributed after encryption.

${\chi }^2={\displaystyle \sum _{i=0}^L}\frac{{\left(f_i-p_i\right)}^2}{p_i}(15)$

Figure 9

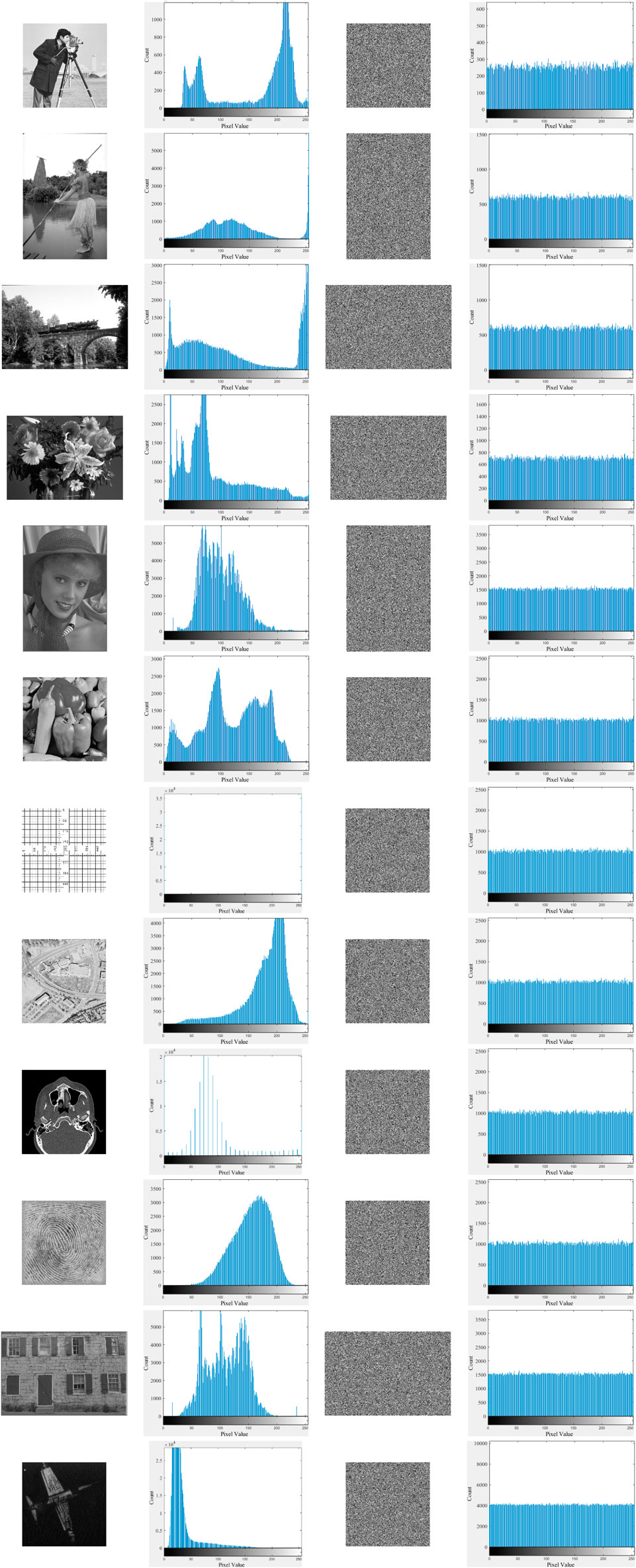
Figure 9. Results of histogram test. The original images, the cipher images, and the decrypted images in second to fourth columns respectively, and their sizes are listed in the first column. Moreover, the chi-square (χ2) test [as defined in Equation 15] is utilized to further assess the uniformity of histograms in a more rigorous manner.

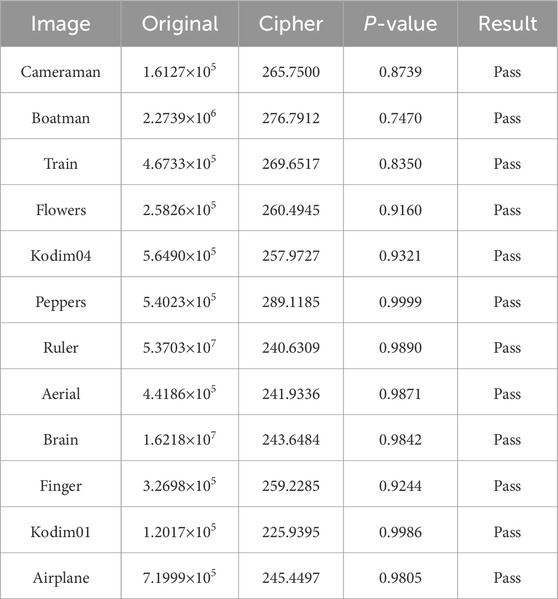
As an 8-bit gray pixel, it has 255 possible values indicating that L∈[0, 255]. Then, the f_i represents the true proportion of the pixel value i in a cipher image, while p_i represents its expected proportion. The ideal cipher image should have an expected χ² value of 293.24783 when the significance level α is set to 0.05. The χ² test results, as presented in Table 2, demonstrate that all cipher images successfully pass the test, aligning with the findings of the preceding histogram analysis. Consequently, the proposed algorithm effectively withstands diverse attacks rooted in frequency analysis.

Table 2

Table 2. Results of χ² test.

4.2 Statistical analysis

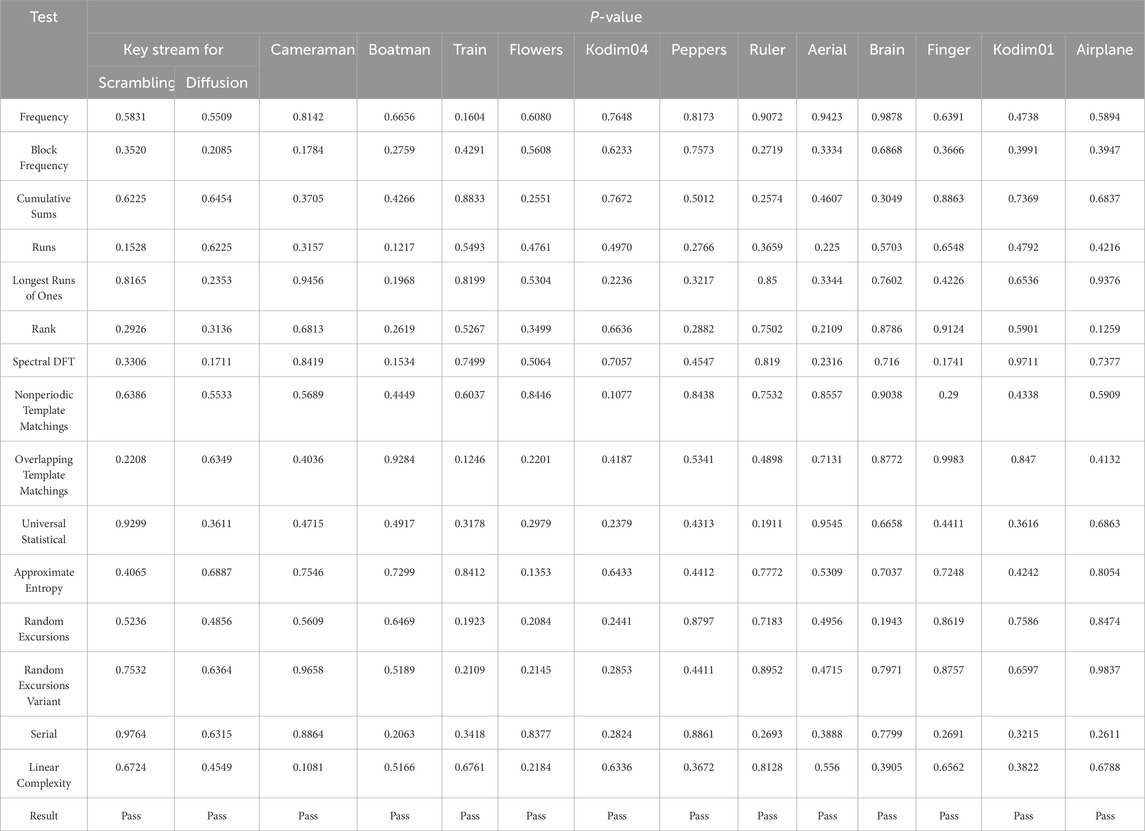
Sufficient level of randomness is a fundamental prerequisite to effectively counter attacks that rely on statistical analysis. To comprehensively validate the resistance against statistical attacks, we utilize the SP 800-22 randomness test suite, comprising of 15 tests endorsed by NIST [46], on both cipher images and key streams. The P-values of all randomness tests significantly exceed the significant level (let α = 0.01), as indicated in Table 3. Therefore, it can be concluded that both the cipher images and key streams exhibit a high degree of statistical randomness. Hence, attacker cannot rely on statistical analysis to obtain useful information facing the proposed algorithm.

Table 3

Table 3. Results of randomness tests (set α = 0.01).

4.3 Information entropy analysis

The information entropy, as defined in Equation 16, is commonly employed as a metric for quantifying the level of uncertainty inherent in data. As an 8-bit digital image, the ideal entropy of 8 after encryption will protect it from entropy attacks.

$H\left(g\right)=-{\displaystyle \sum _{i=1}^L}p\left(g_i\right){\log }_{2}p\left(g_i\right)(16)$

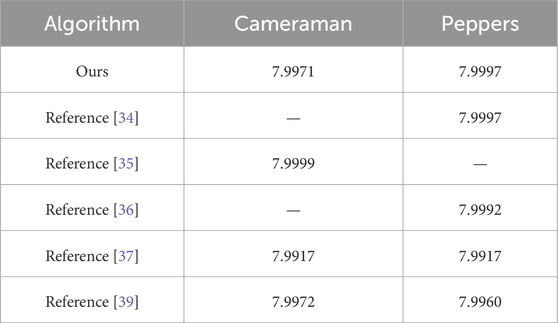
The experimental results of the proposed algorithm are presented in Table 4, whereas Table 5 demonstrates the comparative analysis with other algorithms. The proposed algorithm effectively enhances the entropy of any original image to exceeding 7.99, comparable to other established algorithms, which provide sufficient security to resist attacks based on information entropy analysis.

Table 4

Table 4. Results of information entropy test.

Table 5

Table 5. Comparisons with other works.

The information entropy is a reliable metric for assessing image uncertainty, but it is important to acknowledge the potential risk of local information leakage. Hence, we further employ a more stringent metric called local information entropy [49], which is computed using Equation 17, to evaluate cipher images.

${\overline{H}}_{k,Tb}\left(S\right)={\displaystyle \sum _{i=1}^k}\frac{H\left(S_i\right)}{k}(17)$

When set image blocks k = 30 and non-overlapping pixels T_B = 1936, an ideal average local information entropy of S_i should be 7.902469317. However, since all results in Table 6 fall within the confidence interval of 7.901901305–7.903037329, it can be confirmed that the proposed algorithm effectively safeguards images against local entropy analysis based attacks.

Table 6

Table 6. Results of Local Shannon entropy.

4.4 The correlation between adjacent pixels analysis

To provide comprehensive and intricate information, image data contains a significant amount of redundancy, resulting in high correlation between adjacent pixels. Thus, the primary objective of image encryption is to eliminate these correlations to render the image undecipherable. The image ‘Peppers’ serves as an example. The first row of Figure 10 illustrates that the strong correlations confine most pixels to a specific area in all directions. Subsequently, in the second row of Figure 10, when applying the proposed algorithm, the strong internal relationships within the image are disrupted, resulting in pixels scattering randomly throughout.

Figure 10

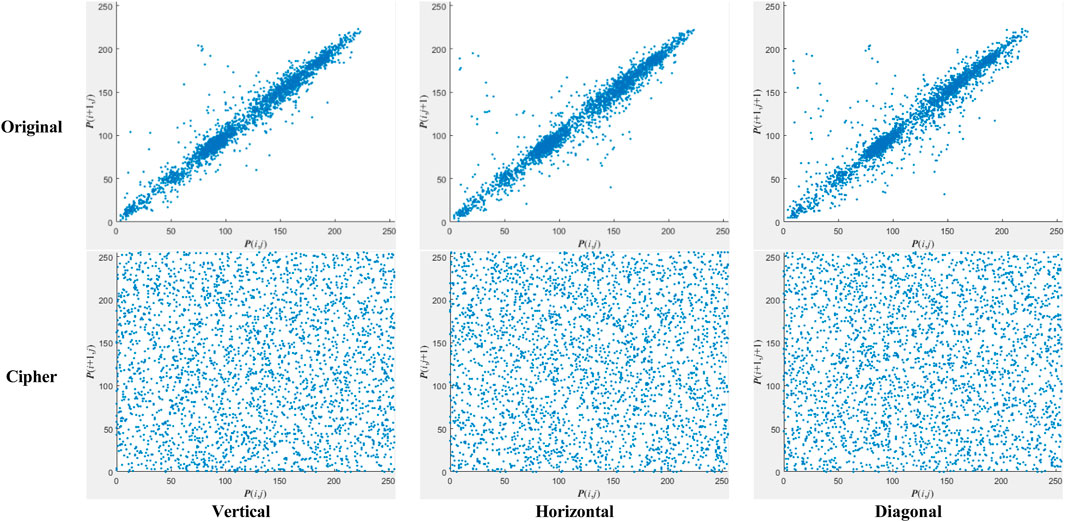
Figure 10. Scatter diagram of original image “Peppers” in the first row, and of cipher image “Peppers” in the second row.

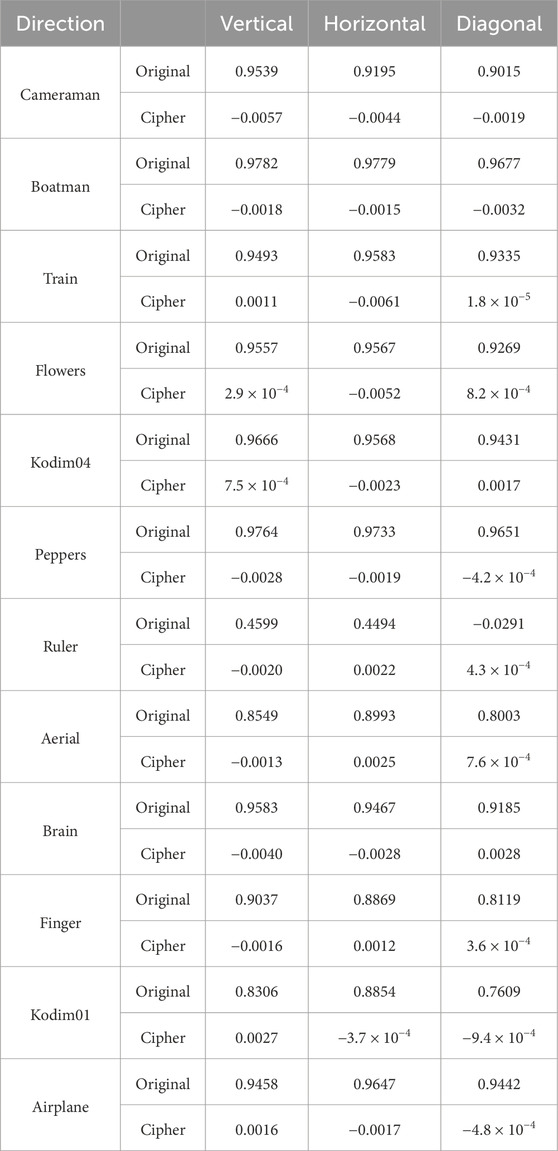
The proposed algorithm is further evaluated by an important indicator (γ_xy, correlation coefficient) to characterize the effect of correlation reduction. Suppose x_i and y_i are two adjacent pixels, then the calculation of γ_xy is given by Equation 18

$\begin{array}{l}\overline{x}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{x}_i,\overline{y}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{y}_i\\ {\gamma }_{xy}=\frac{{\displaystyle \sum _{i=1}^N}\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{\left({\displaystyle \sum _{i=1}^N}{\left(x_i-\overline{x}\right)}^2\right)\left({\displaystyle \sum _{i=1}^N}{\left(y_i-\overline{y}\right)}^2\right)}}\end{array}(18)$

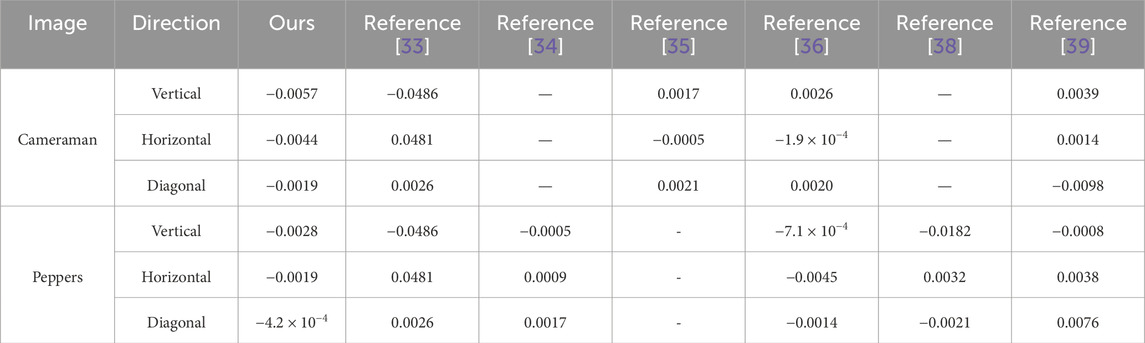
By randomly selecting 10,000 pairs of vertically, horizontally, and diagonally adjacent pixels, the γ_xy tests are conducted both on original images and their corresponding cipher images. The proposed algorithm effectively minimizes the correlations in the cipher image, regardless of the high γ_xy value of the original images, as demonstrated in Table 7. Thus, attacker cannot perform attacks by analyzing correlation coefficient.

Table 7

Table 7. Results of γ_xy tests.

The comparisons with other works are presented in Table 8. It can be observed that the proposed algorithm demonstrates equivalent or even superior ability to conceal correlations between adjacent pixels compared to existing algorithms.

Table 8

Table 8. Comparisons with other works.

4.5 Plaintext sensitivity analysis

In general, the differential attacks pose the greatest threat to a cryptosystem. To cope with this problem, the proposed algorithm must be extremely sensitive to plaintext changes. It means that the slightest alteration in the original image will result in significant changes to the cipher image. There are two indictors, NPCR (Number of Pixels Change Rate) and UACI (Unified Average Changing Intensity), to quantitative analyze the plaintext sensitivity of a cryptosystem (Suppose C₁ and C₂ are two cipher images with one bit difference in their corresponding original images), which are given by Equations 19–21

$D\left(i,j\right)=\left\{\begin{array}{l}0,{\mathit{C}}_1\left(i,j\right)={\mathit{C}}_2\left(i,j\right)\\ 1,{\mathit{C}}_1\left(i,j\right)\ne {\mathit{C}}_2\left(i,j\right)\end{array}\right.(19)$

$\text{NPCR}=\frac{{\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}\mathit{D}\left(i,j\right)\times 100\%}{H\times W}(20)$

$\text{UACI}=\frac{{\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}\frac{\left|{\mathit{C}}_1\left(i,j\right)-{\mathit{C}}_2\left(i,j\right)\right|}{255}}{H\times W}\times 100\%(21)$

The NPCR/UACI tests are conducted 100 times for each original image by randomly selecting a pixel and modifying its least significant bit. As illustrated in Table 9, all results of NPCR and UACI closely match their expected values of 99.6094% and 33.4635%, exhibiting the excellent security performance of the proposed algorithm in countering differential attacks.

Table 9

Table 9. Results of NPCR and UACI test (Unit: %).

Moreover, the proposed algorithm exhibits superior resistance to differential attacks compared to other algorithms as demonstrated in Table 10.

Table 10

Table 10. Comparisons with other algorithms (Unit: %).

4.6 Key sensitivity analysis

In general, the session key should be the sole confidential element within a practical cryptosystem. Thus, we introduce a true random number to ensure the unpredictability during the generation of session key. Furthermore, the cryptosystem must be sensitive to the session key in two aspects: On one hand, even slight modifications to the session key can have a significant impact on the cipher image; on the other hand, minor errors in the session key cannot yield any useful information from the cipher image.

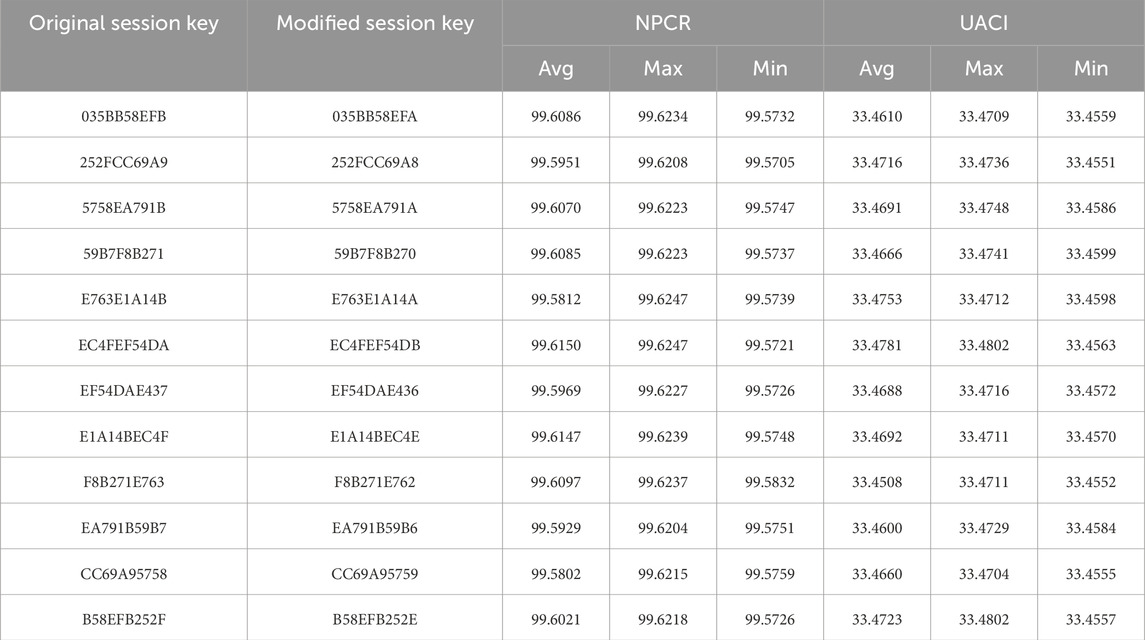
To verify the key sensitivity performance of the proposed algorithm, we take a used session key SK = {035bb58efb252fcc69a95758ea791b59b7f8b271e763e1a14bec4fef54dae437} as a test object. As described in Step A1-A3, the round keys will be computed from the session key. Subsequently, they will be further divided into 12 parts to generate initial values for chaotic systems. Thus, we also extract 12 parts from SK and apply NPCR/UACI tests. Hint: The original byte is highlighted in green, while the modified one is highlighted in red, with only a single bit being flipped in each test. Firstly, the key sensitivity test results in encryption end are listed in Table 11. Obviously, the proposed algorithm can effectively transform the original image into distinct cipher images using session keys with only one-bit difference, demonstrating its sufficient sensitivity to the session key in encryption end.

Table 11

Table 11. The key sensitivity test results in encryption end (Unit: %).

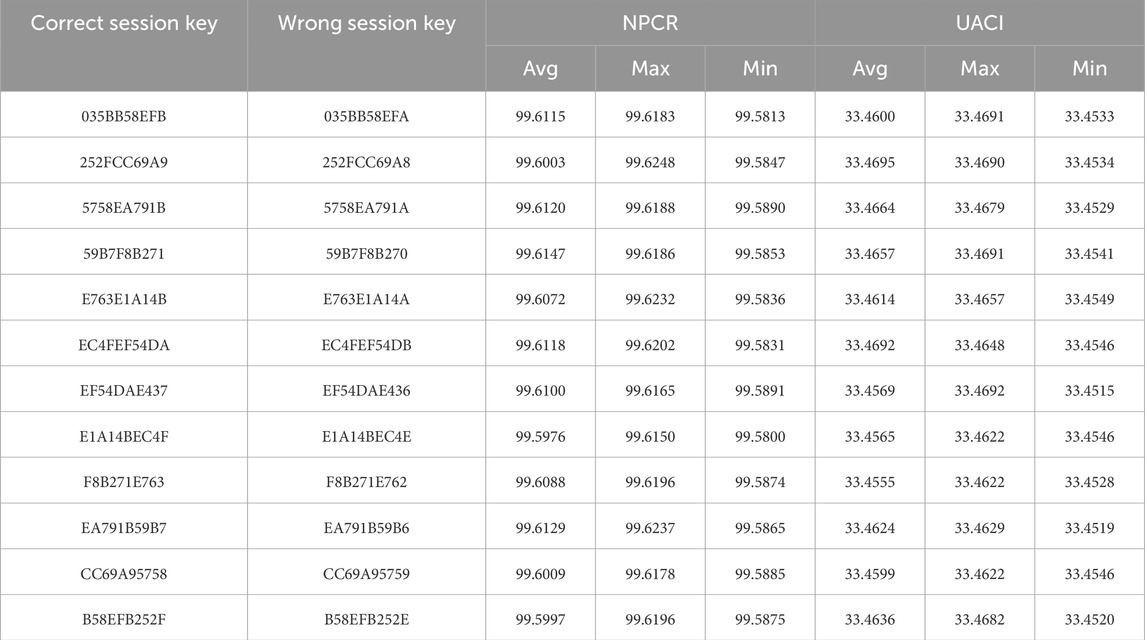
Next, the above modified session keys are served as error session keys to decrypt cipher image. Take image ‘Peppers’ as an example, the decrypted images are shown in Figure 11, and the results of NPCR/UACI tests are listed in Table 12. Hence, attackers cannot obtain any useful information by trying different session keys even being close to the correct session key.

Figure 11

Figure 11. The decrypted results of (A) cipher image ‘Peppers’ with (B) the correct session key, and with bit flipped at (C) SK(40), (D) SK(80), (E) SK(120), (F) SK(160), (G) SK(200), (H) SK(240), (I) SK(56), (J) SK(96), (K) SK(136), (L) SK(176), (M) SK(216), (N) SK(256).

Table 12

Table 12. The key sensitivity test results in decryption end (Unit: %).

4.7 Key space analysis

The session key in this paper is derived by combining a 256-bit true random number with the hash value of all original images. Subsequently, round keys can be computed based on the session key to generate initial values for chaotic systems. The above experimental results demonstrate that any alteration in the session key can potentially impact the encryption/decryption outcomes. Consequently, the proposed algorithm ensures a 256-bit key space.

Some literature suggest that a larger key space enhances the overall security of a cryptosystem. However, an excessively large key space also introduces additional challenges in terms of key exchange. In this paper, the 256-bit key space surpasses the theoretically secure 128-bit key space [50, 51], thus validating our algorithm’s ability to effectively withstand exhaustive attacks while maintaining efficient session key transmission.

4.8 Chosen-plaintext attack analysis

The attackers may exhaust all methods to compromise a cryptosystem, with chosen-plaintext attacks (CPA) being considered the most potent and practical tool in this regard. To perform CPA on image cryptosystems, a particular image with all pixel values being 0 (naming image ‘Black’) or 255 (naming image ‘White’) is consistently considered an optimal carrier. The security performances of the proposed algorithm in handling the image ‘Black’ and ‘White’ are comprehensively evaluated based on the above analyses. The results depicted in Figure 12 and Table 13 demonstrate that attackers are unable to differentiate such specific images from ordinary ones using any analytical tools. Thus, the proposed algorithm can resist CPA attacks.

Figure 12

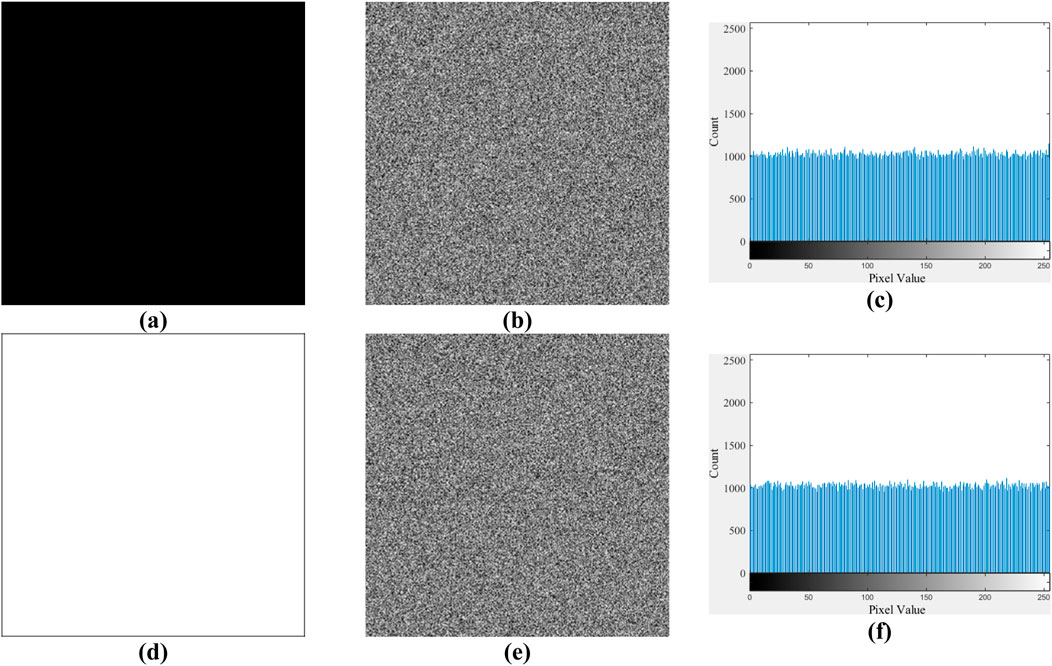
Figure 12. Encryption results and histogram analysis of image (A) “Black” and (D) “White”, shown in the first row and second row respectively.

Table 13

Table 13. Experimental results for images ‘Black’ and ‘White’.

4.9 Robustness analysis

The public communication channel often experiences disturbances like noise and data loss, but images remain useable even with some pollution in daily use. Therefore, the ability of an image cryptosystem to decrypt corrupted cipher images becomes crucial.

Taking the image ‘Airplane’ as an example, we sequentially cropped 1/16, 1/8, 1/4, and 1/2 portions and subsequently decrypted them using the appropriate session key. As illustrated in Figure 13, although there is some loss of data in the decrypted images, they can still be discerned as representing the ' Airplane ' image to a certain extent. The recognition of the decrypted image becomes increasingly challenging with higher levels of data loss during transmission.

Figure 13

Figure 13. Cipher images with data loss 1/16, 1/8, 1/4, 1/2 in the first row and their decrypted image in the second row.

The image ‘Airplane’ is subjected to Salt&Pepper noise and Gaussian noise, which are two common types of noise. Subsequently, the correct session key is used to decrypt the image. As depicted in Figure 14, the proposed algorithm successfully restores a recognizable image even when it is contaminated by different types of noise with varying degrees. Therefore, we can assert that the proposed algorithm exhibits resilience against minor noise interference in a vulnerable channel.

Figure 14

Figure 14. Decrypted image from cipher images polluted with Gaussian noise of 0.001, 0.005, 0.01 in the first row, and with Salt&Pepper noise of 0.01, 0.05; (f) 0.1 in the second row.

4.10 Computational cost analysis

The practicality of encryption algorithms is not solely determined by security, it also relies on high operational efficiency, which should be considered a crucial criterion. In this paper, by introducing multi-thread technique, four images (even with different sizes) can be parallel encrypted on four threads using a single image encryption algorithm. Moreover, the counter mode is utilized to derive round keys from a session key that is associated with all original images, to effectively address the issue of secure key transmission.

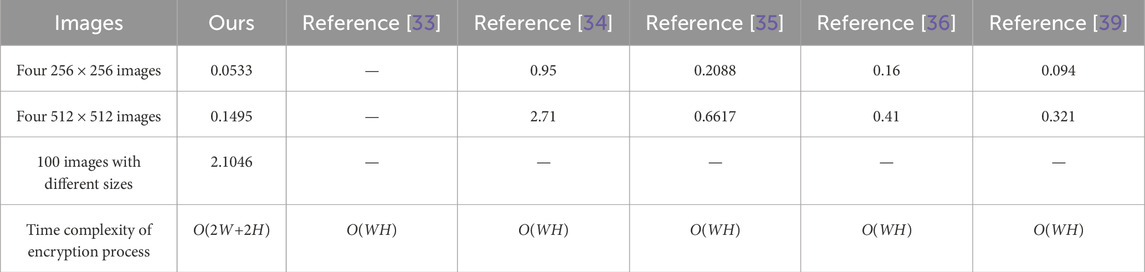
As illustrated in Figure 4, the counter mode can generate round keys far before encryption process. Thus, the time complexity of the proposed algorithm depends almost entirely on the following parts: 1) The generation of key streams for diffusion, which has a time complexity of O(WH); 2) the generation of key streams for initial vectors, which has a time complexity of O(W); 3) the generation of key streams for initial scrambling, which has a time complexity of O(W + H); and 4) the Algorithm SSDIEA, which has a time complexity of O(2W+2H). Overall, the time complexity of the proposed algorithm is square order O(WH). However, due to the linear order time complexity O(2W+2H) of the Algorithm SSDIEA, the proposed algorithm presents the superior speed advantage compared with other algorithms, as shown in Table 14.

Table 14

Table 14. Results of time consumption tests (Unit: second).

5 Conclusion

This paper presents a novel batch images encryption algorithm using the counter mode and a multi-channel processing scheme. Firstly, by combining the hash value of all original images with a 256-bit true random number, the proposed algorithm’s session key not only exhibits ample sensitivity to plaintext but also possesses strong unpredictability. Subsequently, the counter mode is introduced to generate round keys for encrypting each four images, thereby significantly simplifying session key management when dealing with massive images. Secondly, a multi-channel pseudo random number generator is constructed using two discrete hyperchaotic systems (2D-SCCM and 2D-SIDCM), which ensures rapid provision of four diffusion key streams. Moreover, by designing an adapter, the proposed algorithm can easily employ the multi-thread technique to parallel encrypt four different sized images during each encryption round without additional operations on the original images. Thirdly, the encryption speed can be further accelerated by employing a simultaneous scrambling and diffusion image encryption algorithm on each thread, which leverages its vectorized CBC-based structure to efficiently and securely encrypt every single image. Finally, common security analyses are performed on the proposed algorithm. The results of χ² and randomness tests are all over the confidential value 0.01, thus the cipher images can resist attacks based on any statistical analysis. The results of information entropy or correlation coefficient tests are close to the ideal value eight or 0, which indicate that the proposed algorithm can sufficiently hide relations between original and cipher images to prevent attacker obtain any useful information from cipher images. The results of NPCR and UACI tests being close to 99.6094% and 33.4635% reveal that the proposed algorithm has enough sensitivity to both plaintext and session key changes to resist brute-force, differential, or even chosen-plaintext attacks. In addition, due to the multi-thread technique, the proposed algorithm can parallel encrypted four images at once using a simultaneous scrambling and diffusion image encryption with a linear time complexity of O(2W+2H), thus 100 images can be encrypted in about 2.1 s. In the following research, first, we will try to extend the proposed algorithm to batch color images encryption, and dedicate to implement the proposed algorithm on different kinds of IoT devices, such as the Lora node, Zigbee node, to further optimize its security and efficiency performances.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BG: Conceptualization, Methodology, Software, Validation, Writing–original draft. GQ: Writing–review and editing. ZS: Investigation, Methodology, Writing–review and editing. JL: Conceptualization, Formal Analysis, Software, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (62004108) and in part by the Natural Science Foundation of China (No. 62341118); The program of Entrepreneurship and Innovation Ph.D. in Jiangsu Province (JSSCBS20211175). “Huaishang Talent Plan” for Outstanding Doctoral Program in Huai’an Universities (Z302J23212).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Li H, et al. Optimization of graph clustering inspired by dynamic belief systemsKnowl IEEE T. Data En (2024) 36(11):6773–85. doi:10.1109/TKDE.2023.3274547

CrossRef Full Text | Google Scholar

2. Li H, et al. Overlapping graph clustering in attributed networks via generalized cluster potential game. ACM Trans Knowl Discov Data (2023) 18(1):1–26. doi:10.1145/3597436

CrossRef Full Text | Google Scholar

3. Chen J, Li T, Zhang Y, You T, Lu Y, Tiwari P, et al. Global-and-Local attention-based reinforcement learning for cooperative behaviour control of multiple UAVs. IEEE T Veh Technol (2024) 73(3):4194–206. doi:10.1109/TVT.2023.3327571

CrossRef Full Text | Google Scholar

4. Hosseinzadeh R, Zarebnia M, Parvaz R. Hybrid image encryption algorithm based on 3D chaotic system and choquet fuzzy integral. Opt Laser Technol (2019) 120:105698. doi:10.1016/j.optlastec.2019.105698

CrossRef Full Text | Google Scholar

5. Vaidyanathan S, Kammogne AST, Tlelo-Cuautle E, Talonang CN, Abd-El-Atty B, Abd El-Latif AA, et al. A novel 3-D jerk system, its bifurcation analysis, electronic circuit design and a cryptographic application. Electronics (2023) 12(13):2818. doi:10.3390/electronics12132818

CrossRef Full Text | Google Scholar

6. Han B, Jhaveri RH, Wang H, Qiao D, Du J. Application of robust zero-watermarking scheme based on federated learning for securing the healthcare data. IEEE J Biomed Health (2023) 27(2):804–13. doi:10.1109/JBHI.2021.3123936

CrossRef Full Text | Google Scholar

7. Gong L, Luo H. Dual color images watermarking scheme with geometric correction based on quaternion FrOOFMMs and LS-SVR. Opt Laser Technol (2023) 167:109665. doi:10.1016/j.optlastec.2023.109665

CrossRef Full Text | Google Scholar

8. Tan J, Liao X, Liu J, Cao Y, Jiang H. Channel attention image steganography with generative adversarial networks. IEEE T Netw Sci Eng (2022) 9(2):2021888–903. doi:10.1109/TNSE.2021.3139671

CrossRef Full Text | Google Scholar

9. Zhou Z, Wan Y, Cui Q, Yu K, Mumtaz S, Yang CN, et al. Blockchain-based secure and efficient secret image sharing with outsourcing computation in wireless networks. IEEE T Wirel Commun (2024) 23(1):423–35. doi:10.1109/TWC.2023.3278108

CrossRef Full Text | Google Scholar

10. Hsieh PA, Wu J. A review of the asymmetric numeral system and its applications to digital images. Entropy (2022) 24(3):e24030375. doi:10.3390/e24030375

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Kolivand H, Hamood SF, Asadianfam S, Rahim MS. RETRACTED ARTICLE: image encryption techniques: a comprehensive review. Multimed Tools Appl (2024) 83:73789. to be published. doi:10.1007/s11042-023-17896-0

CrossRef Full Text | Google Scholar

12. Guvenoglu E, Tunali V. ZigZag transform with Durstenfeld shuffle for fast and secure image encryption. Connect Sci (2023) 35(1):2162000. doi:10.1080/09540091.2022.2162000

CrossRef Full Text | Google Scholar

13. Lu H, Teng L, Du L. Image encryption with 1D-MS chaotic systems and improved zigzag disambiguation. Eur Phys J Plus (2024) 139:350. doi:10.1140/epjp/s13360-024-05146-7

CrossRef Full Text | Google Scholar

14. Alexan W, Korayem Y, Gabr M, El-Aasser M, Maher EA, El-Damak D, et al. AntEater: when arnold's cat meets langton's ant to encrypt images. IEEE Access (2023) 11:106249–76. doi:10.1109/ACCESS.2023.3319335

CrossRef Full Text | Google Scholar

15. Inam S, Kanwal S, Firdous R, Hajjej F. Blockchain based medical image encryption using Arnold's cat map in a cloud environment. Sci Rep (2024) 14(1):5678. doi:10.1038/s41598-024-56364-z

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Rani N, Sharma SR, Mishra V. Grayscale and colored image encryption model using a novel fused magic cube. Nonlinear Dyn (2022) 108(2):1773–96. doi:10.1007/s11071-022-07276-y

CrossRef Full Text | Google Scholar

17. Ko HJ, Huang CT, Tseng HW, Wang SJ. Efficient cost-reduced with high-quality image of imperceptible steganography using modulo and magic cube. IEEE Access (2022) 10:67686–93. doi:10.1109/ACCESS.2022.3185120

CrossRef Full Text | Google Scholar

18. Bezerra J. I. M., Machado G, Molter A, Soares RI, Camargo V. A novel simultaneous permutation-diffusion image encryption scheme based on a discrete space map. Chaos Soliton. Fract. (2023) 168:113160. doi:10.1016/j.chaos.2023.113160

CrossRef Full Text | Google Scholar

19. Li T., Fan W, Wu J, Zhang D. Image encryption based on a fractional-order hyperchaotic system and fast row-column-level joint permutation and diffusion. Nonlinear Dyn (2024) 112:10555–81. doi:10.1007/s11071-024-09597-6

CrossRef Full Text | Google Scholar

20. Murillo-Escobar M.A., Cruz-Hernández C, Cardoza-Avendaño L, Méndez-Ramírez R. A novel pseudorandom number generator based on pseudorandomly enhanced logistic map. Nonlinear Dyn. (2017) 87:407–25. doi:10.1007/s11071-016-3051-3

CrossRef Full Text | Google Scholar

21. Barani M.J., et al. A new Pseudo random number generator based on generalized Newton complex map with dynamic key. J. Inf. Secur. Appl. (2020) 53:102509. doi:10.1016/j.jisa.2020.102509

CrossRef Full Text | Google Scholar

22. Benkouider K., Sambas A, Bonny T, Al Nassan W, Moghrabi IAR, Sulaiman IM, et al. A comprehensive study of the novel 4D hyperchaotic system with self-exited multistability and application in the voice encryption. Sci. Rep. (2024) 14:12993. doi:10.1038/s41598-024-63779-1

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Hua Z., Zhu Z, Chen Y, Li Y. Color image encryption using orthogonal Latin squares and a new 2D chaotic system. Nonlinear Dyn. (2021) 104:4505–22. doi:10.1007/s11071-021-06472-6

CrossRef Full Text | Google Scholar

24. Gao X., Sun B, Cao Y, Banerjee S, Mou J. A color image encryption algorithm based on hyperchaotic map and DNA mutation. Chin. Phy. B (2023) 32(3):030501. doi:10.1088/1674-1056/ac8cdf

CrossRef Full Text | Google Scholar

25. Huang X., Dong Y, Ye G, Shi Y. Meaningful image encryption algorithm based on compressive sensing and integer wavelet transform. Front. Comput. Sci. (2023) 17(3):173804. doi:10.1007/s11704-022-1419-8

CrossRef Full Text | Google Scholar

26. Teng L., Wang X., Xian Y. Image encryption algorithm based on a 2D-CLSS hyperchaotic map using simultaneous permutation and diffusion. Inform. Sci. (2022) 605:71–85. doi:10.1016/j.ins.2022.05.032

CrossRef Full Text | Google Scholar

27. Huang Z., Zhou N. Image encryption scheme based on discrete cosine Stockwell transform and DNA-level modulus diffusion. Opt. Laser. Technol. (2022) 149:107879. doi:10.1016/j.optlastec.2022.107879

CrossRef Full Text | Google Scholar

28. Sambas A., Miroslav M, Vaidyanathan S, Ovilla-Martínez B, Tlelo-Cuautle E, El-Latif AAA, et al. A New Hyperjerk System With a Half Line Equilibrium: Multistability, Period Doubling Reversals, Antimonotonocity, Electronic Circuit, FPGA Design, and an Application to Image Encryption. IEEE Access (2024) 12:9177–94. doi:10.1109/ACCESS.2024.3351693

CrossRef Full Text | Google Scholar

29. Li Y., Wang Q., Yu S. A novel hybrid scheme for chaotic image encryption. Phys. Scr. (2024) 99(4):045244. doi:10.1088/1402-4896/ad3171

CrossRef Full Text | Google Scholar

30. Sangavi V., Thangavel P. An exquisite multiple image encryption harnessing multi-scroll Lu–Chen and Chua chaotic systems employing domino strategy. J. Inf. Secur. Appl. (2023) 72:103408. doi:10.1016/j.jisa.2022.103408

CrossRef Full Text | Google Scholar

31. Kumar Y., Guleria V. A novel multiple image encryption technique based on asymmetric cryptosystem with HCM in frequency domain. Multimed. Tools Appl. (2024) 83:72253–78. to be published. doi:10.1007/s11042-024-18347-0

CrossRef Full Text | Google Scholar

32. Morteza S. K., Amirabbas G., Mehdi Y. A comprehensive survey on image encryption: Taxonomy, challenges, and future directions. Chaos Soliton. Fract. (2024) 178:114361. doi:10.1016/j.chaos.2023.114361

CrossRef Full Text | Google Scholar

33. Sahasrabuddhe A., Laiphrakpam D. S. Multiple images encryption based on 3D scrambling and hyper-chaotic system. Inform. Sciences (2021) 550:252–67. doi:10.1016/j.ins.2020.10.031

CrossRef Full Text | Google Scholar

34. Zhang X., Liu M., Tian J. Multiple-image encryption algorithm based on Sarrus rule and 3D Fibonacci matrix. Phys. Scr. (2023) 98:055208. doi:10.1088/1402-4896/acc905

CrossRef Full Text | Google Scholar

35. Zhou Z., Xu X, Yao Y, Jiang Z, Sun K Novel multiple-image encryption algorithm based on a two-dimensional hyperchaotic modular model. Chaos Soliton. Fract. (2023) 173:113630. doi:10.1016/j.chaos.2023.113630

CrossRef Full Text | Google Scholar

36. Wang X., Liu H. Cross-plane multi-image encryption using chaos and blurred pixels. Chaos Soliton. Fract. (2022) 164:112586. doi:10.1016/j.chaos.2022.112586

CrossRef Full Text | Google Scholar

37. Tao L., Liang X, Hu B, Han L Compound encryption of multiple images by utilizing a novel chaos and nonlinear transform. Neural Comput.&lic., DPTA- (2022) 2021. doi:10.1007/s00521-022-07849-3

CrossRef Full Text | Google Scholar

38. Xiao D., Zhao M., Wang M. Low-cost and secure multi-image encryption scheme based on P-tensor product compressive sensing. Opt. Laser. Technol. (2021) 140:107077. doi:10.1016/j.optlastec.2021.107077

CrossRef Full Text | Google Scholar

39. Gao X., Mou J, Xiong L, Sha Y, Yan H, Cao Y A fast and efficient multiple images encryption based on single-channel encryption and chaotic system. Nonlinear Dyn. (2022) 108:613–36. doi:10.1007/s11071-021-07192-7

CrossRef Full Text | Google Scholar

40. Liu X., Wang J., Li J. URTSegNet: A real-time segmentation network of unstructured road at night based on thermal infrared images for autonomous robot system. Control Eng. Pract. (2023) 137:105560. doi:10.1016/j.conengprac.2023.105560

CrossRef Full Text | Google Scholar

41. Chen J., Du C, Zhang Y, Han P, Wei W A Clustering-Based Coverage Path Planning Method for Autonomous Heterogeneous UAVs. IEEE T. Veh. Technol. (2022) 23(12):25546–56. doi:10.1109/TITS.2021.3066240

CrossRef Full Text | Google Scholar

42. Zhou S., Qiu Y, Wang X, Zhang Y Novel image cryptosystem based on new 2D hyperchaotic map and dynamical chaotic S-box. Nonlinear Dyn (2023) 111:9571–89. doi:10.1007/s11071-023-08312-1

CrossRef Full Text | Google Scholar

43. Wen J., Xu X, Sun K, Jiang Z, Wang X Triple-image bit-level encryption algorithm based on double cross 2D hyperchaotic map. Nonlinear Dyn. (2023) 11:6813–38. doi:10.1007/s11071-022-08158-z

CrossRef Full Text | Google Scholar

44. Yuan F., Li Y., Wang G. A universal method of chaos cascade and its applications. Chaos (2021) 31(2):021102. doi:10.1063/5.0041518

PubMed Abstract | CrossRef Full Text | Google Scholar

45. El-Semary A.M., Abdel-Azim M. M. Counter Chain: A New Block Cipher Mode of Operation. J. Inf. Process. Syst. (2015) 11:266–279. doi:10.3745/JIPS.03.0031

CrossRef Full Text | Google Scholar

46. Haider T., Blanco S.A., Hayat U. A novel pseudo-random number generator based on multivariable optimization for image-cryptographic applications. Expert. Syst. Appl. (2024) 240:122446. doi:10.1016/j.eswa.2023.122446

CrossRef Full Text | Google Scholar

47. Haahr M. RANDOM.ORG: True Random Number Service. Available from: https://www.random.org (Accessed August 5, 2024).

Google Scholar

48. Pareschi F., Rovatti R., Setti G. On Statistical Tests for Randomness Included in the NIST SP800-22 Test Suite and Based on the Binomial Distribution. IEEE T. Inf. Foren. Sec. (2012) 7(2):491–505. doi:10.1109/TIFS.2012.2185227

CrossRef Full Text | Google Scholar

49. Wu Y., Zhou Y., Saveriades G., Agaian S, Noonan JP, Natarajan P Local Shannon entropy measure with statistical tests for image randomness. Inform. Sciences (2013) 222:323–42. doi:10.1016/j.ins.2012.07.049

CrossRef Full Text | Google Scholar

50. Liu L., Lei Y., Wang D. A fast chaotic image encryption scheme with simultaneous permutation-diffusion operation. IEEE Access (2020) 8:27361–74. doi:10.1109/ACCESS.2020.2971759

CrossRef Full Text | Google Scholar

51. Murillo-Escobar M.A., Meranza-Castillón MO, López-Gutiérrez RM, Cruz-Hernández C Suggested Integral Analysis for Chaos-Based Image Cryptosystems. Entropy (2019) 21(8):815. doi:10.3390/e21080815

PubMed Abstract | CrossRef Full Text | Google Scholar