Divertor Tokamak Test: Impact of NBI shine-through and beam-plasma interaction on Divertor Tokamak Test facility

Introduction: In this work, we aim to explore numerically the behavior of beam energetic particles in the Divertor Tokamak Test (DTT), a superconductive device equipped with a Neutral Beam Injection (NBI) system capable of injecting neutrals up to 510 keV.

Method: We explore beam ionization and beam slowing down for different DTT plasma scenarios. Numerical simulations are performed using the ASCOT suite of codes, including a wide-range scan of plasma density and beam injection energy. For different plasma conditions, we estimate shine-through losses, including the heat fluxes on the first wall thanks to dedicated particle tracing simulations. Orbits of newly-born fast ions are characterized by means of the constant of motion phase space, showing how trapped energetic particles’ population and prompt losses change with plasma density and NBI energy.

Results and discussion: Slowing down simulations show that NBI injection at 510 keV is well coupled to DTT plasmas. DTT NBI will be one of the sources of auxiliary ion heating, with an absorbed power ratio of up to ∼50% depending on plasma and beam parameters. At low plasma densities, energetic particle confinement is less efficient, and NBI power and/or energy reduction is expected.

1 Introduction

The Divertor Tokamak Test (DTT) facility is a superconductive device (R₀ = 2.19 m, a = 0.7 m, B₀ ≤ 6 T, I_p ≤ 5.5 MA) proposed to support ITER operations and DEMO design [1–3]. DTT aims to investigate solutions to the power exhaust problem in future fusion power plants, with adimensional plasma parameters relevant to ITER and DEMO. To obtain reactor-relevant plasmas, DTT will be equipped with three different auxiliary heating systems [4] capable of providing up to 45 MW of power to the plasma. Among these, a high energy, high power (≤510 keV, ≤10 MW) Neutral Beam Injection (NBI) is included [5]. High-density plasmas, such as DTT ones, require a high-energy beam to reach the plasma core. The NBI auxiliary system aims to heat the plasma to fusion relevant temperatures and provide current and torque to the plasma. The design of DTT NBI is still ongoing and modelling studies on DTT beam-plasma interaction are essential to support it and to investigate an efficient application of NBI in future DTT plasmas. The present work numerically explores all the steps of an ideal neutral beam path in DTT plasmas, from neutrals injection and ionization to beam Energetic Particle (EP) slowing down and losses. We present a first estimate of the NBI footprint on machine Plasma-Facing Components (PFCs) due to shine-through losses (i.e., beam neutral particles not ionized in the plasma that reach the opposite machine sector). Shine-through losses can exceed PCFs power load limits, leading to a restriction of the NBI operability in DTT. Therefore power density load quantification is of primary importance for the DTT design and scenario optimization. The impact of parameters such as beam particle energy and plasma kinetic profiles is discussed, since they strongly affect the beam-plasma coupling and the resulting NBI sources in DTT plasmas. We investigate for the first time NBI in low-density, low-current/magnetic field scenarios and update DTT reference scenario results. A first complete characterization of newly born beam-fast ions through the Constant of Motion (CoM) phase space is presented. We study how different plasma and neutral beam parameters affect the initial particle orbits, that are shown with a CoM analysis to relate with fast ion losses. The results presented are supported by state-of-the-art numerical simulations, performed in the so-called “stand-alone” mode, i.e., acting on a “frozen” plasma that is not modified by the simulated beam itself. The present paper is organized as follows. Section 2 describes the input of the analysis work performed, i.e., the selected plasma scenarios, the DTT NBI system and the First Wall (FW) of DTT, i.e., the boundary of our simulations. The structure of the paper is then organized to follow the path of beam energetic particles: ionization, first orbits in the plasma, Coulomb collisions and possible loss channels. Section 3 starts with the analysis of beam ionization and shine-through losses calculated with the BBNBI Monte Carlo code [6]. A heuristic formula is obtained to estimate NBI shine-through from plasma density and NBI energy rapidly. In this section, the quantification of the peak power density loads on DTT PFCs is given thanks to a particle tracing study. The orbits of newly-born beam-fast ions are characterized in Section 4. The description of the global confinement properties of Energetic Particles (EPs) is provided, predicting the so-called prompt (also known as first orbit losses), due to unconfined trajectories on time scales shorter than collisional times. Section 5 presents results of NBI sources in DTT plasmas and fast ion distributions. The slowing-down process due to EP Coulomb collisions with the background plasma, simulated using the orbit-following Monte Carlo ASCOT code [7], is described. Section 6 concludes the paper with a summary of the results.

2 Analyzed DTT plasma scenarios and device description

2.1 DTT scenarios

NBI EP confinement and beam-plasma interaction are analyzed for three selected baseline H-mode DTT scenarios at the stationary flat-top phase of Deuterium (D) plasmas. They are all characterized by a single null divertor configuration with positive triangularity. The three selected scenarios (called “A,” “C” and “E”) have different plasma currents, vacuum magnetic fields and auxiliary installed heating power, as shown in Table 1. A full description of A and C plasmas can be found in [8] where JINTRAC [9] and ASTRA [10] simulation settings, defined according to a mixed iterative approach discussed in [11], are also described. E plasma is instead described in [12]. All plasmas have a “seeding impurity” varied among the scenarios, and a smaller concentration of tungsten (W), added to simulate the source from the DTT FW. Table 1 reports the plasma composition and effective charge values Z_eff of each flat-top plasma considered in this work. The axis-symmetric plasma magnetic equilibria used as input of the numerical simulations in this work are calculated by CREATE-NL code [13]. Figure 1 shows the Last Closed Flux Surface (LCFS) and the 2D wall for the 3 cases. In the present work, we consider only axis-symmetric magnetic equilibria. The effects of 3D magnetic perturbations due to toroidal field ripple have been investigated in, e.g., [14, 15], and show that ripple losses are negligible (0.12%) in the DTT reference scenario. In the current work ripple losses are not considered.

Table 1

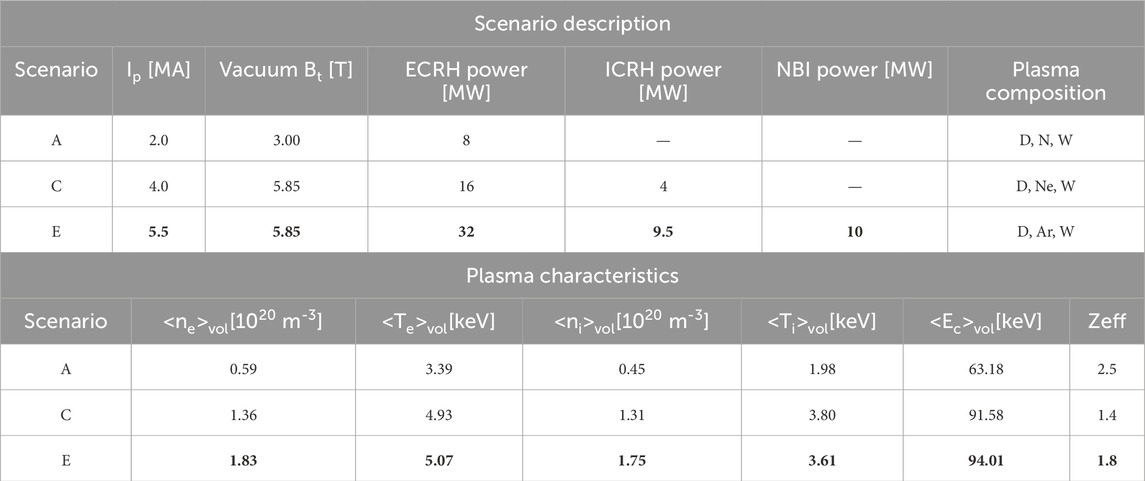
Table 1. Main parameters and plasma properties of analyzed DTT scenarios. In bold the DTT target reference scenario “E”.

Figure 1

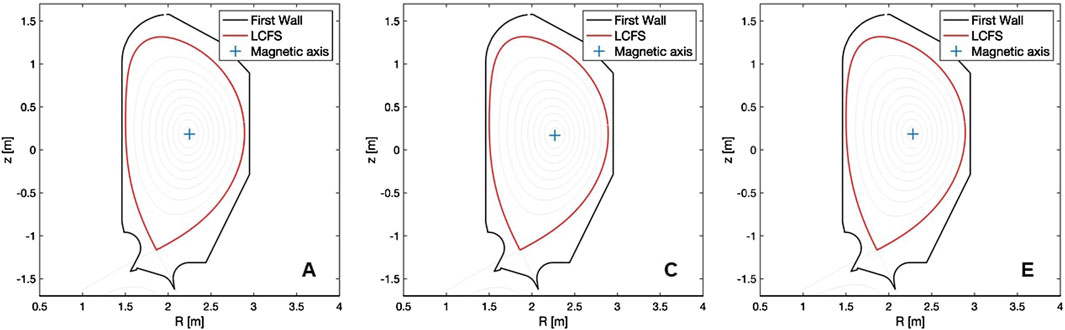
Figure 1. Sketch of the Last Closed Flux Surface (LCFS), First Wall (FW) and magnetic axis of A, C, and E scenarios.

The E scenario is the DTT reference scenario exploiting full machine performance. Early phase A and C scenarios are called in the following sections as A* and C* given that we simulate NBI injection even if they do not include NBI, since they are foreseen before DTT NBI installation. Since half-field/reduced-current scenarios will still be used in the DTT NBI phase – though not yet simulated – we decided to use them as illustrative cases. Our stand-alone NBI simulations do not provide any feedback to the plasma. The volume-averaged density and temperature for plasma electrons and ions are reported in Table 1, where the volume averaged critical energy <E_c>_vol is reported too. E_c corresponds to the value of the fast ion energy when the collisional energy transfer to the background plasma is equally shared by electron and ion species. For completeness, the radial profiles of electron temperature T_e, ion temperature T_i, electron density n_e and deuterium (main) ion density n_D are also reported in Figure 2 for all the analysed plasmas.

Figure 2

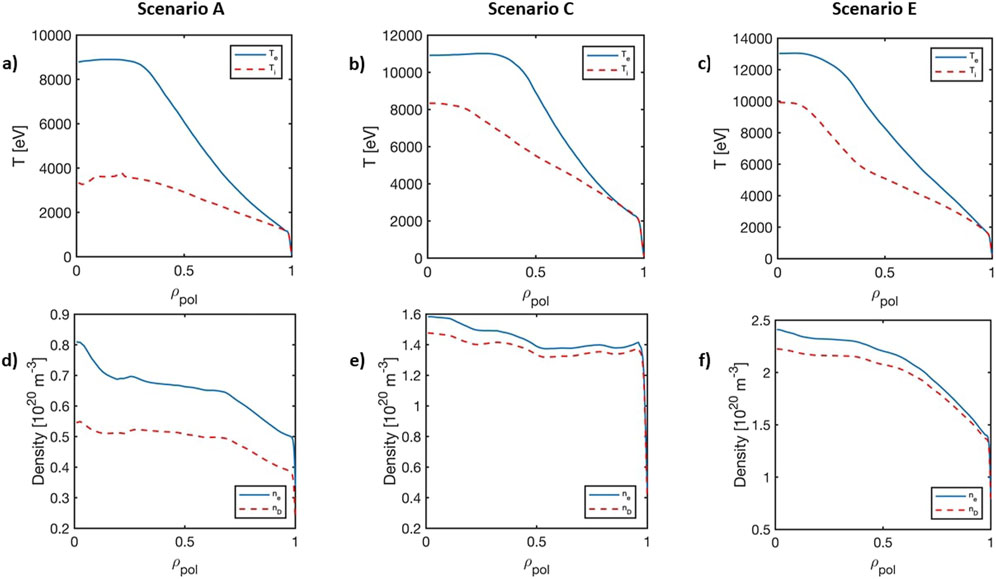
Figure 2. Kinetic profiles for all the analyzed scenarios [8]: (A–C) represent plasma temperature profiles while (D–F) the plasma density profiles of electron (blue) and Deuterium (red) species.

2.2 NBI geometry and first wall geometry

The NBI system [5, 16] designed for DTT is capable of injecting neutrals (H or D; in our work, we considered D injection) up to 510 keV of energy, i.e., the highest beam energy before ITER. The beam energy can be varied in the range of ∼255:510 keV, with beam optics designed to provide NBI power proportional to the injection energy. The high energy needed to heat the plasma core at the high density foreseen in the reference DTT plasma scenario requires using a negative ion source. The beam injection geometry is shown in Figure 3, where the trajectories of a few beamlets are depicted as representative of the total beam. The poloidal view in Figure 3A shows that the injection of DTT NBI is below the equatorial plane of the machine. With the toroidal view (Figure 3B) we can appreciate the tangential direction of the beam injection, with an averaged beam tangency radius $R_{tang}\sim$ 1.95 m. DTT NBI is directed co-current, to avoid a significant fraction of prompt losses, due to unfavourable trapped orbit trajectories.

Figure 3

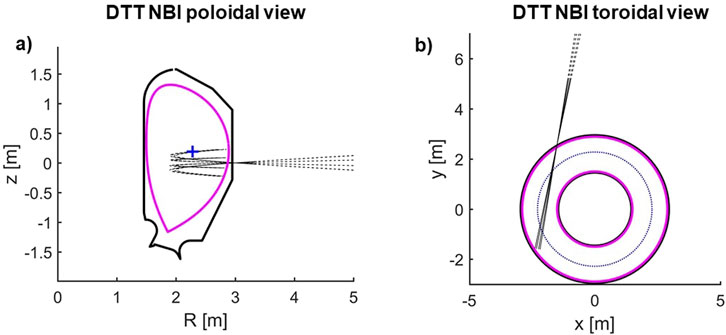
Figure 3. Injection geometry of the DTT neutral beam system in the R, z plane (A) and x, y plane (B). Dashed lines represent each different group of 85 beamlets in the DTT NBI source. DTT FW (solid black) and plasma LCFS (solid magenta) are plotted too.

3 Beam ionization, shine through losses, and consequent PFCs heat loads

Preliminary studies on beam shine-through losses for the DTT full power scenario have already been performed [17, 18], showing that shine-through losses are negligible at the reference E density and may be significant only at plasma densities lower than the reference one. This work presents shine-through analyses for the up-to-date E scenario, not considered in previous publications, and, for the first time, results on low-density, low-current/magnetic field scenarios (A* and C* described in Section 2.1), which also present different shapes of density profiles (see Figure 2). Beam ionization modelling described in Section 3.1 is used to retrieve a heuristic formula for DTT NBI shine-through, in a similar way to what was done for ITER [19] and DEMO [20]. Shine-through losses may represent a significant issue for highly energetic NBI systems, with the risk of causing hot spots on the machine’s first wall. To avoid that, NBI operation may be restricted to specific plasma densities. A necessary step to evaluate NBI operability is the evaluation of shine-through power loads on DTT PFCs, done in Section 3.2, to be then compared to plasma-facing component material limits, which are still to be defined entirely for DTT. Similar studies have also been conducted for current machines, such as EAST [21] and Wendelstein-7X [22].

3.1 Monte Carlo simulations of DTT beam ionization

BBNBI [6] of the ASCOT suite of codes [7] is the state-of-the-art Monte Carlo code used in this work for beam ionization modelling. BBNBI is a beamlet-based neutral beam ionization model capable of following injected neutrals until ionization, providing the input source of fast particles for slowing down simulations. In this work, BBNBI follows neutral particles originating from the 1360 beamlets of the DTT NBI source and calculates the 3D ionization position in the plasma of each injected test particle (50 k per simulation), considering the beamlet divergence and Suzuki cross-section for the collisional ionization [23]. If a test particle is not ionized in the torus and hits the opposite wall, it is counted in the shine-through losses. Shine-through losses strongly depend on beam injection energy and plasma density. Indeed, the beam penetration length ${\lambda }_{beam}$, i.e., the characteristic distance travelled by an energetic neutral before being ionized in the plasma can be approximated to depend linearly on E_NBI and inversely on n_e $\left({\lambda }_{beam}\sim \frac{E_{NBI}}{n_e}\right)$, where E_NBI is the injection energy and n_e the plasma electron density. BBNBI (as well as ASCOT code), considers an exponential decay of plasma kinetic profiles in the Scrape-Off Layer (SOL) region. Therefore, the ionization outside the Last Closed Flux Surface (LCFS) is negligible due to the low-density in the SOL. To explore the DTT NBI operability space, a wide-range parameter scan has been carried out to estimate the shine-through fractions for different plasma conditions and beam energies starting from the three scenarios considered (A*, C* and E). Four different beam energies have been simulated for each scenario covering the range from 255 to 510 keV (see Supplementary Table S3). The injected beam power P_NBI is set to decrease linearly with energy, for consistency (though not influencing shine-through fractions). For each beam energy, the plasma density is varied from the scenario reference value to lower densities since shine-through losses become relevant at low-densities, which may characterize DTT operations in specific scenarios or plasma pulse phases. Other plasma parameters do affect the shine-through losses, though with smaller effects than beam injection energy and plasma density. Those are plasma temperature, injection geometry (which determines the actual local density/temperature seen by beam particles, not necessarily equal to the average value), beam particle species (here only D injection is considered), plasma composition, impurity concentration and even less, magnetic field [23]. In this analysis, we concentrate only on the main dependences, though the BBNBI code takes into account all of them for the ionization. Figure 4 represents the plasma density profiles used in the analysis.

Figure 4

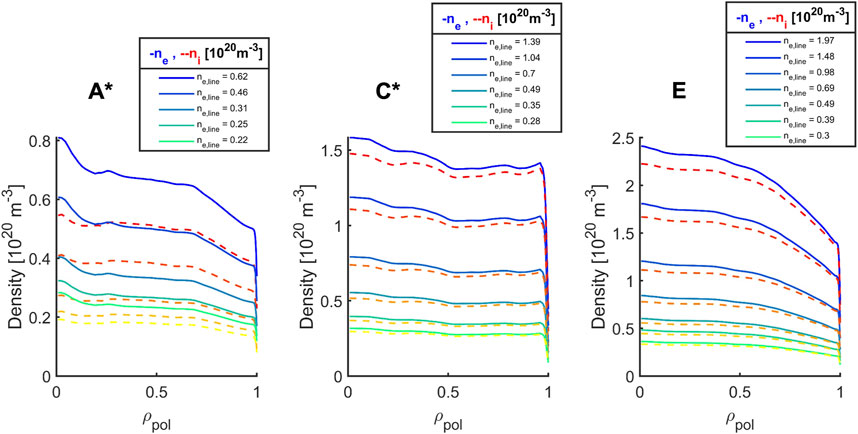
Figure 4. Scaled density profiles used for the shine-through study. Solid blue and dashed red lines represent each scenarios’s reference electron and main ion density. The other profiles are obtained with scaling factors, which resulted in line-averaged electron densities, as shown in the legends above the respective plots.

DTT ref. scenario E foresees a line-averaged plasma electron density of <n_e >_line = 1.97×10²⁰ m^-3, enough to ionize all beam neutrals inside the plasma. The beam ionization cloud for E scenario at full beam energy/power is located from the outer part of the plasma up to the magnetic axis, as shown in Figure 5A. Decreasing the plasma density, the beam penetrates deeper and some energetic neutrals start to cross the whole plasma, reaching the opposite wall. This is the case shown in Figure 5B, for a lower plasma density of <n_e >_line = 0.49×10²⁰ m^-3 and an injection energy of 510 keV. Figure 5C shows instead an opposite situation, where the ionization particle flux is even closer to the plasma edge, happening when decreasing the energy from 510 to 255 keV at fixed ref. E plasma density.

Figure 5

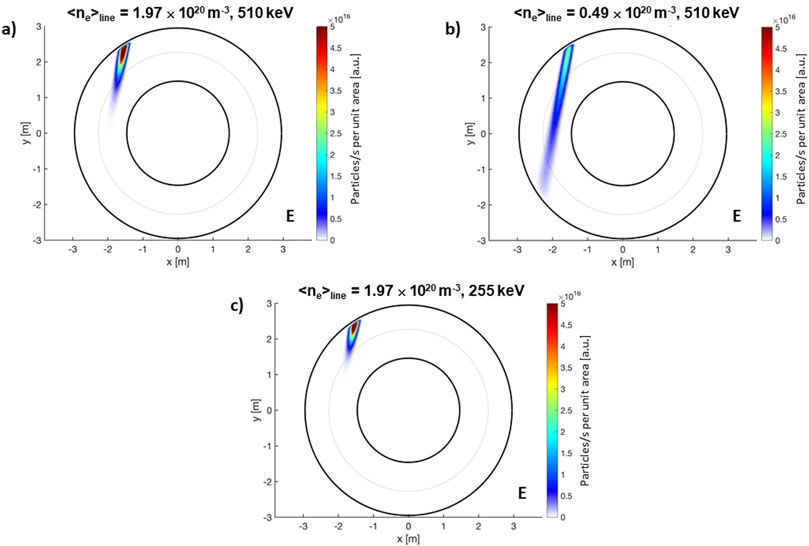
Figure 5. Top view of the beam particle ionization flux for the reference target scenario E (A), at lower plasma electron density (B) and reduced injection energy (C).

Supplementary Table S3 in collects the shine-through fraction values obtained by the BBNBI code as a function of density and energy for all scenarios. Figure 6A shows the shine-through fraction versus the line-averaged plasma electron density of all analyzed scenarios at 510 keV. Shine-through fractions at the same density/energy are not the same for the three analyzed scenarios (Figure 6A). Beam injection geometry, plasma volumes, and flux surface topology are almost identical, implying that, in all the three scenarios, the beam path inside the plasma is virtually equal. Shine-through loss differences can be then explained by the diverse plasma density profile shape in the three cases (see Figure 2). When the plasma density shape is different, even if the average density is the same, the neutral beam ionization rate, which is a local phenomenon, is affected. The fraction of shine-through is always lower in the A*-like plasmas, which present the highest density peaking factor, i.e., the ratio of the core density to the volume-averaged density (n_pf = n_e,0/<n_e>_vol ∼1.37). A larger peaking factor implies a larger core density, and since DTT NBI aims at the plasma core region, the ionization results more efficient. On the contrary, the peaking factor of scenario C* is the smallest (∼1.16), resulting in the highest shine-through fraction at equal energy and density. n_pf and the pedestal density n_ped of the three scenarios are reported in Table 2.

Figure 6

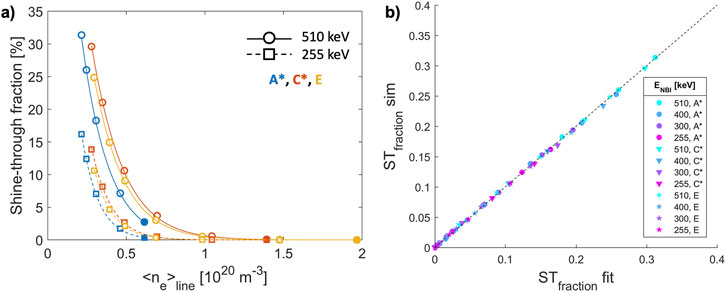
Figure 6. (A) DTT NBI shine-through fractions of A*, C*, and E plasmas, with density profiles scaled as in Figure 4. Simulation points (circles for 510 keV case and squares for 255 keV case) are obtained with BBNBI simulations (full circles and squares represent the reference density values); the curves (solid for 510 keV case and dashed for 255 keV case) are the fit obtained by Equation 1; (B) Comparison of DTT NBI shine-through values obtained by Monte Carlo BBNBI simulations (ST_fraction sim) and by Equation 1 (ST_fraction fit), for all the plasmas considered in this work (Figure 2).

Table 2

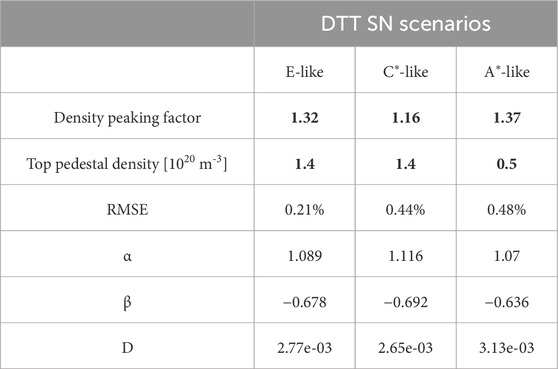
Table 2. Regression coefficients for Equation 1 for each plasma case analyzed. The root mean square error (RMSE) of the regression is also reported as a percentage.

To extend the applicability of this study to any DTT SN plasma with similar characteristics to the cases analyzed here but with different plasma density/beam energy, we retrieve a heuristic formula (Equation 1) similar to what was done for ITER [19] and DEMO [20]. This formula takes into account the exponential dependencies on plasma density (in 10²⁰ m^-3) and beam energy (in keV), and can be used to estimate NBI shine-through (ST) rapidly in future works or design calculation.

$ST=e^{\left(-\frac{<n_e\left[{10}^{20}{m}^{-3}\right]{>}_{line}^{\alpha }{E_{NBI}\left[keV\right]}^{\beta }}{D}\right)}(1)$

Coefficients $\alpha ,\beta ,D$ are obtained from a multilinear regression, using the log (log ()) of shine-through fractions computed by BBNBI code and reported in Supplementary Table S3. Due to differences in plasma density shape, but with too few points to include n_pf or n_ped in the regression, we performed a different fit for each scenario, with the results reported in Table 2. Equation 1 well describes the shine-through dependencies, as proved by the low RMSE reported in Table 2. This can also be seen from Figure 6B, where shine-through values calculated by BBNBI are compared to values obtained with Equation 1, showing a good agreement. For ITER a similar formula has been retrieved and it is currently used to design NBI operative boundaries in terms of plasma density and beam injection energy [24].

3.2 Computation of first wall power loads due to NBI shine-through

In Section 3.1 we analyzed shine-through fraction dependencies in three DTT plasma scenarios. In order to obtain the associated power density load on DTT plasma-facing components due to shine-through losses, a separate, dedicated analysis by particle tracing simulations has been carried out. The code used is the commercial Finite Element Method (FEM) code COMSOL^® Multiphysics [25], which is capable of tracking the trajectories of the NBI particles both during the negative-ion acceleration phase and then, when neutralized, ballistically inside the torus. Before negative-ion neutralization, the effect of the external electromagnetic (EM) fields generated by Beam Line Components (BLCs) or by the tokamak itself is taken into account. The last one is significant, because while the toroidal component of the tokamak magnetic field is fairly enclosed within the tokamak volume itself, the poloidal component (aptly named “stray field”) is virtually free to expand in the Tokamak Hall, potentially affecting everything susceptible to a magnetic disturbance in a radius of tens of meters. Being mainly poloidal (hence “vertical” with respect to the tokamak reference system), it deflects the charged beam exiting the accelerator sideways with respect to the central NBI axis. This potentially reduces the NBI power due to particle collision with BLCs. This NBI power reduction mechanism follows the poloidal field changes during a tokamak plasma pulse, which are also responsible for shifting the shine-through footprint on the PFCs horizontally. Therefore, it is essential to consider this phenomenon both to determine the NBI power reaching the plasma and to localize the shine-through losses on the PFCs. A system dedicated to the suppression of this effect, denominated Stray Field Shielding System (SFSS) [26], is currently under study. A purely passive magnetic shield has been adopted, protecting the region between the grounded grid and the end of the neutralizer where the beam is still charged and susceptible to the magnetic fields. Including all this information in a single time-dependent simulation for each scenario would require a non-trivial setup and computational power, so the poloidal stray field worst-case scenario has been studied here. The following steps have been undertaken:

1. Identification of the highest poloidal stray field in the NBI region in the analyzed DTT plasma scenarios.

2. Setting of DTT magnetic coil currents corresponding to the worst-case scenario (point 1) in a simplified COMSOL magnetostatic model, including the SFSS shielding system [26].

3. Generating a starting set of test particles (with positions and directions) with boundary conditions determined by the poloidal stray field worst-case scenario chosen. In this step, test particles start from the grounded grid, stopping shortly before the end of the connection duct to the tokamak.

4. Simulating a completely neutral beam traveling through the beamline, taking as input the trajectories obtained in step 3 and projecting them to the opposite tokamak wall. This step includes:

4.1. The neutralization due to the background gas, with an efficiency determined by the beam particle energy;

4.2. The suppression of non-neutralized particles in the Residual Ion Dump (RID);

4.3. The deflection due to the stray fields;

4.4. The final impact zone on the opposite First Wall due to the ballistic motion of neutrals, without considering the plasma ionization effects.

The step 4.4 would formally require some integration between COMSOL and the, e.g., BBNBI code to also include the plasma ionization effect. We adopt a more straightforward method, i.e., simulating the full-power beam traveling in the tokamak without ionization reactions by COMSOL, obtaining the power density load and scaling it successively by the expected shine-through fraction calculated by BBNBI (see Section 3.1). The starting COMSOL beam is generated approximating the 1360 DTT NBI beamlets sampling random particles from two overlapped Gaussian beams for each beamlet, to account for a more focused “core” and a less focused “halo” beamlet component. The core-to-halo power ratio adopted is 85:15, with nominal (510 keV) divergence respectively of ${\sigma }_{core}$ = 3 mrad and ${\sigma }_{halo}$ = 30 mrad. For the reduced energy case (255 keV), other particle tracing simulations of the extraction phase [16] showed how the single beamlet divergence roughly doubles when halving the nominal energy. For this reason, the reduced energy divergences have been set to ${\sigma }_{core}$ = 6 mrad and ${\sigma }_{halo}$ = 60 mrad. The particles are emitted with a negative-ion extraction current density of 254 A m⁻². Considering an accelerator efficiency of 0.8, for the nominal energy, the available beam power at the Grounded Grid results in 22.21 MW (at reduced energy 255 keV it results 11.10 MW). The estimated gas density inside the NBI has also been scaled separately for the nominal and reduced energy case to account for the dependency on the energy of the reaction cross-sections. By combining the nominal and reduced energy NBI components in the 3 A*, C*, and E plasma scenarios, six different cases have been investigated.

The first result presented is the NBI power density load without the plasma (vacuum case) at a position corresponding to the opposite DTT FW sector. Figure 7A depicts the NBI port from which the beam enters the tokamak and the beam impact zone on the DTT PFCs. The NBI power density loads estimates on the impact zone are performed considering a detailed geometry of the FW, sketched in Figure 7B, where, ICRH and ECRH ports are shown in addition to the FW section. Figure 8 reports the NBI footprints and the power density loads on the FW section for all scenarios, for both reduced energy and nominal cases. Derived quantities such as the total injected power, the toroidal coordinate of the center of impact, the size of the impact (“NBI footprint”) zone, etc., are reported in Table 3.

Figure 7

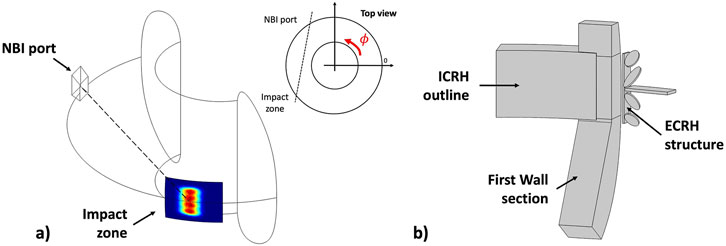
Figure 7. (A) Sketch of the NBI footprint in the toroidal geometry with respect to the NBI injection port. (B) Sketch of the structure of the first wall in the region of the NBI footprint. Location of the footprint in this structure is shown in Figure 8.

Figure 8

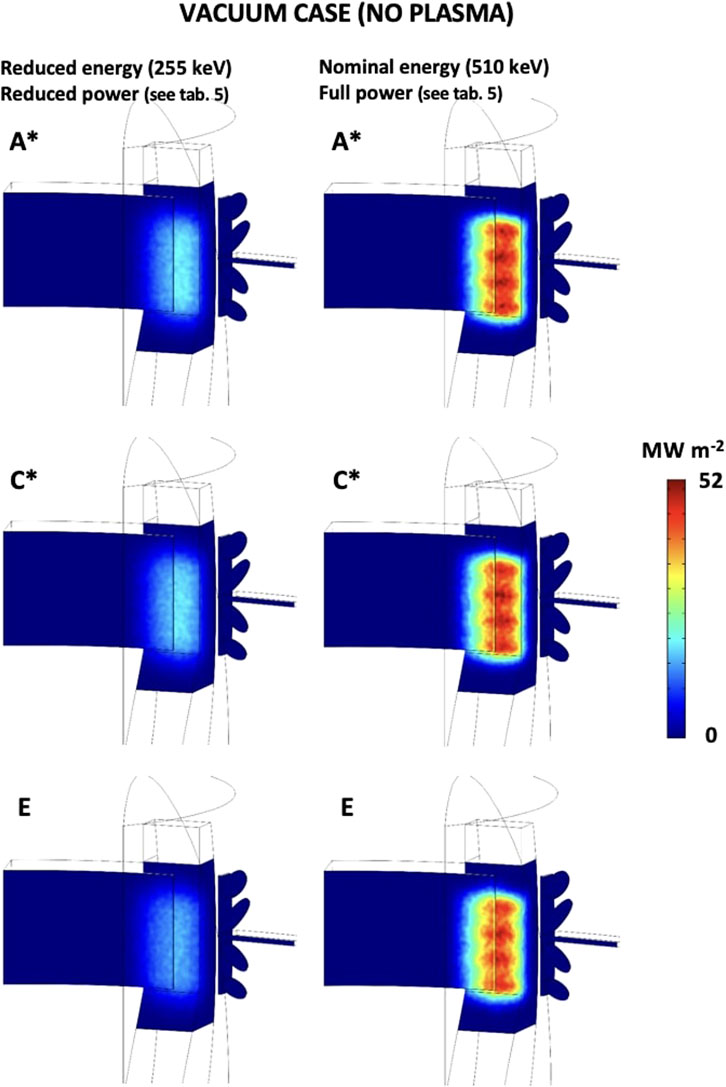
Figure 8. NBI power density loads in the vacuum case (no plasma) projected on the DTT FW section and ICRH, ECRH ports. Nominal and reduced beam energy/power injection cases are reported. The width and heigh of the NBI footprints are noted in the Table 3.

Table 3

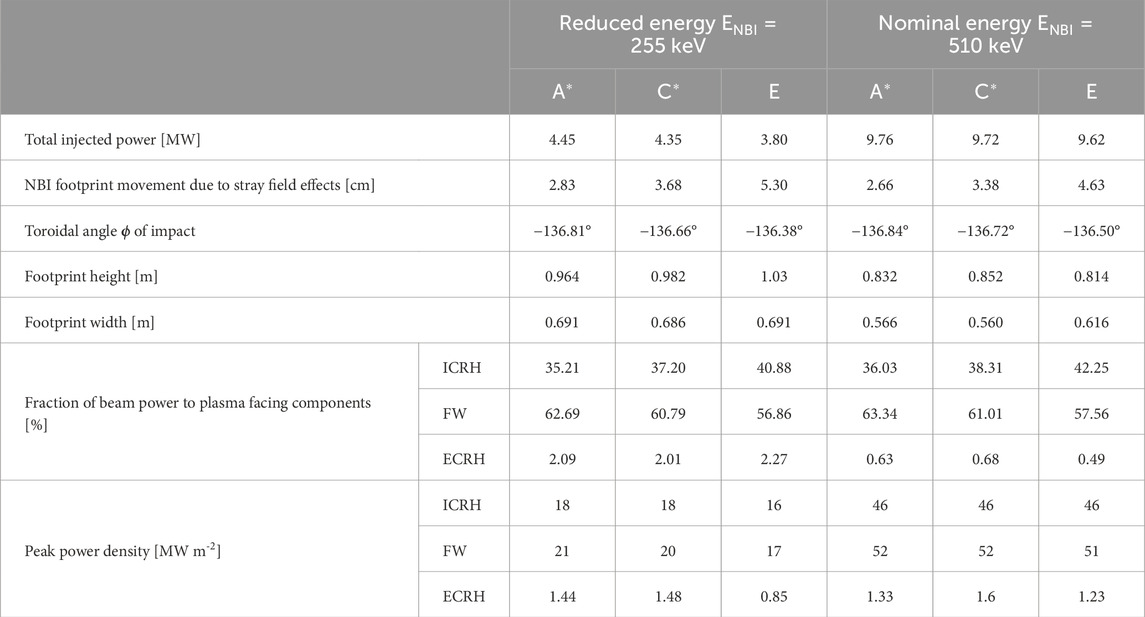
Table 3. Results of the power density load simulations for each considered case and beam power delivered in vacuum (no plasma) to plasma-facing components (FW, ICRH, and ECRH ports), located on the section opposite to the NBI port. When considering a plasma, these power values must be scaled with shine-through fraction (see “supplementary materials”). In bold the DTT target reference scenario “E”.

The results show how the change in the scenario and beam energy affect the strike footprint. A* and C* scenarios feature a reduced plasma current and coil currents, resulting in a lower poloidal field, i.e., in a reduced stray field effect, and thus in a less deviated and more powerful neutral beam with respect to the E scenario. The deviation from the ideal strike point position of the NBI footprint can be expressed in terms of the toroidal angle $\varphi$ of impact, defined in Figure 7. Looking at Figure 7, the ideal strike point ($\varphi$ = −137.31°) is moved anticlockwise while passing from scenarios A* to C* to E (see respective $\varphi$ values in Table 3). The energy modulation of the beam shows a slightly less than linear dependency with the total injected power, due to stray field effect, which is not considered in the BBNBI and ASCOT simulations presented respectively in Sections 3.1 and Section 5. Results are therefore rescaled according to Table 3 estimates. The energy scaling also affects the shape of the impact zone, enlarging and leveling the footprint, as can be seen in Figure 8. At the nominal energy, the footprint is narrower as more particles are removed at the connection duct, due to their excessive lateral movement, than the half-energy case. Width and height of the footprint reported in Table 3. Their values are approximately computed considering as footprint limit the 5% of the peak, i.e., ∼ 2.5 MW m⁻².

As shown in Figure 8, ICRH and ECRH port regions are also affected by the NBI footprint. Considering the beam injection in vacuum (without any plasma) at nominal parameters, about 42% of the beam power is delivered to the ICRH port area (with a peak of 46 MW m⁻²). The ECRH ports receive a small portion of power with respect to the FW and ICRH structure (0.49% at the nominal case, and 2.27% at the reduced energy case). Table 3 reports the fraction of power delivered to the various components (ICRH, FW, ECRH) and the corresponding expected vacuum power density peak load for all scenarios, both at the half and nominal beam energies. The impact of the beam on ICRH and ECRH ports may set a lower operability limit for NBI application since these components are able to withstand a lower power load than the FW section, being not protected by a specific coating like the rest of the wall.

Up to now, we have evaluated the power density loads due to the NBI in the absence of a plasma. When considering the plasma, the power density peak loads reported in Table 3 can be rescaled through the estimated shine-through fractions obtained in Section 3.1. In Supplementary Table S4, all the rescaled values of the power density peak loads on the FW for the reduced energy (255 keV) and the nominal energy (510 keV) cases of the three scenarios are reported. Figure 9 shows the estimates of the FW power density peak load (in log scale) at different plasma densities for both the reduced energy (dashed line) and nominal cases (solid line). The FW power density peak values for the vacuum case (no plasma) are reported too. We can observe that the C* scenario presents the largest power density peak at all densities, while scenario A* presents the lowest, as discussed in the previous section. The design of DTT FW and the consequent PFCs limits is still to be fixed. In particular, additional protection on the NBI footprint would allow the operation of the beam at lower plasma densities.

Figure 9

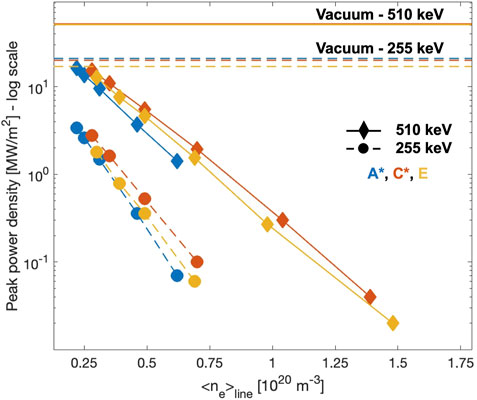
Figure 9. Peak power density plotted versus DTT line-averaged plasma electron densities considering both nominal (510 keV, solid line) and reduced energy (255 keV, dashed lines) NBI injection energies. These values are estimated on the FW section represented in Figure 7B). The data used for this plot are reported in Supplementary Table S4. The peak power density expected with no plasma (vacuum case) are also reported (solid and dashed horizontal lines) for each scenario. These values are reported in Table 3.

4 Orbit characterization of beam newly-born fast ions

After discussing beam trajectory, ionization and shine-through losses in Section 3, we now characterize the beam newly born fast ion orbits for the three DTT plasma scenarios A*, C*, and E. Once ionized, fast ions start to feel the magnetic field and follow orbits depending on their position and velocity. Fast ions typically perform several toroidal turns before experiencing a Coulomb collision with the background plasma particles, i.e., in this phase, their motion is only guided by the magnetic field. In this analysis, the magnetic field fluctuations are neglected but further analyses could be performed to evaluate their impact on the initial beam particle orbits. When evaluating the efficiency of NBI in a plasma, the topology of newly-born fast ion first orbits is an essential feature to be checked to assess the amount of EPs born on unconfined orbits (prompt losses) or the ratio of passing/trapped EPs which can affect beam source in the plasma as, e.g., the driven current. The orbit characterization is here performed in the Constant of Motion (CoM) phase space [27]. Background thermal particles typically follow passing and banana orbits. However, a larger drift affects energetic particles during their motion in the plasma, opening the possibility of the so-called non-standard orbits, as stagnation orbits (i.e., orbits of particles not moving significantly in the poloidal direction) and potato orbits (i.e., trapped orbits that encircle the magnetic axis) [28]. In the following subsections, we present the analyses of first orbits and prompt losses in 2D axial symmetric magnetic equilibria, discussing the effect of plasma density (affecting fast ion birth position) and beam injection energy (affecting both fast ion birth position and EP velocity).

4.1 DTT beam EP constant of motion phase space

In an axisymmetric geometry and in a collisionless plasma, the particle motion can be described by three variables: the particle energy E, the toroidal canonical angular momentum $P_{\varphi }=q\mathrm{\psi }+{\text{mRv}}_{\mathrm{\varphi }}\approx q\mathrm{\psi }+{\text{mRv}}_{\parallel }$ and the magnetic moment $\mu =\frac{m{v}_{\perp }^2}{2B_{tot}}$. Here q and m are the charge and mass of the particle, $\psi$ is the poloidal flux function, R is the radial coordinate, $v_{\varphi }$ is the toroidal velocity and $v_{\perp },v_{\parallel }$ are respectively the perpendicular and parallel components of the particle velocity, $B_{tot}$ is the total magnetic field. In $P_{\varphi }$, the toroidal velocity is assumed as $v_{\varphi }\approx v_{\parallel }$ since we are considering the guiding center motion of the particles [29]. E and $P_{\varphi }$ variables are conserved during the particle motion while $\mu$ is an adiabatic invariant. Together, these three variables define the so-called Constant of Motion (CoM) phase space [27]. A topological map can be built in this phase space, exploiting the relation between $P_{\varphi }$ and $\mu$:

$P_{\varphi }^{\pm }\left(\mathrm{\psi },\mathrm{\mu },\mathrm{E}\right)=q\psi \pm \frac{g\left(R_{\psi }\right)}{B_{\varphi }\left(R_{\psi }\right)}\sqrt{2m\left[E-\mu B_{tot}\left(R_{\psi }\right)\right]}(2)$

where $g$ is the free function defined as $g=R_{\psi }{B}_{\varphi }$, with $B_{\varphi }$ the toroidal magnetic field, and $R_{\psi }$ represents the particle radial position. In this work, for the construction of the topological map, the values of $R_{\psi }$ are taken in the so-called stagnation surface [30], i.e., the surface where the extreme values of $\psi$ along an orbit are met. In up-down symmetric plasmas, the equatorial plane can be considered as the stagnation surface. However, in a tokamak with divertor configuration, like DTT, the up-down symmetry is usually broken, and the stagnation surface must be calculated to define $R_{\psi }$ properly [31]. The condition to obtain this surface is given by Equation 3, with $\mathit{B}=\left(B_R,B_z,B_{\varphi }\right)$ and $\nabla B={\partial }_R{B}_R+{\partial }_z{B}_z$ due to toroidal symmetry.

$\mathit{B}\cdot \nabla B=0(3)$

In “supplementary materials” (Supplementary Figures S1A, B) the stagnation surface for DTT E flat-top plasma in the poloidal plane and the domains of the topological map, obtained by solving Equation 2 at different $R_{\psi }$ positions, are shown. The domains are related to different particle orbits [27]: confined and lost co-passing orbits, confined and lost trapped orbits, stagnation orbits and potato orbits. The boundaries of these regions change with the particle energy and the plasma toroidal magnetic field. These effects can be seen in Supplementary Figure S2. Only co-passing orbits, i.e., orbits defined by particles directed in the same direction as the current, are relevant for DTT, since the DTT injection geometry implies the generation of co-current fast ions only (with pitch $\lambda =\frac{v_{\parallel }}{v}<0$, defined with respect to the toroidal magnetic field, opposite to I_p in DTT). More information on DTT CoM construction and dependencies can be found in [11].

4.2 Orbit classification

Combining CoM boundaries calculated as described in Section 4.1 and BBNBI ionization results reported in Section 3.1, we can classify the orbits of newly-born fast ions for DTT scenarios A*, C*, and E. Differences among plasma scenarios permit also to investigate how plasma parameters play a role in the fast ion orbit topology, at different NBI energies. For each scenario, we obtained 2D histograms of newly born fast ions in CoM phase space, at 510 keV and 255 keV beam injection energy, as shown in Figure 10.

Figure 10

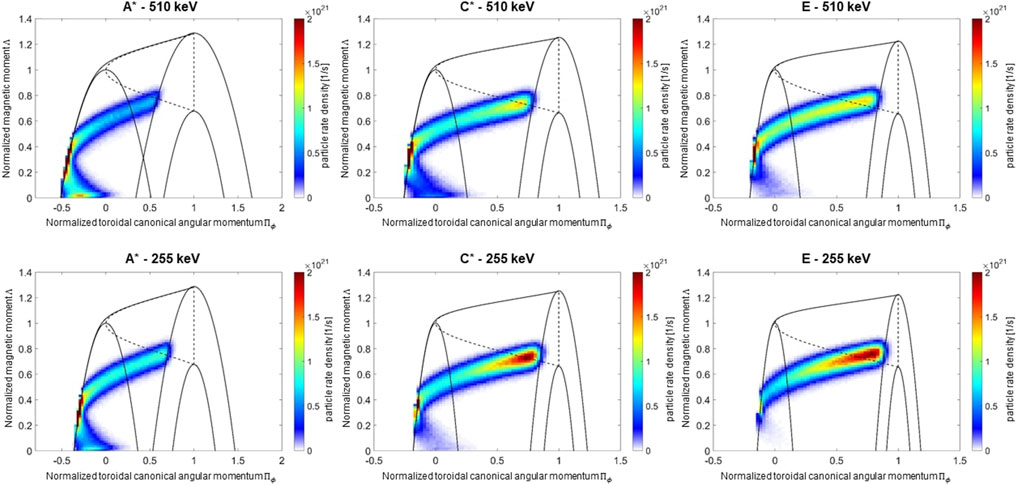
Figure 10. Histograms in the CoM phase space of newly-born fast ions (particle rate density [1/s]). Two beam injection energy cases are shown for each DTT scenario: 510 keV (top row) and 255 keV (bottom row).

As shown in Figure 10, particle energies and scenario properties affect fast ion orbit topology. Confined passing orbits characterize the large majority of the DTT beam EPs. The number of newly-born fast ions with confined passing orbits decreases when the injection energy is reduced (see Supplementary Table S1). This decrease is evident for high density scenario E and almost negligible for low density, low B_T scenario A*. At the same magnetic field and the same injection energy (C* and E scenarios), the percentage of passing orbits increases when decreasing the plasma density. A decrease of EP energy determines an increase of trapped orbits. These effects depend on the penetration of the beam into the plasma. Passing particles are likely to form close to the plasma center, where the ions are born with a larger particle velocity component parallel to the magnetic field. Trapped particles instead are likely to form on the edge of the plasma due to a larger perpendicular velocity component. Therefore, the larger the beam penetration (e.g., due to a higher beam energy or lower plasma density), the higher the fraction of confined passing particles. EP non-standard orbits will not significantly characterize DTT scenarios. However, a small fraction (∼0.8–5%) of stagnation orbits is present (potato orbits are not predicted at all). For all the analyzed cases, lost (or unconfined) orbits contribute up to ∼1% (“prompt losses”). In the CoM phase space analysis, a particle is considered lost when it crosses the Last Closed Flux Surface (LCFS). However, a fast ion that crosses the LCFS can re-enter the plasma, especially if the LCFS is far enough from the FW as in DTT. The lost particle fractions from COM analysis are therefore overestimated. The orbit-following Monte Carlo ASCOT code shows that prompt losses in the reference scenario E, without collisions, reduce to <0.1% with simulation domain up to DTT FW. This result is in agreement with ORBIT simulations [15]. The effect of collisions is taken into account in Section 5.

The complete quantitative estimate of the observed orbit types as fractions of the total fast ion population is reported in Supplementary Table S1, as well as some examples of particle orbits expected in DTT, reported in Supplementary Figure S3.

5 NBI collisional slowing down, fast ion distribution functions and EP confinement

DTT NBI fast ions interact with the plasma particles through Coulomb collisions, providing heat, inducing current drive and injecting torque to the plasma. The orbit-following Monte Carlo ASCOT code [7] is used as modelling tool for the numerical exploration of the collisional slowing down of the beam’s fast ions and to obtain fast ion distributions and sources to the plasma. ASCOT solves the Fokker-Planck equation of charged particles, both in gyro-orbit or guiding center motion. Simulations performed for this work consider a hybrid method, that consists of following particles in their guiding center motion until the guiding center of the particles is closer to the wall than the particle Larmor radius. At this point, the code starts to follow the particle in the gyro-orbit reference. This hybrid method allows to reduce the computational demand required for gyro-orbit simulations, while keeping high accuracy on the evaluation of fast particle losses position close to the wall. The Coulomb collisions happening inside the 2D wall between beam particles and the plasma are implemented using Monte Carlo operator. In our ASCOT simulations, we used the inputs described in Section 2, plus BBNBI outputs which provide the ensemble of newly-born fast ions in the plasma. In this work we neglect the effects of different beam injection options, such as power and energy, on the background magnetic fields. EPs are followed until they are lost or thermalized, i.e., when beam particles reach an energy equal to 1.5 the energy of a thermal ion in the core of the plasma (∼10 keV in the DTT E scenario). This condition is usually done in ASCOT studies.

The fast ion collisional slowing-down until thermalization has been studied for the three scenarios A*, C*, and E. Collisions are responsible for energy and momentum transfer, which may also result in fast ion losses due to, e.g., scattering into an unconfined orbit. The generation of a fast-ion population moving toroidally in the tokamak also gives rise to the current-drive phenomenon. -Charge-exchange fast ion losses with background neutrals are not computed in this work and assumed to be negligible due to the high density of DTT plasmas that likely prevents cold and thermal neutrals from penetrating deep in the core. Future neutral transport studies for DTT will clarify this point. The amount of power absorbed is larger than 99% for all scenarios except the A* scenario at 510 keV, where shine-through losses (2.74%) and orbit losses (0.14%) cause a slightly reduced beam power absorption. As discussed in sec. 4, co-current injection prevents unfavorable (e.g., “outward banana”) fast ion orbits, resulting in negligible prompt losses in all scenarios. Orbit losses due to scattering processes do not change significantly in this picture, with a negligible amount of lost particles. Regarding the power transferred to plasma species, electron heating is dominant at E_NBI = 510 keV, with ∼55–60% of the power absorbed by the electrons for all scenarios. Ion heating instead is larger at 255 keV (up to ∼55%). At 255 keV, particle energy is closer to the critical energy and a larger ion heating is observed during the slowing down, as well as an increasing ion-beam collision frequency (${\nu }_{ib}\propto v_{beam}^{-3}$, where $v_{beam}$ is the beam particle velocity) [32]. DTT NBI can transfer relevant energy to both plasma species with ratios depending on external parameters. DTT NBI can also contribute to the sustainment of the plasma current, thanks to high-energy co-current injection. In absolute terms, NBI can drive up to 1.1 MA, in the low-density plasma (scenario A*). In terms of the Current Drive (CD) efficiency, ${\eta }_{CD}=\frac{I_{CD}}{P_{NBI}}{R}_0{n}_e$, where $I_{CD}$ is the current driven by the beam, it results ∼0.10–0.15 ∙ 10²⁰ A/Wm², with a clear dependence on the beam injection energy. NBI injection transfers momentum to the plasma. ASCOT calculates the torque contributions from collisions and JxB effects [33]. The total torque provided is almost halved when halving the injection energy. Quantitative results for each scenario, at full and half injection energy, of the volume integrated quantities for power absorption, current drive, torque, and losses are collected in Supplementary Table S2.

Figure 11 shows the deposited power and toroidal current density profiles versus the normalized poloidal flux ${\rho }_{pol}$. Power deposition is affected by energy reduction both in profile shape and in absolute values, due also to the power reduction caused by the stray fields (see Section 3.2). More power is deposited in the outer plasma for high-density scenario as C* and E. Current drive, as well as power deposition, is off-axis due to the injection geometry. DTT can produce a large variety of plasma shapes, including plasmas where the beam deposition will result on-axis (not considered in this work).

Figure 11

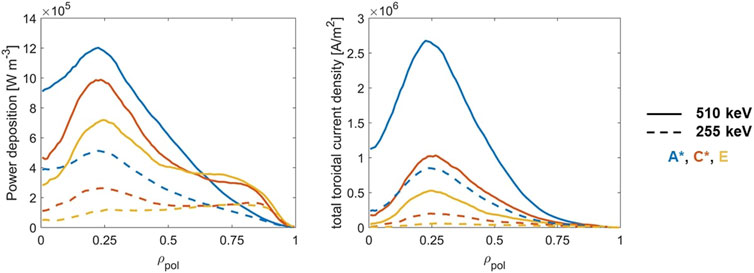
Figure 11. Power deposition and total toroidal current density radial profiles for different DTT scenarios. Solid lines represent the results of ASCOT simulations with a beam injection energy of 510 keV, while dashed lines with an injection energy of 255 keV.

Figure 12 shows the energy-pitch distribution functions for the steady-state scenarios at 510 keV (top) and 255 keV (bottom). These distributions are affected both by plasma parameters and EP initial energy. The source of EPs, originated by the NBI injection, has a negative pitch (peak at $\lambda \sim$ - 0.69 for the DTT reference scenario E), as discussed in sec 4.1. Among the scenarios, the initial source pitch value peak slightly shifts due to the different ionization positions of newly-born fast ions among scenarios. The lower the plasma density, the more tangential the ionization (i.e., $\left|\lambda \right|\sim 1$) due to deeper beam penetration. Each distribution spreads towards positive pitch values when the fast ion energy decreases, due to the pitch-angle scattering effect, which becomes more relevant when particle energy E approaches the critical energy E_c. Even if E_c varies with local plasma parameters, the volume-averaged values (see Table 1), plotted in Figure 12, can already highlight the effect of the pitch angle-scattering becoming dominant at E $\sim$ <E_c>.

Figure 12

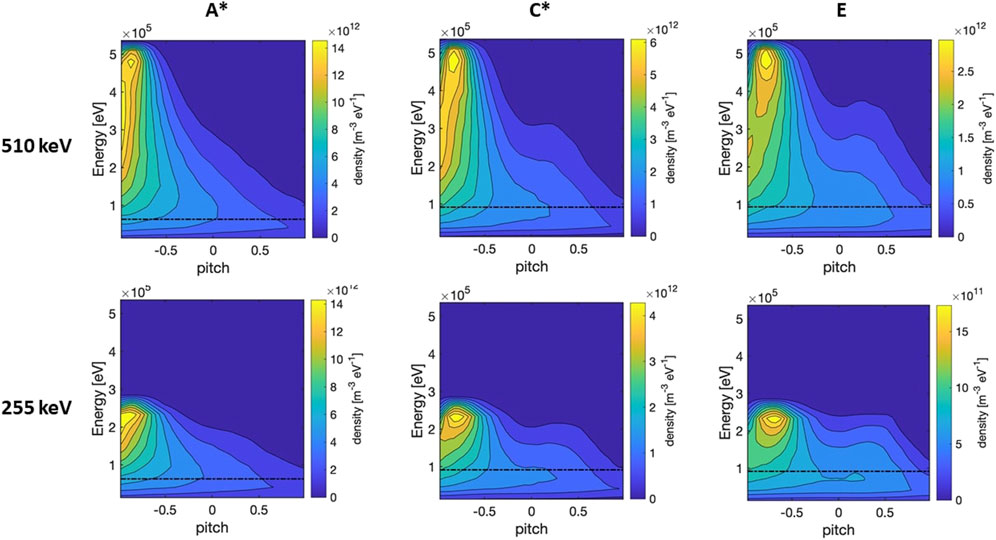
Figure 12. DTT beam EP energy-pitch distributions for A*, C*, and E scenarios, considering an injection energy of 510 keV (top row) and 255 keV (bottom row). The black dashed line represents the critical energy E_c.

6 Conclusion

DTT NBI will be one of the NBI systems with the highest injection energy in the future fusion scene, the only one in a full-metal FW machine besides ITER. This work, which explores numerically the impact of the NBI system in DTT plasmas, supports the design of the system, plasma scenario simulation activities and the DTT Research Plan development [3]. Conditions for efficient beam operability in terms of. e.g., injection energy and power are discussed for various plasma conditions. In this study, beam ionization and beam-plasma interaction are numerically explored for three different plasmas, with a single null divertor configuration, a 2D axis-symmetric magnetic equilibrium, at diverse B_t/I_p values, considering a wide-range scan in plasma density and beam energy. Low B_t, I_p, and plasma density DTT scenarios are explored for the first time in this work, together with an extended analysis of the DTT target reference scenario. Shine-through losses are one of the significant challenges that characterize high-energy beam injection. An effective NBI ionization is shown for high-density DTT plasmas, while low-density plasmas may require reduced beam energy and power due to significant shine-through losses. We also propose a heuristic formula to evaluate NBI shine-through dependence on n_e and E_NBI, that can be used for fast shine-through evaluations on future DTT plasmas and for future analyses to define NBI operational boundaries in terms of plasma density and beam injection energy. The effects of the poloidal magnetic “stray” fields on the beam optics are included in the study, showing a decrease in the injected beam power due to beam scraping by the beam-line components. The stray fields significantly affect the injected beam power at low beam energy and high plasma current. Power density loads due to NBI shine-through on the DTT PFCs are presented, with an estimate of the peak power density in the various plasma-facing components hit by the beam footprint. This analysis shows that ICRH and ECRH ports, located in the area of the NBI footprint on the wall, are partly hit by the beam projection and provides a first estimate of the peak power density loads expected in these regions. The minimum density for safe NBI operation in DTT will have to consider shine-through heat loads, especially on delicate plasma-facing components, such as in the ICRH and ECRH port areas. The analysis through the Constant of Motion phase space provides a picture of NBI EP orbits and prompt losses, showing how the plasma density and beam energy influence the orbit topology of newly-born fast particles. The ratio between confined passing/trapped orbits varies when the plasma density and injection energy changes. Passing orbits dominate the reference DTT plasma. A small fraction of non-standard orbits that includes only stagnation particles is observed, which may be interesting for EP stability studies foreseen in future DTT activities. The beam-plasma coupling results efficient for all the analyzed scenarios ($\sim$ 99% of absorbed power), except in the lowest density scenario at E_NBI = 510 keV, which shows slightly larger EP losses. DTT NBI can transfer relevant energy to both plasma species with ratios depending on external parameters. Electron-to-ion power deposition ratio varies from 60:40 to 45:55 depending on the NBI energy and plasma temperature. NBI CD in the order of 0.24 MA is predicted for the ref. scenario. Current drive increases for the low-density scenarios at high injection energy. The beam power deposition (and current-drive) is deposited off-axis (${\mathit{\rho }}_{\mathit{p}\mathit{o}\mathit{l}}\sim \mathbf{0.25}$) for all scenarios due to a vertical shift of the plasma with respect to the geometrical equatorial plane of the machine. DTT NBI is shown to be an efficient auxiliary system, thanks also to injection energy and power modulation, capable of unique features, like torque injection, relevant ion heating, high-efficiency current drive and the generation of a mostly passing and confined, high energy, fast ion population. Besides robustly delivering power to DTT plasmas to achieve reactor-relevant conditions for power exhaust studies, DTT NBI can be the actuator of exciting and diverse fusion-relevant physics studies.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

CD: Writing–original draft, Writing–review and editing. PV: Writing–original draft, Writing–review and editing. FV: Writing–original draft, Writing–review and editing. PA: Writing–review and editing. IC: Writing–review and editing. AC: Writing–review and editing. PM: Writing–review and editing. AM: Writing–review and editing. TB: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 — EUROfusion). Views and opinions expressed are however those of the authors only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.

Acknowledgments

The authors thank Mireille Schneider, Lars-Goran Eriksson, and Dirk Van Eester for the discussions on energetic particle physics, which greatly improved the manuscripts. A special thanks also to the support given by the ASCOT team of Aalto University and VTT Technical Research Centre, Finland.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1492095/full#supplementary-material

References

1. ENEA. DTT interim design report (2019). Available from: https://www.dtt-dms.enea.it/share/s/avvglhVQT2aSkSgV9vuEtw (Accessed 2019).

Google Scholar

2. Romanelli F, et al. Divertor Tokamak Test facility project: status of design and implementation. Nucl Fusion (2024) 64:112015.

Google Scholar

3. Crisanti F, Giruzzi G, Martin P, et al. Divertor tokamak test facility research plan version 1.0. Rome, Italy: ENEA (2024).

Google Scholar

4. Granucci G, Ceccuzzi S, Giruzzi G, Sonato P, Agostinetti P, Bolzonella T, et al. The DTT device: system for heating. Fusion Eng Des (2017) 122:349–55. doi:10.1016/j.fusengdes.2017.04.124

CrossRef Full Text | Google Scholar

5. Agostinetti P, et al. Improved conceptual design of the beamline for the DTT neutral beam injector. IEEE Transaction on Plasma Science (2022).

Google Scholar

6. Asunta O, Govenius J, Budny R, Gorelenkova M, Tardini G, Kurki-Suonio T, et al. Modelling neutral beams in fusion devices: beamlet-based model for fast particle simulations. Computer Phys Commun (2015) 188:33–46. doi:10.1016/j.cpc.2014.10.024

CrossRef Full Text | Google Scholar

7. Hirvijoki E, Asunta O, Koskela T, Kurki-Suonio T, Miettunen J, Sipilä S, et al. ASCOT: solving the kinetic equation of minority particle species in tokamak plasmas. Computer Phys Commun (2014) 185:1310–21. doi:10.1016/j.cpc.2014.01.014

CrossRef Full Text | Google Scholar

8. Casiraghi I, Mantica P, Ambrosino R, Aucone L, Baiocchi B, Balbinot L, et al. Core integrated simulations for the Divertor Tokamak Test facility scenarios towards consistent core-pedestal-SOL modelling. Plasma Phys Controlled Fusion (2023) 65:035017. doi:10.1088/1361-6587/acb6b1

CrossRef Full Text | Google Scholar

9. Romanelli M, Corrigan G, Parail V, Wiesen S, Ambrosino R, Da Silva Aresta Belo P, et al. JINTRAC: a system of codes for integrated simulation of tokamak scenarios. Plasma Fusion Res (2014) 9:3403023. doi:10.1585/pfr.9.3403023

CrossRef Full Text | Google Scholar

10. Pereverzev GV, Yushmanov e PN. ASTRA automated system for transport analysis in a tokamak. IPP Rep (2002) 5:98.

Google Scholar

11. Casiraghi I, Mantica P, Koechl F, Ambrosino R, Baiocchi B, Castaldo A, et al. First principle-based multi-channel integrated modelling in support of the design of the Divertor Tokamak Test facility. Nucl Fusion (2021) 61:116068. doi:10.1088/1741-4326/ac21b9

CrossRef Full Text | Google Scholar

12. Crisanti F, et al. Physics basis for the divertor tokamak test facility. Nucl Fusion (2024) 64:106040. doi:10.1088/1741-4326/ad6e06

CrossRef Full Text | Google Scholar

13. Albanese R, Ambrosino R, Mattei M. CREATE-NL+: a robust control-oriented free boundary dynamic plasma equilibrium solver. Fusion Eng Des (2015) 96-97:664–7. doi:10.1016/j.fusengdes.2015.06.162

CrossRef Full Text | Google Scholar

14. Spizzo G, Gobbin M, Agostinetti P, Albanese R, Ambrosino R, Casiraghi I, et al. Collisionless losses of fast ions in the Divertor Tokamak Test due to toroidal field ripple. Nucl Fusion (2021) 61:116016. doi:10.1088/1741-4326/ac1e08

CrossRef Full Text | Google Scholar

15. Spizzo G, Gobbin M. ORBIT simulations of fast ion power loads on the wall of the Divertor Tokamak Test. Plasma Phys Controlled Fusion (2023) 65:075013. doi:10.1088/1361-6587/acd71d

CrossRef Full Text | Google Scholar

16. Veronese F, Agostinetti P, Dima R, Murari A, Pepato A, Romanato M. The spherical and lemon hyperlens grids concept applied to the DTT neutral beam injector. IEEE Trans Plasma Sci (2024) 1–6. doi:10.1109/tps.2024.3353349

CrossRef Full Text | Google Scholar

17. Vincenzi P, et al. Interaction of high-energy neutral beams with Divertor Tokamak Test plasma. Fusion Eng Des (2023):113463. doi:10.1016/j.fusengdes.2023.113436

CrossRef Full Text | Google Scholar

18. De Piccoli C. DTT NBI fast particle modelling with Monte Carlo ASCOT code. Padova, Italy: University of Padova (2022).

Google Scholar

19. Vincenzi P, Snicker A, Schneider M. Modelling of NBI shine-through in ITER non-nuclear phase to limit heat fluxes on first wall. Fusion Eng Des (2024) 200:114178. doi:10.1016/j.fusengdes.2024.114178

CrossRef Full Text | Google Scholar

20. Vincenzi P, Agostinetti P, Artaud JF, Bolzonella T, Kurki-Suonio T, Mattei M, et al. Optimization-oriented modelling of neutral beam injection for EU pulsed DEMO. Plasma Phys Controlled Fusion (2021) 63:065014. doi:10.1088/1361-6587/abf402

CrossRef Full Text | Google Scholar

21. Xingquan W, Luo J, Wu B, Wang J, Hu C. Calculation of shinethrough and its power density distribution for EAST NBI. Plasma Sci Technology (2013) 15:480–4. doi:10.1088/1009-0630/15/5/17

CrossRef Full Text | Google Scholar

22. Rust N, et al. Neutral-Beam-Injection on Wendelstein 7-X: beam transmission, shine through and effect of plasma current. In: 46th EPS conference on plasma physics. Milan (2019).

Google Scholar

23. Suzuki S, Shirai T, Nemoto M, Tobita K, Kubo H, Sugie T, et al. Attenuation of high-energy neutral hydrogen beams in high-density plasmas. Plasma Phys Controlled Fusion (1998) 40:2097–111. doi:10.1088/0741-3335/40/12/009

CrossRef Full Text | Google Scholar

24. Vincenzi P, et al. ITER NBI operational window and power availability constraints due to shine-through losses. Submitted Nucl Fusion.

Google Scholar

25. Guide SMU. COMSOL Multiphysics v.6.0. Stockholm, Sweden: COMSOLAB (2021).

Google Scholar

26. Veronese F, Agostinetti P, Calabrò G, Crisanti F, Fanelli P, Lombroni R, et al. Comparison among possible design solutions for the stray field shielding system of the DTT neutral beam injector. J instrumentation (2023) 18:C06018. doi:10.1088/1748-0221/18/06/c06018

CrossRef Full Text | Google Scholar

27. White RB. The theory of toroidally confined plasmas. London, United Kingdom: Imperial college press (2014).

Google Scholar

28. Eriksson LG, Porcelli F. Dynamics of energetic ion orbits in magnetically confined plasmas. Plasma Phys Controlled Fusion (2001) 43:R145–82. doi:10.1088/0741-3335/43/4/201

CrossRef Full Text | Google Scholar

29. Tenney F. Confinement of energetic alphas in TCT and tritons in PLT. Tech Rep Princeton Univerisity (1975).

CrossRef Full Text | Google Scholar

30. Egedal J. Drift orbit topology of fast ions in tokamaks. Nucl Fusion (2000) 40(9):1597–610. doi:10.1088/0029-5515/40/9/304

CrossRef Full Text | Google Scholar

31. Bierwage A, Fitzgerald M, Lauber P, Salewski M, Kazakov Y, Štancar Ž. Representation and modeling of charged particle distributions in tokamaks. Comput Phys Commun (2022) 275:108305. doi:10.1016/j.cpc.2022.108305

CrossRef Full Text | Google Scholar

32. Wesson J. Tokamaks. Oxford University Press (2004).

Google Scholar

33. Hinton FL, Rosenbluth MN. The mechanism for toroidal momentum input to Tokamak plasmas from neutral beams. Phys Lett (1999) A(259):267–75. doi:10.1016/S0375-9601(99)00453-3

CrossRef Full Text | Google Scholar