Lightweight multi-stage temporal inference network for video crowd counting

Crowd density is an important metric for preventing excessive crowding in a particular area, but it still faces challenges such as perspective distortion, scale variation, and pedestrian occlusion. Existing studies have attempted to model the spatio-temporal dependencies in videos using LSTM and 3D CNNs. However, these methods suffer from large computational costs, excessive parameter redundancy, and loss of temporal information, leading to difficulties in model convergence and limited recognition performance. To address these issues, we propose a lightweight multi-stage temporal inference network (LMSTIN) for video crowd counting. LMSTIN effectively models the spatio-temporal dependencies in video sequences at a fine-grained level, enabling real-time and accurate video crowd counting. Our proposed method achieves significant performance improvements on three public crowd counting datasets.

1 Introduction

Crowd counting technology has broad application prospects in fields such as video surveillance, traffic control, and emergency management, and it has been widely applied in urban public safety. In recent years, due to the great success of Convolutional Neural Networks (CNNs) in image classification and object detection, many researchers have introduced CNNs into the crowd counting task to learn the mapping from input images to their corresponding density maps. CNNs are highly favored in the field of crowd counting due to their strong feature learning capabilities, leading to the emergence of numerous outstanding works. Although CNNs have significantly improved the performance of crowd counting methods, most efforts focus on learning feature representations from a single image. These image-based methods still face several challenges that need to be overcome. This is mainly because crowd gatherings can occur in any scenario, such as indoors, outdoors, or in the wild, and both individuals and crowds exhibit rich visual variations. These complex variation factors pose challenges to crowd counting methods, such as occlusion and scale variations, as illustrated in Figure 1.

Figure 1

Figure 1. Examples of existing challenges in crowd counting. (A) Occlusion. (B) Complex backround. (C) Scale change.

Existing research has shown that the spatio-temporal information in video sequences contains a wealth of valuable deep semantic information. Modeling the temporal sequence of videos can significantly enhance the feature learning capabilities and discrimination performance of deep networks. Motion information not only helps produce higher-quality density maps by combining feature representations of adjacent frames, but also improves pedestrian discrimination in occluded scenes. Even if pedestrians are occluded in specific frames, the missing information can still be captured from adjacent frames. Recently, some researchers have attempted to use variants of Long Short-Term Memory (LSTM) networks and 3D Convolutional Neural Networks (3DCNNs) to model the spatio-temporal dependencies in videos, implicitly combining spatial and temporal features [1–6]. Although these methods have achieved some promising results, they suffer from high computational complexity, difficulty in training the related parameters, and the inability to effectively extract long-range temporal context information. These problems lead to low training efficiency and excessive redundant parameters, which limit the model’s performance. The Temporal Convolutional Network (TCN) is a neural network model specifically designed for processing time series data. Compared to traditional recurrent neural networks (such as LSTM and GRU), TCN offers the advantages of parallel computation, efficient long-term dependency capture, stable gradients, and flexibility in handling time series of varying lengths. Additionally, the crowd density maps produced by existing methods only offer a rough estimate of crowd distribution and fail to accurately capture individual pedestrian positions or detailed crowd patterns. This limitation significantly hinders further crowd analysis and reduces their practical applicability.

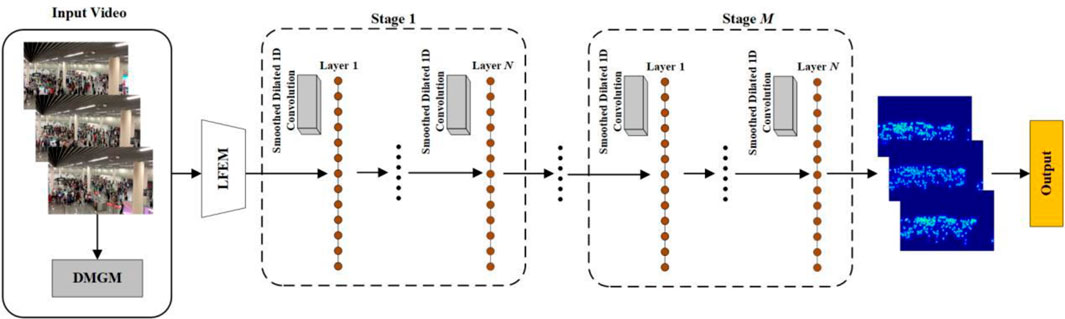
To address these problems, we propose a lightweight multi-stage temporal inference network (LMSTIN) for video crowd counting, which consists of three components: a density map generation module, a lightweight feature extraction module, and a refined temporal inference module. The input to LMSTIN is a sequence of consecutive video frames, and the output is the corresponding crowd density maps. The number of people in each frame is obtained by integrating the density map. Specifically, the density map generation module first uses a focal inverse distance transform to convert the input video frames into crowd density maps with accurate pedestrian positions, which are used as ground truth labels for network training. Then, a lightweight feature extraction module is designed to reduce computational cost while maintaining effective spatial feature extraction, thereby improving the overall efficiency of the network. Finally, a refined temporal inference module is constructed to focus on modeling the dependencies along the temporal dimension. It repeatedly refines the important temporal context information through multiple stages of refined temporal inference to learn better video-level semantic features, further improving crowd counting accuracy. Compared to existing video-based crowd counting methods, LMSTIN achieves promising results on three public video crowd counting datasets. Testing shows that our proposed method demonstrates outstanding performance, meeting the requirements of practical applications in terms of both speed and accuracy.

2 Related work

In recent years, with the rapid development of deep learning, there have been significant improvements in the performance of crowd counting methods. Both the accuracy and speed of counting in crowded scenes have notably increased. Fu et al. [7] proposed the first crowd counting model based on Convolutional Neural Networks (CNNs). This model removed some similar network connections in the feature maps and cascaded two CNN classifiers, effectively enhancing the speed and accuracy of crowd counting. Wang et al. [8] introduced a deep network based on the AlexNet structure [9] for extremely dense crowd counting. This network added extra negative samples during training, setting their true values to zero, to reduce the interference from complex backgrounds. Zhang et al. [10] proposed a cross-scene counting network called CrowdCNN based on the AlexNet structure. This network alternately trains on two related tasks (crowd density and crowd counting) to achieve locally optimal results and then fine-tunes the model using pre-training. The multi-column CNN network includes multiple columns of convolutions to extract multi-scale features, thus generating high-quality crowd density maps. Zhang et al. [11] were the first to use a multi-column structure for crowd counting, addressing the problem of scale variation in crowd counting. They proposed the Multi-Column Convolutional Neural Network (MCNN), which consists of different columns, each using filters with varying receptive fields to extract multi-scale features adapted to scene changes. Zhang et al. [12] utilized Local Self-attention (LSA) and Global Self-attention (GSA) to capture short-term and long-term dependencies between pixels and introduced a relation module to fuse LSA and GSA for richer feature representation. Compared to multi-column CNN methods, single-column CNN methods use a deeper single network structure for feature representation, resulting in a simpler network architecture and easier training convergence. Hu et al. [13] proposed a refinement distance compensation method based on a quantum scale perception learning framework to address crowd counting and localization tasks. This method uses a classic CNN architecture and calculates crowd features through qubit rotation and Pauli operators to generate the final density map. Liu et al. [14] proposed a deformable convolutional network with attention, ADCrowdNet, which consists of an Attention Map Generator (AMG) and a Density Map Estimator (DME). AMG estimates the crowd region and its density in the image, while DME uses multi-scale deformable convolutional layers to generate the crowd density map. Given the great success of Vision Transformers (ViT) in image processing, methods based on ViT have also begun to appear in the field of crowd counting. Liang et al. [15] proposed a crowd counting model called TransCrowd, which was the first to introduce ViT into the crowd counting task, redefining the weakly supervised crowd counting problem from the perspective of image patch sequences based on ViT. TransCrowd effectively utilizes ViT’s self-attention mechanism to extract semantic information about crowds, achieving significant crowd counting results. Li et al. [16] improved the ViT model by proposing a new network called CCTrans. This network first uses a pyramid vision transformer backbone to capture global crowd information, then merges low-level and high-level features through a pyramid feature aggregation module, and finally predicts the crowd density map with an efficient multi-scale dilated convolution. Bai et al. [17] proposed an end-to-end crowd counting method called CounTr, which consists of a ViT-based hierarchical encoder-decoder architecture. The encoder inputs image patch sequences to obtain multi-scale features, while the decoder merges features from different layers and aggregates both local and global contextual feature representations.

Deep learning-based crowd counting methods have demonstrated significant capabilities in feature learning for image-level tasks due to the powerful feature learning capabilities of deep neural networks. However, their performance still faces bottlenecks. Recently, many researchers have suggested that modeling the spatio-temporal information contained in video sequences could further overcome these performance limitations. However, research on this approach for crowd counting tasks remains relatively scarce.

3 Method

When addressing challenges such as significant scale variation and frequent occlusions in crowd counting, a key issue is how to extract contextual information across video frames and effectively model spatio-temporal dependencies, all while maintaining real-time algorithmic performance. To tackle this, we propose a novel framework, LMSTIN, which achieves fast and accurate video crowd counting by constructing finer-grained spatio-temporal dependencies. Figure 2 presents the overall structure of LMSTIN. LMSTIN consists of three components: a density map generation module, a lightweight feature extraction module, and a refined temporal inference module. Specifically, LMSTIN first employs a density map generation module (DMGM) to produce density maps with precise pedestrian locations, which serve as ground truth for network training. Following this, a lightweight feature extraction module (LFEM) is designed to reduce computational complexity and improve the network’s overall efficiency. Lastly, a refined temporal inference module (RTIM) is developed to capture video-level semantic features, ultimately delivering accurate crowd counting results.

Figure 2

Figure 2. Overall structure of LMSTIN.

3.1 Density map generation module

Suppose the position of a person’s head annotation is $x_i$, which can be represented by a shock pulse function $\delta \left(x-x_i\right)$. If there are $N$ head annotations in a crowd image, it can be represented by the following Formula 1:

$H\left(x\right)={\displaystyle \sum _{i=1}^N}\delta \left(x-x_i\right)(1)$

After annotating the crowd image, by performing convolution with a two-dimensional Gaussian kernel function $G_{\sigma }$, the corresponding crowd density map $F\left(x\right)$ of the image can be represented by the following Formula 2:

$F\left(x\right)={\displaystyle \sum _{i=1}^N}\delta \left(x-x_i\right)·G_{\sigma }\left(x\right)(2)$

Due to the “size varies with distance” problem of head scales in the image scene, which results in significant differences in head sizes at different positions, Zhang et al. [11] proposed using a geometric adaptive Gaussian kernel $G_{{\sigma }_i}$ instead of a fixed-size two-dimensional Gaussian kernel function $G_{\sigma }$ to generate the crowd density map. In crowded scenes, the size of a head is often related to the distance between it and the centers of adjacent heads. Therefore, in such scenes, the standard deviation ${\sigma }_i$ of the geometric adaptive Gaussian kernel can be determined by the average distance $\overline{d_i}$ between a given head position $x_i$ and its neighboring $k$ heads. The generated crowd density map $F\left(x\right)$ is defined as following Formula 3:

$F\left(x\right)={\displaystyle \sum _{i=1}^N}\delta \left(x-x_i\right)·G_{{\sigma }_i}\left(x\right)(3)$

Here, ${\sigma }_i=\beta \bullet \overline{d_i}$ and $\beta$ represent weight coefficients. Zhang et al. [11] demonstrated through extensive experiments that the results are optimal when $\beta =0.3$ is used.

In the crowd density maps using the two types of Gaussian kernel functions described above, the spatial distribution information is represented by a series of blurred Gaussian spots, which cannot provide the precise locations of each person. This limits subsequent crowd analysis and practical applications. Therefore, we introduce the focal inverse distance transform (FIDT) to generate crowd density maps with accurate pedestrian locations [18]. Next, we first introduce the Euclidean Distance Transform mapping, which generates density map annotations by calculating the Euclidean distance between each pixel and its nearest annotation point. The Formula 4 is defined as follows:

$D\left(x,y\right)=\begin{array}{l}\min \\ \left(x^{\prime },y^{\prime }\right)\in S\end{array}\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2}(4)$

Here, $S$ represents the set of all head annotations, and $D\left(x,y\right)$ denotes the Euclidean distance between the head annotation position $\left(x,y\right)$ and the nearest head annotation position $\left(x^{\prime },y^{\prime }\right)$. Due to the significant variation in distances between different heads, directly regressing the crowd density map can result in it approaching zero overall. To address this issue, the Inverse Distance Transform (IDT) can be applied to smooth out the distance variation. The Formula 5 is defined as follows:

$I^{\prime }\left(x,y\right)=\frac{1}{D\left(x,y\right)+C}(5)$

Here, $I^{\prime }\left(x,y\right)$ represents the density map generated using IDT, and $C$ is a constant. To prevent the denominator from being zero, $C=1$ is usually set. However, while the pixel values generated by IDT decay rapidly at locations far from the head annotation centers, the decay in the background is not sufficiently pronounced. Building upon this, FIDT is further proposed to make the decay near the heads slower while accelerating the decay to zero at farther locations. The Formula 6 is defined as follows:

$I\left(x,y\right)=\frac{1}{{D\left(x,y\right)}^{\left(\alpha ·D\left(x,y\right)+\beta \right)}+C}(6)$

Here, $I\left(x,y\right)$ represents the density map generated using FIDT, and $\alpha$ and $\beta$ are set to 0.02 and 0.75, respectively.

3.2 Lightweight feature extraction module

The VGG-16 network, due to its excellent performance in image feature extraction, has been favored by many researchers in the field of crowd counting [19, 20]. This network consists of 13 convolutional layers with 3 × 3 kernels, 5 pooling layers with 2 × 2 kernels, and 3 fully connected layers. When applied to different tasks, the fully connected layers are usually removed, retaining only the convolutional and pooling layers to extract features from crowd images. Unlike ResNet, VGG-16 has a relatively moderate number of network layers and consumes fewer computational resources, which allows it to improve convergence speed while ensuring effective feature extraction. Nevertheless, VGG-16 still does not meet the high real-time requirements of video crowd counting tasks effectively.

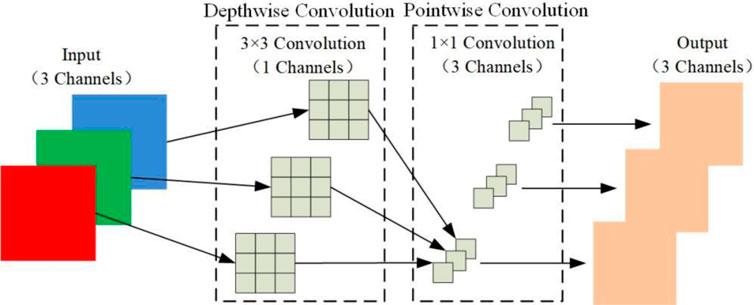
Therefore, this section designs a Lightweight Feature Extraction Module (LFEM) that replaces traditional convolutions with depthwise separable convolutions to reduce network parameters, thus improving operational efficiency while achieving feature extraction results comparable to VGG-16. Depthwise separable convolution, proposed by Chollet et al. [21], is an efficient convolution operation that consists of two main steps: Depthwise Convolution and Pointwise Convolution, as shown in Figure 3. Specifically, Depthwise Convolution performs convolution operations across channels, where each channel has its own kernel, and the kernel size is the same as the traditional convolution kernel being replaced. Thus, the number of input and output channels remains consistent throughout the process. Pointwise Convolution, composed of 1 × 1 kernels, is used to weight the output features from the previous step and adjust the number of output feature channels. The number of kernels depends on the required number of output feature channels, so this process does not change the feature map size. Figure 3 illustrates the specific operation process of depthwise separable convolution. Finally, an additional fully connected layer is added to LFEM to generate a feature vector that meets the input dimensions of the next module. Experimental results indicate that, despite having significantly fewer parameters than VGG-16, LFEM can still achieve results comparable to VGG-16. This provides a solid foundation for achieving real-time performance with our method.

Figure 3

Figure 3. The operation process of depthwise separable convolution.

3.3 Refined temporal inference module

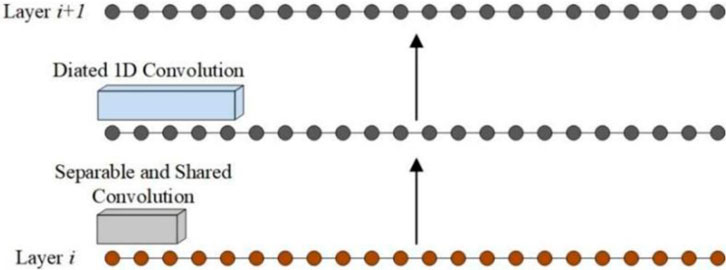
Modeling spatio-temporal information in video sequences has shown good performance in addressing problems such as person occlusion, background interference, and scale variation in crowd counting problems. To address these problems, we construct a refined temporal inference module (RTIM), which includes multiple stages of temporal inference modules. The output of the previous stage module serves as the input for the next stage module. Each stage’s temporal inference module is composed of multiple smooth dilated 1D convolutions stacked together, with a loss layer at the end of each stage to adjust the output features. The final stage outputs the counting results. Since smooth dilated 1D convolution can learn temporal information with a larger receptive field using fewer parameters [22], RTIM can maintain a low computational complexity while focusing on useful temporal information to achieve efficient and reliable temporal video modeling. The following will provide a detailed description of smooth dilated 1D convolution and the loss function.

3.3.1 Smooth dilated 1D convolution

Dilated convolution can effectively expand the receptive field of the filter without increasing the number of parameters and computational load, allowing it to process information over a larger area. In recent years, dilated convolution has gained widespread attention in the field of deep learning. However, it also has some drawbacks, such as the loss of local spatial information, as noted by Chen et al. [22]. Additionally, there is no dependency between input units or output units in dilated convolution, leading to ineffective acquisition of contextual information during network training [23]. For fine recognition tasks such as image segmentation and crowd counting, dilated convolution can result in the loss of local spatial information and lack of contextual information during training, severely impacting the final recognition results.Since RTIM mainly consists of a set of dilated 1D convolution layers, it also suffers from problems of local temporal information loss and lack of relevance in long-range temporal information. To address this, we introduce smooth dilated 1D convolution. Next, we will briefly introduce dilated 1D convolution and then provide a detailed description of smooth dilated 1D convolution.

For a dilated 1D convolution with a filter of size $k$ and dilation rate $w$, the output $Z$ at position $i$ is defined as following Formula 7:

$Z\left[i\right]={\displaystyle \sum _{s=1}^k}f\left[i+r\times s\right]w\left[i\right](7)$

Here, $f$ represents the one-dimensional input, and $r$ represents the dilation rate. When $r=1$, the dilated 1D convolution reduces to a standard 1D convolution. To intuitively understand dilated 1D convolution, it can be viewed as inserting $r-1$ zeros between two adjacent weights of $w$. Therefore, its receptive field becomes $r\times \left(k-1\right)+1$.

To address the issues related to dilated convolutions, we propose a smooth dilated 1D convolution method. This approach uses “separable” and “shared” operations to smooth the dilated 1D convolution before applying the dilated 1D convolution operation. This enables the network to enhance the dependencies between local temporal features in advance, allowing it to capture a broader range of temporal context without increasing computational complexity, effectively reducing the loss of local temporal information. “Separable” refers to the separable convolution mentioned in existing literature [21], while “shared” means that the convolution weights are shared across all channels [23]. Specifically, a separable and shared convolution with a kernel size of $\left(2r-1\right)$ is inserted before the dilated 1D convolution to capture the temporal dependencies between feature maps generated by periodic subsampling. During the smoothing operation (including “separable” and “shared”), there is only one constant parameter that is independent of the number of channels, with a size of $\left(2r-1\right)$. Therefore, the additional computational cost is negligible. Figure 4 shows a schematic of a smooth dilated 1D convolution. As illustrated in the figure, it depicts a smooth dilated 1D convolution with a kernel size of 3 and a dilation rate of 2. The gray circles represent the feature maps after the smoothing operation, while the brown circles represent the original feature maps. Smooth dilated 1D convolution increases the dependencies between input units by adding separable and shared convolutions before the dilated 1D convolution. In short, when using smooth dilated 1D convolution, the features at non-zero positions can incorporate local temporal information from their adjacent zero-value positions. This effectively mitigates the loss of local temporal information and enhances long-range temporal dependencies.

Figure 4

Figure 4. Schematic of smooth dilated 1D convolution.

3.3.2 Loss function

In crowd counting algorithms based on density maps, the Euclidean distance (denoted as $L_E$) is primarily used to measure the error between the actual and predicted crowd counts. The Formula 8 is defined as follows:

$L_E=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(C_i^p-C_i^{gt}\right)}^2(8)$

Here, $N$ represents the number of frames in the video, $C_i^p$ denotes the estimated count for the image in frame $i$, and $C_i^{gt}$ denotes the actual count for the image in frame $i$. Although $L_E$ loss has performed well in image crowd counting tasks, it does not account for spatio-temporal consistency in video sequences. To further improve the accuracy of video crowd counting, this section introduces a smoothing loss (denoted as $L_S$) by incorporating the similarity between video frames to reduce prediction errors between consecutive video frames. The Formulas 9–11 is defined as follows:

$L_S=\frac{1}{N}{\displaystyle \sum _i}{\stackrel{\sim }{\Delta }}_i^2(9)$

${\stackrel{\sim }{\Delta }}_i=\left\{\begin{array}{l}{\Delta }_i:{\Delta }_i\le \tau \\ \tau :\text{otherwise}\end{array}\right.(10)$

${\Delta }_i=\left|\mathit{log}{C}_i^p-\mathit{log}{C}_{i-1}^p\right|(11)$

Here, $\tau$ represents the hyperparameter $L_S$. Combining the above loss functions, the final form of the loss function is as following Formula 12:

$L=L_E+\lambda L_S(12)$

Here, $\lambda$ represents the hyperparameter that adjusts the weight of $L_S$. The values of all hyperparameters will be provided in the subsequent experimental section.

4 Experimental setup

4.1 Implementation details

The experiments are implemented using PyTorch for LMSTIN. The RTIM consists of four stages, each with 10 smooth dilated 1D convolutional layers, where the dilation rate of each layer is twice that of the previous layer. After each convolutional layer, a dropout with a rate of 0.5 is applied, with a kernel size of 3 and 64 convolutional filters. Additionally, the loss function of LMSTIN is a combination of Euclidean distance loss and smoothing loss, with the parameters set to $\tau =10$ and $\lambda =0.15$. In all experiments, Adam is used to optimize the network parameters, with a learning rate of 0.0005 and no weight decay.

4.2 Datasets

In this paper, we evaluate the performance of the proposed LMSTIN on three public video crowd counting datasets: Mall [24], UCSD [25], and WorldExpo’10 [10]. The Mall dataset was collected using surveillance cameras installed in a shopping mall. It consists of 2000 frames of video with a resolution of 320 × 240 pixels per frame, and a total of 62,325 pedestrians are labeled. The number of people per frame ranges from a minimum of 11 to a maximum of 53, with an average of approximately 31 people per frame. The Mall dataset features high crowd density and diverse scenes, and it is divided into a training set and a test set, with the first 800 frames used for training and the remaining 1200 frames used for testing.The UCSD dataset was collected using cameras installed in a pedestrian-only corridor at the University of California, San Diego. The original videos were collected at a resolution of 740 × 480 and a frame rate of 30 FPS, then downsampled to 238 × 158 and 10 FPS. The UCSD dataset contains 2000 frames with a total of 49,885 labeled pedestrians. To exclude unnecessary objects (such as trees and cars), an interest region is defined within which annotations are made manually every 5 frames, with linear interpolation used for the remaining frames. The UCSD dataset is collected from a fixed position, so the scene perspective remains unchanged throughout the video.The WorldExpo’10 dataset is a large-scale cross-scene crowd counting dataset. It was collected from the 2010 Shanghai Expo, including 1132 video sequences with manual annotations captured by 108 surveillance cameras. The dataset consists of 3920 frames with a resolution of 576 × 720 pixels, and a total of 199,923 people are labeled, with an average of 50 people per frame.

4.3 Evaluation metrics

The experiments use two evaluation metrics, namely, Mean Absolute Error (MAE) and Mean Squared Error (MSE), to assess the accuracy and robustness of the method. The specific formulas are as following Formulas 13, 14:

$MAE=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\left|C_i^p-C_i^{gt}\right|(13)$

$MSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(C_i^p-C_i^{gt}\right)}^2}(14)$

Here, $N$ represents the number of frames in the video, and $C_i^p$ and $C_i^{gt}$ denote the estimated count and the actual count for the image in frame $i$, respectively. MAE measures the accuracy of the counting method, while MSE evaluates the robustness of the counting method. The smaller the values of MAE and MSE, the better the accuracy and robustness of the method, and thus, the better its performance.

5 Experimental results and analysis

5.1 Quantitative and qualitative analysis

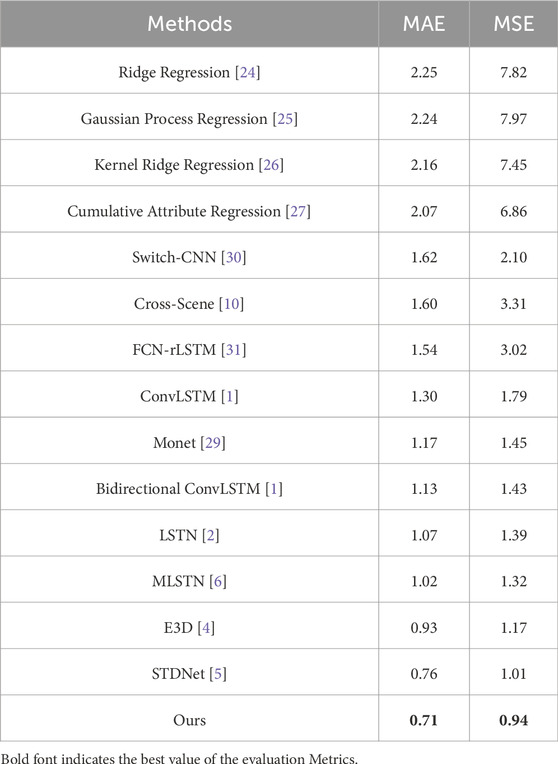
We compared the crowd counting results of our proposed method with several state-of-the-art video crowd counting methods on the Mall, UCSD, and WorldExpo’10 datasets. The comparison results are shown in Tables 1–3.

Table 1

Table 1. Comparison of our method with existing methods on the mall dataset.

Table 2

Table 2. Comparison of our method with existing methods on the UCSD dataset.

Table 3

Table 3. Comparison of our method with existing methods on the WorldExpo’10 dataset.

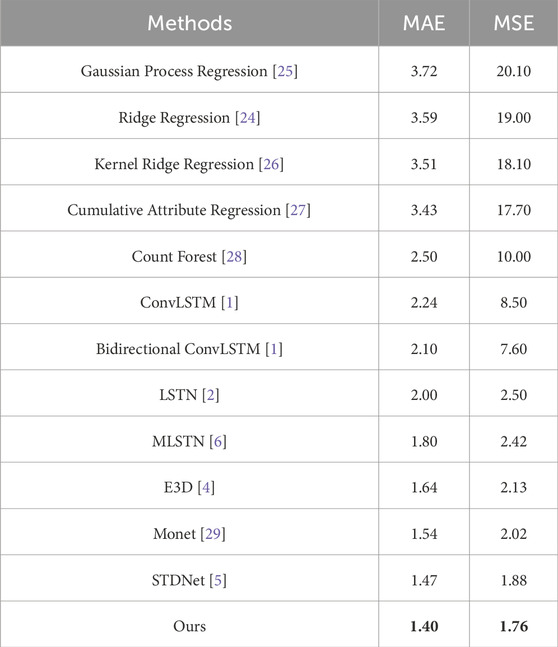
Comparing with 12 advanced video crowd counting methods, our proposed LMSTIN achieved the best results across all metrics, as detailed in Table 1. From Table 1, it can be observed that LMSTIN shows a further improvement over the current state-of-the-art method (STDNet), reducing the MAE by 0.07 and the MSE by 0.12. Additionally, the Mall dataset presents more complex scenarios compared to the UCSD dataset, such as higher levels of perspective distortion and occlusion, which can lead to inaccuracies or imprecisions in annotations. In this context, LMSTIN addresses this problem by modeling spatio-temporal consistency between video frames. Experimental results demonstrate that LMSTIN effectively models temporal dependencies between video frames, thereby extracting more robust spatio-temporal features to enhance the network’s capability for crowd counting tasks.

Table 2 presents a comparison of LMSTIN with 14 state-of-the-art video crowd counting methods. The experimental results show that LMSTIN outperforms all previous methods in both MAE and MSE metrics, achieving reductions of 0.05 in MAE and 0.07 in MSE compared to STDNet.Notably, the improvements on the UCSD dataset have two important implications. First, with a frame rate of 10 FPS, the UCSD dataset allows the network to learn multi-scale temporal features due to the high correlation between consecutive frames. For instance, in a video segment with 20 frames, if a person appears continuously from frame 1 to frame 20, LMSTIN can extract both short-term information (e.g., from frame 1 to frame 2) and long-term information (e.g., from frame 1 to frame 20) from the video frames. Second, since individuals typically move at varying speeds, multi-scale temporal information helps account for people moving at different velocities, which is beneficial for density map estimation in crowded scenes. The experimental results indicate that effectively modeling both short-term and long-term temporal information provides robust performance against crowd occlusion and scale variations in complex environments, leading to improved crowd counting results.

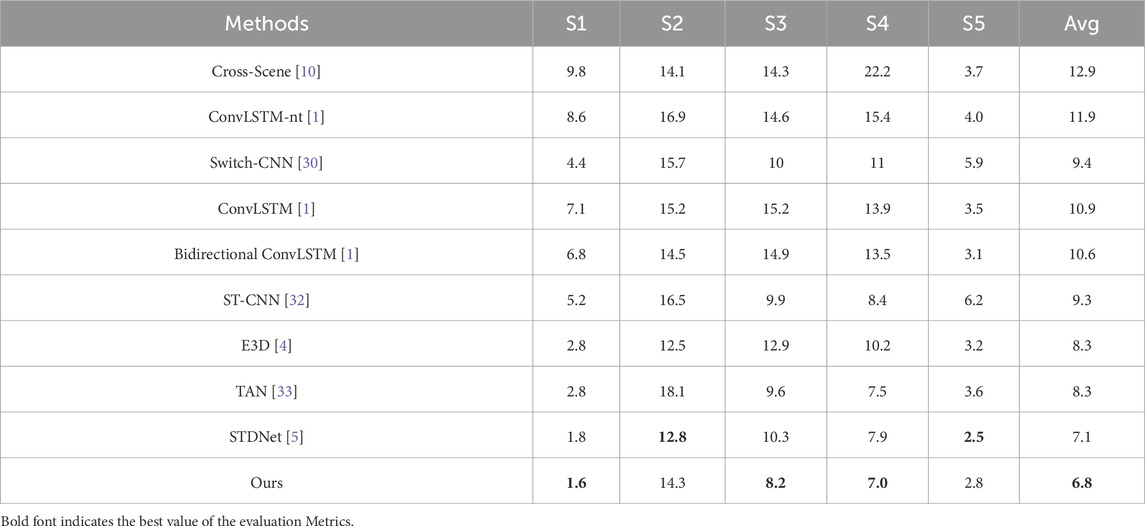
Table 3 summarizes the experimental results of LMSTIN compared with 9 state-of-the-art video crowd counting methods. In this experiment, 16 consecutive frames were used as input, and MAE and average MAE (Avg) across 5 scenes (S1, S2, S3, S4, S5) were used as evaluation metrics. The results show that, compared to the current best method STDNet, LMSTIN has achieved an overall improvement in accuracy, reducing the average MAE by 0.3. However, its performance varies across different scenes: it decreased by 0.2, 2.1, and 0.9 in scenes S1, S3, and S4, respectively, but increased by 1.5 and 0.3 in scenes S2 and S5. This discrepancy is because the temporal correlation between consecutive frames in scenes S2 and S5 is not strong, and these scenes are relatively sparse, which conflicts with our design objectives. Nevertheless, LMSTIN still achieved the best accuracy in 3 out of 5 scenes and provided the lowest average MAE (Avg). This indicates that LMSTIN not only effectively models both short-term and long-term video temporal information but also demonstrates good robustness across datasets with varying scales and scene differences.

In order to facilitate observation and comparative analysis, the final crowd density maps generated by LMSTIN and STDNet are visualized respectively, because this method is one of the most advanced methods in the field of video crowd counting. The visualization results are shown in Figure 5. In Figure 5, the first row is the visualization result of the Mall dataset, the second row is the visualization result of the UCSD dataset, and the third row is the visualization result of the WorldExpo’10 dataset. The first column is the input original image, the second column is the FIDT real density map, and the third and fourth columns represent the corresponding output density maps of STDNet and the method in this chapter, respectively. The numbers in the figure represent the real annotation (GT) and the predicted number of people (Pred). As can be seen from Figure 5, the density map generated by the method in this chapter is closer to the real density map than the density map generated by STDNet, so the counting results and pedestrian locations are also more accurate. The visualization results intuitively demonstrate the effectiveness and robustness of the method in this chapter on the video crowd counting task, and the output crowd density map can provide accurate pedestrian location information, which provides the necessary prerequisite for subsequent crowd analysis tasks.

Figure 5

Figure 5. Qualitative results.

5.2 Structural analysis and efficiency comparison

To validate the effectiveness of each module in LMSTIN, we first analyze the impact of different structures on video crowd counting results by examining LFEM and RTIM. Then, we compare LMSTIN with current state-of-the-art video crowd counting methods from multiple aspects to demonstrate LMSTIN’s real-time performance and effectiveness.

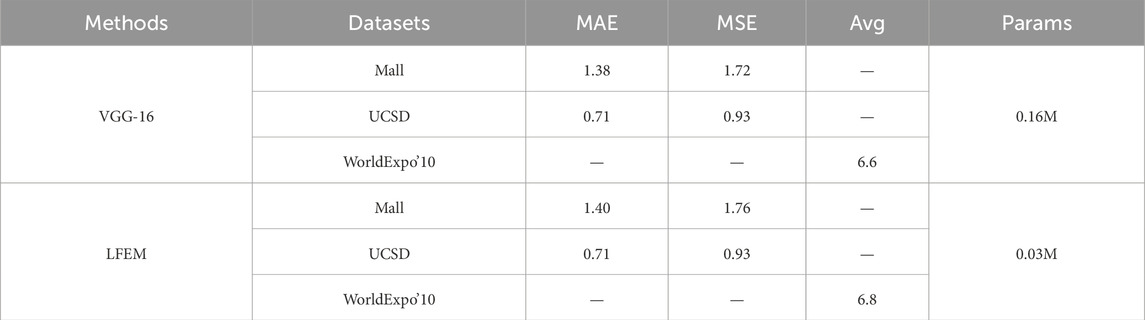
First, we evaluate the performance of LFEM. The VGG-16 network, known for its excellent feature extraction capabilities, has become a mainstream feature extraction method in the field of crowd counting. Specifically, the VGG-16 network consists of 16 layers, including 13 convolutional layers with 3 × 3 kernels, 5 pooling layers with 2 × 2 kernels, and 3 fully connected layers. In crowd counting tasks, the fully connected layers of VGG-16 are typically discarded, retaining only the convolutional and pooling layers to extract features from crowd images. Our proposed LFEM is an improvement based on the VGG-16 network, aiming to reduce the computational load of the network while maintaining its feature extraction capabilities, thus enhancing the overall operational efficiency of the network. Therefore, in the ablation experiments evaluating LFEM’s performance, in addition to using MAE, MSE, and Avg as evaluation metrics, we also introduce the number of module parameters (Params) as an important indicator of computational complexity. Table 4 presents the experimental results of LFEM and VGG-16 on the three datasets.

Table 4

Table 4. Comparison of Experimental Results between LFEM and VGG-16 on three Datasets.

To visually compare the performance differences between LFEM and VGG-16, the experiment involved replacing only the feature extraction module in the entire method while keeping the other modules unchanged. From Table 4, it is evident that LFEM performs similarly to VGG-16 across all datasets, achieving the same accuracy on the UCSD dataset. However, LFEM’s parameter count is only about one-fifth of that of VGG-16. The experimental results demonstrate that LFEM is an effective feature extraction module for video crowd counting tasks, significantly reducing the network’s computational complexity and thereby enhancing the overall efficiency of the method.

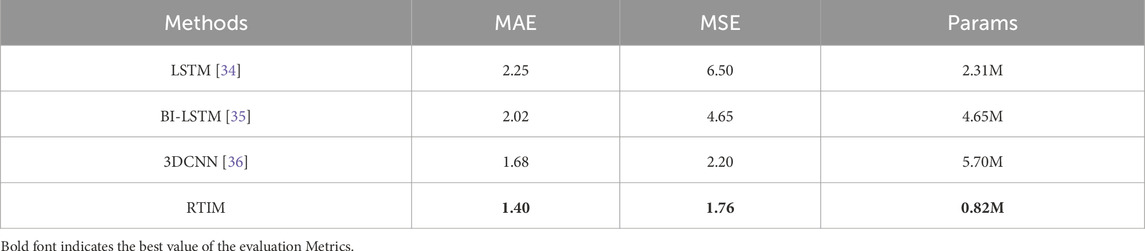
Next, we evaluate the performance of RTIM. In crowd counting tasks, the current methods for modeling spatio-temporal relationships between video frames mainly use LSTM, Bi-directional LSTM (BI-LSTM), and 3DCNN as the foundational frameworks. To intuitively compare the performance differences between RTIM and other temporal modeling networks, we replace only the temporal inference part in the entire method, keeping the other modules unchanged. Since the ablation experiments yield consistent conclusions across the three datasets, we present the results using the Mall dataset as an example. The results are shown in Table 5.

Table 5

Table 5. Comparison of RTIM with other temporal modeling networks on the Mall Dataset.

Table 5 lists the MAE, MSE, and Params for different temporal modeling networks tested on the Mall dataset. From Table 5, it is evident that RTIM significantly improves accuracy compared to LSTM, BI-LSTM, and 3DCNN, while also substantially reducing the network parameter count. RTIM achieves the best results in both MAE and MSE and has less than one-seventh of the network parameters compared to 3DCNN. The experimental results demonstrate that RTIM can effectively model the temporal relationships between video frames with minimal parameters, thus further enhancing the overall efficiency of the method. This is critically important for the practical application of video crowd counting methods.

Finally, the overall operating efficiency of LMSTIN is evaluated. Taking the Mall dataset as an example, the differences in operating efficiency of the method in this chapter are illustrated by comparing it with four state-of-the-art video crowd counting methods, STDNet, Monet, E3D, and MLSTN. Table 6 lists the parameter amount (Params), computation amount (FLOPs), and training time (Training Time) of different networks. As can be seen from Table 6, LMSTIN is significantly more efficient than networks such as STDNet, Monet, E3D, and MLSTN. For example, in terms of computation amount, the value of STDNet is about 2.5 times that of the method in this chapter, the value of E3D is about 11 times that of E3D, the value of Monet is about 20 times that of E3D, and the value of MLSTN is about 23 times that of E3D. In terms of parameter amount, the value of STDNet is about 3 times that of the method in this chapter, the value of E3D is about 8 times that of E3D, the value of Monet is about 13 times that of E3D, and the value of MLSTN is about 14 times that of E3D. The training time in Table 3.6 is the running time for training the Mall dataset for 50 cycles (Epoch) on a single GTX TitanXp GPU. It can be seen that the training time of this chapter’s method is shorter than that of all other networks. The experimental results show that this chapter’s method is significantly better than the existing methods in terms of network parameters, computational complexity and running time, and the overall network operation efficiency has been significantly improved compared with other methods. It is worth noting that for videos with a resolution of 320 × 240 pixels, this chapter’s method only occupies less than 500 MB of GPU memory on the Nvidia TitanXp GPU to achieve a detection speed of 120FPS, and also achieves a real-time crowd counting speed of 25FPS on the daily home Intel Core i5-8400 CPU.

Table 6

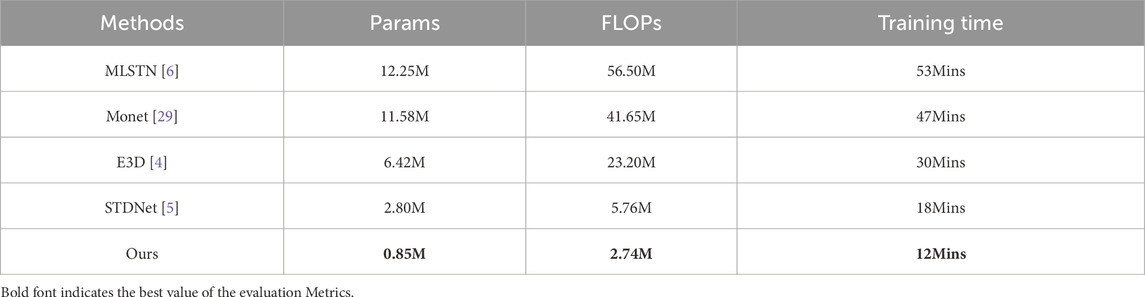
Table 6. Comparison of parameters, computation and training time of different methods on the Mall dataset.

Overall, extensive experiments demonstrate that each module within LMSTIN, performs exceptionally well, significantly surpassing existing advanced methods in both speed and accuracy. This advancement has substantial implications for the practical application of crowd counting methods in real-world monitoring scenarios.

6 Conclusion

We propose a lightweight multi-stage temporal inference network for video crowd counting, named LMSTIN. Specifically, LMSTIN first utilizes the focal inverse distance transformation to convert input video frames into crowd density maps with accurate pedestrian locations, which serve as the ground truth labels for network training. Secondly, we design a lightweight feature extraction module to reduce the computational load of the model, enhancing overall efficiency while maintaining effective spatial feature extraction. Finally, we build a multi-stage temporal inference module with minimal parameters that performs well, focusing on modeling temporal relationships to efficiently extract spatio-temporal information from video frames. Experimental results demonstrate that our method achieves excellent performance across various datasets and is capable of real-time crowd counting at 25 frames per second on an Intel Core i5-8400 CPU. LMSTIN have great potential for future development, especially in handling more complex video scenes, different crowd movement patterns, and integrating other functionalities. By combining with features like behavior recognition, they can achieve comprehensive monitoring and analysis of crowd behavior, providing stronger technical support for public safety, traffic management, and business decision-making.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WG: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Writing–original draft, Writing–review and editing. RF: Data curation, Formal Analysis, Investigation, Methodology, Supervision, Writing–review and editing. XS: Investigation, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is funded by National Social Science Foundation Project (Project Title: Research on the Generation Mechanism and Public Governance of Online Disputes in Public Events, Grant No. 20BXW109) and the 2020 general project of philosophy and social sciences research in colleges and universities of Jiangsu Province (Project Title: Research and Evaluation of Learning Performance based on MOOC platform, Grant No. 2020SJA1173).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Xiong F, Shi X, Yeung DY. Spatiotemporal modeling for crowd counting in videos. Proc IEEE Int Conf Computer Vis (2017) 5151–9. doi:10.1109/ICCV.2017.551

CrossRef Full Text | Google Scholar

2. Fang Y, Zhan B, Cai W, et al. Locality-constrained spatial transformer network for video crowd counting. In: 2019 IEEE international conference on multimedia and Expo (ICME). IEEE (2019) p. 814–9.

CrossRef Full Text | Google Scholar

3. Wu X, Xu B, Zheng Y, et al. Video crowd counting via dynamic temporal modeling (2019) p. 19. arXiv:1907.02198.

Google Scholar

4. Zou Z, Shao H, Qu X, et al. Enhanced 3D convolutional networks for crowd counting. arXiv:1908.04121 (2019). doi:10.48550/arXiv.1908.04121

CrossRef Full Text | Google Scholar

5. Ma YJ, Shuai HH, Cheng WH. Spatiotemporal dilated convolution with uncertain matching for video-based crowd estimation. IEEE Trans Multimedia (2021) 24:261–73. doi:10.1109/tmm.2021.3050059

CrossRef Full Text | Google Scholar

6. Fang Y, Gao S, Li J, Luo W, He L, Hu B. Multi-level feature fusion based locality-constrained spatial transformer network for video crowd counting. Neurocomputing (2020) 392:98–107. doi:10.1016/j.neucom.2020.01.087

CrossRef Full Text | Google Scholar

7. Fu M, Xu P, Li X, Liu Q, Ye M, Zhu C. Fast crowd density estimation with convolutional neural networks. Eng Appl Artif Intelligence (2015) 43:81–8. doi:10.1016/j.engappai.2015.04.006

CrossRef Full Text | Google Scholar

8. Wang C, Zhang H, Yang L, et al. Deep people counting in extremely dense crowds Proceedings of the 23rd ACM International Conference on Multimedia (2015) p. 1299–1302.

Google Scholar

9. Krizhevsky A, Sutskever I, Hinton GE. Imagine classification with deep convolutional neural networks. Adv Neural Inf Process Syst (2012) 25. doi:10.1145/3065386

CrossRef Full Text | Google Scholar

10. Zhang C, Li H, Wang X, et al. Cross-scene crowd counting via deep convolutional neural networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2015) p. 833–41. doi:10.1109/CVPR.2015.7298684

CrossRef Full Text | Google Scholar

11. Zhang Y, Zhou D, Chen S, et al. Single-image crowd counting via multi-column convolutional neural network. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2016) p. 589–97.

CrossRef Full Text | Google Scholar

12. Zhang A, Shen J, Xiao Z, et al. Relational attention network for crowd counting. Proc IEEE/CVF Int Conf Computer Vis (2019) 6788–97. doi:10.1109/ICCV.2019.00689

CrossRef Full Text | Google Scholar

13. Hu R, Tang ZR, Wu EQ, Mo Q, Yang R, Li J. RDC-SAL: refine distance compensating with quantum scale-aware learning for crowd counting and localization. Appl Intelligence (2022) 52(12):14336–48. doi:10.1007/s10489-022-03238-4

CrossRef Full Text | Google Scholar

14. Liu N, Long Y, Zou C, et al. Adcrowdnet: an attention-injective deformable convolutional network for crowd understanding. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (2019) p. 3225–34.

CrossRef Full Text | Google Scholar

15. Liang D, Chen X, Xu W, Zhou Y, Bai X. TransCrowd: weakly-supervised crowd counting with transformers. Sci China Inf Sci (2022) 65(6):160104–14. doi:10.1007/s11432-021-3445-y

CrossRef Full Text | Google Scholar

16. Li B, Zhang Y, Xu H, Yin B. CCST: crowd counting with swin transformer. Vis Computer (2022) 39:2671–82. doi:10.1007/s00371-022-02485-3

CrossRef Full Text | Google Scholar

17. Bai H, He H, Peng Z, et al. CounTr: an end-to-end transformer approach for crowd counting and density estimation European conference on computer vision. Cham: Springer (2023) p. 207–222.

CrossRef Full Text | Google Scholar

18. Liang D, Xu W, Zhu Y, et al. Focal inverse distance transform maps for crowd localization and counting in dense crowd. arXiv preprint arXiv:2102.07925 (2021). doi:10.1109/CVPR.2016.70

CrossRef Full Text | Google Scholar

19. Cao X, Wang Z, Zhao Y, et al. Scale aggregation network for accurate and efficient crowd counting. In: Proceedings of the European conference on computer vision. ECCV (2018) p. 734–50.

CrossRef Full Text | Google Scholar

20. Hossain MA, Cannons K, Jang D, et al. Video-based crowd counting using a multi-scale optical flow pyramid network. In: Proceedings of the asian conference on computer vision (2020).

Google Scholar

21. Chollet F. Xception: deep learning with depthwise separable convolutions. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2017) p. 1251–8.

CrossRef Full Text | Google Scholar

22. Chen W, Chai Y, Qi M, Sun H, Pu Q, Kong J, et al. Bottom-up improved multistage temporal convolutional network for action segmentation. Appl Intelligence (2022) 52(12):14053–69. doi:10.1007/s10489-022-03382-x

CrossRef Full Text | Google Scholar

23. Wang Z, Ji S. Smoothed dilated convolutions for improved dense prediction. Data Mining Knowledge Discov (2021) 35(4):1470–96. doi:10.1007/s10618-021-00765-5

CrossRef Full Text | Google Scholar

24. Chen K, Loy CC, Gong S, et al. Feature mining for localised crowd counting. Bmvc (2012) 1(2):3.

CrossRef Full Text | Google Scholar

25. Chan AB, Liang ZSJ, Vasconcelos N. Privacy preserving crowd monitoring: counting people without people models or tracking. In: 2008 IEEE conference on computer vision and pattern recognition. IEEE (2008) p. 1–7. doi:10.1109/CVPR.2008.4587569

CrossRef Full Text | Google Scholar

26. An S, Liu W, Venkatesh S. Face recognition using kernel ridge regression. In: 2007 IEEE conference on computer vision and pattern recognition. IEEE (2007) p. 1–7. doi:10.1109/CVPR.2007.383105

CrossRef Full Text | Google Scholar

27. Chen K, Gong S, Xiang T, et al. Cumulative attribute space for age and crowd density estimation. Proc IEEE Conf Computer Vis Pattern Recognition (2013) 2467–74.

CrossRef Full Text | Google Scholar

28. Pham VQ, Kozakaya T, Yamaguchi O, et al. Count forest: Co-voting uncertain number of targets using random forest for crowd density estimation. Proc IEEE Int Conf Computer Vis (2015) 3253–61. doi:10.1109/ICCV.2015.372

CrossRef Full Text | Google Scholar

29. Bai H, Chan SHG. Motion-guided non-local spatial-temporal network for video crowd counting. arXiv preprint arXiv:2104.13946 (2021).

Google Scholar

30. Babu Sam D, Surya S, Venkatesh Babu R. Switching convolutional neural network for crowd counting. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2017) p. 5744–52.

CrossRef Full Text | Google Scholar

31. Zhang S, Wu G, Costeira JP, et al. Fcn-rlstm: deep spatio-temporal neural networks for vehicle counting in city cameras. Proc IEEE Int Conf Computer Vis (2017) 3667–76.

CrossRef Full Text | Google Scholar

32. Miao Y, Han J, Gao Y, Zhang B. ST-CNN: spatial-temporal convolutional neural network for crowd counting in videos. Pattern Recognition Lett (2019) 125:113–8. doi:10.1016/j.patrec.2019.04.012

CrossRef Full Text | Google Scholar

33. Wu X, Xu B, Zheng Y, Ye H, Yang J, He L. Fast video crowd counting with a temporal aware network. Neurocomputing (2020) 403:13–20. doi:10.1016/j.neucom.2020.04.071

CrossRef Full Text | Google Scholar

34. Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput (1997) 9(8):1735–80. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Graves A, Schmidhuber J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Networks (2005) 18(5-6):602–10. doi:10.1016/j.neunet.2005.06.042

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Ji S, Xu W, Yang M, Yu K. 3D convolutional neural networks for human action recognition. IEEE Trans Pattern Anal Machine Intelligence (2012) 35(1):221–31. doi:10.1109/tpami.2012.59

CrossRef Full Text | Google Scholar