Mixing of isoscalar and isovector characteristics in the low-energy dipole mode

We investigated isospin splitting in low-energy dipole (LED) states of spherical nuclei such as ⁴⁰Ca, ⁹⁰Zr, ¹³²Sn, ²⁰⁸Pb, and several $N=50$ isotones using self-consistent Hartree–Fock plus random phase approximation calculations. Our analysis of isovector dipole (IVD) and isoscalar dipole (ISD) strengths, along with transition densities, reveals a clear energy-dependent relationship between IS and IV modes in ⁴⁰Ca and ⁹⁰Zr. For ²⁰⁸Pb and ¹³²Sn, LED states show mixed IS + IV characteristics due to different neutron and proton shell structures. In $N=50$ isotones, $E1$ modes exhibit varying IS and IV properties with smooth transitions as neutron excess increases. Our results suggest that compressional ISD strengths could provide valuable insights into the slope parameter of the nuclear equation of state. The observed dependence on nuclear shell structures and neutron–proton correlations highlights the need for precise measurements and further research in nuclear physics.

1 Introduction

Low-energy dipole (LED) excitation is one of the key ingredients to investigate nuclear properties. The LED states appear in low excitation energy compared with the excitation energy of giant dipole resonance (GDR), having sizable strengths up to several percentage of the Thomas–Reiche–Kuhn sum rule. They have been observed in wide nuclear mass regions, e.g., ⁴⁸Ca [1], ⁶⁸Ni [2], ⁹⁰Zr [3, 4], ¹³²Sn [5], and ²⁰⁸Pb [6]. The systematic calculations for the dipole mode $(E1)$ [7–9] show that the LED state appears in many isotopes. The LED state on a neutron-rich nucleus has been called the pygmy dipole resonance, which is often interpreted as a collective oscillation of the neutron skin and the remnant core [10, 11] (skin-core oscillation). There have been many studies for the LED to probe the properties of neutron matter, nuclear symmetry energy, and the slope parameter in the equation of state of neutron matter. However, its nature is still under debate.

It is found from recent experiments [12–19] that the LED state has two components in its lower- and higher-energy regions. The lower LED has an isoscalar (IS) + isovector (IV) characteristic, whereas the higher LED has IV dominant characteristic. These characteristics are indicated by comparing the $E1$ strengths induced by $(\alpha ,{\alpha }^{\prime })$ scattering for the IS characteristic and $(\gamma ,{\gamma }^{\prime })$ scattering for the IV characteristic. This phenomenon is called LED isospin splitting. Several theoretical calculations [20–31] using the (quasi-particle) random-phase approximation (RPA) show that the calculated LED state in magic nuclei has both IS and IV characteristics in its strengths and transition densities. However, the underlying structure of LED isospin splitting is not well-understood yet.

To investigate LED isospin splitting, we systematically study the LED states of several spherical nuclei and $N=50$ isotones, using the RPA calculation, which describes the IV dipole (IVD) and the compressional IS dipole (ISD) modes. We obtain the pure IS characteristic (and pure IV character) in the $E1$ modes of ⁴⁰Ca and ⁹⁰Zr, while the isospin-mixed LED strengths appear in $N\gg Z$ nuclei. Isospin-mixing is induced by proton and neutron shell structures near the Fermi levels. Our calculation for $N=50$ isotone shows that the $E1$ mode with the pure IS characteristic varies smoothly to the lower component in LED isospin splitting. The LED is expected to be a substitute for observing the slope parameter $L$ of the nuclear equation of state (EOS). There have been many studies to investigate which observable LED has the strongest correlation with $L$, but we have not yet pinned down the value of $L$. We show that low-energy compressional ISD strengths might be a suitable probe of $L$.

The manuscript is organized as follows: Section 2 reviews briefly the Hartree–Fock (HF) and the RPA calculation. In Section 3, we calculate the LED states in ⁴⁰Ca, ⁹⁰Zr, ²⁰⁸Pb, and ¹³²Sn and analyze the properties of LED isospin splitting. Changes in the LED properties in $N=50$ isotones are shown. We mention the relation between the ISD strength and $L$. Conclusions are given in Section 4.

2 Methods

We employ the HF + RPA approach to describe LED states. The numerical code used in the present calculation is a revised version of the code developed in [32].

We use the Skyrme effective interaction and the minimal nuclear energy density functional (EDF) [33]. The Skyrme interaction is an EDF often used in mean-field model calculations and is characterized by being expanded in terms of delta functions in space. The parameter set is determined according to each protocol. The adopted Skyrme interactions are ${\text{SkM}}^{*}$ [34], SLy4 [35], UNEDF1 [36], SkI2, and SkI3 [37] parameter sets. The minimal EDF has been recently presented as an EDF with the smallest number of possible phenomenological parameters. The SeaLL1 parameter set is used in this work. The pairing correlation is ignored in this paper because its contribution to LEDs is small, as shown in [9]. We only restrict our consideration to spherical nuclei to avoid complicating the discussion with nuclear deformation and pairing effects. Therefore, the HF + RPA approach is a sufficient model for our purpose, when we discuss the LED in closed-shell and spherical nuclei.

Here, two operators for IVD and compressional ISD are introduced to investigate isovector and isoscalar characteristics in LED. The IVD operator $\widehat{D}$ is expressed as

$\widehat{D}=\frac{N}{A}{\displaystyle \sum _{i\in p}}{r}_i{Y}^{\left(1\right)}\left({\mathrm{\Omega }}_i\right)-\frac{Z}{A}{\displaystyle \sum _{i\in n}}{r}_i{Y}^{\left(1\right)}\left({\mathrm{\Omega }}_i\right),$

where $Y^{(1)}$ denotes the spherical harmonics for the dipole mode $\ell =1$. The index $i\in p$ $(i\in n)$ indicates that the sum runs over protons (neutrons). For the compressional ISD mode, the operator,

${\widehat{D}}_{\text{IS}}={\displaystyle \sum _{i\in n,p}}\left(r_i^2-\frac{5}{3}⟨r^2⟩\right)r_i{Y}^{\left(1\right)}\left({\mathrm{\Omega }}_i\right),$

is adopted where $5⟨r^2⟩/3$ is introduced to eliminate the center-of-mass contribution.

The $E1$ transition strength from the ground state $|0\rangle$ to the excited state $|\alpha \rangle$ by $\widehat{D}$ or ${\widehat{D}}_{\text{IS}}$ in an even-even nucleus is $B(E1;\alpha )={\left|\langle \alpha |\widehat{D}|0\rangle \right|}^2$ or $B(\text{IS}E1;\alpha )={\left|\langle \alpha |{\widehat{D}}_{\text{IS}}|0\rangle \right|}^2$. The transition amplitude $\langle \alpha |\widehat{D}|0\rangle$ can be calculated within HF + RPA for the one-particle-one-hole excitations. Using them, the strength function is given by smearing out with the Lorentzian and is written by

$S\left(E1,E\right)=\frac{\gamma }{\pi }{\displaystyle \sum _{\alpha }}\left[\frac{1}{{\left(E-E_{\alpha }\right)}^2+{\gamma }^2}-\frac{1}{{\left(E+E_{\alpha }\right)}^2+{\gamma }^2}\right]{\left|⟨\alpha |\widehat{D}|0⟩\right|}^2,$

where $E_{\alpha }$ is the energy of the excited state $|\alpha \rangle$ and the strength function is denoted as $S(\mathrm{I}\mathrm{S}E1;\alpha )$ for ${\widehat{D}}_{\text{IS}}$. We adopt $2\gamma =1$ MeV throughout this paper.

The excited states are analyzed by using particle–hole (ph) contribution $C_{ph}$ and transition density $\delta \rho$, which are obtained in the HF + RPA calculations. The ph contribution of an excitation from the $i$ orbit to the $m$ orbit is evaluated, with the forward and backward amplitudes $X_i(\text{r})$ and $Y_i(\text{r})$, as

$C_{mi}={\left|X_{im}\right|}^2-{\left|Y_{im}\right|}^2,$

in which $X_{im}$ is extracted from $X_i(\text{r})$ as

$X_{im}=\int d\text{r}{\varphi }_m^{*}\left(\text{r}\right)X_i\left(\text{r}\right)$

and similar for $Y_{im}$. Here, ${\varphi }_m$ is the $m$th wave function and the spin index is omitted for simplicity. The transition density $\delta \rho$ is expressed as

$\delta \rho \left(\text{r}\right)={\displaystyle \sum _{i\in n,p}}\left\{{\varphi }_i^{*}\left(\text{r}\right)X_i\left(\text{r}\right)+Y_i^{*}\left(\text{r}\right){\varphi }_i\left(\text{r}\right)\right\}.$

The radial dipole transition density $\delta {\rho }_{L=1}(r)$ is calculated from $\delta \rho$ as

$\delta {\rho }_{L=1}\left(r\right)=\int d\mathrm{\Omega }r{Y}^{\left(1\right)}\left(\mathrm{\Omega }\right)\delta \rho \left(\text{r}\right).$

The size of the RPA matrix is reduced by assuming the reflection symmetry of the ground state with respect to $x=0$, $y=0$, and $z=0$ planes. We adopt the three-dimensional coordinate (3D) representation within a sphere of radius $R_{\text{box}}=25$ fm with a uniform mesh spacing of 0.6 fm.

Furthermore, we introduce an index for the isospin structure $(I_{\text{iss}})$ of the excited state to quantify the isospin characteristic of the dipole mode. $I_{\text{iss}}$ is obtained from the transition densities of the neutron and proton at the state with an excitation energy $E$ as

$I_{\text{iss}}\left(E\right)=\frac{\int d\text{r}\left|Z\delta {\rho }^{\nu }\left(\text{r};E\right)-N\delta {\rho }^{\pi }\left(\text{r};E\right)\right|}{\int d\text{r}\left|Z\delta {\rho }^{\nu }\left(\text{r};E\right)\right|+\left|N\delta {\rho }^{\pi }\left(\text{r};E\right)\right|},$

where $\delta {\rho }^{\pi (\nu )}$ denotes the transition density on protons (neutrons). If $I_{\text{iss}}(E)\simeq 0$, it means that the transition density has almost the same distributions in both the proton and neutron, and the state with energy $E$ has a pure IS characteristic. On the contrary, if $I_{\text{iss}}(E)\simeq 1$, the transition densities are out of phase over the space $\text{r}$, and the state has a pure IV characteristic. Then, $I_{\text{iss}}(E)$ with less than or over 0.5 means the state has an IS or IV dominant characteristic, and the $I_{\text{iss}}(E)\sim 0.5$ state has an IS + IV mixed characteristic.

3 Results and discussion

We calculate the E1 strengths and transition densities of the IVD and ISD modes, focusing mainly on their LED states. First, we show the LED modes in ⁴⁰Ca and ⁹⁰Zr, which hold isospin symmetry in their excited states. Next, we investigate the LED states in both stable (²⁰⁸Pb) and unstable (¹³²Sn) nuclei, where $N\gg Z$, demonstrating the emergence of isospin mixing in the excited states. We also investigate the interaction dependence of the LED properties for ⁹⁰Zr and ¹³²Sn. Then, we show how the LED properties change in $N=50$ isotones: ¹⁰⁰Sn, ⁹⁰Zr, ⁸²Ge, ⁷⁸Ni, and ⁷⁰Ca. Finally, we evaluate the relations between the slope parameter $L$ and some quantities of dipole strengths. We can guess that the strength of compressional ISD modes is a more suitable value to probe the slope parameter than the IVD strength, dipole polarization, and partial cross sections of the LED.

3.1 ⁴⁰Ca and ⁹⁰Zr

For the $N=Z$ nucleus, ⁴⁰Ca, Figures 1A, B show the IVD and ISD transition strengths, $B(E1;E)$ and $B(\text{IS}E1;E)$, and the strength functions $S(E1;E)$ and $S(\text{IS}E1;E)$. They are calculated with the ${\text{SkM}}^{*}$ interaction. The $E1$ mode with a large ISD strength appears at the excitation energy 7.2 MeV, which is the lowest in the LED states, while it has a negligibly small IVD strength. The radial transition densities $r^2\delta {\rho }_{L=1}$ of the lowest state are plotted in Figure 1C. Proton $(\pi )$ and neutron $(\nu )$ transition densities, $\delta {\rho }_{L=1}^{\pi }$ and $\delta {\rho }_{L=1}^{\nu }$, are in phase and almost the same, indicating pure IS characteristic. Its index for isospin structure $I_{\text{iss}}=0.044$ also signifies the pure IS characteristic. A coherent superposition of proton and neutron excitations $\pi ,\nu$:$1d_{3/2}\to 2p_{3/2}$ and $1d_{5/2}\to 1f_{7/2}$ generates the state at 7.2 MeV. This isospin-symmetric mechanism is a characteristic transition on the $E1$ excitation in $N=Z$ nuclei, due to the similar shell structures near the Fermi levels in both the proton and neutron. It should be noted that the low-energy ISD mode is also obtained in another isospin-symmetric $N=Z$ stable nucleus, ¹⁶O [21, 31].

Figure 1

Figure 1. IVD and ISD strength and strength functions of ⁴⁰Ca are shown in (A, B), respectively. The arrow indicates the neutron threshold energy. (C) Neutron (solid) and proton (dashed) transition densities $r^2\delta {\rho }_{L=1}$ of the $E1$ mode at 7.2 MeV.

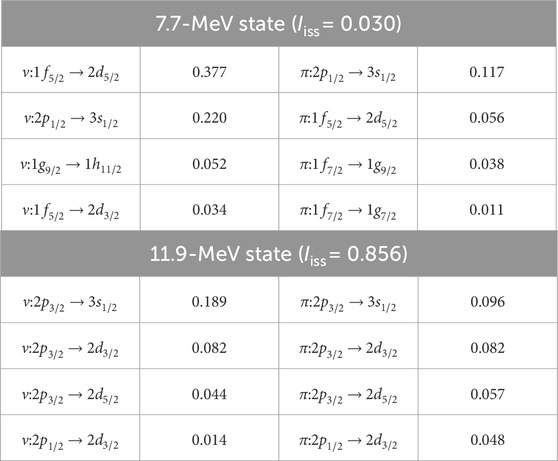
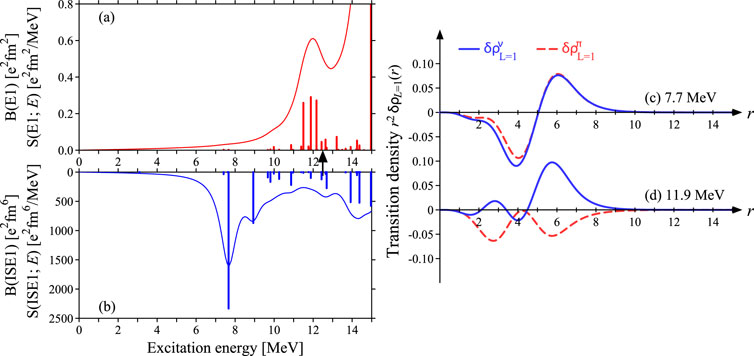
Figures 2A, B show $E1$ strengths for ⁹⁰Zr, same as Figure 1. Similar to ⁴⁰Ca, the $E1$ state at 7.7 MeV has a large ISD strength and a negligibly small IVD strength. Its transition density is displayed in Figure 2C, which seems to have a pure IS characteristic and indicates $I_{\text{iss}}=0.030$. The state is generated by coherent superposition of proton and neutron excitations, $\pi ,\nu$: $1f_{5/2}\to 2d_{5/2}$ and $2p_{1/2}\to 3s_{1/2}$, as listed in Table 1 where we list large contributions $C_{\text{ph}}$ of the decomposed ph excitations. The highest occupied neutron orbit is $1g_{9/2}$, which only contributes to the LED state at 7.7 MeV. The $E1$ transition between $1g_{9/2}$ and $1h_{11/2}$ is the one major shell excitation and a node-less excitation, which needs nodes to be orthogonal to the center-of-mass mode. Then, its contribution $C_{\text{ph}}$ gets small, $C_{\text{ph}}=0.052$ (Table 1). Therefore, although ⁹⁰Zr has 10 more neutrons than protons, its LED properties are almost the same as those of the $N=Z$ nuclide (⁴⁰Ca), which has a large ISD strength.

Figure 2

Figure 2. Same as Figure 1 but for ⁹⁰Zr. (A) IVD strength, (B) ISD strength, (C, D) transition densities of the 7.7, and 11.9-MeV states, respectively.

Table 1

Table 1. Calculated ph contributions $C_{\text{ph}}$ of LED states in ⁹⁰Zr.

The LED states with large IVD and small ISD strengths appear at approximately 12 MeV. Three peaks appear in the IVD strengths, but their transition densities and $C_{\text{ph}}$s are similar to each other. The transition densities of the $E1$ mode at 11.9 MeV are shown in Figure 2D. The aspect of the out-of-phase $\delta {\rho }^{\nu }$ and $\delta {\rho }^{\pi }$ indicates a result of the fragmentation of the GDR due to their two bumps. The $E1$ mode has the transition densities of a typical pure IV characteristic, also shown in its $I_{\text{iss}}=0.856$.

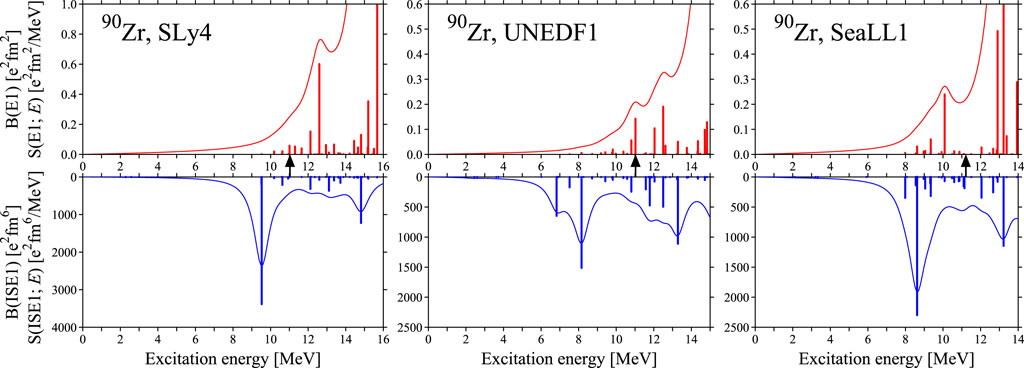
The $E1$ modes with pure IV and IS characteristics with energetic differences appear in the LED strengths of ⁹⁰Zr. The LED modes with large ISD and small IVD strengths appear in lower energy (at 7.2 MeV), and the LED modes with the opposite $E1$ strength distribution in higher energy (at approximately 12 MeV). This property of strength is consistent with that of LED isospin splitting. Furthermore, similar results can be obtained in other interactions shown in Figure 3. For SLy4, UNEDF1, and SeaLL1 interactions, the lower-LED modes with large ISD and negligibly small IVD strengths appear at $\approx$ 8 $-$ 10 MeV, and the higher-LED modes with large IVD and small ISD strengths appear around the neutron threshold energy.

Figure 3

Figure 3. IVD and ISD strengths in ⁹⁰Zr are displayed in upper and lower panels, respectively. The results were obtained using SLy4, UNEDF1, and SeaLL1 parameter sets.

The mechanism to induce LED is the same for all interactions in this work. The interaction dependence appears in the strengths and energy position of the LED, which is a result of the chemical potential and nuclear shell structure.

3.2 ²⁰⁸Pb and ¹³²Sn

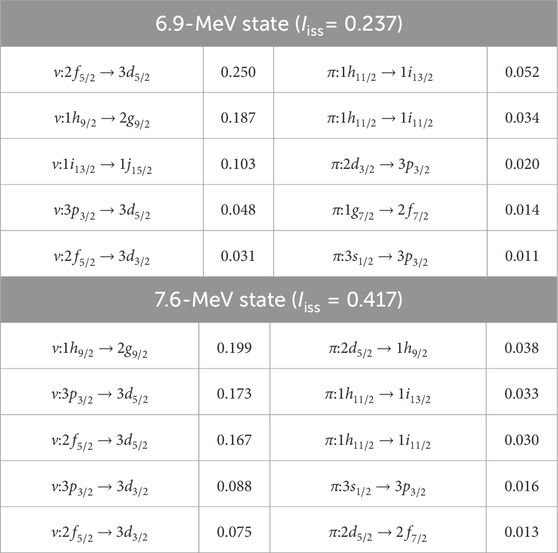
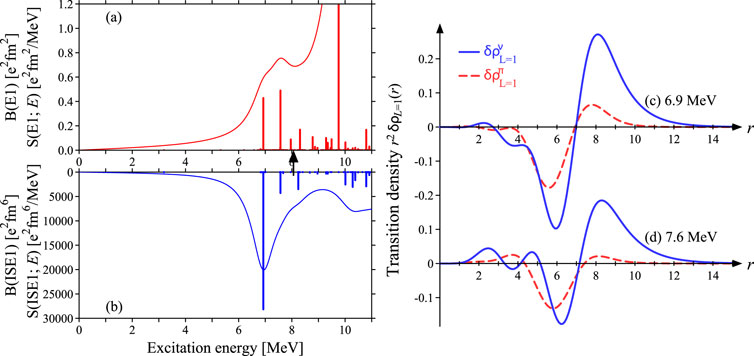
Here, we show $E1$ strengths and transition densities of LED states in $N\gg Z$ nuclei: ²⁰⁸Pb and ¹³²Sn. Figure 4 shows the $E1$ strengths and transition densities in ²⁰⁸Pb, similar to Figure 1, calculated with the ${\text{SkM}}^{*}$ interaction. The lowest $E1$ mode at 6.9 MeV has both large ISD and IVD strengths, which is clearly different from ⁴⁰Ca and ⁹⁰Zr. The second-lowest $E1$ mode appears at 7.6 MeV, with a large IVD strength and small but non-negligible ISD strength. Their transition densities of 6.9 MeV and 7.6 MeV states, displayed in Figures 4C, D, can be interpreted as the skin-core oscillation. This $E1$ mode of ²⁰⁸Pb differs from that of $N=Z$ nuclei, in which protons and neutrons act coherently. The differences come from the nuclear structures near the Fermi levels of nucleons. The $E1$ excitation mode in ²⁰⁸Pb is described by the superposition of neutron (proton) single ph excitations over the $N=126$ $(Z=82)$ gap. This mechanism makes it difficult to induce purely the in-phase transition densities of neutrons and protons, unlike ⁴⁰Ca and ⁹⁰Zr, and causes mixing of the ISD and IVD modes, namely, the IS + IV characteristic in the LED states. The ph contributions of the 6.9 and the 7.6 MeV states, listed in Table 2, are not much different. In both states, significant contributions from four neutron ph excitations, namely, $2f_{5/2}\to 3d_{5/2}$, $1h_{9/2}\to 2g_{9/2}$, $3p_{3/2}\to 3d_{5/2}$, and $2f_{5/2}\to 3d_{3/2}$, exhaust 50% of the total. $I_{\text{iss}}$s of the 6.9 MeV and 7.6 MeV states are 0.237 and 0.417, respectively. Both modes should be interpreted as IS + IV characteristic modes, although the transition densities of the 7.6 MeV state seem to have a dominant IV characteristic trend.

Figure 4

Figure 4. Same as Figure 1 but for ²⁰⁸Pb. (A) IVD strength, (B) ISD strength, (C) transition density of the 6.9-MeV state, and (D) transition density of the 7.6-MeV state.

Table 2

Table 2. Calculated ph contribution $C_{\text{ph}}$ of LED states in ²⁰⁸Pb.

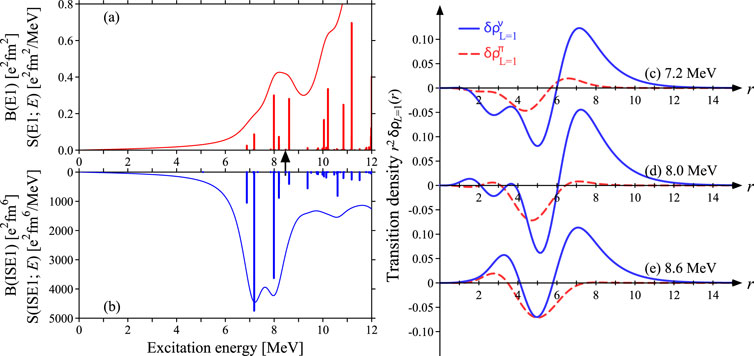
Figure 5 shows the LED states of a neutron-rich unstable nucleus ¹³²Sn which are calculated with the ${\text{SkM}}^{*}$ interaction. Similar to ²⁰⁸Pb, some $E1$ modes appear around the neutron threshold energy with large IVD and ISD strengths. We pick up three $E1$ states with large strengths at 7.2 MeV, 8.0 MeV, and 8.6 MeV. The 7.2-MeV state has the largest ISD strength lower than 10 MeV, and its $I_{\text{iss}}$ is 0.237. The 8.0-MeV state has large ISD and IVD strengths and $I_{\text{iss}}=0.448$, indicating the IS + IV characteristic. The 8.6-MeV state has large IVD and small ISD strengths with $I_{\text{iss}}=0.388$, which also indicates the IS + IV characteristic. At a glance, three states have the characteristics of IS, IS + IV, and IV dominances in their $E1$ strengths, respectively, but their $I_{\text{iss}}$ signify IS + IV characteristics of three modes. To investigate the isospin characteristic of the $E1$ state, not only the strength but also the transition density are necessary. It is not easy to separate pure IS and IV characteristics of the LED modes in $N\gg Z$ nuclei because different proton and neutron shell structures near the Fermi levels hardly induce in-phase transition densities of protons and neutrons, irrespective of the interactions used.

Figure 5

Figure 5. Same as Figure 1 but for ¹³²Sn. (A) IVD strength, (B) ISD strength, (C–E) transition densities of the 7.2, 8.0, and 8.6-MeV states, respectively.

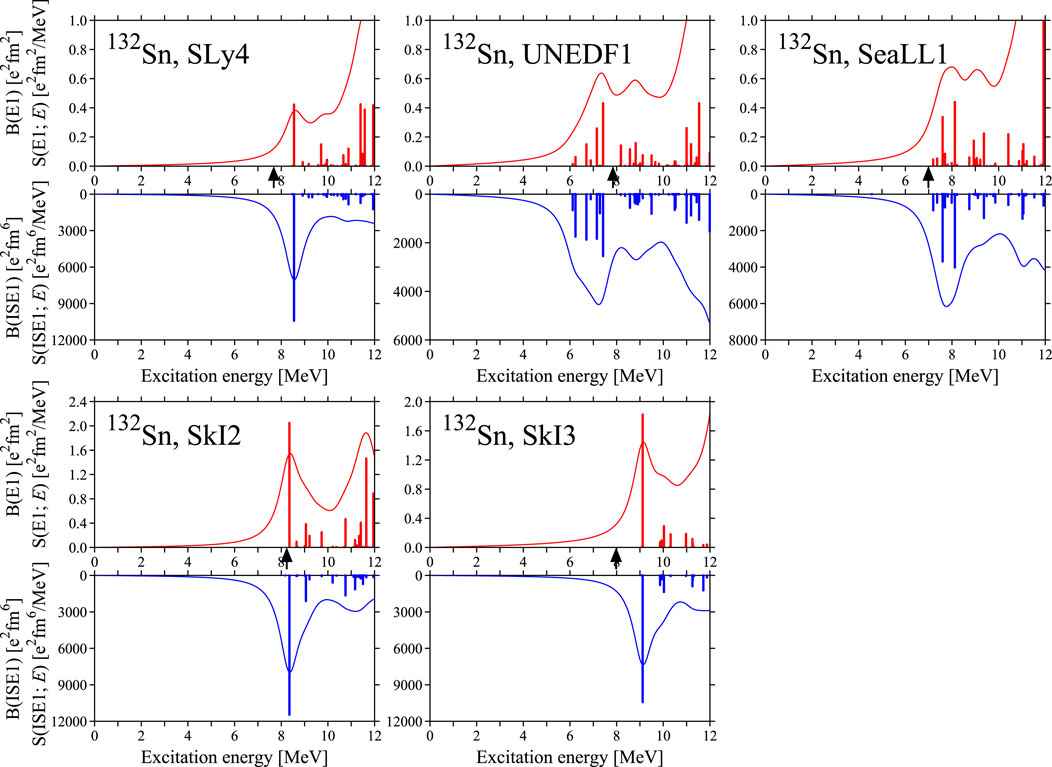
Figure 6 shows the LED strengths calculated with other interactions to compare with them. The LED modes in ¹³²Sn occupy $\sim 2\%$ of the ISD energy-weighted sum rule value, regardless of which interaction is used. We can see similar LED strengths of the ${\text{SkM}}^{*}$ in other interactions, although some detail differences exist, similar to the case of ⁹⁰Zr. From the $E1$ strength distribution viewpoint, LED isospin splitting is less clear than SkM* in the results using SLy4, UNEDF1, SkI2, SkI3, and SeaLL1 due to large ISD and IVD strengths in the states. These interaction differences in LED isospin splitting are attributed to different structures of single-particle states near the Fermi levels and to the correlation between protons and neutrons, which induces the IS + IV characteristic of the LED modes.

Figure 6

Figure 6. Same as Figure 3 but for ¹³²Sn. The results were obtained using SLy4, UNEDF1, SeaLL1, SkI2, and SkI3 parameter sets.

3.3 Transition of LED isospin splitting in $N=50$ isotones

The LED strengths and its transition densities for ⁴⁰Ca, ⁹⁰Zr, and $N\gg Z$ nuclei are investigated in the above sections. For the LED states of ⁹⁰Zr, we obtained LED isospin splitting, where the lower LED mode exhibits large ISD and small IVD strengths, while the higher LED mode shows the opposite. Furthermore, the transition densities of the lower and higher LED modes can take pure IS and pure IV characteristics due to the similar proton and neutron shell structures. On the other hand, in the $N\gg Z$ nuclei, the isospin characteristics of the LED modes mix due to the difference between proton and neutron shell structures near the Fermi levels. This is a general property, irrespective of the used interactions.

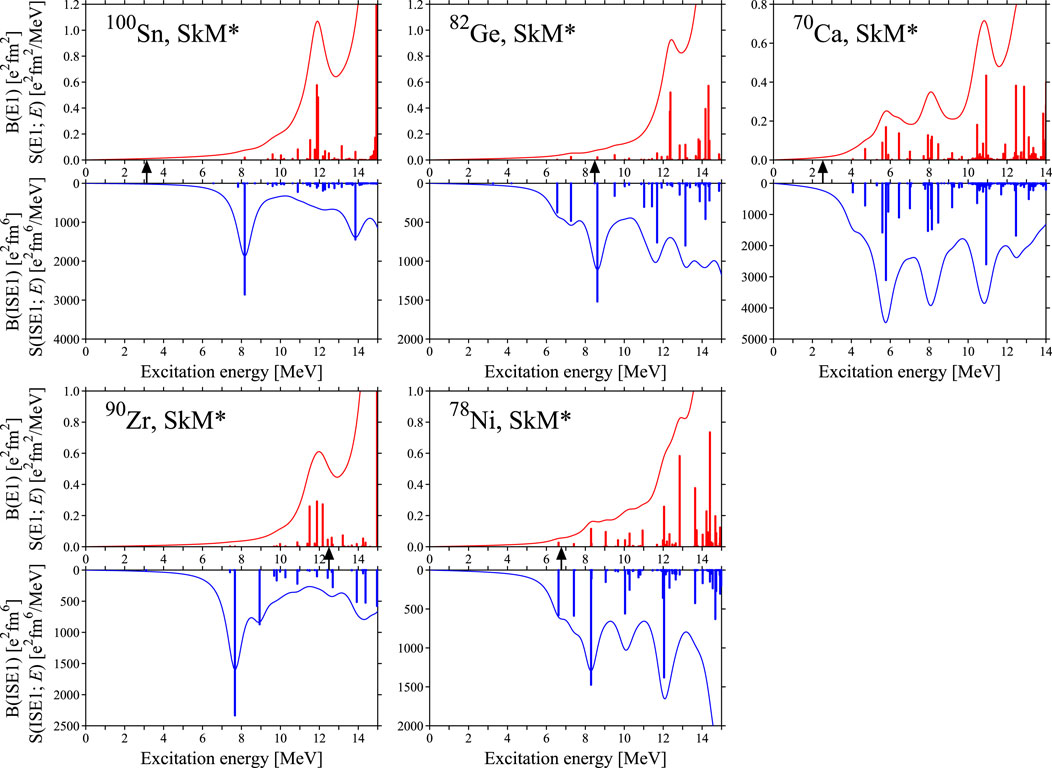
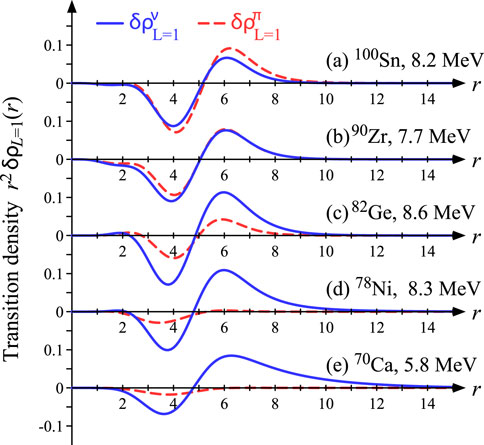
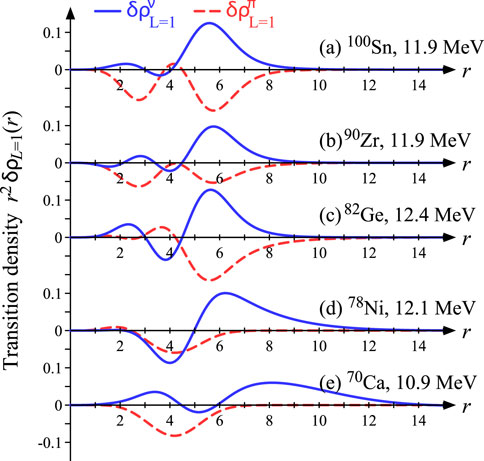
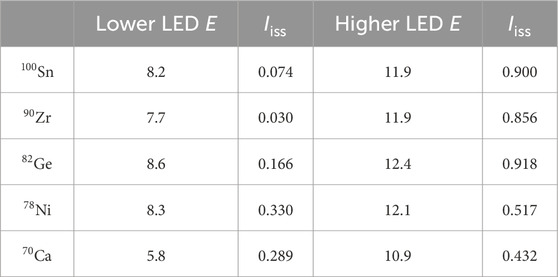
Here, we show the transition of LED isospin splitting in $N=50$ isotones from $N=Z$ to $N\gg Z$. Figure 7 shows the $E1$ strengths calculated with the ${\text{SkM}}^{*}$ interaction in $N=50$ isotones, ¹⁰⁰Sn, ⁹⁰Zr, ⁸²Ge, ⁷⁸Ni, and ⁷⁰Ca. Interestingly, the lowest ISD mode on the proton-drip-line nucleus ¹⁰⁰Sn is essentially the same as that of the stable nucleus ⁹⁰Zr, as well as with its higher LED mode at 12 MeV. The transition densities of the lower LED modes for $N=50$ isotones are shown in Figure 8, and the higher LED modes, in Figure 9. Table 3 shows the excitation energies of lower and higher LED modes and $I_{\text{iss}}$s. From the viewpoints of the strengths and $I_{\text{iss}}$s, the $E1$ states of ¹⁰⁰Sn, ⁹⁰Zr, and ⁸²Ge have the characteristic of LED isospin splitting, which is also shown in their transition densities from Figures 8, 9. The higher LED has out-of-phase two-bump transition densities regarding the fragmentation of the GDR for ¹⁰⁰Sn, ⁹⁰Zr, and ⁸²Ge in Figure 9. However, a small mixing of IS and IV characteristics is seen in the transition densities of the LED states in ⁸²Ge [Figures 8C, 9C]. $\delta {\rho }^{\pi }$ and $\delta {\rho }^{\nu }$ have different behaviors inside the nucleus ($r\lesssim 5$ fm). Considering ⁷⁸Ni, the $E1$ transition strengths at 8.3 MeV seem to have the IS dominant characteristic and its transition density and $I_{\text{iss}}$ indicate the IS + IV characteristic, like the case of ¹³²Sn. The higher LED mode at 12.4 MeV has both large ISD and IVD strengths, but this is the neutron emission mode from the $g_{9/2}$ orbit to the continuum, which has a long tail of neutron transition density. For the LED modes of ⁷⁰Ca, the ISD and IVD strength distributions are similar. The lower LED at 5.8 MeV, which is composed mainly of the neutron excitation from $1f_{5/2}$ to the resonant $2d_{3/2}$ orbit, has $I_{\text{iss}}\sim 0.5$, indicating the IS + IV characteristic, while the higher LED at 10.9 MeV keeps the IV characteristic $(I_{\text{iss}}=0.86)$.

Figure 7

Figure 7. $E1$ strengths in $N=50$ isotones, ¹⁰⁰Sn, ⁹⁰Zr, ⁸²Ge, ⁷⁸Ni, and ⁷⁰Ca, with the SkM^* interaction. For ⁹⁰Zr, the figure shows the same results in Figures 2A, B.

Figure 8

Figure 8. Transition densities of lower LED modes, (A) at 8.2 MeV in ¹⁰⁰Sn, (B) 7.7 MeV in ⁹⁰Zr, (C) 8.6 MeV in ⁸²Ge, (D) 8.3 MeV in ⁷⁸Ni, and (E) 5.8 MeV in ⁷⁰Ca.

Figure 9

Figure 9. Transition densities of higher LED modes, (A) at 11.9 MeV in ¹⁰⁰Sn, (B) 11.9 MeV in ⁹⁰Zr, (C) 12.4 MeV in ⁸²Ge, (D) 12.1 MeV in ⁷⁸Ni, and (E) 10.9 MeV in ⁷⁰Ca.

Table 3

Table 3. $I_{\text{iss}}$ of lower and higher LED modes for $N=50$ isotones: Excitation energy (MeV) and $I_{\text{iss}}$ of the lower LED mode and of the higher LED mode, for each isotone.

As one approaches from $N=Z$ nuclei to $N\gg Z$ nuclei, the characteristic of the LED modes changes from the pure IS or pure IV characteristic to the IS + IV characteristic, although many of the higher LED modes in $N\gg Z$ drip-line nuclei are neutron emission modes.

3.4 ISD strength and the slope parameter L

We investigate the relation between the low-energy $E1$ strengths in ¹³²Sn and the slope parameter $L$ of EOS. The LED has attracted much attention because the LED observables strongly correlate with $L$ [38, 39, 40]. However, the value of $L$ has not yet been completely determined. The candidates observable have been suggested to access and determine the value of $L$. They are the summation of LED strength $\sum B(E1)$, the LED cross section ${\sigma }_{\text{LED}}$, and the LED dipole polarizability ${\alpha }_{\text{LED}}$.

${\sigma }_{\text{LED}}=\frac{16{\pi }^3{e}^2}{9\hslash c}{\int }_0^{E_{\text{dip}}}dEES\left(E1,E\right),$

${\alpha }_{\text{LED}}=\frac{8\pi e^2}{9}{\int }_0^{E_{\text{dip}}}dE\frac{S\left(E1,E\right)}{E},$

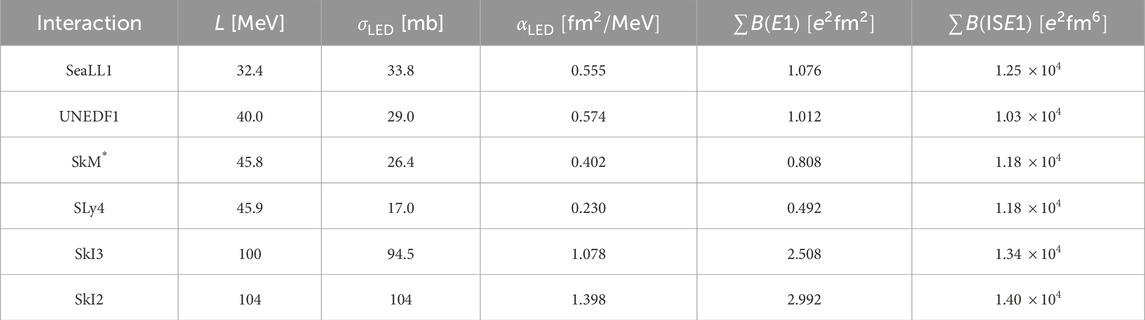
where $E_{\text{dip}}$ is defined as the energy corresponding to the minimum of the strengths $S(E1;E)$ and $S(\mathrm{I}\mathrm{S}E1;E)$ that exist between the LED peak and the GDR on each nucleus. The upper limit of the summation of LED strength is also $E_{\text{dip}}$. The $E_{\text{dip}}$ values for IVD and ISD of ¹³²Sn were all within $10\pm 1$ MeV, as shown in Figure 6. Although the values depend on the smearing parameter $\gamma$, they hardly change in the range $\gamma =$ 0.4 $-$ 0.6 MeV. Table 4 lists the $L$ values and the calculated LED observables, ${\sigma }_{\text{LED}}$, ${\alpha }_{\text{LED}}$, and $\sum B(E1)$, sorted by the value of $L$. In this work, we add the summation of low-energy compressional ISD strength $\sum B(\mathrm{I}\mathrm{S}E1)$ to the candidates.

Table 4

Table 4. Slope parameter $L$ and LED observables for ¹³²Sn; ${\sigma }_{\text{LED}}$, ${\alpha }_{\text{LED}}$, and the summations of IVD and ISD strength ${\sum }^{E_{\text{dip}}}B(E1)$, ${\sum }^{E_{\text{dip}}}B(\mathrm{I}\mathrm{S}E1)$. The interactions are sorted by the order of $L$ value.

Table 4 shows linear relations between $E1$ strength observables and values of $L$ in the Skyrme parameter sets, excluding minimal EDF SeaLL1. The linear correlations between ${\sigma }_{\text{LED}}$, ${\alpha }_{\text{LED}}$, and $\sum B(E1)$ and $L$ can be confirmed, although the linearity deviates locally. However, the sequence of $L$ values and $\sum B(\mathrm{I}\mathrm{S}E1)$ calculated with Skyrme interactions aligns in Figure 10. Its Pearson correlation coefficient is $r=0.93$ and the standard deviation is $\sigma =624$ $[{\mathrm{e}}^{2}f{m}^6]$ in this work. More detailed data are required, but this suggests that $\sum B(\mathrm{I}\mathrm{S}E1)$ might also be a suitable quantity for investigating $L$. ${\widehat{D}}_{\text{IS}}$ contains $r^2$, so it can be expected to be an operator that probes the nuclear surface more than the IVD operator $\widehat{D}$. Therefore, the strength of the ISD of neutron-rich nuclei may be an important quantity for extracting $L$ information.

Figure 10

Figure 10. ${\sum }^{E_{\text{dip}}}B(\mathrm{I}\mathrm{S}E1)$ of ¹³²Sn and the parameter $L$ calculated with Skyrme interactions. The Pearson correlation coefficient is denoted as $r$. The shaded area means the standard deviation $\sigma$ of the linear chi-squared fit.

4 Conclusion

We investigated LED isospin splitting in spherical nuclei (⁴⁰Ca, ⁹⁰Zr, ¹³²Sn, ²⁰⁸Pb, and several $N=50$ isotones). Using fully self-consistent HF + RPA calculations with Skyrme interactions and minimal EDF in 3D Cartesian coordinates, we analyzed the isospin splitting mechanism through IVD and ISD strength functions and transition densities, introducing the isospin structure index $I_{\text{iss}}$ for analysis.

Their LED modes vary with excitation energy for ⁴⁰Ca and ⁹⁰Zr. Below 10 MeV, $E1$ modes show large ISD and minimal IVD strengths, with transition densities in-phase for neutrons and protons (IS characteristic, $I_{\text{iss}}\sim 0$). In contrast, higher-energy $E1$ modes exhibit out-of-phase densities (IV characteristic, $I_{\text{iss}}\sim 1$). This indicates a fundamental energy-position relation between IS and IV modes in ⁴⁰Ca and ⁹⁰Zr, as confirmed by HF + RPA calculations with various interactions.

We investigated the LED states of nuclei with more neutrons than protons, stable ²⁰⁸Pb, and unstable ¹³²Sn. The states differ from those in nuclei with $N=Z$. In both cases, the LED modes below 9 MeV show both IS and IV characteristics, with an IS + IV mixed characteristic $(I_{\text{iss}}\sim 0.5)$. This mixed characteristic is expected due to different neutron and proton shell structures near the Fermi levels. In ²⁰⁸Pb and ¹³²Sn, the transition densities with the IS characteristic are less favored due to the distinct shell structures. We also examined how different interactions affect the LED states of ¹³²Sn. Our HF + RPA results with SLy4 and SeaLL1 show unclear isospin splitting, whereas ${\text{SkM}}^{*}$ and UNEDF1 better reproduce the LED isospin splitting.

We calculated the LED states for spherical $N=50$ isotones: ¹⁰⁰Sn, ⁹⁰Zr, ⁸²Ge, ⁷⁸Ni, and ⁷⁰Ca. We found a smooth evolution in the transition densities of E1 modes with the largest strengths below 10 MeV. In ¹⁰⁰Sn and ⁹⁰Zr, the $E1$ modes show pure IS or IV characteristic. In ⁸²Ge, there is a slight mixing of IS and IV due to neutron excess. For ⁷⁸Ni, the LED mode exhibits skin-core oscillation, while at ⁷⁰Ca, it shows neutron emission. As we approach the neutron drip line, the IS characteristic of the LED modes gradually shifts to a mixed IS + IV characteristic.

Finally, we showed the behaviors of the low-energy $E1$ strengths in ¹³²Sn and the slope parameter $L$ of EOS. It was shown that the sum of the compressional ISD strengths in the low-energy region might be an important quantity for exploring the slope parameter $L$. This is also conjectured from the form of the ISD operator, which includes a term that probes the nuclear surface.

LED isospin splitting is characterized by the isospin (IS, IV, and IS + IV) on the dipole transition, which strongly depends on the nuclear shell structures and the neutron–proton correlation. Therefore, to measure and analyze more precisely the isospin splitting will give the fundamental knowledge of the neutron–proton correlation, and pure IS or neutron characteristic might also be extracted. In the future work, we should proceed to study isospin splitting, considering the nuclear deformation and pairing correlation theoretically.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.

Author contributions

TI: writing–original draft and writing–review and editing. SE: writing–original draft and writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the MEXT Leading Initiative for Excellent Young Researchers Grant in Japan.

Acknowledgments

The authors thank K. Hagino for the fruitful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hartmann T, Babilon M, Kamerdzhiev S, Litvinova E, Savran D, Volz S, et al. Microscopic nature of the pygmy dipole resonance: the stable Ca isotopes. Phys Rev Lett (2004) 93:192501. doi:10.1103/PhysRevLett.93.192501

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Wieland O, Bracco A, Camera F, Benzoni G, Blasi N, Brambilla S, et al. Search for the Pygmy Dipole Resonance in ⁶⁸Ni at 600 MeV/nucleon. Phys Rev Lett (2009) 102:092502. doi:10.1103/PhysRevLett.102.092502

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Schwengner R, Rusev G, Tsoneva N, Benouaret N, Beyer R, Erhard M, et al. Pygmy dipole strength in ⁹⁰Zr. Phys Rev C (2008) 78:064314. doi:10.1103/PhysRevC.78.064314

CrossRef Full Text | Google Scholar

4. Iwamoto C, Utsunomiya H, Tamii A, Akimune H, Nakada H, Shima T, et al. Separation of pygmy dipole and M1 resonance in ⁹⁰Zr by a high-resolution inelastic proton scattering near 0°. Phys Rev Lett (2012) 108:262501. doi:10.1103/PhysRevLett.108.262501

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Adrich P, Klimkiewicz A, Fallot M, Boretzky K, Aumann T, Cortina-Gil D, et al. Evidence for pygmy and giant dipole resonances in ¹³⁰Sn and ¹³²Sn. Phys Rev Lett (2005) 95:132501. doi:10.1103/PhysRevLett.95.132501

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Tamii A, Poltoratska I, von Neumann-Cosel P, Fujita Y, Adachi T, Bertulani CA, et al. Complete electric dipole response and the neutron skin in 208Pb. Phys Rev Lett (2011) 107:062502. doi:10.1103/PhysRevLett.107.062502

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ebata S, Nakatsukasa T, Inakura T, Yoshida K, Hashimoto Y, Yabana K. Canonical-basis time-dependent Hartree-Fock-Bogoliubov theory and linear-response calculations. Phys Rev C (2010) 82:034306. doi:10.1103/physrevc.82.034306

CrossRef Full Text | Google Scholar

8. Inakura T, Nakatsukasa T, Yabana K. Emergence of pygmy dipole resonances: magic numbers and neutron skins. Phys Rev C (2011) 84:021302(R). doi:10.1103/physrevc.84.021302

CrossRef Full Text | Google Scholar

9. Ebata S, Nakatsukasa T, Inakura T. Systematic investigation of low-lying dipole modes using the canonical-basis time-dependent Hartree-Fock-Bogoliubov theory. Phys Rev.C (2014) 90:024303. doi:10.1103/physrevc.90.024303

CrossRef Full Text | Google Scholar

10. Vretenar D, Paar N, Ring P, Lalazissis GA. Collectivity of the low-lying dipole strength in relativistic random phase approximation. Nucl Phys A (2001) 692:496–517. doi:10.1016/s0375-9474(01)00653-4

CrossRef Full Text | Google Scholar

11. Paar N, Vretenar D, Khan E, Colò G. Exotic modes of excitation in atomic nuclei far from stability. Rep Prog Phys (2007) 70:691. doi:10.1088/0034-4885/70/5/R02

CrossRef Full Text | Google Scholar

12. Savran D, Babilon M, van den Berg AM, Harakeh MN, Hasper J, Matic A, et al. Nature of the pygmy dipole resonance in ¹⁴⁰Ce studied in (alpha, alpha' gamma) experiments. Phys Rev Lett (2006) 97:172502. doi:10.1103/PhysRevLett.97.172502

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Endres J, Savran D, van den Berg AM, Dendooven P, Fritzsche M, Harakeh MN, et al. Splitting of the pygmy dipole resonance in ¹³⁸Ba and ¹⁴⁰Ce observed in the (alpha, alpha’ gamma) reaction. Phys Rev C (2009) 80:034302. doi:10.1103/PhysRevC.80.034302

CrossRef Full Text | Google Scholar

14. Endres J, Litvinova E, Savran D, Butler PA, Harakeh MN, Harissopulos S, et al. Isospin character of the pygmy dipole resonance in ¹²⁴Sn. Phys Rev Lett (2010) 105:212503. doi:10.1103/PhysRevLett.105.212503

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Roming C, Beller J, Glorius J, Isaak J, Kelley JH, Kwan E, et al. Low-lying dipole strength of the open-shell nucleus ⁹⁴Mo. Phys Rev C (2013) 88:044331. doi:10.1103/PhysRevC.88.044331

CrossRef Full Text | Google Scholar

16. Derya V, Savran D, Endres J, Harakeh M, Hergert H, Kelley J, et al. Isospin properties of electric dipole excitations in 48Ca. Phys Lett B (2014) 730:288–92. doi:10.1016/j.physletb.2014.01.050

CrossRef Full Text | Google Scholar

17. Negi D, Wiedeking M, Lanza EG, Litvinova E, Vitturi A, Bark RA, et al. Nature of low-lying electric dipole resonance excitations in ⁷⁴Ge. Phys Rev C (2016) 94:024332. doi:10.1103/PhysRevC.94.024332

CrossRef Full Text | Google Scholar

18. Nakatsuka N, Baba H, Aumann T, Avigo R, Banerjee SR, Bracco A, et al. Observation of isoscalar and isovector dipole excitations in neutron-rich ²⁰O. Phys Lett B (2017) 768:387. doi:10.1016/j.physletb.2017.03.017

CrossRef Full Text | Google Scholar

19. Savran D, Derya V, Bagchi S, Endres J, Harakeh MN, Isaak J, et al. Multi-messenger investigation of the pygmy dipole resonance in ¹⁴⁰Ce. Phys Lett B (2018) 786:16. doi:10.1016/j.physletb.2018.09.025

CrossRef Full Text | Google Scholar

20. Paar N, Niu YF, Vretenar D, Meng J. Isoscalar and isovector splitting of pygmy dipole structures. Phys Rev Lett (2009) 103:032502. doi:10.1103/physrevlett.103.032502

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Papakonstantinou P, Ponomarev VY, Roth R, Wambach J. Isoscalar dipole coherence at low energies and forbidden E1 strength. Eur Phys J A (2011) 47:14. doi:10.1140/epja/i2011-11014-7

CrossRef Full Text | Google Scholar

22. Yüksel E, Khan E, Bozkurt K. Analysis of the neutron and proton contributions to the pygmy dipole mode in doubly magic nuclei. Nucl Phys A (2012) 877:35–50. doi:10.1016/j.nuclphysa.2012.01.006

CrossRef Full Text | Google Scholar

23. Papakonstantinou P, Hergert H, Ponomarev VY, Roth R. Low-energy dipole strength and the critical case of 48Ca. Phys Lett B (2014) 709:270–5. doi:10.1016/j.physletb.2012.02.024

CrossRef Full Text | Google Scholar

24. Vretenar D, Niu YF, Paar N, Meng J. Low-energy isovector and isoscalar dipole response in neutron-rich nuclei. Phys Rev C (2012) 85:044317. doi:10.1103/physrevc.85.044317

CrossRef Full Text | Google Scholar

25. Nakada H, Inakura T, Sawai H. Crossover from skin mode to proton-neutron mode inE1excitations of neutron-rich nuclei. Phys Rev C (2013) 87:034302. doi:10.1103/physrevc.87.034302

CrossRef Full Text | Google Scholar

26. Papakonstantinou P, Hergert H, Ponomarev VY, Roth R. Low-energy electric dipole response of Sn isotopes. Phys Rev C (2014) 89:034306. doi:10.1103/physrevc.89.034306

CrossRef Full Text | Google Scholar

27. Lanza EG, Vitturi A, Litvinova E, Savran D. Dipole excitations via isoscalar probes: the splitting of the pygmy dipole resonance in124Sn. Phys Rev C (2014) 89:041601. doi:10.1103/physrevc.89.041601

CrossRef Full Text | Google Scholar

28. Knapp F, Lo Iudice N, Veselý P, Andreozzi F, De Gregorio G, Porrino A. Dipole response inSn132within a self-consistent multiphonon approach. Phys Rev C (2014) 90:014310. doi:10.1103/physrevc.90.014310

CrossRef Full Text | Google Scholar

29. Papakonstantinou P, Hergert H, Roth R. Isoscalar and neutron modes in theE1spectra of Ni isotopes and the relevance of shell effects and the continuum. Phys Rev C (2015) 92:034311. doi:10.1103/physrevc.92.034311

CrossRef Full Text | Google Scholar

30. Hamamoto I, Sagawa H. Interplay between isoscalar and isovector correlations in neutron-rich nuclei. Phys Rev C (2017) 96:064312. doi:10.1103/physrevc.96.064312

CrossRef Full Text | Google Scholar

31. Inakura T, Togano Y. Skyrme random-phase approximation analysis of low-energy dipole states in oxygen isotopes. Phys Rev C (2018) 97:054330. doi:10.1103/physrevc.97.054330

CrossRef Full Text | Google Scholar

32. Inakura T, Imagawa H, Hashimoto Y, Mizutori S, Yamagami M, Matsuyanagi K. Mixed representation RPA calculation for octupole excitations on superdeformed states in the 40Ca and neutron-rich sulfur regions. Nucl Phys A (2006) 768:61–79. doi:10.1016/j.nuclphysa.2006.01.008

CrossRef Full Text | Google Scholar

33. Bulgac A, Forbes MM, Jin S, Perez RN, Schunck N. Minimal nuclear energy density functional. Phys Rev C (2018) 97:044313. doi:10.1103/physrevc.97.044313

CrossRef Full Text | Google Scholar

34. Bartel J, Quentin P, Brack M, Guet C, Håkansson HB. Towards a better parametrisation of Skyrme-like effective forces: a critical study of the SkM force. Nucl Phys A (1982) 386:79–100. doi:10.1016/0375-9474(82)90403-1

CrossRef Full Text | Google Scholar

35. Chabanat E, Bonche P, Heenen P, Meyer J, Schaeffer R. A skyrme parametrization from subnuclear to neutron star densities part II. Nuclei far from stabilities Nucl Phys A (1998) 635:231. doi:10.1016/S0375-9474(98)00180-8

CrossRef Full Text | Google Scholar

36. Kortelainen M, McDonnell J, Nazarewicz W, Reinhard P-G, Sarich J, Schunck N, et al. Nuclear energy density optimization: large deformations. Phys Rev C (2012) 85:024304. doi:10.1103/physrevc.85.024304

CrossRef Full Text | Google Scholar

37. Reinhard P-G, Flocard H. Nuclear effective forces and isotope shifts. Nucl Phys A (1995) 584:467–88. doi:10.1016/0375-9474(94)00770-n

CrossRef Full Text | Google Scholar

38. Carbone A, Col ò G, Bracco A, Cao L-G, Bortignon PF, Camera F, et al. Constraints on the symmetry energy and neutron skins from pygmy resonances in ⁶⁸Ni and ¹³²Sn. Phys Rev C (2010) 81:041301(R). doi:10.1103/PhysRevC.81.041301

CrossRef Full Text | Google Scholar

39. Reinhard P-G, Nazarewicz W. Information content of a new observable: the case of the nuclear neutron skin. Phys Rev C (2010) 81:051303. doi:10.1103/physrevc.81.051303

CrossRef Full Text | Google Scholar

40. Rossi DM, Adrich P, Aksouh F, Alvarez-Pol H, Aumann T, Benlliure J, et al. Measurement of the dipole polarizability of the unstable neutron-rich nucleus ⁶⁸Ni. Phys Rev Lett (2013) 111:242503. doi:10.1103/PhysRevLett.111.242503

PubMed Abstract | CrossRef Full Text | Google Scholar